1994复赛试题
非负数及其应用

(
)(
)
= −5+ 2 6
(第四届“希望杯”全国数学邀请赛初二第一试试题) 第四届“希望杯”全国数学邀请赛初二第一试试题) 第四届
[例3]
2u − v v − 2u 解: Q ≥ 0, ≥ 0. 4 u + 3v 4 u + 3v
∴ 2 u − v = 0. 即v = 2u.
v − 2u 3 2u − v 若u、、满足v = + + , 4u + 3v 4u + 3v 2 2 2 求u − uv + v 的值.
定理
定理2 如果两个图形关于某直线对称,那么对称 如果两个图形关于某直线对称, 定理 轴是对称点连线的垂直平分线。 轴是对称点连线的垂直平分线。 定理3 两个图形关于某直线对称,如果它们的对 两个图形关于某直线对称, 定理 称直线或延长线相交,那么交点在对称轴上。 称直线或延长线相交,那么交点在对称轴上。
(
)
则 a − b >0.
2
(
( )
2
−2 a • b +
)
( )
b = −
2
(
a− b .
)
2
2
2 ab − a − b = =
( − a) + 2 − a ( − a + − b)
2 2
−b + −b
( )
2
Hale Waihona Puke = − a + −b.
(1997年重庆市初中数学竞赛决赛试题) 年重庆市初中数学竞赛决赛试题) 年重庆市初中数学竞赛决赛试题
[例2] 已知
解: Q
b a−b−2 3 +(a+b−2 2) =0,求 的值 。 a
六年级下册奥数专题练习-分数与繁分数化简-全国通用

分数与繁分数化简【分数化简】讲析:容易看出,分子中含有因数37,分母中含有因数71。
所以可得(长沙地区小学数学奥林匹克选拔赛试题)讲析:注意到,4×6=24,2+4=6,由此产生的一连串算式:16×4=64166×4=6641666×4=6664……(全国“育苗杯”小学数学竞赛试题)讲析:容易看出分子中含有因数3。
把48531分解为48531=3×16177,然后可试着用16177去除分母:【繁分数化简】(1990年马鞍山市小学数学竞赛试题)讲析:如果分别计算出分子与分母的值,则难度较大。
观察式子,可发现分子中含有326×274,分母中含有275×326。
于是可想办法化成相同的数:(全国第三届“华杯赛”复赛试题)讲析:可把小数化成分数,把带分数都化成假分数,并注意将分子分母同乘以一个数,以消除各自中的分母。
于是可得例3 化简(全国第三届“华杯赛”复赛试题)讲析:由于分子与分母部分都比较复杂,所以只能分别计算。
计算时,哪一步中能简算的,就采用简算的办法去计算。
所以,原繁分数等于1。
(北京市第一届“迎春杯”小学数学竞赛试题)讲析:连分数化简,通常要从最下层的分母开始,自下而上逐步化简。
依此法计算,题目的得数是2。
(计算过程略)55、对称变换【将军饮马】据说古代希腊有一位将军向当时的大学者海伦请教一个问题:从A地出发到河边饮马,再到B地(如图4.32所示),走什么样的路最近?如何确定饮马的地点?海伦的方法是这样的:如图4.33,设L为河,作AO⊥L交L于O点,延长AO至A',使A'O=AO。
连结A'B,交L于C,则C点就是所要求的饮马地点。
再连结AC,则路程(AC+CB)为最短的路程。
为什么呢?因为A'是A点关于L的对称点,AC与A'C是相等的。
而A'B 是一条线段,所以A'B是连结A'、B这两点间的所有线中,最短的一条,所以AC+CB=A'C+CB=A'B也是最短的一条路了。
1994年全国初中应用物理知识竞赛(复赛)

1994年全国初中应用物理知识竞赛复赛一、选择题(每小题4分,共48分)1.长200米的列车用120秒匀速通过1.6千米的长江大桥,列车运行的速度是:[ ]A.11.7米/秒B.15米/秒C.13.3米/秒D.1.7米/秒2.有一架飞机沿水平向左做匀速直线运动,每隔1秒钟从飞机上轻轻释放一小球,当三只小球落下且均未落至地面时,若不计空气阻力,则这三只小球在空中的排列情况应是下图中的哪一个[ ]3.以下几种关于摩擦的利弊的说法中,正确的是:[ ]A.人走路时,脚与地面的摩擦是有害的B.骑自行车时,自行车轮胎与地面的摩擦是有害的C.机车起动时,轮与钢轨间的摩擦是有益的D.皮带传动时,皮带与皮带轮之间的摩擦是有害的4.在江河湖海游泳的人上岸时,在由深水走向浅水的过程中,如果水底布满石头,以下体验和分析合理的是:[ ]A.脚不痛。
因人越来越轻B.脚越来越痛。
因人越来越重C.脚不痛。
因水底对人的支持力越来越小D.脚越来越痛。
因水底对人的支持力越来越大5.我国北方冬天,河流会结上厚厚的一层冰,冰的温度有时低达-40℃,假如在-40℃的冰下有流动的河水,那么水与冰交界处的温度是:[ ]A.4℃B.0℃C.-40℃D.略高于-40℃6.下图的四种河堤的设计中,最不合理的是[ ]7.为了防盗,在门上装上一个“猫眼”,使屋内的人能看清屋外的人是一个正立缩小的像,屋外面的人却看不清屋内的人,则“猫眼”应该是:[ ]A.凸镜B.凹镜C.凹透镜D.凸透镜8.冻豆腐里面有小孔的成因是:[ ]A.豆腐自身冻缩而成B.豆腐自身膨胀而成C.外界的冰雪扎进豆腐里而成D.豆腐里面的水受冻先结冰,再熔化成水后而成9.用一重锤从相同的高度落下敲击质量和温度分别相同的钢块和铅块,重锤打在钢块上时,重锤会跳起,打在铅块上时,重锤没有弹起,这时:[ ]A.钢块的温度比铅块高B.铅块的温度比钢块高C.钢块与铅块的温度一样高D.无法判断谁的温度高10.一台“220V,60W”的电扇,一只“220V,60W”的白炽灯,一只“220V,60W”的电热器,将它们同时接在220V的电压下,在相同的时间内,它们产生的热量[ ]A.电扇最多B.白炽灯最多C.电热器最多D.都一样多11.在暗室的红灯下看一张白纸和白纸上的红字,得到的感觉是:[ ]A.纸是白色的,字能看清楚B.纸是白色的,字看不清楚C.纸是红色的,字能看清楚D.纸是红色的,字看不清楚12.密度是物质的属性之一,至今人们知道具有最大密度和最小密度的物质分别是:[ ]A.黑洞、星际物质B.中子星、慧星C.巨星、氢气D.白矮星、氢气二、填空题(每小题3分,共12分)1.夏天,在天平左盘中放一敞口玻璃杯,杯中有一冰块,右盘中放有一定质量的砝码,这时天平是平衡的,过了几分钟后,天平失去了平衡,天平向______倾斜了,原因是__________________________________。
小学数学难题解法大全 第五部分 典型难题讲析(七~一) 数的计算

小学数学难题解法大全第五部分典型难题讲析(七之一)数的计算(一)数的计算1.四则计算【基本题】例1 计算7142.85÷3.7÷2.7×1.7×0.7(1991年全国小学数学奥林匹克初赛试题)讲析:本题的两个除数和乘数依次是3.7,2.7,1.7,0.7。
从数字上分析,不能运用简便运算。
所以,只能从左至右依次计算。
结果是850.85。
(1990年江西省“八一杯”小学数学竞赛试题)成假分数之后,分子都含有22的约数,于是可采用分配律计算。
(1994年全国小学数学奥林匹克决赛试题)讲析:两个分数的分母都是3,所以,可把小数化成分数计算。
【巧算题】(全国第三届“华杯赛”初赛试题)讲析:括号中的三个数如果直接通分,则比较繁琐。
经观察,可将三个分母分解质因数,求出公分母;在求公分母的过程中,不必急于求出具体的数,而可边算边约分,能使计算简便一些。
(1993年全国小学数学奥林匹克决赛试题)讲析:当把两个带分数化成假分数时,分子都是65。
于是,第一个括号中可提出一个65,第二个括号中可提出一个5,能使计算变得比较简便。
例3 计算:(全国第四届“华杯赛”复赛试题)讲析:经观察发现,可将整数部分与分数部分分开计算。
这时,每个带分数的分数部分,都可以拆分成两个单位分数之差,然后互相抵消。
计算就很简便了例4 计算:(1990年《小学生数学报》小学数学竞赛试题)除以两数之积,就等于分别除以这两个数。
然后可将它们重新组合计算为法分配律计算。
于是可将10.375分开,然后重新组合。
(1990年小学数学奥林匹克初赛试题)用字母代替去计算。
(长沙市小学数学奥林匹克集训队选拔赛试题)26.3乘以2.5。
这样计算,可较为简便。
原式=2.5×24.7+29×2.5+26.3×2.5=2.5×(24.7+29+26.3)=200。
例8 已知11×13×17×19=46189计算:3.8×8.5×11×39(广州市小学数学竞赛试题)讲析:根据已知条件来计算另一个算式的结果,应尽量将计算式化成与已知条件式相同或相似的式子。
1994年普通高等学校招生全国统一考试(全国)
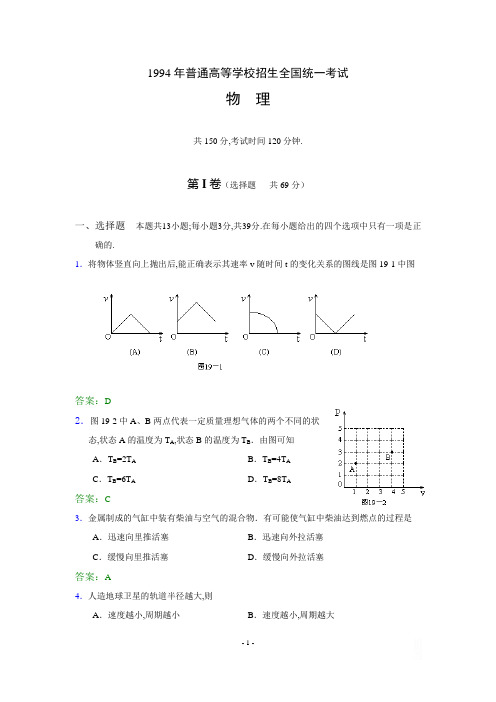
1994年普通高等学校招生全国统一考试物理共150分,考试时间120分钟.第I卷(选择题共69分)一、选择题本题共13小题;每小题3分,共39分.在每小题给出的四个选项中只有一项是正确的.1.将物体竖直向上抛出后,能正确表示其速率v随时间t的变化关系的图线是图19-1中图答案:D2.图19-2中A、B两点代表一定质量理想气体的两个不同的状态,状态A的温度为T A,状态B的温度为T B.由图可知A.T B=2T A B.T B=4T AC.T B=6T A D.T B=8T A答案:C3.金属制成的气缸中装有柴油与空气的混合物.有可能使气缸中柴油达到燃点的过程是A.迅速向里推活塞B.迅速向外拉活塞C.缓慢向里推活塞D.缓慢向外拉活塞答案:A4.人造地球卫星的轨道半径越大,则A.速度越小,周期越小B.速度越小,周期越大C.速度越大,周期越小D.速度越大,周期越大答案:B5.如图19-3所示的电路中,电源的电动势为ε,内阻为r.当可变电阻的滑片P向b点移动时,电压表V1的读数U1与电压表V2的读数U2的变化情况是A.U1变大,U2变小B.U1变大,U2变大C.U1变小,U2变小D.U1变小,U2变大答案:A6.太阳的连续光谱中有许多暗线,它们对应着某些元素的特征谱线.产生这些暗线是由于A.太阳表面大气层中缺少相应的元素B.太阳内部缺少相应的元素C.太阳表面大气层中存在着相应的元素D.太阳内部存在着相应的元素答案:C7.若带正电荷的小球只受到电场力作用,则它在任意一段时间内A.一定沿电力线由高电势处向低电势处运动B.一定沿电力线由低电势处向高电势处运动C.不一定沿电力线运动,但一定由高电势处向低电势处运动D.不一定沿电力线运动,也不一定由高电势处向低电势处运动答案:D8.两个电阻,R1=8欧,R2=2欧,并联在电路中.欲使这两个电阻消耗的电功率相等,可行的办法是A.用一个阻值为2欧的电阻与R2串联B.用一个阻值为6欧的电阻与R2串联C.用一个阻值为6欧的电阻与R1串联D.用一个阻值为2欧的电阻与R1串联答案:A9.一个带正电的质点,电量q=2.0×10-9库,在静电场中由a点移到b点,在这过程中,除电场力外,其他力作的功为6.0×10-5焦,质点的动能增加了8.0×10-5焦,则a、b两点间的电势差Ua-Ub为A.3×104伏B.1×104伏C.4×104伏D.7×104伏答案:B10.质子和α粒子在同一匀强磁场中作半径相同的圆周运动.由此可知质子的动能E1和α粒子的动能E2之比E1:E2等于A.4:1 B.1:1 C.1:2 D.2:1答案:B11.如图19-4所示,一个横截面积为S的圆筒形容器竖直放置.金属圆板A的上表面是水平的,下表面是倾斜的,下表面与水平面的夹角为θ,圆板的质量为M.不计圆板与容器内壁之间的摩擦.若大气压强为p0,则被圆板封闭在容器中的气体的压强p等于答案:D12.图19-5中A是一边长为l的方形线框,电阻为R.今维持线框以恒定的速度v沿x轴运动,并穿过图中所示的匀强磁场B区域.若以x轴正方向作为力的正方向,线框在图示位置的时刻作为时间的零点,则磁场对线框的作用力F随时间t的变化图线为图19-6中的图答案:B13.图19-7A.是演示简谐振动图象的装置.当盛沙漏斗下面的薄木板N被匀速地拉出时,摆动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系,板上的直线CO1代表时间轴.图B.是两个摆中的沙在各自木板上形成的曲线,若板N1和板N2拉动的速度v1和v2的关系为v2=2v1,则板N1、N2上曲线所代表的振动的周期T1和T2的关系为答案:D14.连接在电池两极上的平行板电容器,当两极板间的距离减小时,则A.电容器的电容C变大B.电容器极板的带电量Q变大C.电容器两极板间的电势差U变大D.电容器两极板间的电场强度E变大答案:A、B、D15.若物体在运动过程中受到的合外力不为零,则A.物体的动能不可能总是不变的B.物体的动量不可能总是不变的C.物体的加速度一定变化D.物体的速度的方向一定变化答案:B16.如图19-8所示,C是水平地面,A、B是两个长方形物块,F是作用在物块B上沿水平方向的力,物体A和B以相同的速度作匀速直线运动.由此可知,A、B间的滑动摩擦系数μ1和B、C间的滑动摩擦系数μ2有可能是A.μ1=0,μ2=0 B.μ1=0,μ2≠0C.μ1≠0,μ2=0 D.μ1≠0,μ2≠0答案:B、D17.图19-9为L-C振荡电路中电容器极板上的电量q随时间t变化的图线,由图可知时刻,电路中的磁场能最小A.在tB.从t1到t2,电路中的电流值不断变小C.从t2到t3,电容器不断充电D.在t4时刻,电容器的电场能最小答案:A、C、D18.如图19-10所示,在xy平面内有一沿x轴正方向传播的简谐横波,波速为1米/秒,振幅为4厘米,频率为2.5赫.在t=0时刻,P点位于其平衡位置上方最大位移处,则距P为0.2米的Q点A.在0.1秒时的位移是4厘米B.在0.1秒时的速度最大C.在0.1秒时的速度向下D.在0到0.1秒时间内的路程是4厘米答案:B、D19.图19-11中A、B是一对平行的金属板.在两板间加上一周期为T的交变电压u.A板的电势UA=0,B板的电势UB随时间的变化规律为:在0到T/2的时间内,UB=U0(正的常数);在T/2到T的时间内.U B= U0;在T到3T/2的时间内,U B=U0;在3T/2到2T的时间内.U B= U0……,现有一电子从A板上的小孔进入两板间的电场区内.设电子的初速度和重力的影响均可忽略,则A.若电子是在t=0时刻进入的,它将一直向B板运动B.若电子是在t=T/8时刻进入的,它可能时而向B板运动,时而向A板运动,最后打在B 板上C.若电子是在t=3T/8时刻进入的,它可能时而向B板运动,时而向A板运动,最后打在B 板上D.若电子是在t=T/2时刻进入的,它可能时而向B板、时而向A板运动答案:A、B二、填空题本题共8小题;其中第24、25题每题6分,其余各题每题5分,把答案填在题中的横线上.20.质量为4.0千克的物体A静止在水平桌面上.另一个质量为2.0千克的物体B以5.0米/秒的水平速度与物体A相撞,碰撞后物体B以1.0米/秒的速度反向弹回.相撞过程中损失的机械能是焦.答案:621.一个轴核衰变为钍核时释放出一个α粒子.已知铀核的质量为3.853131×10-25千克,钍核的质量为3.786567×10-25千克,α粒子的质量为6.64672×10-27千克.在这个衰变过程中释放出的能量等于焦.(保留两位数字)答案:8.7×10-13(答9.0×10-13到8.6×-13都算对)三、实验题22.将橡皮筋的一端固定在A点,另一端拴上两根细绳,每根细绳分别连着一个量程为5牛、最小刻度为0.1牛的弹簧测力计.沿着两个不同的方向拉弹簧测力计.当橡皮筋的活动端拉到O点时,两根细绳相互垂直,如图19-12所示.这时弹簧测力计的读数可从图中读出.(1)由图可读得两个相互垂直的拉力的大小分别为牛和牛.(只须读到0.1牛)(2)在本题的虚线方格纸上按作图法的要求画出这两个力及它们的合力.答案:(1)4.0 2.5(2)如图19-20所示23.如图19—13所示,一个面积为S 的矩形线圈在匀强磁场中以其一条边为轴做匀速转动,磁场方向与转轴垂直,线圈中感应电动势e 与时间t 的关系如图所示,感应电动势最大值和周期可由图中读出。
复旦大学经济学历年真题

复旦大学经济学历年真题2004复旦经济学基础试题1,选择4题共20分, a,某企业支付工资2万元,原材料价格3万元,销售收入8万元,则创造的附加值是b 蛛网模型收敛的条件是c,效用函数为u(x,y)=xy,则与之表示相同偏好次序的是u=(x+1)(x-1) u=xy/5 u=(x+5)(x-5)d,凯恩斯陷阱发生在债券价格高位时债券价格低位时2,名词2题共10分,赫克谢尔-俄林模型,经常项目差额第二定理3,简答2题共30分,劳动生产率提高会使商品价值降低,为什么厂商要提高劳动生产率/资本有机构成提高会使利润率降低,为什么资本家还要提高有机构成4,论述2题60分,用AD_AS模型分析通货膨胀的原因/用罗伯特-弗伦克尔模型分析货币金融危机的原因5,计算1题30分。
已知效用函数为U(X1,X2)=(lnx1+2lnx2)/3, p1,p2为价格,m为收入a,效用最大化条件b,求x1和x2的需求函数c,当p1=p2=1时,画出x1,x2的恩格尔线,纵轴为收入d,x1,x2 为正常品还是劣质品?普通品还是吉芬品?替代品还是互补品原题之二版[转帖]一,选择题(每题5分)1,一个公司除了支付一亿美圆的中间产品费用,两亿美圆的工资之外,再没有其他的投入,而它的总销售额是八亿美圆,问其附加值是多少?2,在蛛网模型中,收敛的条件是什么?即需求曲线斜率和供给曲线斜率之间的关系3,下列效用函数中,与u=xy小时的偏好次序相同的是:A,U=(X+5)*(Y+5)B,U=(X/5)*(Y/5)C,U=(X+5)*(Y-5)D,U=(X-5)*(Y-5)4, 凯恩斯陷阱是指证券价格的:A,高位区,B,中位区C,低位区D,无法确定二,名词解释(每题5分)1,赫克歇尔-俄林模型2,经常项目差额第二定理三,简答题(每题15分)1,既然劳动生产率与商品的价值成反比,为何资本家还要提高劳动生产率?2,资本有机构成的提高会导致利润率下降,则资本家为何还有积极提高资本有机构成?四,论述题(每题30分)1,请用AD-AS模型分析通货膨胀产生的原因2,请用弗伦克儿模型分析金融危机产生的原因五,计算题(30分)消费者效用函数为:U=(lnX1+2lnX2)/3,X1,X2表示两种商品,起价格分别为P1,P2 消费者的收入为m1,写出消费者的效用极大化2,写出对X1,X2的需求函数,X1=X1(m,P1,P2),X2=X2(m,P1,P2)3,P1=P2=1,请画出两种商品的恩格儿曲线,该曲线表示消费者收入和需求量间的关系,一般经济学家习惯用纵轴表示收入4,m=10,P2=5,请画出X1的需求曲线,该曲线表示商品价格和商品需求量间的关系,经济学家习惯用纵轴表示商品的价格5,分析X1,X2是正常商品还是劣质商品,是普通品还是吉芬品,是替代品还是互补品2001年经济学试题[转帖]一选择题(每题3分,共30分)1、下列生产资料属于劳动对象的是:——A、原材料;B、厂房;C、工具;D、机器设备。
1994年老高考语文试卷及答案

1994年普通高等学校招生全国统一考试语文本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分。
共五大题,30小题。
满分120分。
考试时间150分钟。
第Ⅰ卷(选择题共40分)一.(24分)1.下列成语中加点字的字的读音、字形全都正确的一组是()(2分)A.为虎作伥.(chānɡ)良莠.(yǒu)不分不径.(jìnɡ)而走惴惴.(zhuì)不安B.无庸赘.(zhuì)述烜.(xuǎn)赫一时畏葸.(xǐ)不前生死攸.(yōu)关C.矫.(jiǎo)揉造作得不偿.(chánɡ)失神采弈.(yì)弈并行不悖.(bèi)D.垂涎.(yán)三尺扑朔.(shuò)迷离谬.(miù)种流传沸.(fèi)反盈天2.下列成语没有错别字的一组是()(2分)A.招摇撞骗一望无垠妄费心机肆无忌惮B.惨绝人寰缄口不言磐竹难书心怀叵测C.望风披靡脍炙人口蜂涌而上短小精悍D.蓬荜生辉呕心沥血含辛茹苦动辄得咎3.下列句子中,加点的词语使用正确的一句是()(3分)A.煤炭、石油、钢铁等是发展工业所必须..的原料。
B.随地吐痰不文明,是一种违犯..社会公德的行为。
C.有的城市缺乏统一规划,经营出租汽车的单位太多,以致..供过于求。
D.他是梨园世家出生..,耳濡目染,各种戏路子都熟悉了。
4.)(3分)宋代四大家。
A.B.独树一帜、别具一格、匠心独运、不落窠臼C.匠心独运、不落窠臼、独树一帜、别具一格D.别具一格、独树一帜、不落窠臼、匠心独运5.两句话所表达的意思不相同的一组是()(2分)A.(1)非经批准不能动用流动资金。
(2)非得经过批准才能动用流动资金。
B.(1)除非你去请,他才会来。
(2)除非你去请,他是不会来的。
C.(1)这样的事,我何尝愿意做?(2)这样的事,我何尝不愿意做?D.(1)他缺乏工作经验,难免会出现一些差错。
(2)他缺乏工作经验,难免不出现一些差错。
(详细解析)1994年普通高等学校招生全国统一考试数学试题及答案(理)

1994年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.第Ⅰ卷(选择题共65分)一、选择题:本大题共15小题;第(1)—(10)题每小题4分,第(11)—(15)题每小题5分,共65分,在每小题给出的四个选项中,只有一项是符合题目要求的1.设全集{0,1,2,3,4}I =,集合{0,1,2,3}A =,集合{2,3,4}B =,则ABA .{0}B .{0,1}C .{0,1,4}D .{0,1,2,3,4} 【答案】C【解析】由于{4},{0,1}A B ==,所以{0,1,4}A B =.2.如果方程222x ky +=表示焦点在y 轴上的椭圆,那么实数k 的取值范围是 A .(0,)+∞ B .(0,2) C .(1,)+∞ D .((0,1) 【答案】D【解析】222x ky +=化为22122x y k+=,则22k >且0k >,所以(0,1)k ∈.3.极坐标方程cos()4πρθ=-所表示的曲线是A .双曲线B .椭圆C .抛物线D .圆 【答案】D【解析】cos()sin )()422x yπθθθρρ-=+=+,即22()02x y x y +-+=.4.设θ是第二象限的角,则必有A .tan cot22θθ> B .tancot22θθ<C .2cos 2sinθθ> D .2cos 2sin θθ< 【答案】A 【解析】22()2k k k Z ππθππ+<<+∈,()422k k k Z πθπππ+<<+∈,所以tan1cot22θθ>>.5.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个).经过3小时,这种细菌由1个可繁殖成A .511个B .512个C .1023个D .1024个 【答案】B 【解析】18092022512==.6.在下列函数中,以2π为周期的函数是 A .sin 2cos 4y x x =+ B .sin 2cos 4y x x = C .sin 2cos 2y x x =+ D .sin 2cos 2y x x = 【答案】D【解析】A 、B 、C 中函数周期均为π;而1sin 2cos 2sin 42y x x x ==,周期为2π.7.已知正六棱台的上、下底面边长分别为2和4,高为2,则其体积为A .B .C .D .【答案】B【解析】上下底面的面积分别为11()33V S S h =+=下上2+⨯=.8.设1F 和2F 为双曲线2214x y -=的两个焦点,点P 在双曲线上且满足1290F PF ∠=︒,则12F PF ∆的面积是A .1B .25C .2D .5 【答案】A【解析】由题设222121212,2,PF PF F F PF PF a ⎧+=⎪⎨-=⎪⎩则22121220,4,PF PF PF PF ⎧+=⎪⎨-=⎪⎩,可得122PF PF ⋅=,面积为12112S PF PF =⋅=.9.如果复数z 满足2z i z i ++-=,那么1z i ++的最小值是 A .1 B .2 C .2 D .5 【答案】A【解析】本题考查复数的几何意义.满足2z i z i ++-=的复数z 对应的点表示以点(0,1)-以及(0,1)为端点的线段,1z i ++表示该线段上的点到点(1,1)--的距离,从而知距离的最小值为1.10.有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担.从10人中选派4人承担这三项任务,不同的选法共有A .1260种B .2025种C .2520种D .5040种 【答案】C【解析】按分步计数原理考虑:第一步安排甲任务有210C 种方法,第二步安排乙任务有18C 种方法,第三步安排丙任务有17C 种方法,所以总共有2111087C C C 种.11.对于直线,m n 和平面,αβ,αβ⊥的一个充分条件是 A .,//,//m n m n αβ⊥ B .,,m n m m αβα⊥=⊂C .//,,m n n m βα⊥⊂D .//,,m n m n αβ⊥⊥ 【答案】C 【解析】略.12.设函数2()11(10)f x x x =---≤≤,则函数1()y fx -=的图像是【答案】B【解析】当10x -≤≤时,2()11(0,1)f x x =--∈,所以易知12()2f x x x -=--+,(0,1)x ∈.13.已知过球面上,,A B C 三点的截面和球心的距离等于球半径的一半,且AB BC ==2CA =,则球面面积是A .169π B .83π C .4π D .649π 【答案】D【解析】如图,设球的半径为R ,O '是ABC ∆的外心,外接圆半径为r ,则OO '⊥面ABC .在Rt ACD ∆中,3CD =,则233O C '=,所以222223()()32R R O C OO ''=+=+,则43R =,所以球面面积为26449S R ππ==.14.函数2arccos(sin )()33y x x ππ=-<<的值域是 A .⎪⎭⎫⎝⎛656ππ, B .⎪⎭⎫⎢⎣⎡650π, C .⎪⎭⎫ ⎝⎛323ππ, D .⎪⎭⎫⎢⎣⎡326ππ, 【答案】B 【解析】由已知3sin 12x -<≤,因余弦函数在[0,]π上递减,所以值域是⎪⎭⎫⎢⎣⎡650π,.15.定义在(,)-∞+∞上的任意函数()f x 都可以表示成一个奇函数()g x 和一个偶函数()h x 之和,如果()lg(101),(,)x f x x =+∈-∞+∞,那么A .(),()lg(10102)xxg x x h x -==++B .11()[(101)],()[(101)]22x x g x x h x x =++=+- C .(),()lg(101)22x x xg x h x ==+-D .(),()lg(10122x x xg x h x =-=++【答案】C【解析】根据题意()()()()()22f x f x f x f x f x --+-=+. ()()lg(101)lg(101)()222x x f x f x xg x ---+-+===,lg(101)lg(101)()lg(101)22x x x xh x -+++==+-.第Ⅱ卷(非选择题共85分)二、填空题 (本大题共5小题,共6个空格;每空格4分,共24分.把答案填在题中横线上)16.在7(3)x -的展开式中,5x 的系数是 .(用数字作答) 【答案】189-【解析】771773()(1)3r r r r r r r r T C x C x --+=⋅⋅-=-⋅⋅,5x 的系数是57557(1)3189C --⋅=-.17.抛物线284y x =-的准线方程是 ,圆心在该抛物线的顶点且与其准线相切的圆的方程是 .【答案】223,(2)1x x y =-+=【解析】原方程化为24(2)y x =-,其顶点为(2,0),准线方程是3x =;圆的方程是22(2)1x y -+=.18.已知1sin cos ,(0,)5θθθπ+=∈,则cot θ的值是 . 【答案】43-【解析】221112sin cos (sin cos )()sin cos 5525θθθθθθ+=⇒+=⇒=-,则(,)2πθπ∈, 从而得7sin cos 5θθ-=解得43sin ,cos 55θθ==-,故cos 3cot sin 4θθθ==-.19.设圆锥底面圆周上两点,A B 间的距离为2,圆锥顶点到直线AB 的距离为3,AB 和圆锥的轴的距离为1,则该圆锥的体积为 . 【答案】π322,则圆锥的体积为π322.20.在测量某物理量的过程中,因仪器和观察的误差,使得n 次测量分别得到12,,...,n a a a ,共n 个数据,我们规定所测量物理量的“最佳近似值”a 是这样一个量:与其他近似值比较,a 与各数据的差的平方和最小.依此规定,从12,,...,n a a a 推出的a = . 【答案】121()n a a a n+++【解析】本题考查构建二次函数求最值.由已知即求22212()()...()n y a a a a a a =-+-++-的最小值,上式化简为2222121212()()(...nn a a a a a a y n a a a nn++++++=--+++2)n a +,当12na a a a n+++=时,y 取最小值.三、解答题(本大题共5小题,共61分;解答应写出文字说明、证明过程或推演步骤)21.(本小题满分11分)已知1z i =+.(Ⅰ)设234z z ω=+-,求ω的三角形式;(Ⅱ)如果i z z baz z -=+-++1122,求实数,a b 的值. 【解】本小题考查共轭复数、复数的三角形式等基础知识及运算能力. (Ⅰ)由1z i =+,有2234(1)3(1)423(1)41z z i i i i i ω=+-=+++-=+--=--,ω55sin )44i ππ+.(Ⅱ)由1z i =+,有()()()()()()2222112(2)()1111i a i b a b a iz az b a a b i z z i i i +++++++++===+-+-++-++. 由题设条件知(2)()1a a b i i +-+=-.根据复数相等的定义,得21,() 1.a a b +=⎧⎨-+=-⎩解得⎩⎨⎧=-=.2,1b a22.(本小题满分12分)已知函数()tan ,(0,)2f x x x π=∈.若12,(0,)2x x π∈,且12x x ≠,证明11[()2f x + 122()]()2x x f x f +>. 【证明】本小题考查三角函数基础知识、三角函数性质及推理能力. ()1212121212121212sin sin sin sin cos cos sin tan tan cos cos cos cos cos cos x x x x x x x x x x x x x x x x +++=+== ()()()1212122sin cos cos x x x x x x +=++-.∵12,(0,)2x x π∈,12x x ≠,∴()12122sin 0,cos cos 0x x x x +>>,且()120cos 1x x <-<, 从而有()()()1212120cos cos 1cos x x x x x x <++-<++,由此得()()1212122sin tan tan 1cos x x x x x x ++>++,∴12121(tan tan )tan 22x x x x ++>,即12121[()()]()22x x f x f x f ++>.23.(本小题满分12分)如图,已知111A B C ABC -是正三棱柱,D 是AC 中点. (Ⅰ)证明1//AB 平面1DBC ;(Ⅱ)假设11AB BC ⊥,求以1BC 为棱,1DBC 与1CBC 为面的二面角α的度数.【解】本小题考查空间线面关系、正棱柱的性质、空间想象能力和逻辑推理能力.(Ⅰ)证明:∵111A B C ABC -是正三棱柱,∴四边形11B BCC 是矩形.连结1B C 交1BC 于E ,则1B E EC =.连结DE . 在1AB C ∆中,∵AD DC =,∴1//DE AB . 又1AB ⊄平面1DBC ,DE ⊂平面1DBC , ∴1//AB 平面1DBC .(Ⅱ)作DF BC ⊥,垂足为F ,则DF ⊥面11B BCC ,连结EF ,则EF 是ED 在平面11B BCC 上的射影.∵11AB BC ⊥,由(Ⅰ)知1//AB DE ,∴1DE BC ⊥,则1BC EF ⊥, ∴DEF ∠是二面角α的平面角. 设1AC =,则12DC =. ∵ABC ∆是正三角形,∴在Rt DCF ∆中,31sin ,cos 44DF DC C CF DC C =⋅==⋅=.取BC 中点G .∵EB EC =,∴EG BC ⊥. 在Rt BEF ∆中,2EF BF GF =⋅,又31,44BF BC FC GF =-==, ∴23144EF =⋅,即34EF =. ∴34tan 134DFDEF EF ∠===.∴45DEF ∠=︒.故二面角α为45︒.24.(本小题满分12分)已知直线l 过坐标原点,抛物线C 顶点在原点,焦点在x 轴正半轴上.若点)0,1(-A 和点(0,8)B 关于l 的对称点都在C 上,求直线l 和抛物线C 的方程. 【解】本小题考查直线与抛物线的基本概念和性质,解析几何的基本思想方法以及综合运用知识解决问题的能力.解法一:依题设抛物线C 的方程可写为22(0)y px p =>,且x 轴和y 轴不是所求直线,又l 过原点,因而可设l 的 方程为(0)y kx k =≠). ①设,A B ''分别是,A B 关于l 的对称点,因而AA l '⊥,直线AA '方程为()11+-=x ky ② 由①、②联立解得AA '与l 的交点M 的坐标为⎪⎭⎫ ⎝⎛+-+-11122k k k ,.又M 为AA '的中点,从而点A '的坐标为2222211221,201111A A k k k x y k k k k ''--⎛⎫⎛⎫=-+==+=- ⎪ ⎪++++⎝⎭⎝⎭. ③同理得点B '的坐标为222168(1),11B B k k x y k k ''-==++. ④ 又,A B ''均在抛物线22(0)y px p =>上,由③得112122222+-⋅=⎪⎭⎫ ⎝⎛+-k k p k k , 由此知1k ≠±,即1242-=k k p . ⑤同理由④得()11621182222+⋅=⎪⎪⎭⎫ ⎝⎛+-k k p k k .即()()k k k p 112222+-=. 从而1242-k k =()()kk k 112222+-,整理得210k k --=.解得12k k ==. 但当251-=k 时,由③知055<-='A x , 这与A'在抛物线22(0)y px p =>上矛盾,故舍去2512-=k . 设251+=k ,则直线l 的方程为x y 251+=. 将251+=k 代入⑤,求得552=p . 所以直线方程为x y 251+=. 抛物线方程为x y 5542=. 解法二:设点,A B 关于l 的对称点分别为1122(,),(,)A x y B x y '',则1,8OA OA OB OB ''====.设由x 轴正向到OB '的转角为α,则228cos ,8sin x y αα==.①因为,A B ''为,A B 关于直线l 的对称点,而BOA ∠为直角,故B OA ''∠为直角,因此11cos()sin ,sin()cos 22x y ππαααα=-==-=-, ②由题意知120,0x x >>,故α为第一象限角.因为,A B ''都在抛物线22y px =上,将①、②代入得22cos 2sin ,64sin 28cos p p αααα=⋅=⋅.∴338sin cos αα=,∴2sin cos αα=,解得52cos 51sin ==αα,. 将52cos 51sin ==αα,代入2cos 2sin p αα=⋅得552sin 2cos 2==ααp , ∴抛物线C 的方程为x y 5542=. 因为直线l 平分B OB '∠,故l 的斜率sin 1cos 1222241sin 21cos 2k tg tg παπαπαααπαα⎛⎫+ ⎪⎡⎤⎛⎫⎛⎫⎝⎭=+-=+=== ⎪ ⎪⎢⎥-⎛⎫⎝⎭⎝⎭⎣⎦++ ⎪⎝⎭. ∴直线l 的方程为x y 215+=.25.(本小题满分14分)设{}n a 是正数组成的数列,其前n 项和为n S ,并且对于所有的自然数n ,n a 与2的等差中项等于n S 与2的等比中项.(Ⅰ)写出数列{}n a 的前3项;(Ⅱ)求数列{}n a 的通项公式(写出推证过程); (Ⅲ)令()N ∈⎪⎪⎭⎫ ⎝⎛+=++n a a a a b n n n n n 1121,求12lim()n n b b b n →∞+++-.【解】本小题考查等差数列、等比数列、数列极限等基础知识考查逻辑推理能力和分析问题与解决问题的能力.(Ⅰ)由题意,当1n =时有11222S a =+,11S a =,∴11222a a =+,解得12a =. 当2n =时有22222S a =+,212S a a =+,将12a =代入,整理得22(2)16a -=.由20a >,解得26a =.当3n =时有33222S a =+,3123S a a a =++,将122,6a a ==代入, 整理得23(2)64a -=.由30a >,解得310a =.故该数列的前3项为2,6,10.(Ⅱ)解法一:由(Ⅰ)猜想数列{}n a 有通项公式42n a n =-.下面用数学归纳法证明数列{}n a 的通项公式是42()n a n n N =-∈. ①当1n =时,因为4122⨯-=,又在(Ⅰ)中已求出12a =,所以上述结论成立. ②假设n k =时结论成立,即有42k a k =-.由题意,有k k S a 222=+,将42k a k =-代入上式,得2k =22k S k =. 由题意,有11222++=+k k S a ,11k k k S S a ++=+, 将22k S k =代入,得221122(2)2k k a a k +++⎛⎫=+ ⎪⎝⎭,整理得 221144160k k a a k ++-+-=. 由10k a +>,解得124k a k +=+.所以1244(1)2k a k k +=+=+-. 这就是说,当1n k =+时,上述结论成立.根据①、②,上述结论对所有的自然数n 成立.解法二:由题意,有)22n a n N +=∈,整理得21(2)8n n S a =+, 由此得2111(2)8n n S a ++=+, ∴2211111[(2)(2)]88n n n n n a S S a a +++=-=+-+, 整理得11()(4)0n n n n a a a a +++--=,由题意知10n n a a ++≠,∴14n n a a +-=.即数列{}n a 为等差数列,其中12a =,公差4d =. ∴1(1)24(2)n a a n d n =+-=+-,即通项公式为42n a n =-. (Ⅲ)令1n n c b =-,则11112121112112221212121n n n n n a a n n c a a n n n n ++⎛⎫⎡+-⎤⎛⎫⎛⎫=+-=-+-=- ⎪ ⎪ ⎪⎢⎥-+-+⎝⎭⎝⎭⎣⎦⎝⎭, 12121111113352121n n b b b n c c c n n ⎛⎫⎛⎫⎛⎫+++-=+++=-+-++- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭1211+-=n . ∴()121lim lim 1121n n n b b b n n →∞→∞⎛⎫+++-=-= ⎪+⎝⎭.。
历年迎春杯高年级决赛(5年级)经典试题汇编

数论
21. (2009 年数学解题能力展示中年级组初试试题)将 1、2、3、4、5、6、7、8、9 这九个数排成一 行,使得第一个数是第二个数的整数倍,前两个数的和是第三个数的整数倍,前三个数的和是第 四个数的整数倍,……,前八个数的和是第九个数的整数倍.如果第一个数是 6,第四个数是 2, 第五个数是 1,最后一个数是_____________.
22. (2009 年迎春杯高年级决赛试题)三个两两不同的正整数,和为 126,则它们两两最大公约数之 和的最大值为 .
23. (1993 年第 9 届迎春杯决赛试题) 设 a 与 b 是两个不相等的自然数, 如果它们的最小公倍数是 72, 那么 a 与 b 之和可以有 种不同的值.
9 历年数学解题能力展示高年级经典试题汇编(1984?~2010)
11 历年数学解题能力展示高年级经典试题汇编(1984?~2010)
31. 从甲地到乙地,需先走一段下坡路,再走一段平路,最后再走一段上坡路。其中下坡路与上坡路 的距离相等。陈明开车从甲地到乙地共用了 3 小时,其中第一小时比第二小时多走 15 千米,第二 小时比第三小时多走 25 千米。如果汽车走上坡路比走平路每小时慢 30 千米,走下坡路比走平路 每小时快 15 千米。那么甲乙两地相距多少千米?
C
B
A
E D
4 历年数学解题能力展示高年级经典试题汇编(1984?~2010)
11. (迎春杯模拟题)如图,求 x 的度数。
80° 20°
20° 20°
12. (2010 年数学解题能力高年级复试试题)现有一块 L 形的蛋糕如图所示,现在要求一刀把它切成 3 部分,因此只能按照如图的方式切,但不能斜着切或横着切.要使得到的最小的那块面积尽可能 大,那么最小的面积为 平方厘米. 10 厘米
华杯赛历届试题

第一届华杯赛决赛一试试题1. 计算:2.975×935×972×(),要使这个连乘积的最后四个数字都是“0”,在括号内最小应填什么数?3.把+、-、×、÷分别填在适当的圆圈中,并在长方形中填上适当的整数,可以使下面的两个等式都成立,这时,长方形中的数是几?9○13○7=100 14○2○5=□4.一条1米长的纸条,在距离一端0.618米的地方有一个红点,把纸条对折起来,在对准红点的地方涂上一个黄点然后打开纸条从红点的地方把纸条剪断,再把有黄点的一段对折起来,在对准黄点的地方剪一刀,使纸条断成三段,问四段纸条中最短的一段长度是多少米?5.从一个正方形木板锯下宽为米的一个木条以后,剩下的面积是平方米,问锯下的木条面积是多少平方米?6.一个数是5个2,3个3,2个5,1个7的连乘积。
这个数当然有许多约数是两位数,这些两位的约数中,最大的是几?7.修改31743的某一个数字,可以得到823的倍数,问修改后的这个数是几?8.蓄水池有甲、丙两条进水管,和乙、丁两条排水管,要灌满一池水,单开甲管需3小时,单开丙管需要5小时,要排光一池水,单开乙管需要4小时,单开丁管需要6小时,现在池内有池水,如果按甲、乙、丙、丁的顺序,循环各开水管,每天每管开一小时,问多少时间后水清苦始溢出水池?9.一小和二小有同样多的同学参加金杯赛,学校用汽车把学生送往考场,一小用的汽车,每车坐15人,二小用的汽车,每车坐13人,结果二小比一小要多派一辆汽车,后来每校各增加一个人参加竞赛,这样两校需要的汽车就一样多了,最后又决定每校再各增加一个人参加竞赛,二小又要比一小多派一辆汽车,问最后两校共有多少人参加竞赛?10.如下图,四个小三角形的顶点处有六个圆圈。
如果在这些圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个顶点上的数之和相等。
问这六个质数的积是多少?11.若干个同样的盒子排成一排,小明把五十多个同样的棋子分装在盒中,其中只有一个盒子没有装棋子,然后他外出了,小光从每个有棋子的盒子里各拿一个棋子放在空盒内,再把盒子重新排了一下,小明回来仔细查看了一番,没有发现有人动过这些盒子和棋子,问共有多少个盒子?12.如右图,把1.2,3.7, 6.5, 2.9, 4.6,分别填在五个○内,再在每个□中填上和它相连的三个○中的数的平均值,再把三个□中的数的平均值填在△中,找出一个填法,使△中的数尽可能小,那么△中填的数是多少?13.如下图,甲、乙、丙是三个站,乙站到甲、丙两站的距离相等。
销售数学题

商品销售方面的数学题我们在日常生活中经常接触到商品买卖问题。
商品买卖,涉及进货价(成本)、售出价(定价)、利润;如果降价销售,涉及原价、降价幅度(折扣)、降价后的价格。
此外,商品在运输、储存、销售过程中还存在损耗问题。
现将商品销售方面的有关知识介绍如下:一、商品的价格和利润某种商品的进货价(成本)是100元,售出价(定价)是120元,就获得利润20元。
利润也可以用百分数表示,20÷100=20%,我们就说获得20%的利润,或者说,利润率为20%。
进货价+利润=售出价;利润率=(售出价-进货价)÷进货价×100%;售出价=进货价×(1+利润率);进货价=售出价÷(1+利润率)。
二、商品价格的打折扣商品的定价按照期望的利润来确定,即成本(进货价)+期望的利润=定价(售出价)。
定价高了,商品积压卖不掉,只能降低利润(甚至亏本)减价销售。
减价也可以用百分数表示,这就是通常所说的打折扣。
如某种商品原来定价50元,现在降价10元,以40元价格出售,10÷50=20%,我们可以说减价20%,就是按定价的(1-20%)80%出售,也就是打八折出售。
三、商品的损耗商品在运输、储存和销售过程中损坏、变质或减轻重量,形成商品的损耗。
原有商品数量-损耗商品数量=现有商品数量;损耗率=损耗的商品数量÷原有商品数量×100%;现有商品数量=原有商品数量×(1-损耗率)。
这类商品销售方面的数学题属于百分数应用题,因此解题时与解其他百分数应用题一样:(1)要确定单位“1”的量(标准量),再分析其他量是标准量的百分之几(百分率);(2)确定某一个数量与百分率的对应关系。
正确找出量率对应是解百分数应用题的关键。
下面列举几道竞赛题,说明这类问题的解法。
例1一商店以每3盘16元的价格购进一批录音带,又从另一处以每4盘21元的价格购进比前一批加倍的录音带。
心理知识竞赛复赛资料及情景题

经管心协心理知识竞赛复赛复习资料一、常见的心理效应1、共生效应自然界有这样一种现象:当一株植物单独生长时,显得矮小、单调,而与众多同类植物一起生长时,则根深叶茂,生机盎然。
人们把植物界中这种相互影响、相互促进的现象,称之为“共生效应”。
事实上,我们人类群体中也存在“共生效应”。
英国“卡迪文实验室”从1901年至1982年先后出现了25位诺贝尔获奖者,便是“共生效应”一个杰出的典型。
2、刻板效应社会心理学认为,那种用老眼光看人造成的影响称为“刻板效应”。
它是对人的一种固定而笼统的看法,从而产生一种刻板印象。
在学校经常可见到这种现象,教师对那些天资聪颖、学习成绩优秀的学生,脸上往往流露出喜爱的神色,并受到器重和青睐。
而天资愚笨、学习成绩较差的学生则往往受到歧视,教师表现出急躁、厌烦的情绪,令人沮丧的话常挂在嘴边。
3、首因效应指的是知觉对象给知觉者留下第一印象对社会知觉的影响作用。
具体说,就是初次与人或事接触时,在心理上产生对某人或某事带有情感因素的定势,从而影响到以后对该人或该事的评价。
4、近因效应近因效应指的是某人或某事的近期表现在头脑中占据优势,从而改变了对该人或该事的一贯看法。
近因效应与首因效应是相对应的两种效应。
首因效应一般在较陌生的情况下产生影响,而近因效应一般在较熟悉的情况下产生影响。
两者都是对人或事的片面了解而主观臆断,使得决策信息失真。
5、晕轮效应(光环效应)晕轮效应是指某人或某事由于其突出的特征留下了深刻的印象,而忽视了其它的心理和行为品质。
它有时会产生“积极肯定的晕轮”,有时会产生“消极否定的晕轮”,这都会干扰对信息的评价,要克服晕轮效应就必须坚持客观,不掺杂主观成分。
6、蝴蝶效应1960年,美国麻省理工学院教授洛伦兹研究“长期天气预报”问题时,出现了疑难问题:她在计算机上用一组简化数据模拟天气的演变,原本是想利用计算机的高速运算来提高天气预报的准确性。
但是,事与愿违,多次计算表明,初始条件的极微小差异,会导致错误的结论。
小学数学难题解法大全 第五部分 典型难题讲析(七~二)数字谜与数字问题

小学数学难题解法大全第五部分典型难题讲析(七之二)数字谜与数字问题(二)数字谜与数字问题1.数字串问题【找规律填数】例1 找规律填数(杭州市上城区小学数学竞赛试题)(1992年武汉市小学数学竞赛试题)讲析:数列填数问题,关键是要找出规律;即找出数与数之间有什么联系。
第(1)小题各数的排列规律是:第1、3、5、……(奇数)个数分别别是4和2。
第(2)小题粗看起来,各数之间好像没有什么联系。
于是,运用分数得到了例2 右表中每竖行的三个数都是按照一定的规律排列的。
按照这个规律在空格中填上合适的数。
(1994年天津市小学数学竞赛试题)讲析:根据题意,可找出每竖行的三个数之间的关系。
不难发现每竖行中的第三个数,是由前两数相乘再加上1得来的。
所以空格中应填33。
【数列的有关问题】数是几分之几?(第一届《从小爱数学》邀请赛试题)讲析:经观察发现,分母是1、2、3、4、5……的分数个数,分别是1、3、5、7、9……。
所以,分母分别为1、2、3……9的分数共例2 有一串数:1,1993,1992,1,1991,1990,1,1989,1988,…这个数列的第1993个数是______(首届《现代小学数学》邀请赛试题)讲析:把这串数按每三个数分为一组,则每组第一个数都是1,第二、三个数是从1993开始,依次减1排列。
而1993÷3=664余1,可知第1993个数是1。
例3 已知小数0.12345678910111213……9899的小数点后面的数字,是由自然数1—99依次排列而成的。
则小数点后面第88位上的数字是______。
(1988年上海市小学数学竞赛试题)讲析:将原小数的小数部分分成A、B两组:A中有9个数字,B中有180个数字,从10到49共有80个数字。
所以,第88位上是4。
例4 观察右面的数表(横排为行,竖排为列);几行,自左向右的第几列。
(全国第三届“华杯赛”决赛试题)讲析:第一行每个分数的分子与分母之和为2,第二行每个分数的分子与分母之和为3,第三行每个分数的分子与分母之和为4,……即每行各数的分子与分母之和等于行数加1。
四边形(竞赛题)[1]
![四边形(竞赛题)[1]](https://img.taocdn.com/s3/m/a8cd445b284ac850ac024201.png)
第一节 四边形的分类与判定【知识点拨】1、四边形的性质:四边形的内角和等于360°.2、四边形的的分类:(1)对边平行;(2)对边不平行。
本节研究是对边不平行的四边形,常用方法是转化为三角形进行研究。
【赛题精选】【例1】如图,四边形ABCD 有4个直角三角形拼凑而成,它们的公共顶点为O,已知△AOB 、△BOC 、△COD 的面积分别为20、10、16,求△AOD 的面积。
(1992年北京市“迎春杯”竞赛题)【注释】求三角形的面积,通常需要求出底和高,当这两个值不易求出时,常把它们的积作为一个整体,设法求出它们的积。
【例2】如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数。
(1999年重庆市竞赛题)【注释】求凹多边形的内角和,常利用四边形和三角形的内角和进行计算,有事需要添加辅助线,将其转化为求一个凸多边形的和或一个凸多边形和一个三角形的内角和,如本题连接BF 、CE ,则所求的值等于四边形ABFG 的内角和加上△DCE 的内角和。
【例3】如图,在四边形ABCD 中,∠B=∠D=90°,∠A=60°,AB=4,AD=5,求CDBC 的值。
(1993年“祖冲之杯”邀请赛试题)【注释】有些几何题,按原有的图形很难求解,可根据图形的特点,将原图形补成特殊图形,利用特殊图形的性质进行求解。
【例4】(1)是否存在这样的四边形,它的4条边依次是1、2、4、7?(2)是否存在这样的四边形,它的一组对角是直角,其中一个直角的两条边分别为3、4,另一个直角的边为6?【注释】探索存在型问题是指在一定条件下,判断是否存在某个结论。
解答这类问题,先假设结论存在,从假设出发,根据题设条件及有关性质进行推理论证,若推出矛盾,则不定假设,若推出合理的结果,则说明假设正确。
这种方法叫“假设法"。
【例5】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形ABCD的周长为32,求BC和CD的长。
1994年第11届全国中学生物理竞赛决赛试题及参考答案

第11届全国中学生物理竞赛决赛试题一、照相机镜头L 前2.28m 处的物体被清晰地成像在镜头后面12.0cm 处的照相胶片P 上。
今将一折射率为1.50、厚0.90AB cm =、两面平行的玻璃平板插入镜头与胶片之间,与光轴垂直,位置如图所示。
设照相机镜头可看作一个简单薄凸透镜,光线为近轴光线。
(1)求插入玻璃板后,像的新位置。
(2)如果保持镜头、玻璃板、胶片三者间距离不变,并要求物体仍然清晰地成像于胶片上,则物体应放在何处?二、1964年制成了世界上第一盏用海浪发电的航标灯,它的气室示意图如图所示。
利用海浪上下起伏的力量,空气能被吸进来,压缩后再推入工作室,推动涡轮机带动发电机发电。
当海水下降时,阀门K 1关闭,K 2打开。
设每次吸入压强为51.010Pa ⨯,温度为7C ︒的空气30.233m (空气可视为理想气体)。
当海水上升时,K 2关闭,海活塞绝热压缩空气,空气压强达到53210Pa ⨯时,阀门K 1才打开。
K 1打开后,活塞继续推动空气,直到气体全部被推入工作室为止,同时工作室的空气推动涡轮机工作。
设打开K 1后,活塞附近的压强近似保持不变,活塞的质量及活塞与筒壁间的摩擦忽略不计。
问海水每次上升时所作功是多少?已知空气从压强为p 1、体积为V 1的状态绝热地改变到压强为p 2、体积为V 2的状态过程中,近似遵循关系式5/31212(//)p p V V =。
1mol 理想气体温度升高1K 时,内能改变为3/2R (8.31/()R J mol K =⋅)。
三、如图所示,一质量为0.10kg 、电量为4810C -⨯的带正小球,从水平地面上A 点以与X 轴正方向成30︒夹角的初速度0v 抛出(0v 在XOY 竖直平面内)。
当达到最高点B 时(B 点恰好处在OY 轴上),在全空间立刻产生一个匀强电场E ,场强为32.5010/N C ⨯,方向平行于XOY 平面,并与X 轴负方向成θ夹角。
1994年复赛解析(1)

)复赛试卷解析说明:1.本试卷共有七大题,答题时间为120分钟,试卷满分为100分。
2.试题中“[]”内的内容是供使用新编物理教材的学生用。
一.填空题(每题2分,共10分)1.居民生活用液化石油气,是在常温条件下,用__加压__的方法,使它成为液体储存在钢罐里的。
解:液化石油气,就是在常温下用加压的方法,使石油气变成液体储存在钢瓶里的.故本题答案为:加压2.某家庭所用的电度表[瓦时计]上标有“1200R/kWh”的字样。
如果这个家庭的一些用电器在正常工作时,电度表[瓦时计]的铝盘在5分钟里转过30圈,则这些用电器在正常工作时的总功率为_300_瓦特。
3.某人驾驶小艇,沿河逆流而上,从甲地到乙地,又立即从乙地返回甲地。
若小艇在静水中的速率为8米/秒,河水流速为2米/秒,则小艇往返于甲、乙两地之间的平均速率为______米/秒。
图14.在图1所示的电路图中,电阻R 1=20欧姆,R 3=8欧姆;伏待表V 1的读数是5伏特,伏特表V 2的读数是3伏特。
由此可见电阻R 2的阻值为______欧姆。
5.已知铜的密度大于铝的密度。
把质量相等的实心铜球和实心铝球,静止地放在同一水平桌面上,如图2所示,则铜球具有的机械能______(填“大于”、“小于”或“等于”)铝球具有的机械能。
解:小于,比较两者重心高低即可.二.1.某人骑自行车以一定的速度沿水平道路匀速行驶,当他经过路口的横道线时,从口袋里掉下一串钥匙,钥匙落地时的位置应在(A)横道线上;(B)横道线后;(C)自行车后;(D)自行车下。
( )解:某人骑自行车以一定的速度沿平直道路匀速前进,当他经过横道线时,口袋里的钥匙落下时,由于要使原来与人和自行车一起运动,速度相同,依靠惯性,仍要保持原来的速度运动一段路程(忽略空气阻力),因此这串钥匙会超过横道线,落在横道线前,且落在自行车的正下方. 故选D .2.如图3所示,许多轿车的后窗内壁都平行地装有若干条金属丝,估计它们的用途可能是(A)为了美观用作装饰;(B)不让车外的行人看到车内的乘客; (C)通电后可以防止后窗积灰;(D)通电后可消除附在后窗内壁上的小水珠。
94年六年级试卷【含答案】

94年六年级试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个事件发生在1994年?A. 互联网正式诞生B. 中国加入世界贸易组织C. 北约成立D. 南非举行首次种族平等选举2. 1994年世界杯足球赛冠军是哪个国家?A. 巴西B. 意大利C. 德国D. 阿根廷3. 1994年中国国内生产总值(GDP)增长率大约为?A. 6%B. 8%C. 10%D. 12%4. 下列哪位科学家在1994年获得了诺贝尔奖?A. 爱因斯坦B. 杨振宁C. 丁肇中D. 崔琦5. 1994年,以下哪部电影获得了奥斯卡最佳影片奖?A. 《辛德勒的名单》B. 《阿甘正传》C. 《肖申克的救赎》D. 《低俗小说》二、判断题(每题1分,共5分)6. 1994年是闰年。
()7. 1994年,香港回归中国。
()8. 1994年,欧洲联盟正式成立。
()9. 1994年,美国成功发射了“火星探路者”探测器。
()10. 1994年,世界人口达到60亿。
()三、填空题(每题1分,共5分)11. 1994年,中国首次实现了全功能接入国际互联网,该事件通常被称作“______”。
12. 1994年,______在法国举办了夏季奥林匹克运动会。
13. 1994年,______成为世界首富。
14. 1994年,______获得了诺贝尔文学奖。
15. 1994年,______发生了严重的核事故。
四、简答题(每题2分,共10分)16. 简述1994年中国经济体制改革的主要方向。
17. 描述1994年美国世界杯足球赛的一件重要事件。
18. 解释1994年“世界贸易组织”的成立对全球经济的影响。
19. 1994年,互联网在中国的发展有哪些标志性事件?20. 1994年,南非历史上首次种族平等选举的意义是什么?五、应用题(每题2分,共10分)21. 如果1994年中国的GDP为4.8万亿元,按照当时汇率计算,相当于多少美元?22. 假设1994年世界人口为5.6亿,计算当时中国人口占世界人口的比例。
1994年全国高中数学联赛试题

1994年全国高中数学联赛试题第 一 试一、选择题(每小题6分,共36分)1、设a,b,c 是实数,那么对任何实数x, 不等式a x b x c sin cos .++>0都成立的充要条件是(A)a,b 同时为0,且c >0 (B)a b c 22+=(C)a b c 22+< (D)a b c 22+>2、给出下列两个命题:(1).设a,b,c 都是复数,如果a b c 222+>,则a b c 2220+->.(2).设a,b,c 都是复数,如果a b c 2220+->,则a b c 222+>.那么下述说法正确的是(A)命题(1)正确,命题(2)也正确 (B)命题(1)正确,命题(2)错误(C)命题(1)错误,命题(2)也错误 (D)命题(1)错误,命题(2)正确3、已知数列{}a n 满足3411a a n n n ++=≥(),且a 19=,其前n 项之和为S n ,则满足不等式||S n n --<61125的最小整数n 是 (A)5 (B)6 (C)7 (D)84、已知0104<<<<b a ,π,则下列三数:x a b a =(sin )log sin ,y a b a =(cos )log cos ,z a b a =(sin )log cos 的大小关系是(A)x<z<y (B)y<z<x (C)z<x<y (D)x<y<z5、在正n 棱锥中,相邻两侧面所成的二面角的取值范围是(A)(,)n n -2ππ (B)(,)n n -1ππ (C)(,)02π (D)(,)n n n n --21ππ 6、在平面直角坐标系中,方程||||x y a x y b ++-=221(a,b 是不相等的两个正数)所代表的曲线是(A)三角形 (B)正方形(C)非正方形的长方形 (D)非正方形的菱形二、填空题(每小题9分,共54分)1.已知有向线段PQ 的起点P 和终点Q 的坐标分别为(-1,1)和(2,2),若直线l x my m :++=0与PQ 的延长线相交,则m 的取值范围是______.2.已知x y a R ,[,],∈-∈ππ44且x x a y y y a 332040+-=++=⎧⎨⎩sin sin cos 则cos()x y +2=_____.3.已知点集A x y x y =-+-≤{(,)|()()()}3452222,B x y x y =-+->{(,)|()()()}4552222,则点集A B 中的整点(即横、纵坐标均为整数的点)的个数为_____.4.设0<<θπ,则sin (cos )θθ21+的最大值是______. 5.已知一平面与一正方体的12条棱的夹角都等于α,则sin α=___6.已知95个数a a a a 12395,,,, , 每个都只能取+1或-1两个值之一,那么它们的两两之积的和a a a a a a 12139495+++ 的最小值是___.。
1994年试题

百度文库专用百度文库专用1994年试题试题六(15分)完成下列叙述,把应填入____(n)____处的字句,写在答案的对应栏内。
(1)设在计算表达式‖k+=i>j? i++:--j‖之前,变量i,j,k分别有值i=6,j=6,k=3,则该表达式的值为______(1)_______。
(2)设有变量定义:int a[ ][4]={1,2,3,4,5,6,7,8}, (*p)[4]=a:则表达式―**(p+1)-*(*p+1)‖的值为____(2)_____(3)设函数m()的说明形式为void m(int, int * );利用函数m()对数5和整型变量j作函数m()定义的计算,正确的调用形式为______(3)_____(4)以下程序输出是______(4)_______int test(){int x=0;static int y=2;y+=++xreturn x+y;}main(){printf(―%d\n‖,(test(),test()));}(5)下面的C函数s()用于求级数s(x)的近似值(精确到0.00001),其中s(x)定义为s(x)=x-x3/3!+x5/5!–x7/7!+…double s(double x){int n=0;double u=x, t=x;while (fabs(t)> 0.00001){n++;u+=(t=____(5)_____);}return u;}试题七(15分)阅读以下C程序,回答问题,把解答写在答案的(1)——(5)栏内。
[程序]void u(int i, char *cp){for (;i;i--)printf (―%c‖, *cp++);}main(){char b[ ][3]={―eof‖, ―EGF‖,‖AB‖};char (*q)[3]=b;char *pL1: p=b[0]; u(1,p++); u(1,p++); u(1,p); printf(―\n‖);L2: p=b[1]; u(3,p++); u(2,p++); u(1,p); printf(―\n‖);L3: printf(―%s\n‖,b[1])L4: u(1,q++); u(1,q++); u(1,q); printf(―\n‖);}问题(1)该程序编译时,会有警告信息输出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1994年第四届全国初中应用物理知识竞赛复赛试题
一、选择题。
(每小题4分,共48分)
1.长200米的列车用120秒匀速通过1.6千米的长江大桥,列车运行的速度是:( )
A.11.7米/秒 B.15米/秒 C.13.3米/秒D.1.7米/秒
2.有一架飞机沿水平向左做匀速直线运动,每隔1秒钟从飞机上轻轻释放一小球,当三只小球落下且均未落至地面时,若不计空气阻力,则这三只小球在空中的排列情况应是下图中的哪一个( )
3.以下几种关于摩擦的利弊的说法中,正确的是:( )
A.人走路时,脚与地面的摩擦是有害的 B.骑自行车时,自行车轮胎与地面的摩擦是有害的
C.机车起动时,轮与钢轨间的摩擦是有益的 D.皮带传动时,皮带与皮带轮之间的摩擦是有害的
4.在江河湖海游泳的人上岸时,在由深水走向浅水的过程中,如果水底布满石头,以下体验和分析合理的是:( )
A.脚不痛。
因人越来越轻 B.脚越来越痛。
因人越来越重
C.脚不痛。
因水底对人的支持力越来越小 D.脚越来越痛。
因水底对人的支持力越来越大
5.我国北方冬天,河流会结上厚厚的一层冰,冰的温度有时低达-40℃,假如在-40℃的冰下有流动的河水,那么水与冰交界处的温度是:( )
A.4℃ B.0℃ C.-40℃ D.略高于-40℃
6.右图的四种河堤的设计中,最不合理的是( )
7.为了防盗,在门上装上一个“猫眼”,使屋内的人能看清屋
外的人是一个正立缩小的像,屋外面的人却看不清屋内的人,
则“猫眼”应该是:( )
A.凸镜B.凹镜 C.凹透镜D.凸透镜
8.冻豆腐里面有小孔的成因是:( )
A.豆腐自身冻缩而成 B.豆腐自身膨胀而成
C.外界的冰雪扎进豆腐里而成 D.豆腐里面的水受冻先结冰,再熔化成水后而成
9.用一重锤从相同的高度落下敲击质量和温度分别相同的钢块和铅块,重锤打在钢块上时,重锤会跳起,打在铅块上时,重锤没有弹起,这时:( )
A.钢块的温度比铅块高 B.铅块的温度比钢块高 C.钢块与铅块的温度一样高D.无法判断谁的温度高10.一台“220V,60W”的电扇,一只“220V,60W”的白炽灯,一只“220V,60W”的电热器,将它们同时接在220V的电压下,在相同的时间内,它们产生的热量( )
A.电扇最多B.白炽灯最多 C.电热器最多 D.都一样多
11.在暗室的红灯下看一张白纸和白纸上的红字,得到的感觉是:( )
A.纸是白色的,字能看清楚 B.纸是白色的,字看不清楚
C.纸是红色的,字能看清楚 D.纸是红色的,字看不清楚
12.密度是物质的属性之一,至今人们知道具有最大密度和最小密度的物质分别是:( )
A.黑洞、星际物质 B.中子星、慧星 C.巨星、氢气D.白矮星、氢气
二、填空题。
(每小题3分,共12分)
1.夏天,在天平左盘中放一敞口玻璃杯,杯中有一冰块,右盘中放有一定质量的砝码,这时天平是平衡的,过了几分钟后,天平失去了平衡,天平向______倾斜了,原因是__________________________________。
2.一杯中装有冰水混合物,冰完全溶解后,杯中水面高度将______;碗中水面木板上放一石块,石块掉入水中被水淹没,水面高度将______。
3.一只“220V,100W”的白炽灯在室温时的电阻约为40Ω,开灯瞬间的电功率为______,正常工作时的电阻是______。
4.修理家用电器时需要一只4.75kΩ的电阻,但手头只有10kΩ、8kΩ、500Ω和300Ω的电阻若干,要用最
少个数的电阻得到最接近所需要的电阻值,连接方法是____________________________,得
到的电阻阻值为______。
三、(6分)右图为建造房屋用的钢筋混凝土预制板,其a面为钢筋钢
架,B面为混凝土,根据混凝土具有抗压能力,钢筋具有抗拉的能力,
在用这种预制板建设楼板时,你认为如何放置才合适,并说明理由。
四、(6分)用两块平面镜做成如图所示的潜望镜,两平面镜中心的距离为L,现在用此
潜望镜观察正前方一物体AB ,那么人从潜望镜中看到AB 的像距物体AB 的水平距离是多少?(作图并说明)
五、(7分)一把一段长约5厘米的蜡烛,粘牢在一个碗底,然后把水装入碗内,使
水面刚好到蜡烛的边缘,然后点燃蜡烛(如图),试说明你观察到的现象,并解释
出现这种现象的原因。
六、(7分)一个照明用的灯具如图所示,接上电源后按下开关K 1、K 2时两灯都发光;断开K 1,
两灯都不发光;接通K 1,断开K 2则L 1发光,L 2不发光,试根据这些现象画出灯具内的电路图。
八、(7分)下面为照明电路中使用的电度表表面示图;
(1)说明表面上3000R/kWh 的含意。
(2)若单独接入一电炉,2分钟内电表盘转了50转,这个电炉的电功率是多大? (3)此电炉通电2小时放出了多少热量?用了多少度电?
1994年第四届全国初中应用物理知识竞赛复赛
一、选择题
1、B 解:列车通过长江大桥行驶的路
距为s=1600米+200米=1800米,
2、C 解:三只小球从匀速直线运动的
飞机上释放后,间隔时间很短,由于惯性,释放后的小球仍能保持原来的运动状态,继续向左运动一段路程,故三只小球在空中的排列情况应是C 图。
3、C 解:四种情况中,两物体间的摩擦都是有益,都是为了防止打滑。
故正确答案是C 。
4、D 解:在江河湖海游泳的人上岸时,由深水走向浅水的过程中,人的重力不变,但水对人的浮力越来越小,水底对人的支持力越来越大,故脚越来越痛。
D 对。
5、B 解:冰水交界处可视为冰水混合物,其温度是0℃。
B 对。
6
、B 解:因为液体内部向各个方向都有压强,压强随着深度的增加而增大,所以河坝、塘坝都是下宽上窄。
故四种设计中,最不合理的是B 。
7、C 解:根据面镜和透镜的成像规律,能成正立缩小的像是凸镜和凹透镜;但要使屋内的人看屋外的人;只能用凹透镜。
应选C 。
8、D 解:冻豆腐里面有小孔的成因是:豆腐里面的水受冻先结冰,再熔化成水体积减小而成。
9、B 解:重锤打在钢块上时重锤会跳起,说明重锤原有的机械能一部分转化为钢块的热能,另一部分转化为重锤的机械能;重锤打在铅块上时重锤没有弹起,说明重锤原有的机械能几乎都转化为铅块的热能。
故这时铅块的温度比钢块高。
B 对。
10、C 解:虽然电扇、白炽灯、电热器工作时消耗的电能相同,但它们工作时,电扇主要是电能转化为机械能和热能;白炽灯是电能转化成光能和热能;电热器是电能转化为热能。
故电热器产生的热量最多。
选C 。
11、D 解:不透明体的颜色是由它反射的色光决定的。
白纸可以反射各种色光,红字只能反射红光,故白纸上写红字,在红色灯光照射下,白纸变成了红色,红字也是红色,字看不清楚。
应选D 。
12、A 解:至今人们知道具有最大密度的物质是黑洞,最小密度的物质是星际物质。
选A 。
二、填空题
1、左;左盘冰块使空气中的水蒸气凝结成水附着在冰块上,使左盘质量增加。
2、不变;下降。
3
、1210瓦,484欧。
4、一只10kΩ的电阻和一只8kΩ的电阻并联再与一只300Ω的电阻串联;4.74kΩ。
三、解答:应把预制板的a面放在下面。
由于预制板的自重和承重,会使预制板发生向下弯曲,使楼板上部成为受压区,下部成为受拉区,因而a面向下,b面向上,才不会使预制板受压而折断。
四、解:图形右图所示。
根据平面镜成像规律, AB与其在M1镜的像A'B'关于M1对称,A'B'对于M2镜为物,它的像
A"B"距O2距离为L+h,所以A"B"距AB水平距离为L。
五、解:点燃蜡烛后,过一会蜡烛会烧到水面以下,这时蜡烛呈四周的壁很薄的漏斗状。
出
现这种现象的原因是蜡烛燃烧后,烛芯四周的蜡熔化,当熔化到四周只剩很薄的一层蜡时,
热从蜡层传递到水,使这层蜡达不到熔化的温度,因而呈漏斗状。
六、解:电路图右图所示。
七、解:作用在活塞表面上的压力:
做功冲程每次的功:W=F·L=35325×0.4=14130(焦耳)
柴油机每分钟转360转,即每秒转6转,对外做功3次。
答:这台柴油机的功率约为58马力。
八、解:(1)3000R/kWh字样表示电流每做1千瓦时的功,转盘转动3000转。
(2)电炉的电功率
消耗的电能: W=Pt=0.5×2=1(度)或W=Pt=500×2×3600=3.6×106(焦)=1度
答:这个电炉的电功率是500瓦特;通电2小时放出8.57×105卡的热量;用了1度电。
