外啮合圆柱齿轮传动计算
齿轮传动的设计参数、许用应力与精度选择

齿轮传动的设计参数、许用应力与精度选择(一)齿轮传动设计参数的选择压力角α的选择由机械原理可知,增大压力角α,轮齿的齿厚及节点处的齿廓曲率半径亦皆随之增加,有利于提高齿轮传动的弯曲强度及接触强度。
我国对一般用途的齿轮传动规定的标准压力角为α=20°。
为增强航空用齿轮传动的弯曲强度及接触强度,我国航空齿轮传动标准还规定了α=25°的标准压力角。
但增大压力角并不一定都对传动有利。
对重合度接近2的高速齿轮传动,推荐采用齿顶高系数为1~1.2 ,压力角为16°~18°的齿轮,这样做可增加轮齿的柔性,降低噪声和动载荷。
小齿轮齿数 z1 的选择若保持齿轮传动的中心距 a 不变,增加齿数,除能增大重合度、改善传动的平稳性外,还可减小模数,降低齿高,因而减少金属切削量,节省制造费用。
另外,降低齿高还能减小滑动速度,减少磨损及减小胶合的可能性。
但模数小了,齿厚随之减薄,则要降低轮齿的弯曲强度。
不过在一定的齿数范围内,尤其是当承载能力主要取决于齿面接触强度时,以齿数多一些为好。
闭式齿轮传动一般转速较高,为了提高传动的平稳性,减小冲击振动,以齿数多一些为好。
小齿轮的齿数可取为 z1=20~40。
开式(半开式)齿轮传动,由于轮齿主要为磨损失效,为使轮齿不至过小,故小齿轮不宜选用过多的齿数,一般可取z1=17~20。
为使轮齿免于根切,对于α=20°的标准直齿圆柱齿轮,应取z1≥17。
齿宽系数φd的选择由齿轮的强度计算公式可知,轮齿愈宽,承载能力愈高;但增大齿宽又会使齿面上的载荷分布趋不均匀,故齿宽系数应取得适当。
圆柱齿轮齿宽系数的荐用值见下表。
对于标准圆柱齿轮减速器,齿宽系数取为,所以对于外啮合齿轮传动:。
φa的值规定为0.2,0.25,0.30,0.40,0.50,0.60,0.80,1.0,1.2。
运用设计计算公式时,对于标准减速器,可先选定φa后再用上式计算出相应的φd值。
齿轮各参数计算公式

模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) (d为分度圆直径,z为齿数)齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径 d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶高ha ha=m=p/π齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2=πm/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1 什么是分度圆?标准齿轮的分度圆在什么位置上?13-2 一渐开线,其基圆半径r b=40 mm,试求此渐开线压力角=20°处的半径r和曲率半径ρ的大小。
13-3 有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径d a=106.40 mm,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4 两个标准直齿圆柱齿轮,已测得齿数z l=22、z2=98,小齿轮齿顶圆直径d al=240 mm,大齿轮全齿高h=22.5 mm,试判断这两个齿轮能否正确啮合传动?13-5 有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z1=19、z2=81,模数m=5 mm,压力角=20°。
若将其安装成a′=250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C 是多少?13-6 已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数z1=21、z2=66,模数m=3.5 mm,压力角=20°,正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7 已知一标准渐开线直齿圆柱齿轮,其齿顶圆直径d al=77.5 mm,齿数z1=29。
圆柱齿轮传动强度的计算

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效,应进行齿面接触疲劳强度计算。
因此,齿轮接触疲劳强度计算准则为:齿面接触应力σH小于或等于许用接触应力σHP,即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区,轮齿受力较大,故点蚀首先出现在节点附近。
因此,通常计算节点的接触疲劳强度。
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。
为了简化计算,用一对轴线平行的圆柱体代替它。
两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径,如图b所示。
由弹性力学可知,当一对轴线平行的圆柱体相接触并受压力作用时,将由线接触变为面接触,其接触面为一狭长矩形,在接触面上产生接触应力,并且最大接触应力位于接触区中线上,其数值为式中σH-接触应力(Mpa)Fn-法向力(N)L-接触线长度(mm)rS-综合曲率半径(mm);±-正号用于外接触,负号用于内接触ZE-材料弹性系数(),,其中E1、E2分别为两圆柱体材料的弹性模量(MPa);m1、m2分别为两圆柱体材料的泊松比。
上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同,且靠近节点的齿根处最大(图c、d)。
但为了简化计算,通常控制节点处的接触应力。
节点处的参数(1)综合曲率半径由图可知,,代入rE公式得式中:,称为齿数比。
对减速传动,u=i;对增速传动,u=1/i。
因,则有(2)计算法向力(3)接触线长度L引入重合度系数Ze,令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令,称为节点区域系数。
则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数,并将代入上式,则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径(mm);ZE-材料弹性系数(),按下表查取;注:泊松比m1=m2=0.3Z H-节点区域系数,考虑节点处轮廓曲率对接触应力的影响,可由下左图查取。
已知一对外啮合正常齿标准直齿圆柱齿轮3mm-推荐下载

第5章 习题5-1 已知一对外啮合正常齿标准直齿圆柱齿轮=3mm ,z1=19,z2=41,试m 计算这对齿轮的分度圆直径、齿顶高、齿根高、顶隙、中心距、齿顶圆直径、齿根圆直径,基圆直径、齿距、齿厚和齿槽宽。
5-2 已知一正常具标准直齿圆柱的a=20°=mm ,=40,试分别求出分m z 度圆、基圆、齿顶圆上渐开线齿廓的曲率半径和压力角。
5-3 如图5-3所示一渐开线齿轮在半径为A =95mm 处的齿轮的齿廓压力r 角为8°26′49″,齿厚为A =10.088mm 。
试计算齿廓压力角为B =25°处的s a 齿厚B 及半径B 。
s r5-4 在某项技术革新中,需要采用一对齿轮传动,其中心距=144mm ,a 传动比=2。
现在库房中存有四种现成的齿轮,压力角都是20°,这四种齿轮i 的齿数和齿顶圆直径a 分别为:1=24,al =104mm ;2=47,a2=196mm ;z d z d z d 3=48,a3=250mm ;4=48,a4=200mm 。
试分析能否从这四种齿轮中选出z d z d 符合要求的一对齿轮。
5-5 有一个渐开线直齿圆柱齿轮如图5-4所示,用卡尺测量三个齿和两个齿的公法线长度为3=61.84mm ,2=37.56mm ,齿顶圆直径a =208mm ,齿根W W d 圆直径f =172mm ,数得其齿数=24。
试求:d z(1)该齿轮的模数、分度圆压力角、齿顶高系数a *和顶隙系数c *;m a h(2)该齿轮的基圆距P b 和基圆齿厚b 。
s 5-6 一对渐开线外啮合直齿柱齿轮机构,两轮的分度半径分别为r 1=30mm,r 2=54mm ,=20°,试求:a (1)当中心距′=86mm 时,啮合角′是多少?两个齿轮的节圆半径a a 1和2各为多少?r 'r '(2)当中心距变为′=87mm 时,啮合角′和节圆半径1和2又各为a a r 'r '多少?(3)以上两种中心距情况下的两对节圆半径的比值是否相等,为什么?5-7 已知一对渐开线外啮合标准直齿柱齿轮,1=18, 2=41,=4mm ,z z m =20°,a *=1,试求:a h (1)两轮的几何尺寸、b 、f 、a 和标准中心距,以及重合度εa ;r r r r a (2)用长度度比例尺=0.5mm/mm 画出理论啮合线N 1N 2在其上标出实际ul 啮合线B 1B 2,并标出一对啮合区和两对啮合区,以及节点C 的位置。
齿轮各参数计算公式知识讲解

齿轮各参数计算公式13-1什么是分度圆?标准齿轮的分度圆在什么位置上? 13-2 一渐开线,其基圆半径r b = 40 mm ,试求此渐开线压力角 =20。
处的半径r 和曲率半径p的大小。
13-3有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径 da = 106.40 mm ,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4两个标准直齿圆柱齿轮,已测得齿数 z i = 22、z 2 = 98,小齿轮齿顶圆直径d ai = 240 mm ,大 齿轮全齿高h = 22.5 mm ,试判断这两个齿轮能否正确啮合传动 ?名称 代号 计算公式 模数 m m=p/n =d/z=da/(z+2)(d 为分度圆直径齿距 P p= n m=t d/z 齿数 z z=d/m=n d/p 分度圆直径 d d=mz=da-2m齿顶圆直径 da da=m(z+2)=d+2m=p(z+2)/ n 齿根圆直径 df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶咼 ha ha=m=p/n 齿根高 hf hf=1.25m齿高 h h=2.25m 齿厚 s s=p/2= n m/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数 k k=z/9+0.5公法线长度ww=m[2.9521(k-0.5)+0.014z]模数齿轮计算公式 ,z 为齿数)13-5有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z i = 19、Z2 = 81,模数m= 5 mm,压力角=20°若将其安装成a' = 250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数Z1 = 21、Z2 = 66,模数m =3.5 mm,压力角 =20°正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
齿轮传动的作用力及计算

11-4直齿圆柱齿轮传动的作用力及计算载荷:一、齿轮上的作用力:为了计算齿轮的强度,设计轴和选用轴承,有必要分析轮齿上的作用力。
当不计齿面的摩擦力时,作用在主动轮齿上的总压力将垂直于齿面,(因为齿轮传动一般都加以润滑,齿轮在齿啮合时,摩擦系数很小,齿面所受的摩擦力相对载荷很小,所以不必考虑),即为P175图11-5b所示的F n(沿其啮合线方向),Fn可分解为两个分力:圆周力:Ft=2T1/d1 N径向力:Fr=Fttgα N而法向力:Fn=Ft/cosα NT1:小齿轮上的扭矩 T1=9550000p/n1 n·mmP:传递的功率(KW) d1:小齿轮分度圆直径 mmα:压力角 n1:小齿轮的转速(r·p·m)Ft1:与主动轮运动方向相反;Ft2与从动轮运动方向一致。
各力的方向 Fr:分别由作用点指向各轮轮心。
Fn:通过节点与基圆相切(由法切互为性质)。
根据作用力与反作用力的关系,主从动轮上各对的应力应大小相等,方向相反。
二、计算载荷:Fn是根据名义功率求得的法向力,称为名义载荷,理论上Fn沿齿宽均匀分布,但由于轴和轴承的变形,传动装置的制造安装误差等原因,载荷沿齿宽的分布并不均匀,即出现载荷集中现象(如P176图11-6所示,齿轮相对轴承不对称布置,由于轴的弯曲变形,齿轮将相互倾斜,这时,轮齿左端载荷增大,轴和轴承刚度越小,b越宽,载荷集中越严重。
此外,由于各种原动机和工作机的特性不同,齿轮制造误差以及轮齿变形等原因,还会引起附加动载荷。
精度越低,圆周速度V越大,附加载荷越大。
因此在计算强度时,通常以计算载荷K·Fn代替名义载荷Fn,以考虑上两因素的影响。
K—载荷系数表达式11-311-5 直齿圆柱齿轮的齿面接触强度计算:一、设计准则:齿轮强度计算是根据齿轮失效形式来决定的,在闭式传动中,轮齿的失效形式主要是齿面点蚀,开式传动中,是齿轮折断,在高速变截的齿轮传动中,还会出现胶合破坏,因胶合破坏的计算方法有待进一步验证和完善。
齿轮各参数计算公式

模数齿轮计算公式名称代号计算公式模数m m=p/n =d/z=da/(z+2)(d为分度圆直径,z为齿数)齿距P p= n m=t d/z齿数Z z=d/m=n d/p分度圆直径d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/ n齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶咼ha ha=m=p/n齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2= n m/2中心距a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1什么是分度圆?标准齿轮的分度圆在什么位置上?13-2 一渐开线,其基圆半径r b= 40 mm ,试求此渐开线压力角:■ = 20°处的半径r和曲率半径p的大小。
13-3有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径da = 106.40 mm ,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4两个标准直齿圆柱齿轮,已测得齿数z i= 22、Z2= 98,小齿轮齿顶圆直径d ai= 240 mm ,大齿轮全齿高h=22.5 mm,试判断这两个齿轮能否正确啮合传动?13-5有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为Z1= 19、Z2= 81,模数m= 5 mm,压力角«= 20°若将其安装成a'= 250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数Z1 = 21、Z2= 66,模数m = 3.5 mm ,压力角□= 20°正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7已知一标准渐开线直齿圆柱齿轮,其齿顶圆直径d ai= 77.5 mm,齿数z1=29。
4种齿轮计算公式
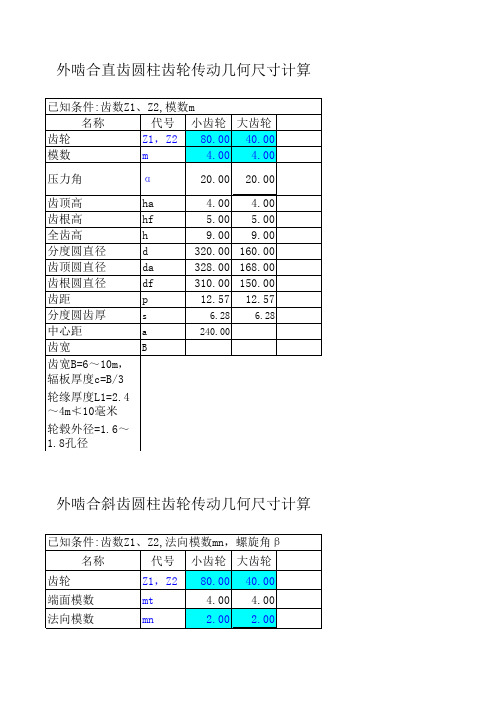
外啮合直齿圆柱齿轮传动几何尺寸计算外啮合斜齿圆柱齿轮传动几何尺寸计算压力角α20.0020.00齿顶高ha 2.00 2.00齿根高hf 2.50 2.50全齿高h 4.50 4.50分度圆直径d320.00160.00齿顶圆直径da324.00164.00齿根圆直径df315.00155.00分度圆齿厚s 6.28 6.28中心距a240.00齿宽计算m n=(da-df)/4.5计算螺旋角cosβ =m n z/(da-2mn)注注:☆蜗杆齿宽:当注:☆最大外圆直注:☆蜗轮齿宽:当注:模数为12,10注注:☆蜗杆螺纹长注:蜗杆在分度圆外啮合直齿锥齿轮传动几何尺齿顶高h a 齿根高hf 分度圆直径d1节圆直径dje1齿顶圆直径da1齿根圆直径df1分度圆螺旋导程角(弧度)γ法向模数m f 轴向齿距Px 分度圆柱螺旋导程P Z螺牙沿分度圆柱上的轴向齿厚S z1螺牙沿分度圆柱上的法向齿厚S f1齿厚测量高度h~齿数Z 2分度圆直径d2齿根圆直径df2齿顶圆直径da2最大外圆直径D2蜗轮宽度b2齿顶圆弧半径R a 齿根圆弧半径Rf注:☆磨削蜗杆需加长:m≤10时,加长25mm;10≤m≤16时,加长35mm;m>16时,加长40-50mm 注:☆蜗杆齿宽:当Z=1~2时取(13~16)m, 当Z=3~4时取(15~21)m注:☆最大外圆直径:当Z=1取≤da2+2m,当Z=2~3取≤da2+1.5m,当Z=4取≤da2+m注:☆蜗轮齿宽:当Z≤3时取≤0.75Ddi1, 当Z=4时取≤0.67Ddi1,包角2θ=45°~130°注:模数为12,10,8,6,5,4,3,2.5,2,1.5,1蜗 轮蜗 杆螺旋长度L☆注:蜗杆特性系数q为14,13,12,11,10,9,8注:☆蜗杆螺纹长度L:当Z=1~2时取大于(11+0.06Z2)m, 当Z=3~4时取大于(12.5+0.09Z2)m 注:蜗杆在分度圆上的轴向齿厚=1.498m,分度圆上的法向齿厚=1.498mcos γ齿齿齿轴向齿距轴向齿形齿齿分h高h 顶高h 根高 3:1a压力角齿根圆弧半d 顶圆直径L切制螺纹部分长度d 根圆直径d 度圆直径21f 1a 1P xa 1f 1(a )蜗杆(b几何尺寸计算mm;m>16时,加长40-50mm+1.5m,当Z=4取≤da2+m67Ddi1,包角2θ=45°~130°时取大于(12.5+0.09Z2)m向齿厚=1.498mcos γ齿顶圆弧半径R 齿根圆弧半径R a 2(b )蜗轮。
齿轮计算公式

由齿轮各部分名称的定义可以得到标准齿轮的几何尺寸计算公式,如(外齿轮):分度圆直径d=mz基圆直径db=dcosα齿顶圆直径齿根圆直径标准齿轮的几何尺寸计算公式详见付表圆柱齿轮根据轮齿的方向,可分为直齿圆柱齿轮、斜齿圆柱齿轮和人字齿圆柱齿轮。
这里主要介绍直齿圆柱齿轮。
图2 齿轮工作图在投影为非圆的外形视图中,齿根线与齿顶线在啮合区内均不画出,而节线用粗实线表示。
图3圆柱齿轮的画法a)直齿(外形视图) b)直齿(全剖) c)斜齿(半剖) d)人字齿(局部剖)(1)直齿圆柱齿轮各部分名称图4a为互相啮合的两齿轮的一部分;图4b为单个齿轮的投影图。
l)节圆直径d’、分度圆直径 d——连心线 O1O2上两相切的圆称为节圆。
对单个齿轮而言,作为设计、制造齿轮时进行各部分尺寸计算的基准圆,也是分齿的圆,称为分度圆。
标准齿轮d=d’。
图4直齿圆柱齿轮各部分名称a)啮合图b)单个齿轮图2)齿顶圆直径da—通过轮齿顶部的圆,称为齿顶圆。
3)齿根圆直径df—通过齿槽根部的圆,称为齿根圆。
4)齿顶高ha 齿根高hf齿高h—齿顶圆与分度圆的径向距离称为齿顶高;分度圆与齿根圆的径向距离称为齿根高;齿顶圆与齿根圆的径向距离称为齿高。
其尺寸关系为:h=ha +hf5)齿厚s、槽宽e、齿距p——每个轮齿在分度圆上的弧长称为齿厚;每个齿槽在分度圆上的孤长称为槽宽;相邻两齿廓对应点间在分度圆上的弧长称为齿距。
两啮合齿轮的齿距必须相等。
齿距p、齿厚S、槽宽e间的尺寸关系为:p=s+e,标准齿轮的s=e。
6)模数——若以Z表示齿轮的齿数,则:分度圆周长=πd=zp,即d=zp/π。
令p/π=m,则d=mz式中。
称为模数。
因为两齿轮的齿距p必须相等,所以它们的模数也相等。
为了齿轮设计与加工的方便,模数的数值已标准化。
如表1所列。
模数越大,轮齿的高度、厚度也越大,承受的载荷也越大,在相同条件下,模数越大,齿轮也越大。
表1 标准模数(GB1357—78)注:选用模数时应选用第一系列:其次选用第二系列;括号内的模数尽可能不用。
直齿轮、斜齿轮、圆锥齿轮、蜗杆蜗轮计算

外啮合直齿圆柱齿轮传动几何尺寸计算外啮合斜齿圆柱齿轮传动几何尺寸计算压力角α20.0020.00齿顶高ha 2.00 2.00齿根高hf 2.50 2.50全齿高h 4.50 4.50分度圆直径d320.00160.00齿顶圆直径da324.00164.00齿根圆直径df315.00155.00分度圆齿厚s 6.28 6.28中心距a240.00齿宽计算m n=(da-df)/4.5计算螺旋角cosβ =m n z/(da-2mn)注注:☆蜗杆齿宽:当注:☆最大外圆直注:☆蜗轮齿宽:当注:模数为12,10注:蜗杆特性系数注:☆蜗杆螺纹长注外啮合直齿锥齿轮传动几何尺齿顶高h di 齿根高hg 分度圆直径D fe1节圆直径D je1齿顶圆直径D di1齿根圆直径D g1分度圆螺旋导角(弧度)λ法向模数m f 轴截面齿距P 螺旋导程P Z 螺牙沿分度圆柱上的轴向齿厚S z1螺牙沿分度圆柱上的法向齿厚S f1齿厚测量高度h~齿数Z 2分度圆直径D fe2节圆直径D je2齿根圆直径D g2齿顶圆直径D di2最大外圆直径Dw 2轮缘宽度b 齿顶圆弧半径R 1齿根圆弧半径R 2注:☆磨削蜗杆需加长:Mdu≤10时,加长25MM;10≤Mdu≤16时,加长35M 注:☆蜗杆齿宽:当Z=1~2时取(13~16)Mdu, 当Z=3~4时取(15~21)Mdu注:☆最大外圆直径:当Z=1取≤Ddi2+2Mdu,当Z=2~3取≤Ddi2+1.5Mdu,当Z=4取≤Ddi2+Mdu 注:☆蜗轮齿宽:当Z≤3时取≤0.75Ddi1, 当Z=4时取≤0.67Ddi1,包角2θ=45°~130°注:模数为12,10,8,6,5,4,3,2.5,2,1.5,1注:蜗杆特性系数q为14,13,12,11,10,9,8注:☆蜗杆螺纹长度L:当Z=1~2时取大于(11+0.06Z2)Mdu, 当Z=3~4时取大于(12.5+0.09Z2)蜗 轮蜗 杆螺旋长度L☆齿根圆弧半注:蜗杆在分度圆上的轴向齿厚=1.498m,分度圆上的法向齿厚=1.498λ齿齿轴向齿形齿齿分h 顶高h 根高轴向齿距 3:1a压力角齿根圆弧半d 顶圆直径d 根圆直径d 度圆直径21f 1a 1P xa 1f 1(a )蜗杆(b几何尺寸计算长35MM;Mdu>16时,加长40-50MM 15~21)MduDdi2+1.5Mdu,当Z=4取≤Ddi2+Mdu 67Ddi1,包角2θ=45°~130°当Z=3~4时取大于(12.5+0.09Z2)Mdu齿顶圆弧半径R 齿根圆弧半径R f a向齿厚=1.498mcosλ齿顶圆弧半径齿根圆弧半径RR f a 2(b)蜗轮。
齿轮变位系数计算公式
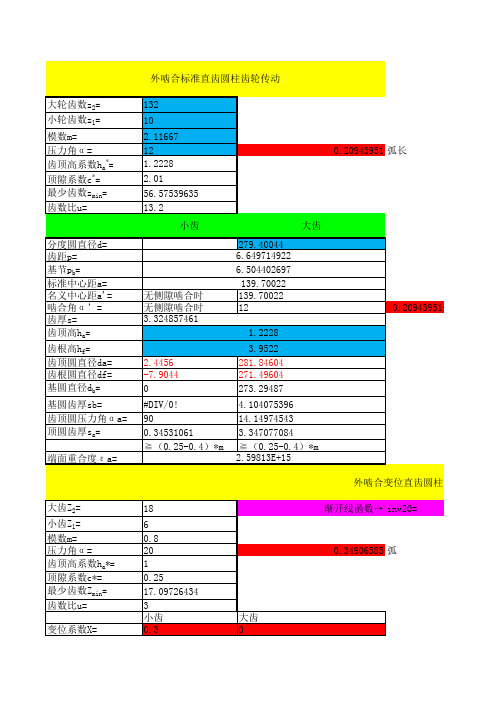
1.743355127
1.622393438
27.87834641
0.295868875
直齿外齿轮
公法线长度
公法线长度的计算 Wk=
标准齿轮 9.70116265
直齿外齿轮 斜齿外齿轮
跨测齿数 公法线长度 跨测齿厚
k= Wkn= k=
5.055555556
直齿外齿轮
公法线长度 跨测齿数
齿顶高hae1= 齿根高hfe1= 全齿高he1= 齿顶圆直径dae1= 分度圆直径de1= 齿根角Øf1= 齿顶角Øa1= 顶锥角δa1= 根锥角δf1= Ak1=
14.212488
齿根圆直径df=
11.14560191
基圆直径db=
12.5630209
法向齿距pn=
端面齿距pt=
5.199545947
法向基圆齿距pbn=
端面基圆齿距pbt=
基圆螺旋角βb=
21.46902352
法向齿厚sn=
2.35619449
端面齿厚st=
2.599772973
端面基圆齿厚sbt= 2.474242055
0.003117051
0.019 要查出,我没查,用时一定要
0.01
查
弧长
αa1
αa2
1.570796327 0.246959646
位直齿圆柱齿轮传动 0.014904
给定x∑求a' 0.320442451
αa1 0.743891086
αa2 0.479274389
inv20= invαa1= invαa2=
变位系数X=
18
6 0.8 20 1 0.25 17.09726434 3 小齿 0.3
关于标准齿轮的公式计算-基本公式

关于标准齿轮的公式计算:
标准齿轮传动的几何计算
注:有“±”或“”号处,上面的符号用于外啮合,下面的符号用于内啮合。
图1 端面重合度εa
注:
1、本图适用于a(或a n)=20°的各种平行轴齿轮传动。
对于外啮合的标准齿轮和高变位齿轮传动,使用图2则更为方便。
2、使用方法:按αt′和d a1
d1′查εα1
z1
出,按αt′和d a2
d2′
查出εα2
z2
,则εα=z1(εα1
z1
)±z2(εα2
z2
),式中“+”用于外啮
合,“-”用于内啮合。
3、αt′可由图3查得。
图2 外啮合标准齿轮传动和高变位齿轮传动的端面
重合度εα(a=a n=20°、ℎa∗=ℎan∗=1)
注:使用方法如下。
1.标准齿轮(ℎa1=ℎa2=m n):按z1和β查出εα1,按z2和β查出εα2,εα=εα1+εα2
2。
和β查出εα1,按和β查出εα2,2.高变位齿轮[ℎa1=(1+x n1)m n、ℎa2=(1−x n1)m n]:按z1
1+x n1
εα=(1+x n1)εα1+(1−x n1)εα2。
图3 端面啮合角αwt(αp=20°)。
一对外啮合的直齿圆柱标准齿轮,小轮的齿根厚度和大轮的齿根厚度关系;

外啮合的直齿圆柱标准齿轮,小轮的齿根厚度和大轮的齿根厚度关系1. 引言1.1 概述直齿圆柱标准齿轮是一种常见的机械传动元件,广泛应用于各个领域。
在齿轮啮合过程中,齿根厚度是当今研究的一个重要方面,因为它对齿轮的强度和工作性能有着重要的影响。
而在外啮合直齿圆柱标准齿轮中,小轮的齿根厚度与大轮的齿根厚度之间存在着一定的关系。
1.2 文章结构本文将首先介绍外啮合的直齿圆柱标准齿轮的基本概念和特性,包括其定义、特点以及应用领域。
接下来,将详细讨论小轮的齿根厚度与大轮的齿根厚度之间的关系,并分析其中的影响因素。
随后,将介绍相关计算模型及仿真验证方法,以进一步验证前述理论分析结果。
最后,通过总结研究结果提出结论,并展望未来该领域研究可能发展的方向。
1.3 目的本文旨在深入研究外啮合的直齿圆柱标准齿轮中小轮的齿根厚度与大轮的齿根厚度之间的关系,探讨影响因素,并提出相关计算模型和仿真验证方法。
通过该研究,可以为设计者提供有关在不同应用场景中优化选择齿根厚度的参考指导,以提高齿轮传动系统的可靠性和工作效率。
此外,本文也希望培养读者对于直齿圆柱标准齿轮特性及其在机械传动中的应用领域有更全面的了解。
2. 外啮合的直齿圆柱标准齿轮介绍:2.1 定义与特性:外啮合的直齿圆柱标准齿轮是一种常见的机械传动元件, 具有两个相互啮合的齿轮: 大轮和小轮。
它们由金属材料加工而成,具有相对简单的结构。
其中大轮拥有较大的直径,而小轮则比大轮尺寸更小。
这种齿轮常用于各种工业领域,如汽车、机床等,用于实现速度转换、扭矩传递和运动分配。
2.2 齿轮应用领域:外啮合的直齿圆柱标准齿轮广泛应用于许多行业。
在汽车行业中,它们被用作变速箱和传动系统中关键组件,实现不同挡位之间的变速。
此外,在航空航天、能源发电以及其他工程应用中也可以找到这种类型的齿轮。
2.3 标准规范概述:为了确保外啮合的直齿圆柱标准齿轮在各种应用中具有良好的兼容性和互换性,相关机构制定了一系列标准规范。
外啮合变位圆柱齿轮传动几何尺寸计算

外啮合变位圆柱齿轮传动几何尺寸计算外啮合变位圆柱齿轮传动的几何尺寸计算是指根据给定的齿轮参数,计算其相关的几何尺寸。
这些几何尺寸包括齿轮的齿数、模数、齿顶高、齿根高、齿轮间隙等,这些参数是设计和制造齿轮传动系统的重要依据。
下面将详细介绍外啮合变位圆柱齿轮传动几何尺寸的计算方法。
1.齿数计算:齿数是齿轮传动中的重要参数,它决定了齿轮的大小和转速比。
在外啮合变位圆柱齿轮传动中,齿数的计算一般按照下面的公式进行:N=Z1+Z2=(p1-p2)/m+2,其中,N表示齿数,Z1和Z2分别为两个齿轮的齿数,p1和p2表示两个齿轮的啮合位置,m表示模数。
2.模数计算:模数是齿轮传动中的重要参数,它决定了齿轮的尺寸和载荷能力。
在外啮合变位圆柱齿轮传动中,模数的计算一般按照下面的公式进行:m=(p1-p2)/(Z1+Z2),其中,m表示模数,p1和p2表示两个齿轮的啮合位置,Z1和Z2分别为两个齿轮的齿数。
3.齿顶高计算:齿顶高是齿轮传动中的重要参数,它决定了齿轮的强度和传动效率。
在外啮合变位圆柱齿轮传动中,齿顶高的计算一般按照下面的公式进行:h=2.2*m,其中,h表示齿顶高,m表示模数。
4.齿根高计算:齿根高是齿轮传动中的重要参数,它决定了齿轮的强度和传动效率。
在外啮合变位圆柱齿轮传动中,齿根高的计算一般按照下面的公式进行:h=2.2*m,其中,h表示齿根高,m表示模数。
5.齿轮间隙计算:齿轮间隙是齿轮传动中的重要参数,它决定了齿轮的啮合性能和传动精度。
在外啮合变位圆柱齿轮传动中,齿轮间隙的计算一般按照下面的公式进行:C=0.25*m,其中,C表示齿轮间隙,m表示模数。
以上是外啮合变位圆柱齿轮传动几何尺寸的计算方法。
通过这些计算,可以确定齿轮的相关几何参数,为设计和制造齿轮传动系统提供重要的参考依据。
同时,还需要根据具体的传动要求和工作条件,进行更详细的设计和计算。
齿轮齿条传动过程中是怎么计算的

齿轮齿条传动过程中是怎么计算的齿轮齿条传动是一种常见的机械传动方式,广泛应用于各种机械装置中。
它通过齿轮齿条的啮合形成传动,将驱动力传递给被传动部分。
在设计和计算齿轮齿条传动时,需要考虑一系列参数和因素,包括齿轮模数、齿数、啮合角、压力角等。
本文将介绍齿轮齿条传动的计算方法和相关参数。
首先需要了解的是一些基本概念和术语:1. 齿轮模数(Module):齿轮模数是指齿轮齿条传动中齿轮齿数与其分度圆直径的比值。
通常用符号m表示。
模数是确定齿轮尺寸和传动比的重要参数。
2. 齿数(Number of teeth):齿数是指齿轮上齿的数量。
齿数通常用符号z表示。
3. 锥角(Pressure angle):指齿轮齿条传动中齿轮齿面上法线与切线之间的夹角。
通常用符号α表示。
4. 圆周速度(Peripheral velocity):指齿轮齿条传动中两个啮合齿轮分度圆上点的速度。
圆周速度是计算齿轮传动时的重要参数。
5. 啮合角(Pressure angle):指两个啮合齿轮轴线的夹角。
通常用符号β表示。
1.齿轮模数的选择:根据传动比和工作条件选择合适的齿轮模数。
一般来说,齿轮模数越大,齿轮尺寸越大,传动能力越强。
2.齿轮齿数的确定:根据传动比和齿轮模数计算齿轮齿数。
一般情况下,齿数为整数。
3.齿轮副的选择:根据工作条件和传动要求选择合适的齿轮副类型,如直齿轮副、斜齿轮副、锥齿轮副等。
不同类型的齿轮副具有不同的应用特点和适用范围。
4.齿轮啮合角和压力角的计算:根据齿轮模数、齿数和齿轮副类型计算齿轮的啮合角和压力角。
这两个参数影响着齿轮传动的平稳性和传动效率。
5.齿轮啮合的计算:根据齿轮齿数、模数、啮合角等参数计算齿轮的几何尺寸,包括齿高、齿根径等。
6.齿轮传动的力学计算:根据预定的传动功率、转速和工作条件计算齿轮的传动力学参数,如转矩、齿轮强度等。
7.齿轮传动的动力学计算:根据齿轮的几何参数和运动条件进行动力学计算,包括速度、加速度、振动等。
给定中心距计算外啮合渐开线圆柱齿轮传动编程计算

外啮合渐开线圆柱齿轮传动计算--给定中心距输入数据1 模数: mn=1.752 齿数: z1=16z2=433 螺旋角: helix=19+31/60+33/3600= 19.5258334 基本齿廓齿形角: an=20齿顶高系数: ha_m=1.0径向间隙系数: c_m=0.25齿根圆角半径系数: p_m=0.385 工作中心距: a_work=54.2756 精度等级: pgrade=77 齿宽: gw1=25gw2=208 工作齿宽: gw_work=MIN[gw1,gw2]= 209 当量齿数: zv1=z1/(cos(helix)^3)= 19.111224zv2=z2/(cos(helix)^3)= 51.36141410 传动比: u=z2/z1= 2.6875主要几何参数计算1 分度(标准)中心距: a_bz=(z1+z2)*mn/cos(helix)*0.5= 54.7750652 中心距变动系数: ya=(a_work-a_bz)/mn= -0.2857523 端面齿形角: at=atan(tan(an)/cos(helix))= 21.1155164 端面啮合角: at1=acos[a_bz/a_work*cos(at)]= 19.7033355 变位系数和:x_sum=[(z1+z2)*(inv(at1)-inv(at))/(2*tan(an))]= -0.2767336 补偿变位系数: deta_y=x_sum-ya= 0.0090187 分度圆直径: d1=mn*z1/cos(helix)= 29.708510d2=mn*z2/cos(helix)= 79.8416218 基圆直径: db1=d1*cos(at)= 27.713762db2=d2*cos(at)= 74.4807369 分配变位系数(原则:大小轮的滑动比相等):x1=rote[x1,-1 to 1,(1+u)*(tan(acos(db2/(d2+2*mn*(ha_m+x_sum-x1-deta_y))))-tan(at1 ))/(tan(at1)-u*(tan(acos(db2/(d2+2*mn*(ha_m+x_sum-x1-deta_y))))-ta n(at1)))-(1+u)*(tan(acos(db1/(d1+2*mn*(ha_m+x1-deta_y))))-tan(at1)) /(u*tan(at1)-(tan(acos(db1/(d1+2*mn*(ha_m+x1-deta_y))))-tan(at1)))] = 0.273863也可以自选小轮变位系数: x1=x1= 0.273863x2=x_sum-x1= -0.55059710 节圆直径: d_node1=2*a_work/(u+1)= 29.437288d_node2=2*a_work*u/(u+1)= 79.11271211 齿顶圆直径: da1=d1+2*(ha_m+x1-deta_y)*mn= 34.135468da2=d2+2*(ha_m+x2-deta_y)*mn= 81.382969 12 齿根圆直径: df1=d1-2*(ha_m+c_m-x1)*mn= 26.292031df2=d2-2*(ha_m+c_m-x2)*mn= 73.53953213 齿高: h1=(da1-df1)/2= 3.921718h2=(da2-df2)/2= 3.92171814 法面分度圆齿厚: sn1=[pi/2+2*x1*tan(an)]*mn= 3.097767sn2=[pi/2+2*x2*tan(an)]*mn= 2.04749115 基圆螺旋角: Bb=asin[sin(helix)*cos(an)]= 18.304993齿厚测量尺寸计算1 固定弦齿厚: s_c1=mn*[pi/2*cos(an)^2+x1*sin(2*an)]=2.735397s_c2=mn*[pi/2*cos(an)^2+x2*sin(2*an)]=1.8079802 固定弦齿高: h_c1=0.5*[da1-d1-s_c1*tan(an)]= 1.715677h_c2=0.5*[da2-d2-s_c2*tan(an)]= 0.4416493 分度圆弦齿厚:deta1=tod[pi/2/z1+2*x1*tan(an)/z1]*[cos(helix)^3]= 5.306948deta2=tod[pi/2/z2+2*x2*tan(an)/z2]*[cos(helix)^3]= 1.305177齿厚: s_1=mn*z1*sin(deta1)/[cos(helix)^3]=3.093339s_2=mn*z2*sin(deta2)/[cos(helix)^3]=2.0473144 分度圆弦齿高:ha_1=0.5*{da1-[cos(deta1)-sin(helix)^2]/[cos(helix)^2]*d1}=2.285159ha_2=0.5*{da2-[cos(deta2)-sin(helix)^2]/[cos(helix)^2]*d2}=0.7823345 公法线长度:z'1=z1*inv(at)/inv(an)= 18.940755z'2=z2*inv(at)/inv(an)= 50.903280跨齿数:k1=toint{z'1/180*acos[z'1*cos(an)/(z'1+2*x1)]+0.5}= 3k2=toint{z'2/180*acos[z'2*cos(an)/(z'2+2*x2)]+0.5}= 5w1=mn*cos(an)*[pi*(k1-0.5)+z1*inv(at)+2*x1*tan(an)]=13.707641w2=mn*cos(an)*[pi*(k2-0.5)+z2*inv(at)+2*x2*tan(an)]=23.836556公法线长度可以测量吗?结果为True(真),表示可以测量;结果为False(假),表示不能测量,需要减少跨齿数再计算:CanMeasure1=among[helix>0,w1< gw1/sin(Bb),True]= TrueCanMeasure2=among[helix>0,w2< gw2/sin(Bb),True]= True改变跨齿数,计算公法线:k1_change=among[k1>2,k1-1,k1]= 2k2_change=among[k2>2,k2-1,k2]= 4 w1_change=mn*cos(an)*[pi*(k1_change-0.5)+z1*inv(at)+2*x1*t an(an)]= 8.541411w2_change=mn*cos(an)*[pi*(k2_change-0.5)+z2*inv(at)+2*x2*t an(an)]= 18.670326公法线长度可以测量吗?结果为True(真),表示可以测量;结果为False(假),表示不能测量:CanMeasure1=among[helix>0,w1_change< gw1/sin(Bb),True]= TrueCanMeasure2=among[helix>0,w2_change< gw2/sin(Bb),True]= True6 量棒(球)跨距M值计算:量棒直径: dp=1.728*mn= 3.024或自定直径: dp=dp= 3.024量棒中心所在圆上的压力角:ad1=ainv{dp/[z1*mn*cos(an)]+inv(at)-pi/2/z1+2*x1*tan(an)/z1}= 28.754439ad2=ainv{dp/[z2*mn*cos(an)]+inv(at)-pi/2/z2+2*x2*tan(an)/z2}= 19.848843M1=among[ceil(z1/2) eq z1/2 ,d1*cos(at)/cos(ad1)+dp,d1*cos(at)/cos(ad1)*cos(90/z1)+dp]= 34.635834M2=among[ceil(z2/2) eq z2/2 ,d2*cos(at)/cos(ad2)+dp,d2*cos(at)/cos(ad2)*cos(90/z2)+dp]= 82.1561567 斜齿轮轴向齿距: px=among[helix> 0 , pi*mn/sin(helix),0]= 16.4490238 斜齿轮导程: pz1=among[helix > 0 ,z1*px,0]= 263.184364pz2=among[helix > 0 ,z2*px,0]= 707.307978 传动质量指标计算1 齿顶点压力角: aa1=acos(db1/da1)= 35.720385aa2=acos(db2/da2)= 23.7675272 端面重合度:ea=0.5*/pi*[ z1*tan(aa1)+z2*tan(aa2)-(z1+z2)*tan(at1)]= 1.4822143 斜齿轮纵向重合度: eB=among[helix> 0 ,gw_work/px,0]= 1.2158784 总重合度: er=ea+eB= 2.6980915 斜齿轮齿顶螺旋角: Ba1=atan[da1/d1*tan(helix)]= 22.169422Ba2=atan[da2/d2*tan(helix)]= 19.873512 6 法面齿顶厚:san1=da1*{[0.5*pi+2*x1*tan(an)]/z1+inv(at)-inv(aa1)}*cos(Ba1) = 1.030677san2=da2*{[0.5*pi+2*x2*tan(an)]/z2+inv(at)-inv(aa2)}*cos(Ba2) = 1.477061判断齿顶厚度是否足够?齿面类型(硬或软): Tooth_face="硬齿面"Thickness1_OK=among[Tooth_face eq "硬齿面",san1 >= 0.25*mn, san1 > 0.4*mn]= TrueThickness2_OK=among[Tooth_face eq "硬齿面",san2 >= 0.25*mn, san2 > 0.4*mn]= True7 滑动比:η1=(1+u)*[tan(aa2)-tan(at1)]/[tan(at1)-u*(tan(aa2)-tan(at1))]= 2.213282η2=(1+u)*[tan(aa1)-tan(at1)]/[u*tan(at1)-(tan(aa1)-tan(at1))]= 2.213282 滑动比的绝对值是否小于等于3?η1_Ok=abs(η1) <= 3= Trueη2_Ok=abs(η2) <= 3= True齿轮精度数据计算(GB/T10095-2001):1 齿距累积总公差Fp: Fp1=table[GB10095_2001_Fp,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.029Fp2=table[GB10095_2001_Fp,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.0372 齿圈径向跳动公差Fr: F r1=table[GB10095_2001_Fr,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.023Fr2=table[GB10095_2001_Fr,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.0293 单个齿距极限偏差±fpt: fpt1=table[GB10095_2001_fpt,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.01fpt2=table[GB10095_2001_fpt,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.0114 齿廓总公差Fa: Fa1=table[GB10095_2001_Fa,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.01Fa2=table[GB10095_2001_Fa,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级eq pgrade,公差值]/1000= 0.0125 齿廓形状公差ffa: ffa1=table[GB10095_2001_ffa,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.008ffa2=table[GB10095_2001_ffa,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.0096 齿廓倾斜极限偏差±fHa: fHa1=table[GB10095_2001_fHa,分度圆1<d1,分度圆2 >= d1,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.0065fHa2=table[GB10095_2001_fHa,分度圆1<d2,分度圆2 >= d2,模数1<mn,模数2 >= mn,精度等级 eq pgrade,公差值]/1000= 0.00757 螺旋线总公差FB: FB1=table[GB10095_2001_FB,分度圆1<d1,分度圆2 >= d1,齿宽1<gw1,齿宽2>= gw1,精度等级 eq pgrade,公差值]/1000= 0.016FB2=table[GB10095_2001_FB,分度圆1<d2,分度圆2 >= d2,齿宽1<gw2,齿宽2>= gw2,精度等级 eq pgrade,公差值]/1000= 0.0158 螺旋线形状公差ffB: ffB1=table[GB10095_2001_ffB,分度圆1<d1,分度圆1<d1,分度圆2 >= d1,齿宽1<gw1,齿宽2>= gw1,精度等级eq pgrade,公差值]/1000= 0.012ffB2=table[GB10095_2001_ffB,分度圆1<d2,分度圆2 >= d2,齿宽1<gw2,齿宽2 >= gw2,精度等级eq pgrade,公差值]/1000= 0.0119 螺旋线倾斜极限偏差±fHB: fHB1=table[GB10095_2001_fHB,分度圆1<d1,分度圆2 >= d1,齿宽1<gw1,齿宽2 >= gw1,精度等级eqpgrade,公差值]/1000= 0.012fHB2=table[GB10095_2001_fHB,分度圆1<d2,分度圆2 >= d2,齿宽1<gw2,齿宽2 >= gw2,精度等级eq pgrade,公差值]/1000= 0.011。
已知一对外啮合正常齿标准直齿圆柱齿轮3mm

第5章习题5-1 已知一对外啮合正常齿标准直齿圆柱齿轮m=3mm,z1=19,z2=41,试计算这对齿轮的分度圆直径、齿顶高、齿根高、顶隙、中心距、齿顶圆直径、齿根圆直径,基圆直径、齿距、齿厚和齿槽宽。
5-2 已知一正常具标准直齿圆柱的a=20°m=mm,z=40,试分别求出分度圆、基圆、齿顶圆上渐开线齿廓的曲率半径和压力角。
5-3 如图5-3所示一渐开线齿轮在半径为r A=95mm处的齿轮的齿廓压力角为8°26′49″,齿厚为s A=10.088mm。
试计算齿廓压力角为a B=25°处的齿厚s B及半径r B。
5-4 在某项技术革新中,需要采用一对齿轮传动,其中心距a=144mm,传动比i=2。
现在库房中存有四种现成的齿轮,压力角都是20°,这四种齿轮的齿数z和齿顶圆直径d a分别为:z1=24,d al=104mm;z2=47,d a2=196mm;z3=48,d a3=250mm;z4=48,d a4=200mm。
试分析能否从这四种齿轮中选出符合要求的一对齿轮。
5-5 有一个渐开线直齿圆柱齿轮如图5-4所示,用卡尺测量三个齿和两个齿的公法线长度为W3=61.84mm,W2=37.56mm,齿顶圆直径d a=208mm,齿根圆直径d f=172mm,数得其齿数z=24。
试求:(1)该齿轮的模数m、分度圆压力角a、齿顶高系数h a*和顶隙系数c*;(2)该齿轮的基圆距P b和基圆齿厚s b。
5-6 一对渐开线外啮合直齿柱齿轮机构,两轮的分度半径分别为r1=30mm,r2=54mm,a=20°,试求:(1)当中心距a′=86mm时,啮合角a′是多少?两个齿轮的节圆半径r'1和r'2各为多少?(2)当中心距变为a′=87mm时,啮合角a′和节圆半径r'1和r'2又各为多少?(3)以上两种中心距情况下的两对节圆半径的比值是否相等,为什么?5-7 已知一对渐开线外啮合标准直齿柱齿轮,z1=18, z2=41,m=4mm,a=20°,h a*=1,试求:(1)两轮的几何尺寸r、r b、r f、r a和标准中心距a,以及重合度εa;(2)用长度度比例尺ul=0.5mm/mm画出理论啮合线N1N2在其上标出实际啮合线B1B2,并标出一对啮合区和两对啮合区,以及节点C的位置。
齿轮传动的计算载荷

恰好相切;受载后,轴产生弯曲变形(图<轮齿所受的载荷分布不均>),轴上的齿轮也就随之偏斜,这就使作用在齿面的载荷沿接触线分布不均匀(图<轮齿所受的载荷分布不均>)。
图<轮齿所受的载荷分布不均>当然,轴的扭转变形,轴承、支座的变形以及制造,装配的误差也是使齿面上载荷分布不均的因素。
计算轮齿强度时,为了计及齿面上载荷沿接触线分布不均的现象,通常以系数Kβ来表示齿面上分布不均的程度对轮齿强度的影响。
为了改善载荷沿接触线分布不均的程度,可以采用增大轴、轴承及支座的刚度,对称的配置轴承,以及适当的限制轮齿的宽度等措施。
同时应尽可能避免齿轮作悬臂布置(即两个支承皆在齿轮的一边)。
对高速、重载(如航空发动机)的齿轮传动应更加重视。
除上述一般措施外,也可把一个齿轮的轮齿做成鼓形(右图)。
当轴产生弯曲变形而导致齿轮偏斜时,鼓形齿齿面上载=1.11+0.18+0.15×=1.11+0.18(1+0.6)+0.15× =1.11+0.18(1+6.7)+0.15× =1.12+0.18+0.23×=1.12+0.18(1+0.6)+0.23× =1.12+0.18(1+6.7)+0.23× =1.15+0.18+0.31×=1.15+0.18(1+0.6)+0.31× =1.15+0.18(1+6.7)+0.31×=1.05+0.26+0.10×=1.05+0.26(1+0.6) +0.10×=1.05+0.26(1+6.7) +0.10×=0.99+0.31+0.12×=0.99+0.31(1+0.6) +0.12×=0.99+0.31(1+6.7) +0.12×=1.05+0.26+0.16×=1.05+0.26(1+0.6) +0.16×=1.05+0.26(1+6.7) +0.16×=1.0+0.31+0.19×=1.0+0.31(1+0.6) +0.19×=1.0+0.31(1+6.7) +0.19×。
