专题:抛物线与圆综合探究题(含答案)
抛物线专题(附答案)

抛物线专题考点1 抛物线的定义题型 利用定义,实现抛物线上的点到焦点的距离与到准线的距离之间的转换1.已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和的最小值为【[解析]过点P 作准线的垂线l 交准线于点R ,由抛物线的定义知,PR PQ PF PQ +=+,当P 点为抛物线与垂线l 的交点时,PR PQ +取得最小值,最小值为点Q 到准线的距离 ,因准线方程为x=-1,故最小值为32. 已知点),4,3(A F 是抛物线x y 82=的焦点,M 是抛物线上的动点,当MF MA +最小时, M 点坐标是 ( )A. )0,0(B. )62,3(C. )4,2(D. )62,3(-[解析] 设M 到准线的距离为MK ,则MK MA MF MA +=+|||,当MK MA +最小时,M 点坐标是)4,2(,选C考点2 抛物线的标准方程题型:求抛物线的标准方程3.求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:(1)过点(-3,2) (2)焦点在直线上【解题思路】以方程的观点看待问题,并注意开口方向的讨论.[解析] (1)设所求的抛物线的方程为22y px =-或22(0)x py p =>, ∵过点(-3,2) ∴229)3(24⋅=--=p p 或 ∴2934p p ==或 ∴抛物线方程为243y x =-或292x y =,前者的准线方程是1,3x =后者的准线方程为98y =- (2)令0x =得2y =-,令0y =得4x =,∴抛物线的焦点为(4,0)或(0,-2),当焦点为(4,0)时,42p =, ∴8p =,此时抛物线方程216y x =;焦点为(0,-2)时22p = ∴4p =,此时抛物线方程28x y =-.∴所求抛物线方程为216y x =或28x y =-,对应的准线方程分别是4,2x y =-=.4.对于顶点在原点的抛物线,给出下列条件:①焦点在y 轴上;②焦点在x 轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④抛物线的通径的长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).能使这抛物线方程为y 2=10x 的条件是____________.(要求填写合适条件的序号)[解析] 用排除法,由抛物线方程y 2=10x 可排除①③④,从而②⑤满足条件.5. 若抛物线的顶点在原点,开口向上,F 为焦点,M 为准线与Y 轴的交点,A 为抛物线上一点,且3||,17||==AF AM ,求此抛物线的方程[解析] 设点'A 是点A 在准线上的射影,则3|'|=AA ,由勾股定理知22|'|=MA ,点A 的横坐标为)23,22(p -,代入方程py x 22=得2=p 或4,抛物线的方程y x 42=或y x 82= 考点3 抛物线的几何性质题型:有关焦半径和焦点弦的计算与论证6.设A 、B 为抛物线px y22=上的点,且 90=∠AOB (O 为原点),则直线AB 必过的定点坐标为__________.【解题思路】由特殊入手,先探求定点位置 [解析]设直线OA 方程为kx y =,由⎩⎨⎧==px y kx y 22解出A 点坐标为)2,2(2k p k p ⎪⎩⎪⎨⎧=-=px y x k y 212解出B 点坐标为)2,2(2pk pk -,直线AB 方程为221)2(2k pk x k pk y ---=+,令0=y 得p x 2=,直线AB 必过的定点)0,2(p【指引】(1)由于是填空题,可取两特殊直线AB, 求交点即可;(2)B 点坐标可由A 点坐标用k1-换k 而得。
初中数学圆形专题训练50题含(参考答案)

初中数学圆形专题训练50题含参考答案一、单选题1.如图,A ,B ,C 是⊙O 上的三点,且⊙ACB =35°,则⊙AOB 的度数是( )A .35°B .65°C .70°D .90°【答案】C 【分析】根据圆周角定理即可得.【详解】解:由圆周角定理得:223570AOB ACB ∠=∠=⨯︒=︒,故选:C .【点睛】本题考查了圆周角定理,熟练掌握圆周角定理是解题关键.2.如图,在半径为R 的圆内作一个内接正方形,⊙然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n 个内切圆,它的半径是( )A .RB .(12)RC .(12)n -1RD .n R3.如图,在ABC中,以A为圆心,任意长为半径画弧,分别交AB、AC于点M、N;再分别以M、N为圆心,大于12MN的长为半径画弧,两弧交于点P;连结AP并延长交BC于点D.则下列说法正确的是()A.AD BD AB+<B.AD一定经过ABC的重心C.BAD CAD∠=∠D.AD一定经过ABC的外心【答案】C【分析】根据题意易得AD平分⊙BAC,然后根据三角形的重心、外心及三边关系可排除选项.【详解】解:⊙AD平分⊙BAC,⊙BAD CAD∠=∠,故C正确;在⊙ABD中,由三角形三边关系可得AD BD AB+>,故A错误;由三角形的重心可知是由三角形三条中线的交点,所以AD不一定经过ABC的重心,故B选项错误;由三角形的外心可知是由三角形三条边的中垂线的交点,所以AD不一定经过ABC的外心,故D选项错误;故选C.【点睛】本题主要考查三角形的重心、外心及角平分线的尺规作图,熟练掌握三角形的重心、外心及角平分线的尺规作图是解题的关键.4.如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若⊙D=40°,则⊙A的度数为()A.20°B.25°C.30°D.40°【点睛】此题主要考查了切线的性质,正确得出⊙DOC =50°是解题关键.5.如图,点A ,B ,C 在圆O 上,65∠=︒ABO ,则ACB ∠的度数是( )A .50︒B .25︒C .35︒D .20︒6.如图4,在Rt ABC △中,90C =∠,3AC =.将其绕B 点顺时针旋转一周,则分别以BA ,BC 为半径的圆形成一圆环.该圆环的面积为( )AB .3πC .3πD .3π 【答案】C 【分析】根据勾股定理,得两圆的半径的平方差即是AC 的平方.再根据圆环的面积计算方法:大圆的面积减去小圆的面积,即9π.【详解】解:圆环的面积为πAB 2-πBC 2,=π(AB 2-BC 2),=πAC 2,=32π,=9π.故选C.7.已知水平放置半径为6cm的球形容器中装有溶液,容器内液面的面积为27πcm2,如图,是该球体的一个最大纵截面,则该截面O中阴影部分的弧长为()A.2πcm B.4πcm C.6πcm D.8πcm意,灵活运用所学知识解决问题,属于中考常考题型.8.如图,点A,B,C都在圆O上,若⊙C=34°,则⊙AOB为()A.34⊙B.56⊙C.60⊙D.68⊙【答案】D【分析】由题意直接根据圆周角定理中同圆同弧所对的圆周角等于这条弧所对的圆心角的一半进行分析即可求解.【详解】解:⊙⊙C=34°,⊙⊙AOB=2⊙C=68°.故选:D.【点睛】本题考查圆周角定理,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.9.下列命题中,真命题的个数是()⊙同位角相等⊙经过一点有且只有一条直线与这条直线平行⊙长度相等的弧是等弧⊙顺次连接菱形各边中点得到的四边形是矩形.A.1个B.2个C.3个D.4个【答案】A【详解】解:两直线平行,同位角相等,⊙错误;经过直线外一点有且只有一条直线与这条直线平行,⊙错误;在同圆或等圆中,长度相等的弧是等弧,⊙错误;顺次连接菱形各边中点得到的四边形是矩形,⊙正确.故选A.【点睛】本题考查命题与定理.10.AB是⊙O的直径,PB、PC分别切⊙O于点B、C,弦CD AB∥,若PB=AB=10,则CD的长为()A .6B C .D .3 OCF CPE ,四边形12BE OF OF ==,【详解】解:过点⊙OCF CPE , OF OC CE PC =, PB 、PC 分别切⊙O PB PC =,10PB AB ==,11.如图,AB 是O 的直径,ACD 是O 的内接三角形,若6AB =,105ADC ∠=︒,则BC 的长为( )A .8πB .4πC .2πD .π【答案】C【分析】连接OC 、BC ,根据四边形ABCD 是圆的内接四边形和⊙D 的度数,即可求出303602π=,【点睛】本题考查了圆内接四边形的性质、圆周角定理以及弧长公式等知识,根据圆12.将一把直尺、一个含60°角的直角三角板和一个光盘按如图所示摆放,直角三角板的直角边AD 与直尺的一边重合,光盘与直尺相切于点B ,与直角三角板相切于点C ,且3AB =,则光盘的直径是( )A .6B .C .3D .【答案】D13.如图,正五边形ABCDE,则⊙DAC的度数为()A.30°B.36°C.60°D.72°【答案】B【分析】根据正五边形和等腰三角形的性质即可得到结论.【详解】⊙在正五边形ABCDE中,AE=DE=AB=BC,⊙E=⊙B=⊙EAB=108°,⊙⊙EAD=⊙BAC=36°,⊙⊙DAC=108°﹣36°﹣36°=36°,故选:B.【点睛】此题考查正多边形和圆,等腰三角形的性质,熟练掌握等腰三角形的性质是解题的关键.14.菱形对角线的交点为O,以O为圆心,以O到菱形一边的距离为半径的圆与其他几边的关系为()A.相交B.相切C.相离D.不能确定【答案】B【分析】首先根据菱形的性质可知:菱形的对角线将菱形分成四个全等的直角三角形,故四个三角形面积相等且斜边相等,然后根据等面积法得出斜边的高相等,这样问题就容易解决了.【详解】如图:⊙菱形对角线互相垂直平分,⊙AO=CO,BO=DO,AB=BC=CD=DA.⊙⊙ABO⊙⊙BCO⊙⊙CDO⊙⊙DAO.⊙⊙ABO、△BCO、△CDO、△DAO的面积相等.又⊙AB=BC=CD=DA,⊙⊙ABO、△BCO、△CDO、△DAO斜边上的高相等.即O到AB、BC、CD、DA的距离相等.⊙O到菱形一边的距离为半径的圆与另三边的位置关系是相切.故选B..【点睛】本题考查了直线与圆的位置关系,解题的关键是画出图形进行分析.15.如图,已知AB是⊙O的直径,弦CD⊙AB于点E,G是弧AB的中点,连接AD,AG ,CD ,则下列结论不一定成立的是( )A .CE =DEB .⊙ADG =⊙GABC .⊙AGD =⊙ADC D .⊙GDC =⊙BAD 【答案】D 【详解】⊙AB 是⊙O 的直径,弦CD ⊙AB ,⊙CE =DE ,A 成立;⊙G 是AB 的中点,⊙AG BG =,⊙⊙ADG =⊙GAB ,B 成立;⊙AB 是⊙O 的直径,弦CD ⊙AB ,⊙AC AD =,⊙⊙AGD =⊙ADC ,C 成立;⊙GDC =⊙BAD 不成立,D 不成立,故选D .16.如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O 为圆心,OA ,OB 长分别为半径,圆心角120O ∠=︒形成的扇面,若3m OA =, 1.5m OB =,则阴影部分的面积为( )A .24.25m πB .23.25m πC .23m πD .22.25m π【答案】D 【分析】根据S 阴影=S 扇形AOD -S 扇形BOC 求解即可.17.下列命题为真命题的是( )A .同旁内角互补B .三角形的外心是三条内角平分线的交点C .平行于同一条直线的两条直线平行D .若甲、乙两组数据中,20.8S =甲,2 1.4S =乙,则乙组数据较稳定【答案】C【分析】根据平行线的性质和判定,三角形的外心性质,方差一一判断即可.【详解】解:A 、两平行线被第三直线所截,同旁内角互补,原命题是假命题,不符合题意;B 、三角形的外心是三条边垂直平分线的交点,原命题是假命题,不符合题意;C 、平行于同一条直线的两条直线平行,是真命题,符合题意;D 、若甲、乙两组数据的平均数都是3,S 甲2=0.8,S 乙2=1.4,则甲组数据较稳定,原命题是假命题,不符合题意;故选:C .【点睛】考查了命题与定理的知识,解题的关键是根据平行线的性质和判定,三角形的外心性质,方差解答.18.如图,C 为⊙O 直径AB 上一动点,过点C 的直线交⊙O 于D ,E 两点,且⊙ACD=45°,DF⊙AB 于点F ,EG⊙AB 于点G ,当点C 在AB 上运动时,设AF=x ,DE=y ,下列中图象中,能表示y 与x 的函数关系式的图象大致是( )A.B.C.D.19.如图,AB为⊙O的直径,AB=AC,AC交⊙O于点E,BC交⊙O于点D,F为CE 的中点,连接DF.给出以下四个结论:⊙BD=DC;⊙AD=2DF;⊙BD DE;⊙DF是⊙O的切线.其中正确结论的个数是:()A.4B.3C.2D.1【答案】B【详解】连接AD,OD,⊙AB是直径,⊙⊙ADB=⊙AEB=90°,又⊙AB=AC,⊙BD=DC,故⊙正确;⊙F是CE中点,BD=CD,⊙BE//DF,BE=2DF,但没有办法证明AD与BE相等,故⊙错误;⊙AB=AC,BD=CD,⊙⊙BAD=⊙CAD,⊙BD=DE,⊙BD=DE,故⊙正确;⊙⊙AEB=90°,⊙⊙BEC=180°-⊙AEB=90°,⊙BE//DF,⊙⊙DFC=⊙BEC=90°,⊙O为AB的中点,D为BC的中点,⊙OD//AC,⊙⊙ODF=⊙DFC=90°,⊙OD是半径,⊙DF是⊙O的切线,故⊙正确,所以正确的结论有3个,故选B.【点睛】本题主要考查了圆周角定理,切线的判定,等腰三角形的性质、三角形的中位线等,能根据具体的图形选择和灵活运用相关性质解题是关键.二、填空题20.如图,若正五边形和正六边形有一边重合,则⊙BAC=_____.【答案】132°##132度【详解】解:⊙正五边形的内角=180°-360°÷5=108°,正六边形的内角=180°-360°÷6=120°,⊙⊙BAC=360°-108°-120°=132°.故答案为132°.21.已知直角⊙ABC中,⊙C=90°,BC=3,AC=4,那么它的内切圆半径为_______.【答案】1【分析】O分别与BC、AC、AB切于点D、E、F,连接OD、OE、OF,由切线的性质可得:⊙ODC=⊙OEC=90°,设OD=OE=r根据正方形的判定即可证出四边形OECD是正方形,从而得出:EC=CD=OD=OE=r,再根据切线长定理可得:BF=BD =3-r,AF=AE =4-r,再根据勾股定理求出AB,利用AB的长列方程即可.【详解】解:如图所示,O分别与BC、AC、AB切于点D、E、F,连接OD、OE、OF⊙⊙ODC=⊙OEC=90°22.如图,AB ,BC ,CD 分别与⊙O 相切于E ,F ,G ,BE =4,CG =6,则BC =_______.【答案】10【分析】从圆外一点可以引圆的两条切线,它们的切线长相等,据此分析解答.【详解】⊙AB ,BC ,CD 分别与⊙O 相切于E ,F ,G ,BE =4,CG =6,⊙BF =BE =4,CF =CG =6,⊙BC =BF +FC =10,故填:10.【点睛】此题主要是综合运用了切线长定理和切线的性质定理.23.若一个扇形的圆心角为60︒,面积为26cm π,则这个扇形的弧长为__________ cm(结果保留π)24.如图,在O 中,弦AC =B 是圆上一点,且=45ABC ∠︒,则O 的半径R =_____.25.如图,⊙O 的内接四边形ABCD 中,⊙A =45°,则⊙C 的度数 _____________ .【答案】135°【分析】根据圆内接四边形的对角互补可得结论.【详解】∵⊙O的内接四边形ABCD中,⊙A=45°,⊙⊙C=135°.故答案为135°.【点睛】本题考查了圆内接四边形,关键是掌握圆内接四边形的性质:①圆内接四边形的对角互补.②圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).26.如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若⊙BAD=105°,则⊙DCE的度数是________°.【答案】105【详解】⊙四边形ABCD是圆内接四边形,⊙⊙DAB+⊙DCB=180°,⊙⊙BAD=105°,⊙⊙DCB=180°﹣⊙DAB=180°﹣105°=75°,⊙⊙DCB+⊙DCE=180°,⊙⊙DCE=⊙DAB=105°.故答案为10527.如图,圆O的半径OA=5cm,弦AB=8cm,点P为弦AB上一动点,则点P到圆心O的最短距离是____cm.【答案】3【分析】由当OP⊙AB时,OP最短,根据垂径定理,可求得AP的长,然后由勾股定28.如图,在矩形ABCD 中,AB a ,BC b =,点P 是BC 上的一个动点,连接AP ,把PAB 沿着AP 翻折到⊙PB C '(点B '在矩形的内部),连接B C ',B D '.点P 在整个运动过程中,若存在唯一的位置使得⊙B CD 为直角三角形,则a ,b 之间的数量关系是 __.为直径作O ,当点为直角三角形且唯一,在Rt ADO 中,根据22OD OA ,可得,计算可得答案. 为直径作O ,当点到O 的最小距离等于得B CD '为直角三角形且唯一,Rt ADO 中,2AD OD +22211())22b a a +=+,整理得22b =,a>,∴=2b29.尺规作图特有的魅力曾使无数人沉湎其中,传说拿破仑通过下列尺规作图考他的大臣:⊙将半径2的⊙O六等分,依次得到A,B,C,D,E,F六个分点;⊙分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;⊙连结OG.问:OG的长是多少?大臣给出的正确答案是_________2222OA,(23)222.【点睛】本题考查了圆周角定理,等腰三角形三线合一的性质以及勾股定理解直角三30.半径为O是锐角三角形ABC的外接圆,AB=AC,连接OB、OC,延长CO交弦AB于点D.若⊙OBD是直角三角形,则弦BC的长为_______________.31.如图,P A,PB是⊙O的切线,A,B是切点,点C是⊙O上异于A、B的一点,若⊙P=40°,则⊙ACB的度数为_________________.【答案】110°【分析】连接OA,OB,在优弧AB上任取一点D(不与A、B重合),连接BD,AD,如图所示,由PA与PB都为圆O的切线,利用切线的性质得到OA与AP垂直,OB与BP垂直,在四边形APBO中,根据四边形的内角和求出⊙AOB的度数,再利用同弧所对的圆周角等于所对圆心角的一半求出⊙ADB的度数,再根据圆内接四边形的对角互补即可求出⊙ACB的度数.【详解】连接OA,OB,在优弧AB上任取一点D(不与A、B重合),连接BD,AD,如图所示:⊙PA、PB是⊙O的切线,⊙OA⊙AP,OB⊙BP,⊙⊙OAP=⊙OBP=90°,又⊙⊙P=40°,⊙⊙AOB=360°-(⊙OAP+⊙OBP+⊙P)=140°,32.如图,矩形ABCD 中,6AB =,9BC =.将矩形沿EF 折叠,使点A 落在CD 边中点M 处,点B 落在N 处.连接EM ,以矩形对称中心O 为圆心的圆与EM 相切于点P ,则圆的半径为________.33.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则AMN周长的最小值为________.34.如图所示,在⊙O 中,AB 是⊙O 的直径,⊙ACB 的角平分线CD 交⊙O 于D ,则⊙ABD=_________ 度.【答案】45.【详解】试题解析:⊙CD 平分⊙ACB⊙⊙ACD=⊙BCD=45°⊙⊙ABD=⊙ACD=45°.考点:圆周角定理.35.如图,在平面直接坐标系xOy 中,()40A ,,()03B ,,()43C ,,I 是ABC ∆的内心,将ABC ∆绕原点逆时针旋转90°后,I 的对应点'I 的坐标为________.【答案】(-2,3)【分析】直接利用直角三角形的性质得出其内切圆半径,进而得出I点坐标,再利用旋转的性质得出对应点坐标.【详解】解:过点作IF⊙AC于点F,IE⊙OA于点E,⊙A(4,0),B(0,3),C(4,3),⊙BC=4,AC=3,则AB=5,⊙I是⊙ABC的内心,⊙I到⊙ABC各边距离相等,等于其内切圆的半径,⊙IF=1,故I到BC的距离也为1,则AE=1,故IE=3-1=2,OE=4-1=3,则I(3,2),⊙⊙ABC绕原点逆时针旋转90°,⊙I的对应点I'的坐标为:(-2,3).故答案为:(-2,3).【点睛】此题主要考查了旋转的性质以及直角三角形的性质,得出其内切圆半径是解题关键.36.一个半径为4cm的圆内接正六边形的面积等于_______cm2.S=ABC⊙内接正六边形的面积是故答案是:37.圆心角为40°,半径为2的扇形面积为________.38.如图,在半圆O中,直径AE=10,四边形ABCD是平行四边形,且顶点A、B、C在半圆上,点D在直径AE上,连接CE,若AD=8,则CE长为_____【答案】【详解】连接OC,过O点作BC垂线,设垂足为F,根据垂径定理、勾股定理可以得到OC=5,CF=4,OF=3,在等腰三角形CDE中,高=OF=3,底边长DE=10-8=2,根据勾股定理即可求出CE.解:连接OC,过O点作OF⊙BC,垂足为F,交半圆与点H,⊙OC=5,BC=8,⊙根据垂径定理CF=4,点H为弧BC的中点,且为半圆AE的中点,⊙由勾股定理得OF=3,且弧AB=弧CE⊙AB=CE,又⊙ABCD为平行四边形,⊙AB=CD,⊙CE=CD,⊙⊙CDE为等腰三角形,在等腰三角形CDE中,DE边上的高CM=OF=3,⊙DE=10-8=2,⊙由勾股定理得,CE2=OF2+(DE)2,⊙CE=,故答案为.本题考查了勾股定理和垂径定理以及平行四边形的性质,是基础知识要熟练掌握.39.如图,⊙O是⊙ABC的外接圆,连接OB、OC,若OB=BC,则⊙BAC的度数是_____.三、解答题40.如图,AB是⊙O的直径,C是半圆上的一点,CD是⊙O的切线,AD⊙CD于点D,交⊙O于点E.(1)求证:AC平分⊙DAB;(2)若点E为弧AC的中点,⊙O的半径为1,求图中阴影部分的面积.41.如图,AB是⊙O的直径,点C、E位于⊙O上AB两侧.在BA的延长线上取点D,使⊙ACD=⊙B.(1)求证:DC是⊙O的切线;(2)当BC=EC时,求证:AC2=AE•AD;(3)在(2)的条件下,若BC=AD:AE=5:9,求⊙O的半径.【点睛】本题考查了切线的判定,圆周角定理,相似三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.42.如图,已知、是⊙的切线,、为切点.直径的延长线与的延长线交于点.(1)求证:;(2)若,.求图中阴影部分的面积(结果保留根号与).【答案】(1)证明见解析;(2).【详解】试题分析:(1)连接,根据是⊙的切线,由切线长定理得到AP=BP,OP平分⊙APB,根据等腰三角形的性质三线合一得到OP⊙AB,再根据AC是⊙O的直径,得到⊙ABC=90°,即AB⊙BC,BC⊙OB,得到内错角相等,由等量代换得到结果.(2)根据切线长定理和三角形全等,S△OPA=S△OPB,通过解直角三角形得到OB,PB,再根据三角形的面积和扇形的面积推出结论.试题解析:(1)证明:连接. 1分⊙是⊙的切线,⊙平分. 2分.⊙是⊙的直径,⊙, 即:. 3分⊙.⊙. 4分,⊙. 5分(2) 连接.⊙,⊙⊙、是⊙的切线,⊙,,又⊙⊙⊙⊙.⊙. 6分在中,,. 7分在中,,⊙. 8分⊙.⊙,.⊙. 9分⊙所求的阴影面积:. 10分考点:1.切线的性质;2.扇形面积的计算.43.数学课上,王老师画好图后并出示如下内容:“已知AB为O的直径,O过AC 的中点D.DE为O的切线.(1)求证:DE BC ⊥(2)王老师说:如果添加条件“1DE =,1tan 2C =”,则能求出O 的直径.请你写出求解过程.DE 为O 的切线,OD DE ∴⊥,即∠AB 为O 的直径,OA OB ∴=,即点点D 为AC 的中点,OD BC ∴∥,CED ODE ∴∠=∠=BC .DE BC ⊥1tan DE CE ∴=O∴的直径为【点睛】本题考查了圆的切线的性质、圆周角定理、三角形中位线定理、解直角三角形等知识点,熟练掌握圆的切线的性质和圆周角定理是解题关键.44.如图,点A、B、C分别是⊙O上的点,⊙B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.(1)求证:AP是⊙O的切线;(2)求PD的长.45.如图,在O 中,弦AB 与CD 相交于点E ,AB CD =,连接AD BC ,,25ADC ∠=︒.(1)求证:AD BC =;(2)求证:AE CE =;(3)若弦BD 经过点O ,求BEC ∠的度数. 【答案】(1)见解析(2)见解析(3)65︒【分析】(1)由AB CD =,推出AB CD =,推出BC AD =;(2)证明AED CEB ≌可得结论;(3)先求出90BCD ︒∠=,再求出25CBE,即可得答案. 【详解】(1)解:AB CD =,C ABD ∴=, AB AC CD AC ∴-=-,BC AD ∴=;(2)BC AD ,BC AD ∴=,ADE ∠和CBE ∠都是AC 的圆周角,ADE CBE ∴∠=∠,AED CEB ,AED CEB ∴≌,AE CE ∴=;(3)25ADC ,25CBE ,弦BD 经过点O ,BD ∴是O 的直径,90BCD ︒∴∠=,⊙在CEB 中,18065BEC BCD CBE .【点睛】本题考查了圆心角、弧、弦之间的关系,全等三角形的判定和性质,直径所对的圆周角是90︒,三角形的内角和,解题的关键是正确寻找全等三角形解决问题. 46.如图,在ABC 中,90ABC ∠=,O 是AB 上一点,以O 为圆心OB 为半径的圆与AB 交于点E ,与AC 交于点D ,连接DE 、DE 、OC ,且//DE OC .()1求证:AC 是O 的切线;()2若8DE OC ⋅=,求O 的半径.【答案】(1)证明见解析;(2)2. 【分析】(1)先由OD=OE ,利用等边对等角可得⊙2=⊙3,再利用DE⊙OC ;进而利用平行线的性质,可得⊙3=⊙4,⊙1=⊙2,等量代换可得⊙1=⊙4;再结合OB=OD ,OC=OC ,利用SAS 可证△DOC⊙⊙BOC ,那么⊙CDO=⊙CBO ,而⊙ABC=90°,于是⊙CDO=90°,即CD 是 O 的切线;(2)由(1)可知⊙2=⊙4,而⊙CDO=⊙BDE=90°,易证△CDO⊙⊙BDE ,可得比例线段,OD :DE=OC :BE ,又BE=2OD ,可求OD .【详解】()1证明:连接OD ,⊙OE OD =,⊙23∠=∠,又⊙//DE OC ,⊙12∠=∠,34∠=∠,⊙14∠=∠;在DOC 和BOC 中,OD OB =,14∠=∠,OC OC =,⊙DOC BOC ≅,⊙CDO CBO ∠=∠;⊙90ABC ∠=,⊙90CDO ∠=,⊙CD 是O 的切线;()2⊙BE 是直径,⊙90BDE ∠=,在COD 和BED 中,24∠=∠,90EDB ODC ∠=∠=,⊙COD BED ∽,⊙::OD DE OC BE =;又⊙2BE OD =,⊙22OD DE OC =⋅,⊙2OD =.【点睛】考查了等边对等角,平行线的性质,全等三角形的判定与性质,切线的判定,直径所对的圆周角是直角,相似三角形的判定与性质.综合性比较强,难度较大. 47.已知:对于平面直角坐标系xOy 中的点P 和O ,O 的半径为4,交x 轴于点A ,B ,对于点P 给出如下定义:过点C 的直线与O 交于点M ,N ,点P 为线段MN 的中点,我们把这样的点P 叫做关于MN 的“折弦点”.(1)若()2,0C -⊙点()10,0P ,()21,1P -,()32,2P中是关于MN 的“折弦点”的是______;⊙若直线y kx =0k ≠)上只存在一个关于MN 的“折弦点”,求k 的值;(2)点C 在线段AB 上,直线y x b =+上存在关于MN 的“折弦点”,直接写出b 的取值范围.与D相交或相切,分两种情况利用勾股定理求出【详解】(1))与D相切,与D相交或相切,=+垂直直线y xy轴交于点重合时,b有最大值,此时48.如图1,AB 为O 的直径,C 为O 上一点,连接CB ,过C 作CD AB ⊥于点D ,过点C 作BCE ∠,使BCE BCD ∠=∠,其中CE 交AB 的延长线于点E .(1)求证:CE 是O 的切线.(2)如图2,点F 在O 上,且满足2FCE ABC ∠=∠,连接AF 并延长交EC 的延长线于点G .若4CD =,3BD =,求线段FG 的长.CD OB ⊥DCB ∴∠+∠BCE ∠=∠OC OB=OCB∴∠=OCB∴∠+即:OC⊥CE∴是O的切线.(2)过点O作OHFCE∠=FCE∴∠=FCE∠=FCO∴∠OC CE⊥DCO∴∠+DCO∴∠=DCO∴∠=CDO∠=OCH∴∆≅CH CD∴=8CF∴=设OB OC=2OC OD=2(x x∴=解得:256 x.256OB OC∴==.CDB中,OC CG ⊥GCF ∴∠GCF ∴∠AFCB 是圆的内接四边形,GFC ∴∠GFC∴∆∽∴GF CF BC OC=GF =49.问题探究:(1)如图⊙,已知在⊙ABC 中,BC =4,⊙BAC =45°,则AB 的最大值是 . (2)如图⊙,已知在Rt ⊙ABC 中,⊙ABC =90°,AB =BC ,D 为⊙ABC 内一点,且AD=BD =2.,CD =6,请求出⊙ADB 的度数.问题解决:(3)如图⊙,某户外拓展基地计划在一处空地上修建一个新的拓展游戏区⊙ABC ,且AB =A C .⊙BAC =120°,点A 、B 、C 分别是三个任务点,点P 是⊙ABC 内一个打卡点.按照设计要求,CP =30米,打卡点P 对任务点A 、B 的张角为120°,即⊙APB =120°.为保证游戏效果,需要A 、P 的距离与B 、P 的距离和尽可能大,试求出AP +BP 的最大值.的外接圆O,连接)如图⊙,作⊙的外接圆O,连接BAC=90°,OB是等腰直角三角形的外接圆O,连接AKC=⊙APB 是等边三角形。
高中数学抛物线经典例题(含解析)

抛物线大题一.解答题(共7小题)1.已知P(4,y0)是抛物线C:y2=2px(p>0)上位于第一象限的一点,且P到C的焦点的距离为5.(1)求抛物线C的方程;(2)设O为坐标原点,F为C的焦点,A,B为C上异于P的两点,且直线P A与PB 斜率乘积为﹣4.(i)证明:直线AB过定点;(ii)求|F A|•|FB|的最小值.2.已知抛物线C:y2=2px(p>0),其准线方程为x=﹣2.(1)求抛物线C的方程;(2)不过原点O的直线l:y=x+m与抛物线交于不同的两点P,Q,且OP⊥OQ,求m 的值.3.已知抛物线C的顶点在原点,对称轴为坐标轴,开口向右,且经过点P(1,2).(1)求抛物线C的标准方程;(2)过点M(2,0)且斜率为2的直线与抛物线C相交于A,B两点,求AB的长.4.在平面直角坐标系xOy中,抛物线y2=2px(p>0)上一点P的横坐标为4,且点P到焦点F的距离为5.(1)求抛物线的方程;(2)若直线l:x=my+t交抛物线于A,B两点(位于对称轴异侧),且,问:直线l是否过定点?若过定点,请求出该定点:若不过,请说明理由.5.已知抛物线C:y2=2px(p为常数,p>0)的焦点F与椭圆的右焦点重合,过点F的直线与抛物线交于A,B两点.(1)求抛物线C的标准方程;(2)若直线AB的斜率为1,求|AB|.6.设O为坐标原点,直线x=2与抛物线C:y2=2px(p>0)交于A,B两点,若OA⊥OB.(1)求抛物线C的方程;(2)若斜率为的直线l过抛物线C的焦点,且与抛物线C交于D,E两点,求|DE|的值.7.设抛物线C:y2=2px(p>0)的焦点为F,点P(4,m)(m>0)是抛物线C上一点,且|PF|=5.(1)求抛物线C的方程;(2)过点Q(2,0)斜率存在的直线l与C相交于A,B两点,在x轴上是否存在点M 使得∠AMQ=∠BMQ?若存在,请求出点M的坐标;若不存在,请说明理由.抛物线大题参考答案与试题解析一.解答题(共7小题)1.已知P(4,y0)是抛物线C:y2=2px(p>0)上位于第一象限的一点,且P到C的焦点的距离为5.(1)求抛物线C的方程;(2)设O为坐标原点,F为C的焦点,A,B为C上异于P的两点,且直线P A与PB 斜率乘积为﹣4.(i)证明:直线AB过定点;(ii)求|F A|•|FB|的最小值.【分析】(1)由题意,结合所给信息列出等式,求出p的值,进而可得抛物线C的方程;(2)(i)结合(1)中所得信息得到点P的坐标,设出A,B两点的坐标,利用斜率公式得到4(y1+y2)+y1y2+20=0,对直线AB的斜率是否存在进行讨论,进而即可求解;(ii)设出A,B两点的坐标,分别讨论直线AB的斜率是否存在,当直线AB的斜率存在时,设出直线AB的方程,将直线方程与抛物线方程联立,利用韦达定理即可得到|F A|•|FB|的最小值,当直线AB的斜率不存在时,结合抛物线的定义即可得到|F A|•|FB|的最小值,两者比较即可求解.2.已知抛物线C:y2=2px(p>0),其准线方程为x=﹣2.(1)求抛物线C的方程;(2)不过原点O的直线l:y=x+m与抛物线交于不同的两点P,Q,且OP⊥OQ,求m 的值.【分析】(1)由抛物线的准线方程求出p,可得抛物线C的方程;(2)设P(x1,y1),Q(x2,y2),联立直线l和抛物线C的方程,消元写出韦达定理,将OP⊥OQ用坐标表示,代入韦达定理化简计算,可得m的值.3.已知抛物线C的顶点在原点,对称轴为坐标轴,开口向右,且经过点P(1,2).(1)求抛物线C的标准方程;(2)过点M(2,0)且斜率为2的直线与抛物线C相交于A,B两点,求AB的长.【分析】(1)由题意,先设出抛物线C的方程,将点P的坐标代入抛物线方程中,求出p的值,进而可得抛物线C的标准方程;(2)设出直线AB的方程和A,B两点的坐标,将直线AB的方程与抛物线方程联立,求出A,B两点的坐标,进而即可求解.4.在平面直角坐标系xOy中,抛物线y2=2px(p>0)上一点P的横坐标为4,且点P到焦点F的距离为5.(1)求抛物线的方程;(2)若直线l:x=my+t交抛物线于A,B两点(位于对称轴异侧),且,问:直线l是否过定点?若过定点,请求出该定点:若不过,请说明理由.【分析】(1)由题意,结合题目所给信息建立有关p的等式,进而即可求解;(2)设出A,B两点的坐标,将直线l的方程与抛物线方程联立,利用向量的坐标运算以及韦达定理再进行求解即可.5.已知抛物线C:y2=2px(p为常数,p>0)的焦点F与椭圆的右焦点重合,过点F的直线与抛物线交于A,B两点.(1)求抛物线C的标准方程;(2)若直线AB的斜率为1,求|AB|.【分析】(1)由题意,先求出的右焦点,根据抛物线C的焦点F与椭圆的右焦点重合,可得,进而求出抛物线方程;(2)结合(1)中所得信息得到直线AB的方程,将直线AB的方程与抛物线方程联立,利用韦达定理以及弦长公式再进行求解即可.6.设O为坐标原点,直线x=2与抛物线C:y2=2px(p>0)交于A,B两点,若OA⊥OB.(1)求抛物线C的方程;(2)若斜率为的直线l过抛物线C的焦点,且与抛物线C交于D,E两点,求|DE|的值.【分析】(1)由题意,得到点A的坐标,代入抛物线方程中进行求解即可;(2)先得到直线l的方程,将直线方程与抛物线方程联立,利用韦达定理以及抛物线的定义再进行求解即可.7.设抛物线C:y2=2px(p>0)的焦点为F,点P(4,m)(m>0)是抛物线C上一点,且|PF|=5.(1)求抛物线C的方程;(2)过点Q(2,0)斜率存在的直线l与C相交于A,B两点,在x轴上是否存在点M 使得∠AMQ=∠BMQ?若存在,请求出点M的坐标;若不存在,请说明理由.【分析】(1)利用|PF|=5,根据抛物线的定义,求出p的值,即可得解;(2)设A(x1,y1),B(x2,y2),M(s,0),直线l的方程为x=ty+2(t≠0),将其与抛物线的方程联立,利用韦达定理,根据k AM=﹣k MB,求出s的值,即可得解.。
抛物线与圆专题讲解

抛物线与圆专题讲解抛物线与圆综合探究题,综合性强,难度较大,通常都作为“压轴题”,解此类题通常需要熟练掌握抛物线与圆相关的基本知识和基本技能(切线的性质与判定、切线长定理、圆与点、线、圆的位置关系等),求解时注意运用有关性质,进行综合、分析、探究解题思路。
在解答中常渗透6大数学思想:数形结合思想、分类思想、化归与转化思想、函数与方程思想、整体思想、建模思想。
你想快速进步请注意:独立思考,与他人合作,题后析题总结。
1.如图,在平面直角坐标系中,二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点,与y 轴交于C 点,与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),OB =OC ,tan∠ACO=31.(1)求这个二次函数的表达式.(2)若平行于x 轴的直线与该抛物线交于M 、N 两点,且以MN 为直径的圆与x 轴相切,求该圆半径的长度.2、已知:如图,抛物线m x x y +-=332312与x 轴交于A 、B 两点,与y 轴交于C 点,∠ACB =90°, ⑴求m 的值及抛物线顶点坐标; ⑵过A 、B 、C 的三点的⊙M 交y 轴于另一点D ,连结DM 并延长交⊙M 于点E ,过E 点的⊙M 的切线分别交x 轴、y 轴于点F 、G ,求直线FG 的解析式; ⑶在条件⑵下,设P 为上的动点(P 不与C 、D 重合),连结PA 交y 轴于点H ,问是否存在一个常数k ,始终满足AH ·AP =k ,如果存在,请写出求解过程;如果不存在,请说明理由.3、如图3已知抛物线2y ax bx c=++,经过点A(0,5)和点B(3 ,2)(1)求抛物线的解析式:(2)现有一半径为l,圆心P在抛物线上运动的动圆,问⊙P在运动过程中,是否存在⊙P与坐标轴相切的情况?若存在,请求出圆心P的坐标:若不存在,请说明理由;(3)若⊙Q的半径为r,点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值课后巩固:1、已知:如图,抛物线233y x x =--+x 轴分别交于A B ,两点,与y轴交于C 点,经过原点O 及点A C ,,点D 是劣弧⋂OA 上一动点(D 点与A O ,不重合).(1)求抛物线的顶点E 的坐标; (2)求的面积;(3)连CD 交AO 于点F ,延长CD 至G ,使2FG =,试探究当点D 运动到何处时,直线GA 与⊙M 相切,并请说明理由.2、如图,在平面直角坐标系中,已知点(B -,(0)A m,(0)m <<,以AB 为边在x 轴下方作正方形ABCD ,点E 是线段OD 与正方形ABCD 的外接圆除点D 以外的另一个交点,连结BE 与AD 相交于点F . (1)求证:BF DO =;(2)设直线l 是BDO △的边BO 的垂直平分线,且与BE 相交于点G .若G 是BDO △的外心,试求经过BF O ,,三点的抛物线的解析表达式;3、如图1,直线y =43x -1与抛物线y =-41x 2交于A ,B 两点(A 在B 的左侧),与y 轴交于点C .(1)求线段AB 的长;(2)若以AB 为直径的圆与直线x =m 有公共点,求m 的取值范围;(3)如图2,把抛物线向右平移2个单位,再向上平移n 个单位(n >0),抛物线与x 轴交于P ,Q 两点,过C ,P ,Q 三点的圆的面积是否存在最小值的情况?若存在,请求出这个最小值和此时n 的值,若不存在,请说明理由.图2图1。
(完整版)抛物线练习题(含答案)

抛物线练习题一、选择题1.在直角坐标平面内,到点(1,1)和直线 x+ 2y= 3 距离相等的点的轨迹是 ()A .直线B.抛物线C.圆D.双曲线2.抛物线 y2= x 上一点 P 到焦点的距离是 2,则 P 点坐标为 ()3,± 67,± 79,± 35,± 10A. 22B. 42C. 42D. 223.抛物线 y= ax2的准线方程是y= 2,则 a 的值为 ()11A. 8 B .-8C. 8D.- 84.设抛物线 y2= 8x 上一点 P 到 y 轴的距离是4,则点 P 到该抛物线焦点的距离是 ()A .4B . 6C. 8D. 125.设过抛物线的焦点 F 的弦为 AB,则以 AB 为直径的圆与抛物线的准线的地址关系是()A .订交B .相切C.相离D.以上答案都有可能6.过点 F(0,3)且和直线 y+ 3=0 相切的动圆圆心的轨迹方程为 ()A .y2= 12xB .y2=- 12x C. x2= 12y D .x2=- 12y7.抛物线 y2= 8x 上一点 P 到 x 轴距离为12,则点 P 到抛物线焦点 F 的距离为 ()A .20B .8C. 22D. 248.抛物线的极点在坐标原点,焦点是椭圆4x2+ y2= 1 的一个焦点,则此抛物线的焦点到准线的距离为 ()11A. 2 3 B. 3 C.2 3 D.4 39.设抛物线的极点在原点,其焦点F 在 y 轴上,又抛物线上的点(k,- 2)与 F 点的距离为4,则 k 的值是 ()A. 4 B . 4 或- 4C.- 2 D .2 或- 212的焦点坐标是 ()10.抛物线 y=m x (m<0)A.0,mB. 0,-mC. 0,1D. 0,-1 444m4m11.抛物线的极点在原点,对称轴是x 轴,抛物线上的点(-5,2 5) 到焦点的距离是6,则抛物线的方程为 ()A. y2=- 2x B .y2=- 4x C. y2= 2x D. y2=- 4x 或 y2=- 36x12.已知抛物线y2=2px(p>0) 的准线与圆 (x- 3)2+ y2= 16 相切,则p 的值为 () 1A. 2 B . 1C.2 D .4二、填空题13.过抛物线焦点 F 的直线与抛物线订交于A 、B 两点,若A 、B 在抛物线准线上的射影是A 1、B 1,则∠ A 1FB 1=。
圆与抛物线的综合练习(专题)

专题三:圆与函数例1、(2011•潍坊)如图,y关于x的二次函数y=﹣(x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m >0)(1)写出A、B、D三点的坐标;(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.例2、(2011•德州)在直角坐标系xoy中,已知点P是反比例函数(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:①求出点A,B,C的坐标.②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的.若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.及时练习1、(2011•湖北荆州)如图甲,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA 所在直线为x2、(2011•襄阳)如图,在平面直角坐标系xoy中,AB在x轴上,AB=10,以AB为直径的⊙O'与y轴正半轴交于点C,连接BC,AC.CD是⊙O'的切线,AD丄CD于点D,tan∠CAD=,抛物线y=ax2+bx+c过A,B,C三点.(1)求证:∠CAD=∠CAB;(2)①求抛物线的解析式;②判断抛物线的顶点E是否在直线CD上,并说明理由;(3)在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由.。
专题3.4 以解析几何中与圆相关的综合问题为解答题(原卷版)

专题三 压轴解答题第四关 以解析几何中与圆相关的综合问题【名师综述】纵观近三年的高考题,解析几何题目是每年必考题型,主要体现在解析几何知识内的综合及与其它知识之间的综合,圆不会单独出大题,一般是结合椭圆、抛物线一起考查,预计在15年高考中解答题仍会重点考查圆与椭圆、抛物线相结合的综合问题,同时可能与平面向量、导数相交汇,每个题一般设置了两个问,第(1)问一般考查曲线方程的求法,主要利用定义法与待定系数法求解,而第(2)问主要涉及最值问题、定值问题、对称问题、轨迹问题、探索性问题、参数范围问题等.这类问题综合性大,解题时需根据具体问题,灵活运用解析几何、平面几何、函数、不等式、三角知识,正确构造不等式,体现了解析几何与其他数学知识的密切联系.这体现了考试中心提出的“应更多地从知识网络的交汇点上设计题目,从学科的整体意义、思想含义上考虑问题”的思想. 类型一 以圆的切线为背景的相关问题典例1(2019·山东省实验中学高考模拟(文))已知椭圆()2222:10x y O a b a b+=>>的左、右顶点分别为A ,B ,点P 在椭圆O 上运动,若△PAB 面积的最大值为23,椭圆O 的离心率为12. (1)求椭圆O 的标准方程;(2)过B 点作圆E :()()2222,02x y r r +-=<<的两条切线,分别与椭圆O 交于两点C ,D(异于点B),当r 变化时,直线CD 是否恒过某定点?若是,求出该定点坐标,若不是,请说明理由.【名师指点】圆的切线的应用,往往从两个方面进行考查,一是设切线方程,利用圆心到切线的距离等于半径列方程求解;二是结合切线长定理与勾股定理求解. 【举一反三】【浙江省台州市2019届高三上学期期末质量评估】设点为抛物线外一点,过点作抛物线的两条切线,,切点分别为,.(Ⅰ)若点为,求直线的方程; (Ⅱ)若点为圆上的点,记两切线,的斜率分别为,,求的取值范围.类型二 与圆有关的面积问题典例2 (2019·山东高考模拟(理))已知椭圆22122:1(0)x y C a b a b+=>>的左、右焦点分别为1F 、2F ,椭圆的离心率为12,过椭圆1C 的左焦点1F ,且斜率为1的直线l ,与以右焦点2F 为圆心,半径为2的圆2C 相切.(1)求椭圆1C 的标准方程;(2)线段MN 是椭圆1C 过右焦点2F 的弦,且22MF F N λ=,求1MF N ∆的面积的最大值以及取最大值时实数λ的值.【名师指点】对于平面图形的面积问题,可以直接表示或者可以利用割补的办法,以及弦长公式等,将面积科学有效表示,其中通过设直线和曲线的交点,利用韦达定理是解决该种问题的关键.【举一反三】设圆x 2+y 2+2x -15=0的圆心为A ,直线l 过点B (1,0)且与x 轴不重合,l 交圆A 于C ,D 两点,过B 作AC 的平行线交AD 于点E .(1)证明|EA |+|EB |为定值,并写出点E 的轨迹方程;(2)设点E 的轨迹为曲线C 1,直线l 交C 1于M ,N 两点,过B 且与l 垂直的直线与圆A 交于P ,Q 两点,求四边形MPNQ 面积的取值范围. 类型三 圆与其他圆锥曲线的结合问题典例3【山东省济南外国语学校2019届高三1月份阶段模拟】抛物线的焦点为F ,圆,点为抛物线上一动点.已知当的面积为.(I )求抛物线方程; (II )若,过P 做圆C 的两条切线分别交y 轴于M ,N 两点,求面积的最小值,并求出此时P点坐标.【名师指点】圆与圆锥曲线的交汇问题以公共点为基点,派生出弦长问题、中点问题、垂直问题、切线问题、恒过定点问题、定长问题等等,应对不同的题目,会采用不同的方式方法,但总体上仍以设而不求的处理策略为主.常规的策略是数形结合,将数反映的形画出来,结合图形解决问题.【举一反三】(2019·山东高三月考(文))已知椭圆C :22221(0)x y a b a b+=>>的离心率为12,以原点为圆120+=相切. (1)求椭圆C 的方程;(2)设(4,0)A -,过点(3,0)R 作与x 轴不重合的直线l 交椭圆C 于P ,Q 两点,连接AP ,AQ 分别交直线163x =于M ,N 两点,若直线MR 、NR 的斜率分别为1k 、2k ,试问:12k k 是否为定值?若是,求出该定值,若不是,请说明理由. 【精选名校模拟】1.(2019·山东新泰市第一中学高三月考(文))已知抛物线C 的顶点在坐标原点,焦点为圆22:40M x y x +-=的圆心,直线l 与抛物线C 的准线和y 轴分别交于点P 、Q ,且P 、Q 的纵坐标分别为13t t-、()2,0t t R t ∈≠. (1)求抛物线C 的方程;(2)求证:直线l 恒与圆M 相切.2.(2020·山东高三期末)设中心在原点O ,焦点在x 轴上的椭圆C 过点12A ⎫⎪⎭,F 为C 的右焦点,⊙F的方程为221104x y +-+= (1)求C 的方程;(2)若直线:(l y k x =(0)k >与⊙O 相切,与⊙F 交于M 、N 两点,与C 交于P 、Q 两点,其中M 、P 在第一象限,记⊙O 的面积为()S k ,求(||||)()NQ MP S k -⋅取最大值时,直线l 的方程. 3.(2020·山东高三期末)在平面直角坐标系中,()()1 ,0,1,0A B -,设ABC 的内切圆分别与边,,AC BC AB 相切于点,,P Q R ,已知1CP =,记动点C 的轨迹为曲线E .(1)求曲线E 的方程;(2)过()2,0G 的直线与y 轴正半轴交于点S ,与曲线E 交于点,H HA x ⊥轴,过S 的另一直线与曲线E 交于M N 、两点,若6SMGSHNSS=,求直线MN 的方程.4.(2020·山东高三期末)已知椭圆E :()222210y x a b a b+=>>的一个焦点为()0,3,长轴与短轴的比为2:1.直线l y kx m =+:与椭圆E 交于P 、Q 两点,其中k 为直线l 的斜率. (1)求椭圆E 的方程;(2)若以线段PQ 为直径的圆过坐标原点O ,问:是否存在一个以坐标原点O 为圆心的定圆O ,不论直线l 的斜率k 取何值,定圆O 恒与直线l 相切?如果存在,求出圆O 的方程及实数m 的取值范围;如果不存在,请说明理由.5.(2012·山东高三月考(理))如图,椭圆G 的中心在坐标原点,其中一个焦点为圆F :x 2+y 2﹣2x =0的圆心,右顶点是圆F 与x 轴的一个交点.已知椭圆G 与直线l :x ﹣my ﹣1=0相交于A 、B 两点. (I )求椭圆的方程;(Ⅱ)求△AOB 面积的最大值.6.(2019·山东高三月考)已知椭圆L :()222210x y a b a b +=>>32.(1)求椭圆L 的标准方程;(2)过点()0,2Q 的直线l 与椭圆L 交于A 、B 两点,若以AB 为直径的圆恰好过坐标原点,求直线l 的方程及AB 的大小.7.(2019·济南市历城第二中学高二月考)已知椭圆C :()222210x y a b a b+=>>,圆Q (x ﹣2)2+(y 2)2=2的圆心Q 在椭圆C 上,点P (02)到椭圆C 6 .(1)求椭圆C 的方程;(2)过点P 作互相垂直的两条直线l 1 .l 2 , 且l 1交椭圆C 于A ,B 两点,直线l 2交圆Q 于C ,D 两点,且M 为CD 的中点,求△MAB 的面积的取值范围.8.【河北省邢台市2018届高三上学期期末考试】已知椭圆2222:1(0)y x W a b a b +=>>的焦距与椭圆22:14x y Ω+=的短轴长相等,且W 与Ω的长轴长相等,这两个椭圆在第一象限的交点为A ,与直线OA(O 为坐标原点)垂直的直线l 与W 交于,M N 两点,且l 与圆222:C x y R +=相切.(1)求W 的方程; (2)若2030MN =,求圆C 的方程. 9.【河南省郑州市2019届高中毕业年级第一次(1月)质量预测】已知抛物线的焦点为,过的直线与抛物线交于,两点,过,分别向抛物线的准线作垂线,设交点分别为,,为准线上一点. (1)若,求的值; (2)若点为线段的中点,设以线段为直径的圆为圆,判断点与圆的位置关系.10.在平面直角坐标系xOy 中,O 为坐标原点,以O 为圆心的圆与直线x-y-4=0相切.(1)求圆O 的方程;(2)直线l:y=kx+3与圆O 交于A,B 两点,在圆O 上是否存在一点M,使得四边形OAMB 为菱形,若存在,求出此时直线l 的斜率;若不存在,说明理由.11.已知抛物线2:2(0)C y px p =>的焦点为F ,过F 且倾斜角为45︒的直线与抛物线C 相交于,P Q 两点,且线段PQ 被直线2y =平分.(1)求p的值;,求以A为圆心且与PQ相切的圆的标准方程. (2)直线l是抛物线C的切线,A为切点,且l PQ12.【山东省新泰市第一中学2019届高三上学期第二次质量检测】已知抛物线的顶点在坐标原点,焦点为圆的圆心,直线与抛物线的准线和轴分别交于点、,且、的纵坐标分别为、.(1)求抛物线的方程;(2)求证:直线恒与圆相切.13. 【安徽省黄山市2019届高三第一次质量检测】设椭圆()的左、右焦点分别为,以线段为直径的圆与直线相切,若直线与椭圆交于两点,坐标原点为. (Ⅰ)求椭圆的离心率;(Ⅱ)若,求椭圆的方程.14.【陕西省榆林市2019届高考模拟第一次测试】已知椭圆的离心率,左顶点到直线的距离,为坐标原点.(1)求椭圆的方程;(2)设直线与椭圆相交于两点,若以为直径的圆经过坐标原点,证明:到直线的距离为定值. 15.【黑龙江省哈尔滨市第三中学2019届高三上学期期末考试】在圆上取一点,过点作轴的垂线段,为垂足,当点在圆上运动时,设线段中点的轨迹为.(1)求的方程;(2)试问在上是否存在两点关于直线对称,且以为直径的圆恰好经过坐标原点?若存在,求出直线的方程;若不存在,请说明理由.。
高考数学抛物线大题专练30题(含详解)经典收藏版

目录目录-------------------------------------------------------------------------------------------------1抛物线大题专练(一)--------------------------------------------------------------------------------2抛物线大题专练(二)--------------------------------------------------------------------------------5抛物线大题专练(三)--------------------------------------------------------------------------------8抛物线大题专练---------------------------------------------------------------------------------------11参考答案与试题解析---------------------------------------------------------------------------------11抛物线大题专练(一)1.已知抛物线C的方程为x2=2py,设点M(x0,1)(x0>0)在抛物线C上,且它到抛物线C的准线距离为;(1)求抛物线C的方程;(2)过点M作倾斜角互补的两条直线分别交抛物线C于A(x1,y1),B(x2,y2)两点(M、A、B三点互不相同),求当∠MAB为钝角时,点A的纵坐标y1的取值范围.2.在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为x=﹣,过点M(0,﹣2)作抛物线的切线MA,切点为A(异于点O).直线l过点M与抛物线交于两点B,C,与直线OA交于点N.(1)求抛物线的方程;(2)试问:的值是否为定值?若是,求出定值;若不是,说明理由.3.如图所示,设F是抛物线E:x2=2py(p>0)的焦点,过点F作斜率分别为k1、k2的两条直线l1、l2,且k1•k2=﹣1,l1与E相交于点A、B,l2与E相交于点C,D.已知△AFO外接圆的圆心到抛物线的准线的距离为3(O为坐标原点).(1)求抛物线E的方程;(2)若•+•=64,求直线l1、l2的方程.4.已知抛物线C:y2=2px(p>0),点A、B在抛物线C上.(Ⅰ)若直线AB过点M(2p,0),且|AB|=4p,求过A,B,O(O为坐标原点)三点的圆的方程;(Ⅱ)设直线OA、OB的倾斜角分别为α,β且α+β=,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.5.已知点A(2,1)在抛物线E:x2=ay上,直线l1:y=kx+1(k∈R,且k≠0)与抛物线E相交于B,C两点,直线AB,AC分别交直线l2:y=﹣1于点S,T.(1)求a的值;(2)若|ST|=2,求直线l1的方程;(3)试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.6.已知抛物线y2=2px(p>0),焦点为F,一直线l与抛物线交于A、B两点,且|AF|+|BF|=8,且AB的垂直平分线恒过定点S(6,0)①求抛物线方程;②求△ABS面积的最大值.7.已知抛物线y2=4x,直线l:y=﹣x+b与抛物线交于A,B两点.(Ⅰ)若x轴与以AB为直径的圆相切,求该圆的方程;(Ⅱ)若直线l与y轴负半轴相交,求△AOB面积的最大值.8.抛物线M:y2=2px(p>0)的准线过椭圆N:+y2=1的左焦点,以原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的图象以及y轴的正半轴相交于点A和B,直线AB与x轴相交于点C.(Ⅰ)求抛物线M的方程;(Ⅱ)设点A的横坐标为a,点C的横坐标为c,抛物线M上点D的横坐标为a+2,求直线CD的斜率.9.已知抛物线y2=4x的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C,过点(1,),(Ⅰ)求椭圆C的标准方程;(Ⅱ)设T(2,0),过点F2作直线l与椭圆C交于A,B两点,且=λ,若λ∈[﹣2,﹣1],求|+|2的最小值.抛物线大题专练(二)10.(2015•福建模拟)如图,已知抛物线y2=4x的焦点为F,过点P(2,0)且斜率为k1的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF、BF分别与抛物线交于点M、N.(Ⅰ)证明•的值与k1无关;(Ⅱ)记直线MN的斜率为k2,证明为定值.11.已知过点M(,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且•=﹣3,其中O为坐标原点.(1)求p的值;(2)当|AM|+4|BM|最小时,求直线l的方程.12.已知过点M(,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且•=﹣3,其中O为坐标原点.(1)求p的值;(2)若圆x2+y2﹣2x=0与直线l相交于以C,D(A,C两点均在第一象银),且线段AC,CD,DB长构成等差数列,求直线l的方程.13.已知点A(﹣4,4)、B(4,4),直线AM与BM相交于点M,且直线AM的斜率与直线BM的斜率之差为﹣2,点M的轨迹为曲线C.(Ⅰ)求曲线C的轨迹方程;(Ⅱ)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值.14.如图所示,已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A,B两点.(1)求证:以AF为直径的圆与x轴相切;(2)设抛物线x2=4y在A,B两点处的切线的交点为M,若点M的横坐标为2,求△ABM的外接圆方程:(3)设过抛物线x2=4y焦点F的直线l与椭圆+=1的交点为C、D,是否存在直线l使得|AF|•|CF|=|BF|•|DF|,若存在,求出直线l的方程,若不存在,请说明理由.15.已知抛物线C:y2=2px(p>0),直线交此抛物线于不同的两个点A(x1,y1)、B(x2,y2)(1)当直线过点M(p,0)时,证明y1.y2为定值;(2)如果直线过点M(p,0),过点M再作一条与直线垂直的直线l′交抛物线C于两个不同点D、E.设线段AB的中点为P,线段DE的中点为Q,记线段PQ的中点为N.问是否存在一条直线和一个定点,使得点N到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.16.(2014•陕西)如图,曲线C由上半椭圆C1:+=1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为.(Ⅰ)求a,b的值;(Ⅱ)过点B的直线l与C1,C2分别交于点P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.17.(2014•山东)已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有丨FA丨=丨FD丨.当点A的横坐标为3时,△ADF为正三角形.(Ⅰ)求C的方程;(Ⅱ)若直线l1∥l,且l1和C有且只有一个公共点E,(ⅰ)证明直线AE过定点,并求出定点坐标;(ⅱ)△ABE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.18.(2014•安徽)如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点.(Ⅰ)证明:A1B1∥A2B2;(Ⅱ)过O作直线l(异于l1,l2)与E1、E2分别交于C1、C2两点.记△A1B1C1与△A2B2C2的面积分别为S1与S2,求的值.19.(2014•福建)已知曲线Γ上的点到点F(0,1)的距离比它到直线y=﹣3的距离小2.(Ⅰ)求曲线Γ的方程;(Ⅱ)曲线Γ在点P处的切线l与x轴交于点A.直线y=3分别与直线l及y轴交于点M,N,以MN为直径作圆C,过点A作圆C的切线,切点为B,试探究:当点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度是否发生变化?证明你的结论.20.(2014•江西)如图,已知抛物线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).(1)证明:动点D在定直线上;(2)作C的任意一条切线l(不含x轴),与直线y=2相交于点N1,与(1)中的定直线相交于点N2,证明:|MN2|2﹣|MN1|2为定值,并求此定值.抛物线大题专练(三)21.(2014•杭州二模)设抛物线Γ:y2=2px(p>0)过点(t,)(t是大于0的常数).(Ⅰ)求抛物线Γ的方程;(Ⅱ)若F是抛物线Γ的焦点,斜率为1的直线交抛物线Γ于A,B两点,x轴负半轴上的点C,D满足|FA|=|FC|,|FD|=|FB|,直线AC,BD相交于点E,当时,求直线AB的方程.22.(2014•包头一模)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,l与x轴交于点R,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.(1)若∠BFD=120°,△ABD的面积为8,求p的值及圆F的方程;(2)在(1)的条件下,若A,B,F三点在同一直线上,FD与抛物线C交于点E,求△EDA的面积.23.(2014•长春三模)已知抛物线C:y2=2px(p>0)的焦点为F,若过点F且斜率为1的直线与抛物线相交于M,N两点,且|MN|=8.(1)求抛物线C的方程;(2)设直线l为抛物线C的切线,且l∥MN,P为l上一点,求的最小值.24.(2014•长沙二模)已知A、B为抛物线C:y2=4x上的两个动点,点A在第一象限,点B在第四象限,l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.(Ⅰ)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;(Ⅱ)设C、D为直线l1、l2与直线x=4的交点,求△PCD面积的最小值.25.(2015•上海模拟)如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2﹣x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).(1)用k、b表示出C点、D点的坐标,并证明CD垂直于x轴;(2)求△ABC的面积,证明△ABC的面积与k、b无关,只与h有关;(3)小张所在的兴趣小组完成上面两个小题后,小张连AC、BC,再作与AC、BC平行的切线,切点分别为E、F,小张马上写出了△ACE、△BCF的面积,由此小张求出了直线l与抛物线围成的面积,你认为小张能做到吗?请你说出理由.26.(2014•乌鲁木齐三模)已知抛物线y2=2px(p>0)的焦点过F,过H(﹣,0)引直线l交此抛物线于A,B两点.(1)若直线AF的斜率为2,求直线BF的斜率;(2)若p=2,点M在抛物线上,且+=t,求t的取值范围.27.(2014•太原二模)已知抛物线y2=4x的焦点为F,直线l1与抛物线交于不同的两点A、B,直线l2与抛物线交于不同的两点C、D.(Ⅰ)当l1过F时,在l1上取不同于F的点P,使得=,求点P的轨迹方程;(Ⅱ)若l1与l2相交于点Q,且倾斜角互补时,|QA|•|QB|=a|QC|•|QD|,求实数a的值.28.(2014•合肥一模)已知△ABC的三个顶点都在抛物线y2=2px(p>0)上,且抛物线的焦点F满足,若BC边上的中线所在直线l的方程为mx+ny﹣m=0(m,n为常数且m≠0).(Ⅰ)求p的值;(Ⅱ)O为抛物线的顶点,△OFA、△OFB、△OFC的面积分别记为S1、S2、S3,求证:为定值.29.(2014•呼和浩特一模)已知抛物线C:y2=2px(p>0),直线l过定点A(4,0)且与抛物线C交于P、Q两点,若以弦PQ为直径的圆E过原点O.(Ⅰ)求抛物线C的方程;(Ⅱ)当圆E的面积最小时,求E的方程.30.(2014•普陀区一模)已知点P(2,0),点Q在曲线C:y2=2x上.(1)若点Q在第一象限内,且|PQ|=2,求点Q的坐标;(2)求|PQ|的最小值.抛物线大题专练参考答案与试题解析1.已知抛物线C的方程为x2=2py,设点M(x0,1)(x0>0)在抛物线C上,且它到抛物线C的准线距离为;(1)求抛物线C的方程;(2)过点M作倾斜角互补的两条直线分别交抛物线C于A(x1,y1),B(x2,y2)两点(M、A、B三点互不相同),求当∠MAB为钝角时,点A的纵坐标y1的取值范围.考点:抛物线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:(1)由抛物线的定义,求出p,即可求抛物线C的方程;(2)设直线AM的方程为:y=k(x﹣1)+1,与抛物线方程联立,求出k的范围,利用,即可求出点A的纵坐标y1的取值范围.解答:解:(1)由定义得,则抛物线C的方程:x2=y(2)设直线AM的方程为:y=k(x﹣1)+1联立方程得x2﹣kx+k﹣1=0,A(k﹣1,(k﹣1)2),△1>0即k≠2同理B(﹣k﹣1,(﹣k﹣1)2),△2>0即k≠﹣2,令,则所以k>2或,所以点评:本题考查抛物线的定义与方程,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.2.(2015•淮安一模)在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为x=﹣,过点M(0,﹣2)作抛物线的切线MA,切点为A(异于点O).直线l过点M与抛物线交于两点B,C,与直线OA交于点N.(1)求抛物线的方程;(2)试问:的值是否为定值?若是,求出定值;若不是,说明理由.考点:抛物线的简单性质.专题:计算题;直线与圆;圆锥曲线的定义、性质与方程.分析:(1)由抛物线的准线方程可得p,进而得到抛物线方程;(2)求出函数y=﹣的导数,求出切线的斜率,以及切线方程,联立切线方程和抛物线方程求得切点A,进而直线OA的方程,设出直线BC的方程,联立抛物线方程运用韦达定理,求出N的坐标,代入所求式子化简即可得到定值2.解答:解:(1)由题设知,,即,所以抛物线的方程为y2=x;(2)因为函数的导函数为,设A(x0,y0),则直线MA的方程为,因为点M(0,﹣2)在直线MA上,所以﹣2﹣y0=﹣•(﹣x0).联立,解得A(16,﹣4),所以直线OA的方程为.设直线BC方程为y=kx﹣2,由,得k2x2﹣(4k+1)x+4=0,所以.由,得.所以,故的为定值2.点评:本题考查抛物线的方程和性质,考查直线方程和抛物线方程联立,运用韦达定理,以及导数的运用:求切线方程,考查运算能力,属于中档题和易错题.3.(2014•九江三模)如图所示,设F是抛物线E:x2=2py(p>0)的焦点,过点F作斜率分别为k1、k2的两条直线l1、l2,且k1•k2=﹣1,l1与E相交于点A、B,l2与E相交于点C,D.已知△AFO外接圆的圆心到抛物线的准线的距离为3(O为坐标原点).(1)求抛物线E的方程;(2)若•+•=64,求直线l1、l2的方程.考点:抛物线的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(1)确定△AFO外接圆的圆心在线段OF的垂直平分线y=上,求出p,即可求抛物线E的方程;(2)利用•+•=64,结合韦达定理,基本不等式,即可求直线l1、l2的方程.解答:解:(1)由题意,F(0,),△AFO外接圆的圆心在线段OF的垂直平分线y=上,∴+=3,∴p=4.∴抛物线E的方程是x2=8y;(2)设直线l1的方程y=k1x+2,代入抛物线方程,得y2﹣(8k12+4)y+4=0设A(x1,y1),B(x2,y2),则y1+y2=8k12+4,y1y2=4设C(x3,y3),D(x4,y4),同理可得y3+y4=+4,y3y4=4∴•+•=32+16(k12+)≥64,当且仅当k12=,即k1=±1时取等号,∴直线l1、l2的方程为y=x+2或y=﹣x+2.点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查向量知识的运用,属于中档题.4.(2014•浙江二模)已知抛物线C:y2=2px(p>0),点A、B在抛物线C上.(Ⅰ)若直线AB过点M(2p,0),且|AB|=4p,求过A,B,O(O为坐标原点)三点的圆的方程;(Ⅱ)设直线OA、OB的倾斜角分别为α,β且α+β=,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.考点:抛物线的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(Ⅰ)求出A,B的坐标,可得三角形ABO是Rt△,从而可求过A,B,O三点的圆方程;(Ⅱ)直线AB的方程为:x=my+b,代入抛物线方程,利用韦达定理,结合α+β=,可得b=﹣2p﹣2mp,即可得出结论.解答:解:(Ⅰ)∵直线AB过点M(2p,0),且|AB|=4p,∴直线x=2p与抛物线y2=2px的两个交点坐标分别是:A(2p,2p),B(2p,﹣2p),∴三角形ABO是Rt△,∴过A,B,O三点的圆方程是:(x﹣2p)2+y2=4p2;(Ⅱ)设点,直线AB的方程为:x=my+b,它与抛物线相交,由方程组消去x可得y2﹣2mpy﹣2pb=0,故y1+y2=2mp,y1y2=﹣2pb,这样,tan==即1=,所以b=﹣2p﹣2mp,∴直线AB的方程可以写成为:x=my﹣2p﹣2mp,即x+2p=m(y﹣2p),∴直线AB过定点(﹣2p,2p).点评:本题考查圆的方程,考查直线与抛物线的位置关系,考查和角的正切公式,考查直线过定点,属于中档题.5.(2014•广州二模)已知点A(2,1)在抛物线E:x2=ay上,直线l1:y=kx+1(k∈R,且k≠0)与抛物线E相交于B,C两点,直线AB,AC分别交直线l2:y=﹣1于点S,T.(1)求a的值;(2)若|ST|=2,求直线l1的方程;(3)试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.考点:抛物线的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(1)根据点A(2,1)在抛物线E:x2=ay上,可求a的值;(2)y=kx+1代入抛物线方程,利用韦达定理,确定S,T的坐标,根据|ST|=2,即可求直线l1的方程;(3)确定以线段ST为直径的圆的方程,展开令x=0,即可求这两个定点的坐标.解答:解:(1)∵点A(2,1)在抛物线E:x2=ay上,∴a=4.…(1分)(2)由(1)得抛物线E的方程为x2=4y.设点B,C的坐标分别为(x1,y1),(x2,y2),依题意,,y=kx+1代入抛物线方程,消去y得x2﹣4kx﹣4=0,解得.∴x1+x2=4k,x1x2=﹣4.…(2分)直线AB的斜率,故直线AB的方程为.…(3分)令y=﹣1,得,∴点S的坐标为.…(4分)同理可得点T的坐标为.…(5分)∴=.…(6分)∵,∴.由,得20k2=16k2+16,解得k=2,或k=﹣2,…(7分)∴直线l1的方程为y=2x+1,或y=﹣2x+1.…(9分)(3)设线段ST的中点坐标为(x0,﹣1),则=.…(10分)而|ST|2=,…(11分)∴以线段ST为直径的圆的方程为=.展开得.…(12分)令x=0,得(y+1)2=4,解得y=1或y=﹣3.…(13分)∴以线段ST为直径的圆恒过两个定点(0,1),(0,﹣3).…(14分)点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查圆的方程,考查学生的计算能力,属于中档题.6.(2015•兴国县一模)已知抛物线y2=2px(p>0),焦点为F,一直线l与抛物线交于A、B两点,且|AF|+|BF|=8,且AB的垂直平分线恒过定点S(6,0)①求抛物线方程;②求△ABS面积的最大值.考点:抛物线的标准方程;抛物线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:①利用点差法,确定AB中点M的坐标,分类讨论,根据AB的垂直平分线恒过定点S(6,0),即可求抛物线方程;②分类讨论,求出△ABS面积的表达式,即可求得其最大值.解答:解:①设A(x1,y1),B(x2,y2),AB中点M(x0,y0)当直线的斜率存在时,设斜率为k,则由|AF|+|BF|=8得x1+x2+p=8,∴又得,∴所以依题意,∴p=4∴抛物线方程为y2=8x﹣﹣﹣﹣(6分)当直线的斜率不存在时,2p=8,也满足上式,∴抛物线方程为y2=8x②当直线的斜率存在时,由(2,y0)及,令y=0,得又由y2=8x和得:∴=﹣﹣﹣﹣(12分)当直线的斜率不存在时,AB的方程为x=2,|AB|=8,△ABS面积为∵,∴△ABS面积的最大值为.点评:本题考查抛物线的标准方程,考查三角形面积的计算,考查学生的计算能力,属于中档题.7.(2015•路南区二模)已知抛物线y2=4x,直线l:y=﹣x+b与抛物线交于A,B两点.(Ⅰ)若x轴与以AB为直径的圆相切,求该圆的方程;(Ⅱ)若直线l与y轴负半轴相交,求△AOB面积的最大值.考点:抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)联立得y2+8y﹣8b=0.由此利用根的判别式、弦长公式,结合已知条件能求出圆的方程.(Ⅱ)由直线l与y轴负半轴相交,得﹣1<b<0,由点O到直线l的距离d=,得S△AOB=|AB|d=4.由此利用导数性质能求出△AOB的面积的最大值.解答:解:(Ⅰ)联立得:y2+8y﹣8b=0.依题意应有△=64+32b>0,解得b>﹣2.设A(x1,y1),B(x2,y2),设圆心Q(x0,y0),则应有x0=,y0==﹣4.因为以AB为直径的圆与x轴相切,得到圆半径为r=|y1|=4,又|AB|==.所以|AB|=2r,即=8,解得b=﹣.所以x0==2b+8=,所以圆心为(,﹣4).故所求圆的方程为(x﹣)2+(y+4)2=16..(Ⅱ)因为直线l与y轴负半轴相交,∴b<0,又l与抛物线交于两点,由(Ⅰ)知b>﹣2,∴﹣2<b<0,直线l:y=﹣x+b整理得x+2y﹣2b=0,点O到直线l的距离d==,所以∴S△AOB=|AB|d=﹣4b=4.令g(b)=b3+2b2,﹣2<b<0,g′(b)=3b2+4b=3b(b+),∴g(b)在(﹣2,﹣)增函数,在(﹣,0)是减函数,∴g(b)的最大值为g(﹣)=.∴当b=﹣时,△AOB的面积取得最大值.点评:本题主要考查圆的方程的求法,考查三角形面积的最大值的求法,考查直线与抛物线、圆等知识,同时考查解析几何的基本思想方法和运算求解能力.8.(2015•大庆二模)抛物线M:y2=2px(p>0)的准线过椭圆N:+y2=1的左焦点,以原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的图象以及y轴的正半轴相交于点A和B,直线AB与x轴相交于点C.(Ⅰ)求抛物线M的方程;(Ⅱ)设点A的横坐标为a,点C的横坐标为c,抛物线M上点D的横坐标为a+2,求直线CD的斜率.考点:抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)由椭圆方程求出椭圆左焦点坐标,得到抛物线准线方程,从而求得p值,则抛物线方程可求;(Ⅱ)写出A的坐标,由|OA|=t列式求得t与A的坐标间的关系,求出直线BC的方程,把A代入BC方程,得到a,c的关系,然后直接代入斜率公式求直线CD的斜率.解答:解:(Ⅰ)∵椭圆N:+y2=1,∴c2=a2﹣b2=﹣1=,∴椭圆的左焦点为F1(﹣,0),∴﹣=﹣,则p=1.故M:y2=2x;(Ⅱ)由题意知,A(a,2a),∵|OA|=t,∴a2+2a=t2.由于t>0,故有t=①由点B(0,t),C(c,0)的坐标知,直线BC的方程为+=1.又∵A在直线BC上,故有+=1.将①代入上式,得:+=1,解得c=a+2+.又∵D(a+2,2),∴直线CD的斜率为:k CD====﹣1.点评:本题主要抛物线方程的求法,考查了直线与圆锥曲线位置关系的应用,解答此题的关键是对抛物线定义的灵活应用,是高考试卷中的压轴题.9.(2015•黄冈模拟)已知抛物线y2=4x的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C,过点(1,),(Ⅰ)求椭圆C的标准方程;(Ⅱ)设T(2,0),过点F2作直线l与椭圆C交于A,B两点,且=λ,若λ∈[﹣2,﹣1],求|+|2的最小值.考点:抛物线的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(Ⅰ)设椭圆的半焦距为c,由y2=4x求得c=1.设椭圆C的标准方程为(a>b>0),由于椭圆C过点(1,),代入椭圆方程结合a2=b2+c2,联立解得即可;(II)设l:x=ky+1,与椭圆的方程联立可得根与系数的关系,由λ∈[﹣2,﹣1)可得到k2的取值范围.由于=(x1﹣2,y1),=(x2﹣2,y2),通过换元,令t=∈[,],即可得出|+|2的最小值.解答:解:(Ⅰ)设椭圆的半焦距为c,由y2=4x得c=1,设椭圆C的标准方程为(a>b>0),∵椭圆C过点(1,),∴,又a2=b2+1,联立解得b2=1,a2=2.故椭圆C的标准方程为椭圆方程为+y2=1…(5分)(Ⅱ)由题意可设l:x=ky+1,由得(k2+2)y2+2ky﹣1=0…(6分)设A(x1,y1),B(x2,y2),则有将①2÷②得+2=﹣⇒λ++2=…(8分)由λ∈[﹣2,﹣1]得﹣≤λ++2≤0⇒﹣≤≤0,0≤k2≤…(9分)=(x1﹣2,y1),=(x2﹣2,y2),+=(x1+x2﹣4,y1+y2)x1+x2﹣4=k(y1+y2)﹣2=﹣,|+|=+==16﹣+令t=∈[,],|+|2=8t2﹣28t+16∴t=时|+|2的最小值是4点评:本题综合考查了椭圆与抛物线的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数、换元法、分类讨论、向量相等及其向量运算和向量的模等基础知识与基本技能方法,考查了分析问题和解决问题的能力,考查了推理能力和计算能力,属于中档题.10.(2015•福建模拟)如图,已知抛物线y2=4x的焦点为F,过点P(2,0)且斜率为k1的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF、BF分别与抛物线交于点M、N.(Ⅰ)证明•的值与k1无关;(Ⅱ)记直线MN的斜率为k2,证明为定值.考点:抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)依题意,设直线AB的方程为x=my+2,与抛物线方程联立消x得关于y的一元二次方程,根据韦达定理即可求得y1y2,进而求出x1x2,根据向量数量积运算公式,可得•的值与k1无关;(Ⅱ)设M(x3,y3),N(x4,y4),设直线AM的方程为x=ny+1,将其代入y2=4x,消去x,得到关于y的一元二次方程,从而得y1y3=﹣4,同理可得y2y4=﹣4,根据斜率公式可把表示成关于y1与y2的表达式,再借助(Ⅰ)的结果即可证明.解答:证明:(Ⅰ)依题意,设直线AB的方程为x=my+2(m≠0).…(1分)将其代入y2=4x,消去x,整理得y2﹣4my﹣8=0.…(2分)从而y1y2=﹣8,于是,…(3分)∴与k 1无关.…(5分)(Ⅱ)设M(x3,y3),N(x4,y4).则.…(8分)设直线AM的方程为x=ny+1(n≠0),将其代入y2=4x,消去x,整理得y2﹣4ny﹣4=0∴y1y3=﹣4.同理可得y2y4=﹣4.…(10分)故,…(11分)由(Ⅰ)知,y1y2=﹣8,∴为定值.…(12分)点评:本题考查直线与圆锥曲线的位置关系及抛物线的简单性质,考查学生综合运用知识分析问题解决问题的能力,难度较大.11.(2015•洛阳一模)已知过点M(,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且•=﹣3,其中O为坐标原点.(1)求p的值;(2)当|AM|+4|BM|最小时,求直线l的方程.考点:直线与圆锥曲线的关系.专题:计算题;平面向量及应用;直线与圆;圆锥曲线的定义、性质与方程.分析:(1)设A(x1,y1),Bx2,y2),直线l:x=my+,代入抛物线方程,运用韦达定理,及平面向量的数量积的坐标表示,即可得到p=2;(2)运用抛物线的定义,及均值不等式,即可得到最小值9,注意等号成立的条件,求得B的坐标,代入直线方程,求得m,即可得到直线l的方程.解答:解:(1)设A(x1,y1),Bx2,y2),直线l:x=my+,代入抛物线方程,消去x,得,y2﹣2pmy﹣p2=0,y1+y2=2pm,y1y2=﹣p2,由于•=﹣3,即x1x2+y1y2=﹣3,x1x2==,即有﹣p2=﹣3,解得,p=2;(2)由抛物线的定义,可得,|AM|=x1+1,|BM|=x2+1,则|AM|+4|BM|=x 1+4x2+5+5=9,当且仅当x1=4x2时取得最小值9.由于x1x2=1,则解得,x2=(负的舍去),代入抛物线方程y2=4x,解得,y2=,即有B(),将B的坐标代入直线x=my+1,得m=.则直线l:x=y+1,即有4x+y﹣4=0或4x﹣y﹣4=0.点评:本题考查抛物线的定义、方程和性质,考查直线方程和抛物线方程联立,消去未知数,运用韦达定理,考查基本不等式的运用:求最值,考查运算能力,属于中档题.12.(2015•洛阳一模)已知过点M(,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且•=﹣3,其中O为坐标原点.(1)求p的值;(2)若圆x2+y2﹣2x=0与直线l相交于以C,D(A,C两点均在第一象银),且线段AC,CD,DB长构成等差数列,求直线l的方程.考点:直线与圆锥曲线的关系;直线的一般式方程.专题:计算题;平面向量及应用;圆锥曲线的定义、性质与方程.分析:(1)设A(x1,y1),Bx2,y2),直线l:x=my+,代入抛物线方程,运用韦达定理,及平面向量的数量积的坐标表示,即可得到p=2;(2)求出AB的长,用m表示,再由等差数列的性质,以及CD为圆的直径,即可得到m的方程,解出m,即可得到直线l的方程.解答:解:(1)设A(x1,y1),Bx2,y2),直线l:x=my+,代入抛物线方程,消去x,得,y2﹣2pmy﹣p2=0,y1+y2=2pm,y1y2=﹣p2,由于•=﹣3,即x1x2+y1y2=﹣3,x1x2==,即有﹣p2=﹣3,解得,p=2;(2)由(1)得,y1+y2=4m,y1y2=﹣4,则(y1﹣y2)2=(y1+y2)2﹣4y1y2=16(1+m2),|AB|2=(y1﹣y2)2+(x1﹣x2)2=(y1﹣y2)2+()2=y1﹣y2)2[1+()2]=16(1+m2)2,即有|AB|=4(1+m2),由于线段AC,CD,DB长构成等差数列,则2|CD|=|AC|+|DB|=|AC|+|BC|﹣|CD|=|AB|﹣|CD|,又CD为圆x2+y2﹣2x=0的直径,即有|CD|=2,则4(1+m2)=6,解得,m=,则直线l的方程是x+y﹣=0或x﹣y﹣=0.点评:本题考查抛物线的定义、方程和性质,考查直线方程和抛物线方程联立,消去未知数,运用韦达定理,考查等差数列的性质,考查运算能力,属于中档题.13.(2015•衡水模拟)已知点A(﹣4,4)、B(4,4),直线AM与BM相交于点M,且直线AM的斜率与直线BM的斜率之差为﹣2,点M的轨迹为曲线C.(Ⅰ)求曲线C的轨迹方程;(Ⅱ)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(I)设M(x,y),由题意可得:,化简可得曲线C的轨迹方程为x2=4y且(x≠±4).(II)设Q(m,﹣1),切线方程为y+1=k(x﹣m),与抛物线方程联立化为x2﹣4kx+4(km+1)=0,由于直线与抛物线相切可得△=0,即k2﹣km﹣1=0.解得x=2k.可得切点(2k,k2),由k2﹣km﹣1=0.可得k1+k2=m,k1•k2=﹣1.得到切线QD⊥QE.因此△QDE为直角三角形,|QD|•|QE|.令切点(2k,k2)到Q的距离为d,则d2=(2k﹣m)2+(k2+1)2=(4+m2)(k2+1),利用两点之间的距离公式可得|QD|=,|QE|=,代入即可得出.解答:解:(I)设M(x,y),由题意可得:,化为x2=4y.∴曲线C的轨迹方程为x2=4y且(x≠±4).(II)设Q(m,﹣1),切线方程为y+1=k(x﹣m),联立,化为x2﹣4kx+4(km+1)=0,由于直线与抛物线相切可得△=0,即k2﹣km﹣1=0.∴x2﹣4kx+4k2=0,解得x=2k.可得切点(2k,k2),由k2﹣km﹣1=0.∴k1+k2=m,k1•k2=﹣1.∴切线QD⊥QE.∴△QDE为直角三角形,|QD|•|QE|.令切点(2k,k2)到Q的距离为d,则d2=(2k﹣m)2+(k2+1)2=4(k2﹣km)+m2+(km+2)2=4(k2﹣km)+m2+k2m2+4km+4=(4+m2)(k2+1),∴|QD|=,|QE|=,∴(4+m2)=≥4,当m=0时,即Q(0,﹣1)时,△QDE的面积S取得最小值4.点评:本题考查了直线与抛物线相切的性质、切线方程、相互垂直的斜率之间的关系、两点之间的距离公式、三角形的面积计算公式、二次函数的性质,考查了推理能力与计算能力,属于难题.14.(2015•郴州二模)如图所示,已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A,B两点.(1)求证:以AF为直径的圆与x轴相切;(2)设抛物线x2=4y在A,B两点处的切线的交点为M,若点M的横坐标为2,求△ABM的外接圆方程:(3)设过抛物线x2=4y焦点F的直线l与椭圆+=1的交点为C、D,是否存在直线l使得|AF|•|CF|=|BF|•|DF|,若存在,求出直线l的方程,若不存在,请说明理由.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(1)如图所示,设线段AF的中点为O1,过O1作O1O2⊥x轴,垂足为点O2,作AA1⊥x轴.利用抛物线的定义及梯形的中位线定理可得可得r====|O1O2|,即可证明;(2)设直线AB的方程为y=kx+1,A(x1,y1),B(x2,y2).与抛物线方程联立化为x2﹣4kx﹣4=0,可得根与系数的关系,由x2=4y,可得.可得k MA•k MB==﹣1,可得△MAB为直角三角形,可得△MAB的外接圆的圆心为线段AB的中点.设线段AB的中点为P,可得⊙P与抛物线的准线相切,切点为点M,利用中点坐标公式与根与系数的关系可得圆心P(2,3),半径r=|MP|=|3﹣(﹣1)|=4,即可得出所求的△MAB的外接圆的方程.(3)假设存在直线l使得|AF|•|CF|=|BF|•|DF|,设=λ,可得,,设C(x3,y3),D (x4,y4).利用向量的坐标运算可得x1=﹣λx2,x4=﹣λx3.把x1=﹣λx2代入根与系数的关系可得.把y=kx+1代入椭圆方程可得(3k2+6)x2+6kx﹣1=0,把根与系数的关系与x4=﹣λx3联立可得,联立解得即可.解答:(1)证明:如图所示,设线段AF的中点为O1,过O1作O1O2⊥x轴,垂足为点O2,作AA1⊥x轴.则r====|O1O2|,∴r=|O1O2|,∴以AF为直径的圆与x轴相切;(2)解:设直线AB的方程为y=kx+1,A(x1,y1),B(x2,y2).联立,化为x2﹣4kx﹣4=0,∴x1+x2=4k,x1x2=﹣4.。
专题复习:抛物线与圆的综合探究

课堂总结
抛物线与圆综合探究题,综合性强,难度较大, 通常都作为“压轴题”,解此类题通常需要熟练掌 握抛物线与圆相关的基本知识和基本技能(切线的 性质与判定、切线长定理、点、线、圆的位置关系 等),求解时注意运用有关性质,进行综合分析, 探究解题思路。
方法3:(利用斜率)
设直线F1M的斜率为 K1 ,直线FN1的斜率为 K2;
2
2
K1 x1 , K2 x2
K1
K2
4 x1x2
1
M1F FN1
∴△M1FN1是直角三角形.
方法4:(利用平分角)
中考模拟 (2015长沙模拟卷六T26)
如图,已知抛物线 y ax2 bx c(a 0)的顶点为(0, 1),且与x轴两 个交点之间的距离为4,直线l1经过点(0, 2)且与x轴平行,直线l2经过 原点且交抛物线于点A和点B(点A在y轴的右侧,点B在y轴的左侧). (1)求抛物线的解析式; (2ቤተ መጻሕፍቲ ባይዱ过点A作AC⊥l1于点C,连接OC,以AB为直径作⊙P,
挑战中考
如图所示,过点F(0,1)的直线y=kx+b与抛物线 交于M(x1,y1)
和N(x2,y2)两点(其中x1<0,x2>0).
1 -4 (1)填空:b=_______.x1•x2=_____________ ;
(2)分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,
判断△M1FN1的形状,并证明你的结论.
M1F 2 FN12 M1N12
M1FN1 90
∴△M1FN1是直角三角形.
方法2(利用相似)
设M1N1交y轴于F1 ∵ M(x1,y1)和N(x2,y2) , ∴ F1M1•F1N1=-x1•x2=4, ∵FF1=2, ∴F1M1•F1N1=F1F2, 又∵∠M1F1F=∠FF1N1=90°, ∴ Rt△M1FF1∽Rt△N1FF1, ∴ ∠M1FF1=∠FN1F1, ∴∠M1FN1=∠M1FF1+∠F1FN1=∠FN1F1+∠F1FN1=90°, ∴△M1FN1是直角三角形
高二下学期数学人教A版选择性必修第二册:抛物线专题练习

抛 物 线题型一 抛物线的定义与方程1.已知点(2,3)A -在抛物线C :22y px =的准线上,过点A 的直线与C 在第一象限相切于点B ,记C 的焦点为F ,则直线BF 的斜率为( ) A .12 B .23 C .34 D .432.如图,正方形ABCD 和正方形DEFG 的边长分别为(),a b a b <,原点O 为AD 的中点,抛物线)0(22>=p px y 经过F C ,两点,则_____=ab.3.已知抛物线C :x y 82=的焦点为F,准线为l ,P 是l 上一点,Q 是直线PF 与C 得一个焦点,若FQ PF 4=,则=QF ( ) A. 27 B. 3 C. 25D. 24.设F 为抛物线C:23y x =的焦点,过F 且倾斜角为30°的直线交C 于A,B 两点,O 为坐标原点,则△OAB 的面积为( ) A. 33 B.938 C. 6332 D. 94题型二 抛物线的性质1. 抛物线26y x =,过点()4,1P 引一条弦,使它恰好被P 点平分,则该弦所在的直线方程为______.2.抛物线22(0)y px p =>的焦点为F ,准线为l ,A ,B 是抛物线上的两个动点,且满足23AFB π∠=,设线段AB 的中点M 在l 上的投影为N ,则||||MN AB 的最大值是( ) A 33 C 3 D 33.直线l 过抛物线C:y 2=2px(p>0)的焦点F(1,0),且与C 交于A,B 两点,则p= ,+= .4.设F 1,F 2分别为椭圆C 1:22221x y a b+=(a >b >0)与双曲线C 2:2222111x y a b -= (a 1>0,b 1>0)的公共左,右焦点,它们在第一象限内交于点M ,∠F 1MF 2=90°,若椭圆C 1的离心率e ∈33[]42,则双曲线C 2的离心率e 1的取值范围是________________.5.已知F 是抛物线()220y px p =>的焦点,过F 的直线与抛物线交于A ,B 两点,AB 的中点为C ,过C 作抛物线准线的垂线交准线于1C ,若1CC 的中点为()1,4M ,则p =( ) A. 4 B. 8C. 42D. 826.已知双曲线C :22221(0,0)x y a b a b-=>>的左焦点为F ,M 为虚轴的一端点,若以M 为圆心的圆与C 的一条渐近线相切于点N ,且M ,N ,F 三点共线,则该双曲线的离心率为________.7.(多选)设抛物线y 2=2px (p >0)的焦点为F ,P 为其上一动点,当P 运动到(2,t )时,|PF |=4,直线l 与抛物线相交于A ,B 两点,点M (4,1),下列结论正确的是( ) A .抛物线的方程为y 2=4x B .|PM |+|PF |的最小值为6 C .存在直线l ,使得A 、B 两点关于x +y ﹣6=0对称D .当直线l 过焦点F 时,以AF 为直径的圆与y 轴相切题型三 抛物线与其它曲线综合1. 抛物线22(0)x py p =>的焦点为F,其准线与双曲线221x y -=相交于,A B 两点,若△ABF 为等边三角形,则p = .2.抛物线)0(42>=p px y 与双曲线)0,0(12222>>=-b a by a x 有相同的焦点F ,点A 是两曲线的交点,且AF ⊥x 轴,则双曲线的离心率为A.215+B.12+C.13+D.2122+题型四 切线问题1.过点M(2,-2p)作抛物线x 2=2py(p>0)的两条切线,切点分别为A,B,若线段AB 的中点的纵坐标为6,则p 的值是________.2.已知抛物线1C :212y x p =(0)p >的焦点与双曲线2C :2213x y -=的右焦点的连线交1C 于第一象限的点M .若1C 在点M 处的切线平行于2C的一条渐近线,则p =( )A .316B .38C .233D .433题型五 斜率、弦长、面积1.已知F 是抛物线2y x =的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,2OA OB ⋅=(其中O 为坐标原点),则ABO ∆与AFO ∆面积之和的最小值是( ) A .2 B .3 C .1728D .102.已知A 、B 是过抛物线22(0)y px p =>焦点F 的直线与抛物线的交点,O 是坐标原点,满足2AF FB =,3||OABSAB =,则p 的值为3.如图,已知抛物线的方程为22(0)x py p =>,过点(0,1)A -作直线l 与抛物线相交于,P Q 两点,点B 的坐标为(0,1),连接,BP BQ ,设,QB BP 与x 轴分别相交于,M N 两点.如果QB 的斜率与PB 的斜率的乘积为3-,则MBN ∠的大小等于 .题型六 范围与最值1.已知抛物线y 2=4x ,过点p (4,0)的直线与抛物线相交于A (x 1, y 1)B (x 2, y 2)两点,则y 12+y 22的最小值是_______2.已知抛物线y2=8x,定点A (3,2),F 为焦点,P 为抛物线上的动点,则|PF |+|PA |的最小值为( ) A .5 B .6C .7D .8 A3.如图,已知抛物线的顶点在坐标原点,焦点在x 轴上,且过点(2,4),圆,过圆心的直线l 与抛物线和圆分别交于P ,Q,M,N,则的最小值为( )A . 36B . 42C . 49D . 50设抛物线方程为由抛物线过定点得,抛物线方程,焦点为,4.已知F 为抛物线212y x =的焦点,过F 作两条夹角为045的直线12,l l , 1l 交抛物线于,A B 两点, 2l 交抛物线于,C D 两点,则11AB CD+的最大值为( ) A . 124+ B . 122+ C . 12+ D . 22+题型七 直线与抛物线位置关系1.在平面直角坐标系xOy 中,点M 到点()1,0F 的距离比它到y 轴的距离多1,记点M 的轨迹为C .(1)求轨迹为C 的方程;(2)设斜率为k 的直线l 过定点()2,1p -,求直线l 与轨迹C 恰好有一个公共点,两个公共点,三个公共点时k 的相应取值范围.2.已知抛物线21:4C x y =的焦点F 也是椭圆22222:1(0)y x C a b a b+=>>的一个焦点,1C 与2C 的公共弦的长为26(1)求2C 的方程;(2)过点F 的直线l 与1C 相交于A ,B 两点,与2C 相交于C ,D 两点,且AC 与BD 同向(ⅰ)若||||AC BD =,求直线l 的斜率 (ⅱ)设1C 在点A 处的切线与x 轴的交点为M ,证明:直线l 绕点F 旋转时,MFD ∆总是钝角三角形3.已知抛物线2:2(0)E y px p =>,直线3x my =+与E 交于A B 、两点,且6OA OB =,其中O 为坐标原点.(1)求抛物线E 的方程;(2)已知点C 的坐标为(3,0)-,记直线CA CB 、的斜率分别为12k k ,,证明22212112m k k +-为定值.4.设点30,2F ⎛⎫ ⎪⎝⎭,动圆P 经过点F 且和直线32y =-相切 .记动圆的圆心P 的轨迹为曲线W .(Ⅰ)求曲线W 的方程;(Ⅱ)过点F 作互相垂直的直线12,l l ,分别交曲线W 于,A B 和,C D . 求四边形ACBD 面积的最小值 .5.已知抛物线S 的顶点在坐标原点,焦点在x 轴上,ABC ∆的三个顶点都在抛物线上,且ABC ∆的重心为抛物线的焦点,若BC 所在直线l 的方程为4200.x y +-=(I )求抛物线S 的方程;(II )若O 是坐标原点,P 、Q 是抛物线S 上的两动点,且满足PO OQ ⊥.试说明动直线PQ 是否过一个定点.6.设抛物线C :22(0)y px p =>过点(3,6)H -,其准线为l ,焦点为F 。
中考数学压轴必刷 专题17函数与圆综合问题(学生版)

【压轴必刷】中考数学压轴大题之经典模型培优案专题17函数与圆综合问题【例1】如图,抛物线y=ax2+bx+2经过A(﹣1,0),B(4,0)两点,与y轴交于点C.(1)求该抛物线的解析式;(2)在y轴上是否存在点P使得∠OBP+∠OBC=45°,若存在,求出点P的坐标,若不存在,请说明理由;(3)点M是BC为直径的圆上的动点,将点M绕原点O顺时针旋转90°得点N,连接NA,求NA的取值范围.【例2】如图1:抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0),与y轴交于点C.动点E(m,0)(0<m<3),过点E作直线l⊥x轴,交抛物线于点M.(1)求抛物线的解析式及C点坐标;(2)连接BM并延长交y轴于点N,连接AN,OM,若AN∥OM,求m的值.(3)如图2.当m=1时,P是直线l上的点,以P为圆心,PE为半径的圆交直线l于另一点F(点F 在x轴上方),若线段AC上最多存在一个点Q使得∠FQE=90°,求点P纵坐标的取值范围.【例3】如图,抛物线y=ax2+bx+2与直线AB相交于A(﹣1,0),B(3,2),与x轴交于另一点C.(1)求抛物线的解析式;(2)在y上是否存在一点E,使四边形ABCE为矩形,若存在,请求出点E的坐标;若不存在,请说明理由;(3)以C为圆心,1为半径作⊙O,D为⊙O上一动点,求DA+DB的最小值【例4】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+3的对称轴是直线x=2,与x轴相交于A,B 两点(点A在点B的左侧),与y轴交于点C.(Ⅰ)求抛物线的解析式及顶点坐标;(Ⅱ)M为第一象限内抛物线上的一个点,过点M作MN⊥x轴于点N,交BC于点D,连接CM,当线段CM=CD时,求点M的坐标;(Ⅲ)以原点O为圆心,AO长为半径作⊙O,点P为⊙O上的一点,连接BP,CP,求2PC+3PB的最小值.1.如图,在平面直角坐标系上,一条抛物线y=ax2+bx+c(a≠0)经过A(1,0)、B(3,0)、C(0,3)三点,连接BC并延长.(1)求抛物线的解析式;(2)点M是直线BC在第一象限部分上的一个动点,过M作MN∥y轴交抛物线于点N.1°求线段MN的最大值;2°当MN取最大值时,在线段MN右侧的抛物线上有一个动点P,连接PM、PN,当△PMN的外接圆圆心Q在△PMN的边上时,求点P的坐标.2.如图1,已知抛物线y=ax2﹣12ax+32a(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C.(1)连接BC,若∠ABC=30°,求a的值.(2)如图2,已知M为△ABC的外心,试判断弦AB的弦心距d是否有最小值,若有,求出此时a的值,若没有,请说明理由;(3)如图3,已知动点P(t,t)在第一象限,t为常数.问:是否存在一点P,使得∠APB达到最大,若存在,求出此时∠APB的正弦值,若不存在,也请说明理由.3.如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE.(1)求抛物线的表达式;(2)判断△BCE的形状,并说明理由;(3)如图2,以C为圆心,为半径作⊙C,在⊙C上是否存在点P,使得BP+EP的值最小,若存在,请求出最小值;若不存在,请说明理由.4.如图,已知二次函数y=ax2+bx+c的图象经过点C(2,﹣3),且与x轴交于原点及点B(8,0).(1)求二次函数的表达式;(2)求顶点A的坐标及直线AB的表达式;(3)判断△ABO的形状,试说明理由;(4)若点P为⊙O上的动点,且⊙O的半径为2,一动点E从点A出发,以每秒2个单位长度的速度沿线段AP匀速运动到点P,再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动,求点E的运动时间t的最小值.5.如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:x…﹣10123…y…03430…(1)求出这条抛物线的解析式及顶点M的坐标;(2)PQ是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求AQ+QP+PC的最小值;(3)如图2,点D是第四象限内抛物线上一动点,过点D作DF⊥x轴,垂足为F,△ABD的外接圆与DF相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.6.如图,抛物线的顶点为A(0,2),且经过点B(2,0).以坐标原点O为圆心的圆的半径r=,OC ⊥AB于点C.(1)求抛物线的函数解析式.(2)求证:直线AB与⊙O相切.。
专题:抛物线与圆综合探究题(含答案)

专题:抛物线与圆综合探究题抛物线与圆综合探究题,综合性强,难度较大,通常都作为“压轴题”,解此类题通常需要熟练掌握抛物线与圆相关的基本知识和基本技能,求解时注意运用有关性质,进行综合、分析、探究解题思路。
例1、抛物线2y ax bx c =++交x 轴于A 、B 两点,交y 轴于点C ,已知抛物线的对称轴为1x =,(3,0)B ,(0,3)C -, ⑴求二次函数2y ax bx c =++的解析式;⑵在抛物线对称轴上是否存在一点P ,使点P 到B 、C 两点距离之差最大?若存在,求出P 点坐标;若不存在,请说明理由; ⑶平行于x 轴的一条直线交抛物线于M N 、两点,若以MN 为直径的圆恰好与x 轴相切,求此圆的半径.解:(1)将(0,3)C -代入c bx ax y ++=2,得 3-=c .将3-=c ,(3,0)B 代入c bx ax y ++=2,得 039=++c b a .∵1x =是对称轴,∴12=-ab.将(2)代入(1)得1=a , 2-=b .二次函数得解析式是322--=x x y .(2)AC 与对称轴的交点P 即为到B C 、的距离之差最大的点.∵C 点的坐标为(0,3)-,A 点的坐标为(1,0)-,∴ 直线AC 的解析式是33--=x y ,又对称轴为1x =,∴ 点P 的坐标(1,6)-. (3)设1(,)M x y 、2(,)N x y ,所求圆的半径为r ,则 r x x 212=-,.(1) ∵ 对称轴为1x =,∴ 212=+x x . .(2)由(1)、(2)得:12+=r x ..(3) 将(1,)N r y +代入解析式322--=x x y ,得 3)1(2)1(2-+-+=r r y ,.(4)整理得: 42-=r y .由于 r=±y ,当0>y 时,042=--r r ,解得,21711+=r , 21712-=r (舍去),当0<y 时,042=-+r r ,解得,21711+-=r , 21712--=r (舍去).所以圆的半径是2171+或2171+-.例2、已知:在平面直角坐标系xOy 中,一次函数y=kx-4k 的图象与x 轴交于点A ,抛物线y ax bx c=++2经过O 、A 两点。
函数的实际应用--抛物线型问题(专题训练)(解析版)-中考数学重难点题型专题汇总
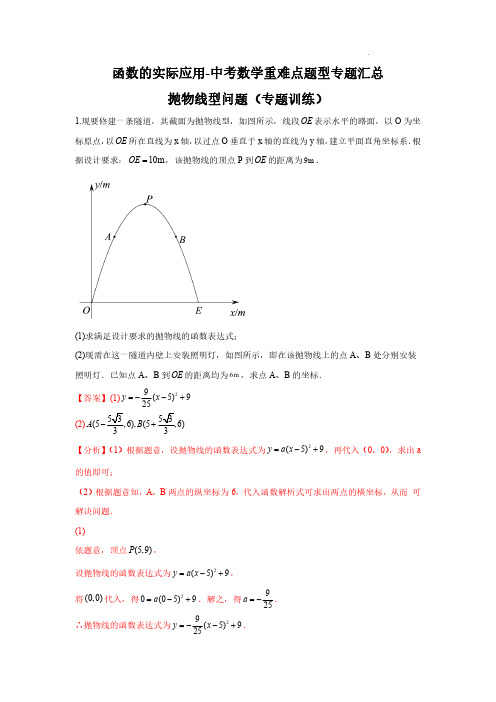
函数的实际应用-中考数学重难点题型专题汇总抛物线型问题(专题训练)1.现要修建一条隧道,其截面为抛物线型,如图所示,线段OE 表示水平的路面,以O 为坐标原点,以OE 所在直线为x 轴,以过点O 垂直于x 轴的直线为y 轴,建立平面直角坐标系.根据设计要求:10m OE =,该抛物线的顶点P 到OE 的距离为9m .(1)求满足设计要求的抛物线的函数表达式;(2)现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A 、B 处分别安装照明灯.已知点A 、B 到OE 的距离均为6m ,求点A 、B 的坐标.【答案】(1)29(5)925y x =--+(2)(5(5A B +【分析】(1)根据题意,设抛物线的函数表达式为2(5)9y a x =-+,再代入(0,0),求出a 的值即可;(2)根据题意知,A ,B 两点的纵坐标为6,代入函数解析式可求出两点的横坐标,从而可解决问题.(1)依题意,顶点(5,9)P ,设抛物线的函数表达式为2(5)9y a x =-+,将(0,0)代入,得20(05)9a =-+.解之,得925a =-.∴抛物线的函数表达式为29(5)925y x =--+.(2)令6y =,得29(5)9625x --+=.解之,得125,5x x +=+.∴(5(5A B +.【点睛】本题考查了运用待定系数法求二次函数的解析式的运用,由函数值求自变量的值的运用,解答时求出二次函数的解析式是关键.2.甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面OBA 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽8m OA =,桥拱顶点B 到水面的距离是4m .(1)按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;(2)一只宽为1.2m 的打捞船径直向桥驶来,当船驶到桥拱下方且距O 点0.4m 时,桥下水位刚好在OA 处.有一名身高1.68m 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);(3)如图③,桥拱所在的函数图象是抛物线()20y ax bx c a =++≠,该抛物线在x 轴下方部分与桥拱OBA 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移()0m m >个单位长度,平移后的函数图象在89x ≤≤时,y 的值随x 值的增大而减小,结合函数图象,求m 的取值范围.【答案】(1)y=14-x 2+2x (0≤x≤8);(2)他的头顶不会触碰到桥拱,理由见详解;(3)【分析】(1)设二次函数的解析式为:y=a(x-8)x ,根据待定系数法,即可求解;(2)把:x =1,代入y=14-x 2+2x ,得到对应的y 值,进而即可得到结论;(3)根据题意得到新函数解析式,并画出函数图像,进而即可得到m 的范围.【详解】(1)根据题意得:A(8,0),B(4,4),设二次函数的解析式为:y=a(x-8)x ,把(4,4)代入上式,得:4=a×(4-8)×4,解得:14a =-,∴二次函数的解析式为:y=14-(x-8)x=14-x 2+2x (0≤x≤8);(2)由题意得:x=0.4+1.2÷2=1,代入y=14-x 2+2x ,得y=14-×12+2×1=74>1.68,答:他的头顶不会触碰到桥拱;(3)由题意得:当0≤x≤8时,新函数表达式为:y=14x 2-2x ,当x <0或x >8时,新函数表达式为:y=-14x 2+2x ,∴新函数表达式为:2212(08)41(08)4x x x y x x x ⎧-≤≤⎪⎪=⎨⎪-+⎪⎩或,∵将新函数图象向右平移()0m m >个单位长度,∴O '(m ,0),A '(m+8,0),B '(m+4,-4),如图所示,根据图像可知:当m+4≥9且m≤8时,即:5≤m≤8时,平移后的函数图象在89x ≤≤时,y 的值随x 值的增大而减小.本题主要考查二次函数的实际应用,掌握二次函数的待定系数法,二次函数的图像和性质,二次函数图像平移和轴对称变换规律,是解题的关键.3.2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x 轴,过跳台终点A 作水平线的垂线为y 轴,建立平面直角坐标系.图中的抛物线2117C :1126y x x =-++近似表示滑雪场地上的一座小山坡,某运动员从点O 正上方4米处的A 点滑出,滑出后沿一段抛物线221:8C y x bx c =-++运动.(1)当运动员运动到离A 处的水平距离为4米时,离水平线的高度为8米,求抛物线2C 的函数解析式(不要求写出自变量x 的取值范围);(2)在(1)的条件下,当运动员运动水平线的水平距离为多少米时,运动员与小山坡的竖直距离为1米?(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b 的取值范围.【答案】(1)213482y x x =-++;(2)12米;(3)3524b ≥.【分析】(1)根据题意可知:点A (0,4)点B (4,8),利用待定系数法代入抛物线221:8C y x bx c=-++即可求解;(2)高度差为1米可得21=1C C -可得方程,由此即可求解;(3)由抛物线2117C :1126y x x =-++可知坡顶坐标为61(7,)12,此时即当7x =时,运动员运动到坡顶正上方,若与坡顶距离超过3米,即2161773812y b c =-⨯++≥+,由此即可求出b的取值范围.【详解】解:(1)根据题意可知:点A (0,4),点B (4,8)代入抛物线221:8C y x bx c =-++得,2=4144=88c b c ⎧⎪⎨-⨯++⎪⎩,解得:=43=2c b ⎧⎪⎨⎪⎩,∴抛物线2C 的函数解析式213482y x x =-++;(2)∵运动员与小山坡的竖直距离为1米,∴221317(4)(1)182126x x x x -++--++=,解得:14x =-(不合题意,舍去),212x =,故当运动员运动水平线的水平距离为12米时,运动员与小山坡的竖直距离为1米;(3)∵点A (0,4),∴抛物线221:48C y x bx =-++,∵抛物线2211761C :1=7)12612y x x x =-++-+,∴坡顶坐标为61(7,12,∵当运动员运动到坡顶正上方,且与坡顶距离超过3米时,∴21617743812y b =-⨯++≥+,解得:3524b ≥.【点睛】本题属二次函数应用中的难题.解决函数应用问题的一般步骤为:(1)审题:弄清题意,分清条件和结论,理清数量关系;(2)建模:将文字语言转化为数学语言,利用数学知识建立相应的数学模型;(3)求模:求解数学模型,得到数学结论;(4)还原:将用数学方法得到的结论还原为实际问题.4.如图是一块铁皮余料,将其放置在平面直角坐标系中,底部边缘AB 在x 轴上,且8AB =dm ,外轮廓线是抛物线的一部分,对称轴为y 轴,高度8OC =dm .现计划将此余料进行切割:(1)若切割成正方形,要求一边在底部边缘AB 上且面积最大,求此正方形的面积;(2)若切割成矩形,要求一边在底部边缘AB 上且周长最大,求此矩形的周长;(3)若切割成圆,判断能否切得半径为3dm 的圆,请说明理由.【答案】(1)296-;(2)20dm ;(3)能切得半径为3dm 的圆.【分析】(1)先把二次函数解析式求出来,设正方形的边长为2m ,表示在二次函数上点的坐标,代入即可得到关于m (2)如详解2中图所示,设矩形落在AB 上的边DE=2n ,利用函数解析式求解F 点坐标,进而表示出矩形的周长求最大值即可;(3)为了保证尽可能截取圆,应保证圆心H 坐标为(0,3),表示出圆心H 到二次函数上个点之间的距离与半径3进行比较即可.(1)由题目可知A (-4,0),B (4,0),C (0,8)设二次函数解析式为y=ax²+bx+c ,∵对称轴为y 轴,∴b=0,将A 、C 代入得,a=12-,c=8则二次函数解析式为2182y x =-+,如下图所示,正方形MNPQ 即为符合题意得正方形,设其边长为2m ,则P 点坐标可以表示为(m ,2m )代入二次函数解析式得,21822m m -+=,解得122,2m m =-=-(舍去),∴2m=4,()()222496m =-=-则正方形的面积为296-;(2)如下如所示矩形DEFG ,设DE=2n ,则E (n ,0)将x=n 代入二次函数解析式,得2182y n =-+,则EF=2182n -+,矩形DEFG 的周长为:2(DE+EF )=2(2n+2182n -+)=22416(2)20n n n -++=--+,当n=2时,矩形的周长最大,最大周长为20dm ;(3)如下图所示,为了保证尽可能截取圆,应保证圆心H 坐标为(0,3),则圆心H 到二次函数上个点之间的距离为3≥,∴能切得半径为3dm 的圆.【点睛】本题考查了二次函数与几何结合,熟练掌握各图形的性质,能灵活运用坐标与线段长度之间的转换是解题的关键.5.跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图中实线部分所示),落地点在着陆坡(如图中虚线部分所示)上,着陆坡上的基准点K 为飞行距离计分的参照点,落地点超过K 点越远,飞行距离分越高.2022年北京冬奥会跳台滑雪标准台的起跳台的高度OA 为66m ,基准点K 到起跳台的水平距离为75m ,高度为m h (h 为定值).设运动员从起跳点A 起跳后的高度(m)y 与水平距离(m)x 之间的函数关系为2(0)y ax bx c a =++.(1)c 的值为__________;(2)①若运动员落地点恰好到达K 点,且此时19,5010a b =-=,求基准点K 的高度h ;②若150a =-时,运动员落地点要超过K 点,则b 的取值范围为__________;(3)若运动员飞行的水平距离为25m 时,恰好达到最大高度76m ,试判断他的落地点能否超过K点,并说明理由.【答案】(1)66(2)①基准点K的高度h为21m;②b>9 10;(3)他的落地点能超过K点,理由见解析.【分析】(1)根据起跳台的高度OA为66m,即可得c=66;(2)①由a=﹣150,b=910,知y=﹣150x2+910x+66,根据基准点K到起跳台的水平距离为75m,即得基准点K的高度h为21m;②运动员落地点要超过K点,即是x=75时,y>21,故﹣150×752+75b+66>21,即可解得答案;(3)运动员飞行的水平距离为25m时,恰好达到最大高度76m,即是抛物线的顶点为(25,76),设抛物线解析式为y=a(x﹣25)2+76,可得抛物线解析式为y=﹣2125(x﹣25)2+76,当x=75时,y=36,从而可知他的落地点能超过K点.(1)解:∵起跳台的高度OA为66m,∴A(0,66),把A(0,66)代入y=ax2+bx+c得:c=66,故答案为:66;(2)解:①∵a=﹣150,b=910,∴y=﹣150x2+910x+66,∵基准点K到起跳台的水平距离为75m,∴y=﹣150×752+910×75+66=21,∴基准点K的高度h为21m;②∵a=﹣1 50,∴y=﹣150x2+bx+66,∵运动员落地点要超过K点,∴当x=75时,y>21,即﹣150×752+75b+66>21,解得b>9 10,故答案为:b>9 10;(3)解:他的落地点能超过K点,理由如下:∵运动员飞行的水平距离为25m时,恰好达到最大高度76m,∴抛物线的顶点为(25,76),设抛物线解析式为y=a(x﹣25)2+76,把(0,66)代入得:66=a(0﹣25)2+76,解得a=﹣2 125,∴抛物线解析式为y=﹣2125(x﹣25)2+76,当x=75时,y=﹣2125×(75﹣)2+76=36,∵36>21,∴他的落地点能超过K点.【点睛】本题考查二次函数的应用,解题的关键是读懂题意,能根据题意把实际问题转化为数学问题.6.根据以下素材,探索完成任务.如何设计拱桥景观灯的悬挂方案?素材1图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽20m,拱顶离水面5m.据调查,该河段水位在此基础上再涨1.8m达到最高.素材2为迎佳节,拟在图1桥洞前面的桥拱上悬挂40cm 长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m ;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m ;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.问题解决任务1确定桥拱形状在图2任务2探究悬挂范围在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.任务3拟定设计方案给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.【答案】任务一:见解析,2120y x =-;任务二:悬挂点的纵坐标的最小值是 1.8-;66x -≤≤;任务三:两种方案,见解析【分析】任务一:根据题意,以拱顶为原点,建立如图1所示的直角坐标系,待定系数法求解析式即可求解;任务二:根据题意,求得悬挂点的纵坐标5 1.810.4 1.8y ≥-+++=-,进而代入函数解析式即可求得横坐标的范围;任务三:有两种设计方案,分情况讨论,方案一:如图2(坐标系的横轴,图3同),从顶点处开始悬挂灯笼;方案二:如图3,从对称轴两侧开始悬挂灯笼,正中间两盏与对称轴的距离均为0.8m ,根据题意求得任意一种方案即可求解.【详解】任务一:以拱顶为原点,建立如图1所示的直角坐标系,则顶点为(0,0),且经过点(10,5)-.设该抛物线函数表达式为2(0)y ax a =≠,则5100a -=,∴120a =-,∴该抛物线的函数表达式是2120y x =-.任务二:∵水位再上涨1.8m 1m ,灯笼长0.4m ,∴悬挂点的纵坐标5 1.810.4 1.8y ≥-+++=-,∴悬挂点的纵坐标的最小值是 1.8-.当 1.8y =-时,211.820x -=-,解得16x =或26x =-,∴悬挂点的横坐标的取值范围是66x -≤≤.任务三:有两种设计方案方案一:如图2(坐标系的横轴,图3同),从顶点处开始悬挂灯笼.∵66x -≤≤,相邻两灯笼悬挂点的水平间距均为1.6m ,∴若顶点一侧挂4盏灯笼,则1.646⨯>,⨯<,若顶点一侧挂3盏灯笼,则1.636∴顶点一侧最多可挂3盏灯笼.∵挂满灯笼后成轴对称分布,∴共可挂7盏灯笼.-.∴最左边一盏灯笼悬挂点的横坐标是 4.8方案二:如图3,从对称轴两侧开始悬挂灯笼,正中间两盏与对称轴的距离均为0.8m,+⨯->,∵若顶点一侧挂5盏灯笼,则0.8 1.6(51)6+⨯-<,若顶点一侧挂4盏灯笼,则0.8 1.6(41)6∴顶点一侧最多可挂4盏灯笼.∵挂满灯笼后成轴对称分布,∴共可挂8盏灯笼.-.∴最左边一盏灯笼悬挂点的横坐标是 5.6【点睛】本题考查了二次函数的应用,根据题意建立坐标系,掌握二次函数的性质是解题的关键.7.公路上正在行驶的甲车,发现前方20m处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程s(单位:m)、速度v(单位:m/s)与时间t(单位:s)的关系分别可以用二次函数和一次函数表示,其图象如图所示.(1)当甲车减速至9m/s时,它行驶的路程是多少?(2)若乙车以10m/s的速度匀速行驶,两车何时相距最近,最近距离是多少?【答案】(1)87.5m ;(2)6秒时两车相距最近,最近距离是2米【分析】(1)根据图像分别求出一次函数和二次函数解析式,令v=9求出t ,代入求出s 即可;(2)分析得出当v=10m/s 时,两车之间距离最小,代入计算即可.【详解】解:(1)由图可知:二次函数图像经过原点,设二次函数表达式为2s at bt =+,一次函数表达式为v kt c =+,∵一次函数经过(0,16),(8,8),则8816k c c =+⎧⎨=⎩,解得:116k c =-⎧⎨=⎩,∴一次函数表达式为16v t =-+,令v=9,则t=7,∴当t=7时,速度为9m/s ,∵二次函数经过(2,30),(4,56),则423016456a b a b +=⎧⎨+=⎩,解得:1216a b ⎧=-⎪⎨⎪=⎩,∴二次函数表达式为21162s t t =-+,令t=7,则s=491672-+⨯=87.5,∴当甲车减速至9m/s 时,它行驶的路程是87.5m ;(2)∵当t=0时,甲车的速度为16m/s ,∴当10<v <16时,两车之间的距离逐渐变小,当0<v <10时,两车之间的距离逐渐变大,∴当v=10m/s 时,两车之间距离最小,将v=10代入16v t =-+中,得t=6,将t=6代入21162s t t =-+中,得78s =,此时两车之间的距离为:10×6+20-78=2m ,∴6秒时两车相距最近,最近距离是2米.【点睛】本题考查了二次函数与一次函数的实际应用,理解题意,读懂函数图像,求出表达式是解题的基本前提.8.如今我国的大棚(如图1)种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在离地面高1米的墙体A 处,另一端固定在离地面高2米的墙体B 处,现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度y (米)与其离墙体A 的水平距离x (米)之间的关系满足216y x bx c =-++,现测得A ,B 两墙体之间的水平距离为6米.图2(1)直接写出b ,c 的值;(2)求大棚的最高处到地面的距离;(3)小明的爸爸欲在大棚内种植黄瓜,需搭建高为3724米的竹竿支架若干,已知大棚内可以根竹竿,则共需要准备多少根竹竿?【答案】(1)76b =,1c =;(2)7324米;(3)352【分析】(1)根据题意,可直接写出点A 点B 坐标,代入216y x bx c =-++,求出b 、c 即可;(2)根据(1)中函数解析式直接求顶点坐标即可;(3根据2173716624y x x =-++=,先求得大棚内可以搭建支架的土地的宽,再求得需搭建支架的面积,最后根据每平方米需要4根竹竿计算即可.【详解】解:(1)由题意知点A 坐标为(0)1,,点B 坐标为(6)2,,将A 、B 坐标代入216y x bx c =-++得:21=12666c b c ⎧⎪⎨=-⨯++⎪⎩解得:761b c ⎧=⎪⎨⎪=⎩,故76b =,1c =;(2)由221717731666224y x x x ⎛⎫=-++=--+ ⎪⎝⎭,可得当72x =时,y 有最大值7324,即大棚最高处到地面的距离为7324米;(3)由2173716624y x x =-++=,解得112x =,2132x =,又因为06x ≤≤,可知大棚内可以搭建支架的土地的宽为111622-=(米),又大棚的长为16米,故需要搭建支架部分的土地面积为1116882⨯=(平方米)共需要884352⨯=(根)竹竿.【点睛】本题主要考查根据待定系数法求函数解析式,根据函数解析式求顶点坐标,以及根据函数值确定自变量取值范围,掌握此题的关键是熟练掌握二次函数图像的性质.9.如图1是一座抛物线型拱桥侧面示意图.水面宽AB 与桥长CD 均为24m ,在距离D 点6米的E 处,测得桥面到桥拱的距离EF 为1.5m ,以桥拱顶点O 为原点,桥面为x 轴建立平面直角坐标系.(1)求桥拱项部O 离水面的距离.(2)如图2,桥面上方有3根高度均为4m 的支柱CG ,OH ,DI ,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m .①求出其中一条钢缆抛物线的函数表达式.②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.【答案】(1)6m ;(2)①21'(6)112y x =++;②2m 【分析】(1)设211y a x =,由题意得(6,1.5)F -,求出抛物线图像解析式,求当x=12或x=-12时y 1的值即可;(2)①由题意得右边的抛物线顶点为(6,1),设222(6)1y a x =-+,将点H 代入求值即可;②设彩带长度为h ,则12h y y =-,代入求值即可.【详解】解(1)设211y a x =,由题意得(6,1.5)F -,11.536a ∴-=,1124a ∴=-,21124y x ∴=-,∴当12x =时,21112624y =-⨯=-,∴桥拱顶部离水面高度为6m .(2)①由题意得右边的抛物线顶点为(6,1),∴设222(6)1y a x =-+,(0,4)H ,224(06)1a ∴=-+,2112a ∴=,221(6)112y x ∴=-+,(左边抛物线表达式:21'(6)112y x =++)②设彩带长度为h ,则22221111(6)1()412248h y y x x x x =-=-+--=-+,∴当4x =时,2min h =,答:彩带长度的最小值是2m .【点睛】本题主要考查待定系数法求二次函数的解析式,以及二次函数最值得求解方法,结合题意根据数形结合的思想设出二次函数的顶点式方程是解题的关键.。
专题12 抛物线及其性质(知识梳理+专题过关)(解析版)

专题12抛物线及其性质【考点预测】知识点一、抛物线的定义平面内与一个定点F 和一条定直线()l F l ∉的距离相等的点的轨迹叫做抛物线,定点F 叫抛物线的焦点,定直线l 叫做抛物线的准线.注:若在定义中有F l ∈,则动点的轨迹为l 的垂线,垂足为点F .知识点二、抛物线的方程、图形及性质抛物线的标准方程有4种形式:22y px =,22y px =-,22x py =,22(0)x py p =->,其中一次项与对称轴一致,一次项系数的符号决定开口方向图形标准方程22(0)y px p =>22(0)y px p =->22(0)x py p =>22(0)x py p =->顶点(00)O ,范围0x ≥,y R ∈0x ≤,y R∈0y ≥,x R ∈0y ≤,x R∈对称轴x 轴y 轴焦点(0)2pF ,(0)2p F -,(0)2p F ,(0)2pF -,离心率1e =准线方程2p x =-2p x =2p y =-2p y =焦半径11()A x y ,12pAF x =+12p AF x =-+12p AF y =+12p AF y =-+【方法技巧与总结】1、点00(,)P x y 与抛物线22(0)y px p =>的关系(1)P 在抛物线内(含焦点)2002y px ⇔<.(2)P 在抛物线上2002y px ⇔=.(3)P 在抛物线外2002y px ⇔>.2、焦半径抛物线上的点00(,)P x y 与焦点F 的距离称为焦半径,若22(0)y px p =>,则焦半径02pPF x =+,max2p PF =.3、(0)p p >的几何意义p 为焦点F 到准线l 的距离,即焦准距,p 越大,抛物线开口越大.4、焦点弦若AB 为抛物线22(0)y px p =>的焦点弦,11(,)A x y ,22(,)B x y ,则有以下结论:(1)2124p x x =.(2)212y y p =-.(3)焦点弦长公式1:12AB x x p =++,12x x p +≥=,当12x x =时,焦点弦取最小值2p ,即所有焦点弦中通径最短,其长度为2p .焦点弦长公式2:22sin pAB α=(α为直线AB 与对称轴的夹角).(4)AOB ∆的面积公式:22sin AOB p S α∆=(α为直线AB 与对称轴的夹角).5、抛物线的弦若AB 为抛物线22(p 0)y px =>的任意一条弦,1122(,),(,)A x y B x y ,弦的中点为000(,)(0)M x y y ≠,则(1)弦长公式:1212(0)AB AB x y k k =-=-=≠(2)0AB p k y =(3)直线AB 的方程为000()py y x x y -=-(4)线段AB 的垂直平分线方程为000()y y y x x p-=--6、求抛物线标准方程的焦点和准线的快速方法(4A法)(1)2(0)y Ax A =≠焦点为(,0)4A ,准线为4Ax =-(2)2(0)x Ay A =≠焦点为(0,)4A ,准线为4Ay =-如24y x =,即24y x =,焦点为1(0,)16,准线方程为116y =-7、参数方程22(0)y px p =>的参数方程为222x pt y pt ⎧=⎨=⎩(参数t R ∈)8、切线方程和切点弦方程抛物线22(0)y px p =>的切线方程为00()y y p x x =+,00(,)x y 为切点切点弦方程为00()y y p x x =+,点00(,)x y 在抛物线外与中点弦平行的直线为00()y y p x x =+,此直线与抛物线相离,点00(,)x y (含焦点)是弦AB 的中点,中点弦AB 的斜率与这条直线的斜率相等,用点差法也可以得到同样的结果.9、抛物线的通径过焦点且垂直于抛物线对称轴的弦叫做抛物线的通径.对于抛物线22(0)y px p =>,由()2p A p ,,()2p B p -,,可得||2AB p =,故抛物线的通径长为2p .10、弦的中点坐标与弦所在直线的斜率的关系:0py k=11、焦点弦的常考性质已知11()A x y ,、22()B x y ,是过抛物线22(0)y px p =>焦点F 的弦,M 是AB 的中点,l 是抛物线的准线,MN l ⊥,N 为垂足.(1)以AB 为直径的圆必与准线l 相切,以AF (或BF )为直径的圆与y 轴相切;(2)FN AB ⊥,FC FD⊥(3)2124p x x =;212y y p =-(4)设BD l ⊥,D 为垂足,则A 、O 、D 三点在一条直线上【专题过关】【考点目录】考点一:抛物线的定义与方程考点二:抛物线的轨迹方程考点三:与抛物线有关的距离和最值问题考点四:抛物线中三角形,四边形的面积问题考点五:焦半径问题考点六:抛物线的性质【典型考题】考点一:抛物线的定义与方程1.(2022·江苏·高二)已知抛物线的顶点在原点,对称轴为y 轴,其上一点(),4A m -到焦点F 的距离为6.求抛物线的方程及点A 的坐标.【解析】由题意,设抛物线方程为()220x py p =->,则其准线方程为2p y =,∴462p+=,得p =4,故抛物线方程为28x y =-;又∵点(),4A m -在抛物线上,∴232m =,∴m =±即点A 的坐标为()4-或()4--.2.(多选题)(2022·全国·高二单元测试)下列方程的图形为抛物线的是()A .10x +=B .2y -=C D .2230x x y --+=【答案】ACD【解析】对于A ,方程10x +=化为1x +=(,)x y 到定点(0,0)的距离与到定直线1x =-的距离相等,且定点(0,0)不在定直线1x =-上,原方程表示的图形是抛物线,A 是;对于B ,方程2y -=(,)x y 到定点(1,2)-的距离与到定直线2y =的距离相等,而定点(1,2)-在定直线2y =上,原方程表示的图形不是抛物线,B 不是;对于C (,)x y 到定点(2,3)的距离与到定直线3410x y +-=的距离相等,且定点(2,3)不在定直线3410x y +-=上,原方程表示的图形是抛物线,C 是;对于D ,方程2230x x y --+=化为223y x x =-+,方程表示的图形是抛物线,D 是.故选:ACD3.(多选题)(2022·广东清远·高二期末)已知0mn ≠,则方程221mx ny +=与2ny mx =在同一坐标系内对应的图形可能是()A .B .C .D .【答案】BC【解析】将对应方程化为标准方程得22111x ym n+=,2m y x n=,所以抛物线2my x n=的焦点在x 轴上,故排除D 选项,对于A 选项,由图可知0mn>,0m <,0n >,矛盾,故A 错误;对于B 选项,由图可知0mn<,0m <,0n >,满足,故B 正确;对于C 选项,由图可知,0mn>,0m >,0n >,满足,故C 正确;故选:BC.4.(2022·江西吉安·高二期末(理))已知抛物线C :()220y px p =>的焦点为F ,准线l 上有两点A ,B ,若FAB 为等腰直角三角形且面积为8,则抛物线C 的标准方程是()A .2y =B .28y x =C .2y =或28y x =D .24y x=【答案】C【解析】由题意得,当2AFB π∠=时,1282AFB S p p =⨯⨯=△,解得p =;当2FAB π∠=或2FBA π∠=时,2182AFB S p ==△,解得4p =,所以抛物线的方程是2y =或28y x =.故选:C.5.(2022·全国·高二课时练习)下列条件中,一定能得到抛物线的标准方程为28y x =的是______(填序号)(写出一个正确答案即可).①焦点在x 轴上;②焦点在y 轴上;③抛物线上横坐标为1的点到焦点的距离为3;④焦点到准线的距离为4;⑤由原点向过焦点的某直线作垂线,垂足坐标为()1,1-.【答案】①③(答案不唯一)【解析】若要得到抛物线的方程为28y x =,则焦点一定在x 轴上,故①必选,②不选.若选①③,由抛物线的定义可知132p+=,得4p =,则抛物线的方程为28y x =.若选①⑤,设焦点,02p F ⎛⎫⎪⎝⎭()0p >,()1,1A -,112AF k p =-,1OA k =-,由1AF OA k k ⋅=-,得1112p =-,解得4p =,故抛物线的方程为28y x =.由④可知4p =,故还可选择①④.故答案可为①③或①⑤或①④.故答案为:①③(答案不唯一)6.(2022·全国·高二课时练习)位于德国东部萨克森州的莱科勃克桥(如图所示)有“仙境之桥”之称,它的桥形可以近似地看成抛物线,该桥的高度为5m ,跨径为12m ,则桥形对应的抛物线的焦点到准线的距离为______m .【答案】185【解析】以抛物线的最高点O 为坐标原点,建立如图所示的平面直角坐标系,设抛物线的解析式为22x py =-,0p >,因为抛物线过点()6,5-,所以3610p =,可得185p =,所以抛物线的焦点到准线的距离为18m 5.故答案为:1857.(2022·全国·高二课时练习)设抛物线C 的顶点在坐标原点,焦点F 在坐标轴上,点P 在抛物线C 上,52PF =,若以线段PF 为直径的圆过坐标轴上距离原点为1的点,试写出一个满足题意的抛物线C 的方程为______.【答案】22x y =(答案不唯一)【解析】由题意,若抛物线的焦点F 在y 轴正半轴上,则可设抛物线方程为22x py =(0p >),()00,P x y ,0,2p F ⎛⎫ ⎪⎝⎭,由焦半径公式可知0522p y +=,圆的半径为54,得052p y -=,并且线段PF 中点的纵坐标是05224py +=,所以以线段PF 为直径的圆与x 轴相切,切点坐标为()1,0-或()1,0,所以02x =±,即点P 的坐标为52,2p -⎛⎫± ⎝⎭,代入抛物线方程22x py =(0p >)得5422p p -=⋅,解得1p =或4p =,即当点F 在y 轴正半轴上时,抛物线方程是22x y =或28x y =.同理,当点F 在y 轴负半轴时,抛物线方程为22x x =-或28x y =-,当点F 在x 轴正半轴时,抛物线方程为22y x =或28y x =,当点F 在x 轴负半轴时,抛物线方程为22y x =-或28y x =-.故答案为:22x y =(答案不唯一).8.(2022·山西·怀仁市第一中学校高二期中(理))设抛物线2:2(0)C y px p =>的焦点为F ,准线为l ,A 为C 上一点,以F 为圆心,FA 为半径的圆交l 于B ,D 两点.若90ABD ∠=︒,且ABF的面积为C 的方程为()A .22y x =B .24y x =C .28y x =D .216y =【答案】B【解析】∵以F 为圆心,FA 为半径的圆交l 于B ,D 两点,90ABD ∠=︒,结合抛物线的定义可得:AB AF BF==ABF ∴是等边三角形,30FBD ∴∠=︒.ABF2=4BF ∴=.又点F 到准线的距离为sin 302BF p ︒==,则该抛物线的方程为24y x =.故选:B .9.(2022·全国·高二课时练习)如图,过抛物线()220y px p =>的焦点F 的直线交抛物线于点,A B ,交其准线l 于点C ,若2BC BF =,且3AF =,则此抛物线的方程为()A .29y x =B .26y x =C .23y x =D .212y x=【答案】C【解析】作AD l ⊥,BE l ⊥,垂足分别为,D E ,设l 与x 轴交于点G ,由抛物线定义知:BE BF =,3AD AF ==,设BF a =,则BE a =,2BC a =,1sin 22a BCE a ∴∠==,则6BCE π∠=,26AC AD ∴==,又33AC AF BF BC a =++=+,1a \=,1BE ∴=,23BE BC FGCF==,32FG ∴=,即32p =,∴抛物线方程为:23y x =.故选:C.10.(2022·全国·高二课时练习)已知抛物线y 2=2px (p >0)经过点M (x 0,),若点M 到准线l 的距离为3,则该抛物线的方程为()A .y 2=4xB .y 2=2x 或y 2=4xC .y 2=8xD .y 2=4x 或y 2=8x【答案】D【解析】∵抛物线y 2=2px (p >0)经过点M (x 0,),∴202px =,可得04x p=.又点M 到准线l 的距离为3,∴432pp +=,解得p =2或p =4.则该抛物线的方程为y 2=4x 或y 2=8x .故选:D.11.(2022·全国·高二课时练习)苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑(如图1所示),“门”的内侧曲线呈抛物线形.图2是“东方之门”的示意图,已知30m CD =,60m AB =,点D 到直线AB 的距离为150m ,则此抛物线顶端O 到AB 的距离为()A .180mB .200mC .220mD .240m【答案】B【解析】以O 为坐标原点,建立如图所示的平面直角坐标系,设抛物线的方程为()220x py p =->,由题意设()15,D h ,0h <,()30,150B h -,则()22152302150php h ⎧=-⎪⎨=--⎪⎩,解得502.25h p =-⎧⎨=⎩,所以此抛物线顶端O 到AB 的距离为()50150200m +=.故选:B .考点二:抛物线的轨迹方程12.(2022·全国·高二课时练习)点()1,0A ,点B 是x 轴上的动点,线段PB 的中点E 在y 轴上,且AE 垂直PB ,则点P 的轨迹方程为______.【答案】24y x =()0x ≠【解析】设(),P x y ,(),0B m ,则,22x m y E +⎛⎫⎪⎝⎭.由点E 在y 轴上,得02x m +=,则m x =-,即0,2y E ⎛⎫⎪⎝⎭.又AE PB ⊥,若0x ≠,则21012AE PB yy k k x⋅=⨯=--,即24y x =.若0x =,则0m =,此时点P ,B 重合,直线PB 不存在.所以点P 的轨迹方程是24y x =()0x ≠.故答案为:24y x =()0x ≠.13.(2022·全国·高二课时练习)若动点(,)M x y 满足()()225123412x y x y -+-=-+,则点M 的轨迹是()A .圆B .椭圆C .双曲线D .抛物线【答案】D【解析】由题意,动点(,)M x y 满足()()225123412x y x y -+-=-+,()()223412125x y x y -+-+-=,即动点(,)M x y 到定点(1,2)的距离等于动点(,)M x y 到定直线34120x y -+=的距离,又由点(1,2)不在直线34120x y -+=上,根据抛物线的定义,可得动点M 的轨迹为以(1,2)为焦点,以34120x y -+=的抛物线.故选:D.14.(2022·江西·赣州市赣县第三中学高二开学考试(理))已知动圆⊙M 经过定点(1,0)A ,且和直线1x =-相切,则点M 的轨迹方程为()A .22y x=B .24y x=C .22y x=-D .24y x=-【答案】B【解析】因为动圆⊙M 经过定点(1,0)A ,且和直线1x =-相切,所以点M 到点(1,0)A 的距离等于它到直线1x =-的距离,即M 的轨迹为以点(1,0)A 为焦点,直线1x =-为准线的抛物线,所以12p=,解得2p =,轨迹方程为24y x =.故选:B .15.(2022·全国·高二课时练习)若动圆M 经过双曲线2213y x -=的左焦点且与直线x =2相切,则圆心M 的坐标满足的方程是______.【答案】28y x=-【解析】双曲线2213y x -=的左焦点为F (-2,0),动圆M 经过F 且与直线x =2相切,则圆心M 到点F 的距离和到直线x =2的距离相等,由抛物线的定义知圆心的轨迹是焦点为F ,准线为x =2的抛物线,其方程为28y x =-.故答案为:28y x =-.16.(2022·全国·高二课时练习)若点(),P x y 满足方程3412x y =++,则点P 的轨迹是______.【答案】抛物线【解析】由|3412|x y =++|3412|5x y ++=,等式左边表示点(),x y 和点()1,2的距离,等式的右边表示点(),x y 到直线34120x y ++=的距离.整个等式表示的意义是点(),x y 到点()1,2的距离和到直线34120x y ++=的距离相等,其轨迹为抛物线.故答案为:抛物线17.(2022·全国·高二课时练习)与点()0,3F -和直线30y -=的距离相等的点的轨迹方程是______.【答案】212x y=-【解析】由抛物线的定义可得平面内与点()0,3F -和直线30y -=的距离相等的点的轨迹为抛物线,且()0,3F -为焦点,直线3y =为准线,设抛物线的方程为22(0)x py p =->,可知32p=,解得6p =,所以该抛物线方程是212x y =-,故答案为:212x y=-18.(2022·河北唐山·高二期中(理))已知动点(,)P x y 满足341x y =+-,则点P 的轨迹为()A .直线B .抛物线C .双曲线D .椭圆【答案】B【解析】把341x y =+-3415x y +-,3415x y +-可看做(,)x y 与(1,2)的距离等于(,)x y 到直线3410x y +-=的距离,由于点(1,2)不在直线3410x y +-=上,满足抛物线的定义,则点P 的轨迹为抛物线,故选:B19.(2022·全国·高二课时练习)平面上动点M 到定点()3,0F 的距离比M 到直线l :10x +=的距离大2,求动点M 满足的方程.【解析】因为动点M 到定点()3,0F 的距离比M 到直线l :10x +=的距离大2,所以动点M 到定点()3,0F 的距离与M 到直线l :30x +=的距离相等,所以M 的轨迹是以()3,0F 为焦点,直线l :3x =-为准线的抛物线,此时6p =,故所求的点M 满足的方程是212y x =.20.(2022·全国·高二课时练习)已知点M 与点(4,0)F 的距离比它到直线:60l x +=的距离小2,求点M 的轨迹方程.【解析】由题意知动点M 到(4,0)的距离比它到直线:6l x =-的距离小2,即动点M 到(4,0)的距离与它到直线4x =-的距离相等,由抛物线定义可知动点M 的轨迹为以(4,0)为焦点的抛物线,则点M 的轨迹方程为216y x =.21.(2022·全国·高二课时练习)已知圆A :(x +2)2+y 2=1与定直线l :x =1,且动圆P 和圆A 外切并与直线l 相切,求动圆的圆心P 的轨迹方程.【解析】由题意知:点P 到圆心A (-2,0)的距离和到定直线x =2的距离相等,所以点P 的轨迹为抛物线,且焦点为A ,准线为x =2,故点P 的轨迹方程为y 2=-8x .22.(2022·全国·高二课时练习)已知点()1,0A ,直线:1l x =-,两个动圆均过A 且与l 相切,若圆心分别为1C 、2C ,则1C 的轨迹方程为___________;若动点M 满足22122C M C C C A =+,则M 的轨迹方程为___________.【答案】24y x =221y x =-【解析】由抛物线的定义得动圆的圆心轨迹是以()1,0A 为焦点,直线l :1x =-为准线的抛物线,所以1C 的轨迹方程为24y x =,设()1,C a b ,()2,C m n ,(),M x y ,因为动点M 满足22122C M C C C A =+,所以()()()2,,1,x m y n a m b n m n --=--+--,即21x a =+,2y b =,所以21a x =-,2b y =,因为24b a =,所以()()22421y x =-,所以221y x =-,即M 的轨迹方程为221y x =-.故答案为:24y x =;221y x =-.考点三:与抛物线有关的距离和最值问题23.(2022·全国·高二课时练习)已知点()2,0P ,点Q 在曲线2:2C y x =上.(1)若点Q 在第一象限内,且2PQ =,求点Q 的坐标;(2)求PQ 的最小值.【解析】(1)设()(),0,0Q x y x y >>,则22y x =,由已知条件得2PQ ==,将22y x =代入上式,并变形得,220,x x -=解得x=0(舍去)或x =2.当x =2时,2y =±,只有x =2,y =2满足条件,所以()2,2Q ;(2)PQ ,其中22y x =,所以()()()22222224130PQ x x x x x x =-+=-+=-+≥,所以当x =1时,min PQ =24.(2022·全国·高二课时练习)若M 是抛物线22y x =上一动点,点103,3P ⎛⎫⎪⎝⎭,设d 是点M 到准线的距离,要使d MP +最小,求点M 的坐标.【解析】由题意,可知抛物线的焦点1(,0)2F ,由抛物线的定义有||||d MP MF MP PF +=+≥,所以d MP +最小值为||PF ,此时点M 为直线PF 与抛物线的交点,而直线PF 的方程求得为:4233y x =-,所以有242332y x y x ⎧=-⎪⎨⎪=⎩,解得4143x y =⎧⎪⎨=⎪⎩或1413x y ⎧=⎪⎪⎨⎪=-⎪⎩(舍),所以14(4,)3M 25.(2022·全国·高二课时练习)已知抛物线22y x =的焦点是F ,点P 是抛物线上的动点,若()3,2A ,则PA PF +的最小值为______,此时点P 的坐标为______.【答案】72【解析】易知点A 在抛物线内部,设抛物线的准线为l ,则l 的方程为12x =-,过点P 作PQ l ⊥于点Q ,则PA PF PA PQ +=+,当PA l ⊥,即A ,P ,Q 三点共线时,PA PF +最小,最小值为17322+=,此时点P 的纵坐标为2,代入22y x =,得2x =,所以此时点P 的坐标为()2,2.故答案为:72;()2,2.26.(2022·全国·高二课时练习)设P 是抛物线24y x =上的一个动点,点F 是焦点.(1)求点P 到点()1,1A -的距离与点P 到直线1x =-的距离之和的最小值;(2)若()3,2B ,求PB PF +的最小值.【解析】(1)抛物线24y x =的焦点为()1,0F ,准线是1x =-.由抛物线的定义,知点P 到直线1x =-的距离等于点P 到焦点F 的距离,所以问题转化为求抛物线上一点P 到点()1,1A -的距离与其到点()1,0F 的距离之和的最小值,如图,当A ,P ,F 共线时上述距离之和最小,连接AF 交抛物线于点P ,此时所求的最小值为||AF =(2)由题意()3,2B ,可知2243<⨯,故点B 在抛物线内部(焦点所在一侧),如图,作BQ 垂直准线于点Q ,交抛物线于点1P ,连接1PF ,此时11PQ PF =,当点P 与点1P 重合时,PB PF +的值最小,此时3(1)4PB PF BQ +==--=,即PB PF +的最小值为4.27.(多选题)(2022·全国·高二单元测试)已知F 是抛物线24y x =的焦点,P 是抛物线24y x =上一动点,Q 是()()22:411C x y -+-=上一动点,则下列说法正确的有()A .PF 的最小值为1B .QFC .PF PQ +的最小值为4D .PF PQ +1+【答案】AC【解析】抛物线焦点为()1,0F ,准线为1x =-,作出图象,对选项A :由抛物线的性质可知:PF 的最小值为1OF =,选项A 正确;对选项B :注意到F 是定点,由圆的性质可知:QF 的最小值为1CF r -=,选项B 错误;对选项CD :过点P 作抛物线准线的垂线,垂足为M ,由抛物线定义可知PF PM =,故PF PQ PM PQ +=+,PM PQ +的最小值为点Q 到准线1x =-的距离,故最小值为4,从而选项C 正确,选项D 错误.故选:AC.28.(2022·河南·襄城县实验高级中学高二阶段练习(文))已知P 为抛物线()2:20C y px p =>上的动点,C 的准线l 与x 轴的交点为A ,当点P 的横坐标为1时,2PF =,则PF PA的取值范围是()A .⎤⎥⎣⎦B .⎤⎥⎣⎦C .⎣⎦D .22⎡⎢⎣⎦【答案】B【解析】因为抛物线C 的方程为()22 0y px p =>,所以其准线方程为2p x =-.因为当点P 的横坐标为1时,2PF =,所以122p+=,所以 2p =,故拋物线C 的方程为24y x =.设直线PA 的倾斜角为θ,PP l '⊥垂足为P ',()1,0A -,由抛物线的性质可得PP PF '=,所以cos PF PP PAPAθ'==,所以当直线PA 与抛物线C 相切时,cos θ最小.设直线PA 的方程为1x my =-,联立方程组214x my y x=-⎧⎨=⎩,得2440y my -+=,由216160m ∆=-=,得1m =±,2tan 1,cos 2θθ==,所以cos 12θ≤≤,故PF PA ⎤∈⎥⎣⎦.故选:B29.(2022·四川·阆中中学高二阶段练习(理))已知抛物线21:8C y x =的焦点为F ,P 为C 上的动点,直线PF 与C 的另一交点为Q ,P 关于点(4,12)N 的对称点为M .当PQ QM +的值最小时,直线PQ 的方程为________.【答案】20x y -+=【解析】设A 为PQ 的中点,连接NA ,设抛物线C 的准线为l ,作QD l ⊥,AG l ⊥,PE l ⊥,垂足分别为D ,G ,E .则2MQ NA =,2PQ PF QF PE QD AG =+=+=,()2PQ QM AG NA ∴+=+,又点N 到直线l 的距离为13,13AG NA ∴+≥,当G ,N ,A 三点共线且A 在G ,N 之间时,13AN AG NG +==,此时,点A 的横坐标为4A x =.PQ ∵过点()0,2F ,故设PQ 方程为2y kx =+,代入218y x =,得28160x kx --=()11,P x y ,()22,Q x y ,则128x x k +=.当G ,N ,A 三点共线时,12288A x x x k +===,解得1k =,直线AM 的方程为2y x =+,此时()4,6A 点A 在G ,N 之间,13AN AG NG +==成立.所以当PQ QM +的值最小时,直线PQ 的方程为20x y -+=故答案为:20x y -+=30.(2022·天津一中高二期中)已知抛物线C :22y px =的准线为1x =-,若M 为C 上的一个动点,设点N 的坐标为()3,0,则MN 的最小值为___________.【答案】【解析】由题意知,2p =,∴抛物线C :24y x =.设()()000,0M x y x ≥,由题意知2004y x =,则()()()2222200000334188x y x x MN x =-+=-+=-+≥,当01x =时,2MN 取得最小值8,∴MN 的最小值为.故答案为:31.(2022·河南·濮阳一高高二期中(文))抛物线y 2=4x 的焦点为F ,点A (2,1),M 为抛物线上一点,且M 不在直线AF 上,则△MAF 周长的最小值为____.【答案】3【解析】如图所示,过M 作MN 垂直于抛物线的准线l ,垂足为N .易知F (1,0),因为△MAF 的周长为|AF |+|MF |+|AM |,|AF ||MF |+|AM |=|AM |+|MN |,所以当A 、M 、N 三点共线时,△MAF 的周长最小,最小值为2+13=.故答案为:332.(2022·上海市长征中学高二期中)抛物线2y x =,其上一点P 到A (3,-1)与到焦点距离之和为最小,则P 点坐标为________【答案】(1,1)-【解析】因为点(3,1)A -在抛物线内部,如图所示,设抛物线的准线为l ,过抛物线上一点P ,作PQ l ⊥于Q ,过A 作AB l ⊥于B .||||||||||PA PF PA PQ AB +=+≥,故当且仅当,,P A B 共线时,||||PA PF +的值最小.此时点P 坐标为0(,1)P x -,代入2y x =,得01x =.故点P 的坐标为(1,1)-.故答案为:(1,1)-33.(2022·河南·高二期中(文))如图所示,已知P 为抛物线()2:20C y px p =>上的一个动点,点()1,1Q ,F 为抛物线C 的焦点,若PF PQ +的最小值为3,则抛物线C 的标准方程为______.【答案】28y x=【解析】过点P 、Q 分别作准线的垂线,垂直分别为M 、N ,由抛物线定义可知PF PQ PM PQ NQ +=+≥,当P ,M ,Q 三点共线时等号成立所以132pNQ =+=,解得4p =所以抛物线C 的标准方程为28y x =.故答案为:28y x=34.(2022·上海·华东师范大学附属东昌中学高二期中)已知点()6,0A ,点P 在抛物线216y x=上运动,点B 在曲线()2241x y -+=上运动,则2PAPB的最小值是___________.【答案】6【解析】抛物线216y x =的焦点为(4,0)F ,设P 点坐标(,)x y ,则||4PF x =+22222||(6)(6)16436PA x y x x x x =-+=-+=++,由题意当||||15PB PF x =+=+时,225436P P x B x Ax +=++,令5x t +=,则5x t =-,222(5)4(5)36466141PAt t t PB t t t tt -++=+=+--=-,由基本不等式知41t t+≥t =时等号成立故2PA PB的最小值为6.故答案为:635.(多选题)(2022·福建泉州·高二期中)在平面直角坐标系xOy 中,(3,2)M -,F 为抛物线2:2(0)C x py p =->的焦点,点P 在C 上,PA x ⊥轴于A ,则()A .当2p =时,||||PF PM +的最小值为3B .当4p =时,||||PF PM +的最小值为4C .当4p =时,||||PA PM -的最大值为1D .当PF x ∥轴时,cos OPF ∠为定值【答案】BCD【解析】对于A :2p =时抛物线2:4C x y =-,焦点()0,1F -,点(3,2)M -在抛物线外,所以||||PF PM FM +≥当且仅当M 、P 、F 三点共线且P 在MF 之间时取等号(如下图所示),故A 错误;对于B 、C :当4p =时抛物线2:8C x y =-,焦点()0,2F -,准线方程为2y =,点(3,2)M -在抛物线内,设PA 与准线交于点N ,则||||PF PN =,所以()||||||||224PF PM PN PM MN +=+≥=--=,当且仅当M 、P 、N 三点共线且P 在MN 之间时取等号(如下图所示),故B 正确;||||||2||||||2||21PA PM PN PM PF PM FM -=--=--≤-=,当且仅当M 、P 、F 三点共线且F 在MP 之间时取等号(如下图所示),故C 正确;对于D :抛物线2:2C x py =-,焦点0,2p F ⎛⎫- ⎪⎝⎭,准线方程为2p y =,当//PF x ,此时2P p y =-,则222p x p ⎛⎫=-⨯- ⎪⎝⎭,解得p x p =±,即,2p P p ⎛⎫-- ⎪⎝⎭或,2p P p ⎛⎫- ⎪⎝⎭,如图取,2p P p ⎛⎫-- ⎪⎝⎭,则PF p =,()2252p OP p ⎛⎫=-+- ⎪⎝⎭,所以25cos 552PFp OPF OPp ∠==D 正确;故选:BCD36.(2022·江西赣州·高二期中(理))已知抛物线216y x =的焦点为F ,P 点在抛物线上,Q 点在圆()()22:624C x y -+-=上,则PQ PF +的最小值为()A .4B .6C .8D .10【答案】C【解析】如图,过点P 向准线作垂线,垂足为A ,则PF PA =,当CP 垂直于抛物线的准线时,CP PA +最小,此时线段CP 与圆C 的交点为Q ,因为准线方程为4x =-,()6,2C ,半径为2,所以PQ PF +的最小值为21028AQ CA =-=-=.故选:C37.(2022·新疆维吾尔自治区喀什第二中学高二期中(理))已知A ()4,2-,F 为抛物线28y x =的焦点,点M 在抛物线上移动,当MA MF +取最小值时,点M 的坐标为()A .()0,0B .(1,-C .()2,2-D .1,22⎛⎫- ⎪⎝⎭【答案】D【解析】如图所示,过M 点作准线l 的垂线,垂足为E ,由抛物线定义,知MF .ME =当M 在抛物线上移动时,ME MA +的值在变化,显然M 移动到M '时,,,A M E 三点共线,ME MA +最小,此时//AM Ox ',把2y =-代入28y x =,得12x =,所以当MA MF +取最小值时,点M 的坐标为1,22⎛⎫- ⎪⎝⎭.故选:D.38.(2022·黑龙江·哈师大附中高二期中(文))若点P 为抛物线2:2C y x =上的动点,F 为抛物线C 的焦点,则PF 的最小值为()A .1B .12C .14D .18【答案】D【解析】由22y x =,得212x y =,∴122p =,则128p =,所以焦点10,8F ⎛⎫⎪⎝⎭,由抛物线上所有点中,顶点到焦点的距离最小,得PF 的最小值为18.故选:D .39.(2022·黑龙江·大兴安岭实验中学高二期中)已知抛物线28y x =,定点A (4,2),F 为焦点,P 为抛物线上的动点,则PF PA +的最小值为()A .5B .6C .7D .8【答案】B【解析】如图,作,PQ AN 与准线2x =-垂直,垂足分别为,Q N ,则PQ PF =,6PF PA PQ PA AN +=+≥=,当且仅当,,Q P A 三点共线即P 到M 重合时等号成立.故选:B .40.(2022·四川省资阳中学高二开学考试(理))已知点P 是抛物线2:8C y x =上的动点,过点P 作圆()22:21M x y -+=的切线,切点为Q ,则PQ 的最小值为()A .1B 2C 3D .32【答案】C【解析】设点P 的坐标为(),m n ,有28n m =,由圆M 的圆心坐标为()2,0,是抛物线C 的焦点坐标,有22PM m =+≥,由圆的几何性质可得PQ QM ⊥,又由22221213PM P P M Q QM=-=-≥-=PQ 3故选:C.41.(2022·全国·高二期中)已知抛物线的方程为24y x =,焦点为F ,点A 的坐标为()3,4,若点P 在此抛物线上移动,记P 到其准线的距离为d ,则d PA +的最小值为______,此时P 的坐标为______.【答案】5355+⎝【解析】过点P 作抛物线准线的垂线,垂足为H ,连接PF ,作图如下:根据抛物线的定义,d PH PF ==,数形结合可知,当且仅当,,A P F 三点共线,且P 在,A F 之间时取得最小值;即d PA +的最小值为AF ,又()()3,4,1,0A F ,故()2231425AF =-+=此时直线AF 的方程为:()21y x =-,联立抛物线方程24y x =,可得:2310x x -+=,解得35x -=35x +=15y =即此时点P 的坐标为355+⎝.故答案为:253552⎛ ⎝.考点四:抛物线中三角形,四边形的面积问题42.(2022·河南洛阳·高二期末(理))已知点()1,0A ,点B 为直线1x =-上的动点,过B 作直线1x =-的垂线1l ,线段AB 的中垂线与1l 交于点P .(1)求点P 的轨迹C 的方程;(2)若过点()2,0E 的直线l 与曲线C 交于M ,N 两点,求MOE △与NAE 面积之和的最小值.(O 为坐标原点)【解析】(1)如图所示,由已知得点P 为线段AB 中垂线上一点,即PA PB =,即动点P 到点()1,0A 的距离与点P 到直线1x =-的距离相等,所以点P 的轨迹为抛物线,其焦点为()1,0A ,准线为直线1x =-,所以点P 的轨迹方程为24y x =,(2)如图所示:设2x ty =+,点()11,M x y ,()11N x y ,,联立直线与抛物线方程242y x x ty ⎧=⎨=+⎩,得2480y ty --=,()()2244816320t t ∆=--⨯-=+>,124y y t +=,128y y ⋅=-,1112MOE S OE y y =×=V ,21122NAE N S AE y y =×=V ,所以1212112422MOE ANE S S y y y y +=+³=V V ,当且仅当1212y y =,即12y =,24y =-时取等号,此时1224y y t +=-=,即12t =-,所以当直线直线1:22l x y =-+,时MOE ANE S S +V V 取得最小值为4.43.(2022·陕西西安·高二期末(文))已知抛物线C :()220y px p =>上的点()()4,0A m m >到其准线的距离为5.(1)求抛物线C 的方程;(2)已知O 为原点,点B 在抛物线C 上,若AOB 的面积为6,求点B 的坐标.【解析】(1)由抛物线C 的方程可得其准线方程2p x =-,依抛物线的性质得452p+=,解得2p =.∴抛物线C 的方程为24y x =.(2)将()4,A m 代入24y x =,得4m =.所以()4,4A ,直线OA 的方程为y x =,即0x y -=.设()2,2B t t ,则点B 到直线OA 的距离222t t d -=,又42OA =由题意得22142622t t -⨯=,解得1t =-或3t =.∴点B 的坐标是()1,2-或()9,6.44.(2022·新疆石河子一中高二阶段练习(理))已知抛物线()2:20C y px p =>的焦点为F ,点M 为C 上一点,点N 为x 轴上一点,若FMN 是边长为2的正三角形,则抛物线的方程为___________.【答案】22y x =或26y x=【解析】抛物线()2:20C y px p =>的焦点为,02p F ⎛⎫ ⎪⎝⎭,由抛物线的对称性,不妨设点M 为第一象限的点,因为点M 为C 上一点,点N 为x 轴上一点,FMN 是边长为2的正三角形,所以当N 在,02p F ⎛⎫ ⎪⎝⎭的右边时,点M 的坐标为2p M ⎛+ ⎝,所以2212p p ⎛⎫=+ ⎪⎝⎭,化简得2230p p +-=,解得1p =或3p =-(舍去),所以抛物线的方程为22y x =,当N 在,02p F ⎛⎫ ⎪⎝⎭的左边时,点M 的坐标为2p M ⎛- ⎝,所以2212p p ⎛⎫=- ⎪⎝⎭,化简得2230p p --=,解得1p =-或3p =,所以抛物线的方程为26y x =,综上,所求的抛物线方程为22y x =或26y x =故答案为:22y x =或26y x=45.(2022·全国·高二单元测试)抛物线()220y px p =>的焦点为F ,过抛物线上一点P 作x轴的平行线交y 轴于M 点,抛物线的准线交x 轴于点N ,四边形PMNF 为平行四边形,则点P 到x 轴的距离为___________.(用含P 的代数式表示)【解析】由題意可知,,02p F ⎛⎫⎪⎝⎭,准线方程为2p x =-,,02p N ⎛⎫- ⎪⎝⎭,不妨设(P x ,四边形PMNF 为平行四边形,||||,PM NF ∴=∴,x p =∴点P 到x .46.(2022·陕西咸阳·高二期末(理))已知双曲线2222:1(0,0)x y C a b a b -=>>的离心率54e =,且双曲线C 的两条渐近线与抛物线22(0)y px p =>的准线围成的三角形的面积为3,则p 的值为()A .1B .2C .22D .4【答案】D【解析】根据题意,2514c b e a a ⎛⎫==+= ⎪⎝⎭,可得2916b a ⎛⎫= ⎪⎝⎭,所以双曲线的渐近线方程为34y x =±,抛物线的准线方程为2p x =-,设准线与抛物线的交点分别为M ,N ,则,23,4p x y x ⎧=-⎪⎪⎨⎪=-⎪⎩,可解得3,28p p M ⎛⎫- ⎪⎝⎭,同理3,28p p N ⎛⎫-- ⎪⎝⎭,所以2133322416OMNp p Sp =⨯-⨯==,解得4p =.故选:D .47.(2022·四川师范大学附属中学高二阶段练习(理))已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线与抛物线22(0)y px p =>的准线分别交于点A 、B ,O 为坐标原点,若双曲线的离心率为2,三角形AOB 3p =()A .1B .32C .2D .3【答案】C【解析】由双曲线的离心率为2知,3ba=3y x =,又抛物线的准线方程为2p x =-,则设渐近线与准线的交点为3(,22p A --,3(,)22p B -,三角形AOB 的面积为133(322p p p⨯⨯=(0p >)解得2p =,故选:C48.(2022·湖北咸宁·高二期末)已知O 是坐标原点,F 是抛物线C :()220y px p =>的焦点,()0,4P x 是C 上一点,且4=PF ,则POF 的面积为()A .8B .6C .4D .2【答案】C【解析】由题可知0042162p x px ⎧+=⎪⎨⎪=⎩,解得024x p =⎧⎨=⎩,所以POF 的面积为12442⨯⨯=,故选:C49.(2022·黑龙江·哈师大附中高二开学考试)已知点()0,1F ,点()(),0A x y y ≥为曲线C 上的动点,过A 作x 轴的垂线,垂足为B ,满足1AF AB +=.(1)曲线C 的方程(2)若,G H 为曲线C 上异于原点的两点,且满足0FG FH ⋅=,延长,GF HF 分别交曲线C 于点,M N ,求四边形GHMN 面积的最小值.【解析】(1)1AF AB +=,∴点A 到直线1y =-的距离等于其到点()0,1F 的距离,∴点A 轨迹是以F 为焦点的抛物线,∴曲线C 方程为:24x y =.(2)由题意知:直线,GM HN 斜率都存在,不妨设直线:1GM y kx =+,()11,G x y ,()22,M x y ,由214y kx x y =+⎧⎨=⎩得:2440x kx --=,则121244x x k x x +=⎧⎨=-⎩,()241GM k ∴==+;设直线1:1HN y x k =-+,同理可得:2141HN k ⎛⎫=+ ⎪⎝⎭,∴四边形GHMN 面积()2222111811822S GM HN k k k k ⎛⎫⎛⎫=⋅=++=++ ⎪ ⎪⎝⎭⎝⎭,又2212k k +≥(当且仅当221k k =,即1k =±时取等号),()82232S ∴≥⨯+=,即四边形GHMN 面积的最小值为32.50.(2022·黑龙江·大庆实验中学高二期中(理))设点30,2F ⎛⎫⎪⎝⎭,动圆P 经过点F 且和直线32y =-相切,记动圆的圆心P 的轨迹为曲线w .(1)求曲线w 的方程;(2)过点F 作互相垂直的直线1l 、2l ,分别交曲线w 于A 、C 和B 、D 两个点,求四边形ABCD 面积的最小值.【解析】(1)由抛物线的定义知点P 的轨迹为以F 为焦点的抛物线,322p =,即3p =,∴2:6w x y =.(2)设3:2AC y kx =+,由223,069026y kx k x kx x y⎧=+≠⎪⇒--=⎨⎪=⎩.设()11,A x y ,()22,C x y ,236360k ∆=+>121269x x kx x +=⎧⎨=-⎩()261AC k ==+,∵1l 与2l 互相垂直,∴以1k -换k 得2161BD k ⎛⎫=+ ⎪⎝⎭,()22111616122ABCD S AC BD k k ⎛⎫==⨯+⨯+ ⎪⎝⎭()221182182272k k ⎛⎫=++⨯+= ⎪⎝⎭≥,当1k =±时取等号,∴四边形ABCD 面积的最小值为72.51.(2022·全国·高二期中)已知曲线C :y =22x ,D 为直线y =12-上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点:(2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE的面积.【解析】(1)证明:设1(,2D t -,11(,)A x y ,则21112y x =.又因为212y x =,所以y'x =.则切线DA 的斜率为1x ,故1111()2y x x t +=-,整理得112210tx y -+=.设22(,)B x y ,同理得222210tx y -+=.11(,)A x y ,22(,)B x y 都满足直线方程2210tx y -+=.于是直线2210tx y -+=过点,A B ,而两个不同的点确定一条直线,所以直线AB 方程为2210tx y -+=.即2(21)0tx y +-+=,当20,210x y =-+=时等式恒成立.所以直线AB 恒过定点1(0,)2.(2)由(1)得直线AB 的方程为12y tx =+.。
2022年沪科版九年级数学下册第24章圆综合测试试题(含答案及详细解析)

沪科版九年级数学下册第24章圆综合测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、点P(-3,1)关于原点对称的点的坐标是()A.(-3,1) B.(3,1) C.(3,-1) D.(-3,-1)2、如图,AB为O的直径,C为D外一点,过C作O的切线,切点为B,连接AC交O于D,38∠=︒,点E在AB右侧的半圆周上运动(不与A,B重合),则AEDC∠的大小是()A.19°B.38°C.52°D.76°3、ABC的边BC经过圆心O,AC与圆相切于点A,若20∠=︒,则CB∠的大小等于()A .50︒B .25︒C .40︒D .20︒4、随着2022年北京冬奥会日渐临近,我国冰雪运动发展进入快车道,取得了长足进步.在此之前,北京冬奥组委曾面向全球征集2022年冬奥会会徵和冬残奥会会徽设计方案,共收到设计方案4506件,以下是部分参选作品,其中既是轴对称图形又是中心对称图形的是( )A .B .C .D .5、如图,PA 是O 的切线,切点为A ,PO 的延长线交O 于点B ,若40P ∠=︒,则B 的度数为( ).A .20°B .25°C .30°D .40°6、下列叙述正确的有( )个.(1)y y =随着x 的增大而增大; (2)如果直角三角形斜边的长是斜边上的高的4倍,那么这个三角形两个锐角的度数分别是75和15;(3)斜边为BC 的直角三角形顶点A 的轨迹是以BC 中点为圆心,BC 长为直径的圆;(4)三角形三边的垂直平分线的交点到三角形三个顶点的距离相等;(5)以2211(1)22m m m m -+>、、为三边长度的三角形,不是直角三角形. A .0 B .1 C .2 D .37、如图,A ,B ,C ,D 都是O 上的点,OA BC ⊥,垂足为E ,若26OBC ∠=︒,则ADC ∠的度数为( )A .26︒B .32︒C .52︒D .64︒8、如图是一个含有3个正方形的相框,其中∠BCD =∠DEF =90°,AB =2,CD =3,EF =5,将它镶嵌在一个圆形的金属框上,使A ,G , H 三点刚好在金属框上,则该金属框的半径是( )A B C .D 9、如图,C 与AOB ∠的两边分别相切,其中OA 边与C 相切于点P .若90AOB ∠=︒,4OP =,则OC 的长为( )A .8B .C .D .10、如图,四边形ABCD 内接于O ,如果它的一个外角64DCE ︒∠=,那么BOD ∠的度数为( )A .20︒B .64︒C .116︒D .128︒第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,在Rt ABC △中,90ACB ∠=︒,D 是ABC 内的一个动点,满足222AC AD CD -=.若AB =4BC =,则BD 长的最小值为_______.2、如图,在平行四边形ABCD 中,7AB =,3AD =,120A ︒∠=,以点B 为圆心,BC 为半径的圆弧交AB 于点E ,连接DE ,则图中黑色阴影部分的面积为________.(结果保留π)3、如图,已知,在ABC 中,AB AC =,30BAC ∠=︒.将ABC 绕点A 逆时针旋转一个α角()0180α︒<<︒至ADE 位置,连接BD ,CE 交于点F .(I )求证:ABD ACE △△≌;(2)若四边形ABFE 为菱形,求α的值;(3)在(2)的条件下,若2AB =,直接写出CF 的值.4、如图,A 与x 轴交于()2,0B 、()4,0C 两点,3OA =,点P 是y 轴上的一个动点,PD 切O 于点D ,则△ABD 的面积的最大值是________;线段PD 的最小值是________.5、如图,将半径为10cm 的圆形纸片沿一条弦AB 折叠,折叠后弧AB 的中点C 与圆心O 重叠,则弦AB 的长度为________cm .三、解答题(5小题,每小题10分,共计50分)1、如图,抛物线y =-212x +32x +2与x 轴负半轴交于点A ,与y 轴交于点B . (1)求A ,B 两点的坐标;(2)如图1,点C 在y 轴右侧的抛物线上,且AC =BC ,求点C 的坐标;(3)如图2,将△ABO 绕平面内点P 顺时针旋转90°后,得到△DEF (点A ,B ,O 的对应点分别是点D ,E ,F ),D ,E 两点刚好在抛物线上.①求点F 的坐标;②直接写出点P 的坐标.2、已知,P 是直线AB 上一动点(不与A ,B 重合),以P 为直角顶点作等腰直角三角形PBD ,点E 是直线AD 与△PBD 的外接圆除点D 以外的另一个交点,直线BE 与直线PD 相交于点F .(1)如图,当点P 在线段AB 上运动时,若∠DBE =30°,PB =2,求DE 的长;(2)当点P在射线AB上运动时,试探求线段AB,PB,PF之间的数量关系,并给出证明.⊥,并经过圆心O).3、如图,已知弓形的长12AB=,弓高2CD=,(CD AB(1)请利用尺规作图的方法找到圆心O;(2)求弓形所在O的半径的长.4、下面是小明设计的“作圆的内接等腰直角三角形”的尺规作图过程.已知:⊙O.求作:⊙O的内接等腰直角三角形ABC.作法:如图,①作直径AB;②分别以点A, B为圆心,以大于12AB的长为半径作弧,两弧交于M点;③作直线MO交⊙O于点C,D;④连接AC,BC.所以△ABC就是所求的等腰直角三角形.根据小明设计的尺规作图过程,解决下面的问题:(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.证明:连接MA,MB.∵MA=MB,OA=OB,∴MO是AB的垂直平分线.∴AC= .∵AB是直径,∴∠ACB= ( ) (填写推理依据) .∴△ABC是等腰直角三角形.5、解题与遐想.如图,Rt△ABC的内切圆与斜边AB相切于点D,AD=4,BD=5.求Rt△ABC的面积.王小明:这道题算出来面积刚好是20,太凑巧了吧.刚好是4×5=20,有种白算的感觉…赵丽华:我把4和5换成m、n再算一遍,△ABC的面积总是m•n!确实非常神奇了…数学刘老师:大家想一想,既然结果如此简单到极致,不计算能不能得到呢?比如,拼图?霍佳:刘老师,我在想另一个东西,这个图能不能尺规画出来啊感觉图都定了.我怎么想不出来呢?计算验证(1)通过计算求出Rt△ABC的面积.拼图演绎(2)将Rt△ABC分割放入矩形中(左图),通过拼图能直接“看”出“20”请在图中画出拼图后的4个直角三角形甲、乙、丙、丁的位置,作必要标注并简要说明.尺规作图(3)尺规作图:如图,点D在线段AB上,以AB为斜边求作一个Rt△ABC,使它的内切圆与斜边AB 相切于点D.(保留作图的痕迹,写出必要的文字说明)-参考答案-一、单选题1、C【分析】据平面直角坐标系中任意一点P (x ,y ),关于原点的对称点是(-x ,-y ),然后直接作答即可.【详解】解:根据中心对称的性质,可知:点P (-3,1)关于原点O 中心对称的点的坐标为(3,-1). 故选:C .【点睛】本题考查关于原点对称的点坐标的关系,是需要熟记的基本问题,记忆方法可以结合平面直角坐标系的图形.2、B【分析】连接,BD 由AB 为O 的直径,求解903852,CBD ∠=︒-︒=︒ 结合CB 为O 的切线,求解905238,ABD ABC DBC ∠=∠-∠=︒-︒=︒ 再利用圆周角定理可得答案.【详解】解:连接,BD AB 为O 的直径,90,90,ADB BDC ∴∠=︒∠=︒38,C ∠=︒903852,CBD ∴∠=︒-︒=︒CB 为O 的切线,90,905238,ABC ABD ABC DBC ∴∠=︒∠=∠-∠=︒-︒=︒38,AED ABD ∴∠=∠=︒故选B【点睛】本题考查的是三角形的内角和定理,直径所对的圆周角是直角,圆周角定理,切线的性质定理,熟练运用以上知识逐一求解相关联的角的大小是解本题的关键.3、A【分析】连接OA ,根据圆周角定理求出AOC ∠,根据切线的性质得到90OAC ∠=︒,根据直角三角形的性质计算,得到答案.【详解】解:连接OA ,20B ︒∠=,240AOC B ∴∠=∠=︒, AC 与圆相切于点A ,90OAC ∴∠=︒,904050C ∴∠=︒-︒=︒,故选:A .【点睛】本题考查的是切线的性质、圆周角定理,掌握圆的切线垂直于经过切点的半径是解题的关键.4、C【分析】根据轴对称图形与中心对称图形的概念求解.【详解】A.是轴对称图形,不是中心对称图形,故此选项不合题意;B.不是轴对称图形,是中心对称图形,故此选项不符合题意;C.是轴对称图形,也是中心对称图形,故此选项合题意;D.不是轴对称图形,也不是中心对称图形,故此选项不合题意.故选:C.【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.5、B【分析】连接OA,如图,根据切线的性质得∠PAO=90°,再利用互余计算出∠AOP=50°,然后根据等腰三角形的性质和三角形外角性质计算∠B的度数.【详解】解:连接OA,如图,∵PA是⊙O的切线,∴OA ⊥AP ,∴∠PAO =90°,∵∠P =40°,∴∠AOP =50°,∵OA =OB ,∴∠B =∠OAB ,∵∠AOP =∠B +∠OAB ,∴∠B =12∠AOP=12×50°=25°.故选:B .【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.6、D【分析】根据反比例函数的性质,得当0x <或者0x >时,y 随着x 的增大而增大;根据直径所对圆周角为直角的性质,得斜边为BC 的直角三角形顶点A 的轨迹是以BC 中点为圆心,BC 长为直径的圆;根据垂直平分线的性质,得三角形三边的垂直平分线的交点到三角形三个顶点的距离相等;根据勾股定理逆定理、完全平方公式的性质计算,可判断直角三角形,即可完成求解.【详解】y =当0x <或者0x >时,y 随着x 的增大而增大,故(1)不正确; 如果直角三角形斜边的长是斜边上的高的4倍,那么这个三角形两个锐角的度数分别是75和15;,故(2)正确;∵圆的直径所对的圆周角为直角∴斜边为BC 的直角三角形顶点A 的轨迹是以BC 中点为圆心,BC 长为直径的圆,故(3)正确; 三角形三边的垂直平分线的交点到三角形三个顶点的距离相等,故(4)正确; ∵224212124m m m ⎛⎫--+= ⎪⎝⎭ ∴242422221211442m m m m m m ⎛⎫-+++++== ⎪⎝⎭∴以2211(1)22m m m m -+>、、为三边长度的三角形,是直角三角形,故(5)错误; 故选:D .【点睛】本题考查了三角形、垂直平分线、反比例函数、圆、勾股定理逆定理的知识;解题的关键是熟练掌握反比例函数、垂直平分线、圆周角、勾股定理逆定理的性质,从而完成求解.7、B【分析】连接OC .根据OA BC ⊥确定AC AB =,90OEB ∠=︒,进而计算出AOB ∠,根据圆心角的性质求出AOC ∠,最后根据圆周角的性质即可求出ADC ∠.【详解】解:如下图所示,连接OC .∵OA BC ⊥,∴AC AB =,90OEB ∠=︒.∴AOC AOB ∠=∠.∵26OBC ∠=︒.∴64AOB ∠=︒.∴64AOC ∠=︒∵ADC ∠和AOC ∠分别是AC 所对的圆周角和圆心角, ∴3122A ADC OC ∠=︒∠=.故选:B .【点睛】本题考查垂径定理,圆心角的性质,圆周角的性质,综合应用这些知识点是解题关键.8、A【分析】如图,记过A ,G , H 三点的圆为,Q 则Q 是HG ,AG 的垂直平分线的交点,,QH QG QA 记,PM EF 的交点为,N ,HG PM 的交点为,M 延长AB 交QM 于,P PM 为HG 的垂直平分线,结合正方形的性质可得:,AP PM 再设,PQ x 利用勾股定理建立方程,再解方程即可得到答案.【详解】 解:如图,记过A ,G , H 三点的圆为,Q 则Q 是HG ,AG 的垂直平分线的交点,,QH QG QA 记,PM EF 的交点为,N ,HG PM 的交点为,M 延长AB 交QM 于,P PM 为HG 的垂直平分线,结合正方形的性质可得:,AP PM四边形HGFE 为正方形,则,HG EF ∥,,QM HG QM EF设,PQ x 而AB =2,CD =3,EF =5,结合正方形的性质可得:5,NQ x而222,HM MQ HQ 115,5,5510,222HM HG EF MN EF MQ x x 222510,4HQ x 又222,AQ PQ AP 而51523,22AP 22215,2AQ x222522510,44x x 解得:5,2x 25225250510.4442AQ 故选A【点睛】本题考查的是正方形的性质,三角形外接圆圆心的确定,圆的基本性质,勾股定理的应用,二次根式的化简,确定过A,G,H三点的圆的圆心是解本题的关键.9、C【分析】如图所示,连接CP,由切线的性质和切线长定理得到∠CPO=90°,∠COP=45°,由此推出CP=OP=4,再根据勾股定理求解即可.【详解】解:如图所示,连接CP,∵OA,OB都是圆C的切线,∠AOB=90°,P为切点,∴∠CPO=90°,∠COP=45°,∴∠PCO=∠COP=45°,∴CP=OP=4,∴OC=,故选C.【点睛】本题主要考查了切线的性质,切线长定理,等腰直角三角形的性质与判定,勾股定理,熟知切线长定理是解题的关键.10、D【分析】由平角的性质得出∠BCD =116°,再由内接四边形对角互补得出∠A =64°,再由圆周角定理即可求得∠BOD =2∠A =128°.【详解】∵64DCE ∠=︒∴18064116BCD ∠=︒-︒=︒∵四边形ABCD 内接于O∴180********A BCD ∠=︒-∠=︒-︒=︒又∵2BOD A ∠=∠∴264128A ∠=⨯︒=︒.故选:D .【点睛】本题考查了圆内接四边形的性质、圆周角定理,圆内接四边形的对角互补,并且任何一个外角都等于它的内对角;在同圆或等圆中,一条弧所对的圆周角等于它所对的圆心角的一半.二、填空题1、2【分析】取AC 中点O ,由勾股定理的逆定理可知∠ADC =90°,则点D 在以O 为圆心,以AC 为直径的圆上,作△ADC 外接圆,连接BO ,交圆O 于1D ,则BD 长的最小值即为1BD ,由此求解即可.【详解】解:如图所示,取AC 中点O ,∵222AC AD CD -=,即222=AC AD CD +,∴∠ADC =90°,∴点D 在以O 为圆心,以AC 为直径的圆上,作△ADC 外接圆,连接BO ,交圆O 于1D ,则BD 长的最小值即为1BD ,∵AB =4BC =,∠ACB =90°,∴AC =, ∴1132OC OD AC ===,∴5OB =,∴112BD OB OD =-=,故答案为:2.【点睛】本题主要考查了一点到圆上一点的最短距离,勾股定理的逆定理,勾股定理,解题的关键在于确定点D 的运动轨迹.232π 【分析】过点C 作CH AB ⊥于点H ,根据正弦定义解得CH 的长,再由扇形面积公式、三角形的面积公式解题即可.【详解】解:过点C 作CH AB ⊥于点H ,在平行四边形ABCD 中,120A ∠=︒18012060B ∴∠=︒-︒=︒=sin sin 603CH BC B AD ∴⋅=⨯︒=平行四边形ABCD 的面积为:7AB CH ⨯= 图中黑色阴影部分的面积为:()2216016037323602360BC AE CH ππ⋅⨯⋅⋅-=⨯-=32π,32π. 【点睛】 本题考查平行四边形的性质、扇形面积等知识,是基础考点,掌握相关知识是解题关键.3、(1)见解析;(2)120°;(3)2【分析】(1)根据旋转的性质和全等三角形的判定解答即可;(2)根据等腰三角形的性质求得∠ABD =90°-12α,∠BAE =α+30°,根据菱形的邻角互补求解即可;(3)连接AF ,根据菱形的性质和全等三角形的性质可求得∠FAC =45°,∠FCA =30°,过F 作FG ⊥AC 于G ,设FG=x ,根据等腰直角三角形的性质和含30°角的直角三角形的性质求解即可.【详解】解:(1)由旋转得:AB=AD ,AC=AE ,∠BAD =∠CAE =α,∵AB=AC ,∴AB=AC =AD=AE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△ACE (SAS );(2)∵AB=AD ,∠BAD =α,∠BAC =30°,∴∠ABD =(180°-∠BAD )÷2=(180°-α)÷2=90°-12α,∠BAE =α+30°,∵四边形ABFE 是菱形,∴∠BAE +∠ABD=180°,即α+30°+90°-12α=180°,解得:α=120°;(3)连接AF ,∵四边形ABFE 是菱形,∠BAE =α+30°=150°,∴∠BAF =12∠BAE =75°,又∠BAC =30°,∴∠FAC =75°-30°=45°,∵△ABD ≌△ACE ,∴∠FCA =∠ABD =90°-12α=30°, 过F 作FG ⊥AC 于G ,设FG=x ,在Rt△AGF 中,∠FAG =45°,∠AGF=90°,∴∠AFG =∠FAG =45°,∴△AGF 是等腰直角三角形,∴AG=FG=x ,在在Rt△AGF 中,∠FCG =30°,∠FGC =90°,∴CF =2FG =2x ,CG ==,∵AC=AB=2,又AG+CG=AC ,∴2x =,解得:1x =,∴CF =2x = 2.【点睛】本题考查全等三角形的判定与性质、旋转的性质、菱形的性质、等腰三角形的判定与性质、含30°角的直角三角形的性质、三角形的内角和定理、解一元一次方程等知识,熟练掌握相关知识的联系与运用是解答的关键.4、12 【分析】根据题中点的坐标可得2BC =圆的直径,半径为1,分析ABD 以AB 定长为底,点D 在圆上,高最大为圆的半径,即可得出三角形最大的面积;连接AP ,设点()0,P y ,根据切线的性质及勾股定理可得PD【详解】解:如图所示:当点P 到如图位置时,ABD 的面积最大,∵()2,0B 、()4,0C ,∴2BC =圆的直径,半径为1,∴ABD 以AB 定长为底,点D 在圆上,高最大为圆的半径,如图所示:此时ABD 面积的最大值为:111122⨯⨯=; 如图所示:连接AP ,∵PD 切A 于点D ,∴AD PD ⊥,∴90ADP ∠=︒,设点()0,P y ,在Rt AOP 中,3OA =,OP y =,∴22229AP OA OP y =+=+,在Rt APD 中,1AD =,∴22222918PD AP AD y y =-=+-=+,则PD当0y =时,PD 取得最小值,=故答案为:①12;②【点睛】题目主要考查切线的性质及勾股定理的应用,理解题意,作出相应图形求出解析式是解题关键.5、【分析】连接OC 交AB 于点D ,再连接OA .根据轴对称的性质确定OC AB ⊥,OD =CD ;再根据垂径定理确定AD =BD ;再根据勾股定理求出AD 的长度,进而即可求出AB 的长度.【详解】解:如下图所示,连接OC 交AB 于点D ,再连接OA .∵折叠后弧AB 的中点C 与圆心O 重叠,∴OC AB ⊥,OD =CD .∴AD =BD .∵圆形纸片的半径为10cm ,∴OA =OC =10cm .∴OD =5cm .∴AD =.∴BD =.∴AB AD BD =+=.故答案为:【点睛】本题考查轴对称的性质,垂径定理,勾股定理,综合应用这些知识点是解题关键.三、解答题1、(1)A (-1,0),B (0,2);(2)点C );(3)①求点F 的坐标(1,2);②点P 的坐标(32,12) 【分析】(1)令x =0,求得y 值,得点B 的坐标;令y =0,求得x 的值,取较小的一个即求A 点的坐标;(2)设C 的坐标为(x ,-212x +32x +2),根据AC =BC ,得到22AC BC =,令t =-212x +32x ,解方程即可;(3)①根据题意,得∠BPE =90°,PB =PE 即点P 在线段BE 的垂直平分线上,根据B ,E 都在抛物线上,则B ,E 是对称点,从而确定点P 在抛物线的对称轴上,点F 在BE 上,且BE ∥x 轴,点E (3,2),确定BE =3,根据旋转性质,得EF =BO =2,从而确定点F 的坐标;②根据BE =3,∠BPE =90°,PB =PE ,确定P 到BE 的距离,即可写出点P 的坐标.【详解】(1)令x =0,得y =2,∴点B 的坐标为B (0,2);令y =0,得-212x +32x +2=0, 解得 121,4,x x =-=∵点A 在x 轴的负半轴;∴A 点的坐标(-1,0);(2)设C 的坐标为(x ,-212x +32x +2), ∵AC =BC ,A (-1,0),B (0,2),∴22AC BC =,∵A (-1,0),B (0,2), ∴2222221313(1)(2)(22)2222x x x x x x ++-++=+-++-, 即2222221313(1)(2)()2222x x x x x x ++-++=+-+, 设t =-212x +32x , ∴2222(1)(2)x t x t +++=+,∴22222144x x t t x t +++++=+,∴2450x t ++=,∴21324()5022x x x +-++=, 整理,得22850x x --=,解得12x x == ∵点C 在y 轴右侧的抛物线上,∴x =,此时y∴点C ); (3)①如图,根据题意,得∠BPE =90°,PB =PE 即点P 在线段BE 的垂直平分线上,∵B ,E 都在抛物线上,∴B ,E 是对称点,∴点P 在抛物线的对称轴上,点F 在BE 上,且BE ∥x 轴,∵抛物线的对称轴为直线x =32,B (0,2), ∴点E (3,2),BE =3,∵EF=BO=2,∴BF=1,∴点F的坐标为(1,2);②如图,设抛物线的对称轴与BE交于点M,交x轴与点N,∵BE=3,∴BM=32,∵∠BPE=90°,PB=PE,∴PM=BM=32,∴PM=BM=32,∴PN=2-32=12,∴点P的坐标为(32,12).【点睛】本题考查了抛物线与坐标轴的交点,旋转的性质,两点间的距离公式,一元二次方程的解法,换元法解方程,熟练掌握抛物线的对称性,灵活理解旋转的意义,熟练解一元二次方程是解题的关键.2、(1(2)PF=AB-PB或PF=AB+PB,理由见解析【分析】(1)根据△PBD等腰直角三角形,PB=2,求出DB的长,由⊙O是△PBD的外接圆,∠DBE=30°,可得答案;(2)根据同弧所对的圆周角,可得∠ADP=∠FBP,由△PBD等腰直角三角形,得∠DPB=∠APD=90°,DP=BP,可证△APD≌△FPB,可得答案.【详解】解:(1)由题意画以下图,连接EP ,∵△PBD 等腰直角三角形,⊙O 是△PBD 的外接圆, ∴∠DPB =∠DEB =90°,∵PB =2,∴DB ,∵∠DBE =30°,∴1122DE DB ==⨯=(2)①点P 在点A 、B 之间,由(1)的图根据同弧所对的圆周角相等,可得: ∠ADP =∠FBP ,又∵△PBD 等腰直角三角形,∴∠DPB =∠APD =90°,DP =BP ,在△APD 和△FPB 中ADP FBP DP BPDPB APD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△APD ≌△FPB∴AP =FP ,∵AP +PB =AB∴FP +PB =AB ,∴FP =AB -PB ,②点P 在点B 的右侧,如下图:∵△PBD 等腰直角三角形,∴∠DPB =∠APF =90°,DP =BP ,∵∠PBF+∠EBP =180°,∠PDA +∠EBP =180°,∴∠PBF =∠PDA ,在△APD 和△FPB 中DPB APF DP BPPBF PDA ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△APD ≌△FPB∴AP =FP ,∴AB +PB =AP ,∴AB +PB =PF ,∴PF = AB +PB .综上所述,FP =AB -PB 或PF = AB +PB .【点睛】本题考查了圆的性质,等腰直角三角形,三角形全等的判定,做题的关键是注意(2)的两种情况. 3、(1)见解析(2)10【分析】(1)作BC 的垂直平分线,与直线CD 的交点即为圆心;(2)连接OA ,根据勾股定理列出方程即可求解.(1)解:如图所示,点O 即是圆心;(2)解:连接OA ,∵CD AB ⊥,并经过圆心O ,12AB =, ∴162AD BD AB ===, ∵2CD =,∴2226(2)OA OA +-=解得,10OA =,答:半径为10.【点睛】本题考查了垂径定理和确定圆心,解题关键是熟练作图确定圆心,利用垂径定理和勾股定理求半径.4、(1)见解析;(2)BC,90°,直径所对的圆周角是直角【分析】(1)过点O任作直线交圆于AB两点,再作AB的垂直平分线OM,直线MO交⊙O于点C,D;连结AC、BC即可;(2)根据线段垂直平分线的判定与性质得出AC=BC,根据圆周角定理得出∠ACB=90°即可.【详解】(1)①作直径AB;②分别以点A, B为圆心,以大于12AB的长为半径作弧,两弧交于M点;③作直线MO交⊙O于点C,D;④连接AC,BC.所以△ABC就是所求的等腰直角三角形.(2)证明:连接MA,MB.∵MA=MB,OA=OB,∴MO是AB的垂直平分线.∴AC=BC.∵AB是直径,∴∠ACB=90°(直径所对的圆周角是直角) .∴△ABC是等腰直角三角形.故答案为:BC,90°,直径所对的圆周角是直角.【点睛】本题考查尺规作圆内接等腰直角三角形,圆周角定理,线段垂直平分线判定与性质,掌握尺规作圆内接等腰直角三角形,圆周角定理,线段垂直平分线判定与性质是解题关键.5、(1)S△ABC=20;(2)见解析;(3)见解析.【分析】(1)设⊙O的半径为r,由切线长定理得,AE=AD=4,BF=BD=5,CE=CF=r,由勾股定理得,(r+4)2+(r+5)2=92,进而求得结果;(2)根据切线长定理可证明甲和乙两个三角形全等,丙丁两个三角形全等,故将甲乙图形放在OE为边的上方,将丙丁以OP为边放在右侧,围成矩形的边长是4和5;(3)可先计算∠AFB=135°,根据“定弦对定角”作F点的轨迹,根据切线性质,过点F作AB的垂线,再根据直径所对的圆周角是90°,确定点C.【详解】解:(1)如图1,设⊙O的半径为r,连接OE,OF,∵⊙O内切于△ABC,∴OE⊥AC,OF⊥BC,AE=AD=4,BF=BD=5,∴∠OEC=∠OFC=∠C=90°,∴四边形ECFO 是矩形,∴CF =OE =r ,CE =OF =r ,∴AC =4+r ,BC =5+r ,在Rt△ABC 中,由勾股定理得,(r +4)2+(r +5)2=92,∴r 2+9r =20,∴S △ABC =12AC BC ⋅ =1(4)(5)2r r +⋅+ =21(920)2x r ++ =1(2020)2⨯+ =20;(2)如图2,(3)设△ABC 的内切圆记作⊙F ,∴AF 和BF 平分∠BAC 和∠ABC ,FD ⊥AB ,∴∠BAF=12∠CAB,∠ABF=12ABC∠,∴∠BAF+∠ABF=12(∠BAC+∠ABC)=1902⨯︒=45°,∴∠AFB=135°,可以按以下步骤作图(如图3):①以BA为直径作圆,作AB的垂直平分线交圆于点E,②以E为圆心,AE为半径作圆,③过点D作AB的垂线,交圆于F,④连接EF并延长交圆于C,连接AC,BC,则△ABC就是求作的三角形.【点睛】本题考查三角形的内切圆性质、切线长定理、勾股定理、矩形的判定与性质、尺规作图-作垂线,熟练掌握相关知识的联系与运用是解答的关键.。
专题15 抛物线中的三类直线与圆相切问题-高中数学经典二级结论解读与应用训练(解析版)

解
读
圆锥曲线中的定值问题一直是近几年来高考试题中的热点问题。解决这类问题时,要善于在动点的“变”中寻求定值或定点的“不变”性,常用特殊值法先确定定点,再转化为有目标的一般性证明,从而达到解决问题的方法。
典
例
在平面直角坐标系中,已知点 ,直线 ,动直线 垂直于 于点 ,线段 的垂直平分线交 于点 ,设 的轨迹为 .
即 由 得
∴
令 则 ∴
令 则 ,∴
点 到切线 的距离 (当且仅当 时取等号)
∴当点 的坐标为 时,满足题意的圆 的面积最小,
此时
∴ 即 与 的面积比为 .
反ቤተ መጻሕፍቲ ባይዱ
思
本题考查了抛物线的标准方程,抛物线的几何性质,以及直线和圆,直线和抛物线的位置关系的相关问题,当题设涉及直线,圆,圆锥曲线时,一般是直线与圆锥曲线相交于两点,需联立方程,得到根与系数的关系,而直线与圆经常利用圆的几何性质,得到一些常量,这些不变的量和圆锥曲线建立联系,从而进一步求解.
【答案】-2
【解析】设切点 抛物线:
因此: 直线MA:
,直线MB:
联立两直线方程得到: 即为M点
故:
又以AB为直径的圆过点M,故 即
故 ,故答案为:-2
4.已知抛物线 的焦点为 ,直线 与抛物线 相切于 点, 是 上一点(不与 重合),若以线段 为直径的圆恰好经过 ,则 的最小值是__________.
所以 , ,
,
因为
所以 ,
(2)假设存在这样的 点,并设 是过抛物线的弦,其方程为 ,
代入 得 ,
此时 , ,计算两直线的斜率之积,
所以 ,
所以 (定值),故存在这样的点 满足题意,
(完整版)《抛物线》典型例题12例(含标准答案解析)

《抛物线》典型例题12 例典型例题一例 1 指出抛物线的焦点坐标、准线方程.22(1)x24 y (2)x ay2(a 0)分析:(1)先根据抛物线方程确定抛物线是四种中哪一种,求出p,再写出焦点坐标和准线方程.(2)先把方程化为标准方程形式,再对 a 进行讨论,确定是哪一种后,求p 及焦点坐标与准线方程.解:(1)p 2 ,∴焦点坐标是(0,1),准线方程是:y 12 1 1(2)原抛物线方程为:y2 1 x, 2 p 1 a a①当 a 0时,p 1,抛物线开口向右,2 4a11∴焦点坐标是(1 ,0),准线方程是:x 1.4a 4a②当a 0 时,p 1,抛物线开口向左,2 4a11∴焦点坐标是( ,0),准线方程是:x .4a 4a2 1 1 综合上述,当a 0时,抛物线x ay2的焦点坐标为(1 ,0),准线方程是:x14a 4a 典型例题二例 2 若直线y kx 2与抛物线y28x交于A、B两点,且AB中点的横坐标为2,求此直线方程.分析:由直线与抛物线相交利用韦达定理列出k 的方程求解.另由于已知与直线斜率及弦中点坐标有关,故也可利用“作差法”求 k .故所求直线方程为: y 2x 2 .则所求直线方程为: y 2x 2 .典型例题三例 3 求证:以抛物线的焦点弦为直径的圆心与抛物线的准线相切. 分析:可设抛物线方程为 y 2 2px(p 0).如图所示,只须证明 A 2B MM 1 ,解法一:设 A(x 1, y 1) 、 B(x 2, y 2 ) ,则由:y kx 22y 28x可得:k 2x 2 (4k 8)x 4 0.∵直线与抛物线相交, k 0 且 0, 则k1.∵AB 中点横坐标为: x 1 x 2 4k 82 k 22,解得: k 2 或 k 1舍去).解法二: 设A(x 1,y 1)、B(x 2,y 2) ,则有 y 1 28x 12y28x 2 .两式作差解: ( y 1 y 2)(y 1 y 2) 8(x 1 x 2) ,即y 1 y 2 x 1x28 y 1 y 2x 1 x 2 4 y 1y 2 kx 1 2 kx 2 2 k( x 1 x 2) 4 4k 4 ,k 4k 8 4 故 k2或 k 1 (舍去).1MM 1AB ,故以 AB 为直径的圆,必与抛物线的准线相切.12说明:类似有: 以椭圆焦点弦为直径的圆与相对应的准线相离, 以双曲线焦点弦为直径的圆与相应的准线相交.典型例题四例4(1)设抛物线 y 2 4x 被直线 y 2x k 截得的弦长为 3 5,求 k 值.为 9 时,求 P 点坐标.求 P 点坐标.k 2x 1 x 2 1 k, x 1 x 242 解:( 1)由 yy4x 2x 得: 4x 2 k2(4k 4)x k 2 0AB (1 22)( x 1 x 2)2 5( x 1 x 2)2 4x 1x 2 5 (1 k)2 k 2 5(1 2k)AB 3 5, 5(1 2k) 3 5 ,即 k 4 2)S 9 ,底边长为 3 5 ,∴三角形高 h 2 9 6 535 ∵点 P 在x 轴上,∴设 P 点坐标是 (x 0,0) 则点 P 到直线 y 2x 4的距离就等于 h ,即 0 2 2 22 12655x1或 x 0 5,即所求 P 点坐标是(- 1,0)或( 5,0).典型例题五MM 111 12( AA 1 BB 1) 12(AF2)以(1)中的弦为底边,以x 轴上的点 P 为顶点作三角形,当三角形的面积 分析:(1)题可利用弦长公式求 k ,(2)题可利用面积求高,再用点到直线距离设直线与抛物线交于 A (x 1,y 1)与B (x 2,y 2) 两点.则有:BF )范文 范例 指导 参考例5 已知定直线 l 及定点 A (A 不在 l 上),n 为过A 且垂直于 l 的直线,设 N 为 l 上任一点, AN 的垂直平分线交 n 于 B ,点 B 关于 AN 的对称点为 P ,求证 P 的轨迹为抛物线.分析:要证 P 的轨迹为抛物线, 有两个途径, 一个证明 P 点的轨迹符合抛物线的 定义,二是证明 P 的轨迹方程为抛物线的方程, 可先用第一种方法,由 A 为定点, l 为定直线,为我们提供了利用定义的信息,若能证明 PA PN 且 PN l 即可. 证明: 如图所示,连结 PA 、PN 、NB .由已知条件可知: PB 垂直平分 NA ,且 B 关于 AN 的对称点为 P . ∴ AN 也垂直平分 PB .则四边形 PABN 为菱形.即有 PA PN .AB l. PN l.则 P 点符合抛物线上点的条件:到定点 A 的距离与到定直线的距离相等,所以 P 点的轨迹为抛物线.典型例题六例6 若线段 P 1P 2为抛物线 C:y 2 2px(p 0)的一条 分析: 此题证的是距离问题,如果把它们用两点间 的距离表示出来,其计算量是很大的.我们可以用 抛物线的定义,巧妙运用韦达定理,也可以用抛物线的定义与平面几何知识,把结论证明出来.证法一:F(2p ,0),若过 F 的直线即线段 P 1P 2所在直线斜率不存在时,则有 P 1F P 2F p,111 1 2P 1F P 2F p p p焦点弦, F 为 C 的焦点,求证:1 12 P 1F P 2F p若线段P1P2 所在直线斜率存在时,设为k,则此直线为:y k(x 2p)(k 0) ,且设P1(x1,y1),P2(x2,y2) .k(x p )2得:k(x p )2 k2x2p(k22)xk2p24x 1 x22p(k 22)k2x 1 x 2根据抛物线定义有:P1 F x1 2p,P2F x12p , P1P2 x1 x2 p则 1 1 P1F P2F P1F P2 F P1F P2Fx1x2(x1 2p)(x2 2 )x2 p2p4x1x1x2 2p (x1 x2)1请将①②代入并化简得:112P1F P2F p证法二:如图所示,设P1、P2 、F点在C的准线l 上的射影分别是P1 、P2 、F ,且不妨设P2P2 n m P1P1 ,又设P2 点在FF P1P1 上的射影分别是A、B点,由抛物线定义知,P2 F n, P1F m, FF p又P2 AF ∽P2 BP1 ,AF P2 F BP1 P2P1p(m n ) 2mn 112 m n p即 AB 2psin 2故原命题成立.典型例题七例 7 设抛物线方程为 y 2 2px(p 0) ,过焦点 F 的弦 AB 的倾斜角为 焦点弦长为 AB 2 2p .sin分析: 此题做法跟上题类似,也可采用韦达定理与抛物线定义解决问题. 证法一: 抛物线 y 2 2px( p 0)的焦点为 (2p ,0), 过焦点的弦 AB 所在的直线方程为: y tan ( x 2p ) 由方程组 y tan (x 2p)消去 y 得: y 2 2 px2 2 2 2 24 x 2 tan 2 4 p(tan 2 ) p 2 tan 2,求证:x 1 x2设 A(x 1, y 1),B(x 2,y 2) ,则x1x2p(tan 22)tan 22p4p(1 2cot 2 )又 y 1 y 2 tan ( x 1 x 2 )AB (1 tan 2 )( x 1 x 2)2 (1 tan 2 ) (x 1 x 2) 2 4x 1x 2 (1 tan 2 ) p 2 (1 cot 2 ) 4 p4sec 2 4p 2 cot 2 (1 cot 2 )2p 2 sin1 4 sin证法二: 如图所示,分别作 AA 1、 BB 1垂直于准线 l .由抛物线定义有:AFAA 1 AF cos p BFBB 1pBF cos典型例题八例 8 已知圆锥曲线 C 经过定点 P (3,2 3) ,它的一个焦点为 F (1,0),对应于该 焦点的准线为 x 1,过焦点 F 任意作曲线 C 的弦 AB ,若弦 AB 的长度不超过 8, 且直线 AB 与椭圆 3x 2 2y 2 2 相交于不同的两点,求 ( 1) AB 的倾斜角 的取值范围.(2)设直线 AB 与椭圆相交于 C 、 D 两点,求 CD 中点 M 的轨迹方程. 分析:由已知条件可确定出圆锥曲线 C 为抛物线, AB 为抛物线的焦点弦,设其 斜率为 k ,弦 AB 与椭圆相交于不同的两点, 可求出 k 的取值范围, 从而可得 的 取值范围,求 CD 中点 M 的轨迹方程时,可设出 M 的坐标,利用韦达定理化简即 可.于是可得出:AFp1 cosBFp1 cosABAF BFpp1 cos1 cos2p21 cos2p2sin故原命题成立.解:(1)由已知得PF 4 .故P到x 1 的距离 d 4 ,从而PF d ∴曲线C是抛物线,其方程为y24x .设直线AB的斜率为k,若k 不存在,则直线AB与3x2∴k 存在.设AB的方程为y k ( x 1)4 x 2可得:ky24 y 4k 0 k( x 1)2 y22 无交点.2 由y2y设A、B坐标分别为(x1,y1)、(x2, y2),则:y1y2y1y2 4AB12 (1 k2 )(y1y2)2 1k k2 (y1 y2)2 k4(1 k2 )4y1 y2 k2∵弦AB的长度不超过8,24(1 k 2)k28即k2由y2k(x21)得:(2k23x22 y223)x24k 2x 2(k21)∵AB与椭圆相交于不同的两点,k2由k21和k2 3可得: 1 k故1 tan 3 或 3 tan又0 ,∴所求的取值范围是:3或232) 设CD中点M ( x, y) 、C( x3, y3 )、D(x4,y4)由y2k(x21)得:(2k23)x24k2x3x22 y222(k 21) 0典型例题九例 9 定长为 3的线段 AB 的端点 A 、 B 在抛物线 y 2 x 上移动,求 AB 的中点到 y 轴的距离的最小值,并求出此时 AB 中点的坐标.分析: 线段 AB 中点到 y 轴距离的最小值,就是其横坐标的最小值.这是中点坐 标问题,因此只要研究 A 、 B 两点的横坐标之和取什么最小值即可.解:如图,设 F 是y 2 x 的焦点, A 、 B 两点到准线的垂线分别是 AC 、BD , 又M 到准线的垂线为 MN , C 、 D 和N 是垂足,则x34k 22, x 3 x 12k 232 x3 x 42k 2 2k 2 3 1 232k 2 3 k 2 322k 23 9x42(k 2 1) 2k 2 3则2 51 2k 21 2223即25yx12k 2 2k 2322 y 2 2 (x 1)2 22 y 22 ( x 1) 2化简得: 3x 2 2 y 2 3x∴所求轨迹方程为: 3x 22y 23x 0( 2 x 2) 531 3 1 设M 点的横坐标为 x ,纵坐标为 y , MN x ,则 x 42 4等式成立的条件是 AB 过点 F .2 2 21(y 1 y 2) y 1 y 2 2y 1y 2 2x 2 2,y 1 y 2 2 , y5 2 5 所以 M(54, 22) ,此时 M 到y 轴的距离的最小值为 45 .说明:本题从分析图形性质出发, 把三角形的性质应用到解析几何中, 解法较简.典型例题十例 10 过抛物线 y 2 px 的焦点 F 作倾斜角为 的直线,交抛物线于 A 、B 两点, 求 AB 的最小值.分析:本题可分 2 和 2两种情况讨论.当 2 时,先写出 AB 的表达式, 再求范围.解:(1) 若 2 ,此时 AB 2p .11 12( AC BD) 21( AFBF)12AB当x 45时, y 1y 2 P 214,故MN1AB :y tan (x 2p ),即 x ta y n说明:(2) 若 2 ,因有两交点,所以 0.代入抛物线方程,有 ta 2 3n p y tan p 2 0 .故 ( y 2 y 1 ) 2 4 p 2tan 2 4p 2 4p 2 csc( x 2 x 1) 2 ( y 2 y 1)2tan 2 22 csc4 p 2 2tan 故 AB 22 4 p csc (1 12 ) 4p 2 csc 4 tan 2所以 AB 2p 2 sin 2p .因 2 ,所以这里不能取“=” 综合(1)(2) ,当 2 时, AB 最小值 2p .(1) 此题须对 分 2 和 2两种情况进行讨论;的大小以及判定直线与圆是否相切.解:①点 A 在抛物线上,由抛物线定义,则 AA ' AF 1 2, 又 AA ' // x 轴 1 3 . ∴ 2 3,同理 4 6 , 而 2 3 6 4 180 ,∴ 3 6 90 ,∴ A 'FB ' 90 .选 C .②过AB 中点 M 作MM ' l ,垂中为 M ',∴以 AB 为直径的圆与直线 l 相切,切点为 M ' .又 F ' 在圆的外部,∴ AF 'B 90 . 特别地,当 AB x 轴时, M '与 F '重合, AF 'B 90 .即 AF 'B 90 ,选 B .典型例题十二例 12 已知点 M(3,2), F 为抛物线 y 2 2x 的焦点,点 P 在该抛物线上移动, 当 PM PF 取最小值时,点 P 的坐标为 __________ .分析: 本题若建立目标函数来求 PM PF 的最小值是困难的,若巧妙地利用抛则 MM1(AA ' BB ' ) 2 1 12( AF BF ) 1 AB 2物线定义,结合图形则问题不难解决.1 由定义知PF PE ,故PM PF PF PM ME MN 3 .取等号时,M 、P、E三点共线,∴ P点纵坐标为2,代入方程,求出其横坐标为2,所以P点坐标为(2, 2) .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:抛物线与圆综合探究题抛物线与圆综合探究题,综合性强,难度较大,通常都作为“压轴题”,解此类题通常需要熟练掌握抛物线与圆相关的基本知识和基本技能,求解时注意运用有关性质,进行综合、分析、探究解题思路。
例1抛物线2y axbx c =++交x 轴于A 、B 两点,交y 轴于点C ,已知抛物线的对称轴为1x =,(3,0)B ,(0,3)C -,⑴求二次函数2y ax bx c =++的解析式;⑵在抛物线对称轴上是否存在一点P ,使点P 到B 、C 两点距离之差最大?若存在,求出P 点坐标;若不存在,请说明理由⑶平行于x 轴的一条直线交抛物线于M N 、两点,若以MN 为直径的圆恰好与x 轴相切,求此圆的半径.解:(1)将(0,3)C -代入c bx ax y ++=2,得 3-=c .将3-=c ,(3,0)B 代入c bx ax y ++=2,得 039=++c b a (1).∵1x =是对称轴,∴12=-ab(2).将(2)代入(1)得1=a ,2-=b . 二次函数得解析式是322--=x x y .(2)AC 与对称轴的交点P 即为到B C 、的距离之差最大的点.∵C 点的坐标为(0,3)-,A 点的坐标为(1,0)-,∴ 直线AC 的解析式是33--=x y ,又对称轴为1x =,∴ 点P 的坐标(1,6)-. (3)设1(,)M x y 、2(,)N x y ,所求圆的半径为r ,则 r x x 212=- (1) ∵ 对称轴为1x =,∴ 212=+x x (2) 由(1)、(2)得:12+=r x (3)将(1,)N r y +代入解析式322--=x x y ,得 3)1(2)1(2-+-+=r r y ,.(4) 整理得:42-=r y .由于 r=±y ,当0>y 时,042=--r r ,解得,21711+=r ,21712-=r (舍去), 当0<y 时,042=-+r r ,解得,21711+-=r , 21712--=r (舍去). 所以圆的半径是2171+或2171+-. 例2、已知:在平面直角坐标系xOy 中,一次函数y=kx-4k 的图象与x 轴交于点A ,抛物线y ax bx c =++2经过O 、A 两点。
⑴试用含a 的代数式表示b ; ⑵设抛物线的顶点为D ,以D 为圆心,DA 为半径的圆被x 轴分为劣弧和优弧两部分。
若将劣弧沿x 轴翻折,翻折后的劣弧落在⊙D 内,它所在的圆恰与OD 相切,求⊙D 半径的长及抛物线的解析式;⑶设点B 是满足⑵中条件的优弧上的一个动点,抛物线在x 轴上方的部分上是否存在这样的点P ,使得∠∠POA OBA =43?若存在,求出点P 的坐标;若不存在,请说明理由。
解:(1)法一:∵一次函数y kx k =-4的图象与x 轴交于点A ,∴点A 的坐标为(4,0)∵抛物线c bx ax y++=2经过O 、A 两点04160=+=∴b a c ,a b 4-=∴ 法二:∵一次函数y kx k =-4的图象与x 轴交于点A ∴点A 的坐标为(4,0)∵抛物线y ax bx c =++2经过O 、A 两点 ∴抛物线的对称轴为直线x =2∴=-=x ba22 (2)由抛物线的对称性可知,DO =DA ∴点O 在⊙D 上,且∠DOA =∠DAO 又由(1)知抛物线的解析式为yax ax =-24,∴点D 的坐标为(24,-a )① 当a>0时, 如图1,设⊙D 被x 轴分得的劣弧为OmA⌒,它沿x 轴翻折后所得劣弧为OnA ⌒,显然OnA ⌒所在的圆与⊙D 关于x 轴对称,设它的圆心为D',∴点D'与点D 也关于x 轴对称,∵点O 在⊙D'上,且OD 与⊙D'相切,∴点O 为切点,∴D'O ⊥OD ,∴∠DOA =∠D'OA =45°,∴△ADO 为等腰直角三角形 ∴=OD 22∴点D 的纵坐标为-2 242124-=-==∴-=-∴a b a a , ∴抛物线的解析式为x x y 2212-=②当a<0时,同理可得:22=OD ,抛物线的解析式为x x y 2212+-=综上,⊙D 半径的长为22,抛物线的解析式为y x x =-1222或x x y 2212+-= (3)抛物线在x 轴上方的部分上存在点P ,使得OBA POA∠∠34=, 设点P 的坐标为(x ,y ),且y >0 ①当点P 在抛物线y x x =-1222上时(如图2),∵点B 是⊙D 的优弧上的一点,∴==︒∠∠OBA ADO 1245 ︒==∴6034OBA POA ∠∠, 过点P 作PE ⊥x 轴于点 E xy xy OEEPPOE 360tan tan =∴︒=∴=∴∠由⎪⎩⎪⎨⎧-==xx y x y 22132解得:⎩⎨⎧==⎪⎩⎪⎨⎧+=+=003463242211y x y x ,(舍去) ∴点P 的坐标为()346324++, ②当点P 在抛物线y x x =-+1222上时(如图3),同理可得,y x =3, 由⎪⎩⎪⎨⎧+-==x x y xy 22132解得:⎩⎨⎧==⎪⎩⎪⎨⎧+-=-=003463242211y x y x ,(舍去) ∴点P 的坐标为()346324+--, 综上,存在满足条件的点P ,点P 的坐标为 ()346324++,或()346324+--,例3、如图,在直角坐标系中,⊙C 过原点O ,交x 轴于点A (2,0),交y 轴于点B (0,.⑴求圆心的坐标;⑵抛物线y =ax 2+bx +c 过O 、A 两点,且顶点在正比例函数yx 的图象上,求抛物线的解析式;⑶过圆心C 作平行于x 轴的直线DE ,交⊙C 于D 、E 两点,试判断D 、E 两点是否在⑵中的抛物线上; ⑷若⑵中的抛物线上存在点P (x 0,y 0),满足∠APB 为钝角,求x 0的取值范围。
解:(1)∵⊙C 经过原点O ,∴AB 为⊙C 的直径. ∴C 为AB 的中点, 过点C 作CH 垂直x 轴于点H , 则有CH =12OBOH =12OA =1。
∴圆心C 的坐标为(1(2)∵抛物线过O 、A 两点,∴抛物线的对称轴为x =1。
∵抛物线的顶点在直线yx 上, ∴顶点坐标为(1)把这三点的坐标代入抛物线抛物线y =ax 2+bx +c ,得0420c a b c a b c ⎧⎪=⎪⎪++=⎨⎪⎪++=⎪⎩解得0a b c ⎧⎪⎪⎪⎪=⎨⎪=⎪⎪⎪⎩∴抛物线的解析式为2y x =。
(3)∵OA =2,OB =4AB ==.即⊙C 的半径r =2。
∴D (3E (-12y x x =检验,知点D 、E 均在抛物线上 (4)∵AB 为直径,∴当抛物线上的点P 在⊙C 的内部时,满足∠APB 为钝角。
∴-1<x 0<0,或2<x 0<3。
例4、如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x 轴交于A 、B 两点(点A 在点B 左侧),与y 轴交于点C 。
⑴求抛物线的解析式及点A 、B 、C 的坐标; ⑵若直线y=kx+t 经过C 、M 两点,且与x 轴交于点D ,试证明四边形CDAN 是平行四边形; ⑶点P 在抛物线的对称轴x=1上运动,请探索:在x 轴上方是否存在这样的P 点,使以P 为圆心的圆经过A 、B 两点,并且与直线CD 相切,若存在,请求出点P 的坐标;若不存在,请说明理由。
解:(1)由抛物线的顶点是M (1,4),设解析式为2y a x 1 4 a 0=(-)+(<)又抛物线经过点N (2,3),所以23a 214=(-)+ 解得a =-1,所以所求抛物线的解析式为y =22x 14x 2x 3.-(-)+=-++令y =0,得2x 2x 30-++=,解得:12x 1 x 3.=-,=得A (-1,0),B (3,0) ;令x =0,得y =3,所以 C (0,3). (2)直线y=kx+t 经过C 、M 两点,所以t 3k t 4⎧⎨⎩=+=即k =1,t =3 ,直线解析式为y =x +3.令y =0,得x =-3,故D (-3,0),CD=AN ,过N 做x 轴的垂线,垂足为F.设过A 、N 两点的直线的解析式为y =mx +n ,则m n 02m n 3⎧⎨⎩-+=+=解得m =1,n =1,所以过A 、N 两点的直线的解析式为y =x +1,所以DC ∥AN.在Rt △ANF 中,AN =3,NF =3,所以AN=DC =AN 。
因此四边形CDAN 是平行四边形.(3)假设在x 轴上方存在这样的P 点,使以P 为圆心的圆经过A 、B 两点,并且与直线CD 相切,设P (1,u ) 其中u >0,则PA 是圆的半径且222PA u 2=+过P 做直线CD 的垂线,垂足为Q ,则PQ =PA 时以P 为圆心的圆与直线CD 相切。
由第(2)小题易得:△MDE 为等腰直角三角形,故△PQM 也是等腰直角三角形,由P (1,u )得PE =u , PM =|4-u|,PQ|4-u|由22PQ PA =得方程:2224u u 22(-)=+,解得u 4±=-舍去负值u=4--, 符合题意的u=4-+,所以,满足题意的点P 存在,其坐标为(1,4-+).例5、已知:如图,抛物线m x x y +-=332312与x 轴交于A 、B 两点, 与y 轴交于C 点,∠ACB =90°,⑴求m 的值及抛物线顶点坐标;⑵过A 、B 、C 的三点的⊙M 交y 轴于另一点D ,连结DM 并延长交⊙M 于点E , 过E 点的⊙M 的切线分别交x 轴、y 轴于点F 、G ,求直线FG 的解析式; ⑶在条件⑵下,设P 为上的动点(P 不与C 、D 重合),连结PA 交y 轴于点H ,问是否存在一个常数k ,始终满足AH ²AP =k ,如果存在,请写出求解过程;如果不存在,请说明理由.解:⑴由抛物线可知,点C 的坐标为(0,m ),且m <0.设A (x 1,0),B (x 2,0).则有x 1²x 2=3m , 又OC 是Rt △ABC 的斜边上的高,∴△AOC ∽△COB ∴OB OC OC OA = ∴21x m m x -=--,即x 1²x 2=-m 2, ∴-m 2=3m ,解得 m =0或m =-3,而m <0, 故只能取m =-3,这时,4)3(3133323122--=--=x x x y 故抛物线的顶点坐标为(3,-4)⑵法一:由已知可得:M (3,0),A (-3,0),B (3 3,0),C (0,-3),D (0, 3) ∵抛物线的对称轴是x =3,也是⊙M 的对称轴,连结CE ∵DE 是⊙M 的直径,∴∠DCE =90°, ∴直线x =3垂直平分CE ,∴E 点的坐标为(2 3,-3),∵33==OD OM OC OA ,∠AOC =∠DOM =90°, ∴∠ACO =∠MDO =30°,∴AC ∥DE ∵AC ⊥CB ,∴CB ⊥DE 又FG ⊥DE ,∴FG ∥CB , 由B (33,0)、C (0,-3)两点的坐标易求直线CB 的解析式为:y =x 33-3 可设直线FG 的解析式为y =x 33+n ,把(23,-3)代入求得n =-5,故直线FG 的解析式为y =x 33-5法二:令y =0,解x x 332312--3=0得x 1=-3,x 2=33 ,即A (-3,0),B (3 3,0) 根据圆的对称性,易知::⊙M 半径为23,M (3,0)在Rt △BOC 中,∠BOC =90°,OB =33,OC =3, ∴∠CBO =30°,同理,∠ODM =30°。
