SPSS多元回归分析实例
SPSS—回归—多元线性回归结果分析

SPSS—回归—多元线性回归结果分析(二),最近一直很忙,公司的潮起潮落,就好比人生的跌岩起伏,眼看着一步步走向衰弱,却无能为力,也许要学习“步步惊心”里面“四阿哥”的座右铭:“行到水穷处”,”坐看云起时“。
接着上一期的“多元线性回归解析”里面的内容,上一次,没有写结果分析,这次补上,结果分析如下所示:结果分析1:由于开始选择的是“逐步”法,逐步法是“向前”和“向后”的结合体,从结果可以看出,最先进入“线性回归模型”的是“price in thousands"建立了模型1,紧随其后的是“Wheelbase"建立了模型2,所以,模型中有此方法有个概率值,当小于等于0.05时,进入“线性回归模型”(最先进入模型的,相关性最强,关系最为密切)当大于等0.1时,从“线性模型中”剔除结果分析:1:从“模型汇总”中可以看出,有两个模型,(模型1和模型2)从R2 拟合优度来看,模型2的拟合优度明显比模型1要好一些(0.422>0.300)2:从“Anova"表中,可以看出“模型2”中的“回归平方和”为115.311,“残差平方和”为153.072,由于总平方和=回归平方和+残差平方和,由于残差平方和(即指随即误差,不可解释的误差)由于“回归平方和”跟“残差平方和”几乎接近,所有,此线性回归模型只解释了总平方和的一半,3:根据后面的“F统计量”的概率值为0.00,由于0.00<0.01,随着“自变量”的引入,其显著性概率值均远小于0.01,所以可以显著地拒绝总体回归系数为0的原假设,通过ANOVA方差分析表可以看出“销售量”与“价格”和“轴距”之间存在着线性关系,至于线性关系的强弱,需要进一步进行分析。
结果分析:1:从“已排除的变量”表中,可以看出:“模型2”中各变量的T检的概率值都大于“0.05”所以,不能够引入“线性回归模型”必须剔除。
从“系数a” 表中可以看出:1:多元线性回归方程应该为:销售量=-1.822-0.055*价格+0.061*轴距但是,由于常数项的sig为(0.116>0.1) 所以常数项不具备显著性,所以,我们再看后面的“标准系数”,在标准系数一列中,可以看到“常数项”没有数值,已经被剔除所以:标准化的回归方程为:销售量=-0.59*价格+0.356*轴距2:再看最后一列“共线性统计量”,其中“价格”和“轴距”两个容差和“vif都一样,而且VIF 都为1.012,且都小于5,所以两个自变量之间没有出现共线性,容忍度和膨胀因子是互为倒数关系,容忍度越小,膨胀因子越大,发生共线性的可能性也越大从“共线性诊断”表中可以看出:1:共线性诊断采用的是“特征值”的方式,特征值主要用来刻画自变量的方差,诊断自变量间是否存在较强多重共线性的另一种方法是利用主成分分析法,基本思想是:如果自变量间确实存在较强的相关关系,那么它们之间必然存在信息重叠,于是就可以从这些自变量中提取出既能反应自变量信息(方差),而且有相互独立的因素(成分)来,该方法主要从自变量间的相关系数矩阵出发,计算相关系数矩阵的特征值,得到相应的若干成分。
SPSS多元线性回归分析实例操作步骤

SPSS多元线性回归分析实例操作步骤在数据分析领域,多元线性回归分析是一种强大且常用的工具,它能够帮助我们理解多个自变量与一个因变量之间的线性关系。
接下来,我将为您详细介绍使用 SPSS 进行多元线性回归分析的具体操作步骤。
首先,准备好您的数据。
数据应该以特定的格式整理,通常包括自变量和因变量的列。
确保数据的准确性和完整性,因为这将直接影响分析结果的可靠性。
打开 SPSS 软件,在菜单栏中选择“文件”,然后点击“打开”,找到您存放数据的文件并导入。
在导入数据后,点击“分析”菜单,选择“回归”,再点击“线性”。
这将打开多元线性回归的对话框。
在“线性回归”对话框中,将您的因变量拖放到“因变量”框中,将自变量拖放到“自变量”框中。
接下来,点击“统计”按钮。
在“统计”对话框中,您可以选择一些常用的统计量。
例如,勾选“估计”可以得到回归系数的估计值;勾选“置信区间”可以得到回归系数的置信区间;勾选“模型拟合度”可以评估模型的拟合效果等。
根据您的具体需求选择合适的统计量,然后点击“继续”。
再点击“图”按钮。
在这里,您可以选择生成一些有助于直观理解回归结果的图形。
比如,勾选“正态概率图”可以检查残差的正态性;勾选“残差图”可以观察残差的分布情况等。
选择完毕后点击“继续”。
然后点击“保存”按钮。
您可以选择保存预测值、残差等变量,以便后续进一步分析。
完成上述设置后,点击“确定”按钮,SPSS 将开始进行多元线性回归分析,并输出结果。
结果通常包括多个部分。
首先是模型摘要,它提供了一些关于模型拟合度的指标,如 R 方、调整 R 方等。
R 方表示自变量能够解释因变量变异的比例,越接近 1 说明模型拟合效果越好。
其次是方差分析表,用于检验整个回归模型是否显著。
如果对应的p 值小于给定的显著性水平(通常为 005),则说明模型是显著的。
最重要的是系数表,它给出了每个自变量的回归系数、标准误差、t 值和 p 值。
回归系数表示自变量对因变量的影响程度,p 值用于判断该系数是否显著不为 0。
spss多元回归分析案例

spss多元回归分析案例SPSS多元回归分析案例。
在统计学中,多元回归分析是一种用于探究多个自变量与因变量之间关系的方法。
通过多元回归分析,我们可以了解不同自变量对因变量的影响程度,以及它们之间的相互作用情况。
在本篇文档中,我将通过一个实际案例来介绍如何使用SPSS软件进行多元回归分析。
案例背景:假设我们是一家电子产品公司的市场营销团队,在推出新产品之前,我们希望了解不同因素对产品销量的影响。
我们收集了一些数据,包括产品的售价、广告投入、竞争对手的售价、季节等因素,以及产品的销量作为因变量。
数据准备:首先,我们需要将数据录入SPSS软件中。
在SPSS中,我们可以通过导入Excel文件的方式将数据导入到软件中,并进行必要的数据清洗和处理。
确保数据的准确性和完整性对于后续的多元回归分析非常重要。
模型建立:接下来,我们需要建立多元回归模型。
在SPSS中,我们可以通过依次选择“分析”-“回归”-“线性回归”来进行多元回归分析。
在“因变量”栏中输入销量,然后将所有自变量依次输入到“自变量”栏中。
在建立模型之前,我们还需要考虑是否需要进行变量转换或交互项的添加,以更好地拟合数据。
模型诊断:建立模型后,我们需要对模型进行诊断,以确保模型的准确性和有效性。
在SPSS中,我们可以通过查看残差的正态性、异方差性以及自相关性来进行模型诊断。
如果模型存在严重的偏差或违反了多元回归分析的假设,我们需要进行相应的修正或改进。
模型解释:最后,我们需要解释多元回归模型的结果。
在SPSS的输出结果中,我们可以看到各个自变量的系数、显著性水平、调整R方等统计指标。
通过这些指标,我们可以了解不同自变量对销量的影响程度,以及它们之间的相互作用情况。
同时,我们还可以进行各种假设检验,来验证模型的有效性和可靠性。
结论:通过以上多元回归分析,我们可以得出不同自变量对产品销量的影响程度,以及它们之间的相互作用情况。
这些结果对于我们制定产品的定价策略、广告投放策略以及市场营销策略都具有重要的指导意义。
基于SPSS多元线性回归分析的案例
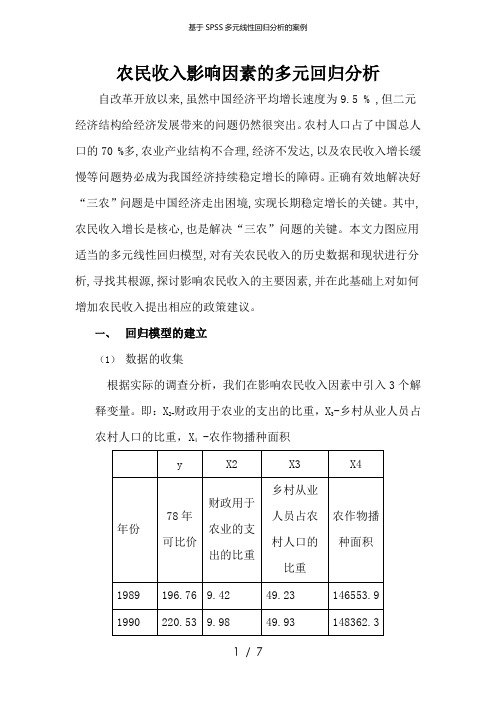
农民收入影响因素的多元回归分析自改革开放以来,虽然中国经济平均增长速度为9.5 % ,但二元经济结构给经济发展带来的问题仍然很突出。
农村人口占了中国总人口的70 %多,农业产业结构不合理,经济不发达,以及农民收入增长缓慢等问题势必成为我国经济持续稳定增长的障碍。
正确有效地解决好“三农”问题是中国经济走出困境,实现长期稳定增长的关键。
其中,农民收入增长是核心,也是解决“三农”问题的关键。
本文力图应用适当的多元线性回归模型,对有关农民收入的历史数据和现状进行分析,寻找其根源,探讨影响农民收入的主要因素,并在此基础上对如何增加农民收入提出相应的政策建议。
一、回归模型的建立(1)数据的收集根据实际的调查分析,我们在影响农民收入因素中引入3个解释变量。
即:X2-财政用于农业的支出的比重,X3-乡村从业人员占农村人口的比重,X4 -农作物播种面积1991223.2510.2650.92149585.8 1992233.1910.0551.53149007.1 1993265.679.4951.86147740.7 1994335.169.252.12148240.6 1995411.298.4352.41149879.3 1996460.688.8253.23152380.6 1997477.968.354.93153969.2 1998474.0210.6955.84155705.7 1999466.88.2357.16156372.8 2000466.167.7559.33156299.9 2001469.87.7160.62155707.9 2002468.957.1762.02154635.5 2003476.247.1263.721524152004499.399.6765.64153552.6 2005521.27.2267.59155487.7(1)回归模型的构建Y i=1+2X2+3X3+4X4+u i二、回归模型的分析(1)多重共线性检验系数a(2)模型异方差的检验异方差产生的原因有:数据质量原因、模型设定原因。
SPSS多元回归分析报告实例
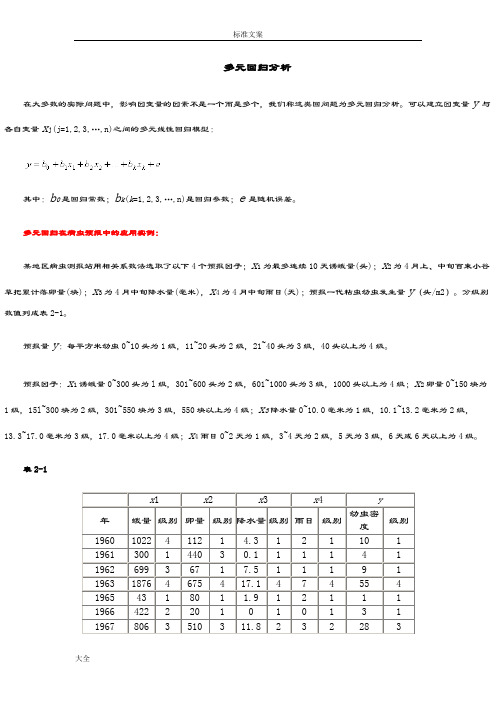
多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量x j(j=1,2,3,…,n)之间的多元线性回归模型:其中:b0是回归常数;b k(k=1,2,3,…,n)是回归参数;e是随机误差。
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1x1 x2 x3 x4 y年蛾量级别卵量级别降水量级别雨日级别幼虫密度级别1960 1022 4 112 1 4.3 1 2 1 10 1 1961 300 1 440 3 0.1 1 1 1 4 1 1962 699 3 67 1 7.5 1 1 1 9 1 1963 1876 4 675 4 17.1 4 7 4 55 4 1965 43 1 80 1 1.9 1 2 1 1 1 1966 422 2 20 1 0 1 0 1 3 1 1967 806 3 510 3 11.8 2 3 2 28 3数据保存在“DATA6-5.SAV”文件中。
1)准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据。
SPSS中多元回归分析实例解析

SPSS中多元回归分析实例解析多元回归分析是一种统计方法,用于研究一个因变量与多个自变量之间的关系。
在SPSS中,可以使用该方法来构建、估计和解释多元回归模型。
下面将以一个实例来解析SPSS中的多元回归分析。
假设我们想要研究一个教育投资项目的效果,该项目包括多个自变量,例如教育资金、教育设施、学生人数等,并且我们希望预测该项目对学生学习成绩的影响。
首先,我们需要准备好数据并导入SPSS中。
数据应包含每个教育投资项目的多个观测值,以及与之相关的自变量和因变量。
例如,可以将每个项目作为一个观测值,并将教育资金、教育设施、学生人数等作为自变量,学生学习成绩作为因变量。
在SPSS中,可以通过选择“Analyze”菜单中的“Regression”选项来打开回归分析对话框。
然后,选择“Linear”选项来进行多元回归分析。
接下来,可以将自变量和因变量添加到对话框中。
在自变量列表中,选择教育资金、教育设施、学生人数等自变量,并将它们移动到“Independent(s)”框中。
在因变量框中,选择学生学习成绩。
然后,点击“OK”按钮开始进行分析。
SPSS将输出多元回归的结果。
关键的统计指标包括回归系数、显著性水平和拟合度。
回归系数表示每个自变量对因变量的影响程度,可以根据系数的大小和正负来判断影响的方向。
显著性水平表示自变量对因变量的影响是否显著,一般以p值小于0.05为标准。
拟合度指示了回归模型对数据的拟合程度,常用的指标有R方和调整后的R方。
在多元回归分析中,可以通过检查回归系数的符号和显著性水平来判断自变量对因变量的影响。
如果回归系数为正且显著,表示该自变量对因变量有正向影响;如果回归系数为负且显著,表示该自变量对因变量有负向影响。
此外,还可以使用其他方法来进一步解释和验证回归模型,例如残差分析、模型诊断等。
需要注意的是,在进行多元回归分析时,需要满足一些前提条件,例如自变量之间应该独立、与因变量之间应该是线性关系等。
spss多元回归分析案例

spss多元回归分析案例SPSS多元回归分析是一种常用的统计方法,可以通过分析多个自变量对一个或多个因变量的影响程度,帮助研究者理解变量之间的关系以及预测变量之间的变化情况。
以下是一个关于人们消费意愿的多元回归分析的案例。
假设我们想研究人们的消费意愿受到收入水平、年龄和受教育水平的影响程度。
我们收集了100个参与者的数据,包括他们的收入、年龄、受教育水平以及消费意愿。
下面将介绍如何使用SPSS进行多元回归分析。
首先,在SPSS软件中打开数据文件,并选择"回归"菜单下的"线性回归"选项。
然后将因变量(消费意愿)拉入"因变量"框中,将自变量(收入、年龄、受教育水平)拉入"自变量"框中。
其次,点击"统计"按钮,在弹出的对话框中勾选"无多重共线性检验"、"离群值"和"样本相关矩阵"选项,并点击"确定"按钮。
接下来,点击"模型"按钮,在弹出的对话框中选择"全量"和"因素样本相关系数"选项,并点击"确定"按钮。
然后,点击"保存"按钮,在弹出的对话框中输入保存路径和文件名,并勾选"标准化残差"、"标准化预测值"和"离群值的DFITS"选项,并点击"确定"按钮。
最后,点击"OK"按钮开始进行多元回归分析。
在分析结果中,我们可以查看每个自变量的回归系数、标准误、t值以及显著性水平。
还可以查看整体模型的解释力、统计显著性和调整R 平方。
根据分析结果,我们可以得出结论:收入水平、年龄和受教育水平对消费意愿有显著影响。
收入水平对消费意愿的影响最大,其次是受教育水平,年龄对消费意愿的影响较小。
多元回归分析SPSS案例

多元回归分析SPSS案例
一、案例背景
一所大学学术部门进行了一项有关学生毕业的调查,主要是为了探讨
学生毕业的影响因素,通过这个调查,大学试图及早发现潜在的学术发展
问题,从而改善学术教育和服务质量。
调查采用SPSS软件分析,将来自
一所大学学生的有关信息作为研究目标,本研究的研究对象为大学学生。
二、研究目的
1、探索影响大学生毕业的主要因素;
2、研究各变量对大学生毕业的影响程度;
3、提出适合大学学生的毕业提升策略。
三、研究变量
本研究采用多元线性回归分析方法,研究变量有:(1)身体健康程
度(即体检结果);(2)现金流(即家庭收入);(3)家庭教育水平;(4)学习成绩;(5)家庭状况,即与家庭成员的关系;(6)个人情感
状况;(7)考试作弊。
四、研究方法
1、获取研究数据:
通过与学校协商,确定调查对象,以及采集问卷的方法(如发放问卷、网络调查等),以获取有关学生毕业的数据;
2、数据处理:
清洗数据,将数据分类进行处理,去除无关信息;
3、多元回归分析:
计算自变量与因变量之间的线性关系,分析变量间关系,建立多元回归模型;。
SPSS中多元回归分析实例解析

1965 43 1 80 1 1.9 1 2 1 1
1
1966 422 2 20 1 0 1 0 1 3
1
1967 806 3 510 3 11.8 2 3 2 28 3
1976 115 1 240 2 0.6 1 2 1 7
1
1971 718 3 1460 4 18.4 4 4 2 45 4
1972 803 3 630 4 13.4 3 3 2 26 3
某地区病虫测报站用相关系数法选取了以下 4 个预报因子;x1 为最多连续 10 天 诱蛾量(头);x2 为 4 月上、中旬百束小谷草把累计落卵量(块);x3 为 4 月中旬降 水量(毫米),x4 为 4 月中旬雨日(天);预报一代粘虫幼虫发生量 y(头/m2)。 分级别数值列成表 2-1。
预报量 y:每平方米幼虫 0~10 头为 1 级,11~20 头为 2 级,21~40 头为 3 级, 40 头以上为 4 级。
1978 255 1 65 1 0 1 0 1 11 2
数据保存在“DATA6-5.SAV”文件中。
1)准备分析数据
在 SPSS 数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼 虫密度”变量,并输入数据。再创建蛾量、卵量、降水量、雨日和幼虫密度的分 级变量“x1”、“x2”、“x3”、“x4”和“y”,它们对应的分级数值可以在 SPSS 数据编 辑窗口中通过计算产生。编辑后的数据显示如图 2-1。
本例选中“Unstandardized”非标准化预测值。
②“Distances”距离栏选项:
Mahalanobis: 距离。 Cook’s”: Cook 距离。 Leverage values: 杠杆值。
③“Prediction Intervals”预测区间选项:
SPSS--回归-多元线性回归模型案例解析

SPSS--回归-多元线性回归模型案例解析多元线性回归,主要是研究⼀个因变量与多个⾃变量之间的相关关系,跟⼀元回归原理差不多,区别在于影响因素(⾃变量)更多些⽽已,例如:⼀元线性回归⽅程为:毫⽆疑问,多元线性回归⽅程应该为:上图中的 x1, x2, xp分别代表“⾃变量”Xp截⽌,代表有P个⾃变量,如果有“N组样本,那么这个多元线性回归,将会组成⼀个矩阵,如下图所⽰:那么,多元线性回归⽅程矩阵形式为:其中:代表随机误差,其中随机误差分为:可解释的误差和不可解释的误差,随机误差必须满⾜以下四个条件,多元线性⽅程才有意义(⼀元线性⽅程也⼀样)1:服成正太分布,即指:随机误差必须是服成正太分别的随机变量。
2:⽆偏性假设,即指:期望值为03:同共⽅差性假设,即指,所有的随机误差变量⽅差都相等4:独⽴性假设,即指:所有的随机误差变量都相互独⽴,可以⽤协⽅差解释。
今天跟⼤家⼀起讨论⼀下,SPSS---多元线性回归的具体操作过程,下⾯以教程教程数据为例,分析汽车特征与汽车销售量之间的关系。
通过分析汽车特征跟汽车销售量的关系,建⽴拟合多元线性回归模型。
数据如下图所⽰:点击“分析”——回归——线性——进⼊如下图所⽰的界⾯:将“销售量”作为“因变量”拖⼊因变量框内,将“车长,车宽,耗油率,车净重等10个⾃变量拖⼊⾃变量框内,如上图所⽰,在“⽅法”旁边,选择“逐步”,当然,你也可以选择其它的⽅式,如果你选择“进⼊”默认的⽅式,在分析结果中,将会得到如下图所⽰的结果:(所有的⾃变量,都会强⾏进⼊)如果你选择“逐步”这个⽅法,将会得到如下图所⽰的结果:(将会根据预先设定的“F统计量的概率值进⾏筛选,最先进⼊回归⽅程的“⾃变量”应该是跟“因变量”关系最为密切,贡献最⼤的,如下图可以看出,车的价格和车轴跟因变量关系最为密切,符合判断条件的概率值必须⼩于0.05,当概率值⼤于等于0.1时将会被剔除)“选择变量(E)" 框内,我并没有输⼊数据,如果你需要对某个“⾃变量”进⾏条件筛选,可以将那个⾃变量,移⼊“选择变量框”内,有⼀个前提就是:该变量从未在另⼀个⽬标列表中出现!,再点击“规则”设定相应的“筛选条件”即可,如下图所⽰:点击“统计量”弹出如下所⽰的框,如下所⽰:在“回归系数”下⾯勾选“估计,在右侧勾选”模型拟合度“ 和”共线性诊断“ 两个选项,再勾选“个案诊断”再点击“离群值”⼀般默认值为“3”,(设定异常值的依据,只有当残差超过3倍标准差的观测才会被当做异常值)点击继续。
SPSS多元线性回归分析实例操作步骤

SPSS多元线性回归分析实例操作步骤在数据分析领域,多元线性回归分析是一种非常实用且强大的工具,它可以帮助我们探究多个自变量与一个因变量之间的线性关系。
下面,我将为您详细介绍使用 SPSS 进行多元线性回归分析的实例操作步骤。
首先,打开 SPSS 软件,我们需要准备好数据。
假设我们有一组关于房屋价格的数据集,其中包含房屋面积、房间数量、地理位置等自变量,以及房屋的销售价格作为因变量。
在 SPSS 中,通过“文件”菜单中的“打开”选项,找到并导入我们的数据文件。
确保数据的格式正确,并且变量的名称和类型都符合我们的预期。
接下来,选择“分析”菜单中的“回归”,然后点击“线性”选项,这就开启了多元线性回归分析的设置窗口。
在“线性回归”窗口中,将我们的因变量(房屋销售价格)放入“因变量”框中,将自变量(房屋面积、房间数量、地理位置等)放入“自变量”框中。
然后,我们可以点击“统计”按钮,在弹出的“线性回归:统计”窗口中,根据我们的需求选择合适的统计量。
通常,我们会勾选“估计”“置信区间”“模型拟合度”等选项,以获取回归系数的估计值、置信区间以及模型的拟合优度等信息。
接着,点击“图”按钮,在“线性回归:图”窗口中,我们可以选择绘制一些有助于分析的图形,比如“标准化残差图”,用于检查残差的正态性;“残差与预测值”图,用于观察残差的分布是否均匀。
再点击“保存”按钮,在这里我们可以选择保存一些额外的变量,比如预测值、残差等,以便后续的进一步分析。
设置完成后,点击“确定”按钮,SPSS 就会开始进行多元线性回归分析,并输出相应的结果。
结果中首先会给出模型的汇总信息,包括 R 方(决定系数)、调整后的 R 方等。
R 方表示模型对因变量的解释程度,越接近 1 说明模型的拟合效果越好。
调整后的 R 方则考虑了自变量的个数,对模型的拟合优度进行了更合理的修正。
接着是方差分析表,用于检验整个回归模型是否显著。
如果 F 值对应的显著性水平小于设定的阈值(通常为 005),则说明回归模型是显著的,即自变量整体上对因变量有显著的影响。
多元线性回归spss案例

多元线性回归spss案例【篇一:多元线性回归spss案例】多元线性回归,主要是研究一个因变量与多个自变量之间的相关关系,跟一元回归原理差不多,区别在于影响因素(自变量)更多些而已,例如:一元线性回归方程为:毫无疑问,多元线性回归方程应该为:上图中的x1, x2, xp分别代表自变量xp截止,代表有p个自变量,如果有 n组样本,那么这个多元线性回归,将会组成一个矩阵,如下图所示:那么,多元线性回归方程矩阵形式为:其中:代表随机误差,其中随机误差分为:可解释的误差和不可解释的误差,随机误差必须满足以下四个条件,多元线性方程才有意义(一元线性方程也一样)1:服成正太分布,即指:随机误差必须是服成正太分别的随机变量。
2:无偏性假设,即指:期望值为03:同共方差性假设,即指,所有的随机误差变量方差都相等4:独立性假设,即指:所有的随机误差变量都相互独立,可以用协方差解释。
今天跟大家一起讨论一下,spss---多元线性回归的具体操作过程,下面以教程教程数据为例,分析汽车特征与汽车销售量之间的关系。
通过分析汽车特征跟汽车销售量的关系,建立拟合多元线性回归模型。
数据如下图所示:点击分析回归线性进入如下图所示的界面:将销售量作为因变量拖入因变量框内,将车长,车宽,耗油率,车净重等10个自变量拖入自变量框内,如上图所示,在方法旁边,选择逐步,当然,你也可以选择其它的方式,如果你选择进入默认的方式,在分析结果中,将会得到如下图所示的结果:(所有的自变量,都会强行进入)如果你选择逐步这个方法,将会得到如下图所示的结果:(将会根据预先设定的 f统计量的概率值进行筛选,最先进入回归方程的自变量应该是跟因变量关系最为密切,贡献最大的,如下图可以看出,车的价格和车轴跟因变量关系最为密切,符合判断条件的概率值必须小于0.05,当概率值大于等于0.1时将会被剔除)选择变量(e) 框内,我并没有输入数据,如果你需要对某个自变量进行条件筛选,可以将那个自变量,移入选择变量框内,有一个前提就是:该变量从未在另一个目标列表中出现!,再点击规则设定相应的筛选条件即可,如下图所示:点击统计量弹出如下所示的框,如下所示:在回归系数下面勾选估计,在右侧勾选模型拟合度和共线性诊断两个选项,再勾选个案诊断再点击离群值一般默认值为 3 ,(设定异常值的依据,只有当残差超过3倍标准差的观测才会被当做异常值)点击继续。
SPSS多元回归分析实例

SPSS多元回归分析实例多元回归分析是一种多变量统计分析方法,它用于探讨自变量与因变量之间的关系。
在实际应用中,可以通过SPSS软件进行多元回归分析。
以下是一个关于房屋价格的多元回归分析实例。
假设我们想要解释一些城市房屋价格与房屋的面积、年龄和地理位置之间的关系。
首先,我们需要收集相关数据,包括房屋价格作为因变量,房屋的面积、年龄和地理位置作为自变量。
我们可以通过SPSS软件建立一个数据文件,将这些数据输入到相应的变量中。
然后,我们需要进行数据预处理,包括缺失值处理和异常值处理。
在SPSS中,可以使用"Transform"菜单中的"Recode"功能来处理缺失值和异常值。
接下来,我们可以建立一个多元回归模型,通过分析自变量与因变量之间的关系。
在SPSS中,可以使用"Analyze"菜单中的"Regression"功能来进行多元回归分析。
在多元回归分析的对话框中,我们需要选择因变量和自变量,然后点击"OK"按钮运行分析。
在本例中,我们可以选择价格作为因变量,面积、年龄和地理位置作为自变量。
SPSS将输出分析结果,包括回归系数、标准误差、显著性水平等信息。
我们可以根据这些结果来解释自变量与因变量之间的关系。
例如,回归系数表示自变量对因变量的影响程度。
正的回归系数表示自变量与因变量呈正相关关系,负的回归系数表示自变量与因变量呈负相关关系。
标准误差用于评估回归模型的准确性。
较小的标准误差表示模型的预测能力较强,较大的标准误差表示模型的预测能力较弱。
显著性水平用于判断自变量与因变量之间的关系是否显著。
通常情况下,显著性水平小于0.05时,表示自变量与因变量之间的关系是显著的。
最后,我们可以通过图表来展示多元回归分析的结果。
在SPSS中,可以使用"Graphs"菜单中的"Chart Builder"功能来绘制相关的图表,如散点图、线性回归图等。
SPSS多元回归分析实例教程
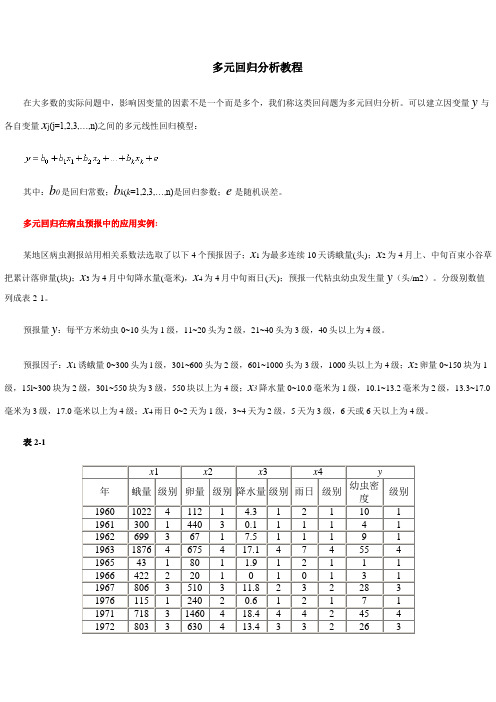
多元回归分析教程在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量x j(j=1,2,3,…,n)之间的多元线性回归模型:其中:b0是回归常数;b k(k=1,2,3,…,n)是回归参数;e是随机误差。
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1数据保存在“DATA6-5.SAV”文件中。
1)准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据。
再创建蛾量、卵量、降水量、雨日和幼虫密度的分级变量“x1”、“x2”、“x3”、“x4”和“y”,它们对应的分级数值可以在SPSS数据编辑窗口中通过计算产生。
编辑后的数据显示如图2-1。
图2-1或者打开已存在的数据文件“DATA6-5.SAV”。
2)启动线性回归过程单击SPSS主菜单的“Analyze”下的“Regression”中“Linear”项,将打开如图2-2所示的线性回归过程窗口。
SPSS多元线性回归分析实例操作步骤

SPSS多元线性回归分析实例操作步骤在数据分析的领域中,多元线性回归分析是一种强大且常用的工具,它能够帮助我们理解多个自变量与一个因变量之间的线性关系。
下面,我们将通过一个具体的实例来详细介绍 SPSS 中多元线性回归分析的操作步骤。
假设我们正在研究一个人的体重与身高、年龄和每日运动量之间的关系。
首先,打开 SPSS 软件,并将我们收集到的数据输入或导入到软件中。
数据准备阶段是至关重要的。
确保每个变量的数据格式正确,没有缺失值或异常值。
如果存在缺失值,可以根据具体情况选择合适的处理方法,比如删除包含缺失值的样本,或者使用均值、中位数等进行填充。
对于异常值,需要仔细判断其是否为真实的数据错误,如果是,则需要进行修正或删除。
接下来,点击“分析”菜单,选择“回归”,然后再选择“线性”。
在弹出的“线性回归”对话框中,将我们的因变量(体重)选入“因变量”框中,将自变量(身高、年龄、每日运动量)选入“自变量”框中。
然后,我们可以在“方法”选项中选择合适的回归方法。
SPSS 提供了几种常见的方法,如“进入”“逐步”“向后”“向前”等。
“进入”方法会将所有自变量一次性纳入模型;“逐步”方法则会根据一定的准则,逐步选择对因变量有显著影响的自变量进入模型;“向后”和“向前”方法则是基于特定的规则,逐步剔除或纳入自变量。
在这个例子中,我们先选择“进入”方法,以便直观地看到所有自变量对因变量的影响。
接下来,点击“统计”按钮。
在弹出的“线性回归:统计”对话框中,我们通常会勾选“描述性”,以获取自变量和因变量的基本统计信息,如均值、标准差等;勾选“共线性诊断”,用于检查自变量之间是否存在严重的多重共线性问题;勾选“模型拟合度”,以评估回归模型的拟合效果。
然后,点击“绘制”按钮。
在“线性回归:图”对话框中,我们可以选择绘制一些有助于分析的图形,比如“正态概率图”,用于检验残差是否服从正态分布;“残差图”,用于观察残差的分布情况,判断模型是否满足线性回归的假设。
SPSS多元回归分析实例共11页

多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量x j(j=1,2,3,…,n)之间的多元线性回归模型:其中:b0是回归常数;b k(k=1,2,3,…,n)是回归参数;e是随机误差。
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1x1 x2 x3 x4 y年蛾量级别卵量级别降水量级别雨日级别幼虫密度级别1960 1022 4 112 1 4.3 1 2 1 10 1 1961 300 1 440 3 0.1 1 1 1 4 1 1962 699 3 67 1 7.5 1 1 1 9 1 1963 1876 4 675 4 17.1 4 7 4 55 4 1965 43 1 80 1 1.9 1 2 1 1 1 1966 422 2 20 1 0 1 0 1 3 1 1967 806 3 510 3 11.8 2 3 2 28 3 1976 115 1 240 2 0.6 1 2 1 7 1 1971 718 3 1460 4 18.4 4 4 2 45 4 1972 803 3 630 4 13.4 3 3 2 26 3数据保存在“DATA6-5.SAV”文件中。
spss多元回归分析案例
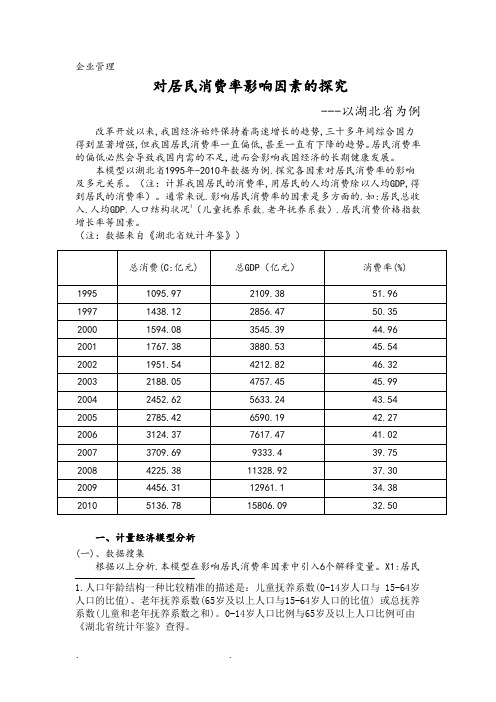
企业管理对居民消费率影响因素的探究---以湖北省为例改革开放以来,我国经济始终保持着高速增长的趋势,三十多年间综合国力得到显著增强,但我国居民消费率一直偏低,甚至一直有下降的趋势。
居民消费率的偏低必然会导致我国内需的不足,进而会影响我国经济的长期健康发展。
本模型以湖北省1995年-2010年数据为例.探究各因素对居民消费率的影响及多元关系。
(注:计算我国居民的消费率,用居民的人均消费除以人均GDP,得到居民的消费率)。
通常来说.影响居民消费率的因素是多方面的.如:居民总收入.人均GDP.人口结构状况1(儿童抚养系数.老年抚养系数).居民消费价格指数增长率等因素。
(注:数据来自《湖北省统计年鉴》)总消费(C:亿元) 总GDP(亿元)消费率(%)1995 1095.97 2109.38 51.96 1997 1438.12 2856.47 50.35 2000 1594.08 3545.39 44.96 2001 1767.38 3880.53 45.54 2002 1951.54 4212.82 46.32 2003 2188.05 4757.45 45.99 2004 2452.62 5633.24 43.54 2005 2785.42 6590.19 42.27 2006 3124.37 7617.47 41.02 2007 3709.69 9333.4 39.75 2008 4225.38 11328.92 37.30 2009 4456.31 12961.1 34.38 2010 5136.78 15806.09 32.50一、计量经济模型分析(一)、数据搜集根据以上分析.本模型在影响居民消费率因素中引入6个解释变量。
X1:居民1.人口年龄结构一种比较精准的描述是:儿童抚养系数(0-14岁人口与 15-64岁人口的比值)、老年抚养系数(65岁及以上人口与15-64岁人口的比值〉或总抚养系数(儿童和老年抚养系数之和)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t i e an dl l t 多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y 与各自变量x j (j=1,2,3,…,n)之间的多元线性回归模型:其中:b 0是回归常数;b k (k =1,2,3,…,n)是回归参数;e 是随机误差。
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x 1为最多连续10天诱蛾量(头);x 2为4月上、中旬百束小谷草把累计落卵量(块);x 3为4月中旬降水量(毫米),x 4为4月中旬雨日(天);预报一代粘虫幼虫发生量y (头/m2)。
分级别数值列成表2-1。
预报量y :每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x 1诱蛾量0~300头为l 级,301~600头为2级,601~1000头为3级,1000头以上为4级;x 2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x 3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x 4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1x 1x 2x 3x 4y 年 蛾量 级别 卵量 级别 降水量 级别 雨日 级别 幼虫密度级别1960102241121 4.31211011961300144030.111141196269936717.511191196318764675417.14745541965431801 1.9121111966422220101013119678063510311.82322831976115124020.612171197171831460418.444245419728033630413.433226319735722280213.224216219742641330342.243219219751981165271.84532331976461214017.515328319777693640444.7432444197825516510101112数据保存在“DATA6-5.SAV”文件中。
1)准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据。
再创建蛾量、卵量、降水量、雨日和幼虫密度的分级变量“x1”、“x2”、“x3”、“x4”和“y”,它们对应的分级数值可以在SPSS数据编辑窗口中通过计算产生。
编辑后的数据显示如图2-1。
图2-1或者打开已存在的数据文件“DATA6-5.SAV”。
2)启动线性回归过程单击SPSS主菜单的“Analyze”下的“Regression”中“Linear”项,将打开如图2-2所示的线性回归过程窗口。
图2-2 线性回归对话窗口3) 设置分析变量设置因变量:用鼠标选中左边变量列表中的“幼虫密度[y]”变量,然后点击“Dependent”栏左边的向右拉按钮,该变量就移到“Dependent”因变量显示栏里。
设置自变量:将左边变量列表中的“蛾量[x1]”、“卵量[x2]”、“降水量[x3]”、“雨日[x4]”变量,选移到“Independent(S)”自变量显示栏里。
设置控制变量: 本例子中不使用控制变量,所以不选择任何变量。
选择标签变量: 选择“年份”为标签变量。
选择加权变量: 本例子没有加权变量,因此不作任何设置。
4)回归方式本例子中的4个预报因子变量是经过相关系数法选取出来的,在回归分析时不做筛选。
因此在“Method”框中选中“Enter”选项,建立全回归模型。
5)设置输出统计量单击“Statistics”按钮,将打开如图2-3所示的对话框。
该对话框用于设置相关参数。
其中各项的意义分别为:图2-3 “Statistics”对话框①“Regression Coefficients”回归系数选项:“Estimates”输出回归系数和相关统计量。
“Confidence interval”回归系数的95%置信区间。
“Covariance matrix”回归系数的方差-协方差矩阵。
本例子选择“Estimates”输出回归系数和相关统计量。
②“Residuals”残差选项:“Durbin-Watson”Durbin-Watson 检验。
“Casewise diagnostic”输出满足选择条件的观测量的相关信息。
选择该项,下面两项处于可选状态:“Outliers outside standard deviations”选择标准化残差的绝对值大于输入值的观测量;“All cases”选择所有观测量。
本例子都不选。
③其它输入选项“Model fit”输出相关系数、相关系数平方、调整系数、估计标准误、ANOVA 表。
“R squared change”输出由于加入和剔除变量而引起的复相关系数平方的变化。
“Descriptives”输出变量矩阵、标准差和相关系数单侧显著性水平矩阵。
“Part and partial correlation”相关系数和偏相关系数。
“Collinearity diagnostics”显示单个变量和共线性分析的公差。
本例子选择“Model fit”项。
6)绘图选项在主对话框单击“Plots”按钮,将打开如图2-4所示的对话框窗口。
该对话框用于设置要绘制的图形的参数。
图中的“X”和“Y”框用于选择X轴和Y轴相应的变量。
左上框中各项的意义分别为:∙“DEPENDNT”因变量。
∙“ZPRED”标准化预测值。
∙“ZRESID”标准化残差。
∙“DRESID”删除残差。
∙“ADJPRED”调节预测值。
∙“SRESID”学生氏化残差。
∙“SDRESID”学生氏化删除残差。
“Standardized Residual Plots”设置各变量的标准化残差图形输出。
其中共包含两个选项:“Histogram”用直方图显示标准化残差。
“Normal probability plots”比较标准化残差与正态残差的分布示意图。
“Produce all partial plot”偏残差图。
对每一个自变量生成其残差对因变量残差的散点图。
本例子不作绘图,不选择。
7) 保存分析数据的选项所示的对话框。
在主对话框里单击“Save”按钮,将打开如图2-5①“Predicted Values”预测值栏选项:Unstandardized 非标准化预测值。
就会在当前数据文件中新添加一个以字符“PRE_”开头命名的变量,存放根据回归模型拟合的预测值。
Standardized 标准化预测值。
Adjusted 调整后预测值。
S.E. of mean predictions 预测值的标准误。
本例选中“Unstandardized”非标准化预测值。
②“Distances”距离栏选项:Mahalanobis:距离。
Cook’s”: Cook距离。
Leverage values: 杠杆值。
③“Prediction Intervals”预测区间选项:Mean:区间的中心位置。
Individual: 观测量上限和下限的预测区间。
在当前数据文件中新添加一个以字符“LICI_”开头命名的变量,存放预测区间下限值;以字符“UICI_”开头命名的变量,存放预测区间上限值。
Confidence Interval:置信度。
本例不选。
④“Save to New File”保存为新文件:选中“Coefficient statistics”项将回归系数保存到指定的文件中。
本例不选。
⑤ “Export model information to XML file”导出统计过程中的回归模型信息到指定文件。
本例不选。
⑥“Residuals” 保存残差选项:“Unstandardized”非标准化残差。
“Standardized”标准化残差。
“Studentized”学生氏化残差。
“Deleted”删除残差。
“Studentized deleted”学生氏化删除残差。
本例不选。
⑦“Influence Statistics” 统计量的影响。
“DfBeta(s)”删除一个特定的观测值所引起的回归系数的变化。
“Standardized DfBeta(s)”标准化的DfBeta 值。
“DiFit” 删除一个特定的观测值所引起的预测值的变化。
“Standardized DiFit”标准化的DiFit 值。
“Covariance ratio”删除一个观测值后的协方差矩隈的行列式和带有全部观测值的协方差矩阵的行列式的比率。
本例子不保存任何分析变量,不选择。
8)其它选项在主对话框里单击“Options”按钮,将打开如图2-6所示的对话框。
图2-6 “Options”设置对话框①“Stepping Method Criteria”框用于进行逐步回归时内部数值的设定。
其中各项为:“Use probability of F”如果一个变量的F值的概率小于所设置的进入值(Entry),那么这个变量将被选入回归方程中;当变量的F值的概率大于设置的剔除值(Removal),则该变量将从回归方程中被剔除。
由此可见,设置“Use probability of F”时,应使进入值小于剔除值。
“Ues F value”如果一个变量的F值大于所设置的进入值(Entry),那么这个变量将被选入回归方程中;当变量的F值小于设置的剔除值(Removal),则该变量将从回归方程中被剔除。
同时,设置“Use F value”时,应使进入值大于剔除值。
本例是全回归不设置。
②“Include constant in equation”选择此项表示在回归方程中有常数项。
本例选中“Include constant in equation”选项在回归方程中保留常数项。
③“Missing Values”框用于设置对缺失值的处理方法。
其中各项为:“Exclude cases listwise”剔除所有含有缺失值的观测值。
“Exchude cases pairwise”仅剔除参与统计分析计算的变量中含有缺失值的观测量。
“Replace with mean”用变量的均值取代缺失值。
本例选中“Exclude cases listwise”。
9)提交执行在主对话框里单击“OK”,提交执行,结果将显示在输出窗口中。
主要结果见表2-2至表2-4。
10) 结果分析主要结果:表2-2表2-2 是回归模型统计量:R 是相关系数;R Square 相关系数的平方,又称判定系数,判定线性回归的拟合程度:用来说明用自变量解释因变量变异的程度(所占比例);Adjusted R Square 调整后的判定系数;Std. Error of the Estimate 估计标准误差。
