【20套精选试卷合集】广东省广州铁一中学2019-2020学年高考数学模拟试卷含答案
广东省广州市2019-2020学年高考数学三模试卷含解析

广东省广州市2019-2020学年高考数学三模试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数为纯虚数(为虚数单位),则实数( ) A .-1 B .1C .0D .2【答案】B 【解析】 【分析】 化简得到,根据纯虚数概念计算得到答案.【详解】为纯虚数,故且,即.故选:. 【点睛】本题考查了根据复数类型求参数,意在考查学生的计算能力.2.已知实数,x y 满足,10,1,x y x y y ≥⎧⎪+-≤⎨⎪≥-⎩则2z x y =+的最大值为( )A .2 B.32C .1D .0【答案】B 【解析】 【分析】作出可行域,平移目标直线即可求解. 【详解】 解:作出可行域:由2z x y =+得,1122y x z =-+ 由图形知,1122y x z =-+经过点时,其截距最大,此z 时最大10y x x y =⎧⎨+-=⎩得1212x y ⎧=⎪⎪⎨⎪=⎪⎩,11,22C ⎛⎫ ⎪⎝⎭ 当1212x y ⎧=⎪⎪⎨⎪=⎪⎩时,max 1232222z =+⨯=故选:B 【点睛】考查线性规划,是基础题.3.设曲线(1)ln y a x x =--在点()1,0处的切线方程为33y x =-,则a =( ) A .1 B .2 C .3 D .4【答案】D 【解析】 【分析】利用导数的几何意义得直线的斜率,列出a 的方程即可求解 【详解】 因为1y a x'=-,且在点()1,0处的切线的斜率为3,所以13a -=,即4a =. 故选:D 【点睛】本题考查导数的几何意义,考查运算求解能力,是基础题4.已知数列{}n a 是公比为2的正项等比数列,若m a 、n a 满足21024n m n a a a <<,则()21m n -+的最小值为( ) A .3 B .5C .6D .10【答案】B 【解析】 【分析】利用等比数列的通项公式和指数幂的运算法则、指数函数的单调性求得110m n <-<再根据此范围求()21m n -+的最小值.【详解】Q 数列{}n a 是公比为2的正项等比数列,m a 、n a 满足21024n m n a a a <<,由等比数列的通项公式得11111122210242n m n a a a ---⋅<⋅<⋅,即19222n m n -+<<,10222m n -∴<<,可得110m n <-<,且m 、n 都是正整数,求()21m n -+的最小值即求在110m n <-<,且m 、n 都是正整数范围下求1m -最小值和n 的最小值,讨论m 、n 取值.∴当3m =且1n =时,()21m n -+的最小值为()23115-+=.故选:B . 【点睛】本题考查等比数列的通项公式和指数幂的运算法则、指数函数性质等基础知识,考查数学运算求解能力和分类讨论思想,是中等题.5.在ABC ∆中,,A B C ∠∠∠所对的边分别是,,a b c ,若3,4,120a b C ︒==∠=,则c =( )A .37B .13C D【答案】D 【解析】 【分析】直接根据余弦定理求解即可. 【详解】解:∵3,4,120a b C ︒==∠=,∴2222cos 9161237c a b ab C =+-=++=,∴c = 故选:D . 【点睛】本题主要考查余弦定理解三角形,属于基础题. 6.已知集合A {}0,1,2=,B={}(2)0x x x -<,则A∩B= A .{}1 B .{}0,1C .{}1,2D .{}0,1,2【答案】A 【解析】 【分析】先解A 、B 集合,再取交集。
【20套精选试卷合集】广东省重点名校2019-2020学年高考数学模拟试卷含答案

高考模拟数学试卷一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设i 为虚数单位,复数21ii -等于A .l +iB .-l -iC .l -iD .-l+i2.(理)在6的二项展开式中,x2的系数为A .427-B .227-C .227D .427(文)已知集合M={y|y=sinx, x ∈R},N={0,1,2}, 则M I N= A .{-1,0,1} B .[0,1] C .{0,1} D .{0,1,2}3.下列有关命题说法正确的是A .命题p :“∃x ∈R ,”,则⌝p 是真命题 B .“x=-1”是“x2-5x -6=0”的必要不充分条件C .命题“∃x ∈R ,使得x2 +x+1<0“的否定是:“∀x ∈R ,x2+x+1<0”D .“a>l”是“y=logax (a >0且a≠1)在(0,+∞)上为增函数”的充要条件4.设m ,n 是两条不同的直线,,αβ是两个不同的平面,给出下列条件,能得到m β⊥的是 A .αβ⊥,m α⊂ B .m ⊥α,αβ⊥ C .m ⊥n,n β⊂ D .m ∥n,n β⊥5.设函数f (x )=32sin tan 3x θθ++,其中θ∈50,12π⎡⎤⎢⎥⎣⎦,则导数f '(1)的取值范围是A .[-2,2]B. C.2⎤⎦ D.2⎤⎦ 6.甲、乙、丙三人投掷飞镖,他们的成绩(环数)如下面的频数条形统计图所示.则甲、乙、丙三人训练成绩方差222s s s 甲乙丙,,的大小关系是( )A .222s s s <<乙甲丙 B .222s s s <<甲乙丙C .222s s s <<甲乙丙 D .222s s s <<乙甲丙7.设b a <,函数)()(2b x a x y --=的图象可能是频数环数环数甲乙丙环数8.(理)己知等差数列{an}的首项为a1,公差为d ,其前n 项和为Sn ,若直线y = a1x+m 与圆(x -2)2+ y2 =1的两个交点关于直线x+y+d=0对称,则Sn= A . n2 B .-n2 C .2n -n2 D .n2-2n(文)已知圆C 的方程为012222=+-++y x y x ,当圆心C 到直线04=++y kx 的距离最大时,k 的值为A .51-B .51C .5-D .59.(理)设两个向量)cos ,2(22αλλ-+=a 和,(m b =)sin 2α+m,其中αλ,,m 为实数,若b a 2=,则m λ的取值范围是A .]1,6[-B .[4,8]C .]1,6(-D .]6,1[-(文)已知向量),1(m a =,),2(n b =,),3(t c =,且b a //,c b ⊥,则22||||c a +的最小值为A .4B .10C .16D .2010.(理)设抛物线2:2(0)C y px p =>的焦点为F ,点M 在C 上,5MF =,若以MF 为直径的圆过点)2,0(,则C 的方程为A .24y x =或28y x =B .22y x =或28y x = C .24y x =或216y x = D .22y x =或216y x = (文)已知斜率为2的直线l 过抛物线ax y =2的焦点F ,且与y 轴相交于点A ,若△OAF(O 为坐标原点)的面积为4,则抛物线方程为( )A .x y 42= B .x y 82= C .x y 42=或x y 42-= D .x y 82=或x y 82-=二、填空题(本大题共5小题,每小题5分共25分.把答案填在答题卷中的横线上.)11.(理)如果在一周内(周一至周日)安排三所学校的学生参观某展览馆,每天最多只安排一所学校,要求甲学校的学生连续参观两天,其余学校的学生均只参观一天,则不同的安排方法共有(文)如果函数)0)(6sin()(>+=ωπωx x f 的两个相邻零点之间的距离为12π,则ω的值为12.按如下程序框,最后输出i 的结果是题号 1 2 3 4 5 6 7 8 9 10 答案13已知变量y x ,满足约束条件⎪⎩⎪⎨⎧≥+-≥≤+-042042k y x y y x ,且目标函数y x z +=3的最小值为1-,则常数=k _______.14. 已知四棱柱1111D C B A ABCD -中,侧棱⊥1AA 底面ABCD ,且21=AA ,底面ABCD 的边长均大于2,且︒=∠45DAB ,点P 在底面ABCD 内运动,且在AB ,AD 上的射影分别为M ,N ,若|PA|=2,则三棱锥MN D P 1-体积的最大值为______.15.(理)(在下列两题中任选一题,若两题都做,按第①题给分)①.以平面直角坐标系的原点为极点,以x 轴的正半轴为极轴,建立极坐标系,则曲线x y ϕϕ⎧=⎪⎨=⎪⎩(ϕ为参数,R ϕ∈)上的点到曲线cos sin 4(,)R ρθρθρθ+=∈的最短距离是 ②.(不等式选做题)若存在实数x 使|||1|3x a x -+-≤成立,则实数a 的取值范围是 .. 15(文). 若存在实数x 使|||1|3x a x -+-≤成立,则实数a 的取值范围是 . 三、解答题(本大题共6小题共75分.解答应写出文字说明、证明过程或演算步骤) 16、(本题满分12分)在△ABC 中,7cos 25A =-,3cos 5B =.(1)求sinC 的值;(2)设BC =5,求△ABC 的面积.17、(本题满分12分)(理)已知数列{an}满足:a1=1,1n na +=2(n 十1)an +n (n +1),(*n N ∈),(1)若1nn a b n =+,试证明数列{bn}为等比数列;(2)求数列{an}的通项公式an 与前n 项和Sn .(文)已知数列{an}的各项均为正数,其前n 项和为Sn,且n a =1,*n N ∈,数列1b ,21b b -,32b b -……,1n n b b --是首项为1,公比为12的等比数列.(1)求证:数列{an}是等差数列; (2)若n n n c a b =,求数列{cn}的前n 项和Tn.18. (本题满分12分)(理)已知正方形ABCD 的边长为2,E F G H 、、、分别是边AB BC CD DA 、、、的中点. (1)在正方形ABCD 内部随机取一点P,求满足||PH <(2)从A B C D E F G H 、、、、、、、这八个点中,随机选取两个点,记这两个点之间的距离为ξ,求随机变量ξ的分布列与数学期望E ξ.(2)已知其余五个班学生视力的平均值分别为4.3、4.4、4.5、4.6、4.8.若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.QPABC19. (本题满分12分)(理)如图,在四棱锥ABCD P -中,⊥PC 底面ABCD , 底面ABCD 是直角梯形,AD AB ⊥,CD AB //,222===CD AD AB ,E 是PB 的中点.(1)求证:平面⊥EAC 平面PBC ;(2)若二面角E AC P --的余弦值为36,求直线PA 与平面EAC 所成角的正弦值.(文)在空间几何体PQ ABC -中,PA ⊥平面ABC , 平面QBC ⊥平面ABC ,AB AC =,QB QC =. (1)求证://PA 平面QBC ; (2)如果PQ ⊥平面QBC ,求证:Q PBC P ABCV V --=.20. (本题满分13分)(理)在平面直角坐标系xOy 中,椭圆G 的中心为坐标原点,左焦点为)0,1(1-F ,P 为椭圆G 的上顶点,且︒=∠451O PF(1)求椭圆G 的标准方程;(2)已知直线11:m kx y l +=与椭圆G 交于A 、B 两点,直线)(:2122m m m kx y l ≠+=与椭圆G 交于C 、D 两点,且CDAB =,如图所示.(i )证明:021=+m m ;(ii )求四边形ABCD 的面积S 的最大值.(文)四边形ABCD 的四个顶点都在抛物线2y x =上,A ,C 关于y 轴对称,BD 平行于抛物线在点C 处的切线.(1)证明:AC 平分BAD ∠;(2)若点A 坐标为(1,1)-,四边形ABCD 的面积为4,求直线BD 的方程.21. (本题满分14分)(理)已知)(,2121xxxx=/是函数)0()(223>-+=axabxaxxf的两个极值点.(1)若11-=x,22=x,求函数)(xf的解析式;(2)若22||||21=+xx,求实数b的最大值;(3)设函数)()()(1xxaxfxg--'=,若21xx<,且ax=2,求函数)(xg在),(21xx内的最小值.(用a表示)(文)若函数()x f 满足:在定义域内存在实数0x ,使()()()k f x f k x f +=+00(k 为常数),则称“f (x )关于k 可线性分解”.(1)函数()22x x f x +=是否关于1可线性分解?请说明理由;(2)已知函数()1ln +-=ax x x g ()0>a 关于a 可线性分解,求a 的取值范围; 参考答案一、选择题:每小题5分,共50分.二、填空题:每小题5分,共25分.11.(理)120(文)12; 12.i =7; 13.9; 14.312-;15.1;○242≤≤-a (文)42≤≤-a 三、解答题:(本大题共6小题共75分)16、解:(1)在ABC ∆中,∵7cos 25A =-,24sin 25A ∴=又∵34c o s s i n 55B B =∴=Q 12544sin cos cos sin )sin(sin =+=+=∴B A B A B A C ;(2)由正弦定理知:625sin sin ==A B BC AC311sin 21=⋅⋅=∴∆C AC BC S ABC17.(理)解:(1)121)1()1(211+=+⇒+++=++n a n a n n a n na nn n n ,)1(222111+=+=+++n an a n a n n n 得,即n n b b 21=+, 21=b 又,{}n b 所以是以2为首项,2为公比的等比数列.(2)由(1)知),12(212b -=⇒=+⇒=n n n nn n n a n a∴231(21)2(21)3(21)(21)nnS n =⨯-+⨯-+⨯-++-K 231222322(123)n n n =⨯+⨯+⨯++⋅-++++K K23(1)12223222n n n n +=⨯+⨯+⨯++⋅-K .令231222322nn T n =⨯+⨯+⨯++⋅K , 则234121222322n n T n +=⨯+⨯+⨯++⋅K ,两式相减得:23112(12)22222212n n n n n T n n ++--=++++-⋅=-⋅-K ,22)1(2)21(211+⋅-=⋅+-=++n n n n n n T .∴2)1(22)1(1+-+⋅-=+n n n S n n .(文)解(1)∵1n a =-,21(1)4n n S a ∴=+当2211112,(1)(1)44n n n n n n a S S a a --≥=-=+-+22111(22)4n n n n a a a a --=+--即11()(2)0n n n n a a a a --+--=,12n n a a -∴-= 又11a =故数列{}n a 是等差数列.且21na n =-;(2)∵12132111()()()22n n n n b b b b b b b b --=+-+-++-=-L L∴11121(21)(2)2(21)22n n n n c n n ---=--=--先求数列1212n n --⎧⎫⎨⎬⎩⎭的前n 项和n A . ∵2313572112222n n n A --=+++++K2312311135232122222212222211222222n n n n n nn n A n A ----=+++++-∴=+++++-K K211123232336262222n n n n n n n n n A A T n --+++=-∴=-∴=+-.18.(理)解:(1)所有点P 构成的平面区域是正方形ABCD 的内部,其面积是224⨯=.满足||PH <P 构成的平面区域是以H为半径的圆的内部与正方形ABCD 内部的公共部分,它可以看作是由一个以H为半径、圆心角为2π的扇形HEG 的内部(即四分之一个圆)与两个直角边为1的等腰直角三角形(△AEH 和△DGH )内部 构成.其面积是2112111422π⨯π⨯+⨯⨯⨯=+.所以满足||PH <112484π+π=+. (2)从A B C D E F G H 、、、、、、、这八个点中,任意选取两个点,共可构成28C 28=条不同的线段.其中长度为1的线段有84条,长度为2的线段有6的线段有8条,长度为的线段有2条.所以ξ所有可能的取值为12.且()821287P ξ===,(41287P ξ===, ()6322814P ξ===,(82287P ξ===,(212814P ξ===.所以随机变量ξ的分布列为:ξ122522P27 1731427114随机变量ξ的数学期望为213211225227714714E ξ=⨯++⨯++52225++=4.42 4.62 4.82 4.95.14.78⨯+⨯+⨯++=.所以任意抽取两个文科班学生视力的平均值数对有()4.34.4,,()4.34.5,,()4.34.6,,()4.34.7,,()4.34.8,,()4.44.5,,()4.44.6,,()4.44.7,,()4.44.8,,()4.54.6,,()4.54.7,,()4.54.8,,()4.64.7,,()4.64.8,,()4.74.8,,共15种情形.其中抽取的两个班学生视力的平均值之差的绝对值不小于0.2的有()4.34.5,,()4.34.6,,()4.34.7,,()4.34.8,,()4.44.6,,()4.44.7,,()4.44.8,,()4.54.7,,()4.54.8,,()4.64.8,,共10种.所以抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率为102=153 19.(理)解:(1)⊥PC Θ平面ABCD ,⊂AC 平面ABCD ,PC AC ⊥∴,2=AB Θ,1==CD AD ,2==∴BC AC222AB BC AC =+∴,BC AC ⊥∴又C PC BC =I ,⊥∴AC 平面PBC ,⊂AC Θ平面EAC ,∴平面⊥EAC 平面PBC(2)以C 为原点,建立空间直角坐标系如图所示,则C (0,0,0),A (1,1,0),B (1,-1,0).设P (0,0,a )(a>0),则E (21,21-,2a ),)0,1,1(=CA ,),0,0(a CP =,)2,21,21(aCE -=,取m u r=(1,-1,0)则0m CP m CA ⋅=⋅=u r u u u r u r u u u r ,∴m u r 为面PAC 的法向量设(,,)n x y z =r 为面EAC 的法向量,则0n CA n CE ⋅=⋅=r u u u r r u u u r ,即⎩⎨⎧=+-=+0,0az y x y x ,取a x =,a y -=,2-=z , 则(,,2)n a a =--r,依题意,26cos ,2m n m n m na ⋅<>===+u r r u r ru r r ,则2=a于是(2,2,2)n =--r设直线PA 与平面EAC 所成角为θ,则sin cos ,PA n PA n PA nθ⋅=<>==u u u r r u u u r r u u u r r ,即直线PA 与平面EAC 所成角的正弦值为32(文)解:(I )如图,取BC 中点D ,连QD ,由QB QC =得QD BC ⊥,∵平面QBC ⊥平面ABC , ∴QD ⊥平面ABC ,又∵PA ⊥平面ABC , ∴QD ∥PA , 又∵QD ⊆平面QBC , ∴PA ∥平面QBC .(2)连接AD ,则AD BC ⊥.∵平面QBC ⊥平面ABC ,面QBC ∩面ABC BC =, ∴AD ⊥平面QBC .又∵PQ QBC ⊥平面,∴PQ ∥AD . 又由(1)知,四边形APQD 是矩形, ∴PQ AD =,PA QD =.∴11()32Q PBC P QBC V V BC QD PQ--==⋅⋅⋅⋅,而11()32P ABC V BC AD PA -=⋅⋅⋅⋅,则Q PBC P ABCV V --=.20.(理)解:(1)设椭圆G 的标准方程为12222=+b y a x (a>b>0)因为)0,1(1-F ,︒=∠451O PF ,所以b=c=12222=+=∴c b a∴椭圆G 的标准方程为1222=+y x(2)设A (11,y x ),B (22,y x ),),(33y x C ,D (44,y x )(i )证明:由⎪⎩⎪⎨⎧=++=12,221y x m kx y ,消去y 得0224)21(21122=-+++m x km x k 则0)12(8212>+-=∆m k ,且⎪⎪⎩⎪⎪⎨⎧+-=+-=+2212121212122,214k m x x k km x xPA2122122212214)(1)()(x x x x k y y x x AB -++=-+-=∴2212222122122112122212242141k m k k k m k km k++-+=+-⋅-⎪⎭⎫ ⎝⎛+-+=同理222222112122k m k kCD ++-+=ΘCD AB =,∴222222212221121222112122k m k k km k k ++-+=++-+Θ21m m ≠,∴021=+m m(ii )解:由题意得四边形ABCD 是平行四边形,设两平行线AB ,CD 间的距离为d ,则2211k m m d +-=,因为021=+m m ,∴2112k m d +=∴2122122122112122k m k m k k d AB S +⋅++-+=⋅=22212122421)12(24221212221212=+++-≤++-=k m m k k m m k当且仅当212212m k =+时,四边形ABCD 的面积S 取得最大值,且最大值为22(文)(1)设A(x0,x20),B(x1,x21),C(-x0,x20),D(x2,x22). 对y =x2求导,得y '=2x ,则抛物线在点C 处的切线斜率为-2x0. 直线BD 的斜率k =x22-x21x2-x1=x1+x2,依题意,有x1+x2=-2x0.记直线AB ,AD 的斜率分别为k1,k2,与BD 的斜率求法同理,得 k1+k2=(x0+x1)+(x0+x2)=2x0+(x1+x2)=0, 所以∠CAB =∠CAD ,即AC 平分∠BAD .(2)由题设,x0=-1,x1+x2=2,k =2.四边形ABCD 的面积 S = 1 2|AC|·|x22-x21|= 1 2|AC|·|x2+x1|·|x22-x1| =12×2×2×|2-2x1|=4|1-x1|, 由已知,4|1-x1|=4,得x1=0,或x1=2. 所以点B 和D 的坐标为(0,0)和(2,4), 故直线BD 的方程为y =2x .21.(理)解:)0(23)(22>-+='a a bx ax x f .(1)因为11-=x ,22=x 是函数)(x f 的两个极值点,所以0)1(=-'f ,0)2(='f .(2分)所以0232=--a b a ,04122=-+a b a ,解得6=a ,9-=b .所以x x x x f 3696)(23--=.(4分)(2)因为)(,2121x x x x =/是函数)0()(223>-+=a x a bx ax x f 的两个极值点, 所以0)()(21='='x f x f ,所以21,x x 是方程)0(02322>=-+a a bx ax 的两根,因为32124a b +=∆,所以0>∆对一切0>a ,R b ∈恒成立,而a b x x 3221-=+,321ax x -=,又0>a ,所以021<x x ,所以||||||2121x x x x -=+=-+=212214)(x x x x a a b a a b 3494)3(4)32(222+=---, 由22||||21=+x x ,得22349422=+a a b ,所以-=6(322a b )a . 因为02≥b ,所以0)6(32≥-a a ,即60≤<a . 令)6(3)(2a a a h -=,则a a a h 369)(2+-='.当40<<a 时,0)(>'a h ,所以)(a h 在(0,4)上是增函数; 当64<<a 时,0)(<'a h ,所以)(a h 在(4,6)上是减函数.所以当4=a 时,)(a h 有极大值为96,所以)(a h 在]6,0(上的最大值是96, 所以b 的最大值是64.(3)因为21,x x 是方程0)(='x f 的两根,且)0(23)(22>-+='a a bx ax x f ,所以321a x x -=,又a x =2,311-=x ,所以))((3)(21x x x x a x f --='))(31(3a x x a -+=,所以)()()(1x x a x f x g --'=+--+=x a a x x a ())(31(3)31)(31(3)31--+=a x x a , 其对称轴为2a x =,因为0>a ,所以),31(2a a -∈,即),(221x x a ∈,所以在),(21x x 内函数)(x g 的最小值==)2()(mina g x g )312)(312(3--+a a a a 221(32)3()=2312a a a a +=-+-(文)解:(1)函数()22x x f x +=的定义域是R ,若是关于1可线性分解,则定义域内存在实数0x ,使得()()()1100f x f x f +=+.构造函数()()()()11f x f x f x h --+=()12212221----++=+x x x x ()1221-+=-x x .∵()10-=h ,()21=h 且()x h 在[]0,1上是连续的,∴()x h 在[]0,1上至少存在一个零点. 即存在[]00,1x ∈,使()()()1100f x f x f +=+.另解:函数()22x x f x +=关于1可线性分解,由()()()11f x f x f +=+,得()3212221++=+++x x x x . 即222+-=x x.作函数()xx g 2=与()22+-=x x h 的图象,由图象可以看出,存在∈0x R ,使222+-=x x ,即()()()1100f x f x f +=+)成立.(2)()x g 的定义域为()+∞,0. 由已知,存在00>x ,使()()()a g x g a x g +=+00.即()()1ln 1ln 1ln 20000+-++-=++-+a a ax x a x a a x . 整理,得()1ln ln ln 00++=+a x a x ,即())e ln(ln 00ax a x =+.∴e 00ax x a =+,所以1e 0-=a ax .由01e 0>-=a a x 且0>a ,得e 1>a . ∴a 的取值范围是⎪⎭⎫⎝⎛+∞,e1.高考模拟数学试卷一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数i ii z (1)1(2+-=为虚数单位)的虚部为( )A .1 B. -1 C. 1± D. 2.已知全集U=R ,设函数y=lg(x-1)的定义域为集合A ,函数y=22+x 的值域为集合B ,则A∩(C U B)= ( ) A .[1,2] B .[1, 2) C .(1,2]D .(1,2)3. 设βα、为两个不同的平面,m 、n 为两条不同的直线,且,m n αβ⊂⊂,有两个命题:p :若//m n ,则//αβ;q :若m β⊥,则αβ⊥;那么( )A .“p 或q ”是假命题B .“p 且q ”是真命题C .“非p 或q ” 是假命题D .“非p 且q ”是真命题 4.在应用数学归纳法证明凸n 变形的对角线为)3(21-n n 条时,第一步检验n 等于( ) A. 1 B.2 C .3 D .05.函数log (3)1(0,1)a y x a a =+->≠的图象恒过定点A ,若点A 在直线10mx ny ++= 上,其中0mn >,则12m n+的最小值为( ) A .8 B .4 C .1 D .146.已知5OA 1,OB AOB 6π==∠=u u u r u u u r ,点C 在∠AOB 外且OB OC 0.•=u u u r u u u r 设实数,m n 满足OC mOA nOB =+u u u r u u u r u u u r ,则mn等于( )A .2BC .-2D .7. 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这 个几何体的外接球的表面积为( )A .23π B.8π3 C .4 3 D.16π38.若将函数y =tan ⎝⎛⎭⎪⎫ωx+π4(ω>0)的图象向右平移π6个单位长度后,与函数y = tan ⎝⎛⎭⎪⎫ωx+π6的图象重合,则ω的最小值为( ) A.16B. 12C.13D. 14A. 0B. ln 2C. 2ln 2e -+D.1ln 2+10.能够把圆O 1622=+y x 的周长和面积同时分为相等的两部分的函数称为圆O 的 “和谐函数”,下列函数不是..圆O 的“和谐函数”的是( ) A .()xxf x e e-=+ B . 5()15x f x nx -=+ C .()tan 2x f x = D .3()4f x x x =+ 11.设二元一次不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+014y 2x 0,8y x 0,192y x 所表示的平面区域为M ,使函数y=a x(a>0, a≠1)的图象过区域M 的a 的取值范围是( ) A .[1, 3]B .[2, 10]C .[2, 9]D .[10, 9]12.给出下列四个结论: ①“22ab >”是 “22log log a b >”的充要条件;②命题“若m >0,则方程20x x m +-=有实数根”的逆否命题为:“若方程20x x m +-=没有实数根,则0≤m ”; ③函数(4)ln(2)()3x x f x x --=-只有1个零点。
广东省广州市2019-2020学年高考数学一模试卷含解析
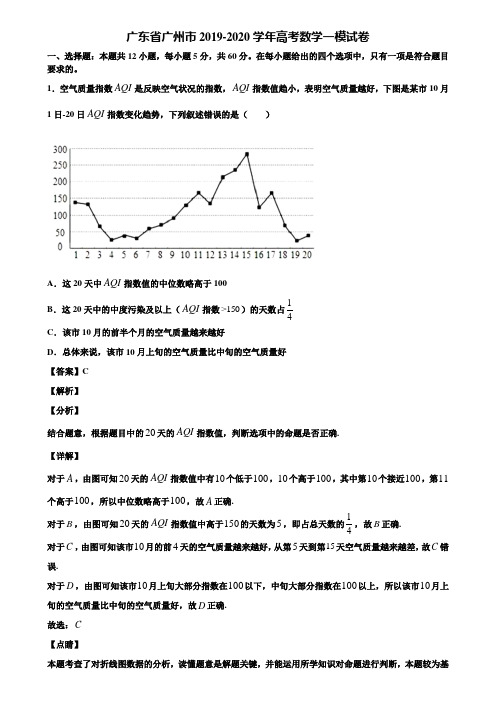
广东省广州市2019-2020学年高考数学一模试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.空气质量指数AQI是反映空气状况的指数,AQI指数值趋小,表明空气质量越好,下图是某市10月1日-20日AQI指数变化趋势,下列叙述错误的是()A.这20天中AQI指数值的中位数略高于100B.这20天中的中度污染及以上(AQI指数>150)的天数占1 4C.该市10月的前半个月的空气质量越来越好D.总体来说,该市10月上旬的空气质量比中旬的空气质量好【答案】C【解析】【分析】结合题意,根据题目中的20天的AQI指数值,判断选项中的命题是否正确.【详解】对于A,由图可知20天的AQI指数值中有10个低于100,10个高于100,其中第10个接近100,第11个高于100,所以中位数略高于100,故A正确.对于B,由图可知20天的AQI指数值中高于150的天数为5,即占总天数的14,故B正确.对于C,由图可知该市10月的前4天的空气质量越来越好,从第5天到第15天空气质量越来越差,故C错误.对于D,由图可知该市10月上旬大部分指数在100以下,中旬大部分指数在100以上,所以该市10月上旬的空气质量比中旬的空气质量好,故D正确.故选:C础.2.《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“”表示一个阳爻,“”表示一个阴爻).若从含有两个及以上阳爻的卦中任取两卦,这两卦的六个爻中都恰有两个阳爻的概率为()A.13B.12C.23D.34【答案】B【解析】【分析】基本事件总数为6个,都恰有两个阳爻包含的基本事件个数为3个,由此求出概率.【详解】解:由图可知,含有两个及以上阳爻的卦有巽、离、兑、乾四卦,取出两卦的基本事件有(巽,离),(巽,兑),(巽,乾),(离,兑),(离,乾),(兑,乾)共6个,其中符合条件的基本事件有(巽,离),(巽,兑),(离,兑)共3个,所以,所求的概率3162 P==.故选:B.【点睛】本题渗透传统文化,考查概率、计数原理等基本知识,考查抽象概括能力和应用意识,属于基础题.3.已知1111143579π≈-+-+-L,如图是求π的近似值的一个程序框图,则图中空白框中应填入A .121i n =-- B .12i i =-+ C .(1)21ni n -=+D .(1)2ni i -=+【答案】C 【解析】 【分析】 【详解】由于111113579-+-+-L 中正项与负项交替出现,根据S S i =+可排除选项A 、B ;执行第一次循环:011S =+=,①若图中空白框中填入(1)21n i n -=+,则13i =-,②若图中空白框中填入(1)2ni i -=+,则13i =-,此时20n >不成立,2n =;执行第二次循环:由①②均可得113S =-,③若图中空白框中填入(1)21ni n -=+,则15i =,④若图中空白框中填入(1)2ni i -=+,则35i =,此时20n >不成立,3n =;执行第三次循环:由③可得11135S =-+,符合题意,由④可得13135S =-+,不符合题意,所以图中空白框中应填入(1)21ni n -=+,故选C .4.如图,平面四边形ACBD 中,AB BC ⊥,3AB =,2BC =,ABD △为等边三角形,现将ABD △沿AB 翻折,使点D 移动至点P ,且PB BC ⊥,则三棱锥P ABC -的外接球的表面积为( )A .8πB .6πC .4πD .823【答案】A将三棱锥P ABC -补形为如图所示的三棱柱,则它们的外接球相同,由此易知外接球球心O 应在棱柱上下底面三角形的外心连线上,在Rt OBE V 中,计算半径OB 即可. 【详解】由AB BC ⊥,PB BC ⊥,可知BC ⊥平面PAB .将三棱锥P ABC -补形为如图所示的三棱柱,则它们的外接球相同.由此易知外接球球心O 应在棱柱上下底面三角形的外心连线上, 记ABP △的外心为E ,由ABD △为等边三角形, 可得1BE =.又12BCOE ==,故在Rt OBE V 中,2OB =, 此即为外接球半径,从而外接球表面积为8π. 故选:A 【点睛】本题考查了三棱锥外接球的表面积,考查了学生空间想象,逻辑推理,综合分析,数学运算的能力,属于较难题.5.如图是一个几何体的三视图,则该几何体的体积为( )A .3B .3C 23D 43【答案】A根据三视图可得几何体为直三棱柱,根据三视图中的数据直接利用公式可求体积. 【详解】由三视图可知几何体为直三棱柱,直观图如图所示:其中,底面为直角三角形,2AD =,3AE =2AB =.∴该几何体的体积为1232232V =⨯= 故选:A. 【点睛】本题考查三视图及棱柱的体积,属于基础题.6.已知抛物线y 2= 4x 的焦点为F ,抛物线上任意一点P ,且PQ ⊥y 轴交y 轴于点Q ,则 PQ PF ⋅u u u r u u u r的最小值为( ) A .-14B .-12C .-lD .1【答案】A 【解析】 【分析】设点2,4y P y ⎛⎫⎪⎝⎭,则点()0,Q y ,()1,0F ,利用向量数量积的坐标运算可得()22112164PQ PF y =⋅--u u u r u u u r ,利用二次函数的性质可得最值. 【详解】解:设点2,4y P y ⎛⎫⎪⎝⎭,则点()0,Q y ,()1,0F , 22,0,1,44PQ P y F y y ⎛⎫⎛⎫∴=-=-- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r ,()22422211,01,244164164PQ P y y y y y F y ⎛⎫⎛⎫∴=-⋅--=-=-- ⎪ ⎪⎝⎭⎝⎭⋅u u u r u u u r ,当22y =时,PQ PF ⋅u u u r u u u r 取最小值,最小值为14-.本题考查抛物线背景下的向量的坐标运算,考查学生的计算能力,是基础题.7.一个几何体的三视图及尺寸如下图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是 ( )A .16216πB .1628πC .8216πD .828π 【答案】D 【解析】 【分析】 【详解】由三视图可知该几何体的直观图是轴截面在水平面上的半个圆锥,表面积为2111442226828222πππ⋅⋅+⋅⋅=,故选D . 8.已知抛物线C :22y px =(0p >)的焦点为F ,01,2M y ⎛⎫⎪⎝⎭为该抛物线上一点,以M 为圆心的圆与C 的准线相切于点A ,120AMF ∠=︒,则抛物线方程为( ) A .22y x = B .24y x =C .26y x =D .28y x =【答案】C 【解析】 【分析】不妨设M 在第一象限,由于M 在抛物线上,所以1,2M p ⎛⎫⎪⎝⎭,由于以M 为圆心的圆与C 的准线相切于点A ,根据抛物线的定义可知,MA MF =、//MA x 轴,且,02p F ⎛⎫⎪⎝⎭.由于120AMF ∠=︒,所以直线MF 的倾斜角α为120o ,所以tan1203122MF p k p-===--o ,解得3p =,或13p =(由于10,122pp -<>,故舍去).所以抛物线的方程为26y x =. 故选:C【点睛】本小题主要考查抛物线的定义,考查直线的斜率,考查数形结合的数学思想方法,属于中档题. 9.刘徽(约公元225年-295年),魏晋期间伟大的数学家,中国古典数学理论的奠基人之一他在割圆术中提出的,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的佳作,割圆术的核心思想是将一个圆的内接正n 边形等分成n 个等腰三角形(如图所示),当n 变得很大时,这n 个等腰三角形的面积之和近似等于圆的面积,运用割圆术的思想,得到sin 2o 的近似值为( )A .π90B .π180C .π270D .π360【答案】A 【解析】 【分析】圆的面积为221360sin 2r n r n π︒=⋅,整理可得3602sin n nπ︒=,当180n =时即可为所求. 【详解】由割圆术可知当n 变得很大时,这n 个等腰三角形的面积之和近似等于圆的面积, 设圆的半径为r ,每个等腰三角形的顶角为360n︒, 所以每个等腰三角形的面积为21360sin 2r n ︒, 所以圆的面积为221360sin2r n r n π︒=⋅,即3602sin n n π︒=, 所以当180n =时,可得3602sin sin 218018090ππ︒=︒==, 故选:A 【点睛】本题考查三角形面积公式的应用,考查阅读分析能力.10.已知函数()2xf x x a =+⋅,()ln 42xg x x a -=-⋅,若存在实数0x ,使()()005f x g x -=成立,则正数a 的取值范围为( )A .(]01,B .(]04,C .[)1+∞,D .(]0,ln2 【答案】A 【解析】 【分析】根据实数0x 满足的等量关系,代入后将方程变形0000242ln 5x x a a x x -⋅+⋅=+-,构造函数()ln 5h x x x =+-,并由导函数求得()h x 的最大值;由基本不等式可求得00242x x a a -⋅+⋅的最小值,结合存在性问题的求法,即可求得正数a 的取值范围. 【详解】函数()2xf x x a =+⋅,()ln 42x gx x a -=-⋅,由题意得()()0000002ln 425x x f x g x x a x a --=+⋅-+⋅=,即0000242ln 5x x a a x x -⋅+⋅=+-,令()ln 5hx x x =+-,∴()111xh x x x-'=-=, ∴()h x 在()01,上单调递增,在()1+∞,上单调递减,∴44a ≤, ∴01a <≤. 故选:A. 【点睛】本题考查了导数在求函数最值中的应用,由基本不等式求函数的最值,存在性成立问题的解法,属于中档题.11.已知复数z 满足0z z -=,且9z z ⋅=,则z =( ) A .3 B .3iC .3±D .3i ±【答案】C 【解析】 【分析】设z a bi =+,则z a bi =-,利用0z z -=和9z z ⋅=求得a ,b 即可. 【详解】设z a bi =+,则z a bi =-,因为0z z -=,则()()20a bi a bi bi +--==,所以0b =, 又9z z ⋅=,即29a =,所以3a =±, 所以3z =±, 故选:C 【点睛】本题考查复数的乘法法则的应用,考查共轭复数的应用. 12.已知变量的几组取值如下表:若y 与x 线性相关,且ˆ0.8yx a =+,则实数a =( ) A .74B .114C .94D .134【答案】B 【解析】 【分析】求出,x y ,把坐标(,)x y 代入方程可求得a .据题意,得()()151191234, 2.4 4.3 5.374244x y =+++==+++=,所以1950.842a =⨯+,所以114a =. 故选:B . 【点睛】本题考查线性回归直线方程,由性质线性回归直线一定过中心点(,)x y 可计算参数值. 二、填空题:本题共4小题,每小题5分,共20分。
【20套精选试卷合集】广东广雅中学2019-2020学年高考数学模拟试卷含答案

高考模拟数学试卷一选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.)1. 已知集合{}4,3,2,1=A ,集合{}6,5,4,3=B ,集合B A C ⋂=,则集合C 的真子集...的个数为( ) A. 1 B. 2 C. 3 D. 42.已知复数1z i =+,则下列命题中正确的个数是( )①2z = ②1z i =- ; ③的虚部为i ; ④z 在复平面上对应的点位于第一象限. A. 1 B. 2 C. 3 D. 4 3. 命题“[]1,0∈∀m ,21≥+xx ”的否定形式是( ) A. []1,0∈∀m ,21<+x x B. []1,0∈∃m ,21≥+xx C. ()()+∞∞-∈∃,00, m ,21≥+x x D. []1,0∈∃m ,21<+xx 4.已知ABC ∆中,=A 6π,=B 4π,a 1=,则b 等于( ) A .2 B .1 C .3 D .25.在区间(0,4)上任取一实数x ,则22<x 的概率是( ) A .43B .21 C .31 D .416. 若y x ,满足约束条件⎪⎩⎪⎨⎧≤+≥+≥32320y x y x x ,则y x z -=的最小值是( )A . 0B . 3-C .23D .3 7.{}n a 是公差不为0的等差数列,满足27262524a a a a +=+,则该数列的前10项和10S =( )A .10-B .5-C .0D .58.已知()222,03,0x x f x x x ⎧-≥=⎨-+<⎩,若()2f a =,则a 的取值为( )A .2B . -1或2 C. 1±或2 D .1或29.双曲线)0,0(12222>>=-b a by a x 的一条渐近线与圆()()11322=-+-y x 相切,则此双曲线的离心率为( )A. 2B. 5C.3 D.210. 某几何体的三视图如右图,若该几何体的所有顶点都在一个球3面上,则该球面的表面 积为( ) A . 4πB .283πC .443πD . 20π11.中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N 除以正整数m 后的余数为n ,则记为()m n N m od ≡,例如()3m od 211≡.现将该问题以程序框图的算法给出,执行该程序框图,则输出的n 等于( ) A .21B .22C .23D .2412.若函数()()()2122ln 02ax f x a x x a =-++>在区间1,12⎛⎫ ⎪⎝⎭内有极大值,则a 的取值范围是( )A . 1,e ⎛⎫+∞ ⎪⎝⎭ B .()1,+∞ C. ()1,2 D .()2,+∞二、填空题(本大题共4小题,每小题5分)13、已知平面向量→a =(k ,3),→b =(1,4),若→→⊥b a ,则实数k = .14.设ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若ABC ∆的面积为22243,则C = .15. 将1,2,3,4…正整数按如图所示的方式排成三角形数组,则第10行左数第10个数为 .16.设函数()⎪⎪⎩⎪⎪⎨⎧->++--≤⎪⎭⎫⎝⎛-=1,3234311,2log 22x x x x x x f ,若()f x 在区间[],4m 上的值域为[]1,2-,则实数m 的取值范围为 .三、解答题(解答应写出文字说明,证明过程或演算步骤) 17.(本题满分12分)已知数列{}n a 是公差不为0的等差数列,首项11=a ,且421,,a a a 成等比数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设数列{}n b 满足n an n a b 2+=,求数列{}n b 的前n 项和n T .18.(本题满分12分)“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:(Ⅰ)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率; (Ⅱ)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的22⨯列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关? 附: ()()()()()22n ad bc k a b c d a c b d -=++++,()20P K k ≥ 0.10 0.05 0.025 0.010 0k2.7063.8415.0246.63518.(本题满分12分)在三棱柱ABC ﹣A 1B 1C 1中,侧面AA 1C 1C ⊥底面ABC ,AA 1=A 1C=AC=AB=BC=2,且点O 为AC 中点. (Ⅰ)证明:A 1O ⊥平面ABC ; (Ⅱ)求三棱锥C 1﹣ABC 的体积. 19.(本题满分12分)已知直线01034:=++y x l ,半径为2的圆C 与l相切,圆心C 在x 轴上且在直线l 的上方.(Ⅰ)求圆C 的标准方程;(Ⅱ)过点()0,1M 的直线与圆C 交于B A ,两点(A 在x 轴上方),问在x 轴正半轴上是否存在点N ,使得x 轴平分ANB ∠?若存在,请求出点N 的坐标;若不存在,请说明理由. 21.(本题满分12分) 已知函数()()211ln ,.2f x x a x a x a R =+--∈ (Ⅰ)若()f x 存在极值点1,求a 的值; (Ⅱ)若()f x 存在两个不同的零点,求证:2ea >(e 为自然对数的底数,ln 20.6931=) 请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题计分 22.(本题满分10分)选修4-4:坐标系与参数方程已知极坐标系的极点为直角坐标系xOy 的原点,极轴为x 轴的正半轴,两种坐标系中的长度单位相同,圆C 的直角坐标方程为22220x y x y ++-=,直线l 的参数方程为1x ty t=-+⎧⎨=⎩(t 为参数),射线OM 的极坐标方程为34πθ=. (Ⅰ)求圆C 和直线l 的极坐标方程;(Ⅱ)已知射线OM 与圆C 的交点为,O P ,与直线l 的交点为Q ,求线段PQ 的长. 23.(本题满分10分)选修4-5:不等式选讲 已知()13++-=x x x f ,()a a x x x g -+-+=1.(Ⅰ)解不等式()6f x ≥;(Ⅱ)若不等式()()f x g x ≥恒成立,求实数a 的取值范围. 一、选择题二、填空题13. ____-12_________ 14. _____6π_____________ 15.______91_________ 16. ______[]1-8-,___________ 三、解答题17.(本题满分12分)解:(Ⅰ)设数列{a n }的公差为d ,由题设,,…(2分)即(1+d )2=1+3d ,解得d=0或d=1…(4分) 又∵d ≠0,∴d=1,可以求得a n =n…(6分) (Ⅱ)由(Ⅰ)得,=(1+2+3+…+n )+(2+22+ (2))=…(12分)18.解:(Ⅰ)由题知,40人中该日走路步数超过5000步的有35人,频率为4035,所以估计他的所有微信好友中每日走路步数超过5000步的概率为87; (Ⅱ)()22401412684038412020221811K ⋅⨯⨯-⨯==<⨯⨯⨯ ,故没有95%以上的把握认为二者有关. 19.证明:(Ⅰ)∵AA 1=A 1C ,且O 为AC 的中点, ∴A 1O ⊥AC ,…(2分) 又∵平面AA 1C 1C ⊥平面ABC , 平面AA 1C 1C ∩平面ABC=AC …(4分) 且A 1O ⊂平面AA 1C 1C ,题号 1 234 5 6 7 8 9 10 11 12 答案CC DADBCBABCC积极型 懈怠型 总计 男 14 6 20 女 8 12 20 总计221840∴A 1O ⊥平面ABC …(6分)(Ⅱ)∵A 1C 1∥AC ,A 1C 1⊄平面ABC ,AC ⊂平面ABC , ∴A 1C 1∥平面ABC ,即C 1到平面ABC 的距离等于A 1到平面ABC 的距离…(8分) 由(Ⅰ)知A 1O ⊥平面ABC 且,…(9分)∴三棱锥C 1﹣ABC 的体积:…(12分)20.解:(Ⅰ)设圆心5(,0)()2C a a >-,则4102055a a a +=⇒==-或(舍去). ·················· 2分 所以圆C 的标准方程为224x y +=. ···················· 4分 (Ⅱ)当直线AB x ⊥轴,在x 轴正半轴上任一点,都可使x 轴平分ANB ∠; ··· 5分 当直线AB 斜率存在时,设直线AB 方程为(1)y k x =-,1122(,0),(,),(,),N t A x y B x y ··········· 6分 联立圆C 的方程和直线AB 的方程得,2222224,(1)240(1)x y k x k x k y k x ⎧+=⇒+-+-=⎨=-⎩, ················ 7分 故2212122224,11k k x x x x k k -+==++, ····················· 8分 若x 轴平分ANB ∠,则12121212(1)(1)00AN BN y y k x k x k k x t x t x t x t--=-⇒+=⇒+=---- 221212222(4)2(1)2(1)()2020411k k t x x t x x t t t k k -+⇒-+++=⇒-+=⇒=++.当点N 的坐标为(4,0)时,能使得ANM BNM ∠=∠成立. ············ 12 21.解:(1) ()1'=+--af x x a x,因为()f x 存在极值点为1,所以(1)0'=f ,即220,1-==a a ,经检验符合题意,所以1=a . ····················· (4分) (2) ()1(1)(1)(0)'=+--=+->a af x x a x x x x①当0≤a 时,()0'>f x 恒成立,所以()f x 在(0,)+∞上为增函数,不符合题意; ②当0>a 时,由()0'=f x 得=x a , 当>x a 时,()0'>f x ,所以()f x 为增函数, 当0<<x a 时,()0'<f x ,所()f x 为增函减数, 所以当=x a 时,()f x 取得极小值()f a又因为()f x 存在两个不同零点,所以()0<f a ,即21(1)ln 02+--<a a a a a整理得1ln 12>-a a ,令1()ln 12h a a a =+-,11()02h a a '=+>,()h a 在定义域内单调递增,()()(ln 1)(ln 1)(ln 2)224224e e e e e eh h e e ⋅=+-+-=-, 由ln 20.6931, 2.71828e ≈≈知ln 204e -<,故2ea >成立. (12分)22.解(1)∵222x y ρ=+,cos x ρθ=,sin y ρθ=, 圆C 的普通方程为22220x y x y ++-=, ∴22cos 2sin 0ρρθρθ+-=, ∴圆C的极坐标方程为)4πρθ=-.1x ty t=-+⎧⎨=⎩(t 为参数)消去t 后得1y x =+, ∴直线l 的极坐标方程为1sin cos θθρ-=.(2)当34πθ=时,3||sin()44OP ππ=-=,∴点P的极坐标为3)4π,||2OQ ==,所以点Q的极坐标为3)4π,故线段PQ, 23.解:(1)()22,34,1322,1x x f x x x x -≥⎧⎪=-<<⎨⎪-+≤-⎩,当3x ≥时,226x -≥解得4x ≥,当13x -<<时,46≥无解,当1x ≤-时,226x -+≥解得2x ≤-. ∴()6f x ≥的解集为{}|24x x x ≤-≥或.(2)由已知311x x x x a a -++≥+-+-恒成立, ∴3x x a a -++≥-恒成立,又3333x x a x x a a a -++≥---=--=+, ∴3a a +≥-,解得32a ≥-,3,2a ⎡⎫∈-+∞⎪⎢⎣⎭时,不等式()()f x g x ≥恒成立.高考模拟数学试卷数 学(理科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,其中第II 卷第22题~第24题为选考题,其它题为必考题.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.第I 卷一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{}2,ln A x =,{},B x y =,若{}0A B =,则y 的值为( ) A .0 B .1 C .e D .1e2.设复数11iz i-=+,则z 为( )A .1B .1-C .iD .i -3. 计算sin 47cos17cos47cos73︒︒-︒︒的结果为( ) A.21 B. 33C.22D.23 4. 61()x x-展开式中的常数项为( )A. -20B. 20C. -15D.155. 三位男同学和三位女同学站成一排,要求任何两位男同学都不相邻,则不同的排法总数为( ) A.720B.144C.36D.126.曲线()sin f x x =,()cos f x x =与直线0x =,2x π=所围成的平面区域的面积为( )A .20(sin cos )x x dx π-⎰ B .402(sin cos )x x dx π-⎰C .424cos +sin xdx xdx πππ⎰⎰ D .402(cos sin )x x dx π-⎰7. 已知函数()sin()(R,0,0,||)2f x A x x A πωϕωϕ=+∈>><的图象(部分)如图所示,则ωϕ,分别为( ) A. ,3πωπϕ==B. 2,3πωπϕ==C. ,6πωπϕ==D. 2,6πωπϕ==8.已知定义在R 上的偶函数)(x f 满足(1)(1)f x f x +=-,且]1,0[∈x 时,7()8f x x =-,则方程1)21()(||-=x x f 在区间[3,3]-零点的个数为( )A .5B .4C .3D .29.已知,A B 两点均在焦点为F 的抛物线22(0)y px p =>上,若||||4AF BF +=,线段AB 的中点到直线2px =的距离为1,则p 的值为( ) A .1 B .1或3 C .2 D .2或6 10.如图是用模拟方法估计椭圆1422=+y x 面积的程序框图,S 表示估计 的结果,则图中空白处应 该填入( ) A .250NS = B .125NS =C .250MS =D .125M S =11.定义在R 上的函数()f x 满足(3)1f =,(2)3f -=,()f x '为()f x 的导函数,已知()y f x '=的图象如图所示,且()f x '有且只有一个零点,若非负实数,a b 满足(2)1f a b +≤,(2)3f a b --≤,则21b a ++的取值范围是( ) A.4[,3]5 B.4(0,][3,)5+∞ C.4[,5]5D.4(0,][5,)5+∞ 12.等腰Rt △ACB ,2AB =,2ACB π∠=.以直线AC 为轴旋转一周得到一个圆锥,D 为圆锥底面一点,BD CD ⊥,CH AD ⊥于点H ,M 为AB 中点,则当三棱锥C HAM -的体积最大时,CD 的长为 ( ) A .53 B .253 C .63 D .263第II 卷本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二.填空题(本大题共4小题,每小题5分,共20分,把答案填在答卷卡的相应位置上) 13.已知△ABC 三个内角A 、B 、C ,且sin :sin :sin 2:3:4A B C =, 则cos C 的值为 .14.如图,格纸是边长为1的小正方形,在其上用粗线开始0,0,1M N i ===产生0~2之间的两个随机数分别赋值给i i y x ,1422≤+i i y x 是否1+=i i1+=M M 1+=N N 2000>i否是输出S 结束画出了某多面体的三视图,则该多面体的体15.已知双曲线C :22221y x a b-=(0,0)a b >>,P 为x 轴上一动点,经过P 的直线2(0)y x m m =+≠与双曲线C 有且只有一个交点,则双曲线C 的离心率为 .16. 设R a ∈,对于0x ∀>,函数()(1)[ln(1)1]f x ax x =-+-恒为非负数,则a 的取值所组成的集合为 .三.解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)已知各项均为正数的数列{}n a 满足11a =,11+0n n n n a a a a ++-=. (Ⅰ)求证:数列1n a ⎧⎫⎨⎬⎩⎭是等差数列,并求数列{}n a 的通项公式; (Ⅱ)求数列2n n a ⎧⎫⎨⎬⎩⎭前n 项和n S .18.(本小题满分12分)某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[]21,7,22.3(单位:cm )之间的零件,把零件尺寸在)1.22,9.21[的记为一等品,尺寸在)2.22,1.22[)9.21,8.21[ 的记为二等品,尺寸在]3.22,2.22[)8.21,7.21[ 的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:()21122122121+2++1+2-=n n n n n n n n n χ,(Ⅱ)以上述各种产品的频率作为各种产品发生的概率,若一等品、二等品、三等品的单件利润分别为/cm/cm30元、20元、15元,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.19.(本小题满分12分)如图,正三棱柱ABC -A 1B 1C 1中,底面边长为2,D 为11A C 中点. (Ⅰ)求证;1BC ∥平面1AB D ; (Ⅱ)求二面角A 1-AB 1-D 的大小.20. (本小题满分12分)设离心率12e =的椭圆2222:1(0)x y M a b a b +=>>的左、右焦点分别为12F F 、,P 是x 轴正半轴上一点,以1PF 为直径的圆经过椭圆M 短轴端点,且该圆和直线30x ++=相切,过点P 的直线与椭圆M 相交于相异两点A 、C . (Ⅰ)求椭圆M 的方程;(Ⅱ)若相异两点A B 、关于x 轴对称,直线BC 交x 轴与点Q ,求QA QC ⋅的取值范围.21.(本小题满分12分)D已知R m ∈,函数2()2x f x mx e =-. (Ⅰ)当2m =时,求函数()f x 的单调区间;(Ⅱ)若()f x 有两极值点,()a b a b <,(ⅰ)求m 的取值范围;(ⅱ)求证:()2e f a -<<-.请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑.22.(本小题满分10分)选修4-1:几何证明选讲 如图,已知圆上的AC BD =,过C 点的圆的 切线与BA 的延长线交于E 点. (Ⅰ)证明:ACE BCD ∠=∠; (Ⅱ)若9,1BE CD ==,求BC 的长.23.(本小题满分10分)选修4-4:坐标系与参数方程 在直角坐标系xOy 中,曲线1C 的参数方程为2cos 22sin x y αα=⎧⎨=+⎩(α为参数),曲线2C 的参数方程为22cos 2sin x y ββ=+⎧⎨=⎩(β为参数),P 是2C 上的点,线段OP 的中点在1C 上. (Ⅰ)求1C 和2C 的公共弦长;(Ⅱ)在以O 为极点,x 轴的正半轴为极轴的极坐标系中,求点P 的一个极坐标.24.(本小题满分10分)选修4-5:不等式选讲 已知512)(-+-=ax x x f (a 是常数,a ∈R) (Ⅰ)当a=1时求不等式0)(≥x f 的解集.(Ⅱ)如果函数)(x f y =恰有两个不同的零点,求a 的取值范围.数学(理科) 参考答案与评分标准说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分. 一.选择题1.A ;2.D ;3. A ;4. D ;5. B ;6.D ;7.C ;8.A ;9.B ;10.D ;11.A ;12.C . 二.填空题13.14-;14.16;15.2;16.11e ⎧⎫⎨⎬-⎩⎭. 三.解答题17.解:(Ⅰ)∵11+0n n n n a a a a ++-=,∴1110n n n nn n a a a a a a ++++-=,∴1111n na a +-=, ·························· 3分 111a =,∴数列1n a ⎧⎫⎨⎬⎩⎭是以1为首项,1为公差的等差数列. ········ 4分 11(1)1n n n a =+-⨯=,1n a n=. ··················· 6分 (Ⅱ)法一:由(Ⅰ)知2=2nn nn a .12=12+22++2n n S n ⨯⨯⨯. ························································ ① 23+12=12+22++2n n S n ⨯⨯⨯. ···················································· ②······························································································· 9分由①-②得121=2+2++22n n n S n +--⨯.∴1=(1)22n n S n +-+. ······························································· 12分法二:令212n n n b n c c +==-,令()2nn c An B =+, ∴11()2()22n n nn n n b c c An A B An B n ++=-=++-+=.∴12A B ==-,. ···································································· 9分 ∴122132111n n n n b b b c c c c c c c c +++++=-+-++-=-1(12)2(12)2=(1)22n n n n +=+----+. ··································· 12分18.解:(Ⅰ)22⨯列联表如下2分841.302.290110100100)50604050(20022<≈⨯⨯⨯⨯-⨯⨯=χ,所以没有理由认为选择不同的工艺与生产出一等品有关. ······································································································ 4分(Ⅱ)由题知运用甲工艺生产单件产品的利润X 的分布列为242.0153.0205.0=⨯+⨯+,X 的方差为392.0)2415(3.0)2420(5.0)2430(222=⨯-+⨯-+⨯-=DX . ·· 7分乙工艺生产单件产品的利润Y 的分布列为Y 30 20 15 P0.60.10.3Y 的数学期望为5.243.0151.0206.030=⨯+⨯+⨯=EY ,Y 的方差为25.473.0)5.2415(1.0)5.2420(6.0)5.2430(222=⨯-+⨯-+⨯-=DY . ···· 10分答案一:由上述结果可以看出EY EX <,即乙工艺的平均利润大,所以以后应该选择乙工艺. 答案二:由上述结果可以看出DY DX <,即甲工艺波动小,虽然EY EX <,但相差不大,所以以后选择甲工艺. ······························ 12分19.解:(Ⅰ)如图,连结A 1B 与AB 1交于E ,连结DE ,则E 为A 1B 的中点,∴BC 1∥DE ,DE ⊂平面1AB D ,1BC ⊄平面1AB D ,∴1BC ∥平面1AB D . ········································································ 6分(Ⅱ)过D 作DF ⊥A 1B 1于F ,由正三棱柱的性质,AA 1⊥DF ,∴DF ⊥平面ABB 1A 1, 连结EF ,DE ,在正三角形A 1B 1C 1中, ∵D 是A 1C 1的中点,∴11132B D A B ==3, ······································ 8分 又在直角三角形AA 1D 中,∵AD =AA 21+A 1D 2=3,∴AD =B 1D . ∴DE ⊥AB 1,∴可得EF ⊥AB 1,则∠DEF 为二面角A 1-AB 1-D 的平面角. ········································ 10分 可求得32DF =, ∵△B 1FE ∽△B 1AA 1,得32EF =,∴∠DEF =π4,即为所求. ·································································· 12分(2)解法(二)(空间向量法)建立如图所示空间直角坐标系,则A (0,-1,0),B 1(0,1), C 1),A 1(0,-1),D12-). 8分 ∴AB 1=(0,1),B 1D,-32,0). 设n 1=(x ,y ,z )是平面AB 1D 的一个法向量,则可得 ⎩⎪⎨⎪⎧n 1·AB 1=0n 1·B 1D =0,即20,30.22y x y ⎧+=⎪⎨--=⎪⎩. ∴n 1=(-3,1,-2). ······························································ 10分 又平面ABB 1A 1的一个法向量n 2=OC,0,0), 设n 1与n 2的夹角是θ,则 cosθ=n 1·n 2|n 1|·|n 2|=22. 又可知二面角A 1-AB 1-D 是锐角.∴二面角A 1-AB 1-D 的大小是π4. ··························································· 12分20. 解:(Ⅰ)设以1||PF 为直径的圆经过椭圆M 短轴端点N , ∴1||NF a =,∵12e =,∴2a c =, ∴13NF P π∠=, 1||2PF a =. ····································································· 2分∴2(,0)F c 是以|1PF |为直径的圆的圆心,∵该圆和直线30x ++=相切,∴2c =1,2,c a b ===∴椭圆M 的方程为:22143x y +=. ····························································· 4分 (Ⅱ)设点11(,)A x y ,22(,)C x y ,则点11(,)B x y -,法一:设直线PA 的方程为(3)y k x =-,联立方程组22143(3).x y y k x ⎧+=⎪⎨⎪=-⎩, 化简整理得2222(43)2436120k x k x k +-+-=, 由2222(24)4(34)(3612)0k k k ∆=-⋅+⋅->得2305k <<. ································· 6分 则22121222243612,4343k k x x x x k k -+==++.直线BC 的方程为:211121()y y y y x x x x ++=--,令0y =,则22221221121221212272247223()44343==2463643k k y x y x x x x x k k x k y y x x k --+-+++==++--+. ∴Q 点坐标为4(,0)3. ··············································································· 8分2121212124444()()()()(3)(3)3333QA QC x x y y x x k x x ⋅=--+=--+--=2221212416(1)(3)()939k x x k x x k +-++++=2222222361242416(1)(3)9433439k k k k k k k -+⋅-+⋅++++ =222191216235105439361612k k k -+=-++. ···························································· 10分 ∵2305k << ∴205(,)93QA QC ⋅∈-. ················· 12分 法二:设直线方程为3x my =+.由2231.43x my x y =+⎧⎪⎨+=⎪⎩,得22(34)18150m y my +++=, 由22(18)415(34)0m m ∆=-⋅⋅+>得253m >. ················································· 6分 12212218,3415.34m y y m y y m ⎧+=-⎪⎪+⎨⎪=⎪+⎩直线BC 的方程为:211121()y y y y x x x x ++=--,令0y =,则212211212122152(3)(3)24343=3+=18334my my y my my y m x m y y y y m ++++==+++-+. ∴Q 点坐标为4(,0)3. ··············································································· 8分121212124444()()()()3333QA QC x x y y my my y y ⋅=--+=+++=21212525(1)()39m y y m y y ++++=2221551825(1)()343349m m m m m +⋅+⋅-+++=23520349m -+.································ 10分∵253m >, ∴205(,)93QA QC ⋅∈-.综上,205(,)93QA QC ⋅∈-. ······················ 12分 21.解:(Ⅰ)2m =时,2()22x f x x e =-,()422(2)x x f x x e x e '=-=-.令()2x g x x e =-,()2x g x e '=-, ································································ 2分 当(,ln 2)x ∈-∞时,()0g x '>,(ln 2,)x ∈+∞时,()0g x '< ∴()(ln 2)2ln 220g x g =-<≤.∴()0f x '<.∴()f x 在(,)-∞+∞上是单调递减函数. ··········· 4分 (Ⅱ)若()f x 有两个极值点,()a b a b <,则,a b 是方程()220x f x mx e '=-=的两不等实根.解法一:∵0x =显然不是方程的根,∴xe m x =有两不等实根. ·························· 6分令()x e h x x =,则2(1)()x e x h x x -'=当(,0)x ∈-∞时,()0h x '<,()h x 单调递减,()(,0)h x ∈-∞(0,1)x ∈时,()0h x '<,()h x 单调递减,(1,)x ∈+∞时,()0h x '>,()h x 单调递增,要使xe m x=有两不等实根,应满足(1)m h e >=,∴m 的取值范围是(,)e +∞.(注意:直接得()h x 在(,1)-∞上单调递减,(1,)+∞上单调递增扣2分). ················· 8分 ∵2()2a f a ma e =-,且()220a f a ma e '=-=2()22(2)a a a a a e f a a e a e e e a a=⋅-=⋅-=-,∵(0)20h =-<,()h x 在区间(0,ln )m 上单调递增,(1)2()0h m e =->,∴(0,1)a ∈ 设()(2)(01)x x e x x ϕ=-<< ,则()(1)0x x e x ϕ'=-<,()x ϕ在(0,1)上单调递减∴(1)()(0)f f a f << 即()2e f a -<<-. ······················································ 12分 解法二:()()22x h x f x mx e '==-,则,a b 是方程()0h x =的两不等实根. ∵()2()x h x m e '=-,当0m ≤时,()0h x '<,()h x 在(,)-∞+∞上单调递减,()0h x =不可能有两不等实根 当0m >时,由()0h x '=得ln x m =,当(,ln )x m ∈-∞时,()0h x '>,(ln ,)x m ∈+∞时,()0h x '<∴当max ()(ln )2(ln )0h x h m m m m ==->,即m e >时,()0h x =有两不等实根∴m 的取值范围是(,)e +∞. ······················· 8分 ∵2()2a f a ma e =-,且()220a f a ma e '=-=2()22(2)a a a a a e f a a e a e e e a a=⋅-=⋅-=-,∵(0)20h =-<,()h x 在区间(0,ln )m 上单调递增,(1)2()0h m e =->,∴(0,1)a ∈设()(2)(01)x x e x x ϕ=-<< ,则()(1)0x x e x ϕ'=-<,()x ϕ在(0,1)上单调递减∴(1)()(0)f f a f << 即()2e f a -<<-. ······················································ 12分解:(Ⅰ)证明,AC BD ABC BCD =∴∠=∠. ··············································· 2分 又EC 为圆的切线,,ACE ABC ∴∠=∠∴ACE BCD ∠=∠. ······················ 5分 (Ⅱ)EC 为圆的切线,∴CDB BCE ∠=∠,由(Ⅰ)可得BCD ABC ∠=∠ ·································································· 7分 ∴△BEC ∽△CBD ,∴CD BCBC EB=,∴BC =3. ······································ 10分 23.解:(Ⅰ)曲线1C 的一般方程为4)2(22=-+y x ,曲线2C 的一般方程为4)2(22=+-y x . ·················································· 2分 两圆的公共弦所在直线为x y =,)0,2(到该直线距离为2,所以公共弦长为2222222=-. ·················· 5分 (Ⅱ)曲线1C 的极坐标方程为θρsin 4=,曲线2C 的极坐标方程为θρcos 4=. ························································ 7分 设),(θρM ,则),2(θρP ,两点分别代入1C 和2C 解得554=ρ, θ不妨取锐角55arcsin, 所以)55arcsin ,558(P . ····································································· 10分 24.解:(Ⅰ)136(),2()14().2x x f x x x ⎧-≥⎪⎪=⎨⎪--<⎪⎩∴0)(≥x f 的解为{}42-≤≥x x x 或 . ·················· 5分 (Ⅱ)由0)(=x f 得,=-12x 5+-ax . ················· 7分 令12-=x y ,5+-=ax y ,作出它们的图象,可以知道,当22<<-a 时, 这两个函数的图象有两个不同的交点,所以,函数)(x f y =有两个不同的零点. ················· 10分。
广东省广州市2019-2020学年高考数学五月模拟试卷含解析
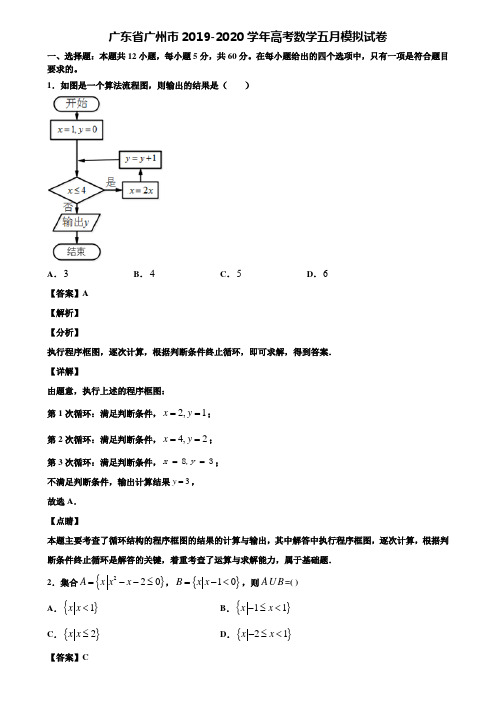
广东省广州市2019-2020学年高考数学五月模拟试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图是一个算法流程图,则输出的结果是( )A .3B .4C .5D .6【答案】A 【解析】 【分析】执行程序框图,逐次计算,根据判断条件终止循环,即可求解,得到答案. 【详解】由题意,执行上述的程序框图:第1次循环:满足判断条件,2,1x y ==; 第2次循环:满足判断条件,4,2x y ==; 第3次循环:满足判断条件,8,3x y ==; 不满足判断条件,输出计算结果3y =, 故选A . 【点睛】本题主要考查了循环结构的程序框图的结果的计算与输出,其中解答中执行程序框图,逐次计算,根据判断条件终止循环是解答的关键,着重考查了运算与求解能力,属于基础题. 2.集合}{220A x x x =--≤,{}10B x x =-<,则A B U =( )A .}{1x x < B .}{11x x -≤< C .{}2x x ≤ D .{}21x x -≤<【答案】C【解析】 【分析】先化简集合A,B ,结合并集计算方法,求解,即可. 【详解】解得集合()(){}{}21012A x x x x x =-+≤=-≤≤,{}1B x x =< 所以{}2A B x x ⋃=≤,故选C . 【点睛】本道题考查了集合的运算,考查了一元二次不等式解法,关键化简集合A,B ,难度较小.3.函数()y f x =满足对任意x ∈R 都有()()2f x f x +=-成立,且函数()1y f x =-的图象关于点()1,0对称,()14f =,则()()()201620172018f f f ++的值为( )A .0B .2C .4D .1【答案】C 【解析】 【分析】根据函数()1y f x =-的图象关于点()1,0对称可得()f x 为奇函数,结合()()2f x f x +=-可得()f x 是周期为4的周期函数,利用()00f =及()14f =可得所求的值. 【详解】因为函数()1y f x =-的图象关于点()1,0对称,所以()y f x =的图象关于原点对称, 所以()f x 为R 上的奇函数.由()()2f x f x +=-可得()()2f x f x +=-,故()()()42f x f x f x +=-+=, 故()f x 是周期为4的周期函数.因为20164504,201745041,201845042=⨯=⨯+=⨯+,所以()()()()()()()20162017201012428f f f f f f f +=+=+++. 因为()()2f x f x +=-,故()()()02000f f f +=-=-=, 所以()()()2016201720148f f f +=+. 故选:C. 【点睛】本题考查函数的奇偶性和周期性,一般地,如果R 上的函数()f x 满足()()()0f x a f x a +=-≠,那么()f x 是周期为2a 的周期函数,本题属于中档题.4.()f x 是定义在()0,∞+上的增函数,且满足:()f x 的导函数存在,且()()f x x f x '<,则下列不等式成立的是( ) A .()()221f f < B .()()3344ff <C .()()2334f f <D .()()3223f f <【答案】D 【解析】 【分析】根据()f x 是定义在()0,∞+上的增函数及()()f x f x '有意义可得()0f x '>,构建新函数()()f xg x x=,利用导数可得()g x 为()0,∞+上的增函数,从而可得正确的选项. 【详解】因为()f x 是定义在()0,∞+上的增函数,故()0f x '≥.又()()f x f x '有意义,故()0f x '≠,故()0f x '>,所以()()f x f x x <'. 令()()f xg x x =,则()()()20'-'=>xf x f x g x x, 故()g x 在()0,∞+上为增函数,所以()()32g g >即()()3232f f >, 整理得到()()2332f f >. 故选:D. 【点睛】本题考查导数在函数单调性中的应用,一般地,数的大小比较,可根据数的特点和题设中给出的原函数与导数的关系构建新函数,本题属于中档题. 5.已知函数()22cos sin 4f x x x π⎛⎫=++⎪⎝⎭,则()f x 的最小值为( )A .12+B .12C .12-D .14-【答案】C 【解析】【分析】利用三角恒等变换化简三角函数为标准正弦型三角函数,即可容易求得最小值. 【详解】由于()221cos 21cos 22cos sin 422x x f x x x ππ⎛⎫-+ ⎪+⎛⎫⎝⎭=++=+ ⎪⎝⎭ cos 2sin 2122x x=++1224x π⎛⎫=++ ⎪⎝⎭,故其最小值为:12-. 故选:C. 【点睛】本题考查利用降幂扩角公式、辅助角公式化简三角函数,以及求三角函数的最值,属综合基础题. 6.P 是正四面体ABCD 的面ABC 内一动点,E 为棱AD 中点,记DP 与平面BCE 成角为定值θ,若点P 的轨迹为一段抛物线,则tan θ=( ) AB.CD.【答案】B 【解析】 【分析】设正四面体的棱长为2,建立空间直角坐标系,求出各点的坐标,求出面BCE 的法向量,设P 的坐标,求出向量DP u u u r,求出线面所成角的正弦值,再由角θ的范围0,2π⎡⎤⎢⎥⎣⎦,结合θ为定值,得出sin θ为定值,且P 的轨迹为一段抛物线,所以求出坐标的关系,进而求出正切值. 【详解】由题意设四面体ABCD 的棱长为2,设O 为BC 的中点,以O 为坐标原点,以OA 为x 轴,以OB 为y 轴,过O 垂直于面ABC 的直线为z 轴,建立如图所示的空间直角坐标系O xyz -,则可得1OB OC ==,323OA ==OA 的三等分点G 、F 如图, 则133OG OA ==2233AG OF OA ===2226DG AD AG =-=,162EF DG ==,所以()0,1,0B 、()0,1,0C -、()3,0,0A、32633D ⎛ ⎝⎭、236,0,33E ⎛⎫⎪ ⎪⎝⎭, 由题意设(),,0P x y ,326,33DP x y ⎛=-- ⎝⎭u u u r , QV ABD 和ACD V 都是等边三角形,E 为AD 的中点,BE AD ∴⊥,CE AD ⊥,BE CE E =Q I ,AD ∴⊥平面BCE ,2326AD ⎛∴= ⎝⎭u u u r 为平面BCE 的一个法向量, 因为DP 与平面BCE 所成角为定值θ,则0,2π⎡⎤θ∈⎢⎥⎣⎦,由题意可得222223326333sin cos ,326233x AD DP AD DP AD DPx y θ⎛⎫⎛⎫-⨯-- ⎪ ⎪⋅⎝⎭⎝⎭=<>==⋅⎛⎫⎛⎫⨯-++- ⎪ ⎪⎝⎭⎝⎭u u u r u u u ru u u r u u u ru u u r u u u r ()()222222223323333239332393138x x x x x y x x y x x y ++++===+-++-+-++ 因为P 的轨迹为一段抛物线且tan θ为定值,则sin θ也为定值,22223339323x x x y x ==-,可得233y x =,此时3sin 3θ=,则6cos 3θ=,sin 2tan cos 2θθθ==. 故选:B. 【点睛】考查线面所成的角的求法,及正切值为定值时的情况,属于中等题.7.等差数列{}n a 的前n 项和为n S ,若13a =,535S =,则数列{}n a 的公差为( ) A .-2 B .2 C .4 D .7【答案】B 【解析】 【分析】在等差数列中由等差数列公式与下标和的性质求得3a ,再由等差数列通项公式求得公差. 【详解】在等差数列{}n a 的前n 项和为n S ,则()155********a a S a a +===⇒=则3123272a a d d d =+=+=⇒= 故选:B 【点睛】本题考查等差数列中求由已知关系求公差,属于基础题.8.如图,在矩形OABC 中的曲线分别是sin y x =,cos y x =的一部分,,02A π⎛⎫⎪⎝⎭,()0,1C ,在矩形OABC 内随机取一点,若此点取自阴影部分的概率为1P ,取自非阴影部分的概率为2P ,则( )A .12P P <B .12P P >C .12P P =D .大小关系不能确定【答案】B 【解析】 【分析】先用定积分求得阴影部分一半的面积,再根据几何概型概率公式可求得. 【详解】根据题意,阴影部分的面积的一半为:()4cos sin 21x x dx π-=⎰,于是此点取自阴影部分的概率为)()12142141.41122 3.22P ππ--=⨯=>=. 又21112P P =-<,故12P P >. 故选B .【点睛】本题考查了几何概型,定积分的计算以及几何意义,属于中档题.9.如图所示的“数字塔”有以下规律:每一层最左与最右的数字均为2,除此之外每个数字均为其两肩的数字之积,则该“数字塔”前10层的所有数字之积最接近()lg 20.3≈( )A .30010B .40010C .50010D .60010【答案】A 【解析】 【分析】结合所给数字特征,我们可将每层数字表示成2的指数的形式,观察可知,每层指数的和成等比数列分布,结合等比数列前n 项和公式和对数恒等式即可求解 【详解】如图,将数字塔中的数写成指数形式,可发现其指数恰好构成“杨辉三角”,前10层的指数之和为29101222211023+++⋅⋅⋅+=-=,所以原数字塔中前10层所有数字之积为10231023lg230021010=≈.故选:A 【点睛】本题考查与“杨辉三角”有关的规律求解问题,逻辑推理,等比数列前n 项和公式应用,属于中档题 10.已知复数21aibi i-=-,其中a ,b R ∈,i 是虚数单位,则a bi +=( ) A .12i -+ B .1C .5D 5【答案】D 【解析】 试题分析:由21aibi i-=-,得()21,1,2ai i bi b i a b -=-=+∴=-=,则()2212,12125a bi i a bi i +=-+∴+=-+=-+= D.考点:1、复数的运算;2、复数的模. 11.已知01a b <<<,则( )A .()()111b b a a ->-B .()()211bb a a ->- C .()()11a b a b +>+ D .()()11a ba b ->- 【答案】D 【解析】 【分析】根据指数函数的单调性,即当底数大于1时单调递增,当底数大于零小于1时单调递减,对选项逐一验证即可得到正确答案. 【详解】因为01a <<,所以011a <-<,所以()1xy a =-是减函数, 又因为01b <<,所以1b b >,2b b >, 所以()()111b b a a -<-,()()211bb a a -<-,所以A,B 两项均错; 又111a b <+<+,所以()()()111aaba b b +<+<+,所以C 错; 对于D ,()()()111abba ab ->->-,所以()()11aba b ->-, 故选D. 【点睛】这个题目考查的是应用不等式的性质和指对函数的单调性比较大小,两个式子比较大小的常用方法有:做差和0比,作商和1比,或者直接利用不等式的性质得到大小关系,有时可以代入一些特殊的数据得到具体值,进而得到大小关系.12.把函数2()sin f x x =的图象向右平移12π个单位,得到函数()g x 的图象.给出下列四个命题①()g x 的值域为(0,1] ②()g x 的一个对称轴是12x π=③()g x 的一个对称中心是1,32π⎛⎫⎪⎝⎭ ④()g x 存在两条互相垂直的切线 其中正确的命题个数是( ) A .1 B .2C .3D .4【答案】C 【解析】 【分析】由图象变换的原则可得11()cos 2262g x x π⎛⎫=--+ ⎪⎝⎭,由cos 2[1,1]6x π⎛⎫-∈- ⎪⎝⎭可求得值域;利用代入检验法判断②③;对()g x 求导,并得到导函数的值域,即可判断④. 【详解】由题,21cos 2()sin 2xf x x -==, 则向右平移12π个单位可得,1cos 21112()cos 22262x g x x ππ⎛⎫-- ⎪⎛⎫⎝⎭==--+ ⎪⎝⎭ cos 2[1,1]6x π⎛⎫-∈- ⎪⎝⎭Q ,()g x ∴的值域为[0,1],①错误;当12x π=时,206x π-=,所以12x π=是函数()g x 的一条对称轴,②正确;当3x π=时,226x ππ-=,所以()g x 的一个对称中心是1,32π⎛⎫⎪⎝⎭,③正确; ()sin 2[1,1]6g x x π⎛⎫'=-∈- ⎪⎝⎭,则1212,,()1,()1x x R g x g x ''∃∈=-=,使得12()()1g x g x ''⋅=-,则()g x 在1x x =和2x x =处的切线互相垂直,④正确.即②③④正确,共3个. 故选:C 【点睛】本题考查三角函数的图像变换,考查代入检验法判断余弦型函数的对称轴和对称中心,考查导函数的几何意义的应用.二、填空题:本题共4小题,每小题5分,共20分。
广东省广州市2019-2020学年高考数学一月模拟试卷含解析
广东省广州市2019-2020学年高考数学一月模拟试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.用一个平面去截正方体,则截面不可能是( ) A .正三角形 B .正方形C .正五边形D .正六边形【答案】C 【解析】试题分析:画出截面图形如图显然A 正三角形,B 正方形:D 正六边形,可以画出五边形但不是正五边形;故选C . 考点:平面的基本性质及推论.2.若()5211x a x ⎛⎫+- ⎪⎝⎭的展开式中的常数项为-12,则实数a 的值为( ) A .-2 B .-3 C .2 D .3【答案】C 【解析】 【分析】先研究511x ⎛⎫- ⎪⎝⎭的展开式的通项,再分()2x a +中,取2x 和a 两种情况求解.【详解】因为511x ⎛⎫- ⎪⎝⎭的展开式的通项为()5151r r r r T C x -+=-,所以()5211x a x ⎛⎫+- ⎪⎝⎭的展开式中的常数项为:()32320551112(1)0x C C x a a -+--=--=-,解得2a =, 故选:C. 【点睛】本题主要考查二项式定理的通项公式,还考查了运算求解的能力,属于基础题.3.某几何体的三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是( )A .203π B .6πC .103π D .163π 【答案】C 【解析】由三视图可知,该几何体是下部是半径为2,高为1的圆柱的一半,上部为底面半径为2,高为2的圆锥的一半,所以,半圆柱的体积为2112122V ππ=⨯⨯⨯=,上部半圆锥的体积为2211422233V ππ=⨯⨯⨯=,所以该几何体的体积为12410233V V V πππ=+=+=,故应选C . 4.已知双曲线()2222:10,0x y C a b a b-=>>的左,右焦点分别为12,F F ,O 为坐标原点,P 为双曲线在第一象限上的点,直线PO ,2PF 分别交双曲线C 的左,右支于另一点12,,3M N PF PF =若,且260MF N ∠=o ,则双曲线的离心率为( )A 5B .3C .2D .72【答案】D 【解析】 【分析】本道题结合双曲线的性质以及余弦定理,建立关于a 与c 的等式,计算离心率,即可. 【详解】结合题意,绘图,结合双曲线性质可以得到PO=MO ,而12F O F O =,结合四边形对角线平分,可得四边形12PF MF 为平行四边形,结合0260MF N ∠=,故01260F MF ∠=对三角形12F MF 运用余弦定理,得到,222121212122cos F M F M F F MF MF F MF +-=⋅⋅⋅∠而结合213PF PF =,可得12,3MF a MF a ==,122F F c =,代入上式子中,得到 2222943a a c a +-=,结合离心率满足c e a =,即可得出72c e a ==,故选D . 【点睛】本道题考查了余弦定理以及双曲线的性质,难度偏难.5.已知定义在R 上的奇函数()f x 和偶函数()g x 满足()()2x x f x g x a a -+=-+(0a >且1a ≠),若(2)g a =,则函数()22f x x +的单调递增区间为( )A .(1,1)-B .(,1)-∞C .(1,)+∞D .(1,)-+∞【答案】D 【解析】 【分析】根据函数的奇偶性用方程法求出(),()f x g x 的解析式,进而求出a ,再根据复合函数的单调性,即可求出结论. 【详解】依题意有()()2xxf xg x a a-+=-+, ①()()2()()--+-=-+=-+x x f x g x a a f x g x , ②①-②得(),()2-=-=x x f x a a g x ,又因为(2)g a =, 所以2,()22-==-x x a f x ,()f x 在R 上单调递增, 所以函数()22f x x +的单调递增区间为(1,)-+∞. 故选:D. 【点睛】本题考查求函数的解析式、函数的性质,要熟记复合函数单调性判断方法,属于中档题.6.函数2sin cos ()20x x xf x x =+在[2,0)(0,2]ππ-⋃上的图象大致为( ) A . B .C .D .【答案】A 【解析】 【分析】首先判断函数的奇偶性,再根据特殊值即可利用排除法解得; 【详解】解:依题意,22sin()()cos()sin cos ()()2020x x x x x xf x f x x x ----=+=+=-,故函数()f x 为偶函数,图象关于y 轴对称,排除C ; 而2()020f ππ=-<,排除B ;2(2)05f ππ=>,排除D.故选:A . 【点睛】本题考查函数图象的识别,函数的奇偶性的应用,属于基础题.7.为了加强“精准扶贫”,实现伟大复兴的“中国梦”,某大学派遣甲、乙、丙、丁、戊五位同学参加、、A B C三个贫困县的调研工作,每个县至少去1人,且甲、乙两人约定去同一个贫困县,则不同的派遣方案共有( ) A .24 B .36 C .48 D .64【答案】B 【解析】 【分析】根据题意,有两种分配方案,一是3:1:1,二是2:2:1,然后各自全排列,再求和. 【详解】当按照3:1:1进行分配时,则有133318C A =种不同的方案;当按照2:2:1进行分配,则有233318C A =种不同的方案. 故共有36种不同的派遣方案, 故选:B. 【点睛】本题考查排列组合、数学文化,还考查数学建模能力以及分类讨论思想,属于中档题. 8.设数列{}()*n a n N ∈的各项均为正数,前n 项和为nS ,212log 1log n n a a +=+,且34a =,则6S =( )A .128B .65C .64D .63【答案】D 【解析】 【分析】根据212log 1log n n a a +=+,得到212log l g 2o n n a a +=,即12n n a a +=,由等比数列的定义知数列{}n a 是等比数列,然后再利用前n 项和公式求6S . 【详解】因为212log 1log n n a a +=+, 所以212log l g 2o n n a a +=, 所以12n n a a +=,所以数列{}n a 是等比数列, 又因为34a =, 所以312414a a q ===,()()6616111263112a q S q-⨯-===--.故选:D 【点睛】本题主要考查等比数列的定义及等比数列的前n 项和公式,还考查了运算求解的能力,属于中档题. 9.已知函数()f x 满足()()11f x f x -=+,当1x ≥时,()2f x x x=-,则()}{21x f x +>=( )A .{3x x <-或}0x > B .{0x x <或}2x > C .{2x x <-或}0x > D .{2x x <或}4x >【答案】C 【解析】 【分析】简单判断可知函数关于1x =对称,然后根据函数()2f x x x =-的单调性,并计算210x xx ⎧-=⎪⎨⎪≥⎩,结合对称性,可得结果. 【详解】由()()11f x f x -=+, 可知函数()f x 关于1x =对称 当1x ≥时,()2f x x x=-, 可知()2f x x x=-在[)1,+∞单调递增 则2120x x xx ⎧-=⎪⇒=⎨⎪≥⎩ 又函数()f x 关于1x =对称,所以()01f = 且()f x 在(),1-∞单调递减,所以20x +<或22x +>,故2x <-或0x > 所以()}{21x f x +>={2x x <-或}0x > 故选:C 【点睛】本题考查函数的对称性以及单调性求解不等式,抽象函数给出式子的意义,比如:()()11f x f x -=+,()()110f x f x -++=,考验分析能力,属中档题.10.设2log 3a =,4log 6b =,0.15c -=,则( ) A .a b c >> B .b a c >>C .c a b >>D .c b a >>【答案】A 【解析】 【分析】先利用换底公式将对数都化为以2为底,利用对数函数单调性可比较,a b ,再由中间值1可得三者的大小关系. 【详解】()2log 31,2a =∈,()422log 6log 1,log 3b ==,()0.150,1c -=∈,因此a b c >>,故选:A.【点睛】本题主要考查了利用对数函数和指数函数的单调性比较大小,属于基础题.11.设α,β是方程210x x --=的两个不等实数根,记n nn a αβ=+(n *∈N ).下列两个命题( )①数列{}n a 的任意一项都是正整数; ②数列{}n a 存在某一项是5的倍数. A .①正确,②错误 B .①错误,②正确 C .①②都正确 D .①②都错误【答案】A 【解析】 【分析】利用韦达定理可得1αβ+=,1αβ=-,结合n nn a αβ=+可推出1n a +1n n a a -=+,再计算出11a =,23a =,从而推出①正确;再利用递推公式依次计算数列中的各项,以此判断②的正误. 【详解】因为α,β是方程210x x --=的两个不等实数根, 所以1αβ+=,1αβ=-,因为n nn a αβ=+,所以111n n n a αβ+++=+()()n n n n n n αβααβββααβ=+++-- ()()()11n n n n αβαβαβαβ--=++-+ ()()111n n n n n n a a αβαβ---=+++=+,即当3n ≥时,数列{}n a 中的任一项都等于其前两项之和, 又11a αβ=+=,()222223a αβαβαβ=+=+-=, 所以3214a a a =+=,4327a a a =+=,54311a a a =+=, 以此类推,即可知数列{}n a 的任意一项都是正整数,故①正确; 若数列{}n a 存在某一项是5的倍数,则此项个位数字应当为0或5, 由11a =,23a =,依次计算可知,数列{}n a 中各项的个位数字以1,3,4,7,1,8,9,7,6,3,9,2为周期, 故数列{}n a 中不存在个位数字为0或5的项,故②错误; 故选:A. 【点睛】本题主要考查数列递推公式的推导,考查数列性质的应用,考查学生的综合分析以及计算能力.12.过抛物线22(0)y px p =>的焦点作直线交抛物线于A B ,两点,若线段AB 中点的横坐标为3,且8AB =,则抛物线的方程是( )A .22y x =B .24y x =C .28y x =D .210y x =【答案】B 【解析】 【分析】利用抛物线的定义可得,12||||||22p pAB AF BF x x =+=+++,把线段AB 中点的横坐标为3,||8AB =代入可得p 值,然后可得出抛物线的方程. 【详解】设抛物线22(0)y px p =>的焦点为F,设点()()1122,,,A x y B x y ,由抛物线的定义可知()1212||||||22p pAB AF BF x x x x p =+=+++=++,线段AB 中点的横坐标为3,又||8AB =,86p ∴=+,可得2p =, 所以抛物线方程为24y x =. 故选:B. 【点睛】本题考查抛物线的定义、标准方程,以及简单性质的应用,利用抛物线的定义是解题的关键. 二、填空题:本题共4小题,每小题5分,共20分。
广东省广州市2019-2020学年高考数学四月模拟试卷含解析

广东省广州市2019-2020学年高考数学四月模拟试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.关于函数22tan ()cos 21tan xf x x x=++,下列说法正确的是( )A .函数()f x 的定义域为RB .函数()f x 一个递增区间为3,88ππ⎡⎤-⎢⎥⎣⎦ C .函数()f x 的图像关于直线8x π=对称D .将函数2y x =图像向左平移8π个单位可得函数()y f x =的图像 【答案】B 【解析】 【分析】化简到()24f x x π⎛⎫=+ ⎪⎝⎭,根据定义域排除ACD ,计算单调性知B 正确,得到答案.【详解】22tan ()cos 2sin 2cos 221tan 4x f x x x x x x π⎛⎫=+=+=+ ⎪+⎝⎭,故函数的定义域为,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭,故A 错误; 当3,88x ππ⎡⎤∈-⎢⎥⎣⎦时,2,224x πππ⎡⎤+∈-⎢⎥⎣⎦,函数单调递增,故B 正确;当4πx =-,关于8x π=的对称的直线为2x π=不在定义域内,故C 错误.平移得到的函数定义域为R ,故不可能为()y f x =,D 错误. 故选:B . 【点睛】本题考查了三角恒等变换,三角函数单调性,定义域,对称,三角函数平移,意在考查学生的综合应用能力.2.直线1y kx =+与抛物线C :24x y =交于A ,B 两点,直线//l AB ,且l 与C 相切,切点为P ,记PABV 的面积为S ,则S AB -的最小值为( ) A .94-B .274-C .3227-D .6427-【答案】D【解析】 【分析】设出,A B 坐标,联立直线方程与抛物线方程,利用弦长公式求得AB ,再由点到直线的距离公式求得P 到AB 的距离,得到PAB ∆的面积为S ,作差后利用导数求最值.【详解】设()11,A x y ,()22,B x y ,联立214y kx x y=+⎧⎨=⎩,得2440x kx --= 则124x x k +=,()21212242y y k x x k +=++=+则21244AB y y p k =++=+由24x y =,得24x y =12y x ⇒'= 设()00,P x y ,则012x k = 02x k ⇒=,20y k =则点P 到直线1y kx =+的距离1d =≥从而()21212S AB d k =⋅=+()()()22322141241S AB k k d d d -=++=-≥.令()3224f x x x =- ()()2681f x x x x ⇒-'=≥当413x ≤≤时,()0f x '<;当43x >时,()0f x '>故()min 464327f x f ⎛⎫==-⎪⎝⎭,即S AB -的最小值为6427- 本题正确选项:D 【点睛】本题考查直线与抛物线位置关系的应用,考查利用导数求最值的问题.解决圆锥曲线中的面积类最值问题,通常采用构造函数关系的方式,然后结合导数或者利用函数值域的方法来求解最值. 3.设函数()sin (0)5f x x πωω⎛⎫=+> ⎪⎝⎭,若()f x 在[0,2]π上有且仅有5个零点,则ω的取值范围为( ) A .1229,510⎡⎫⎪⎢⎣⎭ B .1229,510⎛⎤⎥⎝⎦ C .1229,510⎛⎫⎪⎝⎭ D .1229,510⎡⎤⎢⎥⎣⎦ 【答案】A 【解析】 【分析】由02x π≤≤求出5x ωπ+范围,结合正弦函数的图象零点特征,建立ω不等量关系,即可求解. 【详解】当[0,2]x πÎ时,,2555x πππωπω⎡⎤+∈+⎢⎥⎣⎦, ∵()f x 在[]0,2π上有且仅有5个零点, ∴5265ππωππ≤+<,∴1229510ω≤<. 故选:A. 【点睛】本题考查正弦型函数的性质,整体代换是解题的关键,属于基础题.4.如图是国家统计局于2020年1月9日发布的2018年12月到2019年12月全国居民消费价格的涨跌幅情况折线图.(注:同比是指本期与同期作对比;环比是指本期与上期作对比.如:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比)根据该折线图,下列结论错误的是( )A .2019年12月份,全国居民消费价格环比持平B .2018年12月至2019年12月全国居民消费价格环比均上涨C .2018年12月至2019年12月全国居民消费价格同比均上涨D .2018年11月的全国居民消费价格高于2017年12月的全国居民消费价格 【答案】D 【解析】 【分析】先对图表数据的分析处理,再结简单的合情推理一一检验即可 【详解】由折线图易知A 、C 正确;2019年3月份及6月份的全国居民消费价格环比是负的,所以B 错误;设2018年12月份,2018年11月份,2017年12月份的全国居民消费价格分别为,,a b c ,由题意可知,b a =,1.9%a c c -=,则有1 1.9%ac a b =<=+,所以D 正确.故选:D 【点睛】此题考查了对图表数据的分析处理能力及进行简单的合情推理,属于中档题.5.已知双曲线221:110x y C m m +=-与双曲线222:14y C x -=有相同的渐近线,则双曲线1C 的离心率为( )A .54B .5CD 【答案】C 【解析】 【分析】由双曲线1C 与双曲线2C 有相同的渐近线,列出方程求出m 的值,即可求解双曲线的离心率,得到答案. 【详解】由双曲线221:110x y C m m +=-与双曲线222:14y C x -=有相同的渐近线,2=,解得2m =,此时双曲线221:128x y C -=,则曲线1C 的离心率为c e a ===C . 【点睛】本题主要考查了双曲线的标准方程及其简单的几何性质的应用,其中解答中熟记双曲线的几何性质,准确运算是解答的关键,着重考查了运算与求解能力,属于基础题.6.在平面直角坐标系中,经过点P ,渐近线方程为y =的双曲线的标准方程为( )A .22142-=x yB .221714x y -=C .22136x y -=D .221147y x -=【答案】B 【解析】 【分析】根据所求双曲线的渐近线方程为y =,可设所求双曲线的标准方程为222x y -=k .再把点(代入,求得 k 的值,可得要求的双曲线的方程.【详解】∵双曲线的渐近线方程为y =∴设所求双曲线的标准方程为222x y -=k .又(在双曲线上,则k=16-2=14,即双曲线的方程为222x y 14-=,∴双曲线的标准方程为22x y 1714-=故选:B 【点睛】本题主要考查用待定系数法求双曲线的方程,双曲线的定义和标准方程,以及双曲线的简单性质的应用,属于基础题.7.已知椭圆C :()222210x y a b a b+=>>的左,右焦点分别为1F ,2F ,过1F 的直线交椭圆C 于A ,B 两点,若290ABF ∠=︒,且2ABF V 的三边长2BF ,AB ,2AF 成等差数列,则C 的离心率为( )A .12B .3C D .2【答案】C 【解析】 【分析】根据等差数列的性质设出2BF ,AB ,2AF ,利用勾股定理列方程,结合椭圆的定义,求得21BF a BF ==.再利用勾股定理建立,a c 的关系式,化简后求得离心率.【详解】由已知2BF ,AB ,2AF 成等差数列,设2BF x =,AB x d =+,22AF x d =+.由于290ABF ∠=︒,据勾股定理有22222BF AB AF +=,即()()2222x x d x d ++=+,化简得3x d =; 由椭圆定义知2ABF V 的周长为233124x x d x d x d d a ++++=+==,有3a d =,所以x a =,所以21BF a BF ==;在直角21BF F V 中,由勾股定理,2224a c =,∴离心率2e =. 故选:C 【点睛】本小题主要考查椭圆离心率的求法,考查椭圆的定义,考查等差数列的性质,属于中档题.8.设非零向量a r ,b r ,c r,满足||2b =r ,||1a =r ,且b r 与a r 的夹角为θ,则“||b a -=r r 是“3πθ=”的( ). A .充分非必要条件 B .必要非充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】C利用数量积的定义可得θ,即可判断出结论. 【详解】解:||b a -=r r ∴2223b a a b +-=r r r r g ,221221cos 3θ∴+-⨯⨯⨯=,解得1cos 2θ=,[0θ∈,]π,解得3πθ=,∴ “||b a -=r r 是“3πθ=”的充分必要条件.故选:C . 【点睛】本题主要考查平面向量数量积的应用,考查推理能力与计算能力,属于基础题.9.已知抛物线2:8C y x =的焦点为F ,A B 、是抛物线上两个不同的点,若||||8AF BF +=,则线段AB的中点到y 轴的距离为( ) A .5 B .3C .32D .2【答案】D 【解析】 【分析】由抛物线方程可得焦点坐标及准线方程,由抛物线的定义可知12||||228AF BF x x +=+++=,继而可求出124x x +=,从而可求出AB 的中点的横坐标,即为中点到y 轴的距离. 【详解】解:由抛物线方程可知,28p =,即4p =,()2,0F ∴.设()()1122,,,A x y B x y 则122,2AF x BF x =+=+,即12||||228AF BF x x +=+++=,所以124x x +=. 所以线段AB 的中点到y 轴的距离为1222x x +=. 故选:D. 【点睛】本题考查了抛物线的定义,考查了抛物线的方程.本题的关键是由抛物线的定义求得A B 、两点横坐标的和.10.已知双曲线()2222:10,0x y C a b a b-=>>的一条渐近线经过圆22:240E x y x y ++-=的圆心,则双曲线C 的离心率为( )A B .CD .2【答案】B求出圆心,代入渐近线方程,找到a b 、的关系,即可求解. 【详解】 解:()1,2E -,()2222:10,0x y C a b a b-=>>一条渐近线b y x a =-()21ba=-⨯-,2a b =()222222+b ,2,c a c a a e ==+=故选:B 【点睛】利用a b 、的关系求双曲线的离心率,是基础题.11.已知某批零件的长度误差(单位:毫米)服从正态分布()20,3N ,从中随机取一件,其长度误差落在区间(3,6)内的概率为( )(附:若随机变量ξ服从正态分布()2,N μσ,则()68.26%P μσξμσ-<<+=,()2295.44%P μσξμσ-<<+=.)A .4.56%B .13.59%C .27.18%D .31.74%【答案】B 【解析】 试题分析:由题意13368.26%6695.44%3695.44%68.26%13.59%2P P P (<<),(<<),(<<)().ξξξ-=-=∴=-=故选B . 考点:正态分布12.已知集合{}0,1,2,3A =,{|22}B x x =-≤≤,则A B I 等于( )A .{}012,, B .{2,1,0,1,2}-- C .{}2,1,0,1,2,3-- D .{}12, 【答案】A 【解析】 【分析】进行交集的运算即可. 【详解】{0A =Q ,1,2,3},{|22}B x x =-剟, {0A B ∴=I ,1,2}.故选:A . 【点睛】本题主要考查了列举法、描述法的定义,考查了交集的定义及运算,考查了计算能力,属于基础题. 二、填空题:本题共4小题,每小题5分,共20分。
广州市铁一中学2025届高考仿真卷数学试题含解析

广州市铁一中学2025届高考仿真卷数学试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭,1,03A ⎛⎫ ⎪⎝⎭为()f x 图象的对称中心,若图象上相邻两个极值点1x ,2x 满足121x x -=,则下列区间中存在极值点的是( ) A .,06π⎛⎫-⎪⎝⎭B .10,2⎛⎫ ⎪⎝⎭C .1,3π⎛⎫⎪⎝⎭D .,32ππ⎛⎫ ⎪⎝⎭2.如图,这是某校高三年级甲、乙两班在上学期的5次数学测试的班级平均分的茎叶图,则下列说法不正确的是( )A .甲班的数学成绩平均分的平均水平高于乙班B .甲班的数学成绩的平均分比乙班稳定C .甲班的数学成绩平均分的中位数高于乙班D .甲、乙两班这5次数学测试的总平均分是1033.函数2()ln(1)x xe ef x x --=+在[3,3]-的图象大致为( ) A . B .C .D .4.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则A B =A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,75.《九章算术》中将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的外接球的表面积为( )A .4πB .8πC .642+D .83π6.已知函数()()2,211,22xa x x f x x ⎧-≥⎪=⎨⎛⎫-<⎪ ⎪⎝⎭⎩,满足对任意的实数12x x ≠,都有()()12120f x f x x x -<-成立,则实数a 的取值范围为( ) A .()1,+∞B .13,8⎛⎤-∞ ⎥⎝⎦C .13,8⎛⎫-∞ ⎪⎝⎭D .13,8⎛⎫+∞⎪⎝⎭7.一个算法的程序框图如图所示,若该程序输出的结果是34,则判断框中应填入的条件是( )A .5?i >B .5?i <C .4?i >D .4?i <8.在ABC 中,3AB =,2AC =,60BAC ∠=︒,点D ,E 分别在线段AB ,CD 上,且2BD AD =,2CE ED =,则BE AB ⋅=( ). A .3-B .6-C .4D .99.如图,在ABC ∆中,点Q 为线段AC 上靠近点A 的三等分点,点P 为线段BQ 上靠近点B 的三等分点,则PA PC +=( )A .1233BA BC + B .5799BA BC + C .11099BA BC + D .2799BA BC + 10.若干年前,某教师刚退休的月退休金为6000元,月退休金各种用途占比统计图如下面的条形图.该教师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该教师的月退休金为( ).A .6500元B .7000元C .7500元D .8000元11.设实数满足条件则的最大值为( ) A .1B .2C .3D .412.若不等式22ln x x x ax -+对[1,)x ∈+∞恒成立,则实数a 的取值范围是( ) A .(,0)-∞B .(,1]-∞C .(0,)+∞D .[1,)+∞二、填空题:本题共4小题,每小题5分,共20分。
2019-2020学年广东省广州市铁一中学新高考化学模拟试卷含解析

2019-2020学年广东省广州市铁一中学新高考化学模拟试卷一、单选题(本题包括15个小题,每小题4分,共60分.每小题只有一个选项符合题意)1.X、Y、Z、W是四种短周期主族元素,X原子最外层电子数是次外层的2倍,Y是地壳中含量最多的元素,Z元素在短周期中金属性最强,W与Y位于同一主族。
下列叙述正确的是A.原子半径:r(W)>r(Z)>r(Y)>r(X)B.Y的简单气态氢化物的热稳定性比W的强C.X的最高价氧化物对应水化物的酸性比W的强D.Y与Z形成的两种常见化合物化学键类型相同【答案】B【解析】【分析】X、Y、Z、W是短周期主族元素,X原子最外层电子数是次外层的两倍,最外层电子数不超过8个,则其K层为次外层,故X是C元素;Y元素在地壳中的含量最高的元素,则Y是O元素;W与Y属于同一主族,则为W为S元素;Z元素在短周期中金属性最强,则Z是Na元素;据此答题。
【详解】根据分析,X是C元素,Y是O元素,Z是Na元素,W为S元素;A.X、Y为第二周期,Z、W为第三周期,则X、Y原子半径小于Z、W,同周期元素原子半径随核电荷数增大半径减小,原子半径:r(Z)>r(W)>r(X)>r(Y),故A错误B.非金属性越强,简单气态氢化物的稳定性越强,非金属性:Y>W,则Y的简单气态氢化物的热稳定性比W的强,故B正确;C.非金属性越强,最高价氧化物对应水化物的酸性越强,非金属性:X<W,X的最高价氧化物对应水化物的酸性比W的弱,故C错误;D.Y是O元素,Z是Na元素,Y与Z形成的两种化合物为Na2O、Na2O2,含有的阴阳离子数目之比均为1:2,前者只含离子键,后者含有离子键、共价键,故D错误;答案选B。
【点睛】非金属性越强,简单气态氢化物的稳定性越强,最高价氧化物对应水化物的酸性越强。
2.短周期元素W、X、Y、Z的原子序数依次增加,Y和W、Y和Z分别相邻,且W、Y和Z三种元素的原子最外层电子数之和为19,x原子的电子层数与最外层电子数相等。
广东省广州市铁一中学2024届高三上学期一模数学试题(高频考点版)

一、单选题二、多选题三、填空题四、解答题1. 已知若关于的方程恰有两个不同的实数解,则实数k 的取值范围是( )A.B.C.D.2. 下列函数中,在上是偶函数,且在上为单调递增函数的是A.B.C.D.3. 已知在复平面内对应的点在第四象限,则实数的取值范围是( )A.B.C.D.4. 在长方体中,,,为棱的中点,动点满足,则点的轨迹与长方体的面的交线长等于( )A.B .C.D.5. 已知集合,,则( )A.B.C.D.6. 函数的增区间是( )A.B.C.D.7. 将函数向右平移个单位长度得到函数,若函数在上的值域为,则实数的取值可以是( )A.B.C.D.8. 已知椭圆的左、右焦点分别为,点在上,且的最大值为3,最小值为1,则( )A .椭圆的离心率为B .的周长为4C .若,则的面积为3D .若,则9. 88键钢琴从左到右各键的音的频率组成一个递增的等比数列.若中音A (左起第49个键)的频率为,钢琴上最低音的频率为,则左起第61个键的音的频率为___________.10. 设是定义在上的偶函数,对任意的,都有,且当时,.若在区间内关于的方程,恰有3个不同的实数根,则实数的取值范围是__________.11. 设的内角,,所对的边分别为,,,若,且的面积等于,则边上的中线的长的最小值是______.12. (1)函数的导数是________;(2)函数的导数是________;(3)函数的导数是________.广东省广州市铁一中学2024届高三上学期一模数学试题(高频考点版)广东省广州市铁一中学2024届高三上学期一模数学试题(高频考点版)13. 已知x,y,m,,则试用向量方法求的最值.14. 已知定义域为,对任意都有,当时,,.(1)试判断在上的单调性,并证明;(2)解不等式:.15. 解关于x的不等式ax2﹣(a+1)x+1<0(a>0).16. 设集合A={x|ax2+x+1=0},构成集合A的元素是什么?。
广东省广州市市铁一中学2021-2022学年高三数学理模拟试卷含解析

广东省广州市市铁一中学2021-2022学年高三数学理模拟试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知非零常数α是函数y=x+tanx的一个零点,则(α2+1)(1+cos2α)的值为()A.2 B.C.D.参考答案:A【考点】函数与方程的综合运用;二倍角的余弦.【分析】由题意可得,tanα=﹣α,利用二倍角公式可得(α2+1)?(cos2α+1)=(1+tan2α)(2cos2α),化简可求.【解答】解:由题意非零常数α是函数y=x+tanx的一个零点,可得,tanα=﹣α,可得(α2+1)?(1+cos2α)=(1+tan2α)(2cos2α)=2(cos2α)×(+1)=2.故选:A.2. 若P(2,﹣1)为圆(x﹣1)2+y2=25的弦AB的中点,则直线AB的方程是()A. x﹣y﹣3=0 B.2x+y﹣3=0 C.x+y﹣1=0 D.2x﹣y﹣5=0参考答案:A略3. 若,则()A. B. C. D.参考答案:A【分析】求出共轭复数,根据复数运算法则即可得解.【详解】,,.故选:A【点睛】此题考查复数的概念辨析和基本运算,关键在于熟练掌握复数的运算法则,根据法则求解.4. “sinθ?cosθ>0”是“θ是第一象限角”的()A.充分必要条件B.充分非必要条件C.必要非充分条件D.非充分非必要条件参考答案:C略5. 设点P是曲线上的任意一点,P点处切线倾斜角为α,则角α的取值范围是( )A.B.C.D.参考答案:C【考点】利用导数研究曲线上某点切线方程;直线的倾斜角.【专题】计算题.【分析】求出曲线解析式的导函数,根据完全平方式大于等于0求出导函数的最小值,由曲线在P点切线的斜率为导函数的值,且直线的斜率等于其倾斜角的正切值,从而得到tanα的范围,由α的范围,求出α的范围即可.【解答】解:∵y′=3x2﹣≥﹣,∴tanα≥﹣,又∵0≤α≤π,∴0≤α<或.则角α的取值范围是[0,)∪[,π).故选C.【点评】考查学生会利用导数求曲线上过某点切线方程的斜率,会利用切线的斜率与倾斜角之间的关系k=tanα进行求解.6. 命题“使得”的否定是 ( )A.均有B.均有C.使得D.均有参考答案:B7. 已知i是虚数单位,则()A. 2+iB. 2-iC. 1+2iD. 1-2i参考答案:D略8. 已知点O是边长为1的等边的中心,则= ()A. B. C. D.参考答案:D9. 已知集合,,则( )A.B. C. D.参考答案:C10. 若集合A={x|3+2x﹣x2>0},集合B={x|2x<2},则A∩B等于()A.(1,3)B.(﹣∞,﹣1)C.(﹣1,1)D.(﹣3,1)参考答案:C【考点】1E:交集及其运算.【分析】分别求出关于集合A、B中x的范围,取交集即可.【解答】解:∵集合A={x|3+2x﹣x2>0}={x|﹣1<x<3},集合B={x|2x<2}={x|x<1},则A∩B={x|﹣1<x<1},故选:C.二、填空题:本大题共7小题,每小题4分,共28分11. 已知,求(1)的值;(2)的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知 a i 1 b(1 i) (其中 i 为虚数单位, a, b R),则 a 等于 1i 2
(A) 2
(B) 2
(C) 1
(D) 1 2
(2)设非负实数 x,
y
满足约束条件
x y 3≤ 0, 2x y 4≤ 0.
参考公式:
• 如果事件 A,B 互斥,那么 P(A B) P(A) P(B) .
• 柱体的体积公式V Sh . 其中 S 表示 柱体的底面积, h 表示柱体的高.
• 如果事件 A,B 相互独立,那么 P(A B) P(A) P(B) .
• 球的体积公式V 4 R3 . 其中 R 表示 3
(Ⅰ)求证 数列{ 1 } 为等差数列; an 3
(Ⅱ)求数列{an} 的通项公式;
(Ⅲ)设 bn
an (n 1)2
,求数列{bn} 的前 n
项和 Tn .
(19)(本小题满分 14 分)
如图,椭圆 C :
x2 a2
y2 b2
1( a b 0 )的左、右焦点
分别为
F1 、
F2
,离心率
e
1 2
b 0) 上一点 P 作直线 PA,
PB 交双曲线于 A,
B 两点,且斜率分别为
k1, k2 ,若直线 AB 过原点, k1 k2 2 ,则双曲线的离心率 e 等于
(A) 3
(B) 3
(C) 6 2
(D) 3 2
(5)如图,在△ ABC 中, AD 2 AC , BP 1 BD ,若 AP AB AC ,则 的值为
D
且 PAB 过 O 点,若 PB 10 , PD 8 ,给出下列四个结论
C
① CD 3 ;② BC 5 ;③ BD 2AC ;④ CBD 30 . B
O•
A
P
则所有正确结论的序号是
(A)①③
(B)①④
(C)①②③
(D)①③④
(8)关于 x 的方程 (x2 1)2 3 x2 1 2 0 的不相同实根的个数是
高考模拟数学试卷
第Ⅰ卷 选择题(共 40 分)
注意事项
1. 答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上。 2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后, 再选涂其他答案标号。答在试卷上的无效。 3. 本卷共 8 小题,每小题 5 分,共 40 分。
3
3
C
(A) 8 9
(B) 4 9
D P
A
B
(C) 8 3
(D) 4 3
(6)函数 f (x) 2 x1 m 的图象与 x 轴有交点的充要条件为
(A) m (0, 1) (B) m (0, 1] (C) m [0, 1]
(D) m [1, 0)
(7)如图,已知圆 O 半径是 3 , PAB 和 PCD 是圆 O 的两条割线, Nhomakorabea(A) 3
(B) 4
(C) 5
(D) 8
第Ⅱ卷 非选择题(共 110 分)
注意事项
1. 用钢笔或圆珠笔直接答在答题卷上,答在本试卷上的无效。 2. 本卷共 12 小题,共 110 分。
二、填空题:本大题共 6 小题,每小题 5 分,共 30 分.把答案填在答题卷上.
(9)一个几何体的三视图如图所示(单位 cm),则该几何体
已知函数 f (x) sin(2x ) sin(2x ) a cos2 x b , x R,且 f (0) f ( ) 1.
3
3
4
(Ⅰ)求 a, b 的值及 f (x) 的最小正周期;
(Ⅱ)求函数 f (x) 在区间 [ , ]上的最大值和最小值. 44
(16)(本小题满分 13 分) 盒子中装有“黑桃、红桃、梅花、方块” 4 种不同花色的扑克牌各 3 张,从中一次任取 3 张牌,每张牌
C
到直线
l
距离为
.
( 14 ) 已 知 Sn 3 7 13 (2n 2n 1) , S10 a b c , 其 中 a, b, c N*, 则 a b c 的 最 小 值
为
.
三、解答题:本大题共 6 小题,共 80 分.解答应写出文字说明,证明过程或演算步骤.
(15)(本小题满分 13 分)
2
的体积为
cm³.
(10)抛物线 y x2 与直线 2x y 3 0 所围成图形的面积
2
正视图
4
侧视图
等于
.
(11)若函数
f (x) loga (ax2
x) 在[1 , 2
3] 上单调递增,则实
数 a 的取值范围是
.
4
俯视图
(12)在△ ABC 中,内角 A, B, C 所对的边分别是 a, b, c .
已知 b c 12, C 120 , sin B 5 3 ,则 cos A cos B 的值为
.
14
(13)在极坐标系中,圆 C 的方程为 2 2 sin( ) ,以极点为坐标原点,极轴为 x 轴的正半轴建立平面直 4
角坐标系,直线
l
的参数方程为
x y
t 1 ( 2t 1
t
为参数),则圆心
被取出的可能性都相等. (Ⅰ)求取出的 3 张牌中的花色互不相同的概率; (Ⅱ)用 X 表示取出的 3 张牌中花色是“黑桃”的张数,求随机变量 X 的分布列和数学期望.
(17)(本小题满分 13 分)理科
如图,在直三棱柱 ABC A1B1C1 中, AB BC 2BB1 , ABC 90 , D 为 BC 的中点.
.过
F2
的直线交椭圆
C
于
A
、
y A
B 两点,且△ ABF1 的周长为 8 . (Ⅰ)求椭圆 C 的方程;
O
F1 F2
x
B
(Ⅱ)若直线 l : y kx m 与椭圆 C 相切于 P 点,且与直线 x 4 相交于 Q 点,求证直线 PF1 垂直于直线
则 z 2x 3y 的最大值为
(A) 4
(B) 8
(C) 9
(3)阅读右面的程序框图,当该程序运行后输出的 x 值是
(A) 2
(B) 5
(C) 1 3
(D) 5
(D)12
开始
x 2,i 1
i 10?
否 x 3x
1 x
i i 1
是
输出x 结束
(4)过双曲线
x2 a2
y2 b2
1 (a 0,
(Ⅰ)求证 A1B // 平面 ADC1 ;
B1
C1
E
(Ⅱ)求二面角 C AD C1 的余弦值;
(Ⅲ)若 E 为 A1B1 的中点,求 AE 与 DC1 所成的角. A1
B
D
C
A
(18)(本小题满分 13 分)
已知数列{an} 满足 a1 6 , an1 an 6an1 9 0 , n N*且 n ≥ 2 .
