高中数学线面角与线线角例题、习题-学生

合集下载

高中数学必修2立体几何专题线面角典型例题求法总结

线面角的求法1．直接法：平面的斜线与斜线在平面内的射影所成的角即为直线与平面所成的角。

通常是解由斜线段，垂线段，斜线在平面内的射影所组成的直角三角形，垂线段是其中最重要的元素，它可以起到联系各线段的作用。

例1 （如图1 ）四面体ABCS 中，SA,SB,SC 两两垂直，∠SBA=45°, ∠SBC=60°, M 为 AB 的中点，求（1）BC 与平面SAB 所成的角。

（2）SC 与平面ABC 所成的角。

BMHSCA解:（1） ∵SC ⊥SB,SC ⊥SA,图1∴SC ⊥平面SAB 故 SB 是斜线BC 在平面SAB 上的射影， ∴∠SBC 是直线BC 与平面SAB 所成的角为60°。

（2）连结SM,CM ，则SM ⊥AB,又∵SC ⊥AB,∴AB ⊥平面SCM, ∴面ABC ⊥面SCM过S 作SH ⊥CM 于H, 则SH ⊥平面ABC ∴CH 即为 SC 在面ABC 内的射影。

∠SCH 为SC 与平面ABC 所成的角。

sin ∠SCH=SH ／SC∴SC 与平面ABC 所成的角的正弦值为√7／7（“垂线”是相对的，SC 是面 SAB 的垂线，又是面 ABC 的斜线. 作面的垂线常根据面面垂直的性质定理，其思路是：先找出与已知平面垂直的平面，然后一面内找出或作出交线的垂线，则得面的垂线。

） 2. 利用公式sin θ=h ／ι其中θ是斜线与平面所成的角， h 是垂线段的长，ι是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可用三棱锥的体积自等来求垂线段的长。

例2 （如图2）长方体ABCD-A 1B 1C 1D 1 , AB=3 ,BC=2, A 1A= 4 ，求AB 与面 AB 1C 1D 所成的角。

A 1C 1D 1H4C123BAD解：设点 B 到AB 1C 1D 的距离为h ，∵V B ﹣AB 1C 1=V A ﹣BB 1C 1∴1／3 S △AB 1C 1·h= 1／3 S △BB 1C 1·AB，易得h=12／5 ，设AB 与面 A B 1C 1D 所成的角为θ,则sin θ=h ／AB=4／5，∴AB 与面AB 1C 1D 所成的角为arcsin0.83. 利用公式cos θ=cos θ1·cosθ2（如图3）若 OA 为平面的一条斜线，O 为斜足，OB 为OA 在面α内的射影，OC 为面α内的一条直线，其中θ为OA 与OC 所成的角，B αOAC图3θ1为OA 与OB 所成的角，即线面角，θ2为OB 与OC 所成的角，那么 cos θ=cos θ1·cosθ2，它揭示了斜线和平面所成的角是这条斜线和这个平面内的直线所成的一切角中最小的角（常称为最小角定理）1．平面的斜线和平面所成的角：已知，如图，AO 是平面α的斜线，A 是斜足，OB 垂直于平面α，B 为垂足，则直线AB 是斜线在平面α内的射影。

高考数学一轮复习全套课时作业7-6-1线线角与线面角

题组层级快练7.6.1线线角与线面角一、单项选择题1．(2021·宁夏银川高级中学)在各棱长均相等的直三棱柱ABC －A 1B 1C 1中，已知M 是棱BB 1的中点，N 是棱AC 的中点，则异面直线A 1M 与BN 所成角的正切值为()A.3B ．1C.63D.222．已知直四棱柱ABCD －A 1B 1C 1D 1中，底面ABCD 为正方形，AA 1＝2AB ，E 为AA 1的中点，则异面直线BE 与CD 1所成角的余弦值为()A.1010B.15C.31010D.353.(2021·河北辛集中学月考)如图所示，在长方体ABCD －A 1B 1C 1D 1中，AB ＝BC ＝2，AA 1＝1，则BC 1与平面BB 1D 1D 所成角的正弦值为()A.63B.255C.155D.1054．(2020·福建厦门二模)一副三角板由一块有一个内角为60°的直角三角形和一块等腰直角三角形组成，如图所示，∠B ＝∠F ＝90°，∠A ＝60°，∠D ＝45°，BC ＝DE.现将两块三角板拼接在一起，取BC 中点O 与AC 中点M ，则下列直线与平面OFM 所成的角不为定值的是()A ．ACB ．AFC ．BFD ．CF5.(2021·湖南、江西十四校联考)如图，已知棱长为2的正方体ABCD －A 1B 1C 1D 1，点E 为线段CD 1的中点，则直线AE 与平面A 1BCD 1所成角的正切值为()A.22B.12C.32D.26．(2021·四川雅安期末)如图，将矩形ABCD 沿对角线BD 把△ABD 折起，使点A 移到点A 1处，且A 1在平面BCD 上的射影O 恰好在CD 上，则BC 与A 1D 所成角是()A ．30°B ．45°C ．60°D ．90°7．(2021·河北示范性高中联合体3月联考)正方体ABCD －A 1B 1C 1D 1的棱上到直线A 1B 与CC 1的距离相等的点有3个，记这3个点分别为E ，F ，G ，则直线AC 1与平面EFG 所成角的正弦值为()A.2613B.22613C.27839D.478398．(2021·保定模拟)在直三棱柱ABC －A 1B 1C 1中，底面是等腰直角三角形，∠ACB ＝90°，侧棱AA 1＝2，D ，E 分别是CC 1与A 1B 的中点，点E 在平面ABD 上的射影是△ABD 的重心G.则A 1B 与平面ABD 所成角的余弦值是()A.2 3B.73C.32D.37二、多项选择题9.(2021·山东青岛期末)如图，正方体ABCD－A1B1C1D1的棱长为1，则下列四个结论正确的是()A．直线BC与平面ABC1D1所成的角为π4B．点C到平面ABC1D1的距离为22C．异面直线D1C与BC1所成的角为π4D．三棱柱AA1D1－BB1C1外接球的半径为32三、填空题与解答题10．(2018·课标全国Ⅱ)已知圆锥的顶点为S，母线SA，SB所成角的余弦值为78.SA与圆锥底面所成角为45°.若△SAB的面积为515，则该圆锥的侧面积为________．11．(2021·河北承德二中期末)已知四棱锥P－ABCD的底面是菱形，∠BAD＝60°，PD⊥平面ABCD，且PD＝AB，点E是棱AD的中点，F在棱PC上．若PF∶FC＝1∶2，则直线EF与平面ABCD所成角的正弦值为________．12.(2021·鲁西部分重点中学期末)已知四棱锥P－ABCD的底面ABCD是菱形，∠ADC＝120°，AD的中点M是顶点P在底面ABCD的射影，N是PC的中点．(1)求证：平面MPB⊥平面PBC；(2)若MP＝MC，求直线BN与平面PMC所成角的正弦值．13．(2021·山东德州模拟)如图，P－ABC是一个三棱锥，AB是圆的直径，C是圆上的点，PC垂直圆所在的平面，D，E分别是棱PB，PC的中点．(1)求证：DE⊥平面PAC；(2)若二面角A－DE－C是45°，AB＝PC＝4，求AE与平面ACD所成角的正弦值．14.(2020·浙江)如图，在三棱台ABC－DEF中，平面ACFD⊥平面ABC，∠ACB＝∠ACD＝45°，DC＝2BC.(1)证明：EF⊥DB；(2)求直线DF与平面DBC所成角的正弦值．7.6.1线线角与线面角参考答案1．答案C解析本题考查异面直线所成角的正切值的求法．设直三棱柱ABC －A 1B 1C 1的棱长为2，如图所示，以A 为原点，AC 所在直线为y 轴，AA 1所在直线为z 轴，建立空间直角坐标系，则A 1(0，0，2)，M(3，1，1)，B(3，1，0)，N(0，1，0)，则A 1M →＝(3，1，－1)，BN →＝(－3，0，0)．设异面直线A 1M 与BN 所成角为θ，则cos θ＝|A 1M →·BN →||A 1M →||BN →|＝35×3＝155，∴sin θ＝1－cos 2θ＝105，∴tan θ＝sin θcos θ＝63.∴异面直线A 1M 与BN 所成角的正切值为63.故选C.2．答案C解析以D 为坐标原点建立如图所示的空间直角坐标系．设AA 1＝2AB ＝2，则B(1，1，0)，E(1，0，1)，C(0，1，0)，D 1(0，0，2)．∴BE →＝(0，－1，1)，CD 1→＝(0，－1，2)．∴cos 〈BE →，CD 1→〉＝1＋22×5＝31010.3.答案D解析本题考查线面角的计算．如图所示，在平面A 1B 1C 1D 1内过点C 1作B 1D 1的垂线，垂足为E ，连接BE.1E ⊥B 1D 1，1E ⊥BB 1，1D 1∩BB 1＝B 1，得C 1E ⊥平面BDD 1B 1，∴∠C 1BE 的正弦值即为所求．∵BC 1＝22＋12＝5，C 1E ＝2×222＝2，∴sin ∠C 1BE ＝C 1E BC 1＝25＝105.4．答案B解析本题考查直线与平面垂直的判定定理，直线与平面所成角．因为O ，M 分别为BC ，AC 的中点，所以OM ∥AB ，所以OM ⊥BC.又OF ⊥BC ，且OM ∩OF ＝O ，所以BC ⊥平面OMF ，所以BF ，CF 与平面OFM 所成的角分别为∠BFO 和∠CFO ，它们相等，均为45°.根据直线与平面所成角的定义知，AC 与平面OFM 所成的角为∠CMO ＝∠CAB ＝60°.故只有AF 与平面OFM 所成的角不为定值．5.答案A解析连接AB 1，AB 1与A 1B 交于点F ，由于AF ⊥A 1B ，AF ⊥BC ，且A 1B ∩BC ＝B ，所以AF ⊥平面A 1BCD 1.连接EF ，则∠AEF 是直线AE 与平面A 1BCD 1所成角，tan ∠AEF ＝AF EF ＝22.故选A.6．答案D解析本题主要考查异面直线所成角及线面垂直的判定与性质．因为A 1在平面BCD 上的射影O 恰好在CD 上，所以A 1O ⊥平面BCD.因为BC ⊂平面BCD ，所以A 1O ⊥BC.又因为BC ⊥CD ，A 1O ∩CD ＝O ，所以BC ⊥平面A 1CD.又A 1D ⊂平面A 1CD ，所以BC ⊥A 1D ，故BC 与A 1D 所成的角为90°.故选D.7．答案D解析正方体ABCD －A 1B 1C 1D 1的棱上到直线A 1B 与CC 1的距离相等的点分别为D 1，BC 的中点，B 1C 1的四等分点(靠近B 1)，不妨设D 1与G 重合，BC 的中点为E ，B 1C 1的四等分点(靠近B 1)为F.以D 为坐标原点，建立空间直角坐标系D －xyz ，如图．设AB ＝2，则E(1，2，0)，2，G(0，0，2)，A(2，0，0)，C 1(0，2，2)，从而EF →0，GF →2，AC 1→＝(－2，2，2)．设平面EFG 的法向量为n ＝(x ，y ，z)·EF →＝0，·GF →＝0，＋2z ＝0，＋2y ＝0，令x ＝4，得n ＝(4，－3，－1)．设直线AC 1与平面EFG 所成角为θ，则sin θ＝|cos 〈n ，AC 1→〉|＝|n ·AC 1→||n |·|AC 1→|＝47839.故选D.8．答案B解析以C 为坐标原点，CA 所在直线为x 轴，CB 所在直线为y 轴，CC 1所在直线为z 轴，建立空间直角坐标系如图，设CA ＝CB ＝a ，则A(a ，0，0)，B(0，a ，0)，A 1(a ，0，2)，D(0，0，1)，∴，a 2，，a 3，GE →，a 6，BD →＝(0，－a ，1)，∵点E 在平面ABD 上的射影是△ABD 的重心G ，∴GE →⊥平面ABD ，∴GE →·BD →＝0，解得a ＝2.∴GE →，13，BA 1→＝(2，－2，2)，∵GE →⊥平面ABD ，∴GE →为平面ABD 的一个法向量．∵cos 〈GE →，BA 1→〉＝GE →·BA 1→|GE →|·|BA 1→|＝4363×23＝23，∴A 1B 与平面ABD 所成的角的余弦值为73.9.答案ABD解析本题考查异面直线所成角、线面角、点到平面距离及外接球问题．正方体ABCD －A 1B 1C 1D 1的棱长为1，直线BC 与平面ABC 1D 1所成的角为∠CBC 1＝π4，故A 正确；连接B 1C ，由B 1C ⊥BC 1，B 1C ⊥AB ，BC 1∩AB ＝B ，得B 1C ⊥平面ABC 1D 1，所以点C 到平面ABC 1D 1的距离为B 1C 长度的一半，即22，故B 正确；因为BC 1∥AD 1，所以异面直线D 1C 与BC 1所成的角为∠AD 1C ，连接AC ，则△AD 1C 为等边三角形，故异面直线D 1C 与BC 1所成的角为π3，故C 错误；三棱柱AA 1D 1－BB 1C 1的外接球也是正方体ABCD－A 1B 1C 1D 1的外接球，故外接球半径为12＋12＋122＝32，故D 正确．故选ABD.10．答案402π解析如图所示，设S 在底面的射影为S ′，连接AS ′，SS ′.△SAB 的面积为12SA ·SB ·sin ∠ASB ＝12·SA 2·1－cos 2∠ASB ＝1516·SA 2＝515，∴SA 2＝80，SA ＝4 5.∵SA 与底面所成的角为45°，∴∠SAS ′＝45°，AS ′＝SA·cos45°＝45×22＝210.∴底面周长l ＝2π·AS ′＝410π，∴圆锥的侧面积为12×45×410π＝402π.11．答案43535解析如图，以D 点为坐标原点建立如图所示的空间直角坐标系D －xyz.设菱形ABCD 的边长为2，则D(0，0，0)，E(32，－12，0)，，23，EF →－32，76，又平面ABCD 的一个法向量为n ＝(0，0，1)，所以cos 〈EF →，n 4＝43535，即直线EF 与平面ABCD 所成角的正弦值为43535.12.答案(1)略(2)267解析(1)证明：如图，连接BD ，∵四边形ABCD 为菱形，∠ADC ＝120°，且M 为AD 的中点，∴△ABD 为等边三角形．∴MB ⊥AD ，∴MB ⊥BC.∵P 在底面ABCD 的射影M 是AD 的中点，∴PM ⊥平面ABCD ，又∵BC ⊂平面ABCD ，∴PM ⊥BC ，又PM ∩MB ＝M ，PM ，MB ⊂平面MPB ，∴BC ⊥平面MPB ，又BC ⊂平面PBC ，∴平面MPB ⊥平面PBC.(2)方法一：过点B 作BH ⊥MC 于点H ，连接HN(图略)．∵PM ⊥平面ABCD ，BH ⊂平面ABCD ，∴BH ⊥PM.又∵PM ，MC ⊂平面PMC ，PM ∩MC ＝M ，∴BH ⊥平面PMC.∴直线HN 为直线BN 在平面PMC 上的射影，∴∠BNH 为直线BN 与平面PMC 所成的角．在菱形ABCD 中，设AB ＝2a ，则MB ＝AB·sin60°＝3a ，MC ＝MB 2＋BC 2＝7a ，PC ＝MC 2＋MP 2＝2MC 2＝14a ，∴在Rt △MBC 中，BH ＝2a·3a 7a＝2217 a.由(1)知BC ⊥平面MPB ，PB ⊂平面MPB ，∴PB ⊥BC ，∴BN ＝12PC ＝142a ，∴sin ∠BNH ＝BH BN ＝2217a142a ＝267，即直线BN 与平面PMC 所成角的正弦值为267.方法二：由(1)知MA ，MB ，MP 两两垂直，以M 为坐标原点，以MA ，MB ，MP 所在直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系M －xyz ，不妨设MA ＝1.∴M(0，0，0)，A(1，0，0)，B(0，3，0)，C(－2，3，0)，P(0，0，7)．∵N 是PC 的中点，∴1，32，设平面PMC 的法向量为n ＝(x 0，y 0，z 0)，又∵MP →＝(0，0，7)，MC →＝(－2，3，0)，·MP →＝0，·MC →＝0，0＝0，0＋3y 0＝0，令y 0＝1，则n1，|n |＝72.又∵BN →1，－32，|BN →|＝142，∴|cos 〈BN →，n 〉|＝|BN →·n ||BN →||n |＝267.∴直线BN 与平面PMC 所成角的正弦值为267.13．答案(1)略(2)4214解析(1)证明：因为AB 是圆的直径，所以BC ⊥AC ，因为PC 垂直圆所在的平面，所以PC ⊥BC ，又因为AC ∩PC ＝C ，所以BC ⊥平面PAC.因为D ，E 分别是棱PB ，PC 的中点，所以BC ∥DE ，从而有DE ⊥平面PAC.(2)由(1)可知，DE ⊥AE ，DE ⊥EC ，所以∠AEC 为二面角A －DE －C 的平面角，从而有∠AEC ＝45°，则AC ＝EC ＝12PC ＝2，又BC ⊥AC ，AB ＝4，得BC ＝23.以C 为坐标原点，CB →，CA →，CP →的方向分别为x 轴，y 轴，z 轴的正方向，建立如图所示的空间直角坐标系C －xyz.则C(0，0，0)，A(0，2，0)，E(0，0，2)，B(23，0，0)，P(0，0，4)，D(3，0，2)，AE →＝(0，－2，2)，CA →＝(0，2，0)，CD →＝(3，0，2)．设n ＝(x ，y ，z)是平面ACD ·CA →＝0，·CD →＝0，0，＋2z ＝0.可取n ＝(2，0，－3)．故|cos 〈n ，AE →〉|＝|n ·AE →||n |·|AE →|＝4214.所以直线AE 与平面ACD 所成角的正弦值为4214.14.思路(1)通过添加辅助线，利用面面垂直得到线面垂直，进而得到DO ⊥BC ，再根据题中所给的已知条件，证得BO ⊥BC ，由此可得BC ⊥平面DBO ，BC ⊥DB ，由BC ∥EF 即可得证；(2)可通过作辅助线找到直线DF 与平面DBC 所成角，利用解三角形知识求得直线DF 与平面DBC 所成角的正弦值，也可以建立合适的空间直角坐标系，通过计算直线DF 的方向向量与平面DBC 的法向量求解直线DF 与平面DBC 所成角的正弦值．答案(1)略(2)33解析(1)证明：如图，过点D 作DO ⊥AC ，交直线AC 于点O ，连接OB.由∠ACD ＝45°，DO ⊥AC 得CD ＝2CO.由平面ACFD ⊥平面ABC ，DO ⊥AC ，平面ACFD ∩平面ABC ＝AC ，得DO ⊥平面ABC ，所以DO ⊥BC.由∠ACB ＝45°，BC ＝12CD ＝22CO 得BO ⊥BC ，又DO ⊥BC ，DO ∩BO ＝O ，所以BC ⊥平面BDO ，故BC ⊥DB.由三棱台ABC －DEF 得BC ∥EF ，所以EF ⊥DB.(2)方法一：如图，过点O 作OH ⊥BD ，交直线BD 于点H ，连接CH.由三棱台ABC －DEF 得DF ∥CO ，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角．由BC ⊥平面BDO 得OH ⊥BC ，又OH ⊥BD ，BC ∩BD ＝B ，故OH ⊥平面BCD ，所以∠OCH 为直线CO 与平面DBC 所成角．设CD ＝22，则DO ＝OC ＝2，BO ＝BC ＝2，所以BD ＝6，OH ＝233，所以sin ∠OCH ＝OH OC ＝33，因此，直线DF 与平面DBC 所成角的正弦值为33.方法二：由三棱台ABC －DEF 得DF ∥CO ，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角，记为θ.如图，以O 为原点，分别以射线OC ，OD 为y ，z 轴的正半轴，建立空间直角坐标系O －xyz.设CD ＝22，则O(0，0，0)，B(1，1，0)，C(0，2，0)，D(0，0，2)．因此OC →＝(0，2，0)，BC →＝(－1，1，0)，CD →＝(0，－2，2)．设平面BCD 的法向量n ＝(x ，y ，z)，n ·BC →＝0，n ·CD →＝0，－x ＋y ＝0，－2y ＋2z ＝0，可取n ＝(1，1，1)．所以sin θ＝|cos 〈OC →，n 〉|＝|OC →·n ||OC →|·|n |＝33.因此，直线DF与平面DBC所成角的正弦值为3 3 .。

高中数学线面角与线线角例题、习题-学生

线面角与线线角专练（小练习一）【知识网络】1、异面直线所成的角：（1）范围：(0,]2πθ∈；（2）求法；2、直线和平面所成的角：（1）定义：（2）范围：[0,90]；（3）求法；【典型例题】例1：（1）在正方体1111ABCD A BC D -中，下列几种说法正确的是（）A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角D 、11AC 与1BC 成60角（2）在正方体AC 1中，过它的任意两条棱作平面，则能作得与A 1B 成300角的平面的个数为（）A 、2个B 、4个C 、6个D 、8个（3）正六棱柱ABCDEF －A 1B 1C 1D 1E 1F 1底面边长是1，2则这个棱柱的侧面对角线E 1D 与BC 1所成的角是（）A ．90ºB ．60ºC ．45ºD ．30º（4）在空间四边形ABCD 中，AB ⊥CD ，BC ⊥DA ，那么对角线AC 与BD 的位置关系是。

（5）点AB 到平面α距离距离分别为12，20，若斜线AB 与α成030的角，则AB 的长等于__ ___.例2：．如图：已知直三棱柱ABC —A 1B 1C 1，AB ＝AC ，F 为棱BB 1上一点，BF ∶FB 1＝2∶1，BF ＝BC ＝2a 。

（I ）若D 为BC 的中点，E 为AD 上不同于A 、D 的任意一点，证明EF ⊥FC 1；（II ）试问：若AB ＝2a ，在线段AD 上的E点能否使EF 与平面BB 1C 1C 成60°角，为什么？证明你的结论。

例3：如图, 四棱锥P-ABCD 的底面是AB=2, BC =2的矩形, 侧面PAB 是等边三角形, 且侧面PAB ⊥底面ABCD.(Ⅰ)证明:BC ⊥侧面PAB;(Ⅱ)证明: 侧面PAD ⊥侧面PAB;(Ⅲ)求侧棱PC 与底面ABCD 所成角的大小; A B C DPA B C H S M 线面角与线线角专练（小练习二）例4：设△ABC 内接于⊙O ，其中AB 为⊙O 的直径，PA ⊥平面ABC 。

线线角和线面角

线线角和线面角[重点]：确定点、斜线在平面内的射影。

[知识要点]：一、线线角1、定义：设a、b是异面直线，过空间一点O引a′//a,b′//b,则a′、b′所成的锐角(或直角),叫做异面直线a、b所成的角.2、范围:(0,]3. 向量知识：对异面直线AB和CD(1)；(2) 向量和的夹角<,>(或者说其补角)等于异面直线AB和CD的夹角；(3)二、线面角1、定义：平面的一条斜线和它在这个平面内的射影所成的锐角，斜线和平面所成角的范围是(0,).2、直线在平面内或直线与平面平行，它们所成角是零角；直线垂直平面它们所成角为，3、范围: [0,]。

4、射影定理：斜线长定理：从平面外一点向这个平面所引的垂线段和斜线段中：（1）射影相等的两条斜线段相等，射影较长的斜线段也较长；（2）相等的斜线段的射影相等，较长的斜线段的射影也较长；（3）垂线段比任何一条斜线段都短。

5、最小角定理：平面的一条斜线与平面所成的角，是这条直线和平面内过斜足的直线所成的一切角中最小的角。

6、向量知识（法向量法）与平面的斜线共线的向量和这个平面的一个法向量的夹角<,>(或者说其补角)是这条斜线与该平面夹角的余角.[例题分析与解答]例1．如图所示，在棱长为a的正方体ABCD-A1B1C1D1中，求：异面直线BA1与AC所成的角.分析：利用，求出向量的夹角,再根据异面直线BA1，AC所成角的范围确定异面直线所成角.解：∵，，∴∵AB⊥BC，BB1⊥AB，BB1⊥BC，∴∴又∴∴所以异面直线BA1与AC所成的角为60°.点评：求异面直线所成角的关键是求异面直线上两向量的数量积，而要求两向量的数量积，必须会把所求向量用空间的一组基向量来表示.例2．如图(1)，ABCD是一直角梯形，AD⊥AB，AD//BC，AB=BC=a, AD=2a,且PA⊥平面ABCD，PD与平面ABCD成30°角.(1)若AE⊥PD，E为垂足，求证：BE⊥PD；(2)求异面直线AE与CD所成角的大小（用反三角函数表示）解法一：（1）证明：∵PA⊥平面ABCD，∴PA⊥AB，∵AD⊥AB，∴AB⊥平面PAD，∴AB⊥PD，又AE⊥PD，∴PD⊥平面ABE，∴BE⊥PD.(2)解：设G、H分别为ED、AD的中点，连BH、HG、GB（图（1））易知，∴BH//CD.∵G、H分别为ED、AD的中点，∴HG//AE则∠BHG或它的补角就是异面直线AE、CD所成的角，而，，，在ΔBHG中，由余弦定理，得，∴.∴异面直线AE、CD所成角的大小为.解法二：如图（2）所示建立空间直角坐标系A-xyz，则，，，，，（1）证明：∵∴∴∴（2）解：∵∴∴异面直线AE、CD所成角的大小为例3．如图，在正方体ABCD-A1B1C1D1中，，求BE1与DF1所成角的余弦值.解：以D为坐标原点，为x,y,z轴，建立空间直角坐标系D-xyz，设正方体的棱长为4，则D(0,0,0)，B(4,4,0),E1(4,3,4), F1(0,1,4).则，∴，∵.∴∴BE1与DF1所成角的余弦值为点评：在计算和证明立体几何问题中，若能在原图中建立适当的空间直角坐标系，把图形中的点的坐标求出来，那么图形有关问题可用向量表示.利用空间向量的坐标运算来求解，这样可以避开较为复杂的空间想象。

高考理科数学必考——几何证明与利用空间向量求线面角、面面角

高考理科数学必考——几何证明与利用空间向量求线面角、面
面角
时间过的飞快，距离高考的时间就只剩76天了，同学和老师也越来越紧张了，有些地方欠缺的同学开始寝食难安，老师也赶快奉献点干货来帮助几何证明欠缺的学生。

立体几何其实难度不大，只要你会空间向量，会建系，一切就自然而然水到渠成了。

在这先分析这些立体几何的解题思路。

在立体几何中，第一问一般会让你证明线面平行、线面垂直、面面平行、面面垂直
1、证明线面平行的方法1、平移的方法，找到直线与平面内一条直线平行
2、利用面面平行、证明线面平行
2、证明线面垂直的方法1、证明直线与平面内相交的两直线垂直
3、证明面面平行的方法1、证明一个平面内两相交的直线与另一个平面内两相交的直线互相平行
2、证明平面内两相交的直线分别平行另一个平面
4、证明面面垂直的方法1、先证明一条直线垂直于一个平面，这条直线还在另一个平面内
利用这些方法第一问就可以轻松解决了。

在立体几何第二中，会求线面角、面面角，在第二步中，利用空间向量解决就可以
利用空间向量解决第二问的步骤1、找三垂，建立空间直角坐标系
2、写出各个点的坐标
3、求出直线向量、面的法向量
4、利用夹角公式算出余弦值
下面通过两个例题说明一下这个空间几何。

最新-2018年高考数学考点解析：线线角与线面角的题型与解法精品

线线角与线面角高考考纲透析：线线,线面,面面的平行与垂直,异面直线所成角,直线与平面所成角高考热点：异面直线所成角,直线与平面所成角知识整合:1.转化思想:将异面直线所成的角,直线与平面所成的角转化为平面角,然后解三角形;⇔⇔⊥⇔⊥⇔⊥线线平行线面平行面面平行,线线线面面面2.求角的三个步骤:一猜,二证,三算.猜是关键,在作线面角时,利用空间图形的平行,垂直,对称关系,猜斜线上一点或斜线本身的射影一定落在平面的某个地方,然后再证热点题型1例1、如图, 在直三棱柱111ABC A B C -中，13,4,5,4AC BC AB AA ==== ，点D 为AB 的中点.(Ⅰ)求证1AC BC ⊥; (Ⅱ) 求证11AC CDB 平面;(Ⅲ)求异面直线1AC 与1B C 所成角的余弦值.解析;异面直线所成角的平面角顶点O 的选取一般选在两异面直线的端点处,初学者或观察能力有限者可采用穷举法,实行逐个端点考察,也有取在某线段的中点处. 解：（I ）直三棱柱ABC －A 1B 1C 1，底面三边长AC=3，BC=4AB=5，∴ AC ⊥BC ，且BC 1在平面ABC 内的射影为BC ，∴ AC ⊥BC 1；（II ）设CB 1与C 1B 的交点为E ，连结DE ，∵ D 是AB 的中点，E 是BC 1的中点，∴ DE//AC 1， ∵ DE ⊂平面CDB 1，AC 1⊄平面CDB 1，∴ AC 1//平面CDB 1；（III ）∵ DE//AC 1，∴ ∠CED 为AC 1与B 1C 所成的角，在△CED 中，ED=21AC 1=25，CD=21AB=25，CE=21CB 1=22， ∴8cos 522CED ∠==⋅ ∴ 异面直线 AC 1与 B 1C所成角的余弦值5.1A1A解法二： ∵直三棱锥111ABC A B C -底面三边长3,4,5AC BC AB ===，1,,AC BC CC 两两垂直.如图建立坐标系，则C(0,0,0),A(3,0,0),C 1(0, 0,4),B(0,4,0),B 1(0,4,4),D(32,2,0) (Ⅰ)11(3,0,0),(0,4,4)AC BC =-=,11110,AC BC AC BC ∴⋅=∴⊥.(Ⅱ)设1CB 与1C B 的交点为E ，则E(0,2,2)13(,0,2),(3,0,4),2DE AC =-=-111,//2DE AC DE AC ∴=∴111,,DE CDB AC CDB ⊂⊄平面平面11//AC CDB ∴平面.(Ⅲ)11(3,0,4),(0,4,4),AC CB =-=1111112cos ,5||||AC CB AC CBAC CB ∴<>==∴异面直线1AC 与1B C 所成角的余弦值为5. 热点题型2例2、如图，在斜三棱柱111C B A ABC -中，a B A A A AC AB AC A AB A ===∠=∠1111,,，侧面11BCC B 与底面ABC 所成的二面角为120， E 、F 分别是棱A A C B 111、的中点（Ⅰ）求A A 1与底面ABC 所成的角（Ⅱ）证明E A 1∥平面FC B 1（Ⅲ）求经过C B A A 、、、1四点的球的体积.解：（Ⅰ）过1A 作⊥H A 1平面ABC ，垂足为H ．连结AH ，并延长交BC 于G ，于是AH A 1∠为A A 1与底面ABC 所成的角．1∵AC A AB A 11∠=∠，∴AG 为BAC ∠的平分线．又∵AC AB =，∴BC AG ⊥，且G 为BC 的中点．因此，由三垂线定理BC A A ⊥1．∵B B A A 11//，且B B EG 1//，∴BC EG ⊥．于是AGE ∠为二面角E BC A --的平面角，即120=∠AGE ．由于四边形AGE A 1为平行四边形，得601=∠AG A ．（Ⅱ）证明：设EG 与C B 1的交点为P ，则点P 为EG 的中点．连结PF ．在平行四边形1AGEA 中，因F 为A A 1的中点，故FP E A //1．而⊂FP 平面FC B 1，⊄E A 1平面FC B 1，所以//1E A 平面FC B 1．（Ⅲ）连结C A 1．在AC A 1∆和AB A 1∆中，由于AB AC =，AC A AB A 11∠=∠，A A A A 11=，则AC A 1∆≌AB A 1∆，故B A C A 11=．由已知得a C A B A A A ===111．又∵⊥H A 1平面ABC ，∴H 为ABC ∆的外心．设所求球的球心为O ，则H A O 1∈，且球心O 与A A 1中点的连线A A OF 1⊥．在FO A Rt 1∆中，3330cos 21cos 111a aH AA F A O A ===．故所求球的半径a R 33=，球的体积33273434a R V ππ==．热点题型3例3、如图，在四棱锥P —ABC 右，底面ABCD 为矩形，侧棱PA ⊥底面ABCD ，AB=3，BC=1，PA=2，E 为PD 的中点.（Ⅰ）求直线AC 与PB 所成角的余弦值；（Ⅱ）在侧面PAB 内找一点N ，使NE ⊥面PAC ，并求出N 点到AB 和AP 的距离.解法一：（Ⅰ）建立如图所示的空间直角坐标系，则A 、B 、C 、D 、P 、E 的坐标分别为A （0，0，0），B （3，0，0），C （3，1，0），D （0，1，0）， P （0，0，2），E （0，21，2）. 从而AC =（3，1，0），PB =（3，0，-2）. 设AC 与PB 的夹角为θ，则1473723||||cos ==⋅=PB AC PB AC θ， ∴AC 与PB 所成角的余弦值为1473. （Ⅱ）由于N 点在侧面PAB 内，故可设N 点坐标为（x ，0，z ），则)1,21,(z x ME --=.由NE ⊥面PAC可得：⎪⎩⎪⎨⎧=⋅=⋅,0,0AC NE AP NE 即⎪⎪⎩⎪⎪⎨⎧=⋅--=⋅--,0)0,1,3()1,21,(,0)2,0,0()1,21,(z x z x化简得⎪⎩⎪⎨⎧==⇒⎪⎩⎪⎨⎧=+-=-.1,63.0213,01z x x z即N 点的坐标为（63，0，1），从而N 点到AB 、AP 的距离分别为1，63解法二：（Ⅰ）设AC ∩BD=O ，连OE ，则OE//PB ，∴∠EOA 即为AC 与PB 所成的角或其补角.在ΔAOE 中，AO=1，OE=21PB=27，AE=21PD=25，∴14173127245471cos =⨯⨯-+=EOA . 即AC 与PB 所成角的余弦值为14173.（Ⅱ）在面ABCD 内过D 作AC 的垂线交AB 于F ，则6π=∠ADF .连PF ，则在Rt ΔADF 中DF=33tan ,332cos ===ADF AD AF ADF AD .设N 为PF 的中点，连NE ，则NE//DF ，∵DF ⊥AC ，DF ⊥PA ，∴DF ⊥面PAC 从而NE ⊥面PAC. ∴N 点到AB 的距离=21AP=1，N 点到AP 的距离=21AF=63.。

线面角练习题

线面角练习题在数学中，线面角是一种常见的概念，用于描述线与面之间的相对关系。

本文将为你提供一系列线面角练习题，帮助你加深对线面角概念的理解并提高解题能力。

练习题一：线与平面的关系1. 建立直角坐标系，并画出平面P：4x - 2y + z = 6。

a) 在该平面上选择一点A(x1, y1, z1)，其中x1, y1, z1为任意实数。

画出该平面与点A的关系示意图。

b) 选择另一点B(x2, y2, z2)，其中x2, y2, z2为任意实数。

画出该平面、点A和点B之间的关系示意图。

练习题二：线与平面上的点的关系2. 平面P：2x + 3y - 4z = 12与直线L：x = 2 + t, y = 3 - t, z = -1 + 2t相交于点A。

求出点A的坐标。

练习题三：线面角的计算3. 已知平面P：2x - y + 3z = 1和直线L：x = 3 - t, y = 2 + 2t, z = -1 + t。

求出直线L与平面P的线面角。

练习题四：垂直线面角的判断4. 平面P1：2x - y + 2z = 5与平面P2：4x - 2y + 4z = 9之间的夹角为α。

判断平面P1与平面P2是否垂直。

练习题五：平行线面角的计算5. 平面P：3x - 2y + 4z = 7和直线L：x = 1 + 2t, y = -2 + 3t, z = 3 - t 之间的夹角为β。

判断直线L与平面P是否平行。

练习题六：点到平面的距离计算6. 平面P：2x - y + z = 5上有一点A(1, -3, 2)。

求出点A到平面P的距离。

练习题七：平行平面之间的距离计算7. 已知平面P1：2x - 3y + z = 4和平面P2：4x - 6y + 2z = 8平行。

求出平面P1与平面P2之间的距离。

练习题八：垂直线面之间的距离计算8. 平面P：2x - y + 3z = 5与直线L：x = 1 + t, y = 2 - t, z = 3t之间的距离为d。

线线角_线面角_二面角的一些题目

线线角与线面角、二面角一、目标1.理解异面直线所成角的概念,并掌握求异面直线所成角的常用方法．2.理解直线与平面所成角的概念，并掌握求线面角常用方法．并了解求线二面角常用方法3.掌握求角的计算题步骤是“一作、二证、三计算”,思想方法是将空间图形转化为平面图形即“降维”的思想方法.三、典型例题例1. 如图,正方形ABCD所在平面与正方形ABEF所在平面成60ο角,求异面直线AD与BF所成角的余弦值.例2.如图在正方体AC1中, (1) 求BC1与平面ACC1A1所成的角; (2) 求A1B1与平面A1C1B所成的角.例3. 如图，在棱长为a的正方体ABCD—A1B1C1D1中，求：（1）面A1ABB1与面ABCD所成角的大小；（2）二面角C1—BD—C的正切值。

ADC1D1A1B1CBDACB F EA BC DAD CBB 1D 1ADC 1BC A 1二、重要题型1.在空间四边形ABCD 中，AD=BC=2, E 、F 分别为AB 、CD 的中点且EF=3，AD 、BC 所成的角为 .2.如图,在长方体ABCD-A 1B 1C 1D 1中，B 1C 和C 1D 与底面所成的角分别为60ο和45ο，则异面直线B 1C 和C 1D 所成角的余弦值为 ( ) (A).46(B).36 (C).62(D).633.平面α与直线a 所成的角为3π,则直线a 与平面α内所有直线所成的角的取值范围是． 4.如图,ABCD 是正方形,PD ⊥平面ABCD,PD=AD,则PA 与BD 所成的角的度数为(A).30ο (B).45ο (C).60ο (D).90ο5.有一个三角尺ABC,∠A=30ο, ∠C=90ο,BC 是贴于桌面上,当三角尺与桌面成45ο角时,AB 边与桌面所成角的正弦值是．6. 在四棱锥P-ABCD 中，ABCD 是正方形，PA ⊥平面ABCD ，PA=AB=a ，求二面角B-PC —-D 的大小。

高中立体几何专题：线面角与线线角

线面角与线线角1、异面直线所成的角：（1）范围：(0,]2πθ∈；（2）求法；2、直线和平面所成的角：（1）定义：（2）范围：[0,90]o o ；（3）求法；【典型例题】例1：（1）在正方体1111ABCD A B C D -中，下列几种说法正确的是（）A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45o 角D 、11AC 与1B C 成60o 角答案：D 。

解析：A 1C 1与AD 成45°，D 1C 1与AB 平行，AC 1与DC。

（2）在正方体AC 1中，过它的任意两条棱作平面，则能作得与A 1B 成300角的平面的个数为（）A 、2个B 、4个C 、6个D 、8个答案：B 。

解析：平面A 1ACC 1，平面BB 1D 1D ，平面ABC 1D 1，平面A 1D 1CC 1。

（3）正六棱柱ABCDEF －A 1B 1C 1D 1E 1F 1底面边长是1面对角线E 1D 与BC 1所成的角是（）A ．90ºB ．60ºC ．45ºD ．30º答案：B 。

解析将BC 1平移到E 1F 即可。

（4）在空间四边形ABCD 中，AB ⊥CD ，BC ⊥DA ，那么对角线AC 与BD 的位置关系是。

答案：AC ⊥BD 。

解析：过A 作AH ⊥平面BCD ，垂足为H ，因为CD ⊥AB ，BC ⊥AD ，所以CD ⊥BH ，BC ⊥DH ，故H 为△BCD 的垂心，从而BD ⊥CH ，可得BD ⊥AC 。

（5）点AB 到平面α距离距离分别为12，20，若斜线AB 与α成030的角，则AB 的长等于__ ___.答案：16或64。

解析：分A 、B 在平面α的同侧和异侧进行讨论。

例3：如图, 四棱锥P-ABCD 的底面是AB=2, BC =2的矩形, 侧面PAB 是等边三角形, 且侧面 PAB ⊥底面ABCD.(Ⅰ) 证明:BC ⊥侧面PAB;(Ⅱ) 证明: 侧面PAD ⊥侧面PAB;(Ⅲ) 求侧棱PC 与底面ABCD 所成角的大小;答案： (Ⅰ)证: ∵侧面PAB ⊥底面ABCD, 且侧面PAB 与底面ABCD 的交线是AB, 在矩形ABCD 中, BC ⊥AB ，.∴BC ⊥侧面PAB.(Ⅱ)证: 在矩形ABCD 中, AD ∥BC, BC ⊥侧面PAB, ∴AD ⊥侧面PAB. 又AD ⊂平面PAD, ∴侧面PAD ⊥侧面PAB.(Ⅲ)解: 在侧面PAB 内, 过点P 做PE ⊥AB, 垂足为E, 连结EC, ∵侧面PAB 与底面ABCD 的交线是AB, PE ⊥AB, ∴PE ⊥底面ABCD. 于是EC 为PC 在底面ABCD 内的射影.A BC D PAB C H S M ∴∠PCE 为侧棱PC 与底面ABCD 所成的角. 在△PAB 和△BEC 中, 易求得PE=3, EC=3.在Rt △PEC 中, ∠PCE=45°.例4：设△ABC 内接于⊙O ，其中AB 为⊙O 的直径，PA ⊥平面ABC 。

空间角(空间线线、线面、面面成角问题)练习题(答案)

空间角练习题1．二面角是指（ D ）A 两个平面相交所组成的图形B 一个平面绕这个平面内一条直线旋转所组成的图形C 从一个平面内的一条直线出发的一个半平面与这个平面所组成的图形D 从一条直线出发的两个半平面所组成的图形2．平面α与平面β、γ都相交，则这三个平面可能有（ D ）A 1条或2条交线B 2条或3条交线C 仅2条交线D 1条或2条或3条交线3．在300的二面角的一个面内有一个点，若它到另一个面的距离是10，则它到棱的距离是( B )A 5B 20 CD4．在直二面角α-l-β中，RtΔABC在平面α内，斜边BC在棱l上，若AB 与面β所成的角为600，则AC与平面β所成的角为（ A ）A 300B 450 C600 D 12005．如图，射线BD、BA、BC两两互相垂直，AB=BC=1，BD=，则弧度数为的二面角是（ A ）A D-AC-B B A-CD-BC A-BC-D D A-BD-C6．△ABC在平面α的射影是△A1B1C1，如果△ABC所在平面和平面α成θ角，有（B）A S△A1B1C1=S△ABC·sinθB S△A1B1C1=S△ABC·cosθC S△ABC =S△A1B1C1·sinθD S△ABC=S△A1B1C1·cosθ7．如图，若P为二面角M-l-N的面N内一点，PB⊥l，B为垂足，A为l上一点，且∠PAB=α，PA与平面M所成角为β，二面角M-l-N的大小为γ，则有（ B ）A sinα=sinβsinγB sinβ=sinαsinγC sinγ=sinαsinβD 以上都不对8．在600的二面角的棱上有两点A、B，AC、BD分别是在这个二面角的两个面内垂直于AB的线段，已知：AB=6，AC=3，BD=4，则CD= 7cm 。

9．已知△ABC和平面α，∠A=300，∠B=600，AB=2，ABα，且平面ABC与α所成角为300，则点C到平面α的距离为。

高考文科：点面距离、线线角、线面角练习(含解析)

高考文科：点面距离、线线角、线面角练习1．在四棱锥P ABCD -中，底面ABCD 是平行四边形，PD ⊥底面ABCD ，1PD AD ==，5AB =，5sin 5ABD ∠=．（1）证明：PA BD ⊥；（2）求D 到平面ABP 的距离．2．如图，已知四棱锥P ABCD -的底面为矩形，PA ⊥平面ABCD ，3AB =，4AD AP ==，E 为PD 的中点．（1）证明：AE PC ⊥．（2）若M 为线段BC 上的一点，且1BM =，求点M 到平面PCD 的距离．3．如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，//AD BC ，90DAB ∠=︒，122AB BC PA AD ====，E 为PB 的中点，F 是PC 上的点．（1）若//EF 平面PAD ，证明：F 为PC 的中点．（2）求点C 到平面PBD 的距离．4．如图，四边形ABCD 为平行四边形，点E 在AB 上，22AE EB ==，且DE AB ⊥．以DE 为折痕把ADE ∆折起，使点A 到达点F 的位置，且60FEB ∠=︒．（Ⅰ）求证：平面BFC ⊥平面BDC ；（Ⅱ）若直线DF 与平面BCDE 所成角的正切值为155，求点C 到平面DEF 的距离．5．如图．在长方体1111ABCD A B C D -中，2AB AD ==，14AA =，M 是AC 与BD 的交点．求证：（1）1//D M 平面11A C B ；（2）求1BC 与1D M 的所成角的正弦值．6．如图，在正三棱柱111ABC A B C -中，2AB =，侧棱12AA =，且E ，F 分别是BC ，1CC 的中点．（1）求证：1//BC 平面AEF ；（2）求异面直线AE 与1A B 所成角的大小．7．如图，在直棱柱111ABC A B C -中，1AC BC CC ==，AC BC ⊥，D ，E 分别是棱AB ，AC上的点，且//BC 平面1A DE ．（1）证明：11//DE B C ；（2）若D 为AB 中点，求直线1A D 与直线1AC 所成角的余弦值．8．如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥底面ABCD ，1AB PA ==，3AD =，E ，F 分别为棱PD ，PA 的中点．（1）求证：B 、C 、E 、F 四点共面；（2）求异面直线PB 与AE 所成的角．9．如图，在多面体ABCDEF 中，底面ABCD 是正方形，梯形ADEF ⊥底面ABCD ，且12AF EF DE AD ===．（Ⅰ）证明：平面ABF⊥平面CDF；（Ⅱ）求直线AF与平面CDE所成角的大小．10．如图，四棱锥P ABCD-中，底面ABCD是边长为4的菱形，5PA PC==，点M，N 分别是AB，PC的中点．（1）求证：//MN平面PAD；（2）若4cos5PCD∠=，60DAB∠=︒，求直线AN与平面PAD所成角的正弦值．11．如图，四棱锥P ABCD-中，PAB∆是等边三角形，底面ABCD是直角梯形，//AB CD，AB AD ⊥，2AB BC ==，3ABC π∠=，F ，G 分别是PC ，AD 的中点．（1）①求证：//FG 平面PAB ； ②求线段FG 的长度；（2）若3PC =，求直线FG 与平面PBC 所成角的正弦值．12．如图，三棱锥P ABC -中，PA PC =，AB BC =，120APC ∠=︒，90ABC ∠=︒，3AC PB =．（1）求证：AC PB ⊥；（2）求直线AC 与平面PAB 所成角的正弦值．高考文科：点面距离、线线角、线面角练习参考答案与试题解析1．在四棱锥P ABCD-中，底面ABCD是平行四边形，PD⊥底面ABCD，1PD AD==，5AB=，5sin5ABD∠=．（1）证明：PA BD⊥；（2）求D到平面ABP的距离．【解答】解：（1）证明：在ABD∆中，由正弦定理可得：sin sinAB ADADB ABD=∠∠．∴sin1AB ABDADBAD∠∠==g，90ADB∴∠=︒，BD AD∴⊥．PD⊥平面ABCD，PD BD∴⊥．BD∴⊥平面PAD，PA BD∴⊥．（2）1PD AD==Q，5AB=，2BD∴=．∴5PB=，2PA=，1ABDS∆=，32ABPS∆=．设D到平面ABP的距离为h，则D ABP P ABDV V--=，即：1133ABP ABDS h S PD∆∆⨯⨯=⨯⨯，∴23ABDABPS PDhS∆∆⨯==，故D到平面ABP的距离为23．2．如图，已知四棱锥P ABCD -的底面为矩形，PA ⊥平面ABCD ，3AB =，4AD AP ==，E 为PD 的中点．（1）证明：AE PC ⊥．（2）若M 为线段BC 上的一点，且1BM =，求点M 到平面PCD 的距离．【解答】解：（1）PA ⊥Q 平面ABCD ，CD 在平面ABCD 内，PA CD ∴⊥，又四边形ABCD 为矩形，CD AD ∴⊥，又PA AD A =I ，且都在平面PAD 内，CD ∴⊥平面PAD ，又AE 在平面PAD 内，AE CD ∴⊥，AD AP =Q ，且E 为PD 中点， AE PD ∴⊥，又CD PD D =I ，且都在平面PCD 内，AE ∴⊥平面PCD ，又PC 在平面PCD 内，AE PC ∴⊥；（2）由（1）可知，CD PD ⊥，即PCD ∆为直角三角形，又22161642PD AD AP =+=+3CD AB ==， ∴113426222PCD S CD PD ∆==⨯⨯=g 又1BM =，4BC AD ==， ∴11933222MCD S CM CD ∆==⨯⨯=g ，设点M 到平面PCD 的距离为h ，则由P MCD M PCD V V --=可知，1133MCD PCDS AP S h ∆∆=g g ，则94322262MCD PCD S AP h S ∆∆⨯===g ， ∴点M 到平面PCD 的距离为322．3．如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，//AD BC ，90DAB ∠=︒，122AB BC PA AD ====，E 为PB 的中点，F 是PC 上的点．（1）若//EF 平面PAD ，证明：F 为PC 的中点．（2）求点C 到平面PBD 的距离．【解答】（1）证明：因为//BC AD ，BC ⊂/平面PAD ，AD ⊂平面PAD ，所以//BC 平面PAD ．因为P ∈平面PBC ，P ∈平面PAD ，所以可设平面PBC ⋂平面PAD PM =，又因为BC ⊂平面PBC ，所以//BC PM ．因为//EF 平面PAD ，EF ⊂平面PBC ，所以//EF PM ，从而得//EF BC ．因为E 为PB 的中点，所以F 为PC 的中点．（2）解：因为PA ⊥底面1,90,22ABCD DAB AB BC PA AD ∠=︒====，所以222222,25PB PA AB PD PA AD =+==+=，2225BD BA AD =+=，所以2211()622DPB S PB DP PB ∆=-=g ．设点C 到平面PBD 的距离为d ，由C PBD P BCD V V --=，得11113332DPB BCD S d S PA BC AB PA ∆∆==⨯⨯⨯⨯g g ，即11622236d =g g g g ，解得23d =．4．如图，四边形ABCD 为平行四边形，点E 在AB 上，22AE EB ==，且DE AB ⊥．以DE 为折痕把ADE ∆折起，使点A 到达点F 的位置，且60FEB ∠=︒．（Ⅰ）求证：平面BFC ⊥平面BDC ；（Ⅱ）若直线DF 与平面BCDE 所成角的正切值为15，求点C 到平面DEF 的距离．【解答】解：（Ⅰ）证明：DE AB ⊥Q ，DE EB ∴⊥，DE EF ⊥， EB EF E =Q I ，DE ∴⊥平面BEF ，BF ⊂Q 平面BEF ，DE BF ∴⊥， 22AE EB ==Q ，2EF ∴=，1EB =，60FEB ∠=︒Q ，222cos 3BF EF EB EF EB FEB ∴+-⨯⨯∠=222EF EB BF ∴=+，FB EB ∴⊥，DE BE E =Q I ，BF ∴⊥平面BCDE ，BF ⊂Q 平面BFC ，∴平面BFC ⊥平面BDC ．（Ⅱ）解：以B 为原点，BA 为x 轴，在平面ABCD 中过B 作AB 的垂线为y 轴，BP 为z 轴，建立空间直角坐标系，如图，设DE a =，则(1D ，a ，0)，(1E ，0，0)，(0F ，0，3)，(1DF =-u u u r，a -，3)， Q 直线DF 与平面BCDE 所成角的正切值为15， ∴直线DF 与平面BCDE 所成角的正弦值为6，平面BCDE 的法向量(0n =r，0，1)， Q 直线DF 与平面BCDE 所成角的正切值为15， 2||36|cos ,|||||4n DF n DF n DF a∴<>===+u u u r r u u ur g r u u u r r g ，解得2a =，(1D ∴，2，0)，(2C -，2，0)，∴(0ED =u u u r ，2，0)，(1DF =-u u u r ，2-，3)，(3DC =-u u u r，0，0)，设平面EDF 的法向量(m x =r，y ，)z ，则20230m ED y m DF x y z ⎧==⎪⎨=--+=⎪⎩u u u r r g u u u r r g ，取1z =，得(3,0,1)m =r ， ∴点C 到平面DEF 的距离||33||DC m d m ==u u u r rg r．5．如图．在长方体1111ABCD A B C D -中，2AB AD ==，14AA =，M 是AC 与BD 的交点．求证：（1）1//D M 平面11A C B ；（2）求1BC 与1D M 的所成角的正弦值．【解答】解：（1）证明：连结11B D 交11A C 于点N ，连结BN ，由11//DD BB ，11DD BB =，所以平行四边形11D B BD ，所以11//D B DB ，?D N BM =，所以?//D M NB ，又?D M 不在平面11A C B ，BN ⊂平面11A C B ，故?//D M 平面11A C B ；（2）由（1）可知1BC 与1D M 的所成角为?AD M ∠，由?AC MD ⊥，?AC DD ⊥，故AC ⊥平面?D DM ，在Rt AMD?∆中， 1210sin ?20AM AMD AD ∠===，故1BC 与1D M 的所成角的正弦值为10．6．如图，在正三棱柱111ABC A B C -中，2AB =，侧棱12AA =且E ，F 分别是BC ，1CC 的中点．（1）求证：1//BC 平面AEF ；（2）求异面直线AE 与1A B 所成角的大小．【解答】解：（1）证明：在正三棱柱111ABC A B C -中，E ，F 分别是BC ，1CC 的中点，所以1//EF BC ，又EF ⊂平面AEF ，1BC ⊂平面AEF ，所以1//BC 平面AEF ．（2）解：取11B C 的中点O ，连接BO ，1A O ，在正三棱柱111ABC A B C -中，有1//AO AE ，所以1BAO ∠为异面直线AE 与1A B 所成角，又因为111AO B C ⊥，平面111A B C ⊥平面11BCC B ，所以1A O ⊥平面11BCC B ，1AO BO ⊥，又因为12,2AB AA ==，所以在Rt △1AOB 中，1116,3,90A B A O A OB ==∠=︒，即12cos BA O ∠=，故异面直线AE 与1A B 所成角的大小为45︒．7．如图，在直棱柱111ABC A B C -中，1AC BC CC ==，AC BC ⊥，D ，E 分别是棱AB ，AC 上的点，且//BC 平面1A DE ．（1）证明：11//DE B C ；（2）若D 为AB 中点，求直线1A D 与直线1AC 所成角的余弦值．【解答】（1）证明：//BC Q 平面1A DE ．平面ABC ⋂平面1A DE DE =．//BC DE ∴，又11//BC B C ，11//DE B C ∴．（2）解：建立如图所示的空间直角坐标系，不妨设12AC BC CC ===．则(0C ，0，0)，(2A ，0，0)，(0B ，2，0)，(1D ，1，0)，1(0C ，0，2)，1(2A ，0，2)， ∴1(1DA =u u u u r ，1-，2)，1(2AC =-u u u u r，0，2)，∴112042DA AC =-++=u u u u r u u u u r g ，1||6DA =u u uu r ，1||22AC =u u u u r，1cos DA ∴<u u u u r ，111113||||62DA AC AC DA AC >===⨯u u u u r u u u u ru u u u r g u u u u r u u u u r g ．∴直线1A D 与直线1AC 所成角的余弦值为3．8．如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥底面ABCD ，1AB PA ==，3AD =，E ，F 分别为棱PD ，PA 的中点．（1）求证：B 、C 、E 、F 四点共面；（2）求异面直线PB 与AE 所成的角．【解答】解：（1）在PAD ∆中，由E 、F 为PD ，PA 中点得，EF 为中位线，即//EF AD ，又Q 底面为矩形，//AD BC ，//EF BC ∴，∴由平行线确定唯一平面得E 、F 、B 、C 在同一平面上．（2）如图，以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴建立空间直角坐标系，依题意得：(0A ，0，0)，(1B ，0，0)，(0P ，0，1)，(0E ，3，1)2， (1PB =u u u r ，0，1)-，(0AE =u u u r ，3，1)2，1||22cos ||||21PB AE PB AE θ===u u u r u u u rg u u ur u u u r g g ， ∴异面直线PB 与AE 夹角为：2arccos．9．如图，在多面体ABCDEF 中，底面ABCD 是正方形，梯形ADEF ⊥底面ABCD ，且12AF EF DE AD ===．（Ⅰ）证明：平面ABF ⊥平面CDF ；（Ⅱ）求直线AF 与平面CDE 所成角的大小．【解答】（Ⅰ）证明：Q 梯形ADEF ⊥底面ABCD ，且梯形ADEF ⋂底面ABCD AD =，又AB AD ⊥，AB DF ∴⊥，在梯形ADEF 中，过F 作FG AD ⊥，垂足为G ，设2AD =，可得112AF EF DE AD ====，则12AG =，3GF = 2222233()()32FD FG GD =+=+=，则222AF FD AD +=，即AF FD ⊥，又AB AF A =I ，FD ∴⊥平面ABF ，而FD ⊂平面CDF ， ∴平面ABF ⊥平面CDF ；（Ⅱ）解：以A 为坐标原点，分别以AB ，AD 所在直线为x ，y 轴建立空间直角坐标系，则(0A ，0，0)，(0D ，2，0)，(2C ，2，0)，(0E ，323，(0F ，123，(2,0,0)DC =u u u r ，13(0,2DE =-u u u r ，13(0,2AF =u u u r ，设平面CDE 的一个法向量为(,,)n x y z =r，由201302n DC x n DE y z ⎧==⎪⎨=-=⎪⎩u u u r r g u u u r r g ，取1z =，得3,1)n =r ．设直线AF 与平面CDE 所成角的大小为θ，则||33sin |cos ,|||||AF n AF n AF n θ=<>===u u u r r u u u r g r u u u r r g ，3πθ∴=，即直线AF 与平面CDE 所成角的大小为3π．10．如图，四棱锥P ABCD -中，底面ABCD 是边长为4的菱形，5PA PC ==，点M ，N 分别是AB ，PC 的中点．（1）求证：//MN 平面PAD ；（2）若4cos 5PCD ∠=，60DAB ∠=︒，求直线AN 与平面PAD 所成角的正弦值．【解答】（1）证明：取PD 的中点H ，连接NH ，AH ．N Q 是PC 的中点，1//2NH DC =∴，又1//2AM DC =，//NH AM =∴，∴四边形AMNH 是平行四边形．//MN AH ∴，又MN ⊂/平面PAD ，AH ⊂平面PAD ，//MN ∴平面PAD ．（2）解：5PC =Q ，4DC =，4cos 5PCD ∠=，3PD ∴=，222PC PD CD =+，PD DC ∴⊥，同理可得：PD AD ⊥，又AD CD D =I ，PD ∴⊥平面ABCD ．连接AC ，BD ，设AC BD O =I ，则AC BD ⊥，建立空间直角坐标系O xyz -．(23A ，0，0)，(3C -0，0)，(0D ，2-，0)，(0P ，2-，3)，(3N ，1-，3)2，(33AN =-u u u r ，1-，3)2，(23AD =-u u u r ，2-，0)，(0DP =u u u r ，0，3)．设平面PAD 的法向量为(n x =r，y ，)z ，则0n AD n DP ==u u ur u u u r r r g g ，则2320x y --=，30z =，取(1n =r ，3-，0)．sin |cos AN θ∴=<u u u r ，2323|111122n >==⨯r． ∴直线AN 与平面PAD 所成角的正弦值为2311．11．如图，四棱锥P ABCD -中，PAB ∆是等边三角形，底面ABCD 是直角梯形，//AB CD ，AB AD ⊥，2AB BC ==，3ABC π∠=，F ，G 分别是PC ，AD 的中点．（1）①求证：//FG 平面PAB ； ②求线段FG 的长度；（2）若3PC =，求直线FG 与平面PBC 所成角的正弦值．【解答】解：（1）①证明：取BC 中点I ，则//GI AB ，//FI PB ， GI FI I =Q I ，AB BP B =I ， ∴平面//GFI 平面PAB ，//FG ∴平面PAB ；②由①可知，31,,602FI IG FIG PBA ==∠=∠=︒，由余弦定理有，937121cos60422FG =+-⨯⨯⨯︒=；（2）Q 3,3PO OC PC ===，120POC ∴∠=︒，又EO AB ⊥，OC AB ⊥，AB ∴⊥平面POC ，∴平面POC ⊥平面ABC ，延长CO 到H ，使得PH OH ⊥，则PH ⊥平面ABC ，32PH =， 2PB BC ==Q ，3PC =，∴374GBC S ∆=，设G 到平面PBC 的距离设为h ，则37333424h ⨯=⨯， ∴32114h =， ∴直线FG 与平面PBC 所成角的正弦值为337h FG =．12．如图，三棱锥P ABC -中，PA PC =，AB BC =，120APC ∠=︒，90ABC ∠=︒，3AC PB =．（1）求证：AC PB ⊥；（2）求直线AC 与平面PAB 所成角的正弦值．【解答】解：（1）证明：取AC 中点O ，连结PO ，BO ，PA PC =Q ，AB BC =，PO AC ∴⊥，BO AC ⊥，PO BO O =Q I ，AC ∴⊥平面PBO ，PB ⊂Q 平面PBO ，AC PB ∴⊥．（2）解：设23AC =，则1PO =，2PA PC PB ===，3BO =， 222PO BO PB ∴+=，PO BO ∴⊥，以O 为原点，OB 为x 轴，OC 为y 轴，OP 为z 轴，建立空间直角坐标系，则(0A ，3-，0)，(0C ，3，0)，(0P ，0，1)，(3B ，0，0)， (0AC =u u u r ，23，0)，(0PA =u u u r ，3-，1)-，(3PB =u u u r，0，1)-，设平面PAB 的法向量(n x =r，y ，)z ，则3030n PA y z n PB x z ⎧=--=⎪⎨=-=⎪⎩u u u r r g u u u r r g ，取1x =，得(1n =r ，1-，3)，设直线AC 与平面PAB 所成角为θ，则直线AC 与平面PAB 所成角的正弦值为： ||235sin ||||235AC n AC n θ===u u u r rg u u u r r g g ．。

【高中数学】立体几何(线线、线面、面面成角)解答题A

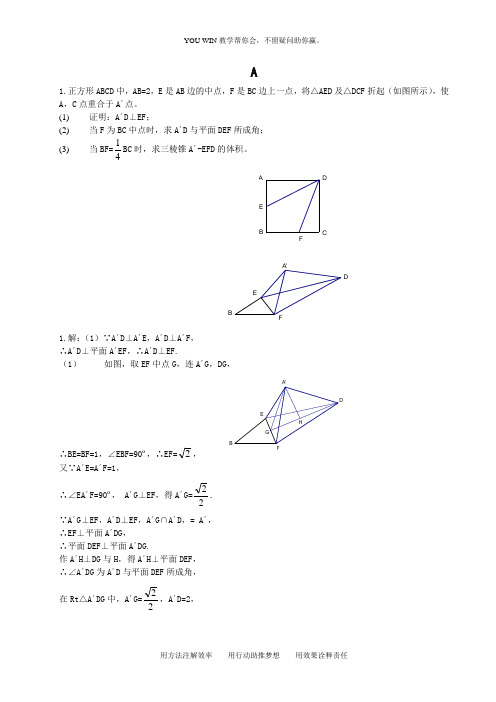
A1.正方形ABCD 中，AB=2，E 是AB 边的中点，F 是BC 边上一点，将△AED 及△DCF 折起（如图所示），使A ，C 点重合于A ´点。

(1) 证明：A ´D ⊥EF ； (2) 当F 为BC 中点时，求A ´D 与平面DEF 所成角； (3)当BF=41BC 时，求三棱锥A ´-EFD 的体积。

FEDCBABEFDA'1.解：（1）∵A ´D ⊥A ´E ，A ´D ⊥A ´F ， ∴A ´D ⊥平面A ´EF ，∴A ´D ⊥EF. （1）如图，取EF 中点G ，连A ´G ，DG ，∴BE=BF=1，∠EBF=90º，∴EF=2， HBEGFDA'又∵A ´E=A ´F=1，∴∠EA ´F=90º， A ´G ⊥EF ，得A ´G=22. ∵A ´G ⊥EF ，A ´D ⊥EF ，A ´G ∩A ´D ，= A ´， ∴EF ⊥平面A ´DG ，∴平面DEF ⊥平面A ´DG.作A ´H ⊥DG 与H ，得A ´H ⊥平面DEF ， ∴∠A ´DG 为A ´D 与平面DEF 所成角，在Rt △A ´DG 中，A ´G=22，A ´D=2，∴∠A ´DG=arctan42. （3）∵A ´D ⊥平面A ´EF ， ∴A ´D 是三棱锥D- A ´EF 的高. 又由BE=1，BF=21推出EF=25，又∵A ´F=23，A ´E =1，∴∠A ´EF=90º，可得：S △A ´EF=45.VA ´-EFD=VD-A ´EF=31 S △A ´EF* A ´D=31*45*2=65.∵A ´D ⊥平面A ´EF ，∴A ´D 是平面A ´EF 的高。

高中数学线面角与线线角例题、习题-学生

高中数学必修2立体几何专题线面角典型例题求法总结

高考数学一轮复习全套课时作业7-6-1线线角与线面角

高中数学线面角与线线角例题、习题-学生

线线角和线面角

高考理科数学必考——几何证明与利用空间向量求线面角、面面角

最新-2018年高考数学考点解析：线线角与线面角的题型与解法 精品

线面角练习题

线线角_线面角_二面角的一些题目

高中立体几何专题：线面角与线线角

空间角(空间线线、线面、面面成角问题)练习题(答案)

高考文科：点面距离、线线角、线面角练习(含解析)

【高中数学】立体几何(线线、线面、面面成角)解答题A

最新-2018年高考数学考点解析：线线角与线面角的题型与解法精品