构造可以使N个城市连接的最小生成树
最小生成树的构造离散数学

最小生成树的构造离散数学
最小生成树的构造是离散数学技术的重要组成部分,用于解决图形中的最小树问题。
能够有效地构造最小生成树,有助于我们解决复杂的网络优化等问题。
最小生成树是指一个边数最少的连接结点的树,即所有点之间只建立最少的边,使得所有点都连接在一起,称为一棵生成树。
最小生成树建立在图上,是多重图G(V,E)的一棵子树,它满足以下三个条件:1、包含G中的所有n个结点;2、只包含G中m-n+1条边;3、权值最小。
使用最小生成树的边,可以把n个节点连接成一个树,所有边的权重总和最小。
最小生成树的步骤是:1、选择一个结点作为树的根,将它加入到树中;2、以选定的结点为根,从剩余结点中选择权值最小的边,加入到树中;3、继续重复步骤2,直到n-1条边全部加入到树中,从而完成树的构造。
最小生成树有多种构造方式,如Prim和Kruskal算法、动态规划算法等,可以快速和有效地构建最小生成树。
Prim算法从图中原始结点出发,每一步都把一条最短边加入进去;Kruskal算法从图中原始边出发,每次都把一条最短边加入进去;动态规划算法是在Graph-MST网络上使用的,可以用来解决复杂的路径优化等问题。
总之,最小生成树的构造是离散数学的重要技术,能够有效地构建最小生成树,从而解决复杂的网络优化问题。
最小生成树的构造有不同的方法,要想更好地理解和使用,就需要深刻掌握其原理和实现方法。
最小生成树求解无向的最小连接子

最小生成树求解无向的最小连接子最小生成树(Minimum Spanning Tree)是图论中的一个概念,指的是在一个联通图中,找出一个子集,使得所有节点都能连接起来,并且边的权值之和最小。
在实际应用中,最小生成树常用于优化网络通信、城市规划、电力传输等问题。
一、什么是最小生成树在图论中,最小生成树是指在一个具有n个顶点的联通图中,选择n-1条边,将n个顶点相互连接,形成具有最小总权值的树形结构。
这里的总权值是指选择的n-1条边的权值之和。
二、Kruskal算法Kruskal算法是一种经典的求解最小生成树问题的算法。
其基本思想是先将所有边按照权值从小到大进行排序,然后依次加入到最小生成树中,直到满足n-1条边的条件。
具体步骤如下:1. 创建一个空的最小生成树集合,初始化为0条边。
2. 将图中的所有边按照权值从小到大排序。
3. 依次遍历排序后的边,如果该边的两个顶点不在同一个连通分量中,则将该边加入到最小生成树集合中,并合并两个连通分量。
4. 重复步骤3,直到最小生成树集合中边的数量达到n-1条。
三、Prim算法Prim算法是另一种常用的最小生成树算法,其基本思想是从一个顶点开始,每次选择一个和当前最小生成树集合相邻的最小权值边,并将该边的另一个顶点加入到最小生成树集合中。
具体步骤如下:1. 创建一个空的最小生成树集合,初始化为0条边。
2. 随机选择一个顶点作为起始点,将其加入到最小生成树集合中。
3. 每次从最小生成树集合中选出一个顶点,遍历其邻接边,选择权值最小的边,并将该边的另一个顶点加入到最小生成树集合中。
4. 重复步骤3,直到最小生成树集合中顶点的数量达到n个。
四、应用示例假设有一个无向图如下所示:```A---4---B/ \ / \2 3 6 8/ \ \C---9---D---5--E```我们可以使用Kruskal算法或Prim算法求解最小生成树。
使用Kruskal算法的步骤如下:1. 将所有边按照权值从小到大排序:AC, AB, AD, BC, BD, BE, CD, DE。
最小生成树题目

最小生成树题目 最小生成树是图论中的一个重要概念,被广泛应用于路由算法、网络设计、电力传输等领域。
最小生成树问题可以简单描述为:给定一个连通图,选择一些边使得图中所有节点都能够连接,并且总边权之和最小。
最小生成树题目是在解决最小生成树问题时所遇到的具体情境。
以下通过分析两个不同的最小生成树题目,来理解最小生成树算法的应用。
题目1:某城市的道路规划 假设一个城市有多个地区,每个地区之间需要建立道路来连接。
已知每条道路的长度,在保证每个地区都能连通的情况下,设计一个道路规划方案,使得总道路长度最小。
解题思路: 1、首先,根据题目中给出的道路长度,建立一个无向带权图。
其中,每个地区对应图的节点,道路对应图的边,道路长度对应边的权值。
2、通过使用Kruskal或Prim算法,从这个带权图中构建最小生成树,即选取一些道路使得所有地区连通,并且这些道路的权值之和最小。
3、最小生成树即为最优的道路规划方案,输出最小生成树的边集合即可。
题目2:电力传输网络设计 某地区有多个居民点,需要建立电力传输网络来确保每个居民点都能接收到电力供应。
已知每个居民点之间建立电力线路的成本,在保证每个居民点都能接收到电力供应的情况下,设计一个电力传输网络,使得总成本最小。
解题思路: 1、根据题目给出的电力线路成本,建立一个带权完全图。
其中,每个居民点对应图的节点,电力线路对应图的边,电力线路成本对应边的权值。
2、通过使用Kruskal或Prim算法,从这个带权图中构建最小生成树,即选取一些电力线路使得所有居民点都能接收到电力供应,并且这些电力线路的成本之和最小。
3、最小生成树即为最优的电力传输网络设计方案,输出最小生成树的边集合即可。
最小生成树问题是一个经典的优化问题,通过构建最小生成树,我们可以找到图中连接所有节点的最优边集合。
在实际应用中,最小生成树算法可以帮助我们进行有效的资源分配、网络规划等决策。
总体来说,最小生成树题目涉及到图的建模和优化算法的运用。
构造可以使n个城市连接的最小生成树

《数据结构》课程设计报告设计题目:构造可以使n个城市连接的最小生成树姓名:学号:专业:物联网工程(嵌入式培养)院系:计算机技术与科学学院班级:1405指导教师:2016年01 月09 日摘要本次课程设计的要求是给定一个地区的n个城市间的距离网,用Prim算法建立最小生成树,并计算得到的最小生成树的代价。
将该地区的城市用顶点表示,城市间的公路用边表示,公路的长度作为边的权值,最终这个问题可以归结为网图中,求顶点A到顶点B的所有路径中,边的权值之和最少的那条路径。
关键词:最小生成树Prim算法C++语言源程序AbstractThe curriculum design requirements is given a region n city, the distance between the net with the Prim algorithm to establish minimum spanning tree, and calculated the price of minimum spanning tree. Cities in the region with vertex said, between highway in the city edge, said the length of the road as the edge of the right values, finally the problem can be summed up in network diagram, and all the paths of vertex A to B, the edge of the weights of the sum of the minimum path.Keywords:minimum spanning treePrim algorithmC++ language source program目录一、问题描述 (4)1.1题目内容 (4)1.2基本要求 (4)二、需求分析 (4)三、概要设计 (4)3.1邻接矩阵的建立 (5)3.2图的建立 (5)3.3求最小生成树 (6)四、数据结构设计 (7)五、算法设计 (8)5.1算法分析 (8)5.2算法实现 (8)六、程序测试与实现 (9)6.1主程序 (9)6.2测试结果 (10)七、调试分析 (10)八、遇到的问题及解决办法 (10)九、心得体会 (10)十、附录 (11)一、问题描述1.题目内容:给定一个地区的n个城市间的距离网,用Prim算法建立最小生成树,并计算得到的最小生成树的代价。
建立n个城市间的最小生成树.doc

建立n个城市间的最小生成树目录设计要求- 1 -问题重述- 1 -基本要求- 2 -概要设计- 2 -2.1 主界面的设计- 2 -2.2 存储结构的设计本系统- 3 -2.2.1 顺序表的基本概念- 3 -2.2.2 图的邻接矩阵的基本概念- 4 -2.2.3 最小生成树的基本概念- 5 -模块设计- 6 -3.1 n个城市连接的最小生成树- 6 -3.2 模块作用用途中的顶点表示- 6 -3.3 模块及模块调用关系- 6 -3.2.1 “SeqList.h”顺序存储结构存放结点信息- 7 -3.2.2“AdjMGraph.h”邻接矩阵存储结构存放边的信息- 7 -3.2.3 最小生成树的生成过程- 8 -3.3 系统子程序及功能设计- 9 -3.3.1 定义数组- 9 -3.3.2 定义集合- 10 -3.3.3 定义lowcost - 10 -3.3.4 修改权值- 10 -3.3.5 带权图- 10 -3.4 算法描述- 12 -3.4.1 流程图- 12 -测试结果及分析- 14 -测试结果- 14 -4.2 结果分析- 17 -4.3 错误分析- 17 -源程序- 17 -1 设计要求1.1 问题重述选择6-10个城市模拟在城市之间建立通信网络,只需要架设通信路线就可以,以最低的经济花费建设通信网,即用Prim算法或Kreskas算法生成一个网的最小生成树,并计算得到的最小生成树的代价。
1.2 基本要求u 城市间的距离网采用邻接矩阵表示,邻接矩阵的存储结构定义采用课本上的定义,若两个城市之间不存在道路,则将相应边的权值设为自己定义的无穷大值。
要求在屏幕上显示得到的最小生成树中包括那些城市间的道路,并显示得到的最小生成树的代价。
u 表示城市间距离网的邻接矩阵u 最小生成树中包括的边及其权值,并显示得到的最小生成树的代价。
2 概要设计为了实现以上功能,可以从以下主界面构造、存储结构采用、系统功能设置等三个方面进行分析设计。
构造可以使N个城市连接的最小生成树

构造可以使N个城市连接的最小生成树专业:_________ 班级:_________ 姓名:_________ 学号:_________ 完成日期:_________【问题描述】给定一个地区的n个城市间的距离网,用Prim算法或Kruskal算法建立最小生成树,并计算得到的最小生成树的代价。
【设计需求及分析】1、城市间的距离网采用邻接矩阵表示,邻接矩阵的存储结构定义采用课本中给出的定义,若两个城市之间不存在道路,则将相应边的权值设为自己定义的无穷大值。
2、要求在屏幕上显示得到的最小生成树中包括了哪些城市间的道路,并显示得到的最小生成树的代价。
3、表示城市间距离网的邻接矩阵(要求至少6个城市,10条边)。
【设计功能的实现】(用C或C++语言描述)#include <iostream.h>#include <stdio.h>#include <string.h>#include <windows.h>#include "TypeDefine.h"#include "AdjacencyMatrix.h"#include "InitializeFunction.h"#include "MiniSpanTree_KRUSKAL.h"#include "MiniSpanTree_PRIM.h"#include "DisplayNet.h"#include "DeleteInfo.h"MGraph G; //全局变量Gint main(int argc, char * argv[]);//主函数Status LocateVex(MGraph G, VertexType v);//判断城市v 在网G 中的位置Status CreateUDN(MGraph &G);//创建网G 的邻接矩阵void DisplayNet(MGraph G);//以邻接矩阵的形式显示网Gvoid MiniSpanTree_KRUSKAL(MGraph G);//最小生成树的Kruskal 算法void MiniSpanTree_PRIM(MGraph G, VertexType u);//最小生成树的Prim 算法Status Minimum(closedge closeEdge, int n);//Prim 算法中求下一个城市的函数void DeleteInfo(MGraph &G);//释放堆内存上动态申请的空间int main(int argc, char * argv[]){CreateGraph(G);DisplayNet(G);MiniSpanTree_KRUSKAL(G);MiniSpanTree_PRIM(G, G.vexs[0]);DeleteInfo(G);cout<<endl<<endl;system("pause");return 0;}//intializeFunction.hStatus CreateDG(MGraph &G){return 0;};Status CreateDN(MGraph &G){return 0;};Status CreateUDG(MGraph &G){return 0;};Status CreateUDN(MGraph &G);Status LocateVex(MGraph G, VertexType v)//判断输入的顶点v在G中的位置。
最小生成树问题

榆林学院12届课程设计《最小生成树问题》课程设计说明书学生姓名:赵佳学号:1412210112院系:信息工程学院专业:计算机科学与技术班级:计14本1指导教师:答辩时间:年月日最小生成树问题一、问题陈述最小生成树问题设计要求:在n个城市之间建设网络,只需保证连通即可,求最经济的架设方法。
存储结构采用多种。
求解算法多种。
二、需求分析1.在n个城市之间建设网络,只需保证连通即可。
2.求城市之间最经济的架设方法。
3.采用多种存储结构,求解算法也采用多种。
三、概要设计1、功能模块图2、功能描述(1)CreateUDG()创建一个图:通过给用户信息提示,让用户将城市信息及城市之间的联系关系和连接权值写入程序,并根据写入的数据创建成一个图。
(2)Switch()功能选择:给用户提示信息,让用户选择相应功能。
(3)Adjacency_Matrix()建立邻接矩阵:将用户输入的数据整理成邻接矩阵并显现在屏幕上。
(4)Adjacency_List()建立邻接表:将用户输入的数据整理成临接表并显现在屏幕上。
(5)MiniSpanTree_KRSL()kruskal算法:利用kruskal算法求出图的最小生成树,即:城市之间最经济的连接方案。
(6)MiniSpanTree_PRIM()PRIM算法:利用PRIM算法求出图的最小生成树,即:城市之间最经济的连接方案。
四、详细设计本次课程设计采用两种存储结构以及两种求解算法。
1、两种存储结构的存储定义如下:typedef struct Arcell{double adj;}Arcell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef struct{char vexs[MAX_VERTEX_NUM]; //节点数组AdjMatrix arcs; //邻接矩阵int vexnum,arcnum; //图的当前节点数和弧数}MGraph;typedef struct Pnode //用于普利姆算法{ char adjvex; //节点double lowcost; //权值}Pnode,Closedge[MAX_VERTEX_NUM];//记录顶点集U到V-U的代价最小的边的辅助数组定义typedef struct Knode//用于克鲁斯卡尔算法中存储一条边及其对应的2个节点{char ch1; //节点1char ch2; //节点2double value;//权值}Knode,Dgevalue[MAX_VERTEX_NUM];2、求解算法采用Prim算法和Kruskal算法。
《数据结构》课程设计 普里姆算法 最小生成树

[i].stop_vex,lge[i].weight); /*输出N-1条最小边的信息*/
for(i=0;i<12;i++)
{
line(vex[lge[i].start_vex][0],vex[lge[i].start_vex][1],vex[lge
lge[min]=lge[i];
lge[i]=edge;
vx=lge[i].stop_vex;
for(j=i+1; j<pgraph->n-1; j++)
{
vy=lge[j].stop_vex;
weight=pgraph->arcs[vx][vy];
if(weight<lge[j].weight)
{
{550,250},{520,330},{430,400},{350,450},{270,400},{200,330}};
/*初始化个顶点的坐标*/
int info[12][12];
char *text;
void initalGraph(int vec[][2]) /*画出顶点函数*/
{
int gd=DETECT,gm;
[i].stop_vex][0],vex[lge[i].stop_vex][1]);
}
/*根据生成的最小边数组连线*/
printf("---It is done!---");
getch();
exit(1);
}
此程序再TURBOC2.0环境中编译通过运行.TURBOC2.0下载的地址
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)
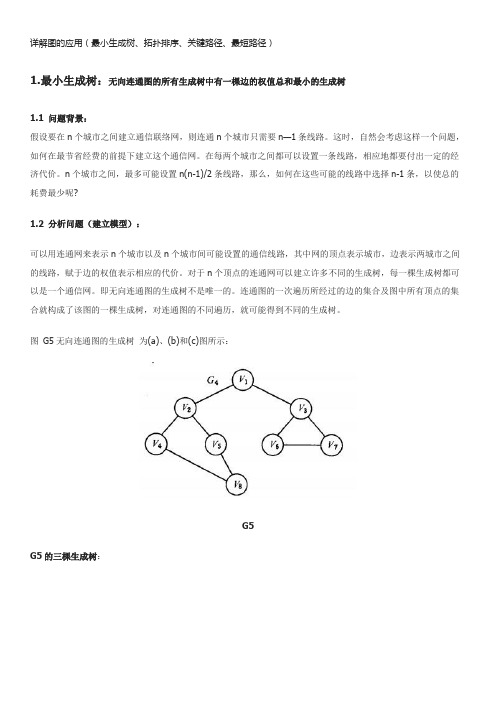
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)1.最小生成树:无向连通图的所有生成树中有一棵边的权值总和最小的生成树1.1 问题背景:假设要在n个城市之间建立通信联络网,则连通n个城市只需要n—1条线路。
这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?1.2 分析问题(建立模型):可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树,对连通图的不同遍历,就可能得到不同的生成树。
图G5无向连通图的生成树为(a)、(b)和(c)图所示:G5G5的三棵生成树:可以证明,对于有n 个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有n-1 条边。
1.3最小生成树的定义:如果无向连通图是一个网,那么,它的所有生成树中必有一棵边的权值总和最小的生成树,我们称这棵生成树为最小生成树,简称为最小生成树。
最小生成树的性质:假设N=(V,{ E}) 是个连通网,U是顶点集合V的一个非空子集,若(u,v)是个一条具有最小权值(代价)的边,其中,则必存在一棵包含边(u,v)的最小生成树。
1.4 解决方案:两种常用的构造最小生成树的算法:普里姆(Prim)和克鲁斯卡尔(Kruskal)。
他们都利用了最小生成树的性质1.普里姆(Prim)算法:有线到点,适合边稠密。
时间复杂度O(N^2)假设G=(V,E)为连通图,其中V 为网图中所有顶点的集合,E 为网图中所有带权边的集合。
【算法】关于图论中的最小生成树(MinimumSpanningTree)详解

【算法】关于图论中的最⼩⽣成树(MinimumSpanningTree)详解什么是图(network)什么是最⼩⽣成树 (minimum spanning tree)最⼩⽣成树的算法这⾥的图当然不是我们⽇常说的图⽚或者地图。
通常情况下,我们把图看成是⼀种由“顶点”和“边”组成的抽象⽹络。
在各个“顶点“间可以由”边“连接起来,使两个顶点间相互关联起来。
图的结构可以描述多种复杂的数据对象,应⽤较为⼴泛,看下图:为了更好地说明问题,下⾯我们看⼀个⽐较⽼套的通信问题:在各⼤城市中建设通信⽹络,如下图所⽰,每个圆圈代表⼀座城市,⽽边上的数字代表了建⽴通信连接的价格。
那么,请问怎样才能以最⼩的价格使各⼤城市能直接或者间接地连接起来呢?我们需要注意两点:最⼩的价格各⼤城市可以是直接或者间接相连的稍稍留⼼可以发现,题⽬的要求是,城市只需要直接或者间接相连,因此,为了节省成本,我们稍稍优化⼀下上述⽅案如下:可以看到,我们砍掉了原先在AD,BE之间的两条道路,建设价格⾃然就降下来了。
当然这个⽅案也是符合我们题⽬的要求的。
按照国际惯例,这⾥要说蛋是了。
上⾯的实例由于数据很简单,优化的⽅案很easy就看出来了。
但在实际中,数据量往往是⾮常庞⼤的。
所以,我们更倾向于设计⼀种⽅法,然后利⽤计算机强⼤的运算能⼒帮我们处理这些数据得出最优的⽅案。
那么,针对上述问题,我们⼀起来看看如何应⽤图的相关知识来实现吧。
为了直观,还是⽤图⽚给⼤家解释⼀下:对于⼀个图⽽⾔,它可以⽣成很多树,如右侧图2,图3就是由图1⽣成的。
从上⾯可以看出⽣成树是将原图的全部顶点以最少的边连通的⼦图,对于有n个顶点的连通图,⽣成树有n-1条边,若边数⼩于此数就不可能将各顶点连通,如果边的数量多于n-1条边,必定会产⽣回路。
对于⼀个带权连通图,⽣成树不同,树中各边上权值总和也不同,权值总和最⼩的⽣成树则称为图的最⼩⽣成树。
基本思想:假设有⼀个⽆向带权图G=(V,E),它的最⼩⽣成树为MinTree=(V,T),其中V为顶点集合,T为边的集合。
构造可以使n个城市连接的最小生成树

数据结构课程设计说明书学院:信息科学与工程学院班级:计算机11-2完成人:姓名:学号:************ 姓名:学号:************ 指导教师:山东科技大学2012年12月13日课程设计任务书一、课程设计题目:构造可以使n个城市连接的最小生成树二、课程设计应解决的主要问题:(1)邻接矩阵的构造及其存储(2)判断是否能够生成最小生成树(3)克鲁斯算法的设计(4)利用克鲁斯算法构造最小生成树时是否产生回路的判断(5)界面的设计三、任务发出日期:2012-11-28 课程设计完成日期:2012-12-13小组分工说明小组编号 35 题目:构造可使n个城市连接的最小生成树小组分工情况:王露:算法设计,void Kruskal()函数,void set ()函数,void find()函数,void Union()函数王炜程:void creat()函数,void judge()函数,int main()函数;int menu()函数,void display()函数组长签字:年月日指导教师对课程设计的评价成绩:指导教师签字:年月日目录一、主要问题------------------------------------------------------------------5二、基本要求------------------------------------------------------------------5三、算法基本思想描述------------------------------------------------------5四、详细设计------------------------------------------------------------------51、数据结构的设计----------------------------------------- 5<1> 存储结构------------------------------------------------------- 5<2> 图的表示--------------------------------------------------------62、算法的设计---------------------------------------------6<1> 克鲁斯卡尔算法设计----------------------------------------------6<2> 防止不能构成最小生成树的图--------------------------------------6<3> 模块结构及功能-------------------------------------------------- 7<4> 主要模块算法描述------------------------------------------------ 7五、源程序清单-----------------------------------------------------------------9六、测试数据及测试结果-----------------------------------------------------91、开始画面--------------------------------------------------------- 92、输入信息--------------------------------------------------------- 103、数据处理---------------------------------------------------------10(1)判断能否构成最小生成树--------------------------------------- 10(2)遍历所有的最小生成树----------------------------------------- 10(3)退出--------------------------------------------------------- 11七、课程设计总结--------------------------------------------------------------11八、附录--------------------------------------------------------------------------------11 参考书目--------------------------------------------------------------------------15构造可以使n个城市连接的最小生成树一、主要问题给定一个地区的n个城市间的距离网,用Prim算法或Kruskal算法建立最小生成树,并计算得到的最小生成树的代价。
数据结构毕业设计论文题目整理

数据结构课程设计题目1.飞机订票系统(限1 人完成)(顺序或链式存储)任务:通过此系统可以实现如下功能:录入:可以录入航班情况(数据可以存储在一个数据文件中,数据结构、具体数据自定)查询:可以查询某个航线的情况(如,输入航班号,查询起降时间,起飞抵达城市,航班票价,票价折扣,确定航班是否满仓);可以输入起飞抵达城市,查询飞机航班情况;订票:(订票情况可以存在一个数据文件中,结构自己设定)可以订票,如果该航班已经无票,可以提供相关可选择航班;退票:可退票,退票后修改相关数据文件;客户资料有姓名,证件号,订票数量及航班情况,订单要有编号。
修改航班信息:当航班信息改变可以修改航班数据文件要求:根据以上功能说明,设计航班信息,订票信息,客户信息的存储结构,设计程序完成功能;2.宿舍管理查询软件(限1 人完成)任务:为宿舍管理人员编写一个宿舍管理查询软件, 程序设计要求:采用交互工作方式建立数据文件,包括学生信息、宿舍信息、住宿信息,学生信息按关键字(姓名、学号)进行排序(排序方法自选,不能相同);查询: (用二分查找实现以下操作)按姓名查询按学号查询(用顺序查找实现以下操作)按房号查询3.校园导航问题(限1 人完成)设计要求:设计你的学校的平面图,至少包括10个以上的场所,每两个场所间可以有不同的路,且路长也可能不同,找出从任意场所到达另一场所的最佳路径(最短路径)。
要求:能增加场所4.图书借阅管理系统(限1 人完成)(顺序或链式存储)主要分为两大功能:1)图书管理(增加图书、查询图书、删除图书、图书借阅、还书);2)会员管理(增加会员、查询会员、删除会员、借书信息);5.学生成绩管理(限1 人完成)(顺序或链式存储)包括:课程信息,学生信息等;能增加课程或学生。
实现功能:输入、输出、插入、删除、查找、显示、保存、排序、退出。
6.活期储蓄帐目管理(限1 人完成)活期储蓄处理中,储户开户、销户、存入、支出活动频繁,系统设计要求:1)能比较迅速地找到储户的帐户,以实现存款、取款记账;2)能比较简单,迅速地实现插入和删除,以实现开户和销户的需要。
普里姆算法求最小生成树

沈阳航空航天大学课程设计报告课程设计名称:数据结构课程设计课程设计题目:Prim算法求最小生成树院(系):计算机学院专业:计算机科学与技术(物联网方向)班级:学号:姓名:指导教师:学术诚信声明本人声明:所呈交的报告(含电子版及数据文件)是我个人在导师指导下独立进行设计工作及取得的研究结果。
尽我所知,除了文中特别加以标注或致谢中所罗列的内容以外,报告中不包含其他人己经发表或撰写过的研究结果,也不包含其它教育机构使用过的材料。
与我一同工作的同学对本研究所做的任何贡献均己在报告中做了明确的说明并表示了谢意。
报告资料及实验数据若有不实之处,本人愿意接受本教学环节“不及格”和“重修或重做”的评分结论并承担相关一切后果。
本人签名: 日期: 2015 年 1 月 15 日沈阳航空航天大学课程设计任务书目录学术诚信声明............................................... - 0 -一课程设计目的和要求..................................... - 5 -1.1课程设计目的 (5)1.2课程设计的要求 (5)二实验原理分析............................................ - 6 -2.1最小生成树的定义.. (6)2.2P RIM算法的基本思想 (7)三概要分析和设计......................................... - 10 -3.1概要分析 (10)3.2概要设计 (11)四测试结果.............................................. - 18 -4.1实验一.. (18)4.2实验二 (18)4.3实验三 (18)参考文献.................................................. - 19 -附录(关键部分程序清单)............................... - 20 -一课程设计目的和要求1.1 课程设计目的(一)根据算法设计需要,掌握连通网的数据表示方法;(二)掌握最小生成树的Prim算法;(三)学习独立撰写报告文档。
数据结构最小生成树

数据结构最小生成树数据结构最小生成树(Minimum Spanning Tree,简称MST)是一种常用的图算法,用来找到一个无向图中权重最小的连通子图,使得该子图包含图中的所有顶点,并且任意两个顶点之间的路径都是该子图中的边。
MST问题在许多实际应用中都有广泛的应用,例如电力传输网络、通信网络、交通网络等。
通过求解MST问题,可以找到一个连接所有节点且总权重最小的网络。
本文将介绍MST问题的定义、经典算法以及一些相关扩展。
MST问题的定义非常直观,即在一个加权无向图G=(V,E)中,找到一个子图T=(V,E'),其中V为图中所有节点的集合,E为图中所有边的集合,E'为E的子集,使得T满足以下条件:1.T是一个连通图,即任意两个节点之间都存在路径。
2.T中不包含回路,即不存在闭合的路径。
3.T的边权重之和最小。
典型的MST算法有Prim算法和Kruskal算法。
Prim算法是通过贪心策略逐步扩展子图T的边集合来构造最小生成树。
算法的基本思想是,从任意一个节点开始,选择一个权重最小的边,将其加入到T的边集合E'中。
然后,将新加入的边连接的节点加入到T的节点集合V中,并以它们为起点,选择与之相连的权重最小的边加入到E'中。
重复这个过程直到图中所有的节点都加入到V中。
Kruskal算法则是通过将图中的所有边按照权重排序,然后逐步将权重最小的边加入到T的边集合E'中,并保证E'中不存在回路,直到E'中的边数达到n-1(其中n为图中节点的个数)或者图中的所有边都加入完毕。
算法的关键在于判断新加入的边是否会形成回路,通常能够通过并查集等数据结构来帮助解决这个问题。
除了Prim和Kruskal算法之外,还存在其他一些改进或者特殊情况下的MST算法。
例如,如果图是稠密图,即边的数量非常多,可以使用优先队列等数据结构来快速找到权重最小的边,提高算法的效率。
如果图是带权的有向图,可以将其转化为无向图再求解MST。
建立n个城市间的最小生成树

目录设计要求........................................................ - 1 - 问题重述........................................................ - 1 - 基本要求........................................................ - 2 - 概要设计........................................................ - 2 - 2.1 主界面的设计............................................... - 2 - 2.2 存储结构的设计本系统...................................... - 3 - 2.2.1 顺序表的基本概念......................................... - 3 - 2.2.2 图的邻接矩阵的基本概念................................... - 4 - 2.2.3 最小生成树的基本概念..................................... - 5 - 模块设计........................................................ - 6 - 3.1 n个城市连接的最小生成树................................... - 6 - 3.2 模块作用用途中的顶点表示................................... - 6 - 3.3 模块及模块调用关系......................................... - 6 - 3.2.1 “SeqList.h”顺序存储结构存放结点信息..................... - 7 - 3.2.2“AdjMGraph.h”邻接矩阵存储结构存放边的信息................ - 7 - 3.2.3 最小生成树的生成过程..................................... - 8 - 3.3 系统子程序及功能设计........................................ - 9 - 3.3.1 定义数组................................................. - 9 - 3.3.2 定义集合................................................ - 10 - 3.3.3 定义lowcost ............................................ - 10 - 3.3.4 修改权值................................................ - 10 - 3.3.5 带权图.................................................. - 10 - 3.4 算法描述.................................................. - 12 - 3.4.1 流程图.................................................. - 12 - 测试结果及分析................................................. - 14 - 测试结果....................................................... - 14 - 4.2 结果分析.................................................. - 16 - 4.3 错误分析.................................................. - 16 - 源程序......................................................... - 17 -1 设计要求1.1 问题重述选择6-10个城市模拟在城市之间建立通信网络,只需要架设通信路线就可以,以最低的经济花费建设通信网,即用Prim算法或Kreskas算法生成一个网的最小生成树,并计算得到的最小生成树的代价。
数据结构(最小生成树)

例如:
a 19
b5
14 12
18
7
c
16 e 8
3
g
d
27
21
f
例如:
a
19
b
14 12
18
7
16 e 8
5
c
3
g
d
27
21
f
克鲁斯卡尔算法
TE
AC
A
6
5
1
B5
1
D
DF
5
C
36
4
2
2 BE
E6
F
3
CF
4
BC
5
算法分析:
• 克鲁斯卡尔算法的时间复杂度为O(eloge)。
• 该算法与网中的边的数目有关。 • 适用于求边稀疏的网的最小生成树。
最小生成树
(Minimum Cost Spanning Tree)
问题:
假设要在 n 个城市之间建立通信联 络网,则连通 n 个城市只需要修建 n-1 条线路,如何在最节省经费的前提下 建立这个通信网?
问题分析:
• 由于在每两个城市之间都可以建立一
条通信线路,n个城市之间最多可能设 置n(n-1)/2条线路,而每条线路都要
最小生成树的定义:
• 按照生成树的定义,含n个顶点的连 通网的生成树有n个顶点、n-1条边。
因此,可以建立许多不同的生成树, 如果一棵生成树的代价等于树上各 边权值之和,那么肯定有一棵生成 树的代价最小,称为最小代价生成 树(简称最小生成树)。
MST性质:
• 假设N=(V,{E})是一个连通网,U是顶点 集V的一个非空子集。若(u,v)是一条具
构造n个城市连接的最小生成树

③主函数: 调用各函数,并输出最后结果
3、 总结: 在做课程设计的时候,我们要先搞清楚原理,再考虑如何去实现! 对于城市的最小生成树问题,让我认识到图能够在计算机中存在,首先 要捕捉它有哪些具体化、数字化的信息,比如说权值、顶点个数等,这 也是说明了想要把生活中的信息转化成到计算机中必须用数字来完整的 构成一个信息库,而图的存在,又涉及到了顶点与顶点之间的联系,图 分为有向图和无向图,而无向图又是有向图在权值双向相等下的一种特 例。
1.构造n个城市连接的最小生成树
一个地区的n个城市间的距离网,用Prim算法或Kruskal算法建 立最小生成树,并计算得到的最小生成树的代价。基本要求: 1) 城市间的距离网采用邻接矩阵表示,邻接矩阵的存储结构定义 采用课本中给出的定义,若两个城市之间不存在道路,则将相应边的 权值设为自己定义的路,并显示得到的最小生成树的代价。 2)表示城市间距离网的邻接矩阵(要求至少6个城市,10条边) (1)代码: #include<stdio.h> #include<stdlib.h> #define MaxVextexNum 30 /* 最大顶点数为30 */ #define INFINITY 32767 typedef struct{ int vexs[MaxVextexNum] ; /* 顶点表 */ int arcs[MaxVextexNum][MaxVextexNum] ; /* 邻接矩阵,即边表 */ int n ,e ; }MGraph ; typedef struct{ int adjvertex ; /* 某顶点与已构造好的部分生成树的顶点 之间权值最小的顶点 */ int lowcost ; /* 某顶点与已构造好的部分生成树的顶点之 间 的最小权值 */ /* 顶点数和边数 */ /* MGragh是以邻接矩阵存储的图类型 */ /* 定义一个权值的最大值 */
prim算法建立n个城市间的最小生成树

数据结构课程设计报告设计题目:n个城市连接的最小生成树专业通信工程班级0903 班学生彭焱学号指导教师起止时间2012.2.14~2012. 3.132012 年 2 学期目录一.设计题目........................................................................................................... - 3 - 【问题描述】.................................................................................................... - 3 - 【基本要求】.................................................................................................... - 3 - 【实现提示】.................................................................................................... - 3 - 二.设计内容........................................................................................................... - 3 -1.分析问题及解决问题.................................................................................... - 3 -三、基本概念........................................................................................................... - 4 -1、顺序表的基本概念...................................................................................... - 4 -2、图的邻接矩阵的基本概念.......................................................................... - 4 -3、最小生成树的基本概念.............................................................................. - 5 -4.普利姆算法思想............................................................................................ - 6 - 四.概要设计........................................................................................................... - 6 -1、模块作用...................................................................................................... - 6 -2、模块及模块调用关系.................................................................................. - 6 -(1)“SeqList.h”顺序存储结构存放结点信息..................................... - 7 -(2).“AdjMGraph.h”邻接矩阵存储结构存放边的信息....................... - 7 -(3)本课程设计中最小生成树的生成过程............................................... - 8 - 五.算法描述......................................................................................................... - 12 -1.流程图.......................................................................................................... - 12 - 六.测试结果及分析............................................................................................. - 14 -1、测试结果.................................................................................................... - 14 -2、结果分析.................................................................................................... - 16 -3、错误分析.................................................................................................... - 16 -七、心得体会和参考资料..................................................................................... - 17 -1.心得体会.................................................................................................... - 17 -2.参考资料...................................................................................................... - 17 - 附录:源代码......................................................................................................... - 17 -一.设计题目【问题描述】给定一个地区的n个城市间的距离网,用Prim算法或Kreskas算法建立最小生成树,并计算得到的最小生成树的代价。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
构造可以使N个城市连接的最小生成树专业:_________ 班级:_________ 姓名:_________ 学号:_________ 完成日期:_________【问题描述】给定一个地区的n个城市间的距离网,用Prim算法或Kruskal算法建立最小生成树,并计算得到的最小生成树的代价。
【设计需求及分析】1、城市间的距离网采用邻接矩阵表示,邻接矩阵的存储结构定义采用课本中给出的定义,若两个城市之间不存在道路,则将相应边的权值设为自己定义的无穷大值。
2、要求在屏幕上显示得到的最小生成树中包括了哪些城市间的道路,并显示得到的最小生成树的代价。
3、表示城市间距离网的邻接矩阵(要求至少6个城市,10条边)。
【设计功能的实现】(用C或C++语言描述)#include <iostream.h>#include <stdio.h>#include <string.h>#include <windows.h>#include "TypeDefine.h"#include "AdjacencyMatrix.h"#include "InitializeFunction.h"#include "MiniSpanTree_KRUSKAL.h"#include "MiniSpanTree_PRIM.h"#include "DisplayNet.h"#include "DeleteInfo.h"MGraph G; //全局变量Gint main(int argc, char * argv[]);//主函数Status LocateVex(MGraph G, VertexType v);//判断城市v 在网G 中的位置Status CreateUDN(MGraph &G);//创建网G 的邻接矩阵void DisplayNet(MGraph G);//以邻接矩阵的形式显示网Gvoid MiniSpanTree_KRUSKAL(MGraph G);//最小生成树的Kruskal 算法void MiniSpanTree_PRIM(MGraph G, VertexType u);//最小生成树的Prim 算法Status Minimum(closedge closeEdge, int n);//Prim 算法中求下一个城市的函数void DeleteInfo(MGraph &G);//释放堆内存上动态申请的空间int main(int argc, char * argv[]){CreateGraph(G);DisplayNet(G);MiniSpanTree_KRUSKAL(G);MiniSpanTree_PRIM(G, G.vexs[0]);DeleteInfo(G);cout<<endl<<endl;system("pause");return 0;}//intializeFunction.hStatus CreateDG(MGraph &G){return 0;};Status CreateDN(MGraph &G){return 0;};Status CreateUDG(MGraph &G){return 0;};Status CreateUDN(MGraph &G);Status LocateVex(MGraph G, VertexType v)//判断输入的顶点v在G中的位置。
//根据顶点的类型,可重载此函数。
目前为charint i=0;while (strcmp(G.vexs[i], v)) {i++;}return i;}Status CreateGraph(MGraph &G){//采用数组(邻接矩阵)表示法,构造图G.G.kind = UDN; //默认构造无向网/* printf("+~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\n");printf("|1:有向图2:无向图3:有向网4:无向网\n");printf("|请选择:[ ]\b\b");scanf("%d", &G.kind);printf("+~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\n");*/switch (G.kind){case DG: return CreateDG(G); //构造有向图Gcase DN: return CreateDN(G); //构造有向网Gcase UDG: return CreateUDG(G); //构造无向图Gcase UDN: return CreateUDN(G); //构造无向网Gdefault : return ERROR;}}//CreateGraphStatus CreateUDN(MGraph &G){//采用数组(邻接矩阵)表示法,构造图G.int i, j, k;VertexType v1, v2;VRType w;printf(" 构造可以使N个城市连接的最小生成树\n"); printf("请输入城市数、道路数(至少6个城市,10条道路):");cin>>G.vexnum>>G.arcnum;for (i=0; i<G.vexnum; ++i) //构造顶点向量{printf("请输入第%d 个城市名(共%d 个):", i+1, G.vexnum);cin>>G.vexs[i];}for (i=0; i<G.vexnum; ++i) //初始化邻接矩阵{for (j=0; j<G.vexnum; ++j){G.arcs[i][j].adj = INFINITY;// G.arcs[i][j].info = NULL;}}printf("请输入一条道路连接的两个城市名及权值:\n");for (k=0; k<G.arcnum; ++k) //构造邻接矩阵{printf("共%3d条道路,第%3d条道路:", G.arcnum,k+1);cin>>v1>>v2>>w; //输入一条边依附的顶点及权值i = LocateVex(G, v1); //确定v1、v2在G中的位置j = LocateVex(G, v2);G.arcs[i][j].adj = w; //弧<v1,v2>的权值G.arcs[j][i] = G.arcs[i][j]; //置<v1,v2>的对称弧<v2,v1>}return OK;}//CreateUDN//MiniSpan Tree PRIM.hStatus Minimum(closedge closeEdge, int n){int i, flag, minTemp = INFINITY;for (i=0; i<n; ++i){if ((closeEdge[i].lowcost != 0) && (minTemp > closeEdge[i].lowcost)){minTemp = closeEdge[i].lowcost;flag = i;}}return flag;}void MiniSpanTree_PRIM(MGraph G, VertexType u){//用普里姆算法从第u 个顶点出发构造网G 的最小生成树T,输出T 的各条边。
//记录从顶点集U 到V-U 的代价最小的边的辅助数组定义见"AdjacencyMatrix.h"int i, j, k, totalCost=0;closedge closeEdge;k = LocateVex(G, u);for (j=0; j<G.vexnum; ++j) //辅助数组初始化{if (j != k){strcpy(closeEdge[j].adjvex, u);closeEdge[j].lowcost = G.arcs[k][j].adj;}}cout<<"\n\n+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^\\\n";cout<<"|用Prim算法求最小生成树的各条边依次为:\n-----";closeEdge[k].lowcost = 0; //初始,U={u};for (i=1; i<G.vexnum; ++i) //选择其余G.vexnum-1 个顶点{k = Minimum(closeEdge, G.vexnum); //求出T 的下一个结点:第k 顶点//此时closeEdge[k].lowcost = MIN{closeEdge[vi].lowcost | closeEdge[vi].lowcost > 0, vi∈V-U}cout<<'<'<<closeEdge[k].adjvex<<','<<G.vexs[k]<<'>'; //输出生成树的边totalCost += closeEdge[k].lowcost;closeEdge[k].lowcost = 0; //第k 顶点并入U 集for (j=0; j<G.vexnum; ++j){if (G.arcs[k][j].adj < closeEdge[j].lowcost) //新顶点并入U 后重新选择最小边{strcpy(closeEdge[j].adjvex, G.vexs[k]);closeEdge[j].lowcost = G.arcs[k][j].adj;}}}cout<<"\n|总代价:"<<totalCost<<endl;cout<<"+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^/\n"; }//MiniSpanTree【实例测试及运行结果】【使用说明】心得体会:【选作内容】。
