江苏省泰兴市第一高级中学2014-2015学年高一下学期期末模拟考试(一)数学试题word版 含答案
江苏省泰兴市第一高级中学2014-2015学年高一数学下学期期末模拟考试试题(一)

泰兴市第一高级中学2014—2015学年度第二学期期末模拟考试(一)高一数学试卷卷面总分:160分 考试时间:120分钟一、填空题:本大题共14小题,每小题5分,共70分。
不需要写出解答过程,请把答案直接填空在答题卡相应位置上........ 1. 已知直线4:=-y mx l 若直线l 与直线2)1(=-+y m m x 垂直,则m 的值为______. 2.若等比数列{}n a 的前n 项和为n S ,且141,8a a ==,则5S = .3. 已知圆222:C x y r +=与直线34100x y -+=相切,则圆C 的半径r =4.若x >y ,a >b ,则在①a -x >b -y ,②a +x >b +y ,③ax >by ,④x -b >y -a ,⑤a y >bx这五个式子中,恒成立的所有不等式的序号是________.5.在等差数列{n a }中,已知1083=+a a ,则375a a += . 6.过圆422=+y x 上一点()3,1-P 的切线方程为___________________.7.设实数y x ,满足⎪⎩⎪⎨⎧≤-≥-+≤--,032,042,02y y x y x 则x y 的最大值为___________8. 设直线x -my -1=0与圆(x -1)2+(y -2)2=4相交于A 、B 两点,且弦AB 的长为23,则实数m 的值是________. 9. 设,l m 是两条不同的直线,,αβ是两个不同的平面,则下列命题为真命题的序号是____. (1).若//,//,//m l m l αα则;(2).若,,//m l m l αα⊥⊥则; (3).若//,,//,l m l m αβαβ⊥⊥则; (4).若,//,,//,//m m l l αββααβ⊂⊂则10. 已知正四棱锥的底面边长是6,则该正四棱锥的侧面积为 .11.己知a ,b 为正数,且直线 60ax by +-=与直线 2(3)50x b y +-+=互相平行,则2a +3b 的最小值为 .12.如果关于x 的不等式22(1)(1)10m x m x --+-<的解集是R ,则实数m 的取值范围是 .2200013.:x 1,(,):3240,O y P x y l x y O OA OB OP x +=+-=+=已知圆点是直线上的动点,若在圆上总存在不同的两点A,B 使得则的取值范围为________.2222214.,,24,1,1x y x y x y R y x x xy x y ++-+∈≤≤-≥-+-已知满足则的最大值为_______.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15. (本题满分14分)已知ABC △的顶点()()()4,1,0,1,23-C B A ,,求: (1)AB 边上的高所在直线的方程; (2)AC 边上的中线所在直线的方程;(3)ABC △外接圆方程. 16、(本题满分14分)等比数列{}n a 的各项均为正数,且21252643,9a a a a a -== .(1)求数列{}n a 的通项公式;(2)设3log n n b a =,求数列{}n n a b +的前n 项和n S .如图所示,矩形ABCD 中,AD ⊥平面ABE ,2AE EB BC ===,F 为CE 上的点,且BF ⊥平面ACE (1) 求证:AE ⊥平面BCE ;(2) 求证://AE 平面BFD ;(3) 求三棱锥C BGF -的体积.18.(本题满分16分)某加工厂需定期购买原材料,已知每千克原材料的价格为1.5元,每次购买原材料需支付运费600元,每千克原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400千克,每次购买的原材料当天即开始使用(即有400千克不需要保管).(1)设该厂每x 天购买一次原材料,试写出每次购买的原材料在x 天内总的保管费用y 1关于x 的函数关系式;(2)求该厂多少天购买一次原材料才能使平均每天支付的总费用y 最小,并求出这个最小值.G BAD C FE已知以点C ⎝⎛⎭⎪⎫t ,2t (t ∈R ,t ≠0)为圆心的圆与x 轴交于点O ,A ,与y 轴交于点O ,B ,其中O为原点.(1)求证:△AOB 的面积为定值;(2)设直线2x +y -4=0与圆C 交于点M ,N ,若OM ON =,求圆C 的方程;(3)在(2)的条件下,设P ,Q 分别是直线l :x +y +2=0和圆C 上的动点,求PB PQ +的最小值及此时点P 的坐标.20.(本题满分16分)已知 n S 是数列{}n a 的前n 项和,且244n S n n =-+ (1)求数列{}n a 的通项公式;(2)设各项均不为零的数列{}n c 中,所有满足01<⋅+k k c c 的正整数k 的个数称为这个数列{}n c 的变号数,令nn a c 41-=(n 为正整数),求数列{}n c 的变号数; (3)记数列1{}na 的前n 的和为n T ,若2n+115n m T T -≤对+∈N n 恒成立,求正整数m 的最小值。
《解析》江苏省泰州市泰兴一中2014-2015学年高一下学期期末数学补考试卷Word版含解析

江苏省泰州市泰兴一中2014-2015学年高一下学期期末数学补考试卷一、填空题(每题5分)1.已知集合A=[1,4),B=(﹣∞,a),若A⊆B,则实数a的取值范围为.2.设函数f(x)=则的值为.3.函数的定义域是.4.若点A(x,y)是300°角终边上异于原点的一点,则的值为.5.求值:=.6.已知向量=(﹣1,1),=(1,2),且(2+)∥(﹣λ),则λ=.7.已知向量与的夹角为θ,且||=3,||=4,|+|=5,则θ=.8.△ABC中,已知AB=2,BC=5,S△ABC=4,∠ABC=θ,则cosθ=.9.已知0<<β<π,且cos,sin(α+β)=,则sinα=.二、解答题10.已知函数f(x)=2sin2x.(Ⅰ)求函数f(x)最小正周期;(Ⅱ)若f(x)=2,求x的值;(Ⅲ)写出函数f(x)的单调递减区间.11.已知向量||=1,||=.(Ⅰ)若向量的夹角为60°,求的值;(Ⅱ)若,求的值;(Ⅲ)若,求的夹角.12.已知向量=(1,cosx),=(,sinx),x∈(0,π).(Ⅰ)若∥,分别求tanx和的值;(Ⅱ)若⊥,求sinx﹣cosx的值.江苏省泰州市泰兴一中2014-2015学年高一下学期期末数学补考试卷一、填空题(每题5分)1.已知集合A=[1,4),B=(﹣∞,a),若A⊆B,则实数a的取值范围为a≥4.考点:集合的包含关系判断及应用.专题:计算题.分析:集合A=[1,4),B=(﹣∞,a),A⊆B,根据子集的定义可求.解答:解:由题意,集合A=[1,4)表示大于等于1而小于4的数,B=(﹣∞,a)表示小于a的数,∵A⊆B,∴a≥4故答案为a≥4点评:本题的考点是集合关系中的参数取值问题,主要考查集合中的子集关系,关键是理解集合表达的数的范围..2.设函数f(x)=则的值为.考点:函数的值;分段函数的解析式求法及其图象的作法.专题:计算题.分析:本题是分段函数求值,规律是先内而外逐层求值,先求f(2)值,再根据的取值范围判断应该用那一段上的函数解析式,代入求值即为的值.解答:解:由于2>1,故f(2)=22+2﹣2=4故=≤1故=1﹣=故答案为.点评:本题考点是求函数的值,本题是一个分段复合型函数,此类题易出错,错因在解析式选用不当.3.函数的定义域是[1,2).考点:函数的定义域及其求法;对数函数的定义域.专题:计算题.分析:根据对数函数的真数一定要大于0,可以得2﹣x>0;又有偶次开方的被开方数非负,得到:x﹣1≥0,进而求出x的取值范围.解答:解:∵2﹣x>0,且x﹣1≥0,解得1≤x<2,∴函数的定义域为[1,2)故答案为:[1,2).点评:本题考查对数函数求定义域问题,注意对数函数的真数一定大于0,偶次开方的被开方数一定非负,属基础题.4.若点A(x,y)是300°角终边上异于原点的一点,则的值为.考点:任意角的三角函数的定义.专题:计算题.分析:根据三角函数的定义,是300°角的正切值,求解即可.解答:解:点A(x,y)是300°角终边上异于原点的一点,则的值就是:tan300°= 所以=tan300°=﹣tan60°=故答案为:﹣点评:本题是基础题,考查任意角的三角函数的定义,诱导公式的应用,考查计算能力.5.求值:=.考点:诱导公式的作用.专题:计算题.分析:直接利用诱导公式,化简表达式为特殊角以及锐角的三角函数,然后求出值即可.解答:解:===.故答案为:.点评:本题是基础题,考查诱导公式的应用,注意特殊角的三角函数值,考查计算能力.6.已知向量=(﹣1,1),=(1,2),且(2+)∥(﹣λ),则λ=.考点:平行向量与共线向量.专题:平面向量及应用.分析:利用向量坐标运算、向量共线定理即可得出.解答:解:2+=2(﹣1,1)+(1,2)=(﹣1,4),=(﹣1,1)﹣λ(1,2)=(﹣1﹣λ,1﹣2λ),∵(2+)∥(﹣λ),∴﹣(1﹣2λ)﹣4(﹣1﹣λ)=0,化为6λ=﹣3,解得λ=﹣.故答案为:﹣.点评:本题考查了向量坐标运算、向量共线定理,属于基础题.7.已知向量与的夹角为θ,且||=3,||=4,|+|=5,则θ=90°.考点:数量积表示两个向量的夹角.专题:计算题.分析:由题意可得=,再利用两个向量的数量积的定义解得cosθ=0,根据θ的范围求出θ的值.解答:解:由题意可得==9+16+2=25+2×3×4cosθ=25,解得cosθ=0.再由0°≤θ≤180°可得θ=90°,故答案为90°.点评:本题主要考查两个向量的数量积的定义,两个向量数量积的运算,根据三角函数的值求角,属于中档题.8.△ABC中,已知AB=2,BC=5,S△ABC=4,∠ABC=θ,则cosθ=.考点:三角形中的几何计算.专题:解三角形.分析:根据三角形的面积公式进行求解即可.解答:解:∵AB=2,BC=5,S△ABC=4,∴S△ABC=AB•BCsinθ=4,即sinθ=4,则sinθ=,则cosθ==,故答案为:点评:本题主要考查三角形面积的计算以及同角的三角函数的基本关系,比较基础.9.已知0<<β<π,且cos,sin(α+β)=,则sinα=.考点:两角和与差的正弦函数.专题:计算题;三角函数的求值.分析:运用同角的平方关系,分别求得sinβ,cos(α+β),再由sinα=sin(α+β﹣β)运用两角差的正弦公式,计算即可得到.解答:解:由于0<<β<π,cos,则sinβ==.由于,则cos(α+β)=﹣=﹣,则有sinα=sin(α+β﹣β)=sin(α+β)cosβ﹣cos(α+β)sinβ=×(﹣)﹣(﹣)×=.故答案为:.点评:本题考查同角的基本关系式,考查两角的正弦公式,考查角的变换的方法,考察运算能力,属于中档题和易错题.二、解答题10.已知函数f(x)=2sin2x.(Ⅰ)求函数f(x)最小正周期;(Ⅱ)若f(x)=2,求x的值;(Ⅲ)写出函数f(x)的单调递减区间.考点:三角函数的周期性及其求法;正弦函数的单调性.专题:三角函数的图像与性质.分析:(1)按三角函数周期公式直接求解;(2)把f(x)=2带入,解三角函数2=2sin2x;(3)根据正弦函数的单调性进行分析;解答:解:(1)T==π…4分(2)∵f(x)=2∴2=2sin2x即sin2x=1∴2x=x=…9分(3)函数f(x)=2sin2x的单调递减区间为2x即x…14分点评:考查了三角函数的基本性质,属于基础题.11.已知向量||=1,||=.(Ⅰ)若向量的夹角为60°,求的值;(Ⅱ)若,求的值;(Ⅲ)若,求的夹角.考点:数量积表示两个向量的夹角;平面向量数量积的运算.专题:计算题;平面向量及应用.分析:(I)根据向量数量积的定义,结合题中数据直接计算,可得的值;(II)将平方,结合题中数据可得=5,代入数据得=1;(III)由已知等式算出==1,再根据平面向量的夹角公式算出夹角的余弦值,即可得到夹角的大小.解答:解:(I)当向量的夹角为60°时,求==;(II)∵||=1,||=.∴由,得()2=1+2+2=5解之得=1;(III)∵∴==1,设的夹角为α则cosα==,可得α=.点评:本题给出向量满足的条件,求的数量积和夹角大小.着重考查了平面向量数量积的定义及其运算性质等知识,属于基础题.12.已知向量=(1,cosx),=(,sinx),x∈(0,π).(Ⅰ)若∥,分别求tanx和的值;(Ⅱ)若⊥,求sinx﹣cosx的值.考点:平面向量共线(平行)的坐标表示;平面向量数量积的运算;同角三角函数基本关系的运用.专题:三角函数的求值;平面向量及应用.分析:(I)利用向量共线定理、同角三角函数基本关系式即可得出;(II)利用向量垂直与数量积的关系、同角三角函数基本关系式即可得出.解答:解:(Ⅰ)∵,∴(Ⅱ)∵,∴,又∵.∴.点评:本题考查了向量共线定理、向量垂直与数量积的关系、同角三角函数基本关系式,考查了推理能力和计算能力,属于中档题.。
江苏省泰兴市第一高级中学2014-2015学年高一语文下学期调研测试试题(一)不分版本

江苏省泰兴市第一高级中学2014-2015学年高一语文下学期调研测试试题(一)不分版本2015年春学期高一年级调研测试〔一〕高一语文〔说明:1.总分值160分,150分钟。
2.所有选择题的答案,请按照相应序号填涂到答题卡上。
〕一、语言文字运用〔21分〕1.在下面一段话空缺处依次填入词语,最恰当的一组是〔3分〕〔〕亚太地区历史悠久,灿烂文明___________至今。
如今,各国正___________改革和经贸合作,着力构建面向未来的新型亚太伙伴关系。
2014年北京APEC会议期间,各国领导人及官员___________了中国的巨大变化,对中国梦和亚太梦的圆满实现充满期待。
A.流传大肆耳濡目染B.留传大事耳闻目睹C.流传大事耳闻目睹D.留传大肆耳濡目染2.以下最适宜做“雪映梅花梅映雪〞下联的是〔3分〕〔〕A.河开镜湖花醉人B.莺宜柳絮柳宜莺C.菊香四野人忘归D.蜂闹花丛蝶伴舞3.下面是四种不同情境的讲话,且都与“笑〞有关。
根据情境推断,表达不得体的一项为哪一项〔〕〔3分〕A.初次见面时的讲话:我不会讲话,您可别见笑。
B.再次遇到朋友时的讲话:去岁路过贵地,本要登堂求教;但愧知识短浅,诚恐贻笑大方。
C.接受别人礼物时的讲话:恭敬不如从命,我就笑纳了。
D.在追悼大会上的讲话:凶手被抓捕,正气得弘扬,愿我们的英雄含笑九泉。
4.在下面一段文字横线处填入语句,衔接最恰当的一项为哪一项〔3分〕〔〕无题诗是李商隐独创的一种诗歌体式。
他创作的无题诗颇多,而这种寄寓又往往是模糊隐晦,在有无之间,所谓不便明言的情感隐秘。
①由于表达隐晦曲折,历代的研究者解说各异,更有不少穿凿附会。
②其中不乏直接写爱情相思的,但更多借“香草美人〞的比兴传统抒发身世感喟。
③往往以男女爱情相思为题材。
④这些诗篇是诗人人生感受与情感的原生态的展现。
⑤辞藻精丽,意境要妙,情思婉转,读来令人荡气回肠。
A.③①②⑤④ B.③⑤①④② C.④①②③⑤ D.④②⑤③①5.对下面句子中加点的实词解释有错误的一项为哪一项〔3分〕〔〕A.时北兵已迫.修门外迫:逼近B.众谓予一行为可以纾.祸纾:祸害C.会.使辙交驰会:适逢D.予更欲一觇.北觇:窥视6.下面四个句子中文言虚词“其〞的用法,与其他三项不一样的一项为哪一项〔3分〕〔〕A.行李之往来,共其.乏困B.越国以鄙远,君知其.难也C.失其.所与,不知D.吾其.还也7.下面四句话中的文言句式,与其它三项不一样的一项为哪一项〔3分〕〔〕A.以其无礼于晋B.夫晋,何厌之有C.因人之力而敝之,不仁D.假设亡郑而有益于君二、文言文阅读〔19分〕阅读下面的文言文,完成8~11题。
江苏省泰兴市第一高级中学2014-2015学年高一语文下学期期末模拟试题(二)不分版本

江苏省泰兴市第一高级中学2014-2015学年高一语文下学期期末模拟试题(二)不分版本泰兴市第一高级中学2014—2015学年度第二学期期末模拟考试〔二〕高一语文试卷卷面总分:160分考试时间:150分钟一、语言文字运用(15分)1. 在下面一段话空缺处依次填入词语,最恰当的一组是(3分)( )网络上大规模________的“挖掘机哪家强?〞造句热,使蓝翔技校________。
事实上,现在“蓝翔〞已经和“土豪〞等词语一样,成了某种文化的象征。
“蓝翔〞两个字早已不再是蓝翔技校的代名词,而逐步________成了类似“高深莫测,咋咋呼呼〞的含义。
A. 爆发名声大噪演绎B. 爆发名声大噪演化C. 爆发声名鹊起演化D. 爆发声名鹊起演绎2.以下古代诗句所蕴含的理趣与故事内容最不相符的一项为哪一项〔〕〔3分〕相传,古希腊有位国王做了一顶纯金王冠,便疑心工匠在王冠中掺假。
如何临别真假又不损坏原物?国王将这个难题交给了阿基米德。
阿基米德尝试过很多方法都失败了。
有一天他去洗澡,踏入浴盆,水往外溢。
他恍然大悟,终于找到了答案。
A.路曼曼其修远兮,吾将上下而求索。
B.山重水复疑无路,柳暗花明又一村C.踏破铁鞋无觅处,得来全不费功夫D.众里寻他千百度,蓦然回首,那人却在,灯火阑珊处。
3. 顾城有这样一首诗:“鸟儿在疾风中/迅速转向/少年去捡拾/一枚分币/葡萄藤因梦想/而延伸的触丝/海浪因退缩/而耸起的背脊。
〞请问这首诗的题目是(3分)( )A. 一种灵魂在歌唱B. 弧线C. 世界中的主人公D. 向往4. 以下是剧中有关人物的描述和对白,在横线上依次填写人物姓名正确的一项为哪一项(3分)〔〕〔1〕_______的语言谦恭、周到,与各种人物应酬反响机敏、对答如流,符合他的身份。
〔2〕_______的语言那么豪爽耿直,带有闯荡多年的侠气和饱经沧桑的沉重感。
〔3〕_______努力改进,终逃不了艰难处境,最后破产自杀;A.王利发马五爷松二爷 B.松二爷马五爷王利发C.秦仲义常四爷松二爷 D.王利发常四爷王利发5.下面选项中符合横线上情节表述的一项为哪一项(3分)〔〕过了七十六岁的葛朗台在看到女儿把玩金梳妆匣时,竟〞身子一纵,扑上梳妆匣,好似一头老虎扑上一个睡着的婴儿〞。
泰兴一中2014-2015年第二学期高一生物期末模拟试卷及答案

泰兴市第一高级中学2014—2015学年度第二学期期末模拟考试(一)高一生物试卷2015.6.22卷面总分:100分 考试时间:100分钟第Ⅰ卷 选择题(共60分)一、选择题:每小题只有一个选项最符合题意(本题共40小题,每小题1.5分)1.下列哪项不属于孟德尔进行遗传实验研究获得成功的原因A .正确地选用豌豆作为实验材料B .先分析多对性状后分析一对相对性状的遗传C .运用统计学方法分析实验结果D .科学地设计实验程序,提出假说并进行验证2.两株高茎豌豆杂交,后代高茎和矮茎的比例如图所示,则亲本的基因型为A .GG×ggB .GG×GgC .Gg×GgD .gg×gg3. 豌豆中高茎(T )对矮茎(t )是显性,绿豆荚(G )对黄豆荚(g )是显性,这两对基因是自由组合的,则Ttgg 与TtGg 杂交后代的基因型和表现型的种类依次是A .5和3B .6和4C .8和6D .9和44. 基因型为YyRr 的个体不可能...产生的配子是 A .YR B .yR C .Yr D .Yy5.以下所示为人类精子形成的过程:精原细胞→初级精母细胞――→减数第一次分裂次级精母细胞――→减数第二次分裂精细胞→精子。
下列关于描述错误的是A.染色体数目减半发生在减数第二次分裂结束时B.精细胞到精子的过程是精子形成中特有的变形过程C.减数第一次分裂中联会的同源染色体彼此分离非同源染色体自由组合D.减数第二次分裂方式和有丝分裂相似 6. 下列曲线表示减数分裂过程中DNA 含量变化的是:A B C D高 矮7.下列对四分体的叙述正确的是A.一个细胞中含有4条染色体B.一个细胞中含有4对染色体C.一个细胞中含有4条染色单体D.一对同源染色体含4条染色单体8.右图是某家族红绿色盲的遗传系谱图,正确的分析是A.父亲是色盲,女儿一定是色盲B.双亲色觉正常,子女色觉一定正常C.图中1、4是色盲基因的携带者D.图中2、7是色盲基因的携带者9.对染色体、DNA、基因三者来说,错误的是A.染色体由DNA和蛋白质组成 B.一般一条染色体上有一个DNAC.基因在染色体上呈线性排列 D.一个DNA上有一个基因10.下列关于生物的遗传物质的叙述中,不正确的是A.某一生物体内的遗传物质只能是DNA或RNAB.除少数病毒外,生物的遗传物质都是DNAC.核酸的基本组成单位是脱氧核糖核酸D.组成核酸的碱基有5种:A、T、G、C、U11.关于DNA分子结构的叙述不.正确的是A.每个DNA分子一般都含有四种脱氧核苷酸B.DNA分子中的碱基之间的化学键是氢键C.DNA分子中的基本骨架脱氧核糖和磷酸交替连接排列在内侧D.DNA一般是双链的,两条链按反向平行方式盘旋成双螺旋结构,12.下列关于DNA复制的叙述,正确的是A.在细胞分裂间期,复制时遵循的碱基互补配对原则是A与T配对,G与C配对B.DNA通过一次复制后产生四个DNA分子C.DNA双螺旋结构全部解链后,开始与原来DNA的一条链为模板复制新的DNAD.单个脱氧核苷酸在DNA连接酶的作用下连接合成新的子链13.DNA分子的一条链中(A+G)/(T+C)=0.4,上述比例在其互补链和整个DNA分子中分别是A. 0.4和0.6B. 2.5和1C. 0.6和1D. 0.6和0.414.有关下图的叙述,正确的是①甲→乙表示DNA转录②共有5种碱基③甲、乙中的A表示同一种核苷酸④共有4个密码子⑤甲→乙过程主要在细胞核中进行A.①②④ B.①②⑤ C.②③⑤ D.①③⑤15.下面是关于基因、蛋白质和性状三者间的关系叙述,其中不正确的是A. 生物体的性状完全由基因控制B. 蛋白质的结构可以直接影响性状C. 基因控制性状是通过控制蛋白质的合成来实现的D. 蛋白质的功能可以影响性状16.我国著名的女子花样游泳运动员蒋雯雯和蒋婷婷是同卵孪生姊妹,长得十分相像。
江苏省泰州市2014-2015学年高一下学期期末统考数学试题 含解析

一、填空题:(本大题共14题,每小题5分,共70分,请将答案填入答题纸填空题的相应答题线上)1。
直线30x y -+=的倾斜角为__________ 【答案】4π【解析】试题分析:由直线方程可知斜率1tan 14k παα=∴=∴=考点:直线倾斜角与斜率2。
若直线1ax y +=与(1)23a x y -+=直线平行,则实数a 的值是_______ 【答案】1- 【解析】试题分析:两直线平行则系数满足211a a a =-∴=- 考点:两直线平行的判定3。
在长方体1111ABCD A BC D -的棱所在直线中,与直线AB 异面的条数为________ 【答案】4 【解析】试题分析:与直线AB 异面的直线有111111,,,A D B C DD CC 共4条考点:异面直线4。
在等比数列{}na 中,45a=,则17a a =_________【答案】25 【解析】试题分析:由等比数列性质可知217425a aa ==考点:等比数列性质5.不等式2111x x ->+的解集为________【答案】(,1)(2,)-∞-+∞【解析】试题分析:原不等式2111x x ->+化为()()2021021x x x x x ->∴-+>∴>+或1x <-,因此不等式的解集为(,1)(2,)-∞-+∞考点:分式不等式解法6。
0,0,1x y x y ≥≥+≤,则x y -的最大值为__________ 【答案】1考点:线性规划问题7.正方体的表面积为24,则该正方体的内切球的体积为____________ 【答案】43π【解析】试题分析:正方形边长设为x 26242x x ∴=∴=,内切球的直径为2,所以体积为34433V Rππ== 考点:正方体与球的基本知识 8。
若圆22(2)()1x y a ++-=与圆22()(5)16x a y -+-=相交,则实数a 的取值范围是_______ 【答案】12a <<【解析】试题分析:两圆相交,则圆心距满足()()221212325512r r d r r a a a -<<+∴<++-<∴<<考点:两圆的位置关系9。
江苏省泰兴市第一高级中学高一英语下学期期末模拟考试试题(一)

泰兴市第一高级中学2014—2015学年度第二学期期末模拟考试(一)高一英语试卷2015.6.23卷面总分:120分考试时间:120分钟第一部分:听力(共15小题;每题1分, 满分15分)第一节:听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有l0秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
()1. What does the man usually do on Sunday afternoon?A. Work in the garden.B. G o to church.C. Do some reading.()2. Which book is the most expensive?A. The blue one.B. The green one.C. The red one. ()3. What is the man going to do?A. Ask the woman to join him.B. Found his own company.C. Find a new job.()4. What does the woman mean?A. It is unfair that the man's wife should stay at home.B. it is impossible to repair the pipes again.C. It is not the first time that the pipes leaked.()5. What does the man mean?A. The price for rent is beyond their reach.B. The neighborhood is too far away.C. They don't need a new apartment.第二节听下面5段对话或独白。
江苏省泰兴市第一高级中学高一下学期期末模拟考试(二)物理试卷.pdf

泰兴市第一高级中学2014—2015学年度第二学期期末模拟考试(一) 高一物理试卷 2015.6.30 卷面总分:120分 考试时间:100分钟 第Ⅰ卷(选择题 共4分) 一、单项选择题:本题共8小题,每小题3分,共24分,每小题只有一个选项符合题意。
1下面关于丹麦天文学家第谷,对行星的位置进行观察所记录的数据,说法正确的是( ) 这些数据误差相当大 B这些数据说明太阳绕地球运动 C这些数据与以行星绕太阳做匀速圆周运动为模型得到的结果相吻合 D这些数据与以行星绕太阳做椭圆运动为模型得到的结果相吻合 25颗地球同步卫星和30非地球同步卫星,如图所示。
下列说法中正确的是 ( ) A.这5颗地球同步卫星离地面的高度不一定相同 B.这5颗地球同步卫星的运行周期都与地球自转周期相等 C.这5颗地球同步卫星的加速度不一定相同 D.为避免卫星相撞,不同国家发射的地球同步卫星必须运行在不同的轨道上 3.如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以地面为参考平面,且不计空气阻力,则下列选项错误的是( ) A.物体落到海平面时的势能为mgh B.重力对物体做的功为mgh C.物体在海平面上的动能为mv02+mgh D.物体在海平面上的机械能为mv02 一个人站在商店的自动扶梯的水平踏板上,随扶梯向上加速运动,如图所示,则 A.人对踏板的压力大小等于人受到的重力大小 B.人只受到重力和踏板的支持力作用 C.人受到的力的合力对人所做的功等于人的重力势能和动能的增加量 D.踏板对人做的功等于人的机械能的增加量5. 足够长的传送带以v匀速传动,一质量为m的小物块A由静止轻放于传送带上,若小物体与传送带之间的动摩擦因数为,如图所示,当物体与传送带相对静止时,转化为内能的能量为 ) A. B. C. D. .空间中P、Q两点处各固定一个点电荷其中P点处为正电荷P、Q两点附近电场的等势面分布如图所示,a、b、c、d为电场中的4个点。
江苏省泰兴中学高一数学2014-2015学年高一数学必修四复习数学试题

江苏省泰兴中学高一数学必修四复习卷(1)一.填空题(共14题,每题5分共70分。
请把答案填写在答题卡相应的位置上..........) 1.计算sin690o = ___ .2.函数y =tan(错误!未找到引用源。
-x)的定义域是 ____ .3.若角α满足条件:sin2α<0,cosα<0,则α是第 ____ 象限角.4.已知向量a =(2,- 4)与向量b =(-1,λ)所成的角为钝角,则λ的取值范围是 _____ _.5.向量a 与b =(2,-1)满足a 错误!未找到引用源。
b =0,|a |=错误!未找到引用源。
,则向量a = ____ .6.点E 是正方形ABCD 边DC 的中点,且错误!未找到引用源。
a ,错误!未找到引用源。
b ,则错误!未找到引用源。
________(用a , b 表示).7.把函数x x y sin 3cos -=的图象向左平移m (其中m >0)个单位,所得图象关于y 轴对称,则m 的最小值是 __.8.设a 错误!未找到引用源。
,b 错误!未找到引用源。
,且a ∥b ,则锐角x 为 ______ .9.设tanθ= 3, π<θ<0,那么cosθ+tan2θ的值等于 _______ .10.在一个半径为2的半圆上截取一个矩形,则矩形的最大面积为____________ .11.已知f (x )=错误!未找到引用源。
,则错误!未找到引用源。
_________ .12.已知AB 是圆O 的一条弦,M 是AB 中点,且AB=2,则错误!未找到引用源。
= ______ .13.设f (x)是定义域为R ,最小正周期为3π的函数,且在区间错误!未找到引用源。
上的表达式为错误!未找到引用源。
,则错误!未找到引用源。
的值为 _________ .14.下面有四个命题: ①函数错误!未找到引用源。
的一条对称轴为错误!未找到引用源。
; ②把函数错误!未找到引用源。
江苏省泰兴市第一高级中学高一地理下学期期末模拟考试
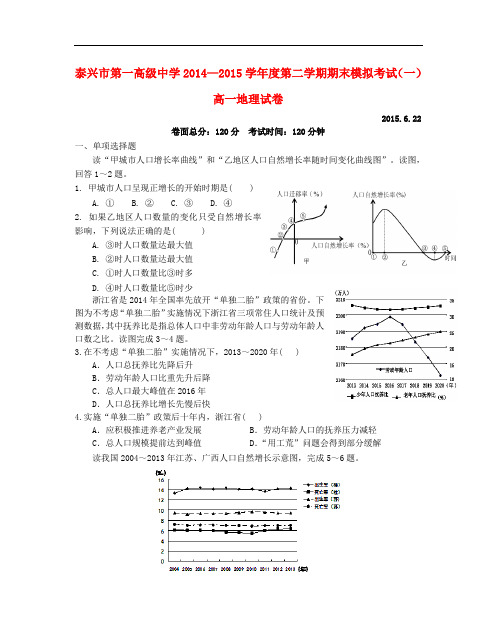
泰兴市第一高级中学2014—2015学年度第二学期期末模拟考试(一)高一地理试卷2015.6.22卷面总分:120分考试时间:120分钟一、单项选择题读“甲城市人口增长率曲线”和“乙地区人口自然增长率随时间变化曲线图”。
读图,回答1~2题。
1. 甲城市人口呈现正增长的开始时期是( )A. ①B. ②C. ③D. ④2. 如果乙地区人口数量的变化只受自然增长率影响,下列说法正确的是( )A. ③时人口数量达最大值B. ②时人口数量达最大值C. ①时人口数量比③时多D. ④时人口数量比⑤时少浙江省是2014年全国率先放开“单独二胎”政策的省份。
下图为不考虑“单独二胎”实施情况下浙江省三项常住人口统计及预测数据,其中抚养比是指总体人口中非劳动年龄人口与劳动年龄人口数之比。
读图完成3~4题。
3.在不考虑“单独二胎”实施情况下,2013~2020年( )A.人口总抚养比先降后升B.劳动年龄人口比重先升后降C.总人口最大峰值在2016年D.人口总抚养比增长先慢后快4.实施“单独二胎”政策后十年内,浙江省( )A.应积极推进养老产业发展B.劳动年龄人口的抚养压力减轻C.总人口规模提前达到峰值D.“用工荒”问题会得到部分缓解读我国2004~2013年江苏、广西人口自然增长示意图,完成5~6题。
5.关于近十年江苏、广西人口自然增长状况,说法正确的是()A.江苏人口出现了负增长B.广西的自然增长率逐年递增C.江苏的人口数量不断增加D.广西人口增长的特点是高出生率、低死亡率和高自然增长率6.江苏人口死亡率相对广西较高的原因主要是因为江苏()A.自然环境质量好B.人口基数大C.人口老龄化 D.出生率较高读江苏城市化与经济发展水平的关系图,回答7~8题。
7.关于江苏城市化的叙述,正确的是( )A.城市化速度不断加快B.城市化水平逐年提高C.20世纪90年代以后,城市化速度快于90年代之前D.城市化速度始终快于人均GDP的增长速度8.下列关于江苏城市化发展的叙述,正确的是( )A.城市化发展过程中出现逆城市化现象B.城市化的发展不断拉大城乡之间差距C.城市化水平是指二三产业占国民经济的比重D.城市化水平与经济发展水平呈正相关下图是北京城市发展示意图。
江苏省泰兴市第一高级中学2014-2015学年高一语文下学期期末考试补考试题不分版本

江苏省泰兴市第一高级中学2014-2015学年高一语文下学期期末考试补考试题不分版本2015春学期期初考试暨2014秋学期期末补考试卷高一语文〔考试时间45分钟,卷面总分100分〕一、选择题〔5分一条,共60分〕1. 在以下句子空缺处依次填入词语,最恰当的一组是〔5分〕①大家推举在学界______的朱德熙先生担任学会主席。
②为维护汉语的纯洁,禁止在广告中用谐音字______成语。
③公元6年,罗马帝国____犹太傀儡王,犹太国从此灭亡。
④政府领导作为人们的公仆,要______关心群众的疾苦。
A.深孚众望篡改废除无时无刻B.不负众望窜改废除时时刻刻C.深孚众望窜改废黜时时刻刻D.不负众望篡改废黜无时无刻2.下面是一首题为“秦淮晓渡〞的绝句,填入横线处的句子意境和谐、对仗工整的一项为哪一项〔5分〕潮长波平岸,。
一声孤棹响,残梦落清淮。
A.乌啼月满街B.月辉洒长街C.莺啼花满枝D.草青风低树3.下面是一封求职信的主要内容,加横线的词语全部..使用得体的一项为哪一项〔5分〕日前①光临贵社网站,得知招聘编辑的消息,我决定应聘。
本人写作才能②超群绝伦,如能③加盟贵社,定当④鼎力工作。
现寄上我的相关资料,如有⑤意向,请与我⑥洽谈。
A.②④ B.①③ C.④⑤ D.③⑤4、邓明为爷爷祝寿写了一副对联“逾古稀又十年可喜慈颜久驻,去期颐尚廿载预征后福无疆〞,请问邓明的爷爷今年高寿?〔5分〕A.七十岁 B.一百岁 C.八十岁 D.六十岁5. 把以下句子组成语意连贯的语段,排序最恰当的一组是〔5分〕①比方告诉你的父母,陪他们一起逛街感觉非常开心②如果只是将快乐私藏,积极的情绪便会很快消失③它不仅有助于快乐感的延续,还能拉近人与人之间的关系④告诉你的朋友,很思念在一起时开心的时光,并开始筹划新的聚会等等⑤传递快乐其实很简单⑥积极与他人分享快乐的记忆和经历,是放大快乐感的最正确方法A.⑥③②⑤①④ B.⑤①④②⑥③ C.⑥③①④⑤② D.⑤①③④②⑥6、在以下句子空缺处依次填入成语,恰当的一项为哪一项〔5分〕①在“假设我是效劳对象〞的大讨论中,人们对如何提高机关行政效率,我认为,单纯的提高行政效率却不转变政府职能实属。
江苏省泰兴市第一高级中学高三数学下学期学情监测试题

2014-2015学年高三学情监测数 学 试 卷一、填空题:(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.)1. 已知集合{}lg M x y x ==,{N x y ==,则M∩N= ▲ . 2. 已知复数()2i+1(1i)z =-为虚数单位),则z = ▲ .3. 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为 ▲ .4. 阅读下面的流程图,若输入a =10,b =6,则输出的结果是 ▲ .5. 盒中装有形状、大小完全相同的5个球,其中红色球3个,黄色球2个.若从中随机取出2个球,则所取出的2个球颜色不同的概率等于 ▲ . 6. 函数a x f x +-=131)( ()0≠x ,则“1)1(=f ”是“函数)(x f 为奇函数”的 ▲ 条件(用“充分不必要”,“必要不充分”“充要”“既非充分又非必要”)7. 在平面直角坐标系xOy 中,双曲线22221(0,0)x y a b a b-=>>的两条渐近线与抛物线y2=4x 的准线相交于A ,B 两点.若△AOB 的面积为2,则双曲线的离心率为 ▲ . 8. 过点(2,0)引直线l 与曲线21x y -=相交于A ,B 两点,O 为坐标原点,当△AOB的面积取最大值时,直线l 的斜率等于 ▲ .9. 已知ABC ∆中,cos tan tan 210A B C =⋅=,且B C <,则B = ▲ . 10.在ABC ∆中,90,1A AB AC ∠===,点P 在边BC 上,则2PB PC +的最大值为 ▲ .11.若关于x 的方程3232ln 21x m x x =++在区间)2,1(上有解,则实数m 的取值范围是▲ .12.在正三棱锥S ABC -中,1,30SA ASB =∠=︒,过A 作三棱锥的截面AMN ,则截面三角形AMN 的周长的最小值为 ▲ .13.已知实数a x f x x x ax x x f a 232167)(1,log 1;2)(,0=⎩⎨⎧>≤+-=>,若方程,有且仅有两个不等实根,且较大的实根大于3,则实数a 的取值范围 ▲ .14.若等差数列{}n a 满足2212015110a a +≤,则2015201620174029S a a a a =++++L 的最大值为 ▲ . 二、解答题:(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.) 15.(本题满分14分)已知向量()sin 2,1m x =-,向量()3cos 2,0.5n x =-,函数x f ⋅+=)()(.⑴求)(x f 的最小正周期T ;⑵已知c b a ,,分别为ABC ∆内角CB A ,,的对边,A 为锐角,2a c =,且()f A 恰是()f x 在0,4π⎡⎤⎢⎥⎣⎦上的最大值,求A 和b .16.(本题满分14分)如图,在四棱锥P ﹣ABCD 中,侧棱PA 丄底面ABCD 底面ABCD 为矩形,E 为PD 上一点,AD =2AB =2AP =2,PE =2DE .⑴若F 为PE的中点,求证BF ∥平面ACE ; ⑵求三棱锥P ﹣ACE 的体积.17.(本题满分14分)北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估.该商品原来每件售价为25元,年销售8万件.⑴据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?⑵为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到x 元.公司拟投入21(600)6x -万作为技改费用,投入50万元作为固定宣传费用,投入5x万元作为浮动宣传费用.试问:当该商品改革后的销售量a 至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价. 18.(本题满分16分)如图,圆O 与离心率为23的椭圆T :12222=+by a x (0>>b a )相切于点M )1,0(.⑴求椭圆T 与圆O 的方程;⑵过点M 引两条互相垂直的两直线1l 、2l 与两曲线分别交于点A 、C 与点B 、D (均不重合). ①若P 为椭圆上任一点,记点P 到两直线的距离分别为1d 、2d ,求2221d d +的最大值; ②若⋅=⋅43,求1l 与2l 的方程.19.(本题满分16分)已知数列{a n }的首项a 1=2,且对任意n ∈N *,都有a n +1=ba n +c ,其中b ,c 是常数. ⑴若数列{a n }是等差数列,且c =2,求数列{a n }的通项公式;⑵若数列{a n }是等比数列,且|b |<1,当从数列{a n }中任意取出相邻的三项,按某种顺序排列成等差数列,求使数列{a n }的前n 项和S n <341256成立的n 的取值集合.20.(本题满分16分)已知函数2()6f x ax x=++,其中a 为实常数. ⑴若()3f x x >在(1,)+∞上恒成立,求a 的取值范围;⑵已知34a =,12,P P 是函数()f x 图象上两点,若在点12,P P 处的两条切线相互平行,求这两条切线间距离的最大值;⑶设定义在区间D 上的函数()y s x =在点00(,)P x y 处的切线方程为:()l y t x =,当0x x ≠时,若()()0s x t x x x ->-在D 上恒成立,则称点P 为函数()y s x =的“好点”.试问函数2()()g x x f x =是否存在“好点”.若存在,请求出所有“好点”坐标,若不存在,请说明理由.AMCO DE2014-2015学年高三学情监测数 学(附加) 试 卷1.(本题满分10分)已知曲线2:2C y x = ,在矩阵M 1002⎡⎤=⎢⎥⎣⎦对应的变换作用下得到曲线1C ,1C 在矩阵N 0110-⎡⎤=⎢⎥⎣⎦对应的变换作用下得到曲线2C ,求曲线2C 的方程. 2.(本题满分10分)在平面直角坐标系xOy 中,已知直线l 的参数方程为⎩⎪⎨⎪⎧x =3+32t ,y =2+12t(t 为参数 ),圆C 的参数方程为⎩⎪⎨⎪⎧x =3+cos θ,y =sin θ(θ为参数).若点P 是圆C 上的动点,求点P 到直线l 的距离的最小值.3.(本题满分10分)如图,平面ABDE ⊥平面ABC ,ABC ∆是等腰直角三角形,4AC BC ==,四边形ABDE 是直角梯形,BD ∥AE,BD ⊥BA ,122BD AE ==,O M 、分别为CE AB 、的中点.(Ⅰ) 求异面直线AB 与CE 所成角的大小; (Ⅱ) 求直线CD 和平面ODM 所成角的正弦值. 4.(本题满分10分)设i 为虚数单位,n 为正整数.⑴证明:(cos isin )cos isin n x x nx nx +=+;⑵结合等式“[][]1(cos isin )(1cos )isin nnx x x x ++=++”证明:121C cos C cos2C cos nn n n x x nx +++⋅⋅⋅+2cos cos 22n n x nx =.2014-2015学年高三数学学情监测参考答案1. (]0,1 3. 480 4. 2 5. 35 6. 充要- 339.4π 10. 110,ln 263⎛⎫- ⎪⎝⎭13. ]4,774( 14.2015215.解:(1)()21()sin 212cos 22f x m n m x x x =+⋅=+++……2分1cos 4114sin 42226x x x π-⎛⎫=++=-+ ⎪⎝⎭,……………… 4分 2.42T ππ∴== ……………… 6分 (2) 由(1)知:()sin(4)26f x x π=-+,当0,4x π⎡⎤∈⎢⎥⎣⎦时,54666x πππ-≤-≤ ∴当462x ππ-=时()f x 取得最大值3,此时6x π=.………………10分∴由3)(=A f 得.6A π=由余弦定理,得2222cos a b c bc A =+-∴222222cos 6b b π=+-⨯, ∴b =14分16. 解:(1)若F 为PE 的中点,由于底面ABCD 为矩形,E 为PD 上一点,AD=2AB=2AP=2,PE=2DE ,故E 、F 都是线段PD 的三等分点.设AC 与BD 的交点为O ,则OE 是△BDF 的中位线,故有BF∥OE,而OE 在平面ACE 内,BF 不在平面ACE 内,故BF∥平面ACE .………6分 (2)由于侧棱PA 丄底面ABCD ,且ABCD 为矩形, 故有CD⊥PA,CD⊥AD,故CD⊥平面PAE ,.……………8分 三棱锥P ﹣ACE 的体积V P ﹣ACE =V C ﹣PAE ………………10分=S △PAE •CD=•(•S △PAD)•AB=(••PA•PD)•AB=•PA•PD•AB=•1•2•1=.………………………………14分 17. 解:(1)设每件定价为t 元,依题意得⎝⎛⎭⎪⎫8-t -251×0.2t ≥25×8,整理得t 2-65t +1000≤0,解得25≤t ≤40.所以要使销售的总收入不低于原收入,每件定价最多为40元. (2)依题意知当x >25时,不等式ax ≥25×8+50+16(x 2-600)+15x 有解,等价于x >25时,a ≥150x +16x +15有解.由于150x +16x ≥2150x ×16x =10,当且仅当150x=x6,即x =30时等号成立,所以a ≥10.2.当该商品改革后的销售量a 至少达到10.2万件时,才可能使改革后的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元.18. 解: (1)由题意知:222,1,23a b c b a c =+==解得3,1,2===c b a 可知: 椭圆C 的方程为1422=+y x 与圆O 的方程122=+y x ……………………4分(2)设),(00y x P 因为1l ⊥2l ,则202022221)1(++==+y x PM d d 因为142020=+y x所以316)31(3)1(442020202221++-=++-=+y y y d d ,………………………7分 因为110≤≤-y 所以当310-=y 时2221d d +取得最大值为316,此时点)31,324(-±P …………9分 (3)设1l 的方程为1+=kx y ,由⎩⎨⎧=++=1122y x kx y 解得)11,12(222k k k k A +-+-; 由⎪⎩⎪⎨⎧=++=14122y x kx y 解得)4141,148(222k k k k C +-+-…………………………11分 把C A ,中的k 置换成k 1-可得)11,12(222+-+k k k k B ,)44,48(222+-+k k k k D ………………12分 所以)12,12(222k k k k +-+-=,)418,148(222kk k k +-+- )12,12(22+-+=k k k ,)48,48(22+-+=k k k由34MA MC MB MD ⋅=⋅得44413222+=+k k k 解得2±=k ……………………15分 所以1l 的方程为12+=x y ,2l 的方程为122+-=x y 或1l 的方程为12+-=x y ,2l 的方程为122+=x y ………………………16分 19.解: (1) 当c =2时,由已知得a 1=2,a 2=ba 1+2=2b +2,a 3=ba 2+2=2b 2+2b +2,因为{a n }是等差数列,所以a 1,a 2,a 3成等差数列,所以a 1+a 3=2a 2, 即2+(2b 2+2b +2)=2(2b +2),所以b 2-b =0,解得b =0,或b =1.(2分) 当b =0时,a n =2,对n∈N *,a n +1-a n =0成立,所以数列{a n }是等差数列, 当b =1时,a n +1=a n +2,对n∈N *,a n +1-a n =2成立,所以数列{a n }是等差数列; 所以数列{a n }的通项公式分别为a n =2或a n =2n.(4分)(2) 因为{a n }是等比数列,所以a 1,a 2,a 3成等比数列,所以a 1a 3=a 22, 即2[b(2b +c)+c]=(2b +c)2,化简得2bc +c 2=2c ,所以c =0或2b +c =2.当2b +c =2时,a 2=ba 1+c =2b +c =2,所以a n =2,不满足S n <341256.当c =0时,若b =0,则与a 1=2矛盾,所以b≠0,因此a n =2b n -1.(8分)则a n +1=2b n,a n +2=2bn +1,因为a n ,a n +1,a n +2按某种顺序排列成等差数列,所以有1+b =2b 2,或1+b 2=2b ,或b +b 2=2,解之得b =1或b =-12或b =-2.(12分)又因为|b|<1,所以b =-12,所以S n =2⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫-12n 1-⎝ ⎛⎭⎪⎫-12=43⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫-12n ,由S n <341256,得43⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫-12n <341256,即⎝ ⎛⎭⎪⎫-12n>11 024,因为n 是正整数,所以n 的取值集合为{2,4,6,8}.(16分)20. 解:(1)方法一:()3f x x >在(1,)+∞上恒成立,即为2(3)620a x x -++>在(1,)+∞上恒成立,①3a =时,结论成立;②3a >时,函数2()(3)62h x a x x =-++图象的对称轴为602(3)x a =-<-,所以函数2()(3)62h x a x x =-++在(1,)+∞单调递增,依题意(1)0h >,即5a >-,所以3a >;③3a <不合要求,综上可得,实数a 的取值范围是3a ≥. 4分 方法二:()3f x x >在(1,)+∞上恒成立等价于2263a x x>--+, 令()222613153222h x x x x ⎛⎫=--+=-++ ⎪⎝⎭因为1x >,所以101x <<,故()53h x -<<所以3a ≥.(2)232'()4f x x =-设111(,)P x y ,222(,)P x y ,过点12,P P 的两切线互相平行, 则2212323244x x -=-,所以12x x =(舍去),或12x x =-, 过点1P 的切线1l :111'()()y y f x x x -=-,即1111'()()'()0f x x y f x x f x -+-=,6分 过点2P 的切线2l :2222'()()'()0f x x y f x x f x -+-=两平行线间的距离是d =1132322|()()|x x +--=8==因为2121254516x x +≥=,所以d ≤=即两平行切线间的最大距离是 ·················· 10分 (3)232()()62g x x f x ax x x ==++,设()g x 存在“好点”00(,)P x y ,由2'()3122g x ax x =++,得000()'()()()h x g x x x g x =-+,依题意0()()0g x h x x x ->-对任意0x x ≠恒成立, 因为0000()['()()()]g x g x x x g x x x --+-0000[()()]'()()g x g x g x x x x x ---=-, 323220000000[(62)(62)](3122)()ax x x ax x x ax x x x x x ++-++-++-=- 22200000[()6()2](3122)a x x x x x x ax x =+++++-++22000(6)(26)ax ax x ax x =++-+13分所以22000(6)(26)0ax ax x ax x ++-+>对任意0x x ≠恒成立,① 若0a ≤,22000(6)(26)0ax ax x ax x ++-+>不可能对任意0x x ≠恒成立,即0a ≤时,不存在“好点”;②若0a >,因为当0x x =时,22000(6)(26)0ax ax x ax x ++-+=,要使22000(6)(26)0ax ax x ax x ++-+>对任意0x x ≠恒成立,2014-2015学年高三数学(附加)学情监测参考答案1.解:设A NM = 则A 011002100210--⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦, ………………3分 设()','P x y 是曲线C 上任一点,在两次变换下,在曲线2C 上的对应的点为(),P x y ,则 02'2'10''x x y y y x --⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦,即2',',x y y x =-⎧⎨=⎩∴',1'.2x y y x =⎧⎪⎨=-⎪⎩ ……………7分 又点()','P x y 在曲线2:2C y x = 上,∴ 21()22x y -=,即218y x =.…………10分 2.解:(方法一)直线l 的普通方程为x -3y +3=0. ……………… 3分因为点P 在圆C 上,故设P (3+cos θ,sin θ),从而点P 到直线l 的距离d =|3+cos θ-3sin θ+3|12+(-3)2=|23-2sin(θ-π6)|2. …………………… 7分 所以d min =3-1.即点P 到直线l 的距离的最小值为3-1. …………… 10分 (方法二) 直线l 的普通方程为x -3y +3=0. ……………… 3分 圆C 的圆心坐标为(3,0),半径为1.从而圆心C 到直线l 的距离为d =|3-0+3|12+(-3)2=3. ………………………… 6分所以点P 到直线l 的距离的最小值为3-1. ………………………… 10分3.如图,平面ABDE ⊥平面ABC ,ABC ∆是等腰直角三角形,4AC BC ==,四边形ABDE 是直角梯形,BD ∥AE,BD ⊥BA ,122BD AE ==,O M 、分别为CE AB 、的中点. (Ⅰ) 求异面直线AB 与CE 所成角的大小;(Ⅱ) 求直线CD 和平面ODM 所成角的正弦值.解:∵DB BA ⊥,又∵面ABDE ⊥面ABC ,面ABDE 面ABC AB =,DB ABDE ⊂面,∴DB ABC ⊥面,∵BD∥AE,∴EA ABC ⊥面,…… 2分如图所示,以C 为原点,分别以CA ,CB 为x ,y 轴,以过点C 且与平面ABC 垂直的直线为z 轴,建立空间直角坐标系,∵4AC BC ==,∴设各点坐标为(0,0,0)C ,(4,0,0)A ,(0,4,0)B ,(0,4,2)D ,(4,0,4)E ,则(2,0,2)O ,(2,2,0)M ,(4,4,0),CE (4,0,4)AB =-=,(0,4,2)CD =,(2,4,0)OD =-,(2,2,2)MD =-.(1)1cos ,2AB CE <>==-, 则AB 与CE 所成角为3π. ……5分 (2)设平面ODM 的法向量(,,)x y z =n ,则由OD ⊥n ,且MD ⊥n 可得240,2220,x y x y z -+=⎧⎨-++=⎩令2x =,则1y =,1z =,∴(2,1,1)=n ,设直线CD 和平面ODM 所成角为θ,则(2,1,1)(0,4,2)sin cos ,|(2,1,1)||(0,4,2)|||||CD CD CD θ⋅⋅=<>===n n n ∴直线CD 和平面ODM . ……10分4. 设i 为虚数单位,n 为正整数.(1)证明:(cos isin )cos isin n x x nx nx +=+;(2)结合等式“[][]1(cos isin )(1cos )isin n nx x x x ++=++”证明:121C cos C cos2C cos n n n n x x nx +++⋅⋅⋅+2cos cos 22n n x nx =. 证明:(1)①当1n =时,cos isin cos isin x x x x +=+,即证;……………… 1分②假设当n k =时,(c o s i s i n )c o s i s i k x x k x k x +=+成立,则当1n k =+时,()1(c o s i s i n )c o s i s i n (c o s i s i n )k x x k x k x x x ++=++()()cos cos sin sin sin cos sin cos i kx x kx x kx x x kx =-++()()cos 1isin 1k x k x=+++, 故命题对1n k =+时也成立,由①②得,(cos isin )cos isin n x x nx nx +=+;……… 4分z(2)由(1)知,[]001(cos isin )C (cos isin )C (cos isin )n nn rrrn n r r x x x x rx rx ==++=+=+∑∑,其实部为121C cos C cos2C cos n n n n x x nx +++⋅⋅⋅+;……… 6分[](1cos )isin n x x ++=()()22cos 2isin cos 2cos cos isin 222222nnn n x x x x x x +=+……… 8分 ()2cos cos isin 222n n x nx nx =+ 其实部为2cos cos 22n n x nx , 根据两个复数相等,其实部也相等可得: 121C cos C cos2C cos n n n n x x nx +++⋅⋅⋅+2cos cos 22n n x nx=.……… 10分。
江苏省泰州市泰兴一中2014_2015学年高一化学下学期期末补考试卷(含解析)

2014-2015学年江苏省泰州市泰兴一中高一(下)期末化学补考试卷一、填空题(本题共18小题,每题只有1个正确答案,每小题4分,共72分)1.(4分)(2015春•泰兴市校级期末)光纤通信是70年代后期发展起来的一种新型通信技术,目前长距离光纤通信系统已投入使用,光纤通信的光导纤维是由下列哪种物质经特殊工艺制成的()A.石墨B.石英C.石灰石D.高纯硅考点:硅和二氧化硅.分析:根据光纤通信的光导纤维是二氧化硅经特殊工艺制成的,光导纤维的主要成分是二氧化硅进行解答.解答:解:A.二氧化硅不是由碳制成的,故A错误;B.光导纤维的主要成分是二氧化硅,而石英的主要成分是二氧化硅,所以光纤通信的光导纤维是由石英经特殊工艺制成,故B正确;C.石灰石高温锻烧生成生石灰,不是制光导纤维的原料,故C错误;D.硅常用于半导体材料,制作太阳能电池,故D错误.故选B.点评:本题考查硅及化合物的组成和用途,题目简单,注意基础知识的学习积累.2.(4分)(2015•怀化模拟)下列物质,不属于合金的是()A.硬铝B.青铜C.水银D.钢考点:生活中常见合金的组成.专题:元素及其化合物.分析:合金是指在一种金属中加热熔合其它金属或非金属而形成的具有金属特性的物质;合金具有以下特点:①一定是混合物;②合金中至少有一种金属等,以此解答该题.解答:解:A.硬铝是铝、铜、镁、硅的合金,故A不选;B.青铜是铜和锡的合金,故B不选;C.水银为汞,为纯净物,不属于合金,故C选;D.钢为铁与碳、镍等的合金,故D不选.故选C.点评:本题考查合金知识,为高频考点,侧重化学与生活、生成的考查,有利于培养学生良好的科学素养,提高学习的积极性,难度不大,注意相关知识的积累.3.(4分)(2015春•泰兴市校级期末)下列物质属于纯净物的是()A.液氯B.漂白粉C.新制氯水D.水玻璃考点:混合物和纯净物.分析:纯净物是由一种物质组成的物质,混合物是由多种物质组成的物质;据此结合常见物质的组成成分逐项分析即可.解答:解:A.液氯是氯气的液态形式,液氯中只含有一种物质,属于纯净物.故A正确;B.工业用氯气和冷的消石灰反应制备漂白粉,发生2Ca(OH)2+2Cl2=CaCl2+Ca(ClO)2,成分为CaCl2、Ca(ClO)2,所以漂白粉为混合物,故B错误;C.新制的氯水中含有氯气分子,水分子和次氯酸分子,属于混合物,故C错误;D.水玻璃是硅酸钠的溶液,属于混合物,故D错误;故选A.点评:本题考查纯净物的判别,解答本题要充分理解纯净物和混合物的区别,要分析物质是由几种物质组成的,如果只有一种物质组成就属于纯净物,如果有多种物质就属于混合物,题目难度不大.4.(4分)(2010秋•宁波期末)胶体区别于其他分散系的本质特征是()A.胶体的分散质能通过滤纸空隙,而浊液的分散质不能B.产生丁达尔现象C.分散质粒子直径在1nm~100nm之间D.胶体在一定条件下能稳定存在考点:胶体的重要性质.专题:溶液和胶体专题.分析:胶体区别于其他分散系的本质特征是分散质微粒直径的大小不同.解答:解:胶体区别于其它分散系的本质特征是胶体粒子直径在1﹣100nm之间,溶液的粒子直径小于1nm,浊液的子直径大于100nm.故选:C.点评:本题比较简单,考查学生教材基本知识,可以根据所学知识进行回答.5.(4分)(2015春•泰兴市校级期末)下列反应中需要加入还原剂才能进行的是()A.H2→H2O B.Zn→Zn2+C.Fe3+→Fe2+ D.CuO→CuCl2考点:氧化还原反应.分析:需要加入还原剂才能实现,选项中为氧化剂发生还原的反应,氧化剂中某元素的化合价降低,以此来解答.解答:解:A.H元素化合价升高,应加入氧化剂,故A错误;B.Zn元素化合价升高,被氧化,应加入氧化剂,故B错误;C.Fe元素化合价降低,被还原,应加入还原剂,故C正确;D.元素化合价没有发生变化,属于复分解反应,故D错误.故选C.点评:本题考查氧化还原反应,侧重氧化剂、还原剂的考查,明确氧化剂在反应中元素的化合价降低为解答的关键,题目难度不大.6.(4分)(2012秋•盐津县期末)铝合金在日常生活、建筑装潢、航空航天和汽车制造等方面均有着广泛的用途.下列关于铝合金具有广泛用途的分析不正确的是()A.铝元素在地壳中的含量高,储量丰富B.铝容易形成致密的氧化膜,抗腐蚀性能好C.铝化学性质稳定,常温下不与任何酸碱反应D.铝的冶炼技术基本成熟,可以大量生产考点:生活中常见合金的组成;铝的化学性质.专题:几种重要的金属及其化合物.分析:A、根据Al元素在地壳中的含量来分析;B、金属铝易被氧气氧化形成氧化铝;C、金属铝化学性质活泼,可以和酸反应;D、金属铝的冶炼技术在工业生产中已经成熟,可以大量生产.解答:解:A、Al元素在地壳中是含量最多的金属元素,含量高,储量丰富,故A正确;B、金属铝易被氧气氧化形成致密的氧化膜氧化铝,抗腐蚀性能好,故B正确;C、金属铝化学性质活泼,常温下可以和酸反应,故C错误;D、现在生活和生产中对金属铝的需求量大,金属铝的冶炼利用电解技术在工业生产中已经成熟,可以大量生产,故D正确.故选C.点评:本题考查学生金属铝的有关知识,可以根据教材知识来回答,难度中等,注意平时知识的积累是解题的关键.7.(4分)(2015春•泰兴市校级期末)钾离子是细胞内液的主要阳离子,体内98%的钾存在于细胞内.经检测某饮用矿泉水中K+浓度为5.85mg/L,该矿泉水中c(K+)/mmol•L﹣1为()A. 1.5 B.0.10 C.0.15 D.1.00考点:物质的量浓度.分析:依据质量浓度计算物质的量浓度,n=,注意单位的换算应用.解答:解:检测某饮用矿泉水中K+浓度为5.85mg/L,该矿泉水中c(K+)/mol•L﹣1==0.15mol/L,故选C.点评:本题考查物质的量有关计算,比较基础,侧重对基础知识的巩固,注意对公式的理解与灵活应用.8.(4分)(2012秋•无锡期末)U是制造原子弹的材料和核反应堆的燃料.U的原子核内的中子数与核外电子数之差是()A.235 B.143 C.92 D.51考点:质量数与质子数、中子数之间的相互关系.分析:在原子的表示方法中元素符号左下角的数字为质子数,左上角的数字为质量数,并利用质量数=质子数+中子数、核外电子数等于核内质子数来分析.解答:解:核素92235U的质子数是92,质量数是235,中子数=质量数﹣质子数=235﹣92=143,所以故中子数与核外电子数之差为:143﹣92=51,故选D.点评:本题考查原子的组成以及数量关系,明确质子数+中子数=质量数、核外电子数等于核内质子数是解答的关键.9.(4分)(2015春•泰兴市校级期末)某无色溶液能与铁粉反应放出大量氢气,此溶液中可能大量共存的离子组是()A.H+、K+、Mg2+、Cl﹣B. Ba2+、SO42﹣、Cl﹣、OH﹣C.K+、OH﹣、CO32﹣、MnO4﹣D. Ca2+、H+、Cl﹣、HCO3﹣考点:离子共存问题.分析:无色时可排除 Cu2+、Fe2+、Fe3+、MnO4﹣等有色离子的存在,与铁粉反应放出大量氢气的溶液中存在大量氢离子,A.四种离子之间不反应,都是无色离子,加入铁粉能够放出氢气;B.钡离子与硫酸根离子反应生成硫酸钡沉淀,氢氧根离子与氢离子反应;C.高锰酸根离子为有色离子,不满足溶液无色的条件;D.氢离子与碳酸氢根离子反应生成二氧化碳气体.解答:解:无色时可排除 Cu2+、Fe2+、Fe3+、MnO4﹣等有色离子的存在,与铁粉反应放出大量氢气的溶液中存在大量氢离子,A.H+、K+、Mg2+、Cl﹣之间不发生反应,都是无色离子,加入铁粉后能够产生大量氢气,故A 正确;B.Ba2+、SO42﹣之间反应生成难溶物硫酸钡,在溶液中不能大量共存,故B错误;C.MnO4﹣为有色离子,不满足溶液无色的要求,故C错误;D.H+、HCO3﹣之间发生反应生成二元化气体和水,在溶液中不能大量共存,故D错误;故选A.点评:本题考查离子共存的判断,题目难度中等,注意掌握离子反应发生条件,明确离子不能大量共存的一般情况,如:能发生复分解反应的离子之间,能发生络合反应的离子之间(如Fe3+和 SCN﹣)等;还应该注意题目所隐含的条件,如:溶液的酸碱性,据此来判断溶液中是否有大量的 H+或OH﹣;溶液的颜色,如无色时可排除 Cu2+、Fe2+、Fe3+、MnO4﹣等有色离子的存在.10.(4分)(2015春•泰兴市校级期末)下列操作中,溶液的颜色不发生变化的是()A.氯化铁溶液中加入足量铁粉,充分振荡B.氯化铁溶液中滴加硫氰化钾(KSCN)溶液C.氧化铜固体加入稀盐酸中,完全溶解D.碳酸氢钠溶液中滴加稀盐酸考点:铁盐和亚铁盐的相互转变;二价Fe离子和三价Fe离子的检验.专题:几种重要的金属及其化合物.分析:A.氯化铁溶液中加入足量铁粉反应生成氯化亚铁;B.三价铁离子与硫氰根离子发生络合反应生成血红色络合物;C.氧化铜为黑色固体,加入稀盐酸反应生成氯化铜;D.碳酸氢钠溶液中滴加稀盐酸反应生成氯化钠和二氧化碳、水.解答:解:A.氯化铁溶液中加入足量铁粉反应生成氯化亚铁,溶液颜色由黄色变化为浅绿色,故A错误;B.三价铁离子与硫氰根离子发生络合反应生成血红色络合物,溶液颜色由黄色变化为血红色,故B错误;C.氧化铜为黑色固体,加入稀盐酸反应生成氯化铜,溶液变成蓝色,故C错误;D.碳酸氢钠溶液为无色,滴加稀盐酸反应生成氯化钠溶液为无色,故D正确;故选:D.点评:本题考查了反应的现象,题目难度不大,熟悉三价铁离子、二价铁离子、铜离子的性质及颜色是解题关键,注意对相关知识的积累.11.(4分)(2015春•泰兴市校级期末)下列物质可以用作药物,用于治疗胃酸过多的是()A.BaCO3B.NaOH C.CuSO4D.A l(OH)3考点:药物的主要成分和疗效.分析:根据酸碱中和反应的知识进行分析,胃酸的主要成分是盐酸,所以治疗胃酸过多所用的物质需具有碱性且不能具有腐蚀性.解答:解:A.BaCO3能和盐酸反应生成钡离子,钡离子是重金属盐离子,有毒,故A错误;B.氢氧化钠虽都是碱,有腐蚀性,但碱性太强,会进一步伤害胃,不能食用,故B错误;C.硫酸铜是重金属盐,有毒,故C错误;D.Al(OH)3能与盐酸反应从而减少胃中盐酸的量,故D正确.故选D.点评:本题考查了常见物质的用途,题目难度不大,注意胃酸的主要成分是盐酸.12.(4分)(2015春•泰兴市校级期末)下列离子方程式书写正确的是()A.烧碱溶液与小苏打溶液反应:OH﹣+HCO3﹣═H2O+CO2↑B.碳酸钙溶于醋酸:CaCO3+2H+═Ca2++H2O+CO2C.氯气与水反应:H2O+Cl2═2H++Cl﹣+ClO﹣D.钠与水反应:2Na+2H2O═2Na++2OH﹣+H2↑考点:离子方程式的书写.分析:A.小苏打为碳酸氢钠,碳酸氢钠与氢氧化钠反应生成碳酸钠和水,不会生成二氧化碳气体;B.醋酸为弱酸,离子方程式中醋酸不能拆开;C.次氯酸为弱酸,离子方程式中次氯酸需要保留分子式;D.钠与水反应生成氢氧化钠和氢气.解答:解:A.烧碱溶液与小苏打溶液反应生成碳酸钠和水,反应的离子方程式为:OH﹣+HCO3﹣═H2﹣,故A错误;2O+CO3B.醋酸为弱电解质,需要保留分子式,正确的离子方程式为:CaCO3+2CH3COOH=Ca2++H2O+CO2↑+2CH3COO﹣,故B错误;C.氯气与水反应生成氯化氢和次氯酸,次氯酸不能拆开,正确的离子方程式为:H2O+Cl2⇌H++Cl ﹣+HClO,故C错误;D.钠与水反应生成氢氧化钠和氢气,反应的离子方程式为:2Na+2H2O═2Na++2OH﹣+H2↑,故D 正确;故选D.点评:本题考查了离子方程式的判断,为高考的高频题,属于中等难度的试题,注意掌握离子方程式的书写原则,明确离子方程式正误判断常用方法:检查反应物、生成物是否正确,检查各物质拆分是否正确,如难溶物、弱电解质等需要保留化学式,检查是否符合原化学方程式等.13.(4分)(2014秋•大连期末)下列溶液中,跟100mL 0.5mol/L NaCl溶液所含的Cl﹣物质的量浓度相同的是()A.100mL 0.5mol/L MgCl2溶液B.200mL 0.25mol/L AlCl3溶液C.50mL 1mol/L NaCl溶液D.25mL 0.5mol/L HCl溶液考点:物质的量浓度.专题:物质的量浓度和溶解度专题.分析:根据溶液中离子的物质的量浓度=溶质的物质的量浓度×化学式中离子的个数,与溶液的体积无关.解答:解:100mL 0.5mol/L NaCl溶液所含的Cl﹣物质的量浓度为 0.5mol/L;A、100mL 0.5mol/L MgCl2溶液所含的Cl﹣物质的量浓度为0.5mol/L×2=1mol/L,故A错误;B、200mL 0.25mol/L AlCl3溶液所含的Cl﹣物质的量浓度为0.25mol/L×3=0.75mol/L,故B 错误;C、50ml 1mol/L NaCl溶液所含的Cl﹣物质的量浓度为 1mol/L,故C错误;D、25ml 0.5mol/L HCl溶液所含的Cl﹣物质的量浓度为0.5mol/L,故D正确;故选:D.点评:本题考查了溶质年度和离子浓度的关系分析,抓住“溶液中离子的物质的量浓度=溶质的物质的量浓度×化学式中离子的个数,与溶液的体积无关”是解本题的关键,难度不大.(4分)(2015春•泰兴市校级期末)用N A表示阿伏加德罗常数的值,下列叙述正确的是()14.A.在常温常压下,11.2LCl2含有的分子数为0.5N AB.常温常压下,2.3gNa+中含有的电子数为N AC.标准状况下,11.2L臭氧含有的氧原子数为N AD.0.1 mol•L﹣1Na2CO3溶液中含有的钠离子数为0.2N A考点:阿伏加德罗常数.分析:A、常温常压下,气体摩尔体积大于22.4L/mol;B、求出钠离子的物质的量,然后根据1mol钠离子含10mol电子来分析;C、求出臭氧的物质的量,然后根据1mol臭氧中含3mol氧原子来分析;D、溶液体积不明确.解答:解:A、常温常压下,气体摩尔体积大于22.4L/mol,故11.2L氯气的物质的量小于0.5mol,故含有的分子数小于0.5N A个,故A错误;B、2.3g钠离子的物质的量n==0.1mol,而1mol钠离子含10mol电子,故0.1mol钠离子中含1mol电子即N A个,故B正确;C、标况下,11.2L臭氧的物质的量为0.5mol,而1mol臭氧中含3mol氧原子,则0.5mol臭氧中含1.5mol氧原子即1.5N A个,故C错误;D、溶液体积不明确,故溶液中的钠离子的个数无法计算,故D错误.故选B.点评:本题考查了阿伏伽德罗常数的有关计算,熟练掌握公式的使用和物质的结构及状态是解题的关键,难度不大.15.(4分)(2015春•泰兴市校级期末)下列各组混合物的分离或提纯方法(括号内)中,正确的是()A.初步分离酒精和水的混合物(蒸发)B.除去FeCl2溶液中的少量铁粉(过滤)C.提纯NaCl和KNO3的混合物中的KNO3(萃取)D.分离溴的四氯化碳溶液中的溴(分液)考点:物质的分离、提纯的基本方法选择与应用.分析:A.酒精和水都易挥发;B.铁粉不溶于水,可过滤分离;C.NaCl的溶解度受温度影响不大,但硝酸钾的溶解度受温度影响较大;D.溴易溶于四氯化碳.解答:解:A.酒精和水都易挥发,应用蒸馏的方法分离,故A错误;B.铁粉不溶于水,可过滤分离,故B正确;C.NaCl的溶解度受温度影响不大,但硝酸钾的溶解度受温度影响较大,则用蒸发结晶法提纯NaCl和KNO3混合物中的KNO3,故C错误;D.溴易溶于四氯化碳,但二者沸点不同,应用蒸馏的方法分离,故D错误.故选B.点评:本题考查混合物的分离、提纯,为高频考点,侧重于学生的分析、实验能力的考查,熟悉物质的性质及常见混合物分离、提纯的方法即可解答,难度不大.16.(4分)(2015春•泰兴市校级期末)检验SO2中是否混有CO2气体,可采用的方法是()A.通过品红溶液,若品红溶液褪色,则说明混有CO2气体B.通过澄清石灰水,若变混浊,则说明混有CO2气体C.先通过足量NaOH溶液,再通过澄清石灰水,若变混浊,则说明混有CO2气体D.先通过足量KMnO4溶液(具有强氧化性),再通过澄清石灰水,若变混浊,则说明混有CO2气体考点:物质的检验和鉴别的基本方法选择及应用.分析:均为酸性氧化物,但二氧化硫具有还原性,检验是否有二氧化碳,应先排除二氧化硫的干扰,以此来解答.解答:解:A.二氧化硫可使品红褪色,只能检验二氧化硫,不能检验二氧化碳,故A错误;B.均能使石灰水变浑浊,不能检验,故B错误;C.均与NaOH、石灰水反应,不能检验,故C错误;D.先通过酸性高锰酸钾溶液将二氧化硫反应掉,再通过品红溶液,说明没有二氧化硫,最后通过澄清的石灰水,变浑浊可检验二氧化碳存在,故D正确;故选D.点评:本题考查物质的检验和鉴别,为高频考点,把握物质的性质及性质差异为解答的关键,注意二氧化硫具有还原性,明确检验中应排除干扰,题目难度不大.17.(4分)(2013•天津校级学业考试)漂白粉的有效成分是()A.次氯酸钙B.氯化钙C.次氯酸D.次氯酸钙与氯化钙考点:氯、溴、碘及其化合物的综合应用.专题:物质的组成专题.分析:漂白粉的主要成分是次氯酸钙和氯化钙,有效成分是次氯酸钙.解答:解:漂白粉的有效成分是次氯酸钙,由于次氯酸的酸性比碳酸弱,次氯酸钙能与二氧化碳和水反应生成具有漂白性的次氯酸,故选A.点评:本题考查物质的组成,题目难度不大,注意相关基础知识的积累.18.(4分)(2012•湖南校级学业考试)实验室配制1mol/L 250mL NaCl溶液,下列仪器中不需要的是()A.玻璃棒B.分液漏斗C.胶头滴管D.250mL容量瓶考点:配制一定物质的量浓度的溶液;计量仪器及使用方法.专题:化学实验常用仪器.分析:配制1mol/L250mLNaCl溶液,配制步骤有:计算、称量、稀释、移液、洗涤移液、定容、摇匀等操作,根据实验操作选择使仪器即不需要的仪器.解答:解:配制1mol/L250mLNaCl溶液,配制步骤有:计算、称量、稀释、移液、洗涤移液、定容、摇匀等操作;一般用天平称量氯化钠质量,在烧杯中溶解,并用玻璃棒搅拌,冷却后转移到250mL容量瓶中,并用玻璃棒引流,当加水至液面距离刻度线1~2cm时,改用胶头滴管滴加,滴加至溶液凹面与刻度线水平相切,盖好瓶塞,摇匀,所以需要的仪器为:天平、药匙、烧杯、玻璃棒、250mL容量瓶、胶头滴管,不需要的仪器是分液漏斗,故选B.点评:本题考查了配制一定物质的量浓度的溶液使用的仪器,该题是中等难度的试题,试题基础性强,贴近高考;该题难易适中,注重灵活性,侧重对学生能力的培养和解题方法的指导和训练,有利于培养学生的逻辑思维能力和严谨的规范实验操作能力.二、解答题(共2小题,满分28分)19.(10分)(2015春•泰兴市校级期末)写出实验室利用MnO2跟浓盐酸在加热条件下制取氯气反应的化学方程式:MnO2+4HCl(浓)MnCl2+Cl2↑+2H2O ,该反应中还原剂与氧化剂物质的量之比是2:1 .考点:氯气的化学性质;氧化还原反应.分析:M nO2与浓盐酸在加热条件下发生氧化还原反应生成氯气;元素化合价升高的做还原剂,元素化合价降低的做氧化剂,据此分析计算二氧化锰与浓盐酸发生反应MnO2+4HCl(浓)MnCl2+Cl2↑+2H2O,Mn元素化合价由+4价降低到+2价,Cl元素化合价由﹣1价升高,根据化合价的变化可知电子的转移方向和数目;得电子化合价降低的反应物是氧化剂、失电子化合价升高的反应物是还原剂.解答:解:二氧化锰与浓盐酸发生反应MnO2+4HCl(浓)MnCl2+Cl2↑+2H2O,Mn元素化合价由+4价降低到+2价,Cl元素化合价由﹣1价升高,,Mn元素化合价由+4价降低到+2价,所以二氧化锰为氧化剂,Cl元素化合价由﹣1价升高为0价,结合化学方程式中元素化合价变化,所以HCl为还原剂,反应中还原剂与氧化剂物质的量之比是2:1,故答案为:MnO2+4HCl(浓)MnCl2+Cl2↑+2H2O,2:1.点评:本题考查了氯气的实验室制法、氧化还原反应的规律以及根据氧化还原反应方程式进行计算,解题关键在于明氧化还原反应关系,题目难度不大.20.(18分)(2015春•泰兴市校级期末)现有金属单质A、B、C和气体甲、乙、丙及物质D、E、F、G、H,它们之间能发生如下反应(图中有些反应的产物和反应的条件没有全部标出).请根据以上信息回答下列问题:(1)写出下列物质的化学式:丙HCl G FeCl3(2)写出下列反应的离子方程式:反应①2Na+2H2O═2Na++2OH﹣+H2↑反应⑤2Fe2++Cl2═2Fe3++2Cl﹣(3)写出乙+D的化学方程式Cl2+2NaOH=NaCl+NaClO+H2O .考点:无机物的推断.分析:金属A焰色反应为黄色,故A为金属Na,由反应①可知,D为NaOH,气体甲为H2;氢氧化钠与金属B反应生成氢气,故金属B为Al.黄绿色气体乙为Cl2,与氢气反应生成丙为HCl,HCl溶于水得物质E为盐酸.氢氧化钠与物质G反应生成红褐色沉淀是Fe(OH)3,故物质G中含有Fe3+,由转化关系HCl物质F物质G,可知金属C为Fe,物质F为FeCl2,物质G为FeCl3,结合物质的性质解答该题结合物质的性质解答该题.解答:解:金属A焰色反应为黄色,故A为金属Na,由反应①可知,D为NaOH,气体甲为H2;氢氧化钠与金属B反应生成氢气,故金属B为Al.黄绿色气体乙为Cl2,与氢气反应生成丙为HCl,HCl溶于水得物质E为盐酸.氢氧化钠与物质G反应生成红褐色沉淀是Fe(OH)3,故物质G中含有Fe3+,由转化关系HCl物质F物质G,可知金属C为Fe,物质F为FeCl2,物质G为FeCl3,(1)由以上分析可知丙为HCl,G为FeCl3,故答案为:HCl;FeCl3;(2)反应①为Na和水的反应,离子方程式为2Na+2H2O═2Na++2OH﹣+H2↑,反应⑤为氯气氧化氯化亚铁,离子方程式为2Fe2++Cl2═2Fe3++2Cl﹣,故答案为:2Na+2H2O═2Na++2OH﹣+H2↑;2Fe2++Cl2═2Fe3++2Cl﹣;(3)乙为Cl2,D为NaOH,乙+D的化学方程式为Cl2+2NaOH=NaCl+NaClO(次氯酸钠)+H2O,故答案为:Cl2+2NaOH=NaCl+NaClO+H2O.点评:本题考查无机物的推断,题目难度中等,解答本题的关键是能根据物质的特性如颜色为突破口进行推断,答题时注意体会.。
江苏省泰兴市第一高级中学2014-2015学年高一下学期期末模拟考试(一)语文试卷 Word版含答案

资料概述与简介 泰兴市第一高级中学2014—2015学年度第二学期期末模拟考试(一) 高一语文试卷 2015.6.21 卷面总分:160分考试时间:150分钟 一、语言文字运用(21分) 1.在下面一段话空缺处依次填入词语,最恰当的一组是(3分) 现在有种观点认为,英语与汉语的学习彼此是▲的,要想学好汉语,就得弱化英语。
这一观点虽说十分流行,但实际上却相当荒谬。
看看钱钟书看看林语堂看看胡适,他们都是▲的文化大师,他们的国学功底异常深厚,他们的英语水准堪称世界一流,他们的出现,正是对这一观点的有力驳斥。
可想而知,随着高考英语分数的下降,学校对英语的教学将会弱化,学生的英语水平将会降低。
这一切,完全与时代的发展▲,是不折不扣的倒退。
这种倒退,令人担忧。
A.针锋相对学富五车南辕北辙 B.针锋相对学贯中西背道而驰 C.势不两立学贯中西背道而驰 D.势不两立学富五车南辕北辙 2.下列各句中,没有语病的一项是(3分) A.只有当促进艺术电影繁荣成为社会共识,从源头的创作方到受众方的各环节都得到强有力的支持,艺术电影才能真正实现飞跃。
B.据说当年徽州男人大多外出经商,家中皆是妇孺及孩童,为了安全,徽州的古村落老宅子大多为高墙深院、重门窄窗的建筑。
C.工作之余,大家闲谈话题脱不开子女教育、住房大小、职务升迁,也照样脱不开为饭菜咸淡、暖气冷热、物价高低吐槽发声。
D.我国重新修订《食品安全法》,目的是用更严格的监管、更严厉的处罚、更严肃的问责,切实保障“舌尖上的安全”,被称为“最严食品安全法”。
3.下列诗句与“秋草独寻人去后”对仗工整的一项是(3 分)A. 海燕双栖玳瑁梁B. 长堤春水绿悠悠C. 寒林空见日斜时D. 孤城遥望玉门关 4. 下列交际用语使用不得体的一项是(3 分) A.欢迎光临阳光小区,这是我公司近年来鼎力打造的又一绿色生态小区! B.本人才疏学浅,刚才一些想法仅是一孔之见,接下来还请在座大方之家批评指正! C.在这特殊的日子里,我向母校致以最诚挚的祝福,愿母校永远年轻,永生机6. 阅读右边这幅漫画,对它的寓意理解不正确的一项是(3分) A.有人把它作前进的路标,结合自身实际,灵活运用 B.有人亦步亦趋,只知道生搬硬套,不顾自身的实际 C.生活中不同的人对待成功者的经验态度也不尽相同 D.将成功者足迹视为路标实际上是犯了经验主义错误 7.葛朗台的妻子生病,治病需要花钱,这简直就是“____________”。
江苏省泰兴一中2014-2015学年高一下学期期末考试补考英语试卷

2015春学期期初考试暨2014秋学期期末补考试卷高一英语2015.2.27 一.单项选择(20条,总分40分)1. The president hopes that the people will be better off when he quits than when he_______.A. has startedB. startsC. startedD. will start2. Not until he retired from teaching three years ago ________ having a holiday abroad.A. he had consideredB. had he consideredC. he consideredD. did he consider3. The manager was concerned to hear that two of his trusted workers ______.A. will leaveB. are leavingC. have leftD. were leaving4.—Can I call you back at two o’clock this afternoon?—I’m sorry, but by then I______ to Beijing. How about five?A. flyB. will flyC. will be flyingD. am flying5. --- I just received an email from one of my former classmates. I ___ from him for years.--- Just like you, I _____ out of touch with most of my old friends--- only one or two still drop me a line occasionally.A. haven’t heard; will beB. hadn’t heard; wasC. hadn’t heard; have beenD. haven’t heard; had been6. Life is like a long race____ we compete with others to go beyond ourselves.A. whyB. whatC. thatD. where7. Whenever I met her, ______was fairly often,she greeted me with a sweet smile.A. whoB. whichC. whenD. that8. The school shop,_______ customers are mainly students, is closed for the holidays.A. whichB. whoseC. whenD. where9.In the dark forest _____, some large enough to hold several English towns.A. stand many lakesB. lie many lakesC. many lakes lieD. many lakes stand10.______ is known to all, China will be an ______ and powerful country in 20 or 30 years’ time.A. That; advancingB. This; advancedC. As; advancedD. It; advancing11. When ______ why he walked in without permission, he just stared at us and said nothing.A. been askedB. askedC. askingD. to be asked12. On August 7,2009 Typhoon Morakot swept across Taiwan, ______a lot of villagesdamaged.A. leftB. leavingC. to leaveD. having left13. I think you can have the copy of the newspaper _______ I finish reading it myself.A. the momentB. unlessC. so thatD. because14. He got well-prepare d for the job interview , for he couldn’t risk __ the good opportunity.A. to loseB. losingC. to be lostD. being lost15. of herself , she left the room with nobody her.A. Being ashamed, noticingB. Ashamed, to noticeC. Ashamed, noticing D .To be ashamed, noticing16. In Britain, students can ___________ some subjects if they don’t like them.A. stopB. dropC. skipD. limit17. As ______ matter of fact, p eople who are on ______ diet can’t lose weight easily.A. a; aB. the; aC. the; theD. a; the18. Although the accident happened all of a sudden, it didn’t affect the ______ work here.A. regularB. commonC. usualD. normal19. — People have reported seeing a wild man-like creature in the Himalayas called a Yeti.— Did you see _______ when you were traveling there?A. itB. oneC. thatD. them20. Ronaldo was ______ to win the 100-meter hurdles race, but he fell to the ground and missedthe chance.A. possibleB. probableC. likelyD. maybe二.完形填空(20条,总分40分)Show yourselfOn the course of life, the first step of the lead is likely to mean the final victory, so the success and failure, or 21 and loss of your life may lie in 22 you dare to show yourself or not.As a student, I was most 23 to answer questions in class, and I found that the students around were just like me. At the beginning of each class, when the professor asked a question, I always 24 my head, for fear that the professor saw me.In a foreign language class, an expert from the Commercial Bank delivered a lecture. The speaker always wanted 25 to be in communication with him, so he asked how many students in the classroom learned Economics, but no one 26 . The expert said with a smile, “Let me tell you a(n) 27 first.”“When I came to the United States to study, there are often lectures delivered in the 28 . Each time, they invite an expert from Wall Street or a transnational company to make a speech.”“Before the beginning of every lectu re, I found a(n) 29 phenomenon(现象). Thestudents around me always took a cardboard folded in half, wrote their 30 with the most eye-catching color, and then placed it on the seat. 31 , when the speaker needed the response, he could see and call a listener’s name 32 .”“I couldn’t 33 why they did that, so I asked the student in front of me. He told me with a smile, ‘the speakers are all top-ranking people, who 34 chances. When your answer is to his 35 or surprise, it is very possible that he will give you more 36 . This is a very simple reason.’“The fact was also like that. I really saw a few students around me went to 37 in the first class company 38 their excellent insights (洞察力). This had a great influence on me. The chance will not find you 39 . Y ou must show yourself constantly to 40 others’ attention for you to find a chance on the cards.”21. A. win B. beat C. gain D. defeat22. A. how B. what C. that D. whether23. A. proud B. ready C. excited D. afraid24. A. raised B. shook C. lowered D. nodded25. A. anyone B. someone C. everyone D. no one26. A. replied B. agreed C. reported D. admitted27. A. idea B. fact C. truth D. story28. A. company B. hospital C. university D. business29. A. tense B. interesting C. attractive D. dull30. A. addresses B. numbers C. names D. cards31. A. Besides B. However C. Otherwise D. Thus32. A. directly B. loudly C. firstly D. rapidly33. A. make for B. make up C. make out D. make sense34. A. present B. mean C. multiply D. add35. A. disappointment B. amusement C. satisfaction D. astonishment36. A. chances B. questions C. responses D. jobs37. A. approve B. employ C. manage D. work38. A. in spite of B. because of C. aside from D. as to39. A. themselves B. himself C. yourself D. itself40. A. pay B. draw C. focus D. fix三.单词拼写(10条,总分10分)1.We started talking about the movie. _______________ (不知怎么的),we got onto the topicof education and culture.2.To my _____________ (满意),the hotel we booked doesn’t charge us for the breakfast.3.As a news agency run by high school students, SENTS not only passes down messages topeople, but also provide students with the spirit of ________________ (独立) thought.4.The country is making (准备) for war.5.T___________(容忍) your carelessness means destroying the whole project.6. We can’t rule out the p that the boy was taken by aliens and murdered by others.7. -- Are you going to the lecture on human development this afternoon?--- Sure, I’m c________________ about the origin of mankind.8. She opened the door quietly so as not to d____________ the sleeping child.9. If b__________ in,these viruses can result in illness or even death.10. I bought this shirt at a d_________, so it was very cheap.四.完成句子(10条,总分10分)1. He was ________ __________ (经历) a difficult time then.2.She _________ ________ (坚持) going to Africa to study wild animals there, although herfamily asked her not to.3. It was really_____ ____to be ready on time.要按时做好准备确非易事。
江苏省泰兴市第一高级中学2014-2015学年高一下学期期末模拟考试(一)化学试卷 Word版含答案.pdf

③,
④。
高一化学期末模拟考试(一)参考答案
题号1234567891011答案DCADBCCCBAC题号1213141516171819202122答案DDDDBBBDCABD23(15分,每空3分).(1)H
SH
(2)Na>C>N
(3)H2O>CH4>SiH4
(4)H++HSO3-=H2O+SO2↑ (5)HClO4
B.升高温度可加快逆反应速率但不能改变正反应速率
C.一定条件下,SO2可100%转化为SO3
D.任何条件下,反应达到平衡,SO2的浓度一定等于SO3的浓度
11.下列物质既能与溴水反应又能与酸性高锰酸钾溶液反应的是
A.甲烷B.四氯化碳C.乙烯D.苯
12.下列物质中,既含离子键又含非极性共价键的是
A.H2B.H2OC.NaOHD.Na2O2
13.氢氧燃料电池已用于航天飞机。以20%NaOH溶液为电解质溶液的这种电池在使用时的电极反应如下:
2H2+4OH--4e-=4H2O O2+2H2O+4e-=4OH- 据此判断,下列说法中正确的是
A.H2在正极发生氧化反应B.燃料电池属二次电池
(1)若A为Zn,B为石墨,电解质溶液为稀硫酸,则A极的电极反应式为______________________________。
(2)若A为铜,B为铁,电解质溶液为Fe2(SO4)3溶液,则铜片为______极(填正或负);该极电极反应式为
______________________________。
D. 反应④中1 mol苯可与3mol H2发生加成反应,说明苯分子中含有三个碳碳双键
19.用下列实验装置完成对应的实验(部分仪器已省略),能达到实验目的的是
江苏省泰州市泰兴一中高一数学下学期期末模拟试卷(含解析)-人教版高一全册数学试题

某某省某某市泰兴一中2014-2015学年高一(下)期末数学模拟试卷一、填空题:本大题共14小题,每小题5分,共70分.不需要写出解答过程,请把答案直接填空在答题卡相应位置上1.不等式(x﹣1)x≥2的解集是.2.已知直线ax+by+1=0与直线4x+3y+5=0平行,且直线ax+by+1=0在y轴上的截距为,则a+b=.3.等差数列{a n}的前n项和S n,若a1=2,S3=12,则a6=.4.设S n为等比数列{a n}的前n项和,已知3S3=a4﹣2,3S2=a3﹣2,则公比q=.5.(理科)若x,y满足约束条件,则z=x﹣y的最小值是.6.已知不等式ax2+bx﹣1>0的解集为{x|3<x<4},则实数a=.7.设m>0,则直线(x+y)+1+m=0与圆x2+y2=m的位置关系为.8.若圆C的半径为1,圆心在第一象限,且与直线4x﹣3y=0和x轴都相切,则该圆的标准方程是.9.已知点P(x,y)在经过两点A(3,0),B(1,1)的直线上,那么2x+4y的最小值是.10.已知一圆锥的底面是半径为1cm的圆,若圆锥的侧面积是底面积的3倍,则该圆锥的体积是cm3.11.等比数列{a n}前n项的积为T n,若a3a6a18是一个确定的常数,那么数列T10,T13,T17,T25中也是常数的项是.12.已知f(x)=x2+2(a﹣2)x+4,如果对x∈[﹣3,1],f(x)>0恒成立,则实数a的取值X围为.13.过圆x2+y2=1上一点作圆的切线与x轴、y轴的正半轴交于A、B两点,则|AB|的最小值为.14.若实数x,y满足x2+y2=1,则的取值X围是.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.已知数列{a n}的前n项和为S n,且S n=n2+2n.(1)求数列{a n}的通项公式;(2)令b n=,且数列{b n}的前n项和为T n,求T n.16.在三棱柱ABC﹣A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=1,A1B=.(1)求证:平面A1BC⊥平面ACC1A1;(2)如果D为AB的中点,求证:BC1∥平面A1CD.17.已知f(x)=ax2+x﹣a,a∈R.(1)若a=1,解不等式f(x)≥1;(2)若不等式f(x)>﹣2x2﹣3x+1﹣2a对一切实数x恒成立,某某数a的取值X围;(3)若a<0,解不等式f(x)>1.18.已知圆C:(x﹣3)2+(y﹣4)2=4,直线l1过定点A (1,0).(1)若l1与圆C相切,求l1的方程;(2)若l1的倾斜角为,l1与圆C相交于P,Q两点,求线段PQ的中点M的坐标;(3)若l1与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时l1的直线方程.19.某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=,∠ABC=,点D在AC上,点E在斜边BC上,且点F在AB上,AC=40米,设AD=x米.(1)试用x表示S,并求S的取值X围;(2)若矩形健身场地面积不小于144平方米,求x的取值X围;(3)设矩形健身场地每平方米的造价为,再把矩形ADEF以外(阴影部分)铺上草坪,每平方米的造价为,求总造价T关于S的函数T=f(S);并求出AD的长使总造价T最低(不要求求出最低造价).20.已知数列{a n}是等差数列,数列{b n}是等比数列,且对任意的n∈N*,都有.(1)若{b n}的首项为4,公比为2,求数列{a n+b n}的前n项和S n;(2)若a1=8,①求数列{a n}与{b n}的通项公式;②试探究:数列{b n}中是否存在某一项,它可以表示为该数列中其它r(r∈N*,r≥2)项的和?若存在,请求出该项;若不存在,请说明理由.某某省某某市泰兴一中2014-2015学年高一(下)期末数学模拟试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.不需要写出解答过程,请把答案直接填空在答题卡相应位置上1.不等式(x﹣1)x≥2的解集是(﹣∞,﹣1]∪[2,+∞).考点:一元二次不等式的解法.专题:不等式的解法及应用.分析:将不等式化为(x+1)(x﹣2)≥0,进而根据大于看两边,小于看中间,求出不等式的解集.解答:解:(x﹣1)x≥2,整理得(x+1)(x﹣2)≥0,解得x≤﹣1,或x≥2,故答案为:(﹣∞,﹣1]∪[2,+∞).点评:本题考查的知识点是一元二次不等式,其中熟练掌握一元二次不等式的解法步骤是解答的关键.2.已知直线ax+by+1=0与直线4x+3y+5=0平行,且直线ax+by+1=0在y轴上的截距为,则a+b= ﹣7 .考点:直线的一般式方程与直线的平行关系.专题:直线与圆.分析:由平行关系和截距可得ab的两个方程,联立解方程组可得.解答:解:∵ax+by+1=0与直线4x+3y+5=0平行,∴4b=3a,又直线ax+by+1=0在y轴上的截距为,∴b+1=0,解得b=﹣3,∴a=﹣4,∴a+b=﹣7故答案为:﹣7点评:本题考查直线的一般式方程和平行关系,属基础题.3.等差数列{a n}的前n项和S n,若a1=2,S3=12,则a6= 12 .考点:等差数列的前n项和.专题:等差数列与等比数列.分析:根据等差数列的通项公式以及前n项和公式进行求解即可.解答:解:∵S3=12,∴S3=3a1+d=3a1+3d=12.解得d=2,则a6=a1+5d=2+2×5=12,故答案为:12点评:本题主要考查等差数列的通项公式的求解和应用,根据条件求出公差是解决本题的关键.4.设S n为等比数列{a n}的前n项和,已知3S3=a4﹣2,3S2=a3﹣2,则公比q= 4 .考点:等比数列的前n项和;等比数列的通项公式.专题:计算题.分析:由于{a n} 为等比数列,由可求得q.解答:解:∵{a n} 为等比数列,S n为其前n项和,公比为q,又∴①﹣②得:3a3=a4﹣a3=a3(q﹣1),∵a3≠0,∴q﹣1=3,q=4.故答案为:4.点评:本题考查等比数列的通项公式与前n项和公式,着重考查公式的应用与解方程的能力,属于基础题.5.(理科)若x,y满足约束条件,则z=x﹣y的最小值是﹣3 .考点:简单线性规划.专题:不等式的解法及应用.分析:先根据条件画出可行域,设z=x﹣y,再利用几何意义求最值,将最小值转化为y轴上的截距最大,只需求出直线z=x﹣y,过可行域内的点A(0,3)时的最小值,从而得到z 最小值即可.解答:解:设变量x、y满足约束条件,在坐标系中画出可行域三角形,将z=x﹣y整理得到y=x﹣z,要求z=x﹣y的最小值即是求直线y=x﹣z的纵截距的最大值,当平移直线x﹣y=0经过点A(0,3)时,x﹣y最小,且最小值为:﹣3,则目标函数z=x﹣y的最小值为﹣3.故答案为:﹣3.点评:借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.线性规划中的最优解,通常是利用平移直线法确定.6.已知不等式ax2+bx﹣1>0的解集为{x|3<x<4},则实数a= ﹣.考点:一元二次不等式的解法.专题:不等式的解法及应用.分析:由题意可知3,4是方程ax2+bx﹣1=0的两个实根,利用韦达定理即可求得a值.解答:解:∵等式ax2+bx﹣1>0的解集为(x|3<x<4},∴3,4是方程ax2+bx﹣1=0的两个实根,则=12,解得a=﹣,故答案为:﹣.点评:本题主要考查一元二次不等式的解法,考查根与系数的关系,深刻理解“三个二次”间的关系是解决相关问题的关键.7.设m>0,则直线(x+y)+1+m=0与圆x2+y2=m的位置关系为相切或相离.考点:直线与圆的位置关系.专题:直线与圆.分析:利用点到直线的距离距离可得圆心到直线的距离d,把d与r比较即可得出.解答:解:圆心(0,0)到直线(x+y)+1+m=0的距离d==.d﹣r==.因此直线与圆相切或相离.故答案为:相切或相离.点评:本题考查了直线与圆的位置关系、点到直线的距离公式、基本不等式等基础知识与基本技能方法,属于基础题.8.若圆C的半径为1,圆心在第一象限,且与直线4x﹣3y=0和x轴都相切,则该圆的标准方程是(x﹣2)2+(y﹣1)2=1 .考点:圆的标准方程;圆的切线方程.专题:计算题.分析:依据条件确定圆心纵坐标为1,又已知半径是1,通过与直线4x﹣3y=0相切,圆心到直线的距离等于半径求出圆心横坐标,写出圆的标准方程.解答:解:∵圆C的半径为1,圆心在第一象限,且与直线4x﹣3y=0和x轴都相切,∴半径是1,圆心的纵坐标也是1,设圆心坐标(a,1),则1=,又 a>0,∴a=2,∴该圆的标准方程是(x﹣2)2+(y﹣1)2=1;故答案为(x﹣2)2+(y﹣1)2=1.点评:本题考查利用圆的切线方程求参数,圆的标准方程求法.9.已知点P(x,y)在经过两点A(3,0),B(1,1)的直线上,那么2x+4y的最小值是.考点:基本不等式在最值问题中的应用.专题:计算题.分析:由题意知2x+4y=.由此可知2x+4y的最小值.解答:解:由题意知点P(x,y)在经过两点A(3,0),B(1,1)的直线上,∴x+2y=32x+4y=.∴2x+4y的最小值是4 .故答案为:.点评:本题考查不等式的性质和应用,解题时要认真审题,仔细解答,解答关键是利用基本不等式求出最值.10.已知一圆锥的底面是半径为1cm的圆,若圆锥的侧面积是底面积的3倍,则该圆锥的体积是cm3.考点:棱柱、棱锥、棱台的体积.专题:空间位置关系与距离.分析:由已知中,圆锥的底面半径为1,侧面积是底面积的3倍,分析圆锥的母线长,进而求出圆锥的高,结合圆锥的体积公式即可获得问题的解答.解答:解:∵圆锥的底面半径r=1cm,侧面积是底面积的3倍,∴圆锥的母线长l=3cm,故圆锥的高h==2cm,故圆锥的体积V=Sh=πr2•h==cm3,故答案为:.点评:本题考查的是圆锥的体积求解问题.在解答的过程当中充分体现了圆锥体积公式的应用以及转化思想的应用.值得同学们体会反思.11.等比数列{a n}前n项的积为T n,若a3a6a18是一个确定的常数,那么数列T10,T13,T17,T25中也是常数的项是T17.考点:等比数列的性质;等比数列的前n项和.专题:等差数列与等比数列.分析:利用等比数列的通项公式、化简a3•a6•a12 =a93 是一个确定的常数,利用等比数列的性质得到T13 =a913,即可得到T19为常数.解答:解:在等比数列中,设公比为q,∵a3•a6•a18=a1q2•a1q5•a1 q17=(a1 q8)3 =为常数,∴a9为常数,则 T17=a1•a2…a17=(a1•a17)(a2•a16)(a3•a15)(a4•a14)(a5 •a13)(a6•a12)•( a7•a11)•(a8•a10)a9=,即T17为常数.故答案为:T17点评:本题主要考查等比数列的性质,考查学生的运算能力.12.已知f(x)=x2+2(a﹣2)x+4,如果对x∈[﹣3,1],f(x)>0恒成立,则实数a的取值X围为(﹣,4).考点:二次函数在闭区间上的最值.专题:函数的性质及应用.分析:对x∈[﹣3,1],f(x)>0恒成立,需讨论对称轴与区间[﹣3,1]的位置关系,确定出最小值建立不等式,解之即可.解答:解:∵f(x)=x2+2(a﹣2)x+4,对称轴x=﹣(a﹣2),对x∈[﹣3,1],f(x)>0恒成立,∴讨论对称轴与区间[﹣3,1]的位置关系得:或或,解得a∈ϕ或1≤a<4或﹣<a<1,∴a的取值X围为(﹣,4)点评:本题主要考查了函数恒成立问题,以及函数在闭区间上恒成立问题,属于基础题.13.过圆x2+y2=1上一点作圆的切线与x轴、y轴的正半轴交于A、B两点,则|AB|的最小值为 2 .考点:直线与圆的位置关系.专题:直线与圆.分析:用截距式设出切线方程,由圆心到直线的距离等于半径以及基本不等式可得:,令t=,可得t的最小值为 2,进而得到答案.解答:解:设切线方程为+=1(a>0,b>0),即 bx+ay﹣ab=0,∵圆心(0,0)到直线的距离等于半径得=1,∴ab=≤,令t=,则有t2﹣2t≥0,t≥2,则t的最小值为2,即|AB|的最小值为2.故答案为:2点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,基本不等式的运用,直线的截距式方程,利用了换元的思想,熟练掌握公式及性质是解本题的关键.14.若实数x,y满足x2+y2=1,则的取值X围是(﹣∞,1﹣]∪(+1,+∞).考点:圆的标准方程.专题:直线与圆.分析:令x=cosθ,y=sinθ,θ∈[0,2π),x+y=t=sin(θ+)∈[﹣,].则=化简为++1,分类讨论,利用基本不等式求得它的X围,综合可得结论.解答:解:∵实数x,y满足x2+y2=1,可令x=cosθ,y=sinθ,θ∈[0,2π),则x+y=t=sin(θ+)∈[﹣,].则=====+ +1,当t∈(1,]时,利用基本不等式可得++1≥+1,当期仅当t=1+时,取等号,而t=1+不可能,故++1>+1.当t<1时,﹣+(﹣)≥,当且仅当t=1﹣时,取等号,故+≤﹣,故++1≤1﹣.综上可得,≤1﹣或>+1,故答案为:(﹣∞,1﹣]∪(+1,+∞).点评:本题考查三角恒等变换,基本不等式的应用,考查计算能力,属于中档题.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.已知数列{a n}的前n项和为S n,且S n=n2+2n.(1)求数列{a n}的通项公式;(2)令b n=,且数列{b n}的前n项和为T n,求T n.考点:数列的求和;数列递推式.专题:等差数列与等比数列.分析:(1)利用S n+1﹣S n可知a n+1=2(n+1)+1,通过a1=S1=3满足上式,进而即得结论;(2)通过S n=n2+2n,裂项可知b n=(﹣),并项相加即得结论.解答:解:(1)∵S n=n2+2n,∴S n+1=(n+1)2+2(n+1),∴a n+1=S n+1﹣S n=[(n+1)2+2(n+1)]﹣(n2+2n)=2(n+1)+1,又∵a1=S1=1+2=3满足上式,∴a n=2n+1;(2)∵S n=n2+2n,∴b n===(﹣),∴T n=(1﹣+﹣+…+﹣+﹣)=(1+﹣﹣)=.点评:本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.16.在三棱柱ABC﹣A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=1,A1B=.(1)求证:平面A1BC⊥平面ACC1A1;(2)如果D为AB的中点,求证:BC1∥平面A1CD.考点:平面与平面垂直的判定;直线与平面平行的判定.专题:空间位置关系与距离.分析:(1)利用等边三角形的判定、勾股定理的逆定理、及线面、面面垂直的判定定理和性质定理即可证明;(2)利用平行四边形的性质、三角形的中位线定理、线面平行的判定定理即可证明.解答:证明:(1)在,∴A1C=1,在△A1BC中,BC=1,A1C=1,,∴,∴∠A1CB=90°,∴BC⊥A1C,又AA1⊥BC,AA1∩A1C=A1,∴BC⊥平面ACC1A1,∵BC⊂平面A1BC,∴平面A1BC⊥平面ACC1A1.(2)连接A1C交AC1于O,连接DO,则由D为AB中点,O为AC1中点得,OD∥BC1,∵OD⊂平面A1DC,BC1⊄平面A1DC,∴BC1∥平面A1DC.点评:熟练掌握等边三角形的判定、勾股定理的逆定理、及线面、面面垂直与平行的判定定理和性质定理、平行四边形的性质、三角形的中位线定理是证明问题的关键.17.已知f(x)=ax2+x﹣a,a∈R.(1)若a=1,解不等式f(x)≥1;(2)若不等式f(x)>﹣2x2﹣3x+1﹣2a对一切实数x恒成立,某某数a的取值X围;(3)若a<0,解不等式f(x)>1.考点:其他不等式的解法;函数恒成立问题;一元二次不等式的解法.专题:不等式的解法及应用.分析:(1)当a=1,不等式即(x+2)(x﹣1)≥0,解此一元二次不等式求得它的解集.(2)由题意可得(a+2)x2+4x+a﹣1>0恒成立,当a=﹣2 时,显然不满足条件,故有,由此求得a的X围.(3)若a<0,不等式为 ax2+x﹣a﹣1>0,即(x﹣1)(x+)<0.再根据1和﹣的大小关系,求得此不等式的解集.解答:解:(1)当a=1,不等式f(x)≥1即 x2+x﹣1≥1,即(x+2)(x﹣1)≥0,解得x≤﹣2,或x≥1,故不等式的解集为{x|x≤﹣2,或x≥1}.(2)由题意可得(a+2)x2+4x+a﹣1>0恒成立,当a=﹣2 时,显然不满足条件,∴.解得 a>2,故a的X围为(2,+∞).(3)若a<0,不等式为 ax2+x﹣a﹣1>0,即(x﹣1)(x+)<0.∵1﹣(﹣)=,∴当﹣<a<0时,1<﹣,不等式的解集为 {x|1<x<﹣};当 a=﹣时,1=﹣,不等式即(x﹣1)2<0,它的解集为∅;当a<﹣时,1>﹣,不等式的解集为 {x|﹣<x<1}.点评:本题主要考查一元二次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.18.已知圆C:(x﹣3)2+(y﹣4)2=4,直线l1过定点A (1,0).(1)若l1与圆C相切,求l1的方程;(2)若l1的倾斜角为,l1与圆C相交于P,Q两点,求线段PQ的中点M的坐标;(3)若l1与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时l1的直线方程.考点:点与圆的位置关系;中点坐标公式;点到直线的距离公式.专题:计算题;分类讨论.分析:(1)通过直线l1的斜率存在与不存在两种情况,利用直线的方程与圆C相切,圆心到直线的距离等于半径,判断直线是否存在,求出k,即可求l1的方程;(2)l1的倾斜角为,直接求出l1的方程,利用直线l1与圆C相交于P,Q两点,求线段PQ的中点M的坐标,直接转化为过圆心与直线l1垂直的中垂线方程,解两条直线方程的交点即可;(3)l1与圆C相交于P,Q两点,直线与圆相交,斜率必定存在,且不为0,设直线方程为kx﹣y﹣k=0,求出圆心到直线的距离,弦长,得到三角形CPQ的面积的表达式,利用二次函数求出面积的最大值时的距离,然后求出直线的斜率,得到l1的直线方程.解答:解:(1)解:①若直线l1的斜率不存在,则直线x=1,圆的圆心坐标(3,4),半径为2,符合题意.②若直线l1斜率存在,设直线l1为y=k(x﹣1),即kx﹣y﹣k=0.由题意知,圆心(3,4)到已知直线l1的距离等于半径2,即:,解之得.所求直线方程是:x=1,或3x﹣4y﹣3=0.(2)直线l1方程为y=x﹣1.∵PQ⊥CM,∴CM方程为y﹣4=﹣(x﹣3),即x+y﹣7=0.∵∴∴M点坐标(4,3).(3)直线与圆相交,斜率必定存在,且不为0,设直线方程为kx﹣y﹣k=0,则圆.又∵三角形CPQ面积∴当d=时,S取得最大值2.∴.∴直线方程为y=x﹣1,或y=7x﹣7.点评:本题考查直线与圆的位置关系,直线与圆相切,相交,直线的交点,弦的中点,三角形的面积的最值直线方程等有关知识,考查计算能力,转化思想,注意直线的斜率不存在的情况,容易疏忽,是易错点.19.某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=,∠ABC=,点D在AC上,点E在斜边BC上,且点F在AB上,AC=40米,设AD=x米.(1)试用x表示S,并求S的取值X围;(2)若矩形健身场地面积不小于144平方米,求x的取值X围;(3)设矩形健身场地每平方米的造价为,再把矩形ADEF以外(阴影部分)铺上草坪,每平方米的造价为,求总造价T关于S的函数T=f(S);并求出AD的长使总造价T最低(不要求求出最低造价).考点:函数模型的选择与应用.专题:应用题;函数的性质及应用.分析:(1)根据题意,分析可得,欲求健身场地占地面积,只须求出图中矩形的面积即可,再结合矩形的面积计算公式求出它们的面积即得,最后再根据二次函数的性质得出其X 围;(2)利用矩形健身场地面积不小于144平方米,建立不等式,即可求x的取值X围;(3)求出总造价,考虑到其中两项之积为定值,可利用基本不等式求它的最大值,从而解决问题.解答:解:(1)在Rt△EDC中,显然|DC|=40﹣x,∠ECD=60°∴|ED|=|DC|tan60°=(40﹣x),矩形ADEF的面积S=|AD||AF|=x(40﹣x),x∈(0,40)于是0<S≤400为所求;(2)∵矩形健身场地面积不小于144平方米,∴x(40﹣x)≥144,∴4≤x≤36;(3)矩形ADEF健身场地造价T1=37又△ABC的面积为800,即草坪造价T2=(800﹣S)由总造价T=T1+T2,∴T=25(+)≥200当且仅当=即S=384时等号成立,此时x(40﹣x)=384,解得x=16或x=24,∴选取|AD|的长为16米或24米时总造价T最低.点评:本小题主要考查函数模型的选择与应用、基本不等式的应用、矩形的面积等基础知识,属于中档题.20.已知数列{a n}是等差数列,数列{b n}是等比数列,且对任意的n∈N*,都有.(1)若{b n}的首项为4,公比为2,求数列{a n+b n}的前n项和S n;(2)若a1=8,①求数列{a n}与{b n}的通项公式;②试探究:数列{b n}中是否存在某一项,它可以表示为该数列中其它r(r∈N*,r≥2)项的和?若存在,请求出该项;若不存在,请说明理由.考点:数列的求和.专题:等差数列与等比数列.分析:(1)由已知条件,先求出b n=2n+1,再由,分别求出a1,a2,由此能求出数列{a n+b n}的前n项和S n.(2)①由已知条件求出a1=8,b1=2,设等差数列{a n}的公差为d,等比数列{b n}的公比为q,列出方程组求出d=4,q=2,由此能求出数列{a n}与{b n}的通项公式.②由b n=2n,能推导出数列{b n}中不存在某一项可以表示为该数列中其它r(r∈N*,r≥2)项的和.解答:解:(1)∵{b n}是等比数列,首项为4,公比为2,∴b n=4•2n﹣1=2n+1,∵数列{a n}是等差数列,且对任意的n∈N*,都有,∴a1b1=24,∴=4,,∴,∴a2===6,∴d=a2﹣a1=6﹣4=2,∴a n=4+(n﹣1)×2=2n+2.∴S n=(a1+a2+a3+…+a n)+(b1+b2+…+b n)=[4n+]+=n2+3n+2n+2﹣4.(2)①∵a1=8,,∴8b1=24,解得b1=2,设等差数列{a n}的公差为d,等比数列{b n}的公比为q,则,解得d=4,q=2,或d=﹣2,q=4(舍).∴a n=8+(n﹣1)×4=4n+4,=2n.②∵b n=2n,∴数列{b n}中不存在某一项可以表示为该数列中其它r(r∈N*,r≥2)项的和.理由如下:假设存在第λ项可以表示为该数列中其它r(r∈N*,r≥2)项的和,则2λ=2m+1+2m+2+…+2m+r=2m+1(1+2+…+2r﹣1),∴2λ﹣(m+1)=1+2+…+2r﹣1,∵2λ﹣(m+1)是偶数,1+2+…+2r﹣1是奇数,∴2λ﹣(m+1)=1+2+…+2r﹣1不成立.∴数列{b n}中是不存在某一项,它可以表示为该数列中其它r(r∈N*,r≥2)项的和.点评:本题考查数列的前n项和的求法,考查数列的通项公式的求法,考查数列中的某一项能否表示为其他几项和的判断,解题时要认真审题,要熟练掌握等差数列、等比数列的性质.。
江苏省泰兴市第一高级中学高一英语下学期期末模拟考试试题(一)

泰兴市第一高级中学2014—2015学年度第二学期期末模拟考试(一)高一英语试卷2015.6.23卷面总分:120分考试时间:120分钟第一部分:听力(共15小题;每题1分, 满分15分)第一节:听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有l0秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
()1. What does the man usually do on Sunday afternoon?A. Work in the garden.B. Go to church.C. Do some reading.()2. Which book is the most expensive?A. The blue one.B. The green one.C. The red one. ()3. What is the man going to do?A. Ask the woman to join him.B. Found his own company.C. Find a new job.()4. What does the woman mean?A. It is unfair that the man's wife should stay at home.B. it is impossible to repair the pipes again.C. It is not the first time that the pipes leaked.()5. What does the man mean?A. The price for rent is beyond their reach.B. The neighborhood is too far away.C. They don't need a new apartment.第二节听下面5段对话或独白。
高一历史月考试题及答案-江苏省泰兴市第一高级中学2014-2015学年高一下学期调研测试(一)

2015年春学期高一年级调研测试(一)高一历史(满分100分) 2015.3.29一、单选选择题(每小题2分,共计70分)1、“(王景)迁庐江(位于安徽)太守。
先是,百姓不知牛耕,致地力有余而食常不足。
……景乃驱率吏民,修起荒废,教用犁耕,由是垦劈倍多,境内丰给。
”《后汉书》的这段记载反映当地:A、大力治理黄河基本消除了水患B、采用铁犁牛耕提高了农业产量C、推广曲辕犁后增加了耕地面积D、农民丰衣足食促进了商业发展2、右图是陕西米脂出土的东汉画像石,从图中我们能读出的正确的历史信息有:①牛耕在当时得到了推广②基本定型③东汉绘画技术高超④东汉精工细作技术得到提高A、①②④B、①③④C、①③D、②③④3、殷墟甲骨文中有“(王)令众人曰,協田”的卜辞。
“協”字在甲骨文中象形成三耒共耕。
该甲骨文反映的殷商时期农业发展的信息有:①已经使用耒耜的锄耕方式②当时是集体耕作方式③证明商代已经有了井田制了④商王朝非常重视农业生产A、①③④B、①②③C、②③④D、①②③④4、《新全球史》记载,从公元前6世纪开始,铁制农具在中国骤然增加,铁犁、铁镐、铁锹、铁锄、铁镰刀和铁耙在乡村成为日常常用工具。
这一现象给当时社会发展带来了影响包括:①“分地则速,无所匿其力也”②“秋七月,初税亩”③“宗庙之牲,变为畎亩之勤”④“庶人食力,工商食官”A、①②③B、①②C、③④D、①②③④5、某古代水利工程“旱则引水浸润,雨则杜塞水门。
故记曰:‘水旱从人,不知饥谨’”。
后来,三国时蜀相诸葛亮“征丁千二百人护之”。
据此判断,这项水利工程是:A、都江堰B、郑国渠 C 、灵渠 D、白守渠6、宋人诗云“小麦青青大麦黄,原头日出天色惊妇姑相呼有忙事,舍后煮茧门前香。
繅车嘈嘈似风雨,茧厚丝长无断缕。
今年那暇织绢着,明日西门卖丝去。
”诗中反映了:A、手工产品质量低下B、农业生产规模庞大C、农民家庭生活闲适D、农户经营方式多样7、《荀子王制》“凡农之道,厚(候)之为宝。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
泰兴市第一高级中学2014—2015学年度第二学期期末模拟考试(一)高一数学试卷卷面总分:160分 考试时间:120分钟一、填空题:本大题共14小题,每小题5分,共70分。
不需要写出解答过程,请把答案直接填空在答题卡相应位置上........1. 已知直线4:=-y mx l 若直线l 与直线2)1(=-+y m m x 垂直,则m 的值为______.2.若等比数列{}n a 的前n 项和为n S ,且141,8a a ==,则5S = .3. 已知圆222:C x y r +=与直线34100x y -+=相切,则圆C 的半径r =4.若x >y ,a >b ,则在①a -x >b -y ,②a +x >b +y ,③ax >by ,④x -b >y -a ,⑤a y >bx这五个式子中,恒成立的所有不等式的序号是________.5.在等差数列{n a }中,已知1083=+a a ,则375a a += . 6.过圆422=+y x 上一点()3,1-P 的切线方程为___________________.7.设实数y x ,满足⎪⎩⎪⎨⎧≤-≥-+≤--,032,042,02y y x y x 则x y 的最大值为___________8. 设直线x -my -1=0与圆(x -1)2+(y -2)2=4相交于A 、B 两点,且弦AB 的长为23,则实数m 的值是________. 9. 设,l m 是两条不同的直线,,αβ是两个不同的平面,则下列命题为真命题的序号是____. (1).若//,//,//m l m l αα则;(2).若,,//m l m l αα⊥⊥则; (3).若//,,//,l m l m αβαβ⊥⊥则; (4).若,//,,//,//m m l l αββααβ⊂⊂则10. 已知正四棱锥的底面边长是6,则该正四棱锥的侧面积为 .11.己知a ,b 为正数,且直线 60ax by +-=与直线 2(3)50x b y +-+=互相平行,则2a +3b 的最小值为 .12.如果关于x 的不等式22(1)(1)10m x m x --+-<的解集是R ,则实数m 的取值范围是 .2200013.:x 1,(,):3240,O y P x y l x y O OA OB OP x +=+-=+=已知圆点是直线上的动点,若在圆上总存在不同的两点A,B 使得则的取值范围为________.2222214.,,24,1,1x y x y x y R y x x xy x y ++-+∈≤≤-≥-+-已知满足则的最大值为_______.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15. (本题满分14分)已知ABC △的顶点()()()4,1,0,1,23-C B A ,,求: (1)AB 边上的高所在直线的方程; (2)AC 边上的中线所在直线的方程;(3)ABC △外接圆方程. 16、(本题满分14分)等比数列{}n a 的各项均为正数,且21252643,9a a a a a -== .(1)求数列{}n a 的通项公式;(2)设3log n n b a =,求数列{}n n a b +的前n 项和n S .17. (本题满分14分)如图所示,矩形ABCD 中,AD ⊥平面ABE ,2AE EB BC ===,F 为CE 上的点,且BF ⊥平面ACE (1) 求证:AE ⊥平面BCE ;(2) 求证://AE 平面BFD ;(3) 求三棱锥C BGF -的体积.18.(本题满分16分)某加工厂需定期购买原材料,已知每千克原材料的价格为1.5元,每次购买原材料需支付运费600元,每千克原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400千克,每次购买的原材料当天即开始使用(即有400千克不需要保管).(1)设该厂每x 天购买一次原材料,试写出每次购买的原材料在x 天内总的保管费用y 1关于x 的函数关系式;(2)求该厂多少天购买一次原材料才能使平均每天支付的总费用y 最小,并求出这个最小值. 19.(本题满分16分)G BAD C FE已知以点C ⎝⎛⎭⎪⎫t ,2t (t ∈R ,t ≠0)为圆心的圆与x 轴交于点O ,A ,与y 轴交于点O ,B ,其中O为原点.(1)求证:△AOB 的面积为定值;(2)设直线2x +y -4=0与圆C 交于点M ,N ,若OM ON =,求圆C 的方程;(3)在(2)的条件下,设P ,Q 分别是直线l :x +y +2=0和圆C 上的动点,求PB PQ +的最小值及此时点P 的坐标.20.(本题满分16分)已知 n S 是数列{}n a 的前n 项和,且244n S n n =-+(1)求数列{}n a 的通项公式;(2)设各项均不为零的数列{}n c 中,所有满足01<⋅+k k c c 的正整数k 的个数称为这个数列{}n c 的变号数,令nn a c 41-=(n 为正整数),求数列{}n c 的变号数; (3)记数列1{}na 的前n 的和为n T ,若2n+115n m T T -≤对+∈N n 恒成立,求正整数m 的最小值。
高一数学期末模拟(一)参考答案1、0或2;2、31;3、2;4、②、④;5、20;6、043=--y x7、 32;8±、 9、③; 10、48;11、25;12、5m m 13>≤-或; 13、240,13⎛⎫ ⎪⎝⎭;14、10315:解:()03:1=-+y x l …………4分()()2221.927503.14339x x y =⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭分分16、解:(1)3n n a =…………4分(2)1(1)13,9314222n n n n n b n S ++==+⨯-分;分. 17、 (1)证明:∵AD ⊥平面ABE ,//AD BC ,∴BC ⊥平面ABE ,则AE BC ⊥又BF ⊥平面ACE ,则AE BF ⊥AE ∴⊥平面BCE(2)由题意可得G 是AC 的中点,连接FGBF ⊥平面ACE ,则CE BF⊥,而BC BE =,F∴是EC 中点,在AEC ∆中,//FG AE ,//AE ∴平面BFD(3)//AE 平面BFD ,//AE FG ∴,而AE ∴⊥平面BCE,FG ∴⊥平面BCFG 是AC 中点,F 是CE 中点,//FG AE ∴且112FG AE ==,BF ⊥平面ACE ,BF CE∴⊥,Rt BCE ∴∆中,12BF CE CF ===, 1CFB S ∆∴==1133C BG F G BC F CFB V V S FG --∆∴==⋅⋅=GBADCFE18、解:(I)每次购买原材料后,当天用掉的400公斤原材料不需要保管费用,第二天用掉的400公斤原材料需保管1天,第三天用掉的400公斤原材料需保管2天,第四天用掉的400公斤原材料需保管3天,……,第x 天(也就是下次购买原材料的前一天)用掉最后的400公斤原材料需保管x-1天. 每次购买的原材料在x 天内总的保管费用 y 1=400×O .03[1+2+3+…+(x -1)]=6x 2-6x(元).…………7分 (Ⅱ)由上问可知,购买一次原材料的总的费用为6x 2-6x+600+1.5×400x 元,∴ 购买一次原材料平均每天支付的总费用∴. 当且仅当,即x=10时,取等号. …………15分∴该厂10天购买一次原材料可以使平均每天支付的总费用y 最少,为714元.…………16分 19:(1)证明:由题设知,圆C 的方程为(x -t )2+⎝⎛⎭⎫y -2t 2=t 2+4t 2,化简得x 2-2tx +y 2-4t y =0, 当y =0时,x =0或2t ,则A (2t,0); 当x =0时,y =0或4t,则B ⎝⎛⎭⎫0,4t , ∴S △AOB =12|OA |·|OB |=12|2t |·⎪⎪⎪⎪4t =4为定值. …………5分(2)解:∵|OM |=|ON |,则原点O 在MN 的中垂线上,设MN 的中点为H ,则CH ⊥MN ,∴C ,H ,O 三点共线,则直线OC 的斜率k =2t t =2t 2=12,∴t =2或t =-2.∴圆心为C (2,1)或(-2,-1),∴圆C 的方程为(x -2)2+(y -1)2=5或(x +2)2+(y +1)2=5,由于当圆方程为(x +2)2+(y +1)2=5时,直线2x +y -4=0到圆心的距离d >r ,此时不满足直线与圆相交,故舍去,∴圆C 的方程为(x -2)2+(y -1)2=5. …………10分 (3)解:点B (0,2)关于直线x +y +2=0的对称点为B ′(-4,-2),则|PB |+|PQ |=|PB ′|+|PQ |≥|B ′Q |,又B ′到圆上点Q 的最短距离为|B ′C |-r =-2+-2-5=35-5=2 5. 所以|PB |+|PQ |的最小值为25,直线B ′C 的方程为y =12x ,则直线B ′C 与直线x +y +2=0的交点P 的坐标为⎝⎛⎭⎫-43,-23. …………16分(2)由题设⎪⎩⎪⎨⎧≥--=-=2n 5n 2411n 3c n 3,129,225n n n n -=⎧⎪=-⎨≥⎪-⎩ …………7分 当2n ≥时,令03272529201<--⋅--<⋅+n n n n c c n n 得4229272523==<<<<n n n n 或解得或即 …………………………9分 又5c ,3c 21=-= 1n =∴时也有0c c 21<⋅ 综上得数列{}n c 共有3个变号数,即变号数为3…………11分(3)令n n S S n g -=+12)(,)()()()()1(1123212132n n n n n n n n S S S S S S S S n g n g ---=---=-+++++++23221111n n n a a a +++=+-=111241414123(41)(41)(23)n n n n n n n -++-=+--+-- …………13分当2n ≥时,(1)()g n g n +<所以)(n g 单调递减;因而)(n g 的最大值为521123(2)15315g S S =-=++=当1n =时,(2)(1)0g g ->,所以(2)(1)g g > …………15分 所以:231515m ≥,即23m ≥,又m 为正整数;所以m 的最小值为23.……………16分。
