R语言 t检验实例程序及答案

合集下载

r语言t检验例题

r语言t检验例题如何理解r语言t检验例题例题，遗传算法（GeneticAlgorithm）是一种基于自然选择模拟进化机制的算法，通过对个体间竞争或协作、变异和遗传实现目标优化求解。

主要包括种群初始化、选择和变异、遗传迭代等步骤，能够很好地应用于简单或复杂的求解问题上。

例题检验，通常，例题检验指的是一种研究方法，它利用小规模的试题或案例来测试和验证某种理论或假设。

这种检验可以实施一系列步骤，其中包括收集例题数据、对假设进行建模、应用统计分析等，最后形成结论。

例题检验通常是在一个更大的实验中完成的，例如，在一个企业发展计划中，用例题检验来决定计划是否可行。

r语言t检验例题，假设有一组数据，20个男性和20个女性的身高分别记录在表中：| 性别 | 身高（cm） || --- | ---------- || 男 | 172 || 女 | 158 || 男 | 176 || 女 | 167 || 男 | 187 || 女 | 149 || 男 | 159 || 女 | 151 || ... | ... |要检验两性之间身高是否存在显著差异，使用 R 语言可以使用 t 检验：为什么需要r语言t检验例题1. 检验某种假设是否成立。

2. 批判性和客观地评估数据。

3. 确定总体参数是否有效。

怎么进一步推进完成r语言t检验例题一、针对性地掌握t检验的相关基础知识，如t统计量、特征参数、抽样分布、假设检验、显著性水平等。

二、通过阅读和实践，学习r语言中t检验的应用，如如何使用t检验方法检验两组样本的均值是否不同、如何使用t检验方法检验单样本的均值和总体均值是否不同等。

三、练习针对t检验的实际例题，根据所提供的数据计算t统计量、计算抽样分布的参数、进行假设检验等。

四、解决t检验实际例题时，可以多使用r语言编程过程，包括数据准备、t检验分析和结果展示。

五、总结学习经验，查阅有关文献，不断学习t检验的先进理论和实践技能，充分发挥R语言在t检验中的优势。

R语言聚类分析、因子分析、t检验程序

R语言聚类分析、因子分析、t检验相关程序及程序运行结果相关程序：#####读入数据x=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1)####作系统聚类d=dist(scale(x))hc1=hclust(d);hc1hc2=hclust(d,"average")hc3=hclust(d,"centroid")hc4=hclust(d,"ward")####绘出谱系图和聚类情况（最长距离法、类平均法）opar=par(mfrow=c(2,1),mar=c(5.2,4,0,0))plclust(hc1,hang=-1)re1=rect.hclust(hc1,k=3,border="red")plclust(hc2,hang=-1)re2=rect.hclust(hc2,k=3,border="red")par(opar)####绘出谱系图和聚类情况（重心法和Ward法）opar<-par(mfrow=c(2,1),mar=c(5.2,4,0,0))plclust(hc3,hang=-1)re3=rect.hclust(hc3,k=3,border="red")plclust(hc4,hang=-1)re4=rect.hclust(hc4,k=3,border="red")par(opar)####动态聚类法km<-kmeans(scale(x),3,nstart=35);kmsort(km$cluster)####因子分析y=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1)R=cov(scale(y))fa<-factanal(factors=4,covmat=R);fa####计算因子得分y=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1)fa<-factanal(~.,factors=4,data=y,scores="Bartlett");fafa$scores ####输出因子得分####画出散点图plot(fa$scores[,1:2],type="n")text(fa$scores[,1],fa$scores[,2])plot(fa$scores[,3:4],type="n")text(fa$scores[,3],fa$scores[,4])####t检验a1=fa$scores[,1]a2=fa$scores[,2]a3=fa$scores[,3]a4=fa$scores[,4]t.test(a1,a2,alternative="greater")t.test(a1,a3,alternative="greater")t.test(a1,a4,alternative="greater")t.test(a2,a3,alternative="greater")t.test(a2,a4,alternative="greater")t.test(a3,a4,alternative="greater")程序运行结果：> rm(list=ls(all=TRUE))> #####读入数据> x=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1) > ####作系统聚类> d=dist(scale(x))> hc1=hclust(d);hc1Call:hclust(d = d)Cluster method : completeDistance : euclideanNumber of objects: 35> hc2=hclust(d,"average")> hc3=hclust(d,"centroid")> hc4=hclust(d,"ward")> ####绘出谱系图和聚类情况（最长距离法、类平均法）> opar=par(mfrow=c(2,1),mar=c(5.2,4,0,0))> plclust(hc1,hang=-1)> re1=rect.hclust(hc1,k=3,border="red")> plclust(hc2,hang=-1)> re2=rect.hclust(hc2,k=3,border="red")> par(opar)> ####绘出谱系图和聚类情况（重心法和Ward法）> opar<-par(mfrow=c(2,1),mar=c(5.2,4,0,0))> plclust(hc3,hang=-1)> re3=rect.hclust(hc3,k=3,border="red")> plclust(hc4,hang=-1)> re4=rect.hclust(hc4,k=3,border="red")> par(opar)> ####动态聚类法> km<-kmeans(scale(x),3,nstart=35);kmK-means clustering with 3 clusters of sizes 21, 6, 8Cluster means:工业生产总值.亿元. 财政收入.万元. 人均财政收入社会消费品零售总额.万元.1 -0.6065578 -0.6358116 -0.492914324 -0.387692232 0.7021330 0.9565806 1.730190783 0.061577083 1.0656146 0.9515700 -0.003742987 0.97150928外贸出口额外资利用总额.万美元. 新增固定资产投资.万元. 职工平均工资.元.1 -0.4402834 -0.6033739 -0.5009169 -0.59498172 0.4309513 1.4647875 0.8770164 1.47480543 0.8325306 0.4852659 0.6571445 0.4557230农民人均纯收入.元. 城镇固定资产投资人均固定资产投资万人拥有工业企业数量1 -0.5985518 -0.6641800 -0.50088606 -0.40066112 1.3534617 1.1106089 1.78476822 1.57153573 0.5561021 0.9105157 -0.02375026 -0.1269165 人均科教文卫.事业费支出1 -0.218176242 0.809047653 -0.03407311Clustering vector:长丰县肥东县肥西县天长市明光市来安县全椒县定远县3 3 3 3 1 1 1 1凤阳县当涂县庐江县无为县含山县和县芜湖县繁昌县1 2 1 3 1 3 2 2南陵县宁国市郎溪县广德县泾县绩溪县旌德县铜陵县3 2 1 2 1 1 1 2东至县石台县青阳县桐城市怀宁县枞阳县潜山县太湖县1 1 1 3 1 1 1 1宿松县望江县岳西县1 1 1Within cluster sum of squares by cluster:[1] 91.95071 40.32272 74.39793(between_SS / total_SS = 53.2 %)Available components:[1] "cluster" "centers" "totss" "withinss"[5] "tot.withinss" "betweenss" "size"> sort(km$cluster)明光市来安县全椒县定远县凤阳县庐江县含山县郎溪县1 1 1 1 1 1 1 1泾县绩溪县旌德县东至县石台县青阳县怀宁县枞阳县1 1 1 1 1 1 1 1潜山县太湖县宿松县望江县岳西县当涂县芜湖县繁昌县1 1 1 1 12 2 2宁国市广德县铜陵县长丰县肥东县肥西县天长市无为县2 2 23 3 3 3 3和县南陵县桐城市3 3 3>> ####因子分析> y=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1)> R=cov(scale(y))> fa<-factanal(factors=4,covmat=R);faCall:factanal(factors = 4, covmat = R)Uniquenesses:工业生产总值.亿元. 财政收入.万元. 人均财政收入0.131 0.005 0.017 社会消费品零售总额.万元. 外贸出口额外资利用总额.万美元.0.135 0.757 0.466 新增固定资产投资.万元. 职工平均工资.元. 农民人均纯收入.元.0.278 0.249 0.228城镇固定资产投资人均固定资产投资万人拥有工业企业数量0.005 0.014 0.213 人均科教文卫.事业费支出0.518Loadings:Factor1 Factor2 Factor3 Factor4工业生产总值.亿元. 0.164 0.863 0.306财政收入.万元. 0.270 0.904 0.252 0.204人均财政收入0.911 0.257 0.236 0.177社会消费品零售总额.万元. -0.334 0.662 0.529 0.188外贸出口额0.144 0.255 0.396外资利用总额.万美元. 0.418 0.441 0.405新增固定资产投资.万元. 0.171 0.485 0.675职工平均工资.元. 0.669 0.446 0.322农民人均纯收入.元. 0.528 0.453 0.501 0.192城镇固定资产投资0.304 0.893 0.293 -0.142人均固定资产投资0.888 0.272 0.263 -0.231万人拥有工业企业数量0.838 0.271人均科教文卫.事业费支出0.659 -0.197Factor1 Factor2 Factor3 Factor4SS loadings 4.009 3.838 1.891 0.247Proportion Var 0.308 0.295 0.145 0.019Cumulative Var 0.308 0.604 0.749 0.768The degrees of freedom for the model is 32 and the fit was 1.9244>> ####计算因子得分> y=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1)> fa<-factanal(~.,factors=4,data=y,scores="Bartlett");faCall:factanal(x = ~., factors = 4, data = y, scores = "Bartlett")Uniquenesses:工业生产总值.亿元. 财政收入.万元. 人均财政收入0.131 0.005 0.017 社会消费品零售总额.万元. 外贸出口额外资利用总额.万美元.0.135 0.757 0.466 新增固定资产投资.万元. 职工平均工资.元. 农民人均纯收入.元.0.278 0.249 0.228城镇固定资产投资人均固定资产投资万人拥有工业企业数量0.005 0.014 0.213 人均科教文卫.事业费支出0.518Loadings:Factor1 Factor2 Factor3 Factor4工业生产总值.亿元. 0.164 0.863 0.306财政收入.万元. 0.270 0.904 0.252 0.204人均财政收入0.911 0.257 0.236 0.177社会消费品零售总额.万元. -0.334 0.662 0.529 0.188外贸出口额0.144 0.255 0.396外资利用总额.万美元. 0.418 0.441 0.405新增固定资产投资.万元. 0.171 0.485 0.675职工平均工资.元. 0.669 0.446 0.322农民人均纯收入.元. 0.528 0.453 0.501 0.192城镇固定资产投资0.304 0.893 0.293 -0.142人均固定资产投资0.888 0.272 0.263 -0.231万人拥有工业企业数量0.838 0.271人均科教文卫.事业费支出0.659 -0.197Factor1 Factor2 Factor3 Factor4SS loadings 4.009 3.838 1.891 0.247Proportion Var 0.308 0.295 0.145 0.019Cumulative Var 0.308 0.604 0.749 0.768Test of the hypothesis that 4 factors are sufficient.The chi square statistic is 50.36 on 32 degrees of freedom.The p-value is 0.0206> fa$scores ####输出因子得分Factor1 Factor2 Factor3 Factor4 长丰县-0.183962645 1.07142140 -0.80273922 -0.55908770 肥东县-0.178091207 2.78806120 -1.86999699 0.68363597 肥西县0.348674595 3.12457544 -1.98272073 -0.50108034 天长市-0.328662939 0.11159589 1.52736647 0.46407338 明光市-0.963771018 -0.86354966 0.47002776 0.81176717 来安县-0.396419372 -0.49065354 0.31428314 -0.67509321 全椒县-0.127042257 -0.41988953 0.37755024 -0.37704456 定远县-1.024098347 -0.26034805 -0.17002711 -0.38265932凤阳县-0.688874840 -0.11971576 -0.14932367 0.36608860 当涂县0.703717153 1.67027029 0.79034965 0.31755372 庐江县-1.347580892 -0.10296382 1.40239214 0.73197698 无为县-1.808834990 1.38504818 2.96739685 -0.89328453 含山县-0.097182092 -0.62906939 -0.01725782 0.69586421 和县-0.633409518 -0.22667039 1.11273582 -0.23828640 芜湖县 1.465823581 0.20925937 0.70918377 -0.98730471 繁昌县 2.663194026 -0.03934722 -0.09699698 1.76758867 南陵县-0.121028895 -0.24059956 1.31746506 1.09467594 宁国市 2.176051304 0.26146591 2.18212596 0.98305592 郎溪县0.322546258 -0.51458155 -0.18277513 -2.09016770广德县0.458900888 0.38443902 1.34637112 -1.52375887 泾县0.066399254 -0.78667484 0.12591414 -0.17464409 绩溪县 1.630369791 -1.37642108 0.12958686 -1.09105223 旌德县0.015581604 -1.38966324 -0.22472503 -0.02326432铜陵县 2.352685506 0.08194171 -0.90854462 -1.71218909 东至县-0.420839170 -0.45254138 -0.45157759 0.05270322 石台县0.004431299 -1.12401413 -1.86938404 0.42232027 青阳县0.395060735 -0.98715620 -0.51665248 2.04123624 桐城市-0.359873784 0.44887271 0.56934952 0.74475186 怀宁县-0.022961863 0.38101100 -0.97991722 2.45423594 枞阳县-0.666759401 0.68399096 -1.01032266 -0.08880833 潜山县-0.659551399 -0.59777412 -0.59583407 0.51402884 太湖县-0.654810156 -0.58593199 -0.98967268 -0.43277938宿松县-0.920198188 -0.28228760 -0.27058925 -0.98831067 望江县-0.825113048 -0.70444337 -0.56674157 -0.10014261 岳西县-0.174369973 -0.40765667 -1.68629963 -1.30659888 > ####画出散点图> plot(fa$scores[,1:2],type="n")> text(fa$scores[,1],fa$scores[,2])> plot(fa$scores[,3:4],type="n")> text(fa$scores[,3],fa$scores[,4])>> ####t检验> a1=fa$scores[,1]> a2=fa$scores[,2]> a3=fa$scores[,3]> a4=fa$scores[,4]> t.test(a1,a2,alternative="greater")> t.test(a11,b11,alternative="greater")Welch Two Sample t-testdata: a11 and b11t = 1.9772, df = 9.704, p-value = 0.03855alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:0.06604808 Infsample estimates:mean of x mean of y0.9958313 0.1749454> t.test(a11,c11,alternative="greater")Welch Two Sample t-testdata: a11 and c11t = 4.3788, df = 9.086, p-value = 0.0008671alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:1.039104 Infsample estimates:mean of x mean of y0.9958313 -0.7901305> t.test(b11,c11,alternative="greater")Welch Two Sample t-testdata: b11 and c11t = 5.8762, df = 21.925, p-value = 3.299e-06alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:0.6830173 Infsample estimates:mean of x mean of y0.1749454 -0.7901305> t.test(a12,b12,alternative="greater")Welch Two Sample t-testdata: a12 and b12t = 2.994, df = 10.814, p-value = 0.006212alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:0.5557607 Infsample estimates:mean of x mean of y0.9931852 -0.3988946> t.test(a12,c12,alternative="greater")Welch Two Sample t-testdata: a12 and c12t = 2.5917, df = 10.145, p-value = 0.01329alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:0.356743 Infsample estimates:mean of x mean of y0.9931852 -0.1893416> t.test(b12,c12,alternative="greater")Welch Two Sample t-testdata: b12 and c12t = -0.8809, df = 22.84, p-value = 0.8062alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:-0.6173701 Inf sample estimates:mean of x mean of y -0.3988946 -0.1893416。

r语言中t检验置信区间

r语言中t检验置信区间t检验是一种常用的统计方法，用于比较两个样本均值之间是否存在显著差异。

而置信区间则是用来估计总体参数的范围。

本文将介绍如何使用R语言进行t检验，并计算出置信区间。

我们需要明确t检验的原假设和备择假设。

原假设（H0）通常是指两个样本均值之间没有显著差异，而备择假设（H1）则是指两个样本均值之间存在显著差异。

在进行t检验前，我们需要确保样本数据满足一些基本假设，如样本数据应当近似正态分布并且两个样本是独立的。

假设我们有两组样本数据，分别为样本1和样本2。

我们可以使用R 语言中的t.test函数来进行t检验。

假设我们的样本1数据存储在变量x中，样本2数据存储在变量y中，我们可以使用以下代码进行t检验：```# 进行独立样本t检验result <- t.test(x, y)# 输出检验结果print(result)```在上述代码中，我们使用了t.test函数对样本1和样本2进行了独立样本t检验，并将结果存储在result变量中。

然后，我们使用print函数输出检验结果。

t.test函数输出的结果包括了t统计量、自由度、p值以及置信区间。

其中，p值用于判断两个样本均值是否存在显著差异，而置信区间则用于估计总体均值的范围。

在进行t检验时，我们可以通过设置conf.level参数来指定置信水平。

例如，如果我们想要使用95%的置信水平，可以将conf.level 参数设置为0.95。

默认情况下，R语言中的t.test函数使用95%的置信水平。

除了独立样本t检验，R语言还提供了配对样本t检验的函数。

配对样本t检验用于比较同一组样本在不同条件下的均值差异。

使用配对样本t检验的方法与独立样本t检验类似，只是需要将样本数据作为一个矩阵输入。

除了输出整体的检验结果，我们还可以提取出置信区间的上限和下限。

例如，如果我们想要提取置信区间的上限，可以使用以下代码：```# 提取置信区间的上限upper <- result$conf.int[2]# 输出置信区间的上限print(upper)```在上述代码中，我们使用了result$conf.int[2]来提取出置信区间的上限，并将结果存储在变量upper中。

R语言聚类分析、因子分析、t检验程序

R语言聚类分析、因子分析、t检验相关程序及程序运行结果相关程序: #####读入数据x=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1####作系统聚类d=dist(scale(xhc1=hclust(d;hc1hc2=hclust(d,"average"hc3=hclust(d,"centroid"hc4=hclust(d,"ward"####绘出谱系图和聚类情况(最长距离法、类平均法opar=par(mfrow=c(2,1,mar=c(5.2,4,0,0plclust(hc1,hang=-1re1=rect.hclust(hc1,k=3,border="red"plclust(hc2,hang=-1re2=rect.hclust(hc2,k=3,border="red"par(opar####绘出谱系图和聚类情况(重心法和Ward法opar<-par(mfrow=c(2,1,mar=c(5.2,4,0,0plclust(hc3,hang=-1re3=rect.hclust(hc3,k=3,border="red"plclust(hc4,hang=-1re4=rect.hclust(hc4,k=3,border="red"par(opar####动态聚类法km<-kmeans(scale(x,3,nstart=35;kmsort(km$cluster####因子分析y=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1 R=cov(scale(yfa<-factanal(factors=4,covmat=R;fa####计算因子得分y=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1 fa<-factanal(~.,factors=4,data=y,scores="Bartlett";fafa$scores ####输出因子得分####画出散点图plot(fa$scores[,1:2],type="n"text(fa$scores[,1],fa$scores[,2]plot(fa$scores[,3:4],type="n"text(fa$scores[,3],fa$scores[,4]####t检验a1=fa$scores[,1]a2=fa$scores[,2]a3=fa$scores[,3]a4=fa$scores[,4]t.test(a1,a2,alternative="greater"t.test(a1,a3,alternative="greater"t.test(a1,a4,alternative="greater"t.test(a2,a3,alternative="greater"t.test(a2,a4,alternative="greater"t.test(a3,a4,alternative="greater"程序运行结果:> rm(list=ls(all=TRUE> #####读入数据> x=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1 > ####作系统聚类> d=dist(scale(x> hc1=hclust(d;hc1Call:hclust(d = dCluster method : completeDistance : euclideanNumber of objects: 35> hc2=hclust(d,"average"> hc3=hclust(d,"centroid"> hc4=hclust(d,"ward"> ####绘出谱系图和聚类情况(最长距离法、类平均法> opar=par(mfrow=c(2,1,mar=c(5.2,4,0,0> plclust(hc1,hang=-1> re1=rect.hclust(hc1,k=3,border="red"> plclust(hc2,hang=-1> re2=rect.hclust(hc2,k=3,border="red"> par(opar> ####绘出谱系图和聚类情况(重心法和Ward法> opar<-par(mfrow=c(2,1,mar=c(5.2,4,0,0> plclust(hc3,hang=-1> re3=rect.hclust(hc3,k=3,border="red"> plclust(hc4,hang=-1> re4=rect.hclust(hc4,k=3,border="red"> par(opar> ####动态聚类法> km<-kmeans(scale(x,3,nstart=35;kmK-means clustering with 3 clusters of sizes 21, 6, 8Cluster means:工业生产总值.亿元. 财政收入.万元. 人均财政收入社会消费品零售总额.万元.1 -0.6065578 -0.6358116 -0.492914324 -0.387692232 0.7021330 0.9565806 1.730190783 0.061577083 1.0656146 0.9515700 -0.003742987 0.97150928外贸出口额外资利用总额.万美元. 新增固定资产投资.万元. 职工平均工资.元.1 -0.4402834 -0.6033739 -0.5009169 -0.59498172 0.4309513 1.4647875 0.8770164 1.47480543 0.8325306 0.4852659 0.6571445 0.4557230农民人均纯收入.元. 城镇固定资产投资人均固定资产投资万人拥有工业企业数量1 -0.5985518 -0.6641800 -0.50088606 -0.40066112 1.3534617 1.1106089 1.78476822 1.57153573 0.5561021 0.9105157 -0.02375026 -0.1269165 人均科教文卫.事业费支出1 -0.218176242 0.809047653 -0.03407311Clustering vector:长丰县肥东县肥西县天长市明光市来安县全椒县定远县3 3 3 3 1 1 1 1凤阳县当涂县庐江县无为县含山县和县芜湖县繁昌县1 2 1 3 1 3 2 2南陵县宁国市郎溪县广德县泾县绩溪县旌德县铜陵县3 2 1 2 1 1 1 2东至县石台县青阳县桐城市怀宁县枞阳县潜山县太湖县1 1 1 3 1 1 1 1宿松县望江县岳西县1 1 1Within cluster sum of squares by cluster:[1] 91.95071 40.32272 74.39793(between_SS / total_SS = 53.2 %Available components:[1] "cluster" "centers" "totss" "withinss"[5] "tot.withinss" "betweenss" "size"> sort(km$cluster明光市来安县全椒县定远县凤阳县庐江县含山县郎溪县1 1 1 1 1 1 1 1泾县绩溪县旌德县东至县石台县青阳县怀宁县枞阳县1 1 1 1 1 1 1 1潜山县太湖县宿松县望江县岳西县当涂县芜湖县繁昌县1 1 1 1 12 2 2宁国市广德县铜陵县长丰县肥东县肥西县天长市无为县2 2 23 3 3 3 3和县南陵县桐城市3 3 3>> ####因子分析> y=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1> R=cov(scale(y> fa<-factanal(factors=4,covmat=R;faCall:factanal(factors = 4, covmat = RUniquenesses:工业生产总值.亿元. 财政收入.万元. 人均财政收入0.131 0.005 0.017 社会消费品零售总额.万元. 外贸出口额外资利用总额.万美元.0.135 0.757 0.466 新增固定资产投资.万元. 职工平均工资.元. 农民人均纯收入.元.0.278 0.249 0.228城镇固定资产投资人均固定资产投资万人拥有工业企业数量0.005 0.014 0.213 人均科教文卫.事业费支出0.518Loadings:Factor1 Factor2 Factor3 Factor4工业生产总值.亿元. 0.164 0.863 0.306财政收入.万元. 0.270 0.904 0.252 0.204人均财政收入0.911 0.257 0.236 0.177社会消费品零售总额.万元. -0.334 0.662 0.529 0.188外贸出口额0.144 0.255 0.396外资利用总额.万美元. 0.418 0.441 0.405新增固定资产投资.万元. 0.171 0.485 0.675职工平均工资.元. 0.669 0.446 0.322农民人均纯收入.元. 0.528 0.453 0.501 0.192城镇固定资产投资0.304 0.893 0.293 -0.142人均固定资产投资0.888 0.272 0.263 -0.231万人拥有工业企业数量0.838 0.271人均科教文卫.事业费支出0.659 -0.197Factor1 Factor2 Factor3 Factor4SS loadings 4.009 3.838 1.891 0.247Proportion Var 0.308 0.295 0.145 0.019Cumulative Var 0.308 0.604 0.749 0.768The degrees of freedom for the model is 32 and the fit was 1.9244 >> ####计算因子得分> y=read.delim("G:\\上机考试数据.txt",header=TRUE,s=1> fa<-factanal(~.,factors=4,data=y,scores="Bartlett";faCall:factanal(x = ~., factors = 4, data = y, scores = "Bartlett"Uniquenesses:工业生产总值.亿元. 财政收入.万元. 人均财政收入0.131 0.005 0.017 社会消费品零售总额.万元. 外贸出口额外资利用总额.万美元.0.135 0.757 0.466 新增固定资产投资.万元. 职工平均工资.元. 农民人均纯收入.元.0.278 0.249 0.228城镇固定资产投资人均固定资产投资万人拥有工业企业数量0.005 0.014 0.213 人均科教文卫.事业费支出0.518Loadings:Factor1 Factor2 Factor3 Factor4工业生产总值.亿元. 0.164 0.863 0.306财政收入.万元. 0.270 0.904 0.252 0.204人均财政收入0.911 0.257 0.236 0.177社会消费品零售总额.万元. -0.334 0.662 0.529 0.188外贸出口额0.144 0.255 0.396外资利用总额.万美元. 0.418 0.441 0.405新增固定资产投资.万元. 0.171 0.485 0.675职工平均工资.元. 0.669 0.446 0.322农民人均纯收入.元. 0.528 0.453 0.501 0.192城镇固定资产投资0.304 0.893 0.293 -0.142人均固定资产投资0.888 0.272 0.263 -0.231万人拥有工业企业数量0.838 0.271人均科教文卫.事业费支出 0.659 -0.197 Factor1 Factor2 Factor3 Factor4 SS loadings 4.009 3.838 Proportion Var 0.308 0.295 Cumulative Var 0.308 0.604 1.8910.145 0.749 0.247 0.019 0.768 Test of the hypothesis that 4 factors are sufficient. The chi square statistic is 50.36 on 32 degrees of freedom. The p-value is 0.0206 > fa$scores####输出因子得分 Factor1 Factor2 Factor3 Factor4 长丰县 -0.183962645 1.07142140 -0.80273922 -0.55908770 肥东县 -0.178091207 2.78806120 -1.86999699 0.68363597 肥西县 0.348674595 3.12457544 -1.98272073 -0.50108034 天长市 -0.3286629390.11159589 1.52736647 0.46407338 明光市 -0.963771018 -0.86354966 0.47002776 0.81176717 来安县 -0.396419372 -0.49065354 0.31428314 -0.67509321 全椒县 -0.127042257 -0.41988953 0.37755024 -0.37704456 定远县 -1.024098347 -0.26034805 -0.17002711 -0.38265932 凤阳县 -0.688874840 -0.11971576 -0.14932367 0.36608860 当涂县 0.703717153 1.67027029 0.79034965 0.31755372 庐江县 -1.347580892 -0.10296382 1.40239214 0.73197698 无为县 -1.808834990 1.38504818 2.96739685 -0.89328453 含山县 -0.097182092 -0.62906939 -0.01725782 0.69586421 和县 -0.633409518 -0.22667039 1.11273582 -0.23828640 芜湖县 1.465823581 0.20925937 0.70918377 -0.98730471 繁昌县 2.663194026 -0.03934722 -0.09699698 1.76758867 南陵县 -0.121028895 -0.24059956 1.31746506 1.09467594 宁国市 2.1760513040.26146591 2.18212596 0.98305592 郎溪县 0.322546258 -0.51458155 -0.18277513 -2.09016770 广德县 0.458900888 0.38443902 1.34637112 -1.52375887 泾县0.066399254 -0.78667484 0.12591414 -0.17464409 绩溪县 1.630369791 -1.37642108 0.12958686 -1.09105223 旌德县 0.015581604 -1.38966324 -0.22472503 -0.02326432 铜陵县 2.352685506 0.08194171 -0.90854462 -1.71218909 东至县 -0.420839170 -0.45254138 -0.45157759 0.05270322 石台县 0.004431299 -1.12401413 -1.86938404 0.42232027 青阳县 0.395060735 -0.98715620 -0.51665248 2.04123624 桐城市 -0.359873784 0.44887271 0.56934952 0.74475186 怀宁县 -0.022961863 0.38101100 -0.97991722 2.45423594 枞阳县 -0.666759401 0.68399096 -1.01032266 -0.08880833 潜山县 -0.659551399 -0.59777412 -0.59583407 0.51402884 太湖县 -0.654810156 -0.58593199 -0.98967268 -0.43277938宿松县 -0.920198188 -0.28228760 -0.27058925 -0.98831067 望江县 -0.825113048 -0.70444337 -0.56674157 -0.10014261 岳西县 -0.174369973 -0.40765667 -1.68629963 -1.30659888 > ####画出散点图 > plot(fa$scores[,1:2],type="n" >text(fa$scores[,1],fa$scores[,2] > plot(fa$scores[,3:4],type="n" >text(fa$scores[,3],fa$scores[,4] > > ####t 检验 > a1=fa$scores[,1] > a2=fa$scores[,2] > a3=fa$scores[,3] > a4=fa$scores[,4] > t.test(a1,a2,alternative="greater" >t.test(a11,b11,alternative="greater" Welch Two Sample t-test data: a11 and b11 t =1.9772, df = 9.704, p-value = 0.03855 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval: 0.06604808 Inf sample estimates: mean of x mean of y 0.9958313 0.1749454 > t.test(a11,c11,alternative="greater" Welch Two Sample t-test data: a11 and c11 t = 4.3788, df = 9.086, p-value = 0.0008671 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:1.039104 Inf sample estimates: mean of x mean of y 0.9958313 -0.7901305 >t.test(b11,c11,alternative="greater" Welch Two Sample t-testdata: b11 and c11 t = 5.8762, df = 21.925, p-value = 3.299e-06 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:0.6830173 Inf sample estimates: mean of x mean of y 0.1749454 -0.7901305 >t.test(a12,b12,alternative="greater" Welch Two Sample t-test data: a12 and b12 t = 2.994, df = 10.814, p-value = 0.006212 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval: 0.5557607 Inf sample estimates: mean of x mean of y 0.9931852 -0.3988946 > t.test(a12,c12,alternative="greater" Welch Two Sample t-test data: a12 and c12 t = 2.5917, df = 10.145, p-value = 0.01329 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:0.356743 Inf sample estimates: mean of x mean of y 0.9931852 -0.1893416 >t.test(b12,c12,alternative="greater" Welch Two Sample t-test data: b12 and c12 t = -0.8809, df = 22.84, p-value = 0.8062 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval:-0.6173701 Inf sample estimates: mean of x mean of y -0.3988946 -0.1893416。

R语言各种假设检验实例整理（常用）

现测得16只元件的寿命如下：159 280 101 212 224 379 179 264222 362 168 250 149 260 485 170问是否有理由认为元件的平均寿命⼤于255⼩时？解：按题意，需检验H0： µ ≤ 225H1: µ >225此问题属于单边检验问题可以使⽤R语⾔t.testt.test(x,y=NULL,alternative=c("two.sided","less","greater"),mu=0,paired=FALSE,var.equal=FALSE,conf.level=0.95)其中x,y是⼜数据构成e向量，（如果只提供x,则作单个正态总体的均值检验，如果提供x,y则作两个总体的均值检验)，alternative表⽰被则假设，two.sided(缺省)，双边检验(H1:µ≠H0),less表⽰单边检验(H1:µ<µ0),greater表⽰单边检验(H1:µ>µ0)，mu表⽰原假设µ0，conf.level置信⽔平，即1-α，通常是0.95，var.equal是逻辑变量，var.equal=TRUE表⽰两样品⽅差相同，var.equal=FALSE（缺省）表⽰两样本⽅差不同。

R代码：X<-c(159, 280, 101, 212, 224, 379, 179, 264,222, 362, 168, 250, 149, 260, 485, 170)t.test(X,alternative = "greater",mu=225)结果：可见P值为0.257 > 0.05 ，不能拒绝原假设，接受H0，即平均寿命不⼤于225⼩时。

r语言 t函数

r语言 t函数R语言是一种广泛使用的统计分析软件，它具有强大的数据分析和可视化功能。

在R语言中，t函数是一个非常重要的函数，它可以用来计算样本均值的置信区间和假设检验。

t函数的语法如下：t.test(x, y = NULL, alternative = c("two.sided", "less", "greater"), mu = 0, paired = FALSE, var.equal = FALSE, conf.level = 0.95)其中，x是一个数值向量，表示样本数据；y是一个可选的数值向量，表示第二组样本数据；alternative表示备择假设，可以是双侧检验（"two.sided"）、左侧检验（"less"）或右侧检验（"greater"）；mu表示假设的总体均值；paired表示是否进行配对样本检验；var.equal表示是否假设两个总体方差相等；conf.level表示置信水平。

t函数的返回值是一个列表，包含了假设检验的结果和置信区间的计算结果。

其中，p.value表示假设检验的p值，如果p值小于显著性水平（通常为0.05），则拒绝原假设；conf.int表示置信区间的计算结果，包括置信水平和置信区间的上下限。

下面是一个例子，演示如何使用t函数进行假设检验和置信区间计算：```{r}# 生成两组样本数据x <- c(1.2, 2.3, 3.4, 4.5, 5.6)y <- c(1.5, 2.6, 3.7, 4.8, 5.9)# 双侧检验，假设总体均值为0t.test(x, y, alternative = "two.sided", mu = 0)# 输出结果：## Welch Two Sample t-test## data: x and y# t = -0.19803, df = 7.998, p-value = 0.8473# alternative hypothesis: true difference in means is not equal to 0# 95 percent confidence interval:# -1.242926 1.042926# sample estimates:# mean of x mean of y# 3.4 3.5# 左侧检验，假设总体均值为3t.test(x, y, alternative = "less", mu = 3)# 输出结果：## Welch Two Sample t-test## data: x and y# t = -1.198, df = 7.998, p-value = 0.1383# alternative hypothesis: true difference in means is less than 3 # 95 percent confidence interval:# -Inf 1.104852# sample estimates:# mean of x mean of y# 3.4 3.5# 右侧检验，假设总体均值为4t.test(x, y, alternative = "greater", mu = 4)# 输出结果：## Welch Two Sample t-test# data: x and y# t = -2.197, df = 7.998, p-value = 0.03186# alternative hypothesis: true difference in means is greater than 4# 95 percent confidence interval:# -Inf 0.005074# sample estimates:# mean of x mean of y# 3.4 3.5```从上面的例子可以看出，t函数可以方便地进行假设检验和置信区间计算。

t检验例题解析

t检验例题解析摘要：1.引言2.t检验的原理和方法3.例题解析4.结论与启示正文：**引言**在统计分析中，t检验是一种常用的方法，用于检验两组数据之间是否存在显著差异。

t检验的原理和步骤相对简单，但其在实际应用中的正确性和实用性却非常重要。

本文将通过例题解析的方式，帮助你更好地理解和掌握t检验的方法和技巧。

**t检验的原理和方法**t检验主要包括两种类型：独立样本t检验（比较两组独立样本）和配对样本t检验（比较同一组样本的两个时间点）。

其基本步骤如下：1.建立原假设：H0表示两组样本的均值相等，H1表示存在显著差异。

2.收集数据并计算统计量：如平均值、标准差等。

3.计算t值：t = （样本均值差- 总体均值差）/ 标准误差。

4.计算p值：根据t值和自由度（df）查找t分布表，得到p值。

5.判断结论：如果p值小于显著性水平（通常为0.05），则拒绝原假设，认为存在显著差异。

**例题解析**例题1：比较两组独立样本的均值差异。

数据如下：样本1：均值= 50，标准差= 10样本2：均值= 55，标准差= 10假设检验：H0：μ1 = μ2，H1：μ1 ≠ μ2计算过程：1.计算t值：t = (50 - 55) / sqrt((10^2 + 10^2) / 2) = -2.52.计算p值：p = 2 * (1 - (1 - 0.025) / 2) = 0.0253.结论：p值小于0.05，拒绝原假设，认为两组样本存在显著差异。

例题2：比较同一组样本的两个时间点的均值差异。

数据如下：时间1：均值= 50，标准差= 10时间2：均值= 55，标准差= 10假设检验：H0：μ1 = μ2，H1：μ1 ≠ μ2计算过程：1.计算t值：t = (50 - 55) / sqrt((10^2 + 10^2) / 2) = -2.52.计算p值：p = 2 * (1 - (1 - 0.025) / 2) = 0.0253.结论：p值小于0.05，拒绝原假设，认为同一组样本的两个时间点存在显著差异。

t检验例题

t检验例题假设我们有两组数据，分别是A组和B组。

我们想要检验A组和B组的平均值是否有显著差异。

以下是一个t检验的例题：假设A组是一组人的体重数据，B组是另一组人的体重数据。

我们想要检验A组和B组的平均体重是否有显著差异。

A组的体重数据：[60, 65, 70, 75, 80]B组的体重数据：[55, 60, 65, 70, 75]首先，我们需要计算出每组数据的平均值和标准差。

A组的平均值：(60 + 65 + 70 + 75 + 80) / 5 = 70B组的平均值：(55 + 60 + 65 + 70 + 75) / 5 = 65A组的标准差：sqrt(((60-70)^2 + (65-70)^2 + (70-70)^2 + (75-70)^2 + (80-70)^2) / 4) = sqrt(250) ≈ 15.81B组的标准差：sqrt(((55-65)^2 + (60-65)^2 + (65-65)^2 + (70-65)^2 + (75-65)^2) / 4) = sqrt(62.5) ≈ 7.91然后，我们可以使用t检验来确定这两组数据的平均值是否有显著差异。

t值的计算公式为：t = (A组的平均值 - B组的平均值) / sqrt((A组的标准差^2/ A组的样本数) + (B组的标准差^2/ B组的样本数))t值 = (70 - 65) / sqrt((15.81^2 / 5) + (7.91^2 / 5)) ≈ 0.71最后，我们需要查找t分布表，确定给定的t值对应的p值。

假设显著性水平为0.05，自由度为8（A组样本数 - 1 + B组样本数 - 1 = 4 + 4 = 8）。

查表得到，当自由度为8时，t分布的临界值为±2.306。

因为0.71 < 2.306，所以我们无法拒绝原假设，即A组和B组的平均体重没有显著差异。

这就是一个t检验的例题。

通过计算t值并查找t分布表中的临界值，我们可以得出结论是否拒绝原假设。

r语言t检验相关检验案例代码

confidence=read.table("data1.txt")# （1 将上述数据输入r，保存为数据框格式，数据框名为confidence，编号对应变量名为id，方法1 对应method1，方法二method2.写输出数据代码#confidence=as.data.frame(confidence)colnames(confidence)=c("id", "method1" ,"method2")# 2）请求两种测评方法之间的均值差的95%置信区间，并据此判断两种方法的是否有显著差异。

写代码#t.test(confidence$method1,confidence$method2)#### Welch Two Sample t-test#### data: confidence$method1 and confidence$method2## t = 1.7058, df = 17.959, p-value = 0.1053## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval:## -2.550565 24.550565## sample estimates:## mean of x mean of y## 72.6 61.6# 95 percent confidence interval:# -2.550565 24.550565mean(confidence$method1 -confidence$method2)+1.64*sd( confidence$method 1 -confidence$method2 )## [1] 21.71244mean(confidence$method1 -confidence$method2)-1.64*sd( confidence$method 1 -confidence$method2 )## [1] 0.2875649# 3）用t检验判别两种方法得到的结果之间是否存在差异，说明p值在此情景中的具体含义，和2）比较t.test(confidence$method1,confidence$method2)#### Welch Two Sample t-test#### data: confidence$method1 and confidence$method2## t = 1.7058, df = 17.959, p-value = 0.1053## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval:## -2.550565 24.550565## sample estimates:## mean of x mean of y## 72.6 61.6#p值大于0.05，因此结果之间不存在差异# p值是在假两种方法没有差异为真时，得到与样本相同或者更极端的结果的概率。

R语言中的t-test和ANOVA_13965

score mean Z standard deviation
Shrinking drug (non-effect value=64)
Vasishth’s Height Example
大部分情况下我们并不知道σ ——T分布
> pt(-3.02, df = 10) + (1 - pt(3.02, df = 10)) [1] 0.01289546
> n <- length(mpg)
> t.test(mpg,mu=17,alternative="less") > c(xbar, s, n)
[1] 14.870000 1.572012 10.000000 > SE <- s/sqrt(n)
> (xbar - 17)/SE
[1] -4.284732 > pt(-4.285, df = 9, lower.tail = T) [1] 0.001017478
两正态总体参数检验
> x<-c(20.5, 19.8, 19.7, 20.4, 20.1, 20.0, 19.0, 19.9) > y<-c(20.7, 19.8, 19.5, 20.8, 20.4, 19.6, 20.2) > t.test(x, y, var.equal=TRUE) Two Sample t-test data: x and y t = -0.8548, df = 13, p-value = 0.4081 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.7684249 0.3327106 sample estimates: mean of x mean of y 19.92500 20.14286

【原创】R语言自编t检验和z检验函数附代码数据

【原创】R语言自编t检验和z检验函数附代码数据有问题到淘宝找“大数据部落”就可以了R语言自编t检验和z检验函数代码myt.test(1:10 ,alternative="less")#### One Sample t-test#### data: 1:10## t = 5.7446, df = 9, p-value = 0.9999## alternative hypothesis: true mean is less than 0## 95 percent confidence interval:## -Inf 7.255072## sample estimates:## mean of x## 5.5My.z.test(x,sigma.x=1)#### One-sample z-Test#### data: x## z = 0.68502, p-value = 0.4933## alternative hypothesis: true mean is not equal to 0## 95 percent confidence interval:## -0.3680456 0.7635401## sample estimates:## mean of x## 0.1977473myt.test <-function(x, y =NULL, alternative =c("two.sided", "less","greater"), mu =0, paired =FALSE, var.equal =FALSE, conf.level =0.95 ){if( !is.null(y) ) {有问题到淘宝找“大数据部落”就可以了dname <-paste(deparse(substitute(x)),"and",deparse(substitute(y)))if(paired)xok <-yok <-complete.cases(x,y)else {yok <-!is.na(y)xok <-!is.na(x)}y <-y[yok]}else {dname <-deparse(substitute(x))if (paired) stop("'y' is missing for paired test")xok <-!is.na(x)yok <-NULL}x <-x[xok]if (paired) {x <-x-yy <-NULL}nx <-length(x)mx <-mean(x)vx <-var(x)if(is.null(y)) {if(nx <2) stop("not enough 'x' observations")df <-nx-1stderr <-sqrt(vx/nx)if(stderr <10 *.Machine$double.eps *abs(mx))stop("data are essentially constant")tstat <-(mx-mu)/stderrmethod <-if(paired) "Paired t-test" else "One Sample t-test" estimate <-setNames(mx, if(paired)"mean of the differences" else "mean of x") } else {ny <-length(y)if(nx <1 ||(!var.equal &&nx <2))stop("not enough 'x' observations")if(ny <1 ||(!var.equal &&ny <2))stop("not enough 'y' observations")if(var.equal &&nx+ny <3) stop("not enough observations") my <-mean(y)vy <-var(y)method <-paste(if(!var.equal)"Welch", "Two Sample t-test") estimate <-c(mx,my)names(estimate) <-c("mean of x","mean of y")有问题到淘宝找“大数据部落”就可以了if(var.equal) {df <-nx+ny-2v <-0if(nx >1) v <-v +(nx-1)*vxif(ny >1) v <-v +(ny-1)*vyv <-v/dfstderr <-sqrt(v*(1/nx+1/ny))} else {stderrx <-sqrt(vx/nx)stderry <-sqrt(vy/ny)stderr <-sqrt(stderrx^2 +stderry^2)df <-stderr^4/(stderrx^4/(nx-1) +stderry^4/(ny-1))}if(stderr <10 *.Machine$double.eps *max(abs(mx), abs(my))) stop("data are essentially constant")tstat <-(mx -my -mu)/stderr}if (alternative =="less") {pval <-pt(tstat, df)cint <-c(-Inf, tstat +qt(conf.level, df) )}else if (alternative =="greater") {pval <-pt(tstat, df, lower.tail =FALSE)cint <-c(tstat -qt(conf.level, df), Inf)}else {pval <-2 *pt(-abs(tstat), df)alpha <-1 -conf.levelcint <-qt(1 -alpha/2, df)cint <-tstat +c(-cint, cint)}cint <-mu +cint *stderrnames(tstat) <-"t"names(df) <-"df"names(mu) <-if(paired ||!is.null(y)) "difference in means" else "mean" attr(cint,"conf.level") <-conf.levelrval <-list(statistic = tstat, parameter = df, p.value = pval, conf.int = cint, estimate = estimate, null.value = mu,alternative = alternative,method = method, /doc/f53000839.html, = dname)class(rval) <-"htest"return(rval)}myt.test(1:10 ,alternative="less")。

用R进行差异检验之t检验

用R进行差异检验之t检验t检验t检验是用t分布理论来推论差异发生的概率，是通过统计检验分析两个群体差异的方法之一。

t检验分为单样本检验和双样本检验两种。

1.单样本检验其中，单样本t检验是指已知总体平均数、样本数据的均值和标准差，以及样本分布正态。

在R中t检验的函数为t.test其格式为t.test(x, y = NULL,alternative = c('two.sided', 'less', 'greater'),mu = 0, paired = FALSE, var.equal = FALSE,conf.level = 0.95, ...)##其中，x，y为数据名称，alternative为检验方式(单侧还是双侧)，mu为总体平均数，当为配对样本时paired设置为TURE，var.equal为样本方差情况(FALSE为默认情况，即样本方差不相等；TURE为认为样本方差相等)，conf.level为置信区间。

本次以嫉妒研究中的数据进行单因素t检验。

首先，对嫉妒进行简单的描述性统计。

了解其均值、标准差和分布情况。

在这里我们可以看到嫉妒的偏度和峰度都<>，可以认为其分布为正态分布。

下面进行单样本t检验假设嫉妒的总体平均数为2.5，那么其t检验如下：t.test(mydata2$jealou, alternative = 'two.sided', mu = 2.5)其中，t＝－10.421，df＝491，p<>。

表明样本嫉妒水平要显著低于总体平均水平。

2.双样本t检验其零假设为两个正态分布的总体的均值之差为某实数，例如检验二群人的身高之平均是否相等。

但具体而言，只有两个总体的方差是相等的情况下，才称为student t检验；否则，有时被称为Welch t检验。

另外，双样本t检验又可以分为独立双样本t检验和配对样本t检验2.1独立双样本t检验例如，我们需要研究嫉妒的男女性别差异，这种双个独立的样本(男性样本vs女性样本)比较均值的情况就可以说是独立双样本t检验其代码如下：t.test(jealou~gender,mydata2)#其中jealou为变量名称，gender为性别，mydata2为变量所在的数据集其中，t=－2.1264,df=488.02,p=0.03397。

t检验例题以及解析

t检验例题以及解析
当进行 t 检验时，我们通常会比较两组数据的平均值，以确定
它们是否存在显著差异。

下面我将以一个例题为例，然后给出解析。

假设我们对一种新药的疗效进行了测试。

我们有两组患者，一
组接受了新药，另一组接受了安慰剂。

我们想知道新药是否比安慰
剂更有效。

假设我们的零假设是，新药的疗效与安慰剂相同，备择假设是，新药的疗效比安慰剂更好。

我们进行了实验，并记录了两组患者的治疗效果数据。

现在我
们要进行 t 检验来确定这两组数据的平均值是否存在显著差异。

首先，我们计算每组数据的平均值和标准差。

然后，我们使用
t 检验的公式计算 t 值。

接下来，我们查找 t 分布表，确定 t 临
界值。

最后，我们将计算得到的 t 值与 t 临界值进行比较，以确
定是否拒绝零假设。

解析：
假设我们进行 t 检验后得到的 t 值为2.31，而自由度为28（假设样本量为30，因此自由度为30-1=29），在显著性水平为0.05的情况下，t 分布表告诉我们 t 临界值为2.045。

因为我们得到的 t 值大于 t 临界值，所以我们可以拒绝零假设，即可以得出结论，新药的疗效与安慰剂存在显著差异。

除了这种数值计算的方法，我们还可以从 t 检验的原理、假设条件、实际应用等多个角度进行解析。

希望这个例题和解析能够帮助你更好地理解 t 检验的应用和原理。

t检验例题

t检验例题【最新版】目录1. t 检验简介2. t 检验的步骤3. t 检验例题解析正文一、t 检验简介t 检验，又称为 t 分布检验，是一种用于检验两组样本均值差异是否显著的统计方法。

它适用于总体分布未知、样本量较小的情况。

t 检验的基本思想是通过计算样本均值的 t 分布来判断样本均值与总体均值之间是否存在显著差异。

二、t 检验的步骤1.假设设定：H0：两组样本均值相等H1：两组样本均值不相等2.收集数据：收集两组样本的数据，并计算它们的均值。

3.计算 t 值：根据样本均值、标准差和自由度，计算 t 值。

4.查表比较：将计算得到的 t 值与 t 分布表中的临界值进行比较。

5.判断结论：如果 t 值大于临界值，则拒绝原假设，认为两组样本均值存在显著差异；如果 t 值小于临界值，则不能拒绝原假设，认为两组样本均值没有显著差异。

三、t 检验例题解析假设我们有两组样本数据，分别是 A 组：2, 3, 4, 5；B 组：1, 3, 5, 7。

现在我们想要检验这两组样本的均值是否存在显著差异。

1.假设设定：H0：A 组和 B 组的均值相等H1：A 组和 B 组的均值不相等2.收集数据：A 组均值 = (2+3+4+5)/4 =3.5，B 组均值 =(1+3+5+7)/4 = 4。

3.计算 t 值：根据公式 t = (样本均值差 - 总体标准差差) / (标准差 / √n)，我们可以得到 t 值。

其中，总体标准差差 = (标准差 A^2 + 标准差 B^2) / (n-1) = ((2^2+1^2)/3 + (3^2+5^2)/4) / (4-1) = 2.83，标准差 A = 1.41，标准差 B = 2.24，n = 4。

带入公式，得到 t 值约为-1.41。

4.查表比较：根据自由度（n-1 = 3）和显著性水平（一般取 0.05），查找 t 分布表，得到临界值约为 -1.999。

5.判断结论：由于计算得到的 t 值（-1.41）大于临界值（-1.999），我们不能拒绝原假设，认为 A 组和 B 组的均值没有显著差异。

R语言学习系列26-均值的t检验

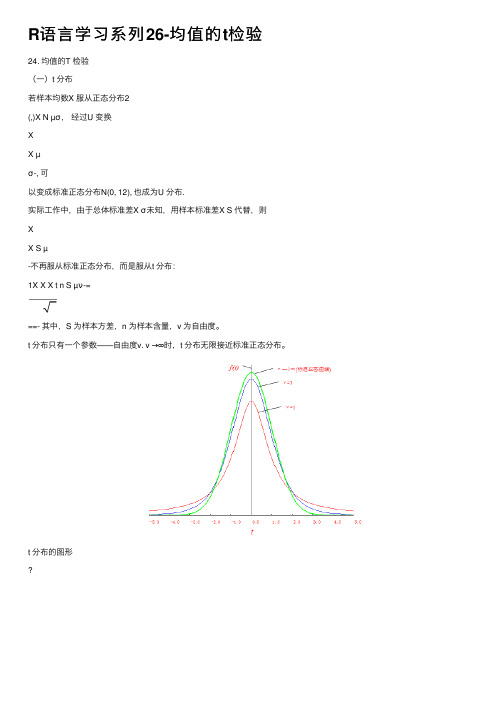
R语⾔学习系列26-均值的t检验24. 均值的T 检验（⼀）t 分布若样本均数X 服从正态分布2(,)X N µσ，经过U 变换XX µσ-, 可以变成标准正态分布N(0, 12), 也成为U 分布.实际⼯作中，由于总体标准差X σ未知，⽤样本标准差X S 代替，则XX S µ-不再服从标准正态分布，⽽是服从t 分布：1X X X t n S µν-===- 其中，S 为样本⽅差，n 为样本含量，v 为⾃由度。

t 分布只有⼀个参数——⾃由度v. v →∞时，t 分布⽆限接近标准正态分布。

t 分布的图形说明：单侧概率（单侧尾部⾯积）⽤,t αν表⽰；双侧概率（双侧尾部⾯积）⽤/2,t αν表⽰；例如，,10=, 则P(t ≤=P(t ≥= 2,10=, 则P(t ≤+P(t ≥=（⼆）t 检验t 检验，是⼀种针对连续变量的参数假设检验，⽤来检验“单样本均值与已知均值（单样本t 检验）、两独⽴样本均值（独⽴样本t 检验）、配对设计资料的均值（配对样本t 检验）”是否存在差异，这种差异是否能推论⾄总体。

T 检验适⽤于样本含量较⼩（⽐如n<60，⼤样本数据可以⽤U 检验），适⽤条件：①数据服从正态分布；。

②满⾜⽅差齐性（⽅差相等）；注：若数据不满⾜①，②，可以尝试对数据做变量变换：对数变换、平⽅根变换、倒数变换、平⽅根反正弦变换等。

⽅差齐性检验要求两样本数据的总体均服从正态分布，统计量F 为为较⼤的⽅差与较⼩的⽅差的⽐值：21112222, 1, 1S F n n S νν==-=-原假设H 0：两总体⽅差相等； H 1：两总体⽅差不相等。

使⽤car 包中的函数leveneTest()实现，基本格式为：leveneTest(y, group, center=, ...) leveneTest(formula,data,subset,...)其中，y 为样本数据； #group 为因⼦型的分组变量；center 指定计算每组的中⼼的⽅法，默认是中位数median ，也可以⽤均值meanformula 设置公式格式：formula=定量变量~分组变量⽰例：setwd("E:/办公资料/R 语⾔/R 语⾔学习系列/codes") load("")head(chengji,3)class sex Math English Rank 1 1 1 60 66 4 2 1 1 42 58 5 3 1 1 78 95 3~library(car)leveneTest(Math~(class),data=chengji)Levene's Test for Homogeneity of Variance (center = median)Df F value Pr(>F)group 148说明：P值=>, 接受原假设，即⽅差齐。

【原创】R语言自编t检验和z检验函数附代码数据

有问题到淘宝找“大数据部落”就可以了R语言自编t检验和z检验函数代码myt.test(1:10 ,alternative="less")#### One Sample t-test#### data: 1:10## t = 5.7446, df = 9, p-value = 0.9999## alternative hypothesis: true mean is less than 0## 95 percent confidence interval:## -Inf 7.255072## sample estimates:## mean of x## 5.5My.z.test(x,sigma.x=1)#### One-sample z-Test#### data: x## z = 0.68502, p-value = 0.4933## alternative hypothesis: true mean is not equal to 0## 95 percent confidence interval:## -0.3680456 0.7635401## sample estimates:## mean of x## 0.1977473myt.test <-function(x, y =NULL, alternative =c("two.sided", "less", "greater"), mu =0, paired =FALSE, var.equal =FALSE, conf.level =0.95 ){if( !is.null(y) ) {有问题到淘宝找“大数据部落”就可以了dname <-paste(deparse(substitute(x)),"and",deparse(substitute(y)))if(paired)xok <-yok <-complete.cases(x,y)else {yok <-!is.na(y)xok <-!is.na(x)}y <-y[yok]}else {dname <-deparse(substitute(x))if (paired) stop("'y' is missing for paired test")xok <-!is.na(x)yok <-NULL}x <-x[xok]if (paired) {x <-x-yy <-NULL}nx <-length(x)mx <-mean(x)vx <-var(x)if(is.null(y)) {if(nx <2) stop("not enough 'x' observations")df <-nx-1stderr <-sqrt(vx/nx)if(stderr <10 *.Machine$double.eps *abs(mx))stop("data are essentially constant")tstat <-(mx-mu)/stderrmethod <-if(paired) "Paired t-test" else "One Sample t-test" estimate <-setNames(mx, if(paired)"mean of the differences" else "mean of x") } else {ny <-length(y)if(nx <1 ||(!var.equal &&nx <2))stop("not enough 'x' observations")if(ny <1 ||(!var.equal &&ny <2))stop("not enough 'y' observations")if(var.equal &&nx+ny <3) stop("not enough observations")my <-mean(y)vy <-var(y)method <-paste(if(!var.equal)"Welch", "Two Sample t-test") estimate <-c(mx,my)names(estimate) <-c("mean of x","mean of y")有问题到淘宝找“大数据部落”就可以了if(var.equal) {df <-nx+ny-2v <-0if(nx >1) v <-v +(nx-1)*vxif(ny >1) v <-v +(ny-1)*vyv <-v/dfstderr <-sqrt(v*(1/nx+1/ny))} else {stderrx <-sqrt(vx/nx)stderry <-sqrt(vy/ny)stderr <-sqrt(stderrx^2 +stderry^2)df <-stderr^4/(stderrx^4/(nx-1) +stderry^4/(ny-1))}if(stderr <10 *.Machine$double.eps *max(abs(mx), abs(my)))stop("data are essentially constant")tstat <-(mx -my -mu)/stderr}if (alternative =="less") {pval <-pt(tstat, df)cint <-c(-Inf, tstat +qt(conf.level, df) )}else if (alternative =="greater") {pval <-pt(tstat, df, lower.tail =FALSE)cint <-c(tstat -qt(conf.level, df), Inf)}else {pval <-2 *pt(-abs(tstat), df)alpha <-1 -conf.levelcint <-qt(1 -alpha/2, df)cint <-tstat +c(-cint, cint)}cint <-mu +cint *stderrnames(tstat) <-"t"names(df) <-"df"names(mu) <-if(paired ||!is.null(y)) "difference in means" else "mean" attr(cint,"conf.level") <-conf.levelrval <-list(statistic = tstat, parameter = df, p.value = pval, conf.int = cint, estimate = estimate, null.value = mu,alternative = alternative,method = method, = dname)class(rval) <-"htest"return(rval)}myt.test(1:10 ,alternative="less")。

R语言 t检验实例程序及答案

r语言t检验例题

R语言聚类分析、因子分析、t检验程序

r语言中t检验置信区间

R语言聚类分析、因子分析、t检验程序

R语言各种假设检验实例整理（常用）

r语言 t函数

t检验例题解析

t检验例题

r语言t检验 相关检验案例代码

R语言中的t-test和ANOVA_13965

【原创】R语言自编t检验和z检验函数附代码数据

用R进行差异检验之t检验

t检验例题以及解析

t检验例题

R语言学习系列26-均值的t检验

【原创】R语言自编t检验和z检验函数 附代码数据

r语言t检验相关检验案例代码

【原创】R语言自编t检验和z检验函数附代码数据