【数学】北京昌平临川育人学校2017届高三12月月考(文)(word版,附答案)
北京市昌平临川育人学校_学年高一数学12月月考试题(PDF)

北京临川学校2016-2017学年上学期12月月考高一数学试题注:本试卷满分150分,考试时间120分钟一、选择题:(每题5分,共12题,共60分) 1.下列说法正确的是( )A.终边相同的角一定相等B.第一象限的角都是锐角C.锐角都是第一象限角D.小于 的角都是锐角 2.如果角的终边经过点(,),那么 的值是( )A. B.C. D.3.如果,那么 ( ) A.B.C.D.4.函数 的定义域是 ( )A .2,2()33k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦B .2,2()66k k k Z ππππ-+∈⎡⎤⎢⎥⎣⎦C .22,2()33k k k Z ππππ++∈⎡⎤⎢⎥⎣⎦D .5.函数)652cos(3π-=x y 的最小正周期是( )A .52πB .25πC .π2D .π56.要得到函数 的图象,只需将函数的图象( ) A.向左平移 个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向右平移 个单位长度 7.已知函数 在同一周期内,当时有最大值2,当时有最小值,那么函数的解析式为( )A.B.C.D.8.下列函数中,最小正周期为,且图象关于直线对称的是( )A. B. C. D.9.A 为三角形ABC 的一个内角,若,则这个三角形的形状为( ) A.锐角三角形 B.钝角三角形 C.等腰直角三角形 D.等腰三角形10.已知4sin 5α=,并且α是第二象限的角,那么tan α的值等于( ) A .43- B .34- C .43 D .3411函数xx x x x x y tan tan cos cos sin sin ++=的值域是( )A .{}3,1,0,1-B .{}3,0,1-C .{}3,1-D .{}1,1- 12. 下列函数是奇函数的是( ).A.B.C.D.二填空题:(每题5分、共4题,共20分)13.已知,则.14.设扇形的周长为8cm ,面积为24cm ,则扇形的圆心角的弧度数是 . 15.若)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2,则ϖ= .16.函数的图象为,如下结论中正确的是 .(写出所有正确结论的编号) ⑴图象关于直线对称 ⑵图象关于点对称;⑶函数在区间上是增函数;⑷由的图象向右平移个单位长度可以得到图象.数学答题卡一. 单选题(每题5分,总分 60 分)二填空题(每题5分,共4题计20分)13 14 15 16三解答题(共6题,其中16题10分,17-21每题12分,计70分)17(1)求值22sin 120cos180tan 45cos (330)sin(210)︒+︒+︒--︒+-︒(2)已知方程,求的值.18已知.求:⑴的值;⑵的值.19.求函数 的最大值和最小值.20已知函数,.⑴求函数的最小正周期和单调递增区间;⑵求函数在区间上的最小值和最大值,并求出取得最值时的值.21对于函数.⑴用“五点法”作出其在一个周期的图象;⑵指出其图象可由的图象经过怎样的变换而得到.22.已知函数f(x)=A sin(ωx+φ) (A>0,ω>0,|φ|<2)在一个周期内的图像如图所示.(1)求函数的解析式;(2)设0<x<π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.。
北京昌平临川育人学校2016-2017学年高二上学期期末考试数学(文)试题 (word版含答案)

2016---2017学年北京临川学校高二期末数学试卷(北京卷)一、选择题:(12小题,共60分)1. 已知椭圆x 225+y 216=1上一点P 到椭圆一个焦点的距离为7,则点P 到另一个焦点的距离为( )A .3B .4C .5D .6 2.直线x -√3y =3的倾斜角的大小为( ) A .30° B .60° C.120° D.150° 3.已知抛物线4y =x 2,则它的焦点坐标是( ) A .(0,2) B .(1,0) C .(2,0) D . (0,1)4. 焦点在y 轴上,虚半轴的长为4,半焦距为6的双曲线的标准方程为( ) A.y 220-x 216=1 B.y 216-x 220=1 C.y 216-x 236=1 D.y 236-x 216=1 5. 运动物体的位移s =3t 2-2t +1,则此物体在t =10时的瞬时速度为( ) A .281 B .58 C .85 D .106. 若f (x )=ax 3+3x 2+2,f ′(-1)=3,则a 的值等于( ) A .5 B .4 C .3 D .67.为了调查全国人口的寿命,抽查了十一个省(市)的2 500名城镇居民,这个问题中“2 500名城镇居民的寿命的全体”是( )A .总体B .个体C .样本D .样本容量 8. 给出下列命题,其中真命题为( )A .对任意x ∈R ,x 是无理数B .对任意x ,y ∈R ,若xy ≠0,则x ,y 至少有一个不为0C .存在实数既能被3整除又能被19整除D .x >1是1x<1的充要条件9..一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+错误!未找到引用源。
B .2+错误!未找到引用源。
C .1+2错误!未找到引用源。
D .2错误!未找到引用源。
10.已知圆(x+1)2+y2=2,则其圆心和半径分别为()A.(1,0),2 B.(﹣1,0),2 C. D.11.抛物线x2=4y的焦点到准线的距离为()A.B.1 C.2 D.412.双曲线4x2﹣y2=1的一条渐近线的方程为()A.2x+y=0 B.2x+y=1 C.x+2y=0 D.x+2y=1二、填空题(本大题共4小题,每小题5分,共20分)13.已知函数f(x)=x3+2,则f′(2)=________.14.已知命题p:“∀x∈R,x2≥0”,则¬p:.15.如图,函数y=f(x)的图像在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.16.椭圆x2+9y2=9的长轴长为.三.解答题(六大题,共70分)17(10分).已知曲线C:y=x3+5x2+3x(1)求曲线C导函数.(2)求曲线C在x=1处的切线方程.18.(12分)(1) 设命题p:(4x-3)2≤1,若p是真命题,求x的取值范围。
北京市昌平临川育人学校2016-2017学年高一数学12月月考试题(PDF)

9.A 为三角形 ABC 的一个内角,若
,则这个三角形的形状为(
)
A.锐角三角形
B.钝角三角形 C.等腰直角三角形 D.等腰三角形
10.已知 sin 4 ,并且 是第二象限的角,那么 tan 的值等于( ) 5
A. 4
B. 3
C. 3
D. 4
3
4
4
3
11 函数 y sin x cos x tan x 的值域是( ) sin x cos x tan x
)
A.
B.
C.
D.
3.如果
,那么
(
)
A.
B.
C.
D.
4.函数
的定义域是
()
A.
2k
3
,
2k
3
(k
Z)
B.
2k
6
,
2k
6
(k
Z)
C.
2kk
Z
)
D.
5.函数 y 3cos( 2 x ) 的最小正周期是( ) 56
A. 2 5
B. 5 2
C. 2
D. 5
6.要得到函数
A.1,0,1,3 B.1,0,3 C.1,3
D. 1,1
12. 下列函数是奇函数的是(
).
A.
B.
C.
D.
二填空题:(每题 5 分、共 4 题,共 20 分)
13.已知
,则
.
14.设扇形的周长为 8cm ,面积为 4cm2 ,则扇形的圆心角的弧度数是 15.若 f (x) 2sinx(0 1) 在区间[0, ] 上的最大值是 2 ,则 =
北京临川学校 2016-2017 学年上学期 12 月月考
北京市昌平临川育人学校2017-2018学年高一12月月考数学试题

北京临川育人2017-2018学年12月月考高一数学试卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}13A x x =<<,{}12B x x =-<≤,则( C ) A .[]1,2 B .(],2-∞ C .(]1,2 D .()1,3- 2.已知30.2a =,0.2log 3b =,0.23c =,则,,a b c 的大小关系是( C ) A .a c b << B .a b c << C .b a c << D .b c a << 3.函数()()2lg 4f x x =-的定义域为( A )A .()2,2-B .[]2,2-C .[)2,+∞D .()(),22,-∞+∞4.与30°角终边相同的角的集合是( D )A.⎩⎨⎧⎭⎬⎫α|α=k ·360°+π6,k ∈Z B .{α|α=2k π+30°,k ∈Z }C .{α|α=2k ·360°+30°,k ∈Z }D.⎩⎨⎧⎭⎬⎫α|α=2k π+π6,k ∈Z 5.下列函数中在定义域上为增函数的是( A )A .y x x =B .xy e = C .1xy e =- D .12xy ⎛⎫= ⎪⎝⎭6.函数f (x )=2x +x-7的零点所在的区间是( C ) A .(0,1)B .(1,2)C .(2,3)D .(3,4)7.图中函数图象所表示的解析式为( B )A .)20(123≤≤-=x x y B .)20(12323≤≤--=x x y C .)20(123≤≤--=x x y D .)20(11≤≤--=x x y 8.已知函数()()22111xa x x f x a x ⎧-+<⎪=⎨+≥⎪⎩在R 上是增函数,则实数a 的取值范围是( D )Oxy1223A .()1,2B .3,22⎛⎫ ⎪⎝⎭C .31,2⎛⎤ ⎥⎝⎦D .3,22⎡⎫⎪⎢⎣⎭9.cos ⎝ ⎛⎭⎪⎫-163π+sin ⎝ ⎛⎭⎪⎫-163π的值为( C )A.-1+32 B .1-32 C .3-12 D .3+1210.若sin αcos α>0,则α在( B )A .第一、二象限B .第一、三象限C .第一、四象限D .第二、四象限11.点⎝ ⎛⎭⎪⎫π4,b 在函数y =2sin x +1的图像上,则b 等于( C )A.22 B .2 C .2 D .3 12.终边经过点(b ,b )(b ≠0)的角α的集合是( D )A.⎩⎨⎧⎭⎬⎫π4B .⎩⎨⎧⎭⎬⎫π4,5π4C.⎩⎨⎧⎭⎬⎫α|α=π4+2k π,k ∈ZD .⎩⎨⎧⎭⎬⎫α|α=π4+k π,k ∈Z 二、填空题(每题5分,满分20分,将答案填在答题纸上)13.某人定制了一批地砖,每块地砖(如图(1)所示)是边长为40 cm 的正方形ABCD ,点E ,F 分别在边BC 和CD 上,△CFE ,△ABE 和四边形AEF D 均由单一材料制成,制成△CFE ,△ABE 和四边形AEFD 的三种材料的每平方米价格之比依次为3∶2∶1.若将此种地砖按图(2)所示的形式铺设,能使中间的阴影部分构成四边形EFGH.则当CE= cm 时,定制这批地砖所需的材料费用最省?解析:设CE=x ,则FC=x ,BE=40-x ,设△CFE ,△ABE 和四边形AEFD 的面积分别为S 1,S 2,S 3,地砖的总费用为y ,则y=3S 1+2S 2+S 3=x 2+402-40x+402-x 2-20×40+20x=x 2-20x+2 400,二次函数开口向上,其对称轴为x=10,所以当x=10,即CE=10时费用最少. 答案:1014.若296a b ==,则21a b+= . 15.函数()()22log 23f x x x =--的单调递减区间为 . 14.2 15.(),1-∞-16.函数y =1+sin x ,x ∈的图像与直线y =32有________个交点.【解析】 在同一坐标系中作出函数y =1+s in x ,y =32的图像,如图所示.在x ∈内共有两个交点.【答案】 两三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知角α终边上一点P (-4,3), 求cos ⎝ ⎛⎭⎪⎫π2+αsin (-π-α)cos ⎝ ⎛⎭⎪⎫11π2-αsin ⎝ ⎛⎭⎪⎫9π2+α的值.【解】 点P 到原点O 的距离|OP |=(-4)2+32=5,根据三角函数的定义得,sin α=35,cos α=-45.cos ⎝ ⎛⎭⎪⎫π2+αsin ()-π-αcos ⎝ ⎛⎭⎪⎫11π2-αsin ⎝ ⎛⎭⎪⎫9π2+α=-sin α·[-sin (π+α)]cos ⎣⎢⎡⎦⎥⎤6π-⎝ ⎛⎭⎪⎫π2+αsin ⎝ ⎛⎭⎪⎫4π+π2+α=sin α·sin (π+α)cos ⎝ ⎛⎭⎪⎫π2+αsin ⎝ ⎛⎭⎪⎫π2+α=sin α(-sin α)-sin α·cos α=sin αcos α=35×⎝ ⎛⎭⎪⎫-54=-34. 18.已知-π6≤x ≤3π4,f (x )=sin 2x +2sin x +2,求f (x )的最大值和最小值,并求出相应的x 值.【解】 令t =sin x ,则由-π6≤x ≤34π知,-12≤t ≤1, ∴f (x )=g (t )=t 2+2t +2=(t +1)2+1,当t =1时,f (x )max =5,此时,sin x =1,x =π2; 当t =-12时,f (x )min =54,此时,sin x =-12,x =-π6. 19.已知幂函数()()2157m f x m m x -=-+为偶函数. (1)求()f x 的解析式;(2)若()()3g x f x ax =--在[]1,3上不是单调函数,求实数a 的取值范围. 19.解:(1)由2571m m -+=⇒25602m m m -+=⇒=或3m = 又()f x 为偶函数,则:3m =此时:()2f x x =(2)()()3g x f x ax =--在[]1,3上不是单调函数,则()g x 的对称轴2ax =满足 13262aa <<⇒<<即:()2,6a ∈ 20.已知半径为10的圆O 中,弦AB 的长为10. (1)求弦AB 所对的圆心角α的大小;(2)求α所在的扇形的弧长l 及弧所在的弓形的面积S.解:(1)由圆O 的半径r=10=AB ,知△AOB 是等边三角形,∴α=∠AOB=60°= rad .(2)由(1)可知α= rad,r=10,∴弧长l=α·r=×10=,∴S 扇形=lr=×10=,而S △AOB =·AB ·×10×,∴S=S 扇形-S △AOB =50.21.已知函数213)(-+=x x f ,]6,3[∈x . (1)试判断函数)(x f 的单调性,并用定义加以证明; (2)求函数)(x f 的最大值和最小值. 21. 解:已知函数213)(-+=x x f ,]6,3[∈x . (1)函数)(x f 在]6,3[∈x 时为减函数。
北京昌平临川育人学校2016-2017学年高二12月月考数学理试题 含答案 精品
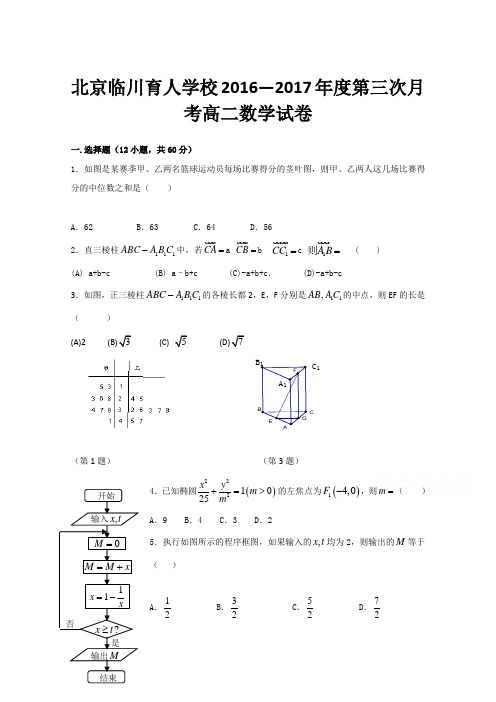
C1C北京临川育人学校2016—2017年度第三次月考高二数学试卷一.选择题(12小题,共60分)1.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是()A.62 B .63 C.64 D.562.直三棱柱111ABC A B C-中,若CA=a CB=b1CC=c1A B=则 ( )(A) a+b-c (B) a–b+c (C)-a+b+c. (D)-a+b-c3.如图,正三棱柱111ABC A B C-的各棱长都2,E,F分别是11,AB AC的中点,则EF的长是()(A)2(C)(第1题)(第3题)4.已知椭圆()2221025x ymm+=>的左焦点为()14,0F-,则m=()A.9 B.4 C.3 D.25.执行如图所示的程序框图,如果输入的tx,均为2,则输出的M等于()A.21B.23C.25D.276.设抛物线:C 24y x =上一点P 到y 轴的距离为4,则点P 到抛物线C 的焦点的距离是( )A .4B .5C .6D .77.实数m 是[0,6]上的随机数,则关于x 的方程240x mx -+=有实根的概率为( ) A .14 B .13 C .12 D .238.命题“R,x ∃∈使得210x x ++<”的否定是 ( )A .R,x ∀∈均有210x x ++< B .R,x ∀∈均有210x x ++≥ C .R,x ∃∈使得210x x ++≥ D .R,x ∀∈均有210x x ++> 9.已知a ,b 都是实数,则“a b 〉”是“22a b 〉”的( ) (A )充分不必要条件 (B )必要不充分条件 (C )充分必要条件 (D )既不充分又不必要条件10.若点A 的坐标为(3,2),F 是抛物线x y 22=的焦点,点M 在抛物线上移动时,使MA MF +取得最小值的M 的坐标为( )A .()6,3 B .⎪⎭⎫ ⎝⎛1,21 C .()2,1 D .()2,211.过抛物线28y x =的焦点F 的直线交抛物线于()()1122,,,A x y B x y 两点,若125x x +=,则AB =( )A .10B .9C .8D .712.已知x y 21=是双曲线2222a y a x =-的一条渐近线,则双曲线的离心率等于( )A .23B .3C . 25D . 5二.填空题(4小题,共20分)13.已知在长方体1111ABCD A BC D -中,底面是边长为2的正方形,高为4,则点1A 到截面11AB D 的距离是______.14.如图1,已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1C l D1的棱AA1、BB1、DD1的中点,点M、N、P、Q分别在线段AG、 CF、BE、C1D1上运动,当以M、N、P、Q为顶点的三棱锥Q-PMN的俯视图是如图2所示的正方形时,则点P到QMN的距离为__________.15.已知点12(F F动点P满足21||||2PF PF-=,当点P的纵坐标为12时,点P到坐标原点的距离为16.设双曲线22221x ya b-=(a>0,b>0)与抛物线y2=8x有一个公共的焦点F,两曲线的一个交点为P.若|PF|=5,则双曲线的渐近线方程为____.三.解答题(6小题,共70分)17(10分).如图,在四棱锥P—ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB是等边三角形.(1)求PC与平面ABCD所成角的正弦值;(2)求二面角B—AC—P的余弦值;(3)求点A到平面PCD的距离.18(12分.设命题2000:,220p x R x ax a∃∈+-=,命题22:,421q x R ax x a x∀∈++>-+,如果命题“p q∨”为真命题,“p q∧”为假命题,求实数a的取值范围.B CDPA19(12分).如图所示,1F 、2F 分别为椭圆C :22221x y a b+=(0)a b >>的左、右两个焦点,A 、B 为两个顶点,已知顶点B 到1F 、2F 两点的距离之和为2.(1)求椭圆C 的方程;(2)求椭圆C 上任意一点00(,)M x y 到右焦点2F 的距离的最小值;(3)作AB 的平行线交椭圆C 于P 、Q 两点,求弦长||PQ 的最大值,并求||PQ 取最大值时1F PQ ∆的面积.20(12分).经销商经销某种产品,在一个销售周期内,每售出1件产品获得利润500元,未售出的产品每件亏损100元,根据过去的市场记录,得到了60个销售周期的市场需求量的频率分布表:经销商为了下一个销售周期购进了130件产品,以(100150)X X ≤≤表示下一个销售周期内的市场需求量,Y 表示下一个销售周期内的经销产品的利润.(1)画出市场需求量的频率分布直方图,并以各组的区间中点值代表该组的各个需求量,估计一个销售周期内的市场需求量的平均数;(2)根据市场需求量的频率分布表提供的数据,估计下一个销售周期内的经销产品的利润Y 不少于53000元的概率.21(12分).如图,边长为1的正三角形SAB 所在平面与直角梯形ABCD 所在平面垂直,且CD AB //,AB BC ⊥,1=BC ,2=CD ,E 、F 分别是线段SD 、CD 的中点.(1)求证:平面//AEF 平面SBC ; (2)求二面角F AC S --的余弦值.22(12分).如图,圆C 与x 轴相切于点(2,0)T ,与y 轴正半轴相交于,M N 两点(点M 在点N 的下方),且3MN =.(1)求圆C 的方程;(2)过点M 任作一条直线与椭圆22184x y +=相交于两点,A B ,连接,AN BN ,求证:ANM BNM ∠=∠.参考答案一.选择题(12小题,共60分)1.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )A .62B .63C .64D .56 【答案】C试题分析:根据茎叶图,可知甲、乙的中位数分别为:28,36,所以两个中位数之和为64,所以答案为C.2.直三棱柱111ABC A B C -中,若CA =a CB =b 1CC =c 1A B =则 (A) a+b-c (B) a –b+c (C)-a+b+c . (D)-a+b-c 【答案】D【解析】要表示向量 1AB ,只需要用给出的基底ab c ,, 表示出来即可,要充分利用图形的直观性,熟练利用向量加法的三角形法则进行运算.解答:解:1AB =11A A AB CC CB CA +=-+-=-a b c +-故选D .3.如图,正三棱柱111ABC A B C -的各棱长都2,E ,F 分别是11,AB AC 的中点,则EF 的长是 (A)2(C)C 1C【答案】C【解析】如图所示,取AC 的中点G ,连EG ,FG ,则易得 EG =2,E G =1,故EFC4.已知椭圆()2221025x y m m +=>的左焦点为()14,0F -,则m =( ) A .9 B .4 C .3 D .2 【答案】C试题分析:根据焦点坐标可知焦点在x 轴,所以252=a ,22m b =,162=c ,又因为92222=-==c a b m ,解得3=m ,故选C.考点:椭圆的基本性质5.执行如图所示的程序框图,如果输入的t x ,均为2,则输出的M 等于A .21 B .23 C .25 D .27 【答案】B 【解析】试题分析:当2x =时,2M =,11122x -=<;12x =,52M =,1112x -=-<;1x =-,32M =,1122x-=≥, 程序结束.输出32M =,故应选B . 考点:1、算法与程序框图.6.设抛物线:C 24y x =上一点P 到y 轴的距离为4,则点P 到抛物线C 的焦点的距离是( )A .4B .5C .6D .7 【答案】B 【解析】试题分析:抛物线C 的准线方程为1x =-,设抛物线C 的焦点为F ,由抛物线的定义知:F d P =(d 为点P 到抛物线C 的准线的距离),而415d =+=,所以F 5P =,故选B . 考点:抛物线的定义.7.实数m 是[0,6]上的随机数,则关于x 的方程240x mx -+=有实根的概率为( )A .14 B .13 C .12 D .23【答案】B 【解析】试题分析:∵方程240x mx -+=有实根,∴判别式2160m ∆=-≥,∴4m ≤-或4m ≥时方程有实根,∵实数m 是[0,6]上的随机数,区间长度为6,[0,6]的区间长度为2,∴所求的概率为2163P ==. 故选:B . 考点:几何概型.8.命题“R,x ∃∈使得210x x ++<”的否定是 ( )A .R,x ∀∈均有210x x ++< B .R,x ∀∈均有210x x ++≥ C .R,x ∃∈使得210x x ++≥ D .R,x ∀∈均有210x x ++>【答案】B 【解析】试题分析:存在性命题的否定是全称命题. 命题“R,x ∃∈使得210x x ++<”的否定是R,x ∀∈均有210x x ++≥ ,故选B .9.已知a ,b 都是实数,则“a b 〉”是“22a b 〉”的( ) (A )充分不必要条件 (B )必要不充分条件 (C )充分必要条件 (D )既不充分又不必要条件 【答案】D【解析】本题考查充分必要条件、不等式的性质。
北京昌平临川育人学校届高三12月月考数学(文)试题Word版含答案

北京临川学校2016—2017学年上学期12月考 高三文科数学试卷---命题人李永刚第Ⅰ卷(选择题,共60分)一、选择题:每小题5分,共60分,在每小题给出的四个选项中,只有一个选项是正确的,请把正确地选项填在题后的括号内. 1.若集合{1,2,3}A =,{0,1,2}B =,则A B =A .{0,1,2,3}B .{0,1,2}C .{1,2}D .{1,2,3}2.设3log 2a =,21log 8b=,c = A .ab c >> B .c b a >> C .a c b >> D .c a b >>3.“数列{}n a 既是等差数列又是等比数列”是“数列{}n a 是常数列”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.若实数,x y 满足010x y x y x -≤⎧⎪+≤⎨⎪≥⎩,则2z x y =+的最大值为A .0B .1C .32D .25.从,,,,A B C D E 5名学生中随机选出2人,A 被选中的概率为A .15B .25C .825 D .9256. 下列函数中,其定义域和值域分别与函数lg 10x y =的定义域和值域相同的是A .y x = B .lg y x = C .2x y = D.y =7.执行如图所示的程序框图,输出的k 的值为A .3B .4C .5D .6 8.函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( ) A .2,3π-B .2,6π-C .4,6π-D .4,3π9、直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为(A )13 (B )12 (C ) 23 (D )3410、如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A)18+(B)54+(C )90 (D )8111、过点(1,1)P 的直线,将圆形区域{}22(,)|4x y xy +≤分两部分,使得这两部分的面积之差最大,则该直线的方程为( )A .20x y +-=B .10y -= C.x y -=D .340x y +-=12、为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是(A )13 (B )12(C )23(D )56第Ⅱ卷(非选择题,共90分)二、填空题:每小题5分,共20分,把正确答案填写在题中的横线上,或按题目要求作答. 13、已知()f x 为偶函数,当0x ≤ 时,1()x f x e x --=-,则曲线()y f x =在点(1,2)处的切线方程式________▲_____________________. 14、(2016年全国III卷高考)函数sin y x x =的图像可由函数2sin y x =的图像至少向右平移____▲_________个单位长度得到.15、已知{a n }是等差数列,S n 是其前n 项和.若a 1+a 22=-3,S 5=10,则a 9的值是 ▲.16、已知函数2(43)3,0()(01)log (1)1,0a x a x a x f x a a x x ⎧+-+<⎪=>≠⎨++≥⎪⎩且在R 上单调递减,且关于x 的方程|()|23xf x =-恰有两个不相等的实数解,则a 的取值范围是____▲_____. 三、解答题:解答题应写出文字说明、证明过程或演算步骤.第17题—第21题每题12分,选考题10分,共70分。
北京昌平临川育人学校2016-2017学年高一上学期12月月考数学试题 含答案

高一数学试题一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列说法正确的是( )A .终边相同的角一定相等B .第一象限的角都是锐角C .锐角都是第一象限角D .小于90的角都是锐角 2.如果角θ的终边经过点31()22-,那么tan θ的值是( )A 3B .33C .3-D .33-3.如果1cos()2πα+=-,那么sin α=( ) A .12- B .12C .32-D .32±4。
函数2sin 1y x -)A .[2,2]()33k k k Z ππππ-+∈ B .[2,2]()66k k k Z ππππ-+∈ C 。
2[2,2]()33k k k Z ππππ++∈ D .5[2,2]()66k k k Z ππππ++∈5.函数23cos()56y x π=-的最小正周期是( ) A .25π B .52π C.2πD .5π6。
要得到函数sin 2y x =的图象,只需将函数sin(2)3y x π=-的图象( ) A .向左平移3π个单位长度 B .向右平移3π个单位长度C 。
向左平移6π个单位长度 D .向右平移6π个单位长度7。
已知函数sin()y A x ωϕ=+在同一周期内,当3x π=时有最大值2,当0x =时有最小值—2,那么函数的解析式为( ) A .32sin 2y x = B .2sin(3)2y x π=+ C 。
2sin(3)2y x π=-D .1sin 32y x =8.下列函数中,最小正周期为π,且函数关于直线3x π=对称的是( )A .sin(2)6y x π=+ B .sin()26x y π=+ C.sin(2)6y x π=-D .sin(2)3y x π=-9. A 为三角形ABC 的一个内角,若2sin cos 5A A +=,则这个三角形的形状为( )A . 锐角三角形B .钝角三角形 C. 等腰直角三角形 D .等腰三角形10。
2017昌平临川育人学校高三(上)期末数学(理科)

9.(5 分)已知 f(x)=asinx+cosx,若 f ( +x) =f( ﹣x),则 f (x)的最大值为(
)
A.1 B. C. 2 D.2 10.( 5 分)设数列 { an} 的前 n 项和为 Sn,若 Sn+1,Sn,Sn+2 成等差数列,且 a2=﹣2,则 a7=( ) A.16 B.32 C. 64 D.128
A. B. C.
D.
5.(5 分)如图,网格纸上小正方形的边长为 1,粗线画出的为某几何体的三视图,则此几何体的体
积为( ) A. B.1 C.
D.2
6.(5 分)已知 2sin2 α =+1cos2 α,则 tan(α+ )的值为( )
A.﹣ 3 B.3 C.﹣ 3 或 3 D.﹣ 1 或 3 7.(5 分)执行如图所示的程序框图,则输出的 c 的值是( )
选考题(二选一) [ 选修 4-4:坐标系与参数方程 ] .
22.( 10 分)在平面直角坐标系 xoy 中,直线
相交于横坐标分别为 x1,x2 的 A, B 两点 ( 1)求证: x02=x1x2; ( 2)若 OA⊥OB,求 x0 的值.
,(t 为参数)与抛物线 y2=2px( p> 0)
[ 选修 4-5:不等式选讲 ] 23.已知 a,b∈R+,设 x= ,y=
( 1)若椭圆 C 的离心率为 ,求 P 点的坐标
( 2)证明四边形 AMBN 的面积 S> 8 . 21.( 12 分)已知函数 f(x)=aex+bxlnx 图象上 x=1 处的切线方程为 y=2ex﹣ e. (Ⅰ)求实数 a 和 b 的值; (Ⅱ)求函数 g(x)=f( x)﹣ ex2 的最小值.
昌平区临川育人学校2017届高三12月月考(解析版)

北京市昌平区临川育人学校2017届高三12月月考化学试卷1.化学与生活密切相关,下列对应关系错误的是()化学性质实际应用A Al2(SO4)3和小苏打反应泡沫灭火器灭火B 铁比铜金属性强刻制印刷电路板C 次氯酸盐具有氧化性作杀菌消毒剂D 二氧化硫具有漂白性漂白纸浆2.A. NaHCO3B. NaHSO4C. NH4NO3D. HBr3.关于溶液的酸碱性说法正确的是()A.C(H+)很小的溶液一定呈碱性B. PH=7的溶液一定呈中性C. C(OH-)= C(H+)的溶液一定呈中性D. 不能使酚酞试液变红的溶液一定呈酸性4. 下列物质对应的用途不正确...的是()A B C D物质Fe2O3 NH3Si Na2O用途作红色涂料制硝酸作半导体材料作供氧剂5.下列氧化物中,能与水反应生成酸的是()A.SiO2B.NO C.SO3D.Al2O36. 下列反应中,属于水解反应的是()A.HCO 3-+H2O H3O++CO32-B.HCO3-+H3O+= 2H2O +CO2↑ C.CO 2+H2O H2CO3D.CO32-+H2O HCO3-+OH-7. 分枝酸可用于生化研究,其结构简式如图。
下列关于分枝酸的叙述正确的是()A.可与乙醇、乙酸反应,且反应类型相同B.1 mo1分枝酸最多可与3 mol NaOH发生中和反应C.分枝酸的分子式为C10H8O6D.分枝酸分子中含有2种官能团8. 下列关于实验的描述中,正确的是()A.用湿润的pH试纸测定溶液的pH,测定结果偏小,该溶液一定呈酸性B.中和滴定实验中,锥形瓶用蒸馏水洗净后即可使用,滴定管用蒸馏水洗净后,须干燥或用待装液润洗后方可使用C.将碘水倒入分液漏斗,加入适量乙醇,振荡后静置,能将碘萃取到乙醇中D.向含FeCl2杂质的FeCl3溶液中通是量Cl2后,充分加热蒸干,得到纯净的FeCl3固体9. 对以下描述的解释或结论中,正确的是()10. 下列事实不能用勒沙特列原理解释的是()A.用排饱和食盐水的方法收集氯气B.在沸腾的蒸馏水中滴加FeCl3溶液,制Fe(OH)3胶体C.在FeCl3溶液中加AgNO3溶液,产生白色沉淀D.向AgCl 和水的悬浊液中加入足量的Na2S溶液并振荡,白色固体转化为黑色固体11. 常温下,下列各组离子在指定溶液中一定能大量共存的是()A.1.0 mol·L-1的KNO3溶液:H+、Fe2+、Cl-、SO2-4B.甲基橙呈红色的溶液:NH+4、Ba2+、AlO-2、Cl-C.与铝反应产生大量氢气的溶液:Na+、K+、CO2-3、Cl-D.pH=12的溶液:K+、Na+、CH3COO-、Br-12. 工业上制备纯硅反应的热化学方程式为:SiCl 4(g)+2H2(g)Si(s)+4HCl(g);△H = + QkJ/mol (Q>0),一定温度、压强下,将一定量反应物通入密闭容器进行以上反应(此条件下为可逆反应),下列叙述正确的是()A. 反应过程中,若将硅移出体系,能提高SiCl4的转化率B. 若反应开始时SiCl4为1mol,则达平衡时,吸收热量为QkJC. 反应至4min 时,若HCl 浓度为0.12mol/L ,则H 2的反应速率为0.03mol/(L min)D. 当反应吸收热量为0.025QkJ 时,生成的HCl 通入100mL 1mol/L 的NaOH 溶液恰好完全反应13. 下列解释事实的方程式不正确...的是( ) A .向氯化铝溶液中滴加过量氨水,生成白色胶状沉淀: Al 3++ 3NH 3·H 2O =Al(OH)3+ 3NH 4+B .加入足量的氢氧化镁以除去氯化镁溶液中的少量氯化铁:Fe 3+ + 3OH —= Fe(OH)3↓C .常温下0.1mol/L 氯化铵溶液pH=5:NH 4+ +H 2ONH 3·H 2O+ H +D .电解精炼铜时阳极铜溶解:Cu — 2e — = Cu 2+14.北京大学和中国科学院的化学工作者已成功研制出碱金属与C 60形成的球碳盐K 3C 60,实验测知该物质属于离子化合物,具有良好的超导性。
2016-2017年北京市昌平区临川育人学校高三(上)期末数学试卷和答案(文科)

2016-2017学年北京市昌平区临川育人学校高三(上)期末数学试卷(文科)一、选择题:共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={0,l,3},B={x|x2﹣3x=0},则A∩B=()A.{0}B.{0,1}C.{0,3}D.{0,1,3}2.(5分)已知z=(i为虚数单位),则复数z=()A.﹣1 B.l C.i D.﹣i3.(5分)设命题p:∀x>0,x>lnx.则¬p为()A.∀x>0,x≤lnx B.∀x>0,x<lnxC.∃x0>0,x0>lnx0D.∃x0>0,x0≤lnx04.(5分)已知向量、,其中||=,||=2,且(﹣)⊥,则向量和的夹角是()A.B.C. D.5.(5分)如图,网格纸上小正方形的边长为1,粗线画出的为某几何体的三视图,则此几何体的体积为()A.B.1 C.D.26.(5分)已知2sin2α=1+cos2α,则tan(α+)的值为()A.﹣3 B.3 C.﹣3或3 D.﹣1或37.(5分)执行如图所示的程序框图,则输出的c的值为()A.6 B.8 C.13 D.218.(5分)同步通讯卫星B定位于地球赤道上一点C的上空,且与地面的距离等于地球的半径,点C与地球上某点A在同一条子午线上,若A点的纬度60°,则从A点看B点的结果是()A.在地平线上B.仰角为30°C.仰角为45°D.仰角为60°9.(5分)已知f(x)=asinx+cosx,若f(+x)=f(﹣x),则f(x)的最大值为()A.1 B.C.2 D.210.(5分)设数列{a n}的前n项和为S,若S n+1,S n,S n+2成等差数列,且a2=﹣2,则a7=()A.16 B.32 C.64 D.12811.(5分)设双曲线=1的两焦点分别为F1,F2,P为双曲线上的一点,若PF1与双曲线的一条渐近线平行,则•=()A.B.C.D.12.(5分)已知f′(x)是函数f(x)(x∈R)的导函数,满足f′(x)=f(x),且f(0)=2,设函数g(x)=f(x)﹣lnf3(x)的一个零点为x0,则以下正确的是()A.x0∈(0,1)B.x0∈(1,2)C.x0∈(2,3)D.x0∈(3,4)二、填空题:本大题共4小题,每小题5分13.(5分)已知实数x,y满足,若x﹣y的最大值为6,则实数m=.14.(5分)曲线f(x)=x3+x在(1,f(1))处的切线方程为.15.(5分)已知{a n}是公差不为0的等差数列,{b n}为等比数列,满足a1=3,b1=1,a2=b2,3a5=b3,若对于每一个正整数n,均有a n=a1+log a b n,则常数a=.16.(5分)已知△ABC的三个顶点均在抛物线y2=x上,边AC的中线BM∥x轴,|BM|=2,则△ABC的面积为.三、解答题:第17-21题每题12分,解答赢下答卷的相应各题中写出文字说明,证明过程或演算步骤.17.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且3acosA=bcosC+ccosB (1)求cosA(2)若a=3,求△ABC的面积的最大值.18.(12分)如图,已知直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.(Ⅰ)求证B1F⊥平面BEC1;(Ⅱ)求三棱锥B1﹣BEC1的体积.19.(12分)某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:甲运动员得分:34,21,13,30,29,33,28,27,10乙运动员得分:49,24,12,31,31,44,36,15,37,25,36(Ⅰ)根据两组数据完成甲、乙两名运动员得分的茎叶图,并通过茎叶图比较两名运动员成绩的平均值及稳定程度;(不要求计算出具体值,给出结论即可)(Ⅱ)若从甲运动员的9次比赛的得分中选2个得分,求两个得分都超过25分的概率.20.(12分)在直角坐标系xOy中,圆x2+y2=4上一点P(x0,y0)(x0y0>0)处的切线l分别交x轴、y轴于点A,B,以A,B为顶点且以O为中心的椭圆记作C,直线OP交C于M,N两点.(Ⅰ)若P点坐标为(,1),求椭圆C的离心率;(Ⅱ)证明|MN|<4.21.(12分)已知函数f(x)=+elnx﹣ax在x=1处取的极值.(Ⅰ)求实数a的值;(Ⅱ)求证:f(x)≥0.请考生在第23、24题中任选一题作答,如果多做,则按所做的第一题记分,满分10分.[选修4-4:坐标系与参数方程].22.(10分)在平面直角坐标系xoy中,直线,(t为参数)与抛物线y2=2px(p>0)相交于横坐标分别为x1,x2的A,B两点(1)求证:x02=x1x2;(2)若OA⊥OB,求x0的值.[选修4-5:不等式选讲]23.已知a,b∈R+,设x=,y=,求证:(1)xy≥ab;(2)x+y≤a+b.2016-2017学年北京市昌平区临川育人学校高三(上)期末数学试卷(文科)参考答案与试题解析一、选择题:共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={0,l,3},B={x|x2﹣3x=0},则A∩B=()A.{0}B.{0,1}C.{0,3}D.{0,1,3}【解答】解:由B中方程变形得:x(x﹣3)=0,解得:x=0或x=3,即B={0,3},∵A={0,1,3},∴A∩B={0,3},故选:C.2.(5分)已知z=(i为虚数单位),则复数z=()A.﹣1 B.l C.i D.﹣i【解答】解:z==.故选:C.3.(5分)设命题p:∀x>0,x>lnx.则¬p为()A.∀x>0,x≤lnx B.∀x>0,x<lnxC.∃x0>0,x0>lnx0D.∃x0>0,x0≤lnx0【解答】解;∵命题是全称命题的否定,是特称命题,只否定结论.∴¬p:x0≤lnx0故选:D.4.(5分)已知向量、,其中||=,||=2,且(﹣)⊥,则向量和的夹角是()A.B.C. D.【解答】解:设两个向量的夹角为θ∵∴∴即∴∵θ∈[0,π]∴故选:A.5.(5分)如图,网格纸上小正方形的边长为1,粗线画出的为某几何体的三视图,则此几何体的体积为()A.B.1 C.D.2【解答】解:依三视图知该几何体为三棱锥P﹣ABC且PD⊥平面ABD,AD⊥BD,C是AD的中点,PD=AD=BD=2,所以其体积,故选:A.6.(5分)已知2sin2α=1+cos2α,则tan(α+)的值为()A.﹣3 B.3 C.﹣3或3 D.﹣1或3【解答】解:∵2sin2α=1+cos2α,∴4sinαcosα=1+2cos2α﹣1,即2sinαcosα=cos2α,①当cosα=0时,,此时,②当cosα≠0时,,此时,综上所述,tan(α+)的值为﹣1或3.故选:D.7.(5分)执行如图所示的程序框图,则输出的c的值为()A.6 B.8 C.13 D.21【解答】解:模拟执行程序,可得a=1,b=1,k=0k=1,满足条件k<6,执行循环体,c=2,a=1,b=2,k=2满足条件k<6,执行循环体,c=3,a=2,b=3,k=3满足条件k<6,执行循环体,c=5,a=3,b=5,k=4满足条件k<6,执行循环体,c=8,a=5,b=8,k=5满足条件k<6,执行循环体,c=13,a=8,b=13,k=6不满足条件k<6,退出循环,输出c的值为13.故选:C.8.(5分)同步通讯卫星B定位于地球赤道上一点C的上空,且与地面的距离等于地球的半径,点C与地球上某点A在同一条子午线上,若A点的纬度60°,则从A点看B点的结果是()A.在地平线上B.仰角为30°C.仰角为45°D.仰角为60°【解答】解:在△ABC中,∠B=60°,AB=R,BC=2R,由余弦定理得,AC2=AB2+BC2﹣2AB•BCcos60°=R2+(2R)2﹣2R•2R×=3R2,∴AC=R,∴BC2=AB2+AC2,则BA⊥AC,∴从A点看B点的结果是在地平线上.故选:A.9.(5分)已知f(x)=asinx+cosx,若f(+x)=f(﹣x),则f(x)的最大值为()A.1 B.C.2 D.2【解答】选B.解:由题意得f(x)的对称轴为,f(x)=asinx+cosx=sin(x+α)当时,f(x)取得最值即,得a=1,∴f(x)的最大值为.故选:B.10.(5分)设数列{a n}的前n项和为S,若S n+1,S n,S n+2成等差数列,且a2=﹣2,则a7=()A.16 B.32 C.64 D.128【解答】解:∵数列{a n}的前n项和为S n,若S n+1,S n,S n+2成等差数列,且a2=﹣2,∴由题意得S n+2+S n+1=2S n,得a n+2+a n+1+a n+1=0,即a n+2=﹣2a n+1,∴{a n}从第二项起是公比为﹣2的等比数列,∴a7=a2q5=64.故选:C.11.(5分)设双曲线=1的两焦点分别为F1,F2,P为双曲线上的一点,若PF1与双曲线的一条渐近线平行,则•=()A.B.C.D.【解答】解:由双曲线=1的a=,b=1,c=2,得F1(﹣2,0),F2(2,0),渐近线为,由对称性,不妨设PF1与直线平行,可得,由得,即有,,•=﹣×+(﹣)2=﹣.故选:B.12.(5分)已知f′(x)是函数f(x)(x∈R)的导函数,满足f′(x)=f(x),且f(0)=2,设函数g(x)=f(x)﹣lnf3(x)的一个零点为x0,则以下正确的是()A.x0∈(0,1)B.x0∈(1,2)C.x0∈(2,3)D.x0∈(3,4)【解答】解:设f(x)=ke x,则f(x)满足f′(x)=f(x),而f(0)=2,∴k=2,∴f(x)=2e x,∴g(x)=2e x﹣3x﹣3ln2,∴g(0)=2﹣3ln2<0,g(1)=2e﹣3﹣3ln2>0,即在(0,1)上存在零点,故选:A.二、填空题:本大题共4小题,每小题5分13.(5分)已知实数x,y满足,若x﹣y的最大值为6,则实数m= 8.【解答】解:由约束条件作出可行域如图,图形可知,要使直线x﹣y=6经过该平面区域内的点时,其在x轴上的截距达到最大,直线x+y﹣m=0必经过直线x﹣y=6与直线y=1的交点A(7,1),于是有7+1﹣m=0,即m=8.故答案为:8.14.(5分)曲线f(x)=x3+x在(1,f(1))处的切线方程为4x﹣y﹣2=0.【解答】解:f(x)=x3+x的导数为f′(x)=3x2+1,可得在(1,f(1))处的切线斜率为4,切点为(1,2),即切线的方程为y﹣2=4(x﹣1),即为4x﹣y﹣2=0.故答案为:4x﹣y﹣2=0.15.(5分)已知{a n}是公差不为0的等差数列,{b n}为等比数列,满足a1=3,b1=1,a2=b2,3a5=b3,若对于每一个正整数n,均有a n=a1+log a b n,则常数a=.【解答】解:设等差数列{a n}的公差为d,等比数列{b n}的公比为q,∵a1=3,b1=1,a2=b2,3a5=b3,∴,解得d=6,q=9,∴a n=3+6(n﹣1)=6n﹣3,,代入a n=a1+log a b n得,,即log a9=6,∴.故答案为:.16.(5分)已知△ABC的三个顶点均在抛物线y2=x上,边AC的中线BM∥x轴,|BM|=2,则△ABC的面积为.【解答】解:根据题意设A(a2,a),B(b2,b),C(c2,c),不妨设a>c,∵M为边AC的中点,∴,又BM∥x轴,则,故,∴(a﹣c)2=8,即,作AH⊥BM交BM的延长线于H.故.故答案为:.三、解答题:第17-21题每题12分,解答赢下答卷的相应各题中写出文字说明,证明过程或演算步骤.17.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且3acosA=bcosC+ccosB (1)求cosA(2)若a=3,求△ABC的面积的最大值.【解答】解:(1)在△ABC中,∵3acosA=bcosC+ccosB,∴3sinAcosA=sinBcosC+sinCcosB=sin(B+C)=sinA,即3sinAcosA=sinA,又A∈(0,π),∴sinA≠0,∴.(2)∵a2=b2+c2﹣2bccosA,即,∴b2+c2=9+bc≥2bc,∴.∵sinA==,∴△ABC的面积,(时取等号)∴.18.(12分)如图,已知直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.(Ⅰ)求证B1F⊥平面BEC1;(Ⅱ)求三棱锥B1﹣BEC1的体积.【解答】证明:(Ⅰ)分别取BC1,BC中点D,G,连结DE,AG,DG,∵D,G分别是BC1,BC的中点,∴DG CC1,又AE CC1,∴四边形AGDE是平行四边形,∴DE∥AG.∵△ABC是等边三角形,G是BC的中点,∴AG⊥BC,∵BB1⊥平面ABC,AG⊂平面ABC,∴AG⊥BB1,又BB1⊂平面BCC1B1,BC⊂平面BCC1B1,BB1∩BC=B,∴AG⊥平面BCC1B1,∵B1F⊂平面BCC1B1,∴AG⊥B1F,又∵DE∥AG.∴DE⊥B1F,又B1F⊥BE,BE⊂平面BEC1,DE⊂平面BEC1,BE∩DE=E,∴B1F⊥平面BEC1.(Ⅱ)∵B1F⊥平面BEC1.BC1⊂平面BEC1,∴B1F⊥BC1,∴Rt△B1C1F∽Rt△BB1C1,∴,设BB1=a,则C1F=,∴,解得a=2.∵G是BC的中点,∴AG=.∴V=V=S•AG==.19.(12分)某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:甲运动员得分:34,21,13,30,29,33,28,27,10乙运动员得分:49,24,12,31,31,44,36,15,37,25,36(Ⅰ)根据两组数据完成甲、乙两名运动员得分的茎叶图,并通过茎叶图比较两名运动员成绩的平均值及稳定程度;(不要求计算出具体值,给出结论即可)(Ⅱ)若从甲运动员的9次比赛的得分中选2个得分,求两个得分都超过25分的概率.【解答】(12分)解:(Ⅰ)茎叶图由茎叶图得,乙的平均值大于甲的平均数,甲比乙稳定.…(6分)(Ⅱ)从9次比赛的得分中选2个得分,共有{34,21},{34,13},{34,30},{34,29},{34,33},{34,28},{34,27},{34,10},{21,13},{21,30},{21,29},{21,33},{21,28},{21,27},{21,10},{13,30},{13,29},{13,33},{13,28},{13,27},{13,10},{30,29},{30,33},{30,28},{30,27},{30,10},{29,33},{29,28},{29,27},{29,10},{33,28},{33,27},{33,10},{28,27},{28,10},{27,10},共36种,得分都超过25分的有15种,∴两个得分都超过25分的概率p==.…(12分)20.(12分)在直角坐标系xOy中,圆x2+y2=4上一点P(x0,y0)(x0y0>0)处的切线l分别交x轴、y轴于点A,B,以A,B为顶点且以O为中心的椭圆记作C,直线OP交C于M,N两点.(Ⅰ)若P点坐标为(,1),求椭圆C的离心率;(Ⅱ)证明|MN|<4.【解答】解:(Ⅰ)k OP=,可得k1=﹣,直线l的方程为y﹣1=﹣(x﹣),令x=0,得y=4,令y=0,得x=,可得A(,0)B(0,4).即有椭圆C的方程为+=1,离心率e===;(Ⅱ)证明:直线OP的斜率为k,依题意有k>0且k≠1,直线OP的方程为y=kx,直线l的方程为,令x=0,得,令y=0,得x=ky0+x0,可得,椭圆C的方程,联立,解出,可得,,即有===4(1+)<4(1+)=8,可得|OM|<2,即有|MN|=2|OM|<4.21.(12分)已知函数f(x)=+elnx﹣ax在x=1处取的极值.(Ⅰ)求实数a的值;(Ⅱ)求证:f(x)≥0.【解答】解:(Ⅰ)∵f′(x)=+﹣a…①,依题意知f′(1)=0,∴a=e;…(4分)(Ⅱ)由(Ⅰ)知f(x)=+elnx﹣ex,(x>0),则f′(x)=,令g(x)=e x﹣ex…②,则g′(x)=e x﹣e,由g′(x)=0,得x=1,∵当0<x≤1时,g′(x)≤0,当x>1时,g′(x)>0,∴函数y=g(x)在(0,1]上递减,在[1,+∞)上递增,∴当0<x≤1时,g(x)≥g(1)=0,当x>1时,g(x)>g(1)=0,∴对∀x∈(0,+∞),g(x)≥0,即e x≥ex…③∴由②③,当0<x≤1时,x﹣1≤0,f′(x)≤0,当x>1时,x﹣1>0,f′(x)>0,∴函数y=f(x)在(0,1]上递减,在[1,+∞)上递增,∴f(x)≥f(1)=0.…(12分)请考生在第23、24题中任选一题作答,如果多做,则按所做的第一题记分,满分10分.[选修4-4:坐标系与参数方程].22.(10分)在平面直角坐标系xoy中,直线,(t为参数)与抛物线y2=2px(p>0)相交于横坐标分别为x1,x2的A,B两点(1)求证:x02=x1x2;(2)若OA⊥OB,求x0的值.【解答】(10分)解:(1)设直线…①与抛物线y2=2px(p>0)…②交于点A(x1,y1),B(x2,y2),∴α≠0把①代入②,得关于t的一元二次方程t2sin2α﹣2tpcosα﹣2px0=0,设点A,B所对应的参数分别为t1,t2,则,…③∴…④把③代入④得…(5分).(2)∵OA⊥OB,∴x1x2+y1y2=0,由(Ⅰ)知,又y1=t1sinα,y2=t2sinα,∴,由③知,∴x0=2p.…(10分)[选修4-5:不等式选讲]23.已知a,b∈R+,设x=,y=,求证:(1)xy≥ab;(2)x+y≤a+b.【解答】证明:(1)∵a,b∈R,x=,y=,+∴xy=≥=ab,当且仅当a=b时取等号.,x+y=+,(2)∵a,b∈R+则(a+b)2﹣(x+y)2=(a+b)2﹣=﹣,而(a+b)4﹣(a﹣b)4=8ab(a2+b2),∴(a+b)4﹣8ab(a2+b2)=(a﹣b)4,∴(a+b)2≥,∴(a+b)2﹣(x+y)2≥0,∴a+b≥x+y.。
北京昌平临川育人学校届高三12月月考化学试题Word版含答案

北京临川学校2016-2017学年上学期12月考高三化学试卷注:本试卷满分100分,考试时间90分钟可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 Cl 35.5 K 39 Fe 56 Cu 64 Ag 108第Ⅰ卷(选择题 共44分)一、选择题:(每小题只有1个正确答案,共22小题,每小题2分,共44分)1.化学与生活密切相关,下列对应关系错误的是( )) ( )A. NaHCO 3B. NaHSO 4C. NH 4NO 3D. HBr3. 关于溶液的酸碱性说法正确的是 ( )A. C(H +)很小的溶液一定呈碱性 B. PH=7的溶液一定呈中性C. C(OH -)= C(H +)的溶液一定呈中性D. 不能使酚酞试液变红的溶液一定呈酸性4. 下列物质对应的用途不正确...的是 5.下列氧化物中,能与水反应生成酸的是A .SiO 2B .NOC .SO 3D .Al 2O 36. 下列反应中,属于水解反应的是 ( )A .HCO 3- + H 2OH 3O + + CO 32- B .HCO 3- + H 3O + = 2H 2O + CO 2↑ C .CO 2 + H 2O H 2CO 3 D .CO 32- + H 2O HCO 3- + OH -7. 分枝酸可用于生化研究,其结构简式如图。
下列关于分枝酸的叙述正确的是()A.可与乙醇、乙酸反应,且反应类型相同B.1 mo1分枝酸最多可与3 mol NaOH发生中和反应C.分枝酸的分子式为C10H8O6D.分枝酸分子中含有2种官能团8. 下列关于实验的描述中,正确的是()A.用湿润的pH试纸测定溶液的pH,测定结果偏小,该溶液一定呈酸性B.中和滴定实验中,锥形瓶用蒸馏水洗净后即可使用,滴定管用蒸馏水洗净后,须干燥或用待装液润洗后方可使用C.将碘水倒入分液漏斗,加入适量乙醇,振荡后静置,能将碘萃取到乙醇中D.向含FeCl2杂质的FeCl3溶液中通是量Cl2后,充分加热蒸干,得到纯净的FeCl3固体9. 对以下描述的解释或结论中,正确的是()10. 下列事实不能用勒沙特列原理解释的是()A.用排饱和食盐水的方法收集氯气B.在沸腾的蒸馏水中滴加FeCl3溶液,制Fe(OH)3胶体C.在FeCl3溶液中加AgNO3溶液,产生白色沉淀D.向AgCl 和水的悬浊液中加入足量的Na2S溶液并振荡,白色固体转化为黑色固体11. 常温下,下列各组离子在指定溶液中一定能大量共存的是A.1.0 mol·L-1的KNO3溶液:H+、Fe2+、Cl-、SO2-4B.甲基橙呈红色的溶液:NH+4、Ba2+、AlO-2、Cl-C.与铝反应产生大量氢气的溶液:Na+、K+、CO2-3、Cl-D.pH=12的溶液:K+、Na+、CH3COO-、Br-12. 工业上制备纯硅反应的热化学方程式为:SiCl4(g)+2H2(g)Si(s)+4HCl(g);△H = + QkJ/mol (Q>0),一定温度、压强下,将一定量反应物通入密闭容器进行以上反应(此条件下为可逆反应),下列叙述正确的是()A. 反应过程中,若将硅移出体系,能提高SiCl4的转化率B. 若反应开始时SiCl4为1mol,则达平衡时,吸收热量为QkJC. 反应至4min时,若HCl浓度为0.12mol/L,则H2的反应速率为0.03mol/(L min)D. 当反应吸收热量为0.025QkJ时,生成的HCl通入100mL 1mol/L的NaOH溶液恰好完全反应13.下列解释事实的方程式不.正确..的是A.向氯化铝溶液中滴加过量氨水,生成白色胶状沉淀: Al3++ 3NH3·H2O=Al(OH)3+ 3NH4+ B.加入足量的氢氧化镁以除去氯化镁溶液中的少量氯化铁:Fe3+ + 3OH—= Fe(OH)3↓C.常温下0.1mol/L 氯化铵溶液pH=5:NH4+ +H2O NH3·H2O+ H+D.电解精炼铜时阳极铜溶解:Cu — 2e—= Cu2+14.北京大学和中国科学院的化学工作者已成功研制出碱金属与C60形成的球碳盐K3C60,实验测知该物质属于离子化合物,具有良好的超导性。
北京市昌平一中2017届高三上学期12月月考数学理试题

昌平一中2016—2017学年高三年级第一学期十二月月考数学(理科)试卷一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项,并把答案填在题后的表格中.1. 已知集合,,若,则的取值范围为().A. B. C. D.【答案】B【解析】由数轴可知,,故选B。
2. 已知命题,,则为().A. ,B. ,C. ,D. ,【答案】A【解析】由特称命题的否定是全称命题,所以是“”,故选A。
3. 已知直线,,若,则的值为().A. B. C. 或 D. 或【答案】C【解析】由题意,则或,故选C。
4. 已知,表示不重合的两个平面,,表示不重合的两条直线,则下列命题中正确的是().A. 若,且,则B. 若且,则C. 若,且,则D. 若,且,则【答案】C【解析】A、存在,但与不垂直,所以错误;B、存在,所以错误;C、正确;D、存在,所以错误;故选C。
5. 某三棱锥的三视图如图所示,则该三棱锥四个面的面积中最大的是().A. B. C. D.【答案】D【解析】四个面的面积分别为,所以最大的是,故选D。
6. 若,满足,且的最大值为,则的值为().A. B. C. D.【答案】A【解析】由题可知,过点,,,故选A。
7. 设,则“”是“”成立的().A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A【解析】若恒成立,则,令,则单调递减,所以,所以,所以是的充分不必要条件,故选A。
点睛:对条件成立的分析,利用分离参数法,得到,令,通过观察,我们可知单调递减,则,集合间的推到关系是小集合能推出大集合,所以是充分不必要条件。
8. 曲线是平面内与两个定点和的距离的积等于常数的点的轨迹.下列四个论断中一定错误的是().A. 曲线关于坐标原点对称B. 曲线与轴恰有两个不同交点C. 若点在曲线上,则的面积不大于D. 椭圆的面积不小于曲线所围成的区域的面积【答案】D【解析】设该点为,则,,A、对称点为,代入曲线方程成立,正确;B、当时,则,所以恰有两个不同交点,正确;C、由函数曲线的对称性可知,曲线是形式椭圆的封闭对称曲线,所以当时,,则,正确;D、,与的大小不确定,所以椭圆与曲线的面积大小不确定,错误,故选D。
北京昌平临川育人学校2016-2017学年八年级数学12月月考试题

北京昌平临川育人学校2016-2017学年八年级数学12月月考试题注:本试卷满分120分,考试时间120分钟 出题人:汤士钢 审核人:汤士钢 时间:12.14 一、选择题:(每题3分、共10题,共30分)1、下列函数关系式中,y 不是x 的函数的是 ( ) A .x y -= B .xy 2= C .xy 2= D .422+=x y2、二元一次方程组⎩⎨⎧=-=+623y x y x 的解是 ( )A.⎩⎨⎧-==36y x B.⎩⎨⎧-==30y x C.⎩⎨⎧==12y x D.⎩⎨⎧==03y x3、已知函数k x k y 3)1(2+-=是一次函数,则k 的取值范围是( ) A .1-≠k B .1≠k C .1±≠k D .k 为一切实数4、8名学生在一次数学测试中的成绩分别为80,81,80,69,74,78,x ,81.这组学生成绩的平均分为77分,则x 的值为 ( ) A.73 B.74 C.75 D.765、在2016年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是 ( ) A .18,18,1 B .18,17.5,3 C .18,18,3 D .18,17.5,16、下列方程组中,是二元一次方程组的是 ( ) ⎪⎩⎪⎨⎧==+2131.xy x A ⎩⎨⎧=-=-6253.z y y x B ⎪⎩⎪⎨⎧==+1125.xy y x C ⎪⎩⎪⎨⎧=-=4232.x y x D7、有19位同学参加歌咏比赛,成绩互不相同,前10名的同学进入决赛。
某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学成绩的 ( ) A.平均数 B.标准差 C.中位数 D.方差8、如图,函数y=kx-2中,y 随x 的增大而减小,则它的图像是( ) 9、无论m 为何实数,直线m x y 2+=与4+-=x y 的交点不可能在( ). A.第一象限 B.第二象限 C.第三象限 D.第四象限 10、对于函数y=﹣x+3,下列说法错误的是 ( ) A .图象经过点(2,2) B .y 随着x 的增大而减小C .图象与y 轴的交点是(6,0)D .图象与坐标轴围成的三角形面积是9二、填空题:(每题3分、共8题,共24分)11、在一次函数y=kx+3中,y 的值随着x 值得增大而增大,请你写出一个符合条件的一次函数解析式________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京昌平临川育人学校2017届高三12月月考(文)本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页,满分150分,考试时间120分钟. 注意事项:1. 答第Ⅰ卷前,考生务必将自己的姓名、考试号、考试科目填涂在答题卡的相应位置.2. 每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.3. 第Ⅱ卷要用钢笔或圆珠笔写在给定答题纸的相应位置,答卷前请将答题纸密封线内的学校、班级、姓名、考试号填写清楚.考试结束,监考人员将答题卡和答题纸按顺序一并收回.第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中, 只有一项是符合题目要求的.1.设 ,,R ∈a b c ,且a>b ,则 ( )A.11a b< B.22a b > C.a c b c ->- D.ac>bc 2.等差数列的前n 项和为,且S 8=-24,=4,则公差d 等于( )A .1 B.C. 3D. -2 3.的内角A 、B 、C 的对边分别为a 、b 、c ,若,则等于( ) A .2B .3C .2D .64.在等比数列{}n a 中,221=+a a ,643=+a a ,则87a a +等于( ) A .52 B .53 C .54 D.555.如图所示,为了测量某障碍物两侧A ,B 间的距离,给定下列四组数据,不能确定A ,B 间距离的是 ( ){}n a n S 1a 53ABC △120c b B ===aA .α,β,bB .α,β,aC . a ,b ,γD .α,a ,b 6.△ABC 满足:cos cos cos ==a b cA B C,那么此三角形的形状是( ) A. 直角三角形 B. 正三角形 C. 任意三角形 D. 等腰三角形 7.下列函数中,最小值为4的是( ) A .4y x x =+B .4sin sin y x x =+(0)<<πx C. 4x x y e e=+ D. 3log 4log 3x y x =+ 8.某企业生产甲、乙两种产品,已知生产每吨甲产品要用A 原料3吨,B 原料2吨;生产每吨乙产品要用A 原料1吨,B 原料3吨. 销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A 原料不超过13吨,B 原料不超过18吨.那么该企业可获得最大利润是( )A. 12万元B. 20万元C. 25万元D. 27万元9.已知等差数列的前n 项和为n S ,且150S >,160S <,则此数列中绝对值最小的项为() A.第9项 B.第8项 C. 第7项 D.第6项10.当1x >时,不等式21mx mx x ++≥恒成立,则实数m 的取值范围是( ) A.)3⎡-+∞⎣B.)3⎡++∞⎣C.(,3-∞-D.(,3-∞+第Ⅱ卷(非选择题,共100分)二、填空题:(本大题共5小题,每小题5分,共25分.把答案填在题中横线上). 11.2242M a b a b =+-+的值与5-的大小关系是M -5; 12.已知等差数列{}n a 中,满足2136=+a a ,则18S =;13. 设0>a ,0>b ,若3是a 3与b3的等比中项,则ba 11+的最小值为; 14.数列{}n a 的前n 项和为n S ,若)12(1-221n -⨯=+n nn a )(,则n S =; 15.如图,测量河对岸的塔高时,可以选与塔底在同一水平面内的两个测点与.现测得,并在点测得塔顶的仰角为,则塔高AB =.AB B C D BCD BDC CD s αβ∠=∠==,,C A θ三、解答题(本大题共6小题,满分共75分) 16.(本小题满分12分)在ABC ∆中,角A ,B ,C 的对边分别为c b a ,,,且3=a ,3=b ,060=A ,求角B 和ABC ∆的面积.17.(本小题满分12分) 设函数2()f x x ax b =-+(Ⅰ)若不等式()0f x <的解集是{}|23x x <<,求不等式012>+-ax bx 的解集;(Ⅱ)当3b a =-时,()0f x ≥恒成立,求实数a 的取值范围.18.(本小题满分12分)已知数列{}n a 的前n 项和为2n S n n =+.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若n b na n +=)21(,求数列{}n b 的前n 项和n T .19.(本小题满分12分)在∆ABC 中,角A ,B ,C 的对边长分别为c b a ,,,且满足 (Ⅰ)求角B 的值;(Ⅱ)若,求∆ABC 的面积.20、(本小题满分13分)如图,将宽和长都为x ,y (x<y )的两个矩形部分重叠放在一起后形成的正十字形面积为45.(注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形)(Ⅰ)求y 关于x 的函数解析式;(Ⅱ)当x ,y 取何值时,该正十字形的外接圆直径d 最小,并求出其最小值.21.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,且22n n S a +=,且数列{}n b 满足11b =,12n n b b +=+.(Ⅰ)求数列{}n a ,{}n b 的通项公式;(2)cos cos 0c a B b A --=7,13b a c =+=(Ⅱ)设1(1)1(1)22n nn n n c a b --+-=-,求数列{}n c 的前2n 项和2n T . (III )求数列{}n n a b ⋅的前n 项和n R .参考答案一、选择题:(本大题共10小题,每小题5分,共50分) 1-5 CDACD 6-10 BCDBD二、填空题:(本大题共5小题,每小题5分,共25分) 11.≥12. 18 13. 4 14.12111--=+n n S 15.sin tan sin()⋅⋅+s βθαβ三、解答题(本大题共6小题,满分共75分)16.(12分)解:由正弦定理得213233sin sin =⨯==aAb B o 30=∴B 或 o 150,o 60=A 且 b a >,o 30=∴B . …………………6分090180=--=∴B A C ,23313321sin 21=⨯⨯⨯==∴∆C ab S ABC . …………………12分 17.(12分)解:(Ⅰ)因为不等式20x ax b -+<的解集是{}|23x x <<,所以2,3x x ==是方程20x ax b -+=的解,…… 2分由韦达定理得:5,6a b ==,故不等式210bx ax -++>为26510x x -+>, …… 4分解不等式26510x x -+>得其解集为11|,32x x x ⎧⎫<>⎨⎬⎩⎭或.……6分 (Ⅱ)据题意,2()30f x x ax a =-+-≥恒成立,则24(3)0a a ∆=--≤,…… 10分整理得:01242≤-+a a ,解得62a -≤≤. …… 12分18.(12分)解:(Ⅰ)当2≥n 时,221(1)(1)2n n n a S S n n n n n -=-=+----=,……4分 当1=n 时,12a =也适合上式,∴n a n 2=. …………………………6分 (Ⅱ)由(I )知,n n b n a n n+=+=)41()21(. ………………………8分∴211[(1())]111(1)44()()(12)444214n n n n n T n -+=+++++++=+- 11(1)[1()]342n n n +=-+. ………………………12分 19.(12分)解:(Ⅰ)由正弦定理得因为0sin ≠C ,所以21cos =B , 所以π3=B ……………………………………6分 (Ⅱ)因为B ac ac c a B ac c a b cos 22)(cos 22222--+=-+= 因为,π3=B分 20.(13分)解:(Ⅰ)因为5422=-x xy ,则x x y 2542+=,因为x y >,所以x xx >+2542,故4520<<x .所以解析式为xx y 2542+=(4520<<x ).(未给出x 的范围,酌情扣分)…6分(Ⅱ)由图可知+=+=2222x y x d 22)254(x x +=52204522++xx5210+≥ 当且仅当2=x ,15+=y 时,正十字形的外接圆直径d 最小,最小为5210+……………………………………13分21.(14分)解:(Ⅰ)由22n n S a +=,当2n ≥时,1122n n S a --+= 两式相减得,122n n n a a a -=-12n n a a -∴=,又因为当1n =时,1122S a +=,1122S a +=12a ∴={}n a ∴是等比数列,首项12a =,公比2q =,2n n a ∴=…………4分又有12n n b b +=+,所以12n n b b +-=,{}n b ∴是等差数列,首项11b =,公差2d =,21n b n ∴=-…………6分(2sin sin )cos sin cos 0,C A B B A --=2sin cos sin()0,sin (2cos 1)0C B A B C B ∴-+=∴-=7,13b a c =+=40ac ∴=1sin 2S ac B ∴==(Ⅱ)当n 为奇数时,2n n c =,当n 为偶数时,21n c n =-,352123521212232527...2(41)(222...2)[3711...(41)]2(14)(341)1422123n n n n n T n n n n n n--+∴=-+-+-++--=+++-++++--+-=---=--………………………………10分(III )由题意得231123252...(23)2(21)2n n n R n n -=⋅+⋅+⋅++-+-……①23412123252...(23)2(21)2n n n R n n +∴=⋅+⋅+⋅++-+-……②①-②得341+12(22...2)(21)2n n n R n +-=++++--3112(12)=2+(21)212n n n -+----1(23)26n n R n +∴=-+…………………14分。
