2018年中考备战策略数学《圆》阶段练习

合集下载

备战中考数学圆的综合综合题含详细答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．（1）如图1，在矩形ABCD 中，点O 在边AB 上，∠AOC =∠BOD ，求证：AO =OB ；（2）如图2，AB 是⊙O 的直径，PA 与⊙O 相切于点A ，OP 与⊙O 相交于点C ，连接CB ，∠OPA =40°，求∠ABC 的度数．【答案】（1）证明见解析；（2）25°.【解析】试题分析：（1）根据等量代换可求得∠AOD=∠BOC ，根据矩形的对边相等，每个角都是直角，可知∠A=∠B=90°，AD=BC ，根据三角形全等的判定AAS 证得△AOD ≌△BOC ，从而得证结论．（2）利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠POA 的度数，然后利用圆周角定理来求∠ABC 的度数．试题解析：（1）∵∠AOC=∠BOD∴∠AOC -∠COD=∠BOD-∠COD即∠AOD=∠BOC∵四边形ABCD 是矩形∴∠A=∠B=90°，AD=BC∴AOD BOC ∆≅∆∴AO=OB（2）解：∵AB 是O 的直径，PA 与O 相切于点A ， ∴PA ⊥AB ，∴∠A=90°.又∵∠OPA=40°，∴∠AOP=50°，∵OB=OC ，∴∠B=∠OCB.又∵∠AOP=∠B+∠OCB ， ∴1252B OCB AOP ∠=∠=∠=︒.2．如图,四边形ABCD 是⊙O 的内接四边形,AB=CD ．(1)如图(1),求证:AD ∥BC ；(2)如图(2),点F 是AC 的中点,弦DG ∥AB,交BC 于点E,交AC 于点M,求证:AE=2DF ；(3)在(2)的条件下,若DG 平分∠3∠3,求⊙O 的半径。

【答案】(1)证明见解析；（2）证明见解析；（3）129【解析】试题分析：(1)连接AC．由弦相等得到弧相等，进一步得到圆周角相等，即可得出结论．（2）延长AD到N，使DN=AD，连接NC．得到四边形ABED是平行四边形，从而有AD=BE，DN=BE．由圆内接四边形的性质得到∠NDC=∠B．即可证明ΔABE≌ΔCND，得到AE=CN，再由三角形中位线的性质即可得出结论．（3）连接BG，过点A作AH⊥BC，由（2）知∠AEB=∠ANC，四边形ABED是平行四边形，得到AB=DE．再证明ΔCDE是等边三角形，ΔBGE是等边三角形，通过解三角形ABE，得到AB，HB，AH，HE的长，由EC=DE=AB，得到HC的长．在Rt△AHC中，由勾股定理求出AC的长．作直径AP，连接CP，通过解△APC即可得出结论．试题解析：解：(1)连接AC．∵AB=CD，∴弧AB=弧CD，∴∠DAC=∠ACB，∴AD∥BC．（2）延长AD到N，使DN=AD，连接NC．∵AD∥BC，DG∥AB，∴四边形ABED是平行四边形，∴AD=BE，∴DN=BE．∵ABCD是圆内接四边形，∴∠NDC=∠B．∵AB=CD，∴ΔABE≌ΔCND，∴AE=CN．∵DN=AD，AF=FC，∴DF=1CN，∴AE=2DF．2（3）连接BG，过点A作AH⊥BC，由（2）知∠AEB=∠ANC，四边形ABED是平行四边形，∴AB=DE．∵DF∥CN，∴∠ADF=∠ANC，∴∠AEB=∠ADF，∴tan∠AEB= tan∠ADF=3DG平分∠ADC，∴∠ADG=∠CDG．∵AD∥BC，∴∠ADG=∠CED，∠NDC=∠DCE．∵∠ABC=∠NDC，∴∠ABC=∠DCE．∵AB∥DG，∴∠ABC=∠DEC，∴∠DEC=∠ECD=∠EDC，∴ΔCDE是等边三角形，∴AB=DE=CE．∵∠GBC=∠GDC=60°，∠G=∠DCB=60°，∴ΔBGE是等边三角形，BE= GE=53．∵tan∠AEB= tan∠ADF=43，设HE=x，则AH=43x．∵∠ABE=∠DEC=60°，∴∠BAH=30°，∴BH=4x，AB=8x，∴4x+x=53，解得：x=3，∴AB=83，HB=43，AH=12，EC=DE=AB=83，∴HC=HE+EC=383+=93．在Rt△AHC中，AC=222212(93)AH HC+=+=343．作直径AP，连接CP，∴∠ACP=90°，∠P=∠ABC=60°，∴sin∠P=AC AP，∴3432129sin603ACAP===︒，∴⊙O的半径是129．3．如图，在以点O为圆心的两个同心圆中，小圆直径AE的延长线与大圆交于点B，点D 在大圆上，BD与小圆相切于点F，AF的延长线与大圆相交于点C，且CE⊥BD．找出图中相等的线段并证明．【答案】见解析【解析】试题分析：由AE是小⊙O的直径，可得OA=OE，连接OF，根据切线的性质，可得OF⊥BD，然后由垂径定理，可证得DF=BF，易证得OF∥CE，根据平行线分线段成比例定理，可证得AF=CF，继而可得四边形ABCD是平行四边形，则可得AD=BC，AB=CD．然后连接OD、OC，可证得△AOD≌△EOC，则可得BC=AD=CE=AE．试题解析：图中相等的线段有：OA=OE，DF=BF，AF=CF，AB=CD，BC=AD=CE=AE．证明如下：∵AE是小⊙O的直径，∴OA=OE．连接OF，∵BD与小⊙O相切于点F，∴OF⊥BD．∵BD是大圆O的弦，∴DF=BF．∵CE⊥BD，∴CE∥OF，∴AF=CF．∴四边形ABCD是平行四边形．∴AD=BC，AB=CD．∵CE：AE=OF：AO，OF=AO，∴AE=EC．连接OD、OC，∵OD=OC，∴∠ODC=∠OCD．∵∠AOD=∠ODC，∠EOC=∠OEC，∴∠AOC=∠EOC，∴△AOD≌△EOC，∴AD=CE．∴BC=AD=CE=AE．【点睛】考查了切线的性质，垂径定理，平行线分线段成比例定理，平行四边形的判定与性质以及全等三角形的判定与性质等知识．此题综合性很强解题的关键是注意数形结合思想的应用，注意辅助线的作法，小心不要漏解．4．如图，已知在△ABC中，∠A=90°，（1）请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）．（2）若∠B=60°，AB=3，求⊙P的面积．【答案】（1）作图见解析；（2）3π【解析】【分析】（1）与AB、BC两边都相切．根据角平分线的性质可知要作∠ABC的角平分线，角平分线与AC的交点就是点P的位置．（2）根据角平分线的性质和30°角的直角三角形的性质可求半径，然后求圆的面积．【详解】解：（1）如图所示，则⊙P为所求作的圆．（2）∵∠ABC=60°，BP平分∠ABC，∴∠ABP=30°，∵∠A=90°，∴BP=2APRt△ABP中,AB=3，由勾股定理可得：3，∴S⊙P=3π5．已知：如图，在四边形ABCD中，AD∥BC．点E为CD边上一点，AE与BE分别为∠DAB和∠CBA的平分线．（1）请你添加一个适当的条件，使得四边形ABCD是平行四边形，并证明你的结论；（2）作线段AB的垂直平分线交AB于点O，并以AB为直径作⊙O（要求：尺规作图，保留作图痕迹，不写作法）；（3）在（2）的条件下，⊙O交边AD于点F，连接BF，交AE于点G，若AE=4，sin∠AGF=45，求⊙O的半径．【答案】（1）当AD=BC时，四边形ABCD是平行四边形，理由见解析；（2）作出相应的图形见解析；（3）圆O的半径为2.5．【解析】分析：（1）添加条件AD=BC，利用一组对边平行且相等的四边形为平行四边形验证即可；（2）作出相应的图形，如图所示；（3）由平行四边形的对边平行得到AD与BC平行，可得同旁内角互补，再由AE与BE为角平分线，可得出AE与BE垂直，利用直径所对的圆周角为直角，得到AF与FB垂直，可得出两锐角互余，根据角平分线性质及等量代换得到∠AGF=∠AEB，根据sin∠AGF的值，确定出sin∠AEB的值，求出AB的长，即可确定出圆的半径．详解：（1）当AD=BC时，四边形ABCD是平行四边形，理由为：证明：∵AD∥BC，AD=BC，∴四边形ABCD为平行四边形；故答案为：AD=BC；（2）作出相应的图形，如图所示；（3）∵AD∥BC，∴∠DAB+∠CBA=180°，∵AE与BE分别为∠DAB与∠CBA的平分线，∴∠EAB+∠EBA=90°，∴∠AEB=90°，∵AB为圆O的直径，点F在圆O上，∴∠AFB=90°，∴∠FAG+∠FGA=90°，∵AE平分∠DAB，∴∠FAG=∠EAB，∴∠AGF=∠ABE，∴sin∠ABE=sin∠AGF=45AE AB ，∵AE=4，∴AB=5，则圆O 的半径为2.5．点睛：此题属于圆综合题，涉及的知识有：圆周角定理，平行四边形的判定与性质，角平分线性质，以及锐角三角函数定义，熟练掌握各自的性质及定理是解本题的关键．6．如图，已知AB 是⊙O 的直径，P 是BA 延长线上一点，PC 切⊙O 于点C ，CD ⊥AB ，垂足为D ．（1）求证：∠PCA ＝∠ABC ；（2）过点A 作AE ∥PC 交⊙O 于点E ，交CD 于点F ，交BC 于点M ，若∠CAB ＝2∠B ，CF ＝3，求阴影部分的面积．【答案】（1）详见解析；（2）633π-. 【解析】【分析】（1）如图，连接OC ，利用圆的切线的性质和直径对应的圆周角是直角可得∠PCA=∠OCB ，利用等量代换可得∠PCA=∠ABC.（2）先求出△OCA 是等边三角形，在利用三角形的等边对等角定理求出FA=FC 和CF=FM,然后分别求出AM 、AC 、MO 、CD 的值，分别求出0A E S ∆、BOE S 扇形、ABM S ∆ 的值，利用0A E ABM BOE S S S S ∆∆=+-阴影部分扇形，然后通过计算即可解答.【详解】解：（1）证明：连接OC ，如图，∵PC 切⊙O 于点C ，∴OC ⊥PC,∴∠PCA+∠ACO=90º,∵AB 是⊙O 的直径，∴∠ACB=∠ACO+OCB=90º∴∠PCA=∠OCB,∵OC=OB,∴∠OBC=∠OCB,∴∠PCA=∠ABC ；（2）连接OE ，如图，∵△ACB 中，∠ACB ＝90º,∠CAB ＝2∠B,∴∠B ＝30º,∠CAB ＝60º,∴△OCA 是等边三角形，∵CD ⊥AB,∴∠ACD+∠CAD ＝∠CAD ＋∠ABC ＝90º,∴∠ACD ＝∠B ＝30º,∵PC ∥AE,∴∠PCA ＝∠CAE ＝30º,∴FC=FA,同理，CF ＝FM,∴AM ＝2CF=23,Rt △ACM 中，易得AC=23×3=3＝OC, ∵∠B ＝∠CAE ＝30º,∴∠AOC=∠COE=60º,∴∠EOB=60º,∴∠EAB=∠ABC=30º,∴MA=MB,连接OM,EG ⊥AB 交AB 于G 点，如图所示，∵OA=OB,∴MO ⊥AB,∴MO ＝3∵△CDO ≌△EDO(AAS)，∴332 ∴1332ABM S AB MO ∆=⨯= 同样，易求93AOE S ∆=， 260333602BOE S ππ⨯==扇形 ∴0A E ABM BOE S S S S ∆∆=+-阴影部分扇形933633332ππ-+-=. 【点睛】本题考查了切线的性质、解直角三角形、扇形面积和识图的能力，综合性较强，有一定难度，熟练掌握定理并准确识图是解题的关键.7．如图，已知AB为⊙O的直径，AB=8，点C和点D是⊙O上关于直线AB对称的两个点，连接OC、AC，且∠BOC＜90°，直线BC和直线AD相交于点E，过点C作直线CG与线段AB的延长线相交于点F，与直线AD相交于点G，且∠GAF＝∠GCE（1）求证：直线CG为⊙O的切线；（2）若点H为线段OB上一点，连接CH，满足CB＝CH，①△CBH∽△OBC②求OH＋HC的最大值【答案】（1）证明见解析；（2）①证明见解析；②5.【解析】分析：（1）由题意可知：∠CAB=∠GAF，由圆的性质可知：∠CAB=∠OCA，所以∠OCA=∠GCE，从而可证明直线CG是⊙O的切线；（2）①由于CB=CH，所以∠CBH=∠CHB，易证∠CBH=∠OCB，从而可证明△CBH∽△OBC；②由△CBH∽△OBC可知：BC HBOC BC＝，所以HB=24BC，由于BC=HC，所以OH+HC=4−24BC+BC，利用二次函数的性质即可求出OH+HC的最大值．详解：（1）由题意可知：∠CAB=∠GAF，∵AB是⊙O的直径，∴∠ACB=90°∵OA=OC，∴∠CAB=∠OCA，∴∠OCA+∠OCB=90°，∵∠GAF=∠GCE，∴∠GCE+∠OCB=∠OCA+∠OCB=90°，∵OC是⊙O的半径，∴直线CG是⊙O的切线；（2）①∵CB=CH，∴∠CBH=∠CHB，∵OB=OC，∴∠CBH=∠OCB，∴△CBH∽△OBC②由△CBH ∽△OBC 可知：BC HB OC BC ＝ ∵AB=8，∴BC 2=HB•OC=4HB ， ∴HB=24BC ， ∴OH=OB-HB=4-24BC ∵CB=CH ，∴OH+HC=4−24BC +BC ，当∠BOC=90°，此时BC=42 ∵∠BOC ＜90°， ∴0＜BC ＜42，令BC=x 则CH=x ，BH=24x ()221142544OH HC x x x ∴+=-++=--+ 当x=2时，∴OH+HC 可取得最大值，最大值为5点睛：本题考查圆的综合问题，涉及二次函数的性质，相似三角形的性质与判定，切线的判定等知识，综合程度较高，需要学生灵活运用所知识．8．如图，是大半圆的直径，是小半圆的直径，点是大半圆上一点，与小半圆交于点，过点作于点. （1）求证：是小半圆的切线；（2）若，点在上运动（点不与两点重合），设，. ①求与之间的函数关系式，并写出自变量的取值范围； ②当时，求两点之间的距离.【答案】（1）见解析；（2）①，，②两点之间的距离为或.【解析】【分析】（1）连接CO、CM，只需证到CD⊥CM．由于CD⊥OP，只需证到CM∥OP，只需证到CM 是△AOP的中位线即可．（2）①易证△ODC∽△CDP，从而得到CD2=DP•OD，进而得到y与x之间的函数关系式．由于当点P与点A重合时x=0，当点P与点B重合时x=4，点P在大半圆O上运动（点P不与A，B两点重合），因此自变量x的取值范围为0＜x＜4．②当y=3时，得到-x2+4x=3，求出x．根据x的值可求出CD、PD的值，从而求出∠CPD，运用勾股定理等知识就可求出P，M两点之间的距离．【详解】（1）连接，如图1所示∵是小半圆的直径，∴即∵∴∵∴∴，∵∴，∴∴.，即∵经过半径的外端，且∴直线是小半圆的切线.（2）①∵，，∴∴∴∽∴∴∵,,，∴当点与点重合时，；当点与点重合时，∵点在大半圆上运动（点不与两点重合），∴∴与之间的函数关系式为，自变量的取值范围是.②当时，解得,Ⅰ当时，如图2所示在中，∵，∴，∴∵，∴是等边三角形∵∴∴.Ⅱ当时，如图3所示，同理可得∵∴∴过点作，垂足为，连接，如图3所示∵，∴同理在中，∵，∴综上所述，当时，两点之间的距离为或.【点睛】考查了切线的判定、平行线的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质、特殊角的三角函数值、勾股定理等知识，综合性比较强．9．结果如此巧合!下面是小颖对一道题目的解答．题目：如图，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积．解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x．根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x．根据勾股定理，得（x+3）2+（x+4）2=（3+4）2．整理，得x2+7x=12．所以S△ABC=12 AC•BC=12（x+3）（x+4）=12（x2+7x+12）=12×（12+12）=12．小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积．这仅仅是巧合吗？请你帮她完成下面的探索．已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n．可以一般化吗？（1）若∠C=90°，求证：△ABC的面积等于mn．倒过来思考呢？（2）若AC•BC=2mn，求证∠C=90°．改变一下条件……（3）若∠C=60°，用m、n表示△ABC的面积．【答案】（1）证明见解析；（2）证明见解析；（3）S△ABC=3mn；【解析】【分析】（1）设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，仿照例题利用勾股定理得（x＋m）2＋（x＋n）2＝（m＋n）2，再根据S△ABC＝AC×BC，即可证明S△ABC＝mn.（2）由AC•BC＝2mn，得x2＋（m＋n）x＝mn，因此AC2＋BC2＝（x＋m）2＋（x＋n）2＝AB2，利用勾股定理逆定理可得∠C＝90°.（3）过点A作AG⊥BC于点G，在Rt△ACG中，根据条件求出AG、CG，又根据BG＝BC－CG得到BG .在Rt△ABG中，根据勾股定理可得x2＋（m＋n）x＝3mn，由此S△ABC＝BC•AG＝mn.【详解】设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，根据切线长定理，得：AE＝AD＝m、BF＝BD＝n、CF＝CE＝x，（1）如图1，在Rt△ABC中，根据勾股定理，得：（x＋m）2＋（x＋n）2＝（m＋n）2，整理，得：x2＋（m＋n）x＝mn，所以S△ABC＝AC•BC＝（x＋m）（x＋n）＝[x2＋（m＋n）x＋mn]＝（mn＋mn）＝mn;（2）由AC•BC＝2mn，得：（x＋m）（x＋n）＝2mn，整理，得：x2＋（m＋n）x＝mn，∴AC2＋BC2＝（x＋m）2＋（x＋n）2＝2[x2＋（m＋n）x]＋m2＋n2＝2mn＋m2＋n2＝（m＋n）2＝AB2，根据勾股定理逆定理可得∠C＝90°；（3）如图2，过点A作AG⊥BC于点G，在Rt△ACG中，AG＝AC•sin60°＝（x＋m），CG＝AC•cos60°＝（x＋m），∴BG＝BC﹣CG＝（x＋n）﹣（x＋m），在Rt△ABG中，根据勾股定理可得：[（x＋m）]2＋[（x＋n）﹣（x＋m）]2＝（m＋n）2，整理，得：x2＋（m＋n）x＝3mn，∴S△ABC＝BC•AG＝×（x＋n）•（x＋m）＝3x2＋（m＋n）x＋mn]＝3（3mn＋mn）3．【点睛】本题考查了圆中的计算问题、与圆有关的位置关系以及直角三角形，注意掌握方程思想与数形结合思想的应用.10．如图，AB是⊙O的直径，∠ACB的平分线交AB于点D，交⊙O于点E，过点C作⊙O 的切线CP交BA的延长线于点P，连接AE．（1）求证：PC=PD；（2）若AC=5cm，BC=12cm，求线段AE，CE的长．【答案】(1)见解析 (2) EC=172AE=132【解析】试题分析：（1）如图1中，连接OC、OE．利用等角的余角相等，证明∠PCD=∠PDC即可；（2）如图2中．作EH⊥BC于H，EF⊥CA于F．首先证明Rt△AEF≌Rt△BEH，推出AF=BH，设AF=BH=x，再证明四边形CFEH是正方形，推出CF=CH，可得5+x=12﹣x，推出x=72，延长即可解决问题；试题解析：（1）证明：如图1中，连接OC、OE．∵AB直径，∴∠ACB=90°，∴CE平分∠ACB，∴∠ECA=∠ECB=45°，∴AE=BE，∴OE⊥AB，∴∠DOE=90°．∵PC是切线，∴OC⊥PC，∴∠PCO=90°．∵OC=OE，∴∠OCE=∠OEC．∵∠PCD+∠OCE=90°，∠ODE+∠OEC=90°，∠PDC=∠ODE，∴∠PCD=∠PDC，∴PC=PD．（2）如图2中．作EH⊥BC于H，EF⊥CA于F．∵CE平分∠ACB，EH⊥BC于H，EF⊥CA于F，∴EH=EF，∠EFA=∠EHB=90°．∵AE=BE，∴AE=BE，∴Rt△AEF≌Rt△BEH，∴AF=BH，设AF=BH=x．∵∠F=∠FCH=∠CHE=90°，∴四边形CFEH是矩形．∵EH=EF，∴四边形CFEH是正方形，∴CF=CH，∴5+x=12﹣x，∴x =72，∴CF =FE =172，∴EC CF =2，AE 点睛：本题考查了切线的性质、圆周角定理、勾股定理、垂径定理、正方形的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．。

2018中考数学中考数学复习模块4圆之典型中考题讲解有详细答案.docx

《中考数学复习模块4•圆》之典型中考题讲解1、（2017-金华）如图，已知：AB是的直径，点C在（DO上，CD是（DO的切线，AD丄CD于点D.E是AB延长线上一点，CE交（DO于点F,连结OC,AC.（1）求证:AC平分ZDA0.（2）若ZDAO=105°, ZE=30°.①求ZOCE的度数.②若的半径为2运，求线段EF的长.2、（2017浙江台州）.如图，已知等腰直角三角形ABC,点P是斜边BC 上一点（不与B, C重合），PE是△ ABP的外接圆（DO的直径.（1）求证：△ APE是等腰直角三角形；（2）若的直径为2,求PC2+PB2的值.3、（2017山东枣庄）.如图，在△ ABC中，ZC=90°, ZBAC的平分线交BC于点D,点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D,分别交AC, AB于点E, F.（1）试判断直线BC与。

0的位置关系，并说明理由；（2）若BD=2V3, BF=2,求阴影部分的面积（结果保留兀）. 4、（2017山东聊城）.如图，OO是△ ABC的外接圆，O点在BC边上，ZBAC的平分线交于点D,连接BD、CD,过点D 作BC的平行线，与AB的延长线相交于点P.（1）求证：PD是（DO的切线；（2）求证：APBDsADCA；D （3）当AB=6, AO8时，求线段PB的长.5、（2017山东东营）.如图，在△ ABC中，AB=AC,以AB为直径的（DO交BC于点D,过点D作的切线DE,交AC于点E, AC 的反向延长线交于点F.（1）求证：DE丄AG；（2）若DE+EA=8, OO的半径为10,求AF的长度.6、（2017山东潍坊）.如图，AB为半圆O的直径，AC是（DO 的一条弦，D为辰的中点，作DE丄AC,交AB的延长线于点F,连接DA.（1）求证：EF为半圆O的切线；（2）若DA=DF=6J5,求阴影区域的面积.（结果保留根号和兀）7、（2017江苏无锡）.如图，以原点O为圆心，3为半径的圆与x轴分别交于4, B两点（点B在点4的右边），P是半径OB上一点，过P且垂直于AB的直线与分别交于C, D两点（点C在点D的上方），直线AC, DB交于点E.若AC：CE=1： 2.（1）求点P的坐标；（2）求过点4和点E,且顶点在直线CD上的抛物线的函数表达式.8、（2017江苏盐城）.如图，在平面直角坐标系中，RtA ABC的斜边AB在y 轴9、(2017湖北襄阳).如图，AB为(DO的直径，C、D为©O ±的两点，ZBAOZDAC,过点C做直线EF丄AD,交AD的延长线于点E,连接BC.(1)求证：EF是(DO的切线；(2)若DE=1, BC=2,求劣弧晓的长1.10、(2017湖北恩施).如图，AB、CD是(DO的直径，BE是(DO 的弦，且BE〃CD,过点C的切线与EB的延长线交于点P,连接BC.(1)求证：BC平分ZABP；(2)求证：PC2=PB«PE；(3)若BE-BP=PC=4,求(DO 的半径.11、（2017 湖北随州）.如图，在RtA ABC 中，ZC=90°, AC=BC,点O在AB上，经过点A的（DO与BC相切于点D,交AB于点E.（1）求证：AD平分ZBAC；（2）若CD=1,求图中阴影部分的面积（结果保留兀）.12、（2017湖北宜昌）.已知，四边形ABCD中，E是对角线AC上一点，DE=EC, 以AE为直径的与边CD相切于点D. B点在（DO上，连接0B.（1）求证：DE=OE；/一:（2）若CD〃AB,求证：四边形ABCD是菱形. / 丿/答案：1、(1)解：•.•直线与(DO相切，AOC 丄CD；又VAD丄CD,.•.AD//OC,/.ZDAC=ZOCA;又VOC=OA,.*.ZOAC=ZOCA,.*.ZDAC=ZOAC;••.AC 平分ZDA.O.(2)解:①TAD//OC, ZDAO=105°,ZEOC=ZDAO=105°;T ZE=30°,ZOCE=45°.②作OG丄CE于点G,可得FG=CG,VOC=2\P,ZOCE=45°..\CG=OG=2,.*.FG=2;*.•在RTA OGE 中,ZE=30°,:.GE=2^, .\EF=GE-FG=2V3-2.2、(1)证明：VAB=AC, ZBAC=90°,/.ZC=ZABC=45°,A ZAEP=ZABP=45°,VPE是直径，/. ZPAB=90°,A ZAPE=ZAEP=45°,.*.AP=AE,•••△PAE是等腰直角三角形.(2)作PM丄AC于M, PN丄AB于N,则四边形PMAN是矩形, .*.PM=AN,「△PCM, △ PNB都是等腰直角三角形，.•.PCpPM, PBpPN,/.PC2+PB2=2 (PM2+PN2) =2 (AN2+PN2) =2PA2=PE2=22=4.3、解：(1) BC与(DO相切. 证明：连接OD.TAD是ZBAC的平分线，.*.ZBAD=ZCAD.又TODOA,.*.ZOAD=ZODA./.ZCAD=ZODA..•.OD〃AC..•.ZODB=ZC=90°,即0D±BC. 又TBC过半径OD的外端点D, ABC与(DO相切.(2)设0F=OD=x,则OB=OF+BF=x+2, 根据勾股定理得：OB2=C)D2+BD2,即(x+2) 2=X2+12,解得：x=2,即OD=OF=2,/. OB=2+2=4,VRtA ODB 中，OD=*3B,:.ZB=30°,/.ZDOB=60°,• u_60K X4_2H••S 號AOB-，则阴影部分的面积为S A ODB -S麻DOF=*X2X2*\/^-2? -故阴影部分的面积为2^3 -写.4、(1)证明：•.•圆心0在BC±,ABC是圆O的直径，.\ZBAC=90o, 连接OD,TAD 平分ZBAC,ZBAO2ZDAC,VZDOC=2ZDAC,.•.ZDOC=ZBAC=90°,即OD丄BC,VPD/7BC,AOD 丄PD,TOD为圆O的半径，.•.PD是圆O的切线；(2)证明：•.•PD〃BC,.*.ZP=ZABC,T ZABOZADC,.*.ZP=ZADC,T ZPBD+ZABD=180°, ZACD+ZABD=180°,A ZPBD=ZACD,.•.APBD^ADCA；(3)解：••'△ABC为直角三角形，BC2=AB2+AC2=62+82=100,.\BC=10,TOD垂直平分BC,.*.DB=DC,VBC为圆O的直径，.•.ZBDC=90°,在RtA DBC 中，DB2+DC2=BC2,即2DC2=BC2=100,.\DC=DB=5V2-V APBD^ADCA,.PB_BD''~DC~W川"9_DC・BD_Sx奶_25人AC 8 4 -5、(1)证明：VOB=OD,.*.ZABC=ZODB,VAB=AC,.•.ZABOZACB,.*.ZODB=ZACB,.•.OD〃AC.「DE是(DO的切线，OD是半径,.'.DE 丄OD,A DEX AC；(2)如图，过点0 作OH丄AF于点H,则ZODE= ZDEH= ZOHE=90°, •••四边形ODEH是矩形，.*.OD=EH, OH=DE.设AH=x.VDE+AE=8, OD=10,/. AE=10 - x, 0H=DE=8 - ( 10 - x) =x - 2.在RtA AOH中，由勾股定理知：AH2+OH2=OA2,即x2+ (x-2) 2=102,解得xi=8, x2= - 6 (不合题意，舍去)..\AH=8.TOHIAF,.*.AH=FH=—AF,2・：AF=2AH=2x8 二16.6、(1)证明：连接OD,VD为说的中点，/.ZCAD=ZBAD,VOA=OD,A ZBAD=ZADO,.•.ZCAD=ZADO,VDE 丄AC,ZE=90°,ZCAD+ZEDA=90°,即ZADO+ZEDA=90°,AOD 丄EF,・・.EF为半圆O的切线；(2)解：连接OC与CD,VDA=DF,A ZBAD=ZF,A ZBAD=ZF=ZCAD,又T ZBAD+ ZCAD+ ZF=90°,A ZF=30°, ZBAC=60°,VOC=OA,AAOC为等边三角形，ZAOC=60°, ZCOB=120°,TOD丄EF, ZF=30°,.•.ZDOF=60°,在RtA ODF 中,DF=6屈OD=DF *tan3 0°=6,在RtA AED 中，D26胰,ZCAD=30°, /. DE=DA*sin30 "晶,EA=DA*cos30°=9, T ZCOD=180° - ZAOC - ZDOF=60°, /. CD/7 AB,故S △ACD-S A COD，•'•S 阴萨S A AED -S扇旳COD=*<9X3后-~^Q nX^2=~^~ ~ ^71-7、解：(1)如图，作EF丄y轴于F, DC的延长线交EF于H.设H (m, “), 则P (m, 0), PA=m+3, PB=3 - m.EH//AP,△ACPs&CH,AC = PC = AP=j_CE_CH_'^7，CH=2n, EH=2m=6,CD 丄AB,PC=PD=n,PB//HE,ADPB s'DHE,PB」)P_ n _13-m _ 12nH-6 4'm=l,P (1, 0).(2)由(1)可知，PA=4, HE=8, EF=9, 连接OP,在R仏OCP中，PC=7OC^O P=2V2-:.CH=2PC=4皈 PH=6屈:.E (9, 6冋,•••抛物线的对称轴为CD,:.(-3, 0)和(5, 0)在抛物线上，设抛物线的解析式为尸a (x+3) (%-5), 把E (9, 6迈)代入得到a欝,•••抛物线的解析式为尸誓.&+3) &-5),即尸导2-孚-耳Z8、(1)证明：连接EF,TAE 平分ZBAC,/. ZFAE=ZCAE,VFA=FE,ZFAE=ZFEA, /. ZFEA=ZEAC,.・.FE〃AC,ZFEB=ZC=90°,即BC 是OF 的切线;(2)解：连接FD,设。

中考数学复习《圆》专题训练-附带有答案

中考数学复习《圆》专题训练-附带有答案一、选择题1．下列有关圆的一些结论：①平分弧的直径垂直于弧所对的弦；②平分弦的直径垂直于弦；③在同圆或等圆中，相等的弦所对的圆周角相等；④同弧或等弧所对的弦相等，其中正确的有（）A．①④B．②③C．①③D．②④2．在同一平面内，已知⊙O的半径为3cm，OP＝4cm，则点P与⊙O的位置关系是（）A．点P在⊙O圆外B．点P在⊙O上C．点P在⊙O内D．无法确定3．如图，AB是⊙O的直径，C是⊙O上一点．若∠BOC＝66°（）A．66°B．33°C．24°D．30°4．如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠CDA＝118°，则∠C的度数为（）A．32°B．33°C．34°D．44°5．如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=26°，则∠D等于（）A．26°B．48°C．38°D．52°6．如图，四边形ABCD内接于⊙O，∠C＝100°，那么∠A是（）A．60°B．50°C．80°D．100°7．如图，AB为⊙O的直径，C是⊙O上的一点，若∠BCO=35°，AO=2，则AC⌢的长度为（）A．29πB．59πC．πD．79π8．如图，点A、B、C、D、E都是⊙O上的点AC⌢=AE⌢，∠D=130°则∠B的度数为（）A．130°B．128°C．115°D．116°二、填空题9．半径为6的圆上，一段圆弧的长度为3π，则该弧的度数为°.10．如图，在△ABC中，∠ACB= 130°，∠BAC=20°，BC=2．以C为圆心，CB为半径的圆交AB于点D，则BD的长为.11．如图，⊙O是△ABC的外接圆，BC是⊙O的直径，AB=AC．∠ABC的平分线交AC于点D，交⊙O于点E，连结CE．若CE= √2，则BD的长为.12．如图，四边形ABCD为⊙O的内接四边形，若∠ADC=85°，则∠B=．13．如图，在△ABC中∠ACB=90°，O为BC边上一点CO=2.以O为圆心，OC为半径作半圆与AB边交π，则阴影部分的面积为.于E，且OE⊥AB.若弧CE的长为43三、解答题14．如图，AB是⊙O的直径，四边形ABCD内接于⊙O，OD交AC于点E，OD∥BC（1）求证：AD＝CD；（2）若AC＝8，DE＝2，求BC的长.15．如图，AB是⊙O的直径，F为⊙O上一点，AC平分∠FAB交⊙O于点C.过点C作CD⊥AF交AF的延长线于点D.（1）求证：CD是⊙O的切线.（2）若DC＝3，AD＝9，求⊙O半径.⌢上一点，AG与DC的延长线交于点F．16．已知，如图，AB是⊙O的直径，弦CD⊥AB于点E，G是AC（1）如CD=8，BE=2，求⊙O的半径长；（2）求证：∠FGC=∠AGD．17．如图，在△ABC中AB=AC，以底边BC为直径的⊙O交两腰于点D，E .（1）求证：BD=CE；⌢的长.（2）当△ABC是等边三角形，且BC=4时，求DE18．如图，在△ABC中，经过A，B两点的⊙O与边BC交于点E，圆心O在BC上，过点O作OD⊥BC交⊙O 于点D，连接AD交BC于点F，且AC＝FC．（1）试判断AC与⊙O的位置关系，并说明理由；（2）若FC＝√3，CE＝1．求图中阴影部分的面积（结果保留π）．参考答案1．A2．A3．B4．C5．C6．C7．D8．C9．9010．2√311．2√212．95°π13．4√3−4314．（1）证明：∵AB是⊙O的直径∴∠ACB＝90°∵OD∥BC∴∠AEO＝∠ACB＝90°⌢＝CD⌢∴AD∴AD＝CD；（2）解：∵OD⊥AC，AC＝8AC＝4∴AE＝12设⊙O的半径为r∵DE＝2∴OE＝OD﹣DE＝r﹣2在Rt△AEO中，AE2+OE2＝AO2∴16+（r﹣2）2＝r2解得：r＝5∴AB＝2r＝10在Rt△ACB中，BC＝√AB2−AC2＝√102−82＝6∴BC的长为6.15．（1）证明：连接OC∵AC平分∠FAB∴∠FAC＝∠CAO∵AO＝CO∴∠ACO＝∠CAO∴∠FAC＝∠ACO∴AD∥OC∵CD⊥AF∴CD⊥OC∵OC为半径∴CD是⊙O的切线；（2）解：过点O作OE⊥AF于EAF，∠OED＝∠EDC＝∠OCD＝90°∴AE＝EF＝12∴四边形OEDC为矩形∴CD＝OE＝3，DE＝OC设⊙O的半径为r，则OA＝OC＝DE＝r∴AE＝9﹣r∵OA2﹣AE2＝OE2∴r2﹣（9﹣r）2＝32解得r＝5.∴⊙O半径为5.16．（1）解：连接OC．设⊙O的半径为R．∵CD⊥AB∴DE=EC=4在Rt △OEC中，∵OC2=OE2+EC2∴R2=(R−2)2+42解得R=5．（2）解：连接AD∵弦CD⊥AB̂ = AĈ∴AD∴∠ADC=∠AGD∵四边形ADCG是圆内接四边形∴∠ADC=∠FGC∴∠FGC=∠AGD．17．（1）证明：∵AB=AC∴∠B=∠C⌢=BE⌢∴CD⌢=CE⌢∴BD∴BD=CE；（2）解：连接OD、OE∵△ABC 是等边三角形∴∠B =∠C =60°∴∠COD =120°∴∠COD +∠BOE =∠COE +∠DOE +∠BOD +∠DOE =240° ∴∠DOE =240°−180°=60°∵BC =4∴⊙O 的半径为 2∴DE ⌢ 的长 =60π×2180=2π3 .18．（1）解：AC 与⊙O 的相切，理由如下∵AO =DO∴∠D =∠OAD∵CF =CA∴∠CAF =∠CFA又∵∠CFA =∠OFD∴∠CAF =∠OFD∵OD ⊥BC∴∠OFD +∠ODF =90°∴∠CAF +∠OAF =90°∴OA ⊥AC∵OA 是半径∴AC 是⊙O 的切线∴ AC 与⊙O 的相切；（2）解：过A 作AM ⊥BC 于M ，如图设OA=OE=r∵FC=√3，CE=1在Rt△CAO中AO=r，AC=FC=√3，OC=OE+EC=r+1AO2+AC2=OC2∴r2+(√3)2=(r+1)2解得r=1∴OC=OE+EC=2∴AO=12 OC∴∠C=30°∴∠AOC=60°∴∠AOB=180−∠AOC=120°在Rt△CAM中AM=12AC=12FC=√32∴S△AOB=12⋅OB⋅AM=12×1×√32=√34∴S扇形AOB=120360π×1=π3∴S阴影部分=S△AOB−S扇形AOB=π3−√34．。

2018年中考数学压轴题之圆题例题

广东中考数学专题训练（二）：几何综合题（圆题）例题训练1．如图，⊙O 为∆ABC 外接圆，BC 为⊙O 直径，BC =4．点D 在⊙O 上，连接OA 、CD 和BD ，AC 与BD 交于点E ，并作AF ⊥BC 交BD 于点G ，点G 为BE 中点，连接OG ．（1）求证：OA ∥CD ；（2）若∠DBC =2∠DBA ，求BD 的长；（3）求证：FG =2DE ．2．如图，⊙O 为∆ABC 外接圆，AB 为⊙O 直径，AB =4．⊙O 切线CD 交BA 延长线于点D ，∠ACB 平分线交⊙O 于点E ，并以DC为边向下作∠DCF =∠CAB 交⊙O 于点F ，连接AF ．（1）求证：∠DCF =∠D +∠B ；（2）若AF =32，AD =52，求线段AC 的长；（3）若CEAB ⊥CF ．3．如图，⊙O为 ABC外接圆，BC为⊙O直径．作»AD=»AC，连接AD、CD和BD，AB与CD交于点E，过点B作⊙O 切线，并作点E作EF⊥DC交切线于点G．（1）求证：∠DAC=∠G+90°；（2）求证：CF=GF；（3）若EFBD=23，求证：AE=DE．4．如图，⊙O 为 ABC 外接圆，AB 为⊙O 直径．连接CO ，并作AD ∥CO 交⊙O 于点D ，过点D 作⊙O 切线DE 交CO 延长线于点E ，连接BE ，作AF ⊥CO 交BC 于点G ，交BE 于点H ，连接OG ．（1）若CF =2，OF =3，求AC 的长；（2）求证：BE 是⊙O 的切线；（3）若2AF AHDE g =23，求证：OG ⊥AB ．。

浙江省2018年中考数学《圆》总复习阶段检测试卷含答案

为
.
三、解答题 (本大题有 8 小题，第 17～ 20 题每题 8 分，第 21 题 10 分，第 22、 23 题每
题 12 分，第 24 题 14 分，共 80 分 )
17．如图， AB 是 ⊙ O 的直径， C， D 两点在 ⊙ O 上，若 ∠C ＝ 45° .
第 17 题图 (1)求 ∠ ABD 的度数； (2)若 ∠ CDB ＝ 30°， BC ＝ 3，求 ⊙ O 的半径．
第 11 题图
第 12 题图
第 13 题图
12．将量角器按如图所示的方式放置在三角形纸板上，使顶点的读数分别为 100°、 150°，则 ∠ ACB 的大小为
C 在半圆上，点 A 、B 度．
13．如图，正方形 ABCD 内接于半径为 2 的 ⊙ O，则图中阴影部分的面积为 ___________．
阶段检测 7 圆
一、选择题 (本大题有 10 小题，每小题 4 分，共 40 分．请选出各小题中唯一的正确选项，不选、多选、错选，均不得分 )
1．在公园的 O 处附近有 E 、F 、 G、 H 四棵树，位置如图所示 (图中小正方形的边长均
相等 )现计划修建一座以 O 为圆心， OA 为半径的圆形水池，要求池中不留树木，则
C．∠ CAD 绕点 A 顺时针旋转一定能与 ∠ DAB 重合 D．线段 ID 绕点 I 顺时针旋转一定能与线段 IB 重合 8．已知 ∠ BAC ＝ 90°，半径为 r 的圆 O 与两条直角边 AB， AC 都相切，设 AB ＝ a(a ＞r )，BE 与圆 O 相切于点 E. 现给出下列命题： ① 当 ∠ ABE ＝ 60°时，BE＝ 3r ；② 当∠ ABE ＝90°时， BE ＝ r；则下列判断正确的是 ( )

2018年中考冲刺---圆的综合题-学习文档

教学内容知识精要一、圆1、圆的有关概念与性质圆的概念：圆是到定点的距离等于定长的点的集合。

圆的内部：圆的内部可以看作是到圆心的距离小于半径的点的集合。

圆的外部：圆的外部可以看作是到圆心的距离大于半径的点的集合。

直径与弧：连结圆上任意两点的线段叫做弦，经过圆心的弦叫直径。

圆上任意两点间的部分叫圆弧，简称弧。

优弧劣弧：圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫半圆，大于半圆的弧叫优弧；小于半圆的弧叫劣弧。

由弦及其所对的弧组成的图形叫弓形。

同心圆与等圆等弧：圆心相同，半径不相等的两个圆叫同心圆，能够重合的两个圆叫等圆，同圆或等圆的半径相等，在同圆或等圆中，能够互相重合的弧叫等弧。

二、过三点的圆过三点的圆的作法：利用中垂线找圆心定理：不在同一直线上的三个点确定一个圆。

经过三角形各顶点的圆叫三角形的外接圆，外接圆的圆心叫外心，这个三角形叫圆的内接三角形。

三、垂直于弦的直径圆是轴对称图形，经过圆心的每一条直线都是它的对称轴。

垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

推理1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对两条弧。

弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。

推理2：圆两条平行弦所夹的弧相等。

四、圆心角、弧、弦、弦心距之间的关系圆是以圆心为对称中心的中心对称图形。

实际上，圆绕圆心旋转任意一个角度，都能够与原来的图形重合。

顶点是圆心的角叫圆心角，从圆心到弦的距离叫弦心距。

定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距相等。

推理：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中，有一组量相等，那么它们所对应的其余各组量都分别相等。

五、圆周角顶点在圆上，并且两边都和圆相交的角叫圆周角。

推理1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等。

推理2：半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径。

2018中考数学总复习圆训练题(江西含答案和解释)

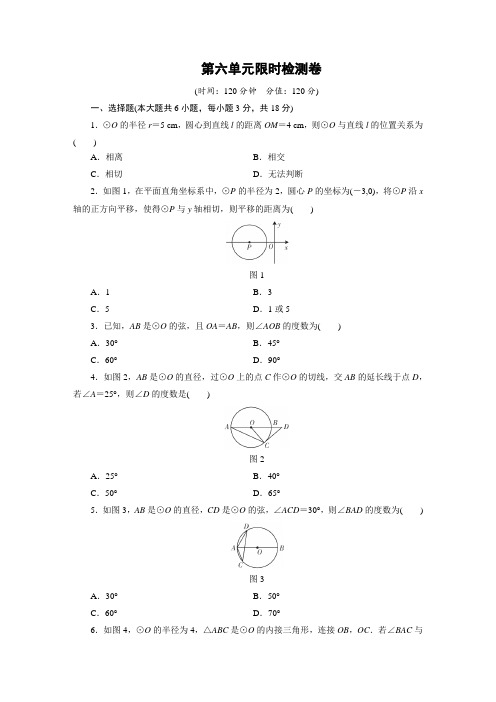
第六单元限时检测卷(时间：120分钟分值：120分)一、选择题(本大题共6小题，每小题3分，共18分)1．⊙O的半径r＝5 cm，圆心到直线l的距离OM＝4 cm，则⊙O与直线l的位置关系为()A．相离B．相交C．相切D．无法判断2．如图1，在平面直角坐标系中，⊙P的半径为2，圆心P的坐标为(－3,0)，将⊙P沿x 轴的正方向平移，使得⊙P与y轴相切，则平移的距离为()图1A．1 B．3C．5 D．1或53．已知，AB是⊙O的弦，且OA＝AB，则∠AOB的度数为()A．30°B．45°C．60°D．90°4．如图2，AB是⊙O的直径，过⊙O上的点C作⊙O的切线，交AB的延长线于点D，若∠A＝25°，则∠D的度数是()图2A．25°B．40°C．50°D．65°5．如图3，AB是⊙O的直径，CD是⊙O的弦，∠ACD＝30°，则∠BAD的度数为()图3A．30°B．50°C．60°D．70°6．如图4，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB，OC．若∠BAC与∠BOC 互补，则弦BC 的长为( )图4A ．3 3B ．4 3C ．5 3D ．6 3二、填空题(本大题共6小题，每小题3分，共18分)7．已知扇形的面积为3π，圆心角为120°，则它的半径为__________．8．如图5，C ，D 是以线段AB 为直径的⊙O 上的两点，若CA ＝CD ，且∠ACD ＝40°，则∠CAB 的度数为__________．图59．如图6，CD 为⊙O 的弦，直径AB 为4，AB ⊥CD 于E ，∠A ＝30°，则BC ︵的长为__________．(结果保留π)图610．如图7，四边形ABCD 内接于⊙O ，F 是CD ︵上一点，且DF ︵＝BC ︵，连接CF 并延长交AD 的延长线于点E ，连接AC ．若∠ABC ＝105°，∠BAC ＝25°，则∠E 的度数为__________．图711．将直角△ABC 绕顶点B 旋转至如图8位置，其中∠C ＝90°，AB ＝4，BC ＝2，点C ，B ，A ′在同一直线上，则阴影部分的面积是__________．图812．如图9，直线AB，CD相交于点O，∠AOC＝30°，⊙P的半径为1 cm，且OP＝4 cm，如果⊙P以1 cm/s的速度沿由A向B的方向移动，那么__________秒后⊙P与直线CD相切．图9三、(本大题共5小题，每小题6分，共30分)13．赵州桥是我国建筑史上的一大创举，它距今约1 400年，历经无数次洪水冲击和8次地震却安然无恙．如图10，若桥跨度AB约为40米，主拱高CD约10米，求桥弧AB所在圆的半径．图1014．如图11，四边形ABCD内接于⊙O，AC平分∠BAD，延长DC交AB的延长线于点E.若AC＝EC，求证：AD＝BE.图1115．如图12，AB是⊙O的直径，且AB＝4，AC是弦，∠CAB＝40°，求劣弧BC和弦AC的长．(参考数据：sin 40°≈0.643，cos 40°≈0.766，tan 40°≈0.839，弧长计算结果保留π，弦长精确到0.01)图1216．如图13，△ABC 是⊙O 的内接三角形，点D ，E 在⊙O 上，连接AE ，DE ，CD ，BE ，CE ，∠EAC ＋∠BAE ＝180°，AB ︵＝CD ︵.图13(1)判断BE 与CE 之间的数量关系，并说明理由； (2)求证：△ABE ≌△DCE .17．(2017贵阳)如图14，C ，D 是半圆O 上的三等分点，直径AB ＝4，连接AD ，AC ，DE ⊥AB ，垂足为E ，DE 交AC 于点F .图14(1)求∠AFE 的度数；(2)求阴影部分的面积．(结果保留π和根号) 四、(本大题共3小题，每小题8分，共24分)18．如图15，在平面直角坐标系中，△ABC 内接于⊙P ，AB 是⊙P 的直径，A (－1,0)，C (3,2 2)，BC 的延长线交y 轴于点D ，点F 是y 轴上的一动点，连接FC 并延长交x 轴于点E .图15(1)求⊙P的半径；(2)当∠A＝∠DCF时，求证：CE是⊙P的切线．19．(2017南充)如图16，在Rt△ACB中，∠ACB＝90°，以AC为直径作⊙O交AB于点D，E为BC的中点，连接DE并延长交AC的延长线于点F.图16(1)求证：DE是⊙O的切线；(2)若CF＝2，DF＝4，求⊙O直径的长．20．如图17，在Rt△ABC中，∠ACB＝90°，以点A为圆心，AC为半径，作⊙A，交AB 于点D，交CA的延长线于点E，过点E作AB的平行线交⊙A于点F，连接AF，BF，DF.(1)求证：△ABC≌△ABF；(2)当∠CAB＝60°时，判断四边形ADFE是什么特殊四边形？说明理由．图17五、(本大题共2小题，每小题9分，共18分)21．如图18，OA，OB是⊙O的半径，且OA⊥OB，点C是OB延长线上任意一点，过点C作CD切⊙O于点D，连接AD交OC于点E.(1)求证：CD＝CE；(2)如图19，若将图18中的半径OB所在直线向上平移，交OA于F，交⊙O于B′，其他条件不变，求证：∠C＝2∠A；图18 图1922．如图20，已知⊙O 的半径为2，AB 为直径，CD 为弦．AB 与CD 交于点M ，将CD ︵沿着CD 翻折后，点A 与圆心O 重合，延长OA 至P ，使AP ＝OA ，连接PC ．(1)求CD 的长；(2)求证：PC 是⊙O 的切线；(3)点G 为ADB ︵的中点，在PC 延长线上有一动点Q ，连接QG 交AB 于点E ，交BC ︵于点F (F 与B ，C 不重合)．GE ·GF 是否为定值？如果是，求出该定值；如果不是，请说明理由．图20六、(本大题共12分)23．如图21所示，点A 为半圆O 的直径MN 所在直线上的一点，射线AB 垂直于MN ，垂足为A ，半圆绕M 点顺时针转动，转过的角度记作α.设半圆O 的半径为R ，AM 的长度为m ，回答下列问题：探究：(1)若R ＝2，m ＝1，如图21，当旋转30°时，圆心O ′到射线AB 的距离是________；如图22，当α＝________°时，半圆O 与射线AB 相切；(2)如图23，在(1)的条件下，为了使得半圆O 转动30°即能与射线AB 相切，在保持线段AM 长度不变的条件下，调整半径R 的大小，请你求出满足要求的R ，并说明理由．发现：(3)如图24，在0°＜α＜90°时，为了对任意旋转角都保证半圆O 与射线AB 能够相切，小明探究了cos α与R ，m 两个量的关系，请你帮助他直接写出这个关系：cos α＝________.(用含有R ，m 的代数式表示)拓展：(4)如图25，若R ＝m ，当半圆弧线与射线AB 有两个交点时，α的取值范围是__________，并求出在这个变化过程中阴影部分(半圆与射线AB 所形成的弓形)面积的最大值．(用m 表示)图21 图22 图23 图24 图25第六单元限时检测卷1．B 2.D 3.C 4.B 5.C 6.B 7.3 8.20° 9.23π 10.50°11.163π－2 3 12.2或6 13．解：根据垂径定理，得AD ＝12AB ＝20米．设圆的半径是R ，根据勾股定理，得R 2＝202＋(R －10)2，解得R ＝25(米)．答：桥弧AB 所在圆的半径为25米． 14．证明：∵AC ＝EC ，∴∠E ＝∠CAE .∵AC 平分∠BAD ，∴∠DAC ＝∠CAB .∴∠DAC ＝∠E . ∵四边形ABCD 内接于⊙O ， ∴∠ADC ＋∠ABC ＝180°.又∠CBE ＋∠ABC ＝180°，∴∠ADC ＝∠CBE . 在△ADC 和△EBC 中，⎩⎪⎨⎪⎧∠ADC ＝∠EBC ，∠DAC ＝∠E ，AC ＝EC ，∴△ADC ≌△EBC . ∴AD ＝BE . 15．解：连接OC ，BC ，如图1，图1∵∠CAB ＝40°，∴∠COB ＝80°.∴劣弧BC 的长＝80·π·2180＝8π9.∵AB 为直径，∴∠ACB ＝90°. 在Rt △ACB 中，cos 40°＝AC AB ＝AC4，∴AC ＝4cos 40°＝4×0.766≈3.06. 16．(1)解：BE ＝CE .理由如下：∵∠EAC ＋∠BAE ＝180°，∠BCE ＋∠BAE ＝180°， ∴∠BCE ＝∠EAC . ∴BE ︵＝CE ︵.∴BE ＝CE .(2)证明：∵AB ︵＝CD ︵，∴AB ＝CD . ∵BE ︵＝CE ︵，∴AE ︵＝ED ︵.∴AE ＝ED . 由(1)得BE ＝CE ，在△ABE 和△DCE 中，∵⎩⎪⎨⎪⎧AE ＝DE ，AB ＝DC ，BE ＝CE ，∴△ABE ≌△DCE (SSS)．17．解：(1)如图2，连接OD ，OC ，图2∵C ，D 是半圆O 上的三等分点， ∴AD ︵＝CD ︵＝BC ︵.∴∠AOD ＝∠DOC ＝∠COB ＝60°. ∴∠CAB ＝30°.∵DE ⊥AB ，∴∠AEF ＝90°. ∴∠AFE ＝90°－30°＝60°. (2)由(1)知，∠AOD ＝60°， ∵OA ＝OD ，AB ＝4，∴△AOD 是等边三角形，OA ＝2. ∵DE ⊥AO ，∴DE ＝ 3.∴S 阴影＝S 扇形AOD －S △AOD ＝60·π×22360－12×2×3＝23π－ 3.18．(1)解：如图3，作CG ⊥x 轴于G ，则AC 2＝AG 2＋CG 2＝(3＋1)2＋(2 2)2＝24， ∵AB 是⊙P 的直径， ∴∠ACB ＝90°. ∴cos ∠CAB ＝AG AC ＝AC AB .∴AB ＝AC 2AG ＝244＝6.∴⊙P 的半径为3.(2)证明：如图3，连接PC ，图3∵∠ACB ＝90°， ∴∠CAB ＋∠CBA ＝90°. ∵PC ＝PB ， ∴∠PCB ＝∠PBC . ∵∠A ＝∠DCF ＝∠ECB ， ∴∠ECB ＋∠PCB ＝90°. ∵C 在⊙P 上， ∴CE 是⊙P 的切线．19．(1)证明：如图4，连接OD ，CD ，图4∵AC 为⊙O 的直径， ∴△BCD 是直角三角形．∵E 为BC 的中点，∴BE ＝CE ＝DE . ∴∠CDE ＝∠DCE .∵OD ＝OC ，∴∠ODC ＝∠OCD . ∵∠ACB ＝90°，∴∠OCD ＋∠DCE ＝90°. ∴∠ODC ＋∠CDE ＝90°，即OD ⊥DE .∴DE 是⊙O 的切线． (2)解：设⊙O 的半径为r ， ∵∠ODF ＝90°，∴OD 2＋DF 2＝OF 2，即r 2＋42＝(r ＋2)2. 解得r ＝3. ∴⊙O 的直径为6. 20．(1)证明：∵EF ∥AB ， ∴∠E ＝∠CAB ，∠EF A ＝∠F AB . ∵∠E ＝∠EF A ，∴∠F AB ＝∠CAB . 在△ABC 和△ABF 中，⎩⎪⎨⎪⎧AC ＝AF ，∠CAB ＝∠F AB ，AB ＝AB ，∴△ABC ≌△ABF .(2)解：当∠CAB ＝60°时，四边形ADFE 为菱形．理由：∵∠CAB ＝60°，由(1)得∠F AB ＝∠CAB ， ∴∠F AB ＝∠CAB ＝∠F AE ＝60°. 又AD ＝AE ＝AF ，∴△AEF ，△AFD 为等边三角形． ∴EF ＝AD ＝AE ＝DF . ∴四边形ADFE 是菱形．21．证明：(1)连接OD ，如图5所示，图5∵OA ⊥OB ，∴∠AOE ＝90°. ∴∠A ＋∠AEO ＝90°， ∵CD 是⊙O 的切线，∴∠ODC ＝90°，即∠CDE ＋∠ODE ＝90°. 又OA ＝OD ，∴∠A ＝∠ODE .∴∠AEO ＝∠CDE .∵∠CED ＝∠AEO ，∴∠CDE ＝∠CED .∴CD ＝CE . (2)连接OD ，作CM ⊥AD 于M ，如图6所示，图6同(1)可证得CD ＝CE .则∠ECM ＝∠DCM ＝12∠DCE ，DE ＝2DM ，∠CME ＝90°. ∴∠ECM ＋∠CEM ＝90°.∵∠A ＋∠AEF ＝90°，∠AEF ＝∠CEM ，∴∠A ＝∠ECM .∴∠A ＝12∠DCE ，即∠DCE ＝2∠A . 22．(1)解：如图7，连接OC ，图7∵CD ︵沿CD 翻折后，点A 与圆心O 重合，∴OM ＝12OA ＝12×2＝1，CD ⊥OA . ∵OC ＝2，∴CD ＝2CM ＝2OC 2－OA 2＝222－12＝2 3.(2)证明：∵P A ＝OA ＝2，AM ＝OM ＝1，CM ＝12CD ＝3，∠CMP ＝∠OMC ＝90°，∴PM ＝3.∴PC ＝MC 2＋PM 2＝(3)2＋32＝2 3.∵OC ＝2，PO ＝2＋2＝4，∴PC 2＋OC 2＝(2 3)2＋22＝16＝PO 2.∴∠PCO ＝90°.∴PC 是⊙O 的切线．(3)解：GE ·GF 是定值．如图8，连接GO 并延长，交⊙O 于点H ，连接HF ，图8∵点G 为ADB ︵的中点，∴∠GOE ＝90°.∵∠HFG ＝90°，∴∠GOE ＝∠GFH .又∠OGE ＝∠FGH ，∴△OGE ∽△FGH .∴OG GF ＝GE GH. ∴GE ·GF ＝OG ·GH ＝2×4＝8.23．解：(1)3＋1；60°.(2)设切点为P ，如图9，连接O ′P ，作MQ ⊥O ′P ，则四边形APQM 是矩形．图9∴O ′P ＝O ′Q ＋QP ＝R .由题知，∠α＝30°，∴O ′Q ＝cos 30°·R ，AM ＝QP ＝1.∴R ＝32R ＋1.∴R ＝4＋2 3. (3)R －m R. (4)当半圆与射线AB 相切时，之后开始出现两个交点，此时α＝90°；当N ′落在AB 上时，为半圆与AB 有两个交点的最后时刻，此时∵MN ′＝2AM ，∴∠AMN ′＝60°.∴α＝120°.∴当半圆弧线与射线AB 有两个交点时，α的取值范围是90°＜α≤120°.当N ′落在AB 上时，阴影部分面积最大，∴S ＝120·π·m 2360－12·3m ·12m ＝πm 23－34m 2.。

2018届湘教版数学中考专项训练(六)圆(含答案)

专项训练六圆一、选择题1.如图，圆O 是△ABC 的外接圆，∠A ＝68°，则∠OBC 的大小是（） A.22° B.26° C.32° D.68°第1题图第2题图第3题图第4题图 2.如图，已知⊙O 的半径OA ＝6，∠AOB ＝90°，则∠AOB 所对的劣弧AB 的长为（） A.2π B.3π C.4π D.6π3.如图，AB 是⊙O 的直径，CD 切⊙O 于点C ，若∠BCD ＝25°，则∠B 等于（） A.25° B.65° C.75° D.90°4.如图，两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB 与小圆有公共点，则弦AB 的取值范围是（）A.8≤AB ≤10B.8＜AB ≤10C.4≤AB ≤5D.4＜AB ≤55.如图，AB 是⊙O 的直径，AC 是⊙O 的切线，A 为切点，连接BC 交⊙O 于点D ，连接AD ，若∠ABC ＝45°，则下列结论正确的是（）A.AD ＝12BCB.AD ＝12AC C.AC ＞AB D.AD ＞DC第5题图第6题图第7题图第8题图6.（2016·邵东县一模）如图，线段AB 是⊙O 的直径，弦CD ⊥AB ，∠CAB ＝20°，则∠AOD 等于（） A.120° B.140° C.150° D.160°7.（2016·枣庄中考）如图，AB 是⊙O 的直径，弦CD ⊥AB ，∠CDB ＝30°，CD ＝23，则阴影部分的面积为（）A.2πB.π C .π3 D.23 8.如图，已知AB ＝AC ＝AD ，∠CBD ＝2∠BDC ，∠BAC ＝44°，则∠CAD 的度数为（） A.68° B.88° C.90° D.112° 二、填空题 9.（2016·怀化中考）已知扇形的半径为6cm ，面积为10πcm 2，则该扇形的弧长等于 .10.如图所示，在⊙O 中，直径CD 垂直弦AB 于点E ，连接BO ，已知⊙O 的半径为2，AB ＝23，则∠OBA ＝ °.第10题图第12题图第13题图11.从圆外一点向半径为5的圆作切线，已知切线长为12，从这点到圆的最短距离为.12.如图，过⊙O外一点P作圆的切线P A，PB，F是劣弧AB上任一点，过F作⊙O的切线分别交P A，PB于D，E，如果P A＝8，∠P＝40°，则△PED的周长为，∠DOE＝.13.如图所示，已知⊙O的半径为5，点O到弦AB的距离为3，则⊙O上到弦所在直线的距离为2的点有个.14.如图，OD是⊙O的半径，弦AB⊥OD于E，若∠O＝70°，则∠A＋∠C＝°.第14题图第15题图第16题图15.如图，将一个半径为2的圆等分成四段弧，再将这四段弧围成星形，则该图形的面积与原来圆的面积之比是.16.★如图，在扇形OAB中，∠AOB＝60°，扇形半径为r，点C在上，CD⊥OA，垂足为D，当△OCD的面积最大时，的长为.三、解答题17.如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上.（1）若∠AOD＝52°，求∠DEB的度数；（2）若OC＝3，OA＝5，求AB的长.18.如图，在△ABC中，∠C＝90°，AC＋BC＝8，点O是斜边AB上一点，以O为圆心的⊙O分别与AC，BC 相切于点D，E.（1）当AC＝2时，求⊙O的半径；（2）设AC＝x，⊙O的半径为y，求y与x的函数关系式.19.（2016·长沙中考）如图，四边形ABCD 内接于⊙O ，对角线AC 为⊙O 的直径，过点C 作AC 的垂线交AD 的延长线于点E ，点F 为CE 的中点，连接DB ，DC ，DF .（1）求∠CDE 的度数；（2）求证：DF 是⊙O 的切线；（3）若AC ＝25DE ，求tan ∠ABD 的值.参考答案与解析1．A 2.B 3.B 4.A 5.A 6.B7．D 解析：∵∠CDB ＝30°，∴∠COB ＝60°.又∵弦CD ⊥AB ，CD ＝23，∴OC ＝12CD sin60°＝332＝2，∴S阴影＝S 扇形COB ＝60×π×22360＝2π3.故选D.8．B 解析：以点A 为圆心，AB 为半径画圆，则点C ，D 都在圆上．∵∠CBD ＝2∠BDC ，∴CD ︵＝2BC ︵，∴∠CAD ＝2∠BAC ＝88°.故选B.9.103πcm 10.30 11.8 12.16 70° 13.3 14．55 解析：如图，连接OB .∵OA ＝OB ，∴∠A ＝∠ABO .又∵OD 是⊙O 的半径，弦AB ⊥OD 于E ，∠O ＝70°，∴AD ︵＝BD ︵，∠AOB ＝140°，∴∠C ＝12∠AOD ＝35°，∠A ＝∠ABO ＝20°，∴∠A ＋∠C ＝55°.15.4－ππ 解析：由题意得圆的面积＝π×22＝4π，星形的面积＝4×4－4π＝16－4π，该图形的面积与原来圆的面积之比为(16－4π)∶4π＝4－ππ.16.14πr 解析：∵OC ＝r ，点C 在AB ︵上，CD ⊥OA ，∴DC ＝OC 2－OD 2＝r 2－OD 2，∴S △OCD ＝12OD ·r 2－OD 2，∴(S △OCD )2＝14OD 2·(r 2－OD 2)＝－14OD 4＋14r 2OD 2＝－14(OD 2－r 22)2＋r 416，∴当OD 2＝r 22，即OD ＝22r 时，△OCD 的面积最大，∴∠OCD ＝45°，∴∠COA ＝45°，∴AC ︵的长为45πr 180＝14πr .17．解：(1)连接OB .∵OD ⊥AB ，∴AC ＝BC ，AD ︵＝BD ︵，∴∠AOD ＝∠BOD .又∵∠DEB ＝12∠DOB ，∴∠DEB＝12∠AOD ＝12×52°＝26°； (2)在Rt △ACO 中，∵OC ＝3，OA ＝5，∴AC ＝OA 2－OC 2＝4.又∵AC ＝BC ＝12AB ，∴AB ＝2AC ＝2×4＝8.18．解：(1)连接OE ，OD .∵AC ＋BC ＝8，AC ＝2，∴BC ＝6.∵∠C ＝90°，∴tan B ＝AC BC ＝13.∵以O 为圆心的⊙O分别与AC ，BC 相切于点D ，E ，∴∠ODC ＝∠OEC ＝90°.又∵∠C ＝90°，∴四边形OECD 是矩形．∵OE ＝OD ，∴四边形OECD 是正方形，∴∠ADO ＝∠C ＝90°，CD ＝OD ，OD ∥BC ，∴∠B ＝∠AOD ，∴tan B ＝tan ∠AOD ，∴AD OD ＝2－OD OD ＝13，解得OD ＝32，∴⊙O 的半径为32；(2)∵AC ＝x ，∴BC ＝8－x .在Rt △ABC 中，tan B ＝AC BC ＝x 8－x .又由(1)知tan B ＝tan ∠AOD ＝AD OD ＝x －y y ，∴x 8－x ＝x －y y ，解得y ＝－18x 2＋x . 19．(1)解：∵AC 为⊙O 直径，∴∠ADC ＝90°，∴∠CD E ＝90°；(2)证明：连接OD .∵∠CDE ＝90°，F 为CE 中点，∴DF ＝12CE ＝CF ，∴∠FDC ＝∠FCD .又∵OD ＝OC ，∴∠ODC＝∠OCD ，∴∠ODC ＋∠FDC ＝∠OCD ＋∠FCD ，∴∠ODF ＝∠OCF .∵EC ⊥AC ，∴∠OCF ＝90°，∴∠ODF ＝90°，即DF 为⊙O 的切线；(3)解：在△ACD 与△ACE 中，∠ADC ＝∠ACE ＝90°，∠EAC ＝∠CAD ，∴△ACD ∽△AEC ，∴AC AE ＝ADAC ，∴AC 2＝AD ·AE .又∵AC ＝25DE ，∴20DE 2＝(AE －DE )·AE ，∴(AE －5DE )(AE ＋4DE )＝0，∴AE ＝5DE ，∴AD ＝4DE .在Rt △ACD 中，CD ＝AC 2－AD 2＝（25DE ）2－（4DE ）2＝2DE .又∵在⊙O 中，∠AB D ＝∠ACD ，∴tan ∠ABD ＝tan ∠ACD ＝AD CD ＝4DE 2DE＝2.。

2018年中考数学总复习圆试题

2018年中考数学总复习圆试题D∠ABC=60°,∠ACB=40°,则∠BOC=(A)A.130°B.135°C.120°D.150°二、填空题(每小题5分,共20分)11.如图,☉O的两条弦AB,CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则☉O的半径是.(第11题图)(第12题图)12.如图,AB是☉O的直径,OA=1,AC是☉O的弦,过点C的切线交AB的延长线于点 D.若BD=-1,则∠ACD=112.5°.13.如下图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是.14.如图,从☉O外的两点C和D分别引圆的两线DA,DC,CB,切点分别为点A、点E和点B,AB是☉O的直径,连接OC,连接OD交CB延长线于F,给出如下结论:①AD+BC=CD;②OD2=DE·CD;③OD=OC;④CD=CF.其中正确的是①②④.(把所有正确结论序号都填在横线上)三、解答题(共70分)15.(6分)如图,PA,PB是☉O的两条切线,A,B分别是切点,点C是上任意一点,连接OA,OB,CA,CB,∠P=70°,求∠ACB的度数.解∵PA,PB是☉O的切线,OA,OB是半径,∴∠PAO=∠PBO=90°.又∵∠PAO+∠PBO+∠AOB+∠P=360°,∠P=70°,∴∠AOB=110°.∵∠AOB是圆心角,∠ACB是圆周角,∴∠ACB=55°.16.(6分)已知在以点O为圆心的两个同心圆中,大圆的弦AB 交小圆于点C,D(如图所示).(1)求证:AC=BD;(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.(1)证明过点O作OE⊥AB于点E,则CE=DE,AE=BE.∴AE-CE=BE-DE,即AC=BD.(2)解由(1)可知,OE⊥AB且OE⊥CD,∴CE===2.AE===8.∴AC=AE-CE=8-2.〚导学号92034207〛17.(6分)已知A,B,C,D是☉O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求☉O的半径.图1图2(1)证明∵∠ADC=∠BCD=90°,∴AC,BD是☉O的直径,且交点为圆心O.∵AD=CD,AO=CO,∴AC⊥BD.(2)解如图,画直径CK,连接DK,BC,则∠KDC=90°,∴∠K+∠KCD=90°.∵AC⊥BD,∴∠ACB+∠EBC=90°.∵∠EBC=∠K,∴∠ACB=∠KCD,∴=,∴DK=AB=2.∵DC=4,∴KC==2,∴☉O的半径为.〚导学号92034208〛18.(6分)如图,O是△ABC的内心,BO的延长线和△ABC 的外接圆相交于点D,连接DC,DA,OA,OC,四边形OADC 为平行四边形.(1)求证:△BOC≌△CDA:(2)若AB=2,求阴影部分的面积.(1)证明∵O为△ABC的内心,∴∠2=∠3,∠5=∠6.∵∠1=∠2,∴∠1=∠3,由AD∥CO,AD=CO,∴∠4=∠5,∴∠4=∠6,∴△BOC≌△CDA.(2)解由(1)得BC=AC,∠3=∠4=∠6,∴∠ABC=∠ACB,∴AB=AC,△AB C为等边三角形,∴O为△ABC的内外心,∴OA=OB=OC.设E为BD与AC的交点,BE垂直平分AC.在Rt△O CE 中,CE=AB=1,∠OCE=30°,∴OA=OB=OC=,∵∠AOB=120°,∴S阴=S扇形AOB-S△AOB=-×2×=.19.(8分)如图,在边长为1的正方形网格中,△ABC 的顶点均在格点上,点A,B的坐标分别是A(4,3),B(4,1),把△ABC绕点C逆时针旋转90°后得到△A 1B1C.(1)画出△A1B1C,直接写出点A1,B1的坐标;(2)求在旋转过程中,△ABC所扫过的面积.解(1)所求作△A1B1C如图所示:由A(4,3),B(4,1)可建立如图所示坐标系,则点A1的坐标为(-1,4),点B1的坐标为(1,4);(2)∵AC===,∠ACA1=90°,∴在旋转过程中,△ABC所扫过的面积为+S△ABC=+×3×2=+3.20.(10分)已知在△ABC中,∠ABC=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB 于点E.(1)求证:AC·AD=AB·AE;(2)如果BD是☉O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.(1)证明连接DE.∵AE是直径,∴∠ADE=90°,∴∠ADE=∠ABC.在Rt△ADE和Rt△ABC中,∠A是公共角,故△ADE∽△ABC,则=,即AC·AD=AB·AE.(2)解连接OD.∵BD是圆O的切线,∴OD⊥BD.在Rt△OBD中,OE=BE=OD,∴OB=2OD,∴∠OBD=30°.同理∠BAC=30°.在Rt△ABC中,AC=2BC=2×2=4.〚导学号92034209〛21.(8分)如图,AB为☉O的直径,F为弦AC的中点,连接OF并延长交于点D,过点D作☉O的切线,交BA的延长线于点E.(1)求证:AC∥DE;(2)连接CD,若OA=AE=a,求四边形ACDE的面积.(1)证明∵ED与☉O相切于D,∴OD⊥DE.∵F为弦AC 中点,∴OD⊥AC,∴AC∥DE.(2)解作DM⊥OA于M,连接CD,CO,AD.∵AC∥DE,AE=AO,∴OF=DF.∵AF⊥DO,∴AD=AO,∴AD=AO=OD,∴△ADO是等边三角形,同理△CDO也是等边三角形,∴∠CDO=∠DOA=60°,AE=CD=AD=AO=CO=a,∴AO ∥CD,又AE=CD,∴四边形ACDE是平行四边形,易知DM=a,∴平行四边形ACDE面积为a2.22.(10分)已知:如图,☉O是△ABC的外接圆,=,点D 在边BC上,AE∥BC,AE=BD.(1)求证:AD=CE;(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.(1)证明在☉O 中,∵=,∴AB=AC,∴∠B=∠ACB.∵AE∥BC,∴∠EA C=∠ACB,∴∠B=∠EAC.在△ABD和△CAE 中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE.(2)解连接AO并延长,交边BC于点H,∵=,OA为半径,∴AH⊥BC,∴BH=CH.∵AD=AG,∴DH=HG,∴BH-DH= CH-GH,即BD=CG.∵BD=AE,∴CG=AE.∵CG∥AE,∴四边形AGCE是平行四边形.23.(10分)如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.(1)求证:∠ACD=∠B.(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;①求tan∠CFE的值;②若AC=3,BC=4,求CE的长.图1图2(1)证明如图中,连接OC.∵OA=OC,∴∠1=∠2.∵CD是☉O切线,∴OC⊥CD,∴∠DCO=90°,∴∠3+∠2=90°.∵AB是直径,∴∠1+∠B=90°,∴∠3=∠B.∴∠ACD=∠B.(2)解①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,∠CDE=∠FDB,∠ECD=∠B,∴∠CEF=∠CFE,∵∠ECF=90°,∴∠CEF=∠CFE=45°,∴tan∠CFE=tan 45°=1.②在Rt△ABC中,∵AC=3,BC=4,∴AB==5.∵∠CDA=∠BDC,∠DCA=∠B,∴△DCA∽△DBC,∴===.∵∠CDE=∠BDF,∠DCE=∠B,∴△DCE∽△DBF,∴=.设EC=CF=x,∴=,∴x=.∴CE=.。

2018年中考数学考前冲刺系列专题05 圆

专题05 圆一、选择题（本大题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．下列说法正确的是A．长度相等的两条弧是等弧B．平分弦的直径垂直于弦C．直径是同一个圆中最长的弦D．过三点能确定一个圆2．如图，在半径为5 cm的⊙O中，弦AB=6 cm，OC⊥AB于点C，则OC=A．3 cm B．4 cmC．5 cm D．6 cm3．如图，AB是⊙O的直径，直线DA与⊙O相切于点A，DO交⊙O于点C，连接BC，若∠ABC=21°，则∠ADC 的度数为A．46° B．47°C．48° D．49°4．如图，在⊙O中，相等的弦AB、AC互相垂直，OE⊥AC于E，OD⊥AB于D，则四边形OEAD为A．正方形B．菱形C．矩形D．平行四边形5．如图，⊙O的半径为4，点P是⊙O外的一点，PO=10，点A是⊙O上的一个动点，连接PA，直线l垂直平分PA，当直线l与⊙O相切时，PA的长度为A．10 B．212C．11 D．4346．如图，⊙C过原点，与x轴、y轴分别交于A、D两点．已知∠OBA=30°，点D的坐标为（0，2），则⊙C半径是A B C．D．27．如图，在矩形ABCD中，AB=4，AD=2，分别以点A、C为圆心，AD、CB为半径画弧，交AB于点E，交CD 于点F，则图中阴影部分的面积是A．4–2πB．8–π2C．8–2πD．8–4π8．如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是 EB的中点，则下列结论不成立的是A．OC∥AE B．EC=BC C．∠DAE=∠ABE D．AC⊥OE 二、填空题（本大题共4个小题，每小题6分，共24分）9．一个扇形的面积是12πcm²，圆心角是60°，则此扇形的半径是________cm.10．如图，半径为1的⊙O与正五边形ABCDE相切于点A、C，则劣弧 AC的长度为__________．11．如图，⊙O的半径是4，△ABC是⊙O的内接三角形，过圆心O分别作AB、BC、AC的垂线，垂足为E、F、G，连接EF．若OG﹦1，则EF为__________．12．如图，已知矩形ABCD中，AB=4，AD=3，P是以CD为直径的半圆上的一个动点，连接BP．（1）半圆 CD=________；（2）BP的最大值是________．三、解答题（本大题共3个小题，每小题12分，共36分．解答应写出文字说明、证明过程或演算步骤）13．如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，CE平分∠ACB，交AB于点E．（1）求证：AC平分∠DAB；（2）求证：△PCE是等腰三角形.15．已知△ABC内接于⊙O，AC是⊙O的直径，D是 AB的中点．过点D作CB的垂线，分别交CB、CA延长线于点F、E．（1）判断直线EF与⊙O的位置关系，并说明理由；（2）若CF=6，∠ACB=60°，求阴影部分的面积．参考答案一、选择题1．【答案】C2．【答案】B3．【答案】C4．【答案】A5．【答案】B6．【答案】B7．【答案】C8．【答案】D二、填空题9．【答案】12．【答案】（1）2π；（2）三、解答题13．【解析】（1）如图，连接OC，∵PD切⊙O于点C，∴OC⊥PD．（2分）又∵AD⊥PD，∴OC∥AD．∴∠ACO=∠DAC．又∵OC=OA，∴∠ACO=∠CAO，∴∠DAC=∠CAO，即AC平分∠DAB．（5分）（2）∵AD⊥PD，∴∠DAC+∠ACD=90°．又∵AB为⊙O的直径，∴∠ACB=90°．（7分）∴∠PCB+∠ACD=90°，∴∠DAC=∠PCB．又∵∠DAC=∠CAO，∴∠CAO=∠PCB．（9分）∵CE平分∠ACB，∴∠ACE=∠BCE，∴∠CAO+∠ACE=∠PCB+∠BCE，∴∠PEC=∠PCE，∴PC=PE，即△PCE是等腰三角形．（12分）15．【解析】如图，连接OD．∵AC为圆O的直径，∴∠CBA=90°.（2分）（2）在Rt△CEF中，∠ACB=60°，∴∠E=30°，又∵CF=6，∴CE=2CF=12，根据勾股定理得：EF （6分）在Rt △ODE 中，∠E =30°，∴OD =12OE ，又OA =OD ，∴OA =AE =OC =13CE =4，OE =8，又∵∠ODE =∠F =90°，∠E =∠E ， ∴△ODE ∽△CFE ，∴OD DEFC EF = 解得DE （9分）又∵Rt △ODE 中，∠E =30°，∴∠DOE =60°，则12ODE OADS S S =-=△阴影扇形（12分）。

2018全国各地中考数学试题《圆》试题汇编(解答题)

2018全国各地中考数学试题《圆》试题汇编(解答题)2018全国各地中考数学试题《圆》解答题汇编1. 如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．求证：∠CBP=∠ADB．若OA=2，AB=1，求线段BP的长．2.如图，AB是⊙O的直径，AC切⊙O于点A，BC交⊙O 于点D．已知⊙O的半径为6，∠C=40°．求∠B的度数．求AD的长．3.如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E，点C是BF的中点．求证：AD⊥CD；若∠CAD=30°，⊙O的半径为3，一只蚂蚁从点B出发，沿着BE-EC-CB爬回至点B，求蚂蚁爬过的路程．第 1 页共 27 页4. 如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．求证：OP ⊥CD；连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．5. 如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O 于点F，AC平分∠BAD，连接BF．求证：AD⊥ED；若CD=4，AF=2，求⊙O的半径．6. 如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE 丄AB，交AB的延第 2 页共 27 页长线于点E．求证：CB平分∠ACE；若BE=3，CE=4，求⊙O的半径．7.如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB 于点F．求证：BC是⊙O的切线；若⊙O的半径是2cm，E 是AD的中点，求阴影部分的面积8.已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，如图①，若D为AB的中点，求∠ABC和∠ABD的大小；如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，第 3 页共 27 页求∠OCD的大小．9. 如图，D是△ABC外接圆上的动点，且B，D位于AC 的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG ⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．求证：BG∥CD；设△ABC外接圆的圆心为O，若AB=3DH，∠OHD=80°，求∠BDE的大小．10. 如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．求证：AE与⊙O相切于点A；若AE∥BC，BC=27，AC=22，求AD的长．第 4 页共 27 页11.如图所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．12.如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．求证：DA=DE；若AB=6，CD=43，求图中阴影部分的面积．13.如图，△ABC中，AB=AC，以AB为直径的⊙O交BC 于点D，交AC于点E，过点D作DF⊥AC于点F，交AB的延长线于点G．求证：DF是⊙O的切线；已知BD=25 第 5 页共27 页25. 如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D．过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F．求证：PC是⊙O的切线；若∠ABC=60°，AB=10，求线段CF的长．26. 如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．试判断直线DE与⊙O的位置关系，并说明理；若⊙O的半径为2，∠B=50°，AC=，求图中阴影部分的面积．第 11 页共 27 页27.如图，AB是⊙O的直径，点C为⊙O上一点，CN为⊙O的切线，OM⊥AB于点O，分别交AC、CN于D、M两点．求证：MD=MC；若⊙O的半径为5，AC=45，求MC的长．27. 如图，在⊙O中，AB为直径，AC为弦．过BC延长线上一点G，作GD⊥AO于点D，交AC于点E，交⊙O于点F，M是GE的中点，连接CF，CM．判断CM与⊙O的位置关系，并说明理；若∠ECF=2∠A，CM=6，CF=4，求MF的长．第 12 页共 27 页28.如图，在△ABC中，AB=AC，以AB为直径的圆交AC 于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC．求证：四边形ABFC是菱形；若AD=7，BE=2，求半圆和菱形ABFC的面积．29.如图，已知A、B、C、D、E是⊙O上五点，⊙O的直径BE=23，∠BCD=120°，A为BE的中点，延长BA到点P，使BA=AP，连接PE．求线段BD的长；求证：直线PE是⊙O的切线．第 13 页共 27 页30.如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB的延长线于点E、F．求证：EF是⊙O的切线；若AC=4，CE=2，求 BD的长度．31.已知：如图，AB是⊙O的直径，AB=4，点F，C是⊙O上两点，连接AC，AF，OC，弦AC平分∠FAB，∠BOC=60°，过点C作CD⊥AF交AF的延长线于点D，垂足为点D．求扇形OBC的面积；求证：CD是⊙O的切线．32.已知：如图，以等边△ABC的边BC为直径作⊙O，分别交AB，AC于点D，E，过点D作DF⊥AC交AC于点F．求证：DF是⊙O的切线；若等边△ABC的边长为8，求第 14 页共 27 页DE、DF、EF围成的阴影部分面积．33.如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．求证：AE=ED；若AB=10，∠CBD=36°，求AC的长．34.如图，△ABC为等腰三角形，O是底边BC的中点，腰AB与⊙O相切于点D，OB与⊙O相交于点E．求证：AC是⊙O 的切线；若BD=3，BE=1．求阴影部分的面积．第 15 页共 27 页35.如图，已知⊙O是等边三角形ABC的外接圆，点D在圆上，在CD的延长线上有一点F，使DF=DA，AE∥BC交CF于E．求证：EA是⊙O的切线；求证：BD=CF．36. 如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C．若∠ADE=25°，求∠C的度数；若AB=AC，CE=2，求⊙O半径的长．37. 如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，点D是AM上一点，连接OD，过点B作BE∥OD交⊙O于点E，连接DE并延长交BN于点C．求证：DE是⊙O的切线；第 16 页共 27 页若AD=l，BC=4，求直径AB的长．38. 如图所示，PB是⊙O的切线，B为切点，圆心O在PC上，∠P=30°，D为弧BC的中点．求证：PB=BC；试判断四边形BOCD的形状，并说明理．39. 某居民小区的一处圆柱形的输水管道破裂，维修人员为更换管道，需要确定管道圆形截面的半径．如图，若这个输水管道有水部分的水面宽AB=16cm，水最深的地方的高度为4cm，求这个圆形截面的半径．40. 如图，AB是⊙O的直径，弦CD⊥AB于点E，过点C 的切线交AB的延长线于点F，连接DF．求证：DF是⊙O的切线；连接BC，若∠BCF=30°，BF=2，求CD的长．第 17 页共 27 页41. 已知，如图AB是⊙O的直径，点P在BA的延长线上，弦BC平分∠PBD，且BD⊥PD于点D．求证：PD是⊙O 的切线．若AB=8cm，BD=6cm，求CD的长．42. 如图，AB是⊙O的直径，∠BAC=90°，四边形EBOC 是平行四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．求证：CF是⊙O的切线；若∠F=30°，EB=8，求图中阴影部分的面积．43.如图，已知△ABC内接于⊙O，AB是直径，OD∥AC， AD=OC．求证：四边形OCAD是平行四边形；第 18 页共 27 页探究：①当∠B= °时，四边形OCAD是菱形；②当∠B满足什么条件时，AD与⊙O相切？请说明理．43. 如图，AB是⊙O的一条弦，OD⊥AB，垂足为点C，交⊙O于点D，点E在⊙O上．若∠AOD=52°，求∠DEB的度数；若OC=3，OA=5，求AB的长．44.如图，在⊙O中，弦AD、BC相交于点E，连接OE，已知AD=BC，AD⊥CB．求证：AB=CD；如果⊙O的半径为5，DE=1，求AE的长．第 19 页共 27 页45.如图，⊙O的直径AB=12，弦AC=6，∠ACB的平分线交⊙O于D，过点D作DE∥AB交CA的延长线于点E，连接AD，BD． AB，BD，AD围成的阴影部分的面积是；求线段DE的长．46.如图，在△ABC中，AB=AC，O为边AC上一点，以OC 为半径的圆分别交边BC，AC于点D，E，过点D作DF⊥AB于点F．求证：直线DF是⊙O的切线；若∠A=45°，OC=2，求劣弧DE的长．第 20 页共 27 页2018全国各地中考数学试题《圆》解答题汇编1. 如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．求证：∠CBP=∠ADB．若OA=2，AB=1，求线段BP的长．2.如图，AB是⊙O的直径，AC切⊙O于点A，BC交⊙O 于点D．已知⊙O的半径为6，∠C=40°．求∠B的度数．求AD的长．3.如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E，点C是BF的中点．求证：AD⊥CD；若∠CAD=30°，⊙O的半径为3，一只蚂蚁从点B出发，沿着BE-EC-CB爬回至点B，求蚂蚁爬过的路程．第 1 页共 27 页4. 如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．求证：OP ⊥CD；连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．5. 如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O 于点F，AC平分∠BAD，连接BF．求证：AD⊥ED；若CD=4，AF=2，求⊙O的半径．6. 如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE 丄AB，交AB的延第 2 页共 27 页长线于点E．求证：CB平分∠ACE；若BE=3，CE=4，求⊙O的半径．7.如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB 于点F．求证：BC是⊙O的切线；若⊙O的半径是2cm，E是AD的中点，求阴影部分的面积8.已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，如图①，若D为AB的中点，求∠ABC和∠ABD的大小；如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，第 3 页共 27 页求∠OCD的大小．9. 如图，D是△ABC外接圆上的动点，且B，D位于AC 的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG ⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．求证：BG∥CD；设△ABC外接圆的圆心为O，若AB=3DH，∠OHD=80°，求∠BDE的大小．10. 如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．求证：AE与⊙O相切于点A；若AE∥BC，BC=27，AC=22，求AD的长．第 4 页共 27 页11.如图所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．12.如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．求证：DA=DE；若AB=6，CD=43，求图中阴影部分的面积．13.如图，△ABC中，AB=AC，以AB为直径的⊙O交BC 于点D，交AC于点E，过点D作DF⊥AC于点F，交AB的延长线于点G．求证：DF是⊙O的切线；已知BD=25 第 5 页共27 页。

2018全国各地中考数学试题《圆》试题汇编（解答题）

2018全国各地中考数学试题《圆》试题汇编（解答题）2018全国各地中考数学试题《圆》解答题汇编1.（2018?黄冈）如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．（1）求证：∠CBP=∠ADB．（2）若OA=2，AB=1，求线段BP的长．2.（2018?长春）如图，AB是⊙O的直径，AC切⊙O于点A，BC交⊙O于点D．已知⊙O的半径为6，∠C=40°．（1）求∠B的度数．（2）求AD的长．（结果保留π）3.（2018?德州）如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E，点C是BF的中点．（1）求证：AD⊥CD；（2）若∠CAD=30°，⊙O的半径为3，⼀只蚂蚁从点B出发，沿着BE-EC-CB爬回⾄点B，求蚂蚁爬过的路程（π≈3.14，3≈1.73，结果保留⼀位⼩数）．4.（2018?北京）如图，AB是⊙O的直径，过⊙O外⼀点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．（1）求证：OP⊥CD；（2）连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．5.（2018?昆明）如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O于点F，AC平分∠BAD，连接BF．（1）求证：AD⊥ED；（2）若CD=4，AF=2，求⊙O的半径．6.（2018?兰陵县⼆模）如图，已知三⾓形ABC的边AB是⊙O的切线，切点为B．AC经过圆⼼O并与圆相交于点D、C，过C作直线CE丄AB，交AB的延长线于点E．（1）求证：CB平分∠ACE；（2）若BE=3，CE=4，求⊙O的半径．7.（2018?⾚峰）如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB于点F．（1）求证：BC是⊙O的切线；（2）若⊙O的半径是2cm，E是AD的中点，求阴影部分的⾯积（结果保留π和根号）8.（2018?天津）已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，（I）如图①，若D为AB的中点，求∠ABC和∠ABD的⼤⼩；（Ⅱ）如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，求∠OCD的⼤⼩．9.（2018?福建）如图，D是△ABC外接圆上的动点，且B，D位于AC的两侧，DE⊥AB，垂⾜为E，DE的延长线交此圆于点F．BG⊥AD，垂⾜为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．（1）求证：BG∥CD；⼩．10.（2018?潍坊）如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．（1）求证：AE与⊙O相切于点A；11.（2018?邵阳）如图所⽰，AB是⊙O的直径，点C为⊙O上⼀点，过点B作BD⊥CD，垂⾜为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．12.（2018?襄阳）如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上⼀点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．（1）求证：DA=DE；13.（2018?孝感）如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E，过点D作DF⊥AC于点F，交AB 的延长线于点G．（1）求证：DF是⊙O的切线；，CF=2，求AE和BG的长．14.（2018?抚顺）如图，Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，点D为⊙O上⼀点，且CD=CB，连接DO并延长交CB的延长线于点E．（1）判断直线CD与⊙O的位置关系，并说明理由；（2）若BE=4，DE=8，求AC的长．15.（2018?泰州）如图，AB为⊙O的直径，C为⊙O上⼀点，∠ABC的平分线交⊙O于点D，DE⊥BC于点E．（1）试判断DE与⊙O的位置关系，并说明理由；（2）过点D作DF⊥AB于点F，若BE=33，DF=3，求图中阴影部分的⾯积．15.（2018?攀枝花）如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC、AC交于点D、E，过点D作DF⊥AC于点F．（1）若⊙O的半径为3，∠CDF=15°，求阴影部分的⾯积；（2）求证：DF是⊙O的切线；（3）求证：∠EDF=∠DAC．16.（2018?扬州）如图，在△ABC中，AB=AC，AO⊥BC于点O，OE⊥AB于点E，以点O为圆⼼，OE为半径作半圆，交AO于点F．（1）求证：AC是⊙O的切线；（2）若点F是OA的中点，OE=3，求图中阴影部分的⾯积；（3）在（2）的条件下，点P是BC边上的动点，当PE+PF取最⼩值时，直接写出BP的长．17.（2018?云南）如图，已知AB是⊙O的直径，C是⊙O上的点，点D在AB 的延长线上，∠BCD=∠BAC．（1）求证：CD是⊙O的切线；（2）若∠D=30°，BD=2，求图中阴影部分的⾯积．18.（2018?聊城）如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，作ED⊥EB交AB于点D，⊙O是△BED的外接圆．（1）求证：AC是⊙O的切线；（2）已知⊙O的半径为2.5，BE=4，求BC，AD的长．19.（2018?长沙）如图，在△ABC中，AD是边BC上的中线，∠BAD=∠CAD，CE ∥AD，CE交BA的延长线于点E，BC=8，AD=3．（1）求CE的长；（2）求证：△ABC为等腰三⾓形．（3）求△ABC的外接圆圆⼼P与内切圆圆⼼Q之间的距离．20.（2018?河南）如图，AB是⊙O的直径，DO⊥AB于点O，连接DA交⊙O于点C，过点C作⊙O的切线交DO于点E，连接BC 交DO于点F．（1）求证：CE=EF；（2）连接AF并延长，交⊙O于点G．填空：21.（2018?咸宁）如图，以△ABC的边AC为直径的⊙O恰为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE∥AC 交BC的延长线于点E．（1）求证：DE是⊙O的切线；（2）若AB=25，BC=5，求DE的长．22.（2018?齐齐哈尔）如图，以△ABC的边AB为直径画⊙O，交AC于点D，半径OE∥BD，连接BE，DE，BD，设BE交AC于点F，若∠DEB=∠DBC．（1）求证：BC是⊙O的切线；（2）若BF=BC=2，求图中阴影部分的⾯积．23.（2018?郴州）已知BC是⊙O的直径，点D是BC延长线上⼀点，AB=AD，AE是⊙O的弦，∠AEC=30°．（1）求证：直线AD是⊙O的切线；（2）若AE⊥BC，垂⾜为M，⊙O的半径为4，求AE的长．24.（2018?陕西）如图，在Rt△ABC中，∠ACB=90°，以斜边AB上的中线CD为直径作⊙O，分别与AC、BC交于点M、N．（1）过点N作⊙O的切线NE与AB相交于点E，求证：NE⊥AB；（2）连接MD，求证：MD=NB．25.（2018?宿迁）如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D．过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F．（1）求证：PC是⊙O的切线；（2）若∠ABC=60°，AB=10，求线段CF的长．26.（2018?淮安）如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．（1）试判断直线DE与⊙O的位置关系，并说明理由；（2）若⊙O的半径为2，∠B=50°，AC=4.8，求图中阴影部分的⾯积．27.（2018?随州）如图，AB是⊙O的直径，点C为⊙O上⼀点，CN为⊙O的切线，OM⊥AB于点O，分别交AC、CN于D、M两点．（1）求证：MD=MC；（2）若⊙O的半径为5，AC=45，求MC的长．27.（2018?湖北）如图，在⊙O中，AB为直径，AC为弦．过BC延长线上⼀点G，作GD⊥AO于点D，交AC于点E，交⊙O于点F，M是GE的中点，连接CF，CM．（1）判断CM与⊙O的位置关系，并说明理由；（2）若∠ECF=2∠A，CM=6，CF=4，求MF的长．28.（2018?宜昌）如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE⾄点F，使EF=AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD=7，BE=2，求半圆和菱形ABFC的⾯积．29.（2018?黄⽯）如图，已知A、B、C、D、E是⊙O上五点，⊙O的直径BE=2 3，∠BCD=120°，A为BE的中点，延长BA到点P，使BA=AP，连接PE．（1）求线段BD的长；（2）求证：直线PE是⊙O的切线．30.（2018?衡阳）如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB 的延长线于点E、F．（1）求证：EF是⊙O的切线；（2）若AC=4，CE=2，求BD的长度．（结果保留π）31.（2018?怀化）已知：如图，AB是⊙O的直径，AB=4，点F，C是⊙O上两点，连接AC，AF，OC，弦AC平分∠FAB，∠BOC=60°，过点C作CD⊥AF交AF 的延长线于点D，垂⾜为点D．（1）求扇形OBC的⾯积（结果保留π）；（2）求证：CD是⊙O的切线．32.（2018?达州）已知：如图，以等边△ABC的边BC为直径作⊙O，分别交AB，AC于点D，E，过点D作DF⊥AC交AC于点F．（1）求证：DF是⊙O的切线；（2）若等边△ABC的边长为8，求由DE、DF、EF围成的阴影部分⾯积．33.（2018?湖州）如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．（1）求证：AE=ED；（2）若AB=10，∠CBD=36°，求AC的长．34.（2018?临沂）如图，△ABC为等腰三⾓形，O是底边BC的中点，腰AB与⊙O相切于点D，OB与⊙O相交于点E．（1）求证：AC是⊙O的切线；（2）若BD=3，BE=1．求阴影部分的⾯积．35.（2018?常德）如图，已知⊙O是等边三⾓形ABC的外接圆，点D在圆上，在CD的延长线上有⼀点F，使DF=DA，AE∥BC 交CF于E．（1）求证：EA是⊙O的切线；（2）求证：BD=CF．36.（2018?沈阳）如图，BE是O的直径，点A和点D是⊙O上的两点，过点A 作⊙O的切线交BE延长线于点C．（1）若∠ADE=25°，求∠C的度数；（2）若AB=AC，CE=2，求⊙O半径的长．37.（2018?官渡区⼆模）如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，点D是AM上⼀点，连接OD，过点B作BE∥OD 交⊙O于点E，连接DE并延长交BN于点C．（1）求证：DE是⊙O的切线；（2）若AD=l，BC=4，求直径AB的长．38.（2018?⾦⽔区校级模拟）如图所⽰，PB是⊙O的切线，B为切点，圆⼼O在PC上，∠P=30°，D为弧BC的中点．（1）求证：PB=BC；（2）试判断四边形BOCD的形状，并说明理由．39.（2018?历城区⼀模）某居民⼩区的⼀处圆柱形的输⽔管道破裂，维修⼈员为更换管道，需要确定管道圆形截⾯的半径．如图，若这个输⽔管道有⽔部分的⽔⾯宽AB=16cm，⽔最深的地⽅的⾼度为4cm，求这个圆形截⾯的半径．40.（2018?昌平区⼆模）如图，AB是⊙O的直径，弦CD⊥AB于点E，过点C 的切线交AB的延长线于点F，连接DF．（1）求证：DF是⊙O的切线；（2）连接BC，若∠BCF=30°，BF=2，求CD的长．41.（2018?天⽔模拟）已知，如图AB是⊙O的直径，点P在BA的延长线上，弦BC平分∠PBD，且BD⊥PD于点D．（1）求证：PD是⊙O的切线．（2）若AB=8cm，BD=6cm，求CD的长．42.（2018?葫芦岛⼀模）如图，AB是⊙O的直径，∠BAC=90°，四边形EBOC 是平⾏四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．（1）求证：CF是⊙O的切线；（2）若∠F=30°，EB=8，求图中阴影部分的⾯积．（结果保留根号和π）43.（2018?内乡县⼀模）如图，已知△ABC内接于⊙O，AB是直径，OD∥AC，AD=OC．（1）求证：四边形OCAD是平⾏四边形；（2）探究：②当∠B满⾜什么条件时，AD与⊙O相切？请说明理由．43.（2018?资中县⼀模）如图，AB是⊙O的⼀条弦，OD⊥AB，垂⾜为点C，交⊙O于点D，点E在⊙O上．（1）若∠AOD=52°，求∠DEB的度数；（2）若OC=3，OA=5，求AB的长．44.（2018?合肥模拟）如图，在⊙O中，弦AD、BC相交于点E，连接OE，已知AD=BC，AD⊥CB．（1）求证：AB=CD；（2）如果⊙O的半径为5，DE=1，求AE的长．。

中考复习备战策略数学《圆》阶段练习

宇轩图书
11．(2013·常德)连接一个几何图形上任意两点间的线段中，最长的线段称为这个几何图形的直径，根据此定义，下图(扇形、菱形、直角梯形、红十字图标) 中“直径” 最小的是( C )
宇轩图书
解析：如图①，连接 BC，则 BC 为这个几何图形的直径，
图①
宇轩图书
过点 O 作 OM⊥BC 于点 M，∵OB＝OC，∴∠BOM
A. 45° B. 53° C. 56° D. 71°
宇轩图书
解析：∵∠ABC＝71°，∠CAB＝53°，∴∠C＝180° －71°－53°＝56°.∵∠ADB 和∠C 都是 AB 所对的圆周角，∴∠ADB＝∠C＝56°.故选 C.
宇轩图书
5．(2013·海南)如图，在⊙O 中，弦 BC＝1，点 A 是圆上一点，且∠BAC＝30°，则⊙O 的半径是( A )
A．3
B．4
C．6
D．9
宇轩图书
解析：连接 PC，则 PC⊥AB，过点 O 作 OE⊥AB 于点 E ，则四边形 OECP 是矩形， ∴OE ＝ PC ，又∵S 阴影＝S⊙O－S⊙P＝π·OA2－π·PC2＝π(OA2－OE2) ＝π·AE2＝9π，∴AE＝3，∴AB＝2AE＝6.故选 C.
1
3
2
3
A. 2
B.连接 OC，∵CE 为⊙O 的切线， ∴△OCE 为直角三角形．∵∠CDB＝30°，∴∠COB ＝60°，∴∠E＝30°，∴sin E＝sin 30°＝12.故选 A.
宇轩图书
7．(2013·宁夏)如图，以等腰直角△ABC 两锐角顶点 A，B 为圆心作等圆，⊙A 与⊙B 恰好外切，若 AC＝2，那么图中两个扇形(即阴影部分)的面积之和为

【中考数学】2018最新版本中考数学专项训练-圆(含解析)(历年真题-可打印)

中考数学专项训练-圆附参考答案
1．（2015•贵阳）如图，⊙O是△ABC的外接圆，AB是⊙O的直径，FO⊥AB，垂足为点O，连接AF并延长交⊙O 于点D，连接OD交BC于点E，∠B=30°，FO=2．
（1）求AC的长度；
（2）求图中阴影部分的面积．（计算结果保留根号）
2．（2015•丹东）如图，AB是⊙O的直径，=，连接ED、BD，延长AE交BD的延长线于点M，过点D作⊙O的切线交AB的延长线于点C．
（1）若OA=CD=2，求阴影部分的面积；
（2）求证：DE=DM．
3．（2015•青海）如图，在△ABC中，∠B=60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点M，CM交⊙O于点D．
（1）求证：AM=AC；
（2）若AC=3，求MC的长．
4．（2015•庆阳）如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线，交AB 于点E，交CA的延长线于点F．
（1）求证：FE⊥AB；
（2）当EF=6，=时，求DE的长．
5．（2015•呼伦贝尔）如图，已知直线l与⊙O相离．OA⊥l于点A，交⊙O于点P，OA=5，AB与⊙O相切于点B，BP的延长线交直线l于点C．。

河南地区2018年中考数学总复习：专题检测(6)圆(Word版,含答案)

章节检测卷6圆(建议时间：90分钟总分：100分)一、选择题(本大题共7个小题，每小题4分，共28分)1．如图，△ABC内接于⊙O，若∠A＝α，则∠OBC等于(D) A．180°－2αB．2αC．90°＋αD．90°－α第1题图第2题图2．如图，AB是⊙O的直径，P A切⊙O于点A，PO交⊙O于点C.连接BC，若∠P＝40°，则∠B等于(B)A．20°B．25°C．30°D．40°3．如图，四边形ABCD内接于⊙O，AB经过圆心，∠B＝3∠BAC，则∠ADC等于(B)A．100°B．112.5°C．120°D．135°第3题图第5题图4．已知圆锥的底面面积为9π cm2，母线长为6 cm，则圆锥的侧面积是(A) A．18π cm2B．27π cm2C．18 cm2D．27 cm2 5．如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A＝15°，半径为2，则弦CD的长为(A)A．2 B．－1 C.2D．46．已知一个扇形的圆心角为60°，它所对的弧长为2π cm，则这个扇形的半径为(A)A．6 cm B．12cm C．2 3 cm D. 6 cm 7．如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC＝∠AEC；③BC平分∠ABD；④AF＝DF；⑤DB＝2OF；⑥△CEF≌△BED，其中一定成立的是(D)A．②④⑤⑥B．①③⑤⑥C．②③④⑥D．①③④⑤二、填空题(本大题共6个小题，每小题4分，共24分)8．如图，AB是⊙O的直径，AC与⊙O相切，CO交⊙O于点D.若∠CAD＝30°，则∠BOD＝120°.第8题图第9题图9．如图，AB为⊙O的直径，C，D为⊙O上的点，︵AD＝︵CD.若∠CAB＝40°，则∠CAD＝25°.10．在半径为20的⊙O中，弦AB＝32，点P在弦AB上，且OP＝15，则AP＝7或25.11．如图，小明自制一块乒乓球拍，正面是半径为8 cm的⊙O，︵AB＝90°，弓形ACB(阴影部分)粘贴胶皮，则胶皮面积为(48π＋32)cm2.第11题图第12题图12．如图，扇形OAB中，∠AOB＝60°，扇形半径为4，点C在︵AB上，CD⊥OA，垂足为点D，当△OCD的面积最大时，图中阴影部分的面积为2π－4. 13．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝1，E为BC边上的一点，以A为圆心，AE为半径的圆弧交AB于点D，交AC的延长线于点F，若图中两个阴影部分的面积相等，则AF的长为π(结果保留根号)．三、解答题(本大题共4个小题，共48分)14．(12分)如图，⊙O是△ABC的外接圆，BC为⊙O的直径，点E为△ABC的内心，连接AE并延长交⊙O于D点，连接BD并延长至F，使得BD＝DF，连接CF，BE.(1)求证：DB＝DE；(2)求证：直线CF为⊙O的切线．证明：(1)∵E是△ABC的内心，∴∠BAE＝∠CAE，∠EBA＝∠EBC.∵∠BED＝∠BAE＋∠EBA，∠DBE＝∠EBC＋∠DBC，∠DBC＝∠EAC，∴∠DBE＝∠DEB，∴DB＝DE；(2)连接CD，如解图所示．∵E是△ABC的内心，∴∠DAB＝∠DAC，∴BD＝CD.∵BD＝DF，∴CD＝DB＝DF，∴∠BCF＝90°，∴BC⊥CF，∴CF是⊙O的切线．15．(12分)如图，AB为⊙O的直径，C，D为⊙O上两点，∠BAC＝∠DAC，过点C作直线EF⊥AD，交AD的延长线于点E，连接BC.(1)求证：EF是⊙O的切线；(2)若DE ＝1，BC ＝2，求劣弧BC ︵)的长l . (1)证明：连接OC ，如解图所示． ∵OA ＝OC ，∴∠OAC ＝∠OCA .又∵∠OAC ＝∠DAC ，∴∠DAC ＝∠OCA ， ∴AD ∥OC .∵EF ⊥AD ，∴EF ⊥OC ， ∴EF 是⊙O 的切线；(2)解：连接OD ，DC ，如解图所示．∵∠DAC ＝12∠DOC ， ∠OAC ＝12∠BOC ，∴∠DOC ＝∠BOC ，∴CD ＝CB . ∵ED ＝1，DC ＝BC ＝2， ∴sin ∠ECD ＝DE DC ＝12，∴∠ECD ＝30°，∴∠OCD ＝60°. ∵OC ＝OD ，∴△DOC 是等边三角形，∴∠BOC ＝∠COD ＝60°，OC ＝2， ∴l ＝60π×2180＝2π3.16．(12分)如图，C ，D 是半圆O 上的三等分点，直径AB ＝4，连接AD ，AC ，DE ⊥AB ，垂足为E ，DE 交AC 于点F .(1)求∠AFE的度数；(2)求阴影部分的面积(结果保留π和根号)．解：(1)连接OD，OC，如解图所示.∵C，D是半圆O上的三等分点，∴︵AD＝︵CD＝︵BC，∴∠AOD＝∠DOC＝∠COB＝60°，∴∠CAB＝30°.∵DE⊥AB，∴∠AEF＝90°，∴∠AFE＝90°－30°＝60°；(2)由(1)知，∠AOD＝60°.∵OA＝OD，AB＝4，∴△AOD是等边三角形，OA＝2. ∵DE⊥AO，∴DE＝ 3.∴S阴影＝S扇形AOD－S△AOD＝60π×22360－12×2×3＝2π3－ 3.17．(12分)如图，AB是⊙O的直径，且AB＝6，C是⊙O上一点，D是︵BC的中点，过点D作⊙O的切线，与AB，AC的延长线分别交于点E，F，连接AD.(1)求证：AF⊥EF；(2)填空：①当BE＝__________时，点C是AF的中点；②当BE＝__________时，四边形OBDC是菱形．(1)证明：连接OD，如解图所示．∵EF为⊙O的切线，∴OD⊥EF.∵点D是︵BC的中点，∴∠CAD＝∠OAD. 又∵OA＝OD，∴∠OAD＝∠ODA，∴∠CAD＝∠ODA，∴OD∥AF，∴AF⊥EF；(2)解：①6；②3.。