2019重庆中考数学第24题专题训练四(含答案解析)
2019重庆中考数学第24题专题训练---矩形(含答案)

2019重庆中考数学第24题专题训练---矩形1、沙坪坝区2017—2018学年度第二学期期末调研测试八年级数学试题如图,在矩形ABCD 中,点E 为AD 上一点,连接BE 、CE ,∠ABE =45°. (1)如图1,若32BE,BC =4,求EC 的长.(2)如图2,点P 是EC 的中点,连接BP 并延长交CD 于F ,H 为AD 上一点,连接HF ,且∠DHF =∠CBF ,求证:BP=PF+FH .2、重庆市南开(融侨)中学初2019级暑假作业数学综合练习 已知,如图所示,在矩形ABCD 中,点E 为BC 边上,∠AEF=90°.(1)如图1,已知点F 在CD 边上,AD=AE,AD=5,AB=4,求DF 的长; (2)如图2,已知AE=EF,点G 为AF 的中点,求证:2.AB BE BG +=FCDFG图1 图23、重庆第二外国语学校初2019级初三年级第二学月质量检测如图,在矩形ABCD 中,点E 为BC 边上一点,过点E 作EF ⊥DE 于点E. (1)如图1,已知F 在AB 上,AD=DE,AD=10, CD=6, 求BF 的长; (2)如图2,已知DE=EF ,点G 为DF 的中点,求证:2.CD EC CG +=4、已知:在矩形ABCD 中,点H 是对角线AC 与BD 交点,点E 是AB 上的一点,连接HE,连接CE 交BD于F.(1) 如图1,若HE ⊥AC.且BC=3,AB=4,求△BEH 的面积; (2) 如图2,若∠AEB=∠BEC,求证:F 是BH 的中点.5、重庆巴蜀中学2019届初三下半期如图1,在矩形ABCD 中,AC 为矩形的对角线,点E 为AD 边上一点,连接BE. (1)若045EBC ∠=,且BE=CB ,AB=2,求AC 的长;(2)如图2,过B 作BF ⊥BE,使得BF=CD,连接CF 交BE 于点G,,当G 为CF 的中点时,求证:AE=2BG.6、重庆南开(融侨)中学初2018届初三下入学在矩形ABCD 中,点F 在AD 延长线上,且DF=DC,M 为AB 边上一点,N 为MD 的中点,点E 在直线CF 上,且BN=NE.(1)如图1,若AB=BC=6,13BM AB =,E 为线段FC 上的点,求NE 的长;(2)如图2.若AB<BC,E 为线段FC 延长线上的点,连结BE,求证:2.BE NE =7、重庆一中初2018级17—18学年度下期第一次定时作业如图1:在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE,F为AB上一点,且BF=DE,连接FC.(1)若DE=1,CF=22,求CD的长;(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=3AC.8、重庆巴蜀中学初2018级17—18学年度下期第一次月考在矩形ABCD中,对角线AC、BD交于点O,E为OB上一点,连接CE,G为CE中点.(1)如图1,连接AE,OG,若∠DAC=60°,BE=2,AB=53,求OG的长;(2)如图2,点F为线段OC上一点,连接BF,BG,若∠COB=∠OBG=∠CBF,求证:BE+CF=OA.2019重庆中考数学第24题专题训练---矩形答案1、沙坪坝区2017—2018学年度第二学期期末调研测试八年级数学试题如图,在矩形ABCD 中,点E 为AD 上一点,连接BE 、CE ,∠ABE =45°. (1)如图1,若32BE,BC =4,求EC 的长.(2)如图2,点P 是EC 的中点,连接BP 并延长交CD 于F ,H 为AD 上一点,连接HF ,且∠DHF =∠CBF ,求证:BP=PF+FH .解:(1)∵矩形ABCD ,∴∠A =∠D =90° 又∵∠ABE =45° ∴AB =AE设AB =AE =x 在Rt △ABE 中,∠A =90° 222AB AE BE += 即(22233x x += 解得:13x = 23x =-(舍) ∴AB =AE =3∵矩形ABCD ∴ AB =CD =3, BC =AD =4 ∴ED =AD -AE =4-3=1 在Rt △CDE 中,∠D =90° 22223110CE CD ED =++ (2)如答图,延长BF 交AD 的延长线于G ∵AG ∥BC , ∴∠G =∠PBC 又∵P 为CE 的中点, ∴EP =CP 在△EPG 和△CPB 中 G PBCEPG CPB EP CP ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△EPG ≌△CPB (AAS ) ∴BP =GP∵∠DHF =∠CBF ,∠CBF=∠G ∴∠DHF=∠G ∴FH =FG ∴GP =PF +FG =PF +FH2、重庆市南开(融侨)中学初2019级暑假作业数学综合练习 已知,如图所示,在矩形ABCD 中,点E 为BC 边上,∠AEF=90°. (1)如图1,已知点F 在CD 边上,AD=AE,AD=5,AB=4,求DF 的长; (2)如图2,已知AE=EF,点G 为AF 的中点,求证:2.AB BE BG +=ABCDEFABCDFEGH图1 图23、重庆第二外国语学校初2019级初三年级第二学月质量检测如图,在矩形ABCD 中,点E 为BC 边上一点,过点E 作EF ⊥DE 于点E. (1)如图1,已知F 在AB 上,AD=DE,AD=10, CD=6, 求BF 的长;(2)如图2,已知DE=EF ,点G 为DF 的中点,求证:.CD EC +=解答:M4、已知:在矩形ABCD中,点H是对角线AC与BD交点,点E是AB上的一点,连接HE,连接CE交BD 于F.(3)如图1,若HE⊥AC.且BC=3,AB=4,求△BEH的面积;(4)如图2,若∠AEB=∠BEC,求证:F是BH的中点.解答:M5、重庆巴蜀中学2019届初三下半期如图1,在矩形ABCD 中,AC 为矩形的对角线,点E 为AD 边上一点,连接BE. (1)若045EBC ∠=,且BE=CB ,AB=2,求AC 的长;(2)如图2,过B 作BF ⊥BE,使得BF=CD,连接CF 交BE 于点G,,当G 为CF 的中点时,求证:AE=2BG.解法一:解法二:解法三:解法四:6、重庆南开(融侨)中学初2018届初三下入学在矩形ABCD 中,点F 在AD 延长线上,且DF=DC,M 为AB 边上一点,N 为MD 的中点,点E 在直线CF 上,且BN=NE.(1)如图1,若AB=BC=6,13BM AB =,E 为线段FC 上的点,求NE 的长; (2)如图2.若AB<BC,E 为线段FC 延长线上的点,连结BE,求证:2.BE NE =如图1:在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE,F为AB上一点,且BF=DE,连接FC.(1)若DE=1,CF=22,求CD的长;(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=3AC. 解答:在矩形ABCD中,对角线AC、BD交于点O,E为OB上一点,连接CE,G为CE中点. (3)如图1,连接AE,OG,若∠DAC=60°,BE=2,AB=53,求OG的长;(4)如图2,点F为线段OC上一点,连接BF,BG,若∠COB=∠OBG=∠CBF,求证:BE+CF=OA.。
2019重庆中考数学第24题专题训练---- 平行四边形(含大部分题目答案)
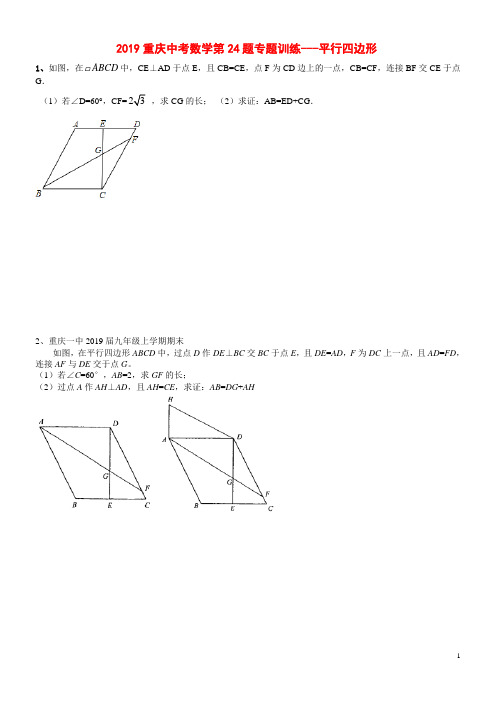
6、重庆市沙坪坝区 2019 届九年级上学期期末
A E
D
G
F
A
D
G
E
F
B
C
第 24 题图 1
B
C
第 24 题图 2
3
7、已知,在平行四边形 ABCD 中,AE⊥BC,且 E 为 BC 的中点,AE=2BE,P 为 BC 上一点,连接 DP,作 EF⊥DP 于点 F,连接 AF. (1)若 AD=4,求 AE 的长; (2)求证: 2 AF+EF=DF.
G.点 H 在 BC 的延长线上,且 CH=AG, 连接 EH.
(1)若 BC 12 2 ,AB=13,求 AF 的长; (2)求证:EB=EH.
9
19、重庆市 2018 年初中学业水平暨高中招生考试数学( A 卷)
A
F
D
O
H
G
B
E
C
10
2019 重庆中考数学第 24 题专题训练---平行四边形答案
连接 AF 与 DE 交于点 G。 (1)若∠C=60°,AB=2,求 GF 的长; (2)过点 A 作 AH⊥AD,且 AH=CE,求证:AB=DG+AH
1
3、如图,已知 ABCD 中,DE⊥BC 于点 E,DH⊥AB 于点 H,AF 平分∠BAD,分别交 DC、DE、DH 于点 F、G、M,
(1)若∠F=60°,∠C=45°,BC= 2 6 ,请求出 AB 的长;(2)求证:CD=BF+DF.
F
E
D
A
B
G
C
6
13、重庆一中初 2019 级 17-18 学年度下期期末
已知在平行四边形 ABCD 中,过点 D 作 DE BC 于点 E ,且 AD DE .连接 AC 交 DE 于点 F ,作 DG AC 于点 G . (1)如图 1,若 EF 1 , AF 13 ,求 DG 的长;
2019重庆中考数学第24题专题训练十一

2019重庆中考数学第24题专题训练十一
2018、12
1、重庆实验外国语学校2018-2019学年度度上期2020级八年级第二次月考(2018年12月中旬)
2、2018-2019学年重庆实验外国语学校九年级数学定时练习试题
如图△ABC,以AC为斜边向下作等腰直角△ADC,直角边AD交BC于点E
BC=+求线段DC的长;
(1)如图1,若∠ACB=30°,∠B=45°,BC=2
(2)如图2,若等腰R△ADC的直角顶点D恰好落在线段BC的垂直平分线上,过点A作AF⊥BC于点F,连接DF,
求证:AB=.
3、重庆第一中学2018-2019学年初2019级初三年级上学期第二次定时作业数学试题
4、2018-2019学年重庆外国语学校初三上第2次月考数学试题
5、重庆八中2019届初三上期第三学月
6、重庆第十一中学珊瑚校区2018-2019学年上学期初2019届初三年级第二次月考。
2019重庆中考数学第24题专题训练---三角形
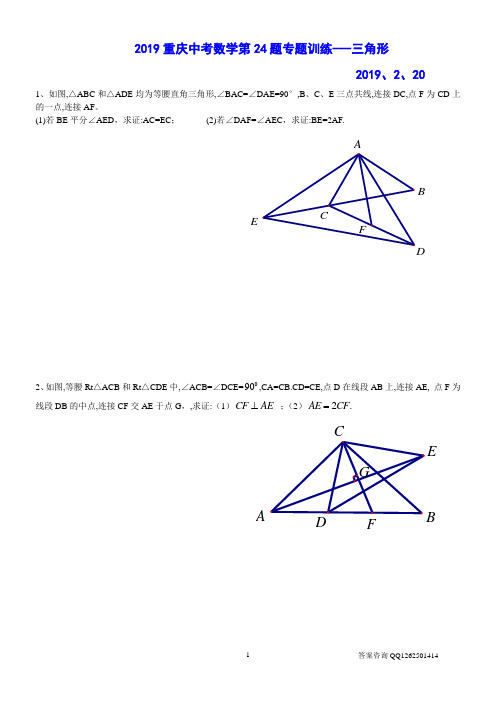
2019重庆中考数学第24题专题训练---三角形2019、2、201、如图,△ABC 和△ADE 均为等腰直角三角形,∠BAC=∠DAE=90°,B 、C 、E 三点共线,连接DC,点F 为CD 上的一点,连接AF 。
(1)若BE 平分∠AED ,求证:AC=EC ; (2)若∠DAF=∠AEC ,求证:BE=2AF.ACBEDF2、如图,等腰Rt △ACB 和Rt △CDE 中,∠ACB=∠DCE=090,CA=CB.CD=CE,点D 在线段AB 上,连接AE, 点F 为线段DB 的中点,连接CF 交AE 于点G ,,求证:(1)CF AE ⊥ ;(2)2.AE CF =GABCDEF3、如图,等腰Rt △ACB 和Rt △CDE 中,∠ACB=∠DCE=090,CA=CB.CD=CE,点D 在线段AB 上,连接AE,过C 作CF ⊥AE 于G ,交AB 于点F,求证:(1)点F 为线段DB 的中点;(2)2.AE CF =GABCDEF4、如图,等腰直角三角形ABC 中,090ACB ∠=,,CE CD ⊥ 且,CE CD = 连接AD ,过C 作CF AD ⊥于F ,交AB 于点G .求证:G 为BE 的中点.FACBDE G5、重庆市巴川中学2018-2019学年度上学期(秋季)初2020届初二年级半期考试 已知在△ABC 中,AB=AC,0120BAC ∠=,,点E 是AD 上一点,AD=CE,060AEC ∠= ,(1)如图1,求证:△ACE ≌△BAD(2)如图2,连接BE 并廷长,交AC 于点H,点E 恰好是BH 的中点,∠BAC 的角平分线交CE 于点F,求证:DE=AE+EF6、八中2019级周考157、重庆八中初2018届初三上期期末考试已知Rt ABC ∆中, CD 是斜边AB 边上的中线,点E 是直角边AC 上一点,连接DE ,.BE (1)如图1,若DE AB ⊥,且3BC =,4AC =,求CDE ∆的,面积;. (2)如图2,若AED BEC ∠=∠,求证:F 是CD 的中点.DF ACBEAC BE图1 图28、如图1,在五边形 ABCDE 中,∠E=90°,BC=DE 连接AC,AD,且AB=AD,AC ⊥BC(1)求证:AC=AE ; (2)如图2,若∠ABC=∠CAD ,AF 为BE 边上的中线,求证:AF ⊥CD.BB图1 图29、如图在ABC中,过点A作AE⊥BC交BC于E,D为△BC外一点且AD⊥DC,AD交BC于F,连接、D,已知AE=BE,AD= DC.(1) AB=22,BC=35,求DC长度;(2)求证:∠CBD+∠ACE=045.AB CED10、在等腰直角△ABC中,AC=BC,∠ACB=90°,CF⊥AB交AB于点F,点D在AC上,连接BD,交CF 于点G,过点C作BD的垂线交BC于点H,交AB于点E:(1)如图1,∠ABD=∠CBD,CG=1,求AB;BH AH.(2)如图2,连接AH、FH,∠AHF=90°,求证:211、如图1,△AOB 中,∠AOB= 90°,AO=BO,点C 在边AB 上,连接CO ,过点O 作CO 的垂线,在垂线上取点D ,使DO=CO,连接BD ,CD.(1)已知AC=2,BC=6,求CD 的长;(2)如图2,取线段BC 的中点E ,连接OE ,AD ,求证:OE ⊥AD 且AD=2OE.AOBDCFAOBDCE图1 图212、如图,△ABC 和△DEC 都是等腰直角三角形,C 为它们的公共直角顶点,连AD ,BE ,F 为线段AD 的中点,连接CF(1)如图1,当D 点在BC 上时,CE=4,BD=2,求CF;(2)如图2,把△DEC 绕C 点顺时针旋转一个锐角,其他条件不变,求证:BE=2CF .13、已知:△AOB 和△COD 均为等腰直角三角形,∠AOB=∠COD=90°.连接AD ,BC ,点H 为BC 中点,连接OH .(1)如图1所示,若AB =8,CD =2,求OH 的长。
2019重庆中考数学第24题专题训练四(含答案解析)

图1图2 2019重庆中考数学第24题专题训练四(含答案解析)2018.8.31、沙坪坝区2017—2018学年度第二学期期末调研测试八年级数学试题如图,在矩形ABCD 中,点E 为AD 上一点,连接BE 、CE ,∠ABE =45°. (1)如图1,若BE =,BC =4,求EC 的长.(2)如图2,点P 是EC 的中点,连接BP 并延长交CD 于F ,H 为AD 上一点,连接HF ,且∠DHF =∠CBF ,求证:BP=PF+FH .2、重庆八中2017-2018学年度下期期末考试八年级数学试题3、重庆育才中学2017-2018学年度初三上入学数学试题菱形ABCD中,一射线BE分∠ABC为∠ABE与∠CBE,且∠ABE:∠CBE=7:3.BE交对角线AC 于F,交CD于E.过B作BK⊥AD于K点,交AC于M,且∠DAC=15°.(1)求∠DEB的度数;(2)求证:2CF=CM+2FB.4、重庆市南开(融侨)中学初2019级暑假作业数学综合练习6、重庆市南开(融侨)中学初2019级暑假作业数学综合练习ABFBF图1 图28、如图,在Rt ABC ∆中,0,ABC=90∠D 为AB 的中点,E 为AC 上一点,且DE DB =,连接.BE(1)如图1,连接,CD 若,4,BE BD AC ==求DC 的长;(2)如图2,若,BD BC =F 为EC 的中点,过E 作BC 的平行线交BF 的延长线于点,G 连接,DG 延长BE 交DG 于点,H 连接,HC求证:.DHHC +=ABCDBG图1 图2图1图22019重庆中考数学第24题专题训练四答案解析2018.8.31、沙坪坝区2017—2018学年度第二学期期末调研测试八年级数学试题如图,在矩形ABCD 中,点E 为AD 上一点,连接BE 、CE ,∠ABE =45°. (1)如图1,若BE =,BC =4,求EC 的长.(2)如图2,点P 是EC 的中点,连接BP 并延长交CD 于F ,H为AD 上一点,连接HF ,且∠DHF =∠CBF ,求证:BP=PF+FH .解:(1)∵矩形ABCD ,∴∠A ∠=D =90°又∵∠ABE ∴=45° AB =AE 设AB =AE =x在△Rt ABE 中,∠A =90° 222AB AE BE +=即(222x x +=解得:13x = 23x =-(舍) 24(2)答图∴AB =AE =3 ---------------------------------------------------------------2分∵ 矩形ABCD∴ AB =CD =3, BC =AD =4∴ ED =AD -AE =4-3=1 -----------------------------------------------------3分 在△Rt CDE 中,∠D =90°CE === -------------------------------------------------5分 (2)如答图,延长BF 交AD 的延长线于G ∵ AG ∥BC ,∴∠ G ∠=PBC在△EPG 和△CPB 中 G PBC EPG CPB EP CP ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ EPG ≌△CPB (AAS ) ------------------------------------------------------------7分 ∴ BP =GP∵∠ DHF ∠=CBF ,∠∠CBF=G ∴∠∠ DHF=G∴ FH =FG ------------------------------------------------------------------9分 ∴GP =PF +FG =PF +FH∴BP =PF +FH ------------------------------------------------------------------10分3、重庆育才中学2017-2018学年度初三上入学数学试题菱形ABCD中,一射线BE分∠ABC为∠ABE与∠CBE,且∠ABE:∠CBE=7:3.BE交对角线AC 于F,交CD于E.过B作BK⊥AD于K点,交AC于M,且∠DAC=15°.(2)求∠DEB的度数;(2)求证:2CF=CM+2FB.5、重庆市南开(融侨)中学初2019级暑假作业数学综合练习6、重庆市南开(融侨)中学初2019级暑假作业数学综合练习A BFBFE图1 图27、重庆市南开(融侨)中学初2019级暑假作业数学综合练习8、如图,在Rt ABC ∆中,0,ABC=90∠D 为AB 的中点,E 为AC 上一点,且DE DB =,连接.BE(1)如图1,连接,CD 若,4,BE BD AC ==求DC 的长;(2)如图2,若,BD BC =F 为EC 的中点,过E 作BC 的平行线交BF 的延长线于点,G 连接,DG 延长BE 交DG 于点,H 连接,HC求证:.DHHC +=DGG图1 图2。
2019重庆中考数学第24题专题训练---正方形(含答案)

2019重庆中考数学第24题专题训练---正方形201902121、重庆第一中学2018-2019学年初2019级初三年级上学期第二次定时作业数学试题如图,点M 是正方形ABCD 的边BC 上一点,连接AM ,点E 是线段AM 上一点,CDE ∠的平 分线交AM 延长线于点F .(1)如图1,若点E 为线段AM 的中点,:1:2BM CM =,BE =AB 的长;(2)如图2,若G 为AE 中点,延长DG 至N ,使DG NG =,连接EN ,且EDG ENG ∠=∠,求证:BF DF +=.2、在正方形ABCD 中,点F 是BC 延长线上一点,过点B 作BE ⊥DF 于点E ,交CD 于点G ,连接CE . (1)若正方形ABCD 边长为3,DF =4,求CG 的长; (2)求证:EF+EG =2CE .GEA B CDF3、如图1,在正方形ABCD 中,对角线AC 与BD 交于点,O H 为CD 边上一点,连接BH 交AC 于K ,E 为BH 上一点,连接AE 交BD 于点.F(1)若AE BH ⊥于E ,且6,CK ==求AF 的长; (2)如图2,若=AE BE ,且,BEO EAO ∠=∠求证:.AEH图1 图24、重庆市南开(融侨)中学初2019级暑假作业数学综合练习如图,正方形ABCD 中,CB 的延长线上有一点E,连接AC 、AE. (1)如图1,若AC=4,∠CAE=75°,求△ACE 的面积; (2)如图2,连接BD 交AC 于点O ,在线段AB 上取点F ,使BE=BF ,连接CF ,过点B 作BG ∥CF ,交AE 于点G ,连接OG 、BG.求证:.BG AG +=5、重庆市南岸区11中、二外、珊瑚2018-2019学年度上期三校期末联考九年级数学如图1,以正方形ABCD 边AD 为边作等边三角形ADE ,EF ⊥AD 于点F ,连接BE 交AD 于G . (1)若正方形的边长为2,求AG 的长;(2)如图2,∠EAD 的平分线交BE 于点P ,连接CP ,求证:AP +PC6、在正方形ABCD 中,对角线AC,BD 交于点O,E 为OB 上一点,连接CE,F 为CE 的中点.(1)如图1,连接AE,OF,若 AB=6,求OF 的长;(2)如图2,连接BF,作BG ⊥BF 交CA 的延长线于点G ,求证:.CG BE =7、已知正方形ABCD如图所示,连接其对角线AC,∠BCA的平分线CF交AB于点F,过点B作BM⊥C F于点N,交AC于点M,过点C作CP⊥CF,交AD延长线于点P.(1)若正方形ABCD的边长为4,求△ACP的面积;(2)求证:CP=BM+2FN.8、重庆巴蜀中学初2018届九年级下第二次周考如图1,正方形ABCD中,AE为过顶点A的任意一条射线,过C作CE⊥AE于E.(1)己知AB=6.AE=8,求CE的长;(2)如图2,过D作DF⊥AE于F,求证:DF=EF.图1 图29、重庆一中初2018级初三下期期中如图,在正方形ABCD 中,点M 是边BC 上一点,连接AM ,过点C 作CH ⊥AM 交AM 的延长线于点H ,延长CH 于点M 连接MN 、BN . (1)若AB =4,AH =528,求线段CH 的长度; (2)若∠MAD =∠BMN ,求证:AM =MN +CN .2019重庆中考数学第24题专题训练---正方形答案1、重庆第一中学2018-2019学年初2019级初三年级上学期第二次定时作业数学试题如图,点M 是正方形ABCD 的边BC 上一点,连接AM ,点E 是线段AM 上一点,CDE ∠的平 分线交AM 延长线于点F .(3)如图1,若点E 为线段AM 的中点,:1:2BM CM =,BE =AB 的长;(4)如图2,若G 为AE 中点,延长DG 至N ,使DG NG =,连接EN ,且EDG ENG ∠=∠,求证:BF DF +=.(1):1:2BM CM ==,2BM x CM x ∴=设则∵正方形ABCD 3,90AB x ABC ∴=∠=︒Rt ABM AM ∆在中,∵点E 为线段AM 的中点2AM BM ∴== 2x ∴=36AB x ∴==(2)G AE 为中点AG EG ∴=AGD EGN AG EG AGD EGN DG NG ∆∆=⎧⎪∠=∠⎨⎪=⎩在和中AGD EGN ∴∆≅∆ 4N ∴∠=∠ EDG ENG ∠=∠,34ED EN ∴=∠=∠ DG NG = 90EGD ∴∠=︒AF CDE ∠平分12∴∠=∠123452FDG CDA ∴∠=∠+∠=∠=︒,90A AH AF FD H FAH ⊥∠=︒过作交延长线于即//DG AH ∴45H FDG ∴∠=∠=︒AHF ∴∆为等腰直角三角形,AH AF FH ∴=90DAB HAF ∴∠=∠=︒ DAH BAF ∴∠=∠DAH BAF AH AF DAH BAF AD AB DAH BAF DH BF∆∆=⎧⎪∠=∠⎨⎪=⎩∴∆≅∆∴=在和中BF DF DH DF FH ∴+=+==2、在正方形ABCD 中,点F 是BC 延长线上一点,过点B 作BE ⊥DF 于点E ,交CD 于点G ,连接CE . (1)若正方形ABCD 边长为3,DF =4,求CG 的长; (2)求证:EF+EG =2CE .解答:(1)∵四边形ABCD 是正方形∴∠BCG =∠DCB=∠DCF=90°,BC=DC .∵BE ⊥DF∴∠CBG+∠F=∠CDF+∠F .∴∠CBG=∠CDF . ∴△CBG ≌△CDF .∴BG=DF=4.∴在Rt △BCG 中,222BG BC CG =+∴CG =73422=-. …………………………4分 (2)过点C 作CM ⊥CE 交BE 于点M∵∠BCG=∠MCE =∠DCF =90° ∴∠BCM=∠DCE ,∠MCG=∠ECF ∵BC=DC ,∠CBG=∠CDF∴△CBM ≌△CDE ∴CM=CE∴△CME 是等腰直角三角形∴ME=CE 2 ,即MG+EG=CE 2 又∵△CBG ≌△CDF ∴CG=CF∴△CMG ≌△FCE ∴MG=EF∴EF+EG =2CEGEA B CDFM3、如图1,在正方形ABCD 中,对角线AC 与BD 交于点,O H 为CD 边上一点,连接BH 交AC 于K ,E 为BH 上一点,连接AE 交BD 于点.F(1)若AE BH ⊥于E ,且6,CK ==求AF 的长; (2)如图2,若=AE BE ,且,BEO EAO ∠=∠求证:.AEH图1图2解答:4、重庆市南开(融侨)中学初2019级暑假作业数学综合练习如图,正方形ABCD中,CB的延长线上有一点E,连接AC、AE.(1)如图1,若AC=4,∠CAE=75°,求△ACE的面积;(2)如图2,连接BD交AC于点O,在线段AB上取点F,使BE=BF,连接CF,过点B作BG∥CF,交AE于点G,连接OG、BG.求证:.+=BG AG5、重庆市南岸区11中、二外、珊瑚2018-2019学年度上期三校期末联考九年级数学如图1,以正方形ABCD边AD为边作等边三角形ADE,EF⊥AD于点F,连接BE交AD于G.(1)若正方形的边长为2,求AG的长;(2)如图2,∠EAD的平分线交BE于点P,连接CP,求证解法一:解法二:6、在正方形ABCD 中,对角线AC,BD 交于点O,E 为OB 上一点,连接CE,F 为CE 的中点.(1)如图1,连接AE,OF,若 AB=6,求OF 的长;(2)如图2,连接BF,作BG ⊥BF 交CA 的延长线于点G ,求证:.CG BE =7、已知正方形ABCD 如图所示,连接其对角线AC ,∠BCA 的平分线CF 交AB 于点F ,过点B 作BM⊥C F 于点N ,交AC 于点M ,过点C 作CP⊥CF,交AD 延长线于点P .(1)若正方形ABCD 的边长为4,求△ACP 的面积;(2)求证:CP=BM+2FN .解:∵∠1=∠2=22.5°,又CP⊥CF,∴∠3+∠FCD=∠1+∠FCD=90°∴∠3=∠1=22.5°∴∠P=67.5°又∵四边形ABCD 为正方形,∴∠ACP=45+22.5=67.5°∴∠P=∠ACP∴AP=AC又∵AB=4 ∴AP=42 ∴S △A P C =12AP•CD=82(2)∵在△PDC 和△FBC 中,{ ∠PDC=∠FBCCD=BC∠1=∠3∴△PDC≌△FBC∴CP=CF 在CN 上截取NH=FN ,连接BH∵FN=NH,且BN⊥FH∴BH=BF∴∠4=∠5∴∠4=∠1=∠5=22.5°又∠4+∠BFC=∠1+∠BFC=90°∴∠HBC=∠BAM=45°在△AMB 和△BHC 中,{ ∠1=∠4AB=BC∠HBC=∠BAM,∴△AMB≌△BHC,∴CH=BM∴CF=BM+2FN∴CP=BM+2FN.8、重庆巴蜀中学初2018届九年级下第二次周考如图1,正方形ABCD 中,AE 为过顶点A 的任意一条射线,过C 作CE ⊥AE 于E.(1)己知AB=6.AE=8,求CE 的长;(2)如图2,过D 作DF ⊥AE 于F,求证:DF=EF.图1 图29、重庆一中初2018级初三下期期中如图,在正方形ABCD 中,点M 是边BC 上一点,连接AM ,过点C 作CH ⊥AM 交AM 的延长线于点H ,延长CH 于点M 连接MN 、BN .(1)若AB =4,AH =528,求线段CH 的长度; (2)若∠MAD =∠BMN ,求证:AM =MN +CN .。
2019重庆中考数学第24题专题训练十二((含答案)
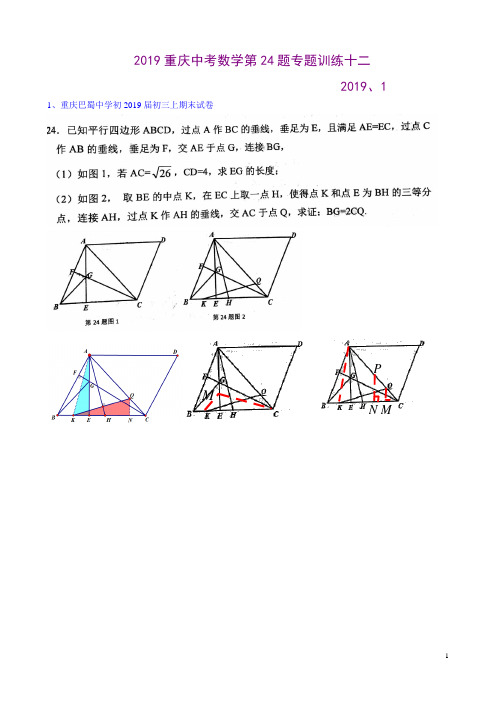
2019重庆中考数学第24题专题训练十二2019、11、重庆巴蜀中学初2019届初三上期末试卷MMPN2、重庆市南岸区11中、二外、珊瑚2018-2019学年度上期三校期末联考九年级数学4、2018-2019学年重庆实验外国语学校九年级数学定时练习试题如图△ABC,以AC为斜边向下作等腰直角△ADC,直角边AD交BC于点EBC=+求线段DC的长;(1)如图1,若∠ACB=30°,∠B=45°,BC=2(2)如图2,若等腰R△ADC的直角顶点D恰好落在线段BC的垂直平分线上,过点A作AF⊥BC于点F,连接DF,求证:AB.BB图1图2B6、如图,△ABC中,∠BAC=5°,点D是AB边上一点,且CB=CD,过点B作BH⊥CD于H,交AC于E(1)若CH=4,DH=2,求△BCD的面积;(2)求证:∠BEC=∠A+12∠BCD;(3)用等式表示AE与BD之间的数量关系;并证明。
7、如图1,在五边形 ABCDE 中,∠E=90°,BC=DE 连接AC,AD,且AB=AD,AC ⊥BC (1)求证:AC=AE; (2)如图2,若∠ABC=∠CAD,AF 为BE 边上的中线,求证:AF ⊥CDABB图1 图2方法一:方法二:MN方法三:8、如图①,在等腰Rt △ABC 中,∠ACB=90°,点D 在AC 上(且不与点A,C 重合),以AD 为直角边向外作等腰Rt △ADE,使∠ADE=90°,连接CE,再以CE 、CB 为邻边作平行四边形CBFE (1)已知求线段CF 的长;(2)将Rt △ADE 绕点A 逆时针旋转角a(90°<a<180°),如图②,连接CD 、CE,再以CE 、CB 为邻边作平行四边形CBFE,设线段AB 、CE 交于点G ,求证BECF图① 图②9、已知,在△ABC中,∠ABC=45,高线AD、BE相交于点G,(1)如图,若∠CAD=30°,GE=2,求DG的长(2)如图2,连接DE,过点D作DF⊥DE交BE于点F,连接AF,过点D作DH⊥AF于点H交BE于点M求证:AF=2DM10、如图在ABC中,过点A作AE⊥BC交BC于E,D为△BC外一点且AD⊥DC,AD交BC 于F,连接、D,已知AE=BE,AD= DC.(1) AB=BC=,求DC长度;(2)求证:∠CBD+∠ACE=45B CADEMM11、八中2019级周考1512、如图,平行四边形ABCD 中,过点B 作BE⊥CD 于点E ,点F 是AD 上一点,连接BF 、CF,交BE 于点G.. (1)若CF 平分∠BCD,∠A=60°,BC=8,求线段CG 的长。
2019重庆中考数学第24题专题训练八
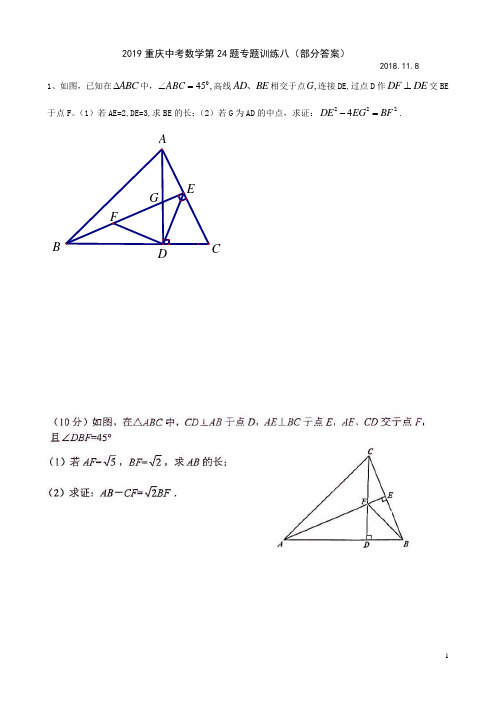
2019重庆中考数学第24题专题训练八(部分答案)2018.11.81、如图,已知在ABC ∆中,045,ABC ∠=高线AD BE 、相交于点,G 连接DE,过点D 作DF DE ⊥交BE 于点F 。
(1)若AE=2,DE=3,求BE 的长;(2)若G 为AD 的中点,求证:2224DE EG BF -=.BDA3、重庆八中初2019级初三上第七次周考如图1、在Rt△ABC中,点D为边AC上一点,DE AB于点E,点M为BD的中点,CM的延长线交AB于点F(1)若∠A=50°,求∠EMC的大小(2)如图2,若△ABC是等腰直角三角形,且EA=EM,AN//EM,求证:CN=NM4、在等腰要三角形ABC中AB=AC,BD是AC边的中线,过点C作CE⊥BC,交BD的延长现于点E,连接AE.(1)如图1,若∠ABC=60º,BE=4,求AE的长;(2)如图2,求证:BE=2AE.BBMN图1 图25、西南大学 附属中学2018--2019学年度上期期中考试八年级数学试题求证:(1);AD DG = (2)1.2AF BE =FDEABC HGDEAM7、如图等腰直角△ABC中,∠ACB= 90°,点D在BA的延长线上,连接CD,过C作CE⊥CD,使CE=CD,连接BE,若点N为BD 的中点,连接CN、BE. (1)求证:AB⊥BE; (2)AE=2CN.M8、如图,等腰直角三角形ABC 中,090ACB ∠=,,CE CD ⊥ 且,CE CD = 连接AD ,过C 作CF AD⊥于F ,交AB 于点G .求证:G 为BE 的中点.FACBDE G9、如图,Rt ABC ∆中,090ACB ∠=,CD AB ⊥于,E ,CD AB DA BC =、的延长线交于.F(1)若.DA = 012,30,AC ABC =∠= 求DE 的长;(2)若2,BC AC =求证:.DA =B。
2019中考数学狙击重难点系列专题24----反比例函数与一次函数综合(含答案)

反比例函数与一次函数综合1. 如图,一次函数 ( )与反比例函数( )的图象交于点 , .(1)求这两个函数的表达式;(2)在 轴上是否存在点 ,使 为等腰三角形?若存在,求 的值;若不存在,说明理由.2. 如图,一次函数 的图象与反比例函数的图象交于点A ﹙−2,−5﹚、C ﹙5,n ﹚,交y 轴于点B ,交x 轴于点D .(1)求反比例函数和一次函数 的表达式; (2)连接OA 、OC .求△AOC 的面积.3. 如图,一次函数y=kx+b 与反比例函数( ) 的图象交于A (m ,6),B (3,n )两点. (Ⅰ)求一次函数的解析式;(Ⅱ)根据图象直接写出的x 的取值范围; (Ⅲ)求△AOB 的面积.4. 已知正比例函数y=2x 的图象与反比例函数y=(k≠0)在第一象限的图象交于A 点,过A 点作x 轴的垂线,垂足为P 点,已知△OAP 的面积为1. (1)求反比例函数的解析式;(2)如果点B 为反比例函数在第一象限图象上的点(点B 与点A 不重合),且点B 的横坐标为2,在x 轴上求一点M ,使MA+MB 最小.5. 已知:一次函数y=﹣2x+10的图象与反比例函数(k >0)的图象相交于A ,B 两点(A 在B 的右侧).(1)当A (4,2)时,求反比例函数的解析式及B 点的坐标;(2)在1的条件下,反比例函数图象的另一支上是否存在一点P ,使△PAB 是以AB 为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,请说明理由.(3)当A (a ,﹣2a+10),B (b ,﹣2b+10)时,直线OA 与此反比例函数图象的另一支交于另一点C ,连接BC 交y 轴于点D .若,求△ABC 的面积.6. 已知:如图,直线AB 与x 轴y 轴分别交于A ,B 两点,与双曲线y=在第一象限内交于点C ,BO=2AO=4,△AOC 的面积为2 +2.(1)求点C 的坐标和k 的值;(2)若点P 在双曲线y=上,点Q 在y 轴上,且以A ,B ,P ,Q 为顶点的四边形为平行四边形,求所有符合题意的点Q 的坐标.7. 如图,反比例函数y=的图象与一次函数y=x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积。
2019重庆中考数学第24题专题训练十五
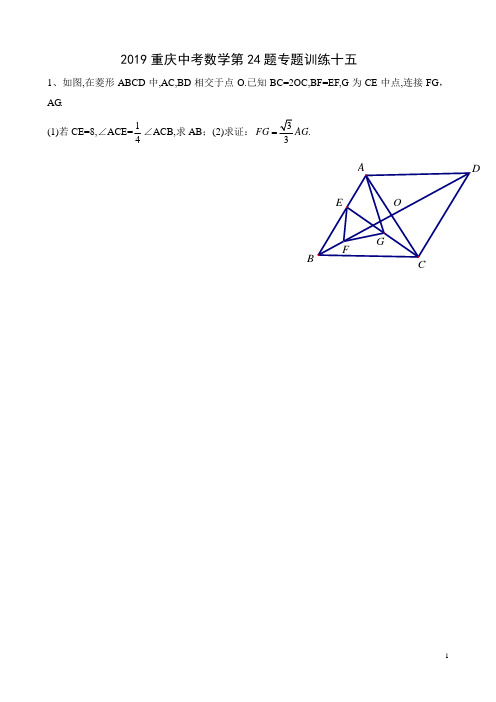
图1
图2
3
4、如图,在菱形 ABCD 中, ABC 600 , AE CF , 点 G 为 BE 的中点。 (1)若 E 是 AC 的中点,AB=6,求 AG 的长;(2)求证: FG 3AG.
4
5、重庆一中初 2019 级 18-19 学年度下期定时练习
(1)如图 1,若 DE 平分 ADC ,点 G 为 AB 的中点, CD 2 3CF 6 ,求平行四边形 ABCD 的面 积. (2)如图 2,点 P 在 GF 上,且 PE PF ,延长 EP 交 AC , CD 于点 O , Q ,连接 AQ ,若 AC BC EQ , EQC 45 ,求证: CE 2BG DQ .
10
10、重庆二外初 2019 级一诊模拟
11
A
D
OG
F
B
E
C
图1
图2
12
已知:在▱ABCD 中,过点 D 作 DE 延长线于点 F.
交 BC 延长线于点 E,且
,连接 AC 并延长交
如图 1,若
,
,求 AD 的长;
如图 2,作
于点 G,作
于点 M,连接 DM,求证:
解: 四边形 ABCD 是平行四边形,
5
6
6、南开(融侨)中学初 2019 届(下)阶段检测二
7
7、八中初 2019 级初三下第一次月考
8
8、2019 届一外第一次模拟考试
9
9、重庆巴蜀中学初 2019 届初三(下)第二次定时作业 如图,四边形 ABCD 是平行四边形,点 E 、 F 在 BC 上,且 CF BE ,连接 DE ,过点 F 作 FG AB 于 点 G ,交 DE 于点 P .
2019重庆中考数学第24题专题训练二(含部分答案)
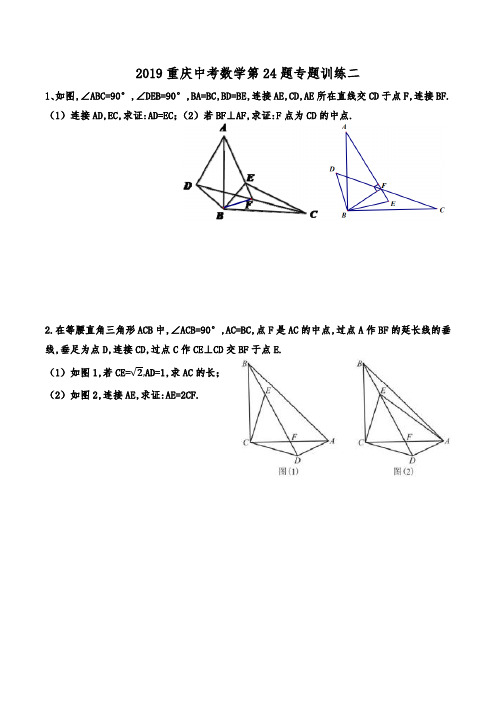
2019重庆中考数学第24题专题训练二1、如图,∠ABC=90°,∠DEB=90°,BA=BC,BD=BE,连接AE,CD,AE所在直线交CD于点F,连接BF.(1)连接AD,EC,求证:AD=EC;(2)若BF⊥AF,求证:F点为CD的中点.2.在等腰直角三角形ACB中,∠ACB=90°,AC=BC,点F是AC的中点,过点A作BF的延长线的垂线,垂足为点D,连接CD,过点C作CE⊥CD交BF于点E.(1)如图1,若CE=AD=1,求AC的长;(2)如图2,连接AE,求证:AE=2CF.3、如图,矩形ABCD中,BC=2AB,点E是边AD的中点,点F是线段AE上ー点(点F不与点A,E重合)连接BF,过点F作直线BF的垂线,与线段CE交于点G,点H是线段BG的中点.(1)若CE=2求矩形ABCD的面积;(2)求证:BF=EH.4、如图1,在正方形ABCD中,对角线AC与BD交于点O,H为CD边上一点,连接BH交AC于K,E 为BH上一点,连接AE交BD于点F.(1)若AE⊥BH于E,且CK=,AD=6,求AF的长;(2)如图2,若AE=BE,且∠BEO=∠EAO,求证:AE=2OE.5、如图,在△ABC中,∠BAC=90°,AB=AC,点D为形外一点,BD⊥CD于点D,CD交AB于E. (1)如图1,若∠ABD=15°,BE=6,求BC的长;(2)如图2,连接AD,作AF⊥BC于F,交CD于M,若DA=DB,求证:CE=CM.6.(2017春・垫江县期末)已知,如图1在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.(1)若BF=5,DC=3,求AB的长;(2)在图1上过点F作BE的垂线,过点A作AB 的垂线,两条垂线交于点G,连接BG,得如图2。
①求证:∠BGF=45°;②求证:AB=AG+AF.2019重庆中考数学第24题专题训练二答案解析。
2019重庆中考数学第24题专题训练七
2019重庆中考数学第24题专题训练七(部分答案)
2018.10.16
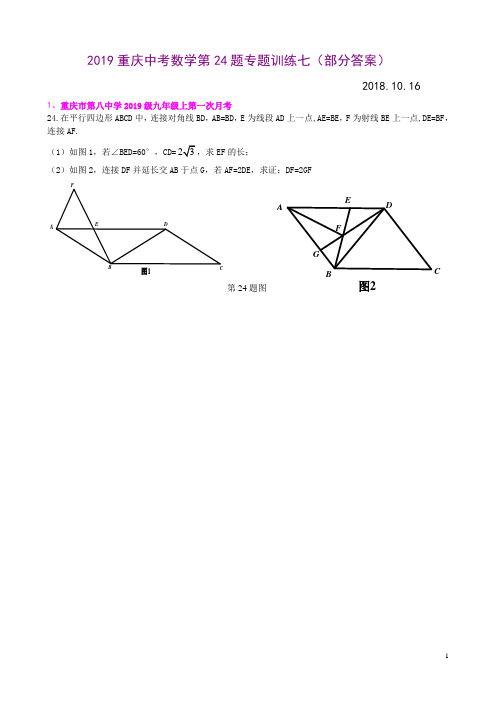
1、重庆市第八中学2019级九年级上第一次月考 24.在平行四边形ABCD 中,连接对角线BD ,AB=BD ,E 为线段AD 上一点,AE=BE ,F 为射线BE 上一点,DE=BF ,连接AF.
(1)如图1,若∠BED=60°,
CD=EF 的长;
(2)如图2,连接DF 并延长交AB 于点G ,若AF=2DE ,求证:DF=2GF
图1
A
图2
C
A
第24题图
2、重庆南开中学2019届九上第一次月考(阶段测试二)
H
K
3、重庆市实验外国语学校初2019级第一次月考
4、重庆一中初2019级2018-2019学年度上期第一次定时作业
5、在ABCD 中,AC CD ⊥,点E 为边BC 上一点,点F 为AE 的中点,点G 为ABCD 外一点,连接AG CG DG 、、,已知AGC ADC ∠=∠.
(1) 如图1,若tan 2ADC ∠=,点E 为边BC 中点,1AF =,求线段CD 的长; (2) 如图2,若2ACG ACB ∠=∠,DG BE =,求证:2.CG BF =
B
D
B
D
如图1 如图2
H。
2019重庆中考数学第24题专题训练十
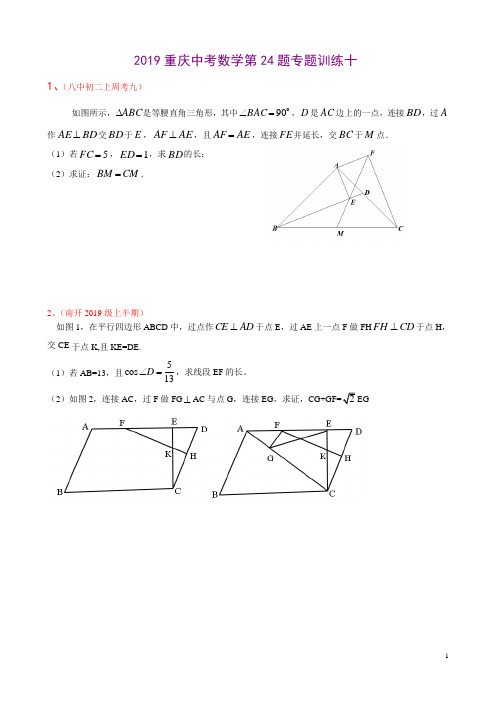
2019重庆中考数学第24题专题训练十1、(八中初二上周考九)如图所示,ABC ∆是等腰直角三角形,其中o90=∠BAC ,D 是AC 边上的一点,连接BD ,过A 作BD AE ⊥交BD 于E ,AE AF ⊥,且AE AF =,连接FE 并延长,交BC 于M 点.(1)若5=FC ,1=ED ,求BD 的长; (2)求证:CM BM =.2、(南开2019级上半期)如图1,在平行四边形ABCD 中,过点作CE AD ⊥于点E ,过AE 上一点F 做FH FH CD ⊥于点H ,交CE 于点K,且KE=DE. (1)若AB=13,且5cos 13D ∠=,求线段EF 的长。
(2)如图2,连接AC ,过F 做FG ⊥AC 与点G ,连接EG ,求证,EG3、(一中2019级上半期)在平行四边形ABCD中,点E为CD边上一点,点F为BC中点,连接BE,DF 交于点G,且GA=GD,(1)如图1,若AB=AE=BG=,AE⊥CD,求AG2的值(2)如图2,若EM平分∠BEC,且EM//DF,过点G做GN⊥BE交AE于点N且GN=GE,求证:AE⊥CD4、(西附2019级上第一次月考)如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上一点,连接AC, E为AD延长线上一点,连接BE并延长,交AC延长线于点G,(1)如图,若BE⊥AE,∠BAD=15°,BC=1,求△ABG的面积。
(2)如图2,连接EC,过点A做AF⊥EC交EC延长线于点F,且∠FAC=∠BAE.求证:CE5、(巴川2019级上半期)在△ABC中,以AB为斜边,做直角△ABD,使点D落在△ABC内,∠ADB=90°,(1)如图1,若AB=AC,∠ABD=60°,BD= 点P, M分别为BC, AB边的中点,连接PM,求线段PM的长。
(2)如图2,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC 于点P,求证:BP=CP(3)如图3,若AD=BD,过点D的直线交AC于点E,交BC于点F,且EF AC, AE=EC, 请直接写出线段BF,FC , AD之间的关系,(不需证明)6、(一外2019级上周考10)如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF, E为△ADC内一点,连接AE, BE, AE平分∠CAD,AE BE.(1)若∠EBD=15°,求∠ADF;(2)求证:BE-AE=DF.7、重庆一中2018-2019学年度上期初2020级八年级数学半期考试8、西南大学附属中学2018-2019学年上学期初2019级初三年级第三次月考10、重庆市巴川中学2018-2019学年度上学期(秋季)初2020届初二年级半期考试11、已知△ABC 中,AB AC =,过B 点作射线BE ,过C 点作射线CF ,使ABE ACF ∠=∠,且射线BE ,CF 交于点D ,过A 点作AM BD ⊥于M .(1)如图1所示,若CF BE ⊥,4=AB ,︒=∠30ABE ,求CD ; (2)如图2所示,求证:DC DM BM -=.图1A BC EFMD图2。
2019重庆中考数学第24题专题训练二(含答案解析)
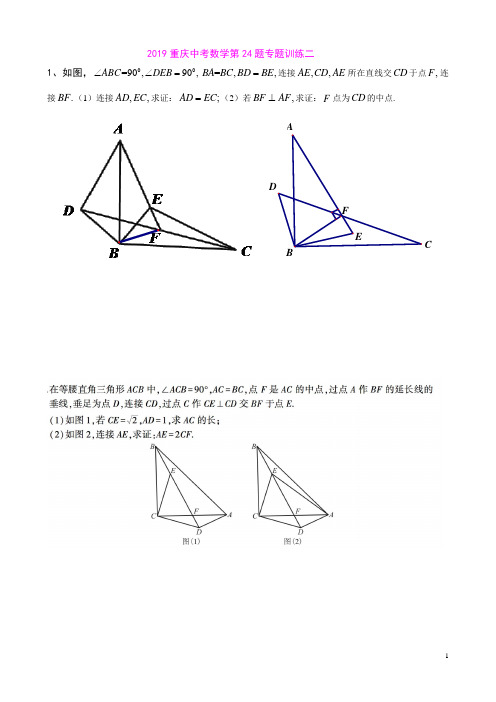
2019重庆中考数学第24题专题训练二1、如图,00=90,90,ABC DEB ∠∠==,,BA BC BD BE =连接,,AE CD AE 所在直线交CD 于点,F 连接.BF (1)连接,,AD EC 求证:;AD EC =(2)若,BF AF ⊥求证:F 点为CD 的中点.BBCADF E3、如图,矩形ABCD 中,2BC AB =,点E 是边AD 的中点,点F 是线段AE 上一点(点F 不与点,A E 重合)连接BF ,过点F 作直线BF 的垂线,与线段CE 交于点,G 点H 是线段BG 的中点. (1)若CE =求矩形ABCD 的面积;(2)求证:.BF =B4、如图1,在正方形ABCD 中,对角线AC 与BD 交于点,O H 为CD 边上一点,连接BH 交AC 于K ,E 为BH 上一点,连接AE 交BD 于点.F (1)若AE BH ⊥于E ,且6,CK ==求AF 的长;(2)如图2,若=AE BE ,且,BEO EAO ∠=∠求证:.AEBHBH图1 图25、如图,在ABC ∆中,090BAC ∠=,AB AC =,点D 为形外一点,BD CD ⊥于点D ,CD 交AB 于E , (1)如图1,若015ABD ∠=,6,BE =求BC 的长;(2)如图2,连接AD ,作AF BC ⊥于,F 交CD 于,M 若DA DB =,求证:2.CE CM =EBC ADEMBCA DF图1 图22019重庆中考数学第24题专题训练二答案解析1、如图,00=90,90,ABC DEB ∠∠==,,BA BC BD BE =连接,,AE CD AE 所在直线交CD 于点,F 连接.BF (1)连接,,AD EC 求证:;AD EC =(2)若,BF AF ⊥求证:F 点为CD 的中点.MG3、如图,矩形ABCD 中,2BC AB =,点E 是边AD 的中点,点F 是线段AE 上一点(点F 不与点,A E 重合)连接BF ,过点F 作直线BF 的垂线,与线段CE 交于点,G 点H 是线段BG 的中点. (1)若22,CE =求矩形ABCD 的面积;(2)求证: 2.BF EH =EABCDFGH。
2019重庆中考数学第24题专题训练九

2019重庆中考数学第24题专题训练九
2018.11.25 重庆八中初2019级初三上第六次周考数学试题
C
重庆八中2018-2019学年上学期2019届初三半期考试
M
重庆第二外国语学校初2019级初三年级第二学月质量检测
重庆市第八中学初2019级初三上学期第十次周考
重庆市第八中学初2019级初三上学期第八次周考
重庆外国语学校2018—2019学年度(上)初三年级半期考试
如图,ABC
∠90
BCD
ABC.
=
∠
Rt∆与BCD
AB=,︒
Rt∆在线段BC的同侧,BC
=
(1)如图1,已知2
=
BD,求CD的长;
=
6
AC,41
(2)如图2,将BCD
Rt∆,点C、D的对应点分别是
90得到BAF
Rt∆绕着点B逆时针旋转︒
点A、F,连接CF和AD.过点B作CF
BH⊥于点H,交AD于点M,求证:BM
=.
CF2。
2019重庆中考数学第24题专题训练十三(含答案)

2019重庆中考数学第24题专题训练十三(答案在后面)1、重庆一中2019届九年级上学期期末24、如图,在平行四边形ABCD中,过点D作DE⊥BC交BC于点E,且DE=AD,F为DC上一点,且AD=FD,连接AF与DE交于点G。
(1)若∠C=60°,AB=2,求GF的长;(2)过点A作AH⊥AD,且AH=CE,求证:AB=DG+AHY中,DE⊥BC于点E,DH⊥AB于点H,AF平分∠BAD,分别交DC、DE、DH于点F、G、2、如图,已知ABCDM,且DE=AD.(1)求证:△ADG≌△FDM.(2)求证:AB=DG+EC3、如图,已知▱ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D 作DC的垂线,分别交AE、AB于点M、N.(1)若M为AG中点,且DM=2,求DE的长;(2)求证:AB=CF+DM.4、如图,在ABCD 中,CE ⊥AD 于点E ,且CB=CE ,点F 为CD 边上的一点,CB=CF ,连接BF 交CE 于点G . (1)若∠D=60°,CF=,求CG 的长; (2)求证:AB=ED+CG .5、重庆市沙坪坝区2019届九年级上学期期末BGDB第24题图1 第24题图26、重庆实验外国语学院2018-2019学年上期期末考试初三数学试题在△ABC 中,D 为BC 上一点,连接AD,过点B 作BE 垂直于CA 的廷长线于点E,BE 与DA 的延长线相交于点F(1)如图1,若AB 平分∠CBE,∠ADB=30·,AE=3,AC=7,求C 的长;(2)如图2,若AB=AC,∠ADB=45°,求证:.BC =7、重庆南开中学2019届九年级上学期期末如图,在平行四边形ABCD 中,对角线BD ⊥AD,E 为CD 上一点,连接AE 交BD 于F.G 为AF 的中点,连接DG.(1)如图1,若DG=DF=1,BF=3,求CD 的长;(2)如图2,连接BE,且BE=AD,090,AEB ∠= M 、N 分别为DG ,BD 上的点,且DM=BN,H 为AB 的中点,连接HM 、HN,求证:∠MHN=∠AFB.8、重庆巴蜀中学初2019届初三上期末试卷9、重庆市两江新区2018-2019学年八年级第一学期期末如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,B、C、E三点共线,连接DC,点F为CD上的一点,连接AF。
2019重庆中考数学第24题专题训练之二------平行四边形(Word版含答案)
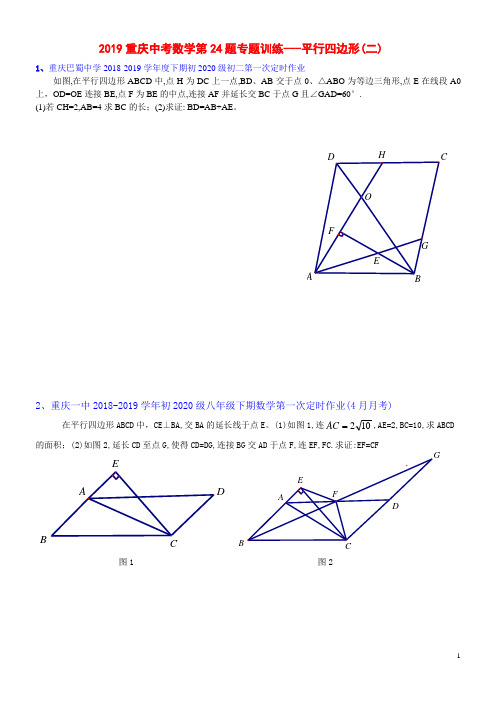
2019重庆中考数学第24题专题训练---平行四边形(二)1、重庆巴蜀中学2018-2019学年度下期初2020级初二第一次定时作业如图,在平行四边形ABCD 中,点H 为DC 上一点,BD 、AB 交于点0、△ABO 为等边三角形,点E 在线段A0上,OD=OE 连接BE,点F 为BE 的中点,连接AF 并延长交BC 于点G 且∠GAD=60°. (1)若CH=2,AB=4求BC 的长;(2)求证: BD=AB+AE 。
2、重庆一中2018-2019学年初2020级八年级下期数学第一次定时作业(4月月考)在平行四边形ABCD 中,CE ⊥BA,交BA 的延长线于点E 。
(1)如图1,连102 AC ,AE=2,BC=10,求ABCD 的面积;(2)如图2,延长CD 至点G,使得CD=DG,连接BG 交AD 于点F,连EF,FC.求证:EF=CFBDB图1 图23、重庆市巴蜀中学、育才中学、南开中学三校联考初2019级一诊4、重庆西南大学附属中学2019级第六次月考在ABCD中,AC=AD,(1)如图1,过点A作AE⊥AC于E,若BC=10,AE=6,求AB边的长;(2)如图2,过点C作CF⊥CD交DD于F,在ABCD外有一点G,连接AG,使得AG=2OF,且∠BAG=∠BFC,连接BG.、DC,若CD=CF,求证:BG⊥BC.图1 图25、如图,ABCD的对角线AC、BD相交于点O,AC=BC.(1)如图1,过点B作BE⊥AC于点E,若AC=8,BE=6,求OE的长;(2)如图2,若∠BDC=045,过点C作CF⊥CD交BD于F,过B作BG⊥BC,且BG=BC,.连接AG、DG,求证:AG=2OF.图1 图26、重庆一中初2019级18-19学年度下期定时练习7、南开(融侨)中学初2019届(下)阶段检测二8、八中初2019级初三下第一次月考9、2019届一外第一次模拟考试如图,在菱形ABCD 中,∠A=60°,点E 、F 分别在边AB 、BC 上。
2019重庆中考数学第24题专题训练十四

2019重庆中考数学第24题专题训练十四1、重庆育才中学初2019级初三(下)2019年入学考试如图,在平行四边形 A BCD 中,对角线 B D ∞ AD ,E 为 C D 上一点,连接 A E 交 B D 于点 F ,G 为 A F 的中点,连接 D G . (1)如图 1,若 D G =DF =1,BF =3,求 C D 的长;(2)如图 2,连接 B E ,且 B E =AD , ∠AEB = 90 ,M 、N 分别为 D G ,BD 上的点,且 D M =BN ,H 为 A B的中点,连接 H M 、HN ,求证: ∠MHN = ∠AFB .2、重庆市融汇清华中学2019届九年级下学期数学入学考试如图一所示,△ABC 是等腰直角三角形,其中∠BAC =090,D 是AB 边上的一点,连接CD,过A 作AE CD ⊥.垂足为E ,,,AF AE AF AE ⊥= 连接.FB(1)求证:;CF FB =(2)如图二,延长FE ,交BC 于G ,若G 点正好为BC 的中点,求证:2.EG AE BF +=3、重庆外国语学校初2019级(九年级)2018-2019学年度下期入学考试45,点E在对角线AC上,BE的延长线交CD于点F,交AD的延长线于点在平行四边形ABCD中,∠ABE=0G过点C作CH⊥AB于点H,交BF于点M。
(1)若BE=AE=ABE的面积;(2)若∠ABC=3∠EBC,CA=CB,求证:CM=FG.4、重庆育才中学初2019级九年级上期末考试试题已知平行四边形ABCD中,连接AC,AC=AB,过点B作BE⊥AC,垂足为E,延长BE与CD相交于点F. (1)如图1,若AE=3,CE=2,求线段AD的长;AC=(2)如图2,若∠BAC=45°,过点F作FG⊥AD于点G,连接AF、EG,求证:.如图,在ABCD 中,AD ⊥AC,点E 是AC 上一点,且∠ADE =45°,连接DE 并延长交BC 于点F. (1)若3,2AE CD CE == 求ABCD 的面积; (2)过点A 作AG ⊥CD 于点G ,交DF 于点M ,点N 是CA 延长线上一点,连接MN ,若∠ACD =∠ANM ,求证:AC=CB+AN.6、如图,在ABCD 中,E 是AD 上一点,连接BE ,AH ⊥BC 交BE 于G ,连接CG 并延长交AB 于F,已知GC=CD,090GCD ∠=.(1) 若∠BAG=30°,GC=4,2AG =,求ABCD 的面积; (2)求证:.DE =BH8、重庆南开(融侨)中学初2019届(下)阶段一(入学)检测 如图,对角线AC ,BD 交交于点O ,AD =BD .(1)如图1,若BD =10,ABCD 的面积为60,求AB 的长;(2)如图2,若sin ∠ACD=sin 2ACD ∠=,过D 作DE ⊥DC 交AC 于点E ,过A 在△ACD 的同侧作AF ⊥AC ,且使AF =2OE ,连接BF ,求证:BF ⊥BC 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图1
图2 2019重庆中考数学第24题专题训练四(含答案解析)
2018.8.3
1、沙坪坝区2017—2018学年度第二学期期末调研测试八年级数学试题
如图,在矩形ABCD 中,点E 为AD 上一点,连接BE 、CE ,∠ABE =45°. (1)如图1,若BE =,BC =4,求EC 的长.
(2)如图2,点P 是EC 的中点,连接BP 并延长交CD 于F ,H 为AD 上一点,连接HF ,且∠DHF =∠
CBF ,求证:BP=PF+FH .
2、重庆八中2017-2018学年度下期期末考试八年级数学试题
3、重庆育才中学2017-2018学年度初三上入学数学试题
菱形ABCD中,一射线BE分∠ABC为∠ABE与∠CBE,且∠ABE:∠CBE=7:3.BE交对角线AC 于F,交CD于E.过B作BK⊥AD于K点,交AC于M,且∠DAC=15°.
(1)求∠DEB的度数;(2)求证:2CF=CM+2FB.
4、重庆市南开(融侨)中学初2019级暑假作业数学综合练习
6、重庆市南开(融侨)中学初2019级暑假作业数学综合练习
A
B
F
B
F
图1 图2
8、如图,在Rt ABC ∆中,0,ABC=90∠D 为AB 的中点,E 为AC 上一点,且DE DB =,连接.BE
(1)如图1,连接,CD 若,4,BE BD AC ==求DC 的长;
(2)如图2,若,BD BC =F 为EC 的中点,过E 作BC 的平行线交BF 的延长线于点,G 连接,DG 延长BE 交DG 于
点,H 连接,HC
求证:.DH
HC +=
A
B
C
D
B
G
图1 图2
图
1
图2
2019重庆中考数学第24题专题训练四答案解析
2018.8.3
1、沙坪坝区2017—2018学年度第二学期期末调研测试八年级数学试题
如图,在矩形ABCD 中,点E 为AD 上一点,连接BE 、CE ,∠ABE =45°. (1)如图1,若BE =,BC =4,求EC 的长.
(2)如图2,点P 是EC 的中点,连接BP 并延长交CD 于F ,H
为AD 上一点,连接HF ,且∠DHF =∠
CBF ,求证:BP=PF+FH .
解:(1)∵矩形ABCD ,∴∠A ∠=D =90°
又∵∠ABE ∴=45° AB =AE 设AB =AE =x
在△Rt ABE 中,∠A =90° 222AB AE BE +=
即(2
2
2
x x +=
解得:13x = 23x =-(舍) 24(2)答图
∴AB =AE =3 ---------------------------------------------------------------2分
∵ 矩形ABCD
∴ AB =CD =3, BC =AD =4
∴ ED =AD -AE =4-3=1 -----------------------------------------------------3分 在△Rt CDE 中,∠D =90°
CE === -------------------------------------------------5分 (2)如答图,延长BF 交AD 的延长线于G ∵ AG ∥BC ,∴∠ G ∠=PBC
在△EPG 和△CPB 中 G PBC EPG CPB EP CP ∠=∠⎧⎪
∠=∠⎨⎪=⎩
∴△ EPG ≌△CPB (AAS ) ------------------------------------------------------------7分 ∴ BP =GP
∵∠ DHF ∠=CBF ,∠∠CBF=G ∴∠∠ DHF=G
∴ FH =FG ------------------------------------------------------------------9分 ∴GP =PF +FG =PF +FH
∴BP =PF +FH ------------------------------------------------------------------10分
3、重庆育才中学2017-2018学年度初三上入学数学试题
菱形ABCD中,一射线BE分∠ABC为∠ABE与∠CBE,且∠ABE:∠CBE=7:3.BE交对角线AC 于F,交CD于E.过B作BK⊥AD于K点,交AC于M,且∠DAC=15°.
(2)求∠DEB的度数;(2)求证:2CF=CM+2FB.
5、重庆市南开(融侨)中学初2019级暑假作业数学综合练习
6、重庆市南开(融侨)中学初2019级暑假作业数学综合练习
A B
F
B
F
E
图1 图2
7、重庆市南开(融侨)中学初2019级暑假作业数学综合练习
8、如图,在Rt ABC ∆中,0,ABC=90∠D 为AB 的中点,E 为AC 上一点,且DE DB =,连接.BE
(1)如图1,连接,CD 若,4,BE BD AC ==求DC 的长;
(2)如图2,若,BD BC =F 为EC 的中点,过E 作BC 的平行线交BF 的延长线于点,G 连接,DG 延长BE 交DG 于
点,H 连接,HC
求证:.DH
HC +=
D
G
G
图1 图2。
