最新整理小学几何图形知识点汇总
小学五年级数学解析:几何图形的分类与性质

小学五年级数学解析:几何图形的分类与性质一、几何图形的分类1. 三角形的分类按边分类:等边三角形、等腰三角形、不等边三角形。
按角分类:锐角三角形、直角三角形、钝角三角形。
例题解析:例题1:识别并分类下列三角形:一个等边三角形、一个直角三角形、一个钝角三角形。
解答:按边分类,等边三角形的三边相等;按角分类,直角三角形有一个角为90度,钝角三角形有一个角大于90度。
2. 四边形的分类类型:正方形、长方形、平行四边形、梯形、菱形。
例题解析:例题2:识别并分类下列四边形:一个正方形、一个长方形、一个平行四边形。
解答:正方形的四边相等且四个角都是直角,长方形的对边相等且四个角都是直角,平行四边形的对边平行。
3. 多边形的分类定义:多边形是由多条线段组成的封闭图形。
常见的有五边形、六边形等。
例题解析:例题3:识别并分类下列多边形:一个五边形、一个六边形。
解答:五边形有五条边,六边形有六条边。
二、几何图形的性质1. 三角形的性质三角形内角和:任何三角形的内角和都是180度。
例题解析:例题4:已知一个三角形的两个角分别为50度和60度,求第三个角的度数。
解答:第三个角的度数 = 180度 - 50度 - 60度 = 70度。
2. 四边形的性质四边形内角和:任何四边形的内角和都是360度。
例题解析:例题5:已知一个四边形的三个角分别为90度、85度和95度,求第四个角的度数。
解答:第四个角的度数 = 360度 - 90度 - 85度 - 95度 = 90度。
3. 多边形的性质多边形的内角和:多边形的内角和 = (n - 2) × 180度,其中n为边的数量。
例题解析:例题6:求一个五边形的内角和。
解答:五边形的内角和 = (5 - 2) × 180度 = 540度。
三、几何图形的实际应用1. 建筑设计中的几何图形例题解析:题目:设计一个正方形花坛,要求每边长为5米,问花坛的面积是多少?解答:正方形的面积 = 边长×边长 = 5米× 5米 = 25平方米。
图形知识点总结五年级

图形知识点总结五年级在小学五年级的数学课程中,图形知识是一个重要的组成部分,它帮助学生建立空间观念,理解图形的基本属性以及它们之间的关系。
以下是对五年级图形知识点的总结:一、平面图形1. 直线与射线:直线是无限延伸的,射线有一个端点,从端点向一个方向无限延伸。
2. 线段:线段有起点和终点,长度有限。
3. 角:角由两条射线组成,它们的端点重合形成角的顶点。
角的大小可以通过度量器测量。
4. 平行线:在同一平面内,不相交的两条直线称为平行线。
5. 垂直线:当两条直线相交,形成90度的角时,它们是垂直的。
二、几何图形1. 三角形:由三条线段围成的图形,内角和为180度。
三角形可以分为等边三角形、等腰三角形和一般三角形。
2. 四边形:由四条线段围成的图形,包括正方形、长方形、平行四边形、梯形等。
3. 圆:所有点到中心点的距离相等的平面图形,圆心是圆的中心,半径是圆心到圆上任意一点的距离。
三、图形的属性1. 周长:图形边缘的长度总和。
2. 面积:图形内部的区域大小。
3. 对称性:图形的对称轴可以是一条直线或一个点。
四、图形的变换1. 平移:图形在平面内沿着某一方向移动,不改变其形状和大小。
2. 旋转:图形绕某一点旋转一定角度,不改变其形状和大小。
3. 反射:图形沿某一条直线翻转,形成镜像。
五、图形的组合1. 组合图形:将多个基本图形组合在一起,形成新的图形。
2. 分割图形:将一个图形分割成几个部分,每个部分可以是基本图形。
六、图形的测量1. 长度测量:使用直尺测量线段的长度。
2. 角度测量:使用量角器测量角的大小。
3. 面积测量:计算图形的面积,常用的公式包括三角形面积公式、四边形面积公式等。
七、图形的应用1. 日常生活:在日常生活中,我们经常需要用到图形知识,比如测量房间的面积,计算材料的用量等。
2. 艺术设计:在艺术和设计领域,图形知识是构图和创造美的基础。
通过这些知识点的学习,学生不仅能够理解平面图形的基本性质,还能够将这些知识应用到实际生活中,提高解决问题的能力。
小学生必背几何知识点总结

小学生必背几何知识点总结一、基本概念1. 点、线、面:点是没有长度、宽度和高度的;线是由无限多个点连在一起形成的;面是由无限多条线连在一起形成的。
2. 直线、射线、线段:直线是没有端点的;射线是一个端点发散而出的,另一个方向无限延伸的部分;线段是由两个端点确定的部分。
3. 角:由两条射线的公共端点所围成的图形称为角,公共端点称为角的顶点,两条射线称为角的两边。
4. 三角形:由三条线段所围成的图形称为三角形。
5. 四边形:由四条线段所围成的图形称为四边形。
二、基本图形的性质1. 三角形的内角和:所有内角和为180°。
2. 三角形的外角和:所有外角和为360°。
3. 直角三角形:一个角为90°的三角形称为直角三角形。
4. 等边三角形:三条边相等的三角形称为等边三角形。
5. 等腰三角形:两条边相等的三角形称为等腰三角形。
6. 直线上的角:直线上的两个相邻角互为补角,补角的和为180°。
三、平行线和垂直线1. 平行线:在同一平面内,不相交且方向相同的两条直线称为平行线。
2. 垂直线:在同一平面内,相交且相交角为90°的两条直线称为垂直线。
3. 平行线交叉:平行线交叉时,所得的对应角相等、内错角相加为180°、外错角相加为180°。
4. 垂直线交叉:垂直线交叉时,所得的相邻角相加为180°。
四、长方形、正方形、菱形和梯形1. 长方形:对角线相等、相对边相等且两两平行的四边形称为长方形。
2. 正方形:对角线相等、四个边相等且四个角为90°的四边形称为正方形。
3. 菱形:对角线相等、四个边相等的四边形称为菱形。
4. 梯形:有两边平行的四边形称为梯形。
五、圆的基本性质1. 圆心和半径:圆心是圆的中心点,半径是圆心到圆上任意一点的距离。
2. 圆的周长:圆的周长等于直径乘以π,即C=πd。
3. 圆的面积:圆的面积等于半径平方乘以π,即A=πr²。
(完整)小学几何图形必考知识点汇总,
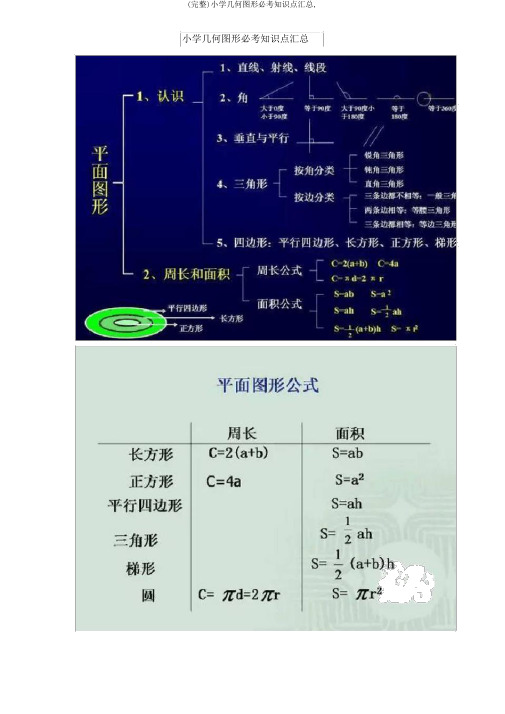
小学几何图形必考知识点汇总小学阶段常考的几何易错知识点1线、角1.直线没有端点,没有长度,可以无限延伸。
2.射线只有一个端点,没有长度,射线可以无限延伸,并且射线有方向。
3.在一条直线上的一个点可以引出两条射线。
4.线段有两个端点,可以测量长度。
圆的半径、直径都是线段。
5.角的两边是射线,角的大小与射线的长度没有关系,而是跟角的两边叉开的大小有关,叉得越大角就越大。
6.几个易错的角边关系:(1 〕平角的两边是射线,平角不是直线。
(2 〕三角形、四边形中的角的两边是线段。
(3 〕圆心角的两边是线段。
7.两条直线相交成直角时,这两条直线叫做互相垂直。
其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
8.从直线外一点到这条直线所画的垂直线段的长度叫做点到直线的距离。
9.在同一个平面上不相交的两条直线叫做平行线。
2三角形1.任何三角形内角和都是 18 0 度。
2.三角形具有稳定的特性,三角形两边之和大于第三边,三角形两边之差小于第三边。
3.任何三角形都有三条高。
4.直角三角形两个锐角的和是 90 度。
5.两个三角形等底等高,那么它们面积相等。
6.面积相等的两个三角形,形状不一定相同。
3正方形面积1.正方形面积:边长×边长2.正方形面积:两条对角线长度的积÷24三角形、四边形的关系1.两个完全一样的三角形能组成一个平行四边形。
2.两个完全一样的直角三角形能组成一个长方形。
3.两个完全一样的等腰直角三角形能组成一个正方形。
4.两个完全一样的梯形能组成一个平行四边形。
5圆1.把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,宽相当于圆的半径。
那么长方形的面积等于圆的面积,长方形的周长比圆的周长增加 r ×2。
2.半圆的周长等于圆的周长的一半加直径。
3.半圆的周长公式:C= pd?2+ d 或C= pr +2 r4.在同一个圆里,半径扩大或缩小多少倍,直径和周长也扩大或缩小相同的倍数。
小学生必背几何知识点总结

小学生必背几何知识点总结小学生在学习几何时,需要掌握一些基础的几何知识点,这不仅有助于他们更好地理解数学概念,还能培养他们的空间想象力。
以下是小学生必背的几何知识点总结:1. 点、线、面:点是几何图形的基本元素,没有大小只有位置;线是由无数个点组成的,有长度但没有宽度;面是由无数条线组成的,有长度和宽度但没有厚度。
2. 平面图形:平面图形是指所有点都在同一个平面上的图形。
常见的平面图形有三角形、四边形、圆形等。
3. 三角形:三角形是由三条线段首尾相连形成的封闭图形。
根据边和角的不同,三角形可以分为等边三角形、等腰三角形、直角三角形和不等边三角形。
4. 四边形:四边形是由四条线段首尾相连形成的封闭图形。
常见的四边形有正方形、长方形、平行四边形、梯形和菱形。
5. 圆:圆是由一个中心点和所有与中心点等距离的点组成的平面图形。
圆的周长称为圆周,圆的面积可以通过公式 \( A = \pi r^2 \) 计算,其中 \( r \) 是圆的半径。
6. 立体图形:立体图形是指具有长度、宽度和高度的三维图形。
常见的立体图形有立方体、长方体、圆柱体、圆锥体和球体。
7. 立方体和长方体:立方体是所有边长相等的长方体,而长方体的长、宽、高可以不同。
它们的表面积和体积可以通过特定的公式计算。
8. 圆柱体和圆锥体:圆柱体由两个平行且相等的圆面和连接它们的侧面组成。
圆锥体是一个圆面和一个顶点组成,侧面收缩到一个点。
9. 球体:球体是由所有与中心点等距离的点组成的三维图形。
球体的表面积和体积也可以通过公式计算。
10. 对称性:许多几何图形具有对称性,例如轴对称和中心对称。
轴对称图形可以沿一条直线(称为对称轴)对折后两部分完全重合,中心对称图形则是围绕一个中心点旋转180度后与原图形重合。
11. 角度:角度是用来描述两条射线(或线段)的夹角大小的度量。
角度的单位是度(°),直角是90°,平角是180°,周角是360°。
小学三年级数学几何的初步认识知识点

1.几何图形的认识:-点:没有大小和形状的位置。
-线段:由两个端点和之间的所有点组成,没有曲线。
-直线:在平面上的无限延伸得两个方向上的点组成。
-尖角:小于90度的角。
-钝角:大于90度但小于180度的角。
-直角:等于90度的角。
-平行线:永远不会相交的线。
-垂直线:相交的角度为90度的线。
2.几何图形的识别和分类:-三角形:有三条边的图形。
-矩形:有四个直角的四边形。
-正方形:四个边相等且四个直角的四边形。
-平行四边形:有两组对边平行的四边形。
-圆形:由一个圆心和一条半径相等的弧线组成。
-弧:圆形的一部分。
-曲线:线条在不同点上的变向。
3.几何图形的特征:-边:图形的边缘。
-角:两条线相交所形成的区域。
-顶点:两条边或多条边的交点。
-对称性:图形左右或上下对折后完全相同。
-线对称:通过中心线对折后完全一样。
-中心对称:图形可通过其中一点为中心旋转180度后重合。
4.几何图形的关系和组合:-图形的包含和相交关系:一个图形是否被另一个图形包围或相交。
-集合:一个或多个物体的组合。
-二维几何体:平面上的图形。
-三维几何体:有长度、宽度和高度的立体图形。
-分解和组合:将复杂的图形分解成简单的图形,并将简单的图形组合成复杂的图形。
以上是小学三年级数学几何初步认识的一些重要知识点。
随着学习的深入,孩子们还将学习到更多有关几何的概念和技能,如相似、等边、等腰三角形等。
这些基础知识为孩子打下了坚实的几何基础,为将来更深入的数学学习奠定了基础。
小学平面几何重点总结

小学平面几何重点总结
1. 直线、线段和射线
- 直线是由无数个点连成的轨迹,没有起点和终点。
- 线段是直线上的两个点及其之间的部分,有起点和终点。
- 射线是直线上的一个点及其之后的部分,有一个起点但没有终点。
2. 角
- 角是由两条射线共享一个端点组成的图形。
- 角的大小可用角度来量度,角度的单位可以是度或弧度。
- 锐角是小于90度的角,直角是90度的角,而钝角是大于90度但小于180度的角。
3. 三角形
- 三角形是由三条线段组成的图形。
- 三角形的三条边和三个内角的关系:任意两边之和大于第三边,任意两角之和小于180度。
- 常见的三角形类型包括等边三角形、等腰三角形和直角三角形。
4. 矩形
- 矩形是一个有四个直角(90度)的四边形。
- 矩形的特点:对角线相等,相对边相等,相邻边互相垂直。
5. 正方形
- 正方形是一个具有四条相等边和四个直角的矩形。
- 正方形的特点:对角线相等,所有边相等,所有角均为直角。
6. 圆
- 圆是由与一个固定点的距离相等的点构成的图形。
- 圆的特征:半径是从圆心到圆上的任意一点的距离,直径是
通过圆心的两个点的距离,圆周是圆的边界。
以上是小学平面几何的一些重点总结,请您参考。
小学图形与几何知识点

小学图形与几何知识点在小学阶段,图形与几何是数学学习中的重要组成部分。
它不仅能帮助孩子们建立空间观念,还能培养他们的逻辑思维和解决实际问题的能力。
接下来,咱们就一起梳理一下小学图形与几何的主要知识点。
一、平面图形1、线段、射线和直线线段有两个端点,可以度量长度;射线有一个端点,一端可以无限延伸;直线没有端点,两端都可以无限延伸。
2、角从一点引出两条射线所组成的图形叫做角。
角通常用符号“∠”来表示。
角的大小与两条边张开的程度有关,与边的长短无关。
角可以分为锐角、直角、钝角、平角和周角。
锐角小于 90 度,直角等于 90 度,钝角大于 90 度小于 180 度,平角等于 180 度,周角等于 360 度。
3、三角形由三条线段围成的图形叫做三角形。
三角形具有稳定性。
三角形按角可以分为锐角三角形、直角三角形和钝角三角形;按边可以分为等边三角形、等腰三角形和不等边三角形。
三角形的内角和是 180 度。
4、四边形由四条线段围成的封闭图形叫做四边形。
常见的四边形有平行四边形、长方形、正方形和梯形。
平行四边形两组对边分别平行且相等。
长方形对边平行且相等,四个角都是直角。
正方形四条边都相等,四个角都是直角。
梯形只有一组对边平行。
5、圆圆是一种曲线图形。
圆心用字母 O 表示,半径用字母 r 表示,直径用字母 d 表示。
在同一个圆中,直径是半径的 2 倍,即 d = 2r。
圆的周长计算公式是 C =2πr 或 C =πd,圆的面积计算公式是 S =πr²。
二、立体图形1、长方体长方体有 6 个面,相对的面完全相同;有 12 条棱,相对的棱长度相等;有 8 个顶点。
长方体的棱长总和=(长+宽+高)× 4长方体的表面积=(长×宽+长×高+宽×高)× 2长方体的体积=长×宽×高2、正方体正方体有 6 个面,每个面都是正方形,6 个面完全相同;有 12 条棱,12 条棱长度都相等;有 8 个顶点。
(完整版)小学几何知识

小学数学知识点:几何的初步知识一、线和角(1)线直线直线没有端点;长度无限;过一点可以画无数条,过两点只能画一条直线。
射线射线只有一个端点;长度无限。
线段线段有两个端点,它是直线的一部分;长度有限;两点的连线中,线段为最短。
平行线在同一平面内,不相交的两条直线叫做平行线。
两条平行线之间的垂线长度都相等。
垂线两条直线相交成直角时,这两条直线叫做互相垂直,其中一条直线叫做另一条直线的垂线,相交的点叫做垂足。
从直线外一点到这条直线所画的垂线的长叫做这点到直线的距离。
(2)角从一点引出两条射线,所组成的图形叫做角。
这个点叫做角的顶点,这两条射线叫做角的边。
角的分类锐角:小于90°的角叫做锐角。
直角:等于90°的角叫做直角。
钝角:大于90°而小于180°的角叫做钝角。
平角:角的两边成一条直线,这时所组成的角叫做平角。
平角180°。
周角:角的一边旋转一周,与另一边重合。
周角是360°。
二、平面图形1.长方形(1)特征对边相等,4个角都是直角的四边形。
有两条对称轴。
(2)计算公式c=2(a+b)s=ab2.正方形(1)特征:四条边都相等,四个角都是直角的四边形。
有4条对称轴。
(2)计算公式c=4as=a23.三角形(1)特征由三条线段围成的图形。
内角和是180度。
三角形具有稳定性。
三角形有三条高。
(2)计算公式s=ah/2(3)分类按角分锐角三角形:三个角都是锐角。
直角三角形:有一个角是直角。
等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
按边分不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
4.平行四边形(1)特征两组对边分别平行的四边形。
相对的边平行且相等。
对角相等,相邻的两个角的度数之和为180度。
平行四边形容易变形。
几何图形有哪些知识点总结

几何图形有哪些知识点总结1. 几何图形的分类几何图形可以分为基本图形和复合图形两类。
基本图形包括圆、正方形、矩形、三角形等,它们是由相应的基本几何体所组成的。
复合图形是由多个基本几何体组合而成的图形,比如梯形、菱形等。
掌握这些基本图形的性质和计算方法是学习几何图形的第一步。
2. 图形的性质每种几何图形都有其独特的性质,这些性质可以帮助我们更好地理解和利用这些图形。
比如,圆形的性质包括直径、半径、周长、面积等;矩形的性质包括长、宽、周长、面积等。
了解图形的性质可以帮助我们更好地应用这些知识点来解决实际问题。
3. 图形的面积计算计算图形的面积是学习几何图形的重要内容之一。
不同类型的图形有不同的面积计算公式,比如矩形的面积等于长乘以宽,三角形的面积等于底边乘以高再除以二。
掌握这些面积计算公式可以帮助我们更快地计算图形的面积。
4. 图形的周长计算周长是指图形的边缘的长度之和。
计算图形的周长也是学习几何图形的重要内容之一。
不同类型的图形有不同的周长计算公式,比如矩形的周长等于长加宽乘以二,三角形的周长等于三条边的长度之和。
掌握这些周长计算公式可以帮助我们更快地计算图形的周长。
5. 图形的相似相似图形指的是形状相同,但大小不同的图形。
学习几何图形的过程中,我们也需要掌握相似图形的性质和计算方法。
相似图形的性质包括对应边成比例、对应角相等等。
掌握相似图形的性质可以帮助我们更好地理解这些图形之间的关系。
6. 图形的投影在实际生活中,我们经常会遇到图形的投影问题。
比如,当太阳光线照射到地面上时,物体的影子就是物体的投影。
学习几何图形的过程中,我们也需要了解图形的投影性质和计算方法。
掌握图形的投影性质可以帮助我们更好地理解这些现象。
总之,学习几何图形需要掌握许多知识点,包括图形的分类、性质、面积计算、周长计算、相似性质以及投影性质等。
只有深入理解这些知识点,我们才能更好地应用几何图形知识来解决实际问题。
希望本文的总结可以帮助读者更好地掌握几何图形的相关知识点。
几何知识总结小学二年级

几何知识总结小学二年级小学二年级的几何知识是数学课程中的基础部分,它为学生日后学习更复杂的几何概念打下了坚实的基础。
以下是对小学二年级几何知识的总结:一、平面图形的认识1. 点:点是最基本的几何元素,没有大小,只有位置。
2. 线:线由无数个点组成,有长度但没有宽度。
3. 面:面由无数条线组成,有长度和宽度,但没有厚度。
二、基本平面图形1. 正方形:四条边相等,四个角都是直角。
2. 长方形:对边相等,四个角都是直角。
3. 三角形:由三条边组成,内角和为180度。
4. 圆:所有点到中心点的距离相等,周长称为圆周长,面积称为圆面积。
三、图形的属性1. 边:图形的边界线。
2. 角:两条线相交形成的点。
3. 周长:图形边界线的总长度。
4. 面积:图形内部的区域大小。
四、图形的分类1. 规则图形:所有边和角都相等的图形,如正方形和圆。
2. 不规则图形:边和角不相等的图形。
五、图形的对称性1. 轴对称:图形沿某条线折叠后,两边完全重合。
2. 中心对称:图形绕某一点旋转180度后,与原图形重合。
六、图形的变换1. 平移:图形沿着直线移动,不改变形状和大小。
2. 旋转:图形绕某一点旋转一定角度,不改变形状和大小。
七、图形的组合与分割1. 组合:将两个或多个图形拼接在一起,形成新的图形。
2. 分割:将一个图形分割成两个或多个部分。
八、图形的测量1. 长度测量:使用直尺测量线段的长度。
2. 角度测量:使用量角器测量图形中的角度大小。
九、图形的绘制1. 使用工具:直尺、三角板、圆规等。
2. 绘制技巧:学习如何使用工具绘制直线、曲线、圆等。
十、实际应用1. 生活中的几何:识别和应用几何知识解决日常生活中的问题。
2. 艺术与设计:在艺术和设计中运用几何知识创造图案和结构。
通过这些基础知识的学习,二年级的学生能够对几何概念有一个初步的了解,并能够运用这些知识解决一些简单的问题。
随着年级的提高,学生将学习到更多复杂的几何知识,这将有助于他们更好地理解数学和自然界中的几何现象。
小学数学几何图形知识点公式大全

小学数学几何图形知识点公式大全一、长方形
►长方形的周长=(长+宽)×2
C=(a+b)×2
►长方形的面积=长×宽
S=ab
二、正方形
►正方形的周长=边长×4
C=4a
►正方形的面积=边长×边长
S=a.a=a
三、三角形
►三角形的面积=底×高÷2
S=ah÷2
►三角形的内角和=180度
四、平行四边形
►平行四边形的面积=底×高
S=ah
五、梯形
►梯形的面积=(上底+下底)×高÷2
S=(a+b)h÷2
六、圆形
►圆的直径=半径×2(d=2r)
►圆的半径=直径÷2(r=d÷2)
►圆的周长=圆周率×直径=圆周率×半径×2
C=πd=2πr
►圆的面积=圆周率×半径×半径
S=πr×r
七、长方体
►长方体的体积=长×宽×高
V=abh
八、正方体
►正方体的体积=棱长×棱长×棱长
V=aaa
九、圆柱
►圆柱的侧面积:圆柱的侧面积等于底面的周长乘高
S=ch=πdh=2πrh
►圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积
S=ch+2s=ch+2πr×
r►圆柱的体积:圆柱的体积等于底面积乘高
V=Sh
十、圆锥
►圆锥的体积=1/3底面×积高
V=1/3Sh。
几何知识点总结小学三年级

几何知识点总结小学三年级几何学是数学中研究形状、大小和相对位置的分支。
对于小学三年级的学生来说,几何知识点的总结应该简单易懂,并且与他们日常所见的物体和形状相关联。
以下是对小学三年级几何知识点的总结:认识基本几何图形1. 点、线、面:点是几何图形的起点,线是由点组成的,面是二维的平面图形。
2. 直线、射线、线段:直线没有端点,射线有一个端点,线段有两个端点。
3. 角:由两条射线组成的图形,两条射线的交点称为顶点,射线称为边。
4. 平面图形:如三角形、正方形、长方形、圆形等。
理解基本几何属性1. 边:图形的边缘,可以是直线段。
2. 顶点:图形的角点,两条边的交点。
3. 周长:图形边界的总长度。
4. 面积:平面图形所覆盖的空间大小。
学习基本的几何运算1. 角度测量:使用量角器测量角的大小。
2. 周长计算:计算图形的周长,例如正方形的周长是边长的四倍。
3. 面积计算:计算图形的面积,如正方形的面积是边长的平方。
探索几何图形的性质1. 对称性:图形是否可以通过一条线(对称轴)折叠后两边完全重合。
2. 相似性:两个图形的形状相同,但大小可能不同。
3. 全等性:两个图形不仅形状相同,大小也完全一样。
几何图形的分类1. 三角形:三条边,三个角的图形。
2. 四边形:四条边,四个角的图形,如正方形、长方形、平行四边形。
3. 圆:所有点到中心点的距离相等的平面图形。
几何图形的实际应用1. 日常生活中的几何:如桌子、窗户、地板砖等。
2. 艺术和设计中的几何:如图案设计、建筑装饰。
通过这些知识点的学习,三年级的学生可以开始理解基本的几何概念,并能够将它们应用到实际问题中。
几何学不仅是一门学科,更是一种思维方式,它帮助我们更好地理解周围的世界。
希望这些知识点能够帮助学生们建立起对几何学的初步认识,并激发他们对数学的兴趣。
图形与几何知识点整理图形与几何复习知识点

图形与几何知识点整理图形与几何复习知识点一、平面几何知识点:1.点、直线、线段、射线的基本定义和性质:点是没有大小和形状的,直线是由无数个点组成的,线段是由两个端点和这两个端点之间的所有点组成的,射线是由一个端点和这个端点到无限远方的所有点组成的。
2.角的基本概念和性质:角是由两条边和它们的公共端点组成的,以顺时针或逆时针方向为正方向。
角的度量是以度为单位,一个圆周角等于360度。
3.三角形的性质:三角形是由三条边和三个顶点组成的,根据边长和角度可以分为等边三角形、等腰三角形、直角三角形等,根据角度可以分为锐角三角形、钝角三角形、直角三角形等,根据边的关系可以分为全等三角形、相似三角形等。
4.四边形的性质:四边形是由四条边和四个顶点组成的,根据边的关系可以分为平行四边形、矩形、正方形、菱形等。
5.圆的性质:圆是由一个固定点和到这个点距离相等的所有点组成的,圆的中心到圆上任意一点的距离称为半径,关于半径的线称为半径。
6.整除性质:整除指的是一个数能够被另一个数整除,可以整除的数称为约数,而可以被整除的数称为倍数。
7.直角三角形的勾股定理:直角三角形中,两直角边的平方和等于斜边的平方。
8.相似三角形的性质:两个三角形对应的角相等,对应边的比值相等。
二、立体几何知识点:1.立体图形的基本概念:包括点、线、面、体的概念。
2.立体图形的展开与视图:通过展开立体图形可以得到平面的投影视图,包括正交投影和斜投影。
3.三棱柱、四棱柱、五棱柱等的性质:包括底面类型、侧面类型、轴线类型、全等类型等。
4.三棱锥、四棱锥、五棱锥等的性质:包括底面类型、侧面类型、轴线类型、全等类型等。
5.正多面体的性质:包括正方体、正六面体、正八面体、正十二面体等的性质。
三、向量几何知识点:1.向量的基本概念和性质:向量是有大小和方向的,用箭头表示。
2.向量的加减法:向量的加法是对应分量相加,向量的减法是对应分量相减。
3.向量的数量积和向量积:数量积是两个向量的乘积,向量积是两个向量的叉乘。
小学数学总复习-图形与几何

小学数学图形与几何一、图形的认识和测量1、图形知识大盘点(1)点、线、角○1从一点出发可以画无数条射线,过一点可以画无数条直线,过两点只能画一条直线○2直线没有端点,可以向两端无限延伸,所以直线长度无法测量。
射线有一个端点,可以向一端无限延伸,所以直线长度无法测量。
线段有两个端点,长度可以测量。
○3从一点引出两条射线,就组成了一个角。
角的大小和角两边的长短无关。
(2)平面图形○1三角形三角形具有稳定性三角形任意两条边之和大于第三条边。
任意两条边之差都小于第三条边。
三条线段,如果两条短的线段长度之和小于第三条,则一定能围城三角形。
三角形的内角和是180度。
一个三角形,至少有2个锐角。
三角形的三个内角中,有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形。
三个角都是锐角的三角形叫做锐角三角形。
○2四边形两组对边分别平行四边形叫做平行四边形。
平行四边形具有不稳定性,容易变形。
只有一组对边平行的四边形叫做梯形。
两组对边分别平行且相等,四个角都是直角的四边形是长方形。
有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
四条边都相等的长方形是正方型。
长方形是特殊的平行四边形正方形是特殊的长方形、平行四边形。
○3圆圆是曲线图形在同一个圆内,所有的半径都相等,所有的直径都相等。
○4平面图形的面积和周长计算公式(3)立体图形○1长方体和正方体长方体是由6个长方形围成的立体图形。
在一个长方体中,相对的面完全相等。
(特殊情况是有两个相对的面是正方形,其它四个面都是长方形,且完全相等)长方体有12条棱,相对的棱长度相等。
可分为三组,每一组有4条棱。
长方体有8个顶点。
每个顶点连接三条棱。
长方体相邻的两条棱互相(相互)垂直。
正方体是由6个完全相同的正方形围成的立体图形。
在一个正方体中,6个面完全相等。
○2圆柱和圆锥圆柱的两个圆面叫做地面,周围的面叫做侧面;两个底面之间的距离叫做高。
圆柱的侧面是曲面,展开后可能是长方形,也可能是正方形,还可能是平行四边形。
小学平面几何基础要点总结

小学平面几何基础要点总结
在小学阶段研究平面几何时,有一些基本要点需要理解和掌握。
下面是对这些基础要点的总结:
1. 图形的命名:了解常见的几何图形,如:三角形、正方形、
矩形、圆形等,并学会用适当的符号和名称来命名它们。
2. 图形的特征:掌握各种图形的特征。
例如,了解三角形有三
条边和三个角,正方形的四边相等且四个角都是直角等。
3. 图形的性质:研究图形的性质,例如正方形的对角线相等且
垂直、矩形的对边相等且平行等。
4. 图形的分类:研究将图形进行分类,根据不同的属性进行划分。
例如,可以将三角形按照角的大小分类为锐角三角形、钝角三
角形和直角三角形。
5. 图形的面积和周长:了解如何计算图形的面积和周长。
研究不同图形的计算公式,如正方形的面积公式为边长的平方,矩形的面积公式为长乘以宽。
6. 图形的变换:了解平面几何中的常见变换,如平移、旋转和翻转,并研究如何描述这些变换对图形的影响。
以上是小学平面几何基础要点的总结。
通过掌握这些要点,学生能够更好地理解和应用平面几何的知识。
小学数学几何知识

小学数学几何知识在小学数学学科中,几何是一个重要的部分,它涉及到空间中的图形、尺寸和位置关系等内容。
通过学习几何知识,学生能够培养观察力、想象力和逻辑思维能力,并且为后续学习更高级的数学知识打下坚实的基础。
本文将介绍小学阶段学生需要掌握的基本几何知识。
一、平面图形1. 点、线段和直线在几何学中,点是最基本的图形元素,它没有长度、宽度和厚度,只有位置。
线段是由两个端点连接而成的线段,它有固定的长度。
直线是由无数个点连接而成的,它没有端点,可以无限延伸。
2. 三角形三角形是由三条线段组成的图形,它的特点是三边和三个内角的大小固定。
根据三角形内角的大小,可以将三角形分为锐角三角形、钝角三角形和直角三角形。
3. 长方形和正方形长方形是由两对平行线段和四个直角组成的四边形,它的相邻边相等。
正方形是一种特殊的长方形,它四条边相等且都是直角。
4. 圆圆是由一条曲线组成的,它的每个点到圆心的距离都相等。
圆由圆心、半径和圆周组成。
二、空间图形1. 立体图形立体图形是具有长度、宽度和高度的图形,在三维空间中存在。
常见的立体图形有长方体、正方体、圆柱体、圆锥体和球体等。
2. 轴对称图形轴对称图形是指能够沿着一个轴线进行对称的图形。
轴对称图形的两侧是完全一样的,常见的轴对称图形有正方形、矩形和心形等。
3. 镜像图形镜像图形是指通过一面镜子观察到的图形,它和实际图形是左右对称的。
镜像图形的左侧和右侧是完全一样的。
三、位置关系1. 平行和垂直平行是指两条直线在同一平面内永不相交,它们的方向永远相同或者相反。
垂直是指两条直线相交,且相交的角度为90度。
2. 内部和外部在几何学中,我们经常讨论图形的内部和外部。
对于一个给定的图形,它的内部是指图形所包围的区域,而外部则是指不在图形内部的区域。
3. 点、线和面的位置关系在空间中,点可以在直线上,直线可以在平面内。
同样,直线也可以不在平面内,而是与平面平行或垂直。
小学数学几何知识的学习不仅仅是为了应付考试,更重要的是培养学生的观察力、想象力和逻辑思维能力。
(完整版)小学阶段学过的几何图形相关知识

小学阶段学过的几何图形相关知识一、平面图形:长方形、正方形、平行四边形、梯形、三角形、圆形1、长方形:对边相等,四个角都是直角的四边形,叫做长方形.长方形的对边相等,并且四个角都是直角;对角线长度相等,又互相平行分.长方形的周长:长方形的周长=(长+宽)×2通常用C表示周长,a表示长,b表示宽,那么C=(a+b)×2长方形的面积:长方形的面积=长×宽字母公式:S=a×b长方形是轴对称图形,有2条对称轴2、正方形:长和宽相等的长方形,叫做正方形.正方形又是特殊的长方形.对角线的长度相等,又互相垂直且平分.正方形的周长:正方形的周长=边长×4 字母公式:C=4a正方形的面积:正方形的面积=边长×边长字母公式:S=a×a或S=a的平方正方形是轴对称图形,有4条对称轴3、平行四边形:两组对边分别平行的四边形,叫做平行四边形.平行四边行对边相等,对角相等4、梯形:只有一组对边平行的四边形,叫做梯形.在梯形中,互相平行的一组对边,分别叫做梯形的上底和下底.不平行的一组对边,叫做梯形的腰.梯形的两底之间的距离,叫做梯形的高.梯形的面积:梯形的面积=(上底+下底)×高÷25、三角形:由三条线段围成的图形(每相邻两条线段的的端点相连)叫做三角形.从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底.三角形具有稳定性. 三角形的高:任意三角形的三条高都相交于一点.三角形边的性质:a、三角形任何两边的长度和大于第三边.b、三角形的任何两边的差小于第三边.c、三角形的内角和是180度.三角形的分类:(1)按边分:三条边都不相等的三角形,叫不等边三角形;三条边中有两条边相等的三角形,叫等腰三角形.三条边都相等的三角形,叫做等边三角形,也叫正三角形.(2)、按角分:三个角都是锐角的三角形,叫做锐角三角形.有一个角是直角的三角形,叫做直角三角形.有一个角是钝角的三角形,叫做钝角三角形.(锐角三角形和钝角三角形合称为斜三角形.三角形的面积:三角形的面积=底×高÷2 通常用S表示三角形的面积,用a表示底,用h表示高.那么:S=ah÷2 或S=1/2ah6、圆:在平面上,以一个定点为中心,以一定长度为距离而运动一周形成的轨迹,叫做圆周,简称圆.这个定点叫做圆心,圆心通常用字母O表示.连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示.通过圆心,并且两端都在圆上的线段叫做直径.一般用字母d表示.圆的性质:在同一个圆内,所有的半径都相等,所有的直径都相等;直径等于半径的2倍圆周率:圆的周长与这个圆的直径长度的比,叫做圆周率.一般取它的近似值,即π=3.14.圆的周长:圆的周长=圆周率×直径用字母示:C=πd 或C=2πr圆的面积:圆的面积=圆周率×半径的平方字母公式:S=πr的平方环形的面积:即圆环.两个半径不相等的同心圆的圆周之间所夹的平面部分,叫做环形.面积等于外圆的面积减去内圆的面积.扇形:由圆心角和圆心角所对的弧围成的图形,叫做扇形.扇形面积:扇形面积等于所在圆的面积除以360,再乘以圆心角的度数值.用n表示圆心角的度数,那么:S=πr 的平方/360×n.。
小学图形知识总结

小学图形知识总结小学阶段的图形知识是数学学习中的重要组成部分,它不仅帮助学生建立起空间观念,还能培养学生的观察能力和逻辑思维能力。
以下是对小学图形知识的总结:一、平面图形1. 点:点是图形的最小单位,没有大小和形状,只有位置。
2. 线:线由点组成,有长度但没有宽度,直线是两点之间的最短路径。
3. 角:角由两条射线组成,它们的端点重合形成顶点,角的大小由两条射线张开的程度决定。
4. 三角形:由三条线段首尾相连形成的封闭图形,根据边长或角度的不同,可以分为等边三角形、等腰三角形和普通三角形。
5. 四边形:由四条线段首尾相连形成的封闭图形,包括正方形、长方形、平行四边形等。
6. 圆:所有点到中心点距离相等的平面图形,圆周角是360度。
二、立体图形1. 立方体:六个面都是正方形的立体图形,有12条边和8个顶点。
2. 长方体:六个面都是矩形的立体图形,有12条边和8个顶点。
3. 圆柱体:由两个平行的圆形底面和连接这两个底面的侧面组成,侧面展开是一个矩形。
4. 圆锥体:一个圆形底面和一个顶点组成,侧面展开是一个扇形。
5. 球体:所有点到中心点距离相等的立体图形,表面是连续的曲面。
三、图形的属性1. 周长:图形边界的长度,平面图形的周长是边界线段的总和,立体图形的周长可能包括底面和侧面。
2. 面积:平面图形内部的空间大小,可以通过不同的公式计算。
3. 体积:立体图形所占空间的大小,可以通过公式计算得出。
四、图形的变换1. 平移:图形在平面上沿着某一方向移动,不改变图形的形状和大小。
2. 旋转:图形绕着某一点或轴进行转动,不改变图形的形状和大小。
3. 反射:图形关于某一条直线进行翻转,图形的形状和大小不变。
五、图形的组合与拆分1. 组合:将两个或多个图形拼接在一起,形成新的图形。
2. 拆分:将一个图形分割成两个或多个部分。
六、图形的对称性1. 轴对称:图形关于某条直线对称,这条直线称为对称轴。
2. 中心对称:图形关于某一点对称,这个点称为对称中心。
