2018届全国名校高三新题试卷(二)文科数学
2018文科数学高考真题全国卷Ⅱ试卷及答案详解-最全word版本

2018年普通高等学校招生全国统一考试文科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.()i 23i += A .32i -B .32i +C .32i --D .32i -+2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB =A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数()2e e x xf x x --=的图像大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为 A .0.6B .0.5C .0.4D .0.36.双曲线22221(0,0)x y a b a b-=>>3A .2y x =±B .3y x =±C .2y = D .3y = 7.在ABC △中,5cos 2C =1BC =,5AC =,则AB = A .42B 30C 29D .258.为计算11111123499100S =-+-++-,设计了如图的程序框图,则在空白框中应填入A .1i i =+B .2i i =+ C.3i i =+D .4i i =+9.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为 A B C D 10.若()cos sin f x x x =-在[0,]a 是减函数,则a 的最大值是A .π4B .π2C .3π4D .π11.已知1F ,2F 是椭圆C的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C的离心率为 A .1 B .2C D 112.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)f f f ++(50)f ++=A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分. 13.曲线2ln y x =在点(1,0)处的切线方程为__________.14.若,x y 满足约束条件250,230,50,x y x y x +-⎧⎪-+⎨⎪-⎩≥≥≤ 则z x y =+的最大值为__________.15.已知5π1tan()45α-=,则tan α=__________. 16.已知圆锥的顶点为S ,母线SA ,SB 互相垂直,SA 与圆锥底面所成角为30︒,若SAB △的面积为8,则该圆锥的体积为__________.三、解答题:共70分。
2018年高考全国II卷数学(文科)真题与答案
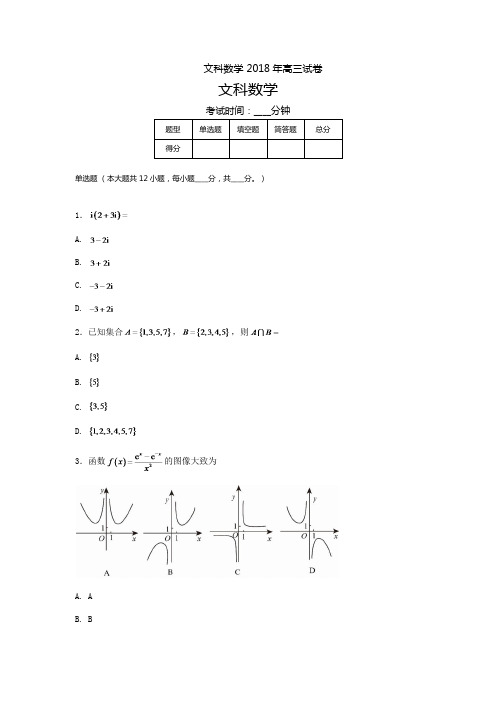
文科数学 2018年高三试卷文科数学单选题(本大题共12小题,每小题____分,共____分。
)1.A.B.C.D.2.已知集合,,则A.B.C.D.3.函数的图像大致为A. AB. BC. CD. D4.已知向量,满足,,则A. 4B. 3C. 2D. 05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为A.B.C.D.6.双曲线的离心率为,则其渐近线方程为A.B.C.D.7.在中,,,,则A.B.C.D.8.为计算,设计了如图的程序框图,则在空白框中应填入A.B.C.D.9.在正方体中,为棱的中点,则异面直线与所成角的正切值为A.B.C.D.10.若在是减函数,则的最大值是A.B.C.D.11.已知,是椭圆的两个焦点,是上的一点,若,且,则的离心率为A.B.C.D.12.已知是定义域为的奇函数,满足.若,则A.B. 0C. 2D. 50填空题(本大题共4小题,每小题____分,共____分。
)13.曲线在点处的切线方程为__________.14.若满足约束条件则的最大值为__________.15.已知,则__________.16.已知圆锥的顶点为,母线,互相垂直,与圆锥底面所成角为,若的面积为,则该圆锥的体积为__________.简答题(综合题)(本大题共6小题,每小题____分,共____分。
)17.(12分)记为等差数列的前项和,已知,.(1)求的通项公式;(2)求,并求的最小值.18.(12分)下图是某地区2000年至2016年环境基础设施投资额(单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了与时间变量的两个线性回归模型.根据2000年至2016年的数据(时间变量的值依次为)建立模型①:;根据2010年至2016年的数据(时间变量的值依次为)建立模型②:.(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;(2)你认为用哪个模型得到的预测值更可靠?并说明理由.19.(12分)如图,在三棱锥中,,,为的中点.(1)证明:平面;(2)若点在棱上,且,求点到平面的距离.20.(12分)设抛物线的焦点为,过且斜率为的直线与交于,两点,.(1)求的方程;(2)求过点,且与的准线相切的圆的方程.21.(12分)已知函数.(1)若,求的单调区间;(2)证明:只有一个零点.(二)选考题:共10分。
2018年高考全国二卷数学文科(word版)试题(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
学@科网 1.()i 23i += A .32i -B .32i +C .32i --D .32i -+2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB =A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数()2e e x xf x x --=的图像大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为 A .0.6B .0.5C .0.4D .0.36.双曲线22221(0,0)x y a b a b-=>>3则其渐近线方程为A .2y x =B .3y x =±C .2y = D .3y = 7.在ABC △中,5cos 2C =1BC =,5AC =,则AB = A .42B 30C 29D .258.为计算11111123499100S =-+-++-,设计了如图的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+9.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为 A B C D 10.若()cos sin f x x x =-在[0,]a 是减函数,则a 的最大值是A .π4B .π2C .3π4D .π11.已知1F ,2F是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为 A .1-B .2CD 112.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)f f f ++(50)f ++=A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分。
2018文数全国二卷及答案

高考真题汇编卷 第1页(共8页) 高考真题汇编卷 第2页(共8页)2018年普通高等学校招生全国统一考试(新课标II 卷)文 科 数 学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.()i 23i +=( ) A .32i -B .32i +C .32i --D .32i -+2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则A B =( )A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数()2e e x xf x x --=的图象大致为( )4.已知向量a ,b 满足1=a ,1⋅=-a b ,则()2⋅-=a a b ( ) A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为( ) A .0.6B .0.5C .0.4D .0.36.双曲线()222210,0x y a b a b-=>>的离心率为3,则其渐近线方程为( )A .2y x =±B .3y x =±C .22y x =±D .32y x =±7.在ABC △中,5cos25C =,1BC =,5AC =,则AB =( ) A .42 B .30C .29D .258.为计算11111123499100S =-+-++-,设计了右侧的程序框图,则在空白框中应填入( )A .i i 1=+B .i i 2=+C .i i 3=+D .i i 4=+9.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为( ) A .22B .32C .52D .7210.若()cos sin f x x x =-在[]0,a 是减函数,则a 的最大值是( ) A .π4B .π2C .3π4D .π11.已知1F ,2F 是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为( ) A .312-B .23-C .312- D .31-12.已知()f x 是定义域为(),-∞+∞的奇函数,满足()()11f x f x -=+.若()12f =, 则()()()()12350f f f f ++++=( ) A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分。
2018年高考全国二卷数学文科(word版)试题(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
学@科网1ABCD2ABCD34,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为A B C D6A B C D7ABCD899100+-A B CD9值为 A B C D 10A B C D 11. A B C D 12A B .0 C .2 D .50二、填空题:本题共4小题,每小题5分,共20分。
13__________.14__________.15.16.__________.三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23为选考题。
考生根据要求作答。
(一)必考题:共60分。
17.(12分)(1(218.(12分)下图是某地区2000年至2016为了预测该地区2018归模型.根据2000年至2016根据2010年至2016年的数据(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;(2)你认为用哪个模型得到的预测值更可靠?并说明理由.19.(12分)如图,点.(1(220.(12分)(1(221.(12分)(1(2(二)选考题:共10分。
请考生在第22、23题中任选一题作答。
如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分).(1(223.[选修4-5:不等式选讲](10分)(1(2绝密★启用前2018年普通高等学校招生全国统一考试文科数学试题参考答案一、选择题1.D 2.C 3.B 4.B 5.D 6.A7.A 8.B 9.C 10.C 11.D 12.C二、填空题13.y=2x–2 14.9 1516.8π三、解答题17.解:(1)设{a n}的公差为d,由题意得3a1+3d=–15.由a1=–7得d=2.所以{a n}的通项公式为a n=2n–9.(2)由(1)得S n=n2–8n=(n–4)2–16.所以当n=4时,S n取得最小值,最小值为–16.18.解:(1)利用模型①,该地区2018年的环境基础设施投资额的预测值为–30.4+13.5×19=226.1(亿元).利用模型②,该地区2018年的环境基础设施投资额的预测值为×9=256.5(亿元).(2)利用模型②得到的预测值更可靠.理由如下:(i)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=–30.4+13.5t上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立t可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.(ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分.学科@网19.解:(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP连结OB.因为AB=BC ABC为等腰直角三角形,且OB⊥AC,OB=2.OP⊥OB.由OP⊥OB,OP⊥AC知PO⊥平面ABC.(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM.故CH的长为点C到平面POM的距离.由题设可知OC,CM ACB=45°.所以OMCH所以点C 到平面20.解:(1)由题意得F (1,0),l 的方程为y =k (x –1)(k >0).设A (x 1,y 1),B (x 2,y 2).因此l 的方程为y =x –1.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为设所求圆的圆心坐标为(x 0,y 0),则因此所求圆的方程为21.解:(1)当a =3时,f (x )f ′(x )令f ′(x )=0解得xx当x +∞)时,f ′(x )>0;当x f ′(x )<0.故f(x+单调递减.(2g ′(x)0,仅当x=0时g ′(x)=0,所以g(x)在(–∞,+∞)单调递增.故g(x)至多有一个零点,从而f(x)至多有一个零点.学·科网又f(3a–1)f(3a+1)f(x)有一个零点.综上,f(x)只有一个零点.22.解:(1(2又由①得,,于是直的斜率23.解:(1(2。
2018年高考全国二卷数学文科(word版)试题(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上. 2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
学@科网 1.()i 23i += A .32i -B .32i +C .32i --D .32i -+2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB =A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数()2e e x xf x x --=的图像大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为 A .0.6B .0.5C .0.4D .0.36.双曲线22221(0,0)x y a b a b-=>>3则其渐近线方程为A .2y x =B .3y x =±C .2y = D .3y = 7.在ABC △中,5cos 2C =1BC =,5AC =,则AB = A .42B 30C 29D .258.为计算11111123499100S =-+-++-,设计了如图的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+9.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为 A B C D 10.若()cos sin f x x x =-在[0,]a 是减函数,则a 的最大值是A .π4B .π2C .3π4D .π11.已知1F ,2F是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为A .1-B .2CD 112.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)f f f ++(50)f ++=A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分. 13.曲线2ln y x =在点(1,0)处的切线方程为__________.14.若,x y 满足约束条件250,230,50,x y x y x +-⎧⎪-+⎨⎪-⎩≥≥≤ 则z x y =+的最大值为__________.15.已知5π1tan()45α-=,则tan α=__________. 16.已知圆锥的顶点为S ,母线SA ,SB 互相垂直,SA 与圆锥底面所成角为30︒,若SAB △的面积为8,则该圆锥的体积为__________.三、解答题:共70分。
2018年高考文科数学全国卷2含答案

绝密★启用前2018年普通高等学校招生全国统一考试文科数学(全国II 卷)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上. 2.作答时,务必将答案写在答题卡上.写在本试卷及草稿纸上无效. 3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.()i 23i +=【D 】 A .32i -B .32i +C .32i --D .32i -+2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则A B = 【C 】 A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数()2e e x xf x x --=的图象大致为【B 】4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b 【B 】 A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为【D 】 A .0.6B .0.5C .0.4D .0.36.双曲线22221(0,0)x y a b a b -=>>,则其渐近线方程为【A 】A .y =B .y =C .y =D .y =7.在ABC △中,cos 2C ,1BC =,5AC =,则AB =【A 】 A. BCD.8.为计算11111123499100S =-+-++- ,设计了如图的程序框图,则在空白框中应填入【B 】A .1i i =+B .2i i =+ C .3i i =+D .4i i =+9.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为【C 】 A B C D 10.若()cos sin f x x x =-在[0,]a 是减函数,则a 的最大值是【C 】A .π4B .π2C .3π4D .π11.已知1F ,2F是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为【D 】 A .1 B .2-C D 1-12.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)f f f ++(50)f ++= 【C 】A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分.、13.曲线2ln y x =在点(1,0)处的切线方程为 y =2x –2 .14.若,x y 满足约束条件250,230,50,x y x y x +-⎧⎪-+⎨⎪-⎩≥≥≤ 则z x y =+的最大值为 9 .15.已知5π1tan(45α-=,则tan α=32 .16.已知圆锥的顶点为S ,母线SA ,SB 互相垂直,SA 与圆锥底面所成角为30︒,若SAB△的面积为8,则该圆锥的体积为8π .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23为选考题.考生根据要求作答. (一)必考题:共60分.17.(本小题满分12分)记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-. (1)求{}n a 的通项公式;(2)求n S ,并求n S 的最小值.解:(1)设{a n }的公差为d ,由题意得3a 1+3d =–15. 由a 1=–7得d =2.所以{a n }的通项公式为a n =2n –9. (2)由(1)得S n =n 2–8n =(n –4)2–16. 所以当n =4时,S n 取得最小值,最小值为–16.18.(本小题满分12分) 下图是某地区2000年至2016年环境基础设施投资额y (单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了y 与时间变量t 的两个线性回归模型.根据2000年至2016年的数据(时间变量t 的值依次为1,2,,17 )建立模型①:ˆ30.413.5yt =-+;根据2010年至2016年的数据(时间变量t 的值依次为1,2,,7 )建立模型②:ˆ9917.5y t =+. (1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;(2)你认为用哪个模型得到的预测值更可靠?并说明理由.解:(1)利用模型①,该地区2018年的环境基础设施投资额的预测值为y $=–30.4+13.5×19=226.1(亿元).利用模型②,该地区2018年的环境基础设施投资额的预测值为y $=99+17.5×9=256.5(亿元).(2)利用模型②得到的预测值更可靠. 理由如下:(i )从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y =–30.4+13.5t 上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型y $=99+17.5t 可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.(ii )从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分.19.(本小题满分12分)如图,在三棱锥P ABC -中,AB BC ==,4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且2MC MB =,求点C 到平面POM 的距离.解:(1)因为AP =CP =AC =4,O 为AC 的中点,所以OP ⊥AC ,且OP =.连结OB .因为AB =BC AC ,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB =12AC =2.由222OP OB PB +=知,OP ⊥OB . 由OP ⊥OB ,OP ⊥AC 知PO ⊥平面ABC .(2)作CH ⊥OM ,垂足为H .又由(1)可得OP ⊥CH ,所以CH ⊥平面POM . 故CH 的长为点C 到平面POM 的距离.由题设可知OC =12AC =2,CM =23BC ACB =45°.所以OM ,CH =sin OC MC ACB OM ⋅⋅∠.所以点C 到平面POM . 20.(本小题满分12分)设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l与C 交于A ,B 两点,||8AB =.(1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.解:(1)由题意得F (1,0),l 的方程为y =k (x –1)(k >0). 设A (x 1,y 1),B (x 2,y 2).由2(1)4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++=. 216160k ∆=+=,故212224k x x k ++=.所以212244(1)(1)k AB AF BF x x k +=+=+++=.由题设知22448k k +=,解得k =–1(舍去),k =1. 因此l 的方程为y =x –1.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为 2(3)y x -=--,即5y x =-+.设所求圆的圆心坐标为(x 0,y 0),则00220005(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩,解得0032x y =⎧⎨=⎩,或00116.x y =⎧⎨=-⎩, 因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=.21.(本小题满分12分)已知函数()()32113f x x a x x =-++.(1)若3a =,求()f x 的单调区间;(2)证明:()f x 只有一个零点.解:(1)当a =3时,f (x )=3213333x x x ---,f ′(x )=263x x --.令f ′(x )=0解得x=3-或x=3+.当x ∈(–∞,3-)∪(3++∞)时,f ′(x )>0; 当x∈(3-3+ f ′(x )<0.故f (x )在(–∞,3-),(3++∞)单调递增,在(3-3+单调递减.(2)由于210x x ++>,所以()0f x =等价于32301x a x x -=++. 设()g x =3231x a x x -++,则g ′(x )=2222(23)(1)x x x x x ++++≥0,仅当x =0时g ′(x )=0, 所以g (x )在(–∞,+∞)单调递增.故g (x )至多有一个零点,从而f (x )至多有一个零点.又f (3a –1)=22111626()0366a a a -+-=---<,f (3a +1)=103>, 故f (x )有一个零点. 综上,f (x )只有一个零点.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.【选修4-4:坐标系与参数方程】(本小题满分10分)在直角坐标系xOy 中,曲线C 的参数方程为2cos ,4sin x θy θ=⎧⎨=⎩(θ为参数),直线l 的参数方程为1cos ,2sin x t αy t α=+⎧⎨=+⎩(t 为参数).(1)求C 和l 的直角坐标方程;(2)若曲线C 截直线l 所得线段的中点坐标为(1,2),求l 的斜率.解:(1)曲线C 的直角坐标方程为221416x y +=. 当cos 0α≠时,l 的直角坐标方程为tan 2tan y x αα=⋅+-, 当cos 0α=时,l 的直角坐标方程为1x =.(2)将l 的参数方程代入C 的直角坐标方程,整理得关于t 的方程 22(13cos )4(2cos sin )80t t ααα+++-=.①因为曲线C 截直线l 所得线段的中点(1,2)在C 内,所以①有两个解,设为1t ,2t ,则120t t +=.又由①得1224(2cos sin )13cos t t ααα++=-+,故2cos sin 0αα+=,于是直线l 的斜率tan 2k α==-.23.【选修4-5:不等式选讲】(本小题满分10分) 设函数()5|||2|f x x a x =-+--.(1)当1a =时,求不等式()0f x ≥的解集;(2)若()1f x ≤,求a 的取值范围.解:(1)当1a =时,24,1,()2,12,26, 2.x x f x x x x +≤-⎧⎪=-<≤⎨⎪-+>⎩可得()0f x ≥的解集为{|23}x x -≤≤. (2)()1f x ≤等价于|||2|4x a x ++-≥.而|||2||2|x a x a ++-≥+,且当2x =时等号成立.故()1f x ≤等价于|2|4a +≥. 由|2|4a +≥可得6a ≤-或2a ≥,所以a 的取值范围是(,6][2,)-∞-+∞ .。
2018高考全国2卷文科数学带答案(汇编)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学本试卷共23题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.i(2+3i)=A .32i -B .32i +C .32i --D .32i -+ 2.已知集合{}1,3,5,7A =,{}2,3,4,5B =则A B = A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数2e e ()x xf x x--=的图象大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a bA .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中2人都是女同学的概率为 A .0.6 B .0.5 C .0.4 D .0.36.双曲线22221(0,0)x ya b a b -=>>A .y =B .y =C .y =D .y =7.在ABC △中,cos 2C =1BC =,5AC =,则AB =A .BCD .8.为计算11111123499100S =-+-++-,设计了右侧的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+9.在长方体1111ABCD A B C D -中,E为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为ABCD 10.若()cos sin f x x x =-在[0,]a 是减函数,则a 的最大值是A .π4 B .π2 C .3π4D .π 11.已知1F ,2F 是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为A.1-B.2CD 1 12.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++=A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分。
2018年高考全国二卷数学文科(word版)试题(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上. 2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
学@科网 1.()i 23i += A .32i -B .32i +C .32i --D .32i -+2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB =A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数()2e e x xf x x --=的图像大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为 A .0.6B .0.5C .0.4D .0.36.双曲线22221(0,0)x y a b a b-=>>3A .2y x =B .3y x =±C .2y = D .3y = 7.在ABC △中,5cos 2C =1BC =,5AC =,则AB = A .42B 30C 29D .258.为计算11111123499100S =-+-++-,设计了如图的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+9.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为 A B C D 10.若()cos sin f x x x =-在[0,]a 是减函数,则a 的最大值是A .π4B .π2C .3π4D .π11.已知1F ,2F 是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为A .1-B .2CD 112.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)f f f ++(50)f ++=A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分。
2018年高考全国二卷数学文科(word版)试题(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上.写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.学@科网 1.()i 23i += A .32i -B .32i +C .32i --D .32i -+2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB =A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数()2e e x xf x x --=的图像大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为 A .0.6B .0.5C .0.4D .0.36.双曲线22221(0,0)x y a b a b-=>>3A .2y x =±B .3y x =±C .2y =D .3y x = 7.在ABC △中,5cos 2C 1BC =,5AC =,则AB = A .42B 30 C 29D .258.为计算11111123499100S =-+-++-,设计了如图的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+9.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为 A B C D 10.若()cos sin f x x x =-在[0,]a 是减函数,则a 的最大值是A .π4B .π2C .3π4D .π11.已知1F ,2F是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为A .1B .2CD 112.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)f f f ++(50)f ++=A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分.13.曲线2ln y x =在点(1,0)处的切线方程为__________.14.若,x y 满足约束条件250,230,50,x y x y x +-⎧⎪-+⎨⎪-⎩≥≥≤ 则z x y =+的最大值为__________.15.已知5π1tan()45α-=,则tan α=__________. 16.已知圆锥的顶点为S ,母线SA ,SB 互相垂直,SA 与圆锥底面所成角为30︒,若SAB △的面积为8,则该圆锥的体积为__________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23为选考题。
2018届全国名校高三新题试卷(二)数 学 试 卷(文科)

2018届全国名校高三新题试卷(二)数 学 试 卷(文科)本试题卷共10页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}0,1,3A =,()(){}120B x x x =+-<,则A B =I ( ) A .{}0 B .{}0,1,3 C .{}0,1 D .{}0,1,2 2.若复数3i12iz -+=-(i 是虚数单位),则4i z +=( )A B .2 D .43.若,,a b c ∈R ,且a b >,则下列不等式一定成立的是( )A .c c a b >B .20c a b >-C .22a b >D .2211a bc c >++ 4.下列结论中正确的个数是( ) ①“3x π=”是“1sin 22x π⎛⎫+= ⎪⎝⎭”的充分不必要条件; ②命题“,sin 1x x ∀∈≤R ”的否定是“,sin 1x x ∀∈>R ”;③函数()cos f x x =在区间[)0,+∞内有且仅有两个零点.A .1B .2C .3D .05.已知关于x 的不等式2680kx kx k -++≥对任意的x ∈R 恒成立,若k 的取值范围为区间D ,在区间[]1,3-上随机取一个数k ,则k D ∈的概率是( ) A .12 B .13 C .14 D .156.我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,目取其半,万事不竭”,其意思是:一尺长木棍,每天截取一半,永远截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则空白处可填入的是( ) A .S S i =- B .1S S i =- C .2S S i =- D .12S S i=-7.如图所示是一个几何体的三视图,则该几何体的体积为( )A .163π B .643 C .16643π+ D .1664π+ 8.已知某函数在[],ππ-上的图象如图所示,则该函数的解析式可能是( )A .sin 2xy = B .cos y x x =+ C .ln cos y x = D .sin y x x =+9.《九章算术》卷第五《商功》中有记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍,如图,四边形ABCD 为正方形,四边形ABFE 、CDEF 为两个全等的等腰梯形,4AB =,12EF AB ∥,若这个刍甍的体积为403,则CF 的长为( )A .1B .2C .3D .410.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,cos cos 2cos a B b A c C +=,c =且ABC ∆,则ABC ∆的周长为( )A .1+.2+.4.511.设12,F F 分别是椭圆()2222:10x y E a b a b+=>>的左,右焦点,过点1F 的直线交椭圆E于,A B 两点,若12AF F ∆的面积是12BF F ∆的三倍,23cos 5AF B ∠=,则椭圆E 的离心率为( )A .12 B .23C .212.已知定义在区间0,2π⎛⎫⎪⎝⎭上的函数()f x ,()f x '为其导函数,且()()sin cos 0f x x f x x '->恒成立,则( )A .226f f ππ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭ B 43ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭C 63f ππ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭ D .()12sin16f f π⎛⎫< ⎪⎝⎭第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.某乡镇中学有初级职称教师160人,中级职称教师30人,高级职称教师10人,要从其中抽取20人进行体检,如果采用分层抽样的方法,则高级职称教师应该抽取的人数为 .14.已知平面向量,a b r r ,4a b ==rr ,且6a b +=r r ,则a r 在b r 方向上的投影是 .15.若双曲线()222210,0x y a b a b-=>>的渐近线与圆(222x y +=相交,则此双曲线的离心率的取值范围是 .16.已知三棱锥P ABC -的各顶点都在同一球面上,且PA ⊥平面ABC ,若2AB =,1AC =,60BAC ∠=︒,4PA =,则球的体积为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知数列{}n a 满足11a =,()1n n n na na a n +=-∈*N .(1)求数列{}n a 的通项公式;(2)若数列{}n b 的前n 项和为n S ,23n n S b =-,求数列{}n n b a ⋅的前n 项和n T . 18. 在直三棱柱111ABC A B C -中,AD ⊥平面1A BC ,其垂足D 落在直线1A B 上. (1)求证:BC ⊥平面1A AB ;(2)若AD =2AB BC ==,P 为AC 的中点,求三棱锥1P A BC -的体积.19. 某市甲、乙两地为了争创“市级文明城市”,现市文明委对甲、乙两地各派10名专家进行打分评优,所得分数情况如下茎叶图所示.(1)分别计算甲、乙两地所得分数的平均值,并计算乙地得分的中位数;(2)从乙地所得分数在[)60,80间的成绩中随机抽取2份做进一步分析,求所抽取的成绩中,至少有一份分数在[)75,80间的概率;(3)在甲、乙两地所得分数超过90分的成绩中抽取其中2份分析其合理性,求这2份成绩都是来自甲地的概率.20. 已知点()00,M x y 在圆22:4O x y +=上运动,且存在一定点()6,0N ,点(),P x y 为线段MN 的中点.(1)求点P 的轨迹C 的方程; (2)过()0,1A 且斜率为k 的直线l 与点P 的轨迹C 交于不同的两点,E F ,是否存在实数k 使得12OE OF ⋅=uu u r uu u r,并说明理由.21. 已知函数()()ln f x x ax a =-∈R . (1)求函数()f x 的单调区间;(2)当1a =时,方程()()2f x m m =<-有两个相异实根12,x x ,且12x x <,证明:2122x x ⋅<.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,曲线C 的参数方程为,sin x y αα⎧=⎪⎨=⎪⎩(α是参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为sin 4πρθ⎛⎫-= ⎪⎝⎭. (1)将直线l 的极坐标方程化为普通方程,并求出直线l 的倾斜角; (2)求曲线C 上的点到直线l 的最大距离. 23.选修4-5:不等式选讲已知函数()()22f x x x a a =++->-,若()7f x ≥的解集是{3x x ≤-或}4x ≥. (1)求实数a 的值;(2)若x ∀∈R ,不等式()()31f x f m ≥+恒成立,求实数m 的取值范围.文数参考答案一、选择题1-5:CBDAC 6-10:BCACD 11、12:DC二、填空题13.1 14.13815.( 16三、解答题17.解:(1)∵1n n n na na a +=-, ∴11n n a n a n++=. ∴121121n n n n n a a a a a a a a ---=⋅⋅⋅⋅L 121121n n n n n -=⋅⋅⋅⋅=--L , ∴数列{}n a 的通项公式为n a n =. (2)由23n n S b =-,得13b =, 又()11232n n S b n --=-≥,∴1122n n n n n b S S b b --=-=-, 即()122,n n b b n n -=≥∈*N ,∴数列{}n b 是以3为首项,2为公比的等比数列, ∴()132n n b n -=⋅∈*N ,∴132n n n b a n -⋅=⋅,∴()012131222322n n T n -=⋅+⋅+⋅++⋅L ,()123231222322n n T n =⋅+⋅+⋅++⋅L ,两式相减,得()0121322222n n n T n --=++++-⋅L ()3121nn ⎡⎤=--⎣⎦,∴()3123nn T n =-+.18.解:(1)∵三棱柱111ABC A B C -为直三棱柱, ∴1A A ⊥平面ABC .又BC ⊂平面ABC ,∴1A A BC ⊥. ∵AD ⊥平面1A BC ,且BC ⊂平面1A BC , ∴AD BC ⊥.又1A A ⊂平面1A AB ,AD ⊂平面1A AB ,1A A AD A =I , ∴BC ⊥平面1A AB .(2)在直三棱柱111ABC A B C -中,1A A AB ⊥. ∵AD ⊥平面1A BC ,其垂足D 落在直线1A B 上, ∴1AD A B ⊥.在Rt ABD ∆中,AD =2AB BC ==,∴sin 2AD ABD AB ∠==, 即60ABD ∠=︒,在1Rt ABA ∆中,1tan60A A AB =︒=由(1)知,BC ⊥平面1A AB ,AB ⊂平面1A AB , 从而BC AB ⊥, ∴1122222ABC S AB BC =⋅=⨯⨯=. ∵F 为AC 的中点, ∴112BCF ABC S S ∆==.∴11113P A BC A PBC BCF V V S AA --∆==⋅=1133⨯⨯=. 19.解:(1)由题得,甲地得分的平均数为()17778838580898892979986.810⨯+++++++++=, 乙地得分的平均数为()1657275798280848696918110⨯+++++++++=,乙地得分的中位数为8280812+=.(2)由茎叶图可知,乙地得分中分数在[)60,80间的有65,72,75,79四份成绩,随机抽取2份的情况有:()65,72,()65,75,()65,79,()72,75,()72,79,()75,79,共6种,其中至少有一份分数在[)70,80间的情况有:()65,75,()65,79,()72,75,()72,79,()75,79,共5种.故所求概率56P =. (3)甲、乙两地所得分数中超过90分的一共有5份,记甲地中的三份分别为,,A B C ,乙地中的两份分别为,a b .随机抽取其中2份,所有情况如下:(),A B ,(),A C ,(),B C ,(),a b ,(),A a ,(),A b ,(),B a ,(),B b ,(),C a ,(),C b ,一共10种.其中两份成绩都来自甲地的有3种情况:(),A B ,(),A C ,(),B C ,. 故所求概率310p =.20.解:(1)由中点坐标公式,得00622x x y y +⎧=⎪⎪⎨⎪=⎪⎩即()f x ,()f x .∵点()00,M x y 在圆224x y +=上运动,∴22004x y +=,即()()222624x y -+=, 整理,得()2231x y -+=.∴点P 的轨迹C 的方程为()2231x y -+=.(2)设()11,E x y ,()22,F x y ,直线l 的方程是1y kx =+,代入圆()2231x y -+=.可得()()2212390k x k x +--+=, 由232240k k ∆=-->,得304k -<<, 且()122231k x x k -+=+,12291x x k =+, ∴()()()2212121212291111k y y kx kx k x x k x x k =++=+++=++()()22222432391111k k k k k k k--+=++++. ∴2121228610121k k AB AB x x y y k ++⋅=+==+uu u r uu u r , 解得12k =或1,不满足0∆>. ∴不存在实数12k =使得OF .21.解:(1)由题得,()()110axf x a x x x-=-=>.当0a <时,由于0x >,可得10ax ->,即()0f x '>.∴()f x 在区间()0,+∞内单调递增, 当0a >时,由()0f x '>,得10x a<<, 由()0f x '<,得1x a>, ∴()f x 在区间10,a ⎛⎫ ⎪⎝⎭内单调递增,在区间1,a ⎛⎫+∞ ⎪⎝⎭内单调递减. (2)由(1)可设,方程()()2f x m m =<-的两个相异实根12,x x ,满足ln 0x x m --=, 且101x <<,21x >,即1122ln ln 0x x m x x m --=--=. 由题意,可知11ln 2ln 22x x m -=<-<-,又由(1)可知,()ln f x x x =-在区间()1,+∞内单调递减,故22x >. 令()ln g x x x m =--, 则()1112211223ln ln 2g x g x x x x ⎛⎫-=-++-⎪⎝⎭. 令()()223lnt ln 22h t t t t =-++->, 则()()()2221t t h t t -+'=-.当2t >时,()0h t '<,()h t 是减函数, ∴()()322ln 202h t h <--<. ∴当22x >时,()12220g x g x ⎛⎫-<⎪⎝⎭, 即()1212g x g x ⎛⎫<⎪⎝⎭. ∵()g x 在区间()0,1内单调递增,∴1222x x <,故2122x x ⋅<.22.解;(1)由sin 4πρθ⎛⎫-= ⎪⎝⎭,得sin cos 2ρθρθ-=,将cos sin x y ρθρθ=⎧⎨=⎩代入上式,化简,得2y x =+.所以直线l 的倾斜角为4π.(2)在曲线C上任取一点),sin A αα,则点A 到直线l的距离d =当()sin 601α-︒=-时,d取得最大值,且最大值是23.解:(1)∵2a >-,∴()22,2,2,2,22,.x a x f x a x a x a x a -+-<-⎧⎪=+-≤≤⎨⎪+->⎩作出函数()f x 的图象,如图所示:由()7f x ≥的解集为{3x x ≤-或4x ≥及函数图象,可得627,827,a a +-=⎧⎨+-=⎩解得3a =.(2)由题知,x ∀∈R ,不等式()()31f x f m ≥+恒成立, 即x ∀∈R ,不等式32332x x m m ⎡++-⎤≥++-⎣⎦恒成立,由(1)可知,235x x ++-≥(当且仅当23x -≤≤时取等号), ∴3235m m ++-≤⨯,当3m ≤-时,3215m m ---+≤,∴8m ≥-,∴83m -≤≤-,当32m -<<时,3215m m +-+≤,成立;当2m ≥时,3215m m ++-≤,∴7m ≤,∴27m ≤≤,综上所述,实数m 的取值范围为[]8,7-.。
2018年高考全国2卷文科数学带答案解析-精选.pdf

A. 4
B. 3
C. 2Biblioteka D. 05.从 2 名男同学和 3 名女同学中任选 2 人参加社区服务,则选中 2 人都是女同学的概率为
A. 0.6
6.双曲线
x2
2
a
B. 0.5
C. 0.4
D. 0.3
y2 2 1( a 0, b 0) 的离心率为
b
3 ,则其渐近线方程为
A. y
2x
B. y
3x
C. y
2 x
2 x 3) x 1)2 ≥0,仅当 x=0 时 g ′( x) =0,
所以 g(x)在(–∞, +∞)单调递增.故 g( x)至多有一个零点,从而 f ( x)至多有一
个零点.
又 f ( 3a–1) =
2
6a
2a
1
3
零点.
6(a
12 )
1
0 , f ( 3a+1) = 1
0 ,故 f ( x)有一个
( 2)证明: f (x) 只有一个零点.
(二)选考题:共 10 分。请考生在第 22、23 题中任选一题作答。如果多做,则按所做的第
一题计分。
22. [ 选修 4- 4:坐标系与参数方程 ] (10 分)
x 2cos θ,
在直角坐标系 xOy 中,曲线 C 的参数方程为
( θ为参数),直线 l 的参数方
y? 30.4 13.5t ;根据 2010 年至 2016 年的数据(时间变量 t 的值依次为 1, 2, , 7 )建立模
型②: y? 99 17.5t .
( 1)分别利用这两个模型,求该地区 2018 年的环境基础设施投资额的预测值;
( 2)你认为用哪个模型得到的预测值更可靠?并说明理由.
2018年高考全国二卷数学文科(word版)试题(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
学@科网 1.()i 23i += A .32i -B .32i +C .32i --D .32i -+2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB =A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数()2e e x xf x x --=的图像大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为 A .0.6B .0.5C .0.4D .0.36.双曲线22221(0,0)x y a b a b-=>>3A .2y x =B .3y x =±C .2y = D .3y = 7.在ABC △中,5cos 2C =1BC =,5AC =,则AB = A .42B 30C 29D .258.为计算11111123499100S =-+-++-,设计了如图的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+9.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为 A B C D 10.若()cos sin f x x x =-在[0,]a 是减函数,则a 的最大值是A .π4B .π2C .3π4D .π11.已知1F ,2F是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为A .1-B .2CD 112.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)f f f ++(50)f ++=A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018届全国名校高三新题试卷(二)文科数学本试题卷共10页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}3,2,1,0,1,2,3A =---,集合{}1,0,1,3A =-,集合{}3,2,1,3B =---,则()U C A B ⋃=( )A .{}3,2,1--B .{}2,1,1--C .{}2D .{}1,2,3-2. 已知复数z 满足()20181z i i +=(i 是虚数单位),则复数z 在复平面内对应的点所在象限为( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.函数()()ln 21f x x ++的定义域为( )A .1,22⎡⎤-⎢⎥⎣⎦B .1,22⎡⎫-⎪⎢⎣⎭C .1,22⎛⎤- ⎥⎝⎦D .1,22⎛⎫- ⎪⎝⎭4.三世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法.所谓割圆术,就是不断倍增圆内接正多边形的边数求出圆周率的方法.如图是刘徽利用正六边形计算圆周率时所画的示意图,现项园中随机投掷一个点,则该点落在正六边形内的概率为( )A B C D5.已知双曲线()222210,0x y a b a b-=>>的一条渐近线与直线4310x y ++=垂直,且焦点在圆()22126x y +-=上,则该双曲线的标准方程为( )A .221916x y -=B .221169x y -=C .22134x y -=D .22143x y -=6.执行如图所示的程序框图,若输入的0.05t =,则输出的n 为( )A .3B .4C .5D .67.已知数列{}n a 的前n 项和为n S ,1133,2n n a a S ++==,则5a =( ) A .33 B .43 C .53 D .638.已知将函数()()sin 206f x x πωω⎛⎫=+> ⎪⎝⎭的图象向左平移3π个单位长度得到函数()g x 的图象,若函数()g x 图象的两条相邻的对称轴间的距离为2π,则函数()g x 的—个对称中心为( )A .,06π⎛⎫- ⎪⎝⎭B .,06π⎛⎫ ⎪⎝⎭C .,012π⎛⎫- ⎪⎝⎭D .,012π⎛⎫⎪⎝⎭9.榫卯是在两个木构件上所采用的一中凹凸结合的连接方式,凸出部分叫榫,凹进部分叫卯,榫和卯咬合,起到连接作用,代表建筑有:北京的紫禁城、天坛祈年殿、山西悬空寺等,如图所示是一种榫卯的三视图,其表面积为( )A .812π+B .816π+C .912π+D .916π+10.已知实数,x y 满足约束条件0,20,3,x y x y x -≥⎧⎪+-≥⎨⎪≤⎩当且仅当1x y ==时,目标函数z kx y =+取大值,则实数k 的取值范围是( )A .(),1-∞B .(),1-∞-C .()1,-+∞D .()1,+∞11.已知0a >,命题:p 函数()()2lg 23f x ax x =++的值域为R ,命题:q 函数()ag x x x=+在区间()1,+∞内单调递增.若p q ⌝∧是真命题,则实数a 的取值范围是( ) A .(],0-∞ B .1,3⎛⎤-∞ ⎥⎝⎦ C .10,3⎛⎤ ⎥⎝⎦ D .1,13⎛⎤⎥⎝⎦12.若函数()ln ,0x x f x x >⎧⎪=⎨≤⎪⎩与()1g x x a =++的图像上存在关于y 轴对称的点,则实数a的取值范围是( )A .RB .(],e -∞-C .[),e +∞D .∅第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知在ABC ∆中,D 为BC 边上的点,20BD CD +=,若(),AD mAB nAC m n R =+∈,则n = .14.已知焦点在x 轴上的椭圆222121x y m m +=+20y -+=上,则椭圆的离心率为 .15.在锐角ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若()sin cos sin 1cos C A B C =-,且,3A b π==c = .16.如图,在矩形ABCD 中,2AD =,E 为AB 边上的点,项将ADE ∆沿DE 翻折至A DE '∆,使得点A '在平面EBCD 上的投影在CD 上,且直线A D '与平面EBCD 所成角为30︒,则线段AE 的长为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知等差数列{}n a 的前n 项和为n S ,15965,3a a a S =+=. (1)求数列{}n a 的通项公式;(2)若数列{}n b 满足11n n n b a a ++=,且16b a =,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T .18.如图,四棱锥P ABCD -的底面ABCD 是边长为2的正方形,平面PAB ⊥平面ABCD ,点E 是PD 的中点,棱PA 与平面BCE 交于点F .(1)求证://AD EF ;(2)若PAB ∆是正三角形,求三棱锥P BEF -的体积.19.某市统计局就某地居民的收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[)1000,1500).(1)求居民收入在[)3000,3500的频率;(2)根据频率分布直方图算出样本数据的中位数及样本数据的平均数;(3)为了分析居民的收人与年龄、职业等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在[)2500,3000内应抽取多少人? 20.已知点F 为抛物线()2:20C y px p =>的焦点,过F 的直线l 交抛物线于,A B 两点. (1)若直线l 的斜率为1,8AB =,求抛物线C 的方程;(2)若抛物线C 的准线与x 轴交于点()1,0P -,(:2:1APF BPF S S ∆∆=,求PA PB ⋅的值. 21.已知函数()2ln ,f x x x ax a R =++∈.(1)当1a =时,求曲线()f x 在1x =处的切线方程;(2)若()1212,x x x x <是函数()f x 的导函数()f x '的两个零点,当(),3a ∈-∞-时,求证:()()123ln 24f x f x ->-. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,已知曲线1C 的参数方程为2143x t y t =-⎧⎨=-+⎩(t 为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为4πρθ⎛⎫=- ⎪⎝⎭.(1)求曲线1C 的普通方程与2C 的直角坐标方程; (2)判断曲线12,C C 是否相交,若相交,求出相交弦长. 23.选修4-5:不等式选讲 已知函数()212f x x x =-++. (1)求不等式()0f x >的解集;(2)若对任意的[),x m ∈+∞,都有()f x x m ≤-成立,求实数m 的取值范围.试卷答案一、选择题1-5: CBDAB 6-10: CCDBB 11、12:DC二、填空题13.1314. 23三、解答题17. 解:(1)设等差数列{}n a 的公差为d , 由15965,3a a a S =+=, 得 ()()6535458652d d d ⨯+++=⨯+, 解得2d =.所以()()()*1152123n a a n d n n n N =+-=+-=+∈. (2)由(1)得,1626315b a ==⨯+=. 又因为11n n n b a a ++=,所以当2n ≥时,()()12321n n n b a a n n -==++ 当1n =时,15315b =⨯=,符合上式,所以()()2321n b n n =++. 所以()()11111232122123n b n n n n ⎛⎫==- ⎪++++⎝⎭. 所以1111111235572123n T n n ⎛⎫=-+-++- ⎪++⎝⎭()1112323323nn n ⎛⎫=-= ⎪++⎝⎭. 18. 解:(1)因为底面ABCD 是边长为2的正方形, 所以//BC AD .又因为BC ⊄平面PAD ,AD ⊂平面PAD , 所以//BC 平面PAD .又因为,,,B C E F 四点共面,且平面BCEF ⋂平面PAD EF =, 所以//BC EF .又因为//BC AD ,所以//AD EF . (2)因为//AD EF ,点E 是PD 的中点, 所以点F 为PA 的中点,112EF AD ==. 又因为平面PAB ⊥平面ABCD ,平面PAB ⋂平面,ABCD AB AD AB =⊥, 所以AD ⊥平面PAB ,所以EF ⊥平面PAB . 又因为PAB ∆是正三角形, 所以2PA PB AB ===,所以12PBF PBA S S ∆∆==. 又1EF =,所以113P BEF B PEF V V --===故三棱锥P BEF -19.解:(1)由题知,月收入在[)3000,3500的频率为0.00035000.15⨯=.(2)从左数第一组的频率为0.00025000.1⨯=,第二组的频率为0.00045000.2⨯=, 第三组的频率为0.00055000.25⨯=, ∴中位数在第三组, 设中位数为2000x +,则0.00050.50.10.2x ⨯=--,解得400x =,∴中位数为2400.由12500.117500.222500.2527500.2532500.1537500.052400⨯+⨯+⨯+⨯+⨯+⨯=, 得样本数据的平均数为2400.(3)月收入在[)2500,3000的频数为0.25100002500⨯=(人), ∵抽取的样本容量为100, ∴抽取的比例为100110000100=, ∴月收入在[)2500,3000内应抽取的人数为1250025100⨯=(人). 20.解:(1)由题意知,直线l 的方程为2p y x =-. 联立2,22,p y x y px ⎧=-⎪⎨⎪=⎩得22304p x px -+=.设,A B 两点的坐标分别为()(),,,A A B B x y x y , 则3A B x x p +=.由抛物线的性质,可得4822A B A B p pAB FA FB x x x x p p =+=+++=++==, 解得2p =,所以抛物线C 的方程为24y x =.(2)由题意,得()1,0F ,抛物线2:4C y x =, 设直线l 的方程为1x my =+,()()1122,,,A x y B x y , 联立21,4,x my y x =+⎧⎨=⎩得2440y my --=.所以12124,4,y y m y y +=⎧⎨=-⎩①因为(:2:1APF BPF S S ∆∆=,所以2AF BF=-因为,,A F B 三点共线,且,AF FB 方向相同,所以()23AF FB =-,所以()(()11221,21,x y x y --=--, 所以)122y y =,代入①,得))22214,2 4.y m y⎧=⎪⎨=-⎪⎩解得212m =, 又因为()1,0P -,所以()()11221,,1,PA x y PB x y =+=+, 所以()()11221,1,PA PB x y x y ⋅=+⋅+ ()1212121x x x x y y =++++()()()1212111114my my my my =+++++++-()212122m y y m y y =++ 2224842m m m =-+==.21.解:(1)当1a =-时,()2ln f x x x x =+-,()121f x x x'=+-, 所以()1ln1110f =+-=,()11212f '=+-=. 所以曲线()f x 在1x =处的切线方程为()21y x =-, 即220x y --=.(2)由题得,()()212120x ax f x x a x x x ++'=++=>.因为12,x x 是导函数()f x '的两个零点, 所以12,x x 是方程210ax ax ++=的两根, 故121210,22a x x x x +=->=. 令()221g x x ax =++, 因为(),3a ∈-∞-,所以13022a g +⎛⎫=< ⎪⎝⎭,()130g a =+<, 所以()1210,,1,2x x ⎛⎫∈∈+∞ ⎪⎝⎭,且22112221,21ax x ax x =--=--,所以()()()()()2222111212121222lnln x x f x f x x x ax ax x x x x -=+-+-=--+, 又因为1212x x =,所以1212x x =,所以()()()()2212121221ln 2,1,4f x f x x x x x -=--∈+∞,令()2222,t x =∈+∞,()()()121ln 22t h t f x f x t t=-=--. 因为()()22211110222t h t t t t -'=+-=>, 所以()h t 在区间()2,+∞内单调递增, 所以()()32ln 24h t h >=-, 即()()123ln 24f x f x ->-. 22.解:(1)由题知,将曲线1C 的参数方程消去参数t , 可得曲线1C 的普通方程为210x y +-=.由4πρθ⎛⎫=- ⎪⎝⎭,得()22cos sin ρρθρθ=+.将222x y ρ=+,cos ,sin x y ρθρθ==代入上式, 得2222x y x y +=+, 即()()22112x y -+-=.故曲线2C 的直角坐标方程为()()22112x y -+-=. (2)由(1)知,圆2C 的圆心为()1,1,半径R = 因为圆心到直线1C的距离d ==<所以曲线12,C C 相交,所以相交弦长为=.23.解:(1)当2x ≤-时,不等式转化为()()2120x x --++>,解得2x ≤-; 当122x -<<时,不等式转化为()()2120x x ---+>,解得123x -<<-;当12x ≥ 时,不等式转化为()()2120x x --+>,解得3x >. 综上所述,不等式()0f x >的解集为{13x x <-或}3x >.(2)由(1)得,()3,2,131,2,213,,2x x f x x x x x ⎧⎪-+≤-⎪⎪=---<<⎨⎪⎪-≥⎪⎩作出其函数图象如图所示:令y x m =-,若对任意的[),x m ∈+∞,都有()f x x m ≤-成立, 即函数()f x 的图象在直线y x m =-的下方或在直线y x m =-上. 当2m ≤-时,30m -+≤,无解;当122m -<<时,310m --≤,解得1132m -≤<; 当12m ≥时,30m -≤,解得132m ≤≤.综上可知,当133m -≤≤时满足条件,故实数m 的取值范围是1,33⎡⎤-⎢⎥⎣⎦.。
