寒假作业6

合集下载

小学语文一年级上册寒假作业 (6)

一、比一比，再组词。

目（）毛（）羊（）月（）八（）九（）耳（）自（）手（）半（）用（）入（）力（）儿（）二、选字填空。

木，目耳（）（）光（）头（）耳树（）妈妈让我吃（）耳。

老师的（）光很慈祥（cíxiánɡ）。

十石时识．早上，（）针指向点，我就起床了。

．妈妈说她不认（）这个人。

．哥哥今年（）岁了。

．司马光用（）头砸破了大水缸。

三、填一填。

一（）水牛一（）图书一（）小树一（）小鸡四、选择正确的读音。

．行：①xíng ②háng（）穿过人行( )道，就是中国银行( )。

（）因为下雨，路上的行( )人少了。

（）道路的两旁各有一行( )小树。

五、乱词组句。

今天一班的同学去植物园参观一年级_______________________________________________六、扩词。

入_______ _______ _____大_______ _______ ____天_______ _______ _____一、比一比，再组词。

目（）生（）一（）又（）木（）木（）升（）衣（）右（）禾（）二、选字填空。

耳，儿，二花（）（）只（）朵（）子（）光（）个女（）木（）王爷爷有（）个女（）。

我在听（）机。

喜欢高兴．小猴子找到一些桃子，非常（）。

．动画片是我最（）看的。

三、填一填。

一（）小河一（）白云一（）木船一（）野花四、选择正确的读音。

.只：①zhī②zhǐ（）一只（）小鸟在天上飞。

（）我只（）有一个娃娃。

五、乱词组句。

悄悄地月亮窗户离开了______________________________六、扩词。

人_______ _______ ____火_______ _______ _____文_______ _______ _____一、比一比，再组词。

目（）毛（）羊（）月（）八（）九（）耳（）自（）手（）半（）用（）入（）力（）儿（）二、选字填空。

升生声（）日（）旗上（）花（）笑（）大（）在走廊（lánɡ）上要小（）说话。

南京市高一上学期物理寒假作业(含答案) (6)

南京市高一上学期物理寒假作业06一、单选题（本大题共11小题，共44.0分）1.物体从斜面顶端由静止开始滑下，经t秒到达中点，则物体从斜面顶端到底端共用时间为（）A. B. t C. 2t D. t2.图为蹦极运动的示意图．弹性绳的一端固定在O点，另一端和运动员相连．运动员从O点自由下落，至B点弹性绳自然伸直，经过合力为零的C点到达最低点D，然后弹起．整个过程中忽略空气阻力．分析这一过程，下列表述正确的是（）①经过B点时，运动员的速率最大②经过C点时，运动员的速率最大③从C点到D点，运动员的加速度增大④从C点到D点，运动员的加速度不变．A. ①③B. ②③C. ①④D. ②④3.如图，桌面上有一光滑的木块，木块上有一小球，推动木块，小球的位置可能在桌面上的（）A. A点B. B点C. O点D. 无法确定4.用手握重为1N的圆柱形瓶子，握力为20N，使其在竖直方向处于静止状态，则手与瓶子间的摩擦力为（）A. 21NB. 20NC. 19ND. 1N5.如图所示，甲、乙、丙三个物体质量相同，与地面的动摩擦因数相同，受到三个大小相同的作用力F，当它们滑动时，受到的摩擦力大小是（）A. 甲、乙、丙所受摩擦力相同B. 甲受到的摩擦力最大C. 乙受到的摩擦力最大D. 丙受到的摩擦力最大6.关于自由落体运动，下列说法正确的是（）A. 从地球表面附近做自由落体运动的物体，加速度都是不同的B. 下落快慢与物体质量有关，在同一地点，重物体下落的加速度较大C. 下落快慢与物体质量无关，但与物体所在地理位置有关，赤道上自由落体加速度最大D. 同一地点，两个质量不等，高度不同但同时自由下落的物体，下落过程中任何时刻的速度、加速度一定相同7.在半球形光滑容器内，放置一细杆，如图所示，细杆与容器的接触点分别为A、B两点，则容器上A、B两点对细杆m的作用力的方向分别为（）A. 均竖直向上B. 均指向球心C. A点处的弹力指向球心O，B点处的弹力竖直向上D. A点处的弹力指向球心O，B点处的弹力垂直于细杆向上8.物体做匀加速直线运动，加速度为2m/s2，那么（）A. 在任意时间内，物体的末速度一定等于初速度的2倍B. 在任意时间内，物体的末速度一定比初速度大2m/sC. 在任意1s内，物体的末速度一定等于初速度的2倍D. 在任意1s内，物体的末速度一定比初速度大2m/s9.关于位移和路程，下列说法中正确的是（）A. 位移是矢量，位移的方向即物体运动的方向B. 位移的大小不会比路程大C. 路程是标量，即位移的大小D. 物体通过一段路程，则它通过的位移不可能为零10.一辆汽车从静止开始做匀加速直线运动，5s末的速度达到15m/s，汽车的加速度是（）A. 15m/s2B. 1m/s2C. 5m/s2D. 3m/s211.小球从靠近竖直砖墙的某位置由静止释放，用频闪方法拍摄的小球位置如图中1、2、3和4所示．已知连续两次闪光的时间间隔均为T，每块砖的厚度为d．由此可知小球（）A. 下落过程中的加速度大小约为B. 经过位置3时的瞬时速度大小约为2gTC. 经过位置4时的瞬时速度大小约为D. 从位置1到4过程中的平均速度大小约为二、多选题（本大题共5小题，共20.0分）12.A、B、C三个物体如图所示放置在水平面上，所有接触面均不光滑，有一个水平向右的力F作用在物体C上，使A、B、C一起向右做匀速运动，则（）A. B对A的静摩擦力方向水平向左B. B对A的静摩擦力方向水平向右C. C对A的静摩擦力方向水平向左D. C对A的静摩擦力方向水平向右13.下列说法正确的是（）A. 每个力都必有施力物体和受力物体B. 网球运动员用球拍击球，对网球施力的物体是运动员C. 两个力的大小都是5N，则这两个力一定相同D. 施力物体同时也是受力物体，受力物体同时也是施力物体14.下列说法中与人们的日常习惯相吻合的是（）A. 测量三楼楼道内日光灯的高度，选择三楼地板为参考系B. 测量井的深度，以井底为参考系，井“深”为0米C. 以卡车司机为参考系，卡车总是静止的D. 以路边的房屋为参考系判断自己是否运动15.下列说法中正确的是（）A. 力的合成遵循平行四边形定则B. 一切矢量的合成都遵循平行四边形定则C. 以两个分力为邻边的平行四边形的两条对角线都是它们的合力D. 以两个分力为邻边的平行四边形中，与两个分力共点的那一条对角线所表示的力是它们的合力16.如图所示，粗糙的水平地面上有三块材料完全相同的木块A、B、C，质量均为m，B、C之间用轻质细绳连接。

2023年高三生物寒假作业(六)

生物寒假作业（六）——《选三》专项练习一、单选题1．为避免航天器在执行载人航天任务时出现微生物污染风险，需要对航天器及洁净的组装车间进行环境微生物检测。

下列叙述错误的是（）A．航天器上存在适应营养物质匮乏等环境的极端微生物B．细菌形成菌膜粘附于航天器设备表面产生生物腐蚀C．在组装车间地面和设备表面采集环境微生物样品D．采用平板划线法等分离培养微生物，观察菌落特征2．下列是某同学分离高产脲酶菌的实验设计，不合理的是（）A．选择农田或公园土壤作为样品分离目的菌株B．在选择培养基中需添加尿素作为唯一氮源C．适当稀释样品是为了在平板上形成单菌落D．可分解酚红指示剂使其褪色的菌株是产脲酶菌3．为探究校内植物园土壤中的细菌种类，某兴趣小组采集园内土壤样本并开展相关实验。

下列有关叙述错误．．的是（）A．采样时应随机采集植物园中多个不同地点的土壤样本B．培养细菌时，可选用牛肉膏蛋白胨固体培养基C．土壤溶液稀释倍数越低，越容易得到单菌落D．鉴定细菌种类时，除形态学鉴定外，还可借助生物化学的方法4．废水、废料经加工可变废为宝。

某工厂利用果糖生产废水和沼气池废料生产蛋白质的技术路线如图所示。

下列叙述正确的是（）A．该生产过程中，一定有气体生成B．微生物生长所需碳源主要来源于沼气池废料C．该生产工艺利用微生物厌氧发酵技术生产蛋白质D．沼气池废料和果糖生产废水在加入反应器之前需要灭菌处理5．关于白酒、啤酒和果酒的生产，下列叙述错误的是（）A．在白酒、啤酒和果酒的发酵初期需要提供一定的氧气B．白酒、啤酒和果酒酿制的过程也是微生物生长繁殖的过程C．葡萄糖转化为乙醇所需的酶既存在于细胞质基质，也存在于线粒体D．生产白酒、啤酒和果酒的原材料不同，但发酵过程中起主要作用的都是酵母菌6．青霉菌的代谢类型为异养需氧型，其处在葡萄糖浓度不足的环境中时，会通过分泌青霉素杀死细菌，以保证自身生存所需的能量供应。

目前已实现青霉素的工业化生产，关于该生产过程，下列说法错误的是A．发酵液中的碳源不宜使用葡萄糖B．可用深层通气液体发酵技术提高产量C．选育出的高产菌株经扩大培养后才可接种到发酵罐中D．青霉素具有杀菌作用，因此发酵罐不需严格灭菌7．植物体细胞通常被诱导为愈伤组织后才能表现全能性。

北师大版八年级数学寒假作业练习6

八年级数学练习61、下列命题中正确的是（）A 、若a<b<0，则不等式ax<b 的解集为x<baC 、相等的角是对顶角B 、一般而言,一组数据的极差、标准差越小,数据就越稳定 D 、一组数据的众数只有一个 2、已知直角三角形的三边分别为a 、a+b 、a+2b ，其中a>0,b>0,则a 与b 的比为（） A 、1∶3 B 、1∶4C 、2∶1D 、3∶13、如果一个三角形的两个外角的和是270°，则这个三角形一定是（） A 、锐角三角形 B 、直角三角形 C 、钝角三角形 D 、等腰三角形4、直角三角形的周长为48,一锐角的平分线分对边为3∶5,则斜边长为（） A 、20 B 、15 C 、25 D 、165、如果正比例函数x y 3=和一次函数k x y +=2的图像的交点在第三象限，那么k 的取值范围是( ) A 、k ＞0 B 、k ＜0 C 、k ≤0 D 、k ≥06、若3===c z b y a x ，则=+-+-c b a z y x 3232 ；若_____,432=++==yz y x z y x 则。

7的解是；不等式的解集是．8、如图，某测量工作人员的眼与标杆顶端F ，电视塔顶端E 在同一直线上，已知此人身高为1.6米，标杆为3.2米，且BC=1米，CD=5米，则电视塔的高ED= 米。

9、如右图，在正方形ABCD 的边BC 的延长线上取一点E ，使CE=AC ，AE 与CD 交于点F ，那么∠AEC ＝________度； 10、如图，在△ABC 中，∠C 的平分线CD 交AB 于D ，过D 作DE ∥BC ，交AC 于E ，AE=4,EC=5，那么11、如图，AD ⊥BC ，垂足为D ，且CD BD AD ⋅=2,求证：(1)△ADB ∽△CDA ；(2)∠BAC=90°；12、一条河的两岸有一段是平行的．在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆．在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽．C A ED A C D B13、随着苏州人民生活水平的不断提高，青少年的肥胖问题正在受到大家的关注，初中阶段是控制肥胖的重要阶段，营养学家总结出了如下初中阶段计算超重公式：超重y(千克)=体重x(千克)—身高h(厘米)+105， y为正值属于超重。

寒假作业(6) 2022—2023学年部编版语文七年级上册(古诗文默写。有答案)

寒假作业（6）——2022-2023学年七年级语文人教部编版1.诗句默写。

（1）成长的路上，总有先贤为我们点亮思想的明灯：路过潼关，少年谭嗣同意气风发地吟诵“______________，山入潼关不解平”；虽至暮年，犹思报国的陆游，发出“僵卧孤村不自哀，_____________________”的呐喊。

（2）思乡是戍边将士、在外游子共有的情怀。

“______________，一夜征人尽望乡”，乡思，在征人的失眠时；“乡书何处达？___________________”，乡思，在游子的书信里。

2.诗句默写。

（1）《夜雨寄北》中，蕴含羁旅他乡的抑郁之情，并把愁苦之情融入凄凉萧瑟的景色之中的诗句是：____________________，____________________。

（2）在《十一月四日风雨大作》（其二）一诗中，爱国诗人陆游年迈苍老，但他“____________________”，内心燃烧的是为国戍边的志愿；听着窗外肆虐的风雨，“____________________”，做梦都在想为国征战，收复失地！3.默写。

（1）孔子认为一个人的志向很重要，他说：“____________________，____________________。

”（2）《江南逢李龟年》一诗中，表达出“同是天涯沦落人”的感慨的诗句是：“____________________，____________________。

”（3）《夜上受降城闻笛》一诗中，表现出征人满怀愁绪，凝望故乡，思念故乡的诗句是：“____________________，____________________。

”4.按要求默写诗句。

（1）日月之行，________________；________________，若出其里。

（曹操《观沧海》）（2）《次北固山下》一诗中，借景抒情又蕴含自然理趣的两句是：________________，________________；描绘涨潮时水面宽阔，帆船顺风而行的句子是：________________，________________；抒发乡愁的句子是：________________？________________。

九年级数学寒假作业(6)

九年级数学寒假作业（6）1．在Rt △ABC 中，∠C=90°，下列式子不一定成立的是（）A ．sinA=sinB B ．cosA=sinBC ．sinA=cosBD ．∠A+∠B=90°2．直角三角形的两边长分别是6，8，则第三边的长为（）A ．10B ．C ．10或．无法确定3．在Rt △ABC 中，∠C=90°，当已知∠A 和a 时，求c ，应选择的关系式是（）A ．c=sin a AB ．c=cos a AC ．c=a ·tanAD ．c=a ·cotA 4．如图是一个棱长为4cm 的正方体盒子，一只蚂蚁在D 1C 1的中点M 处，它到BB 的中点N 的最短路线是（）A ．8B ．C ．．5．已知∠A 是锐角，且，那么∠A 等于（） A ．30° B ．45° C ．60° D ．75°6．当锐角α>30°时，则cos α的值是（）A ．大于12B ．小于12CD7．已知Rt △ABC 中，∠C=90°，tanA=43，BC=8，则AC 等于（） A ．6 B ．323 C ．10 D ．12 8．已知sin α=12，求α，若用计算器计算且结果为“”，最后按键（） A ．AC10N B ．SHIET C ．MODE D ．SHIFT “”9．如图，3×3•网格中一个四边形ABCD ，•若小方格正方形的边长为1，•则四边形ABCD 的周长是_______．10．计算2sin30°+2cos60°+3tan45°=_______．11．若sin28°=cos α，则α=________．12．已知△ABC 中，∠C=90°，AB=13，AC=5，则tanA=______．13．如图所示的一只玻璃杯，最高为8cm ，将一根筷子插入其中，杯外最长4厘米，•最短2厘米，那么这只玻璃杯的内径是________厘米．14．由下列条件解题：在Rt △ABC 中，∠C=90°：（1）已知a=4，b=8，求c ．（2）已知b=10，∠B=60°，求a ，c ．（3）已知c=20，∠A=60°，求a ，b ．15．计算下列各题．（1）s in230°+cos245°°·tan45°；（2）22cos30cos60tan60cot30︒+︒︒︒+tan60°（3）tan2°tan4°·tan6°…tan88°16．已知等腰△ABC中，AB=AC=13，BC=10，求顶角∠A的四种三角函数值．17．如图所示，平地上一棵树高为5米，两次观察地面上的影子，•第一次是当阳光与地面成45°时，第二次是阳光与地面成30°时，第二次观察到的影子比第一次长多少米？。

人教_B_版高一寒假作业_6：平面向量初步

人教B 版高一寒假作业6：平面向量初步【基础巩固】1.(2023·陕西省宝鸡市·期末考试)下列命题不正确的是()A.若向量,a b 满足3a b =- ，则,a b 为平行向量B.已知平面内的一组基底12,e e ，则向量1212,e e e e +- 也能作为一组基底C.模等于1个单位长度的向量是单位向量，所有单位向量均相等D.若ABC 是等边三角形，则2,3AB BC π<>= 2.(2023·吉林省·单元测试)在ABC 中，点D 为BC 边的中点，点F 为线段AD 的中点，点E 满足2AE EC = ，则EF =()A.11212AB AC - B.1123AB AC - C.11412AB AC - D.15412AB AC - 3.已知e 为直线l 上的一个单位向量，向量a 与b 都是直线l 上的向量，且3a e = ，2b e =- ，则,a b 的坐标分别为()A.3，2-B.3，2C.3-，2D.3-，2-4.已知一艘船以5/km h 的速度行驶，同时河水的流速为2/km h ，则船的实际航行速度(单位：/)km h 的取值范围是()A.[2,5] B.[2,7] C.[5,7] D.[3,7]5.(2023·山东省·单元测试)已知正方形ABCD 的边长为1，,,,AB a BC b AC c === 则||a b c ++ 等于()A.0B.3C.D.6.(2023·山东省菏泽市·月考试卷)已知向量(1,2)a = ，(1,0)b = ，(3,4).c = 若()//()a b c R λλ+∈ ，则实数λ=()A.2B.1C.12 D.147.(2023·安徽省·月考试卷)已知(5,2)a =- ，(4,3)b =-- ，(,)c x y = ，若230a b c -+= ，则c = ()A.81,3⎛⎫⎪⎝⎭ B.138,33⎛⎫- ⎪⎝⎭ C.134,33⎛⎫- ⎪⎝⎭ D.134,33⎛⎫-- ⎪⎝⎭8.(2022·湖南省·月考试卷)如图，在ABC 中，点D 是线段BC 上的动点(端点除外)，且AD x AB y AC =+ ，则91x y +的最小值为()A.16B.17C.18D.199.(多选)(2023·河南省·月考试卷)如图所示，在ABC 中，点D 在边BC 上，且2CD DB =，点E 在边AD 上，且3AD AE =，则()A.13CE AD AC =+B.13CE AD AC =-C.2899CE AB AC =+D.2899CE AB AC =- 10.(多选)(2022·全国·同步练习)八卦是中国古代哲学的基本概念之一，如图1是八卦模型图，其平面图形记为图2中的正八边形ABCDEFGH ，其中1OA =，则下列结论中正确的是()A.//AD BCB.0OA OD OE OH +++=C.OA OC +=D.AD =【拓展提升】11.(多选)(2023·四川省成都市·月考试卷)如图，正方形ABCD 中，E 为AB 中点，M 为线段AD 上的动点，若BM BE BD λμ=+，则λμ+的值可以是()A.32 B.12 C.1 D.212.(2023·北京市·原创试题)已知向量(3,2),(2,1),a b t R =-=∈ ，则a tb + 的最小值为__________此时t为__________13.(2023·安徽省合肥市·期中考试)在平面向量中有如下定理：设点O ，P ，Q ，R 为同一平面内的点．则P ，Q ，R 三点共线的充要条件是：存在实数t ，使(1).OP t OQ tOR =-+ 试利用该定理解答下列问题：如图，在ABC 中，E 为边AB 的中点，点F 在边AC 上，且2CF FA =，BF 交CE 于点M ，设AM xAE y AF =+，则x y +=__________.14.(2023·河南省·联考题)已知E 为ABC 内一点，F 为AC 边的中点.(1)若30EA EB EC ++= ，求证：52;BE BF = (2)若230EA EB EC ++= ，EBC ，ABC 的面积分别为S '，S ，求证：6.S S ='15.(2022·全国·模拟题)如图，在梯形ABCD 中，2AB DC =，E ，F 是DC 的两个三等分点，G ，H 是AB 的两个三等分点，线段BC 上一动点P 满足(01)BP BC λλ= ，AP 分别交EG ，FH 于M ，N 两点，记AB a = ，.AD b = (1)当12λ=时，用a ，b 表示AP ；(2)若MN AP μ= ，试写出λ和μ的关系，并求出μ的取值范围．1.【答案】C【解析】【分析】本题考查零向量、单位向量，相等向量，共线向量，基底的概念，属于中档题.由平行向量定义判断A ，根据基底的定义判断B ，由相等向量的定义判断C ，由向量夹角的定义判断.D 【解答】解：对于A ，因为3a b =- ，所以当b 为零向量时，0a b == ，,a b 是平行向量，当b 不是零向量时，3a b =- ，,a b 也是平行向量，A 正确；对于B ，12,e e 为一组基底，12,e e ∴ 不共线，假设1212,e e e e +- 共线，则()1212e e e e λ+=- ，所以()()12110e e λλ-++= ，所以10,10λλ-=+=，矛盾，所以1212,e e e e +- 不共线，所以1212,e e e e +- 可以作为一组基底，B 正确；对于C ，虽然单位向量模长相等，但方向可以不同，故不是所有单位向量均相等，C 错误；对于D ，ABC 为等边三角形，2,33AB BC ABC ππππ∴<>=-∠=-= ，D 正确.故选：.C 2.【答案】C【解析】【分析】本题考查向量的加减与数乘混合运算，属于基础题．由题意结合向量的加减与数乘混合运算，用AB 与AC 表示出.EF【解答】解：因为点D 为BC 边的中点，点F 为线段AD 的中点，所以()1124AF AD AB AC ==+ ，又2AE EC = ，所以13AE AC = ，所以()111111.2343412EF AF AE AD AC AB AC AC AB AC =-=-=+-=- 故选：.C 3.【答案】A【解析】【分析】本题主要考查了单位向量的概念，直线上向量的计算，考查了推理与计算能力，属于基础题.由单位向量e 在数轴上对应的坐标表示1，根据3a e = ，2b e =- ，即可求解,a b 在数轴上对应的坐标，得到答案.【解答】解：由题意，向量e 在数轴上对应的坐标表示1，因为3a e = ，所以a 在数轴上对应的坐标为3，又由2b e =- ，所以b在数轴上对应的坐标为 2.-故选：.A 4.【答案】D【解析】【分析】本题考查了共线向量时取得最值的性质，属于基础题．利用共线向量时取得最值即可得出．【解答】解：由一艘船以5/km h 的速度在行驶，同时河水的流速为2/km h ，则船的实际航行速度最大是527(/)km h +=，最小是523(/).km h -=故选.D 5.【答案】D【解析】【分析】本题考查两个向量的加减法的法则及其几何意义，求向量的模的方法，属于基础题．由题意得a b c += ，||c = ，故有|||2|a b c c ++= ，由此求出结果．【解答】解：由题意得，a b c += ，且||c =，|||2|a b c c ∴++==故答案选.D【解析】【分析】本题考查了向量运算和向量共线定理，属于基础题．利用向量运算和向量共线定理即可得出．【解答】解：向量(1,2)a = ，(1,0)b = ，(3,4).c = (1,2)(1,0)(1,2)a b λλλ∴+=+=+ ，()//()a b c R λλ+∈ ，4(1)320λ∴+-⨯=，解得1.2λ=故选：.C 7.【答案】D【解析】【分析】本题考查向量的坐标运算，考查计算能力，是基础题.直接利用向量的坐标运算求解即可.【解答】解：230a b c -+=，1212333c a b b a →→→→→⎛⎫∴=--=- ⎪⎝⎭，又(5,2)a =- ，(4,3)b =-- ，(,)c x y = ，()()()21134,4,35,2,.3333x y ⎛⎫∴=----=-- ⎪⎝⎭故选.D 8.【答案】A【解析】【分析】本题考查了平面向量基本定理、基本不等式的运用，属于基础题．利用平面向量基本定理，由题意可得1x y +=，则9191()()x y x y x y +=++，化简后利用基本不等式即可得出最小值．解：如图可知x ，y 均为正，AD x AB y AC =+ ，B ，D ，C 三点共线，1x y ∴+=，且0x >，0y >，91x y∴+91()()x y x y=++910y x x y=++1016+，当且仅当9y x x y =，即34x =，14y =时取等号，则91x y+的最小值为16，故选.A 9.【答案】BD【解析】【分析】本题主要考查了向量的线性表示及平面向量的基本定理，根据三角形法则，结合向量的线性运算是求解问题的关键，属于基础题．由已知结合向量的线性表示及向量加法的三角形法则即可求解．【解答】解：因为CE CA AE =+ ，13AE AD = ，AD AB BD =+ ，12BD BC = ，BC BA AC =+ ，所以13CE AD AC =- ，1()3BD BA AC =+ ，所以1133AD AB BD AB BA AC =+=++ ，所以111()333AE AB BA AC =++ ，所以11128.39999CE CA AB BA AC AB AC =+++=- 故选：.BD 10.【答案】ABC【解析】【分析】本题考查平面向量的坐标运算，向量的模，属于中档题.利用向量平行关系的坐标表示判断A ；利用向量线性运算的坐标表示判断BC ；利用向量模的坐标表示判断.D 【解答】解：将题干图2中的正八边形进行适当旋转，得到下图，虽然改变了向量，但不影响各向量之间的位置关系和线性运算及模长的结果，故以点O 为坐标原点，建立如图所示的平面直角坐标系，故(0,0)O ，(0,1)A -，(,22B -，(1,0)C ，)22D ，(0,1)E ，(,22F -，(,22H --对于A 选项，,1)22AD =+ ，(1,)22BC =- ，满足111)(1(1)0222222⨯-+-=--=，所以//AD BC ，故A 正确.对于B 选项，(0,1)OA =- ，(,22OD = ，(0,1)OE = ，(22OH =-- ，所以0OA OD OE OH +++= ，故B 正确.对于C 选项，(0,1)OA =- ，(1,0)OC = ，(22OF =- ，所以22(1,1),)22OA OC +=-=-= ，故C 正确.对于D 选项，1)22AD =+ ，所以||AD == D 错误；故选.ABC 11.【答案】ACD【解析】【分析】本题考查向量的加减与数乘混合运算，平面向量基本定理，属于中档题.设AM k AD = ，其中01k ，利用平面向量的线性运算可得出()21k k λμ⎧=-⎨=⎩，求出λμ+的取值范围，即可得出合适的选项.【解答】解：因为M 在线段AD 上，设AM k AD = ，其中01k ，则()BM BA k BD BA -=- ，所以，()1BM k BA k BD =-+ ，因为E 为BA 的中点，则2BA BE = ，所以()21BM k BE k BD =-+ ，又因为BM BE BD λμ=+ 且BE 、BD 不共线，则()21k kλμ⎧=-⎨=⎩，所以，()[]2121,2k k k λμ+=-+=-∈，故ACD 选项满足条件.故选：.ACD12.【答案】5；45【解析】【分析】本题考查平面向量的坐标运算以及向量模的知识，考查二次函数的性质，题目常规.首先求得()23,2a tb t t +=-+ ，故||a tb += ，因为t R ∈，所以当45t =时，||a tb +取得最小值，问题得解.【解答】解：因为(3,2),(2,1)a b =-= ，所以()()()3,22,23,2a tb t t t t +=-+=-+ ，所以||a t b →→+=因为t R ∈，所以当45t =时，||a tb + 取得最小值5故答案为5；4.513.【答案】75【解析】【分析】本题考查对给出的定理的运用，共面向量基本定理，共线向量基本定理．由图形知道E ，M ，C 三点共线，从而存在实数λ，使(1)AM AE AC λλ=+- ，根据2CF FA =，可得3(1)AM AE AF λλ=+- ，这样即可得到：3(1)x y λλ=⎧⎨-=⎩，所以消去λ可得关于x ，y 的方程，同样根据B ，M ，F 三点共线又可得到一个关于x ，y 的方程，这两个方程联立即可求出x ，y ，从而求出.x y +【解答】解：如图，E ，M ，C 三点共线，∴存在实数λ，使(1)AM AE AC λλ=+- ，2CF FA = ，3AC AF ∴=，3(1)AM AE AF λλ∴=+- ，又AM xAE y AF =+ ；3(1)x y λλ=⎧∴⎨-=⎩，3(1)x y ∴-=①；同样，B ，M ，F 三点共线，所以存在实数μ，使(1)AM AB u AF μ=+- ，E 为AB 边的中点，2AB AE ∴=，2(1)AM AE AF μμ∴=+- ，又AM xAE y AF =+ ；21x y μμ=⎧∴⎨=-⎩，112y x ∴=-②；∴联立①②可得：45x =，35y =，7.5x y ∴+=故答案为7.514.【答案】解：(1)证明：30EA EB EC ++= ，3.EA EC EB ∴+=- 又F 为AC 边的中点，233.EF EB BE ∴=-= BE EF BF += ，32BE BE BF ∴+= ，52.BE BF ∴= (2)证明：如图，设BC 边的中点为P ，连接EF ，.EP 230EA EB EC ++= ，2()EA EC EB EC ∴+=-+ ，24EF EP ∴=- ，即2EF EP =- ，F ∴，E ，P 三点共线.设点E ，F 到BC 的距离分别为1d ，2d ，则12:1:3.d d =设点A 到BC 的距离为3.d F 是AC 的中点，23:1:2d d ∴=，13:1:6d d ∴=，13::1:6S S d d ∴'==，即6.S S ='【解析】本题考查向量的线性运算和向量在平面几何中的应用，是中档题.(1)由向量的线性运算即可得证；(2)由230EA EB EC ++= 化简得2EF EP =- ，则F ，E ，P 三点共线，再根据三角形高的关系即可得证.15.【答案】解：(1)当12λ=时，12BP BC = ，则11()22AP AB BP AB BC AB BA AD DC AB =+=+=+++= 113131().224242AB AD AB AB AD a b +-++=+=+ 所以3142AP a b =+ ；(2)连结AE ，AF ，所以MN AN AM =- ，11113326AE AD DC b a a b =+=+⨯=+ ，22113323AF AD DC b a a b =+=+⨯=+ ，因为E ，M ，G 三点共线，F ，N ，H 三点共线，所以11(1)()36AM x AE x AG xb x a =+-=+- ，21(1)()33AN y AF y AH yb y a =+-=+- ，因为BP BC λ= ，所以()AP AB AC AB λ-=- ，可得(1)(12AP AC AB b a λλλλ=+-=+- ，111()()336MN AN AM y x b y x a =-=-+-+ ，因为//AN AM ，所以21331136y y x x -=-，可得22xy x y =-①，又MN AP μ= ，则有1113362y x y x λμλμμ-=⎧⎪⎨-+=-⎪⎩，即26262y x λμμλμμ=-+⎧⎨=-+⎩②，将②代入①可得，2(3)(6)(36)0λλμλμ--+-=，因为0μ≠，则(3)(6)3(2)0λλμλ--+-=，故3(2)34(3)(6)(2)52λμλλλλ---==---+--，因为[0,1]λ∈，令2t λ=-，则[2,1]t ∈--，则4y t t=+在[2,1]t ∈--上单调递减，所以4[5,4]t t +∈--，则31[,]103μ∈，故μ的取值范围为31[,].103【解析】本题考查了平面向量的综合应用，涉及了平面向量基本定理、三点共线、向量平行的应用，利用单调性求解函数取值范围的应用，考查了逻辑推理能力、化简运算能力与转化化归能力，属于较难题．(1)利用向量的线性运算即可求解；(2)利用三点共线得到11(1)()36AM x AE x AG xb x a =+-=+- ，21(1)()33AN y AF y AH yb y a =+-=+- ，再利用BP BC λ= ，MN AP μ= ，//AN AM ，得到x ，y ，λ，μ之间的关系，用λ表示出μ，然后利用函数的单调性求解取值范围即可．。

专题06第六章统计-寒假作业(六)(解析版)

专题06第六章统计-寒假作业（六）一、单选题1．为调查某地区中学生每天睡眠时间，采用样本量比例分配的分层随机抽样，现抽取初中生800人，其每天睡眠时间均值为9小时，方差为1，抽取高中生1200人，其每天睡眠时间均值为8小时，方差为0.5，则估计该地区中学生每天睡眠时间的方差为（）A．0.96B．0.94C．0.79D．0.752．16名跳高运动员参加一项校际比赛，成绩分别为1.70、1.65、1.68、1.69、1.72、1.59、1.60、1.67、1.74、1.78、1.55、1.56、1.64、1.76、1.75、1.79（单位：m），则比赛成绩的75%分位数是（）A．1.755B．1.75C．1.745D．1.74⨯160.75故选：C.3．宏伟公司有职工750人，其中青年职工350人，中年职工250人，老年职工150人，为了了解该公司职工的健康状况，用分层抽样的方法从中抽取样本，若样本中的中年职工为5人，则样本容量为（）A．7 B．15 C．25 D．35故选：B.4．第24届冬奥会于2022年2月4日在国家体育场鸟巢举行了盛大开幕式.在冬奥会的志愿者选拔工作中，某高校承办了面试工作，面试成绩满分100分，现随机抽取了80名候选者的面试成绩并分为五组，绘制成如图所示的频率分布直方图，则下列说法错误的是（每组数据以区间的中点值为代表）（）A ．直方图中b 的值为0.025B ．候选者面试成绩的中位数约为69.4C ．在被抽取的学生中，成绩在区间[)65,75之间的学生有30人D ．估计候选者的面试成绩的平均数约为69.5分【答案】C【分析】根据在频率分布直方图中所有小矩形的面积之和为1，结合中位数、平均数的定义、频数的定义逐一判断即可.【详解】对于A ，∵()0.0050.0450.020.005101b ++++⨯=，∴0.025b =，故A 正确；对于B ，设候选者面试成绩的中位数为x ，则()()0.0050.02510650.0450.5x +⨯+-⨯=，解得69.4x ≈，故B 正确；对于C ，成绩在区间[)65,75的频率为0.045100.45⨯=，故人数有800.4536⨯=，故C 错误；对于D ，500.00510600.02510700.04510800.0210900.0051069.5⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=，故D正确．故选：C5．若样本数据122018,,,x x x 的标准差为3，则数据12201841,41,,41x x x ---的方差为（） A ．11 B ．12C ．143D ．144【答案】D【分析】根据数据方差公式()()2D aX b a D X +=求解即可.【详解】因为样本数据122018,,,x x x 的标准差为3，所以方差为9，所以数据12201841,41,,41---x x x 的方差为249144⨯=.故选：D.6．最早发现于2019年7月的某种流行疾病给世界各国人民的生命财产带来了巨大的损失.近期某市由于人员流动出现了这种疾病，市政府积极应对，通过3天的全民核酸检测，有效控制了疫情的发展，决定后面7天只针对41类重点人群进行核酸检测，下面是某部门统计的甲､乙两个检测点7天的检测人数统计图，则下列结论不正确的是（）A ．甲检测点的平均检测人数多于乙检测点的平均检测人数B ．甲检测点的数据极差大于乙检测点的数据极差C ．甲检测点数据的中位数大于乙检测点数据的中位数D ．甲检测点数据的方差大于乙检测点数据的方差【答案】C【分析】根据题意分别求甲乙监测点的平均人数,极差,中位数及方差判断即可. 【详解】对于A :甲检测点的平均检测人数为2000160012001200800160012001371.437++++++≈乙检测点的平均检测人数为160018001600800120080016001342.867++++++≈故甲检测点的平均检测人数多于乙检测点的平均检测人数，故A 正确; 对于B :甲检测点的数据极差20008001200-= 乙检测点的数据极差180********-=，故B 正确;对于C :甲检测点数据为800,1200,1200,1200,1600,1600,2000,中位数为1200, 乙检测点数据为800,800,1200,1600,1600,1600,1800,中位数为1600，故C 错误; 对于D :通过观察平均数附近数据个数,极差等或计算甲乙数据的方差,都可以判断乙检测点数据比甲检测点数据稳定性强,故甲检测点数据的方差大于乙检测点数据的方差,故D 正确. 故选: C .7．第24届冬季奥运会于2022年2月4日至20日在北京举行，中国代表团取得了9枚金牌，4枚银牌，2枚铜牌的历史最好成绩.已知六个裁判为某一运动员这一跳的打分分别为95，95，95，93，94，94，评分规则为去掉六个原始分中的一个最高分和一个最低分，剩下四个有效分的平均数即为该选手的本轮得分.设这六个原始分的中位数为a ，方差为2S ；四个有效分的中位数为1a ，方差为21S .则下列结论正确的是（）A ．1a a ≠，221S S <B ．1a a ≠，221S S <C ．1a a =，221S S <D ．1a a =，221S S <8．甲、乙、丙、丁四人各掷骰子5次（骰子每次出现的点数可能为1，2，3，4，5，6），并分别记录每次出现的点数，四人根据统计结果对各自的试验数据分别做了如下描述：①中位数为3，众数为5；②中位数为3，极差为3；③中位数为1，平均数为2；④平均数为3，方差为2；可以判断一定没有出现6点的描述共有（） A ．1人 B ．2人C ．3人D ．4人【答案】B【分析】根据数据的特征，写出满足要求的数据集判断①②③；写出一个含6的数据集判断是否存在满足的情况判断④.【详解】①5出现两次，又中位数为3，则数据从小到大为{m ,n ,3,5,5}，一定没有6； ②中位数为3，极差为3，则数据从小到大为{1,m ,3,n ,4}、{2,m ,3,n ,5}、{3,3,3,m ,6}，故可能出现6；③中位数为1，平均数为2，则数据从小到大为{1,1,1,m ,n }，即7m n +=，故可能出现6； ④平均数为3，方差为2，则满足要求且含6的数据从小到大为{a ,b ,c ,d ,6}，故9a b c d +++=且2222(3)(3)(3)(3)1a b c d -+-+-+-=、a b c d ≤≤≤，显然不能同时满足，故一定没有6. 综上，①④一定没有6. 故选：B二、多选题9．下列抽样方法是简单随机抽样的是（） A ．质检员从50个零件中一次性抽取5个做质量检验B ．“隔空不隔爱，停课不停学”，网课上，李老师对全班45名学生中点名表扬了3名发言积极的C ．老师要求学生从实数集中逐个抽取10个分析奇偶性D ．某运动员从8条跑道中随机抽取一条跑道试跑【答案】AD【分析】根据简单随机抽样的定义，逐项分析判断即可.【详解】选项A ：“一次性”抽取与逐个不放回的抽取等价，符合不放回简单随机抽样要求，故正确；选项B ：老师表扬的是发言积极的，对每一个个体而言，不具备“等可能性”，故错误；选项C ：因为总体容量是无限的，不符合简单随机抽样要求，故错误；选项D ：8条跑道，抽取1条，总体有限，每个个体被抽到的机会均等，是简单随机抽样，故正确. 故选：AD10．秋季开学前，某学校要求学生提供由当地社区医疗服务站或家长签字认可的返校前一周（7天）的体温测试记录，已知小明在一周内每天自测的体温（单位：C ）依次为36.0,36.2,36.1,36.4,36.3,36.1,36.3，则该组数据的（）A ．极差为0.4CB ．平均数为36.2C C ．中位数为36.1CD ．第75百分位数为36.3C【答案】ABD【分析】根据极差、平均数、中位数和百分位数的定义判断即可.0.4C ，故36.336.2C 7++=，故36.2C ，故C 错误； 5.25=，所以体温的第75百分位数为从小到大排列的第36.3C ，三、填空题11．总体是由编号为01,02,,29,30的30个个体组成.利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为__________. 7816157208026315021643199714019832049234493682003623486969387181【答案】19【分析】根据随机数表选取编号的方法求解即可.【详解】随机数表第1行的第5列和第6列数字为15，则选取的5个个体依次为：15，08,02,16,19，故选出来的第5个个体的编号为19.故答案为:19.12．已知样本数据12,,,n x x x 的均值5x =，则样本数据1221,21,,21n x x x +++的均值为_____ (2n x +++1nx n+++=1113．已知一组样本数据1、2、m 、8的极差为8，若0m >，则其方差为______．【答案】252##12.5 【分析】根据极差的定义可求得m 的值，再根据方差的定义可求得这组数据的方差. 【详解】因为该组数据的极差为8，所以18m -=，解得9m =．因为这组数据的平均数为128954x+++==，所以，这组数据的方差为()()()()22222152585952542 s-+-+-+-==.故答案为：25 2.14．雅言传承文明，经典浸润人生，南宁市某校每年举办“品经诵典浴书香，提雅增韵享阅读”中华经典诵读大赛，比赛内容有三类：“诵读中国”、“诗教中国”、“笔墨中国”．已知高一、高二、高三报名人数分别为：100人、150人和250人．现采用分层抽样的方法，从三个年级中抽取25人组成校代表队参加市级比赛，则应该从高一年级学生中抽取的人数为______．【答案】5【分析】根据分层抽样的性质运算求解.【详解】根据题意可得：高一、高二、高三报名人数之比为100:150:2502:3:5=，故从高一年级学生中抽取的人数为2255235⨯=++.故答案为：5.四、解答题15．新冠肺炎疫情期间，某地为了了解本地居民对当地防疫工作的满意度，从本地居民中随机抽取若干居民进行评分（满分为100分），根据调查数据制成如图频率分布直方图，已知评分在[70，90]的居民有2200人．(1)求频率分布直方图中a的值及所调查的总人数；(2)从频率分布直方图中，估计本次评测分数的众数、中位数（精确到0.1)．【答案】(1)0.025a=，4000；(2)众数为85.0，中位数约为82.9.16．2022年2月4日—2月20日，北京冬奥会顺利召开，全民关注冬奥赛事.为了更好的普及冬奥知识，某中学举办了冬奥知识竞赛，并随机抽取了100名学生的成绩，且这100名学生的成绩（单位：分）都在[]50,100，其频数分布表如下图所示.由分布表得知该中学冬奥知识竞赛成绩的中位数的估计值为82分. (1)求a ，b 的值；(2)该中学冬奥知识竞赛成绩的平均数与标准差的估计值（同一组中的数据用该组区间的中点值为代表）. 5.1）。

高一寒假作业(六)氧化还原反应

高一寒假作业（六）氧化还原反应1．下列有关氧化还原反应的叙述中正确的是( )A ．在反应中不一定所有元素化合价都发生变化B ．肯定有一种元素被氧化另一种元素被还原C ．非金属单质在反应中只能得电子D ．金属单质在反应中失电子被还原解析：氧化还原反应的宏观特征是元素化合价有升降，但不一定是所有元素化合价均有升降，如Fe 2O 3＋3CO=====高温2Fe ＋3CO 2，氧元素没有化合价变化；化合价变化的元素可以是不同种元素，也可以是同种元素，如CO 2＋C=====高温2CO ；作为非金属，在反应中可以得到电子，但也有失去电子的可能，如C ＋O 2=====点燃CO 2；金属在反应中失去电子被氧化，而不是失去电子被还原。

答案： A2．(2011·吉林一中高一期中)古诗词是古人为我们留下的宝贵精神财富。

下列诗句中不涉及氧化还原反应的是( )A ．野火烧不尽，春风吹又生B ．爆竹声中一岁除，春风送暖入屠苏C ．春蚕到死丝方尽，蜡炬成灰泪始干D ．粉身碎骨浑不怕，要留清白在人间解析：诗句“野火烧不尽、蜡炬成灰泪始干、爆竹声中一岁除”都包含有物质的燃烧，涉及了氧化还原反应；“粉身碎骨浑不怕，要留清白在人间”则包含有以下三个反应：CaCO 3=====高温CaO ＋CO 2↑、CaO ＋H 2O===Ca(OH)2和Ca(OH)2＋CO 2===CaCO 3↓＋H 2O ，以上三个化学反应中均无元素化合价的升降，都不是氧化还原反应。

答案： D3．(2011·长春外国语学校高一期中)下列化学反应中，属于氧化还原反应的是( )A ．Na 2CO 3＋CaCl 2===CaCO 3↓＋2NaClB ．Fe ＋CuSO 4===Cu ＋FeSO 4C ．2NaHCO 3=====△Na 2CO 3＋CO 2↑＋H 2OD ．CaO ＋H 2O===Ca(OH)2解析：氧化还原反应的特征是有元素化合价的升降，B 正确。

寒假作业(6)语文九上部编版(古诗文默写)

寒假作业（6）九年级语文部编版（古诗文默写）1.名句默写。

（1）_______________，况乃未休B。

（杜甫《月夜忆舍弟》）（2）_______________，肯将衰朽惜残年！（韩愈《左迁至蓝关示侄孙湘》）（3）李白在《行路难》（其一）中用典故表达了自己渴望得到明君重用、成就功名愿望的诗句是：_________________，_________________。

（4）刘长卿在《长沙过贾谊宅》中溯古思今，把自己的遭遇同贾谊、屈原两位先哲联系在一起，从而深化了咏叹主题的诗句是：__________，__________。

（5）岳阳楼的一副长联里有“范希文两字关情，滕子京百废俱兴”的佳句，《岳阳楼记》中对应“两字关情”的句子是：___________，____________。

2.根据提示填空。

（1）_________，高处不胜寒。

（苏轼《水调歌头》）（2）金樽清酒斗十千，_________。

（李白《行路难》（其一））（3）春蚕到死丝方尽，_________。

（李商隐《无题》）（4）《岳阳楼记》中动静结合、描写洞庭湖月夜美景的句子是：“________，________。

”3.默写。

（1）戍鼓断人行，____________。

（杜甫《月夜忆舍弟》）（2）春蚕到死丝方尽，____________。

（李商隐《无题》）（3）____________，月有阴晴圆缺。

（苏轼《水调歌头》）（4）刘禹锡在《酬乐天扬州初逢席上见赠》一诗中借用典故来写自己离开家乡之久的诗句是：“____________，____________”。

（5）《行路难》（其一）中象征人生路上的艰难险阻的诗句是：“_______，_________。

”4.根据原文默写。

（1）__________，病树前头万木春。

（刘禹锡《酬乐天扬州初逢席上见赠》）（2）_____________，怜君何事到天涯！（刘长卿《长沙过贾谊宅》）（3）《岳阳楼记》中揭示了范仲淹先忧后乐抱负的句子是：“_______________，________________。

初三化学寒假作业6

沭阳银河学校初三化学寒假作业（6）2.15号前完成1．关于海水晒盐原理的说法中，正确的是（）A．利用阳光和风力，使氯化钠蒸发出来B．利用阳光和风力，使水分蒸发，析出盐C．降低温度使氯化钠析出D．通过化学反应产生沉淀而得到食盐2．将ag食盐投入到bg水中，搅拌，所得溶液的质量是（）A．等于(a＋b)g B．小于(a＋b)gC．小于或等于(a＋b)g D．大于或等于(a＋b)g3．向一定温度下的氯化钠饱和溶液中加入少量的硝酸钾固体（假设溶液温度不变），则（）A．溶液饱和，硝酸钾不再溶解B．硝酸钾溶解，氯化钠质量分数不变C．硝酸钾溶解，氯化钠质量分数减小D．硝酸钾溶解，溶液变为氯化钠的不饱和溶液4．下列有关氯化钠的用途的说法错误的是（）A．氯化钠是一种重要的调味品B．农业上可用氯化钠溶液来选种C．氯化钠可以帮助消除公路上的积雪D．可以用氯化钠溶液来清除铁锈5．现有一杯20℃的饱和硝酸钾溶液，欲改变其溶质质量分数，下列方法可行的是A．加入一定量的水B．恒温蒸发部分水C．升温到60℃D．加入一定量的硝酸钾6．目前从海水中提取食盐的方法主要是利用海水晒盐，它所利用的物质分离的方法是（）A．溶解法B．过滤法C．蒸馏法D．结晶法7．下列关于溶液的说法中，不正确的是（）A．溶液中各部分性质相同，是一种高级混合物B．氢氧化钠溶液能导电，是因为溶液中含有自由移动的离子C．接近饱和的硝酸钾溶液，通过蒸发溶剂或加溶质的方法都可以达到饱和状D．20℃，氯化钠饱和溶液100g，升温到100℃仍为饱和溶液8．20℃时，向一盛有40 g氯化钠的烧杯内加入100 g水，充分搅拌后静置，烧杯底部仍有未溶解的氯化钠固体，过滤得到4 g 固体和澄清溶液。

下列有关叙述错误的是（）A．该溶液中溶质的质量等于36 g B．过滤后所得溶液为饱和溶液C．该溶液中溶质的质量分数等于36% D．所得溶液质量为136g9．含有蔗糖晶体的溶液A，从冰箱冷藏室中取出，放置一段时间后，晶体慢慢消失，形成溶液B。

高一上学期数学寒假作业(每天一套)(含答案) (6)

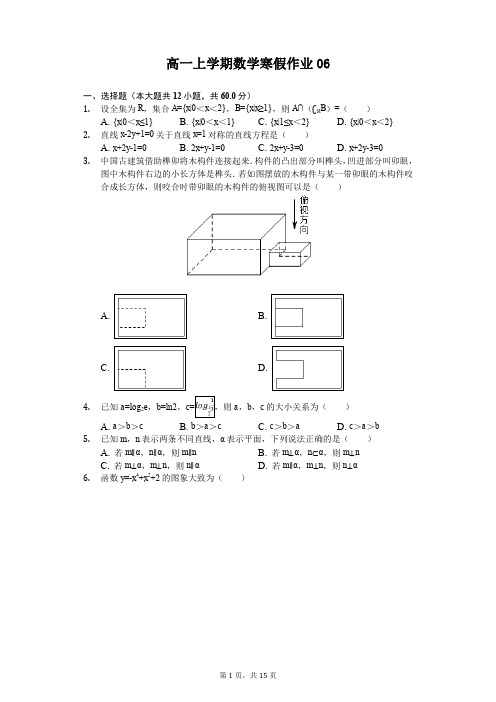
高一上学期数学寒假作业06一、选择题（本大题共12小题，共60.0分）1.设全集为R，集合A={x|0＜x＜2}，B={x|x≥1}，则A∩（∁R B）=（）A. {x|0＜x≤1}B. {x|0＜x＜1}C. {x|1≤x＜2}D. {x|0＜x＜2}2.直线x-2y+1=0关于直线x=1对称的直线方程是（）A. x+2y-1=0B. 2x+y-1=0C. 2x+y-3=0D. x+2y-3=03.中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）4.已知a=log2e，b=ln2，c a，b，c的大小关系为（）A. a＞b＞cB. b＞a＞cC. c＞b＞aD. c＞a＞b5.已知m，n表示两条不同直线，α表示平面，下列说法正确的是（）A. 若m∥α，n∥α，则m∥nB. 若m⊥α，n⊂α，则m⊥nC. 若m⊥α，m⊥n，则n∥αD. 若m∥α，m⊥n，则n⊥α6.函数y=-x4+x2+2的图象大致为（）7.x2+y2-4y所截得的弦长为（）A. B. 28.根据有关资料，汽车二级自动驾驶仪能够处理空间复杂度的上限M约为1010，目前人类可预测的地面危机总数N约为36×230．（）（参考数据：lg2≈0.30，lg3≈0.48）9.设四面体的六条棱的长分别为2，2，2，2和的两条棱是异面直线，则该四面体的外接球的表面积为（）A. 5πB. 20πC. 12πD. 3π10.已知函数f（x）=ln x）+1，f（a）=4，则f（-a）=（）A. -4B. 2C. -2D. 311.如图，在正方形SG1G2G3中，E、F分别是G1G2及G2G3的中点，D是EF的中点，现在沿SE、SF及EF把这个正方形折成一个四面体，使G1、G2、G3三点重合，重合后的点记为G，那么，二面角S-EF-G的正切值是（）A. C. 2 D. 312.设函数f（x）f（x）+f（1的x的取值范围是（）A. （）B. （-∞，0）C.D.二、填空题（本大题共4小题，共20.0分）13.已知函数f（x）g（x）=f（x）所有零点之积为______．15.过点A（4，1）的圆C与直线x-y-1=0相切于点B（2，1），则圆C的方程为______．16.如图，在棱长为1的正方体ABCD-A1B1C1D1中，E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为______．三、解答题（本大题共6小题，共70.0分）17.（Ⅰ（Ⅱ）在△ABC中，∠B，∠C的内角平分线分别为x=0，y=x，A（3，-1），求BC 边所在的直线方程．18.如图，在正方体ABCD-A1B1C1D1中．（Ⅰ）求证：B1D⊥平面A1C1B；（Ⅱ）求BD1与平面A1C1B所成角的正弦值．19.设函数f（x）是二次函数，且f（x+1）-f（x-1）=3x-2对一切实数x成立，若f（0）=1．（Ⅰ）求f（x）的表达式；（Ⅱ）设A={x|f（x）=x，x∈R}，B={x|f（f（x））=x，x∈R}．（i）求证A⊆B；（ii）若2∈A，函数f（x）在区间[m，m+1]上的最小值大于2，求实数m的取值范围．20.视某地全体中小学生为群体S，S的人均回家时间是指某次S中成员从学校到家的平均用时．S的成员以乘私家车方式或绿色出行（乘公交、骑自行车、步行、家长骑电动车接）方式回家．调查发现：当S中x%（0＜x＜100）的成员乘私家车时，乘私家车群体的人均回家时间为f（x）均回家时间不受x的影响，恒为40分钟，根据上述分析结果回答下列问题：（Ⅰ）当x在什么范围内时，绿色出行群体的人均回家时间小于乘私家车群体的人均回家时间？（Ⅱ）求该地中小学生群体S的人均回家时间g（x）的表达式，讨论g（x）的单调性，求g（x）的最小值，并说明其实际意义．21.如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长P为侧棱SD上的点．（1）求证：AC⊥SD；（2）若SD⊥平面PAC，求二面角P-AC-D的大小；（3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC．若存在，求SE：EC的值；若不存在，试说明理由．22.已知圆C经过点P（1，3），Q（2，0），且圆心在直线y=x+1上．（Ⅰ）求圆C的标准方程；（Ⅱ）已知点A与点Q关于y轴对称，点B在圆C上（与点A不重合），记AB的中点为M，且|OA|=|OM|，求直线AB的方程．答案和解析1.【答案】B【解析】【分析】本题考查了集合的化简与运算问题，是基础题．根据补集、交集的定义即可求出．【解答】解：∵A={x|0＜x＜2}，B={x|x≥1}，∴∁R B={x|x＜1}，∴A∩（∁R B）={x|0＜x＜1},故选B．2.【答案】D【解析】解：解法一（利用相关点法）设所求直线上任一点（x，y），则它关于x=1对称点为（2-x，y）在直线x-2y+1=0上，∴2-x-2y+1=0化简得x+2y-3=0故选答案D．解法二：根据直线x-2y+1=0关于直线x=1对称的直线斜率是互为相反数得答案A或D，再根据两直线交点在直线x=1选答案D故选：D．设所求直线上任一点（x，y），关于x=1的对称点求出，代入已知直线方程，即可得到所求直线方程．本题采用两种方法解答，一是相关点法：求轨迹方程法；法二筛选和排除法．本题还有点斜式、两点式等方法．3.【答案】A【解析】【分析】本题看出简单几何体的三视图的画法，是基本知识的考查．直接利用空间几何体的三视图的画法，判断选项的正误即可．【解答】解：由题意可知，如图摆放的木构件与某一带卯眼的木构件咬合成长方体，小的长方体，是榫头，从图形看出，轮廓是长方形，内含一个长方形，并且一条边重合，另外3边是虚线，所以木构件的俯视图是A．故选：A．4.【答案】D【解析】【分析】本题考查了对数函数及其性质的运用，比较大小，考查了对数运算和变形能力，属于基础题.根据对数函数的单调性和对数运算法则，求出a、b、c的大致范围，即可作出比较．【解答】则a，b，c的大小关系c＞a＞b，故选D．5.【答案】B【解析】【分析】本题考查空间直线与平面的位置关系，考查直线与平面的平行、垂直的判断与性质，记熟这些定理是迅速解题的关键，注意观察空间的直线与平面的模型,属于基础题.A．运用线面平行的性质，结合线线的位置关系，即可判断；B．运用线面垂直的性质，即可判断；C．运用线面垂直的性质，结合线线垂直和线面平行的位置即可判断；D．运用线面平行的性质和线面垂直的判定，即可判断．【解答】解：A．若m∥α，n∥α，则m，n相交或平行或异面，故A错；B．若m⊥α，n⊂α，则m⊥n，故B正确；C．若m⊥α，m⊥n，则n∥α或n⊂α，故C错；D．若m∥α，m⊥n，则n∥α或n⊂α或n⊥α或n与α相交，故D错．故选B．6.【答案】D【解析】【分析】本题主要考查函数的图象的识别和判断，利用函数过定点以及判断函数的单调性是解决本题的关键．属于基础题.根据函数图象的特点，求函数的导数利用函数的单调性进行判断即可．【解答】解：函数过定点（0，2），排除A，B．函数的导数f′（x）=-4x3+2x=-2x（2x2-1），由f′（x）＞0得2x（2x2-1）＜0，得x＜0＜x由f′（x）＜0得2x（2x2-1）＞0，得x x＜0，此时函数单调递减，排除C，也可以利用f（1）=-1+1+2=2＞0，排除A，B，故选D．7.【答案】A【解析】解：根据题意：直线方程为：y，∵圆x2+y2-4y=0，∴圆心为：（0，2），半径为：2，圆心到直线的距离为：d=1，∴弦长为故选：A．先由题意求得直线方程，再由圆的方程得到圆心和半径，再求得圆心到直线的距离，即可求解．8.【答案】B【解析】解：汽车二级自动驾驶仪能够处理空间复杂度的上限M约为1010，目前人类可预测的地面危机总数N约为36×230．两边取常用对数，可得-6×0.48-30×0.30=-1.88．故选：B．本题考查对数的运算性质，考查运算求解能力，是基础题．9.【答案】A【解析】【分析】将四面体放在长方体中，设长方体的长、宽、高分别为x、y、z，根据题中条件列勾股定理，可得出长方体的体对角线长，即为四面体的外接球直径，再利用球体表面积公式可得出答案．本题考查球体表面积的计算，解决本题的关键在于找出合适的模型计算处球体的半径，考查计算能力，属于中等题．【解答】解：如下图所示，四面体ABCD AC=AD=BC=BD=2，可将四面体ABCD放在长方体AEDF-GBHC，设BG=x，CG=y，AG=z，2（x2+y2+z2）=10，则x2+y2+z2=5，设四面体ABCD的外接球直径为2R，则（2R）2=x2+y2+z2=5，因此，该四面体外接球的表面积为4πR2=π×（2R）2=5π．故选：A．10.【答案】C【解析】【分析】根据对数函数的运算性质，结合条件建立方程关系进行求解即可．本题主要考查函数值的计算，结合对数函数的运算性质进行转化是解决本题的关键．【解答】解：∵f（a）=4，。

高三历史寒假作业(六)

高三历史寒假作业（六）一、选择题，每小题的四个选项中，只有一项符合题意。

1.某史学家认为：“后世官制，变化繁赜。

而其原理，不能出于治民、治军、监察官吏三者之外；此亦可见秦之定制，非漫然而设也。

”以下相关评述正确的是A．文中“原理”指分权与制衡 B．秦朝中央官制体现此“原理”C．作者反对“原理”的长期不变 D．作者否定了“后世”官制2.《礼记·王制》：“山川神祗有不举者为不敬，不敬者君削以地。

宗庙有不顺者为不孝，不孝者君绌以爵。

变礼易乐者为不从，不从者君流。

革制度衣服者为畔，畔者君讨。

”材料表明西周礼乐制的特点是A．威慑性、实效性 B．制度性、强制性C．等级性、仪式性 D．规范性、持久性3.下面是中国青年报的特别报道《变迁：从“一五”到“十一五”》的部分主题词摘要。

从“一五”到“十一五”主题词的变化不能反映出A.对经济发展规律认识不断深化B.中国共产党治国方略日益成熟C.社会主义建设道路逐步完善D.社会主义民主法制进程不断加快4.国庆，这种特殊纪念方式一旦成为新的、全民性的节日形式，便承载了反映这个国家、民族的凝聚力的功能。

下列国家国庆日的确定的时间顺序是A.法国、德国、美国、中国B.美国、法国、中国、德国C.法国、美国、德国、中国D.法国、美国、中国、德国5.基辛格在《大外交》中提到：“美国采取措施以强化受到苏联侵略或共产党颠覆威胁的国家，这也就是保护美国的安全——它就是保护自由!”为此，美国首先采取的措施是A．推行杜鲁门主义 B．实施马歇尔计划C．成立北约组织 D．发动局部“热战”6.马克思、恩格斯指出：“当工业和商业进一步发展了私有制的时候，详细拟定的罗马法便立即得到恢复并重新取得威信。

……即使在英国，为了私法的进一步发展，也不得不参照罗马法的诸原则。

”材料说明( )A．罗马法完全适应了资本主义发展的需要B．罗马法因具有资产阶级性质得以在近代推广C．罗马法对近代西方的立法产生了重大影响D．近代英国非常重视法制建设7.亚里士多德说:“不容许所有公民共享的制度是寡头的，容许所有公民共享的制度是民主的。

八年级上数学寒假作业6

八年级数学寒假作业（六）相似图形Ⅰ. 梳理知识1.三角形相似的条件(1) ，两三角形相似.(2) ，两三角形相似.(3) ，两三角形相似.2.如何寻找和发现相似三角形两个三角形相似，一般说来必须具备下列六种图形之一：只要能在复杂图形中辨认出上述基本图形，并能根据问题需要舔加适当的辅助线，构造出基本图形，从而使问题得以解决.3.相似三角形与相似多边形的性质(1)相似三角形的性质①相似三角形的三边，三角.②相似三角形的，与都等于相似比.③相似三角形周长之比等于，相似三角形面积之比等于.(2)相似多边形的性质①相似多边形的对应边，对应角.②相似多边形的对角线之比、周长之比都等于.③相似多边形面积之比等于.4.几何变换(按一定的方法把一个图形变成另一个图形)(1)相似变换：保持图形的形状不变的几何变换叫做相似变换(2)位似变换①位似图形：如果两个图形不仅是图形，而且每组对应点所在的直线都，那么这样的两个图形叫做位似图形，这个点叫做，这时的相似比又称为.②位似图形的性质：位似图形上任意一对对应点到的距离之比等于位似比.5.相似三角形的应用——测量旗杆的高度(利用阳光下的影子；利用标杆；利用镜子的反射.) Ⅱ. 典例剖析例1.如图，DE∥BC，SΔDOE∶SΔCOB=4∶9，求AD∶BD. 例2.如图，四边形ABCD是平行四边形，AE⊥BC于E，AF⊥CD于F.(1)ΔABE与ΔADF相似吗？说明理由.(2)ΔAEF与ΔABC相似吗？说说你的理由.例3.如图，在RtΔABC中，∠C=90°，AC=4，BC=3.(1)如图(1)，四边形DEFG为ABC的内接正方形，求正方形的边长.(2)如图(2)，三角形内有并排的两个相等的正方形，它们组成的矩形内接于ΔABC，求正方形的边长.(3)如图(3)，三角形内有并排的三个相等的正方形，它们组成的矩形内接于ΔABC，求正方形的边长.(4) 如图(4)，三角形内有并排的n个相等的正方形，它们组成的矩形内接于ΔABC，请写出正方形的边长.Ⅲ.同步测试一、选择题(每小题3分，共30分)1、在相同时刻的物高与影长成比例，如果高为1.5米的测竿的影长为2.5米，那么影长为30米的旗杆的高是（）A.20米.B.18米C.16米D.15米2、如图，D、E分别是AB、AC上两点，CD与BE相交于点O，下列条件中不能使ΔABE和ΔACD相似的是（）A.∠B=∠CB.∠ADC=∠AEBC.BE=CD，AB=ACD.AD∶AC=AE∶AB3、如图所示，D、E分别是ΔABC的边AB、AC上的点，DE∥BC，并且AD∶BD=2，那么S ΔADE∶S四边形DBCE=（）(A)32(B)43(C)54(D)944.在矩形ABCD中，E、F分别是CD、BC上的点，若∠AEF=90°，则一定有（）(A)ΔADE∽ΔAEF (B)ΔECF∽ΔAEF (C)ΔADE∽ΔECF (D)ΔAEF∽ΔABF(第2题图) (第3题图) (第4题图) (第5题图)5、厨房角柜的台面是三角形(如图所示)，如果把各边中点连线所围成的三角形铺成黑色大理石(图中阴影部分)，其余部分铺成白色大理石，则黑色大理石面积与白色大理石的面积之比是（）A.1∶2B.1∶3C.1∶4D.1∶56、如图，在大小为4×4的正方形网格中，是相似三角形的是（）① ② ③ ④A.①和②B.②和③C.①和③D.②和④7、如图是圆桌正上方的灯泡O 发出的光线照射桌面后，在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m ，桌面距离地面1m ，若灯泡O 距离地面3m ，则地面上阴影部分的面积为（）A.0.36πm 2B.0.81πm 2C.2πm 2D.3.24πm 28、如图，直线l 1∥l 2，AF ∶FB=2∶3，BC ∶CD=2∶1，则AE ∶EC 是（） A.5∶2 B.4∶1 C.2∶1 D.3∶29、如图，三个正六边形全等，其中成位似图形关系的有（） A.4对 B.1对 C.2对 D.3对(第7题图) (第8题图) (第9题图) (第10题图)10、平面直角坐标系中，有一条“鱼，它有六个顶点”，则（） A.将各点横坐标乘以2，纵坐标不变，得到的鱼与原来的鱼位似 B.将各点纵坐标乘以2，横坐标不变，得到的鱼与原来的鱼位似 C.将各点横、纵坐标都乘以2，得到的鱼与原来的鱼位似 D.将各点横坐标乘以2，纵坐标乘以21，得到的鱼与原来的鱼位似二、填空题(每小题4分，共20分)11、两个相似多边形的一组对应边分别为3cm 和4.5cm ，如果它们的面积之和为130cm 2，那么较小的多边形的面积是 cm 2. 12、如图，DE 与BC 不平行，当ACAB= 时，ΔABC 与ΔADE 相似.(第12题图) (第13题图) (第14题图) (第15题图)13、如图，AD=DF=FB ，DE ∥FG ∥BC ，则S Ⅰ∶S Ⅱ∶S Ⅲ= .14、如图，正方形ABCD 的边长为2，AE=EB ，MN=1，线段MN 的两端在CB 、CD 上滑动，当CM= 时，ΔAED 与N ，M ，C 为顶点的三角形相似.15、如图，在直角坐标系中有两点A(4,0)、B(0,2)，如果点C 在x 轴上(C 与A 不重合)，当点C 的坐标为或时，使得由点B 、O 、C 组成的三角形与ΔAOB 相似(至少写出两个满足条件的点的坐标).三、解答题(每小题8分，共40分)16、如图，ΔABC 中，BC=a .(1)若AD 1=31AB ，AE 1=31AC ，则D 1E 1= ； (2)若D 1D 2=31D 1B ，E 1E 2=31E 1C ，则D 2E 2= ；(3)若D 2D 3=31D 2B ，E 2E 3=31E 2C ，则D 3E 3= ；(4)若D n -1D n =31D n -1B ，E n -1E n =31E n -1C ，则D n E n = .17、已知：如图，ΔABC 中，∠B=∠C=30°.请你设计三种不同的分法，将ΔABC 分割成四个三角形，使得其中两个是全等三角形，而另外两个是相似三角形但不全等的直角三角形.请画出分割线段，标出能够说明分法的所得三角形的顶点和内角度数或记号，并在各种分法的空格线上填空.(画图工具不限，不要求写出画法，不要求说明理由).分法一分法二分法三分法一：分割后所得的四个三角形中，Δ ≌Δ ，Rt Δ ∽Rt Δ . 分法二：分割后所得的四个三角形中，Δ ≌Δ ，Rt Δ ∽Rt Δ . 分法三：分割后所得的四个三角形中，Δ ≌Δ ，Rt Δ ∽Rt Δ。

_统编版七年级上学期语文寒假作业(6)金牌语文资料

2020-2021学年初一语文人教统编版寒假作业（6）一、下列加粗字的注音完全正确的一项是（）A.花瓣（bàn）并蒂（tì）覆盖（fù）B.祷告（dăo）嗅觉（xiù）徘徊（huái ）C.匿笑（nì）菡萏（dàn）攲斜（qí）D.姊妹（zĭ）繁衍（yán）遮拦（zhē）二、下列词语中，书写完全正确的一项是（）A.莲篷遮蔽凌霄花绿树成荫B.姊妹繁杂捉迷藏絮絮叨叨C.覆盖慈怜笑嘻嘻丰富多彩D.庭院花瑞花瓣儿烩炙人口三、下列句子中加粗成语使用正确的一项是（）A.湛蓝的海，洁白的云，时而有几只海鸥掠过船舷，眼前的一切真是栩栩如生。

B.它们的叶子和花都不一样，各有各的鲜为人知的秘密，可惜我知道得太迟了。

C.多年来，老校长为了这群孩子成长，起早贪黑，处心积虑，他的功劳不能忘。

D.到新学校后，班集体相敬如宾的和谐氛围让张晓亮很快适应了新的学习环境。

四、给下列句子排序，最恰当的一项是（）①当阳光洒在身上时，它更坚定了心中的信念——要开出一朵鲜艳的花。

②不久，它从泥土里探出了小脑袋，渐渐地，种子变成了嫩芽。

③从此，它变得沉默，只有它知道，它在努力，它在默默地汲取土壤中的养分。

④虽然它经受着黑暗的恐惧，暴雨的侵袭，但是它依然努力地生长着。

⑤种子在这块土地上的生活并不那么顺利，周围的各种杂草都嘲笑它，排挤它，认为它只是一粒平凡的种子。

A.①⑤②③④B.①③②⑤④C.⑤③④②①D.⑤④②③①五、从传统文化的角度来看，下列各项中的表述不正确的一项是（）A．家慈是旧时对别人称自己母亲的谦辞。

旧俗有“严父慈母”之说，故有此称。

B．在没有发明造纸术之前，我国曾用削成狭长的竹片作为书写材料，人们把这种竹片称为简。

C．诗句“灯树千光照，花焰七枝开”描写的是我国传统节日——春节的盛况。

D．现代所说的书信，古代通称为“书”，如诸葛亮的《诫子书》就是写给儿子的一封家书，即家信。