青岛版2018-2019学年六年级数学下册期中测试题
青岛版六年级下册数学期末测试题一套附答案【历年真题】

青岛版六年级下册数学期末测试题一.选择题(共6题, 共12分)1.有一种商品, 甲店进价比乙店进价便宜10%, 甲店按20%的利润定价, 乙店按15%的利润定价, 甲店的定价比乙店的定价便宜11.2元.则甲店的进价是()。
A.160元B.124元C.150元D.144元2.等底等高的圆柱、正方体、长方体的体积相比较()。
A.一样大B.长方体体积大C.圆柱体体积大D.正方体体积大3.一种饼干包装袋上标着: 净重(200±5克), 表示这种饼干标准的质量是200克, 实际每袋最少不少于()克。
A.205B.200C.195D.2104.一件衬衫按进价提高50%后标价, 后因季节关系按标价8折出售, 此时仍获利12元, 则这批衬衫的进价是()。
A.48元B.60元C.90元D.180元5.一个圆柱形橡皮泥, 底面积是12平方厘米, 高15厘米。
如果把它捏成同样底面大小的圆锥, 这个圆锥的高是()厘米。
A.15B.45C.56.下面四句话中正确的一句是( )。
A.18的所有因数都是合数B.一条线段长0.75m, 可以改写成75%mC.位置数对是(3, 2)的物体和(2, 3)的物体处于同一位置D.通常情况下, 盈利用正数表示, 亏损用负数表示二.判断题(共6题, 共12分)1.圆柱的体积比与它等底等高的圆锥大2倍。
()2.正数都比0大, 负数都比0小。
()3.一个比例的外项之积是1.2,若一个内项是0.6,则另一个内项是0.2。
()4.如果4a=5b, 则a∶b=4∶5并且a与b成反比例。
()5.圆柱的侧面沿着高展开后会得到一个长方形或者正方形。
()6.在+/、-4.0、6.-2.7这5个数中, 整数有2个。
()三.填空题(共6题, 共12分)1.做一个圆柱形厨师帽底面圆周长为45厘米, 高是底面直径的2倍, 至少需要()平方厘米布料。
2.如果收入600元, 记作+600元, 那么支出300元, 记作________元。
2018-2019年度青岛版(六三制)小学数学六年级下册-选择合适的统计图-教学设计、教案

选择合适的统计图1.教学目标1知识与技能:通过情境创设,使学生将三种统计图进行系统的复习,知道每种统计图的不同作用,并能够根据实际情况进行合理的选择和使用。
2过程与方法:在教学过程中,引导学生通过探索、交流活动,经历统计图辨析的过程,点和作用,增强统计观念。
3情感态度与价值观:体会数学与日常生活的紧密联系,感受统计在生产、生活中的广泛应用和统计的价值。
2. 教学重点侬点1教学重点:辨析三种统计图的特点和作用,能从统计图中读出必要的信息。
2教学难点:根据不同的统计图进行简单的数据分析。
3.教学用具多媒体设备教学过程1回顾旧知1、某校六年级有120人,英语竞赛中优秀的有24人,占六年级学生的(20 ) %,若制成扇形统计图,对应的扇形圆心角的度数为( 72 )2、下图是王大妈批发的三种蔬菜。
其中茄子的千克数是三种蔬菜总量的(40 ) %。
黄瓜的千克数是西红柿的(50 ) %。
其中,茄子是32千克, 黄瓜是(16 )千克。
3、下图是某班一次数学考试成绩统计图。
已知不及格的有3人。
请你算出各种成绩的人数填入统计表内。
成绩人数优36良15及格6不及格3一、比例的意义1、出示情境图例2、下面几组数据分别选用哪种统计图表示更合适?(1)绿荫小学2007— 2011年校园内树木总量变化情况统计表(2) 2011年绿荫小学校园内各种树木所占百分比情况统计表。
(3) 2011年绿荫小学校园内各种树木数量统计表。
2、小组分工合作,完成统计图的绘制任务。
同的能够时思考一下,为什么你要绘制这样的统计图?3、小组汇报。
(1)第一个统计表。
预设:1、学生绘制成条形统计图。
师:为什么你们组选择条形统计图?说说你们的理由。
生:可以看到每一年树木总量,也可以根据条形的高低大致看出变化趋势。
预设:2、学生绘制成折线统计图。
师:你们又是怎么想的?生:折线统计图可以清晰地看出变化趋势。
师:同学们观察这两个统计图,针对绿荫小学2007-2011年校园内树木总量变化情况的统计表,哪种统计图更清楚地表示出变化情况呢?生回答。
青岛版2018-2019学年度九年级数学上册期中测试卷及答案

2018-2019学年度上学期期中考试九年级数学试题一、选择题(本大题共12小题,共48.0分)1.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图1中的三角形与△ABC相似的是()A. B. C. D.2.在Rt△ABC中,∠C=90°,sin A=,BC=6,则AB=()A. 4B. 6C. 8D. 103.如图2,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是()A. B. C. ∠ ∠ D. ∠ ∠图1 图2 图34.下列语句正确的个数是()①过平面上三点可以作一个圆;②平分弦的直径垂直于弦;③在同圆或等圆中,相等的弦所对的圆周角相等;④三角形的内心到三角形各边的距离相等.A. 1个B. 2个C. 3个D. 4个5.如图3,在△ABC中,中线BE,CD相交于点O,连线DE,下列结论:①;△△ ;③;④△△其中正确的个数有()A. 1个B. 2个C. 3个D. 4个6.已知在△ABC中,∠A、∠B都是锐角,,则∠C的度数是()A. B. C. D.7.如图4,水库大坝截面的迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,则下底AB的长为()A. 55mB. 60mC. 65mD. 70m8.在RT△ABC中,∠C=90°,BC=3cm,AC=4cm,以点C为圆心,以2.5cm为半径画圆,则⊙C与直线AB的位置关系是()A. 相交B. 相切C. 相离D. 不能确定9.如图5,在等腰Rt△ABC中,AC=BC=2,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是()A. B. C. D. 2图4 图5 图610.已知:如图6,在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为()A. B. C. D.11.如图7,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)()A. 16B.C.D.12.如图8,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH•PC其中正确的是()A. B. C. D.图7 图8 图9二、填空题(本大题共8小题,共32.0分)13.如图9,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为______时,△ADP和△ABC相似.14.如图10,在平行四边形ABCD中,E为边BC上一点,AC与DE相交于点F,若CE=2EB,S△AFD=9,则S四边形ABEF等于_____.15.已知在平面直角坐标系中,点A(-3,-1)、B(-2,-4)、C(-6,-5),以原点为位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为______.16.某兴趣小组借助无人飞机航拍,如图11,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)______ 米.图10 图11 图1217.如图12,点E(0,3),O(0,0),C(4,0)在⊙A上,BE是⊙A上的一条弦.则cos∠OBE=______.18.如图13,在⊙O中,弦AB=8,M是弦AB上的动点,且OM的最小值为3.则⊙O的半径为______.19.半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为______.20.如图14,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为________图13 图14三、解答题(本大题共6小题,共70.0分)21.(10分)某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米),tan48°≈,sin64°≈,tan64°≈2)(参考数据:sin48°≈22.(12分)在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E,F分别是AC,BC边上一点.(1)求证:=;(2)若CE=AC,BF=BC,求∠EDF的度数.23.(12分)如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.(1)求证:CB是⊙O的切线;(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.24.(12分)如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.(1)①求证:AP=CQ;②求证:PA2=AF•AD;(2)若AP:PC=1:3,求tan∠CBQ.25.(12分)如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE(1)求证:AC2=AE•AB;(2)过点B作⊙O的切线交EC的延长线于点P,试判断PB与PE是否相等,并说明理由;(3)设⊙O半径为4,点N为OC中点,点Q在⊙O上,求线段PQ的最小值.答案和解析1.【答案】B【解析】解:根据勾股定理,,BC=,所以,夹直角的两边的比为,观各选项,只有B选项三角形符合,与所给图形的三角形相似.故选:B.可利用正方形的边把对应的线段表示出来,利用三边对应成比例两个三角形相似,分别计算各边的长度即可解题.此题考查了勾股定理在直角三角形中的运用,三角形对应边比值相等判定三角形相似的方法,本题中根据勾股定理计算三角形的三边长是解题的关键.2.【答案】D【解析】解:在Rt△ABC中,∠C=90°,sinA==,BC=6,∴AB===10,故选:D.在直角三角形ABC中,利用锐角三角函数定义表示出sinA,将sinA的值与BC的长代入求出AB的长即可.此题考查了解直角三角形,熟练掌握锐角三角函数定义是解本题的关键.3.【答案】A【解析】解:∵∠DAE=∠CAB,∴当∠AED=∠B或∠ADE=∠C时,△ABC∽△AED;当=即=时,△ABC∽△AED.故选:A.根据相似三角形的判定定理进行判定即可.本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.4.【答案】A【解析】解:过平面上不在同一直线上的三点可以作一个圆,错误;平分弦(不是直径)的直径垂直于弦,故错误;在同圆或等圆中,相等的弦所对的圆周角相等,错误;三角形的内心到三角形各边的距离相等,正确,正确的有1个,故选A.利用确定圆的条件、垂径定理、圆周角定理及三角形的内心的性质分别判断后即可确定正确的选项;本题考查了确定圆的条件、垂径定理、圆周角定理及三角形的内心的性质等知识,解题的关键是能够了解有关的定义及定理,难度不大.5.【答案】B【解析】解:∵BE、CD是△ABC的中线,∴DE是△ABC的中位线,∴,正确;=,错误;∵D是AB的中点,∴=,由题意得,点O是△ABC的重心,∴=,∴,正确;=,错误,故选:B.根据三角形的重心的概念和性质、相似三角形的性质计算即可.本题考查的是三角形的重心的概念和性质、相似三角形的性质,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.6.【答案】C【解析】解:∵,∴sinA=,cosB=,∴∠A=60°,∠B=60°,故可得∠C=180°-∠A-∠B=60°.故选C.根据绝对值及完全平方的非负性可得出sinA及cosB的值,继而可得出∠A及∠B的度数,利用三角形的内角和定理求解即可.此题考查了特殊角的三角函数值、非负数的性质,属于基础题,解答本题的关键是根据特殊角的三角函数值得出∠A及∠B的度数.7.【答案】C【解析】解:∵DE=20m,DE:AE=4:3,∴AE=15m,∵CF=DE=20m,CF:BF=1:2,∴BF=40m,∴AB=AE+EF+BF=15+10+40=65m.故选C.利用坡比的比值关系,求出AE与BF的长度即可得出下底的长.本题考查了坡度和坡角的知识,解答本题的关键是根据坡比和已知条件求出三角形的边长.8.【答案】A【解析】解:过C作CD⊥AB于D,如图所示:∵在Rt△ABC中,∠C=90,AC=4,BC=3,∴AB==5,∵△ABC的面积=AC×BC=AB×CD,∴3×4=5CD,∴CD=2.4<2.5,即d<r,∴以2.5为半径的⊙C与直线AB的关系是相交;故选A.过C作CD⊥AB于D,根据勾股定理求出AB,根据三角形的面积公式求出CD,得出d<r,根据直线和圆的位置关系即可得出结论.本题考查了直线和圆的位置关系,用到的知识点是勾股定理,三角形的面积公式;解此题的关键是能正确作出辅助线,并进一步求出CD的长,注意:直线和圆的位置关系有:相离,相切,相交.9.【答案】B【解析】解:取AB的中点O、AE的中点E、BC的中点F,连结OC、OP、OM、OE、OF、EF,如图,∵在等腰Rt△ABC中,AC=BC=2,∴AB=BC=4,∴OC=AB=2,OP=AB=2,∵M为PC的中点,∴OM⊥PC,∴∠CMO=90°,∴点M在以OC为直径的圆上,当P点在A点时,M点在E点;当P点在B点时,M点在F点,易得四边形CEOF为正方形,EF=OC=2,∴M点的路径为以2为直径的半圆,∴点M运动的路径长=•π•2=π.故选B.取AB的中点O、AE的中点E、BC的中点F,连结OC、OP、OM、OE、OF、EF,如图,利用等腰直角三角形的性质得到AB=BC=4,则OC=AB=2,OP=AB=2,再根据等腰三角形的性质得OM⊥PC,则∠CMO=90°,于是根据圆周角定理得到点M在以OC为直径的圆上,由于点P点在A点时,M点在E点,点P点在B点时,M点在F点,则利用四边形CEOF为正方得到EF=OC=2,所以M点的路径为以2为直径的半圆,然后根据圆的周长公式计算点M运动的路径长.本题考查了轨迹:点按一定规律运动所形成的图形为点运动的轨迹.解决此题的关键是利用等腰三角形的性质和圆周角定理确定M 点的轨迹为以2为直径的半圆. 10.【答案】B 【解析】解:∵OA ⊥BC ,∠AOB=70°, ∴=,∴∠ADC=∠AOB=35°. 故选:B .先根据垂径定理得出=,再由圆周角定理即可得出结论.本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键. 11.【答案】B 【解析】解:连接AD ,OD , ∵等腰直角△ABC 中,∴∠ABD=45°. ∵AB 是圆的直径,∴∠ADB=90°, ∴△ABD 也是等腰直角三角形,∴=.∵AB=8,∴AD=BD=4, ∴S 阴影=S △ABC -S △ABD -S 弓形AD=S △ABC -S △ABD -(S 扇形AOD -S △ABD )=×8×8-×4×4-+××4×4=16-4π+8=24-4π. 故选B .连接AD ,因为△ABC 是等腰直角三角形,故∠ABD=45°,再由AB 是圆的直径得出∠ADB=90°,故△ABD 也是等腰直角三角形,所以=,S 阴影=S △ABC -S △ABD -S 弓形AD 由此可得出结论.本题考查的是扇形面积的计算,根据题意作出辅助线,构造出三角形及扇形是解答此题的关键.12.【答案】C【解析】解:∵△BPC是等边三角形,∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,在正方形ABCD中,∵AB=BC=CD,∠A=∠ADC=∠BCD=90°∴∠ABE=∠DCF=30°,∴BE=2AE;故正确;∵PC=CD,∠PCD=30°,∴∠PDC=75°,∴∠FDP=15°,∵∠DBA=45°,∴∠PBD=15°,∴∠FDP=∠PBD,∵∠DFP=∠BPC=60°,∴△DFP∽△BPH;故正确;∵∠FDP=∠PBD=15°,∠ADB=45°,∴∠PDB=30°,而∠DFP=60°,∴∠PFD≠∠PDB,∴△PFD与△PDB不会相似;故错误;∵∠PDH=∠PCD=30°,∠DPH=∠DPC,∴△DPH∽△CPD,∴,∴DP2=PH•PC,故正确;故选C.由正方形的性质和相似三角形的判定与性质,即可得出结论.本题考查的正方形的性质,等边三角形的性质以及相似三角形的判定和性质,解答此题的关键是熟练掌握性质和定理.13.【答案】4或9【解析】【分析】此题主要考查了相似三角形的判定与性质,利用倒推法以及分类讨论得出是解题关键.分别根据当△ADP∽△ACB时,当△ADP∽△ABC时,求出AP的长即可.【解答】解:当△ADP∽△ACB时,∴=,∴=,解得:AP=9,当△ADP∽△ABC时,∴=,∴=,解得:AP=4,∴当AP的长度为4或9时,△ADP和△ABC相似.故答案为4或9.14.【答案】11【解析】【分析】此题主要考查了相似三角形的判定与性质,解题首先利用平行四边形的构造相似三角形的相似条件,然后利用其性质即可求解.由于四边形ABCD是平行四边形,所以得到BC∥AD、BC=AD,而CE=2EB,由此即可得到△AFD∽△CFE,它们的相似比为3:2,最后利用相似三角形的性质即可求解.【解答】解:∵四边形ABCD是平行四边形,∴BC∥AD、BC=AD,而CE=2EB,∴△AFD∽△CFE,且它们的相似比为3:2,∴S△AFD:S△EFC=()2,而S△AFD=9,∴S△EFC=4,∴S△DFC=9×=6,∴S△ADC=15,S=15-4=11.四边形ABEF故答案为11.15.【答案】(1,2)或(-1,-2)【解析】解:∵点B的坐标为(-2,-4),以原点为位似中心将△ABC缩小,位似比为1:2,∴点B的对应点的坐标为(1,2)或(-1,-2),故答案为:(1,2)或(-1,-2).根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k解答.本题考查的是位似变换的概念和性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.16.【答案】9+9【解析】解:如图,作AD⊥BC,BH⊥水平线,由题意得:∠ACH=75°,∠BCH=30°,AB∥CH,∴∠ABC=30°,∠ACB=45°,∵AB=3×12=36m,∴AD=CD=18m,BD=AB•cos30°=18m,∴BC=CD+BD=(18+18)m,∴BH=BC•sin30°=(9+9)m.故答案为:9+9.作AD⊥BC,BH⊥水平线,根据题意确定出∠ABC与∠ACB的度数,利用锐角三角函数定义求出AD与BD的长,由CD+BD求出BC的长,即可求出BH的长.此题考查了解直角三角形的应用-仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.17.【答案】【解析】解:连接EC,由∠EOC=90°得到BC为圆A的直径,∴EC过点A,又OE=3,OC=4,根据勾股定理得:EC=5,∵∠OBE和∠OCE为所对的圆周角,∴∠OBE=∠OCE,则cos∠OBE=cos∠OCE==.故答案为:连接EC,由90°的圆周角所对的弦为直径,根据∠EOC=90°得到EC为圆A的直径,所以点A在EC上且为EC中点,在直角三角形EOC中,由OE和OC的长,利用勾股定理求出EC的长,根据同弧所对的圆周角都相等得到∠EBO与∠ECO相等,而∠ECO在直角三角形EOC中,根据余弦函数定义即可求出cos∠ECO的值,进而得到cos∠EBO.此题考查学生掌握90°的圆周角所对的弦为直径以及同弧所对的圆周角相等,考查了数形结合以及转化的数学思想,是一道中档题.连接EC且得到EC为圆A的直径是解本题的突破点.18.【答案】5【解析】解:根据垂线段最短知,当OM⊥AB时,OM有最小值,此时,由垂径定理知,点M是AB的中点,连接OA,AM=AB=4,由勾股定理知,OA2=OM2+AM2.即OA2=42+32,解得OA=5.所以⊙O的半径为5;故答案为5.根据垂线段最短知,当OM⊥AB时,OM有最小值.根据垂径定理和勾股定理求解.本题考查了垂径定理和勾股定理,根据垂线段最短知,当OM⊥AB时,OM有最小值是解题的关键.19.【答案】1::【解析】解:由题意可得,正三角形的边心距是:2×sin30°=2×=1,正四边形的边心距是:2×sin45°=2×,正六边形的边心距是:2×sin60°=2×,∴半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为:1::,故答案为:1::.根据题意可以求得半径为2的圆内接正三角形,正四边形,正六边形的边心距,从而可以求得它们的比值.本题考查正多边形和圆,解答本题的关键是明确题意,求出相应的图形的边心距.20.【答案】.【解析】【分析】本题考查了圆的切线的性质,矩形的性质,平行线的性质,勾股定理的应用以及三角形相似的判定和性质,本题的关键是判断出P处于什么位置时面积最大.当P点移动到平行于OA且与⊙D相切时,△AOP面积的最大,由于P为切点,得出MP垂直与切线,进而得出PM⊥AC,根据勾股定理先求得AC的长,进而求得OA的长,根据△ADM∽△ACD,求得DM的长,从而求得PM的长,最后根据三角形的面积公式即可求得.【解答】解:当P点移动到平行于OA且与⊙D相切时,△AOP面积的最大,如图,菁优网∵P是⊙D的切线,∴DP垂直与切线,延长PD交AC于M,则DM⊥AC,∵在矩形ABCD中,AB=3,BC=4,∴.∴.∵∠AMD=∠ADC=90°,∠DAM=∠CAD,∴△ADM∽△ACD,∴,∵AD=4,CD=3,AC=5,∴DM=,∴,∴△AOP的最大面积=.故答案为.21.【答案】解:根据题意,得∠ADB=64°,∠ACB=48°在Rt△ADB中,tan64°=,则BD=≈AB,在Rt△ACB中,tan48°=,则CB=≈AB,∴CD=BC-BD即6=AB-AB解得:AB=≈14.7(米),∴建筑物的高度约为14.7米.【解析】Rt△ADB中用AB表示出BD、Rt△ACB中用AB表示出BC,根据CD=BC-BD可得关于AB 的方程,解方程可得.本题考查解直角三角形的应用-仰角俯角问题,解题的关键是利用数形结合的思想找出各边之间的关系,然后找出所求问题需要的条件.22.【答案】解:(1)∵CD⊥AB,∴∠A+∠ACD=90°又∵∠A+∠B=90°∴∠B=∠ACD∴Rt△ADC∽Rt△CDB∴=;(2)∵==,又∵∠ACD=∠B,∴△CED∽△BFD;∴∠CDE=∠BDF;∴∠EDF=∠EDC+∠CDF=∠BDF+∠CDF=∠CDB=90°.【解析】(1)证相关线段所在的三角形相似即可,即证Rt△ADC∽Rt△CDB;(2)易证得CE:BF=AC:BC,联立(1)的结论,即可得出CE:BF=CD:BD,由此易证得△CED∽△BFD,即可得出∠CDE=∠BDF,由于∠BDF和∠CDF互余,则∠EDC和∠CDF也互余,由此可求得∠EDF的度数.此题考查的是相似三角形的判定和性质;识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.23.【答案】(1)证明:连接OD,与AF相交于点G,∵CE与⊙O相切于点D,∴OD⊥CE,∴∠CDO=90°,∵AD∥OC,∴∠ADO=∠DOC,∠DAO=∠BOC,∵OA=OD,∴∠ADO=∠DAO,∴∠DOC=∠BOC,在△CDO和△CBO中,\∠ ∠ ,∴△CDO≌△CBO,∴∠CBO=∠CDO=90°,∴CB是⊙O的切线.(2)由(1)可知∠DOA=∠BOC,∠DOC=∠BOC,∵∠ECB=60°,∴∠DCO=∠BCO=∠ECB=30°,∴∠DOC=∠BOC=60°,∴∠DOA=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠GOF=∠ADO,在△ADG和△FOG中,∠ ∠∠ ∠ ,∴△ADG≌△FOG,∴S△ADG=S△FOG,∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF==π.【解析】(1)欲证明CB是⊙O的切线,只要证明BC⊥OB,可以证明△CDO≌△CBO解决问题.(2)首先证明S阴=S扇形ODF,然后利用扇形面积公式计算即可.本题考查切线的性质和判定、扇形的面积公式,记住切线的判定方法和性质是解决问题的关键,学会把求不规则图形面积转化为求规则图形面积,属于中考常考题型.24.【答案】解:(1)①∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∴∠ABP+∠PBC=90°,∵△BPQ是等腰直角三角形,∴BP=BQ,∠PBQ=90°,∴∠PBC+∠CBQ=90°∴∠ABP=∠CBQ,∴△ABP≌△CBQ,∴AP=CQ;②∵四边形ABCD是正方形,∴∠DAC=∠BAC=∠ACB=45°,∵∠PQB=45°,∠CEP=∠QEB,∴∠CBQ=∠CPQ,由①得△ABP≌△CBQ,∠ABP=∠CBQ∵∠CPQ=∠APF,∴∠APF=∠ABP,∴△APF∽△ABP,∴,∴AP2=AF•AB=AF•AD;(本题也可以连接PD,证△APF∽△ADP)(2)由①得△ABP≌△CBQ,∴∠BCQ=∠BAC=45°,∵∠ACB=45°,∠PCQ=45°+45°=90°,∴tan∠CPQ=,由①得AP=CQ,又∵AP:PC=1:3,∴tan∠CPQ=,由②得∠CBQ=∠CPQ,∴tan∠CBQ=tan∠CPQ=.【解析】(1)证出∠ABP=∠CBQ,由SAS证明△ABP≌△CBQ可得结论;根据正方形的性质和全等三角形的性质得到∠DAC=∠BAC,∠APF=∠ABP,根据AA 证明△APF∽△ABP,再根据相似三角形的性质即可求解;(2)根据全等三角形的性质得到∠BCQ=∠BAC=45°,可得∠PCQ=90°,根据三角函数和已知条件得到tan∠CPQ=,由中∠CBQ=∠CPQ即可求解.本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质等知识;本题综合性强,有一定难度.25.【答案】证明:(1)如图1,连接BC,∵CD为⊙O的直径,AB⊥CD,∴=,∴∠A=∠ABC,∵EC=AE,∴∠A=∠ACE,∴∠ABC=∠ACE,∵∠A=∠A,∴△AEC∽△ACB,∴,∴AC2=AE•AB;(2)PB=PE,理由是:如图2,连接OB,∵PB为⊙O的切线,∴OB⊥PB,∴∠OBP=90°,∴∠PBN+∠OBN=90°,∵∠OBN+∠COB=90°,∴∠PBN=∠COB,∵∠PEB=∠A+∠ACE=2∠A,∠COB=2∠A,∴∠PEB=∠COB,∴∠PEB=∠PBN,∴PB=PE;(3)如图3,∵N为OC的中点,∴ON=OC=OB,Rt△OBN中,∠OBN=30°,∴∠COB=60°,∵OC=OB,∴△OCB为等边三角形,∵Q为⊙O任意一点,连接PQ、OQ,因为OQ为半径,是定值4,则PQ+OQ的值最小时,PQ最小,当P、Q、O三点共线时,PQ最小,∴Q为OP与⊙O的交点时,PQ最小,∠A=∠COB=30°,∴∠PEB=2∠A=60°,∠ABP=90°-30°=60°,∴△PBE是等边三角形,Rt△OBN中,BN==2,∴AB=2BN=4,设AE=x,则CE=x,EN=2-x,Rt△CNE中,x2=22+(2-x)2,x=,∴BE=PB=4-=,Rt△OPB中,OP===,∴PQ=-4=.则线段PQ的最小值是.【解析】(1)证明△AEC∽△ACB,列比例式可得结论;(2)如图2,证明∠PEB=∠COB=∠PBN,根据等角对等边可得:PB=PE;(3)如图3,先确定线段PQ的最小值时Q的位置:因为OQ为半径,是定值4,则PQ+OQ 的值最小时,PQ最小,当P、Q、O三点共线时,PQ最小,先求AE的长,从而得PB的长,最后利用勾股定理求OP的长,与半径的差就是PQ的最小值.本题是圆的综合题,考查了三角形相似的性质和判定、等腰三角形、等边三角形的性质和判定、垂径定理、切线的性质、勾股定理等知识,第三问有难度,确定PQ最小值时Q的位置是关键,根据两点之间线段最短,与勾股定理、方程相结合,解决问题.。
(完整版)青岛版六年级数学下册第三单元测试题

(完整版)青岛版六年级数学下册第三单元测试题五年级数学下册第三单元《⽐例》测试题⼀、填空:1. 在4 :5 = 1.2中,4叫⽐的(),5叫⽐的(),1.2叫⽐)。
在8 :14=48 :84中,8和84是⽐例的(),14和48是⽐例的()。
2.两种()的量,⼀种量变化,另⼀种量也随着变化,如果这两种量中相对应的两个数的()⼀定,这两种量就叫做成正⽐例的量,它们的关系叫做()。
3.如果4A= 5B,那么AB =();5 = 24 ÷()= ():15 。
4.如果X=6 Y,那么X和Y成()⽐例。
5.():25 = 13 :166.单价⼀定,总价和数量成()⽐例。
总价⼀定,单价和数量成()⽐例;数量⼀定,总价和单价成()⽐例。
7. ⼀种盐⽔是由盐和⽔按1 :19 的重量配制⽽成的。
其中,盐的重量占盐⽔的(),⽔的重量占盐⽔的()。
8. 根据8a=9b,那么a:b=( )9. 根据关系式填空⼯作效率*⼯作时间=⼯作总量,因为()/()=⼯作效率,如果()⼀定,()和()成正⽐例;因为()/()=⼯作时间,如果()⼀定,()和()成正⽐例;⼆.判断。
1.两个⽐就能组成⼀个⽐例。
()2.正⽅形的⾯积⼀定,它的边长和边长不成⽐例。
()3.在⼀个⽐例⾥,两个内项的积与两个外项的积的⽐值是1。
()4.圆的⾯积和半径成正⽐例。
()5.长⽅形⾯积⼀定,长和宽成反⽐例。
()6.把10克盐放⼊100克⽔中,盐与盐⽔的重量的⽐是1 :10。
()7.⼀批货物,运⾛的和剩下的成反⽐例。
()8.如果ab + 5 = 15,则a与b成反⽐例。
()三、判断下⾯两种量是否成正⽐例、反⽐例或不成⽐例。
(在括号内⽤⽂字注明)1. 烧煤的天数⼀定,每天的烧煤量和煤的总量。
()2. 修路的总⽶数⼀定,修好了的⽶数和剩下的⽶数。
()3. 排印⼀本书,每页的字数和页数。
()4. 图上距离⼀定,实际距离和⽐例尺。
()5. 长⽅形的周长⼀定,它的长和宽。
青岛版六年级下册数学期中测试题(附答案)

六年级数学学科试题答案
一、用心填空( 25 分、每个 1 分)
1、 2 2、 196 3、 760 4、 1.5 3.2 5、 4:5
6、 3.145 3.14% 7、 85 10 8、 9 9、 正 反 10、 0.08 11、 1:600000 12、 6 12 13、 20 15 18 60 六 14、 70 15、 40 2、合理判断。正确的涂 A,不正确的涂 B(6 分、每个 1 分) BBABBA
二、合理判断。正确的涂 A,不正确的涂 B(12 分、每个 2 分)
1、刘老师看一本 80 页的故事书、第一天看了 35%、第二天应从第 28 页看起。( )
2、半径为 2 米的圆柱体 , 它的底面周长和底面积相等.
()
3、 2011 年苹果的产量比 2010 年增加了 15%、2011 年的产量是 2010 年的 115%。()
四、细心计算
1、直接写得数( 12 分、每个 1 分)
1
1
7× 7 ÷7× 7 =
3 4 ×10% =
1.25 × 8=
11 2-5=
23 3÷ 2=
15÷( 1+50 ℅) =
9 10 ÷ 9=
14 6+7=
3553 4× 6 ÷6 × 4 =
0.6 ÷3 ℅=
70÷ 1.4=
90 ℅×90=
2、脱式计算、怎样简便就怎样算。(每题 3 分、共 12 分)
)
A 、扩大 2 倍
B、扩大 3 倍
C、扩大 4 倍 D、扩大 5 倍
6、把一个棱长是 4 分米的正方形木块削成一个最大的圆柱、圆柱的体积是( 方分米。 A 、 50.24 B、100.48 C、64 D、5
青岛版2018-2019学年六年级上学期期末测试数学试卷考试数学试卷含解析

青岛版2018-2019学年六年级上学期期末测试数学试卷考试数学试卷一、填空题1.一座楼高6层,每层有16个台阶,上到第四层,共有台阶____个.【答案】48【解析】相邻两层之间有16个台阶,上到第四层有16×3=48(个)台阶.2.0.4的倒数是(______),(______)没有倒数。
【答案】52【分析】根据倒数的意义,乘积是1的两个数互为倒数;求一个数的倒数就是用1除以这个数,0没有倒数。
由此解答。
【详解】0.4=25,因为25×52=1,所以0.4的倒数是52;0没有倒数。
【点睛】此题考查的目的是理解倒数的意义,掌握求倒数的方法及应用。
3.把5克盐放入100克水中,盐占盐水的() ().【答案】1 21【详解】5÷(5+100)=1 21;答:盐占盐水的1 21.故答案为:1 21.4.【答案】5.有10箱桔子,最少的一箱装了50个,如果每两箱中放的桔子都不一样多,那么这10只箱子一共至少装了____个桔子.【答案】545【解析】由于每两箱中放的桔子都不一样多,因此,这10只箱子一共至少装了50+51+52+…+59=545(个)桔子6.【答案】7.(A是非0自然数)的分数单位是________,当A=________时,这个数的倒数是。
【答案】 3【解析】把单位“1”平均分成若干份,表示其中一份的数叫做分数单位;判断出的倒数即可确定A的值。
8.2800dm3=________m3 3.26L=________mL【答案】2.8 3260【解析】1m³=1000dm³,1L=1000mL,把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
2800÷1000=2.8,所以2800dm³=2.8m³;3.26×1000=3260,所以3.26L=3260mL。
故答案为:2.8;3260。
青岛版数学六年级上册期中测试题及答案(共3套)

青岛版数学六年级上册期中测试题(一)一、我来填一填。
1.如果m ×15=m ÷15,则m=( )。
2.一块正方形木板,周长是45 dm,它的边长是( )dm,面积是( )dm2。
3.如图,涂色部分的面积是20平方厘米,空白部分的面积是( )平方厘米。
4.6∶5=( )20=18÷( )=12∶( )=( )(填小数)5.晨晨看一本书,已看页数与剩下的页数之比是7∶3。
已看页数是剩下的页数的( );剩下的页数是已看页数的( );已看页数占全书的( );剩下的页数占全书的( )。
6.a=5b ,则a∶b=( )∶( ),b∶a=( )∶( )。
7.把5∶7的前项加上6,要使比值不变,后项应加上( )。
二、我来判一判。
1.如果a ÷b=14,那么b 是a 的4倍。
( )2.47÷34=47×43。
( )3.两个真分数相除,商一定小于被除数。
( )4.85克盐水中含有5克盐,那么盐和水的质量比是1∶17。
( )5.走完同一段路,甲用7分钟,乙用8分钟,甲和乙所用的时间之比是7∶8,速度之比也是7∶8。
( ) 三、我来选一选。
1.一个比的前项是6,比值是512,这个比的后项是( )。
A.10B.725C.572 2.一项工作,甲单独做10天完成,乙单独做8天完成,甲和乙工作效率的最简单的整数比是( )。
A.8∶10B.5∶4C.4∶53.一个长方形的周长是24厘米,长与宽的比是2∶1,这个长方形的面积是( )平方厘米。
A.32B.128C.5763.红花和黄花一共有30朵,其中黄花占23,黄花有( )朵,红花有( )朵。
A.20 B.15 C.10 四、我来算一算。
1.直接写得数。
0÷512=1213÷4= 35÷7= 38÷1920= 1736÷49= 713÷1439= 13÷34= 89÷59= 2.计算下面各题。
青岛版数学六年级下1-5单元测试题和期中期末试题答案
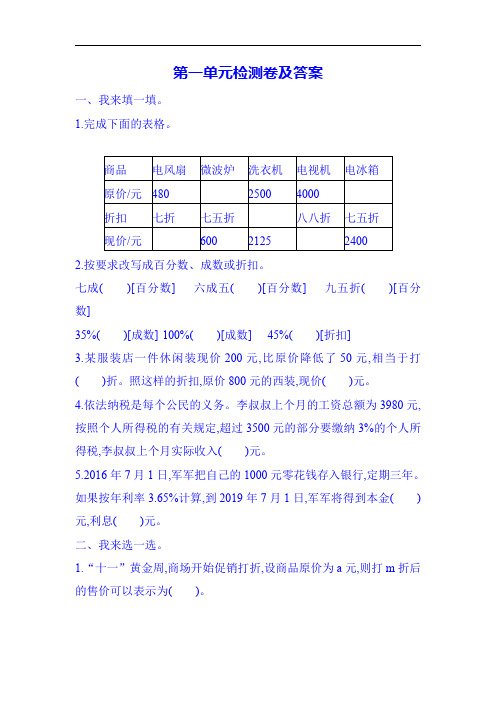
第一单元检测卷及答案一、我来填一填。
1.完成下面的表格。
商品电风扇微波炉洗衣机电视机电冰箱原价/元48025004000折扣七折七五折八八折七五折现价/元600212524002.按要求改写成百分数、成数或折扣。
七成()[百分数]六成五()[百分数]九五折()[百分数]35%()[成数]100%()[成数]45%()[折扣]3.某服装店一件休闲装现价200元,比原价降低了50元,相当于打()折。
照这样的折扣,原价800元的西装,现价()元。
4.依法纳税是每个公民的义务。
李叔叔上个月的工资总额为3980元,按照个人所得税的有关规定,超过3500元的部分要缴纳3%的个人所得税,李叔叔上个月实际收入()元。
5.2016年7月1日,军军把自己的1000元零花钱存入银行,定期三年。
如果按年利率3.65%计算,到2019年7月1日,军军将得到本金()元,利息()元。
二、我来选一选。
1.“十一”黄金周,商场开始促销打折,设商品原价为a元,则打m折后的售价可以表示为()。
A.amB.C. D.2.小英把1000元钱按年利率2.45%存入银行,存期为两年,那么计算到期时她可以从银行取回多少钱,列式正确的是()。
A.1000×2.45%×2B.(1000×2.45%+1000)×2C.1000×2.45%×2+1000D.1000×2.45%+10003.苏果超市和华联超市以同样的价格销售同一品牌的洗发液。
为了促销,两家超市打出优惠广告(如下所示)。
下面几种说法中,正确的是()。
苏果超市××牌洗发液买三送一!华联超市××牌洗发液降价25%销售!A.苏果超市的便宜B.华联超市的便宜C.两家超市折扣相同,到哪家购买都可以D.两家超市折扣相同,但在苏果超市要买3瓶以上才有优惠,应到华联超市购买4.“个人所得税起征点调整至3500元,一级(应纳税额1500元以内)税率降至3%。
青岛版六年级下册数学期中测试卷(及答案)

青岛版六年级数学(下)期中测试卷一、填空。
1、3÷( )= 18( )=( ):12= 七成五=( )% 2.李婷在1:8000000的地图上量得北京到南京的距离约为15厘米,两地实际距离约为( )千米。
3、一个比例里,两个外项正好互为倒数,其中一个内项是2,另一个内项是( )。
4、一件衣服200元,降低20元出售,这件衣服是打( )折出售的。
5、一个圆柱的底面半径是3分米,高2分米,它的侧面积是( )平方分米,表面积是( )平方分米,体积是( )立方分米。
6、一种大豆的出油率为 24% ~ 32% , 300 千克这样的大豆最少可以出油( )千克。
如果要榨出 64 千克油,最少需要( )千克这种大豆。
7、一个圆柱形水杯的底面直径是8cm ,高是8cm 。
如果杯子里水面的高度是5cm ,那么水的体积是( )cm ³,杯子的内壁与水接触的面积是多少( )cm ²8、一个圆柱和圆锥的底面半径和高分别相等,已知圆柱体积比圆锥的体积多12cm ³,圆柱的体积是( ) cm ³,圆锥的体积是( ) cm ³。
9、六(1)班男生人数是女生人数的32,女生人数占全班人数的( )。
10、甲乙两数的比是5:4,那么甲数比乙数多( )%,乙数比甲数少( )%。
11、已知4X=3Y , X :Y =( ):( )。
12、M 与N 是两种相关联的量,a 、b 、c 、d(都不为零)是它们其中的两组 相对应的值。
如下表:(1)如果a :c=b :d ,那么M 、N 成( )比例;(2)如果a ×c=b ×d ,那么M 、N 成( )比例。
13、圆柱底面半径扩大2倍,高不变,侧面积就扩大( )倍,体积扩大( )倍。
14、如右下图所示,把底面直径8厘米的圆柱切成若干等分,拼成一个近似的长方体。
这个长方体的表面积比原来增加80平方厘米,那么长方体的体积是( )立方厘米。
青岛版数学六年级下册期中测试题

2022-2023学年度第二学期六年级数学期中检测题一、用心思考,我会填 23% 1.二十四节气是我国劳动人民在长期实践中总结出来的,凝聚了劳动人民的智慧与心血,也是世界天文史上的一个重要发现。
“夏至”是第10个节气,也是一年中白昼最长,黑夜最短的一天。
2022年6月21日夏至这天,这一天,潍坊地区的黑夜将近10个小时,潍坊的白昼和黑夜时间的比是( ),白昼的时间比黑夜的时间长( )%。
同一天,在北京地区,白昼的时长将长达15个小时,是北半球得到太阳最多的一天,那北京的白昼和黑夜时间的比是( ),白昼的时间比黑夜的时间长约( )%。
(保留一位小数)这两个比( )组成比例(填“能”或“不能” ),是因为( ) 。
2. 25米:0.1千米=15( ) =( )360=( )(填小数)=( )% 3.李明将微信零钱里的10000元钱转入零钱通,年收益率为2.45%,一年后,他打算转出收益的80%,他打算转出( )元。
4. 制作一个无盖的圆柱形水桶,有以下几种型号的铁皮可供选择。
你选择的材料是( )和( )。
用你选择的材料做成的水桶容积是( )。
5. 32米减少25%是( )米。
40千克增加25%是( )千克。
6. 一件羽绒服原价400元,现在打六五折出售,现价比原价便宜了( )元。
7.如右图,涂色的小平行四边形按( ):1放大得到大平行四边形。
如果小平行四边形的面积是5平方厘米,空白部分的面积是( )平方厘米。
8.独立完成一项工程,甲用41小时,乙用51小时,甲乙的工作效率之比是( )。
9.如右图,先将甲容器注满水,再将水倒入乙容器,连续倒入两杯,这时乙容器中的水深( )cm 。
10.一个直角三角形的两条直角边长分别是6厘米和8厘米,把这个三角形缩小,使缩小后的图形与原图形对应边长的比为1:2,则缩小后的图形的两条直角边长分别是( )厘米和( )厘米,面积是( )平方厘米。
二、细心读,用心选一选10%1.50÷(200+50)表示的意思是()。
第3-4单元测试题B卷-六年级数学下册阶段测试(青岛版,六三制)

第3-4单元测试题B 卷 六年级数学下册阶段测试题号 一 二 三 四 五 六 总分得分一、选择题(每题2分,共16分)1.下列图形中,将图(1)按2∶1画出来的是( )。
A .①B .②C .③2.在比例尺是( )的地图上,8厘米的线段表示实际240米的距离。
A .1∶30B .1∶300C .1∶30003.下列几组量中,成反比例关系的是( )。
A .房间面积一定,一块方砖的面积和所需块数 B .6x =7y C .圆的周长一定,半径和圆周率4.下面各题中的两种量,成正比例的是( )。
A .小东的身高和体重 B .修一条水渠,每天修的米数和天数C .正方形的周长和边长5.下面三组数中,不能组成比例的是( )。
A .3、4、6、8B .1、2、3、4C .14、13、4、36.下面说法错误的是( )。
A .两种量相对应的两个数的比值-定,这两种量之间就是正比例关系。
B .同一幅地图,图上距离和实际距离之间成正比例关系。
C .如果两种相关联的量相对应的两个数的乘积一定,它们之间就是反比例关系。
7.在比例尺是1∶150000的地图上,3厘米表示实际距离( )千米。
A .15B .45C .4.58.实际距离为240千米,如果用1∶5000000的比例尺画在地图上,图上距离应画( )。
A .4.8厘米B .524厘米 C .48厘米二、填空题(每题2分,共16分)9.在比例18∶3=12∶2里,两个外项的积是( )。
10.一种微型零件的长4毫米,画在图纸上长20厘米,这幅图的比例尺是( )。
11.小明按4∶1的比例放大一个20°的角,放大后角的度数是( )。
12.把下面的线段比例尺改写成数值比例尺是( )。
13.如果x 与y 成反比例,a 是( );如果x 与y 成正比例,a 是( )。
x618y 150 a14.4∶9的后项加上27,要使比值不变,前项应加上________。
青岛版六年级数学下册期中测试题1

青岛版六年级数学第二学期期中测试题一、填空(30分)1、3÷()=18( )=():12= 七成五=()%2.写出1个用18的因数组成的比例:()。
3.一种药品的售价比过去降低了15%,现价是原价的()%4、在一个比例里,两个内项互为倒数,一个外项为92,则另一个外项为()。
5、20千克比()千克少20%。
6、把底面半径是2厘米的圆柱的侧面展开,得到一个正方形,这个圆柱的高为()。
7、在一幅地图上,用3厘米的线段表示18千米的实际距离,这幅地图的比例尺是()。
8、在一个比例中,两个外项互为倒数,其中一个内项是37,另一个内项是()。
9、一个圆柱体的底面直径4分米,高0.5分米,它的侧面积是()平方分米;它的表面积是()平方分米;它的体积是()立方分米。
10.圆锥的体积是100立方厘米,底面积是50平方厘米它的高是()厘米二、判断(5分)1、甲数比乙数多25%,乙数就比甲数少25%()2、一件上衣200元先提价10%,又降价10%,这时价格和原价相等。
()3、圆柱体的体积与圆锥体的体积比是3∶1。
()4、由两个比组成的式子叫做比例。
()5.订阅<<小学生数学报>>的份数和钱数不成比例. ( )三、选择题(16分)1、把10克糖放入100克水中,糖与糖水的重量比是()。
①、1:10 ②、1:11 ③、10:112、求5千克比8千克少百分之几?正确的列式为()A、5÷8B、8÷5C、(8-5)÷5D、(8-5)÷83、下面第( )组的两个比不能组成比例① 7:8和14:16 ②0.6:0.2和3:1 ③19:110 和10:94、圆柱体的底面半径扩大3倍,高不变,体积扩大()①3倍②9倍③6倍5、把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是()立方分米。
①50.24 ②100.48 ③646、在一个比例尺是200︰1的图纸上,量得一个零件的长是2厘米,这个零件实际长①4米②1米③ 0.1毫米④ 0.4毫米7、把一张长方形的图按1:20的比例缩小后,长和宽的比()A、不变B、变了C、无法确定8、一种长5毫米的机器零件,画在图纸上长10厘米,图纸的比例尺是()A、1:2B、2:1C、1:20D、20:1四、计算(27分)1、直接写得数。
青岛版六年级数学下册第一单元测试题及答案一

第一单元检测卷(1)(时间:60分钟分数: )一、填一填。
(27分)1.一种国产冰箱原来每台售价是2800元,现在比原来降低了5%,现在每台售价是多少元?(1)此题应该把( )看作单位“1”。
(2)2800×5%求的是( )。
(3)1-5% 求的是( )。
(4)2800×95%求的是( )。
2.今年小麦的亩产量是去年的115%,今年小麦的亩产量比去年增加( )%。
3.25比20多( )% ,20比25少( )%。
4.某化工厂今年的收入额比去年同期增加了10%,也可以说今年的收入额是去年同期的( )%。
5.找出各题中的单位“1”,并写出等量关系式。
(1)杨树比柳树多25% ,单位“1”是( ),数量关系式是( )。
(2)8月份的用电量比7月份降低了8%,单位“1”是( ),数量关系式是( )。
6.某种彩电打八六折销售,现在的价钱是( )的86%。
7.九折是百分之( ),改写成百分数是( );七五折改写成百分数是( )。
某种服装原价每套500元,现价每套475元,现价是打( )折出售的。
8.八成改写成百分数是( ),四成二改写成百分数是( ),九成九改写成百分数是( )。
9.今年某旅游区接待的游客比去年多了二成,今年接待的游客是去年的( )%。
10.今年到北京旅游的人数比去年增加50%,就是比去年增加( )成。
11.应纳税额=( ),本金是( ),利息是( ),利率是( ),利息的计算公式是( )。
二、辨一辨。
(正确的画“√”,错误的画“✕”)(8分)1.一件衣服200元,先提价10%,在提价的基础上又降价10%,这时的价格和原价相等。
() 2.甲数比乙数多25%,乙数就比甲数少25%。
( )3.甲数比乙数多20,乙数就比甲数少20。
( )4.今年我县粮食比去年增产一成八,是指今年我县粮食比去年增产的部分占去年的1.8%。
( )5.万叔叔说:“我付出劳动,得到工资,不需要纳税。
”( )6.税率与应纳税额有关,与总收入无关。
第3-4单元测试题C卷-六年级数学下册阶段测试(青岛版,六三制)

第3-4单元测试题C卷六年级数学下册阶段测试一、选择题(每题2分,共16分)1.王亮的身高与体重成()。
A.正比例B.反比例C.不成比例2.在一个比例里,两个内项的积是最小的质数。
一个外项是5,另一个外项是()。
A.0.2 B.0.4 C.0.83.在比例尺是()的平面图上,5厘米表示实际距离50米。
A.1∶100 B.1∶1000 C.1000∶14.能和4∶0.3组成比例的是()。
A.0.8∶0.6 B.8∶0.6 C.0.8∶65.下面各数量关系中,成正比例关系的是()。
A.圆的半径与它的面积B.圆柱的底面积不变,它的体积与高C.一批货物,运走的吨数与剩下的吨数。
6.一块计算机芯片实际尺寸是4mm×4mm,下图是按照一定比例所画的图。
图中所用的比例尺是()。
A.1∶5 B.1∶2 C.5∶17.一个长方形的运动场长108米、宽65米。
小东想在练习本上画出这个操场的平面图,下面比例尺比较合适的是()。
A.11000B.1100C.1508.一种零件长0.5毫米,画在图纸上长5厘米,这幅图的比例是()。
A.1∶10 B.10∶1 C.100∶1二、填空题(每题2分,共16分)9.在比例20∶4=35∶7里,外项有20和( );内项有4和( )。
10.XY+6=25,X和Y成( )比例,X=32Y,X和Y成( )比例。
11.比例尺800∶1表示图上距离是实际距离的( )倍,实际距离是图上距离的( )。
12.在一个比例中,两个内项的积是最小的合数,一个外项是58,另一个外项是( )。
13.在比例尺是1∶1500的图纸上量得一个学校操场长8厘米、宽6厘米,这个学校操场的实际面积是( )平方米。
14.火箭中有一种精密零件,该精密零件长3毫米,画在图纸上长9厘米,这幅图纸的比例尺是( )。
15.某工厂按照1:500的比制造了一列火车的模型,模型长1.1米。
这列火车的实际长度是( )米。
16.写出由6、9、12、18组成的两个不同的比例式:( )。
六年级青岛版数学测试题

一、填空题1. 一个数由5 个千万、4 个十万、8 个千、3 个百和7 个十组成,这个数写作(50408370),省略万位后面的尾数约是(5041 万)。
-解析:写数时从高位写起,哪一位上是几就写几,没有单位的用0 占位。
省略万位后面的尾数,就看千位上的数,进行四舍五入。
2. 把3 米长的铁丝平均分成5 段,每段长(0.6)米,每段占全长的(1/5)。
-解析:求每段长,用总长度除以段数;求每段占全长的几分之几,把全长看成单位“1”,平均分成5 段,每段就占全长的1/5。
3. 12 和18 的最大公因数是(6),最小公倍数是(36)。
-解析:分别列出12 和18 的因数,找出最大公因数;用短除法求最小公倍数。
4. 一个圆柱的底面半径是2 厘米,高是5 厘米,它的侧面积是(62.8)平方厘米,体积是(62.8)立方厘米。
-解析:圆柱侧面积= 底面圆周长×高,底面圆周长= 2πr;圆柱体积= 底面积×高,底面积= πr²。
二、选择题1. 下面图形中,对称轴最多的是(C)。
A. 正方形B. 长方形C. 圆D. 等边三角形-解析:正方形有4 条对称轴,长方形有2 条对称轴,圆有无数条对称轴,等边三角形有3 条对称轴。
2. 把10 克盐溶解在100 克水中,盐和盐水的比是(B)。
A. 1:10B. 1:11C. 10:11D. 11:1-解析:盐水的质量是10 + 100 = 110 克,盐和盐水的比是10:110 = 1:11。
3. 一个圆锥的体积是12 立方厘米,底面积是4 平方厘米,高是(C)厘米。
A. 3B. 6C. 9D. 12-解析:圆锥的高= 体积×3÷底面积,即12×3÷4 = 9 厘米。
三、计算题1. 直接写出得数。
- 3.14×5 = 15.7- 12.56÷3.14 = 4- 1/4 + 1/5 = 9/20- 2/3×3/4 = 1/22. 解方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019学年六年级数学期中第二学期测试卷
一、填空。
1.李婷在1:8000000的地图上量得北京到南京的距离约为15厘米,两地实际距离约为( )千米。
2、3÷( )= 18( )
=( ):12= 七成五=( )% 3、一个比例里,两个外项正好互为倒数,其中一个内项是2,另一个内项是( )。
4、一件衣服200元,降低20元出售,这件衣服是打( )折出售的。
5、一个圆柱的底面半径是3分米,高2分米,它的侧面积是( )平方分米,表面积是( )平方分米,体积是( )立方分米。
6、一种大豆的出油率为 24%--32% , 300 千克这样的大豆最少可以出油( )千克。
如果要榨出 64 千克油,最少需要( )千克这种大豆。
7、一个圆柱形水杯的底面直径是8cm ,高是8cm 。
如果杯子里水面的高度是5cm ,那么水的体积是( )cm ³,杯子的内壁与水接触的面积是多少( )cm ²
8、一个圆柱和圆锥的底面半径和高分别相等,已知圆柱体积比圆锥的体积多12cm ³,圆柱的体积是( ) cm ³,圆锥的体积是( ) cm ³。
9、六(1)班男生人数是女生人数的3
2,女生人数占全班人数的( )。
10、甲乙两数的比是5:4,那么甲数比乙数多( )%,乙数比甲数少( )%。
11、已知4X=3Y , X :Y =( ):( )。
12、M 与N 是两种相关联的量,a 、b 、c 、d(都不为零)是它们其中的两组
(1 (2)如果a ×c=b ×d ,那么M 、N 成( )比例。
13、圆柱底面半径扩大2倍,高不变,侧面积就扩大( )倍,体积扩大( )倍。
14、如右下图所示,把底面直径8厘米的圆柱切成若干等分,拼成一个近似的长方体。
这个长方体的表面积比原来增加80平方厘米,那么长方体的体积是( )立方厘米。
二、选择(把正确答案的序号填入括号里)。
1、( )能与 41:3
1组成比例。
A 、3∶4
B 、4∶3
C 、3:41
D 、34 :4
3 2、把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。
A 、200.96
B 、100.48
C 、64
D 、50.24
3、在一个比例尺是200︰1的图纸上,量得一个零件的长是2厘米,这个零件的实际长是( )
A 、4米
B 、1米
C 、0.1毫米
D 、 0.4毫米
4、一个圆柱体杯中盛满15升水,把一个与它等底等高的铁圆锥倒放入水中,杯中还有
( )水。
A 、5升
B 、7.5升
C 、10升
D 、9升
5、某班女生人数减少3
1,就与男生人数相等。
下面( )是不正确的。
A .女生是男生的150% B .女生比男生多20%
C .女生人数占全班的53
D .男生比女生少3
1 三、判断(正确的在括号里打“√”,错误的打“×” )。
1、一种商品打“八五折”出售,也就是把这种商品优惠了85%。
( )
2、两种相关联的量,一定成比例关系。
( )
3、甲数比乙数多10%,乙数就比甲数少10%。
( )
4、圆锥的体积一定,它的底面积和高成反比例。
( )
5、 5、一件商品,先涨价20%,然后又降价20%,结果现价与原价相等。
( )
四、计算。
1、直接写得数。
6÷43 = 4
3×10% = 1÷100%÷25= 15÷1%= 1.05-21 = 32÷23 = (41-51 )×201= 43×65÷65×4
3= 2、解比例。
X 21=8
32 201:51=X :41 X 2.3=0.5
3、计算(能简算的要简算)。
65÷(1-209)×51 52×116+40%×11
5
169÷(83+161) (1924+17
16)×81+1715
(31-61+41)×12 47×85+41÷5
8
五、解决问题
1、水果店买进橘子150千克,比苹果的75%还少30千克。
水果店买进苹果多少千克?(列方程)
3、数学兴趣小组的同学测量一棵大树的高度,因工具有限只测得了这棵树的影长是5米,同时还测得旁边的一棵小树高1.8米,影长1米。
请你计算出这棵大树的高度?
4、 左图是王老师在电脑上下载一份文件的过程示意图
电脑显示,下载这份文件已经用了16分钟,照这样的速度,王老师还要等多少分钟才能下载完这份文件。
5、用边长3分米的方砖给一间教室铺地,要600块,如果改用边长5分米的方砖来铺,需要多少块?(用比例解)
6、一个用塑料薄膜制作的蔬菜大棚,长20米,横截面是一个半径2米的半圆。
(1)这个大棚的种植面积是多少平方米?
(2) 制作这个大棚用塑料薄膜约多少平方米?
(3) 大棚内的空间大约有多大?
7、圆柱的底面半径和高都是2厘米,把它浸入一个均匀水槽内的水中,量得水位上升了4厘
米。
再把一个底面直径为6厘米的圆锥浸入水中,水位又上升了4.5厘米。
求圆锥的高。
8、一个圆锥形的沙堆,底面周长是18.84米,高1.2米。
把它均匀铺在宽为10米的公路上,厚度为2厘米,
可以铺多少米?。
