常用体积和表面积计算公式

合集下载

几何体的表面积和体积公式大全

几何体的表面积和体积公式大全几何体的表面积,体积计算公式1、圆柱体:表面积:2πRr+2πRh 体积:πR²h (R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR²+πR[(h²+R²)的平方根] 体积:πR²h/3 (r为圆锥体低圆半径,h为其高, 3、正方体a－边长,S＝6a²,V＝a³4、长方体a－长,b－宽,c－高S＝2(ab+ac+bc) V＝abc5、棱柱S－底面积h－高V＝Sh6、棱锥S－底面积h－高V＝Sh/37、棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S2)^1/2]/38、拟柱体S1－上底面积,S2－下底面积,S0－中截面积h－高,V＝h(S1+S2+4S0)/69、圆柱r－底半径,h－高,C—底面周长S底—底面积,S侧—侧面积,S表—表面积C＝2πrS底＝πr²,S侧＝Ch ,S表＝Ch+2S底,V＝S底h＝πr²h10、空心圆柱R－外圆半径,r－内圆半径h－高V＝πh(R^2-r^2)11、直圆锥r－底半径h－高V＝πr^2h/312、圆台r－上底半径,R－下底半径,h－高V＝πh(R²＋Rr＋r²)/313、球r－半径d－直径V＝4/3πr^3＝πd^3/614、球缺h－球缺高,r－球半径,a－球缺底半径V＝πh(3a²+h²)/6 ＝πh²(3r-h)/315、球台r1和r2－球台上、下底半径h－高V＝πh[3(r1²＋r2²)+h²]/616、圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr²＝π2Dd²/417、桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D²＋d²)/12 ,(母线是圆弧形,圆心是桶的中心)V＝πh(2D²＋Dd＋3d²/4)/15 (母线是抛物线形)。

体积、表面积计算公式大全

图形
立方体
长方体 ∧ 棱柱 ∨
三棱柱
学习必备
欢迎下载
多面体的体积和表面积
尺寸符号
棱锥柱 ∧ 管 ∨
斜线直圆柱
直圆锥
圆台
球
球扇形 ∧ 球楔 ∨
学习必备
欢迎下载
球缺
圆环体 ∧ 胎 ∨
球带体
桶形
椭
球
a,b,c-半轴
欢迎下载
新月形
抛物线形
等多边形
体
交叉圆柱体
学习必备
欢迎下载
梯形体
常用图形求面积公式
图形
正方形
长方形
三角形
平行四边形任意四边形
正多边形
尺寸符号
面积（F）表面积（S）
学习必备
欢迎下载
菱形
梯形
圆形
椭
圆
a·b-主轴
F= (π/4) a·b
形
扇形
弓形
圆环
部分圆环
学习必备

常用图形周长面积体积计算公式

常⽤图形周长⾯积体积计算公式常⽤图形周长⾯积体积计算公式:1、正⽅形C周长S⾯积a边长周长=边长×4⾯积=边长×边长C=4aS=a×a S=a22、正⽅体V体积a棱长(1)表⾯积=棱长×棱长×6 (2)体积=棱长×棱长×棱长S表=a×a×6 表=6a2 V=a×a×a V= a33、长⽅形C周长S⾯积a边长周长=(长+宽)×2C=2(a+b)⾯积=长×宽S=ab4、长⽅体V体积S⾯积a长b宽h⾼(1)表⾯积=(长×宽+长×⾼+宽×⾼)×2(2)体积=长×宽×⾼S=2(ab+ah+bh)V=abh5、三⾓形S⾯积a底h⾼⾯积=底×⾼÷2S=ah÷2三⾓形⾼=⾯积×2÷底三⾓形底=⾯积×2÷⾼6、平⾏四边形S⾯积a底h⾼⾯积=底×⾼S=ah7、梯形S⾯积a上底b下底h⾼⾯积=(上底+下底)×⾼÷2S=(a+b)×h÷28、圆形S⾯积C周长π圆周率d直径r半径周长=直径×π周长=2×π×半径⾯积=半径×半径×πC=πd C=2πrS=πr2 d=C÷πd=2r r=d÷2r=C÷2÷πS环=π(R2-r2)9、圆柱体V体积h⾼S底⾯积r底⾯半径C底⾯周长侧⾯积=底⾯周长×⾼(2)表⾯积=侧⾯积+底⾯积×2(3)体积=底⾯积×⾼S侧=ChS侧=πdhV=Sh V=πr2h圆柱体积=侧⾯积÷2×半径10、圆锥体V体积h⾼S底⾯积r底⾯半径体积=底⾯积×⾼÷3V=Sh÷3长度单位换算1千⽶=1000⽶；1⽶=10分⽶；1分⽶=10厘⽶；1⽶=100厘⽶；1厘⽶=10毫⽶⾯积单位换算1平⽅千⽶=100公顷；1公顷=10000平⽅⽶；1平⽅⽶=100平⽅分⽶；1平⽅分⽶=100平⽅厘⽶；1平⽅厘⽶=100平⽅毫⽶；1平⽅⽶＝0.0015亩；1万平⽅⽶=15亩；1公顷＝15亩＝100公亩＝10000平⽅⽶；1公亩等于100平⽅⽶；1(市)亩等于666.66平⽅⽶体(容)积单位换算1⽴⽅⽶=1000⽴⽅分⽶；1⽴⽅分⽶=1000⽴⽅厘⽶；1⽴⽅分⽶=1升；1⽴⽅厘⽶=1毫升；1⽴⽅⽶=1000升重量单位换算1吨=1000千克；1千克=1000克；1千克=1公⽄⼈民币单位换算1元=10⾓；1⾓=10分；1元=100分时间单位换算1世纪=100年；1年=12⽉；⼤⽉(31天)有:1\3\5\7\8\10\12⽉；⼩⽉(30天)的有:4\6\9\11⽉平年2⽉28天,闰年2⽉29天；平年全年365天,闰年全年366天1⽇=24⼩时1时=60分；1分=60秒1时=3600秒总数÷总份数＝平均数和差问题的公式：(和＋差)÷2＝⼤数；(和－差)÷2＝⼩数和倍问题：和÷(倍数－1)＝⼩数⼩数×倍数＝⼤数(或者和－⼩数＝⼤数)差倍问题：差÷(倍数－1)＝⼩数⼩数×倍数＝⼤数(或⼩数＋差＝⼤数)植树问题1、⾮封闭线路上的植树问题主要可分为以下三种情形:⑴如果在⾮封闭线路的两端都要植树,那么:株数＝段数＋1＝全长÷株距－1全长＝株距×(株数－1)株距＝全长÷(株数－1)⑵如果在⾮封闭线路的⼀端要植树,另⼀端不要植树,那么:株数＝段数＝全长÷株距全长＝株距×株数株距＝全长÷株数⑶如果在⾮封闭线路的两端都不要植树,那么:株数＝段数－1＝全长÷株距－1全长＝株距×(株数＋1)株距＝全长÷(株数＋1)2、封闭线路上的植树问题的数量关系如下株数＝段数＝全长÷株距全长＝株距×株数株距＝全长÷株数盈亏问题(盈＋亏)÷两次分配量之差＝参加分配的份数(⼤盈－⼩盈)÷两次分配量之差＝参加分配的份数(⼤亏－⼩亏)÷两次分配量之差＝参加分配的份数相遇问题相遇路程＝速度和×相遇时间相遇时间＝相遇路程÷速度和速度和＝相遇路程÷相遇时间追及问题追及距离＝速度差×追及时间追及时间＝追及距离÷速度差速度差＝追及距离÷追及时间顺流速度＝静⽔速度＋⽔流速度逆流速度＝静⽔速度－⽔流速度静⽔速度＝(顺流速度＋逆流速度)÷2⽔流速度＝(顺流速度－逆流速度)÷2浓度问题溶质的重量＋溶剂的重量＝溶液的重量溶质的重量÷溶液的重量×100%＝浓度溶液的重量×浓度＝溶质的重量溶质的重量÷浓度＝溶液的重量利润与折扣问题利润＝售出价－成本利润率＝利润÷成本×100%＝(售出价÷成本－1)×100%涨跌⾦额＝本⾦×涨跌百分⽐折扣＝实际售价÷原售价×100%(折扣＜1)利息＝本⾦×利率×时间税后利息＝本⾦×利率×时间×(1－20%)定义定理公式（⼀）三⾓形的⾯积＝底×⾼÷2。

体积与表面积的关系

体积与表面积的关系体积与表面积是几何学中的两个重要概念，它们在数学和物理学等领域中具有广泛的应用。

本文将探讨体积与表面积之间的关系，并分析其中的数学原理和物理应用。

一、体积的定义与计算公式体积是三维物体所占据的空间大小。

对于规则几何体，我们可以使用特定的公式来计算其体积：1. 正方体和长方体的体积公式：正方体的体积公式为V = a³，其中a表示正方体的边长。

长方体的体积公式为V = l × w × h，其中l、w和h分别表示长方体的长、宽和高。

2. 圆柱体和圆锥体的体积公式：圆柱体的体积公式为V = πr²h，其中r表示底面半径，h表示高度。

圆锥体的体积公式为V = (1/3)πr²h，其中r表示底面半径，h表示高度。

3. 球体的体积公式：球体的体积公式为V = (4/3)πr³，其中r表示球体的半径。

二、表面积的定义与计算公式表面积是三维物体外部所占据的面积大小。

同样地，对于规则几何体，我们可以使用特定的公式来计算其表面积：1. 正方体和长方体的表面积公式：正方体的表面积公式为A = 6a²，其中a表示正方体的边长。

长方体的表面积公式为A = 2lw + 2lh + 2wh，其中l、w和h分别表示长方体的长、宽和高。

2. 圆柱体和圆锥体的表面积公式：圆柱体的表面积公式为A = 2πr² + 2πrh，其中r表示底面半径，h表示高度。

圆锥体的表面积公式为A = πr² + πrl，其中r表示底面半径，l表示斜高线（母线）的长度。

3. 球体的表面积公式：球体的表面积公式为A = 4πr²，其中r表示球体的半径。

三、体积与表面积的关系体积和表面积之间存在一定的关系，特别是对于某些几何体而言。

以立方体为例，我们可以观察到体积和表面积之间的关系：对于边长为a的正方体来说，它的体积和表面积分别为V = a³、A = 6a²。

常用面积体积计算公式

常用面积、体积计算公式长方形的周长=（长+宽）×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=（长×宽+长×高＋宽×高）×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体（正方体、圆柱体）的体积=底面积×高平面图形名称符号周长C和面积S正方形a—边长C＝4aS＝a2长方形a和b－边长C＝2(a+b) S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πrS＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα) ＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－内圆半径D－外圆直径d－内圆直径S＝π(R2-r2)＝π(D2-d2)/4椭圆D－长轴d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3 拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积S表—表面积C＝2πrS底＝πr2S侧＝ChS表＝Ch+2S底V＝S底h＝πr2h空心圆柱R－外圆半径r－内圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6 ＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6 圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D2＋d2)/12(母线是圆弧形,圆心是桶的中心) V＝πh(2D2＋Dd＋3d2/4)/15 (母线是抛物线形)。

长方体、正方体的表面积和体积计算

复习三长方体和正方体的表面积和体积计算一、基本公式：正方体表面积 = 棱长×棱长×6= 一个面的面积×6正方体体积 = 棱长×棱长×棱长长方体表面积 = （长×宽＋长×高＋宽×高）×2长方体体积 = 长×宽×高正方体、长方体都有12条棱、6个面。

正方体的棱长和=棱长×12长方体的棱长和=（长＋宽＋高）×4二、认识表面积和体积做一个长12厘米，宽6厘米，高5厘米的长方体框架，至少需要铁丝多少厘米？在这个框架外糊一层纸，至少需多少平方厘米的纸，这个纸盒占空间多少立方厘米？三、典型习题1、用铁丝焊成图形/绣花边棱长例题：用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米,宽7厘米的长方体框架,它的高应该是多少厘米?2、占地面积即底面的面积例题：有一个长20米，宽15米，深5米的长方体游泳池，该游泳池占地面积有多大？3、贴瓷砖/给墙壁粉刷面积，要注意是几个面，是否要减门窗等例题：天天游泳池,长25米,宽10米,深1.6米,在游泳池的四周和池底砌瓷砖,如果瓷砖的边长是1分米的正方形,那么至少需要这种瓷砖多少块？4例题：一个带盖的长方体木箱,体积是0.576立方米,它的长是12分米,宽是8分米,做这样一个木箱至少要用木板多少平方米?5、一物体放置入令一盛水容器体积不变，上升水的体积即该物体的体积例题：有一个底面积是300平方厘米、高10厘米的长方体，里面盛有5厘米深的水。

现在把一块石头浸没到水里，水面上升2厘米。

这块石头的体积是多少立方厘米？6、铁块熔铸成另一图形前后体积不变例题：有一块棱长是80厘米的正方体的铁块，现在要把它溶铸成一个横截面积是20平方厘米的长方体，这个长方体的长是多少厘米？7、切锯后截面积截a次，增加2a个截面，成为a＋1段例题：把长1.2米的长方体木料锯成3段，表面积增加48平方分米，原来木料的体积是多少？解题的方法：1、判断是求体积、表面积、棱长、还是单个面的面积？2、根据单位来帮助判断是面积还是体积，还是棱长；练习巩固一、判断1．体积单位比面积单位大，面积单位比长度单位大．（）2．正方体和长方体的体积都可以用底面积乘高来进行计算．（）3．表面积相等的两个长方体，它们的体积一定相等．（）4．长方体的体积就是长方体的容积．（）5．如果一个长方体能锯成四个完全一样的正方体，那么长方体前面的面积是底面积的4倍．（）6、正方体的棱长扩大3倍，体积就扩大9倍。

表面积与体积公式

在数学中，表面积和体积是基本的几何概念。

表面积指物体外部所覆盖的空间面积，体积则指物体占据的空间大小。

对于各种形状的物体，我们可以通过不同的公式来计算它们的表面积和体积。

一、常见几何图形的表面积和体积公式1.立方体立方体是一种正六面体，所有六个面都是正方形。

它的表面积和体积公式如下：表面积S = 6a²其中，a为立方体的边长。

体积V = a³2.正方体正方体也是一种正六面体，但是它的所有面都是正方形且相等。

它的表面积和体积公式如下：表面积S = 6a²其中，a为正方体的边长。

体积V = a³3.圆柱体圆柱体是一种由两个平行圆面和一个侧面组成的几何图形。

它的表面积和体积公式如下：表面积S = 2πrh + 2πr²其中，r为圆柱体底面半径，h为圆柱体的高度。

体积V = πr²h4.圆锥体圆锥体是一种由一个圆锥面和一个底面组成的几何图形。

它的表面积和体积公式如下：表面积S = πr√(r²+h²) + πr²其中，r为圆锥底面半径，h为圆锥的高度。

体积V = 1/3πr²h5.球体球体是一种三维的几何图形，由所有与一个特定点的距离相等的点组成。

它的表面积和体积公式如下：表面积S = 4πr²其中，r为球体的半径。

体积V = 4/3πr³二、总结通过以上几种几何图形的表面积和体积公式，我们可以看出它们的计算方式都是基于图形的不同属性进行推导的。

在应用时，我们需要了解图形的性质和特征，然后选择适当的公式进行计算。

掌握这些公式可以帮助我们更好地理解几何概念，同时也方便我们在实际生活和工作中应用数学知识。

常用面积体积公式

常用面积体积公式在几何学中，面积和体积是两个十分重要的概念。

面积是用来衡量平面上的二维形状所占据的空间大小，而体积则是用来衡量三维形状所占据的空间大小。

在计算面积和体积时，我们可以利用一些常用的公式来简化计算过程。

下面是一些常用的面积和体积公式：1.矩形的面积公式：矩形的面积可以通过其宽度w和长度l相乘得到。

公式为：面积=长度×宽度，即A=l×w。

2.正方形的面积公式：正方形的面积可以通过其边长s的平方得到。

公式为：面积=边长×边长，即A=s^23.三角形的面积公式：三角形的面积可以通过其底边长b和高h的乘积再除以2得到。

公式为：面积=(底边长×高)/2，即A=(b×h)/24.平行四边形的面积公式：平行四边形的面积可以通过其底边长b和高h的乘积得到。

公式为：面积=底边长×高，即A=b×h。

5.梯形的面积公式：梯形的面积可以通过其上底a、下底b和高h的乘积再除以2得到。

公式为：面积=(上底+下底)×高/2，即A=(a+b)×h/26.圆的面积公式：圆的面积可以通过其半径r的平方乘以圆周率π得到。

公式为：面积=半径^2×π，即A=r^2×π。

7.球体的表面积和体积公式：球体的表面积可以通过其半径r的平方乘以4再乘以圆周率π得到。

公式为：表面积=4×半径^2×π，即A=4×r^2×π。

球体的体积可以通过其半径r的立方乘以4再除以3再乘以圆周率π得到。

公式为：体积=4/3×半径^3×π，即V=4/3×r^3×π。

8.立方体的体积公式：立方体的体积可以通过其边长s的立方得到。

公式为：体积=边长^3，即V=s^39.长方体的体积公式：长方体的体积可以通过其长l、宽w和高h的乘积得到。

公式为：体积=长×宽×高，即V=l×w×h。

常用面积体积公式大全

常用面积体积公式大全在日常生活和学习中，我们经常会遇到需要计算面积和体积的问题。

掌握常用的面积和体积公式可以帮助我们更快、更准确地解决这些问题。

下面是一些常见的面积和体积公式：1.矩形的面积公式：矩形的面积=长×宽2.正方形的面积公式：正方形的面积=边长×边长3.三角形的面积公式：三角形的面积=底边长×高÷24.梯形的面积公式：梯形的面积=(上底+下底)×高÷25.平行四边形的面积公式：平行四边形的面积=底边长×高6.圆的面积公式：圆的面积=π×半径×半径7.正圆锥的体积公式：正圆锥的体积=圆锥的底面积×高÷3=π×半径×半径×高÷38.球体的体积公式：球体的体积=4/3×圆的面积×半径9.直角梯形的体积公式：直角梯形的体积=(上面积+下面积+上底×下底)×高÷310.圆柱体的体积公式：圆柱体的体积=圆的面积×高=π×半径×半径×高11.弧长公式：弧长=θ×半径其中，θ为弧度（以弧长所对的圆心角所对应的弧长）12.扇形面积公式：扇形的面积=θ×π×半径×半径÷360°其中，θ为弧度（以弧长所对的圆心角所对应的弧度）13.椭圆的面积公式：椭圆的面积=π×长轴×短轴14.菱形的面积公式：菱形的面积=对角线1×对角线2÷215.立方体的体积公式：立方体的体积=边长×边长×边长16.正方体的表面积公式：正方体的表面积=6×边长×边长17.圆柱体的侧面积公式：圆柱体的侧面积=π×直径×高18.圆锥的侧面积公式：圆锥的侧面积=π×半径×斜高19.球体的表面积公式：球体的表面积=4×π×半径×半径20.圆锥的全面积公式：圆锥的全面积=圆锥的侧面积+圆锥的底面积通过掌握上述面积和体积公式，我们可以在实际问题中快速准确地进行求解。

几何体的表面积和体积公式

几何体的表面积和体积公式一、柱体。

1. 棱柱。

- 表面积公式：- 直棱柱的表面积S = 2S_底+S_侧，其中S_底为底面多边形的面积，S_侧为侧面积。

若直棱柱底面多边形的边长为a，边数为n，棱柱的高为h，则S_侧=nah。

- 体积公式：V = S_底h，h为棱柱的高。

2. 圆柱。

- 表面积公式：S = 2π r^2+2π rh，其中r为底面半径，h为圆柱的高。

- 体积公式：V=π r^2h。

二、锥体。

1. 棱锥。

- 表面积公式：S = S_底+S_侧，棱锥的侧面积S_侧等于各个侧面三角形面积之和。

若棱锥底面多边形的边长为a，边数为n，斜高（侧面三角形底边上的高）为h'，则S_侧=(1)/(2)nah'。

- 体积公式：V=(1)/(3)S_底h，h为棱锥的高。

2. 圆锥。

- 表面积公式：S=π r^2+π rl，其中r为底面半径，l为母线长。

- 体积公式：V = (1)/(3)π r^2h，h为圆锥的高。

三、台体。

1. 棱台。

- 表面积公式：S = S_上底+S_下底+S_侧，棱台的侧面积S_侧=(1)/(2)(n(a + b)h')，其中n为底面边数，a为上底面多边形的边长，b为下底面多边形的边长，h'为斜高。

- 体积公式：V=(1)/(3)h(S_上底+S_下底+√(S_上底)S_{下底})，h为棱台的高。

2. 圆台。

- 表面积公式：S=π r^2+π R^2+π l(R + r)，其中r为上底面半径，R为下底面半径，l为母线长。

- 体积公式：V=(1)/(3)π h(r^2+R^2+rR)，h为圆台的高。

四、球体。

- 表面积公式：S = 4π R^2，其中R为球的半径。

- 体积公式：V=(4)/(3)π R^3。

各种形体面积体积计算公式

各种形体面积体积计算公式以下是一些常见的形体面积和体积计算公式，其中包括平面图形、三维立体图形和球体的计算公式。

平面图形的面积计算公式：1.长方形的面积：面积=长×宽2.正方形的面积：面积=边长×边长3.圆的面积：面积=π×半径×半径4.椭圆的面积：面积=π×长半轴×短半轴5.三角形的面积（已知底和高）：面积=底×高÷26.三角形的面积（已知三边）：面积=√[s×(s-a)×(s-b)×(s-c)]，其中s=(a+b+c)÷2，a、b、c分别为三角形的三边。

三维立体图形的表面积和体积计算公式：1.立方体的表面积：表面积=6×边长×边长2.立方体的体积：体积=边长×边长×边长3.直方体的表面积：表面积=2×(长×宽+长×高+宽×高)4.直方体的体积：体积=长×宽×高5.圆柱体的表面积：表面积=2×π×半径×(半径+高)6.圆柱体的体积：体积=π×半径×半径×高7.圆锥体的表面积：表面积=π×半径×(半径+斜高)8.圆锥体的体积：体积=1/3×π×半径×半径×高9.球体的表面积：表面积=4×π×半径×半径10.球体的体积：体积=(4/3)×π×半径×半径×半径还有一些特殊形状的面积和体积计算公式：1.梯形的面积：面积=(上底+下底)×高÷22.抛物线围成的区域的面积：面积=π×（r2^2-r1^2），其中r1和r2分别是抛物线上两个不同半径的值3.球冠体的表面积：表面积=2×π×半径×（半径+斜高）4.球冠体的体积：体积=(1/3)×π×(高×高×高-底面积×高)，其中底面积为半径×半径×π以上公式只是一些常见形体的面积和体积计算公式，实际应用中可能会遇到更多特殊的情况需要使用其他公式进行计算。

空间几何体的表面积和体积公式大全

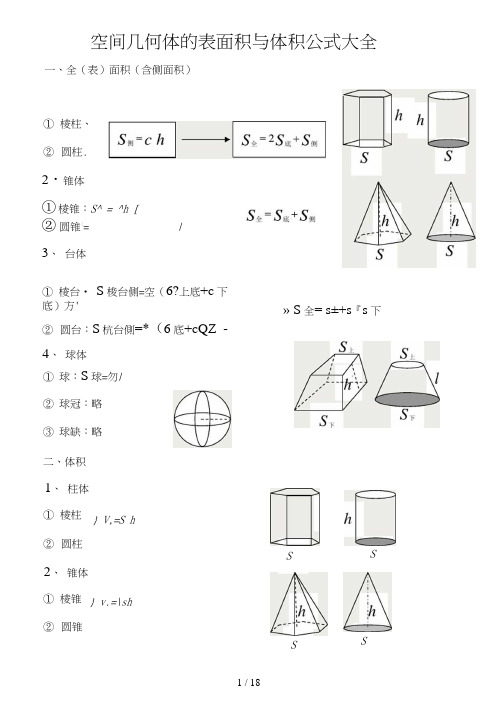
空间几何体的表面积与体积公式大全一、全（表）面积（含侧面积）①棱柱、②圆柱.2・锥体①棱锥：S^ = ^h [②圆锥:= /3、台体①棱台• S梭台侧=空（6?上底+c下底）方'» S全= s±+s『s下②圆台：S杭台側=*（6底+cQZ -4、球体①球：S球=勿/②球冠：略③球缺：略二、体积1、柱体①棱柱} V,=S h②圆柱S S 2、锥体①棱锥} v.=\sh②圆锥S S3、台体V 台肓//（S 匕+ JS 上S F + S 下）台=齐方（厂上+Jr 上厂下+厂下） 4、球体①球：V 球② 球冠：略VyT/③ 球缺：略说明：棱锥、棱台计算侧面积时使用侧面的斜高力计算；而圆锥、圆台的侧面积计算时使用母线/计算。

三、拓展提高1、祖眶原理：（祖璀：祖冲之的儿子）夹在两个平行平面间的两个几何体，如果它们在任意高度上的平行截面面积都相等，那么这两个几何体的体积相等。

最早推导出球体体积的祖冲之父子便是运用这个原理实现的。

2、阿基米德原理：（圆柱容球）圆柱容球原理：在一个高和底面直径都是2厂的圆柱形容器内装一个最大的球体，则该球体的全面积等于圆柱的侧面积，体积等于圆柱体积的？。

①棱台 ②圆台丿分析：圆柱体积：V H1 = s h =（^r）x2r = 2^/圆柱侧面积：S叭削= c/z = （2岔）X2广=4兀/2 彳4 彳因lit :球体体积：|/厅=—x2/r^ =_龙厂球体表面积：S球=4兀厂通过上述分析，我们可以得到一个很重要的关系（如图）即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和3、台体体积公式公式：几冷〃（S上+、恳瓦+ S』证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD。

延长两侧棱相交于一点P 0设台体上底面积为Si，下底面积为S下高为// °易知：\PDCs 型AB，设卩£ =人，则Pf+h由相似三角形的性质得：孚=袋AB PF即：（相似比等于面积比的算术平方根）、用hi整理得：人=尺刃又因为台体的体积二大锥体体积一小锥体体积u台=§s下（九+力r s上人人（S下-S上）+§s下方即：（、瓦+丫瓦）+扣下力=|/z $ + 应7+S卜）4、球体体积公式推导分析：将半球平行分成相同高度的若干层（兀层），〃越大，每一层越近似于圆柱'"T -HZ）时»每一层都可以看作是一个圆柱。

体积和表面积的计算公式

体积和表面积的计算公式体积和表面积是数学和物理中非常重要的概念，广泛应用于各个领域。

无论是求解立方体、球体还是其他各种几何体的体积和表面积问题，我们都可以套用相应的计算公式进行计算。

1. 立方体的计算公式立方体是最简单的一种几何体，其形状规则且具有六个相等的面。

根据立方体的定义我们知道，其体积等于边长的立方，表面积等于六个面的总和。

- 体积计算公式：V = a^3，其中V表示体积，a表示边长。

- 表面积计算公式：S = 6a^2，其中S表示表面积，a表示边长。

2. 圆柱体的计算公式圆柱体是由两个平行的圆面和一个侧面围成的几何体，体积和表面积的计算公式需要考虑到圆的性质。

- 体积计算公式：V = πr^2h，其中V表示体积，r表示圆的半径，h 表示圆柱体的高度。

- 表面积计算公式：S = 2πrh + 2πr^2，其中S表示表面积，r表示圆的半径，h表示圆柱体的高度。

3. 球体的计算公式球体是由所有距离球心相等的点组成的几何体，是一种完整封闭的几何体。

求解球体的体积和表面积需要用到球的半径。

- 体积计算公式：V = (4/3)πr^3，其中V表示体积，r表示球的半径。

- 表面积计算公式：S = 4πr^2，其中S表示表面积，r表示球的半径。

4. 锥体的计算公式锥体是由一个底面和一个顶点以及连接两者的曲面组成的几何体。

计算锥体的体积和表面积需要考虑到锥的底面和侧面的形状。

- 体积计算公式：V = (1/3)πr^2h，其中V表示体积，r表示底面的半径，h表示锥体的高度。

- 表面积计算公式：S = πr(r + l)，其中S表示表面积，r表示底面的半径，l表示锥体的斜高。

综上所述，体积和表面积的计算公式因几何体的不同而不同。

通过套用相应的计算公式，我们可以准确地求解各种几何体的体积和表面积问题。

这些公式在实际应用中非常重要，特别是在工程建模、几何计算和物理相关领域中发挥着重要作用。

体积面积计算公式大全

体积面积计算公式大全一、二维图形1.正方形-面积公式：A=a×a，其中a为正方形的边长。

2.长方形-面积公式：A=l×w，其中l为长方形的长度，w为长方形的宽度。

3.圆4.三角形-面积公式：A=0.5×b×h，其中b为三角形的底边长，h为三角形的高度。

5.梯形-面积公式：A=0.5×(a+b)×h，其中a为梯形的上底边长，b为梯形的下底边长，h为梯形的高度。

6.平行四边形-面积公式：A=b×h，其中b为平行四边形的底边长，h为平行四边形的高度。

7.菱形-面积公式：A=0.5×d1×d2，其中d1和d2为菱形的对角线。

二、三维图形1.立方体-体积公式：V=a×a×a，其中a为立方体的边长。

-表面积公式：S=6×a×a，其中a为立方体的边长。

2.长方体-体积公式：V=l×w×h，其中l为长方体的长度，w为长方体的宽度，h为长方体的高度。

- 表面积公式：S = 2lw + 2lh + 2wh。

3.圆柱体-体积公式：V=π×r²×h，其中r为圆柱体的底面半径，h为圆柱体的高度。

- 表面积公式：S = 2πrh + 2πr²。

4.圆锥体-体积公式：V=(1/3)×π×r²×h，其中r为圆锥体的底面半径，h为圆锥体的高度。

-表面积公式：S=πr(r+√(r²+h²))。

5.球体-体积公式：V=(4/3)×π×r³，其中r为球体的半径。

-表面积公式：S=4πr²。

6.棱锥体-体积公式：V=(1/3)×Bh，其中B为棱锥体的底面积，h为棱锥体的高度。

-表面积公式：S=B+L，其中B为底面积，L为斜面面积。

7.棱柱体-体积公式：V=Bh，其中B为棱柱体的底面积，h为棱柱体的高度。

数学高中所有体积,表面积的计算公式

数学高中所有体积，表面积的计算公式长方形的周长=（长+宽）×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=（长×宽+长×高＋宽×高）×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体（正方体、圆柱体）的体积=底面积×高平面图形名称符号周长C和面积S正方形a—边长C＝4aS＝a2长方形a和b－边长C＝2(a+b) S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πrS＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα) ＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－内圆半径D－外圆直径d－内圆直径S＝π(R2-r2)＝π(D2-d2)/4椭圆D－长轴d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3 拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积S表—表面积C＝2πrS底＝πr2S侧＝ChS表＝Ch+2S底V＝S底h＝πr2h空心圆柱R－外圆半径r－内圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6 ＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6 圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D2＋d2)/12 (母线是圆弧形,圆心是桶的中心) V＝πh(2D2＋Dd＋3d2/4)/15 (母线是抛物线形)。

小学数学公式：面积与体积

小学数学公式：面积与体积1、长方形的周长=(长+宽)×2C=(a+b)×22、正方形的周长=边长×4C=4a3、长方形的面积=长×宽S=ab4、正方形的面积=边长×边长S=a.a=a5、三角形的面积=底×高÷2S=ah÷26、平行四边形的面积=底×高S=ah7、梯形的面积=(上底+下底)×高÷2S=(a+b)h÷28、直径=半径×2d=2r半径=直径÷2r=d÷29、圆的周长=圆周率×直径=圆周率×半径×2c=πd=2πr10、圆的面积=圆周率×半径×半径？=πr11、长方体的表面积=(长×宽+长×高+宽×高)×212、长方体的体积=长×宽×高V=abh13、正方体的表面积=棱长×棱长×6S=6a14、正方体的体积=棱长×棱长×棱长V=a.a.a=a15、圆柱的侧面积=底面圆的周长×高S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr+2πrh=2π(d÷2)+2π(d÷2)h=2π(C÷2÷π)+Ch17、圆柱的体积=底面积×高V=ShV=πrh=π(d÷2)h=π(C÷2÷π)h唐宋或更早之前，针对“经学”“律学”“算学”和“书学”各科目，其相应传授者称为“博士”，这与当今“博士”含义差不多相去甚远。

而对那些专门讲授“武事”或讲解“经籍”者，又称“讲师”。

“教授”和“助教”均原为学官称谓。

前者始于宋，乃“宗学”“律学”“医学”“武学”等科目的讲授者；而后者则于西晋武帝时代即已设立了，要紧协助国子、博士培养生徒。