(冲刺高考)2021年春辉教育云平台高考考前提分试卷 理 科 数 学 (十) 学生版 含答案
2021年春辉教育云平台高三最新金牌试卷 理科数学 (十一) 教师版

2021年春辉教育云平台高三最新金牌试卷理 科 数 学(十一)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4、考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2019·焦作模拟]已知集合,,则的所有元素之和为( )A .21B .17C .15D .13 【答案】C【解析】依题意,得,所以,所以的所有元素之和为.故答案为C .2.[2019·宣城调研]复数满足,为虚数单位,则的共轭复数( )A .1B .C .2D .【答案】D【解析】由,,所以的共轭复数为,故选D .3.[2019·南开中学]在平面直角坐标系中,角的顶点与原点重合,始边与的非负半轴重合,终边过点,则( )A .B .C .D .【答案】A【解析】角的终边过点,则,则,故选A .4.[2019·汉中质检]双曲线的离心率恰为它一条渐近线斜率的2倍,则离心率为( )A .B .C .D .【答案】A【解析】由题意可知,即,而,得,因此本题选A .5.[2019·维吾尔适应]正项等差数列的前项和为,已知,则( )A .35B .36C .45D .55 【答案】D 【解析】由是等差数列,得, 因为,所以,或,又,得,所以,故选D .6.[2019东北模拟]已知,为两条不重合直线,,为两个不重合平面,下列条件中,的充分条件是( ) A .,, B .,,C .,,D .,,【答案】B 【解析】当时,若,可得,此卷只装订不密封班级 姓名 准考证号 考场号 座位号又,可知本题正确选项B.7.[2019·广州毕业]函数的部分图像如图所示,先把函数图像上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的图像向右平移个单位长度,得到函数的图像,则函数的图像的一条对称轴为()A.B.C.D.【答案】C【解析】由图得,,,从而,,,,,,故选C.8.[2019·邯郸一模]过点引曲线的两条切线,这两条切线与轴分别交于,两点,若,则()A.B.C.D.【答案】B【解析】设切点坐标为,,,即,解得或.,,即,故,故选B.9.[2019·宣城调研]一个几何体的三视图如图所示,在该几何体的各个面中,最大面积是()A.2B.C.D.4【答案】C【解析】如图所示,由三视图可知:该几何体是四棱锥截去三棱锥后得到的三棱锥.其中四棱锥中,底面是正方形,底面,且,最大面为,,故选C.10.[2019·唐山二模]割补法在我国古代数学著作中称为“出入相补”,刘徽称之为“以盈补虚”,即以多余补不足,是数量的平均思想在几何上的体现.如图揭示了刘徽推导三角形面积公式的方法.在内任取一点,则该点落在标记“盈”的区域的概率为()A.B.C.D.【答案】B【解析】由题“盈”部分的面积为,又的面积为,则该点落在标记“盈”的区域的概率为,故选B.11.[2019·大连模拟]已知抛物线的焦点为,点在抛物线上,以为边作一个等边三角形,若点在抛物线的准线上,则()A.1B.2C.D.【答案】B【解析】抛物线的焦点坐标,由抛物线的定义可得等于到准线的距离,因为,在准线上,所以与准线垂直与轴平行,因为三角形为正三角形,所以,可得直线,可得,可得,则,,等于到准线的距离,故选B.12.[2019·唐山二模]已知,,,则,,的大小关系是()A.B.C.D.【答案】B【解析】,故,又,故,故,即,又,故,故,即,所以,综上,故选B.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2019·黄山质检]若整数..,满足不等式组,则的最小值为_______.【答案】【解析】画出可行域如下图所示,依题意只取坐标为整数的点.由图可知,在点处,目标函数取得最小值为.14.[2019·保定期末]元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,若最终输出的,则开始时输入的的值为_______.【答案】【解析】第一次输入,,执行循环体,,,执行循环体,,,执行循环体,,,输出的值为0,解得,故答案为.15.[2019·南阳一中]已知非零向量满足则向量与的夹角为______.【答案】【解析】对进行平方,可得,化简整理得,,故,所以,又因为,所以.16.[2019·海安中学]已知数列的通项公式是,数列的通项公式是,集合,,,将集合中的元素按从小到大的顺序排列构成的数列记为,则数列的前45项和_______.【答案】2627【解析】因为数列的通项公式是,所以集合,随着增大时,数列中前后连续两项之间的差值越来越大,故考虑在中的前后连续两项之间插入数列中相应大小的项,因为是选取新数列的前45项,故,,数列中无项可插入,,,数列中无项可插入,,,数列中可插入,增加1项,共5项,,,数列中可插入,,增加2项,共8项,,,数列中可插入,增加5项,共14项,,,数列中可插入,增加10项,共25项,接下来只需再增加中的20项即可,也就是中从(含)开始的连续的20项,因为,故终止于.则.三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.17.(12分)[2019·桂林一模]如图所示,在平面四边形中,,的面积是2.(1)求的大小;(2)若,求线段的长.【答案】(1);(2).【解析】(1)在中,,,解得,.(2)由,,得到,,,,,在中,由正弦定理有,即,在中由余弦定理有:,.18.(12分)[2019·四川质检]如图,在三棱柱,侧面,.(1)求证:平面平面;(2)若,,求二面角的余弦值.【答案】(1)见解析;(2).【解析】(1)如图,设,连接.因为三棱柱的侧面为平行四边形,所以为的中点,因为,所以为等腰三角形,所以,又因为侧面,且平面,所以,又因为,所以平面,又因为平面,所以平面平面.(2)由(1)知平面,所以,以为坐标原点,以的方向为轴正方向,以的方向为轴正方向,建立如图所示的空间直角坐标系.由易知四边形为菱形,因为,,所以,,则可得,,,,所以,,设平面的法向量,由,得,取,所以,由(1)知为平面的法向量,则,易知二面角的余弦值.19.(12分)[2019·安庆联考]2018年“双十一”全网销售额达亿元,相当于全国人均消费225元,同比增长,监测参与“双十一”狂欢大促销的22家电商平台有天猫、京东、苏宁易购、网易考拉在内的综合性平台,有拼多多等社交电商平台,有敦煌网、速卖通等出口电商平台.某大学学生社团在本校1000名大一学生中采用男女分层抽样,分别随机调查了若干个男生和60个女生的网购消费情况,制作出男生的频率分布表、直方图(部分)和女生的茎叶图如下:男生直方图男生的频率分布表女生茎叶图(1)请完成频率分布表的三个空格,并估计该校男生网购金额的中位数(单位:元,精确到个位). (2)若网购为全国人均消费的三倍以上称为“剁手党”,估计该校大一学生中的“剁手党”人数为多少?从抽样数据中网购不足200元的同学中随机抽取2人发放纪念品,则2人都是女生的概率为多少?(3)用频率估计概率,从全市所有高校大一学生中随机调查5人,求其中“剁手党”人数的分布列和期望.【答案】(1)见解析;(2);(3)见解析.【解析】(1)表格数据依次为,8,40,中位数是元.(2)由图表可知样本中消费675元以上的男生有2人,女生有8人,共有10人,样本容量共100人,故该校大一学生中的“剁手党”人数为100人,抽样数据中网购不足200元的同学中男生有4人,女生有3人,随机抽取2人发放纪念品,则2人都是女生的概率为.(3)全市所有高校大一学生中,为“剁手党”的概率为,故随机调查的5人中“剁手党”人数的分布列为,分布表为数学期望为.20.(12分)[2019·白银联考]设椭圆的左、右焦点分别为,,下顶点为,为坐标原点,点到直线的距离为,为等腰直角三角形.(1)求椭圆的标准方程;(2)直线与椭圆交于,两点,若直线与直线的斜率之和为2,证明:直线恒过定点,并求出该定点的坐标.【答案】(1);(2)见解析.【解析】(1)解:由题意可知:直线的方程为,即,则,因为为等腰直角三角形,所以,又,可解得,,,所以椭圆的标准方程为.(2)证明:由(1)知,当直线的斜率存在时,设直线的方程为,代入,得,所以,即,设,,则,,因为直线与直线的斜率之和为2,所以,整理得,所以直线的方程为,显然直线经过定点,当直线的斜率不存在时,设直线的方程为,因为直线与直线的斜率之和为2,设,则,所以,解得,此时直线的方程为,显然直线也经过该定点,综上,直线恒过点.21.(12分)[2019·新疆诊断]已知函数.(1)若在处的切线与直线垂直,求实数的值;(2)当时,求证.【答案】(1);(2)见证明.【解析】(1)由,因为在处的切线与直线垂直,,.(2)由,设,则,①若时,,在单调递增,而,在上递减,在上递增,,显然满足,②若时,,在上递减,在上递增,,同①则,也满足,③若时,,,在上递减,在上递增,,在上存在两个零点,,且,,在和上是减函数,在和上是增函数,在和处取得极小值,由,又,,即,,同理,,记,则,,时,,综上所述,时,成立.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(10分)【选修4-4:坐标系与参数方程】[2019·常德检测]在平面直角坐标系中,已知曲线(为参数),.以原点为极点,轴的非负半轴为极轴建立极坐标系.(1)写出曲线与圆的极坐标方程;(2)在极坐标系中,已知射线分别与曲线及圆相交于,,当时,求的最大值.【答案】(1),;(2).【解析】(1)曲线的普通方程为,由普通方程与极坐标方程的互化公式,的极坐标方程为.曲线的极坐标方程为.(2)因为与以点为顶点时,它们的高相同,即,由(1)知,,,所以,由,得,所以当,即时,有最大值为,因此的最大值为.23.(10分)【选修4-5:不等式选讲】[2019·湖南联考]已知函数.(1)设,求不等式的解集;(2)已知,且的最小值等于3,求实数的值.【答案】(1);(2).【解析】(1)时,.当时,,即为,解得.当时,,解得.当时,,解得.综上,的解集为.(2),,由的图象知,,.。
(冲刺高考)2021年春辉教育云平台高考考前提分试卷 英语(含听力) (十)教师版

(冲刺高考)2021年春辉教育云平台高考考前提分试卷英 语(十)注意事项:1、答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3、考试结束后,请将本试题卷和答题卡一并上交。
第一部分 听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5个小题;每小题1. 5分,满分7. 5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A 、B 、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt? A. £19.15.B. £9.18.C. £9.15.答案是C 。
1. What does the man suggest doing during spring vacation? A. Going back home. B. Having a trip. C. Looking for a job.2. What is the woman probably? A. A teacher. B. A journalist. C. A guider.3. What time is it now?A. 9:30 a.m.B. 10:00 a.m.C. 10:30 a.m. 4. How does the woman sound? A. Nervous. B. Sad. C. Angry.5. What is the probable relationship between the speakers? A. Teacher and students.B. Workmates.C. Boss and employee.第二节 (共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
(冲刺高考)2021年春辉教育云平台高考考前提分试卷 英语 (十)学生版

(冲刺高考)2021年春辉教育云平台高考考前提分试卷英 语(十)注意事项:1、答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3、考试结束后,请将本试题卷和答题卡一并上交。
第一部分 听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5个小题;每小题1. 5分,满分7. 5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A 、B 、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt? A. £19.15.B. £9.18.C. £9.15.答案是C 。
1. What does the man suggest doing during spring vacation? A. Going back home.B. Having a trip.C. Looking for a job.2. What is the woman probably? A. A teacher. B. A journalist. C. A guider.3. What time is it now?A. 9:30 a.m.B. 10:00 a.m.C. 10:30 a.m. 4. How does the woman sound? A. Nervous. B. Sad. C. Angry.5. What is the probable relationship between the speakers? A. Teacher and students. B. Workmates. C . Boss and employee. 第二节 (共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
(冲刺高考)2021年春辉教育云平台高考考前提分试 地理 (六) 教师版

(冲刺高考)2021年春辉教育云平台高考考前提分试卷地 理(六)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4、考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题)本卷共11个小题,每小题4分,共44分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
从1996年正式实施国际化行动以来,华为在海外的扩张之路艰难而成功。
2018年10月18日,华为公布Mate20Pro 支持40W 的快速充电技术,充电速度更快,且实现无线反向快充,被称为“华为领先方案”。
据此完成1~3题。
1.俄罗斯是华为国际化的第一站,从1997年起合资或收购了贝托康采恩等多家公司,最主要目的是为了( )A .降低内部交易成本B .分散投资风险C .拓展更大市场D .利用廉价原料2.2015年起华为在印度筹建海外最大研发中心及全球服务中心,地点在有“印度硅谷”之称的班加罗尔。
其选址主要考虑( )①协作条件好 ②市场广阔 ③中印地缘优势 ④技术人才优势 A .①②B .②③C .③④D .①④3.“华为领先方案”推行产生的环境效益是( )A .增强市场竞争力B .减少温室气体排放C .方便人们生活D .树立品牌意识【解析】第1题,华为在俄罗斯合租收购多家公司,降低了市场交易成本,而不是内部交易成本;华为公司不是原料指向型企业,海外投资依然有风险;最主要目的是开拓俄罗斯广阔的市场。
第2题,班加罗尔软件业世界领先,技术人才优势和良好的协作条件,并非主要因为中印为邻国,建立研发中心和全球服务中心,面向的是国际市场。
第3题,快速充电节约能源,可以减少温室气体排放;而且此题干指向“环境效益”。
(冲刺高考)2021年春辉教育云平台高考考前提分试卷 文科数学 (十)学生版
(冲刺高考)2021年春辉教育云平台高考考前提分试卷文 科 数 学(十)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4、考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2019·宁波期末]已知集合,,则( )A .B .C .D .2.[2019·江南十校]的值为( )A .B .C .D .3.[2019·西安适应]设复数,,则( )A .B .C .D .4.[2019·湖北联考]设双曲线的右焦点与抛物线的焦点相同,双曲线的一条渐近线方程为,则双曲线的方程为( )A .B .C .D .5.[2019·延边质检]下列函数中,既是奇函数,又是上的单调函数的是( )A .B .C .D .6.[2019·江南十校]已知边长为1的菱形中,,点满足,则的值是( )A .B .C .D .7.[2019·江西联考]将函数的图像沿轴向左平移个单位后,得到一个函数的图像,则“是偶函数”是“”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件8.[2019·长春质检]一个几何体的三视图如图所示,则这个几何体的体积为( )A .32B .C .D .89.[2019·江西联考]程序框图如下图所示,若上述程序运行的结果,则判断框中应填入( )A .B .C .D .10.[2019·滨州期末]已知抛物线的焦点为,准线为,是上一点,是直线与抛物线的一个交点,若,则( )此卷只装订不密封班级 姓名 准考证号 考场号 座位号A.3B.C.4或D.3或411.[2019·珠海期末]若、满足约束条件,目标函数取得最大值时的最优解仅为,则的取值范围为()A.B.C.D.12.[2019·东师附中]已知函数有且只有一个极值点,则实数构成的集合是()A.B.C.D.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2019·中山一中]假设要考察某公司生产的狂犬疫苗的剂量是否达标,现从500支疫苗中抽取50支进行检验,利用随机数表抽取样本时,先将500支疫苗按000,001,,499进行编号,如果从随机数表第7行第8列的数开始向右读,请写出第3支疫苗的编号______________________.(下面摘取了随机数表第7行至第9行)84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 7663 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54 14.[2019·武威十八中]学校艺术节对、、、四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:甲说:“是或作品获得一等奖”;乙说:“作品获得一等奖”;丙说:“、两件作品未获得一等奖”;丁说:“是作品获得一等奖”.评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.15.[2019·江西联考]函数,则不等式的解集是_________.16.[2019·茂名一模]《九章算术》中记载了一个“折竹抵地”问题,今年超强台风“山竹”登陆时再现了这一现象(如图所示),不少大树被大风折断.某路边一树干被台风吹断后(没有完全断开),树干与底面成角,折断部分与地面成角,树干底部与树尖着地处相距10米,则大树原来的高度是_________米(结果保留根号).三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(12分)[2019·河南期末]在公差为的等差数列中,.(1)求的取值范围;(2)已知,试问:是否存在等差数列,使得数列的前项和为?若存在,求的通项公式;若不存在,请说明理由.18.(12分)[2019·淄博模拟]某商店销售某海鲜,统计了春节前后50天该海鲜的需求量(,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为元.(1)求商店日利润关于需求量的函数表达式;(2)假设同组中的每个数据用该组区间的中点值代替.①求这50天商店销售该海鲜日利润的平均数;②估计日利润在区间内的概率.19.(12分)[2019·柳州模拟]已知四棱锥中,底面为等腰梯形,如,,,底面.(1)证明:平面平面;(2)过的平面交于点,若平面把四棱锥分成体积相等的两部分,求三棱锥的体积.20.(12分)[2019·十堰模拟]已知椭圆过点.(1)求椭圆的方程,并求其离心率;(2)过点作轴的垂线,设点为第四象限内一点且在椭圆上(点不在直线上),点关于的对称点为,直线与交于另一点.设为原点,判断直线与直线的位置关系,并说明理由.21.(12分)[2019·吕梁一模]已知函数.(1)求函数在点处的切线方程;(2)证明:.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(10分)【选修4-4:坐标系与参数方程】[2019·渭南质检]在直角坐标系中,直线的参数方程为(为参数),以原点为极点,轴正半轴为极轴建立极坐标系,圆的极坐标方程为.(1)若,求圆的直角坐标方程与直线的普通方程;(2)设直线截圆的弦长等于圆的半径长的倍,求的值.23.(10分)【选修4-5:不等式选讲】[2019·银川一中]设不等式的解集是,,.(1)试比较与的大小;(2)设表示数集的最大数.,求证:.(冲刺高考)2021年春辉教育云平台高考考前提分试卷文科数学答案(十)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】B【解析】∵集合,,∴,故选B.2.【答案】A【解析】,故选A.3.【答案】A【解析】∵,∴.故选A.4.【答案】B【解析】由题意得双曲线的渐近线方程为,又双曲线的一条渐近线方程为,∴,故,∴双曲线方程为,∴双曲线的右焦点坐标为.又抛物线的焦点坐标为,双曲线的右焦点与抛物线的焦点相同,∴,,∴双曲线的方程为.故选B.5.【答案】B【解析】对于A,,有,则函数为偶函数,不符合题意;对于B,,有,函数为奇函数,且在上的单调递增,符合题意;对于C,,有,函数为奇函数,但在上不是单调函数,不符合题意;对于D,,的定义域为,在上不是单调函数,不符合题意;故选B.6.【答案】D【解析】由题意可得大致图像如下:;,∴,又,,∴.故选D.7.【答案】B【解析】函数的图像沿轴向左平移个单位后,得到,当为偶函数时,,.故“是偶函数”是“”的必要不充分条件.故选B.8.【答案】B【解析】由题意,根据给定的三视图可知,该几何体表示底面是边长为4的正方形,高为4的四棱锥,∴该四棱锥的体积为,故选B.9.【答案】D【解析】初始值,;执行框图如下:,;不能满足条件,进入循环;,;不能满足条件,进入循环;,,此时要输出,因此要满足条件,∴.故选D.10.【答案】B【解析】设到的距离为,则由抛物线的定义可得,∵,∴,,∴直线的斜率为,∵抛物线方程为,∴,准线,∴直线的方程为,与联立可得或(舍去),∴,故选B.11.【答案】A【解析】结合不等式组,绘制可行域,得到:目标函数转化为,当时,则,此时的范围为,当时,则,此时的范围为,综上所述,的范围为,故选A.12.【答案】A【解析】由题意,求得函数的导数,令,得,即.设,则,当时,得;当时,得或,∴函数在区间和上单调递减,在区间上单调递增.∵函数有且只有一个极值点,∴直线与函数的图象有一个交点,∴或.当时,恒成立,∴无极值,∴.故选A.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.【答案】068【解析】由题意,根据简单的随机抽样的方法,利用随机数表从第7行的第8列开始向右读取,依次为,,,,∴第3支疫苗的编号为.14.【答案】B【解析】若A为一等奖,则甲、乙、丙、丁的说法均错误,不满足题意;若B为一等奖,则乙、丙的说法正确,甲、丁的说法错误,满足题意;若C为一等奖,则甲、丙、丁的说法均正确,不满足题意;若D为一等奖,则乙、丙、丁的说法均错误,不满足题意;综上所述,故B获得一等奖.15.【答案】【解析】当时,不等式可化为,解得,结合可得;当时,不等式可化为,解得,结合可得,故答案为.16.【答案】【解析】如图所示,设树干底部为,树尖着地处为,折断点为,则,,∴.由正弦定理知,,∴(米),(米),∴(米).答案:.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.【答案】(1);(2)存在,通项公式为.【解析】(1)∵,∴,整理得,则,解得,则的取值范围为.(2)∵,∴,即,则.假设存在等差数列,则,即,解得,从而,此时,,故存在等差数列,且,使得数列的前项和为.18.【答案】(1);(2)①元;②.【解析】(1)商店的日利润关于需求量的函数表达式为:,化简得.(2)①由频率分布直方图得:海鲜需求量在区间的频率是;海鲜需求量在区间的频率是;海鲜需求量在区间的频率是;海鲜需求量在区间的频率是;海鲜需求量在区间的频率是;这50天商店销售该海鲜日利润的平均数为:(元)②由于时,,显然在区间上单调递增,,得;,得;日利润在区间内的概率即求海鲜需求量在区间的频率:.19.【答案】(1)见解析;(2).【解析】(1)证明:在等腰梯形,,,易得,在中,,则有,∴,又∵,即平面平面.(2)在梯形中,设,∴,∴,∴,而,即,∴,∴,而,∴,故三棱锥的体积为.20.【答案】(1)椭圆的方程为,离心率;(2)直线与直线平行,理由见解析.【解析】(1)由椭圆方程椭圆过点,可得,∴,∴椭圆的方程为,离心率.(2)直线与直线平行.证明如下:设直线,,设点的坐标为,,由得,∴,∴,同理,∴,由,,有,∵在第四象限,∴,且不在直线上.∴,又,故,∴直线与直线平行.21.【答案】(1);(2)见解析.【解析】(1),,又由题意得,,∴,即切线方程为.(2)证明:由(1)知,易知在区间单调递增,,且,∴,使得,即有唯一的根,记为,则,对两边取对数,得整理得,∵时,,,函数单调递减,时,,,函数单调递增,∴,当且仅当,即时,等号成立,∵,∴,即.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.【答案】(1),;(2)或.【解析】(1)当时,转化为,整理成直角坐标方程为,直线的参数方程为(为参数),转化成直角坐标方程为.(2)圆的极坐标方程转化成直角坐标方程为:,直线截圆的弦长等于圆的半径长的倍,∴,整理得,利用平方法解得或.23.【答案】(1);(2)见解析.【解析】由得,解得,∴.(1)由,,得,,∴,故.(2)由,得,,,∴,故.。
2021年春辉教育云平台高三最新金牌试卷 理科数学 (三) 学生版

2021年春辉教育云平台高三最新金牌试卷理 科 数 学(三)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4、考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.[2019·江师附中]集合,,则( )A .B .C .D .2.[2019·呼和浩特调研]若复数(为虚数单位)在复平面内所对应的点在虚轴上,则实数为( )A .B .2C .D .3.[2019·蚌埠质检]某电商为某次活动设计了“和谐”、“爱国”、“敬业”三种红包,活动规定每人可以依次点击4次,每次都会获得三种红包的一种,若集全三种即可获奖,但三种红包出现的顺序不同对应的奖次也不同员工甲按规定依次点击了4次,直到第4次才获奖则他获得奖次的不同情形种数为( ) A .9B .12C .18D .244.[2019·惠来一中]平面向量与的夹角为,,,则( )A .B .C .0D .25.[2019·江西联考]程序框图如下图所示,若上述程序运行的结果,则判断框中应填入( )A .B .C .D .6.[2019·四川诊断]几何体的三视图如图所示,该几何体的体积为( )A .729B .428C .356D .243 7.[2019·唐山一中]已知,则在,,,中最大值是( )A .B .C .D .8.[2019·宜宾诊断]已知直线:与圆心为,半径为的圆相交于,两点,另一直线:与圆交于,两点,则四边形面积的最大值为( )A .B .C .D .9.[2019·吉林实验中学]一个正三棱锥(底面积是正三角形,顶点在底面上的射影为底面三角形的中心)的四个顶点都在半径为的球面上,球心在三棱锥的底面所在平面上,则该正三棱锥的体积是( )A .B .C .D .10.[2019·四川诊断]已知函数的最小正周期为,其图象向左平移个单位后所得图象关于轴对称,则的单调递增区间为( )A .,B .,C .,D .,此卷只装订不密封 班级 姓名 准考证号 考场号 座位号11.[2019·厦门一中]已知数列的前项和为,直线与圆交于,两点,且.若对任意恒成立,则实数的取值范围是()A.B.C.D.12.[2019·四川诊断]已知定义在上的函数关于轴对称,其导函数为.当时,不等式.若对,不等式恒成立,则正整数的最大值为()A.1B.2C.3D.4第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2019·全国大联考]若实数,满足,则的最小值为_______.14.[2019·云师附中]在1和2之间插入2016个正数,使得这2018个数成为等比数列,则这个数列中所有项的乘积为______.15.[2019·南洋中学]已知函数是定义在上的奇函数,当时,,则时,不等式的解集为_______.16.[2019·扬州中学]已知双曲线的左、右焦点分别为、,直线过,且与双曲线右支交于、两点,若,,则双曲线的离心率等于_______.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(12分)[2019·保山统测]在中,内角,,的对边分别为,,,且.(1)求角;(2)若,求周长的最大值.18.(12分)[2019·柳州模拟]某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.(1)以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况,则2018年11月中有多少天的空气质量达到优良?(2)从这10天的空气质量指数监测数据中,随机抽取三天,求恰好有一天空气质量良的概率;(3)从这10天的数据中任取三天数据,记表示抽取空气质量良的天数,求的分布列和期望.19.(12分)[2019·全国大联考]如图,在四棱锥中,已知四边形是边长为的正方形,点是的中点,点在底面上的射影为点,点在棱上,且四棱锥的体积为.(1)若点是的中点,求证:平面平面;(2)若,且二面角的余弦值为,求的值.20.(12分)[2019·柳州模拟]如图,已知椭圆的左、右焦点分别为、,点为椭圆上任意一点,关于原点的对称点为,有,且的最大值.(1)求椭圆的标准方程;(2)若是关于轴的对称点,设点,连接与椭圆相交于点,直线与轴相交于点,试求的值.21.(12分)[2019·石室中学]已知函数,.(1)当,函数图象上是否存在3条互相平行的切线,并说明理由?(2)讨论函数的零点个数.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(10分)【选修4-4:坐标系与参数方程】[2019·执信中学]极坐标系与直角坐标系有相同的长度单位,以原点为极点,以轴正半轴为极轴.已知曲线的极坐标方程为,曲线的极坐标方程为,射线,,,与曲线分别交异于极点的四点,,,.()若曲线关于曲线对称,求的值,并把曲线和化成直角坐标方程.()求,当时,求的值域.23.(10分)【选修4-5:不等式选讲】[2019·衡阳联考]已知函数.(1)若的最小值为3,求实数的值;(2)若时,不等式的解集为,当,时,求证:.2021年春辉教育云平台高三最新金牌试卷理科数学答案(三)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】D【解析】∵,∴,故选D.2.【答案】D【解析】∵在复平面内所对应的点在虚轴上,∴,即.故选D.3.【答案】C【解析】根据题意,若员工甲直到第4次才获奖,则其第4次才集全“和谐”、“爱国”、“敬业”三种红包,则甲第4次获得的红包有3种情况,前三次获得的红包为其余的2种,有种情况,则他获得奖次的不同情形种数为种;故选C.4.【答案】D【解析】∵,∴,∴,∴.故选D.5.【答案】D【解析】初始值,,执行框图如下:,;不能满足条件,进入循环,;不能满足条件,进入循环;,,此时要输出,因此要满足条件,∴.故选D.6.【答案】D【解析】由题得几何体原图是如图所示的四棱锥,底面是边长为9的正方形,高,∴几何体的体积为.故选D.7.【答案】C【解析】∵,∴和均为减函数,∴,,又∵在为增函数,∴,即在,,,中最大值是,故选C.8.【答案】A【解析】以为圆心,半径为的圆的方程为,联立,解得,,∴中点为,而直线:恒过定点,要使四边形的面积最大,只需直线过圆心即可,即为直径,此时垂直,,∴四边形的面积最大值为.故选A.9.【答案】C【解析】设正三棱锥底面中心为,连接,延长交于,则.∵是三棱锥的外接球球心,∴,∴,∴.∴.故选C.10.【答案】B【解析】由的最小正周期为,∴,的图象向左平移个单位后所得图象对应的函数为,因其图象关于轴对称,∴,,∵,则,∴,由,,得,.即的单调递增区间为,.故选B.11.【答案】B【解析】圆心到直线,即的距离,由,且,得,∴,即且;∴是以为首项,2为公比的等比数列.由,取,解得,∴,则;∴,适合上式,∴;设,,∴;∴,若对任意恒成立,即对任意恒成立,即对任意恒成立.设,∵,∴,故的最大值为,∵,∴.故选B.12.【答案】B【解析】∵,∴,令,则,又∵是在上的偶函数,∴是在上的奇函数,∴是在上的单调递增函数,又∵,可化为,即,又∵是在上的单调递增函数,∴恒成立,令,则,∵,∴在单调递减,在上单调递增,∴,则,∴,∴正整数的最大值为2.故选B.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.【答案】【解析】作出不等式组表示的平面区域,如图中阴影部分所示.平移直线,可知当直线过点时,有最小值,联立,解得,故,则的最小值为.故答案为.14.【答案】【解析】根据等比数列的性质可得,∴这个数列中所有项的乘积为,故答案为.15.【答案】【解析】∵函数是定义在上的奇函数,∴当时,,∴,由奇函数可,∴不等式可化为,解得;∴时,不等式的解集为,故答案为.16.【答案】2【解析】如图,由可得,∴,,由双曲线的定义可得,,∴,在中由余弦定理得,在中由余弦定理得,∵,∴,整理得,∴,解得或(舍去).∴双曲线的离心率等于2.故答案为2.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.【答案】(1);(2).【解析】(1)由得.根据正弦定理,得,化为,整理得到,∵,故,又,∴.(2)由余弦定理有,故,整理得到,故,当且仅当时等号成立,∴周长的最大值为.18.【答案】(1)11月中平均有9天的空气质量达到优良;(2);(3)见解析.【解析】(1)由频率分布直方图,知这10天中1级优1天,2级良2天,3-6级共7天.∴这10天中空气质量达到优良的概率为,∵,∴11月中平均有9天的空气质量达到优良.(2)记“从10天的空气质量指数监测数据中,随机抽取三天,恰有一天空气质量优良”为事件,则,即恰好有一天空气质量良的概率.(3)由题意得的所有可能取值为0,1,2,;;.∴的分布列为:∴.19.【答案】(1)见解析;(2).【解析】(1)∵点在底面上的射影为点,∴平面,又四边形是边长为的正方形,且四棱锥的体积为,∴,即,∴,又,点是的中点,∴,同理可得.又,∴平面,又平面,∴平面平面.(2)如图,连接,易得,,互相垂直,分别以,,的方向为轴、轴、轴的正方向建立空间直角坐标系,则,,,,∵,点在棱上,∴,又,∴,∴,设平面的法向量为,则,∵,,∴,令,可得,∴平面的一个法向量为,又平面的一个法向量为,二面角的余弦值为,∴,即,解得(负值舍去).20.【答案】(1);(2).【解析】(1)∵点为椭圆上任意一点,关于原点的对称点为,∴,又,∴,∴,又的最大值为,知当为上顶点时,最大,∴,∴,∴,∴椭圆的标准方程为.(2)由题意可知直线存在斜率,设直线的方程为,由消去并整理得.∵直线与椭圆交于两点,∴,解得.设,,则,且,,①直线的方程为,令,得,②由①②得.∴点为左焦点,因此,,∴.21.【答案】(1)存在;(2)见解析.【解析】(1),,,则函数在单调递减,上单调递增,上单调递减,∵,,,,,∴存在切线斜率,使得,,,,∴函数图象上是存在3条互相平行的切线.(2),当,有;,在上单调递增;∴函数存在唯一一个零点在内;当,有,;,在上单调递增;∴函数存在唯一一个零点在内;当,有,∴在上单调递增,在上单调递减,在上单调递增,,,,,,∴函数一个零点在区间内,一个零点在区间内,一个零点在内.∴函数有三个不同零点.综上所述:当函数一个零点;当函数三个零点.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.【答案】(1),,;(2).【解析】(),即,化为直角坐标方程为.把的方程化为直角坐标方程为,∵曲线关于曲线对称,故直线经过圆心,解得,故的直角坐标方程为.()当时,,,,,∴,当时,,,故的值域为.23.【答案】(1)或;(2)见解析.【解析】(1)∵,(当且仅当时取=号)∴,解得或.(2)当时,,当时,由,得,解得;又,∴不等式无实数解;当时,恒成立,∴;当时,由,得,解得;∴的解集为..∵,,∴,,∴,即,∴.。
(冲刺高考)2021年春辉教育云平台高考考前提分试卷 物理(十) 教师版

(冲刺高考)2021年春辉教育云平台高考考前提分试卷物 理(十)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4、考试结束,将本试卷和答题卡一并交回。
二、选择题:本题共8小题,每题6分,在每小题给出的四个选项中,第14~18题只有一个选项符合题目要求。
第19~21题有多选项符合题目要求。
全部答对的得6分,选对但不全的得3分,有选错的得0分。
14.氡气有天然放射性,其衰变产生的粒子可对人的呼吸系统造成辐射损伤。
氡衰变方程为 86222Rn→ 84218Po +X ,衰变过程中同时产生γ射线,半衰期为3.8天,以下说法正确的是A .该衰变过程为β衰变B .对一个特定的氡核,在3.8天内一定会衰变C .γ射线是由处于高能级的 84218Po 核向低能级跃迁时产生的D .衰变后, 84218Po 核与X 粒子的质量之和等于衰变前 86222Rn 核的质量 【答案】C15.如图所示,直线a 与半圆周b 分别表示两质点A 、B 从同一地点出发,沿同一方向做直线运动的v -t 图。
当B 的速度变为0时,A 恰好追上B ,则A 的加速度为(B 质点的运动为理想模型)A .1 m/s 2B .2 m/s 2C .m/s 2D .m/s 2【答案】C【解析】设A 的加速度为a .两质点A 、B 从同一地点出发,A 追上B 时两者的位移相等,即x a=x b .根据v-t 图象的“面积”表示位移,得,由题知 t =4s ,解得 a =m/s 2,故选C 。
16.如图所示的电路中,变压器为理想变压器,开关S 闭合,交流电源电压恒定,电阻R 1=R 2,通过R 1的电流与通过R 3的电流相等,R 1两端的电压为电源总电压的71,则若断开开关S ,R 1与R 3的电功率之比为A .1∶3B .1∶9C .2∶9D .1∶18 【答案】D【解析】开关S 闭合时,设电源的电压为U ,变压器的匝数比为n ;R 1两端的电压为U R ,变压器输入端的电压为U 1,输出端的电压为U 2;原线圈上的电流为I 1,流过R 2的电流为I 2,流过R 3的电流为I 3,则:U R =71U ,U 1=U -U R =U -71U =76U ,由于:U2U1=n ,所以:U 2=n U1,由欧姆定律得:I 1=R1UR =7R1U ;I 2=R2U2=7nR26U =7nR16U ,由题:I 1=I 3,由电流关系可得:I2+I3I1=n 1,联立可得:n =3,R 3=I3U2=2R 1,若断开开关S ,则:I 1′=31I 3′,由功率的表达式:P =I 2R ,联立可得R 1与R 3的电功率之比为:P3P1=I3′2R3I1′2R1=181,故D 正确。
考前冲刺卷01-2021年高考数学(理)一模考前冲刺集训卷(解析版)

2021年高考模拟冲刺卷一(全国卷)理科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数1iz i-=(i 为虚数单位),则复数z 的虚部是( ) A .1 B .-1C .iD .i -【答案】B 【解析】 ∵1i z i-=11i +=-1i =--, ∴复数z 的虚部是1-, 故选:B .2.已知集合{}23100A x x x =--<,集合{}16B x x =-≤<,则A B 等于( )A .{}15x x -<<B .{}15x x -≤<C .{}26x x -<<D .{}25x x -<<【答案】B 【解析】由{}()(){}{}2310025025A x x x x x x x x =--<=+-<=-<<,所以{}15A B x x ⋂=-≤<, 故选:B.3.某口罩厂一年中各月份的收入、支出情况如图所示(单位:万元,下列说法中错误的是(注:月结余=月收入一月支出)( )A .上半年的平均月收入为45万元B .月收入的方差大于月支出的方差C .月收入的中位数为70D .月结余的众数为30【答案】C 【解析】由图可得,上半年的平均月收入为406030305060456+++++=万元,故A 正确由图可得,月收入的方差大于月支出的方差,故B 正确由图可得,112-月的月收入(单位:万元)分别为:40、60、30、30、50、60、80、70、70、80、90、80 所以月收入的中位数为:6070652+=,故C 错误 由图可得,112-月的月结余(单位:万元)分别为:20、30、20、10、30、30、60、40、30、30、50、30所以月结余的众数为30,故D 正确 故选:C4.记n S 为等比数列{a n }的前n 项和,已知S 2=2,S 3=–6.则{a n }的通项公式为A .(2)nn a =- B .2nn a =-C .(3)nn a =-D .3nn a =-【答案】A【解析】根据题意,设等比数列{}n a 的首项为1a ,公比为q ,又由22S =,36S =-,则有()()1211216a q a q q ⎧+=⎪⎨++=-⎪⎩,解得12a =-,2q =-,则()2nn a =-,故选A . 5.若点P 在函数3()3f x x x =-+的图象上,且函数3()3f x x x =-+的图象在点P 处的切线平行于直线21y x =+,则点P 的坐标为( ) A .(1,3) B .(1,3)- C .(1,3)和(1,3)- D .(1)3-,【答案】B 【解析】设P 点坐标为(,)P m n ,则33n m m =-+2()31x f x '=-由于在点P 处的切线平行于直线21y x =+ 故2312m -=,1m ∴=±,代入33n m m =-+,故点P 坐标为(1,3)和(1,3)-又点(1,3)在直线21y x =+,此时切线与21y x =+重合,排除 故点P 坐标为(1,3)- 故选:B6.已知非零向量,a b ,满足||4||,a b =||[1,3]b ∈且()1,a b b -⋅=记θ是向量a 与b 的夹角,则θ的最小值是( )A .6π B .4π C .13D .3π【答案】D【解析】由题意知非零向量a ,b 满足4||||b a =,[1,3]b ∈且()1,a b b -⋅=,可得21a b b -=,即2cos 1a b b θ=+,所以22221111cos 444b b a bbb θ++===+ 因为1,3b ⎡⎤∈⎣⎦,所以[]21,3b ∈,所以21111cos ,4324b θ⎡⎤=+∈⎢⎥⎣⎦因为[]0,θπ∈,且余弦函数cos y x =在[]0,π上单调递减, 所以min 3πθ=7.一个球体被挖去一个圆锥,所得几何体的三视图如图所示,则该几何体的体积为( )A .403πB .56πC .1843πD .104π【答案】C 【解析】由题意可知该几何体是球体被挖去一个圆锥,圆锥底面半径为3232=6, 设球的半径为R ,可得(()222236R R =+-,解得4R =,所以该几何体的体积为(23411846333R π⨯π⨯-⨯⨯π=.故选:C .8.抛物线24y x =的焦点为F ,点()3,2A ,P 为抛物线上一点,且P 不在直线AF 上,则PAF △周长的最小值为( )A. 4B. 5C.4+D.5+【答案】C 【解析】【分析】将问题转化为求PA PF +的最小值,根据抛物线的定义可知PF PD =,即求PA PD +的最小值,当P 、A 、D 三点共线时,PA PD +最小,由()()min1314A PA PD x +=--=+=即可求解.【详解】由抛物线为24y x =可得焦点坐标()1,0F ,准线方程为1x =-. 由题可知求PAF △周长的最小值.即求PA PF +的最小值. 设点p 在准线上的射影为点D . 则根据抛物线的定义.可知PF PD =.因此求PA PF +的最小值即求PA PD +的最小值.根据平面几何知识,当P 、A 、D 三点共线时,PA PD +最小. 所以()()min 1314A PA PD x +=--=+=.又因为AF ==所以PAF △周长的最小值为4+. 故选:C .9.已知函数12,0()21,0x e x f x x x x -⎧>⎪=⎨--+≤⎪⎩,若关于x 的方程23())0()(f f x a x a -+=∈R 有8个不等的实数根,则a 的取值范围是( )A .10,4⎛⎫⎪⎝⎭B .1,33⎛⎫ ⎪⎝⎭C .(1,2)D .92,4⎛⎫ ⎪⎝⎭【答案】D【解析】绘制函数()12,021,xe xf xx x x-⎧>⎪=⎨--+≤⎪⎩的图象如图所示,令()f x t=,由题意可知,方程230t t a-+=在区间()1,2上有两个不同的实数根,令()()2312g t t t a t=-+<<,由题意可知:()()11302460399242g ag ag a⎧⎪=-+>⎪⎪=-+>⎨⎪⎛⎫⎪=-+<⎪⎪⎝⎭⎩,据此可得:924a<<.即a的取值范围是92,4⎛⎫⎪⎝⎭.本题选择D选项.10.已知函数()()lg,1lg2,1x xf xx x≥⎧=⎨--<⎩,()3g x x=,则方程()()1f xg x=-所有根的和等于()A.1 B.2 C.3 D.4【答案】C【解析】设点(),x y是函数lg,1y x x=≥图象上任意一点,它关于点()1,0的对称点为()'',x y,则22,x x x xy y y y+==-⎧⎧∴⎨⎨+=='-''⎩'⎩,代入lgy x=,得()()'''''lg2,lg2,1y x y x x-=-∴=--≤.∴函数lg ,1y x x =≥的图象与函数()lg 2,1y x x =--≤的图象关于点()1,0对称,即函数()()lg ,1lg 2,1x x f x x x ≥⎧=⎨--<⎩的图象关于点()1,0对称,易知函数()f x 在定义域R 上单调递增.又函数()3g x x =的图象关于原点()0,0对称,∴函数()1y g x =-的图象关于点()1,0对称,且函数()1y g x =-在定义域R 上单调递增.又()()0111,1f g x =-=∴=是方程()()1f x g x =-的一个根.当1x ≥时,令()()()()31lg 1h x x x g x f x -=--=-,则()h x 在[)1,+∞上单调递减.()()33331313lg 210,lg lg lg100,202222822h h h h ⎛⎫⎛⎫⎛⎫-<=-=-=>∴< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=根据零点存在定理,可得()h x 在3,22⎛⎫ ⎪⎝⎭上有一个零点1x ,根据()h x 的单调性知()h x 在()1,+∞上有且只有一个零点1x ,即方程()()1f x g x =-在()1,+∞上有且只有一个根1x .根据图象的对称性可知方程()()1f x g x =-在(),1-∞上有且只有一个根2x ,且122x x +=.故方程()()1f x g x =-所有根的和等于1213x x ++=.11.已知椭圆22221x y a b+=的左右焦点分别为12,F F ,过1F 作倾斜角为45︒的直线与椭圆交于,A B 两点,且112F B AF =,则椭圆的离心率= ABCD【答案】D【解析】椭圆22221x y a b+=的左右焦点分别为12F F 、,过10F c -(,)且斜率为1k =的直线为y x c =+,联立直线与椭圆方程22221x y a b y x c ⎧+=⎪⎨⎪=+⎩,消x 后,化简可得2222222220a b y cb y c b a b +++-=(), 因为直线交椭圆于A ,B ,设1122A x y B x y (,),(,),由韦达定理可得22222121222222,cb c b a b y y y y a b a b -+=-=++, 且112F B AF =,可得212y y =-,代入韦达定理表达式可得2222221122222,2cb c b a b y y a b a b --=--=++,即222222222222cb c b a b a b a b ⎛⎫--= ⎪++⎝⎭,化简可得229c 2a =,所以3c e a ==,故选D . 12.三棱锥P ABC -中,,,PA PB PC 互相垂直,1PA PB ==,M 是线段BC 上一动点,若直线AM 与平面PBC 则三棱锥P ABC -的外接球的体积是( ) A .2π B .4πC .83πD .43π【答案】D 【解析】M 是线段BC 上一动点,连接PM ,PA PB PC ,,互相垂直,AMP ∴∠就是直线AM 与平面PBC 所成角,当PM 最短时,即PM BC ⊥时直线AM 与平面PBC 所成角的正切的最大.此时2AP PM =,PM =在直角PBC 中,3PB PC BC PM PC PC ⋅=⋅⇒=⇒=三棱锥P ABC -2=.∴三棱锥P ABC -的外接球的半径为1R =, ∴三棱锥P ABC -的外接球的体积为34433R ππ=.故选:D.二、填空题:本题共4小题,每小题5分,共20分。
【原创】(新高考)2021届高考考前冲刺卷 数学(十) 解析版

(新高考)2021届高考考前冲刺卷数 学(十)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(选择题)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{}3,2,0,2,3U =--,{}3,3A =-,()(){}320B x x x =--=,则图中阴影部分所表示的集合为( )A .{}3,2,3-B .{}3,2,0,2--C .{}3D .{}2,0-2.设z 是复数z 的共轭复数,若10i 5z z z ⋅+=,则2i z=+( ) A .2 B .34i 55+ C .2或43i 55+ D .2或34i 55+ 3.已知数列{}n a 是公差为d 的等差数列,n S 为其前n 项和,若45S =,232S =,则公差d =( )A .14B .1C .34D .124.设m ∈R ,则“12m ≤≤”是“直线:0l x y m +-=和圆()()22:123C x y m -+-=-有公共点”的( ) A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件5.已知抛物线2:(0)E y ax a =≠的焦点为F ,准线为l ,一圆以F 为圆心且与l 相切,若该圆与抛物线E 交于点00(,)M x y ,则0y x 的值为( ) A .2a -或2aB .2-或2C .2-D .2a6.我国东汉末数学家赵爽在《周牌算经》中利用一幅“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示若E 为AF 的中点,EG AB AD λμ=+,则λμ+=( )A .12B .35C .23D .457.已知在锐角三角形ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若()2b a ac =+,则sin cos cos a Ab A a B -的取值范围是( )A .20,⎛⎫ ⎪ ⎪⎝⎭B .30,⎛⎫⎪ ⎪⎝⎭C .12,2⎛⎫⎪⎪⎝⎭D .13,2⎛⎫⎪⎪⎝⎭8.已知定义在R 上的函数()y f x =,对任意x 都满足(2)()f x f x +=,且当11x -≤≤时2()2f x x =,则函数()()ln ||g x f x x =-的零点个数为( )A .12B .14C .15D .16二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列选项中,与sin π6的值相等的是( ) A .22cos 151︒-B .cos18cos 42sin18sin 42︒︒-︒︒C .2sin15sin 75︒︒D .tan 30tan151tan 30tan15︒︒-︒+︒此卷只装订不密封班级 姓名 准考证号 考场号 座位号10.下列命题中,正确的命题有( )A .已知随机变量服从二项分布(),B n p ,若()30E X =,()20D X =,则23p = B .将一组数据中的每个数据都加上同一个常数后,方差恒不变C .设随机变量ξ服从正态分布()0,1N ,若()1P p ξ>=,则()1102P p ξ-<≤=- D .若某次考试的标准分X 服从正态分布()90,900N ,则甲、乙、丙三人恰有2人的标准分超过90分的概率为3811.连接正方体每个面的中心构成一个正八面体(如图),则( )A .以正八面体各面中心为顶点的几何为正方体B .直线AE 与CF 是异面直线C .平面ABF ⊥平面ABED .平面//ABF 平面CDE12.已知曲线2()(0)x f x ae a -=>与曲线2()(0)g x x m m =->有公共点,且在第一象限内的公共点处的切线相同(e 是自然对数的底数),则当m 变化时,实数a 取以下哪些值能满足以上要求( ) A .1 B .eC .2eD .2e第Ⅱ卷(非选择题)三、填空题:本大题共4小题,每小题5分.13.在二项式()51x +的展开式中任取两项,则所取两项中至少有一项的系数为偶数的概率是_____. 14.已知函数()22xxa f x a -=+是奇函数,则()f a 的值等于_________. 15.最大视角问题是1471年德国数学家米勒提出的几何极值问题,故最大视角问题一般称为“米勒问题”.如图,树顶A 离地面a 米,树上另一点B 离地面b 米,在离地面()c c b <米的C 处看此树,离此树的水平距离为_________米时看A ,B 的视角最大.16.已知区域D 表示不在直线()212223m x my m -+=+(m ∈R )上的点构成的集合,则区域D的面积为________,若在区域D 内任取一点(),P x y 22x y +的取值范围为_________.四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.17.(10分)在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c )22232sin a c b bc A +-=.(1)求B ;(2)若ABC △23,2c a =,求b .18.(12分)已知数列{}n a 的前n 项和为n A ,数列{}n b 的前n 项和为n B ,且122n n n A B +-=-.(1)求{}n n a b -的通项公式;(2)若n n a b n +={}n n a b ⋅的前n 项和n T .19.(12分)某乒乓球教练为了解某同学近期的训练效果,随机记录了该同学40局接球训练成绩,每局训练时教练连续发100个球,该同学每接球成功得1分,否则不得分,且每局训练结果相互独立,得到如图所示的频率分布直方图.(1)同一组数据用该区间的中点值作代表, ①求该同学40局接球训练成绩的样本平均数x ;②若该同学的接球训练成绩X 近似地服从正态分布(),100N μ,其中μ近似为样本平均数x , 求()5464P X <<的值;(2)为了提高该同学的训练兴趣,教练与他进行比赛.一局比赛中教练连续发100个球,该同学得分达到80分为获胜,否则教练获胜.若有人获胜达3局,则比赛结束,记比赛的局数为Y .以频率分布直方图中该同学获胜的频率作为概率,求()E Y .参考数据:若随机变量()2~,N ξμσ,则()0.6827P μσξμσ-<<+≈,()220.9545P μσξμσ-<<+≈,()330.9973P μσξμσ-<<+≈.20.(12分)如图,在三棱柱111ABC A B C -中,四边形11BCC B 是菱形,AB BC ⊥,1C 在底面ABC上的射影是BC 的中点. (1)证明:1CB ⊥平面1ABC ;(2)若2BC AB =,求1CB 与平面11ACC A 所成角的正弦值.21.(12分)已知圆(22:12C x y+=,动圆M过点)D且与圆C相切.(1)求动圆圆心M的轨迹E的方程;(2)假设直线l与轨迹E相交于A,B两点,且在轨迹E上存在一点P,使四边形OAPB为平行四边形,试问平行四边形OAPB的面积是否为定值?若是,求出此定值;若不是,请说明理由.22.(12分)已知函数()212ln2f x x mx x=++在点()()1,1f处的切线垂直于y轴.(1)求()f x的单调区间;(2)若存在a,b,c()0a b c<<<使得()()()f a f b f c==,求证:2c a-<.(新高考)2021届高考考前冲刺卷数 学(十)答 案注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2021年春辉教育云平台高考一轮复习精品资源 理数 第十章(章测试) 解析版

2021年春辉教育云平台高考一轮复习精品资源理数 第十章 测试题一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选择中,只有一个是符合题目要求的.)1.【云南省昆明一中2018届高三第一次摸底测试】二项式展开式中的常数项为( )A.B.C.D.【答案】B【解析】展开式的通项为,令得,所以展开式中的常数项为,故选B.2.【北京市朝阳区2017届高三二模】现将5张连号的电影票分给甲、乙等5个人,每人一张,且甲、乙分得的电影票连号,则共有不同分法的种数为A. 12B. 24C. 36D. 48 【答案】D【解析】甲、乙分得的电影票连号有 种情况,其余三人有分法,所以共有,选D.3.【安徽省合肥市2018届高三调研性检测】用数字0,1,2,3,4组成没有重复数字且大于3000的四位数,这样的四位数有( )A. 250个B. 249个C. 48个D. 24个 【答案】C4.【2015高考四川,理6】用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )(A )144个 (B )120个 (C )96个 (D )72个 【答案】B 【解析】据题意,万位上只能排4、5.若万位上排4,则有个;若万位上排5,则有个.所以共有个.选B.5.【四川省德阳市2018届高三三校联合测试】从5名学生中选出4名分别参加数学,物理,化学,生物四科竞赛,其中甲不能参加生物竞赛,则不同的参赛方案种数为A. 48B. 72C. 90D. 96【答案】D6.除以100的余数是( )A .1B .79C .21D .81 【答案】C 【解析】 试题分析:==4,即除以100的余数为21。
7.【广西桂林市柳州市2018年届高三综合模拟金卷】已知的展开式中第4项的二项式系数为20,则的展开式中的常数项为( )A. 60B.C. 80D.此卷只装订不密封 班级 姓名 准考证号 考场号 座位号【答案】A【解析】由题意可得=20,求得n=6,则=的展并式的通项公式为T r+1=••,令6﹣=0,求得r=4,可得展并式中的常数项为•4=60.8.【安徽省六校教育研究会2018届高三上学期第一次联考】某学校有5位教师参加某师范大学组织的暑期骨干教师培训,现有5个培训项目,每位教师可任意选择其中一个项目进行培训,则恰有两个培训项目没有被这5位教师中的任何一位教师选择的情况数为()A. 5400种B. 3000种C. 150种D. 1500种【答案】D9.【四川省双流中学2018届高三上学期9月月考】在展开式中,二项式系数的最大值为,含项的系数为,则()A. B. C. D.【答案】D【解析】因为是偶数,所以展开式共有7项,其中中间一项的二项式系数最大,其二项式系数为时,含项的系数为,则,应选答案D。
(冲刺高考)2021年春辉教育云平台高考考前提分试卷 理科综合能力测试 (十)学生版

(冲刺高考)2021年春辉教育云平台高考考前提分试卷理科综合能力测试(十)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3.回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4.考试结束,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 S 32 Cl 35.5 K 39第Ⅰ卷(选择题,共126分)一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图表示某细胞正在进行正常的减数分裂,有关该图的叙述正确的是A .处于减数第一次分裂,有4个四分体B .有四对同源染色体,8条染色单体C .1和2间的片段互换可导致基因重组D .A 和C 间的片段互换可导致染色体结构变异 2.以下实验观察到的现象与结论匹配正确的是A .洋葱表皮细胞质壁分离复原后,细胞不再吸水,说明细胞液浓度与外界溶液浓度一致B .动物脂肪细胞用苏丹Ⅲ染色后,能观察到橘黄色的脂肪微滴,说明脂肪细胞代谢旺盛C .层析分离结果显示在相邻色素带之间,叶绿素a 与叶黄素间距最大,说明相邻色素间,此二者在层析液中的溶解度差异最大D .低温处理的洋葱根尖制成装片,高倍镜下观察分裂期细胞,均看不到纺锤体,说明低温能抑制纺锤体的形成。
3.已知5%葡萄糖溶液的渗透压与动物血浆渗透压基本相同。
现给正常小鼠输入一定量的该溶液,一段时间后小鼠体内会发生的生理变化是A .血浆中胰岛素与胰高血糖素的比值下降B .位于胰岛组织的血糖感受器产生兴奋C .下丘脑分泌的抗利尿激素释放量减少,尿量增多D .肾小管和集合管对葡萄糖的重吸收减少,尿液中葡萄糖含量增加4.化疗药物长春碱能够与微管蛋白结合阻碍纺锤体形成,从而抑制癌细胞增殖。
2021-2022年高三下学期高考前冲刺模拟数学试题 含答案

2021年高三下学期高考前冲刺模拟数学试题 含答案xx.6一. 填空题1. 两数和的几何平均数为 ;【解析】几何平均数为,顺便复习一下其他几个平均数,算术平均数,平方平均 数为,调和平均数为211a b +2112a b a b +≥≥≥+,本 题易错点在于几何平均数没有正负【答案】2. 设复数,,在复平面的对应的向量分别为,,则向量对应的复数所对应的点的坐标为 ;【解析】点坐标对应为,点坐标对应为,∴【答案】3. 已知幂函数过点,则的反函数为 ;【解析】将点代入,得,即幂函数为,∴;本题容易忘写定义域,考试时务必谨记定义域!【答案】4. 若无穷等比数列满足:,则首项的取值范围为 ;【解析】根据题意,即,∵,∴,本题易被忽略,是一个易错点;【答案】5. 在△中,,则的最大值是 ;【解析】3sin sin sin sin()sin )4A C A A A A A π⋅=⋅-=⋅12cos 2)sin(2)24A A A π=-=-≤ 的常用套路必须烂熟于心!【答案】6. 在极坐标中,直线被圆截得的弦长为 ;【解析】根据极坐标与直角坐标的换算公式,,可知直线为,圆两边同时乘以,即,即,图形如图所示,易得弦长为【答案】7. 若不等式对于任意正整数恒成立,则实数的取值范围是 ;【解析】当为奇数,,即恒成立,所以;当为偶数,恒成立,所以;综上,;本题易错点在是否取得到【答案】8. 如图,某地一天中6时至14时的温度变化曲线近似满足函数(其中,),则估计中午12时的温度近似为 ;(精确到)【解析】根据图像解得函数解析式为,代入,【答案】9. 《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有 系统的数学典籍,其中记载有求“盖”的术:置如其周,令相承也,又以高乘之,三十六成 一,该术相当于给出了由圆锥的底面周长与高,计算其体积的近似公式,它实际上是将圆锥体积公式中的圆周率近似取3,那么近似公式相当于将圆锥体积公式中的近似取为 ;【解析】,∴,2222122437575V r h L h r h ππ=⋅⋅≈=⋅⋅,解得; 【答案】10. 数列是公差不为零的等差数列,其前项和为,若记数据的方差为,数据的方程为,则 ;【解析】根据题意,数据为等差数列,公差为;而等差数列 的公差为,即21224()2d d λλ== 【答案】11. 已知数列满足,,222(1cos)sin 22n n n n a a ππ+=++,则该数列的前 项和是 ;【解析】通过不完全归纳法,不难发现,,,…为等差数列;而,,,…为等比数列;∴分类讨论可得1222(3)(1)22,218(2)22,28n n n n n n k S n n n k ++⎧+++-=+⎪⎪=⎨+⎪+-=⎪⎩ 【答案】1222(3)(1)22,218(2)22,28n n n n n n k S n n n k ++⎧+++-=+⎪⎪=⎨+⎪+-=⎪⎩ 12. 已知是定义在上的奇函数,当时,,函数 ,如果对于任意,存在,使得,则实数的取值范围是 ;【解析】根据题意,在的值域在的值域,而在的图像如图所示(红线部分),即要满足:且,解得【答案】13. 在面积为2的△中,、分别是、的中点,点在直线上,则的最小值是 ;【解析】建立直角坐标系,设,,因为△面积为2,则点纵坐标为,∴点纵坐 标为,设点,∴222(,)(,)PC PB BC x t t x x⋅+=--⋅--22243()024x x t x =-++≥+= 【答案】14. 如图,已知抛物线及两点和,其中,过、分别作轴的垂线,交抛物线于、两点,直线与轴交于点,依次类推得,,若,,则的坐标为 ;【解析】依题意得:、、、、、、、、、,观察分母1、2、3、5、8、…、的规律即可【答案】二. 选择题15. 对一个容量为的总体抽取容量为的样本,当选取简单随机抽样、系统抽样和分层抽样三种方法抽取样本时,总体中每个个体被抽中的概率分别为、、,则( )A. B.C. D.【解析】如果每个个体被抽中的概率不一样,则无法保证总体统计的公平性,所以无论是以何种抽样方式,必须要保证个体被抽中的概率一致!【答案】D16. 数列是由实数构成的等比数列,,则数列中( )A. 任一项均不为0B. 必有一项为0C. 至多有有限项为0D. 或无一项为0,或有无穷多项为0【解析】当时,中有无穷多项为0,排除AC ;当时,没有一项为0,排除B ,所以选D【答案】D17. 若等比数列的公比为,则关于、的二元一次方程组的解的情况的下列说法中正确的是( )A. 对任意,方程组都有唯一解B. 对任意,方程组都无解C. 当且仅当时,方程组有无穷多解D. 当且仅当时,方程组无解【解析】当且仅当时,,∴方程组有无穷多解【答案】C18. 如图,在△中,,,,点、分别在轴、轴上,当点在轴上运动时,点随之在轴上运动,在运动过程中,点到原点的最大距离是( )A. B.C. D.【解析】如图,,,,∴点坐标,点到原点的距离222sin (2sin cos )3)4OB πθθθθ=++=+-, ∴,即【答案】C三. 解答题19. 已知向量,,,函数的最大值为,求实数的值【解析】21sin cos sin )242a b x x x x π⋅=⋅+=-+,∵, ∴,,∴当,;当,,即【评析】本题容易漏解,注意有两种情况!20. 如图在三棱锥中,平面,且垂足在棱上,,,,(1)证明:△为直角三角形(2)求直线与平面所成角的正弦值【解析】(1)取中点,联结、∵,∴∵,,∴∴,,∵平面,∴,∴在△,∴△为直角三角形(2)等体积法,设点到平面的距离为,∵∴,即,∴∴,即直线与平面所成角的正弦值为【评析】当垂线不好找或者不好作时,用等体积法可以很快求出点到平面的距离;当然如果建立空间直角坐标系的话,肯定是可以做出来的,计算量偏大一些21. 如图,公路、围成的是一块顶角为的角形耕地,其中,在该块土地中处有一小型建筑,经测量它到公路、的距离分别为、,现要过点修建一条直线公路,将三条公路围成的区域建成一个工业区,为尽量减少耕地占用,问如何确定点的位置,使该工业园区的面积最小?并求最小面积【解析】,∴3sin BC B == 由正弦定理得,∴1113sin 33)2222sin sin C B S AC AB C B +=⋅⋅⋅=⋅115sin 15sin ()4sin sin C B C B C B ++=+1(30)4sin sin B C C B=++,当且仅当时等号成立,即,解得∴当时,该工业园区的面积最小值为【评析】本题不容易形成思路,做不好就容易卡在这,不妨以为原点建立直角坐标系,用直线方程的方法会比较好想22. 已知过椭圆方程右焦点、斜率为的直线交椭圆于、两点(1)求椭圆的两个焦点和短轴的两个端点构成的四边形的面积(2)当直线的斜率为1时,求△的面积(3)在线段上是否存在点,使得以、为邻边的平行四边形是菱形?若存在,求出的取值范围;若不存在,说明理由【解析】(1)四个点分别为、、、,(2)直线的方程为,代入椭圆方程,解得或∴、两点坐标分别为、,(3)设点坐标,点坐标,中点坐标为∴,,点差可得,又因为解得,,即中点坐标为∴中垂线方程为22212()2121k ky xk k k--=--++,代入点∴【评析】要看懂“以、为邻边的平行四边形是菱形”这句话的意思即23. 若对任意的正整数,总存在正整数,使得数列的前项和,则称是“回归数列”(1)①前项和为的数列是否是“回归数列”?并请说明理由②通项公式为的数列是否是“回归数列”?并请说明理由(2)设是等差数列,首项,公差,若是“回归数列”,求的值(3)是否对任意的等差数列,总存在两个“回归数列”和,使得成立,请给出你的结论,并说明理由【解析】(1)①∵,作差法可得当时,;当时,,存在,使得∴数列是“回归数列”②∵,∴前项和,根据题意∵一定是偶数,∴存在,使得∴数列是“回归数列”(2),根据题意,存在正整数,使得成立即,,,∴,即(3)1111(1)(1)(1)(1)n a a n d a n a n a n d =+-=--+-+- 设,数列前项和,根据题意即1111(1)(1)2n n na a a m a --=--,化简得 时,;时,;,为正整数∴存在正整数,使得,是“回归数列” 数列前项和,根据题意即11(1)()(1)()2n n a d m a d -+=-+,化简得 ∵,∴为正整数,∴存在正整数, 使得,是“回归数列”,所以结论成立。
2021年高三下学期考前冲刺卷(一)数学(理)试题 含答案

绝密★启封并使用完毕前2021年高三下学期考前冲刺卷(一)数学(理)试题含答案一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设复数,则a+b等于( ).A. 1B. 3C. -1D. -32.已知全集U={x∈Z|x2-9x+8<0},M={3,5,6},N={x|x-9x+20=0},则集合{2,7}为( ).A. M∪NB. M∩NC. CU(M∪N)D. CU(M∩N)3.设x∈R,向量a=(2,x),b=(3,-2),且a⊥b,则|a-b|等于( ).A. 5B.C.D. 64.一个几何体的三视图如图所示,则这个几何体的体积为().A. B. C. D.5.将函数的图象向右平移个单位后得到函数y=g(x)的图象,则g(x)的单调递增区间为().A. B.C. D.6.如果执行如图所示的程序框图,输出的S=240,那么判断框中为().A. k≥15?B. k≤16?C. k≤15?D. k≥16?7.已知中心在坐标原点的双曲线C与拋物线x2=2py(p>0)有相同的焦点F,点A是两曲线的交点,且AF⊥y轴,则双曲线的离心率为().A. B. C. D.8.已知实数x,y满足如果目标函数z=5x-4y的最小值为-3,那么实数m等于().A. 3B. 2C. 4D.9.已知四面体ABCD中,AB=AD=6,AC=4,CD=,AB⊥平面ACD,则四面体ABCD外接球的表面积为().A. 36πB. 88πC. 92πD. 128π10.设函数f(x)=2a-x-2kax(a>0且a≠1)在(-∞,+∞)上既是奇函数又是减函数,则g(x)=loga(x-k)的图象是().11.若直线y=-nx+4n(n∈N*)与两坐标轴所围成封闭区域内(不含坐标轴)的整点的个数为an(其中整点是指横、纵坐标都是整数的点),则等于().A. 1012B. 2012C. 3021D. 400112.定义在实数集R上的函数y=f(x)的图象是连续不断的,若对任意实数x存在实常数t使得f(t+x)=-tf(x)恒成立,则称f(x)是一个“关于t函数”.有下列“关于t函数”的结论:①f(x)=0是常数函数中唯一一个“关于t函数”;②“关于函数”至少有一个零点;③f(x)=x2是一个“关于t函数”.其中正确结论的个数是().A. 1B. 2C. 3D. 0二、填空题:本大题共4小题,每小题5分,共20分。
2021-2022年高三高冲刺考试 理科数学试题

2021-2022年高三高冲刺考试 理科数学试题命题:高三数学组周东生 xx.5.25一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.的值A .大于B .等于C .小于D .不存在2.已知集合22{|60},{|60},{2},M x x px N x x x q MN p q =-+==+-==+若则的值为A .B .C .D .3.已知复数的虚部为,则实数的值为A .B .C .D .4.正方形的边长为,A .B .C .D .5.在四面体中,2ABC ABD ADC π∠=∠=∠=,则下列是直角的为A .B .C .D .6.已知000()()lim1,3x f x x f x x x∆→+∆--∆=∆则的值为 A . B . C . D .7. 若数列满足:12211,2,(3),n n n a a a a a n --===≥则的值为A .B .C .D .8.在中,则A .B .C .或D .或9.将一枚骰子先后抛掷两次,若第一次朝上一面的点数为,第二次朝上一面的点数为,则函数在上为减函数的概率是A .B .C .D . 10.函数的大致图像为A .B .C .D .11.已知直线与抛物线相交于、两点,为抛物线的焦点,若,则=A .B .C .D .12.已知二元函数2cos (,)(,),sin 2x f x x R R x x θθθθ=∈∈++则的最大值和最小值分别为A .B .,C .D .二、填空题:本大题共4小题,每小题5分,共20分。
13.若2012220120122012(12)x a a x a x a x -=++++,则 .14已知随机变量的分布列如右表,其中, 随机变量满足则___________________.15.如图:已知四面体的外接球的球心在线段上,且平面,,若四面体的体积为,则球的表面积为 .16.已知直线与圆交于、两点,且,其中为坐标原点,则正实数的值为 .三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
2021年全国100所普通高等学校高考数学冲刺试卷(理科)
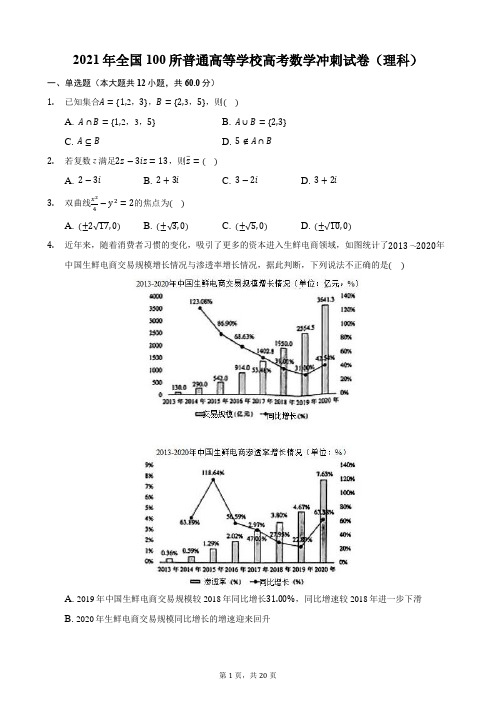
2021年全国100所普通高等学校高考数学冲刺试卷(理科)一、单选题(本大题共12小题,共60.0分)1.已知集合A={1,2,3},B={2,3,5},则()A. A∩B={1,2,3,5}B. A∪B={2,3}C. A⊆BD. 5∉A∩B2.若复数z满足2z−3iz=13,则z−=()A. 2−3iB. 2+3iC. 3−2iD. 3+2i3.双曲线x2−y2=2的焦点为()4A. (±2√17,0)B. (±√3,0)C. (±√5,0)D. (±√10,0)4.近年来,随着消费者习惯的变化,吸引了更多的资本进入生鲜电商领域,如图统计了2013~2020年中国生鲜电商交易规模增长情况与渗透率增长情况,据此判断,下列说法不正确的是()A. 2019年中国生鲜电商交易规模较2018年同比增长31.00%,同比增速较2018年进一步下滑B. 2020年生鲜电商交易规模同比增长的增速迎来回升C. 2013~2020年中国生鲜电商渗透率同比增长逐年上升D. 可能受疫情催化的影响,2020年中国生鲜电商渗透率增速加快5.若(1x +√x2)n(n∈N∗)的展开式中第5项与第6项的二项式系数相等,则n=()A. 11B. 10C. 9D. 86.已知函数f(x)为奇函数,当x<0时,f(x)=2x+2,则f(1)=()A. −4B. −52C. 4 D. 527.若sin37°=a,则cos16°=()A. 2a2−1B. 1−2a2C. 2a√1−a2D. a√2a2−18.声音通过空气的振动所产生的压强叫作声压强,简称声压,声压的单位为帕斯卡(Pa),把声压的有效值取对数来表示声音的强弱,这种表示声音强弱的数值叫声压级,声压级以符号SPL表示,单位为分贝(dB).在空气中声压级的计算公式为SPL(声压级)=20lg p p0(dB),其中p为待测声压的有效值,p0为参考声压,在空气中,一般参考声压取2×10−5Pa.据此估计,声压为1Pa的声压级为()(lg2≈0.301)A. 92dBB. 94dBC. 95dBD. 96dB9.过圆x2+y2=4上一点P作圆O:x2+y2=m2(m>0)的两条切线,切点分别为A,B,若∠APB=π3,则实数m=()A. 13B. 12C. 1D. 210.已知ω>0,顺次连接函数y=√2sinωx与y=√2cosωx的任意三个相邻的交点都构成一个等腰直角三角形,则ω=()A. 12B. √6π2C. πD. π211.已知四棱锥D1−ABCD的底面ABCD为平行四边形,M是棱DD1上靠近点D的三等分点,N是BD1的中点,平面AMN∩CD1=H,则D1HD1C=()A. 12B. 23C. 14D. 2512.已知a>1,b>1,且e aa =e b+1+1b+1,则下列结论一定正确的是()A. ln(a+b)>2B. ln(a−b)>0C. 2a+1<2bD. 2a+2b<23二、单空题(本大题共4小题,共20.0分)13. 已知实数x ,y 满足{2x −y ≥3x +2y ≤4y ≥0,则z =x −3y 的最小值是______.14. 已知向量a ⃗ =(2,2),<a ⃗ ,b ⃗ >=π4,b ⃗ 2−a ⃗ 2=a ⃗ ⋅b ⃗ ,则|b ⃗ |=______. 15. 莱昂哈德⋅欧拉,瑞士数学家和物理学家,近代数学先驱之一.他的研究论著几乎涉及到所有数学分支,有许多公式、定理、解法、函数、方程、常数等是以欧拉名字命名的.欧拉发现,不论什么形状的凸多面体,其顶点数V 、棱数E 、面数F 之间总满足数量关系V +F −E =2,此式称为欧拉公式.已知某凸32面体,12个面是五边形,20个面是六边形,则该32面体的棱数为______,顶点的个数为______. 16. 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,A 为锐角,tanBcosC =1−sinC ,△ABC 的面积为2,则△ABC 的周长的最小值为______. 三、解答题(本大题共7小题,共82.0分)17. 已知等差数列{a n }的前n 项和为S n ,a 1=2,且满足nS n =An 3+3n 2+B .(1)求数列{a n }的通项公式;(2)若a m ,6−2Am ,S 3−5A+B 成等比数列,求正整数m 的值.18. 如图,在直三棱柱ABC −A 1B 1C 1中,AC =2AA 1=2,AB =BC ,D 为AC的中点.(1)证明:DC 1⊥平面A 1BD ;(2)若BD =1,求二面角B −DB 1−C 1的余弦值.19.在近日结束的全国扶贫开发工作会议上,国务院扶贫办表示,2021年要把巩固拓展脱贫攻坚成果摆在头等重要的位置来抓,当前和未来一段时间是我国脱贫攻坚和乡村振兴战略实施交汇的特殊时期.为解决果农农产品滞销问题,进一步提升电子商务专业师生新媒体营销应用能力,某财经学校电商专业教师经过认真策划、精心组织,开启了以“情系三农、爱心助力”为主题的直播带货活动.在最近一个月(按30天算)的直播带货中,A,B,C三种水果的成交订单数统计如表:将调查的每种水果在30天中的成交订单数的频率视为概率,每种水果的销售相互独立,三种水果一天中成交订单的总数记为X.(1)求P(X≥1000);(2)试估计下个月某天中该校电子商务专业师生直播带货三种水果成交订单的总数X最可能的取值并求出其概率.20.椭圆E:x2a2+y2b2=1(a>b>0)的右焦点为F(c,0),规定直线x=a2c为椭圆E的右准线,椭圆E上的任意一点到右焦点F的距离与其到右准线的距离之比为ca .已知椭圆E:x24+y23=1.(1)若点D(−1,1),P是椭圆E上的任意一点,求|PD|+2|PF|的最小值;(2)若M,N分别是椭圆E的左、右顶点,过点F的直线l与椭圆E交于A,B两点(A,B非顶点),证明:直线AM与BN的交点在椭圆E的右准线上.21. 设函数f(x)=(1−a2)x 2+ax −2lnx .(1)若曲线y =f(x)在点(2,f(2))处的切线方程为2x −y +b =0,求a ,b 的值; (2)若函数f(x)有零点,求实数a 的取值范围.22. 在平面直角坐标系xOy 中,曲线C 1的参数方程为{x =2costy =1+cos 4t −sin 4t(t 为参数),以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=−2(sinθ+cosθ). (1)求曲线C 1与C 2的直角坐标方程;(2)已知直线l 的极坐标方程为θ=α(ρ∈R,0<α<π2),直线l 与曲线C 1、C 2分别交于M 、N(异于点O 两点,若|OM||ON|=8,求α.23.已知a,b,c∈R,a+b+c=2.(1)证明:a2+b2+c2≥43;(2)若(a−1)2+(b+t)2+c2≥34,证明:t≥12或t≤−52.答案和解析1.【答案】D【解析】解:∵A={1,2,3},B={2,3,5},∴A∩B={2,3},A∪B={1,2,3,5},∴5∉A∩B.故选:D.进行交集和并集的运算可求出A∩B和A∪B,然后即可判断每个选项的正误.本题考查了集合的列举法的定义,交集和并集的定义及运算,元素和集合的关系,子集的定义,考查了计算能力,属于基础题.2.【答案】A【解析】解:因为2z−3iz=13,所以z=132−3i =13(2+3i)(2−3i)(2+3i)=2+3i,则z−=2−3i.故选:A.利用复数的除法运算法则求出z,然后由共轭复数的定义求解即可.本题考查了复数的除法运算法则的运用,共轭复数定义的理解与应用,属于基础题.3.【答案】D【解析】解:双曲线x24−y2=2,化为x28−y22=1,所以c=√10,所以双曲线的焦点坐标(±√10,0).故选:D.利用双曲线方程求解c,即可得到焦点坐标.本题考查双曲线的简单性质的应用,考查转化思想以及计算能力,是基础题.4.【答案】C【解析】解:由上图可知,2019年中国生鲜电商交易规模同比增长31.00%,2018年中国生鲜电商交易规模同比增长39.01%,故选项A正确;由上图可知,2020年生鲜电商交易规模同比增长的增长分别为42.54%,31%,故选项B正确;由下图可知,2014~2015年中国生鲜电商渗透率同比增长上升,2015~2019年中国生鲜电商渗透率同比增长下降,故选项C错误;由下图可知,2019,2020年中国生鲜电商渗透率增速依次为22.89%,63.38%,故增速加快,故选项D正确.故选:C.利用题中条形图和折线图中的数据信息以及变化趋势,对四个选项逐一分析判断即可.本题考查了条形图和折线图的应用,读懂统计图并能从统计图得到必要的信息是解决问题的关键,属于基础题.5.【答案】C【解析】解:由题意可得:C n4=C n5,n∈N+,可得n=4+5=9.故选:C.由题意可得:C n4=C n5,n∈N+,即可得出.本题考查了二项式定理的性质,考查了推理能力与计算能力,属于基础题.6.【答案】B【解析】解:∵函数f(x)为奇函数,当x<0时,f(x)=2x+2,,则f(1)=−f(−1)=−(2−1+2)=−52故选:B.由题意根据函数的解析式,利用函数的奇偶性求函数的值.本题主要考查利用函数的奇偶性求函数的值,属于基础题.7.【答案】C【解析】解:因为sin37°=a,可得cos37°=√1−a2,所以cos16°=sin(90°−16°)=sin74°=sin2×37°=2sin37°cos37°=2a√1−a2.故选:C.由已知利用同角三角函数基本关系式可求cos37°=√1−a2,进而根据诱导公式,二倍角的正弦公式即可求解.本题主要考查了同角三角函数基本关系式,诱导公式,二倍角的正弦公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.8.【答案】B【解析】解:结合题意可知,声压为1Pa的声压级为20lg12×10−5=20lg1052=20(lg105−lg2)=20(5−0.301)=93.98≈94dB.故选:B.直接把数据代入声压级的计算公式即可得答案.本题考查函数的实际应用,考查对数的运算,属于基础题.9.【答案】C【解析】解:根据题意,如图:x2+y2=4的圆心为(0,0),半径R=2,即|OP|=2,圆O:x2+y2=m2,圆心为(0,0),半径r=m,则|OA|=|OB|=m,若∠APB=π3,则∠OPA=π6,又由OA⊥AP,则|OP|=2|OA|,则m=1,故选:C.根据题意,由圆的方程求出圆的圆心和半径,作出草图,由圆的切线性质分析可得|OP|=2|OA|,据此分析可得答案.本题考查圆的切线的性质,注意分析两圆半径的关系,属于基础题.10.【答案】D【解析】解:如图所示,在函数y=√2sinωx与y=√2cosωx的交点中,|AC|=T=2πω,令√2sinωx=√2cosωx,即tanωx=1,不妨取ωx1=π4,ωx2=9π4,即|AC|=x2−x1=2πω,因为三个相邻的交点构成一个等腰直角三角形,则12|AC|=2,即|AC|=2πω=4,所以ω=π2.故选:D.根据题意作出图形,结合图形求出函数y=√2sinωx与y=√2cosωx的交点中相邻的三个交点,利用等腰三角形的性质,求解即可.本题考查了三角函数的图形和性质的运用,三角函数周期的公式的运用,等腰直角三角形性质的运用,考查了逻辑推理能力与数形结合法的运用,属于中档题.11.【答案】D【解析】解:如图所示,补全四棱锥为三棱柱,其中H为ME与CD1的交点,四边形CDD1E为平行四边形,易知△D1MH∽△CEH,则D1HCH =D1MCE=23,则D1HD1C=25.故选:D.补全四棱锥为三棱柱,根据相似关系易知D1HCH =D1MCE=23,进而得解.本题主要考查立体几何中线段比值的求解,考查分割补形法的运用,考查数形结合思想及运算求解能力,属于中档题.12.【答案】B【解析】解:令f(x)=e xx,x∈(0,+∞),f′(x)=e x(x−1)x2,可得x>1时,函数f(x)单调递增,∵a>1,b>1,且e aa =e b+1+1b+1=e b+1b+1+1b+1,,∴e aa −e b+1b+1=1b+1∈(0,12),∴a>b+1,∴Ln(a−b)>0,因此B正确;∴ln(a+b)>ln(2b+1)>ln3,ln(a+b)>2不一定成立,因此A不正确;2a+1>2b+2>2b,因此C不正确;2a+2b>2b+1+2b=3×2b.因此2a+2b<23不一定成立,因此不正确.故选:B.令f(x)=e xx,x∈(0,+∞),利用导数研究函数的单调性即可判断出结论.本题考查了利用导数研究函数的单调性、不等式的性质、指数与对数函数的单调性,考查了推理能力与计算能力,属于中档题.13.【答案】−1【解析】解:由约束条件作出可行域如图,联立{2x −y =3x +2y =4,解得A(2,1),由z =x −3y ,得y =x3−z3,由图可知,当直线y =x3−z3过A 时,直线在y 轴上的截距最大, z 有最小值为−1. 故答案为:−1.由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.本题考查简单的线性规划,考查数形结合思想,是中档题.14.【答案】4【解析】解:∵a ⃗ =(2,2),∴|a ⃗ |=√4+4=2√2,∵<a ⃗ ,b ⃗ >=π4,b ⃗ 2−a ⃗ 2=a ⃗ ⋅b ⃗ , ∴b ⃗ 2−8=|a ⃗ ||b ⃗ |cos π4=2√2×√22|b ⃗ |=2|b ⃗ |, 即|b ⃗ |−2|b ⃗ |−8=0, 得(|b ⃗ |+2)(|b ⃗ |−4)=0, 得|b ⃗ |=−2,(舍)或|b ⃗ |=4, 故答案为:4.根据向量数量积以及一元二次方程进行转化求解即可.本题主要考查向量数量积的应用,根据条件建立方程,利用一元二次方程的解法是解决本题的关键,是中档题.15.【答案】90 60【解析】解:根据题意,某凸32面体,12个面是五边形,20个面是六边形,即面数F=32,则其棱数E=12(12×5+20×6)=90,其顶点数V=2+E−F=2+90−32=60;故答案为:90,60.根据题意,结合凸多面体的几何结构,可得棱数E=12(12×5+20×6),计算可得E的值,又由“欧拉公式”,计算可得答案.本题考查合情推理的应用,注意理解“欧拉公式”以及凸32面体的几何结构,属于基础题.16.【答案】4+2√2【解析】解:∵tanBcosC=1−sinC,∴sinBcosC=cosB−cosBsinC,即sinBcosC+cosBsinC=sin(B+C)=cosB,∵B+C=π−A,∴sinA=cosB,∴△ABC是∠C=π2的直角三角形,故S△ABC=12ab=2,即ab=4,c=√a2+b2,∴△ABC的周长a+b+√a2+b2=√a2+b2+2ab+√a2+b2≥√4ab+√2ab=4+2√2,当且仅当a=b=2时,等号成立.故答案为:4+2√2.由题意可得,sin(B+C)=cosB,根据三角形内角的性质,可得∴△ABC是∠C=π2的直角三角形,再结合基本不等式的公式,即可求解.本题主要考查了三角函数与不等式的综合应用,需要学生较强的综合能力,属于中档题.17.【答案】解:(1)设等差数列的公差为d,因为a1=2,所以前n项和S n=na1+n(n−1)d2=d2n2+(2−d2)n,所以nS n=d2n3+(2−d2)n2,又nS n=An3+3n2+B,所以{A =d22−d 2=3B =0,解得{d =−2A =−1B =0,所以a n =a 1+(n −1)d =2−2(n −1)=−2n +4, 即数列{a n }的通项公式为a n =−2n +4.(2)由(1)可知S n =−n 2+3n ,6−2Am =6+2m ,3−5A +B =8, a m =−2m +4,S 3−5A+B =S 8=−8²+3×8=−40, 因为a m ,6−2Am ,S 3−5A+B 成等比数列, 所以(6+2m)²=(−2m +4)×(−40), 即m²−14m +49=0,解得m =7.【解析】(1)设等差数列的公差为d ,由等差数列的前n 项和公式求得S n ,从而可得nS n ,结合已知及对应项系数相等即可求解d ,A ,B 的值,从而得到数列的通项公式;(2)由(1)可求得a m ,6−2Am ,S 3−5A+B ,然后根据等比数列的性质可得关于m 的方程,再求出m 的值. 本题考查等差数列的通项公式及前n 项和公式,等比数列的性质,考查运算求解能力,属于中档题.18.【答案】解:(1)证明:∵AB =BC ,D 为AC 的中点,∴BD ⊥AC ,∵直三棱柱ABC −A 1B 1C 1,∴CC 1⊥平面ABC , ∵BD ⊂平面ABC ,∴CC 1⊥BD , ∵CC 1∩AC =C ,∴BD ⊥平面ACC 1A 1, ∵C 1D ⊂平面ACC 1A 1,∴BD ⊥DC 1,∵在直三棱柱ABC −A 1B 1C 1中,AC =2AA 1=2,AB =BC ,D 为AC 的中点.∴DA 1=DC 1=√12+12=√2,A 1C 1=2,∴DC 12+DA 12=A 1C 12,∴DA 1⊥DC 1,∵BD ∩DA 1=D ,∴DC 1⊥平面A 1BD ;(2)∵在直三棱柱ABC −A 1B 1C 1中,AC =2AA 1=2,AB =BC ,D 为AC 的中点,BD =1, ∴BA ⊥BC ,以B 为原点,BA 为x 轴,BC 为y 轴,BB 1为z 轴,建立空间直角坐标系,B(0,0,0),D(√22,√22,0),B 1(0,0,1),C 1(0,√2,1),BB 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,1),BD ⃗⃗⃗⃗⃗⃗ =(√22,√22,0),B 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =(√22,√22,−1),B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,√2,0), 设平面BDB 1的法向量n⃗ =(x,y ,z), 则{n ⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =√22x +√22y =0n ⃗ ⋅BB 1⃗⃗⃗⃗⃗⃗⃗ =z =0,取x =1,得n ⃗ =(1,−1,0), 设平面DB 1C 1的法向量m⃗⃗⃗ =(a,b ,c), 则{m ⃗⃗⃗ ⋅B 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =√22a +√22b −c =0m ⃗⃗⃗ ⋅B 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =√2b =0,取a =2,得m ⃗⃗⃗ =(2,0,√2), 设二面角B −DB 1−C 1的平面角为θ, 则二面角B −DB 1−C 1的余弦值为: cosθ=|m ⃗⃗⃗ ⋅n ⃗⃗ ||m ⃗⃗⃗ |⋅|n ⃗⃗ |=√2⋅√6=√33.【解析】(1)推导出BD ⊥AC ,CC 1⊥BD ,从而BD ⊥平面ACC 1A 1,进而BD ⊥DC 1,由勾股定理得DA 1⊥DC 1,由此能证明DC 1⊥平面A 1BD ;(2)推导出BA ⊥BC ,以B 为原点,BA 为x 轴,BC 为y 轴,BB 1为z 轴,建立空间直角坐标系,利用向量法能求出二面角B −DB 1−C 1的余弦值.本题考查线面垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.19.【答案】解:(1)将频率看作概率,则有每天成交订单数200300400频数(天数)水果A02313水果B5616水果C131216设A2表示水果A卖出200单,以此类推,又P(X≥1000)=P(X=1000)+P(X=1100)=P(A3)P(B3)P(C4)+P(A4)P(B3)P(C3)+P(A4)P(B2)P(C4)+P(A4)P(B3)P(C4)=23×16×16+13×16×12+13×56×16+13×16×16=11108;(2)X的可能取值为700,800,900,1000,1100,则P(X=700)=P(A3)P(B2)P(C2)=23×56×13=527,P(X=800)=P(A3)P(B3)P(C2)+P(A3)P(B2)P(C3)+P(A4)P(B2)P(C2)=23×16×13+23×56×12+13×56×13=1127,P(X=900)=P(A3)P(B2)P(C4)+P(A3)P(B3)P(C3)+P(A4)P(B2)P(C3)+P(A4)P(B3)P(C2)=23×56×16+23×16×12+13×56×12+13×16×13=1136,P(X=1000)=P(A3)P(B3)P(C4)+P(A4)P(B3)P(C3)+P(A4)P(B2)P(C4)=23×16×16+13×16×12+13×56×16=554,P(X=1100)=P(A4)P(B3)P(C4)=13×16×16=1108.【解析】(1)将频率看作概率,求出每天成交订单数的概率,由概率的乘法公式分析求解即可;(2)先确定X的可能取值,然后利用相互独立事件的概率乘法公式分别求解概率即可.本题考查概率的求法,考查离散型随机变量的分布列的求法,相互独立事件概率乘法公式的应用等,考查运算求解能力,是中档题.20.【答案】解:(1)根据条件可得椭圆E的右准线为x=4,e=ca =12,若PA垂直于右准线,如图,则|PF|=e|PA|,即|PA|=2|PF|,所以|PD|+2|PF|=|PD|+|PA|,故当仅当D ,P ,A 三点共线时,|PD|+|PA|最短,即为D 到右准线的距离d =5, 故|PD|+2|PF|的最小值为5;证明:(2)由题意,设l :x =ky +1,A(x 1,y 1),B(x 2,y 2), 联立{x =ky +1x 24+y 23=1得:(3k²+4)y²+6ky −9=0,则y 1+y 2=−6k 3k 2+4,y 1y 2=−93k 2+4, 又M(−2,0),N(2,0),则AM :y =y 1x 1+2(x +2),BN :y =y 2x 2−2(x −2),当x =4时,y AM =6y 1x 1+2=6y 1ky1+3,y BN =2y 2x 2−2=2y 2ky 2−1,而6y 1ky 1+3−2y 2ky2−1=6ky 1y 2−6y 1−6ky 1y 2−6y 2(ky 1+3)(ky 2−1)=4ky 1y 2−6(y 1+y 2)(ky 1+3)(ky 2−1)=4k⋅(−93k 2+4)−6⋅(−6k3k 2+4)(ky 1+3)(ky 2−1)=0,即y AM =y BN ,所以直线AM 与BN 的交点在椭圆E 的右准线x =4上,得证.【解析】(1)若PA 垂直于右准线x =4于A ,由题设可得|PA|=2|PF|,则|PD|+2|PF|=|PD|+|PA|,易知当D ,P ,A 共线时有最小值,即可求最小值;(2)设l :x =ky +1,A(x 1,y 1),B(x 2,y 2),联立椭圆与直线方程,并应用韦达定理可求y 1+y 2,y 1y 2,写出直线AM ,BN 的方程,令x =4求对应的纵坐标,利用作差法判断它们是否相等,即可证明结论. 本题考查直线与椭圆的综合,熟练应用题设所给条件是关键,涉及韦达定理得应用,属于中档题.21.【答案】解:由题可得f′(x)=(2−a)x +a −2x ,(1)则f′(2)=2(2−a)+a −1=3−a =2,解得a =1, 又f(2)=4(1−a2)+2a −2ln2=4−2ln2, 且直线2x −y +b =0过点(2,f(2)), 所以4−4+2ln2+b =0,解得b =−2ln2, 综上:a =1,b =−2ln2; (2)f′(x)=(2−a)x +a −2x =(2−a)x 2+ax−2x=(x−1)[(2−a)x+2]x(x >0),①当a =2时,f′(x)=2(x−1)x ,所以x ∈(0,1),f(x)递减,x ∈(1,+∞),f(x)递增;则f(x)min =f(1)=2>0,所以f(x)无零点,不符题意; ②当a ≠2时,令f′(x)=0,则x =1或x =2a−2,(i)当a <2时,f(x)在(0,1)上递减,在(1,+∞)上递增,则f(x)min =f(1)=1+a2, 若1+a2≤0,即a ≤−2时,f(1)≤0,当x →0时,f(x)>0, 所以f(x)有零点,符合题意;(ii)当1=2a−2,即a =4时,则f′(x)≤0,所以f(x)在(0,+∞)上递减,f(x)=−x²+4x −2lnx ,f(1e )=−1e 2+4e +2>0,f(e³)=−e 6+4e 3−6<0, 所以函数f(x)存在零点,即a =4符合题意; (iii)当1<2a−2,即2<a <4时,则函数f(x)在(0,1)和(2a−2,+∞)上递减,在(1,2a−2)上递增, f(1)=1+a2>0,当x →+∞时,f(x)<0, 所以f(x)存在零点,即a >4符合题意, 综上所述:a ∈(−∞,−2]∪(2,+∞).【解析】(1)先求出函数的导函数,然后根据导数的几何意义求出a ,再将点(2,f(2))代入切线方程即可求出b ;(2)线求出函数的导函数,再讨论a 是否为0,然后求出导函数的零点,讨论零点的大小,再根据零点存在定理即可求出a 的取值范围.本题考查函数零点与方程根的关系,涉及分类讨论思想,属于中档题.22.【答案】解:(1)由曲线C 1的参数方程为{x =2costy =1+cos 4t −sin 4t (t 为参数),得y =1+cos 4t −sin 4t =1+(cos 2t +sin 2t)(cos 2t −sin 2t) =1+(cos 2t −sin 2t)=2cos 2t ,∴曲线C 1的直角坐标方程为y =2⋅(x2)2=12x 2; 又曲线C 2的极坐标方程为ρ=−2(sinθ+cosθ), ∴ρ2=−2(ρsinθ+ρcosθ),则x 2+y 2=−2x −2y , 可得曲线C 2的直角坐标方程为(x +1)2+(y +1)2=2;(2)曲线C 1的极坐标方程为ρsinθ=12ρ2cos 2θ,即ρ=2sinθcos 2θ,把θ=α分别代入曲线C 1与C 2的极坐标方程,得|ρ1|=|OM|=2sinαcos 2α,|ρ2|=|ON|=2(sinα+cosα), ∴|ON||ON|=2sinα⋅2(sinα+cosα)cos 2α=4(tan 2α+tanα)=8,解得tanα=1或tanα=−2. ∵0<α<π2,∴tanα=1,则α=π4.【解析】(1)把曲线C 1的参数方程中的参数t 消去,可得曲线C 1的直角坐标方程;把曲线C 2的极坐标方程两边同时乘以ρ,结合极坐标与直角坐标的互化公式可得C 2的直角坐标方程;(2)写出曲线C 1的极坐标方程,把θ=α分别代入曲线C 1、C 2的极坐标方程,结合|OM||ON|=8求解tanα,进一步得到角α的值.本题考查简单曲线的极坐标方程,考查参数方程化普通方程,考查运算求解能力,是中档题.23.【答案】证明:(1)∵a +b +c =2,∴a 2+b 2+c 2+2ab +2ac +2bc =4,∵a 2+b 2≥2ab ,a 2+c 2≥2ac ,b 2+c 2≥2bc ,∴a 2+b 2+c 2+2ab +2ac +2bc ≤a 2+b 2+c 2+a 2+b 2+a 2+c 2+b 2+c 2, 即3(a 2+b 2+c 2)≥4,可得a 2+b 2+c 2≥43; (2)由柯西不等式可得:[(a −1)2+(b +t)2+c 2]⋅(12+12+12)≥(a −1+b +t +c)2=(1+t)2, 当且仅当a −1=b +t =c ,又a =b +c =2,即a =4+t 3,b =1−2t 3,c =1+t 3时取等号,∴(a −1)2+(b +t)2+c 2≥13(1+t)2,又(a −1)2+(b +t)2+c 2≥34,∴13(1+t)2≥34, 解得t ≥12或t ≤−52.【解析】(1)把已知等式两边平方,然后结合基本不等式即可证明a 2+b 2+c 2≥43;(1)由柯西不等式得到(a −1)2+(b +t)2+c 2≥13(1+t)2,结合已知得到13(1+t)2≥34,求解得结论. 本题考查不等式的证明,训练了基本不等式及柯西不等式的应用,考查逻辑思维能力及推理论证能力,是中档题.。
2021年高考数学冲刺卷02 理(新课标Ⅰ卷)答案

2021年高考数学冲刺卷02 理(新课标Ⅰ卷)答案第Ⅰ卷(共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.【命题意图】本题考查不等式解法、集合的交集运算,容易题.【答案】A【解析】由128x ≤<,解得03x ≤<,所以{}|03P x x =≤<,所以{}1,2P Q =,故选A .2.【命题意图】本题考查复数的运算与几何意义,容易题.【答案】A【解析】由(1)|1|2z i i i i -=-+=+,得2(2)(1)2121i i i z i +++-+===+,则z 的实部为212-,故选A . 3.【命题意图】本题考查等差数列的前n 项和与性质,容易题.【答案】A【解析】根据等差数列的性质,535S a =,所以533255S a ==. 4.【命题意图】本题考查函数奇偶性、充要条件判断,容易题.【答案】C5.【命题意图】本题考频率分布直方图及性质,容易题.【答案】B【解析】设中间一个长方形的面积为x ,则其他8个小长方形面积和为52x ,则512x x +=,所以27x =,所以中间一组的频数为2140407⨯=,故选B . 6.【命题意图】本题考查推理与证明、球的体积,中档题.【答案】B【解析】所求的空间几何体是以原点为球心,1为半径的球位于第一象限的部分,体积为3141836ππ⨯⨯⨯=,故选B .7.【命题意图】本题考查线性回归的基本思想,中档题.【答案】D【解析】由题意可得18131012434386410,40 44x y++-+++====,代入到线性回归方程2y x a=-+,可得60,260a y x=∴=-+,由26072y x=-+=,可得6x=-,故选D.8.【命题意图】本题考查程序框图、对数运算,中档题.【答案】B【解析】11,lg lg31,3i S===->-否;1313,lg+lg lg lg51,355i S====->-否;1515,lg+lg lg lg71,577i S====->-否;1717,lg+lg lg lg91,799i S====->-否;1919,lg+lg lg lg111,91111i S====-<-是,输出9,i=故选B.9.命题意图】本题考查线性规划问题,中档题.【答案】B10.【命题意图】本题考查平面向量的几何意义、平行关系,中档题.【答案】A【解析】由()22PA PB PC AB PB PA++==-,得3PA PB PC CB=-=,所以PA BC,且13PA BC=,ABC∆的边AB上的高是ABP∆边AB上的高的3倍,所以13ABPABCSS∆∆=,由12,4ABC ABPS S∆∆=∴=.11.【命题意图】本题考查双曲线的定义与几何意义,中档题.【答案】A【解析】由题意不妨设223,4,5AB BF AF ===,因为22222AB BF AF +=,所以290ABF ∠=,又由双曲线的定义得12122,2BF BF a AF AF a -=-=,所以1113453AF AF AF +-=-⇒=,所以1222BF BF a -==,所以1a =,在直角12BFF ∆中,222121252F F BF BF =+=,因为22124F F c =,所以2452c =,所以52c =,所以双曲线的离心率为13ce a==,故选A . 12.【命题意图】本题考查函数的单调性、复合函数,较难题. 【答案】B第Ⅱ卷(共90分)二、填空题(本大题共4小题,每小题5分,共20分) 13.【命题意图】本题考查二项式定理,容易题.【答案】15【解析】由题意得,二项式的展开式662166((1)r r rrr r r r T C xC xx---+==-,当4r =时,常数项为446(1)15C -=.14.【命题意图】本题考查三视图、棱柱与圆柱的体积计算,中档题.【答案】32165++π【解析】由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为16242=⨯⨯,两个底面面积之和为3232212=⨯⨯⨯;半圆柱的侧面积为ππ44=⨯,两个底面面积之和为ππ=⨯⨯⨯21212,所以几何体的表面积为32165++π. 15.【命题意图】本题考查两圆位置关系、直线与圆的位置关系,中档题.【答案】3216.【命题意图】本题考查等比数列的前n 项和、不等式恒成立问题,较难题.【答案】272≥k 【解析】()2323313131++-=--=n n n T ,所以23231+=+n n T ,将不等式转化为()n n n n k 32232)63(1-⨯=⨯-≥+恒成立,所以只需求数列n n 342-的最大值.因为当1=n 时,nn 342-=23-,当2=n 时,n n 342-=0,当3=n 时,n n 342-=272,当4=n 时,n n 342-=814,即数列值是先增后减,当3=n 时,取得最大值272,所以272≥k . 三、解答题(解答应写出文字说明、证明过程或演算步骤)17.【命题意图】本题考查三角恒等变换、三角函数的性质、正弦定理与余弦定理的应用,以及考查转化能力、逻辑思维能力、运算求解能力、整体思想的应用.【解析】(1)2()2sin cos 233sin 232f x x x x x x =+=+ 2sin(2)3x π=+,因此()f x 的最小正周期为22T ππ==.………………(3分) 因为3222232k x k πππππ≤≤+++, 所以,()f x 的单调递减区间为7[,]1212x k k ππππ∈++()k Z ∈.………………(5分) (2) 由()2sin(2())2sin 326263A A f A πππ-=-+==, 又∵A 为锐角,∴3A π=.………………(7分)由正弦定理可得2sin 33a R A ===,133sin sin 2b c B C R ++==,………………(9分)则1331413143b c +=⋅=. 由余弦定理可知,22222()21cos 222b c a b c bc a A bc bc +-+--===, 整理,得40bc =.………………(12分)18.【命题意图】本题考查空间直线和平面间的垂直关系、二面角、空间向量的应用,以及考查空间想象能力、逻辑推证能力、运算求解能力、转化的思想.(2)由(1)可建立分别以直线,,CA CB CF 为轴轴轴,z y x ,,建立如图所示的空间直角坐标系,令)30(≤≤=λλFM ,则)0,0,3(),0,0,0(A C ,()()1,0,,0,1,0λM B ,∴ ()()1,1,,0,1,3-=-=λBM AB .………………(7分) 设1(,,)n x y z =为平面MAB 的一个法向量,由110n AB n BM ⎧=⎪⎨⋅=⎪⎩ ,联立得⎩⎨⎧=+-=+-003z y x y x λ ,取1=x ,则1n ()λ-=3,3,1.…………(9分)∵()21,0,0n =是平面FCB 的一个法向量, ∴=θcos 1212||||||n n n n ⋅⋅()234λ=-+.………………(10分)∵03λ≤≤, ∴ 当0λ=时,θcos 有最小值77,当3λ=时,θcos 有最大值12, ∴71cos ,72θ⎡⎤∈⎢⎥⎣⎦.………………(12分)19.【命题意图】本题考查古典概型的概率、离散型随机变量分布列与期望,以及考查分类讨论思想、运算求解能力、数据处理能力.(2)计算10名同学的综合指标,可得下表: 人员编号 1A2A3A4A5A6A7A8A9A10A综合指标4461453543其中综合指标是一级的4≥有1235689,,,,,,A A A A A A A ,共7名, 综合指标不是一级的()4ω<有1710,,A A A 共3名. ………………(7分) 随机变量X 的所有可能取值为:1,2,3,4,5.()114211738121C C P X C C ===,()()11111122411211117373462,32121C C C C C C P X P X C C C C +======, ()()1111121111117373214,52121C C C C P X P X C C C C ======,………………(9分) 所以X 的分布列为:X 1 2 3 4 5P821 421 621 221 121所以12345212121212121EX =⨯+⨯+⨯+⨯+⨯=.………………(12分) 20.【命题意图】本题考查椭圆的方程与几何性质、直线与椭圆的位置关系,以及考查方程思想、逻辑思维能力、运算求解能力.(2)设直线l 的方程为:1-=my x ()R m ∈,则由⎪⎩⎪⎨⎧=+-=134122y x my x ,得()0964322=--+my y m .设()11y ,x C ,()22y ,x D ,则436221+=+m m y y ,0439221<+-=⋅m y y . 所以,2121y AB S ⋅=,1221y AB S ⋅=, ()21122142121y y y y AB S S +⨯⨯=-=-43122+=m m ………………(8分) 当0m ≠时,=-21S S 343212431222=⨯≤+=mmm m ()R m ∈. 由432=m ,得 332±=m ; 当0=m 时,3021<=-S S 从而,当332±=m 时,21S S -取得最大值3.………………(12分) 21.【命题意图】本题考查利用导数研究函数的单调性与极值、不等式恒成立问题,以及考查等价转化思想、方程思想、逻辑思维能力、运算求解能力.请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(冲刺高考)2021年春辉教育云平台高考考前提分试卷理 科 数 学(十)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4、考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2019·宁波期末]已知集合,,则( )A .B .C .D .2.[2019·江南十校]的值为( )A .B .C .D .3.[2019·西安适应]设复数,,则( )A .B .C .D .4.[2019·湖北联考]设双曲线的右焦点与抛物线的焦点相同,双曲线的一条渐近线方程为,则双曲线的方程为( )A .B .C .D .5.[2019·延边质检]下列函数中,既是奇函数,又是上的单调函数的是( )A .B .C .D .6.[2019·江南十校]已知边长为1的菱形中,,点满足,则的值是( )A .B .C .D .7.[2019·江西联考]将函数的图像沿轴向左平移个单位后,得到一个函数的图像,则“是偶函数”是“”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件8.[2019·长春质检]一个几何体的三视图如图所示,则这个几何体的体积为( )A .32B .C .D .89.[2019·江西联考]程序框图如下图所示,若上述程序运行的结果,则判断框中应填入( )A .B .C .D .10.[2019·滨州期末]已知抛物线的焦点为,准线为,是上一点,是直线与抛物线的一个交点,若,则( )此卷只装订不密封班级 姓名 准考证号 考场号 座位号A.3B.C.4或D.3或411.[2019·珠海期末]若、满足约束条件,目标函数取得最大值时的最优解仅为,则的取值范围为()A.B.C.D.12.[2019·荆门检测]设函数(,为自然对数的底数),定义在上的函数满足,且当时,.令,已知存在,且为函数的一个零点,则实数的取值范围为()A.B.C.D.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2019·中山一中]假设要考察某公司生产的狂犬疫苗的剂量是否达标,现从500支疫苗中抽取50支进行检验,利用随机数表抽取样本时,先将500支疫苗按000,001,,499进行编号,如果从随机数表第7行第8列的数开始向右读,请写出第3支疫苗的编号______________________.(下面摘取了随机数表第7行至第9行)84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 7663 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54 14.[2019·武威十八中]学校艺术节对、、、四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:甲说:“是或作品获得一等奖”;乙说:“作品获得一等奖”;丙说:“、两件作品未获得一等奖”;丁说:“是作品获得一等奖”.评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.15.[2019·江西联考]函数,则不等式的解集是_________.16.[2019·湛江二模]如图,游客从景点下山至有两种路径:一种是从沿直线步行到,另一种是先从乘缆车到,然后从沿直线步行到.现有甲、乙两位游客从下山,甲沿匀速步行,速度为米/分钟.在甲出发分钟后,乙从乘缆车到,在处停留分钟后,再从匀速步行到.已知缆车从到要分钟,长为米,若,.为使两位游客在处互相等待的时间不超过分钟,则乙步行的速度(米/分钟)的取值范围是__________.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(12分)[2019·河南期末]在公差为的等差数列中,.(1)求的取值范围;(2)已知,试问:是否存在等差数列,使得数列的前项和为?若存在,求的通项公式;若不存在,请说明理由.18.(12分)[2019·深圳调研]某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如下图所示:(1)将去年的消费金额超过 3200 元的消费者称为“健身达人”,现从所有“健身达人”中随机抽取2人,求至少有1位消费者,其去年的消费金额超过4000元的概率; (2)针对这些消费者,该健身机构今年欲实施入会制,详情如下表:预计去年消费金额在内的消费者今年都将会申请办理普通会员,消费金额在内的消费者都将会申请办理银卡会员,消费金额在内的消费者都将会申请办理金卡会员.消费者在申请办理会员时,需一次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:方案1:按分层抽样从普通会员,银卡会员,金卡会员中总共抽取25位“幸运之星”给予奖励:普通会员中的“幸运之星”每人奖励500元;银卡会员中的“幸运之星”每人奖励600元; 金卡会员中的“幸运之星”每人奖励800元.方案2:每位会员均可参加摸奖游戏,游戏规则如下:从一个装有3个白球、2个红球(球只有颜色不同)的箱子中,有放回地摸三次球,每次只能摸一个球.若摸到红球的总数为2,则可获得200元奖励金;若摸到红球的总数为3,则可获得300元奖励金;其他情况不给予奖励.规定每位普通会员均可参加1次摸奖游戏;每位银卡会员均可参加2次摸奖游戏;每位金卡会员均可参加3次摸奖游戏(每次摸奖的结果相互独立).以方案2的奖励金的数学期望为依据,请你预测哪一种方案投资较少?并说明理由.19.(12分)[2019·咸阳模拟]如图,在四棱锥中,底面是菱形,,,,.(1)求证:平面; (2)若与平面所成的角为,求二面角的余弦值.20.(12分)[2019·十堰模拟]已知椭圆过点.(1)求椭圆的方程,并求其离心率;(2)过点作轴的垂线,设点为第四象限内一点且在椭圆上(点不在直线上),点关于的对称点为,直线与交于另一点.设为原点,判断直线与直线的位置关系,并说明理由.21.(12分)[2019·吕梁一模]已知函数,若曲线在点处的切线方程为.(1)求实数、的值;(2)证明:.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(10分)【选修4-4:坐标系与参数方程】[2019·渭南质检]在直角坐标系中,直线的参数方程为(为参数),以原点为极点,轴正半轴为极轴建立极坐标系,圆的极坐标方程为.(1)若,求圆的直角坐标方程与直线的普通方程;(2)设直线截圆的弦长等于圆的半径长的倍,求的值.23.(10分)【选修4-5:不等式选讲】[2019·银川一中]设不等式的解集是,,.(1)试比较与的大小;(2)设表示数集的最大数.,求证:.(冲刺高考)2021年春辉教育云平台高考考前提分试卷理科数学答案(十)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】B 【解析】∵集合,,∴,故选B .2.【答案】A【解析】,故选A .3.【答案】A【解析】∵,∴.故选A .4.【答案】B【解析】由题意得双曲线的渐近线方程为,又双曲线的一条渐近线方程为,∴,故,∴双曲线方程为,∴双曲线的右焦点坐标为.又抛物线的焦点坐标为,双曲线的右焦点与抛物线的焦点相同,∴,,∴双曲线的方程为.故选B .5.【答案】B 【解析】对于A ,,有,则函数为偶函数,不符合题意;对于B ,,有,函数为奇函数,且在上的单调递增,符合题意;对于C ,,有,函数为奇函数,但在上不是单调函数,不符合题意;对于D ,,的定义域为,在上不是单调函数,不符合题意;故选B .6.【答案】D【解析】由题意可得大致图像如下:;,∴,又,,∴.故选D .7.【答案】B【解析】函数的图像沿轴向左平移个单位后,得到,当为偶函数时,,.故“是偶函数”是“”的必要不充分条件.故选B .此卷只装订不密封班级 姓名 准考证号 考场号 座位号8.【答案】B【解析】由题意,根据给定的三视图可知,该几何体表示底面是边长为4的正方形,高为4的四棱锥,∴该四棱锥的体积为,故选B.9.【答案】D【解析】初始值,;执行框图如下:,;不能满足条件,进入循环;,;不能满足条件,进入循环;,,此时要输出,因此要满足条件,∴.故选D.10.【答案】B【解析】设到的距离为,则由抛物线的定义可得,∵,∴,,∴直线的斜率为,∵抛物线方程为,∴,准线,∴直线的方程为,与联立可得或(舍去),∴,故选B.11.【答案】A【解析】结合不等式组,绘制可行域,得到:目标函数转化为,当时,则,此时的范围为,当时,则,此时的范围为,综上所述,的范围为,故选A.12.【答案】D【解析】∵,∴,∴为奇函数,当时,,∴在上单调递减,∴在上单调递减.∵存在,∴,∴,即.令,,∵为函数的一个零点,∴在时有一个零点.∵当时,,∴函数在时单调递减,由选项知,,又∵,∴要使在时有一个零点,只需使,解得,∴的取值范围为,故选D.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.【答案】068【解析】由题意,根据简单的随机抽样的方法,利用随机数表从第7行的第8列开始向右读取,依次为,,,,∴第3支疫苗的编号为.14.【答案】B【解析】若A为一等奖,则甲、乙、丙、丁的说法均错误,不满足题意;若B为一等奖,则乙、丙的说法正确,甲、丁的说法错误,满足题意;若C为一等奖,则甲、丙、丁的说法均正确,不满足题意;若D为一等奖,则乙、丙、丁的说法均错误,不满足题意;综上所述,故B获得一等奖.15.【答案】【解析】当时,不等式可化为,解得,结合可得;当时,不等式可化为,解得,结合可得,故答案为.16.【答案】【解析】在中解三角形:已知,,,则,由正弦定理可得,乙从出发时,甲已经走了,还需走才能到达C.设乙步行的速度为,由题意得,解得,∴为使两位游客在处互相等待的时间不超过3分钟,乙步行的速度应控制在范围内.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.【答案】(1);(2)存在,通项公式为.【解析】(1)∵,∴,整理得,则,解得,则的取值范围为.(2)∵,∴,即,则.假设存在等差数列,则,即,解得,从而,此时,,故存在等差数列,且,使得数列的前项和为.18.【答案】(1);(2)预计方案2投资较少;见解析.【解析】(1)设随机抽取的2人中,去年的消费金额超过4000元的消费者有人,则的可能值为“0,1,2”,∴.或者.(2)方案1:按分层抽样从普通会员,银卡会员,金卡会员中总共抽取25位“幸运之星”,则“幸运之星”中的普通会员,银卡会员,金卡会员的人数分别为:,,,∴按照方案1奖励的总金额为:元,方案2:设表示参加一次摸奖游戏所获得的奖励金,则的可能值为“0,200,300”,∵摸到红球的概率:,∴,,,∴的分布列为∴元,∴按照方案2奖励的总金额为:元,∵方案1奖励的总金额多于方案1奖励的总金额,∴预计方案2投资较少.19.【答案】(1)见解析;(2).【解析】(1)证明:∵四边形是菱形,∴为,的中点,又,,∴,,∵,且、平面,∴平面.(2)设菱形的边长为,∵,∴,∴.由(1)知平面,∴与平面所成的角为,得到,建立如图所示的空间直角坐标系:则,,,,得到,.设平面的法向量,平面的法向量.则,即,令,则,得到.同理可得,∴.∵二面角为钝二面角,则余弦值为.20.【答案】(1)椭圆的方程为,离心率;(2)直线与直线平行,理由见解析.【解析】(1)由椭圆方程椭圆过点,可得,∴,∴椭圆的方程为,离心率.(2)直线与直线平行.证明如下:设直线,,设点的坐标为,,由得,∴,∴,同理,∴,由,,有,∵在第四象限,∴,且不在直线上.∴,又,故,∴直线与直线平行.21.【答案】(1),;(2)见解析.【解析】(1),,又由题意得,,∴,∴可得,构造函数,则在区间内恒大于0,∴在区间内单调递增,又,∴关于的方程的根为,把代入,解得,∴,.(2)证明:由(1)知,则,∵在区间单调递增,,,∴有唯一实根,记为,即,∴,由得,整理得,∵时,,函数单调递减,时,,函数单调递增,∴,当且仅当,即时取等号,∵,∴,即.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.【答案】(1),;(2)或.【解析】(1)当时,转化为,整理成直角坐标方程为,直线的参数方程为(为参数),转化成直角坐标方程为.(2)圆的极坐标方程转化成直角坐标方程为:,直线截圆的弦长等于圆的半径长的倍,∴,整理得,利用平方法解得或.23.【答案】(1);(2)见解析.【解析】由得,解得,∴.(1)由,,得,,∴,故.(2)由,得,,,∴,故.。
