2020年新高考数学二轮复习练习:小题强化练 小题强化练(八)
2020版高考数学二轮复习第一部分小题强化练小题强化练(四)(含解析)(最新整理)

(京津鲁琼专用)2020版高考数学二轮复习第一部分小题强化练小题强化练(四)(含解析)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((京津鲁琼专用)2020版高考数学二轮复习第一部分小题强化练小题强化练(四)(含解析))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(京津鲁琼专用)2020版高考数学二轮复习第一部分小题强化练小题强化练(四)(含解析)的全部内容。
小题强化练(四)一、选择题1.设集合A={y|y=log2x,0〈x≤4},B={x|e x〉1},则A∩B=()A.(0,2)B.(0,2]C.(-∞,2)D.R2.若i为虚数单位,复数z满足z(1+i)=|1-i|+i,则z的虚部为()A。
错误!B。
错误!-1C.错误!iD.错误!3.设随机变量X~N(1,1),其正态分布密度曲线如图所示,那么向正方形ABCD中随机投掷10 000个点,则落入阴影部分的点的个数的估计值是( )注:若X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ〈X≤μ+2σ)=0。
954 5.A.6 038 B.6 587C.7 028 D.7 5394.《九章算术》中的“竹九节"问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,现自上而下取第1,3,9节,则这3节的容积之和为()A。
133升B。
错误!升C.199升D。
2512升5.某城市有连接8个小区A,B,C,D,E,F,G,H和市中心O的整齐方格形道路网,每个小方格均为正方形,如图所示.某人从道路网中随机地选择一条最短路径,由小区A前往小区H,则他经过市中心O的概率为( )A.13B。
高考数学二轮复习题型强化练1 客观题8+4+4标准练(A) (2)

题型强化练1 客观题8+4+4标准练(A )一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2020天津滨海新区联考,1)设集合U={x|x ≥-1},A={1,3,5,7},B={x|x>5},则A ∩∁U B=( ) A.{1,3,5} B.{3,5}C.{1,3}D.{1,3,5,7}2.(2020山东日照二模,2)在复平面内,已知复数z 对应的点与复数1+i 对应的点关于实轴对称,则z i=( )A.1+iB.-1+iC.-1-iD.1-i 3.(2020北京西城二模,6)设a=30.2,b=log 32,c=log 0.23,则 ( )A.a>c>bB.a>b>cC.b>c>aD.b>a>c4.(2020山东日照一模,3)南北朝时代的伟大数学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”.其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,如图,夹在两个平行平面之间的两个几何体的体积分别为V 1,V 2,被平行于这两个平面的任意平面截得的两个截面的面积分别为S 1,S 2,则“S 1,S 2总相等”是“V 1,V 2相等”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件5.(2019广东深圳适应性考试,文8)已知△ABC 是边长为1的等边三角形,D ,E 分别是边AB ,BC 的中点,连接DE 并延长到点F ,使得DE=2EF ,则AF ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ 的值为 ( ) A.-58 B.118C.14D.186.(2020广东东莞一模,8)函数y=cos x ·2x +12x -1的部分图象大致为( )7.(2020河北石家庄5月检测,8)若双曲线C:x 2a2−y2b2=1(a>0,b>0)的一条渐近线被圆x2+y2-4y+2=0所截得的弦长为2,则双曲线C的离心率为()A.√3B.2√33C.2D.√28.(2020山东聊城一模,8)高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,为了纪念数学家高斯,人们把函数y=[x],x∈R称为高斯函数,其中[x]表示不超过x的最大整数.设{x}=x-[x],则函数f(x)=2x{x}-x-1的所有零点之和为()A.-1B.0C.1D.2二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分.9.(2020海南线上诊断测试,9)如图所示的曲线图是2020年1月25日至2020年2月12日陕西省及西安市新冠肺炎累计确诊病例的曲线图,则下列判断正确的是()A.1月31日陕西省新冠肺炎累计确诊病例中西安市占比超过了13B.1月25日至2月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势C.2月2日后到2月10日陕西省新冠肺炎累计确诊病例增加了97例D.2月8日到2月10日西安市新冠肺炎累计确诊病例的增长率大于2月6日到2月8日的增长率10.(2020山东德州一模,10)1970年4月24日,我国发射了自己的第一颗人造地球卫星“东方红一号”,从此我国开始了人造卫星的新篇章.人造地球卫星绕地球运行遵循开普勒行星运动定律:卫星在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为2a ,2c ,下列结论正确的是( )A.卫星向径的取值范围是[a-c ,a+c ]B.卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间C.卫星向径的最小值与最大值的比值越大,椭圆轨道越扁平D.卫星运行速度在近地点时最大,在远地点时最小11.(2020山东淄博一模,10)在正方体ABCD-A 1B 1C 1D 1中,P ,Q 分别为棱BC 和棱CC 1的中点,则下列说法正确的是( ) A.BC 1∥平面AQPB.平面APQ 截正方体所得截面为等腰梯形C.A 1D ⊥平面AQPD.异面直线QP 与A 1C 1所成的角为60°12.(2020海南海南中学月考,12)已知函数f (x )=A sin(ωx+φ)(A>0,ω>0)在x=1处取得最大值,且最小正周期为2,则下列说法正确的有( ) A.函数f (x-1)是奇函数B.函数f (x+1)是偶函数C.函数f (x+2)在[0,1]上单调递增D.函数f (x+3)是周期函数三、填空题:本题共4小题,每小题5分,共20分.13.(2020山东泰安考前模拟,14)(x -1x )(1-x )4的展开式中x 3的系数为 .14.《九章算术》中的“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则该竹子最上面一节的容积为 升. 15.(2019四川攀枝花统考,文16)已知函数f (x )=(x -b )2-lnx x (b ∈R ).若存在x ∈[1,2],使得f (x )+xf'(x )>0,则实数b 的取值范围是 .16.已知正三棱柱ABC-A 1B 1C 1的六个顶点都在球O 的表面上,AB=3,异面直线AC 1与BC 所成角的余弦值为310,则球O 的表面积为 .题型强化练题型强化练1 客观题8+4+4标准练(A )1.A 解析 由题意∁U B={x|-1≤x ≤5},∴A ∩∁U B={1,3,5}. 2.C 解析 由题意得z=1-i,所以zi =1-ii =i+1-1=-1-i .3.B 解析 指数函数y=3x 为R 上的增函数,则a=30.2>30=1;对数函数y=log 3x 为(0,+∞)内的增函数,则log 31<log 32<log 33,即0<b<1;对数函数y=log 0.2x 为(0,+∞)内的减函数,则c=log 0.23<log 0.21=0.故a>b>c.4.A 解析 根据祖暅原理,当S 1,S 2总相等时,V 1,V 2相等,所以充分性成立;当两个完全相同的四棱台,一正一反的放在两个平面之间时,此时体积固然相等但截得的面积未必相等,所以必要性不成立.所以“S 1,S 2总相等”是“V 1,V 2相等”的充分不必要条件.5.D 解析 由DE=2EF ,可得DE ⃗⃗⃗⃗⃗ =2EF ⃗⃗⃗⃗⃗ ,EF ⃗⃗⃗⃗⃗ =12DE ⃗⃗⃗⃗⃗ .如图所示,连接AE ,则AE ⊥BC ,所以BC ⃗⃗⃗⃗⃗ ·AE ⃗⃗⃗⃗⃗ =0,AF ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =(AE ⃗⃗⃗⃗⃗ +EF ⃗⃗⃗⃗⃗ )·BC ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ ·AE ⃗⃗⃗⃗⃗ +12DE ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =0+12·|DE ⃗⃗⃗⃗⃗ |·|BC ⃗⃗⃗⃗⃗ |·cos π3=0+12×12×1×12=18.故选D .6.A 解析 令f (x )=y=cos x ·2x+12x -1(x ≠0),则f (-x )=cos(-x )·2-x+12-x -1=cos x ·12x +112x -1=cos x ·2x +11-2x =-f (x ),所以函数f (x )为奇函数,可排除B,D; 当x ∈(0,π2)时,cos x>0,2x +12x -1>0,所以f (x )>0,故排除C.7.C 解析 双曲线C :x 2a 2−y 2b2=1(a>0,b>0)的渐近线方程为y=±ba x ,由对称性,不妨取y=ba x ,即bx-ay=0.圆x 2+y 2-4y+2=0可化为x 2+(y-2)2=2,其圆心的坐标为(0,2),半径为√2. 圆心(0,2)到渐近线的距离d=√(√2)2-12=1. 由点到直线的距离公式,可得√b +a 2=2a c =2e =d=1,所以e=2.8.A 解析 由题意知,当x=0时,f (x )=-1,所以0不是函数f (x )的零点.当x ≠0时,由f (x )=2x {x }-x-1=0可得,2{x }=1x +1,令y 1=2{x }=2x-2[x ],y 2=1x +1,作出函数y 1=2{x }=2x-2[x ],y 2=1x +1的图象如图所示, 由图象可知,除点(-1,0)外,函数y 1=2{x }=2x-2[x ],y 2=1x +1图象其余交点关于(0,1)中心对称,所以横坐标互为相反数.由函数零点的定义知,函数f (x )=2x {x }-x-1的所有零点之和为-1.9.ABC 解析 1月31日陕西省新冠肺炎累计确诊病例共有87例,其中西安32例,所以西安所占比例为3287>13,故A 正确;由曲线图可知,1月25日至2月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势,故B 正确;2月2日后到2月10日陕西省新冠肺炎累计确诊病例增加了213-116=97(例),故C 正确;2月8日到2月10日西安市新冠肺炎累计确诊病例的增长率为98-8888=544,2月6日到2月8日西安新冠肺炎累计确诊病例的增长率为88-7474=737,显然737>544,故D 错误.10.ABD解析根据椭圆定义知卫星向径的取值范围是[a-c,a+c],故A正确;当卫星在左半椭圆弧运行时,对应的面积更大,根据面积守恒规律,速度应更慢,故B 正确;a-c a+c =1-e1+e=21+e-1,比值越大,则e越小,椭圆轨道越接近于圆,故C错误.根据面积守恒规律,卫星在近地点时向径最小,故速度最大,在远地点时向径最大,故速度最小,故D正确.11.ABD解析如图,因为P,Q分别为棱BC和棱CC1的中点,所以PQ∥BC1, 又因为BC1⊄平面AQP,PQ⊂平面AQP,由线面平行的判定定理,知BC1∥平面AQP,故A正确;由AD1∥PQ,知平面APQ截正方体所得截面为四边形APQD1,又因为PQ≠AD1,所以四边形APQD1是等腰梯形,故B正确;若A1D⊥平面AQP,则A1D⊥AP,又因为AA1⊥AP,AA1∩A1D=A1,所以AP⊥平面A1AD,而AB⊥平面A1AD,这与垂直于同一平面的两条直线平行矛盾,故C不正确;异面直线QP与A1C1所成的角为∠A1C1B,而△A1C1B为等边三角形,故D正确. 12.BCD解析因为f(x)=A sin(ωx+φ)的最小正周期为2,所以2=2πω,所以ω=π.又因为f(x)=A sin(ωx+φ)在x=1处取得最大值,所以ω+φ=2kπ+π2(k∈Z).所以φ=2kπ-π2(k∈Z).所以f(x)=A sin(ωx+φ)=-A cos πx.设g(x)=f(x-1)=-A cos [π(x-1)]=A cos πx,因为g(-x)=A cos [π(-x)]=A cos πx=g(x),所以g(x)=f(x-1)是偶函数,故A不正确;设h (x )=f (x+1)=-A cos [π(x+1)]=A cos πx ,因为h (-x )=A cos [π(-x )]=A cos πx=h (x ),所以h (x )=f (x+1)是偶函数,故B 正确; 设m (x )=f (x+2)=-A cos [π(x+2)]=-A cos πx ,因为x ∈[0,1],所以πx ∈[0,π],又因为A>0,所以函数m (x )=f (x+2)在[0,1]上单调递增,故C 正确; 设n (x )=f (x+3)=-A cos [π(x+3)]=A cos πx ,函数n (x )最小正周期为2ππ=2,故D 正确.13.5 解析 (1-x )4的通项为T r+1=C 4r 14-r (-x )r =(-1)r C 4r x r ,令r=2,此时x 3的系数为(-1)2C 42=6,令r=4,此时x 3的系数为-(-1)4C 44=-1,则x 3的系数为6-1=5.14.1322 解析 设竹子自上而下各节的容积分别为a 1,a 2,…,a 9,且为等差数列,根据题意得{a 1+a 2+a 3+a 4=3,a 7+a 8+a 9=4,即{4a 1+6d =3,3a 1+21d =4,解得a 1=1322,故最上面一节的容积为1322升.15.-∞,74解析 ∵f (x )=(x -b )2-lnx x ,x>0,∴f'(x )=2x (x -b )-1-(x -b )2+lnxx 2,∴f (x )+xf'(x )=(x -b )2-lnx x +2x (x -b )-1-(x -b )2+lnxx=2x (x -b )-1x. 存在x ∈[1,2],使得f (x )+xf'(x )>0,即2x (x-b )-1>0,∴b<x-12x 在[1,2]上有解. 设g (x )=x-12x (1≤x ≤2),∴b<g (x )max .g (x )=x-12x 在[1,2]上为增函数, 故g (x )max =g (2)=74,∴b<74. 故实数b 的取值范围是-∞,74. 16.28π 解析 由题意BC ∥B 1C 1,所以∠AC 1B 1或其补角为异面直线AC 1与BC 所成的角.设AA 1=b ,在△AC 1B 1中,AB 1=AC 1,则cos ∠AC 1B 1=12B 1C 1AC 1=12·√32+b =310,所以AA 1=b=4.设外接球的半径为R ,底面外接圆的半径为r ,则R 2=r 2+(b 2)2.因为底面为等边三角形,所以2r=3sin π3,即r=√3,所以R 2=3+4=7,所以球O 的表面积为4π×7=28π.。
2020年新高考数学二轮复习练习:小题强化练 小题强化练(二)

小题强化练(二)一、选择题1.设集合M ={x |x 2-x ≥0},N ={x |x <2},则M ∩N =( ) A .{x |x <0}B .{x |1≤x <2}C .{x |x ≤0或1≤x <2}D .{x |0≤x ≤1}2.复数i 51-i 的虚部是( )A.12B.i 2 C .-12D .-i 23.∃x ≥0,使2x +x -a ≤0,则实数a 的取值范围是( ) A .(1,+∞) B .[1,+∞) C .(-∞,1)D .(-∞,1]4.设向量a ,b 满足a +b =(3,1),a ·b =1,则|a -b |=( ) A .2 B. 6 C .2 2D.105.设数列{a n }为等差数列,a 1=22,S n 为其前n 项和,若S 10=S 13,则公差d =( ) A .-2 B .-1 C .1D .26.在⎝⎛⎭⎪⎫x 2-2x 6的二项展开式中,x 2的系数为( )A.154 B .-154C.38D .-387.已知F 是抛物线C :y 2=4x 的焦点,抛物线C 的准线与双曲线Г:x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线交于A ,B 两点,若△ABF 为等边三角形,则Γ的离心率e =( )A.32B.233C.217D.2138.将甲、乙等6位同学平均分成正方、反方两组举行辩论赛,则甲、乙被分在不同组中的概率为( )A.310B.12C.35D.259.若函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,0<φ≤π2的图象关于点⎝⎛⎭⎫π6,0对称,且f (x )在⎣⎡⎦⎤0,π6上单调递减,则ω=( )A .1B .2C .3D .410.已知点P 在圆x 2+y 2=4上,A (-2,0),B (2,0),M 为BP 中点,则sin ∠BAM 的最大值为( )A.12B.13C.1010D.1411.(多选)某电视台主办的歌手大奖赛上七位评委为甲、乙两名选手打出的分数为甲:81,84,m ,70,85,85,85;乙:93,84,79,86,84,84,87(其中m 为数字90~99中的一个).则下列结论不正确的是( )A .甲选手的平均分有可能和乙选手的平均分相等B .甲选手的平均分有可能比乙选手的平均分高C .甲选手得分的中位数比乙选手得分的中位数低D .甲选手得分的众数比乙选手得分的众数高12.(多选)如图,棱长为1的正方体ABCD -A1B 1C 1D 1中,P 为线段A 1B 上的动点,则下列结论正确的是( )A .平面D 1A 1P ⊥平面A 1APB .∠APD 1的取值范围是⎝⎛⎭⎫0,π2C .三棱锥B 1D 1PC 的体积为定值 D .DC 1⊥D 1P13(多选)若定义域为(0,+∞)的函数f (x )的导函数f ′(x )满足xf ′(x )+1>0,且f (1)=1,则下列结论中不成立的是( )A .f (e)>1B .f ⎝⎛⎭⎫1e <0C .∀x ∈(1,e),f (x )>0D .∃x ∈(1,e),f (x )-f ⎝⎛⎭⎫1x +2<0 二、填空题14.已知如表所示的数据的回归直线方程为y ^=4x +242,则实数a =________.15.已知函数f (x )=⎩⎪⎨⎪⎧x ln (x +1),x ≥0,则不等式f (x )<1的解集为______.16.已知S n 是数列{a n }的前n 项和,S n =2-2a n +1,若a 2=12,则S 5=______.17.已知F 1,F 2分别为椭圆C :x 2a 2+y 2=1(a >1)的左、右焦点,点F 2关于直线y =x 的对称点Q 在椭圆上,则长轴长为________;若P 是椭圆上的一点,且|PF 1|·|PF 2|=43,则S △F 1PF 2=________.小题强化练(二)1.解析:选C.由x 2-x ≥0,解得x ≥1或x ≤0,所以集合M ={x |x ≥1或x ≤0}.因为N ={x |x <2},所以M ∩N ={x |x ≤0或1≤x <2},故选C.2.解析:选A.由i 51-i =i 1-i =i (1+i )(1-i )(1+i )=-1+i 2=-12+12i ,可知复数的虚部为12,故选A.3.解析:选B.因为∃x ≥0,使2x +x -a ≤0,所以a ≥2x +x ,易知f (x )=2x +x 在[0,+∞)上单调递增,所以f (x )min =f (0)=1,所以a ≥1,故选B.4.解析:选B.因为a +b =(3,1),所以|a +b |=32+1=10,所以|a -b |2=|a +b |2-4a ·b =10-4×1=6,所以|a -b |=6,故选B.5.解析:选A.法一:设等差数列{a n }的公差为d ,由a 1=22,S 10=S 13得10×22+10×92d =13×22+13×122d ,解得d =-2,故选A.法二:由题意可得3a 12=a 11+a 12+a 13=S 13-S 10=0,则a 12=0,所以公差d =a 12-a 112-1=0-2211=-2. 6.解析:选D.由二项式定理可得⎝⎛⎭⎪⎫x 2-2x 6的通项为T r +1=C r 6⎝⎛⎭⎫x 26-r ⎝⎛⎭⎫-2x r =C r 6⎝⎛⎭⎫126-r(-2)r x3-r(r =0,1,2,3,…,6),令3-r =2,则r =1,所以x 2的系数为C 16⎝⎛⎭⎫126-1×(-2)1=-38,故选D.7.解析:选D.由题意可得,抛物线y 2=4x 的焦点为F (1,0),准线为直线x =-1,双曲线的渐近线方程为y =±b a x .设点A 在第二象限,由等边三角形的性质可知A ⎝⎛⎭⎫-1,233.又因为点A 在双曲线的渐近线y =-b a x 上,所以渐近线方程为y =-233x ,所以b a =233,则e =ca =1+b 2a 2=213. 8.解析:选C.由题可知,所有的分组组数为C 36,甲、乙被分在不同组中的基本事件为C 12C 24,故所求的概率P =C 12C 24C 36=35.9.解析:选C.由函数f (x )的图象关于点⎝⎛⎭⎫π6,0对称,且在⎣⎡⎦⎤0,π6上单调递减,可知π6ω+φ=k 1π,k 1∈Z ①,且在⎣⎡⎦⎤0,π3上单调递减,则函数f (x )的最小正周期T ≥2×π3②,⎣⎡⎦⎤φ,π3ω+φ⊆⎣⎡⎦⎤2k 2π+π2,2k 2π+3π2,k 2∈Z ③,由③可得⎩⎨⎧φ≥2k 2π+π2,π3ω+φ≤2k 2π+3π2,其中k 2∈Z .④因为0<φ≤π2,所以φ=π2,由①②④及φ=π2,ω>0可得⎩⎪⎨⎪⎧π6ω+π2=k 1π,2πω≥2×π3,π3ω+π2≤2k 2π+3π2,k 1,k 2∈Z ,即⎩⎪⎨⎪⎧ω=6k 1-3,0<ω≤3,k 1,k 2∈Z ,ω≤6k 2+3,解得ω=3.故选C.10.解析:选B.设点M 的坐标为(x ,y ),则P (2x -2,2y ),将点P 的坐标代入圆的方程可得点M 的轨迹方程为(x -1)2+y 2=1,如图所示,当AM 与圆K 相切时,sin ∠BAM 取得最大值,此时sin ∠BAM =|MK ||AK |=13.11.解析:选ABC.由题意知,甲选手的平均分为x 甲=17×(70+81+85+85+85+84+m )=70+m7,m ∈[90,99],且m ∈Z ;乙选手的平均分为x 乙=17×(79+84+84+84+86+87+93)=8527,令70+m 7=8527,解得m =107,这与m 的取值范围不符,所以A ,B 选项错误;对于C ,甲选手得分的中位数是85,乙选手得分的中位数为84,甲的中位数比乙的中位数高,C 错误;对于D ,甲选手得分的众数是85,乙选手得分的众数是84,甲的众数高于乙的众数,D 正确.12.解析:选ACD.在A 中,因为A 1D 1⊥平面A 1AP ,A 1D 1⊂平面D 1A 1P ,所以平面D 1A 1P ⊥平面A 1AP ,故A 正确;对B 中,当P 与A 1重合时,∠APD 1=π2,故B 错误;在C 中,因为△B 1D 1C 的面积是定值,A 1B ∥平面B 1D 1C ,所以点P 到平面B 1D 1C 的距离是定值,所以三棱锥B 1D 1PC 的体积为定值,故C 正确;在D 中,因为DC 1⊥D 1C ,DC 1⊥BC ,D 1C ∩BC =C ,D 1C ,BC ⊂平面BCD 1A 1,所以DC 1⊥平面BCD 1A 1,所以DC 1⊥D 1P ,故D 正确.13.解析:选ABD.根据题意,若定义域为(0,+∞)的函数f (x )的导函数f ′(x )满足xf ′(x )+1>0,则有f ′(x )+1x >0,则有(f (x )+ln x )′>0,设g (x )=f (x )+ln x ,则g ′(x )=f ′(x )+1x >0,则g (x )在(0,+∞)上为增函数,依次分析选项:对于A ,e >1,则g (e)>g (1),即f (e)+ln e >1,则有f (e)>0,不能得到f (e)>1,A 不成立;对于B ,1e <1,则g ⎝⎛⎭⎫1e <g (1),即f ⎝⎛⎭⎫1e +ln 1e =f ⎝⎛⎭⎫1e -1<1,即有f ⎝⎛⎭⎫1e <2,f ⎝⎛⎭⎫1e <0不一定成立,故B 不成立;对于C ,g (x )在(1,e)上为增函数,且g (1)=1,则有f (x )+ln x >1,则f (x )>1-ln x ,又当1<x <e 时,0<ln x <1,则f (x )>0,符合题意;对于D ,当x ∈(1,e)时,有x >1x >1e >0,此时有g (x )>g ⎝⎛⎭⎫1x ,即f (x )+ln x >f ⎝⎛⎭⎫1x +ln ⎝⎛⎭⎫1x ,变形可得f (x )-f ⎝⎛⎭⎫1x +2ln x >0,又当1<x <e 时,0<ln x <1,则f (x )-f ⎝⎛⎭⎫1x +2>0恒成立,不符合题意.故选ABD.14.解析:回归直线y ^=4x +242必过样本点的中心(x ,y ),而x =2+3+4+5+65=4,y=251+254+257+a +2665=1 028+a 5,所以1 028+a5=4×4+242,解得a =262.答案:26215.解析:当x <0时,f (x )=x 2<1,解得-1<x <0;当x ≥0时,f (x )=ln(x +1)<1,解得0≤x <e -1,综上,不等式f (x )<1的解集为(-1,e -1).答案:(-1,e -1)16.解析:法一:由题意可知S 1=2-2a 2=1,且S n =2-2(S n +1-S n ),整理可得S n +1-2=12(S n -2).因为S 1-2=-1,所以数列{S n -2}是以-1为首项,12为公比的等比数列,故S 5-2=(-1)×⎝⎛⎭⎫124=-116,所以S 5=3116. 法二:根据S n =2-2a n +1,所以a 1=S 1=2-2a 2=1.当n ≥2时,由S n =2-2a n +1①,得S n-1=2-2a n ②,①-②可得a n =-2a n +1+2a n ,所以a n =2a n +1,即a n +1=12a n .因为a 2=12a 1,所以数列{a n }是首项为1,公比为12的等比数列,所以S 5=1×⎣⎡⎦⎤1-⎝⎛⎭⎫1251-12=3116. 答案:311617.解析:由椭圆C :x 2a 2+y 2=1(a >1),知c =a 2-1,所以F 2(a 2-1,0),点F 2关于直线y =x 的对称点Q (0,a 2-1),由题意可得a 2-1=1,即a =2,则长轴长为2 2.所以椭圆方程为x 22+y 2=1,则|PF 1|+|PF 2|=2a =22,又|PF 1|·|PF 2|=43,所以cos ∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|=(|PF 1|+|PF 2|)2-2|PF 1|·|PF 2|-|F 1F 2|22|PF 1|·|PF 2|=8-83-483=12, 所以sin ∠F 1PF 2=32,则S △F 1PF 2=12|PF 1|·|PF 2|·sin ∠F 1PF 2=12×43×32=33. 答案:22 33。
2020新课标高考数学二轮习题:小题强化练(一) Word版含解析

小题强化练 小题强化练(一)一、单项选择题1.i 为虚数单位,a ∈R .若z =a -ia +i +i 为实数,则实数a =( )A .-1B .-12C .1D .22.已知集合U ={x |x 2≥2x },A ={x |log 2x ≥2},则∁U A =( ) A .{x |x ≤0或2≤x <4} B .{x |x ≤-2或0≤x <4} C .{x |x ≤0或1≤x <2}D .{x |x ≤-2或x >4}3.已知数列{a n }为等差数列,若a 3+6=2a 5,则3a 6+a 10=( ) A .18 B .24 C .30D .324.如图,在△ABC 中,AD ⊥AB ,DC →=2BD →,|AB →|=2,则AC →·AB →的值为( )A .-4B .-3C .-2D .-85.若将函数f (x )=sin ⎝⎛⎭⎫2x +π6的图象向左平移φ(φ>0)个单位长度,所得图象关于y 轴对称,则当φ最小时,函数g (x )=cos ⎝⎛⎭⎫12x +2φ-1图象的一个对称中心的坐标是( )A.⎝⎛⎭⎫π3,0 B.⎝⎛⎭⎫-π3,-1 C.⎝⎛⎭⎫-π3,1 D.⎝⎛⎭⎫π3,-1 6.已知一个三棱锥的六条棱的长分别为1,1,1,1,2,a ,且长为a 的棱与长为2的棱所在直线是异面直线,则三棱锥的体积的最大值为( )A.212 B.312 C.26D.367.已知F 为双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点,过点F 向C 的一条渐近线引垂线,垂足为A ,交一条渐近线于点B ,O 为坐标原点.|OF |=|FB |,则C 的渐近线方程为( )A .y =±33xB .y =±2xC .y =±3xD .y =±x8.已知函数f (x )=⎩⎪⎨⎪⎧|ln x |,x >0,x +2,x ≤0,若存在实数x 1,x 2,x 3,且x 1<x 2<x 3,使f (x 1)=f (x 2)=f (x 3),则x 1f (x 2)的取值范围是( )A .[-2,0]B .[-1,0] C.⎣⎡⎦⎤-23,0 D.⎣⎡⎦⎤-12,0 二、多项选择题9.(2020·山东省普通高等学校统一考试)下图为某地区2006年~2018年地方财政预算内收入、城乡居民储蓄年末余额折线图.根据该折线图可知,该地区2006年~2018年( ) A .财政预算内收入、城乡居民储蓄年末余额均呈增长趋势 B .财政预算内收入、城乡居民储蓄年末余额的逐年增长速度相同 C .财政预算内收入年平均增长量高于城乡居民储蓄年末余额年平均增长量 D .城乡居民储蓄年末余额与财政预算内收入的差额逐年增大10.函数f (x )=x1+x 2,x ∈(-∞,0)∪(0,+∞),则下列等式成立的是( )A .f (x )=f ⎝⎛⎭⎫1x B .-f (x )=f ⎝⎛⎭⎫1x C.1f (x )=f ⎝⎛⎭⎫1x D .f (-x )=-f (x )11.如图,在平面直角坐标系xOy 中,角α以Ox 为始边,终边与单位圆O 交于点P .过点P 的圆O 的切线交x 轴于点T ,点T 的横坐标关于角α的函数记为f (α),则下列关于函数f (α)的说法错误的是( )A .f (α)的定义域是⎩⎨⎧⎭⎬⎫α⎪⎪α≠2k π+π2,k ∈ZB .f (α)的图象的对称中心是⎝⎛⎭⎫k π+π2,0,k ∈ZC .f (α)的单调递增区间是[2k π,2k π+π],k ∈ZD .f (α)对定义域内的α均满足f (π+α)=f (α)12.已知O 是坐标原点,A ,B 是抛物线y =x 2上不同于O 的两点,OA ⊥OB ,下列四个结论中,所有正确的结论是( )A .|OA |·|OB |≥2 B .|OA |+|OB |≥2 2C .直线AB 过抛物线y =x 2的焦点D .O 到直线AB 的距离小于等于1 三、填空题13.已知f (x )是(0,+∞)上的可导函数,f (e x )=xe x ,则f ′(e)的值为________.14.若α∈⎝⎛⎭⎫0,π2,cos ⎝⎛⎭⎫π4-α=22cos 2α,则sin 2α=________.15.记S n 为数列{a n }的前n 项和,S n =1-a n ,记T n =a 1a 3+a 3a 5+…+a 2n -1a 2n +1,则a n=________,T n =________.16.在三棱锥D -ABC 中,DC ⊥底面ABC ,AD =6,AB ⊥BC ,且三棱锥D -ABC 的每个顶点都在球O 的表面上,则球O 的表面积为________.小题强化练 小题强化练(一)1.解析:选C.因为z =a -i a +i +i =(a -i )(a -i )(a +i )(a -i )+i =a 2-1-2a i a 2+1+i =a 2-1a 2+1+(a -1)2a 2+1i ,所以由z 为实数得(a -1)2a 2+1=0,解得a =1,故选C.2.解析:选A.U ={x |x 2≥2x }={x |x ≤0或x ≥2},A ={x |log 2x ≥2}={x |x ≥4},则∁U A ={x |x ≤0或2≤x <4},故选A.3.解析:选B.法一:设等差数列{a n }的公差为d ,由a 3+6=2a 5,得a 1+2d +6=2(a 1+4d ),整理得a 1+6d =6,所以3a 6+a 10=3(a 1+5d )+(a 1+9d )=4(a 1+6d )=4×6=24,故选B.法二:由等差数列的性质知a 3+a 7=2a 5,结合条件a 3+6=2a 5,得a 7=6,则3a 6+a 10=2a 6+(a 6+a 10)=2a 6+2a 8=4a 7=24.4.解析:选D.由AD ⊥AB ,DC →=2BD →,|AB →|=2,得AC →·AB →=(AB →+BC →)·AB →=(AB →+3BD →)·AB →=|AB →|2+3AB →·BD →=|AB →|2-3|AB →|·|BD →|cos ∠ABD =|AB →|2-3|AB →|2=-2|AB →|2=-2×22=-8,故选D.5.解析:选D.将函数f (x )=sin ⎝⎛⎭⎫2x +π6的图象向左平移φ(φ>0)个单位长度,可得函数的解析式为h (x )=sin ⎣⎡⎦⎤2(x +φ)+π6=sin ⎝⎛⎭⎫2x +2φ+π6.又函数h (x )的图象关于y 轴对称,所以2φ+π6=k π+π2(k ∈Z ),即φ=k π2+π6(k ∈Z ).又φ>0,则当k =0时,φmin =π6,此时函数g (x )=cos ⎝⎛⎭⎫12x +2×π6-1=cos ⎝⎛⎭⎫12x +π3-1.由12x +π3=k π+π2(k ∈Z ),得x =2k π+π3(k ∈Z ).当k =0时,x =π3,由选项知A ,B ,C 中的点均不是函数g (x )图象的对称中心,故选D.6.解析:选A.如图,在三棱锥A -BCD 中,设AD =a ,BC =2,AB =AC =BD =CD =1,则该三棱锥为满足题意的三棱锥.易知BD ⊥CD ,AB ⊥AC .将△BCD 看作底面,假设平面ABD ⊥平面BCD ,因为平面ABD ∩平面BCD =BD ,CD ⊥BD ,所以CD ⊥平面ABD ,所以CD ⊥AD .在△ACD 中,已知AC =CD =1,所以CD ⊥AD 不成立,即平面ABD 不垂直于平面BCD .同理可知平面ACD 不垂直于平面BCD .则当平面ABC ⊥平面BCD 时,该三棱锥的体积有最大值,此时三棱锥的高h =22.△BCD 是等腰直角三角形,则S △BCD =12×1×1=12.所以此三棱锥的体积的最大值为13×12×22=212,故选A. 7.解析:选A.如图,过点F 向C 的一条渐近线引垂线,垂足为D .双曲线的渐近线方程为y =±ba x ,则点F (c ,0)到渐近线的距离d =|bc |a 2+b 2=b ,即|F A |=|FD |=b ,则|OA |=|OD |=a .又|OF |=|FB |,则|AB |=b +c .△OFB 为等腰三角形,则D 为OB 的中点,所以|OB |=2a .在Rt △OAB 中,则|OB |2=|OA |2+|AB |2,即4a 2=a 2+(b +c )2,整理得c 2-bc -2b 2=0,解得c =2b .又c 2=a 2+b 2,则4b 2=a 2+b 2,即b a =33,所以双曲线的渐近线方程为y =±33x ,故选A.8.解析:选B.作出函数f (x )=⎩⎪⎨⎪⎧|ln x |,x >0,x +2,x ≤0的图象,如图所示.由题设f (x 1)=f (x 2)=f (x 3)=m ,由图易知m ∈(0,2],且x 1∈(-2,0],x 2∈⎣⎡⎭⎫1e 2,1,x 3∈(1,e 2].则由f (x 1)=m ,得x 1+2=m ,解得x 1=m -2,所以x 1f (x 2)=(m -2)·m =(m -1)2-1,则当m =1时,x 1f (x 2)取得最小值-1,当m =2时,x 1f (x 2)取得最大值0,所以x 1f (x 2)的取值范围是[-1,0],故选B.9.解析:选AD.根据题目提供的图表分析题目,区分好两条折线即可.故选AD. 10.解析:选AD.根据题意得f (x )=x 1+x 2,所以f ⎝⎛⎭⎫1x =1x1+⎝⎛⎭⎫1x 2=x 1+x 2,所以f (x )=f ⎝⎛⎭⎫1x ;f (-x )=-x 1+(-x )2=-x1+x 2=-f (x ),所以f (-x )=-f (x ).故AD 正确,BC 错误. 11.解析:选ACD.由三角函数的定义可知P (cos α,sin α),则以点P 为切点的圆的切线方程为x cos α+y sin α=1,由已知有cos α≠0,令y =0,得x =1cos α,即函数f (α)=1cos α.由cos α≠0,得α≠2k π±π2,即函数f (α)的定义域为⎩⎨⎧⎭⎬⎫α⎪⎪α≠2k π±π2,k ∈Z ,故A 错误;函数f (α)的对称中心为⎝⎛⎭⎫k π+π2,0,k ∈Z ,故B 正确;由复合函数的单调性可知,函数f (α)的增区间为⎣⎡⎭⎫2k π,2k π+π2,⎝⎛⎦⎤2k π+π2,2k π+π,k ∈Z ,故C 错误;由函数的周期T =2πω可得f (α)的周期为2π,故D 错误.12.解析:选ABD.设A (x 1,x 21),B (x 2,x 22),则OA →·OB →=0,即x 1x 2·(1+x 1x 2)=0,所以x 2=-1x 1.对于A ,|OA |·|OB |=x 21(1+x 21)·1x 21⎝⎛⎭⎫1+1x 21=1+x 21+1x 21+1≥2,当且仅当x 1=±1时取等号,正确;对于B ,|OA |+|OB |≥2|OA |·|OB |≥22,正确;对于C ,直线AB 的方程为y -x 21=⎝⎛⎭⎫x 1-1x 1(x -x 1),不过点⎝⎛⎭⎫0,14,错误;对于D ,原点到直线AB :⎝⎛⎭⎫x 1-1x 1x -y +1=0的距离d =1⎝⎛⎭⎫x 1-1x 12+1≤1,正确. 13.解析:因为f (e x )=x e x ,所以f (x )=ln xx (x >0),所以f ′(x )=1x ·x -ln x x 2=1-ln xx 2,所以f ′(e)=0. 答案:014.解析:由已知得22(cos α+sin α)=22(cos α-sin α)·(cos α+sin α),所以cos α+sin α=0或cos α-sin α=14,由cos α+sin α=0得tan α=-1,因为α∈⎝⎛⎭⎫0,π2,所以cos α+sin α=0不满足条件;由cos α-sin α=14,两边平方得1-sin 2α=116,所以sin 2α=1516.答案:151615.解析:由题意有a 1=1-a 1,故a 1=12.当n ≥2时,由⎩⎪⎨⎪⎧S n =1-a n ,S n -1=1-a n -1两式相减得a n =S n -S n -1=-a n +a n -1,则a n a n -1=12,故数列{a n }是以12为首项,12为公比的等比数列,可得数列{a n }的通项公式为a n =12n .由等比数列性质可得a 1a 3=a 22,a 3a 5=a 24,…,a 2n -1a 2n +1=a 22n ,所以数列{a 2n -1a 2n +1}是以a 22=116为首项,116为公比的等比数列,则T n =a 22+a 24+…+a 22n =116⎝⎛⎭⎫1-116n 1-116=115⎝⎛⎭⎫1-116n . 答案:12n 115⎝⎛⎭⎫1-116n 16.解析:取AD 的中点为E ,连接EC ,EB .因为DC ⊥平面ABC ,所以DC ⊥AC ,DC ⊥AB ,所以在Rt △ACD 中,EA =ED =EC .因为AB ⊥BC ,且BC ∩DC =C ,所以AB ⊥平面BCD ,所以AB ⊥DB ,所以在Rt △ABD 中,EA =ED =EB ,所以球心O 与AD 的中点E 重合,所以球O 的半径为3,所以球O 的表面积为4π×32=36π.答案:36π。
2020江苏高考数学二轮微专题 巩固强化

.--------------------------------------------------------.
.
.
.
.
.
.
.
.
.
.
.
!"# 1-'1-,-
.
.
.
.
总分!,!分!建议用时!#$*!分钟
.
.
.
.
.
.
姓名!!!!!!!!!!班级!!!!!!!!!!学号!!!!!!!!!!得分!!!!!!!
$ (
$'!
&"#则下列命题为真命题的是!!!!#"填序号$
. . .
. .
"0&$1"0-$*"0&$2"0-$*"0&$2-*&2-#
. .
.
.
.
.
.
"-% 给出以下四个结论!
.
.
.
.
命题'若$!'($'3&"#则$&3(的逆否命题为'若$33#则$!'($'33"(*
.
.
.
.
'$&3(是'$!'($'3&"(的充分条件*
.
.
.
.
.
. . .
&% "!"$-扬州月考$若函数+"$$&$,'$)'$是奇函数#则 )&!!!!#
. . .
.
.
.
高考数学二轮复习练习:专项限时集训8 函数最值、恒成立及存在性问题 含答案

专项限时集训(八) 函数最值、恒成立及存在性问题(限时:60分钟)1.(本小题满分14分)(镇江市2019届高三上学期期末)已知函数f (x )=x ln x ,g (x )=λ(x 2-1)(λ为常数).(1)若函数y =f (x )与函数y =g (x )在x =1处有相同的切线,求实数λ的值; (2)若λ=12,且x ≥1,证明:f (x )≤g (x );(3)若对任意x ∈[1,+∞),不等式f (x )≤g (x )恒成立,求实数λ的取值范围. [解](1)f ′(x )=ln x +1,则f ′(1)=1且f (1)=0. 所以函数y =f (x )在x =1处的切线方程为:y =x -1, 从而g ′(x )=2λx ,g ′(1)=2λ=1,即λ=12.2分(2)证明:由题意知:设函数h (x )=x ln x -12(x 2-1),则h ′(x )=ln x +1-x ,设p (x )=ln x +1-x ,从而p ′(x )=1x-1≤0对任意x ∈[1,+∞)恒成立,所以p (x )=ln x +1-x ≤p (1)=0,即h ′(x )≤0, 因此函数h (x )=x ln x -12(x 2-1)在[1,+∞)上单调递减,即h (x )≤h (1)=0,所以当x ≥1时,f (x )≤g (x )成立. 6分(3)设函数H (x )=x ln x -λ()x 2-1,从而对任意x ∈[1,+∞),不等式H (x )≤0=H (1)恒成立. 又H ′(x )=ln x +1-2λx ,当H ′(x )=ln x +1-2λx ≤0,即ln x +1x≤2λ恒成立时,函数H (x )单调递减.设r (x )=ln x +1x ,则r ′(x )=-ln x x2≤0, 所以r (x )max =r (1)=1,即1≤2λ⇒λ≥12,符合题意;当λ≤0时,H ′(x )=ln x +1-2λx ≥0恒成立,此时函数H (x )单调递增. 于是,不等式H (x )≥H (1)=0对任意x ∈[1,+∞)恒成立,不符合题意;当0<λ<12时,设q (x )=H ′(x )=ln x +1-2λx ,则q ′(x )=1x -2λ=0⇒x =12λ>1,当x ∈⎝ ⎛⎭⎪⎫1,12λ时,q ′(x )=1x -2λ>0,此时q (x )=H ′(x )=ln x +1-2λx 单调递增,所以H ′(x )=ln x +1-2λx >H ′(1)=1-2λ>0, 故当x ∈⎝ ⎛⎭⎪⎫1,12λ时,函数H (x )单调递增.于是当x ∈⎝ ⎛⎭⎪⎫1,12λ时,H (x )>0成立,不符合题意; 综上所述,实数λ的取值范围为λ≥12.14分2.(本小题满分14分)已知函数f (x )=a ln x -bx 3,a ,b 为实数,b ≠0,e 为自然对数的底数,e≈2.71828.(1)当a <0,b =-1时,设函数f (x )的最小值为g (a ),求g (a )的最大值; (2)若关于x 的方程f (x )=0在区间(1,e]上有两个不同的实数解,求a b的取值范围.【导学号:56394114】[解](1)b =-1时,f (x )=a ln x +x 3,则f ′(x )=a +3x 3x,令f ′(x )=0,解得:x =3-a3,∵a <0,∴3-a3>0, x ,f ′(x ),f (x )的变化如下:故g (a )=f ⎝⎛⎭⎪⎫3-a 3=a 3ln ⎝ ⎛⎭⎪⎫-a 3-a3, 令t (x )=-x ln x +x ,则t ′(x )=-ln x ,令t ′(x )=0,解得:x =1, 且x =1时,t (x )有最大值1, 故g (a )的最大值是1,此时a =-3;8分(2)由题意得:方程a ln x -bx 3=0在区间(1,e]上有2个不同的实数根,故a b =x 3ln x在区间(1,e]上有2个不同实数根, 即函数y 1=a b 的图象与函数m (x )=x 3ln x 的图象有2个不同的交点,∵m ′(x )=x 2 3ln x -1 ln x 2,令m ′(x )=0,得:x =3e , x ,m ′(x ),m (x )的变化如下:∴x ∈(1,3e)时,m (x )∈(3e ,+∞),x ∈(3e ,e]时,m (x )∈(3e ,e 3], 故a ,b 满足的关系式是3e <a b≤e 3,即a b的范围是(3e ,e 3].14分3.(本小题满分14分)(江苏省镇江市丹阳高中2019届高三下学期期中)已知函数f (x )=x -1x,(1)函数F (x )=f (e x)-k ⎝ ⎛⎭⎪⎫x +x 36,其中k 为实数, ①求F ′(0)的值;②对∀x ∈(0,1),有F (x )>0,求k 的最大值;(2)若g (x )=x 2+2ln xa(a 为正实数),试求函数f (x )与g (x )在其公共点处是否存在公切线,若存在,求出符合条件的a 的个数,若不存在,请说明理由. [解](1)由F (x )=e x-1e x -k ⎝ ⎛⎭⎪⎫x +x 36得F ′(x )=e x+1e x -k ⎝ ⎛⎭⎪⎫1+x 22,①F ′(0)=2-k ,②记h (x )=F ′(x ),则h ′(x )=e x-1ex -kx ,记m (x )=h ′(x ),则m ′(x )=e x +1e x -k ,当x ∈(0,1)时,e x+1e x ∈⎝ ⎛⎭⎪⎫2,e +1e .3分(ⅰ)当k ≤2时,m ′(x )>2-k ≥0,x ∈(0,1),即m (x )在(0,1)上是增函数, 又m (0)=0,则h ′(x )>0,x ∈(0,1),即h (x )在(0,1)上是增函数,又F ′(0)=2-k ≥0, 则F ′(x )>0,x ∈(0,1),即F (x )在(0,1)上是增函数,故F (x )>F (0)=0,x ∈(0,1). (ⅱ)当k >2时,则存在x 0∈(0,1),使得m ′(x )在(0,x 0)小于0,即m (x )在(0,x 0)上是减函数,则h ′(x )<0,x ∈(0,x 0), 即h (x )在(0,x 0)上是减函数,又F ′(0)=2-k <0, 则F ′(x )<0,x ∈(0,x 0),又F ′(0)=2-k <0, 即F (x )在(0,x 0)上是减函数, 故F (x )<F (0)=0,x ∈(0,x 0),矛盾. 故k 的最大值为2.8分(2)设函数f (x )与g (x )在其公共点x =x 1处存在公切线,则⎩⎨⎧x 1-1x 1=x 21+2ln x 1a, ①1+1x 21=2x 1+2x 1a , ②由②得(2x 1-a )(x 21+1)=0,即x 1=a2,代入①得8ln a -8ln2-a 2+8=0,记G (a )=8ln a -8ln2-a 2+8,则G ′(a )=8a-2a ,得G (a )在(0,2)上是增函数,(2,+∞)上是减函数, 又G (2)=4>0,G (4)=8ln2-8<0,G ⎝ ⎛⎭⎪⎫2e =-4e 2<0, 得符合条件的a 的个数为2.(未证明小于0的扣2分)14分4.(本小题满分16分)(无锡市2019届高三上学期期末)已知f (x )=x 2+mx +1(m ∈R ),g (x )=e x.(1)当x ∈[0,2]时,F (x )=f (x )-g (x )为增函数,求实数m 的取值范围; (2)若m ∈(-1,0),设函数G (x )=f xg x ,H (x )=-14x +54,求证:对任意x 1,x 2∈[1,1-m ],G (x 1)<H (x 2)恒成立.[解](1)∵F (x )=x 2+mx +1-e x ,∴F ′(x )=2x +m -e x. ∵当x ∈[0,2]时,F (x )=f (x )-g (x )为增函数, ∴F ′(x )≥0即2x +m -e x≥0在[0,2]上恒成立, 即m ≥e x-2x 在[0,2]上恒成立. 令h (x )=e x-2x ,x ∈[0,2],则h ′(x )=e x-2,令h ′(x )=0,则x =ln2.∴h (x )在[0,ln2]上单调递减,在[ln2,2]上单调递增. ∵h (0)=1,h (2)=e 2-4>1, ∴h (x )max =h (2)=e 2-4, ∴m ≥e 2-4.6分(2)证明:G (x )=x 2+mx +1ex,则G ′(x )=-x 2+ 2-m x +m -1e x =- x -1 [x - 1-m ]e x. 要证任给x 1,x 2∈[1,1-m ],G (x 1)≤H (x 2)恒成立,即证G (x )max ≤H (x )min , ∵x ∈[1,1-m ],∴G (x )在[1,1-m ]上单调递增,G (x )max =G (1-m )=2-me 1-m ,∵H (x )在[1,1-m ]上单调递减,H (x )min =H (1-m )=-14(1-m )+54.10分要证G (x )max ≤H (x )min ,即证2-m e 1-m ≤-14(1-m )+54,即证4(2-m )≤e1-m[5-(1-m )].令1-m =t ,则t ∈(1,2).设r (x )=e x(5-x )-4(x +1),x ∈[1,2],即r (x )=5e x-x e x-4x -4.r ′(x )=(4-x )e x -4≥2e x -4>0,∴r (x )=e x(5-x )-4(x +1)在[1,2]上单调递增, ∵r (1)=4e -8>0,∴e x(5-x )≥4(x +1),从而有-14(1-m )+54≥2-m e ,即当x ∈[1,1-m ]时,G (x )max ≤H (x )min 成立.16分5.(本小题满分16分)(苏北四市(徐州、淮安、连云港、宿迁)2019届高三上学期期末)已知函数f (x )=x 22e-ax ,g (x )=ln x -ax ,a ∈R .(1)解关于x (x ∈R )的不等式f (x )≤0; (2)证明:f (x )≥g (x );(3)是否存在常数a ,b ,使得f (x )≥ax +b ≥g (x )对任意的x >0恒成立?若存在,求出a ,b 的值;若不存在,请说明理由.【导学号:56394115】[解](1)当a =0时,f (x )=x 22e,所以f (x )≤0的解集为{0};当a ≠0时,f (x )=x ⎝⎛⎭⎪⎫x 2e -a , 若a >0,则f (x )≤0的解集为[0,2e a ]. 若a <0,则f (x )≤0的解集为[2e a,0]. 综上所述,当a =0时,f (x )≤0的解集为{0};当a >0时,f (x )≤0的解集为[0,2e a ]; 当a <0时,f (x )≤0的解集为[2e a,0].4分(2)证明:设h (x )=f (x )-g (x )=x 22e -ln x ,则h ′(x )=x e -1x =x 2-ee x.令h ′(x )=0,得x =e ,列表如下:所以函数h (x )所以h (x )=x 22e-ln x ≥0,即f (x )≥g (x ).8分(3)假设存在常数a ,b 使得f (x )≥ax +b ≥g (x )对任意的x >0恒成立, 即x 22e≥2ax +b ≥ln x 对任意的x >0恒成立. 而当x =e 时,ln x =x 22e =12,所以12≥2a e +b ≥12,所以2a e +b =12,则b =12-2a e ,所以x 22e -2ax -b =x 22e -2ax +2a e -12≥0(*)恒成立,①当a ≤0时,2a e -12<0,所以(*)式在(0,+∞)上不恒成立;②当a >0时,则4a 2-2e (2a e -12)≤0,即⎝ ⎛⎭⎪⎫2a -1e 2≤0,所以a =12e,则b =-12. 令φ(x )=ln x -1ex +12,则φ′(x )=e -x e x,令φ′(x )=0,得x =e ,当0<x <e 时,φ′(x )>0,φ(x )在(0,e)上单调递增; 当x >e 时,φ′(x )<0,φ(x )在(e ,+∞)上单调递减. 所以φ(x )的最大值为φ(e)=0.所以ln x -1ex +12≤0恒成立.所以存在a =12e,b =-12符合题意.16分6.(本小题满分16分)(江苏省南京市、盐城市2019届高三第一次模拟)设函数f (x )=ln x ,g (x )=ax +a -1x-3(a ∈R ). (1)当a =2时,解关于x 的方程g (e x)=0(其中e 为自然对数的底数);(2)求函数φ(x )=f (x )+g (x )的单调增区间;(3)当a =1时,记h (x )=f (x )·g (x ),是否存在整数λ,使得关于x 的不等式2λ≥h (x )有解?若存在,请求出λ的最小值:若不存在,请说明理由.(参考数据:ln2≈0.6931,ln3≈1.0986)[解](1)当a =2时,方程g (e x )=0即为2e x+1e x -3=0,去分母,得2(e x )2-3e x +1=0,解得e x =1或e x=12,故所求方程的根为x =0或x =-ln2. 2分(2)因为φ(x )=f (x )+g (x )=ln x +ax +a -1x-3(x >0), 所以φ′(x )=1x +a -a -1x 2=ax 2+x - a -1 x2= ax - a -1 x +1x2(x >0), ①当a =0时,由φ′(x )>0,解得x >0; ②当a >1时,由φ′(x )>0,解得x >a -1a; ③当0<a <1时,由φ′(x )>0,解得x >0; ④当a =1时,由φ′(x )>0,解得x >0; ⑤当a <0时,由φ′(x )>0,解得0<x <a -1a . 综上所述,当a <0时,φ(x )的增区间为⎝⎛⎭⎪⎫0,a -1a ; 当0≤a ≤1时,φ(x )的增区间为(0,+∞);a >1时,φ(x )的增区间为⎝⎛⎭⎪⎫a -1a ,+∞.6分(3)法一:当a =1时,f (x )=ln x ,g (x )=x -3,h (x )=(x -3)ln x ,所以h ′(x )=ln x +1-3x 单调递增,h ′⎝ ⎛⎭⎪⎫32=ln 32+1-2<0,h ′(2)=ln2+1-32>0, 所以存在唯一x 0∈⎝ ⎛⎭⎪⎫32,2,使得h ′(x 0)=0,即ln x 0+1-3x 0=0,当x ∈(0,x 0)时,h ′(x )<0,当x ∈(x 0,+∞)时,h ′(x )>0,所以h (x )min =h (x 0)=(x 0-3)ln x 0=(x 0-3)⎝ ⎛⎭⎪⎫3x 0-1=- x 0-3 2x 0=6-⎝⎛⎭⎪⎫x 0+9x 0,记函数r (x )=6-⎝ ⎛⎭⎪⎫x +9x ,则r (x )在⎝ ⎛⎭⎪⎫32,2上单调递增,所以r ⎝ ⎛⎭⎪⎫32<h (x 0)<r (2),即h (x 0)∈⎝ ⎛⎭⎪⎫-32,-12,由2λ≥-32,且λ为整数,得λ≥0,所以存在整数λ满足题意,且λ的最小值为0. 16分法二:当a =1时,f (x )=ln x ,g (x )=x -3, 所以h (x )=(x -3)ln x ,由h (1)=0得,当λ=0时,不等式2λ≥h (x )有解,下证:当λ≤-1时,h (x )>2λ恒成立,即证(x -3)ln x >-2恒成立. 显然当x ∈(0,1]∪[3,+∞)时,不等式恒成立, 只需证明当x ∈(1,3)时,(x -3)ln x >-2恒成立. 即证明ln x +2x -3<0.令m (x )=ln x +2x -3, 所以m ′(x )=1x -2 x -3 2=x 2-8x +9x x -3 2,由m ′(x )=0,得x =4-7,当x ∈(1,4-7)时,m ′(x )>0;当x ∈(4-7,3)时,m ′(x )<0; 所以m (x )max =m (4-7)=ln(4-7)-7+13<ln(4-2)-2+13=ln2-1<0. 所以当λ≤-1时,h (x )>2λ恒成立.综上所述,存在整数λ满足题意,且λ的最小值为0. 16分。
高考数学二轮复习之专练二中档小题(八)
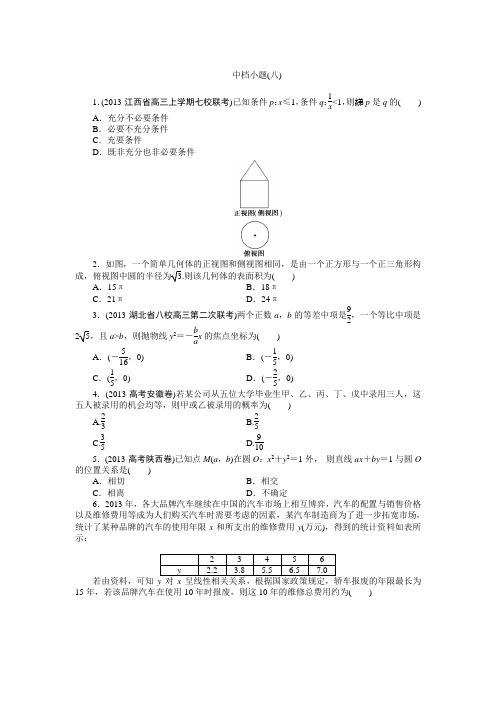
中档小题(八)1.(2013·江西省高三上学期七校联考)已知条件p :x ≤1,条件q :1x<1,则綈p 是q 的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既非充分也非必要条件2.如图,一个简单几何体的正视图和侧视图相同,是由一个正方形与一个正三角形构成,俯视图中圆的半径为 3.则该几何体的表面积为( )A .15πB .18πC .21πD .24π3.(2013·湖北省八校高三第二次联考)两个正数a ,b 的等差中项是92,一个等比中项是25,且a >b ,则抛物线y 2=-b ax 的焦点坐标为( ) A .(-516,0) B .(-15,0) C .(15,0) D .(-25,0) 4.(2013·高考安徽卷)若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为( ) A.23 B.25C.35D.9105.(2013·高考陕西卷)已知点M (a ,b )在圆O :x 2+y 2=1外, 则直线ax +by =1与圆O 的位置关系是( )A .相切B .相交C .相离D .不确定6.2013年,各大品牌汽车继续在中国的汽车市场上相互博弈,汽车的配置与销售价格以及维修费用等成为人们购买汽车时需要考虑的因素,某汽车制造商为了进一步拓宽市场,统计了某种品牌的汽车的使用年限x 和所支出的维修费用y (万元),得到的统计资料如表所示:若由资料,可知15年,若该品牌汽车在使用10年时报废,则这10年的维修总费用约为( )A .11.28万元B .11.38万元C .12.28万元D .12.38万元 7.设变量x ,y 满足约束条件⎩⎪⎨⎪⎧2x +y -2≥0x -2y +k ≥0x -1≤0,如果目标函数z =3x -2y 的取值范围为[-4,3],则k 的值为( )A .5B .4C .3D .28.若不等式|a -2x |≤x +3对任意x ∈[0,2]恒成立,则实数a 的取值范围是( )A .(-1,3)B .[-1,3]C .(1,3)D .[1,3]9.(2013·郑州市高中毕业年级第一次质量预测))设函数f (x )=sin x +cos x ,把f (x )的图象按向量a =(m ,0)(m >0)平移后的图象恰好是函数y =-f ′(x )的图象,则m 的最小值为( ) A.π4 B.π3C.π2D.2π310.执行如图所示的程序框图,则输出的S 的值为( )A .25B .9C .17D .20 11.(2013·广东省惠州市高三第三次调研考试)sin(α+π4)=24,则sin 2α=________. 12.(2013·安徽省“江南十校”高三联考)若不等式组⎩⎪⎨⎪⎧x -y +2≥0ax +y -2≤0y ≥0表示的平面区域的面积为3,则实数a 的值是________.13.(2013·海淀区高三年级第二学期期中练习)某几何体的三视图如图所示,则它的体积为________.14.设A 是整数集的一个非空子集,对于k ∈A ,如果k -1∉A 且k +1∉A ,那么称k 是集合A 的一个“好元素”.给定集合S ={1,2,3,4,5,6,7,8},由S 的3个元素构成的所有集合中,不含“好元素”的集合共有________个.备选题1.(2013·高考课标全国卷Ⅰ)已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,23cos 2A +cos 2A =0,a =7,c =6,则b =( )A .10B .9C .8D .52.函数f (x )=log a |x |+1(0<a <1)的图象大致为( )3.已知函数f (x )=2x -12x ,函数g (x )=⎩⎪⎨⎪⎧f (x ),x ≥0,f (-x ),x <0,则函数g (x )的最小值是________. 4.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a ,b ,c 成递减的等差数列.若A =2C ,则a c的值为________.答案:1.【解析】选A.由x >1得1x <1;反过来,由1x<1不能得知x >1,即綈p 是q 的充分不必要条件.2.【解析】选C.由三视图可知,该几何体是圆锥与等底面的圆柱组合而成的几何体,所以该几何体的表面积是圆锥的侧面积、圆柱的侧面积和底面圆的面积的和,所以该几何体的表面积S =12×2π×3×23+2π×3×23+π×(3)2=21π.3.【解析】选B.由两个正数a ,b 的等差中项是92得a +b =9;a ,b 的一个等比中项是25得ab =20,且a >b ,故a =5,b =4,又由b a =45=2p 得p 2=15,故抛物线y 2=-b ax 的焦点坐标为(-15,0). 4.【解析】选D.由题意,从五位大学毕业生中录用三人,所有不同的可能结果有(甲,乙,丙),(甲,乙,丁),(甲,乙,戊),(甲,丙,丁),(甲,丙,戊),(甲,丁,戊),(乙,丙,丁),(乙,丙,戊),(乙,丁,戊),(丙,丁,戊),共10种,其中“甲与乙均未被录用”的所有不同的可能结果只有(丙、丁、戊)这1种,故其对立事件“甲或乙被录用”的可能结果有9种,所求概率P =910. 5.【解析】选B.由题意知点在圆外,则a 2+b 2>1,圆心到直线的距离d =1a 2+b2<1,故直线与圆相交. 6.【解析】选D.x =15(2+3+4+5+6)=4,y =15(2.2+3.8+5.5+6.5+7.0)=5,b = 错误!=1.23,a =5-1.23×4=0.08.所以回归直线方程为错误!=0.08+1.23x ,当x =10时,y ^=0.08+1.23×10=12.38(万元).7.【解析】选B.作出不等式组对应的可行域,如图中阴影部分所示,由z =3x -2y 得y=32x -z 2,由图象可知当直线y =32x -z 2经过点C (4-k 5,2+2k 5)时,直线y =32x -z 2的截距最大,而此时z =3x -2y 取得最小值-4,所以12-3k 5-4+4k 5=-4,解得k =4. 8.【解析】选B.不等式|a -2x |≤x +3等价于-x -3≤a -2x ≤x +3,即x -3≤a ≤3x +3对任意x ∈[0,2]恒成立.所以当x ∈[0,2]时,(x -3)max ≤a ≤(3x +3)min ,即-1≤a ≤3.9.【解析】选C.f (x )=sin x +cos x =2sin(x +π4),y =-f ′(x )=-(cos x -sin x )=2sin(x -π4),∵将f (x )的图象按向量a =(m ,0)(m >0)平移后得到y =2sin(x -π4)的图象,∴2sin(x +π4-m )=2sin(x -π4).故m =π2+2k π,k ∈N ,故m 的最小值为π2. 10.【解析】选C.由题知,第一次运行:S =1,T =0,不满足T >S ,则S =1+8=9,n =0+2=2,T =0+22=4;第二次运行:S =9,T =4,不满足T >S ,则S =9+8=17,n =2+2=4,T =4+24=20,此时20>17满足T >S ,故输出的S 的值为17.11.【解析】sin(α+π4)=22sin α+22cos α=24,∴sin α+cos α=12,(sin α+cos α)2=sin 2α+cos 2α+2sin αcos α=1+sin 2α=14,故sin 2α=-34. 【答案】-3412.【解析】作出可行域,如图中阴影部分所示,区域面积S =12(2a+2)×2=3,解得a =2.【答案】213.【解析】依题意得,该几何体是一个四棱锥,其中底面是一个直角梯形(上底长是2、下底长是4、高是4),一个侧面垂直于底面,因此该几何体的体积等于13×12×(2+4)×4×4=16.【答案】1614.【解析】依题意可知,若由S 的3个元素构成的集合不含“好元素”,则这3个元素一定是紧邻的3个数,故这样的集合共有6个.【答案】6备选题1.【解析】选D.由23cos 2A +cos 2A =0,得23cos 2A +2cos 2A -1=0,解得cos A =±15. ∵A 是锐角,∴cos A =15. 又a 2=b 2+c 2-2bc cos A ,∴49=b 2+36-2×b ×6×15, ∴b =5或b =-135. 又∵b >0,∴b =5.2.【解析】选A.由函数f (x )的解析式可确定该函数为偶函数,图象关于y 轴对称,设g (x )=log a |x |,先画出x >0时,g (x )的图象,然后根据g (x )的图象关于y 轴对称画出x <0时g (x )的图象,最后由函数g (x )的图象向上整体平移一个单位即得f (x )的图象,结合图象知选A.3.【解析】当x ≥0时,g (x )=f (x )=2x -12x 为单调增函数,所以g (x )≥g (0)=0;当x <0时,g (x )=f (-x )=2-x -12-x 为单调减函数,所以g (x )>g (0)=0,所以函数g (x )的最小值是0. 【答案】04.【解析】依题意知b =a +c 2,a c =sin A sin C =sin2C sin C =2cos C =2×a 2+b 2-c 22ab ,即a c =a 2+b 2-c 2ab=(a +c )(a -c )+b 2ab =2b (a -c )+b 2ab =2(a -c )+b a ,所以a 2=c [2(a -c )+a +c 2],即(2a -3c )(a -c )=0,又由a >c ,因此有2a =3c ,故a c =32. 【答案】32。
2020年新高考数学二轮复习练习:小题强化练小题强化练(一)

小题强化练
小题强化练 (一 )
1.解析 :选 C.因为
z=
a- a+
i i
+
i=
( (
a- a+
i)( i)(
a- a-
i i
) )
+
i=
a2- 1-2ai a2+ 1
+
i
=
a a
2- 2+
1 1+
( a-1) a2+1
2
(a- 1) 2 i,所以由 z 为实数得 a2+ 1 = 0,解得 a=1,故选 C.
B. - π,- 1 3
D. π3,- 1
8.已知一个三棱锥的六条棱的长分别为 1,1,1, 1, 2,a,且长为 a 的棱与长为 2的
棱所在直线是异面直线,则三棱锥的体积的最大值为
()
2 A. 12
3 B. 12
2 C. 6
3 D. 6
x2 y2 9.已知 F 为双曲线 C:a2-b2= 1(a>0 ,b>0) 的右焦点, 过点 F 向 C 的一条渐近线引垂线,
π
π
解析式为 h(x)= sin 2( x+ φ)+ 6 = sin 2x+ 2φ+ 6 .又函数 h(x)的图象关于 y 轴对称,所以
π
π
kπ π
π
2φ+ 6 = kπ + 2 ( k∈ Z ),即 φ= 2 + 6 (k∈ Z ).又 φ>0,则当 k= 0 时, φ min= 6 ,此时函数
1
1 C.f( x)
=
f
1 x
D. f( -x)=- f( x)
12.(多选 )如图,在平面直角坐标系 xOy 中,角 α以 Ox 为始边,终边 与单位圆 O 交于点 P.过点 P 的圆 O 的切线交 x 轴于点 T,点 T 的横坐标
2020年新高考数学二轮复习练习:小题强化练小题强化练(三)

小题强化练(三)、选择题已知集合 A = {x € N x < 3} , B = {xx 2 + 6x — 16<0},贝V AA B =( ){x|— 8<x<2}1 + z已知复数—1 + i(i 是虚数单位),则三=( 1 1 2 + 2i 1 2 C.1—2i3 .我国古代数学著作《九章算术》有如下问题:“今有金棰,长五尺.斩本一尺,重四 斤.斩末一尺,重二斤.问次一尺各重几何?”意思是:“现有一根金棰,长五尺,一头粗,在粗的一端截下一尺,重四斤;在细的一端截下一尺,重二斤.问依次每一尺各重根据已知条件,若金棰由粗到细是均匀变化的,则中间三尺的重量为C . {1}{0 , 1 , 2}{0,1} 1 2. 5—5i几C. 10斤D. 12 斤设点F2分别是双曲线x29 = 1的左、右焦点.若点P在双曲线上,且P F1• P F2=0,则 |陥+ P F2|=( )A. .10 C. .5B. 2 ,10 D. 2 55.在直三棱柱ABC-A1B1C1中, AA1= 2A1B1 = 2B1C1,且AB 丄BC,点M 是A1C1 的中点, 则异面直线MB与AA1所成角的余弦值为(A1A.3C雪C. 46.在区间[—2, 2]上随机取一个数b,若使直线y = x+ b与圆x2+ y2= a有交点的概率为*,1B.1C. 17.已知定义在R上的函数f(x)满足:(1)f(x+ 2) = f(x); (2)f(x —2)为奇函数;(3)当x€ [0 ,11.(多选)在平面直角坐标系 xOy 中,角a 以Ox 为始边,终边经过点 P(— 1, m )(m > 0), 则下列各式的值一定为负的是( )A . sin a + cos a C . sin a cos a12. (多选)(2019湖南长沙一模)设a , b , c 表示不同直线,a , B 表示不同平面,下列结 论不正确的是() A .若 a // c , b // c,贝U a // b1)时,f (x1)— f >0(x 1工x 2)恒成立,贝y f —15I f (4),住 ;的大小关系正确的是( )f(4)> f8.已知函数f (x )= 2x — log/,且实数a>b>c>0满足2f(a)f(b)f(c)<0.若实数 x o 是函数 y = f(x) 的一个零点,那么下列不等式中不可能成立的是(A . x o <a x o >a C . x o <b X o <c9.已知抛物线的最大值为(A. .32 ;3 D. 310.将函数 y = sin 2x 的图象向右平移$ 0<林守 个单位长度得到y = f (x )的图象.若函数 71f (x )在区间0,—单调递增,且f (x )的最大负零点在区间12, — nn 上,贝y $的取值范围B. 6,,B . sin a — cos a r sin a D.tan aX 1 —X A .C . f2D . ff(4)B. 若a // b, b// a,贝U a // aC . 若 a //a, b // a ,贝U a // bD .若 a? a , b? 3 , a / 3,贝U a // b13. (多选)已知函数f(x)及其导函数f'(x),若存在x o 使得f(x o ) = f'(x o ),则称x o 是f(x )的一个“巧值点”•下列选项中有“巧值点”的函数是2A . f(x) = x C . f(x) = In x 二、填空题14. 二项式2一 x 展开式中含x 3项的系数为 15.设数列{a n }是由正数组成的等比数列, S n 是{a n }的前n 项和,已知a 2a 4= 16, S 3= 28, 则当a i a 2…a n 最大时,n 的值为16. 已知扇形 OAB 的圆心角/ AOB = 90°,半径为2, C 是其弧上一点.若 OC =入OA + QB ,贝U 入卫的最大值为 ________->-> n17. 如图,在△ ABC 中,已知 M 为边 BC 上一点,BC = 4BM ,/ AMC = -3 , AM = 2, △小题强化练(三)21 .解析:选 B.由 A = {x € N X W 3} = {0 , 1 , 2, 3}, B = {x|x + 6x — 16<0} = {x|— 8<x<2}, 得 A n B = {0 , 1},故选 B.1 + z 2.解析:选B.因为Z =- 1 + i ,所以三= 1+ 5i.故选 B. 5 53.解析:选B.由题意知金杖由粗到细每一尺构成一个等差数列,且首项 a 1 = 4, a5=2,1一 xf(x) = ef(x) = tan xAMC 的面积为1 — 1 + i 1—(— 1 + i )i (2+ i ) (2 — i )( 2+ i )则公差d =害=3 3,贝U CM =2.所以a3= a1+ 2d= 4 —1 = 3,所以a2+ a3+ a4= 3a3= 9,故选B.4 .解析:选B.由双曲线方程知a = 1, b= 3,则c=J10, |F1F2|=刃70.由PF1 • P?2= 0,2AA i 所成角的余弦值为,故选B.3x 2 + y 2 = a 有交点,得圆心到直线的距离 d =^ W ,a ,解得b € [— 近,2a]•又b € [ — 2, 2],且直线y = x + b 与圆x 2 + y 2= a 有交点的概率为g, 所以由几何概型的概率计算公式可知P =2a —(—,2a)= £,解得a =i ,故选B.2 — (— 2) 2 27.解析:选C.由f(x + 2) = f(x)可知函数f(x)的周期为2,可知f(x) = f(x — 2).又f(x — 2)为 奇函数,可知 f(x)为奇函数.所以 f —号=f —多+ 2X 4 = f , f(4) = f(4 — 2X 2)= f(0) = 0, f 乎=f 牙一2 X3 = f — 2 .又x € [0, i)时,f(x)单调递增,故奇函数 f(x)在(—i , i)内单调递 增,所以 f 2 >f(0)>f — 2,即 f —号 >f(4)>f ¥,故选 C.8.解析:选D.由f(x) = 2x — log 」x ,可知函数f(x)在区间(0,+^ )上单调递增.因为实数得PF i 丄 PF 2,则 |PF i + PF 2|= |2PO|= |F^1F 2|= 2屮0,故选 B.5.解析:选B.法一:由题知AA i 〃 BB i ,则异面直线 MB 与AA i 所成角 为/ MBB i ,如图•又△ BB i M 为直角三角形,cos / MBB i =器.在直三棱柱1ABC-A i B i C i 中,设 AA i = 2A i B i = 2B i C i = 2,由 AB 丄 BC ,得 B i M = QA i C i ¥•故MB =冷22+普:=希,所以 cos / MBB i = MBB = ^2^2,故选 B.法二:以B 为原点,BA , BC , BB i 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,如图.设 AA i = 2A i B i = 2B i C i = 2,贝V M g, i , 2 }B(0, 0, 0), A(1 , 0, 0), A i (1 , 0, 2),所以 MB =―;1, — 2 , A A i = (0, 0 , 2).设异面直线MB 与AA i 所成角为0,则cosa _ |MB AA i |0 =|MB||A A i |4= 2子,所以异面直线MB 与 A 2 36 .解析:选B.由直线y = x + b 与圆Clx € 0 +时,2x — 2n€ —今,—严I,函数f(x)先减后增,不符合题意,排除B , D ;取©—41 3 - 3 61=6,易得函数f(x) = singx —"3在0,亍 上单调递增,令 2x —n^ = k n (k € Z ),得x =~6 + ? n (k € Z ),则函数f(x)取得的最大负零点为 x =— n 3 € — ,—n 6,符合题意,排除 A ,故选C.a>b>c>0满足f(a)f(b)f(c)<0 ,贝U f(a), f(b), f(c)可能都小于0或有1个小于0, 2个大于0,如 图•贝U A , B , C 可能成立,9.解析:选D.设抛物线上点 M (m, n)( m>0),则 由抛物线的定义得n 2 = 2pm ,可得 |MO |= < m 2 + n 2=寸 m 2 + 2pm.m 2 + 2pm 2 =2pm + pm+7眄=m + P ,所以鋼=m + P2 2浩,即t =晋时,等号成立,故选D.10•解析:选C.法一:函数y = sin 2x 的图象向右平移 © 0<强石 个单位长度得到函数 f(x)=sin(2xnn—2© — — 2© 由函数f(x)在区间0, —2 —■ ■— ^4上单调递增,可知厂 n\ — ~ + 2k nW — 2 ©— 2n1(k € Z ),解得一k nW © W —— k n (k € Z ).又由nn 〜4—2 ©W — + 2k nnn 10< ©<~2,可知 0<©W 4①屈数 f(x)的所有零点满足 2x — 2 ©= k n (k € Z ),即 x = ~k n+©k € Z ),由最大负零点在 一5n ,—才 内,得一5f2<2k n + © < —-6(k € Z),即一5n — fk n <© < — -6 — ~k n (k € Z ),由 0<©<亍可知当k = — 1时,$< © <-3②.由①②,©的取值范围为 盘,亍,故 选C.法二:由题意得f(x)= sin(2x — 2 ©)观察选项可取n©=§,可得 f (x )= sin 2x —,可知当 ,当且仅当2t>-7,则吩P + P ,所以黑1 + ~2 t2 =討尹霍11.解析:选 CD.由已知得 r = |0P|= ;J m 2+ 1,则 sin a = — ?> 0, cos a = -------- 2V m + 1 寸 m + 1V 0, tan a =— m v 0,所以 sin x + cos a 的符号不确定, sin a — cos a > 0, sin a cos a V 0 sin a = cos a V 0.故选 CD.'tan a12. 解析:选BCD.由a , b , c 表示不同直线,a , 3表示不同平面知: 在A 中,若a // c , b // c ,则由平行公理得 a // b ,故A 正确; 在B 中,若a // b , b // a ,贝U a // a 或a? a ,故B 错误;在C 中,若a // a, b // a ,贝U a 与b 相交、平行或异面,故 C 错误; 在D 中,若a? a , b? 3 , a // 3,则a 与b 平行或异面,故 D 错误.13. 解析:选AC.若f(x) = x 2,则f'(x) = 2x ,令x 2= 2x ,得x = 0或x = 2,方程显然有解, 故A 符合要求;若f(x)= e —x ,则f'(x) = — e —x ,令e —x =— e —x ,此方程无解,故 B 不符合要求;1 11若f(x) = In x ,则f '(x) = -,令In x = -,在同一直角坐标系内作出函数y = In x 与y = -的图象(作x x所以方程f(x) = f'(x)存在实数解,故C 符合要求;若f(x)tan x = —,化简得 sin xcos x = 1,变形可得 sin 2x = 2, cos x 无解,故D 不符合要求•故选 AC.T r 十 C 9(x 「—= (- 1)r - 29—也2「— 9.令2r — 9 =3,解得r = 8,可知所求二项式展开式中含x 3项的系数为(一1)8- 29—8C 9= 2X 9= 18.答案:18(9— n ) n=a 3q n —3= 25—n .则 a 1a 2 …a .= 24x 23 x-x 25—n = 22a 1a 2…a n 取得最大值,此时整数n = 4或5.答案:4或516. 解析:由题 |(0A|= |0B |= |0C| = 2,且 OA OB = 0.由 0C =活A + 卩 OB ,两边平方得 OC 2=(?O A +(J OB)2= f OA 2+ 2 入 OA OB + a 2OB 2= 4 f + 4『,可得 4= 4 *+ 4『,即卩 *+『=1,所 以入详三护=2当且仅当f=尸爭时取得等号,故 入J 的最大值为;图略),可得两函数的图象有一个交点,=tan x ,贝U f (x)='=」^,令 9os x jcos x14.解析:二项式展开式的通项为 15.解析:由数列{a n }是各项均为正数的等比数列,且12」丄3= a 2a 4 = 16,可得 a 3= 4.又 S 3=a 3 F+ J + 1 = 28‘ 可得扌 + 十 1= 7’ 即 J -+ 3 = 0,q = — 3舍去,故a n,可知当 (9 — n ) n2 取得最大值时,1答案:217. 解析:因为在△ AMC中,/ AMC = n3, AM = 2, △ AMC的面积为3 3,则有3.3=1AM CM sin / AMC = 2 X 2X CM xf ,所以解得 CM = 6.因为BC = 4E 3M ,所以BM = 2, BC = 8,因为/ AMB = n -Z AMC = 年,所以由余弦定理 3 可得AB = AM 2+ BM 2-2AM BM c os / BMAAC = AM 2+ CM 2- 2AM CM cos / AMC所以 cos Z BAC = AB 2+ A C 2- BC 2 = 12+ 28— 6仁」2AB - AC 2X 2羽 X 2曲7 答案:6 —甲+ 22- 2X 2X 2X+ 62-2X 2X 6X 1 = 2 7,2 3,。
2020年新高考数学二轮复习练习:小题强化练小题强化练(七)

、选择题小题强化练(七)2 z1.若复数z 满足(篙)2= 1 —i,其中i为虚数单位,则复数z在复平面内对应的点位于A.第一象限B.第二象限C.第三象限 D .第四象限2.已知集合M ={x|2x2 * * * * 7—x—3<0} , N={x|X|(x—2)>0},全集U= R,则下列关于集合M, N叙述正确的是() A . M n N= M B . M U N= NC. (?U M) n N= ?23 .若双曲线予一;D. N? (?U M) 2詁=1(a>0, b>0)的一个顶点到一条渐近线的距离等于,则双曲线的离心率为()C.|D. ,34.已知等差数列{a n}, a1 = 2,若a1, a3+ 2, a§+ 8成等比数列,则S10 =(A.85B. —16C.—70 或855.已知角a+n T的终边与单位圆/+宀1交于点P x o,3,贝U sin 2 a等于(D. a<c<ba , b, c,且(b + c)sin B = (a +A.2n3B.c) 则A=(9 .有一个公用电话亭,在观察使用这个电话亭的人流量时,设在某一时刻,有 个人正在使用或等待使用电话的概率为P( n),且P( n)与时刻P( 0)( 1三n 三5),那么P(0)的值是() 0 (n > 6),点F 的直线与抛物线 C 交于A , B 两点,贝U |AF|+ 2|BF|的最小值为( )D . 10b<0 且 c>0 a — b + c>0a +b + c>0不等式ax 2 + bx + c>0的解集是(—2, 1)(多选)已知函数f(x)=|sin x||cos x|,则下列说法正确的是( )nC.6nD・38.函数 f(x)=n(n € N )t 无关,统计得到P(n)=10.已知抛物2 Xa + 22 y= 1(a>0)的焦点重合,过 aC . 7 11.(多选)若不等式ax 2— bx + c>0的解集是(—1 , 2),则下列选项正确的是(C . 12.10x + 1 lg x 2的图象大致为(n f(x)的图象关于直线x=~2对称n f(x)的周期为—C . (n, 0)是f (x )的一个对称中心D . f (x )在区间才,~2上单调递减13. (多选)如图,已知在矩形 ABCD 中,AB = 2AD , E 为边AB 的中点,将△ ADE 沿直线DE 翻折成△ A I DE ,若M 为线段A i C 的 中点,则△ ADE 在翻折过程中,下列命题正确的是( )A .线段BM 的长是定值:B •存在某个位置,使 DE 丄A iC C .点M 的运动轨迹是一个圆D •存在某个位置,使 MB 丄平面 A i DE 二、填空题14. _______________________________________________________________ 已知向量 a = (x ,2),b = (— 2,1),若 a 与 2a — b 共线,则 = ___________________________ .15. 已知等比数列{a n }的公比q>0,其前n 项和为S n ,且S 2= 6,S 4= 30,数列{b n }满足 b n = log 2a 2— 1,则数列 佃匕岀勺前n 项和T n = ____________ .2 216. 已知椭圆C :拿+治=1(a>b>0),A 是椭圆的右顶点,B 为椭圆的上顶点,点 F ( — c , 0)是椭圆的左焦点,椭圆的长轴长为 __________ 4,且BF 丄AB ,则c =.17. (2019 •西北海联考改编)设函数f (x ) = ax 3+ bx 2 + cx (a ,b ,c € R ,a ^ 0)•若不等式b +c xf'(x )— af (x )< 2对一切x € R 恒成立,则 a = _____ , 的取值范围为 ____________ .a小题强化练(七). . 21.解析:选 A.由题意,得 z =(1— i1 + i }= 2i( ;-I )= i (1 — i ) = 1 + i ,则复数 z在复平面内对应的点为(1,1),位于第一象限,故选A.2.解析:选 D.由 2x 2 — x — 3< 0,得(2x — 3)(x + 1) w 0,则 M = — 1, ~ L 所以?U M =(——1,2 U (2,+o ),(?U M)Q N = (2,+o ),(2,+o )? (— o ,— 1) U3.解析:选C.根据双曲线的对称性,不妨取双曲线的一个顶点为 (a ,0),一条渐近线方o o,—1) U 2,+o .由凶(x — 2)>0,得 [XM 0, 贝y N = (2,+o ).因此 M n N = ?,M U N = x — 2>0,3,+o ,故选 D.程为bx — ay = 0•由题意,得一a b —尸ab = 4a ,即-=4所以双曲线的离心率e = c =“1+ -" J b + a 2 c 3c a 3 a 讨 丿=3,故选C . 34.解析:选A.设等差数列{a n }的公差为d ,由a i , a 3+ 2, a 6+ 8成等比数列,得 a i (a 6 + 8) = (a 3+ 2)2,即 2(10 + 5d)= (4 + 2d)2,解得 d i = — 2, d 2=舟•当 d = — 2 时,a 3 + 2= 0, a i , 83 + 2, a 6 + 8不成等比数列,故舍去,所以 d = 2 S 10 = 10X 2 + 10; 9X*= 85,故选A.5 •解析:选B.因为角a+n^的终边与单位圆x 2+ y 2= 1交于点P X 0, 1,所以sin a+寸 =3,所以 cos||2a+ 4 = 1 — 2sin 2 a+-4 = 1 — 2 X 9 = 7 .又因为 cos ||2 a+-4 = cos 2 a+ 2 = — sin 2 a ,所以 sin 2 a = —£,故选 B.20 in 216. 解析:选B.因为in 2 = log e 2,所以0<ln 2<1,所以c = (in 2) <1.因为2 <2 <2,所以1<a<2.又 b = 2 + 2ln 2>2,所以 c<a<b ,故选 B.7.解析:选A.由已知可得(b + c)sin B = (a + c)(sin A — sin C),由正弦定理可得(b + c)b = (a2 2 2b +c — a 1+ c)(a — c),整理得 b 2 + c 2— a 2=— bc ,由余弦定理可得 cos A ==—;.又 A € (0, n , 2bc 22 n 所以A =寸.血—x —n8 .解析:选B.由题意知f(x)的定义域为X M 0•由f(1) = 0排除C.因为f( — x) = 10-x + 1 |g(— X)2= 1— 10x• lg x 2=— f(x),所以 f(x)为奇函数,故排除 A.当 x>1 时,, 0<'10x +1 i1 +1010 + 1钉0 +1 丿lg x 2<lg x 2,即f(x)<2lg x ,因此当x>1时,f(x)的图象在y = 2lg x 图象的下方,故排除 D.故选 B.9 •解析:选C.由题意知,在任意时刻,该公用电话亭不超过5人正在使用或等待使用电话,所以“有0, 1, 2, 3, 4或5个人正在使用或等待使用电话”是必然事件.因为P(1) =11 1 1 1P(0), P(2) = 4P(0) , P(3) = 8P(0), P(4) = 16P(0), P(5)=五p (0),所以 P(0) = 1 — [P(1) + P(2) + -1 汨 32P(3) + P(4) + P(5)] = 1— 1— $丿 P(0),所以 P(0)=云.故选 C. 10.解析:选B.由所以 a n = 2n ,所以 b n = log 2a 叮—1 = 2n — 1 ,所以题意得抛物线C的焦点为F(2a, 0),则由2a= . a+ 2+ a,解得a = 1, 所以F(2, 0),抛物线C: y2= 8x.由题知,直线AB的斜率不为零,所以设其方程为x= my+ 2, x = my+ 2,y2= 8xy2 ,联立2 得y2—8my —16= 0,所以y1y2=—16.由抛物线的定义,2> 6 +乙严 =6 + 4 2,当且仅当y 2= 2y 2,即=1 = b ,— 1 x 2= c ,所以 b = a , c =— 2a ,所以 b<0, aac ,对于B ,由题意可知f(1) = a — b + c>0,所以B 正确;对于 C , f( — 1) = a + b + c = 0,所以C b错误,对于D ,因为对于方程ax + bx + c = 0,设其两根x 1, x 2,所以x 1+ x 2= — = — 1, x 1x 2ac=— 2,所以两根分别为—2和1•所以不等式ax 2 + bx + c>0的解集是(—2, 1),所以D 正确. a12.解析:选 BCD. f(x)= |sin x||cos x|= |sin xcos x|= * |sin 2x|,则 f 专=psin n |= 0,则f(x)的图象不关于直线x =^对称,故A 错误;函数周期T = |x 今=2,故B 正确;f(n ) =2此时sin 2x>0,且sin 2x 为减函数,故 D 正确.13.解析:选AC.取CD 的中点F ,连接MF , BF ,则MF // DA 1, BF // DE ,所以平面 MBF //平面 A 1DE ,所以 MB //平面 A 1DE , D n1错误;由前面的讨论可知/ A 1DE = Z MFB = — ,MF = -A 1D =定值, FB = DE =定值,因此由余弦定理可得MB 2 = MF 2 + FB 2 -2MF F B cos / MFB ,所以 MB 是定值,故 AC 正确;由题可知 DE = CE = . 2AD =^AB ,贝UDE 丄CE ,若B 成立,可得DE 丄平面 A 1EC ,此时DE 丄A 1E 与DA 1丄A J E 矛盾,故B 错误.综 上可得AC 正确.14.解析:由题意,得 2a — b = (2x + 2, 3).因为a 与2a — b 共线,所以x 3— 2 (2x + 2)=0,解得 x =— 4,所以 a = (— 4, 2) = 2b,所以耳=£|a I 2|sin 2n |= 0,则(n, 0)是f(x)的一个对称中心,故C 正确;当x €nn 4,n .…y 时,2X € —15.解析:由题意,知q 丰1,所以r a 1 (1 — q 2)°=6, 1 — q a 1 (1 — q 4)-=30,1 — qa 1= 2,解得/ q = 2 a 1 = — 6, 或q_ 2(舍去),1 b n b n +1(2n — 1) ( 2n + 1)” 4血或;y1 = —即,时取等号,故选 夕=—2^8 目2= 2簪B.11. 解析:选 ABD.对于 A , a<0, - 1,2是方程 ax 2— bx + c = 0的两个根,所以一 1 + 2得 |AF|+ 2|BF|=洱+ 2+ 28c>0,所以 A 正确;令 f(x)= ax 2— bx +答案:16. 解析:由题意得 |BO|2=|OF| |OA|,即卩 b 2= 则 c = \.;5 — 1.答案:5— 117. 解析:由题可得f'(x)= 3ax 2 + 2bx + c ,不等式xf'(x) — af(x)<2对一切x € R 恒成立, 可化为(3a — a 2)x 3 + (2b — ab)x 2 + (c — ac)x — 2< 0 对一切 x € R 恒成立,所以 3a — a 2= 0,解得 a =3或a = 0(舍).所以bx 2 + 2cx + 2> 0对一切x € R 恒成立.当 b = 0, c = 0时,有2> 0,符2合题意,此时b +c= 0;当b 工0时,需满足b>0且△= (2c)2— 8b w 0,所以b >,a2 (c + 1) 21 2 1 12>— 1,当且仅当c =— 1, b = £时等号成立•综上所述,6 2值范围是答案:3亠—— n — 1 2n + 1 ,所以 T n = 2^1— 1+ -由卜11 —2n + 1丿=2n + 1.A(a , 0), B(0, b),由BF 丄AB 及OB 丄AF ,其中O 为坐标原点,得 ac ,又 a 2= b 2+ c 2,所以 ac = a 2— c 2,又 a = 2,所以 c 2 + 2c — 4= 0,2 b + c 2+ c> - 33 b + c 曲弟的取 a2 1C•- 3 D.36•已知实数a= 2ln 2, b = 2 + 2ln 2 , c= (In 2)2,贝V a, b, c 的大小关系是() A• c<b<a B• c<a<bC. b<a<c7 .已知△ ABC中,角A, B, C的对边分别为。
2020年新高考数学二轮复习练习:小题强化练小题强化练(六)

小题强化练(六)一、选择题11.已知全集 U = R ,集合 A = {x|y = . Inx} , B = {y|y = x 2, x>0},那么(?u A)Q B =()的离心率为()4 .下列结论正确的是()1A .当x>0且X M 1时,In x +订;》2B .当 x>0 时,x>ln x 1C.当x >2时,x — -无最小值x1D .当 x >2 时,x + ->2xA . — 14 C. — 2 6.已知定义在 R 上的奇函数f(x)满足f(x + 2) = f(x — 2),且当x € (— 2, 0)时,f(x)= Iog 2(x + 3) + a.若 f(13) = 2f(7) + 1,贝U a =( )7.已知 AB = (COS 22° , cos 68° ), AC = (2cos 52°, 2cos 38° ),则厶 ABC 的面积为(A. ? C . (0, 1)2 .已知等差数列{a n }中,前n 项和S 满足 A. 54 C . 722 2y x3 .已知双曲线 C : 9 — b 2= 1(b>0),其焦点 B. (0, 1] D . (1 ,+^ ) S y — S 2= 35,贝 U 0=()B. 63 D . 81F 到C 的一条渐近线的距离为2,则该双曲线A.,13 "V的展开式中,常数项为B . 14 D . 24 34B .1B.A.29 .已知函数f(x)= 3sin 2x + . 3cos 2x ,将f(x)图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再向左平移n个单位长度,得到函数g(x)的图象,已知 g(x)分别在x 2处取得最6 大值和最小值,则 %+ X 2|的最小值为()2nBE4 n C . n D.-^10.已知抛物线C : y = ax 2的焦点坐标为(0, 1),点P(0, 3),过点P 作直线l 交抛物线C 于A , B 两点,过点A , B 分别作抛物线C 的切线,两切线交于点 0,则厶QAB 面积的最小值为()A . 6 2B . 6.3 C.12 .3 D . 12.211(多选)如图,如果在每格中填上一个数, 每一横行成等差数列, 每一纵列成等比数列,那么( )2412xyzA.x = 1B . y = 2C . z = 3D . x + y + z 的值为 212.(多选)甲罐中有5个红球,2个白球和3个黑球,乙罐中有 6个红球,2个白球和2 个黑球,先从甲罐中随机取出 1个球放入乙罐,分别以 A 1, A 2, A 3表示事件“由甲罐取出的球是红球、白球和黑球”,再从乙罐中随机取出 1个球,以B 表示事件“由乙罐取出的球是红球”,下列结论正确的是 ()C. 8•函数f(x)的大致图象如图所示,则函数f(x)的解析式可以是(A . f(x) = x 2 • sin|x|f(x) = x - cos 2xC .f(x)=xln |x|凶x— xf(x) = (e — e )cosA .事件B与事件A1不相互独立B . A i, A2, A3是两两互斥的事件C. P(BA i) = 1D . P(B) = 313. (多选)如图,四边形ABCD是边长为1的正方形,ED丄平面ABCD,FB丄平面ABCD,且ED = FB = 1, G为线段EC上的动点,则下列结论中正确的是()A . EC 丄AFB .该几何体外接球的表面积为 3 nC.若G为EC的中点,贝U GB//平面AEFD . AG2+ BG2的最小值为3.二、填空题14. ________________________________________________________________ 已知平面向量a与b的夹角为—,|a| = 2, |b|= 1,贝V a (a- b) = _____________________________ .315. 已知关于x的不等式2x2+ ax—a2>0的解集中的一个元素为2,则实数a的取值范围为________ .16. _____________________________________ 已知数列{a n}中,a n +1 = 2a n—1, a1 = 2,设其前n项和为Si,若对任意的n€ N , (S n + 1—n)k> 2n—3恒成立,则k的最小值为 .17. 已知函数f(x)= x3+ ax2+ bx(a, b€ R),若函数f(x)在x= 1处有极值—4,则函数f(x)的单调递减区间为________ ;函数f(x)在[—1, 2]上的最大值与最小值的和为___________ .小题强化练(六)1 .解析:选C.解In x>0得x> 1,所以A= [1 ,+s ).所以?U A = (— ^, 1).又因为B =(0, +m),所以(?U A) n B = (0, 1),故选C.a3+ a4+ a5+ a6+ a7= 5a5= 35,所以a5= 7,贝U S92 .解析:选B.由等差数列的性质可得9 ( a1 + a?)=9a5= 63,故选 B.22倉=1(b>0)中,a 2= 9,所以a = 3•根据双曲线的对称性,不妨设焦点F(0, c),一条渐近线方程为y = :x ,即ax — by = 0,则点F(0 , c)到渐近线的3 .解析:选A.因为在双曲线2C: y 94. 解析:选B.A 选项,0<x<1时,In x<0,不等式不成立,-1在X 》2时单调递增,所以函数y =x -£在x =2处取得最小值,1 1 5X + -在 X 》2时单调递增,所以函数y = X +X 在 x = 2处取得最小值5, D 错误;B 选项,构造函1数 f(x) = x — In x ,贝y f'(x) = 1 — 一,易得 x € (0, 1)时,f ' (x)<0,所以 f(x)在(0, 1)上单调递减, X X € (1 ,+s )时,f ' (X)>0,所以 f(x)在(1 ,+s )上单调递增,故 f(x)min = f(1) = 1 ,所以 f(x)>0 , 即x>ln x 在x>0时恒成立,B 正确.5. 解析:选 D. 能)展开式的通项为 T r +1= C7[J2j •— ^x)r = C%— 1)r a7 — rx 7 • — 14,人76令3「— 14 = 0,得 r = 6,贝U C 7a = 14,即 a = 2,故选 D.6.解析:选 A.由题知函数 f(x)的周期为 4, f(13) = f(1) = — f( — 1), f(7) = f(— 1).因为 f(13)1=2f ⑺ + 1,所以一f( — 1) = 2f( — 1) + 1,从而 f(— 1) = — ~.当 x € (— 2, 0)时,f(x) = log 2(x + 3) 1 4+ a ,所以 f(— 1) = a + 1 = — 3,解得 a =—-,故选 A.3 37. 解析:选 A.根据题意,AB = (cos 22°, sin 22° ), AC = (2sin 38° , 2cos 38° ),所以 |AB|= 1, |AC|= 2.所以 AB AC = 2(cos 22° sin 38 ° + sin 22 ° cos 38° )= 2sin 60 ° = ,3,可得 cos A = AB AC 二宁,贝V A = 30°,故 ABC = 2|AB| |AC| sin A = 一X 1 X 2 X *= *,故选 A.AB||AC| 8.解析:选D.由题中图象可知,在原点处没有图象.故函数的定义域为{X |X M 0},故排 除选项A , C ;又函数图象与x 轴只有两个交点,f(x) = \x — - • cos 2x 中cos 2x = 0有无数个根, 故排除选项B ,正确选项是D.9. 解析:选 B.因为 f(x) = 3sin 2x + . 3cos 2x = 2 , 3sin 2x + 卡,所以 g(x) = 2 . 3sin X +nn,n n nn n所以冷+"3 = 2k 1 n + y(k 1 Z ),即 X 1= 2&冗+石(匕€ Z ), x ? +§ = 2k ?n —Z ),即 x ? 5 n2=2k 2 n — 6 (k 2 € Z ),则 |x 1 + x 2|= 2 (+ k 2) n —3 (k 1,k 2Z ),当 +k 2= 0 时,恢 + x 2|距离d = 」—bc|_ .a 2+ b 2琴=b ,由题意得 b = 2,所以c=“...,a 2+ b 2= 13,所以双曲线的离心率 ,13 .故选A.A 错误;C 选项,函数y = x C 错误;D 选项,函数y =取得最小值牛,故选B.310. 解析:选C.因为抛物线y= ax2的焦点坐标为(0, 1),所以抛物线方程为y=〔x2.设42 2(X1、厂X2、 1 x iX1, 4,B X2, 4 .因为y'= 2X,所以抛物线在点A处的切线方程的斜率k i—2,所以点A2 2处的切线方程为y —X = X1(x —x1),化简得y= 1x1x —彳①.同理得点B处的切线方程为y= ^x2x 2—乎②.联立①②,消去y得x= x1"2~,代入点A处的切线方程得Q x^2―,卑护.因为直线AB 过点P(0,3),所以设直线I的方程为y= kx+ 3(由题可知直线I的斜率不存在时不满足题意)•联"='J,得x^ —4kx—12 = 0,所以严x2 =4k,所以Q(2k, —3), 所以点Q 到AB 的距y= &x ,区伙2=—12.2 ( k2+ 3) 1离d=—k2+1—.又因为|AB|=寸k2+ 1 凶—x?|= 4pk2+ 1 • k2+ 3,所以S^QAB = ^|AB| d =1 2 / I 2 _3) 3-4^;J k2+ 1 •k2+ 3 •2= 4(k2+ 3)2,所以当k= 0 时,S^AQB取得最小值12叮3.故选C.2 k +1 '1 111. 解析:选AD.因为每一纵列成等比数列,所以第一列的第3, 4, 5个数分别是2, 2, 1 1 1 8;第三列的第3, 4, 5个数分别是1,夕才.所以x= 1.又因为每一横行成等差数列,所以y=1 — 11+ 3X丄匕=5.又z—£= 2 X1,所以z= 3所以x+ y+ z= 2.故A , D正确,B , C错误.4 2 8 8 8 85 1 2 112. 解析:选ABC.由题意A1, A2, A3是两两互斥事件,P(A1) = 10 = -, P(A2) =石=-,、1X Z3 P (BA1) 2 11 7 6 6P(A3)= -, P(B|A" = p((Ai1)=^— = 11,P(B|A2)= 11,P(B|A3)=石,P(B)= P("B) + P(A2B)2+ P(A3B)=P(A”P(B|A1)+ P(A2)P(B|A2)+ P(A3)P(B|A3)1 7 1 6 3 6 13=_X —+ -X —+ —X —=—所以D 不正确2 11 5 11 10 11 22•所以不正确.13. 解析:选ABC.如图所示,几何体可补形为正方体,以D为坐标原点,DA , DC, DE所在直线分别为x轴、y轴、z轴建立空间直角坐标系.A,由正方体的性质易得EC丄AF.B,该几何体的外接球与正方体的外接球相同,外接球半径为~,故外接球表面积为3n .C, A(1 , 0, 0),E(0, 0, 1), F(1 , 1 , 1), B(1 , 1 , 0) , C(0 , 1, 0),则A E = (—1, 0 , 1) , A F = (0 , 1, 1).设n AE = 0, — x + z = 0,平面AEF 的法向量为n = (x , y ,乙).由$得] 令z = 1,得x = 1, y =— 1, 』A F =oi y +z =0,则 n = (1, — 1, 1).当 G 为 EC 的中点时,G [0, 1, 1 ],则GB = [l, 1, — 2 ],所以 G B n = 0, 可得GB //平面AEF(也可由平面平行来证明线面平行 ).D ,设G(0, t , 1 — t)(0< t < 1),则AG 22+ BG 2= 4t 2 — 6t + 5= 4 t — 3 + 11,故当 t = 3时,AG 2+ BG 2 的最小值为 普.故选 ABC.22n2114. 解析:由已知得 a (a — b ) = a —a b = |a | —|a | |b |cos — = 2 — 2 x 1x ^= 3.答案:315. 解析:因为关于x的不等式2x 2+ ax — a 2>0的解集中的一个元素为 2,所以8+ 2a —2 a >0,即(a — 4)(a + 2)<0,解得-2<a<4.答案:(一2, 4)16. 解析:由 a n +1 = 2a n — 1 可得 a n +1 — 1 = 2(a n — 1),且 a 1 — 1 = 1,所以{a n — 1}是首项为 1,公比为2的等比数列,所以a n = 2"1+1,所以S n =,一 1+n.由(5+ 1—n)k 》2n—3恒成立,2n — 3,一、2n — 3— 2n+5得k 》一2^ —恒成立.令 b n = ~2^ —,贝U b n + 1—b n= ~?n +1 ~,所以数列{ bn }的前3项单调递增,3 33从第3项起单调递减,所以{b n }的最大值为b 3 = 8所以k >3所以k 的最小值为;.答案:817. 解析:f'(x) = 3x 2+ 2ax + b ,依题意有 f'(1)= 0, f(1) = — 4, a = 2,.b = — 7.所以 f'(x)= 3x 2+ 4x — 7= (3x + 7)(x — 1),由f'(x)<0,得一7<x<1,所以函数f(x)的单调递减区间为 一3, 1 .f ' (x), f(x)在[—1 , 2]上随x 的变化情况如下表:由上表知,在[—1, 2] 上, f(x)min = f(1) =— 4 , f(x)max = f( — 1) = 8 , f(X )max + f(X )min = 4.答案:-3,14即’3+ 2a+b= 0 ,1 + a + b = — 4。
2020年新高考数学二轮复习练习:小题强化练小题强化练(五)

、选择题已知集合A= {x|x2- 16W 0}, B = {x|lg|x- 2|>0},则 A n B=( )28.已知抛物线x2=8y与双曲线?-X2小题强化练(五)C. [-4, (-4,1) U (3, 4] 1)U (3, 4) B . [ —4,- 3) U (—1 , 4] D . (-4,- 3) U (- 1, 4)若复数z= 在复平面内对应的点在第四象限,则实数m的取值范围是(C.C.C.C. (-1,1)(1,+m)B. (- 1, 0)D. (-m,- 1)1若a>0, b>0且2a+ b = 4,则品的最小值为()已知f(x)= (-3, 2)1B.1警(1X),x<1,则(2, 3)若 a = log32, b= lg 0.2 , c= 2 .,贝V ( c<b<aa<b<c 的解集为((-2, 3) (-3,- 2)b<a<cb<c<a6本不同的书在书架上摆成一排,要求甲、乙两本书必须摆放在两端,丙、丁两本书必须相邻,则不同的摆放方法有 (A. 24 种 D . 60 种得图象的一条对称轴方程为 ( )2nA.x=3nc . x = 71(a>0)的一个交点为 M , F 为抛物线的焦点,=5,则该双曲线的渐近线方程为( )B . 36种C . 48 种7.把函数 y = ,2sin x + ~ + 1图象上各点的横坐标缩短为原来的 1-(纵坐标不变),那么所若 |MF|A . 5x ± 3y = 0 C . 4x ± 5y = 02 2nx y9.倾斜角为的直线经过椭圆a 2 3+ b 2^ 1(a>b>0)的右焦点F ,与椭圆交于 A 、B 两点,且AF = 2FB ,则该椭圆的离心率为()11.(多选)下列说法正确的是( )A .回归直线过样本点的中心(x , y )B .在回归分析模型中,残差平方和越小,说明模型的拟合效果越好C .从独立性检验可知有 95%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么 他有95%的可能患有肺病D .从统计量中得知有 99%的把握认为吸烟与患肺病有关系,是指有 1%的可能性使得推断出现错误12.(多选)下列函数中,满足“对任意的 X 1,2B. f (x ) = x —-x C. f (x ) = x + 1D. f (x ) = log 1(2x ) + 1313.(多选)以等腰直角三角形 ABC 的斜边BC 上的中线AD 为折痕,将△ ABD 与厶ACD 折成互相垂直的两个平面.下列说法正确的是 ()A . BD 丄平面ACDB . △ ABC 为等边三角形 C .平面 ADC 丄平面 ABCB . 3x ± 5y = 0D . 5x ± 4y = 0C.~2D. 且恒有 cos x f (x) + sin x •f(x)<0成立,则有(10.定义在 f (x ),已知f'(x )是它的导函数,(0 ,+^ ),使得f(x1)- x2)v 0”X1 —x2成立的是()2A . f(x)= —x —2x+ 1D .点D 在平面ABC 内的射影为△ ABC 的外接圆圆心 二、填空题14. 已知函数 f(x) = x 3+ alog 3x ,若 f(2) = 6,贝U f 2 = _______________ .15. △ ABC 的内角 A , B , C 的对边分别为 a , b , c ,若 2acos( 0- B)+ 2bcos(B+ A)+ c = 0, 贝U cos 0的值为 _________ .16. 已知三棱锥 P-ABC 的底面 ABC 是等腰三角形, AB 丄AC , PA 丄底面 ABC , PA = AB = 1,则这个三棱锥内切球的半径为 ___________ .117. 已知数列{a n }是公差为3的等差数列,数列{b n }满足b 1= 1 , b 2 = -, a n b n + 1+ b n + 1 = nb n . 则{a n }的通项公式为 ______ ; {b n }的前n 项和为 ________小题强化练(五)1 .解析:选A.由题意得A = {x|-4W X W 4} , B = {x|x>3或x<1},结合交集的定义知 A A B =[—4, 1)U (3, 4].故选 A.2 .解析:选A.法一:因为z =啓=篇)(二)=学+号i 在复平面内对1 1 — i1 1 法二:当m = 0时,z=, = i ) = 7—7i ,在复平面内对应的点在第四象限,1 + i (1 + i )( 1 — i ) 22所以排除选项B , C , D ,故选A.3.解析:选B.因为a>0, b>0,故2a + b > 2,2ab(当且仅当2a = b 时取等号).又因为2a + b = 4,所以 2 2ab < 4? 0<ab < 2,4. 解析:选 A.当 x<1 时,f(x)<2 可化为 log 2(1 — x)<2,即 0<1 — x<4,解得一3<x<1;当 x > 1 时,f(x)<2可化为3x — 7<2,即3x <9,得1 W x<2.综上,不等式f(x)<2的解集为(—3, 1) U [1 , 2) = (— 3, 2).5.解析:选B.由对数函数的性质可得 a = log 32 € (0, 1),b = lg 0.2<0,由指数函数的性 质可得c = 2 . >1,所以b<a<c ,故选B.应的点为1+2m , 等,且在第四象限,所以>0,解得—1<m<1,故选A.所以新2故ab 的最小值为1,故选B.1 + m2 m — 1 〒<0,6.解析:选A.由题意知将甲、乙两本书放在两端有A 2种放法,将丙、丁两本书捆绑,与剩余的两本书排列,有 A 3种放法,将相邻的丙、丁两本书排列,有A 2种放法,所以不同的摆放方法有A 2X A 2= 24(种),n「 n k nn ,, Xf[ 4 =_2 + k n (k € Z ),则 x = 8 +2(k €Z ),取k = 0,得x= §,故选D.解析:选 B.设点 M (X 0, y °),则有 |MF| = y ° + 2 = 5, y °= 3, x 0= 24,由点 M(x 0, y °)在双2 2 2— x 2= 1上,得^2— x 0= 1,爲一24= 1, a 2=',所以双曲线^2— x 2=1的渐近线方程为^2a a 25 aa—x 2= 0,即 3x±5y = 0,选 B.卓 1 29 •解析:选B.由题可知,直线的方程为y = x — c ,与椭圆方程联立得 ab ,所以(by = x — c+ a 2)y 2 + 2b 2cy — b 4= 0,由于直线过椭圆的右焦点,故必与椭圆有两个交点,则 40.设A(x i , —2b 2ca 2 +b 2 ,又 AF = 2FB ,所以(c — X i ,— y i ) = 2(x 2 — c , y 2),所以一y i11.解析:选ABD.对于A ,回归直线一定过样本点的中心点(x , y),正确;对于B ,回归分析模型中,残差平方和越小,说明模型的拟合效果越好,正确;对于C ,从独立性检验知:有 95%的把握认为吸烟与患肺病有关系时,我们说某人吸烟, 他有95%的可能与患有肺病有关, C 错误;故选A.7.解析:选所得图象对应的函数解析式为f(x)= , 2sin 2x +~令2x +8.2曲线^2a y i + y 2 =y i ), B(X 2, y 2),则.yiy2=a ^+Pf- 2b2c—y2=齐扌 =2y 2,可得 川―2y 2= 2. b 2 i a + b4c,所以,故选B.3[ n ) r10. 解析:选 C.因为 cos x • f ' (x) + sin x • f(x)<0,所以在 0, ?上,~f (x ) -cos x<0,所以函数y =f (x )cos x 在 0(0, n 上是减函数,所以2冗> 2冗,所以cos青cos 专—b 4专,故选c.对于D,从统计量中得知有99%的把握认为吸烟与患肺病有关系,是指有1%的可能性使得推断出现错误,D正确.12. 解析:选AD.根据题意,“对任意的x i,(0,+^ ),使得f (xi)一 f (x2)v 0”,x i —X2则函数f(x)在(0,+8 )上为减函数,据此依次分析选项:对于选项 A , f(x) = —x2—2x+ 1,为1B二次函数,其对称轴为 x =- 1,在(0,+8 )上递减,符合题意;对于选项 1导数f(x)= 1 + X 2>0,所以f(x)在(0,+^ )上递增,不符合题意;对于选项 C , f(x)= X + 1为次函数,所以f(x)在(0,+^ )上递增,不符合题意;对于选项D , f(x)= log 1(2x) + 1,在(0, +2g )上单调递减,符合题意.13. 解析:选ABD.在A 中,以等腰直角三角形 ABC 的斜边BC 上的 中线AD 为折痕,将△ ABD 与厶ACD 折成互相垂直的两个平面,所以AD 丄 BD ,CD 丄 BD ,因为 AD n CD = D ,AD ,CD?平面 ACD ,所以 BD 丄 平面ACD ,故A 正确;在B 中,因为 AD ,CD ,BD 两两垂直, AD = CD = BD ,所以 AB = AC = BC ,所以△ ABC 为等边三角形,故 B 正确;在C 中,取AC 中点0,连接DO ,BO ,贝U BO 丄AC ,DO 丄AC ,所以/ BOD 是平面ADC 与平面ABC 所成角的平面角,设CD = 1,则OD = |A C = ;,AD 4+ CD 2=4 17B , f(x) = x —,其xOB = (,2) 2 * - ; 2= 26,所以cos / BOD = 0D 2+OB 2-BD 2 =2X OD X OB1B所以平面ADC 与平面ABC 不垂直,故C 错误;在D 中,因为 AD , CD , BD 两两垂直,AD = CD = BD ,所以AB = CA = BC ,所以△ ABC 为等边三角形,所以点 D 在平面ABC 内的射影为△ ABC 的外接圆圆心,故 D 正确.2 “ \ 1 1 1 114. 解析:由 f(2) = 8+ alog 32 = 6,解得 a =-匸扁2,所以 f? = 8+ alog 3^=?— alo g 32 = 816.解析:如图所示,依题意可得PAB_1 X 1 = 2,S A PAC= 2X 1 X 1 = 2 S A PBC = 2X 2 X 2 X sin6° °= £.设这个三棱锥内切球的半径11 11 1为 r ,则有 V p -ABC = 3XSA ABCX PA = 3(S ^ PAB + S ^ PAC + S ^ ABC + & PBC ) X r ,得到 3X X1 =X 2 + 1 + 2+于 X r ,解得 r = 士答案:55严617.解析:、 1因为 a n b n +1+ 5+1 = nb n .当 n = 1 时,a 1b 2+ b 2= B,因为1, b 2= 3,所以5 1答案:a n = 3n — 1 3—】n -12 2 31=b n .即数列{b n }是以1为首项,以3为公比的等比数列,所以{b n }的前n 项和S n =1- 1n33 V = 2(1 -3-n )=32 3n -1a 1 = 2,又因为{ a n }是公差为3的等差数列,所以 a n = 3n — 1.(3n —1)b n + 1 + b n + 1 = nb n ,知3b n + 1+ 血 lOg32=亍17答案:¥ 8 15. 解析:由正弦定理,得 2sin Acos( 0— B)+ 2sin Bcos( 0+ A) + sin C = 0,展开得到 2sin Acos 0 cos B + 2sin Asin 0 sin B + 2sin Bcos 0 cos A - 2sin Bsin 0 sin A + sin C = 0,化简得 2cos 0 (sin AcosB + sin Bcos A) + sinC = 0,即 2cos 0 sin(A + B) + sin C = 0,由三角形内角和定理, 得” 1sin(A + B)= sin C 丰0,故 cos 0 =-。
2020新课标高考数学二轮习题:小题强化练(五) Word版含解析

小题强化练(五)一、单项选择题1.已知集合A ={x |x 2-16≤0},B ={x |lg|x -2|>0},则A ∩B =( ) A .[-4,1)∪(3,4] B .[-4,-3)∪(-1,4] C .(-4,1)∪(3,4)D .(-4,-3)∪(-1,4)2.若复数z =1+m i1+i 在复平面内对应的点在第四象限,则实数m 的取值范围是( )A .(-1,1)B .(-1,0)C .(1,+∞)D .(-∞,-1)3.若a >0,b >0且2a +b =4,则1ab 的最小值为( )A .2 B.12 C .4D.144.若a =log 32,b =lg 0.2,c =20.2,则( ) A .c <b <a B .b <a <c C .a <b <cD .b <c <a5.6本不同的书在书架上摆成一排,要求甲、乙两本书必须摆放在两端,丙、丁两本书必须相邻,则不同的摆放方法有( )A .24种B .36种C .48种D .60种6.已知抛物线x 2=8y与双曲线y 2a2-x 2=1(a >0)的一个交点为M ,F 为抛物线的焦点,若|MF |=5,则该双曲线的渐近线方程为( )A .5x ±3y =0B .3x ±5y =0C .4x ±5y =0D .5x ±4y =07.倾斜角为π4的直线经过椭圆x 2a 2+y 2b 2=1(a >b >0)的右焦点F ,与椭圆交于A 、B 两点,且AF →=2FB →,则该椭圆的离心率为( )A.32B.23C.22D.338.定义在⎝⎛⎭⎫0,π2上的函数f (x ),已知f ′(x )是它的导函数,且恒有cos x ·f ′(x )+sin x ·f (x )<0成立,则有( )A .f ⎝⎛⎭⎫π6>2f ⎝⎛⎭⎫π4B.3f ⎝⎛⎭⎫π6>f ⎝⎛⎭⎫π3C .f ⎝⎛⎭⎫π6>3f ⎝⎛⎭⎫π3D .f ⎝⎛⎭⎫π6>3f ⎝⎛⎭⎫π4二、多项选择题9.下列说法正确的是( ) A .回归直线过样本点的中心(x ,y )B .在回归分析模型中,残差平方和越小,说明模型的拟合效果越好C .从独立性检验可知有95%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有95%的可能患有肺病D .从统计量中得知有99%的把握认为吸烟与患肺病有关系,是指有1%的可能性使得推断出现错误10.下列函数中,满足“对任意的x 1,x 2∈(0,+∞),使得f (x 1)-f (x 2)x 1-x 2<0”成立的是( )A .f (x )=-x 2-2x +1B .f (x )=x -1xC .f (x )=x +1D .f (x )=log 12(2x )+111.把函数y =2sin ⎝⎛⎭⎫x +π4+1图象上各点的横坐标缩短为原来的12(纵坐标不变),那么所得图象的一条对称轴方程为( )A .x =2π3B .x =5π8C .x =π4D .x =π812.以等腰直角三角形ABC 的斜边BC 上的中线AD 为折痕,将△ABD 与△ACD 折成互相垂直的两个平面.下列说法正确的是( )A .BD ⊥平面ACDB .△ABC 为等边三角形 C .平面ADC ⊥平面ABCD .点D 在平面ABC 内的射影为△ABC 的外接圆圆心 三、填空题13.已知函数f (x )=x 3+a log 3x ,若f (2)=6,则f ⎝⎛⎭⎫12=________.14.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若 2a cos(θ-B )+2b cos(θ+A )+c =0,则cos θ的值为________.15.已知数列{a n }是公差为3的等差数列,数列{b n }满足b 1=1,b 2=13,a n b n +1+b n +1=nb n .则{a n }的通项公式为________;{b n }的前n 项和为________.16.已知三棱锥P -ABC 的底面ABC 是等腰三角形,AB ⊥AC ,P A ⊥底面ABC ,P A =AB =1,则这个三棱锥内切球的半径为________.小题强化练(五)1.解析:选A.由题意得A ={x |-4≤x ≤4},B ={x |x >3或x <1},结合交集的定义知A ∩B =[-4,1)∪(3,4].故选A.2.解析:选A.法一:因为z =1+m i 1+i =(1+m i )(1-i )(1+i )(1-i )=1+m 2+m -12i 在复平面内对应的点为⎝⎛⎭⎫1+m 2,m -12,且在第四象限,所以⎩⎨⎧1+m2>0,m -12<0,解得-1<m <1,故选A. 法二:当m =0时,z =11+i =1-i (1+i )(1-i )=12-12i ,在复平面内对应的点在第四象限,所以排除选项B ,C ,D ,故选A.3.解析:选B.因为a >0,b >0,故2a +b ≥22ab (当且仅当2a =b 时取等号). 又因为2a +b =4, 所以22ab ≤4⇒0<ab ≤2,所以1ab ≥12,故1ab 的最小值为12,故选B.4.解析:选B.由对数函数的性质可得a =log 32∈(0,1),b =lg 0.2<0,由指数函数的性质可得c =20.2>1,所以b <a <c ,故选B.5.解析:选A.由题意知将甲、乙两本书放在两端有A 22种放法,将丙、丁两本书捆绑,与剩余的两本书排列,有A 33种放法,将相邻的丙、丁两本书排列,有A 22种放法,所以不同的摆放方法有A 22×A 33×A 22=24(种),故选A.6.解析:选B.设点M (x 0,y 0),则有|MF |=y 0+2=5,y 0=3,x 20=24,由点M (x 0,y 0)在双曲线y 2a 2-x 2=1上,得y 20a 2-x 20=1,9a 2-24=1,a 2=925,所以双曲线y 2a 2-x 2=1的渐近线方程为y 2a 2-x 2=0,即3x ±5y =0,选B.7.解析:选B.由题可知,直线的方程为y =x -c ,与椭圆方程联立得⎩⎪⎨⎪⎧x 2a 2+y 2b 2=1y =x -c ,所以(b 2+a 2)y 2+2b 2cy -b 4=0,由于直线过椭圆的右焦点,故必与椭圆有两个交点,则Δ>0.设A (x 1,y 1),B (x 2,y 2),则⎩⎪⎨⎪⎧y 1+y 2=-2b 2ca 2+b 2y 1y 2=-b 4a 2+b 2,又AF →=2FB →,所以(c -x 1,-y 1)=2(x 2-c ,y 2),所以-y 1=2y 2,可得⎩⎪⎨⎪⎧-y 2=-2b 2c a 2+b 2-2y 22=-b4a 2+b2,所以12=4c 2a 2+b 2,所以e =23,故选B.8.解析:选C.因为cos x ·f ′(x )+sin x ·f (x )<0,所以在⎝⎛⎭⎫0,π2上,⎣⎡⎦⎤f (x )cos x ′<0,所以函数y =f (x )cos x 在⎝⎛⎭⎫0,π2上是减函数,所以f ⎝⎛⎭⎫π6cos π6>f ⎝⎛⎭⎫π3cosπ3,所以f ⎝⎛⎭⎫π6>3f ⎝⎛⎭⎫π3,故选C.9.解析:选ABD.对于A ,回归直线一定过样本点的中心点(x ,y ),正确; 对于B ,回归分析模型中,残差平方和越小,说明模型的拟合效果越好,正确; 对于C ,从独立性检验知:有95%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,他有95%的可能与患有肺病有关,C 错误;对于D ,从统计量中得知有99%的把握认为吸烟与患肺病有关系,是指有1%的可能性使得推断出现错误,D 正确.10.解析:选AD.根据题意,“对任意的x 1,x 2∈(0,+∞),使得f (x 1)-f (x 2)x 1-x 2<0”,则函数f (x )在(0,+∞)上为减函数,据此依次分析选项:对于选项A ,f (x )=-x 2-2x +1,为二次函数,其对称轴为x =-1,在(0,+∞)上递减,符合题意;对于选项B ,f (x )=x -1x ,其导数f ′(x )=1+1x 2>0,所以f (x )在(0,+∞)上递增,不符合题意;对于选项C ,f (x )=x +1为一次函数,所以f (x )在(0,+∞)上递增,不符合题意;对于选项D ,f (x )=log 12(2x )+1,在(0,+∞)上单调递减,符合题意.11.解析:选BD.根据题中变换,所得图象对应的函数解析式为f (x )=2sin ⎝⎛⎭⎫2x +π4+1,令2x +π4=π2+k π(k ∈Z ),则x =π8+k π2(k ∈Z ),取k =0,得x =π8,取k =1得,x =5π8,故选BD.12.解析:选ABD.在A 中,以等腰直角三角形ABC 的斜边BC 上的中线AD 为折痕,将△ABD 与△ACD 折成互相垂直的两个平面,所以AD ⊥BD ,CD ⊥BD ,因为AD ∩CD =D ,AD ,CD ⊂平面ACD ,所以BD ⊥平面ACD ,故A 正确;在B 中,因为AD ,CD ,BD 两两垂直,AD =CD =BD ,所以AB =AC =BC ,所以△ABC 为等边三角形,故B 正确;在C 中,取AC 中点O ,连接DO ,BO ,则BO ⊥AC ,DO ⊥AC ,所以∠BOD 是平面ADC 与平面ABC 所成角的平面角,设CD =1,则OD =12AC =12AD 2+CD 2=22,OB =(2)2-⎝⎛⎭⎫222=62,所以cos ∠BOD =OD 2+OB 2-BD 22×OD ×OB =12+32-12×22×62=33,所以平面ADC 与平面ABC 不垂直,故C 错误;在D 中,因为AD ,CD ,BD 两两垂直,AD =CD =BD ,所以AB =CA =BC ,所以△ABC 为等边三角形,所以点D 在平面ABC 内的射影为△ABC 的外接圆圆心,故D 正确.13.解析:由f (2)=8+a log 32=6,解得a =-2log 32,所以f ⎝⎛⎭⎫12=18+a log 312=18-a log 32=18+2log 32×log 32=178. 答案:17814.解析:由正弦定理,得2sin A cos(θ-B )+2sin B cos(θ+A )+sin C =0,展开得到2sin A cosθcos B +2sin A sin θsin B +2sin B cos θcos A -2sin B sin θsin A +sin C =0,化简得2cos θ(sin A cos B +sin B cos A )+sin C =0,即2cos θsin(A +B )+sin C =0,由三角形内角和定理,得sin(A +B )=sin C ≠0,故cos θ=-12.答案:-1215.解析:因为a n b n +1+b n +1=nb n .当n =1时,a 1b 2+b 2=b 1,因为b 1=1,b 2=13,所以a 1=2,又因为{a n }是公差为3的等差数列,所以a n =3n -1.(3n -1)b n +1+b n +1=nb n ,知3b n +1=b n .即数列{b n }是以1为首项,以13为公比的等比数列,所以{b n }的前n 项和S n =1-⎝⎛⎭⎫13n1-13=32(1-3-n )=32-12·3n -1.答案:a n =3n -1 32-12·3n -116.解析:如图所示,依题意可得S △ABC =12×1×1=12,S △P AB =12×1×1=12,S △P AC =12×1×1=12,S △PBC =12×2×2×sin 60°=32.设这个三棱锥内切球的半径为r,则有V PABC=13×S△ABC×P A=13(S△P AB+S△P AC+S△ABC+S△PBC)×r,得到13×12×1=13×⎝⎛⎭⎫12+12+12+32×r,解得r=3-36. 答案:3-36。
2020新课标高考数学二轮习题:小题强化练(三) Word版含解析

小题强化练(三)一、单项选择题1.已知集合A ={x ∈N |x ≤3},B ={x |x 2+6x -16<0},则A ∩B =( ) A .{x |-8<x <2} B .{0,1} C .{1}D .{0,1,2}2.已知复数z =-1+i(i 是虚数单位),则1+z1-z =( )A.15+25i B .-15+25iC.15-25i D .-15-25i3.我国古代数学著作《九章算术》有如下问题:“今有金棰,长五尺.斩本一尺,重四斤.斩末一尺,重二斤.问次一尺各重几何?”意思是:“现有一根金棰,长五尺,一头粗,一头细.在粗的一端截下一尺,重四斤;在细的一端截下一尺,重二斤.问依次每一尺各重几斤?”根据已知条件,若金棰由粗到细是均匀变化的,则中间三尺的重量为( )A .6斤B .9斤C .10斤D .12斤4.在直三棱柱ABC -A 1B 1C 1中,AA 1=2A 1B 1=2B 1C 1,且AB ⊥BC ,点M 是A 1C 1的中点,则异面直线MB 与AA 1所成角的余弦值为( )A.13B.223C.324D.125.在区间[-2,2]上随机取一个数b ,若使直线y =x +b 与圆x 2+y 2=a 有交点的概率为12,则a =( )A.14B.12 C .1D .26.已知定义在R 上的函数f (x )满足:(1)f (x +2)=f (x );(2)f (x -2)为奇函数;(3)当x ∈[0,1)时,f (x 1)-f (x 2)x 1-x 2>0(x 1≠x 2)恒成立,则f ⎝⎛⎭⎫-152,f (4),f ⎝⎛⎭⎫112的大小关系正确的是( ) A .f ⎝⎛⎭⎫112>f (4)>f ⎝⎛⎭⎫-152 B .f (4)>f ⎝⎛⎭⎫112>f ⎝⎛⎭⎫-152 C .f ⎝⎛⎭⎫-152>f (4)>f ⎝⎛⎭⎫112 D .f ⎝⎛⎭⎫-152>f ⎝⎛⎭⎫112>f (4)7.已知抛物线y 2=2px (p >0)的焦点为F ,O 为坐标原点.设M 为抛物线上的动点,则|MO ||MF |的最大值为( )A. 3 B .1 C.33D.2338.将函数y =sin 2x 的图象向右平移φ⎝⎛⎭⎫0<φ<π2个单位长度得到y =f (x )的图象.若函数f (x )在区间⎣⎡⎦⎤0,π4上单调递增,且f (x )的最大负零点在区间⎝⎛⎭⎫-5π12,-π6上,则φ的取值范围是( )A.⎝⎛⎦⎤π6,π4 B.⎝⎛⎭⎫π6,π2 C.⎝⎛⎦⎤π12,π4 D.⎝⎛⎭⎫π12,π2 二、多项选择题9.在平面直角坐标系xOy 中,角α以Ox 为始边,终边经过点P (-1,m )(m >0),则下列各式的值一定为负的是( )A .sin α+cos αB .sin α-cos αC .sin αcos αD.sin αtan α 10.(2019·湖南长沙一模)设a ,b ,c 表示不同直线,α,β表示不同平面,下列结论不正确的是( )A .若a ∥c ,b ∥c ,则a ∥bB .若a ∥b ,b ∥α,则a ∥αC .若a ∥α,b ∥α,则a ∥bD .若a ⊂α,b ⊂β,α∥β,则a ∥b11.已知函数f (x )=2x -log 12x ,且实数a >b >c >0满足f (a )f (b )f (c )<0.若实数x 0是函数y =f (x )的一个零点,那么下列不等式中可能成立的是( )A .x 0<aB .x 0>aC .x 0<bD .x 0<c12.已知函数f (x )及其导函数f ′(x ),若存在x 0使得f (x 0)=f ′(x 0),则称x 0是f (x )的一个“巧值点”.下列选项中有“巧值点”的函数是( )A .f (x )=x 2B .f (x )=e -x C .f (x )=ln x D .f (x )=tan x三、填空题13.二项式⎝⎛⎭⎫2x -x 9展开式中含x 3项的系数为________.14.设数列{a n }是由正数组成的等比数列,S n 是{a n }的前n 项和,已知a 2a 4=16,S 3=28,则当a 1a 2…a n 最大时,n 的值为________.15.如图,在△ABC 中,已知M 为边BC 上一点,BC →=4BM →,∠AMC =π3,AM =2,△AMC 的面积为33,则CM =________;cos ∠BAC =________.16.已知扇形OAB 的圆心角∠AOB =90°,半径为2,C 是其弧上一点.若OC →=λOA →+μOB →,则λ·μ的最大值为________.小题强化练(三)1.解析:选B.由A ={x ∈N |x ≤3}={0,1,2,3},B ={x |x 2+6x -16<0}={x |-8<x <2},得A ∩B ={0,1},故选B.2.解析:选B.因为z =-1+i ,所以1+z 1-z =1-1+i 1-(-1+i )=i 2-i =i (2+i )(2-i )(2+i )=-15+25i.故选B. 3.解析:选B.由题意知金杖由粗到细每一尺构成一个等差数列,且首项a 1=4,a 5=2,则公差d =a 5-a 15-1=-12.所以a 3=a 1+2d =4-1=3,所以a 2+a 3+a 4=3a 3=9,故选B.4.解析:选B.法一:由题知AA 1∥BB 1,则异面直线MB 与AA 1所成角为∠MBB 1,如图.又△BB 1M 为直角三角形,cos ∠MBB 1=BB 1MB.在直三棱柱ABC -A 1B 1C 1中,设AA 1=2A 1B 1=2B 1C 1=2,由AB ⊥BC ,得B 1M =12A 1C 1=22.故MB =22+⎝⎛⎭⎫222=32,所以cos ∠MBB 1=BB 1MB =223,故选B.法二:以B 为原点,BA ,BC ,BB 1所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,如图.设AA 1=2A 1B 1=2B 1C 1=2,则M ⎝⎛⎭⎫12,12,2,B (0,0,0),A (1,0,0),A 1(1,0,2),所以MB →=⎝⎛⎭⎫-12,-12,-2,AA 1→=(0,0,2).设异面直线MB 与AA 1所成角为θ,则cos θ=|MB →·AA 1→||MB →||AA 1→|=492×2=223,所以异面直线MB 与AA 1所成角的余弦值为223,故选B.5.解析:选B.由直线y =x +b 与圆x 2+y 2=a 有交点,得圆心到直线的距离d =|b |2≤a ,解得b ∈[-2a ,2a ].又b ∈[-2,2],且直线y =x +b 与圆x 2+y 2=a 有交点的概率为12,所以由几何概型的概率计算公式可知P =2a -(-2a )2-(-2)=12,解得a =12,故选B. 6.解析:选C.由f (x +2)=f (x )可知函数f (x )的周期为2,可知f (x )=f (x -2).又f (x -2)为奇函数,可知f (x )为奇函数.所以f ⎝⎛⎭⎫-152=f ⎝⎛⎭⎫-152+2×4=f ⎝⎛⎭⎫12,f (4)=f (4-2×2)=f (0)=0,f ⎝⎛⎭⎫112=f ⎝⎛⎭⎫112-2×3=f ⎝⎛⎭⎫-12.又x ∈[0,1)时,f (x )单调递增,故奇函数f (x )在(-1,1)内单调递增,所以f ⎝⎛⎭⎫12>f (0)>f ⎝⎛⎭⎫-12,即f ⎝⎛⎭⎫-152>f (4)>f ⎝⎛⎭⎫112,故选C. 7.解析:选D.设抛物线上点M (m ,n )(m >0),则n 2=2pm ,可得|MO |=m 2+n 2=m 2+2pm .由抛物线的定义得|MF |=m +p 2,所以|MO ||MF |=m 2+2pmm +p 2=m 2+2pmm 2+pm +p 24=1+pm -p 24m 2+pm +p 24.令pm -p 24=t ,t >-p 24,则m =t p +p 4,所以|MO ||MF |=1+tt 2p 2+3t 2+9p 216=1+1t p 2+32+9p 216t≤1+13=233,当且仅当t p 2=9p 216t ,即t =3p 24时,等号成立,故选D. 8.解析:选C.法一:函数y =sin 2x 的图象向右平移φ⎝⎛⎭⎫0<φ<π2个单位长度得到函数f (x )=sin (2x -2φ)的图象,则当x ∈⎣⎡⎦⎤0,π4时,2x -2φ∈⎣⎡⎦⎤-2φ,π2-2φ.由函数f (x )在区间⎣⎡⎦⎤0,π4上单调递增,可知⎩⎨⎧-π2+2k π≤-2φ,π2-2φ≤π2+2k π(k ∈Z ),解得-k π≤φ≤π4-k π(k ∈Z ).又由0<φ<π2,可知0<φ≤π4①.函数f (x )的所有零点满足2x -2φ=k π(k ∈Z ),即x =12k π+φ(k ∈Z ),由最大负零点在⎝⎛⎭⎫-5π12,-π6内,得-5π12<12k π+φ<-π6(k ∈Z ),即-5π12-12k π<φ<-π6-12k π(k ∈Z ),由0<φ<π2可知当k =-1时,π12<φ<π3②.由①②,φ的取值范围为⎝⎛⎦⎤π12,π4,故选C.法二:由题意得f (x )=sin(2x -2φ)观察选项可取φ=π3,可得f (x )=sin ⎝⎛⎭⎫2x -2π3,可知当x ∈⎣⎡⎦⎤0,π4时,2x -2π3∈⎣⎡⎦⎤-2π3,-π6,函数f (x )先减后增,不符合题意,排除B ,D ;取φ=π6,易得函数f (x )=sin ⎝⎛⎭⎫2x -π3在⎣⎡⎦⎤0,π4上单调递增,令2x -π3=k π(k ∈Z ),得x =π6+k 2π(k ∈Z ),则函数f (x )取得的最大负零点为x =-π3∈⎝⎛⎭⎫-5π12,-π6,符合题意,排除A ,故选C.9.解析:选CD.由已知得r =|OP |=m 2+1,则sin α=m m 2+1>0,cos α=-1m 2+1<0,tan α=-m <0,所以sin x +cos α的符号不确定,sin α-cos α>0,sin αcos α<0,sin αtan α=cos α<0.故选CD. 10.解析:选BCD.由a ,b ,c 表示不同直线,α,β表示不同平面知: 在A 中,若a ∥c ,b ∥c ,则由平行公理得a ∥b ,故A 正确; 在B 中,若a ∥b ,b ∥α,则a ∥α或a ⊂α,故B 错误;在C 中,若a ∥α,b ∥α,则a 与b 相交、平行或异面,故C 错误; 在D 中,若a ⊂α,b ⊂β,α∥β,则a 与b 平行或异面,故D 错误.11.解析:选ABC.由f (x )=2x -log 12x ,可知函数f (x )在区间(0,+∞)上单调递增.因为实数a >b >c >0满足f (a )f (b )f (c )<0,则f (a ),f (b ),f (c )可能都小于0或有1个小于0,2个大于0,如图.则A ,B ,C 可能成立,x 0>c ,D 不可能成立.12.解析:选AC.若f (x )=x 2,则f ′(x )=2x ,令x 2=2x ,得x =0或x =2,方程显然有解,故A 符合要求;若f (x )=e -x ,则f ′(x )=-e -x ,令e -x =-e -x ,此方程无解,故B 不符合要求;若f (x )=ln x ,则f ′(x )=1x ,令ln x =1x ,在同一直角坐标系内作出函数y =ln x 与y =1x 的图象(作图略),可得两函数的图象有一个交点,所以方程f (x )=f ′(x )存在实数解,故C 符合要求;若f (x )=tan x ,则f ′(x )=⎝⎛⎭⎫sin x cos x ′=1cos 2x ,令tan x =1cos 2x ,化简得sin x cos x =1,变形可得sin 2x =2,无解,故D 不符合要求.故选AC.13.解析:二项式展开式的通项为T r +1=C r 9⎝⎛⎭⎫2x 9-r(-x )r =(-1)r ·29-r C r 9x 32r -9.令32r -9=3,解得r =8,可知所求二项式展开式中含x 3项的系数为(-1)8·29-8C 89=2×9=18.答案:1814.解析:由数列{a n }是各项均为正数的等比数列,且a 2a 4=16,可得a 3=4.又S 3=a 3⎝⎛⎭⎫1q 2+1q +1=28,可得1q 2+1q +1=7,即⎝⎛⎭⎫1q -2·⎝⎛⎭⎫1q +3=0,解得q =12⎝⎛⎭⎫q =-13舍去,故a n =a 3qn -3=25-n.则a 1a 2…a n =24×23×…×25-n=2(9-n )n 2,可知当(9-n )n2取得最大值时,a 1a 2…a n 取得最大值,此时整数n =4或5.答案:4或515.解析:因为在△AMC 中,∠AMC =π3,AM =2,△AMC 的面积为33,则有33=12AM ·CM ·sin ∠AMC =12×2×CM ×32,所以解得CM =6. 因为BC →=4BM →,所以BM =2,BC =8,因为∠AMB =π-∠AMC =2π3,所以由余弦定理可得AB =AM 2+BM 2-2AM ·BM ·cos ∠BMA =22+22-2×2×2×⎝⎛⎭⎫-12=23, AC =AM 2+CM 2-2AM ·CM ·cos ∠AMC =22+62-2×2×6×12=27,所以cos ∠BAC =AB 2+AC 2-BC 22AB ·AC =12+28-642×23×27=-217.答案:6 -21716.解析:由题|OA →|=|OB →|=|OC →|=2,且OA →·OB →=0.由OC →=λOA →+μOB →,两边平方得OC →2=(λOA →+μOB →)2=λ2OA →2+2λμOA →·OB →+μ2OB →2=4λ2+4μ2,可得4=4λ2+4μ2,即λ2+μ2=1,所以λ·μ≤λ2+μ22=12,当且仅当λ=μ=22时取得等号,故λ·μ的最大值为12.1答案:2。
2020版新高考数学二轮复习第一部分 小题强化练 小题强化练(七)

小题强化练(七)一、选择题 1.若复数z 满足2z(1+i )2=1-i ,其中i 为虚数单位,则复数z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2.已知集合M ={x |2x 2-x -3≤0},N ={x ||x |(x -2)>0},全集U =R ,则下列关于集合M ,N 叙述正确的是( )A .M ∩N =MB .M ∪N =NC .(∁U M )∩N =∅D .N ⊆(∁U M )3.若双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一个顶点到一条渐近线的距离等于4a 23c ,则双曲线的离心率为( )A.54 B. 2 C.53D. 34.已知等差数列{a n },a 1=2,若a 1,a 3+2,a 6+8成等比数列,则S 10=( ) A.852 B .-16 C .-70或852D .-16或1325.已知角α+π4的终边与单位圆x 2+y 2=1交于点P ⎝⎛⎭⎫x 0,13,则sin 2α等于( ) A.19 B .-79C .-23D.136.已知实数a =2ln 2,b =2+2ln 2,c =(ln 2)2,则a ,b ,c 的大小关系是( ) A .c <b <a B .c <a <b C .b <a <cD .a <c <b7.已知△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且(b +c )sin B =(a +c )⎣⎡⎦⎤cos ⎝⎛⎭⎫A -π2+cos ⎝⎛⎭⎫π2+C ,则A =( ) A.2π3B.5π6C.π6D.π38.函数f (x )=⎝ ⎛⎭⎪⎫10x-110x +1lg x 2的图象大致为( )9.有一个公用电话亭,在观察使用这个电话亭的人流量时,设在某一时刻,有n (n ∈N )个人正在使用或等待使用电话的概率为P (n ),且P (n )与时刻t 无关,统计得到P (n )=⎩⎪⎨⎪⎧⎝⎛⎭⎫12n·P (0)(1≤n ≤5),0(n ≥6),那么P (0)的值是( ) A .0 B .1 C.3263D.1210.已知抛物线C :y 2=8ax (a >0)的焦点F 与双曲线D :x 2a +2-y 2a =1(a >0)的焦点重合,过点F 的直线与抛物线C 交于A ,B 两点,则|AF |+2|BF |的最小值为( )A .3+4 2B .6+4 2C .7D .1011.(多选)若不等式ax 2-bx +c >0的解集是(-1,2),则下列选项正确的是( ) A .b <0且c >0 B .a -b +c >0 C .a +b +c >0D .不等式ax 2+bx +c >0的解集是(-2,1)12.(多选)已知函数f (x )=|sin x ||cos x |,则下列说法正确的是( ) A .f (x )的图象关于直线x =π2对称B .f (x )的周期为π2C .(π,0)是f (x )的一个对称中心D .f (x )在区间⎣⎡⎦⎤π4,π2上单调递减13.(多选)如图,已知在矩形ABCD 中,AB =2AD ,E 为边AB的中点,将△ADE 沿直线DE 翻折成△A 1DE ,若M 为线段A 1C 的中点,则△ADE 在翻折过程中,下列命题正确的是( )A .线段BM 的长是定值B .存在某个位置,使DE ⊥A 1C C .点M 的运动轨迹是一个圆D .存在某个位置,使MB ⊥平面A 1DE 二、填空题14.已知向量a =(x ,2),b =(-2,1),若a 与2a -b 共线,则|b ||a |=________.15.已知等比数列{a n }的公比q >0,其前n 项和为S n ,且S 2=6,S 4=30,数列{b n }满足b n =log 2a 2n-1,则数列⎩⎨⎧⎭⎬⎫1b n b n +1的前n 项和T n =________. 16.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0),A 是椭圆的右顶点,B 为椭圆的上顶点,点F (-c ,0)是椭圆的左焦点,椭圆的长轴长为4,且BF ⊥AB ,则c =________.17.(2019·广西北海联考改编)设函数f (x )=ax 3+bx 2+cx (a ,b ,c ∈R ,a ≠0).若不等式xf ′(x )-af (x )≤2对一切x ∈R 恒成立,则a =________,b +c a 的取值范围为________.小题强化练(七)1.解析:选A.由题意,得z =(1-i )(1+i )22=2i (1-i )2=i(1-i)=1+i ,则复数z在复平面内对应的点为(1,1),位于第一象限,故选A.2.解析:选D.由2x 2-x -3≤0,得(2x -3)(x +1)≤0,则M =⎣⎡⎦⎤-1,32,所以∁U M =(-∞,-1)∪⎝⎛⎭⎫32,+∞.由|x |(x -2)>0,得⎩⎪⎨⎪⎧x ≠0,x -2>0,则N =(2,+∞).因此M ∩N =∅,M ∪N =⎣⎡⎦⎤-1,32∪(2,+∞),(∁U M )∩N =(2,+∞),(2,+∞)⊆(-∞,-1)∪⎝⎛⎭⎫32,+∞,故选D.3.解析:选C.根据双曲线的对称性,不妨取双曲线的一个顶点为(a ,0),一条渐近线方程为bx -ay =0.由题意,得ab b 2+a 2=ab c =4a 23c ,即b a =43,所以双曲线的离心率e =ca =1+⎝⎛⎭⎫b a 2=53,故选C. 4.解析:选A.设等差数列{a n }的公差为d ,由a 1,a 3+2,a 6+8成等比数列,得a 1(a 6+8)=(a 3+2)2,即2(10+5d )=(4+2d )2,解得d 1=-2,d 2=12.当d =-2时,a 3+2=0,a 1,a 3+2,a 6+8不成等比数列,故舍去,所以d =12,S 10=10×2+10×92×12=852,故选A.5.解析:选B.因为角α+π4的终边与单位圆x 2+y 2=1交于点P ⎝⎛⎭⎫x 0,13,所以sin ⎝⎛⎭⎫α+π4=13,所以cos ⎣⎡⎦⎤2⎝⎛⎭⎫α+π4=1-2sin 2⎝⎛⎭⎫α+π4=1-2×19=79.又因为cos ⎣⎡⎦⎤2⎝⎛⎭⎫α+π4=cos ⎝⎛⎭⎫2α+π2=-sin 2α,所以sin 2α=-79,故选B.6.解析:选B.因为ln 2=log e 2,所以0<ln 2<1,所以c =(ln 2)2<1.因为20<2ln 2<21,所以1<a <2.又b =2+2ln 2>2,所以c <a <b ,故选B.7.解析:选A.由已知可得(b +c )sin B =(a +c )(sin A -sin C ),由正弦定理可得(b +c )b =(a +c )(a -c ),整理得b 2+c 2-a 2=-bc ,由余弦定理可得cos A =b 2+c 2-a 22bc =-12.又A ∈(0,π),所以A =2π3.8.解析:选B.由题意知f (x )的定义域为x ≠0.由f (1)=0排除C.因为f (-x )=⎝ ⎛⎭⎪⎫10-x-110-x +1lg(-x )2=1-10x 1+10x ·lg x 2=-f (x ),所以f (x )为奇函数,故排除A.当x >1时,0<10x -110x +1<1,0<⎝ ⎛⎭⎪⎫10x -110x +1lg x 2<lg x 2,即f (x )<2lg x ,因此当x >1时,f (x )的图象在y =2lg x 图象的下方,故排除D.故选B.9.解析:选C.由题意知,在任意时刻,该公用电话亭不超过5人正在使用或等待使用电话,所以“有0,1,2,3,4或5个人正在使用或等待使用电话”是必然事件.因为P (1)=12P (0),P (2)=14P (0),P (3)=18P (0),P (4)=116P (0),P (5)=132P (0),所以P (0)=1-[P (1)+P (2)+P (3)+P (4)+P (5)]=1-⎣⎡⎦⎤1-⎝⎛⎭⎫125P (0),所以P (0)=3263.故选C.10.解析:选B.由题意得抛物线C 的焦点为F (2a ,0),则由2a =a +2+a ,解得a =1,所以F (2,0),抛物线C :y 2=8x .由题知,直线AB 的斜率不为零,所以设其方程为x =my +2,A ⎝⎛⎭⎫y 218,y 1,B ⎝⎛⎭⎫y 228,y 2,联立⎩⎪⎨⎪⎧x =my +2,y 2=8x 得y 2-8my -16=0,所以y 1y 2=-16.由抛物线的定义,得|AF |+2|BF |=y 218+2+2⎝⎛⎭⎫y 228+2=6+y 21+2y 228≥6+22y 21y 228=6+42,当且仅当y 21=2y 22,即⎩⎨⎧y 1=442,y 2=-248或⎩⎨⎧y 1=-442,y 2=248时取等号,故选B. 11.解析:选ABD.对于A ,a <0,-1,2是方程ax 2-bx +c =0的两个根,所以-1+2=1=b a ,-1×2=ca ,所以b =a ,c =-2a ,所以b <0,c >0,所以A 正确;令f (x )=ax 2-bx+c ,对于B ,由题意可知f (1)=a -b +c >0,所以B 正确;对于C ,f (-1)=a +b +c =0,所以C 错误,对于D ,因为对于方程ax 2+bx +c =0,设其两根x 1,x 2,所以x 1+x 2=-ba =-1,x 1x 2=ca =-2,所以两根分别为-2和1.所以不等式ax 2+bx +c >0的解集是(-2,1),所以D正确.12.解析:选BCD.f (x )=|sin x ||cos x |=|sin x cos x |=12·|sin 2x |,则f ⎝⎛⎭⎫π2=12|sin π|=0,则f (x )的图象不关于直线x =π2对称,故A 错误;函数周期T =12×2π2=π2,故B 正确;f (π)=12|sin 2π|=0,则(π,0)是f (x )的一个对称中心,故C 正确;当x ∈⎣⎡⎦⎤π4,π2时,2x ∈⎣⎡⎦⎤π2,π,此时sin 2x >0,且sin 2x 为减函数,故D 正确.13.解析:选AC.取CD 的中点F ,连接MF ,BF ,则MF ∥DA 1,BF ∥DE ,所以平面MBF ∥平面A 1DE ,所以MB ∥平面A 1DE ,D 错误;由前面的讨论可知∠A 1DE =∠MFB =π4,MF =12A 1D =定值,FB =DE =定值,因此由余弦定理可得MB 2=MF 2+FB 2-2MF ·FB ·cos ∠MFB ,所以MB 是定值,故AC 正确;由题可知DE =CE =2AD =22AB ,则DE ⊥CE ,若B 成立,可得DE ⊥平面A 1EC ,此时DE ⊥A 1E 与DA 1⊥A 1E 矛盾,故B 错误.综上可得AC 正确.14.解析:由题意,得2a -b =(2x +2,3).因为a 与2a -b 共线,所以x ·3-2·(2x +2)=0,解得x =-4,所以a =(-4,2)=2b ,所以|b ||a |=12.答案:1215.解析:由题意,知q ≠1,所以⎩⎪⎨⎪⎧a 1(1-q 2)1-q=6,a 1(1-q 4)1-q =30,解得⎩⎪⎨⎪⎧a 1=2,q =2或⎩⎪⎨⎪⎧a 1=-6,q =-2(舍去),所以a n =2n ,所以b n =log 2a 2n -1=2n -1,所以1b n b n +1=1(2n -1)(2n +1)=12⎝⎛⎭⎫12n -1-12n +1, 所以T n =12⎣⎡⎝⎛⎭⎫1-13+⎝⎛⎭⎫13-15+⎝⎛⎭⎫15-17+…⎦⎤+⎝⎛⎭⎫12n -1-12n +1=12⎝⎛⎭⎫1-12n +1=n2n +1.答案:n2n +116.解析:由题意得A (a ,0),B (0,b ),由BF ⊥AB 及OB ⊥AF ,其中O 为坐标原点,得|BO |2=|OF |·|OA |,即b 2=ac ,又a 2=b 2+c 2,所以ac =a 2-c 2,又a =2,所以c 2+2c -4=0,则c =5-1.答案:5-117.解析:由题可得f ′(x )=3ax 2+2bx +c ,不等式xf ′(x )-af (x )≤2对一切x ∈R 恒成立,可化为(3a -a 2)x 3+(2b -ab )x 2+(c -ac )x -2≤0对一切x ∈R 恒成立,所以3a -a 2=0,解得a =3或a =0(舍).所以bx 2+2cx +2≥0对一切x ∈R 恒成立.当b =0,c =0时,有2≥0,符合题意,此时b +c a =0;当b ≠0时,需满足b >0且Δ=(2c )2-8b ≤0,所以b ≥c 22,所以b +c a =b +c 3≥c 22+c 3=(c +1)22-123≥-16,当且仅当c =-1,b =12时等号成立.综上所述,b +c a 的取值范围是⎣⎡⎭⎫-16,+∞. 答案:3 ⎣⎡⎭⎫-16,+∞。
2020年高考数学二轮复习小题押题(12+4)提速综合练习7-8(含答案解析)

2020年高考数学二轮复习小题押题(12+4)提速综合练习7-8“12+4”小题提速综合练(七)一、选择题1.(2016·浙江高考)命题“∀x ∈R ,∃n ∈N *,使得n ≥x 2”的否定形式是( ) A .∀x ∈R ,∃n ∈N *,使得n <x 2 B .∀x ∈R ,∀n ∈N *,使得n <x 2 C .∃x ∈R ,∃n ∈N *,使得n <x 2 D .∃x ∈R ,∀n ∈N *,使得n <x 2解析:选D 由于特称命题的否定形式是全称命题,全称命题的否定形式是特称命题,所以“∀x ∈R ,∃n ∈N *,使得n ≥x 2”的否定形式为“∃x ∈R ,∀n ∈N *,使得n <x 2”.2.(2017·南京模拟)若复数z =(a -1)+3i(a ∈R)在复平面内对应的点在直线y =x +2上,则a 的值等于( ) A .1 B .2 C .5D .6解析:选B 因为复数z =(a -1)+3i(a ∈R)在复平面内对应的点为(a -1,3),所以由题意得点在直线y =x +2上,则3=a -1+2,解得a =2.3.把函数y =sin ⎝⎛⎭⎫x +π3的图象上各点的横坐标缩短到原来的12(纵坐标不变),再将图象向右平移π3个单位,所得图象对应的函数为( )A .y =sin ⎝⎛⎭⎫2x -π3B .y =sin 2xC .y =sin ⎝⎛⎭⎫12x +π6 D .y =sin 12x解析:选A 把函数y =sin ⎝⎛⎭⎫x +π3的图象上各点的横坐标缩短到原来的12(纵坐标不变),得到y =sin ⎝⎛⎭⎫2x +π3的图象,再将图象向右平移π3个单位,所得图象对应的函数为y =sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π3+π3=sin ⎝⎛⎭⎫2x -π3. 4.如图所示的程序框图,程序运行时,若输入的S =-12,则输出S 的值为( ) A .4 B .5C .8D .9解析:选C 第一次循环,得S =-10,n =2;第二次循环,得S =-6,n =3;第三次循环,得S =0,n =4;第四次循环,得S =8,n =5.此时S >n ,不满足循环条件,退出循环,输出S 的值为8,故选C.5.已知等差数列{a n }的前n 项和为S n ,且满足S 33-S 22=1,则数列{a n }的公差d 是( )A .1B .2C .4D .6解析:选B 法一:等差数列{a n }的前n 项和为S n =na 1+12n (n -1)d ,所以有S n n =a 1+12(n -1)d ,代入S 33-S 22=1中,得a 1+12(3-1)d -a 1+12(2-1)d =12d =1,所以d =2.法二:易知数列⎩⎨⎧⎭⎬⎫S n n 是公差为d2的等差数列,所以d =2.6.在[-2,6]上随机取一个数m ,则使关于x 的一元二次方程x 2-4x +m 2=0有实数根的概率是( ) A.12 B.13C.14D.15解析:选A 由关于x 的一元二次方程x 2-4x +m 2=0得(-4)2-4m 2≥0,解得-2≤m ≤2,所以所求概率P =2-(-2)6-(-2)=12.7.函数y =e x cos e xe 2x -1的图象大致为( )解析:选D 设f (x )=e x cos e xe 2x -1,则易得函数f (x )的定义域为(-∞,0)∪(0,+∞),且f (-x )=e -x cos (-e x )e -2x -1=e x cos e x 1-e 2x=-f (x ),所以函数f (x )为奇函数,函数图象关于原点中心对称,排除A ;当0<x <π2e 时,f (x )>0,排除B ;当x增大时,函数值的符号正负交替出现,排除C ,故选D.8.(2017·南京模拟)某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是( )A.323B.643C .16D .32解析:选A 由三视图可知该几何体如图所示,此几何体是三棱锥,且底面是腰长为4的等腰直角三角形,高为4,故该几何体的体积V =13×⎝⎛⎭⎫12×4×4×4=323. 9.(2017·惠州模拟)设直线l 过双曲线C 的一个焦点,且与C 的一条对称轴垂直,l 与C交于A ,B 两点,|AB |为C 的实轴长的2倍,则C 的离心率为( )A. 3B. 2 C .2D .3解析:选A 设双曲线C 的标准方程为x 2a 2-y 2b2=1(a >0,b >0),由于直线l 过双曲线的焦点且与对称轴垂直,因此直线l 的方程为x =c 或x =-c ,代入x 2a 2-y 2b 2=1中得y 2=b 2⎝⎛⎭⎫c 2a 2-1=b 4a2,∴y =±b 2a ,故|AB |=2b 2a ,依题意2b 2a =4a ,∴b 2a 2=2,∴e =1+b 2a2= 3. 10.(2017·湘中名校联考)已知函数f (x )=sin(2x +φ),其中φ为实数,若f (x )≤⎪⎪⎪⎪f ⎝⎛⎭⎫π6对x ∈R 恒成立,且f ⎝⎛⎭⎫π2>f (π),则f (x )的单调递增区间是( )A.⎣⎡⎦⎤k π-π3,k π+π6(k ∈Z) B.⎣⎡⎦⎤k π,k π+π2(k ∈Z) C.⎣⎡⎦⎤k π+π6,k π+2π3(k ∈Z) D.⎣⎡⎦⎤k π-π2,k π(k ∈Z) 解析:选C 因为f (x )≤⎪⎪⎪⎪f ⎝⎛⎭⎫π6对x ∈R 恒成立,即⎪⎪⎪⎪f ⎝⎛⎭⎫π6=⎪⎪⎪⎪sin ⎝⎛⎭⎫π3+φ=1,所以φ=k π+π6(k ∈Z).因为f ⎝⎛⎭⎫π2>f (π),所以sin(π+φ)>sin(2π+φ),即sin φ<0,所以φ=-5π6+2k π(k ∈Z),所以f (x )=sin ⎝⎛⎭⎫2x -5π6,所以由三角函数的单调性知2x -5π6∈⎣⎡⎦⎤2k π-π2,2k π+π2(k ∈Z),得x ∈k π+π6,k π+2π3(k ∈Z). 11.已知曲线C :y =18x 2的焦点为F ,过点F 的直线l 与曲线C 交于P ,Q 两点,且|FP |=2|FQ |,则△OPQ 的面积等于( )A .6 2 B.322C .12 2D.324解析:选A 由题意得抛物线的标准方程为x 2=8y ,所以焦点F (0,2),易得直线l 的斜率一定存在,则不妨设直线l 的方程为y =kx +2,与抛物线的方程联立,消去y 得x 2-8kx -16=0,则x P x Q =-16, ①又因为|FP |=2|FQ |,所以x P =-2x Q , ②联立①②,解得⎩⎨⎧ x P =42,x Q =-22或⎩⎨⎧x P =-42,x Q =22,所以S △OPQ =12(|x P |+|x Q |)·|OF |=6 2.12.(2018届高三·昆明两区七校调研)若f (x )+1=1f (x +1),当x ∈[0,1]时,f (x )=x ,在区间(-1,1]内,g (x )=f (x )-mx -m2有两个零点,则实数m 的取值范围是( )A.⎣⎡⎭⎫0,13B.⎝⎛⎦⎤0,23 C.⎝⎛⎦⎤0,13 D.⎣⎡⎭⎫23,+∞解析:选B 依题意,f (x )=1f (x +1)-1,当x ∈(-1,0)时,x +1∈(0,1), f (x )=1f (x +1)-1=1x +1-1, 由g (x )=0得f (x )=m ⎝⎛⎭⎫x +12. 在同一坐标系上画出函数y =f (x )与y =m ⎝⎛⎭⎫x +12在区间(-1,1]内的图象, 结合图象可知,要使g (x )有两个零点,只需函数y =f (x )与y =m ⎝⎛⎭⎫x +12该直线斜率为m ,过点-12,0在区间(-1,1]内的图象有两个不同的交点,故实数m 的取值范围是⎝⎛⎦⎤0,23,选B. 二、填空题13.(2017·合肥模拟)某同学在高三学年的五次阶段性考试中,数学成绩依次为110,114,121,119,126,则这组数据的方差是________.解析:因为对一组数据同时加上或减去同一个常数,方差不变,所以本题中可以先对这5个数据同时减去110,得到新的数据分别为0,4,11,9,16,其平均数为x =15(0+4+11+9+16)=8,根据方差公式可得s 2=(0-8)2+(4-8)2+(11-8)2+(9-8)2+(16-8)25=30.8. 答案:30.814.(2018届高三·广西五校联考)已知向量a =(1,3),b =(3,m ),且b 在a 上的投影为3,则向量a 与b 的夹角为________.解析:因为a ·b =3+3m ,|a |=12+(3)2=2,|b |=9+m 2,由|b |cos 〈a ,b 〉=3,可得a ·b|a |=3,故3+3m 2=3,解得m =3,故|b |=9+3=23,故cos 〈a ,b 〉=323=32,故〈a ,b 〉=π6,即向量a 与b 的夹角为π6. 答案:π615.(2017·西安八校联考)设实数x ,y 满足⎩⎪⎨⎪⎧x -y ≤0,x +y ≥0,y ≤a ,若z =x +2y 的最大值为3,则a 的值是________.⎩⎪⎨⎪⎧x -y ≤0,x +y ≥0,y ≤a表示的平解析:依题意得a >0,在平面直角坐标系内大致画出不等式组面区域如图所示,结合图形可知,直线z =x +2y 经过直线y =a 与直线x -y =0的交点,即点A (a ,a )时,z =x +2y 取得最大值3,因此a +2a =3,a =1.答案:116.(2017·福建质检)数列{a n }的前n 项和为S n ,且a 1=23,a n +1-S n =23.用[x ]表示不超过x 的最大整数,如:[-0.4]=-1,[1.6]=1.设b n =[a n ],则数列{b n }的前2n 项和为________.解析:当n ≥2时,由题意,得S n =a n +1-23,S n -1=a n -23,两式相减得,a n =a n +1-a n ,即a n +1a n =2(n ≥2),又当n =1时,a 1=23,a 2-a 1=23,所以a 2=43,即a 2a 1=2,所以数列{a n }是首项为23,公比为2的等比数列,所以a n =23·2n -1=13·2n.所以b 1=0,b 2=1=2b 1+1, b 3=2=2b 2,b 4=5=2b 3+1, b 5=10=2b 4,b 6=21=2b 5+1, b 7=42=2b 6,b 8=85=2b 7+1, …,b 2n -1=2b 2n -2,b 2n =2b 2n -1+1, 所以b 1+b 2=21-1,b 3+b 4=23-1, b 5+b 6=25-1,b 7+b 8=27-1,…, b 2n -1+b 2n =22n -1-1,设数列{b n }的前2n 项和为T 2n , 则T 2n =2(1-4n )1-4-n =22n +13-n -23.答案:22n +13-n -23“12+4”小题提速综合练(八)一、选择题1.(2017·湘中名校联考)已知集合A ={x |x 2-11x -12<0},B ={x |x =2(3n +1),n ∈Z},则A ∩B 等于( ) A .{2} B .{2,8} C .{4,10}D .{2,4,8,10}解析:选B 因为集合A ={x |x 2-11x -12<0}={x |-1<x <12},集合B 为被6整除余数为2的数.又集合A 中的整数有0,1,2,3,4,5,6,7,8,9,10,11,故被6整除余数为2的数有2和8,所以A ∩B ={2,8}.2.(2017·兰州模拟)下列命题中的真命题为( ) A .∃x 0∈R ,e x 0≤0 B .∀x ∈R,2x ≥x 2C .已知a ,b 为实数,则a +b =0的充要条件是ab=-1D .已知a ,b 为实数,则a >1,b >1是ab >1的充分不必要条件解析:选D 选项A 为假命题,理由是对∀x ∈R ,e x >0;选项B 为假命题,不妨取x =3,则23<32,显然不满足∀x ∈R,2x ≥x 2;选项C 为假命题,当b =0时,由a +b =0推不出a b =-1,但由ab =-1可推出a +b =0,即a +b =0的充分不必要条件是ab =-1.3.(2017·石家庄模拟)已知等差数列{a n }的公差为5,前n 项和为S n ,且a 1,a 2,a 5成等比数列,则S 6=( ) A .80 B .85 C .90D .95解析:选C 由题意,得(a 1+5)2=a 1(a 1+4×5),解得a 1=52,所以S 6=6×52+6×52×5=90.4.(2017·合肥模拟)设向量a ,b 满足|a +b |=4,a ·b =1,则|a -b |=( ) A .2 B .2 3 C .3D .2 5解析:选B 因为|a +b |2=a 2+2a ·b +b 2,|a -b |2=a 2-2a ·b +b 2,以上两式相减可得,4a ·b =|a +b |2-|a -b |2,所以|a -b |2=|a +b |2-4a ·b =16-4=12,即|a -b |=2 3.5.(2018届高三·湖北五校联考)已知数列{a n }的前n 项和S n =Aq n +B (q ≠0),则“A =-B ”是“数列{a n }是等比数列”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:选B 若A =B =0,则S n =0,故数列{a n }不是等比数列;若数列{a n }是等比数列,则a 1=Aq +B ,a 2=Aq 2-Aq ,a 3=Aq 3-Aq 2,由a 3a 2=a 2a 1,得A =-B .6.一个凸多面体,其三视图如图,则该几何体体积为( )A .5 2B .6 2C .9D .10解析:选C 由三视图知,该几何体是一个四棱锥,画出该几何体的直观图如图中实线所示,所以该四棱锥由两个三棱锥组成,其体积V =2×13×12×32×3=9.7.(2017·云南模拟)执行如图所示的程序框图,如果输入的N =30,则输出的S =( )A .26B .57C .225D .256解析:选B 第一次循环,得S =1,n =3;第二次循环,得S =4,n =7;第三次循环,得S =11,n =15;第四次循环,得S =26,n =31;第五次循环,S =57,n >30.所以此时退出循环,故输出的S =57.8.(2018届高三·玉溪四校联考)已知函数f (x )=⎩⎪⎨⎪⎧x +2,x >a ,x 2+5x +2,x ≤a ,函数g (x )=f (x )-2x 恰有三个不同的零点,则实数a 的取值范围是( )A .[-1,1)B .[0,2]C .[-2,2)D .[-1,2)解析:选D 由题意知g (x )=⎩⎪⎨⎪⎧2-x ,x >a ,x 2+3x +2,x ≤a ,因为g (x )有三个不同的零点,所以2-x =0在x >a 时有一个解,由x =2得a <2;由x 2+3x +2=0得x =-1或x =-2,则由x ≤a 得a ≥-1.综上,a 的取值范围为[-1,2).9.(2017·广西三市联考)已知在(0,+∞)上函数f (x )=⎩⎪⎨⎪⎧-2,0<x <1,1,x ≥1,则不等式log 2x -(log 144x -1)f (log 3x +1)≤5的解集为( )A.⎝⎛⎭⎫13,1 B .[1,4] C.⎝⎛⎦⎤13,4D .[1,+∞)解析:选C 原不等式等价于⎩⎪⎨⎪⎧log 3x +1≥1,log 2x -⎝⎛⎭⎫log 144x -1≤5 或⎩⎪⎨⎪⎧0<log 3x +1<1,log 2x +2⎝⎛⎭⎫log 144x -1≤5,解得1≤x ≤4或13<x <1,∴原不等式的解集为⎝⎛⎦⎤13,4. 10.(2017·安徽二校联考)在边长为1的正三角形ABC 中,D ,E 是边BC 的两个三等分点(D 靠近点B ),则AD ―→·AE ―→等于( )A.16B.29C.1318D.13解析:选C 法一:因为D ,E 是边BC 的两个三等分点,所以BD =DE =CE =13,在△ABD 中,AD 2=BD 2+AB 2-2BD ·AB ·cos 60° =⎝⎛⎭⎫132+12-2×13×1×12=79, 即AD =73,同理可得AE =73, 在△ADE 中,由余弦定理得 cos ∠DAE =AD 2+AE 2-DE 22AD ·AE=79+79-⎝⎛⎭⎫1322×73×73=1314,所以AD ―→·AE ―→=|AD ―→|·|AE ―→|cos ∠DAE =73×73×1314=1318. A ⎝⎛⎭⎫0,32,D ⎝⎛⎭⎫-16,0,法二:如图,建立平面直角坐标系,由正三角形的性质易得E ⎝⎛⎭⎫16,0,所以AD ―→=⎝⎛⎭⎫-16,-32,AE ―→=⎝⎛⎭⎫16,-32,所以AD ―→·AE ―→=⎝⎛⎭⎫-16,-32·⎝⎛⎭⎫16,-32=-136+34=1318.11.(2018届高三·贵州摸底)已知函数f (x )=sin ωx -3cos ωx (ω>0),若方程f (x )=-1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )A.⎝⎛⎦⎤136,72 B.⎝⎛⎦⎤72,256 C.⎝⎛⎦⎤256,112D.⎝⎛⎦⎤112,376解析:选B 因为f (x )=2sin ⎝⎛⎭⎫ωx -π3, 方程2sin ⎝⎛⎭⎫ωx -π3=-1在(0,π)上有且只有四个实数根,即sin ⎝⎛⎭⎫ωx -π3=-12在(0,π)上有且只有四个实数根.设t =ωx -π3,因为0<x <π,所以-π3<t <ωπ-π3,所以19π6<ωπ-π3≤23π6,解得72<ω≤256.12.(2018届高三·石家庄调研)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过点F 1且垂直于x 轴的直线与该双曲线的左支交于A ,B 两点,AF 2,BF 2分别交y 轴于P ,Q 两点,若△PQF 2的周长为12,则ab 取得最大值时该双曲线的离心率为( )A. 2B. 3C .2 2D.233解析:选D 由题意,得|AF 1|+|BF 1|=|AB |=2b 2a , ①且P ,Q 分别为AF 2,BF 2的中点. 由双曲线的定义,知|AF 2|-|AF 1|=2a , ② |BF 2|-|BF 1|=2a , ③联立①②③,得|AF 2|+|BF 2|=4a +2b 2a .因为△PQF 2的周长为12,所以△ABF 2的周长为24, 即4a +4b 2a =24,亦即b 2=6a -a 2, 所以(ab )2=6a 3-a 4. 令f (a )=6a 3-a 4,则f ′(a )=18a 2-4a 3=4a 2⎝⎛⎭⎫92-a , 所以f (a )在⎝⎛⎭⎫0,92上单调递增, 在⎝⎛⎭⎫92,+∞上单调递减, 所以当a =92时,f (a )取得最大值,此时b 2=6×92-⎝⎛⎭⎫922=274,所以c =a 2+b 2=33, 所以e =c a =233.二、填空题13.若函数f (x )=(x -a )(x +3)为偶函数,则f (2)=________.解析:由f (x )=x 2+(3-a )x -3a 为偶函数,知其奇次项的系数为0,所以3-a =0,a =3,所以f (2)=22-9=-5.答案:-514.(2017·贵阳模拟)已知不等式1+14<32,1+14+19<53,1+14+19+116<74,照此规律总结出第n 个不等式为________________________________.解析:由已知,三个不等式可以写成1+122<2×2-12,1+122+132<2×3-13,1+122+132+142<2×4-14,所以照此规律可得到第n 个不等式为1+122+132+…+1n 2+1(n +1)2<2(n +1)-1n +1=2n +1n +1.答案:1+122+132+…+1n 2+1(n +1)2<2n +1n +115.(2017·广西五校联考)两圆x 2+y 2+2ax +a 2-4=0和x 2+y 2-4by -1+4b 2=0恰有三条公切线,若a ∈R ,b ∈R 且ab ≠0,则1a 2+1b2的最小值为________.解析:两圆x 2+y 2+2ax +a 2-4=0和x 2+y 2-4by -1+4b 2=0分别配方得,(x +a )2+y 2=4,x 2+(y -2b )2=1,依题意得两圆相外切,故a 2+4b 2=1+2=3,即a 2+4b 2=9,则1a 2+1b 2=⎝⎛⎭⎫a 29+4b 29⎝⎛⎭⎫1a 2+1b 2=19+a 29b 2+4b 29a 2+49≥59+2a 29b 2·4b 29a 2=1,当且仅当a 29b 2=4b 29a 2,即a 2=2b 2时等号成立,故1a 2+1b 2的最小值为1. 答案:116.设A ,B 是球O 的球面上两点,∠AOB =π3,C 是球面上的动点,若四面体OABC 的体积V 的最大值为934,则此时球的表面积为________.解析:在四面体OABC 中,显然△OAB 的面积一定,设球O 的半径为R ,则S △OAB =12×R ×32R =34R 2,要使四面体的体积最大,则只需球上的点到平面OAB 的距离最大,显然,到平面OAB 距离的最大值为球的半径,所以(V C -OAB )max =13×34R 2×R =312R 3=934,解得R =3,由球的表面积公式得S 球=4πR 2=4×32×π=36π. 答案:36π。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小题强化练(八)一、选择题1.已知集合M ={1,a 2},P ={-1,-a },若M ∪P 有三个元素,则M ∩P =( ) A .{0,1} B .{-1,0} C .{0}D .{-1}2.若复数z =a +i1-i ,且z ·i 3>0,则实数a 的值等于( )A .1B .-1 C.12D .-123.已知条件甲:a >0,条件乙:a >b 且1a >1b ,则甲是乙的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知数列{a n }满足3a n +1=9·3a n (n ∈N *)且a 2+a 4+a 6=9,则log 13(a 1+a 9+a 11)=( )A .-13B .3C .-3D.135.已知非零向量a ,b 满足|a +b |=|a -b |=2,|a |=1,则a +b 与a -b 的夹角为( ) A.π6 B.π3 C.2π3D.5π66.函数f (x )=sin(πx )e -⎪⎪⎪⎪x 2的图象可能是( )7.已知函数f (x )=sin ⎝⎛⎭⎫2x -3π2(x ∈R ),下列说法错误的是( )A .函数f (x )的最小正周期是πB .函数f (x )是偶函数C .函数f (x )的图象关于⎝⎛⎭⎫π4,0对称 D .函数f (x )在⎣⎡⎦⎤0,π2上是增函数8.某市教育局卫生健康所对全市高三年级的学生身高进行抽样调查,随机抽取了100名学生,他们的身高都处于A ,B ,C ,D ,E 五个层次,根据抽样结果得到如图所示的统计图,则从图中不能得出的信息是( )A .样本中男生人数少于女生人数B .样本中B 层次身高的人数最多C .样本中D 层次身高的男生多于女生 D .样本中E 层次身高的女生有3人9.如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为1,M ,N 分别是棱AA 1,BC 上的动点,若MN =2,则线段MN 的中点P 的轨迹是( )A .一条线段B .一段圆弧C .一个球面区域D .两条平行线段10.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,O 为坐标原点,以线段F 1F 2为直径的圆与双曲线的右支交于P 点,且以线段OF 2为直径的圆与直线PF 1相切,若|PF 1|=8,则双曲线的焦距等于( )A .6 2B .6C .3 2D .311.(多选)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,则( ) A .若2cos C (a cos B +b cos A )=c ,则角C =π3B .若2cosC (a cos B +b cos A )=c ,则角C =π6C .若边BC 上的高为36a ,则当c b +bc 取得最大值时,角A =π3 D .若边BC 上的高为36a ,则当c b +bc 取得最大值时,角A =π612.(多选)如图,正方体ABCD -A 1B 1C 1D 1的棱长为3,线段B 1D 1上有两个动点E ,F 且EF =1,则当E ,F 移动时,下列结论正确的是( )A .AE ∥平面C 1BDB .四面体ACEF 的体积不为定值C .三棱锥A -BEF 的体积为定值D .四面体ACDF 的体积为定值 13.(多选)某同学在研究函数f (x )=x1+|x |(x ∈R )时,分别得出下面几个结论,其中正确的结论是( )A .等式f (-x )+f (x )=0在x ∈R 时恒成立B .函数f (x )的值域为(-1,1)C .若x 1≠x 2,则一定有f (x 1)≠f (x 2)D .函数g (x )=f (x )-x 在R 上有三个零点 二、填空题14.设a ∈{1,3,5,7},b ∈{2,4,6},则函数f (x )=log a bx 是增函数的概率为________.15.已知正实数a ,b 满足ab -b +1=0,则1a+4b 的最小值是________.16.已知数列{a n }的首项a 1=1,函数f (x )=x 3+⎝⎛⎭⎫a n +1-a n -cos n π2为奇函数,记S n 为数列{a n }的前n 项和,则S 2 019的值为________.17.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的两个焦点分别为F 1,F 2,若B 为短轴的一个端点,且∠F 1BF 2=90°,则椭圆C 的离心率为________;若椭圆C 上存在点P ,使得PF 1⊥PF 2,则椭圆C 的离心率的取值范围为________.小题强化练(八)1.解析:选C.要使M ∪P 有三个元素,则a 2=-a ,即a =0或a =-1,若a =-1,则有a 2=1不合题意,所以a =0,则M ∩P ={0}.2.解析:选A.z ·i 3=z ·(-i)=(a +i )(-i )1-i =1-a i 1-i=(1+a )+(1-a )i2,因为z ·i 3>0,所以z ·i 3为正实数,则有⎩⎪⎨⎪⎧1-a =0,1+a >0,所以a =1.3.解析:选B.若1a >1b ,则b -a ab >0.又a >b ,所以ab <0,即a >0>b ,故甲是乙的必要不充分条件.4.解析:选C.由题意得3a n +1=3a n+2即,a n +1-a n =2,所以{a n }是公差为2的等差数列.由a 2+a 4+a 6=3a 4=9得a 4=3,所以a n =3+(n -4)×2=2n -5,所以log 13(a 1+a 9+a 11)=log 13(-3+13+17)=log 1327=-3.5.解析:选C.法一:由|a +b |=|a -b |=2可得a ·b =0,则有|a +b |2=|a |2+|b |2=4,所以|b |2=4-|a |2=3.因为|a -b |=2,所以cos 〈a +b ,a -b 〉=(a +b )·(a -b )|a +b |·|a -b |=1-34=-12.因为〈a +b ,a -b 〉∈[0,π],所以〈a +b ,a -b 〉=2π3.法二:由题设|a +b |=|a -b |=2及向量的加减运算的几何意义可知以a ,b 为邻边的平行四边形是矩形,即a ⊥b ,如图.由于|a +b |=|a -b |=2,|a |=1,则OA =OC =AC =1,则∠ACO =π3,则向量a +b 与a -b 的夹角∠ACD =2π3. 6.解析:选A.因为f (-x )=sin(-πx )e -⎪⎪⎪⎪-x 2=-sin(πx )e -⎪⎪⎪⎪x 2=-f (x ),所以f (x )为奇函数,故排除C ;令0<x <12,则有0<πx <π2,此时f (x )>0,故排除D ;因为|sin(πx )|≤1,e-⎪⎪⎪⎪x 2≤1,故|f (x )|≤1,故排除B ,故选A.7.解析:选D.函数f (x )=sin ⎝⎛⎭⎫2x -3π2(x ∈R )的最小正周期为2π2=π,故A 正确;由于f (x )=cos 2x ,故函数f (x )是偶函数,故B 正确;令x =π4,求得f (x )=cos π2=0,故函数f (x )的图象关于⎝⎛⎭⎫π4,0对称,故C 正确;当x ∈⎣⎡⎦⎤0,π2时,2x ∈[0,π],函数f (x )=cos 2x 在⎣⎡⎦⎤0,π2上是减函数,故D 错误,故选D.8.解析:选C.由男生身高情况统计图知100名学生中,男生有4+12+10+8+6=40(人),女生有100-40=60(人),所以选项A 正确;因为身高处于B 层次的男生人数最多,有12人,在扇形统计图中,B 层次身高的女生占的比例为40%,也最多,所以样本中B 层次身高的人数最多,选项B 正确;身高处于D 层次的男生有8人,女生有(100-40)×15%=9(人),8<9,所以选项C 不正确;身高处于E 层次的女生有(100-40)×(1-40%-15%-25%-15%)=3(人),所以选项D 正确.故选C.9.解析:选B.连接AN ,AP ,易知△MAN 为直角三角形.因为MN =2,P 为线段MN 的中点,所以AP =22,因此点P 到A 的距离为定值,所以点P 在以点A 为球心,22为半径的球面上运动,记此球为球O ,分别取A 1B 1,D 1C 1,DC ,AB 的中点E ,F ,G ,H ,并顺次连接,则MA ∥平面EFGH .记AN ∩HG =Q ,则易知HQ 为△ABN 的中位线,故Q 为AN 的中点.连接PQ ,则PQ 为△AMN 的中位线,得MA ∥PQ ,又点Q 在平面EFGH 内,MA ∥平面EFGH ,所以点P 在平面EFGH 内运动,故点P 的轨迹为平面EFGH 与球O 的球面的交线,所以点P 的轨迹是一段圆弧.故选B.10.解析:选A.如图,连接PF 2,依题意知PF 1⊥PF 2,设以线段OF 2为直径的圆与直线PF 1相切于点N ,圆心为M ,连接MN ,则NM ⊥PF 1,因此Rt △PF 1F 2∽Rt △NF 1M ,所以|NM ||PF 2|=|F 1M ||F 1F 2|,若设双曲线的焦距为2c ,则c 2|PF 2|=3c 22c ,解得|PF 2|=2c3,由勾股定理可得|PF 1|=|F 1F 2|2-|PF 2|2=(2c )2-⎝⎛⎭⎫2c 32=42c 3,于是42c3=8,则c =32,故焦距2c =6 2.11.解析:选AC.因为在△ABC 中,0<C <π,所以sin C ≠0.对于A ,已知等式利用正弦定理化简得2cos C (sin A cos B +sin B cos A )=sin C ,整理得2cos C sin(A +B )=sin C ,即2cos C ·sin[π-(A +B )]=sin C ,即2cos C sin C =sin C ,又sin C ≠0,所以cos C =12,所以C =π3.故A 正确,同理B 错误.由等面积法得12×36a 2=12bc sin A ,所以a 2=23bc sin A ,又b 2+c 2=a 2+2bc cos A =23bc sin A +2bc cos A ,则c b +b c =b 2+c2bc =23sin A +2cos A =4sin ⎝⎛⎭⎫A +π6≤4,当且仅当A +π6=π2+2k π,k ∈Z 时,即A =π3+2k π,k ∈Z 时,c b +bc 取得最大值4,又0<A <π,所以A =π3.故C 正确,D 错误.12.解析:选ACD.对于A ,如图1,AB 1∥DC 1,易证AB 1∥平面C 1BD ,同理AD 1∥平面C 1BD ,且AB 1∩AD 1=A ,所以平面AB 1D 1∥平面C 1BD ,又AE ⊂平面AB 1D 1,所以AE ∥平面C 1BD ,A 正确;对于B ,如图2,S △AEF =12EF ·h 1=12×1×(32)2-⎝⎛⎭⎫3222=364,点C 到平面AEF的距离为点C 到平面AB 1D 1的距离d 为定值,所以V A CEF =V C AEF =13×364×d =64d 为定值,所以B 错误;对于C ,如图3,S △ BEF =12×1×3=32,点A 到平面BEF 的距离为点A 到平面BB 1D 1D 的距离d 为定值,所以V A BEF =13×32×d =12d 为定值,C 正确;对于D ,如图4,四面体ACDF 的体积为V A CDF =V F ACD =13×12×3×3×3=92为定值,D正确.13.解析:选ABC.易知函数的定义域为R ,且f (-x )=-f (x ),故函数为奇函数,故A 正确;当x >0时,f (x )=x 1+x=11+1x ,该函数在(0,+∞)上递增,且当x →0时,f (x )→0;当x →+∞时,f (x )→1.结合奇偶性,作出f (x )的图象如图所示:易知函数的值域是(-1,1),故B 正确;结合函数f (x )为定义域内的增函数,所以C 正确;当x ≥0时,g (x )=f (x )-x =x1+x -x =-x 21+x ,令g (x )=0得x =0,故此时g (x )只有一个零点0,g (x )显然是奇函数,故该函数只有一个零点,所以D 错误.14.解析:由题知a b 所有可能取值有12,32,52,72,14,34,54,74,16,36,56,76,共12个.当a b >1时,f (x )为增函数,此时a b 的可能取值有32,52,72,54,74,76,共6个.故所求概率P =612=12. 答案:1215.解析:由ab -b +1=0可得a =b -1b ,由a =b -1b >0得b >1,所以1a +4b =bb -1+4b=1b -1+4(b -1)+5.因为1b -1+4(b -1)≥4,所以1a +4b ≥9,当且仅当a =13,b =32时等号成立.答案:916.解析:因为f (x )为奇函数,所以f (-x )=-f (x ),则根据函数f (x )的表达式易知必有a n+1-a n -cos n π2=0,即a n +1=a n +cos n π2.于是由a 1=1,得a 2=a 1+cos π2=1,a 3=a 2+cos2π2=0,a 4=a 3+cos 3π2=0,a 5=a 4+cos 4π2=1,…如此继续下去,知a n +4=a n .所以数列{a n }是周期数列,其周期为4,所以S 2 019=504(a 1+a 2+a 3+a 4)+a 1+a 2+a 3=504×2+1+1+0=1 010.答案:1 01017.解析:由题知b =c ,所以a 2=b 2+c 2=2c 2,所以a =2c ,所以e =c a =c 2c =22.由题知F 1(-c ,0),F 2(c ,0),c 2=a 2-b 2,设点P (x ,y ),由PF 1⊥PF 2,得(x -c ,y )·(x +c ,y )=0,化简得x 2+y 2=c 2,联立方程组⎩⎪⎨⎪⎧x 2+y 2=c 2,x 2a 2+y 2b 2=1,整理得x 2=(2c 2-a 2)·a 2c 2≥0,解得e ≥22,又0<e <1,所以22≤e <1. 答案:22 ⎣⎡⎭⎫22,1。
