人教A版高中数学必修一第一章第2节《函数及其表示》课时作业
2017-2018学年高中数学人教A版必修一课时作业:1-2函数及其表示-1 含解析 精品

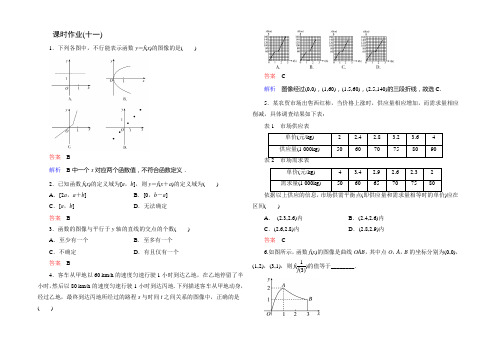
第一章 1.2 1.2.1A 级 基础巩固一、选择题1.下列四种说法中,不正确的是导学号 69174212( B ) A .在函数值域中的每一个数,在定义域中都至少有一个数与之对应 B .函数的定义域和值域一定是无限集合C .定义域和对应关系确定后,函数的值域也就确定了D .若函数的定义域中只含有一个元素,则值域也只含有一个元素 2.f (x )=1+x +x1-x的定义域导学号 69174213( D ) A .[-1,+∞) B .(-∞,-1] C .RD .[-1,1)∪(1,+∞)[解析] ⎩⎪⎨⎪⎧ 1+x ≥01-x ≠0,解得⎩⎪⎨⎪⎧x ≥-1,x ≠1,故定义域为[-1,1)∪(1,+∞),选D . 3.各个图形中,不可能是函数y =f (x )的图象的是导学号 69174214( A )[解析] 因为垂直x 轴的直线与函数y =f (x )的图象至多有一个交点,故选A . 4.(2016·曲阜二中月考试题)集合A ={x |0≤x ≤4},B ={y |0≤y ≤2},下列不表示从A 到B 的函数是导学号 69174215( C )A .f x →y =12xB .f x →y =13xC .f x →y =23xD .f x →y =x[解析] 对于选项C ,当x =4时,y =83>2不合题意.故选C .5.下列各组函数表示相等函数的是导学号 69174216( C ) A .y =x 2-9x -3与y =x +3B .y =x 2-1与y =x -1C .y =x 0(x ≠0)与y =1(x ≠0)D .y =x +1,x ∈Z 与y =x -1,x ∈Z[解析] A 项中y =x 2-9x -3可化为y =x +3(x ≠3),∴定义域不同;B 项中y =x 2-1=|x |-1.∴定义域相同,但对应关系不同;D 项中定义域相同,但对应关系不同;C 项正确,故选C .6.函数y =f (x )的图象与直线x =m 的交点个数为导学号 69174217( C ) A .可能有无数个 B .只有一个 C .至多一个D .至少一个[解析] 根据函数定义,一个自变量x 只能对应一个函数值y ,而y =f (x )的定义域中不一定含有m .二、填空题7.已知函数f (x )=11+x ,又知f (t )=6,则t =__-56__.导学号 69174218[解析] f (t )=1t +1=6.∴t =-56.8.用区间表示下列数集:导学号 69174219 (1){x |x ≥1}=__[1,+∞)__; (2){x |2<x ≤4}=__(2,4]__;(3){x |x >-1且x ≠2}=__(-1,2)∪(2,+∞)__. 三、解答题9.求下列函数的定义域,并用区间表示:导学号 69174220 (1)y =(x +1)2x +1-1-x ;(2)y =5-x|x |-3. [解析] (1)要使函数有意义,自变量x 的取值必须满足⎩⎪⎨⎪⎧x +1≠01-x ≥0,解得x ≤1且x ≠-1,即函数定义域为{x |x ≤1且x ≠-1}=(-∞,-1)∪(-1,1].(2)要使函数有意义,自变量x 的取值必须满足⎩⎪⎨⎪⎧5-x ≥0|x |-3≠0,解得x ≤5,且x ≠±3,即函数定义域为{x |x ≤5,且x ≠±3}=(-∞,-3)∪(-3,3)∪(3,5]. [点评] 定义域的求法:(1)如果f (x )是整式,那么函数的定义域是实数集R ;(2)如果f (x )是分式,那么函数的定义域是使分母不为0的实数的集合;(3)如果f (x )为偶次根式,那么函数的定义域是使根号内的式子大于或等于0的实数的集合;(4)如果f (x )是由几个部分的数学式子构成的,那么函数的定义域是使各部分式子都有意义的实数的集合.(5)如果函数有实际背景,那么除符合上述要求外,还要符合实际情况. 函数定义域要用集合或区间形式表示,这一点初学者易忽视. 10.已知函数f (x )=x 2-2x (-1≤x ≤2).导学号 69174221 (1)画出f (x )的图象; (2)根据图象写出f (x )的值域. [解析] (1)f (x )的图象如图所示.(2)观察f (x )的图象可知,f (x )图象上所有点的纵坐标的取值范围是[-1,3],故f (x )的值域是[-1,3].B 级 素养提升一、选择题1.给出下列从A 到B 的对应:①A =N ,B ={0,1},对应关系是:A 中的元素除以2所得的余数 ②A ={0,1,2},B ={4,1,0},对应关系是f :x →y =x 2 ③A ={0,1,2},B ={0,1,12},对应关系是f :x →y =1x其中表示从集合A 到集合B 的函数有( )个.导学号 69174222( B ) A .1B .2C .3D .0[解析] 由于③中,0这个元素在B 中无对应元素,故不是函数,因此选B . 2.下列函数中,不满足:f (2x )=2f (x )的是导学号 69174223( C ) A .f (x )=|x | B .f (x )=x -|x | C .f (x )=x +1D .f (x )=-x[解析] f (x )=kx 与f (x )=k |x |均满足:f (2x )=2f (x )得:A ,B ,D 满足条件.3.A ={x |0≤x ≤2},B ={y |1≤y ≤2},下列图形中能表示以A 为定义域,B 为值域的函数的是导学号 69174224( B )[解析] A 、C 、D 的值域都不是[1,2],故选B . 4.(2016~2017·盘锦高一检测)函数f (x )=11-2x的定义域为M ,g (x )=x +1的定义域为N ,则M ∩N =导学号 69174225( B )A .[-1,+∞)B .[-1,12)C .(-1,12)D .(-∞,12)二、填空题5.若函数f (x )的定义域为[2a -1,a +1],值域为[a +3,4a ],则a 的取值范围是__(1,2)__.导学号 69174226[解析] 由区间的定义知⎩⎪⎨⎪⎧2a -1<a +1,a +3<4a ⇒1<a <2.6.函数y =f (x )的图象如图所示,那么f (x )的定义域是__[-3,0]∪[2,3]__;其中只与x 的一个值对应的y 值的范围是__[1,2)∪(4,5]__.导学号 69174227[解析] 观察函数图象可知 f (x )的定义域是[-3,0]∪[2,3];只与x 的一个值对应的y 值的范围是[1,2)∪(4,5]. 三、解答题7.求下列函数的定义域:导学号 69174228 (1)y =31-1-x ;(2)y =(x +1)0|x |-x ;(3)y =2x +3-12-x +1x. [解析] (1)要使函数有意义,需⎩⎨⎧1-x ≥0,1-1-x ≠0⇔⎩⎪⎨⎪⎧x ≤1,x ≠0⇔x ≤1且x ≠0,所以函数y =31-1-x的定义域为(-∞,0)∪(0,1]. (2)由⎩⎪⎨⎪⎧ x +1≠0,|x |-x ≠0得⎩⎪⎨⎪⎧x ≠-1,|x |≠x ,∴x <0且x ≠-1, ∴原函数的定义域为{x |x <0且x ≠-1}. (3)要使函数有意义,需⎩⎪⎨⎪⎧2x +3≥0,2-x >0,x ≠0.解得-32≤x <2且x ≠0,所以函数y =2x +3-12-x +1x 的定义域为[-32,0)∪(0,2).[点评] 求给出解析式的函数的定义域的步骤为:(1)列出使函数有意义的x 所适合的式子(往往是一个不等式组);(2)解这个不等式组;(3)把不等式组的解表示成集合(或者区间)作为函数的定义域.C 级 能力拔高1.已知函数f (x )=1+x 21-x 2,导学号 69174229(1)求f (x )的定义域. (2)若f (a )=2,求a 的值. (3)求证:f ⎝⎛⎭⎫1x =-f (x ).[解析] (1)要使函数f (x )=1+x 21-x 2有意义,只需1-x 2≠0,解得x ≠±1, 所以函数的定义域为{x |x ≠±1}. (2)因为f (x )=1+x 21-x 2,且f (a )=2,所以f (a )=1+a 21-a 2=2,即a 2=13,解得a =±33.(3)由已知得f ⎝⎛⎭⎫1x =1+⎝⎛⎭⎫1x 21-⎝⎛⎭⎫1x 2=x 2+1x 2-1,-f (x )=-1+x 21-x 2=x 2+1x 2-1,∴f ⎝⎛⎭⎫1x =-f (x ).2.已知函数f (x )=12x 2-x +32,是否存在实数m ,使得该函数在x ∈[1,m ]时,f (x )的取值范围也是[1,m ](m >1)?若存在,求出m 的值;若不存在,请说明理由.导学号 69174230[解析] f (x )=12x 2-x +32=12(x -1)2+1的图象是一条抛物线,它的对称轴为直线x =1,顶点坐标为(1,1),开口向上,若存在实数m ,使该函数在x ∈[1,m ]时,f (x )的取值范围也是[1,m ],则需m >1,且f (m )=m ,即12m 2-m +32=m ,即m 2-4m +3=0, 解得m =3或m =1(舍去m =1). 故存在实数m =3满足条件.。
新人教A版高中数学【必修1】 1.2.2第1课时函数的表示法课时作业练习含答案解析

1.2.2 函数的表示法 第1课时 函数的表示法课时目标 1.掌握函数的三种表示方法——解析法、图象法、列表法.2.在实际情境中,会根据不同的需要选择恰当方法表示函数.函数的三种表示法(1)解析法——用____________表示两个变量之间的对应关系; (2)图象法——用______表示两个变量之间的对应关系; (3)列表法——列出______来表示两个变量之间的对应关系.一、选择题1.一个面积为100 cm 2的等腰梯形,上底长为x cm ,下底长为上底长的3倍,则把它的高y 表示成x 的函数为( )A .y =50x (x >0)B .y =100x (x >0)C .y =50x (x >0)D .y =100x (x >0)2.一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则正确论断的个数是( )A .0B .1C .2D .3 1xA.1xB.1x -1C.11-xD.1x -1 4.已知f (x )=2x +3,g (x +2)=f (x ),则g (x )等于( ) A .2x +1 B .2x -1 C .2x -3 D .2x +7 5.若g (x )=1-2x ,f [g (x )]=1-x 2x 2,则f (12)的值为( ) A .1 B .15 C .4 D .306.在函数y =|x |(x ∈[-1,1])的图象上有一点P (t ,|t |),此函数与x 轴、直线x =-1及x =t 围成图形(如图阴影部分)的面积为S ,则S 与t 的函数关系图可表示为( )二、填空题7.一个弹簧不挂物体时长12 cm ,挂上物体后会伸长,伸长的长度与所挂物体的质量成正比例.如果挂上3 kg 物体后弹簧总长是13.5 cm ,则弹簧总长y (cm)与所挂物体质量x (kg)之间的函数关系式为_________________________________________________________ _______________. 8.已知函数y =f (x )满足f (x )=2f (1x )+x ,则f (x )的解析式为____________.9.已知f (x )是一次函数,若f (f (x ))=4x +8,则f (x )的解析式为__________________. 三、解答题10.已知二次函数f (x )满足f (0)=f (4),且f (x )=0的两根平方和为10,图象过(0,3)点,求f (x )的解析式.11.画出函数f (x )=-x 2+2x +3的图象,并根据图象回答下列问题: (1)比较f (0)、f (1)、f (3)的大小; (2)若x 1<x 2<1,比较f (x 1)与f (x 2)的大小; (3)求函数f (x )的值域.能力提升12.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于..6·时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为( )A .y =[x10] B .y =[x +310] C .y =[x +410] D .y =[x +510]13.设f (x )是R 上的函数,且满足f (0)=1,并且对任意实数x ,y ,有f (x -y )=f (x )-y (2x -y +1),求f (x )的解析式.1.如何作函数的图象一般地,作函数图象主要有三步:列表、描点、连线.作图象时一般应先确定函数的定义域,再在定义域内化简函数解析式(可能有的要表示为分段函数),再列表描出图象,并在画图象的同时注意一些关键点,如与坐标轴的交点、分段函数的区间端点等.2.如何求函数的解析式求函数的解析式的关键是理解对应关系f的本质与特点(对应关系就是对自变量进行对应处理的操作方法,与用什么字母表示无关),应用适当的方法,注意有的函数要注明定义域.主要方法有:代入法、待定系数法、换元法、解方程组法(消元法).第1课时 函数的表示法知识梳理(1)数学表达式 (2)图象 (3)表格 作业设计1.C [由x +3x2·y =100,得2xy =100. ∴y =50x (x >0).]2.B [由题意可知在0点到3点这段时间,每小时进水量为2,即2个进水口同时进水且不出水,所以①正确;从丙图可知3点到4点水量减少了1,所以应该是有一个进水口进水,同时出水口也出水,故②错;当两个进水口同时进水,出水口也同时出水时,水量保持不变,也可由题干中的“至少打开一个水口”知③错.]3.B [令1x =t ,则x =1t ,代入f (1x )=x1-x ,则有f (t )=1t1-1t=1t -1,故选B.]4.B [由已知得:g (x +2)=2x +3,令t =x +2,则x =t -2,代入g (x +2)=2x +3,则有g (t )=2(t -2)+3=2t -1,故选B.] 5.B [令1-2x =12,则x =14, ∴f (12)=1-142142=15.]6.B [当t <0时,S =12-t 22,所以图象是开口向下的抛物线,顶点坐标是(0,12);当t >0时,S =12+t 22,开口是向上的抛物线,顶点坐标是(0,12).所以B 满足要求.] 7.y =12x +12解析 设所求函数解析式为y =kx +12,把x =3,y =13.5代入,得13.5=3k +12,k =12. 所以所求的函数解析式为y =12x +12. 8.f (x )=-x 2+23x (x ≠0) 解析 ∵f (x )=2f (1x )+x ,① 111由①②消去f (1x ),得f (x )=-23x -x3, 即f (x )=-x 2+23x (x ≠0). 9.f (x )=2x +83或f (x )=-2x -8 解析 设f (x )=ax +b (a ≠0), 则f (f (x ))=f (ax +b )=a 2x +ab +b .∴⎩⎪⎨⎪⎧a 2=4ab +b =8,解得⎩⎪⎨⎪⎧a =2b =83或⎩⎪⎨⎪⎧a =-2b =-8. 10.解 设f (x )=ax 2+bx +c (a ≠0).由f (0)=f (4)知⎩⎪⎨⎪⎧f 0=c ,f 4=16a +4b +c ,f 0=f 4,得4a +b =0.① 又图象过(0,3)点, 所以c =3.②设f (x )=0的两实根为x 1,x 2, 则x 1+x 2=-b a ,x 1·x 2=ca .所以x 21+x 22=(x 1+x 2)2-2x 1x 2=(-b a )2-2·c a =10. 即b 2-2ac =10a 2.③由①②③得a =1,b =-4,c =3.所以f (x )=x 2-4x +3. 11.解 因为函数f (x )=-x 2+2x +3的定义域为R ,列表:(1)根据图象,容易发现f (0)=3,f (1)=4,f (3)=0, 所以f (3)<f (0)<f (1).(3)根据图象,可以看出函数的图象是以(1,4)为顶点,开口向下的抛物线,因此,函数的值域为(-∞,4].12.B [方法一 特殊取值法,若x =56,y =5,排除C 、D ,若x =57,y =6,排除A ,所以选B. 方法二 设x =10m +α(0≤α≤9),0≤α≤6时, [x +310]=[m +α+310]=m =[x 10],当6<α≤9时,[x +310]=[m +α+310]=m +1=[x10]+1, 所以选B.]13.解 因为对任意实数x ,y ,有 f (x -y )=f (x )-y (2x -y +1), 所以令y =x ,有f (0)=f (x )-x (2x -x +1), 即f (0)=f (x )-x (x +1).又f (0)=1, ∴f (x )=x (x +1)+1=x 2+x +1.。
人教A版高中数学第一册(必修1)课时作业2:第一课时 函数的单调性

3.2 函数的基本性质 3.2.1 单调性与最大(小)值第一课时 函数的单调性基础达标一、选择题1.函数y =f (x ),x ∈『-4,4』的图象如图所示,则f (x )的增区间是( )A.『-4,4』B.『-4,-3』∪『1,4』C.『-3,1』D.『-3,4』『解 析』 由图象知增区间为『-3,1』,故选C. 『答 案』 C2.下列说法中,正确的有( )①若任意x 1,x 2∈I ,当x 1<x 2时,f (x 1)-f (x 2)x 1-x 2>0,则y =f (x )在I 上是增函数;②函数y =x 2在R 上是增函数;③函数y =-1x 在定义域上是增函数;④函数y =1x 的单调区间是(-∞,0)∪(0,+∞). A.0个 B.1个 C.2个D.3个『解 析』 当x 1<x 2时,x 1-x 2<0,由f (x 1)-f (x 2)x 1-x 2>0知f (x 1)-f (x 2)<0,∴f (x 1)<f (x 2),①正确;②③④均不正确. 『答 案』 B3.下列函数中,在区间(0,2)上为增函数的是( ) A.y =5-x B.y =x 2+2 C.y =1xD.y =-|x |『解 析』 选项A ,C ,D 中的函数在(0,2)上是减函数,只有函数y =x 2+2在(0,2)上是增函数. 『答 案』 B4.若函数y =x 2+(2a -1)x +1在区间(-∞,2』上是减函数,则实数a 的取值范围是( ) A.⎝ ⎛⎭⎪⎫-32,+∞ B.⎝ ⎛⎦⎥⎤-∞,-32 C.(3,+∞)D.(-∞,-3』『解 析』 ∵函数y =x 2+(2a -1)x +1的图象是开口向上,直线x =2a -1-2为函数的对称轴,又∵函数在区间(-∞,2』上是减函数,故2≤2a -1-2,解得a ≤-32.『答 案』 B5.已知定义域为R 的函数f (x )在(4,+∞)上为减函数,且函数y =f (x )的对称轴为x =4,则( ) A.f (2)>f (3) B.f (2)>f (5) C.f (3)>f (5)D.f (3)>f (6)『解 析』 ∵f (x )关于x =4对称且在(4,+∞)上为减函数, ∴f (x )在(-∞,4)上为增函数,且f (5)=f (3),f (6)=f (2), ∴f (3)>f (2)=f (6),故选D. 『答 案』 D二、填空题 6.函数f (x )=1x +1在(a ,+∞)上单调递减,则a 的取值范围是________. 『解 析』 函数f (x )=1x +1的单调减区间为(-1,+∞),(-∞,-1),又f (x )在(a ,+∞)上单调递减,所以a ≥-1. 『答 案』 『-1,+∞)7.下列函数中满足“对任意x 1,x 2∈(0,+∞),都有f (x 1)-f (x 2)x 1-x 2>0”的是________(填序号).①f (x )=-2x ; ②f (x )=-3x +1; ③f (x )=x 2+4x +3;④f (x )=x -1x .『解 析』 由题意知f (x )在(0,+∞)上为增函数,①③④在(0,+∞)上均为增函数.『答 案』 ①③④8.函数y =f (x )在(-2,2)上为增函数,且f (2m )>f (-m +1),则实数m 的取值范围是________.『解 析』由题意知⎩⎪⎨⎪⎧-2<2m <2,-2<-m +1<2,2m >-m +1,解得13<m <1. 『答 案』 ⎝ ⎛⎭⎪⎫13,1三、解答题9.已知函数f (x )=mx +1nx +12(m ,n 是常数),且f (1)=2,f (2)=114. (1)求m ,n 的值;(2)当x ∈『1,+∞)时,判断f (x )的单调性并用定义证明.解 (1)因为f (1)=m +1n +12=2, f (2)=2m +12n +12=114. 所以⎩⎪⎨⎪⎧m =1,n =2.(2)由(1)知f (x )=x +12x +12,f (x )在x ∈『1,+∞)上为增函数,证明如下: 设1≤x 1<x 2,f (x 1)-f (x 2)=x 1+12x 1+12-⎝ ⎛⎭⎪⎫x 2+12x 2+12=(x 1-x 2)⎝ ⎛⎭⎪⎫1-12x 1x 2=(x 1-x 2)(2x 1x 2-1)2x 1x2.因为1≤x 1<x 2,所以x 1-x 2<0,x 1x 2>1, 所以2x 1x 2>2>1,所以(x 1-x 2)(2x 1x 2-1)2x 1x2<0,即f (x 1)<f (x 2),所以f (x )在『1,+∞)上单调递增. 10.求函数f (x )=x +9x (x >0)的单调区间.解 设x 1,x 2是(0,+∞)上的任意两个实数,且x 1<x 2,则f (x 1)-f (x 2)=⎝ ⎛⎭⎪⎫x 1+9x 1-⎝ ⎛⎭⎪⎫x 2+9x 2 =(x 1-x 2)-9(x 1-x 2)x 1x 2=(x 1-x 2)(x 1x 2-9)x 1x2.∵0<x 1<x 2,∴x 1-x 2<0,x 1x 2>0.由于x 1x 2-9的符号不能确定,因此需要对x 1,x 2的取值进行讨论. 当x 1,x 2∈(0,3』时,有x 1x 2-9<0,所以(x 1-x 2)(x 1x 2-9)x 1x 2>0,即f (x 1)>f (x 2),∴f (x )在区间(0,3』上是减函数;当x 1,x 2∈『3,+∞)时,x 1x 2-9>0,所以(x 1-x 2)(x 1x 2-9)x 1x 2<0,即f (x 1)<f (x 2),∴f (x )在区间『3,+∞)上是增函数.综上可知,函数f (x )=x +9x (x >0)的单调递减区间是(0,3』, 单调递增区间是『3,+∞).能力提升11.讨论函数f (x )=axx 2-1(a ≠0)在区间(-1,1)上的单调性. 解x 1,x 2∈(-1,1)且x 1<x 2.则f (x 1)-f (x 2)=ax 1x 21-1-ax 2x 22-1=ax 1(x 22-1)-ax 2(x 21-1)(x 21-1)(x 22-1)=ax 1x 2(x 2-x 1)+a (x 2-x 1)(x 21-1)(x 22-1) =a (x 2-x 1)(x 1x 2+1)(x 21-1)(x 22-1) ∵x 21-1<0,x 22-1<0,x 1x 2+1>0,x 2-x 1>0.∴当a >0时,a (x 2-x 1)(x 1x 2+1)(x 21-1)(x 22-1)>0. 即f (x 1)>f (x 2),∴f (x )在(-1,1)上为减函数.当a <0时,a (x 2-x 1)(x 1x 2+1)(x 21-1)(x 22-1)<0, 即f (x 1)<f (x 2),∴f (x )在(-1,1)上为增函数.12.若f (x )是定义在(0,+∞)上的增函数,且对一切x ,y >0,满足f (xy )=f (x )-f (y ). (1)求f (1)的值;(2)若f (6)=1,解不等式f (x +3)-f (13)<2.解 (1)在f (xy )=f (x )-f (y )中, 令x =y =1,则有f (1)=f (1)-f (1), ∴f (1)=0. (2)∵f (6)=1,∴f (x +3)-f (13)<2=f (6)+f (6), ∴f (3x +9)-f (6)<f (6), 即f (x +32)<f (6).∵f (x )是(0,+∞)上的增函数,∴⎩⎨⎧x +32>0,x +32<6,解得-3<x <9.即不等式的解集为{x |-3<x <9}.。
高中数学第一章集合与函数概念1.2.1函数概念课时作业(含解析)新人教A版必修1

高中数学第一章集合与函数概念1.2.1函数概念课时作业(含解析)新人教A 版必修1[基础巩固](25分钟,60分)一、选择题(每小题5分,共25分) 1.下列对应:①M =R ,N =N *,对应关系f :“对集合M 中的元素,取绝对值与N 中的元素对应”; ②M ={1,-1,2,-2},N ={1,4},对应关系f :x →y =x 2,x ∈M ,y ∈N ;③M ={三角形},N ={x |x >0},对应关系f :“对M 中的三角形求面积与N 中元素对应.” 是集合M 到集合N 上的函数的有( ) A .1个 B .2个 C .3个 D .0个解析:①M 中有的元素在N 中无对应元素.如M 中的元素0;③M 中的元素不是实数,即M 不是数集;只有②满足函数的定义,故选A.答案:A2.函数f (x )=x +3+2x +303-2x的定义域是( )A.⎣⎢⎡⎦⎥⎤-3,32B.⎣⎢⎡⎭⎪⎫-3,-32∪⎝ ⎛⎭⎪⎫-32,32C.⎣⎢⎡⎭⎪⎫-3,32 D.⎣⎢⎡⎦⎥⎤-3,-32 解析:由题意得⎩⎪⎨⎪⎧x +3≥0,3-2x >0,2x +3≠0,解得-3≤x <32且x ≠-32,故选B.答案:B3.已知函数f (x )=-1,则f (2)的值为( ) A .-2 B .-1 C .0 D .不确定解析:因为函数f (x )=-1,所以不论x 取何值其函数值都等于-1,故f (2)=-1.故选B. 答案:B4.下列各组函数中,表示同一函数的是( )A .y =x +1和y =x 2-1x -1B .y =x 2和y =(x )2C .f (x )=x 2和g (x )=(x +1)2D .f (x )=x 2x和g (x )=x x2解析:只有D 是相同的函数,A 与B 中定义域不同,C 是对应法则不同. 答案:D5.函数f (x )=11+x 2(x ∈R )的值域是( )A .[0,1]B .[0,1)C .(0,1]D .(0,1) 解析:因为x 2≥0, 所以x 2+1≥1, 所以0<1x 2+1≤1, 所以值域为(0,1],故选C. 答案:C二、填空题(每小题5分,共15分) 6.用区间表示下列数集. (1){x |x ≥2}=________; (2){x |3<x ≤4}=________; (3){x |x >1且x ≠2}=________. 解析:由区间表示法知:(1)[2,+∞); (2)(3,4];(3)(1,2)∪(2,+∞).答案:(1)[2,+∞) (2)(3,4] (3)(1,2)∪(2,+∞)7.函数f (x )的图象如图所示,则f (x )的定义域为________,值域为________.解析:由f (x )的图象可知 -5≤x ≤5,-2≤y ≤3. 答案:[-5,5] [-2,3]8.若A ={x |y =x +1},B ={y |y =x 2+1},则A ∩B =________. 解析:由A ={x |y =x +1},B ={y |y =x 2+1}, 得A =[-1,+∞),B =[1,+∞), ∴A ∩B =[1,+∞). 答案:[1,+∞)三、解答题(每小题10分,共20分) 9.(1)求下列函数的定义域: ①y =4-x ; ②y =1|x |-x ;③y =5-x +x -1-1x 2-9; (2)将长为a 的铁丝折成矩形,求矩形面积y 关于一边长x 的解析式,并写出此函数的定义域.解析:(1)①4-x ≥0,即x ≤4,故函数的定义域为{x |x ≤4}. ②分母|x |-x ≠0, 即|x |≠x ,所以x <0. 故函数的定义域为{x |x <0}. ③解不等式组⎩⎪⎨⎪⎧5-x ≥0,x -1≥0,x 2-9≠0,得⎩⎪⎨⎪⎧x ≤5,x ≥1,x ≠±3.故函数的定义域是{x |1≤x ≤5,且x ≠3}. (2)设矩形一边长为x ,则另一边长为12(a -2x ),所以y =x ·12(a -2x )=-x 2+12ax ,函数的定义域为⎩⎪⎨⎪⎧x >012a -2x >0⇒0<x <a2,定义域为⎝ ⎛⎭⎪⎫0,a 2.10.求下列各函数的值域:(1)y =x +1,x ∈{2,3,4,5,6}; (2)y =x 2-4x +6; (3)y =x +2x -1.解析:(1)因为当x 分别取2,3,4,5,6时,y =x +1分别取3,4,5,6,7, 所以函数的值域为{3,4,5,6,7}. (2)函数的定义域为R .因为y =x 2-4x +6=(x -2)2+2≥2, 所以该函数的值域为[2,+∞). (3)设t =2x -1,则x =t 2+12,且t ≥0.问题转化为求y =1+t22+t (t ≥0)的值域.因为y =1+t 22+t =12(t +1)2(t ≥0),所以y 的取值范围为⎣⎢⎡⎭⎪⎫12,+∞.故该函数的值域为⎣⎢⎡⎭⎪⎫12,+∞. [能力提升](20分钟,40分)11.下表表示y 是x 的函数,则函数的值域是( )A.{y |-1≤y ≤1} B .C .{y |2≤y ≤3} D.{-1,0,1}解析:函数值只有-1,0,1三个数值,故值域为{-1,0,1}. 答案:D12.设函数f (x )=41-x ,若f (a )=2,则实数a =________.解析:因为f (x )=41-x ,所以f (a )=41-a=2,所以a =-1. 答案:-113.(1)已知函数f (x )的定义域为[-1,5],求函数f (x -5)的定义域; (2)已知函数f (x -1)的定义域是[0,3],求函数f (x )的定义域.解析:(1)由-1≤x -5≤5,得4≤x ≤10,所以函数f (x -5)的定义域是[4,10]. (2)由0≤x ≤3,得-1≤x -1≤2,所以函数f (x )的定义域是[-1,2]. 14.已知f (x )=11+x(x ≠-1),g (x )=x 2+2. (1)求f (2)和g (2); (2)求g (f (2)),f (g (x )); (3)若1f g x=4,求x .解析:(1)f (2)=11+2=13,g (2)=22+2=6. (2)g (f (2))=g ⎝ ⎛⎭⎪⎫13=⎝ ⎛⎭⎪⎫132+2=199,f (g (x ))=11+g x =11+x 2+2=1x 2+3. (3)1f g x=x 2+3=4,即x 2=1,解得x =±1.。
高中数学人教版A版必修一课时作业及解析:第一章1-2函数及其表示

高中数学人教版A版必修一第一章集合与函数概念§1.2函数及其表示1.2.1 函数的概念课时目标 1.理解函数的概念,明确函数的三要素.2.能正确使用区间表示数集,表示简单函数的定义域、值域.3.会求一些简单函数的定义域、值域.1.函数(1)设A、B是非空的数集,如果按照某种确定的__________,使对于集合A中的____________,在集合B中都有________________和它对应,那么就称f:________为从集合A到集合B的一个函数,记作__________________.其中x 叫做________,x的取值范围A叫做函数的________,与x的值相对应的y值叫做________,函数值的集合{f(x)|x∈A}叫做函数的________.(2)值域是集合B的________.2.区间(1)设a,b是两个实数,且a<b,规定:①满足不等式__________的实数x的集合叫做闭区间,表示为________;②满足不等式__________的实数x的集合叫做开区间,表示为________;③满足不等式________或________的实数x的集合叫做半开半闭区间,分别表示为______________.(2)实数集R可以用区间表示为__________,“∞”读作“无穷大”,“+∞”读作“__________”,“-∞”读作“________”.我们把满足x≥a,x>a,x≤b,x<b的实数x的集合分别表示为________,________,________,______.一、选择题1.对于函数y=f(x),以下说法正确的有()①y 是x 的函数②对于不同的x ,y 的值也不同③f (a )表示当x =a 时函数f (x )的值,是一个常量 ④f (x )一定可以用一个具体的式子表示出来 A .1个B .2个 C .3个D .4个2.设集合M ={x |0≤x ≤2},N ={y |0≤y ≤2},那么下面的4个图形中,能表示集合M 到集合N 的函数关系的有( )A .①②③④B .①②③C .②③D .②3.下列各组函数中,表示同一个函数的是( ) A .y =x -1和y =x 2-1x +1B .y =x 0和y =1C .f (x )=x 2和g (x )=(x +1)2D .f (x )=(x )2x 和g (x )=x(x )24.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为y =2x 2-1,值域为{1,7}的“孪生函数”共有( )A .10个B .9个C .8个D .4个 5.函数y =1-x +x 的定义域为( )A .{x |x ≤1}B .{x |x ≥0}C .{x |x ≥1或x ≤0}D .{x |0≤x ≤1} 6.函数y =x +1的值域为( ) A .[-1,+∞) B .[0,+∞) C .(-∞,0] D .(-∞,-1]二、填空题7.已知两个函数f (x )和g (x )的定义域和值域都是{1,2,3},其定义如下表:8.如果函数f (x )满足:对任意实数a ,b 都有f (a +b )=f (a )f (b ),且f (1)=1,则f (2)f (1)+f (3)f (2)+f (4)f (3)+f (5)f (4)+…+f (2011)f (2010)=________. 9.已知函数f (x )=2x -3,x ∈{x ∈N |1≤x ≤5},则函数f (x )的值域为______________.10.若函数f (x )的定义域是[0,1],则函数f (2x )+f (x +23)的定义域为________. 三、解答题11.已知函数f (1-x1+x )=x ,求f (2)的值.能力提升12.如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.根据这个曲线图,请你回答下列问题:(1)最初到达离家最远的地方是什么时间?离家多远?(2)何时开始第一次休息?休息多长时间?(3)第一次休息时,离家多远?(4)11∶00到12∶00他骑了多少千米?(5)他在9∶00~10∶00和10∶00~10∶30的平均速度分别是多少?(6)他在哪段时间里停止前进并休息用午餐?13.如图,某灌溉渠的横断面是等腰梯形,底宽为2m,渠深为1.8m,斜坡的倾斜角是45°.(临界状态不考虑)(1)试将横断面中水的面积A(m2)表示成水深h(m)的函数;(2)确定函数的定义域和值域;(3)画出函数的图象.1.函数的判定判定一个对应关系是否为函数,关键是看对于数集A 中的任一个值,按照对应关系所对应数集B 中的值是否唯一确定,如果唯一确定,就是一个函数,否则就不是一个函数.2.由函数式求函数值,及由函数值求x ,只要认清楚对应关系,然后对号入座就可以解决问题.3.求函数定义域的原则:①当f (x )以表格形式给出时,其定义域指表格中的x 的集合;②当f (x )以图象形式给出时,由图象范围决定;③当f (x )以解析式给出时,其定义域由使解析式有意义的x 的集合构成;④在实际问题中,函数的定义域由实际问题的意义确定.§1.2 函数及其表示 1.2.1 函数的概念知识梳理1.(1)对应关系f 任意一个数x 唯一确定的数f (x ) A →B y =f (x ),x ∈A 自变量 定义域 函数值 值域 (2)子集2.(1)①a ≤x ≤b [a ,b ] ②a <x <b (a ,b ) ③a ≤x <b a <x ≤b [a ,b ),(a ,b ] (2)(-∞,+∞) 正无穷大 负无穷大 [a ,+∞) (a ,+∞) (-∞,b ] (-∞,b ) 作业设计1.B [①、③正确;②不对,如f (x )=x 2,当x =±1时y =1;④不对,f (x )不一定可以用一个具体的式子表示出来,如南极上空臭氧空洞的面积随时间的变化情况就不能用一个具体的式子来表示.]2.C [①的定义域不是集合M ;②能;③能;④与函数的定义矛盾.故选C.] 3.D [A 中的函数定义域不同;B 中y =x 0的x 不能取0;C 中两函数的对应关系不同,故选D.]4.B [由2x 2-1=1,2x 2-1=7得x 的值为1,-1,2,-2,定义域为两个元素的集合有4个,定义域为3个元素的集合有4个,定义域为4个元素的集合有1个,因此共有9个“孪生函数”.]5.D [由题意可知⎩⎨⎧1-x ≥0,x ≥0,解得0≤x ≤1.]6.B 7.3 2 1解析 g [f (1)]=g (2)=3,g [f (2)]=g (3)=2, g [f (3)]=g (1)=1. 8.2010解析 由f (a +b )=f (a )f (b ),令b =1,∵f (1)=1, ∴f (a +1)=f (a ),即f (a +1)f (a )=1,由a 是任意实数,所以当a 取1,2,3,…,2010时,得f (2)f (1)=f (3)f (2)=…=f (2011)f (2010)=1.故答案为2010. 9.{-1,1,3,5,7}解析 ∵x =1,2,3,4,5,∴f (x )=2x -3=-1,1,3,5,7. 10.[0,13]解析 由⎩⎪⎨⎪⎧0≤2x ≤1,0≤x +23≤1,得⎩⎪⎨⎪⎧0≤x ≤12,-23≤x ≤13,即x ∈[0,13].11.解 由1-x 1+x=2,解得x =-13,所以f (2)=-13.12.解 (1)最初到达离家最远的地方的时间是12时,离家30千米. (2)10∶30开始第一次休息,休息了半小时. (3)第一次休息时,离家17千米. (4)11∶00至12∶00他骑了13千米.(5)9∶00~10∶00的平均速度是10千米/时;10∶00~10∶30的平均速度是14千米/时.(6)从12时到13时停止前进,并休息用午餐较为符合实际情形.13.解 (1)由已知,横断面为等腰梯形,下底为2m ,上底为(2+2h )m ,高为h m ,∴水的面积A=[2+(2+2h)]h2=h2+2h(m2).(2)定义域为{h|0<h<1.8}.值域由二次函数A=h2+2h(0<h<1.8)求得.由函数A=h2+2h=(h+1)2-1的图象可知,在区间(0,1.8)上函数值随自变量的增大而增大,∴0<A<6.84.故值域为{A|0<A<6.84}.(3)由于A=(h+1)2-1,对称轴为直线h=-1,顶点坐标为(-1,-1),且图象过(0,0)和(-2,0)两点,又考虑到0<h<1.8,∴A=h2+2h的图象仅是抛物线的一部分,如下图所示.1.2.2 函数的表示法 第1课时 函数的表示法课时目标 1.掌握函数的三种表示方法——解析法、图象法、列表法.2.在实际情境中,会根据不同的需要选择恰当方法表示函数.函数的三种表示法(1)解析法——用____________表示两个变量之间的对应关系; (2)图象法——用______表示两个变量之间的对应关系; (3)列表法——列出______来表示两个变量之间的对应关系.一、选择题1.一个面积为100cm 2的等腰梯形,上底长为x cm ,下底长为上底长的3倍,则把它的高y 表示成x 的函数为( ) A .y =50x (x >0) B .y =100x (x >0)C .y =50x (x >0)D .y =100x (x >0)2.一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则正确论断的个数是( ) A .0B .1C .2D .33.如果f (1x )=x1-x,则当x ≠0时,f (x )等于( )A.1xB.1x -1C.11-xD.1x-1 4.已知f (x )=2x +3,g (x +2)=f (x ),则g (x )等于( )A .2x +1B .2x -1C .2x -3D .2x +75.若g (x )=1-2x ,f [g (x )]=1-x 2x 2,则f (12)的值为( ) A .1B .15C .4D .306.在函数y =|x |(x ∈[-1,1])的图象上有一点P (t ,|t |),此函数与x 轴、直线x =-1及x =t 围成图形(如图阴影部分)的面积为S ,则S 与t 的函数关系图可表示为( )二、填空题7.一个弹簧不挂物体时长12cm ,挂上物体后会伸长,伸长的长度与所挂物体的质量成正比例.如果挂上3kg 物体后弹簧总长是13.5cm ,则弹簧总长y (cm)与所挂物体质量x (kg)之间的函数关系式为________________________________________________________________________.8.已知函数y =f (x )满足f (x )=2f (1x )+x ,则f (x )的解析式为____________. 9.已知f (x )是一次函数,若f (f (x ))=4x +8,则f (x )的解析式为__________________.三、解答题10.已知二次函数f (x )满足f (0)=f (4),且f (x )=0的两根平方和为10,图象过(0,3)点,求f (x )的解析式.11.画出函数f (x )=-x 2+2x +3的图象,并根据图象回答下列问题: (1)比较f (0)、f (1)、f (3)的大小;(2)若x 1<x 2<1,比较f (x 1)与f (x 2)的大小; (3)求函数f (x )的值域.能力提升12.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于..6·时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为( )A .y =[x10] B .y =[x +310]C .y =[x +410]D .y =[x +510]13.设f (x )是R 上的函数,且满足f (0)=1,并且对任意实数x ,y ,有f (x -y )=f (x )-y (2x -y +1),求f (x )的解析式.1.如何作函数的图象一般地,作函数图象主要有三步:列表、描点、连线.作图象时一般应先确定函数的定义域,再在定义域内化简函数解析式(可能有的要表示为分段函数),再列表描出图象,并在画图象的同时注意一些关键点,如与坐标轴的交点、分段函数的区间端点等. 2.如何求函数的解析式求函数的解析式的关键是理解对应关系f 的本质与特点(对应关系就是对自变量进行对应处理的操作方法,与用什么字母表示无关),应用适当的方法,注意有的函数要注明定义域.主要方法有:代入法、待定系数法、换元法、解方程组法(消元法).1.2.2 函数的表示法 第1课时 函数的表示法知识梳理(1)数学表达式 (2)图象 (3)表格 作业设计1.C [由x +3x2·y =100,得2xy =100.∴y =50x (x >0).]2.B [由题意可知在0点到3点这段时间,每小时进水量为2,即2个进水口同时进水且不出水,所以①正确;从丙图可知3点到4点水量减少了1,所以应该是有一个进水口进水,同时出水口也出水,故②错;当两个进水口同时进水,出水口也同时出水时,水量保持不变,也可由题干中的“至少打开一个水口”知③错.]3.B [令1x =t ,则x =1t ,代入f (1x )=x1-x,则有f (t )=1t 1-1t=1t -1,故选B.] 4.B [由已知得:g (x +2)=2x +3,令t =x +2,则x =t -2,代入g (x +2)=2x +3,则有g (t )=2(t -2)+3=2t -1,故选B.]5.B [令1-2x =12,则x =14,∴f (12)=1-(14)2(14)2=15.] 6.B [当t <0时,S =12-t 22,所以图象是开口向下的抛物线,顶点坐标是(0,12);当t >0时,S =12+t 22,开口是向上的抛物线,顶点坐标是(0,12).所以B 满足要求.]7.y =12x +12解析 设所求函数解析式为y =kx +12,把x =3,y =13.5代入,得13.5=3k+12,k =12.所以所求的函数解析式为y =12x +12.8.f (x )=-x 2+23x (x ≠0)解析 ∵f (x )=2f (1x )+x ,①∴将x 换成1x ,得f (1x )=2f (x )+1x .②由①②消去f (1x ),得f (x )=-23x -x3,即f (x )=-x 2+23x (x ≠0).9.f (x )=2x +83或f (x )=-2x -8 解析 设f (x )=ax +b (a ≠0), 则f (f (x ))=f (ax +b )=a 2x +ab +b .∴⎩⎨⎧a 2=4ab +b =8,解得⎩⎪⎨⎪⎧a =2b =83或⎩⎨⎧a =-2b =-8.10.解 设f (x )=ax 2+bx +c (a ≠0).由f (0)=f (4)知⎩⎨⎧f (0)=c ,f (4)=16a +4b +c ,f (0)=f (4),得4a +b =0.① 又图象过(0,3)点, 所以c =3.②设f (x )=0的两实根为x 1,x 2,则x 1+x 2=-b a ,x 1·x 2=ca . 所以x 21+x 22=(x 1+x 2)2-2x 1x 2=(-b a)2-2·c a=10.即b 2-2ac =10a 2.③由①②③得a =1,b =-4,c =3.所以f (x )=x 2-4x +3.11.解 因为函数f (x )=-x 2+2x +3的定义域为R ,列表:x … -2 -1 0 1 2 3 4 … y … -5 0 3 4 3 0 -5 …连线,描点,得函数图象如图:(1)根据图象,容易发现f (0)=3,f (1)=4,f (3)=0, 所以f (3)<f (0)<f (1).(2)根据图象,容易发现当x 1<x 2<1时,有f (x 1)<f (x 2). (3)根据图象,可以看出函数的图象是以(1,4)为顶点,开口向下的抛物线,因此,函数的值域为(-∞,4].12.B [方法一 特殊取值法,若x =56,y =5,排除C 、D ,若x =57,y =6,排除A ,所以选B.方法二 设x =10m +α(0≤α≤9),0≤α≤6时, [x +310]=[m +α+310]=m =[x 10],当6<α≤9时,[x +310]=[m +α+310]=m +1=[x10]+1, 所以选B.]13.解 因为对任意实数x ,y ,有 f (x -y )=f (x )-y (2x -y +1), 所以令y =x ,有f (0)=f (x )-x (2x -x +1),即f (0)=f (x )-x (x +1).又f (0)=1, ∴f (x )=x (x +1)+1=x 2+x +1.第2课时分段函数及映射课时目标 1.了解分段函数的概念,会画分段函数的图象,并能解决相关问题.2.了解映射的概念.1.分段函数(1)分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的____________的函数.(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的______;各段函数的定义域的交集是空集.(3)作分段函数图象时,应_____________________________________.2.映射的概念设A、B是两个非空的集合,如果按某一个确定的对应关系f,使对于集合A 中的任意一个元素x,在集合B中____________确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的__________.一、选择题1.已知,则f(3)为()A.2B.3C.4D.52.下列集合A到集合B的对应中,构成映射的是()3.一旅社有100间相同的客房,经过一段时间的经营实践,发现每间客房每天的定价与住房率有如下关系:A.100元B.90元C.80元D.60元4.已知函数,使函数值为5的x的值是()A.-2B.2或-5 2C.2或-2D.2或-2或-5 25.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为() A.13立方米B.14立方米C.18立方米D.26立方米6.已知集合P={x|0≤x≤4},Q={y|0≤y≤2},下列不能表示从P到Q的映射的是()A.f:x→y=12x B.f:x→y=13xC.f:x→y=23x D.f:x→y=x二、填空题7.已知,则f(7)=____________.8.设则f {f [f (-34)]}的值为________,f (x )的定义域是______________.9.已知函数f (x )的图象如下图所示,则f (x )的解析式是__________________.三、解答题 10.已知,(1)画出f (x )的图象; (2)求f (x )的定义域和值域.11.如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C、D、A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.能力提升12.设f:x→x2是集合A到集合B的映射,如果B={1,2},则A∩B一定是() A.∅B.∅或{1}C.{1}D.∅13.在交通拥挤及事故多发地段,为了确保交通安全,规定在此地段内,车距d是车速v(公里/小时)的平方与车身长S(米)的积的正比例函数,且最小车距不得小于车身长的一半.现假定车速为50公里/小时,车距恰好等于车身长,试写出d关于v的函数关系式(其中S为常数).1.全方位认识分段函数(1)分段函数是一个函数而非几个函数.分段函数的定义域是各段上“定义域”的并集,其值域是各段上“值域”的并集.(2)分段函数的图象应分段来作,特别注意各段的自变量取区间端点处时函数的取值情况,以决定这些点的实虚情况.2.对映射认识的拓展映射f:A→B,可理解为以下三点:(1)A中每个元素在B中必有唯一的元素与之对应;(2)对A中不同的元素,在B中可以有相同的元素与之对应;(3)A中元素与B中元素的对应关系,可以是:一对一、多对一,但不能一对多.3.函数与映射的关系映射f:A→B,其中A、B是两个“非空集合”;而函数y=f(x),x∈A为“非空的实数集”,其值域也是实数集,于是,函数是数集到数集的映射.由此可知,映射是函数的推广,函数是一种特殊的映射.第2课时 分段函数及映射知识梳理1.(1)对应关系 (2)并集 (3)分别作出每一段的图象 2.都有唯一 一个映射 作业设计 1.A [∵3<6,∴f (3)=f (3+2)=f (5)=f (5+2)=f (7)=7-5=2.] 2.D3.C [不同的房价对应着不同的住房率,也对应着不同的收入,因此求出4个不同房价对应的收入,然后找出最大值对应的房价即可.] 4.A [若x 2+1=5,则x 2=4,又∵x ≤0,∴x =-2, 若-2x =5,则x =-52,与x >0矛盾,故选A.]5.A [该单位职工每月应缴水费y 与实际用水量x 满足的关系式为y =⎩⎨⎧mx , 0≤x ≤10,2mx -10m ,x >10. 由y =16m ,可知x >10.令2mx -10m =16m ,解得x =13(立方米).]6.C [如果从P 到Q 能表示一个映射,根据映射的定义,对P 中的任一元素,按照对应关系f 在Q 中有唯一元素和它对应,选项C 中,当x =4时,y =23×4=83∉Q ,故选C.] 7.6解析 ∵7<9,∴f (7)=f [f (7+4)]=f [f (11)]=f (11-3)=f (8). 又∵8<9,∴f (8)=f [f (12)]=f (9)=9-3=6. 即f (7)=6.8.32 {x |x ≥-1且x ≠0}解析 ∵-1<-34<0,∴f (-34)=2×(-34)+2=12.而0<12<2,∴f (12)=-12×12=-14.∵-1<-14<0,∴f (-14)=2×(-14)+2=32.因此f {f [f (-34)]}=32.函数f (x )的定义域为{x |-1≤x <0}∪{x |0<x <2}∪{x |x ≥2}={x |x ≥-1且x ≠0}.9.f (x )=⎩⎨⎧ x +1, -1≤x <0,-x ,0≤x ≤1解析 由图可知,图象是由两条线段组成,当-1≤x <0时,设f (x )=ax +b ,将(-1,0),(0,1)代入解析式,则⎩⎨⎧ -a +b =0,b =1.∴⎩⎨⎧a =1,b =1.当0<x <1时,设f (x )=kx ,将(1,-1)代入,则k =-1. 10.解 (1)利用描点法,作出f (x )的图象,如图所示.(2)由条件知,函数f (x )的定义域为R .由图象知,当-1≤x ≤1时,f (x )=x 2的值域为[0,1],当x >1或x <-1时,f (x )=1,所以f (x )的值域为[0,1].11.解 当点P 在BC 上运动,即0≤x ≤4时,y =12×4x =2x ;当点P 在CD 上运动,即4<x ≤8时,y =12×4×4=8;当点P 在DA 上运动,即8<x ≤12时,y =12×4×(12-x )=24-2x .综上可知,f (x )=⎩⎨⎧ 2x , 0≤x ≤4,8,4<x ≤8,24-2x ,8<x ≤12.12.B [由题意可知,集合A 中可能含有的元素为:当x 2=1时,x =1,-1;当x 2=2时,x =2,- 2. 所以集合A 可为含有一个、二个、三个、四个元素的集合.无论含有几个元素,A ∩B =∅或{1}.故选B.]13.解 根据题意可得d =k v 2S .∵v =50时,d =S ,代入d =k v 2S 中,解得k =12500.∴d =12500v 2S .当d =S 2时,可解得v =25 2.∴d =⎩⎪⎨⎪⎧ S 2 (0≤v <252)12500v 2S (v ≥252).§1.2习题课课时目标 1.加深对函数概念的理解,加深对映射概念的了解.2.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.3.通过具体实例,理解简单的分段函数,并能简单应用.1.下列图形中,不可能作为函数y=f(x)图象的是()2.已知函数f:A→B(A、B为非空数集),定义域为M,值域为N,则A、B、M、N的关系是()A.M=A,N=B B.M⊆A,N=BC.M=A,N⊆B D.M⊆A,N⊆B3.函数y=f(x)的图象与直线x=a的交点()A.必有一个B.一个或两个C.至多一个D.可能两个以上4.已知函数,若f(a)=3,则a的值为()A.3B.- 3C.±3D.以上均不对5.若f(x)的定义域为[-1,4],则f(x2)的定义域为()A.[-1,2]B.[-2,2]C.[0,2]D.[-2,0]6.函数y=xkx2+kx+1的定义域为R,则实数k的取值范围为() A.k<0或k>4B.0≤k<4C.0<k<4D.k≥4或k≤0一、选择题1.函数f (x )=xx 2+1,则f (1x )等于( )A .f (x )B .-f (x )C.1f (x )D.1f (-x )2.已知f (x 2-1)的定义域为[-3,3],则f (x )的定义域为( )A .[-2,2]B .[0,2]C .[-1,2]D .[-3,3]3.已知集合A ={a ,b },B ={0,1},则下列对应不是从A 到B 的映射的是()4.与y =|x |为相等函数的是( )A .y =(x )2B .y =x 2C .D .y =3x 35.函数y =2x +1x -3的值域为( )A .(-∞,43)∪(43,+∞)B .(-∞,2)∪(2,+∞)C .RD .(-∞,23)∪(43,+∞)6.若集合A ={x |y =x -1},B ={y |y =x 2+2},则A ∩B 等于( )A .[1,+∞)B .(1,+∞)C .[2,+∞)D .(0,+∞)二、填空题7.设集合A=B={(x,y)|x∈R,y∈R},点(x,y)在映射f:A→B的作用下对应的点是(x-y,x+y),则B中点(3,2)对应的A中点的坐标为____________.8.已知f(x+1)=x+2x,则f(x)的解析式为___________________________________.9.已知函数,则f(f(-2))=______________________________.三、解答题10.若3f(x-1)+2f(1-x)=2x,求f(x).11.已知,若f(1)+f(a+1)=5,求a的值.能力提升12.已知函数f(x)的定义域为[0,1],则函数f(x-a)+f(x+a)(0<a<12)的定义域为()A.∅B.[a,1-a] C.[-a,1+a]D.[0,1]13.已知函数(1)求f(-3),f[f(-3)];(2)画出y=f(x)的图象;(3)若f(a)=12,求a的值.1.函数的定义域、对应关系以及值域是构成函数的三个要素.事实上,如果函数的定义域和对应关系确定了,那么函数的值域也就确定了.两个函数是否相同,只与函数的定义域和对应关系有关,而与函数用什么字母表示无关.求函数定义域时,要注意分式的字母不能为零;偶次根式内的被开方式子必须大于或等于零.2.函数图象是描述函数两个变量之间关系的一种重要方法,它能够直观形象地表示自变量、函数值的变化趋势.函数的图象可以是直线、光滑的曲线,也可以是一些孤立的点、线段或几段曲线等.3.函数的表示方法有列举法、解析法、图象法三种.根据解析式画函数的图象时,要注意定义域对函数图象的制约作用.函数的图象既是研究函数性质的工具,又是数形结合方法的基础.§1.2习题课双基演练1.C[C选项中,当x取小于0的一个值时,有两个y值与之对应,不符合函数的定义.]2.C[值域N应为集合B的子集,即N⊆B,而不一定有N=B.]3.C[当a属于f(x)的定义域内时,有一个交点,否则无交点.]4.A[当a≤-1时,有a+2=3,即a=1,与a≤-1矛盾;当-1<a<2时,有a2=3,∴a=3,a=-3(舍去);当a≥2时,有2a=3,∴a=32与a≥2矛盾.综上可知a = 3.]5.B [由-1≤x 2≤4,得x 2≤4,∴-2≤x ≤2,故选B.]6.B [由题意,知kx 2+kx +1≠0对任意实数x 恒成立,当k =0时,1≠0恒成立,∴k =0符合题意.当k ≠0时,Δ=k 2-4k <0,解得0<k <4,综上,知0≤k <4.]作业设计1.A [f (1x )=1x 1x 2+1=x 1+x 2=f (x ).] 2.C [∵x ∈[-3,3],∴0≤x 2≤3,∴-1≤x 2-1≤2,∴f (x )的定义域为[-1,2].]3.C [C 选项中,和a 相对应的有两个元素0和1,不符合映射的定义.故答案为C.]4.B [A 中的函数定义域与y =|x |不同;C 中的函数定义域不含有x =0,而y =|x |中含有x =0,D 中的函数与y =|x |的对应关系不同,B 正确.]5.B [用分离常数法.y =2(x -3)+7x -3=2+7x -3. ∵7x -3≠0,∴y ≠2.] 6.C [化简集合A ,B ,则得A =[1,+∞),B =[2,+∞).∴A ∩B =[2,+∞).]7.(52,-12)解析 由题意⎩⎨⎧ x -y =3x +y =2,∴⎩⎪⎨⎪⎧ x =52y =-12.8.f (x )=x 2-1(x ≥1)解析 ∵f (x +1)=x +2x=(x )2+2x +1-1=(x +1)2-1,∴f (x )=x 2-1. 由于x +1≥1,所以f (x )=x 2-1(x ≥1).9.4解析 ∵-2<0,∴f (-2)=(-2)2=4,又∵4≥0,∴f (4)=4,∴f (f (-2))=4.10.解 令t =x -1,则1-x =-t ,原式变为3f (t )+2f (-t )=2(t +1),①以-t 代t ,原式变为3f (-t )+2f (t )=2(1-t ),②由①②消去f (-t ),得f (t )=2t +25. 即f (x )=2x +25.11.解 f (1)=1×(1+4)=5,∵f (1)+f (a +1)=5,∴f (a +1)=0.当a +1≥0,即a ≥-1时,有(a +1)(a +5)=0,∴a =-1或a =-5(舍去).当a +1<0,即a <-1时,有(a +1)(a -3)=0,无解.综上可知a =-1.12.B [由已知,得⎩⎨⎧ 0≤x +a ≤1,0≤x -a ≤1⇒⎩⎨⎧-a ≤x ≤1-a ,a ≤x ≤1+a . 又∵0<a <12,∴a ≤x ≤1-a ,故选B.]13.解 (1)∵x ≤-1时,f (x )=x +5,∴f (-3)=-3+5=2,∴f [f (-3)]=f (2)=2×2=4.(2)函数图象如右图所示.(3)当a ≤-1时,f (a )=a +5=12,a =-92≤-1; 当-1<a <1时,f (a )=a 2=12,a =±22∈(-1,1); 当a ≥1时,f (a )=2a =12,a =14∉[1,+∞),舍去. 故a 的值为-92或±22.。
【新教材】新人教A版必修一 函数及其表示 课时作业

2019-2020学年新人教A版必修一函数及其表示课时作业1.设全集U是实数集R,函数y=ln(x2—4)的定义域为M,N=(1,3),则N∩(U M)= ( )A.{x|-2≤x<1}B.{x|—2≤x≤2}C.{x|x<2}D.{x|1<x≤2}【解析】选D.M={x|x2—4〉0}=(—∞,-2)∪(2,+∞),所以N∩(U M)=(1,3)∩[-2,2]=(1,2]。
2。
已知函数f(x)=则f的值为( )A。
B。
C.- D.18【解析】选A.f(2)=4,f=f=1—=。
3。
已知f=+,则f(x)等于( )A。
(x+1)2(x≠1)B。
(x-1)2(x≠1)C。
x2—x+1(x≠1)D。
x2+x+1(x≠1)【解析】选C。
f=+=—+1,令=t(t≠1),则f(t)=t2—t+1,即f(x)=x2-x+1(x≠1)。
4.(2019·太原模拟)若函数f(x)满足f(1—lnx)=,则f(2)等于( )A。
B.eC.D。
-1【解析】选B。
令1-lnx=t,则x=e1-t,于是f(t)=,即f(x)=,故f(2)=e.【一题多解】本题还可以采用如下解法:选B.由1—ln x=2,得x=,这时==e,即f(2)=e。
5.已知函数f(x)的定义域为[0,2],则函数g(x)=f(2x)+的定义域为()A。
[0,1]B。
[0,2] C。
[1,2] D.[1,3]【解析】选A.由题意,得解得0≤x≤1.【变式备选】设函数f(x)=lg(1—x),则函数 f[f(x)]的定义域为( )A。
(—9,+∞)B.(—9,1)C.[-9,+∞)D。
[—9,1)【解析】选B.f[f(x)]=f[lg(1—x)]=lg[1-lg(1—x)],其定义域为解得—9〈x〈1,所以f[f(x)]的定义域为(-9,1).二、填空题(每小题5分,共10分)6。
(2018·泉州模拟)已知函数f(x)=若f(x0)=2,则x0的值为.【解析】若x0≤1,则=2,解得x0=—1,若x0>1,则log3x0=2,解得x0=7。
【红对勾】人教版高中数学必修一第1章课件+课时作业+章末总结(41份)(1.2.2.1)

第一章·1.2·1.2.2·第1课时
学习目标 1.掌握函数的三种表示方法——解析法、图象法、列
表法 2.会求函数解析式,并正确画出函数的图象 3.在实际情境中,会根据不同的需要选择恰当的方法
表示函数
RJA版·数学·必修1
进入导航
第一章·1.2·1.2.2·第1课时
重点难点 重点:函数解析式的求法及函数图象的画法 难点:求函数解析式的两种通法
RJA版·数学·必修1
进入导航
第一章·1.2·1.2.2·第1课时
通法提炼 求函数解析式的常用方法: 1待定系数法:若已知函数的类型,可用待定系数法 求解,即由函数类型设出函数解析式,再根据条件列方程 组,通过解方程组求出待定系数,进而求出函数解析式. 2换元法有时可用“配凑法”:已知函数f[gx]的解 析式求fx的解析式,可用换元法或“配凑法”,即令gx =t,反解出x,然后代入f[gx]中求出ft,从而求出fx.
第一章·1.2·1.2.2·第1课时
(2)列表法,就是 列出表格 来表示两个变量之间的对 应关系;
(3)图象法,就是用 图象 表示两个变量之间的对应关 系.
RJA版·数学·必修1
进入导航
第一章·1.2·1.2.2·第1课时
1.任何一个函数都可以用解析法表示吗? 提示:不一定.如学校安排的月考.某一地区绿化面 积与年份关系等受偶然因素影响较大的函数关系就无法用 解析法表示.
RJA版·数学·必修1
进入导航
第一章·1.2·1.2.2·第1课时
预习篇01
新知导学
RJA版·数学·必修1
进入导航
第一章·1.2·1.2.2·第1课时
函数的表示法
函数有 解析法、列表法、图象法 三种表示法. (1)解析法,就是用 数学表达式 表示两个变量之间 的对应关系;
人教A版数学必修一§1.2.2(1)函数的表示法(课时练).docx

§1.2.2(1)函数的表示法(课时练)一、选择题:1. 若正比例函数()321--=m x m y 的图象经过二、四象限,则m 等于( )A . 1B .2C .1-D .2-2.某同学从家里到学校,为了不迟到,先跑,跑累了再走余下的路,设在途中花的时间为t ,离开家里的路程为d ,下面图形中,能反映该同学的行程的是( ).3.已知正方形的边长为x ,它的外接圆的半径为y ,则y 关于x 的解析式为( )A .x y 22=B .x y 42=C .x y 82=D .x y 162= 4.已知函数()f x 满足()()()f ab f a f b =+,且(2)f p =,(3)f q =,那么(12)f 等于( ). A. p q + B. 2p q +C. 2p q +D. 2p q + 二、填空题:5.已知函数(),m f x x x=+且此函数图象过点(1,5),实数m 的值为 . 6.24,02(),(2)2,2x x f x f x x ⎧-≤≤==⎨>⎩ ;若00()8,f x x == . 7.已知f (2x +1)=3x -2且f (a )=4,则a 的值为________.8.已知f (x )与g (x )分别由下表给出 x1 2 3 4 f (x ) 43 2 1Od t O d t O d t O dt A. B. C. D.x1 2 3 4 g (x )3 14 2那么f (g (3))=________. 三、解答题:9.邮局寄信,不超过 20g 重时付邮资 0.5 元,超过20g 重而不超过40g 重付邮资1元. 一封x 克( 0<x ≤40)重的信应付邮资数y (元). 试写出y 关于x 的函数解析式,并画出函数的图象.10.已知函数⎪⎩⎪⎨⎧>+-≤<-≤+=.4,2,40,2,,4)(2x x x x x x x x f(1)求{})]5([f f f 的值;(2)画出函数的图象.§1.2.2(1)函数的表示法答案一、选择题:1.D2.C3.A4.B二、填空题:5. 4 .6. 0,4.7. 5.8. 1.三、解答题:9.⎩⎨⎧≤<≤<=.4020,1200,5.0x x y 10. (1) 3, (2)略.。
人教版高中数学A版必修1课后习题及答案(全)

高中数学必修1课后习题答案第一章 集合与函数概念1.1集合1.1.1集合的含义与表示练习(第5页)1.(1)中国∈A ,美国∉A ,印度∈A ,英国∉A ;中国和印度是属于亚洲的国家,美国在北美洲,英国在欧洲.(2)1-∉A 2{|}{0,1}A x x x ===.(3)3∉B 2{|60}{3,2}B x x x =+-==-.(4)8∈C ,9.1∉C 9.1N ∉.2.解:(1)因为方程290x -=的实数根为123,3x x =-=,所以由方程290x -=的所有实数根组成的集合为{3,3}-;(2)因为小于8的素数为2,3,5,7,所以由小于8的所有素数组成的集合为{2,3,5,7}; (3)由326y x y x =+⎧⎨=-+⎩,得14x y =⎧⎨=⎩,即一次函数3y x =+与26y x =-+的图象的交点为(1,4),所以一次函数3y x =+与26y x =-+的图象的交点组成的集合为{(1,4)};(4)由453x -<,得2x <,所以不等式453x -<的解集为{|2}x x <.1.1.2集合间的基本关系练习(第7页)1.解:按子集元素个数来分类,不取任何元素,得∅;取一个元素,得{},{},{}a b c ;取两个元素,得{,},{,},{,}a b a c b c ;取三个元素,得{,,}a b c ,即集合{,,}a b c 的所有子集为,{},{},{},{,},{,},{,},{,,}a b c a b a c b c a b c ∅.2.(1){,,}a a b c ∈ a 是集合{,,}a b c 中的一个元素;(2)20{|0}x x ∈= 2{|0}{0}x x ==;(3)2{|10}x R x ∅=∈+= 方程210x +=无实数根,2{|10}x R x ∈+==∅;(4){0,1}N (或{0,1}N ⊆) {0,1}是自然数集合N 的子集,也是真子集; (5){0}2{|}x x x = (或2{0}{|}x x x ⊆=) 2{|}{0,1}x x x ==;(6)2{2,1}{|320}x x x =-+= 方程2320x x -+=两根为121,2x x ==.3.解:(1)因为{|8}{1,2,4,8}B x x ==是的约数,所以A B ;(2)当2k z =时,36k z =;当21k z =+时,363k z =+,即B 是A 的真子集,B A ;(3)因为4与10的最小公倍数是20,所以A B =.1.1.3集合的基本运算练习(第11页)1.解:{3,5,6,8}{4,5,7,8}{5,8}A B ==,{3,5,6,8}{4,5,7,8}{3,4,5,6,7,8}A B ==.2.解:方程2450x x --=的两根为121,5x x =-=,方程210x -=的两根为121,1x x =-=,得{1,5},{1,1}A B =-=-,即{1},{1,1,5}A B A B =-=-.3.解:{|}AB x x =是等腰直角三角形, {|}AB x x =是等腰三角形或直角三角形. 4.解:显然{2,4,6}U B =,{1,3,6,7}U A =, 则(){2,4}U A B =,()(){6}U U A B =.1.1集合习题1.1 (第11页) A 组1.(1)237Q ∈ 237是有理数; (2)23N ∈ 239=是个自然数; (3)Q π∉π是个无理数,不是有理数; (42R 2是实数; (59Z 93=是个整数; (6)25)N ∈ 2(5)5=是个自然数.2.(1)5A ∈; (2)7A ∉; (3)10A -∈.当2k =时,315k -=;当3k =-时,3110k -=-;3.解:(1)大于1且小于6的整数为2,3,4,5,即{2,3,4,5}为所求;(2)方程(1)(2)0x x -+=的两个实根为122,1x x =-=,即{2,1}-为所求;(3)由不等式3213x -<-≤,得12x -<≤,且x Z ∈,即{0,1,2}为所求.4.解:(1)显然有20x ≥,得244x -≥-,即4y ≥-,得二次函数24y x =-的函数值组成的集合为{|4}y y ≥-; (2)显然有0x ≠,得反比例函数2y x =的自变量的值组成的集合为{|0}x x ≠; (3)由不等式342x x ≥-,得45x ≥,即不等式342x x ≥-的解集为4{|}5x x ≥. 5.(1)4B -∉; 3A -∉; {2}B ; B A ;2333x x x -<⇒>-,即{|3},{|2}A x x B x x =>-=≥;(2)1A ∈; {1}-A ; ∅A ; {1,1}-=A ; 2{|10}{1,1}A x x =-==-;(3){|}x x 是菱形{|}x x 是平行四边形;菱形一定是平行四边形,是特殊的平行四边形,但是平行四边形不一定是菱形;{|}x x 是等边三角形{|}x x 是等腰三角形. 等边三角形一定是等腰三角形,但是等腰三角形不一定是等边三角形.6.解:3782x x -≥-,即3x ≥,得{|24},{|3}A x x B x x =≤<=≥, 则{|2}A B x x =≥,{|34}A B x x =≤<.7.解:{|9}{1,2,3,4,5,6,7,8}A x x ==是小于的正整数,则{1,2,3}AB =,{3,4,5,6}AC =, 而{1,2,3,4,5,6}BC =,{3}B C =, 则(){1,2,3,4,5,6}A B C =,(){1,2,3,4,5,6,7,8}A B C =.8.解:用集合的语言说明这项规定:每个参加上述的同学最多只能参加两项,即为()A B C =∅.(1){|}A B x x =是参加一百米跑或参加二百米跑的同学; (2){|}A C x x =是既参加一百米跑又参加四百米跑的同学.9.解:同时满足菱形和矩形特征的是正方形,即{|}BC x x =是正方形, 平行四边形按照邻边是否相等可以分为两类,而邻边相等的平行四边形就是菱形, 即{|}A B x x =是邻边不相等的平行四边形, {|}S A x x =是梯形.10.解:{|210}AB x x =<<,{|37}A B x x =≤<, {|3,7}R A x x x =<≥或,{|2,10}R B x x x =≤≥或,得(){|2,10}R A B x x x =≤≥或, (){|3,7}R A B x x x =<≥或,(){|23,710}R A B x x x =<<≤<或, (){|2,3710}R A B x x x x =≤≤<≥或或.B 组1.4 集合B 满足A B A =,则B A ⊆,即集合B 是集合A 的子集,得4个子集.2.解:集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示两条直线21,45x y x y -=+=的交点的集合, 即21(,)|{(1,1)}45x y D x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭,点(1,1)D 显然在直线y x =上,得D C .3.解:显然有集合{|(4)(1)0}{1,4}B x x x =--==,当3a =时,集合{3}A =,则{1,3,4},AB A B ==∅; 当1a =时,集合{1,3}A =,则{1,3,4},{1}AB A B ==; 当4a =时,集合{3,4}A =,则{1,3,4},{4}A B A B ==;当1a ≠,且3a ≠,且4a ≠时,集合{3,}A a =,则{1,3,4,},A B a A B ==∅.4.解:显然{0,1,2,3,4,5,6,7,8,9,10}U =,由U AB =, 得U B A ⊆,即()U U A B B =,而(){1,3,5,7}U A B =, 得{1,3,5,7}U B =,而()U U B B =,即{0,2,4,6,8.9,10}B =.第一章 集合与函数概念1.2函数及其表示1.2.1函数的概念练习(第19页)1.解:(1)要使原式有意义,则470x +≠,即74x ≠-, 得该函数的定义域为7{|}4x x ≠-; (2)要使原式有意义,则1030x x -≥⎧⎨+≥⎩,即31x -≤≤,得该函数的定义域为{|31}x x -≤≤. 2.解:(1)由2()32f x x x =+,得2(2)322218f =⨯+⨯=,同理得2(2)3(2)2(2)8f -=⨯-+⨯-=,则(2)(2)18826f f +-=+=,即(2)18,(2)8,(2)(2)26f f f f =-=+-=;(2)由2()32f x x x =+,得22()3232f a a a a a =⨯+⨯=+,同理得22()3()2()32f a a a a a -=⨯-+⨯-=-,则222()()(32)(32)6f a f a a a a a a +-=++-=,即222()32,()32,()()6f a a a f a a a f a f a a =+-=-+-=.3.解:(1)不相等,因为定义域不同,时间0t >;(2)不相等,因为定义域不同,0()(0)g x x x =≠.1.2.2函数的表示法练习(第23页) 1.解:显然矩形的另一边长为2250x cm -,222502500y x x x x =-=-,且050x <<,即22500(050)y x x x =-<<.2.解:图象(A )对应事件(2),在途中遇到一次交通堵塞表示离开家的距离不发生变化; 图象(B )对应事件(3),刚刚开始缓缓行进,后来为了赶时间开始加速; 图象(D )对应事件(1),返回家里的时刻,离开家的距离又为零;图象(C )我出发后,以为要迟到,赶时间开始加速,后来心情轻松,缓缓行进.2,2|2|2,2x x y x x x -≥⎧=-=⎨-+<⎩,图象如下所示. 3.解:4.解:因为3sin 602=,所以与A 中元素60相对应的B 中的元素是32; 因为2sin 452=,所以与B 中的元素22相对应的A 中元素是45. 1.2函数及其表示习题1.2(第23页) 1.解:(1)要使原式有意义,则40x -≠,即4x ≠,得该函数的定义域为{|4}x x ≠;(2)x R ∈,2()f x x =都有意义,即该函数的定义域为R ;(3)要使原式有意义,则2320x x -+≠,即1x ≠且2x ≠,得该函数的定义域为{|12}x x x ≠≠且;(4)要使原式有意义,则4010x x -≥⎧⎨-≠⎩,即4x ≤且1x ≠, 得该函数的定义域为{|41}x x x ≤≠且.2.解:(1)()1f x x =-的定义域为R ,而2()1x g x x=-的定义域为{|0}x x ≠, 即两函数的定义域不同,得函数()f x 与()g x 不相等;(2)2()f x x =的定义域为R ,而4()()g x x =的定义域为{|0}x x ≥,即两函数的定义域不同,得函数()f x 与()g x 不相等;(3)对于任何实数,都有362x x =,即这两函数的定义域相同,切对应法则相同,得函数()f x 与()g x 相等.3.解:(1)定义域是(,)-∞+∞,值域是(,)-∞+∞;(2)定义域是(,0)(0,)-∞+∞,值域是(,0)(0,)-∞+∞;(3)定义域是(,)-∞+∞,值域是(,)-∞+∞;(4)定义域是(,)-∞+∞,值域是[2,)-+∞.4.解:因为2()352f x x x =-+,所以2(2)3(2)5(2)2852f -=⨯--⨯-+=+,即(2)852f -=+;同理,22()3()5()2352f a a a a a -=⨯--⨯-+=++,即2()352f a a a -=++;22(3)3(3)5(3)231314f a a a a a +=⨯+-⨯++=++,即2(3)31314f a a a +=++;22()(3)352(3)3516f a f a a f a a +=-++=-+,即2()(3)3516f a f a a +=-+. 5.解:(1)当3x =时,325(3)14363f +==-≠-, 即点(3,14)不在()f x 的图象上;(2)当4x =时,42(4)346f +==--, 即当4x =时,求()f x 的值为3-;(3)2()26x f x x +==-,得22(6)x x +=-, 即14x =.6.解:由(1)0,(3)0f f ==,得1,3是方程20x bx c ++=的两个实数根,即13,13b c +=-⨯=,得4,3b c =-=,即2()43f x x x =-+,得2(1)(1)4(1)38f -=--⨯-+=,即(1)f -的值为8.7.图象如下:8.解:由矩形的面积为10,即10xy =,得10(0)y x x=>,10(0)x y y =>,由对角线为d,即d =(0)d x =>, 由周长为l ,即22l x y =+,得202(0)l x x x =+>, 另外2()l x y =+,而22210,xy d x y ==+,得0)l d ===>,即(0)l d =>.9.解:依题意,有2()2dx vt π=,即24v x t dπ=, 显然0x h ≤≤,即240v t h dπ≤≤,得204h d t v π≤≤, 得函数的定义域为2[0,]4h d vπ和值域为[0,]h . 10.解:从A 到B 的映射共有8个.分别是()0()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()0()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩.B组1.解:(1)函数()r f p =的定义域是[5,0][2,6)-;(2)函数()r f p =的值域是[0,)+∞;(3)当5r >,或02r ≤<时,只有唯一的p 值与之对应.2.解:图象如下,(1)点(,0)x 和点(5,)y 不能在图象上;(2)省略.3.解:3, 2.522,211,10()[]0,011,122,233,3x x x f x x x x x x --<<-⎧⎪--≤<-⎪⎪--≤<⎪==≤<⎨⎪≤<⎪≤<⎪⎪=⎩图象如下4.解:(1)驾驶小船的路程为222x +,步行的路程为12x -,得2221235x xt +-=+,(012)x ≤≤, 即241235x xt +-=+,(012)x ≤≤. (2)当4x =时,2441242583()3535t h +-=+=+≈.第一章 集合与函数概念1.3函数的基本性质1.3.1单调性与最大(小)值练习(第32页)1.答:在一定的范围内,生产效率随着工人数量的增加而提高,当工人数量达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率随着工人数量的增加而降低.由此可见,并非是工人越多,生产效率就越高.2.解:图象如下[8,12]是递增区间,[12,13]是递减区间,[13,18]是递增区间,[18,20]是递减区间. 3.解:该函数在[1,0]-上是减函数,在[0,2]上是增函数,在[2,4]上是减函数,在[4,5]上是增函数. 4.证明:设12,x x R ∈,且12x x <,因为121221()()2()2()0f x f x x x x x -=--=->, 即12()()f x f x >,所以函数()21f x x =-+在R 上是减函数. 5.最小值.1.3.2单调性与最大(小)值练习(第36页)1.解:(1)对于函数42()23f x x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有4242()2()3()23()f x x x x x f x -=-+-=+=, 所以函数42()23f x x x =+为偶函数;(2)对于函数3()2f x x x =-,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有33()()2()(2)()f x x x x x f x -=---=--=-, 所以函数3()2f x x x =-为奇函数;(3)对于函数21()x f x x+=,其定义域为(,0)(0,)-∞+∞,因为对定义域内每一个x 都有22()11()()x x f x f x x x -++-==-=--, 所以函数21()x f x x+=为奇函数;(4)对于函数2()1f x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有22()()11()f x x x f x -=-+=+=, 所以函数2()1f x x =+为偶函数.2.解:()f x 是偶函数,其图象是关于y 轴对称的; ()g x 是奇函数,其图象是关于原点对称的.习题1.3A 组1.解:(1)函数在5(,)2-∞上递减;函数在5[,)2+∞上递增; (2)函数在(,0)-∞上递增;函数在[0,)+∞上递减.2.证明:(1)设120x x <<,而2212121212()()()()f x f x x x x x x x -=-=+-,由12120,0x x x x +<-<,得12()()0f x f x ->,即12()()f x f x >,所以函数2()1f x x =+在(,0)-∞上是减函数;(2)设120x x <<,而1212211211()()x x f x f x x x x x --=-=, 由12120,0x x x x >-<,得12()()0f x f x -<,即12()()f x f x <,所以函数1()1f x x=-在(,0)-∞上是增函数. 3.解:当0m >时,一次函数y mx b =+在(,)-∞+∞上是增函数; 当0m <时,一次函数y mx b =+在(,)-∞+∞上是减函数, 令()f x mx b =+,设12x x <, 而1212()()()f x f x m x x -=-,当0m >时,12()0m x x -<,即12()()f x f x <, 得一次函数y mx b =+在(,)-∞+∞上是增函数;当0m <时,12()0m x x ->,即12()()f x f x >,得一次函数y mx b =+在(,)-∞+∞上是减函数. 4.解:自服药那一刻起,心率关于时间的一个可能的图象为5.解:对于函数21622100050x y x =-+-, 当162405012()50x =-=⨯-时,max 307050y =(元), 即每辆车的月租金为4050元时,租赁公司最大月收益为307050元. 6.解:当0x <时,0x ->,而当0x ≥时,()(1)f x x x =+,即()(1)f x x x -=--,而由已知函数是奇函数,得()()f x f x -=-,得()(1)f x x x -=--,即()(1)f x x x =-, 所以函数的解析式为(1),0()(1),0x x x f x x x x +≥⎧=⎨-<⎩.B 组1.解:(1)二次函数2()2f x x x =-的对称轴为1x =,则函数()f x 的单调区间为(,1),[1,)-∞+∞,且函数()f x 在(,1)-∞上为减函数,在[1,)+∞上为增函数, 函数()g x 的单调区间为[2,4], 且函数()g x 在[2,4]上为增函数; (2)当1x =时,min ()1f x =-, 因为函数()g x 在[2,4]上为增函数,所以2min ()(2)2220g x g ==-⨯=.2.解:由矩形的宽为x m ,得矩形的长为3032xm -,设矩形的面积为S , 则23033(10)22x x x S x --==-,当5x =时,2max 37.5S m =,即宽5x =m 才能使建造的每间熊猫居室面积最大,且每间熊猫居室的最大面积是237.5m . 3.判断()f x 在(,0)-∞上是增函数,证明如下: 设120x x <<,则120x x ->->,因为函数()f x 在(0,)+∞上是减函数,得12()()f x f x -<-, 又因为函数()f x 是偶函数,得12()()f x f x <, 所以()f x 在(,0)-∞上是增函数.复习参考题A 组1.解:(1)方程29x =的解为123,3x x =-=,即集合{3,3}A =-; (2)12x ≤≤,且x N ∈,则1,2x =,即集合{1,2}B =;(3)方程2320x x -+=的解为121,2x x ==,即集合{1,2}C =. 2.解:(1)由PA PB =,得点P 到线段AB 的两个端点的距离相等, 即{|}P PA PB =表示的点组成线段AB 的垂直平分线;(2){|3}P PO cm =表示的点组成以定点O 为圆心,半径为3cm 的圆. 3.解:集合{|}P PA PB =表示的点组成线段AB 的垂直平分线, 集合{|}P PA PC =表示的点组成线段AC 的垂直平分线,得{|}{|}P PA PB P PA PC ==的点是线段AB 的垂直平分线与线段AC 的 垂直平分线的交点,即ABC ∆的外心.4.解:显然集合{1,1}A =-,对于集合{|1}B x ax ==, 当0a =时,集合B =∅,满足B A ⊆,即0a =; 当0a ≠时,集合1{}B a =,而B A ⊆,则11a =-,或11a=, 得1a =-,或1a =, 综上得:实数a 的值为1,0-,或1. 5.解:集合20(,)|{(0,0)}30x y AB x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭,即{(0,0)}A B =;集合20(,)|23x y A C x y x y ⎧-=⎫⎧==∅⎨⎨⎬-=⎩⎩⎭,即A C =∅;集合3039(,)|{(,)}2355x y BC x y x y ⎧+=⎫⎧==-⎨⎨⎬-=⎩⎩⎭; 则39()(){(0,0),(,)}55AB BC =-.6.解:(1)要使原式有意义,则2050x x -≥⎧⎨+≥⎩,即2x ≥,得函数的定义域为[2,)+∞; (2)要使原式有意义,则40||50x x -≥⎧⎨-≠⎩,即4x ≥,且5x ≠,得函数的定义域为[4,5)(5,)+∞.7.解:(1)因为1()1x f x x -=+, 所以1()1a f a a -=+,得12()1111a f a a a -+=+=++, 即2()11f a a +=+;(2)因为1()1xf x x-=+,所以1(1)(1)112a af a a a -++==-+++, 即(1)2af a a +=-+.8.证明:(1)因为221()1x f x x +=-,所以22221()1()()1()1x x f x f x x x+-+-===---, 即()()f x f x -=;(2)因为221()1x f x x +=-,所以222211()11()()111()x x f f x x x x++===---, 即1()()f f x x=-.9.解:该二次函数的对称轴为8k x =, 函数2()48f x x kx =--在[5,20]上具有单调性,则208k ≥,或58k≤,得160k ≥,或40k ≤, 即实数k 的取值范围为160k ≥,或40k ≤.10.解:(1)令2()f x x -=,而22()()()f x x x f x ---=-==,即函数2y x -=是偶函数;(2)函数2y x -=的图象关于y 轴对称; (3)函数2y x -=在(0,)+∞上是减函数; (4)函数2y x -=在(,0)-∞上是增函数.B 组1.解:设同时参加田径和球类比赛的有x 人,则158143328x ++---=,得3x =,只参加游泳一项比赛的有15339--=(人),即同时参加田径和球类比赛的有3人,只参加游泳一项比赛的有9人. 2.解:因为集合A ≠∅,且20x ≥,所以0a ≥. 3.解:由(){1,3}UA B =,得{2,4,5,6,7,8,9}A B =,集合AB 里除去()U A B ,得集合B ,所以集合{5,6,7,8,9}B =.4.解:当0x ≥时,()(4)f x x x =+,得(1)1(14)5f =⨯+=; 当0x <时,()(4)f x x x =-,得(3)3(34)21f -=-⨯--=;(1)(5),1(1)(1)(3),1a a a f a a a a ++≥-⎧+=⎨+-<-⎩.5.证明:(1)因为()f x ax b =+,得121212()()222x x x x af a b x x b ++=+=++,121212()()()222f x f x ax b ax b ax x b ++++==++, 所以1212()()()22x x f x f x f ++=; (2)因为2()g x x ax b =++,得22121212121()(2)()242x x x x g x x x x a b ++=++++, 22121122()()1[()()]22g x g x x ax b x ax b +=+++++2212121()()22x x x x a b +=+++,因为2222212121212111(2)()()0424x x x x x x x x ++-+=--≤,即222212121211(2)()42x x x x x x ++≤+, 所以1212()()()22x x g x g x g ++≤. 6.解:(1)函数()f x 在[,]b a --上也是减函数,证明如下:设12b x x a -<<<-,则21a x x b <-<-<,因为函数()f x 在[,]a b 上是减函数,则21()()f x f x ->-,又因为函数()f x 是奇函数,则21()()f x f x ->-,即12()()f x f x >, 所以函数()f x 在[,]b a --上也是减函数;(2)函数()g x 在[,]b a --上是减函数,证明如下: 设12b x x a -<<<-,则21a x x b <-<-<,因为函数()g x 在[,]a b 上是增函数,则21()()g x g x -<-, 又因为函数()g x 是偶函数,则21()()g x g x <,即12()()g x g x >, 所以函数()g x 在[,]b a --上是减函数.7.解:设某人的全月工资、薪金所得为x 元,应纳此项税款为y 元,则0,02000(2000)5%,2000250025(2500)10%,25004000175(4000)15%,40005000x x x y x x x x ≤≤⎧⎪-⨯<≤⎪=⎨+-⨯<≤⎪⎪+-⨯<≤⎩由该人一月份应交纳此项税款为26.78元,得25004000x <≤, 25(2500)10%26.78x +-⨯=,得2517.8x =, 所以该人当月的工资、薪金所得是2517.8元.新课程标准数学必修1第二章课后习题解答第二章 基本初等函数(I ) 2.1指数函数 练习(P54)1. a 21=a ,a 43=43a ,a53-=531a,a32-=321a.2. (1)32x =x 32, (2)43)(b a +=(a +b )43, (3)32n)-(m =(m -n )32, (4)4n)-(m =(m -n )2,(5)56q p =p 3q 25,(6)mm 3=m213-=m 25.3. (1)(4936)23=[(76)2]23=(76)3=343216;(2)23×35.1×612=2×321×(23)31×(3×22)61=231311--×3613121++=2×3=6;(3)a 21a 41a 81-=a814121-+=a 85; (4)2x 31-(21x 31-2x 32-)=x 3131+--4x 3221--=1-4x -1=1x4-.练习(P58)1.如图图2-1-2-142.(1)要使函数有意义,需x -2≥0,即x ≥2,所以函数y =32-x 的定义域为{x |x ≥2};(2)要使函数有意义,需x ≠0,即函数y =(21)x 1的定义域是{x ∣x ≠0}.3.y =2x (x ∈N *)习题2.1 A 组(P59)1.(1)100;(2)-0.1;(3)4-π;(4)x -y .2解:(1)623b a ab=212162122123)(⨯⨯⨯b a a b =23232121--⨯b a =a 0b 0=1. (2)a aa2121=212121a a a⨯=2121a a ⨯=a 21.(3)415643)(mm m m m •••=4165413121mm m m m ••=4165413121+++mm=m 0=1.点评:遇到多重根号的式子,可以由里向外依次去掉根号,也可根据幂的运算性质来进行.3.解:对于(1),可先按底数5,再按键,再按12,最后按,即可求得它的值.答案:1.710 0; 对于(2),先按底数8.31,再按键,再按12,最后按即可. 答案:2.881 0; 对于(3)这种无理指数幂,先按底数3,再按键,再按键,再按2,最后按即可.答案:4.728 8;对于(4)这种无理指数幂,可先按底数2,其次按键,再按π键,最后按即可.答案:8.825 0.4.解:(1)a 31a 43a127=a 1274331++=a 35; (2)a 32a 43÷a 65=a654332-+=a 127;(3)(x 31y43-)12=12431231⨯-⨯yx =x 4y -9;(4)4a 32b 31-÷(32-a 31-b 31-)=(32-×4)31313132+-+b a =-6ab 0=-6a ;(5))2516(462rt s -23-=)23(4)23(2)23(6)23(2)23(452-⨯-⨯-⨯--⨯-⨯rts=6393652----rt s =36964125s r r ; (6)(-2x 41y31-)(3x21-y 32)(-4x 41y 32)=[-2×3×(-4)]x 323231412141++-+-yx=24y ;(7)(2x 21+3y41-)(2x 21-3y41-)=(2x 21)2-(3y 41-)2=4x -9y 21-;(8)4x 41 (-3x 41y31-)÷(-6x21-y32-)=3231214141643+-++-⨯-y x =2xy 31. 点评:进行有理数指数幂的运算时,要严格按法则和运算顺序,同时注意运算结果的形式,但结果不能既有分数指数又有根式,也不能既有分母又有负指数.5.(1)要使函数有意义,需3-x ∈R ,即x ∈R ,所以函数y =23-x 的定义域为R . (2)要使函数有意义,需2x +1∈R ,即x ∈R ,所以函数y =32x +1的定义域为R . (3)要使函数有意义,需5x ∈R,即x ∈R,所以函数y =(21)5x的定义域为R . (4)要使函数有意义,需x ≠0,所以函数y =0.7x1的定义域为{x |x ≠0}.点评:求函数的定义域一是分式的分母不为零,二是偶次根号的被开方数大于零,0的0次幂没有意义.6.解:设经过x 年的产量为y ,一年内的产量是a (1+100p ),两年内产量是a (1+100p )2,…,x 年内的产量是a (1+100p )x ,则y =a (1+100p )x(x ∈N *,x ≤m ). 点评:根据实际问题,归纳是关键,注意x 的取值范围.7.(1)30.8与30.7的底数都是3,它们可以看成函数y =3x ,当x =0.8和0.7时的函数值;因为3>1,所以函数y =3x 在R 上是增函数.而0.7<0.8,所以30.7<30.8.(2)0.75-0.1与0.750.1的底数都是0.75,它们可以看成函数y =0.75x ,当x =-0.1和0.1时的函数值; 因为1>0.75,所以函数y =0.75x 在R 上是减函数.而-0.1<0.1,所以0.750.1<0.75-0.1.(3)1.012.7与1.013.5的底数都是1.01,它们可以看成函数y =1.01x ,当x =2.7和3.5时的函数值; 因为1.01>1,所以函数y =1.01x 在R 上是增函数.而2.7<3.5,所以1.012.7<1.013.5. (4)0.993.3与0.994.5的底数都是0.99,它们可以看成函数y =0.99x ,当x =3.3和4.5时的函数值; 因为0.99<1,所以函数y =0.99x 在R 上是减函数.而3.3<4.5,所以0.994.5<0.993.3.8.(1)2m ,2n 可以看成函数y =2x ,当x =m 和n 时的函数值;因为2>1,所以函数y =2x 在R 上是增函数.因为2m <2n ,所以m <n . (2)0.2m ,0.2n 可以看成函数y =0.2x ,当x =m 和n 时的函数值;因为0.2<1, 所以函数y =0.2x 在R 上是减函数.因为0.2m <0.2n ,所以m >n . (3)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为0<a <1, 所以函数y =a x 在R 上是减函数.因为a m <a n ,所以m >n . (4)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为a >1, 所以函数y =a x 在R 上是增函数.因为a m >a n ,所以m >n . 点评:利用指数函数的单调性是解题的关键.9.(1)死亡生物组织内碳14的剩余量P 与时间t 的函数解析式为P=(21)57301.当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量为P=(21)573057309⨯=(21)9≈0.002. 答:当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前含量的2‰, 因此,还能用一般的放射性探测器测到碳14的存在.(2)设大约经过t 万年后,用一般的放射性探测器测不到碳14,那么(21)537010000t <0.001,解得t >5.7.答:大约经过6万年后,用一般的放射性探测器是测不到碳14的. B 组1. 当0<a <1时,a 2x -7>a 4x -12⇒x -7<4x -1⇒x >-3;当a >1时,a 2x -7>a 4x -1⇒2x -7>4x -1⇒x <-3. 综上,当0<a <1时,不等式的解集是{x |x >-3};当a >1时,不等式的解集是{x |x <-3}.2.分析:像这种条件求值,一般考虑整体的思想,同时观察指数的特点,要注重完全平方公式的运用. 解:(1)设y =x 21+x21-,那么y 2=(x 21+x21-)2=x +x -1+2.由于x +x -1=3,所以y =5.(2)设y =x 2+x -2,那么y =(x +x -1)2-2.由于x +x -1=3,所以y =7.(3)设y =x 2-x -2,那么y =(x +x -1)(x -x -1),而(x -x -1)2=x 2-2+x -2=5,所以y =±35. 点评:整体代入和平方差,完全平方公式的灵活运用是解题的突破口. 3.解:已知本金为a 元.1期后的本利和为y 1=a +a ×r =a (1+r ), 2期后的本利和为y 2=a (1+r )+a (1+r )×r =a (1+r )2, 3期后的本利和为y 3=a (1+r )3, …x 期后的本利和为y =a (1+r )x .将a =1 000,r =0.022 5,x =5代入上式得y =a (1+r )x =1 000×(1+0.022 5)5=1 000×1.02255≈1118. 答:本利和y 随存期x 变化的函数关系式为y =a (1+r )x ,5期后的本利和约为1 118元. 4.解:(1)因为y 1=y 2,所以a 3x +1=a -2x .所以3x +1=-2x .所以x =51-. (2)因为y 1>y 2,所以a 3x +1>a -2x . 所以当a >1时,3x +1>-2x .所以x >51-. 当0<a <1时,3x +1<-2x .所以x <51-.2.2对数函数 练习(P64)1.(1)2log 83=; (2)2log 325=; (3)21log 12=-; (4)2711log 33=-2.(1)239=; (2)35125=; (3)2124-=; (4)41381-=3.(1)设5log 25x =,则25255x ==,所以2x =; (2)设21log 16x =,则412216x -==,所以4x =-; (3)设lg1000x =,则310100010x ==,所以3x =; (4)设lg 0.001x =,则3100.00110x -==,所以3x =-;4.(1)1; (2)0; (3)2; (4)2; (5)3; (6)5.练习(P68)1.(1)lg()lg lg lg xyz x y z =++;(2)222lg lg()lg lg lg lg lg 2lg lg xy xy z x y z x y z z =-=++=++;(3)33311lg()lg lg lg lg 3lg lg22xy x y z x y z =-=+-=+-;(4)2211lg()lg (lg lg )lg 2lg lg 22y z x y z x y z ==-+=--. 2.(1)223433333log (279)log 27log 9log 3log 3347⨯=+=+=+=;(2)22lg1002lg1002lg104lg104====;(3)5lg 0.00001lg105lg105-==-=-; (4)11ln 22e ==3. (1)22226log 6log 3log log 213-===; (2)lg5lg 2lg101+==; (3)555511log 3log log (3)log 1033+=⨯==;(4)13333351log 5log 15log log log 31153--====-. 4.(1)1; (2)1; (3)54练习(P73)1.函数3log y x =及13log y x =的图象如右图所示.相同点:图象都在y 轴的右侧,都过点(1,0) 不同点:3log y x =的图象是上升的,13log y x =的图象是下降的关系:3log y x =和13log y x =的图象是关于x 轴对称的.2. (1)(,1)-∞; (2)(0,1)(1,)+∞; (3)1(,)3-∞; (4)[1,)+∞3. (1)1010log 6log 8< (2)0.50.5log 6log 4< (3)2233log 0.5log 0.6> (4) 1.5 1.5log 1.6log 1.4>习题2.2 A 组(P74) 1. (1)3log 1x =; (2)41log 6x =; (3)4log 2x =; (4)2log 0.5x = (5) lg 25x = (6)5log 6x =2. (1)527x = (2) 87x = (3) 43x = (4)173x= (5) 100.3x = (6) 3xe =3. (1)0; (2) 2; (3) 2-; (4)2; (5) 14-; (6) 2. 4. (1)lg 6lg 2lg3a b =+=+; (2) 3lg 42lg 22log 4lg3lg3ab===; (3) 2lg122lg 2lg3lg3log 1222lg 2lg 2lg 2b a +===+=+; (4)3lg lg3lg 22b a =-=- 5. (1)x ab =; (2) mx n=; (3) 3n x m =; (4)b x =.6. 设x 年后我国的GDP 在1999年的GDP 的基础上翻两番,则(10.073)4x+=解得 1.073log 420x =≈. 答:设20年后我国的GDP 在1999年的GDP 的基础上翻两番.7. (1)(0,)+∞; (2) 3(,1]4. 8. (1)m n <; (2) m n <; (3) m n >; (4)m n >.9. 若火箭的最大速度12000v =,那么62000ln 112000ln(1)61402M M M M e mm m m ⎛⎫+=⇒+=⇒+=⇒≈ ⎪⎝⎭答:当燃料质量约为火箭质量的402倍时,火箭的最大速度可达12km/s. 10. (1)当底数全大于1时,在1x =的右侧,底数越大的图象越在下方.所以,①对应函数lg y x =,②对应函数5log y x =,③对应函数2log y x =. (2)略. (3)与原函数关于x 轴对称. 11. (1)235lg 25lg 4lg92lg52lg 22lg3log 25log 4log 98lg 2lg3lg5lg 2lg3lg5⋅⋅=⨯⨯=⨯⨯= (2)lg lg lg log log log 1lg lg lg a b c b c a b c a a b c⋅⋅=⨯⨯= 12. (1)令2700O =,则312700log 2100v =,解得 1.5v =. 答:鲑鱼的游速为1.5米/秒. (2)令0v =,则31log 02100O=,解得100O =. 答:一条鱼静止时的耗氧量为100个单位.B 组1. 由3log 41x =得:143,43xx-==,于是11044333x x -+=+= 2. ①当1a >时,3log 14a<恒成立; ②当01a <<时,由3log 1log 4a a a <=,得34a <,所以304a <<.综上所述:实数a 的取值范围是3{04a a <<或1}a >3. (1)当1I = W/m 2时,112110lg 12010L -==;(2)当1210I -= W/m 2时,121121010lg 010L --==答:常人听觉的声强级范围为0120dB .4. (1)由10x +>,10x ->得11x -<<,∴函数()()f x g x +的定义域为(1,1)- (2)根据(1)知:函数()()f x g x +的定义域为(1,1)-∴ 函数()()f x g x +的定义域关于原点对称又∵ ()()log (1)log (1)()()a a f x g x x x f x g x -+-=-++=+ ∴()()f x g x +是(1,1)-上的偶函数.5. (1)2log y x =,0.3log y x =; (2)3xy =,0.1x y =.习题2.3 A 组(P79) 1.函数y =21x是幂函数.2.解析:设幂函数的解析式为f (x )=x α,因为点(2,2)在图象上,所以2=2α.所以α=21,即幂函数的解析式为f (x )=x 21,x ≥0.3.(1)因为流量速率v 与管道半径r 的四次方成正比,所以v =k ·r 4; (2)把r =3,v =400代入v =k ·r 4中,得k =43400=81400,即v =81400r 4;(3)把r =5代入v =81400r 4,得v =81400×54≈3 086(cm 3/s ), 即r =5 cm 时,该气体的流量速率为3 086 cm 3/s .第二章 复习参考题A 组(P82)1.(1)11; (2)87; (3)10001; (4)259. 2.(1)原式=))(()()(212121212212122121b a b a b a b a -+++-=b a b b a a b b a a -++++-2121212122=ba b a -+)(2;(2)原式=))(()(1121----+-a a a a a a =aa a a 11+-=1122+-a a .3.(1)因为lg 2=a ,lg 3=b ,log 125=12lg 5lg =32lg 210lg2•=3lg 2lg 22lg 1+-,所以log 125=ba a +-21. (2)因为2log 3a =,3log 7b =37147log 27log 56log 27⨯=⨯=2log 112log 377++=7log 2log 11)7log 2(log 33333÷++÷=b ab a ÷++÷111)1(3=13++ab ab . 4.(1)(-∞,21)∪(21,+∞);(2)[0,+∞).5.(32,1)∪(1,+∞);(2)(-∞,2);(3)(-∞,1)∪(1,+∞).6.(1)因为log 67>log 66=1,所以log 67>1.又因为log 76<log 77=1,所以log 76<1.所以log 67>log 76. (2)因为log 3π>log 33=1,所以log 3π>1.又因为log 20.8<0,所以log 3π>log 20.8.7.证明:(1)因为f (x )=3x ,所以f (x )·f (y )=3x ×3y =3x +y .又因为f (x +y )=3x +y ,所以f (x )·f (y )=f (x +y ).(2)因为f (x )=3x ,所以f (x )÷f (y )=3x ÷3y =3x -y . 又因为f (x -y )=3x -y ,所以f (x )÷f (y )=f (x -y ).8.证明:因为f (x )=lgxx+-11,a 、b ∈(-1,1), 所以f (a )+f (b )=lgbb a a +-++-11lg11=lg )1)(1()1)(1(b a b a ++--, f (ab b a ++1)=lg (abb a ab ba +++++-1111)=lg b a ab b a ab +++--+11=lg )1)(1()1)(1(b a b a ++--. 所以f (a )+f (b )=f (abba ++1). 9.(1)设保鲜时间y 关于储藏温度x 的函数解析式为y =k ·a x (a >0,且a ≠1).因为点(0,192)、(22,42)在函数图象上,所以022192,42,k a k a ⎧=⋅⎪⎨=⋅⎪⎩解得⎪⎩⎪⎨⎧≈==.93.0327,19222a k 所以y =192×0.93x ,即所求函数解析式为y =192×0.93x . (2)当x =30 ℃时,y ≈22(小时);当x =16 ℃时,y ≈60(小时),即温度在30 ℃和16 ℃的保鲜时间约为22小时和60小时. (3)图象如图:图2-210.解析:设所求幂函数的解析式为f (x )=x α,因为f (x )的图象过点(2,22), 所以22=2α,即221-=2α.所以α=21-.所以f (x )=x 21-(x >0).图略,f (x )为非奇非偶函数;同时它在(0,+∞)上是减函数.B 组1.A2.因为2a =5b =10,所以a =log 210,b =log 510,所以a 1+b 1=10log 12+10log 15=lg 2+lg 5=lg 10=1. 3.(1)f (x )=a 122+-x 在x ∈(-∞,+∞)上是增函数. 证明:任取x 1,x 2∈(-∞,+∞),且x 1<x 2.f (x 1)-f (x 2)=a 122+-x -a +1222+x =1222+x -1221+x =)12)(12()22(21221++-x x x x .因为x 1,x 2∈(-∞,+∞),所以.012.01212>+>+x x 又因为x 1<x 2, 所以2122x x <即2122x x <<0.所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).所以函数f (x )=a 122+-x 在(-∞,+∞)上是增函数. (2)假设存在实数a 使f (x )为奇函数,则f (-x )+f (x )=0,即a 121+--x +a 122+-x =0⇒a =121+-x +121+x =122+x +121+x=1, 即存在实数a =1使f (x )=121+--x 为奇函数.4.证明:(1)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以[g (x )]2-[f (x )]2=[g (x )+f (x )][g (x )-f (x )]=)22)(22(xx x x x x x x e e e e e e e e -----++++ =e x ·e -x =e x -x =e 0=1, 即原式得证.(2)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以f (2x )=222x x e e -+,2f (x )·g (x )=2·2x x e e --·2x x e e -+=222xx e e --.所以f (2x )=2f (x )·g (x ).(3)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以g (2x )=222x x e e -+,[g (x )]2+[f (x )]2=(2x x ee -+)2+(2xx e e --)2=4222222x x x x e e e e --+-+++=222xx e e -+.所以g (2x )=[f (x )]2+[g (x )]2.5.由题意可知,θ1=62,θ0=15,当t =1时,θ=52,于是52=15+(62-15)e -k ,解得k ≈0.24,那么θ=15+47e -0.24t . 所以,当θ=42时,t ≈2.3;当θ=32时,t ≈4.2.答:开始冷却2.3和4.2小时后,物体的温度分别为42 ℃和32 ℃.物体不会冷却到12 ℃. 6.(1)由P=P 0e -k t 可知,当t =0时,P=P 0;当t =5时,P=(1-10%)P 0.于是有(1-10%)P 0=P 0e -5k ,解得k =51-ln 0.9,那么P=P 0e t )9.0ln 51(.所以,当t =10时,P=P 0e 9.01051n I ⨯⨯=P 0e ln 0.81=81%P 0.答:10小时后还剩81%的污染物. (2)当P=50%P 0时,有50%P 0=P 0et )9.0ln 51(,解得t =9.0ln 515.0ln ≈33.答:污染减少50%需要花大约33h . (3)其图象大致如下:图2-3新课程标准数学必修1第三章课后习题解答第三章 函数的应用 3.1函数与方程 练习(P88)1.(1)令f (x )=-x 2+3x +5,作出函数f (x )的图象(图3-1-2-7(1)),它与x 轴有两个交点,所以方程-x 2+3x +5=0有两个不相等的实数根.(2)2x (x -2)=-3可化为2x 2-4x +3=0,令f (x )=2x 2-4x +3,作出函数f (x )的图象(图3-1-2-7(2)),它与x 轴没有交点,所以方程2x (x -2)=-3无实数根. (3)x 2=4x -4可化为x 2-4x +4=0,令f (x )=x 2-4x +4,作出函数f (x )的图象(图3-1-2-7(3)), 它与x 轴只有一个交点(相切),所以方程x 2=4x -4有两个相等的实数根. (4)5x 2+2x =3x 2+5可化为2x 2+2x -5=0,令f (x )=2x 2+2x -5,作出函数f (x )的图象(图3-1-2-7(4)), 它与x 轴有两个交点,所以方程5x 2+2x =3x 2+5有两个不相等的实数根.图3-1-2-72.(1)作出函数图象(图3-1-2-8(1)),因为f(1)=1>0,f(1.5)=-2.875<0,所以f(x)=-x3-3x+5在区间(1,1.5)上有一个零点.又因为f(x)是(-∞,+∞)上的减函数,所以f(x)=-x3-3x+5在区间(1,1.5)上有且只有一个零点.(2)作出函数图象(图3-1-2-8(2)),因为f(3)<0,f(4)>0,所以f(x)=2x·ln(x-2)-3在区间(3,4)上有一个零点.又因为f(x)=2x·ln(x-2)-3在(2,+∞)上是增函数,所以f(x)在(3,4)上有且仅有一个零点. (3)作出函数图象(图3-1-2-8(3)),因为f(0)<0,f(1)>0,所以f(x)=e x-1+4x-4在区间(0,1)上有一个零点.又因为f(x)=e x-1+4x-4在(-∞,+∞)上是增函数,所以f(x)在(0,1)上有且仅有一个零点.(4)作出函数图象(图3-1-2-8(4)),因为f(-4)<0,f(-3)>0,f(-2)<0,f(2)<0,f(3)>0,所以f(x)=3(x+2)(x-3)(x+4)+x在(-4,-3),(-3,-2),(2,3)上各有一个零点.图3-1-2-8练习(P91)1.由题设可知f(0)=-1.4<0,f(1)=1.6>0,于是f(0)·f(1)<0,所以函数f(x)在区间(0,1)内有一个零点x0.下面用二分法求函数f(x)=x3+1.1x2+0.9x-1.4在区间(0,1)内的零点.取区间(0,1)的中点x1=0.5,用计算器可算得f(0.5)=-0.55.因为f(0.5)·f(1)<0,所以x0∈(0.5,1).再取区间(0.5,1)的中点x2=0.75,用计算器可算得f(0.75)≈0.32.因为f(0.5)·f(0.75)<0,所以x0∈(0.5,0.75).同理,可得x0∈(0.625,0.75),x0∈(0.625,0.687 5),x0∈(0.656 25,0.687 5).由于|0.687 5-0.656 25|=0.031 25<0.1,所以原方程的近似解可取为0.656 25.2.原方程可化为x+lgx-3=0,令f(x)=x+lgx-3,用计算器可算得f(2)≈-0.70,f(3)≈0.48.于是f(2)·f(3)<0,所以这个方程在区间(2,3)内有一个解x0.下面用二分法求方程x=3-lgx在区间(2,3)的近似解.取区间(2,3)的中点x1=2.5,用计算器可算得f(2.5)≈-0.10.因为f(2.5)·f(3)<0,所以x0∈(2.5,3).再取区间(2.5,3)的中点x2=2.75,用计算器可算得f(2.75)≈0.19.因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75).同理,可得x0∈(2.5,2.625),x0∈(2.562 5,2.625),x0∈(2.562 5,2.593 75),x0∈(2.578 125,2.593 75),x0∈(2.585 937 5,2.59 375).由于|2.585 937 5-2.593 75|=0.007 812 5<0.01,所以原方程的近似解可取为2.593 75.习题3.1 A组(P92)1.A,C 点评:需了解二分法求函数的近似零点的条件.2.由x,f(x)的对应值表可得f(2)·f(3)<0,f(3)·f(4)<0,f(4)·f(5)<0,又根据“如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点.”可知函数f(x)分别在区间(2,3),(3,4),(4,5)内有零点.3.原方程即(x+1)(x-2)(x-3)-1=0,令f(x)=(x+1)(x-2)(x-3)-1,可算得f(-1)=-1,f(0)=5.于是f(-1)·f(0)<0,所以这个方程在区间(-1,0)内有一个解.下面用二分法求方程(x+1)(x-2)(x-3)=1在区间(-1,0)内的近似解.取区间(-1,0)的中点x1=-0.5,用计算器可算得f(-0.5)=3.375.因为f(-1)·f(-0.5)<0,所以x0∈(-1,-0.5).再取(-1,-0.5)的中点x2=-0.75,用计算器可算得f(-0.75)≈1.58.因为f(-1)·f(-0.75)<0,所以x0∈(-1,-0.75).同理,可得x0∈(-1,-0.875),x0∈(-0.937 5,-0.875).由于|(-0.875)-(-0.937 5)|=0.062 5<0.1,所以原方程的近似解可取为-0.937 5.4.原方程即0.8x-1-lnx=0,令f(x)=0.8x-1-lnx,f(0)没有意义,用计算器算得f(0.5)≈0.59,f(1)=-0.2.于是f(0.5)·f(1)<0,所以这个方程在区间(0.5,1)内有一个解.下面用二分法求方程0.8x-1=lnx在区间(0,1)内的近似解.取区间(0.5,1)的中点x1=0.75,用计算器可算得f(0.75)≈0.13.因为f(0.75)·f(1)<0,所以x0∈(0.75,1).再取(0.75,1)的中点x2=0.875,用计算器可算得f(0.875)≈-0.04.。
2021-2022学年高一数学(人教A版必修一)课时作业:1-2函数及其表示 习题课
课时作业(十一)1.下列各图中,不行能表示函数y=f(x)的图像的是()答案 B解析B中一个x对应两个函数值,不符合函数定义.2.已知函数f(x)的定义域为[a,b],则y=f(x+a)的定义域为()A.[2a,a+b]B.[0,b-a]C.[a,b] D.无法确定答案 B3.函数的图像与平行于y轴的直线的交点的个数()A.至少有一个B.至多有一个C.不确定D.有且仅有一个答案 B4.客车从甲地以60 km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80 km/h的速度匀速行驶1小时到达丙地.下列描述客车从甲地动身,经过乙地,最终到达丙地所经过的路程s与时间t之间关系的图像中,正确的是()答案 C解析图像经过(0,0),(1,60),(1.5,60),(2.5,140)的三段折线,故选C.5.某农贸市场出售西红柿,当价格上涨时,供应量相应增加,而需求量相应削减,具体调查结果如下表:表1市场供应表单价(元/kg)2 2.4 2.8 3.2 3.6 4供应量(1 000kg)506070758090 表2市场需求表单价(元/kg)4 3.4 2.9 2.6 2.3 2需求量(1 000kg)506065707580 依据以上供应的信息,市场供需平衡点(即供应量和需求量相等时的单价)应在区间()A.(2.3,2.6)内B.(2.4,2.6)内C.(2.6,2.8)内D.(2.8,2.9)内答案 C6.如图所示,函数f(x)的图像是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(1f(3))的值等于________.答案 2解析 ∵f (3)=1,1f (3)=1,∴f (1f (3))=f (1)=2.7.若函数f (x )的定义域为[-1,2],则y =f (x )+f (-x )的定义域为________. 答案 [-1,1]8.设函数y =f (x )的定义域为R +,且f (xy )=f (x )+f (y ),f (8)=3,则f (2)等于__________.答案 12解析 ∵f (8)=f [(2)6]=6f (2)=3,∴f (2)=12. 9.设f (x )=2x +3,g (x +2)=f (x ),则g (x )=________. 答案 2x -110.已知函数f (x )满足f (x +4)=x 3+2,当f (x )=1时,x 的值为________. 答案 311.已知函数f (1-x1+x )=x ,求f (2)的值.解析 由1-x 1+x=2,解得x =-13.所以f (2)=-13.12.(1)已知函数f (x )的定义域是[1,5],求函数f (x 2+1)的定义域. (2)已知函数f (2x 2-1)的定义域是[1,5],求f (x )的定义域.解析 (1)由f (x )定义域为[1,5],知f (x 2+1)中需1≤x 2+1≤5,解得-2≤x ≤2. (2)由f (2x 2-1)定义域为[1,5],得1≤x 2≤25,1≤2x 2-1≤49,故f (x )定义域为[1,49].13.周长为l 的铁丝弯成下部为矩形,上部为半圆形的框架(如图所示),若矩形底边长为2x ,求此框架围成图形的面积y 与x 的函数解析式y =f (x ),并写出它的定义域.【思路】 这是一个有实际意义的问题,应依据几何学问,先写出y =f (x ),再依据实际意义求出函数f (x )的定义域.解析 AB =2x ,CD ︵=πx ,于是AD =12(l -2x -πx ).因此, y =2x ·l -2x -πx 2+12πx 2 =-π+42x 2+lx .函数y =f (x )的定义域由下列不等式组确定, ⎩⎪⎨⎪⎧2x >0,l -2x -πx 2>0,解得0<x <l2+π.故所求函数解析式为y =-π+42x 2+lx ,定义域为⎝ ⎛⎭⎪⎪⎫0,l 2+π. 14.如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.依据这个曲线图,请你回答下列问题:。
2019-2019学年人教A版必修一1.2.2.1函数的表示法课时作业

1.2.2函数的表示法第1课时函数的表示法课后篇巩固提升A组基础巩固1.已知函数f(x)由下表给出,则f(3)等于()A.1B.2C.3D.不存在解析:因为2<3≤4,所以由题中表格可知f(3)=3.答案:C2.已知f-=x,则f(x)=()A.-B.- C.-D.解析:令-=t,则x=-,故f(t)=-,即f(x)=-.答案:B3.若f(x)对于任意实数x恒有3f(x)-2f(-x)=5x+1,则f(x)=()A.x+1B.x-1C.2x+1D.3x+3解析:因为3f(x)-2f(-x)=5x+1,所以3f(-x)-2f(x)=-5x+1,解得f(x)=x+1.答案:A4.已知函数f(x)是反比例函数,且f(-1)=2,则f(x)=.解析:设f(x)=(≠0),∵f(-1)=2,∴- =2,即 =-2.∴f(x)=-.答案:-5.已知函数f(x)的图象如图所示,则f(-5)=,f(f(2))=.解析:由题图可知f(-5)=,f(2)=0,f(0)=4,故f(f(2))=4.答案: 46.对于定义域为R的函数y=f(x),部分x与y的对应关系如下表:则f(f(f(0)))=.解析:由列表表示的函数可得f(0)=3,则f(f(0))=f(3)=-1,f(f(f(0)))=f(-1)=2.答案:27.作出下列函数的图象,并指出其值域:(1)y=x2+x(-1≤x≤1);(2)y=(-2≤x≤1,且x≠0).解(1)用描点法可以作出所求函数的图象如图所示.由图可知y=x2+x(-1≤x≤1)的值域为-.(2)用描点法可以作出函数的图象如图所示.由图可知y=(-2≤x≤1,且x≠0)的值域为(-∞,-1 ∪[2,+∞).8.已知f(x)为二次函数,其图象的顶点坐标为(1,3),且过原点,求f(x)的解析:式.解(方法一)由于函数图象的顶点坐标为(1,3),则设f(x)=a(x-1)2+3(a≠0).∵函数图象过原点(0,0),∴a+3=0,∴a=-3.故f(x)=-3(x-1)2+3.(方法二)设f(x)=ax2+bx+c(a≠0),依题意得--即--解得-∴f(x)=-3x2+6x.B组能力提升1.小明在如图1所示的跑道上匀速跑步,他从点A出发,沿箭头方向经过点B跑到点C,共用时30 s,他的教练选择了一个固定的位置观察小明跑步的过程,设小明跑步的时间为t(s),他与教练间的距离为y(m),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的()A.点MB.点NC.点PD.点Q解析:由图知固定位置到点A距离大于到点C距离,所以舍去N,M点,不选A,B;若是P点,则从最高点到C点依次递减,与图1矛盾,因此取Q,即选D.答案:D2.已知正方形的周长为x,它的外接圆的半径为y,则y关于x的函数解析:式为()A.y=x(x>0)B.y=x(x>0)C.y=x(x>0)D.y=x(x>0)解析:正方形外接圆的直径是它的对角线,因为正方形的边长为,由勾股定理得(2y)2=, 所以y2=,即y=x(x>0).答案:C3.定义两种运算:a b=-,a b=-,则函数f(x)=-的解析:式为()A.f(x)=-,x∈[-2,0)∪(0,2B.f(x)=-,x∈(-∞,-2 ∪[2,+∞)C.f(x)=--,x∈(-∞,-2 ∪[2,+∞)D.f(x)=--,x∈[-2,0)∪(0,2解析:∵f(x)=-------.由---得-2≤x≤2,且x≠0.∴f(x)=--,x∈[-2,0)∪(0,2 .答案:D4.已知f=1+x2,则f(x)=.解析:令=t(t≠0),则x=-1.所以f=f(t)=1+-+2.故f(x)=+2.答案:+25.已知函数f(x),g(x)由下表给出:x87654g(x)65874则g(f(7))=;不等式g(x)<f(x)的解集为.解析:f(7)=7,g(f(7))=g(7)=5.当x=4时,f(4)=5,g(4)=4,所以f(4)>g(4),满足不等式;当x=5时,f(5)=4,g(5)=7,不满足不等式;当x=6时,f(6)=8,g(6)=8,不满足不等式;当x=7时,f(7)=7,g(7)=5,满足不等式;当x=8时,f(8)=6,g(8)=6,不满足不等式,所以不等式g(x)<f(x)的解集为{4,7}.答案:5{4,7}6.定义在R上的函数f(x)对任意的实数x,y满足f(x+y)=f(x)+f(y)+2xy,f(1)=2,则f(3)=.解析:令x=y=1,则f(1+1)=f(1)+f(1)+2.∵f(1)=2,∴f(2)=6.令x=2,y=1,则f(2+1)=f(2)+f(1)+2×2,∴f(3)=6+2+4=12.答案:127.如图所示,用长为l的铁丝弯成下半部分为矩形,上半部分为半圆形的框架,若矩形的底边长为2x,求此框架围成的图形的面积y与x的函数关系式,并指出其定义域.解由题意知此框架是由一个矩形和一个半圆组成的图形,而矩形的边AB=2x,设AD=a,则有2x+2a+πx=l,即a=x-x,其中半圆的直径为2x,半径为x.所以框架围成的图形的面积y=πx2+--·2x=-x2+lx.根据实际意义知x-x>0,又x>0,解得0<x<.故函数y=-x2+lx,其定义域为.8.导学号03814013已知函数f(x)=(a,b为常数,且a≠0)满足f(2)=1,方程f(x)=x有唯一解,求函数f(x)的解析式,并求f(f(-3))的值.解由f(x)=x,得=x,即ax2+(b-1)x=0.∵方程f(x)=x有唯一解,∴Δ=(b-1)2=0,即b=1.∵f(2)=1,∴=1.∴a=.∴f(x)=.∴f(f(-3))=f(6)=.。
人教A版高中数学必修一课时达标作业1.2.2.1函数的表示法

课时提升作业(八)函数的表示法(30分钟50分)一、选择题(每小题3分,共18分)1.(2014·西双版纳高一检测)由下表给出函数y=f(x),若f(m)=3,则m的值为()A.-1B.1C.±1D.3【解析】选C.由表知当m=-1,1时f(m)=3.【变式训练】某班连续进行了5次数学测试,其中刘勇同学的成绩如表所示,在这个函数中,定义域为()A.{1,2,3,4,5}B.{x|1≤x≤5}C.{80,85,83,90,95}D.{x|80≤x≤95}【解析】选A.由题意知定义域是自变量x的取值范围,故这个函数的定义域为{1,2,3,4,5}.2.(2013·济宁高一检测)设函数f(x)=2x+3,g(x+2)=f(x),则g(x)=()A.2x+1B.2x-1C.2x-3D.2x+7【解析】选B.由g(x+2)=f(x)=2x+3,所以g(x+2)=2(x+2)-1,所以g(x)=2x-1.3.(2014·石家庄高一检测)给如图的容器甲注水,下面图象中哪一个图象可以大致刻画容器中水的高度与时间的函数关系()【解析】选B.容器下端较窄,上端较宽,当均匀注入水时,刚开始的一段时间高度变化较大,随着时间的推移,高度的变化速度开始减小,即高度变化不太明显,四个图象中只有B项符合特点.4.(2013·北京高一检测)如果常数项为0的二次函数f(x)的图象经过点M(1,5),N(-1,-3),那么这个函数的解析式为()A.f(x)=x2-2xB.f(x)=x2+4x-1C.f(x)=x2+4xD.f(x)=-x2+4x【解题指南】根据条件设出二次函数的解析式,再根据图象经过两点,代入求解.【解析】选 C.设二次函数的解析式为f(x)=ax2+bx(a≠0),因为函数的图象经过点M(1,5),N(-1,-3),所以得解得所以函数的解析式为f(x)=x2+4x.5.(2014·合肥高一检测)已知f(+1)=x+1,则函数f(x)的解析式为()A.f(x)=x2B.f(x)=x2+1(x≥1)C.f(x)=x2-2x+2(x≥1)D.f(x)=x2-2x(x≥1)【解析】选C.设+1=t(t≥1),则x=(t-1)2,f(t)=(t-1)2+1=t2-2t+2,所以f(x)=x2-2x+2(x≥1). 【误区警示】利用换元法求解析式时,要注意所换新元的取值范围,如本题,因为+1=t,故t ≥1.6.(2014·武安高一检测)若f(x)满足关系式f(x)+2f=3x,则f(2)的值为() A.1 B.-1 C.- D.【解析】选B.①-②×2得-3f(2)=3,所以f(2)=-1,选B.【一题多解】选B.由f(x)+2f=3x①以代x,得f+2f(x)=②②×2-①得3f (x)=-3x,所以f(x)=-x,所以f(2)=-2=-1.二、填空题(每小题4分,共12分)7.函数y=f(x)的图象如图,则函数的定义域为.【解析】根据图象,可知函数y=f(x)的自变量的取值范围为[-3,0]∪[1,2).答案:[-3,0]∪[1,2)8.(2014·淮安高一检测)已知函数f(x)=2x-1,则f(x-1)=.【解析】f(x-1)=2(x-1)-1=2x-3.答案:2x-39.(2014·哈尔滨高一检测)已知f(x)=2x+3,g(x)=4x-5,则使得f(h(x))=g(x)成立的h(x)=. 【解析】由f(x)=2x+3,所以f(h(x))=2h(x)+3=4x-5,所以h(x)= 2x-4.答案:2x-4三、解答题(每小题10分,共20分)10.已知f(x)是一次函数,且满足3f(x+1)-f(x)=2x+9,求f(x)的解析式.【解析】设f(x)=kx+b,则f(x+1)=k(x+1)+b=kx+k+b,所以3f(x+1)-f(x)=3kx+3k+3b-kx-b=2kx+3k+2b=2x+9,所以解得所以f(x)=x+3.【变式训练】已知f(x)=kx+b,f(1)=0,f(3)=-,求f(4)的值.【解析】因为f(1)=0,f(3)=-,所以解得所以f(x)=-x+,所以f(4)=-×4+=-.11.(2014·杭州高一检测)某企业生产某种产品时的能耗y与产品件数x之间适合关系式:y=ax+.且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.(1)写出函数y关于x的解析式.(2)用列表法表示此函数.【解题指南】根据已知数据求出a,b的值,从而写出解析式,然后列表表示函数.【解析】(1)将代入y=ax+,得即解得所以所求函数解析式为y=x+(x∈N*,0<x≤20).(2)当x∈{1,2,3,4,5,…,20}时,列表:(30分钟50分)一、选择题(每小题4分,共16分)1.(2014·济宁高一检测)已知f=,则f(x)的解析式为()A.f(x)=B.f(x)=C.f(x)=D.f(x)=1+x【解析】选C.因为f==,所以f(x)=,故选C.2.(2014·三明高一检测)已知函数y=f(x)的对应关系如下表,函数y=g(x)的图象是如图的曲线ABC,其中A(1,3),B(2,1),C(3,2),则f(g(2))的值为()A.3B.2C.1D.0【解析】选 B.由y=g(x)的图象与y=f(x)的对应关系表可知g(2)=1,f(1)=2,所以f=f(1)=2.3.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程,如图,纵轴表示离学校的距离,横轴表示出发后的时间,则图中较符合此学生走法的是()【解析】选D.由于纵轴表示离学校的距离,所以距离应该越来越小,排除A,C,又一开始跑步,速度快,所以D符合.4.(2014·德州高一检测)已知f(x)是一次函数,若2f(2)-3f(1)=5,2f(0)-f(-1)=1,则f(x)的解析式为()A.f(x)=3x+2B.f(x)=3x-2C.f(x)=2x+3D.f(x)=2x-3【解析】选B.设f(x)=ax+b(a≠0),由已知得即解得故选B.【变式训练】(2014·临沂高一检测)已知g(x)=1-2x,f(g(x))=(x≠0),则f等于() A.1 B.3 C.15 D.30【解析】选C.令g(x)=,得1-2x=,所以x=,所以f==15.二、填空题(每小题5分,共10分)5.(2013·慈溪高一检测)如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2, 0),(6,4),则f(f(f(3)))=.【解析】由图可知f(3)=1,所以f(f(f(3)))=f(f(1)),而f(1)=2,所以f(f(f(3)))=f(2)=0.答案:0【举一反三】本题条件不变,则f(f(f(4)))=.【解析】由图可知:f(f(f(4)))=f(f(2))=f(0)=4.答案:46.(2014·宿迁高一检测)已知b为常数,若f(x)=x2+4x+3,f(x+b)=x2+10x+24,则b=. 【解析】由f(x)=x2+4x+3,得f(x+b)=(x+b)2+4(x+b)+3=x2+(4+2b)x+b2+4b+3,所以所以b=3.答案:3三、解答题(每小题12分,共24分)7.(2013·晋江高一检测)某省在两座重要城市之间修了一条专用铁路,用一列火车作为直通车,已知该列火车的车头,每次拖4节车厢,每天可以来回16次,如果每次拖7节车厢,则每天可以来回10次.(1)设车头每次拖挂车厢节数为x节,每天来回的次数为y次,如果y是x的一次函数,求此一次函数的解析式.(2)在(1)的条件下,每节车厢来回一次能载乘客110人.问这列火车每天来回多少次才能使所载的人数最多?最多能载多少人?【解析】(1)由题意可设y=kx+b(k≠0).当x=4时,y=16,当x=7时,y=10,得方程组:解得k=-2,b=24,所以y=-2x+24.(2)由题意,一天所挂车厢总数最多时,所载人数就最多,设S为每天所挂的车厢数,则:S=xy=x(-2x+24)=-2x2+24x=-2(x-6)2+72,所以当x=6时,S max=72,此时y=12,则一天最多载的人数为110×72=7920(人).答:这列火车每天来回12次才能使所载的人数最多,最多能载7920人.8.设f(x)是R上的函数,且满足f(0)=1,并且对任意的实数x,y,都有f(x-y)=f(x)-y(2x-y+1),求f(x)的解析式.【解题指南】对y赋值,使得出现f(0)的结论,利用条件f(0)=1求出f(x).【解析】因为对任意实数x,y,都有f(x-y)=f(x)-y(2x-y+1),所以令y=x,有f(0)=f(x)-x(2x-x+1),即f(0)=f(x)-x(x+1),又f(0)=1,所以f(x)=x(x+1)+1=x2+x+1.。
高中数学第一章集合与函数概念1.2.2.1函数的表示法课时作业(含解析)新人教A版必修1

1.2.2.1 函数的表示法[基础巩固](25分钟,60分)一、选择题(每小题5分,共25分) 1.已知f (x -1)=1x +1,则f (x )的解析式为( ) A .f (x )=11+x B .f (x )=1+xxC .f (x )=1x +2D .f (x )=1+x 解析:令x -1=t ,则x =t +1,∴f (t )=1t +1+1=12+t,∴f (x )=1x +2. 答案:C2.星期天,小明从家出发,出去散步,图中描述了他散步过程中离家的距离s (m)与散步所用的时间t (min)之间的函数关系,根据图象,下面的描述符合小明散步情况的是( )A .从家出发,到一个公共阅报栏,看了一会儿报,就回家了B .从家出发,到一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了C .从家出发,散了一会儿步(没有停留),然后回家了D .从家出发,散了一会儿步,就找同学去了,18 min 后才回家解析:水平线段表明小明离家的距离始终是300米,然后离家距离达到500米,说明小明从家出发后,到一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了.答案:B3.将函数y =2(x +1)2-3的图象向右平移1个单位长度,再向上平移3个单位长度,所得的图象对应的函数解析式为( )A .y =2(x +2)2-6 B .y =2x 2-6 C .y =2x 2D .y =2(x +2)2解析:根据函数图象的平移原则——“左加右减,上加下减”,可知平移后的图象对应的解析式为y =2[(x -1)+1]2-3+3=2x 2.答案:C4.已知函数f (x )由下表给出,则f (f (3))等于( )A.1 B .2 C .3 D .4解析:∵f (3)=4,∴f (f (3))=f (4)=1. 答案:A5.设函数f (x )=2x +3,g (x +2)=f (x ),则g (x )的解析式是( ) A .g (x )=2x +1 B .g (x )=2x -1 C .g (x )=2x -3 D .g (x )=2x +7 解析:因为g (x +2)=f (x )=2x +3,所以令x +2=t ,则x =t -2,g (t )=2(t -2)+3=2t -1.所以g (x )=2x -1. 答案:B二、填空题(每小题5分,共15分)6.如图,函数f (x )的图象是折线段ABC ,其中A ,B ,C 的坐标分别为(0,4),(2,0),(6,4),则f [f (0)]=________.解析:由图象可知f (0)=4,f (4)=2,f [f (0)]=2. 答案:27.已知x ≠0,函数f (x )满足f ⎝⎛⎭⎪⎫x -1x =x 2+1x2,则f (x )=________.解析:f ⎝⎛⎭⎪⎫x -1x =x 2+1x2=⎝ ⎛⎭⎪⎫x -1x 2+2,所以f (x )=x 2+2.答案:x 2+28.已知函数f (2x +1)=3x +2,且f (a )=4,则a =________.解析:因为f (2x +1)=32(2x +1)+12,所以f (a )=32a +12.又f (a )=4,所以32a +12=4,a=73.答案:73三、解答题(每小题10分,共20分)9.如图,函数f (x )的图象是曲线OAB ,其中点O ,A ,B 的坐标分别为(0,0),(1,2),(3,1),求f ⎝⎛⎭⎪⎫1f的值. 解析:由f (3)=1得1f=1,故f ⎝⎛⎭⎪⎫1f=f (1)=2. 10.已知函数f (x )=x 2+px +q 且满足f (-1)=f (2)=0,求函数f (x )的解析式.解析:因为f (-1)=f (2)=0,所以有⎩⎪⎨⎪⎧1-p +q =0,4+2p +q =0,解得⎩⎪⎨⎪⎧p =-1,q =-2,故f (x )=x 2-x -2.[能力提升](20分钟,40分)11.某学校要召开学生代表大会,规定根据班级人数每10人给一个代表名额,当班级人数除以10的余数大于6时,再增加一名代表名额.那么各班代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可表示为( )A .y =⎣⎢⎡⎦⎥⎤x 10B .y =⎣⎢⎡⎦⎥⎤x +310C .y =⎣⎢⎡⎦⎥⎤x +410 D .y =⎣⎢⎡⎦⎥⎤x +510解析:因为是大于6而非大于等于6,故要加3. 答案:B12.若f (x )-12f (-x )=2x (x ∈R ),则f (2)=________.解析:∵f (x )-12f (-x )=2x ,∴⎩⎪⎨⎪⎧f -12f -=4,f--12f =-4,得⎩⎪⎨⎪⎧2f -f -=8,f --12f =-4,相加得32f (2)=4,f (2)=83.答案:8313.作出下列函数的图象并写出其值域: (1)y =2x,x ∈[2,+∞);(2)y =x 2+2x ,x ∈[-2,2]. 解析:(1)列表当x ∈[2,+∞)时,图象是反比例函数y =x的一部分,观察图象可知其值域为(0,1].(2)列表:由图可得函数的值域是[-1,8].14.已知函数f (x )=xax +b(a ,b 为常数,且a ≠0)满足f (2)=1,且f (x )=x 有唯一解,求函数y =f (x )的解析式和f (f (-3))的值.解析:因为f (2)=1,所以22a +b =1,即2a +b =2,①又因为f (x )=x 有唯一解,即x ax +b=x 有唯一解,所以ax 2+(b -1)x =0有两个相等的实数根,所以Δ=(b -1)2=0,即b =1.代入①得a =12.所以f (x )=x12x +1=2x x +2. 所以f (f (-3))=f ⎝ ⎛⎭⎪⎫-6-1=f (6)=2×66+2=32.。
人教A版高中数学第一册(必修1)课时作业1:第二课时 指数函数的图象和性质的应用

第二课时 指数函数的图象和性质的应用基础达标一、选择题 1.函数f (x )=3x -1的定义域为( )A.(-∞,1)B.(-∞,1』C.『1,+∞)D.(1,+∞)『解 析』 由x -1≥0可得x ≥1,所以函数f (x )=3x -1的定义域为『1,+∞).『答 案』 C2.若⎝ ⎛⎭⎪⎫142a +1<⎝ ⎛⎭⎪⎫148-2a ,则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫74,+∞B.(1,+∞)C.(-∞,1)D.⎝ ⎛⎭⎪⎫-∞,74 『解 析』 函数y =⎝ ⎛⎭⎪⎫14x在R 上为减函数,所以2a +1>8-2a ,所以a >74.故选A.『答 案』 A3.已知a =30.2,b =0.2-3,c =(-3)0.2,则a ,b ,c 的大小关系为( ) A.a >b >c B.b >a >c C.c >a >bD.b >c >a『解 析』 a =30.2∈(1,3),b =0.2-3=⎝ ⎛⎭⎪⎫15-3=53=125,c =(-3)0.2=()-315<0,所以b >a >c . 『答 案』 B4.同一直角坐标系中函数y =⎝ ⎛⎭⎪⎫12x ,y =⎝ ⎛⎭⎪⎫13x,y =3x ,y =2x 的图象如图所示,则上述函数分别对应的图象是( )A.①②③④B.②①③④C.④③②①D.③④②①『解 析』 由指数函数的图象在y 轴右侧“底大图高”的特点知,选A. 『答 案』 A5.比较⎝ ⎛⎭⎪⎫1323,34,⎝ ⎛⎭⎪⎫13-2的大小关系为( )A.34>⎝ ⎛⎭⎪⎫13-2>⎝ ⎛⎭⎪⎫1323B.⎝ ⎛⎭⎪⎫1323>34>⎝ ⎛⎭⎪⎫13-2C.34>⎝ ⎛⎭⎪⎫1323>⎝ ⎛⎭⎪⎫13-2D.⎝ ⎛⎭⎪⎫13-2>⎝ ⎛⎭⎪⎫1323>34 『解 析』 因为y =⎝ ⎛⎭⎪⎫13x 是R 上的减函数,所以⎝ ⎛⎭⎪⎫1323<⎝ ⎛⎭⎪⎫130=1,34=81,⎝ ⎛⎭⎪⎫13-2=(3-1)-2=9,所以34>⎝ ⎛⎭⎪⎫13-2>⎝ ⎛⎭⎪⎫1323.『答 案』 A 二、填空题6.已知函数f (x )=n ·3x -23x +1为奇函数,则n 的值为________.『解 析』 由f (0)=n -21+1=0,解得n =2,当n =2时,f (x )=2×(3x -1)3x+1,易证其是奇函数. 『答 案』 27.函数y =2-x 2+ax 在(-∞,1)内单调递增,则a 的取值范围是________.『解 析』 由复合函数的单调性知,y =-x 2+ax 的对称轴x =a2≥1,即a ≥2. 『答 案』 『2,+∞)8.设函数y =1+2x +a ·4x ,若函数在(-∞,1』上有意义,则实数a 的取值范围是________.『解 析』 设t =2x ,∵x ∈(-∞,1』,∴0<t ≤2.则原函数有意义等价于1+t +at 2≥0在t ∈(0,2』上恒成立,∴a ≥-t +1t 2,设f (t )=-1+t t 2,则f (t )=-1+t t 2=-⎝ ⎛⎭⎪⎫1t +122+14,∵0<t ≤2,所以1t ∈⎣⎢⎡⎭⎪⎫12,+∞,∴f (t )≤f ()2=-34,∴a ≥-34. 『答 案』 ⎣⎢⎡⎭⎪⎫-34,+∞三、解答题9.设0≤x ≤2,y =4x -12-3·2x +5,试求该函数的最值. 解 令t =2x ,0≤x ≤2,∴1≤t ≤4. 则y =22x -1-3·2x +5=12t 2-3t +5. 配方得y =12(t -3)2+12,t ∈『1,4』,∴y =12(t -3)2+12,t ∈『1,3』上是减函数;t ∈『3,4』上是增函数, ∴当t =3时,y min =12;当t =1时,y max =52. 故函数的最大值为52,最小值为12.10.已知函数f (x )=⎝ ⎛⎭⎪⎫13ax 2-4x +3.(1)若a =-1时,求函数f (x )的单调增区间; (2)如果函数f (x )有最大值3,求实数a 的值.解 (1)当a =-1时,f (x )=⎝ ⎛⎭⎪⎫13-x 2-4x +3,令g (x )=-x 2-4x +3=-(x +2)2+7,由于g (x )在(-2,+∞)上递减,y =⎝ ⎛⎭⎪⎫13x在R 上是减函数,∴f (x )在(-2,+∞)上是增函数,即f (x )的单调增区间是(-2,+∞). (2)令h (x )=ax 2-4x +3,f (x )=⎝ ⎛⎭⎪⎫13h (x ),由于f (x )有最大值3,所以h (x )应有最小值-1. 因此必有⎩⎪⎨⎪⎧a >0,12a -164a =-1,解得a =1,即当f (x )有最大值3时,实数a 的值为1.能力提升11.已知函数g (x )=ax 2-2ax +1+b (a >0)在区间『2,3』上有最大值4和最小值1.设f (x )=g (x )x .(1)求a ,b 的值.(2)若不等式f (2x )-k ·2x ≥0在x ∈『-1,1』上有解,求实数k 的取值范围. 解 (1)g (x )=a (x -1)2+1+b -a ,因为a >0,所以g (x )在区间『2,3』上是增函数,故⎩⎪⎨⎪⎧g (2)=1+b =1,g (3)=3a +1+b =4,解得⎩⎪⎨⎪⎧a =1,b =0.(2)由(1)可得f (x )=x +1x -2,所以f (2x )-k ·2x ≥0可化为2x +12x -2≥k ·2x , 化为1+⎝ ⎛⎭⎪⎫12x 2-2·12x ≥k .令t =12x ,则k ≤t 2-2t +1. 因x ∈『-1,1』,故t ∈⎣⎢⎡⎦⎥⎤12,2.记h (t )=t 2-2t +1,因为t ∈⎣⎢⎡⎦⎥⎤12,2,故h (t )max =1,所以实数k 的取值范围是(-∞,1』.12.设函数f (x )=e x a +ae x ,(e 为无理数,且e ≈2.718 28…)是R 上的偶函数且a >0. (1)求a 的值;(2)判断f (x )在(0,+∞)上的单调性.解 (1)∵f (x )是R 上的偶函数,∴f (-1)=f (1), ∴e -1a +a e -1=e a +a e ,即1a e -a e =ea -a e. ∴1e ⎝ ⎛⎭⎪⎫1a -a =e ⎝ ⎛⎭⎪⎫1a -a , ∴1a -a =0,∴a 2=1,又a >0,∴a =1. (2)f (x )=e x +e -x .设x 1,x 2>0,且x 1<x 2,f (x 2)-f (x 1)=e x 2+e -x 2-e x 1-e -x 1=e x 2-e x 1+1e x 2-1e x 1=e x 2-e x 1+e x 1-e x 2e x 1e x 2=(e x 2-e x 1)⎝ ⎛⎭⎪⎫1-1e x 1e x 2.∵x 1,x 2>0,x 1<x 2,∴e x 2>e x 1且e x 1e x 2>1, ∴(e x 2-e x 1)⎝ ⎛⎭⎪⎫1-1e x 1e x 2>0,即f (x 2)>f (x 1), ∴f (x )在(0,+∞)上为增函数.。
高中数学 1.2.1函数的概念课时作业(含解析)新人教A版必修1

课时作业(六) 函数的概念[学业水平层次]一、选择题1.对于函数y =f (x ),以下说法中正确的个数为( )①y 是x 的函数;②对于不同的x ,y 值也不同;③f (a )表示当x =a 时函数f (x )的值,是一个常量.A .0B .1C .2D .3【解析】 ①③正确;②不正确;如f (x )=x 2,f (-1)=f (1).【答案】 C2.下列各组函数中,表示同一函数的是( ) A .y =x 2-9x -3与y =x +3 B .y =x 2-1与y =x -1C .y =x 0(x ≠0)与y =1(x ≠0)D .y =2x +1,x ∈Z 与y =2x -1,x ∈Z【解析】 A 项中两函数的定义域不同;B 项,D 项中两函数的对应关系不同,故选C.【答案】 C3.下列图形中不是函数图象的是( )A B C D【解析】 由函数的定义,即对于任一自变量,都有唯一确定的函数值与之对应来验证图象是否为函数图象.选项B 、C 、D 都符合函数定义的要求,而选项A ,自变量都有两个值与之对应,不符合函数定义,故选A.【答案】 A4.(2014·广西桂林中学段考)已知函数f (x )=12-x 的定义域为M ,g (x )=x +2的定义域为N ,则M ∩N =( ) A.{}x |x ≥-2 B.{}x |x <2C.{}x |-2<x <2D.{}x |-2≤x <2【解析】 ∵M ={}x |x <2,N {}x |x ≥-2,∴M ∩N ={}x |-2≤x <2,故选D.【答案】 D二、填空题5.(2013·渐江高考)已知函数f (x )=x -1.若f (a )=3,则实数a =________.【解析】 f (a )=3,得a -1=3,解得a =10.【答案】 106.函数y =x 2-2x 的定义域为{0,1,2,3},那么其值域为________.【解析】 由函数的定义可知,当x =0时,y =0;当x =1时,y =1-2=-1;当x =2时,y =4-4=0;当x =3时,y =9-6=3,∴值域为{-1,0,3}.【答案】 {-1,0,3}7.若A ={x |y =x +1},B ={}y |y =x 2+1,则A ∩B =________. 【解析】 由A ={x |y =x +1},B ={}y |y =x 2+1,得A =[-1,+∞),B =[1,+∞),∴A ∩B =[1,+∞). 【答案】 [1,+∞)三、解答题8.求下列函数的定义域:(1)y =2x +1+3-4x ;(2)y =1|x +2|-1. 【解】 (1)由已知得⎩⎪⎨⎪⎧2x +1≥0,3-4x ≥0,∴⎩⎪⎨⎪⎧x ≥-12,x ≤34,∴-12≤x ≤34,∴函数的定义域为⎣⎢⎡⎦⎥⎤-12,34. (2)由已知得:∵|x +2|-1≠0,∴|x +2|≠1,∴函数的定义域(-∞,-3)∪(-3,-1)∪(-1,+∞).9.已知函数f (x )=x +1x. (1)求f (x )的定义域;(2)求f (-1),f (2)的值;(3)当a ≠-1时,求f (a +1)的值.【解】 (1)要使函数f (x )有意义,必须使x ≠0,∴f (x )的定义域是(-∞,0)∪(0,+∞).(2)f (-1)=-1+1-1=-2, f (2)=2+12=52.(3)当a ≠-1时,a +1≠0,∴f (a +1)=a +1+1a +1. [能力提升层次]1.若函数f (x )=ax 2-1,a 为一个正实数,且f (f (-1))=-1,那么a 的值是( )A .1B .0C .-1D .2【解析】 f (-1)=a ·(-1)2-1=a -1,f [f (-1)]=a ·(a -1)2-1=a 3-2a 2+a -1=-1.∴a 3-2a 2+a =0,∴a =1或a =0(舍去).【答案】 A2.(2014·湖北襄阳四中、龙泉中学、荆州中学联考)已知函数f (2x +1)的定义域为⎝⎛⎭⎪⎫-2,12,则f (x )的定义域为( ) A.⎝ ⎛⎭⎪⎫-32,14 B.⎝⎛⎭⎪⎫-1,32 C .(-3,2)D .(-3,3) 【解析】 由于函数f (2x +1)的定义域为⎝⎛⎭⎪⎫-2,12,即-2<x <12,所以-3<2x +1<2,故函数f (x )的定义域为(-3,2),选C.【答案】 C3.已知集合A ={x |x ≥4},g (x )=11-x +a 的定义域为B ,若A ∩B =∅,则实数a 的取值范围是________. 【解析】 g (x )的定义域B ={x |x <a +1},由于A ∩B =∅,画数轴:易得a +1≤4,即a ≤3.【答案】 (-∞,3]4.已知函数f (x )=x 2+1,x ∈R.(1)分别计算f (1)-f (-1),f (2)-f (-2),f (3)-f (-3)的值;(2)由(1)你发现了什么结论?并加以证明.【解】(1)f(1)-f(-1)=(12+1)-[(-1)2+1]=2-2=0;f(2)-f(-2)=(22+1)-[(-2)2+1]=5-5=0;f(3)-f(-3)=(32+1)-[(-3)2+1]=10-10=0.(2)由(1)可发现结论:对任意x∈R,有f(x)-f(-x)=0.证明如下:∵f(-x)=(-x)2+1=x2+1=f(x),∴对任意x∈R,总有f(x)-f(-x)=0.。
人教A版数学必修一绥化市第九中学高一《函数表示》课时作业(2).docx

高中数学学习材料唐玲出品绥化市第九中学高一《函数表示》课时作业(2)1. 设集合2{|430}A x x x =-+< ,{|230}B x x =->,则AB = ( ) A.3(3,)2-- B.3(3,)2- C.3(1,)2 D .3(,3)22. 已知集合{}{}213,4,P x x Q x x =∈≤≤=∈≥R R 则()P Q =R C ( )A .[2,3]B .( -2,3 ]C .[1,2)D .(,2][1,)-∞-⋃+∞3.下列从P 到Q 的各对应关系f 中,不是映射的是( )A .P =N ,Q =N *,f :x →|x -8|B .P ={1,2,3,4,5,6},Q ={-4,-3,0,5,12},f :x →x (x -4)C .P =N *,Q ={-1,1},f :x →(-1)xD .P =Z ,Q ={有理数},f :x →x 24.已知函数()||f x x x =,若0()4f x =,则0x 的值为( )A.-2 B.2 C.-2或2 D.25. 函数y =232x x -- 的定义域是 .6.已知21(1)()2(1)x x f x x x ⎧-≥=⎨--<⎩,(1)求[(1)]f f -的值(2)若0()9f x =,求实数0x 的值.7.画出下列函数的图象,并根据图象写出函数的值域(1)|2|y x =- (2)22(1)(24)y x x =-++ (3)22||y x x =- (4)2|2|y x x =- 能力提升题1.已知函数2[1,1]()[1,1]x f x x x ∈-⎧=⎨∉-⎩,若f [f (x )]=2,则x 的取值范围是______.2.已知函数10()10x x f x x x -+<⎧=⎨-≥⎩,则不等式()1(1)1x x f x +++≤的解集是________ 3.已知函数22()12,()2f x x g x x x =-=-,若(),()()()(),()()g x f x g x F x f x f x g x ≥⎧=⎨<⎩,则()F x 的值域是____ 4.设函数⎩⎨⎧<+≥+-=0,60,64)(2x x x x x x f 则不等式)1()(f x f >的解集是____. 参考答案:1. D2. B3.A4. B5. []3,1-6.解:(1)(1)(1)23f -=--+=,2[(1)](3)318f f f ∴-==-=(2)当01x ≥时200()19f x x =-=,010x ∴=±,由01x ≥,得010x =; 当01x <时00()29f x x =--=,0111x ∴=-<,011x ∴=-从而实数0x 的值为10与11-7. 解:(1)2(2)|2|2(2)x x y x x x -≥⎧=-=⎨-<⎩,由图知:函数的值域为[0,)+∞(2)2233(1)(1)(24)|1||24|5(21)33(2)x x y x x x x x x x x +≥⎧⎪=-++=-++=+-≤<⎨⎪--<-⎩由图知:函数的值域为[3,)+∞(3)2222(0)2||2(0)x x x y x x x x x ⎧-≥⎪=-=⎨+<⎪⎩由图知:函数的值域为[1,)-+∞(4)2222(20)|2|2(02)x x x x y x x x x x ⎧-≥≤⎪=-=⎨-+<<⎪⎩或由图知:函数的值域为:[0,)+∞能力提升题1. {2}∪[-1,1];2. 1,12⎡⎤--+⎣⎦;3. 7(,]9-∞;4.=),3()1,3(+∞⋃-。
