全等三角形证明辅助线分析实例
辅助线证明题三角形全等

做辅助线证明三角形全等1、如图,等腰直角三角形ABC 中,∠ACB =90°,AD 为腰CB 上的中线,CE ⊥AD 交AB 于E .求证∠CDA =∠EDB .2、在Rt △ABC 中,∠A =90°,CE 是角平分线,和高AD 相交于F ,作FG ∥BC 交AB 于G ,求证:AF =BG .3、如图,已知△ABC 是等边三角形,∠BDC =120º,说明AD=BD+CD 的理由4、如图,在△ABC 中,AD 是中线,BE 交AD 于F,且AE=EF,说明AC=BF 的理由5、如图,在△ABC 中,∠ABC=100º,AM=AN,CN=CP,求∠MNP 的度数C 1 2 A B CD E6、用两个全等的等边三角形△ABC 和△ACD 拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A 重合,两边分别与AB 、AC 重合.将三角尺绕点A 按逆时针方向旋转.(1)当三角尺的两边分别与菱形的两边BC 、CD 相交于点E 、F 时(如图所示),通过观察或测量BE 、CF 的长度,你能得出什么结论?并证明你的结论;B(2)当三角尺的两边分别与菱形的两边BC 、CD 的延长线相交于点E 、F 时(如图所示),你在(1)中得到的结论还成立吗?说明理由。
B7、.在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE =AD +BE ;(2)当直线MN 绕点C 旋转到图2的位置时,求证:DE =AD -BE ;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.C B A ED 图1 N M A B C DE M N 图2 A C B E D N M 图3。
初中数学中考复习考点知识与题型专题讲解20 全等三角形的辅助线问题(解析版)

初中数学中考复习考点知识与题型专题讲解专题20全等三角形的辅助线问题【考点题型】考点题型一连接两点做辅助线典例1.把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC 交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.【解析】试题分析:要证明HG与HB是否相等,可以把线段放在两个三角形中证明这两个三角形全等,或放在一个三角形中证明这个三角形是等腰三角形,而图中没有这样的三角形,因此需要作辅助线,构造三角形.试题解析:HG=HB,证法1:连接AH,∵四边形ABCD,AEFG都是正方形,∴∠B=∠G=90°,由题意知AG=AB,又AH=AH,∴Rt△AGH≌Rt△ABH(HL),∴HG=HB.证法2:连接GB,∵四边形ABCD,AEFG都是正方形,∴∠ABC=∠AGF=90°,由题意知AB=AG,∴∠AGB=∠ABG,∴∠HGB=∠HBG,∴HG=HB.变式1-1.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形画出图形,写出结论不证明.【答案】(1)见解析;(2)见解析【分析】(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;(2)根据题意画出图形,连接AD,构造△DAF≌△DBE.得出FD=ED ,∠FDA=∠EDB,再算出∠EDF=90°,即可得出△DEF是等腰直角三角形.【详解】解:(1)连结AD ,∵AB=AC ,∠BAC=90°,D为BC中点,∴AD⊥BC ,BD=AD ,∴∠B=∠BAD=∠DAC=45°,又∵BE=AF ,∴△BDE≌△ADF(SAS),∴ED=FD ,∠BDE=∠ADF,∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,∴△DEF为等腰直角三角形.(2)连结AD∵AB=AC ,∠BAC=90°,D 为BC 中点 , ∴AD=BD ,AD ⊥BC ,∴∠DAC=∠ABD=45°, ∴∠DAF=∠DBE=135°, 又∵AF=BE ,∴△DAF ≌△DBE (SAS ),∴FD=ED ,∠FDA=∠EDB,∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°. ∴△DEF 为等腰直角三角形.变式1-2.如图,以O 为直角顶点作两个等腰直角三角形Rt OAB 和Rt OCD △,且点C 在线段AB 上(A B 、除外),求证:222AC BC CD +=【答案】证明见解析【分析】连接BD ,证明△AOC ≌△BOD (SAS ),得到△CBD 为直角三角形,再由勾股定理即可证明.【详解】解:连接BD ,∵△AOB 与△COD 为等腰直角三角形,∴AO=BO ,CO=DO ,∠AOB=∠COD=90°,∠A=∠ABO=45°,∴∠AOC+∠BOC=∠BOD+∠BOC∴∠AOC=∠BOD ,在△AOC 与△BOD 中,AO BO AOC BOD CO DO =⎧⎪∠=∠⎨⎪=⎩,∴△AOC ≌△BOD (SAS )∴∠A=∠OBD=45°,AC=BD ,∴∠ABO+∠OBD=90°,即∠CBD=90°,∴在Rt △CBD 中,222BD BC CD +=即222AC BC CD +=.考点题型二全等三角形 -倍长中线模型典例2.已知,在Rt ABC △中,90BAC ∠=︒,点D 为边AB 的中点,AE CD ⊥分别交CD ,BC 于点F ,E .(1)如图1,①若AB AC =,请直接写出EAC BCD ∠-∠=______;②连接DE ,若2AE DE =,求证:DEB AEC ∠=∠;(2)如图2,连接FB ,若FB AC =,试探究线段CF 和DF 之间的数量关系,并说明理由.【答案】(1)①45°;②见解析;(2)2CF DF =,理由见解析【分析】(1)①利用直角三角形两个锐角相加得90︒和三角形的外角等于不相邻的两个内角和的性质结合题干已知即可解题.②延长ED 至点G ,使得DG DE =,连接AG ,从而可证明ADG ≌BDE (SAS ),再利用全等的性质,可知DGA DEB ∠=∠,即可知道//AG BC ,所以GAE AEC ∠=∠,根据题干又可得到AE EG =,所以DGA GAE ∠=∠,从而得出结论.(2)延长CD 至点H ,使得DH DF =,连接BH ,从而可证明HDB ≌FDA △(SAS ),再利用全等的性质,可知BH AF =,90H AFD AFC ∠=∠=∠=︒,根据题干即可证明Rt HBF △≌Rt FAC △(HL ),即得出结论.【详解】(1)①∵90EAC ACD ∠+∠=︒,90AEC BCD ∠+∠=︒∴EAC BCD AEC ACD ∠-∠=∠-∠∵90EAC BAE ∠+∠=︒∴ACD BAE ∠=∠又∵AEC B BAE ∠=∠+∠∴EAC BCD B BAE ACD ∠-∠=∠+∠-∠∴45EAC BCD B ∠-∠=∠=︒故答案为45︒.②如图,延长ED 至点G ,使得DG DE =,连接AG ,∵点D 为AB 的中点,∴BD AD =,又∵ADG BDE ∠=∠,∴ADG ≌BDE ,∴DGA DEB ∠=∠,∴//AG BC ,∴GAE AEC ∠=∠,又∵2AE DE =,∴AE EG =,∴DGA GAE ∠=∠,∴DEB AEC ∠=∠.(2)2CF DF =.如图,延长CD 至点H ,使得DH DF =,连接BH ,∵AD BD =,ADF BDH ∠=∠,∴HDB ≌FDA △,∴BH AF =,90H AFD AFC ∠=∠=∠=︒,∵BF AC =.∴Rt HBF △≌Rt FAC △,∴2CF HF DF ==.变式2-1.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.(探究与发现)(1)如图1,AD 是ABC 的中线,延长AD 至点E ,使ED AD =,连接BE ,证明:ACD EBD △≌△.(理解与应用)(2)如图2,EP 是DEF 的中线,若5EF =,3DE =,设EP x =,则x 的取值范围是________.(3)如图3,AD 是ABC 的中线,E 、F 分别在AB 、AC 上,且DE DF ⊥,求证:BE CF EF +>.【答案】(1)见解析;(2)14x <<;(3)见解析【分析】(1)根据全等三角形的判定即可得到结论;(2)延长EP 至点Q ,使PQ PE =,连接FQ ,根据全等三角形的性质得到3FQ DE ==,根据三角形的三边关系即可得到结论;(3)延长FD 至G ,使得GD DF =,连接BG ,EG ,结合前面的做题思路,利用三角形三边关系判断即可.【详解】(1)证明:CD BD =,ADC EDB ∠=∠,AD ED =,ACD EBD ∴≌,(2)14x <<;如图,延长EP 至点Q ,使PQ PE =,连接FQ ,在PDE ∆与PQF ∆中,PE PQ EPD QPF PD PF =⎧⎪∠=∠⎨⎪=⎩,PEP QFP ∴∆≅∆,3FQ DE ∴==,在EFQ ∆中,EF FQ QE EF FQ -<<+,即53253x -<<+, x 的取值范围是14x <<;故答案为:14x <<;(3)延长FD 至G ,使得GD DF =,连接BG ,EG ,在DFC △和DGB 中,DF DG =,CDF BDG ∠=∠,DC DB =,(SAS)DFC DGB ∴≌,BG CF ∴=,在EDF 和EDG △中,DF DG =,90FDE GDE ∠=∠=︒,DE DE =,(SAS)EDF EDG ∴≌,EF EG ∴=,在BEG 中,两边之和大于第三边,BG BE EG ∴+>,又EF EG =,BG CF =,BE CF EF ∴+>变式2-2.倍长中线的思想在丁倍长某条线段(被延长的线段a 要满足两个条件:①线段a 一个端点是图中一条线段b 的中点;②线段a 与这条线段b 不共线),然后进行连接,构造三角形全等,再进一步将某些线段进行等量代换,再证明全等或其他的结论,从而解决问题.(应用举例)如图(1),已知:AD 为ABC ∆的中线,求证:2AB AC AD +>.简证:如图(2),延长AD 到E ,使得DE AD =,连接CE ,易证ABD ECD ∆≅∆,得AB =,在ACE ∆中,AC CE +>,2AB AC AD +>.(问题解决)(1)如图(3),在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,求证:AF EF =.(2)如图(4),在ABC ∆中,90,A D ∠=︒是BC 边的中点,E F 、分别在边AB AC 、上,DE DF ⊥,若3,4BE CF ==,求EF 的长.(3)如图(5),AD 是ABC ∆的中线,,AB AE AC AF ==,且90BAE FAC ∠=∠=︒,请直接写出AD 与EF 的数量关系_及位置关系_.【答案】,CE AE ;(1)详见解析;(2)5;(3)2EF AD =,EF AD ⊥【应用举例】由全等的性质可得AB=EC ,由三角形三边关系可得AC+CE>AE ,即AB+AC>2AD ;故答案为EC ,AE ;【问题解决】(1)由题意不难得到,ACD GBD ∆≅∆所以∠BGD=∠BED=∠AEF=∠DAC ,∴有AF=EF ;(2)延长ED 到G ,使DG=ED ,连结CG 、FG ,不难得到EF=FG ,另同(1)有△BDE ≌△CDG ,所以∠FCG=∠FCD+∠GCD=∠FCD+∠EBD=90°,CG=BE=3,由勾股定理可得FG 即EF 的长;(3)由全等三角形的性质可以得到解答.【详解】【应用举例】,CE AE【问题解决】()1如图()1延长AD 到G ,使得,DG AD =连接,BG易证,ACD GBD ∆≅∆得,BG AC G DAC =∠=∠,,BE AC =,BE BG ∴=,G BEG ∴∠=∠,BEG AEF ∠=∠,AEF EAC ∴∠=∠AF EF ∴=.()2如图()2,延长ED 到G ,使得,DG ED =连接,CG FG 、易证,BDE CDG ∆≅∆得,,CG BE ED GD B DCG ==∠=∠,,DE DF ⊥DF ∴垂直平分,EG,FE FG ∴=90,A ∠=︒90,B ACB ∴∠+∠=︒90,DCG ACB ∴∠+∠=︒即90,FCG ∠=︒在Rt FCG ∆中,3,4CG BE CF ===,5,FG ∴=5,EF ∴=()32EF AD EF AD =⊥,,理由如下:如图3,延长AD 到G ,使AD=DG ,延长DA 交EF 于P ,连结BG ,则不难得到△BGD≌△CAD,∴BG=AC,∠GBD=∠ACD,∠DGB=∠DAC,又AF=AC,∴BG=AF,∴∠ABG=∠ABD+∠GBD=∠ABD+∠ACD=180°-∠BAC=∠EAF,∴在△ABG和△EAF中,AB AEABG EAF BG AF=⎧⎪∠=∠⎨⎪=⎩,∴△ABG≌△EAF,∴EF=AG=2AD,∠EFA=∠DGB=∠DAC,∵∠DAC+∠PAF=180°-∠FAC=180°-90°=90°,∴∠EFA+∠PAF=90°,∴∠APF=90°,∴EF⊥AD .考点题型三全等三角形–旋转模型典例3.在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度α得到△AED,点B、C的对应点分别是E、D.(1)如图1,当点E恰好在AC上时,求∠CDE的度数;(2)如图2,若α=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.【答案】(1)15°;(2)证明见解析.【分析】(1)如图1,利用旋转的性质得CA=DA,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,再根据等腰三角形的性质求出∠ADC,从而计算出∠CDE的度数;(2)如图2,利用直角三角形斜边上的中线性质得到BF=12AC,利用含30度的直角三角形三边的关系得到BC=12AC,则BF=BC,再根据旋转的性质得到∠BAE=∠CAD=60°,AB=AE,AC=AD ,DE=BC,从而得到DE=BF,△ACD和△BAE为等边三角形,接着由△AFD≌△CBA得到DF=BA,然后根据平行四边形的判定方法得到结论.【详解】解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,∴∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,∵CA=DA,∴∠ACD=∠ADC=12(180°−30°)=75°,∠ADE=90°-30°=60°,∴∠CDE=75°−60°=15°;(2)证明:如图2,∵点F是边AC中点,∴BF=12 AC,∵∠BAC=30°,∴BC=12 AC,∴BF=BC,∵△ABC绕点A顺时针旋转60°得到△AED,∴∠BAE=∠CAD=60°,AB=AE,AC=AD,DE=BC,∴DE=BF,△ACD和△BAE为等边三角形,∴BE=AB,∵点F为△ACD的边AC的中点,∴DF⊥AC,易证得△AFD≌△CBA,∴DF=BA,∴DF=BE,而BF=DE,∴四边形BEDF是平行四边形.变式3-1.给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.①求证:△BCE是等边三角形;②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.【答案】(1)正方形、矩形、直角梯形均可;(2)①证明见解析②证明见解析【分析】(1)根据定义和特殊四边形的性质,则有矩形或正方形或直角梯形;(2)①首先证明△ABC≌△DBE,得出AC=DE,BC=BE,连接CE,进一步得出△BCE 为等边三角形;②利用等边三角形的性质,进一步得出△DCE是直角三角形,问题得解.【详解】解:(1)正方形、矩形、直角梯形均可;(2)①∵△ABC≌△DBE,∴BC=BE,∵∠CBE=60°,∴△BCE是等边三角形;②∵△ABC≌△DBE,∴BE=BC,AC=ED;∴△BCE为等边三角形,∴BC=CE,∠BCE=60°,∵∠DCB=30°,∴∠DCE=90°,在Rt △DCE 中,DC 2+CE 2=DE 2,∴DC 2+BC 2=AC 2.变式3-2.如图,在ABC △中,90BAC ∠=︒,E 为边BC 上的点,且AB AE =,D 为线段BE 的中点,过点E 作EF AE ⊥,过点A 作AF BC ,且AF 、EF 相交于点F .(1)求证:C BAD ∠=∠(2)求证:AC EF =【答案】(1)见解析;(2)见解析【分析】(1)由等腰三角形的性质可得AD ⊥BC ,由余角的性质可得∠C=∠BAD ;(2)由“ASA”可证△ABC ≌△EAF ,可得AC=EF .【详解】(1)如图∵AB AE =,∴ABE ∆是等腰三角形 又∵D 为BE 的中点, ∴AD BE ⊥(等腰三角形三线合一) 在Rt ABC ∆和Rt DBA ∆中, ∵B 为公共角,90BAC BDA ∠=∠=︒, ∴C BAD ∠=∠.另解:∵D 为BE 的中点, ∵BD ED =,又AB AE =,AD AD =, ∴ADB ADE ∆≅∆,∴ADB ADE ∠=∠,又180ADB ADE ∠+∠=︒, ∴90ADB ADE ∠=∠=︒ ∴AD BC ⊥,在Rt ABC ∆和Rt DBA ∆中, ∵B 为公共角,90BAC BDA ∠=∠=︒, ∴C BAD ∠=∠.(2)∵AF BC ,∴EAF AEB ∠=∠,∵AB AE =,∴ABE AEB ∠=∠,∴EAF ABC ∠=∠,又∵90BAC AEF ∠=∠=∠︒, ∴BAC AEF ∆≅∆,∴AC EF =.考点题型四全等三角形– 垂线模型典例4.在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证:△ADC ≌△CEB ;(2)当直线MN 绕点C 旋转到图2的位置时,试问DE 、AD 、BE 的等量关系?并说明理由. 【答案】(1)见解析;(2)DE=AD-BE ,理由见解析【分析】(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE ,根据AAS 即可得到答案;(2)与(1)证法类似可证出∠ACD=∠EBC ,能推出△ADC ≌△CEB ,得到AD=CE ,CD=BE ,即可得到答案.【详解】解:(1)证明:如图1,∵AD ⊥DE ,BE ⊥DE ,∴∠ADC=∠BEC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,∴∠DAC=∠BCE ,在△ADC 和△CEB 中, CDA BEC DAC ECB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS );(2)结论:DE=AD-BE .理由:如图2,∵BE ⊥EC ,AD ⊥CE ,∴∠ADC=∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB=90°,∴∠ECB+∠ACE=90°,∴∠ACD=∠EBC ,在△ADC 和△CEB 中,ACD CBE ADC BEC AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS ),∴AD=CE ,CD=BE ,∴DE=EC-CD=AD-BE .变式4-1.在直角三角形ABC 中,90,30︒︒∠=∠=ACB BAC ,分别以AB 、AC 为边在ABC ∆外侧作等边ABE ∆和等边ACD ∆,DE 交AB 于点F ,求证:=EF FD .【答案】详见解析【分析】过点E 作EG AB ⊥于点G ,则有1122AG BG AE AB ===,再证 ()SAS ACB EGA ≅,得到EG AC =.从而得到90DAF DAC CAB ∠=∠+∠=︒,所以(AAS)ADF GEF ≅,即可完成证明。
初中几何辅助线解题举例大全(最全版)

初中几何辅助线解题举例大全(最全版) 三角形中作辅助线的常用方法举例一、延长已知边构造三角形:分析:欲证 AD =BC ,先证分别含有AD ,BC 的三角形全等,有几种方案:△ADC 与△BCD ,△AOD 与△BOC ,△ABD 与△BAC ,但根据现有条件,均无法证全等,差角的相等,因此可设法作出新的角,且让此角作为两个三角形的公共角。
证明:分别延长DA ,CB ,它们的延长交于E 点, ∵AD ⊥AC BC ⊥BD (已知) ∴∠CAE =∠DBE =90° (垂直的定义) 在△DBE 与△CAE 中∵⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已知已证公共角AC BD CAE DBE E E∴△DBE ≌△CAE (AAS )∴ED =EC EB =EA (全等三角形对应边相等) ∴ED -EA =EC -EB 即:AD =BC 。
(当条件不足时,可通过添加辅助线得出新的条件,为证题创造条件。
)二 、连接四边形的对角线,把四边形的问题转化成为三角形来解决。
三、有和角平分线垂直的线段时,通常把这条线段延长。
分析:要证BD =2CE ,想到要构造线段2CE ,同时CE 与∠ABC 的平分线垂直,想到要将其延长。
证明:分别延长BA ,CE 交于点F 。
∵BE ⊥CF (已知)DAEF 12ABCDE17-图O∴∠BEF =∠BEC =90° (垂直的定义)在△BEF 与△BEC 中,∵ ⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(21已证公共边已知BEC BEF BE BE ∴△BEF ≌△BEC (ASA )∴CE=FE=21CF (全等三角形对应边相等) ∵∠BAC=90° BE ⊥CF (已知)∴∠BAC =∠CAF =90° ∠1+∠BDA =90°∠1+∠BFC =90° ∴∠BDA =∠BFC在△ABD 与△ACF 中⎪⎩⎪⎨⎧∠=∠∠=∠)()()(已知=已证已证AC AB BFC BDA CAF BAC∴△ABD ≌△ACF (AAS )∴BD =CF (全等三角形对应边相等) ∴BD =2CE四、取线段中点构造全等三有形。
初中几何全等三角形常见辅助线作法

全等三角形常见辅助线作法【例1】.已知:如图6, 4BCE、△ACO分别是以8E、为斜边的直角三角形,且= ACDE是等边三角形.求证:△ A3c是等边三角形.【例2】、如图,已知BC>AB, AD=DCo BD 平分NABC。
求证:ZA+ZC=180°.线段的数量关系: 通过添加辅助线构造全等三角形转移线段到一个三角形中证明线段相等。
1、倍长中线法【例.3]如图,己知在△ABC中,ZC = 90°, ZB = 30°, A。
平分NB4C,交BC于点D.求证:BD = 2CD证明:延长DC到E,使得CE=CD,联结AEZC=90°A AC ± CDVCD=CEAD=AEVZB=30° ZC=90°ZBAC=60°YAD 平分NBACJ ZBAD=30°A DB=DA ZADE=60°VDB=DA:.BD=DE/. BD=2DC4B D笫3题•/ ZADE=60° AD=AEA △ ADE为等边三角形,AD=DE【例4.】如图,。
是AABC的边上的点,且CD = AB, ZADB = ZBAD, AE是AARD的中线。
求证:AC = 2AEo 证明:延长AE至IJ点F,使得EF=AE联结DF在4ABE和4FDE中BE=DEZAEB=ZFEDAE=FE/.△ABE 也AFDE (SAS) A AB=FD ZABE=ZFDE VAB=DCJ FD = DCZADC=ZABD+ZBAD ZADB = ZBAD,ZADC=ZABD+ZBDA VZABE=ZFDE・・・NADONADB+NFDE即ZADC= ZADF ffiAADF 和AADC 中AD=AD< ZADF= ZADC、DF =DC・•・△ ADF也ADC(SAS) AAF=ACAC=2AE【变式练习】、如图,AABC中,BD二DOAC, E是DC的中点,求证:AD平分NBAE.【小结】熟悉法一、法三“倍长中线”的辅助线包含的基本图形“八字型”和“倍长中线”两种基本操作方法, 倍长中线,或者倍长过中点的一条线段以后的对于解决含有过中点线段有很好的效果。
(完整版)几种证明全等三角形添加辅助线的方法

教学过程构造全等三角形几种方法在几何解题中,常常需要添加辅助线构造全等三角形,以沟通题设与结论之间的联系。
现分类加以说明。
一、延长中线构造全等三角形例1. 如图1,AD是△ABC的中线,求证:AB+AC>2AD。
证明:延长AD至E,使AD=DE,连接CE。
如图2。
∵AD是△ABC的中线,∴BD=CD。
又∵∠1=∠2,AD=DE,∴△ABD≌△ECD(SAS)。
AB=CE。
∵在△ACE中,CE+AC>AE,∴AB+AC>2AD。
二、沿角平分线翻折构造全等三角形例2. 如图3,在△ABC中,∠1=∠2,∠ABC=2∠C。
求证:AB+BD=AC。
证明:将△ABD沿AD翻折,点B落在AC上的E点处,即:在AC上截取AE=AB,连接ED。
如图4。
∵∠1=∠2,AD=AD,AB=AE,∴△ABD≌△AED(SAS)。
∴BD=ED,∠ABC=∠AED=2∠C。
而∠AED=∠C+∠EDC,∴∠C=∠EDC。
所以EC=ED=BD。
∵AC=AE+EC,∴AB+BD=AC。
三、作平行线构造全等三角形例3. 如图5,△ABC中,AB=AC。
E是AB上异于A、B的任意一点,延长AC到D,使CD=BE,连接DE交BC于F。
求证:EF=FD。
证明:过E作EM∥AC交BC于M,如图6。
则∠EMB=∠ACB,∠MEF=∠CDF。
∵AB=AC,∴∠B=∠ACB。
∴∠B=∠EMB。
故EM=BE。
∵BE=CD,∴EM=CD。
又∵∠EFM=∠DFC,∠MEF=∠CDF,∴△EFM≌△DFC(AAS)。
EF=FD。
四、作垂线构造全等三角形例4. 如图7,在△ABC中,∠BAC=90°,AB=AC。
M是AC边的中点。
AD ⊥BM交BC于D,交BM于E。
求证:∠AMB=∠DMC。
证明:作CF⊥AC交AD的延长线于F。
如图8。
∵∠BAC=90°,AD⊥BM,∴∠FAC=∠ABM=90°-∠BAE。
∵AB=AC,∠BAM=∠ACF=90°,∴△ABM≌△CAF(ASA)。
全等三角形(辅助线)
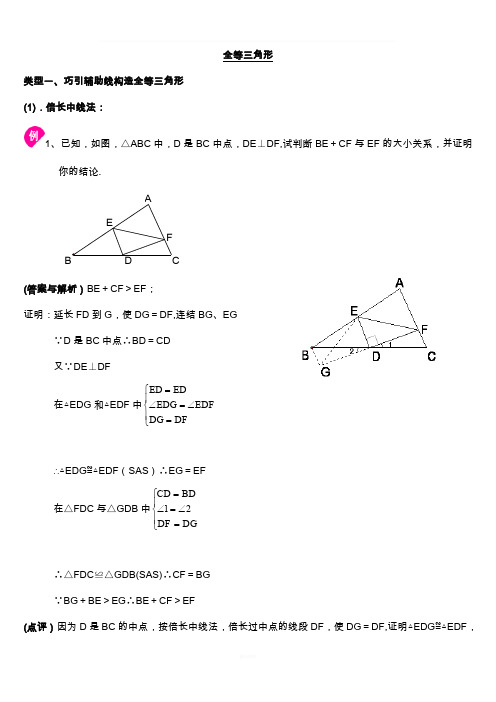
全等三角形类型一、巧引辅助线构造全等三角形(1).倍长中线法:1、已知,如图,△ABC 中,D 是BC 中点,DE ⊥DF,试判断BE +CF 与EF 的大小关系,并证明你的结论. FED C B A(答案与解析)BE +CF >EF ;证明:延长FD 到G ,使DG =DF,连结BG 、EG∵D 是BC 中点∴BD =CD又∵DE ⊥DF在△EDG 和△EDF 中ED ED EDG EDF DG DF =⎧⎪∠=∠⎨⎪=⎩∴△EDG ≌△EDF (SAS )∴EG =EF在△FDC 与△GDB 中⎪⎩⎪⎨⎧=∠=∠=DG DF BD CD 21∴△FDC ≌△GDB(SAS)∴CF =BG∵BG +BE >EG ∴BE +CF >EF(点评)因为D 是BC 的中点,按倍长中线法,倍长过中点的线段DF ,使DG =DF,证明△EDG ≌△EDF ,△FDC≌△GDB,这样就把BE、CF与EF线段转化到了△BEG中,利用两边之和大于第三边可证.有中点的时候作辅助线可考虑倍长中线法(或倍长过中点的线段).举一反三:(变式)已知:如图所示,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.(答案)证明:延长CE至F使EF=CE,连接BF.∵EC为中线,∴AE=BE.在△AEC与△BEF中,,,,AE BEAEC BEFCE EF=⎧⎪∠=∠⎨⎪=⎩∴△AEC≌△BEF(SAS).∴AC=BF,∠A=∠FBE.(全等三角形对应边、角相等)又∵∠ACB=∠ABC,∠DBC=∠ACB+∠A,∠FBC=∠ABC+∠A.∴AC=AB,∠DBC=∠FBC.∴AB=BF.又∵BC为△ADC的中线,∴AB=BD.即BF=BD.在△FCB与△DCB中,,,,BF BDFBC DBCBC BC=⎧⎪∠=∠⎨⎪=⎩∴△FCB≌△DCB(SAS).∴CF=CD.即CD=2CE.(2).作以角平分线为对称轴的翻折变换构造全等三角形2、已知:如图所示,在△ABC中,∠C=2∠B,∠1=∠2.求证:AB=AC+CD.(答案与解析)证明:在AB上截取AE=AC.在△AED 与△ACD 中,()12()()AE AC AD AD =⎧⎪∠=∠⎨⎪=⎩已作,已知,公用边,∴ △AED ≌△ACD (SAS ).∴ ∠AED =∠C(全等三角形对应边、角相等).又∵ ∠C =2∠B ∴∠AED =2∠B .由图可知:∠AED =∠B +∠EDB ,∴ 2∠B =∠B +∠EDB .∴ ∠B =∠EDB .∴ BE =ED .即BE =CD .∴ AB =AE +BE =AC +CD(等量代换).(点评)本题图形简单,结论复杂,看似无从下手,结合图形发现AB >AC .故用截长补短法.在AB 上截取AE =AC .这样AB 就变成了AE +BE ,而AE =AC .只需证BE =CD 即可.从而把AB =AC +CD 转化为证两线段相等的问题.举一反三:(变式)如图,AD 是ABC ∆的角平分线,H ,G 分别在AC ,AB 上,且HD =BD.(1)求证:∠B 与∠AHD 互补;(2)若∠B +2∠DGA =180°,请探究线段AG 与线段AH 、HD 之间满足的等量关系,并加以证明.(答案)证明:(1)在AB 上取一点M, 使得AM =AH, 连接DM.∵ ∠CAD =∠BAD, AD =AD, ∴ △AHD ≌△AMD. ∴ HD =MD, ∠AHD =∠AMD.∵ HD =DB, ∴ DB = MD. ∴ ∠DMB =∠B. ∵ ∠AMD +∠DMB =180︒,∴ ∠AHD +∠B =180︒. 即 ∠B 与∠AHD 互补.(2)由(1)∠AHD =∠AMD, HD =MD, ∠AHD +∠B =180︒.∵ ∠B +2∠DGA =180︒,∴ ∠AHD =2∠DGA.∴ ∠AMD =2∠DGM.∵ ∠AMD =∠DGM +∠GDM. ∴ 2∠DGM =∠DGM +∠GDM.∴ ∠DGM =∠GDM. ∴ MD =MG.∴ HD = MG.∵ AG = AM +MG, ∴ AG = AH +HD.(3).利用截长(或补短)法作构造全等三角形:M G H D CB A3、如图所示,已知△ABC 中AB >AC ,AD 是∠BAC 的平分线,M 是AD 上任意一点,求证:MB -MC <AB -AC .(答案与解析)证明:因为AB >AC ,则在AB 上截取AE =AC ,连接ME .在△MBE 中,MB -ME <BE (三角形两边之差小于第三边).在△AMC 和△AME 中,()()()AC AE CAM EAM AM AM =⎧⎪∠=∠⎨⎪=⎩所作,角平分线的定义,公共边,∴ △AMC ≌△AME (SAS ).∴ MC =ME (全等三角形的对应边相等).又∵ BE =AB -AE ,∴ BE =AB -AC ,∴ MB -MC <AB -AC .(点评)因为AB >AC ,所以可在AB 上截取线段AE =AC ,这时BE =AB -AC ,如果连接EM ,在△BME中,显然有MB -ME <BE .这表明只要证明ME =MC ,则结论成立.充分利用角平分线的对称性,截长补短是关键.举一反三:(变式)如图,AD 是△ABC 的角平分线,AB >AC,求证:AB -AC >BD -DC(答案)证明:在AB 上截取AE =AC,连结DE∵AD 是△ABC 的角平分线,∴∠BAD =∠CAD⎪⎩⎪⎨⎧=∠=∠=AD AD CAD BAD AC AE 在△AED 与△ACD 中∴△AED ≌△ADC (SAS )∴DE =DC 在△BED 中,BE >BD -DC即AB -AE >BD -DC ∴AB -AC >BD -DCE DC B A(4).在角的平分线上取一点向角的两边作垂线段.4、如图所示,已知E 为正方形ABCD 的边CD 的中点,点F 在BC 上,且∠DAE=∠FAE .求证:AF =AD +CF .(答案与解析)证明: 作ME ⊥AF 于M ,连接EF .∵ 四边形ABCD 为正方形,∴ ∠C =∠D =∠EMA =90°.又∵ ∠DAE =∠FAE ,∴ AE 为∠FAD 的平分线,∴ ME =DE .在Rt △AME 与Rt △ADE 中,()()AE AE DE ME =⎧⎨=⎩公用边,已证, ∴ Rt △AME ≌Rt △ADE(HL).∴ AD =AM(全等三角形对应边相等).又∵ E 为CD 中点,∴ DE =EC .∴ ME =EC .在Rt △EMF 与Rt △ECF 中,()(ME CE EF EF =⎧⎨=⎩已证,公用边), ∴ Rt △EMF ≌Rt △ECF(HL).∴ MF =FC(全等三角形对应边相等).由图可知:AF =AM +MF ,∴ AF =AD +FC(等量代换).(点评)与角平分线有关的辅助线: 在角两边截取相等的线段,构造全等三角形;在角的平分线上取一点向角的两边作垂线段. 四边形ABCD 为正方形,则∠D =90°.而∠DAE =∠FAE 说明AE 为∠FAD 的平分线,按常规过角平分线上的点作出到角两边的距离,而E 到AD 的距离已有,只需作E 到AF 的距离EM 即可,由角平分线性质可知ME =DE .AE =AE .Rt △AME 与Rt △ADE全等有AD =AM .而题中要证AF =AD +CF .根据图知AF =AM +MF .故只需证MF =FC 即可.从而把证AF =AD +CF 转化为证两条线段相等的问题.5、如图所示,在△ABC 中,AC=BC ,∠ACB=90°,D 是AC 上一点,且AE 垂直BD 的延长线于E ,12AE BD ,求证:BD 是∠ABC 的平分线. (答案与解析)证明:延长AE 和BC ,交于点F ,∵AC ⊥BC ,BE ⊥AE ,∠ADE=∠BDC (对顶角相等),∴∠EAD+∠ADE=∠CBD+∠BDC .即∠EAD=∠CBD . 在Rt △ACF 和Rt △BCD 中.所以Rt △ACF ≌Rt △BCD (ASA ).则AF=BD (全等三角形对应边相等).∵AE=BD ,∴AE=AF ,即AE=EF . 在Rt △BEA 和Rt △BEF 中,则Rt △BEA ≌Rt △BEF (SAS ).所以∠ABE=∠FBE (全等三角形对应角相等),即BD 是∠ABC 的平分线.(点评)如果由题目已知无法直接得到三角形全等,不妨试着添加辅助线构造出三角形全等的条件,使问题得以解决.平时练习中多积累一些辅助线的添加方法.类型二、全等三角形动态型问题6、在△ABC 中,∠ACB =90°,AC =BC ,直线l 经过顶点C ,过A ,B 两点分别作l 的垂线AE ,BF ,垂足分别为E ,F 。
全等三角形问题中常见的8种辅助线的作法(有答案)

全等三角形问题中常见的辅助线的作法(有答案)总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
.1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”:遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
;常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二DCB AA个角之间的相等。
1) 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”法构造全等三角形.2) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转” 法构造全等三角形.3) 遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
全等三角形证明之辅助线,附练习题含答案

全等三角形证明之辅助线讲义➢ 知识与方法梳理1. 为了解决几何问题,在原图的基础上另外添加的直线或线段称为辅助线.辅助线通常画成虚线.辅助线的原则:添加辅助线,构造新图形,形成新关系,建立已知和未知之间的桥梁,把问题转化成自己已经会解的情况. 辅助线的作用:①把分散的条件转为集中; ②把复杂的图形转化为基本图形.添加辅助线的注意事项:明确目的,多次尝试.2. 要证明边相等(或角相等),可以考虑证明它们所在的三角形全等;要证全等,需要找3组条件. ➢ 例题示范例:已知:如图,在△ABC 中,∠C =90°,D 是AB 边上一点,AD =AC ,过点D 作DE ⊥AB ,交BC 于点E . 求证:CE =DE . 【思路分析】 ① 读题标注:② 梳理思路:要证CE =DE ,考虑把这两条线段放在两个三角形中证全等,利用全等三角形对应边相等来证明.观察图形,发现不存在全等的三角形.结合条件,AC =AD ,∠C =∠ADE =90°,考虑连接AE ,证明△ACE ≌△ADE . 【过程书写】 证明:如图,连接AE ∵DE ⊥AB ∴∠ADE =90° ∵∠C =90° ∴∠C =∠ADE在Rt △ACE 和Rt △ADE 中AE AE AC AD=⎧⎨=⎩(公共边)(已知)∴Rt △ACE ≌Rt △ADE (HL ) ∴CE =DE (全等三角形对应边相等)EDC AEDBAEDBCA➢练习题BFEAC D7. 已知:如图,BD ,CE 是△ABC 的高,点P 在BD 的延长线上,BP =AC ,点Q 在CE 上,CQ =AB .判断线段AP 和AQ 的数量和位置关系,并加以证明.8. 已知:如图,∠B =∠D ,AB =CD ,AD ∥BC ,E ,F 分别是AD ,BC 的中点.求证:AF =CE .9. 已知:如图,B ,C ,F ,E 在同一条直线上,AB ,DE 相交于点G ,且BC =EF ,GB =GE ,∠A =∠D .求证:DC =AF .10. 已知:如图,∠C =∠F ,AB =DE ,DC =AF ,BC =EF .求证:AB ∥DE .11. 已知:如图,AB ∥CD ,AD ∥BC ,E ,F 分别是AD ,BC 的中点.求证:BE =DF .QPEDCBACAEF B DDGC AB EFFEBAD CF E B A DC12. 已知:如图,在正方形ABCD 中,AD =AB ,∠DAB =∠B =90°,点E ,F 分别在AB ,BC 上,且AE =BF ,AF 交DE 于点G . 求证:DE ⊥AF .连接BM ,交CN 于点F .有下列结论:①∠AMB =∠ANB ;②△ACE ≌△MCF ;③CE =CF ;④EN =FB .其中正确结论的序号是_________________.【参考答案】1. 证明:如图,连接AD在△ABD 和△DCA 中AB DCBD CAAD DA =⎧⎪=⎨⎪=⎩(已知)(已知)(公共边) ∴△ABD ≌△DCA (SSS )∴∠ABO=∠DCO (全等三角形对应角相等) 2. 证明:如图,连接AC∵AB ∥CDGFEDCBANM EB AFC∴∠CAB =∠ACD ∵AD ∥BC ∴∠DAC =∠BCA 在△ABC 和△CDA 中CAB ACDAC CABCA DAC ∠=∠⎧⎪=⎨⎪∠=∠⎩(已证)(公共边)(已证) ∴△ABC ≌△CDA (ASA )∴AB =CD ,BC =DA (全等三角形对应边相等) 3. 证明:如图,连接AC ,AD在△ABC 和△AED 中,AB AE B EBC ED =⎧⎪∠=∠⎨⎪=⎩(已知)(已知)(已知) ∴△ABC ≌△AED (SAS )∴AC =AD (全等三角形对应边相等) ∵F 是CD 的中点 ∴CF =DF在△ACF 和△ADF 中,AC AD AF AFCF DF =⎧⎪=⎨⎪=⎩(已证)(公共边)(已证) ∴△ACF ≌△ADF (SSS )∴∠CFA =∠DFA (全等三角形对应角相等) ∵∠CFA +∠DFA =180° ∴∠CFA =90° ∴AF ⊥CD4. 证明:如图,过点A 作AD ⊥BC 于点D∵AD ⊥BC∴∠ADB =∠ADC=90° 在△ADB 和△ADC 中,B CADB ADCAD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(公共边) ∴△ADB ≌△ADC (AAS )∴AB =AC (全等三角形对应边相等) 5. 证明:如图,过点B 作BF ⊥AC 于点FA DBCFCBEDAAD B C6. ∵BC ⊥AD∴∠ACE =∠BCD =90° 在Rt △ACE 和Rt △BCD 中AE BD CE CD =⎧⎨=⎩(已知)(已知)∴Rt △ACE ≌Rt △BCD (HL )∴∠CAE =∠CBD (全等三角形对应角相等) ∵∠ACE =90° ∴∠CAE +∠AEC =90° ∵∠AEC =∠BEF ∴∠CBD +∠BEF =90° ∴∠BFE =90° ∴AF ⊥BD7. 解:AP =AQ 且AP ⊥AQ ,理由如下:如图,∵BD ⊥AC ,CE ⊥AB ∴∠BEQ =∠BDC =∠ADP =90° ∴∠1+∠3=90° ∠2+∠4=90° ∵∠3=∠4 ∴∠1=∠2在△ABP 和△QCA 中54321QCB PE DA1 2 AB QC BP CA =⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(已知) ∴△ABP ≌△QCA (SAS )∴AP =AQ (全等三角形对应边相等) ∠P =∠5(全等三角形对应角相等) ∵∠ADP =90° ∴∠P +∠PAD =90° ∴∠5+∠PAD =90° 即∠QAP =90° ∴AP =AQ 且AP ⊥AQ 8. 证明:如图,连接AC∵AD ∥BC ∴∠DAC =∠BCA 在△ABC 和△CDA 中,∴△ABC ≌△CDA (AAS )∴BC =DA (全等三角形对应边相等) ∵E ,F 分别是AD ,BC 的中点 ∴1122BF BC DE AD ==, ∴BF =DE在△ABF 和△CDE 中,∴△ABF ≌△CDE (SAS )∴AF =CE (全等三角形对应边相等)9. 证明:如图,过点G 作GH ⊥BE 于点H∵GH ⊥BE∴∠GHB =∠GHE =90° 在Rt △GHB 和Rt △GHE 中,BCA DAC B DAB CD (已证)(已知)(公共边)∠=∠⎧⎪∠=∠⎨⎪=⎩AB CD B DBF DE (已知)(已知)(公共边)=⎧⎪∠=∠⎨⎪=⎩H FBA C GDGB GEGH GH=⎧⎨=⎩(已知)(公共边) ∴Rt △GHB ≌Rt △GHE (HL )∴∠B =∠E (全等三角形对应角相等) ∵BC =EF ∴BC +CF =EF +CF 即BF =EC在△ABF 和△DEC 中,A DB EBF EC ∠=∠⎧⎪∠=∠⎨⎪=⎩(已知)(已证)(已证) ∴△ABF ≌△DEC (AAS ) ∴DC =AF10. 证明:如图,连接BE在△AEF 和△DBC 中,AF DCF CEF BC =⎧⎪∠=∠⎨⎪=⎩(已知)(已知)(已知) ∴△AEF ≌△DBC (SAS )∴AE =DB (全等三角形对应边相等) 在△ABE 和△DEB 中,AE DB AB DEEB BE =⎧⎪=⎨⎪=⎩(已证)(已知)(公共边) ∴△ABE ≌△DEB (SSS )∴∠ABE =∠DEB (全等三角形对应角相等) ∴AB ∥DE11. 证明:如图,连接BDCD ABE F∵AB ∥CD ,AD ∥BC∴∠ABD =∠CDB ,∠ADB =∠CBD 在△ABD 和△CDB 中,ABD CDBBD DBADB CBD ∠=∠⎧⎪=⎨⎪∠=∠⎩(已证)(公共边)(已证) ∴△ABD ≌△CDB (ASA )∴AD =CB (全等三角形对应边相等) ∵E ,F 分别是AD ,BC 的中点 ∴DE =BF在△BED 和△DFB 中,DE BF ADB CBDBD DB =⎧⎪∠=∠⎨⎪=⎩(已证)(已证)(公共边) ∴△BED ≌△DFB (SAS )∴BE =DF (全等三角形对应边相等) 12. 证明:如图,在△DAE 和△ABF 中AD BA DAE B AE BF =⎧⎪=⎨⎪=⎩(已知)∠∠(已知)(已知) ∴△DAE ≌△ABF (SAS )∴∠1=∠2(全等三角形对应角相等) ∵∠DAB =90° ∴∠2+∠3=90° ∴∠1+∠3=90° ∴∠AGD =90° ∴DE ⊥AF 13. B 14. ②③④CDA B E F ABCDEF G第7题图312。
(完整版)全等三角形常用辅助线做法

五种辅助线助你证全等姚全刚在证明三角形全等时有时需增加辅助线,对学习几何证明不久的学生而言常常是难点.下面介绍证明全等常常有的五种辅助线,供同学们学习时参照.一、截长补短一般地,当所证结论为线段的和、差关系,且这两条线段不在同素来线上时,平时能够考虑用截长补短的方法:或在长线段上截取一部分使之与短线段相等;或将短线段延长使其与长线段相等.例 1.如图 1,在△ ABC 中,∠ ABC=60 °, AD 、CE 分别均分∠ BAC 、∠ ACB .求证:AC=AE+CD .解析:要证AC=AE+CD ,AE 、CD 不在同素来线上.故在AC 上截取 AF=AE ,则只要证明 CF=CD .证明:在 AC 上截取 AF=AE ,连接 OF.∵ AD 、 CE 分别均分∠ BAC 、∠ ACB ,∠ ABC=60 °∴∠ 1+∠ 2=60 °,∴∠ 4=∠ 6=∠ 1+∠ 2=60 °.显然,△ AEO ≌△ AFO ,∴∠ 5=∠4=60°,∴∠ 7=180°-(∠ 4+ ∠ 5) =60 °在△ DOC 与△ FOC 中,∠ 6=∠ 7=60°,∠ 2=∠ 3, OC=OC∴△ DOC ≌△ FOC, CF=CD∴ AC=AF+CF=AE+CD.截长法与补短法,详尽作法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明。
这种作法,适合于证明线段的和、差、倍、分等类的题目。
例2:如图甲, AD∥BC,点 E 在线段 AB上,∠ ADE=∠CDE,∠ DCE=∠ECB。
求证: CD=AD+BC。
思路解析:1)题意解析:此题观察全等三角形常有辅助线的知识:截长法或补短法。
2)解题思路:结论是CD=AD+BC,可考虑用“截长补短法”中的“截长”,即在 CD上截取 CF=CB,只要再证 DF=DA即可,这就转变成证明两线段相等的问题,进而达到简化问题的目的。
构造全等三角形(常见辅助线法)

练习1
如图,已知△ABC中,AD是∠BAC的角平分线,AB=AC+CD,求证:∠C=2∠B
证明:
延长AC到F,使CF=CD,连结DF。
∵ AD是∠BAC的角平分线(已知) ∴∠1=∠2(角平分线定义) ∵ AB=AC+CD,CF=CD(已知) ∴ AB=AC+CF=AF(等量代换)
A 12
在△ABD和△AFD中 ∵ AB=AF(已证)
C D
B E
Ⅴ.“周长问题”的转化 借助“垂直平分线性质”
2.如图,△ABC中, D在AB的垂直平分线上, E在AC的垂直平分线上.若BC=6cm,求△ADE的周长.
AD+AE+DE BD+CE+DE BC
A
B
D
E
C
Ⅴ.“周长问题”的转化 借助“等腰三角形性质”
5.如图, △ABC中,BP、CP是△ABC的角平分线,MN//BC. 若BC=6cm, △AMN周长为13cm,求△ABC的周长.
D
1 2
A 在AB上取点F使得AF=AD,连接EF
截
E
C
长 补
短
4 3
B F
已知:如图,在四边形ABCD中,BD是∠ABC的角平分线,AD=CD,求证:
例1
∠A+∠C=180°
证明:
在BC上截取BE,使BE=AB,连结DE。
∵ BD是∠ABC的角平分线(已知) ∴∠1=∠2(角平分线定义) 在△ABD和△EBD中 ∵ AB=EB(已知)
构造全等三角形(常见辅助线法)
如图,AB=AD,BC=DC,求证:∠B=∠D.
A 连接AC 构造全等三角形
连 线 B 构 造 全 等 C
全等三角形问题中常见的8种辅助线的作法(有答案)

全等三角形问题中常见的辅助线的作法(有答案)总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”:遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变D C BAED F CB A换中的“对折”法构造全等三角形.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”法构造全等三角形.3)遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
(完整版)全等三角形经典题型——辅助线问题

全等三角形问题中常见的辅助线的作法(含答案) 总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”:遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”法构造全等三角形.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,D C BAED F CB A利用的思维模式是全等变换中的“旋转”法构造全等三角形.3)遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
(完整版)全等三角形问题中常见的8种辅助线的作法(有答案解析)

全等三角形问题中常见的辅助线的作法(有答案)总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一”法:遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”:遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”法构造全等三角形.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”法构造全等三角形.3)遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
专题 全等三角形的常见辅助线

方法一作平行线法变式12.如图,△ABC 中,AB =AC ,在AB 上取一点E ,在AC 的延长线上取一点F ,使CF =BE ,连接EF ,交BC 于点D .求证:DE =DF 作平行,构造全等.利用的思维模式是全等变换中的“平移”.【例题1】1.△ABC 中,∠BAC =60°,∠C =40°,AP 平分∠BAC 交BC 于P ,BQ 平分∠ABC 交AC 于Q ,求证:AB +BP=BQ +AQ .(有多种辅助线作法).专题 全等三角形的常见辅助线变式23.如图,在Rt △ABC 中,∠ACB =90°,点D ,E 分别是边AB ,AC 的中点,延长BC 到点F ,使CF =12BC .连结CD 、EF ,那么CD 与EF 相等吗?请证明你的结论.变式34.如图所示,ABC ∆为等边三角形,边长为4,点O 为BC 边中点,120EOF ∠=︒,其两边分别交AB 和CA 的延长线于E ,F ,求AE AF -的值.变式45.如图,将一把三角尺放在边长为1的正方形ABCD 上使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与射线DC 相交于点Q ,当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的大小关系?试证明你观察得到的结论.培优变式56.如图1,已知ABC 和EFC 都是等边三角形,且点E 在线段AB 上.(1)过点E 作//EG BC 交AC 于点G ,试判断AEG △的形状并说明理由;(2)求证://BF AC ;(3)如图2,若点D 在射线CA 上,且ED EC =,求证:AB AD BF =+.方法二作垂直法作垂直,构造全等.分为做1条垂直辅助线和2条垂直辅助线.可以利用通过作角平分线上的点两边的距离得全等,或截取等长线段得全等;思维模式是全等变换中的“轴对称”即“对折”.【例题2】7.如图,△ABC中,AB=2AC,AD平分∠BAC,且AD=BD.求证:CD⊥AC.变式18.如图所示,在四边形ABCD 中,AC 平分,DAB CD CB ∠=,求证:180B D ∠+∠= .变式29.已知:∠AOB+∠CPD =180°,OM 是∠AOB 的平分线,将三角板的直角顶P 在射线OM 上滑动,两直角边分别与OA 、OB 交于C 、D .求证:PC=PD .变式310.如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.变式411.如图,在梯形ABCD中,∠A=∠B=90°,点E为AB的中点,DE平分∠ADC.(1)求证:CE平分∠BCD;(2)求证:AD+BC=CD.培优变式512.已知如图,在△ABC中,以AB、AC为直角边,分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.(1)用圆规比较EM与FM的大小.(2)你能说明由(1)中所得结论的道理吗?方法三倍长中线法倍长中线主要用于证明全等三角形,其主要是在全等三角形的判定过程中,遇到一般三角形边上的中线或中点,考虑中线倍长;思维模式是全等变换中的“旋转”,可转移元素或将分散的条件聚集拢来.其主要的图形特征和证明方法如图:已知:在三角形ABC中,O为BC边中点,辅助线:延长AO到点D使AO=DO,结论:△AOB≌△DOC证明:延长AO到点D使AO=DO,由中点可知,OB=OC,在△AOB 和△DOC 中OA OD AOB DOC OB OC =⎧⎪∠=∠⎨⎪=⎩∴△AOB ≌△DOC同理在下图中仍能得到△AOB ≌△DOC规律总结:由倍长中线法证明三角形全等的过程一般均是用SAS 的方法,这是由于作出延长线后出现的对顶角决定的.补充:关于倍长中线的其他方法①向中线做垂直,易证△BEO ≌△CDO步骤:延长AO 到点D ,过点B ,C 分别向AD 作垂线,垂足为E ,D ,易证△BEO ≌△CDO (AAS )②过中线做任意三角形证明全等,易证△BDO ≌△CEO步骤:在AC 上任意选取一点E ,连接EO 并延长到点D ,使EO =DO ,连接BD ,易证△BDO ≌△CEO (SAS )点拨:倍长中线的思路:已知中线——作中线倍长线——证全等——找大小关系【例题3】13.如图,AD 是ABC 的中线,,E F 分别在边,AB AC 上(,E F 不与端点重合),且DE DF ⊥,则().A .BE CF EF+>B .BE CF EF +=C .BE CF EF+<D .BE CF +与EF 的长短关系不确定变式14.如图,901,2,AB CD BCD AB BC CD E ∠=︒=== ,,为AD 上的中点,则BE =______.变式15.如图,ABC ∆中,D 为BC 的中点,E 是AD 上一点,连接BE 并延长交AC 于F ,BE AC =,且9BF =,6CF =,那么AF 的长度为__.变式16.如图,E 是BC 的中点,点A 在DE 上,且∠BAE =∠CDE.求证:AB =CD .变式17.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.【探究与发现】(1)如图1,AD 是ABC 的中线,延长AD 至点E ,使ED AD =,连接BE ,证明:ACD EBD △≌△.【理解与应用】(2)如图2,EP 是DEF 的中线,若5EF =,3DE =,设EP x =,则x 的取值范围是________.(3)如图3,AD 是ABC 的中线,E 、F 分别在AB 、AC 上,且DE DF ⊥,求证:BE CF EF +>.培优变式18.问题探究:小红遇到这样一个问题:如图1,ABC 中,6AB =,4AC =,AD 是中线,求AD 的取值范围.她的做法是:延长AD 到E ,使DE AD =,连接BE ,证明BED CAD △≌△,经过推理和计算使问题得到解决.请回答:(1)小红证明BED CAD △≌△的判定定理是:__________________________________________;(2)AD 的取值范围是________________________;方法运用:(3)如图2,AD 是ABC 的中线,在AD 上取一点F ,连结BF 并延长交AC 于点E ,使AE EF =,求证:BF AC =.(4)如图3,在矩形ABCD 中,12AB BC =,在BD 上取一点F ,以BF 为斜边作Rt BEF △,且12EF BE =,点G 是DF 的中点,连接EG ,CG ,求证:=EG CG .方法四截长补短法基本方法已知条件在ABC 中,,AB AC AM >平分BAC∠辅助线作(1)在AB 上截取AD AC =;(2)把AC 延长到点E ,使AB AE =法可用结论截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长:在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;补短:将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段.理论依据(1)因为AM 平分BAC ∠,且AD AC =,所以(SAS)AMD AMC ≌;(2)因为AM 平分BAC ∠,且AE AB=,所以(SAS)AMB AME ≌【例题4】19.在ABC 中,60ABC ∠=︒,点D 、E 分别在AC 、BC 上,连接BD 、DE 和AE ;并且有AB BE =,AED C ∠=∠.(1)求CDE ∠的度数;(2)求证:AD DE BD +=.变式120.如图,在ABC 中,AD 为BAC ∠的平分线,如图,若2,12,7.2C B AB AC ∠=∠==,求线段CD 的长度.变式221.如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.(1)求证:DP=DB;(2)求证:DA+DB=DC;变式322.在等边△ABC中,E为BC边上一点,G为BC延长线上一点,过点E作∠AEM=60°,交∠ACG的平分线于点M.(1)如图1,当点E在BC边的中点位置时,求证:AE=EM;(2)如图2,当点E在BC边的任意位置时,(1)中的结论是否成立?请说明理由.变式423.如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.(1)当点E在线段BD上移动时,如图(1)所示,求证:AE=EF;(2)当点E在直线BD上移动时,如图(2)、图(3)所示,线段AE与EF又有怎样的数量关系?请直接写出你的猜想,不需证明.变式524.如图1,在四边形ABCD 中,AB=AD ,∠B+∠ADC=180°,点E ,F 分别在四边形ABCD 的边BC ,CD 上,∠EAF=12∠BAD ,连接EF ,试猜想EF ,BE ,DF 之间的数量关系.(1)思路梳理将△ABE 绕点A 逆时针旋转至△ADG ,使AB 与AD 重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F ,D ,G 三点共线,易证△AFG ≌△AFE ,故EF ,BE ,DF 之间的数量关系为__;(2)类比引申如图2,在图1的条件下,若点E ,F 由原来的位置分别变到四边形ABCD 的边CB ,DC 延长线上,∠EAF=12∠BAD ,连接EF ,试猜想EF ,BE ,DF 之间的数量关系,并给出证明.(3)联想拓展如图3,在△ABC 中,∠BAC=90°,AB=AC ,点D ,E 均在边BC 上,且∠DAE=45°,若BD=1,EC=2,直接写出DE 的长为________________.培优变式625.通过类比联想、引申拓展典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.【解决问题】如图,点E 、F 分别在正方形ABCD 的边BC 、CD 上,45EAF ∠=︒,连接EF ,则EF BE DF =+,试说明理由.证明:延长CD 到G ,使DG BE =,在ABE 与ADG △中,90AB AD B ADG BE DG =⎧⎪∠=∠=︒⎨⎪=⎩∴ABE ADG △≌△理由:(SAS )进而证出:AFE △≌___________,理由:(__________)进而得EF BE DF =+.【变式探究】如图,四边形ABCD 中,AB AD =,90BAD ∠=︒点E 、F 分别在边BC 、CD 上,45EAF ∠=︒.若B ∠、D ∠都不是直角,则当B ∠与D ∠满足等量关系________________时,仍有EF BE DF =+.请证明你的猜想.【拓展延伸】如图,若AB AD =,90≠︒∠BAD ,45EAF ∠≠︒,但12EAF BAD ∠=∠,90B D ∠=∠=︒,连接EF ,请直接写出EF 、BE 、DF 之间的数量关系.方法五补全图形法补全定理图形或基本图形,运用定理或基本结论解题.【例题5】26.如图,已知等腰直角三角形ABC 中,AB AC =,90BAC ∠=︒,BF 平分ABC ∠,CD BD ⊥交BF 的延长线于点D ,试说明:2BF CD =.变式127.如图,在ABC ∆中,,90,AC BC ACB BD =∠= 平分ABC ∠,且AE 垂直于BD 的延长线于点E ,求证:2BD AE =.变式228.如图,已知△ABC 中,AB =AC ,∠BAC =90°,直角EPF ∠的顶点P 是BC 中点,两边PE 、PF 分别交AB 、CA 的延长线于点E 、F .(1)求证:AE =CF ;(2)求证:△EPF 是等腰直角三角形;(3)求证:∠FEA +∠PFC =45°;(4)求证:S △PFC -S △PBE =12S △ABC .方法六旋转法常见通过旋转构造全等的情况1、等腰三角形的旋转2、等边三角形的旋转3、四边形旋转4、正方形旋转根据想要转换的线段以及“共顶点等线段"的特点锁定旋转目标,添加辅助线促成全等,实现线段或角度在位置上的变化,再根据题目中的具体条件从而解决问题.【例题6】29.如图,在四边形ABCD 中,AB =AD ,∠BAD =60°,∠BCD =120°,AC =2,则四边形ABCD 的面积为________变式130.在ABC 中,90,ACB CA CB ∠=︒=,点,E F 在AB 边上,45ECF ∠=︒.若10,15AE EF ==,则BF 的长为__________.变式231.如图,在Rt △ABC 和Rt △BCD 中,∠BAC =∠BDC =90°,BC =8,AB =AC ,∠CBD =30°,BD =M ,N 分别在BD ,CD 上,∠MAN =45°,则△DMN 的周长为_____.变式332.如图,等腰三角形ABC 中,BA BC =,ABC α∠=.作AD BC ⊥于点D ,将线段BD 绕着点B 顺时针旋转角α后得到线段BE ,连接CE .(1)求证:BE CE ⊥;(2)延长线段AD ,交线段CE 于点F .求CFA ∠的度数(用含有α的式子表示).培优变式433.阅读下面材料:小炎遇到这样一个问题:如图1,点E 、F 分别在正方形ABCD 的边BC ,CD 上,∠EAF=45°,连结EF ,则EF=BE+DF ,试说明理由.小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB ,AD 是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE 绕着点A 逆时针旋转90°得到△ADG ,再利用全等的知识解决了这个问题(如图2).参考小炎同学思考问题的方法,解决下列问题:(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D 都不是直角,则当∠B与∠D满足_关系时,仍有EF=BE+DF;(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1,EC=2,求DE的长.。
全等三角形辅助线总结3

图2-1D CBA图3-1FED CB A三角形全等辅助线探索一、基础知识点:1、在利用三角形三边关系证明线段不等关系时,若直接证不出来,可连接两点或延长某边构成三角 典型例题1-1:D 、E 为△ABC 内两点,求证:AB +AC >BD +DE +CE.2、在利用三角形的外角大于任何和它不相邻的内角时如直接证不出来时,可连接两点或延长某边,构造三角形,使求证的大角在某个三角形的外角的位置上,小角处于这个三角形的内角位置上,再利用外角定理:例:如图2-1:已知D 为△ABC 内的任一点,求证:∠BDC >∠BAC 。
证明:由三角形内角和为180°可知:∠A=180°-∠ABC -∠ACB∠D=180°-∠DBC -∠DCB 又点D 为三角形ABC 内任意一点,可知:∠ABC>∠DBC、∠ACB>∠DCB∴∠ABC+∠ACB>∠DBC+∠DCB∴∠A=180°-∠ABC -∠ACB<∠D=180°-∠DBC -∠DCB,即∠BDC>∠BAC3、有角平分线时,通常在角的两边截取相等的线段,构造全等三角形,如: 例:如图3-1:已知AD 为△ABC 的中线,且DE 平分∠ADB,DF 平分∠ADC, 求证:BE +CF >EF 。
过B 点作BG 平行AC 交FD 延长线于G,连接GF 因BG 平行AC ,则BD/CD=BG/CF=DG/DF又因D 是BC 中点即BD=DC ,则BG=CF,DG=DF因DE 、DF 分别平分∠ADB ,∠ADC,∠ADB+ADC=180度则∠EDF=∠EDA+∠ADf=∠ADB/2+∠ADC/2=(∠ADB+∠ADC)/2=180/2=90度 则∠EDG=180-∠EDF=180-90=90度又DE 为共边,DG=DF 则三角形EDG 与EDF 全等 则EG=EF因EG=EF,BG=CF ,EG<BE+BG (三角形两边之和大于第三边) 所以EF<BE+CF4、有以线段中点为端点的线段时,常延长加倍此线段,构造全等三角形。
专项练习(五) 证明三角形全等四种添加辅助线的方法

专项练习(五)证明三角形全等四种添加辅助线的方法►方法一直接连线构造全等三角形1.如图5-ZT-1所示,AB=AD,BC=DC.求证:∠ABC=∠ADC.图5-ZT-12.如图5-ZT-2,AB=AE,∠ABC=∠AED,BC=ED,AF⊥CD.求证:F是CD的中点.图5-ZT-23.如图5-ZT-3,AC,BD相交于点O,且AB=DC,AC=DB.求证:∠ABO=∠DCO.图5-ZT-3►方法二倍长中线构造全等三角形4.如图5-ZT-4,AD是△ABC的边BC上的中线,AB=4,AC=8,求中线AD的取值范围.图5-ZT-45.如图5-ZT-5,CE,CB分别是△ABC,△ADC的中线,且AB =AC.求证:CD=2CE.(提示:等腰三角形的两底角相等)图5-ZT-5►方法三作垂直构造全等三角形6.如图5-ZT-6,四边形ABCD中,BC<BA,AD=CD,BD平分∠ABC.求证:∠A+∠C=180°.图5-ZT-67.如图5-ZT-7,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边与OA,OB分别交于点C,D,PC 与PD相等吗?试说明理由.图5-ZT-7►方法四翻折构造全等三角形8.如图5-ZT -8所示,BE 平分∠ABC ,E 为AD 的中点,且BC =B A +CD.求证:CE 平分∠BCD.图5-ZT -89.2019·南京二模命题:有两个角相等的三角形是等腰三角形(简称〝等角对等边〞).:如图5-ZT -9,△ABC 中,∠B =∠C.求证:AB =AC.三名同学作出了三种不同的辅助线,并完成了命题的证明.小刚的方法:作∠BAC 的平分线AD ,可证△ABD ≌△ACD ,得AB =AC ;小亮的方法:作BC 边上的高AD ,可证△ABD ≌△ACD ,得AB =AC ;小莉的方法:作BC 边上的中线AD.(1)请你写出小刚与小亮的方法中△ABD ≌△ACD 的理由:________________;(2)请你按照小莉的思路完成命题的证明.图5-ZT -9详解详析1.证明:连接AC , 在△ABC 与△ADC 中,∵⎩⎪⎨⎪⎧AB =AD ,BC =DC ,AC =AC ,∴△ABC ≌△ADC ,(SSS) ∴∠ABC =∠ADC.2.证明:如图,连接AC ,AD. 在△ABC 和△AED 中,∵⎩⎪⎨⎪⎧AB =AE ,∠ABC =∠AED ,BC =ED ,∴△ABC ≌△AED ,(SAS) ∴AC =AD.∵AF ⊥AD ,∴∠AFC =∠AFD =90°.在Rt △ACF 和Rt △ADF 中, ∵⎩⎪⎨⎪⎧AC =AD ,AF =AF , ∴Rt △ACF ≌Rt △ADF ,(HL)∴CF =DF ,∴F 是CD 的中点.3.证明:连接BC. 在△ABC 和△DCB 中,∵⎩⎪⎨⎪⎧AB =DC ,AC =DB ,BC =CB ,∴△ABC ≌△DCB ,(SSS) ∴∠ABC =∠DCB ,∠ACB =∠DBC ,∴∠ABC -∠DBC =∠DCB -∠ACB ,即∠ABO =∠DCO.4.[解析] 通过作辅助线,把AB ,AD ,AC 转化到同一个三角形中,如图,证△ADB ≌△EDC ,推出EC =AB ,在△ACE 中,利用三角形的三边关系求解.解:如图,延长AD 到点E ,使AD =DE ,连接CE.∵D 是BC 的中点,∴BD =CD. 在△ADB 和△EDC 中,∵⎩⎪⎨⎪⎧AD =ED ,∠ADB =∠EDC ,BD =CD ,∴△ADB ≌△EDC ,(SAS) ∴EC =AB =4,∴AC -EC =AC -AB =8-4=4,AC +EC =AC +AB =12.在△ACE 中,根据三角形的三边关系,得4<AE<12.∵AE =2AD ,∴2<AD<6.5.证明:延长CE 到点F ,使EF =CE ,连接FB.∵CE 是△ABC 的中线,∴AE =EB. 在△AEC 和△BEF 中,∵⎩⎪⎨⎪⎧AE =EB ,∠AEC =∠BEF ,CE =EF ,∴△AEC ≌△BEF ,(SAS) ∴∠A =∠EBF ,AC =BF.∵AB =AC ,∴∠ABC =∠ACB ,∴∠CBD =∠A +∠ACB =∠EBF +∠ABC =∠CBF.∵CB 是△ADC 的中线,∴AB =BD ,又∵AB =AC ,AC =BF ,∴BF =BD. 在△CBF 和△CBD 中,∵⎩⎪⎨⎪⎧BF =BD ,∠CBF =∠CBD ,CB =CB ,∴△CBF ≌△CBD ,(SAS) ∴CD =CF =CE +EF =2CE.6.证明:如图,过点D 作DE ⊥BA 于点E ,DF ⊥BC 交BC 的延长线与点F.∵BD 平分∠ABC ,∴∠DBE =∠DBF.∵DE ⊥AB ,DF ⊥BC ,∴∠BED =∠BFD =90°. 在△DBE 和Rt △DBF 中,∵⎩⎪⎨⎪⎧∠BED =∠BFD ,∠DBE =∠DBF ,BD =BD , ∴△DBE ≌△DBF ,(AAS)∴DE =DF. 在Rt △DEA 和Rt △DFC 中,∵⎩⎪⎨⎪⎧AD =CD ,DE =DF , ∴Rt △DEA ≌Rt △DFC ,(HL)∴∠A =∠DCF.∵∠BCD +∠DCF =180°,∴∠A +∠BCD =180°.7.解:PC 与PD 相等.理由如下:过点P 作PE ⊥OA 于点E ,PF ⊥OB 于点F.∵OM 平分∠AOB ,∴∠POE =∠POF. 在△OPE 与△OPF 中,∵⎩⎪⎨⎪⎧∠OEP =∠OFP ,∠POE =∠POF ,OP =OP ,∴△OPE ≌△OPF ,(AAS)∴PE =PF.∵∠AOB =90°,∠PEO =∠PFO =90°,∴∠EPF =90°,∴∠EPC +∠CPF =90°.又∵∠CPD =90°,∴∠CPF +∠FPD =90°,∴∠EPC =∠FPD =90°-∠CPF. 在△PCE 与△PDF 中,∵⎩⎪⎨⎪⎧∠PEC =∠PFD ,PE =PF ,∠EPC =∠FPD ,∴△PCE ≌△PDF ,(ASA)∴PC =PD.8.[解析] 在BC 上截取BF =BA.根据SAS 证明△BAE ≌△BFE ,再证明△CEF ≌△CED 即可.证明:如图,在BC 上截取BF =BA ,连接EF.∵BE 平分∠ABC ,∴∠ABE =∠FBE. 在△BAE 和△BFE 中,∵⎩⎪⎨⎪⎧BA =BF ,∠ABE =∠FBE ,BE =BE ,∴△BAE ≌△BFE ,(SAS)∴AE =FE.∵E 是AD 的中点,∴DE =AE =FE.又∵BC =BA +CD ,BA =BF ,∴CD =CF. 在△CED 和△CEF 中,⎩⎪⎨⎪⎧CD =CF ,DE =FE ,CE =CE ,∴△CED ≌△CEF ,(SSS) ∴∠FCE =∠DCE ,即CE 平分∠BCD.9.解:(1)AAS(2)证明:过点D 作DE ⊥AB 于点E ,DF ⊥AC 于点F.∵AD 是BC 边上的中线,∴BD =CD.在△BDE 和△CDF 中, ∵⎩⎪⎨⎪⎧∠BED =∠CFD =90°,∠B =∠C ,BD =CD , ∴△BDE ≌△CDF ,(AAS)∴BE =CF ,DE =DF. 在Rt △AED 和Rt △AFD 中,∵⎩⎪⎨⎪⎧AD =AD ,DE =DF , ∴Rt △AED ≌Rt △AFD ,(HL)∴AE =AF ,∴AE +BE =AF +CF ,即AB =AC.。
全等三角形问题中常见的8种辅助线的作法(有答案解析)

全等三角形问题中常见的辅助线的作法(有答案 )总论:全等三角形问题最主要的是构造全等三角形,构造二条边之间的相等,构造二个角之间的相等【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接那么成中位线。
三角形中有中线,延长中线等中线。
1.等腰三角形“三线合一〞法:遇到等腰三角形,可作底边上的高,利用“三线合一〞的性质解题2.倍长中线:倍长中线,使延长线段与原中线长相等,构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法〞或“补短:法〞遇到有二条线段长之和等于第三条线段的长,6.图形补全法:有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为 30 、60 度的作垂线法:遇到三角形中的一个角为30 度或 60 度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90 的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种:最主要的是构造全等三角形,构造二条边之间的相等,二个角之间的相等。
1)遇到等腰三角形,可作底边上的高,利用“三线合一〞的性质解题,思维模式是全等变换中的“对折〞法构造全等三角形.2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转〞法构造全等三角形.3)遇到角平分线在三种添辅助线的方法,〔1〕可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折〞,所考知识点常常是角平分线的性质定理或逆定理.〔2〕可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。
全等三角形中的辅助线的作法

全等三角形中的辅助线的作法在《全等三角形》的解题中,在解决一些复杂的全等三角形问题中往往需要构造辅助线,本文将对添加辅助线的一些常用方法进行介绍,通常有连线构全等、截长补短法、倍长中线法、角平分线构全等等四种常见辅助线。
一、连线构全等例1:已知,如图,AD =BC ,AC =BD ,求证:D C ∠=∠分析:此题是一道易错的全等三角形证明题,很多学生会错误地认为需要证明的是ADO ∆和BCO ∆,但条件明显是不能证明的,所以本题的正确解法是连结AB (或者CD )构造ADB ∆和BCA ∆全等,再得到D C ∠=∠证明:连结AB在ADB ∆和BCA ∆中⎪⎩⎪⎨⎧===BA AB BD AC BC ADADB ∆∴≌BCA ∆ (SSS )D C ∠=∠∴练习1:如图,CD AB =,DC BC =,求证:D B ∠=∠.练习2:如图,CD AB //,CD AB =,求证:BC AD =练习3:如图,AB=AC ,BD=CD ,M 、N 分别是BD 、CD 的中点,求证:ANC AMB ∠=∠二、截长补短法截长补短法:在某条线段上截取一条线段与特定线段相等,或者将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明。
这种作法,适合于证明线段的和、差、倍、分等类的题目。
例2:已知在ABC ∆,B C ∠=∠2,21∠=∠,求证:CD AC AB +=分析:本题证明的是线段的和差问题,可考虑利用截长或补短法。
方法一(截长法):如图1,在AB 上截取AE=AC ,连结BE ,易证ADE ∆≌ADC ∆,从而得DC DE =,AED C ∠=∠,AC AE =又因为B C ∠=∠2所以得B AED ∠=∠2,又因为BDE B AED ∠+∠=∠所以得BDE B ∠=∠可得DE BE =从而得CD AC AB +=方法二(补短法):如图2,延长AC 到点E ,使得AE=AB ,易证ADE ∆≌ADB ∆,从而得AE AB =,E B ∠=∠又因为B ACB ∠=∠2所以得E ACB ∠=∠2,又因为E CDE ACB ∠+∠=∠所以得E CDE ∠=∠可得CE CD =从而得CD AC AB +=练习1:如图所示,已知BC AD //,AE 平分DAB ∠,BE 平分ABC ∠,线段CD 经过点E 交AD 于点D ,交BC 于点C ,求证:AB BC AD =+图1图2练习2:如图,在四边形ABDE 中,C 是BD 边的中点,若AC 平分BAE ∠,︒=∠90ACE ,猜想线段AE 、AB 、DE 的长度满足的数量关系,并证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形综合复习
切记:“有三个角对应相等”和“有两边及其中一边的对角对应相等”的两个三角形不一定全等。
例1. 如图,,,,A F E B 四点共线,AC CE ⊥,BD DF ⊥,AE BF =,AC BD =。
求证:
ACF BDE ∆≅∆。
思路:从结论A C F B D E ∆≅∆入
手,全等条件只有A C B D =;由A E B F =两边同时减去EF 得到AF BE =,又得到一个全等条件。
还缺少一个全等条件,可以是CF DE =,也可以是A B ∠=∠。
由条件AC CE ⊥,BD DF ⊥可得90ACE BDF ∠=∠=,再加上AE BF =,AC BD =,可以证明ACE BDF ∆≅∆,从而得到A B ∠=∠。
证明AC CE ⊥,BD DF ⊥
∴90ACE BDF ∠=∠=
在Rt ACE ∆与Rt BDF ∆中
AE BF AC BD =⎧⎨=⎩
∴Rt ACE Rt BDF ∆≅∆(HL)
∴A B ∠=∠
AE BF =
∴AE EF BF EF -=-,即AF BE =
在ACF ∆与BDE ∆中
AF BE A B AC BD =⎧⎪∠=∠⎨⎪=⎩
∴ACF BDE ∆≅∆(SAS)
思考:本题的分析方法实际上是“两头凑”的思想方法:一方面从问题或结论入手,看还需要什么条件;另一方面从条件入手,看可以得出什么结论。
再对比“所需条件”和“得出结论”之间是否吻合或具有明显的联系,从而得出解题思路。
小结:本题不仅告诉我们如何去寻找全等三角形及其全等条件,而且告诉我们如何去分析一个题目,得出解题思路。
例2. 如图,在ABC ∆中,BE 是∠ABC 的平分线,AD BE ⊥,垂足为D 。
求证:
21C ∠=∠+∠。
思路:直接证明21C ∠=∠+∠比较困难,我们可以间接证明,即找到α∠,证明2α∠=∠且1C α∠=∠+∠。
也可以看成将2∠“转移”到α∠。
那么α∠在哪里呢?角的对称性提示我们将AD 延长交BC 于F ,则构造了△FBD ,可以通过证明三角形全等来证明∠2=∠DFB ,可以由三角形外角定理得∠DFB=∠1+∠C 。
证明:延长AD 交BC 于F
在ABD ∆与FBD ∆中
90
ABD FBD BD BD
ADB FDB ⎧∠=∠⎪=⎨⎪∠=∠=⎩ ∴ABD FBD ∆≅∆(ASA ∴2D FB ∠=∠ 又1DFB C ∠=∠+∠ ∴21C ∠=∠+∠。
思考:由于角是轴对称图形,所以我们可以利用翻折来构造或发现全等三角形。
例3. 如图,在ABC ∆中,AB BC =,90ABC ∠=。
F 为AB 延长线上一点,点E 在BC 上,BE BF =,连接,AE EF 和CF 。
求证:AE CF =。
思路:可以利用全等三角形来证明这两条线段相等,关键是要找到这两个三角形。
以线段AE 为边的ABE ∆绕点B 顺时针旋转90到CBF ∆的位置,而线段CF 正好是CBF ∆的边,故只要证明它们全等即可。
证明:90ABC ∠=,F 为AB 延长线上一点
∴90ABC CBF ∠=∠=
在ABE ∆与CBF ∆中
AB BC ABC CBF BE BF =⎧⎪∠=∠⎨⎪=⎩
∴ABE CBF ∆≅∆(SAS)
∴AE CF =。
思考:利用旋转的观点,不但有利于寻找全等三角形,而且有利于找对应边和对应角。
小结:利用三角形全等证明线段或角相等是重要的方法,但有时不容易找到需证明的三角形。
这时我们就可以根据需要利用平移、翻折和旋转等图形变换的观点来寻找或利用辅助线构造全等三角形。
例4. 如图,AB //CD ,AD //BC ,求证:AB CD =。
思路:关于四边形我们知之甚少,通过连接四边形的对角线,可以把原问题转化为全等三角形的问题。
证明:连接AC
AB //CD ,AD //BC
∴12∠=∠,34∠=∠
在ABC ∆与CDA ∆中
1243AC CA ∠=∠⎧⎪=⎨⎪∠=∠⎩
∴ABC CDA ∆≅∆(ASA)
∴AB CD =。
思考:连接四边形的对角线,是构造全等三角形的常用方法。
例5. 如图,,AP CP 分别是ABC ∆外角MAC ∠和NCA ∠的平分线,它们交于点P 。
求证:BP 为MBN ∠的平分线。
思路:要证明“BP 为MBN ∠的平分线”,可以利用点P 到,BM BN 的距离相等来证明,
故应过点P 向,BM BN 作垂线;另一方面,为了利用已知条件“,AP CP 分别是MAC ∠和NCA ∠的平分线”,也需要作出点P 到两外角两边的距离。
证明:过P 作PD BM ⊥于D ,PE AC ⊥于E ,PF BN ⊥于F
AP 平分MAC ∠,PD BM ⊥于D ,PE AC ⊥于E
∴PD PE =
CP 平分NCA ∠,PE AC ⊥于E ,PF BN ⊥于F
∴PE PF =
PD PE =,PE PF =
∴PD PF =
PD PF =,且PD BM ⊥于D ,PF BN ⊥于F
∴BP 为MBN ∠的平分线。
思考:题目已知中有角平分线的条件,或者有要证明角平分线的结论时,常过角平分线上的一点向角的两边作垂线,利用角平分线的性质或判定来解答问题。
例6. 如图,D 是ABC ∆的边BC 上的点,且CD AB =,ADB BAD ∠=∠,AE 是ABD ∆的中线。
求证:2AC AE =。
思路:要证明“2AC AE =”,不妨构造出一条等于2AE 的线段,然后证其等于AC 。
因此,延长AE 至F ,使EF AE =。
证明:延长AE 至点F ,使EF AE =,连接DF
在ABE ∆与FDE ∆中
AE FE AEB FED BE DE =⎧⎪∠=∠⎨⎪=⎩
∴ABE FDE ∆≅∆(SAS)
∴B EDF ∠=∠
ADF ADB EDF ∠=∠+∠,ADC BAD B ∠=∠+∠ 又ADB BAD ∠=∠
∴ADF ADC ∠=∠
AB DF =,AB CD =
∴DF DC =
在ADF ∆与ADC ∆中
AD AD ADF ADC DF DC =⎧⎪∠=∠⎨⎪=⎩
∴ADF ADC ∆≅∆(SAS)
∴AF AC =
又2AF AE =
∴2AC AE =。
思考:三角形中倍长中线,可以构造全等三角形,继而得出一些线段和角相等,甚至可以证明两条直线平行。
例7. 如图,在ABC ∆中,A B A C >,12∠=∠,P 为AD 上任意一点。
求证:AB AC PB PC ->-。
原图 法一图 法二图
思路:欲证AB AC PB PC ->-,不难想到利用三角形中三边的不等关系来证明。
由于结论中是差,故用两边之差小于第三边来证明,从而想到构造线段AB AC -。
而构造AB AC -可以采用“截长”和“补短”两种方法。
证明:法一:
在AB 上截取AN AC =,连接PN
在APN ∆与APC ∆中
12AN AC AP AP =⎧⎪∠=∠⎨⎪=⎩
∴APN APC ∆≅∆(SAS)
∴PN PC =
在BPN ∆中,PB PN BN -<
∴-<-PB PC AB AC ,即AB -AC>PB -PC 。
法二:
延长AC 至M ,使AM AB =,连接PM
在ABP ∆与AM P ∆中
12AB AM AP AP =⎧⎪∠=∠⎨⎪=⎩
∴ABP AM P ∆≅∆(SAS)
∴PB PM =
在PCM ∆中,CM PM PC >-
∴AB AC PB PC ->-。
思考:当已知或求证中涉及线段的和或差时,一般采用“截长补短”法。
具体作法是:在较长的线段上截取一条线段等于一条较短线段,再设法证明较长线段的剩余线段等于另外的较短线段,称为“截长”;或者将一条较短线段延长,使其等于另外的较短线段,然后证明这两条线段之和等于较长线段,称为“补短”。
小结:本题组总结了本章中常用辅助线的作法,以后随着学习的深入还要继续总结。
我们不光要总结辅助线的作法,还要知道辅助线为什么要这样作,这样作有什么用处。
