广东省汕头市潮阳一中高二物理竞赛专题:6.磁场
高二物理竞赛静磁场课件

5
5
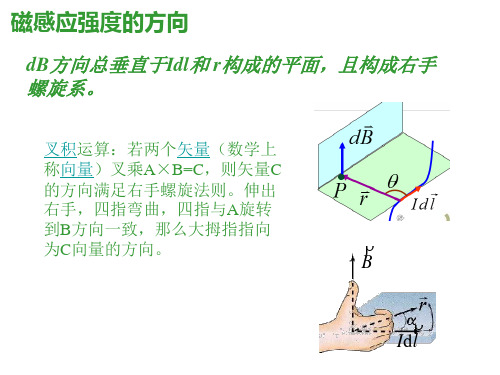
v 二 磁感强度 B 的定义
安培提出:一切磁现象起源于电荷运动
本质
运动电 荷载流 导线磁 体
磁
运动电
荷载流
场
导线磁
体
6
6
磁场的性质 (1) 对运动电荷(或电流)有力的作用 (2) 磁场有能量
磁感应强度有各种定义方法,除上述方法外,我 们还可以用运动电荷在磁场中的受力来定义。
9
9
一 毕奥-萨伐尔定律
(电流元在空间产生的磁场)
dB
0
4π
Idl sin
r2
v dB
0
4π
v Idl
r3
v r
真空磁导率 0 4 π10 7 N A2
rv
v dB
P*v v r Idl
v dB
v Idl
I
B 的方向沿 x 轴负方向
14
14
B
0I
4 π r0
(cos
1
cos 2 )
无限长载流长直导线
z
D 2
1 0 2 π
B 0I
2 π r0
I
xo
C 1
v
B
×
P
y
半无限长载流长直导线
1
π 2
2 π
BP
0I
4πr
15
15
静磁场
1
1
磁现象(1)
磁现象(2)
磁体 SN
磁体 磁 场 SN
电流
高中物理竞赛课件:磁场(共80张PPT)
6 10
专题21-例4 一N匝密绕的螺线管长L,半径r,且L >> r.当通有
恒定电流I时,试求作用在长螺线管侧面上的压强p .
解:解题方向: 求出电流元所处磁场磁感 应强度,即可求安培力及其对螺线管
Fi
侧面压强
电流元所在处磁场设为B其它;
B其余 Bi
Bi
电流元内侧有
B B其余 Bi B I
dB 只有x,y方向上的分量
B dB
dx I
2b
o
r
d
r
dB
P
dB
y
x
iˆ
dB x
ˆj
dB y
dx
由于铜片对y 轴对称,所有长条电流的
dB
dBy
dB
x
dB 分量的代数和等于零 y
dB y
B
iˆ
dB x
dI I dx dB 0dI
x
2b
2r
I
n 1
2
a
P
变式训练
电流为I的一无限长直导线在C点被折成60°角,若用同样导 线将A,B两点连接,且AB=BC=L,求三角形中心点O的磁感 应强度。
变式训练
从无限远来的直电流从A点流入正方形导体框,又从B点沿 直线流向无限远。若正方形边长为l,且导体粗细均匀,流 入的总电流强度为I。求正方形中心O处的磁感应强度。
电流元外侧有
0 B其余 Bi
B其余
B 2 Fi Fi
0BrIN2lI 2
2nL
P Fi 0 N 2 I 2
高二物理竞赛利用安培环路定理求磁场的分布PPT(课件)

真空中两无限大的均匀带电平行板?
解: 0 r R, B d l 0 l
B0
r R,
l B d l 0I
B 0I 2 r
例4 在一无限大的导体平板上均匀流有电流密度为 j 的面电流,求平板两侧的磁感应强度。
解:
j
dI
dI’
dB
俯视图
1) 对称性分析:载流平面产生的磁场,其方向与平面 平行,与平面电流成右手螺旋方向。
2) 选回路 L:矩形环路 有对称性分布电流的磁感应强度。
例1 求载流螺绕环的磁场分布
解:1) 对称性分析;B 线为与 螺绕环共轴的圆周。
2) 选回路 L。
L B dl B L dl B2 r
L
0 Iint 0NI
L d
B 0 NI 2 r
(R1 r R2 )
L
r
B 0 (r R1, r R2 )
静电场的高斯定理: (1) 均匀密绕螺线管
E dS q 且与轴线距离相同的各点的磁感强度B值相同.故可以
真空中两无限大的均匀带电平行板?
r
为半径、以轴线为圆心、过P点作一圆形环S路
对均匀密绕螺绕环,磁场几乎全部集中于管内,在环的外部空间,磁感应强度处处为零。
l
为积分路径,利用安培环路定理i求ntB 0
I . dB
dI B
B 的方向与 I 成右螺旋
0 r R,
r R,
B
0 Ir 2 R2
B 0I 2 r
I
R
0I
B
2 R
oR r
例3 无限长载流圆柱面的磁场
L1
(2) 求通过两柱面间长度为L的径向纵截面的磁通量。
r
例3 无限长载流圆柱面的磁场
高二物理竞赛电磁学磁场的高斯定理安培环路定理PPT(课件)

dB
dB
d
P. P.
d B
c
B a b B c d 2Bab i
而0Ii0i ab
i
... . d l
.o.
.
dl
.
.
.
B
1 2
0i
均匀场!
i
i
a
.B b 与P点到平板的距离无关!
P
例8. 求通电流I, 环管轴线半径为R的螺绕环的 磁场分布。已知环上均匀密绕N 匝线圈。
解:由电流对称性,与环共轴的圆周
Bdl L
B2r
0
0r2R 1 2 0I
Ii r 2 R12 R22 R12
.
r
R1
R2
B 0I
2 R22R12
rRr12
I
R22 R12
当 当
R1 0 r R1
;B ;B
0 Ir
2
R
2 2
0 当 r
实心圆柱体内部
的磁感应强度
R2
;B
0I 2 R2
圆柱体内外 壁的磁感应 强度
当
;
r Ampere’s Law
o 1º 静电场中,任意闭合曲面S的电通量:
d drl' 各点产生的B都不为0。
L dl
dsrd
且有
(B dl)90o
(B dl)90o
B d l B d l
B d l c o s B d l c o s
B d s B d s
20Irrdds 20Irdr sd = 0
B
2
0I
R22 R12
rRr12
r
I
R1
R2
高中物理竞赛电磁学专题练习20题(带答案详解)

高中物理竞赛电磁学专题练习20题(带答案详解)一、解答题1.如图所示,长直螺旋管中部套有一导线围成的圆环,圆环的轴与螺旋管的轴重合,圆环由电阻不同的两半圆环组成,其阻值1R 、2R 未知.在两半圆环的结合点A 、B 间接三个内阻均为纯电阻的伏特表,且导线0A V B --准确地沿圆环直径安放,而1A V B --、2A V B --分置螺旋管两边,长度不拘,螺旋管中通有交流电时发现,0V 、1V 的示数分别为5V 、10V ,问:1V 的示数为多少?螺旋管外的磁场及电路的电感均忽略不计2.图1、2、3所示无限长直载流导线中,如果电流I 随时间t 变化,周围空间磁场B 也将随t 变化,从而激发起感应电场E .在载流导线附近空间区域内,B 随t 的变化,乃至E 随t 的变化可近似处理为与I 随时间t 变化同步.距载流导线足够远的空间区域,B 、E 随t 的变化均会落后于I 随t 的变化.考虑到电磁场变化传播的速度即为光速,如果题图讨论的空间区域线度尽管很大,题图讨论的空间区域线度尽管很大,即模型化为图中即模型化为图中x 可趋向无穷,可趋向无穷,但这一距离造成的但这一距离造成的B 、E 随t 的变化滞后于I 随t 变化的效应事实上仍可略去.在此前提下,求解下述问题(1)系统如图1、2所示,设()I I t =①通过分析,判定图1的xOy 平面上P 处感应电场场强P E 的三个分量Px E 、Py E 、PzE中为零的分量中为零的分量②图2中12l l ⨯长方形框架的回路方向已经设定,试求回路电动势ε③将图1中的P 、Q 两处感应电场场强的大小分别记为P E 、Q E ,试求P Q -E E 值 (2)由两条无限长反向电流导线构成的系统如图3所示,仍设()I I t =,试求P 处感应电场场强P E 的方向和大小3.现构造如图1所示网络,该网络为无穷正方形网络,以A 为原点,B 的坐标为()1985,930.现在两个这样的网络C C A B 和L L A B ,其单位长度上所配置的电学元件分别为电容为C 的电容器及电感为L 的线圈,且网络中的电阻均忽略不计,并连接成如图2所示的电路S 为调频信号发生器,可发出频率()0,f Hz ∈+∞的电学正弦交流信号.即()0sin 2πS U U ft =,0U 为一已知定值,R 为一已知保护电阻为一已知保护电阻试求干路电流达到最大时,S 的频率m f 以及此时干路的峰值电流max I4.在空间中几个点依次放置几个点电荷1q ,2q ,3q ,4q ,…,n q ,对于点i ,其余1n -个点电荷在这一点上的电势和为i U ,若在这n 个点上换上另n 个点电荷1q ',2q ',3q ',…,n q ',同理定义()1,2,,i U i n '=L(1)证明:()112nni i i i i i qU q U n ==''=≥∑∑(2)利用(1)中结论,证明真空中一对导体电容器的电容值与这两个导体的带电量无关.(这对导体带等量异号电荷)(3)利用(1)中的结论,中的结论,求解如下问题:求解如下问题:求解如下问题:如图所示,如图所示,如图所示,正四面体正四面体ABCD各面均为导体,但又彼此绝缘.已知带电后四个面的静电势分别为1ϕ、2ϕ、3ϕ和4ϕ,求四面体中心O点的电势O ϕ5.有七片完全相同的金属片,有七片完全相同的金属片,面积为面积为S ,放置在真空中,放置在真空中,除除4和5两板间的间距为2d 外,其他相邻两板间距均为d ,且1和5、3和7用导线相连,试求:(1)4与6两板构成的电极的电容(2)若在4和6间加上电压U ,求各板的受力.6.如图所示,一电容器由一圆形平行金属板构成,金属板的半径为R ,间距为d ,现有一点P ,在两金属板的中位面(即平行于两板,且平分两极板所夹区域的平面)上,P 到两中心O 的距离为()0R r r +>R ,已知极板所带的面电荷密度为σ±,且R r d ??,试求P 点的场强大小P E7.在一环形铁芯上绕有N 匝外表绝缘的导线,导线两端接到电动势为ε的交流电源上,一电阻为R 、自感可略去不计的均匀细圆环套在这环形铁芯上,细圆环上a 、b 两点间的环长(劣弧)为细圆环长度的1n.将电阻为r 的交流电流计G 接在a 、b 两点,有两种接法,分别如图1、图2所示,试分别求这两种接法时通过G 的电流8.有一个平面正方形无限带电网络,每个格子边长均为r ,线电荷密度为()0λλ>,有一带电电量为()0Q Q >、质量为m 的粒子恰好处于一个格子的中心,若给它某个方向的微扰,使其位移d ,d r =.试求它受到电场力的大小,并描述它以后的运动.(提示:可能用到的公式2222π11116234=++++L )9.(1)一维电磁驻波()()sin x E x A k x =在x 方向限制在0x =和x a =之间.在两个端点处驻波消失,求x k 的可能值.的可能值.(2)弦理论认为物理空间多于三维,多出的隐藏维空间像细圆柱的表面一样卷了起来,如图中y 坐标所示,设圆柱的半径为()b a =,在圆柱面上电磁波的形式为()()(),sin cos x y E x y A k x k y =,其中y 是绕圆柱的折叠空间的坐标.求y k 的可能值.的可能值.(3)光子能量222πx yhc W k k =+,其中()1239hc eV nm =⨯,eV 表示1电子伏特,1nm 等于910m -.目前人类能产生的最高能量的光子大约为121.010eV ⨯.如果该能量能够产生一个折叠空间的光子,b 的值满足什么条件?10.在图1所示的二极管电路中,所示的二极管电路中,从从A 端输入图2所示波形的电压,所示波形的电压,若各电容器最初都若各电容器最初都没有充电,试画出B 、D 两点在三个周期内的电压变化.将三极管当作理想开关,B 点电压的极限是多少?电压的极限是多少?11.理想的非门可以视为一个受控电压源:理想的非门可以视为一个受控电压源:当输入端电压小于当输入端电压小于6C U V =时,输出端相当于和地线之间有一个理想电压源,电源电压012U V =;当输入端电压大于C U 时,输出端相当于和地线之间短路.出端相当于和地线之间短路.等效电路图如图等效电路图如图1所示.不同非门中接地点可以视为是同一个点,我们利用非门、电容和电阻能够做成一个输出方波信号的多谐振荡器.给出图2电路中02U 随着时间的变换关系.提示:如图3的RC 电路,从刚接通电路开始,电容上的电压随时间变化规律为()()01t RC U t U e -=- 12.如图所示,在圆形区域中(足够大),有垂直于纸面向内随时间均匀增加的磁场B kt∆=∆.在与圆心O 距离为d 的位置P 处有一个钉子,钉住了一根长度为l ,质量为m 的均匀绝缘棒的中心,绝缘棒能在平面内自由无摩擦地自由转动.绝缘棒能在平面内自由无摩擦地自由转动.绝缘棒上半截均匀带绝缘棒上半截均匀带正电,电量为Q ,下半截均匀带负电,电量为Q -.初始时刻绝缘棒垂直于OP(1)计算在P 点处钉子受到的压力(2)若绝缘棒受到微小扰动,在平面内来回转动起来(速度很小,洛仑兹力可以忽略),求证此运动是简谐振动,并计算周期.(绝缘棒绕质心的转动惯量为2112I ml =)13.如图1所示的电阻网络中,图中各段电阻的阻值均为r(1)试求AB R 、AC R(2)现将该网络接入电路中,如图2所示.AC 间接电感L ,A 、B 间接一交流电源,其角频率为ω,现为提高系统的动率因数,在A 、B 间接一电容C ,试求使功率因数为1的电容C ,已知rL αω=14.两个分别绕有1N 和2N 匝的圆线圈,半径分别为1r ,2r 且21r r =,设大圆的电阻为R ,试求:(1)两线圈在同轴共面位置的互惑系数(2)在小线圈中通以稳恒电流I ,并使之沿轴线以速度v 匀速运动.始终保持二者共轴,求两线圈中心相距为x 时,大线圈中的感生电动势(3)若把小线圈从共面移到很远处,求大线圈中通过的感生电量.(忽略所有自感) 15.如图所示为一两端无限延伸的电阻网络,设每小段电阻丝电阻均为1Ω,试问:A 、B 间等效电阻AB R 为多少?(结果保留三位有效数字)为多少?(结果保留三位有效数字)16.如图a 所示,电阻101k R R ==Ω,电动势6V E =,两个相同的二极管D 串联在电路中,二极管D 的D D I U -特性曲线如图b 所示.试求: (1)通过二极管D 的电流;的电流; (2)电阻1R 消耗的功率.17.如图甲所示,两台发电机并联运行,共同供电给负载,负载电阻24R =Ω.由于某种原因,两台发电机的电动势发生差异,1130V ε=、11r =Ω、2117V ε=、20.6r =Ω.求每台发电机中的电流和它们各自发出的功率.18.如图1所示的无限旋转内接正方形金属丝网络由一种粗细一致、所示的无限旋转内接正方形金属丝网络由一种粗细一致、材料相同的金属丝材料相同的金属丝构成,其中每一个内接正方形的顶点都在外侧正方形四边中点上.其中每一个内接正方形的顶点都在外侧正方形四边中点上.已知与最外侧正方形已知与最外侧正方形边长相同的同种金属丝A B ''的电阻为0R ,求网络中 (1)A 、C 两端间等效电阻AC R ; (2)E 、G 两端间等效电阻EC R .19.正四面体框架形电阻网络如图所示,其中每一小段的电阻均为R,试求:(1)AB两点间的电阻;(2)CD两点间的电阻.20.在如图所示的网络中,仅知道部分支路上的电流值及其方向、某些元件参数和支路交点的电势值(有关数值及参数已标在图甲上),请你利用所给的有关数值及参数求出含有电阻x R的支路上的电流值x I及其方向.参考答案1.220V U V =或0. 【解析】【解析】 【详解】因螺旋管中通有交流电,故回路中产生的电动势也是交变的,但可以仅限于某确定时刻的感生电动势、电压和电流的瞬时值,这是因为在无电感、电容的情况下,各量有效值的关系与瞬时值的关系相同.(1)当12R R <,取A B U U >时,回路中的电流如图所示,则时,回路中的电流如图所示,则0001102V I R I R ε+-=,0100102V V I R I R ε'+-=,2202V I R I R ε-+=,0200202V V I R I R ε'-+=.整理可得0120001202V V V V I R I R I R I R ε''=+=-.所以,2201201220V V V V U I R I R I R V ''==+=(2)当12R R >,取A B U U <时,0I 反向,其他不变,则1020010202V V V V I R I R I R I R ε''=-=+所以,221021020V V V V U I R I R I R ''==-=(此时20R =,即2R 段为超导体,10R ≠) 综上所述,220V U V =或02.(1)①0PzE =②012d ln2πd l x l l t x με+⎛⎫= ⎪⎝⎭ ③02d ln 2πd P Q x l I E E t x μ+⎛⎫-= ⎪⎝⎭(2)()0d ln 2πd P I d x E x t x μ-⎛⎫= ⎪⎝⎭,基准方向取为与y 轴反向轴反向 【解析】 【详解】(1)①若0Pz E ≠,则在过P 点且与xOy 坐标面平行的平面上,取一个以x 为半径,以y 轴为中央轴的圆,设定回路方向如题解图所示.由系统的轴对称性,回路各处感应电场E 的角向分量与图中Pz E 方向一致地沿回路方向,且大小相同,由E 的回路积分所得的感应电动势0ε≠.另一方面,电流I 的磁场B 在该回路所包围面上磁通量恒为零,磁通量变化也为零,据法拉第电磁感应定律应有0ε=.两者矛盾,故必定是0Pz E =.若0Py E ≠,由系统的轴对称性,在题解图1的圆柱面上各处场强E 的y 方向分量方向、大小与图中Py E 方向、大小相同.若取一系列不同半径x 的同轴圆柱面,每个圆柱面上场强E 的y 方向分量方向相同、方向分量方向相同、大小也相同,但大小应随大小也相同,但大小应随x 增大而减小.这将使得题文图2中的矩形回路感生感应电动势0ε≠,与法拉第电磁感应定律相符,因此允许0Py E ≠若0Px E ≠,由轴对称性,题解图1的圆柱面上各处场强E E 的径向分量方向与Px E 对应的径向方向一致,两者大小也相同.将题解图1中的圆柱面上、下封顶,成为一个圆筒形高斯面,上、下两个端面d ⋅E S 通量积分之和为零,侧面d ⋅E S 通量积分不为零,这与麦克斯韦假设所得1d d 0se sV V ρε⋅==⎰⎰⎰⎰⎰ÒE S矛盾,故必定是0Px E =②据法拉第定律,参考题文图2,有()21d d d x l xB x l x t ε+=--⎰,其中()02πI B x x μ= 所以,001221d d ln ln d 2π2πd Il x l x l l l t x t x μμε++⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭③据麦克斯韦感应电场假设,结合(1.1)问解答,有)问解答,有 ()()121=d LE l E x l E x l l ε⋅=-+⎰Ñ结合①②问所得结果,有()()012121d ln 2πd l x l I E x l E x l l t x μ+⎛⎫-+= ⎪⎝⎭ ()()022d ln 2πd x l IE x E x l t xμ+⎛⎫-+= ⎪⎝⎭ 即得()()022d ln2πd P Q x l I E E E x E x l t x μ+⎛⎫-=-+=⎪⎝⎭ (2)从物理上考虑,远场应()220l E x l →∞+→代入上式,得()202d ln 2πd Pl x l I E E xt x μ→∞+⎛⎫==→∞⎪⎝⎭为行文方便,将P E 改述为()02d ln2πd z PP l x l IE E xt x μ→∞+⎛⎫→=→∞⎪⎝⎭()P E x 为发散量,系因模型造成,并非真实如图所示,由左侧变化电流贡献的()P x 左E 和右侧变化电流贡献的()P x 右E合成的()PE x ,基准方向取为与y 轴反向.轴反向.即有()()()P P P E x E x E x =-左右()()00d d ln ln 2πd 2πd P x d x lx l I I E x t x t x μμ∞+-++⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭左右()()()00d d ln ln 2πd 2πd P d x l d x x lI I E x t d x t d x μμ∞-+-++⎛⎫⎛⎫== ⎪ ⎪--⎝⎭⎝⎭右左 使得()()0d ln 2πd P I d x E x E x t xμ-⎛⎫== ⎪⎝⎭3.0maxU I R =,12π2πm f LCω== 【解析】【解析】 【详解】不妨设电感网络等效电感AB L L α=,则其阻抗L αω=Z j (j 为单位虚根)为单位虚根) 又由于C C A B 与L L A B 的结构相同,故在阻抗上形式具有相似性,故在阻抗上形式具有相似性,有有1C C αω=⋅Z j ,从而总阻抗11LCRR L RL C C αωααωωω⎛⎫⎛⎫=++=+-=+- ⎪ ⎪⎝⎭⎝⎭ZZZZj j j 又峰值0U I =Z ,所以,1222001I U R L C ααω-⎡⎤⎛⎫⎥=⋅+- ⎪⎢⎝⎭⎣⎦所以,当10L Cωω-=,即1LCω=时,0I 最大 此时,0maxU I R =,而12π2πm f LCω== 4.(1)证明见解析(2)证明见解析(3)12344Oϕϕϕϕϕ+++=【解析】 【详解】(1)设i 点对j 点所产生的电势为ij i a q ,同理易知j 点对i 点产生电势为ji j a q ,而对于此二点系统,我们有ij j ji i U q U q =,即ij i j ji j i a q q a q q = 所以,ij ji a a =,易知ij a 为只与位置有关的参量.又1231231n ni i i i i n ij j j U a q a q a q a q a q ==++++=∑L (令0ii a =)则1231231n nii i i i nij j j U a q a q a q a q a q =''''''=++++=∑L(ij a 只与位置有关)所以,111,1111nnn n n nn i i i ij j ij i j i ij j i i i i j i j i j i qU q a q a q q q a q q U =======⎛⎫⎛⎫'''''==== ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∑∑∑所以原式(格林互易定理)成立(2)分别设两导体前后所带静电分别为1Q ±,2Q ±,其对应的电容分别为1C 、2C则由(1)知,()121122121221ni i i qU QU QU Q U U ='=-=-∑(其中21U ,22U 为带2Q ±时两导体电势)同样()211212211121ni i i q U Q U Q U Q U U ='=-=-∑(其中11U ,12U 为带1Q ±时两导体电势)时两导体电势)由(1)知二者相等,则()()1212221112Q U U Q U U -=-所以,121211122122Q Q C C U U U U ===--即与导体带电量多少无关.即与导体带电量多少无关.(3)由题意,设四个面与中心O 的电荷量分别为1q 、2q 、3q 、4q 、0 同时,四个面与中心的电势分别为1ϕ、2ϕ、3ϕ、4ϕ、O ϕ.现将外面四个面接地,中心放一个电量为Q 的点电荷,中心电势为U ,而四个面产生的感应电荷都相等,为4Q-,则此时四个面与中心O 的电荷和电势分别为4Q -、4Q -、4Q -、4Q-、Q ;0、0、0、0、U由格林互易定理可得123404444O Q Q Q Q U ϕϕϕϕϕ⎛⎫⎛⎫⎛⎫⎛⎫⋅-+⋅-+⋅-+⋅-+⋅=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭即可得12344O ϕϕϕϕϕ+++=5.(1)04616161919S C C d ε==(2)24232361U S F d ε=,方向向上;25213722U S F dε=,方向向下;206216722U S F d ε=,方向向上;207281722U SF d ε=,方向向上【解析】 【详解】【详解】(1)由4与6两板构成的电极的电容结构可等效为图所示的电容网络,其中图101223345667SC C C C C C dε======,04522SC C dε==.由图可知,各电容器所带的电量满足342356Q Q Q =+,451267Q Q Q +=,2312Q Q =. 各支路的电压满足如下关系:各支路的电压满足如下关系:3456Q Q U C C +=,45672Q Q U C C +=,23566712Q Q Q Q C C C C+=-. 由上述各式解得1223119Q Q CU ==,341019Q CU =,45619Q CU =,56919Q CU =,67719Q CU =,则344504616161919Q Q S C C U dε+===.为求4、6端的电容,我们也可通过先求如图左所示的电阻网络的阻值,进而求得电容.将图中O ABC -的Y 形接法部分转化为△接法,得到图2右所示电路,其阻值如图所示,进而易得到进而易得到461916R R =. 直流电路的电阻、电压、电流之间有U I R=. 由电容组成的电路的电容、电压、电量之间有Q CU =. 类比有1C R~.且上述的电阻电路与电容电路匹配,所以,46461C R ~,即有04616161919S C C dε==.(2)由于各板的受力为系统中其他板上的电荷在该板处产生的电场对其板上电荷的作用力,故而通过高斯定理易求得各板处的场强,进而求得各板的受力为2121111202722U S Q F E Q Q dεε==⋅=,方向向下,在原系统中. (1E 求法:1板上侧面不带电,下侧面带电12Q ,正电,即011219USQ Q dε==,由电荷守恒知,27~板带电总量为1Q ,为负电,将27~视为整体,由高斯定理易得到1102Q E ε=)下面符号i Q 表示第i 块板所带的总电量.2220F E Q ==.(该板显然有20Q =)2456701233332009922722Q Q Q Q U S Q Q F E Q Q d εεε⎛⎫++++==-⋅= ⎪⎝⎭,方向向下.,方向向下.式中00033423109191919US US US Q Q Q d d d εεε=-+=-+=-,0434451619US Q Q Q d ε=+=, 054556319US Q Q Q d ε=-+=,656671619US Q Q Q d ε=--=-, 0767719USQ Q d ε=-=-.同理可得:24232361U S F d ε=,方向向上;,方向向上;205213722U SF d ε=,方向向下; 206216722U S F dε=,方向向上; 27281722U SF dε=,方向向上.6.02πP dE rσε=【解析】【解析】 【详解】我们用磁场来类比,引入假想的磁荷1m q 、2m q ,且定义,且定义123014πm m q q r μ==F r ,且1213014πm m q q r μ==F H r . 下面我们通过磁偶极子与环电流找到联系:下面我们通过磁偶极子与环电流找到联系:对于一1m ±q 的磁偶极子,磁矩m m q =p l ,而对于一个电流为I 的线圈,磁矩0m I μ'=p S ,当m m '=p p 时,有0m q I μ=l S .对于此题,我们认为上、下两极板带磁荷面密度为m σ±,则对于S ∆面积中的上、下磁荷,我们看作磁偶极子,则若用环电流代替,有0m Sd I S σμ∆=∆,所以,0m dI σμ=.于是,该两带电磁荷板可等效为许多小电流元的叠加,该两带电磁荷板可等效为许多小电流元的叠加,而这样的电流源会在内部抵消,而这样的电流源会在内部抵消,而这样的电流源会在内部抵消,最后最后只剩下最外层一大圆,且0mdI σμ=.在P 点处的磁场强度,由于R r,故可认为由一距P 距离为r 的无限长通电导线所产生,且其中的电流为I ,则002π2πm Pd B IH r r σμμ===. 由于电、磁场在引入磁荷后,在形式上完全一样,则02πP d E rσε=7.()21n N n R n r ε⎡⎤-+⎣⎦ 【解析】 【详解】【详解】解法(1):细圆环中的电动势为R Nεε=.细圆环上ab 段的电阻为段的电阻为劣弧ab R R n=. 优弧()1ab n R R n-'=.如题图1中接上G 后,G 的电阻r 与ab R 并联,然后再与ab R '串联,这时总电阻便为串联,这时总电阻便为()11ab ab abn RrR rRR R r R nr R n -'=+=+++.于是,总电流(通过优弧ab R '的电流)为()1111RI n R R NrR nr R nεε==⋅-++.(请读者自行推导此式)则通过G 的电流为()11121RR nn i I I Rnr R N n R n r rnε===+⎡⎤-+⎣⎦+.(请读者自行推导此式)解法(2):如题图2中接上G 后,G 的电阻r 与abR '并联,然后再与ab R 串联,这时总电阻便为()()211ab ab abn rRrR R R R nr n Rnr R '-=+=++-'+.于是,总电流(通过劣弧ab R 的电流)为()()22111RI n rR R N R nr n R n εε==⋅-++-,则通过G的电流为()()2211n n i N n R n r ε-=⎡⎤-+⎣⎦8.故对于一微扰位移为d 的粒子,有()20π02Q Q r λλε=->F d ,粒子做简谐振动,20π2Q r mλωε= 【解析】 【详解】引理:线电荷密度为()0λλ>的无限长带电线,其在距带电线r 处产生的场强大小为02πE r λε=,方向垂直于带电线向外.,方向垂直于带电线向外. 证明略.证明略.对于本题所给的模型,对于本题所给的模型,建立图示坐标.建立图示坐标.建立图示坐标.因粒子在因粒子在x 轴方向上的受力只与粒子x 方向上的微扰有关,在y 方向上的受力,也只与y 方向上的微扰有关,设粒子在x 方向上有微扰位移x d ,则110021212π2πd 22xi i x Q Q F i i d r x r λλεε∞∞==∆=---⎛⎫⎛⎫+-+⎪ ⎪⎝⎭⎝⎭∑∑. 又由于x d r =,则()()110022*********π2π22xxx i i d d Q Q F i r i r i r i r λλεε∞∞==⎡⎤⎡⎤∆≈--+⎢⎥⎢⎥--⎛⎫⎛⎫⎣⎦⎣⎦-- ⎪ ⎪⎝⎭⎝⎭∑∑()()22221100441ππ2121x xi i Q d Q d r i r i λλεε∞∞===-=---∑∑.又22222222221111111111113523456246⎛⎫⎛⎫+++=-++++++-+++ ⎪ ⎪⎝⎭⎝⎭LL L222222221111111111234564123⎛⎫⎛⎫=++++++-+++ ⎪ ⎪⎝⎭⎝⎭L L 223ππ468=⨯=,所以,2π2x x Q F d rλε∆=-.同理,20π2y y Q F d rλε∆=-. 故对于一微扰位移为d 的粒子,有()20π02Q Q rλλε=->F Fd , 故粒子做简谐振动,20π2Q r mλωε=9.(1)πx n k a =,1n =,2,3,… (2)y mk b=,1m =,2,3,…(3)12101239102102πb nm nm -->⨯≈⨯【解析】【解析】 【详解】(1)要使得电磁波在两端形成驻波,则长度应是半波长的整数倍,相位满足:πx k a n =,即πx nk a=,1n =,2,3,….(2)要使得电磁波在y 方向上的形式稳定为()()(),sin cos x y E x y A k x k y =,则圆柱的周长应为波长的整数倍,相位满足:2π2πy k b m =,即y mk b=,1m =,2,3,…. (3)由222πx yhc W k k =+得22121239π102πn m a b ⎛⎫⎛⎫+=⎪ ⎪⎝⎭⎝⎭, 所以,121239102πm m b <,即12101239102102πb nm nm -->⨯≈⨯10.02U 【解析】【解析】 【详解】将过程分为三个阶段,记为α、β、γ.在第一个14周期内,A U 增加,0A D U U >>,因此二极管2D 截止;又因0DB U ≥,二极管1D 保持导通,等效电路如图1所示,在此阶段2D B A U U U ==,记为α然后A U 开始减小,但AD U 保持不变,最初D U 仍然大于零,因此,2D 依然截止.不过D U 正在逐渐减小,所以1D 截止.由于电容上的电荷无处可走,B U 保持不变,AD U 也保持不变.这个阶段一直持续到0D U =,这一过程等效电路如图2所示,记为β.不过,0D U <是不可能的,所以0D U =直至0A U U =-.这一过程等效电路如答图3所示,记为γ.下面A U 又从0U -开始增加,然后AD U 又保持在0U -不变(再次处于β阶段),而B D U U >停留在02U ,直到D U 升至B U .当D B U U =时β阶段结束.阶段结束. 而后新的α阶段又开始了.每个周期均按αβγβ---的次序通过各个阶段,但是电路并不是随时间周期变化的,这可以从图4中看出.B U 等比地趋近于02U ,即是说00322B U U U -→,034U ,038U ,0316U ,….这个电路称为电压倍增器 11.见解析.见解析 【解析】 【详解】将多谐振荡器电路等效为图示电路,可见电流只在0102U R C U ---回路中流动.假设系统存在稳态,则电容电量为常数,因而电阻上电流为0,则1G 输入电压等于输出电压,这显然矛盾,因而系统不存在稳态.不失一般性,电容初态电压为0,系统初态010U =,因而0212U V =,电路沿顺时针给电容充电(电阻上的电流I 从下向上为正,电容电量Q 右边记为正).从0C Q Q CU ==时起,图中i U 的大小开始小于6V ,门反转,将此后直到门再次反转的过程记为过程I :此时0112U V =,020U =,由于电容上电量不突变,所以,006iQ U V C=-=-.因而电路沿逆时针给电容反向充电,新充入电量为Q ∆.120Q Q V IR C +∆-=--,即18Q VIR C∆=--.i U 不断上升,到达6C U V =时,10C Q Q Q CU =+∆=-时,门反转,此后进入过程Ⅱ.设过程Ⅰ历时t Ⅰ,将18QV IR C ∆=--与题目中的RC 电路满足的0Q U IR C∆=+类比,过程Ⅰ满足的018U V =,()12Q U t V C∆==,则由电容上的电压随时间变化规律()()01t RCU t U e-=-可得:ln 3tRC =Ⅰ. 对于过程Ⅱ,此时010U =,0212UV =,由于电容上电量不突变,所以,11218i Q U V C=-=.因而电路沿顺时针给电容正向充电,新冲入电量为Q '.1012Q Q V IR C '+∆-=--,即18Q V IR C'∆=+. i U 不断上升,到达6C U V =时,210C Q Q Q CU Q '=+∆==,门再次反转,此后又进入过程Ⅰ.同理可得:1ln 3t RC =. 过程Ⅰ、Ⅱ循环进行.因此得方波的信号周期为2ln3T RC =. 12.(1)4klQ (2)2π2π3d m mlT K k Q== 【解析】 【详解】设由变化的磁场产生的涡旋电场大小为E ,则有22ππB E r r t∆⋅=∆,得到2rE k =⋅,方向垂直于与O 的连线.则杆上场强分量为2x k E y =-⋅,2y kE d =-⋅.(1)由于上下电量相反,y 方向的场强为定值,故钉子在y 方向不受力.在x 方向上,其所受电场力(考虑到上下对称)为202d 224l k Q klQ F y y l ⎛⎫=⨯-⋅⋅=⎪⎝⎭⎰. 故钉子压力为4klQ .(由于电场和y 坐标成正比,因而也可以使用平均电场计算电场力)坐标成正比,因而也可以使用平均电场计算电场力)(2)设绝缘棒转过一微小角度θ,此时,y 方向的电场力会提供回转力矩.(由于力臂是一阶小量,横坐标变化引起的电场力改变也是一阶小量,横坐标变化引起的电场力改变也是一阶小量,忽略二阶以上小量,忽略二阶以上小量,忽略二阶以上小量,因而不必计算电因而不必计算电场力改变量产生的力矩.由于电场几乎是均匀的,所以正电荷受力的合力力臂为4lθ⋅)244k l kdlQM d Q θθ=-⋅⋅⋅⋅=-,而M I θ=,则04kdlQ Iθθ+=.这是简谐方程,故绝缘棒的运动是简谐运动,其周期为2π2π3d m mlT K k Q==. 13.(1)12AB R r =,78AC R r =(2)241916C rααω=+【解析】 【分析】【分析】 【详解】(1)将题图1所示的电阻网络的A 、B 两点接入电路时,可以发现D 、E 等势点,于是DC 、DE 、CE 可去掉.所以,12AB R r =.将A 、C 接入电路时,将原电路进行等效变化,如图甲所示.接入电路时,将原电路进行等效变化,如图甲所示.11711283122AC R r r r r =+=+.(2)将题图1等效为图所示三端网络.等效为图所示三端网络.由(1)知1122AB R R r ==,1278AC R R R r +==,解得114R r =,258R r =.所以图所示虚线框内的等效阻抗为121211121324154496448i Z r r r i L αααω-⎛⎫ ⎪++=++= ⎪+ ⎪+⎝⎭.电路的总复导纳()()()()()22222222214964213244964111213216213216Y i C i C Z r r ααααωωαααα⎛⎫+++ ⎪=+=⋅+-⋅ ⎪++++⎝⎭为使功率因数为1,则复导纳虚部为0.所以,()()2222244964141916213216C r rαααωαωαα+=⋅=⋅+++14.(1) 201221211π2I N r I r μΦ= (2) ()2201212522213π2N N r r Ivx r xμε=+ (3) 201221π2N N r IQ r Rμ=【解析】【解析】 【详解】6.【解析.如图所示,半径为a 的线圈中通以I 的电流,则中轴线上距圆心x 处的磁感强度为()22π00322222022d d 4π2a a II l a B B a x a x a x μμ==⋅=+++⎰⎰P(1)两线圈在同轴共面位置时,1a r =,0x =,当大线圈中通有1I 的电流时,有010112I B N r μ=⋅因为21r r =,所以,212022πB N r Φ=⋅,则201221211π2I N r I r μΦ=(2)当两环中心相距x 时,有()220121211232221π2N N r r I r x μΦ=+,121M I Φ=,12MI Φ=,()22012122121522213πd d d d d d 2N N r r Ivxx t x tr x μεΦΦ=-=-⋅=+(3)d d q I t =220122012211ππ1d 1d d d d 0d 22N N r IN N r I Q q I t t t R R t R rr R μμε⎛⎫Φ⎛⎫====-⋅=-= ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰ 15.112310.465AB I R I I I '⨯==Ω'''++ 【解析】【解析】【分析】 【详解】将该网络压扁,如图1所示,除AB ,BC ,CD ,DA 间各边电阻为1Ω外,其余电阻为12Ω现在我们讨论MNPQ 的内部电阻我们将RSTL 的内部电阻等效为图2所示电路,其中a ,b 为待定值,由于RSTL 与MNPQ全等,则有如图所示的等价关系,此等价关系即1212MQ MQ MP MP R R R R =⎧⎪⎨=⎪⎩下标的1代表图3,2代表图4(1)MP R 的分析的分析①1MP R ,由对称性,去掉NS ,SL ,LQ 得1112112MP ab a b R ab a b ⎛⎫+⋅ ⎪+⎝⎭=⎛⎫++⎪+⎝⎭ ②2MP R ,由对称性,去掉NQ ,得2MP ab R a b=+,从而112112ab ab a b ab a b a b ⎛⎫+⋅ ⎪+⎝⎭=+⎛⎫++ ⎪+⎝⎭,解得312ab a b -=+ (2)MQ R 的分析的分析①1MQ R .如图5所示,取回路MNPQM ,MRLQM ,RSTLR ,RLTR ,QLTPQ 得()()13412255256452566225643301110222334001110222I I I I I I aI I I I I I aI a I I I bI I a I I I I I -+=⎧⎪⎪---=⎪⎪-++-=⎨⎪----=⎪⎪+----=⎪⎩解得1626364655166721162582482562376252222531332225b ab a b aI I a b a b a I I a b ab a b a I I a b a a I I a b b a I I a ⎧++++⎪=⎪+⎪+++⎪=⎪+⎪⎪⎪++++⎨=⎪+⎪⎪++⎪=⎪+⎪⎪++⎪=⎪+⎩ 故1122316167211626016246460MQ b ab a b I a R b I I I ab a b a++++==++++++ ②2MP R 如图6所示,由回路MNPQM ,MQPM 得()79878930I I I aaI bI aI⎧--=⎨--=⎩,解得7898322a bI Iaa bI Ia+⎧=⎪⎪⎨+⎪=⎪⎩,故()27789344MQa b aaIR I I I a b+==+++.于是有()166721163604416246460312bab a ba b a aba bab a baaba b⎧++++⎪+=⎪+⎪++++⎨⎪-⎪=⎪+⎩⑧⑨令1xa=,由,由⑨⑨得()131xb=--⑩由⑩代入代入⑧⑧化简有2210x x--=.则12x=±又0a>,则0x>,所以,21x=+,所以,()()2132ab⎧=-Ω⎪⎨=+Ω⎪⎩于是ABCD如图7所示,同上步骤可得:所示,同上步骤可得:1618.93I I ''=,2614.55I I ''=,367.19I I ''=,462.64I I ''=,5610.57I I ''=.则112310.465ABI R I I I '⨯==Ω'''++ 16.(1) 2mA D I = (2) 211116mW U P R ==【解析】 【详解】(1)设每只二极管两端的电压为D U ,通过二极管的电流为D I ,则有,则有1222D D DU U I R R ε⎛⎫=-+ ⎪⎝⎭ 代入题设数据得代入题设数据得()31.50.2510V DDU I =-⨯这是一个在图c 上横轴截距为1.5,纵轴截距为6,斜率为一4的直线方程,绘于c 图可获一直线一直线(称为二极管的负载线).因D U 、D I 还受二极管D 的伏安线限制,故二极管必然工作在负载线与伏安曲线的交点P 上,如图c 所示.此时二极管两端的电压和电流分别为1VDU =,2mA DI =.(2)电阻1R 上的电压124V D U U ε=-=.其功率211116mW U P R==.【点睛】对于非线元件的伏安特性曲线,一般无法用函数方式表述,用图解的方式确定其静态工作点应该是不二的选择.应该是不二的选择.物理问题中涉及非线性元件或过程时,物理问题中涉及非线性元件或过程时,物理问题中涉及非线性元件或过程时,通过图解法来确定其工作点,通过图解法来确定其工作点,通过图解法来确定其工作点,应应该是这类问题的通行做法.17.110A I =(方向为11I 的方向),25A I =(方向为21I 的方向);11200W P =,2600W P =-. 【解析】 【分析】 【详解】【详解】这个电路的结构,不能简单地等效为一个串联、并联电路.要计算这种较复杂的电路,可有多种解法.下面提供两种较为常用的方法.方法一:用基尔霍夫定律解.方法一:用基尔霍夫定律解.如图乙所示,设各支路的电流分别为1I 、2I 、3I . 对节点1:1230I I I --+=. ① 对回路1:112212I r I r εε-=-. ② 对回路2:2232I r I R ε+=.③解①②③式求得()2121122110A r R RI rrr R r R εε+-==++,()121212215A r R RI r r r R r Rεε+-==-++,2112312215A r r I r r r R r Rεε-==++.2I 为负值,说明实际电流方向与所设方向相反.为负值,说明实际电流方向与所设方向相反. 各发电机输出的功率分别为2111111200W PI I r ε=-=, 221111600W P I I r ε=-=-.这说明第二台发电机不仅没有输出功率,而且还要吸收第一台发电机的功率. 方法二:利用电源的独立作用原理求解.当只考虑发电机1ε的作用时,原电路等效为如图丙所示的电路,的作用时,原电路等效为如图丙所示的电路,由图可知()2111122182A r RI rrr R r R ε+==++,2111280A RI I r R==+. 当只考虑发电机2ε的作用时,原电路等效为如图丁所示的电路. 由图可知由图可知将()1222122175A r RI r r r R r Rε+==++122172A RI I r R ==+两次求得的电流叠加,可得到两台发电机的实际电流分别为两次求得的电流叠加,可得到两台发电机的实际电流分别为11112827210A I I I =-=-=(方向为11I 的方向),2212280755A I I I =-=-=(方向为21I 的方向).同理,可解得各发电机的输出功率同理,可解得各发电机的输出功率 11200W P =,2600W P =-.【点睛】(1)从本题计算结果看出,将两个电动势和内电阻都不同的电源并联向负载供电未必是好事,这样做会形成两电源并联部分的环路电流,使电源发热.(2)运用基尔霍夫定律解题时,对于一个复杂的含有电源的电路,如果有n 个节点、p 条支路所组成,我们可以对每一支路任意确定它的电流大小和方向,我们可以对每一支路任意确定它的电流大小和方向,最后解出值为正说明所设电流最后解出值为正说明所设电流方向与实际方向一致,所得值为负则说明所设电流方向与实际方向相反.这个电路中共有p 个待求电流强度.个待求电流强度.在n 个节点中任意选取其中()1n -个节点,根据基尔霍夫第一定律,列出节点电流方程组,再选择()1m p n =--个独立回路,根据基尔霍夫第二定律,列出回路电压方程组,个独立回路,根据基尔霍夫第二定律,列出回路电压方程组,从而得从而得到p 个方程即可求解.(3)处理复杂的电路的方法有很多,各种方法的优点与不足是在比较中领会的,对于某一道具体的试题,该用何种方法,取决于你的经验与临场的判断.事实上,这些方法也不存在优劣之分,只是在具体的过程中可能存在繁易的差别.18.(1) 00.659AC R R = (2)0321321EG R R -+++=【解析】【分析】【分析】【详解】(1)先考察B 、D 连线上的节点.由于这些节点都处于从A 到C 途径的中点上,在A 、C 两端接上电源时,这些节点必然处在一等势线上.因此可将这些节点“拆开”,将原网络等效成如图2所示网络.所示网络.。
高二物理竞赛磁场磁感强度课件

y
实验发现带电粒 子在磁场中沿某一特定 直线方向运动时不受力, 此直线方向与电荷无关.vvoz
B 沿x方向
F0
+ vv
x
3
带电粒子在磁场中
沿 垂其 直于他方v 向与运特动定时直F 线
所组成的平面. 当带电粒子在磁场
中垂直于此特定直线运 动时受力最大.
4
FF maxF
Fmaxqv F max 大小与 q,v 无关
向定义为该点的 的方向. 解法一 圆电流的磁场
带电粒子在磁场中运动所受的力与运动方向有关. 当正电荷垂直于 特定直线运动时,受力 N、S极同时存在;
正时电,荷受垂力直Fm 于a特x将定F直m线ax运v动方 向定义为该点的 B的方向.
实验发现带电粒子在磁场中沿某一特定直线方向运动时不受力,此直线方向与电荷无关.
磁感强度 的定义:当
时,受力
将
方
当带电粒子在磁场中垂直于此特定直线运动时受力最大.
磁感强度大小 B Fmax
当带电粒子在磁场中垂直于此特定直线运动时受力最大.
正电荷垂直于特定直线运动
二 磁感强度 的定义
qv
Fmax 正电荷垂直于特定直线运动
同名磁极相斥,异名磁极相吸. 当正电荷垂直于 特定直线运动时,受力 二 磁感强度 的定义
S
N
S
正同电名荷 磁垂极直相于斥特,定异直名线磁运极动相吸.
时同,名受 磁力极相斥,将异名磁极相吸方.
时解,法受 一力 圆电流将的磁场 方
磁
铁
磁场
磁铁
1
2 电流的磁场 奥斯特实验
电流
磁场
3 磁现象的起源
运动电荷
磁场
演示动画
高中物理竞赛电学教程第三讲磁场第四讲电磁感应

高中物理比赛电学教程 第四讲 电磁感觉第三 磁 § 3。
1基本磁 象因为自然界中有磁石 ( Fe 3O 4) 存在,人 很早从前就开始了 磁 象的研究。
人 把磁石能吸引 ` ` 等物 的性 称 磁性。
条形磁 或磁 是两头吸引 屑的能力最 , 我 把 吸引 屑能力最 的地区称之 磁极。
将一条形磁 挂起来, 两极 是分 指 向南北方向,指北的一端称北极 (N 表示 ) ;指南的一端称南极(S 表示 ) 。
磁极之 有相互作使劲,同性磁极相互排挤,异性磁极相互吸引。
磁 静止 沿南北方向取向 明地球是一个大磁体,它的N 极位于地理南极邻近,S 极位于地理北极邻近。
1820 年,丹麦科学家奥斯特 了 流的磁效 。
第一个揭露了磁与 存在着 系。
直通 能 磁 作用;通 直螺 管与条形磁 作用 就好像条形磁 一般;两根平行通 直 之 的相互作用⋯⋯,所有 些都启 我 一个: 磁 和 流能否在本源上一致 ? 1822 年,法国科学家安培提出了 成磁 的最小 元就是 形 流, 些分子 流定向摆列,在宏 上就会 示出N 、 S 极的分子 流假 。
近代物理指出,正是 子的 原子核运 以及它自己的自旋运 形成了“分子 流”, 就是物 磁性的基本本源。
全部磁 象的本源是 流,以下我 只研究 流的磁 象。
§ 3。
2 磁感觉强度3.2. 1、磁感 度、 奥伐 定律将一个 L ,I 的 流元放在磁 中某一点, 流元遇到的作使劲F 。
当 流元在某一方向 , 个力最大, 个最大的力 F m和 IL 的比 ,叫做 点的磁感 度。
将一个能自由 的小磁 放在 点,小磁 静止N 极所指的方向,被 定 点磁感 度的方向。
真空中,当 生磁 的 流回路确立后,那空 的磁 就确立了,空 各点的B 也就确定了。
依据 流回路而求出空 各点的 B 要运用一个称 奥— 伐 定律的 定律。
— 定律告 我 :一个 流元IL( 如 3-2-1)在相 流元的地点矢量r 的 P 点所KI L sinr 2L 的方向与 r 方向的 角, 生的磁 的磁感 度B 大小, 着 流 IB 的方向可用右手螺旋法 确立,即伸出右手, 先把四指放在 I L 的方向上, 着小于的角 向 r 方向 大拇指方向即 B 的方向。
高中物理奥林匹克竞赛专题磁场部分精选题(有详细解答)

电流与磁场、电磁感应、自感互感、磁场能量一、选择题1.如图,流出纸面的电流为2I ,流进纸面的电流为I ,则下述各式中哪一个是正确的 (A )12L H dl I =⎰(B )2L H dl I =⎰(C )3L H dl I =-⎰(D )4L H dl I =-⎰分析:选D ,根据安培环路定理LB dl I μ=∑⎰,当电论。
2.如图,M 、N 为水平面内两根平行金属导轨,ab 与cd 为垂直于导轨并可在其上自由滑动的两根直裸导线。
外磁场垂直水平面向上。
当外力使ab 向右平移时,cd(A )不动。
(B )转动(C )向左移动(D )向右移动 分析:选D ,根据楞次定律即判定。
3. A,B 两个电子都垂直于磁场方向射入一均匀磁场而作圆周运动,A 电子的速率是B 电子速率的两倍,设A R ,B R 分别为A 电子与B 电子的轨道半径,A T ,B T 分别为它们各自的周期,则(A ):2,:2AB A B R R T T == (B )1:,:12A B A B R RT T ==(C )1:1,:2A B A B R R T T == (D ):2,:1A B A B R R T T ==分析:根据公式2,mv mR T eB eBπ==,即可得到答案,选D 4.真空中一根无限长直细导线上通电流I ,则距导线垂直距离拉为a 的空间某点处的磁能密度为(A )2001()22I aμμπ (B )2001()22I a μμπ (C )2012()2a I πμ (D )2001()22I a μμ 分析:212m B w μ=,而02IBaμπ=。
代入可得答案B 5.如图,无限长直载流导线与正三角形载流线圈在同一平面内,若长直导线固定不动,则载流三角形线圈将 (A ) 向着长直导线平移(B )离开长直导线平移 (C)转动 (D)不动 分析:利用安培力的方向判定,选A6.如图所示,螺线管内轴上放入一小磁针,当电键K 闭合时,小磁针的N (A)向外转90(B)向里转90(C)保持图示位置不动(D)旋转180。
历年(2008-2014)汕头高二物理统考,中3-1第三章磁场内容部分及答案

历年(2008-2014)汕头高二统考中3-1第三章磁场内容部分(汕头四中陈锐桐)2014年2013年9、下图中标出了磁场B 的方向、通电直导线中电流I 的方向以及通电直导线所受磁场力F 的方向,其中正确的是16、如图,坐标系xOy 在竖直平面内,第一象限内分布匀强磁场,磁感应强度大小为B ,方向垂直纸面向外;第二象限内分布着沿x 轴正方向的水平匀强电场,场强大小m qLB E 62,质量为m 、电荷量为+q 的带电粒子从A 点由静止释放,A 点坐标为(-L ,L23),在静电力的作用下以一定速度进入磁场,最后落在x轴上的P 点.不计粒子的重力.求: (1)带电粒子进入磁场时速度v 的大小. (2) P 点与O 点之间的距离.2012年7.(双选) 如图,把一条导线平行地放在磁针的正上方附近,当导线通有水平向右的电流时A .磁针所在区域磁场方向垂直纸面向里B .磁针所在区域磁场方向垂直纸面向外C .磁针发生偏转,N 极向里,S 极向外D .磁针发生偏转,S 极向里,N 极向外17.(14分)如图所示,在OPNM 区域内有垂直于纸面向里的匀强磁场,磁感应强度大小为B , ∠QOP =60°. 离子源中带电量为+q ,质量为m 的离子(离子初速度可忽略不计)经电场AB 加速后以一定速度从O 点处垂直QN 进入磁场,不计离子的重力. (1)当加速电压U =U 0,求离子进入磁场中做圆周运动的半径r .(2)已知P 点到O 点距离为L ,若要离子恰好从P 点离开磁场,加速电压U 多大?INSBOO ’I a bcd(3)若离子恰好从P 点离开磁场,求该离子在磁场中的运动时间.2011年3.(单选)一矩形通电线框abcd 可绕其中心轴OO ′自 由转动,匀强磁场与转轴OO ′ 垂直,当线框从图示位置由静止释放时 A .线框静止,四边受到指向线框外部的磁场力 B .线框静止,四边受到指向线框内部的磁场力 C .线框转动,ab 转向纸外,cd 转向纸内 D .线框转动,ab 转向纸内,cd 转向纸外17.(14分)图甲是一足够大的光滑绝缘水平面,在t =0时刻,质量m =0.04kg 、电荷量q =0.01C 的带负电小球以初速度v 0=1m/s 从Ο点开始水平向右运动.整个平面处于方向竖直向下的匀强磁场中.(1)若磁感应强度B = 4T 并保持不变,求小球在匀强磁场中运动的半径和周期.(2)若从t =0时刻开始,磁感应强度B 随时间的变化规律如图乙所示,求小球至少经过多长时间才能再次经过Ο点,画出小球在这段时间内的运动轨迹并求小球通过的路程.2010年16. 如图,一束带正电粒子(不计重力)自下而上进入一匀强磁场区域,发现该粒子发生如图的偏转.下列说法正确的是( ) A .磁场方向垂直纸面向里 B .进入磁场后粒子的动能变大C .增大磁场的磁感应强度,其运动周期变大D .增大粒子进入磁场的速度,其轨迹半径变大Οv 0甲4π 0t/sB/T 2π 3π 5π 4π 乙2009年25.(18分)如图,在平面直角坐标系xOy 内,第I 象限存在沿y 轴负方向的匀强电场,第IV 象限以ON 为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B .一质量为m 、电荷量为q 的带正电的粒子,从y 轴正半轴上y h =处的M 点,以速度0v 垂直y 轴射入电场,经x 轴上2x h =处的P 点进入磁场,最后以垂直于y 轴的方向射出磁场.不计粒子重力.求(1)粒子刚进入磁场时的速度v(2)粒子在磁场中运动的轨道半径r 和时间t .2008年19.(17分)质量为m ,电荷量为q 的带负电粒子自静止开始,经M 、N 板间的电场加速后 从A 点垂直于磁场边界射入宽度为d 的匀强磁场中,该粒子离开磁场时的位置P 偏离入 射方向的距离为L ,如图所示.已知M 、N 两板间的电压为U ,粒子的重力不计. (1)正确画出粒子由静止开始至离开匀强磁场时的轨迹图(用直尺和圆规规范作图) (2)求匀强磁场的磁感应强度B.m q汕头高二统考中3-1第三章磁场内容部分答案 2014年9、AC 13、AD17、(1)在不计重力的情况下,粒子在电场中向下运动,则粒子带正电。
高中物理竞赛培训电磁学部分课件

当电容器与电源相连时,电荷会从电源流入电容 器,使电容器两极板间形成电场,电容器的电压 会逐渐升高;当电容器与电源断开时,电荷会从 电容器流出,形成电流。
电容器在电路中的作用
在电路中,电容器可以起到滤波、耦合、旁路、 储能等作用。
电容器的应用实例
在电子设备中,电容器被广泛应用于信号处理、 电源滤波、旁路、谐振等场合。
详细描述
环路定理是由英国物理学家詹姆斯·克拉克·麦克斯韦提出的。该定理表明,磁场沿闭合回路的线积分等于穿过该 回路所围区域的电流总量。这个定理在电磁学中有着广泛的应用,可以用来解决各种与磁场和电流相关的问题。
欧姆定律与基尔霍夫定律
总结词
欧姆定律和基尔霍夫定律是电路分析中的基本定律,它们描述了电路中电流、电压和电阻之间的关系。
VS
详细描述
库仑扭秤实验是电磁学中一个非常著名的 实验,通过这个实验,科学家们验证了库 仑定律,即两个点电荷之间的作用力与它 们的电荷量的乘积成正比,与它们之间的 距离的平方成反比。这个实验对于理解电 磁学中的基本概念和规律非常重要。
法拉第电磁感应实验
总结词
法拉第电磁感应实验揭示了磁场与电场之间的相互作用关系, 是电磁学中的一个里程碑实验。
详细描述
法拉第电磁感应实验是电磁学发展史上的一个重要实验。通 过这个实验,科学家们证明了变化的磁场可以产生电场,从 而揭示了磁场与电场之间的相互作用关系。这个实验对于现 代电磁技术的发展和应用具有重要意义。
霍尔效应实验
总结词
霍尔效应实验揭示了磁场对电流的影响,对 于现代电子技术和磁学研究具有重要意义。
法拉第电磁感应定律
感应电动势的大小与磁通量变 化率成正比。
麦克斯韦方程组
广东省汕头市潮阳第一中学2023-2024学年高二下学期开学考试物理试题

广东省汕头市潮阳第一中学2023-2024学年高二下学期开学考试物理试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图所示,关于电磁现象,下列说法正确的是()A.甲图,用细金属丝将直导线水平悬挂在磁铁的两极间,当通以如图所示的电流时,导线会向左摆动一定角度B.乙图,是真空冶炼炉,当炉外线圈通入高频交流电时,铁块中产生涡流,从而产生大量热量,冶炼金属C.丙图,通电线圈在磁场作用下转动,机械能转化为电能D.丁图,当用力让线圈发生转动时,电流表就有电流通过,利用此原理可制成电动机2.截面为正方形的绝缘弹性长管中心有一固定长直导线,长管外表面固定着对称分布的四I I,电根平行长直导线,若中心直导线通入电流1I,四根平行直导线均通入电流2I,12流方向如图所示,下列截面图中可能正确表示通电后长管发生形变的是()A.B.C.D.3.如图所示,匀强磁场限定在一个圆形区域内,磁感应强度大小为B,一个质量为m,电荷量为q,初速度大小为v的带电粒子沿磁场区域的直径方向从P点射入磁场,从Q点沿半径方向射出磁场,粒子射出磁场时的速度方向与射入磁场时相比偏转了θ角,忽略重力及粒子间的相互作用力,下列说法错误..的是()A.粒子带正电B.粒子在磁场中运动的轨迹长度为mvθBqC.粒子在磁场中运动的时间为mθBqD.圆形磁场区域的半径为tanmvθBq4.如图所示,矩形abcd的边长bc是ab的2倍,两细长直导线通有大小相等、方向相反的电流,垂直穿过矩形平面,与平面交于e、f两点,其中e、f分别为ad、bc的中点。
下列说法正确的是()A.a点与b点的磁感应强度相同B.a点与c点的磁感应强度相同C.a点与d点的磁感应强度相同D.a点与b、c、d三点的磁感应强度均不相同5.如图甲为电动汽车无线充电原理图,M 为受电线圈,N 为送电线圈。
图乙为受电线圈M 的示意图,线圈匝数为n ,电阻为r ,横截面积为S ,两端a 、b 连接车载变流装置,匀强磁场平行于线圈轴线向上穿过线圈。
高二物理竞赛课件:磁场磁感应强度(15张PPT)

磁铁与磁极 (1)N、S极成对出现,
不能单独存在。
(2)同号磁极相斥, 异号磁极相吸。
著名实验
图19-11(a) 磁铁对 载流导线的作用 (导线受到垂直纸 面向外的力)
II
II
奥斯特实验 1820年7月21日
安培分子电流假说(1821年1月)
Fmax qv
磁感强度大小 B Fmax qv
磁感强度单位 特斯拉 1(T) 1N/A m
B
• 曲线切线方向即B方向
• 曲线疏密表示B的大小
规定: B Φm
S
B线性质 :
Φm :磁感线的数目
•闭合曲线, 互不相交, 无起点, 无终点;
• 与电流方向满足右手螺旋关系.
N
S
内容回顾
电动势为描述非静电力作功本领的物理量,只与电源 本身的性质有关。
3.规定电动势方向: 在电源内部由负极指向正极。
-+
+
*
源
电源的电动势 和内阻 Ri
全电路欧姆定律
从点A出发 , 顺时针绕 行一周各部分电势降落(或
C* R D*
增量)总和为零 , 即得回路
电压方程:
*A
分子电流:与分子中所有电子运动磁效应等效的环形电流。
磁铁是环形电流的
s
N 定向排列。宏观上
与表面圆电流等效。
磁铁磁效应的根源是分子电流,即电荷的运动。
• 一切磁现象的根源是电流,即电荷的运动。 磁场:运动电荷或电流周围存在的场。
磁力:运动电荷之间的相互作用力。
运动电荷
磁场
运动电荷
稳恒磁场:稳恒电流产生的磁场。
高二物理竞赛课件:磁现象 磁场(14张PPT)

实验
3. 磁极 :磁体上磁性最强的部位。
实验
小磁针静止后的位置总是指向南北方向
南极(S极):能够自由转动的磁体静止时指南的那个磁极 北极(N极):能够自由转动的磁体静止时指北的那个磁极
如果磁体被分割成两段或几段后,每一段磁 体上是否仍然有N极和S极
每一段磁体上仍然有N极和S极
4.磁极间பைடு நூலகம்互作用的规律:
同名磁极相互排斥, 异名磁极相互吸引。
二、磁化
磁化现象:使原来没有磁性的物体在磁体或电流的作用
下获得磁性的过程。 被磁化的物体如果是铁棒,获得的磁性会立即消失 被磁化的物体如果是钢棒,获得的磁性就会保持较长 的时间
应用:磁悬浮列车
连接上海国际机场与市区的磁悬浮列车最高速度达到 431千米/小时,全线长17.3千米。该列车由德国磁悬浮高 速列车国际公司承建,并于2002年12月31日首次通车。
第二十章 电和磁
第一节
磁现象 磁场
你知道这是做什么用的吗?
动手动脑
通过做实验解决下面的问题: 1.磁体能够吸引桌上的哪些东西? 2.磁体上的磁性强弱处处一样吗? 3.“指南针”是如何得名的?
一、磁现象 1.磁性:能吸引铁、钴、镍 等物质的性质。
2.磁体:具有磁性的物体。
条形、针形、 蹄形、圆柱形
磁现象在现代科技生产生活中的应用
地质工作者正在进行 磁法勘探
磁共振成像的胸部显影片
录音带、录像带
计算机房的磁盘存储器
观察 思考
桌面上放一小磁针, 用条形磁体绕小磁针 转一圈,你观察到了什 么?产生这种现象的原 因是什么?
彼此不接触的两个磁体, 通过什么发生作用?
2021-2022学年高二物理竞赛磁场对电流和电荷的作用课件

F3
M BISsin
M
P
F2
M
ISen
B
m
B
I
B
F1 N
F4
O en
线圈有N匝时
M
NISen
B
M,N
F1
F2 O,P
B en
12
讨论
(1)en 与 B 同向 (2)方向相反 (3)方向垂直
稳定平衡
不稳定平衡
力矩最大
× ×I × × ×
×××××
× × × × × F × × × × ×
d
dFy
dF
I1
dFx
d
I2dl
OR
x
I2
8
为纯科学呼吁 – 美国科学的独立宣言
1883年8月15日,美国著名物理学家、美国物理学会第一任会长亨利·奥古 斯特·罗兰(Henry Augustus Rowland, 1848-1901)在美国科学促进会 (AAAS)年会上做了题为“为纯科学呼吁”的演讲。该演讲的文字后发表 在1883年8月24日出版的Science杂志上,并被誉为“美国科学的独立宣 言"
磁场对电流和电荷的作用
1
一 安培力
洛伦兹力 Fm evd B Fm evd B sin
Fm
Idl
vd
I
S
dl
dF nevdSdlB sin B
I nevdS
dF IdlBsin IdlB sin
安培力 dF Idl B
2
例 1 求如图不
规则的平面载流导线
在均匀磁场中所受的
× × × ×B
0,M 0
. I . . . . . .F . . .
广东省汕头市潮阳第一中学2025届下学期高三物理试题二模考试试卷

广东省汕头市潮阳第一中学2025届下学期高三物理试题二模考试试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、2010 年命名为“格利泽581g”的太阳系外行星引起了人们广泛关注,由于该行星的温度可维持表面存在液态水,科学家推测这或将成为第一颗被发现的类似地球世界,遗憾的是一直到2019 年科学家对该行星的研究仍未有突破性的进展。
这颗行星距离地球约20 亿光年(189.21 万亿公里),公转周期约为37 年,半径大约是地球的 2 倍,重力加速度与地球相近。
则下列说法正确的是A.飞船在Gliese581g 表面附近运行时的速度小于7.9km/sB.该行星的平均密度约是地球平均密度的1 2C.该行星的质量约为地球质量的8 倍D.在地球上发射航天器前往“格利泽581g”,其发射速度不能超过11.2km/s2、如图所示,固定在竖直平面内的大圆环的半径为R。
质量为m的小环套在大圆环上,且与大圆环接触面光滑。
在劲度系数为k的轻弹簧作用下,小环恰静止于大圆环上,弹簧与竖直方向的夹角为30°,则()A.弹簧伸长的长度为3mg kB.弹簧伸长的长度为mg kC.弹簧缩短的长度为3mg kD.弹簧缩短的长度为mg k3、下列关于原子核的说法正确的是()A.质子由于带正电,质子间的核力表现为斥力B.原子核衰变放出的三种射线中, 粒子的穿透能力最强C.铀核发生链式反应后能自动延续下去,维持该反应不需要其他条件D.比结合能小的原子核结合成比结合能大的原子核时一定放出核能4、如图,斜面上a、b、c三点等距,小球从a点正上方O点抛出,做初速为v0的平抛运动,恰落在b点.若小球初速变为v,其落点位于c,则()A.v0< v <2v0B.v=2v0C.2v0< v <3v0D.v>3v05、如图,劲度系数为400N/m的轻弹簧一端固定在倾角为45°的光滑楔形滑块的顶端O处,另一端拴一质量为m=10 10kg的小球。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
磁场一、知识网络与概要1、通过某一平面磁通量的大小,可以用通过这一平面的磁感线条数的多少来形象说明。
理解公式ø=BS ⊥明白磁场中某一点的磁场方向就是通过这一点的磁感线方向。
以上仅是本知识的高考要求初赛要求还有:长直线电流周围的磁感应强度为:如图,设△L 为导线的一段线微元,其电流强度为I ,则在真空中距该“线微元”为r 的P 处,此通电微元产生的磁感应强度为:θπμsin 420L rIB ∆=∆ 式中θ为电流方向与矢径r 之间的夹角,μ0=4π×10-7 T ·m/A ,△B 的方向为右手螺旋定则。
长直线电流周围的磁感应强度有时又写为:B=2kI /r 或B=μ0I /(2πr ),其中r 为P 点到导线的垂直距离,k=10-7 N/A 2,μ0=4π×10-7 T ·m/A2、会判断安培力的方向。
会计算匀强磁场中安培力的大小。
安培力的方向应用左手定则判定。
通电导体在磁场中受到的安培力F =B ⊥IL 。
以上仅是本知识的高考要求初赛要求还有: 通电线圈在匀强磁场中所受的力矩,设通有电流I 的长为l ,宽为b 的矩形线框,在磁场B 中长l 的一边受到安培力F=IlB,如图3所示,线框两边受到的两力大小相等,方向相反,但作用不在一直线上,其力偶矩大小为BIS BIlb Fb M ===,F=qvB 左手定则B △如果线圈共有N 匝,并且线圈平面和磁感应强度互成角度θ, 则总力偶矩为θcos NBIS M =3、会判断洛仑兹力的方向,会计算洛仑兹力的大小f =B ⊥qv 。
了解电子束的磁偏转原理以及在科学技术中的应用。
洛仑兹力的方向应用左手定则判定。
左手定则中四指指向电流的方向,对于负电荷,电流的方向与电荷运动的方向相反。
带电粒子在匀强磁场中的运动,要注意用电场力平衡带电粒子重力的情形。
圆周运动的圆心的确定:①利用洛仑兹力的方向永远指向圆心的特点,只要找到圆运动两个点上的洛仑兹力的方向,其延长线的交点必为圆心.②利用圆上弦的中垂线必过圆心的特点找圆心。
以上仅是本知识的高考要求初赛要求还有: 带电粒子以速度v 进入磁场,速度v 与磁场B 的夹角为θ,此时带电粒子将作等螺距螺旋运动,如图5所示。
将速度v 分解为平行于磁场的v //和垂直于磁场的⊥v 两个速度分量,v //与磁场平行,洛伦磁力为零,故沿x 方向将作匀速直线运动,⊥v 与磁场垂直,洛伦磁力使带电粒子作匀速圆周运动,两个运动合成,带电粒子作等螺距螺旋运动。
作等螺旋运动的向心力B qv Rv F ⊥⊥==2m 向,运动周期qBmv R T ππ22==⊥, 圆轨道半径B m q v R ⊥=, 螺距 qBmv T ////2v h π==二、重点热点透析<一>.安培力改变导线的运动状态Ⅰ、安培力使导线产生平动和转动【例1】如图,导线ab固定,导线cd与ab垂直且与ab相隔一段距离且可以自由移动.试分析cd的运动情况.Ⅱ、安培力使导线产生加速度【例2】如图所示,U形金属导轨与水平面成θ=30°角放置,空间有与导轨平面垂直的匀强磁场B=6×10-2 T,两平行导轨相距L=0.1 m.一质量m=0.01 kg、电阻为R=0.2 Ω的裸导体棒ab搁在导轨上,与导轨串联的电源电动势E=3 V,内阻r=0.1 Ω,导轨电阻不计,导轨与导体间无摩擦.求导体棒刚被释放时的加速度.Ⅲ、安培力的冲量使导线产生动量的变化【例3】两条光滑的水平金属导轨彼此平行,金属棒ab架在两导轨端点并与导轨垂直,导轨区域内有竖直向下的匀强磁场,导轨另一端与电源、电容器连成电路,如图所示.已知金属棒的质量m=5×10-3kg,两导轨间距L=1.0 m,电源电动势E=16 V,电容器的电容C=200 μF,磁场的磁感应强度B=0.5 T.金属棒在通电后受安培力作用而平抛出去,下落高度h=0.8 m,抛出落地水平位移s=0.064 m.试求开关K先接1,再接2,金属棒被抛出后电容器上电压的数值.<二>安培力参与物体的平衡 Ⅰ、安培力参与共点力的平衡正交的匀强磁场和匀强电场组成速度选择器,带电粒子必须以唯一确定的速度(包括大小、方向)进入才能匀速通过速度选择器,否则将发生偏转,这个速度大小可由洛伦兹力和电场力的平衡求得,qvB=Eq ,所以v=BE,速度方向必须向右.(1)这个结论与粒子带何种电荷及所带电荷多少无关.(2)若速度小于这一速度,电场力将大于洛伦兹力,带电粒子将向电场力方向偏转.粒子运动轨迹为一条复杂曲线.若大于这一速度,将向洛伦兹力方向偏转,电场力将做负功,动能减少,粒子轨迹为一条复杂曲线.【例4】. 如图所示,光滑导轨与水平面成α角,导轨宽L 。
匀强磁场磁感应强度为B 。
金属杆长也为L ,质量为m ,水平放在导轨上。
当回路总电流为I 1时,金属杆正好能静止。
求:⑪B 至少多大?这时B 的方向如何?⑫若保持B 的大小不变而将B 的方向改为竖直向上,应把回路总电流I 2调到多大才能使金属杆保持静止?【例5】.磁流体发电机原理图如右。
等离子体高速从左向右喷射,两极板间有如图方向的匀强磁场。
该发电机哪个极板为正极?两板间最大电压为多少?Ⅱ.安培力参与力矩的平衡【例6】.有一均匀细铜棒OA长为l,质量为m,其上端悬在一固定、水平、光滑轴O点,此棒能在垂直平面内绕O点作自由摆动,其下部恒与另一水平、固定铜棒C’C作无摩擦接触。
当开关S接通时,电源对两棒供应回路电流。
已知O点与棒C’C的垂直距离为h,整个回路放在磁感应强度为B的匀强磁场中,磁场方向与两棒组成的平面垂直。
如图所示,若回路电流I值恰好使OA棒与垂线OC’’成成θ角时而平衡,求回路中的电流I。
<三>带电粒子在电磁场中的运动(一)不计重力的带电粒子在电场中的运动1.运动类型:(1)匀速直线运动;(2)匀加速直线运动;(3)电偏转——类平抛运动.2.两种观点解决带电粒子在电场中运动问题:(1)运动学观点:是指用匀变速运动的公式和牛顿运动定律来解决实际问题,一般有两种情况(仅限于匀强电场):①带电粒子的初速度方向与电场线共线,则粒子做匀变速直线运动.②带电粒子的初速度方向垂直电场线,则粒子做类平抛运动.(2)功能观点:首先对带电粒子受力分析,再分析运动情况,然后再根据具体情况选用公式计算.①若选用动能定理,则要分清有多少个力做功,是恒力做功还是变力做功,同时要明确初末状态及运动过程中动能的增量.②若选用能量守恒定律,则分清带电粒子在运动中共有多少种能量参与转化,哪些能量是增加的,哪些能量是减少的,表达式有两种.a.初状态和末状态的能量相等,即E初=E末.b.一种形式的能量增加必然引起另一种形式的能量减少,即E增=E减.这种方法不仅适用于匀变速运动,对非匀变速运动(非匀强电场)也同样适用.(二)不计重力的带电粒子在磁场中的运动1.运动类型:(1)匀速直线运动;(2)磁偏转――匀速圆周运动.2.对于带电粒子在匀强磁场中做匀速圆周运动的问题,应注意把握以下几点:(1)粒子圆轨迹的圆心的确定①若已知粒子在圆周运动中的两个具体位置及通过某一位置的速度方向,可在已知的速度方向的位置作速度的垂线,同时作两位置的中垂线,两垂线交战为圆轨迹的圆心.如图1所示.②若已知做圆周运动的粒子通过某两个具体位置的速度方向,可在两位置上分别作两速度的垂线,两垂线的交点为圆轨迹的圆心.如图2所示.③若已知做圆周运动的粒子通过某一具体位置的速度方向及圆轨迹半径R,可在该位置上作速度的垂线,垂线上距该位置R处的点为圆轨迹的圆心(利用左手定则判断圆心在已知位置的哪一侧),如图3所示.(2)粒子圆轨迹的半径的确定 ①可直接运用公式qBm vR =来确定.②画出几何图形,利用半径R与题中已知长度的几何关系来确定.在利用几何关系时,要注意事项一个重要的几何特点:粒子速度的偏向角ϕ等于转过的圆心,并等于AB 弦与切线的夹角(弦切角θ)的2倍.如图4所示.(3)粒子做圆周运动的周期的确定 ①可直接运用公式qBmT π2=来确定.②利用周期T与题中已知时间t 的关系来确定.若粒子在时间t 内通过的圆弧所对应的圆心角为α,则有:T t ︒=360α(或Tt πα2=)(4)圆周运动中有关对称的规律①从磁场的直边界射入的粒子,若再从此边界射出,则速度方向与边界的夹角相等,如图5所示.②在圆形磁场区域内,沿径向射入的粒子必沿径向射出,如图6所示.(5)洛伦兹力多解问题①带电粒子电性不确定形成双解;②磁场方向不确定形成双解.③临界状态不唯一形成多解:带电粒子在洛伦兹力作用下飞越有界磁场时,由于粒子的运动轨迹是圆弧状,因此,它可能穿过去了,也可能转过180°从入射界面这边反向飞出,于是形成了多解.④运动的重复性形成多解:带电粒子在部分是电场、部分是磁场的空间中运动时往往运动具有往复性,因而形成了多解。
(三)带电粒子在复合场中的运动 1.复合场及分类复合场是指重力场、电场、磁场并存的场,在中学阶段常有四种组合:①电场与磁场的复合场;②磁场与重力场的复合场;③电场与重力场的复合场;④电场、磁场与重力场的复合场。
2.处理复合场问题的前提判断带电粒子的重力是否可以忽略,这要依据具体情况而定,电子、质子、离子等微观粒子无特殊说明一般不计重力;带电小球、尘埃、油滴、液滴等带电颗粒无特殊说明一般要考虑重力;如果有具体数据,可通过比较确定是否考虑重力。
3.带电粒子在复合场中的运动性质带电粒子在复合场中做什么运动,取决于带电粒子所受的合外力及其初速度,因此应把带电粒子的运动情况和受力情况结合起来进行分析:⑪当带电粒子在复合场中所受的合外力为零时,带电粒子做匀速直线运动.⑫当带电粒子所受的重力与电场力等值反向,洛仑兹力提供向心力时,带电粒子在垂直于磁场的平面内做匀速圆周运动.⑬当带电粒子所受的合外力是变力,且与初速度方向不在一条直线上时,粒子的运动轨迹既不是圆弧,也不是抛物线.粒子做变速曲线运动.4.带电粒子在复合场中的处理方法特别提醒:由于带电粒子在复合场中的受力情况复杂,运动情况多变,往往出现临界问题,此时应以题目中出现的“恰好”、“最大”、“最高”、“至少”等词语为突破口挖掘隐含条件,根据临界条件列出辅助方程,再与其他方程联立求解。
(四)带电粒子在交变电场或磁场中的运动带电粒子在交变电场或磁场中的运动情况比较复杂,其运动情况不仅与场变化的规律有关,还与粒子进入场的时刻有关。
对此类问题,一定要从粒子的受力情况入手,分析清楚粒子在不同时间间隔内的运动情况(其运动情况通常具有某种对称性)。
另外,对于偏转电压是交变电压的情况,若交变电压的变化周期远大于穿越电场的时间,则在粒子穿越电场过程中,电场可看做匀强电场处理。
