(完整版)六年级奥数讲义第31讲逻辑推理(一)
小学六年级数学知识点学习之逻辑推理

小学六年级数学知识点学习之逻辑推理
今天学习方法网小编为大家带来了小学六年级数学知识点:逻辑推理,供大家学习。
小学六年级数学知识点:逻辑推理
基本方法简介:
①条件分析假设法:假设可能情况中的一种成立,然后按照这个假设去判断,如果有与题设条件矛盾的情况,说明该假设情况是不成立的,那么与他的相反情况是成立的。
例如,假设a是偶数成立,在判断过程中出现了矛盾,那么a一定是奇数。
②条件分析列表法:当题设条件比较多,需要多次假设才能完成时,就需要进行列表来辅助分析。
列表法就是把题设的条件全部表示在一个长方形表格中,表格的行、列分别表示不同的对象与情况,观察表格内的题设情况,运用逻辑规律进行判断。
③条件分析图表法:当两个对象之间只有两种关系时,就可用连线表示两个对象之间的关系,有连线则表示“是,有”等肯定的状态,没有连线则表示否定的状态。
例如A和B两人之间有认识或不认识两种状态,有连线表示认识,没有表示不认识。
④逻辑计算:在推理的过程中除了要进行条件分析的推理之
外,还要进行相应的计算,根据计算的结果为推理提供一个新的判断筛选条件。
⑤简单归纳与推理:根据题目提供的特征和数据,分析其中存在的规律和方法,并从特殊情况推广到一般情况,并递推出相关的关系式,从而得到问题的解决。
希望这篇文章对大家有用,更多内容请关注学习方法网。
小学六年级奥数第31讲 逻辑推理(一)(含答案分析)

第31讲逻辑推理(一)一、知识要点逻辑推理题不涉及数据,也没有几何图形,只涉及一些相互关联的条件。
它依据逻辑汇率,从一定的前提出发,通过一系列的推理来获取某种结论。
解决这类问题常用的方法有:直接法、假设法、排除法、图解法和列表法等。
逻辑推理问题的解决,需要我们深入地理解条件和结论,分析关键所在,找到突破口,进行合情合理的推理,最后作出正确的判断。
推理的过程中往往需要交替运用“排除法”和“反正法”。
要善于借助表格,把已知条件和推出的中间结论及时填入表格内。
填表时,对正确的(或不正确的)结果要及时注上“√”(或“×”),也可以分别用“1”或“0”代替,以免引起遗忘或混乱,从而影响推理的速度。
推理的过程,必须要有充足的理由或重复内的根据,并常常伴随着论证、推理,论证的才能不是天生的,而是在不断的实践活动中逐渐锻炼、培养出来的。
二、精讲精练【例题1】星期一早晨,王老师走进教室,发现教室里的坏桌凳都修好了。
传达室人员告诉他:这是班里四个住校学生中的一个做的好事。
于是,王老师把许兵、李平、刘成、张明这四个住校学生找来了解。
(1)许兵说:桌凳不是我修的。
(2)李平说:桌凳是张明修的。
(3)刘成说:桌凳是李平修的。
(4)张明说:我没有修过桌凳。
后经了解,四人中只有一个人说的是真话。
请问:桌凳是谁修的?根据“两个互相否定的思想不能同真”可知:(2)、(4)不能同真,必有一假。
假设(2)说真话,则(4)为假话,即张明修过桌凳。
又根据题目条件了:只有1人说的是真话:可退知:(1)和(3)都是假话。
由(1)说的可退出:桌凳是许兵修的。
这样,许兵和张明都修过桌凳,这与题中“四个人中只有一个人说的是真话”相矛盾。
因此,开头假设不成立,所以,(2)李平说的为假话。
由此可退知(4)张明说了真话,则许兵、刘成说了假话。
所以桌凳是许兵修的。
练习1:1、小华、小红、小明三人中,有一人在数学竞赛中得了奖。
老师问他们谁是获奖者,小华说是小红,小红说不是我,小明也说不是我。
六年级奥数——逻辑推理

教学课题逻辑推理教学目标会找突破口,学会条理性分析题目。
教学重点找突破口教学难点逻辑推理逻辑问题是一类非常规的数学问题,不需要过多的计算,只需对问题分析,综合、判断、推理论证。
运用逻辑推理时,要有条理,要从众多条件中理清头绪,选准突破口,以事实为根据,使问题水落石出。
像这样有根有据的推理过程叫做“逻辑推理”。
例1、学校举行数学竞赛,A、B、C、D、E五位同学进入前5名。
他们猜测各人的名次如下:A:B第三名,C第五名;B:D第二名,E第四名;C:A第一名,E第四名;D:C第一名,B第二名;E:D第二名,A第三名。
老师说他们各猜对了一半。
你能推算他们的名次吗?练习:甲乙丙丁四位同学的运动衫上印有不同的号码:赵说:甲是2号,乙是3号。
钱说:丙是2号,乙是4号。
孙说:丁是2号,丙是3号。
李说:丁是1号,乙是3号。
又知赵钱孙李每人都说对了一半,那么丙是几号?例2、四(1)班为了表扬好人好事核实一件事,老师找了a、b、c三位同学。
a说:是b做的。
b说:不是我做的。
c说:不是我做的。
这三人只有一人说了实话,问这件事是谁做的?练习:甲乙丙三个孩子踢球打碎了玻璃。
甲说:是丙打碎的。
乙说:我没有打碎玻璃。
丙说:是乙打碎的。
他们当中只有一人说了谎话。
问到底是谁打碎了玻璃?例3、甲乙丙丁在谈论他们及他们的同学何伟栋的居住地。
甲说:我住在北京,乙住在北京,丙住在天津。
乙说:我住在上海,丁住在上海,丙住在天津。
丙说:我和甲都不住在北京,何伟栋住在南京。
丁说:甲住在北京,乙住在北京,我住在广州。
假设他们每人都说了两句真话,一句假话,问:不在场的何伟栋住在哪儿?练习:要选派ABCDE五人中若干人去执行某项任务,选派时需考虑以下条件:(1)若A去,则B也去;(2)D、E两人中至少去一人;(3)B、C两人中只去一人;(4)C、D两人都去或都不去;(5)若E去,则A、D都去。
问:应该选派谁去?例4、某宾馆住着ABCDEF六个不同国籍的客人,他们来自美、英、法、德、俄、意大利,现在知道:(1)A和美国人是医生。
六年级奥数:第31讲 逻辑推理(一)

第31講邏輯推理(一)一、知識要點邏輯推理題不涉及數據,也沒有幾何圖形,只涉及一些相互關聯的條件。
它依據邏輯匯率,從一定的前提出發,通過一系列的推理來獲取某種結論。
解決這類問題常用的方法有:直接法、假設法、排除法、圖解法和列表法等。
邏輯推理問題的解決,需要我們深入地理解條件和結論,分析關鍵所在,找到突破口,進行合情合理的推理,最後作出正確的判斷。
推理的過程中往往需要交替運用“排除法”和“反正法”。
要善於借助表格,把已知條件和推出的中間結論及時填入表格內。
填表時,對正確的(或不正確的)結果要及時注上“√”(或“×”),也可以分別用“1”或“0”代替,以免引起遺忘或混亂,從而影響推理的速度。
推理的過程,必須要有充足的理由或重複內的根據,並常常伴隨著論證、推理,論證的才能不是天生的,而是在不斷的實踐活動中逐漸鍛煉、培養出來的。
二、精講精練【例題1】星期一早晨,王老師走進教室,發現教室裏的壞桌凳都修好了。
傳達室人員告訴他:這是班裏四個住校學生中的一個做的好事。
於是,王老師把許兵、李平、劉成、張明這四個住校學生找來瞭解。
(1)許兵說:桌凳不是我修的。
(2)李平說:桌凳是張明修的。
(3)劉成說:桌凳是李平修的。
(4)張明說:我沒有修過桌凳。
後經瞭解,四人中只有一個人說的是真話。
請問:桌凳是誰修的?根據“兩個互相否定的思想不能同真”可知:(2)、(4)不能同真,必有一假。
假設(2)說真話,則(4)為假話,即張明修過桌凳。
又根據題目條件了:只有1人說的是真話:可退知:(1)和(3)都是假話。
由(1)說的可退出:桌凳是許兵修的。
這樣,許兵和張明都修過桌凳,這與題中“四個人中只有一個人說的是真話”相矛盾。
因此,開頭假設不成立,所以,(2)李平說的為假話。
由此可退知(4)張明說了真話,則許兵、劉成說了假話。
所以桌凳是許兵修的。
練習1:1、小華、小紅、小明三人中,有一人在數學競賽中得了獎。
老師問他們誰是獲獎者,小華說是小紅,小紅說不是我,小明也說不是我。
精品奥数-高年级-第31讲-逻辑推理-1分析推理

精品奥数-高年级-第31讲-逻辑推理-1分析推理逻辑推理-1分析推理类型一:猜盒子【例1】(★★)有三个盒子,一个装着两个红球,一个装着两个白球,还有一个装着一红一白两个球,三个盒子都盖着盖子,盖子上贴着说明盒内装着是什么颜色的球的标签,但全贴错了。
你能否只从一个盒子里摸出一个球,就准确地判断出三个盒子里各装的是什么球?解:从“红白”口袋里摸出一个球。
①如果是红球,由于此袋内一定不是“红白”,则此袋定是“红红”。
同时可以推出“白白”口袋里装的是一红一白,“红红”口袋里是两个白球。
②如果是白球,那么这个口袋里装的是两个白球,“白白”口袋里装两个红球,“红红“口袋里是一红一白。
答:红红口袋里是两个白球,白白口袋里装两个红球,红红口袋里是一红一白。
练习11、三个贴着标签的盒子,分别装着两个白球,两个黑球以及一黑一白两个球,但是标签全贴错了。
你能从一只盒子里摸一个球就能说出三只盒子里装的是什么颜色的球吗?2、三个袋子分别装着两个红球,两个白球和一红一白两个球,可是袋子外面的标签都贴错了。
你能否只从一个袋子里摸出一个球,就能判断出三个袋子里装的各是什么颜色的球,3、三个口袋里分别装有两个黄色玻璃球,两个绿色玻璃球和一黄一绿两个玻璃球。
口袋外面贴的标签都是错的,请从一个口袋里取出一个玻璃球,从而判断出这三个口袋里玻璃球的颜色?4、三个装笔的包装箱,一个装的全是红笔,一个装的全是蓝笔,还有一个装的既有红笔又有蓝笔。
但包装箱上的标签全都贴错了,你能只拆开一个箱子,就能判断出三个箱子里装的是什么颜色的笔吗?类型二:猜职业【例2】(★★)徐、王、陈、赵四位师傅分别是工厂的木工、车工、电工和钳工,他们都是象棋迷。
⑴木工只和车工下棋,而且总是输给车工;⑵王、陈两位师傅是邻居;⑶陈师傅与电工下棋互有胜负;⑷徐师傅比赵师傅下的好;⑸木工的家离工厂最远。
问:徐、王、陈、赵四位师傅各是什么工种?解:因为:⑵王、陈两位师傅是邻居;⑸木工的家离工厂最远。
小学六年级数学知识点学习之逻辑推理

小学六年级数学知识点学习之逻辑推理
今天学习方法网小编为大家带来了小学六年级数学知识点:逻辑推理,供大家学习。
小学六年级数学知识点:逻辑推理
基本方法简介:
①条件分析假设法:假设可能情况中的一种成立,然后按照这个假设去判断,如果有与题设条件矛盾的情况,说明该假设情况是不成立的,那么与他的相反情况是成立的。
例如,假设a是偶数成立,在判断过程中出现了矛盾,那么a一定是奇数。
②条件分析列表法:当题设条件比较多,需要多次假设才能完成时,就需要进行列表来辅助分析。
列表法就是把题设的条件全部表示在一个长方形表格中,表格的行、列分别表示不同的对象与情况,观察表格内的题设情况,运用逻辑规律进行判断。
③条件分析图表法:当两个对象之间只有两种关系时,就可用连线表示两个对象之间的关系,有连线则表示“是,有”等肯定的状态,没有连线则表示否定的状态。
例如A和B两人之间有认识或不认识两种状态,有连线表示认识,没有表示不认识。
④逻辑计算:在推理的过程中除了要进行条件分析的推理之
外,还要进行相应的计算,根据计算的结果为推理提供一个新的判断筛选条件。
⑤简单归纳与推理:根据题目提供的特征和数据,分析其中存在的规律和方法,并从特殊情况推广到一般情况,并递推出相关的关系式,从而得到问题的解决。
希望这篇文章对大家有用,更多内容请关注学习方法网。
六年级奥数逻辑推理含答案

逻辑推理知识框架逻辑推理作为数学思维中重要的一部分,经常出现在各种数学竞赛中,除此以外,逻辑推理还经常作为专项的内容出现在各类选拔考试,甚至是面向成年人的考试当中。
对于学生学习数学来说,逻辑推理既有趣又可以开发智力,学生自主学习研究性比较高。
本讲我们主要从各个角度总结逻辑推理的解题方法。
一、 列表推理法逻辑推理问题的显著特点是层次多,条件纵横交错.如何从较繁杂的信息中选准突破口,层层剖析,一步步向结论靠近,是解决问题的关键.因此在推理过程中,我们也常常采用列表的方式,把错综复杂的约束条件用符号和图形表示出来,这样可以借助几何直观,把令人眼花缭乱的条件变得一目了然,答案也就容易找到了.二、 假设推理用假设法解逻辑推理问题,就是根据题目的几种可能情况,逐一假设.如果推出矛盾,那么假设不成立;如果推不出矛盾,而是符合题意,那么假设成立.解题突破口:找题目所给的矛盾点进行假设三、 体育比赛中的数学对于体育比赛形式的逻辑推理题,注意“一队的胜、负、平”必然对应着“另一队的负、胜、平”。
有时综合性的逻辑推理题需要将比赛情况用点以及连接这些点的线来表示,从整体考虑,通过数量比较、整数分解等方式寻找解题的突破口。
四、 计算中的逻辑推理能够利用数论等知识通过计算解决逻辑推理题.例题精讲一、列表推理法【例 1】 刘刚、马辉、李强三个男孩各有一个妹妹,六个人进行乒乓球混合双打比赛.事先规定:兄妹二人不许搭伴.第一盘:刘刚和小丽对李强和小英;第二盘:李强和小红对刘刚和马辉的妹妹.问:三个男孩的妹妹分别是谁?【考点】逻辑推理 【难度】2星 【题型】解答【解析】 因为兄妹二人不许搭伴,所以题目条件表明:刘刚与小丽、李强与小英、李强与小红都不是兄妹.由第二盘看出,小红不是马辉的妹妹.将这些关系画在左下表中,由左下表可得右下表.李强马辉刘刚小丽小红小英××××李强马辉刘刚小丽小红小英×√×××××√√刘刚与小红、马辉与小英、李强与小丽分别是兄妹.【答案】刘刚与小红、马辉与小英、李强与小丽分别是兄妹【巩固】王文、张贝、李丽分别是跳伞、田径、游泳运动员,现在知道:⑴张贝从未上过天;⑵跳伞运动员已得过两块金牌;⑶李丽还未得过第一名,她与田径运动员同年出生.请根据上述情况判断王文、张贝、李丽各是什么运动员?【考点】逻辑推理【难度】2星【题型】解答【解析】为了能清楚地找到所给条件之间的关系,我们不妨运用列表法,列出下表,在表中“√”表示是,“×”表示不是,在任意一行或一列中,如果一格是“√”,可推出其它两格是“×”由⑴⑶可知张贝、李丽都不是跳伞运动员,可填出第一行,即王文是跳伞运动员;由⑶可知,李丽也不是田径运动员,可填出第三列,即李丽是游泳运动员,则张贝是田径运动员.【答案】王文是跳伞运动员,李丽是游泳运动员,张贝是田径运动员【例 2】张明、席辉和李刚在北京、上海和天津工作,他们的职业是工人、农民和教师,已知:⑴张明不在北京工作,席辉不在上海工作;⑵在北京工作的不是教师;⑶在上海工作的是工人;⑷席辉不是农民.问:这三人各住哪里?各是什么职业?【考点】逻辑推理【难度】2星【题型】解答【解析】这道题的关系要复杂一些,要求我们通过推理,弄清人物、工作地点、职业三者之间的关系.三者的关系需要两两构造三个表,即人物与地点,人物与职业,地点与职业三个表.我们先将题目条件中所给出的关系用下面的表来表示,由条件⑴得到表1,由条件⑵、⑶得到表2,由条件⑷得到表3.因为各表中,每行每列只能有一个“√”,所以表2可填全为表5.由表5知农民在北京工作,又知席辉不是农民,所以席辉不在北京工作,可以将表1可填全完为表4由表4和表5知得到:张明住在上海,是工人;席辉住在天津,是教师;李刚住在北京,是农民.方法二:由题目条件可知:席辉不在上海工作,而在上海工作的是工人,所以席辉不是工人,又不是农民,那么席辉只能是教师,不在北京工作,就只能是在天津工作,那么张明在上海工作,是工人。
小学奥数六年级举一反三第31周逻辑推理

第三十一周逻辑推理(一)专题简析:逻辑推理题不涉及数据,也没有几何图形,只涉及一些相互关联的条件。
它依据逻辑汇率,从一定的前提出发,通过一系列的推理来获取某种结论。
解决这类问题常用的方法有:直接法、假设法、排除法、图解法和列表法等。
逻辑推理问题的解决,需要我们深入地理解条件和结论,分析关键所在,找到突破口,进行合情合理的推理,最后作出正确的判断。
推理的过程中往往需要交替运用“排除法”和“反正法”。
要善于借助表格,把已知条件和推出的中间结论及时填入表格内。
填表时,对正确的(或不正确的)结果要及时注上“√”(或“×”),也可以分别用“1”或“0”代替,以免引起遗忘或混乱,从而影响推理的速度。
推理的过程,必须要有充足的理由或重复内的根据,并常常伴随着论证、推理,论证的才能不是天生的,而是在不断的实践活动中逐渐锻炼、培养出来的。
例题1:星期一早晨,王老师走进教室,发现教室里的坏桌凳都修好了。
传达室人员告诉他:这是班里四个住校学生中的一个做的好事。
于是,王老师把许兵、李平、刘成、张明这四个住校学生找来了解。
(1)许兵说:桌凳不是我修的。
(2)李平说:桌凳是张明修的。
(3)刘成说:桌凳是李平修的。
(4)张明说:我没有修过桌凳。
后经了解,四人中只有一个人说的是真话。
请问:桌凳是谁修的?根据“两个互相否定的思想不能同真”可知:(2)、(4)不能同真,必有一假。
假设(2)说真话,则(4)为假话,即张明修过桌凳。
又根据题目条件了:只有1人说的是真话:可退知:(1)和(3)都是假话。
由(1)说的可退出:桌凳是许兵修的。
这样,许兵和张明都修过桌凳,这与题中“四个人中只有一个人说的是真话”相矛盾。
因此,开头假设不成立,所以,(2)李平说的为假话。
由此可退知(4)张明说了真话,则许兵、刘成说了假话。
所以桌凳是许兵修的。
练习1:1、小华、小红、小明三人中,有一人在数学竞赛中得了奖。
老师问他们谁是获奖者,小华说是小红,小红说不是我,小明也说不是我。
六年级奥数 第31讲 逻辑推理(1)

第31讲逻辑推理(1)讲义专题简析逻辑推理题不涉及数据,也没有几何图形,只沙一参相互关联的条件。
它依据逻辑规律,从一定的前提出发,通过一系列的推理来获取某种结论。
解决这类间题常用的方法有:直接法、假设法、排除法图解法和列表法等。
逻辑推理问题的解决,需要我们深入地理解条件和结论,分析关键所在,找到突破口,进行合情合理的推理,最后做出正确的判断。
推理的过程中往往需要交替运用“排除法”和“反证法”。
要善于借助表格,把已知条件和推出的中间结论及时填入表格内。
填表时,对正确的(或不正确的)结果要及时注上“√”(或“×”),也可以分别用“1”或“0”代替,以免引起遗忘或混乱,从而影响推理的速度。
推理的过程,必须要有充足的理由或充分的根据,并常,常伴随着论证、推理。
论证的能力不是天生的,而是在不断的实践活动中逐渐锻炼、培养出来的。
例1、已知四人中只有一人说真话,请根据下面四人说的话,判断是哪名同学修好的桌凳。
(1)许兵说:“桌凳不是我修的。
”(2)李平说:“桌凳是张明修的。
”(3)刘成说:“桌凳是李平修的。
”(4)张明说:“我没有修过桌発。
”后经了解,四人中只有一人说的是真话。
请问:桌凳是谁修的?练习:1、小华、小红、小明三人中,有一人在数学竞赛中得了奖。
老师问他们谁是获奖者,小华说是小红,小红说不是自己,小明也说不是自己。
如果他们当中只有一人说了真话,那么,谁是获奖者?2、一位警察,抓获四个盗窃嫌疑犯A,B,C,D,他们的供词如下A说“不是我偷的。
”B说“是A偷的。
”C说:“不是我。
”D说:“是B偷的。
”他们四人中只有一人说的是真话。
你知道谁是小偷吗?3、有500人聚会,其中至少有一人说假话,这500人里任意两人总有一人说真话。
说真话的有多少人,说假话的有多少人?例2、虹桥小学举行科技知识竞赛,同学们对一贯刻苦学习、爱好读书的4名学生的成绩进行了如下估计:(1)丙得第一,乙得第二。
(2)丙得第二,丁得第三。
六年级奥数.逻辑推理(ABC级).教师版

逻辑推理知识框架逻辑推理作为数学思维中重要的一部分,经常出现在各种数学竞赛中,除此以外,逻辑推理还经常作为专项的内容出现在各类选拔考试,甚至是面向成年人的考试当中。
对于学生学习数学来说,逻辑推理既有趣又可以开发智力,学生自主学习研究性比较高。
本讲我们主要从各个角度总结逻辑推理的解题方法。
一、列表推理法逻辑推理问题的显著特点是层次多,条件纵横交错.如何从较繁杂的信息中选准突破口,层层剖析,一步步向结论靠近,是解决问题的关键.因此在推理过程中,我们也常常采用列表的方式,把错综复杂的约束条件用符号和图形表示出来,这样可以借助几何直观,把令人眼花缭乱的条件变得一目了然,答案也就容易找到了.二、假设推理用假设法解逻辑推理问题,就是根据题目的几种可能情况,逐一假设.如果推出矛盾,那么假设不成立;如果推不出矛盾,而是符合题意,那么假设成立.解题突破口:找题目所给的矛盾点进行假设三、体育比赛中的数学对于体育比赛形式的逻辑推理题,注意“一队的胜、负、平”必然对应着“另一队的负、胜、平”。
有时综合性的逻辑推理题需要将比赛情况用点以及连接这些点的线来表示,从整体考虑,通过数量比较、整数分解等方式寻找解题的突破口。
四、计算中的逻辑推理能够利用数论等知识通过计算解决逻辑推理题.例题精讲一、列表推理法【例 1】刘刚、马辉、李强三个男孩各有一个妹妹,六个人进行乒乓球混合双打比赛.事先规定:兄妹二人不许搭伴.第一盘:刘刚和小丽对李强和小英;第二盘:李强和小红对刘刚和马辉的妹妹.问:三个男孩的妹妹分别是谁?【考点】逻辑推理【难度】2星【题型】解答【解析】 因为兄妹二人不许搭伴,所以题目条件表明:刘刚与小丽、李强与小英、李强与小红都不是兄妹.由第二盘看出,小红不是马辉的妹妹.将这些关系画在左下表中,由左下表可得右下表.李强马辉刘刚小丽小红小英××××李强马辉刘刚小丽小红小英×√×××××√√刘刚与小红、马辉与小英、李强与小丽分别是兄妹. 【答案】刘刚与小红、马辉与小英、李强与小丽分别是兄妹【巩固】 王文、张贝、李丽分别是跳伞、田径、游泳运动员,现在知道:⑴张贝从未上过天;⑵跳伞运动员已得过两块金牌;⑶李丽还未得过第一名,她与田径运动员同年出生.请根据上述情况判断王文、张贝、李丽各是什么运动员?【考点】逻辑推理 【难度】2星 【题型】解答【解析】 为了能清楚地找到所给条件之间的关系,我们不妨运用列表法,列出下表,在表中“√”表示是,“×”表示不是,在任意一行或一列中,如果一格是“√”,可推出其它两格是“×”由⑴⑶可知张贝、李丽都不是跳伞运动员,可填出第一行,即王文是跳伞运动员;由⑶可知,李丽也不是田径运动员,可填出第三列,即李丽是游泳运动员,则张贝是田径运动员.【答案】王文是跳伞运动员,李丽是游泳运动员,张贝是田径运动员【例 2】 张明、席辉和李刚在北京、上海和天津工作,他们的职业是工人、农民和教师,已知:⑴张明不在北京工作,席辉不在上海工作;⑵在北京工作的不是教师;⑶在上海工作的是工人;⑷席辉不是农民.问:这三人各住哪里?各是什么职业?【考点】逻辑推理 【难度】2星 【题型】解答【解析】 这道题的关系要复杂一些,要求我们通过推理,弄清人物、工作地点、职业三者之间的关系.三者的关系需要两两构造三个表,即人物与地点,人物与职业,地点与职业三个表.我们先将题目条件中所给出的关系用下面的表来表示,由条件⑴得到表1,由条件⑵、⑶得到表2,由条件⑷得到表3.因为各表中,每行每列只能有一个“√”,所以表2可填全为表5.由表5知农民在北京工作,又知席辉不是农民,所以席辉不在北京工作,可以将表1可填全完为表4由表4和表5知得到:张明住在上海,是工人;席辉住在天津,是教师;李刚住在北京,是农民.方法二:由题目条件可知:席辉不在上海工作,而在上海工作的是工人,所以席辉不是工人,又不是农民,那么席辉只能是教师,不在北京工作,就只能是在天津工作,那么张明在上海工作,是工人。
【小学六年级奥数讲义】逻辑推理(二)

1 丁丙乙甲小华【小学六年级奥数讲义】逻辑推理(二)一、知识要点解数学题,从已知条件到未知的结果需要推理,也需要计算,通常是计算与推理交替进行,而且这种推理不仅是单纯的逻辑推理,而是综合运用了数学知识和专门的生活常识相结合来运用。
这种综合推理的问题形式多样、妙趣横生,也是小学数学竞赛中比较流行的题型。
解答综合推理问题,要恰当地选择一个或几个条件作为突破口。
统称从已知条件出发可以推出两个或两个以上结论,而又一时难以肯定或否定其中任何一个时,这就要善于运用排除法、反证法逐一试验。
当感到题中条件不够时,要注意生活常识、数的性质、数量关系和数学规律等方面寻找隐蔽条件。
二、精讲精练【例题1】小华和甲、乙、丙、丁四个同学参加象棋比赛。
每两人要比赛一盘。
到现在为止,小华已经比赛了4盘。
甲赛了3盘,乙赛了2盘,丁赛了1盘。
丙赛了几盘?这道题可以利用画图的方法进行推理,如图所示,用5个点分别表示小华、甲、乙、丙、丁。
如果两人之间已经进行了比赛,就在表示两人的点之间连一条线。
现在小华赛4盘,所以小华应与其余4个点都连线……甲赛了3盘。
由于丁只赛了一盘,所以甲与丁之间没有比赛。
那么,就连接甲、乙和甲、丙。
这时,乙已有了两条线,与题中乙赛2盘相结合,就不再连了。
所以,从中可以看出,丙与小华、甲各赛一盘。
即丙赛了两盘。
练习1:1、A ,B ,C ,D ,E 五位同学一起比赛象棋,每两人都要比赛一盘。
到现在为止,A 已经比赛了4盘。
B 赛了3盘,C 赛了2盘,D 赛了1盘。
E 赛了几盘?。
六年级下册 逻辑推理

六年级下册逻辑推理六年级下册:逻辑推理的提升与实践在六年级下册的学习阶段,学生们将接触到更为复杂的数学概念和逻辑推理。
在这个关键时期,教育者应当关注如何引导学生掌握逻辑推理的技巧,并将其应用于实际生活和学习中。
本文将探讨如何提升六年级学生的逻辑推理能力,并辅以具体的实例。
关键词:六年级下册、逻辑推理、能力提升、实践应用在数学学科中,逻辑推理是一种重要的思维方式,它能够帮助学生在解决数学问题时更加准确地分析和解答。
在六年级下册的教材中,涉及到的逻辑推理问题越来越多,这为学生们提供了更多的实践机会,以提升他们的逻辑推理能力。
要提升六年级学生的逻辑推理能力,首先要让他们明白逻辑推理的概念及重要性。
逻辑推理是指根据已知条件,通过一系列的推导和演绎,得出结论的思维方式。
在数学领域,逻辑推理的应用十分广泛,除了解决数学问题,还可以应用于科学、工程、计算机等领域。
在理解了逻辑推理的概念后,学生们需要掌握逻辑推理的基本步骤。
首先,要明确问题或任务,以便确定推导的方向。
其次,根据已知条件进行推导,找到解决问题的方法。
最后,得出结论并进行验证。
这些步骤在学习数学和应用题解答时尤其重要。
除了理论知识的掌握,实践应用也是提升逻辑推理能力的关键。
教师可以设计一些实际问题,如应用题、几何证明题等,让学生们在实际操作中锻炼逻辑推理能力。
通过不断的实践,学生们可以逐渐掌握逻辑推理的技巧,提高解题效率。
以一道几何证明题为例,题目要求证明一个三角形内角和为180度。
通过逻辑推理,我们可以知道这个三角形三个内角的度数之和为180度。
如果已知其中两个角度,便可以计算出第三个角度的度数。
在实际解题过程中,学生们可以画出这个三角形,标出各个角度,然后根据已知条件进行推导,得出结论。
通过这样的实践操作,学生们可以更加深入地理解逻辑推理的概念和应用。
总之,在六年级下册的学习阶段,学生们应当重视逻辑推理能力的培养和实践应用。
教育者应当引导学生在解决实际问题时运用逻辑推理,提高他们的解题效率和准确性。
小学奥数六年级逻辑推理题解题策略讲解

小学奥数六年级逻辑推理题解题策略讲解逻辑推理题作为小学奥数的一部分,在学生们的学习过程中扮演着重要的角色。
通过解题训练,不仅可以提高学生的逻辑思维能力,还可以培养他们的分析和推理能力。
本文将为大家详细介绍六年级逻辑推理题的解题策略,帮助学生更好地应对这类题目。
六年级逻辑推理题主要涉及到条件判断、排列组合和演绎推理等内容。
下面我们将逐一介绍各类题型的解题策略。
1. 条件判断题条件判断题是逻辑推理题中较为常见的一种题型。
解题时,学生需要根据已给出的条件进行推理和判断。
首先,学生要对条件进行仔细分析和理解。
将条件条目展示在纸上,形成一个条件表格,有助于学生更好地整理信息。
其次,学生要善于利用排除法,通过逐个排除不符合条件的选项,找到正确答案。
2. 排列组合题排列组合题是让学生从给定的元素中按照一定的规则进行组合和排列,然后求解满足特定条件的情况数。
解这类题目时,学生需要了解排列组合的基本原理,并学会运用相关的计算公式。
在实际解题过程中,可以尝试将问题转化为更简单的形式,利用分步计数法或找规律的方法进行求解。
3. 演绎推理题演绎推理题是通过已知条件进行推理,得出结论的题目。
这类题目要求学生运用逻辑思维和推理能力。
在解答演绎推理题时,学生需要仔细阅读题干和给定条件,并建立符号表示法,将已知信息一一列举出来。
然后,通过对已知条件进行逻辑运算,逐步得出结论。
此外,在做逻辑推理题时,学生还需具备良好的表达和推理能力。
他们应该掌握用文字和符号的方式进行推理和证明,能够准确地描述思路和推理过程。
综上所述,解决小学奥数六年级逻辑推理题的关键在于理解和掌握题目要求,并运用相应的解题策略。
通过不断的练习和总结,学生可以提高解题的速度和准确性,培养良好的逻辑思维和分析能力。
希望本文的讲解对同学们的学习有所帮助,祝大家在小学奥数中取得优异的成绩!。
精品奥数-高年级-第31讲-逻辑推理-3计算推理-答案
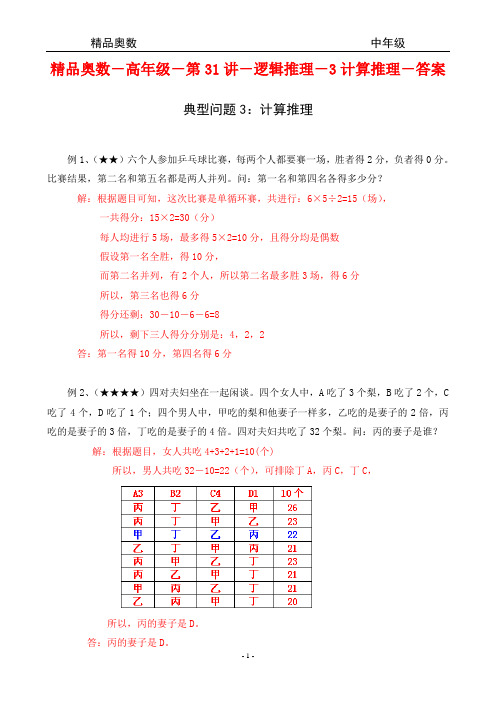
精品奥数-高年级-第31讲-逻辑推理-3计算推理-答案典型问题3:计算推理例1、(★★)六个人参加乒乓球比赛,每两个人都要赛一场,胜者得2分,负者得0分。
比赛结果,第二名和第五名都是两人并列。
问:第一名和第四名各得多少分?解:根据题目可知,这次比赛是单循环赛,共进行:6×5÷2=15(场),一共得分:15×2=30(分)每人均进行5场,最多得5×2=10分,且得分均是偶数假设第一名全胜,得10分,而第二名并列,有2个人,所以第二名最多胜3场,得6分所以,第三名也得6分得分还剩:30-10-6-6=8所以,剩下三人得分分别是:4,2,2答:第一名得10分,第四名得6分例2、(★★★★)四对夫妇坐在一起闲谈。
四个女人中,A吃了3个梨,B吃了2个,C 吃了4个,D吃了1个;四个男人中,甲吃的梨和他妻子一样多,乙吃的是妻子的2倍,丙吃的是妻子的3倍,丁吃的是妻子的4倍。
四对夫妇共吃了32个梨。
问:丙的妻子是谁?解:根据题目,女人共吃4+3+2+1=10(个)所以,男人共吃32-10=22(个),可排除丁A,丙C,丁C,所以,丙的妻子是D。
答:丙的妻子是D。
练习1、(★★★)A,B,C,D四个足球队进行循环比赛,赛了若干场后,A,B,C三队的比赛情况如下:问:D赛了几场?D赛的几场的比分各是多少?解:四个队进行循环赛,则每个队都要其他队赛一场,则每个队均要赛3场。
根据上表可知,A赛了3场,则A与B、C、D均赛过B、C各赛了2场,所以,B、C都未和D赛。
根据比分信息,A胜2场,平1场,B平1场,可知:A与B的那一场,与C、D的两场均胜。
所以:D赛了1场,比分是0:1。
答:D赛了1场。
比分是0:1。
2、六个人参加乒乓球比赛,每两个人都要赛一场,胜者得2分,负者得0分。
比赛结果,第二名和第五名都是两人并列。
问:第一名和第四名各得多少分?解:根据题目可知,这次比赛是单循环赛,共进行:6×5÷2=15(场),一共得分:15×2=30(分)每人均进行5场,最多得5×2=10分,且得分均是偶数假设第一名全胜,得10分,而第二名并列,有2个人,所以第二名最多胜3场,得6分所以,第三名也得6分得分还剩:30-10-6-6=8所以,剩下三人得分分别是:4,2,2答:第一名得10分,第四名得6分3、(★★)A,B,C,D四个队举行足球循环赛(即每两个队都要赛一场),胜一场得3分,平一场得1分,负一场得0分。
六年级逻辑推理

第一章逻辑推理在数学竞赛中,有一类问题似乎不像数学题,这类问题没有或很少给出数量或数量关系,也不出现任何图形。
解答这类问题没有什么现成的公式可用,甚至不需要什么复杂计算。
也有的问题,似乎像算术或几何问题,但解决它却很少用到算术和集合的知识,而是用逻辑推理的知识来解答。
这类问题称为逻辑推理问题。
逻辑推理是运用已知若干判断去获得一个新判断的思维方法。
在推理过程中,常常需要否定一些错误的可能性,去获得正确的结论。
解决这类问题常用的方法有:直接法;假设法;排除法;图解法;列表法和枚举法等。
逻辑推理问题的解决,需要我们深入地理解条件和结论,分析关键所在,找到突破口,进行合情合理的推理,最后做出正确的判断。
推理的过程,必须要有充足的理由和充分的依据。
论证的才能不是天生的,而是在不断的实践活动中逐渐锻炼、培养出来的。
一、直接法例1 张、王、李三个工人,在甲、乙、丙三个工厂里分别当车工、钳工和电工,已知:(1)张不在甲厂;(2)王不在乙厂;(3)在甲厂的不是钳工;(4)在乙厂的是车工;(5)王不是电工,这三个人分别在哪个厂?干什么工作?【分析与解】此题可用直接法解答,即直接从特殊条件出发,再结合其他条件往下推,直到推出结论为止。
由条件(5)可知,王不是电工,那么王必是车工或钳工;由条件(2)可知,王不在乙厂,那么王必在甲厂或丙厂;又由条件(4)可知,在乙厂的是车工,所以王只能是钳工;又因为甲厂的不是钳工,则王必是丙厂的钳工;张不在甲厂,必在乙厂或丙厂,而王在丙厂,则张必在乙厂,是乙厂的车工,剩下的李是甲厂的电工。
所以,张是乙厂的车工,王是丙厂的钳工,李是甲厂的电工。
例2 A 、B 、C 、D 、E 五人参加乒乓球比赛,每两人都要赛一场,并且只赛一场,规定胜者得2分,负者得0分。
现在知道比赛结果是:A 和B 并列第一名;C 是第三名,D 和E 并列第四名,求C 得多少分?【分析与解】我们从A 和B 并列第一名,D 和E 并列第四名的已知条件直接入手分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三十一周逻辑推理(一)专题简析:逻辑推理题不涉及数据,也没有几何图形,只涉及一些相互关联的条件。
它依据逻辑汇率,从一定的前提出发,通过一系列的推理来获取某种结论。
解决这类问题常用的方法有:直接法、假设法、排除法、图解法和列表法等。
逻辑推理问题的解决,需要我们深入地理解条件和结论,分析关键所在,找到突破口,进行合情合理的推理,最后作出正确的判断。
推理的过程中往往需要交替运用“排除法”和“反正法”。
要善于借助表格,把已知条件和推出的中间结论及时填入表格内。
填表时,对正确的(或不正确的)结果要及时注上“√”(或“×”),也可以分别用“1”或“0”代替,以免引起遗忘或混乱,从而影响推理的速度。
推理的过程,必须要有充足的理由或重复内的根据,并常常伴随着论证、推理,论证的才能不是天生的,而是在不断的实践活动中逐渐锻炼、培养出来的。
例题1:星期一早晨,王老师走进教室,发现教室里的坏桌凳都修好了。
传达室人员告诉他:这是班里四个住校学生中的一个做的好事。
于是,王老师把许兵、李平、刘成、张明这四个住校学生找来了解。
(1)许兵说:桌凳不是我修的。
(2)李平说:桌凳是张明修的。
(3)刘成说:桌凳是李平修的。
(4)张明说:我没有修过桌凳。
后经了解,四人中只有一个人说的是真话。
请问:桌凳是谁修的?根据“两个互相否定的思想不能同真”可知:(2)、(4)不能同真,必有一假。
假设(2)说真话,则(4)为假话,即张明修过桌凳。
又根据题目条件了:只有1人说的是真话:可退知:(1)和(3)都是假话。
由(1)说的可退出:桌凳是许兵修的。
这样,许兵和张明都修过桌凳,这与题中“四个人中只有一个人说的是真话”相矛盾。
因此,开头假设不成立,所以,(2)李平说的为假话。
由此可退知(4)张明说了真话,则许兵、刘成说了假话。
所以桌凳是许兵修的。
练习1:1、小华、小红、小明三人中,有一人在数学竞赛中得了奖。
老师问他们谁是获奖者,小华说是小红,小红说不是我,小明也说不是我。
如果他们当中只有一人说了真话。
那么,谁是获奖者?2、一位警察,抓获4个盗窃嫌疑犯A、B、C、D,他们的供词如下:A说:“不是我偷的”。
B说:“是A偷的”。
C说:“不是我”。
D说:“是B偷的”。
他们4人中只有一人说的是真话。
你知道谁是小偷吗?3、有500人聚会,其中至少有一人说假话,这500人里任意两个人总有一个说真话。
说真话的有多少人?说假话的有多少人?例题2:虹桥小学举行科技知识竞赛,同学们对一贯刻苦学习、爱好读书的四名学生的成绩作了如下估计:(1)丙得第一,乙得第二。
(2)丙得第二,丁得第三。
(3)甲得第二,丁得死四。
比赛结果一公布,果然是这四名学生获得前4名。
但以上三种估计,每一种只对了一半错了一半。
请问他们各得第几名?同学们的预测里有真有假。
但是最后公布的结果中,他们都只预测对了一半。
我们可以用假设法假设某人前半句对后半句错,如果不成立,再从相反方向思考推理。
假设(1)中“丙得第一”说错了,则(1)中“乙得第二”说对了;(1)中“乙得第二”说对了,则(2)中“丙得第二”说错了;(2)中“丙得第二”说错了,“丁得第三”说对了;(2)中“丁得第三”说对了,(3)中“丁得第四”说错了;(3)中“丁得第四”说错了,则(3)中“甲得第二”说对了,这与最初的假设相矛盾。
所以,正确答案是:丙得死一,丁得第三,甲得第二,乙得第四。
练习2:1、甲、乙、丙、丁同时参加一次数学竞赛。
赛后,他们四人预测名词的谈话如下:甲:“丙得第一,我第三”。
乙:“我第一,丁第四”。
丙:“丁第二,我第三”。
丁:没有说话。
最后公布结果时,发现甲、乙丙三人的预测都只对了一半。
请你说出这次竞赛中甲、乙、丙、丁四人的名次。
2、某小学最近举行一次田径运动会,人们对一贯刻苦锻炼的5名学生的短跑成绩作了如下的估计:A说:“第二名是D,第三名是B”。
B说:“第二名是C,第四名是E”。
C说:“第一名是E,第五名是A”。
D说:“第三名是C,第四名是A”。
E说:“第二名是B,第五名是D”。
这5位同学每人说对了一半,请你猜一猜5位同学的名次。
3、某次考试考完后,A,B,C,D四个同学猜测他们的考试成绩。
A说:“我肯定考得最好”。
B说:“我不会是最差的”。
C说:“我没有A考得好,但也不是最差的”。
D说:“可能我考得最差”。
成绩一公布,只有一个人说错了,请你按照考试分数由高到低排出他们的顺序。
例题3:张、王、李三个工人,在甲、乙丙三个工厂里分别当车工、钳工和电工。
①张不在甲厂,②王不在乙厂,③在甲厂的不是钳工,④在乙厂的是车工,⑤王不是电工。
这三个人分别在哪个工厂?干什么工作?这题可用直接法解答。
即直接从特殊条件出发,再结合其他条件往下推,直到推出结论为止。
通过⑤可知王不是电工,那么王必是车工或钳工;又通过②可知王不在乙厂,那么,王必在甲厂或丙厂;又由④知道在乙厂的是车工,所以王只能是钳工;又因为甲厂的不是钳工,则晚必是丙厂的钳工;张不在甲厂,必在乙厂或丙厂;王在丙厂,则张必在乙厂,是乙厂的车工,所以张是乙厂的车工。
剩下的李是甲厂的电工。
练习3:1、某大学宿舍里A,B,C,D,E,F,G七位同学,其中两位来自哈尔滨,两位来自天津,两位来自广州,还知道:(1)D,E来自同一地方;(2)B,G,F不是北方人;(3)C没去过哈尔滨。
那么,A来自什么地方?2、每个星期的七天中,甲在星期一、、二、三讲假话,其余四天都讲真话:乙在星期四、五、六讲假话,其余各天都讲真话。
今天甲说:“昨天是我说谎的日子。
”乙说:“昨天也是我说谎的日子。
”今天是星期几?3、王涛、李明、江民三人在一起谈话。
他们当中一位是校长,一位是老师,一位是学生家长。
现在只知道:(1)江民比家长年龄大。
(2)王涛和老师不同岁。
(3)老师比李明年龄小。
你能确定谁是校长、谁是老师,谁是家长吗?例题4:六年级有四个班,每个班都有正、副班长各一人。
平时召开年级班长会议时,各班都只有一人参加。
参加第一次回师的是小马、小张、小刘、小林;参加第二次会议的是小刘、小朱、小马、小宋;参加第三次会议的是小宋、小陈、小马、小张,小徐因有病,三次都没有参加。
你知道他们哪两个是同班的吗?将条件列在一张表格内,借助于表格进行分析、推理、根据题意,可列表如下:由上表可知,小马三次参加会议,而小徐三次都没参加,他们是同一班级的。
小张和小朱是同班的,小刘和小陈是同班的,小林和小宋是同班的。
练习4:1、某市举行家庭普法学习竞赛,有5个家庭进入决赛(每家2名成员)。
决赛时进行四项比赛,每项比赛各家出一名成员参赛,第一项参赛的是吴、孙、赵、李、王;第二项参赛的是郑、孙、吴、李、周;第三项参赛的是赵、张、吴、钱、郑;第四项参赛的是周、吴、孙、张、王。
另外,刘某因故四次均未参赛。
谁和谁是同一家庭呢?2、刘刚、马辉、李强三个男孩各有一个妹妹,六个人进行乒乓球混合双打比赛。
事先规定:兄、妹不许搭伴。
第一局:刘刚和小丽对李强和小英;第二局:李强和小红对刘刚和马辉的妹妹。
那么,三个男孩的妹妹分别是谁?3、有三只小袋,一只小袋有两粒红珠,另一只小袋有两粒蓝珠,第三只小袋装有一粒蓝珠和一粒红珠。
小兰不慎把小袋外面的三只标签都贴错了。
请问从哪只小袋中摸出一粒珠,就可以知道三只小袋中各装有什么颜色的珠?例题5:已知张新、李敏、王强三位同学分别在北京、苏州、南京的大学学习化学、地理、物理。
①张新不在北京学习;②李敏不在苏州学习;③在北京学习的同学不学物理;④在苏州学习的同学是学化学的;⑤李敏不学地理。
三位同学各在什么城市学什么?解答此题的关键是抓住三个人必在三地之一学习三种科目的某一种这个条件。
这种逻辑推理题,须在两方面加以判定。
尽管相对的问题要求增多了,但列表法仍然适用。
综合两方面的交错因素,两表对立,一举两得。
由①、②、⑤可列下表由④可知:李敏不在苏州,不学化学、学物理;张新、王强不学物理。
由③“在北京学习的不学物理”的条件可知:王强在北京,张新在苏州,李敏在南京。
由④“在苏州学习的学的是化学”的条件可知,王强学习地理。
从上表可以看出,张新在苏州学化学,李敏在南京学物理,王强在北京学地理。
练习5:1、甲、乙、丙分别在南京、苏州、西安工作,他们的职业分别是工人、农民和教师。
已知:①甲不在南京工作;②乙不在苏州工作;③在苏州工作的是工人;④在南京工作的不是教师;⑤乙不是农民。
三人各在什么地方工作?各是什么职业?2、小明、小青、小菊读书的学校分别是一小、二小、三小,他们各自爱好游泳、篮球、排球中的一项体育运动。
但究竟谁爱好哪一项运动,在哪个学校读书还不清楚,只知道:(1)小明不在一小。
(2)小青不在二小。
(3)爱好排球的在二小。
(4)爱好游泳的在一小。
(5)爱好游泳的不是小青。
请你说出他们各自就读的学校和爱好的运动项目。
3、甲、乙、丙分别是工程师、会计师和教师。
他们的业余爱好分别是文学、绘画和音乐。
现在知道:(1)爱好音乐、文学者和甲一起看电影。
(2)爱好绘画者常请会计师讲经济学。
(3)乙不爱好文学。
(4)工程师常埋怨自己对绘画和音乐一窍不通。
请问每个人的职业和爱好各是什么?答案:练11 、小明2、C 3、499 1练21、乙、丁、甲、丙2、E、C、B、A、D3、B、A、C、D练31、天津2、星期四3、李明是校长江兵是老师王涛是家长练41、吴和刘一家,孙和钱一家,赵和周一家,李和张一家2、李强的妹妹是小丽,马辉的妹妹是小瑛,刘刚的妹妹是小红3、从标签为“红、蓝”的小袋中摸出一珠,可由表答30-2知:练51、甲在苏州是工人,乙在无锡是教师,丙在南京是农民。
2、小明在二小,爱好排球;小青在三小,爱好篮球;小菊在一小,爱好游泳。
3、甲是教师,爱好绘画;乙是会计师,爱好音乐;丙是工程师,爱好文学。
例题1:星期一早晨,王老师走进教室,发现教室里的坏桌凳都修好了。
传达室人员告诉他:这是班里四个住校学生中的一个做的好事。
于是,王老师把许兵、李平、刘成、张明这四个住校学生找来了解。
(1)许兵说:桌凳不是我修的。
(2)李平说:桌凳是张明修的。
(3)刘成说:桌凳是李平修的。
(4)张明说:我没有修过桌凳。
后经了解,四人中只有一个人说的是真话。
请问:桌凳是谁修的?练习1:1、小华、小红、小明三人中,有一人在数学竞赛中得了奖。
老师问他们谁是获奖者,小华说是小红,小红说不是我,小明也说不是我。
如果他们当中只有一人说了真话。
那么,谁是获奖者?2、一位警察,抓获4个盗窃嫌疑犯A、B、C、D,他们的供词如下:A说:“不是我偷的”。
B说:“是A偷的”。
C说:“不是我”。
D说:“是B偷的”。
他们4人中只有一人说的是真话。
你知道谁是小偷吗?3、有500人聚会,其中至少有一人说假话,这500人里任意两个人总有一个说真话。
说真话的有多少人?说假话的有多少人?例题2:虹桥小学举行科技知识竞赛,同学们对一贯刻苦学习、爱好读书的四名学生的成绩作了如下估计:(1)丙得第一,乙得第二。
