1.16 第16题解答
奥数专题:逻辑推理1。16

一、填空题1. 甲、乙、丙三人进行跑步比赛.A、B、C三人对比赛结果进行预测.A说:“甲肯定是第一名.”B说:“甲不是最后一名.”C说:“甲肯定不是第一名.”其中只有一人对比赛结果的预测是对的.预测对的是.2. A、B、C、D、E和F六人一圆桌坐下.B是坐在A右边的第二人.C是坐在F右边的第二人.D坐在E的正对面,还有F和E不相邻.那么,坐在A和B之间的是.3. 甲、乙、丙、丁与小明五位同学进入象棋决赛.每两人都要比赛一盘,每胜一盘得2分,和一盘得1分,输一盘得0分.到现在为止,甲赛了4盘,共得了2分;乙赛了3盘,得了4分;丙赛了2盘,得了1分;丁赛了1盘,得了2分.那么小明现在已赛了盘,得了分.4. 曹、钱、刘、洪四个人出差,住在同一个招待所.一天下午,他们分别要找一个单位去办事.甲单位星期一不接待,乙单位星期二不接待,丙单位星期四不接待,丁单位只在星期一、三、五接待,星期日四个单位都不接待.曹:“两天前,我去误了一次,今天再去一次,还可以与老洪同走一条路.”钱:“今天我一定得去,要不明天人家就不接待了.”刘:“这星期的前几天和今天我去都能办事.”洪:“我今天和明天去,对方都接待.”那么,这一天是星期,刘要去单位,钱要去单位,曹要去单位,洪要去单位.5. 四位外国朋友住在十八层高的饭店里,他们分别来自埃及、法国、朝鲜和墨西哥.A住的层数比C住的层数高,但比D住的层数低;B住的层数比朝鲜人住的层数低;D住的层数恰好是法国人住的层数的5倍;如果埃及人住的层数增加2层,他与朝鲜人相隔的层数,恰好和他与墨西哥人相隔的层数一样;埃及人住的层数是法国人和朝鲜人住的层数的和.根据上述情况,请你确定A是人,住在层;B是人,住在层;C是人,住在____层;D是人,住在层.6. 小赵的电话号码是一个五位数,它由五个不同的数字组成.小张说:“它是84261.”小王说:“它是26048.”小李说:“它是49280.”小赵说:“谁说的某一位上的数字与我的电话号码上的同一位数字相同,就算谁猜对了这个数字.现在你们每人都猜对了位置不相邻的两个数字.”这个电话号码是.7. 小赵的电话号码是一个五位数,它由五个不同的数字组成.小王说:“它是93715.”小张说:“它是79538.”小李说:“它是15239.”小赵说:“谁说的某一位上的数字与我的电话号码上的同一位数字相同,就算谁猜对了这个数字.现在你们三人猜对的数字个数都一样,并且电话号码上的每一个数字都有人猜对.而每个人猜对的数字的数位都不相邻”.这个电话号码是.8. A、B、C、D四人定期去图书馆,四人中A、B二人每隔8天(中间空7天,下同)、C每隔6天、D每隔4天各去一次,在2月份的最后一天,四人刚好都去了图书馆,那么从3月1日到12月31日只有一个人来图书馆的日子有____ 天.9. 六年级六个班组织乒乓球单打比赛,每班派甲、乙两人参赛,根据规则每两人之间至多赛一场,且同班的两人之间不进行比赛.比赛若干场后发现,除一班队员甲以外,其他每人已比赛过的场数各不相同,那么一班队员乙已赛过____场.二、解答题11. 刘毅、马宏明、张健三个男孩都有一个妹妹,六人在一起打乒乓球,进行男女混合双打,事先规定:兄妹不搭档.第一盘:刘毅和小萍对张健和小英;第二盘:张健和小红对刘毅和马宏明的妹妹.小萍、小红和小英各是谁的妹妹?12. 四位运动员分别来自北京、上海、浙江和吉林,在游泳、田径、乒乓球和足球四项运动中,每人只参加了一项,且四人的运动项目各个不相同,除此以外,只知道一些零碎情况:张明是球类运动员,不是南方人;胡老纯是南方人,不是球类运动员;李勇和北京运动员、乒乓球运动员三人同住一个房间;郑永禄不是北京运动员,年龄比吉林运动员和游泳运动员两人的年龄小;浙江运动员没有参加游泳比赛.根据这些条件,请你分析一下:这四名运动员各来自什么地方?各参加什么运动?13. 老吴、老周、老杨分别是工程师、会计师和农艺师,还分别是业余作家、画家和音乐家,但不知道每人的职业及业余爱好,只知道:业余音乐家、作家常和老吴一起看电影;画家常请会计师讲经济学的道理;老周一点也不爱好文学;工程师埋怨自己对绘画、音乐一窍不通.请你指出每个人的职业和爱好.14. 四个人聚会,每人各带了2件礼品,分赠给其余三个人中的二人,试证明:至少有两对人,每对人是互赠过礼品的.一、填空题1. 从前一个国家里住着两种居民,一个叫宝宝族,他们永远说真话;另一个叫毛毛族,他们永远说假话.一个外地人来到这个国家,碰见三位居民,他问第一个人:“请问,你是哪个民族的人?”“匹兹乌图”.那个人回答.外地人听不懂,就问其他两个人:“他说的是什么意思?”第二个人回答:“他说他是宝宝族的.” 第三个人回答:“他说他是毛毛族的.”那么,第一个人是族,第二个人是族,第三个人是族.2. 有四个人各说了一句话.第一个人说:“我是说实话的人.”第二个人说:“我们四个人都是说谎话的人.”第三个人说:“我们四个人只有一个人是说谎话的人.”第四个人说:“我们四个人只有两个人是说谎话的人.”请你确定第一个人说话,第二个人说话,第三个人说___ 话,第四个人说话.3. 某地质学院的三名学生对一种矿石进行分析.甲判断:不是铁,不是铜. 乙判断:不是铁,而是锡. 丙判断:不是锡,而是铁.经化验证明,有一个人判断完全正确,有一人只说对了一半,而另一人则完全说误了.那么,三人中是对的, 是错的, 只对了一半.4. 甲、乙、丙、丁四人参加一次数学竞赛.赛后,他们四个人预测名次的谈话如下:甲:“丙第一名,我第三名.” 乙:“我第一名,丁第四名.” 丙:“丁第二名,我第三名.” 丁没说话.最后公布结果时,发现他们预测都只对了一半.请你说出这次竞赛的甲、乙、丙、丁四人的名次.甲是第名,乙是第名,丙是第名,丁是第名.5. 王春、陈则、殷华当中有一人做了件坏事,李老师在了解情况中,他们三人分别说了下面几句话:陈:“我没做这件事.殷华也没做这件事.”王:“我没做这件事.陈刚也没做这件事.”殷:“我没做这件事.也不知道谁做了这件事.”当老师追问时,得知他们都讲了一句真话,一句假话,则做坏事的人是.6. 三个班的代表队进行N(N 2)次篮班比赛,每次第一名得a分,第二名得b分,第三名得c分(a、b、c为整数,且a>b>c>0).现已知这N次比赛中一班共得20分,二班共得10分,三班共得9分,且最后一次二班得了a 分,那么第一次得了b 分的是 班.7. A 、B 、C 、D 四个队举行足球循环赛(即每两个队都要赛一场),胜一场得3分,平一场得1分,负一场得0分.已知:(1)比赛结束后四个队的得分都是奇数;(2)A 队总分第一;(3)B 队恰有两场平局,并且其中一场是与C 队平局.那么,D 队得 分.8. 六个足球队进行单循环比赛,每两队都要赛一场.如果踢平,每队各得1分,否则胜队得3分,负队得0分.现在比赛已进行了四轮(每队都已与4个队比赛过),各队4场得分之和互不相同.已知总得分居第三位的队共得7分,并且有4场球赛踢成平局,那么总得分居第五位的队最多可得 分,最少可得 分.由此可推知,甲与丁的比分为 ,丙与丁的比分为 .10. 某俱乐部有11个成员,他们的名字分别是A~K.这些人分为两派,一派人总说实话,另一派人总说谎话.某日,老师问:“11个人里面,总说谎话的有几个人?”那天,J 和K 休息,余下的9个人这样回答: A 说:“有10个人.” B 说:“有7个人.” C 说:“有11个人.” D 说:“有3个人.” E 说:“有6个人.” F 说:“有10个人.” G 说:“有5个人.” H 说:“有6个人.” I 说:“有4个人.” 那么,这个俱乐部的11个成员中,总说谎话的有 个人.二、解答题11. 甲、乙、丙三人,一个姓张,一个姓李和一个姓王,他们一个是银行职员,一个是计算机程序员,一个是秘书.又知甲既不是银行职员也不是秘书;丙不是秘书;张不是银行职员;王不是乙,也不是丙.问:甲、乙、丙三人分别姓什么?12. 世界杯足球小组赛,每组四个队进行单循环比赛.每场比赛胜队得3分,败队记0分.平局时两队各记1分.小组全赛完以后,总积分最高的两个队出线进入下轮比赛.如果总积分相同,还要按小分排序. 问:一个队至少要积几分才能保证本队必然出线?简述理由.在上述世界杯足球小组赛中,若有一个队只积3分,问:这个队有可能出线吗?为什么?13.有一个如图那样的方块网,每1个小方块里有1个人,在这些人中间,有人戴着帽子,有人没戴.每一个人都只能看见自己前方,后方和斜方的人的头,如图1所示A 方块里的人能看见8个人的头,B 方块里的人能看见5个人的头,C 方块里的人能看见3个人的头,自己看不见自已的头.在图2的方格中,写着不同方块里的人能看见的帽子的数量,那么,请在图中找出有戴帽子的人的方块,并把它涂成黑色.14. 某校学生中,没有一个学生读过学校图书馆的所有图书,又知道图书馆内任何两本书至少被一个同学都读过,问:能不能找到两个学生甲、乙和三本书A 、B 、C ,甲读过A 、B ,没读过C ,乙读过B、C ,没读过A?说明判断过程.图1 图2A BCD F E1. CC 的预测截然相反,必一对一错.因为只有一人对,不论A 、C 谁对,B 必 错,所以甲是最后一名,C 对. 2. E如右图,E 坐在A 、B 之间.3. 2,3.由题意可画出比赛图,已赛过的两人之间用线段引连(见右图).由图看出小明赛了2盘.因 为一共赛了六盘,共得12分,所以小明得了12-(2+4+1+2)=3(分).4. 三,丙,丁,甲,乙.由刘的讲话,知这一天是星期三,刘要去丙单位.钱要去丁单位,曹去的是甲单位,洪去的是乙单位. 埃及,8;法国,3;朝鲜,5;墨西哥,15.容易知道,墨西哥人住得最高,埃及人次之,朝鲜人又次之,法国人最低,各层次分别15,8,5和3.由(2)知B 是法国人,由(3)和D 是墨西哥人,由(1)知A 是埃及人,而C 是朝鲜人. 86240.因为每人猜对两个数字,三人共猜对 张:842 1 2⨯3=6(个)数字,而电话号码只有5位, 王:26048 所以必有一位数字被两人同对猜对.如右 李:49 80图所示,猜对的是左起第三位数字2.因为每人猜对的两个数字不相邻,所以张、李猜对的另一个数字分别在两端,推知王猜对的数字是6和4,进一步推知张猜对8,李猜对0.电话号码是86240.7. 19735.因为每个数字都有人猜对,所以每人至少猜对两个数字.下页右上图中,同一位数中只有方框中的两个数相同,如果每人猜对的数字多于两位,相同的数字至少有3⨯3-5=4(组),所以每人恰好猜对两个数字. 王: 9 3 7 1 5三人共猜对2⨯3=6(个)数字,因为电话号码只有 张: 7 9 5 3 8 5位,所以相同的一组是正确的,即左起第四位是 李: 1 5 2 3 9 3.因为每人猜对的数字不相邻,所以张、李猜对的另一个数字都在前两位,王猜对的两个数字是7和5,进而推知张猜对9,李猜对1.电话号码是19735. 8. 51天.因为[8,6,4]=24,所以四人去图书馆的情况每24天循环一次(见下表):1 2 3 4 5 6 7 8 D C A 、B 、D 9 10 11 12 13 14 15 16 C 、DA 、B 、D 17 18 19 20 21 22 23 24CDA 、B 、C 、D每24天有4天只有1人去图书馆.3月1日至12月31日有306天,甲乙 丙 丁小明306÷24=12…18,所以所求天数为4⨯12+3=51(天).9. 5根据题意,有11名队员比赛场数各不相同,并且每人最多比赛10场,所以除甲外的11名队员比赛的场数分别为0~10.已赛10场的队员与除已赛0场外的所有队员都赛过,所以已赛10场的队员与已赛0场的队员同班;已赛9场的队员与除已赛0、1场外的所有队员都赛过,所以已赛9场的队员与已赛1场的队员同班;同理,已赛8、7、6场的队员分别与已赛2、3、4场的队员同班;所以甲与已赛5场的队员同班,即乙赛过5场.注本题可以求出甲也赛了5场,分别与已赛10、9、8、7、6场的队员各赛1场.10. 蓝、黄、红.解法一题中表明,每个孩子的父母是同血型的.具有B型血的孩子,其父母同血型时,由表中可见,只能是B型或AB 型,但题中没有同具B型血的父母,所以戴红帽子的父母的孩子穿蓝上衣.具有A型血的孩子的同血型的父母,只可能同为A型血或同为AB型血.今已知有一对父母为AB型血者,所以穿黄上衣的孩子的父母戴黄帽子.由表中可见,其孩子为O型血时,父母血型只能同为A型或B型或O型.今已知不具有同为B型血的父母,而同为A型血的父母的孩子已知具有A型血.把代表孩子的点与他的可能双亲的代表点之间连一直线段,便可得下面的图;由于孩子与其父母之间是唯一搭配的,所以,保存下来的只有连着红、蓝;黄,黄及蓝,红的三条边.所以,穿红上衣(O型血)孩子的父母戴蓝帽子.孩子衣服颜色父母帽子颜色(O型血)红)(A型血)黄(B型血)蓝所以,穿红上衣的孩子的父母戴蓝帽子;穿黄上衣的孩子的父母戴黄帽子;穿蓝上衣的孩子的父母戴红帽子.11..12.用表格解如下:13.表解如下:由(3)北京运动员是乒乓球运动员, 故张是足球运动员郑是乒乓球运动员由(4)吉林运动员不是游泳运动员,故李是田径运动员,而胡是游泳运动员杨工 会 农作 画 音⨯ ⨯ 吴 ⨯ √ ⨯ ⨯周 ⨯ ⨯ √杨 √⨯⨯工 会 农作 画 音⨯ ⨯ √ 吴 ⨯ √ ⨯ ⨯ √ ⨯ 周 ⨯ ⨯ √ √⨯⨯ 杨 √⨯⨯14. 设此四人为甲、乙、丙、丁并用画在平面上的四个点分别表示他们,称为它们的代表点,当某人(例如甲)赠了1件礼品给另一个(例如乙)时,就由甲向乙的代表点画一条有指向的线,无非有以下两个可能: 甲、乙、丙、丁每人各收到了2件礼品.上面的情形不发生.这时只有以下一个可能,即有一个人接受了3件礼品(即多于2件礼品;因为一人之外总共还有三个人,所以至多收到3件礼品).(或许会有人说,还有两个可能:有人只收到1件礼品及有人什么礼品也没收到.其实,这都可归以“有一人接受了3件礼品”这个情形.因为,当有一人(例如甲)只接受了1件礼品的情形发生时,四人共带来的8件礼品中还剩下7件在甲以外的三个人中分配,如果他们每人至多只收到2件礼品,则收受礼品数将不超过6件,这不可能,所以至少有一人收到2件以上(即3件)礼品,同样,当甲未收到礼品时,8件礼品分给乙、丙、丁三人,也必定有人收到3件礼品). 当(1)发生时,例如甲收到乙、丙的礼品,由于甲发出的礼品中至少有1件给了乙或丙,为确切计,设乙收到了甲的礼品,于是我们先有了一对人:(甲、乙),他们互赠了礼品,如果丙也收到甲的礼品,那么又有了第二对互赠了礼品的人(甲、丙);如果收到甲礼品的另一人是丁(如右图)丁的2件礼品必定分赠了乙及丙(甲已收足了本情形中限定的2件礼品)丙或乙的另一件礼品给了丁,则问题也解决(这时另一对互赠了礼品的人便是(乙、丁)或(丙、丁)但丙的另一件礼品只能给丁,因为这时乙已收足了2件礼品,所以,当本情形发生时,至少能找到两对互赠过1件礼品的人.当(2)发生时,不失一般性,设甲收到了来自乙、丙、丁的各1件礼品,但甲又应向他们之中的某两人(例如乙、丙)各赠送1件礼品,于是(甲、乙),(甲、丙)便是要找的两对人.总上可知,证明完毕.老吴是业余画家,老周是业余音乐家,老杨是业余作家.工程师是老杨,会计师是老周农艺师是老吴.—1. 宝宝,宝宝,毛毛.如果第一个人是宝宝族的,他说真话,那么他说的是“我是宝宝族的”.如果这个人是毛毛族的,他说假话,他说的还是“我是宝宝族的”.所以第二个人是宝宝族的,第三个人是毛毛族的.”2. 真,假,假,不确定.第二个人显然说的是假话.如果第三个人说的是真话,那么第四个人说的也是真话,产生矛盾.所以第三个人说假话.如果第四个人说真话,那么第一个人也说真话.如果第四个人说假话,那么只有第一个人说真话.所以可以确定第一个人主真话,第二、第三个人说假话,第四个人不能确定.3. 丙,乙,甲.如果甲的判断完全正确,那么乙说对了一半“不是铁,”所以这矿石也不是锡,这样丙也说对了一半,矛盾.如果乙的判断完全正确,那么甲对了一半,这矿石应是铜,丙也说对了一半,矛盾.所以丙的判断完全正确,而乙完全错了,甲只说对了一半.4. 三,一,四,二.假设甲说的“丙是第一名”正确,结果推出丙是第三名,矛盾,故甲说的第二句话是正确.由表中可知乙第一名,丁第二名,甲第三名,则第四名是丙.5. 陈刚.如果王春做了坏事,则陈刚的两句话都是真话,不合题意;如果殷华做了坏事,则王春的两句话都是真话,不合题意;如果陈刚做了坏事,符合题意.所以陈刚做了坏事.6. 三.N次比赛共得20+10+9=39(分),39=3⨯13,所以共进行了3次比赛,每次比赛共得13分,即a+b+c=13.因为一班3次比赛共得20分,20÷3=6…2,所以a≥7,a,b,c可能组合为7、5、1;7、4、2;8、4、1;8、3、2;9、3、1,考虑到3次比赛得20分,只有a=8、b=4、c=1时才7. 3B队得分是奇数,并且恰有两场平局,所以B队是平2场胜1场,得5分.A队总分第1,并且没有胜B队,只能是胜2场平1场(与B队平),得7分.因为C队与B队平局,负于A队,得分是奇数,所以只能得1分.D队负于A、B队,胜C队,得3分.8. 3,1.共赛了4⨯6÷2=12(场),其中平了4场,分出胜负的8场,共得3⨯8+2⨯4=32(分).因为前三位的队至少共得7+8+9=24(分),所以后三位的队至多共得32-24=8(分).又因为第四位的队比第五位的队得分多,所以第五位的队至多得3分.因为第六位的队可能得0分,所以第五位的队至少得1分(此时这两队之间必然没有赛过).9. 3:2,3:4.由乙队共进2球,胜2场平1场推知,乙队胜的两场都是1:0,平的一场是0:0.由甲队与乙队是0:0,甲队与丙队未赛,推知甲队所有的进球都来自与丁队的比赛,所以甲队与丁队是3:2.由丙队与乙队是0:1,丙队与甲队未赛,所以丙队与丁队是3:4.10 9.因为9个人回答出了7种不同的人数,所以说谎话的不少于7人.若说谎话的有7人,则除B外,其他回答问题的8人均说了谎话,与假设出现矛盾;若说谎话的有8人,则回答问题的9人均说了谎话,出现矛盾;若说谎话的有10人,则只能1人说实话,而A和F都说了实话,出现了矛盾;若说谎话的有11人,则没有说实话的,而E说了实话,出现矛盾;显然说谎话的有9人,回答问题的9人均说谎话,休息的两人说实话.11. 根据题意有关条件,用“√”表示是、“Х”表示不是,列表所示.这样,可知甲姓王、乙姓张和丙姓李.12. 四个队单循环赛共6场比赛,每场均有胜负,6场最多共计18分.若该队积7分,剩下的11分被3个队去分,那么,不可能再有两个队都得7分,即至多再有一个队可得7分以上.这样该队可以出线.其次,如果该队积6分,则剩下12分,可能有另两队各得6分.如果这另两队小分都比该队高,该队就不能出线了.所以,一个队至少要积7分才能保证必然出线.有可能出线.当6场比赛都是平局时,4个队都得3分,这时两个小分最高的队可以出线.如果这个队恰属于两个小分最高的队,那么这个队就会出线.13.答案如右图所示站在第一行第五列的人能看见1顶帽子,说明他周围的3人中有2人没戴帽子.站在第二行第四列的人能看见7顶帽子,说明他周围的8人中只有1人没戴帽子,综合结论 可知他本人没有戴帽子.站在第二行第五列的人能看到4顶帽子,且他周围的五人中已有1人没戴帽子,说明其余4人均戴帽子,根据结论 可知他本人没戴帽子.利用上下对称原理可以分析出:站在第四行、第五行后三列的6个人中,只有第四行第四列、第五列两人没戴帽子,其他人均戴帽子.站在第四行第二列的人能看到7顶帽子,说明他周围的8人中只有1人没戴帽子.站在第三行第1列的人能看见1顶帽子,说明他周围的5人中只有1人戴帽子.综合结论可知:这1人不可能是第二行第1、2列的人,也不可能是第四行第二列的人.所以只能是站在第三行第二列的人或第四行第1列的人.站在第五行第1列的人能看到2顶帽子,说明结论 所说戴帽子的人站在第四行第一列. 站在第二行第二列的人能看到6顶帽子,说明站在第一行第1、2列的2人都戴帽子.14. 解法一首先从读书数最多的学生中找一人叫他为甲,由题设,甲至少有一本书C未读过,设B是甲读过的书中的一本,根据题设,可找到学生乙,乙读过B、C.由于甲是读书数最多的学生之一,乙读书数不能超过甲的读书数,而乙读过C书,甲未读过C书,所以甲一定读过一本书A,乙没读过A书,否则乙就比甲至少多读过一本书,这样一来,甲读过A、B,未读过C;乙读过B、C,未读过A.因此可以找到满足要求的两个学生.解法二将全体同学分成两组.若某丙学生所读的所有的书,都被另一同学全部读过,而后一同学读过的书中,至少有一本书,丙未读过,则丙同学就分在第一组.另外,凡一本书也未读过的同学也分在第一组,其余的同学就分在第二组.按照以上分组方法,不可能将全体同学都分在第一组,因为读书数最多的同学一定在第二组.在第二组中,任找一位同学叫做甲,由题设有书C,甲未读过.再从甲读过的书中任找一本书叫做B,由题设,可找到同学乙,乙读过B、C书,由于甲属于第二组,所以甲一定读过一本书A,乙未读过A,否则甲只能分在第一组.这样,甲读过A、B,未读过C;乙读过B、C,未读过A.。
湖南省长沙市华益中学2023-2024学年上学期七年级期中考试数学试卷

23年秋初一华益中学期中考试数学试卷 一、选择题 (在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本大题共10个小题,每小题3分,共30分) −1.(3分)2的相反数是()A .2−B .2C .21D . −21 2.(3分)2023年我国高校毕业生近1160万人,教育部等七部门拟联合开展促就业的“国 聘行动”.数据“1160万”用科学记数法表示为()1.1610⨯A .81.1610⨯B .711.610⨯C .6 0.11610⨯D .83.(3分)下列各组数中,相等的一组是()−−A .(2)−−与|2|(1)−−12B .与2(2)−C .3−2与3D .322与 32()2 a b +<4.(3分)若0 ab <,0,则下列说法正确的是()A .a ,b 同号B . a ,b 异号且负数的绝对值较大C .a ,b 异号且正数的绝对值较大D .以上均有可能5.(3分)关于整式,下列说法正确的是() A .x y 2的次数是2B .0不是单项式3πC .mn 的系数是3x x −−D .2332是三次三项式−2a b n 6.(3分)若5 5a b 32m n 与+的差仍是单项式,则m n的值是()A .2B .0 −C .1D .17.(3分)下列各式运用等式的性质变形,错误的是() a b =A .若,则+=+a b =B a c b c .若,则=c ca ba b =C .若,则=a b =D ac bc .若,则−=−a c b c −1A 8.(3分)如果数轴上的点对应的数为,点B 与 A 点相距3个单位长度,则点 B 所对 应的有理数为()A .2−B .4−C .2或4−D .2或49.(3分)某同学在解关于x x mx 的方程−=+313时,把m x =看错了,结果解得4,则该同m 学把看成了()−A .2B .2C .34D .27 10.(3分)《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出八,盈十一;人出五,不足十三.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出八钱,那么多了十一钱;如果每人出五钱,那么少了十三钱.问:共有几个人?”设共有x 个人共同出钱买鸡,则下面所列方程正确的是() x x A .−=+x x B 811513.+=−811513x x C .−=+x x D 511813.+=−8(11)5(13)二、填空题 (本大题共6个小题,每小题3分,共18分)11.(3分)某地上午气温为︒16C ,下午上升︒3C ,到半夜又下降︒ 20C,则该地半夜的气温为. 12.(3分)用“四舍五入”法将3.896精确到0.01,所得到的近似数为.13.(3分)已知a ,b a b ++−=满足|3|(2)02+,则a b ()2023的值是.14.(3分)已知轮船在逆水中前进的速度是a 千米时,水流的速度是5/千米 /时,则这轮船在顺水中前进的速度是/千米时. a a 2+−=1015.(3分)已知,则代数式 a a 2222021++的值是.16.(3分)若k x −−=||4k (5)60− 是关于x的一元一次方程,则k 的值为.三、解答题 (本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每17.(6分)−+−−⨯−2|23|2(1)32023.18.(6分)解方程:x x =−+−6312152.19.(6分)先化简,再求值:+−−−m m n m n 2(32)6()22,其中=−m 3,=n 3.20.(8分)(1)已知有理数a ,b ,c 在数轴上对应的点如图所示,化简:−+−−−b a a c c b ||||||; (2)已知=−A x x 532,=−+B x x 1162,求当=x 1时,求−A B 的值.21.(8分)如图,在长为++a ab 12,宽为−a ab 22的长方形纸板上裁去一个边长为b 的正方形.(1)求剩余纸板的周长C (用含a ,b 的代数式表示); (2)当=a 3,=b 1时,求C 的值.22.(9分)李军大学毕业后返乡创业,成为一名电商老板,把村里农民的苹果放在网上销售,计划每天销售2000千克,实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负.下表是李军某一周苹果的销售情况:(1)李军该周销售苹果最多的一天比最少的一天多销售多少千克? (2)李军该周实际销售苹果的总量是多少千克?(3)若李军按5元/千克收购,按9.5元/千克进行苹果销售,运费及包装费等平均为2.5元/千克,则李军该周销售苹果一共收入多少元?23.(9分)已知关于x 的整式=+−+A x ax x 3322,整式=+−+B x ax x 24222,若a 是常数,且−A B 3不含x 的一次项. (1)求a 的值;(2)若b 为整数,关于x 的一元一次方程+−=bx x 230的解是整数,求+a b 5的值.24.(10分)1990年,著名社会学家费孝通先生总结出了“各美其美,美人之美,美美与共,天下大同”这一处理不同文化关系的十六字“箴言”.在数学上,我们不妨约定:若关于x 的方程110a x b +=与220a x b +=同时满足21221||()0a b a b −+−=,则称方程110a x b +=与220a x b +=互为“美美与共”方程.根据该约定,回答下列问题.(1)已知关于x 的方程20x m −=与0ax b +=互为“美美与共”方程,且方程20x m −=的解为12,则m = ,a = ,b = ; (2)是否存在有理数k ,使关于x 的方程30x k +=与其“美美与共”方程的解都是整数,若存在,求出k 的值,若不存在,请说明理由;(3)若方程12(21)x x −=−的解也是方程0ax b +=的解,求方程0ax b +=的“美美与共”方程的解.25.(10分)如图,在长沙市华益中学迎面50米接力比赛中,设运动时间为t秒,甲班的A 同学在数轴上位置C拿到最后一棒接力棒时,记为0t=,此时乙班的B同学已经位于数轴上数10的位置,A同学以每秒8米向左运动,B同学以每秒5米向左运动,两位同学到达D点立即停止运动.(1)当0t=时,A、B同学相距米;当1t=时,A、B同学在数轴上所表示的数为、.(2)①若t秒后A同学恰好追上B同学,求t;②当A同学到达终点D后,B同学还要经过多少秒到达D点.③分别取线段AC、BD中点为E、F,若在点A、B运动期间,4mEF nDA−始终保持不变(其中m,n为常数),求mn的值.23年秋初一华益中学期中考试数学试卷参考答案与试题解析 一、选择题 (在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本大题共10个小题,每小题3分,共30分)−1.(3分)2的相反数是()A .2−B .2C .21D . −21 【分析】根据相反数的定义进行判断即可.−【解答】解:2的相反数是2,故选:A .【点评】本题考查相反数,掌握相反数的定义是正确判断的前提.2.(3分)2023年我国高校毕业生近1160万人,教育部等七部门拟联合开展促就业的“国聘行动”.数据“1160万”用科学记数法表示为()1.1610⨯A .81.1610⨯B .711.610⨯C .60.11610⨯D .8a ⨯10【分析】将一个数表示成n a 的形式,其中1||10<,n 为整数,这种记数方法叫做科学记数法,据此即可得出答案.【解答】解:1160万 ==⨯11600000 1.16107,故选:B .【点评】本题考查科学记数法表示较大的数,科学记数法是基础且重要知识点,必须熟练掌握.3.(3分)下列各组数中,相等的一组是()−−A .(2)−−与|2|−1B .2(1)−与2(2)−C .3−2与3D .322与32()2【分析】根据有理数的乘方运算法则、绝对值的意义可进行求解.【解答】解:A −−=、(2)2−−=−,|2|2 −−,所以(2)−−与|2|不相等不符合题意;−=−11B 、2 −=,(1)12(1)−2,所以与−12不相等不符合题意;−=−C 、(2)83−=−28,3(2)−,所以3−23与相等符合题意;D 、3924()2=,所以322与23()2不相等不符合题意;C 故选:.【点评】本题主要考查有理数的乘方运算,熟练掌握有理数的乘方运算法则是解题的关键. 4.(3分)若0a b +<,0ab <,则下列说法正确的是( ) A .a ,b 同号B .a ,b 异号且负数的绝对值较大C .a ,b 异号且正数的绝对值较大D .以上均有可能【分析】根据题意得知a 、b 异号,并且负数的绝对值较大,挖掘出这一条件后,再对四个选项逐一分析.【解答】解:0ab <,a ∴、b 异号,又0a b +<,∴负数的绝对值较大, 根据这一条件判断:A 、C 、D 选项错误;B 选项正确; 故选:B .【点评】本题考查了有理数的除法,两个不等于零的数相乘,两数相乘,同号为正,异号为负,并把绝对值相乘.5.(3分)关于整式,下列说法正确的是( ) A .2x y 的次数是2 B .0不是单项式C .3mn π的系数是3D .3223x x −−是三次三项式【分析】根据单项式的系数与单项式的次数的定义对A 、C 进行判断;根据单独的一个数字或字母也是单项式对B 进行判断;根据多项式的次数和项数的定义对D 进行判断. 【解答】解:A 、2x y 的次数是3,所以A 选项错误; B 、数字0是单项式,所以B 选项错误; C 、3mn π的系数是3π,所以C 选项错误;D 、3223x x −−是三次三项式,所以D 选项正确.故选:D .【点评】本题考查了单项式:由数与字母的积或字母与字母的积所组成的代数式叫做单项式(单独的一个数字或字母也是单项式).单项式中的数字因数叫做这个单项式的系数.所有字母的指数之和叫做这个单项式的次数.也考查了多项式的定义. 6.(3分)若52n a b −与325m n a b +的差仍是单项式,则n m 的值是( ) A .2B .0C .1−D .1【分析】由52n a b −与325m n a b +的差仍是单项式知52n a b −与325m n a b +是同类项,据此可得3n =,25m n +=,解之求出m 的值,代入计算可得.【解答】解:52n a b −与325m n a b +的差仍是单项式,52n a b ∴−与325m n a b +是同类项,3n ∴=,25m n +=, 1m ∴=,则311n m ==,故选:D .【点评】本题主要考查同类项,所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.7.(3分)下列各式运用等式的性质变形,错误的是( ) A .若a b =,则a c b c +=+ B .若a b =,则a bc c=C .若a b =,则ac bc =D .若a b =,则a c b c −=−【分析】根据等式的性质,可得答案.【解答】解:A 、若a b =,则a c b c +=+,故A 不符合题意; B 、c 等于零时,除以c 无意义,故B 符合题意; C 、若a b =,则ac bc =,故C 不符合题意;D 、若a b =,则a c b c −=−,故D 不符合题意;故选:B .【点评】本题考查了等式的性质,熟记等式的性质是解题关键.8.(3分)如果数轴上的点A 对应的数为1−,点B 与A 点相距3个单位长度,则点B 所对应的有理数为( ) A .2B .4−C .2−或4D .2或4−【分析】考虑在A 点左边和右边两种情形解答问题.【解答】解:在A 点左边与A 点相距3个单位长度的点所对应的有理数为4−; 在A 点右边与A 点相距3个单位长度的点所对应的有理数为2. 故选:D .【点评】本题考查了数轴上两点间的距离,解题的关键是注意分类讨论.9.(3分)某同学在解关于x 的方程313x mx −=+时,把m 看错了,结果解得4x =,则该同学把m 看成了( ) A .2−B .2C .43D .72【分析】将4x =代入313x mx −=+中解得m 的值即可.x =【解答】解:将4x mx 代入−=+313中可得−=+m 12143m =,解得:2,B 故选:. 【点评】本题考查解一元一次方程,熟练掌握解方程的方法是解题的关键.10.(3分)《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出八,盈十一;人出五,不足十三.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出八钱,那么多了十一钱;如果每人出五钱,那么少了十三钱.问:共有几个人?”设共有x 个人共同出钱买鸡,则下面所列方程正确的是() x x A .−=+x x B 811513.+=−811513x x C .−=+x x D 511813.+=−8(11)5(13)x 【分析】设有个人共同出钱买鸡,根据买鸡需要的总钱数不变,即可得出关于x 的一元一次方程,此题得解.【解答】解:设有x x x 个人共同出钱买鸡,根据题意得:−=+811513.故选:A .【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.二、填空题 (本大题共6个小题,每小题3分,共18分)11.(3分)某地上午气温为︒16C ,下午上升︒3C ,到半夜又下降︒ 20C ,则该地半夜的气温为︒−1C . 【分析】利用题意列出算式解答即可.【解答】解:+− =−163211920︒=−1C .故答案为:︒ −1C .【点评】本题主要考查了有理数的加减混合运算的应用,正确列出算式是解题的关键.3.90. 12.(3分)用“四舍五入”法将3.896精确到0.01,所得到的近似数为【分析】把千分位上的数字6进行“四舍五入”即可.【解答】解:≈3.896 3.900.01)(精确到.故答案为:3.90.【点评】本题考查了近似数与精确度,熟练掌握精确度的定义是解答本题的关键.近似数的最后一个数字实际在什么位上,即精确到了什么位,要求精确到某一位,应当对下一位的数字进行四舍五入.13.(3分)已知a ,a b ++−=b 满足|3|(2)02 +,则a b ()2023−的值是1.【分析】根据绝对值、偶次方的非负性求出a、b ,再根据有理数的乘方法则计算即可.a b 【解答】解:|3|(2)0++−=2∴+=a 30,,b −=20,∴=−a 3b =,2,∴+=−+=−a b ()(32)120232023,−故答案为:1.【点评】本题考查的是非负数的性质,熟记绝对值、偶次方具有非负性是解题的关键.14.(3分)已知轮船在逆水中前进的速度是a 时,水流的速度是5千米/千米/ 时,则这轮 a 船在顺水中前进的速度是+(10)/千米时.【分析】根据顺水速度=逆水速度+⨯2水流速度,把相关数值代入后化简即可.a +【解答】解:由题意得:船在静水中的速度为:5,∴a a ++=+这轮船在顺水中航行的速度是55(10)千米/时,a 故答案为:+(10).【点评】本题考查列代数式,解题的关键是顺水速度=逆水速度+⨯2水流速度.a a +−=15.(3分)已知102 a a 2,则代数式222021++的值是2023.a a +=【分析】根据题意得到12,再将代数式变形即可求值.a a 【解答】解:2+−=10∴+=a a 2,1,∴++=++=⨯+=a a a a 2220212()2021212021202322,故答案为:2023.【点评】本题考查了代数式求值,利用整体代入思想解决问题是解题关键.16.(3分)若k x −−=||4k (5)60−是关于x 的一元一次方程,则k−的值为5.【分析】直接利用一元一次方程的定义得出关于k 的方程求出答案.k x 【解答】解:(5)60−−=||4k −是关于x 的一元一次方程,∴−=k ||41k −≠50且,解得:k =−5.−5故答案为:.【点评】此题主要考查了一元一次方程的定义,正确把握未知数的系数与次数是解题关键.三、解答题 (本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每17.(6分)320232|23|2(1)−+−−⨯−.【分析】先求绝对值和乘方,再作乘法和加减即可.【解答】解:原式812(1)=−+−⨯−812=−++5=−.【点评】本题考查含乘方的有理数运算,掌握相关的运算法则和公式是解题的关键.18.(6分)解方程:2152163x x +−=−. 【分析】先去分母,再去括号,移项,合并同类项,系数化成1即可.【解答】解:2152163x x +−=−,去分母,得2162(52)x x +=−−, 去括号,得216104x x +=−+,移项,得210641x x +=+−,合并同类项,得129x =,系数化成1,得34x =. 【点评】本题考查了解一元一次方程,熟知解一元一次方程的基本步骤是解题的关键.19.(6分)先化简,再求值:,其中,.【分析】直接去括号,再合并同类项,把已知数据代入得出答案.【解答】解:原式2262466m m n m n =+−−+22m n =+,当3m =−,3n =时,原式2(3)23=⨯−+⨯66=−+0=.【点评】此题主要考查了整式的加减—化简求值,正确合并同类项是解题关键.20.(8分)(1)已知有理数,,在数轴上对应的点如图所示,化简:; (2)已知,,求当时,求的值.【分析】(1)根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的意义化简,去括号合并即可得到结果;(2)先化简A B −,然后把1x =代入求值.【解答】解:(1)由数轴可得:0a b c <<<,且||||||a c b >>,0b a ∴−>,0a c −<,0c b −>, ||||||b a a c c b −+−−−()()()b a a c c b =−−−−−b a a c c b =−−+−+22a b =−+;(2)A B −322(5)(116)x x x x =−−−+3225116x x x x =−−+−326116x x x =−+−, 当1x =时,原式3216111160=−⨯+⨯−=.【点评】本题考查整式的加减−化简求值、数轴、绝对值,解题的关键是掌握绝对值性质.21.(8分)如图,在长为,宽为的长方形纸板上裁去一个边长为的正方形.(1)求剩余纸板的周长(用含,的代数式表示); (2)当,时,求的值.【分析】(1)根据长方形的周长公式进行解答即可;(2)把3a =,1b =代入求值即可.【解答】解:(1)剩余纸板的周长:222(12)a ab a ab +++−2222224a ab a ab =+++−2422a ab =−+;(2)把3a =,1b =代入得:243231232C =⨯−⨯⨯+=.【点评】本题主要考查了列代数式,整式加减的应用;解题的关键是熟练掌握整式加减混合运算法则,准确计算.22.(9分)李军大学毕业后返乡创业,成为一名电商老板,把村里农民的苹果放在网上销售,计划每天销售2000千克,实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负.下表是李军某一周苹果的销售情况:(1)李军该周销售苹果最多的一天比最少的一天多销售多少千克?(2)李军该周实际销售苹果的总量是多少千克?(3)若李军按5元千克收购,按9.5元千克进行苹果销售,运费及包装费等平均为2.5元千克,则李军该周销售苹果一共收入多少元?【分析】(1)根据表中数据计算即可;(2)根据表中数据计算即可;(3)根据(2)的数据计算即可.【解答】解:(1)13070200+=(千克),答:李军该周销售苹果最多的一天比最少的一天多200千克;(2)20007305070130205011014180⨯+−−+−++=(千克),答:李军该周实际销售苹果的总量是14180千克;(3)14180(9.55 2.5)28360⨯−−=(元),答:李军该周销售苹果一共收入28360元.【点评】本题主要考查正负数的计算,熟练掌握正负数的计算是解题的关键.23.(9分)已知关于的整式,整式,若是常数,且不含的一次项. (1)求的值;(2)若为整数,关于的一元一次方程的解是整数,求的值.【分析】(1)将A ,B 代入3A B −中计算后根据已知条件即可求得a 的值;(2)解方程并进行分类讨论后确定b 的值,然后将a ,b 的值代入5a b +中计算即可.【解答】解:(1)2332A x ax x =+−+,22422B x ax x =+−+,3A B ∴−223(332)(2422)x ax x x ax x =+−+−+−+2239962422x ax x x ax x =+−+−−+− 2(57)4x a x =+−+,3A B −不含x 的一次项,570a ∴−=,解得:75a =; (2)230bx x +−=,整理得:(2)3b x +=,原方程的解为整数,且b 为整数,1b ∴=±或3−或5−,当1b =时,75517185a b +=⨯+=+=;当1b =−时,75517165a b +=⨯−=−=; 当3b =−时,75537345a b +=⨯−=−=;当5b =−时,75557525a b +=⨯−=−=; 综上,5a b +的值为2或4或6或8.【点评】本题考查整式的化简求值及解一元一次方程,结合已知条件确定a ,b 的值是解题的关键.24.(10分)1990年,著名社会学家费孝通先生总结出了“各美其美,美人之美,美美与共,天下大同”这一处理不同文化关系的十六字“箴言”.在数学上,我们不妨约定:若关于x 的方程110a x b +=与220a x b +=同时满足21221||()0a b a b −+−=,则称方程110a x b +=与220a x b +=互为“美美与共”方程.根据该约定,回答下列问题.(1)已知关于x 的方程20x m −=与0ax b +=互为“美美与共”方程,且方程20x m −=的解为12,则m = 1 ,a = ,b = ;(2)是否存在有理数k ,使关于x 的方程30x k +=与其“美美与共”方程的解都是整数,若存在,求出k 的值,若不存在,请说明理由;(3)若方程12(21)x x −=−的解也是方程0ax b +=的解,求方程0ax b +=的“美美与共”方程的解.【分析】(1)根据题干信息得出12a b =,21a b =,先方程20x m −=的解为12,求出1m =,即可得出答案;(2)先求出方程30x k +=的解为:3k x =−,在求出方程30x k +=的“美美与共”方程30kx +=的解为3x k=−,根据3k −和3k −都为整数,求出结果即可; (3)先求出方程12(21)x x −=−的解为:13x =,得出方程0ax b +=的解为13b x a =−=−,再求出方程0ax b +=的“美美与共”方程为0bx a +=,求出方程0bx a +=的解为:3a x b =−=−. 【解答】解:(1)21221||()0a b a b −+−=,120a b ∴−=,210a b −=,解得:12a b =,21a b =, 方程20x m −=的解为12,∴1202m ⨯−=,解得:1m =, ∴方程20x m −=与0ax b +=互为“美美与共”方程,2b ∴=,m a −=,1a ∴=−, 故答案为:1;1−;2;(2)存在;方程30x k +=的解为:3k x =−, 方程30x k +=的“美美与共”方程为:30kx +=,且其解为3x k=−, 关于x 的方程30x k +=与其“美美与共”方程的解都是整数, ∴3k −和3k−都为整数,3k ∴=±; (3)方程12(21)x x −=−的解为:13x =, 方程12(21)x x −=−的解也是方程0ax b +=的解,∴方程0ax b +=的解为13b x a =−=, 方程0ax b +=的“美美与共”方程为0bx a +=,∴方程0bx a +=的解为:3a x b=−=. 即方程0ax b +=的“美美与共”方程的解为3x =. 【点评】本题主要考查了方程的解,解一元一次方程,解题的关键是熟练掌握解方程的一般步骤准确计算.25.(10分)如图,在长沙市华益中学迎面50米接力比赛中,设运动时间为t 秒,甲班的A 同学在数轴上位置C 拿到最后一棒接力棒时,记为0t =,此时乙班的B 同学已经位于数轴上数10的位置,A 同学以每秒8米向左运动,B 同学以每秒5米向左运动,两位同学到达D 点立即停止运动.(1)当0t =时,A 、B 同学相距 15 米;当1t =时,A 、B 同学在数轴上所表示的数为 、 .(2)①若t 秒后A 同学恰好追上B 同学,求t ;②当A 同学到达终点D 后,B 同学还要经过多少秒到达D 点.③分别取线段AC 、BD 中点为E 、F ,若在点A 、B 运动期间,4mEF nDA −始终保持不变(其中m ,n 为常数),求m n的值. 【分析】(1)根据数轴上两点间距离公式进行解答即可;(2)①根据t 秒后A 恰好追上B 时,A 同学的路程比B 同学的路程多15列方程求解即可; ②先求出A 到达D 所需要的时间,再求出B 到达D 所需要的时间,然后两个时间相减即可; ③分别用t 表示出E 、F 在数轴表示的数,然后求出线段653||2t EF −=,508DA t =−,进而求出6532t EF −=,然后代入4mEF nDA −并化简得出4(86)13050mEF nDA n m t m n −=−+−,根据4mEF nDA −为定值(其中m ,n 为常数)得出860n m −=,即可求解.【解答】解:(1)当0t =时,A 同学所在位置表示的数为25,B 表示的数为10, ∴此时A 、B 同学相距251015−=;当1t =时,A 同学在数轴上所表示的数为251817−⨯=,B 同学在数轴上所表示的数为10155−⨯=;故答案为:15;17;5;(2)解:①根据题意,得852510t t −=−,解得5t =; ②10(25)25(25)0.7558−−−−−=(秒), 答:当A 同学到达终点D 后,B 同学还要经过0.75秒到达D 点;③A 在数轴上所表示的数为258t −,B 在数轴上所表示的数为105t −,故258(25)508DA t t =−−−=−,E 在数轴上所表示的数为(258)252542t t −+=−, F 在数轴上所表示的数为(105)(25)15522t t −+−−−=, 线段长155653|254()|||22t t EF t −−−=−−=, 当B 同学运动到D 点时停止运动,所以总运动时间为10(25)75−−=(秒), ∴65302t −>,则6532t EF −=, 4mEF nDA ∴−,2(653)(508)m t n t =−−−(86)13050n m t m n =−+−,由于4mEF nDA −为定值,故860n m −=,解得43m n =. 【点评】本题主要考查的是数轴上两点之间的距离,一元一次方程的应用,熟练的利用方程思想解决数轴上的动点问题是解题的关键.。
福建省永春县崇贤中学2022-2023学年八年级上学期12月月考数学试题(含答案解析)

19.如图,在 4 3 的正方形网格中, ABC 的顶点都在正方形网格的格点上请你在图① 和图②中分别画出一个三角形,同时满足以下两个条件:
(1)以点 A 为一个顶点,另外两个顶点也在正方形网格点上; (2)与 ABC 全等,且不与 ABC 重合. 20.如图,△ABC 中,AB=AC,点 E,F 在边 BC 上,BE=CF,点 D 在 AF 的延长线上, AD=AC,
在 Rt△ABP 中,BP= 52 -1.42 = 23.04=4.8, ∴AP+BP+CP=AC+BP=5+4.8=9.8. 故选:D.
由勾股定理可得, Rt△ADE 中, DE AD2 AE2 5 , 又CE 3 ,
CD 3 5 ,
故选:C.
答案第 2页,共 16页
【点睛】本题考查了勾股定理的运用,由勾股定理求出 DE 是解决问题的关键. 8.B 【分析】已知,∠C=90°BC=6,AC=8,由勾股定理求 AB,根据翻折不变性,可知 △DAE≌△DBE,从而得到 BD=AD,BE=AE,设 CE=x,则 AE=8-x,在 Rt△CBE 中,由勾 股定理列方程求解. 【详解】∵△CBE≌△DBE, ∴BD=BC=6,DE=CE, 在 RT△ACB 中,AC=8,BC=6, ∴AB= AC2 BC2 = 62 82 =10. ∴AD=AB-BD=10-6=4. 根据翻折不变性得△EDA≌△EDB ∴EA=EB ∴在 Rt△BCE 中,设 CE=x, 则 BE=AE=8-x, ∴BE2=BC2+CE2, ∴(8-x)2=62+x2, 解得 x= 7 .
AutoCAD2005 高级绘图员职业鉴定试题解答1-5单元
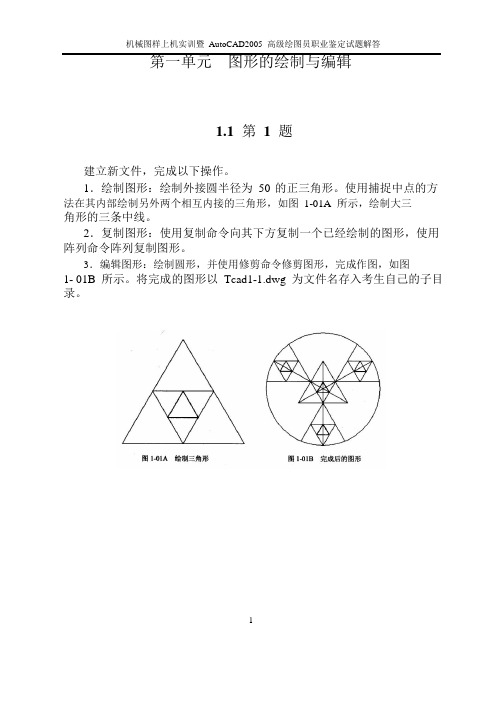
第一单元图形的绘制与编辑1.1第1题建立新文件,完成以下操作。
1.绘制图形:绘制外接圆半径为50 的正三角形。
使用捕捉中点的方法在其内部绘制另外两个相互内接的三角形,如图1-01A 所示,绘制大三角形的三条中线。
2.复制图形:使用复制命令向其下方复制一个已经绘制的图形,使用阵列命令阵列复制图形。
3.编辑图形:绘制圆形,并使用修剪命令修剪图形,完成作图,如图1- 01B 所示。
将完成的图形以Tcad1-1.dwg 为文件名存入考生自己的子目录。
11.2第2题建立新文件,完成以下操作。
1.绘制图形:绘制两个正三角形,第一个正三角形的中心点设置为(190 , 160 ),外接圆半径分别为100。
另一个正三角形的中心点为第一个三角形的任意一个角点,其外接圆半径为70,如图1-02A 所示。
2.复制图形:将大三角形向其外侧偏移复制,将小三角形向其内侧偏移复制,其偏移距离适当即可,使用复制命令复制两小三角形。
3.编辑图形:使用修剪命令将图形中多余的部分修剪掉,如图1-02B所示。
再使用图案填充命令填充图形。
调整图形的线宽(线宽为0.30 毫米),如图1- 02C 所示。
将完成的图形以Tcadl-2.dwg 为文件名存入考生自己的子目录。
1.3第3题建立新文件,完成以下操作。
1.绘制图形:绘制6 个半径分别为120、110、90、80、70、40 的同心圆。
绘制一条一端点为圆心,另一端点在大圆上的垂线,并以该直线与半径为80 的圆的交点为圆心绘制一个半径为 5 的小圆,如图1-03A 所示。
2.复制图形:使用阵列命令阵列复制垂线,数量为20。
绘制直线a,并使用阵列命令阵列复制该直线,如图1-03B 所示。
阵列复制小圆。
3.编辑图形:将半径分别为120、110、80 的圆删除掉。
使用修剪命令修剪图形中多余的部分。
使用图案填充命令填充图形完成作图,如图1-03C 所示。
将完成的图形以Tcad1-3.dwg 为文件名存入考生自己的子目录。
32位汇编语言程序设计部分课后习题答案

3.1 简答题-1
(1)如何修改“MOV ESI, WORD PTR 250”语句使其 正确?
• 删除“WORD PTR”即可
(2)为什么说“XCHG EDX,CX”是一条错误的指令?
32位汇编语言习题解答
课件制作: 钱晓捷
钱晓捷,32位汇编语言程序设计,机械工业出版社
第1章习题:汇编语言基础
1.1 简答题(1、3、6、7、8) 1.2 判断题(1、6、7、8、9) 1.3 填空题(3、4、5、7、10) 1.9、1.13、1.15、1.16
1.1 简答题-1
(1)哪个处理器的指令系统成为Intel
• 没有
(8)汇编语言的标识符大小写不敏感意味着什么?
• 表示字母大小写不同、但表示同一个符号
4
习题解答
1.2 判断题
1)EAX也被称为累加器,因为它使用最频繁。
• 对,EAX中的A来自英文累加器(Accumulator)
6)处理器的传送指令MOV属于汇编语言的执行性语句
•对
7)汇编语言的语句由明显的4部分组成,不需要分隔 符区别。
13,10
byte
'---+-------------------------------',
13,10
byte '20 |',20h,20h,21h,20h,22h,20h,23h,20h,
24h,20h,25h,20h,26h,20h,27h,20h,28h,20h,29h,20h
byte 2ah,20h,2bh,20h,2ch,20h,2dh,20h,2eh,20h,
• 寄存器寻址,立即数寻址
(9)已知ESI=04000H,EBX=20H,指令“MOV EAX, [ESI+EBX*2+8]”中访问的有效地址是__________。
计算机网络计算题

计算机网络计算题在计算机网络领域,计算题是一种重要的学习和测试工具,可帮助学生巩固理论知识并提高实践能力。
本文将为您提供一些计算机网络计算题的例子,并以问题和解答的形式呈现,帮助您更好地理解和应用这些知识。
问题一:IP地址子网划分给定一个IP地址段为192.168.1.0/24,划分出5个子网,请计算每个子网的网络地址、子网掩码、广播地址和可用主机数。
解答:根据题目要求,我们需要从192.168.1.0/24这个IP地址段中划分出5个子网。
首先,我们需要确定每个子网的所需主机数量。
假设子网1需要16个主机,子网2需要32个主机,子网3需要64个主机,子网4需要128个主机,子网5需要256个主机。
1. 子网1:主机数量:16个子网掩码:255.255.255.240网络地址:192.168.1.0广播地址:192.168.1.152. 子网2:主机数量:32个子网掩码:255.255.255.224网络地址:192.168.1.16广播地址:192.168.1.31 3. 子网3:主机数量:64个子网掩码:255.255.255.192网络地址:192.168.1.32广播地址:192.168.1.63 4. 子网4:主机数量:128个子网掩码:255.255.255.128网络地址:192.168.1.64广播地址:192.168.1.127 5. 子网5:主机数量:256个子网掩码:255.255.255.0网络地址:192.168.1.128广播地址:192.168.1.255问题二:TCP/IP分段与重组有一台主机A要向主机B发送一个1500字节大小的数据包,假设链路上最大传输单元(MTU)为500字节,请计算主机A需要将数据包分成多少个片段进行传输,并给出分片的偏移值和标志位。
解答:根据题目要求,我们需要将一个1500字节的数据包分成多个大小为500字节的片段进行传输。
每个片段都需要有偏移值和标志位。
山东省东营市2021年中考数学真题试卷(Word版,含答案与解析)

山东省东营市2021年中考数学试卷一、单选题(共10题;共20分)1.16的算术平方根是()A. 4B. -4C. ±4D. 8【答案】A【考点】算术平方根【解析】【解答】解:∵4的平方是16,∴16的算术平方根是4.故答案为:A .【分析】如果一个非负数x的平方等于a,那么x是a的算术平方根,直接利用此定义即可解决问题.2.下列运算结果正确的是()A. x2+x3=x5B. (−a−b)2=a2+2ab+b2C. (3x3)2=6x6D. √2+√3=√5【答案】B【考点】完全平方公式及运用,合并同类项法则及应用,幂的乘方【解析】【解答】解:A,x2和x3不是同类项,不能够合并,选项A不符合题意;B,根据完全平方公式可得(−a−b)2=(a+b)2=a2+2ab+b2,选项B符合题意;C,根据积的乘方的运算法则可得(3x3)2=9x6,选项C不符合题意;D,√2与√3不能够合并,选项D不符合题意.故答案为:B.【分析】根据合并同类项法则可判断A;根据完全平方公式可判断B;根据积的乘方与幂的乘方运算法则计算可判断C;根据二次根式的加法法则计算可判断D。
3.如图,AB//CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE=()A. 30°B. 40°C. 50°D. 60°【答案】 D【考点】角的运算,平行线的性质【解析】【解答】解:过点E作EH∥CD,如图,∴∠DFE+∠HEF=180°,∵EF⊥CD,∴∠DFE=90°,∴∠HEF=90°,∵∠BEF=150°,∴∠BEH=60°,∵EH∥CD ,AB//CD,∴AB∥EH,∴∠ABE=∠BEH=60°,故答案为:D.【分析】过点E作EH∥CD,利用平行线的性质得到∠DFE+∠HEF=180°,由垂直的定义∠DFE= 90°,进而得出∠HEF=90°,根据角的和差得到∠BEH=60°,再根据平行线的性质求解即可。
专题116 有理数的减法(拓展提高)(解析版)

专题1.16 有理数的减法(拓展提高)一、单选题1.若m 为有理数,则m m +的结果必是( )A .正数B .负数C .非正数D .非负数 【答案】D【分析】根据绝对值的性质:正数的绝对值是它本身、负数的绝对值是它的相反数、0的绝对值是0,可根据m 是正数、负数和0三种情况讨论.【详解】解:①当m >0时,原式=m+m=2m >0;②当m=0时,原式=0+0=0;③当m <0时,原式= m-m =0. ∴m m +的值大于等于0,即为非负数,故选:D .【点睛】本题主要考查绝对值的性质,能够通过讨论去掉绝对值符号是解决本题的关键,难度不大. 2.若||5m =,||2n =.且mn 异号,则||m n -的值为( )A .7B .3或3-C .3D .7或3 【答案】A【分析】先求出m 、n 的值,再将其代入计算m n -的值.【详解】解:∵|m|=5,|n|=2,∴m=±5,n=±2.∵m n 、异号,∴m=-5,n=2或m=5,n=-2. ∴527m n -=--=或()527m n -=--=.故答案为:A .【点睛】本题主要考查了绝对值的定义及有理数的减法运算:正数的绝对值是它本身,负数是它的相反数,零的绝对值是零.3.有理数a b c 、、在数轴上的位置如图所示,则在式子1,a,c b,c a a---+中,值最大的是( )A .a -B .c b -C .c a +D .1a - 【答案】D【分析】根据数轴可得1a 0b c 1-<<<<<,且a c =,然后分别求得1a-,c a +,a -,c b -的取值范围即可.【详解】由数轴可得,1a 0b c 1-<<<<<,且a c =, 0c b 1∴<-<,c a 0+=,01a <-<,11a ->, ∴最大的数为1a-. 故选D . 【点睛】本题考查了数轴,有理数的大小比较,根据数轴判断出a 、b ,c 的正负情况以及绝对值的大小是解题的关键.4.已知7x =,5y =,且0x y +>,那么x y -的值是( )A .2或12B .2或12-C .2-或12D .2-或1- 【答案】A【分析】先根据绝对值运算求出x 、y 的值,再根据0x y +>可得两组x 、y 的值,然后分别代入计算有理数的减法即可得. 【详解】57,x y ==,7,5x y ∴=±=±,又0x y +>,75x y =⎧∴⎨=⎩或75x y =⎧⎨=-⎩, 则752x y -=-=或()757512x y -=--=+=,故选:A .【点睛】本题考查了绝对值、有理数加减法的应用,熟练掌握各运算法则是解题关键.5.若有理数x 、y 满足条件:10=x ,2y =,x y y x -=-,那么2x y -的值是( ) A .-14或-6B .-14或6C .-12或-8D .-14 【答案】A【分析】根据绝对值的定义可得10x =±,2y =±,x y <,所以可能的取值情况只有10x =-,2y =-或10x =-,2y =,再求出2x y -的值.【详解】解:∵10=x ,∴10x =±, ∵2y =,∴2y =±, ∵x y y x -=-,∴x y <,若10x =-,2y =-,则21046x y -=-+=-,若10x =-,2y =,则210414x y -=--=-.故答案是:A .【点睛】本题考查绝对值的性质和有理数的减法运算,解题的关键是掌握绝对值的性质和有理数的减法运算法则.6.陆上最高处是珠穆朗玛峰,峰顶高于海平面约8844米,最低处位于亚洲西部名为死海的湖,死海的水面低于海平面415米,两处高度相差( )A .9259米B .9159米C .8429米D .﹣8429米【答案】A【分析】用珠穆朗玛峰的峰顶高度减去死海最低高度,再根据有理数减法法则进行计算即可.【详解】若海平面以上记为正,则海平面以下记为负,∴珠穆朗玛峰峰顶高约+8844米,死海的水面高为-415米,∴两处高度相差8844-(-415)=8844+415=9259(米),故选:A.【点睛】此题考查有理数的减法计算法则,正确理解题意是解题的关键.二、填空题7.已知A,B,C是数轴上的三个点,且C在B的左侧.点A,B表示的数分别是1,3,如图所示,若BC=2AB,则点C表示的数是___________________.【答案】-1【分析】先利用点A、B表示的数计算出AB,再计算出BC,然后计算点C到原点的距离即可得到C点表示的数.【详解】解:∵点A,B表示的数分别是1,3,∴AB=3-1=2,∵BC=2AB=4,∴OC=BC-OB=4-3=1,∵C在B的左侧,∴点C表示的数是-1.故答案为:-1.【点睛】本题考查了数轴:所有的有理数都可以用数轴上的点表示,但数轴上的点不都表示有理数.(一般取右方向为正方向,数轴上的点对应任意实数,包括无理数.)8.计算:111111 201820172017201620182016-+---=______.【答案】0【分析】原式利用绝对值的代数意义化简,计算即可求出值.【详解】解:111111 201820172017201620182016 -+---111111 201720182016201720162018 =-+--+0=.故答案为:0.【点睛】此题考察了绝对值的化简,熟练掌握运算法则是解本题的关键.9.已知|x |=1,|y |=3,若||x y x y +=+,则x -y =____【答案】-2或-4【分析】已知绝对值的意义和加法的符号规律,求得x =1,y =3或x =-1,y =3,再代入求值即可.【详解】∵|x |=1,|y |=3,∴x =±1,y =±3, ∵x y x y +=+,∴x +y >0,又∵|x |<|y |,∴x =1,y =3或x =-1,y =3,当x =1,y =3时,x -y =1-3=-2;当x =-1,y =3时,x -y =-1-3=-4.综上,当|x |=1,|y |=3,而且x y x y +=+时, x -y =-2或-4.故答案为:-2或-4.【点睛】本题考查了绝对值的性质和意义及有理数的加减法,根据绝对值的意义和性质和有理数加法的符号规律求得x =1,y =3或x =-1,y =3是解决问题的关键.10.东京与北京的时差为1+,巴黎与北京的时差为7-.假如现在是北京时间7:00,那么东京时间是______,巴黎时间是________.【答案】8:00 0:00.【分析】由于带正号的数表示同一时刻比北京时间早的时数,那么用北京时间+时差=东京时间,用北京时间-时差=巴黎时间.【详解】解:7+1=8,所以东京时间为上午8:00.7-7=0,所以巴黎时间为凌晨0:00.故答案为:8:00;0:00.【点睛】此题主要考查了有理数加减法在实际生活中的应用,在学习这一部分内容时一定要联系实际.11.两个小朋友玩跳棋游戏,游戏的规则是:先画一根数轴,棋子落在数轴上0K 点,第一步从0K 点向左跳1个单位到1K ,第二步从1K 向右跳2个单位到2K ,第三步从2K 向左跳3个单位到3K ,第四步从3K ,向右跳4个单位到4K ,…,如此跳20步,棋子落在数轴的20K 点,若20K 表示的数是16,则2019K 的值为_______.【答案】-1004【分析】根据向左减向右加可知每两步跳动向右1个单位,根据20K 表示的数是16,可得0K ,然后先得出2018K 的值,进而得出2019K 的值.【详解】解:由题意得,第一步、第二步后向右跳动1个单位,跳20步后向右20÷2=10个单位, 则K 0的值是16-10=6,因为2019÷2=1009…1,所以跳2018步时,所对应的数是1009+6=1015,跳2019步时,所对应的数是1015-2019=-1004,故答案为:-1004.【点睛】本题考查数轴上动点问题,有理数的减法的应用.解决此题的关键是理解可知每两步跳动向右1个单位.12.如图,是北京S1线地铁的分布示意图,其中桥户营、四道桥、金安桥、苹果园四站在同一条直线上.如果在图中以正东为正方向建立数轴,桥户营站、苹果园站表示的数分别是4-,2,那么金安桥站表示的数是___________.【答案】0【分析】由桥户营站、苹果园站表示的数分别是4-,2,计算出两点之间的距离为6,求出一个单位长度表示的数是2,即可得到答案.【详解】∵桥户营站、苹果园站表示的数分别是4-,2,∴桥户营站与苹果园站的距离是2-(-4)=6,∵桥户营站与苹果园站之间共有三个单位长度,∴每个单位长度表示632÷=,∴金安桥表示的数是2-2=0,故答案为:0.【点睛】此题考查数轴上两点之间的距离,数轴上点的平移规律,有理数的加减法计算,掌握数轴上两点之间的距离公式是解题的关键.13.已知数轴上A 、B 两点所对应的数分别是1和3,P 为数轴上任意一点,对应的数为x .(1)则A 、B 两点之间的距离为________;(2)式子|1||3||2017||2019|x x x x -+-++-+-的最小值为________.【答案】2; 510050.【分析】(1)根据两点间的距离公式解题即可;(2)由绝对值的几何意义,||x a -表示数x 到数a 的距离,要使式子取得最小值,则应找到与最小数和最大数距离相等的x 的值,即可解题.【详解】(1)A 、B 两点之间的距离为3-1=2,故答案为:2;(2)由已知条件可知,||x a -表示数x 到数a 的距离,只有当x 到1的距离等于x 到2019的距离时,式子即可取最小值, ∴当1201910102x +==时,|1||3||2017||2019|x x x x -+-++-+-取最小值,最小值为:|10101||10103||10102017||10102019|-+-++-+-=1009+1007+1005+1+1++1005+1007+1009=2(1009+1007+1005+1)⨯(10091)505=22+⨯⨯ 510050=【点睛】本题考查数轴、绝对值、两点间的距离等知识,是重要考点,难度一般,掌握相关知识是解题关键.14.在日常生活中,“八点五十八”通常可以说成“九点差二分”,有时这样表达更清楚,受此启发,我们设计了一种新的加减计数法.例如:6写成14,141046=-=;191写成209,2092009191=-=.按这个方法请计算:2020=______.【答案】1980【分析】观察例子找到规律,根据有理数的减法法则计算得出答案. 【详解】由例题可得2020=2000-20=1980,故答案为:1980.【点睛】此题考查有理数运算的规律,有理数的减法计算法则,读懂例题的计算方法并应用解决问题是解题的关键.三、解答题15.已知6x =,3y =(1)若x 、y 异号,直接写出x 和y 的差为_____(2)若x y <,直接写出x 与y 的和为_____【答案】(1)9±;(2)3-或9-【分析】(1)先根据绝对值的性质求出x 、y 的值,再由x 、y 异号,分类讨论x y -的值;(2)由x y <,得6x ≠,再分类讨论当=6x -时y 的值;算出+x y .【详解】解:(1)∵6x =,3y =,∴6x =±,3=±y ,∵x 、y 异号,∴ 当=6x 时,3y =-,()=63639x y ---=+=,当6x =-时,3y =,639x y -=--=-,∴9x y -=±;故答案为:9±(2)∵ x y <,∴当=6x 时,x 不可能小于y ,不成立,当6x =-时,3y =时,+6+33x y =-=-,当6x =-时,3y =-时,+639x y =--=-,∴+x y 的值为3-或9-故答案为:3-或9-【点睛】本题考查绝对值的性质和有理数的加减运算,解题的关键是掌握绝对值的性质和有理数加减运算法则.16.某路公交车从起点经过A ,B ,C ,D 站到达终点,各站上下乘客的人数如下(上车为正,下车为负):起点(20,0),(12,4),(8,9),(6,4),(2,7)A B C D ----,终点()0,____.(1)在横线上填写适当的数,并说明该数的实际意义;(2)行驶在哪两站之间时,车上的乘客最多?(3)若乘坐该车的票价为每人2元,则这一趟公交车能收入多少钱?【答案】(1)−24;(2)公交车行驶在C 站和D 站之间车上的乘客最多;(3)96【分析】(1)根据正负数的意义,利用有理数的加法法则计算即可;(2)根据(1)的计算解答即可;(3)根据各站之间的人数,乘以票价2,然后计算即可得解.【详解】解:(1)起点到A 站,车上人数:20,A 站到B 站,车上人数:20+12−4=28,B 站到C 站,车上人数,28+8−9=27,C 站到D 站,车上人数,27+6−4=29,D 站到终点,29+2−7=24,所以,到终点下车还有24人;故答案为:−24;(2)由(1)的计算可知,公交车行驶在C 站和D 站之间车上的乘客最多,为29人;(3)(20+12+8+6+2)×2=96(元).答:这趟出车能收入96元.【点睛】本题考查了正数和负数,有理数的混合运算,读懂图表信息,求出各站点上的人数是解题的关键.17.国内汽油价格每月会有两次调整,如果以今年6月底的油价为基准,涨价记为正方向,7月至10月的油价调整情况记录如下(单位:元/吨):(1)7月至10月之间,今年_______(填时间)的调价令油价与基准价格相差最大.(2)到10月底,油价能否回到基准价格?请说明理由.【答案】(1)8月下旬;(2)不能,理由见解析【分析】(1)计算出每个时间段与基准价格的差,即可得解;(2)将表格中的数据相加,根据结果判断即可.【详解】解:(1)7月上旬与基准价格相差:+100,7月下旬与基准价格相差:+100, 8月上旬与基准价格相差:+100,8月下旬与基准价格相差:+100+85=185,9月上旬与基准价格相差:185,9月下旬与基准价格相差:185-315=-130, 10月上旬与基准价格相差:-130,10月下旬与基准价格相差:-130+70=-60,∴8月下旬的调价令油价与基准价格相差最大;(2)由题意可得: 100+0+0+85+0-315+0+70=-60,∴到10月底,油价不能回到基准价格.【点睛】本题考查的是正数与负数的定义,有理数的加法的实际应用,解答此题的关键是熟知用正负数表示两种具有相反意义的量.具有相反意义的量都是互相依存的两个量,它包含两个要素,一是它们的意义相反,二是它们都是数量.18.(1)填空:①正数:35+= ,8= ; ②负数:0.7-= ,12-= ;③零:0= ;(2)根据(1)中的规律可以发现:无论什么数,它们的绝对值一定是 数,即0a ≥(3)请认真阅读下列材料,求2x +的最小值解:0x ≥,∴当0x =,即0x =时,2x +的最小值是2解答下列问题 ①求2020x +的最小值;②255a --有最大值还是最小值,求出这个值,并求出a 的值【答案】(1)①35,8;②0.7,12;③0;(2)非负;(3)①2020;②最大值25,a =5 【分析】(1)根据绝对值的意义即可得出答案;(2)分析(1)中的结论,即可得到(2)中的答案;(3)①要使2020x +有最小值,则需使x 最小,结合(2)中结论有0x ≥,可得出0,x =时,2020x +最小,即可得出答案; ②由50a -≥,得出当50a -=时,原式有最大值,求出a 的值,代入即可得出答案.【详解】解:(1)①正数:35+=35,8=8; ②负数:0.7-=0.7,12-=12; ③零:0=0;(2)根据(1)中的规律可以发现:无论什么数,它们的绝对值一定是非负数,即0a ≥;(3)①0x ≥ ∴当0,x =即0x =时∴2020x +有最小值是2020②255a --有最大值. 50a -≥∴当50a -=,即50,a -=5a =时255a --有最大值25,此时a =5.【点睛】本题考查了绝对值的相关知识,在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值:正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0.19.学校为了备战校园足球联赛,利用体育课让学生进行足球训练,为了训练学生快速抢断转身,体育老师设计了折返跑训练.老师在东西方向的足球场上画了一条直线插上不同的折返旗帜,如果约定向西为正,向东为负,练习一组的行驶记录如下(单位:米):+40,﹣30,+45,﹣25,+25,﹣35,+15,﹣28,+16,﹣18.(1)学生最后到达的地方在出发点的哪个方向?距出发点多远?(2)学生训练过程中,最远处离出发点多远?(3)学生在一组练习过程中,跑了多少米?【答案】(1)在出发点的正西方向,距出发点5米;(2)最远处离出发点55米;(3)跑了277米【分析】(1)根据加法法则,将正数与正数相加,负数与负数相加,进而得出计算得结果;(2)求出每一段到出发点的距离,即可判断出结果;(3)利用绝对值的性质以及有理数加法法则求出即可.【详解】解:(1)(+40)+(﹣30)+(+45)+(﹣25)+(+25)+(﹣35)+(+15)+(﹣28)+(+16)+(﹣18)=+5(米).答:学生最后到达的地方在出发点的正西方向,距出发点5米;(2)第一段,40米,第二段,40﹣30=10(米),第三段,10+45=55(米),第四段,55﹣25=30(米),第五段,30+25=55(米),第六段,55﹣35=20(米),第七段,20+15=35(米),第八段,35﹣28=7(米),第九段,7+16=23(米),第十段,23﹣18=5(米),故最远处离出发点55米;(3)|+40|+|﹣30|+|+45|+|﹣25|+|+25|+|﹣35|+|+15|+|﹣28|+|+16|+|﹣18|=277(米).答:学生在一组练习过程中,跑了277米.【点睛】此题考查有理数的加减法的实际应用,绝对值的性质,正确理解题意列式进行计算是解题的关键.20.在2020年抗洪抢险中,解放军战士的冲锋舟加满汽油后沿东西方向的河流抢救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天的航行路程记录如下(单位:千米):+15,﹣8,+9,﹣6,+14,﹣5,+13,﹣10.(1)B地位于A地的什么方向?距离A地多少千米?(2)若冲锋舟每千米耗油0.6升,油箱容量为30升,求冲锋舟当天救灾过程中至少还需补充多少升油?(3)救灾过程中,冲锋舟离出发点A最远时,距A地多少千米?【答案】(1)B地在A地的东边22千米;(2)还需补充18升汽油;(3)距A地32千米【分析】(1)把题目中所给数值相加,若结果为正数,则B地在A地的东方,若结果为负数,则B地在A 地的西方;(2)先求出这一天航行的总路程,再计算出一共所需油量,减去油箱容量即可求出途中还需补充的油量;(3)分别计算出各点离出发点的距离,取数值较大的点即可.【详解】解:(1)∵15﹣8+9﹣6+14﹣5+13﹣10=22,∴B地在A地的东边22千米;(2)这一天走的总路程为:15+|﹣8|+9+|﹣6|+14+|﹣5|+13|+|﹣10|=80千米,应耗油80×0.6=48(升),故还需补充的油量为:48﹣30=18(升),答:冲锋舟当天救灾过程中至少还需补充18升油;(3)∵路程记录中各点离出发点的距离分别为:15千米;15﹣8=7千米;7+9=16千米;16﹣6=10千米;10+14=24千米;24﹣5=19千米;19+13=32千米;32﹣10=22千米.∴冲锋舟离出发点A最远时,距A地32千米.【点睛】本题考查的是正数与负数的定义,解答此题的关键是熟知用正负数表示两种具有相反意义的量,注意所走总路程一定是绝对值的和.。
冀教版三年级下册数学 期末整理与复习 教材整理与评价-第16招 智巧问题的应用

第16招 智巧问题的应用
学习教材整理与复习后使用
经Hale Waihona Puke 例题有12人要到河对岸去,现只有一条船。这条船每次最 多只能载4人。这条船至少要载几次才能将所有人都送 到河对岸?
思路分析: 每次最多只能载4人,船返回时必须有1人跟着返回 每次最多只能有3人过河(最后1次4人过河) (12-4)÷3=2(次)……2(人) 要载2+1+1=4(次)
每次最多只能载4人,船返回时必须有1人跟着返回 每次最多只能有3人过河(最后1次4人过河)
16-4=12(人)
4-1=3(人) 12÷3=4(次)
4+1=5(次) 答:至少需要5次才能将所有人都送过河去。
2.一个牧童要带着一只羊和两筐青草过一条河,河面上 只有一条小船,但是船太小,每次只能带一样东西过 去,你能替他想个办法,把三样东西都带过河,又不 让羊吃到青草吗?
6.丽丽唱一首歌要4分钟,全班45名同学合唱这首歌 需要多少分钟?
4分钟。
应用 4 喝牛奶问题
7.丰富营养的早餐需要一杯牛奶,丁丁先喝了半杯, 然后加满水,又喝了半杯,再加满水,最后全部喝 完。那么丁丁喝的牛奶多,还是水多?
加了半杯水 + 加了半杯水 =1杯水 一样多。
4.池塘的水面上有浮萍,浮萍每天增加一倍。经过80 天池塘全部长满浮萍,多是少前天一时天浮的萍两长倍满池塘的一 半?
80-1=79(天) 答:79天时浮萍长满池塘的一半。
应用 3 猫吃鱼问题
5.有5只猫,同时吃5条鱼,需要5分钟吃完。照这样 的速度,100只猫同时吃掉100条鱼,需要多长时间?
1只猫吃完1条鱼需要5分钟 5分钟。
第一次将羊带到河对岸,牧童空船返回;第 二次将一筐青草带到河对岸,放下青草带羊 返回;第三次将另一筐青草带到河对岸,牧 童空船返回;第四次将羊带到河对岸。
人教版四年级上册数学期中测试卷及完整答案(精选题)

人教版四年级上册数学期中测试卷一.选择题(共6题,共12分)1.用计算器计算2896+3514-1234时,应该按怎样的顺序计算()。
A.同级运算,从前往后,先算2896+3514B.先算3514-1234 C.先算哪个都行2.当()整时,时针和分针所成的角是直角。
A.3时B.5时C.6时3.在8和6中间添()个0,这个数才能成为八亿零六。
A.6B.7C.84.下列各数中,一个0也不读的是()。
A.1008000B.10800000C.1008000005.一条()长50厘米。
A.直线B.线段C.射线6.用直尺把纸上的两个点连接起来,就得到一条()。
A.直线B.线段C.射线二.判断题(共6题,共12分)1.线段可以测量它的长度,直线不能测量长度。
()2.边长是300米的正方形,面积是9公顷。
()3.120050000是一个九位数,最高位是亿位。
()4.小红画了一条长20厘米的线段。
()5.因为自然数中,相邻的两个计数单位之间的进率都是十,所以将“5”写在十万位上比写在万位上多10。
()6.边长是100米的正方形的面积是1公顷。
()三.填空题(共10题,共36分)1.12时分针和时针成()角,8时成()角,3时是或9时分针与时针成()角。
2.请给下面的角分类。
80° 26° 150° 170° 92°180° 130°90° 91° 89° 360° 81° 10° 65°周角:________锐角:________钝角:________直角:________平角:________3.写出横线上的数。
(1)2015年,我国粮食总产量为六亿二千一百万吨。
写作:()(2)2014年鲁甸地震后,某地向灾区捐款二百一十四万元。
写作:()(3)太阳系八大行星之一的火星,按离太阳由近而远的次序计为第四颗,与太阳的平均距离约为二亿二千七百九十四万千米。
概率论课后习题解答

一、习题详解:1.1 写出下列随机试验的样本空间:(1) 某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数;解:连续5 次都命中,至少要投5次以上,故}{ ,7,6,51=Ω;(2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和;解:}{12,11,4,3,22 =Ω;(3) 观察某医院一天内前来就诊的人数;解:医院一天内前来就诊的人数理论上可以从0到无穷,所以}{,2,1,03=Ω; (4) 从编号为1,2,3,4,5 的5 件产品中任意取出两件, 观察取出哪两件产品; 解:属于不放回抽样,故两件产品不会相同,编号必是一大一小,故:()}{;51,4≤≤=Ωj i j i(5) 检查两件产品是否合格;解:用0 表示合格, 1 表示不合格,则()()()()}{1,1,0,1,1,0,0,05=Ω;(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2); 解:用x 表示最低气温, y 表示最高气温;考虑到这是一个二维的样本空间,故: ()}{216,T y x T y x ≤≤=Ω ;(7) 在单位圆内任取两点, 观察这两点的距离;解:}{207 x x =Ω;(8) 在长为l 的线段上任取一点, 该点将线段分成两段, 观察两线段的长度.解:()}{l y x y x y x =+=Ω,0,0,8 ;1.2 设A ,B ,C 为三事件, 用A;B;C 的运算关系表示下列各事件:(1) A 与B 都发生, 但C 不发生; C AB ;(2) A 发生, 且B 与C 至少有一个发生;)(C B A ⋃;(3) A,B,C 中至少有一个发生; C B A ⋃⋃;(4) A,B,C 中恰有一个发生;C B A C B A C B A ⋃⋃;(5) A,B,C 中至少有两个发生; BC AC AB ⋃⋃;(6) A,B,C 中至多有一个发生;C B C A B A ⋃⋃; (7) A;B;C 中至多有两个发生;ABC ;(8) A,B,C 中恰有两个发生.C AB C B A BC A ⋃⋃ ;注意:此类题目答案一般不唯一,有不同的表示方式。
(北师大版)初中九年级数学下学期中考复习模拟考试试题卷(含答案详解)

(北师大版)初中九年级数学下学期中考复习模拟考试试题卷(含答案详解)(满分150分 时间:120分钟)一.单选题。
(共40分) 1.16的算术平方根是( )A.±2B.2C.4D.±4 2.下面四个几何体中,左视图为圆的是( )A. B. C. D.3.据5月17日消息,全国各地约42600名医务人员支援湖北抗击新冠肺炎疫情,将42600用科学记数法表示为( )A.0.426×105B.4.26×105C.42.6×104D.4.26×1044.如图,直线a ∥b ,直线c 分别交a ,b 于点A ,C ,∠BAC 的平分线交直线b 于点D ,若∠1=50°,则∠2的度数是( )A.50°B.70°C.80°D.110°(第4题图) (第9题图) (第10题图) 5.下列图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D.6.化简a 2a -1-1-2a 1-a的结果为( )A.a+1a -1B.a ﹣1C.aD.17.从甲、乙、丙、丁四人中抽调两人参加“寸草心”志愿服务队,恰好抽到甲和乙的概率是( )A.112 B.18 C.16 D.128.在同一直角坐标系中,函数y=kx 和y=kx ﹣3的图象大致是( )A. B. C. D.9.在直角坐标系中,等腰直角三角形AOB 在如图所示的位置,点B 的横坐标为2,将△AOB 绕点O 按逆时针方向旋转90°,得到△A’OB’,则点A’的坐标为( ) A.(1,1) B.(√2,√2) C.(﹣1,1) D.(﹣√2,√2)10.在平面直角坐标系内,已知点A (﹣1,0),点B (1,1)都在直线y =12x+12上,若抛物线y =ax 2﹣x+1(a ≠0)与线段AB 有两个不同的交点,则a 的取值范围是( ) A.a ≤﹣2 B.a <98 C.1≤a <98或a ≤﹣2 D.﹣2≤a <98 二.填空题。
数字电子技术基础(数电)课后习题解答

解: ① (0011101)2 =1×24+ 1×23+ 1×22+ 1×20=(29)10
(0011101)2 =(0 011 101)2= (35)8 (0011101)2 =(0001 1101)2= (1D)16 同理:② (27.75)10,(33.6)8,(1B.C)16; ③ (439)10,(667)8,(1B7)16;
(1) Y=AB+BC+A'C'
=B+A'C'
BC
A
00 01 11 10
0
1
11
1
11
(2) Y=AB'C'+A'B'+A'D+C+BD =B’+C+D (或用圈0法)
CD 00 01 11 10
AB
00 1
1
1
1
01
1
1
1
11
1
1
1
10 1
1
1
1
(3) Y=A' (B'C+B(CD'+D))+ABC'D
1
010
1
011
1
100
1
101
1
110
1
111
0
题1.9 在举重比赛中,有甲、乙、丙三名裁判,其中甲为主裁判,乙、丙为副裁判,当主裁判 和一名以上(包括一名)副裁判认为运动员上举合格后,才可发出合格信号。列出该函数的 真值表。
【三套卷】小学数学一年级上册第六单元基础卷

学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.16的前一个数是()。
A. 15B. 16C. 172.一个数,个位上的数字比十位上的数字大2,这个数是几?()A. 13B. 20C. 143.18是由()组成的。
A. 1个十和8个一B. 10个十和8个一C. 8个十和1个一4.一个数,十位上是1,个位上的数字比十位上的数字大4,这个数是()。
A. 5B. 14C. 155.在4,16,7,12,8,20,9,10,14中,比12大的数有()个。
A. 3B. 4C. 56.下面哪个算式的结果大于15()。
A. 10+5B. 15-5C. 7+97.比18多1的数是()。
A. 19B. 18C. 17D. 16 8.从8到16,最中间的数是( )。
A. 11B. 12C. 139.正确答案是(1)6+9= ()A.14B.15(2)17-2= ()A.15B.510.不数,你能看出大约有多少吗?()A. 5个B. 10个C. 15个11.“4+9 13”,比较大小,在里应填的符号是()A. >B. <C. =D. + 12.下面和18最接近的数是几?()A. 10B. 16C. 19二、填空题13.比8大,比12小的数是________、________、________。
14.1个十和8个一合起来是________。
15.15的十位上是________,个位上是________。
16.按顺序填数。
17.在横线上填上“>”“<”或“=”。
8________11 17________12 19________2017________7+7 13+3________16 18-6________1518.20里面有________个十,17里有________个一。
19.________8________10________________________________1520.房子里和外面一共有________人,排在第________位,房子里有________人。
模拟电子技术基础(第四版)习题解答

图 Pl.14
(a)
(b)
解图 Pl.14
8
解: 在场效应管的恒流区作横坐标的垂线 (如解图 Pl.14 (a)所示 ),读出其与各条曲 线交点的纵坐标值及 u G S 值,建立 i D f ( uG S ) 坐标系,描点,连线,即可得到转移 特性曲线,如 解图 Pl.14 (b) 所示。
1.15 电路如 图 P1.15 所示,T 的输出特性如 图 Pl.14 所示 ,分析当 u I =4V、8V 、12V 三种情况下场效应管分别工作在什么区域。
因此, u GD u GS u DS
2V ,小于开启电压,
说明假设成立,即 T 工作在恒流区。
当 u I =12V 时,由于 V DD 12V ,必然使 T 工作在可变电阻区。
图 Pl.15
l.16 分别判断 图 Pl.16 所示各电路中的场效应管是否有可能工作在恒流区。
(a)
(b)
(c)
图 P1.16
其动态电阻 : rD U T / I D 10
故动态电流的有效值: I d U i / rD 1m A
图 P1.4
1.5 现有两只稳压管,稳压值分别是 6V 和 8V,正向导通电压为 (1) 若将它们串联相接,则可得到几种稳压值?各为多少? (2) 若将它们并联相接,则又可得到几种稳压值?各为多少?
U I 15V 时, U O
RL
UI
R RL
5V ;
图 Pl.6
U I 35 V 时, U O
RL
UI
R RL
11.7 V
U Z ,∴ U O U Z 6V 。
0.1 (2) 当负载开路时, I Z
UI UZ R
29 mA I Z max
小学一年级数学20以内的进位加法练习题带解析答案

小学一年级数学20以内的进位加法练习题一.选择题(共6题, 共12分)1.列式计算,正确的是()A.15-8=7B.8-7=1C.8+7=152.树上先飞走4只鸟, 又飞走8只, 一共飞走了()只。
A.4B.7C.12D.113.小明第一天做了7道题, 第二天做了8道题, 两天一共做了多少道题?正确的列式计算是()A.8-7=1(道)B.8+7=13(道)C.8-1=7(道) D.7+8=15(道)4.下面的算式正确的是 ()。
A.9-4=5B.5-4=1C.9+4=13D.5+4=95.小红有7颗糖, 小东的糖和小红的同样多, 小红和小东一共有()颗糖。
A.8B.14C.76.5+○<12。
○内可以填的数字有几个? ( )A.7个B.6个C.3个二.判断题(共6题, 共12分)1.妈妈买来8个梨, 吃了4个, 爸爸又买来8个, 这时有12个梨。
()2.7+8和8+7的得数一样。
()3.18比10多8。
()4.与8相邻的两个数之差为2。
()5.9+3=12, 所以12-9=3。
()6.计算8+9时, 可以先把8凑成10, 也可以先把9凑成10。
()三.填空题(共9题, 共45分)1.写出20以内比15大的数_____。
2.在□里填数(从上到下依次填写)3.填上“>”“<”或“=”15________9 8________18 20________10 0________73+8________12 4+7________19 15________4+9 4+1________9 +64.在○里填上“+”或“-”3○7=10 5○5=0 8○5=3 12○2=9○112○12=0 19○10=9 12○2=10 8○2=16○105.在□里填数(从上到下依次填写)6.在方框里填上合适的数. (从下到上, 从左到右填写)7.在○里填“>”“<”“=”。
8○5 0+6○11 3+9○13 15○170+8○8-0 5○10-2 13○13-2 0+6○6 8.夺红旗。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.16 第16题解答
1.建立文件
第1步“建立一个新文件:16×12cm、72pixels/inch、RGB模式、背景色为黑色。
2.编辑调整
第2步:新建图层1,选择矩形选框工具建立一矩形选区,填充白色,取消选区,如图1-16a 所示。
用字体工具输入“由此前进”,字体为“华文新魏”,大小为20,如图1-16b所示。
第3步:新建图层2,在图案工具里找到箭头,如图1-16c所示。
在路径面板里单击“将路径作为选区载入”按钮,然后填充为深红色,取消选区,如图1-16d所示。
第4步:新建图层3,用矩形选框工具建立一矩形选区,设置渐变色为“蓝—白—蓝”,然后填充矩形选区,取消选区,执行“编辑”>“变换”>“斜切”命令,按回车键应用此命令,移动到适当的位置,如图1-16f所示。
复制图层4为图层4副本,移动到右边,执行“编辑”>“变换”>“水平翻转”命令,如图1-16g所示。
第6步:用同样的方法做出上下两个边框,最终效果如图1-16h所示。
3.保存文件
第7步:将最终效果以Xps1-16.tif为文件名保存在考生文件夹下。
