09年中考各地数学二次函数压轴题
2009中考数学压轴题精选12题

2009中考数学压轴题精选12题2009年9月11日星期五1、(四川省达州市)如图11,抛物线)1)(3(-+=x x a y 与x 轴相交于A 、B 两点(点A 在点B 右侧),过点A 的直线交抛物线于另一点C ,点C 的坐标为(-2,6).(1)求a 的值及直线AC 的函数关系式;(2)P 是线段AC 上一动点,过点P 作y 轴的平行线,交抛物线于点M ,交x 轴于点N.①求线段PM 长度的最大值;②在抛物线上是否存在这样的点M ,使得△CMP 与△APN 相似?如果存在,请直接写出所有满足条件的点M 的坐标(不必写解答过程);如果不存在,请说明理由.2、(四川省资阳市)如图9,已知抛物线y =12x 2–2x +1的顶点为P ,A 为抛物线与y 轴的交点,过A 与y 轴垂直的直线与抛物线的另一交点为B ,与抛物线对称轴交于点O ′,过点B 和P 的直线l 交y 轴于点C ,连结O ′C ,将△ACO ′沿O ′C 翻折后,点A 落在点D 的位置.(1) (3分) 求直线l 的函数解析式; (2) (3分) 求点D 的坐标;(3) (3分) 抛物线上是否存在点Q ,使得S △DQC = S △DPB ? 若存在,求出所有符合条件的点Q 的坐标;若不存在,请说明理由.3、(四川省绵阳市)如图,在平面直角坐标系中,矩形AOBC 在第一象限内,E 是边OB 上的动点(不包括端点),作∠AEF = 90︒,使EF 交矩形的外角平分线BF 于点F ,设C (m ,n ).(1)若m = n 时,如图,求证:EF = AE ;(2)若m ≠n 时,如图,试问边OB 上是否还存在点E ,使得EF = AE ?若存在,请求出点E 的坐标;若不存在,请说明理由.(3)若m = tn (t >1)时,试探究点E 在边OB 的何处时,使得EF =(t + 1)AE 成立?并求图9出点E 的坐标.4、(四川省眉山市)已知:直线112y x =+与y 轴交于A ,与x 轴交于D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x轴交于B 、C 两点,且B点坐标为 (1,0). (1)求抛物线的解析式;(2)动点P 在x 轴上移动,当△P AE 是直角三角形时,求点P 的坐标.(3)在抛物线的对称轴上找一点M ,使||AM MC -的值最大,求出点M 的坐标. 5、(四川省成都市)在平面直角坐标系xOy 中,已知抛物线y=2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,其顶点为M,若直线MC 的函数表达式为3y kx =-,与x 轴的交点为N ,且COS∠BCO=10。
09年中考二次函数考试试题

09年二次函数典型试题一、选择题1、(09年台湾)向上发射一枚炮弹,经x 秒后的高度为y 公尺,且时间与高度关系为y =ax 2+bx 。
若此炮弹在第7秒与第14秒时的高度相等,则再下列哪一个时间的高度是最高的?( ) (A) 第8秒 (B) 第10秒 (C) 第12秒 (D) 第15秒 。
2、(09年上海市)抛物线22()y x m n =++(m n ,是常数)的顶点坐标是( )A .()m n ,B .()m n -,C .()m n -,D .()m n --,3、(09年陕西省)根据下表中的二次函数c bx ax y ++=2的自变量x 与函数y 的对应值,可判断二次函数的图像与x 轴A .只有一个交点B .有两个交点,且它们分别在y 轴两侧C .有两个交点,且它们均在y 轴同侧D .无交点4、(09威海)二次函数2365y x x =--+的图象的顶点坐标是( )A .(18)-,B .(18),C .(12)-,D .(14)-,5、(09湖北省荆门市)函数y =ax +1与y =ax 2+bx +1(a ≠0)的图象可能是( )6、(09年贵州黔东)抛物线的图象如图所示,根据图象可知,抛物线的解析式可能..是( )A 、y=x 2-x-2 B 、y=121212++-x C 、y=121212+--x x D 、y=22++-x x7、(09年齐齐哈尔市)已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论:0ac >①;②方程20ax bx c ++=的两根之和大于0;y ③随x 的增大而增大;④0a b c -+<,其中正确的个数( )A .4个B .3个C .2个D .1个8、(09烟台市)二次函数2y ax bxc =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为( ) A . B . C . D .(15题图)图49、(09年南宁)已知二次函数2y ax bx c =++(0a ≠)的图象如图4所示,有下列四个结论:20040b c b ac <>->①②③④0a b c -+<,其中正确的个数有( A .1个 B .2个 C .3个 D .4个10、(09年孝感)将函数2y x x =+的图象向右平移a (0)a >数232y x x =-+的图象,则a 的值为( ) A .1 B .2 C .3 D .411、(09泰安)抛物线1822-+-=x x y 的顶点坐标为(A )(-2,7) (B )(-2,-25) (C )(2,7) (D )(2,-9)12、(09年新疆)如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系 不正..确.的是( ) A .h m =B .k n =C .k n >D .00h k >>,13、(09年天津市)在平面直角坐标系中,先将抛物线22y x x =+-关于x 轴作轴对称变换,再将所得的抛物线关于y 轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为( ) A .22y x x =--+ B .22y x x =-+-C .22y x x =-++D .22y x x =++14、(09年济宁市)小强从如图所示的二次函数2y ax bx c =++的图象中,观察得出了下面五条信息:(1)0a <;(2) 1c >;(3)0b >;(4) 0a b c ++>; (5中正确信息的个数有A .2个B .3个C .4个D .5个15、(09宁夏)二次函数2(0)y ax bx c a =++≠线1x =,则下列四个结论错误..的是( )D A .0c > B .20a b +=C .240b ac -> D .0a b c -+>16、(09年南充)抛物线(1)(3)(0)y a x x a =+-≠的对称轴是直线( ) A .1x = B .1x =- C .3x =- D .3x =17、(09年兰州)在同一直角坐标系中,函数y mx m =+和函数222y mx x =-++(m 是常数,且0m ≠)的图象可能..是xxxx图618、(09年黄石市)已知二次函数2y ax bx c =++的图象如图所示,有以下结论:①0a b c ++<;②1a b c -+>;③0abc >;④420a b c -+<;⑤1c a ->其中所有正确结论的序号是( )A .①②B . ①③④C .①②③⑤D .①②③④⑤二、填空题1、(09年安徽)已知二次函数的图象经过原点及点(12-x 轴的另一交点到原点的距离为12、(09襄樊市)抛物线2y x bx c =-++的图象如图6为 .3、(09湖北省荆门市)函数(2)(3)y x x =--4、5、(09年贵州省黔东南州)二次函数322--=x x y 的图象的解析式是_________________。
2009年中考试题专题之13-二次函数试题及答

2009年中考试题专题之13-二次函数试题及答案一、选择题1、(2009年台湾)向上发射一枚炮弹,经x 秒后的高度为y 公尺,且时间与高度关系为y =ax 2+bx 。
若此炮弹在第7秒与第14秒时的高度相等,则再下列哪一个时间的高度是最高的?(A) 第8秒 (B) 第10秒 (C) 第12秒 (D) 第15秒 。
2、(2009年泸州)在平面直角坐标系中,将二次函数22x y =的图象向上平移2个单位,所得图象的解析式为A .222-=x yB .222+=x y C .2)2(2-=x y D .2)2(2+=x y3、 (2009年四川省内江市)抛物线3)2(2+-=x y 的顶点坐标是( ) A .(2,3) B .(-2,3) C .(2,-3) D .(-2,-3) 5、(2009年桂林市、百色市)二次函数2(1)2y x =++的最小值是( ). A .2 B .1 C .-3 D .236、(2009年上海市)抛物线22()y x m n =++(m n ,是常数)的顶点坐标是( )A .()m n ,B .()m n -,C .()m n -,D .()m n --,7、(2009年陕西省)根据下表中的二次函数c bx ax y ++=2的自变量x 与函数y 的对应值,可判断二次函数的图像与x 轴【 】x … -112…y … -1 47--2 47- … A .只有一个交点B .有两个交点,且它们分别在y 轴两侧C .有两个交点,且它们均在y 轴同侧D .无交点8、(2009威海)二次函数2365y x x =--+的图象的顶点坐标是( ) A .(18)-, B .(18),C .(12)-,D .(14)-,9、(2009湖北省荆门市)函数y =ax +1与y =ax 2+bx +1(a ≠0)的图象可能是( )解析:本题考查函数图象与性质,当0a >时,直线从左向右是上升的,抛物线开口向上,D 是错的,函数y =ax +1与y =ax 2+bx +1(a ≠0)的图象必过(0,1),所以C 是正确的,故选C .10、(2009年贵州黔东南州)抛物线的图象如图所示,根据图象可知,抛物线的解析式可.能.是( )A 、y=x 2-x-2 B 、y=121212++-x C 、y=121212+--x x D 、y=22++-x x11、(2009年齐齐哈尔市)已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论:0ac >①;②方程2ax bx c ++=的两根之和大于0;y ③随x 的增大而增大;④0a b c -+<,其中正确的个数() A .4个B .3个C .2个D .1个12、(2009年深圳市)二次函数c bx ax y ++=2的图象如图2所示,若点A (1,y 1)、B (2,y 2)是它图象上的两点,则y 1与y 2的大小关系是( ) A .21y y < B .21y y = C .21y y >D .不能确定12、(2009桂林百色)二次函数2(1)2y x =++的最小值是( ).A .B .C .D .A .2B .1C .-3D .2313、(2009丽水市)已知二次函数y =ax 2+bx +c(a ≠0)的图象如图所示,给出以下结论: ①a >0.②该函数的图象关于直线1x =对称. ③当13x x =-=或时,函数y 的值都等于0. 其中正确结论的个数是( ) A .3 B .2 C .1 D .014、(2009烟台市)二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为( )15、(2009年甘肃庆阳)图6(1)是一个横断面为抛物线形状的拱桥,当水面在l 时,拱顶(拱桥洞的最高点)离水面2m ,水面宽4m .如图6(2)建立平面直角坐标系,则抛物线的关系式是( )A .22y x =- B .22y x = C .212y x=-D .212y x =16、(2009年甘肃庆阳)将抛物线22y x =向下平移1个单位,得到的抛物线是( ) A .22(1)y x =+B .22(1)y x =-C .221y x =+D .221y x =-17、(2009年广西南宁)已知二次函数2y ax bx c =++(0a ≠)的图象如图4所示,有下列四个结论:20040b c b ac <>->①②③④0a b c -+<,其中正确的个数有( ) A .1个B .2个C .3个D .4个图6(1) 图6(2)xxxxO18、(2009年鄂州)已知=次函数y =ax 2+bx+c 的图象如图.则下列5个代数式:ac ,a+b+c ,4a -2b+c ,2a+b ,2a -b 中,其值大于0的个数为( ) A .2 B 3 C 、4D 、519、(2009年孝感)将函数2y x x =+的图象向右平移a (0)a >个单位,得到函数232y x x =-+的图象,则a 的值为A .1B .2C .3D .420、(2009泰安)抛物线1822-+-=x x y 的顶点坐标为(A )(-2,7) (B )(-2,-25) (C )(2,7) (D )(2,-9)21、(2009年烟台市)二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为( )22、(2009年嘉兴市)已知0≠a ,在同一直角坐标系中,函数ax y =与2ax y =的图象有可能是( ▲ )图4xxxxxA . C . D .23、(2009年新疆)如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确...的是( ) A .h m = B .k n = C .k n > D .00h k >>,24、(2009年天津市)在平面直角坐标系中,先将抛物线22y x x =+-关于x 轴作轴对称变换,再将所得的抛物线关于y 轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为( )A .22y x x =--+ B .22y x x =-+- C .22y x x =-++D .22y x x =++25、(2009年南宁市)已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列四个结论:20040b c b ac <>->①②③④0a b c -+<,其中正确的个数有( ) A .1个B .2个C .3个D .4个26、(2009年衢州)二次函数2(1)2y x =--的图象上最低点的坐标是A .(-1,-2)B .(1,-2)C .(-1,2)D .(1,2) 27、(2009年舟山)二次函数2(1)2y x =--的图象上最低点的坐标是A .(-1,-2)B .(1,-2)C .(-1,2)D .(1,2) 28、(2009年广州市)二次函数2)1(2+-=x y 的最小值是( )A.2 (B )1 (C )-1 (D )-229、(2009年济宁市)小强从如图所示的二次函数2y ax bx c =++的图象中,观察得出了下面五条信息:(1)0a <;(2) 1c >;(3)0b >;(4) 0a b c ++>; (5)0a b c -+>. 你认为其中正确信息的个数有A .2个B .3个C .4个D .5个30、(2009年广西钦州)将抛物线y =2x 2向上平移3个单位得到的抛物线的解析式是( ) A .y =2x 2+3B .y =2x 2-3C .y =2(x +3)2D .y =2(x -3)231、(2009宁夏)二次函数2(0)y ax bx c a =++≠的图象如图所示,对称轴是直线1x =,则下列四个结论错误..的是( )D A .0c > B .20a b += C .240b ac -> D .0a b c -+>32、(2009年南充)抛物线(1)(3)(0)y a x x a =+-≠的对称轴是直线( )A .1x =B .1x =-C .3x =-D .3x =33、(2009年湖州)已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,请你在图中任意画一条抛物线,问所画的抛物线最多能经过81个格点中的多少个?( ) A .6 B .7 C .8 D .9 34、(2009年兰州)在同一直角坐标系中,函数y mx m =+和函数222y mx x =-++(m 是常数,且0m ≠)的图象可能..是(8题图)(第12题)35、(2009年兰州)把抛物线2y x =-向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 A .2(1)3y x =--- B .2(1)3y x =-+- C .2(1)3y x =--+D .2(1)3y x =-++36、(2009年兰州)二次函数c bx ax y ++=2的图象如图6所示,则下列关系式不正确的是A .a <0 B.abc >0C.c b a ++>0D.ac b 42->037、(2009年遂宁)把二次函数3412+--=x x y 用配方法化成()k h x a y +-=2的形式A.()22412+--=x yB. ()42412+-=x yC.()42412++-=x yD. 321212+⎪⎭⎫ ⎝⎛-=x y 39、(2009年广州市)二次函数2)1(2+-=x y 的最小值是( )A.2 (B )1 (C )-1 (D )-2【关键词】二次函数41、(2009年台湾)向上发射一枚炮弹,经x 秒后的高度为y 公尺,且时间与高度关系为y =ax 2+bx 。
09年中考数学专题训练——二次函数及其应用

中招专题训一一二次函数及其应用一、填空题:(每题 3分,共36分)21、 抛物线 y =— x + 1的开口向 __________ .2、 抛物线 y = 2x 2的对称轴是 __________ .3、 函数y = 2 (x — 1)2图象的顶点坐标为 ______ .4、 将抛物线 y = 2x 2向下平移2个单位,所得的抛物线的解析式为 ___________________5、 函数y = x 2+ bx + 3的图象经过点(一1, 0),贝U b= ________6、 二次函数 y = (x — 1)2+ 2,当x= _______ 时,y 有最小值.1( 6分)如图,矩形的长是 4cm , 长和宽都增加 x cm ,那么面积增加 ycm ,① 求y 与x 之间的函数关系式•② 求当边长增加多少时,面积增加 8cm 2 7、 9、10、 11、 12函数 y = 2 (x — 1)2+ 3,当 x 8、将 y = x 2— 2x + 3 化成 y = a (x — h )2+ k 的形式,则 y =_ 若点 A ( 2, m )在函数y = x 2— 1的图像上,贝U A 点的坐标是. 抛物线y = 2x 2+ 3x — 4与y 轴的交点坐标是 _______________ . 请写出一个二次函数以(2, 3)为顶点,且开口向上• ____________已知二次函数 时,函数值 y 随x 的增大而增大.次函数的解析式是 二、选择题:(每题 1、在圆的面积公式 A 、一次函数关系2、已知函数 A 、土 2y = ax 2 + bx + c 的图像如图所示:则这个二y = _____ .3分,共18分)S = n r 2中,s 与r 的关系是 B 、正比例函数关系 y = (m + 2) x |m|是二次函数,贝U ) C 、反比例函数关系 m 等于( )5、 抛物线A 、开口向 6、 抛物线 A 、0 三、解答题: 2 y =—x 不具有的性质是 B 、对称轴是y 轴y = x 2 — 4x + c 的顶点在 B 、4(共 46 分) x 轴, )C 、与y 轴不相交 贝U c 的值是(C 、一 4 最咼点是原点宽是 .2 3cm ,如果将xx2(8分)已知抛物线的顶点坐标是(一2, 1),且过点(1,—2),求抛物线的解析式3 (8分)用6m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?4(6分)某农场种植一种蔬菜,销售员张平根据往年的销售情况,对今年种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线表示这种蔬菜销售价与月份之间的关系•观察图像,你能得到关于这种蔬菜销售情况的哪些信息?(至少写出四条)6(10分)有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为所示,把它的图形放在直角坐标系中•①求这条抛物线所对应的函数关系式•②如图,在对称轴右边1m处,桥洞离水面的高是多少?*千克销售价(元)和投掷的最大高度4m,。
2009年中考数学压轴汇编

2009年中考数学压轴题汇编(含解题过程) (2009年北京)25.如图,在平面直角坐标系xOy中,ABC三个机战的坐标分别为()6,0A-,()6,0B,(0,C,延长AC到点D,使CD=12AC,过点D作DE∥AB交BC的延长线于点E.(1)求D点的坐标;(2)作C点关于直线DE的对称点F,分别连结DF、EF,若过B点的直线y kx b=+将四边形CDFE分成周长相等的两个四边形,确定此直线的解析式;(3)设G为y轴上一点,点P从直线y kx b=+与y轴的交点出发,先沿y 轴到达G点,再沿GA到达A点,若P点在y轴上运动的速度是它在直线GA上运动速度的2倍,试确定G点的位置,使P点按照上述要求到达A点所用的时间最短。
(要求:简述确定G点位置的方法,但不要求证明)(2009年重庆市)26.已知:如图,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3.过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .(1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为65,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由;(3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在,请说明理由.26.解:(1)由已知,得(30)C ,,(22)D ,,90ADE CDB BCD ∠=-∠=∠ °,1tan 2tan 212AE AD ADE BCD ∴=∠=⨯∠=⨯= .∴(01)E ,. ····················································································································· (1分) 设过点E D C 、、的抛物线的解析式为2(0)y ax bx c a =++≠. 将点E 的坐标代入,得1c =.将1c =和点D C 、的坐标分别代入,得42129310.a b a b ++=⎧⎨++=⎩,············································································································ (2分) 解这个方程组,得56136a b ⎧=-⎪⎪⎨⎪=⎪⎩故抛物线的解析式为2513166y x x =-++. ································································ (3分) (2)2EF GO =成立. ································································································ (4分)点M 在该抛物线上,且它的横坐标为65,26题图x∴点M 的纵坐标为125. ······························································································· (5分) 设DM 的解析式为1(0)y kx b k =+≠, 将点D M 、的坐标分别代入,得1122612.55k b k b +=⎧⎪⎨+=⎪⎩, 解得1123k b ⎧=-⎪⎨⎪=⎩,. ∴DM 的解析式为132y x =-+. ··············································································· (6分) ∴(03)F ,,2EF =. ··································································································· (7分) 过点D 作DK OC ⊥于点K ,则DA DK =.90ADK FDG ∠=∠= °, FDA GDK ∴∠=∠.又90FAD GKD ∠=∠= °, DAF DKG ∴△≌△. 1KG AF ∴==.1GO ∴=.····················································································································· (8分) 2EF GO ∴=.(3) 点P 在AB 上,(10)G ,,(30)C ,,则设(12)P ,.∴222(1)2PG t =-+,222(3)2PC t =-+,2GC =.①若PG PC =,则2222(1)2(3)2t t -+=-+, 解得2t =.∴(22)P ,,此时点Q 与点P 重合.∴(22)Q ,. ···················································································································· (9分) ②若PG GC =,则22(1)22t 2-+=, 解得 1t =,(12)P ∴,,此时GP x ⊥轴.GP 与该抛物线在第一象限内的交点Q 的横坐标为1,∴点Q 的纵坐标为73.∴713Q ⎛⎫⎪⎝⎭,. ················································································································ (10分) ③若PC GC =,则222(3)22t -+=,x解得3t =,(32)P ∴,,此时2PC GC ==,PCG △是等腰直角三角形. 过点Q 作QH x ⊥轴于点H , 则QH GH =,设QH h =,(1)Q h h ∴+,.2513(1)(1)166h h h ∴-++++=.解得12725h h ==-,(舍去).12755Q ⎛⎫∴ ⎪⎝⎭,. ··············································· (12分) 综上所述,存在三个满足条件的点Q ,即(22)Q ,或713Q ⎛⎫⎪⎝⎭,或12755Q ⎛⎫⎪⎝⎭,.x(2009年重庆綦江县)26.(11分)如图,已知抛物线(1)20)y a x a=-+≠经过点(2)A-,0,抛物线的顶点为D,过O作射线OM AD∥.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.(1)求该抛物线的解析式;(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为()t s.问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB=,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t()s,连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.*26.解:(1)抛物线2(1)0)y a x a=-+≠经过点(20)A-,,09a a∴=+=·································································································1分∴二次函数的解析式为:2y x x=+·······················································3分(2)D为抛物线的顶点(1D∴过D作DN OB⊥于N,则DN=3660AN AD DAO=∴==∴∠=,° ························································4分OM AD∥①当AD OP=时,四边形DAOP是平行四边形66(s)OP t∴=∴=·····················································5分②当DP OM⊥时,四边形DAOP是直角梯形过O作OH AD⊥于H,2AO=,则1AH=(如果没求出60DAO∠=°可由Rt RtOHA DNA△∽△求AH55(s)OP DH t∴=== ·····································································································6分③当PD OA =时,四边形DAOP 是等腰梯形 26244(s)OP AD AH t ∴=-=-=∴=综上所述:当6t =、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形. ·· 7分 (3)由(2)及已知,60COB OC OB OCB ∠==°,,△是等边三角形 则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<,,,过P 作PE OQ ⊥于E ,则2PE =················································································ 8分116(62)222BCPQ S t t ∴=⨯⨯⨯-⨯232t ⎫-+⎪⎝⎭·········································································································· 9分当32t =时,BCPQ S ········································································· 10分∴此时3339332444OQ OP OE QE PE ==∴=-==,=,2PQ ∴=== ··························································· 11分(2009年河北省)26.(本小题满分12分)如图16,在Rt △ABC 中,∠C =90°,AC = 3,AB = 5.点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动,到达点A 后立刻以原来的速度沿AC 返回;点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动.伴随着P 、Q 的运动,DE 保持垂直平分PQ ,且交PQ 于点D ,交折线QB -BC -CP 于点E .点P 、Q 同时出发,当点Q 到达点B 时停止运动,点P 也随之停止.设点P 、Q 运动的时间是t 秒(t >0).(1)当t = 2时,AP = ,点Q 到AC 的距离是 ; (2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与t 的函数关系式;(不必写出t 的取值范围)(3)在点E 从B 向C 运动的过程中,四边形QBED 能否成为直角梯形?若能,求t 的值.若不能,请说明理由; (4)当DE 经过点C 时,请直接..写出t 的值.26.解:(1)1,85;(2)作QF ⊥AC 于点F ,如图3, AQ = CP = t ,∴3AP=由△AQF ∽△ABC ,4BC ==, 得45QF t =.∴45QF t =.∴14(3)25S t t =-⋅,即22655S t t =-+.(3)能.①当DE ∥QB 时,如图4. ∵DE ⊥PQ ,∴PQ ⊥QB ,四边形QBED 是直角梯形. 此时∠AQP =90°. 由△APQ ∽△ABC ,得AQ APAC AB =, 即335t t -=. 解得98t =.P图16P图4 P图3F②如图5,当PQ ∥BC 时,DE ⊥BC ,四边形QBED 是直角梯形. 此时∠APQ =90°. 由△AQP ∽△ABC ,得 AQ APAB AC=, 即353t t -=. 解得158t =.(4)52t =或4514t =.【注:①点P由C 向A 运动,DE 经过点C . 方法一、连接QC ,作QG ⊥BC 于点G ,如图6.PC t =,222QC QG CG =+2234[(5)][4(5)]55t t =-+--.由22PC QC =,得22234[(5)][4(5)]55t t t =-+--,解得52t =.方法二、由CQ CP AQ ==,得QAC QCA ∠=∠,进而可得B BCQ ∠=∠,得CQ BQ =,∴52AQ BQ ==.∴52t =. ②点P 由A 向C 运动,DE 经过点C ,如图7.22234(6)[(5)][4(5)]55t t t -=-+--,4514t =】P图5(2009年河南省)23.(11分)如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ①过点E 作EF ⊥AD 于点F ,交抛物线于点G.当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值.解.(1)点A 的坐标为(4,8) …………………1分 将A (4,8)、C (8,0)两点坐标分别代入y=ax 2+bx8=16a +4b得0=64a +8b解 得a =-12,b =4 ∴抛物线的解析式为:y =-12x 2+4x …………………3分(2)①在Rt △APE 和Rt △ABC 中,tan ∠PAE =PE AP =BC AB ,即PE AP =48∴PE =12AP =12t .PB=8-t .∴点E的坐标为(4+12t ,8-t ).∴点G 的纵坐标为:-12(4+12t )2+4(4+12t )=-18t 2+8. …………………5分∴EG=-18t 2+8-(8-t )=-18t 2+t .∵-18<0,∴当t =4时,线段EG 最长为2. …………………7分②共有三个时刻. …………………8分t 1=163, t 2=4013,t 3. …………………11分(2009年山西省)26.(本题14分)如图,已知直线128:33l y x =+与直线2:216l y x =-+相交于点C l l 12,、分别交x 轴于A B 、两点.矩形DEFG 的顶点D E 、分别在直线12l l 、上,顶点F G 、都在x 轴上,且点G 与点B 重合.(1)求ABC △的面积;(2)求矩形DEFG 的边DE 与EF 的长;(3)若矩形DEFG 从原点出发,沿x 轴的反方向以每秒1个单位长度的速度平移,设移动时间为(012)t t ≤≤秒,矩形DEFG 与ABC △重叠部分的面积为S ,求S 关t 的函数关系式,并写出相应的t 的取值范围.26.(1)解:由28033x +=,得4x A =-∴.点坐标为()40-,. 由2160x -+=,得8x B =∴.点坐标为()80,. ∴()8412AB =--=. ·························································································· (2分)由2833216y x y x ⎧=+⎪⎨⎪=-+⎩,.解得56x y =⎧⎨=⎩,.∴C 点的坐标为()56,. ······································· (3分) ∴111263622ABC C S AB y ==⨯⨯=△·.······························································· (4分) (2)解:∵点D 在1l 上且2888833D B D x x y ==∴=⨯+=,.∴D 点坐标为()88,. ······························································································ (5分)又∵点E 在2l 上且821684E D E E y y x x ==∴-+=∴=,..∴E 点坐标为()48,. ····························································································· (6分)∴8448OE EF =-==,. ················································································· (7分)(3)解法一:①当03t <≤时,如图1,矩形DEFG 与ABC △重叠部分为五边形CHFGR (0t =时,为四边形CHFG ).过C 作CM AB ⊥于M ,则Rt Rt RGB CMB △∽△.(第26题)(图3)(图1)(图2)∴BG RG BM CM =,即36t RG=,∴2RG t =. Rt Rt AFH AMC △∽△,∴()()11236288223ABC BRG AFH S S S S t t t t =--=-⨯⨯--⨯-△△△.即241644333S t t =-++.········································································· (10分)(2009年山西省太原市)29.(本小题满分12分) 问题解决如图(1),将正方形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C ,D 重合),压平后得到折痕MN .当12CE CD =时,求AMBN的值.类比归纳在图(1)中,若13CE CD =,则AM BN 的值等于 ;若14CE CD =,则AMBN的值等于 ;若1CE CD n =(n 为整数),则AM BN的值等于 .(用含n 的式子表示) 联系拓广如图(2),将矩形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C D ,重合),压平后得到折痕MN ,设()111AB CE m BC m CD n =>=,,则AMBN的值等于 .(用含m n ,的式子表示)解:方法一:如图(1-1),连接BM EM BE ,,.由题设,得四边形ABNM 和四边形FENM 关于直线MN 对称.∴MN 垂直平分BE .∴BM EM BN EN ==,. ·············································· 1分 ∵四边形ABCD 是正方形,∴902A D C AB BC CD DA ∠=∠=∠=====°,. ∵112CE CE DE CD =∴==,.设BN x =,则NE x =,2NC x =-.在Rt CNE △中,222NE CN CE =+.∴()22221x x =-+.解得54x =,即54BN =. ···················································· 3分 在Rt ABM △和在Rt DEM △中,222AM AB BM +=, 222DM DE EM +=,∴2222AM AB DM DE +=+.············································································· 5分 方法指导:为了求得AMBN 的值,可先求BN 、AM 的长,不妨设:AB =2图(2)NABCD EFM图(1)A BCDEFMNN图(1-1)A BC EFM设AM y =,则2DM y =-,∴()2222221y y +=-+.解得14y =,即14AM =. ······················································································· 6分 ∴15AM BN =.··········································································································· 7分 方法二:同方法一,54BN =. ················································································ 3分如图(1-2),过点N 做NG CD ∥,交AD 于点G ,连接BE .∵AD BC ∥,∴四边形GDCN 是平行四边形. ∴NG CD BC ==.同理,四边形ABNG 也是平行四边形.∴54AG BN ==. ∵90MN BE EBC BNM ⊥∴∠+∠=,°. 90NG BC MNG BNM EBC MNG ⊥∴∠+∠=∴∠=∠ ,°,. 在BCE △与NGM △中90EBC MNG BC NG C NGM ∠=∠⎧⎪=⎨⎪∠=∠=⎩,,°.∴BCE NGM EC MG =△≌△,. ······························· 5分∵114AM AG MG AM =--=5,=.4 ··································································· 6分 ∴15AM BN =.········································································································· 7分 类比归纳25(或410);917; ()2211n n -+ ··············································································· 10分联系拓广2222211n m n n m -++ ············································································································ 12分评分说明:1.如你的正确解法与上述提供的参考答案不同时,可参照评分说明进行估分.2.如解答题由多个问题组成,前一问题解答有误或未答,对后面问题的解答没有影响,可依据参考答案及评分说明进行估分.N图(1-2) A BC DEFMG第23题图(1)第23题图(2)(2009年安徽省)23.已知某种水果的批发单价与批发量的函数关系如图(1)所示. (1)请说明图中①、②两段函数图象的实际意义.【解】(2)写出批发该种水果的资金金额w (元)与批发量m (kg )之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什 么范围内,以同样的资金可以批发到较多数量的该种水果.【解】(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg 以上该种水果, 且当日零售价不变,请你帮助该经销商设计进货和销售的方案, 使得当日获得的利润最大. 【解】)23.(1)解:图①表示批发量不少于20kg 且不多于60kg 的该种水果,可按5元/kg 批发;……3分图②表示批发量高于60kg 的该种水果,可按4元/kg 批发. ………………………………………………………………3分(2)解:由题意得: 2060 6054m m w m m ⎧=⎨⎩≤≤())>(,函数图象如图所示.………………………………………………………………7分由图可知资金金额满足240<w ≤300时,以同样的资金可 批发到较多数量的该种水果.……………………………8分(3)解法一:设当日零售价为x 元,由图可得日最高销量32040w m =- 当m >60时,x <6.5 由题意,销售利润为2(4)(32040)40[(6)4]y x m x =--=--+………………………………12分当x =6时,160y =最大值,此时m =80即经销商应批发80kg 该种水果,日零售价定为6元/kg ,当日可获得最大利润160元.……………………………………………14分 解法二:设日最高销售量为x kg (x >60)则由图②日零售价p 满足:32040x p =-,于是32040xp -=销售利润23201(4)(80)1604040x y x x -=-=--+………………………12分当x =80时,160y =最大值,此时p =6即经销商应批发80kg 该种水果,日零售价定为6元/kg ,当日可获得最大利润160元.……………………………………………14分)。
2009年全国中考数学压轴题2(修订版)

2009年全国中考数学分类试题---综合题压轴题汇编2教师答案版1(09广东广州)25.(本小题满分14分)如图13,二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),ΔABC 的面积为45。
(1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴上午垂线,若该垂线与ΔABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使四边形ABCD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由。
解:(1)OC=1,所以,q=-1,又由面积知0.5OC ×AB=45,得AB=52设A (a,0),B(b,0)AB=b-a=52,解得p=32±,但p<0,所以p=32-。
所以解析式为:2312y x x =-- (2)令y=0,解方程得23102x x --=,得121,22x x =-=,所以A(12-,0),B(2,0),在直角三角形AOC 中可求得同样可求得,显然AC 2+BC 2=AB 2,得三角形ABC 是直角三角形。
AB 为斜边,所以外接圆的直径为AB=52,所以5544m -≤≤. (3)存在,AC ⊥BC,①若以AC 为底边,则BD//AC,易求AC 的解析式为y=-2x-1,可设BD 的解析式为y=-2x+b ,把B(2,0)代入得BD 解析式为y=-2x+4,解方程组231224y x x y x ⎧=--⎪⎨⎪=-+⎩得D (52-,9) ②若以BC 为底边,则BC//AD,易求BC 的解析式为y=0.5x-1,可设AD 的解析式为y=0.5x+b ,把 A(12-,0)代入得AD 解析式为y=0.5x+0.25,解方程组23120.50.25y x x y x ⎧=--⎪⎨⎪=+⎩得D(53,22) 综上,所以存在两点:(52-,9)或(53,22)。
09年数学中考压轴题

09年数学中考压轴题1.(09年.嘉兴中考)如图,已知A、B是线段MN上的两点,4MN,1=MB.以>MA,1= A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设xAB=.Array(1)求x的取值范围;(2)若△ABC为直角三角形,求x的值;(3)探究:△ABC的最大面积?(第24题)2.(09年.兰州中考)如图①,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.3.(09年.杭州中考)已知平行于x 轴的直线)0(≠=a a y 与函数x y =和函数xy 1=的图象分别交于点A 和点B ,又有定点P (2,0) . (1)若0>a ,且tan ∠POB=91,求线段AB 的长; (2)在过A ,B 两点且顶点在直线x y =上的抛物线中,已知线段AB=38,且在它的对称轴左边时,y 随着x 的增大而增大,试求出满足条件的抛物线的解析式; (3)已知经过A ,B ,P 三点的抛物线,平移后能得到259x y =的图象,求点P 到直线AB 的距离 .4.(09年.青岛中考)如图,在梯形ABCD 中,AD BC ∥,6cm AD =,4cm CD =,10cm BC BD ==,点P 由B 出发沿BD 方向匀速运动,速度为1cm/s ;同时,线段EF 由DC 出发沿DA 方向匀速运动,速度为1cm/s ,交BD 于Q ,连接PE .若设运动时间为t (s )(05t <<).解答下列问题: (1)当t 为何值时,PE AB ∥?(2)设PEQ △的面积为y (cm 2),求y 与t 之间的函数关系式; (3)是否存在某一时刻t ,使225PEQ BCD S S =△△?若存在,求出此时t 的值;若不存在,说明理由.(4)连接PF ,在上述运动过程中,五边形PFCDE 的面积是否发生变化?说明理由.第24题图5.(09年.台州中考)如图,已知直线 交坐标轴于B A ,两点,以线段AB 为边向上作正方形ABCD ,过点C D ,A ,的抛物线与直线另一个交点为E . (1)请直接写出点D C ,的坐标; (2)求抛物线的解析式;(3)若正方形以每秒5个单位长度的速度沿射线AB 下滑,直至顶点D 落在x 轴上时停止.设正方形落在x 轴下方部分的面积为S ,求S 关于滑行时间t 的函数关系式,并写出相应自变量t 的取值范围;(4)在(3)的条件下,抛物线与正方形一起平移,同时D 停止,求抛物线上E C , 两点间的抛物线弧所扫过的面积.(第24题)y x121+-=x y6.(09年.金华中考)如图,在平面直角坐标系中,点A (0,6),点B 是x 轴上的一个动点,连结AB ,取AB 的中点M ,将线段MB 绕着点B 按顺时针方向旋转90o ,得到线段BC .过点B 作x 轴的垂线交直线AC 于点D .设点B 坐标是(t ,0). (1)当t =4时,求直线AB 的解析式;(2)当t >0时,用含t 的代数式表示点C 的坐标及△ABC 的面积; (3)是否存在点B ,使△ABD 为等腰三角形?若存在,请求出所有符合条件的点B 的坐标;若不存在,请说明理由.· yO A x 备用图7.(09年义乌.中考).已知点A 、B 分别是x 轴、y 轴上的动点,点C 、D 是某个函数图像上的点,当四边形ABCD (A 、B 、C 、D 各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形。
2009二模压轴

09卢湾.在平面直角坐标系xOy 中,将抛物线22y x =沿y 轴向上平移1个单位,再沿x 轴向右平移两个单位,平移后抛物线的顶点坐标记作A ,直线3x =与平移后的抛物线相交于B ,与直线OA 相交于C . (1)求△ABC 面积;(2)点P 在平移后抛物线的对称轴上,如果△ABP 与△ABC 相似,求所有满足条件的P 点坐标..在等腰△ABC 中,已知AB =AC =3,1cos 3B ∠=,D 为AB 上一点,过点D 作DE ⊥AB 交BC 边于点E ,过点E 作EF ⊥BC 交AC 边于点F .(1)当BD 长为何值时,以点F 为圆心,线段FA 为半径的圆与BC 边相切?(2)过点F 作FP ⊥AC ,与线段DE 交于点G ,设BD 长为x ,△EFG 的面积为y ,求y 关于x的函数解析式及其定义域.12345-1-2-3-4-5-1-2-3-4-512345x y 0 24题图 FE BCAD 25题图FE BCAD 25题图09静安已知:⊙O 的直径AB =8,⊙B 与⊙O 相交于点C 、D ,⊙O 的直径CF 与⊙B 相交于点E ,设⊙B 的半径为x ,OE 的长为y ,(1) 如图7,当点E 在线段OC 上时,求y 关于x 的函数解析式,并写出定义域; (2) 当点E 在直径CF 上时,如果OE 的长为3,求公共弦CD 的长;(3) 设⊙B 与AB 相交于G ,试问△OEG 能否为等腰三角形?如果能够,请直接写出BC 的长度(不必写过程);如果不能,请简要说明理由.闸北如图九,△ABC 中,AB=5,AC=3,cosA=310.D 为射线BA 上的点(点D 不与点B 重合),作DE//BC 交射线CA 于点E..(1) 若CE =x ,BD =y ,求y 与x 的函数关系式,并写出函数的定义域; (2) 当分别以线段BD ,CE 为直径的两圆相切时,求DE 的长度;(3) 当点D 在AB 边上时,BC 边上是否存在点F ,使△ABC 与△DEF 相似?若存在,请求出线段BF 的长;若不存在,请说明理由.AOBCDEFEACB D (备用图二)EACB D (图九) EA CB D (备用图一)G F E D C BA 09黄埔二次函数c bx x y ++-=241的图像经过点()()4,4,0,4--B A ,且与y 轴交于点C . (1)试求此二次函数的解析式;(2)试证明:CAO BAO ∠=∠(其中O 是原点);(3)若P 是线段AB 上的一个动点(不与A 、B 重合),过P 作y 轴的平行线,分别交此二次函数图像及x 轴于Q 、H 两点,试问:是否存在这样的点P ,使QH PH 2=? 若存在,请求出点P 的坐标;若不存在,请说明理由.如图,在ABC ∆中,6,5===BC AC AB ,D 、E 分别是边AB 、AC 上的两个动点(D 不与A 、B 重合),且保持BC DE ∥,以DE 为边,在点A 的异侧作正方形DEFG . (1)试求ABC ∆的面积;(2)当边FG 与BC 重合时,求正方形DEFG 的边长; (3)设x AD =,ABC ∆与正方形DEFG 重叠部分的面积为y ,试求y 关于x 的函数关系式,并写出定义域;(4)当BDG ∆是等腰三角形时,请直接写出AD 的长.09虹口在平面直角坐标系xOy 中(如图7),已知二次函数c bx x y ++=2的图像经过点(0,3)A 和点(3,0)B ,其顶点记为点C .(1)确定此二次函数的解析式,并写出顶点C 的坐标;(2)将直线CB 向上平移3个单位长度,求平移后直线l 的解析式;(3)在(2)的条件下,能否在直线上l 找一点D ,使得以点C 、B 、D 、O 为顶点的四边形是等腰梯形.若能,请求出点D 的坐标;若不能,请说明理由.如图8,在ABC ∆中,90C ∠=︒,6AC =,3tan 4B =,D 是BC 边的中点,E 为AB 边上的一个动点,作90DEF ∠=︒,EF 交射线BC 于点F .设B E x =,BED ∆的面积为y .(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)如果以线段BC 为直径的圆与以线段AE 为直径的圆相切,求线段BE 的长;(3)如果以B 、E 、F 为顶点的三角形与BED ∆相似,求BED ∆的面积.09奉贤.在平面直角坐标系中,矩形ABOC 的边BO 在x 轴正半轴上,边CO 在y 轴的正AC D EFB图8ACD B备用图· O 1 2 3xy图7ABCDEFxyO第24题半轴上,且322==OB AB ,,矩形ABOC 绕点O 逆时针旋转后得到矩形EFOD ,且点A 落在y 轴上的E 点,点B 的对应点为点F ,点C 的对应点为点D . (1)求F 、E 、D 三点的坐标;(2)若抛物线c bx ax y ++=2经过点F 、E 、D , 求此抛物线的解析式;(3)在x 轴上方的抛物线上求点Q 的坐标,使得 三角形QOB 的面积等于矩形ABOC 的面积?已知:在△ABC 中,AB =AC ,∠B =30º,BC =6,点D 在边BC 上,点E 在线段DC 上,DE =3,△DEF 是等边三角形,边DF 、EF 与边BA 、CA 分别相交于点M 、N . (1)求证:△BDM ∽△CEN ;(2)当点M 、N 分别在边BA 、CA 上时,设BD =x ,△ABC 与△DEF 重叠部分的面积为y ,求y 关于x 的函数解析式,并写出定义域.(3)是否存在点D ,使以M 为圆心, BM 为半径的圆与直线EF 相切, 如果存在,请求出x的值;如不存在,请说明理由.09崇明如图,抛物线32++=bx ax y 与y 轴交于点C ,与x 轴交于A 、B 两点,31tan =∠OCA ,ABF DEMNC第25题 ABFD EMNC第25题6=∆ABC S .(1)求点B 的坐标;(2)求抛物线的解析式及顶点坐标;(3)设点E 在x 轴上,点F 在抛物线上,如果A 、C 、E 、F 构成平行四边形,请写出点E 的坐标(不必书写计算过程).在等腰ABC ∆中,已知5==AC AB cm ,6=BC cm ,动点P 、Q 分别从A 、B 两点同时出发,沿AB 、BC 方向匀速移动,它们的速度都是1 cm/秒. 当点P 到达点B 时,P 、Q 两点停止运动,设点P 的运动时间为t (秒). (1)当t 为何值时,PQ ⊥AB ?(2)设四边形APQC 的面积为y cm 2,写出y 关于t 的函数关系式及定义域; (3)分别以P 、Q 为圆心,PA 、BQ 长为半径画圆,若⊙P 与⊙Q 相切,求t 的值; (4)在P 、Q 运动中,BPQ ∆与ABC ∆能否相似?若能,请求出AP 的长;若不能,请说明理由.09徐汇如图,抛物线c bx ax y ++=2与y 轴正半轴交于点C ,与x 轴交于点A BC ABC(备用图)CAB Oy x),(、04)0,1(B A ,OBC OCA ∠=∠.(1)求抛物线的解析式; (2)在直角坐标平面内确定点M ,使得以点C B A M 、、、为顶点的四边形是平行四边形,请直接写出点M 的坐标; (3)如果⊙P 过点C B A 、、三点,求圆心P 的坐标.如图,ABC ∆中,10==AC AB ,12=BC ,点D 在边BC 上,且4=BD ,以 点D 为顶点作B EDF ∠=∠,分别交边AB 于点E ,交射线CA 于点F . (1)当6=AE 时,求AF 的长;(2)当以点C 为圆心CF 长为半径的⊙C 和以点A 为圆心AE 长为半径的⊙A 相切时,求BE 的长; (3)当以边AC 为直径的⊙O 与线段DE 相切时,求BE 的长.杨浦已知一次函数m x y +=43的图像分别交x 轴、y 轴于A 、B 两点(如图),且与反比例函A B CO y x A B C DE F A B CD (备用图)数xy 24=的图像在第一象限交于点C (4,n ),CD ⊥x 轴于D 。
2009年中考试题 二次函数专题

1. (2009杭州) 已知点P (x ,y )在函数x x y -+=21的图象上,那么点P 应在平面直角坐标系中的A.第一象限B. 第二象限C. 第三象限D. 第四象限 2. (2009南州)抛物线的图象如图1所示,根据图象可知,抛物线的解析式可能..是( ) A 、y=x 2-x-2 B 、y=121212++-x C 、y=121212+--x x D 、y=22++-x x 3. (2009莆田)二次函数2241y x x =-++的图象如何平移就褥到22y x =-的图像( )A .向左平移1个单位,再向上平移3个单位.B .向右平移1个单位,再向上平移3个单位.C .向左平移1个单位,再向下平移3个单位.D .向右平移1个单位,再向下平移3个单位。
4. (2009丽水)已知二次函数y =ax 2+bx +c(a ≠0)的图象如图所示,给出以下结论: ①a >0.②该函数的图象关于直线1x =对称. ③当13x x =-=或时,函数y 的值都等于0. 其中正确结论的个数是 A .3 B .2 C .1 D .05. (2009嘉兴)已知0≠a ,在同一直角坐标系中,函数ax y =与2ax y =的图象有可能是( ▲ )6. (2009广州)二次函数2)1(2+-=x y 的最小值是( ) (A )2 (B )1 (C )-1 (D )-27. (2009烟台)二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac=+-与反比例函数a b cy x++=在同一坐标系内的图象大致为( )图1(第7题) OACD xxxx8. (2009黄石)已知二次函数y=ax 2+bx+c (a ≠0)的图象如图3所示, 下列结论:①abc >0 ②2a+b <0 ③4a -2b+c <0 ④a+c >0, 其中正确结论的个数为( )A 、4个B 、3个C 、2个D 、1个9. (2009湖州)已知抛物线2y ax bx c =++(a >0)的对称轴为直线1x =,且经过点()()212y y -1,,,,试比较1y 和2y 的大小:1y _2y (填“>”,“<”或“=”) 10. (2009重庆)某电视机生产厂家去年销往农村的某品牌电视机每台的售价y (元)与月份x 之间满足函数关系260050+-=x y ,去年的月销售量p (万台)与月份x 之间成(1(2)由于受国际金融危机的影响,今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了%m ,且每月的销售量都比去年12月份下降了%5.1m 。
2009年中考数学专题复习——压轴题

2009年中考数学专题复习一一压轴题1. (2008年四川省宜宾市)已知:如图抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点 A (-1, 0)、B (0, 3)两点,其 顶点为D.(1) 求该抛物线的解析式;(2) 若该抛物线与x 轴的另一个交点为 E.求四边形ABDE 的面积;(3) △ AOB 与厶BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由.2. (08浙江衢州)已知直角梯形纸片 OABC 在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为 O (0, 0), A (10 , 0), B (8, 2 3), C (0, 2 3),点T在线段OA 上(不与线段端点重合),将纸片折叠,使点A 落在射线AB 上(记为点 A '),折痕经过点T ,折痕TP 与射线AB 交于点P ,设点T 的横坐标为t ,折叠 后纸片重叠部分(图中的阴影部分)的面积为S ;(1) 求/OAB 的度数,并求当点A '在线段AB 上时,S 关于t 的函数关系式; (2) 当纸片重叠部分的图形是四边形时,求 t 的取值范围;⑶S 存在最大值吗?若存在,求出这个最大值,并求此时 t 的值;若不存在,请 说明理由.3. (08 浙江温州)如图,在 Rt △ ABC 中,• A =90", AB =6, AC =8 , D , E 分别是b2a4ac- b24a 2(注:抛物线 y=ax +bx+c (a 工0)的顶点坐边AB, AC 的中点,点P 从点D 出发沿DE 方向运动,过点P 作PQ _ BC 于Q ,过点Q 作QR // BA 交AC 于R ,当点Q 与点C 重合时,点P 停止运动•设BQ =x , QR = y .(1) 求点D 到BC 的距离DH 的长;(2) 求y 关于x 的函数关系式(不要求写出自变量的取值范围); (3)是否存在点 P ,使△ PQR 为等腰三角形?若存在,请求出所有满足要求的 x 的值;若不存在,请说明理由.4. ( 08山东省日照市)在 △ ABC 中,/ A = 90 ° AB = 4, AC = 3, M 是AB 上的动点(不与 A , B 重合),过 M 点作MN // BC 交AC 于点N .以MN 为直径作O 0,并在O O 内作内接 矩形 AMPN .令 AM = x .(1) 用含x 的代数式表示 A M NP 的面积S ; (2 )当x 为何值时,O 0与直线BC 相切?(3)在动点M 的运动过程中,记 A M NP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求 x 为何值时,y 的值最大,最大值是多少?k5、( 2007浙江金华)如图1,已知双曲线 y= (k>0)与直线y=k ' x 交于A , B 两点,点 A 在x第一象限•试解答下列问题:(1)若点A 的坐标为(4 , 2).则点B 的坐标为 ____________ ;若点A 的横坐标为 m,则点B 的坐标可表示为 ___________ ;k(2)如图2,过原点O 作另一条直线 I ,交双曲线 y= (k>0)于P , C 两点,点P 在第一Cx象限•①说明四边形APBC一定是平行四边形;②设点 A.P的横坐标分别为m, n ,四边形APBQ 可能是矩形吗 ?可能是正方形吗 ?若可能,直接写出mn 应满足的条件;6.( 2008浙江金华)如图1,在平面直角坐标系中,己知△ AOB 是等边三角形,点A 的坐标是(0 , 4),点B 在第一象限,点 P 是 x 轴上的一个动点,连结AP ,并把△ AOP绕着点A 按逆时针方向旋转 .使边AO 与 AB 重合.得到△ ABD. ( 1)求直线 AB 的解析式;7. (2008浙江义乌)如图1,四边形ABCD 是正方形,G 是CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边在正方形 ABCD 外作正方形 CEFG ,连结BG , DE .我们探究下列 图中线段BG 、线段DE 的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG 、线段DE 的长度关系及所在直线的位置关系;②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度:-, 得到如图2、如图3情形•请你通过观察、测量等方法判断①中得到的结论是否 仍然成立,并选取图2证明你的判断.(2)当点P 运动到点(.3 , 0 )时,求此时 DP 的长及点D 的坐标;3)是否存在点卩,使△ OPD 勺面积等于 —,若存在, 4请求出符合条件的点P 的坐标;若不存在,若不可能,请说明理由E(23題團3 )D(2)将原题中正方形改为矩形 (如图4— 6),且AB=a , BC=b ,CE=ka , CG=kb (a= b ,8. (2008浙江义乌)如图1所示,直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半 轴上.过点B 、C 作直线I .将直线l 平移,平移后的直线l 与x 轴交于点D,与y 轴交于点E .(1) 将直线l 向右平移,设平移距离CD 为t (t_0),直角梯形OABC 被直线I 扫过的面积(图中阴影部份)为 s , S 关于t 的函数图象如图2所示,OM 为线段,MN 为抛物 线的一部分,NQ 为射线,N 点横坐标为4.① 求梯形上底AB 的长及直角梯形OABC 的面积; ② 当2 :::t : 4时,求S 关于t 的函数解析式;(2) 在第(1)题的条件下,当直线l 向左或向右平移时(包括 I 与直线BC 重合),在 直线AB 上是否存在点P ,使APDE 为等腰直角三角形?若存在,请直接写出所有满 足条件的点P 的坐标;若不存在,请说明理由.9. (2008山东烟台)如图,菱形 ABCD 的边长为2, BD=2 , E 、F 分别是边AD , CD 上的两个 动点,且满足AE+CF=2.(1) 求证:△ BDE ◎△ BCF ; (2) 判断△ BEF 的形状,并说明理由; (3) 设厶BEF 的面积为S ,求S 的取值范围.以图5为例简要说(3)在第⑵题图5中,连结DG 、1 N280 2 4tk ■ 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,明理由.求BE 2 DG 2的值.(23题图G210.(2008山东烟台)如图,抛物线L i : y - -x -2x 3交x轴于A、B两点,交y轴于M点.抛物线L1向右平移2个单位后得到抛物线L2, L2交x轴于C、D两点.(1 )求抛物线L2对应的函数表达式;(2)抛物线L i或L2在x轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形•若存在,求出点N的坐标;若不存在,请说明理由;(3)若点P是抛物线L i上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线L2上,请说明理由•11.2008淅江宁波)2008年5月1日,目前世界上最长的跨海大桥一一杭州湾跨海大桥通车了•通车后,苏南A地到宁波港的路程比原来缩短了120千米•已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.(1 )求A地经杭州湾跨海大桥到宁波港的路程.D(2)若货物运输费用包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时 28元,那么该车货物从 A 地经杭州湾跨海大桥到宁波港 的运输费用是多少元? (3) A 地准备开辟宁波方向的外运路线,即货物从A 地经杭州湾跨海大桥到宁波港,再从宁波港运到B 地.若有一批货物(不超过10车)从A 地按外运路线运到 B 地的运费需8320 元,其中从A 地经杭州湾跨海大桥到宁波港的每车运输费用与( 2)中相同,从宁波港到B地的海上运费对一批不超过 10车的货物计费方式是:一车 800元,当货物每增加1车时, 每车的海上运费就减少 20元,问这批货物有几车?12. (2008淅江宁波)如图1,把一张标准纸一次又一次对开,得到“ 2 开”纸、“ 4开”纸、“ 8开”纸、“16开”纸….已知标准纸.的 短边长为a .(1) 如图2,把这张标准纸对开得到的“ 16开”张纸按如下步骤折 叠: 第一步 将矩形的短边 AB 与长边AD 对齐折叠,点 B 落在AD 上 的点B •处,铺平后得折痕 AE ;第二步 将长边AD 与折痕AE 对齐折叠,点 D 正好与点E 重合,铺平后得折痕 AF . 则AD: AB 的值是 ____________________ , AD , AB 的长分别是 ________ , ________ .(2) “ 2开”纸、“ 4开”纸、“ 8开”纸的长与宽之比是否都相等?若相等,直接写出这 个比值;若不相等,请分别计算它们的比值.(3) 如图3,由8个大小相等的小正方形构成 “ L ”型图案,它的四个顶点E , F , G , H 分别在“16开”纸的边 AB, BC , CD , DA 上,求DG 的长.(4) 已知梯形 MNPQ 中,MN // PQ , Z M =90: , MN =MQ =2PQ ,且四个顶点M , N , P, Q 都在“ 4开”纸的边上,请直接写出面积.13. (2008 山东威海)如图,在梯形 ABCD 中,AB // CD , AB = 7, CD = 1, AD = BC = 5.点 M , N 分另【J 在边 AD , BC 上运动,并保持 MN // AB , ME 丄AB , NF 丄AB ,垂足分另U 为 E , F .(1) 求梯形ABCD 的面积; (2) 求四边形MEFN 面积的最大值.(3) 试判断四边形 MEFN 能否为正方形,若能, 求出正方形 MEFN 的面积;若不能,请说明理由.2个符合条件且大小不同的直角梯形的BAEHFD G图3k14. (2008山东威海)如图,点A ( m, m+ 1), B ( m+ 3, m—1)都在反比例函数y = —x的图象上.(1)求m, k的值;(2)如果M为x轴上一点,N为y轴上一点,以点A,B, M , N为顶点的四边形是平行四边形,试求直线MN的函数表达式.. _________ ____________ Q友情提示:本大题第(1)小题4分,第(2)小题7分.对完成第(2)小题有困难的同学可以做下面的(3)(3)选做题:在平面直角坐标系中,点P的坐标为(5, 0),点Q的坐标为(0, 3),把线段PQ向右平移4个单位,然后再向上平移2个单位,得到线段P1Q1, 则点P1的坐标为____________________,点Q1的坐标为________ .15. ( 2008湖南益阳)我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线如图12,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0 , -3), AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.(1) 请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;(2) 你能求出经过点C的“蛋圆”切线的解析式吗?试试看;(3) 开动脑筋想一想,相信你能求出经过点D的“蛋圆”切线的解析式•O M—x16.(2008年浙江省绍兴市)将一矩形纸片OABC放在平面直角坐标系中,0(0,0) , A(6,0),2C(0,3) •动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动一秒时,3动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t (秒).(1)用含t的代数式表示OP, OQ ;(2)当t =1时,如图1,将厶OPQ沿PQ翻折,点O恰好落在CB边上的点D处,求点D 的坐标;(4) 连结AC,将△ OPQ沿PQ翻折,得到△ EPQ,如图2.问:PQ与AC能否平行?PE与AC能否垂直?若能,求出相应的t值;若不能,说明理由.16.(2008年浙江省绍兴市)将一矩形纸片OABC放在平面直角坐标系中,0(0,0) , A(6,0),17.(2008年辽宁省十二市)如图16,在平面直角坐标系中,直线y = i、3x-;3与X轴交于点A,与y轴交于点C ,抛物线y = ax2-2 3 x c( 0)经过A, B, C三点.3(1)求过A B, C三点抛物线的解析式并求出顶点F的坐标;(2)在抛物线上是否存在点P,使△ ABP为直角三角形,若存在,直接写出P点坐标;若不存在,请说明理由;(3)试探究在直线AC上是否存在一点M ,使得△ MBF的周长最小,若存在,求出M点的坐标;若不存在,请说明理由.18.(2008年沈阳市)如图所示,在平面直角坐标系中, 上,边OC在y轴的正半轴上,且AB =1, OB 矩形ABOC的边BO在x轴的负半轴=3,矩形ABOC绕点O按顺时针方向x17.(2008年辽宁省十二市)如图16,在平面直角坐标系中,直线y = i、3x-;3与X轴交于旋转60后得到矩形EFOD •点A的对应点为点E,点B的对应点为点F,点C的对应点20.(2008年成都市)如图,在平面直角坐标系 xOy 中,△ OAB 的顶点A 的坐标为(10, 0), 为点D ,抛物线y =ax 2 • bx c 过点A, E , D . (1) 判断点E 是否在y 轴上,并说明理由; (2) 求抛物线的函数表达式;(3) 在x 轴的上方是否存在点 P ,点Q ,使以点O, B, P ,Q 为顶点的平行四边形的面 积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点 P ,点Q 的坐标;若3 2 _19.(2008年四川省巴中市)已知:如图14,抛物线y x 3与x 轴交于点A ,点B ,433与直线y x b 相交于点B ,点C ,直线y x b 与y 轴交于点E .4 4(1 )写出直线BC 的解析式. )求△ ABC 的面积.(3) 若点M 在线段AB 上以每秒1个单位长度的速度从 A 向B 运动(不与 A B 重合), 同时,点N 在射线BC 上以每秒2个单位长度的速度从 B 向C 运动.设运动时间为t 秒, 请写出△MNB 的面积S 与t 的函数关系式,并求出点M 运动多少时间时, △MNB 的面积S14x(1) 若点C 是点B 关于x 轴的对称点,求经过 O 、C 、A 三点的抛物线的函数表达式;(2) 在(1)中,抛物线上是否存在一点 P ,使以P 、O 、C 、A 为顶点的四边形为梯形?若存 在,求出点P 的坐标;若不存在,请说明理由;(3) 若将点O 、点A 分别变换为点 Q ( -2k ,0)、点R (5k , 0) ( k>1的常数),设过 Q 、 R 两点,且以 QR 的垂直平分线为对称轴的抛物线与 y 轴的交点为N ,其顶点为 M ,记△ QNM 的面积为S QMN , △ QNR 的面积S QNR ,求S QMN:S QNR 的值.21. (2008年乐山市)在平面直角坐标系中△ ABC 的边AB 在x 轴上,且 OA>OB,以AB 为直 径的圆过点 C 若C 的坐标为(0,2),AB=5, A,B 两点的横坐标 X A ,X B 是关于 X 的方程2x -(m 2)x n-1=0 的两根:(1) 求m , n 的值(2) 若Z ACB 的平分线所在的直线 I 交x 轴于点D ,试求直线l 对应的一次函数的解析式- 1丄1 ⑶ 过点D 任作一直线I 分别交射线CA , CB (点C 除外)于点M , N ,则+— 的值CM CN是否为定值,若是,求出定值,若不是,请说明理由顶点B 在第一象限内,且AB =3 ^5, sin ZOAB=20.(2008年成都市)如图,在平面直角坐标系 xOy 中,△ OAB 的顶点A 的坐标为(10, 0),22. (2008年四川省宜宾市)已知:如图抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点 A (-1 , 0)、B ( 0,3)两点,其顶点为 D. (1)求该抛物线的解析式;⑵若该抛物线与x 轴的另一个交点为 E.求四边形ABDE 的面积;⑶△ AOB 与厶BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由‘‘ b 4ac —b 2 "(注:抛物线 y=ax 2+bx+c (a 丰0)的顶点坐标为 -------------- -——, )I 2a 4a 丿23. (天津市2008年)已知抛物线y =3ax 2 2bx c ,(I )若a=b=1 , c = -1,求该抛物线与x 轴公共点的坐标;L'备用图(n)若a =b =1,且当x ,1时,抛物线与x 轴有且只有一个公共点, 求c 的取值范围;(川)若a b c =0,且x i =0时,对应的y i . 0 ; X 2 =1时,对应的 y 0,试判断当0 ::: x ::: 1 时,抛物线与x 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.24. (2008年大庆市)如图①,四边形 AEFG 和ABCD 都是正方形,它们的边长分别为 a , b ( b > 2a ),且点 F 在AD 上(以下问题的结果均可用 a , b 的代数式表示).(1) 求 S A DBF ; (2) 把正方形 AEFG 绕点A 按逆时针方向旋转 45°得图②,求图②中的 S A DBF ;(3)把正方形 AEFG 绕点A 旋转一周,在旋转的过程中,S A DBF 是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由.25. (2008 年上海市)已知 AB =2, AD =4 , DAB =90 , AD // BC (如图 13). E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.(1 )设BE 二x , △ ABM 的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域; (2) 如果以线段 AB 为直径的圆与以线段 DE 为直径的圆外切,求线段 BE 的长;(3) 联结BD ,交线段AM 于点N ,如果以A, N , D 为顶点的三角形与 △ BME 相似, 求线段BE 的长.CBCB26. (2008年陕西省)某县社会主义新农村建设办公室, 为了解决该县甲、 乙两村和一所中 学长期存在的饮水困难问题, 想在这三个地方的其中一处建一所供水站. 由供水站直接铺设 管道到另外两处.如图,甲,乙两村坐落在夹角为 30的两条公路的 AB 段和CD 段(村子和公路的宽均不计), 点M 表示这所中学.点B 在点M 的北偏西30的3km 处,点A 在点M 的正西方向,点D 在点M 的南偏西60的2、、3 km 处.为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:方案一:供水站建在点 M 处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小 值; 方案二:供水站建在乙村(线段 CD 某处),甲村要求管道建设到 A 处,请你在图①中,画 出铺设到点 A 和点M 处的管道长度之和最小的线路图,并求其最小值;方案三:供水站建在甲村(线段AB 某处),请你在图②中,画出铺设到乙村某处和点 M 处 的管道长度之和最小的线路图,并求其最小值.综上,你认为把供水站建在何处,所需铺设的管道最短?图① 图②27. (2008年山东省青岛市) 已知:如图①,在 Rt △ ACB 中,/ C = 90°, AC = 4cm BC = 3cm,点P 由B 出发沿BA 方向向点 A 匀速运动,速度为 1cm/s ;点Q 由A 出发沿AC 方向向 点C 匀速运动,速度为 2cm/s ;连接PQ 若设运动的时间为t (s ) ( 0v t v 2),解答下列 问题: (1 )当t 为何值时,PQ// BC ?2(2) 设厶AQP 的面积为y ( cm ),求y 与t 之间的函数关系式;(3) 是否存在某一时刻t ,使线段PQ 恰好把Rt △ ACB 的周长和面积同时平分?若存在,求 出此时t 的值;若不存在,说明理由;(4) 如图②,连接 PC,并把△ PQC 沿QC 翻折,得到四边形 PQP C,那么是否存在某一时 刻t ,使四边形PQP C 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.北k 上的点M( m n )(在A 点左侧)是双曲线 y 上的动点.过点B 作BD// y 轴于点D.过Nxk (0, - n )作NC// x 轴交双曲线y 于点E ,交BD 于点C. x(1) 若点D 坐标是(—8, 0),求A 、B 两点坐标及k 的值.(2) 若B 是CD 的中点,四边形 OBCE 勺面积为4,求直线CM 的解析式.(3) 设直线 AM BM 分别与y 轴相交于 P 、Q 两点,且 MA= pMR MB= qMQ 求p — q 的值.29. (2008年江苏省无锡市) 一种电讯信号转发装置的发射直径为 31km .现要求:在一边长为30km 的正方形城区选择若干个安装点, 每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:(1 )能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求? 答题要求:请你在解答时,画出必要的示意图, 并用必要的计算、推理和文字来说明你的理由•(下面给出了几个边长为30km 的正方形城区示意图,供解题时选用)图1 图2 图3 图 428. (2008年江苏省南通市)已知双曲线 y 二一与直线y x 相交于Ax4B 两点•第一象限图①BC压轴题答案「c = 31. 解:(1)由已知得:解得…1 - b ■ c = 0c=3,b=2•••抛物线的线的解析式为y = -x2• 2x • 3(2)由顶点坐标公式得顶点坐标为(1 , 4)所以对称轴为x=1,A,E关于x=1对称,所以E(3,0)设对称轴与x轴的交点为F所以四边形ABDE的面积=S ABO ' S梯形BOFD ' S.QFE1 1 1=—AO BO —(BO DF) OF —EF DF2 221 1 1=—1 3 — (3 4) 1 2 42 22=9(3)相似如图,BD= BG2DG^ 1212 = 2BE= ,BO2OE2二3232DE= DF2EF2二2242=2,5BD2BE2=DE2,所以BDE是直角三角形所以BD2 BE2=20 , DE2=20 即:所以.AOB =. DBE =90 ,且 二 2,BD BE 2所以:AOBL DBE •2. (1) T A , B 两点的坐标分别是 A(10 , 0)和B(8 , 2.3),tan ZOAB ---------- 3 ,10—8■OAB =60当点A '在线段AB 上时,••• • OAB =60 , TA=TA ■ △ A 'TA 是等边三角形,且 TP _ TA :33(10 — t) , AP2当t=2时,S 的值最大是 4.3 ;^-A P TP 3(10 —t)2,2 82^3当A '与B 重合时,AT=AB=4 ,si n60°所以此时6 mt :: 10.x⑵当点A '在线段AB 的延长线,且点 P 在线段AB (不与B 重合)上时, 纸片重叠部分的图形是四边形 (如图(1),其中E 是TA '与CB 的交点), 当点P 与B 重合时,AT=2AB=8,点T 的坐标是(2, 又由⑴中求得当A '与B 重合时,T 的坐标是(6, 0) 所以当纸片重叠部分的图形是四边形时, 2 t <6.(3)S 存在最大值32①当 6 汨 <10时,S (10 — t ),8x在对称轴t=10的左边,S 的值随着t 的增大而减小,•••当t=6时,S 的值最大是 2 3.㈢当2 < t :: 6时,由图。
2009年中考数学试题与二次函数有关的题目(绝对的精品)

25.(12分)已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0),与y 轴的正半轴交于点C .⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标; ⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式;⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.25.解:⑴对称轴是直线:1=x ,点B 的坐标是(3,0). ……2分说明:每写对1个给1分,“直线”两字没写不扣分.⑵如图,连接PC ,∵点A 、B 的坐标分别是A (-1,0)、B (3,0),∴AB =4.∴.AB PC 242121=⨯==在Rt △POC 中,∵O P =PA -OA =2-1=1, ∴.PO PC OC 3122222=-=-=∴b =.3 ………………………………3分 当01=-=,y x 时,,a a 032=+--∴.a 33=………………………………4分 ∴.x x y 3332332++-= ………………5分 ⑶存在.……………………………6分理由:如图,连接AC 、BC .设点M 的坐标为),(y x M .①当以AC 或BC 为对角线时,点M 在x 轴上方,此时CM ∥AB ,且CM =AB . 由⑵知,AB =4,∴|x |=4,3==OC y .∴x =±4.∴点M 的坐标为)3,4()3,4(-或M .…9分说明:少求一个点的坐标扣1分.②当以AB 为对角线时,点M 在x 轴下方.过M 作MN ⊥AB 于N ,则∠MNB =∠AOC =90°.∵四边形AMBC 是平行四边形,∴AC =MB ,且AC ∥MB .∴∠CAO =∠MBN .∴△AOC ≌△BNM .∴BN =AO =1,MN =CO =3. ∵OB =3,∴0N =3-1=2.∴点M 的坐标为(2,3)M -. ……………………………12分说明:求点M 的坐标时,用解直角三角形的方法或用先求直线解析式,然后求交点M 的坐标的方法均可,请参照给分.综上所述,坐标平面内存在点M ,使得以点A 、B 、C 、M 为顶点的四边形是平行四边形.其坐标为123(4,3),(4,3),(2,3)M M M --.说明:①综上所述不写不扣分;②如果开头“存在”二字没写,但最后解答全部正确,不扣分。
2009年全国各地中考数学压轴题精选
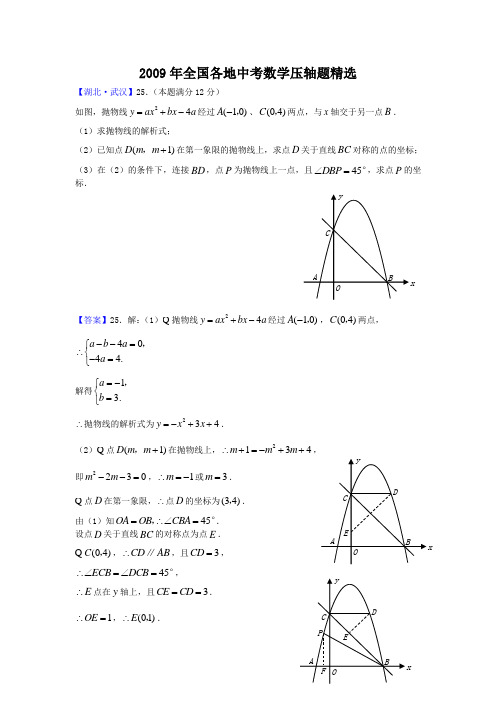
2009年全国各地中考数学压轴题精选【湖北·武汉】25.(本题满分12分)如图,抛物线24y ax bx a =+-经过(10)A -,、(04)C ,两点,与x 轴交于另一点B . (1)求抛物线的解析式;(2)已知点(1)D m m +,在第一象限的抛物线上,求点D 关于直线BC 对称的点的坐标; (3)在(2)的条件下,连接BD ,点P 为抛物线上一点,且45DBP ∠=°,求点P 的坐标.【答案】25.解:(1) 抛物线24y ax bx a =+-经过(10)A -,,(04)C ,两点,404 4.a b a a --=⎧∴⎨-=⎩, 解得13.a b =-⎧⎨=⎩,∴抛物线的解析式为234y x x =-++.(2) 点(1)D m m +,在抛物线上,2134m m m ∴+=-++,即2230m m --=,1m ∴=-或3m =.点D 在第一象限,∴点D 的坐标为(34),. 由(1)知45OA OB CBA =∴∠=,°. 设点D 关于直线BC 的对称点为点E .(04)C ,,CD AB ∴∥,且3CD =,45ECB DCB ∴∠=∠=°,E ∴点在y 轴上,且3CE CD ==.1OE ∴=,(01)E ∴,.即点D 关于直线BC 对称的点的坐标为(0,1).(3)方法一:作PF AB ⊥于F ,DE BC ⊥于E . 由(1)有:445OB OC OBC ==∴∠=,°, 45DBP CBD PBA ∠=∴∠=∠ °,.(04)(34)C D ,,,,CD OB ∴∥且3CD =.45DCE CBO ∴∠=∠=°,DE CE ∴==. 4OB OC ==,BC ∴=2BE BC CE ∴=-= 3tan tan 5DE PBF CBD BE ∴∠=∠==. 设3PF t =,则5BF t =,54OF t ∴=-,(543)P t t ∴-+,.P 点在抛物线上,∴23(54)3(54)4t t t =--++-++, 0t ∴=(舍去)或2225t =,266525P ⎛⎫∴- ⎪⎝⎭,. 方法二:过点D 作BD 的垂线交直线PB 于点Q ,过点D 作DH x ⊥轴于H .过Q 点作QG DH ⊥于G .45PBD QD DB ∠=∴= °,. QDG BDH ∴∠+∠90=°,又90DQG QDG ∠+∠=°,DQG BDH ∴∠=∠.QDG DBH ∴△≌△,4QG DH ∴==,1DG BH ==.由(2)知(34)D ,,(13)Q ∴-,.(40)B ,,∴直线BP 的解析式为31255y x =-+.解方程组23431255y x x y x ⎧=-++⎪⎨=-+⎪⎩,,得1140x y =⎧⎨=⎩,;222566.25x y ⎧=-⎪⎪⎨⎪=⎪⎩,∴点P 的坐标为266525⎛⎫- ⎪⎝⎭,.【重庆·綦江】*26.(11分)如图,已知抛物线(1)20)y a x a =-+≠经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC . (1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.【答案】*26.解:(1)抛物线2(1)0)y a x a =-+≠经过点(20)A -,,093a a ∴=+=-························· 1分 ∴二次函数的解析式为:2333y x x =-++ ············· 3分 (2)D为抛物线的顶点(1D ∴过D 作DN OB ⊥于N,则DN =3660AN AD DAO =∴==∴∠=,° ·············· 4分OM AD ∥①当AD OP =时,四边形DAOP 是平行四边形 66(s)OP t ∴=∴= ············· 5分②当DP OM ⊥时,四边形DAOP 是直角梯形过O 作OH AD ⊥于H ,2AO =,则1AH =(如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求1AH =)55(s)OP DH t ∴===·························· 6分 ③当PD OA =时,四边形DAOP 是等腰梯形 26244(s)OP AD AH t ∴=-=-=∴=综上所述:当6t =、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形. 7分(3)由(2)及已知,60COB OC OB OCB ∠==°,,△是等边三角形 则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<,,,过P 作PE OQ ⊥于E,则PE =···················· 8分116(62)22BCPQ S t ∴=⨯⨯⨯-=2322t ⎫-+⎪⎝⎭··························· 9分 当32t =时,BCPQ S··················· 10分 ∴此时33393324444OQ OP OE QE PE ==∴=-==,=,2PQ ∴=== ··············· 11分【浙江·丽水】24. 已知直角坐标系中菱形ABCD 的位置如图,C ,D 两点的坐标分别为(4,0),(0,3).现有两动点P ,Q 分别从A ,C同时出发,点P 沿线段AD 向终点D 运动,点Q 沿折线CBA 向终点A 运动,设运动时间为t 秒.(1)填空:菱形ABCD 的边长是 ▲ 、面积是 ▲ 、Oxy ABC DE(第24题)高BE 的长是 ▲ ; (2)探究下列问题:①若点P 的速度为每秒1个单位,点Q 的速度为每秒2个单位.当点Q 在线段BA 上时,求△APQ 的面积S 关于t 的函数关系式,以及S 的最大值; ②若点P 的速度为每秒1个单位,点Q 的速度变为每秒k 个单位,在运动过程中,任何时刻都有相应的k 值,使得 △APQ 沿它的一边翻折,翻折前后两个三角形组成的四边 形为菱形.请探究当t =4秒时的情形,并求出k 的值.【答案】24.(本题12分)解:(1)5 , 24,524.......................................3分 (2)①由题意,得AP =t ,AQ =10-2t. (1)分如图1,过点Q 作QG ⊥AD ,垂足为G ,由QG ∥BE 得△AQG ∽△ABE ,∴BAQABE QG =, ∴QG =2548548t-, …………………………1分 ∴t t QG AP S 5242524212+-=⋅=(25≤t ≤5).……1分∵6)25(25242+--=t S (25≤t ≤5).∴当t =25时,S 最大值为6.…………………1分② 要使△APQ 沿它的一边翻折,翻折前后的两个三角形组成的四边形为菱形,根据轴对称的性质,只需△APQ 为等腰三角形即可. 当t =4秒时,∵点P 的速度为每秒1个单位,∴AP =4.………………1分 以下分两种情况讨论:第一种情况:当点Q 在CB 上时, ∵PQ ≥BE >PA ,∴只存在点Q 1,使Q 1A =Q 1P .如图2,过点Q 1作Q 1M ⊥AP ,垂足为点M ,Q 1M 交AC 于点F ,则AM =122AP =.由△AMF ∽△AOD ∽△CQ 1F ,得4311===AO OD CQ F Q AM FM , ∴23=FM , ∴103311=-=FM MQ F Q . ………………1分∴CQ 1=QF 34=225.则11CQ AP t k t =⋅⨯,∴11110CQ k AP == .……………………………1分 第二种情况:当点Q 在BA 上时,存在两点Q 2,Q 3,分别使A P = A Q 2,PA =PQ 3.①若AP =A Q 2,如图3,CB +BQ 2=10-4=6.则21BQ CB AP t k t +=⋅⨯,∴232CB BQ k AP +==.……1分②若PA =PQ 3,如图4,过点P 作PN ⊥AB ,垂足为N ,由△ANP ∽△AEB ,得ABAPAE AN =. ∵AE =5722=-BE AB , ∴AN =2825. ∴AQ 3=2AN=5625, ∴BC+BQ 3=10-251942556=则31BQ CB APt k t +=⋅⨯.∴50973=+=AP BQ CB k . ………………………1分综上所述,当t = 4秒,以所得的等腰三角形APQ沿底边翻折,翻折后得到菱形的k 值为1011或23或5097.【湖南·益阳】六、解答题:本题满分14分. 20.阅读材料:如图12-1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法:ah S ABC21=∆,即三角形面积等于水平宽与铅垂高乘积的一半. 解答下列问题:如图12-2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆;(3)是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.图12-2xC O yABD11图12-1【答案】六、解答题:本题满分14分.20.解:(1)设抛物线的解析式为:4)1(21+-=x a y ············· 1分把A (3,0)代入解析式求得1-=a所以324)1(221++-=+--=x x x y ·············· 3分设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( ··········· 4分 把)0,3(A ,)3,0(B 代入b kx y +=2中 解得:3,1=-=b k所以32+-=x y ······················· 6分 (2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2所以CD =4-2=2 ························ 8分32321=⨯⨯=∆CAB S (平方单位) ················10分 (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△PAB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-= ······· 12分 由S △PAB =89S △CAB 得:389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中, 解得P 点坐标为)415,23( ···················· 14分【遂宁市】25.如图,二次函数的图象经过点D(0,397),且顶点C 的横坐标为4,该图象在x 轴上截得的线段AB 的长为6.⑴求二次函数的解析式;⑵在该抛物线的对称轴上找一点P ,使PA+PD 最小,求出点P 的坐标;⑶在抛物线上是否存在点Q ,使△QAB 与△ABC 相似?如果存在,求出点Q 的坐标;如果不存在,请说明理由.【答案】25.⑴设二次函数的解析式为:y=a(x-h)2+k∵顶点C 的横坐标为4,且过点(0,397)∴y=a(x-4)2+k k a +=16397 ………………①又∵对称轴为直线x=4,图象在x 轴上截得的线段长为6 ∴A(1,0),B(7,0) ∴0=9a+k ………………② 由①②解得a=93,k=3-∴二次函数的解析式为:y=93(x-4)2-3⑵∵点A 、B 关于直线x=4对称 ∴PA=PB∴PA+PD=PB+PD ≥DB∴当点P 在线段DB 上时PA+PD 取得最小值 ∴DB 与对称轴的交点即为所求点P 设直线x=4与x 轴交于点M∵PM ∥OD ,∴∠BPM=∠BDO ,又∠PBM=∠DBO ∴△BPM ∽△BDO∴BO BM DO PM = ∴3373397=⨯=PM ∴点P 的坐标为(4,33)⑶由⑴知点C(4,3-),又∵AM=3,∴在Rt △AMC 中,cot ∠ACM=33,∴∠ACM=60o,∵AC=BC ,∴∠ACB=120o①当点Q 在x 轴上方时,过Q 作QN ⊥x 轴于N 如果AB=BQ ,由△ABC ∽△ABQ 有 BQ=6,∠ABQ=120o,则∠QBN=60o∴QN=33,BN=3,ON=10, 此时点Q(10,33),如果AB=AQ ,由对称性知Q(-2,33) ②当点Q 在x 轴下方时,△QAB 就是△ACB , 此时点Q 的坐标是(4,3-),经检验,点(10,33)与(-2,33)都在抛物线上 综上所述,存在这样的点Q ,使△QAB ∽△ABC 点Q 的坐标为(10,33)或(-2,33)或(4,3-).【江西】24.如图,抛物线223y x x =-++与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连接BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF DE ∥交抛物线于点F ,设点P 的横坐标为m ;①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设BCF △的面积为S ,求S 与m 的函数关系式.【答案】24.解:(1)A (-1,0),B (3,0),C (0,3). ············ 2分(第24题)抛物线的对称轴是:x =1. ······················ 3分(2)①设直线BC 的函数关系式为:y=kx+b .把B (3,0),C (0,3)分别代入得:303k b b +=⎧⎨=⎩,解得:k = -1,b =3. 所以直线BC 的函数关系式为:3y x =-+. 当x =1时,y = -1+3=2,∴E (1,2). 当x m =时,3y m =-+,∴P (m ,-m +3). ························· 4分 在223y x x =-++中,当1x =时,4y =.∴()14D ,.当x m =时,223y m m =-++,∴()223F m m m -++,. ········ 5分∴线段DE =4-2=2,线段()222333PF m m m m m =-++--+=-+. ··· 6分∵PF DE ∥,∴当PF ED =时,四边形PEDF 为平行四边形.由232m m -+=,解得:1221m m ==,(不合题意,舍去).因此,当2m =时,四边形PEDF 为平行四边形. ··········· 7分②设直线PF 与x 轴交于点M ,由()()3000B O ,,,,可得:3OB OM MB =+=. ∵BPF CPF S S S =+△△. ······················· 8分即1111()2222S PF BM PF OM PF BM OM PF OB =+=+= . ∴()()221393303222S m m m m m =⨯-+=-+≤≤.········· 9分 说明:1.第(1)问,写对1个或2个点的坐标均给1分,写对3个点的坐标得2分;2.第(2)问,S 与m 的函数关系式未写出m 的取值范围不扣分.【江西】25.如图1,在等腰梯形ABCD 中,AD BC ∥,E 是AB 的中点,过点E 作EF BC ∥交CD 于点F .46AB BC ==,,60B =︒∠. (1)求点E 到BC 的距离; (2)点P 为线段EF 上的一个动点,过P 作PM EF ⊥交BC 于点M ,过M 作MN AB ∥交折线ADC 于点N ,连结PN ,设EP x =. ①当点N 在线段AD 上时(如图2),P M N △的形状是否发生改变?若不变,求出PMN △的周长;若改变,请说明理由;②当点N 在线段DC 上时(如图3),是否存在点P ,使PMN △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.【答案】25.(1)如图1,过点E 作EG BC ⊥于点G .1分∵E 为AB 的中点,∴122BE AB ==.在Rt EBG △中,60B =︒∠,∴30BEG =︒∠. ··· 2分∴112BG BE EG ====, 即点E 到BC ··········· 3分(2)①当点N 在线段AD 上运动时,PMN △的形状不发生改变. ∵PM EF EG EF ⊥⊥,,∴PM EG ∥. ∵EF BC ∥,∴EP GM =,PM EG ==同理4MN AB ==. ·························· 4分 如图2,过点P 作PH MN ⊥于H ,∵MN AB ∥, ∴6030NMC B PMH ==︒=︒∠∠,∠. ∴122PH PM == ∴3cos302MH PM =︒= .则35422NH MN MH =-=-=.A D E BFC图4(备用)AD EBF C图5(备用)A D E BF C 图1图2 A D E BF C PNM图3A D EBFCPN M(第25题) 图1A D E BF CG图2A DEBF CPNMG H在Rt PNH △中,PN === ∴PMN △的周长=4PM PN MN ++=. ············ 6分 ②当点N 在线段DC 上运动时,PMN △的形状发生改变,但MNC △恒为等边三角形.当PM PN =时,如图3,作PR MN ⊥于R ,则MR NR =.类似①,32MR =. ∴23MN MR ==.··························· 7分 ∵MNC △是等边三角形,∴3MC MN ==.此时,6132x EP GM BC BG MC ===--=--=. ··········· 8分当MP MN =时,如图4,这时MC MN MP ===此时,615x EP GM ===-=当NP NM =时,如图5,30NPM PMN ==︒∠∠.则120PMN =︒∠,又60MNC =︒∠, ∴180PNM MNC +=︒∠∠.因此点P 与F 重合,PMC △为直角三角形. ∴tan301MC PM =︒= .此时,6114x EP GM ===--=.综上所述,当2x =或4或(5-时,PMN △为等腰三角形. ······ 10分【济南】24.(本小题满分9分)已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.图3A D E BFCPNM图4A D EBFCP MN 图5A D E BF (P ) CMN GGRG(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.【答案】24.(本小题满分9分)解:(1)由题意得129302ba abc c ⎧=⎪⎪⎪-+=⎨⎪⎪=-⎪⎩ ···················· 2分解得23432a b c ⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩∴此抛物线的解析式为224233y x x =+- ··············· 3分 (2)连结AC 、BC .因为BC 的长度一定,所以PBC △周长最小,就是使PC PB +最小.B 点关于对称轴的对称点是A 点,AC 与对称轴1x =-的交点即为所求的点P .设直线AC 的表达式为y kx b =+则302k b b -+=⎧⎨=-⎩,···························································· 4分解得232k b ⎧=-⎪⎨⎪=-⎩∴此直线的表达式为223y x =--. ·················· 5分(第24题图)(第24题图)把1x =-代入得43y =- ∴P 点的坐标为413⎛⎫--⎪⎝⎭, ····················· 6分 (3)S 存在最大值························· 7分 理由:∵DE PC ∥,即DE AC ∥. ∴OED OAC △∽△.∴OD OE OC OA =,即223m OE-=.∴333322OE m AE OE m =-==,,方法一:连结OPOED POE POD OED PDOE S S S S S S =-=+-△△△△四边形=()()13411332132223222m m m m ⎛⎫⎛⎫⨯-⨯+⨯-⨯-⨯-⨯- ⎪ ⎪⎝⎭⎝⎭=23342m m -+ ························· 8分 ∵304-<∴当1m =时,333424S =-+=最大 ················· 9分方法二:OAC OED AEP PCD S S S S S =---△△△△=()1131341323212222232m m m m ⎛⎫⨯⨯-⨯-⨯--⨯⨯-⨯⨯ ⎪⎝⎭ =()22333314244m m m -+=--+ ················· 8分 ∵304-<∴当1m =时,34S =最大 ····················· 9分【衡阳】26、(本小题满分9分)如图12,直线4+-=x y 与两坐标轴分别相交于A 、B 点,点M 是线段AB 上任意一点(A 、B 两点除外),过M 分别作MC ⊥OA 于点C ,MD ⊥OB 于D .(1)当点M 在AB 上运动时,你认为四边形OCMD 的周长是否发生变化?并说明理由;(2)当点M 运动到什么位置时,四边形OCMD 的面积有最大值?最大值是多少?(3)当四边形OCMD 为正方形时,将四边形OCMD 沿着x 轴的正方向移动,设平移的距离为)40<<a a (,正方形OCMD 与△AOB 重叠部分的面积为S .试求S 与a 的函数关系式并画出该函数的图象.【答案】解:(1)设点M 的横坐标为x ,则点M 的纵坐标为-x+4(0<x<4,x>0,-x+4>0); 则:MC =∣-x+4∣=-x+4,MD =∣x ∣=x ;∴C 四边形OCMD =2(MC+MD )=2(-x+4+x )=8∴当点M 在AB 上运动时,四边形OCMD 的周长不发生变化,总是等于8;(2)根据题意得:S 四边形OCMD =MC ·MD =(-x+4)· x =-x 2+4x =-(x-2)2+4∴四边形OCMD 的面积是关于点M 的横坐标x (0<x<4)的二次函数,并且当x =2,即当点M 运动到线段AB 的中点时,四边形OCMD 的面积最大且最大面积为4; (3)如图10(2),当20≤<a 时,42121422+-=-=a a S ; 如图10(3),当42<≤a 时,22)4(21)4(21-=-=a a S ;∴S 与a 的函数的图象如下图所示:【鄂州】27.如图所示,将矩形OABC 沿AE 折叠,使点O 恰好落在BC 上F 处,以CF 为边作正方形CFGH ,延长BC 至M ,使CM =|CF —EO |,再以CM 、CO 为边作矩形CMNO (1)试比较EO 、EC 的大小,并说明理由 (2)令;四边形四边形CNMN CFGHS S m =,请问m 是否为定值?若是,请求出m 的值;若不是,请说明理由(3)在(2)的条件下,若CO =1,CE =31,Q 为AE 上一点且QF =32,抛物线y =mx 2+bx+c经图12(1)图12(2)图12(3)))4<≤a过C 、Q 两点,请求出此抛物线的解析式.(4)在(3)的条件下,若抛物线y =mx 2+bx+c 与线段AB 交于点P ,试问在直线BC 上是否存在点K ,使得以P 、B 、K 为顶点的三角形与△AEF 相似?若存在,请求直线KP 与y 轴的交点T 的坐标?若不存在,请说明理由。
中考二次函数压轴题经典例题

中考二次函数压轴题经典例题一、一类中考二次函数高分难题:如考题:“某费用与生产成本的平方成正比,生产成本为每件5元时,总费用为125元,生产成本为每件10元时,总费用为多少元?”解:依题意可知费用与生产成本的平方之间的关系式为y=kx²,经过点(5,125),代入上式得k=5。
于是,当生产成本为每件10元时,总费用y=5x²=5×10²=500元。
二、二次函数的解析式与图像:题目:“已知函数y = ax² + bx + c(a ≠ 0)如果x1、x2是y = 0的解,试求函数的解析式。
”解:如果已知x1、x2是y=0的解,那么二次函数的解析式可以表示为y=a(x-x1)(x-x2)。
对x进行配平方,得y=ax²-(x1+x2)ax+ax1x2,与y=ax²+bx+c相比,可以得出b=-(x1+x2)a, c=ax1x2。
由此可以看出,二次函数的系数与其解之间存在着规律性的联系。
三、二次函数的最值问题:题目:“设函数y=ax²+bx+c,在点(0,c)处取得最值,已知a,c>0, c是常数,求a,b 的取值范围。
”解:本题主要考查了函数的极值点。
首先明确这样一个概念:一个函数在它的极值点处的导数等于0。
设二次函数y=ax²+bx+c的极值点为x0,将它代入导数等于0的方程式得到x0=-b/2a,所以二次函数的对称轴为x=-b/2a。
因为函数在点(0,c)处取得最值,那么有x0=0,将x0=0代入上式,解得b=0。
又因为a,c>0,且当a>0时,抛物线开口朝上,函数的最小值点在对称轴上,与题意相符。
故a>0,所以a,b的取值范围是:a>0,b=0。
2009年中考试题专题之13-二次函数试题及答案

2、(2009年株洲市)已知ABC ∆为直角三角形,90ACB ∠=︒,AC BC =,点A 、C 在x 轴上,点B 坐标为(3,m )(0m >),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B 、D . (1)求点A 的坐标(用m 表示); (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连结PQ 并延长交BC 于点E ,连结 BQ 并延长交AC 于点F ,试证明:()FC AC EC +为定值.3、(2009年重庆市江津区)某商场在销售旺季临近时 ,某品牌的童装销售价格呈上升趋势,假如这种童装开始时的售价为每件20元,并且每周(7天)涨价2元,从第6周开始,保持每件30元的稳定价格销售,直到11周结束,该童装不再销售。
(1)请建立销售价格y (元)与周次x 之间的函数关系;(2)若该品牌童装于进货当周售完,且这种童装每件进价z (元)与周次x之间的关系为12)8(812+--=x z , 1≤ x ≤11,且x 为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?4、(2009年重庆市江津区)如图,抛物线c bx x y ++-=2与x 轴交与A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式; (2)设(1)中的抛物线交y 轴与C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由.5、(2009年滨州)某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:(1)若设每件降价x 元、每星期售出商品的利润为y 元,请写出y 与x 的函数关系式,并求出自变量x 的取值范围;(2)当降价多少元时,每星期的利润最大?最大利润是多少? (3)请画出上述函数的大致图象. 6、(2009年滨州) 如图①,某产品标志的截面图形由一个等腰梯形和抛物线的一部分组成,在等腰梯形ABCD 中,AB DC ∥,20cm 30cm 45AB DC ADC ==∠=,,°.对于抛物线部分,其顶点为CD 的中点O ,且过A B 、两点,开口终端的连线MN 平行且等于DC .(1)如图①所示,在以点O 为原点,直线OC 为x 轴的坐标系内,点C 的坐标为(150),,试求A B 、两点的坐标;(2)求标志的高度(即标志的最高点到梯形下底所在直线的距离);(3)现根据实际情况,需在标志截面图形的梯形部分的外围均匀镀上一层厚度为3cm 的保护膜,如图②,请在图中补充完整镀膜部分的示意图,并求出镀膜的外围周长.7、 (2009年四川省内江市)如图所示,已知点A (-1,0),B (3,0),C (0,t ),且t >0,tan ∠BAC=3,抛物线经过A 、B 、C 三点,点P (2,m )是抛物线与直线)1(:+=x k y l 的一个交点。
2009年二次函数压轴题
不存在,请说明理由.
y M
C
B
D O (A) 图1
Ex
y M
N
C
B
P
DO A 图2
Ex
2
11. 如图,已知抛物线 C1: y a x 2 5 的顶点为 P,与 x 轴相交于 A、B 两点(点 A 在点 B
否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
y
D
C
9. 如图 1,已知抛物线经过坐标原点
O 和 x 轴上另一点
E ,顶点AM
的坐标为 O(2,4)
;B矩形
ABCD
x
的
Q C
顶点 A 与点 O 重合, AD、AB 分别在 x 轴、 y 轴上,且 AD 2 , AB 3 .
( 1)求该抛物线所对应的函数关系式;
请直接写出相应的 t 值.
y
AF D
G
PE
Q
O
B
C
x
13. 如图 1,已知正比例函数和反比例函数的图像都经过点
M(- 2, - 1),且 P( - 1,- 2)为双曲线上
的一点, Q 为坐标平面上一动点, PA 垂直于 x 轴, QB 垂直于 y 轴,垂足分别是 A、B.
( 1)写出正比例函数和反比例函数的关系式;
( 1)当矩形 OEDC 的顶点 D 在直线 AB 上时,求 t 的值;
( 2)当 t 4 时,求 S 的值;
y
B
( 3)直接写出 S 与 t 的函数关系式; (不必写出解题过程)
( 4)若 S 12 ,则 t
[学子教育]2009年全国中考数学压轴题5(修订版)
![[学子教育]2009年全国中考数学压轴题5(修订版)](https://img.taocdn.com/s3/m/c2c939529b6648d7c1c7464a.png)
年全国中考数学分类试题综合题压轴题汇编教师答案版(湖南长沙).(本题满分分)如图,二次函数()的图象与轴交于两点,与轴相交于点.连结两点的坐标分别为、,且当和时二次函数的函数值相等.()求实数的值;()若点同时从点出发,均以每秒个单位长度的速度分别沿边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为秒时,连结,将沿翻折,点恰好落在边上的处,求的值及点的坐标;()在()的条件下,二次函数图象的对称轴上是否存在点,使得以为项点的三角形与相似?如果存在,请求出点的坐标;如果不存在,请说明理由.(湖南衡阳)、(本小题满分分)如图,直线与两坐标轴分别相交于、点,点是线段上任意一点(、两点除外),过分别作⊥于点,⊥于.()当点在上运动时,你认为四边形的周长是否发生变化?并说明理由;()当点运动到什么位置时,四边形的面积有最大值?最大值是多少? ()当四边形为正方形时,将四边形沿着轴的正方向移动,设平移的距离为,正方形与△重叠部分的面积为.试求与的函数关系式并画出该函数的图象.解:()设点的横坐标为,则点的纵坐标为-(<<,>,->); 则:=∣-∣=-,=∣∣=;∴四边形=()=(-)=∴当点在上运动时,四边形的周长不发生变化,总是等于; ()根据题意得:四边形=·=(-)· =-=-()∴四边形的面积是关于点的横坐标(<<)的二次函数,并且当=,即当点运动到线段的中点时,四边形的面积最大且最大面积为; ()如图(),当时,; 如图(),当时,;∴与的函数的图象如下图所示:(湖南娄底).(本小题分)如图,在△中,∠°,,,另有一直角梯形图()图()图()· ·(∥,∠°)的底边落在上,腰落在上,且,∠∠,∶∶()延长交于,求△的面积.()操作:固定△,将直角梯形以每秒个单位的速度沿方向向右移动,直到点与点重合时停止,设运动的时间为秒,运动后的直角梯形为′(如图).探究:在运动中,四边形′能否为正方形?若能,请求出此时的值;若不能,请说明理由.探究:在运动过程中,△与直角梯形′重叠部分的面积为,求与的函数关系..(分)解:()∵∶∶,∴×又∵∥,∴∥,∴△∽△…………………………分∴,即,∴…………………………………分∴△·××……………………………………分()①能为正方形…………………………………………………………………分∵′∥,∥′,∴四边形′为平行四边形又∠°,∴四边形′为矩形…………………………………分又∴当时,四边形′为正方形此时可得秒时,四边形′为正方形…………………………分②(Ⅰ)∵∠∠,∴∥∴当秒时,直角梯形的腰与重合.当≤≤时,重叠部分的面积为直角梯形′的面积.…………分过作⊥于,∠∠∴×,∴直角梯形′的面积为()×∴………………………………………………………………分(Ⅱ)∵当<≤时,重叠部分的面积为四边形的面积矩形′的面积.…………………………………………………………分而边形△△××矩形′∴……………………………………………………………………分 (Ⅲ)当<≤时,如图,设′交于.又∠∴()………………分∴重叠部分的面积△··()()()∴重叠部分面积与的函数关系式:(≤≤)(<≤)(<≤)(注:评分时,考生未作结论不扣分)(湖南益阳)六、解答题:本题满分分. .阅读材料:如图,过△的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△的“水平宽”(),中间的这条直线在△内部线段的长度叫△的“铅垂高()”.我们可得出一种计算三角形面积的新方法:,即三角形面积等于水平宽与铅垂高乘积的一半.解答下列问题:如图,抛物线顶点坐标为点(),交轴于点(),交轴于点.()求抛物线和直线的解析式;()点是抛物线(在第一象限内)上的一个动点,连结,,当点运动到顶点时,求△的铅垂高及;()是否存在一点,使△△,若存在,求出点的坐标;若不存在,请说明理由.……………………………………分图六、解答题:本题满分分..解:()设抛物线的解析式为: ·················································分把()代入解析式求得所以 ···············································分设直线的解析式为:由求得点的坐标为·········································分把,代入中解得:所以 ···········································································分()因为点坐标为(1)所以当=1时,=,=所以== ······················································································分(平方单位) ·······················································分()假设存在符合条件的点,设点的横坐标为,△的铅垂高为,则··························分由△△得:化简得:解得,将代入中,解得点坐标为 ·····································································分(湖南株洲).(本题满分分)如图,已知为直角三角形,,,点、在轴上,点坐标为(,)(),线段与轴相交于点,以(,)为顶点的抛物线过点、. ()求点的坐标(用表示);()求抛物线的解析式; ()设点为抛物线上点至点之间的一动点,连结并延长交于点,连结并延长交于点,试证明:为定值..()由可知,,又△为等腰直角三角形,∴,,所以点的坐标是(). ………………… 分()∵ ∴,则点的坐标是(). 又抛物线顶点为,且过点、,所以可设抛物线的解析式为:,得:解得∴抛物线的解析式为 ………分()过点作于点,过点作于点,设点的坐标是,则,. ∵ ∴∽ ∴ 即,得∵ ∴∽ ∴ 即,得又∵∴即为定值. ……………………分个人整理,仅供交流学习--------------------------------------------------------------------------------------------------------------------。
2009年中考压轴题精选

2009年中考压轴题精选/台州9.已知二次函数c bx ax y ++=2的y 与x 的部分对应值如下表:x… 1- 0 1 3 … y…3-131…则下列判断中正确的是( )A .抛物线开口向上B .抛物线与y 轴交于负半轴C .当x =4时,y >0D .方程02=++c bx ax 的正根在3与4之间 10.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式.....,如a b c ++就是完全对称式.下列三个代数式:①2)(b a -;②ab bc ca ++;③222a b b c c a ++.其中是完全对称式的是( )A .①②B .①③C . ②③D .①②③ 15.如图,三角板ABC 中,︒=∠90ACB ,︒=∠30B ,6=BC .三角板绕直角顶点C 逆时针旋转,当点A 的对应点'A 落在AB 边的起始位置上时即停止转动,则点B 转过的路径长为 .16.将正整数1,2,3,…从小到大按下面规律排列.若第4行第2列的数为32,则①n = ;②第i 行第j 列的数为 (用i ,j 表示).第1列 第2列 第3列… 第n 列第1行12 3 … n第2行 1+n 2+n 3+n … n 2 第3行 12+n 22+n 32+n… n 3………………23.定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内..点..如图1,PH PJ =,PI PG =,则点P 就是四边形ABCD 的准内点.(1)如图2, AFD ∠与DEC ∠的角平分线,FP EP 相交于点P .求证:点P 是四边形ABCD 的准内点.(2)分别画出图3平行四边形和图4梯形的准内点.(作图工具不限,不写作法,但要有必要的说明) (3)判断下列命题的真假,在括号内填“真”或“假”. ①任意凸四边形一定存在准内点.( ) ②任意凸四边形一定只有一个准内点.( )③若P 是任意凸四边形ABCD 的准内点,则PD PC PB PA +=+ 或PD PB PC PA +=+.( )(第23题)图3 图2图4 F E D C B A P G HJ I 图1 B J IH GDC AP24.如图,已知直线121+-=x y 交坐标轴于B A ,两点,以线段AB 为边向上作 正方形ABCD ,过点C D ,A ,的抛物线与直线另一个交点为E . (1)请直接写出点D C ,的坐标; (2)求抛物线的解析式;(3)若正方形以每秒5个单位长度的速度沿射线AB 下滑,直至顶点D 落在x 轴上时停止.设正方形落在x 轴下方部分的面积为S ,求S 关于滑行时间t 的函数关系式,并写出相应自变量t 的取值范围;(4)在(3)的条件下,抛物线与正方形一起平移,同时D 停止,求抛物线上E C , 两点间的抛物线弧所扫过的面积.2009年中考压轴题精选/河南5.如图所示,在平面直角坐标系中,点A 、B 的坐标分别为(﹣2,0)和(2,0).月牙①绕点B 顺时针旋转900得到月牙②,则点A 的对应点A ’的坐标为( ) (A )(2,2) (B )(2,4) (C)(4,2) (D)(1,2)6.一个几何体由一些大小相同的小正方体组成,如图 是它的主视图和俯视图,那么组成该几何体所需小正 方体的个数最少为( )(A )3 (B ) 4 (C) 5 (D)6 14.动手操作:在矩形纸片ABCD 中,AB =3,AD =5.如图所示, 折叠纸片,使点A 落在BC 边上的A ’处,折痕为PQ ,当点 A ’在BC 边上移动时,折痕的端点P 、Q 也随之移动.若限定 点P 、Q 分别在AB 、AD 边上移动,则点A ’在BC 边上可移 动的最大距离为 .(第24题)y x121+-=x y15.如图,在半径为5,圆心角等于450的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在AB上,则阴影部分的面积为(结果保留 ).21. 如图,在Rt△ABC中,∠ACB=90°, ∠B =60°,BC=2.点0是AC的中点,过点0的直线l从与AC重合的位置开始,绕点0作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.(1)①当α=________度时,四边形EDBC是等腰梯形,此时AD的长为_________;②当α=________度时,四边形EDBC是直角梯形,此时AD的长为_________;(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.23.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值.2009年中考压轴题精选/长春7.菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC=2,则点B的坐标为( )(A)(2,1). (B)(1, 2).(第7题)(C )(2+1,1). (D )(1,2+1).8.如图,动点P 从点A 出发,沿线段AB 运动至点B 后,立即按原路返回.点P 在运动过程中速度大小不变.则以点A 为圆心,线段AP 长为半径的圆的面积S 与点P 的运动时间t 之间的函数图象大致为( )13.用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n 个图案中正三角形的个数为 (用含n 的代数式表示).14.如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为(结果保留π).25.某部队甲、乙两班参加植树活动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为y 甲(棵),乙班植树的总量为y 乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x (时).y 甲、y 乙分别与x 之间的部分函数图象如图所示.(1)当0≤x ≤6时,分别求y 甲、y 乙与x 之间的函数关系式.(3分)(2)如果甲、乙两班均保持前6个小时的工作效率,通过计算说明,当x=8时,甲、乙两班植树的总量之和能否超过260棵.(3分)(3)如果6个小时后,甲班保持前6个小时的工作效率,乙班通过增加人数,提高了工作效率,这样继续植树2小时,活动结束.当x=8时,两班之间植树的总量相差20棵,求乙班增加人数后平均每小时植树多少棵.(4分)26.如图,直线643+-=x y 分别与x 轴、y 轴交于A 、B 两点;直线x y 45=与AB 交于点C ,与过点A 且平行于y 轴的直线交于点D.点E 从点A 出发,以每秒1个单位的速度沿x 轴向左运动.过点E 作x 轴的垂线,分别交直线AB 、OD 于P 、Q 两点,以PQ 为边向右作正方形PQMN.设正方形PQMN 与△ACD 重叠部分(阴影部分)的面积为S(第8题)(第13题)(第14题)(平方单位),点E 的运动时间为t (秒). (1)求点C 的坐标.(1分)(2)当0<t<5时,求S 与t 之间的函数关系式.(4分) (3)求(2)中S 的最大值.(2分) (4)当t>0时,直接写出点(4,29)在正方形PQMN 内部时t 的取值范围.(3分) 【参考公式:二次函数y=ax 2+bx+c 图象的顶点坐标为(ab ac a b 44,22--).】2009年中考压轴题精选/黄石9.如图,ABC △为O ⊙的内接三角形,130AB C =∠=,°,则O ⊙的内接正方形的面积为( ) A .2 B .4 C .8 D .16 10.已知二次函数2y ax bx c =++的图象如图所示,有以下结论: ①0a b c ++<;②1a b c -+>;③0abc >;④420a b c -+<; ⑤1c a ->其中所有正确结论的序号是( ) A .①② B . ①③④ C .①②③⑤ D .①②③④⑤15.下图中正比例函数与反比例函数的图象相交于A B 、两点, 分别以A B 、两点为圆心,画与x 轴相切的两个圆,若点A 的坐 标为(2,1),则图中两个阴影部分面积的和是 . 16.若抛物线23y ax bx =++与232y x x =-++的两交点关 于原点对称,则a b 、分别为 . 25.(本小题满分10分)正方形ABCD 在如图所示的平面直角坐标系中,A 在x 轴正半轴上,D 在y 轴的负半轴上,AB 交y 轴正半轴于E BC ,交x 轴负半轴于F ,1OE =,抛物线24y ax bx =+-过A D F 、、三点.(1)求抛物线的解析式;(3分)11 1- (第10题图)OxyA xyOB(第15题图)(2)Q 是抛物线上D F 、间的一点,过Q 点作平行于x 轴的直线交边AD 于M ,交BC 所在直线于N ,若32FQN AFQM S S =△四边形,则判断四边形AFQM 的形状;(3分) (3)在射线DB 上是否存在动点P ,在射线CB 上是否存在动点H ,使得AP PH ⊥且AP PH =,若存在,请给予严格证明,若不存在,请说明理由.(4分)2009年中考压轴题精选/青海11.如图4,函数y x =与4y x=的图象交于A 、B 两点, 过点A 作AC 垂直于y 轴,垂足为C ,则ABC △的面积 为 .12.观察下面的一列单项式:x ,22x -,34x ,48x -,…根据你发现的规律,第7个单项式为 ;第n 个单项式为 .19.如图7是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为( )20.将三个均匀的六面分别标有1、2、3、4、5、6的正方体同时掷出,出现的数字分别为a b c 、、,则a b c 、、正好是直角三角形三边长的概率是( ) A .1216B .172C .112D .13627.请阅读,完成证明和填空.(第25题图)O y xB E AD CF OAC Bxy图41 3 21 图7 A . B . C . D .九年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:(1)如图12-1,正三角形ABC 中,在AB AC 、边上分别取点M N 、,使BM AN =,连接BN CM 、,发现BN CM =,且60NOC ∠=°. 请证明:60NOC ∠=°.(2)如图12-2,正方形ABCD 中,在AB BC 、边上分别取点M N 、,使A M B N =,连接AN DM 、,那么AN = ,且DON ∠= 度.(3)如图12-3,正五边形ABCDE 中,在AB BC 、边上分别取点M N 、,使A M B N =,连接AN EM 、,那么AN = ,且EON ∠= 度.(4)在正n 边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现: . 28.矩形OABC 在平面直角坐标系中位置如图13所示,A C 、两点的坐标分别为(60)A ,,(03)C -,,直线34y x =-与BC 边相交于D 点.(1)求点D 的坐标;(2)若抛物线294y ax x =-经过点A ,试确定此抛物线的表达式;(3)设(2)中的抛物线的对称轴与直线OD 交于点M ,点P 为对称轴上一动点,以P O M 、、为顶点的三角形与OCD △相似,求符合条件的点P 的坐标.9.如图,P A 、PB 分别与⊙O 相切于点A 、B ,⊙O 的切线EF 分别交P A 、PB 于点E 、F ,切点C 在AB 上,若PA 长为2,则△PEF 的周长是 .A A AB B BC C CD D O O O MM MN N N E图12-1 图12-2 图12-3… yO 3- CD B6 A x34y x=-图1310.一组按一定规律排列的式子:-2a ,52a ,-83a ,114a ,…,(a ≠0)则第n 个式子是______________(n 为正整数).17.如图,AC =AD ,BC =BD ,则有( )A .AB 垂直平分CD B .CD 垂直平分ABC .AB 与CD 互相垂直平分D .CD 平分∠ACB18.如图,有一长为4cm ,宽为3cm 的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上的顶点A 的位置变化为A →A 1→A 2,其中第二次翻滚被桌面上一小木块挡住,使木板边沿A 2C 与桌面成30°角,则点A 翻滚到A 2位置时,共走过的路径长为( ) A .10cm B .3.5πcm C .4.5πcmD .2.5πcm25.(本题满分10分)已知:如图,在Rt △ABC 中,∠ABC =90°,以AB 上的点O 为圆心,OB 的长为半径的圆与AB 交于点E ,与AC 切于点D .(1)求证:BC =CD ; (2)求证:∠ADE =∠ABD ;(3)设AD =2,AE =1,求⊙O 直径的长.26.(本题满分10分)如图,已知抛物线y =34x 2+bx +c 与坐标轴交于A 、B 、C 三点, A 点的坐标为(-1,0),过点C 的直线y =34tx -3与x 轴交于点Q ,点P 是线段BC 上的一个动点,过P 作PH ⊥OB 于点H .若PB =5t ,且0<t <1.(1)填空:点C 的坐标是 ,b = ,c = ; (2)求线段QH 的长(用含t 的式子表示);(3)依点P 的变化,是否存在t 的值,使以P 、H 、Q 为顶点的三角形与△COQ 相似?若存在,求出所有t 的值;若不存在,说明理由.A1A 2A BCA B xyOQH PCABCD EO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
09年中考各地数学试题汇编——二次函数(能力)1、(09安徽芜湖)如图,在平面直角坐标系中放置一直角三角板,其顶点为(10)A -,,B ,(00)O ,,将此三角板绕原点O 顺时针旋转90°,得到A B O ''△. (1)如图,一抛物线经过点A B B '、、,求该抛物线解析式;(2)设点P 是在第一象限内抛物线上一动点,求使四边形PBAB '的面积达到最大时点P 的坐标及面积的最大值.2、(09甘肃庆阳)如图18,在平面直角坐标系中,将一块腰长为5的等腰直角三角板ABC 放在第二象限,且斜靠在两坐标轴上,直角顶点C 的坐标为(1-,0),点B 在抛物线22y ax ax =+-上.(1)点A 的坐标为 ,点B 的坐标为 ; (2)抛物线的关系式为 ;(3)设(2)中抛物线的顶点为D ,求△DBC 的面积; (4)将三角板ABC 绕顶点A 逆时针方向旋转90°,到达AB C ''△的位置.请判断点B '、C '是否在(2)中的抛物线上,并说明理由.3、(09福建莆田)已知,如图抛物线23(0)y ax ax c a =++>与y 轴交于C 点,与x 轴交于A 、B 两点,A 点在B 点左侧。
点B 的坐标为(1,0),OC=30B . (1)、抛物线的解析式;(2)、点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值:(3)、点E 在x 轴上,点P 在抛物线上。
是否存在以A 、C 、E 、P 为顶点且以AC 为一边的平行四边形?若存在,求点P 的坐标;若不存在,请说明理由.x4(((5线上,A 、B 点在地面OM 上,则这个“支撑架”总长的最大值是多少?6、(09广东深圳)如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB .(1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由. (4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△P AB 是否有最大面积?若有,求出此时P 点的坐标及△P AB7、(09福建漳州)如图1,已知:抛物线212y x bx c =++与x 轴交于A B 、两点,与y 轴交于点C ,经过B C 、两点的直线是122y x =-,连结AC . (1)B 、C 两点坐标分别为B ( , )、C ( , ),抛物线的函数关系式为 ; (2)判断ABC △的形状,并说明理由;(3)若ABC △内部能否截出面积最大的矩形DEFC (顶点D E F 、、、G 在ABC △各边上)?若能,求出在AB 边上的矩形顶点的坐标;若不能,请说明理由.[抛物线2y ax bx c =++的顶点坐标是24,24b ac b aa ⎛⎫-- ⎪⎝⎭]8、(09甘肃定西)如图14(1),抛物线22y x x k =-+与x 轴交于A 、B 两点,与y 轴交于点C (0,3-).[图14(2)、图14(3)为解答备用图] (1)k=,点A 的坐标为 ,点B 的坐标为 ; (2)设抛物线22y x x k =-+的顶点为M ,求四边形ABMC的面积;(3)在x 轴下方的抛物线上是否存在一点D ,使四边形ABDC 的面积最大?若存在,请求出点D 的坐标;若不存在,请说明理由; (4)在抛物线22y x x k =-+上求点Q ,使△BCQ 是以BC为直角边的直角三角形.9、(09广东广州)如图13,二次函数)0(2<++=p q px x y的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),ΔABC 的面积为45。
(1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴上午垂线,若该垂线与ΔABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使四边形ABCD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由。
x 图1图2(备用)(第26题)图14(1) 图14(2) 图14(3)10、(09广西贵港)如图,抛物线y =ax 2+bx +c 的交x 轴于点A 和点B (-2,0),与y 轴的负半轴交于点C ,且线段OC 的长度是线段OA 的2倍,抛物线的对称轴是直线x =1. (1)求抛物线的解析式;(2)若过点(0,-5)且平行于x 轴的直线与该抛物线交于M 、N 两点,以线段MN 为一边抛物线上与M 、N 不重合的任意一点P (x ,y )为顶点作平行四边形,若平行四边形的面积为S ,请你求出S 关于点P 的纵坐标y 的函数解析式;(3)当0<x ≤ 10 3时,(2)中的平行四边形的面积是否存在最大值?若存在,请求出来;若不存在,请说明理由.11、(09广西河池)如图12,已知抛物线243y x x =++交x 轴于A 、B 两点,交y 轴于点C ,•抛物线的对称轴交x 轴于点E ,点B 的坐标为(1-,0). (1)求抛物线的对称轴及点A 的坐标;(2)在平面直角坐标系xoy 中是否存在点P ,与A 、B 、C 三点构成一个平行四边形?若存在,请写出点P 的坐标;若不存在,请说明理由;(3)连结CA点M ,使得直线CM 若存在,请求出直线12、(09广西柳州)如图,已知抛物线b ax ax y--=22(0>a )与x 轴的一个交点为(10)B -,,与y 轴的负半轴交于点C ,顶点为D .(1)直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点A 的坐标;(2)以AD 为直径的圆经过点C . ①求抛物线的解析式; ②点E在抛物线的对称轴上,点F在抛物线上,且以E F A B ,,,四点为顶点的四边形为平行四边形,求点F 的坐标.图11(09广西钦州)如图,已知抛物线y =34x 2+bx +c 与坐标轴交于A 、B 、C 三点, A 点的坐标为(-1,0),过点C 的直线y =34tx -3与x 轴交于点Q ,点P 是线段BC 上的一个动点,过P 作PH ⊥OB 于点H .若PB =5t ,且0<t <1. (1)填空:点C 的坐标是 ,b = ,c = ; (2)求线段QH 的长(用含t 的式子表示);(3)依点P 的变化,是否存在t 的值,使以P 、H 、Q 为顶点的三角形与△COQ 相似?若存在,求出所有t 的值;若不存在,说明理由.(09广西梧州)如图(9)-1,抛物线23y ax ax b =-+经过A (1-,0),C (3,2-)两点,与y 轴交于点D ,与x 轴交于另一点B .(1)求此抛物线的解析式; (2)若直线)0(1≠+=k kx y 将四边形ABCD 面积二等分,求k 的值;(3)如图(9)-2,过点E (1,1)作EF ⊥x 轴于点F ,将△AEF 绕平面内某点旋转180°得△MNQ (点M 、N 、Q 分别与点A 、E 、F 对应),使点M 、N 在抛物线上,作MG ⊥x 轴于点G ,若线段MG ︰AG =1︰2,求点M ,N 的坐标.(09贵州安顺)如图,已知抛物线与x 交于A(-1,0)、E(3,0)两点,与y 轴交于点B(0,3)。
(1) 求抛物线的解析式;(2) 设抛物线顶点为D ,求四边形AEDB 的面积; (3) △AOB 与△DBE 是否相似?如果相似,请给以证明;如果不相似,请说明理由。
图(9)-1图(9)-2(09贵州黔东南)已知二次函数22-++=a ax x y 。
(1)求证:不论a 为何实数,此函数图象与x 轴总有两个交点。
(2)设a<0,当此函数图象与x 轴的两个交点的距离为13时,求出此二次函数的解析式。
(3)若此二次函数图象与x 轴交于A 、B 两点,在函数图象上是否存在点P ,使得△PAB 的面积为2133,若存在求出P 点坐标,若不存在请说明理由。
(09湖北黄冈)新星电子科技公司积极应对2008年世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y (万元)与销售时间第x (月)之间的函数关系式(即前x 个月的利润总和y 与x 之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA 、曲线AB 和曲线BC ,其中曲线AB 为抛物线的一部分,点A 为该抛物线的顶点,曲线BC 为另一抛物线252051230y x x =-+-的一部分,且点A ,B ,C 的横坐标分别为4,10,12(1)求该公司累积获得的利润y (万元)与时间第x (月)之间的函数关系式;(2)直接写出第x 个月所获得S (万元)与时间x (月)之间的函数关系式(不需要写出计算过程);(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?(09湖北黄冈) (满分14分)如图,在平面直角坐标系xoy 中,抛物线21410189y x x =--与x 轴的交点为点B ,过点B 作x 轴的平行线BC ,交抛物线于点C ,连结AC .现有两动点P ,Q 分别从A,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动,点P 停止运动时,点Q 也同时停止运动,线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于点E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒)(1)求A,B,C 三点的坐标和抛物线的顶点的坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当0<t <92时,△PQ F 的面积是否总为定值?若是,求出此定值,若不是,请说明理由;(4)当t 为何值时,△PQF 为等腰三角形?请写出解答过程.(09湖北荆州)一开口向上的抛物线与x 轴交于A (m -2,0),B (m +2,0)两点,记抛物线顶点为C ,且AC ⊥BC . (1)若m 为常数,求抛物线的解析式;(2)若m 为小于0的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点?(3)设抛物线交y 轴正半轴于D 点,问是否存在实数m ,使得△BCD 为等腰三角形?若存在,求出m 的值;若不存在,请说明理由.(09湖北十堰) 如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式;(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.(3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.(09湖北武汉) 如图,抛物线24y ax bx a =+-经过(10)A -,、(04)C ,两点,与x 轴交于另一点B . (1)求抛物线的解析式;(2)已知点(1)D m m +,在第一象限的抛物线上,求点D 关于直线BC 对称的点的坐标;(3)在(2)的条件下,连接BD ,点P 为抛物线上一点,且45DBP ∠=°,求点P(09湖北仙桃) )如图,已知抛物线y =x 2+bx +c 经过矩形ABCD 的两个顶点A 、B ,AB 平行于x 轴,对角线BD 与抛物线交于点P ,点A 的坐标为(0,2),AB =4(1)求抛物线的解析式;(2)若S △APO =23,求矩形ABCD(09湖南娄底) 已知关于x的二次函数y =x 2-(2m -1)x +m 2+3m + (1)探究m 满足什么条件时,二次函数y 的图象与x 轴的交点的个数.(2)设二次函数y 的图象与x 轴的交点为A (x 1,0),B (x 2,0),且21x +22x =5,与y 轴的交点为C ,它的顶点为M ,求直线CM 的解析式.(09湖南湘西) 在直角坐标系xoy 中,抛物线2y x bx c =++与x 轴交于两点A 、B ,与y 轴交于点C ,其中A 在B 的左侧,B 的坐标是(3,0).将直线y kx =沿y 轴向上平移3个单位长度后恰好经过点B 、C . (1) 求k 的值;(2) 求直线BC 和抛物线的解析式; (3) 求△ABC 的面积;(4)设抛物线顶点为D ,点P 在抛物线的对称轴上,且∠APD =∠ACB ,求点P 的坐标.(09山东德州)如图,已知抛物线21y x =-与x 轴交于A 、B两点,与y 轴交于点C .(1)求A 、B 、C 三点的坐标.(2)过点A 作AP ∥CB 交抛物线于点P ,求四边形ACBP 的面积.(3)在x 轴上方的抛物线上是否存在一点M ,过M 作MG ⊥x轴于点G ,使以A 、M 、G 三点为顶点的三角形与∆PCA 相似.若存在,请求出M 点的坐标;否则,请说明理由.(09湖南益阳) 20.阅读材料:如图12-1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法:ah S ABC 21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.解答下列问题:如图12-2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结P A ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆;(3)是否存在一点P ,使S △P AB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.(09湖南株洲) 如图,已知ABC ∆为直角三角形,90ACB ∠=︒,AC BC =,点A 、C 在x 轴上,点B 坐标为(3,m )(0m >),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B 、D .(1)求点A 的坐标(用m 表示);(2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连结PQ 并延长交BC 于点E ,连结 BQ 并延长交AC 于点F ,试证明:()FC AC EC +为定值.(09浙江绍兴)图12-2 xOy ABD 11C图12-1A2(09吉林长春)如图,在直角坐标系中,矩形ABCD 的边AD 在y 轴正半轴上,点A 、C 的坐标分别为(0,1)、(2,4).点P 从点A 出发,沿A →B →C 以每秒1个单位的速度运动,到点C 停止;点Q 在x 轴上,横坐标为点P 的横、纵坐标之和.抛物线c bx x y ++-=241经过A 、C 两点.过点P 作x 轴的垂线,垂足为M ,交抛物线于点R .设点P 的运动时间为t (秒),△PQR 的面积为S (平方单位).(1)求抛物线对应的函数关系式.(2分) (2)分别求t=1和t=4时,点Q 的坐标.(3分)(3)当0<t ≤5时,求S 与t 之间的函数关系式,并直接写出S 的最大值.(5分) 【参考公式:抛物线2y ax bx c =++的顶点坐标为2b a⎛- ⎝,244ac b a ⎫-⎪⎭.】(09江西省)如图,抛物线223y x x =-++与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连接BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF DE ∥交抛物线于点F ,设点P 的横坐标为m ;①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设BCF △的面积为S ,求S 与m 的函数关系式.(09内蒙包头)已知二次函数2y ax bx c =++(0a≠)的图象经过点(10)A ,,(20)B ,,(02)C -,,直线x m =(2m >)与x 轴交于点D . (1)求二次函数的解析式; (2)在直线x m =(2m >)上有一点E (点E 在第四象限),使得E D B 、、为顶点的三角形与以A O C 、、为顶点的三角形相似,求E 点坐标(用含m 的代数式表示);(3)在(2)成立的条件下,抛物线上是否存在一点F ,使得四边形ABEF 为平行四边形?若存在,请求出m 的值及四边形ABEF 的面积;若不存在,请说明理由.(第24(09山东济南)已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y轴交于点C 其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.(09山东威海)如图,在直角坐标系中,点A B C ,,的坐标分别为(10)(30)(03)-,,,,,,过A B C ,,三点的抛物线的对称轴为直线l D ,为对称轴l 上一动点. (1)、求抛物线的解析式;(2)、求当AD CD +最小时点D 的坐标; (3)、以点A 为圆心,以AD 为半径作A . ①证明:当AD CD +最小时,直线BD 与A相切.②写出直线BD 与A 相切时,D 点的另一个坐标:_________.(09山东德州)如图,在平面直角坐标系xOy 中,半径为1的圆的圆心O 在坐标原点,且与两坐标轴分别交于A B C D 、、、四点.抛物线2y ax bx c =++与y轴交于点D ,与直线y x =交于点M N 、,且MA NC 、分别与圆O 相切于点A 和点C .(1)求抛物线的解析式;(2)抛物线的对称轴交x 轴于点E ,连结DE ,并延长DE 交圆O 于F ,求EF 的长.(3)过点B 作圆O 的切线交DC 的延长线于点P ,判断点P 是否在抛物线上,说明理由.(第24题图)(09山东烟台)如图,抛物线23y ax bx =+-与x 轴交于A B ,两点,与y 轴交于C 点,且经过点(23)a -,,对称轴是直线1x =,顶点是M .(1)求抛物线对应的函数表达式;(2)经过C,M 两点作直线与x 轴交于点N ,在抛物线上是否存在这样的点P ,使以点P A C N ,,,为顶点的四边形为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)设直线3y x =-+与y 轴的交点是D ,在线段BD 上任取一点E (不与B D ,重合),经过A B E ,,三点的圆交直线BC 于点F ,试判断AEF △的形状,并说明理由;(4)当E 是直线3y x =-+上任意一点时,(3)中的结论是否成立?(请直接写出结论).(09浙江台州)如图,已知直线121+-=x y 交坐标轴于B A ,两点,以线段AB 为边向上作正方形ABCD ,过点C D ,A ,的抛物线与直线另一个交点为E . (1)请直接写出点D C ,的坐标;(2)求抛物线的解析式;(3)若正方形以每秒5个单位长度的速度沿射线AB 下滑,直至顶点D 落在x 轴上时停止.设正方形落在x 轴下方部分的面积为S ,求S 关于滑行时间t 的函数关系式,并写出相应自变量t 的取值范围;(4)在(3)的条件下,抛物线与正方形一起平移,同时D 停止,求抛物线上E C , 两点间的抛物线弧所扫过的面积.(09浙江湖州)已知抛物线22y x x a =-+(0a <)与y 轴相交于点A ,顶点为M .直线12y x a =-分别与x 轴,y 轴相交于B C ,两点,并且与直线AM 相交于点N.(1)填空:试用含a 的代数式分别表示点M 与N 的坐标,则()()M N , , , ;(2)如图,将NAC △沿y 轴翻折,若点N 的对应点N′恰好落在抛物线上,AN ′与x 轴交于点D ,连结CD ,求a 的值和四边形ADCN 的面积; (3)在抛物线22y x x a =-+(0a <)上是否存在一点P ,使得(第24题)yx121+-=x y备用图以P A C N ,,,为顶点的四边形是平行四边形?若存在,求出P 点的坐标;若不存在,试说明理由.(09天津)已知函数212y x y x bx c αβ==++,,,为方程120y y -=的两个根,点()1M T ,在函数2y 的图象上.(Ⅰ)若1132αβ==,,求函数2y 的解析式;(Ⅱ)在(Ⅰ)的条件下,若函数1y 与2y 的图象的两个交点为A B ,,当ABM △的面积为112时,求t 的值;(Ⅲ)若01αβ<<<,当01t<<时,试确定T αβ,,三者之间的大小关系,并说明理由.(09四川遂宁)如图,二次函数的图象经过点D(0,397),且顶点C 的横坐标为4,该图象在x 轴上截得的线段AB 的长为6.⑴求二次函数的解析式;⑵在该抛物线的对称轴上找一点P ,使PA+PD 最小,求出点P 的坐标;⑶在抛物线上是否存在点Q ,使△QAB 与△ABC 相似?如果存在,求出点Q 的坐标;如果不存在,请说明理由.(09四川内江)如图所示,已知点(10)A -,,(30)B ,,(0)C t ,,且0t>,tan 3BAC ∠=,抛物线经过A 、B 、C 三点,点(2)P m ,是抛物线与直线:(1)l y k x =+的一个交点. (1)求抛物线的解析式;(2)对于动点(1)Q n ,,求PQ QB +的最小值;(3)若动点M 在直线l 上方的抛物线上运动,求AMP △的边AP 上的高h 的最大值.第(2)题备用图(第24题)(09四川南充)如图9,已知正比例函数和反比例函数的图象都经过点(33)A ,.(1)求正比例函数和反比例函数的解析式;(2)把直线O A 向下平移后与反比例函数的图象交于点(6)B m ,,求m 的值和这个一次函数的解析式; (3)第(2)问中的一次函数的图象与x 轴、y 轴分别交于C 、D ,求过A 、B 、D 三点的二次函数的解析式;(4)在第(3)问的条件下,二次函数的图象上是否存在点E ,使四边形O ECD 的面积1S 与四边形O ABD 的面积S 满足:123S S=?若存在,求点E 的坐标;若不存在,请说明理由.(09四川眉山)如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
