安徽大学信号系统例题分析
安徽大学电子科学与技术学院信号与线性系统第四章

3.拉氏变换对
F s L f t f t e s t d t 0 σ j 1 1 st F s e d s f t L f t 2 π j σ j
与傅氏变换的区别p187 单边拉氏变换
L[ f (at b)u (at b)]
1
F ( )e a a
s
s
b a
《信号与线性系统》
7
第四章 连续时间系统的s域分析
(七)
初值定理
f (0 ) lim f (t ) lim sF ( s)
t 0 s
注:初值定理应用的条件是F(s)是真分式,若不是,则在t=0 处有冲激及其导数产生。 F(s)可写成多项式和真分式之和。
p1 , p2 , p3 pn为不同的实数根
F ( s) k1 s p1 k2 s p2 kn s pn
(m<n)
《信号与线性系统》
12
第四章 连续时间系统的s域分析
例F ( s )
2s 3s 3
2
s 6s 11s 6
3 2
2
,求f(t)
(1)找极点 F s
f t e
t
2π
1
F j e
j t
d
两边同乘以 e t:
f t
2π
1
1
F j e
st
j t
d
f t j F s e d s 至4.11节之前只讨论单边拉氏变换 2π j
j
《信号与线性系统》
s 3 ( s 2)( s 2s 5)
安大信号系统课程考试试题出题范围基本要求

《信号与系统》课程考试出题范围的基本要求1、掌握下列信号的FT、LT、ZTFT、LT:阶跃信号、冲激信号、斜坡信号、指数信号、矩形脉冲、三角脉冲、梯形脉冲、符号函数、正弦函数、余弦函数ZT:单位样值、单位阶跃、斜坡、矩形、正弦、复指数2、考试卷型:填空题<10分):各章的基本概念、简单的计算选择题<10分):各章的基本概念、简单的计算计算分析题<65分):基本按卷积1题、FT 2题、 LT2题、ZT 2T比例分配<1)求解微分方程及冲激响应<可利用LT);<2)连续及离散域的卷积<可利用LT及ZT求解);<3)求非周期信号、周期信号的FT<可利用FT线性、对称性、时移、频移等性质);<4)求解周期信号的FS<从周期信号中取单周期做FT计算FS);<5)求解抽样信号的FT、抽样定理及应用;<6)求解信号的LT及逆变换<可利用LT的性质、部分分式法、留数法);<7)求解信号的初值和终值<可利用S域和Z域的初值和终值定理);<8)利用S域元件模型求解电路的系统函数、冲激响应、各种解、画系统的零极点、频率响应曲线、判定系统的稳定性、讨论解与系统函数、激励函数零极点的关系;<9)建立和求解差分方程<对框图描述的系统建立其差分方程,并利用ZT求解差分方程、冲激响应);<10)求解信号的ZT及逆变换<对应不同收敛域、可利用ZT的性质、掌握ZT 的收敛域);<11)求解离散系统的系统函数、确定收敛域、稳定性、求解系统的冲激响应、对给定激励信号的系统响应、画出零极点及频率响应曲线。
简答题<15分)通过信号与系统的学习,应该具备以下基本分析方法和基本思想:<1)为什么要对信号进行分解?常用的分解方法有哪些?<2)什么样的系统<微分方程)是线性时不变系统?线性时不变系统的意义与应用?<3)阐述时域分析中系统响应的各种分类及物理含义,解的形式与微分方程特征方程特征根的关系,解的形式与S域激励信号、系统函数零极点的关系,微分方程特征根与系统稳定性的关系。
安徽大学2013-2014学年度第1学期信号与系统(A)及答案

安徽大学2013—2014学年第 1 学期《信号与系统 》考试试卷(A 卷)(闭卷 时间120分钟)考场登记表序号一、填空题(每小题2分,共10分)1.某LTI 系统在()e t 激励下响应为()r t ,则当激励0()e t t -时,系统响应为 。
2.若信号()f t 的傅里叶变换为F(j ω),则信号()f at (a ≠0)的傅里叶变换为 。
3.已知某LTI 系统对激励信号e(t)的零状态响应为4(2)de t dt-,则系统函数()H s = 。
4.某全通系统的系统函数2()s H s s a-=+,则a 取值为 。
5.某线性时不变因果系统为稳定系统,其单位样值响应为h(n),则|)n (h |0n ∑+∞=应满足______。
二、选择题(每小题2分,共10分)1.已知 f (t) ,为求 f (5-2t) 则下列运算正确的是( )。
A .f (-2t) 左移2.5B .f (-2t) 右移2.5C .f (2t) 左移5D .f (2t) 右移52.下列关于冲激函数性质的表达式不正确的是( )。
A .)()1()()1(t f t t f δδ=+ B. )0(d )()(f t t t f '='⎰∞∞-δ C.()d ()tu t δττ-∞=⎰D.)0(d )()(f t t t f =⎰+∞∞-δ院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------3.已知某LTI 连续系统的冲激响应为)(t h ,当激励为()f t 时,该系统的零状态响应为)(t y zs ,零输入响应为)(t y zi ,全响应为)(1t y 。
信号与系统第六章习题答案

第六章 离散系统的Z域分析 6.1学习重点 1、离散信号z 域分析法—z变换,深刻理解其定义、收敛域以及基本性质;会根据z变换的定义以及性质求常用序列的z变换;理解z变换与拉普拉斯变换的关系。
2、熟练应用幂级数展开法、部分分式法及留数法,求z 反变换。
3、离散系统z 域分析法,求解零输入响应、零状态响应以及全响应。
4、z 域系统函数()z H 及其应用。
5、离散系统的稳定性。
6、离散时间系统的z 域模拟图。
7、用MATLAB 进行离散系统的Z 域分析。
6.2 教材习题同步解析 6.1 求下列序列的z 变换,并说明其收敛域。
(1)n 31,0≥n (2)n−−31,0≥n(3)nn−+ 3121,0≥n (4)4cos πn ,0≥n(5)+42sin ππn ,0≥n 【知识点窍】本题考察z 变换的定义式 【逻辑推理】对于有始序列离散信号[]n f 其z 变换的定义式为()[]∑∞=−=0n nzn f z F解:(1)该序列可看作[]n nε31()[][]∑∑∞=−∞=− == =010313131n n n nn n z z n n Z z F εε对该级数,当1311<−z ,即31>z 时,级数收敛,并有 ()13331111−=−=−z zz z F其收敛域为z 平面上半经31=z 的圆外区域 (2)该序列可看作[]()[]n n nnεε331−=−−()()[][]()[]()∑∑∞=−∞=−−=−=−=010333n nn nnnzzn n Z z F εε对该级数,当131<−−z ,即3>z 时,级数收敛,并有()()33111+=−−=−z zz z F 其收敛域为z 平面上半经3=z 的圆外区域(3)该序列可看作[][]n n nn n n εε+ = + −3213121()[][]()∑∑∑∞=−∞=−∞=−+ =+ = + =01010*********n nn n n nn n n n z z z n n Z z F εε对该级数,当1211<−z 且131<−z ,即3>z 时,级数收敛,并有 ()3122311211111−+−=−+−=−−z zz z z zz F 其收敛域为z 平面上半经3=z 的圆外区域(4)该序列可看作[]n n επ4cos()[]∑∑∑∑∞=−−∞=−−∞=−∞=−+=+== =0140140440*******cos 4cos n nj n nj nn j j n n z e z e z e e z n n n Z z F πππππεπ对该级数,当114<−ze j π且114<−−zejπ,即1>z 时,级数收敛,并有()122214cos 24cos 21112111212222441414+−−=+−−=−+−=−×+−×=−−−−z z zz z z z z e z z e z z z eze z F j j j j ππππππ其收敛域为z 平面上半经1=z 的圆外区域 (5)该序列可看作[][][]n n n n n n n n εππεππππεππ+=+= +2cos 2sin 222sin 4cos 2cos 4sin 42sin()[]()122212212212cos 22cos 2212cos 22sin 222cos 222sin 222cos 2sin 222222222200++=+++=+−−++−=+=+=∑∑∞=−∞=−z z z z z z z z z z z z z z z n z n n n n Z z F n nn n ππππππεππ 其收敛域为z 平面上半经1=z 的圆外区域 6.2 已知[]1↔n δ,[]a z z n a n −↔ε,[]()21−↔z z n n ε, 试利用z 变换的性质求下列序列的z 变换。
安徽大学2010-2011信号A及答案

安徽大学20 10 —20 11 学年第 2 学期《 信号与系统 》考试试卷(A 卷)(闭卷 时间120分钟)一、填空题(每小题2分,共10分) 1. 对于一个因果系统()n h 来说,当0<n 时,()n h _________。
2. 若激励信号为()t x ,响应信号为()t y ,则无失真传输的条件是_________。
3. 如果一个系统函数的极点位于左半平面,零点位于右半平面,而且零点与极点对于_________互为镜像,那么我们称这种系统函数为全通函数。
4. 若系统的单位冲激响应为()t h ,单位阶跃响应为()t g ,则二者的关系为_____________。
5. 设()n x 是一序列且[)+∞-∈,5n ,则它的收敛域是________。
二、选择题(每小题2分,共10分)1.已知()t f ,为求()at t f -0()0,0>t a 应按( )运算求得正确结果。
A. ()at f -左移0t B. ()at f 右移0t C. ()at f 左移a t 0 D. ()at f -右移a t 02. 对于信号f (t )及单位冲激信号)(t δ,则()()=-⎰+∞∞-0t t t f δ( )。
A.()0f B.()t f C. ()0t f D.03. 已知()t f 的拉氏变换为()F s ,则1()2f t 的拉式变换是( )。
A.()22s F B. ()s F 22C. ()212-s FD. ()2s e s F -4. 由S 平面与Z 平面的映射关系ST e Z =可知,S 平面的垂直带区域[]()21σσσ,∈映射为Z 平面上的( )区域。
A .环状的 B.某个圆以内 C.某个圆以外 D.带状的院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------5. 带通滤波器的品质因数Q 定义为( )。
2014-2015-2学年信号与系统试卷A

安徽大学2014—2015学年第 2 学期《信号与系统 》考试试卷(A 卷)(闭卷 时间120分钟)考场登记表序号一、填空题(每小题1分,共10分)1.利用单位冲激信号)(t δ的性质,有()=-⎰+∞∞--dt t e t 23δ ; 2.描述离散时间系统输入输出关系的数学模型是 方程; 3.已知信号()t f 的单边拉普拉斯变换()21++=s s s F ,则该信号的傅里叶变换为 ; 4.全通系统的系统函数()as s s F +-=2,则a 的取值为 ; 5.根据响应产生的原因,完全响应等于零输入响应与 响应相加; 6.()()()t f t f t y 211*=,则()()()=-*-=22112t t f t t f t y ;7.离散时间系统的单位样值响应为()n h ,则该系统因果稳定的充分必要条件为 ;8.根据傅里叶变换的性质可知,当信号在时域中压缩时,其频谱将会 ; 9.s 平面上的虚轴对应z 平面上的 ;10.设激励信号为)(t e ,响应信号为)(t r ,则无失真传输条件为 。
二、选择题(每小题2分,共10分)1.一个线性定常系统,若要使其稳定,则它的极点不该出现在( ) A . 实轴 B . 虚轴 C . 右半平面 D . 左半平面院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------2.已知()()11+=s s s F ,则)(∞f 等于( )A. 0B. 1C. 2D. 33.已知连续系统二阶微分方程的零输入响应()t y zi 的形式为t t Be Ae 2--+,则其2个特 征根为( )。
安徽大学-信号与系统C卷(含答案)

安徽大学《 信号与系统 》考试试卷(C 卷答案)(闭卷 时间120分钟)一、填空题(每小题2分,共10分) 1.对于信号f (t ),单位冲激信号)(t δ,有)()(0t t t f -⎰∞∞-δ= 0()f t 。
2.已知信号f (t )的傅立叶变换为)(ωF ,则f (2t )的傅立叶变换为1()22F ω。
3.若系统的起始状态为0,在x (t )的激励下,所得的响应为 零状态响应 。
4.已知信号()f t 在-=0t 时刻的值为)0(-f ,()f t 的单边拉普拉斯变换为)(s F ,则dtt df )(的单边拉普拉斯变换为()(0)sF s f --。
5.已知时域x (n )、h (n )、y (n )的Z 变换为X(z)、H(z)、Y(z),且)()()(n h n x n y *=,则 有Y(z)= ()()X z H z 。
二、选择题(每小题2分,共10分) 1.f (5-2t )是如下运算的结果(C )A 、 f (-2t )右移5B 、 f (-2t )左移5C 、 f (-2t )右移25D 、 f (-2t )左移252.已知系统的激励e (t )与响应r (t )的关系为:)()(t ke t r =,k 为常数, 则该系统为(A )A 、线性时不变系统B 、线性时变系统C 、非线性时不变系统D 、非线性时变系统3..一连续时间系统,其单位冲击响应为h (t ),则该系统是因果系统的条件是(C ) A 、0)(lim =∞→t h t ; B 、∞→∞→)(lim t h t ;C 、h (t )=h (t )u (t );D 、h (t )=h (-t )。
4.一连续信号x (t )的最高频率是π1000Hz ,对x (t )抽样成离散时间信号,为了满足抽样院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------定理,则抽样的最大间隔T s 是(D )A 、0.02sB 、0.002sC 、0.004sD 、0.001s5.一个因果稳定的离散系统,其H (z )的全部极点须分布在z 平面的(B ) A 、单位圆外 B 、单位圆内 C 、单位圆上 D 、单位圆内或单位圆上三、计算分析题(1、2题10分,3、6题15分,4题7分,5题8分,共65分) 1.求图1所示信号()f t 的傅立叶变换。
安徽大学信号与系统试卷及答案

安徽大学2006—2007学年第二学期 《 信号与系统 》考试试卷(A 卷)(时间120分钟)院/系 专业 姓名 学号一、填空题(每小题2分,共20分)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?)2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常 数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8.为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
信号与系统教程习题解析(前七章)
题 4-1(a) 图
解
对于 于周期锯齿波 波信号,在 在周期( 0,T )内可表示 示为 At A f t t T A T T a 1 T f t dt d 1 T At T A dt A T t 2T t A 2 0
∵ω T 2 T 2A 2 T b 2 T
2π, 2 ∴
sinnω tdt t 2 2A T
《信 信号与系 系统教程 程》习题 题解析
第1 章 导论 导
1-1 题 1-1 图示信号中, 图 哪些是连续 续信号?哪 哪些是离散信 信号?哪些 些是周期信号 号? 哪些 些是非周期 期信号?哪些 些是有始信 信号?
题 1-1 图
解
图(a a)、(c)、( (d)为连续信 信号;(b)为 为离散信号 号;(d)为周 周期信号;其 其余
(a)和(b)的波形如图 p2-1 所示。
2
图 p2-1
2-2 试用 用阶跃函数的组合表示 示题 2-2 图所 所示信号。 解 (a) f t (b) f t ε t ε t 2ε t ε t 1 T ε t ε t 2 2T T
题 2-2 图
2-3 如题 题 2-3 图所示 示f t ,试画 画出如下信 信号的波形。 。 (a) f (b) f t (c) f t (d) f 2t (e) f t/2 (f) f 2t 2
cosn nω tdt A 2A T
a
f t cosnω ω tdt tsinnω ω t nω f t sinnω ω tdt
tcosn nω tdt
cosnω ω tdt
sinnω t dt nω 2 2A T
0 2A A T
tsinn nω tdt
sinnω tdt
安徽大学-数字信号处理试卷

安徽大学2009 — 2010学年第 一 学期《 数字信号处理 》试题一、 对于连续非周期信号)(t f ,对应的频谱函数为)(ωF ,现对 )(t f 进行单位冲击周期序列抽样,形成抽样信号)(t f s ,抽样间隔为T,试详细推导抽样后信号的傅立叶变换)(ωs F 表达式,并说明其与)(ωF 的关系。
(15分)解:⎰∞∞--=dt e t f w F jwt)()(; 冲击利用傅式级数展开有:∑∑∑∞-∞=∞-∞=∞-∞===-=m t jmw Tm tjm m n s e eC nT t t P 12)()(πδδ , T s w π2=∑⎰⎰∑⎰∞-∞=--∞∞--∞∞-∞-∞=∞∞--=-==m t mw w j Tjwtn jwts s dt e t f dt enT t t f dt et f w F s )(1)()()()()(δ∑∑∞-∞=∞-∞=-=-=m T Tm s Ts m w F mw w F w F )()()(211π;二、 推导离散傅立叶级数公式,并说明离散傅立叶变换与离散傅立叶级数的关系。
(15分) 解: 我们知道,非周期离散信号的傅里叶变换为:∑∞-∞=-=n jwnjwen x eX )()(由于)(jwe X 是周期的,我们在)(jwe X 上加以表示周期性的上标“~”,并重写如下:∑∞-∞=-=n jwnjw en x e X )()(~;设)(n x 的列长为N ,则上式为:∑-=-=1)()(~N n jwn jwe n x e X ;现在对)(~jw e X 取样,使其成为周期性离散频率函数,并导致时域序列)(n x 周期化为)(~n x ,时域取样间隔为T ,在一个周期内取样点数为N 。
现在序列的周期为NT ,所以对频谱取样的谱间距是NT 1。
以数字频率表示时,则谱间距是I w π2=。
因此,上述以数字频率w 为变量的)(jwe X 被离散化时,其变量w 则成为k kw w NI π2== k=0,1,2…N-1所以离散周期序列)(~n x 的傅里叶级数可写成 ∑∑-=-=-====1010)(~)(~|)(~)(~22N n knN N n kn j k w jw W n x e n x e X k X Nππ k=0,1,2,…N-1上面公式中k 为整数,而且由于)(~jw e X 的周期是π2,所以k 只有0至(N-1)个值。
安徽大学数字信号处理-复习(含答案)

判断题1.数字信号处理的主要对象是数字信号,且是采用数值运算的方法达到处理目的的。
(对)2.因果系统一定是稳定系统。
(错)3.如果系统对输入信号的运算关系在整个运算过程中不随时间变化,则这种系统称为时不变系统。
(对)4.所谓稳定系统是指有界输入、有界输出的系统。
(对)5. 差分方程本身能确定该系统的因果和稳定性。
(错)6. 若连续信号属带限信号,最高截止频率为Ωc ,如果采样角频率Ωs<2Ωc ,那么让采样信号通过一个增益为T 、 截止频率为Ωs/2的理想低通滤波器,可以唯一地恢复出原连续信号。
(错)7.一个系统是因果系统的充要条件是,单位序列响应h(n)是因果序列。
(错)8.()nx n cos=5是周期信号。
(错) 9.设某系统输入为()x n ,输出为()y n ,且()()y n ax n b,=+(a 和b 是常数)。
则该系统是线性系统。
(错)10.设某系统输入为()x n ,输出为()y n ,且()()y n nx n =。
则该系统是时变系统。
(对)11.设LTI 系统的单位系统脉冲响应()()n h n a u n =,式中a 是实常数。
则该系统一定是因果、稳定系统。
(错)12.设LTI 系统的单位系统脉冲响应()()h n n δ=+4,则该系统一定是非因果、稳定系统。
(对) 13.LTI 系统稳定的充分必要条件:系统的单位脉冲响应绝对可和,即()n h n +∞=-∞<+∞∑。
(对)14.单位阶跃序列与矩形序列的关系是()()()N R n u n N u n =--。
(错) 15.时域离散信号傅里叶变换存在的充分条件是序列绝对可和。
( 对 ) 16.序列的傅里叶变换是频率ω非周期函数。
(错) 17.序列z 变换的收敛域内可以含有极点。
(错)18.离散傅里叶变换中,有限长序列都是作为周期序列的一个周期来表示的,都隐含有周期性的意思。
(对)19.单位圆上的Z 变换就是序列的傅里叶变换。
《信号与系统》课程习题与解答
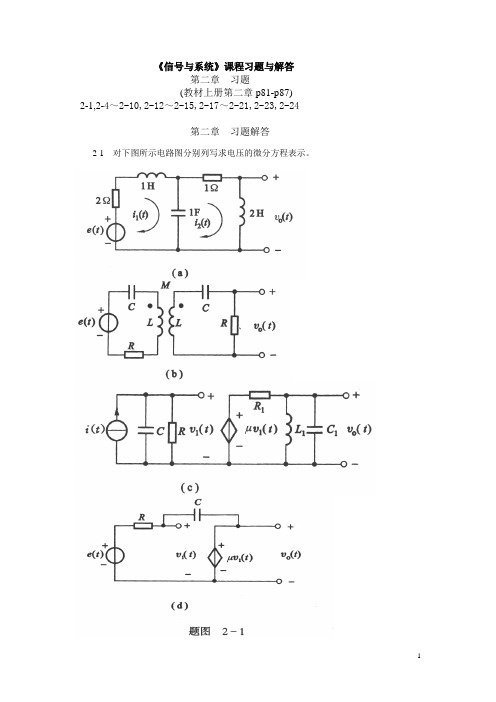
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
安徽大学信号(A)及答案

安徽大学2011—2012学年第 2 学期《信号与系统 》考试试卷(A 卷)(闭卷 时间120分钟)考场登记表序号一、选择题(每小题2分,共10分) 1.已知()f t ,为求(25)f t -应按照下列哪种运算求得正确结果( D ) A .(5)f t -左移2 B.(5)f t 右移2 C.(5)f t 左移25 D.(5)f t -右移252.已知系统的激励e (t )与响应r (t )的关系为:()()de t r t dt=,则该系统为( A ) A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 3.若信号f(t)的最高频率是4kHz ,则2tf()的乃奎斯特抽样频率为( B ) A .4kHz B. 2kHz C. 8kHz D.3kHz4. 因果序列的Z 变换1121 1.50.5z X(z)z z---=-+,则该因果序列的终值()x ∞为( A ) A . 0 B. 1 C. 2 D. 3 5.若系统函数23()32s H s s s +=-+,则该系统(A ) A .不稳定 B. 稳定 C. 临界稳定 D. 以上均不对院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------二、填空题(每小题2分,共10分)1.求()()f t u t *= 。
2.某连续时间系统由两个冲击响应分别为1h (t)和2h (t)子系统串联构成,则该系 统的冲击响应为 。
3.对连续时间最小相移系统,其在S 平面的________平面无零点。
4.若信号的113s F(s)=(s+)(s+)-,求该信号的=)j (F ω 。
2011-2012信号与系统(B卷)参考答案

安徽大学2011—2012学年第2学期《信号与系统》(B 卷)考试试题参考答案及评分标准一、 选择题1.C2.A3.D4.B5. B 每小题2分,共计10分 二、 填空题1. 0()f t2. 1(/3)3F w 3. 零状态响应 4. ()(0)sF s f --5. X(z)H(z)每小题2分,共计10分 三、 简述题1、调制过程将信号频谱搬移到任何所需的较高频率范围,这就容易以电磁波形式辐射出去。
(+2分)调制作用的实质是把各种信号的频谱搬移,使它们互不相重叠地占据不同的频率范围,也即信号分别托附于不同频率的载波上,接收机就可以分离出所需频率的信号,不致互相干扰。
(+3分)2、连续时间域就是以连续时间t 为自变量,频率域则是以变化的频率w 对其进行研究,傅里叶变换就是将连续的时间域信号转变到频率域,拉氏变换是傅里叶变换的推广,是将连续的时间域信号变换到复频率域(拉氏变换,此时看成仅在j Ω轴);而z 变换则是连续信号经过理想采样之后的离散信号的拉氏变换,再令STz e =时的变换结果,所对应的域为数字复频率域,此时数字频率ω=ΩT 。
(+5分)3、系统零状态响应的拉式变换与激励的拉式变换之比称为“系统函数”,以(s)H 表示。
在S 域中,系统函数非常重要,系统函数零、极点分布与冲激响应的有着对应关系。
利用()H s 在s 平面的零极点分布情况可以分析系统的时域特性。
由()H s 可直接写出系统的微分方程,因而系统也就可以用具有微分方程特性的网络来实现。
可研究()H s 的零极点分布对()h t 的影响。
(+10分)四、计算题1、解:()()()-(t)y t h t *x t =*()d tdh x dtττ∞=⎰ (+1分)()()()()()()=[t 1t 2][t 2u t 2t 4u t 4]δδ---*-----(+1分)=(3)(3)(4)(4)(5)(5)(6)(6)t u t t u t t u t t u t --------+--(+1分)2、解:(n)*y(n)={4,3,2,1}*{2,3,4}={8,18,29,20,11,4}x(+5分)3、解:由图可得:0,(),t t f t tt τττττ<->⎧⎪=⎨-<≤⎪⎩或 (+3分)令1(),tf t t τττ=-<≤,2()0,f t t t ττ=<->或,则1()1/[()()]1/[()()()()]df t u t u t dtu t u t u t u t ττττττ=+--=+-+-- (+3分)122()11()(/2)(/2)j j df t F Sa e Sa e dt ττωωωτωτττ-=+(+2分)所以频谱 1()()()(0)()df t F dt F F j ωπδωω=+ 2211(/2)(/2)2j j Sa e Sa ej ττωωωτωτπττωτ-+=+(+2分)4、解:(1)211()3+2(s 2)(s 1)F s s s ==--- =111()s 12s -∙--- (+2分)⇒ 2(t )=e tt f e -(+3分)(2)由于收敛域为0.5Z >,因此(n)x 为右边序列(+1分)2(z )=(z 0.5)(z 0.3)z X --=2.5 1.50.50.3z zz z --- (+2分)⇒ ()x (n )=[2.5(0.5)1.50.3]u (n )nn -(+2分)五、综合题1、 解:(1)由于2()(1)()t g t e u t -=-则系统的冲击响应为2()()2t dg t h t e dt-== (+2分)所以,系统函数2()2H s s =+ (+3分)(2)2()2H j j ωω=+,得到其幅频特性如图1所示 (+2分)()arctan ϕωω=-,得到其相频特性如图2所示(+2分)图1 图2(3)由2111()11/22(2)()()22R s s s s E s H s s s s --++===-++ (+3分)可得:21()(1)()2t e t e u t -=-(+3分)2、解:(1)(n)+0.2y(n 1)0.24y(n 2)=x(n)+x(n 1)y ---- 对差分方程表达式进行Z 变换,得:121()0.2(z)0.24(z)=X(z)+X(z)Y z z Y z Y z ---+-(+2分)⇒12122()1+()=()10.20.24+0.20.24Y Z z z zH Z X Z z z z z ---+==+-- 22()(z+1)()=()+0.20.24(z 0.4)(z+0.6)Y Z z z z H Z X Z z z +==-- (+2分)()H Z 的两个极点分别位于0.4和—0.6,它们都在单位圆内,对此因果系统的收敛域为0.6z >,且包含=z ∞点,是一个稳定的因果系统。
安徽大学信号与系统期末复习题【精选】

第一章 P.40 ~ P.44
[§1-1] [§1-2] [§1-3] [§1-4]
[§1-5] [§1-6] [§1-7]
[§1-8]
2, 4[图形位于P.13], 7, 10[用阶跃函数表示分段函数], 11(1,3,5), 12(1,3,5,7), 14(1,3,5,7), 17(2,4), 18,
[§5-10] [§5-11] [§5-12]
第五章 P.325 ~ P.331
1, 2, 6[表达式和图形位于P.286], 11,
17[画图证明,或用数学表达式证明]
2019/10/1
共5大题
第十一章 P.316 ~ P.323
[§11-1] [§11-2] [§11-3] [§11-4]
[§11-5] [§11-6]
20(1,3,4,5,7)[要证明。证明非时变时,对e( ·)括号内进行变换], 21[可逆:能根据输出唯一地确定输入], 23[ f (t)·(t) = f (0)·(t) ]
2019/10/1
共12大题
[§2-1] [§2-2] [§2-3] [§2-4] [§2-5] [§2-6] [§2-7] [§2-8]
2019/10/1
共16大题
[§4-1] [§4-2] [§4-3] [§4-4] [§4-5] [§4-6] [§4-7] [§4-8] [§4-9] [§4-10] [§4-11] [§4-12] [§4-13]
2019/10/1
第四章 P.261 ~ P.276
1(13,15,16,18,20)[利用性质求解], 3(1,2,3), 5[不求原函数,利用定理求解], 4(3,4,7,12,16,19,20),
安徽大学信号与系统课件

由系统框图列写微分(或差分)方程的步骤
• 选中间变量x(· )。对于连续系统,设其最右端积分 器的输出为x(t);对于离散系统,设其最左端迟延 单元的输入为x(n); • 写出各加法器输出信号的方程; • 消去中间变量x(· )。 如果已知系统的微分或差分方程,也可以画出相应的 框图。但解不是惟一的。
e t cos t sin t ut t
t
波形如下图
π 2 e cos t ut t 4
1
O
f 2 (t )
3 4
7 4
t
1
X
例1-2
求下列函数值
t d t e t e t (2) f t 3 τ d τ (1) f dt
X
第
12 页
由加法器的输出,得
yt a1 yt a0 yt f t
将上式除f(t)以外的各项移到等号左端,得
yt a1 yt a0 yt f t
连续系统或离散系统除用数学方程描述外,还可用 框图表示系统的激励与响应之间的数学运算关系, 一个方框图可以表示一个具有某种功能的部件,也 可以表示一个子系统。每个方框内部的具体结构并 非是考察重点,只注重其输入输出之间的关系。
习题课1
内容摘要
信号的定义、分类、描述 典型的连续时间信号
第 1 页
信号
信号的运算 奇异信号 信号的分解
信号的自变量的变换 信号的时域运算
系统
系统的定义、分类 线性时不变系统
线性特性 时不变性 微分特性 因果性
X
例题
• 例题1:画函数波形 • 例题2:冲激函数的性质
第 2 页
信号与系统阶跃响应例题

信号与系统阶跃响应例题
在信号与系统中,阶跃响应是一个常见的概念,它描述了系统在输入信号为阶跃函数时的响应情况。
下面是一个阶跃响应的例题:假设有一个系统的传递函数为H(s) = 1/(s+2),求该系统在输入信号为阶跃函数时的阶跃响应。
解题步骤如下:
1. 将传递函数H(s)中的s替换为jω,得到H(jω) = 1/(jω +
2)。
2. 计算系统的单位阶跃响应h(t),即系统在输入信号为u(t)
时的响应。
根据拉普拉斯变换的定义可知,h(t) = L^{-1}[H(s)/s],其中L^{-1}表示拉普拉斯反变换。
将H(s)/s代入上式中,得到h(t) = L^{-1}[1/(s(s+2))]。
3. 对于L^{-1}[1/(s(s+2))],可以使用部分分式分解的方法将其拆分为L^{-1}[1/s]和L^{-1}[-1/(s+2)]两部分。
具体地,对于1/(s(s+2)),可以拆分为A/s + B/(s+2),其中A 和B是待求系数。
将A/s + B/(s+2)代入原式中,得到1/s = A/(s+2) + B/s。
将s分别取0和-2,得到A = -1/2,B = 1/2。
因此,1/(s(s+2)) = -1/(2(s+2)) + 1/(2s)。
将-1/(2(s+2))和1/(2s)分别代入拉普拉斯反变换的公式中,可得到L^{-1}[-1/(2(s+2))] = -1/2 e^{-2t}和L^{-1}[1/(2s)] = 1/2。
因此,h(t) = L^{-1}[1/(s(s+2))] = -1/2 e^{-2t} + 1/2。
这就是该系统在输入信号为阶跃函数时的阶跃响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现在的响应=现在的激励+以前的激励 所以该系统为因果系统。
微分方程r (t ) = e (t ) + e (t + 2)代表的系统是否是因果 系统。
t=0
r (0 ) = e (0 ) + e (+ 2 )
未来的激励 所以该系统为非因果系统。
X
第
例2-2-5
t < 0开关S处于1的位置而且已经 给定如图所示电路, 达到稳态。当t = 0时S由1转向2。建立电流i ( t )的微分 方程并求解i ( t )在t ≥ 0时的变化。
3 页
当e1 ( t ) + e2 ( t ) 同时作用于系统时,若该系统为线性系统, 应有
d [r1 (t ) + r2 (t )] + 10[r1 (t ) + r2 (t )] + 5 = e1 (t ) + e2 (t ) dt t>0 ( 5)
(3)+(4)得
d [r1 (t ) + r2 (t )] + 10[r1 (t ) + r2 (t )] + 10 = e1 (t ) + e2 (t ) dt t>0 ( 6)
f ( − t ) → f ( t ) 倒置
f ( t ) = 4δ ( t + 1)
(4) t O 1 2 3 6
X
第
例1-5-1 求f(t)的奇分量和偶分量
f (t ) f (− t )
1 页
O
t
O
t
fe (t ) O t O
fo (t ) t
X
第
例1-6-1
d e( t ) d r (t ) d 2 r (t ) +3 + 2r ( t ) = + e( t ) 2 dt dt dt
t ⋅ f (t − τ )
f (t )
DE
τ
f (t − τ )
H [•]
可见,时移、再经系统 ≠ 经系统、再时移,所以 此系统是时变系统。
X
第
例1-7-4
微分方程r (t ) = e (t ) + e (t − 2)代表的系统是否是因果 系统。
t=0
1 页
r (0 ) = e (0 ) + e (− 2 )
系统框图
X
第
系统框图
e( t )
2 页
∫
∫
−3
r (t )
∫ ∫
−2
r ( t ) = −3 ∫ r ( t ) d t − 2 ∫∫ r ( t ) d t + ∫ e( t ) d t + ∫∫ e( t ) d t
X
第
例1-7-1
判断下述微分方程所对应的系统是否为线性系统?
d r (t ) + 10r ( t ) + 5 = e( t ) t > 0 dt
(t ≥ 0+ )
X
d i (0 + )和 i (0 + ) (3)确定换路后的 dt
换路前
2 S R1 = 1Ω 1
e (t ) = 4 V
第 4 页
iC (t ) i (t ) C = 1F
i L (t )
1 L= H 4 3 R2 = Ω 2
e (t ) = 2 V
2 4 i (0 − ) = i L (0 − ) = = A R1 + R2 5
展宽一倍
O f(-t) 1 2 3
(4) t 6
t f (5 − t ) = 2δ − 3 = 4δ ( t − 6) 2
f (5 − t ) → f ( − t ) 左移5
f ( − t ) = f [5 − ( t + 5)] = 4δ ( t − 1)
(4) O f(t) t 1 2 3 6
X
(5)、(6)式矛盾,该系统为不具有叠加性
第
例1-7-2
判断下列两个系统是否为非时变系统。 系统1:r (t ) = cos[e (t )] 系统2:r (t ) = e (t ) ⋅ cos t
t>0 t>0
1 页
1.系统的作用是对输入信号作余弦运算。
过系统 移t 0 (1)e( t ) 时 → e( t − t 0 ) 经 → r11 ( t ) = cos e( t − t 0 ) t > 0 移t 0 → r12 ( t ) = cos e( t − t 0 ) t > 0 ( 2)e( t ) → cos e( t ) 时
t>0
t>0
t 0→ r ( t ) = e( t − t ) cos(t − t ) ( 2)e( t ) → e( t ) cos t 22 0 0
经过系统
时移
r21 ( t ) ≠ r22 ( t )
此系统为时变系统。
X
第
例1-7-3
y (t ) = t ⋅ f (t )判断系统是否为线性非时变系统。
X
第
(4)求i (t )在t ≥ 0 + 时的完全响应
由i (t )的表示式
8 14 i (0 + ) = A1 + A2 + = 5 5 d i (0 ) = −2 A − 5 A = −2 + 1 2 d t 4 A1 = 3 A = − 2 2 15
1 页
请用积分器画出如下微分方程所代表的系统的系统框图。
方程左端只保留输出的最高阶导数项
d e( t ) d r (t ) d 2 r (t ) = −3 − 2r ( t ) + + e( t ) 2 dt dt dt
积分 n=2 次,使方程左端只剩下r(t) 项
r ( t ) = −3 ∫ r ( t ) d t − 2 ∫∫ r ( t ) d t + ∫ e( t ) d t + ∫∫ e( t ) d t
ih (t ) = A1e −2 t + A2e −5 t
e (t ) = 4V
(t ≥ 0+ )
方程右端自由项为 4 × 4,因此令特解 ip (t ) = B , 代入式(1)
10 B = 4 × 4
要求系统的完全响应为
i (t ) = A1e
−2t
16 8 B= = 10 5
−5t
+ A2e
8 + 5
2
O
1 页
(1)将e(t)代入微分方程,t≥0得
t
d d2 r (t ) + 7 r (t ) + 10r (t ) = 2δ ′(t ) + 12δ (t ) + 8∆u(t ) 2 dt dt
X
第
(2)
d d2 r (t ) + 7 r (t ) + 10r (t ) = 2δ ′(t ) + 12δ (t ) + 8∆u(t ) 2 dt dt 方程右端的冲激函数项最高阶次是 δ ′(t ),因而有 d2 2 r (t ) = aδ ′(t ) + bδ (t ) + c∆u(t ) d t d (0 − < t < 0 + ) r (t ) = aδ (t ) + b∆u(t ) d t r (t ) = a∆u(t )
d i (0 − ) = 0 dt
6 4 3 vC (0 − ) = × V = V 5 5 2
X
d 换路后的 i (0 + )和 i (0 + ) : dt
2 S R1 = 1Ω 1
e (t ) = 4 V
第 5 页
iC (t ) i (t ) C = 1F
i L (t )
1 L= H 4 3 R2 = Ω 2
2 页
原方程两端乘A:
d r (t ) + 10r ( t ) + 5 = Ae( t ) A dt t>0 ( 2)
(1),(2)两式矛盾。故此系统不满足均匀性
X
第
证明叠加性
假设有两个输入信号 e1 ( t )及e2 ( t ) 分别激励系统,则由 所给微分方程式分别有:
d r1 (t ) + 10r1 (t ) + 5 = e1 (t ) dt d r2 (t ) + 10r2 (t ) + 5 = e2 (t ) dt t>0 t>0 ( 3) ( 4)
1 页
分析:根据线性系统的定义,证明此系统是否具有 均匀性和叠加性。可以证明: 系统不满足均匀性 系统不具有叠加性 所以此系统为非线性系统。 请看下面证明过程
X
第
证明均匀性
设信号e(t)作用于系统,响应为r(t) 当Ae(t)作用于系统时,若此系统具有线性,则
d Ar ( t ) + 10 Ar ( t ) + 5 = Ae( t ) dt t>0 (1)
1 页
是否为线性系统?
f 1 (t ) C1 C 1 f 1 (t )
f 2 (t )
f 1 (t )
C2
H [•]
C 2 f 2 (t )
t ⋅ f 1 (t )
∑
C1 C 1 t ⋅ f 1 (t )
H [•]
t ⋅ [C 1 f 1 (t ) + C 2 f 2 (t )]
f 2 (t )
H [•]
t ⋅ f 2 (t )
C2
C 2 t ⋅ f 2 (t )
∑
C 1 tf1 (t ) + C 2 tf 2 (t )
