中考复习专题(填空题)
九年级数学中考复习《分式方程解的相关问题》填空题专题训练

九年级数学中考复习《分式方程解的相关问题》填空题专题训练(附答案)1.若关于x的方程有增根,则a的值.2.若关于x的方程有增根,实数m的值为.3.关于x的方程有增根,则增根是;且k的值是.4.解关于x的分式方程=时不会产生增根,则m的取值范围是.5.若关于x的方程=1﹣无解,则a的值为.6.若关于x的分式方程+=无解,则m的值为.7.已知关于x的方程的解为正数,则m的取值范围是.8.如果关于x的方程=2无解,则a的值为.9.已知关于x的方程的解大于1,则实数m的取值范围是.10.若关于x的分式方程有正整数解,则整数a=.11.若关于x的分式方程=1﹣的解为非负数,则m的取值范围是.12.已知关于x的方程无解,则m=.13.若整数a既使得关于x的分式方程有整数解,又使得关于x,y的方程组的解为正数,则a=.14.已知关于x的不等式组共有三个整数解,关于y的分式方程的解为整数,则整数a的值为.15.关于x的方程=1的解为正数,且关于y的不等式组有解,则符合题意的所有整数m的和为.16.若方程+1=的解使关于x的不等式(2﹣a)x﹣3>0成立,则实数a的取值范围是.17.如果关于x的不等式组的解集为x<1,且关于x的分式方程有非负整数解,则符合条件的m的所有值的和是.18.若关于x的不等式组有且仅有4个整数解,且使得关于y的分式方程﹣1=有整数解,则满足条件整数a的和为.19.若关于x的方程的解为整数,则满足条件的所有整数a的和等于.20.从﹣4,﹣3,1,3,4这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组的解集是x<a,且使关于x的分式方程有整数解,那么这5个数中所有满足条件的a的值之和是.参考答案1.解:去分母,得:2x+a=x+2,由分式方程有增根,得到x+2=0,即x=﹣2,把x=﹣2代入整式方程,﹣4+a=﹣2+2,可得:a=4.故答案为:4.2.解:去分母,得2mx﹣(m+1)=x+1,∵关于x的方程有增根,将增根为x=﹣1代入2mx﹣(m+1)=x+1,得﹣2m﹣(m+1)=0,解得m=﹣,将增根为x=0代入2mx﹣(m+1)=x+1,得﹣(m+1)=1,解得m=﹣2,∴m的值为﹣或﹣2,故答案为:﹣或﹣2.3.解:,x﹣1=2(x﹣3)+k,解得:x=5﹣k,∵方程有增根,∴x=3,把x=3代入x=5﹣k中,3=5﹣k,解得:k=2,∴关于x的方程有增根,则增根是x=3,且k的值是2,答案为:x=3;2.4.解:=,1+x﹣1=﹣m,解得:x=﹣m,∵分式方程不会产生增根,∴x≠1,∴﹣m≠1,∴m≠﹣1,∴m的取值范围是m≠﹣1,故答案为:m≠﹣1.5.解:∵=1﹣,∴ax=x﹣2+6,∴(a﹣1)x=4.当a=1时,方程无解,a=1符合题意;当a≠1时,x=,∵关于x的方程=1﹣无解,∴x﹣2=0,∴=2,∴a=3.∴a的值为1或3.故答案为:1或3.6.解:(1)x=﹣2为原方程的增根,此时有2(x+2)+mx=5(x﹣2),即2×(﹣2+2)﹣2m=5×(﹣2﹣2),解得m=10;(2)x=2为原方程的增根,此时有2(x+2)+mx=5(x﹣2),即2×(2+2)+2m=5×(2﹣2),解得m=﹣4.(3)方程两边都乘(x+2)(x﹣2),得2(x+2)+mx=5(x﹣2),化简得:(m﹣3)x=﹣14.当m=3时,整式方程无解.综上所述,当m=10或m=﹣4或m=3时,原方程无解.故答案为:10或﹣4或3.7.解:去分母,得2x﹣m﹣(x﹣3)=﹣x,解得:x=,∵关于x的方程的解为正数,∴x=>0且x≠3,∴m>3且m≠9;故答案为:m>3且m≠9.8.解:去分母得,ax﹣1=2(x﹣1)ax﹣2x=﹣1,(a﹣2)x=﹣1,当a﹣2=0时,∴a=2,此时方程无解,满足题意,当a﹣2≠0时,∴x=﹣,将x=﹣代入x﹣1=0,解得:a=1,综上所述,a=1或a=2,故答案为:1或2.9.解:方程两边同乘以x﹣5得:x+m=5﹣x,解这个整式方程得:x=,由题意得:>1且≠5,解得:m<3且m≠﹣5,故答案为:m<3且m≠﹣5.10.解:分式方程去分母得1﹣ax+3(x﹣2)=﹣1,整理得(3﹣a)x=4,解得x=,∵分式方程有正整数解,且x﹣2≠0,∴整数a=﹣1或2.故答案为:﹣1或2.11.解:=1﹣,2=x﹣3+m,x=5﹣m,∵方程的解为非负数,∴5﹣m≥0,∴m≤5,∵x≠3,∴5﹣m≠3,∴m≠2,∴m的取值范围为m≤5且m≠2,故答案为:m≤5且m≠2.12.解:去分母得:2x=mx﹣3(x+3),整理为:(5﹣m)x=﹣9,当5﹣m=0,即m=5时,此方程无解,原分式方程也无解,当5﹣m≠0时,由x+3=0得:x=﹣3,把x=﹣3代入(5﹣m)x=﹣9得:(5﹣m)×(﹣3)=﹣9,解得:m=2,∴m=5或2.故答案为:5或2.13.解:解方程得,x=,∵分式方程有整数解,且x≠1,∴a﹣3=﹣4或﹣2或﹣1或1或2或4,且a≠7,∴a=﹣1或1或2或4或5,解方程组得,,∵方程组的解为正数,∴,解得a>4,综上,a=5.故答案为:5.14.解:解不等式3x﹣a>0,得x>.解不等式x﹣4≤﹣x,得x≤2.∵关于x的不等式组有且仅有三个整数解,∴﹣1≤<0,∴﹣3≤a<0,分式方程,去分母,得a+y﹣1=3y﹣6,∴y=,且≠2,∵关于y的分式方程有整数解,∴a=﹣3,故答案为:﹣3.15.解:∵关于x的方程=1的解为正数,∴2﹣x﹣m=x﹣3,解得:x=,∵x﹣3≠0,∴x≠3,∴≠3,m≠﹣1,则5﹣m>0,故m<5,且m≠﹣1,∵关于y的不等式组有解,∴m+3≤y≤3m+6,且m+3≤3m+6,解得:m≥﹣1.5,故m的取值范围是:﹣1.5≤m<5,且m≠﹣1,则符合题意的整数m有:0,1,2,3,4,∴符合题意的所有整数m的和为10.故答案为:10.16.解:+1=,+=,=0,解得:x=1,∵x﹣2≠0,2﹣x≠0,∴x=1是分式方程的解,将x=1代入不等式(2﹣a)x﹣3>0,得:2﹣a﹣3>0,解得:a<﹣1,∴实数a的取值范围是a<﹣1,故答案为:a<﹣1.17.解:,由①得:x<m,由②得:x﹣4>3x﹣6.∴x<1.∵原不等式组的解集为:x<1.∴m≥1.∵﹣=3.∴x+2﹣m=3x﹣3.∴x=,∵方程的解是非负整数,∴符合条件的整数m为:1,3,5.当m=3是,x=1,x﹣1=0不合题意,∴m=1,5.1+5=6.故答案为:6.18.解:,解不等式①,得:x≤3,解不等式②,得:x>﹣,∵该不等式组有且仅有4个整数解,∴﹣1≤﹣<0,解得:﹣4<a≤1,分式方程去分母,得:y﹣(1﹣y)=﹣a,解得:y=,∵分式方程有整数解,且y≠1,∴满足条件的整数a可以取﹣3,1,其和为﹣3+1=﹣2,故答案为:﹣2.19.解:原分式方程可化为:﹣=,去分母,得x﹣3﹣a(x+1)=2a﹣2,解得,x===﹣3+,∵x≠3且x≠﹣1,∴﹣3+≠3且﹣3+≠﹣1,∴a≠且a≠﹣1,a≠1,∵关于x的方程的解为整数,∴a=±1或a=±2或a=±4,∴a=﹣3、0、2、3、5,∴﹣3+0+2+3+5=7,故答案为:7.20.解:不等式组化简为,∵不等式组的解集是x<a,∴a≤3,∴a=﹣4,﹣3,1,3,解分式方程得:x=,∵x≠2,∴≠2,∴a≠1,∵分式方程有整数解,∴x=是整数,∴满足条件的a有:﹣3,3,∴满足条件的a的值之和为﹣3+3=0,故答案为:0.。
中考数学复习专题训练精选试题及答案

中考数学复习专题训练精选试题及答案一、选择题1. 以下哪一个数是最小的无理数?A. √2B. πC. 3.14D. √9答案:A2. 若一个等差数列的首项是2,公差是3,则第8项是多少?A. 17B. 18C. 19D. 20答案:A3. 一个二次函数的图像开口向上,顶点坐标为(3,-4),则该二次函数的一般式为:A. y = x² + 6x - 13B. y = x² - 6x + 13C. y = -x² + 6x - 13D. y = -x² - 6x + 13答案:B4. 在三角形ABC中,a = 5,b = 7,C = 60°,则边c 的长度等于:A. 6B. 8C. 10D. 12答案:C二、填空题1. 已知a = 3,b = 4,则a² + b² = _______。
答案:252. 已知一个等差数列的前5项和为35,首项为7,求公差d = _______。
答案:23. 在梯形ABCD中,AB // CD,AB = 6,CD = 8,AD = BC = 5,求梯形的高h = _______。
答案:34. 若函数f(x) = x² - 2x + 1的最小值为m,求m =_______。
答案:0三、解答题1. 已知一元二次方程x² - 4x - 12 = 0,求解该方程。
解:首先,将方程因式分解为(x - 6)(x + 2) = 0。
然后,解得x = 6或x = -2。
答案:x = 6或x = -22. 已知一个长方体的长为a,宽为b,高为c,且a、b、c成等差数列。
若长方体的体积为V,求V的表达式。
解:由题意可知,a + c = 2b,所以c = 2b - a。
长方体的体积V = abc = ab(2b - a)。
答案:V = ab(2b - a)3. 已知三角形ABC,AB = AC,∠BAC = 40°,BC = 6,求三角形ABC的周长。
通用版中考数学填空题专题训练(附答案)
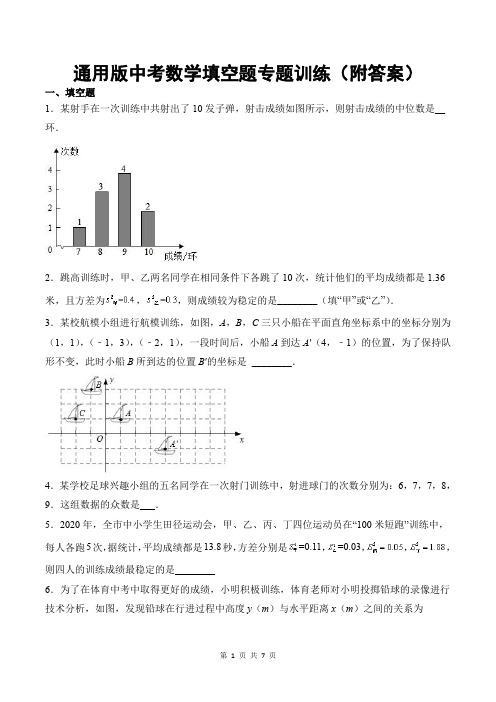
通用版中考数学填空题专题训练(附答案)一、填空题1.某射手在一次训练中共射出了10发子弹,射击成绩如图所示,则射击成绩的中位数是__环.2.跳高训练时,甲、乙两名同学在相同条件下各跳了10次,统计他们的平均成绩都是1.36米,且方差为,,则成绩较为稳定的是________(填“甲”或“乙”).3.某校航模小组进行航模训练,如图,A,B,C三只小船在平面直角坐标系中的坐标分别为(1,1),(﹣1,3),(﹣2,1),一段时间后,小船A到达A′(4,﹣1)的位置,为了保持队形不变,此时小船B所到达的位置B′的坐标是________.4.某学校足球兴趣小组的五名同学在一次射门训练中,射进球门的次数分别为:6,7,7,8,9.这组数据的众数是___.5.2020年,全市中小学生田径运动会,甲、乙、丙、丁四位运动员在“100米短跑”训练中,每人各跑5次,据统计,平均成绩都是13.8秒,方差分别是=0.11,=0.03,,,则四人的训练成绩最稳定的是________6.为了在体育中考中取得更好的成绩,小明积极训练,体育老师对小明投掷铅球的录像进行技术分析,如图,发现铅球在行进过程中高度y(m)与水平距离x(m)之间的关系为,由此可知小明此次投掷的成绩是___.7.为增强学生体质,感受中国的传统文化,某校将“抖空竹”定为特色体育项目每天大课间进行训练,某同学“抖空竹”的一个瞬间如图①所示,若将图①抽象成图①的数学问题:,,,则的大小是____________度.8.甲、乙、丙、丁四位同学在相同条件下进行“立定跳远”训练,每人各跳10次,统计他们的平均成绩(单位:米)和方差如下表所示:则这四名同学“立定跳远”成绩波动最大的是______.9.2022年冬奥会北京赛区,共举办包括滑冰(含短道速滑、速度滑冰、花样滑冰)、冰球、冰壶在内的3个大项5个分项的所有冰上项目比赛,为了迎接2022年的冬奥会,中小学都积极开展冰上运动.小聪和小明进行500米短道速滑训练,他们的五次成绩如表所示:设两个人的五次成绩的平均数依次为小聪,小明,方差依次为S2小聪,S2小明,你认为两人中技术更好的是,你的理由是____.10.甲、乙、丙三人进行羽毛球比赛赛前训练,每局两人进行比赛,第三个人做裁判,每一局。
中考语文复习 词语(填空题)专练-人教版初中九年级全册语文试题

词语1、填空:(1)几个小片_________云霞,_________起来,_________起来,_________而出,原来是出太阳了。
(2)古人写“日”的诗句很多,请你任写两首诗中的名句。
① _____________________________________________________②_____________________________________________________(3)玫瑰汁,___________, __________, ___________, ___________——大量的染工,在层累的云底工作,无数蜿蜒的鱼龙,爬进了苍白色的云堆。
答案:(1)冲破密接融合飞跃(2)略(3)葡萄浆紫荆液玛瑙精霜枫叶2、根据拼音写出汉字,补充完整句子:⑴一片冬意(méng)(lóng)的光照扩展开了,群山像是浮在一片白浪的海中,只有山尖分明突出。
⑵在我没有一点准备、一丝预料的时刻,宇宙便把它那无与(lún)比的光华、风(cǎi),全部展现在我的眼前了。
⑶有一天,他登上山顶,看见一轮太阳正在喷(bó)而出,于是,罗曼·罗兰心目中久久(yùn)(niàng)的英雄在东地平线上出现了。
⑷每天舞蹈般(pó)(suō)变化的只有远远近近的游云,颜色也变(huàn)莫定。
答案:⑴朦胧⑵伦采⑶薄酝酿⑷婆娑幻3、根据括号内的提示,写出相应的词语(1)对待学习应采取认真的态度,那种(只求知道个大概,不求彻底了解,常指学习或研究不认真、不深入)的学习方法是不可取的。
(2)参加某某电影节的女嘉宾们一个个婀娜多姿,(形容女子打扮的十分艳丽),为颁奖盛典带来了一道亮丽的风景。
答案:不求甚解花枝招展4、根据括号里的意思写词语:(1)有(闲适安逸的兴致情趣)的人,自然不喜欢这种紧X的旋律。
▲(2)富有创造性的人总是(勤奋努力,不知疲倦)地汲取知识。
中考物理复习专题训练(共八个专题)含答案

中考物理复习专题训练专题训练一力学专题一、填空题(每空1分,共26分)1.用托盘天平称物体质量时,物体应放在天平的_______盘中,如果发现指针偏向分度盘的左侧,应该_______(填“增加”或“减少”)砝码.2.自行车车轮的外表面都有凹凸不平的花纹,这是为了_______,菜刀的刀刃要做得很薄,这是为了_______.3.在百米跑训练中,测得一短跑运动员起跑后5 s跑完34 m,即可达到最大速度11 m/s,以后保持这一速度跑完全程,则这名运动员这次百米跑的成绩(时间)是_______s,他百米跑的平均速度为_______m/s.4.沿直线运动的物体在一直线上的两个力作用下,其运动的速度越来越小,那么这两个力的合力大小一定_______零.(选填“大于”“小于”“等于”),合力的方向与运动的方向_______.5.木块的密度是0.6 g/cm3,冰块的密度是0.9 g/cm3,若它们的体积相等,都漂浮在水面上,则木块受到的浮力_______冰块受到的浮力,木块露出水面的体积_______冰块露出水面的体积.(选填“大于”“小于”“等于”)6.下列实物属于哪种简单机械:(1)操场上旗杆顶端的小轮属于(2)码头上起重机吊钩上方的铁轮属于(3)家用缝纫机的脚踏板属于7.将以下做法中用到的主要物理知识分别填在题后的横线上(简要写出物理知识的内容)拦河坝总是下部宽上部窄用吸管将杯中的饮料吸入口中自行车的轴承上要经常加油把斧柄的一端在水泥地面撞击几下,斧头就牢牢地套在斧柄上___________8.汽车如果空载和满载时都以相同的速度行驶,空载时具有的动能_______满载时的动能,停在山顶上的卡车具有的重力势能_______该车在山下时具有的重力势能.(填“大于”“等于”或“小于”)9.把一个空杯子底朝上竖直按入水中,随着杯子没入水中深度的增加,杯中空气的压强_______体积_______.10.甲、乙两支完全相同的试管,内装密度相等的同种液体,甲管竖直放置,乙管倾斜放置,两管液面相平,如图所示,设液体对两试管底的压强分别为p甲和p乙,则p甲____p乙(填“大于”“等于”或“小于”)11.用50 N的水平拉力拉着重为200 N的小车沿水平道路在1 min内前进60 m,则拉力做的功为_______J,拉力的功率为_______ W.12.某高层楼房中,五楼水龙头出水口的水的压强是2.5×105 Pa,那么比它高12 m的九楼的出水口的水的压强是_______,比它低12 m的底楼水龙头出水口的压强是_______Pa.(g=10 N/kg)二、选择题(每题3分,共36分)13.甲同学把耳朵贴在长铁管的一端,乙同学在另一端敲一下铁管,甲同学听到两次响声,这是因为( ) A.声音有反射现象B.声音在空气中比在铁中传播的快C.声音有折射现象 D.声音在空气中比在铁中传播的慢14.放在水平桌面上静止不动的电视机,受到彼此平衡的两个力是( )A.电视机受到的重力和桌面对电视机的支持力B.电视机受到的重力和电视机对桌面的压力C.桌面对电视机的支持力和电视机对桌面的支持力D.桌面受到的重力和电视机对桌面的压力15.用1 m的玻璃管做托里拆利实验,下面几种情况中对管内水银柱竖直高度有影响的是( )A.玻璃管的粗细B.玻璃管的长短 C.实验所在的高度D.玻璃管插入水银槽的深度16.如图所示的三只相同的烧杯分别放有质量相等的煤油、水、硫酸,根据液面高度判断盛硫酸的是( )A.甲杯 B.乙杯 C.丙杯 D.无法判断17.三个分别用铜、铁、铝制成的正立方体,它们的质量相等,把它们放在水平桌面上,则对桌面压强大的是( )A.铜立方体B.铁立方体 C.铝立方体D.三个一样大18.有一人用一滑轮组分别将1000 N和2000 N的物体匀速提高相同的高度,动滑轮重200 N,绳重及摩擦都不计,则在上述两种情况中( )A.人做的额外功相等B.滑轮组的机械效率相等C.人做的总功相等D.人做功的功率相等19.下列各现象中不属于惯性现象的是( )A.刹车时,人的身体向前倾B.放入水中的铁球很快沉入水底C.汽车关闭发动机后,车还会向前运动一段距离D.锤头松了,用力将锤柄撞击固定物,使锤头紧套在柄上20.下列工具或仪器中属于省力杠杆的是( )21.用手握住汽水瓶,汽水瓶并不滑落,这是因为( )A.手的握力大于汽水瓶的重力 B.手的握力等于汽水瓶的重力C.手给汽水瓶的摩擦力大于瓶的重力 D.手给汽水瓶的摩擦力等于瓶的重力22.两手对拉一弹簧秤,它的示数是10 N ,这两手的拉力分别为( ) A .5 N ,5 N B .10 N ,10 NC .0 N ,0 ND .20 N ,20 N23.如图所示,原来静止的物体A 在水平拉力F 作用下沿水平面做直线运动,速度逐渐增大,则拉力F ( ) A .一定大于阻力F fB .一定等于阻力F fC .可能等于阻力F f D .可能小于阻力F f24.两个完全相同的容器中分别盛有质量相等的水和酒精,如图所示.下列说法正确的是( )A .两容器底受到的压力相等B .液面下深度相同的两处a 、b 所受液体的压强相等C .盛水容器底部受到的压强较大D .盛水容器底部受到的压强较小三、实验题(每题7分,共14分)25.把从图所示实验中观察到的弹簧秤和量筒的示数记录在表格中,并计算出相应的物理量.(g =9.8 N/kg) 26.在做“研究杠杆平衡条件”的实验中,挂钩码前,使杠杆在水平位置平衡,实验中只有10个相同的钩码,杠杆上每格等距,当在A 点挂上4个钩码时,应怎样挂钩码才可使杠杆在水平位置平衡?请在图中画出两种设计方案.四、计算题(每题8分,共24分)27.一木块浮在水面上,露出水面的体积为32 cm 3,把露出水面的部分截去后,原水下部分又有24 cm 3体积露出水面,求:(1)木块的体积. (2)木块的密度.28.有一个形状不规则的物体,用弹簧秤测得物体在空气中的重力为G ,然后把它全部浸入密度为0的液体中,测出物体在液体中的重力为G ′,求: (1)此物体的体积V ;(2)此物体的密度1.(3)若将一个与它的体积相同的物体用绳子将它们捆在一起,放在原来的液体中恰好悬浮,求另一物体的密度2.29.某人乘坐出租车在平直的公物重(N) 物体在水中弹簧秤的示数(N)物体受到的浮力(N)物体排开水的体积(m 3)物体排开的水重(N)路上匀速行驶,出租车的牵引力为3000 N,下表为他乘车到达目的地的车费发票,求: (1)出租车行驶的时间.(2)出租车的速度. 专题训练一 力学参考答案1.左 增加2.增大摩擦力 增大压强3.11 s 9.09 m/s4.大于 相反5.小于 大于6.定滑轮 动滑轮 费力杠杆7.液体压强随深度增大而增大 大气压强的作用 减小摩擦力 由于惯性8.小于 大于 9.增加 减少10.等于11.300050 12.1.3×105Pa 3.7×105Pa 13.D 14.A 15.C 16.C 17.A 18.A 19.B20.A 21.D 22.B 23.A 24.A25.1.96 0.98 0.98 1×10-40.98 26.略 27.128 cm 30.75×103kg/m 328.略 29.5 min 96 km/h专题训练二 电学专题一、填空题(每空1分,共15分)1.一个导体两端加4 V 电压时,通过它的电流强度为0.8 A ,当把它两端电压变为6 V 时,通过它的电流为_______A ,它的电阻为_______ .2.如图所示的电路中,定值电阻R 2为10 ,闭合开关S 前后干路中总电流的比为2∶3,则R 1的阻值为_______.3.标有“2.5 V 0.3 A ”的小灯泡,正常工作1 min 通过的电量为_______,功率为_______,产生的热量为_______.4.如图所示的电路,用电器的电阻R 0=30 ,要求通过它的电流能在100~200 mA 的范围内变化,选用的电源电压最小应为_______V ,电路中所用滑动变阻器的阻值变化范围应是_______ .5.“220 V 100 W ”的甲灯和“220 V 40 W ”的乙灯相比较,正常工作时_______灯更亮,_______灯的电阻大一些,_______灯的灯丝粗一些.6.如图所示的圆环是由阻值R 、粗细均匀的金属丝制成的.A 、B 、C 三点将圆环分成三等份(每等份电阻为31R ),若将其中任意两点连入电路,则连入电路的电阻值为_________.7.如图所示电路中,电源电压保持不变,当滑动变阻器的滑片P 由中点向右端移动的过程中,电流表的示数将_______,灯泡L 消耗的电功率将_______,变阻器R 上消耗的电功率将_______(选填“变大”“变小”或“不变”)二、选择题(每题3分,共45分)8.阻值为3 与6 的电阻,将它们串联,其总电阻为R1;将它们并联,其总电阻为R2,则R1∶R2等于( )A.2∶1 B.1∶2 C.2∶9 D.9∶29.如图所示的电路中,电源电压不变,闭合开关S后,灯L1、L2都发光,一段时间后,其中一灯突然熄灭,而电流表、电压表的示数都不变,则产生这一现象的原因是( )A.灯L1短路 B.灯L2短路C.灯L1断路D.灯L2断路10.如图所示,V1和V2是完全相同的两个电压表,都有3 V和15 V两个量程,闭合开关后,发现两个电压表偏转的角度相同,则( )A.R1∶R2=1∶4 B.R1∶R2=4∶1C.R1∶R2=1∶5 D.R1∶R2=5∶111.将两只滑动变阻器按图所示的方法连接,如果把a、b两根导线接入电路里,要使这两只变阻器接入电路中的总电阻最大,应把滑片P1、P2放在( )A.P1放在最右端,P2放在最右端B.P1放在最左端,P2放在最左端C.P1放在最右端,P2放在最左端D.P1放在最左端,P2放在最右端12.在图所示的电路中,电源电压保持不变,当开关S闭合,滑动变阻器的滑片P向右移动时,电流表和电压表的示数的变化情况分别为( )A.电流表的示数变小,电压表的示数变大B.电流表的示数变大,电压表的示数变小C.电流表的示数变小,电压表的示数不变D.电流表的示数变小,电压表的示数变小13.如图所示,下列判断错误的是( )A.仅使灯L1工作,应闭合开关S2、S3 B.仅使灯L2工作,应闭合开关S1、S3C.使灯L1工作,应闭合开关S1、S3 D.使灯L2工作,只闭合开关S3也可14.如图所示,电磁铁P和Q通电后( )A.P的右端是N极,Q的左端是S极,它们相互吸引B.P的右端是S极,Q的左端是N极,它们相互吸引C.P的右端是N极,Q的左端是N极,它们相互排斥D.P的右端是S极,Q的左端是S极,它们相互排斥15.有a、b、c、d四个带电体,它们之间的相互作用是:a排斥c,b吸引c,b排斥d,由此判断( ) A.a、d间相互排斥B.a、d间相互吸引C.a一定带正电D.d一定带负电16.用粗细均匀的电热丝加热烧水,通电10 min可烧开一壶水,若将电热丝对折起来使用,电源电压不变,则烧开同样一壶水的时间是( )A.2.5 min B.5 min C.20 min D.30 min17.现有一只“PZ220—60”灯泡L1和一只“PZ220—25”灯泡L2,下列有关说法中正确的是( )A.灯泡L1的电阻小于灯泡L2的电阻 B.它们并联在照明电路中时L2亮C.它们串联在照明电路中时L1亮 D.它们正常发光时,在相同时间内消耗的电能相同18.原来室内的电灯正常发光,当把台灯的插头插入插座时(台灯的开关断开),室内的灯全部熄灭,熔丝熔断,发生这一现象的原因是( )A.台灯的功率太大B.台灯的插头处有短路C.台灯的灯座处有短路D.插座处原来就有短路19.电工修理如图所示的照明电路时,发现电灯R不亮,用测电笔测试C、D后,发现这两处都能使氖管发光,而测试A、B两点时,只有A点氖管发光,则故障可能发生在( )A.AC段B.CD段C.电灯R短路D.BD段20.一个通电螺线管两端磁极的极性决定于()A.螺线管的匝数B.通过螺线管的电流方向C.螺线管内有无铁芯D.通过螺线管的电流21.闭合电路的一部分导体在磁场中运动的方向如下图所示,图中小圆圈表示导体的横截面,箭头表示导体运动的方向,下列各图中不能产生感应电流的是( )22.在如图所示的电路中,电源电压恒定,R1为一定值电阻,R2为滑动变阻器.开关S闭合后,当滑动变阻器的滑片P在a、b之间滑动的过程中,电压表的示数最大为4 V,电阻R1的电功率变化范围是0.8 W~7.2 W,则P从a端滑至b端的过程中,电流表的示数( )A.从1.8 A变化至0.2 A B.从0.4 A变化至1.2 AC.从1.2 A变化至0.4 A D.从0.2 A变化至1.8 A三、作图题(每题5分,共15分)23.根据下图中小磁针静止时的位置,标出电源的正、负极或通电螺线管的绕法.24.下图是安装一盏电灯和一个大功率插座的实物示意图,A、B为保险丝,请在图上画出接线.25.在下图中,A、B、C为三条引出线,由三个阻值相等的电阻组成,现用装有电池和电流表的检测器连接AB时,电流表示数I,当检测器与BC连接时,电流表的示数为I/2;当检测器与AC连接时,电流表的示数为I/3,试画出方框里的电路图.四、实验题(14分)26.测定标有“3.8 V”灯泡的额定功率.(1)画出实验电路图,并根据电路图将下列所需实物连接起来.(10分)(2)电压表所选量程是_______,调节滑动变阻器,应使电压表指针指在_______的位置上.(2分)(3)若此时电流表的示数如图所示,其读数为_______,则灯泡的额定功率约是________.(2分)五、计算题(11分)27.某同学家的电炉铭牌模糊不清了,为了测出电炉的额定功率,他让家里的所有用电器都停止工作,只接入电炉让其正常工作,然后观察家里正在运行的电能表,电能表上标有“3000 R/kWh”,利用手表计时,发现1 min转盘转了50转,那么:(1)电炉的额定功率是多少?(2)小明同学觉得电炉使用不方便,想对电炉进行改装:使电炉的功率可以为额定功率,也可以为额定功率的1/4,请你利用一个开关和一个定值电阻帮他设计一个电路,画出电路图,并计算出定值电阻的大小.专题训练二电学专题参考答案1.1.2 5 2.20 3.18 C 0.75 W 45 J 4.6 0~30 5.甲乙甲 6.2R/97.变小不变变小8.D 9.D 10.A 11.D 12.C 13.C 14.B 15.B 16.A 17.A 18.B 19.D 20.B 21.C 22.C 23.略 24.略 25.略26.(1)略 (2)0~15 V 2.8 V (3)0.34 A 1.3 W 27.(1)1 kW(2)图略将开关与定值电阻并联后再与电炉丝串联R=48.4专题训练三实验一、填空题(每空1分,共37分)1.为测量运动员短跑时的平均速度.在室外测出40 m的路程,每隔10 m作一记号.选出4位记时员分别站在10、20、30、40 m处;让该运动员跑完40 m路程即告实验完毕.(1)实验中所用的主要器材是_______和_______;(2)实验原理是_______________.2.瓶里放少量的碘,并且对烧瓶微微加热,可以观察到碘的_______现象.停止加热,过一会儿,在烧瓶壁上可观察到碘的_______现象.3.做“研究透镜成像规律实验”前,首先要利用_______和_______测出一凸透镜的焦距.做这个实验时,为了使像能成在光屏的中央,应先调节好_______和_______的高度,使它们的中心跟_______的中心大致在同一高度.4.某同学做“平面镜成像的特点”实验时,将一块玻璃板竖直架在一把直尺的上面,再取两段等长的蜡烛A和B一前一后竖放在直尺上,点燃玻璃板前的蜡烛A,用眼睛进行观察,如图所示.在此实验中:(1)直尺的作用是便于比较物与像的______________关系;(2)两段等长的蜡烛是为了比较______________关系;(3)移去蜡烛B,并在其所在位置上放一光屏,则光屏上_______接收到蜡烛A的烛焰的像(填“能”或“不能”).这说明平面镜成的是_______像.5.在实验室里,我们通常用_______法来测定电阻的阻值,即只要测出电阻两端的_______和通过它的_______,就可以用公式_______算出电阻的阻值.根据这一实验要求,除待测电阻外,还必需的器材是_______、_______、_______、_______、_______.6.如果你的家庭电路中有一只表盘上标有3000 R/kWh的电能表,另外你手头还有一块秒表.如何测量你家中某一盏白炽灯的实际电功率?(1)写出测量方法:_______________;(2)要测量哪些物理量:_______________;(3)写出根据测量的物理量,计算灯泡电功率的数学表达式:______________.7.白炽灯的灯丝常在_______时发生断开,如若能接上继续使用,则电功率将比原来_______(填“大”或“小”),这是由于它的电阻变_______了.8.把几滴红墨水滴入清水中,隔一会儿,清水变成红水,这是_______现象.当红墨水分别滴入冷水和热水中,可以看到热水变色比冷水快.这说明温度越高,______________.9.水的比热是_______.装有50 L水的太阳能热水器,在阳光照射下,水温从20℃上升到50℃,该热水器中水吸收的热量是_______.10.黑板的“反光”现象属于光的_______现象;我们能从不同方向看到本身不发光的物体,是由于光射到物体上时,发生了_______反射的缘故.11.普通自行车上,通过增大压力来增大摩擦的装置是_______;在前后轮中减小摩擦的措施是在轮子的轴上安装了_______.二、选择题(每题2分,共24分)12.使用天平时,下列哪种原因会使测量产生误差( )A.天平使用之前忘了调节B.游码所对标尺的读数估计值偏小了C.将砝码放在天平的左盘里,被称物体放在天平的右盘里,并使用了游码D.少加了一个2 g游码标示的质量13.少数不法商贩将煤矸石(矿井下与煤共生一处的石块)破碎后掺在优质煤中高价销售给客户.客户为了防止上当,最恰当的方法是可以检测下述物理量中的( )A.密度B.比热C.熔点D.燃烧值14.若给你一块小木块、一只量筒、水、酒精、一根细针,你能完成下列实验中的哪几种( )①测出木块的质量②测出木块的体积③测出木块的密度④测出酒精的密度⑤测出木块所受水的浮力⑥测出木块所受酒精的浮力A.①②③B.①②③④C.①②③④⑤D.①②③④⑤⑥15.若给你一只弹簧秤、一杯水、细线和一个金属块,你能完成下列四种实验中的哪几种?( )①测金属块的质量②测金属块浸没在水中的浮力③金属块的体积④测金属块的密度A.①B.①②C.①②③D.①②③④16.用一端封闭的足够长的玻璃管做托里拆利实验时,下列哪种情况会影响管内水银柱的高度( )A.改变玻璃管的粗细B.少许改变管的倾斜程度C.改变水银槽内水银面的高低D.玻璃管内漏进少许空气17.放映幻灯时,在屏幕上得到的是幻灯片上景物的( )A.正立放大的虚像 B.正立放大的实像C.倒立放大的虚像 D.倒立放大的实像18.用一滑轮组提升重物,不计摩擦,下列方法中可以提高滑轮组机械效率的是( )A.改变绕绳方法B.增加重物的提升高度C.减少重物的提升高度D.增加提升重物的重力19.下列关于电路的说法中正确的是( )A.电路连接过程中,开关必须处于断开状态B.电路连接必须从电源的正极开始C.电流表测电流时为了安全应选择使用大量程D.滑动变阻器使用时必须串联在电路中20.要改变直流电动机的转向,应采取的方法是( )A.增强磁极的磁性B.增加电源电压C.增大线圈中的电流D.改变线圈中的电流方向或对调磁铁的磁极21.下列测量仪器中,刻度不均匀的是( )A.体温计B.弹簧秤C.量筒D.密度计22.两个相同的烧杯里分别盛有质量和温度都相同的水和煤油,用两个相同的酒精灯给它们加热,可以看到煤油的温度比水的温度升高的快.若水和煤油的比热分别用C水和C煤油表示,则( )A.C水>C煤油 B.C水=C煤油C.C水<C煤油D.条件不足,无法比较23.下列变化不属于物理变化的是( )A.灯泡用久了灯丝变细B.用石灰浆抹墙,经过一段时间后变硬C.用压缩体积的办法,使丁烷气体液化并贮存在打火机内 D.潮湿的衣服变干了三、实验题(每题4分,共20分)24.你能用几种方法判断一蓄电池能否供电?又怎样判别它的正、负极?试设计几个办法,并说明道理.25.联欢会上,某同学从家里带来40只规格为“6 V 0.5 W”的彩灯,通过计算说明他最少应将多少只彩灯接在220 V的照明电路中?应该怎样连接?如果晚会开了5 h,使用这些彩灯一共用了多少kWh的电能?26.用日常生活中装饮料的塑料空瓶,请你设计:做演示液体压强和大气压强存在及其性质的物理实验各一个.要求制作方法简便,并只加少量其他辅助器材.画图并写明制作方法、实验步骤.27.弹簧秤下悬挂着一重物(浸在硫酸铜溶液中,不与溶液反应),若向硫酸铜溶液中逐渐滴加氢氧化钡溶液至恰好完全反应后,弹簧秤的示数将_______(填“变大”“变小”或“不变”);发生反应的化学方程式是_______________28.做“测滑轮组的机械效率”的实验.(1)实验所用的器材除铁架台、滑轮组、细绳和钩码外,还需要____和_______.(2)实验时,除已知钩码重外,需要测量的物理量是____、_____和_______.需要计算的物理量是_______、_______和_______.(3)请设计出实验记录表格.四、计算题(29、题每题9分,30题10分,共19分)29.电饭锅工作时有两种状态:一是锅内水烧干前的加热状态,二是水烧干后的保温状态.下图为CFXB型“220 V 1100 W”电饭锅的简易原理图.已知R=1956 .求:(1)电阻R0的阻值.(2)接通档“1”时,电饭锅处于_______状态(选填“保温”或“加热”),此时电路的总功率为多大?(3)如果用该电饭锅来烧水,其放出的热量全部被水吸收,问需多少分钟可将2.2 kg,初温为20℃的水烧开?(设1标准大气压下)30.同学用弹簧秤、量筒、水、物块做测定浮力的实验,根据图中弹簧秤和量筒的示数,填写记录表格中的各项内容,并分析、比较这些数据,得出的结论用数学式表达为________ ____________.专题训练三 实验参考答案1.卷尺 秒表 v =ts2.升华 凝华3.平行光源 刻度尺 透镜 光屏 烛焰 4.(1)到透镜的距离 (2)物体和像的大小(3)不能 虚5.伏安 电压 电流 R =IU 电源 开关 导线 电压表 电流表6.(1)将家中的其他用电器全都断开,只把白炽灯接入电路,让其工作一段时间,用手表记录时间,用电能表记录它所消耗的电能,最后用P =W /t 计算出它的功率.(2)时间t 消耗的电能W (3) P =W /t 7.刚闭合电路 大 小8.扩散 分子无规则运动越剧烈9.4.2×103J/(kg ·℃) 6300 KJ 10.镜面反射 漫 11.刹车用的闸皮 钢珠 12.B 13.A 14.D 15.D 16.D 17.D 18.D19.A 20.D 21.D 22.A 23.B24.(1)用电表,根据电流的方向.(2)用小磁针来判断,根据奥斯特实验的结论.(3)利用电镀的原理,在碳棒上析出铜的相连的为负极.25.用37个同样的灯泡串联起来就可以了,0.09 kWh26.液体:在塑料瓶的侧壁上打一小孔,就会看到水从侧壁流出来.气体:用抽气机将瓶中的气体抽走,瓶子就会被空气压瘪了.27.变大 CuSO 4+Ba(OH)2=BaSO 4↓+Cu(OH)2↓ 28.(1)重物 刻度尺 (2)s h G 总功 有用功 机械效率 (3)略 29.(1)R 0=44 (2)保温 24.2 W (3)11.2 min 30.F 浮=G 排物体重量(N)物体在水中时弹簧秤示数(N)物体受到的浮力(N) 物体排开的水的体积(cm 3) 物体排开的水的重量(N) 1.960.980.981000.98专题训练四 设计1.(5分)请你利用以下所提供的器材:刻度尺、量杯、细线、烧杯、水、中国地图设计两种办法,分别测量出:(1)一个薄壁圆柱形容器的容积.物体重量(N)物体在水中时弹簧秤示数(N) 物体受到的浮力(N)物体排开的水的体积(cm 3)物体排开的水的重量(N)(2)京沪铁路线长度.2.(5分)如何用一种光学方法,判定一个透镜是凸透镜还是凹透镜?小明的身边有硬纸板、手电筒、笔、玻璃砖、蚊香、空可乐瓶(容积为10 L)等物品,请你从中选择器材设计一个实验验证:“光在空气中是沿直线传播的”.3.(5分)老师给小明布置了一个作业:测量一根电线杆的长度.小明看着高高的电线杆和手中的米尺犯了难:这可怎么办?请你利用你学过的知识帮小明想出一个好办法,说出你这样做的理由.4.(5分)请你利用学过的有关热学的知识设计一个实验,测量水的比热容.5.(5分)如何测量密度大于水的石块的密度,至少设计三个试验并说明方法和过程.6.(5分)如何测量密度小于水、形状不规则的石蜡的密度(试验中用的是水),简述试验办法.7.(5分)请你用一个烧杯、适量的水、托盘天平来测量一种未知液体的密度.简述你的办法及过程并写出未知液体密度的表达式.8.(5分)有一条形磁铁,要想知道它是否有磁性,可以采用哪些办法?请具体说明.9.(5分)对农民来讲,农作物的种子中混有一些杂草的种子是一件很头痛的事情,但是这两种种子的外表面不同,农作物的种子很光滑,杂草的种子表面有很多绒毛,能够吸附靠近它的小颗粒物,当然也能粘在走过的动物身上,因此它可以广为传播.现在,给你一些混有杂草种子的农作物的种子,一些铁屑和一块磁铁,请你替农民将其中的杂草种子从农作物种子中分离出来,说出你的办法和道理.10.(5分)用所学过的知识在家中测苹果的密度.所能利用的器材有:自制的弹簧秤、水桶、水、塑料袋、塑料绳、水瓢.请写出简要的实验步骤及苹果密度表达式的推导过程.11.(5分)一个质量为m人的木工师傅,想粗测一根粗细均匀的长木料的质量m木,找来一块有棱角的石头和一把刻度尺,利用自己的身体便可测出木料的质量.请你说出他测量的方法及依据的原理.12.(5分)已知物体重800 N,滑轮重50 N,要用不大于200 N的力将重物匀速提起,那么动滑轮和重物要用几段绳子来承担?请选择一个合适的滑轮组,并将它的装配图画出来.13.(5分)一个商品仓库,后门进货、前门取货,现有红、绿两只灯泡和一个电铃,一个电池组、两个开关,还有若干条导线,请你为仓库管理员设计一个电路:电铃响同时绿灯亮,表示送货人在后门按开关,电铃响同时红灯亮表示前门取货人在前门按开关.要求画出电路图,图中要标明红灯、绿灯及相应的前门、后门的开关.14.(5分)现有3只电阻值均为R的定值电阻及若干导线,它们分别与图中的虚线框中标有ABCD的有关接线柱相连,经测试发现:(1)接线柱B与C间的电阻值等于R.(2)接线柱AC、AD、DC 间的电阻均为2R.根据上述测试结果在虚线框内有关接线柱间画出电阻或导线的连接情况.。
【精选试卷】(必考题)中考数学填空题专项练习复习题(含答案解析)

一、填空题1.已知圆锥的底面圆半径为3cm ,高为4cm ,则圆锥的侧面积是________cm 2.2.已知反比例函数的图象经过点(m ,6)和(﹣2,3),则m 的值为________.3.如图,将矩形ABCD 沿CE 折叠,点B 恰好落在边AD 的F 处,如果AB 2BC 3=,那么tan ∠DCF 的值是____.4.若a ,b 互为相反数,则22a b ab +=________.5.用一个圆心角为180°,半径为4的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径为_______.6.计算:82-=_______________.7.对于有理数a 、b ,定义一种新运算,规定a ☆b =a 2﹣|b|,则2☆(﹣3)=_____.8.如图,在平行四边形ABCD 中,连接BD ,且BD =CD ,过点A 作AM ⊥BD 于点M ,过点D 作DN ⊥AB 于点N ,且DN =32,在DB 的延长线上取一点P ,满足∠ABD =∠MAP +∠PAB ,则AP =_____.9.如图,已知AB ∥CD ,F 为CD 上一点,∠EFD=60°,∠AEC=2∠CEF ,若6°<∠BAE <15°,∠C 的度数为整数,则∠C 的度数为_____.10.如图,在△ABC 中E 是BC 上的一点,EC=2BE ,点D 是AC 的中点,设△ABC 、△ADF 、△BEF 的面积分别为S △ABC ,S △ADF ,S △BEF ,且S △ABC =12,则S △ADF -S △BEF =_________.11.已知扇形AOB 的半径为4cm ,圆心角∠AOB 的度数为90°,若将此扇形围成一个圆锥的侧面,则围成的圆锥的底面半径为________cm12.如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.在第n 个图形中有______个三角形(用含n 的式子表示)13.如图,边长为2的正方形ABCD 的顶点A ,B 在x 轴正半轴上,反比例函数k y x =在第一象限的图象经过点D ,交BC 于E ,若点E 是BC 的中点,则OD 的长为_____.14.计算:2cos45°﹣(π+1)0111()42-=______. 15.不等式组0125x a x x ->⎧⎨->-⎩有3个整数解,则a 的取值范围是_____. 16.如图,Rt AOB ∆中,90AOB ∠=︒,顶点A ,B 分别在反比例函数()10y x x =>与()50y x x-=<的图象上,则tan BAO ∠的值为_____.17.等腰三角形一腰上的高与另一腰的夹角的度数为20°,则顶角的度数是 .18.关于x 的一元二次方程2310ax x --=的两个不相等的实数根都在-1和0之间(不包括-1和0),则a 的取值范围是___________19.如图,⊙O 是△ABC 的外接圆,∠A =45°,则cos ∠OCB 的值是________.20.如图,在Rt△ABC 中,∠ACB=90°,∠ABC=30°,将△ABC 绕点C 顺时针旋转至△A′B′C,使得点A′恰好落在AB 上,则旋转角度为_____.21.已知关于x 的一元二次方程mx 2+5x+m 2﹣2m=0有一个根为0,则m=_____.22.计算:21(1)211x x x x ÷-+++=________. 23.我国倡导的“一带一路”建设将促进我国与世界各国的互利合作,“一带一路”地区覆盖总人口约为4400000000人,将数据4400000000用科学记数法表示为______.24.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是_____.25.二元一次方程组627x y x y +=⎧⎨+=⎩的解为_____. 26.如图,一张三角形纸片ABC ,∠C=90°,AC=8cm ,BC=6cm .现将纸片折叠:使点A 与点B重合,那么折痕长等于 cm.27.在一个不透明的口袋中,装有A,B,C,D4个完全相同的小球,随机摸取一个小球然后放回,再随机摸取一个小球,两次摸到同一个小球的概率是___.28.如图①,在矩形 MNPQ 中,动点 R 从点 N 出发,沿N→P→Q→M 方向运动至点 M 处停止,设点 R 运动的路程为 x,△MNR 的面积为 y,如果 y 关于 x 的函数图象如图②所示,则矩形 MNPQ 的面积是________.29.如图,点A在双曲线y=4x上,点B在双曲线y=kx(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为____.30.如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC=________.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、填空题1.15π【解析】【分析】设圆锥母线长为l根据勾股定理求出母线长再根据圆锥侧面积公式即可得出答案【详解】设圆锥母线长为l∵r=3h=4∴母线l=∴S侧=×2πr×5=×2π×3×5=15π故答案为15π2.-1【解析】试题分析:根据待定系数法可由(-23)代入y=可得k=-6然后可得反比例函数的解析式为y=-代入点(m6)可得m=-1故答案为:-13.【解析】【分析】【详解】解:∵四边形ABCD是矩形∴AB=CD∠D=90°∵将矩形ABCD沿CE折叠点B恰好落在边AD的F处∴CF=BC∵∴∴设CD=2xCF=3x∴∴tan∠DCF =故答案为:【点4.0【解析】【分析】先提公因式得ab(a+b)而a+b=0任何数乘以0结果都为0【详解】解:∵=ab(a+b)而a+b=0∴原式=0故答案为0【点睛】本题考查了因式分解和有理数的乘法运算注意掌握任何数5.2【解析】【分析】设这个圆锥的底面圆的半径为R根据扇形的弧长等于这个圆锥的底面圆的周长列出方程即可解决问题【详解】设这个圆锥的底面圆的半径为R由题意:2πR=解得R=2故答案为26.【解析】【分析】先把化简为2再合并同类二次根式即可得解【详解】2-=故答案为【点睛】本题考查了二次根式的运算正确对二次根式进行化简是关键7.1【解析】解:2☆(﹣3)=22﹣|﹣3|=4﹣3=1故答案为1点睛:此题考查有理数的混合运算掌握规定的运算方法是解决问题的关键8.6【解析】分析:根据BD=CDAB=CD可得BD=BA再根据AM⊥BDDN⊥AB即可得到DN=AM=3依据∠ABD=∠MAP+∠PAB∠ABD=∠P+∠BAP即可得到△APM是等腰直角三角形进而得到9.36°或37°【解析】分析:先过E作EG∥AB根据平行线的性质可得∠AEF=∠BAE+∠DFE 再设∠CEF=x则∠AEC=2x根据6°<∠BAE<15°即可得到6°<3x-60°<15°解得22°<10.2【解析】由D是AC的中点且S△ABC=12可得;同理EC=2BE即EC=可得又等量代换可知S△ADF-S△BEF=211.1【解析】试题分析:根据圆锥的侧面展开图为一扇形这个扇形的弧长等于圆锥底面的周长和弧长公式可设圆锥的底面圆的半径为rcm根据题意得2πr=解得r=1故答案为:1点睛:本题考查了圆锥的计算:圆锥的侧面12.【解析】【分析】分别数出图①图②图③中的三角形的个数可以发现:第几个图形中三角形的个数就是4与几的乘积减去3如图③中三角形的个数为9=4×3-3按照这个规律即可求出第n各图形中有多少三角形【详解】分13.【解析】【分析】设D(x2)则E(x+21)由反比例函数经过点DE列出关于x的方程求得x的值即可得出答案【详解】解:设D(x2)则E(x+21)∵反比例函数在第一象限的图象经过点D点E∴2x=x+214.【解析】解:原式==故答案为:15.﹣2≤a<﹣1【解析】【分析】先解不等式组确定不等式组的解集(利用含a的式子表示)根据整数解的个数就可以确定有哪些整数解根据解的情况可以得到关于a的不等式从而求出a的范围【详解】解不等式x﹣a>0得16.【解析】【分析】过作轴过作轴于于是得到根据反比例函数的性质得到根据相似三角形的性质得到求得根据三角函数的定义即可得到结论【详解】过作轴过作轴于则∵顶点分别在反比例函数与的图象上∴∵∴∴∴∴∴∴故答案17.110°或70°【解析】试题分析:此题要分情况讨论:当等腰三角形的顶角是钝角时腰上的高在外部根据三角形的一个外角等于与它不相邻的两个内角的和即可求得顶角是90°+20°=110°;当等腰三角形的顶角18.<a<-2【解析】【分析】【详解】解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根∴△=(-3)2-4×a×(-1)>0解得:a>−设f(x)=ax2-3x-1如图∵实数根都在-119.【解析】【分析】根据圆周角定理可得∠BOC=90°易求BC=OC从而可得cos∠OCB的值【详解】∵∠A=45°∴∠BOC=90°∵OB=OC由勾股定理得BC=OC∴cos∠OCB=故答案为【点睛】20.60°【解析】试题解析:∵∠ACB=90°∠ABC=30°∴∠A=90°-30°=60°∵△ABC绕点C顺时针旋转至△A′B′C时点A′恰好落在AB上∴AC=A′C∴△A′AC是等边三角形∴∠ACA21.2【解析】【分析】根据一元二次方程的定义以及一元二次方程的解的定义列出关于m的方程通过解关于m的方程求得m的值即可【详解】∵关于x的一元二次方程mx2+5x+m2﹣2m=0有一个根为0∴m2﹣2m=22.【解析】【分析】先对括号内分式的通分并将括号外的分式的分母利用完全平方公式变形得到÷;接下来利用分式的除法法则将除法运算转变为乘法运算然后约分即可得到化简后的结果【详解】原式=÷=·=故答案为【点睛23.4×109【解析】【分析】科学记数法的表示形式为a×10n的形式其中1≤|a|<10n为整数确定n的值时要看把原数变成a时小数点移动了多少位n的绝对值与小数点移动的位数相同当原数绝对值>10时n是正24.【解析】【分析】根据概率的求法找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率【详解】共个数大于的数有个(大于);故答案为【点睛】本题考查概率的求法:如果一个事件有n种可25.【解析】【分析】由加减消元法或代入消元法都可求解【详解】②﹣①得③将③代入①得∴故答案为:【点睛】本题考查的是二元一次方程组的基本解法本题属于基础题比较简单26.cm【解析】试题解析:如图折痕为GH由勾股定理得:AB==10cm由折叠得:AG=BG=AB=×10=5cmGH⊥AB∴∠AGH=90°∵∠A=∠A∠AGH=∠C=90°∴△ACB∽△AGH∴∴∴G27.【解析】【分析】【详解】试题分析:画树状图如下:∴P(两次摸到同一个小球)==故答案为考点:列表法与树状图法;概率公式28.20【解析】【分析】根据图象横坐标的变化问题可解【详解】由图象可知x=4时点R 到达Px=9时点R到Q点则PN=4QP=5∴矩形MNPQ的面积是20【点睛】本题为动点问题的函数图象探究题考查了动点到达29.12【解析】【详解】解:设点A的坐标为(a)则点B的坐标为()∵AB∥x轴AC=2CD∴∠BAC=∠ODC∵∠ACB=∠DCO∴△ACB∽△DCO∴∵OD=a则AB=2a∴点B的横坐标是3a∴3a=30.【解析】【分析】连接BD根据中位线的性质得出EFBD且EF=BD进而根据勾股定理的逆定理得到△BDC是直角三角形求解即可【详解】连接BD分别是ABAD的中点EFBD且EF=BD又△BDC是直角三角形2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、填空题1.15π【解析】【分析】设圆锥母线长为l根据勾股定理求出母线长再根据圆锥侧面积公式即可得出答案【详解】设圆锥母线长为l∵r=3h=4∴母线l=∴S侧=×2πr×5=×2π×3×5=15π故答案为15π解析:15π【分析】设圆锥母线长为l ,根据勾股定理求出母线长,再根据圆锥侧面积公式即可得出答案.【详解】设圆锥母线长为l ,∵r=3,h=4,∴母线5=,∴S 侧=12×2πr×5=12×2π×3×5=15π, 故答案为15π. 【点睛】本题考查了圆锥的侧面积,熟知圆锥的母线长、底面半径、圆锥的高以及圆锥的侧面积公式是解题的关键.2.-1【解析】试题分析:根据待定系数法可由(-23)代入y=可得k=-6然后可得反比例函数的解析式为y=-代入点(m6)可得m=-1故答案为:-1 解析:-1【解析】试题分析:根据待定系数法可由(-2,3)代入y=k x,可得k =-6,然后可得反比例函数的解析式为y =-6x,代入点(m ,6)可得m=-1. 故答案为:-1. 3.【解析】【分析】【详解】解:∵四边形ABCD 是矩形∴AB =CD ∠D =90°∵将矩形ABCD 沿CE 折叠点B 恰好落在边AD 的F 处∴CF =BC ∵∴∴设CD =2xCF =3x ∴∴tan ∠DCF =故答案为:【点解析:2. 【解析】【分析】【详解】 解:∵四边形ABCD 是矩形,∴AB =CD ,∠D =90°,∵将矩形ABCD 沿CE 折叠,点B 恰好落在边AD 的F 处,∴CF =BC , ∵AB 2BC 3=,∴CD 2CF 3=.∴设CD =2x ,CF =3x ,∴.∴tan ∠DCF =DF =CD 2x 2=.【点睛】 本题考查翻折变换(折叠问题),翻折对称的性质,矩形的性质,勾股定理,锐角三角函数4.0【解析】【分析】先提公因式得ab (a+b )而a+b=0任何数乘以0结果都为0【详解】解:∵=ab(a+b )而a+b=0∴原式=0故答案为0【点睛】本题考查了因式分解和有理数的乘法运算注意掌握任何数解析:0【解析】【分析】先提公因式得ab (a+b ),而a+b=0,任何数乘以0结果都为0.【详解】解:∵22a b ab += ab (a+b ),而a+b=0,∴原式=0.故答案为0,【点睛】本题考查了因式分解和有理数的乘法运算,注意掌握任何数乘以零结果都为零.5.2【解析】【分析】设这个圆锥的底面圆的半径为R 根据扇形的弧长等于这个圆锥的底面圆的周长列出方程即可解决问题【详解】设这个圆锥的底面圆的半径为R 由题意:2πR=解得R=2故答案为2解析:2【解析】【分析】设这个圆锥的底面圆的半径为R ,根据扇形的弧长等于这个圆锥的底面圆的周长,列出方程即可解决问题.【详解】设这个圆锥的底面圆的半径为R ,由题意: 2πR=1804180π⨯, 解得R=2.故答案为2.6.【解析】【分析】先把化简为2再合并同类二次根式即可得解【详解】2-=故答案为【点睛】本题考查了二次根式的运算正确对二次根式进行化简是关键【解析】【分析】.【详解】=..本题考查了二次根式的运算,正确对二次根式进行化简是关键.7.1【解析】解:2☆(﹣3)=22﹣|﹣3|=4﹣3=1故答案为1点睛:此题考查有理数的混合运算掌握规定的运算方法是解决问题的关键解析:1【解析】解:2☆(﹣3)=22﹣|﹣3|=4﹣3=1.故答案为1.点睛:此题考查有理数的混合运算,掌握规定的运算方法是解决问题的关键.8.6【解析】分析:根据BD=CDAB=CD可得BD=BA再根据AM⊥BDDN⊥AB即可得到DN=AM=3依据∠ABD=∠MAP+∠PAB∠ABD=∠P+∠BAP即可得到△APM是等腰直角三角形进而得到解析:6【解析】分析:根据BD=CD,AB=CD,可得BD=BA,再根据AM⊥BD,DN⊥AB,即可得到,依据∠ABD=∠MAP+∠PAB,∠ABD=∠P+∠BAP,即可得到△APM是等腰直角三角形,进而得到AM=6.详解:∵BD=CD,AB=CD,∴BD=BA,又∵AM⊥BD,DN⊥AB,∴,又∵∠ABD=∠MAP+∠PAB,∠ABD=∠P+∠BAP,∴∠P=∠PAM,∴△APM是等腰直角三角形,∴AM=6,故答案为6.点睛:本题主要考查了平行四边形的性质以及等腰直角三角形的性质的运用,解决问题给的关键是判定△APM是等腰直角三角形.9.36°或37°【解析】分析:先过E作EG∥AB根据平行线的性质可得∠AEF=∠BAE+∠DFE再设∠CEF=x则∠AEC=2x根据6°<∠BAE<15°即可得到6°<3x-60°<15°解得22°<解析:36°或37°.【解析】分析:先过E作EG∥AB,根据平行线的性质可得∠AEF=∠BAE+∠DFE,再设∠CEF=x,则∠AEC=2x,根据6°<∠BAE<15°,即可得到6°<3x-60°<15°,解得22°<x <25°,进而得到∠C的度数.详解:如图,过E作EG∥AB,∵AB∥CD,∴GE∥CD,∴∠BAE=∠AEG,∠DFE=∠GEF,∴∠AEF=∠BAE+∠DFE,设∠CEF=x,则∠AEC=2x,∴x+2x=∠BAE+60°,∴∠BAE=3x-60°,又∵6°<∠BAE<15°,∴6°<3x-60°<15°,解得22°<x<25°,又∵∠DFE是△CEF的外角,∠C的度数为整数,∴∠C=60°-23°=37°或∠C=60°-24°=36°,故答案为:36°或37°.点睛:本题主要考查了平行线的性质以及三角形外角性质的运用,解决问题的关键是作平行线,解题时注意:两直线平行,内错角相等.10.2【解析】由D是AC的中点且S△ABC=12可得;同理EC=2BE即EC=可得又等量代换可知S△ADF-S△BEF=2解析:2【解析】由D是AC的中点且S△ABC=12,可得1112622ABD ABCS S∆∆==⨯=;同理EC=2BE即EC=13BC,可得11243ABES∆=⨯=,又,ABE ABF BEF ABD ABF ADFS S S S S S∆∆∆∆∆∆-=-=等量代换可知S△ADF-S△BEF=211.1【解析】试题分析:根据圆锥的侧面展开图为一扇形这个扇形的弧长等于圆锥底面的周长和弧长公式可设圆锥的底面圆的半径为rcm根据题意得2πr=解得r=1故答案为:1点睛:本题考查了圆锥的计算:圆锥的侧面解析:1【解析】试题分析:根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式,可设圆锥的底面圆的半径为rcm,根据题意得2πr=904180π⨯,解得r=1.故答案为:1.点睛:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.12.【解析】【分析】分别数出图①图②图③中的三角形的个数可以发现:第几个图形中三角形的个数就是4与几的乘积减去3如图③中三角形的个数为9=4×3-3按照这个规律即可求出第n 各图形中有多少三角形【详解】分 解析:()43n -【解析】【分析】分别数出图①、图②、图③中的三角形的个数,可以发现:第几个图形中三角形的个数就是4与几的乘积减去3.如图③中三角形的个数为9=4×3-3.按照这个规律即可求出第n 各图形中有多少三角形.【详解】分别数出图①、图②、图③中的三角形的个数,图①中三角形的个数为1=4×1-3; 图②中三角形的个数为5=4×2-3; 图③中三角形的个数为9=4×3-3; …可以发现,第几个图形中三角形的个数就是4与几的乘积减去3.按照这个规律,如果设图形的个数为n ,那么其中三角形的个数为4n-3.故答案为4n-3.【点睛】此题主要考查学生对图形变化类这个知识点的理解和掌握,解答此类题目的关键是根据题目中给出的图形,数据等条件,通过认真思考,归纳总结出规律,此类题目难度一般偏大,属于难题.13.【解析】【分析】设D (x2)则E (x+21)由反比例函数经过点DE 列出关于x 的方程求得x 的值即可得出答案【详解】解:设D (x2)则E (x+21)∵反比例函数在第一象限的图象经过点D 点E∴2x=x+2 解析:12x x 【解析】【分析】设D (x ,2)则E (x+2,1),由反比例函数经过点D 、E 列出关于x 的方程,求得x 的值即可得出答案.【详解】解:设D (x ,2)则E (x+2,1), ∵反比例函数k y x=在第一象限的图象经过点D 、点E , ∴2x =x+2,解得x =2,∴D(2,2),∴OA=AD=2,∴OD==故答案为:【点睛】本题主要考查反比例函数图象上点的坐标特征,解题的关键是根据题意表示出点D、E的坐标及反比例函数图象上点的横纵坐标乘积都等于反比例系数k.14.【解析】解:原式==故答案为:32.【解析】解:原式=121222⨯-++3232.15.﹣2≤a<﹣1【解析】【分析】先解不等式组确定不等式组的解集(利用含a 的式子表示)根据整数解的个数就可以确定有哪些整数解根据解的情况可以得到关于a的不等式从而求出a的范围【详解】解不等式x﹣a>0得解析:﹣2≤a<﹣1.【解析】【分析】先解不等式组确定不等式组的解集(利用含a的式子表示),根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a的不等式,从而求出a的范围.【详解】解不等式x﹣a>0,得:x>a,解不等式1﹣x>2x﹣5,得:x<2,∵不等式组有3个整数解,∴不等式组的整数解为﹣1、 0、1,则﹣2≤a<﹣1,故答案为:﹣2≤a<﹣1.【点睛】本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.16.【解析】【分析】过作轴过作轴于于是得到根据反比例函数的性质得到根据相似三角形的性质得到求得根据三角函数的定义即可得到结论【详解】过作轴过作轴于则∵顶点分别在反比例函数与的图象上∴∵∴∴∴∴∴∴故答案【解析】【分析】过A 作AC x ⊥轴,过B 作BD x ⊥轴于D ,于是得到90BDO ACO ∠=∠=︒,根据反比例函数的性质得到52BDO S ∆=,12AOC S ∆=,根据相似三角形的性质得到25BOD OAC S OB S OA ∆∆⎛⎫== ⎪⎝⎭,求得5OB OA =,根据三角函数的定义即可得到结论. 【详解】过A 作AC x ⊥轴,过B 作BD x ⊥轴于,则90BDO ACO ∠=∠=︒,∵顶点A ,B 分别在反比例函数()10y x x =>与()50y x x -=<的图象上, ∴52BDO S ∆=,12AOC S ∆=, ∵90AOB ∠=︒,∴90BOD DBO BOD AOC ∠+∠=∠+∠=︒,∴DBO AOC ∠=∠,∴BDO OCA ∆∆,∴252512BODOAC S OB S OA ∆∆⎛⎫=== ⎪⎝⎭, ∴5OB OA=, ∴tan 5OB BAO OA ∠==, 故答案为:5.【点睛】本题考查了相似三角形的判定与性质、反比例函数的性质以及直角三角形的性质.解题时注意掌握数形结合思想的应用,注意掌握辅助线的作法.17.110°或70°【解析】试题分析:此题要分情况讨论:当等腰三角形的顶角是钝角时腰上的高在外部根据三角形的一个外角等于与它不相邻的两个内角的和即可求得顶角是90°+20°=110°;当等腰三角形的顶角解析:110°或70°.【解析】试题分析:此题要分情况讨论:当等腰三角形的顶角是钝角时,腰上的高在外部.根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+20°=110°;当等腰三角形的顶角是锐角时,腰上的高在其内部,故顶角是90°﹣20°=70°.故答案为110°或70°.考点:1.等腰三角形的性质;2.分类讨论.18.<a<-2【解析】【分析】【详解】解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根∴△=(-3)2-4×a×(-1)>0解得:a>−设f(x)=ax2-3x-1如图∵实数根都在-1解析:94-<a<-2【解析】【分析】【详解】解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根∴△=(-3)2-4×a×(-1)>0,解得:a>−9 4设f(x)=ax2-3x-1,如图,∵实数根都在-1和0之间,∴-1<−32a-<0,∴a<−32,且有f(-1)<0,f(0)<0,即f(-1)=a×(-1)2-3×(-1)-1<0,f(0)=-1<0,解得:a <-2,∴−94<a <-2, 故答案为−94<a <-2. 19.【解析】【分析】根据圆周角定理可得∠BOC=90°易求BC=OC 从而可得cos ∠OCB 的值【详解】∵∠A=45°∴∠BOC=90°∵OB=OC 由勾股定理得BC=OC ∴cos ∠OCB=故答案为【点睛】【解析】【分析】根据圆周角定理可得∠BOC=90°,易求OC ,从而可得cos ∠OCB 的值.【详解】∵∠A =45°,∴∠BOC=90°∵OB=OC ,由勾股定理得,OC ,∴cos ∠OCB =2OC BC ==.. 【点睛】 本题考查的是圆周角定理、等腰直角三角形的判定及锐角三角函数的定义,属较简单题目题目.20.60°【解析】试题解析:∵∠ACB=90°∠ABC=30°∴∠A=90°-30°=60°∵△ABC 绕点C 顺时针旋转至△A′B′C 时点A′恰好落在AB 上∴AC=A′C∴△A′AC 是等边三角形∴∠ACA解析:60°【解析】试题解析:∵∠ACB=90°,∠ABC=30°,∴∠A=90°-30°=60°,∵△ABC 绕点C 顺时针旋转至△A′B′C 时点A′恰好落在AB 上,∴AC=A′C ,∴△A′AC 是等边三角形,∴∠ACA′=60°,∴旋转角为60°.故答案为60°.21.2【解析】【分析】根据一元二次方程的定义以及一元二次方程的解的定义列出关于m 的方程通过解关于m 的方程求得m 的值即可【详解】∵关于x 的一元二次方程mx2+5x+m2﹣2m=0有一个根为0∴m2﹣2m=解析:2【解析】【分析】根据一元二次方程的定义以及一元二次方程的解的定义列出关于m 的方程,通过解关于m 的方程求得m 的值即可.【详解】∵关于x 的一元二次方程mx 2+5x+m 2﹣2m=0有一个根为0,∴m 2﹣2m=0且m≠0,解得,m=2,故答案是:2.【点睛】本题考查了一元二次方程ax 2+bx+c=0(a≠0)的解的定义.解答该题时需注意二次项系数a≠0这一条件.22.【解析】【分析】先对括号内分式的通分并将括号外的分式的分母利用完全平方公式变形得到÷;接下来利用分式的除法法则将除法运算转变为乘法运算然后约分即可得到化简后的结果【详解】原式=÷=·=故答案为【点睛 解析:11x + 【解析】【分析】先对括号内分式的通分,并将括号外的分式的分母利用完全平方公式变形得到()21xx +÷111x x +-+;接下来利用分式的除法法则将除法运算转变为乘法运算,然后约分即可得到化简后的结果.【详解】原式=()21x x +÷111x x +-+ =()21x x +·1x x+ =11x +. 故答案为11x +. 【点睛】 本题考查了公式的混合运算,解题的关键是熟练的掌握分式的混合运算法则.23.4×109【解析】【分析】科学记数法的表示形式为a×10n 的形式其中1≤|a|<10n 为整数确定n 的值时要看把原数变成a 时小数点移动了多少位n 的绝对值与小数点移动的位数相同当原数绝对值>10时n 是正解析:4×109【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.【详解】4400000000的小数点向左移动9位得到4.4,所以4400000000用科学记数法可表示为:4.4×109,故答案为4.4×109.【点睛】本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.24.【解析】【分析】根据概率的求法找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率【详解】共个数大于的数有个(大于);故答案为【点睛】本题考查概率的求法:如果一个事件有n种可解析:12.【解析】【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【详解】共6个数,大于3的数有3个,P∴(大于3)31 62 ==;故答案为12.【点睛】本题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=mn.25.【解析】【分析】由加减消元法或代入消元法都可求解【详解】②﹣①得③将③代入①得∴故答案为:【点睛】本题考查的是二元一次方程组的基本解法本题属于基础题比较简单解析:15 xy=⎧⎨=⎩【解析】【分析】由加减消元法或代入消元法都可求解.【详解】627x y x y +=⎧⎨+=⎩①②, ②﹣①得1x =③将③代入①得5y =∴15x y =⎧⎨=⎩故答案为:15x y =⎧⎨=⎩【点睛】本题考查的是二元一次方程组的基本解法,本题属于基础题,比较简单.26.cm 【解析】试题解析:如图折痕为GH 由勾股定理得:AB==10cm 由折叠得:AG=BG=AB=×10=5cmGH⊥AB∴∠AGH=90°∵∠A=∠A∠AGH=∠C=90°∴△ACB∽△AGH∴∴∴G 解析:cm .【解析】试题解析:如图,折痕为GH ,由勾股定理得:AB==10cm , 由折叠得:AG=BG=AB=×10=5cm ,GH ⊥AB ,∴∠AGH=90°, ∵∠A=∠A ,∠AGH=∠C=90°,∴△ACB ∽△AGH , ∴, ∴,∴GH=cm.考点:翻折变换27.【解析】【分析】【详解】试题分析:画树状图如下:∴P(两次摸到同一个小球)==故答案为考点:列表法与树状图法;概率公式解析:14.【解析】【分析】【详解】试题分析:画树状图如下:∴P(两次摸到同一个小球)=416=14.故答案为14.考点:列表法与树状图法;概率公式.28.20【解析】【分析】根据图象横坐标的变化问题可解【详解】由图象可知x=4时点R到达Px=9时点R到Q点则PN=4QP=5∴矩形MNPQ的面积是20【点睛】本题为动点问题的函数图象探究题考查了动点到达解析:20【解析】【分析】根据图象横坐标的变化,问题可解.【详解】由图象可知,x=4时,点R到达P,x=9时,点R到Q点,则PN=4,QP=5∴矩形MNPQ的面积是20.【点睛】本题为动点问题的函数图象探究题,考查了动点到达临界点前后图象趋势的趋势变化.解答时,要注意数形结合.29.12【解析】【详解】解:设点A的坐标为(a)则点B的坐标为()∵AB∥x轴AC=2CD∴∠BAC=∠ODC∵∠ACB=∠DCO∴△ACB∽△DCO∴∵OD=a则AB=2a∴点B的横坐标是3a∴3a=解析:12【解析】【详解】解:设点A 的坐标为(a ,4a ),则点B 的坐标为(ak 4,4a ), ∵AB ∥x 轴,AC=2CD ,∴∠BAC=∠ODC ,∵∠ACB=∠DCO ,∴△ACB ∽△DCO , ∴AB AC 2DA CD 1==, ∵OD=a ,则AB=2a ,∴点B 的横坐标是3a ,∴3a=ak 4, 解得:k=12.故答案为12. 30.【解析】【分析】连接BD 根据中位线的性质得出EFBD 且EF=BD 进而根据勾股定理的逆定理得到△BDC 是直角三角形求解即可【详解】连接BD 分别是ABAD 的中点EFBD 且EF=BD 又△BDC 是直角三角形 解析:43【解析】【分析】连接BD ,根据中位线的性质得出EF //BD ,且EF=12BD ,进而根据勾股定理的逆定理得到△BDC 是直角三角形,求解即可.【详解】连接BD ,E F 分别是AB 、AD 的中点∴EF //BD ,且EF=12BD 4EF =8BD ∴= 又8106BD BC CD ===,,∴△BDC 是直角三角形,且=90BDC ∠︒∴tanC=BD DC =86=43. 故答案为:43.。
2021年中考数学填空题专项练习复习题(答案解析)(3)

一、选择题1.如图,在Rt △ABC 中,∠ACB=90°,AC=BC=1,将绕点A 逆时针旋转30°后得到Rt △ADE ,点B 经过的路径为弧BD ,则图中阴影部分的面积是( )A .6πB .3πC .2π-12D .122.一种药品原价每盒25元,经过两次降价后每盒16元,设两次降价的百分率都为x ,则x 满足等式( )A .16(1+2x)=25B .25(1-2x)=16C .25(1-x)²=16D .16(1+x)²=253.若⊙O 的半径为5cm ,点A 到圆心O 的距离为4cm ,那么点A 与⊙O 的位置关系是 A .点A 在圆外B .点A 在圆上C .点A 在圆内D .不能确定 4.将抛物线y=2x 2向右平移3个单位,再向下平移5个单位,得到的抛物线的表达式为( )A .y=2(x ﹣3)2﹣5B .y=2(x+3)2+5C .y=2(x ﹣3)2+5D .y=2(x+3)2﹣5 5.如图,四边形ABCD 是菱形,∠A=60°,AB=2,扇形BEF 的半径为2,圆心角为60°,则图中阴影部分的面积是( )A .2332π-B .233π-C .32π-D .3π-6.下列诗句所描述的事件中,是不可能事件的是( )A .黄河入海流B .锄禾日当午C .大漠孤烟直D .手可摘星辰7.如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )A .15B .25C .35D .458.用配方法解方程x 2+2x ﹣5=0时,原方程应变形为( )A .(x ﹣1)2=6B .(x+1)2=6C .(x+2)2=9D .(x ﹣2)2=9 9.若a 是方程22x x 30--=的一个解,则26a 3a -的值为( )A .3B .3-C .9D .9- 10.如图,某中学计划靠墙围建一个面积为280m 的矩形花圃(墙长为12m ),围栏总长度为28m ,则与墙垂直的边x 为( )A .4m 或10mB .4mC .10mD .8m 11.以3942c x ±+=为根的一元二次方程可能是( ) A .230x x c --=B .230x x c +-=C .230-+=x x cD .230++=x x c 12.如图,在△ABC 中,BC =4,以点A 为圆心,2为半径的⊙A 与BC 相切于点D ,交AB 于点E ,交AC 于点F .P 是⊙A 上一点,且∠EPF =40°,则图中阴影部分的面积是( )A .4-9πB .4-89π C .8-49π D .8-89π 13.下列说法正确的是( ) A .“任意画出一个等边三角形,它是轴对称图形”是随机事件B .某种彩票的中奖率为11000,说明每买1000张彩票,一定有一张中奖 C .抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为13D .“概率为1的事件”是必然事件 14.如图,矩形 ABCD 中,AB=8,BC=6,将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG ,AE ,FG 分别交射线CD 于点 PH ,连结 AH ,若 P 是 CH 的中点,则△APH 的周长为( )A .15B .18C .20D .2415.已知二次函数y =ax 2+bx +c(a≠0)的图象如图所示,当y >0时,x 的取值范围是( )A .-1<x <2B .x >2C .x <-1D .x <-1或x >2二、填空题16.如图,有6张扑克牌,从中任意抽取两张,点数和是偶数的概率是_____.17.已知二次函数y =3x 2+2x ,当﹣1≤x ≤0时,函数值y 的取值范围是_____.18.如图,在边长为2的正方形ABCD 中,以点D 为圆心,AD 长为半径画AC ,再以BC 为直径画半圆,若阴影部分①的面积为S 1,阴影部分②的面积为S 2,则图中S 1﹣S 2的值为_____.(结果保留π)19.已知二次函数y =(x −2)2+3,当x _______________时,y 随x 的增大而减小.20.抛物线21(2)43y x =++关于x 轴对称的抛物线的解析式为_______ 21.半径为2的圆被四等分切割成四条相等的弧,将四个弧首尾顺次相连拼成如图所示的恒星图型,那么这个恒星的面积等于______.22.△ABC 中,∠A =90°,AB =AC ,以A 为圆心的圆切BC 于点D ,若BC =12cm ,则⊙A 的半径为_____cm .23.一元二次方程22x 20-=的解是______.24.若实数a 、b 满足a+b 2=2,则a 2+5b 2的最小值为_____.25.如图,P 是⊙O 的直径AB 延长线上的一点,PC 与⊙O 相切于点C ,若∠P=20°,则∠A=___________°.三、解答题26.在平面直角坐标系中,直线2y x =+与x 轴交于点A ,与y 轴交于点B ,抛物线()20y ax bx c a =++<经过点A 、B .(1)求a 、b 满足的关系式及c 的值.(2)当0x <时,若()20y ax bx c a =++<的函数值随x 的增大而增大,求a 的取值范围. (3)如图,当1a =-时,在抛物线上是否存在点P ,使PAB ∆的面积为1?若存在,请求出符合条件的所有点P 的坐标;若不存在,请说明理由.27.在四张编号为A ,B ,C ,D 的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张,不放回,再从剩下的卡片中随机抽取一张.(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A ,B ,C ,D 表示);(2)我们知道,满足a 2+b 2=c 2的三个正整数a ,b ,c 成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.28.如图,以△ABC 的BC 边上一点O 为圆心的圆,经过A ,B 两点,且与BC 边交于点E ,D 为BE 的下半圆弧的中点,连接AD 交BC 于F ,AC=FC .(1)求证:AC 是⊙O 的切线;(2)已知圆的半径R=5,EF=3,求DF 的长.29.某企业为响应国家教育扶贫的号召,决定对某乡镇全体贫困初、高中学生进行资助,初中学生每月资助200元,高中学生每月资助300元.已知该乡受资助的初中学生人数是受资助的高中学生人数的2倍,且该企业在2018年下半年7﹣12月这6个月资助学生共支出10.5万元.(1)问该乡镇分别有多少名初中学生和高中学生获得了资助?(2)2018年7﹣12月期间,受资助的初、高中学生中,分别有30%和40%的学生被评为优秀学生,从而获得了该乡镇政府的公开表扬.同时,提供资助的企业为了激发更多受资助学生的进取心和学习热情,决定对2019年上半年1﹣6月被评为优秀学生的初中学生每人每月增加a%的资助,对被评为优秀学生的高中学生每人每月增加2a%的资助.在此奖励政策的鼓励下,2019年1﹣6月被评为优秀学生的初、高中学生分別比2018年7﹣12月的人数增加了3a%、a%.这样,2019年上半年评为优秀学生的初、高中学生所获得的资助总金额一个月就达到了10800元,求a的值.30.如图,已知AB为⊙O的直径,点C、D在⊙O上,CD=BD,E、F是线段AC、AB 的延长线上的点,并且EF与⊙O相切于点D.(1)求证:∠A=2∠BDF;(2)若AC=3,AB=5,求CE的长.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1.A2.C3.C4.A5.B6.D7.C8.B9.C10.C11.A12.B13.D14.C15.D二、填空题16.【解析】【分析】列举出所有情况再找出点数和是偶数的情况根据概率公式求解即可【详解】解:从6张牌中任意抽两张可能的情况有:(410)(510)(610)(810)(910)(109)(417.﹣≤y≤1【解析】【分析】利用配方法转化二次函数求出对称轴根据二次函数的性质即可求解【详解】∵y=3x2+2x=3(x+)2﹣∴函数的对称轴为x=﹣∴当﹣1≤x≤0时函数有最小值﹣当x=﹣1时有最大18.π【解析】【分析】如图设图中③的面积为S3构建方程组即可解决问题【详解】解:如图设图中③的面积为S3由题意:可得S1﹣S2=π故答案为π【点睛】本题考查扇形的面积正方形的性质等知识解题的关键是学会利19.<2(或x≤2)【解析】试题分析:对于开口向上的二次函数在对称轴的左边y随x的增大而减小在对称轴的右边y随x的增大而增大根据性质可得:当x<2时y随x的增大而减小考点:二次函数的性质20.【解析】【分析】由关于x轴对称点的特点是:横坐标不变纵坐标变为相反数可求出抛物线关于x轴对称的抛物线解析式【详解】∵∴关于x轴对称的抛物线解析式为-即故答案为:【点睛】此题考查了二次函数的图象与几何21.16﹣4π【解析】【分析】恒星的面积=边长为4的正方形面积-半径为2的圆的面积依此列式计算即可【详解】解:如图2+2=4恒星的面积=4×4-4π=16-4π故答案为16-4π【点睛】本题考查了扇形面22.【解析】【分析】由切线性质知AD⊥BC根据AB=AC可得BD=CD=AD=BC=6【详解】解:如图连接AD则AD⊥BC∵AB=AC∴BD=CD=AD=BC=6故答案为:6【点睛】本题考查了圆的切线性23.x1=1x2=-1【解析】分析:方程整理后利用平方根定义开方即可求出解详解:方程整理得:x2=1开方得:x=±1解得:x1=1x2=﹣1故答案为x1=1x2=﹣1点睛:本题考查了解一元二次方程﹣直接24.4【解析】【分析】由a+b2=2得出b2=2-a代入a2+5b2得出a2+5b2=a2+5(2-a)=a2-5a+10再利用配方法化成a2+5b2=(a-即可求出其最小值【详解】∵a+b2=2∴b225.35【解析】【分析】【详解】解:∵PC与⊙O相切∴∠OCP=90°∴∠COP=90°-∠P=90°-20°=70°∵OA=OC∴∠A=∠ACO∵∠A+∠ACO=∠COP∴∠A=35°故答案为35三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.A解析:A【解析】【分析】先根据勾股定理得到,再根据扇形的面积公式计算出S 扇形ABD ,由旋转的性质得到Rt △ADE ≌Rt △ACB ,于是S 阴影部分=S △ADE +S 扇形ABD -S △ABC =S 扇形ABD .【详解】∵∠ACB=90°,AC=BC=1,∴,∴S 扇形ABD =230=3606ππ⨯,又∵Rt △ABC 绕A 点逆时针旋转30°后得到Rt △ADE ,∴Rt △ADE ≌Rt △ACB ,∴S 阴影部分=S △ADE +S 扇形ABD −S △ABC =S 扇形ABD =6π, 故选A.【点睛】本题考查扇形面积计算,熟记扇形面积公式,采用作差法计算面积是解题的关键. 2.C解析:C【解析】解:第一次降价后的价格为:25×(1﹣x ),第二次降价后的价格为:25×(1﹣x )2.∵两次降价后的价格为16元,∴25(1﹣x )2=16.故选C .3.C解析:C【解析】【分析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系;利用d >r 时,点在圆外;当d=r 时,点在圆上;当d <r 时,点在圆内判断出即可.【详解】解:∵⊙O 的半径为5cm ,点A 到圆心O 的距离为4cm ,∴d <r ,∴点A 与⊙O 的位置关系是:点A 在圆内,故选C .4.A【解析】把22y x =向右平移3个单位长度变为:223()y x =-,再向下平移5个单位长度变为:22(3)5y x =--.故选A .5.B解析:B【解析】【分析】根据菱形的性质得出△DAB 是等边三角形,进而利用全等三角形的判定得出△ABG ≌△DBH ,得出四边形GBHD 的面积等于△ABD 的面积,进而求出即可.【详解】连接BD ,∵四边形ABCD 是菱形,∠A=60°,∴∠ADC=120°,∴∠1=∠2=60°,∴△DAB 是等边三角形,∵AB=2,∴△ABD 3,∵扇形BEF 的半径为2,圆心角为60°,∴∠4+∠5=60°,∠3+∠5=60°,∴∠3=∠4,设AD 、BE 相交于点G ,设BF 、DC 相交于点H ,在△ABG 和△DBH 中,2{34A AB BD ∠=∠=∠=∠,∴△ABG ≌△DBH (ASA ),∴四边形GBHD 的面积等于△ABD 的面积,∴图中阴影部分的面积是:S 扇形EBF -S △ABD =26021233602π⨯-⨯ =233π 故选B .解析:D【解析】【分析】不可能事件是指在一定条件下,一定不发生的事件.【详解】A、是必然事件,故选项错误;B、是随机事件,故选项错误;C、是随机事件,故选项错误;D、是不可能事件,故选项正确.故选D.【点睛】此题主要考查了必然事件,不可能事件,随机事件的概念.理解概念是解决这类基础题的主要方法.必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.7.C解析:C【解析】【分析】【详解】解:根据题意,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有②④⑤,3种情况,因此可知使与图中阴影部分构成轴对称图形的概率为3 355÷=故选C8.B解析:B【解析】x2+2x﹣5=0,x2+2x=5,x2+2x+1=5+1,(x+1)2=6,故选B.9.C解析:C【解析】由题意得:2a2-a-3=0,所以2a2-a=3,所以6a2-3a=3(2a2-a)=3×3=9,故选C.10.C解析:C 【解析】 【分析】设与墙相对的边长为(28-2x )m ,根据题意列出方程x (28-2x )=80,求解即可. 【详解】设与墙相对的边长为(28-2x )m ,则0<28-2x≤12,解得8≤x <14, 根据题意列出方程x (28-2x )=80, 解得x 1=4,x 2=10 因为8≤x <14∴与墙垂直的边x 为10m 故答案为C. 【点睛】本题考查一元二次方程的应用,根据题意列出方程并求解是解题的关键,注意题中限制条件,选取适合的x 值.11.A解析:A 【解析】 【分析】根据一元二次方程根与系数的关系求解即可. 【详解】设x 1,x 2是一元二次方程的两个根, ∵3942cx ±+=∴x 1+x 2=3,x 1∙x 2=-c ,∴该一元二次方程为:21212()0x x x x x x -++=,即230x x c --=故选A. 【点睛】此题主要考查了根据一元二次方程的根与系数的关系列一元二次方程.12.B解析:B 【解析】试题解析:连接AD ,∵BC是切线,点D是切点,∴AD⊥BC,∴∠EAF=2∠EPF=80°,∴S扇形AEF=280?28 3609ππ=,S△ABC=12AD•BC=12×2×4=4,∴S阴影部分=S△ABC-S扇形AEF=4-89π.13.D解析:D【解析】试题解析:A、“任意画出一个等边三角形,它是轴对称图形”是必然事件,选项错误;B. 某种彩票的中奖概率为11000,说明每买1000张,有可能中奖,也有可能不中奖,故B错误;C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为12.故C错误;D. “概率为1的事件”是必然事件,正确.故选D.14.C解析:C【解析】【分析】连结AC,先由△AGH≌△ADH得到∠GHA=∠AHD,进而得到∠AHD=∠HAP,所以△AHP是等腰三角形,所以PH=PA=PC,所以∠HAC是直角,再在Rt△ABC中由勾股定理求出AC的长,然后由△HAC∽△ADC,根据=求出AH的长,再根据△HAC∽△HDA求出DH的长,进而求得HP和AP的长,最后得到△APH的周长.【详解】∵P是CH的中点,PH=PC,∵AH=AH,AG=AD,且AGH与ADH都是直角,∴△AGH≌△ADH,∴∠GHA=∠AHD,又∵GHA=HAP,∴∠AHD=∠HAP,∴△AHP是等腰三角形,∴PH=PA=PC,∴∠HAC是直角,在Rt△ABC中,AC==10,∵△HAC∽△ADC,∴=,∴AH===7.5,又∵△HAC∽△HAD,=,∴DH=4.5,∴HP==6.25,AP=HP=6.25,∴△APH的周长=AP+PH+AH=6.25+6.25+7.5=20.【点睛】本题主要考查直角三角形的性质以及相似三角形的性质,解题的关键是清楚直角三角形斜边上的中线是斜边的一半以及会运用相似三角形线段成比例求出各边长的长.15.D解析:D【解析】【分析】根据已知图象可以得到图象与x轴的交点是(-1,0),(2,0),又y>0时,图象在x 轴的上方,由此可以求出x的取值范围.【详解】依题意得图象与x轴的交点是(-1,0),(2,0),当y>0时,图象在x轴的上方,此时x<-1或x>2,∴x的取值范围是x<-1或x>2,故选D.【点睛】本题考查了二次函数与不等式,解答此题的关键是求出图象与x轴的交点,然后由图象找出当y>0时,自变量x的范围,注意数形结合思想的运用.二、填空题16.【解析】【分析】列举出所有情况再找出点数和是偶数的情况根据概率公式求解即可【详解】解:从6张牌中任意抽两张可能的情况有:(410)(510)(610)(810)(910)(109)(4解析:7 15.【解析】【分析】列举出所有情况,再找出点数和是偶数的情况,根据概率公式求解即可.【详解】解:从6张牌中任意抽两张可能的情况有:(4,10)(5,10)(6,10)(8,10)(9,10)(10,9) (4,9)(5,9)(6,9)(8,9)(9,8)(10,8) (4,8)(5,8)(6,8)(8,6)(9,6)(10,6) (4,6)(5,6)(6,5)(8,5)(9,5)(10,5)(4,5)(5,4)(6,4)(8,4)(9,4)(10,4)∴一共有30种情况,点数和为偶数的有14个,∴点数和是偶数的概率是147 3015;故答案为7 15.【点睛】本题考查概率的概念和求法.解题的关键是找到所求情况数与总情况数,根据:概率=所求情况数与总情况数之比.17.﹣≤y≤1【解析】【分析】利用配方法转化二次函数求出对称轴根据二次函数的性质即可求解【详解】∵y=3x2+2x=3(x+)2﹣∴函数的对称轴为x=﹣∴当﹣1≤x≤0时函数有最小值﹣当x=﹣1时有最大解析:﹣13≤y≤1【解析】【分析】利用配方法转化二次函数求出对称轴,根据二次函数的性质即可求解.【详解】∵y=3x2+2x=3(x+13)2﹣13,∴函数的对称轴为x=﹣13,∴当﹣1≤x≤0时,函数有最小值﹣13,当x=﹣1时,有最大值1,∴y的取值范围是﹣13≤y≤1,故答案为﹣13≤y≤1.【点睛】本题考查二次函数的性质、一般式和顶点式之间的转化,解题的关键是熟练掌握二次函数的性质.18.π【解析】【分析】如图设图中③的面积为S3构建方程组即可解决问题【详解】解:如图设图中③的面积为S3由题意:可得S1﹣S2=π故答案为π【点睛】本题考查扇形的面积正方形的性质等知识解题的关键是学会利解析:1 2π【解析】【分析】如图,设图中③的面积为S 3.构建方程组即可解决问题. 【详解】解:如图,设图中③的面积为S 3.由题意:2132231··241··12S S S S ππ⎧+=⎪⎪⎨⎪+=⎪⎩,可得S 1﹣S 2=12π, 故答案为12π. 【点睛】本题考查扇形的面积、正方形的性质等知识,解题的关键是学会利用参数构建方程组解决问题.19.<2(或x≤2)【解析】试题分析:对于开口向上的二次函数在对称轴的左边y 随x 的增大而减小在对称轴的右边y 随x 的增大而增大根据性质可得:当x <2时y 随x 的增大而减小考点:二次函数的性质解析:<2(或x≤2). 【解析】试题分析:对于开口向上的二次函数,在对称轴的左边,y 随x 的增大而减小,在对称轴的右边,y 随x 的增大而增大.根据性质可得:当x <2时,y 随x 的增大而减小. 考点:二次函数的性质20.【解析】【分析】由关于x 轴对称点的特点是:横坐标不变纵坐标变为相反数可求出抛物线关于x 轴对称的抛物线解析式【详解】∵∴关于x 轴对称的抛物线解析式为-即故答案为:【点睛】此题考查了二次函数的图象与几何 解析:()21243y x =-+- 【解析】 【分析】由关于x 轴对称点的特点是:横坐标不变,纵坐标变为相反数,可求出抛物线21(2)43y x =++关于x 轴对称的抛物线解析式.【详解】 ∵21(2)43y x =++, ∴关于x 轴对称的抛物线解析式为-21(2)43y x =++,即()21243y x =-+-, 故答案为:()21243y x =-+-. 【点睛】此题考查了二次函数的图象与几何变换,解题的关键是抓住关于x 轴、y 轴对称点的特点.21.16﹣4π【解析】【分析】恒星的面积=边长为4的正方形面积-半径为2的圆的面积依此列式计算即可【详解】解:如图2+2=4恒星的面积=4×4-4π=16-4π故答案为16-4π【点睛】本题考查了扇形面解析:16﹣4π 【解析】 【分析】恒星的面积=边长为4的正方形面积-半径为2的圆的面积,依此列式计算即可. 【详解】 解:如图.2+2=4,恒星的面积=4×4-4π=16-4π. 故答案为16-4π. 【点睛】本题考查了扇形面积的计算,关键是理解恒星的面积=边长为4的正方形面积-半径为2的圆的面积.22.【解析】【分析】由切线性质知AD⊥BC 根据AB =AC 可得BD =CD =AD =BC =6【详解】解:如图连接AD 则AD⊥BC∵AB=AC∴BD=CD =AD =BC =6故答案为:6【点睛】本题考查了圆的切线性解析:【解析】 【分析】由切线性质知AD ⊥BC ,根据AB =AC 可得BD =CD =AD =12BC =6. 【详解】解:如图,连接AD ,则AD ⊥BC , ∵AB =AC , ∴BD =CD =AD =12BC =6, 故答案为:6.【点睛】本题考查了圆的切线性质,解题的关键在于掌握圆的切线性质.23.x1=1x2=-1【解析】分析:方程整理后利用平方根定义开方即可求出解详解:方程整理得:x2=1开方得:x=±1解得:x1=1x2=﹣1故答案为x1=1x2=﹣1点睛:本题考查了解一元二次方程﹣直接解析:x 1=1,x 2=-1【解析】分析:方程整理后,利用平方根定义开方即可求出解.详解:方程整理得:x 2=1,开方得:x =±1,解得:x 1=1,x 2=﹣1. 故答案为x 1=1,x 2=﹣1.点睛:本题考查了解一元二次方程﹣直接开平方法,熟练掌握直接开平方法是解答本题的关键.24.4【解析】【分析】由a+b2=2得出b2=2-a 代入a2+5b2得出a2+5b2=a2+5(2-a )=a2-5a+10再利用配方法化成a2+5b2=(a-即可求出其最小值【详解】∵a+b2=2∴b2解析:4 【解析】 【分析】由a+b 2=2得出b 2=2-a ,代入a 2+5b 2得出a 2+5b 2=a 2+5(2-a )=a 2-5a+10,再利用配方法化成a 2+5b 2=(a-2515)24+,即可求出其最小值. 【详解】 ∵a+b 2=2, ∴b 2=2-a ,a≤2,∴a 2+5b 2=a 2+5(2-a )=a 2-5a+10=(a-2515)24+, 当a=2时,a 2+b 2可取得最小值为4. 故答案是:4. 【点睛】考查了二次函数的最值,解题关键是根据题意得出a 2+5b 2=(a-2515)24+. 25.35【解析】【分析】【详解】解:∵PC 与⊙O 相切∴∠OCP=90°∴∠COP=90°-∠P=90°-20°=70°∵OA=OC ∴∠A=∠ACO ∵∠A+∠ACO=∠COP ∴∠A=35°故答案为35解析:35 【解析】 【分析】 【详解】解:∵PC 与⊙O 相切,∴∠OCP=90°, ∴∠COP=90°-∠P=90°-20°=70°, ∵OA=OC ,∴∠A=∠ACO , ∵∠A+∠ACO=∠COP , ∴∠A=35°, 故答案为35.三、解答题 26.(1)21b a =+;2c =;(2)102a -≤<;(3)存在,点()1,2P -或()1-或(1--.【解析】 【分析】(1)求出点A 、B 的坐标,即可求解;(2)当0x <时,若()20y ax bx c a =++<的函数值随x 的增大而增大,则函数对称轴02b x a =-≥,而21b a =+,即:2102a a+-≥,即可求解; (3)过点P 作直线l AB ,作PQ y 轴交BA 于点Q ,作PH AB ⊥于点H ,11122PAB S AB PH PQ ∆=⨯⨯=⨯=,则1P Q y y -=,即可求解.【详解】(1)2y x =+,令0x =,则2y =,令0y =,则2x =-, 故点A 、B 的坐标分别为()2,0-、()0,2,则2c =,则函数表达式为:22y ax bx =++,将点A 坐标代入上式并整理得:21b a =+;(2)当0x <时,若()20y ax bx c a =++<的函数值随x 的增大而增大,则函数对称轴02bx a=-≥,而21b a =+, 即:2102a a +-≥,解得:12a ≥-, 故:a 的取值范围为:102a -≤<; (3)当1a =-时,二次函数表达式为:22y x x =--+, 过点P 作直线lAB ,作PQy 轴交BA 于点Q ,作PH AB ⊥于点H ,∵OA OB =,∴45BAO PQH ∠=∠=︒,112221222PAB S AB PH PQ ∆=⨯⨯=⨯⨯=,则1P Q y y -=,在直线AB 下方作直线m ,使直线m 和l 与直线AB 等距离,则直线m 与抛物线两个交点坐标,分别与点AB 组成的三角形的面积也为1, 故:1P Q y y -=,设点()2,2P x x x --+,则点(),2Q x x +,即:2221x x x --+--=±, 解得:1x =-或12-±故点()1,2P -或 ()12,1-或(12,2---. 【点睛】主要考查二次函数和与几何图形.解题关键在于要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.27.(1)图形见解析(2)12【解析】 【分析】(1)本题属于不放回的情况,画出树状图时要注意;(2)B、C、D三个卡片的上的数字是勾股数,选出选中B、C、D其中两个的即可【详解】(1)画树状图如下:(2)∵共有12种等可能的结果数,抽到的两张卡片上的数都是勾股数的结果数为6种,∴抽到的两张卡片上的数都是勾股数的概率61 122 ==.28.(1)证明见解析;(2)29【解析】【分析】(1)连结OA、OD,如图,根据垂径定理的推理,由D为BE的下半圆弧的中点得到OD ⊥BE,则∠D+∠DFO=90°,再由AC=FC得到∠CAF=∠CFA,根据对顶角相等得∠CFA=∠DFO,所以∠CAF=∠DFO,加上∠OAD=∠ODF,则∠OAD+∠CAF=90°,于是根据切线的判定定理即可得到AC是⊙O的切线;(2)由于圆的半径R=5,EF=3,则OF=2,然后在Rt△ODF中利用勾股定理计算DF的长.【详解】解:(1)连结OA、OD,如图,∵D为BE的下半圆弧的中点,∴OD⊥BE,∴∠D+∠DFO=90°,∵AC=FC,∴∠CAF=∠CFA,∵∠CFA=∠DFO,∴∠CAF=∠DFO,而OA=OD,∴∠OAD=∠ODF,∴∠OAD+∠CAF=90°,即∠OAC=90°,∴OA⊥AC,∴AC 是⊙O 的切线;(2)∵圆的半径R=5,EF=3,∴OF=2,在Rt △ODF 中,∵OD=5,OF=2,∴【点睛】本题考查切线的判定.29.(1)50,25;(2)20【解析】【分析】(1)先将10.5万元化为105000元,设该乡镇有x 名高中学生获得了资助,则该乡镇有2x 名初中学生受到资助,由题意得一元一次方程,求解即可;(2)以“2019年上半年评为优秀学生的初、高中学生所获得的资助总金额一个月就达到了10800元”为等量关系,列出方程,然后设a%=t ,化为关于t 的一元二次方程,求解出t ,再根据a%=t ,求得a 即可.【详解】(1)10.5万元=105000元设该乡镇有x 名高中学生获得了资助,则该乡镇有2x 名初中学生受到资助,由题意得: 20023006105000x x ⨯+⨯=解得:25x =∴250x =∴该乡镇分别有50名初中学生和25名高中学生获得了资助.(2)由题意得:5030%13%2001%2540%1%30012%10800a a a a ⨯⨯+⨯++⨯⨯+⨯+=∴1013%1%101%12%36a a a a ⨯+⨯++⨯+⨯+=设%a t =,则方程化为:22101431013236t t t t +++++=∴2253580t t +=﹣解得 1.6t =﹣(舍)或20%t =∴20a =.【点睛】本题主要考查了由实际问题抽象出一元二次方程和一元一次方程,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.30.(1)见解析:(2)CE =1.【解析】【分析】(1)连接AD ,如图,先证明CD BD =得到∠1=∠2,再根据圆周角定理得到∠ADB =90°,根据切线的性质得到OD⊥EF,然后证明∠1=∠4得到结论;(2)连接BC交OD于F,如图,根据圆周角定理得到∠ACB=90°,再根据垂径定理,由CD BD=得到OD⊥BC,则CF=BF,所以OF=12AC=32,从而得到DF=1,然后证明四边形CEDF为矩形得CE=1.【详解】(1)证明:连接AD,如图,∵CD=BD,∴CD BD=,∴∠1=∠2,∵AB为直径,∴∠ADB=90°,∴∠1+∠ABD=90°,∵EF为切线,∴OD⊥EF,∴∠3+∠4=90°,∵OD=OB,∴∠3=∠OBD,∴∠1=∠4,∴∠A=2∠BDF;(2)解:连接BC交OD于F,如图,∵AB为直径,∴∠ACB=90°,∵CD BD=,∴OD⊥BC,∴CF=BF,∴OF=12AC=32,∴DF=52﹣32=1,∵∠ACB=90°,OD⊥BC,OD⊥EF,∴四边形CEDF为矩形,∴CE=DF=1.【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和勾股定理.。
中考语文复习专题(十):词语的搭配

中考语文复习专题(十):词语的搭配姓名:________ 班级:________ 成绩:________一、填空题 (共4题;共15分)1. (3分) (2019九上·宝鸡月考) 请从所给的三个词语中,选出一个最符合语境的填写在横线上。
①平凡孕育伟大,劳动创造价值,让一切劳动与创新的活力竞相________(迸射迸发迸溅),让一切创造社会财富的源泉充分涌流。
②器成还须久为功,卓越从来都不是速成的,________(齐心协力坚定不移持之以恒)才是关键。
愿年轻人都能沉心静气,积蓄力量,静待花开。
2. (2分)读《乞丐》,词语填空红肿的、流着泪水的眼睛,发青的嘴唇,粗糙、________的衣服,________的伤口……3. (4分)根据下面语境,为空格处选择合适的词语,将其序号填在横线上。
只要拥有一颗纯真的心,就可以________烦恼的枷锁,在欢乐的草坪上自由漫步;就可以________失败的阴影,在胜利的阳光下大步前行;就可以________冷漠的坚冰,在热情的海洋里扬帆远航。
A.驱散B.融化C.摆脱4. (6分)你从括号内选择合适的词语填入文中横线处。
瓦尔杰茨基公国国王弗里德里赫乘着马车,被 ________(狂野狂热热情)的人群簇拥着走得正欢,忽然晴天霹雳似地有一封信________(堕落降落飘落)到他的膝上,不知是谁 ________(扔投射)进来的。
二、单选题 (共31题;共62分)5. (2分) (2017八下·梅江月考) 下列句子中划线的词语使用不恰当的一项是()A . 当四野蛙声和其他虫鸣暂时沉寂时,我所听到的一点歌声则是非常柔和的,与夜色苍茫中的静谧气氛是再合适不过了。
B . 如果一只主教雀对着暖流歌唱起春天来,却发现自己搞错了,它还可以纠正自己的错误,继续保持它在冬季的缄默。
C . “水光潋滟晴方好”,从游船上纵目四望,西子湖春风送暖,碧波荡漾,长堤缀绿,群山围翠,真是赏心悦目。
中考英语总复习专题选词填空练习题基础版含解析

专题:选词填空一、用单词的正确形式完成句子用方框中所给单词的适当形式填空,每词仅用一次(每空一词)。
1.My classmates and I like to go hiking in our ________ time.2.Aunt Li never________ money on things that she doesn’t need.3.Scientists repor t that it’s better to smell________ than to drink it.4.It is known that Mother’s Day is the ________Sunday of May.5.Turn left and you will see the library________ the bank and the supermarket.根据句意,用所给单词、短语的适当形式填空,每词或短语只限使用一次。
6.This cat caught three _____________ in the yard last night.7.His mobile phone rang while he _____________ his new car on the street.8.You’d better stop smoking. It’s _____________ to your health.9.He _____________ the tree and hurt his left leg.10.Next Sunday is my grandmother’s _____________ birthd ay. We will hold a party for her.In a society where people always pay their attention to bad news, the 2012 year’s "Touching China" award definitely 11.. The award honors ten of China’s inspirational role models in 2012.12. the ten are public faces who did good deeds like Luo Yang, the late Commander of the program for 13. the J-15 fighter, who died from overwork. And Lin Junde, a scientist who devoted his whole life to China’s nuclear course. There are also common people who have 14. , like Zhang Lili. She was called "China’s Most Beautiful Teacher" after she saved two students, but lost both her legs in the effort.The award 15. are carefully selected to represent a true moral epic of 2012 in China. The "Touching China" award has been held yearly since 2003.danger, health, lucky, carrot, cross16.---How about the kids in your neighborhood ? --- They are happy and ____________.17.You must be careful when you __________ the street.18.---I passed the last exam. --- Oh, you’re really a _________ dog.19.---Can I help you, madam? ---Two kilos of ___________, please.20.Now lots of wild animals are in _________. We must try our best to protect them.21.Only Mother Love is true love. It gives everybody everything all 56._________ life. When you are still a baby, Mother takes good care of you as possible. In your walking hours she always holds you in herarms. When you are 57.________, she stops her work right now to look after you day and night and 58._________ about herself. When you are growing up day by day, she feels very happy. When you are 59.__________ enough go to school, Mother still looks after you all the time. On cold winter days, she always 60.________ you to put on more clothes. She always stands in the wind 61._________ for you back from school. When you hurry to leave home for school with little breakfast, she always feels 62.________ about you at home. She usually knows about your 63.__________ and spends much money on your school things. When you do well at school, you will see the brightest smile on her face.Mother is 64.__________ ready to give everything she has to her children, not to receive. What true love that is in the 65.__________! We will remember Mother Love for ever!It’s very important for everyone to protect the environment. As a student, I always try my 1 to save energy at home. I turn off 2 when I don’t need them. And I try to save water when I wash the dishes. I don’t 3 bottles or newspaper away because it’s better to recycle them.I think everyday activities at home can make a difference to the environment. I feel proud of 4 , and I will not only keep saving energy but also advise others to do the same things as me. If everyone cares about 5 the environment, I’m sure we’ll have a better life.请根据句意从方框中选择合适的单词,并用其适当形式填空,使句子通顺。
初三中考复习 专题练习题 含答案

参考答案:选择题1-5 B C B B A 6-10 B C B B C二、填空题11、1 12、-1 13、y=-x (答案不唯一) 14、(0,0)15、y=2x(答案不唯一) 16、m=-2三、解答题21、(1)y=3x-5(2)x=222、y=-3+2(x-2) y=-1224、p点坐标为(,4)或(-,-4)二、反比例基础训练2、3、4、5、三、计算题参考答案选择题1-5 AAAAD 6、C 填空题16、-3计算题22、S△aoc=一元二次函数专项训练4、5、6、4、5、6、解答题参考答案圆基础训练的是()参考答案1-5 ADDCC 6.60 7、AB⊥CD 8、8 9、10、11-13 BDD 14、0.115、16、方程组训练1.今有鸡兔同笼,上有三十五头,下有九十四足(问鸡有( )只,A.12B.23C.35D.49 答案:B2.一个长方形的长减少15cm,宽增加6cm,就成为一个正方形,并且这两个图形的面积相等.该长方形的面积是( )cm?(A.90B.100C.120D.150答案:B3.一支部队第一天行军4小时,第二天行军5小时,两天共行军98km,且第一天比第二天少走2km,第一天行军的平均速度是_____km/h. 第二天行军的平均速度_____ km/h.A.12、10B.10、12C.12.5、9.6D.9.6、12.5 答案:A4.某公司有大小两种货车,2辆大车和3辆小车可运货15.5吨,5辆大车和6辆小车可运货35吨.大车每辆运送( )吨,A.2.5B.3C.3.5D.4 答案:D5.某公司用30000元购进两种货物,货物卖出后,一种货物的利润是10%,另一种货物的利润是11%,共获得利润3150元.问两种货物各进货( )元,A.1500、28500B.15000、15000C.1500、2150D.10000、20000 答案:B6.一张方桌由1个桌面、4条桌腿组成(如果1m3木料可以做方桌的桌面50个或做桌腿300条,现有5m3木料,那么用立方米木料做桌面、立方米木料做桌腿,做出的桌面和桌腿,恰好能配成方桌,能配成张方桌,()A.2,3,100B.1,4,50C.3,2,150D.4,1,200 答案:C7.1号仓库与2号仓库共存粮450吨,现从1号仓库运出存粮的60%,从2号仓库运出存粮的40%,结果2号仓库所余的粮食比1号仓库所余的粮食多30吨,1号仓库与2号仓库原来各存粮( )吨,A.210,240B.240,210C.306,144D.126,324答案:B8.一个三位数的数字之和等于12,它的个位数比十位数字小2(若将它的百位数字与个位数字互换,所得的数比原来的数小99,则原数( )A.264B.453C.345D.642 答案:B相似三角形专项、5、6、参考答案1、2、4、5、第三次:平行四边形动态讨论1、已知y=ax+b与反比例函数交点为A(2,2)B(-1,-4),求:(1)表达式(2)C点坐标(-4,m)求S△ABC(3)是否存在一点D,使四边形ABCD若存在,写出来。
中考复习 填空题、选择题专题一 正负数的意义,相反数、倒数、绝对值

填空题、选择题专题一正负数的意义、数轴、相反数、倒数、绝对值一、云南中考原题1.(2016)计算:|3|-= .2.(2017) 2的相反数是 .3.(2018)1-的绝对值是 .4.(2019)若零上8℃记作+8℃,则零下6℃记作 ℃.5.(2020)中国是最早采用正负数表示相反意义的量的国家.某仓库运进面粉7吨,记为7+吨,那么运出面粉8吨应记为___________吨.6. (2021)某地区2021年元旦的最高气温为9℃,最低气温为﹣2℃,那么该地区这天的最低气温比最高气温低( )A .7℃B .﹣7℃C .11℃D .﹣11℃7.(2022)中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.若零上10℃记作+10℃,则零下10℃可记作( )A. 10℃B. 0℃C. -10 ℃D. -20℃二、强化训练1.把上升5m 记为5m +,那么3m -表示______.2.如果向西走30米记作30-米,那么15+米表示:_________.3.将数轴上的点A 向右移动3个单位长度到达点B ,若点B 表示的数是2,则点A 表示的数是________.4.在数轴上与表示﹣2的点相距3个单位长度的点表示的数是 _____.5.13-的绝对值是__________,5的相反数是_________. 6.2022-的相反数是( )A .2022B .12022- C .12022 D .2022-7.12-的绝对值等于( ) A .12-B .12C .2D .-2 8.12-的相反数是( ) A .12- B .12 C .2- D .2 9.12-的倒数等于( ) A .12- B .12 C .2 D .-210.下列说法错误的是( )A .0既不是正数,也不是负数B .零上4摄氏度可以写成4C +︒,也可以写成4C ︒C .若盈利100元记作100+元,则20-元表示亏损20元D .向正北走一定用正数表示,向正南走一定用负数表示11.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )A .B .C .D .12.下列说法正确的是( )A .分数都是有理数B . a -是负数C .有理数不是正数就是负数D .绝对值等于本身的数是正数13.将下列四个数表示在数轴上,它们对应的点中,离原点最近的是( )A .-0.4B .0.6C .1.3D .-214.若a 与﹣6互为相反数,则1a -的值为( )A .﹣6B .﹣5C .5D .615.若a 、b 互为相反数,则2(a +b )+3的值为( )A .-1B .3C .1D .216.下列化简,正确的是( )A .[(10)]=10----B .(3)=3---C .(+5)=5-D .[(+8)]=8---17.下列各式正确的是( )A .﹣|﹣5|=5B .﹣(﹣5)=﹣5C .|﹣5|=﹣5D .﹣(﹣5)=518.在实数3-,12-,0,1中,绝对值最小的数是( )A .3-B .12- C .0 D .119.已知等腰三角形的两边长为x ,y ,且满足24(2)0x x y -+-=,则三角形的周长为( )A .12B .16C .20D .16或20 20.一个数的绝对值为7,则这个数是( )A .7B .﹣7C .±7D .以上都不对 21.已知a >0,b <0,且|a |<|b |,则下列关系正确的是() A .b a a b <-<<- B .a b a b -<<<- C .a b b a -<<-< D .b a b a <<-<-。
中考数学复习专题训练精选试题及答案

中考数学复习专题训练精选试题及答案目录实数专题训练 (2)实数专题训练答案 (4)代数式、整式及因式分解专题训练 (5)代数式、整式及因式分解专题训练答案 (6)分式和二次根式专题训练 (7)分式和二次根式专题训练答案 (8)一次方程及方程组专题训练 (9)一次方程及方程组专题训练答案 (11)一元二次方程及分式方程专题训练 (11)一元二次方程及分式方程专题训练答案 (13)一元一次不等式及不等式组专题训练 (13)一元一次不等式及不等式组专题训练答案 (15)一次函数及反比例函数专题训练 (15)一次函数及反比例函数专题训练答案 (17)二次函数及其应用专题训练 (18)二次函数及其应用专题训练答案 (20)立体图形的认识及角、相交线与平行线专题训练 (20)立体图形的认识及角、相交线与平行线专题训练答案 (22)三角形专题训练 (23)三角形专题训练答案 (25)多边形及四边形专题训练 (25)多边形及四边形专题训练答案 (27)圆及尺规作图专题训练 (28)圆及尺规作图专题训练答案 (30)轴对称专题训练 (30)轴对称专题训练答案 (32)平移与旋转专题训练 (33)平移与旋转专题训练答案 (35)相似图形专题训练 (35)相似图形专题训练答案 (37)图形与坐标专题训练 (38)图形与坐标专题训练答案 (40)图形与证明专题训练 (40)图形与证明专题训练答案 (42)概率专题训练 (42)概率专题训练答案 (44)统计专题训练 (45)统计专题训练答案 (47)实数专题训练一、填空题:(每题 3 分,共 36 分)1、-2 的倒数是____。
2、4 的平方根是____.3、-27 的立方根是____。
4、-2 的绝对值是____。
5、2004年我国外汇储备3275。
34亿美元,用科学记数法表示为____亿美元。
6、比较大小:-____-。
7、近似数0。
020精确到____位,它有____个有效数字.8、若 n 为自然数,那么(-1)2n+(-1)2n+1=____.9、若实数 a、b 满足|a-2|+( b+)2=0,则 ab=____.10、在数轴上表示 a 的点到原点的距离为 3,则 a-3=____。
《好题》中考数学填空题专项练习经典复习题(含答案)
一、选择题1.已知2(0)y ax bx c a =++≠的图象如图,则y ax b =+和c y x=的图象为( )A .B .C .D .2.如图,AB 是⊙O 的直径,AC 是⊙O 的切线,A 为切点,BC 与⊙O 交于点D ,连结OD .若50C ∠=︒,则∠AOD 的度数为( )A .40︒B .50︒C .80︒D .100︒3.下列智能手机的功能图标中,既是轴对称图形又是中心对称图形的是( )A .B .C .D .4.关于x 的一元二次方程2(1)20x k x k ---+=有两个实数根12,x x ,()1212122(2)2x x x x x x -+--+3=-,则k 的值( )A .0或2B .-2或2C .-2D .25.如图,在△ABC 中,∠CAB=65°,在同一平面内,将△ABC 绕点A 旋转到△AB′C′的位置,使得CC′∥AB ,则∠BAB′的度数为( )A .25°B .30°C .50°D .55°6.受益于电子商务发展和法治环境改善等多重因素,“快递业”成为我国经济的一匹“黑马”,2016年我国快递业务量为300亿件,2018年快递量将达到450亿件,若设快递量平均每年增长率为x ,则下列方程中,正确的是( )A .()3001x 450+=B .()30012x 450+=C .2300(1x)450+=D .2450(1x)300-=7.在一个不透明纸箱中放有除了标注数字不同外,其他完全相同的3张卡片,上面分别标有数字1,2,3,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之和为奇数的概率为( )A .59B .49C .56D .138.某同学在解关于x 的方程ax 2+bx +c =0时,只抄对了a =1,b =﹣8,解出其中一个根是x =﹣1.他核对时发现所抄的c 是原方程的c 的相反数,则原方程的根的情况是( ) A .有两个不相等的实数根B .有两个相等的实数根C .有一个根是x =1D .不存在实数根 9.若将抛物线y=x 2平移,得到新抛物线2(3)y x =+,则下列平移方法中,正确的是( )A .向左平移3个单位B .向右平移3个单位C .向上平移3个单位D .向下平移3个单位10.关于下列二次函数图象之间的变换,叙述错误的是( )A .将y =﹣2x 2+1的图象向下平移3个单位得到y =﹣2x 2﹣2的图象B .将y =﹣2(x ﹣1)2的图象向左平移3个单位得到y =﹣2(x+2)2的图象C .将y =﹣2x 2的图象沿x 轴翻折得到y =2x 2的图象D .将y =﹣2(x ﹣1)2+1的图象沿y 轴翻折得到y =﹣2(x+1)2﹣1的图象11.以394c x ±+=为根的一元二次方程可能是( ) A .230x x c --= B .230x x c +-= C .230-+=x x cD .230++=x x c 12.正五边形绕着它的中心旋转后与它本身重合,最小的旋转角度数是( )A .36°B .54°C .72°D .108° 13.如图,在△ABC 中,BC =4,以点A 为圆心,2为半径的⊙A 与BC 相切于点D ,交AB 于点E ,交AC 于点F .P 是⊙A 上一点,且∠EPF =40°,则图中阴影部分的面积是( )A .4-9πB .4-89πC .8-49πD .8-89π 14.某人到瓷砖商店去购买一种多边形形状的瓷砖,用来铺设无缝地板,他购买的瓷砖形状不可以是( )A .正三角形B .矩形C .正八边形D .正六边形15.与y=2(x ﹣1)2+3形状相同的抛物线解析式为( )A .y=1+12x 2B .y=(2x+1)2C .y=(x ﹣1)2D .y=2x 2二、填空题16.抛物线y =(x ﹣1)2﹣2与y 轴的交点坐标是_____.17.如图,在直角坐标系中,已知点30A -(,)、04B (,),对OAB 连续作旋转变换,依次得到1234、、、,则2019的直角顶点的坐标为__________.18.如图,在边长为2的正方形ABCD 中,以点D 为圆心,AD 长为半径画AC ,再以BC 为直径画半圆,若阴影部分①的面积为S 1,阴影部分②的面积为S 2,则图中S 1﹣S 2的值为_____.(结果保留π)19.一个扇形的圆心角为135°,弧长为3πcm ,则此扇形的面积是_____cm 2.20.函数y =x 2﹣4x +3的图象与y 轴交点的坐标为_____.21.在一个不透明的口袋中装有5个红球和3个白球,他们除颜色外其他完全相同,任意摸出一个球是白球的概率为________.22.若点A (-3,y 1)、B (0,y 2)是二次函数y=-2(x -1)2+3图象上的两点,那么y 1与y 2的大小关系是________(填y 1>y 2、y 1=y 2或y 1<y 2).23.某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作,去年已投入5亿元资金,并计划投入资金逐年增长,明年将投入7.2亿元资金用于保障性住房建设,则这两年投入资金的年平均增长率为________.24.若1x 、2x 是方程22x 2mx m m 10-+--=的两个实数根,且x 1+x 2=1-x 1⋅x 2,则 m 的值为________.25.某校组织“优质课大赛”活动,经过评比有两名男教师和两名女教师获得一等奖,学校将从这四名教师中随机挑选两位教师参加市教育局组织的决赛,挑选的两位教师恰好是一男一女的概率为____.三、解答题26.如图,在⊙O 中,点C 为AB 的中点,∠ACB =120°,OC 的延长线与AD 交于点D ,且∠D =∠B .(1)求证:AD 与⊙O 相切;(2)若CE =4,求弦AB 的长.27.用你喜欢的方法解方程(1)x 2﹣6x ﹣6=0(2)2x 2﹣x ﹣15=028.如图,已知二次函数y=-x 2+bx+c 的图象经过A (-2,-1),B (0,7)两点.(1)求该抛物线的解析式及对称轴;(2)当x 为何值时,y >0?(3)在x 轴上方作平行于x 轴的直线l ,与抛物线交于C ,D 两点(点C 在对称轴的左侧),过点C ,D 作x 轴的垂线,垂足分别为F ,E .当矩形CDEF 为正方形时,求C 点的坐标.29.从甲、乙、丙、丁4名同学中随机抽取同学参加学校的座谈会(1)抽取一名同学,恰好是甲的概率为(2) 抽取两名同学,求甲在其中的概率。
中考语文复习:句子成分和主干练习题及答案

中考语文复习:句子成分和主干练习题及答案《句子成分和句子的主干》专题练习一、填空题1.“两千年来,我国修建了无数的石拱桥。
”中的“两千年来”充当。
2.“远寺的钟声突然惊醒了海的醋梦。
”一句中的主语是。
3.“爱因斯坦常忘了兑取支票。
”中的“兑取支票”充当。
4.“祥子的全身没有一点干松的地方。
”一句的主干是。
5.“一张简陋的大竹床铺着厚厚的稻草。
”一句的谓语是。
6.“这种意志和精神才是世界最可贵的财产。
”一句的主干是。
7.“有几个园林还在适当的位置装上一面大镜子。
”一句的宾语是。
8.“在湛蓝的天空下,故宫博物院那金黄色的琉璃瓦重檐屋顶,格外辉煌。
”一句的主语是,谓语是,状语是。
9.“每根大柱上盘绕着矫健的金龙。
”一句的主干是。
10.“冰凉的河水呛得我好难受。
”一句中的划线部分充当。
11.“她对贫苦农民的同情和对为富不仁者的反感却更强烈了。
”一句的主干是。
12.“一把坚实的锁挂在大门上。
”一句中“在大门上”充当。
二、选择题1.选出对下边句子成分分析正确的一项是()十几年来,延安机场上送行的情景时时出现在眼前。
A.这个句子的主语中心语是“情景”,谓语中心语是“出现”,宾语是“在眼前”。
B.这个句子的主语中心语是“延安机场”,谓语中心语是“出现”,补语是“在眼前”。
C.这个句子的主语中心语是“情景”,谓语中心语是“出现”,补语是“在眼前”。
D.这个句子的主语是“十几年来”,谓语是“延安机场送行的情景常常出现在眼前”。
2.主谓短语充当谓语的一项是()A.他身材高大。
B.他的身材高大。
C.他有高大的身材。
D.身材高大的就是他。
3.下列句子中只有一个是错误的,请找出来。
()A.这件事情,使我明白了一个深刻的道理。
B.从这件事情中,使我明白了一个深刻的道理。
C.通过这件事情,我明白了一个深刻的道理。
D.白花不含色素,但组织里面含有空气,会把光束全部反射出来,所以呈现白色。
4.下列句中,划线部分与例句划线部分在结构和充当句子成分方面都相同的一句是()例句:大家都觉得这种做法不合适。
历届中考真题汇总重点复习专题(含解析答案)

一、选择题1.(2015•江苏南京市,第 6题,3分)如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O 相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为()A.133B.92C.4133D.252.(2015•江苏无锡市,第 8题,3分).八边形的内角和为()A.180ºB.360ºC.1080ºD.1440º3.(2015•江苏连云港市,第5题,3分)已知四边形ABCD,下列说法正确的是( )A.当AD=BC,AB//DC时,四边形ABCD是平行四边形B.当AD=BC,AB=DC时,四边形ABCD是平行四边形C.当AC=BD,AC平分BD时,四边形ABCD是矩形D.当AC=BD,AC⊥BD时,四边形ABCD是正方形二、填空题4.(2015•江苏泰州市,第 16题,3分)如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP 沿BP翻折至△EBP, PE与CD相交于点O,且OE=OD,则AP的长为__________.5.(2015•江苏无锡市,第 14题,3分)如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于cm.6.(2015•江苏盐城市,第 16题,3分)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .7.(2015•江苏盐城市,第 17题,3分)如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则弧BE的长度为 .8.(2015•江苏连云港市,第 12题,3分)如图,一个零件的横截面是六边形,这个六边形的内角和为 .三、解答题:9.(2015•江苏泰州市,第 25题,10分)如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA 上的动点,且AE=BF=CG=DH.(1)求证:四边形EFGH是正方形;(2)判断直线EG是否经过一个定点,并说明理由;(3)求四边形EFGH面积的最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考复习专题(填空题)一. 数学填空题的特点与选择题同属客观性试题的填空题,具有客观性试题的所有特点,即题目短小精干,考查目标集中明确,答案唯一正确,答卷方式简便,评分客观公正等。
但是它又有本身的特点,即没有备选答案可供选择,这就避免了选择项所起的暗示或干扰的作用,及考生存在的瞎估乱猜的侥幸心理,从这个角度看,它能够比较真实地考查出学生的真正水平。
考查内容多是“双基”方面,知识复盖面广。
但在考查同样内容时,难度一般比选择题略大。
试看下面二题:例1如图1,已知一块正方形的地瓷砖边长为a,瓷砖上的图案是以各边为直径在正方形内画半圆所围成(阴影部分),那么阴影部分的面积____。
例2 如上图,以正方形各边为直径在正方形内画半圆,求所围成的图形(阴影部分)的面积。
下列计算方法,正确的是()。
A.三个半圆的面积减去正方形的面积;B.四个半圆的面积减去正方形的面积;C.正方形的面积减去两个半圆的面积;D.正方形的面积减去三个半圆的面积;这道题是课本中的解答题,把它编成填空题后,同样要认真计算才能得出结果,而把它编成选择题,不少考生通过比较选择项,通过选择项的暗示作用,可筛选出正确答案(B),花时间比例1少得多。
二.主要题型初中填空题主要题型一是定量型填空题,二是定性型填空题,前者主要考查计算能力的计算题,同时也考查考生对题目中所涉及到数学公式的掌握的熟练程度,后者考查考生对重要的数学概念、定理和性质等数学基础知识的理解和熟练程度。
当然这两类填空题也是互相渗透的,对于具体知识的理解和熟练程度只不过是考查有所侧重而已。
填空题一般是一道题填一个空格,当然个别省市也有例外。
中考南京出了四道类似上题的填空题。
这类有递进层次的试题,实际上是考查解题的几个主要步骤。
中考江西省还出了一道“先阅读,后填空”的试题,它首先列举了30名学生的数学成绩,给出频率分布表,然后要求考生回答六小道填空题,这也可以说是一种新题型。
这种先阅读一段短文,在理解的基础上,要求解答有关的问题,是近年悄然兴起的阅读理解题。
它不仅考查了学生阅读理解和整理知识的能力,同时提醒考生平时要克服读书囫囵吞枣、不求甚解的不良习惯。
这种新题型的出现,无疑给填空题较寂静的湖面投了一个小石子。
三.基本解法一、直接法例1 如图,点C 在线段AB 的延长线上,︒=∠15DAC ,︒=∠110DBC ,则D ∠的度数是_____________分析:由题设知︒=∠15DAC ︒=∠110DBC ,利用三角形的一个外角等于和它不相邻的两个内角的和知识,通过计算可得出D ∠=︒95.二、特例法例2 已知ABC △中,60A ∠=,ABC ∠,ACB ∠的平分线交于点O ,则BOC ∠的度数为 . 分析:此题已知条件中就是ABC △中,60A ∠=说明只要满足此条件的三角形都一定能够成立。
故不妨令ABC △为等边三角形,马上得出BOC ∠=120。
例4、填空题:已知a<0,那么,点P(-a 2-2,2-a)关于x 轴的对称点是在第____解:设a=-1,则P{-3,3}关于x 轴的对称点是 {-3,-3}在第三象限,所以点P(-a^2-2,2-a)关于x 轴的对称点是在第三象限.例5、无论m 为任何实数,二次函数y=x 2+(2-m)x+m 的图像都经过的点是 _____解:因为m 可以为任何实数,所以不妨设m=2,则y=x ^2+2,再设m=0,则y=x ^2+2x 解方程组解得所以二次函数y=x ^2+(2-m)x+m 的图像都经过的点是(1,3).三、数形结合法 "数缺形时少直观,形缺数时难入微。
"数学中大量数的问题后面都隐含着形的信息,图形的特征上也体现着数的关系。
我们要将抽象、复杂的数量关系,通过形的形象、直观揭示出来,以达到"形帮数"的目的;同时我们又要运用数的规律、数值的计算,来寻找处理形的方法,来达到"数促形"的目的。
对于一些含有几何背景的填空题,若能数中思形,以形助数,则往往可以简捷地解决问题,得出正确的结果。
例6、 在直线l 上依次摆放着七个正方形(如图所示)。
已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,,则S1+S2+S3+S4=_______。
D解:四个正方形的面积依次是S1、S2、S3、S4,可设它们的边长分别为a 、b 、c 、d ,由直角三角形全等可得解得a^2+b^2+c^2+d^2=4,则S1+S2+S3+S4=4.四、猜想法例4 用同样大小的黑色棋子按图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).分析:从第1个图中有4枚棋子4=3×1+1,从第2个图中有7枚棋子7=3×2+1, 从第3个图中有10枚棋子10=3×3+1,从而猜想:第n 个图中有棋子3n+1枚.五、整体法例5 如果x+y=-4,x-y=8,那么代数式x2-y2的值是 c 分析:若直接由x+y=-4,x-y=8解得x ,y 的值,再代入求值,则过程稍显复杂,且易出错,而采用整体代换法,则过程简洁,妙不可言.分析:x2-y2=(x+y )(x-y )=-4×8=-32例7已知53=-=-c b b a ,1222=++c b a ,则ca bc ab ++的值等于_____ 分析:运用完全平方公式,得222)()()(a c c b b a -+-+-=2)(222c b a ++-2)(ca bc ab ++,即)(ca bc ab ++=)(222c b a ++-21[222)()()(a c c b b a -+-+-]. ∵ 53=-=-c b b a ,56)()(-=-+-=-a b b c a c ,1222=++c b a , ∴ )(ca bc ab ++=1-21[2)53(+2)53(+2)56(-]=-252. 六、构造法例7 已知反比例函数的图象经过点(m ,2)和(-2,3)则m 的值为 . 分析:采用构造法求解.由题意,构造反比例函数的解析式为xk =y ,因为它过(-2,3)所以把x =-2,y =3代入x k =y 得k=-6. 解析式为x 6-=y 而另一点(m,2)也在反比例函数的图像上,所以把x =m ,y =2代入x 6-=y 得第1个图第2个图第3个图 …m=-3.七、图解法例8如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1= -1, x2= 3③a+b+c>0 ④当x>1时,y随x的增大而增大。
正确的说法有_____________。
(把正确的答案的序号都填在横线上)分析:本题借助图解法来求①利用图像中抛物线开口向上可知a>0,与y轴负半轴相交可知c<0,所以ac<0.②图像中抛物线与x轴交点的横坐标为-1,3可知方程ax2+bx+c=0的根是x1= -1, x2= 3 ③从图中可知抛物线上横坐标为1的点(1,a+b+c)在第四象限内所以a+b+c<0 ④从与x轴两交点的横坐标为-1,3可知抛物线的对称轴为x=1且开口向上,所以当x>1时y随x的增大而增大。
所以正确的说法是:①②④八、等价转化法通过"化复杂为简单、化陌生为熟悉",将问题等价地转化成便于解决的问题,从而得出正确的结果例7、如图10,在△ ABC中,AB=7,AC=11,点M是BC的中点, AD是∠BAC 的平分线,MF∥AD,则FC的长为_________. 解:如图,设点N是AC的中点,连接MN,则MN∥AB.又MF∥AD,所以,所以分析:本题借助图解法来求①利用图像中抛物线开口向上可知a>0,与y轴负半轴相交可知c<0,所以ac<0.②图像中抛物线与x轴交点的横坐标为-1,3可知方程ax2+bx+c=0的根是x1= -1, x2= 3 ③从图中可知抛物线上横坐标为1的点(1,a+b+c)在第四象限内所以a+b+c<0 ④从与x轴两交点的横坐标为-1,3可知抛物线的对称轴为x=1且开口向上,所以当x>1时y随x的增大而增大。
所以正确的说法是:①②④八、等价转化法通过"化复杂为简单、化陌生为熟悉",将问题等价地转化成便于解决的问题,从而得出正确的结果。
.例7、如图10,在△ ABC中,AB=7,AC=11,点M是BC的中点, AD是∠BAC 的平分线,MF∥AD,则FC的长为_________. 解:如图,设点N是AC的中点,连接MN,则MN∥AB.又M F∥AD,所以,所以.因此例8、如图6,在中,E为斜边AB上一点,AE=2,EB=1,四边形DEFC为正方形,则阴影部分的面积为________. 解:将直角三角形EFB绕E点,按逆时针方向旋转,因为CDEF是正方形,所以EF和ED重合,B点落在CD上,阴影部分的面积转化为直角三角形ABE的面积,因为AE=2,EB=1,所以阴影部分的面积为1/2*2*1=1.九、观察法例3 一组按规律排列的式子:2ba-,53ba,83ba-,114ba,…(0ab≠),其中第7个式子是,第n个式子是(n为正整数).分析:通过观察已有的四个式子,发现这些式子前面的符号一负一正连续出现,也就是序号为奇数时负,序号为偶数时正。
同时式子中的分母a的指数都是连续的正整数,分子中的b的指数为同个式子中a的指数的3倍小1,通过观察得出第7个式子是207ba-,第n个式子是31(1)nnnba--。
由以上的例子我们可以看到数学思想方法是处理数学填空题的指导思想和基本策略,是数学的灵魂,它能够帮助我们从多角度思考问题,灵活选择方法,是快速准确地解数学填空题的关键。
因此,我们首先要对初中数学知识和技能做到"透彻理解,牢固掌握,融会贯通"进而领悟和掌握以数学知识为载体的数学思想方法,来提高思维水平,运用数学思想方法达到"举一反三,熟练运用,提升素养"的目的。
四.认真作答,减少失误填空题虽然多是中低档题,但不少考生在答题时往往出现失误,这是要引起师生的足够重视的。
首先,应按题干的要求填空,如有时填空题对结论有一些附加条件,如用具体数字作答,精确到……等,有些考生对此不加注意,而出现失误,这是很可惜的。
例6一个圆柱的底面半径为1米,它的高为2米,则这个圆柱的侧面积为__平方米。
(精确到0.1平方米)。
有的考生直接把求出的4Л作为结果而致错误,正确答案应当是12.6。
其次,若题干没有附加条件,则按具体情况与常规解题。
第三,应认真分析题目的隐含条件。
例8 等腰三角形的一边等于4,一边等于9,则它的周长等于___。
