椭圆几何性质3 胡红
椭圆的简单几何性质课件

椭圆的简单几何性质课件椭圆的简单几何性质椭圆,作为一种常见的几何形状,具有许多有趣的性质和特点。
在这篇文章中,我们将探讨椭圆的一些简单几何性质,帮助读者更好地理解和应用椭圆。
一、椭圆的定义和基本元素椭圆是指平面上到两个固定点F1和F2的距离之和等于常数2a的点的轨迹。
这两个固定点称为焦点,连接两个焦点的线段称为主轴,主轴的中点称为椭圆的中心。
椭圆的两个焦点与中心之间的距离称为焦距,记为c。
椭圆的长轴长度为2a,短轴长度为2b,其中a大于b。
二、椭圆的离心率和焦半径椭圆的离心率是一个重要的参数,用e表示。
离心率的定义是焦距与长轴长度的比值,即e=c/a。
离心率可以用来描述椭圆的扁平程度,当离心率接近于0时,椭圆趋近于圆形;当离心率接近于1时,椭圆趋近于直线。
与离心率相关的概念是焦半径。
焦半径是指从椭圆上的任意一点到两个焦点的距离之和,记为r。
根据焦半径的定义,我们可以得到一个重要的结论:椭圆上的任意一点到两个焦点的距离之和等于2a,即r=2a。
三、椭圆的方程和参数方程椭圆的方程是描述椭圆上的点的数学表达式。
椭圆的标准方程是(x-h)^2/a^2+(y-k)^2/b^2=1,其中(h,k)是椭圆的中心坐标。
根据椭圆的定义,我们可以得到一个重要的性质:椭圆上的任意一点到中心的距离与椭圆的长轴、短轴长度之间存在一定的关系,即(x-h)^2/a^2+(y-k)^2/b^2=1。
除了标准方程,椭圆还可以用参数方程来表示。
参数方程是通过引入一个参数t,将椭圆上的点的坐标表示为x=a*cos(t)+h,y=b*sin(t)+k。
参数方程的优点是可以方便地描述椭圆上的点的运动和变化。
四、椭圆的性质和应用椭圆具有许多有趣的性质和应用。
首先,椭圆是一个闭合曲线,它的形状稳定且对称。
其次,椭圆上的点到两个焦点的距离之和是常数,这个性质可以应用于天文学中的行星轨道计算、卫星轨道设计等领域。
此外,椭圆还有许多与切线、法线、对称性等相关的性质。
苏教版高考总复习一轮数学精品课件 第九章 平面解析几何 第五节 椭圆-第2课时 椭圆的几何性质

4
4
3
4
3
2
2
2
2
2
2
2
2
C. + = 1或 + = 1D. + = 1或 + = 1
6
3
6
3
16
9
9
16
[解析]因为离心率为 ,则有 = = ,所以 = ,又椭圆的面积为
所以 =
+
,又
= .故选B.
=
+ ,解得
=
,
∴ = ,解得 = ,
∵ = × ,∴ = ,
∴椭圆的标准方程为
+ = ;
+
= > > ,∵椭圆过点 , ,
若焦点在轴上,设方程为
= ,
又 = × ,∴ =
+
=
或
1 = + 0 , 2 = − 0 .
自测诊断
1.椭圆3 2 + 4 2 = 12的长轴长、短轴长分别为() C
A.2, 3B. 3,2C.4,2 3D.2 3,4
[解析]把
+
短轴长为 .
=
化成标准形式为
+
= ,得 = , = ,则长轴长为4,
+
= .
3.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为( A )
椭圆的几何性质

1、定义:e=c/a。
2、离心率范围:0<e<1。
3、离心率越大椭圆就越扁,越小则越接近于圆。
面积
S=π×a×b(其中a,b分别是椭圆的长半轴,短半轴的长)。
或S=π×A×B/4(其中A,B分别是椭圆的长轴,短轴的长)。
周长
椭圆周长没有公式,有积分式Fra bibliotek无限项展开式。
椭圆周长的精确计算要用到积分或无穷级数的求和。
chusancom隶属于吉林省春雨秋风科技有限公司其它同名网站均为侵权或假冒
椭圆的几何性质
范围:焦点在x轴上-a≤x≤a,-b≤y≤b;焦点在y轴上-b≤x≤b,-a≤y≤a。对称性:关于x轴对称,关于y轴对称,关于原点中心对称。顶点:(a,0),(-a,0),(0,b),(0,-b)。离心率:e=c/a。离心率范围0<e<1。离心率越大椭圆就越扁,越小则越接近于圆。
椭圆和双曲线的性质

椭圆和双曲线的性质椭圆和双曲线是数学中常见的曲线形状,它们具有一些独特的性质和特点。
本文将介绍椭圆和双曲线的定义、方程、焦点、直径、离心率等基本概念,并探讨它们的性质和应用。
一、椭圆的性质椭圆是平面上一点到两个固定点的距离之和等于常数的轨迹。
这两个固定点称为椭圆的焦点,常数称为椭圆的离心率。
椭圆的方程一般形式为:(x/a)^2 + (y/b)^2 = 1其中a和b分别是椭圆的半长轴和半短轴的长度。
椭圆的中心位于原点(0,0)处。
椭圆的性质有以下几点:1. 椭圆是对称图形,关于x轴和y轴都具有对称性。
2. 椭圆的长轴和短轴分别是直径,且长轴和短轴的长度之比等于椭圆的离心率。
3. 椭圆的焦点到椭圆上任意一点的距离之和等于椭圆的长轴长度。
4. 椭圆的离心率小于1,且越接近于1,椭圆越扁平。
椭圆的应用广泛,例如在天文学中,行星的轨道可以近似看作椭圆;在工程中,椭圆的形状常用于设计汽车、船舶等物体的外形。
二、双曲线的性质双曲线是平面上一点到两个固定点的距离之差等于常数的轨迹。
这两个固定点称为双曲线的焦点,常数称为双曲线的离心率。
双曲线的方程一般形式为:(x/a)^2 - (y/b)^2 = 1其中a和b分别是双曲线的半长轴和半短轴的长度。
双曲线的中心位于原点(0,0)处。
双曲线的性质有以下几点:1. 双曲线是对称图形,关于x轴和y轴都具有对称性。
2. 双曲线的长轴和短轴分别是直径,且长轴和短轴的长度之比等于双曲线的离心率。
3. 双曲线的焦点到双曲线上任意一点的距离之差等于双曲线的长轴长度。
4. 双曲线的离心率大于1,且越接近于1,双曲线越扁平。
双曲线的应用也非常广泛,例如在物理学中,双曲线常用于描述光的折射和反射现象;在经济学中,双曲线常用于描述供需关系和市场变化。
总结:椭圆和双曲线是两种常见的曲线形状,它们具有一些共同的性质,如对称性和焦点到曲线上任意一点的距离关系。
同时,它们也有一些不同的特点,如离心率的大小和形状的扁平程度。
《椭圆的简单几何性质》知识点总结

椭圆的简单几何性质知识点总结椭圆是一种重要的几何图形,具有一些特殊的性质。
在本篇文档中,我们将总结椭圆的一些简单几何性质。
1. 椭圆的定义椭圆可以通过以下定义来描述:对于给定的两个焦点F1和F2,及其到两个焦点的总距离的一半定为常量2a(长轴),椭圆上每一点到两个焦点的距离之和等于常量2a。
椭圆的另一个参数e(离心率)定义为焦点之间的距离与长轴的比值:e = c/a,其中c是焦点之间的距离。
2. 椭圆的焦点和准线椭圆的焦点F1和F2对称分布在长轴上,并且与椭圆的中心O相等。
准线是通过焦点F1和F2垂直于长轴的直线,交于椭圆的中心O。
准线的长度定为2b(短轴)。
椭圆的离心率e= c/a = √(a^2 - b^2)/a。
3. 椭圆的主轴和副轴椭圆的主轴是长轴,长度为2a。
副轴是短轴,长度为2b。
长轴和短轴是椭圆上的两个对称轴。
4. 椭圆的焦准距椭圆上的任意一点P到两个焦点F1和F2的距离之和等于2a,即PF1+PF2=2a。
我们把这个距离之和称为焦准距。
对于同一条主轴上的两个点P1和P2,它们到焦点的距离之和相等。
5. 椭圆的离心率椭圆的离心率是一个反映椭圆形状的重要参数。
离心率e定义为焦点之间的距离与长轴的比值:e = c/a。
当离心率小于1时,椭圆是真椭圆;当离心率等于1时,椭圆是半圆;当离心率大于1时,椭圆是伪椭圆。
离心率越接近于0,椭圆形状越扁。
6. 椭圆的方程椭圆的方程可以通过不同的形式来表示,其中最常用的是标准形式和一般形式。
标准形式的椭圆方程为:x2/a2 + y2/b2 = 1,其中a和b分别为椭圆的长轴和短轴的长度。
一般形式的椭圆方程为:Ax^2 + By^2 + Cx + Dy + E = 0,其中A、B、C、D和E为常数。
7. 椭圆的焦距定理椭圆的焦距定理说明了椭圆上的任意一点P到两个焦点F1和F2的距离之和等于椭圆的主轴长度。
即PF1+PF2=2a。
8. 椭圆的切线椭圆上任意一点P的切线是通过点P且与椭圆仅相交于点P的直线。
椭圆的基本概念与性质

椭圆的基本概念与性质椭圆是一种常见的几何图形,具有许多独特的性质和应用。
本文将介绍椭圆的基本概念和性质,包括定义、标准方程、焦点、直径、离心率、轨道和应用等方面。
1.椭圆的定义椭圆可以定义为平面上到两个固定点(焦点)的距离之和等于常数的点的集合。
这两个固定点称为焦点,常数称为椭圆的离心率。
椭圆也可以视为一个平面上到定点的连线长度之和等于一定长度(主轴)的点的轨迹。
2.椭圆的标准方程以坐标原点为中心的椭圆的标准方程为x²/a² + y²/b² = 1,其中a和b 分别表示椭圆的长短半轴。
可以看出,a表示椭圆离心率对应的焦距长度,b表示椭圆的短半轴长度。
3.焦点和直径椭圆的焦点是椭圆的一个重要属性,它是椭圆离心率定义的核心。
可以通过标准方程中的离心率公式e = c/a(c为焦点到原点的距离),求得焦点的坐标表达式为(c, 0)和(-c, 0)。
椭圆的直径是通过椭圆中心并且同时与椭圆上两个点相交的线段。
对于以坐标原点为中心的椭圆,直径的长度为2a。
4.椭圆的离心率椭圆的离心率是描述椭圆形状的重要指标。
离心率的取值范围为0到1,离心率为0时表示圆形,离心率为1时表示扁平的线段。
椭圆的离心率定义为离心焦距和长半径之比,即e = c/a。
5.椭圆的轨迹椭圆的轨迹是指通过一定规则的运动得到的点所形成的图形。
在天体力学中,行星绕太阳运动的轨迹就是椭圆。
椭圆的轨迹具有许多独特的性质,例如对称性、曲率等。
6.椭圆的应用椭圆在现实生活中有许多重要的应用。
例如,在通信中,为了提高信号传输的质量和距离,卫星轨道通常选择为椭圆轨道。
此外,椭圆也被广泛应用于地理测量、天体力学、光学设计等领域。
总结:椭圆作为几何图形中的重要一员,具有许多独特的概念和性质。
通过本文的介绍,我们了解到椭圆的定义、标准方程、焦点、直径、离心率、轨迹和应用。
对于几何学的学习和实际应用,理解和掌握椭圆的基本概念与性质至关重要。
人教版高中数学课件:8.2椭圆的几何性质3

(c,0)
B2(0,-b)
1.习题8.3 第2题(3) (4)(5)第3题
秦皇岛市职业技术学校 李天乐
一、椭圆的范围
x a
2 2
y b
2 2
1( a b 0 )
x a
2 2
1,
y b
2 2
1
即
x a和 y b
y
B2
A1
F1
O
B1
F2
A2 X
说明:椭圆位于矩形之中。
二、椭圆的对称性
x a
2 2
y b
2 2
1( a b 0 )
y
椭圆关于x轴对称; 椭圆关于y轴对称; 椭圆关于原点对称; 中心:椭圆的对称中心叫做椭圆的中心. o x
四、椭圆的离Βιβλιοθήκη 率离心率:椭圆的焦距与长轴长的比: e y a 叫做椭圆的离心率。 [1]离心率的取值范围: 因为 a > c > 0,所以 0 e 1 o [2]离心率对椭圆形状的影响: 1)e 越接近 1,c 就越接近 a,从而 b就越小,椭圆就 越扁 . 2)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆 就 越圆 . 3)特例:e =0,则 a = b,则 c=0,两个焦点重合, 2 2 2 方程变为 x y a .
由题意,有 2c=8,c=4;2a=10,a=5.
x a
2 2
y b
2 2
1( a b 0 )
又
b2=a2-c2=25-16=9.
故所求方程为x2/25+y2/9=1.
(2)设焦点在y轴上,标准方程为
椭圆的几何性质一览表
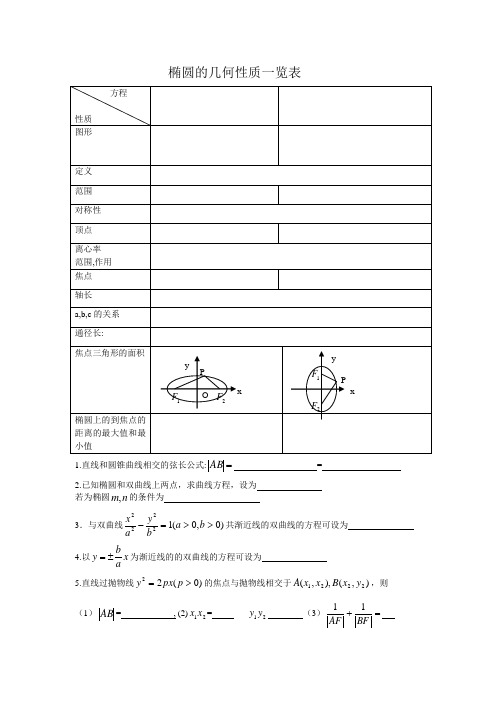
5.直线过抛物线 的焦点与抛物线相交于 ,则
(1) =,(2) = (3)
双曲线的几何性质一览表
方程
性质
图形
范围
对称性
顶点
离心率
对称性
焦点
轴长
的关系
通径长
焦点三角形的面积
渐进线方程
抛物线的几何性质一览表
方程
性质
图形
范围
对称性
顶点
离心率
对称性
焦点
准线方程
焦半径
焦半径的范围
椭圆的几何Leabharlann 质一览表方程性质图形
定义
范围
对称性
顶点
离心率
范围,作用
焦点
轴长
a,b,c的关系
通径长:
焦点三角形的面积
P
x
y
O
x
y
P
O
椭圆上的到焦点的距离的最大值和最小值
1.直线和圆锥曲线相交的弦长公式: =
2.已知椭圆和双曲线上两点,求曲线方程,设为
若为椭圆 的条件为
3.与双曲线 共渐近线的双曲线的方程可设为
椭圆几何性质4 胡红

(适用于任何曲线)
3、弦中点问题的两种处理方法: (1)联立方程组,消去一个未知数,利用韦达定理; (2)设两端点坐标,代入曲线方程相减可求出弦的斜率。
直线和椭圆相交有关弦的中点问题,常用设而不求的 思想方法.
例2.已知椭圆5x2+9y2=45,椭圆的右焦点为F, 判断点A(1,1)与椭圆的位置关系,并求以A为中 点椭圆的弦所在的直线方程.
解 : (2)5 12 9 12 45 A(1,1)在椭圆内。
设以A为中点的弦为MN 且M ( x1 , y1 ), N ( x2 , y2 ) x1 x2 2, y1 y2 2
椭圆几何性质4
பைடு நூலகம்
中点弦问题
知识点3:中点弦问题
例1 :已知椭圆 过点P(2,1)引一弦,使弦在这点被 平分,求此弦所在直线的方程. 解:
韦达定理→斜率 韦达定理法:利用韦达定理及中点坐标公式来构造
2
例 1.已知椭圆 过点P(2,1)引一弦,使弦在这点被 平分,求此弦所在直线的方程.
点 作差
点差法:利用端点在曲线上,坐标满足方程,作差构造 出中点坐标和斜率.
5 x12 9 y12 45 5 x2 2 9 y2 2 45
两式相减得: ( 5 x12 x2 2) ( 9 y12 y2 2) 0 y1 y2 5 5 x1 x2 kMN 9 x1 x2 9 y1 y2 5 以A为中点的弦为MN 方程为:y 1 ( x 1) 5 x 9 y 14 0 9
两式相减得:
b 2 ( x12 x2 2 ) a 2 ( y12 y12 ) 0
由b ( x x2 ) a ( y y ) 0
(整理版)椭圆的几何性质要点梳理

椭圆的几何性质要点梳理一、椭圆两个标准方程的几何性质:二、规律总结1.通过对椭圆的范围、对称性、特殊点〔顶点、焦点、中心〕、对称轴及其他特性的讨论,从整体上把握曲线的形状、大小和位置,进而掌握椭圆的性质。
学习过程中应注意:图形与性质对照,方程与性质对照,通过数形结合的方式牢固掌握椭圆的几何性质。
2 涉及直线与椭圆位置关系问题时,注意判别式及韦达定理的运用,特别是方程思想、整体思想在解题中的应用。
3.待定系数法是解决问题的一种重要方法,同时要注意方程思想、分类讨论思想在解题中的应用。
4.在由椭圆的标准方程写出椭圆的性质,如长轴长、短轴长、顶点坐标、焦点坐标等,要分清焦点在x 轴上还是在y 轴上,不要弄错。
三、范例点悟例1 椭圆()()2230x m y m m ++=>的离心率e =求m 的值及椭圆的长轴和短轴的长、焦点坐标、顶点坐标。
分析:解决此题的关键是确定m 的值,因此,应先将椭圆方程化为标准形式,用m 表示a 、b 、c,再由e =m 的值。
解析:椭圆方程可化为2213x y m mm +=+。
∵()2033m m m m m m +-=>++,∴3m m m >+,即22,,3ma mbc m ====+由e==1m =。
∴椭圆的标准方程为22114y x +=,∴11,,2a b c ===。
∴椭圆的长轴为2,短轴长为1;两焦点坐标分别为1F ⎛⎫ ⎪ ⎪⎝⎭,2F ⎫⎪⎪⎝⎭;四个顶点分别为()()1212111,0,1,0,0,,0,22A A B B ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭。
评注:解决有关椭圆问题,首先应弄清椭圆的类型,而椭圆的类型又决定于焦点的位置。
例2 求长轴长为20,离心率等于35的椭圆的标准方程。
分析:根据椭圆的几何性质确定椭圆的标准方程。
解析:由3220,5c a e a ===,∴2222210,6,12880a c b a c ===-=-=。
人教A版3.1.2椭圆的简单几何性质(第二定义、焦半径和三角型面积)课件

---椭圆第二定义,焦半径和三角形面积
复习:椭圆的简单几何性质
焦点位置 方程
图形 范围
x轴
x2 y2 a2 b2 1 (a b 0)
y B1 M
A1 F•1
O
F• 2
A2 x
B2
a x a, b y b
y轴
y2 x2 a2 b2 1 (a b 0)
x1
x2
6km 3k 2 1
,
x1x2
3(m2 3k 2
1) 1
.
AB
2
(1
k 2 )(x2
x1)2
12(k 2 1)(3k 2 1 m2 ) 3(k 2 1)(9k 2 1)
(3k 2 1)2
(3k 2 1)2
3
12k 2 9k 4 6k 2
1
3
9k 2
12
1 k2
6
(k
0) ≤ 3
12 23 6
(Ⅱ)设 A(x1,y1) , B(x2,y2 ) .
(1)当 AB⊥ x 轴时, AB 3 .
(2)当 AB 与 x 轴不垂直时,设直线 AB 的方程为 y kx m .
由已知 m 3 ,得 m2 3 (k 2 1) .
1 k2 2
4
把 y kx m 代入椭圆方程,整理得 (3k 2 1)x2 6kmx 3m2 3 0 ,
x2 36
y2 20
1上在第一象限的点,且MF1F2
为等腰三角形,则M的坐标为 _(_3_, _1_5_)___ .
y
M
析 : MF1 F1F2 8
由焦半径的公式得 MF1
a exM
6
人教版高中数学必修第二册椭圆的简单几何性质

椭圆的简单几何性质课堂设计理念:授人于鱼不如授人于渔。
通过创设符合学生认知规律的问题情景,挖掘学生内在的研究问题的巨大潜能,使学生在做中学,学中思,亲身体会创造过程,充分展示思维差异,培养学生的自主探究能力,逻辑推理能力,提高学生的思维层次,掌握获取知识的方法和途径,真正体现学生学习知识过程中的主体地位。
教学目标:(1)知识与技能:掌握椭圆的范围、对称性、顶点,掌握ca,,ba,,几何意义以及cb的相互关系,初步学习利用方程研究曲线性质的方法。
(2)过程与方法:利用曲线的方程来研究曲线性质的方法是学习解析几何以来的第一次,通过初步尝试,使学生经历知识产生与形成的过程,不仅注意对研究结果的掌握和应用,更重视对研究方法的思想渗透及分析问题和解决问题能力的培养;以自主探究为主,通过体验数学发现和创造的历程,培养学生观察、分析、逻辑推理、理性思维的能力。
(3)情感、态度与价值观:通过自主探究、交流合作使学生亲身体验研究的艰辛,从中体味合作与成功的快乐,由此激发其更加积极主动的学习精神和探索勇气;通过多媒体展示,让学生体会椭圆方程结构的和谐美和椭圆曲线的对称美,培养学生的审美习惯和良好的思维品质。
教学重点、难点:重点:从知识上来讲,要掌握如何利用椭圆标准方程的结构特征研究椭圆的几何性质;从学生的体验来说,需要关注学生在探究椭圆性质的过程中思维的过程展现,如思维角度和思维方法。
难点:椭圆几何性质的形成过程,即如何从椭圆标准方程的结构特征中抽象出椭圆的几何性质。
通过本节课的教学力求使一个平淡的性质陈述过程成为一个生动而有价值的学生主动交流合作、大胆探究的过程应是教学的难点。
教学策略与学法指导:教学策略:本节课采用创设问题情景——学生自主探究——师生共同辨析研讨——归纳总结组成的“四环节”探究式学习方式,并在教学过程中根据实际情况及时地调整教学方案。
学法指导:通过创设问题情景、学生自主探究、展示学生的研究过程来激励学生的探索勇气。
高中数学第二册(上)椭圆的简单几何性质(3)

椭圆的简单几何性质(3)教学目标:能推导并掌握椭圆的焦半径公式,能利用焦半径公式解决与焦点有关的问题。
教学重点与难点:焦半径公式。
教学过程:一、知识点:若椭圆)0(12222>>=+b a by a x 上任意一点),(00y x P ,焦半径01ex a r +=,02ex a r -=;若椭圆)0(12222>>=+b a b x a y 上任意一点),(00y x P ,焦半径01ey a r +=, 02ey a r -=;其中1r 表示左(下)焦半径,2r 表示右(上)焦半径,且1r +2r a 2=。
二、例题分析:例1.①点P 在椭圆192522=+y x ,它到左焦点的距离是它到右焦点距离的两倍,则点P 的横坐标是 。
②椭圆14922=+y x 的焦点为,点P 为其上的动点,当21PF F ∠为钝角时,则点P 横坐标的取值范围是 。
③已知)0(12222>>=+b a b y a x 上一点P (3,4),21,F F 为椭圆上两焦点,且21PF PF ⊥,则2a 。
例2.设),(11y x A 是椭圆2222=+y x 上一点,过A 点作一条斜率为112y x -的直线l ,d 为原点到直线l 的距离,1r ,2r 分别为点A 到两焦点的距离。
求证:21r r d 为定值。
例3.已知椭圆的焦点是)0,4(),0,4(21F F -,过点2F 并垂直于X 轴的直线与椭圆的一个交点为B ,且10||||21=+B F B F ,椭圆上不同的两点),(),,(2211y x C y x A 满足条件:||2A F 、||2B F 、||2C F 成等差数列。
(1)求该椭圆方程;(2)求弦AC 的中点的横坐标;(3)设弦AC 的垂直平分线的方程为m kx y +=,求m 的取值范围。
(02年高考) 例4.已知21,F F 是椭圆13422=+y x 的两焦点,能否在椭圆上求一点M (M 在Y 轴的左侧),使M 到左准线的距离|MQ|是||1MF 与||2MF 的比例中项,若能,求出该点坐标,若不能,请说明理由。
人教版--2.2.2椭圆的几何性质(教案1)

2.2.2椭圆的几何性质(1)浙江省岱山中学 姜海斌 2009年11月一、教学目标知识目标:通过椭圆标准方程的讨论,使学生掌握椭圆的几何性质(范围、对称性、顶点、离心率),并能正确画出椭圆的图形。
能说明离心率的大小对椭圆形状的影响能力目标:通过对椭圆的几何性质的教学,掌握利用方程研究曲线的基本方法,加深对曲线与方程关系的理解,培养学生分析问题和解决实际问题的能力.德育目标:使学生掌握利用方程研究曲线性质的基本方法,加深对直角坐标系中曲线与方程的关系概念的理解,综合运用方程(组)理论,提高代数运算能力,提高综合分析能力,揭示透过现象看本质的辩证唯物主义观念。
美育渗透点用美学的眼光审视数学,数学中处处闪耀着美的光彩,椭圆代数方程闪耀着数学的简约美、方程形式的对称性显现数学的对称、均衡美.用数学的简约美去研究曲线几何性质的形象美,是学数学、用数学的重要目标。
二、教学重、难点重点是椭圆的几何性质――范围、对称性、顶点、离心率、准线方程;根据方程研究曲线的几何性质的思路与方法;椭圆的几种画法。
难点是椭圆的几何性质的推导,数形结合思想的贯彻,运用曲线方程研究几何性质。
三.教学过程: (一)复习提问1.椭圆的定义是什么? 2.椭圆的标准方程是什么? 学生口述,教师板书. (二)、探索研究⑴研究曲线几何特征有何几何意义?研究曲线的几何性质可以从整体上把握曲线的形状、大小和位置。
(2)研究曲线的几何特征呢?通过对曲线方程的讨论来研究曲线的几何特征。
(3)用椭圆的标准方程12222=+by a x (0>>b a 来研究椭圆的性质(1)范围:从标准方程得出122≤a x ,122≤by ,即有a x a ≤≤-,b y b ≤≤-,可知椭圆落在b y a x ±=±=,组成的矩形中.(2)对称性:把方程中的x 换成x -方程不变,图象关于y 轴对称.y 换成y -方程不变,图象关于x 轴对称.把y x ,同时换成y x --,方程也不变,图象关于原点对称.如果曲线具有关于x 轴对称,关于y 轴对称和关于原点对称中的任意两种,则它一定具有第三种对称原点叫椭圆的对称中心,简称中心.x 轴、y 轴叫椭圆的对称轴.从椭圆的方程中直接可以看出它的范围,对称的截距(3)顶点:椭圆和对称轴的交点叫做椭圆的顶点在椭圆12222=+b y a x 的方程里,令0=y 得a x ±=,因此椭圆和x 轴有两个交点)0,(),0,(2a A a A -,它们是椭圆12222=+by a x 的顶点令0=x ,得b y ±=,因此椭圆和y 轴有两个交),0(),,0(2b B b B -,它们也是椭圆12222=+by a x 的顶点 因此椭圆共有四个顶点: )0,(),0,(2a A a A -,,0(),,0(2b B b B -加两焦点)0,(),0,(21c F c F -共有六个特殊点.21A A 叫椭圆的长轴,21B B 叫椭圆的短轴.长分别为b a 2,2b a ,分别为椭圆的长半轴长和短半轴长.椭圆的顶点即为椭圆与对称轴的交点.至此我们从椭圆的方程中直接可以看出它的范围, 对称性, 顶点.因而只需少量描点就可以较正确的作图了. (4)离心率:椭圆的焦距与长轴的比ce a=叫椭圆的离心率. ∵0a c >>,∴01e <<,且e 越接近1,c 就越接近a ,从而b 就越小,对应的椭圆越扁;反之,e 越接近于0,c 就越接近于0,从而b 越接近于a ,这时椭圆越接近于圆。
31113椭圆的简单的几何性质

大白高中高二数学学练稿 主备:李海红 审核: 数学组 类型: 新授课 日期:31113编号:31113积极思考造成积极人生,消极思考造成消极人生。
2.2.2椭圆的简单的几何性质【学习目标】1.掌握椭圆的简单几何性质; 2.掌握标准方程中a,b 及c,e 的几何意义,a,b ,c,e 之间相互关系;3.能根据已知条件求椭圆的标准方程。
【要点解析】和直线 所围成的矩形里2. a 是 ,b 是 。
3.e 越接近 时椭圆越扁;当e 越接近时椭圆越圆。
【典型应用】例1:求椭圆16x 2+25y 2=400的长轴和短轴的长、离心率、焦点和顶点的坐标.跟踪训练1:已知椭圆方程为6x²+y²=6则它的长轴长是: 短轴长是: 焦距是: . 离心率等于: 焦点坐标是: 顶点坐标是:例2: 长轴在x 轴上,长轴的长等于12,离心率等于23,求椭圆的标准方程.跟踪训练2:椭圆过点(3,0),离心率e =63,求椭圆的标准方程.例3:如图,A 、B 、C 分别为椭圆22221x y a b += (0)a b >>的顶点与焦点,若∠ABC =90°,求该椭圆的离心率。
【自我反馈】1.椭圆25x 2+9y 2=225的长轴长、短轴长、离心率依次是( )A .5、3、0.8B .10、6、0.8C .5、3、0.6D .10、6、0.62.已知椭圆的中心在坐标原点,焦点在x 轴上,且长轴长为12,离心率为13,则椭圆的方程是 ( ) A.221144128x y += B. 2213620x y += C. 2213236x y += D. 2213632x y += 3.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是 ( )A.45B.35C.25D.15 小结:作业:质量监测第29、30页的1—5题必做;第29页第6题、30页第6题选做。
新课程新教材高中数学选择性必修3:椭圆的简单几何性质(第二课时)

数学思想方法:
消元思想
从特殊到一般思想
数形结合思想
大?又在何位置时,∠1 2 最小?
2
探究2:已知椭圆: 2
2
+ 2
= 1( > > 0),1 、2 分别为椭圆的
左、右顶点. 为椭圆上一动点. 探究:当在何位置时,∠1 2 最
大?又在何位置时,∠1 2 最小?
2
且-a≤y≤a
_____________________
_____________________
焦点的位置
顶点
焦点在 x 轴上
焦点在 y 轴上
A1(-a,0),A2(a,0), _____________________
A1(0,-a),A2(0,a),
_____________________
动点(, )与定点(4,0)的距离和到定直线: =
4
常数 ,求动点的轨迹.
5
25
的距离的比是
4
2
探究1:已知椭圆: 2
2
2
+ = 1( > > 0),1 、2 分别为椭圆的
左、右焦点. 为椭圆上一动点. 探究:当在何位置时,∠1 2 最
3.1.2椭圆的简单几何性质
(第二课时)
椭圆的简单几何性质
焦点的位置
焦点在 x 轴上
焦点在 y 轴上
图形
标准方程
范围
2
2
y2 x2
2+ 2=1(a>b>0)
a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x2 y2 1 练习2.无论k为何值,直线y=kx+2和曲线 9 4 交点情况满足( D )
6 6 k< 时没有交点 3 3
A.没有公共点
C.两个公共点
B.一个公共点
D.有公共点
x2 y2 1 , 直线 4 x 5 y 40 0 , 椭圆 例 2: 已知椭圆 25 9 上是否存在一点,到直线 l 的距离最小?最小距离是多少 ? y
椭圆的简单几何性质3
直线与椭圆的位置关系
种类:
相离(没有交点) 相切(一个交点)
相交(二个交点)
直线与椭圆的位置关系的判定
代数方法
Ax By C 0 2 由方程组 x y2 2 2 1 b a
mx 2 nx p 0(m 0)
△=n2 4mp
右焦点F ( 3,0).
y x 3 2 x 2 y 1 4
直线l方程为: y x 3. 消y得: 5x 8 3x 8 0
2
设A( x1, y1 ), B( x2 , y2 )
8 3 8 x1 x2 , x1 x2 5 5
AB 1 k x1 x2 1 k
o
x
.
知识点2:弦长公式
可推广到任意二次曲线
设直线与椭圆交于A(x1,y1),B(x2,y2)两点,直线P1P2的斜率为k.
同理可得
当k=0时,直线平行于x轴所以
当直线斜率不存在时,直线平行于 y 轴所
例3:已知斜率为1的直线L过椭圆 的右焦点,交椭圆于A,B两点,求弦AB之长.
解 :由椭圆方程知 : a2 4, b2 1, c2 3.
解:设直线m平行于l,
则l可写成: 4x 5 y k 0
4 x 5 y k 0 2 2 2 2 消去y,得25x 8kx k - 225 0 由方程组 x y 1 25 9 由 0,得64k 2 - 4 25 (k 2 - 225) 0
题型一:直线与椭圆的位置关系
例1:直线y=x+1与椭圆
x2 y 2 1 m 5
恒有公共点,
求m的取值范围。
变式练习:y=kx+1与椭圆 m的范围( )。 A、(0,1) B、(0,5 ) C、[ 1,5)∪(5,+ ∞ ) D、(1,+ ∞ )
x2 y2 1 恰有公共点,则 5 m
练习1.K为何值时,直线y=kx+2和曲线2x2+3y2=6有两 个公共点?有一个公共点?没有公共点?
2 2
8 ( x1 x2 ) 4 x1 x2 5
2
x y 例 4:已知点 F1 、F2 分别是椭圆 1 的左、右 2 1 焦点,过 F2 作倾斜角为 的直线,求 △F1 AB 的面积. 4 x2
解:∵椭圆
2
2
∴直线 AB 的方程为 y x 1 设 A( x1 , y1 ), B( x2 , y2 )
△ 0
方程组有两解 方程组有一解 方程组无解
两个交点 一个交点 无交点
相交 相切 相离
△=0 △ 0
知识点1.直线与椭圆的位置关系
1.位置关系:相交、相切、相离 2.判别方法(代数法) 联立直线与椭圆的方程 消元得到二元一次方程组 (1)△>0直线与椭圆相交有两个公共点; (2)△=0 直线与椭圆相切有且只有一个公共点; (3)△<0 直线与椭圆相离无公共点. 3.几何法 在平面直角坐标系中画出直线和椭圆,从而观察 直线与椭圆的位置关系。
y x 1 由 x2 消去 y 并化简整理得 2 y 1 2
2
2
y 2 1 的两个焦点坐标 F1 (1, 0), F2 (1, 0)
3x 4x 0
4 2 2 ∴ AB ( x1 x2 )2 ( y1 y2 )2 2( x1 x2 )2 2 = ( x x ) 4 x x 2 1 2 1 3
4 ∴ x1 x2 , x1 x2 0 3
0 ( 1) 1 2
∵点 F1 到直线 AB 的距离 d
∴ S F1 AB
= 2
1 1 4 4 4 d AB = 2 2= . 答: △F1 AB 的面积等于 2 2 3 3 3
解得k1 =25,k 2 =-25
o
x
由图可知k 25.
直线m为: 4 x 5 y 25 0
直线m与椭圆的交点到直线l的距离最近。 15 且d 41 42 52 41 40 25
y
思考:最大的距离是多少?
dmax 65 41 42 52 41 40 25
