岩土力学课件:本构与强度理论
合集下载
岩体本构关系与强度理论

岩体力学
Rockmass Mechanics
第七章 岩体本构关系与强度理论
概述 岩石的本构关系 岩石强度理论 岩体变形及本构关系 岩体破坏机制及破坏判据
概述
--岩体的力学性质表现为弹性、塑性和粘性或三者之间的组合,如
粘弹性、弹粘性、弹塑性、弹塑粘性等。
如何求解岩体的基本力学问题呢?
3
(12c)1
1 3c
3(12)t
那么最大正应变强度判据可写成:
f C tg
1 1 3 c
当岩石应力条件满足以上判据时,岩石发生张破裂。取其中最小的
比较。 该强度理论适用于无围压和低围压及脆性岩石。
0
0
2. (二次)抛物线型 岩性较坚硬至较弱的岩石,
如泥灰岩、泥岩、砂岩、泥页 岩、页岩等岩石的强度包络线 近似于二次抛物线。
3.双曲线型 岩性坚硬、较坚硬的岩石,
如砂岩、灰岩、花岗岩等,其强 度包络线近似于双曲线。
二次抛物线型莫尔强度包络线 双曲线型莫尔强度包络线
0
说明:莫尔-库仑判据(强度理论)实质上是一种剪应力强度判据(理 论),既适用于塑性岩石,又适用于脆性岩石的剪切破坏,应用很广。
那么,岩石承受低于瞬时强度的荷载作用,是否会破坏?
只要收到长期荷载作用下,由于流变作用,岩石完全可能发生破坏。 而且岩石强度随外荷载作用时间的延长而降低,通常将时间t→∞的强度 (最低值)称为岩石的长期强度。
对大多数岩石,长期强度/瞬时强度(S∞/S0)一般为0.4~0.8,软的 和中等坚固岩石为0.4~0.6,坚固岩石为0.7~0.8。
2.莫尔-库仑强度理论
(Coulomb-Mohr Strength theory)
Rockmass Mechanics
第七章 岩体本构关系与强度理论
概述 岩石的本构关系 岩石强度理论 岩体变形及本构关系 岩体破坏机制及破坏判据
概述
--岩体的力学性质表现为弹性、塑性和粘性或三者之间的组合,如
粘弹性、弹粘性、弹塑性、弹塑粘性等。
如何求解岩体的基本力学问题呢?
3
(12c)1
1 3c
3(12)t
那么最大正应变强度判据可写成:
f C tg
1 1 3 c
当岩石应力条件满足以上判据时,岩石发生张破裂。取其中最小的
比较。 该强度理论适用于无围压和低围压及脆性岩石。
0
0
2. (二次)抛物线型 岩性较坚硬至较弱的岩石,
如泥灰岩、泥岩、砂岩、泥页 岩、页岩等岩石的强度包络线 近似于二次抛物线。
3.双曲线型 岩性坚硬、较坚硬的岩石,
如砂岩、灰岩、花岗岩等,其强 度包络线近似于双曲线。
二次抛物线型莫尔强度包络线 双曲线型莫尔强度包络线
0
说明:莫尔-库仑判据(强度理论)实质上是一种剪应力强度判据(理 论),既适用于塑性岩石,又适用于脆性岩石的剪切破坏,应用很广。
那么,岩石承受低于瞬时强度的荷载作用,是否会破坏?
只要收到长期荷载作用下,由于流变作用,岩石完全可能发生破坏。 而且岩石强度随外荷载作用时间的延长而降低,通常将时间t→∞的强度 (最低值)称为岩石的长期强度。
对大多数岩石,长期强度/瞬时强度(S∞/S0)一般为0.4~0.8,软的 和中等坚固岩石为0.4~0.6,坚固岩石为0.7~0.8。
2.莫尔-库仑强度理论
(Coulomb-Mohr Strength theory)
04岩石的本构关系和强度准则1

微分单元体的变形
15
4.2 应变及应变状态分析
微分单元体的变形
16
4.2 应变及应变状态分析
微分单元体的变形
正应变与位移分量之间的关系
显然微分线段伸长,则正应变ε x,ε y,ε z 大于零;反之则小于零。
17
4.2 应变及应变状态分析
微分单元体的变形
剪应变与位移分量之间的关系
xy
19
4.3 岩石的应力应变关系
求解岩石力学问题是从岩石的单元微分体出发,研究微分 体的力的平衡关系(平衡方程)、位移与应变的关系(几何方程) 以及应力与应变的关系(物理方程或本构方程),得到相应的基 本方程,然后结合岩石的边界条件,联立、积分求解这些方程, 从而求得整个岩石内部的应力场和位移场。 平衡方程和几何方程与岩石材料的性质无关,只有本构关 系反映岩石材料的性质。所谓岩石本构关系是指岩石的应力或 应力速率与其应变或应变速率的关系。在只考虑静力问题情况 下,本构关系就是指应力与应变,或者应力增量与应变增量之 间的关系。
11 12 13 11 12 13 22 23 12 22 23 21 31 32 33 13 23 33
7
4.1 应力及应力状态分析
二、一点应力状态的张量表达
20
4.3 岩石的应力应变关系
岩石在弹性阶段的本构关系称为岩石弹性本构关系,岩 石在塑性阶段的本构关系称为岩石塑性本构关系。岩石弹性
本构关系和塑性本构关系通称为弹塑性本构关系。弹性本构 关系按是否为线性又分为线弹性本构关系与非线弹性本构关 系。弹塑性本构关系按物质是否为各向同性又分为各向同性 本构关系和非各向同性本构关系。 如果外界条件不变,岩石的应力或应变随时间而变化, 则称岩石具有流变性。岩石产生流变时的本构关系称为岩石 的流变本构关系。
15
4.2 应变及应变状态分析
微分单元体的变形
16
4.2 应变及应变状态分析
微分单元体的变形
正应变与位移分量之间的关系
显然微分线段伸长,则正应变ε x,ε y,ε z 大于零;反之则小于零。
17
4.2 应变及应变状态分析
微分单元体的变形
剪应变与位移分量之间的关系
xy
19
4.3 岩石的应力应变关系
求解岩石力学问题是从岩石的单元微分体出发,研究微分 体的力的平衡关系(平衡方程)、位移与应变的关系(几何方程) 以及应力与应变的关系(物理方程或本构方程),得到相应的基 本方程,然后结合岩石的边界条件,联立、积分求解这些方程, 从而求得整个岩石内部的应力场和位移场。 平衡方程和几何方程与岩石材料的性质无关,只有本构关 系反映岩石材料的性质。所谓岩石本构关系是指岩石的应力或 应力速率与其应变或应变速率的关系。在只考虑静力问题情况 下,本构关系就是指应力与应变,或者应力增量与应变增量之 间的关系。
11 12 13 11 12 13 22 23 12 22 23 21 31 32 33 13 23 33
7
4.1 应力及应力状态分析
二、一点应力状态的张量表达
20
4.3 岩石的应力应变关系
岩石在弹性阶段的本构关系称为岩石弹性本构关系,岩 石在塑性阶段的本构关系称为岩石塑性本构关系。岩石弹性
本构关系和塑性本构关系通称为弹塑性本构关系。弹性本构 关系按是否为线性又分为线弹性本构关系与非线弹性本构关 系。弹塑性本构关系按物质是否为各向同性又分为各向同性 本构关系和非各向同性本构关系。 如果外界条件不变,岩石的应力或应变随时间而变化, 则称岩石具有流变性。岩石产生流变时的本构关系称为岩石 的流变本构关系。
岩体力学PPT-3岩石的强度理论

3.岩石的强度理论 岩石的强度理论
主讲: 主讲: 林锋 • • • • • • 3.1 概述 3.2 最大正应变理论 3.3 摩尔强度理论 3.4 霍克 布朗岩石破坏经验判据 霍克—布朗岩石破坏经验判据 3.5 考虑中间主应力的强度理论简介 3.6 Griffith强度理论 强度理论
3 岩石的强度理论
3 岩石的强度理论
3.1 概述
破坏判据:表征岩石破坏条件的函数( 破坏判据:表征岩石破坏条件的函数(应力及应变函 破坏条件的函数 ),也称为破坏判据或强度准则。 也称为破坏判据 数),也称为破坏判据或强度准则。破坏判据应反映岩石 的破坏机理。 的破坏机理。 强度理论:所有研究岩石破坏的原因 过程及条件的理 原因、 强度理论:所有研究岩石破坏的原因、过程及条件的理 称为强度理论。 论,称为强度理论。 岩石的破坏机理很复杂,受多种因素影响。 岩石的破坏机理很复杂,受多种因素影响。 目前建立了多种强度理论,其中, 目前建立了多种强度理论,其中,岩石力学中应用较多 的强度理论有: 的强度理论有: ,(2)莫尔强度理论,( ,(2) (1)最大正应变理论,( )莫尔强度理论,( )格 )最大正应变理论,( 里菲斯强度理论,( ,(4)应变能理论等 里菲斯强度理论,( )应变能理论等。 实际上,各种强度理论都有一定的使用范围 使用范围。 实际上,各种强度理论都有一定的使用范围。
3.3 摩尔 摩尔(Mohr)强度理论 强度理论
(一)直线型 直线型摩尔—库仑强度线还有如下表达形式 库仑强度线还有如下表达形式: 直线型摩尔 库仑强度线还有如下表达形式:
σ1 − σ3 sin ϕ = σ1 + σ3 + 2c⋅ ctgϕ
σ1 = σ3tg (45 + ) + 2c ⋅ tg(45 + )
主讲: 主讲: 林锋 • • • • • • 3.1 概述 3.2 最大正应变理论 3.3 摩尔强度理论 3.4 霍克 布朗岩石破坏经验判据 霍克—布朗岩石破坏经验判据 3.5 考虑中间主应力的强度理论简介 3.6 Griffith强度理论 强度理论
3 岩石的强度理论
3 岩石的强度理论
3.1 概述
破坏判据:表征岩石破坏条件的函数( 破坏判据:表征岩石破坏条件的函数(应力及应变函 破坏条件的函数 ),也称为破坏判据或强度准则。 也称为破坏判据 数),也称为破坏判据或强度准则。破坏判据应反映岩石 的破坏机理。 的破坏机理。 强度理论:所有研究岩石破坏的原因 过程及条件的理 原因、 强度理论:所有研究岩石破坏的原因、过程及条件的理 称为强度理论。 论,称为强度理论。 岩石的破坏机理很复杂,受多种因素影响。 岩石的破坏机理很复杂,受多种因素影响。 目前建立了多种强度理论,其中, 目前建立了多种强度理论,其中,岩石力学中应用较多 的强度理论有: 的强度理论有: ,(2)莫尔强度理论,( ,(2) (1)最大正应变理论,( )莫尔强度理论,( )格 )最大正应变理论,( 里菲斯强度理论,( ,(4)应变能理论等 里菲斯强度理论,( )应变能理论等。 实际上,各种强度理论都有一定的使用范围 使用范围。 实际上,各种强度理论都有一定的使用范围。
3.3 摩尔 摩尔(Mohr)强度理论 强度理论
(一)直线型 直线型摩尔—库仑强度线还有如下表达形式 库仑强度线还有如下表达形式: 直线型摩尔 库仑强度线还有如下表达形式:
σ1 − σ3 sin ϕ = σ1 + σ3 + 2c⋅ ctgϕ
σ1 = σ3tg (45 + ) + 2c ⋅ tg(45 + )
岩石力学与工程岩石本构关系与强度理论

其蠕变曲线和弹性后效曲线,如图3-15所示。
蠕变曲线
0 k2
0 k1
弹性后效
0
t1
t
图3-15 广义开尔文体蠕变曲线和卸载曲线
2020/11/3
34
3.4.4.5 饱依丁-汤姆逊体(PTh:H/M)
一、力学模型 k1,1
k2 , 2
图3-16 饱依丁-汤姆逊体力学模型
二、本构方程
本模型是由马克斯威尔体与虎克体并联而成,由并 联规则:
2020/11/3
19
3.4.4 组合流变模型
三种基本元件进行组合时应力、应变的计算规则:
1.串联组合体中各元件的应力相等;应变等于各元件应 变之和。 2.并联组合体中各元件的应变相等;应力等于各元件应 力之和。
5.4.4.1 圣维南体(St.V:H-C)
一、力学模型
图3-5 圣维南体力学模型
2020/11/3
y
x
21
xy E xy
2020/11/3
4
4.边界条件
(1)位移边界条件
us us,vs vs
(2)应力边界条件
l x m yx s f x s
m y
l xy
s
f y s
(3)混合边界条件
(在 su上)
(在 s 上)
2020/11/3
5
3.4 岩石流变理论
3.4.1概念
四、卸载方程
0
k
kt
1 e
在t t1 时卸载,即 0,代入本构方程:
k 0
2020/11/3
28
解上述微分方程可得:
kt
A1e
当t t1 时, 1 ,结合蠕变方程,可得卸载方程 :
岩体本构关系与强度理论

对莫尔强度理论的评价:
优点:①适用于塑性岩石,也适用于脆性岩石的剪切破坏; ②较好解释了岩石抗拉强度远远低于抗压强度特征; ③解释了三向等拉时破坏,三向等压时不破坏现象; ④简单、方便:同时考虑拉、压、剪,可判断破坏方向. 不足:①忽视了σ2 的作用,误差:±10%; ②没有考虑结构面的影响; ③不适用于拉断破坏; ④不适用于膨胀、蠕变破坏。
判据的表达式 剪应力表达式:
4 ) t( t
2
主应力表达式:
2 ( ) 1 3 8 t 1 3 3 t
3 0 1 3 3 0 1 3
由格里菲斯判据得
1.当σ3=0时,σ1=σc=8σt,即 c t =8,与库仑-纳维尔判据接近。 2. 适用脆性岩石拉破坏。 修正的格里菲斯判据(考虑摩擦效应f,C)
b.最大剪应力理论破坏面上剪应力最大; 而岩石破坏面上剪应力不是最大。
④歪形能理论
只与σ1 、σ2 和σ3三者之间的差的绝对值有关;
而与应力大小无关,这与岩石破坏现象不符。
1 2 2 2 [ ( ) ( ) ( )] 1 2 2 3 3 1 2
古典强度理论与岩石强度表现不符:
①最大拉应力理论没有考虑σ
2
和σ
3
的影响。
②最大伸长线应变理论虽考虑σ2 和σ3 的影响,但多向拉 比单向拉安全,与事实矛盾。
③最大剪应力理论与岩石试验结果不符
σ1-σ3≤[σ]
a.最大剪应力理论破坏面与σ1 的夹角为45°;
而岩石破坏面与σ1 的夹角为45°-φ/2。
第七章 岩体本构关系与强度理论
§ 7.1 概述 § 7.2 岩石的本构关系
岩石的本构关系和强度(公式)
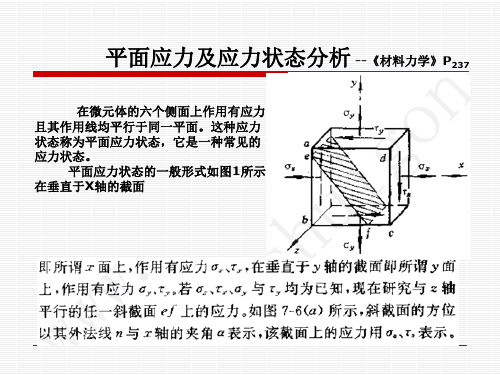
2
平面应力及应力状态分析
计算岩石的抗压强度
ctΒιβλιοθήκη 1 sin o 2C cos c 2C 2Ctg 45 1 sin 2 1 sin
抗拉强度
2C cos Rt 1 sin
内聚力
C
C
t c
2
2
1 sin 2 1 sin 2
1 tg 1 tg 2 2 1 3 1 tg 1 tg 2 2
2
0 0 1 3 tg 45 2C tg 45 2 2
1 3
2
1 3
2
sin
1 1 1 1 n 1 3 1 3 sin 1 3 1 3 cos 2 2 2 2 2 1 1 f 1 3 cos 1 3 sin 2 2 2
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
O1
1 3 / 2 sin 1 3 / 2 c ctg
平面应力及应力状态分析
莫尔-库伦破坏准则:
1
3 / 2 sin 3 / 2 c ctg
平面应力及应力状态分析
计算岩石的抗压强度
ctΒιβλιοθήκη 1 sin o 2C cos c 2C 2Ctg 45 1 sin 2 1 sin
抗拉强度
2C cos Rt 1 sin
内聚力
C
C
t c
2
2
1 sin 2 1 sin 2
1 tg 1 tg 2 2 1 3 1 tg 1 tg 2 2
2
0 0 1 3 tg 45 2C tg 45 2 2
1 3
2
1 3
2
sin
1 1 1 1 n 1 3 1 3 sin 1 3 1 3 cos 2 2 2 2 2 1 1 f 1 3 cos 1 3 sin 2 2 2
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
极值应力与主应力
237
平面应力及应力状态分析 --《材料力学》P
O1
1 3 / 2 sin 1 3 / 2 c ctg
平面应力及应力状态分析
莫尔-库伦破坏准则:
1
3 / 2 sin 3 / 2 c ctg
第7章岩体本构关系与强度理论

σ σc
σ
利用图7-10中的关系,有:
σ3
1 2
(1 3)
1 2
(1
3)
ctg 2
sin 2
1.双向压7 缩应4力2圆,2.双向拉压应力圆,
3..双向拉伸应力圆 图7-10 二次抛物型强度包络线
其中:
n( t )
1 3 2
sin 2
(
1 3 )2 2
2
(
1
3
)
2
规定:
1、σ1为最大主应力 、σ2 为中间主应力、 σ3 为最小主应力 ;
2、压应力为正,拉应力为负,剪应力以逆时 针为正。位移与应变的规定也一样。
二、 岩石弹性本构关系 1.平面弹性本构关系
据广义虎克定理有:
成E/(1- μ 2) ,μ换成μ/(1- μ)。
2. 空间问题弹性本构方程
x
1 E
x
( y
z )
y
1 E
y
( z
x )
z
1 E
z
( x
y )
yz
2(1 E
) yz , zx
1
1 f f2
2
f
f
)
σ1
1 tan2 c
1 3tg 2 (45 / 2) 2ctg(45 / 2)
σc
arc( tan2 θ)
第四章-岩石本构关系与强度理论

•
0
0t + 0
设初始条件 t=0
=
0
K1
+0=
0
K1
0 =
0
K1
4.4 岩石流变理论
4.4.2 流变模型理论
组合模型——马克斯威尔(Maxwell)体
蠕变方程:
=
1
2
0t +
0 =
0
K1
0
K1
蠕变曲线
0
o
等速蠕变,且不稳定
t
(a)蠕变曲线
4.4 岩石流变理论
是弹性变形后的一个阶段,材料进入塑性的特征是当荷
载卸载以后存在不可恢复的永久变形。
(1)屈服条件:材料最先达到塑性状态的应力条件。
(2)加-卸载准则(塑性发展或退化):材料进入塑性状态
以后继续塑性变形或回到弹性状态的准则。
(3)本构方程:材料在塑性阶段的应力应变关系或应力增
量与应变增量间的关系。
1
=
+
K1
2
= 0e
−
K1
2
0
t
o
t
(b)松弛曲线
4.4 岩石流变理论
4.4.2 流变模型理论
组合模型——马克斯威尔(Maxwell)体
瞬变应变量
描述岩石的特点
具有瞬变性
有不稳定的蠕变
有松弛
有残余(永久)变形
0 =
无弹性后效
0
0
K1
o
0
=
1
+ t
——岩石的蠕变特性对于岩石工程稳定意义重大,重点
0
0t + 0
设初始条件 t=0
=
0
K1
+0=
0
K1
0 =
0
K1
4.4 岩石流变理论
4.4.2 流变模型理论
组合模型——马克斯威尔(Maxwell)体
蠕变方程:
=
1
2
0t +
0 =
0
K1
0
K1
蠕变曲线
0
o
等速蠕变,且不稳定
t
(a)蠕变曲线
4.4 岩石流变理论
是弹性变形后的一个阶段,材料进入塑性的特征是当荷
载卸载以后存在不可恢复的永久变形。
(1)屈服条件:材料最先达到塑性状态的应力条件。
(2)加-卸载准则(塑性发展或退化):材料进入塑性状态
以后继续塑性变形或回到弹性状态的准则。
(3)本构方程:材料在塑性阶段的应力应变关系或应力增
量与应变增量间的关系。
1
=
+
K1
2
= 0e
−
K1
2
0
t
o
t
(b)松弛曲线
4.4 岩石流变理论
4.4.2 流变模型理论
组合模型——马克斯威尔(Maxwell)体
瞬变应变量
描述岩石的特点
具有瞬变性
有不稳定的蠕变
有松弛
有残余(永久)变形
0 =
无弹性后效
0
0
K1
o
0
=
1
+ t
——岩石的蠕变特性对于岩石工程稳定意义重大,重点
第七章 岩体本构关系与强度理论

14
最易扩展的裂纹端部附近的最大切向拉应力
第 七 章 岩 石 的 破 坏 判 据
( 1 3 ) 2 b m 4( 1 3 )
用单轴拉伸破坏时的抗拉强度来表示临界值
( 1 3 ) 2 8 t 1 3
1 3 1 2( 1 3 )
σb:椭圆周边切向应力; m=b/a,a为椭圆长半轴,b为椭圆短半轴; α:椭圆偏心角。
11
假定: (1)岩体内裂纹形状是一个很扁平的椭圆; (2)岩石性质的局部变化忽略不计; (3)岩体内裂纹与裂纹之间相互不发生影响; (4)椭圆形裂纹周围的应力系统作为平面问题处理。
裂纹尖端附近,α→0,故sinα→α,cosα→1
12
2、强度准则 (1)以σy 、τxy表示的强度准则
第 七 章 岩 石 的 破 坏 判 据
当单向拉伸破坏时,τxy=0,σy=σt,代入得
b m t t 2 t
或
2 1/ 2 2 t y ( t2 xy )
4 t ( t y )
d b 0 d
sin 2 0
( 1 3 )
2 1 2 3 2 1
12 32
2 3
0
1 2
0
2 cos 2 2 2
1 3 cos2 2(1 3 )
β称为破裂发生角
二、莫尔判据
第 七 章 岩 石 的 f ( ) 破 坏 判 •判断岩石中一点是否会发生剪切破坏时,可在莫尔包络 据 线上,叠加上反映实际研究点应力状态的莫尔应力圆, 如果应力圆与包络线相切或相割,则研究点将产生破坏; 如果应力圆位于包络线下方,则不会产生破坏。 5
本构与强度理论课件

本构与强度理论课件
$number {01}
目录
• 本构理论概述 • 弹性本构理论 • 塑性本构理论 • 强度理论概述 • 材料的强度与断裂 • 本构与强度理论的应用
01
本构理论概述
本构关系的定义
本构关系是指材料在受力状态下,其内部应力、 应变和时间的依赖关系。
它描述了材料在受力过程中,应力与应变之间的 变化规律,是材料力学行为的重要特征。
最大拉应力理论
最大拉应力理论是最早的强度理论之一,它认为材料在拉应 力达到某一极限值时发生破坏。该理论适用于脆性材料,如 玻璃、陶瓷等,因为这些材料的拉伸强度远低于压缩强度。
最大拉应力理论的局限性:最大拉应力理论没有考虑剪切应 力的影响,因此不适用于剪切破坏为主的材料,如某些塑料 和橡胶。此外,该理论也无法解释某些高强度材料的拉伸行 为。
最大伸长应变理论
最大伸长应变理论认为材料在伸长应变达到某一极限值时 发生破坏。该理论适用于韧性材料,如金属和某些聚合物 。这些材料的拉伸强度相对较高,且剪切应力对破坏的影 响较大。
最大伸长应变理论的局限性:最大伸长应变理论忽略了剪 切应变的影响,因此对于剪切破坏为主的材料,该理论可 能不适用。此外,该理论也无法解释某些材料的压缩行为 。
能量准则
能量准则认为材料在能量释放率达到某一极限值时发生破坏。该准则基于能量守 恒定律和材料内部结构的稳定性。能量准则适用于各种类型的材料和应力状态, 具有更广泛的适用范围。
能量准则的局限性:虽然能量准则具有普适性,但由于它涉及到材料的内部结构 和性能,因此需要更深入的材料科学知识来理解和应用。此外,对于某些特殊材 料和复杂应力状态,可能需要更具体的能量准则模型来描述其破坏行为。
增量的关系。
屈服准则和流动法则共 同决定了金属材料在塑 性变形过程中的应力应
$number {01}
目录
• 本构理论概述 • 弹性本构理论 • 塑性本构理论 • 强度理论概述 • 材料的强度与断裂 • 本构与强度理论的应用
01
本构理论概述
本构关系的定义
本构关系是指材料在受力状态下,其内部应力、 应变和时间的依赖关系。
它描述了材料在受力过程中,应力与应变之间的 变化规律,是材料力学行为的重要特征。
最大拉应力理论
最大拉应力理论是最早的强度理论之一,它认为材料在拉应 力达到某一极限值时发生破坏。该理论适用于脆性材料,如 玻璃、陶瓷等,因为这些材料的拉伸强度远低于压缩强度。
最大拉应力理论的局限性:最大拉应力理论没有考虑剪切应 力的影响,因此不适用于剪切破坏为主的材料,如某些塑料 和橡胶。此外,该理论也无法解释某些高强度材料的拉伸行 为。
最大伸长应变理论
最大伸长应变理论认为材料在伸长应变达到某一极限值时 发生破坏。该理论适用于韧性材料,如金属和某些聚合物 。这些材料的拉伸强度相对较高,且剪切应力对破坏的影 响较大。
最大伸长应变理论的局限性:最大伸长应变理论忽略了剪 切应变的影响,因此对于剪切破坏为主的材料,该理论可 能不适用。此外,该理论也无法解释某些材料的压缩行为 。
能量准则
能量准则认为材料在能量释放率达到某一极限值时发生破坏。该准则基于能量守 恒定律和材料内部结构的稳定性。能量准则适用于各种类型的材料和应力状态, 具有更广泛的适用范围。
能量准则的局限性:虽然能量准则具有普适性,但由于它涉及到材料的内部结构 和性能,因此需要更深入的材料科学知识来理解和应用。此外,对于某些特殊材 料和复杂应力状态,可能需要更具体的能量准则模型来描述其破坏行为。
增量的关系。
屈服准则和流动法则共 同决定了金属材料在塑 性变形过程中的应力应
岩石力学课件第四章 岩石本构关系与强度理论

位
形
移
变
应 力
面 力
体 积 力
几何方程
9
物理方程
平衡方程
(一) 平面应力问题与平面应变问题
在实际问题中,任何一个弹性体严格地说都是空间物体, 它所受的外力一般都是空间力系。但是,当所考察的弹性体 的形状和受力情况具有一定特点时,只要经过适当的简化和 力学的抽象处理,就可以归结为弹性力学平面问题。
平面问题分为平面应力问题和平面应变问题。 1、平面应力问题
等厚度薄板,承受平行于 板面并且不沿厚度变化的面力, 同时体力也平行于板面并且不 沿厚度变化。
σz = 0 τzx = 0 τzy = 0
10
特点:
1) 长、宽尺寸远大于厚度
2) 沿板面受有平行板面的面力,且沿厚度均布,体力
平行于板面且不沿厚度变化,在平板的前后表面上
无外力作用。
y
x
注意:平面应力问题z =0,但 z 0,这与平面应变
问题相反。
11
2、平面应变问题 很长的柱体,在柱面上承受平行于柱面并且不沿长度变
化的面力,同时体力也平行于柱面并且不沿长度变化。
εz = 0 τzx = 0 τzy = 0
如:水坝、受内压的圆柱管道和长水平巷道等。
y
x
P
x
图 2-2
注意平面应变问题z = 0,但z 0,这恰与平面应力
问题相反。
12
15 xyd y1Ydxd y10
整理得:
x yx X 0
x y
y xy Y 0
y x
这两个微分方程中包含着三个未知数x,y,xyyx。
因此决定应力分量的问题是超静定的;还必须考虑形变和 位移,才能解决问题。
二讲、本构关系和强度理论

2)
单轴抗压强度的影响因素
(1)承压板给予单轴抗压强度的影响(摩擦力和刚度)
(2)试件尺寸和形状对单轴抗压强度的影响
方形试件的四个边角会产生明显的应力集中现象。试 件的强度通常随其尺寸的增大而减小。高径比在2~3时, 岩石的单轴抗压强度值趋于稳定。 (3) 加载速率对单轴抗压强度的影响
岩石的单轴抗压强度通常随加载速率的提高而增大。 (4)环境对岩石单轴抗压强度的影响 含水量的影响(软化系数)、温度的影响。
图 1-24 根据岩石强度曲线判断岩石破坏状态示意图
图 1-25 斜直线强度曲线
4) 格里菲斯强度理论 1) 格里菲斯强度理论的基本思想 (1) 在脆性材料内部随机地分布着扁平的(用橢圆)裂 纹,在外力作用下,微裂纹尖端附近的应力很大时,裂 纹开始扩展。 (2) 理论分析:裂纹将沿着与最大拉应力成直角的方向 扩展。在单轴压缩的情况下,裂纹最终向最大主应力的 方向过渡,类似于单轴压缩的情况下的劈裂现象。 (3) 当作用在裂纹尖端附近的有效应力达到形成新裂纹 所需能量时,裂纹开始扩展,其表达式为:
1) 位移边界гd,即全部边界上的位移是已知的;
2) 面力边界гt,即全部边界上的面力是已知的;
3) 混合边界,即部分边界(位移边界гd)上的位移 是已知的;而其余边界(面力边界гt)上的面力 是已知的。
边界条件是求解弹性力学问题的重要条件,在位移 边界条件中,所研究物体的边界上的位移分量已知,设 u,v为物体的边界位移。
1e
E
t t1
4 岩石的强度理论 1) 平面问题的简化 平面应力问题,主要特征为:σz=0 εz≠0。
平面应变问题,主要特征为:σz≠0 εz=0。
二维的应力状态
土力学与数值方法:土的本构理论完整ppt课件

εx
σx Eh
νhh
σy Eh
νvh
σz Ev
,
1
γ xy
Gh
τ xy
εy
σy Eh
νhh
σx Eh
νvh
σz ,
Ev
γ yz
1 Gv
τ yz
εz
σz Ev
νhv
σx Eh
νhv
σy ,
Eh
γzpxpt精G选1v版τ zx
Gh2(1E h νhh ),νhvE Eh vνvh
(σ1σ3)f 2cc1 o ss2iσ n 3sin
代入Et公式中后,得到:
包含5个参数:KE、n、c、φ、Rf
E tK Ep a σ p 3 a n 1R 2 fc (1 cs o i s2 )n σ σ 3 (1 sσ i3 n ) 2
ppt精选版
20
k、n为试验常数,正常固结粘性土,n=10,一般情况下 在0.2~1.0之间;k值随土类变化大,可能小于100,也可 能大于数千。
00,G(1Eν)(12ν)
称
G 0
2(1ν)
G
对于各向同性材料,独立的弹性常数只有2个,另外,剪 应变不引起体积应变。
ppt精选版
5
• B-G形式的本构关系
为了将应力和应变的球张量与偏张量分开,将三个正应
力公式相加:
体积弹性模量
, σ m λ 3 2 G ε v B ε εvv = 3ε3 mB ε m
B4G/3 0 0 0
对
G 0 0
称
G 0
G
同样,独立的弹性常数只有2个,相互可以换算。
ppt精选版
7
• 弹性常数
岩石力学第四章岩石本构关系与强度理论PPT课件

介绍了岩石本构关系的定义、分类和特点 ,以及不同类型本构关系的适用范围和局 限性。
介绍了岩石强度理论的定义、分类和特点 ,以及不同类型强度理论的适用范围和局 限性。
岩石本构关系与强度理论的实验 研究
介绍了实验研究在岩石本构关系与强度理 论中的重要性,以及实验研究的方法和步 骤。
岩石本构关系与强度理论的应用 实例
岩石力学第四章:岩石本构关系与 强度理论
目录
• 引言 • 岩石本构关系 • 岩石强度理论 • 岩石破坏准则 • 本章总结与展望
01 引言
课程背景
01
岩石力学是一门研究岩石材料在 各种力场作用下的行为和性能的 科学。
02
本章重点介绍岩石的本构关系和 强度理论,为后续章节的学习奠 定基础。
本章目标
探索新的应用领域
将岩石本构关系与强度理论应用到更广泛的领域,如环境工程、地质 工程和地震工程等,为解决实际问题提供更多帮助。
结合数值计算方法
将岩石本构关系与强度理论结合数值计算方法,实现更加高效、精确 的数值模拟和分析,为工程设计和优化提供更多支持。
THANKS FOR WATCHING
感谢您的观看
3
该准则适用于分析简单应力状态下的岩石破坏, 但在复杂应力状态下需要考虑其他因素。
应变能密度准则
应变能密度准则是基于岩石在受力过 程中储存的应变能密度来描述其应力 状态。
当应变能密度达到一定阈值时,岩石 会发生破坏。该准则适用于分析岩石 在复杂应力状态下的破坏机制。
莫尔-库仑强度理论
01
莫尔-库仑强度理论是岩石力学中最常用的强度理论之一。
弹性本构关系
描述
弹性本构关系描述了岩石在受力后立即发生的弹性变形阶段的应力应变关系。
岩石力学岩体的本构关系与强度理论

eij
si0j
(c 2G
3ip ) 2i0
si0jc
(1
2G
3ip ) 2c i0
eij
sij(21G
3ip ) 2i
令
3G ip ,有 3ip
i
2i
2G
所以: eij
1 2G
sij
这就是Hencky 本构方程,它 包括了弹性变形与塑性变形
eij
eiej
eipj
1 2G
sij
⑶ 应变偏量与应力偏量成比例
(2)非稳定蠕变:岩石承受的恒定荷载较大,当岩石应力超过 某一临界值时,变形随时间增加而增大,其变形速率逐渐增大,最 终导致岩体整体失稳破坏。
(3)岩石的长期强度:岩石的蠕变形式取决于岩石应力大小, 当应力小于某一临界值时,岩石产生稳定蠕变;当应力大于该值时, 岩石产生非稳定蠕变。则将该临界应力称为岩石的长期强度。
可见,σ、ε与时间t无关。
2、粘性介质及粘性元件(牛顿体)
d dt
tc
加载瞬间,无变形 即当t=0时,σ=σ0,ε=0,则 c=0
σ2
ωσ σ1
σ3
e2
ωdε e1
e3
3、Levy-Mises本构方程 因为ε0=0,所以eij=εij,εij=ε0δij+eij
⑴应变偏量的增量与应力偏量的关系
由假定⑴,并参照Page57和Page21
de1p s
de2p s
de3p s
1
2
3
d ip cos d
2 3
i
cos
d ip cos(d
⑴Lode试验 Lode参数代表Mohr圆心的相对位置
=2
岩体本构关系与强度理论

要注重作业的多样性和 实用性,让学生通过实 际操作巩固所学知识
18
注意事项
通过以上教学步骤和注意事项 的安排,相信学生能够更好地 掌握表格数据的图表化技能, 为未来的学习和工作打下坚实
的基础
··· ···
-
谢谢您的 ·观看·
BUSINESS TRIP PROJECT PLAN
汇报人:XXX
汇报时间:XXXXX
了解图表的基本 类型及适用场景
课程目标
Stage 3 学会根据需:求 调整图表的样式 和布局
Stage 5
了解如何根据数 据变化更新图表
Stage 2
掌握在Ex:cel 中创建图表的方 法
Stage 4
掌握数据标签和 图例的添加方法
3 课程内容
1. 图表基础知 识
什么是图表?
图表的基本类型 及特点
岩体本构关系与强度 理论
1 课程简介 3 课程内容 5 教学步骤
-
2 课程目标 4 教学方法 6 注意事项
1 课程简介
课程简介
本课程旨在介绍如何使 用Excel软件进行表格
数据的图表化
通过学习这个课程,你 将掌握如何将表格数据 转化为直观的图表形式, 以更好地分析和理解数 据
2 课程目标
Stage 1ຫໍສະໝຸດ 5. 高级图表的 制作复合图表的制作
自定义图表的制作
数据透视表的创 建和应用
课程内容
4 教学方法
教学方法
5 教学步骤
作业布置:布置与课程内容 相关的作业,让学生进行实 际操作,加深对知识点的理
解和掌握
总结与回顾:对本节课的内 容进行总结与回顾,帮助学
生巩固所学知识
教学步骤
18
注意事项
通过以上教学步骤和注意事项 的安排,相信学生能够更好地 掌握表格数据的图表化技能, 为未来的学习和工作打下坚实
的基础
··· ···
-
谢谢您的 ·观看·
BUSINESS TRIP PROJECT PLAN
汇报人:XXX
汇报时间:XXXXX
了解图表的基本 类型及适用场景
课程目标
Stage 3 学会根据需:求 调整图表的样式 和布局
Stage 5
了解如何根据数 据变化更新图表
Stage 2
掌握在Ex:cel 中创建图表的方 法
Stage 4
掌握数据标签和 图例的添加方法
3 课程内容
1. 图表基础知 识
什么是图表?
图表的基本类型 及特点
岩体本构关系与强度 理论
1 课程简介 3 课程内容 5 教学步骤
-
2 课程目标 4 教学方法 6 注意事项
1 课程简介
课程简介
本课程旨在介绍如何使 用Excel软件进行表格
数据的图表化
通过学习这个课程,你 将掌握如何将表格数据 转化为直观的图表形式, 以更好地分析和理解数 据
2 课程目标
Stage 1ຫໍສະໝຸດ 5. 高级图表的 制作复合图表的制作
自定义图表的制作
数据透视表的创 建和应用
课程内容
4 教学方法
教学方法
5 教学步骤
作业布置:布置与课程内容 相关的作业,让学生进行实 际操作,加深对知识点的理
解和掌握
总结与回顾:对本节课的内 容进行总结与回顾,帮助学
生巩固所学知识
教学步骤
本构与强度理论教学课件

强度理论的应用
金属材料
适用于描述金属材料的强度行为 ,用于设计金属结构、评估金属
材料的承载能力和安全性。
复合材料
适用于描述复合材料的强度行为 ,用于设计复合结构、评估复合
材料的承载能力和安全性。
工程应用
强度理论广泛应用于土木工程、 航空航天、机械工程等领域,用 于评估结构的承载能力和安全性 ,优化结构设计,提高工程安全
02
强度理论是材料力学和断裂力学 中的重要概念,用于评估材料在 不同受力状态下的承载能力和安 全性。
强度理论的分类
01
02
03
最大剪应力理论
认为材料在最大剪应力达 到某一临界值时发生屈服 或断裂。
最大应变理论
认为材料在最大应变达到 某一临界值时发生屈服或 断裂。
米塞斯理论
认为材料在等效应力达到 某一临界值时发生屈服或 断裂。
实际应用的发展趋势
1 2
拓展应用领域
随着新材料和新技术的不断涌现,本构与强度理 论的应用领域将不断拓展,涉及航空航天、能源 、环保等领域。
提高工程安全性和可靠性
通过本构与强度理论研究,提高工程结构和设备 的承载能力和安全性,降低事故风险。
3
智能化和自动化技术的应用
结合智能化和自动化技术,实现本构与强度理论 的在线监测、实时分析和预警等功能。
本构与强度理论教学 课件
目录
• 本构理论概述 • 强度理论概述 • 本构理论与强度理论的联系与区别 • 本构与强度理论的实际应用 • 本构与强度理论的发展趋势与展望
01
本构理论概述
本构关系的定义
总结词
本构关系是描述材料在受力状态下性质如何变化的关系。
详细描述
本构关系是指材料在受到外力作用时,其内部性质如何随外力变化而变化的关 系。这种关系反映了材料的力学特性,是材料科学和工程领域中非常重要的概 念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
A B C
d c
B C
间增长有所增加,但蠕变变形的 速率则随时间增长而减少,最后 变形趋于一个稳定的极限值,这 种蠕变称为稳定蠕变。
a
b
o
t
图 岩石蠕变曲线示意图
2)当荷载较大时, abcd 曲线所示,蠕变不能稳定于某一极限值,
而是无限增长直到破坏,这种蠕变称为不稳定蠕变。这是典 型的蠕变曲线,根据应变速率不同,其蠕变过程可分为三个 阶段,即减速蠕变阶段或初始蠕变阶段、等速蠕变阶段及加 速蠕变阶段。
对于大多数岩石,长期强度/瞬时强度
( s / s0 )一般为0.4~0.8,软的和中等坚固岩 石为0.4~0.6,坚固岩石为0.7~0.8。表7-1中列 出某些岩石瞬时强度与长期强度的比值。
表6-1 几种岩石长期强度与瞬时强度比值
岩石名称
s / s0
粘土 0.74
石灰石 0.73
盐岩 0.70
三、 岩石塑性本构关系
塑性本构关系特点:
1、应力-应变关系的多值性
同一应力有多个应变值 σ 与它相对应。 本构关系采用应力和应 变增量的关系表达。
A 加载 卸载 C B
塑性状态描述:除用应
力、应变,还需用塑性应变, 0
ε
图6-1 加-卸载应力-应变曲线
塑性功等内状态变量来刻画
塑性变形历史。
2、本构关系的复杂性
据广义虎克定理有:
1 ( ) x y z E 1 y ( ) y z x E 1 z ( ) z x y E 1 1 1 yx yz , zx zz , xy xy G G G
| | c tan
σ1 σ σ3 θ
或
| | tan c
(6-1)
L
σ3
Φ c
D
A
σ1
O
Hale Waihona Puke σ3Bσ1 σ图6-6 σ-τ坐标下库仑准则
最大主应力方向与剪切面(指其法线方向)间的夹角 (称为破坏角)恒等为: 2 或 45 o 2 2 另外由图6-6可得: 1 3 sin 2c ctg 1 3
③混合硬化模型:介于等向硬化-软化和随动硬化之间的模型,后继
f f * ( ij ijp ) H ( ) 0
(2)塑性岩石力学最常用的屈服条件
库仑(Coulomb)、德鲁克-普拉格(Drucker-Prager)屈服条件。
2. 塑性状态的加-卸载准则
塑性加载:对材料施加应力增量后,材料从 一种塑性状态变化到另一种塑性状态,且有新的 塑性变形出现; 中性变载:对材料施加应力增量后,材料从一 种塑性状态变化到另一种塑性状态,但没有新的 塑性变形出现; 塑性卸载:对材料施加应力增量后,材料从塑 性状态退回到弹性状态。
E 1 2
中的E换成
,v
换成 1 。
2. 空间问题弹性本构方程
1 x x ( y z ) E 1 y ( ) y z x E 1 z z ( x y ) E 2(1 ) 2(1 ) yz yz , zx zx E E 2(1 ) xy xy E
d ijp F ij
1
F d ij D d ij 其总应变增量表示为: ij
由一致性条件可推出待定有限量 为:
1 F d ij A ij
对于系数A: 理想塑性材料: 硬化材料:
A0
F Q F Q A D ij p ij ij kl u
图
岩石的典型蠕变曲线
典型岩石蠕变方程:幂函数方程、指数方程、幂指数对数混合方程
2. 理论模型模拟法
将介质理想化,归纳成各种模型,模型可用理想化的具有基本性能(包 括弹性、塑性和粘性)的元件组合而成。
岩石的长期强度:由于流变作用,岩石强度随外
载作用时间的延长而降低,通常把作用时间 t 的强度(最低值)称为长期强度。
或处于极限平衡状态截面上的剪应力 和正应力 间的关系方程:
f
§6.3 岩石强度理论与破坏判据
一、 库仑强度准则
二、 莫尔强度理论 三、 格里菲斯强度理论 四、 德鲁克一普拉格准则
一、 库仑强度准则
岩石的破坏:剪切破坏。
认为岩石的剪切强度等于岩石本身的粘结力和剪切面上由法 向力产生的摩擦阻力。平面应力中的剪切强度准则(图)为:
d ijp Q ij
式中: 是一正的待定有限量,它的具体数值和材料硬化法则有关。
式
Q d ij
p ij
称为塑性流动法则,对于稳定的应
变硬化材料,Q 通常取与后继屈服函数F 相同的形式,
当Q=F 时,这种特殊情况称为关联塑性。 对于关联塑性,塑性流动法则可表示为:
通过强度准则来反映。
§6.2 岩石的本构关系
一、 岩石力学中的符号规定
(1)力和位移分量的正方向与坐标轴的正方向 一致; (2)压缩的正应变取为正; (3)压缩的正应力取为正。
假如表面的外法线与坐标轴的正方向一致,则
该表面上正的剪应力的方向与坐标轴的正方向相反,
反之亦然。
二、 岩石弹性本构关系 1.平面弹性本构关系
第6章 岩石本构关系与强度理论
§6.1 概 述
§6.2 岩石的本构关系
§6.3 岩石强度理论与破坏判据
§6.1 概 述
岩体力学研究对象:岩体是岩块和结构面的组合体,其力学性 质往往表现为弹性、塑性、粘性或三者之间的组合。 岩体力学问题求解:是将岩体划分成若干单元或称微分单元, 其求解过程如下:
力的平衡关系(平衡方程) + 边界条件 = 位移和应变的关系(几何方程) 应力和应变的关系(物理方程 或本构方程)
式中: u 为塑性功,这样加载时的本构方程为:
1 1 Q F d ij D d kl A ij kl p 对任何一个状态 kl , kl , u ,只要给出了应力增量,就
可以唯一地确定应变增量 d ij 。 应用增量理论求解塑性问题,能够反映应变历史对塑性 变形的影响,因而比较准确地描述了材料的塑性变形规律。
塑性阶段本构关系包括三组方程:
1)屈服条件:塑性状态的应力条件。
2)加-卸载准则:材料进入塑性状态后继续塑性变形 或回到弹性状态的准则,通式写成:
( ij , Ha ) 0
式中: ij垂直于 i轴的平面上平行于 j 轴的应力 (i x, y, z; j x, y, z) , 。 为某一函数关系,H a为与加载历史有关的参数, a 1, 2 3)本构方程:
应力场
位移场
依据适合的强度理论,判断岩体的破坏及其破坏形式。 岩体本构关系:指岩体在外力作用下应力或应力速率与其应
变或应变速率的关系。
岩石或岩体的变形性质:弹塑性或粘弹塑性。 本构关系:弹塑性或粘弹塑性本构关系。
本构关系分类:
①弹性本构关系:线性弹性、非线性弹性本构关系。 ②弹塑性本构关系:各向同性、各向异性本构关系。 ③流变本构关系:岩石产生流变时的本构关系。流变
对于平面应力问题:σz=τzx=τzy=0
1 x x y E 1 y y x E 2(1 ) xy xy E
对比平面应力问题与平面应变的本构方程,
可以看出,只要将平面应力问题的本构关系式
性是指如果外界条件不变,应变或应力随时间而变化的
性质。
岩石强度理论:研究岩石在一定的假说条件下在各 种应力状态下的强度准则的理论。
岩石的强度是指岩石抵抗破坏的能力。
岩石材料破坏的形式:断裂破坏、流动破坏(出现
显著的塑性变形或流动现象)。断裂破坏发生于应力 达到强度极限,流动破坏发生于应力达到屈服极限。 岩体的力学性质可分为变形性质和强度性质, 变形性质主要通过本构关系来反映,强度性质主要
在一系列的岩石流变试验基础上建立反映岩石流变性 质的流变方程,通常有二种方法:
ε ε 2( t) ε 1( t)
A ε0
O
1.经验法
岩石蠕变经验方程:
D ε 3( t) C
(t ) 0 1 (t ) 2 (t ) 3 (t )
B t
(t )为时间 t 的应变; 式中: 0 瞬时应变; 2 (t ) 等速段应变; 1 (t )初始段应变; 3 (t ) 加速段应变。
3.本构方程
塑性状态时应力-应变关系是多值的,取决材料性质和加 -卸载历史。 1)全量理论:描述塑性变形中全量关系的理论,称形变理 论或小变形理论。 汉基(Hencky)、依留申等依据类似弹性理论的广义胡克
定律,提出如下公式 :
xx m 2G xx m , xy G xy yy m 2G yy m , yz G yz zz m 2G zz m , zx G zx
x
式中:E为物体的弹性模量; 为泊松比;G为剪切弹性模量,
E G 2(1 )
对于平面应变问题:因εz =γzx =γyz = 0 ,故τyz
=τzx=0,可知:
z ( x y )
y x 1 1 2 y x y E 1 2(1 ) xy xy E 1 2 x E
或均匀收缩(软化)。如果 是初始屈服面,后继屈服面为: f* 0
f f * ( ij ) H ( ) 0
②随动硬化模型:塑性变形发展时,屈服面的大小和形状保持不变,
