2016学下学期开学测试性考试
2016届九年级下学期开学数学试卷【解析版】

2021届九年级||下学期开学数学试卷一、选择题(共10小题,每题3分,共30分)1.以下各数中,负数是()A.﹣(1﹣2 ) B.﹣1﹣1C.(﹣1 )0D.1﹣22.以下运算正确的选项是()A.﹣3 (x﹣1 ) =﹣3x﹣1 B.﹣3 (x﹣1 ) =﹣3x +1 C.﹣3 (x﹣1 ) =﹣3x﹣3 D.﹣3 (x﹣1 ) =﹣3x +33.以下命题中,不正确的选项是()A.对角线相等的平行四边形是矩形B.有一个角为60°的等腰三角形是等边三角形C.正方形的两条对角线相等且互相垂直平分D.直角三角形斜边上的高等于斜边的一半4.不等式组的解集在数轴上表示为()A.B.C.D.5.如图,8×8方格纸的两条对称轴EF ,MN相交于点O ,图a到图b的变换是()A.绕点O旋转180°B.先向上平移3格,再向右平移4格C.先以直线MN为对称轴作轴对称,再向上平移4格D.先向右平移4格,再以直线EF为对称轴作轴对称6.如图,将宽为1cm的纸条沿BC折叠,使∠CAB =45° ,那么折叠后重叠局部的面积为()A.cm2B.cm2C.cm2D.cm27.三军受命,我解放军各部队奋力抗战地救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到小镇只有唯一通道,且路程为24km ,如图是他们行走的路线关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是()A.1 B.2 C.3 D.48.在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是()A.B.C.D.9.四边形ABCD中,AC和BD交于点E ,假设AC平分∠DAB ,且AB =AE ,AC =AD ,有以下四个命题:①AC⊥BD;②BC =DE;③∠DBC =∠DAB;④AB =BE =AE.其中命题一定成立的是()A.①②B.②③C.①③D.②④10.二次函数y =ax2+bx +c (a≠0 )的图象如下列图,有以下5个结论:①abc>0;②b<a +c;③4a +2b +c>0;④2c<3b;⑤a +b>m (am +b ) (m≠1的实数).其中正确的结论有()A.2个B.3个C.4个D.5个二、填空题(共10小题,每题3分,共30分)11.分解因式:m2n﹣n =.12.假设一次函数y = (2﹣m )x﹣2的函数值y随x的增大而减少,那么m的取值范围是.13.某市高新技术产业产值突破110亿元,数据"110亿〞用科学记数法可表示为.14.关于x的一元二次方程x2﹣4x +8sinα=0的两根相等,且α是锐角,那么∠α=度.15.如图,梯形ABCD中,AD∥BC ,∠B =30° ,∠C =60° ,AD =4 ,AB =3,那么下底BC的长为.16.如图,在△ABC中,∠C =90° ,AC =8cm ,AB的垂直平分线MN交AC于D ,连接BD ,假设sin∠DBC =,那么BC的长是cm.17.如图,△P1OA1 ,△P2A1A2是等腰直角三角形,点P1 ,P2在函数y =(x>0 )的图象上,斜边OA1 ,A1A2都在x轴上,那么点A2的坐标是.18.如图,△ABC中,∠BAC =90° ,AB =AC.P是AB的中点,正方形ADEF的边在线段CP上,那么正方形ADEF与△ABC的面积的比为.19.如图,抛物线的顶点为P (﹣2 ,2 ) ,与y轴交于点A (0 ,3 ).假设平移该抛物线使其顶点P沿直线移动到点P′ (2 ,﹣2 ) ,点A的对应点为A′ ,那么抛物线上PA段扫过的区域的面积为.20.正方形A1B1C1O ,A2B2C2C1 ,A3B3C3C2 ,… ,按如下列图的方式放置.点A1 ,A2 ,A3 ,… ,和点C1 ,C2 ,C3 ,… ,分别在直线y =kx +b (k>0 )和x轴上,点B1、B2的坐标分别为B1 (1 ,1 ) ,B2 (3 ,2 ) ,那么B8的坐标是.三、解答题21.(1 )计算:(﹣1 )2021﹣|﹣|﹣(﹣)﹣2+2sin45°﹣(π﹣3.14 )0+(2 )先化简,再求值:•+,其中x满足x2﹣3x +2 =0.22.在建筑楼梯时,设计者要考虑楼梯的平安程度,如图(1 ) ,虚线为楼梯的斜度线,斜度线与地板夹角为倾角为θ ,一般情况下,倾角θ愈小,楼梯的平安度就越高.如图(2 ) ,设计者为提高楼梯平安度,要把楼梯倾角由θ1减至||θ2 ,这样楼梯占用地板的长度d1增加到d2 ,d1=4m ,∠θ1=45° ,∠θ2=30° ,求楼梯占用地板的长度增加了多少?23.如图,四边形ABCD是矩形,E是BD上的一点,∠BAE =∠BCE ,∠AED =∠CED ,点G是BC、AE延长线的交点,AG与CD相交于点F.(1 )求证:四边形ABCD是正方形;(2 )当AE =2EF时,判断FG与EF有何数量关系?并证明你的结论.24.如图,反比例函数的图象经过点(,8 ) ,直线y =﹣x +b经过该反比例函数图象上的点Q (4 ,m ).(1 )求上述反比例函数和直线的函数表达式;(2 )设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P ,连接0P、OQ ,求△OPQ的面积.25.我市的重大惠民工程﹣﹣公租房建设已陆续竣工,方案10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积y (单位:百万平方米) ,与时间x的关系是y =﹣x +5 , (x 单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y (单位:百万平方米) ,与时间x的关系是y =﹣x +(x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z (单位:元/m2 )与时间x (单位:年,1≤x≤10且x为整数)满足一次函数关系如表:z (元/m2 ) 50 52 54 56 58 …x (年) 1 2 3 4 5 …(1 )求出z与x的函数关系式;(2 )求政府在第几年投入的公租房收取的租金最||多,最||多为多少百万元.26.如图,在Rt△ABC中,∠A =90° ,AB =6 ,AC =8 ,D ,E分别是边AB ,AC的中点,点P从点D 出发沿DE方向运动,过点P作PQ⊥BC于Q ,过点Q作QR∥BA交AC于R ,当点Q与点C重合时,点P停止运动.设BQ =x ,QR =y.(1 )求点D到BC的距离DH的长;(2 )求y关于x的函数关系式(不要求写出自变量的取值范围);(3 )假设△PQR是以QR为底边的等腰三角形,求的x值.27.如图,在平面直角坐标系中,二次函数y =x2+bx +c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3 ,0 ) ,与y轴交于C (0 ,﹣3 )点,点P是直线BC下方的抛物线上一动点.(1 )求这个二次函数的表达式.(2 )连接PO、PC ,并把△POC沿CO翻折,得到四边形POP′C ,那么是否存在点P ,使四边形POP′C 为菱形?假设存在,请求出此时点P的坐标;假设不存在,请说明理由.(3 )当点P运动到什么位置时,四边形ABPC的面积最||大?求出此时P点的坐标和四边形ABPC的最||大面积.2021届九年级||下学期开学数学试卷参考答案与试题解析一、选择题(共10小题,每题3分,共30分)1.以下各数中,负数是()A.﹣(1﹣2 ) B.﹣1﹣1C.(﹣1 )0D.1﹣2【考点】负整数指数幂;零指数幂.【专题】计算题.【分析】依次计算出各选项的值,然后判断结果为负数的选项.【解答】解:A、﹣(1﹣2 ) =1 ,为正数,故本选项错误;B、﹣1﹣1=﹣1 ,为负数,故本选项正确;C、(﹣1 )0=1 ,为正数,故本选项错误;D、1﹣2=1 ,为正数,故本选项错误;应选B.【点评】此题考查了负整数指数幂及零指数幂的知识,属于根底题,解答此题的关键是正确运算出各项的值,难度一般.2.以下运算正确的选项是()A.﹣3 (x﹣1 ) =﹣3x﹣1 B.﹣3 (x﹣1 ) =﹣3x +1 C.﹣3 (x﹣1 ) =﹣3x﹣3 D.﹣3 (x﹣1 ) =﹣3x +3【考点】去括号与添括号.【分析】去括号时,要按照去括号法那么,将括号前的﹣3与括号内每一项分别相乘,尤其需要注意,﹣3与﹣1相乘时,应该是+3而不是﹣3.【解答】解:根据去括号的方法可知﹣3 (x﹣1 ) =﹣3x +3.应选D.【点评】此题属于根底题,主要考查去括号法那么,理论依据是乘法分配律,容易出错的地方有两处,一是﹣3只与x相乘,忘记乘以﹣1;二是﹣3与﹣1相乘时,忘记变符号.此题直指去括号法那么,没有任何其它干扰,掌握了去括号法那么就能得分,不掌握就不能得分.3.以下命题中,不正确的选项是()A.对角线相等的平行四边形是矩形B.有一个角为60°的等腰三角形是等边三角形C.正方形的两条对角线相等且互相垂直平分D.直角三角形斜边上的高等于斜边的一半【考点】命题与定理.【分析】根据矩形的判定方法对A矩形判断;根据等边三角形的判定对B进行判断;根据正方形的性质对C进行判断;根据直角三角形斜边上的中线性质对D进行判断.【解答】解:A、对角线相等的平行四边形是矩形是正确的,不符合题意;B、有一个角为60°的等腰三角形是等边三角形是正确的,不符合题意;C、正方形的两条对角线相等且互相垂直平分是正确的,不符合题意;D、直角三角形斜边上的中线等于斜边的一半,故原来的命题不正确.应选D.【点评】此题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.4.不等式组的解集在数轴上表示为()A.B.C.D.【考点】解一元一次不等式组;在数轴上表示不等式的解集.【分析】先求出两个不等式的解集,再求其公共解.【解答】解:由得:x≤2.由2﹣x<3得:x>﹣1.所以不等式组的解集为﹣1<x≤2.应选C.【点评】此题主要考查不等式组的解法及在数轴上表示不等式组的解集.不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画) ,数轴上的点把数轴分成假设干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时"≥〞, "≤〞要用实心圆点表示;"<〞, ">〞要用空心圆点表示.5.如图,8×8方格纸的两条对称轴EF ,MN相交于点O ,图a到图b的变换是()A.绕点O旋转180°B.先向上平移3格,再向右平移4格C.先以直线MN为对称轴作轴对称,再向上平移4格D.先向右平移4格,再以直线EF为对称轴作轴对称【考点】利用轴对称设计图案.【分析】根据平移和轴对称的性质,结合图形,对选项进行一一分析,排除错误答案.【解答】解:A、绕点O旋转180° ,两条对称轴EF ,MN不可能相交于点O ,故此选项错误;B、平移后的图形与b形状不同,故此选项错误;C、先以直线MN为对称轴作轴对称,其中平移后与b形状不同,故此选项错误;D、先向右平移4格,再以直线EF为对称轴作轴对称,故此选项正确.应选:D.【点评】此题考查图形的平移变换和旋转性质即轴对称的性质.注意这些变换都不改变图形的形状和大小.注意结合图形解题的思想.6.如图,将宽为1cm的纸条沿BC折叠,使∠CAB =45° ,那么折叠后重叠局部的面积为()A.cm2B.cm2C.cm2D.cm2【考点】翻折变换(折叠问题).【分析】先根据题意得出△ABC是一个顶角为45°的等腰三角形,即∠A =45° ,AC =AB ,过C作CD⊥AB ,垂足为D ,根据三角函数定义求出AC ,AB ,然后就可以求出△ABC面积.【解答】解:∵纸条的两边互相平行,∴∠1 =∠BAC =45° ,∴∠ABC ===67.5° ,同理可得,∠ACB =67.5° ,∴△ABC是一个顶角为45°的等腰三角形,即∠A =45° ,AC =AB.作CD⊥AB ,垂足为D ,那么CD =1.∵sin∠A =,∴AC ===AB ,∴S△ABC=×AB×CD =,∴折叠后重叠局部的面积为cm2.应选B.【点评】此题考查的是图形折叠的性质,熟知图形翻折不变性的性质是解答此题的关键.7.三军受命,我解放军各部队奋力抗战地救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到小镇只有唯一通道,且路程为24km ,如图是他们行走的路线关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是()A.1 B.2 C.3 D.4【考点】一次函数的应用.【专题】压轴题;阅读型;图表型.【分析】此题主要考查的是分段函数的应用,应结合函数的图形,按不同的时间段进行逐段分析.【解答】解:由图可知:甲、乙的起始时间分别为0h和2h;因此甲比乙早出发2小时;在3h﹣4h这一小时内,甲的函数图象与x轴平行,因此在行进过程中,甲队停顿了一小时;两个函数有两个交点:①甲行驶4.5小时、乙行驶2.5小时时,两函数相交,因此乙队出发2.5小时后追上甲队;②甲行驶6小时、乙行驶4小时后,两函数相交,此时两者同时到达目的地.所以在整个行进过程中,乙队用的时间为4小时,行驶的路程为24千米,因此它的平均速度为6km/h.这四个同学的结论都正确,应选D.【点评】此题考查了识别函数图象的能力,是一道较为简单的题,观察图象提供的信息,再分析这四位同学的结论.8.在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是()A.B.C.D.【考点】列表法与树状图法.【专题】转化思想.【分析】列举出所有情况,看两次都摸到红球的情况占总情况的多少即可.【解答】解:∴一共有12种情况,有2种情况两次都摸到红球,∴两次都摸到红球的概率是=.应选:C.【点评】列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.9.四边形ABCD中,AC和BD交于点E ,假设AC平分∠DAB ,且AB =AE ,AC =AD ,有以下四个命题:①AC⊥BD;②BC =DE;③∠DBC =∠DAB;④AB =BE =AE.其中命题一定成立的是()A.①②B.②③C.①③D.②④【考点】全等三角形的判定与性质;等边三角形的性质.【专题】压轴题.【分析】根据等腰三角形的性质,等边三角形的判定,圆内接四边形的性质,全等三角形的性质判断各选项是否正确即可.【解答】解:∵AB =AE ,一个三角形的直角边和斜边一定不相等,∴AC不垂直于BD ,①错误;利用边角边定理可证得△ADE≌△ABC ,那么BC =DE ,②正确;由△ADE≌△ABC可得∠ADE =∠ACB ,那么A ,B ,C ,D四点共圆,∴∠DBC =∠DAC=∠DAB ,③正确;△ABE不一定是等边三角形,那么④不一定正确;②③正确,应选B.【点评】此题主要考查了全等三角形的性质,以及直角三角形中斜边最||长;全等三角形的对应边相等;等边三角形的三边相等.10.二次函数y =ax2+bx +c (a≠0 )的图象如下列图,有以下5个结论:①abc>0;②b<a +c;③4a +2b +c>0;④2c<3b;⑤a +b>m (am +b ) (m≠1的实数).其中正确的结论有()A.2个B.3个C.4个D.5个【考点】二次函数图象与系数的关系.【专题】压轴题;数形结合.【分析】观察图象:开口向下得到a<0;对称轴在y轴的右侧得到a、b异号,那么b>0;抛物线与y轴的交点在x轴的上方得到c>0 ,所以abc<0;当x =﹣1时图象在x轴下方得到y =a﹣b +c =0 ,即a +c =b;对称轴为直线x =1 ,可得x =2时图象在x轴上方,那么y =4a +2b +c>0;利用对称轴x =﹣=1得到a =﹣ b ,而a﹣b +c<0 ,那么﹣b﹣b +c<0 ,所以2c<3b;开口向下,当x =1 ,y有最||大值a +b +c ,得到a +b +c>am2+bm +c ,即a +b>m (am +b ) (m≠1 ).【解答】解:开口向下,a<0;对称轴在y轴的右侧,a、b异号,那么b>0;抛物线与y轴的交点在x轴的上方,c>0 ,那么abc<0 ,所以①不正确;当x =﹣1时图象在x轴下方,那么y =a﹣b +c =0 ,即a +c =b ,所以②不正确;对称轴为直线x =1 ,那么x =2时图象在x轴上方,那么y =4a +2b +c>0 ,所以③正确;x =﹣=1 ,那么a =﹣ b ,而a﹣b +c =0 ,那么﹣b﹣b +c =0 ,2c =3b ,所以④不正确;开口向下,当x =1 ,y有最||大值a +b +c;当x =m (m≠1 )时,y =am2+bm +c ,那么a +b +c>am2+bm +c ,即a +b>m (am +b ) (m≠1 ) ,所以⑤正确.应选:A.【点评】此题考查了二次函数图象与系数的关系:对于二次函数y =ax2+bx +c (a≠0 )的图象,当a>0 ,开口向上,函数有最||小值,a<0 ,开口向下,函数有最||大值;对称轴为直线x =﹣,a与b同号,对称轴在y轴的左侧,a与b异号,对称轴在y轴的右侧;当c>0 ,抛物线与y轴的交点在x 轴的上方;当△=b2﹣4ac>0 ,抛物线与x轴有两个交点.二、填空题(共10小题,每题3分,共30分)11.分解因式:m2n﹣n =n (m +1 ) (m﹣1 ).【考点】提公因式法与公式法的综合运用.【分析】观察原式,找到公因式n ,提取公因式后发现m2﹣1符合平方差公式,再利用平方差公式继续分解即可.【解答】解:m2n﹣n ,=n (m2﹣1 ) ,=n (m +1 ) (m﹣1 ).【点评】此题考查了提公因式法与公式法进行因式分解,一个多项式有公因式首||先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.12.假设一次函数y = (2﹣m )x﹣2的函数值y随x的增大而减少,那么m的取值范围是m>2.【考点】一次函数图象与系数的关系.【分析】根据一次函数y = (2﹣m )x﹣2的增减性知m﹣1<0 ,通过解不等式即可求得m的取值范围.【解答】解:∵函数y = (2﹣m )x﹣2是一次函数,且y随x的增大而减少,∴2﹣m<0 ,解得,m>2.故答案为:m>2.【点评】此题考查了一次函数图象与系数的关系.:在直线y =kx +b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.13.某市高新技术产业产值突破110亿元,数据"110亿〞用科学记数法可表示为 1.1×1010.【考点】科学记数法-表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10 ,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝||对值与小数点移动的位数相同.当原数绝||对值>1时,n 是正数;当原数的绝||对值<1时,n是负数.【解答】解:将110亿用科学记数法表示为:1.1×1010.故答案为:1.1×1010.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10 ,n为整数,表示时关键要正确确定a的值以及n的值.14.关于x的一元二次方程x2﹣4x +8sinα=0的两根相等,且α是锐角,那么∠α=30度.【考点】根的判别式;特殊角的三角函数值.【分析】方程有两相等实数根,那么其根的判别式△=0.由此可以得到关于sinα的方程,解方程求出sinα后再求α的度数.【解答】解:∵a =1 ,b =﹣4 ,c =8sinα ,∴△=b2﹣4ac =16﹣32sinα=0 ,∴sinα=,∴α=30°.【点评】一元二次方程根的情况与判别式△的关系:(1 )△>0⇔方程有两个不相等的实数根;(2 )△=0⇔方程有两个相等的实数根;(3 )△<0⇔方程没有实数根.15.如图,梯形ABCD中,AD∥BC ,∠B =30° ,∠C =60° ,AD =4 ,AB =3,那么下底BC的长为10.【考点】梯形.【专题】压轴题.【分析】过A作AE∥CD ,把梯形分成平行四边形和直角三角形,利用平行四边形的对边相等得到CE =AD ,所以BE可以求出,在直角三角形中,根据∠B =30° ,利用勾股定理求出BE ,BC的长也就可以求出了.【解答】解:如图,过A作AE∥CD交BC于点E ,∵AD∥BC ,∴四边形AECD是平行四边形,∴CE =AD =4 ,∵∠B =30° ,∠C =60° ,∴∠BAE =90° ,∴AE =BE (直角三角形30°角所对的直角边等于斜边的一半) ,在Rt△ABE中,BE2=AB2+AE2 ,即BE2= (3)2+ (BE )2 ,BE2=27 +BE2 ,BE2=36 ,解得BE =6 ,∴BC =BE +EC =6 +4 =10.故答案为:10.【点评】通过作腰的平行线,把梯形分成平行四边形和直角三角形,再利用直角三角形30°角所对的直角边等于斜边的一半和勾股定理求解,考虑此题的突破口在于两个角的和是90°.16.如图,在△ABC中,∠C =90° ,AC =8cm ,AB的垂直平分线MN交AC于D ,连接BD ,假设sin∠DBC =,那么BC的长是4cm.【考点】解直角三角形.【专题】计算题;压轴题.【分析】根据线段垂直平分线的性质进行等量转换,运用三角函数定义解直角三角形.【解答】解:AB的垂直平分线MN交AC于D ,∴AD =BD.∵sin∠DBC ==,设CD =3a ,那么BD =5a ,AC =AD +CD =BD +CD =8 ,∴a =1 ,∴CD =3 ,BD =5 ,BC =4.【点评】此题考查了线段垂直平分线性质和三角函数定义的应用.17.如图,△P1OA1 ,△P2A1A2是等腰直角三角形,点P1 ,P2在函数y =(x>0 )的图象上,斜边OA1 ,A1A2都在x轴上,那么点A2的坐标是(,0 ).【考点】反比例函数图象上点的坐标特征;等腰直角三角形.【专题】数形结合.【分析】作P1B⊥y轴,P1A⊥x轴,根据等腰直角三角形的性质解答即可.【解答】解:作P1B⊥y轴,P1A⊥x轴,∵△P1OA1 ,△P2A1A2是等腰直角三角形,∴AP1=BP1 ,A1D =DA2=DP2 ,那么OA•OB =4 ,∴OA =OB =AA1=2 ,OA1=4 ,设A1D =x ,那么有(4 +x )x =4 ,解得x =﹣2 +2,或x =﹣2﹣2(舍去) ,那么OA2=4 +2x =4﹣4 +4=4,A2坐标为(4,0 ).故答案为:(4,0 ).【点评】此题考查等腰三角形的性质与反比例函数的性质的综合,一定经过某点的函数应符合这个点的横纵坐标.18.如图,△ABC中,∠BAC =90° ,AB =AC.P是AB的中点,正方形ADEF的边在线段CP上,那么正方形ADEF与△ABC的面积的比为.【考点】正方形的性质;勾股定理;等腰直角三角形.【分析】设AC与EF交于点M ,首||先根据∠BAC =90° ,∠DAF =90° ,可知∠PAD =∠MAF ,根据SAS证明△PAD≌△MAF ,可得AP =AM ,P为AB中点,那么知道M为AC中点,又可证明△AFM≌△CEM ,得出M为EF中点,设FM =x ,那么EF =AD =2x ,根据勾股定理得出AP=x ,那么AB =2x ,分别求出△ABC的面积和正方形ADEF的面积,即可求出它们的比值.【解答】解:设AC与EF交于点M ,∵∠BAC =90° ,∠DAF =90° ,∴∠PAD =∠MAF ,在△PAD和△MAF中,,∴△PAD≌△MAF ,那么AP =AM ,∵P为AB中点,AB =AC ,∴M为AC中点,在△AFM和△CEM中,,∴△AFM≌△CEM ,那么M为EF中点,设FM =x ,那么EF =AD =2x ,∴AM ==x ,那么AB =AC =2AM =2x ,∴S△ABC=×2x•2x =10x2 ,=2x•2x =4x2.S正方形ADEF那么正方形ADEF与△ABC的面积的比为==.故答案为:.【点评】此题考查了正方形的性质,涉及了全等三角形的证明,勾股定理的运用,解题关键是根据各边之间的关系求出两图形的面积.19.如图,抛物线的顶点为P (﹣2 ,2 ) ,与y轴交于点A (0 ,3 ).假设平移该抛物线使其顶点P沿直线移动到点P′ (2 ,﹣2 ) ,点A的对应点为A′ ,那么抛物线上PA段扫过的区域的面积为12.【考点】二次函数图象与几何变换.【分析】根据平移的性质得出四边形APP′A′是平行四边形,进而得出AD ,PP′的长,求出面积即可.【解答】解:连接AP ,A′P′ ,过点A作AD⊥PP′于点D ,由题意可得出:AP∥A′P′ ,AP =A′P′ ,∴四边形APP′A′是平行四边形,∵抛物线的顶点为P (﹣2 ,2 ) ,与y轴交于点A (0 ,3 ) ,平移该抛物线使其顶点P沿直线移动到点P′ (2 ,﹣2 ) ,∴PO ==2,∠AOP =45° ,又∵AD⊥OP ,∴△ADO是等腰直角三角形,∴PP′=2×2 =4,∴AD =DO =sin45°•OA =×3 =,∴抛物线上PA段扫过的区域的面积为:4×=12.故答案为:12.【点评】此题主要考查了二次函数图象与几何变换以及平行四边形面积求法和勾股定理等知识,根据得出AD ,PP′是解题关键.20.正方形A1B1C1O ,A2B2C2C1 ,A3B3C3C2 ,… ,按如下列图的方式放置.点A1 ,A2 ,A3 ,… ,和点C1 ,C2 ,C3 ,… ,分别在直线y =kx +b (k>0 )和x轴上,点B1、B2的坐标分别为B1 (1 ,1 ) ,B2 (3 ,2 ) ,那么B8的坐标是(28﹣1 ,28﹣1 )或(255 ,128 ).【考点】一次函数综合题.【专题】压轴题;规律型.【分析】首||先利用待定系数法求得直线的解析式,然后分别求得B1 ,B2 ,B3…的坐标,可以得到规律:B n (2n﹣1 ,2n﹣1 ) ,据此即可求解.【解答】解:∵B1的坐标为(1 ,1 ) ,点B2的坐标为(3 ,2 ) ,∴正方形A1B1C1O1边长为1 ,正方形A2B2C2C1边长为2 ,∴A1的坐标是(0 ,1 ) ,A2的坐标是:(1 ,2 ) ,代入y =kx +b得:,解得:,那么直线的解析式是:y =x +1.∵A1B1=1 ,点B2的坐标为(3 ,2 ) ,∴点A3的坐标为(3 ,4 ) ,∴A3C2=A3B3=B3C3=4 ,∴点B3的坐标为(7 ,4 ) ,∴B1的纵坐标是:1 =20 ,B1的横坐标是:1 =21﹣1 ,∴B2的纵坐标是:2 =21 ,B2的横坐标是:3 =22﹣1 ,∴B3的纵坐标是:4 =22 ,B3的横坐标是:7 =23﹣1 ,∴B n的纵坐标是:2n﹣1 ,横坐标是:2n﹣1 ,那么B n (2n﹣1 ,2n﹣1 ).∴B8的坐标是:(28﹣1 ,28﹣1 ) ,即(255 ,128 ).故答案为:(28﹣1 ,28﹣1 )或(255 ,128 ).【点评】此题主要考查了待定系数法求函数解析式和坐标的变化规律.此题难度较大,注意正确得到点的坐标的规律是解题的关键.三、解答题21.(1 )计算:(﹣1 )2021﹣|﹣|﹣(﹣)﹣2+2sin45°﹣(π﹣3.14 )0+(2 )先化简,再求值:•+,其中x满足x2﹣3x +2 =0.【考点】分式的化简求值;实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.【分析】(1 )先算乘方,绝||对值,负指数幂,特殊角的三角函数,0次幂以及开方,再算加减;(2 )先化简分式,进一步根据式子的特点整理,整体代入求得答案即可.【解答】解:(1 )原式=﹣1﹣﹣4 +2×﹣1 +2=﹣1﹣﹣4 +﹣1 +2=﹣4;(2 )原式=•+=x +=∵x2﹣3x +2 =0 ,∴x2+2 =3x∴原式=3.【点评】此题考查分式的化简求值,实数的混合运算,掌握运算方法是解决问题的关键.22.在建筑楼梯时,设计者要考虑楼梯的平安程度,如图(1 ) ,虚线为楼梯的斜度线,斜度线与地板夹角为倾角为θ ,一般情况下,倾角θ愈小,楼梯的平安度就越高.如图(2 ) ,设计者为提高楼梯平安度,要把楼梯倾角由θ1减至||θ2 ,这样楼梯占用地板的长度d1增加到d2 ,d1=4m ,∠θ1=45° ,∠θ2=30° ,求楼梯占用地板的长度增加了多少?【考点】解直角三角形的应用-坡度坡角问题.【专题】计算题.【分析】由题意得:增加局部是CD长,分别在Rt△ABC ,Rt△ABD中利用三角函数的定义即可求出BC ,BD长,然后利用条件即可求出CD长.【解答】解:在Rt△ABC中,BC =d1=4m ,∠ACB =∠θ1=45° ,∴AB =BC×tan45°=4tan45°=4m ,在Rt△ABD中,BD =d2 ,∠ADB =θ2=30° ,∴BD =AB÷tan30°=4÷=4m∴CD =d2﹣d1=BD﹣CB = (4﹣4 )m.∴楼梯占用地板的长度增加了(4﹣4 )m.【点评】此题考查的知识点是解直角三角形的应用,关键是当两个直角三角形共用一条线段时,应先利用三角函数算出这条线段的长度.23.如图,四边形ABCD是矩形,E是BD上的一点,∠BAE =∠BCE ,∠AED =∠CED ,点G是BC、AE延长线的交点,AG与CD相交于点F.(1 )求证:四边形ABCD是正方形;(2 )当AE =2EF时,判断FG与EF有何数量关系?并证明你的结论.【考点】相似三角形的判定与性质;全等三角形的判定与性质;矩形的性质;正方形的判定.【专题】几何综合题;压轴题.【分析】(1 )由∠BAE =∠BCE ,∠AED =∠CED ,利用三角形外角的性质,即可得∠CBE=∠ABE ,又由四边形ABCD是矩形,即可证得△ABD与△BCD是等腰直角三角形,继而证得四边形ABCD是正方形;(2 )由题意易证得△ABE∽△FDE ,△ADE∽△GBE ,△ADF∽△GCF ,由AE =2EF ,利用相似三角形的对应边成比例,即可求得FG =3EF.【解答】(1 )证明:∵∠CED是△BCE的外角,∠AED是△ABE的外角,∴∠CED =∠CBE +∠BCE ,∠AED =∠BAE +∠ABE ,∵∠BAE =∠BCE ,∠AED =∠CED ,∴∠CBE =∠ABE ,∵四边形ABCD是矩形,∴∠ABC =∠BCD =∠BAD =90° ,AB =CD ,∴∠CBE =∠ABE =45° ,∴△ABD与△BCD是等腰直角三角形,∴AB =AD =BC =CD ,∴四边形ABCD是正方形;(2 )当AE =2EF时,FG =3EF.证明:∵四边形ABCD是正方形,∴AB∥CD ,AD∥BC ,∴△ABE∽△FDE ,△ADE∽△GBE ,∵AE =2EF ,∴BE:DE =AE:EF =2 ,∴BG:AD =BE:DE =2 ,即BG =2AD ,∵BC =AD ,∴CG =AD ,∵△ADF∽△GCF ,∴FG:AF =CG:AD ,即FG =AF =AE +EF =3EF.【点评】此题考查了相似三角形的判定与性质、矩形的性质,正方形的判定与性质、等腰直角三角形的性质以及三角形外角的性质.此题难度适中,注意数形结合思想的应用.24.如图,反比例函数的图象经过点(,8 ) ,直线y =﹣x +b经过该反比例函数图象上的点Q (4 ,m ).(1 )求上述反比例函数和直线的函数表达式;(2 )设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P ,连接0P、OQ ,求△OPQ的面积.【考点】反比例函数综合题.【专题】综合题.【分析】(1 )把点(,8 )代入反比例函数,确定反比例函数的解析式为y =;再把点Q (4 ,m )代入反比例函数的解析式得到Q的坐标,然后把Q的坐标代入直线y =﹣x +b ,即可确定b的值;(2 )把反比例函数和直线的解析式联立起来,解方程组得到P点坐标;对于y =﹣x +5 ,令y =0 ,求出A点坐标,然后根据S△OPQ=S△AOB﹣S△OBP﹣S△OAQ进行计算即可.【解答】解:(1 )把点(,8 )代入反比例函数,得k =×8 =4 ,∴反比例函数的解析式为y =;又∵点Q (4 ,m )在该反比例函数图象上,∴4•m =4 ,解得m =1 ,即Q点的坐标为(4 ,1 ) ,而直线y =﹣x +b经过点Q (4 ,1 ) ,∴1 =﹣4 +b ,解得b =5 ,∴直线的函数表达式为y =﹣x +5;(2 )联立,解得或,∴P点坐标为(1 ,4 ) ,对于y =﹣x +5 ,令y =0 ,得x =5 ,∴A点坐标为(5 ,0 ) ,∴S△OPQ=S△AOB﹣S△OBP﹣S△OAQ=×5×5﹣×5×1﹣×5×1=.【点评】此题考查了点在图象上,点的横纵坐标满足图象的解析式以及求两个图象交点的方法(转化为解方程组);也考查了利用面积的和差求图形面积的方法.25.我市的重大惠民工程﹣﹣公租房建设已陆续竣工,方案10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积y (单位:百万平方米) ,与时间x的关系是y =﹣x +5 , (x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y (单位:百万平方米) ,与时间x的关系是y =﹣x +(x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z (单位:元/m2 )与时间x (单位:年,1≤x≤10且x为整数)满足一次函数关系如表:z (元/m2 ) 50 52 54 56 58 …x (年) 1 2 3 4 5 …。
2016届九年级下学期入学考试数学试题

初三入学考试数学参考答案×1089.(1)(1)ab a a +- 10.3 11.83 12.2m ≤ 13.24514.(0,256) 解析:A (0,1) 1(0,4)A 2(0,16)A 3(0,64)A (0,4)n n A 15.8中位数为3 (2)4950次17.(1)略 (2)4918.(1)2y x =-- (2)6AOB S ∆=(3)40x -<<或2x >19.解析:外国军舰到达C 地需56522135h -≈ 中国海监船到达C 地需101303h =∵2153> ∴能够及时赶到20.解:(1)设甲工厂每天加工x 件,则乙工厂每天加工(8)x +件,依题960960208x x -=+ ∴116x =,224x =-经检验116x =是原分式方程的根且符合题意,224x =-是原分式方程的根但不符合题意 ∴舍去 ∴824x +=∴甲工厂每天加工16件,乙工厂每天加工24件(2)设乙工厂向公司中报加工费用每天y 元,则960960(50)(80050)2416y +⨯+≤ ∴1225y ≤ ∴乙工厂向公司报加工费用每天最多1225元21.解:(1)证ADE CBF ∆≅∆,可证AE CF .(2)∵四边形AECF O 为菱形∴AE CE =∵,EM BC BM CM ⊥= ∴BE=CE∵AE=BE ∴∠1=∠3=∠5=∠6∵∠1+∠3+∠5=90︒∵∠1=∠3=∠5=30︒过E 作EG AB ⊥于G ,则:2:3AE AG =∴:23:23:1AB AE ==22.(1)证明:连接,OD BD∵AB 为直径∴BD AC ⊥ ∵E 为BC 中点∴DE=CE ∴∠1=∠C ∵OA=OD ∴∠A =∠2∥ =∵∠A+∠C=90︒, ∴1290∠+∠=︒∴DE CD ⊥于点D ,又OD 为半径∴DE 为⊙O 相切.(2)证明:∵O 为AB 中点,E 为BC 中点,∴OE 12AC ,∴AC=2OE ∵90,90C CBD C A ∠+∠=︒∠+∠=︒ ∴,2CBD A C C ∠=∠∠=∠ ∴△CBD ∽△CAB ∴CB CD CA CB= ∴2BC CD AC =⋅ ∵2AC OE = ∴22BC CD OE =⋅(3)由(1),1,2DE BC = ∴28BC DE == 在Rt BCD ∆中,cos CD C BC =∴216cos 833CD BC C =⋅=⨯= 在Rt ABC ∆中,cos BC C AC =∴3812cos 2BC AC C ==⨯= ∴16201233AD AC CD =-=-= 23.解:(1)设购买x 台时,单价恰为3900元,则450050(10)3900x --=∴22x = ∴购买22台时,销售单价恰为3900元(2)①当010x ≤≤时,(45003600)900y x x =-=②当1022x <≤时,2[450050(10)3600]501300y x x x x =⋅---=-+ ③当22x >时,(39003600)300y x x =-=综上2900501400(1022)300(22)x y x x x x x ⎧⎪=-+<⎨⎪ >⎩≤①当010x ≤≤时,900y x = ∵900≥0,∴y 随x 增大而增大 ∴当10x =时,y 最大且max 9000y =②当1022x <≤时,2250140050(14)9800y x x x =-+=--+ ∵500-<,对称轴为14x = ∵1022x <≤,∴当14x =时,y 最大且max 9800y =. ③当 22x >时 y=300x ,∵300≥0,∴y 随x 增大而增大 ∵2225x <≤,∴当25x =时,y 最大且max 7500y =,∵750090009800<<∴一次性购买14台电脑时,利润最大且为9800元(3)①当010x ≤≤时 900y x = ∵900>0,∴y 随x 增大而增大 ②当1022x <≤时,2250140050(14)9800y x x x =-+=--+∥ =∵500-<当1014x <≤时,y 随x 增大而增大当1422x <≤时,y 随x 增大而减小∴最低单价应调为450050(1410)4300--=元综上,商场应将最低销售单价调为4300元24.(1)设抛物线的解析式为(2)y ax x =+∵过点(3,3)B - ∴3(1)3x a --⋅= ∴1a = ∴2(2)2y x x x x =+=+(2)存在,且(2,0)G -,最大值为1理由:过G 作GH y 轴交BC 于点H ,设21(2)G x x x +,设:(0)lBC y kx b k =+≠ ∵222(1)1y x x x =+=+- ∴(1,1)C --又(3,3)B - ∴133k b k b -+=-⎧⎨-+=⎩∴23k b =-⎧⎨=-⎩ ∴:23BC l y x =-- ∴(,23)H x x -- ∴21(232)(13)2GBC S x x x ∆=----⋅-+=2243(2)1x x x ---=-++ ∵10-<,对称轴为2x =-∴当2x =-时,max 1S S =最大且,此时,(2,0)G -(3)存在,且17(,)39P 或(3,15) 证明:∵(0,0)O , (3,3),(1,1)B C ---∴2222223318,112OB OC =+==+= 2224220BC =+= ∴222OB OC BC += ∴90BOC PMA ∠=︒=∠设2(,2)P x x x +∴22,2PM x x MA x =+=+①PMA BOC ∆∆ 则PM MA BO OC =,即222322x x x ++= ∴123,2x x ==-(舍) ∴(3,15)P ②△AMP △BOC ,则AM MP BO OC =,即222322x x x ++= ∴1212,3x x =-= ∴17(,)39P 综上,存在P 点,且(3,15)P 或17(,)39(4)123(3,3),(1,3),(1,1)D D D ---。
2016年下期新生入学考试题

2016年下期新生入学测试题(共50分)姓名:考号:一: 按句意填写单词(10分)1. ---What _____is it? ---It’s red.2. ---What’s _____ name? --- My name’s Jenny.3. ---What’s his phone ? --- It’s 281---9176.4. --- this your pencil? ---Yes, it is.5. ---Please Alan at 495---3539.6. ---Is Tom your brother? ---No, isn’t.7. Your uncle’s daughter is your .8. Thanks the photo of your family.9. ---Where my books? ---I don’t know.10. you have a soccer ball?---Yes, I do.二:单项选择(10分)11. ---I’m Gina. Nice to meet you!--- .A. HelloB. I’m Lina.C. Nice to meet you, too.12. --- is Tom?---He is at home.A. WhenB. WhereC. What13. ---Let’s play baseball.--- , but I don’t have a ball.A.OK.B. Yes.C. Thank you.14. Please these things to your brother.A. takeB. bringC. buy15.I like movie Rusb Hour very much. It’s an action movie.A. heB. hisC. him16. Tom’s pictures are here. Please color .A. it greenB. them greenC. green them17.---Come in and sit down.--- .A. Thank you.B. I’m sorryC. Fine.18.How many days has a week? It has .A. sevenB. sixC. five19. is the baby?A. How manyB. How oldC. how much20. these books? In her backpack.A. Are thereB. Where’reC. Are they三:用所给单词的恰当形式填空。
初一下开学测试试题

亲爱的同学,又到了展示你才能的时刻了,请你轻松地走进考场,微笑着拿起语文试卷,愉快地接受检验,相信你平日的辛勤耕耘定会在这里收获到累累硕果。
2015—2016学年度第二学期开学测试七年级语文试卷2016.02试卷满分:100分考试时间:45分钟一、语文基础。
下面各题均有四个选项,其中只有一个符合题意,请将答案写在上面的表格中。
(共18分。
每小题3分)1.阅读下面的文字,完成第(1)—(2)题。
(共6分)人间的天堂,神奇的九寨!九寨沟,位于四川省阿坝州九寨沟县漳扎镇,因曾经仅有九个藏族村寨坐落在此而得名。
沟内遍布原始森林,分布着无数的河湖,飞动与静谧.结合,①无穷,美丽到让人失语。
对于成年人,这里是重归儿时的童话世界;对于都市族,这里是无忧无虑的人间仙境。
这里,就是九寨沟。
九寨沟中的天鹅海海拔2905米,与草海的下游相连,广阔的湖面大部分已淤积成浅滩,半为沼泽湖泊。
浅滩上绿草如茵,一道清流在绿茵中蜿蜒流过,滋养着这一方水草。
天鹅海静静地躺卧在山谷里。
由于这一带②肥美,天鹅常在这里栖.息繁殖,海子也因此得名。
不过因为天鹅是(侯候)鸟,会根据季节的③而去留,所以游人并不容易在此见到它们的芳踪。
(1)对文中加点字的注音和词语的选择,全都正确的一项是(3分)..A.静谧.(bì)栖.息(qī)候鸟B.静谧.(mì)栖.息(qī)候鸟C.静谧.(bì)栖.息(xī)侯鸟D.静谧.(mì)栖.息(xī)侯鸟(2)根据语意,分别在横线①②③处填入词语,最恰当的一项是(3分)..A.①变幻②水草③变换B.①变换②水草③变幻C.①变幻②水藻③变换D.①变换②水藻③变幻的一项是(3分)2.对下列句子中所使用的修辞方法及作用理解不正确...A.盼望着,盼望着,东风来了,春天的脚步近了。
(朱自清《春》)理解:这句话运用排比、拟人的修辞表达了盼春的急切心情。
B.天儿越晴,水藻越绿,就凭这些绿的精神,水也不忍得冻上,况且那些长枝的垂柳还要在水里照个影儿呢!(老舍《济南的冬天》)理解:这句话用了拟人的修辞,突出了济南冬天水的温、清的特点。
2016届九年级下学期开学考试数学试卷【解析版】

2021届九年级||下学期开学考试数学试卷一、选择题(本大题共6题,每题4分,总分值24分)1.抛物线y =﹣(x﹣2 )2+3的顶点坐标是()A.(﹣2 ,3 ) B.(2 ,3 ) C.(2 ,﹣3 ) D.(﹣2 ,﹣3 )2.点D、E分别在△ABC的边AB、AC上,以下给出的条件中,不能判定DE∥BC的是() A.BD:AB =CE:AC B.DE:BC =AB:AD C.AB:AC =AD:AE D.AD:DB=AE:EC3.在4×4网格中,∠α的位置如下列图,那么tanα的值为()A. B.C.2 D.4.在直角△ABC中,∠C =90° ,∠A、∠B与∠C的对边分别是a、b和c ,那么以下关系中,正确的选项是()A.cosA =B.tanA = C.sinA = D.cosA =5.在以下y关于x的函数中,一定是二次函数的是()A.y =x2B.y =C.y =kx2D.y =k2x6.如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE =3米) ,测得自己影子EF的长为2米,小明的身高是1.5米,那么路灯A的高度AB是()A.4.5米B.6米C.7.2米D.8米二、填空题(本大题共12题,每题4分,总分值48分)7.=,那么的值是.8.点P是线段AB的黄金分割点(AP>BP ) ,那么=.9.如图,在平行四边形ABCD中,点E在BC边上,且CE:BC =2:3 ,AC与DE相交于点F ,假设S△AFD=9 ,那么S△EFC=.10.如果α是锐角,且tanα=cot20° ,那么α=度.11.计算:2sin60°+tan45°=.12.如果一段斜坡的坡角是30° ,那么这段斜坡的坡度是.(请写成1:m的形式) 13.如果抛物线y = (m﹣1 )x2的开口向上,那么m的取值范围是.14.将抛物线y =﹣(x﹣3 )2+5向下平移6个单位,所得到的抛物线的顶点坐标为.15.抛物线经过A (0 ,﹣3 )、B (2 ,﹣3 )、C (4 ,5 ) ,判断点D (﹣2 ,5 )是否在该抛物线上.你的结论是:(填"是〞或"否〞).16.如图,正方形DEFG内接于Rt△ABC ,∠C =90° ,AE =4 ,BF =9 ,那么tanA =.17.如图,梯形ABCD中,AD∥BC ,AB =DC ,点P是AD边上一点,联结PB、PC ,且AB2=AP•PD ,那么图中有对相似三角形.18.如图,在Rt△ABC中,∠C =90° ,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果=m ,=n.那么m与n满足的关系式是:m =(用含n的代数式表示m ).三、解答题(本大题共7题,总分值78分)19.解方程:﹣=2.20.二次函数y =﹣2x2+bx +c的图象经过点A (0 ,4 )和B (1 ,﹣2 ).(1 )求此函数的解析式;并运用配方法,将此抛物线解析式化为y =a (x +m )2+k的形式;(2 )写出该抛物线顶点C的坐标,并求出△CAO的面积.21.抛物线y =﹣x2+bx +c的对称轴是直线x =﹣1 ,且经过点(2 ,﹣3 ) ,求这个二次函数的表达式.22.如图7 ,某人在C处看到远处有一凉亭B ,在凉亭B正东方向有一棵大树A ,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574 ,cos35°≈0.819 ,tan35°≈0.700 )23.如图,等腰梯形ABCD中,AD∥BC ,AD =1 ,BC =3 ,AB =CD =2 ,点E在BC边上,AE与BD交于点F ,∠BAE =∠DBC.(1 )求证:△ABE∽△BCD;(2 )求tan∠DBC的值;(3 )求线段BF的长.24.如图,在平面直角坐标系内,直线y =x +4与x轴、y轴分别相交于点A和点C ,抛物线y =x2 +kx +k﹣1图象过点A和点C ,抛物线与x轴的另一交点是B ,(1 )求出此抛物线的解析式、对称轴以及B点坐标;(2 )假设在y轴负半轴上存在点D ,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D 的坐标.25.如图,在等腰Rt△ABC中,∠C =90° ,斜边AB =2 ,假设将△ABC翻折,折痕EF分别交边AC、边BC于点E和点F (点E不与A点重合,点F不与B点重合) ,且点C落在AB边上,记作点D.过点D作DK⊥AB ,交射线AC于点K ,设AD =x ,y =cot∠CFE ,(1 )求证:△DEK∽△DFB;(2 )求y关于x的函数解析式并写出定义域;(3 )联结CD ,当=时,求x的值.2021届九年级||下学期开学考试数学试卷参考答案与试题解析一、选择题(本大题共6题,每题4分,总分值24分)1.抛物线y =﹣(x﹣2 )2+3的顶点坐标是()A.(﹣2 ,3 ) B.(2 ,3 ) C.(2 ,﹣3 ) D.(﹣2 ,﹣3 )【考点】二次函数的性质.【分析】直接根据二次函数的顶点式进行解答即可.【解答】解:∵抛物线的解析式为:y =﹣(x﹣2 )2+3 ,∴其顶点坐标为(2 ,3 ).应选B.【点评】此题考查的是二次函数的性质,熟知二次函数的顶点式是解答此题的关键.2.点D、E分别在△ABC的边AB、AC上,以下给出的条件中,不能判定DE∥BC的是() A.BD:AB =CE:AC B.DE:BC =AB:AD C.AB:AC =AD:AE D.AD:DB=AE:EC【考点】平行线分线段成比例.【分析】根据选项只要能推出=或=,再根据相似三角形的判定推出△ADE∽△ABC ,推出∠ADE =∠B ,根据平行线的判定推出DE∥BC ,即可得出选项.【解答】解:A、∵BD:AB =CE:AC ,∴=,∴=,∴1﹣=1﹣,∴=,∵∠A =∠A ,∴△ADE∽△ABC ,∴∠ADE =∠B ,∴DE∥BC ,正确,故本选项错误;B、∵根据DE:BC =AB:AD不能推出△ADE∽△ABC ,∴不能推出∠ADE =∠B ,∴不能推出DE∥BC ,错误,故本选项正确;C、∵AB:AC =AD:AE ,∴=,∴=,∵∠A =∠A ,∴△ADE∽△ABC ,∴∠ADE =∠B ,∴DE∥BC ,正确,故本选项错误;D、∵AD:DB =AE:EC ,∴=,∴=,∴=,∴﹣1 =﹣1 ,∴=,∵∠A =∠A ,∴△ADE∽△ABC ,∴∠ADE =∠B ,∴DE∥BC ,正确,故本选项错误;应选B.【点评】此题考查了平行线分线段成比例定理和相似三角形的性质和判定,平行线的判定的应用,解此题的关键是能推出△ADE≌△ABC ,题目比较好,难度适中.3.在4×4网格中,∠α的位置如下列图,那么tanα的值为()A. B.C.2 D.【考点】锐角三角函数的定义.【专题】网格型.【分析】根据"角的正切值=对边÷邻边〞求解即可.【解答】解:由图可得,tanα=2÷1 =2.应选C.【点评】此题考查了锐角三角函数的定义,正确理解正切值的含义是解决此题的关键.4.在直角△ABC中,∠C =90° ,∠A、∠B与∠C的对边分别是a、b和c ,那么以下关系中,正确的选项是()A.cosA =B.tanA = C.sinA = D.cosA =【考点】锐角三角函数的定义.【分析】根据三角函数定义:(1 )正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.(2 )余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.(3 )正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.分别进行分析即可.【解答】解:在直角△ABC中,∠C =90° ,那么A、cosA =,故本选项错误;B、tanA =,故本选项错误;C、sinA =,故本选项正确;D、cosA =,故本选项错误;应选:C.【点评】此题主要考查了锐角三角函数的定义,关键是熟练掌握锐角三角函数的定义.5.在以下y关于x的函数中,一定是二次函数的是()A.y =x2B.y =C.y =kx2D.y =k2x【考点】二次函数的定义.【分析】根据二次函数的定义形如y =ax2+bx +c (a≠0 )是二次函数.【解答】解:A、是二次函数,故A符合题意;B、是分式方程,故B错误;C、k =0时,不是函数,故C错误;D、k =0是常数函数,故D错误;应选:A.【点评】此题考查二次函数的定义,形如y =ax2+bx +c (a≠0 )是二次函数.6.如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE =3米) ,测得自己影子EF的长为2米,小明的身高是1.5米,那么路灯A的高度AB是()A.4.5米B.6米C.7.2米D.8米【考点】相似三角形的应用;中|心投影.【专题】计算题.【分析】由MC∥AB可判断△DCM∽△DAB ,根据相似三角形的性质得=,同理可得=,然后解关于AB和BC的方程组即可得到AB的长.【解答】解:∵MC∥AB ,∴△DCM∽△DAB ,∴=,即=① ,∵NE∥AB ,∴△FNE∽△FAB ,∴=,即=② ,∴=,解得BC =3 ,∴=,解得AB =6 ,即路灯A的高度AB为6m.应选B.【点评】此题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和"在同一时刻物高与影长的比相等〞的原理解决.二、填空题(本大题共12题,每题4分,总分值48分)7.=,那么的值是.【考点】比例的性质.【分析】根据分比性质,可得答案.【解答】解:由分比性质,得==,故答案为:.【点评】此题考查了比例的性质,利用了分比性质:=⇒=.8.点P是线段AB的黄金分割点(AP>BP ) ,那么=.【考点】黄金分割.【分析】把一条线段分成两局部,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比.【解答】解:∵点P是线段AB的黄金分割点(AP>BP ) ,∴==.故答案为.【点评】此题考查了黄金分割的定义,牢记黄金分割比是解题的关键.9.如图,在平行四边形ABCD中,点E在BC边上,且CE:BC =2:3 ,AC与DE相交于点F ,假设S△AFD=9 ,那么S△EFC=4.【考点】相似三角形的判定与性质;平行四边形的性质.【专题】推理填空题.【分析】由于四边形ABCD是平行四边形,所以得到BC∥AD、BC =AD ,而CE:BC =2:3 ,由此即可得到△AFD∽△CFE ,它们的相似比为3:2 ,最||后利用相似三角形的性质即可求解.【解答】解:∵四边形ABCD是平行四边形,∴BC∥AD、BC =AD ,而CE:BC =2:3 ,∴△AFD∽△CFE ,且它们的相似比为3:2 ,∴S△AFD:S△EFC= ()2 ,而S△AFD=9 ,∴S△EFC=4.故答案为:4.【点评】此题主要考查了相似三角形的判定与性质,解题首||先利用平行四边形的构造相似三角形的相似条件,然后利用其性质即可求解.10.如果α是锐角,且tanα=cot20° ,那么α=70度.【考点】互余两角三角函数的关系.【分析】根据一个角的正切值等于它的余角的余切值即可求解.【解答】解:∵tanα=cot20° ,∴∠α+20°=90° ,即∠α=90°﹣20°=70°.故答案为70.【点评】此题考查了互为余角的锐角三角函数关系:一个角的正切值等于它的余角的余切值.11.计算:2sin60°+tan45°=+1.【考点】特殊角的三角函数值.【分析】根据特殊三角函数值,可得答案.【解答】解:原式=2×+1=+1 ,故答案为:+1.【点评】此题考查了特殊角的三角函数值,解决此类题目的关键是熟记特殊角的三角函数值.12.如果一段斜坡的坡角是30° ,那么这段斜坡的坡度是1:.(请写成1:m的形式)【考点】解直角三角形的应用-坡度坡角问题.【分析】坡比等于坡角的正切值,据此即可求解.【解答】解:i =tanα=tan30°==1:,故答案是:1:.【点评】此题主要考查了坡比与坡角的关系,注意坡比一般表示成1:a的形式.13.如果抛物线y = (m﹣1 )x2的开口向上,那么m的取值范围是m>1.【考点】二次函数的性质.【分析】根据二次函数的性质可知,当抛物线开口向上时,二次项系数m﹣1>0.【解答】解:因为抛物线y = (m﹣1 )x2的开口向上,所以m﹣1>0 ,即m>1 ,故m的取值范围是m>1.【点评】解答此题要掌握二次函数图象的特点.14.将抛物线y =﹣(x﹣3 )2+5向下平移6个单位,所得到的抛物线的顶点坐标为(3 ,﹣1 ).【考点】二次函数图象与几何变换.【专题】计算题.【分析】根据二次函数的性质得抛物线y =﹣(x﹣3 )2+5的顶点坐标为(3 ,5 ) ,然后根据点平移的规律,点(3 ,5 )经过平移后得到对应点的坐标为(3 ,﹣1 ) ,从而得到新抛物线的顶点坐标.【解答】解:抛物线y =﹣(x﹣3 )2+5的顶点坐标为(3 ,5 ) ,点(3 ,5 )向下平移6个单位得到对应点的坐标为(3 ,﹣1 ) ,所以新抛物线的顶点坐标为(3 ,﹣1 ).故答案为(3 ,﹣1 ).【点评】此题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.15.抛物线经过A (0 ,﹣3 )、B (2 ,﹣3 )、C (4 ,5 ) ,判断点D (﹣2 ,5 )是否在该抛物线上.你的结论是:是(填"是〞或"否〞).【考点】二次函数图象上点的坐标特征.【专题】计算题.【分析】利用点A与点B的坐标特征得到抛物线的对称轴为直线x =1 ,然后根据抛物线的对称性可判断点C (4 ,5与点D (﹣2 ,5 )是抛物线上的对称点.【解答】解:∵抛物线经过A (0 ,﹣3 )、B (2 ,﹣3 ) ,而点A与点B关于直线x =1对称,∴抛物线的对称轴为直线x =1 ,∴点C (4 ,5 )关于直线x =1的对称点D (﹣2 ,5 )在抛物线上.故答案为:是.【点评】此题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了抛物线的对称性.16.如图,正方形DEFG内接于Rt△ABC ,∠C =90° ,AE =4 ,BF =9 ,那么tanA =.【考点】相似三角形的判定与性质;锐角三角函数的定义.【分析】根据条件可证明△ADE∽△GFB ,利用相似三角形的性质可求得DE ,在Rt△ADE中,由正切函数的定义可求得tanA.【解答】解:∵四边形DEFG为正方形,∴∠DEA =∠GFB =90° ,DE =GF ,∵∠C =90° ,∴∠A +∠B =∠A +∠ADE =90° ,∴∠ADE =∠B ,∴△ADE∽△GFB ,∴=,即=,解得DE =6 ,∴tanA ===,故答案为:.【点评】此题主要考查相似三角形的判定和性质,由条件证明三角形相似求得DE的长是解题的关键.17.如图,梯形ABCD中,AD∥BC ,AB =DC ,点P是AD边上一点,联结PB、PC ,且AB2=AP•PD ,那么图中有3对相似三角形.【考点】相似三角形的判定.【分析】由AD∥BC ,AB =DC可判断梯形ABCD为等腰梯形,那么∠A =∠D ,由AB2=AP•PD 得AB•CD =AP•PD ,于是根据两组对应边的比相等且夹角对应相等的两个三角形相似判断△ABP∽△DPC ,由相似的性质得∠ABP =∠DPC ,接着利用AD∥BC得到∠DPC =∠PCB ,∠APB =∠PBC ,那么∠PCB =∠ABP ,于是根据有两组角对应相等的两个三角形相似得到△ABP∽△PCB ,所以△DPC∽△DPC.【解答】解:∵AD∥BC ,AB =DC ,∴梯形ABCD为等腰梯形,∴∠A =∠D ,∵AB2=AP•PD ,∴AB•CD =AP•PD ,即=,∴△ABP∽△DPC ,∴∠ABP =∠DPC ,∵AD∥BC ,∴∠DPC =∠PCB ,∠APB =∠PBC ,∴∠PCB =∠ABP ,∴△ABP∽△PCB ,∴△DPC∽△DPC.故答案为3.【点评】此题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.18.如图,在Rt△ABC中,∠C =90° ,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果=m ,=n.那么m与n满足的关系式是:m =2n +1(用含n的代数式表示m ).【考点】平行线分线段成比例;旋转的性质.【专题】计算题.【分析】作DH⊥AC于H ,如图,根据旋转的性质得DE =DC ,那么利用等腰三角形的性质得EH =CH ,由=n可得AE =2nEH =2nCH ,再根据平行线分线段成比例,由DH∥BC得到=,所以m =,然后用等线段代换后约分即可.【解答】解:作DH⊥AC于H ,如图,∵线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处,∴DE =DC ,∴EH =CH ,∵=n ,即AE =nEC ,∴AE =2nEH =2nCH ,∵∠C =90° ,∴DH∥BC ,∴=,即m ===2n +1.故答案为:2n +1.【点评】此题考查了平行线分线段成比例定理的应用,解此题的关键是能根据定理得出比例式,注意:一组平行线截两条直线,所截得的线段对应成比例.也考查了旋转的性质和等腰三角形的性质.三、解答题(本大题共7题,总分值78分)19.解方程:﹣=2.【考点】解分式方程.【专题】计算题.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:2﹣3x +x +2 =2x2﹣8 ,整理得:x2+x﹣6 =0 ,即(x﹣2 ) (x +3 ) =0 ,解得:x =2或x =﹣3 ,经检验x =2是增根,分式方程的解为x =﹣3.【点评】此题考查了解分式方程,解分式方程的根本思想是"转化思想〞,把分式方程转化为整式方程求解.解分式方程一定注意要验根.20.二次函数y =﹣2x2+bx +c的图象经过点A (0 ,4 )和B (1 ,﹣2 ).(1 )求此函数的解析式;并运用配方法,将此抛物线解析式化为y =a (x +m )2+k的形式;(2 )写出该抛物线顶点C的坐标,并求出△CAO的面积.【考点】二次函数的三种形式.【分析】(1 )将A (0 ,4 )和B (1 ,﹣2 )代入y =﹣2x2+bx +c求得b ,c的值,得到此函数的解析式;再利用配方法先提出二次项系数,然后加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;(2 )由顶点式可得顶点C的坐标,再根据三角形的面积公式即可求出△CAO的面积.【解答】解:(1 )将A (0 ,4 )和B (1 ,﹣2 )代入y =﹣2x2+bx +c ,得,解得,所以此函数的解析式为y =﹣2x2﹣4x +4;y =﹣2x2﹣4x +4 =﹣2 (x2+2x +1 ) +2 +4 =﹣2 (x +1 )2+6;(2 )∵y =﹣2 (x +1 )2+6 ,∴C (﹣1 ,6 ) ,∴△CAO的面积=×4×1 =2.【点评】此题考查了用待定系数法求二次函数的解析式,二次函数解析式的三种形式,二次函数的性质以及三角形的面积,难度适中.正确求出函数的解析式是解题的关键.21.抛物线y =﹣x2+bx +c的对称轴是直线x =﹣1 ,且经过点(2 ,﹣3 ) ,求这个二次函数的表达式.【考点】待定系数法求二次函数解析式.【分析】由抛物线的一般形式可知:a =﹣1 ,由对称轴方程x =﹣,可得一个等式﹣① ,然后将点(2 ,﹣3 )代入y =﹣x2+bx +c即可得到等式﹣4 +2b +c =﹣3② ,然后将①②联立方程组解答即可.【解答】解:根据题意,得:,解得,所求函数表达式为y =﹣x2﹣2x +5.【点评】此题考查了用待定系数法求二次函数的解析式,解题的关键是:熟练掌握待定系数法及对称轴表达式x =﹣.22.如图7 ,某人在C处看到远处有一凉亭B ,在凉亭B正东方向有一棵大树A ,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574 ,cos35°≈0.819 ,tan35°≈0.700 )【考点】解直角三角形的应用-仰角俯角问题.【分析】过点C⊥AB于点D ,在Rt△ACD中,求出AD、CD的值,然后在Rt△BCD中求出BD的长度,继而可求得AB的长度.【解答】解:过点C⊥AB于点D ,在Rt△ACD中,∵∠ACD =35° ,AC =100m ,∴AD =100•sin∠ACD =100×0.574 =57.4 (m ) ,CD =100•cos∠ACD =100×0.819 =81.9 (m ) ,在Rt△BCD中,∵∠BCD =45° ,∴BD =CD =81.9m ,那么AB =AD +BD =57.4 +81.9≈139 (m ).答:A、B之间的距离约为139米.【点评】此题考查了直角三角形的应用,解答此题的关键是根据方向角构造直角三角形,利用三角函数解直角三角形.23.如图,等腰梯形ABCD中,AD∥BC ,AD =1 ,BC =3 ,AB =CD =2 ,点E在BC边上,AE与BD交于点F ,∠BAE =∠DBC.(1 )求证:△ABE∽△BCD;(2 )求tan∠DBC的值;(3 )求线段BF的长.【考点】相似三角形的判定与性质;等腰梯形的性质.【分析】(1 )根据等腰梯形可得到∠ABE =∠C ,结合条件可证得结论;(2 )过D作DG⊥BC ,那么可求得BG、CG ,在Rt△DCG中可求得DG ,在Rt△BGD中由正切函数的定义可求得tan∠DBC;(3 )由(2 )可求得BD ,结合(1 )中的相似可求得BE ,再利用平行线分线段成比例得到=,代入可求得BF.【解答】(1 )证明:∵四边形ABCD为等腰梯形,∴∠ABE =∠C ,且∠BAE =∠DBC ,∴△ABE∽△BCD;(2 )解:过D作DG⊥BC于点G ,∵AD =1 ,BC =3 ,∴CG =(BC﹣AD ) =1 ,BG =2 ,又∵在Rt△DGC中,CD =2 ,CG =1 ,∴DG =,在Rt△BDG中,tan∠DBC ==;(3 )解:由(2 )在Rt△BGD中,由勾股定理可求得BD =,由(1 )△ABE∽△BCD可得=,即==,解得BE =,又∵AD∥BC ,∴=,且DF =BD﹣BF ,∴=,解得BF =.【点评】此题主要考查相似三角形的判定和性质及三角函数的定义,在(2 )中构造直角三角形,求得DG是解题的关键,在(3 )中求得BE、BD的长是解题的关键.24.如图,在平面直角坐标系内,直线y =x +4与x轴、y轴分别相交于点A和点C ,抛物线y =x2 +kx +k﹣1图象过点A和点C ,抛物线与x轴的另一交点是B ,(1 )求出此抛物线的解析式、对称轴以及B点坐标;(2 )假设在y轴负半轴上存在点D ,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D 的坐标.【考点】二次函数综合题.【专题】综合题.【分析】(1 )先求出A、C两点的坐标,再代入抛物线的解析式,就可求出该抛物线的解析式,然后根据抛物线的对称轴方程x =﹣求出抛物线的对称轴,根据抛物线上点的坐标特征求出点B的坐标;(2 )易得∠OAC =∠OCA ,∠ABC>∠ADC ,由此根据条件即可得到△CAD∽△ABC ,然后运用相似三角形的性质可求出CD的长,由此可得到OD的长,就可解决问题.【解答】解:(1 )由x =0得y =0 +4 =4 ,那么点C的坐标为(0 ,4 );由y =0得x +4 =0 ,解得x =﹣4 ,那么点A的坐标为(﹣4 ,0 );把点C (0 ,4 )代入y =x2+kx +k﹣1 ,得k﹣1 =4 ,解得:k =5 ,∴此抛物线的解析式为y =x2+5x +4 ,∴此抛物线的对称轴为x =﹣=﹣.令y =0得x2+5x +4 =0 ,解得:x1=﹣1 ,x2=﹣4 ,∴点B的坐标为(﹣1 ,0 ).(2 )∵A (﹣4 ,0 ) ,C (0 ,4 ) ,∴OA =OC =4 ,∴∠OCA =∠OAC.∵∠AOC =90° ,OB =1 ,OC =OA =4 ,∴AC ==4,AB =OA﹣OB =4﹣1 =3.∵点D在y轴负半轴上,∴∠ADC<∠AOC ,即∠ADC<90°.又∵∠ABC>∠BOC ,即∠ABC>90° ,∴∠ABC>∠ADC.∴由条件"以A、C、D为顶点的三角形与△ABC相似〞可得△CAD∽△ABC ,∴=,即=,解得:CD =,∴OD =CD﹣CO =﹣4 =,∴点D的坐标为(0 ,﹣).【点评】此题主要考查了用待定系数法求二次函数的解析式、解一元二次方程、相似三角形的性质、勾股定理、等腰三角形的性质等知识,弄清两相似三角形的对应关系是解决第(2 )小题的关键.25.如图,在等腰Rt△ABC中,∠C =90° ,斜边AB =2 ,假设将△ABC翻折,折痕EF分别交边AC、边BC于点E和点F (点E不与A点重合,点F不与B点重合) ,且点C落在AB边上,记作点D.过点D作DK⊥AB ,交射线AC于点K ,设AD =x ,y =cot∠CFE ,(1 )求证:△DEK∽△DFB;(2 )求y关于x的函数解析式并写出定义域;(3 )联结CD ,当=时,求x的值.【考点】相似形综合题;等腰三角形的判定与性质;等边三角形的判定与性质;直角三角形斜边上的中线;轴对称的性质;锐角三角函数的定义;特殊角的三角函数值.【专题】综合题;分类讨论.【分析】(1 )要证△DEK∽△DFB ,只需证到∠EKD =∠FBD ,∠EDK =∠FDB即可;(2 )易得DK =DA =x ,DB =2﹣x ,由△DFB∽△DEK可得到=,从而可得y =cot∠CFE=cot∠DFE ===;然后只需先求出在两个临界位置(点F在点B处、点E在点A处)下的x值,就可得到该函数的定义域;(3 )取线段EF的中点O ,连接OC、OD ,根据直角三角形斜边上的中线等于斜边的一半可得OC =OD =EF.设EF与CD交点为H ,根据轴对称的性质可得EF⊥CD ,且CH =DH =CD.由=可得tan∠HOC ==,从而得到∠HOC =60°.①假设点K在线段AC上,如图2 ,由∠HOC=60°可求得∠OFC =30° ,由此可得到y的值,再把y的值代入函数解析式就可求出x的值;②假设点K在线段AC的延长线上,如图3 ,由∠HOC =60°可求得∠OFC =60° ,由此可得到y的值,再把y的值代入函数解析式就可求出x的值.【解答】(1 )证明:如图1 ,由折叠可得:∠EDF =∠C =90° ,∠DFE =∠CFE.∵△ABC是等腰直角三角形,∠C =90° ,∴∠A =∠B =45°.∵DK⊥AB ,∴∠ADK =∠BDK =90° ,∴∠AKD =45° ,∠EDF =∠KDB =90° ,∴∠EKD =∠FBD ,∠EDK =∠FDB ,∴△DEK∽△DFB;(2 )解:∵∠A =∠AKD =45° ,∴DK =DA =x.∵AB =2 ,∴DB =2﹣x.∵△DFB∽△DEK ,∴=,∴y =cot∠CFE =cot∠DFE ===.当点F在点B处时,DB =BC =AB•sinA =2×=,AD =AB﹣AD =2﹣;当点E在点A处时,AD =AC =AB•cosA =2×=;∴该函数的解析式为y =,定义域为2﹣<x<;(3 )取线段EF的中点O ,连接OC、OD ,∵∠ECF =∠EDF =90° ,∴OC =OD =EF.设EF与CD交点为H ,根据轴对称的性质可得EF⊥CD ,且CH =DH =CD.∵=,∴sin∠HOC ==,∴∠HOC =60°①假设点K在线段AC上,如图2 ,∵CO =EF =OF ,∴∠OCF =∠OFC =∠HOC =30° ,∴y =cot30°=,∴=,解得:x =﹣1;②假设点K在线段AC的延长线上,如图3 ,∵OC =OF ,∠FOC =60° ,∴△OFC是等边三角形,∴∠OFC =60° ,∴y =cot60°=,∴=,解得:x =3﹣;综上所述:x的值为﹣1或3﹣.【点评】此题主要考查了相似三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质、锐角三角函数的定义、特殊角的三角函数值、直角三角形斜边上的中线等于斜边的一半等知识,在解决此题的过程中还用到了临界值法、分类讨论的思想,而运用(1 )中的结论那么是解决第(2 )小题的关键,取EF的中点O ,将转化为那么是解决第(3 )小题的关键.。
2016年九年级下学期开学考语文测试卷

2016年九年级下学期开学考语文试卷参考答案一、语文知识积累(本大题含1-7小题,其中1-6小题为选择题,每小题2分,第7小题8分,共20分)1. D2.B3.A4.D5.C6.B7.(1)角声满天秋色里 (2) 雪拥蓝关马不前 (3) 共看明月应垂泪(4)水是眼波横,山是眉峰聚眉眼盈盈处 (5) 已知泉路近,欲别故乡难。
二、口语交际与语文综合运用(本大题含8-10小题,共8分)8.(3分)合作是生存的最高法则。
予人玫瑰,手有余香。
(言之有理也可给分,但要简洁连贯)9.(3分)不给别人添麻烦——是在尊重别人的前提下,一种自觉的行动,应当属于可以学习、借鉴的文化财富。
团结互助是中华民族的传统,我们要继承,但也要注意培养自己的独立意识。
或:帮助别人快乐自己;人是群居动物,既要团结互助,又要有独立意识。
(言之有理可给分)10、略三、阅读(本大题含11—25小题,共42分)(一) 阅读下面诗歌,完成第11-12题。
(4分)11. (2分)“狂”字贯穿全篇,统摄全词,奠定了全词纵情、豪迈的气概。
12.(2分)表达了词人乐观自信的人生态度,坚信终有一天会为国杀敌立功,抒发作者强烈的爱国情怀。
(二)阅读下面文言文,完成13—16题。
(12分)13.(2分)(1)私:偏爱。
(2)孰:通“熟”仔细。
14.(4分)(每题2分)(1)都认为我比徐公美。
(2)满一年以后,即使想进谏也没什么可说的了。
15. 他认为妻是“私我”、妾是“畏我”、客是“有求于我”,故不可信。
面对赞美,并未得意忘形,不盲目轻信,对别人的褒奖能理智判断、冷静思考,能正视自己,可见他有自知之明。
(3分)16我更欣赏邹忌。
因为邹忌能用生动委婉的方式劝说别人,这是一种智慧。
或我更欣赏齐威王。
因为他能够正视自己的不足,虚心接受他人劝谏。
(3分)(三)阅读下面的文字,完成17—20题。
(10分)17 .(2分)逻辑顺序18.(2分)整体呈蛋形(或倒置的气球形);底部宽大,顶部狭小;顶部是削平的凹形的;整体呈白色并点缀着其他颜色的花纹。
2016届九年级下学期开学考试数学试卷【解析版】2

2021届九年级||下学期开学考试数学试卷一、选择题(本大题总分值42分,每题3分)1.﹣3的倒数是()A.3 B.﹣3 C.D.2.一粒米的质量是0.000021千克,这个数字用科学记数法表示为()A.21×10﹣4千克B.2.1×10﹣6千克C.2.1×10﹣5千克D.2.1×10﹣4千克3.分式方程的解为()A.x =1 B.x =2 C.x =3 D.x =44.今年体育学业考试增加了跳绳测试工程,下面是测试时记录员记录的一组(10名)同学的测试成绩(单位:个/分钟).176 180 184 180 170 176 172 164 186 180该组数据的众数、中位数、平均数分别为()A.180 ,180 ,178 B.180 ,178 ,1785.如图是一个用相同的小立方体搭成的几何体的三视图,那么组成这个几何体的小立方体的个数是()A.2 B.3 C.4 D.56.等腰三角形的一个内角为40° ,那么这个等腰三角形的顶角为()A.40°B.100°C.40°或100°D.70°或50°7.如图,直线l∥m ,将含有45°角的三角板ABC的直角顶点C放在直线m上,假设∠1 =25° ,那么∠2的度数为()A.20°B.25°C.30°D.35°8.以下各因式分解正确的选项是()A.﹣x2+ (﹣2 )2= (x﹣2 ) (x +2 ) B.x2+2x﹣1 = (x﹣1 )2C.4x2﹣4x +1 = (2x﹣1 )2D.x2﹣4x =x (x +2 ) (x﹣2 )9.在平面直角坐标系中,点P (﹣1 ,2 )关于x轴的对称点的坐标为()A.(﹣1 ,﹣2 ) B.(1 ,2 ) C.(2 ,﹣1 ) D.(﹣2 ,1 )10.关于x的一元二次方程x2+2x﹣a =0有两个相等的实数根,那么a的值是()A.1 B.﹣1 C.D.﹣11.如果一个扇形的弧长等于它的半径,那么此扇形称为"等边扇形〞,那么半径为2的"等边扇形〞的面积为()A.πB.1 C.2 D.12.该试题已被管理员删除13.一次函数y1=kx +b (k≠0 )与反比例函数,在同一直角坐标系中的图象如下列图,假设y1>y2 ,那么x的取值范围是()A.﹣2<x<0或x>1B.x<﹣2或0<x<1 C.x>1 D.﹣2<x<114.二次函数y =a (x +m )2+n的图象如图,那么一次函数y =mx +n的图象经过()A.第|一、二、三象限B.第|一、二、四象限C.第二、三、四象限 D.第|一、三、四象限二、填空题(本大题总分值16分,每题4分)15.从边长为(a +1 )cm的正方形纸片中剪去一个边长为(a﹣1 )cm的正方形(a>1 ) ,剩余局部沿虚线又剪拼成一个矩形(不重叠无缝隙) ,那么该矩形的面积是.16.函数中,自变量x的取值范围是.17.如图,AC与BD交于P ,AD、BC延长交于点E ,∠AEC =37° ,∠CAE =31° ,那么∠APB的度数为.18.如图,在△ABC中,AB =AC =3cm ,AB的垂直平分线交AC于点N ,△BCN的周长是5cm ,那么BC的长等于cm.三、解答题(本大题总分值62分)19.化简与计算(1 ) (﹣2 )0+ ()﹣1+4cos30°﹣|﹣|.(2 )先化简,再求值:÷ (﹣a﹣2 ) ,其中a =﹣3.20.为了解某中学2021届九年级||学生2021届中|考体育成绩情况,现从中抽取局部学生的体育成绩进行分段(A:50分、B:49~40分、C:39~30分、D:29~0分)统计,统计结果如下列图.根据上面提供的信息,答复以下问题:(1 )本次抽查了多少名学生的体育成绩;(2 )补全图9.1 ,求图9.2中D分数段所占的百分比;(3 )该校2021届九年级||共有900名学生,请估计该校2021届九年级||学生体育成绩到达40分以上的人数.21.为了防控甲型H1N1流感,某校积极进行校园环境消毒,购置了甲、乙两种消毒液共100瓶,其中甲种6元/瓶,乙种9元/瓶.(1 )如果购置这两种消毒液共用780元,求甲、乙两种消毒液各购置多少瓶?(2 )该校准备再次购置这两种消毒液(不包括已购置的100瓶) ,使乙种瓶数是甲种瓶数的2倍,且所需费用不多于1200元(不包括780元) ,求甲种消毒液最||多能再购置多少瓶?22.如图,某校2021届九年级||3班的一个学习小组进行测量小山高度的实践活动.局部同学在山脚点A测得山腰上一点D的仰角为30° ,并测得AD的长度为180米;另一局部同学在山顶点B测得山脚点A的俯角为45° ,山腰点D的俯角为60度.请你帮助他们计算出小山的高度BC.(计算过程和结果都不取近似值)23.正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F ,连接DF ,G为DF中点,连接EG ,CG.(1 )求证:EG =CG;EG⊥CG.(2 )将图①中△BEF绕B点逆时针旋转45° ,如图②所示,取DF中点G ,连接EG ,CG.问(1 )中的结论是否仍然成立?假设成立,请给出证明;假设不成立,请说明理由.24.如图1 ,抛物线y =x2﹣2x +k与x轴交于A、B两点,与y轴交于点C (0 ,﹣3 ).[图2、图3为解答备用图](1 )k =,点A的坐标为,点B的坐标为;(2 )设抛物线y =x2﹣2x +k的顶点为M ,求四边形ABMC的面积;(3 )在x轴下方的抛物线上是否存在一点D ,使四边形ABDC的面积最||大?假设存在,请求出点D 的坐标;假设不存在,请说明理由;(4 )在抛物线y =x2﹣2x +k上求点Q ,使△BCQ是以BC为直角边的直角三角形.2021届九年级||下学期开学考试数学试卷参考答案与试题解析一、选择题(本大题总分值42分,每题3分)1.﹣3的倒数是()A.3 B.﹣3 C.D.【考点】倒数.【专题】常规题型.【分析】直接根据倒数的定义进行解答即可.【解答】解:∵ (﹣3 )× (﹣) =1 ,∴﹣3的倒数是﹣.应选:D.【点评】此题考查的是倒数的定义,即乘积是1的两数互为倒数.2.一粒米的质量是0.000021千克,这个数字用科学记数法表示为()A.21×10﹣4千克B.2.1×10﹣6千克C.2.1×10﹣5千克D.2.1×10﹣4千克【考点】科学记数法-表示较小的数.【分析】绝||对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第|一个不为零的数字前面的0的个数所决定.【解答】解:0.000021 =2.1×10﹣5;应选:C.【点评】此题考查了用科学记数法表示较小的数,一般形式为a×10﹣n ,其中1≤|a|<10 ,n为由原数左边起第|一个不为零的数字前面的0的个数所决定.3.分式方程的解为()A.x =1 B.x =2 C.x =3 D.x =4【考点】解分式方程.【分析】首||先分式两边同时乘以最||简公分母2x (x﹣1 )去分母,再移项合并同类项即可得到x的值,然后要检验.【解答】解:,去分母得:3x﹣3 =2x ,移项得:3x﹣2x =3 ,合并同类项得:x =3 ,检验:把x =3代入最||简公分母2x (x﹣1 ) =12≠0 ,故x =3是原方程的解,故原方程的解为:X =3 ,应选:C.【点评】此题主要考查了分式方程的解法,关键是找到最||简公分母去分母,注意不要忘记检验,这是同学们最||容易出错的地方.4.今年体育学业考试增加了跳绳测试工程,下面是测试时记录员记录的一组(10名)同学的测试成绩(单位:个/分钟).176 180 184 180 170 176 172 164 186 180该组数据的众数、中位数、平均数分别为()A.180 ,180 ,178 B.180 ,178 ,178【考点】众数;算术平均数;中位数.【专题】计算题.【分析】找中位数要把数据按从小到大的顺序排列,位于最||中间的一个数(或两个数的平均数)为中位数,众数是一组数据中出现次数最||多的数据.再根据平均数、众数和中位数的定义求解即可.【解答】解:在这一组数据中180是出现次数最||多的,故众数是180;将这组数据从小到大的顺序排列(164 ,170 ,172 ,176 ,176 ,180 ,180 ,180 ,184 ,186 ) ,处于中间位置的那两个数为176 ,180 ,那么由中位数的定义可知,这组数据的中位数是178;平均数为:(164 +170 +172 +176 +176 +180 +180 +180 +184 +186 )÷10 =176.8.应选C.【点评】此题为统计题,考查平均数、众数与中位数的意义.将一组数据从小到大(或从大到小)重新排列后,最||中间的那个数(或最||中间两个数的平均数)叫做这组数据的中位数;如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.5.如图是一个用相同的小立方体搭成的几何体的三视图,那么组成这个几何体的小立方体的个数是()A.2 B.3 C.4 D.5【考点】由三视图判断几何体.【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,再结合题意和三视图的特点找出每行和每列的小正方体的个数再相加即可.【解答】解:由俯视图易得最||底层有3个立方体,第二层有1个立方体,那么搭成这个几何体所用的小立方体个数是4.应选C.【点评】此题意在考查学生对三视图掌握程度和灵活运用能力,同时也表达了对空间想象能力方面的考查.如果掌握口诀"俯视图打地基,正视图疯狂盖,左视图拆违章〞就更容易得到答案.6.等腰三角形的一个内角为40° ,那么这个等腰三角形的顶角为()A.40°B.100°C.40°或100°D.70°或50°【考点】等腰三角形的性质.【专题】分类讨论.【分析】此题要分情况考虑:40°是等腰三角形的底角或40°是等腰三角形的顶角.再进一步根据三角形的内角和定理进行计算.【解答】解:当40°是等腰三角形的顶角时,那么顶角就是40°;当40°是等腰三角形的底角时,那么顶角是180°﹣40°×2 =100°.应选:C.【点评】注意:当等腰三角形中有一个角是锐角时,可能是它的底角,也可能是它的顶角;当等腰三角形中有一个角是锐角时,只能是它的顶角.7.如图,直线l∥m ,将含有45°角的三角板ABC的直角顶点C放在直线m上,假设∠1 =25° ,那么∠2的度数为()A.20°B.25°C.30°D.35°【考点】平行线的性质.【分析】首||先过点B作BD∥l ,由直线l∥m ,可得BD∥l∥m ,由两直线平行,内错角相等,即可求得答案∠4的度数,又由△ABC是含有45°角的三角板,即可求得∠3的度数,继而求得∠2的度数.【解答】解:过点B作BD∥l ,∵直线l∥m ,∴BD∥l∥m ,∴∠4 =∠1 =25° ,∵∠ABC =45° ,∴∠3 =∠ABC﹣∠4 =45°﹣25°=20° ,∴∠2 =∠3 =20°.应选A.【点评】此题考查了平行线的性质.此题难度不大,注意辅助线的作法,注意掌握两直线平行,内错角相等定理的应用.8.以下各因式分解正确的选项是()A.﹣x2+ (﹣2 )2= (x﹣2 ) (x +2 ) B.x2+2x﹣1 = (x﹣1 )2C.4x2﹣4x +1 = (2x﹣1 )2D.x2﹣4x =x (x +2 ) (x﹣2 )【考点】因式分解-运用公式法;因式分解-提公因式法.【分析】根据完全平方公式与平方差公式分解因式,提公因式法分解因式,对各选项分析判断后利用排除法求解.【解答】解:A、﹣x2+ (﹣2 )2=﹣x2+4 = (2﹣x ) (2 +x ) ,故本选项错误;B、x2+2x﹣1不符合完全平方公式,不能利用公式分解,故本选项错误;C、4x2﹣4x +1 = (2x﹣1 )2 ,故本选项正确;D、x2﹣4x =x (x﹣4 ) ,故本选项错误.应选C.【点评】此题考查了公式法分解因式,提公因式法分解因式,熟记平方差公式与完全平方公式的结构式解题的关键.9.在平面直角坐标系中,点P (﹣1 ,2 )关于x轴的对称点的坐标为()A.(﹣1 ,﹣2 ) B.(1 ,2 ) C.(2 ,﹣1 ) D.(﹣2 ,1 )【考点】关于x轴、y轴对称的点的坐标.【分析】根据"关于x轴对称的点,横坐标相同,纵坐标互为相反数〞解答.【解答】解:点P (﹣1 ,2 )关于x轴对称的点的坐标为(﹣1 ,﹣2 ).应选:A.【点评】此题考查了关于x轴、y轴对称的点的坐标,解决此题的关键是掌握好对称点的坐标规律:(1 )关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2 )关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3 )关于原点对称的点,横坐标与纵坐标都互为相反数.10.关于x的一元二次方程x2+2x﹣a =0有两个相等的实数根,那么a的值是()A.1 B.﹣1 C.D.﹣【考点】根的判别式.【专题】探究型.【分析】根据关于x的一元二次方程x2+2x﹣a =0有两个相等的实数根可知△=0 ,求出a的取值即可.【解答】解:∵关于x的一元二次方程x2+2x﹣a =0有两个相等的实数根,∴△=22+4a =0 ,解得a =﹣1.应选B.【点评】此题考查的是根的判别式,即一元二次方程ax2+bx +c =0 (a≠0 )的根与△=b2﹣4ac 有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.11.如果一个扇形的弧长等于它的半径,那么此扇形称为"等边扇形〞,那么半径为2的"等边扇形〞的面积为()A.πB.1 C.2 D.【考点】扇形面积的计算;弧长的计算.【专题】压轴题;新定义.【分析】根据扇形的面积公式计算.【解答】解:设扇形的半径为r ,根据扇形面积公式得S =lr =r2=2应选C.【点评】此题主要考查了扇形的面积公式.12.该试题已被管理员删除13.一次函数y1=kx +b (k≠0 )与反比例函数,在同一直角坐标系中的图象如下列图,假设y1>y2 ,那么x的取值范围是()A.﹣2<x<0或x>1B.x<﹣2或0<x<1 C.x>1 D.﹣2<x<1【考点】反比例函数与一次函数的交点问题.【分析】先根据图象得出反比例函数与一次函数交点的坐标,再利用数形结合即可解答.【解答】解:由函数图象可知一次函数y1=kx +b与反比例函数的交点坐标为(1 ,4 ) , (﹣2 ,﹣2 ) ,由函数图象可知,当﹣2<x<0或x>1时,y1在y2的上方,∴当y1>y2时x的取值范围是﹣2<x<0或x>1.应选A.【点评】此题考查的是反比例函数与一次函数的交点问题,解答此题的关键是利用数形结合求出x 的取值范围.14.二次函数y =a (x +m )2+n的图象如图,那么一次函数y =mx +n的图象经过()A.第|一、二、三象限B.第|一、二、四象限C.第二、三、四象限 D.第|一、三、四象限【考点】二次函数的图象;一次函数的性质.【分析】根据抛物线的顶点在第四象限,得出n<0 ,m<0 ,即可得出一次函数y =mx +n的图象经过二、三、四象限.【解答】解:∵抛物线的顶点在第四象限,∴﹣m>0 ,n<0 ,∴m<0 ,∴一次函数y =mx +n的图象经过二、三、四象限,应选C.【点评】此题考查了二次函数的图象,用到的知识点是二次函数的图象与性质、一次函数的图象与性质,关键是根据抛物线的顶点在第四象限,得出n、m的符号.二、填空题(本大题总分值16分,每题4分)15.从边长为(a +1 )cm的正方形纸片中剪去一个边长为(a﹣1 )cm的正方形(a>1 ) ,剩余局部沿虚线又剪拼成一个矩形(不重叠无缝隙) ,那么该矩形的面积是4a.【考点】平方差公式的几何背景.【分析】矩形的面积就是边长是a +1的正方形与边长是a﹣1的正方形的面积的差,列代数式进行化简即可.【解答】解:矩形的面积是(a +1 )2﹣(a﹣1 )2=4a (cm2 ).故答案为:4a.【点评】此题考查了平方差公式的几何背景,关键是根据题意列出式子,运用平方差公式进行计算,要熟记公式.16.函数中,自变量x的取值范围是x>﹣5.【考点】函数自变量的取值范围.【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0 ,分母不等于0 ,可以求出x的范围.【解答】解:由题意得,x +5>0 ,解得x>﹣5.故答案为:x>﹣5.【点评】此题考查了函数自变量的范围,一般从三个方面考虑:(1 )当函数表达式是整式时,自变量可取全体实数;(2 )当函数表达式是分式时,考虑分式的分母不能为0;(3 )当函数表达式是二次根式时,被开方数非负.17.如图,AC与BD交于P ,AD、BC延长交于点E ,∠AEC =37° ,∠CAE =31° ,那么∠APB的度数为99°.【考点】圆周角定理.【分析】由∠ACB为△ACE的外角,求得∠ACE =∠A +∠AEC ,由圆周角定理,得∠ADB=∠ACB ,根据三角形外角定理即可求得答案.【解答】解:∵∠ACB为△ACE的外角,∴∠ACE =∠A +∠AEC∵ ,∠AEC =37° ,∠CAE =31° ,∴∠ACE =68°.由圆周角定理,得∠ADB =∠ACB ,∴∠ADB =68° ,∴∠APB =∠A +∠ADB =31°+68°=99° ,故答案为99°.【点评】此题考查了圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,熟练掌握定理是解决问题的关键.18.如图,在△ABC中,AB =AC =3cm ,AB的垂直平分线交AC于点N ,△BCN的周长是5cm ,那么BC的长等于2cm.【考点】线段垂直平分线的性质.【专题】计算题;压轴题.【分析】由AB的垂直平分线交AC于点N ,根据线段的垂直平分线的性质得到NA =NB ,而BC +BN +NC =5cm ,那么BC +AN +NC =5cm ,由AC =AN +NC =3cm ,即可得到BC的长.【解答】解:∵AB的垂直平分线交AC于点N ,∴NA =NB ,又∵△BCN的周长是5cm ,∴BC +BN +NC =5cm ,∴BC +AN +NC =5cm ,而AC =AN +NC =3cm ,∴BC =2cm.故答案为:2.【点评】此题考查了线段的垂直平分线的性质:线段的垂直平分线的点到线段两端点的距离相等;也考查了三角形周长的定义.三、解答题(本大题总分值62分)19.化简与计算(1 ) (﹣2 )0+ ()﹣1+4cos30°﹣|﹣|.(2 )先化简,再求值:÷ (﹣a﹣2 ) ,其中a =﹣3.【考点】分式的化简求值;实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.【专题】计算题;分式.【分析】(1 )原式第|一项利用零指数幂法那么计算,第二项利用负整数指数幂法那么计算,第三项利用特殊角的三角函数值计算,最||后一项利用绝||对值的代数意义化简,计算即可得到结果;(2 )原式括号中两项通分并利用同分母分式的减法法那么计算,同时利用除法法那么变形,约分得到最||简结果,把a的值代入计算即可求出值.【解答】解:(1 )原式=1 +3 +2﹣2=4;(2 )原式=÷=﹣•=﹣,当a =﹣3时,原式=﹣.【点评】此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法那么是解此题的关键.20.为了解某中学2021届九年级||学生2021届中|考体育成绩情况,现从中抽取局部学生的体育成绩进行分段(A:50分、B:49~40分、C:39~30分、D:29~0分)统计,统计结果如下列图.根据上面提供的信息,答复以下问题:(1 )本次抽查了多少名学生的体育成绩;(2 )补全图9.1 ,求图9.2中D分数段所占的百分比;(3 )该校2021届九年级||共有900名学生,请估计该校2021届九年级||学生体育成绩到达40分以上的人数.【考点】条形统计图;用样本估计总体;扇形统计图.【分析】(1 )结合条形统计图和扇形统计图知:A的人数为80人,A占被调查人数的16% ,用除法即可计算总人数;(2 )根据(1 )中计算的总人数以及B所占的百分比进行计算,然后正确补全统计图即可;根据条形统计图中D的具体数据结合总人数计算D所占的比例即可;(3 )根据题意,知达标的即是A类和B类,共占56% ,再进一步结合总体人数计算即可.【解答】解:(1 )根据统计图可知,A的人数为80人,A占被调查人数的16% ,所以本次调查的人数为80÷16% =500 (人);(2 )由分数段百分比统计图知B的人数占被调查人数的40% ,所以B的人数为500×40% =200 (人) 在分数段统计图中将B的局部补充如下列图.D分数段所占的百分比为:×100% =12%;(3 )该校2021届九年级||学生体育成绩到达40分以上的人数为900× (16% +40% ) =504 (人).【点评】此题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个工程的数据;扇形统计图直接反映局部占总体的百分比大小.21.为了防控甲型H1N1流感,某校积极进行校园环境消毒,购置了甲、乙两种消毒液共100瓶,其中甲种6元/瓶,乙种9元/瓶.(1 )如果购置这两种消毒液共用780元,求甲、乙两种消毒液各购置多少瓶?(2 )该校准备再次购置这两种消毒液(不包括已购置的100瓶) ,使乙种瓶数是甲种瓶数的2倍,且所需费用不多于1200元(不包括780元) ,求甲种消毒液最||多能再购置多少瓶?【考点】二元一次方程组的应用;一元一次不等式的应用.【分析】(1 )等量关系为:甲消毒液总价钱+乙消毒液总价钱=780.(2 )关系式为:甲消毒液总价钱+乙消毒液总价钱≤1200.【解答】解:(1 )设甲种消毒液购置x瓶,那么乙种消毒液购置(100﹣x )瓶.依题意得:6x +9 (100﹣x ) =780.解得:x =40.∴100﹣x =100﹣40 =60 (瓶).答:甲种消毒液购置40瓶,乙种消毒液购置60瓶.(2 )设再次购置甲种消毒液y瓶,那么购置乙种消毒液2y瓶.依题意得:6y +9×2y≤1200.解得:y≤50.答:甲种消毒液最||多再购置50瓶.【点评】解决此题的关键是读懂题意,找到符合题意的等量关系和不等关系式.等量关系为:甲消毒液总价钱+乙消毒液总价钱=780.不等关系式为:甲消毒液总价钱+乙消毒液总价钱≤1200.22.如图,某校2021届九年级||3班的一个学习小组进行测量小山高度的实践活动.局部同学在山脚点A测得山腰上一点D的仰角为30° ,并测得AD的长度为180米;另一局部同学在山顶点B测得山脚点A的俯角为45° ,山腰点D的俯角为60度.请你帮助他们计算出小山的高度BC.(计算过程和结果都不取近似值)【考点】解直角三角形的应用-仰角俯角问题.【专题】应用题.【分析】首||先根据题意分析图形;过点D作DE⊥AC于点E ,作DF⊥BC于点F;构造此题涉及到的两个直角三角形,根据图形分别求解可得DE与BF的值,再利用BC =DE +BF ,进而可求出答案.【解答】解:如图,过点D作DE⊥AC于点E ,作DF⊥BC于点F ,那么有DE∥FC ,DF∥EC.∵∠DEC =90° ,∴四边形DECF是矩形,∴DE =FC.∵∠HBA =∠BAC =45° ,∴∠BAD =∠BAC﹣∠DAE =45°﹣30°=15度.又∵∠ABD =∠HBD﹣∠HBA =60°﹣45°=15° ,∴△ADB是等腰三角形.∴AD =BD =180 (米).在Rt△AED中,sin∠DAE =sin30°=,∴DE =180•sin30°=180×=90 (米) ,∴FC =90米.在Rt△BDF中,∠BDF =∠HBD =60° ,sin∠BDF =sin60°=,∴BF =180•sin60°=180×(米).∴BC =BF +FC =90+90 =90 (+1 ) (米).答:小山的高度BC为90 (+1 )米.【点评】此题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.23.正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F ,连接DF ,G为DF中点,连接EG ,CG.(1 )求证:EG =CG;EG⊥CG.(2 )将图①中△BEF绕B点逆时针旋转45° ,如图②所示,取DF中点G ,连接EG ,CG.问(1 )中的结论是否仍然成立?假设成立,请给出证明;假设不成立,请说明理由.【考点】正方形的性质;全等三角形的判定与性质.【分析】(1 )根据直角三角形斜边中线的性质以及三角形外角定理即可证明.(2 )作GM⊥BC于M ,⊥AB于N交CD于H ,只要证明△GNE≌△GMC即可解决问题.【解答】证明:(1 )如图①中,∵四边形ABCD是正方形,∴∠BCD =∠ADC =90° ,∠BDC =,∵EF⊥BD ,∴∠DEF =90° ,∵GF =GD ,∴EG =DG =GF =DF ,GC =DG =GF =DF ,∴EG =GC ,∠GED =∠GDE ,∠GCD =∠GDC ,∵∠EGF =∠GED +∠GDE =2∠EDG ,∠CGF =∠GCD +∠GDC =2∠GDC ,∴∠EGC =∠EGF +∠CGF =2∠EDG +2∠GDC =2 (∠EDG +∠GDC ) =90° ,∴EG⊥GC.(2 )图②中,结论仍然成立.理由:作GM⊥BC于M ,⊥AB于N交CD于H.∵四边形ABCD是正方形,∴∠A =∠ADC =90° ,∠ABD =∠DBC =∠BDC =45°∴GM =GN ,∵∠A =∠ANG =∠ADH =90° ,∴四边形ANHD是矩形,∴∠DHN =90° ,∠GDH =∠HGD =45° ,∴HG =DH =AN ,同理GH =CM ,∵∠ENG =∠A =∠BEF =90° ,∴EF∥GN∥AD ,∵GF =GD ,∴AN =NE =GH =MC ,在△GNE和△GMC中,,∴△GNE≌△GMC ,∴GE =GC ,∠NGE =∠MGC ,∴∠EGC =∠NGM =90° ,∴EG⊥GC.【点评】此题考查全等三角形的判定和性质、正方形的性质、矩形的判定和性质等知识,添加辅助线构造全等三角形是解决问题的关键,属于2021届中|考常考题型.24.如图1 ,抛物线y =x2﹣2x +k与x轴交于A、B两点,与y轴交于点C (0 ,﹣3 ).[图2、图3为解答备用图](1 )k =,点A的坐标为,点B的坐标为;(2 )设抛物线y =x2﹣2x +k的顶点为M ,求四边形ABMC的面积;(3 )在x轴下方的抛物线上是否存在一点D ,使四边形ABDC的面积最||大?假设存在,请求出点D 的坐标;假设不存在,请说明理由;(4 )在抛物线y =x2﹣2x +k上求点Q ,使△BCQ是以BC为直角边的直角三角形.【考点】二次函数综合题.【专题】压轴题;分类讨论.【分析】(1 )把C (0 ,﹣3 )代入抛物线解析式可得k值,令y =0 ,可得A ,B两点的横坐标;(2 )过M点作x轴的垂线,把四边形ABMC分割成两个直角三角形和一个直角梯形,求它们的面积和;(3 )设D (m ,m2﹣2m﹣3 ) ,连接OD ,把四边形ABDC的面积分成△AOC ,△DOC ,△DOB的面积和,求表达式的最||大值;(4 )有两种可能:B为直角顶点、C为直角顶点,要充分认识△OBC的特殊性,是等腰直角三角形,可以通过解直角三角形求出相关线段的长度.【解答】解:(1 )把C (0 ,﹣3 )代入抛物线解析式y =x2﹣2x +k中得k =﹣3∴y =x2﹣2x﹣3 ,令y =0 ,即x2﹣2x﹣3 =0 ,解得x1=﹣1 ,x2=3.∴A (﹣1 ,0 ) ,B (3 ,0 ).(2 )∵y =x2﹣2x﹣3 = (x﹣1 )2﹣4 ,∴抛物线的顶点为M (1 ,﹣4 ) ,连接OM.那么△AOC的面积=,△MOC的面积=,△MOB的面积=6 ,∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9.说明:也可过点M作抛物线的对称轴,将四边形ABMC的面积转化为求1个梯形与2个直角三角形面积的和.(3 )如图(2 ) ,设D (m ,m2﹣2m﹣3 ) ,连接OD.那么0<m<3 ,m2﹣2m﹣3<0且△AOC的面积=,△DOC的面积=m ,△DOB的面积=﹣(m2﹣2m﹣3 ) ,∴四边形ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积=﹣m2+m +6=﹣(m﹣)2+.∴存在点D (,) ,使四边形ABDC的面积最||大为.(4 )有两种情况:如图(3 ) ,过点B作BQ1⊥BC ,交抛物线于点Q1、交y轴于点E ,连接Q1C.∵∠CBO =45° ,∴∠EBO =45° ,BO =OE =3.∴点E的坐标为(0 ,3 ).∴直线BE的解析式为y =﹣x +3.由解得∴点Q1的坐标为(﹣2 ,5 ).如图(4 ) ,过点C作CF⊥CB ,交抛物线于点Q2、交x轴于点F ,连接BQ2.∵∠CBO =45° ,∴∠CFB =45° ,OF =OC =3.∴点F的坐标为(﹣3 ,0 ).∴直线CF的解析式为y =﹣x﹣3.由解得∴点Q2的坐标为(1 ,﹣4 ).综上,在抛物线上存在点Q1 (﹣2 ,5 )、Q2 (1 ,﹣4 ) ,使△BCQ1、△BCQ2是以BC为直角边的直角三角形.说明:如图(4 ) ,点Q2即抛物线顶点M ,直接证明△BCM为直角三角形同样可以.【点评】此题考查了抛物线解析式的求法,运用解析式解决面积问题,及求构成直角三角形的条件等知识.。
2016年高二下学期开学考英语试题

英语注意事项:⒈本卷共150 分,考试时间120 分钟。
⒉答题前,考生在答题卡上用黑色签字笔将自己的姓名、准考证号填写清楚。
⒊请用2B 铅笔在答题卡上各题的答题区域内作答,在试卷上作答无效。
⒋考试结束后上交答题卡。
第I 卷(选择题,共105 分)第一部分:听力理解(共两节,满分30 分)第一节:(共 5 小题;每小题 1.5 分,满分7.5 分)听下面 5 段对话,每段对话后有一个小题,从题中所给的 A 、B 、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Which skirt will the man buy?A. The green one.B. The brown one.C. The red one.2. What does the man think of the car?A. Cheap.B. Old.C. Nice.3. Why can ’t men do better in a computer company than women?A. They are not as careful as women.B. They are too strong.C. Their hands are too big.4. When is the concert going to start?A. At 7:45.B. At 7:30.C. At 7:15.5. Where does this conversation take place?A. In a food store.B. In a restaurant.C. At a vegetable market.第二节:(共15 小题;每小题 1.5 分,满分22.5 分)听下面 5 段对话或独白,每段对话或独白后有几个小题,从题中所给的 A 、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
2016届高三下学期开学考试英语试题(附答案)(2)

英语试题(满分:150分,考试时间:115分钟)第一部分听力(共两节,满分30分)(徐鑫老师提供)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What will the woman probably do?A. Find a project abroad.B. Continue her project.C. Go abroad.2. What do we know about the man?A. He wants to solve easy ones first.B. He wants to give up difficult ones.C. He thinks the problems easy.3. Why is the woman sad?A. She is ill for quite a while.B. She can’t watc h a game.C. She can’t join in a game.4. What information can we get about the woman?A. She is a victim of the quake.B. She is tired and sleepy.C. She is moved by a movie.5. Why does the woman make the call?A. To cancel an appointment.B. To inform about the birthday party.C. To congratulate the man on his birthday.第二节(共15小题, 每题1.5分,满分22.5分)听下面5段对话或独白。
江苏省启东市2016届九年级下学期开学考试数学试题

2016年九年级数学寒假作业检测卷一、填空题(每题3分,共30分)1、下列图案中,不能由一个图形通过旋转而构成的是()A B (: I)2、如图,AB是O O的弦,半径OA=2,/ AOB=120°,则弦AB的长是(A、2 2B、2 3C、,5 D3 23、在一个不透明的袋中,装有若干个除颜色不同外其余都相同的一 1球,如果袋中有3个红球且摸到红球的概率为4,那么袋中球的总个数为()A、15 个B、12 个C、9 个D、3 个4、如图,数轴上A,B两点表示的数分别为一1和3,点B关于点A的对称点C,则点C所表示的数为()A、一2—3B、一1—3—I --------- L 1(C、一2+ 3D、1+ .3 1」5、已知关于x的方程2x2—6x+m=0的两个根互为倒数,则m的值为()1 1A、2B、一2C、2D、一26、如图,若将△ ABC绕点C顺时针旋转90°后得到△ A' 点A'的坐标是())A、(—3,—2)B、(2, 2)1“ 丁B— LI;.C、(3, 0)D、(2,1)7、已知一个圆锥的底面半径为3cm,母线长为二、选择题(每题3分,共24分) 11、 函数y=―1中,自变量x 的取值范围是 ____________ .x -112、 已知点A ( — 2m+4,3m — 1)关于原点的对称点位于第四象限,贝U m 的取值 范围是 ____ . 13、 方程(2x+3) (x — 2) =0 的根是14、 要组织一次篮球联赛,赛制是单循环形式(每两队之间都赛一场) ,计划安 排21场比赛,则参赛球队的个数是 ______________ .10cm ,则这个圆锥的侧面积为A 、15 n cm 2B 、30 cm 2C 、60 n cm 2D 、3 91 cm 28、 若关于x 的一兀二次方程 值范围是()A 、k> — 1B 、k> — 1 且〜0D 、k<1且〜0 9、 如图,FA ,PB 是。
2016年下学期入学考试数学试卷
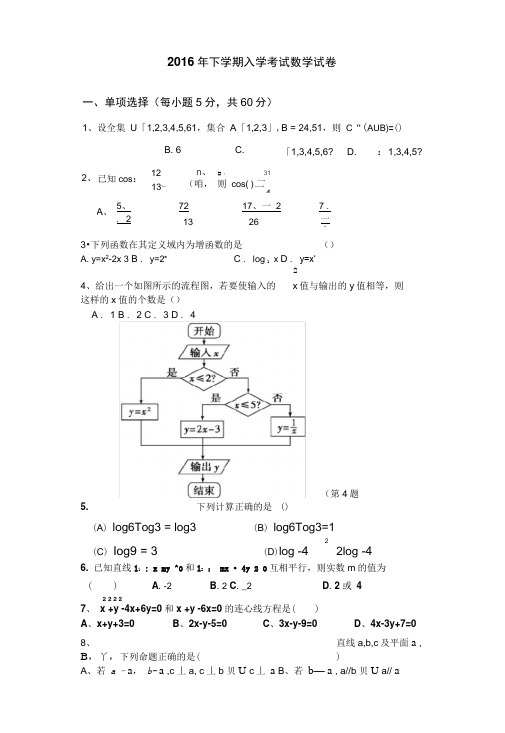
2016年下学期入学考试数学试卷一、单项选择(每小题5分,共60分)1、设全集 U 「1,2,3,4,5,61,集合 A 「1,2,3」,B = 24,51,则 C “(AUB)=()3•下列函数在其定义域内为增函数的是()A. y=x 2-2x 3 B . y=2xC . log 1 xD . y=x‘24、给出一个如图所示的流程图,若要使输入的 x 值与输出的y 值相等,则这样的x 值的个数是() A . 1 B . 2 C . 3 D . 45. 下列计算正确的是 ()(A ) log6Tog3 = log3 (B ) log6Tog3=12(C ) Iog9 = 3(D )log -4 2log -46. 已知直线l 1 : x my ^0和l 2 : mx • 4y 2 0互相平行,则实数m 的值为 ()A . -2B . 2C . _2D . 2 或 4 2 2 2 27、 x +y -4x+6y=0和x +y -6x=0的连心线方程是( )A 、x+y+3=0B 、2x-y-5=0C 、3x-y-9=0D 、4x-3y+7=08、 直线a,b,c 及平面a , B ,丫,下列命题正确的是( )A 、若 a - a , b - a ,c 丄a, c 丄b 贝U c 丄 aB 、若 b — a , a//b 贝U a// a2、 已知cos :12 A 、5、. 2B. 6C.13,_n 、 (咱, 72 13「1,3,4,5,6? D.:1,3,4,5?口 r31 则 cos( )二417、一 2 267 .一2(第4题图)x C、若a// a , a A B =b 则a//b D 、若a丄a , b 丄a 则a//bc9 •函数f(x)= x —x—1的一个零点所在的区间可能是(A • [0,1] B. [1,2] C • [2,3] D • [3,4]10、要得到y =3sin(2 x ')的图象,只需将y=3sin 2x的图象4二、填空题(每小题5分,共20分)13.如果函数y二a x+1在[0 , 2]上的最大值与最小值的和为7 ,则a= _____ .14. f (x)为偶函数,当x>0 时,f(x) = 2x—1,则f ( —5) = _______________ . ______15、有一个正三棱柱的三视图如图所示(俯视图为正三角形),则这个三棱柱的高和底面边长分别为____________ •题号 1 2 3 4 5 6 7 8 9 10 11 12 答案393C.B. D.16164A.向左平移个单位B. 向右平移■—个单位4 4C.向左平移一个单位D. 向左平移二个单位8 811、当〉为第二象限角时,| sin :- 一- COs的值是(sin篇|cos: |12、在区间0,4 ]上随机取两个实数)A • 1B • 2C • 0D • —2x, y,使得x - 2y< 8的概率为(x18、(12分)某地区有100名学员参加交通法规考试,考试成绩的频率分布直方图 如图所示•其中成绩分组区间是:第 i 组:,第2组:,第3组:用y :,第4组: ,第5组:[处 •(1)求图中 的值,并估计此次考试成绩的中位数(结果保留一位小数) ;(2)在第2、4小组中用分层抽样的方法抽取 5人,再从这5人中随机选取2人进 行面试,求至少有一人来自第 2小组的概率.19、(12分)如图,在四棱锥 P-ABCD 中,底面 ABCD 是边长为a 的正方形侧中点.(1)求证:EF //平面PAD ; (2)求证:面 PAB _平面PDC ;B面PAD —底面ABCD且 PA = PD 2 AD ,设 E 、2F 分别为PC 、BD 的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016学下学期开学测试性考试
八年级物理
班别:姓名:学号:
一、选择题(每题4分,共48分)
1.乒乓球被誉为我国的“国球”,其直径约为()
A.40nm B.40μm C.40mm D.40cm
2. 用图象可以表示物体运动的规律,如图所示,表示物体做匀速直线运动的是哪一段()
A.AB段和EF段
B.AB段和DE段
C.BC段和EF段
D.BC段和DE段
3. 下列对声现象四个实验的分析,正确的是
A.图甲正在发声的音叉把静止的乒乓球弹开,说明声音的传播需要介质
B.图乙抽取玻璃罩内的空气,听到罩内的铃声减小,说明声音可以在真空中传播
C.图丙同学把耳朵贴在桌面上,轻敲桌子,听到敲击声,说明声音是由物体的振动产生
D.8个相同的玻璃瓶中灌入不同高度的水,敲击它们,会听到它们发出声音的音调不同
4.如图所示,甲、乙、丙、丁是不同的声音先后输入到同一示波器上所显示的波形图。
则下面说法中正确的是()
A.甲和乙声音的音调相同B.甲和丙声音的响度相同
C.丙声音在真空中传播速度最快D.甲和丁声音的音色相同
5. 对一年四季中的物理现象,解释正确的是()
A.春天,晶莹的露水的形成是熔化现象,吸热B.夏天,飘渺的雾的形成是液化现象,吸热C.秋天,凝重的霜的形成是凝华现象,放热D.冬天,洁白的雪的形成是凝固现象,放热
6. 吃刚从冰箱冷冻室里拿出的冰糕,舌头有时会被冻在冰糕上,这是因为舌头上的水发生了()
A.熔化
B.凝固
C.蒸发
D.凝华
7. 小明在吃鸳鸯火锅时,发现加了辣椒油调料比不加调料的火锅汤会先沸腾,根据这个现象,小明就提出:“火锅汤沸腾的快慢与什么因素有关”,他这一提法属于()
A. 猜想
B. 提出问题
C. 设计实验
D. 评估
8. 下列说法中,正确的是( )
A.月亮是一个巨大的光源B.光在真空中的速度是340 m/s
C.影子是由于光的直线传播形成的D.漫反射不遵守光的反射定律
9. 小汽车前挡风玻璃并不是竖直安装的,其光学原因是( )
A.为了造型美观B.可以有效减小外界噪声干扰
C.扩大视野D.使车内物体通过挡风玻璃所成的像不在车的正前方
10.下列说法中,不正确
...的是( )
A.所有通过透镜光心的光都不会改变传播方向
B.来自凸透镜焦点的光将平行于主光轴射出
C.平行于主光轴的光通过凸透镜后会聚于焦点
D.通过凸透镜的光的光路可逆,通过平面镜的光的光路不可逆
11.下列说法中,不正确
...的是( )
A.穿衣镜成正立、等大的虚像B.照相机成倒立、缩小的实像
C.放大镜成正立、放大的实像D.幻灯机成倒立、放大的实像
12.小红用放大镜看自己的指纹时,觉得看到的指纹太小。
为了看到更大的清晰的指纹,应( ) A.手指与眼睛不动,放大镜离手指远一些B.手指与眼睛不动,放大镜离手指近一些
C.手指与放大镜不动,眼睛离手指远一些D.手指与放大镜不动,眼睛离手指近一些
二、填空题(每空1分,共20分)
13.小强在马路边上拍街景照片,连续拍了两张,如图9甲、乙所示。
如果以轿车为参照物,树是向__ __运动的,卡车向______运动;如果以骑自行车的人为参照物,树是向________运动。
(填“左”或“右”)
14. 请选用描述声现象的“乐音、噪声、音调、响度、音色”等词填写下面的空格:
声音很大是描述声音的;小陈根据声音的判断曲子是由笛子而非钢琴演奏的;能听出是国歌是根据声音的判断;刺耳难听表明对小陈而言,此声音是。
15.2015年春节,小红去北方看雾凇,在公园看到温度计
(寒暑表)如图11所示,其量程为,当
时气温为℃,温度计内的测温液体可能是
表格中的。
16.如图4所示为“充气式太阳能蒸馏器”装置。
它是通过太阳照射充气物内的
海水,产生大量水蒸气,水蒸气在透明罩内壁形成水珠,将水珠收集即可。
在
此过程中发生的物态变化是先____________,后____________。
17.为了验证装在密封试管里的固态碘在受热时能直接变成气态,甲同学
直接把密封试管放在酒精灯火焰上,如图13甲所示;乙同学将密封试管浸
入装有沸水的烧杯中,如图13乙所示,结果两根试管都出现了碘蒸气.已
知:碘的熔点是114℃、沸点是184.35℃;水的沸点是100℃;酒精灯火
焰温度约为400℃.由上述信息判断,
请回答下列问题:
(1)水沸腾后用猛火继续加热,水的温度(选填“可以”或“不可以”)继续上升。
(2)沸水中加热的固态碘(选填“可能”或“不可能)升温到熔点熔化后,再升温到沸点汽化。
(3)酒精灯加热的固态碘(选填“可能”或“不可能)升温到熔点熔化后,再升温到沸点汽化。
(4)分析甲、乙两位同学的实验方法,哪一个更合理?答:。
18. 我们看到的天空中的星星、月亮,都是经过大气层折射后位置(填“变高”或“变低”)了的(填“实像”或“虚像”)。
19.现在有一种微型手电筒,虽然体积很小,但发出的光很集中,在照物体时,被照的物体显得相当明亮。
这种微型手电的灯泡如图所示,它的玻璃泡顶端做成凸起的形状,相当于一个________,对灯丝发出的光起________作用,所以能够很集中地照亮物体。
三、作图题(每图4分,共12分)
20.在图中,利用平面镜成像的特点,画出AB在平面镜中的像。
21.完成下列光路图,画出发射光线金额折射光线
22. 物体在2f和f之间,如图,请画出物体的像
图20 图21
图22
四、解析题(23题4分,24题2分,共20分)
23.科学工作者为了探测海洋某处深度,向海底垂直发射超声波,经过6s收到回波信号,海洋中该处的深度是多少?(声音在海水中传播的速度是1500m/s)
24.下图停表的示数是________ s.
25. 小凡同学在做“观察水的沸腾”实验中
(1)他的操作如图所示,其中错误
..之处是。
(2)纠正错误后进行实验,当看到水中有大量气泡不断上升,变大,到水面破裂开来,里面的散发到空气中,就表明水沸腾了;水沸腾时温度计示数如图所示,所以水当时的沸点为℃。
(3)分析上图9所示图像,可知水在沸腾过程中温度的特点是。
(4)小凡将水加热至沸腾的时间较长,为了减少从开始加热到沸腾时的时间,可以采取的措施:。
(2分)
(5)实验结束时,发现纸盖变湿了,主要原因是______________________。
(2分)
26. 洋洋同学在探究“凸透镜成像规律及应用”的活动中,选用了焦距未知的凸透镜。
(1)将凸透镜安装在光具座上,用平行光作光源,移动光屏,在光屏上得到一个最小最亮的光斑,如图甲所示,则该凸透镜的焦距为cm。
(2)将蜡烛、凸透镜、光屏依次安装在光具座上,并调整蜡烛火焰、凸透镜及光屏三者的中心,使其大致在上,为实验探究做好准备。
(3)如图乙所示,将点燃的蜡烛移到标尺10cm处,再移动光屏,直到在光屏上得到一个清晰的像为止。
生活中就是利用这一成像原理来工作的。
(4)在图乙所示情况下,保持光屏和凸透镜的位置不变,将蜡烛向左移动一段距离后,为了在光屏上再次得到清晰的像,应在凸透镜左侧附近安装一个焦距适当的。
A.凸透镜B.凹透镜
(5)若保持凸透镜位置不变,将蜡烛移动到标尺35cm处,会在光屏上得到一个倒立的实像。
(6)如果用不透明纸板将凸透镜上半部分遮住,结果。
A.没有影响B.不能成像C.成一半的像D.仍能成完整的像,但亮度变暗
2016学下学期开学测试性考试
八年级物理
班别:姓名:学号:
一、选择题(每题4分,共48分)
二、填空题(每空1分,共20分)
13.、、。
14.、、、。
15.、、。
16.、。
17.、、、。
18.、。
19.、。
三、作图题(每图4分,共12分)
四、解析题(23题4分,24题2分,共20分)
23.
24.。
25.(1).
(2).
(3).
(4).
(5). 26.(1).
(2).
(3).
(4).
(5).
(6).。
