2013届湖里区初三毕业班质量检查
厦门市湖里区2013-2014年初中毕业模拟考试(一)试卷 2014313

厦门市湖里区2013-2014年初中毕业模拟考试(一)英语试题(满分:150分;考试时间:120分钟)准考证号_________________ 姓名__________________ 座位号_________考生注意:本试卷分为两大部分,第一部分(1-61小题)为选择题,请考生将答案用2B铅笔填涂在答题卡上;第二部分为非选择题,请考生将答案用0.5毫米的黑色签字笔书写在答题卡上。
第一部分(选择题)(一)听力测试(每小题1.5分,共30分)I. Listen and choose the right pictures.(听音,选择符合内容情景的图片。
听两遍)1.A B C2.A B3.A B C4.II. Listen to some short dialogues and choose the right answers to the questions you hear.(听简短对话,然后挑选最佳答案回答所听到的问题。
听两遍)5. A. Tomorrow evening. B. Tonight. C. This afternoon.6. A. He wants to go out for his vacation.B. He prefers to stay at home.C. He doesn’t like travelling abroad.7. A. Doctor. B. Farmer. C. Worker8. A. It’s 4:55. B. It’s 9:40. C. It’s 10:10.9. A. He is reading a newspaper.B. He is working in his office.C. He is walking in the park.10. A. To tell Lisa to take a message.B. To ask Lisa to go shopping with her.C. To tell Lisa that band practice has been put off to Thursday night at 7:30.III. Listen to a long dialogue and a passage, then choose the right answers to questions 16-20.(听一篇较长对话和一篇短文,然后选择正确答案作答16 – 20小题。
福建省厦门市湖里区中考数学毕业班第二次适应性考试卷
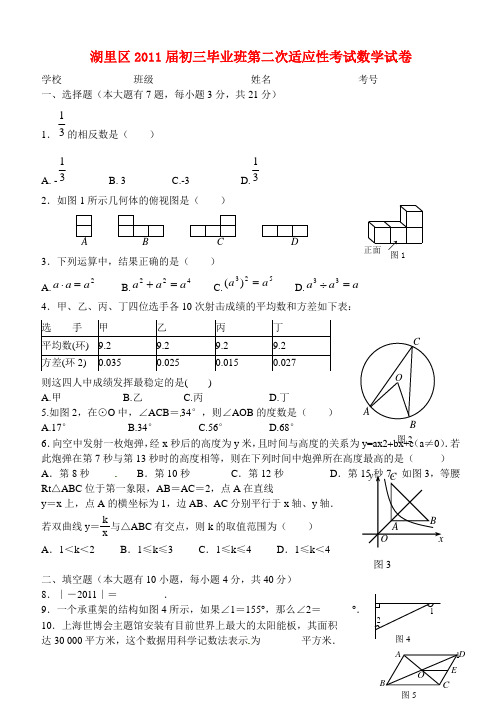
湖里区2011届初三毕业班第二次适应性考试数学试卷学校 班级 姓名 考号 一、选择题(本大题有7题,每小题3分,共21分)1.31的相反数是( )A. -31B. 3C.-3D.312.如图1所示几何体的俯视图是( )3.下列运算中,结果正确的是( )A.2a a a =⋅B.422a a a =+C.523)(a a =D.a a a =÷334.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:则这四人中成绩发挥最稳定的是( )A.甲B.乙C.丙D.丁5.如图2,在⊙O 中,∠ACB =34°,则∠AOB 的度数是( )A.17°B.34°C.56°D.68°6.向空中发射一枚炮弹,经x 秒后的高度为y 米,且时间与高度的关系为y=ax2+bx+c (a ≠0).若此炮弹在第7秒与第13秒时的高度相等,则在下列时间中炮弹所在高度最高的是( ) A .第8秒 B .第10秒 C .第12秒 D .第Rt △ABC 位于第一象限,AB =AC =2,点A 在直线y =x 上,点A 的横坐标为1,边AB 、AC 分别平行于x 轴、y 轴. 若双曲线y = kx与△ABC 有交点,则k 的取值范围为( )A .1<k <2B .1≤k ≤3C .1≤k ≤4D .1≤k <4图3 二、填空题(本大题有10小题,每小题4分,共40分) 8.∣-2011∣=_ _.9.一个承重架的结构如图4所示,如果∠1=155°,那么∠2=_ _°.10.上海世博会主题馆安装有目前世界上最大的太阳能板,其面积达30 000平方米,这个数据用科学记数法表示为_ _ 平方米.图1正面 ↗图212图4图711在实数范围内有意义,则实数a 的取值范 围是 _.12.如图5,□ABCD 的对角线AC 、BD 相交于点O ,点E 是CD 的中点, 若AD =4cm ,则OE 的长为 cm .13.如图6,反比例函数ky x =(k >0)的图象与经过原点的直线l 相交于A 、B 两点,已知A 点的坐标为(2,1),那么B 点的坐标为 .14.已知关于x 的一元二次方程x2 +kx +1 =0有两个相等的实数根, 则k = .15.某盏路灯照射的空间可以看成如图7所示的圆锥, 它的高AO = 8米,母线AB 与底面半径OB 的夹角为α,34tan =α,则圆锥的侧面积是 平方米.(结果保留π).16.抛物线242mx x y +-=与x 轴的一个交点的坐标为)0,1(,则此抛物线与y 轴的交点的坐标是_________.17.已知△ABC 是腰长为1的等腰直角三角形,以Rt △ABC 的斜边AC 为直角边,画第二个等腰Rt △ACD ,再以Rt △ACD 的斜边AD 为直角边,画第三个等腰Rt △ADE ,…,依此类推,第n 个等腰直角三角形的斜边长是 . 三、解答题(本题有9题,共89分) (本题满分18分)(1)计算:3-1×2π⎛⎫-+ ⎪3⎝⎭-tan60° (2)解不等式组:⎩⎪⎨⎪⎧x+4<6 ①3x -12>x ②(3)先化简,再求值: 6)6()3)(3(2+---+a a a a ,其中12-=a .19.(8分)袋子中装有2个红球,1个黄球,它们除颜色外其余都相同。
厦门市湖里区初中毕业班数学第一轮质量检测试卷

湖里区2013届初三毕业班模拟考试数 学 试 题(试卷满分:150分 考试时间:120分钟)学校 班级 姓名 考号 注意事项:1.全卷三大题,26小题,试卷共4页,另有答题卡.2.答案一律写在答题卡上,否则不能得分. 3.可直接用2B 铅笔画图. 一、选择题(本大题有7题,每小题3分,共21分) 1.下列计算正确的是 A .220-+=B .326=C .330--=D .133-=2.化简3a a ÷的结果是A .aB .2a C .3a D .4a3.图1是小华在3月8日“妇女节”送给她妈妈的礼盒,图中所示礼盒的俯视图是4.设10a =,a 在两个相邻整数之间,则这两个整数是A .2和3B .3和4C .4和5D .5和65.PM2.5指数是测控空气污染程度的一个重要指数.在一年中最可靠的一种观测方法是 A .随机选择5天进行观测 B .选择某个月进行连续观测 C .选择在春节7天期间连续观测 D .每个月都随机选中5天进行观测 6.如图2,A 、B 、C 是O 上的三点,点C 是劣弧AB 的中点,40A ∠=︒,则B ∠的度数等于A .40°B .50°C .60°D .70°7.小华的家与学校的距离为s 千米,她从家到学校先以匀速1v 跑步前进,后以匀速2v (21v v <)走完余下的路程,共用了t 小时,下列能大致表示小华离学校的距离 y (千米)与离家时间x (小时)之间关系的图象是二、填空题(本大题有10小题,每小题4分,共40分) 8.已知130A ∠=︒,则A ∠的补角的度数为 °.9.某班6名学生的考试成绩如下(单位:分):45,61,75,95,83,40,则这组数据的极差是 分.10.如图3,菱形ABCD 中,对角线AC 、BD 相交于点O ,A .B .C .D .st st st st OOOOxy xy xy xy A .B . . .正面图1CO A B图2DA O CB图3则______AOB ∠=︒ .11.因式分解:510_________a b -=. 12.若分式13x -有意义,则x 的取值范围为 .13.数学老师布置7道选择题作业,并对批阅后答对题的结果进行统计,根据 右表数据可知,这50名同学答对题数的众数是__ .14.已知关于x 的方程20x bx c ++=有一个根为1,则_______b c +=. 15.某工厂现在比原计划每天多生产50台机器,且现在生产600台机器与原计划生产450台机器所需的时间相同.设原计划每天生产机器x 台, 则可列出方程 (不求解).16.如图4,已知在直角△ABC 中,90C ∠=︒,5AB =,△ABC 的面积为5,则△ABC 的周长为 .17.如图5所示,把一根细线固定在半圆形量角器的的圆心处,另一端系一个小重物,制成简单的测角仪,若细线正好和60°重合,则此时的仰角α是 °,若细线所在位置刻度模糊,请在图6中添加一条直线,就能求出此时的仰角α.三、解答题(本题有9题,共89分) 18.(本题满分18分,每小题6分) (1)计算:20(2)(3)255-⨯-+÷-;(2)如图7,画出与△ABC 关于x 轴对称的△111A B C ;(3)如图8,在等腰梯形ABCD 中,AD ∥BC ,E 为AD 的中点,连接BE 、CE .求证:△ABE ≌△DCE .答对(题) 01 2 3 4 567人数(名)1 123515 16 7C AB图4图5图6图7DBCEA图819.(本题满分7分)解不等式组:10217x x ->⎧⎨+<⎩20.(本题满分8分)如图9,在△ABC 中,90C ∠=︒,设BC x =,AC y =, (1)若1x =,2y =,求AB 的长; (2)若1tan 3A =,求点(,)x y 中纵坐标随横坐标变化的函数解析式,并画图象. 21.(本题满分8分)现有7张形状大小相同的卡片,分别标有数字1、2、3、4、5、6、7,记为甲组, (1)从甲组中随机抽一张卡片,求数字为奇数的概率;(2)从甲组中抽取5张卡片,记为乙组,要求乙组满足两个条件:① 与甲组的中位数相同,② 从乙组中抽取一张卡片,使得数字为奇数的概率小于甲组. 你选取的乙组卡片数字分别是 ,并说明理由.22. (本题满分8分)某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x 人. (1)求第一轮后患病的人数;(用含x 的代数式表示)(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.23.(本题满分9分)四边形ABCD 中,对角线AC 、BD 的交点为O ,(1)如图10,若AD ∥BC ,6AD =,4BC =,求AOCO的值; (2)如图11,若四边形ABCD 是矩形,过点B 作BE AC ⊥,垂足为E ,当30ACB ∠=︒时,有1AC =+,求BC 的长度.24. (本题满分10分)对于双曲线)0(>=k x k y必定过点P ,比如xy 9=必定过(3,3),我们称点P图9图10图11是双曲线)0(>=k x ky 的正方点. (1)画出4y x =的图象,并标出正方点P .(2)若ky x=的正方点在21y x m =+-上,求m 的取值范围.25. (本题满分10分)如图12,已知四边形ABCD 是正方形,以AB 为直径在正方形内作半圆,P 是半圆上的动点(不与点A 、B 重合),连接PA 、PD . (1)若37PAB ∠=︒,正方形的边长为5,求PA 的长度; (sin37︒≈0.60,cos37︒≈0.80,tan37︒≈0.75) (2)若PA PD =,过点P 作PE AD ⊥,垂足为E ,判断直线PE 与半圆的位置关系并说明理由.26. (本题满分11分)已知抛物线22(0)y x bx c c =-+>与y 轴的交点为A , 顶点为(,)M m n . (1)若12-=b c ,点M 在x 轴上,求c 的值. (2)若直线12y x t =-+过点A ,且与x 轴交点为B ,直线和抛物线的另一交点为P ,且P 为线段AB 的中点.当n 取得最大值时,求抛物线的解析式.图12。
湖里区2012—2013学年(上)八年级数学统考试卷

2012—2013学年(上)八年级质量检测数学试题(试卷满分:120分;考试时间:120分钟)考生注意:解答内容一律写在答题卷上,否则不得分,交卷时只交答题卷.一、选择题(本大题有7小题,每小题2分,共14分.每小题都有四个选项,其中有且只有一个选项是正确的)1.在下列实数中,是无理数的为A B.75C.0D2.下列图形是轴对称图形的有A.2个B.3个C.4个D.5个3.下列计算正确的是A.3x2·2x3=6x6B.(-2a)2=-2a2C.y3÷y3=y1D.(-m3)2=m6 4. 如图,ABC∆与'''A B C∆关于直线a对称,且'78A∠=︒,'48C∠=︒,则∠B的度数为A. 48°B. 54°C. 74°D. 78°5.若函数(2)y x a=+-是正比例函数,则a的值为A.0 B.1 C.2 D.36.如图,在△ABC中,C∠=90°,AE平分BAC∠,6CE=,则点E到AB的距离DE是A.9B.8 C.7D.67.如图,已知函数2y x b=+和3y ax=-的图像交于点(P则根据图像可得不等式,23x b ax+>-的解集是A.5->x B.2->x C.5-<x D.<x第6题图第4题图二、填空题(本大题有10小题,其中第8小题7分,其余每小题2分,共25分) 8.计算:(1)9= ;(2)3-= ;(3)01.0±= ;(4)3)2(a = ;(5)423-82x y x y ÷()= ;(6))4)(3-+x x (= ;(7)2)3(y x += . 9.分解因式244x x -+=__________.10.如图,AB 、CD 相交于点O ,且AO OB =,观察图形,只需补充一个条件 ,则有AOC ∆≌BOD ∆. 11.将直线21y x =-向上平移5个单位长度得到直线的解析式为_____.12.若2-6+x x m 是一个完全平方式,则m 的值是 .13.如图是某市乘出租车所付车费y (元)与行车里程x (千米)之间的函数关系图象,根据图象,当行车路程为6千米时,应付车费 元.14.已知一次函数y =kx +b 的图象(如图),当y <0时,x 的取值范围是 .15.如图,等腰△ABC 中,AB =AC=10, AB 的垂直平分线DE交AC 于E ,交AB 于D ,BC =6,则△CEB 的周长为__________. 16.已知直线y =-x+b 经过A (-1,m ),B (2,n )两点,比较大小:m n .17.已知a 2+b 2=13,ab =6,则a +b 的值是________.三、解答题(本大题有9小题,共81分) 18.(本题每小题6分,共18分) (101) (2)因式分解:x x 93-(3)如右图,已知AB =AC ,90B C ∠=∠=︒,求证:ABD ∆≌ACD ∆.19.(本题满分8分)先化简再求值:2(2)(2)(2)4a b a b b a b a b b +-++-÷,其中12a =-,2b = 第10题图第15题图)y 第13题图20.(本题满分6分)如图,在平面直角坐标系xoy 中,(15)A -,,(10)B -,,(43)C -,.(1)在图中作出ABC △关于y 轴的对称图形11A B C △(2)写出点1A 、1B 、1C 的坐标.21.(本题满分7分)小明平时喜欢玩“QQ 农场”游戏,本学期八年级数学备课组组织了几(1)根据表中数据确定数学成绩y 与月份x 之间的函数关系式;(2)若小明继续沉溺于“QQ 农场”游戏,照这样的发展趋势,请你估计12月份的月考小明的数学成绩,并用简要几句话对小明提出一些建议.22.(本题满分8分)如图,ABC ∆中,6AC BC ==,CE 平分ACB ∠,DE ∥BC (1)求证:DE DC =; (2)若2=AE ,求ABC ∆周长.23.(本题满分8分)已知实数,a b ,有以下两个命题: (1)若a =1b =,则122a b+<<; (2)无论,a b 为任何实数,都有222a b ab +<.判断以上两个命题是否正确,如果正确,请说明理由;如果错误,请举一个反例说明.24.(本题满分8分)如图, 已知直线a :y =2x +4与直线b :221+-=x y 相交于点P . (1)请在图中画出直线b :221+-=x y 的图像,并标出直线b 分别与x 轴、y 轴交于E 、F 两点的坐标. (2)若直线a 与x 轴、y 轴分别交于A 、B 两点,求证: AB =EF .25.(本题满分8分)如图1,ABC ∆是等边三角形,点D 、E分别是AC 、BC 边上的点,BEA CDB ∠=∠,BD ,AE 交于点N , (1)求证:BD AE =;(2)如图2,若过点B 作BM AE ⊥,垂足为M , 判断MN 和BN 的数量关系并证明.26.(本题满分10分)已知直角梯形OABC 在如图所示的平面直角坐标系中,∠OAB=90°,AB ∥OC ,AB=10,OC=22,OA=5,动点M 从A 点出发,以每秒一个单位长度的速度沿AB 向点B 运动,同时动点N 从C 点出发,以每秒2个单位长度的速度沿CO 向O 点运动.当其中一个动点运动到终点时,两个动点都停止运动,设运动时间为t 秒.(1)连接OM,假设△OMN 的面积为S,求S 与自变量t 的函数关系式,并求出自变量t 的取值范围以及在这个范围内t 取何值时,△OMN 的面积S 最小; (2)当t=5时,停止运动,在OA 上求作一点P ,使PM+P N 最小,在图中画图表示并说明理由.图2图1。
福建省厦门市湖里区2013届中考模拟试卷物理试题(无答案)

图2准考证号 姓名座位号 考生注意:1.全卷六大题,33小题,试卷共8页,另有答题卡;2.答案一律写在答题卡上,否则不能得分,交卷时只交答题卡; 3.作图题可以直接用2B 笔画; 4.全卷g 取10N/Kg 。
一、选择题(本大题12小题。
每小题2分,共24分。
每小题只有1个选项符合题意)1.为了保持厦门优雅的环境,减少噪声污染,厦门岛内禁止汽车鸣笛。
这种减弱噪声的途径是在A .声源处 B .传播过程中C .人耳处D .声源和人耳处 2.如图1所示的四种现象中,由于光的折射形成的是3.图2中的握力器是一种健身器材,主要是利用金属的A .导热性好B .弹性好C .导电性好 D.光泽度好 4.如图3所示在“探究产生感应电流”的四次实验中,有感应电流产生的是5. 祖国的山河一年四季美景如画,在图4的描述的物态变化中,属于升华的是A BCD图3D.严冬,冰雕逐渐减小 C.秋天,枝头挂上白霜 图1A.手影B. 桥的倒影C.小孔成像D. 筷子变弯折图66.关于0℃,以下说法正确的是A .0℃时,物体的内能为零B . 0℃时,地面的大气压等于零C .0℃时,液体可以继续蒸发D . 0℃时,大部分导体出现超导现象 7.图5所示的电路中,当开关闭合时,甲电流表的示数为0.6A 乙电流表的示数为0.2A ,则下列判断正确是 A .通过灯L 1的电流为0.6A B .通过灯L 1的电流为0.4A C .通过电路总电流为0.8 A D .通过灯L 2的电流为0.4 A8.妈妈要给小亮网上买衣服,用卷尺量他胸围。
小亮则找条塑料带, 在同一位置绕了一周,然后用米尺测这一周的长度,测量结果与妈妈一致。
小亮用了物理学一种重要的方法,这方法是 A .等效替代法 B .微小放大法 C .控制变量法 D .模型法9.体积相等,形状不同的甲、乙两物体悬浮在水中的不同位置(如图6所示), 则它们的密度ρ及其所受到的浮力F大小关系分别是 A .ρ甲<ρ乙 F 甲=F 乙 B.ρ甲<ρ乙F 甲>F 乙 C.ρ甲=ρ乙 F 甲>F 乙 D.ρ甲=ρ乙F 甲=F 乙10.如图7所示,光在玻璃和空气的界面CD ,同时发生了反射和折射,以下说法正确的是 A.入射角为40度,左边是空气 B .入射角为50度,右边是空气C .折射角为20度,右边是玻璃D .折射角为70度,左边是玻璃11.小林连接了一个电路,如图8,电源电压保持不变。
2013年初中毕业班质量检测及答案(1)

莆田市2013年初中毕业班质量检测数 学(满分:150分;考试时间:120分钟)友情提醒:本试卷分为“试题”和“答题卡”两部分,答题时,请按答题卡中的“注意事项”认真作答。
答案写在答题卡上的相应位置.一、精心选一选:本大题共8小题,每小题4分,共32分,每小题给出的四个选项中有且只有一个选项是正确的,答对的得4分;答错、不答或答案超过一个的一律得0分. 1.计算 -3+2的结果是( ).A .1B . 一1C .5D . 一52.不等式组5121213{<-≥+-x xx 的解集在数轴上表示正确的是( )3.如图,A 、B 的坐标分别为(2,0),(0,1),若将线段AB 平移至A 1B 1,则a +b 的值为( ).A .2B .3C .4D .54.一个几何体的三视图如下,其中主视图和左视图都是腰长为4,底边为2的等腰三角形,则这个几何体侧面展开图的面积为( ).A .2πB .12π C .4π D .8π5.如图,OP 平分∠MON ,PA ⊥ON 于点A ,点Q 是射线OM 上一个动点,若PA =2,则PQ 的最小值为( ). A .1 B .2 C .3 D .46.在等腰三角形、梯形、矩形、平行四边形中既是轴对称图形又是中心对称图形的是 ( ). A .等腰三角形 B .梯形 c .矩形 D .平行四边形7.如图,正方形ABCD的边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG= DH,设小正方形EFGH的面积为y),,AE为x,y关于x的函数图象大致是( )8.观察图中正方形四个顶点所标的规律,可知2013应标在( ).A.第503个正方形的左上角B.第503个正方形的右下角C.第504个正方形的左下角D.第504个正方形的右下角二、细心填一填:本大题共8小题,每小题4分,共32分.9.16的算术平方根是___________.10.太阳的半径约是69000千米,用科学记数法表示(保留2个有效数字)约是________千米.11.如图,要测量A、B两点间距离,在0点打桩,取OA的中点C,OB的中点D,测得CD=30米,则AB=________米.12.如图,在平行四边形ABCD中,点E、F分别在边BC、AD上,请添加一个条件_________________________,使四边形AECF是平行四边形.13.已知两圆直径分别为2cm和4cm,圆心距为2.5cm,则这两个圆位置关系是_______.14.抛掷一枚质地均匀的硬币两次,正面都朝上的概率是____________.15.一次函数y=kx+6的图象如图所示,则方程kx+6=0的解为________________.16.如图,∆ABC 的周长为21,底边BC =5,线段AB 的垂直平分线DE 交AB 于点 D ,交AC 于点E ,∆BEC 的周长为______________.三、耐心做一做:本大题共9小题,共86分,解答应写出必要的文字说明、证明过程或演算步骤 17.(本小题满分8分)计算:|一2 |+(一2)0+2sin 300.18.(本小题满分8分)先化简,再求值:12112---x x ,其中x =-2.19.(本小题满分8分) .如图,在矩形ABCD 中,E 是BC 边上的点,将∆DCE 沿DE 折叠,使点c 落在AE 边上的点F 处.(1)(4分)求证:AE =BC ;(2)(4分)若AD =5,AB =3,求sin ∠EDF .我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:根据以上表格信息,解答如下问题::(1)(4分)计算这组数据的三个统计量:平均数、中位数和众数;(2)(4分)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普通身高”的是哪几位男生?并说明理由.21.(本小题满分8分)如图,在Rt∆ABC中,∠C=900,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F(1)(4分)求证:BC是⊙O的切线;(2)(4分)CD=6,AC=8,求AE.如图,一次函数),y = -13 x +2的图象分别与x 轴、y 轴相交于A 、B 两点,点P 为线段AB上一点,PC ⊥x 轴于点C ,延长PC 交反比例函数y =k x (x >0)的图象于点Q ,tan ∠OAQ =13 ,连接DP 、OQ ,四边形OQAP 的面积为6.(1)(6分)求k 的值;(2)(4分)判断四边形OQAP 的形状,并加以证明.23.(本小题满分10分)用长度一定的不锈钢材料设计成外观为矩形的框架(如图1、图2中的一种),设竖档AB =x 米,请根据以下图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有线段的长度和,所有横档和竖档分别与AD 、AB 平行)(1)(5分)在图1中,如果不锈钢材料总长度为12米,当x 为多少时,矩形框架ABCD 的面积为3平方米?(2)(5分)在图2中,如果不锈钢材料总长度为12米,当x 为多少时,矩形框架ABCD 的面积S 最大?最大面积是多少?24.(本小题满分14分)已知:抛物线y =14 x 2+l 的顶点为M ,直线z 过点F (0,2)且与抛物线分别相交于A 、B 两点,过点A ,B 分别作x 轴的垂线,垂足分别为点C ,D ,连接CF ,DF ,. (1)如图1所示:①(3分)若A (一l ,54),求证:AC =AF ;②(6分)若A (m ,n ),判断以CD 为直径的圆与直线l 的位置关系,并加以证明; (2)(5分)若直线l 绕点F 旋转,且与x 轴交于点P ,PC ×PD =8.求直线l 的解析式.25.(本小题满分12分)新知认识:在∆ABC 中,∠A ,∠B ,∠C 所对的边分别用a ,b ,c 表示,如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.(1)(3分)特殊验证:如图1,在△ABC 中,若a=3,b=1,c=2 求证:△ABC 为倍角三角形;(2)(4分)模型探究:如图2,对于任意的倍角三角形,若∠A =2∠B 求证:a 2=b(b+c)(3)(5分)拓展应用:在△ABC 中,若∠C =2∠A =4∠B 求证:b a + bc=1莆田市2013年初中毕业班质量检测数学参考答案与评分标准一、精心选一选(本大题共8小题,每小题4分,共32分) 1.B 2.A 3.A 4.C 5.B 6.C 7.B 8.D二、细心填一填(本大题共8小题,每小题4分,共32分) 9. 4 10. 6.9⨯104 11.6012.AF=CE 或 BE=DF 或∠AEC=∠AFC 等(答案不唯一) 13.相交 14.1/4 15.x=-1 16.13三、耐心做一做(本大题共9小题,共86分) 17.解:原式=2+1+221⨯……………………………………6分 =2+1+1=4 ……………………………………8分18.解:原式=)1)(1(2)1)(1(1+-+-+-x x x x x=)1)(1(1+--x x x =11+x 把x=-2代入原式得:原式=121+-=-119(1)证明:∵将DCE ∆沿DE 折叠。
2013-2014学年厦门市九年级第一学期质量检测-数学试题(含答案)

2013—2014学年(上)厦门市九年级质量检测数学试题(试卷满分:150分考试时间:120分钟)一、选择题(本大题有7小题,每小题3分,共21分。
每小题都有四个选项,其中有且只有一个选项正确)1. 下列计算正确的是( )A.333=⨯B.933=⨯C.333=÷D.633=+2. 一元二次方程x 2+2x=0的根是( )A.x=0B.x=-2C.x=0或x=-2D.x=0或x=2 3. 下列事件中,属于随机事件的是()A.掷一枚质地均匀的正方体股子,向上的一面点数小于7B.某射击运动员射击一次,命中靶心C.在只装了红球的袋子中摸到白球D.在三张分别标有数字2,4,6的卡片中摸两张,数字和是偶数 4. 已知⊙○的半径是3,OP=3,那么点P 和⊙○的位置关系是()A.点P 在⊙○内B.点P 在⊙○上C.点P 在⊙○外D.无法确定 5. 下列图形,属于中心对称图形的是()A.等边三角形B.直角三角形C.矩形D.等腰梯形 6. 反比例函数xm y 2-=的图象在第二,四象限内,则m 的取值范围是( )A.m >0B.m >2C.m <0D.m <27. 如图1,在⊙○中,弦AC 和BD 相交于点E,弧AB=弧BC=弧CD,若∠BEC=1100,则∠BDC=()A.350B.450C.550D.700二、填空题(本大题有10小题,每小题4分,共40分)8. 化简:3-=.9. 一个圆形转盘被平均分成红,黄,蓝,白4个扇形区域,向其投掷一枚飞镖,飞镖落在红色区域的概率是.10. 已知点A (-1,-2)与点B(m,2)关于原点对称,则m=.11. 已知△ABC 的三边的长分别是6,8,10,则△ABC 外接圆的直径是.12. 九年级有一个诗歌朗诵小组,其中男生5人,女生12人,现从中随机抽取一名同学参加表演,抽中男生的概率是.13. 若直线y=(k-2)x+2k-1与y 轴交于点(0,1)则K=.14. 如图,A,B,C 是⊙○上的三个点,若∠AOC=1100则∠ABC=.15. 电流通过导线时会产生热量,设电流是I (安培),导线电阻为R (欧姆),t 秒产生的热量为Q (焦),根据物理公式,Q=I 2Rt ,如果导线电阻为5欧姆,2秒时间导线产生60焦热量,则电流I 的值是安培16. 如图,以正方形ABCD 的顶点D 为圆心画圆,分别交AD,CD 两边于点E,F 。
福建省厦门市2013届九年级数学上学期质量检测试题

2012—2013学年(上)某某市九年级质量检测数 学(试卷满分:150分 考试时间:120分钟)某某号 某某 座位号 注意事项:1.全卷三大题,26小题,试卷共4页,另有答题卡. 2.答案必须写在答题卡上,否则不能得分. 3.可以直接使用2B 铅笔作图.一、选择题(本大题有7小题,每小题3分,共21分.每小题都有四个选项,其中有且只有一个选项正确) 1. 下列计算正确的是A 3-3=0B 3+3=3C 33=633=32. 计算25()的值是 A .±5B .5C .553. 掷一个均匀正方体骰子,当骰子停止后,朝上一面的点数为2的概率是A .1B .12C .13D .164. 若2是方程x 2-2x +c =0的根,则c 的值是A .-3B .-1C .0D .1 5. 下列事件,是随机事件的是A.从0,1,2,3,…,9这十个数中随机选取两个数,和为20 B .篮球队员在罚球线上投篮一次,未投中DC .度量三角形的内角和,结果是360 °D .度量正方形的内角和,结果是360 °6. 如图1,四边形ABCD 是正方形,点E 、F 分别在线段BC 、DC 上, ∠BAE =30°.若线段AE 绕点A 逆时针旋转后与线段AF 重合, 则旋转的角度是A .30°B .45°C .60°D .90°7. 如图2,在△ABC 中,AB =AC =2,BCA 为圆心作 圆弧切BC 于点D ,且分别交边AB 、AC 于点E 、F ,则扇形AEF 的面积是 A .π8B .π4C .π2D .π二、填空题(本大题有10小题,每小题4分,共40分) 8. 二次根式2x 有意义,则x 的取值X 围是 .9. 方程x 2=3的根是.10.如图3,A 、B 、C 、D 是⊙O 上的四点,若∠ACD =30°,则∠ABD =度. 1AB 、CD 是⊙O 的两条弦,若︵AB =︵CD ,且AB =2,则CD =.12. 若一元二次方程x 2+4x +c =0有两个相等的实数根,则c 的值是 .13. 一个圆形转盘被平均分成红、黄、蓝3个扇形区域,向其投掷一枚飞镖,飞镖落在红 色区域的概率是.14. 已知点A (a ,-1)、A 1(3,1)是关于原点O 的对称点,则a =.图3ODCBA图2FECBA15. 把小圆形场地的半径增加5米得到大圆形场地,此时大圆形场地的面积是小圆形x 米,若要求出未知数x , 则应列出方程(列出方程,不要求解方程).16. 如图4,AB 是⊙O 的弦,AB =2,△AOB 的面积是3,则∠AOB =度. 17. 若1x a =+,1y a =-,x 2-y 2=8,则a =.三、解答题(本大题有9小题,共89分) 18.(本题满分18分)(1)计算2(32)26⨯+-;(2)如图5,画出△ABC 关于点C 对称的图形;(3)如图6,已知A 、B 、C 是⊙O 上的三点,∠ACB =90°,BC =3,AC =4,求⊙O 直径的长度.19.(本题满分7分)解方程x 2+2x -2=0.20.(本题满分7分)第一盒乒乓球中有1个白球和2个黄球,第二盒乒乓球中有2个白球和1个黄球.(1)从第一盒乒乓球中随机取出1个球,求这个球恰好是黄球的概率; (2)分别从每盒中随机取出1个球,求这2个球恰好都是黄球的概率.21.(本题满分8分)我们知道,若两个有理数的积是1,则称这两个有理数互为倒数.同样图5CBA图6OC 图4OBA的,当两个实数(a +与(a 的积是1时,我们仍然称这两个实数互为倒数. (1)判断(4+与(4是否互为倒数,并说明理由;(2)若实数是的倒数,求点(x ,y )中纵坐标随横坐标变化的函数解析式,并画出函数图象.22.(本题满分8分)某公司举办产品鉴定会,参加会议的是该公司的林经理和邀请的专家.在专家到会时,林经理和每位专家握一次手表示欢迎;在专家离会时,林经理又和他 们每人握一次手表示道别.且参加会议的每两位专家都握了一次手.(1)若参加会议的专家有a 人,求所有参加会议的人共握手的次数(用含a 的代数式表示);(2)所有参加会议的人共握手10次的情况是否会发生,请说明理由.23.(本题满分9分)如图7,四边形ABCD 是等腰梯形,AD ∥BC ,BC =2.以线段BC 的中点O为圆心,以OB 为半径作圆,连结OA 交⊙O 于点M . (1)若∠ABO =120°,AO 是∠BAD 的平分线,求︵BM 的长;(2)若点E 是线段AD 的中点,AE,OA =2,求证:直线AD 与⊙O 相切.24.(本题满分10分)已知关于x 的方程(a 2+1) x 2-2(a +b ) x +b 2+1=0. (1)若b =2,且2是此方程的根,求a 的值;(2)若此方程有实数根,当-3<a <-1时,求b 的取值X 围.图725.(本题满分10分)已知双曲线y =k x(k >0),过点M (m ,m )(m作MA ⊥x 轴,MB ⊥y 轴,垂足分别是A 和B ,MA 、MB 分别交双曲线y =k x(k >0)于点E 、F . (1)若k =2,m =3,求直线EF 的解析式;(2)O 为坐标原点,连结OF ,若∠BOF °,多边形BOAEF 的面积是2,求k 的值.26.(本题满分12分)已知A 、B 、C 、D 是⊙O 上的四点,︵CD =︵BD ,AC 是四边形ABCD 的对角线.(1) 如图8,连结BD ,若∠CDB =60°,求证:AC 是∠DAB 的平分线;(2) 如图9,过点D 作DE ⊥AC ,垂足为E ,若AC =7, AB =5 ,求线段AE 的长度.学年(上) 3分,共21二、填空题(本大题共10小题,每题4分,共40分)8. x ≥2; 9. ±3; 10. 30; 11. 2; 12. 4; 13. 13;14. -3; 15. 4πx 2=π(x +5)2; 16. 60; 17. 4.说明:☆ 第9题写对1个给2分; 第15题写成4x 2=(x +5)2不扣分. 三、解答题(本大题共9小题,共89分) 18.(本题满分18分)(1)解:2×(3+2)-26;=6+2-26……………………………………………………4分=2- 6. …………………………………………………………6分 说明:☆ 写出正确答案,至少有一步过程,不扣分,只有正确答案,没有过程,只扣1分;☆ 没有写正确答案的,按步给分.(2)能在图中看出对称点是C 点 ……………2分 能画出对称图形是三角形 ……………4分以上两点都有 …………………6分(3)证明:∵∠ACB =90°,…………………………1分 ∴AB 是直径. …………………………3分 在Rt △ABC 中,∵BC =3,AC =4,∴AB =5. ……………………………6分19.(本题满分7分)解法一: x 2+2x -2=0,∵b 2-4ac =22+8=12, …………………………………………2分 ∴x =-b ±b 2-4ac2a ………………………………………… 4分=-2±122…………………………………………5分=-1± 3. ………………………………………………6分 即x 1=-1+3,x 2=-1- 3. ……………………………………………7分 解法二: x 2+2x -2=0,OCB CEDA(x +1)2=3. ………………………………………………4分x +1=± 3. ………………………………………………6分即x 1=-1+3,x 2=-1- 3. ……………………………………………7分 说明:☆x 1=,x 2=,写错一个扣1分.☆ 写出正确答案(即写出x 1=,x 2=,)且至少有一步过程,不扣分. ☆ 只有正确答案,没有过程,只扣1分. ☆ 没有写正确答案的,按步给分.☆ 如果12没有化简(即x 1=-2+122,x 2=-2-122),只扣1分.20.(本题满分7分)(1)解: P ( 恰好是黄球) ……………………………………………1分=23. …………………………………………………………………3分 (2)解: P (两球恰好都是黄球)=29 . ………………………………………7分说明:☆ 第(2)若答案不正确,但分母写对,则只扣2分.☆ 两小题的答案正确,但格式不对,如“事件”没写或写不对,只扣1分.21.(本题满分8分)(1)解法一:(4+2)与(4-2)不是互为倒数. …………………………………1分∵(4+2)(4-2) ……………………………………………………2分 =14. ………………………………………………………3分 而14≠1, ∴(4+2)与(4-2)不是互为倒数.解法二:(4+2)与(4-2)不是互为倒数. …………………………………1分 14+2……………………………………………………2分=4-214………………………………………………………3分 ≠4- 2.∴(4+2)与 (4-2)不是互为倒数.说明:☆ 若没有写“(4+2)与(4-2)不是互为倒数”但最后有写“(4+2)与(4-2)不是互为倒数”,则分数可不扣,若有写“(4+2)与(4-2)不是互为倒数”但最后没有“(4+2)与(4-2)不是互为倒数”,不扣分. ☆ 若写成“(4+2)不是(4-2)的倒数”亦可.(2)解:∵实数(x +y )是(x -y )的倒数,∴(x +y )(x -y )=1. ……………4分 ∴x -y =1. ………………………5分 ∴y =x -1. ………………………6分 画出坐标系,正确画出图象 …………8分说明:若图象画成直线、或自变量的取值不对,可得1分.22.(本题满分8分) (1)解:2a +a (a -1)2……………………………………………………3分说明: 若没有写全对,则写出2a 得1分,写出a (a -1)2得2分.(2)解法一:不会发生. ……………………………………………………4分设参加会议的专家有x 人.若参加会议的人共握手10次,由题意 ……………………………5分2x +x (x -1)2=10. ……………………………………………………6分∴x 2+3x -20=0.∴x 1=-3-892,x 2=-3+892. …………………………………7分∵x 1、x 2都不是正整数, …………………………………8分 ∴ 所有参加会议的人共握手10次的情况不会发生.解法二:不会发生. ……………………………………………………4分 由题意我们知道,参加会议的专家的人数越多,则所有参加会议的人握手 的次数就越多.当参加会议的专家有3人时,所有参加会议的人共握手9次; …6分 当参加会议的专家有4人时,所有参加会议的人共握手14次; …8分 故所有参加会议的人共握手10次的情况不会发生.说明:☆ 若没有写“不会发生”但最后有下结论,则分数可不扣,若有写“不会发生”但最后没有下结论,不扣分.☆ 若没有写“若参加会议的人共握手10次”但列对方程,则此分不扣,列对方程可得2分;☆ 没有写“x 1、x 2都不是正整数,不合题意”而是写“经检验,不合题意” 亦可.23.(本题满分9分)(1)解:∵AD ∥BC ,∠ABO =120°,∴∠BAD =60°.…………………………………………………………1分 ∵AO 是∠BAD 的平分线, ∴∠BAO =30°.∴∠AOB =30°.………………2分∵BC =2,∴BO =1.………………3分MOEDCBA∴︵BM =30π180=π6. ……………4分(2)证明:由题意得,四边形ABCD 是等腰梯形, ∴ 四边形ABCD 是轴对称图形.∵ 点O 、E 分别是底BC 、AD 的中点,连结OE ,∴OE 是等腰梯形ABCD 的对称轴.………………………………………5分 ∴OE ⊥AD .…………………………………………………………6分在Rt △AOE 中,∵AE =3,OA =2,∴OE =1. …………………………………………………………7分即OE 是⊙O 的半径. ……………………………………………………8分 ∴ 直线AD 与⊙O 相切. …………………………………………………9分 24.(本题满分10分)(1)解:∵b =2,且2是方程的根, ∴ 原方程可化为(a 2+1)22-2(a +2)2+1+22=0. ……………………………………1分 即 4a 2-4a +1=0. …………………………………………2分 ∴a =12. ………………………………………………………4分(2)解:△=4(a +b )2-4(a 2+1)(1+b 2) ……………………………………5分 =8ab -4a 2b 2-4=-4(ab -1)2. ………………………………………………6分 ∵ 方程有实数根,∴-4(ab -1)2≥0. 即 4(ab -1)2≤0.∴4(ab -1)2=0. ……………………………………………………7分∴ab -1=0.∴b =1a. ……………………………………………………………8分∵1>0,∴ 在每个象限,b 随a 的增大而减小. ……………………………………9分 ∴ 当-3<a <-1时,-1<b <-13. ……………………………………………………………10分25.(本题满分10分) (1)解:∵k =2,m =3,∴ 点E (3,23),点F (23,3). …………………………………………2分设直线EF 的解析式为y =ax +b , 则得,⎩⎪⎨⎪⎧3a +b =23,23a +b =3.……………………………………………………………3分 解得,⎩⎪⎨⎪⎧a =-1,b =113. ∴直线EF 的解析式为y =-x +113…………4分(2)解法一:由题意得,MA ⊥OA ,MB ⊥OB ,∠BOA =90°,∴ 四边形OAMB 是矩形. 又MA =MB =m , ∴ 四边形OAMB 正方形.点E (m ,km ),F (k m,m ). ……………5分 ∴OA =OB ,AE =BF .连结OE ,∴R t △OBF ≌R t △OAE . ………………6分 ∴∠EOA =∠BOF °.∴∠FOE =45°.连结EF 、OM 交于点C . 又 ∵∠MOA =45°, ∴∠MOE °.同理得,∠FOM °. ∵OF =OE ,∴OC ⊥FE ,且点C 线段EF 的中点.∴R t △FOC ≌R t △EOC . ………………………………………………7分Rt △COE ≌R t △AOE . ………………………………………………8分∴S △AOE =14S 五边形BOAEF . …………………………………………………9分∴12·m ·k m =12. ∴k =1. …………………………………………………………10分 解法二:由题意得,MA ⊥OA ,MB ⊥OB ,∠BOA =90°,∴ 四边形OAMB 是矩形. 又MA =MB =m , ∴ 四边形OAMB 正方形.点E (m ,k m ),F (k m,m ). ………………………………………………5分 ∴OA =OB ,AE =BF .连结OE ,∴R t △OBF ≌R t △OAE . ………………………………………………6分∴∠EOA =∠BOF °.OF =OE .将△OBF 绕点O 顺时针旋转90°,记点F 的对应点是P . ……………7分 则∠EOP =45°. ∵∠EOF =45°,∴△EOF ≌△EOP . …………………………………………………8分 ∴S △EOP =12S BOAEF . ……………………………………………………9分即S △EOP =1. 12·m (k m +km)=1 ∴k =1. …………………………………………………………10分 解法三:由题意得,MA ⊥OA ,MB ⊥OB ,∠BOA =90°,∴ 四边形OAMB 是矩形. 又MA =MB =m , ∴ 四边形OAMB 正方形.点E (m ,km ),F (k m,m ). ………………………………………5分 ∴ME =MF =m -k m.连结EF ,则△MFE 是等腰直角三角形. 连结OM 交EF 于点C .则OM ⊥EF . ∵∠BOM =45°,∠BOF ° ∴∠FOC °.∴R t △FOB ≌R t △FOC . …………………………………………6分∴OC =OB =m .∵点E (m ,km ),F (k m,m ).∴ 直线EF 的解析式是y =-x +m +k m. ∵ 直线OM 的解析式是y =x ,∴ 点C (m 2+k 2m ,m 2+k2m). ……………………………………7分过点C 作⊥x 轴,垂足为N .则(m 2+k 2m )2+(m 2+k 2m)2=m 2.解得,k =(2-1) m 2. ……………………………………8分 由题意得,m 2-12(m -k m )2=2. ……………………………………9分即 m 2-12[ m -(2-1) m ] 2=2.解得,(2-1) m 2=1.∴k =1. ……………………………………10分 26.(本题满分12分) (1)证明:∵︵CD =︵BD ,∴CD =BD . ………………………1分 又∵∠CDB =60°,∴△CDB 是等边三角形. …………………2分 ∴∠CDB =∠DBC . …………………3分 ∴︵CD =︵BC .∴∠DAC =∠CAB .∴AC 是∠DAB 的平分线. ………………………………………………4分 (2)解法一:连结DB .ODB A在线段CE 上取点F ,使EF =AE ,连结DF . ……………………………6分 ∵DE ⊥AC ,∴DF =DA ,∠DFE =∠DAE . ……………………………………7分 ∵︵CD =︵BD , ∴CD =BD . ∴∠DAC =∠DCB . ∴∠DFE =∠DCB .∵ 四边形ABCD 是圆内接四边形,∴∠DAB +∠DCB =180°.………………8分 又∵∠DFC +∠DFE =180°,∴∠DFC =∠DAB .………………………9分 ∵∠DCA =∠ABD ,∴△CDF ≌△BDA . ……………………………………………………10分 ∴CF =AB . …………………………………………………………11分 ∵AC =7, AB =5,∴AE =1. …………………………………………………………12分 解法二:在︵CD 上取一点F ,使得︵DF =︵DA ,…………………………………5分 连结CF ,延长CF ,过D 作DG ⊥CF ,垂足为G . ……………6分 ∵︵DF =︵DA , ∴∠GCD =∠DCE . ∵DC =DC ,∴R t △CGD ≌R t △CED . ……………7分 ∴CG =CE .∴DG =DE . ∵︵DF =︵DA , ∴DF =DA .∴R t △DGF ≌R t △DEA . ………………………………………8分 ∴FG =AE . ………………………………………9分 ∵︵CD =︵BD ,︵DF =︵DA , ∴︵CF =︵AB .∴CF =AB . ………………………………………10分 ∵CG =CE ,∴CF +FG =AC -AE ………………………………………11分 即 AB +AE =AC -AE ∵AC =7, AB =5,∴AE =1. …………………………………………………………12分。
2013-2014厦门市初三(上学期)质量检查语文试卷分析

厦门市2013-2014学年(上)九年级语文质量检测分析一、试卷形式分析这次市质检试卷总体来说难度系数和之前的市质检说明会告知的难度还是比较匹配的,在0.75左右。
本份试卷的构成和以往有一些略微变化,以往的试卷构成是由三大部分组成,这次的质检通过内容的浓缩和考题的微变变成了三大部分构成,分别是:第一部分语言积累与运用(42分),第二部分阅读(48分),第三部分作文(60分)。
从题目的设置上看,题量还是比较适中的18题。
考试的形式也是不变的120分钟。
二、试卷考察内容的分布状况和难易度分析一、语言积累中,九年级上册的古诗文背默13分,考察范围是九年级上册的课内五首词、出师表、课外古诗十首。
这题的难度相比之前还是有所降低的,基本上是给出前句然后填写后一句,课外的背默难度比较一般,选取了学生背诵的比较多的有带“酒”字的古诗词。
二、语言的运用,相比之前的口语交际来说,有所变动,把之前的针对某一话题判断观点的题目变成了语言的得体考察,考察的话题也是比较接近学生的“穿红灯劝阻”问题。
三、字词拼音的考察和以往的一样,从ABCD四个选项中选择完全正确的一项,考察的字音字形也是平时学生接触的比较多的,难度不大。
此题略微修改之处在于把之前的“仿写句子”的考察内容替换成了回忆想象某一情景的描绘,可以说减低的学生的答题难度。
四、名著的考察,范围和去年一样,就考一本水浒传;比之去年的考察二线人物,今年的考察比较注重学生对名著的常识的考察,考察的是最基本的作者和书名。
另一方面降低名著考察的内容体现在故事情节的节选上,本次的内容的节选在课本的名著导读中就可以找到,学生如果有认真阅读课本的话,答此题问题不大。
要求学生读文品人的能力体现在名著的最后一道小题,此题的难度关键在针对故事情节,点评符合的人物性格。
五、综合性学习考察的分值是13分,所选取的题材内容既能和语文息息相关也能结合当今的一些时代关注热点,离学生的日常生活还是很接近的,题材中的“走进汉字”系列活动在厦门的双十中学就开展过。
初中毕业生第三次质量调查

2013年初中毕业生第三次质量调查语文试卷说明:1.试卷满分150分,考试时间为150分钟。
考试结束后,请将本试卷和答题卡一并交回。
2.所有的试题都必须在专用的“答题卡”上作答,选择题用2B铅笔在涂卡区作答,其它题在指定位置用0.5毫米黑色水笔作答。
一、积累与运用(满分30分)1. 请选出下列词语中加点字音形..全都正确的一项(2分)A.绯.闻(fēi)翘.首(qiáo)锋芒毕露.(lù) 栩栩..如生(xǔ)B.剔.除(tì)嫉.妒(jí)莫衷.一是(z hōnɡ)妇儒.皆知(rú)C.烦燥.(zào)处.理(chù)鳞次栉.比(zhì)惟妙惟肖.(xiào)D.祈.祷(qǐ)阔绰.(chuò) 苍.海桑田(cāng)颔.首低眉(hàn)2.下列加点的词语运用正确..的一项是(2分)A. 他自信这一席话委婉得体,尤其最后那一段接得天衣无缝....。
B. 只有拥有了广博的阅历、丰富的语汇,我们创作作品才有可能一鼓作气....。
C. 他感到一种不言而喻....的恐惧,一种同亲人隔绝、同大地分离的孤独感油然而生。
D. 当电影《2012》里每一个生命不断殊死挣扎时,那种生离死别使人感觉到我们似乎太渺小了,渺小得无与伦比....。
3. 选出对下列病句修改正确..的一项(2分)A.只有坚持经久不息的冶炼和艰苦卓绝的开采,才有可能获得一颗光彩夺目的金珠。
将“只有……才”换成“如果……就”。
B.上海科技开发中心聚集了一批热心于科技开发服务、善于经营管理的专业化队伍。
修改:将“热心于科技开发服务”与“善于经营管理”调换位置。
C.无论干部和群众,毫无例外,都必须遵守社会主义法制。
去掉“毫无例外”D.国家免收义务教育阶段学生的学杂费,这一举措降低了家长的经济负担。
修改:将“降低”改为“减轻”。
4. 选出对《水调歌头·明月几时有》赏析有误..的一项(2分)A. 词的上片极写作者在“天上”、“人间”的徘徊、矛盾,下片写对月怀人,以积极乐观的旷达情怀作结。
2013年厦门市九年级初中毕业质量检测语文试卷

2012—2013学年(上)厦门市九年级质量检测语文试题第一部分口语交际(7分)一.完成第1题1.根据对话情境,回答问题。
今年中秋、国庆期间,央视播出了系列调查“你幸福吗?”在此次“幸福调查”采访中,受访者对幸福的回答各不相同:上海外滩一位环卫工人说最大的幸福是外来务工人员都能改善福利;兰州动物园一位游客认为社会安定就是幸福;沈阳北站广场一位老人则认为幸福是儿女孝顺,生活有保障。
其间,“我姓曾”,“没有成功收回钓鱼岛”,“我耳朵不好”等各类“神回复”也频频出现。
一时间,“幸福调查”的播出引起网友热议。
甲:出现这么多“神回复”,可见央视“幸福调查”不会调查出什么事实来,这样的“幸福调查”没有什么实际意义。
乙:我可不这么看。
我觉得这次调查真实的反应了老百姓的心声。
这样将采访的“原汁原味”呈现给大家,给予不同声音同等的表达机会,说明的恰恰是调查本身具有极强的真实性,调查结果有着极高的可信度。
丙:其实,无论是受访者自然朴实的话语,还是受访者答非所问,甚至是“神回复”,“你幸福吗?这看似简单的问题的本身更有价值,它提醒我们问问自己:“你幸福吗?”“什么是幸福?”“怎样才能幸福?”,央视此问是值得称道的。
(1)甲、乙、丙争论的焦点是( )(2分)A.怎样看待“幸福”。
B.怎样看待“幸福调查”的意义。
C.“神回复”到底好不好。
(2)下列说法与乙的观点不相符的一项是()(2分)A.乙认为央视的“幸福调查”难能可贵。
B.乙认为调查的本身具有极强的真实性。
C.乙希望大家都能感受到幸福。
(3)假如你有机会接受央视的“幸福调查”,你会发表怎样的看法?请简要说说。
(3分)_____________________________________________________________________ _____________________________________________________________________ ____第二部分语言积累与运用(满分:36分)二、完成2—5题(36分)2.请根据提示填写相应的古诗文。
【精品·打印版】2013-2014厦门市九年级物理质检试题及答案

2013-2014学年(上)厦门市九年级质量检测物理试题答案及评分标准一、选择题(本大题12小题,每小题2分,共24分) 1-5CACDC 6-10 DCBDB 11-12AB 二、填空题(本大题10小题,每小题2分,共20分) 13.无规则升高 14.B 汽化15.总开关并16.电源不适合 17.13.5 热 18.同种电荷相互排斥从B 到A 19.增加液化过程要放热 20.增大突然增大 21.天然气 7.2×108 22. 小于小于 三、简答题(4分)23.①污水杯中的水汽化成水蒸气,汽化吸热;②水蒸气上升,在塑料罩上遇冷液化成小水珠,液化放热。
四、作图题(本大题共2题。
每小题2分,共4分) 24.25.28分)26.(每小题2分,共4分)(1) 38.5 (2)2014.1 27.(每空1分,共4分)(1) 0 冰(2)小(3)受热均匀 28.(每小题2分,共4分)(1)滑动变阻器的滑片没有放在阻值最大处; (2)移动滑片电阻R 两端的电压(3)电压一定时,通过导体的电流与导体的电阻成反比。
29.(每小题2分,共8分)(1)A 电阻(2)温度计的示数变化比热容 (3)c 水(t 水-t 0)/(t 煤油-t 0)30.(每小题2分,共6分)(1)连接电源负极与滑动变阻器的左下接线柱 (2)滑动变阻器的电阻太大,电流太小(3)D (4)电压表接在滑动变阻器的两端。
六、计算题(本大题3小题,共20分)*其它方法计算正确的,参照评分标准分步给分。
31.解:(1)由Rt I Q 2=, 得A1s6040J4002=⨯Ω==Rt QI ………2分(2)电热丝剪去一半时,R 1=20 Ω,………1分U 总=I R =1 A×40 Ω=40 V ………1分11=R U I A 220V 40=Ω=………1分Q 1=I 12R 1t 1=(2A )2×20 Ω×60 s=4 800J ………1分乙 甲32.解:(1)V =1.5 L=1.5×10-3 m 3kg 5.1m 105.1kg/m 103333=⨯⨯===-V m V mρρ ……1分Q =c mΔt=4.2×103 J/(kg·℃) ×1.5kg×(100 ℃-20 ℃)=5.04×105 J ………………2分(2) J106.590%J 105.0455⨯=⨯==ηQW …………1分 s700W 800J 106.55=⨯===P W t t W P ………2分33.解:(1)当只闭合S 3时,L 与R 2串联,R 2=20 Ω,I 1=0.4 AΩ====30A 4.0V121I U R R U I ……1分R L =R 总-R 2=30 Ω-20 Ω=10 Ω…1分当只闭合S 2时,L 与R 1串联,R L =10 Ω,I 2=0.4 AR ′总=Ω==30A 4.0V 122I UR 1= R ′总- R L =30 Ω-10 Ω=20 Ω……1分(2)只闭合S 3时,L 与R 2串联,灯泡L 正常发光,U L =5 VI L=A 5.010V 5L L =Ω=R U ……1分∵U 2= U -U L=12 V-5 V=7 V ∴R ′2=Ω==14A 5.0V7'22I U ……1分(3)当闭合S 1、S 2、S 3时,L 被短路,R 1与R 2并联,U 1=U 2=U =12 V 1分I 1=A 6.020V1211=Ω=R U∵电流表示数不超过3 A ,∴R 2支路的最大电流 I 2=I -I 1=3 A-0.6 A=2.4 A …………1分R 2的最小阻值为R 2=Ω==5A 4.2V1222I U即R 2的阻值变化范围为5~40 Ω……1分。
厦门市2013—2014学年(上)九年级质量检测化学试题含答案

2013—2014 学年(上)厦门市九年级质量检测化学试题(满分:100 分;时间:60分钟)友情提示:1.本考试有两张试卷,一是答题卡,二是本试题卷(共 5 页,18题);将全部答案填在答题卡的相应答题栏内,否则不能得分。
2.可能用到的相对原子质量:H-1;C-12;N-14;O-16;Cl-35.5;K-39;Ca-40;Mn-55;Cu-63.5 一、选择题(共10题,25分。
1~5题各2分,6~10题各3分。
每题仅一个选项正确)1.下列关于化学发展的看法错误的是()A.导致生态环境恶化B.提升人类健康水平C.有助于人类开发新能源D.帮助人类研制新材料2.属于“空气污染指数”监测的污染物是()A.氮气B.二氧化碳 C.稀有气体D.可吸入颗粒物3.利用化学反应获得能量的是()A.微波炉B.风力发电机 C.酒精灯D.太阳灶4.下列处理方法错误的是()A.进入久未开启的菜窖前,用燃着的蜡烛做“灯火试验”B.电线短路起火,用水泼灭C.炒菜时油锅着火,用锅盖盖灭D.桌面上酒精燃烧,用湿抹布盖灭5.根据右图信息,说法正确的是()A.硫属于金属元素B.硫原子的核电荷数为16C.硫的相对原子质量32.06g D.在化学反应中,硫原子容易失去6 个电子6.下列实验操作正确的是()7.我国长征二F 运载火箭使用的燃料含有液态偏二甲肼(C2H8N2)。
下列关于偏二甲肼说法正确的是()A.含有氮分子B.相对分子质量为27C . C 、H 元素质量比为12 : 1D . 10g偏二甲联含碳元素4gCaO+CO2↑。
下列坐标图能正确反映一定质量碳酸钙充分灼烧过程变化关系的是()8.已知:CaCO3高温====9.在一个密闭容器中放人X 、Y 、Z 、W 四种物质,一定条件下发生化学反应,一段时间后,测得有关数据如下表。
关于此反应的说法正确的是()物质X Y Z W反应前质量(g) 2 1 16 16反应后质量(g)11 m 8 14A . m 的值为0 B.该反应类型为分解反应C.Z 与W 的质量变化比为4 : 1 D.物质Y 是该反应的催化剂选项方案结论A 人呼出的气体全部是CO2B 燃烧条件之一是可燃物的温度达到着火点C 温度升高,分子运动加快D 细铁丝与氧气反应比粗铁丝更激烈二、填空与简答(共5 题,44 分)11. ( 7 分)在宏观、微观和符号之间建立联系是化学学科的特点。
2013厦门市初三质检

一、根据听到的内容选择正确答语(听两遍)。
(5分)()1. A. Yes , you are . B. Yes , we are . C. Yes , they are .()2. A. It’s a watch. B. The watch is over there . C. Yes , it’s a watch .()3. A. That’s all right . B. Yes , it is . C. That’s a good idea .()4. A. Yes , speak ! B. No , you can’t . C. Yes , speaking !()5. A. It’s November 28 . B. It’s eight fifteen . C. It’s . Saturday 二、听对话,选择正确的答语(听两遍)。
(5分)每段对话后各有一个问题,根据对话内容及问题,选择正确的答语。
()6. A. On the 6th floor. B. On the 4th floor C. On the 8th floor()7. A.He is a worker. B.He is a waiter C. He is a doctor.()8. A. 45 yuan B. 55 yuan C. 14 yuan()9. A. In a bookshop. B. In the classroom C. In a clothes shop.()10. A. On Tuesday. B. On Wednesday. C. On Thursday.听下面一段对话,回答第11至第12小题。
()11. Where are the two speakers?A. At a food shop.B. In a library.C. In a bookshop.()12. Who likes maths very much ?A. The man.B. The man’s son.C. The woman.听下面一段对话,回答第13至第15小题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013届湖里区初三毕业班质量检查
数 学 试 题
(试卷满分:150分 考试时间:120分钟)
学校 班级 姓名 考号 一、选择题(本大题有7题,每小题3分,共21分) 1.下列计算正确的是
A .220-+=
B .326=
C .330--=
D .133-=
2.化简3a a ÷的结果是
A .a
B .2a
C .3a
D .4a
3.图1是小华在3月8日“妇女节”送给她妈妈的礼盒,图中所示礼盒的俯视图是 4
.设a =a 在两个相邻整数之间,则这两个整数是
A .2和3
B .3和4
C .4和5
D .5和6
5.PM2.5指数是测控空气污染程度的一个重要指数.在一年中最可靠的一种观测方法是 A .随机选择5天进行观测 B .选择某个月进行连续观测
C .选择在春节7天期间连续观测
D .每个月都随机选中5天进行观测 6.如图2,A 、B 、C 是O ⊙上的三点,点C 是劣弧AB 的中点,
40A ∠=︒,则B ∠的度数等于
A .40°
B .50°
C .60°
D .70°
7.小华的家与学校的距离为s 千米,她从家到学校先以匀速1v 跑步前进,后以匀速
2v (21v v <)走完余下的路程,共用了t 小时,下列能大致表示小华离学校的距离
y (千米)与离家时间x (小时)之间关系的图象是
二、填空题(本大题有10小题,每小题4分,共40分) 8.已知130A ∠=︒,则A ∠的补角的度数为 °.
9.某班6名学生的考试成绩如下(单位:分):45,61,75,95,83,40,则这组数据的极差是 分. 10.如图3,菱形ABCD 中,对角线AC 、BD 相交于点O , 则______AOB ∠=︒ .
A .
B .
C .
D .
A .
B .
C .
D .
图2
图3
11.因式分解:510_________a b -=. 12.若分式
1
3
x -有意义,则x 的取值范围为 . 13.数学老师布置7道选择题作业,并对
批阅后答对题的结果进行统计,根据
右表数据可知,这50名同学答对题数的众数是__ .
14.已知关于x 的方程20x bx c ++=有一个根为1,则_______b c +=.
15.某工厂现在比原计划每天多生产50台机器,且现在生产600台机器与
原计划生产450台机器所需的时间相同.设原计划每天生产机器x 台,
则可列出方程 (不求解).
16.如图4,已知在直角△ABC 中,90C ∠=︒,5AB =,△ABC 的
面积为5,则△ABC 的周长为 .
17.如图5
简单的测角仪,若细线正好和60°重合,则此时的仰角α是
°,若细线所在位置刻度模糊,请在图6中添加一条直线,就能求出此时的仰角α.
三、解答题(本题有9题,共89
分) 18.(本题满分18分,每小题6分) (1)计算:20(2)(3)5-⨯--;
(2)如图7,画出与△ABC 关于x 轴对称的△111A B C ; (3)如图8,在等腰梯形ABCD 中,AD ∥BC ,
E 为AD 的中点,连接BE 、CE . 求证:△ABE ≌△DCE .
图4
图5 图6
图7
图8
19.(7分)解不等式组:10
217
x x ->⎧⎨+<⎩
20.(8分) 如图9,在△ABC 中,90C ∠=︒,设BC x =,AC y =
(1)若1x =,2y =,求AB 的长; (2)若1
tan 3
A =
,求点(,)x y 中纵坐标随横坐标变化的函数解析式,并画图象.
21.(8分) 现有7张形状大小相同的卡片,分别标有数字1、2、3、4、5、6、7,记为甲组, (1)从甲组中随机抽一张卡片,求数字为奇数的概率;
(2)从甲组中抽取5张卡片,记为乙组,要求乙组满足两个条件:① 与甲组的中位数
相同,② 从乙组中抽取一张卡片,使得数字为奇数的概率小于甲组. 你选取的乙组卡片数字分别是 ,并说明理由.
22. (8分)某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x 人. (1)求第一轮后患病的人数;(用含x 的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否
会有21人患病的情况发生,请说明理由.
图9
23.( 9分) 四边形ABCD 中,对角线AC 、BD 的交点为O ,
(1)如图10,若AD ∥BC ,6AD =,4BC =,求
AO
CO
的值; (2)如图11,若四边形ABCD 是矩形,过点B 作BE AC ⊥,垂足为E ,当
30ACB ∠=︒
时,有1AC +,求BC 的长度.
24. (10分)
对于双曲线)0(>=k x k y
必定过点P ,比如x
y 9=必定过(3,3),我们称点P 是双曲线)0(>=
k x k
y 的正方点. (1)画出4
y x =的图象,并标出正方点P .
(2)若k
y x
=的正方点在21y x m =+-上,求m 的取值范围.
25. (10分)
如图12,已知四边形ABCD 是正方形,以AB 为直径在正方形内作半圆,P 是半圆上的动点(不与点A 、B 重合),连接PA 、PD .
(1)若37PAB ∠=︒,正方形的边长为5,求PA 的长度; (sin 37︒≈0.60,cos37︒≈0.80,tan 37︒≈0.75) (2)若PA PD =,过点P 作PE AD ⊥,垂足为E ,
判断直线PE 与半圆的位置关系并说明理由.
图10 图11
图12
26. (11分)
已知抛物线22(0)y x bx c c =-+>与y 轴的交点为A , 顶点为(,)M m n . (1)若12-=b c ,点M 在x 轴上,求c 的值. (2)若直线1
2
y x t =-
+过点A ,且与x 轴交点为B ,直线和抛物线的另一交点为P ,且P 为线段AB 的中点.当n 取得最大值时,求抛物线的解析式.。
