安徽省皖南八校2008届高三第二次联考数学(理)
08届高三年级数学第二次联考试题

5 208届高三年级数学第二次联考试题第I 巻选择题共50 分)、选择题(本题共 10小题,每小题5 分, 是符合题目要求的)共50分.每小题给出的四个选项中,只有一项C . {X |1 _ X _ 3}D . {X | 0 :: X _ 1}2y =3x」(—1 _ X :: 0)的反函数是______ 1y = .1 log 3x (「:xE1)3______ 1y = 1 log 3 x (x 一 -)3______ 1y - -. 1 log 3 x (- < x 乞 1)3______ 1y - - 1 Iog 3 x(x __) 31.集合 A ={x | log 2 x ::1, x R},集合 B 二{x||x-2|:::1,x R },那么 A 一 (C R B )等于2. △ ABC 中,“ A>30 ° ”是 A .充分不必要 C .充要条件 3"x + y 兰 6 已知」 x M y j >1 A . 11 (理) 已知数列{<于A . 48 ,则函数 3. 4. 曰B •必要不充分D .既不充分也不必要条件=2x y 的最大值是C . 5, 若 S 3=18 , S 4- a 1= — 9, S n 为它的前n 项和, 则n m s n 等(B . 32C . 16D .(文)在各项都为正数的等比数列 {a n }中,首项a 1=3,前三项和为21,则a 3+a 4+a 5等于( A . 33B . 72C .84 D . 1896.将4个颜色互不相同的球全部放入编号为 的个数不小于该盒子的编号,则不同的放法有A . 10 种B . 20 种C . 30 种1和2的两个盒子里,使得放入每个盒子里球 ( D . 52 种7•定义在R 上的偶函数y = f (x )满足f (x 1^-f (x ),且当x ,(0,1]时单调递增,则1 5ff(—5) ::f(-)1 5B . fq< f (2)< f(—5)3 2A . {x | x _1}5.函数C .5 2515D . d : f (3):: f (2)1 3 1 — 2」-&已知|a|=2|b 卜0,且关于x 的函数f (x ) x 3 • — |a|x 2 • a bx 在R 上有极值,3 2则a 与b 的夹角范围为A. [°,6)B.(訂]2 x9.如果以原点为圆心的圆经过双曲线2 a 2=1(a - 0,b ■ 0)的焦点,而且被该双曲线bD . 、2|PA| PB| = 2,|PA-PB |=2-5 ,PA PC PBPC , I 为线段PC 上一点,且有Bl =BA ■( |PB| 则BUBA 的值为 |BA|C .5二、填空题(本题共 6小题,每小题4分,共24分,将答案写在题中横线上)(文)某校有老师 200人,男学生1200 ,女学生1000人,现用分层抽样的方法从所有 老师中抽取一个容量的 n 的样本;已知从女学生中抽取的人数为 80人,贝U n=值是14 .已知'2),且切-,tn :是方程x 2 ■ 3 3x 4=0的两个根,则:二2小 兀15 .过抛物线y 2二X 的焦点F 的直线I 的倾斜角 ,l 交抛物线于A , B 两点,且A 点4在x 轴上方,则|AF|的取值范围是的右准线分成弧长为 2:1的两段圆弧, 那么该双曲线的离心离e 等于 10.已知C 为线段AB 上一点,P 为直线AB 外一点,满足11.(理)复数3的虚部为-1 3iC .A . .5|PA|丝舉)(• .0),|AC| |AP|12.(2x-于)9的展开式中,常数项为 13. 设点(m , n )在直线x+y=1位于第一象限内的图象上运动,则log 2 m log 2 n 的最大的通项公式;⑺设b n=o12 a ng,T n 是数列{b n }的前n 项和,求使得T n <2 an 1m 2016.(理)数列{a n }, {b n }( n =1,23 )由下列条件所确定:(i)a , ::: 0,d • O ;(ii )k _ 2时,a k 与b k 满足如下条件:当a kj - b kj _ 0时,a k =a k 」,b k =色“ 也,当2时,用a i , b i 表示{b k }的通项公式b k = ___________ (k=2 , 3,…,n )a +?(文)数列{a n }满足递推式a n =3a n 二-3n -1(n _ 2),又a i = 5,则使得{」—}为 3等差数列的实数丸= ______________ 三、解答题(本大题共 6小题,满分76分) 17. (本小题满分12分)厂1已知函数f (x) = (. 3sin 「x - cos x) cos x .(「- 0)的最小正周期为 4 .(1 )求f (x)的单调递增区间;(2)在厶ABC 中,角A , B , C 的对边分别是 a , b , c 满足(2a -c)cosB = bcosC ,求函数f(A)的取值范围•18. (本小题满分12分)(理)一个小正方体的六个面,三个面上标以数字0.两个面上标以数字1,一个面上标以数字2, (1)甲、乙两人各抛掷一次,谁的点数大谁就胜,求甲获胜的概率; (2)将这个小正方体抛掷两次, 用变量E 表示向上点数之积,求随机变量E 的概率分布列及数学期望E E .23(文)甲、乙两人各进行3次投篮,甲每次投中的概率为,乙每次投中的概率为-,3 4求:(1)甲恰好投中2次的概率;(2)乙至少投中2次的概率;(3)甲、乙两人共投中 5次的概率.19. (本小题满分12分)已知数列{a n }, S n 是其前n 项和,且a n =7S n 4 2(n - 2), a 1 = 2 , (1)求数列{a n }a ki -b k j ::: 0时,ak 」+bk 二,ak,那么,当a i =-5,bi =5时,{a n }的通项公式a nf-5, n = 1_22;当…八皿2)对所有n • N *都成立的最小正整数 m.20. (本小题满分12分)ax(理)已知函数f(x)二二 ,在x=1处取得极值2, (1)求函数f (x)的解析式;(2)x +bm 满足什么条件时,区间(m , 2m+1)为函数f (x)的单调增区间;(3)若P(X o ,y °)为axf(x)二飞图象上的任意一点,直线I 与f (x)的图象切于P 点,求直线I 的倾斜角x +b的取范围•32(文)已知函数 f(x)=2x -6x ,求曲线y 二f(x)的平行于直线18x-y=3的切线 方程;(2)若函数y = f(x) m 在区间[—2, 2]上有最大值3,求常数m 的值及此函 数的最小值.已知椭圆C 的方程是 笃-爲=1(a b 0),a b乂为,%),B(X 2,y 2)两点•(1)若椭圆的离心率e=^,直线I 过点M (b , 0),且2OA OB =32cor AOB ,求椭圆的方程;(2)直线I 过椭圆的右焦点F ,设向量521. (本小题满分14分)斜率为1的直线l 与椭圆C 交于已知函数 f (x)二a(x -1)2 1bx c -b(a,b,c,N)的图象按e = (-1,0)平移后得到的图0P二■ (0A • 0B)( ■0),若点P在椭圆C上,求’的取值范围•22.(本小题满分14分)象关于原点对称,f (2) =2, f (3) ::: 3.(1) 求a, b, c 的值;(2)设0 :::| x |::: 1,0 :::| t 1< 1,求证:| t • x | • 11 -x| :::| f (tx - 1) |;(理科学生)(3)设x是正实数,求证:f n(x T) - f (x n• 1) _2n -2.参考答案(理)1(文)192 12. 6722 二 1 _^2n11——13.—2 14. 15. ( ,1 ]23 4 216 .(理)n 1 \ k」;a「(D -aj(2)(文)~~217 . (1) f (x)=3sin xcos x cos2 1 二x sin(2g............ 2分1. D2. B3. A4.(理)C (文)C5. B6. A7. B8. C9. D 10. D••• T 2 二4 二1 1 二匸f(x)Yi%x石)……4分4 下2*Tf(x)的单调递增区间为[企盲*肓(「)(2)T (2a -c)cosB = bcosC••• 2sin AcosB-sinCcosB=sin BcosC ................... 8 分1 n2sin AcosB =sin(B C)=sin A cosB B ……10 分2 31 兀2兀兀 A 兀兀f(A)二sin(—A ) 0 :: A ::-2 63 6 2 6 21f(A) (?,1) .......... 12 分1 1 118.(理)(1)面上是数字0的概率为一,数字为1的概率为一,数字为2的概率 ---------- 2分2 3 6165 当甲掷出的数字为2,乙掷出的数字为0或1时,甲获胜的概率为丄3611•••甲获胜的概率为 .............. 6分36(2) E的取值为0、1、2、44•- E E = ........................... 12 分9(文)(1)甲恰好投中2次的概率为C:(?)2丄...................... 3分3 3 93 1 3 27(2)乙至少投中2次的概率为Cf (-)2 - C^3)^27……7分4 4 4 32(3)设甲、乙两人共投中5次为事件A,甲恰投中3次且乙恰投中2次的事件B1, 甲恰投中2次且乙恰投中3次为事件B2,则A=B J+B2, B1、B2为互斥事件.32 3 .2 32 11_ 2 2 2_ 1 3 23 P(B1) = C3 ( ) C3 ()J P(B2)= C3 ()C2()…11分3 4 4334165• P(A) =P(B1) P(B2):16 ................ 12分19. (1 )••• n _2时a n二7S nJ1 2■an 1 -7Sn ' 2,-an 1 _ a n~7an• a n 1 =8a n(n 一2) ............ 2 分又a1=2 • a2 =7a1 2=16= 9a1a n彳=8a n (n N*) ...... 4分•- {a n}是一个以2为首项,8为公比的等比数列当甲掷出的数字为1,乙掷出的数字为0时,甲获胜的概率为• a n =2 8n_l =2心 ...................6 分(2)bn ______ 1 _____ _ 1log 2 a n log 2 a n 1 (3n -2)(3n 1)13n 14(1. 1111 10分m 1 ------ —• m_2°•最小正整数m=72二3312分20.(理)(1 )已知函数f(x)二axx2b(x)二-ax2ab(x2b)2y min = f ( 一2) m = m - 40 一37 12分y min = f ( 一2) m = m - 40 一3712分则其斜率为 k =6x 2 -12x 0 =18r x 0 =3或x 0 二-1 当X 。
皖南八校高三第二次联考理科数学.12.26

安徽省皖南八校高三第二次联考理科数学南京考一教育研究所命制 宣城二中承办 2008.12考生注意:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,考试时间120分钟。
2.答题前,请考生务必将答题纸左侧密封线内的项目填写清楚。
请考生按规定用笔将所有试题的答案涂、写在答题纸上,在试题卷上作答无效。
参考公式如果事件A ,B 互斥,那么球的体积公式 ()()()P A B P A P B -=⋅343V R π=如果事件A ,B 相互,那么 其中R 表示球的半径 ()()()P A B P A P B ⋅=⋅棱柱的体积公式如果事忙A 在一次试验中发生的概率 V Sh =是ρ,那么n 次独立重复试验中事件A 其中S 表示棱柱的底面积,h 表示棱柱的高 恰好发生k 次的概率棱锥的体积公式()(1)(0,1,2,)k kn k n n P k C P P k n -=-= 13V Sh =球的表面积公式其中S 表示棱锥的底面积,h 表示棱锥的高24S R π=第Ⅰ卷 (选择题 共6 0分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若12ii 12ia b +=+-(,,i a b R ∈是虚数单位),则a b -等于 A .7-B .1-C .15-D .75-2.从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如右图:若某高校A 专业对视力的要求在0.9以上,则该班学生中能报A 专业的人数为A .10B .20C .8D .163.已知集合222{|0},{|(21)0}()x S x T x x a x a a a R x-=<=-+++≥∈,则S T R =的充要条件是 A .11a -≤≤B .11a -<≤C .01a ≤≤D .01a <≤4.若23123(1)1()n n x a x a x a x x n N +-=+++++∈,且13:1:7a a =,则5a 等于A .56B .56-C .35D .35-5.若20(sin cos )2x a x dx π-=⎰,则实数a 等于A .1-B .1C .3-D .36.已知奇函数()f x 的定义域为R ,当0x >时,()lg f x x =,则不等式()0xf x ≤的解集为A .[(1,0)(0,1)]B .[1,1]-C .(,1][1,)-∞--∞D .(,1]{0}[1,)-∞--∞7.某几何体的三视图如图所示,根据图中数据,可得该几何体的体积是A .323+B .233+C .2233-D . 3223-8.在棱长为a 的正方体1111ABCD A B C D -内任取一点P ,则点P 到点A 的距离小于等于a 的概率为 A .22B .22π C .16D .16π9.若向量(sin(),1),(4,4cos 3)6a ab a π=+=-,若a b ⊥,则4sin()3πα+等于A .34- B .34C .14-D .1410.极坐标方程cos 2sin 2ρθθ=表示的曲线为A .一条射线和一个圆B .两条直线C .一条直线和一个圆D .一个圆11.已知曲线23:2C y x x =-,点(0,4)p -,直线l 过点P 且与曲线C 相切于点Q ,则点Q 的横坐标为 A .1-B .1C .2-D .212.已知(,)P x y 满足102350,4310,x x y x y -≤⎧⎪+-≤⎨⎪+-≥⎩点(,)Q x y 在圆22(2)(2)1x y +-+=,则||PQ 的最大值与最小值分别为A .6,3B .5,3C .6,2D .5,2第Ⅱ卷 (非选择题 共9 0分)二、填空题:本大题共4小题。
安徽省皖南八校高三数学第二次联考试题(理)

安徽省皖南八校2008届高三数学第二次联考试题(理)1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.2.请将各卷答案填在试卷后面的答题卷上.3.本试卷主要考试内容:第一章至第五章占60%,其它占40%.第Ⅰ卷(选择题 共55分)一、选择题:本大题共11小题,每小题5分,共55分.在每小题给出的四个选项中.只有一项是符合题目要求的. 1.设全集1,{|0},{1,}u x U R A x C A a x b-==≥=--+,则a b +等于 A .一2B .2C .1D .02.函数212(log )4(2)y x x =-≥的反函数是A.3)y x =≥- B.23)y x =≥- C.3)y x =-≥-D.23)y x =-≥-3.在等比数列{}n a 中,已知13118a a a =,则28a a 等于A .16B .6C .12D .44.若定义在R 上的函数()f x 满足()()3f x f x π+=-,且()()f x f x -=,则()f x 可以是A .1()2sin3f x x = B .()2sin3f x x = C .1()2cos 3f x x =D .()2cos3f x x =5.已知函数12()3,0log ,0x f x x x x +⎧=≤⎨>⎩,若0()1f x ≥,则0x 的取值范围是A .2x ≥B .10x -≤≤C .10x -≤≤或2x ≥D .1x ≤-或02x <≤6.已知点(cos ,sin )θθ到直线sin cos 10x y θθ+-=的距离是1(0)22πθ≤≤.则θ的值为 A .12πB .512πC .12π或512πD .56π或6π7.已知向量(2,1),(,2),(3,)a b x c y =-=-=,若,()()a b a b b c +⊥-,则x y +为A .0B .2C .4D .一48.某校A 班有学生40名,其中男生24人,B 班有学生50名,其中女生30人,现从A 、B 两班各找一名学生进行问卷调查,则找出的学生是一男一女的概率为A .1225B .1325C .1625D .9259.已知非零向量AB 和AC 满足()0||||AB AC BC AB AC +⋅=,且12||||A B A C A B A C ⋅=,则ABC 为 A .三边均不相等的三角形 B .直角三角形 C .等腰非等边三角形D .等边三角形10.一同学在电脑中打出如下若干个圆:若依此规律继续下去,得到一系列的圆,则在前2007个圆中共有●的个数是A .6lB .62C .63D .6411.已知()f x 是定义在R 上的奇函数.且是以2为周期的周期函数.若当[0,1)x ∈时,()21x f x =-,则12(log 6)f 的值为A .52- B .一5C .12-D .一6第Ⅱ卷(非选择题 共95分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卷中的横线上.12.右图是函数sin()(0,||)2y x πωϕωϕ=+><的图象的一部分,则ϕ= ,ω=13.已知A 、B 为椭圆22:11x y C m m+=+的长轴的两个端点,P 是椭圆C 上的动点,且APB ∠的最大值是23π,则实数m 的值是 .14.若61()x的展开式中的第5项是152,设12n n S x x x ---=++⋅⋅⋅+,则lim n n S →+∞=15.对正整数n ,设曲线(1)n y x x =-在2x =处的切线与y 轴交点的纵坐标为n a ,则数列{}1na n +的前n 项和公式是三、解答题:本大题共6小题,共79分.解答应写出必要的文字说明、证明过程及演算步骤. 16.(本小题满分12分)已知7cos 2,252πθθπ=<<.求: (1)tan θ的值;(2)22cos sin 2)4θθπθ-+的值17.(本小题满分14分)已知在四棱锥P 一ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,PA=AD=1,AB=2,E 、F 分别是AB 、PD 的中点.(1)求证:AF ∥平面PEC ;(2)求PC 与平面ABCD 所成角的大小; (3)求二面角P 一EC 一D 的大小.18.(本小题满分14分)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且满足(2)cos cos a c B b C -= (1)求角B 的大小;(2)设(sin ,cos2),(4,1)(1),m A A n k k m n ==>⋅的最大值为5,求k 的值19.(本小题满分12分)已知椭圆22221(0)x y a b a b+=>>的中心在坐标原点O ,一条准线的方程为4x =,过椭圆的左准点F ,且方向向量为(1,1)a =的直线l 交椭圆于A 、B 两点,AB 的中点为M .(1)求直线OM 的斜率(用a b 、表示);(2)设直线AB 与OM 的夹角为α,当tan 7α=时,求椭圆的方程.20.(本小题满分13分)已知定义域为R 的函数2()(1),()4(1)f x x g x x =-=-,数列{}n a 满足12a =,*1()()()0()n n n n a a g a f a n N +-+=∈(1)求数列{}n a 的通项公式;(2)设13()()n n n b f a g a +=-,求数列{}n b 的最值及相应的n 值.21.(本小题蠛分14分)在数列{}n a 中12a =,且1112212n n n nn a a +++--=(1)求证:2n n a n ≤⋅(2)设数列{}n a 的前n 项和为n S ,求证:1(1)22n n S n +≤-⋅+ (3)求证:122n n n a a +≤+皖南八校2008届高三第二次联考数学参考答案(理科)1.A2.A3.D4.D5.C6.C7.A8.B9.D10.A11.C 12.6π 2 13.1214.115.122n +-提示:1.A 由{1,}u C A a =--,知(,1](,)A a =-∞-⋃-+∞.所以1,a b a =--=-,因此2a b +=-2.A 函数可化为22(log )4y x =-,所以2l o g (3)x y =≥-,则反函数为3)y x =≥-3.D 由312311188a a a q =⇒=(q 为公比),即412a q =,∴42281()4a a a q ==4.D ∵()()f x f x -=,∴排除A 、B ,又∵()()3f x f x π+=-,∴选D5.C 当0x ≤时,13110x x +≥⇒+≥,∴当0x >时,2log 12x x ≥⇒≥,∴2x ≥,综上所述:10x -≤≤或2x ≥ 6.C12=,∴1sin 2(0)22πθθ=≤≤,即12π或512π7.A ∵a b ,∴4x =,∴(4,2)b =-,∴(6,3),(1,3)a b b c y +=--=--,∵()()a b b c +⊥-,∴()()0a b b c +⋅-=,即62(2)0y ---=,∴4y =-,∴0x y +=.8.B A 班男生B 班女生概率为3355⨯,B 班男生A 班女生概率为2255⨯.9.D 由()0||||AB ACBC BAC AB AC +⋅=⇒∠的角平分线与BC 垂直,∴ABC 为等腰三角形.∵12||||AB AC AB AC ⋅=,∴60BAC ∠=︒,∴ABC 为等边三角形 10.A 因为黑圆间隔的白圆数成等差数列,设有n 组白圆,则有1n -个黑圆,所以所有圆的个数为2(1)32122n n n n n ++-+-=,由已知23220072n n +-≤,因为当61n =时,232195120072n n +-=<,当62n =时,232201420072n n +-=>,但第62组中共有62个白圆,所以在前2007个圆中共有61个黑圆11.C ∵123log 62-<<-,∴121log 620-<+<,即1231log 02-<<,∵()f x 是周期为2的奇函数,∴23log 211122223331(log 6)(log )(log )(log )(21)2222f f f f ==--=-=--=-12.6π 2 由图知11()1212T πππ=--=,∴222T ππωπ===,∴sin(2)y x ϕ=+,又点(,0)12π-在图象上,∴sin()06πϕ-+=,∴由06πϕ-+=,知6πϕ= 13.12由椭圆知识知,当点P 位于短轴的端点时APB ∠取得最大值.据题意则有1tan32m π=⇒=14.1 由题意知42456115(()T C xx =-=,又∵5152T =,∴2x =,∴11(1)122lim lim lim (1)11212n n n n n n S →+∞→+∞→+∞-==-=- 15.122n +- ∵(1)n y x x =-,∴1'(1)n n y nx n x -=-+,∴1'(2)2(1)2n n k f n n -==-+12(2)n n -=-+,又切点为(2,2)n -,∴切线方程为122(2)(2)n n y n x -+=-+-,令0x =,则(1)2n n a n =+,∴数列{}1n a n +的通项公式21n na n =+,故前n 项和公式12(21)2221n n n S +-==--16.(1)由7cos 225θ=,得227912sin ,sin 2525θθ-==…………2分∵2πθπ<<,∴34sin ,cos 55θθ==-,∴sin 3tan cos 4θθθ==-…………6分 (2)24312cos sin cos 1sin 552234sin cos )455θθθθπθθθ-+--+-===++-…………12分 17.解法一:(1)取PC 的中点O ,连结OF 、OE .∴FO ∥DC ,且FO=12DC ∴FO ∥AE …………2分又E 是AB 的中点.且AB=DC .∴FO=AE . ∴四边形AEOF 是平行四边形.∴AF ∥OE 又OE ⊂平面PEC ,AF ⊄平面PEC ∴A F ∥平面PEC (2)连结AC∵P A ⊥平面ABCD ,∴∠PCA 是直线PC 与平面ABCD 所成的角……………6分 在Rt △PAC中,tan 5PA PCA AC ∠===即直线PC 与平面ABCD所成的角大小为arctan……………9分 (3)作A M ⊥CE ,交CE 的延长线于M .连结PM ,由三垂线定理.得P M ⊥CE∴∠PMA 是二面角P —EC —D 的平面角. ……11分 由△AM E ∽△CBE,可得2AM =,∴tan PA PMA AM ∠==∴二面角P一EC一D的大小为14分解法二:以A 为原点,如图建立直角坐标系,则A (0.0,0),B (2,0,0),C (2,l ,0),D (0,1,0),F (0,12,12),E (1,0,0),P (0,0,1) (1)取PC 的中点O ,连结OE ,则O (1,12,12),1111(0,,),(0,,)2222AF EO ==∴AF EO ……………………………………5分又OE ⊂平面PEC ,AF ⊄平面PEC ,∴A F ∥平面PEC …………………………6分 (2)由题意可得(2,1,1)PC =-,平面ABCD 的法向量(0,0,1)PA =-cos ,6||||6PA PC PAPC PA PC ⋅<>=== 即直线PC 与平面ABCD 所成的角大小为 ……………9分 (3)设平面PEC 的法向量为(,,),(1,0,1),(1,1,0)m x y z PE EC ==-=则00m PE m EC ⎧⋅=⎪⎨⋅=⎪⎩,可得00x z x y -=⎧⎨+=⎩,令1z =-,则(1,1,1)m =--……………11分由(2)可得平面ABCD 的法向量是(0,0,1)PA =-cos ,3||||3m PA m PA m PA⋅<>=== ∴二面角P 一EC 一D 的大小为……………………………………14分 18.(1)∵(2)cos cos a c B b C -=,∴(2sin sin )cos sin cos A C B B C -=……2分整理得2sin cos sin cos sin cos A B B C C B =+,∴2sin cos sin()sin A B B C A =+=………………………4分∵(0,)A π∈,∴sin 0A ≠,∴1cos ,23B B π==………………………6分 (2)24sin cos22sin 4sin 1m n k A A A k A ⋅=+=-++,其中2(0,)3A π∈……8分 设sin (0,1]A t =∈,则2241,(0,1]m n t kt t ⋅=-++∈ ∴当1t =时,m n ⋅取得最大值………………………12分 依题意2415k -++=,解得32k =,符合题意,∴32k =……………………14分 19.(1)设1122(,),(,)A x y B x y ,∵A 、B 在椭圜上,∴2222112222221,1x y x y a b a b+=+= ………………3分两式相减,得2121221212y y y y b x x x x a-+⋅=--+∵121212121,AB OM y y y y k k x x x x -+===-+∴22OMb k a=-………………6分(2)∵直线AB 与OM 的夹角为α,tan 7α=由(1)知221,AB OMb k k a ==-,∴22221tan 71b a b aα+==- ①………………8分 又椭圆的中心在坐标原点O ,一条准线的方程为4x =,∴24a c= ② 在椭圆中,222a b c =+ ③联立①②③,解得2243a b ⎧=⎪⎨=⎪⎩,∴椭圆的方程为22143x y +=………………12分20.(1)2()(1),()4(1)n n n n f a a g a a =-=-∵21()4(1)(1)0n n n n a a a a +-⋅-+-=,∴1(1)(431)0n n n a a a +---= ∵12a =,∴1n a ≠,∴14310n n a a +--=,∴131(1)4n n a a +-=-………3分 又111a -=,∴数列{1}n a -是首项为1,公比为34的等比数列, ∴131()4n n a --=,∴13()14n n a -=+………………7分(2)21211333(1)4(1)3((())())44n n n n n b a a --+=---=-………………9分 令13,()4n n b y u -==,则2211133(())3()2424y u u =--=--∵*n N ∈,∴()u n 递减,其值分别为39271,,,,41664⋅⋅⋅,经比较916距12最近 ∴当3n =时,n b 有最小值189256-;当1n =时,n b 有最小值0………………13分21.(1)1121222n n n n a a ++-=-<∵11112,2(21)2n n n n n a a a +++==+-,∴110,22n n n n a a a ++>-<, 整理得11122n nn na a ++-<………………2分 则当2n ≥时,1211211,,12222n n n n a a a a ---<⋅⋅⋅-< 叠加得11122n n a a n -<-,即2nn a n <⋅ 当1n =时,1112a =⋅故2n n a n ≤⋅………………………………………………………………4分 (2)由(1)得231222322n n S n ≤⋅+⋅+⋅+⋅⋅⋅+⋅………………………………6分令231222322n n T n =⋅+⋅+⋅+⋅⋅⋅+⋅,则234121222322n n T n +=⋅+⋅+⋅+⋅⋅⋅+⋅∴231122222,(1)22n n n n n T n T n ++-=+++⋅⋅⋅+-⋅=-+ 故1(1)22n n S n +≤-⋅+………………………………9分 (3)由已知得1112222n n nn n n a a a n +++-=-≥-,故只须证明122n n n +->,即2n n > ∵012(11)n n nn n n C C C n =+=++⋅⋅⋅+>,∴结论成立………………………14分。
2008高考安徽数学理科试卷和答案(全word版)080613

2008年普通高等学校招生全国统一考试(安徽卷)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至第4页.全卷满分150分,考试时间120分钟.考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致.2. 答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上书写.在试题卷上作答无效. 4. 考试结束,监考员将试题卷和答题卡一并收回. 参考公式:如果事件A B ,互斥,那么球的表面积公式 24πS R = ()()()P A B P A P B +=+其中R 表示球的半径 如果事件A B ,相互独立,那么()()()P A B P A P B =球的体积公式 34π3V R =如果随机变量(,),B n p ξ 那么 其中R 表示球的半径(1)D np p ξ=-第I 卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1).复数 32(1)i i +=( )A .2B .-2C .2i D . 2i -(2).集合{}|lg ,1A y R y x x =∈=>,}{2,1,1,2B =--则下列结论正确的是( )A .}{2,1A B =-- B . ()(,0)R C A B =-∞ C .(0,)A B =+∞D . }{()2,1R C A B =--(3).在平行四边形ABCD 中,AC 为一条对角线,若(2,4)AB = ,(1,3)AC = ,则BD = ( )A . (-2,-4)B .(-3,-5)C .(3,5)D .(2,4)(4).已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是( )A .,,m n m n αα若则‖‖‖B .,,αγβγαβ⊥⊥若则‖C .,,m m αβαβ若则‖‖‖D .,,m n m n αα⊥⊥若则‖(5).将函数sin(2)3y x π=+的图象按向量α平移后所得的图象关于点(,0)12π-中心对称,则向量α的坐标可能为( ) A .(,0)12π-B .(,0)6π-C .(,0)12πD .(,0)6π(6).设88018(1),x a a x a x +=+++ 则0,18,,a a a 中奇数的个数为( )A .2B .3C .4D .5(7).0a <是方程2210ax x ++=至少有一个负数根的( )A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件(8).若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( ) A .[ B .( C .[ D .( (9).在同一平面直角坐标系中,函数()y g x =的图象与x y e =的图象关于直线y x =对称。
2008届高三第二次月考数学(理科)

安徽省舒城中学2008届高三第二次月考数学(理科)试卷一、选择题:(本大题共12小题,每小题5分,共60分。
在每小题给出的四个备选项中,只有一项是符合题目要求的) 1.已知全集{}1,2,3,4,5U =, 集合{}1,3,5,A =则C U A = ( )A {}2,4B {}1,3,5C {}1,2,3,4,5D ∅ 选A.2.设全集I={1,3,5,7,9},集合A={1,|a -5|,9}, C I A={5,7},则a 的值是 ( ) A.2 B.8 C.-2或8 D.2或8(验证)若a =-2,则A ={1,7,9} C I A ={3,5}不合条件,若a =2,则A ={1,3,9}, C I A ={5,7},满足条件;若a =8则A ={1,3,9},仍符合条件,故选D.3.已知命题p ∶x ≥1,命题q ∶x 2≥x ,则p 是q 的 ( ) A 充分不必要条件 B 必要不充分条件 C 充要条件 D 既不充分也不必要条件 选A. 4.若集合}1|{},2|{-====x y y P y y M X ,则M ∩P= ( )A .}1|{>y yB .}1|{≥y yC .}0|{>y yD .}0|{≥y y 故选C.5.函数13)(23+-=x x x f 是减函数的区间为( )A .),2(+∞B .)2,(-∞C .)0,(-∞D .(0,2)解:由x x x f 63)(2/-=<0,得0<x<2 ∴函数13)(23+-=x x x f 是减函数的区间为(0,2),故选D 6.若复数z 满足|z|-z =i2110-,则z 等于 ( )A .-3+4iB .-3-4iC .3-4iD .3+4i 选D. 7.下列函数中既是奇函数,又在区间[-1,1]上单调递减的是 ( ) A.f(x)= sinx B.f(x)=-|x+1| C.f(x)=21(a x +a -x)D.f(x)=lnxx+-22 解:用排除法,A 是增函数,B 不是奇函数,C 是偶函数.,故选D.8.函数y=log a x 在x ∈[2,+∞]上总有|y|>1,则a 的取值范围是 ( ) A.0<a<21或1<a<2 B.21<a<1或1<a<2 C.1<a<2 D.0<a<21或a>2 解: 由f(x)=|y|=|log a x|的图象可知|log a 2|>1,分a>1与0<a<1求解.,故选B. 9.已知f(x)=⎩⎨⎧>≤+)0( log 0)(),3(3x x x x f ,则f(-9)等于 ( )A.-1B.0C.1D.3解:由题意得f(-9)=f(-9+3)=f(-6)=f(-6+3)=f(-3)=f(-3+3)=f(0)=f(0+3)=f(3)=log 33=1,故选C.点评:本题考查分段函数的运用及其有关计算问题.10.定义在R 上的偶函数f(x)满足对任意x ∈R ,都有f(x+8)=f(x)+f(4),且x ∈[0,4]时f(x)=4-x ,则f(2005)的值为 ( )A.-1B.1C.-2D.0 解: 由f(4)=0知周期为8,则f(2005)=f(5)=f(-3)=f(3)=1.,故选B. 11.已知正实数x 1,x 2及函数f(x),满足4x=)(1)(1x f x f -+,且f(x 1)+f(x 2)=1,则f(x 1+x 2)的最小值( )A.4B.2C.54 D.41 解: 由4x=)(1)(1x f x f -+得出f(x)= 1414+-x x .由4x1=)(1)(111x f x f -+,4x 2=)(1)(122x f x f -+两式相乘,并注意到关系f(x 1)+f(x 2)=1得421x x +=)()()]()([1)()()]()([121212121x f x f x f x f x f x f x f x f ++-+++=)()()()(22121x f x f x f x f +=1+)()(4821x f x f ≥1+221)]()([8x f x f +=9(当f(x 1)=f(x 2)=21时取得等号).于是f(x 1+x 2)=14142121+-++x x x x =1-14221++x x ≥1-192+=54.,故选C.12.已知函数)(x f x y '=的图象如右图所示(其中 )(x f '是函数)(x f 的导函数),下面四个图象中)(x f y =的图象大致是 ( )[解析]:由函数)(x f x y '=的图象可知: 当1-<x 时, )(x f x '<0,)(x f '>0,此时)(x f 增;当01<<-x 时,)(x f x '>0,)(x f '<0,此时)(x f 减;当10<<x 时,)(x f x '<0,)(x f '<0,此时)(x f 减;当1>x 时,)(x f x '>0,)(x f '>0,此时)(x f 增,故选C . 二、填空题:(本大题4个小题,每小题4分,共16分)13. 已知P=}4|{<a x x -,Q=}034|{2<+-x x x ,且x ∈P 是x ∈Q 的必要条件,则实数a 的取值范围是_________________解析]:由 x 2-3x +3<0 得 1<x <3,由4<a x -得a -4<x <a +4, ∵x ∈P 是x ∈Q的必要条件,∴Q ⊆P 则 ⎩⎨⎧≤-≥+1434a a ∴-1≤a ≤514.函数13)(3+-=x x x f 在闭区间[-3,0]上的最大值、最小值分别是 . [解析]:由33)(2'-=x x f =0,得1±=x ,当1-<x 时,)(/x f >0,当11<<-x 时,)(/x f <0,当1>x 时,)(/x f >0,故)(x f 的极小值、极大值分别为1)1(3)1(-==-f f 、,而1)0(17)3(=-=-f f 、 故函数13)(3+-=x x x f 在[-3,0]上的最大值、最小值分别是3、-17。
2008年普通高等学校招生全国统一考试(安徽卷)、数学(理)试卷与答案祥解

2008年普通高等学校招生全国统一考试(安徽卷)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至 第4页。
全卷满分150分,考试时间120分钟。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2.答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮控干净后,再选涂其他答案标号。
3.答第Ⅰ卷时,必须使用0.5毫米的黑色笔迹签字笔在答题卡上书写,要求字体工事、笔迹清晰。
作图题可先铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色笔迹字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、早稿纸上答题无效。
4.考试结束,务必将试题和答题卡一并上交。
参考公式:如果事件A 、B 互斥,那么()()()P A B P A P B +=+ 如果事件A 、B 相互独立,那么()()()P A B P A P B = 如果随机变量~(,)B n p ξ,那么(1-)D np p ξ=球的表面积公式2S=4R π ;球的体积公式34V=3R π,其中R 表示球的半径第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数()231i i += 【 】 (A)2 (B)-2 (C)2i (D )-2i(2)集合{}{}|lg ,1,2,1,1,2A y R y x x B =∈=>=--,则下列结论中正确的是 【 】 (A){}2,1A B =-- (B)()(),0R A B =-∞ð (C)()0,AB =+∞ (D)(){}2,1R A B =--ð(3)在平行四边形ABCD 中,AC 为一条对角线,若AB =(2,4),AC =(1,3) ,BD = 【 】 (A)(-2,-4) (B)(-3,-5) (C)(3,5) (D)(2,4)(4)已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是 【 】 (A)若,m n αα∥∥,则m n ∥ (B)若,αγβγ⊥⊥,则αβ∥ (C)若,m n ββ∥∥,则αβ∥ (B)若,m n αα⊥⊥,则m n ∥ (5)将函数y=sin 23x π⎛⎫+⎪⎝⎭的图象按向量a 平移后所得的图象关于点,012π⎛⎫- ⎪⎝⎭中心对称,则向量a 的坐标可能为 【 】 (A),012π⎛⎫-⎪⎝⎭ (B),06π⎛⎫- ⎪⎝⎭ (C),012π⎛⎫ ⎪⎝⎭(D),06π⎛⎫⎪⎝⎭(6)设()880181...x a a x a x +=+++,则018,,...,a a a 中奇数的个数为 【 】 (A)2 (B)3 (C)4 (D)5(7)0a <是方程2210ax x ++=至少有一个负数根的 【 】 (A)必要不充分条件 (B)充分不必要条件(C)充分必要条件 (D)既不充分也不必要条件(8)若过点()4,0A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为 【 】(A)⎡⎣ (B)((C)33⎡-⎢⎣⎦(D)33⎛- ⎝⎭ (9)在同一平面直角坐标系中,函数()y g x =的图象与xy e =的图象关于直线y x =对称,而函数()y f x =的图象与()y g x =的图象关于y 轴对称,若()1f m =-,则m 的值为 【 】 (A)-e (B )-1e (C)e (D)1e(10)设两个正态分布N(μ1, σ21)(σ 1 >0)和N(μ2, σ22)(σ2>0)的密度函数图象如图所示,则有 【 】(A) 1212,μμσσ<< (B) 1212,μμσσ<> (C) 1212,μμσσ>< (D) 1212,μμσσ>>(11)若函数()(),f x g x 分别为R 上的奇函数、偶函数,且满足()()xf xg x e-=,则有 【 】 (A)()()()230f f g << (B)()()()032g f f << (C)()()()203f g f << (B)()()()023g f f <<(12)12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是 【 】 (A)2283C A (B)2686C A (C)2286C A (D)2285C A2008年普通高等学校招生全国统一考试(安徽卷)数 学(理 科)第Ⅱ卷 (非选择题 共90分)考生注意事项:请用0.5毫米黑色签字笔在答题卡上.....作答,在试题卷上答题无效.........。
08届高三数学第二次联考

08届高三数学第二次联考 数学(理科)试卷 (2008.3)一、填空题:(12×4’=48’)1、集合}2|||{<=x x A 的一个非空真子集是__________2、若(2)a i i b i -=+,其中i R b a ,,∈是虚数单位,则=+b a __________3、在等差数列}{n a 中,2365-==a a ,,则=+++843a a a __________ 4、若1sin()2πα+=,)0,2(πα-∈,则=αtan __________ 5、设函数⎩⎨⎧<-≥+=)0(2)0(1)(2x x x x x f ,那么1(10)f -=_________6、已知圆的半径为2,圆心在x 轴的正半轴上,且圆与直线3x + 4y +4 = 0相切,则圆的标准方程是_______________________7、已知c b a ,,是锐角ABC ∆中C B A ∠∠∠,,的对边,若,4,3==b a ABC ∆的面积为33, 则=c8、某机关的2008年新春联欢会原定10个节目已排成节目单,开演前又增加了两个反映军民联手抗击雪灾的节目,将这两个节目随机地排入原节目单,则这两个新节目恰好排在一起的概率是_______________9、在极坐标系中,O 是极点,设点)6,4(πA ,2(3,)3B π,则O 点到AB 所在直线的距离是10、设定义在R 的函数)(x f 同时满足以下条件:①0)()(=-+x f x f ;②)2()(+=x f x f ;③当10<≤x 时,12)(-=x x f 。
则=++++)25()2()23()1()21(f f f f f _____________11、在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函y=f(x)的图像恰好经过k 个格点,则称函数y=f(x)为k 阶格点函数.已知函数:①y=2sinx ;②y=cos(x+6π);③1x y e =-;④2y x = .其中为一阶格点函数的序号为 (注:把你认为正确论断的序号都填上)12、已知AB 是椭圆)0(12222>>=+b a by a x 的长轴,若把该长轴n 等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点121,,,-n P P P ,设左焦点为1F,则________)(1111111lim=++++-∞→B F P F P F A F nn n二、选择题(4×4’=16’)13、如果a,b,c 满足c<b<a 且ac<0,那么下列选项中不一定成立的是 ---------- ( ) A . ab>ac B . c(b-a)>0 C . 22cb ab < D . ac(a-c)<014、设a,b,c 表示三条直线,βα,表示两个平面,下列命题中不正确的是---------( )A. ⎭⎬⎫⊥βαα//a β⊥⇒a B. c b a c b a ⊥⇒⎪⎭⎪⎬⎫⊥内的射影在是内在ββbC. ααα////c c b cb ⇒⎪⎭⎪⎬⎫内不在内在 D. αα⊥⇒⎭⎬⎫⊥b a b a //15、若c b a 、、是常数,则“0402<->c a b a 且”是“对任意R ∈x ,有02>++c x b x a ”的 --------------------------- ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件16、由方程1||||=+y y x x 确定的函数)(x f y =在),(∞+-∞上是 --------- ( ) A .增函数 B .减函数 C .先增后减 D .先减后增 三、解答题:17、(8+4)已知向量a =(−cosx , sinx ),b =(x ),函数f(x)=a b ⋅ [0,]x π∈ (1)求函数f(x)的最大值 (2)当函数f(x)取得最大值时,求向量a b 与夹角的大小. [解]18、(6+6)在长方体1111ABCD A BC D -中(如图),AD =1AA =1,2AB =,点E 是AB 上的动点 (1)若直线1D E EC 与垂直,请你确定点E 的位置,并求出此时异面直线1AD 与EC 所成的角 (2) 在(1)的条件下求二面角1D EC D --的大小 [解]19、(7+7)已知等比数列{}n a 的首项11=a ,公比为)0(>x x ,其前n 项和为n S(1)求函数1lim )(+∞→=n n n S S x f 的解析式;(2)解不等式8310)(xx f ->.[解]20、(4+6+4)电信局根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,则两种方案付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分)(MN 平行CD ) (1) 若通话时间为两小时,按方案A ,B 各付话费多少元? (2) 方案B 从500分钟以后,每分钟收费多少元?(3) 通话时间在什么范围内,方案B 比方案A 优惠? [解]21、(4+6+6)设12,F F 分别是椭圆C :22221(0)x y a b a b+=>>的左右焦点(1)设椭圆C上的点到12,F F 两点距离之和等于4,写出椭圆C 的方程和焦点坐标 (2)设K 是(1)中所得椭圆上的动点,求线段1KF 的中点B 的轨迹方程(3)设点P 是椭圆C 上的任意一点,过原点的直线L 与椭圆相交于M ,N 两点,当直线PM ,PN 的斜率都存在,并记为,PM PN k K 试探究PM PN k K ⋅的值是否与点P 及直线L 有关,并证明你的结论。
2008年高考安徽理科数学试卷及答案

2008年普通高等学校招生全国统一考试(安徽卷)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至第4页.全卷满分150分,考试时间120分钟.考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致.2. 答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上书写.在试题卷上作答无效. 4. 考试结束,监考员将试题卷和答题卡一并收回. 参考公式:如果事件A B ,互斥,那么球的表面积公式 24πS R = ()()()P A B P A P B +=+其中R 表示球的半径 如果事件A B ,相互独立,那么()()()P A B P A P B =球的体积公式 34π3V R =如果随机变量(,),B n p ξ那么 其中R 表示球的半径(1)D np p ξ=-第I 卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1).复数 32(1)i i +=( )A .2B .-2C .2i D . 2i -(2).集合{}|lg ,1A y R y x x =∈=>,}{2,1,1,2B =--则下列结论正确的是( )A .}{2,1AB =--B . ()(,0)RC A B =-∞C .(0,)AB =+∞D . }{()2,1R C A B =--(3).在平行四边形ABCD 中,AC 为一条对角线,若(2,4)AB =,(1,3)AC =,则AB =( )A . (-2,-4)B .(-3,-5)C .(3,5)D .(2,4)(4).已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是( )A .,,m n m n αα若则‖‖‖B .,,αγβγαβ⊥⊥若则‖C .,,m m αβαβ若则‖‖‖D .,,m n m n αα⊥⊥若则‖(5).将函数sin(2)3y x π=+的图象按向量α平移后所得的图象关于点(,0)12π-中心对称,则向量α的坐标可能为( )A .(,0)12π-B .(,0)6π-C .(,0)12πD .(,0)6π(6).设88018(1),x a a x a x +=+++则0,18,,a a a 中奇数的个数为( )A .2B .3C .4D .5(7).0a <是方程2210ax x ++=至少有一个负数根的( )A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件(8).若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( )A .[3,3]B .(3,3)C .33[ D .33( (9).在同一平面直角坐标系中,函数()y g x =的图象与xy e =的图象关于直线y x =对称。
安徽省皖南八校2008届高三第二次联考-理科综合

安徽省皖南八校2008届高三第二次联考理科综合能力测试本试卷分第I卷(选择题)和第Ⅱ巷(非选择题)两部分,共300分,考试时间150分钟。
可能用到的相对原于质量:H 1 C 12 N 14 Na 23 S 32 Cl 35.5 K 39 Ca 40 Fe 56 Cu 64第I卷(选择题共126分)一、选择题(本题包括13小题.每小题6分,共78分。
每小题只有一个选项符合题意)1.右图表示某基因型为AaBb的二倍体生物某器官细胞榜中DNA含量的变化曲线,下列有关叙述错误的是 A.桉DNA数日的加倍发生在A时期和F时期B.L时期细胞中的基因组成可能为AABB、AAbb、aaBB、aabbC. D 时期细胞中有4个染色体组D.在F时期细胞核中发生了DNA的解旋、转录和翻译等过程2.下列选项中前者随后者变化的情况与右图走势不相符...的是A. T细胞数量一一HIV浓度B.胚芽鞘生长速率——生长素浓度C.洋葱表皮细胞液泡的体积——蔗糖浓度D.消除抗原所需时间——同种抗原侵染的次数3.生产者细胞中的叶绿体可产生ATP,同时生产者、消费者、分解者细胞中的线粒体及细胞质基质也能产生ATP。
在一个处于生长期的森林生态系统中,下列判断正确的是A.生产者叶绿体产生的ATP多于生产者、消费者和分解者的线粒体、细胞质基质产生的ATP之和B.消费者的各细胞中线粒体产生的ATP都多于细胞质礁质产生的ATPC.所有的分解者都可通过线粒体产生的ATP供能D.生产者叶绿体产生的ATP与其线粒体和细胞质基质中产生的ATP之和相等4.下列有关N、P元素的叙述中,正确的是A.根瘤菌和圆褐固氮菌能将N2转化为NO3-B.正常的植物转入无N、P的培养液中,植物顶部叶片首先表现缺素症C.N、P是生物膜系统不可缺少的成分之一D.健康的青少年在其生长发育阶段.摄入的N、P量等于排出的N、P量5.右图是细胞膜结构的亚硅微结构模式图,其中a和b为两种物质的运输方式。
2008年高考理科数学试题及参考答案(安徽卷)

2008年普通高等学校招生全国统一考试(安徽卷)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至 第4页。
全卷满分150分,考试时间120分钟。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2.答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮控干净后,再选涂其他答案标号。
3.答第Ⅰ卷时,必须使用0.5毫米的黑色笔迹签字笔在答题卡上书写,要求字体工事、笔迹清晰。
作图题可先铅笔在答题卡规定的位臵绘出,确认后再用0.5毫米的黑色笔迹字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、早稿纸上答题无效。
4.考试结束,务必将试题和答题卡一并上交。
参考公式:如果事件A 、B 互斥,那么()()()P A B P A P B +=+ 如果事件A 、B 相互独立,那么()()()P A B P A P B = 如果随机变量~(,)B n p ξ,那么(1-)D np p ξ=球的表面积公式2S=4R π ;球的体积公式34V=3R π,其中R 表示球的半径第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数()231i i +=【 】(A)2 (B)-2 (C)2i (D )-2i (2)集合{}{}|l g ,1,2,1,1,2A y R y x x B=∈=>=--,则下列结论中正确的是 【 】(A){}2,1A B =-- (B)()(),0R A B =-∞ ð (C)()0,A B =+∞ (D)(){}2,1R A B =-- ð(3)在平行四边形ABCD 中,AC 为一条对角线,若AB =(2,4),AC =(1,3) ,BD=【 】(A)(-2,-4) (B)(-3,-5) (C)(3,5) (D)(2,4)(4)已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是 【 】(A)若,m n αα∥∥,则m n ∥ (B)若,αγβγ⊥⊥,则αβ∥ (C)若,m n ββ∥∥,则αβ∥ (B)若,m n αα⊥⊥,则m n ∥ (5)将函数y=sin 23x π⎛⎫+ ⎪⎝⎭的图象按向量a 平移后所得的图象关于点,012π⎛⎫-⎪⎝⎭中心对称,则向量a的坐标可能为【 】 (A),012π⎛⎫-⎪⎝⎭ (B),06π⎛⎫- ⎪⎝⎭ (C),012π⎛⎫ ⎪⎝⎭(D),06π⎛⎫⎪⎝⎭(6)设()880181...x a a x a x +=+++,则018,,...,a a a 中奇数的个数为【 】(A)2 (B)3 (C)4 (D)5 (7)a <是方程2210a x x ++=至少有一个负数根的【 】(A)必要不充分条件 (B)充分不必要条件(C)充分必要条件 (D)既不充分也不必要条件(8)若过点()4,0A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为【 】(A)3,3⎡⎤-⎣⎦(B)()3,3-(C)33,33⎡⎤-⎢⎥⎣⎦ (D)33,33⎛⎫- ⎪ ⎪⎝⎭(9)在同一平面直角坐标系中,函数()y g x =的图象与xy e =的图象关于直线y x =对称,而函数()y f x =的图象与()y g x =的图象关于y 轴对称,若()1f m =-,则m 的值为 【 】(A)-e (B )-1e (C)e (D)1e(10)设两个正态分布N(μ1, σ21)(σ 1 >0)和N(μ2, σ22)(σ2>0)的密度函数图象如图所示,则有 【 】(A) 1212,μμσσ<< (B) 1212,μμσσ<> (C) 1212,μμσσ>< (D) 1212,μμσσ>>(11)若函数()(),f x g x 分别为R 上的奇函数、偶函数,且满足()()xf xg x e-=,则有 【 】 (A)()()()230f f g << (B)()()()032g f f << (C)()()()203f g f << (B)()()()023g f f <<(12)12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是 【 】(A)2283C A (B)2686C A (C)2286C A (D)2285C A2008年普通高等学校招生全国统一考试(安徽卷)数 学(理 科)第Ⅱ卷 (非选择题 共90分)考生注意事项:请用0.5毫米黑色签字笔在答题卡上.....作答,在试题卷上答题无效.........。
2008年高考理科数学试题及参考答案(安徽卷)

2008年普通高等学校招生全国统一考试(安徽卷)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至第4页.全卷满分150分,考试时间120分钟.考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致.2. 答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上书写.在试题卷上作答无效. 4. 考试结束,监考员将试题卷和答题卡一并收回. 参考公式:如果事件A B ,互斥,那么球的表面积公式 24πS R = ()()()P A B P A P B +=+其中R 表示球的半径 如果事件A B ,相互独立,那么()()()P A B P A P B =球的体积公式 34π3V R =如果随机变量(,),B n p ξ 那么 其中R 表示球的半径(1)D np p ξ=-第I 卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1).复数 32(1)i i +=( )A .2B .-2C .2i D . 2i -(2).集合{}|lg ,1A y R y x x =∈=>,}{2,1,1,2B =--则下列结论正确的是( )A .}{2,1A B =-- B . ()(,0)R C A B =-∞ C .(0,)A B =+∞D . }{()2,1R C A B =--(3).在平行四边形ABCD 中,AC 为一条对角线,若(2,4)AB = ,(1,3)AC = ,则AB = ( )A . (-2,-4)B .(-3,-5)C .(3,5)D .(2,4)(4).已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是( )A .,,m n m n αα若则‖‖‖B .,,αγβγαβ⊥⊥若则‖C .,,m m αβαβ若则‖‖‖D .,,m n m n αα⊥⊥若则‖(5).将函数sin(2)3y x π=+的图象按向量α平移后所得的图象关于点(,0)12π-中心对称,则向量α的坐标可能为( )A .(,0)12π-B .(,0)6π-C .(,0)12πD .(,0)6π(6).设88018(1),x a a x a x +=+++ 则0,18,,a a a 中奇数的个数为( )A .2B .3C .4D .5(7).0a <是方程2210ax x ++=至少有一个负数根的( )A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件(8).若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( )A .[B .(C .[33-D .(33-(9).在同一平面直角坐标系中,函数()y g x =的图象与x y e =的图象关于直线y x =对称。
2008届安徽皖南八校高三第二次联考理

712008届安徽省皖南八校高三第二次联考数学试题(理科)1.本试卷分第I 卷(选择题)和第n 卷(非选择题)两部分,共分钟.2 .请将各卷答案填在试卷后面的答题卷上.一项是符合题目要求的.x — a1 .设全集 U 二 R,A 二{x|0}, C u A = (-1,-a ],则a b 等于x +b2.函数y =(log 1 x)2 -4(x _2)的反函数是2A .『=2厂4&__3)y - -2-「x _ -3)A . 16 f (X )满足 f ( x) - - f (x),且 f (-x)二 f (x),则 f (x)可以是 31 *6.已知点(cos =,sin r )到直线xsin^ yco^ -1=0的距离是?(0 -二-—).则二的值A . 1f(x) =2sin x3B f (x) = 2sin 3xC. 1 f(x) =2cos —x3D f(x) =2cos3x A . 16B . 6C.12 D 已知函数mx<0 若 f (x 。
)一1,则x0的取值范围是1 log2 x,x 0A . x -2B .—1^x^0C .T 空x 空0或x — 2D.x _ —1 或 0 :: x 乞 2 .45 . 150分.考试时间1203•本试卷主要考试内容:第一章至第五章占60%,其它占40% 第I 卷(选择题共 55 分)、选择题:本大题共 11小题,每小题5分,共55分.在每小题给出的四个选项中.只有y =2”(x _-3)3.在等比数列{a n }中, 已知 a 1a 3a 11 =8,贝U a 2a 8等于C . 124.若定义在R 上的函数为( )71127.已知向量;=(2, _1); =(x, _2);=(3,y),若:左,(;b) _(b —C),则 x y 为(D .一 4&某校A 班有学生40名,其中男生24人,B 班有学生50名,其中女生30人,现从B 两班各找一名学生进行问卷调查,则找出的学生是一男一女的概率为f (x) =2x-1,则 f (log ! 6)的值为3T12 .下图是函数 y 二si n 「x •「)(■ • 0, |的图像的一部分,则-二5兀B .12C .二或兰12 12C . 4 12 A .2513B .25C . 16 259 D .259.已知非零向量AB 和忑满足ABAC|AB| |AC|竺=1,则L ABC 为| AC| 2A •三边均不相等的三角形B •直角三角形C .等腰非等边三角形D .等边三角形10. 一同学在电脑中打出如下若干个圆:若依此规律继续下去,得到一系列的圆,则在前 2007个圆中共有•的个数是(A . 61B . 6263D . 6411.已知f (x)是定义在 R 上的奇函数.且是以2为周期的周期函数.若当[0,1)时,A. -2第n 卷(非选择题2共 95分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卷中的横线上.2 213.已知A 、B 为椭圆C\—— =1的长轴的两个端点,P 是椭圆C 上的动点,且三APB m +1 m的最大值是,则实数m 的值是31 1514若(X 、x)6的展开式中的第5项是 ,设Sn =x 「x ^亠 亠X 』,则x2l in _》15.对正整数n ,设曲线y =x n (1-x)在x =2处的切线与y 轴交点的纵坐标为 a n ,则数列{王}的前n 项和公式是_ n 1三、解答题:本大题共 6小题,共骤.(1) tanv 的值;2 ' .-/小、2cos — -sin 日砧洁 (2) 2 的值-2 sin ( n -")(1)求证:AF //平面PEC ;(2 )求PC 与平面ABCD 所成角的大小; (3 )求二面角 P 一 EC 一 D 的大小.(1)求角B 的大小;79分•解答应写出必要的文字说明、证明过程及演算步16. (本小题满分12分)7 応已知如坛丁八二.求:17. (本小题满分14分)已知在四棱锥 P 一 ABCD 中, 底面ABCD 是矩形,PA 丄平面 ABCD , PA=AD=1 , AB=2 ,E 、F 分别是AB 、PD 的中点.18. (本小题满分14分)在厶ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且满足(2a - c)cos B 二 bcosCH T n 4(2)设m=(si nA,cos2A), n =(4k,1)(k . 1),m n 的最大值为5,求k 的值19. (本小题满分12分)X y2 已知椭圆—2 =i(a .b ■ 0)的中心在坐标原点0, —条准线的方程为x= 4,过椭a b4圆的左准点F,且方向向量为a =(1,1)的直线I交椭圆于A、B两点,AB的中点为M .(1)求直线OM的斜率(用a、b表示);(2)设直线AB与OM的夹角为:•,当tan〉= 7时,求椭圆的方程.20. (本小题满分13分)2已知定义域为R的函数f(x) =(x-1) ,g(x) =4(x -1),数列{a n}满足a^ 2 ,(a n 1 —a n)g(a n) f (a.) =0( n N*)(1)求数列{a n}的通项公式;(2)设b n =3f (a n)-g(a n 1),求数列{b n}的最值及相应的n值.21 .(本小题满分14分)_2n卅2^^ _1 在数列{a n}中心,且丁-宁a(1) 求证:a n辽n 2n(2) 设数列{a n}的前n项和为S n,求证:S n乞(n -1) 2n 1 - 2(3) 求证:a n 1 - 2a n • 2n。
08届高考理科数学联考试卷

08届咼考理科数学联考试卷、填空题(本大题满分 44分,共11题,每题4分,只要求直接填写结果)=log a 2 , n = log a 3,则 a 2m4na ={1,2},b 二{x,1},且 a 2b 与 2a -b 平行,则 x 二的概率是(用分数表示);7、经过点A (a,0) , ( a 0 ),且与极轴正方向夹角为一的直线的极坐标方程42 2&若直线2ax —by+2 = 0 ( a 、b^R ),始终平分圆x + y +2x —4y+1 = 0的周长, 则ab 的最大值为9、已知:函数f (x ) TogNx • 1) ( a 0)在区间[1,::)上单调递减,则实数 a 取2x值范围是10、数列{a n }是等差数列,前 n 项和为S n, S 2 =10 , S 5 =55,则过点P (n ,鱼),nSQ (n ,2,」2)的直线斜率为 _____________ ;1、 已知: a bi = i - i 4 (其中a 、b 为实数,i 为虚数单位)。
则a b =2、已知: 已知2f (x) = sin x 2cosx ,在一个袋子里有 10个红球和x上肴]的最小值为2个白球,现从中随机拿出 3个,则其中至少有一个白球6、参数方程丿x = 1 + 2 cos日 y =cos2v 为参数方程)所表示的曲线的焦点的直角坐标n +211、设集合Sn ={1,2,3,n},若Z丄S n ,则把Z的所有元素的乘积称为Z的容量(若Z中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为(偶)数,则称为奇(偶)子集。
若n = 4 ,则S n的所有奇子集的容量之和为__________________二、选择题(本大题满分16分,共4题,每题有且仅有一个正确答案)12、x _2的必要非充分条件是......................................( )A、X +1<3B、X+1<2C、X +1 兰1D、X—1<113、已知:si n2B =-1 兀——,且一£日<兀,则cs日—n e =.....................( ) 4275A、B、—-- C D、222214、直线a在平面M 内,贝“平面M//平面N”是“直线a//在平面N ”的........ ( )A、充分非必要条件B、必要非充分条件C、充要条件D、既非充分也非必要条件15、函数f(x)的反函数图像向左平移一个单位得到曲线C,函数g(x)的图像与曲线C关于y=x成轴对称,则g(x)等于............................................... ( )A、g(x)二f(x)-1B、g(x)二f(x 1)C、g(x)二f(x)1D、g(x)二f(x-1) 三、解答题16、(本题满分12分,第1小题8分,第2小题4分)若复数z=x+yi ( x、y^R ),且一匚+ —= —1—, i是虚数单位1-i 1 -2i 1 -3i(1)求复数z ;(2)求Z。
08届高三(理科)数学第二次调研考试试题
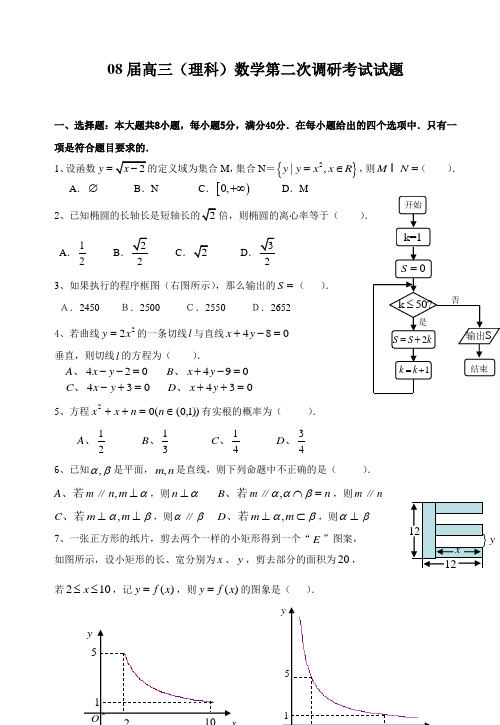
08届高三(理科)数学第二次调研考试试题一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中.只有一项是符合题目要求的. 1、设函数y =M ,集合N ={}2|,y y x x R =∈,则M N =( ).A .∅B .NC .[)0,+∞D .M2)A .12BCD 3、如果执行的程序框图(右图所示),那么输出的S =( ). A.2450 B.2500 C.2550 D.2652 4、若曲线22y x =的一条切线l 与直线084=-+y x 垂直,则切线l 的方程为( ).A 、420x y --=B 、490x y +-=C 、034=+-y xD 、034=++y x5、方程))1,0((02∈=++n n x x 有实根的概率为( ).A 、21B 、31C 、41D 、436、已知βα,是平面,n m ,是直线,则下列命题中不正确的是( ).A 、若m ∥α⊥m n ,,则α⊥nB 、若m ∥n =⋂βαα,,则m ∥nC 、若⊥m βα⊥m ,,则α∥βD 、若⊥m βα⊂m ,,则⊥αβ7、一张正方形的纸片,剪去两个一样的小矩形得到一个“E ”图案, 如图所示,设小矩形的长、宽分别为x 、y ,剪去部分的面积为20, 若210x ≤≤,记()y f x =,则()y f x =的图象是( ).y8、将函数sin(2)3y x π=-的图象先向左平移6π,然后将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应的函数解析式为( ). A .cos y x =- B .sin 4y x =C .sin()6y x π=-D .sin y x =第Ⅱ卷(非选择题,共110分)二、填空题:本大题共7小题,其中13~15题是选做题,考生只能选做两题,三题全答的,只计算前两题得分.每小题5分,满分30分.9、已知向量(21,4)c x →=+,(2,3)d x →=-,若//c d →→,则实数x 的值等于 . 10、已知3,,sin 25πθπθ⎛⎫∈=⎪⎝⎭,则tan θ= .11、i 是虚数单位,则=++++++666556446336226161i C i C i C i C i C i C .12、函数()f x 由下表定义:若05a =,1()n n a f a +=,0,1,2,n =,则2007a = .x2 53 1 4()f x123 452x10D13、(坐标系与参数方程选做题)曲线1C :⎩⎨⎧=+=)y x 为参数θθθ(sin cos 1上的点到曲线2C:12(112x t t y t⎧=-⎪⎪⎨⎪=-⎪⎩为参数)上的点的最短距离为 . 14、(不等式选讲选做题)已知实数a b x y 、、、满足3,12222=+=+y x b a ,则by ax +的最大值为 .15、(几何证明选讲选做题)如图,平行四边形ABCD 中,2:1:=EB AE ,若AEF ∆的面积等于1cm 2,则CDF ∆的面积等于 cm 2.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16、(本小题满分12分)设正项等比数列{}n a 的前n 项和为n S , 已知34a =,124562a a a =. (Ⅰ)求首项1a 和公比q 的值; (Ⅱ)若1021n S =-,求n 的值.17、(本小题满分12分)设函数2()2cos sin 2()f x x x a a R =++∈. (Ⅰ)求函数()f x 的最小正周期和单调递增区间; (Ⅱ)当[0,]6x π∈时,()f x 的最大值为2,求a 的值,并求出()()y f x x R =∈的对称轴方程.A FE D CB18、(本小题满分14分)一个口袋中装有大小相同的2个白球和4个黑球. (Ⅰ)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率; (Ⅱ)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差. (方差:21()ni ii D p E ξξξ==⋅-∑)19、(本小题满分14分)如图,已知四棱锥P ABCD -的底面ABCD 是菱形;PA ⊥平面ABCD ,PA AD AC ==, 点F 为PC 的中点.(Ⅰ)求证://PA 平面BFD ; (Ⅱ)求二面角C BF D --的正切值.20、(本小题满分14分)给定圆P:222xy x +=及抛物线S:24y x =,过圆心P 作直线l ,此直线与上述两曲线 的四个交点,自上而下顺次记为A B C D 、、、,如果线 段AB BC CD 、、的长按此顺序构成一个等差数列,求直 线l 的方程.21、(本小题满分14分)设M 是由满足下列条件的函数)(x f 构成的集合:“①方程xyoABCDPCBADPF)(x f 0=-x 有实数根;②函数)(x f 的导数)(x f '满足1)(0<'<x f ”. (Ⅰ)判断函数4sin 2)(xx x f +=是否是集合M 中的元素,并说明理由; (Ⅱ)集合M 中的元素)(x f 具有下面的性质:若)(x f 的定义域为D ,则对于任意[m ,n]⊆D ,都存在0x ∈[m ,n],使得等式)()()()(0x f m n m f n f '-=-成立”,试用这一性质证明:方程0)(=-x x f 只有一个实数根;(Ⅲ)设1x 是方程0)(=-x x f 的实数根,求证:对于)(x f 定义域中任意的23x x 、,当21||1x x -<,且31||1x x -<时,32|()()|2f x f x -<.数学试题(理科)参考答案一、选择题:题号 1 2 3 4 5 6 7 8 答案DBCACBAD1、解析:{2}M x x =≥,N ={}22|,{0}y y x x R y y x =∈==≥,即M N M N M ⊂⇒⋂=.答案:D .2、解析:由题意得2a a =⇒=,又2222a b c b c a c =+⇒=⇒=. 答案:B .3、解析:程序的运行结果是2550100642=+⋅⋅⋅+++=s .答案:C .4、解析:与直线084=-+y x 垂直的切线l 的斜率必为4,而'4y x =,所以,切点为(1,2).切线为24(1)y x -=-,即420x y --=,答案:A . 5、解析:由一元二次方程有实根的条件41041≤⇒≥-=∆n n ,而)1,0(∈n ,由几何概率得有实根的概率为41.答案:C . 6、解析:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面,所以A 正确;如果两个平面与同一条直线垂直,则这两个平面平行,所以C 正确; 如果一个平面经过了另一个平面的一条垂线,则这两个平面平行,所以D 也正确; 只有B 选项错误.答案:B . 7、解析:由题意,得10(210)y x x=≤≤,答案:A . 8、解析:sin(2)3y x π=-的图象先向左平移sin[2()]sin 2663y x x πππ⇒=+-=,横坐标变为原来的2倍1sin 2()sin 2y x x ⇒==.答案:D . 二、填空题:题号9 10 11 12 13 14 15答案 1234-8i - 4 1399、解析:若//c d →→,则3(21)4(2)0x x +--=,解得12x =. 10、解析:由题意43cos sin tan 54cos -==⇒-=θθθθ. 11、解析:=++++++666556446336226161i C i C i C i C i C i C i i i i 8)2(])1[()1(3326-==+=+12、解析:令0n =,则10()5a f a ==,令1n =,则21()(5)2a f a f ===, 令2n =,则32()(2)1a f a f ===,令3n =,则43()(1)4a f a f ===, 令4n =,则54()(4)5a f a f ===,令5n =,则65()(5)2a f a f ===, …,所以20075014334a a a ⨯+===.13、解析:1C :⎩⎨⎧=+-⇒=+=1)1(sin cos 122y x y x θθ;则圆心坐标为)0,1(.2C :⎪⎩⎪⎨⎧=-++⇒-=+-=01222112122y x ty t x 由点到直线的距离公式得圆心到直线的距离为221221=-+=d ,所以要求的最短距离为11=-d .14、解析:由柯西不等式22222)())((by ax y x b a +≥++,答案:3.15、解析:显然AEF ∆与CDF ∆为相似三角形,又3:1:=CD AE ,所以CDF ∆的面积等于9cm 2.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16、解: (Ⅰ)31244565552216(0)a a a a a a ==⇒==>, ……………………… 2分∴25342a q q a ==⇒=,………………………………………………… 4分 解得11a =.………………………………………………………………… 6分(Ⅱ)由1021n S =-,得:1(1)211n n n a q S q -==--, ……………………… 8分∴1010212122n n -=-⇒= ………………………………… 10分 ∴10n =.…………………………………………………………… 12分17、解:(1)2()2cos sin 21cos 2sin 2)14f x x x a x x a x a π=++=+++=+++ … 2分 则()f x 的最小正周期2T ππω==, …………………………………4分且当222()242k x k k Z πππππ-≤+≤+∈时()f x 单调递增.即3[,]()88x k k k Z ππππ∈-+∈为()f x 的单调递增区间(写成开区间不扣分).………6分 (2)当[0,]6x π∈时724412x πππ⇒≤+≤,当242x ππ+=,即8x π=时sin(2)14x π+=.所以max ()121f x a a =+=⇒= …………………………9分2()4228k x k x k Z πππππ+=+⇒=+∈为()f x 的对称轴. …………………12分 18、解:(Ⅰ)解法一:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”, 记“有放回摸球两次,两球恰好颜色不同”为事件A ,………………………2分 ∵“两球恰好颜色不同”共24+42=16⨯⨯种可能,…………………………5分 ∴164()669P A ==⨯. ……………………………………………………7分 解法二:“有放回摸取”可看作独立重复实验, …………………………2分 ∵每次摸出一球得白球的概率为3162==P .………………………………5分 ∴“有放回摸两次,颜色不同”的概率为1224(1)(1)9P C p p =⋅⋅-=. ……………………………7分 (Ⅱ)设摸得白球的个数为ξ,依题意得:432(0)655P ξ==⨯=,42248(1)656515P ξ==⨯+⨯=,211(2)6515P ξ==⨯=.…………10分∴1812012215153Eξ=⨯+⨯+⨯=,……………………………………12分22222282116(0)(1)(2)3531531545Dξ=-⨯+-⨯+-⨯=.……………………14分19、(Ⅰ)证明: 连结AC,BD与AC交于点O,连结OF.………………………1分ABCD是菱形, ∴O是AC的中点. ………………………………………2分点F为PC的中点, ∴//OF PA. …………………………………3分OF ⊂平面,BFD PA⊄平面BFD, ∴//PA平面BFD. ……………… 6分(Ⅱ)解法一:PA⊥平面ABCD,AC⊂平面ABCD,∴PA AC⊥.//OF PA,∴OF AC⊥. …………………………… 7分ABCD是菱形, ∴AC BD⊥.OF BD O=,∴AC⊥平面BDF. …………………………………………………………8分作OH BF⊥,垂足为H,连接CH,则CH BF⊥,所以OHC∠为二面角C BF D--的平面角. ………………………………… 10分PA AD AC==,∴1,2OF PA BO PA==,BF PA==.在Rt△FOB中,OH=43·=BFBOOFPA,…………………………… 12分∴1tanPAOCOHCOH∠===.…………………………… 13分∴二面角C BF D--………………………… 14分解法二:如图,以点A为坐标原点,线段BC的垂直平分线所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系,令1PA AD AC===,……………2分OCBH DPFA则()()10,0,0,0,0,1,,02A P C ⎫⎪⎪⎝⎭,()1,0,0,1,02B D ⎫-⎪⎪⎝⎭,11,42F ⎫⎪⎪⎝⎭. ∴()310,1,0,,42BC BF ⎛⎫==- ⎪ ⎪⎝⎭.……………4分 设平面BCF 的一个法向量为n (),,x y z =,由n ,BC ⊥n BF ⊥,得003104422y y x y z z x ==⎧⎧⎪⎪⇒⎨⎨-++==⎪⎪⎩⎩,令1x =,则z =,∴31,0,n ⎛= ⎝⎭. …………………7分PA ⊥平面ABCD ,AC ⊂平面ABCD ,∴PA AC ⊥. ………………………………… 8分//OF PA ,∴OF AC ⊥. ABCD 是菱形,∴AC BD ⊥.OF BD O =,∴AC ⊥平面BFD .…………………………… 9分∴AC 是平面BFD 的一个法向量,AC =1,02⎫⎪⎪⎝⎭.………………… 10分∴cos ,7AC n AC n AC n⋅===⋅, ∴sin ,1AC n ==, …………………… 12分∴2tan ,AC n == 13分∴二面角C BF D --的正切值是3. ……………………… 14分 20、解:圆P 的方程为()2211x y -+=,则其直径长2B C =,圆心为()1,0P ,设l 的方程为1ky x =-,即1x ky =+,代入抛物线方程得:244y ky =+,设()()1122,, ,A x y D x y ,有⎩⎨⎧-==+442121y y k y y , ………………………………2分 则222121212()()416(1)y y y y y y k -=+-=+. ……………………4分 故222222212121212||()()()()4y y AD y y x x y y -=-+-=-+ …6分 22221221)1(16])4(1[)(+=++-=k y y y y , ………… 7分 因此)1(4||2+=k AD . ………………………………… 8分 据等差,BC AD CD AB BC -=+=2, …………… 10分 所以63==BC AD ,即6)1(42=+k ,22±=k ,…………… 12分 即:l0y -=0y +=. …………………14分21、解:(1)因为x x f cos 4121)(+=', …………………………2分 所以]43,41[)(∈'x f ,满足条件0()1f x '<<. …………………3分又因为当0=x 时,0)0(=f ,所以方程0)(=-x x f 有实数根0. 所以函数4sin 2)(x x x f +=是集合M 中的元素. …………………………4分 (2)假设方程0)(=-x x f 存在两个实数根βαβα≠(,),则0)(,0)(=-=-ββααf f ,……………………………………5分不妨设βα<,根据题意存在数),,(βα∈c使得等式()()()()f f f c βαβα'-=-成立, ………………………7分因为βαββαα≠==且,)(,)(f f ,所以1)(='c f ,与已知1)(0<'<x f 矛盾, 所以方程0)(=-x x f 只有一个实数根;………………………10分(3)不妨设32x x <,因为,0)(>'x f 所以)(x f 为增函数,所以)()(32x f x f <, 又因为01)(<-'x f ,所以函数x x f -)(为减函数, ……………………11分 所以3322)()(x x f x x f ->-, ………………………………12分所以2323)()(0x x x f x f -<-<,即3232|()()|||f x f x x x -<-, …………13分x y o A B C D P所以323231213121|()()||||()||||2f x f x x x x x x x x x x x -<-=---≤-+-<. …14分。
2008全国高考理科数学试题及答案安徽

2008年普通高等学校招生全国统一考试(安徽卷)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至第4页.全卷满分150分,考试时间120分钟.考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致. 2. 答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上书写.在试题卷上作答无效. 4. 考试结束,监考员将试题卷和答题卡一并收回. 参考公式:如果事件A B ,互斥,那么球的表面积公式 24πS R = ()()()P A B P A P B +=+其中R 表示球的半径 如果事件A B ,相互独立,那么()()()P A B P A P B =球的体积公式 34π3V R =如果随机变量(,),B n p ξ那么 其中R 表示球的半径(1)D np p ξ=-第I 卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. (1).复数 32(1)i i +=( )A .2B .-2C .2i D . 2i -(2).集合{}|lg ,1A y R y x x =∈=>,}{2,1,1,2B =--则下列结论正确的是( )A .}{2,1AB =--B . ()(,0)RC A B =-∞C .(0,)AB =+∞D . }{()2,1R C A B =--(3).在平行四边形ABCD 中,AC 为一条对角线,若(2,4)AB =,(1,3)AC =,则AB =( )A . (-2,-4)B .(-3,-5)C .(3,5)D .(2,4)(4).已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是( )A .,,m n m n αα若则‖‖‖B .,,αγβγαβ⊥⊥若则‖C .,,m m αβαβ若则‖‖‖D .,,m n m n αα⊥⊥若则‖(5).将函数sin(2)3y x π=+的图象按向量α平移后所得的图象关于点(,0)12π-中心对称,则向量α的坐标可能为( )A .(,0)12π-B .(,0)6π-C .(,0)12πD .(,0)6π(6).设88018(1),x a a x a x +=+++则0,18,,a a a 中奇数的个数为( )A .2B .3C .4D .5(7).0a <是方程2210ax x ++=至少有一个负数根的( )A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件(8).若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( )A .[3,3]-B .(3,3)-C .33[,]33-D .33(,)33-(9).在同一平面直角坐标系中,函数()y g x =的图象与xy e =的图象关于直线y x =对称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省皖南八校2008届高三第二次联考数学(理)一、选择题:本大题共11小题,每小题5分,共55分.在每小题给出的四个选项中.只有一项是符合题目要求的. 1.设全集1,{|0},{1,}u x U R A x C A a x b-==≥=--+,则a b +等于 A .一2B .2C .1D .02.函数212(log )4(2)y x x =-≥的反函数是A.3)y x =≥- B.23)y x =≥- C.3)y x =-≥-D.23)y x =-≥-3.在等比数列{}n a 中,已知13118a a a =,则28a a 等于A .16B .6C .12D .44.若定义在R 上的函数()f x 满足()()3f x f x π+=-,且()()f x f x -=,则()f x 可以是A .1()2sin3f x x = B .()2sin3f x x = C .1()2cos 3f x x =D .()2cos3f x x =5.已知函数12()3,0log ,0x f x x x x +⎧=≤⎨>⎩,若0()1f x ≥,则0x 的取值范围是A .2x ≥B .10x -≤≤C .10x -≤≤或2x ≥D .1x ≤-或02x <≤6.已知点(cos ,sin )θθ到直线sin cos 10x y θθ+-=的距离是1(0)22πθ≤≤.则θ的值为A .12πB .512πC .12π或512πD .56π或6π7.已知向量(2,1),(,2),(3,)a b x c y =-=-= ,若,()()a b a b b c +⊥-,则x y +为A .0B .2C .4D .一48.某校A 班有学生40名,其中男生24人,B 班有学生50名,其中女生30人,现从A 、B 两班各找一名学生进行问卷调查,则找出的学生是一男一女的概率为A .1225B .1325 C .1625 D .925 9.已知非零向量AB 和AC 满足()0||||AB AC BC AB AC +⋅= ,且12||||A B A C A B A C ⋅=,则ABC为A .三边均不相等的三角形B .直角三角形C .等腰非等边三角形D .等边三角形10.一同学在电脑中打出如下若干个圆:若依此规律继续下去,得到一系列的圆,则在前2007个圆中共有●的个数是A .6lB .62C .63D .6411.已知()f x 是定义在R 上的奇函数.且是以2为周期的周期函数.若当[0,1)x ∈时,()21x f x =-,则12(log 6)f 的值为A .52-B .一5C .12-D .一6二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卷中的横线上.12.右图是函数sin()(0,||)2y x πωϕωϕ=+><的图象的一部分,则ϕ= ,ω=13.已知A 、B 为椭圆22:11x y C m m+=+的长轴的两个端点,P 是椭圆C 上的动点,且APB ∠的最大值是23π,则实数m 的值是 .14.若61()x的展开式中的第5项是152,设12n n S x x x ---=++⋅⋅⋅+,则lim n n S →+∞=15.对正整数n ,设曲线(1)ny x x =-在2x =处的切线与y 轴交点的纵坐标为n a ,则数列{}1na n +的前n 项和公式是三、解答题:本大题共6小题,共79分.解答应写出必要的文字说明、证明过程及演算步骤.16.(本小题满分12分)已知7cos 2,252πθθπ=<<.求: (1)tan θ的值;(2)22cos sin 2)4θθπθ-+的值17.(本小题满分14分)已知在四棱锥P 一ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,PA=AD=1,AB=2,E 、F 分别是AB 、PD 的中点.(1)求证:AF ∥平面PEC ;(2)求PC 与平面ABCD 所成角的大小; (3)求二面角P 一EC 一D 的大小.18.(本小题满分14分)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且满足(2)cos cos a c B b C -= (1)求角B 的大小;(2)设(sin ,cos2),(4,1)(1),m A A n k k m n ==>⋅的最大值为5,求k 的值19.(本小题满分12分)已知椭圆22221(0)x y a b a b+=>>的中心在坐标原点O ,一条准线的方程为4x =,过椭圆的左准点F ,且方向向量为(1,1)a =的直线l 交椭圆于A 、B 两点,AB 的中点为M .(1)求直线OM 的斜率(用a b 、表示);(2)设直线AB 与OM 的夹角为α,当tan 7α=时,求椭圆的方程. 20.(本小题满分13分)已知定义域为R 的函数2()(1),()4(1)f x xg x x =-=-,数列{}n a 满足12a =,*1()()()0()n n n n a a g a f a n N +-+=∈(1)求数列{}n a 的通项公式;(2)设13()()n n n b f a g a +=-,求数列{}n b 的最值及相应的n 值. 21.(本小题蠛分14分)在数列{}n a 中12a =,且1112212n n n nn a a +++--= (1)求证:2n n a n ≤⋅(2)设数列{}n a 的前n 项和为n S ,求证:1(1)22n n S n +≤-⋅+ (3)求证:122n n n a a +≤+皖南八校2008届高三第二次联考数学参考答案(理科)1.A 2.A3.D4.D5.C6.C7.A8.B9.D10.A11.C 12.6π 2 13.1214.115.122n +-提示:1.A 由{1,}u C A a =--,知(,1](,)A a =-∞-⋃-+∞.所以1,a b a =--=-,因此2a b +=-2.A 函数可化为22(log )4y x =-,所以2l og (3)x y ≥-,则反函数为3)y x =≥-3.D 由312311188a a a q =⇒=(q 为公比),即412a q =,∴42281()4a a a q ==4.D ∵()()f x f x -=,∴排除A 、B ,又∵()()3f x f x π+=-,∴选D5.C 当0x ≤时,13110x x +≥⇒+≥,∴当0x >时,2log 12x x ≥⇒≥,∴2x ≥,综上所述:10x -≤≤或2x ≥ 6.C12=,∴1sin 2(0)22πθθ=≤≤,即12π或512π7.A ∵a b ,∴4x =,∴(4,2)b =- ,∴(6,3),(1,3)a b b c y +=--=--,∵()()a b b c +⊥- ,∴()()0a b b c +⋅-=,即62(2)0y ---=,∴4y =-,∴0x y +=.8.B A 班男生B 班女生概率为3355⨯,B 班男生A 班女生概率为2255⨯.9.D 由()0||||AB AC BC BAC AB AC +⋅=⇒∠的角平分线与BC 垂直,∴ABC 为等腰三角形.∵12||||AB AC AB AC ⋅=,∴60BAC ∠=︒,∴ABC 为等边三角形 10.A 因为黑圆间隔的白圆数成等差数列,设有n 组白圆,则有1n -个黑圆,所以所有圆的个数为2(1)32122n n n n n ++-+-=,由已知23220072n n +-≤,因为当61n =时,232195120072n n +-=<,当62n =时,232201420072n n +-=>,但第62组中共有62个白圆,所以在前2007个圆中共有61个黑圆11.C ∵123log 62-<<-,∴121log 620-<+<,即1231log 02-<<,∵()f x 是周期为2的奇函数,∴23log 211122223331(log 6)(log )(log )(log )(21)2222f f f f ==--=-=--=-12.6π 2 由图知11()1212T πππ=--=,∴222T ππωπ===,∴sin(2)y x ϕ=+,又点(,0)12π-在图象上,∴sin()06πϕ-+=,∴由06πϕ-+=,知6πϕ=13.12由椭圆知识知,当点P 位于短轴的端点时APB ∠取得最大值.据题意则有1tan32m π=⇒=14.1 由题意知42456115(()T C xx=-=,又∵5152T =,∴2x =,∴11(1)122lim lim lim (1)11212n n n n n n S →+∞→+∞→+∞-==-=- 15.122n +- ∵(1)n y x x =-,∴1'(1)n n y nx n x -=-+,∴1'(2)2(1)2n n k f n n -==-+12(2)n n -=-+,又切点为(2,2)n -,∴切线方程为122(2)(2)n n y n x -+=-+-,令0x =,则(1)2n n a n =+,∴数列{}1n a n +的通项公式21n n an =+,故前n 项和公式12(21)2221n n n S +-==--16.(1)由7cos 225θ=,得227912sin ,sin 2525θθ-==…………2分∵2πθπ<<,∴34sin ,cos 55θθ==-,∴sin 3tan cos 4θθθ==-…………6分 (2)24312cos sin cos 1sin 552234sin cos )455θθθθπθθθ-+--+-===++-…………12分 17.解法一:(1)取PC 的中点O ,连结OF 、OE .∴FO ∥DC ,且FO=12DC ∴FO ∥AE …………2分又E 是AB 的中点.且AB=DC .∴FO=AE . ∴四边形AEOF 是平行四边形.∴AF ∥OE 又OE ⊂平面PEC ,AF ⊄平面PEC ∴A F ∥平面PEC (2)连结AC∵P A ⊥平面ABCD ,∴∠PCA 是直线PC 与平面ABCD 所成的角……………6分 在Rt △PAC中,tan 5PA PCA AC ∠===即直线PC 与平面ABCD所成的角大小为arctan……………9分 (3)作A M ⊥CE ,交CE 的延长线于M .连结PM ,由三垂线定理.得P M ⊥CE∴∠PMA 是二面角P —EC —D 的平面角. ……11分 由△AM E ∽△CBE,可得AM =tan PA PMA AM ∠==∴二面角P 一EC 一D的大小为14分解法二:以A 为原点,如图建立直角坐标系,则A (0.0,0),B (2,0,0),C (2,l ,0),D (0,1,0),F (0,12,12),E (1,0,0),P (0,0,1) (1)取PC 的中点O ,连结OE ,则O (1,12,12),1111(0,,),(0,,)2222AF EO ==∴AF EO……………………………………5分又OE ⊂平面PEC ,AF ⊄平面PEC ,∴A F ∥平面PEC …………………………6分(2)由题意可得(2,1,1)PC =- ,平面ABCD 的法向量(0,0,1)PA =-cos ,||||PA PC PA PC PA PC ⋅<>===即直线PC 与平面ABCD所成的角大小为 ……………9分 (3)设平面PEC 的法向量为(,,),(1,0,1),(1,1,0)m x y z PE EC ==-=则0m PE m EC ⎧⋅=⎪⎨⋅=⎪⎩,可得00x z x y -=⎧⎨+=⎩,令1z =-,则(1,1,1)m =-- ……………11分 由(2)可得平面ABCD 的法向量是(0,0,1)PA =-cos ,||||m PA m PA m PA ⋅<>===∴二面角P 一EC 一D的大小为……………………………………14分 18.(1)∵(2)cos cos a c B b C -=,∴(2sin sin )cos sin cos A C B B C -=……2分整理得2sin cos sin cos sin cos A B B C C B =+,∴2sin cos sin()sin A B B C A =+=………………………4分∵(0,)A π∈,∴sin 0A ≠,∴1cos ,23B B π==………………………6分 (2)24sin cos22sin 4sin 1m n k A A A k A ⋅=+=-++ ,其中2(0,)3A π∈……8分 设sin (0,1]A t =∈,则2241,(0,1]m n t kt t ⋅=-++∈∴当1t =时,m n ⋅取得最大值………………………12分依题意2415k -++=,解得32k =,符合题意,∴32k =……………………14分 19.(1)设1122(,),(,)A x y B x y ,∵A 、B 在椭圜上,∴2222112222221,1x y x y a b a b+=+= ………………3分两式相减,得2121221212y y y y b x x x x a-+⋅=--+∵121212121,AB OM y y y y k k x x x x -+===-+∴22OMb k a=-………………6分(2)∵直线AB 与OM 的夹角为α,tan 7α=由(1)知221,AB OMb k k a ==-,∴22221tan 71b a b aα+==- ①………………8分 又椭圆的中心在坐标原点O ,一条准线的方程为4x =,∴24a c= ② 在椭圆中,222a b c =+ ③联立①②③,解得2243a b ⎧=⎪⎨=⎪⎩,∴椭圆的方程为22143x y +=………………12分 20.(1)2()(1),()4(1)n n n n f a a g a a =-=-∵21()4(1)(1)0n n n n a a a a +-⋅-+-=,∴1(1)(431)0n n n a a a +---= ∵12a =,∴1n a ≠,∴14310n n a a +--=,∴131(1)4n n a a +-=-………3分 又111a -=,∴数列{1}n a -是首项为1,公比为34的等比数列, ∴131()4n n a --=,∴13()14n n a -=+………………7分(2)21211333(1)4(1)3((())())44n n n n n b a a --+=---=-………………9分 令13,()4n n b y u -==,则2211133(())3()2424y u u =--=--∵*n N ∈,∴()u n 递减,其值分别为39271,,,,41664⋅⋅⋅,经比较916距12最近 ∴当3n =时,n b 有最小值189256-;当1n =时,n b 有最小值0………………13分21.(1)1121222n n n n a a ++-=-<∵11112,2(21)2n n n n n a a a +++==+-,∴110,22n n n n a a a ++>-<, 整理得11122n nn na a ++-<………………2分 则当2n ≥时,1211211,,12222nn n n a a a a ---<⋅⋅⋅-< 叠加得11122n n a a n -<-,即2nn a n <⋅ 当1n =时,1112a =⋅故2n n a n ≤⋅………………………………………………………………4分 (2)由(1)得231222322n n S n ≤⋅+⋅+⋅+⋅⋅⋅+⋅………………………………6分令231222322n n T n =⋅+⋅+⋅+⋅⋅⋅+⋅,则234121222322n n T n +=⋅+⋅+⋅+⋅⋅⋅+⋅ ∴231122222,(1)22n n n n n T n T n ++-=+++⋅⋅⋅+-⋅=-+ 故1(1)22n n S n +≤-⋅+………………………………9分 (3)由已知得1112222n n n n n n a a a n +++-=-≥-,故只须证明122n n n +->,即2nn > ∵012(11)n n nn n n C C C n =+=++⋅⋅⋅+>,∴结论成立………………………14分薄雾浓云愁永昼, 瑞脑消金兽。
