2011年普通高等学校招生全国统一考试(广东卷)解析
2011年高考英语广东卷(word精校版)

2011年普通高等学校招生全国统一考试(广东A卷)英语Ⅰ. 语言知识及应用(共两节。
满分35分)第一节完形填空(共15小题;每小题2分,满分30分)阅读下面短文,掌握其大意,然后从1~15各题所给的A、B、C和D项中,选出最佳选项,并在答题卡上将该项涂黑。
It has been argued by some that gifted children should be grouped in special classes, The 1 has been on the belief that in regular classes these children are held back in their intellectual (智力的) growth by 2 situation that has designed for the 3 children.There can be little doubt that 4 classes can help the gifted children to graduate earlier and take their place in life sooner. However, to take these 5 out of the regular classes may create serious problems.I observed a number of 6 children who were taken out of a special class and placed in a 7 class. In the special class, they showed little ability to use their own judgment, relying 8 on their teachers‟ directions. In the regular class, having no worry about keeping up, they began to reflect 9 on many problems, some of which were not on the school program.Many are concerned that gifted children become 10 and lose interest in learning. However this 11 is more often from parents and teachers than from students, and some of these 12 simply conclude that special classes should be set up for those who are 13 . Some top students do feel bored in class, but why they 14 so goes far beyond the work they have in school. Studies have shown that to be bored is to be anxious. The gifted child whop is bored is an 15 child.1. A. principle B. theory C. arguments D. classification2. A. designing B. grouping C. learning D. living3. A. smart B. curious C. mature D. average4. A. regular B. special C. small D. creative5. A. children B. programs C. graduates D. designs6. A. intelligent B. competent C. ordinary D. independent7. A. separate B. regular C. new D. boring8. A. specially B. slightly C. wrongly D. heavily9. A, directly B. cleverly C. voluntarily D. quickly10. A. doubted B. bored C. worried D. tired11. A. concern B. conclusion C. reflection D. interest12. A. students B. adults C. scholars D. teachers13. A. talented B. worried C. learned D. interested14. A. believe B. think C. say D. feel15. A. outstanding B. intelligent C. anxious D. ordinary第二节语法填空(共10小题;每小题1.5分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空,并将答案填写在答题卡标号为16~25的相应位置上。
【物理】2011年高考试题——(广东卷)

2011年普通高等学校招生全国统一考试(广东卷)理科综合(物理部分)一、单项选择题:本大题共16小题,每小题小题,每小题4分,共64分。
在每小题给出的四个选项中,只有一个符合题目要求,选对的得4分,选错或不答的得0分。
15、将闭合多匝线圈置于仅随时间变化的磁场中,线圈平面与磁场方向垂直,关于线圈中产生的感应电动势和感应电流,下列表述正确的是 A 、感应电动势的大小与线圈的匝数无关 B 、穿过线圈的磁通量越大,感应电动势越大C 、穿过线圈的磁通量变化越快,感应电动势越大D 、感应电流产生的磁场方向与原磁场方向始终相同 答案:C解析:由法拉第电磁感应定律,S BE n n ttϕ∆∆==∆∆,选项A 错误。
穿过线圈的磁通量越大,并不代表穿过线圈的磁通量变化率大,选项B 错误,C 正确。
由楞次定律感应电流的磁场总是阻碍产生感应电流的磁通量的变化,感应电流的磁场方向与原磁场方向有时相同,有时相反。
选项D 错误。
16、如图5所示,水平面上,橡皮绳一端固定,另一端连接两根弹簧,连接点P 在F 1、F 2和F 3三力作用下保持静止,下列判断正确的是: A 、F 1>F 2>F 3 B 、F 3>F 1>F 2 C 、F 2>F 1>F 3 D 、F 3>F 2>F 1 答案:B图5解析:由于在F1、F2和F3三力作用下保持静止,合力为零,现力F1与F2垂直,根据力的平行四边形定则由角度及几何关系可得:F3>F1>F2,B正确。
二、双项选择题:本大题共9小题,每小题6分,共54分。
在每小题给出的四个选项中,有两个选项符合题目要求,全部选对的得6分,只选1个且正确的得3分,有选错或不答的得0分。
答案:C D解析:光电流的大小与入射光的强度相关,A错误。
产生光电效应的条件是:入射光的频率大于或等于被照射材料的极限频率。
入射光的频率达不到极限频率,增加照射光的强度是不能产生光电流的,所以B错误,C、D正确。
2011广东高考文综地理试题及解析

2011年普通高等学校招生全国统一考试(广东卷)文科综合地理一、选择题:1.读“某区域地质面简图”(图1),图中甲、乙、丙三处的地质构造分别是A.断层、向斜、背斜 B. 断层、背斜、向斜C.向斜、断层、背斜D. 背斜、向斜、断层【解析】结合背斜,向斜,断层相关知识即可得出答案【答案】B2. 研究发现,长江干流江苏段河床在1985年前后平均冲漩状态发生了明显的转变,由淤积转变为冲刷。
其主要原因是A.该河段平均流速下降B.该河段径流量减少C.流域年降水量减少D.上游来沙量减少【解析】从材料来看,由原来的淤积变成冲栓,说明水量在增大,或者流速在加大,故答案ABC就错,还有一个可能就是河流的含沙量将少,故答案D对【答案】D3. 1996~2006年我国城镇人口数量年均增长4.46%,城镇建成区面积年均增长5.23%,2006年人均建设用地面积是发达国家的1.58倍。
由此可推断该阶段我国A.城镇建成区城镇人口密度升高B.城镇化水平已经超过发达国家C.城镇土地集约利用水平高于发达国家D.城镇人口增长速度滞后于城镇扩张速度【解析】从题干来看,城镇人口数量的增长速度明显慢于城市面积增长速度,故答案为D,人均建设面积是发达国家的1.58倍,说明我国土地集约利用水平低于发达国家。
【答案】D读“2007年我国部分省级行政区人均GDP与人均CO2排放量点图”(图2),结合所学知识,完成4~5题。
4.与全国人均水平相比,人均GDP高、人均CO2排放量低的是A.上海、天津B.广东、福建C.海南、贵州D.辽宁、山东5.山西、内蒙古人均GDP不算高,但人均CO2排放量高,其主要原因是A.自然资源贫乏B.交通设施落后C.煤炭消耗量大D.第三产业发达【解析】第4题,与全国平均来比,人均GDP高,人均CO2排放量低的,故答案就是B,第5题,结合中国地理的知识,山西,内蒙古煤炭资源丰富,故二氧化碳的排放量大,故答案为C【答案】B C6.暖锋过境期间的天气一般表现为A.锋前气压急剧升高,常出现雷暴天气B.锋后空气湿度增加,常形成大范围降水C.锋前水汽凝结,常形成雨,雾天气D.锋后气温降低,常出现晴朗天气【解析】暖锋的降水主要位于锋前,降雨的强度比较小,多连续性降水,过境后,气压降低,气温升高,故答案为C,【答案】C读“1995-2009年我国某省级行政区户籍人口迁移变动情况图”(图3),结合所学知识,完成7~8题。
(全国卷)2011年普通高等学校招生全国统一考试

2011年普通高等学校招生全国统一考试(全国卷)语文本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至4页,第Ⅱ卷5至8页。
第Ⅰ卷注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码,请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试卷上作答无效........3.第Ⅰ卷共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项符合题目要求。
一、(12分,每小题3分)1.下列词语中加点的字,读音全都正确的一组是()A.逾.越(yú)鸟瞰.(kàn)一丘之貉.(luò)栩.栩如生(xǔ)B.溃.败(kuì)凹.陷(wā)贻.笑大方(yí)兢.兢业业(jīng)C.咀.嚼(zǔ)桧.柏(guì)罄.竹难书(qìng)饕餮.大餐(tiè)D.觊.觎(jì)攻讦.(jié)光阴荏苒.(rǎn)心怀叵.测(pǒ)【试题解析】本题考查“识记现代汉语普通话的字音”的能力。
本题涉及多音多义字、形声字、形似字的读音、口语读音和书面语读音等。
A.“一丘之貉”的“貉”应读“hé”。
B.“凹陷”的“凹”应读“āo”;这个字是多音多义字,读“wā”时用于地名,属于口语读音。
C.“咀嚼”的“咀”应读“jǔ”;这个字是多音多义字,也读“zuǐ”,义同“嘴”,如山咀、壶咀儿。
D.所有读音都正确,虽然其中非常用字(如“讦”)的读音考生可能未能准确识记,但这并不影响答题,因为确认了前三项中“貉”“凹”“咀”读音的错误,就能判断D项是正确的。
【答案】D2.下列各句中,加点的成语使用恰当的一项是()A.我读过弗莱的著作,很喜欢他那高层建瓴....的气势和包罗万象的体系,更欣赏他努力摆脱主观印象式品评的文学批评方法。
2011年普通高等学校招生全国统一考试数学卷(广东.文)含详解

绝密★启用前 试卷类型:B2011年普通高等学校招生全国统一考试(广东卷)线性回归方程 y bxa =+ 中系数计算公式121()()()niii nii x x y y b x x ==--=-∑∑ , ay bx =- , 样本数据12,,,n x x x 的标准差,222121[()()()]n s x x x x x x n=-+-++- , 其中x ,y 表示样本均值.n 是正整数,则1221()()n n n n n n a b a b a a b ab b -----=-++++ .一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数z 满足1iz =,其中i 为虚数单位,则z =A .i -B .iC .1-D .1 2.已知集合{(,)|,A x y x y =为实数,且221}x y +=,{(,)|,B x y x y =为实数,且1}x y +=,则A B ⋂的元素个数为A .4B .3C .2D .1 3.已知向量(1,2),(1,0),(3,4)===a b c .若λ为实数,()λ+a b ∥c ,则λ=A .14 B .12C .1D .2 4.函数1()lg(1)1f x x x=++-的定义域是 A .(,1)-∞- B .(1,)+∞ C .(1,1)(1,)-⋃+∞ D .(,)-∞+∞5.不等式2210x x -->的解集是A .1(,1)2-B .(1,)+∞C .(,1)(2,)-∞⋃+∞D .1(,)(1,)2-∞-⋃+∞ 6.已知平面直角坐标系xOy 上的区域D 由不等式组0222x y x y⎧⎪⎨⎪⎩≤≤≤≤给定.若(,)M x y 为D 上的动点,点A的坐标为(2,1),则z OM OA=⋅的最大值为A .3B .4C .32D .4223正视图 图1侧视图 图22 俯视图 2图37.正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有A .20B .15C .12D .10 8.设圆C 与圆22(3)1x y +-=外切,与直线0y =相切,则C 的圆心轨迹为A .抛物线B .双曲线C .椭圆D .圆 9.如图1 ~ 3,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为 A .43 B .4 C .23 D .210.设(),(),()f x g x h x 是R 上的任意实值函数,如下定义两个函数()f g ()x 和()f g ()x :对任意x ∈R ,()f g ()x =(())f g x ;()f g ()x =()()f x g x ,则下列等式恒成立的是A .(()f g h )()x =(()f h ()g h )()xB .(()f g h )()x =(()f h ()g h )()xC .(()f g h )()x =(()f g ()g h )()xD .(()f g h )()x =(()f g()g h )()x二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(9 ~ 13题)11.已知{}n a 是递增的等比数列,若22a =,434a a -=,则此数列的公比q = .12.设函数3()cos 1f x x x =+.若()11f a =,则()f a -= .13.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x (单位:小时)与当天投篮命中率y 之间的关系:图4BAC DEF时间x 1 2 3 4 5 命中率y0.40.50.60.60.4小李这5天的平均投篮命中率为 ;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 . (二)选做题(14 ~ 15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)已知两曲线参数方程分别为5cos sin x y θθ⎧=⎪⎨=⎪⎩(0)θπ<≤和254x t y t⎧=⎪⎨⎪=⎩(t ∈)R ,它们的交点坐标为___________.15.(几何证明选讲选做题)如图4,在梯形ABCD 中,AB ∥CD ,4AB =,2CD =,,E F 分别为,AD BC 上的点,且3EF =, EF ∥AB ,则梯形ABFE 与梯形EFCD 的面积比为________.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数1()2sin()36f x x π=-,x ∈R .(1)求(0)f 的值;(2)设,0,2παβ⎡⎤∈⎢⎥⎣⎦,10(3)213f πα+=,6(32)5f βπ+=,求sin()αβ+的值.17.(本小题满分13分)在某次测验中,有6位同学的平均成绩为75分.用n x 表示编号为n (1,2,,6)n = 的同学所得成绩,且前5位同学的成绩如下:编号n 1 2 3 4 5 成绩n x7076727072(1)求第6位同学的成绩6x ,及这6位同学成绩的标准差s ;(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.18.(本小题满分13分)图5所示的几何体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右BAB 'A 'CC 'DD 'EE 'G H '1O2O1O '2O '图5水平平移后得到的.,,,A A B B ''分别为 CD , C D '', DE , D E ''的中点,1122,,,O O O O ''分别为CD ,C D '', DE ,D E ''的中点.(1)证明:12,,,O A O B ''四点共面;(2)设G 为AA '中点,延长1A O ''到H ',使得11O H A O ''''=.证明:2BO '⊥平面H B G ''.19.(本小题满分14分)设0a >,讨论函数2()ln (1)2(1)f x x a a x a x =+---的单调性. 20.(本小题满分14分)设0b >,数列{}n a 满足1a b =,111n n n nba a a n --=+-(n ≥2).(1)求数列{}n a 的通项公式;(2)证明:对于一切正整数n ,2n a ≤11n b ++.21.(本小题满分14分)在平面直角坐标系xOy 上,直线l :2x =-交x 轴于点A .设P 是l 上一点,M 是线段OP 的垂直平分线上一点,且满足MPO AOP ∠=∠.(1)当点P 在l 上运动时,求点M 的轨迹E 的方程;(2)已知(1,1)T -,设H 是E 上动点,求HO HT +的最小值,并给出此时点H 的坐标; (3)过点(1,1)T -且不平行于y 轴的直线1l 与轨迹E 有且只有两个不同的交点,求直线1l 的斜率k 的取值范围.1.(A ).1()iz i i i i -===-⨯- 2.(C ).A B ⋂的元素个数等价于圆221x y +=与直线1x y +=的交点个数,显然有2个交点 3.(B ).(1,2)λλ+=+a b ,由()λ+a b ∥c ,得64(1)0λ-+=,解得λ=124.(C ).10110x x x -≠⎧⇒>-⎨+>⎩且1x ≠,则()f x 的定义域是(1,1)(1,)-⋃+∞5.(D ).21210(1)(21)02x x x x x -->⇒-+>⇒<-或1x >,则不等式的解集为1(,)(1,)2-∞-⋃+∞6.(B ).2z x y =+,即2y x z =-+,画出不等式组表示的平面区域,易知当直线2y x z =-+经过点(2,2)时,z 取得最大值,max 2224z =⨯+=7.(D ).正五棱柱中,上底面中的每一个顶点均可与下底面中的两个顶点构成对角线,所以一个正五棱柱对角线的条数共有5210⨯=条8.(A ).依题意得,C 的圆心到点(0,3)的距离与它到直线1y =-的距离相等,则C 的圆心轨迹为抛物线 9.(C ).该几何体是一个底面为菱形的四棱锥,菱形的面积1223232S =⨯⨯=,四棱锥的高为3,则该几何体的体积112332333V Sh ==⨯⨯= 10.(B ).11.2. 2243224422402(2)(1)0a a a q a q q q q q -=⇒-=⇒--=⇒-+=2q ⇒=或1q =-∵{}n a 是递增的等比数列,∴2q =12.9-3()cos 111f a a a =+=,即3()cos 10f a a a ==,则33()()cos()1cos 11019f a a a a a -=--+=-+=-+=- 13.0.5;0.53小李这5天的平均投篮命中率1(0.40.50.60.60.4)0.55y =++++= 3x =,1222221()()0.2000.1(0.2)0.01(2)(1)012()niii ni i x x y y bx x ==--++++-===-+-+++-∑∑ , 0.47a y bx =-=∴线性回归方程 0.010.47y x =+,则当6x =时,0.53y = ∴预测小李该月6号打6小时篮球的投篮命中率为0.5314.25(1,)5.5cos sin x y θθ⎧=⎪⎨=⎪⎩表示椭圆2215x y +=(5501)x y -<≤≤≤且,254x t y t⎧=⎪⎨⎪=⎩表示抛物线245y x =,22221(5501)5450145x y x y x x x y x ⎧+=-<≤≤≤⎪⎪⇒+-=⇒=⎨⎪=⎪⎩且或5x =-(舍去),又因为01y ≤≤,所以它们的交点坐标为25(1,)515.75如图,延长,AD BC ,AD BC P =∵23CD EF =,∴49PCD PEF S S ∆∆= ∵24CD AB =,∴416PCD PEF S S ∆∆= ∴75ABEF EFCDS S =梯形梯形16.解:(1)(0)2sin()16f π=-=-(2)110(3)2sin[(3)]2sin 232613f πππααα+=+-==,即5sin 13α= 16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=,即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦, ∴212cos 1sin 13αα=-=,24sin 1cos 5ββ=-= ∴5312463sin()sin cos cos sin 13513565αβαβαβ+=+=⨯+⨯=17.解:(1)61(7076727072)756x +++++=,解得690x = PBAC DEFxy O2x =-AP l MM标准差22222222212611[()()()](5135315)766s x x x x x x =-+-++-=+++++= (2)前5位同学中随机选出的2位同学记为(,)a b ,,{1,2,3,4,5}a b ∈且a b ≠则基本事件有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种 这5位同学中,编号为1、3、4、5号的同学成绩在区间(68,75)中设A 表示随机事件“从前5位同学中随机选出2位同学,恰有1位同学成绩在区间(68,75)中” 则A 中的基本事件有(1,2)、(2,3)、(2,4)、(2,5)共4种,则42()105P A == 18.证明:(1)连接2,BO 22,O O '依题意得1122,,,O O O O ''是圆柱底面圆的圆心∴,,,CD C D DE D E ''''是圆柱底面圆的直径∵,,A B B ''分别为 C D '', DE , D E ''的中点∴1290A O D B O D ''''''∠=∠=∴1A O ''∥2BO '∵BB '//22O O ',四边形22O O B B ''是平行四边形∴2BO ∥2BO ' ∴1A O ''∥2BO ∴12,,,O A O B ''四点共面(2)延长1A O '到H ,使得11O H AO ''=,连接1,,HH HO HB '' ∵11O H A O ''''=∴1O H ''//2O B '',四边形12O O B H ''''是平行四边形 ∴12O O ''∥H B ''∵1222O O O O '''⊥,122O O B O ''''⊥,2222O O B O O ''''= ∴12O O ''⊥面22O O B B ''∴H B ''⊥面22O O B B '',2BO '⊂面22O O B B '' ∴2BO H B '''⊥易知四边形AA H H ''是正方形,且边长2AA '=∵11tan 2HH HO H O H '''∠=='',1tan 2A G A H G A H '''∠==''∴1tan tan 1HO H A H G ''''∠⋅∠=∴190HO H A H G ''''∠+∠= ∴1HO H G ''⊥易知12O O ''//HB ,四边形12O O BH ''是平行四边形∴2BO '∥1HO '∴2BO H G ''⊥,H G H B H ''''= ∴2BO '⊥平面H B G ''21.解:(1)如图所示,连接OM ,则PM OM =∵MPO AOP ∠=∠,∴动点M 满足MP l ⊥或M 在x 的负半轴上,设(,)M x yxy O 2x =-TN l HNH∙H xy O TA 1l 1l1l① 当MP l ⊥时,2MP x =+,22OM x y =+222x x y +=+,化简得244y x =+(1)x ≥-② 当M 在x 的负半轴上时,0y =(1)x <-综上所述,点M 的轨迹E 的方程为244y x =+(1)x ≥-或0y =(1)x <-(2)由(1)知M 的轨迹是顶点为(1,0)-,焦点为原点的抛物线和x 的负半轴0y =(1)x <- ① 若H 是抛物线上的动点,过H 作HN l ⊥于N由于l 是抛物线的准线,根据抛物线的定义有HO HN = 则HO HT HN HT +=+当,,N H T 三点共线时,HN HT +有最小值3TN =求得此时H 的坐标为3(,1)4--② 若H 是x 的负半轴0y =(1)x <-上的动点显然有3HO HT +>综上所述,HO HT +的最小值为3,此时点H 的坐标为3(,1)4-- (3)如图,设抛物线顶点(1,0)A -,则直线AT 的斜率12AT k =-∵点(1,1)T -在抛物线内部,∴过点T 且不平行于,x y 轴的直线1l 必与抛物线有两个交点 则直线1l 与轨迹E 的交点个数分以下四种情况讨论: ① 当12k ≤-时,直线1l 与轨迹E 有且只有两个不同的交点 ② 当102k -<<时,直线1l 与轨迹E 有且只有三个不同的交点 ③ 当0k =时,直线1l 与轨迹E 有且只有一个交点 ④ 当0k >时,直线1l 与轨迹E 有且只有两个不同的交点 综上所述,直线1l 的斜率k 的取值范围是1(,](0,)2-∞-+∞。
2012年普通高等学校招生统一理综试题(广东卷)试题解析(生物部分)有答案

2012年普通高等学校招生全国统一考试(广东卷)理综生物部分解析(参考版)1.有关生物膜结构与功能的叙述,正确的是A.膜载体蛋白的合成不需要ATPB.葡萄糖跨膜运输不需要载体蛋白C.线粒体外膜与内膜的主要功能不同D.变形虫和草履虫的细胞膜基本组成成分不同【答案】C【解析】A、任何蛋白质的合成都需要ATP的参入提供能量;B、葡萄糖的跨膜运输方式为主动运输或协助扩散,都需要载体蛋白的参入;D、几乎所有的生物膜的基本结构都是蛋白质和磷脂。
2.培育草莓脱毒苗所采用的主要技术是A.组织培养B.细胞杂交C.显微注射D.核移植【答案】A【解析】草莓植株分生区的细胞含病毒的量比较少,可以利用植物组织培养技术培养出脱毒幼苗。
3.分析下表,可推测注:“+”显色,“++”显色更深;“-”不显色.A.甲溶液含有淀粉酶B.乙溶液含有还原糖C.混合溶液不含淀粉D.混合溶液含有淀粉酶【答案】D【解析】双缩脲试剂、碘液、斐林试剂分别检测蛋白质、淀粉和还原性糖。
据表可以推测,甲含有蛋白质,乙含有淀粉,甲和乙混合能够产生还原性糖,证明甲中含有淀粉酶,将淀粉分解产生还原性糖。
4.有关土壤动物研究的叙述,正确的是A.土壤动物群落不存在分层现象B.土壤动物中间关系主要是互利共生C.土壤盐碱度不同,土壤动物群落结构有差异D.随机扫取表层土取样,可以调查土壤小动物类群丰富度【答案】C【解析】由于不同的土壤层面为不同的生物提供了栖息地,土壤中的群落也存在垂直分布,所以A错;土壤中动物的中间关系,除了互利共生之外,还有捕食、寄生、竞争,这些无主次之分,所以B错;土壤表层只有一部分小动物分布,应该选择取样器取样法调查小动物的丰富度,所以D错。
5、有关人体免疫的叙述,正确的是A 机体主要依赖免疫调节维持内环境稳态B 病原微生物侵袭,可引起机体产生特异性免疫C 特异性免疫过程中,只有T 细胞产生记忆细胞D 如果神经中枢受损,机体的特异性免疫功能完全丧失【答案】B【解析】机体依赖神经-体液-免疫系统共同调节内环境的稳态,所以A错;在特异性免疫的过程中,B淋巴细胞也可以产生记忆细胞,所以C错;神经中枢受损,不会导致特异性免疫功能完全丧失。
2011年普通高等学校招生全国统一考试(广东卷)

2011年普通高等学校招生全国统一考试(广东卷)英语(因扫描版图片不清,信息匹配题没有配插图)Ⅰ. 语言知识及应用(共两节。
满分35分)第一节完形填空(共15小题;每小题2分,满分30分)阅读下面短文,掌握其大意,然后从1~15各题所给的A、B、C和D项中,选出最佳选项,并在答题卡上将该项涂黑。
It has been argued by some that gifted children should be grouped in special classes, The 1 has been on the belief that in regular classes these children are held back in their intellectual (智力的) growth by 2 situation that has designed for the 3 children.There can be little doubt that 4 classes can help the gifted children to graduate earlier and take their place in life sooner. However, to take these 5 out of the regular classes may create serious problems.I observed a number of 6 children who were taken out of a special class and placed ina 7 class. In the special class, they showed little ability to use their own judgment, relying8 on their teachers‟ directions. In the regular class, having no worry about keeping up, they began to reflect 9 on many problems, some of which were not on the school program.Many are concerned that gifted children become 10 and lose interest in learning. However this 11 is more often from parents and teachers than from students, and some of these 12 simply conclude that special classes should be set up for those who are 13 . Some top students do feel bored in class, but why they 14 so goes far beyond the work they have in school. Studies have shown that to be bored is to be anxious. The gifted child whop is bored is an 15 child.1. A. principle B. theory C. arguments D. classification2. A. designing B. grouping C. learning D. living3. A. smart B. curious C. mature D. average4. A. regular B. special C. small D. creative5. A. children B. programs C. graduates D. designs6. A. intelligent B. competent C. ordinary D. independent7. A. separate B. regular C. new D. boring8. A. specially B. slightly C. wrongly D. heavily9. A, directly B. cleverly C. voluntarily D. quickly10. A. doubted B. bored C. worried D. tired11. A. concern B. conclusion C. reflection D. interest12. A. students B. adults C. scholars D. teachers13. A. talented B. worried C. learned D. interested14. A. believe B. think C. say D. feel15. A. outstanding B. intelligent C. anxious D. ordinary第二节语法填空(共10小题;每小题1.5分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空,并将答案填写在答题卡标号为16~25的相应位置上。
2010—2013年广东高考文综地理题及解析

2010年普通高等学校招生全国统一考试(广东卷)文科综合地理部分 一、选择题: 1.利用作物秸秆等农副产品发展农区畜牧业,有利于 A.改善局地气候 B.综合利用资源 C.防止水土流失 D.保护农田作物 2.我国甲、乙两地均位于29°N 附近。
读“1971~2000年甲、乙两地各月气温和降水分布图”(图1),可知 图1A.甲地年平均气温较乙地低B.乙地降水较甲地丰沛C. 乙地是高原山地气候D.甲地属温带季风气候3.卫星遥感监测显示,1999~2008年青藏高原上的色林错湖面扩大了约20%,主要原因是A.冰雪融水增加B.冻土面积扩大C.青藏高原抬升D.湖面蒸发增加4.下列关于河流的叙述,正确的是A.河流右岸更容易遭受侵蚀B.河流最深处位于河床中心C.水面宽度一年中洪水期最大D.自上游向下游流量逐渐增加读“2006年我国水资源、人口、耕地和经济总量区域比重图”(图2),完成5~6题。
图2 5.人口数量最多、经济总量最大的区域是 A.西南区 B.西北区 C.南方区 D.北方区 6.水资源与人口、耕地、经济发展匹配较差的区域是A.北方区和南方区B.北方区和西南区C.西北区和西南区D.西北区和南方区 7.三峡大坝下游附近河床某测点,沉积物粒径的平均值比建坝前大(如图3示意),其成因是A.侵蚀—搬运作用B.搬运—堆积作用C.风化—侵蚀作用D.沉积—固结成岩作用8.下列关于无霜期的叙述,正确的是 A.同一海拔,纬度越高无霜期越长 B.同一纬度,海拔越低无霜期越短C.同一山地,阳坡无霜期短于阴坡D.同一地段,开阔地无霜期长于低洼地 9.沙尘暴对地理环境的影响是多方面的。
华北地区沙尘暴的降尘会 A.导致气候变暖 B.引发草场退化 C.引起地表水体酸化 D.增加土壤肥力读“2005年我国东部沿海某市各图层间人口净迁移模式图”(图4),完成10~11题。
10.可知该市 A.中心区和近郊区为人口净迁出区 B.城区边缘区和远郊区为人口净迁入区 C.城区边缘区人口净迁出量最大 D.近郊区人口净迁入量最大 11.可推测该市 A.处于城市化初级阶段 B.出现郊区城市化现象 C.城市“空心化”现象明显 D.城市人口规模逐渐减少40 80 160 120 200 103020 -5 051525降水量(m m )气温(℃)1 2 3 4 5 6 7 8 9 10 11 12 甲地各月平均气温 乙地各月平均气温 甲地各月平均降水 乙地各月平均降水图3 建坝后 建坝前二、非选择题:40.(26分)中国是贸易大国,政府高度重视出口商品生产的碳排放问题。
2011年普通高等学校招生全国统一考试(广东卷)——理科综合

2 .最近 , 5 可以抵抗多数抗 生素的“ 超级细菌 ” 引人 关注 , 这类细菌含有超强耐药性 基因 N M一 , D 1该基 因编码金属 B 内 一
酰胺酶 , 此菌耐药性产生 的原 因是( )
A 定 向突变 .
第2 7卷第 9期
2 1 0 1经
中学 生物 学
Mide S h o oo y d l c o lBilg
V0 .7 No 9 1 . 2 2 1 0 1
文 件编 号 : 0 3—7 8 (0 10 10 5 6 2 1 )9—0 4 0 4—0 3
2 年普通高等学校招生全国统一考试( 0 1 1 广东卷)
(
2. 4 小杨 同学将部分生物学知识归纳如下 , 中正确 的是 其
)
② ③
④
R R
R
荚膜 多 糖 DA N
D A 经 D A酶 处理 ) N ( N
R型 R型、 型 S
R型
A ①不能证明 s . 型菌的蛋 白质不是转化 因子
B ②说 明 s . 型菌 的荚膜多糖有酶活性
Ⅲ
8 9 1 0 ll
B .Ⅱ一 5是该病致病基因的携带 者
C .Ⅱ一 5和 I— 再生患病男孩 的概率为 1 16 / 2
D I 9与正常女性结婚 , .I一 I 建议生 女孩
二 、双项选择题
实验 组号 接种茵型 加入 S 菌物质 培 养皿 长茵情况 型 ① R 蛋白质 R型
^
…
…
…
…
一
…
』 …
f
…
…
…
2011年普通高等学校招生全国统一考试理综试题(广东卷)

绝密★启用前试卷类型:A 2011年普通高等学校招生全国统一考试(广东卷)理科综合本试卷共10页,41小题,满分300分。
考试用时150分钟。
注意事项:1.答题前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、单项选择题:本大题共16小题,每小题4分,共64分。
在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得4分,选错或不答的得0分。
1.小陈在观察成熟叶肉细胞的亚显微结构照片后得出如下结论,不正确...的是A、叶绿体和线粒体都有双层膜B、核糖体附着在高尔基体上C、内质网膜与核膜相连D、液泡是最大的细胞器2、艾弗里和同事用R型和S型肺炎双球菌进行实验,结果如下表。
从表可知实验组号接种菌型加入S型菌物质培养皿长菌情况①R 蛋白质R型②R 荚膜多糖R型③R DNA R型、S型④R DNA(经DNA酶处理)R型A.①不能证明S型菌的蛋白质不是转化因子B.②说明S型菌的荚膜多糖有酶活性C.③和④说明S型菌的DNA是转化因子D.①~④说明DNA是主要的遗传物质3.华南虎是国家一级保护动物,可采用试管动物技术进行人工繁殖,该技术包括的环节有①转基因②核移植③体外受精④体细胞克隆⑤胚胎移植A. ①③B. ①④C. ②⑤D. ③⑤4.短跑运动员听到发令枪声后迅速起跑,下列叙述正确的是A.起跑动作的产生是非条件反射的结果B.调节起跑动作的神经中枢是听觉中枢C.该反射有多个中间神经元先后兴奋D.起跑反应的快慢取决于小脑兴奋的程度5.以下关于猪血红蛋白提纯的描述,不正确...的是A.洗涤红细胞时,使用生理盐水可防止红细胞破裂B.猪成熟红细胞中缺少细胞器和细胞核,提纯时杂蛋白较少C.血红蛋白的颜色可用于凝胶色谱法分离过程的监测D.在凝胶色谱法分离过程中,血红蛋白比分子量较小的杂蛋白移动慢6.某班同学对一种单基因遗传病进行调查,绘制并分析了其中一个家系的系谱图(如图1).下列说法正确的是A.该病为常染色体显性遗传病B.II-5是该病致病基因的携带者C. II-5与 II-6再生患病男孩的概率为1/2D.III-9与正常女性结婚,建议生女孩7. 下列说法正确的是A.纤维素和淀粉遇碘水均显蓝色B.蛋白质、乙酸和葡萄糖均属电解质C.溴乙烷与NaOH乙醇溶液共热生成乙烯D.乙酸乙酯和食用植物油均可水解生成乙醇8. 能在水溶液中大量共存的一组离子是A. H+、I―、NO3―、SiO32-B. Ag+、Fe3+、Cl―、SO42―C.K+、SO42-、Cu2+、NO3―D.NH4+、OH-、Cl-、HCO3-9.设n A为阿伏伽德罗常数的数值,下列说法正确的是A、常温下,23g NO2含有n A个氧原子B、1L0.1mol•L-1的氨水含有0.1n A个OH―C、常温常压下,22.4LCCl4含有个n A个CCl4分子D、1molFe2+ 与足量的H2O2溶液反应,转移2n A个电子10、某同学通过系列实验探究Mg及其化合物的性质,操作正确且能达到目的的是A、将水加入浓硫酸中得到稀硫酸,置镁片于其中探究讨Mg的活泼性B、将NaOH溶液缓慢滴入MgSO4溶液中,观察Mg(OH)2沉淀的生成C、将Mg(OH)2浊液直接倒入已装好滤纸的漏斗中过滤,洗涤并收集沉淀D、将Mg(OH)2沉淀转入蒸发皿中,加足量稀盐酸,加热蒸干得无水MgCl2固体11、对于0.1mol•L-1 Na2SO3溶液,正确的是A、升高温度,溶液的pH降低B、c(Na+)=2c(SO32―)+ c(HSO3―)+ c(H2SO3)C、c(Na+)+c(H+)=2 c(SO32―)+ 2c(HSO3―)+ c(OH―)D、加入少量NaOH固体,c(SO32―)与c(Na+)均增大12、某小组为研究电化学原理,设计如图2装置。
2011广东高考英语试题及答案解析完整版

2011年普通高等学校招生全国统一考试(广东卷)英语Ⅰ. 语言知识及应用(共两节,满分35分)第一节完形填空(共15小题;每小题2分,满分30分)阅读下面短文,掌握其大意,然后从1~15各题所给的A、B、C和D项中,选出最佳选项,并在答题卡上将该项涂黑。
It has been argued by some that gifted children should be grouped in special classes。
The 1 has been on the belief that in regular classes these children are held back in their intellectual (智力的) growth by 2 situation that has designed for the 3 children.There can be little doubt that 4 classes can help the gifted children to graduate earlier and take their place in life sooner. However, to take these 5 out of the regular classes may create serious problems.I observed a number of 6 children who were taken out of a special class and placed ina 7 class. In the special class, they showed little ability to use their own judgment, relying8 on their teachers’ directions. In the regular class, having no worry about keeping up, they began to reflect 9 on many problems, some of which were not on the school program.Many are concerned that gifted children become 10 and lose interest in learning. However this 11 is more often from parents and teachers than from students, and some of these 12 simply conclude that special classes should be set up for those who are 13 . Some top students do feel bored in class, but why they 14 so goes far beyond the work they have in school. Studies have shown that to be bored is to be anxious. The gifted child who is bored is an 15 child.1. A. principle B. theory C. arguments D. classification2. A. designing B. grouping C. learning D. living3. A. smart B. curious C. mature D. average4. A. regular B. special C. small D. creative5. A. children B. programs C. graduates D. designs6. A. intelligent B. competent C. ordinary D. independent7. A. separate B. regular C. new D. boring8. A. specially B. slightly C. wrongly D. heavily9. A, directly B. cleverly C. voluntarily D. quickly10. A. doubted B. bored C. worried D. tired11. A. concern B. conclusion C. reflection D. interest12. A. students B. adults C. scholars D. teachers13. A. talented B. worried C. learned D. interested14. A. believe B. think C. say D. feel15. A. outstanding B. intelligent C. anxious D. ordinary第二节语法填空(共10小题;每小题1.5分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空,并将答案填写在答题卡标号为16~25的相应位置上。
2011年高考理科综合(广东卷)-物理试题 word 解析版

2011年普通高等学校招生全国统一考试(广东卷)理科综合能力测试-物理试题一、单项选择题:本大题共4小题,每小题4分,共16分。
在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得4分,选错或不答的得0分13.(2011广东理综·13)如图3所示,两个接触面平滑的铅柱压紧后悬挂起来,下面的铅柱不脱落,主要原因是A.铅分子做无规则热运动B.铅柱受到大气压力作用C.铅柱间存在万有引力作用D.铅柱间存在分子引力作用【答案】D【解析】考查分子力、大气压力、万有引力之间的区别。
选D14.(2011广东理综·14)图4为某种椅子与其升降部分的结构示意图,M、N两筒间密闭了一定质量的气体,M可沿N的内壁上下滑动,设筒内气体不与外界发生热交换,在M向下滑动的过程中A.外界对气体做功,气体内能增大B.外界对气体做功,气体内能减小C.气体对外界做功,气体内能增大D.气体对外界做功,气体内能减小【答案】A【解析】由热力学第二定律△U=Q+W,Q=0,W>0,△U>0.选A15. (2011广东理综·15)将闭合多匝线圈置于仅随时间变化的磁场中,线圈平面与磁场方向垂直,关于线圈中产生的感应电动势和感应电流,下列表述正确的是 A.感应电动势的大小与线圈的匝数无关 B.穿过线圈的磁通量越大,感应电动势越大 C.穿过线圈的磁通量变化越快,感应电动势越大 D.感应电流产生的磁场方向与原磁场方向始终相同 【答案】C 【解析】由E =tBNS t N ∆∆=∆∆φ,AB 错,C 正确。
B 原与B 感的方向可相同亦可相反。
D 错。
选C16. (2011广东理综·16)如图5所示的水平面上,橡皮绳一端固定,另一端连接两根弹簧,连接点P 在F 1、F 2和F 3三力作用下保持静止。
下列判断正确的是 A.F 1>F 2>F 3 B.F 3>F 1>F 2 C.F 2>F 3>F 1 D.F 3>F 2>F 1【答案】B【解析】由力的平行四边形法则及三角形知识得B 正确。
2011年广东高考数学理科试卷(带详解)

2011年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数z 满足(1i)2z +=,其中i 为虚数单位,则z = ( ) A . 1i + B . 1i - C . 22i + D . 22i - 【测量目标】复数代数形式的四则运算.【考查方式】给出复数的等式形式,变形为分数形式再通分化简即可求其代数形式. 【难易程度】容易 【参考答案】B【试题解析】∵(1i)2z +=,∴22(1i)1i 1i (1i)(1i)z -===-++-. 2. 已知集合{(,)|,A x y x y =为实数,且221}x y +=,{(,)|,B x y x y =为实数,且}y x =,则A B 的元素个数为 ( )A . 0B . 1C . 2D . 3 【测量目标】集合的交集运算(描述法).【考查方式】给出一个一元二次方程和一个二元二次方程,联立求出解,进而得出交集元素. 【难易程度】容易 【参考答案】C【试题解析】联立两集合的函数解析式得:221x y y x⎧+=⎨=⎩⇒221x =,解得22x =±,分别把22x =±代入y x =,解得22y =±, 所以两函数的交点有两个,坐标分别为22(,)22和22(,)22--,则A B 的元素个数为2个. 3.若向量,a b,c 满足a b ∥且⊥a c ,则(2)c a +b= ( ) A . 4 B . 3 C . 2 D . 0 【测量目标】平面向量的数量积运算.【考查方式】给出向量间垂直或平行的关系,进而求出向量积. 【难易程度】容易【参考答案】D【试题解析】∵a b ∥且⊥a c ,∴(2)20=c a +b c a +c b =. 4.设函数()f x 和()g x 分别是R 上的奇函数和偶函数,则下列结论成立的是 ( )A . ()()f x g x +是偶函数B . ()()f x g x -是奇函数C . ()()f x g x +是偶函数D . ()()f x g x -是奇函数 【测量目标】函数奇偶性的判断.【考查方式】由奇函数和偶函数的特性,考查加上绝对值符号后奇偶性的变化关系. 【难易程度】容易 【参考答案】A【试题解析】∵()g x 是R 上的奇函数,∴ )(x g 是R 上的偶函数,从而()()f x g x +是偶函数,故选A.5. 已知平面直角坐标系xOy 上的区域D 由不等式组0222x y x y⎧⎪⎨⎪⎩剟……给定,若(),M x y 为D 上的动点,点A 的坐标为(2,1),则z OM OA =的最大值为 ( )A .3B .4C .32D .42【测量目标】二元线性规划求目标函数的最值,向量的数量积运算.【考查方式】利用向量积构造出目标函数,由不等式组画出可行域,进而求出其最值. 【难易程度】中等 【参考答案】B【试题解析】作出可行域如图所示(步骤1)∵2z OM OA x y ==+,∴当直线02=+y x 平移到)2,2(M 时,z 取到最大值4.(步骤2)6.甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军. 若两队胜每局的概率相同,则甲队获得冠军的概率为 ( )第5题图A .12 B .35 C .23 D .34【测量目标】随机事件与概率.【考查方式】给出两人获胜概率相等的条件,根据条件求出其中某人获胜的概率. 【难易程度】容易 【参考答案】D 【试题解析】43212121=⨯+=P . 7.如图,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为 ( )A .63B .93C .123D .183 【测量目标】由三视图求几何体(棱柱)的体积.【考查方式】给出几何体的三视图,推测出几何体的形状,进而由线段关系得出体积. 【难易程度】中等 【参考答案】B【试题解析】由三视图可推测该几何体为四棱柱.(步骤1)高为31222=-=h ,底面面积为933=⨯=s ,∴39==sh V .(步骤2)8.设S 是整数集Z 的非空子集,如果,a b S ∀∈,有a b S ∈,则称S 关于数的乘法是封闭的.若,T V 是Z 的两个不相交的非空子集, T V =Z ,且,,a b c T ∀∈,有abc T ∈;,,x y z V ∀∈,有xyz V ∈,则下列结论恒成立的是 ( )第7题图A .,T V 中至少有一个关于乘法是封闭的B . ,T V 中至多有一个关于乘法是封闭的C . ,T V 中有且只有一个关于乘法是封闭的D . ,T V 中每一个关于乘法都是封闭的 【测量目标】集合间的关系.【考查方式】给出集合的特殊关系,利用特殊值法或假设法判断对应的选项. 【难易程度】较难 【参考答案】A【试题解析】 当{=T 奇数},V {=偶数},T ,V 关于乘法都是封闭的,故B,C 错误;(步骤1) ∵T V =Z ,∴整数1一定在T ,V 两个集合中的一个中,不妨设T ∈1,则T b a ∈,,(步骤2)∵T b a ∈1,,,∴ 1a b T ∈,即 a b T ∈ ,∴T 对乘法封闭,即V T ,中至少有一个关于乘法是封闭的;(步骤3)当{=T 非负整数},V {=负整数},T 关于乘法封闭,而V 关于乘法不封闭,故D 错误.(步骤4) 二、填空题:本大题共7小题.考生作答6小题.每小题5分,满分30分. (一)必做题(9~13题)9.不等式130x x +--…的解集是 . 【测量目标】解绝对值不等式.【考查方式】给出绝对值不等式,利用平方去绝对值符号,再进行求解. 【难易程度】容易 【参考答案】),1[+∞【试题解析】∵13x x +-…,∴22(1)(3)x x +-…,解得1x …. 10.7)2(xx x -的展开式中4x 的系数是 (用数字作答). 【测量目标】二项式定理.【考查方式】由二项式展开式的通项公式得出所求系数的通项,再根据所给乘积关系求出所满足项的系数. 【难易程度】中等 【参考答案】84【试题解析】所求的4x 的系数就是7)2(xx -展开式中3x 的系数,(步骤1) ∵7)2(xx -的通项为772177C (2)(2)C r r r r r r r r T x x x ---+=-=-,(步骤2) ∴令327=-r ,解得2=r . ∴令4x 的系数是227(2)C 84-=.(步骤3)11.等差数列{}n a 的前9项和等于前4项和,若0,141=+=a a a k ,则=k . 【测量目标】等差数列的通项.【考查方式】给出等差数列的通项所满足的关系和首项的值,由此求出等式中的对应参数. 【难易程度】中等 【参考答案】10【试题解析】∵}{n a 的前9项和等于前4项和,且11=a ,∴d d 23442899⨯+=⨯+,解得61-=d .(步骤1)∴06223)1(114=+-=++-+=+k d a d k a a a k ,解得10=k .(步骤2) 12.函数13)(23+-=x x x f 在=x 处取得极小值. 【测量目标】利用导数求函数的极值.【考查方式】给出函数的解析式,利用导数求出单调区间和极值点,进而判断得出极小值. 【难易程度】容易 【参考答案】2【试题解析】∵()f x ')2(3632-=-=x x x x ,(步骤1)∴)2,0(∈x 时,()0f x '<;),2(+∞∈x 时,()0f x '>;(步骤2) ∴13)(23+-=x x x f 在2=x 处取得极小值.(步骤3)13.某数学老师身高176cm ,他爷爷,父亲,儿子的身高分别是173cm,170cm 和182cm ,因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高是 cm . 【测量目标】线性回归方程.【考查方式】由所给数据求出直线回归方程,进而求出对应的数值. 【难易程度】中等 【参考答案】185【试题解析】根据题中所提供的信息,可知父亲和儿子的对应数据可列表如下:∵176,173==y x ,∴3132221()()361(3)3()iii ii x x y y b x x ==--⨯===-+-∑∑, 父亲的身高(x ) 173 170 176 儿子的身高(y )1701761821761733a y bx =-=-=, ∴回归直线方程为3+=x y ,(步骤1) ∴预测他孙子的身高是182+3=185cm .(步骤2) (二)选做题(14、15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)已知两曲线参数方程分别为5cos (0π)sin x y θθθ⎧=⎪<⎨=⎪⎩…和⎪⎩⎪⎨⎧==ty t x 245()t ∈R ,它们的交点坐标为.【测量目标】坐标系与参数方程.【考查方式】给出曲线的参数方程形式,转化为普通方程,联立求出交点坐标. 【难易程度】中等 【参考答案】)552,1( 【试题解析】两曲线的方程分别为1522=+y x 和x y 542=,(步骤1) 由05454152222=-+⇒⎪⎪⎩⎪⎪⎨⎧==+x x x y y x ,∴1=x 或5-=x (舍去),∴⎪⎩⎪⎨⎧±==5521y x .(步骤2) ∵sin (0π)y θθ=<…,∴]1,0[∈y ,∴⎪⎩⎪⎨⎧==5521y x (步骤3).15.(几何证明选讲选做题)如图,过圆O 外一点P 分别做圆的切线和割线交圆于A 、B 两点,且7=PB ,C 是圆上一点使得5=BC ,APB BAC ∠=∠,则=AB .第15题图【测量目标】圆的性质与应用.【考查方式】结合三角形和圆的位置关系,利用三角形相似得出比例关系,进而求出对应线段长度. 【难易程度】中等 【参考答案】35【试题解析】∵APB BAC ∠=∠,BCA PAB ∠=∠,∴BAP △∽BCA △,(步骤1)∴ABBCPB AB =,∴35AB PB BC == . (步骤2) 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数1π()2sin(),36f x x x =-∈R .(1)求5π()4f 的值; (2)设π,[0,]2αβ∈,π10(3)213f α+=,6(32π)5f β+=,求cos()αβ+的值.【测量目标】三角函数的图象及其变换,同角三角函数的基本关系,两角和的余弦.【考查方式】给出三角函数的解析式,直接求其对应未知数的函数值;由解析式满足的关系,利用诱导公式和同角三角函数的基本关系变形化简得出余弦值和正弦值,再求出对应的三角函数值. 【难易程度】中等 【试题解析】(1)5π15πππ()2sin()2sin 243464f =⨯-==. (2)∵π1ππ10(3)2sin[(3)]2sin 232613f ααα+=⨯+-==,∴5sin 13α=.(步骤1)∵π6(32π)2sin()2cos 25f βββ+=+==,∴3cos 5β=.(步骤2)∵π,[0,]2αβ∈,∴124cos ,sin 135αβ==.(步骤3)∴16cos()cos cos sin sin 65αβαβαβ+=-=.(步骤4)17.(本小题满分13分)为了解甲,乙两厂的产品质量,采取分层抽样的方法从甲,乙两厂的产品中分别抽取14件和5件,测量产品中微量元素y x ,的含量(单位:毫克).下表是乙厂的5件产品的测量数据:编号1 2 3 4 5 x169 178 166 175 180 y7580777081(1) 已知甲厂生产的产品共有98件,求乙厂生产的产品数量;(2) 当产品中微量元素y x ,满足175x …且75y …时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;(3) 从乙厂抽出的上述5件产品中,随即抽取2件,求抽出的2件产品中优等品数ξ的分布列及其均值(即数学期望).【测量目标】分层抽样,分布列与期望.【考查方式】利用样本和总体的比例关系求出某层的样本容量;由给定条件得出概率进而求出满足的样本容量;直接利用给定条件画出分布列得出离散型随机变量的期望. 【难易程度】中等【试题解析】(1)设乙厂生产的产品数量为m 件,则14985m=,解得35=m . 答:乙厂生产的产品数量为35件.(步骤1)(2)∵产品中微量元素y x ,满足175x …且75y …时的概率为52,(步骤2) ∴用上述样本数据估计乙厂生产的优等品的数量为143552=⨯.(步骤3) (3)∵ξ的可能值为0,1,2,则 2223()C ()()55iiiP i ξ-==, 0,1,2i =.(步骤4)ξ的分布列为∴ξ的数学期望为54522)(=⨯=ξE .(步骤5) 18.(本小题满分13分)如图,在锥体P ABCD -中,A B C D 是边长为1的菱形,且60DAB ∠= ,2PA PD ==,2PB E F =,,分别是BC PC ,的中点.(1) 证明:AD ⊥平面DEF ; (2) 求二面角B AD P --的平面角.第18题图【测量目标】线面垂直和线面平行的判定与线面角的求法. 【考查方式】线线垂直⇒线面垂直,由对应线段关系利用余弦定理求出线面角. 【难易程度】较难【试题解析】(1)设AD 中点为H ,连接BH PH ,,X 012P9251225425,,PA PD PH AD =∴⊥ 1,1,60,2AH AB DAB ==∠= 可得出3,2BH =(步骤1)从而222,,AH BH AB AH HB +=∴⊥即,AD HB ⊥AD ∴⊥平面,PHB (步骤2)又,E F 分别是,BC PC 的中点,,EF PB EF ∴∴∥∥平面,PHB 又显然,BH DE DE ∴∥∥平面,PHB 又,DE EF ⊂平面,,DEF DE EF E = ∴平面DEF ∥平面,PHB (步骤3) AD ⊥ 平面,PHB AD ∴⊥平面.DEF (步骤4)(2)由(1)知,,,PH AD BH AD ⊥⊥且PH ⊂平面,PAD BH ⊂平面,BAD PHB ∴∠就是二面角P AD B --的平面角,(步骤5)22173(2)(),,2,222PH BH PB =-===(步骤6)2227334321442cos ,277321212222PH BH PB PHB PH BH +--+-∴∠====-=-⨯⨯即二面角P AD B --的余弦值为21.7-(步骤7)第18题图19.(本小题满分14分)设圆C 与两圆22(5)4x y ++=,22(5)4x y -+=中的一个内切,另一个外切. (1) 求圆C 的圆心轨迹L 的方程; (2) 已知点M (553,554),)0,5(F ,且P 为L 上的动点,求FP MP -的最大值及此时点P 的坐标.【测量目标】圆与圆的位置关系,双曲线的标准方程,直线与双曲线的位置关系和圆锥曲线的综合应用. 【考查方式】给出曲线与两圆之间的位置关系,利用圆心距求出曲线的轨迹方程;根据双曲线上动点与定点的线段关系,联立直线方程与曲线方程求出交点,进而得出取最值时的点坐标. 【难易程度】较难【试题解析】(1)设两圆22(5)4x y ++=,22(5)4x y -+=的圆心分别为21,O O ,半径为r , 则r CO CO 221=-, ∴点C 轨迹L 为双曲线,其中1,2,5===b a c ,(步骤1)∴圆C 的圆心轨迹L 的方程为1422=-y x .(步骤2) (2)直线MF 的方程为)5(2)5(5553554--=--=x x y ,(步骤3) 由⎪⎪⎩⎪⎪⎨⎧==⇒⎪⎩⎪⎨⎧--==-155215514)5(21422y x x y y x 或⎪⎪⎩⎪⎪⎨⎧-==552556y x .设)552,556(),1552,15514(-Q E , ∴当点P 在点Q处时,满足2MP FPMF -==.(步骤4)20.(本小题满分14分)设0>b ,数列}{n a 满足b a =1,11(2)22n n n nba a n a n --=+-….(1)求数列}{n a 的通项公式;(2)证明:对于一切正整数n ,1112n n n ba +++….【测量目标】已知递推关系求通项,不等式恒成立问题.【考查方式】由递推关系化简变形求出最简式,再利用配凑法或书数学归纳法求出其通项;利用并项求合法、放缩法以及均值不等式得出不等式恒成立的关系. 【难易程度】较难【试题解析】(1)由1122n n n nba a a n --=+-得1211n n n n a b a b--=+ ,当2b =时, 1112n n n n a a ---=, 所以{}n n a 是以首项为1112a =,公差为12的等差数列,所以11(1)222n n nn a =+-= ,从而2n a =.(步骤1)当2b ≠时, 11211()22n n n n a b b a b --+=+--,所以1{}2n n a b +-是首项为11122(2)a b b b +=--,公比为2b 的等比数列,所以11222()2(2)(2)nn n n n a b b b b b b -+==--- ,从而(2)2n n n n nb b a b -=-. 综上所述,数列{}n a 的通项公式为2,2(2),22n n n n b a nb b b b=⎧⎪=⎨-≠⎪-⎩(步骤2) (Ⅱ)当2b =时,不等式显然成立;当2b ≠时,要证1112n n n b a +++…,只需证11(2)122n n n n n nb b b b ++-+-…,即证11122(2)2n n n n n n b n b b b +++-+- …(*) 因为1111122312(2)(2)(222)2n nn n n n n n n n b b b b b b b ++++-----+=+++++- (步骤3) 1122222111(222)(22)n n n n n n n n n b b b b b +-+---+=+++++++ 1112121222[()()]222n n n n nn n n b b b b b b b --++=+++++++ 21122311222[()()()]222n nn n n n b b b b b b b -++=++++++ 2111122311222(222)2(111)2222n nn nn n n n n n b b b b b n b b b b -+++++++=+++= …(步骤4) 所以不等式(*)成立,从而原不等式成立;综上所述,当0b >时,对于一切正整数n ,11 1.2n n n b a +++…(步骤5) 21.(本小题满分14分)在平面直角坐标系xOy 上,给定抛物线21:4L y x =,实数,p q 满足240p q -…,12,x x 是方程20x px q -+=的两根,记12(,)max{||,||}p q x x ϕ=.(1) 过点20001(,)(0)4A p p p ≠作L 的切线交y 轴于点B .证明:对线段AB 上的任一点(,)Q p q ,有0||(,)2p p q ϕ=; (2) 设(,)M a b 是定点,其中,a b 满足240,0a b a ->≠.过(,)M a b 作L 的两条切线12,l l ,切点分别为22112211(,),(,)44E p p E p p ',12,l l 与y 轴分别交于,F F '.线段EF 上异于两端点的点集记为X , 证明:112||(,)||||(,)2p M a b X p p a b ϕ∈⇔>⇔=; (3) 设215{(,)|1,(1)}44D x y y x y x =-+-剠,当点(,)p q 取遍D 时,求(,)p q ϕ的最小值(记为min ϕ)和最大值(记为max ϕ).【测量目标】抛物线与直线的位置关系,导数在实际问题中的应用,不等式的大小比较.【考查方式】应用导数建立直线方程,求出抛物线上点与线段的对应关系,得出证明;利用切线方程的关系,得出不等式的推导关系;在所给范围内代入函数解析式求出对应的最值.【难易程度】较难【试题解析】(1)00011|()|22AB x p x p k y x p =='===, 直线AB 的方程为200011()42y p p x p -=-,即2001124y p x p =-,(步骤1) 2001124q p p p ∴=-,方程20x px q -+=的判别式2204()p q p p ∆=-=-, 两根001,2||22p p p p x ±-==或02p p -,(步骤2) 00p p …,00||||||||22p p p p ∴-=-,又00||||p p 剟, 000||||||||222p p p p ∴--剟,得000||||||||||222p p p p p ∴-=-…,(步骤3) 0(,)||2p p q ϕ∴=.(步骤4) (2)由240a b ->知点(,)M a b 在抛物线L 的下方,(步骤5)①当0,0a b >…时,作图可知,若(,)M a b X ∈,则120p p >…,得12||||p p >; 若12||||p p >,显然有点(,)M a b X ∈; (,)M a b X ∴∈12||||p p ⇔>.(步骤6) ②当0,0a b ><时,点(,)M a b 在第二象限,作图可知,若(,)M a b X ∈,则120p p >>,且12||||p p >; 若12||||p p >,显然有点(,)M a b X ∈;(,)M a b X ∴∈12||||p p ⇔>.(步骤7)根据曲线的对称性可知,当0a <时,(,)M a b X ∈12||||p p ⇔>, 综上所述,(,)M a b X ∈12||||p p ⇔>(*);(步骤8) 由(1)知点M 在直线EF 上,方程20x ax b -+=的两根11,22p x =或12p a -, 同理点M 在直线E F ''上,方程20x ax b -+=的两根21,22p x =或22p a -,(步骤9) 若1(,)||2p a b ϕ=,则1||2p 不比1||2p a -、2||2p 、2||2p a -小, 12||||p p ∴>,又12||||p p >(,)M a b X ⇒∈, 1(,)||2p a b ϕ∴=⇒(,)M a b X ∈;又由(1)知,(,)M a b X ∈1(,)||2p a b ϕ⇒=; 1(,)||2p a b ϕ∴=⇔(,)M a b X ∈,综合(*)式,得证.(步骤10) (3)联立1y x =-,215(1)44y x =+-得交点(0,1),(2,1)-,可知02p 剟,(步骤11)过点(,)p q 作抛物线L 的切线,设切点为2001(,)4x x ,则20001142x q x x p -=-,得200240x px q -+=,解得204x p p q =+-,(步骤12) 又215(1)44q p +-…,即2442p q p --…, 042x p p ∴+-…,设42p t -=,20122x t t ∴-++…215(1)22t =--+,(步骤13) 0max max ||2x ϕ= ,又052x …,max 54ϕ∴=;(步骤14) 1q p - …,2044|2|2x p p p p p ∴+-+=+-=…, 0min min ||12x ϕ∴==.(步骤15)。
2011年广东理解析
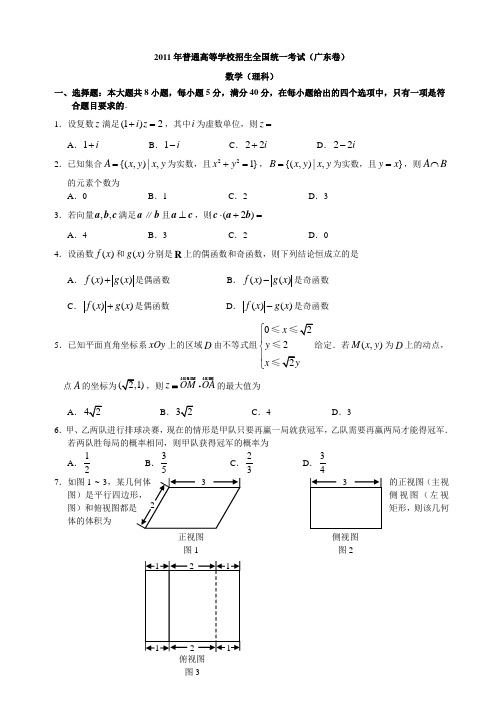
正视图 图1 侧视图 图2俯视图 图32011年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设复数z 满足(1)2i z +=,其中i 为虚数单位,则z =A .1i +B .1i -C .22i +D .22i -2.已知集合{(,)|,A x y x y =为实数,且221}x y +=,{(,)|,B x y x y =为实数,且}y x =,则A B⋂的元素个数为A .0B .1C .2D .3 3.若向量,,a b c 满足a ∥b 且⊥a c ,则(2)⋅+=c a bA .4B .3C .2D .0 4.设函数()f x 和()g x 分别是R 上的偶函数和奇函数,则下列结论恒成立的是A .()()f x g x +是偶函数B .()()f x g x -是奇函数C .()()f x g x +是偶函数D .()()fx g x -是奇函数5.已知平面直角坐标系xOy 上的区域D 由不等式组02x y x ⎧⎪⎨⎪⎩≤≤≤≤给定.若(,)M x y 为D 上的动点,点A 的坐标为,则z OM OA=⋅的最大值为A. B . C .4 D .36.甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军.若两队胜每局的概率相同,则甲队获得冠军的概率为A .12B .35C .23D .347.如图1 ~ 3的正视图(主视侧视图(左视矩形,则该几何体的体积为图4COPBAA .B .C .D .8.设S 是整数集Z 的非空子集,如果,a b S ∀∈,有ab S ∈,则称S 关于数的乘法是封闭的.若,T V 是Z 的两个不相交的非空子集,T V Z ⋃=,且,,a b c T ∀∈,有abc T ∈;,,x y z V ∀∈,有xyz V ∈,则下列结论恒成立的是A .,T V 中至少有一个关于乘法是封闭的B .,T V 中至多有一个关于乘法是封闭的C .,T V 中有且只有一个关于乘法是封闭的D .,T V 中每一个关于乘法都是封闭的 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9 ~ 13题)9.不等式13x x +--≥0的解集是 . 10.72()x x x-的展开式中,4x 的系数是 (用数字作答)11.等差数列{}n a 前9项的和等于前4项的和.若11a =,40k a a +=,则k = . 12.函数32()31f x x x =-+在x = 处取得极小值.13.某数学老师身高176cm ,他爷爷、父亲和儿子的身高分别是173cm 、170cm 和182cm .因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为 cm . 14.(坐标系与参数方程选做题)已知两曲线参数方程分别为sin x y θθ⎧=⎪⎨=⎪⎩(0)θπ<≤和254x t y t ⎧=⎪⎨⎪=⎩(t ∈)R ,它们的交点坐标为___________.15.(几何证明选讲选做题)如图4,过圆O 外一点P 分别作 圆的切线和割线交圆于,A B ,且7P B =,C 是圆上一点使得5B C =,BAC APB ∠=∠,则A B =___________.图5CDPBAEF三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数1()2sin()36f x x π=-,x ∈R .(1)求5()4f π的值;(2)设,0,2παβ⎡⎤∈⎢⎥⎣⎦,10(3)213f πα+=,6(32)5f βπ+=,求cos()αβ+的值.17.(本小题满分13分)为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中微量元素,x y 的含量(单位:毫克).下表是乙厂的5件产品的测量数据:(1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量;(2)当产品中的微量元素,x y 满足175x ≥且75y ≥时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列及其均值(即数学期望).18.(本小题满分13分)如图5,在锥体P A BC D -中,A B C D 是边长为1的 菱形,且60DAB ∠=,PA PD ==2PB =,,E F分别是B C ,PC 的中点.(1)证明:AD ⊥平面DE F ; (2)求二面角P AD B --的余弦值. 19.(本小题满分14分)设圆C 与两圆22(4x y ++=,22(4x y -+=中的一个内切,另一个外切.(1)求C 的圆心轨迹L 的方程; (2)已知点55M ,0)F ,且P 为L 上动点,求M P FP - 的最大值及此时点P的坐标.20.(本小题满分14分)设0b >,数列{}n a 满足1a b =,1122n n n nba a a n --=+-(2)n ≥.(1)求数列{}n a 的通项公式;(2)证明:对于一切正整数n ,1112n n n b a ++≤+.21.(本小题满分14分)在平面直角坐标系xOy 上,给定抛物线L :214y x =.实数,p q 满足24p q -≥0,12,x x 是方程20x px q -+=的两根,记12(,)max{,}p q x x ϕ=.(1)过点2001(,)4A p p 0(0)p ≠作L 的切线交y 轴于点B .证明:对线段A B 上的任一点(,)Q p q ,有0(,)2p p q ϕ=;(2)设(,)M a b 是定点,其中,a b 满足240a b ->,0a ≠.过(,)M a b 作L 的两条切线12,l l ,切点分别为2111(,)4E p p ,2221(,)4E p p ',12,l l 与y 轴分别交于,F F '.线段E F 上异于两端点的点集记为X .证明:112(,)(,)2p M a b X p p a b ϕ∈⇔>⇔=;(3)设{(,)|D x y y =≤1x -,y ≥215(1)}44x +-.当点(,)p q 取遍D 时,求(,)p q ϕ的最小值 (记为m in ϕ)和最大值(记为max ϕ)参考答案 1.(B ).22(1)11(1)(1)i z i ii i -===-++-2.(C ).A B ⋂的元素个数等价于圆221x y +=与直线y x =的交点个数,显然有2个交点 3.(D ).依题意得⊥c a ,⊥c b ,则(2)20⋅+=⋅+⋅=c a b c a c b4.(A ).由()f x 是偶函数、()g x 是奇函数,得()f x 和()g x 都是偶函数,所以()()f x g x +与()()f x g x -都是偶函数,()()f x g x +与()()f x g x -的奇偶性不能确定5.(C ).z y =+,即y z =-+,画出不等式组表示的平面区域,易知当直线y z =+经过点2)时,z取得最大值,max 24z ==6.(D ).乙获得冠军的概率为111224⨯=,则甲队获得冠军的概率为13144-=7.(B ).该几何体是一个底面为平行四边形,高为3,则33V Sh ==⨯=8.(A ).若T 为奇数集,V 为偶数集,满足题意,此时T 与V 关于乘法都是封闭的,排除B 、C 若T 为负整数集,V 为非负整数集,也满足题意,此时只有V 关于乘法是封闭的,排除D 9.[1,)+∞.解析:13x x +--≥0 ⇒1x +≥3x -⇒2(1)x +≥2(3)x -⇒x ≥1 10.84.解析:72()x x x-的通项7821772()(2)r rr r r rr T x C x C xx--+=-=-,由824r -=得2r =,则227(2)84C -=11.10.方法1:由94S S =得93646d d +=+,求得16d =-,则4111(1)()13()066k a a k +=+-⨯-++⨯-=,解得10k =方法2:由94S S =得567890a a a a a ++++=,即750a =,70a =,即104720a a a +==,即10k =12.2.解析:2()363(2)f x x x x x '=-=-,令()0f x '=得0x =或2x =,显然当0x <时()0f x '>;当02x <<时()0f x '<;当2x >时()0f x '>,函数32()31f x x x =-+在2x =处取得极小值 13.185.设父亲的身高为x cm ,儿子的身高为y cm ,则根据上述数据可得到如下表格:上表中的最后一组(182,?)是预测数据,173,176x y ==12221()()00361033()nii i ni i xx yy bx x ==--++⨯===++-∑∑, 3ay b x =-= 线性回归方程 3y x =+,所以当182x =时,185y =,即他孙子的预测身高为185 cm . 14.(1,5.sin x y θθ⎧=⎪⎨=⎪⎩表示椭圆2215x y +=(01)x y <≤≤≤,254x t y t⎧=⎪⎨⎪=⎩表示抛物线245y x =22221(01)5450145x y x y x x x y x ⎧+=<≤≤≤⎪⎪⇒+-=⇒=⎨⎪=⎪⎩或5x =-(舍去), 又因为01y ≤≤,所以它们的交点坐标为(1,515P A B A C B ∠=∠,又B A C A P B ∠=∠,则△P A B ∽△AC B ,则P BA BA B B C=,235AB PB BC =⋅=,即AB =16.解:(1)515()2sin()2sin 43464f ππππ=⨯-==(2)110(3)2sin[(3)]2sin 232613f πππααα+=+-==,即5sin 13α= 16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=,即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦,∴12cos 13α==,4sin 5β==∴1235416cos()cos cos sin sin 13513565αβαβαβ+=-=⨯-⨯=17.解:(1)设乙厂生产的产品数量为a 件,则98145a =,解得35a =所以乙厂生产的产品数量为35件(2)从乙厂抽取的5件产品中,编号为2、5的产品是优等品,即5件产品中有2件是优等品由此可以估算出乙厂生产的优等品的数量为235145⨯=(件)(3)ξ可能的取值为0,1,223253(0),10C P C ξ===1123256(1),10C C P C ξ===22251(2),10C P C ξ===∴ξ的分布列为:CDPBAE FH∴3614012.1010105E ξ=⨯+⨯+⨯=18.(1)证明:取A D 的中点H ,连接,,PH BH BD∵PA PD =,∴AD PH ⊥∵在边长为1的菱形A B C D 中,60DAB ∠= ∴△ABD 是等边三角形∴AD H B ⊥,PH HB H = ∴AD ⊥平面PH B ∴AD PB ⊥∵,E F 分别是B C ,PC 的中点∴E F ∥P B ,H B ∥D E ∴AD D E ⊥,AD EF ⊥,DE EF E = ∴AD ⊥平面D E F(2)解:由(1)知PH AD ⊥,HB AD ⊥∴P H B ∠是二面角P AD B --的平面角,易求得22PH BH ==∴2227334cos 27222PH H B PBPH B PH HB+--+-∠====-⋅∴二面角P AD B--的余弦值为7-19.解:(1)设(0),0)F F ',圆C 的半径为r ,则(2)(2)4CF CF r r '-=+--=< ∴C 的圆心轨迹L 是以,F F '为焦点的双曲线,2a =,c =,1b =∴C 的圆心轨迹L 的方程为2214xy -=(2)2M P FP M F -≤== ∴M P FP - 如图所示,P 必在L 直线M F 的斜率2k =-:2M F y x =-+22142x y y x ⎧-=⎪⎨⎪=-+⎩215280x -+=,6)0--=,12155x x ==∵P x >5P x =5P y =-∴M P FP - 的最大值为2,此时P为55-20.(1)解:∵1122n n n nba a a n --=+-∴1122n n n a ba n a n --=+-∴1211nn n n a b a b --=⋅+ ① 当2b =时,1112nn n n a a ---=,则{}nn a 是以12为首项,12为公差的等差数列∴11(1)22nn n a =+-⨯,即2n a =② 当0b >且2b ≠时,11211()22nn n n a b b a b--+=+-- 当1n =时,122(2)nn a bb b +=--∴1{}2nn a b +-是以2(2)b b -为首项,2b为公比的等比数列∴112()22nnn a bb b +=⋅--∴212(2)2(2)nn nn nnn ba b b b b b -=-=---∴(2)2nn nnn b b a b-=-综上所述(2),02222nn n n n b b b b a b b ⎧->≠⎪=-⎨⎪=⎩ 且, (2)方法一:证明:① 当2b =时,11122n n n b a ++=+=;② 当0b >且2b ≠时,12212(2)(222)n n n n n n b b b bb -----=-++++1221222nnnn n n n n n ba b bb----⋅=≤=++++1112111111222222222n nn n n n n n n n bb b b+++----+++=====<=⋅1112n n b +++∴对于一切正整数n ,1112n n n b a ++≤+.方法二:证明:① 当2b =时,11122n n n b a ++=+=;② 当0b >且2b ≠时, 要证1112n n n b a ++≤+,只需证11(2)122nn nnn nb b b b++-≤+-,即证1(2)122nnn nn b b bb+-≤+-即证1221112222n n n n n nnb b b bb----+≤+++++即证122111()(222)2n n n n n nb b bbn b----++++++≥即证2112231122221()()2222n nn n nn nn b b bb n bbbb---+-+++++++++≥∵2112231122221()()2222n nn n nn nn b b bb bbbb---+-+++++++++2121232111222()()()()2222n n nn nn n nb b bb bbbb----+=++++++++n ≥+= ,∴原不等式成立∴对于一切正整数n ,1112n n n b a ++≤+.21.解:(1)2001(,)4A p p 是抛物线L 上的点,12y x '=,则切线的斜率012k p = 过点A 的抛物线L 的切线方程为A B :200011()42y p p x p -=-,即2001124y p x p =-∵(,)Q p q 在线段A B 上,∴2001124q p p p =-,∴22220001144()()24p q p p p p p p -=--=-≥0不妨设方程20x px q -+=的两根为12x =,22x =则012p p p x --=,022p p p x +-=① 当00p >时,00p p ≤≤,001222p p p x p -==-,022p x =∵00122p p x -<≤,∴12x x ≤,∴122(,)max{,}p q x x x ϕ==02p =② 当00p <时,00p p ≤≤,012p x =,002222p p p x p -==-∵00222p p x ≤<-,∴12x x ≥,∴121(,)max{,}p q x x x ϕ==02p =综上所述,对线段A B 上的任一点(,)Q p q ,有0(,)2p p q ϕ=(2)由(1)知抛物线L 在2001(,)4p p 处的切线方程为2001124y p x p =-,即200240p p x y -+=∵切线恒过点(,)M a b ,则200240p ap b -+=,∴1,2p a =±① 当0a >时,(,)M a b X ∈⇔10a p <<⇔1p a =+,2p a =-⇔12p p >② 当0a <时,(,)M a b X ∈⇔10p a <<⇔1p a =-2p a =+⇔12p p >综合①②可得(,)M a b X ∈⇔12p p >∵由(1)可知,若2111(,)4E p p ,点(,)M a b 在线段E F 上,有1(,)2p a b ϕ=∴(,)M a b X ∈⇒1(,)2p a b ϕ=③由(1)可知,方程20x a x b -+=的两根11,22p x =或12p a -,21,22p x =或22p a -若1(,)2p a b ϕ=,即112max{,}2p x x = 则1122p a p -≥、2122p p ≥、2122p a p -≥∴12p p >∴1(,)2p a b ϕ=⇒12||||p p >⇒(,)M a b X ∈ ④综合③④可得(,)M a b X ∈⇔1(,)2p a b ϕ=综上所述112(,)(,)2p M a b X p p a b ϕ∈⇔>⇔=;(3)由2115(1)44y x y x =-⎧⎪⎨=+-⎪⎩,求得两个交点(0,1),(2,1)-,则02p ≤≤, 过点(,)G p q 作抛物线L 的切线,设切点为N 2001(,)4x x ,切线与y 轴的交点为H由(2)知200240x px q -+=,解得0x p =±,①若0x p =+(,)G p q 在线段N H 上,由1y x ≤-,得1q p ≤-,∴022x p p p p =+≥+=+-=,∴0m min in )12(x ϕ==.由215(1)44y x ≥+-,得221511(1)14442q p p p ≥+-=+-∴2442p q p -≤-,∴0x p p =+≤+令t =,则2122p t =-+,02t ≤≤∴22011552(1)2222x t t t ≤-++=--+≤∴0max max 5)24(x ϕ==②若0x p =-,则点(,)G p q 在线段N H 的延长线上方程20x px q -+=的两根为012p p x x --=,022p p x x +-=即01,22x x =或02x p -∵0x p ≤∴00012(,)max{,}max{,}222x x x p q x x p p ϕ==-=-2p -==51(,)4p q ϕ≤≤综上所述m in 1ϕ=,m ax 54ϕ=。
2011年高考语文试题参考答案(全国卷)

四、文体选择:
写作要求里的“生活体验与认识”告诉考生,可以写成记叙文或者散文、议论文。
根据立意的要求,估计记叙文比例会比往年有增加,亲情、友情将是考生选择最多的题材。考生之中也有单亲家庭的,如果考生来自一个离异家庭,写作一段父母和合的故事,将是佳作。特别是写考生自己游走在父母之间,积极撮合,将是最大的亮点。记叙文要求考生注重细节描写和心理刻画,这是成功的要素。
(二)19.(1)夸张手法。突出了梁宗岱善于跑路,有强健的体格。
(2)比喻。形象生动地写出了梁宗岱擅长且喜欢辩论,辩论的技巧出众,辩论时激情洋溢的性格特点。
20.为人富有激情,尤其在辩论时更能显示雄辩的才华。随性洒脱,朗读起来气势磅礴,任由性情勃发。治学严谨,才华横溢。一个字一个字计较,力求和原作一致,翻译作品达到接近原著。
最佳的立意在于强烈的现实针对性和时效性,以及选取的一个角度:一个家庭的矛盾冲突、一段友情的回归、一段成长道路的自我反思。这些都是考生最熟悉的生活,可以信手拈来。
三、构思:
本题构思的难度在于作文提示语与文题的距离,提示语只简单地提示原点,而文题却多了“回到”,因此,构思全文的关键在于“为什么要回到原点”。也就是说,不论是记叙文还是散文、议论文,都要有这样一个过程:美好的原点——破坏、矛盾冲突——回到原点。例如:纯净的环境——发展破坏——治理、恢复环境;幸福家庭——矛盾冲突——回归幸福;纯洁的友情——伤害——恢复友情。
2011年高考真题详解——广东卷(文科数学)

2011年普通高等学校招生全国统一考试【广东卷】(文科数学)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3页至第4页.全卷满分150分,考试时间120分钟.第Ⅰ卷(选择题 共50分)一、选择题:(每小题5分,共50分)【2011⋅广东文,1】1.设复数z 满足1iz =,其中i 为虚数单位,则z = ( ). A .i - B .i C .1 D .1- 【答案】A . 【解析】 1()iz i i i i -===-⨯-. 【2011⋅广东文,2】2.已知集合(){,|A x y x y =、为实数,且}221xy +=,(){,|B x y x y=、为实数,且}1x y +=,则A B 的元素个数为( ).A .4B .3C .2D .1 【答案】C .【解析】A B 的元素个数等价于圆221x y +=与直线1x y +=的交点个数,显然有2个交点.【2011⋅广东文,3】3.已知向量(1,2),(1,0),(3,4)===a b c .若λ为实数,()λ+a b ∥c ,则λ= ( ). A .14 B .12C .1D .2 【答案】B .【解析】 (1,2)λλ+=+a b ,由()λ+a b ∥c ,得64(1)0λ-+=,解得λ=12. 【2011⋅广东文,4】4.函数1()lg(1)1f x x x=++-的定义域是( ). A .(,1)-∞- B .(1,)+∞ C .(1,1)(1,)-+∞ D .(,)-∞+∞ 【答案】C .【解析】 10110x x x -≠⎧⇒>-⎨+>⎩且1x ≠,则()f x 的定义域是(1,1)(1,)-+∞ .【2011⋅广东文,5】5.不等式2210x x -->的解集是( ). A .1(,1)2-B .(1,)+∞C .(,1)(2,)-∞+∞D .1(,)(1,)2-∞-+∞ 【答案】D .【解析】21210(1)(21)02x x x x x -->⇒-+>⇒<-或1x >,则不等式的解集为1(,)(1,)2-∞-+∞ . 【2011⋅广东文,6】6. 已知平面直角坐标系xOy 上的区域D由不等式组02x y x ⎧≤≤⎪≤⎨⎪≤⎩给定,若(),M x y 为D 上的动点,点A的坐标为),则z OM OA =⋅的最大值为( ).A .3B .4 C. D. 【答案】B .【解析】z y =+,即y z =+,画出不等式组表示的平面区域,易知当直线y z =+经过点时,z取得最大值,max 24z =.【2011⋅广东文,7】7.正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有( ).A .20B .15C .12D .10 【答案】D .【解析】正五棱柱中,上底面中的每一个顶点均可与下底面中的两个顶点构成对角线,所以一个正五棱柱对角线的条数共有5210⨯=条.【2011⋅广东文,8】8.设圆C 与圆22(3)1x y +-=外切,与直线0y =相切.则C 的圆心轨迹为( ).A .抛物线B .双曲线C .椭圆D .圆 【答案】A .【解析】依题意得,C 的圆心到点(0,3)的距离与它到直线1y =-的距离相等,则C 的圆心轨迹为抛物线.【2011⋅广东文,9】9.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别为等边三角形、等腰三角形和菱形,则该几何体体积为( ).A .B .4C .D . 2【答案】C .【解析】该几何体是一个底面为菱形的四棱锥,菱形的面积122S =⨯⨯=,四棱锥的高为3,则该几何体的体积11333V Sh ==⨯=.【2011⋅广东文,10】10.设||||HO HT +是R 上的任意实值函数.如下定义两个函数()()f g x 和()()f g x ;对任意x R ∈,()()()()f g x f g x = ;()()()()f g x f x g x = .则下列等式恒成立的是( ). A .()()()()()()()f g h x f h g h x = B . ()()()()()()()f g h x f h g h x = C . ()()()()()()()f g h x f h g h x =D .()()()()()()()f g h x f h g h x =【答案】B . 【解析】对A 选项 (()f g h )()x =()f g ()()x h x (())()f g x h x =, (()f h ()g h )()x =()f h (()()g h x )=()f h ((()()g x h x ) (()())(()())f g x h x h g x h x = ,故排除A ;对B 选项 (()f g h )()x =()(())f g h x = (())(())f h x g h x ,(()f h ()g h )()x =()()()()f h x g h x (())(())f h x g h x =,故选B ; 对C 选项 (()f g h )()x =()(())f g h x ((()))f g h x =,(()f g ()g h )()x =()(()())()((()))f g g h x f g g h x = . (((())))f g g h x =,故排除C ;对D 选项 (()f g h )()x =()()()()()()f g x h x f x g x h x = ,(()f g ()g h )()x =()()()()()()()()f g x g h x f x g x g x h x = ,故排除D . 解析二:二、填空题:本大题共5小题.考生作答4小题.每小题5分,满分20分. (一)必做题(11~13题)第Ⅱ卷(非选择题 共100分)二、填空题:(每小题5分,共20分)【2011⋅广东文,11】11.已知{}n a 是递增等比数列,2432,4a a a =-=,则此数列的公比=q .【答案】 2.【解析】 2243224422402(2)(1)0a a a q a q q q q q -=⇒-=⇒--=⇒-+=2q ⇒=或1q =- ∵{}n a 是递增的等比数列,∴2q =.【2011⋅广东文,12】12.设函数3()cos 1.f x x x =+若()11f a =,则()f a -= .【答案】 9-.【解析】3()cos 111f a a a =+=,即3()cos 10f a a a ==,则33()()cos()1cos 11019f a a a a a -=--+=-+=-+=-.【2011⋅广东文,13】13.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打时间x (单位:小时)与当于投篮命中率y 之间的关系:小李这 5天的平均投篮命中率为 ,用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 . 【答案】 0.5;0.53.【解析】小李这5天的平均投篮命中率1(0.40.50.60.60.4)0.55y =++++= 3x =,1222221()()0.2000.1(0.2)0.01(2)(1)012()niii nii x x y y bx x ==--++++-===-+-+++-∑∑ , 0.47a y bx =-= ∴线性回归方程 0.010.47y x =+,则当6x =时,0.53y = ∴预测小李该月6号打6小时篮球的投篮命中率为0.53. (二)选做题(14、15题,考生只能从中选做一题)【2011⋅广东文,14】14.(坐标系与参数方程选做题)已知两曲线参数方程分别为⎩⎨⎧==θθsin cos 5y x (0≤θ <π) 和254x ty t⎧=⎪⎨⎪=⎩(t ∈R ),它们的交点坐标为 . 【答案】 (1,)5. 【解析】 sin x y θθ⎧=⎪⎨=⎪⎩表示椭圆2215x y +=(01)x y <≤≤≤,254x t y t⎧=⎪⎨⎪=⎩表示抛物线245y x =,22221(01)5450145x y x y x x x y x ⎧+=≤≤≤⎪⎪⇒+-=⇒=⎨⎪=⎪⎩或5x =-(舍去), 又因为01y ≤≤,所以它们的交点坐标为. 【2011⋅广东文,15】15.(几何证明选讲选做题)如图4,在梯形ABCD 中,AB ∥CD ,AB =4,CD =2,E 、F 分别为AD 、BC 上点,且EF =3,EF ∥AB ,则梯形ABFE 与梯形EFCD 的面积比为 . 【答案】75. 【解析】如图,延长,AD BC ,AD BC P = ,∵23CD EF =,∴49PCD PEF S S ∆∆= ∵24CD AB =,∴416PCD PEF S S ∆∆= ∴75ABEF EFCDS S =梯形梯形. 三、解答题:(本大题共6小题,共80分)【2011⋅广东文,16】16.(本小题满分12分)已知函数()12sin()36f x x π=-,x R ∈.(Ⅰ) 求()0f 的值; (Ⅱ) 设10,0,,(3),2213f ππαβα⎡⎤∈+=⎢⎥⎣⎦6(3),25f πβ+=求()sin αβ+的值. 【解析】 . (Ⅰ) (0)2sin()16f π=-=-;(Ⅱ) 110(3)2sin[(3)]2sin 232613f πππααα+=+-==,即5sin 13α=16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=,即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦,∴12cos 13α==,4sin 5β== ∴5312463sin()sin cos cos sin 13513565αβαβαβ+=+=⨯+⨯=. 【2011⋅广东文,17】17.(本小题满分13分)在某次测验中,有6位同学的平均成绩为75分.用n x 表示编号为()1,2,,6n n = 的同学所得成绩,且前5(Ⅰ) 求第6位同学成绩6,及这6位同学成绩的标准差;(Ⅱ) 从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间()68,75中的概率. 【解析】 .(Ⅰ) 611756n n x x ===∑5616675707672707290,n n x x x =∴=-=⨯-----=∑622222222111()(5135315)4966n n s x x ==-=+++++=∑,7.s ∴=(Ⅱ) 从5位同学中随机选取2位同学,共有如下10种不同的取法: {1,2},{1,3},{1,4},{1,5},{2,3},{2,4},{2,5},{3,4},{3,5},{4,5}, 选出的2位同学中,恰有1位同学的成绩位于(68,75)的取法共有如下4种取法: {1,2},{2,3},{2,4},{2,5},故所求概率为25. 解法二: (1)61(7076727072)756x +++++=,解得690x =, 标准差7s =. (2)前5位同学中随机选出的2位同学记为(,)a b ,,{1,2,3,4,5}a b ∈且a b ≠,则基本事件有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种,这5位同学中,编号为1、3、4、5号的同学成绩在区间(68,75)中设A 表示随机事件“从前5位同学中随机选出2位同学,恰有1位同学成绩在区间(68,75)中”,则A 中的基本事件有(1,2)、(2,3)、(2,4)、(2,5)共4种,则42()105P A ==. 【2011⋅广东文,18】18.(本小题满分12分)如图所示,将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右平移到的,,,A A B B ''分别为,,,,CD C D DE D E ''''的中点,1122,,,O O O O ''分别为,,,CD C D DE D E ''''的中点. (Ⅰ) 证明:12,,,O A O B ''四点共面;(Ⅱ) 设G 为AA '中点,延长1A O ''到H ',使得11O H A O ''''=,证明:2BO H B G '''⊥面.【解析】 .// (Ⅰ) ,,A A CDC D ''' 分别为中点, 11//O A O A ''∴连接BO 2直线BO 2是由直线AO 1平移得到12//AO BO ∴12//O A BO ''∴ 12,,,O A O B ''∴共面.(Ⅱ) 将AO 1延长至H 使得O 1H=O 1A ,连接1,,HO HB H H '' ∴由平移性质得12O O ''=HB21//BO HO ''∴11,,2A G H O H H A H O H H GA H π''''''''''==∠=∠=1GA H O H H ''''∴∆≅∆12H O H GH A π'''∴∠+=1O H H G ''∴⊥ 2BO H G ''∴⊥12212222222,,O O B O O O O O B O O O O '''''''''''⊥⊥⋂= 1222O O B BO O ''''∴⊥平面122O O BO '''∴⊥ 2BO H B '''∴⊥ H B H G H ''''⋂=2.BO H B G '''∴⊥平面解法二:证明:(1)连接2,BO 22,O O '依题意得1122,,,O O O O ''是圆柱底面圆的圆心 ∴,,,CD C D DE D E ''''是圆柱底面圆的直径∵,,A B B ''分别为 CD '', DE , D E ''的中点 ∴1290A O D B O D ''''''∠=∠=∴1A O ''∥2BO '∵BB '//22O ',四边形22O O B B ''是平行四边形 ∴2BO ∥2BO ' ∴1A O ''∥2BO∴12,,,O A O B ''四点共面(2)延长1A O '到H ,使得11O H AO ''=,连接1,,HH HO HB '' ∵11O H A O ''''=∴1O H ''2B '',四边形12O O B H ''''是平行四边形 ∴12O O ''∥H B ''∵1222O O O O '''⊥,122O O B O ''''⊥,2222O O B O O ''''= ∴12O O ''⊥面22O O B B ''∴H B ''⊥面22O O B B '',2BO '⊂面22O O B B '' ∴2BO H B '''⊥易知四边形AA H H ''是正方形,且边长2AA '=,∵11tan 2HH HO H O H'''∠=='',1tan 2A G A H G A H '''∠=='', ∴1tan tan 1HO H A H G ''''∠⋅∠=, ∴190HO H A H G ''''∠+∠= , ∴1HO H G ''⊥易知12O O ''HB ,四边形12O O BH ''是平行四边形, ∴2BO '∥1HO ',∴2BO H G ''⊥,H G H B H ''''= , ∴2BO '⊥平面H B G ''.【2011⋅广东文,19】19.(本小题满分14分)设0a >,讨论函数2()ln (1)2(1)f x x a a x a x =+---的单调性. 【解析】 .函数()f x 的定义域为(0,)+∞.22(1)2(1)1(),a a x a x f x x---+'=当212(1)2(1)1a a a x a x ≠---+时,方程的判别式112(1)()3a a ∆=--.①当10,0,()3a f x '<<∆>时有两个零点,12110,22x x a a =>= 且当12120,()0,()(0,)(,)x x x x f x f x x x '<<>>+∞或时在与内为增函数; 当1212,()0,()(,)x x x f x f x x x '<<<时在内为减函数;②当11,0,()0,()(0,)3a f x f x '≤<∆≤≥+∞时所以在内为增函数;③当11,()0(0),()(0,)a f x x f x x'==>>+∞时在内为增函数;④当111,0,0,2a x a >∆>=>时210,()2x f x a '=+<所以在定义域内有唯一零点1x ,且当110,()0,()(0,)x x f x f x x '<<>时在内为增函数;当1x x >时,1()0,()(,)f x f x x '<+∞在内为减函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东卷解析【试卷亮点】2011高考广东试题的特点是:1.主要考查英语知识的应用,即使对于基础知识的考查也是在具体的语境中进行考查。
2.很好的考查了考生的四项基本能力,尤其是听,读,写的能力。
3.试卷编排具有一定的科学性,由易到难。
能力题的选材多样,可读性强。
4.本套试题词汇量大,对考生的英语水平要求较高。
【命题趋势分析】近年高考广东卷将继续秉承考纲要求,继续贯彻“注重实用,考查基础”的考查思路和方向进行命题,并适当地探索高考改革的新思路,其高考试题大方向和考查思路,考查范围不会有太大变化,仍将保持较大的词汇量和较高层次的考查方向,贯彻“稳定中秋发展”的高考改革思路。
【复习使用指导】在今后的高考复课主要要注意做到以下几点:1.注意词汇的积累。
广东高考试题的最大特点是词汇量要求高,因此在今后的高考复课中对于词汇的记忆和巩固要加强。
2.对于阅读和写作要加大训练力度,坚持每天进行阅读和写作练习。
3.注意英语语言知识的运用的准确性,规范使用英语。
【文章大意】本文是一篇议论文,主题是学校按学生的智力差异分班的方法是错误的,即将智力好的学生分在一个班里会抑制他们的智力发育。
1.【答案】C【命题立意】考查名词辨析。
【解题思路】根据前一句中的argue可知此处选C。
其余选项不符合题意。
2.【答案】C【命题立意】考查动词辨析。
【解题思路】design:设计;group:分组;learn:学会;live:住,生活。
此处所填词做介词by的宾语,意思是:学会,了解到,选C。
其余选项不符合题意。
3.【答案】D【命题立意】考查形容词辨析。
【解题思路】smart:聪敏的,敏捷的;curious:好奇的;mature:成熟的;average:一般的,平均的。
根据前文的regular classes可知此处选D。
其余选项不符合题意。
4.【答案】B【命题立意】考查形容词辨析。
【解题思路】regular:规则的;定期的;special:特殊的;small:小的;creative:有创造力的。
根据后一句中的regular classes可知此处所填词与regular相对,选B。
其余选项与句意不符。
5.【答案】A【命题立意】考查名词辨析。
【解题思路】本句意思是:然而,把这些孩子从普通班里挑出来可能会造成严重的问题。
选A。
其余选项不符合题意。
其余选项不符合题意。
6.【答案】A【命题立意】考查形容词辨析。
【解题思路】intelligent:聪敏的;competent:有能力的, 能胜任的,称职的;ordinary:平凡的;independent:独立的。
根据前一句的意思可知此处选A。
B, C, D三个选项不符合句意。
7.【答案】B【命题立意】考查形容词辨析。
【解题思路】separate:独立的;regular:定期的,规则的;一般的;new:新的;boring:无聊的。
根据前文的regular classes可知此处选B。
其他选项与句意不符。
8.【答案】D【命题立意】考查副词辨析。
所填词修饰rely on,意思是:主要依靠,选D。
其余选项不符合语境。
9.【答案】D【命题立意】考查副词辨析。
【解题思路】directly:直接地,径直地;cleverly:聪明地;voluntarily:志愿地;quickly:快地,迅速地。
句意是:他们开始对很多问题反映很快。
选D。
其余选项不符合语境。
10.【答案】B【命题立意】考查形容词辨析。
【解题思路】所填词做表语,修饰人,根据lose interest可以推断出此处选B。
其余选项形式不准确。
11.【答案】A【命题立意】考查名词辨析。
【解题思路】concern:关心;conclusion:结论;reflection:反映;interest:兴趣。
根据前一句中的concerned 可知此处选A。
其余选项不符合语境。
12.【答案】B【命题立意】考查名词辨析。
【解题思路】根据空前的these和前文的parents and teachers可知此处选B。
其余选项不符合具体语境。
13.【答案】A【命题立意】考查形容词辨析。
【解题思路】由本句中的special classes可知此处所填词意思是:天才的,选A。
其他选项不符合句意。
14.【答案】D【命题立意】考查动词辨析。
【解题思路】根据前一句中的feel bored可知此处选D。
其余选项不符合题意。
15.【答案】C【命题立意】考查形容词辨析。
【解题思路】outstanding:突出的,杰出的;intelligent:聪明的,智商高的;anxious:忧虑的,担心的;ordinary:普通的,平凡的。
由前一句中的anxious可知此处选C。
其他选项不符合语境。
第二节【文章大意】本文是一篇记叙文,内容是关于“我”在公交车上遇见一位看起来精神有些不太正常的人的故事。
当时尽管车上人不多,但没有一位乘客愿意和他搭话,最终为了不使这个人感到不适,“我”主动去和他交谈。
16.【答案】later【命题立意】考查形容词的级。
【解题思路】根据句意可知此处时间状语意思是:当天晚些时候,用late的比较级。
17.【答案】until【命题立意】考查状语从句。
【解题思路】根据句意可以猜测出其意思是:直到,用until。
18.【答案】sitting【命题立意】考查非谓语动词。
【解题思路】做感官动词notice的宾语补足语,与notice的动作同时进行,用v-ing形式。
19.【答案】was pretending【命题立意】考查动词时态。
【解题思路】所填词表示当时正在进行的动作,用过去进行时。
20.【答案】mentally【命题立意】考查副词。
【解题思路】修饰形容词,应用副词。
21.【答案】whom【解题思路】先行词是people,关系词在从句中作介词to的宾语,用whom。
22.【答案】they【命题立意】考查代词。
【解题思路】做句子主语,指代前文中的people,故用人称代词的主格they。
23.【答案】on【命题立意】考查介词。
【解题思路】此处所填词与one’s own构成搭配,做状语,用on。
24.【答案】an【命题立意】考查冠词。
【解题思路】此处所填词构成短语have a/an …conversation,意思是:和……交谈,用冠词an。
25.【答案】both【命题立意】考查不定代词,【解题思路】根据句意可知本句中的us指我和那位乘客,是两个人,故此处用both。
阅读理解A【文章大意】本文是一篇夹叙夹议文章,作者通过介绍自己的亲身经历,讨论的是勇敢地问题。
26.【答案】A【命题立意】细节理解题。
【解题思路】由第一自然段的后两句可知本题选A。
27.【答案】D【命题立意】细节理解题。
【解题思路】根据第二自然段中的From my wheelchair experience, I see the best in people, but sometimes I feel sad because those who appear independent miss the kindness I see daily一句可知本题选D。
28.【答案】B【命题立意】推理判断题。
【解题思路】由第五自然段中的But instead of getting impatient and angry, they waited, knowing the driver in front of them was in some way weak.可知本题选B。
29.【答案】C【命题立意】推理判断题。
【解题思路】根据文章最后一句可知本题C项正确。
30.【答案】B【命题立意】主旨大意题。
【解题思路】根据主题段——第一自然段的前两句可知本文大意思是谈论弱点和好心问题,故本题选B。
B【文章大意】本文是一篇科普说明文,大意是说明科学家们研究发现:猫和狗能否和谐相处主要由它们最初在一起的年龄来决定。
尽管如此,它们有和谐相处的可能,那么我们人类能偶借鉴它们的关系呢!31.【答案】B【命题立意】词义猜测题。
【解题思路】Swimmingly所在句子的意思是:很有可能这两种宠物相处的很甜蜜。
由此可知swimmingly 与sweetly意思相同,选B。
32.【答案】C【命题立意】推理判断题。
【解题思路】根据第二自然段中的One reason for this is probably that some of their body signals were just opposite.一句可知本题选C。
33.【答案】C【解题思路】根据第四自然段的前两句可知奇怪的是:猫合狗开始学习对方的语言,选C。
34.【答案】B【命题立意】段落大意题。
【解题思路】第四自然段中说明毛和狗开始学习对方的语言,所以它们并不是像我们想象的那样水火不容,而是越来越有更多的共同点,选B。
35.【答案】A【命题立意】推理判断题。
【解题思路】根据最后一自然段大意可知本题选A。
C【文章大意】本文是记叙文,大意是记述了作者在教学的过程中一次难忘的经历。
36.【答案】A【命题立意】推理判断题。
【解题思路】根据第一自然段中的as it would allow me to wear a tie and go by the name of Mr. Davis.一句可以推断出本题选A。
37.【答案】C【命题立意】推理判断题。
【解题思路】根据本段中的But when the day eventually came, my nerves kicked in and the true Mr. Davis was there.可知本题选C。
38.【答案】D【命题立意】细节理解题。
【解题思路】根据第三自然段的首句和最后意思可知作者上课的第一件事是让学生把自己的名字鞋在卡片上。
选D。
39.【答案】B【命题立意】细节理解题,根据最后一自然段的首句可知本题选B。
40.【答案】A【命题立意】推理判断题。
【解题思路】根据最后一自然段的大意可知作者让学生这样题目的作文的原因是自己的第一节课上很失望,选A。
D【文章大意】本文是一篇议论文,大意是说明对世界的可持续发展造成负面影响的主要问题之一——环境问题。
41 【答案】D【命题立意】推理判断题。
【解题思路】由第一自然段中的可知传统的商业模式有害的原因中并未提到增长速度问题,选D。
42. 【答案】C【命题立意】推理判断题。
【解题思路】根据本自然段中的…and is spending a huge amount of money majing electric cars and high-speed trains.一句可知本题选C。
43. 【答案】B【命题立意】细节理解题。
【解题思路】由第三自然段的第二句可知本题选B。
