人教版高中数学选修2-3回归分析的基本思想及其初步应用教案
高中数学选修2-3公开课教案3.1回归分析的基本思想及其初步应用

第三章、统计案例3.1回归分析的基本思想及其初步应用(共计4课时) 授课类型:新授课一、教学内容与教学对象分析学生将在必修课程学习统计的基础上,通过对典型案例的讨论,了解和使用一些常用的统计方法,进一步体会运用统计方法解决实际问题的基本思想,认识统计方法在决策中的作用。
二、学习目标1、知识与技能通过本节的学习,了解回归分析的基本思想,会对两个变量进行回归分析,明确建立回归模型的基本步骤,并对具体问题进行回归分析,解决实际应用问题。
2、过程与方法 本节的学习,应该让学生通过实际问题去理解回归分析的必要性,明确回归分析的基本思想,从散点图中点的分布上我们发现直接求回归直线方程存在明显的不足,从中引导学生去发现解决问题的新思路—进行回归分析,进而介绍残差分析的方法和利用R 的平方来表示解释变量对于预报变量变化的贡献率,从中选择较为合理的回归方程,最后是建立回归模型基本步骤。
3、情感、态度与价值观 通过本节课的学习,首先让显示了解回归分析的必要性和回归分析的基本思想,明确回归分析的基本方法和基本步骤,培养我们利用整体的观点和互相联系的观点,来分析问题,进一步加强数学的应用意识,培养学生学好数学、用好数学的信心。
加强与现实生活的联系,以科学的态度评价两个变量的相关系。
教学中适当地增加学生合作与交流的机会,多从实际生活中找出例子,使学生在学习的同时。
体会与他人合作的重要性,理解处理问题的方法与结论的联系,形成实事求是的严谨的治学态度和锲而不舍的求学精神。
培养学生运用所学知识,解决实际问题的能力。
三、教学重点、难点教学重点:熟练掌握回归分析的步骤;各相关指数、建立回归模型的步骤;通过探究使学生体会有些非线性模型通过变换可以转化为线性回归模型,了解在解决实际问题的过程中寻找更好的模型的方法。
教学难点:求回归系数 a , b ;相关指数的计算、残差分析;了解常用函数的图象特点,选择不同的模型建模,并通过比较相关指数对不同的模型进行比较。
人教版高中选修2-3数学3.1回归分析的基本思想及其初步应用教案(2)
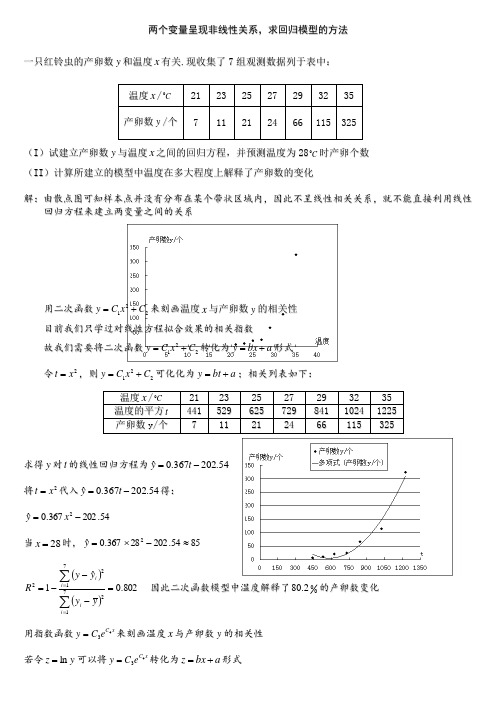
两个变量呈现非线性关系,求回归模型的方法一只红铃虫的产卵数y 和温度x 有关.现收集了7组观测数据列于表中:(I )试建立产卵数y 与温度x 之间的回归方程,并预测温度为28C 0时产卵个数(I I )计算所建立的模型中温度在多大程度上解释了产卵数的变化解:由散点图可知样本点并没有分布在某个带状区域内,因此不呈线性相关关系,就不能直接利用线性 回归方程来建立两变量之间的关系用二次函数221C x C y +=来刻画温度x 与产卵数y 的相关性 目前我们只学过对线性方程拟合效果的相关指数故我们需要将二次函数221C x C y +=转化为a bx y +=形式 令2x t =,则221C x C y +=可化化为a bt y +=;相关列表如下:求得y 对t 的线性回归方程为54.202367.0ˆ-=t y 将2x t =代入54.202367.0ˆ-=t y得: 54.202367.0ˆ2-=x y当28=x 时,8554.20228367.0ˆ2≈-⨯=y()()802.0ˆ17127122=---=∑∑==i i i i y y y y R 因此二次函数模型中温度解释了002.80的产卵数变化用指数函数x C e C y 43=来刻画温度x 与产卵数y 的相关性 若令y z ln =可以将x C e C y 43=转化为a bx z +=形式温度x /C 02123 25 27 293235产卵数y /个 7 11212466 115 325温度x /C 0 21 23 2527 29 32 35 温度的平方t 441 529 625 729 841 1024 1225 产卵数y /个7 11212466 115 325对x C e C y 43=两边取对数343ln ln ln ln 4C x C e C y x C +=+=令y z ln =,b C =4,a C =3ln 则有a bx z +=;相关列表如下:求得z 对x 的线性回归方程为849.3272.0ˆ-=x z将272.04=C ,849.3-3e C =代入x C e C y 43=得:849.3272.0ˆ-=x e y当28=x 时,44ˆ849.328272.0≈=-⨯e y利用计算器求得98.02=R因此二次函数模型中温度解释了0098的产卵数变化综上可得用指数模型拟合效果较好,也就是说刻画产卵数与温度的关系更接近实际情况1.在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( ) A .总偏差平方和 B .残差平方和 C .回归平方和 D .相关指数R 22.回归分析中,相关指数R 2的值越大,说明残差平方和( )A .越小B .越大C .可能大也可能小D .以上都不对3.若对于变量y 与x 的10组统计数据的回归模型中,相关指数95.02=R ,又知残差平方和为53.120,那么∑=-1012)(i i y y 的值为( ) (A ) 06.241 (B )6.2410 (C )08.253 (D )8.25304.在一次抽样调查中测得样本的5个样本点,数据如下: (1)画出散点图;(2)通过作出的散点图发现,y 与x 之间的关系可用函数a xby +=拟合,试确定a b ,的值 温度x /C 021232527293235y z ln = 1.946 2.398 3.405 3.178 4.19 4.745 5.784 产卵数y /个 7 11 21 24 66 115 325 x 0.25 0.5 1 2 4 y 16 125 2 1。
人教版 选修2-3第三章回归分析的基本思想及其初步应用 同步教案
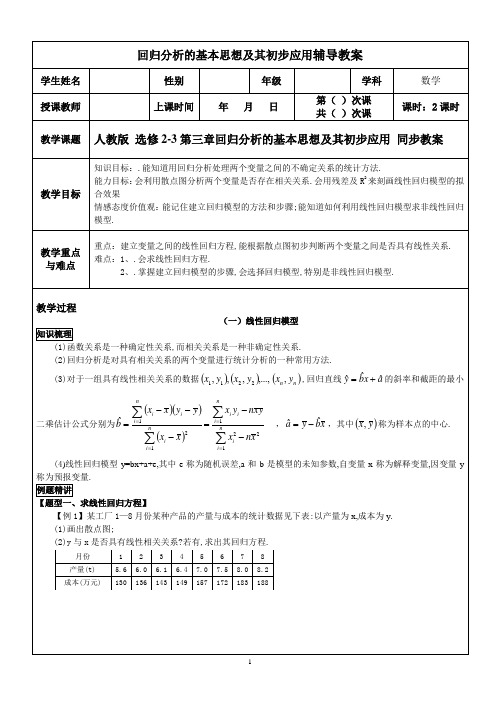
C.=2x+1
D.=x-1
2.某商场经营一批进价是 30 元/台的小商品,在市场试验中发现,此商品的销售单价 x(x 取整数)元与日销售量 y
台之间有如下关系:
x
35 40 45 50
y
56 41 28 11
(1)y 与 x 是否具有线性相关关系?如果具有线性相关关系,求出回归直线方程.(方程的斜率精确到个位)
例题精讲
【题型一、线性回归分析】
【例 1】、某运动员训练次数与运动成绩之间的数据关系如下:
(1)作出散点图;
次数(x) 30 33 35 37 39 44 46 50
(2)求出线性回归方程; (3)作出残差图,并说明模型的拟合效果;
成绩(y) 30 34 37 39 42 46 48 51
(4)计算 R2,并说明其含义.
(2)设经营此商品的日销售利润为 P 元,根据(1)写出 P 关于 x 的函数关系式,并预测当销售单价 x 为多少元时,才
能获得最大日销售利润.
知识梳理
(二)线性回归分析
1、.残差的概念
对于样本点 x1, y1 , x2 , y2 ,..., xn , yn 而言,它们的随机误差为 ei yi bxi a,i 1,2,..., n 其估计值为
【方法技巧】
“相关指数 R2、残差图”在回归分析中的作用:
(1)相关指数 R2 是用来刻画回归效果的,由 R2=1-可知 R2 越大,意味着残差平方和越小,也就是说模型的拟合
效果就越好.
(2)残差图也是用来刻画回归效果的,判断依据是:残差点比较均匀地分布在水平带状区域中,带状区域的宽
度越窄,说明模型拟合精度越高, 回归方程预报精度越高.
月份
3.1《回归分析的基本思想及其初步应用》教案2(新人教选修2-3)

3.1《回归分析的基本思想及其初步应用》教案2(新人教选修2-3)3.1 回归剖析的基本思想及其初步应用(二)教课要求 :经过典型事例的研究,进一步认识回归剖析的基本思想、方法及初步应用 教课要点 :认识评论回归成效的三个统计量:总偏差平方和、残差平方和、回归平方和 教课难点 :认识评论回归成效的三个统计量:总偏差平方和、残差平方和、回归平方和 教课过程 :一、复习准备 :1.由例 1 知,预告变量(体重)的值受解说变量(身高)或随机偏差的影响....2.为了刻画预告变量(体重)的变化在多大程度上与解说变量(身高)有关?在多大程度上与随机偏差有关?我们引入了评论回归成效的三个统计量:总偏差平方和、残差平方和、回归平方和 .二、讲解新课:1. 教课 总偏差平方和、残差平方和、回归平方和:ny) 2 .(1)总偏差平方和 :全部单个样本值与样本均值差的平方和,即SST( y ii 1nμ 2残差平方和: 回归值与样本值差的平方和,即SSE( y i.i 1y i )n回归平方和: 相应回归值与样本均值差的平方和,即SSRμy) 2( y i.i1(2)学习要领: ①注意 y iμ、 y 的差别;②预告变量的变化程度能够分解为由解说变量、 y innμn惹起的变化程度与残差变量的变化程度之和,即( y i y) 2( y i2μy) 2;y i )( y ii 1i 1i1③当总偏差平方和相对固准时,残差平方和越小, 则回归平方和越大, 此时模型的拟合成效n ( y iμ 22y i )越好;④对于多个不一样的模型,我们还能够引入有关指数1i 1来刻画回归Rni1( y iy) 2的成效,它表示解说变量对预告变量变化的贡献率 . R 2的值越大,说明残差平方和越小,也就是说模型拟合的成效越好 .2. 教课例题: 例 2 对于 x 与 Y 有以下数据:x 24 56 8 y3040605070为了对 x 、 Y 两个变量进行统计剖析,现有以下两种线性模型:$ 6.5 x 17.5 ,y $ y 7 x 17 ,试比较哪一个模型拟合的成效更好. 剖析: 既可分别求出两种模型下的总偏差平方和、 残差平方和、回归平方和,也可分别求出两种模型下的有关指数,而后再进行比较,进而得出结论.5μ 25μ 2( y i( y i(答案:R 1 1y i )1550.845 , R 2 1y i )180 , 84.5%> 82% ,因此51510.822i 12i1( yy )21000( yy) 21000iii 1i1甲采用的模型拟合成效较好 . )3. 小结: 分清总偏差平方和、残差平方和、回归平方和,初步认识怎样评论两个不一样模型拟合成效的利害 .。
3.1《回归分析的基本思想及其初步应用》教案4(新人教选修2-3)

3.1《回归分析的基本思想及其初步应用》教案4(新人教选修2-3)3.1 回归剖析的基本思想及其初步应用(四)教课要求:经过典型事例的研究,进一步认识回归剖析的基本思想、方法及初步应用.教课要点:经过研究使学生领会有些非线性模型经过变换能够转变为线性回归模型,认识在解决实质问题的过程中找寻更好的模型的方法,认识可用残差剖析的方法,比较两种模型的拟合成效 .教课难点:认识常用函数的图象特色,选择不一样的模型建模,并经过比较有关指数对不一样的模型进行比较 .教课过程:一、复习准备:1.发问:在例3中,察看散点图,我们选择用指数函数模型来拟合红铃虫的产卵数y 和温度 x 间的关系,还可用其余函数模型来拟合吗?2.议论:能用二次函数模型y c3 x2c4来拟合上述两个变量间的关系吗?(令t x2,则y c3t c4,此时y与t间的关系如t44152962572984110241225y711212466115325 400下:300察看 y 与t的散点图,能够发现样本点其实不散布在一y200条直线的四周,所以不宜用线性回归方程来拟合它,100y c3 x2c4来拟合y与 x 之间的0即不宜用二次曲线050010001500关系 . )小结:也就是说,我们能够经过察看变换后t的散点图来判断可否用此种模型来拟合. 事实上,除了察看散点图之外,我们也可先求出函数模型,然后利用残差剖析的方法来比较模型的利害.二、讲解新课:1.教课残差剖析:①残差:样本值与回归值的差叫残差,即μμe i y i y i.②残差剖析:经过残差来判断模型拟合的成效,判断原始数据中能否存在可疑数据,这方面的剖析工作称为残差剖析 .③残差图:以残差为横坐标,以样本编号,或身高数据,或体重预计值等为横坐标,作出的图形称为残差图 . 察看残差图,假如残差点比较平均地落在水平的带状地区中,说明采用的模型比较适合,这样的带状地区的宽度越窄,模型拟合精度越高,回归方程的预告精度越高.2.例 3 中的残差剖析:计算两种模型下的残差一般状况下,比较两个模型的残差比较困难(某些样本点上一个模型的残差的绝对值比另一个模型的小,而另一些样本点的状况则相反),故经过比较两个模型的残差的平方和的大小来判断模型的拟合成效. 残差平方和越小的模型,拟合的成效越好.因为两种模型下的残差平方和分别为 1450.673 和 15448.432,应采用指数函数模型的拟合成效远远优于采用二次函数模型 . (自然,还可用有关指数刻画回归成效)3.小结:残差剖析的步骤、作用三、稳固练习:练习:教材 P13 第 1 题。
人教版高中数学选修2-3 3.1 回归分析的基本思想及其初步应用教案
小结与练习:
1、回归分析的基本思想是什么?
2、如何进行回归分析。
第一个问题由教师讲解,第二个问题由学生齐答。
1、整理本节课所学习到的知识.
2、体会随机数学的特点.
1、由小结再次明确了回归分析的步骤 以及每一步需要注意的地方。
2、注重数学教学中的思想性,它们是贯穿数学教学过程的“灵魂”.
3、后续问题的提出,给 学生留下思维发展的时空和探索余地,激发学生对知识的进一步渴望.
一、将前面1、2问题改为:
1、两个变量之间有哪几种关系?
2、进行线 性回归分析的一般步骤是什么。
二、学生回答完问题后,教师用计算机演示一遍操作。
1、在学生小组讨论的时候,教师适时参与讨论。
2、教师演示用计算机进行回归分析的方法。
学生小组讨论1、2两个问题。通过小组讨论,使得学困生也能对以前的知识有必要的了解。
例2教学:
提供期中考试400多名考生的成绩数据来进行回归分析,再次让学生体会回归分析的魅力。
提供期中考试4பைடு நூலகம்0多名考生的成绩,简单的部分让学生来操作。并让学生来分析回答。后面的部分教师操作。
认真思考,并感受当数据量很大的时候,残差图的特点。更加直观的理解,当残差点均匀分布在一条水平带状区域上时,模型选 取较合适。
必修三和选修1-2这两本书在教学时间上间隔很远,通过有效的复习让学生为后面新知识的讲授打下良好的基础。
问题呈现:
例1 、统计10名高三女生的身高体重数据,汇总后求出根据身高预报体重的回归方程,并随机调查一名高三女生的身高,然后预报体重。
1、要求学生小组讨论统计方案。并对学生提出的方案做出评价
2、找学生代表上台操作。
人教课标版高中数学选修2-3《回归分析基本思想及其初步应用(第1课时)》教学设计

第3章 统计案例3.1 回归分析基本思想及其初步应用第一课时一、教学目标 1.核心素养:通过学习回归分析的基本思想及其初步应用,初步形成基本的数据分析能力. 2.学习目标(1)1.1.1.1 温习散点图,复习相关关系与函数关系.(2)1.1.1.2 理解回归分析的基本思想,会求线性回归方程.(3)1.1.1.3 理解回归模型与函数模型的差别,了解随机误差产生的原因. 3.学习重点线性回归分析的一般步骤,,回归分析的应用. 4.学习难点理解随机误差产生的原因以及函数模型与回归模型的差别. 二、教学设计 (一)课前设计 1.预习任务 任务1阅读教材P 2-P 4,思考求解线性回归方程一般步骤是什么?回归模型和函数模型有何区别?随机误差产生的原因? 任务2什么是解样本中心点,什么是回归分析?2.预习自测 1.两个变量有线性相关关系且正相关,则回归直线方程中,a bx y +=的系数b ( )A.0>bB.0<bC.0=bD.1=b解:A2.在画两个变量的散点图时,下面哪个叙述是正确的( ) A.预报变量在x 轴上,解释变量在y 轴上 B.解释变量在x 轴上,预报变量在y 轴上 C.可以选择两个变量中任意一个变量在x 轴上D.可以选择两个变量中任意一个变量在y 轴上 解:B3.回归直线y bx a =+必过( )A. (0,0)B. (,0)xC. (0,)yD. (,)x y 解:D (二)课堂设计 1.知识回顾(1)线性回归方程:∧∧∧+=a x b y ,其中.1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx∧====---==--∑∑∑∑, ˆy ab x ∧=- (2)线性相关:如果所有点看上去都在一条直线附近波动,则两个变量间是线性相关,可用一条直线来近似表示(3)非线性相关:若所有点看上去都在某条曲线附近波动,则两个变量间是非线性相关,可用一条曲线来拟合.(4)回归分析:是对具有相关关系的两个变量进行的统计分析的一种常用方法. 2.问题探究问题探究一 相关关系与函数关系是什么,如何画散点图? ●活动一 回顾旧知,回忆相关关系与函数关系在《必修3》中,我们已经学习过函数关系与相关关系,那么什么是函数关系,什么是相关关系?想一想:在以往数学学习和日常生活中,我们接触了哪些函数关系与相关关系? 举例:请大家试着列举生活与学习中的相关例子.例如圆的周长2C r π=,周长C 与半径r 之间就是一种确定性的关系,对于自变量半径的每一个确定的值,都有唯一确定的周长的值与之相对应.又如人的体重y 与身高x ,一般来说,身高越高,体重越重,但不能用一个函数来严格表示它们之间的关系.即变量之间有一定的联系,但取值也具有一定的随机性.即: 1. 函数关系与相关关系 (1) 函数关系是一种确定关系. (2) 相关关系是一种不确定关系.注意:判断两个变量是否具有相关关系,应该先看它们是否有关,再看这种关系是否是确定的函数关系.●活动二 旧知推进,回忆散点图的画法 2. 散点图在分析两个变量的关系时,为了对变量之间的关系有一个大概的了解,我们通常将一个变量的数据作为横坐标,另一个变量的数据作为纵坐标,将这些点描在平面直角坐标系中,形成的图形就是散点图(1)散点图直观反映了实例的成对观测值之间是否存在相关关系和存在什么样的相关关系. (2)若散点图中点的分布由左下方到右上方,则两个变量正相关;点的分析由左上方到右下方,则两个变量负相关问题探究二 线性回归分析步骤是什么?●活动一 通过实例,亲身体验在《必修3》中,我们利用回归分析的方法对两个具有线性相关关系的变量进行了研究,你能利用回归分析对下列实例进行分析吗?例1 从某大学中随机选取8名女大学生,其身高和体重数据如下表所示:求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm 的女大学生的体重.【知识点:线性回归方程,回归分析;】详解:(1) 作散点图,由于问题是根据身高预报体重,因此要求身高与体重的回归直线方程,取身高为自变量x ,体重为因变量y ,作散点图:40455055606570150155160165170175180从散点图可以看出,样本点呈条状分布,身高和体重有比较好的线性相关关系,因此可以用回归直线y =bx +a 来近似刻画它们之间的关系,从而可利用我们学过的最小二乘估计思想及计算公式求得线性回归直线方程.其计算公式如下:1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx∧====---==--∑∑∑∑,y a b x ∧∧=-其中1211,n n i i x x x x x n n =+++==∑…121y y y 1y y ,nn i i n n=+++==∑…根据上面公式,可以得到712.85,849.0-==∧∧a b 于是得到线性回归方程712.85849.0-=∧x y对于身高172cm 女大学生,由回归方程可以预报体重为)(316.60712.85172849.0kg y =-⨯=∧,预测身高为172cm 的女大学生的体重为约60.316kg.点拨:回归分析的基本过程: (1)画出两个变量的散点图; (2)判断是否线性相关;(3)求回归直线方程(利用最小二乘法); (4)并用回归直线方程进行预报 ●活动二 整理旧知,得出新概念 1.样本中心点对于一组具有线性相关关系的数据1122(,),(,),,(,)n n x y x y x y ,1211,nni i x x x x x n n=+++==∑121y y y 1y y ,nni i n n=+++==∑则称点),y x (为样本点的中心.●活动三 总结反思,得出新结论 由上计算过程可以得出:(1)样本点的中心坐标分别是两个变量的观测数据的算术平均数. (2)点),y x (在回归直线上,即回归直线一定过样本点的中心.问题探究三 线性回归模型与函数模型有何差异,随机误差是怎么产生的??●活动一结合实际,反思结果想一想:身高为172cm 的女大学生的体重一定是60.316kg吗?如果不是,你能解释一下原因吗?答:不一定,但一般可以认为她的体重在60.316kg左右.由样本点和回归直线的相互位置可以说明这一点.从散点图可观察出,女大学生的体重y和身高x之间的关系并不能用一次函数y=bx+a来严格刻画(因为所有的样本点不共线,所以线性模型只能近似地刻画身高和体重的关系). 在数据表中身高为165cm的3名女大学生的体重分别为48kg、57kg和61kg,如果能用一次函数来描述体重与身高的关系,那么身高为165cm的3名女在学生的体重应相同. 这就说明体重不仅受身高的影响还受其他因素的影响,这时我们把身高和体重的关系可用下面的线性回归模型y=bx+a+e来表示,其中a和b为模型的未知参数,e称为随机误差.●活动二层层推进,答疑解惑那么,产生随机误差项e的原因是什么呢?实际上,一个人的体重除了受身高影响外,还受其他许多因素的影响,例如饮食习惯、是否喜欢运动、度量误差等.另一方面,没有人知道身高和体重之间的真正关系是什么,现在只是利用线性回归方程来近似这种关系.而这种近似和上面提到的影响因素都会导致随机误差e的产生.即随机误差产生的原因:(1)线性回归方程中的∧b和∧a为估计值,与真实值b和a之间存在误差.(2)影响变量y的因素不止变量x一个,可能还包括许多因素(例如农作物的生长不仅要收日照时间的影响,还会受土壤的肥沃程度,施肥量等影响)(3)观测误差,由于测量工具及测量值一般也存在一定的误差,这样的误差也包含在e中所以随机误差e中包含体重不能由身高的线性函数解释的所有部分. 当残差变量恒等于0时,线性回归模型就变成一次函数模型. 因此,一次函数模型是线性回归模型的特殊形式,线性回归模型是一次函数模型的一般形式.●活动三新知学习在统计中,我们把自变量x称为解释变量,因变量y称为预报变量.线性回归模型与我们熟知的一次函数模型的不同之处就在于增加了随机误差e,预报变量y的值由解释变量x和随机误差e共同决定,即解释变量x只能解释部分预报变量y的变化3.课堂总结【知识梳理】(1)线性回归方程:∧∧∧+=a x b y ,其中.1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx∧====---==--∑∑∑∑,a ∧=x b ∧-y(2)回归分析的基本过程:①画出两个变量的散点图;②判断是否线性相关,③求回归直线方程(利用最小二乘法),④并用回归直线方程进行预报(3)对于一组具有线性相关关系的数据1122(,),(,),,(,)n n x y x y x y ,1211,nni i x x x x x n n=+++==∑121y y y 1y y ,nni i n n=+++==∑则称点),y x (为样本点的中心.(4)线性回归模型:y =bx +a +e ,其中a 和b 为模型的未知参数,e 称为随机误差.【重难点突破】(1)利用回归分析的方法对两个具有线性相关关系的变量进行研究的步骤: ①作出散点图 ②求回归直线方程 ③利用所求方程进行预测.(2) 随机误差产生的原因:①线性回归方程中的∧b 和∧a 为估计值,与真实值b 和a 之间存在误差.②影响变量y 的因素不止变量x 一个,可能还包括许多因素(例如农作物的生长不仅要收日照时间的影响,还会受土壤的肥沃程度,施肥量等影响)③观测误差,由于测量工具及测量值一般也存在一定的误差,这样的误差也包含在e 中. 4.随堂检测1.下面两个变量间的关系不是函数关系的是() A.正方体的棱长与体积 B.角的度数与它的正弦值C.单位产量为常数时,土地面积与粮食总产量 D.日照时间与水稻亩产量【知识点:函数关系,相关关系】解:D2. 设有一个回归方程为25.2+-=∧x y ,则变量x 增加一个单位时,y 的值得变化情况是( ) A.平均增加2.5个单位 B.平均增加2个单位 C.平均减少2.5个单位 D.平均减少2个单位【知识点:回归方程,函数】 答案:C3. 为了研究两个变量x 与y 之间的线性相关性,甲、乙两个同学并且利用线性回归方法,求得回归直线分别为1l 和2l ,已知在两个人的试验中发现y x 和分别相等,那么下列说法正确的是( )A.1l 与2l 一定平行B. 1l 与2l 重合C.1l 与2l 相交于点),y x (D.无法判断1l 与2l 是否相交【知识点:回归方程,样本点中心】 答案:C4.为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据上表可得回归直线方程∧∧∧+=a x b y ,其中 x b y a b ^^,76.0-==∧,据此估计,该社区一户收入为15万元家庭年支出为( ) A. 11.4万元 B. 11.8万元 C.12.0万元 D.12.2万元【知识点:回归方程,回归分析】 答案:B5.已知x 与y 有如下数据:则y 关于x 的回归直线方程∧∧∧+=a x b y 必过点 . 【知识点:回归方程,样本点的中心】 解:(1.5,5) (三)课后作业 基础型 自主突破1.对具有相关关系的两个变量统计分析的一种常用的方法是( ) A.回归分析 B.相关系数分析 C.残差分析 D.相关指数分析 【知识点:回归分析】 解:A2.对于具有线性相关关系的变量x 和y ,由测得的数据已求得回归直线的斜率为 6.5,且恒过点(2,3),则回归直线的方程为 . 【知识点:回归方程,样本点的中心】 解:105.6-=∧x y3.一位母亲记录了儿子3—9岁的身高,数据(略),由此建立的身高与年龄的回归模型为y =7.19x +73.93,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( ) A.身高一定是145.83cm B.身高在145.83cm 以上 C.身高在145.83cm 左右 D.身高在145.83cm 以下【知识点:回归方程,回归分析】 答案:C4.为了了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了他某月1号到5号每天打篮球的时间x (单位:小时)与当天投篮命中率y 之间的关系:小李这5天平均投篮命中率为________;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为_______.【知识点:回归方程,样本点的中心】 解:0.5,0.53 能力型 师生共研1.在一次实验中,测得(x ,y )的四组值分别是A (1,2)、B (2,3)、C (3,4)、D (4,5),则y 与x 之间的回归直线方程为( )A.1ˆ+=x yB.2ˆ+=x yC.12ˆ+=x yD.1ˆ-=x y【知识点:回归直线方程】 解:A2.如果某地的财政收入x 与支出y 满足线性回归方程e a bx y ++=∧(单位:亿元),其中5.0||,2,8.0≤==e a b ,如果今年该地区财政收入10亿元,则年支出预计不会超过( )A.10亿元B.9亿元C.10.5亿元D.9.5亿元【知识点:回归模型,】解:C 点拨:带入数据,得,10e y +=∧又,5.0||≤e 得5.105.9≤≤∧y . 3.已知y x ,的值如下表所示,若y 与x 具有相关关系且其回归直线方程为,2741x y +=∧则a =( )A.4B.5C. 6D. 7【知识点:回归直线方程】解: A 点拨:又表格求得y x ,的值,带入回归直线方程,建立关于a 的方程求解. 4. 有下列关系:①人的年龄与他(她)拥有的财富之间的关系; ②曲线上的点与该点的坐标之间的关系; ③苹果的产量与气候之间的关系;④森林中的同一种树木,其横断面直径与高度之间的关系, ⑤学生他(她)的学号之间的关系.(填序号) 【知识点:函数关系,相关关系】 答案:①③④ 探究型 多维突破1.下表提供了某厂节能降耗技术改造后,生产甲产品过程中记录的产量x (单位:吨)与相应的能耗y (单位:吨标准煤)的几组对照数据(1)请画出上表数据的散点图.(2)y 与x 是否具有线性相关关系?若是,则求出y 关于x 的线性回归方程.(3)已知该厂技术改造前100吨甲产品的生产能耗为90吨标准煤,试根据(2)中求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤(参考值:5.665.4645345.23=⨯+⨯+⨯+⨯) 【知识点:散点图,相关关系,回归分析】 解:(1)略(2)由散点图可知,各数据点大致分布在一条直线的附近,故具有线性相关关系.计算得86412=∑=i ix,5.6641=∑=i i i y x ,,5.3,5.4==y x 又最小二乘法确定的线性回归方程的参数为.35.0,7.0==∧∧a b 故所求的线性回归方程为35.07.0+=∧x y .(3)由(2)中的线性回归方程及技术改造前100吨甲产品的生产能耗,得降低的生产能耗为65.1935.01007.090=+⨯-)((吨标准煤). (四)自助餐1.下面列两个变量之间呈相关关系的是( ) A.圆的面积与半径 B.球的体积与半径 C.角的度数与它的正切值D.一个考生的数学成绩与物理成绩 【知识点:相关关系】 解:D2.下列关于回归分析说法错误的是( ) A.回归分析是研究两个具有相关关系的变量的方法 B.在散点图中,解释变量在x 轴,预报变量在y 轴 C.回归模型中一定存在随机误差 D.散点图能明确反映变量间的关系 【知识点:回归分析】 解:D3.已知变量x 与y 正相关,且由观测数据算得样本平均数5.3,3==y x ,由此该观测数据算得的线性回归方程可能是( ) A.3.24.0+=∧x y B.4.2-2x y =∧ C.5.92-+=∧x y D.4.43.0-+=∧x y【知识点:回归方程,样本点中心】 解:A4.为了了解儿子身高与父亲身高的关系,随机抽取5对父子的身高数据如下则y 对于x 的线性回归方程为( )A.1+=∧x y B.1+=∧x y C.885.0+=∧x y D.12+=∧x y【知识点:回归方程】 解:C5.小李同学根据下表记录的产量x (吨)和能耗y (吨标准煤)对应的四组数据,用最小二乘法求出了y 对于x 的线性回归方程是070.35y x ∧=+.,之后不慎将一滴墨水滴于表内,表中第二行第四列的数据已经无法看清,据你判断这个数据应该是( )A.3.5B.3.75C. 4D. 4.25【知识点:回归方程,样本点中心】 解:C6.四名同学根据各自的样本数据研究变量x ,y 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y 与x 负相关且623.0-347.2x y =∧;②y 与x 负相关且648.5476.3-+=∧x y ;③y 与x 正相关且493.8437.5+=∧x y ;④y 与x 正相关且578.4-326.4-x y =∧. 其中一定不正确的结论序号是( ) A.①② B.②③ C.③④ D.①④【知识点:回归方程,正相关、负相关】 解:D7.若施化肥量x 与小麦产量y 之间的回归直线方程为x y 4250ˆ+=,当施化肥量为50kg 时,预计小麦产量为__________.解析:当50=x 时,450450250ˆ=⨯+=y . 答案:kg 450.8.年或者更少教育的百分比(x )和收入低于官方规定的贫困线人数占本地区的人数的百分比(y )的数据,建立的回归直线方程6.48.0+=∧x y ,斜率的估计值为0.8,说明__________;成年人受过9年或者更少教育的百分比(x )与收入低于官方规定的贫困线的人数占本地区人数的百分比(y )之间的相关系数__________(填“大于0”或“小于0”). 【知识点:回归方程,回归分析】解:一个地区受过9年或者更少教育的百分比每增加1%,收入低于官方规定的贫困线的人数占本地区人数的百分比将增加0.8%左右 大于0.9.对具有线性相关关系的变量x ,y 有一组观测数据),8,,2,1)(, =i y x i i (其回归直线方程是a x y +=∧31,且,6)(2821821=+++=+++y y y x x x 则实数a 的值是__________. 【知识点:回归方程,回归分析】解:8110.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:(1)求回归直线方程y bx a ∧=+,其中20-=b ,a y bx =-;(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本) 【知识点:回归方程,相关关系,回归分析】解:(1)由于x =16(x 1+x 2+x 3+x 4+x 5+x 6)=8.5,y =16(y 1+y 2+y 3+y 4+y 5+y 6)=80,所以a =y -b x =80+20×8.5=250,从而回归直线方程为y =-20x +250. (2)设工厂获得的利润为L 元,依题意得L =x (-20x +250)-4(-20x +250)=-20x 2+330x -1 000=-20(x-334)2+361.25, 当且仅当x =8.25时,L 取得最大值.故当单价定为8.25元时,工厂可获得最大利润.11. 下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图(1)由折线图看出,可用线性回归模型拟合y 与t 的关系,请用相关系数加以说明; (2)建立y 关于t 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量. 参考数据:719.32i i y ==∑,7140.17i i i t y ==∑,()7210.55i i y y=-=∑,7≈2.646.参考公式:相关系数1221t)(y y)(t t)(y y)niii niii r ==--=--∑∑回归方程 中斜率和截距的最小二乘估计公式分别为: 121(t t)(y y)(t t)niii ni i b ∧==--=-∑∑,a y b t =-【知识点:回归方程,相关关系,回归分析】 解:(1)由折线图这数据和附注中参考数据得4=t ,28)(712=-∑=i i t t ,55.0)(712=-∑=i iy y,89.232.9417.40))((717171=⨯-=-=--∑∑∑===i i i iii i iy t yt y y t t,99.0646.2255.089.2≈⨯⨯≈r .因为y 与t 的相关系数近似为0.99,说明y 与t 的线性相关相当高,从而可以用线性回归模型拟合y 与t 的关系.(2)由9.321.3317y =≈及(1)得7121()()2.890.10328()iii ni i t t y y b t t ∧==--==≈-∑∑, 92.04103.0331.1ˆˆ≈⨯-≈-=t b y a .所以,y 关于t 的回归方程为:t y10.092.0ˆ+=. 将2016年对应的9=t 代入回归方程得:82.1910.092.0ˆ=⨯+=y. 所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.。
人教课标版高中数学选修2-3《回归分析基本思想及其初步应用(第3课时)》教学设计

3.1 回归分析基本思想及其初步应用第三课时一、教学目标 1.核心素养:通过学习回归分析的基本思想及其初步应用,初步形成基本的数据分析能力. 2.学习目标(1)1.1.3.1 温习线性回归模型,.理解建立回归模型的基本步骤.(2)1.1.3.2 通过非线性回归分析,能将非线性回归模型转化为线性回归模型. (3)1.1.3.3 通过非线性回归分析,判断几种不同模型的拟合程度. 3.学习重点通过非线性回归分析,能将非线性回归模型转化为线性回归模型. 4.学习难点通过非线性回归分析,判断几种不同模型的拟合程度 二、教学设计 (一)课前设计 1.预习任务 任务1阅读教材P 6-P 8,思考在回归分析中,建立回归模型的基本步骤是什么? 任务2当两个变量不呈线性相关关系时,如何建立回归模型?2.预习自测 1.有下列数据:下列四个函数中,模拟效果最好的为( ) A.132x y -=⨯ B.2log y x = C.3y x =解:A2.已知回归方程ˆ21y x =+,而试验得到一组数据是(2,4.9),(3,7.1),(4,9.1),则残差平方和是( ) A.0.01 B.0.02 C.0.03 D.0.04 解:C(二)课堂设计 1.知识回顾(1)线性回归方程:∧∧∧+=a x b y ,其中.1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx∧====---==--∑∑∑∑,a ∧=x b ∧-y(2)线性回归模型:y =bx +a +e 其中a 和b 为模型的未知参数,e 称为随机误差. (3)数据点和它在回归直线上相应位置的差异是随机误差的效应,称(1,2,3,n)i i e y y i ∧∧=-=…,为残差.由y i i b x a ∧∧∧=+,得i i i e y b x a ∧∧∧=--(1,2,3,)i n =…,.(4)相关系指数: ∑∑==∧---=n i ini iy yy yR 12122)((1)(5)2R 是刻画回归效果的量,除了表示回归模型的拟合效果,也表示解释变量和预报变量的线性相关关系(在线性回归模型中).2R 越大,说明残差平方和越小,模型的拟合效果越好,在线性回归模型中,2R 越接近于1,回归的效果越好(因为2R 越接近于1,表示解释变量和预报变量的线性相关性越强) 2.问题探究问题探究一 建立回归模型的基本步骤是什么?●活动一 归纳提升,总结一般方法例1 某城区为研究城镇居民月家庭人均生活费支出和月人均收入的相关关系,随机抽取10户进行调查,其结果如下:月人均收入x/元300 390 420 520 570 700 760 800 850 1080 月人均生活费y/元255 324 335 360 450 520 580 600 630 750 试预测人均月收入为1100元和人均月收入为1200元的两个家庭的月人均生活费.【知识点:线性回归,线性相关关系】详解:作出散点分布图如图,由图可知,月人均生活费与人均收入之间具有线性相关关系. 通过计算可知4.480,639==yx,46103001012=∑=iix,25405261012=∑=iiy,3417560101=∑=iiiyx,所以10110221100.6599.10i iiiix y x ybx x∧==-=≈-∑∑751.58≈-=∧∧xbya,所以回归直线方程为.751.586599.0^+=xy计算相关系数得r=0.993136,故月人均收入与月人均生活费之间具有显著相关关系.作残差图如图,由图可知,残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适.计算相关指数得2R=0.9863,说明城镇居民的月人均生活费的差异有98.63%是由月人均收入引起的.由以上分析可知,我们可以利用回归方程ˆ0.659958.751.=+来作为月生活费的预报值.y x将x=1100代入回归方程得y=784.59元;将x=1200代入回归方程得y=850.58元.故预测月人均收入分别为1100元和1200元的两家庭的月人均生活费分别为784.59元和850.58元.点拨:建立回归模型的基本步骤(1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量.(2)画出解释变量和预报变量的散点图,观察它们之间的关系(是否存在线性关系等). (3)由经验确定回归方程的类型(如果我们观察到诗句呈线性关系,则选用线性回归方程). (4)按一定的规则(如最小二乘法)估计回归方程中的参数.(5)得出结论后分析残差图是否有异常(如个别数据对应的残差绝对值过大,残差呈现不随机的规律性等),若存在异常,则检查数据是否有误或模型是否合适等.问题探究二若两变量为非线性相关关系,如何建立回归模型?●活动一整合旧知,发现新问题当两个变量呈线性相关关系时,我们通过模拟线性回归模型,用回归分析的基本思想对两个变量进行研究.若当有些变量间的关系并不是线性相关,怎样确定回归模型?例2 一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据列于下表中,试建立y与x之间的回归方程.【知识点:线性回归,线性相关关系】详解:根据收集数据,作散点图:●活动二 观察发现,寻找新模型样本点并没有分布在某个带状区域内,因此两个变量不呈线性相关关系,即不能直接用线性回归方程来建立两个变量之间的关系.怎样确定回归模型?首先要作出散点图,如果散点图中的样本点并没有分布在某个带状区域内,则两个变量不呈现线性相关关系,不能直接利用回归方程来建立两个变量之间的关系,根据已有的函数知识,观察样本点是否呈指数函数关系或二次函数关系,选定适当的回归模型.根据已有的函数知识,从散点图中可以看到样本点分布在某一条指数函数曲线x c e c y 21=的周围.●活动三 非线性转化为线性问题如果两个变量呈现非线性相关关系,怎样求出回归方程?可以通过对解释变量进行变换,如对数变换或平方变换,先得到另外两个变量间的回归方程,再得到所求两个变量的回归方程.现在,我们通过对数变换把指数关系变为线性关系,即对x c e c y 21=两边取自然对数()22111212ln ln ln ln ln ln ln ln c x c x y c e c e c c x e c c e x ==+=+=+令y z ln =,建立z 与x 之间的线性回归方程x c c z 21ln +=12ln a c b c z a bx ===+令,,即分析x 与z 之间的关系,通过画散点图(如下图),可知x 与z 之间是存在着线性回归关系,可以用最小二乘法求出线性回归方程z=a+bx.由表1的数据可以得到变换后的样本数据表x21 23 25 27 29 32 35z 1.946 2.398 3.045 3.178 4.190 4.745 5.784列表计算出各个量编号 1 2 3 4 5 6 7 合计温度x/°C21 23 25 27 29 32 35 192 产卵数y/个7 11 21 24 66 115 325 569 z=ln y 1.946 2.398 3.045 3.178 4.190 4.745 5.784 25.285 x i2441 529 625 729 841 1024 1225 5414 x i z i40.9 55.2 76.1 85.8 121.5 151.8 202.4 733.7=x27.429 =z 3.612∑==niix125414 ∑==niyiyx1733.71272.043.277541461.343.2777.733ˆ22121=⨯-⨯⨯-=--=∑∑==x n xzx n zx bni ini i i 843.3ˆˆ-=⋅-=x b z a843.3272.0ˆ-=x z0.272 3.843ˆˆln ln 0.272 3.843.x z y yx y e -==-=因为,所以,即 问题探究三 能否用其它模型来拟合上述问题?如何判断各种的模型的拟合效果?●活动一 二次曲线模型样本点还可以看作是分布在二次函数曲线221c x c y +=的周围.2t x =令,建立y 与t 之间的线性回归方程21c t c y +=12b c a c y a bt ===+令,,即.分析y 与t 之间的关系,通过画散点图(如下图),可看到y 与t 的散点图并不分布在一条直线的周围,即不宜用线性回归方程来拟合它,即不宜用二次曲线221c x c y +=来拟合y 与x 之间的关系,这个结论还可以用残差分析得到. ●活动二 对比提升为比较两个不同模型的残差,需建立相应的回归模型,用线性回归模型拟合回归方程bt a y +=.0.367-202.543=--=∑∑==2121ˆzn x z x n z x bni ii i i =-=x b z aˆˆ所以543.202367.0-=t y2t x =因为,即y 关于x 的二次回归方程为543.202367.02-=x y .●活动三 残差分析指数回归模型与二次回归模型中哪个能更好地刻画红铃虫的产卵数y 与温度x 的关系?通过什么数据说明?一般在参数个数一定的条件下,相关指数越大或残差平方和越小说明模型拟合得越好.计算每个模型的相关指数,并进行模型的比较.指数函数模型的相关指数i yˆi i i y y e ˆ-=()2ˆˆy y e -=()()98.0ˆ112122=---=∑∑==ni ini ii y yy y R二次函数模型的相关指数从相关指数的计算结果来看,指数函数模型的2R比二次函数模型的2R更接近于1,所以指数函数模型的回归效果好.再从残差图看:从图中可看出指数函数模型的残差点比较均匀地落在水平的带状域中,所以指数函数模型拟合精度较二次函数模型的高.点拨:归纳判断模型拟合效果的方法:(1)可以通过变换后的散点图观察两个新变量之间是否存在线性回归方程;(2)通过残差分析比较两种模型的拟合效果.一般情况下,比较两个模型的残差比较困难(某些样本点上一个模型的残差的绝对值比另一个模型的小,而另一些样本点的情况则相反),故通过比较两个模型的残差的平方和的大小来判断模型的拟合效果.残差平方和越小的模型,拟合的效果越好.3.课堂总结【知识梳理】(1)建立回归模型的基本步骤①确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量.②画出解释变量和预报变量的散点图,观察它们之间的关系(是否存在线性关系等).③由经验确定回归方程的类型(如果我们观察到诗句呈线性关系,则选用线性回归方程).④按一定的规则(如最小二乘法)估计回归方程中的参数.⑤得出结论后分析残差图是否有异常(如个别数据对应的残差绝对值过大,残差呈现不随机的规律性等),若存在异常,则检查数据是否有误或模型是否合适等.(2)归纳判断模型拟合效果的方法:①可以通过变换后的散点图观察两个新变量之间是否存在线性回归方程;②通过残差分析比较两种模型的拟合效果.一般情况下,比较两个模型的残差比较困难(某些样本点上一个模型的残差的绝对值比另一个模型的小,而另一些样本点的情况则相反),故通过比较两个模型的残差的平方和的大小来判断模型的拟合效果.残差平方和越小的模型,拟合的效果越好.【重难点突破】(1)如果两个变量不呈现线性相关关系,常见的两个变量间的关系还有指数函数关系、二次函数关系.(2)两个变量间的非线性关系可以通过对解释变量的变换(对数变换、平方变换等)转化为另外两个变量的线性关系.(3)比较不同模型的拟合效果,可以通过残差平方和的大小,相关指数的大小来判断.4.随堂检测1.变量x,y的散点图如图所示,那么x,y之间的样本相关系数r最接近的值为()A.1B.-0.5C.0D.0.5答案:C解析:【知识点:线性回归,线性相关关系】2.某学校开展研究性学习活动,某同学获得一组实验数据如下表:x 1.9934 5.1 6.12y 1.5 4.047.51218.01对于表中数据,现给出下列拟合曲线,其中拟合程度最好的是( ) A.y =2x -2 B.y =(12)x C.y =log 2x D.y =12(x 2-1)【知识点:线性回归,线性相关关系】解:D4.已知方程y ^=0.85x -82.71是根据女大学生的身高预报她的体重的回归方程,其中x 的单位是cm ,y ^的单位是kg ,那么针对某个体(160,53)的残差是( ) A.-0.29 B.0.29 C.-0.58 D.3【知识点:线性回归,线性相关关系】解:A5.在研究两个变量的相关关系时,观察散点图发现样本点集中于某一条指数曲线bx a y e +=的周围,令ln z y =,求得线性回归方程为 ˆz=0.25x -2.58,则该模型的回归方程为________. 【知识点:线性回归,线性相关关系】解:0.25 2.58x y e -= ∵ z =0.25x -2.58,z =ln y ,∴0.25 2.58x y e -= (三)课后作业基础型 自主突破1.两个变量有线性相关关系且残差的平方和等于0,则( ) A.样本点都在回归直线上 B.样本点都集中在回归直线附近 C.样本点比较分散 D.不存在规律【知识点:线性回归,线性相关关系】解:A2.散点图在回归分析中的作用是( )A.查找个体个数B.比较个体数据大小关系C.探究个体分类D.粗略判断变量是否相关【知识点:线性回归,线性相关关系】解:D3.为了考察两个变量x 和y 之间的线性相关性,甲、乙两位同学各自独立地做了100次和150次试验,并且利用线性回归方法,求得回归直线分别为l 1和l 2.已知两个人在试验中发现对变量x的观测数据的平均值都是s,对变量y 的观测数据的平均值都是t,那么下列说法正确的是( ). A.l 1和l 2有交点(s,t )B.l 1与l 2相交,但交点不一定是(s,t )C.l 1与l 2必定平行D.l 1与l 2必定重合【知识点:线性回归,线性相关关系】 解:A 都过样本中心点(s,t ),但斜率不确定.4.甲、乙、丙、丁四位同学各自对A ,B 两变量做回归分析,分别得到散点图与残差平方和21ˆ()niii y y=-∑如下表甲乙丙丁散点图残差平方和115106124103A.甲B.乙C.丙D.丁【知识点:线性回归,线性相关关系】解:D5.在研究气温和热茶销售杯数的关系时,若求得相关指数R 2≈________,表明“气温解释了85%的热茶销售杯数变化”或者说“热茶销售杯数差异有85%是由气温引起的”. 【知识点:线性回归,线性相关关系】解:0.85 能力型 师生共研6.若一函数模型为)0(2≠++=a c bx ax y ,为将y 转化为关于t 的线性回归方程,则需作的变换t =( ) A.2x B.2)(a x + C.2)2(ab x +D.以上都不对【知识点:线性回归,线性相关关系】答案:C解析:y 关于t 的线性回归方程,实际上就是y 关于t 的一次函数,又因为224()24b ac b y a x a a-=++7.某学生在高三学年最近九次考试中的数学成绩加下表:设回归直线方程y =bx +a ,则点(a ,b )在直线x +5y ﹣10=0的( ) A.左上方 B.左下方 C.右上方 D.右下方【知识点:线性回归,线性相关关系】解:C8. 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:经检验,这组样本数据具有线性相关关系,那么对于加工零件的个数x 与加工时间y 这两个变量,下列判断正确的是( )A.成正相关,其回归直线经过点(30,75)B.成正相关,其回归直线经过点(30,76)C.成负相关,其回归直线经过点(30,76)D.成负相关,其回归直线经过点(30,75) 【知识点:线性回归,线性相关关系】解:B探究型 多维突破9.下表提供了甲产品的产量x (吨)与利润y (万元)的几组对照数据.(1)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆˆybx a =+; (2)计算相关指数2R 的值,并判断线性模型拟合的效果.参考公式:1122211()()ˆˆˆ,()n niii ii i nniii i x x y y x y nx ybay bx x x xnx====---===---∑∑∑∑,22121ˆ()1()niii nii y yR y y ==-=--∑∑【知识点:线性回归方程的算法;,回归方程的应用】 (1) 4.5, 3.5x y ==∴224 4.5 3.563,4 4.581nx y nx ⋅=⨯⨯==⨯=,17.512202766.5ni i i x y ==+++=∑,21916253686ni i x ==+++=∑∴122166.563ˆ0.78681ni ii ni i x y nx ybx nx==--===--∑∑,∴ˆˆ 3.50.7 4.50.35a y bx =-=-⨯= ∴y 关于x 的线性回归方程ˆ0.70.35yx =+(2)222221()(2.5 3.5)(3 3.5)(4 3.5)(4.5 3.5) 2.5ni i y y =-=-+-+--=∑222221ˆ()(2.5 2.45)(3 3.15)(4 3.85)(4.5 4.55)0.05niii y y=-=-+-+--=∑∴22121ˆ()0.05110.982.5()niii nii y yR y y ==-=-=-=-∑∑∴线性模型拟合的效果较好 10.某公司采用众筹的方式募集资金,开发一种创新科技产品,为了解募集资金x (单位:万元)与收益率y 之间的关系,对近6个季度筹到的资金i x 和收益率1y 的数据进行统计,得到如下数据表:(1)通过绘制并观察散点图的分布特征后,分别选用y a bx =+与lg y c d x =+作为众筹到的资金x 与收益率y 的拟合方式,再经过计算,得到这两种拟合方式的回归方0.340.02,0.27 1.47lg y x y x ===-+和下表统计数值,试运用相关指数比较以上两回归方程的拟合效果;(2)根据以上拟合效果较好的回归方程,解答:预测众筹资金为5万元时的收益率.(精确到0.0001)【知识点:线性回归,线性相关关系】解:(1)由已知,得对于方程0.340.02y x =+,相关指数20.1310.1330.15R =-≈;对于方程0.27 1.47lg y x =-+,相关指数20.0110.9330.1330.15R =-≈>,所以方程0.27 1.47lg y x =-+的拟合效果更好. (2)当5x =时,0.27 1.47lg 50.7575y =-+≈;(四)自助餐1.变量x 与y 之间的回归方程表示( ) A.x 与y 之间的函数关系 B.x 与y 之间的不确定性关系 C.x 与y 之间的真实关系形式D.x 与y 之间的真实关系达到最大限度的吻合 【知识点:线性回归,线性相关关系】解:D2.已知回归方程ˆ21y x =+,而试验得到一组数据是(2,4.9),(3,7.1),(4,9.1),则残差平方和是( ) A.0.01 B.0.02 C.0.03 D.0.04【知识点:线性回归,线性相关关系】解:C3.一台机器由于使用时间较长,但还可以使用,它按不同的转速生产出来的某机器零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,下表是抽样试验结果:若实际生产中,允许每小时的产品中有缺点的零件数最多为10个,那么机器的转速应该控制所在的范围是( ) A.10转/s 以下 B.15转/s 以下 C.20转/s 以下 D.25转/s 以下【知识点:线性回归,线性相关关系】解:B4.已知x,y 的取值如下表:y 2.2 4.3 4.8 6.7若x,y 具有线性相关关系,且回归方程为=0.95x +a,则a 的值为( ) A.0.325 B.2.6 C.2.2 D.0【知识点:线性回归,线性相关关系】解:B 由已知得x =2,y =4.5,而回归方程过点(,)x y ,则4.5=0.95×2+a,∴a =2.6.5.某工厂为了新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据: 单位x (元) 4 5 6 7 8 9 销量y (件)908483807568线左下方的概率为( ) A.16 B.13 C.12 D.23【知识点:线性回归,线性相关关系】解:B6.某企业对自己的拳头产品的销售价格(单位:元)与月销售量(单位:万件)进行调查,其中最近五个月的统计数据如下表所示: 价格x 9 9.5m 10.5 11 销售量y11n865==++-=∧n n m x y 则且,20,402.3( ) A.10B.5C.13D.2【知识点:线性回归,线性相关关系】解:A7.以下四个命题,其中正确的序号是________.①从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;②两个随机变量相关性越强,则相关系数的绝对值越接近于1;③在线性回归方程ˆ0.212yx =+中,当解释变量x 每增加一个单位时,预报变量ˆy 平均增加0.2个单位;④对分类变量X 与Y 的随机变量K 2的观测值k 来说,k 越小,“X 与Y 有关系”的把握程度越大.【知识点:线性回归,线性相关关系】解:②③ ①是系统抽样;对于④,随机变量K 2的观测值k 越小,说明两个相关变量有关系的把握程度越小.8.对具有线性相关关系的变量x ,y 有一组观测数据(x i ,y i )(i =1,2,…,8),其线性回归方程是1ˆˆ3yx a=+,且x 1+x 2+x 3+…+x 8=2(y 1+y 2+y 3+…+y 8)=6,则实数ˆa 的值是________. 【知识点:线性回归,线性相关关系】答案:1ˆ8a = 解析:依题意可知样本点的中心为⎝ ⎛⎭⎪⎫34,38,则313ˆ834a=⨯+,解得1ˆ8a =. 9.某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与医院抄录了1至6月份每月10日的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:该兴趣小组确定的研究方案是:先从这六组数据中选举2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.(1)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y 关于x 的线性回归方程ˆybx a =+; (2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?(参考公式:^1122211()()()()nniiiii i nniii i x ynx yx x yy b xn x x x ====---==--∑∑∑∑^^^a yb x =-)【知识点:线性回归,线性相关关系】解:(1)由数据求得11,24x y ==,由公式求得187b =,307a y bx ∴=-=-.所以回归方程是1830ˆ77yx =-. (2)当10x =时,150150ˆ,22277y=-<;同样,当6x =时,7878ˆ,12277y =-<,所以,该小组所得线性回归方程是理想的.10. 某种书每册的成本费y (元)与印刷册数x (千册)有关,经统计得到数据如下:检验每册书的成本费y 与印刷册数的倒数x之间是否具有线性相关关系?如有,求出y 对x 的线性回归方程.【知识点:线性回归,线性相关关系】解:把x 1置换为z ,则有x z 1=可作出散点图,从图可看出,变换后的样本点分布在一条直线的附近,因此可以用线性回归方程来拟合.z =110×(1+0.5+0.333+0.2+0.1+0.05+0.033+0.02+0.01+0.005)=0.2251,y =110×(10.15+5.52+4.08+…+1.15)=3.14, ∑=1012i iz=12+0.52+0.3332+…+0.012+0.0052≈1.415,∑=1012i iy=10.152+5.522+…+1.212+1.152=171.803,∑=101i ii yz =1×10.15+0.5×5.52+…+0.005×1.15=15.221 02,所以,75.09998.0>≈r 具有线性相关关系. 所以8.976b ∧≈,∧a =3.14-8.976×0.2251≈1.120, 所以所求的z 与y 的线性回归方程为 8.976 1.120y z ∧=+.又因为x z 1=,所以 8.976 1.120y x∧=+.数学视野二战后期,美国空军对德国和日本法西斯展开了大规模战略轰炸,美国空军自己也损失惨重.美国空军对此十分头疼.如果要降低损失,就要往飞机上焊防弹钢板,但如果整个飞机都焊上钢板,速度、航程、载弹量等都要受到影响.怎么办?美国空军请来数学家亚伯拉罕沃尔德.亚伯拉罕沃尔德在一张大白纸上画出了飞机的轮廓,再把返回的飞机上的弹洞的位置标出.观察图形,可以看出飞机几乎浑身上下都是窟窿,只有飞行员坐舱和尾翼两个地方几乎是空白.飞行员们一看就明白了:如果座舱中弹,飞行员就牺牲了:如果尾翼中弹,飞机失去平衡就要坠落.这两处如果中弹,飞行员很可能牺牲,因此只需要给这两个部位焊上钢板即可.数学家亚伯拉罕沃尔德灵活地运用了统计的思想,做出了如此睿智的结论.。
高中数学人教A版 选修2-3 3.1.2回归分析的基本思想及其初步应用 教案

3.1回归分析的基本思想及其初步应用(2课时)一、教学目标(一)必备知识:能根据散点分布特点,建立不同的回归模型(二)关键能力:知道有些非线性模型通过变换可以转化为线性回归模型;通过散点图及相关指数比较不同模型的拟合效果.(三)学科素养通过学科教育能给学生终身发展数学运算、数学建模和数据分析的能力。
(四)核心价值:让学生探索、发现数学知识和掌握数学知识的内在规律的过程中不,不断获得成功积累愉快的体验,不断增进学习数学的兴趣,同时还通过探索这一活动培养学生善于和他人合作的精神.二、生情分析:本节课是学生在必修模块《数学3》概率统计知识的基础上,进一步学习用统计方法解决实际问题,主要是通过对典型案例的讨论、解决,让学生初步了解独立性检验的基本思想和操作步骤,认识统计方法在决策中的作用,体验数学的科学价值、应用价值和文化价值.三、过程方法:通过将非线性模型转化为线性回归模型,使学生体会“转化”的思想;让学生经历数据处理的过程,培养他们对数据的直观感觉,体会统计方法的特点,认识统计方法的应用;通过使用转化后的数据,利用计算器求相关指数,使学生体会使用计算器处理数据的方法.四、重点难点:重点:通过探究使学生体会有些非线性模型运用等量变换、对数变换可以转化为线性回归模型;难点:如何启发学生“对变量作适当的变换(等量变换、对数变换)”,变非线性为线性,建立线性回归模型.五、教学用具:黑板、粉笔、多媒体;六、教学课时:1课时七、设计思路:教学模式:本课采用“探究——发现”教学模式.教师的教法:利用多媒体辅助教学,突出活动的组织设计与方法的引导.“抓三线”,即(一)知识技能线(二)过程与方法线(三)能力线.“抓两点”,即一抓学生情感和思维的兴奋点,二抓知识的切入点.学法:突出探究、发现与交流.八、教学过程 (一)创设问题情境我国是世界产棉大国,种植棉花是我国很多地区农民的主要经济来源,在棉花的种植过程中,病虫害的防治是棉农的一项重要任务,如果处置不当就会造成棉花的减产.其中红铃虫就是危害棉花生长的一种常见害虫,在1953年,我国18省曾发生红铃虫大灾害,受灾面积300万公顷,损失皮棉约二十万吨.如图就是红铃虫的有关图片:红铃虫喜高温高湿,适宜各虫态发育的温度为25~32 ℃,相对湿度为80%~100%,低于20 ℃和高于35 ℃卵不能孵化,相对湿度60%以下成虫不产卵.冬季月平均气温低于-4.8 ℃时,红铃虫就不能越冬而被冻死.为采取有效防治方法,有必要研究红铃虫的产卵数和温度之间的关系.现收集了红铃虫的产卵数y 和温度x 之间的7组观测数据列于下表:(1)试建立y 与x 之间的回归方程;并预测温度为28 ℃时产卵的数目. (2)你所建立的模型中温度在多大程度上解释了产卵数的变化? 学生活动:类比前面所学过的建立线性回归模型的步骤,动手实施. 活动结果:(1)画散点图:通过计算器求得线性回归方程:y ^=19.87x -463.73.当x =28 ℃时,y ^=19.87×28-463.73≈93,即温度为28 ℃时,产卵数大约为93. (2)进行回归分析计算得: R 2≈0.746 4,即这个线性回归模型中温度解释了74.64%产卵数的变化.设计目的:通过背景材料,加深学生对问题的理解,并明白“为什么要学”.体会问题产生于生活,并通过问题的解决复习建立回归模型的基本步骤.(二)探究新知提出问题:结合数据可以发现,随着自变量的增加,因变量也随之增加,气温为28 ℃时,估计产卵数应该低于66个,但是从推算的结果来看93个比66个却多了27个,是什么原因造成的呢?学生活动:分组合作讨论交流.学情预测:由于我们所建立的线性回归模型的相关指数约等于0.746 4,即解释变量仅能解释预报变量大约74.64%的变化,所占比例偏小.这样根据我们建立的模型进行预报,会存在较大的误差.我们还可以从残差图上分析一下我们所建立的回归模型的拟合效果:残差数据表:画出残差图根据残差图可以发现,残差点分布的带状区域较宽,并不集中,这表明我们所建立的回归模型拟合效果并不理想.之所以造成预报值偏差太大的原因是所选模型并不理想.实际上根据散点图也可以发现,样本点并没有很好地集中在一条直线附近,故变量之间不会存在很强的线性相关性.设计目的:引导学生对结果进行分析,从而发现存在的问题,激发好奇心、求知欲.同时培养学生对问题的洞悉能力,增强对结果的敏感自检能力.理解新知提出问题:如何选择合适的回归模型进行预测呢?学生活动:学生讨论,教师合理引导学生观察图象特征,联想学过的基本函数.学情预测:方案一:建立二次函数模型y=bx2+a.方案二:建立指数函数模型y=c1ac2x.提出问题:如何求出所建立的回归模型的系数呢?我们不妨尝试解决方案一中的系数.学生活动:分组合作,教师引导学生观察y=bx2+a与y=bx+a的关系.学情预测:通过比较,发现可利用t=x2,将y=bx2+a(二次函数)转化成y=bt+a(一次函数).求出x ,t ,y 间的数据转换表:利用计算器计算出y 和t 的线性回归方程:y ^=0.367t -202.54, 转换回y 和x 的模型:y ^=0.367x 2-202.54.当x =28 ℃时,y ^=0.367×282-202.54≈85,即温度为28 ℃时,产卵数大约为85. 计算相关指数R 2≈0.802,这个回归模型中温度解释了80.2%产卵数的变化. 提出问题:提出问题“如果选用指数模型,是否也能转换成线性模型,如何转化?” 学生活动:独立思考也可相互讨论.教师可启发学生思考“幂指数中的自变量如何转化为自变量的一次幂?”可引导学生回忆对数的运算性质以及指对数关系.学情预测:可利用取对数的方法,即在y =c 1ac 2x 两边取对数,得log a y =c 2x +log a c 1.提出问题:在上面的运算中,由于底数a 不确定,对于x 的值无法求出相应的log a y ,这时可取a =10时的情况,以便利用计算器进行计算,试求出回归模型.学生活动:合作协作,讨论解决. 学情预测:建立数据转换表:根据数据,可求得变量z 关于x 的回归方程:z ^=0.118x -1.665. 转换回y 和x 的模型:y ^=100.118x-1.665.当x =28 ℃时,y ^≈44,即温度为28 ℃时,产卵数大约为44.计算相关指数R 2≈0.985,这个回归模型中温度解释了98.5%产卵数的变化.提出问题:试选择合适的方法,比较方案一和方案二在数据拟合程度上的效果有什么不同? 学生活动:独立思考也可相互讨论,教师加以适当的引导提示. 活动结果:无论从图形上直观观察,还是从数据上分析,指数函数模型都是更好的模型.设计目的:引导学生进行不同模型的比较,体会“虽然任意两个变量的观测数据都可以用线性回归模型来拟合,但不能保证这种模型对数据的拟合效果最好,为更好地刻画两个变量之间的关系,要根据观测数据的特点来选择回归模型”.提出问题:由上面的分析可以看出,回归模型不一定是线性回归模型,对于非线性回归模型,我们的处理方法是什么?学生活动:独立思考,回顾上面的解决过程.学情预测:选用非线性回归模型时,一般思路是转化成线性回归模型,往往要用“等量变换、对数变换”等方法.设计目的:让学生整理建立非线性回归模型的思路.(三)应用巩固例1为了研究某种细菌繁殖个数y与时间x的关系,收集数据如下:试建立y与x之间的回归方程.思路分析:先画出散点图,根据散点图确定回归模型的类型,然后求y与x之间的回归方程.解:根据上表中的数据,作出散点图由图可以看出,样本点分布在某指数函数曲线y=c1ec2x的周围,于是令z=lny,则上表变换后如下:作出散点图从图中可以看出,变换后的样本点分布在某条直线附近,因此可用线性回归模型来拟合. 由表中数据可得,z 与x 之间的线性回归方程为z ^=0.69x +1.112, 则y 与x 之间的回归方程为y ^=e 0.69x+1.112.例2混凝土的抗压强度X 较易测定,其抗弯强度Y 不易测定,已知X 与Y 由关系式Y =AX b 表示,工程中希望由X 估算出Y ,以便应用.现测得一批对应数据如下:试求Y 对X 的回归方程.思路分析:题目中已经给出回归模型为Y =AX b 类型,故只要通过适当的变量置换把非线性回归方程转化为线性回归方程,然后再套用线性回归分析的解题步骤即可.解:对Y =AX b 两边取自然对数得:lnY =blnX +lnA ,做变换y =lnY ,x =lnX ,a =lnA ,则上述数据对应表格如下:根据公式可求得y ^=0.64x +0.017 2,则Y ^=e 0.64lnx +0.017 2=1.02X 0.64.变式1:若X 与Y 的关系由关系式Y ^=β^X b+α^表示,试根据给出的数据求Y 对X 的回归方程.活动设计:学生分组讨论,尝试解决. 活动成果:Y ^=0.086X +13.005.变式2:试选择合适的方法比较上述两种回归模型,相对于给出的数据哪一个的拟合效果更好? 活动成果:计算残差平方和与相关指数,对于模型Y =AX b,残差平方和Q ^(1)=9.819,相关指数R 21=0.930 4;对于模型Y ^=β^X b +α^,残差平方和Q ^(2)=12.306,相关指数R 22=0.908,故模型Y =AX b 的拟合效果较好.设计意图:熟悉判断回归模型拟合效果的方法. (四)达标检测1.相关指数R 2,残差平方和与模型拟合效果之间的关系是( ) A .R 2的值越大,残差的平方和越大,拟合效果越好 B .R 2的值越小,残差的平方和越大,拟合效果越好 C .R 2的值越大,残差的平方和越小,拟合效果越好 D .以上说法都不正确2.如果散点图的所有点都在一条直线上,则残差均为____________________,残差平方和为__________,相关指数为______________.答案:1.C 2.0 0 13.某种书每册的成本费Y 元与印刷册数x(千册)有关,经统计得到数据如下:检验每册书的成本费Y 元与印刷册数的倒数1x 之间是否有线性相关关系,如有,求出Y 对1x 的回归方程.解:把1x 置换为z ,则z =1x,从而z 与Y 的数据为:根据数据可得r≈0.999 8>0.75,故z 与Y 具有很强的线性相关关系. 所以b ^≈8.976,a ^≈1.120,从而y ^=8.976z +1.120.又z =1x ,所以y ^ =8.976x+1.120.(五)、小结1.数学知识:建立回归模型及残差图分析的基本步骤;非线性模型向线性模型的转换方法;不同模型拟合效果的比较方法:相关指数和残差的分析. 2.数学思想:数形结合的思想,化归思想及整体思想. 3.数学方法:数形结合法,转化法,换元法. (六)、作业 1.课时检测九、课后记本课时内容教材中只安排了一道关于“红铃虫”的例题,但是它却代表了一种“回归分析”的类型.如何利用这道例题使学生掌握这类问题的解决方法呢?为此,本课时设计了“引导发现、合作探究”的教学方法.首先展示“红铃虫”的背景资料来激发学生的学习兴趣;鼓励学生用已有知识解决问题,引导学生检查结果从而发现新问题;通过分组合作来对不同方案进行探索;使学生在合作探索的过程中体会“选择模型——将非线性转化成线性”的方法,体会“化未知为已知、用已知探索未知”思想,同时认识不同模型的效果.培养学生观察、类比联想以及分析问题的能力.在教学过程中让学生自主探索、动手实践,养成独立思考、积极探索的习惯.在“选模型”这个环节中,注意引导学生将散点分布和已学函数图象进行比较,从而发现二次函数和指数函数模型.在“转化”这个环节中,通过引导学生观察所选模型,联系已学知识选择“等量变换或对数变换”,从而找到转化的途径.在运算过程中,如求“相关指数”引导学生使用转化后的数据,利用计算器求其相关系数即为相关指数,使学生体会使用计算器处理数据的方法和技能.。
【最新】高中数学人教A版选修2-3教学案:3.1回归分析的基本思想及其初步应用-含解析

回归分析的基本思想及其初步应用预习课本P80~89,思考并完成以下问题1.什么是回归分析?2.什么是线性回归模型?3.求线性回归方程的步骤是什么?[新知初探]1.回归分析(1)回归分析 回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.(2)回归方程的相关计算对于两个具有线性相关关系的变量的一组数据(x 1,y 1),(x 2,y 2),…,(x n ,y n ).设其回归直线方程为y ^=b ^x +a ^,其中a ^,b ^是待定参数,由最小二乘法得b ^=∑i =1n (x i -x )(y i -y )∑i =1n (x i -x )2=∑i =1n x i y i -nx y∑i =1n x 2i -n x 2, a ^=y -b ^x .(3)线性回归模型线性回归模型⎩⎪⎨⎪⎧y =bx +a +e ,E (e )=0,D (e )=σ2,其中a ,b 为模型的未知参数,通常e 为随机变量,称为随机误差.x 称为解释变量,y 称为预报变量.[点睛] 对线性回归模型的三点说明(1)非确定性关系:线性回归模型y =bx +a +e 与确定性函数y =a +bx 相比,它表示y与x 之间是统计相关关系(非确定性关系),其中的随机误差e 提供了选择模型的准则以及在模型合理的情况下探求最佳估计值a ,b 的工具.(2)线性回归方程y ^=b ^x +a ^中a ^,b ^的意义是:以a ^为基数,x 每增加1个单位,y 相应地平均增加b ^个单位.2.线性回归分析(1)残差:对于样本点(x i ,y i )(i =1,2,…,n )的随机误差的估计值 e ^i =y i -y ^i 称为相应于点(x i ,y i )的残差,∑i =1n(y i -y ^i )2称为残差平方和.(2)残差图:利用图形来分析残差特性,作图时纵坐标为残差, 横坐标可以选为样本编号,或身高数据,或体重的估计值等,这样作出的图形称为残差图.(3)R 2=1-∑i =1n (y i -y ^i )2∑i =1n (y i -y )2越接近1,表示回归的效果越好.[小试身手]1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)(1)残差平方和越小, 线性回归方程的拟合效果越好.( )(2)在画两个变量的散点图时, 预报变量在x 轴上,解释变量在y 轴上.( )(3)R 2越小, 线性回归方程的拟合效果越好.( )答案:(1)√ (2)× (3)×2.从散点图上看,点散布在从左下角到右上角的区域内, 两个变量的这种相关关系称为________.答案:正相关3.在残差分析中, 残差图的纵坐标为________.答案:残差4.如果发现散点图中所有的样本点都在一条直线上, 则残差平方和等于________, 解释变量和预报变量之间的相关系数等于________.答案:0 1或-1[典例] 某研究机构对高三学生的记忆力x 和判断力y 进行统计分析,得下表数据。
人教版高中数学选修2-3第三章统计案例3.1回归分析的基本思想及其初步应用教案6
§3.1 独立性检验(1)教学目标(1)通过对典型案例的探究,了解独立性检验(只要求22⨯列联表)的基本思想、方法及初步应用;(2)经历由实际问题建立数学模型的过程,体会其基本方法.教学重点、难点:独立性检验的基本方法是重点.基本思想的领会及方法应用是难点.教学过程一.问题情境5月31日是世界无烟日。
有关医学研究表明,许多疾病,例如:心脏病、癌症、脑血管病、慢性阻塞性肺病等都与吸烟有关,吸烟已成为继高血压之后的第二号全球杀手。
这些疾病与吸烟有关的结论是怎样得出的呢?我们看一下问题:1.某医疗机构为了了解呼吸道疾病与吸烟是否有关,进行了一次抽样调查,共调查了515个成年人,其中吸烟者220人,不吸烟者295人.调查结果是:吸烟的220人中有37人患呼吸道疾病(简称患病),183人未患呼吸道疾病(简称未患病);不吸烟的295人中有21人患病,274人未患病.问题:根据这些数据能否断定“患呼吸道疾病与吸烟有关”?二.学生活动为了研究这个问题,(1)引导学生将上述数据用下表来表示:患病未患病合计吸烟37 183 220不吸烟21 274 295合计58 457 515(2)估计吸烟者与不吸烟者患病的可能性差异:在吸烟的人中,有3716.82%220≈的人患病,在不吸烟的人中,有217.12%295≈的人患病.问题:由上述结论能否得出患病与吸烟有关?把握有多大?三.建构数学1.独立性检验:(1)假设0H :患病与吸烟没有关系.若将表中“观测值”用字母表示,则得下表:患病未患病合计吸烟 ab b a +不吸烟 cd d c + 合计c a +d b +d c b a +++(近似的判断方法:设n a b c d =+++,如果0H 成立,则在吸烟的人中患病的比例与不吸烟的人中患病的比例应差不多,由此可得a ca b c d≈++,即()()0a c d c a b a d b c +≈+⇒-≈,因此,||ad bc -越小,患病与吸烟之间的关系越弱,否则,关系越强.)设n a b c d =+++,在假设0H 成立的条件下,可以通过求 “吸烟且患病”、“吸烟但未患病”、“不吸烟但患病”、“不吸烟且未患病”的概率(观测频率),将各种人群的估计人数用,,,,a b c d n 表示出来.例如:“吸烟且患病”的估计人数为()a b a cn P AB n n n ++⨯≈⨯⨯; “吸烟但未患病” 的估计人数为()a b b dn P AB n n n ++⨯≈⨯⨯; “不吸烟但患病”的估计人数为()c d a cn P AB n n n ++⨯≈⨯⨯; “不吸烟且未患病”的估计人数为()c d b dn P AB n n n++⨯≈⨯⨯. 如果实际观测值与假设求得的估计值相差不大,就可以认为所给数据(观测值)不能否定假设0H .否则,应认为假设0H 不能接受,即可作出与假设0H 相反的结论. (2)卡方统计量:为了消除样本对上式的影响,通常用卡方统计量(χ22()-=∑观测值预期值预期值)来进行估计.卡方χ2统计量公式:χ222a b a c a b b d a n b n n n n n a b a c a b b d n n n n n n ++++⎛⎫⎛⎫-⨯⨯-⨯⨯ ⎪ ⎪⎝⎭⎝⎭=+++++⨯⨯⨯⨯22c d a c c d b d c n d n n n n n c d a c c d b d n n n n n n++++⎛⎫⎛⎫-⨯⨯-⨯⨯ ⎪ ⎪⎝⎭⎝⎭++++++⨯⨯⨯⨯()()()()()2n ad bc a b c d a c b d -=++++(其中n a b c d =+++) 由此若0H 成立,即患病与吸烟没有关系,则χ2的值应该很小.把37,183,21,274a b c d ====代入计算得χ211.8634=,统计学中有明确的结论,在0H 成立的情况下,随机事件“2 6.635χ≥”发生的概率约为0.01,即2( 6.635)0.01P χ≥≈,也就是说,在0H 成立的情况下,对统计量χ2进行多次观测,观测值超过6.635的频率约为0.01.由此,我们有99%的把握认为0H 不成立,即有99%的把握认为“患病与吸烟有关系”.象以上这种用2χ统计量研究吸烟与患呼吸道疾病是否有关等问题的方法称为独立性检验. 说明:(1)估计吸烟者与不吸烟者患病的可能性差异是用频率估计概率,利用χ2进行独立性检验,可以对推断的正确性的概率作出估计,观测数据,,,a b c d 取值越大,效果越好.在实际应用中,当,,,a b c d 均不小于5,近似的效果才可接受.(2)这里所说的“呼吸道疾病与吸烟有关系”是一种统计关系,这种关系是指“抽烟的人患呼吸道疾病的可能性(风险)更大”,而不是说“抽烟的人一定患呼吸道疾病”. (3)在假设0H 下统计量χ2应该很小,如果由观测数据计算得到χ2的观测值很大,则在一定程度上说明假设不合理(即统计量χ2越大,“两个分类变量有关系”的可能性就越大).2.独立性检验的一般步骤:一般地,对于两个研究对象Ⅰ和Ⅱ,Ⅰ有两类取值:类A和类B(如吸烟与不吸烟),Ⅱ也有两类取值:类1和类2(如患呼吸道疾病与不患呼吸道疾病),得到如下表所示:Ⅱ类1类2合计Ⅰ类Aa b ba+类B c d dc+合计ca+db+dcba+++推断“Ⅰ和Ⅱ有关系”的步骤为:第一步,提出假设H:两个分类变量Ⅰ和Ⅱ没有关系;第二步,根据2×2列联表和公式计算χ2统计量;第三步,查对课本中临界值表,作出判断.3.独立性检验与反证法:反证法原理:在一个已知假设下,如果推出一个矛盾,就证明了这个假设不成立;独立性检验(假设检验)原理:在一个已知假设下,如果一个与该假设矛盾的小概率事件发生,就推断这个假设不成立.四.数学运用1.例题:例1.在500人身上试验某种血清预防感冒的作用,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表所示.问:该种血清能否起到预防感冒的作用?未感冒感冒合计使用血清258 242 500未使用血清216 284 500合计474 526 1000分析:在使用该种血清的人中,有24248.4%500=的人患过感冒;在没有使用该种血清的人中,有28456.8%500=的人患过感冒,使用过血清的人与没有使用过血清的人的患病率相差较大.从直观上来看,使用过血清的人与没有使用过血清的人的患感冒的可能性存在差异.解:提出假设0H :感冒与是否使用该种血清没有关系.由列联表中的数据,求得221000(258284242216)7.075474526500500χ⨯⨯-⨯=≈⨯⨯⨯∵当0H 成立时,2 6.635χ≥的概率约为0.01,∴我们有99%的把握认为:该种血清能起到预防感冒的作用.例2.为研究不同的给药方式(口服或注射)和药的效果(有效与无效)是否有关,进行了相应的抽样调查,调查结果如表所示.根据所选择的193个病人的数据,能否作出药的效果与给药方式有关的结论?有效 无效 合计 口服 58 40 98 注射 64 31 95 合计12271193分析:在口服的病人中,有5859%98≈的人有效;在注射的病人中,有6467%95≈的人有效.从直观上来看,口服与注射的病人的用药效果的有效率有一定的差异,能否认为用药效果与用药方式一定有关呢?下面用独立性检验的方法加以说明. 解:提出假设0H :药的效果与给药方式没有关系.由列联表中的数据,求得22193(58314064) 1.3896 2.072122719895χ⨯⨯-⨯=≈<⨯⨯⨯当0H 成立时,2 1.3896χ≥的概率大于15%,这个概率比较大,所以根据目前的调查数据,不能否定假设0H ,即不能作出药的效果与给药方式有关的结论.说明:如果观测值22.706χ≤,那么就认为没有充分的证据显示“Ⅰ与Ⅱ有关系”,但也不能作出结论“0H 成立”,即Ⅰ与Ⅱ没有关系. 2.练习:课本第91页 练习第1、2、3题. 五.回顾小结:1.独立性检验的思想方法及一般步骤;2.独立性检验与反证法的关系.六.课外作业:课本第93页习题3.1 第1、2、3题.。
高中数学选修2-3精品教案7:§3.1 回归分析的基本思想及其初步应用教学设计

§3.1 回归分析的基本思想及其初步应用教学目标知识与技能从相关指数和残差分析角度探讨回归模型的拟合效果,以及建立回归模型的基本步骤.过程与方法在发现直接求回归直线方程存在缺陷的基础上,引导学生去发现解决问题的新思路——进行回归分析,进而介绍残差分析的方法和利用R2来表示解释变量对于预报变量变化的贡献率.情感、态度与价值观通过本节课的学习,加强数学与现实生活的联系,以科学的态度评价两个变量的相关性,掌握处理问题的方法,形成严谨的治学态度和锲而不舍的求学精神.培养学生运用所学知识解决实际问题的能力.教学中适当地利用学生的合作与交流,使学生在学习的同时,体会与他人合作的重要性.重点难点教学重点:从残差分析、相关指数角度探讨回归模型的拟合效果,以及建立回归模型的基本步骤;教学难点:了解评价回归效果的两个统计量:相关指数、残差和残差平方和.教学过程引入新课(幻灯片)编号 1 2 3 4 5 6 7 8身高/cm 165 165 157 170 175 165 155 170体重/kg 48 57 50 54 64 61 43 59 上表是上一节课我们从某大学选取8名女大学生其身高和体重数据组成的数据表,在上一节课中我们通过数据建立了回归直线方程,并根据方程预测了身高为172 cm的女大学生的体重.当时,我们提到根据回归直线方程求得的体重数据,仅是一个估计值,其与真实值之间存在着误差,为了综合分析身高和体重的关系,我们引入了线性回归模型y=bx+a+e 来表示两变量之间的关系,其中e为随机变量,又称随机误差.线性回归模型y=bx+a+e 增加了随机误差项e,因变量y的值由自变量x和随机误差e共同确定.假设随机误差对体重没有影响,也就是说,体重仅受身高的影响,那么散点图中所有的点将完全落在回归直线上.但是,在图中,数据点并没有完全落在回归直线上.这些点散布在回归直线附近,所以一定是随机误差把这些点从回归直线上“推”开了,即自变量x 只能解释部分y 的变化. 同学们考虑一下,随机变量e 的均值是多少?方差又是多少? 活动设计:学生思考回答问题.学情预测:学生回答E (e )=0,D (e )=σ2>0.教师提问:能否通过D (e )来刻画线性回归模型的拟合程度?学情预测:随机误差e 的方差越小,通过回归直线预报真实值y 的精度越高.随机误差是引起预报值与真实值y 之间的误差的原因之一,其大小取决于随机误差的方差.设计意图:说明研究随机误差e 的必要性,通过研究随机误差e 可以分析预报值的可信度. 提出问题:既然可以用随机变量e 的方差来衡量随机误差的大小,即通过方差σ2来刻画预报变量(体重)的变化在多大程度上与随机误差有关,那么如何获得方差σ2呢? 学生活动:学生独立思考,小组合作交流讨论.活动结果:可以采用抽样统计的思想,通过随机变量e 的样本来估计σ2的大小. 设计目的:复习抽样统计思想,以便通过随机变量e 的样本来估计总体.探究新知提出问题:既然e 表示了除解释变量以外其他各种影响预报值的因素带来的误差,那么如何获得e 的样本来计算σ2呢? 学生活动:分组合作讨论交流.学情预测:由函数模型y ^=b ^x +a ^和回归模型y =bx +a +e 可知e =y -y ^,这样根据图表中女大学生的身高求出预报值,再与真实值作差,即可求得e 的一个估计值.教师:由于在计算回归直线方程时,利用公式求得的b ^和a ^为斜率和截距的估计值,它们与真实值a 和b 之间存在误差,因此y ^是估计值,所以e ^=y -y ^也是一个估计值. 由上可知,对于样本点(x 1,y 1),(x 2,y 2),…,(x n ,y n )而言,它们的随机误差为e i =y i -bx i -a ,i =1,2,…n ,称其估计值e ^i =y i -y ^i 为相应于点(x i ,y i )的残差.将所有残差的平方加起来,即 i =1ne ^2i ,这个和称作残差平方和.类比样本方差估计总体方差的思想,可以用σ^2=1n -2∑i =1n e ^2i =1n -2∑i =1n(y i -y ^i )2(n >2)作为σ2的估计量,通常,σ^2越小,预报精度越高.这样,当我们求得回归直线方程后,可以通过残差来判断模型拟合程度的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析. 设计目的:通过问题诱思,引入残差概念.理解新知提出问题:对照女大学生的身高和体重的原始数据,结合求出的回归直线方程,求出相应的残差数据.学生活动:独立完成. 活动结果: 编号 1 2 3 4 5 6 7 8 身高( cm) 165 165 157 170 175 165 155 170 体重( kg) 48 57 50 54 64 61 43 59 残差e ^-6.3732.6272.419-4.6181.1376.627-2.8830.382提出问题:根据表格中的数据,以样本编号为横坐标,残差值为纵坐标,做出散点图(这样的散点图称作残差图).学生活动:分组合作,共同完成. 活动结果:残差图提出问题:观察上面的残差图,你认为哪几个样本点在采集时可能存在人为的错误?为什么?学生活动:分组讨论.活动结果:第一个和第六个样本点在采集过程中可能存在错误,因为其他的样本点基本都集中在一个区域内,只有这两个样本点的残差比较大,相对其他样本点来说,分布得较为分散. 提出问题:如何从残差图来判断模型的拟合程度? 学生活动:独立思考也可相互讨论. 活动结果:因为σ^2越小,预报精度越高,即模型的拟合程度越高,而σ^2越小,e ^的取值越集中,故若残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,且带状区域的宽度越窄,说明拟合精度越高,回归直线的预报精度越高.教师:在统计学上,人们经常用相关指数R 2来刻画回归的效果,其计算公式是:R 2=1-∑i =1n(y i -y ^i )2∑i =1n(y i -y )2提出问题:分析上面计算相关指数R 2的公式,如何根据R 2来判断模型的拟合效果? 学生活动:独立思考也可相互讨论,教师加以适当的引导提示.活动结果:因为对于确定的样本数据而言,∑i =1n(y i -y )2是一个定值,故R 2取值越大,意味着残差平方和越小,也就是说模型的拟合效果越好.提出问题:在线性回归模型中,R2表示解释变量对于预报变量变化的贡献率,R2越接近1,表示回归的效果越好,即解释变量和预报变量的线性相关性越强,试计算关于女大学生身高与体重问题中的相关指数R2.学生活动:学生独立计算获得数据.活动结果:R2≈0.64.根据R2≈0.64就可得出“女大学生的身高解释了64%的体重变化”,或者说“女大学生的体重差异有64%是由身高引起的”.由此就不难理解为什么预报体重和真实值之间有差距了.设计目的:结合图象,让学生直观感受残差图在刻画回归模型拟合效果方面的应用,体会残差分析和相关指数的意义.提出问题:根据前面得到的回归方程,能否预测一名美国女大学生的体重?建立回归模型后能否一劳永逸,在若干年后还可以使用,或者适用于多年以前的女大学生体重预测?学生活动:讨论交流总结发言.活动结果:在使用回归方程进行预报时要注意:(1)回归方程只适用于我们所研究的样本的总体;(2)我们建立的回归方程一般都有时间性;(3)样本取值的范围会影响回归方程的适用范围;(4)不能期望回归方程得到的预报值就是预报变量的精确值.提出问题:结合我们刚学习的概念,现在能否将建立回归模型的步骤补充完整?学生活动:讨论交流,合作完成.活动结果:一般地,建立回归模型的基本步骤为:(1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量.(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系(如是否存在线性关系等).(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性回归方程).(4)按一定规则(如最小二乘法)估计回归方程中的参数.(5)得出结果后分析残差图是否有异常(如个别数据对应残差过大,或残差呈现不随机的规律性,等等).若存在异常,则检查数据是否有误,或模型是否合适等.设计意图:设计问题,让学生讨论分析,得出使用回归方程进行预报需注意的问题,并让学生完善建立回归模型的步骤.在这个过程中,教师不宜做太多引导,要放手给学生,让学生讨论,充分参与进来.运用新知例1一个车间为了规定工时定额,需确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下:编号 1 2 3 4 5 6 7 8 9 10 零件数x /个 10 20 30 40 50 60 70 80 90 100 加工时间y /分626875818995102108115122(1)建立零件数为解释变量,加工时间为预报变量的回归模型,并计算残差; (2)你认为这个模型能较好地刻画零件数和加工时间的关系吗? 解:(1)根据表中数据作出散点图如下:散点图由散点图可知变量之间具有线性相关关系,可以通过求线性回归方程来拟合数据. 根据公式可求得加工时间对零件数的线性回归方程为y ^=0.668x +54.96. 残差数据如下表: 编号 1 2 3 4 5 6 7 8 9 10 残差e ^0.39-0.290.03-0.650.67-0.010.31-0.37 -0.050.27(2)画出残差图残差图由图可知,残差点分布较均匀,即用上述回归模型拟合数据效果很好,但需注意,由残差图也可以看出,第4个样本点和第5个样本点残差较大,需要确认在采集这两个样本点的过程中是否有人为的错误.点评:由散点图判断两个变量的线性相关关系,误差较大,利用残差图可以较好地评价模型的拟合程度,并能发现样本点中的可疑数据.变练演编例2在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据为:价格x/元14 16 18 20 22需求量y/件56 50 43 41 37求出y对x的回归方程,并说明拟合效果的好坏.解:作出散点图:从作出的散点图可以看出,这些点在一条直线附近,可用线性回归模型来拟合数据.由数据可得x =18,y =45.4,由计算公式得b ^=-2.35,a ^=y -b ^x =87.7. 故y 对x 的回归方程为y ^=-2.35x +87.7,列表:y i -y ^i 1.2 -0.1 -2.4 0.3 1 y i -y10.64.6-2.4-4.4-8.4所以∑i =15 (y i -y ^i )2=8.3,∑i =15(y i -y )2=229.2.相关指数R 2=1-∑i =15(y i -y ^i )2∑i =15(y i -y )2≈0.946.因为0.964很接近1,所以该模型的拟合效果很好.变式1:若要分析是否在上述样本的采集过程中存在可疑数据,应如何分析? 活动设计:学生分组讨论,回顾课本解答问题. 活动成果:可以画出残差图来进行分析.变式2:既然利用残差图和相关指数都能够评价回归模型的拟合效果,能否总结一下两种方法各自的特点?活动成果:利用残差图可以直观展示拟合的效果,而且还可以发现样本数据中的可疑数据;而相关指数是把对拟合效果的评价转换为数值大小的判断,易于量化处理,并能在数量上表现解释变量对于预报变量变化的贡献率.设计意图:进一步熟悉判断拟合效果的方法以及各自的特点. 达标检测1.分析下列残差图,所选用的回归模型效果最好的是( )A BC D2.下列说法正确的是()①回归直线方程适用于一切样本和总体;②回归直线方程一般都有时间性;③样本的取值范围会影响回归直线方程的适用范围;④根据回归直线方程得到的预测值是预测变量的精确值.A.①③④B.②③C.①②D.③④3.在研究气温和热茶销售杯数的关系时,若求得相关指数R2≈__________,表明“气温解释了85%的热茶销售杯数变化”或者说“热茶销售杯数差异有85%是由气温引起的”.【答案】1.D 2.B 3.0.85.课堂小结学生回顾本节课学习的内容,尝试总结,然后不充分的地方由学生相互补充,最后在老师的引导下,用精炼的语言进行概括:1.判断变量是否线性相关的方法以及各自的特点;2.在运用回归模型时需注意的事项;3.建立回归模型的基本步骤.设计意图:让学生自己小结,这是一个多维整合的过程,是一个高层次的自我认识过程.补充练习基础练习1.有下列说法:①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适.②用相关指数R2来刻画回归的效果,R2值越接近于1,说明模型的拟合效果越好.③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.正确的是( )A .①②B .②③C .①③D .①②③2.甲、乙、丙、丁四位同学各自对A ,B 两变量做回归分析,分别得到散点图与残差平方和∑i =1n(y i -y ^i )2如下表甲 乙 丙 丁散点图残差平方和115106124103哪位同学的实验结果体现拟合A ,B 两变量关系的模型拟合精度高?( ) A .甲 B .乙 C .丙 D .丁 3.关于x 与y 有如下数据:x 2 4 5 6 8 y3040605070为了对x ,y 两个变量进行统计分析,现有以下两种线性模型:甲:y ^=6.6x +17.5,乙:y ^=7x +17.试比较哪一个模型拟合效果更好. 【答案】1.D 2.D3.解析:设甲模型的相关指数为R 21,则R 21=1-∑i =15(y i -y ^i )2∑i =15(y i -y )2=1-1551 000=0.845;设乙模型的相关指数为R 22,则可求得R 22=0.82,因为R 21>R 22,所以甲模型的拟合效果更好.【拓展练习】4.假设某种农作物基本苗数x 与有效穗数y 之间存在相关关系,今测得5组数据如下:x 15.0 25.8 30.0 36.6 44.4 y39.442.942.943.149.2(1)以x 为解释变量,y 为预报变量,作出散点图;(2)求y 与x 之间的回归方程,对于基本苗数56.7预报有效穗数. (3)计算各组残差;(4)求R 2,并说明随机误差对有效穗数的影响占百分之几? 解:(1)散点图如图:(2)由图可以看出,样本点呈条状分布,有比较好的线性相关关系,因此可用线性回归方程来建立两个变量之间的关系.设线性回归方程为y ^=b ^x +a ^,由数据可以求得:b ^≈0.291, a ^=y -b ^x =34.67.故所求的线性回归方程为y ^=0.291x +34.67. 当x =56.7时,y ^=0.291×56.7+34.67=51.169 7. 估计有效穗数为51.169 7.(3)各组数据的残差分别是e ^1≈0.37,e ^2≈0.72,e ^3≈-0.5,e ^4≈-2.22,e ^5≈1.61.(4)残差平方和:∑i =15(y i -y ^i )2=8.425 8,又∑i =15(y i -y )2=50.18,∴R 2=1-∑i =15(y i -y ^i )2∑i =15(y i -y )2=1-8.425 850.18≈0.832.即解释变量(农作物基本苗数)对有效穗数的影响约占了83.2%,所以随机误差对有效穗数的影响约占1-83.2%=16.8%.设计说明本课时从上一节课的案例出发,通过分析随机误差产生的原因,引入随机变量、残差、残差平方和、相关指数的有关概念,从相关指数和残差分析等角度探讨回归模型拟合的效果,并通过案例说明利用所建立的回归模型进行预报时需要注意的问题,然后总结建立回归模型的基本步骤.在教学过程中以问题为引导思考的动机,注重对学生合作意识的培养,通过对案例的分析,培养学生对数据的处理能力,让学生初步了解回归分析思想在实际生活中的运用.。
数学人教A版选修2-3教案:3.1回归分析的基本思想及其初步应用第四课时含解析

第四课时教学目标 知识与技能通过典型案例的探究,进一步了解回归分析的基本思想和求回归方程的步骤. 过程与方法通过对回归模型的选择,使学生进一步体会建立回归模型的步骤,体会各个步骤的功能和重要性. 情感、态度与价值观通过案例的分析,培养学生的探索精神,提高对数据的处理能力,并且使学生了解回归分析在生活实际中的应用,增强数学的应用意识,提高学习兴趣.重点难点教学重点:掌握在解决实际问题的过程中寻找更好的模型的方法,总结求回归方程的步骤,会用合适的方法进行模型分析.教学难点:如何根据散点图选择合适的回归模型并对其拟合效果进行检验. 错误! 错误!(1)试建立y 与x 之间的回归方程;(2)若体重超过相同身高男性体重平均值的1。
2倍为偏胖,低于平均值的0。
8为偏瘦,那么这个地区一名身高为175 cm ,体重为82 kg 的在校男生的体重是否正常?学生活动:合作交流,探讨方案并计算检验. 学情预测:方案一:计算相关系数r≈0。
96>0。
75,故y 与x 之间具有很强的线性相关性. 设y 与x 之间的回归方程为错误! =错误! x +错误! ,则错误! =错误!≈0.431 9,错误! =错误!-错误! 错误!≈-25.679,故回归方程为: 错误! =0.431 9x -25.679。
当x =175时,错误! ≈55.15。
因为55.15×1。
2=66。
18<82,故这名男生偏胖.方案二:画出散点图如图所示:由表中数据可得z与x之间的回归直线方程为错误!=0.693+0.020x,则有错误!=e0。
693+0。
020x.当x=175时,错误!≈66.22,由于66.22×1.2=79。
464〈82,所以这名男生偏胖.设计目的:复习回归分析的基本步骤,让学生体会回归思想在实际问题中的应用,在操作过程中锻炼学生的数据处理能力.错误!提出问题:虽然两种解法的结论是一致的,但分析过程同学们可以发现,两种解法中求得的体重平均值是不同的,试分析两种模型哪种更合适?学生活动:讨论交流.学情预测:可能学生会出现争论:一种观点:原因出在选取的回归模型不同,从散点图上观察,选取指数型模型可能更好,得到的答案可信度可能更高.另一种观点:计算x与y的相关系数可得:r≈0。
高中数学选修2-3人教A教案导学案3.1.1回归分析的基本思想与其初步应用

从已经学过的知识,截距
n
a 和斜率 b 分别是使 Q( , )
( yi
xi
)2 取最小值时
i1
, 的值,由于
Q( , )
n
[ yi
i1
xi ( y
x) +( y
x) ] 2
n
{[ yi
i1
xi ( y
x) ] 2 2[ yi
xi ( y
x) ] [( y
x) ] [( y
x) ]2}
n
[ yi
i1
xi ( y
7
2
④
1 n2 e
1 Q (a, b)(n 2)
n 2i1
n2
⑤ Q(a, b) 称为残差平方和,
2
越小,预报精度越高。
6 思考 当样本容量为 1 或 2 时,残差平方和是多少?用这样的样本建立的线性回归方程的预报误差 为 0 吗? 7 残差分析
①判断原始数据中是否存在可疑数据;②残差图
n
( yi yi )2
538
484
290
226
204
价格 y (美
答:
x 0, y
10 2
0, xi
i1
10
110, xi yi
i1
110,
10
b
xi yi
i1
10
xi 2
10 x y
2
10x
110 10 0 110 10 0
1,a
y bx 0 0 b 0.
i1
所以所求回归直线方程为 y x
五、课堂小结
1. a 、 b 公式的推到过程。
2. y bx a通过 ( x, y)
2020-2021学年人教A版选修2-3 回归分析的基本思想及其初步应用 学案

3.1 回归分析的基本思想及其初步应用内容 标 准学 科 素 养1.能知道用回归分析处理两个变量之间的不确定关系的统计方法.2.会利用散点图分析两个变量是否存在相关关系,会用残差及R 2来刻画线性回归模型的拟合效果.3.能记住建立回归模型的方法和步骤;能知道如何利用线性回归模型求非线性回归模型.利用数据分析 提升数学建模 及数学运算授课提示:对应学生用书第51页[基础认识]知识点一 线性回归模型预习教材P 80-84,思考并完成以下问题“名师出高徒”这句谚语的意思是什么?有名气的老师就一定能教出厉害的学生吗?这两者之间是否有关?某电脑公司有5名产品推销员,其工作年限与年推销金额数据如下表:推销员编号 1 2 3 4 5 工作年限x /年 3 5 6 7 9 推销金额y /万元23345的线性回归方程是什么?提示:画出散点图,由图可知,样本点散布在一条直线附近,因此可用回归直线表示变量之间的相关关系.设所求的线性回归方程为y ^=b ^x +a ^,则b ^=∑i =15(x i -x )(y i -y )∑i =15(x i -x )2=1020=0.5, a ^=y -b ^x =0.4.所以年推销金额y 关于工作年限x 的线性回归方程为 y ^=0.5x +0.4.知识梳理 1.概念:回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.2.步骤:画散点图→求回归方程→用回归方程进行预报.3.在线性回归方程y ^=a ^+b ^x 中,b ^=∑i =1n (x i -x )(y i -y )∑i =1n(x i -x)2=∑i =1nx i y i -n x y∑i =1nx 2i -n x2,a ^=y -b ^x ,其中x =1n ∑i =1n x i ,y =1n ∑i =1ny i ,(x ,y )称为样本点的中心,回归直线过样本点的中心.4.线性回归模型y =bx +a +e ,其中e 称为随机误差,自变量x 称为解释变量,因变量y 称为预报变量.知识点二 刻画回归效果的方式 预习教材P 84-88,思考并完成以下问题(1)具有相关关系的两个变量的回归方程是唯一的吗? (2)预报变量y ^与真实值y 一样吗?(3)预报值y ^与真实值y 之间误差大了好还是小了好? 提示:(1)不一定. (2)不一样. (3)越小越好.知识梳理 1.残差平方和法(1)e ^i =y i -y ^i =y i -b ^x i -a ^(i =1,2,…,n )称为相应于点(x i ,y i )的残差. (2)残差平方和∑i =1n(y i -y ^i )2越小,模型的拟合效果越好.2.残差图法残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适.这样的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高.3.利用相关指数R2刻画回归效果其计算公式为:R2=1-∑i=1n(y i-y^i)2∑i=1n(y i-y)2,其几何意义:R2越接近于1,表示回归的效果越好.知识点三建立回归模型的基本步骤知识梳理确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量.画出解释变量和预报变量的散点图,观察它们之间的关系(如是否存在线性关系等).由经验确定回归方程的类型(如观察到数据呈线性关系,则选用线性回归方程).按一定规则(如最小二乘法)估计回归方程中的参数.得出结果后分析残差图是否有异常(如个别数据对应残差过大,残差呈现不随机的规律性等).若存在异常,则检查数据是否有误,或模型是否合适等.[自我检测]1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)(1)残差平方和越小,线性回归模型的拟合效果越好.()(2)在画两个变量的散点图时,预报变量在x轴上,解释变量在y轴上.()(3)R2越小,线性回归模型的拟合效果越好.()答案:(1)√(2)×(3)×2.如果记录了x,y的几组数据分别为(0,1),(1,3),(2,5),(3,7),那么y关于x的线性回归直线必过点()A.(2,2)B.(1.5,2)C.(1,2) D.(1.5,4)答案:D3.从散点图上看,点散布在从左下角到右上角的区域内,两个变量的这种相关关系称为________.答案:正相关授课提示:对应学生用书第52页探究一 求线性回归方程[阅读教材P 81例1]从某大学中随机选取8名女大学生,其身高和体重数据如表所示.编号 1 2 3 4 5 6 7 8 身高/cm 165 165 157 170 175 165 155 170 体重/kg4857505464614359重.题型:求线性回归方程 方法步骤:(1)画出散点图.(2)确定身高和体重有很好的线性相关关系. (3)由b ^和a ^的计算公式得出回归直线方程. (4)由所给x 的值进行预报y 的值.[例1] 某商场经营一批进价是30元/件的小商品,在市场试验中发现,此商品的销售单价x (x 取整数)元与日销售量y 台之间有如下关系:x 35 40 45 50 y56412811(1)y 与x (方程的斜率精确到1)(2)设经营此商品的日销售利润为P 元,根据(1)写出P 关于x 的函数关系式,并预报当销售单价x 为多少元时,才能获得最大日销售利润.[解析] (1)散点图如图所示,从图中可以看出这些点大致分布在一条直线附近,因此两个变量线性相关.设回归直线方程为y ^=b ^x +a ^, 由题知x =42.5,y =34,则求得b ^=∑i =14(x i -x )(y i -y )∑i =14(x i -x )2≈-3.a ^=y -b ^x ≈34-(-3)×42.5=161.5. ∴y ^=-3x +161.5.(2)依题意有P =(-3x +161.5)(x -30) =-3x 2+251.5x -4 845=-3⎝⎛⎭⎫x -251.562+251.5212-4 845. ∴当x =251.56≈42时,P 有最大值,约为426.故预报当销售单价为42元时,才能获得最大日销售利润. 方法技巧 1.求线性回归方程的基本步骤(1)列出散点图,从直观上分析数据间是否存在线性相关关系. (2)计算:x ,y ,∑i =1nx 2i ,∑i =1ny 2i ,∑i =1nx i y i .(3)代入公式求出y ^=b ^x +a ^中参数b ^,a ^的值. (4)写出线性回归方程并对实际问题作出估计.2.需特别注意的是,只有在散点图大致呈线性时,求出的回归方程才有实际意义,否则求出的回归方程毫无意义.跟踪探究 1.某研究机构对高三学生的记忆力x 和判断力y 进行统计分析,得下表数据:(1)(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程y ^=b ^x +a ^; (3)试根据求出的线性回归方程,预测记忆力为9的同学的判断力.⎝ ⎛⎭⎪⎪⎫相关公式:b ^=∑i =1nx i y i -n x -·y -∑i =1nx 2i-n x -2,a ^=y --b ^ x -解析:(1)如图:(2)∑i =14x i y i =6×2+8×3+10×5+12×6=158,x -=6+8+10+124=9,y -=2+3+5+64=4,∑i =14x 2i =62+82+102+122=344,b ^=158-4×9×4344-4×92=1420=0.7,a ^=y --b ^ x -=4-0.7×9=-2.3, 故线性回归方程为y ^=0.7x -2.3.(3)由(2)中线性回归方程可知,当x =9时,y ^=0.7×9-2.3=4,预测记忆力为9的同学的判断力约为4.探究二 线性回归分析[阅读教材P 84思考]如何发现数据中的错误?如何衡量模型的拟合效果? 以例1中的女大学生身高和体重的原始数据以及相应的残差数据进行分析. 题型:判断模型的拟合效果 方法步骤:(1)求出残差,并画出残差图进行分析.(2)求出残差平方和进行分析. (3)求出R 2进行分析.[例2] 已知某种商品的价格x (单位:元/件)与需求量y (单位:件)之间的关系有如下一组数据:求y 对x [解析] x -=15(14+16+18+20+22)=18,y -=15(12+10+7+5+3)=7.4,∑i =15x 2i =142+162+182+202+222=1 660,∑i =15y 2i =122+102+72+52+32=327,∑i =15x i y i =14×12+16×10+18×7+20×5+22×3=620,所以b ^=∑i =15x i y i -5x - y-∑i =15x 2i -5x -2=620-5×18×7.41 660-5×182=-1.15,a ^=7.4+1.15×18=28.1,所以所求回归直线方程是y ^=-1.15x +28.1. 列出残差表:所以∑i =15(y i -y ^i )2=0.3,∑i =15(y i -y -)2=53.2,R 2=1-∑i =15(y i -y ^i )2∑i =15(y i -y -)2≈0.994, 所以回归模型的拟合效果很好.方法技巧 1.解答线性回归问题,应通过散点图来分析两变量间的关系是否线性相关,然后再利用求回归方程的公式求解回归方程,并利用残差图或相关指数R 2来分析函数模型的拟合效果,在此基础上,借助回归方程对实际问题进行分析.2.刻画回归效果的三种方法(1)残差图法,残差点比较均匀地落在水平的带状区域内说明选用的模型比较合适. (2)残差平方和法:残差平方和∑i =1n(y i -y ^i )2越小,模型的拟合效果越好.(3)相关指数法:R 2=1-∑i =1ny i -y ^i2∑i =1ny i -y-2越接近1,表明回归的效果越好.跟踪探究 2.关于x 与y 有如下数据:x 2 4 5 6 8 y3040605070有如下的两个线性模型:(1)y =6.5x +17.5;(2)y =7x +17.试比较哪一个拟合效果更好. 解析:由(1)可得y i -y ^i 与y i -y -的关系如下表:y i -y ^i-0.5-3.510-6.50.5y i -y --20 -1010 0 20∴∑i =15(y i -y ^i )2=(-0.5)2+(-3.5)2+102+(-6.5)2+0.52=155,∑i =15(y i -y -)2=(-20)2+(-10)2+102+02+202=1 000.∴R 21=1-∑i =15(y i -y ^i )2∑i =15(y i -y -)2=1-1551 000=0.845.由(2)可得y i -y ^i 与y i -y -的关系如下表:y i -y ^i -1 -5 8 -9 -3 y i -y --20-101020∴∑i =15(y i -y ^i )2=(-1)2+(-5)2+82+(-9)2+(-3)2=180,∑i =15(y i -y -)2=(-20)2+(-10)2+102+02+202=1 000.∴R 22=1-∑i =15(y i -y ^i )2∑i =15(y i -y -)2=1-1801 000=0.82.由于R 21=0.845,R 22=0.82,0.845>0.82, ∴R 21>R 22.∴(1)的拟合效果好于(2)的拟合效果. 探究三 非线性回归模型[阅读教材P86例2]一只红铃虫的产卵数y 和温度x 有关.现收集了7组观测数据列于下表中,试建立y 关于x 的回归方程.温度x /℃ 21 23 25 27 29 32 35 产卵数y /个711212466115325方法步骤:(1)画出散点图(2)写出非线性回归方程:y =c 1e c 2x .(3)通过某种变换令z =ln y ,得出线性回归直线z =bx +a . (4)用线性回归方程来建立y 与x 间的非线性回归方程.[例3] 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t)和年利润z (单位:千元)的影响.对近8年的年宣传费x i 和年销售量y i (i =1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.x - y - w - ∑i =18(x i -x -)2∑i =18(w i -w -)2∑i =18(x i -x -)·(y i -y -) ∑i =18(w i -w -)·(y i -y -) 46.65636.8289.8 1.6 1 469 108.8表中w i =x i ,w -=18∑i =18w i .(1)根据散点图判断,y =a +bx 与y =c +d x 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程;(3)已知这种产品的年利润z 与x ,y 的关系为z =0.2y -x ,根据(2)的结果回答下列问题: ①年宣传费x =49时,年销售量及年利润的预报值是多少? ②年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据(u 1,v 1),(u 2,v 2),…,(u n ,v n ),其回归直线v =α+βu 的斜率和截距的最小二乘估计分别为β^=∑i =1n(u i -u -)(v i -v -)∑i =1n(u i -u -)2,α^=v --β^ u -.[解析] (1)由散点图可以判断,y =c +d x 适宜作为年销售量y 关于年宣传费x 的回归方程类型.(2)令w =x ,先建立y 关于w 的线性回归方程.由于d ^=∑i =18(w i -w -)(y i -y -)∑i =18(w i -w -)2=108.81.6=68, c ^=y --d ^ w -=563-68×6.8=100.6,所以y 关于w 的线性回归方程为y ^=100.6+68w , 因此y 关于x 的回归方程为y ^=100.6+68x . (3)①由(2)知,当x =49时,年销售量y 的预报值y ^=100.6+6849=576.6, 年利润z 的预报值z ^=576.6×0.2-49=66.32. ②根据(2)的结果知,年利润z 的预报值 z ^=0.2(100.6+68x )-x =-x +13.6x +20.12. 所以当x =13.62=6.8,即x =46.24时,z ^取得最大值.故年宣传费为46.24千元时,年利润的预报值最大. 方法技巧 求非线性回归方程的步骤 (1)确定变量,作出散点图.(2)根据散点图,选择恰当的拟合函数.(3)变量置换,通过变量置换把非线性回归问题转化为线性回归问题,并求出线性回归方程.(4)分析拟合效果:通过计算相关指数或画残差图来判断拟合效果. (5)根据相应的变换,写出非线性回归方程.跟踪探究 3.在一次抽样调查中测得样本的5个样本点,数值如下表:x 0.25 0.5 1 2 4 y1612521试建立y 与x 之间的回归方程. 解析:由数值表可作散点图如图,根据散点图可知y 与x 近似地呈反比例函数关系, 设y ^=k x ,令t =1x,则y ^=kt ,原数据变为:t 4 2 1 0.5 0.25 y1612521由置换后的数值表作散点图如下:由散点图可以看出y 与t 呈近似的线性相关关系,列表如下:i t i y i t i y i t 2i 1 4 16 64 16 2 2 12 24 4 3 1 5 5 1 4 0.5 2 1 0.25 5 0.25 1 0.25 0.062 5 ∑7.753694.2521.312 5所以t -=1.55,y -=7.2.所以b ^=∑i =15t i y i -5t - y-∑i =15t 2i -5t-2≈4.134 4,a ^=y --b ^t -≈0.8. 所以y ^=4.134 4t +0.8.所以y 与x 之间的回归方程是y ^=4.134 4x +0.8.授课提示:对应学生用书第54页[课后小结]回归分析的步骤:①确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量;②画出确定好的解释变量和预报变量的散点图,观察它们之间的关系(如是否存在线性关系等);③由经验确定回归方程的类型(如果呈线性关系,则选用线性回归方程y ^=b ^x +a ^); ④按一定规则估算回归方程中的参数;⑤得出结果后分析残差图是否有异常(个别数据对应的残差过大,或残差呈现不随机的规律性等),若存在异常,则检查数据是否有误或模型是否合适等.[素养培优]求回归直线方程的方法和技巧某地最近十年粮食需求量逐年上升,下表是部分统计数据:年 份 2007 2009 2011 2013 2015 需求量/万吨236246257276286(1)利用所给数据求年需求量与年份之间的回归直线方程y =b x +a ; (2)利用(1)中所求出的直线方程预测该地2020年的粮食需求量. 教你审题:分别计算x -,y -,b ^,a ^,把2020代入所求回归直线方程中.解析:(1)由所给数据看出,年需求量与年份之间是近似直线上升,下面来求回归直线方程,先将数据处理如下:对处理的数据,容易算得x -=0,y -=3.2.b ^=(-4)×(-21)+(-2)×(-11)+2×19+4×29-5×0×3.2(-4)2+(-2)2+22+42-5×02=26040=6.5, a ^=y --b ^ x -=3.2.由上述计算结果,知所求回归直线方程为 y ^-257=6.5(x -2 011)+3.2, 即y ^=6.5(x -2 011)+260.2.(2)利用所求得的回归直线方程,可预测2020年的粮食需求量为6.5×(2020-2 011)+260.2=318.7(万吨).方法点睛 求回归直线方程时,重点考查的是计算能力.若本题用一般方法去解,计算比较繁琐(如年份、需求量不做如上处理),所以平时训练时遇到数据较大的要考虑有没有更简便的方法解决.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1回归分析的基本思想及其初步应用(共计4课时)一、教学内容与教学对象分析学生将在必修课程学习统计的基础上,通过对典型案例的讨论,了解和使用一些常用的统计方法,进一步体会运用统计方法解决实际问题的基本思想,认识统计方法在决策中的作用。
二、学习目标1、知识与技能通过本节的学习,了解回归分析的基本思想,会对两个变量进行回归分析,明确建立回归模型的基本步骤,并对具体问题进行回归分析,解决实际应用问题。
2、过程与方法 本节的学习,应该让学生通过实际问题去理解回归分析的必要性,明确回归分析的基本思想,从散点图中点的分布上我们发现直接求回归直线方程存在明显的不足,从中引导学生去发现解决问题的新思路—进行回归分析,进而介绍残差分析的方法和利用R 的平方来表示解释变量对于预报变量变化的贡献率,从中选择较为合理的回归方程,最后是建立回归模型基本步骤。
3、情感、态度与价值观 通过本节课的学习,首先让显示了解回归分析的必要性和回归分析的基本思想,明确回归分析的基本方法和基本步骤,培养我们利用整体的观点和互相联系的观点,来分析问题,进一步加强数学的应用意识,培养学生学好数学、用好数学的信心。
加强与现实生活的联系,以科学的态度评价两个变量的相关系。
教学中适当地增加学生合作与交流的机会,多从实际生活中找出例子,使学生在学习的同时。
体会与他人合作的重要性,理解处理问题的方法与结论的联系,形成实事求是的严谨的治学态度和锲而不舍的求学精神。
培养学生运用所学知识,解决实际问题的能力。
三、教学重点、难点教学重点:熟练掌握回归分析的步骤;各相关指数、建立回归模型的步骤;通过探究使学生体会有些非线性模型通过变换可以转化为线性回归模型,了解在解决实际问题的过程中寻找更好的模型的方法。
教学难点:求回归系数 a , b ;相关指数的计算、残差分析;了解常用函数的图象特点,选择不同的模型建模,并通过比较相关指数对不同的模型进行比较。
四、教学策略:教学方法:诱思探究教学法学习方法:自主探究、观察发现、合作交流、归纳总结。
教学手段:多媒体辅助教学 五、教学过程: (一)、复习引入:回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法。
(二)、新课:探究:对于一组具有线性相关关系的数据:(11,x y ) , (22,x y ) ,…, (,n n x y ),我们知道其回归方程的截距和斜率的最小二乘估计公式分别为:$ay bx =-$ (1)121()()()niii nii x x y y bx x ==--=-∑∑$ (2)其中1111,n ni i i i x x y y n n ====∑∑,(,x y )成为样本点的中心.注:回归直线过样本中心.你能推导出这两个计算公式吗?从我们已经学过的知识知道,截距$a和斜率b $分别是使 21(,)()niii Q y bx a αβ==--∑取到最小值时,αβ的值. 由于 21(,)[()()]niii Q y x y x y x αββββα==---+--∑221{[()]2[()][()][()]}ni i i i i y x y x y x y x y x y x βββββαβα==---+---⨯--+--∑2211[()]2[()]()[()]nni i i i i i y x y x y x y x y x n y x βββββαβα===---+---⨯--+--∑∑注意到1[()]()niii y x y x y x βββα=-----∑1()[()]ni i i y x y x y x βαββ==-----∑11()[()]n ni i i i y x y x n y x βαββ===-----∑∑()[()]0y x n y n x n y x βαββ=-----=.221(,)[()]()ni i i Q y x y x n y x αββββα==---+--∑2222111()2()()()()nn nii i i i i i x x x x y y y y n y x βββα====----+-+--∑∑∑2222211221111()()[()()]()()[]()()()nniii i nni i i i nni i iii i x x y y x x y y n y x x x y y x x x x βαβ======----=--+----+---∑∑∑∑∑∑ 在上式中,后两项和,αβ无关,而前两项为非负数,因此要使Q 取得最小值,当且仅当前两项的值均为0,即有1221niii nii x y nx yy x xnx βαβ==⋅-⋅==--∑∑,.这正是我们所要推导的公式.下面我们从另一个角度来推导的公式. 人教A 版选修2-2P37习题1.4A 组第4题:用测量工具测量某物体的长度,由于工具的精度以及测量技术的原因,测得n 个数据12,,,n a a a L .证明:用这个数据的平均值11ni i x a n ==∑表示这个物体的长度,能使这n 个数据的方差211()()ni i f x x a n ==-∑最小.思考:这个结果说明了什么?通过这个问题,你能说明最小二乘法的基本原理吗?证明:由于211()()n i i f x x a n ==-∑,所以'12()()ni i f x x a n ==-∑,令'()0f x =, 得11ni i x a n ==∑。
可以得到, 11ni i x a n ==∑是函数()f x 的极小值点,也是最小值点.这个结果说明,用n 个数据的平均值11ni i a n =∑表示这个物体的长度是合理的,这就是最小二乘法的基本原理.由最小二乘法的基本原理即得定理 设x R ∈,12nx x x x n+++=L ,则2222222121211[()()()][()()()]n n x x x x x x x x x x x x s n n-+-++-≥-+-++-=L L (*) 当且仅当12nx x x x x n+++==L 时取等号.(*)式说明, 12nx x x x n+++=L 是任何一个实数x 与12,,,n x x x L 的差的平方的平均数中最小的数.从而说明了方差具有最小性,也即定义标准差的合理性.下面借助(*)式求2222211)()()(a bx y a bx y a bx y Q n n --++--+--=Λ的最小值.1122()()()n n y bx y bx y bx n-+-++-L1212n n y y y x x x b y b x n n++++++=-⋅=-⋅L L ,由(*)式知,2221122[()][()][()]n n Q a y bx a y bx a y bx =--+--++--L2221122[()()][()()][()()]n n y b x y bx y b x y bx y b x y bx ≥-⋅--+-⋅--++-⋅--L 2221122[()()][()()][()()]n n x x b y y x x b y y x x b y y =---+---++---L222111()2()()()nnni i i i i i i x x b x x y y b y y ====----+-∑∑∑222211221111()()[()()]()[]()()()nniii i nni i i i nni i iii i x x y y x x y y x x b y y x x x x ======----=--+----∑∑∑∑∑∑222211221111()()[()()]()[]()()()nn iii i nni i i i nni i iii i x x y y x x y y x x b y y x x x x ======----=--+----∑∑∑∑∑∑221211[()()]()()n i i ni i ni ii x x y y y y x x ===--≥---∑∑∑22211121()()[()()]()nnniii i i i i nii x x y y x x y y x x ====-----=-∑∑∑∑当且仅当a y b x =-⋅,且1122211()()()n niii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑时, Q 达到最小值22211121()()[()()]()nnniii i i i i n ii x x y y x x y y x x ====------∑∑∑∑.由此得到,⎪⎪⎩⎪⎪⎨⎧-=-⋅-⋅=---=∑∑∑∑====.,x b y a x n x yx n y xx x y y x x b ni i ni i in i i ni i i 2121121)())((其中b 是回归直线的斜率,a是截距.借助||||||||||||a b a b a b -≤+≤+r r r r r r和配方法,我们给出了人教A 版必修3的第二章统计第三节变量间的相关关系中回归直线方程y bx a =+的一个合理的解释.1、回归分析的基本步骤:(1) 画出两个变量的散点图. (2) 求回归直线方程.(3) 用回归直线方程进行预报.下面我们通过案例,进一步学习回归分析的基本思想及其应用. 2、举例:例1. 从某大学中随机选取 8 名女大学生,其身高和体重数据如表编号 123 4 5 6 7 8 身高/cm 165 165 157 170 175 165155 170 体重/kg48 57505464614359求根据女大学生的身高预报体重的回归方程,并预报一名身高为 172 cm 的女大学生的体重.解:由于问题中要求根据身高预报体重,因此选取身高为自变量 x ,体重为因变量 y . 作散点图(图3 . 1 一 1)从图3. 1一1 中可以看出,样本点呈条状分布,身高和体重有比较好的线性相关关系,因此可以用线性回归方程来近似刻画它们之间的关系.根据探究中的公式(1)和(2 ) ,可以得到ˆˆ0.849,85.712ba ==-. 于是得到回归方程$084985.712y x =-.因此,对于身高172 cm 的女大学生,由回归方程可以预报其体重为$084917285.71260.316y=⨯-= ( kg ) .ˆ0.849b=是斜率的估计值,说明身高 x 每增加1个单位时,体重y就增加0.849 位,这表明体重与身高具有正的线性相关关系.如何描述它们之间线性相关关系的强弱?在必修 3 中,我们介绍了用相关系数;来衡量两个变量之间线性相关关系的方法.本相关系数的具体计算公式为()()12211()()ni iin ni ii ix x y yrx x y y===--=--∑∑∑当r>0时,表明两个变量正相关;当r<0时,表明两个变量负相关.r的绝对值越接近1,表明两个变量的线性相关性越强;r的绝对值接近于0时,表明两个变量之间几乎不存在线性相关关系.通常,当r的绝对值大于0. 75 时认为两个变量有很强的线性相关关系.在本例中,可以计算出r =0. 798.这表明体重与身高有很强的线性相关关系,从而也表明我们建立的回归模型是有意义的.显然,身高172cm 的女大学生的体重不一定是60. 316 kg,但一般可以认为她的体重接近于60 . 316 kg .图3 . 1 一 2 中的样本点和回归直线的相互位置说明了这一点.由于所有的样本点不共线,而只是散布在某一条直线的附近,所以身高和体重的关系可用下面的线性回归模型来表示:y bx a e=++, ( 3 )这里 a 和 b 为模型的未知参数,e是 y 与%y bx a=+之间的误差.通常e为随机变量,称为随机误差,它的均值 E (e)=0,方差D(e)=2()D eσ=>0 .这样线性回归模型的完整表达式为:2,()0,().y bx a eE e D eσ=++⎧⎨==⎩(4)在线性回归模型(4)中,随机误差e的方差护越小,通过回归直线%y bx a =+ (5)预报真实值y 的精度越高.随机误差是引起预报值$y 与真实值 y 之间的误差的原因之一,大小取决于随机误差的方差.另一方面,由于公式(1)和(2)中$a和b $为截距和斜率的估计值,它们与真实值a 和b 之间也存在误差,这种误差是引起预报值$y 与真实值y 之间误差的另一个原因.思考:产生随机误差项e 的原因是什么?一个人的体重值除了受身高的影响外,还受许多其他因素的影响.例如饮食习惯、是否喜欢运动、度量误差等.事实上,我们无法知道身高和体重之间的确切关系是什么,这里只是利用线性回归方程来近似这种关系.这种近似以及上面提到的影响因素都是产生随机误差 e 的原因.因为随机误差是随机变量,所以可以通过这个随机变量的数字特征来刻画它的一些总体特征.均值是反映随机变量取值平均水平的数字特征,方差是反映随机变量集中于均值程度的数字特征,而随机误差的均值为0,因此可以用方差2σ来衡量随机误差的大小. 为了衡量预报的精度,需要估计护的值.一个自然的想法是通过样本方差来估计总体方差.如何得到随机变量e 的样本呢?由于模型(3)或(4)中的e 隐含在预报变量 y 中,我们无法精确地把它从 y 中分离出来,因此也就无法得到随机变量e 的样本.解决问题的途径是通过样本的估计值来估计2σ.根据截距和斜率的估计公式(1)和(2 ) , 可以建立回归方程%y bx a =+,因此y 是(5)中%y 的估计量.由于随机误差%e y y =-,所以e y y =-$是e 的估计量.对于样本点(11,x y ) , (22,x y ) ,…, (,n n x y ) 而言,相应于它们的随机误差为,1,2,,i i i i i e y y y bx a i n =-=--=L ,其估计值为µµ$,1,2,,i i i i ie y y y bx a i n =-=--=$L , µie 称为相应于点(,)i i x y 的残差(residual ).类比样本方差估计总体方差的思想,可以用¶µ$22111(,)(2)22n i i e Q a b n n n σ===>--∑$ 作为2σ的估计量, 其中$a 和b $由公式(1) (2)给出,Q ($a ,b $)称为残差平方和(residualsum of squares ).可以用¶2σ衡量回归方程的预报精度.通常,¶2σ越小,预报精度越高. 在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否线性相关,是否可以用线性回归模型来拟合数据.然后,可以通过残差µµµ12,,,n e e e L来判断模型拟合的效果,判断原始数据中是否存在可疑数据.这方面的分析工作称为残差分析.表3一 2 列出了女大学生身高和体重的原始数据以及相应的残差数据.编号 1 2 3 4 5 6 7 8 身高/cm 165 165 157 170 175 165 155 170 体重/kg4857505464614359残差e$ -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382 我们可以利用图形来分析残差特性作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重的估计值等,这样作出的图形称为残差图.图 3 . 1 一 3 是以样本编号为横坐标的残差图.从图3 . 1 一 3 中可以看出,第 1 个样本点和第 6 个样本点的残差比较大,需要确认在采集这两个样本点的过程中是否有人为的错误.如果数据采集有错误,就予以纠正,然后再重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他的原因.另外,残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适.这样的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高.另外,我们还可以用相关指数2R 来刻画回归的效果,其计算公式是:µ22121()1()niii nii y y R y y ==-=--∑∑显然,2R 取值越大,意味着残差平方和越小,也就是说模型的拟合效果越好.在线性回归模型中,2R 表示解释变量对于预报变量变化的贡献率. 2R 越接近于1,表示回归的效果越好(因为2R 越接近于1,表示解释变量和预报变量的线性相关性越强).如果对某组数据可能采取几种不同的回归方程进行回归分析,也可以通过比较几个2R ,选择2R 大的模型作为这组数据的模型.在例 1 中,2R =0. 64 ,表明“女大学生的身高解释了64 %的体重变化”,或者说“女大学生的体重差异有 64 %是由身高引起的”.用身高预报体重时,需要注意下列问题:1.回归方程只适用于我们所研究的样本的总体.例如,不能用女大学生的身高和体重之间的回归方程,描述女运动员的身高和体重之间的关系.同样,不能用生长在南方多雨地区的树木的高与直径之间的回归方程,描述北方干旱地区的树木的高与直径之间的关系.2.我们所建立的回归方程一般都有时间性.例如,不能用 20 世纪 80 年代的身高体重数据所建立的回归方程,描述现在的身高和体重之间的关系.3.样本取值的范围会影响回归方程的适用范围.例如,我们的回归方程是由女大学生身高和体重数据建立的,那么用它来描述一个人幼儿时期的身高和体重之间的关系就不恰当(即在回归方程中,解释变量 x 的样本的取值范围为[155cm,170cm 〕 ,而用这个方程计算 x-70cm 时的y 值,显然不合适.)4.不能期望回归方程得到的预报值就是预报变量的精确值.事实上,它是预报变量的可能取值的平均值.一般地,建立回归模型的基本步骤为:(1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量;(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系(如是否存在线性关系等) ;(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性回归方程 y=bx+a ) ;(4)按一定规则估计回归方程中的参数(如最小二乘法);(5)得出结果后分析残差图是否有异常(个别数据对应残差过大,或残差呈现不随机的规律性等等),若存在异常,则检查数据是否有误,或模型是否合适等.例2.现收集了一只红铃虫的产卵数y 和温度x 之间的7组观测数据列于下表:温度x oC 21 23 25 27 29 3235产卵数y /个 7 11 21 24 66 115 325(1)试建立y 与x 之间的回归方程;并预测温度为28oC 时产卵数目。
