群的直积
群论讲课提纲

群论讲课提纲第一章 抽象群理论群的大体概念 一、群的概念 实例分析; 群的概念。
二、大体概念有限群与无穷群(群的阶); 持续群与分立群; 阿贝群(互换群),例题;对称群,例题(234444{,,,,,,,}x y C E C C C m m νμνσσ=); 循环群(生成元) 有限群的大体性质一、群的乘法表(群乘表) 群乘表构造方式(SL2群,4C ν群) 群乘表的性质(重排定理及推论) 二、元素的阶 例题分析概念(元素的阶)几点结论 3、元素的共轭概念(共轭元素)共轭的性质(自反、对称、传递) 4、共轭类等价关系与集合的划分 共轭类的概念关于类的几个结论(7条,例题)类的积(i j ijk k kC C a C =∑,例题)子群与商群 一、子群的概念概念、判别条件、一般子群 二、陪集(旁系) 概念 例题与分析 陪集的性质① 子群与它的任何一个陪集没有一起元素, 即&,X G X H XH H HX H Φ∀∈∉⋂=⋂=② 子群的任何两个左(右)陪集要么完全相同,要么完全不同。
即,:XH YH or XH YH Φ=⋂=③ 子群与它的所有相异左(右)陪集概念群的一个划分*。
推论1:群的阶与子群的阶之比为整数,即G nk Hm==;推论2:群阶与元素阶的商为整数。
3、共轭子群定理:以群G 中任何元素为过渡元素对子群1H 作共轭变换取得的集合2H 仍然是G 的子群,称为1H 的共轭子群。
例题4、正规子群(自轭子群、不变子群)例题分析正规子群的两种概念 正规子群的性质 ① 不变子群的任何两个陪集的积仍然是该子群的陪集;② 不变子群与其任何一个陪集的积等于该陪集。
五、商群例题分析定理:由正规子群及其所有相异陪集组成群称为商群。
商群的性质 ① 商群/G H 的幺元是正规子群H ;② 商群的阶数为正规子群的指数/n m ;群的同构与同态 一、 群的同构 ① 例题分析 ② 同构的概念 ③ 注意事项④ 4C 群所有子群的同构关系二、 群的同态① 例题分析 ② 同态的概念③ 注意事项3、有限群的结构① 1~6阶群的结构分析(试探题) ② 关于高阶群结构分析的注意事项 群的生成集存在性素数阶群的结构③ 生成集定理置换群① 置换群的大体概念 ② 3S 群及其乘法表 ③ n S 群的性质④ 任何有限群总同构于n S 群的一个子群。
2.4群的直积

(a,e)(a,e)=(e,e)ein四元群同构, G×G K4 。
2.4.2 群的直积的性质 (Property of Direct Product of Group)
x1=a1b1,x2=a2b2∈G,由(1)(2)及正规子群 的性质,A和B的元素可交换,故有 f(x1x2)=f(a1b1a2b2)=f(a1a2b1b2)=(a1a2,b1b2) = (a1, b1) (a2, b2) = f(x1)f(x2) 保运算
∴G A×B
推论: 设群G有n个不变子群Gi G ,i=1,2,…,n, 使G的每一元均可唯一地表示为G1,G2,…,Gn的 元的积,则 G G1×G2×…×Gn。 注:推论中的两个条件 (1) G1,G2,…,Gn是G的不变子群; (2) G的每一元均可唯一地表示 G1, G2,…,Gn 的元的积,等价于以下三个条件: (1) G=G1G …Gn n2 (2) Gi G j {e}
定义二元运算为乘法 (a1,a2,…,an)(b1,b2,…,bn)=(a1b1,a2b2,…,anbn), 则G关于乘法构成群,
G=G1×G2×…×Gn
为群G1,G2,…,Gn的外直积。 特别地,如果Gi中的二元运算都采用“+”,则称直 积 为直和,记做:G=G1⊕G2 ⊕… ⊕Gn
注1. 设e1,e2 分别是G1,G2的单位元则(e1,e2)是G1×G2 的单位元;
2.4.4 群的内直积 (Internal Direct Product of Group)
定义:设G1,G2是群G的两个正规子群,满足条件 G=G1G2,G1∩G2=e, 则称G是G1和G2的内直积。 定理1设G1,G2是群G的两个子群,则G是G1和G2的内直 积的充要条件是G满足下列条件 ⑴群G中的每个元素都可唯一地表示成hk的形式,其中 h ∈ G1, k ∈ G2 ; ⑵群G1中的每个元素与群G2中的任意元素可交换, hk = kh. 定理2设G是正规子群G1,G2的内直积,则GG1×G2; 反之,若G =G1×G2,则存在群G的两个正规子群G'1, G'2,且G'i与Gi同构,使得G是G'1与G'2的的内直积。
1.5群的直积同构同态
证明: 构成群, 满足群的四个条件) 证明:(证G'构成群,只需证 满足群的四个条件) 构成群 只需证G'满足群的四个条件
●封闭性 ●结合律
由定理给出的假设条件自动满足 中的元素与G'中元素的对应为 设G中的元素与 中元素的对应为 中的元素与 R→R' ,S→S' ,T→T'
则乘积也有对应关系 (RS)T→(R'S')T', R(ST)→R'(S'T') 中的元素满足结合律, 群G中的元素满足结合律,即 中的元素满足结合律 (RS)T=R(ST) 则 (R'S')T'=R'(S'T') 即集合G'中的元素乘积满足结合律 即集合 中的元素乘积满足结合律
7
●H中的元素都属于群 ,则H中元素乘积显然满足结合律 中的元素都属于群G, 中的元素都属于群 中元素乘积显然满足结合律
●综上,子集 在与群 相同乘积规则下满足群的四个条件, 综上,子集H在与群 相同乘积规则下满足群的四个条件, 在与群G相同乘积规则下满足群的四个条件
因此, 是 的子群 因此,H是G的子群 2)(证H是不变子群) 是不变子群) )(证 是不变子群 中的元素RS 中的元素R' 群G中的元素 µR-1→G'中的元素 E'R'-1=E' 中的元素 中的元素 即 RSµR-1=Sν →E' 属于 属于H 由元素的任意性, 则 RSµ=SνR, 由元素的任意性,可知 RH=HR 因此,子群H是 的不变子群 因此,子群 是G的不变子群
5
证明定理( 证明定理(一) 思路: 思路: 证明与G'恒元 对应的G中元素集合 恒元E'对应的 中元素集合H是 的子群 1)证明与 恒元 对应的 中元素集合 是G的子群 再证H是 的不变子群 2)再证 是G的不变子群 最后证与G'其它元素 对应的G中元素集合是 的陪集RH 其它元素R'对应的 中元素集合是H的陪集 3)最后证与 其它元素 对应的 中元素集合是 的陪集 显然与商群G/H同构(见商群定义) 同构( 则G'显然与商群 显然与商群 同构 见商群定义) 证明: 证明: )(H是 的子群 据群的四个条件) 的子群, 1)( 是G的子群,据群的四个条件) ●设H的内容是 H={S1,S2,...,Sh},H中的元素与元素间乘积均 的内容是 中的元素与元素间乘积均 对应于G'中的恒元 中的恒元E',即 对应于 中的恒元 即 Sµ→E', Sν→E', SµSν→E' 因此有 S µ ∈ H , Sν ∈ H , S µ Sν ∈ H 子集H对元素乘积封闭 即子集 对元素乘积封闭 6
自同构和直积

自同构和直积全文共四篇示例,供读者参考第一篇示例:自同构和直积是群论中两个重要的概念,它们在研究群的结构和性质方面起着非常重要的作用。
本文将介绍自同构和直积的定义、性质和应用,并探讨它们在群论中的重要性。
一、自同构在群论中,自同构是指一个群和其自身之间的同态映射。
具体地说,设G是一个群,如果存在一个映射φ: G → G,使得对于所有的a, b ∈ G,有φ(ab) = φ(a)φ(b),且φ是双射,则称φ是一个自同构。
如果存在一个自同构φ,使得φ是恒等映射,则称这个自同构是平凡的。
否则,该自同构被称为非平凡的。
自同构在群论中的研究具有重要的意义。
通过对自同构的研究,我们可以了解群的结构和性质。
自同构可以帮助我们研究群的不变性质,比如正规子群和共轭类等。
自同构还可以帮助我们刻画不同群之间的关系,比如同构和同态等。
二、直积直积是群论中的另一个重要概念。
设G和H是两个群,它们的直积G × H定义为一个新的群,其元素是所有形式为(g, h)的有序对,其中g ∈ G,h ∈ H。
直积的群运算定义为:(g1, h1) * (g2, h2) = (g1*g2, h1*h2),其中*是G和H中的运算符。
直积在群论中的应用广泛。
通过直积,我们可以将两个群的结构和性质相结合,得到一个新的群。
直积还可以帮助我们研究群的子群和同态。
通过对直积的研究,我们可以了解不同群之间的关系,并且探索它们之间的关系。
三、自同构和直积的关系自同构和直积在群论中有着广泛的应用。
它们不仅帮助我们研究群的结构和性质,还可以应用于其他数学领域。
自同构和直积的理论在密码学、代数几何和物理等领域都有着重要的应用。
在密码学中,自同构和直积的概念可以帮助我们设计安全的加密算法。
通过对群的自同构和直积的研究,我们可以设计出不易破解的密码系统,从而保护通信的安全性。
在代数几何中,自同构和直积的理论可以帮助我们研究拓扑空间和代数结构。
自同构和直积的概念可以帮助我们理解复杂的几何结构,揭示其内在的对称性和性质。
2 群的概念

A A E C B
B B C E A
C C B A E
这个群的特点是每个群元素的逆都是其自身。 这个群的特点是每个群元素的逆都是其自身。 可对易( 任意两群元素的乘积是可对易的, 可对易(Abel)群:任意两群元素的乘积是可对易的,aiaj =ajai。 ) 群的例子。 上述例子都是 Abel 群的例子。
G3 E A B E E A B A B A B
G3 E A B
E E B
A B A B E A E
A B
例 2-1 二阶点群 抽象的看,只有一个可能的二阶群,它具有下列乘法表。这个 抽象的看,只有一个可能的二阶群,它具有下列乘法表。 表示。 群用符号 G2 表示。
G2 E A E E A A
G2 = C2 , Ci , Cs
(2) 结合律 群元素相乘满足乘法结合律, 群元素相乘满足乘法结合律,如: ABC = ( AB )C =A( BC ) (3) 恒等元素 群中有且仅有一个恒等元素 E,且有: ,且有: EX = XE = X 为群中的任何元素。 其中 X 为群中的任何元素。
(4) 逆元素 群中任一元素 X 都有一个逆元素 X-1 ,且逆元素 X-1 也 是该群中的元素,且有: 是该群中的元素,且有: X X-1 = X-1 X = E 群元素的数目称为群的阶 h . 从数学的角度看,按一定规则联系起来的任何元素的一个集合, 从数学的角度看,按一定规则联系起来的任何元素的一个集合, 如果满足上述四个条件,就称为群。 如果满足上述四个条件,就称为群。群的特征不在于构成群的是何种 元素,而在于它们共同遵守着某种规则, 元素,而在于它们共同遵守着某种规则,这种规则反映了群元素之间 的内在联系。 的内在联系。
群的基本概念
2.11近世代数

§2.11群的直积和有限交换群§2.11.1群的直积定理1设G1,G2为两个群,G1×G2≡D{(a,b)|a∈G1,b∈G2}。
定义运算(a1,b1)•(a2,b2)=(a1a2,b1b2),则G1×G2关于运算“•”成群。
证明:(a∀1,b1),(a2,b2)∈G1×G2有(a1a2,b1b2) ∈G1×G2,易见 G1×G2对“•”封闭。
若设1为G1的单位元,1’为G2的单位元,易验证(1,1’)为G1×G2的单位元。
运算满足结合律,∀(a1,b1),(a2,b2),(a3,b3)∈G1×G2有[(a1,b1)(a2,b2)] (a3,b3)= (a1,b1)[(a2,b2) (a3,b3)];∀(a,b)∈G1×G2,由(a,b)(a-1,b-1)= (a-1,b-1) (a,b)= (1,1’),知(a,b)-1=(a-1,b-1)。
所以G1×G2对“•”形成一个群。
注:1°群G1×G2称为群G1与群G2的直积。
2°|G1×G2|=|G1||G2|。
3°对于G1×G2来说,含有子群H={(a,1’)|a∈G1},易见H≌G1,并可证明H G1×G2。
4°若G1,G2都为Abel群,则G1×G2也为Abel群。
例子(1)若G={(1,a|a2=1)}⇒G×G为Klein四元群,即G×G≌{1,(12)(34),(12),(34)}。
(2)C n表示阶数为n的循环群,若(m,n)=1,则C m×C n≌C mn。
(3)R为实数域,(R,+)×(R,+)同构于平面上所有向量关于向量加法所成的群。
(位置向量)定理2 . G 为群,A ,B 为群G 的两个正规子群,使得G 的每一个元素均可表为A ,B 中的元素之积,并且表示法是唯一的,则G ≌A ×B 。
D8群直积分解

D8群直积分解在开始本文前,我们默认读者对于Sylow定理、群的直积等群论的基本内容有所了解。
我们知道:群论的一个重要部分就是对于有限群进行基于其阶数的分类。
在有限群的分类理论中,若一个群为Abel群,那么我们总是可以应用有限交换群的分解定理写出其所有同构类。
那么,若没有交换性的条件,分类会变得稍微困难一些,我们需要依赖Sylow定理与群的直积分解定理。
首先举出一些经典的例子:对于p^2 阶群而言(之后默认p,q 等为素数),其分类仅有\mathbb{Z}_{p^2},\mathbb{Z}_p\times\mathbb{Z}_p 。
这是由于p^2 阶群必交换(考虑群的中心),进一步讨论是否存在p^2 阶元素而导致的。
对于36 阶Abel群,其分类仅有\mathbb{Z}_{36},\mathbb{Z}_2\times \mathbb{Z}_{18},\mathbb{Z}_3\times\mathbb{Z}_{12},\mathbb{Z}_6\times \mathbb{Z}_6 。
这是由于考虑36 的素因子分解36=2^2\times 3^2 ,利用有限交换群的结构定理,只能有上述的几种分解形式。
(因为要保证36 的乘积分解中,因子不是互素的,这是因为若(a,b)=1 ,则\mathbb{Z}_a\times\mathbb{Z}_b=\mathbb{Z}_{ab} )对于15 阶群,其必为循环群。
这是由于利用Sylow定理可以得到其 3 阶子群H 与 5 阶子群K 均存在且唯一,故必定正规。
又注意到H\cap K 是平凡的(两个子群均是循环的),且|HK|=\frac{|H||K|}{|H\cap K|}=15 表明HK=G 从而利用群的直积分解定理得到其为H\times K=\mathbb{Z}_{15} 。
然而,注意到直积分解定理适用要求的条件有三个:H\cap K 平凡、HK=G 、H,K \unlhd G 。
群的直积

群的直积(Direct Product of Group )群的直积是群论中的重要概念,也是研究群的重要手段之一,利用群的直积可以从已知的群构出新的群,可以用小群构造大群,也可以将一个群用它的子群来表示,这一节介绍子群的直积及其基本性质。
定义1 设12,G G 是群,121122{(,)|,)G a a a G a G =∈∈为集合G 1与G 2为的卡氏积(Cartesian product ),在G 中定义乘法运算121211221212(,)(,)(,),(,),(,)a a b b a b a b a a b b G ⋅=∈。
则G 关于上述定义的乘法构成群,称为群G 1与G 2的外直积(external direct product ),记作21G G G ⨯=,G 1、G 2称为G 的直积因子(factor of the direct product)。
当G 1、G 2是加群时,G 1与G 2的外直积也可记作21G G ⊕。
定理1 设21G G G ⨯=是群G 1与G 2的外直积,则(1) G 是有限群的充分必要条件是G 1与G 2都是有限群,并且,当G 是有限群时,©©有||||||21G G G =;(2)G 是交换群的充分必要条件是G 1与G 2都是交换群。
(3)1221G G G G ⨯≅⨯; (4) 若令112112{(,)|,A a e a G e =∈为G 2的单位元},则A 1是G 的子群,且11G A ≅;若令212222{(,)|,A e a a G e =∈为的单位元},则A 2是G 的子群,且22G A ≅。
证明 (1)由卡氏积的性质显然。
(2)如果G 1和G 2都是交换群,则对任意的1212(,),(,),a a b b G ∈有),(),(),(),(),(),(2121221122112121a a b b a b a b b a b a b b a a ⋅===⋅,所以G 是交换群。
群的直积

群的直积(Direct Product of Group )群的直积是群论中的重要概念,也是研究群的重要手段之一,利用群的直积可以从已知的群构出新的群,可以用小群构造大群,也可以将一个群用它的子群来表示,这一节介绍子群的直积及其基本性质。
定义1 设12,G G 是群,121122{(,)|,)G a a a G a G =∈∈为集合G 1与G 2为的卡氏积(Cartesian product ),在G 中定义乘法运算121211221212(,)(,)(,),(,),(,)a a b b a b a b a a b b G ⋅=∈。
则G 关于上述定义的乘法构成群,称为群G 1与G 2的外直积(external direct product ),记作21G G G ⨯=,G 1、G 2称为G 的直积因子(factor of the direct product)。
当G 1、G 2是加群时,G 1与G 2的外直积也可记作21G G ⊕。
定理1 设21G G G ⨯=是群G 1与G 2的外直积,则(1) G 是有限群的充分必要条件是G 1与G 2都是有限群,并且,当G 是有限群时,©©有||||||21G G G =;(2)G 是交换群的充分必要条件是G 1与G 2都是交换群。
(3)1221G G G G ⨯≅⨯; (4) 若令112112{(,)|,A a e a G e =∈为G 2的单位元},则A 1是G 的子群,且11G A ≅;若令212222{(,)|,A e a a G e =∈为的单位元},则A 2是G 的子群,且22G A ≅。
证明 (1)由卡氏积的性质显然。
(2)如果G 1和G 2都是交换群,则对任意的1212(,),(,),a a b b G ∈有),(),(),(),(),(),(2121221122112121a a b b a b a b b a b a b b a a ⋅===⋅,所以G 是交换群。
2.14-6.1-6.3 直积群的表示
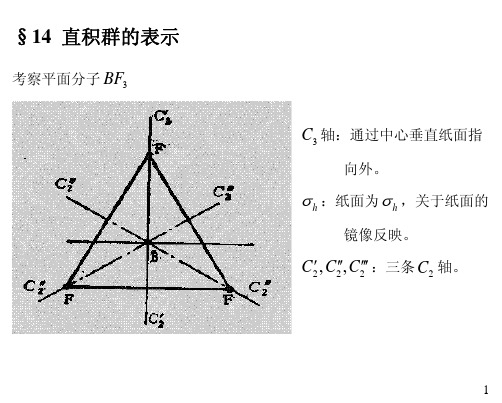
§14 直积群的表示考察平面分子3BF3C 轴:通过中心垂直纸面指向外。
h σ:纸面为h σ,关于纸面的镜像反映。
222,,C C C ′′′′′′:三条2C 轴。
3BF 分子的全部对称操作:233222222222223333312h h h h h h h h h h h ec c c c c c c c c c c c c c c σσσσσσσσσσσσσσ′′′′′′′′′′′′′′′′′′======== 构成直积群{}{}33223322233123,h h h h h D D e e c cc c c c c σσσσσσσ=×′′′′′′=3BF 分子的简并态按直积群{}33,h h D D e σ=×在分子波函数希尔伯特空间上的表示的约化情况进行分类。
直积群的表示:设直积群 12G G G =×()ατ:1G 在线性空间1V 上的不可约表示 ()βτ:2G 在线性空间2V 上的不可约表示基函数()(){}11111:n V φφLL ()(){}22221:n V φφLL则()()()()()()()()111111111111n n ik g g g G αατφφφφτ⎡⎤⎡⎤⎡⎤=∈⎣⎦⎣⎦⎣⎦LL LL ()()()()()()()()222222211222n n jl g g g G ββτφφφφτ⎡⎤⎡⎤⎡⎤=∈⎣⎦⎣⎦⎣⎦LL LL考虑乘积函数()()()()()()()()2112121212121111,,,n n n n φφφφφφφφL L L生成12n n 维线性空间()()121211n n ij i j ij i j V x x x C φφ==⎧⎫==∈⎨⎬⎩⎭∑∑任取12g G G G ∈=×,则必有121122,,g g g g G g G =⋅∈∈令()()()()()()()()()()()()()()()12121212121211k l k l n n i j ikjl i j g g g g g αβαβτφφτφτφφφττ====∑∑()()12g g g ττ=()()()()(),,g x y g x g y x y V ταβατβτ+=+∈则()()g g G τ∈是V 上的线性算符, 且()()()()()12121211n n g τφφφφ⎡⎤⎣⎦L ()()()()()()()()()1212121112n n ik jl g g αβφφφφττ⎡⎤⎡⎤⎡⎤=⊗⎣⎦⎣⎦⎣⎦L任取 12,g h G G G ∈=×,必有12g g g =⋅ 121,g g G ∈ 12h h h =⋅ 122,h h G ∈使得()()()()()()12121212k l k l gh g g h h τφφτφφ=⋅()()()121122k l g h g h τφφ=⋅()()()()()()1212112211n n i j ik jl i j g h g h αβφφττ===∑∑由矩阵直积性质:()()()()()12121211n n gh τφφφφ⎡⎤⎣⎦L ()()()()()()()()()121212111122n n ik jl g h g h αβφφφφττ⎡⎤⎡⎤⎡⎤=⊗⎣⎦⎣⎦⎣⎦L=()()()()12121211n n φφφφ⎡⎤⎣⎦L()()()(){}()()()(){}()1122ikik jl jl g h g h ααββττττ⎡⎤⎡⎤⎡⎤⎡⎤⊗⎣⎦⎣⎦⎣⎦⎣⎦()()()()12121211n n φφφφ⎡⎤=⎣⎦L ()()()(){}()()()(){}()1212ikjlik jl g g h h αβαβττττ⎡⎤⎡⎤⎡⎤⎡⎤⊗⋅⊗⎣⎦⎣⎦⎣⎦⎣⎦()()()()()()()12121211n n g h ττφφφφ⎡⎤=⎣⎦L即 ()()()gh g h τττ=所以线性算符群(){}12g g G G G ττ=∈=×是直积群12G G G =×在V 上的一个表示, 记作()()αβττ× 或 ()αβτ×特征标:()()()()()()()()()()()()()()()121212ik jl ikjl g tr g g tr g tr g g g αβαβαβαβχττττχχ×⎡⎤⎡⎤=⊗⎣⎦⎣⎦⎡⎤⎡⎤=⋅⎣⎦⎣⎦=1212g g g G G G =⋅∈=×, 11g G ∈,22g G ∈。
群论第二章ppt

§2.1 群的概念
(3),存在单位元素 集合中存在一个单位元素或称恒等元素 (Identity Element)而且只存在一个单位元素e
e∈G
(4), 集合总任何元素的逆元素在集合中,a 的逆元 1 为 a −, 有 aa −1 = a −1a = e a −1 ∈ G a −1 是唯一的。 在一定乘法规则下满足以上四条的具有代数结构的集合称 为群。在四条中没有要求满足交换律,如果一个群其元素乘 法满足交换律称为交换群或Abel群 群元的数目称为群的阶,记为g。g为有限称为有限群。元 素无限称为无限阶群。群元可数的无限群为离散无限群,而 群元素不可数的称为连续群。
5
§2.1 群的概念
显然只有群元素比较少时这乘法表才排得出来,在乘法表 中每列与每行,每个元素出现一次,也仅一次,这为乘法表 的重排定理。 若群是Abel群(交换群),则乘法表中对主对角线是对称 的。下面给出几个例子 例1 G = {1, −1} 乘法为普通数乘法,单位元素为1 = e ,a=-1逆元素为 自 己,其乘法定律 ee=e, aa=e, ea=ae=a, 这群在量子力学中很重要,这群与空间反演相对应,三维 v v v v v 空间矢量 r 作用 er = r ar = − r v v e保持 r 不变的恒等变换 a 使 r 反演的反演变换,则 {e, a}构成反演群。 我们称群G与反演群同构。
16ቤተ መጻሕፍቲ ባይዱ
子群, §2.2 子群 同态和同构
2. 同态与同构 定义2.3。若从群G到群F上存在一一对应的映射, 定义 且在映射中群代数结构不变,即乘法规则不变,即 G中两元素乘积的映射等于两元素映射到F的乘积, G F 称群G与群F同构。 φ g• •f 记 G ≅ F 映射称同构映射。 g • •f g •f 即 Φ :G → F •
【抽象代数】03-商群和直积

【抽象代数】03-商群和直积1. 陪集 现在继续研究群的分解,先来讨论⼀般⼦群之间、以及⼦群和⽗群的关系。
⾸先根据⼦群的判定条件,如果H,K⩽,则很容易有H\cap K\leqslant G。
那么H\cup K呢?当然这⾥H,K都是真⼦群,并且不互相包含。
从H中取元素h\not\in K,从K中取元素k\not\in H,则容易证明hk\not\in H\cup G,从⽽H,K⼀定不是G的⼦集。
如果再把hk都包含进来呢,即HK是不是G的⼦集?对h_1k_1,h_2k_2\in HK,如果总有有(h_1k_1)(h_2k_2)=hk,容易证明该条件和HK=KH等价。
所以就有下式结论,但要注意HK=HK并不表⽰hk=kh。
这样的分割需要⼦集满⾜⼀定条件,不符合我们现在的需求,需要另找⽅法。
HK\leqslant G\quad\Leftrightarrow\quad HK=KH\tag{1} 现在看来,我们必须放弃将⽗群分解为若⼲个⼦群的想法,⽽只能以某个⼦群H为参考或划分单位。
我们还希望分成的每⼀块和⼦群⼀样⼤,最好元素与H也有⼀⼀对应的关系。
由此我们想到了考察集合aH,它表⽰a和H每个元素的乘积组成的集合,被称为H的左陪集(left coset),a是左陪集的代表元。
如果a\in H,显然aH=H,现在来研究a\not\in H时,aH之间的关系。
对任意b\in aH,存在b=ah,(h\in H),则bH=ahH=aH,也就是说以aH的中任何元素为代表元的左陪集都与aH完全重合。
换句话说,所有左陪集要么完全相等,要么没有交集,每个元素都被划分到了⼀个左陪集中,且都能作为该左陪集的代表元。
另⼀⽅⾯,对b\in aH,有a^{-1}b=h\in H,容易证明a^{-1}b\in H就是a,b同属于⼀个左陪集的充要条件,它是群元素之间的⼀个等价关系。
同样可以定义右陪集Ha的概念,并有着和左陪集⼀样的结论,只不过同属于⼀个右陪集的条件要改成ab^{-1}。
直积的计算公式

直积是指将两个或多个集合的元素按照一定规则进行组合,形成新的集合。
对于两个集合A 和B的直积,记作A ×B,其中A和B分别为两个集合。
直积的计算公式如下:A ×B = {(a, b) | a ∈A, b ∈B}其中,(a, b)表示一个有序对,a ∈A表示a是集合A中的一个元素,b ∈B表示b是集合B中的一个元素。
换句话说,直积A ×B包含了所有由A和B的元素组成的有序对。
例如,假设集合A = {1, 2},集合B = {a, b, c},则A ×B的计算结果为:A ×B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)}这个结果表示了A和B的所有元素组成的有序对。
当计算两个集合的直积时,可以按照以下步骤进行:定义两个集合:首先,明确给定的两个集合A和B。
这些集合可以是数字、字符、对象或其他类型的集合。
创建直积集合:直积集合是由A和B的元素组成的有序对。
需要创建一个新的集合来容纳这些有序对。
遍历元素:对于集合A中的每个元素a,以及集合B中的每个元素b,生成一个由它们组成的有序对(a, b)。
添加有序对:将生成的有序对(a, b)添加到直积集合中。
完成直积计算:当遍历完集合A和B的所有元素后,直积计算完成。
下面是一个示例程序,用于计算集合A和B的直积:#include <stdio.h>int main() {int A[] = {1, 2, 3}; // 集合Achar B[] = {'a', 'b'}; // 集合Bint sizeA = sizeof(A) / sizeof(A[0]); // A的元素个数int sizeB = sizeof(B) / sizeof(B[0]); // B的元素个数// 创建直积集合int sizeProduct = sizeA * sizeB;int product[sizeProduct][2]; // 二维数组,存储有序对// 计算直积int index = 0; // 直积集合的索引for (int i = 0; i < sizeA; i++) {for (int j = 0; j < sizeB; j++) {product[index][0] = A[i]; // 第一个元素为A中的元素product[index][1] = B[j]; // 第二个元素为B中的元素index++;}}// 输出直积集合printf("直积集合:\n");for (int i = 0; i < sizeProduct; i++) {printf("(%d, %c)\n", product[i][0], product[i][1]);}return 0;}在这个示例程序中,集合A是一个包含整数的数组,集合B是一个包含字符的数组。
群的直积

群的直积(Direct Product of Group )群的直积是群论中的重要概念,也是研究群的重要手段之一,利用群的直积可以从已知的群构出新的群,可以用小群构造大群,也可以将一个群用它的子群来表示,这一节介绍子群的直积及其基本性质。
定义1 设12,G G 是群,121122{(,)|,)G a a a G a G =∈∈为集合G 1与G 2为的卡氏积(Cartesian product ),在G 中定义乘法运算121211221212(,)(,)(,),(,),(,)a a b b a b a b a a b b G ⋅=∈。
则G 关于上述定义的乘法构成群,称为群G 1与G 2的外直积(external direct product ),记作21G G G ⨯=,G 1、G 2称为G 的直积因子(factor of the direct product)。
当G 1、G 2是加群时,G 1与G 2的外直积也可记作21G G ⊕。
定理1 设21G G G ⨯=是群G 1与G 2的外直积,则(1) G 是有限群的充分必要条件是G 1与G 2都是有限群,并且,当G 是有限群时,©©有||||||21G G G =;(2)G 是交换群的充分必要条件是G 1与G 2都是交换群。
(3)1221G G G G ⨯≅⨯; (4) 若令112112{(,)|,A a e a G e =∈为G 2的单位元},则A 1是G 的子群,且11G A ≅;若令212222{(,)|,A e a a G e =∈为的单位元},则A 2是G 的子群,且22G A ≅。
证明 (1)由卡氏积的性质显然。
(2)如果G 1和G 2都是交换群,则对任意的1212(,),(,),a a b b G ∈有),(),(),(),(),(),(2121221122112121a a b b a b a b b a b a b b a a ⋅===⋅,所以G 是交换群。
群论讲义

D3 群的循环子群: D3={e, d, f, a, b, c} 2 阶循环子群:{a, a2=e},{b, b2 =e},{c, c2=e} 3 阶循环子群:{d, d2(=f), d3=e},{f, f2(=d), f3=e}
【定义 1.4】 (左陪集和右陪集)
n 为循环群的阶,循环群是阿贝尔群。
an = e}
例 1.10 从 n 阶有限群 G 的任一元素出发,总可以生成一个 G 的循环子群。
G = {e, , gα , }, ∀gα ∈G
3
作 gα , gα 2 , gα 3 ,…, 存在 k ≤ n, gα k = e ,
则{gα1, gα 2 , ..., gα k = e} 构成循环群 Zk ,且 Zk < G 。
在乘法表中,每行和每列都是群元的重排,每个群元只出现一次。
§1.2 子群和陪集
【定义 1.2】 设 H 是群 G 的一个子集,若对于与群 G 同样的乘法运算,H 也构成一个群,
则称 H 为 G 的子群,记为 H < G 。 ·系 1. H < G 的充要条件为: (1) ∀hα , hβ ∈H,有 h α hβ ∈H
证:f1 ~ h, 故 ∃ g1, 使 f1 = g1hg1-1 ,故有 h=g1-1f1g1 f2 ~ h, 故 ∃ g2, 使 f2 = g2hg2-1 = g2g1-1f1g1g2-1 = (g2g1-1)f1(g2g1-1) -1 故 f1 ~ f2
【定义 1.6】 群 G 的所有相互共轭的元素集合,称为群 G 的一个类。 ·系 1 一个类被类中任意一个元素所决定,知道了类中某一个元素 f,则 f 所属类的所有
群论2-2

C2h
E
C2
I 1 -1 1 -1
σh
D1 D2
D3
1 1 1 1
1 1 -1 -1
1 -1 -1 1
D4
不可约表示符号
A、B:一维的不可约表示.分别指对绕主轴的操作是对称或反对称的表示. E:二维的不可约表示. T:三维的不可约表示. G:四维的不可约表示. H:五维的不可约表示.
a
b
表示,称为直积表示. 直积过程中,对应于同一个元素的不同表示矩阵直积.得到的仍然是这 个元素的表示矩阵,一般情况下,这个新表示矩阵是可约的. 两个可约表示的直积一定是可约的. 群表示的直积得到的表示矩阵数目是不变的.新的表示的维数是原来两 个表示空间维数的乘积. 2.特征标 新表示的特征标是对应的原来表示的特征标乘积.
2.直积群的表示
1.直积群的表示是两个可对易的表示的直积.即
G = Ga ⊗ Gb
若 D G 是G a 的表示,D G 是G
a b
b
a b 的表示,则群G的表示 D G = D G ⊗ D G .
a b 其中G中的元素为 Rij = Ri R j ,对应的表示矩阵为 D ( Rij ) = D a ( Ri ) ⊗ D b ( R j ) .
1.群表示的直积
1.定义:群G的两个(可约或不可约)表示是 D G 和 D G .取这两个表示的直 积,即 D ( R ) = D a ( R ) ⊗ D b ( R ) , 对 ∀R ∈ G成 立
a b D G , G = D G ⊗ D G .而 D G 也是群G的一个 D 得到一个新的矩阵的集合
C2 A B
E
C2 1 -1
Cs
群的直积

群的直积群的直积(Direct Product of Group )群的直积是群论中的重要概念,也是研究群的重要手段之一,利用群的直积可以从已知的群构出新的群,可以用小群构造大群,也可以将一个群用它的子群来表示,这一节介绍子群的直积及其基本性质。
定义1 设12,G G 是群,121122{(,)|,)G a a a G aG =∈∈为集合G 1与G 2为的卡氏积(Cartesian product ),在G 中定义乘法运算121211221212(,)(,)(,),(,),(,)a a b b a b a b a a b b G⋅=∈。
则G 关于上述定义的乘法构成群,称为群G 1与G 2的外直积(external direct product ),记作21G G G ⨯=,G 1、G 2称为G 的直积因子(factor of thedirect product)。
当G 1、G 2是加群时,G 1与G 2的外直积也可记作21G G ⊕。
定理1 设21G G G ⨯=是群G 1与G 2的外直积,则(1) G 是有限群的充分必要条件是G 1与G 2都是有限群,并且,当G 是有限群时,©©有||||||21G GG =;(2) G 是交换群的充分必要条件是G 1与G 2都是交换群。
11:A G →φ),(211e a a →则易知φ是一个同构映射,因此1A 是G 的子群,同理可证另一个结论。
例1 设>=<>=<b G a G21,分别是3阶和5阶的循环群,则21G G G ⨯=是一个15阶的循环群。
证明 首先,由定理1知,G 是一个15阶的交换群,设G b a c ∈=),(,),(21e e 是G 的单位元,则),(),,(225313e a c b e c ==,所以53,c c都不等于),(21e e ,可知ord c 5,3≠由拉格朗日定理知,ord c =15,即>=<c G 是15阶循环群。
1.4---1.7 直积群

§4 直积群设1G 和2G 是群G 的两个子群,如果 1) G 的每一个元素g 都可唯一地表成121122,,g g g g G g G =⋅∈∈2) 1G 的元素与2G 的元素有乘可交换1221g g g g ⋅=⋅则称G 为1G 和2G 的直积群,记作12G G G =×, 称1G 和2G 为G 的直因子直积分解:将群分成直因子群的直积,称为直积分解。
例如:{}{},,,x y e m e m 是2v C 的两个子群,可验证满足上述两条,故2v C 有直积分解{}222,,,,v x y x y y x x x x y y y C e c m m e e e c m m m m m e m m e m e m m e ⎧⎫=⎪⎪=⋅⎪⎪⎪⎪=⋅=⋅⎨⎬⎪⎪=⋅=⋅⎪⎪⎪⎪=⋅=⋅⎩⎭即 {}{}2,,v x y C e m e m =×但是,{},x e m ,{}2,,,x y e c m m 不是2v C 的直因子,因为条件(1)不满足222,x y y y x c ec m m m em m c ====为什么要做群的直积分解1) 由于直因子群的元素个数较少,研究起来较容易2)取直积是扩大群的最简单方法。
这在研究原子、分子、晶体、原子核及基本粒子体系的对称性时有用处。
例如 分子体系22ABC D 。
关于平面ABC 和平面ABD 的镜像反映x m 和y m 之下不变,故有群{},x e m 和{},y e m 的对称性 又由2x y y x m m m m c ==, 故分子体系22ABC D 在直积群{}{}{}22,,,,,x y x y v e m e m e c m m C ×==的所有元素作用下不变。
即具有直积群{}{}2,,v x y C e m e m =×的对称性。
又如乙烷26C H 具有1)C C −连线为轴的3v C 群对称性{}2333123,,,,,v C e c c σσσ=2)C C −中点为中心的反演()I 对称性{},e I⎫⎬⎭反演与轴及镜面可变换过反演中心的旋转及反映33333212133321232113332113321232111213322Ic I Ic c I c Ic ′′′⎫⎪′′′==⎪′′′⎪⎪⇒=⎬⎪′′′⎪′′′==⎪⎪′′′⎭11111232111323232111332311123232311122233I I I I Iσσσσσ′′′⎫⎪′′′==⎪′′′⎪⎪⇒=⎬⎪′′′⎪′′′==⎪⎪′′′⎭{}{}{}{}{}333,,,v v v C e I C e I C e I """"讨论:1),都是群,是的子群2),中元素可乘,相乘可交换,中的元素可唯一地表成和中的元素的乘积故乙烷具有直积群,{}3,v C e I ×的对称性{}{}{}233123223312333123,,,,,,,,,,,,,,,,e c c e I e c c I c I c I I I I σσσσσσσσσ×=,推广,直积群的概念可以推广到多个直因子的情形:12n G G G G =×××"有定义可得直积群的四条简单性质 1)直因子的交集是{}e 2)直因子是正规子群 3)直因子的直积仍为直因子 4)若1212,,j n j j j jn G G G G G G G G =×××=×××""则1j j jn G G G =××××"""§5 共轭类群的内部关系:子群、陪集分解、直积分解、共轭类分解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
群的直积群的直积(Direct Product of Group )群的直积是群论中的重要概念,也是研究群的重要手段之一,利用群的直积可以从已知的群构出新的群,可以用小群构造大群,也可以将一个群用它的子群来表示,这一节介绍子群的直积及其基本性质。
定义1 设12,G G 是群,121122{(,)|,)G a a a G aG =∈∈为集合G 1与G 2为的卡氏积(Cartesian product ),在G 中定义乘法运算121211221212(,)(,)(,),(,),(,)a a b b a b a b a a b b G⋅=∈。
则G 关于上述定义的乘法构成群,称为群G 1与G 2的外直积(external direct product ),记作21G G G ⨯=,G 1、G 2称为G 的直积因子(factor of thedirect product)。
当G 1、G 2是加群时,G 1与G 2的外直积也可记作21G G ⊕。
定理1 设21G G G ⨯=是群G 1与G 2的外直积,则(1) G 是有限群的充分必要条件是G 1与G 2都是有限群,并且,当G 是有限群时,©©有||||||21G GG =;(2) G 是交换群的充分必要条件是G 1与G 2都是交换群。
(3)1221G G G G ⨯≅⨯;(4) 若令112112{(,)|,A a e a G e =∈为G 2的单位元},则A 1是G 的子群,且11G A ≅;若令212222{(,)|,A e a a G e =∈为的单位元},则A 2是G 的子群,且22GA ≅。
证明 (1)由卡氏积的性质显然。
(2)如果G 1和G 2都是交换群,则对任意的1212(,),(,),a a b b G ∈有),(),(),(),(),(),(2121221122112121a a b b a b a b b a b a b b a a ⋅===⋅,所以G 是交换群。
反之,如果G 是交换群,那么对任意的111,G b a ∈,222,G b a ∈有),(),(),(),(21212121a a b b b b a a ⋅=⋅,即),(),(22112211a b a b b a b a =。
故1111a b ba =,2222a b ba =,所以G 1,G 2都是交换群。
(3)构造映射1221:G G G G ⨯→⨯φ),(),(1221a a a a →,2121),(G G a a ⨯∈∀,显然φ是双射,且),(),(),)(,(),(),()),)(,((21211212112222112121b b a a b b a a b a b a b a b a b b a a φφφφ⋅====因此,φ是21G G ⨯到12G G⨯的同构映射,即1221G G G G ⨯≅⨯。
(4)构造映射11:A G →φ),(211e a a →则易知φ是一个同构映射,因此1A 是G 的子群,同理可证另一个结论。
例1 设>=<>=<b G a G21,分别是3阶和5阶的循环群,则21G G G ⨯=是一个15阶的循环群。
证明 首先,由定理1知,G 是一个15阶的交换群,设G b a c ∈=),(,),(21e e 是G 的单位元,则),(),,(225313e a c b e c ==,所以53,c c 都不等于),(21e e ,可知ord c 5,3≠由拉格朗日定理知,ord c =15,即>=<c G 是15阶循环群。
例2,22G Z Z ≅⊕ 这里{})23)(14(),24)(13(),34)(12(),1(=G证明 对于4阶群22Z Z ⊕中的任意元),(b a 有).0,0(),(),(=+b a b a故22Z Z⊕中没有4阶元素,所以22Z Z⊕不是循环群,而4阶群在同构的意义下仅有两个,于是.22G Z Z ≅⊕事实上, 22Z Z ⊕到G 的任意一个将零元)0,0(映到)1(的双射都是一个群同构。
定理2 设21,G G 是群,a 和b 分别是1G 和2G 中的有限阶元素,则对于21),(G G b a ⨯∈有[].,),(o r d b o r d a b a o r d= 证明 设[],,,,n m s n ordb m orda ===则),(),(),(21e e b a b a s s S==从而),(b a 的阶有限,设其为t ,则需证.s t =首先s t |。
又因为).,(),(),(21t t tb a b a e e ==所以21,e b e at t==,于是t m |且tn |,从而t 是m 和n 的公倍数,而s 是m 和n 的最小公倍数,因此t s |,从而t s =。
例3 试确定515Z Z⊕中5阶元素的个数。
解 由定理2,即要确定515Z Z ⊕中满足[]ordb orda b a ord ,),(5==的元素),(b a 的个数。
即要求:或者5=orda 且1=ordb 或5;或者1=orda 且5=ordb 。
分别讨论如下:(1)5==ordb orda ,此时a 可选12,9,6,3,b 可选4,3,2,1,从而共有16个5阶的元。
(2),1,5==ord orda 此时a 如上,而b 为0故共有4个5阶元。
(3)b a ordb orda ,0,5,1===同(1),故也有4个5阶元。
于是515Z Z⊕共有24个5阶元。
定理3 设1G 和2G 分别是m 阶及n 阶的循环群,则21G G ⨯是循环群的充要条件是1),(=n m 。
证明 设,21b G a G==假设21G G ⨯是循环群。
若1),(≠=t n m ,则由于nordb m orda ==,而tm a /和tn b 的阶都是t ,因此),(2e a m 和),(1n b e 是循环群21G G ⨯中的两个不同的t 阶子群,矛盾,所以1),(=n m 。
反之,假设1),(=n m ,则[]2121,),(G G G G mn n m b a ord ⨯====,所以),(b a 是21G G ⨯的生成元,因此21G G ⨯是循环群。
定义2 设H 和K 是群G 的正规子群,如果群G 满足条件,HK G =且{}e K H =⋂,则称G 是H 和K 的内直积(internal direct product )。
定理4 设H 和K 是G 的子群,则G 是H 和K 的内直积的充分必要条件是G 满足以下两个条件:(1)G 中每个元可惟一地表为hk 的形式,其中K k H h ∈∈,;(2)H 中任意元与K 中任意元可交换,即:对任意K k H h ∈∈,,有hk=kh 。
证明 如果G 是H 和K 的内直积,则G=HK ,所以,G 中每个元g 都可表为的hk 形式,其中Kk H h ∈∈,,如果,,,''''K k H h k h hk g ∈∈==则{}e K H k k h h =⋂∈=--1'1',从而ek k h h==--1'1',因此'',k k h h ==,即条件(1)成立。
对任意K k H h ∈∈,,考虑Gk hkh g ∈=--11,则由于G K ,故KKk k hkhg =∈=--11)(,同理H g ∈,所以K H g ⋂∈,即g=e ,于是hk=kh ,条件(2)成立。
反之,若H ,K 是G 的子群,且条件(1)和(2)成立,则G=HK ,又对任意的G hk g H h ∈=∈,1,其中K k H h ∈∈,,则由条件(2)k h kh 11=,所以Hh hh h kk hh h k h hk hk h hk g gh ∈====-------111111111111)()()()(。
于是GH 。
同理可得G K 。
对任意的K H g ⋂∈,有ge = g = eg 而由条件(1),g 表示为hk 的形式是惟一的,故得g = e ,即{}e K H =⋂。
从而G 是H 和K 的内直积。
例4 设G ={})(,),(22121R GL A A A A diag ∈,则易证G 是的)(4R GL 子群,令{}{})(),()(),(2222R GL A A E diag K R GL A E A diag H ∈=∈=则H 和K 是G 的正规子群,显然{}4E K H =⋂,且对G A A diag ∈),(21,有HK A E diag E A diag A A diag ∈⋅=),(),(),(222121。
由定义知G 是H 和K 的内直积。
例 5 将3S 自然地看作4S 的子群,设=K {})23)(14(),24)(13(),34)(12(),1(,则K 是4S 的正规子群。
显然{})1(3=⋂K S。
因此433324S KS H S K S==⋂⋅=⋅。
从而KS S⋅=34。
但是由于3S 不是4S 的正规子群,因此4S 不是3S 和K的内直积。
关于群的内外直积,我们有如下定理: 定理5 如果群G 是正规子群,H 和K 的内直积,则G K H ≅⨯;反之,如果群21G G G ⨯=,则存在G 的正规子群'1G 和'2G ,且'iG 与iG 同构)2,1(=i ,使得G是'1G 和'2G 的内直积。
证明 如果群G 是正规子群H 和K 的内直积,定义映射KH k h hk k h GK H ⨯∈∀→→⨯Φ),(,),(:则由于G=HK ,故Φ是满射,又由定理4知G 中元与表为hk 形式时表法惟一,故Φ是单射,又对任意的K H k h k h ⨯∈),(),,(2211,由于H 中的元与K中的元可交换,故())()())(())((),(),(),(22112211212121212211k h k h k h k h k k h h k k h h k h k h Φ⋅Φ===Φ=⋅Φ所以Φ是同构映射,从而G K H ≅⨯。
如果21G G G ⨯=。
令{}{}2221'21121'1),(,),(G a a e G G a ea G ∈=∈=首先由定理1知'1G ,'2G 都是G 的子群,'iG 与iG同构。
且对任意的'2'121212121),)(,(),(,),(G G a e e a a a G a a ⋅∈=∈,这一表法是惟一的。
且对任意的'221'121),(,),(G a e G e a ∈∈,有),)(,(),(),(),(2121212121e a a e a a a e e a ==⋅。
