初中数学竞赛定理大全

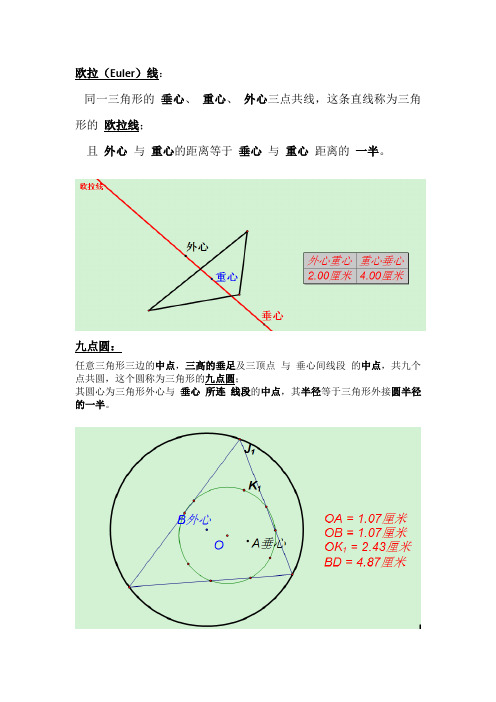
欧拉（Euler）线：同一三角形的垂心、重心、外心三点共线，这条直线称为三角形的欧拉线；且外心与重心的距离等于垂心与重心距离的一半。

九点圆：任意三角形三边的中点，三高的垂足及三顶点与垂心间线段的中点，共九个点共圆，这个圆称为三角形的九点圆；其圆心为三角形外心与垂心所连线段的中点，其半径等于三角形外接圆半径的一半。

费尔马点：已知P为锐角△ABC内一点，当∠APB＝∠BPC＝∠CPA＝120°时，PA＋PB＋PC的值最小，这个点P称为△ABC的费尔马点。

海伦（Heron）公式：塞瓦（Ceva）定理：在△ABC中，过△ABC的顶点作相交于一点P的直线，分别交边BC、CA、AB与点D、E、F，则(BD/DC)·(CE/EA)·(AF/FB)＝1；其逆亦真。

密格尔（Miquel）点：若AE、AF、ED、FB四条直线相交于A、B、C、D、E、F六点，构成四个三角形，它们是△ABF、△AED、△BCE、△DCF，则这四个三角形的外接圆共点，这个点称为密格尔点。

葛尔刚（Gergonne）点:△ABC的内切圆分别切边AB、BC、CA于点D、E、F，则AE、BF、CD三线共点，这个点称为葛尔刚点。

西摩松（Simson）线：已知P为△ABC外接圆周上任意一点，PD⊥BC，PE⊥ACPF⊥AB，D、E、F为垂足，则D、E、F三点共线，这条直线叫做西摩松线。

黄金分割：把一条线段(AB)分成两条线段，使其中较大的线段(AC)是原线段(AB) 与较小线段(BC)的比例中项，这样的分割称为黄金分割。

帕普斯（Pappus）定理：已知点A1、A2、A3在直线l1上，已知点B1、B2、B3在直线l2上，且A1 B2与A2 B1交于点X，A1B3与A3 B1交于点Y，A2B3于A3 B2交于点Z，则X、Y、Z三点共线。

笛沙格（Desargues）定理：已知在△ABC与△A'B'C'中，AA'、BB'、CC'三线相交于点O，BC与B'C'、CA与C'A'、AB与A'B'分别相交于点X、Y、Z，则X、Y、Z三点共线；其逆亦真摩莱（Morley）三角形：在已知△ABC三内角的三等分线中，分别与BC、CA、AB相邻的每两线相交于点D、E、F，则△DEF是正三角形，这个正三角形称为摩莱三角形。

已知圆内接六边形ABCDEF的边AB、DE延长线交于点G，边BC、EF 延长线交于点H，边CD、FA延长线交于点K，则H、G、K三点共线。

托勒密（Ptolemy）定理：在圆内接四边形中，AB·CD＋AD·BC＝AC·BD（任意四边形都可！哇哈哈）设P为△ABC边BC上一点，且BP：PC＝n：m，则m·(AB2)＋n·(AC2)＝m·(BP2 )＋n·(PC2)＋（m＋n）(AP2)梅内劳斯定理：在△ABC中，若在BC、CA、AB或其延长线上被同一条直线截于点X、Y、Z，则(BX/XC)·(CY/YA)·(AZ/ZB)＝1阿波罗尼斯（Apollonius）圆一动点P与两定点A、B的距离之比等于定比m:n，则点P的轨迹，是以定比m:n内分和外分定线段的两个分点的连线为直径的圆，这个圆被称为阿波罗尼斯圆，简称“阿氏圆”。

布拉美古塔（Brahmagupta）定理：在圆内接四边形ABCD中，AC⊥BD，自对角线的交点P向一边作垂线，其延长线必平分对边。

广勾股定理：在任一三角形中，(1)锐角对边的平方，等于两夹边之平方和，减去某夹边和另一夹边在此边上的影射乘积的两倍．(2)钝角对边的平方，等于两夹边的平方和，加上某夹边与另一夹边在此边延长上的影射乘积的两倍．加法原理：做一件事情，完成它有N类办法，在第一类办法中有M1种不同的方法，在第二类办法中有M2种不同的方法，……，在第N类办法中有M(N)种不同的方法，那么完成这件事情共有M1+M2+……+M(N)种不同的方法。

比如说：从北京到上海有3种方法可以直接到达上海，1：火车k12：飞机k23：轮船k3，那么从北京-上海的方法N = k1+k2+k3乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2不同的方法，……，做第n步有m·n不同的方法.那么完成这件事共有 N=m1·m2·m3…mn 种不同的方法.正弦定理在一个三角形中，各边和它所对角的正弦的比相等。

即a/sinA=b/sinB=c/sinC=2R （2R 在同一个三角形中是恒量，是此三角形外接圆的直径）这一定理对于任意三角形ABC ，都有a/sinA=b/sinB=c/sinC=2R （R 为三角形外接圆半径）余弦定理：对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与他们夹角的余弦的两倍积，若三边为a, b, c 三角为A,B,C ，则满足性质：a 2=b 2+c 2-2bc ·Cos A b 2=a 2+c 2-2ac ·Cos B c 2=a 2+b 2-2ab ·Cos C Cos C= (a 2+b 2-c 2)/2ab Cos B= (a 2+c 2-b 2)/2acCos A= (c ^2+b ^2-a ^2)/2bc解析几何中的基本公式1、 两点间距离：若)y ,x (B ),y ,x (A 2211，则212212)()(y y x x AB -+-=2、 平行线间距离：若0C By Ax :l ,0C By Ax :l 2211=++=++则：2221BA C C d +-=注意点：x ，y 对应项系数应相等。

3、 点到直线的距离：0C By Ax :l ),y ,x (P =++则P 到l 的距离为：22BA CBy Ax d +++=4、 直线与圆锥曲线相交的弦长公式：⎩⎨⎧=+=0)y ,x (F bkx y消y ：02=++c bx ax ，务必注意.0>∆若l 与曲线交于A ),(),,(2211y x B y x则：2122))(1(x x k AB -+=5、 若A ),(),,(2211y x B y x ，P （x ，y ）。

P 在直线AB 上，且P 分有向线段AB 所成的比为λ，则⎪⎪⎩⎪⎪⎨⎧λ+λ+=λ+λ+=112121y y y x x x ，特别地：λ=1时，P 为AB 中点且⎪⎪⎩⎪⎪⎨⎧+=+=222121y y y x x x 变形后：yy y y x x x x --=λ--=λ2121或6、 若直线l 1的斜率为k 1，直线l 2的斜率为k 2，则l 1到l 2的角为),0(,π∈αα适用范围：k 1，k 2都存在且k 1k 2≠－1 ， 21121tan k k k k +-=α若l 1与l 2的夹角为θ，则=θtan 21211k k k k +-，]2,0(π∈θ注意：（1）l 1到l 2的角，指从l 1按逆时针方向旋转到l 2所成的角，范围),0(π l 1到l 2的夹角：指 l 1、l 2相交所成的锐角或直角。

（2）l 1⊥l 2时，夹角、到角=2π。

（3）当l 1与l 2中有一条不存在斜率时，画图，求到角或夹角。

7、 （1）倾斜角α，),0(π∈α； （2）]0[,π∈θθ→→，，夹角b a ；（3）直线l 与平面]20[π∈ββα，，的夹角；（4）l 1与l 2的夹角为θ，∈θ]20[π，，其中l 1//l 2时夹角θ=0；（5）二面角,θ],0(π∈α； （6）l 1到l 2的角)0(π∈θθ，，8、 直线的倾斜角α与斜率k 的关系a) 每一条直线都有倾斜角α，但不一定有斜率。

b) 若直线存在斜率k ，而倾斜角为α，则k=tan α。

9、 直线l 1与直线l 2的的平行与垂直（1）若l 1，l 2均存在斜率且不重合：①l 1//l 2⇔ k 1=k 2②l 1⊥l 2⇔ k 1k 2=－1 （2）若0:,0:22221111=++=++C y B x A l C y B x A l若A 1、A 2、B 1、B 2都不为零① l 1//l 2⇔212121C C B B A A ≠=； ② l 1⊥l 2⇔ A 1A 2+B 1B 2=0； ③ l 1与l 2相交⇔2121B B A A ≠ ④ l 1与l 2重合⇔212121C C B B A A ==； 注意：若A 2或B 2中含有字母，应注意讨论字母=0与≠0的情况。

10、 直线方程的五种形式名称 方程 注意点斜截式： y=kx+b 应分①斜率不存在 ②斜率存在 点斜式： )( x x k y y -=- （1）斜率不存在： x x = （2）斜率存在时为)( x x k y y -=-两点式： 121121x x x x y y y y --=--截距式：1=+bya x 其中l 交x 轴于)0,(a ，交y 轴于),0(b 当直线l 在坐标轴上，截距相等时应分：（1）截距=0 设y=kx （2）截距=0≠a 设1=+ay a x 即x+y=a 一般式： 0=++C By Ax （其中A 、B 不同时为零）11、直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系有三种若22BA C Bb Aa d +++=，0<∆⇔⇔>相离r d0=∆⇔⇔=相切r d 0>∆⇔⇔<相交r d13、圆锥曲线定义、标准方程及性质 （一）椭圆定义Ⅰ：若F 1，F 2是两定点，P 为动点，且21212F F a PF PF >=+ （a 为常数）则P 点的轨迹是椭圆。

定义Ⅱ：若F 1为定点，l 为定直线，动点P 到F 1的距离与到定直线l 的距离之比为常数e （0<e<1），则P 点的轨迹是椭圆。

标准方程：12222=+by a x)0(>>b a定义域：}{a x a x ≤≤-值域：}{b y b x ≤≤- 长轴长=a 2，短轴长=2b 焦距：2c准线方程：ca x 2±=焦半径：)(21ca x e PF +=，)(22x ca e PF -=，212PF a PF -=，c a PF c a +≤≤-1等（注意涉及焦半径①用点P 坐标表示，②第一定义。

）注意：（1）图中线段的几何特征：=11F A c a F A -=22，=21F A c a F A +=12 =11F B a F B F B F B ===122221 ，222122b a B A B A +==等等。