初中数学竞赛定理
初中数学竞赛定理大全
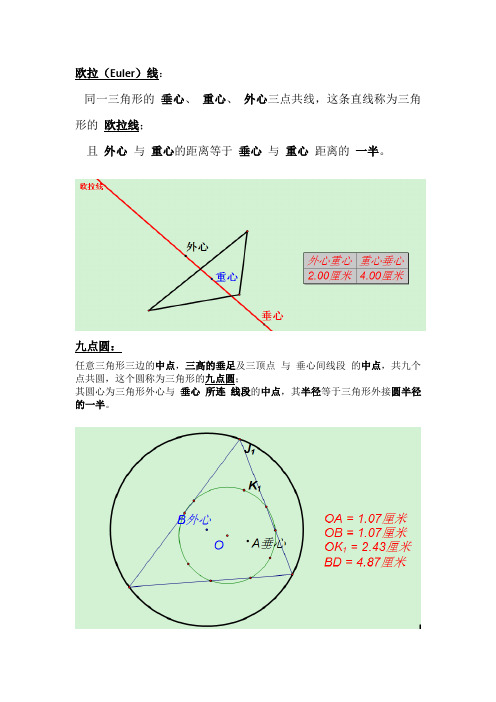
欧拉(Euler)线:同一三角形的垂心、重心、外心三点共线,这条直线称为三角形的欧拉线;且外心与重心的距离等于垂心与重心距离的一半。
九点圆:任意三角形三边的中点,三高的垂足及三顶点与垂心间线段的中点,共九个点共圆,这个圆称为三角形的九点圆;其圆心为三角形外心与垂心所连线段的中点,其半径等于三角形外接圆半径的一半。
费尔马点:已知P为锐角△ABC内一点,当∠APB=∠BPC=∠CPA=120°时,PA+PB+PC的值最小,这个点P称为△ABC的费尔马点。
海伦(Heron)公式:塞瓦(Ceva)定理:在△ABC中,过△ABC的顶点作相交于一点P的直线,分别交边BC、CA、AB与点D、E、F,则(BD/DC)·(CE/EA)·(AF/FB)=1;其逆亦真。
密格尔(Miquel)点:若AE、AF、ED、FB四条直线相交于A、B、C、D、E、F六点,构成四个三角形,它们是△ABF、△AED、△BCE、△DCF,则这四个三角形的外接圆共点,这个点称为密格尔点。
葛尔刚(Gergonne)点:△ABC的内切圆分别切边AB、BC、CA于点D、E、F,则AE、BF、CD三线共点,这个点称为葛尔刚点。
西摩松(Simson)线:已知P为△ABC外接圆周上任意一点,PD⊥BC,PE⊥ACPF⊥AB,D、E、F为垂足,则D、E、F三点共线,这条直线叫做西摩松线。
黄金分割:把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB) 与较小线段(BC)的比例中项,这样的分割称为黄金分割。
帕普斯(Pappus)定理:已知点A1、A2、A3在直线l1上,已知点B1、B2、B3在直线l2上,且A1 B2与A2 B1交于点X,A1B3与A3 B1交于点Y,A2B3于A3 B2交于点Z,则X、Y、Z三点共线。
笛沙格(Desargues)定理:已知在△ABC与△A'B'C'中,AA'、BB'、CC'三线相交于点O,BC与B'C'、CA与C'A'、AB与A'B'分别相交于点X、Y、Z,则X、Y、Z三点共线;其逆亦真摩莱(Morley)三角形:在已知△ABC三内角的三等分线中,分别与BC、CA、AB相邻的每两线相交于点D、E、F,则△DEF是正三角形,这个正三角形称为摩莱三角形。
初中数学竞赛25个定理

初中数学竞赛25个定理
初中数学竞赛25个定理1. 勾股定理:直角三角形斜边的平方等于两腰的平方和。
2. 余弦定理:在任意三角形ABC中,有c²=a²+b²-2abcosC。
3. 正弦定理:在任意三角形ABC中,有a/sinA=b/sinB=c/sinC。
4. 相似三角形的性质:对应角相等,对应边成比例。
5. 平行四边形法则:平行四边形两对邻边互相平分、互为反向共线向量。
6. 向量加减法则:向量之间可以进行加减运算,并且满足交换律、结合律和分配律。
7. 向量数量积公式:设向量a=(x₁,y₁,z₁)和b=(x₂,y₂,z₂),则
a·b=x₁x₂+y₁y₂+z₁z₂。
8. 圆周率π的计算方法及其性质
9. 等差数列通项公式an=a1+(n-1)d
10. 等比数列通项公式an=a1*q^(n-1)
11. 数列求和公式Sn=n(a1+an)/2
12. 柿子(二次根号不含整系数)判别法
13 .一元二次方程求解公式 x=(-b±√(b^2-4ac))/2a
14 .勾股数存在条件与构造方法
15 .正多面体表面积与体积计算公式
16 .圆锥侧面积与体积计算公式
17 .球表面积与体积计算公式
18 .立体图像展开后各部位长度关系推导方法
19 .概率基本定义及常见问题解决思路
20 .排列组合基础知识点总结
21 .函数定义域、值域以及单调性研究方法
22 .极坐标下曲线参数化表示方式
23 .复杂图案拼接技巧总结
24 .代数恒等变换规律总结
25 .空间几何证明题目思考策略。
初中数学竞赛数论定理

初中数学竞赛数论定理
初中数学竞赛中常用的数论定理:
1. 质数与因数:任何一个整数都可以唯一分解成若干质数的乘积,而且所有的因子都由这些质因子的指数作出来。
2. 最大公因数和最小公倍数:两个正整数a和b的最大公因数和最小公倍数分别记作gcd(a,b)和lcm(a,b)。
它们有许多重要性质可以应用。
3. 素性质数列:素数可以用许多方式列举出来,例如欧拉函数、Wilson定理、费马小定理等等。
其中一些方法在竞赛中比较常用。
4. 同余定理:如果a和b除以正整数m的余数相同,即
a≡b(mod m),那么a和b就被称为模m同余。
同余关系具有传递性、对称性和反对称性,可以用来证明各种数学恒等式和不等式。
5. 等比数列:等比数列指的是一个数列中每个数都是前一个数乘以一个固定的比例因子。
一些有用的定理包括调和平均值不小于几何平均值、柯西不等式等等。
6. 解方程:竞赛中常常需要解各种复杂的方程,例如二次方程、方程组、移项变系数、绝对值不等式等等。
有些常见的技巧包括配方法、因式分解、代数恒等式、三角变换等等。
初中数学竞赛知识点归纳(定理)

1.中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)初中竞赛需要,重要2.托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC初中竞赛需要,重要3.梅涅劳斯定理:设△ABC的三边BC、CA、AB或其延长线和一条不经过它们任一顶点的直线的交点分别为P、Q、R则有BPPC×CQQA×ARRB=1初中竞赛需要,重要4.梅涅劳斯定理的逆定理:(略)初中竞赛需要,重要5.梅涅劳斯定理的应用定理1:设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R,、∠B的平分线交边CA于Q,则P、Q、R三点共线。
不用掌握6.梅涅劳斯定理的应用定理2:过任意△ABC的三个顶点A、B、C作它的外接圆的切线,分别和BC、CA、AB的延长线交于点P、Q、R,则P、Q、R三点共线不用掌握7.、塞瓦定理:设△ABC的三个顶点A、B、C的不在三角形的边或它们的延长线上的一点S连接面成的三条直线,分别与边BC、CA、AB或它们的延长线交于点P、Q、R,则BPPC×CQQA×ARRB()=1.初中竞赛需要,重要8.塞瓦定理的应用定理:设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E,又设BE和CD交于S,则AS一定过边BC的中心M不用掌握9.塞瓦定理的逆定理:(略)初中竞赛需要,重要10.塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点这个定理用塞瓦定理来证明将毫无几何美感,应该用中位线证明才漂亮11.塞瓦定理的逆定理的应用定理2:设△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T,则AR、BS、CT交于一点。
不用掌握12.西摩松定理:从△ABC的外接圆上任意一点P向三边BC、CA、AB或其延长线作垂线,设其垂足分别是D、E、R,则D、E、R共线,(这条直线叫西摩松线)初中竞赛的常用定理13.西摩松定理的逆定理:(略)初中竞赛的常用定理14.切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角15.圆的外切四边形的两组对边的和相等16.弦切角定理弦切角等于它所夹的弧对的圆周角17.推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等18.相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等19.推论如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项20.切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项21.推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等斯特瓦特定理有三角形ABC,D为角A平分线与BC边的交点,则有以下定理:AB(2)·DC +AC(2)·BD-AD(2)·BC=BC·BD·DC托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).已知:圆内接四边形ABCD,求证:AC·BD=AB·CD+AD·BC.证明:如图1,过C作CP交BD于P,使∠1=∠2,又∠3=∠4,∴△ACD∽△BCP.得AC:BC=AD:BP,AC·BP=AD·BC ①。
中学数学竞赛中常用的几个重要定理
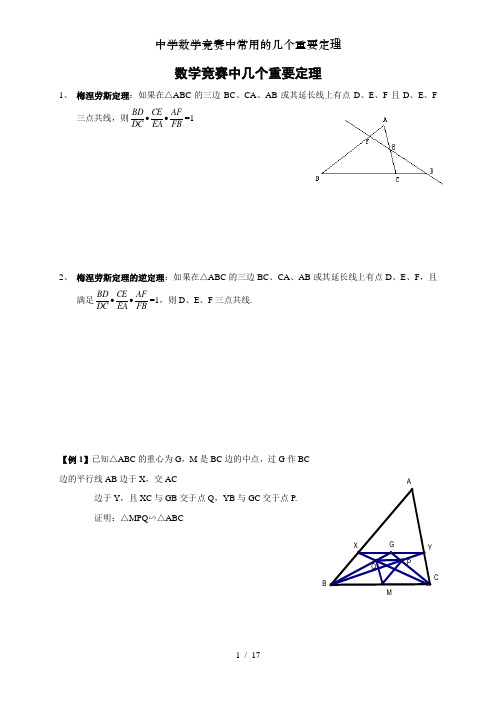
数学竞赛中几个重要定理1、 梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F三点共线,则FBAFEA CE DC BD ••=12、 梅涅劳斯定理的逆定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,且满足FBAFEA CE DC BD ••=1,则D 、E 、F 三点共线.【例1】已知△ABC 的重心为G ,M 是BC 边的中点,过G 作BC 边的平行线AB 边于X ,交AC边于Y ,且XC 与GB 交于点Q ,YB 与GC 交于点P. 证明:△MPQ ∽△ABCj MQGAC BXY P【例2】以△ABC的底边BC为直径作半圆,分别与边AB,AC交于点D和E,分别过点D,E作BC的垂线,垂足依次为F,G,线段DG和EF交于点M.求证:AM⊥BC【例3】四边形ABCD内接于圆,其边AB,DC的延长线交于点P,AD和BC的延长线交于点Q,过Q作该圆的两条切线,切点分别为E,F.求证:P,E,F三点共线.【练习1】设凸四边形ABCD 的对角线AC 和BD 交于点M ,过M 作AD 的平行线分别交AB ,CD于点E ,F ,交BC 的延长线于点O ,P 是以O 为圆心,以OM 为半径的圆上一点. 求证:∠OPF=∠OEP【练习2】 在△ABC 中,∠A=900,点D 在AC 上,点E 在BD 上,AE 的延长线交BC 于F. 若BE :ED=2AC :DC ,则∠ADB=∠FDCD塞瓦定理:设O是△ABC内任意一点,AO、BO、CO分别交对边于N、P、M,则1=••PACPNCBNMBAM塞瓦定理的逆定理:设M、N、P分别在△ABC的边AB、BC、CA上,且满足1=••PACPNCBNMBAM,则AN、BP、CM相交于一点.【例1】B E是△ABC的中线,G在BE上,分别延长AG,CG交BC,AB于点D,F,过D作DN∥CG交BG于N,△DGL及△FGM是正三角形.求证:△LMN为正三角形.GCLMEDFN【例2】在△ABC 中,D 是BC 上的点DC BD =31,E 是AC 中点.AD 与BE 交于O ,CO 交AB 于F 求四边形BDOF 的面积与△ABC 的面积的比【练习1】设P 为△ABC 内一点,使∠BPA=∠CPA ,G 是线段AP 上的一点,直线BG ,CG 分别交边AC ,AB 于E ,F.求证:∠BPF=∠CPE【练习2】 在△ABC 中,∠ABC 和∠ACB 均为锐角.D 是BC 边BC 上的内点,且AD 平分∠BAC ,过点D 作垂线DP ⊥AB 于P ,DQ ⊥AC 于Q ,CP 于BQ 相交于K. 求证:AK ⊥BCCCC托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD【例1】 已知在△ABC 中,AB >AC ,∠A 的一个外角的平分线交△ABC 的外接圆于点E ,过E 作EF ⊥AB ,垂足为F.求证:2AF=AB -AC【例2】经过∠XOY 的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P ,Q.求证:OP 1+OQ1为定值HABCEFAXYPOQ【例3】 解方程42-x+12-x=x 7【练习1】 设AF 为⊙O1与⊙O2的公共弦,点B ,C 分别在⊙O1,⊙O2上,且AB=AC ,∠BAF ,∠CAF 的平分线交⊙O1,⊙O2于点D ,E. 求证:DE ⊥AF【练习2】⊙O 为正△ABC 的外接圆,AD 是⊙O 的直径,在弧BC 上任取一点P (与B ,C不重合).设E ,F 分别为△PAB ,△PAC 的内心.证明:PD=∣PE-PF ∣西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥AC ,PF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线.【例1】过正△ABC 外接圆的弧AC 上点P 作P D ⊥直线AB 于D,作PE ⊥AC 于E,作PF ⊥BC 于F.求证:PF 1+PD 1=PE1【练习1】设P 为△ABC 外接圆周上任一点,P 点关于边BC ,AC 所在的直线的对称点分别为P 1,P 2.求证:直线P 1P 2经过△ABC 的垂心.CABPEFD HABP1P2CP三角形的五心内心【例1】设点M 是△ABC 的BC 边的中点,I 是其内心,AH 是BC 边上的高,E 为直线IM 与AH 的交点.求证:AE 等于内切圆半径r【例2】在△ABC 中,AB=4,AC=6,BC=5,∠A 的平分线AD 交△ABC的外接圆于K.O ,I 分别为△ABC 的外心,内心.求证:OI ⊥AK【练习】 在△ABC 中,∠BAC=300,∠ABC=700,M 为形内一点,∠MAB=∠MCA=200求∠MBA 的度数.B外心【例1】锐角△ABC的外心为O,线段OA,BC的中点为M,N,∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN【例2】在等腰△ABC中,AB=BC,CD是它的角平分线,O是它的外心,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,证明:BE=FD.【练习】1、⊙O 1与⊙O 2相交于P ,Q ,⊙O 1的弦PA 与⊙O 2相切,⊙O 2的弦PB 与⊙O 1相切.设△PAB 的外心为O ,求证:OQ ⊥PQ重心【例1】在△ABC 中,G 为重心,P 是形内一点,直线PG 交直线BC ,CA ,AB 于F ,E ,D.求证:FG FP +EG EP +DGDP=3【例2】已知△ABC 的重心G 和内心I 的连线GI ∥BC ,求证:AB+AC=2BCC【练习】1、设M 为△ABC 的重心,且AM=3,BM=4,CM=5,求△ABC 的面积.2、设O 是△ABC 的外心,AB=AC ,D 是AB 的中点,G 是△ACD 的重心,求证:OG ⊥CD垂心三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍.BCB【例1】△ABC 的外接圆为⊙O ,∠C=600,M 是弧AB 的中点,H 是△ABC 的垂心.求证:OM ⊥OH【例2】已知AD ,BE ,CF 是锐角△ABC 的三条高,过D 作EF 的平行线RQ ,RQ 分别交AB 和AC 于R ,Q ,P 为EF 与CB 的延长线的交点.证明:△PQR 的外接圆通过BC 的中点M.旁心【例1】在锐角∠XAY 内部取一点,使得∠ABC=∠XBD ,∠ACB=∠YCD.证明:△ABC 的外心在线段AD 上.CD【例2】AD是直角△ABC斜边BC上的高(AB<AC),I1,I2分别是△ABD,△ACD的内心,△A I1 I2的外接圆⊙O分别交AB,AC于E,F,直线FE与CB的延长线交于点M.证明:I1,I2分别是△ODM的内心与旁心.相交两圆的性质与应用【例1】证明:若凸五边形ABCDE中,∠ABC=∠ADE,∠AEC=∠ADB. 证明:∠BAC=∠DAEE【例2】已知⊙O1与⊙O2相交于A,B,直线MN垂直于AB且分别与⊙O1与⊙O2交于M,N,P 是线段MN的中点,Q1,Q2分别是⊙O1与⊙O2上的点,∠AO1Q1=∠AO2Q2求证:PQ1=PQ2【练习】梯形ABCD中,AB∥CD,AB>CD,K,M分别是腰AD,CB上的点,∠DAM=∠CBK,求证:∠DMA=∠CKBA其他的一些数学竞赛定理1、 广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和.推论2:设△ABC 三边长分别为a 、b 、c ,对应边上中线长分别为m a 、m b 、m c 则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+2、 三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有ACABDC BD =外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D ,则有ACABDC BD =3、 三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P4、 正弦定理、在△ABC 中有R CcB b A a 2sin sin sin ===(R 为△ABC 外接圆半径) 余弦定理: a 、b 、c 为△ABC 的边,则有: a 2=b 2+c 2-2bc ·cosA;b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;5、欧拉定理:△ABC 的外接圆圆心为O ,半径为R ,内切圆圆心为I ,半径为r,记OI=d,则有:d 2=R 2-2Rr.6、巴斯加线定理:圆内接六边形ABCDEF (不论其六顶点排列次序如何),其三组对边AB 与DE 、BC 与EF 、CD 与FA 的交点P 、Q 、R 共线.。
初中数学竞赛中常用重要定理

3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)ss为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
初中数学竞赛25个定理

初中数学竞赛25个定理在初中数学竞赛中,各种数学定理都是竞赛的基础,熟练掌握各种数学定理可以在竞赛中脱颖而出。
下面将介绍初中数学竞赛中常见的25个定理,希望对竞赛备战有所帮助。
1. 二元一次方程的解法对于形如ax+by=c的二元一次方程,当a、b不为零时,可以利用消元法、代入法等方式求解。
2. 勾股定理直角三角形的两条直角边的平方和等于斜边的平方,即a2+b2=c2。
3. 同底数幂的乘法法则同底数幂相乘,底数不变,指数相加,即 $a^m \\cdot a^n=a^{m+n}$。
4. 相反数的性质两个数的和为0时,互为相反数,即a+(−a)=0。
5. 解三角形内角和三角形内角和等于180°,即 $\\angle A+\\angle B+\\angle C=180°$。
6. 二次根式性质非负实数组的二次根式恒大于等于0,即 $\\sqrt{a} \\geq 0$。
7. 顺序角对应性质顺序角对应,即 $\\angle A | \\angle B$ 且 $\\angle B=\\angle A+k \\cdot 180°$。
8. 同底数幂的除法法则同底数幂相除,底数不变,指数相减,即 $\\dfrac{a^m}{a^n}=a^{m-n}$。
9. 三角形中角平分线性质三角形中角平分线将一个角平分为两个角,且两个角相等。
10. 解一元二次方程一元二次方程一般形式为ax2+bx+c=0,可以利用求根公式求解。
11. 垂直平分线性质垂直平分线将一条线段垂直平分成两段相等的线段。
12. 多边形内角和n边形内角和等于 $(n-2) \\cdot 180°$,其中n表示多边形的边数。
13. 二次函数的顶点坐标二次函数y=ax2+bx+c的顶点坐标为 $\\left(-\\dfrac{b}{2a}, -\\dfrac{\\Delta}{4a} \\right)$。
14. 欧拉公式对于任何凸多面体,顶点数、棱数和面数之差为2。
初中数学竞赛知识点归纳(定理)

1.中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)初中竞赛需要,重要2.托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC初中竞赛需要,重要3.梅涅劳斯定理:设△ABC的三边BC、CA、AB或其延长线和一条不经过它们任一顶点的直线的交点分别为P、Q、R则有BPPC×CQQA×ARRB=1初中竞赛需要,重要4.梅涅劳斯定理的逆定理:(略)初中竞赛需要,重要5.梅涅劳斯定理的应用定理1:设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R,、∠B的平分线交边CA于Q,则P、Q、R 三点共线。
不用掌握6.梅涅劳斯定理的应用定理2:过任意△ABC的三个顶点A、B、C作它的外接圆的切线,分别和BC、CA、AB的延长线交于点P、Q、R,则P、Q、R三点共线不用掌握7.、塞瓦定理:设△ABC的三个顶点A、B、C的不在三角形的边或它们的延长线上的一点S连接面成的三条直线,分别与边BC、CA、AB或它们的延长线交于点P、Q、R,则BPPC×CQQA×ARRB()=1.初中竞赛需要,重要8.塞瓦定理的应用定理:设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E,又设BE和CD交于S,则AS一定过边BC的中心M不用掌握9.塞瓦定理的逆定理:(略)初中竞赛需要,重要10.塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点这个定理用塞瓦定理来证明将毫无几何美感,应该用中位线证明才漂亮11.塞瓦定理的逆定理的应用定理2:设△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T,则AR、BS、CT交于一点。
不用掌握12.西摩松定理:从△ABC的外接圆上任意一点P向三边BC、CA、AB或其延长线作垂线,设其垂足分别是D、E、R,则D、E、R共线,(这条直线叫西摩松线)初中竞赛的常用定理13.西摩松定理的逆定理:(略)初中竞赛的常用定理14.切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角15.圆的外切四边形的两组对边的和相等16.弦切角定理弦切角等于它所夹的弧对的圆周角 第一角元形式的梅涅劳斯定理 且因为AF=BF 所以AF/FB必等于1 所以AF=FB 所以三角形三条中线交于一点 此外,可用定比分点来定义塞瓦定理: 在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
初中数学竞赛必备——42个定理与解题模型

初中数学竞赛必备——42个定理与解题模型一、概述1. 数学竞赛在培养学生的逻辑思维能力、数学解决问题的能力以及快速计算的能力方面具有重要的作用。
2. 初中数学竞赛中,掌握一定的数学定理和解题模型对于取得好成绩至关重要。
3. 本文将介绍初中数学竞赛必备的42个定理与解题模型,希望能为参加数学竞赛的同学们提供帮助。
二、数学定理与解题模型1. 代数部分1.1. 一元二次方程的求解方法1.2. 因式分解1.3. 角平分线定理1.4. 勾股定理1.5. 平方差公式1.6. 公式a^2-b^2=(a+b)(a-b)1.7. a^3-b^3=(a-b)(a^2+ab+b^2)2. 几何部分2.1. 同位角性质2.2. 对顶角性质2.3. 三角形的内角和2.4. 三角形的外角和2.5. 圆的性质2.6. 相似三角形的性质2.7. 三角形的高到底边的距离是线段的中线3. 概率部分3.1. 随机事件的概率计算3.2. 排列组合问题的概率计算3.3. 互斥事件和对立事件4. 数论部分4.1. 奇数与偶数的性质4.2. 质数与合数4.3. 最大公约数与最小公倍数5. 解题模型5.1. 分析题目5.2. 构建数学模型5.3. 运用定理解题5.4. 推理思路与方法三、数学竞赛练习与应用1. 多做数学竞赛题目,提高解题速度和正确率。
2. 运用所学的定理和解题模型解决实际问题,提高数学应用能力。
3. 对于涉及到竞赛的数学知识点,进行整体性的复习和整理。
四、结语1. 数学竞赛对于学生的数学能力提升有着一定的促进作用。
2. 要想在数学竞赛中取得好成绩,掌握基本数学定理和解题模型至关重要。
3. 希望本文介绍的42个定理与解题模型能为广大初中生在数学竞赛中取得优异成绩提供一定帮助。
五、举例演练1. 代数部分:一元二次方程的求解方法:解方程x^2+5x+6=0,可以使用因式分解或者配方法来进行求解。
因式分解:对于表达式x^2-4,可以因式分解为(x+2)(x-2)。
数学竞赛25个定理

数学竞赛25个定理1. 费马大定理:对于n>2时,方程a^n+b^n=c^n没有正整数解。
2. 勾股定理:直角三角形的两条直角边的平方和等于斜边的平方。
3. 柯西不等式:对于n维向量a和b,有|a·b|≤||a||·||b||,其中||a||和||b||分别表示向量a和b的模长。
4. 无理数的存在性:根号2是一个无理数,即不可表示为有理数的分数形式。
5. 威尔逊定理:如果p是质数,则(p-1)!+1能够被p整除。
6. 欧拉公式:对于任意实数x,有e^(ix)=cosx+isinx。
7. 线性规划:在一定条件下,线性规划问题可以通过线性规划算法有效地求解。
8. 奥托-康托定理:对于任意正整数n和正整数m,可以将1~n的全排列映射到1~m的m进制数中。
9. 科赫曲线:科赫曲线是一条典型的分形曲线,具有无限细节和自相似性质。
10. 柯西-黎曼方程:复函数必须满足柯西-黎曼方程,才能够进行解析运算。
11. 供求关系:供求关系是微观经济学中的一个基本概念,描述了在市场中商品的价格和数量之间的关系。
12. 投影定理:向量b在向量a的方向上的投影等于向量a与b的内积除以向量a的模长。
13. 黎曼假设:黎曼猜想认为,所有非平凡的自然数零点都在一条竖线上,即1/2+it,其中t为实数。
14. 矩阵行列式:矩阵的行列式可以表示为对角线上的乘积减去反对角线上的乘积。
15. 平均值不等式:对于正实数a和b,有(a+b)/2≥(ab)^(1/2)。
16. 裴蜀定理:对于整数a和b,存在整数x和y,使得ax+by=(a,b),其中(a,b)表示a和b的最大公约数。
17. 黑斯托夫定理:将一个整数的各位数字全部平方后求和所得到的数,如果最终能够得到1,则该数为幸福数;否则就会进入一个循环,永远无法得到1。
18. 莫比乌斯函数:莫比乌斯函数是数论中一种重要的函数,可以用于求解许多数论问题。
19. 皮克定理:计算凸多边形的面积需要知道其内部的点数和边上的点数,皮克定理给出了一种简单的求解方法。
-初中数学竞赛定理大全

欧拉(Euler)线:同一三角形的垂心、重心、外心三点共线,这条直线称为三角形的欧拉线;且外心与重心的距离等于垂心与重心距离的一半。
九点圆:任意三角形三边的中点,三高的垂足及三顶点与垂心间线段的中点,共九个点共圆,这个圆称为三角形的九点圆;其圆心为三角形外心与垂心所连线段的中点,其半径等于三角形外接圆半径的一半。
费尔马点:已知P为锐角△ABC内一点,当∠APB=∠BPC=∠CPA=120°时,PA+PB+PC的值最小,这个点P称为△ABC的费尔马点。
海伦(Heron)公式:塞瓦(Ceva)定理:在△ABC中,过△ABC的顶点作相交于一点P的直线,分别交边BC、CA、AB与点D、E、F,则(BD/DC)·(CE/EA)·(AF/FB)=1;其逆亦真。
密格尔(Miquel)点:若AE、AF、ED、FB四条直线相交于A、B、C、D、E、F六点,构成四个三角形,它们是△ABF、△AED、△BCE、△DCF,则这四个三角形的外接圆共点,这个点称为密格尔点。
葛尔刚(Gergonne)点:△ABC的内切圆分别切边AB、BC、CA于点D、E、F,则AE、BF、CD三线共点,这个点称为葛尔刚点。
西摩松(Simson)线:已知P为△ABC外接圆周上任意一点,PD⊥BC,PE⊥ACPF⊥AB,D、E、F为垂足,则D、E、F三点共线,这条直线叫做西摩松线。
黄金分割:把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB) 与较小线段(BC)的比例中项,这样的分割称为黄金分割。
帕普斯(Pappus)定理:已知点A1、A2、A3在直线l1上,已知点B1、B2、B3在直线l2上,且A1 B2与A2 B1交于点X,A1B3与A3 B1交于点Y,A2B3于A3 B2交于点Z,则X、Y、Z三点共线。
笛沙格(Desargues)定理:已知在△ABC与△A'B'C'中,AA'、BB'、CC'三线相交于点O,BC与B'C'、CA与C'A'、AB与A'B'分别相交于点X、Y、Z,则X、Y、Z三点共线;其逆亦真摩莱(Morley)三角形:在已知△ABC三内角的三等分线中,分别与BC、CA、AB相邻的每两线相交于点D、E、F,则△DEF是正三角形,这个正三角形称为摩莱三角形。
完整版)初中数学竞赛定理大全

完整版)初中数学竞赛定理大全欧拉线是同一三角形的垂心、重心、外心三点共线的直线,且外心与重心的距离等于垂心与重心距离的一半。
九点圆是任意三角形三边的中点、三高的垂足及三顶点与垂心间线段的中点共九个点共圆,其圆心为三角形外心与垂心所连线段的中点,其半径等于三角形外接圆半径的一半。
费尔马点是△ABC内一点P,当∠APB=∠XXX∠CPA=120°时,PA+PB+PC的值最小,这个点P称为△XXX的费尔马点。
海伦公式是用三角形三边的长度计算其面积的公式,即面积=sqrt[s(s-a)(s-b)(s-c)],其中s=(a+b+c)/2.塞瓦定理是指在△ABC中,过△ABC的顶点作相交于一点P的直线,分别交边BC、CA、AB与点D、E、F,则(BD/DC)·(CE/EA)·(AF/FB)=1;其逆亦真。
密格尔点是指若AE、AF、ED、FB四条直线相交于A、B、C、D、E、F六点,构成四个三角形,它们是△ABF、△AED、△BCE、△DCF,则这四个三角形的外接圆共点,这个点称为密格尔点。
葛尔刚点是指△XXX的内切圆分别切边AB、BC、CA于点D、E、F,则AE、BF、CD三线共点,这个点称为葛尔刚点。
西摩松线是指已知P为△ABC外接圆周上任意一点,PD⊥BC,PE⊥AC,PF⊥AB,D、E、F为垂足,则D、E、F 三点共线,这条直线叫做西摩松线。
黄金分割是指把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB)与较小线段(BC)的比例中项,这样的分割称为黄金分割。
XXX定理是指已知点A1、A2、A3在直线l1上,已知点B1、B2、B3在直线l2上,且A1B2与A2B1交于点X,A1B3与A3B1交于点Y,A2B3于A3B2交于点Z,则X、Y、Z三点共线。
笛沙格定理是指已知在△ABC与△A'B'C'中,AA'、BB'、CC'三线相交于点O,BC与B'C'、CA与C'A'、AB与A'B'分别相交于点X、Y、Z,则X、Y、Z三点共线;其逆亦真。
初中数学竞赛重要定理公式(平面几何篇)

初中数学竞赛重要定理、公式及结论平面几何篇【三角形面积公式(包括海伦公式)】)(为内切圆半径,为外接圆半径,边上的高,表示,其中c b a p R BC h c p b p a p p pr C B A c b a C B A R R abc C ab ah S a a ++=---==++++=====21r ))()(()cot cot (cot 4sin sin sin 24sin 21212222ABC Δ【斯特瓦尔特定理】设已知△ABC 及其底边上B 、C 两点间的一点D ,则有AB 2·DC+AC 2·BD -AD 2·BC =BC·DC·BD .【托勒密定理】圆内接四边形对角线之积等于两组对边乘积之和,即AC·BD=AB·CD+AD·BC ,(逆命题成立).(广义托勒密定理)AB·CD+AD·BC ≥AC·BD .【蝴蝶定理】AB 是△O 的弦,M 是其中点,弦CD 、EF 经过点M ,CF 、DE 交AB 于P 、Q ,则MP=QM .【勾股定理(毕达哥拉斯定理)(广义勾股定理)】(1)锐角对边的平方,等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍.(2)钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍.【中线定理(巴布斯定理)】设△ABC 的边BC 的中点为P ,则有)BP 2(AP AC AB 2222+=+中线长:【垂线定理】AB ⊥CD ⇔AC 2-AD 2=BC 2-BD 2 高线长: 【角平分线定理】三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例如△ABC 中,AD 平分△BAC ,则 (外角平分线定理) 角平分线长:【正弦定理】 222222a c b m a -+=bSinC cSinB SinA a bc c p b p a p p a h a ===---=))()((2ACAB DC BD =为周长一半)其中p A c b bc a p bcp c b t a (2cos 2)(2+=-+=为三角形外接圆半径)其中,R R C c B b A a (2sin sin sin ===【余弦定理】 【张角定理】【圆周角定理】同弧所对的圆周角相等,等于圆心角的一半.【弦切角定理】弦切角等于夹弧所对的圆周角.【圆幂定理】(相交弦定理:垂径定理:切割线定理(割线定理):切线长定理:)【射影定理(欧几里得定理)】直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
初中数学竞赛定理大全
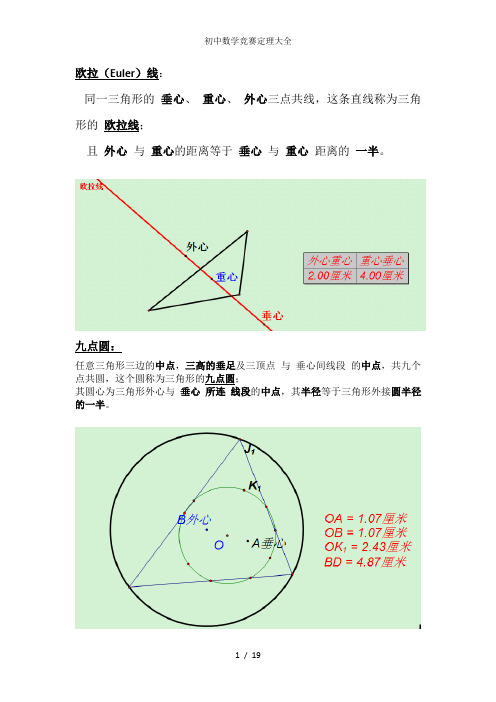
欧拉(Euler)线:同一三角形的垂心、重心、外心三点共线,这条直线称为三角形的欧拉线;且外心与重心的距离等于垂心与重心距离的一半。
九点圆:任意三角形三边的中点,三高的垂足及三顶点与垂心间线段的中点,共九个点共圆,这个圆称为三角形的九点圆;其圆心为三角形外心与垂心所连线段的中点,其半径等于三角形外接圆半径的一半。
费尔马点:已知P为锐角△ABC内一点,当∠APB=∠BPC=∠CPA=120°时,PA+PB+PC的值最小,这个点P称为△ABC的费尔马点。
海伦(Heron)公式:塞瓦(Ceva)定理:在△ABC中,过△ABC的顶点作相交于一点P的直线,分别交边BC、CA、AB与点D、E、F,则(BD/DC)·(CE/EA)·(AF/FB)=1;其逆亦真。
密格尔(Miquel)点:若AE、AF、ED、FB四条直线相交于A、B、C、D、E、F六点,构成四个三角形,它们是△ABF、△AED、△BCE、△DCF,则这四个三角形的外接圆共点,这个点称为密格尔点。
葛尔刚(Gergonne)点:△ABC的内切圆分别切边AB、BC、CA于点D、E、F,则AE、BF、CD三线共点,这个点称为葛尔刚点。
西摩松(Simson)线:已知P为△ABC外接圆周上任意一点,PD⊥BC,PE⊥ACPF⊥AB,D、E、F为垂足,则D、E、F三点共线,这条直线叫做西摩松线。
黄金分割:把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB) 与较小线段(BC)的比例中项,这样的分割称为黄金分割。
帕普斯(Pappus)定理:已知点A1、A2、A3在直线l1上,已知点B1、B2、B3在直线l2上,且A1 B2与A2 B1交于点X,A1B3与A3 B1交于点Y,A2B3于A3 B2交于点Z,则X、Y、Z三点共线。
笛沙格(Desargues)定理:已知在△ABC与△A'B'C'中,AA'、BB'、CC'三线相交于点O,BC与B'C'、CA与C'A'、AB与A'B'分别相交于点X、Y、Z,则X、Y、Z三点共线;其逆亦真摩莱(Morley)三角形:在已知△ABC三内角的三等分线中,分别与BC、CA、AB相邻的每两线相交于点D、E、F,则△DEF是正三角形,这个正三角形称为摩莱三角形。
初中数学竞赛公式定理大全

1.过两点有且只有一条直线2.两点之间线段最短3.同角或等角的补角相等4.同角或等角的余角相等5.过一点有且只有一条直线和已知直线垂直6.直线外一点与直线上各点连接的所有线段中,垂线段最短7.平行公理经过直线外一点,有且只有一条直线与这条直线平行8.如果两条直线都和第三条直线平行,这两条直线也互相平行9.同位角相等,两直线平行10.内错角相等,两直线平行11.同旁内角互补,两直线平行12.两直线平行,同位角相等13.两直线平行,内错角相等14.两直线平行,同旁内角互补15.定理三角形两边的和大于第三边16.推论三角形两边的差小于第三边17.三角形内角和定理三角形三个内角的和等于180°18.推论1 直角三角形的两个锐角互余19.推论2 三角形的一个外角等于和它不相邻的两个内角的和20.推论3 三角形的一个外角大于任何一个和它不相邻的内角21.全等三角形的对应边、对应角相等22.边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23.角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24.推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25.边边边公理(SSS) 有三边对应相等的两个三角形全等26.斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27.定理1 在角的平分线上的点到这个角的两边的距离相等28.定理2 到一个角的两边的距离相同的点,在这个角的平分线上29.角的平分线是到角的两边距离相等的所有点的集合30.等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31.推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32.等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33.推论3 等边三角形的各角都相等,并且每一个角都等于60°34.等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35.推论1 三个角都相等的三角形是等边三角形36.推论2 有一个角等于60°的等腰三角形是等边三角形37.在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38.直角三角形斜边上的中线等于斜边上的一半39.定理线段垂直平分线上的点和这条线段两个端点的距离相等40.逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41.线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42.定理1 关于某条直线对称的两个图形是全等形43.定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44.定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45.逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46.勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^247.勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形48.定理四边形的内角和等于360°49.四边形的外角和等于360°50.多边形内角和定理n边形的内角的和等于(n-2)×180°51.推论任意多边的外角和等于360°52.平行四边形性质定理1 平行四边形的对角相等53.平行四边形性质定理2 平行四边形的对边相等54.推论夹在两条平行线间的平行线段相等55.平行四边形性质定理3 平行四边形的对角线互相平分56.平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57.平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58.平行四边形判定定理3 对角线互相平分的四边形是平行四边形59.平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60.矩形性质定理1 矩形的四个角都是直角61.矩形性质定理2 矩形的对角线相等62.矩形判定定理1 有三个角是直角的四边形是矩形63.矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65.菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66.菱形面积=对角线乘积的一半,即S=(a×b)÷267.菱形判定定理1 四边都相等的四边形是菱形68.菱形判定定理2 对角线互相垂直的平行四边形是菱形69.正方形性质定理1 正方形的四个角都是直角,四条边都相等70.正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71.定理1 关于中心对称的两个图形是全等的72.定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73.逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74.等腰梯形性质定理等腰梯形在同一底上的两个角相等75.等腰梯形的两条对角线相等76.等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77.对角线相等的梯形是等腰梯形78.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79.推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80.推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81.三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82.梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2 S=L×h83.(1)比例的基本性质如果a:b=c:d,那么ad=bc;如果ad=bc,那么a:b=c:d84.(2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85.(3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87.推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88.定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89.平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90.定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91.相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92.直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93.判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94.判定定理3 三边对应成比例,两三角形相似(SSS)95.定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96.性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97.性质定理2 相似三角形周长的比等于相似比98.性质定理3 相似三角形面积的比等于相似比的平方99.任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100.任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101.圆是定点的距离等于定长的点的集合102.圆的内部可以看作是圆心的距离小于半径的点的集合103.圆的外部可以看作是圆心的距离大于半径的点的集合104.同圆或等圆的半径相等105.到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106.和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107.到已知角的两边距离相等的点的轨迹,是这个角的平分线108.到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109.定理不在同一直线上的三点确定一个圆。
初中数学竞赛定理大全

斯图尔特(Stewart)定理:设P为△ABC边BC上一点,且BP:PC=n:m,则m·(AB2)+n·(AC2)=m·(BP2 )+n·(PC2)+(m+n)(AP2)梅内劳斯定理:在△ABC中,若在BC、CA、AB或其延长线上被同一条直线截于点X、Y、Z,则(BX/XC)·(CY/YA)·(AZ/ZB)=1阿波罗尼斯(Apollonius)圆一动点P与两定点A、B的距离之比等于定比m:n,则点P的轨迹,是以定比m:n内分和外分定线段的两个分点的连线为直径的圆,这个圆被称为阿波罗尼斯圆,简称“阿氏圆”。
布拉美古塔(Brahmagupta)定理:在圆内接四边形ABCD中,AC⊥BD,自对角线的交点P向一边作垂线,其延长线必平分对边。
广勾股定理:在任一三角形中,(1)锐角对边的平方,等于两夹边之平方和,减去某夹边和另一夹边在此边上的影射乘积的两倍.(2)钝角对边的平方,等于两夹边的平方和,加上某夹边与另一夹边在此边延长上的影射乘积的两倍.加法原理:做一件事情,完成它有N类办法,在第一类办法中有M1种不同的方法,在第二类办法中有M2种不同的方法,……,在第N类办法中有M(N)种不同的方法,那么完成这件事情共有M1+M2+……+M(N)种不同的方法。
比如说:从北京到上海有3种方法可以直接到达上海,1:火车k12:飞机k23:轮船k3,那么从北京-上海的方法N = k1+k2+k3乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2不同的方法,……,做第n步有m·n不同的方法.那么完成这件事共有 N=m1·m2·m3…mn 种不同的方法.正弦定理在一个三角形中,各边和它所对角的正弦的比相等。
即a/sinA=b/sinB=c/sinC=2R (2R 在同一个三角形中是恒量,是此三角形外接圆的直径)这一定理对于任意三角形ABC ,都有a/sinA=b/sinB=c/sinC=2R (R 为三角形外接圆半径)余弦定理:对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与他们夹角的余弦的两倍积,若三边为a, b, c 三角为A,B,C ,则满足性质:a 2=b 2+c 2-2bc ·Cos A b 2=a 2+c 2-2ac ·Cos B c 2=a 2+b 2-2ab ·Cos C Cos C= (a 2+b 2-c 2)/2ab Cos B= (a 2+c 2-b 2)/2acCos A= (c ^2+b ^2-a ^2)/2bc解析几何中的基本公式1、 两点间距离:若)y ,x (B ),y ,x (A 2211,则212212)()(y y x x AB -+-=2、 平行线间距离:若0C B y A x :l ,0C B y A x :l 2211=++=++则:2221BA C C d +-=注意点:x ,y 对应项系数应相等。
初中数学竞赛模型定理

初中数学竞赛模型定理包括但不限于以下几个:
1. 勾股定理:在直角三角形中,直角边的平方和等于斜边的平方。
即,如果a和b是直角三角形的两条直角边,c是斜边,那么a² + b² = c²。
2. 三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半。
3. 圆的性质:在同一个圆或等圆中,相等的弦所对的弧相等,所对的圆心角也相等。
4. 平行线的性质:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行。
5. 垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
这些定理在初中数学竞赛中经常出现,掌握这些定理可以更好地理解和解决数学问题。
同时,还需要注意这些定理的使用条件和限制,避免在解题过程中出现错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦定理定理概述在一个三角形中,各边和它所对角的正弦的比相等。
即a/sinA=b/sinB=c/sinC=2R(2R在同一个三角形中是恒量,是此三角形外接圆的直径)这一定理对于任意三角形ABC,都有a/sinA=b/sinB=c/sinC=2RR为三角形外接圆半径证明步骤1.在锐角△ABC中,设BC=a,AC=b,AB=c。
作CH⊥AB垂足为点HCH=a·sinBCH=b·sinA∴a·sinB=b·sinA得到a/sinA=b/sinB同理,在△ABC中,b/sinB=c/sinC步骤2.证明a/sinA=b/sinB=c/sinC=2R:如图,任意三角形ABC,作ABC的外接圆O.作直径BD交⊙O于D.连接DA.因为直径所对的圆周角是直角,所以∠DAB=90度因为同弧所对的圆周角相等,所以∠D等于∠C.所以c/sinC=c/sinD=BD=2R类似可证其余两个等式。
意义正弦定理指出了任意三角形中三条边与对应角的正弦值之间的一个关系式。
扩展三角形面积公式1.海伦公式:设P=(a+b+c)/2S△=根号下P(P-a)(P-b)(P-c)解释:假设有一个三角形,边长分别为a、b、c,三角形的面积S可由以下公式求得:S=√[p(p-a)(p-b)(p-c)]而公式里的p为半周长:p=(a+b+c)/22.S△ABC=(ab/2)·sinC=(bc/2)·sinA=(ac/2)·sinB=abc/(4R)[R为外接圆半径]3.S△ABC=ah/2正弦定理的变形公式(1) a=2RsinA, b=2RsinB, c=2RsinC;(2) sinA : sinB : sinC = a : b : c;(条件同上)在一个三角形中,各边与其所对角的正弦的比相等,且该比值都等于该三角形外接圆的直径已知三角形是确定的,利用正弦定理解三角形时,其解是唯一的;已知三角形的两边和其中一边的对角,由于该三角形具有不稳定性,所以其解不确定,可结合平面几何作图的方法及“大边对大角,大角对大边”定理和三角形内角和定理去考虑解决问题(3)相关结论:a/sinA=b/sinB=c/sinC=(a+b)/(sinA+sinB)=(a+b+c)/(sinA+sinB+sinC)c/sinC=c/sinD=BD=2R⑷设R为三角外接圆半径,公式可扩展为:a/sinA=b/sinB=c/sinC=2R,即当一内角为90°时,所对的边为外接圆的直径。
灵活运用正弦定理,还需要知道它的几个变形sinA=a/2R,sinB=b/2R,sinC=c/2RasinB=bsinA,bsinC=csinB,asinC=csinA余弦定理余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
余弦定理性质对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与他们夹角的余弦的两倍积,若三边为a,b,c 三角为A,B,C ,则满足性质——(注:a*b、a*c就是a乘b、a乘c 。
a^2、b^2、c^2就是a的平方,b的平方,c的平方。
)a^2=b^2+c^2-2*b*c*Cos Ab^2=a^2+c^2-2*a*c*Cos Bc^2=a^2+b^2-2*a*b*Cos CCos C=(a^2+b^2-c^2)/2abCos B=(a^2+c^2-b^2)/2acCos A=(c^2+b^2-a^2)/2bc余弦定理证明平面几何证法:在任意△ABC中做AD⊥BC.∠C所对的边为c,∠B所对的边为b,∠A所对的边为a则有BD=cosB*c,AD=sinB*c,DC=BC-BD=a-cosB*c根据勾股定理可得:AC^2=AD^2+DC^2b^2=(sinB*c)^2+(a-cosB*c)^2b^2=sin^2B*c^2+a^2+cos^2B*c^2-2ac*cosBb^2=(sin^2B+cos^2B)*c^2-2ac*cosB+a^2b^2=c^2+a^2-2ac*cosBcosB=(c^2+a^2-b^2)/2ac余弦定理的作用(1)已知三角形的三条边长,可求出三个内角;(2)已知三角形的两边及夹角,可求出第三边.例如:已知△ABC的三边之比为:2:1,求最大的内角.解设三角形的三边为a,b,c且a:b:c=:2:1.由三角形中大边对大角可知:∠A为最大的角.由余弦定理cos A==-所以∠A=120°.再如△ABC中,AB=2,AC=3,∠A=π3,求BC之长.解由余弦定理可知BC2=AB2+AC2-2AB×AC·cos A=4+9-2×2×3×=7,所以BC=7.以上两个小例子简单说明了余弦定理的作用.其他从余弦定理和余弦函数的性质可以看出,如果一个三角形两边的平方和等于第三边的平方,那么第三边所对的角一定是直角,如果小于第三边的平方,那么第三边所对的角是钝角,如果大于第三边的平方,那么第三边所对的角是锐角。
即,利用余弦定理,可以判断三角形形状。
同时,还可以用余弦定理求三角形边长取值范围。
斯特瓦尔特(stewart)定理设已知△ABC及其底边上B、C两点间的一点D,则有AB²·DC+AC²·BD-AD²·BC=BC·DC·BD。
证明:在图2-6中,作AH⊥BC于H。
为了明确起见,设H和C在点D的同侧,那么由广勾股定理有AC²=AD²+DC²-2DC·DH,(1)AB²=AD²+ BD²+2BD·DH。
(2)用BD乘(1)式两边得AC²·BD=AD²·BD+DC²·BD-2DC·DH·BD,(1)′用DC乘(2)式两边得AB²·DC=AD²·DC+BD²·DC+2BD·DH·DC。
(2)′由(1)′+(2)′得到AC²·BD+AB²·DC=AD²(BD+DC)+DC²·BD+BD&sup 2;·DC=AD²·BC+BD·DC·BC。
∴AB²·DC+AC²·BD-AD²·BC=BC·DC·BD。
或者根据余弦定理得AB²=PB²+PA²-2PB·PA·cos∠APBAC²=PA²+PC²-2PA·PC·cos∠APC两边同时除以PB·PA·PC得AC²·PB+AB²·PC=(PB²+PA²)PC+(PA²+PA&sup 2;)PB化简即可(注:图中2-7A点为P点,BDC点依次为ABC)梅涅劳斯(Menelaus)定理简介梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1证明一:过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二:过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立:若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/EA)=1,则F、D、E三点共线。
利用这个逆定理,可以判断三点共线。
梅涅劳斯(Menelaus)定理证明三:过ABC三点向三边引垂线AA'BB'CC',所以AD:DB=AA':BB',BE:EC=BB':CC',CF:FA=CC':AA'所以(AF/FB)×(BD/DC)×(CE/EA)=1证明四:连接BF。
(AD:DB)·(BE:EC)·(CF:FA)=(S△ADF:S△BDF)·(S△BEF:S△CEF)·(S△BCF:S△BAF)=(S△ADF:S△BDF)·(S△BDF:S△CDF)·(S△CDF:S△ADF)=1此外,用定比分点定义该定理可使其容易理解和记忆:在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
于是L、M、N三点共线的充要条件是λμν=1。
第一角元形式的梅涅劳斯定理如图:若E,F,D三点共线,则(sin∠ACF/sin∠FCB)(sin∠BAD/sin∠DAC)(sin∠CBA/sin∠ABE)=1即图中的蓝角正弦值之积等于红角正弦值之积该形式的梅涅劳斯定理也很实用第二角元形式的梅涅劳斯定理在平面上任取一点O,且EDF共线,则(sin∠AOF/sin∠FOB)(sin∠BOD/sin ∠DOC)(sin∠COA/sin∠AOE)=1。
(O不与点A、B、C重合)记忆ABC为三个顶点,DEF为三个分点(AF/FB)×(BD/DC)×(CE/EA)=1(顶到分/分到顶)*(顶到分/分到顶)*(顶到分/分到顶)=1空间感好的人可以这么记:(上1/下1)*(整/右)*(下2/上2)=1实际应用为了说明问题,并给大家一个深刻印象,我们假定图中的A、B、C、D、E、F 是六个旅游景点,各景点之间有公路相连。
