一次函数与几何综合(一)(习题及答案)
一次函数与几何综合(一)(讲义及答案).

一次函数与几何综合(一)(讲义)➢ 课前预习1. 若一次函数经过点 A (2,-1)和点 B (4,3),则该一次函数的表达式为.2. 若直线 l 平行于直线 y =-2x -1,且过点(1,4),则直线 l 的表达式为 .3.如图,一次函数的图象经过点 A ,且与正比例函数 y =-x 的图象交于点 B ,则该一次函数的表达式为.第 3 题图第 4 题图4.如图,点 A 在直线 l 1:y =3x 上,且点 A 在第一象限,过点 A 作 y 轴的平行线交直线 l 2:y =x 于点 B .(1) 设点 A 的横坐标为 t ,则点 A 的坐标为,点 B的坐标为 ,线段 AB 的长为;(用含 t的式子表示)(2) 若 AB =4,则点 A 的坐标是.➢ 知识点睛1. 一次函数与几何综合的处理思路:从已知的表达式、坐标或几何图形入手,分析特征,通过坐标与横平竖直线段长、函数表达式相互转化解决问题.2. 函数与几何综合问题中常见转化方式:(1) 借助表达式设出点坐标,将点坐标转化为横平竖直线段长,结合几何特征利用线段长列方程;(2) 研究几何特征,考虑线段间关系,通过设线段长进而表达点坐标,将点坐标代入函数表达式列方程.表达线段长:横平线段长,横坐标相减,右减左; 竖直线段长,纵坐标相减,上减下.1➢ 精讲精练1.如图,直线 y = - 3x + 3 与 x 轴、y 轴交于 A ,B 两点,点 C4是 y 轴负半轴上一点,若 BA =BC ,则直线 AC 的表达式为.第 1 题图第 2 题图2.如图,在平面直角坐标系中,一次函数 y =kx +b 的图象经过点A (-2,6),且与 x 轴相交于点 B ,与正比例函数 y =3x 的图象交于点 C ,点 C 的横坐标为 1,则△OBC 的面积为 .3.如图,直线l :y = 3x + 6 与 y 轴相交于点 N ,直线l :y = kx -31 42与直线l 1 相交于点 P ,与 y 轴相交于点 M ,若△PMN 的面积为 18,则直线l 2的表达式为.4.如图,一次函数 y = 1x + 2 的图象与 y 轴交于点 A ,与正比例3函数 y =kx 的图象交于第二象限内的点 B ,若 AB =OB ,则 k 的值为.5. 如图,点A,B 的坐标分别为(-8,0),(0,4),点C(a,0)为x轴上一个动点,过点C 作x 轴的垂线,交直线AB 于点D,若CD=5,则a 的值为.6.如图,直线y=kx+6 与x 轴、y 轴分别交于点A,B,点A 的坐标为(6,0),点C 的坐标为(4,0).若点P 是直线y=kx+6 上的一个动点,当点P 的坐标为时,△OPC 的面积为4.7.如图,直线y =-1x +b 与x 轴、y 轴分别交于点A,B,与直2线y=x 交于点M,点M 的横坐标为2,点C 为线段AM 上一点,过点C 作x 轴的垂线,垂足为点D,交直线y=x 于点E.若ED=4CD,则点E 的坐标为.8.如图,直线l1:y=2x+1 与直线l2:y=mx+4 相交于点P(1,b),垂直于x 轴的直线x=a 与直线l1,l2 分别交于点A,B,若线段AB 的长为2,则a 的值为.9.如图,直线AB:y=-x+20 与y 轴交于点A,与直线OB:y =1 x 3交于点B.点C 为线段OB 上一点,过点C 作y 轴的平行线交直线AB 于点D,向y 轴作垂线,垂足为点E.若DC=2CE,则点C 的坐标为.10.如图,在平面直角坐标系中,点A,C 和B,D 分别在直线y=1x+3和x 轴上,若△OAB,△BCD 都是等腰直角三角形,2∠OAB=∠BCD=90°,则点C 的坐标为.11.如图,直线l1:y 3x 与直线l2:y=-x+7 相交于点A.点P 4在x 轴正半轴上,过点P 作x 轴的垂线,与直线l1,l2 分别交于点B,C.设点P 的横坐标为t.(1)当t=1 时,求线段BC 的长;(2)用含t 的式子表达BC 的长;(3)若三个点B,C,P 中恰有一点是其他两点所连线段的中点,则称B,C,P 三点为“共谐点”.请直接写出使得B,C,P 三点成为“共谐点”的t 的值.⎨ 【参考答案】➢ 课前预习1. y = 2x - 52. y = -2x + 63. y = x + 24. (1)(t ,3t ),(t ,t ),2t(2)(2,6)➢ 精讲精练1. y = 1x - 222. 63. y = - 3x - 32 4. - 13 5. 2 或-186. (4,2)或(8,-2)7. (4,4)8. 5 或 13 3 9. (6,2) 10. (30,18) 11. (1) BC =21;4 ⎧- 7t + 7(0 < t ≤ 4) (2) BC = ⎪4 ;7 ⎪ t - 7(t > 4) ⎩ 4(3)当 t 的值为14 ,56或 28 时,B ,C ,P 三点成为“共5 11谐点”⎪。
2021年九年级数学中考复习知识点综合专题训练:一次函数与几何变换1(附答案)

2021年九年级数学中考复习知识点综合专题训练:一次函数与几何变换1(附答案)1.在平面直角坐标系中,把直线y=﹣2x+3沿y轴向上平移两个单位长度后.得到的直线的函数关系式为()A.y=﹣2x+5B.y=﹣2x﹣5C.y=﹣2x+1D.y=﹣2x+72.如图,直线l:与y轴交于点A,将直线l绕点A顺时针旋转75°后,所得直线的解析式为()A.y=x+B.y=x﹣C.y=﹣x+D.y=x+3.在平面直角坐标系中,将直线y=﹣2x+2关于平行于y轴的一条直线对称后得到直线AB,若直线AB恰好过点(6,2),则直线AB的表达式为()A.y=2x﹣10B.y=﹣2x+14C.y=2x+2D.y=﹣x+5 4.将直线y=﹣3x沿着x轴向右平移2个单位,所得直线的表达式为()A.y=﹣3x+6B.y=﹣3x﹣6C.y=﹣3x+2D.y=﹣3x﹣2 5.将直线y=﹣2x+1向上平移2个单位长度,所得到的直线解析式为()A.y=2x+1B.y=﹣2x﹣1C.y=2x+3D.y=﹣2x+3 6.将直线y=﹣2x+1向下平移2个单位,平移后的直线表达式为()A.y=﹣2x﹣5B.y=﹣2x﹣3C.y=﹣2x﹣1D.y=﹣2x+3 7.将直线y=x平移,使得它经过点(﹣2,0),则平移后的直线为()A.y=x﹣2B.y=x+1C.y=﹣x﹣2D.y=x+28.将一次函数y=3x向左平移后所得直线与坐标轴围成的三角形面积是24,则平移距离()A.4B.6C.6D.129.把直线y=2x﹣1向下平移1个单位,平移后直线的关系式为()A.y=2x﹣2B.y=2x+1C.y=2x D.y=2x+210.将直线y=﹣2x﹣1向上平移两个单位,平移后的直线所对应的函数关系式为()A.y=﹣2x﹣5B.y=﹣2x﹣3C.y=﹣2x+1D.y=﹣2x+3 11.将直线y=3x沿y轴向下平移1个单位长度后得到的直线解析式为()A.y=3x+1B.y=3x﹣1C.y=x+1D.y=x﹣112.在平面直角坐标系中,把直线y=2x﹣3沿y轴向上平移2个单位后,得到的直线的函数表达式为()A.y=2x+2B.y=2x﹣5C.y=2x+1D.y=2x﹣113.将直线y=2x+1向上平移3个单位后得到的解析式为.14.如果将直线y=3x平移,使其经过点(0,﹣1),那么平移后的直线表达式是.15.把直线y=2x﹣1向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的解析式为.16.将直线y=2x﹣5向上平移3个单位长度,所得直线的解析式为.17.把直线y=﹣2x+5向下平移2个单位,得到的直线解析式是.18.在平面直角坐标系xOy中,将函数y=3x+3图象向右平移5个单位长度,则平移后的图象与x轴、y轴分别交于A、B两点,则△AOB的面积为.19.将直线y=2x﹣3沿y轴向上平移2个单位后,所得直线的解析式是.20.将直线y=﹣2x+3向下平移5个单位,得到直线.21.将直线y=2x向上平移2个单位后得到的直线解析式为.22.在平面直角坐标系中,把直线y=x沿y轴向上平移后得到直线AB,如果点P(m,n)是直线AB上的一点,且m﹣n+8=0,那么直线AB的函数表达式为.23.在平面直角坐标系中,已知A,B两点的坐标分别(2,4),(﹣3,1).(1)在平面直角坐标系中,描出点A;(2)若函数y=mx的图象经过点A,求m的值;(3)若一次函数y=kx+b的图象由(2)中函数y=mx的图象经过平移,且经过点B得到,求这个一次函数的表达式,并在直角坐标系中画出该函数对应的图象.24.已知一次函数y=kx﹣4,当x=2时,y=﹣3.(1)求一次函数的解析式;(2)将该函数的图象向上平移6个单位长度,求平移后的图象与x轴交点的坐标;(3)在(2)的条件下,直接写出y>0时,x的取值范围.25.在一次函数学习中,我们经历了列表、描点、连线画函数图象,结合图象研究函数性质并对其性质进行应用的过程.小红对函数y=的图象和性质进行了如下探究,请同学们认真阅读探究过程并解答:(1)小红列出了如下表格,请同学们把下列表格补充完整,并在平面直角坐标系中画出该函数的图象:x…﹣10123456…y……(2)根据函数图象,以下判断该函数性质的说法,正确的有(填正确答案的序号).①函数图象关于y轴对称;②此函数无最小值;③当x<3时,y随x的增大而增大;当x≥3时,y的值不变.(3)若直线y=x+b与函数y=的图象只有一个交点,求b的值.26.已知一次函数y=kx+b(k,b是常数,且k≠0)的图象过A,B两点.(1)在图中画出该一次函数并求其表达式;(2)若点(a﹣3,﹣a)在该一次函数图象上,求a的值;(3)把y=kx+b的图象向下平移3个单位后得到新的一次函数图象,在图中画出新函数图形,并直接写出新函数图象对应的表达式.27.有这样一个问题:探究函数y=|x+1|的图象与性质.小明根据学习一次函数的经验,对函数y=|x+1|的图象与性质进行了探究.下面是小明的探究过程,请补充完整:(1)函数y=|x+1|的自变量x的取值范围是;(2)如表是x与y的几组对应值.x…﹣5﹣4﹣3﹣2﹣10123…y…432m01234…m的值为;(3)在如图网格中,建立平面直角坐标系xOy,描出表中各对对应值为坐标的点,并画出该函数的图象;(4)小明根据画出的函数图象,得出了如下几条结论:①函数有最小值为0;②当x>﹣1时,y随x的增大而增大;③图象关于过点(﹣1,0)且垂直于x轴的直线对称.小明得出的结论中正确的是.(只填序号)28.已知正比例函数的图象经过点A(2,3);(1)求出此正比例函数表达式;(2)该直线向上平移3个单位,写出平移后所得直线的表达式,并画出它的图象.29.一次函数y=2x+a的图象与x轴交与点(2,0),(1)求出a的值;(2)将该一次函数的图象向上平移5个单位长度,求平移后的函数解析式.30.表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l'.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.31.已知一次函数y=kx+b(k,b是常数,且k≠0)的图象过A(3,5)与B(﹣2,﹣5)两点.(1)求一次函数的解析式;(2)若点(a﹣3,﹣a)在该一次函数图象上,求a的值;(3)把y=kx+b的图象向下平移3个单位后得到新的一次函数图象,在图中画出新函数图象,并直接写出新函数图象对应的解析式.32.如图,在平面直角坐标系xOy中,直线y=﹣x+8与x、y轴分别相交于点A、B,此直线向下平移后与y轴相交于点C、与x轴相交于点D,四边形ABCD的面积为18.(1)求直线CD的表达式;(2)如果点E在直线CD上,四边形ABED是等腰梯形,求点E的坐标.参考答案1.解:直线y=﹣2x+3沿y轴向上平移2个单位,则平移后直线解析式为:y=﹣2x+3+2=﹣2x+5,故选:A.2.解:由直线l:可知,直线与x轴的夹角为60°,∴与y轴的夹角为30°,∴直线l绕点A顺时针旋转75°后的直线与y轴的夹角为45°,∴旋转后的直线的斜率为1,∵直线l:与y轴交于点A,∴A(0,).∴旋转后的直线解析式为:y=x+,故选:D.3.解:由题意得,直线AB的解析式为y=2x+b,∵直线AB恰好过点(6,2),∴2=2×6+b,解得b=﹣10,∴直线AB的表达式为y=2x﹣10,故选:A.4.解:根据题意,得直线向右平移2个单位,即对应点的纵坐标不变,横坐标减2,所以得到的解析式是y=﹣3(x﹣2)=﹣3x+6.故选:A.5.解:由“上加下减”的原则可知,把直线y=﹣2x+1上平移2个单位长度后所得直线的解析式为:y=﹣2x+1+2,即y=﹣2x+3故选:D.6.解:由题意得:平移后的解析式为:y=﹣2x+1﹣2=﹣2x﹣1,即.所得直线的表达式是y=﹣2x﹣1.故选:C.7.解:设平移后直线的解析式为y=x+b.把(﹣2,0)代入直线解析式得0=﹣2+b解得b=2所以平移后直线的解析式为y=x+2.故选:D.8.解:设平移的距离为k(k>0),则将一次函数y=3x向左平移后所得直线解析式为:y =3(x+k)=3x+3k.易求得新直线与坐标轴的交点为(﹣k,0)、(0,3k)所以,新直线与坐标轴所围成的三角形的面积为:•3k=24,解得k=4或﹣4(舍去).故选:A.9.解:根据题意,把直线y=2x﹣1向下平移1个单位后得到的直线解析式为:y=2x﹣1﹣1,即y=2x﹣2,故选:A.10.解:直线y=﹣2x﹣1向上平移两个单位,所得的直线是y=﹣2x+1,故选:C.11.解:由“上加下减”的原则可知:将直线y=3x沿y轴向下平移1个单位长度后,其直线解析式为y=3x﹣1.故选:B.12.解:由题意得:平移后的解析式为:y=2x﹣3+2,即y=2x﹣1.故选:D.13.解:由“上加下减”的原则可知,把直线y=2x+1上平移3个单位长度后所得直线的解析式为:y=2x+1+3,即y=2x+4,故答案为:y=2x+4.14.解:设平移后直线的解析式为y=3x+b,把(0,﹣1)代入直线解析式得﹣1=b,解得b=﹣1.所以平移后直线的解析式为y=3x﹣1.故答案为:y=3x﹣1.15.解:把直线y=2x﹣1向左平移1个单位长度,得到y=2(x+1)﹣1=2x+1,再向上平移2个单位长度,得到y=2x+3.故答案为:y=2x+3.16.解:由“上加下减”的原则可知,将函数y=2x﹣5向上平移3个单位所得函数的解析式为y=2x﹣5+3,即y=2x﹣2.故答案为:y=2x﹣2.17.解:由“上加下减”的原则可知,把直线y=﹣2x+5向下平移2个单位后所得直线的解析式为:y=﹣2x+5﹣2,即y=﹣2x+3.故答案为:y=﹣2x+3.18.解:根据题意知,平移后直线方程为y=3(x﹣5)+3=3x﹣12.所以A(4,0),B(0,﹣12).故OA=4,OB=12.所以S△AOB=OA•OB==24.故答案是:24.19.解:由“上加下减”的原则可知,直线y=2x﹣3沿y轴向上平移2个单位,所得直线的函数关系式为y=2x﹣3+2,即y=2x﹣1;故答案为y=2x﹣1.20.解:原直线的k=﹣2,b=3.向下平移5个单位长度得到了新直线,那么新直线的k=﹣2,b=3﹣5=﹣2.∴新直线的解析式为y=﹣2x﹣2.故答案为:y=﹣2x﹣2.21.解:直线y=2x向上平移2个单位后得到的直线解析式为y=2x+2.故答案为y=2x+2.22.解:设直线AB的解析式为y=x+b.将(m,n)代入y=x+b,得m+b=n,则m﹣n+8=0,∴b=8,∴直线AB的解析式为y=x+8.故答案为y=x+8.23.解:(1)点A(2,4),如图所示:(2)∵函数y=mx的图象经过点A,∴4=2m,∴m=2;(3)由(2)可得经过点A的函数为y=2x,∵一次函数y=kx+b的图象由函数y=2x经过平移,且经过点B,∴,解得,∴这个一次函数的表达式为y=2x+7,依题意画出图象如图所示;24.解:(1)当x=2时,y=﹣3,∴﹣3=2k﹣4,则,∴,(2)图象向上平移6个单位长度,∴,当y=0时,x=﹣4,∴平移后的图象与x轴交点的坐标为(﹣4,0),(3)y>0时,x的取值范围为x>﹣4.25.解:(1)补充表格:x…﹣10123456…y…﹣2﹣1012222…画出函数图象如图所示:(2)由图象可知,正确的性质为②此函数无最小值;③当x<3时,y随x的增大而增大;当x≥3时,y的值不变.故答案为②③;(3)直线y=x+b与函数y=的图象只有一个交点,根据图象直线y=+b经过点(3,2),∴2=+b,∴b=.26.解:(1)∵一次函数y=kx+b(k,b是常数,k≠0)的图象过A(1,5),B(﹣1,﹣1)两点,∴,得,即该一次函数的表达式是y=3x+2;(2)点(a﹣3,﹣a)在该一次函数y=3x+2的图象上,∴﹣a=3(a﹣3)+2,解得,a=,即a的值是;(3)把y=3x+2向下平移3个单位后可得:y=3x+2﹣3=3x﹣1,图象如图:27.解:(1)在函数y=|x+1|中,自变量x的取值范围是x为任意实数,故答案为:x为任意实数;(2)当x=﹣2时,m=|﹣2+1|=1,故答案为1;(3)画出函数的图象如图:;(4)由函数图象可知,①函数有最小值为0,正确;②当x>﹣1时,y随x的增大而增大,正确;③图象关于过点(﹣1,0)且垂直于x轴的直线对称,正确;.故答案为:①②③.28.解:(1)设正比例函数的解析式为y=kx,把A(2,3),代入得到k=,∴正比例函数的解析式为y=x.(2)将直线y=x向上平移3个单位,得直线y=x+3,如图;29.解:(1)∵一次函数y=2x+a的图象与x轴交与点(2,0),∴4+a=0,解得a=﹣4;(2)将一次函数y=2x﹣4的图象向上平移5个单位长度,得到y=2x﹣4+5,即y=2x+1,故平移后的函数解析式为y=2x+1.30.解:(1)∵直线l:y=kx+b中,当x=﹣1时,y=﹣2;当x=0时,y=1,∴,解得,∴直线l的解析式为y=3x+1;(2)依题意可得直线l′的解析式为y=x+3如图,解得,∴两直线的交点为A(1,4),∵直线l′:y=x+3与y轴的交点为B(0,3),∴直线l'被直线l和y轴所截线段的长为:AB==;(3)把y=a代入y=3x+1得,a=3x+1,解得x=;把y=a代入y=x+3得,a=x+3,解得x=a﹣3;分三种情况:①当第三点在y轴上时,a﹣3+=0,解得a=;②当第三点在直l上时,2×=a﹣3,解得a=7;③当第三点在直线l'上时,2×(a﹣3)=,解得a=;∴直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,则a 的值为或7或.31.解:(1)∵一次函数y=kx+b(k,b是常数,且k≠0)的图象过A(3,5)与B(﹣2,﹣5)两点,∴,解得,即该一次函数的表达式是y=2x﹣1;(2)点(a﹣3,﹣a)在该一次函数y=2x﹣1的图象上,∴﹣a=2(a﹣3)﹣1,解得,a=,即a的值是;(3)把y=2x﹣1向下平移3个单位后可得:y=2x﹣1﹣3=2x﹣4,图象如图:32.解:(1)∵直线y=﹣x+8与x、y轴分别相交于点A、B,∴A(6,0)B(0,8),∴OA=6,OB=8,∴AB===10,∴S△AOB==24,四边形ABCD的面积为18.∴S△COD=24﹣18=6,∵AB∥CD,∴△COD∽△BOA,∴=()2,即=,∴OC=4,∴C(0,4),∴直线CD的解析式为:y=﹣x+4;(2)作DM⊥AB于M,EN⊥AB于N,∵四边形ABED是等腰梯形,∴AD=BE,∠DAB=∠EBA,∵∠DMA=∠ENB=90°,∴△ADM≌△BEN(AAS),∴AM=BN,∵直线CD的解析式为:y=﹣x+4,∴D(3,0),∴OD=3,∴AD=6﹣3=3,∵∠AMD=∠AOB,∠DAM=∠BAO,∴△ADM∽△ABO,∴=,即,∴AM=,∴BN=AM=,∴MN=10﹣2×=,∴ED=MN=,∵OD=3,OC=4,∴CD==5,∴CE=DE﹣CD=﹣5=,作EH⊥x轴于H,则EH∥OC,∴,即=,∴OH=,∴E的横坐标为﹣,把x=﹣代入直线CD:y=﹣x+4得y=,∴点E的坐标为(﹣,).。
一次函数代数几何综合问题

一次函数代几综合问题一.填空题(共6小题)1.如图,直线和x轴、y轴分别交于点A、B.若以线段AB为边作等边三角形ABC,则点C的坐标是.2.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的点C的坐标为.3.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为.4.如图,已知直线l:y=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为.5.在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、A n B n C n C n﹣1按如图所示的方式放置,其中点A1、A2、A3、…、A n均在一次函数y=kx+b的图象上,点C1、C2、C3、…、C n均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点A n的坐标为.6.如图,直线1:与x轴、y轴分别相交于点A、B,△AOB与△ACB关于直线l对称,则点C的坐标为.二.解答题(共24小题)7.已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y 轴的距离分别为d1、d2.(1)当P为线段AB的中点时,求d1+d2的值;(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值.8.在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.(1)如图1,当CG=OD时,直接写出点D和点G的坐标,并求直线DG的函数表达式;(2)如图2,连接BF,设CG=a,△FBG的面积为S.①求S与a的函数关系式;②判断S的值能否等于等于1?若能,求此时m的值,若不能,请说明理由;(3)如图3,连接GE,当GD平分∠CGE时,m的值为.9.认真阅读材料,然后回答问题:我们知道,在数轴上,x=1表示一个点.而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方方程2x﹣y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是方程组在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图2;y≧2x+1也表示一个平面区域,即直线y=2x+1以及它上方的部分,如图3.回答下列问题:请你自己作一个直角坐标系,并在直角坐标系中(1)用作图象的方法求出方程组的解.(2)用阴影表示,所围成的区域.10.如图,直线l1的解析表达式为:y=3x﹣3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求△ADC的面积;(2)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,则点P的坐标为;(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.11.如图,在平面直角坐标系中,已知直线l1和l2相交于点A,它们的解析式分别为l1:y=x,l2:y=﹣x+.直线l2与两坐标轴分别相交于点B和点C,点P在线段OB上从点O出发.以每秒1个单位的速度向点B运动,同时点Q从点B出发以每秒4个单位的速度沿B→O→C→B的方向向点B运动,过点P作直线PM⊥OB分别交l1,l2于点M,N.连接MQ.设点P,Q运动的时间是t秒(t>0)(1)求点A的坐标;(2)点Q在OC上运动时,试求t为何值时,四边形MNCQ为平行四边形;(3)试探究是否存在某一时刻t,使MQ∥OB?若存在,求出t的值;若不存在,请说明理由.12.已知,将边长为5的正方形ABCO放置在如图所示的直角坐标系中,使点A在x轴上,点C在y轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.(1)当t=1时,求直线MC的解析式;(2)设△AMN的面积为S,求S关于t的函数解析式并写出相应t的取值范围;(3)在该平面直角坐标系中,第一象限内取点P(2,y),是否存在以M、N、C、P为顶点的四边形是直角梯形?若存在,直接写出点P的坐标;若不存在,请说明理由.13.如图①,以四边形AOCD的顶点O为原点建立直角坐标系,点A、C、D的坐标分别为(0,2)、(2,0)、(2,2),点P(m,0)是x轴上一动点,m是大于0的常数,以AP为一边作正方形APQR(QR落在第一象限),连接CQ.(1)请判断四边形AOCD的形状,并说明理由:(2)连接RD,请判断△ARD的形状,并说明理由:(3)如图②,随着点P(m,0)的运动,正方形APQR的大小会发生改变,若设CQ所在直线的表达式为y=kx+b(k≠0),求k的值.14.如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,AB在x轴正方向上,E、F分别是AD、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.(1)求点M、P的坐标;(2)求折痕AM所在直线的解析式;(3)设点H为直线AM上的点,是否存在这样的点H,使得以H、A、P为顶点的三角形为等腰三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.15.如图①,在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,4).动点M从点O出发,沿OA方向以每秒1个单位长度的速度向终点A运动;同时,动点N从点A出发沿AB方向以每秒个单位长度的速度向终点B运动.设运动了x秒.(1)点N的坐标为(,);(用含x的代数式表示)(2)当x为何值时,△AMN为等腰三角形;(3)如图②,连接ON得△OMN,△OMN可能为正三角形吗?若不能,点M的运动速度不变,试改变点N的运动速度,使△OMN为正三角形,并求出点N的运动速度.16.已知直线y=﹣x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).(1)求AB、BD的长度,并证明△ABD是直角三角形;(2)在x轴上找点C,使△ACD是以AD为底边的等腰三角形,求出C点坐标;(3)一动点P速度为1个单位/秒,沿A﹣﹣B﹣﹣D运动到D点停止,另有一动点Q从D点出发,以相同的速度沿D﹣﹣B﹣﹣A运动到A点停止,两点同时出发,PQ的长度为y(单位长),运动时间为t(秒),求y关于t的函数关系式.17.如图:直线y=kx+3与x轴、y轴分别交于A、B两点,,点C(x,y)是直线y=kx+3上与A、B不重合的动点.(1)求直线y=kx+3的解析式;(2)当点C运动到什么位置时△AOC的面积是6;(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?若存在,请求出点C的坐标;若不存在,请说明理由.18.如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(﹣5,1),B(﹣2,4),C(5,4),点D在第一象限.(1)写出D点的坐标;(2)求经过B、D两点的直线的解析式,并求线段BD的长;(3)将平行四边形ABCD先向右平移1个单位长度,再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积.19.如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.20.已知,直线y=﹣x+1与x轴,y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90度.且点P(1,a)为坐标系中的一个动点.(1)求三角形ABC的面积S△ABC;(2)证明不论a取任何实数,三角形BOP的面积是一个常数;(3)要使得△ABC和△ABP的面积相等,求实数a的值.21.如图,在直角坐标系xoy中,一次函数的图象与x轴交于点A,与y轴交于点B.(1)已知OC⊥AB于C,求C点坐标;(2)在x轴上是否存在点P,使△PAB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.22.如图1,在正方形ABOC中,BD平分∠OBC,交OA于点D.(1)若正方形ABOC的边长为2,对角线BC与OA相交于点E.则:①BC的长为;②DE的长为;③根据已知及求得的线段OB、BC、DE的长,请找出它们的数量关系?(2)如图2,当直角∠BAC绕着其顶点A顺时针旋转时,角的两边分别与x轴正半轴、y轴正半轴交于点C1和B1,连接B1C1交OA于P.B1D平分∠OB1C1,交OA于点D,过点D作DE⊥B1C1,垂足为E,请猜想线段OB、B1C1、DE三者之间的数量关系,并证明你的猜想;(3)在(2)的条件下,当B1E=6,C1E=4时,求直线B1D的解析式.23.如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°;(1)如果点P(m,)在第二象限内,试用含m的代数式表示四边形AOPB的面积,并求当△APB与△ABC面积相等时m的值;(2)如果△QAB是等腰三角形并且点Q在坐标轴上,请求出点Q所有可能的坐标;(3)是否存在实数a,b使一次函数和y=ax+b的图象关于直线y=x对称?若存在,求出的值;若不存在,请说明理由.24.一次函数的图象与x轴、y轴分别交于点A(8,0)和点B(0,6).(1)确定此一次函数的解析式.(2)求坐标原点O到直线AB的距离.(3)点P是线段AB上的一个动点,过点P作PM垂直于x轴于M,作PN垂直于y轴于N,记L=PM+PN,问L是否存在最大值和最小值?若存在,求出此时P点到原点O的距离,若不存在请说明理由.25.已知直线y=2x+4与x轴交于点A,与y轴交于点B,点P在坐标轴上,且PO=2AO.求△ABP的面积.26.已知A(1,5),B(3,﹣1)两点,在x轴上取一点M,使AM﹣BM取得最大值时,则M的坐标为.27.如图,在平面直角坐标系中,直线分别交于x轴,y轴于B、A两点,D、E分别是OA、OB的中点,点P从点D出沿DE方向运动,过点P作PQ⊥AB于Q,过点Q作QR∥OA交OB于R,当点Q与B点重合时,点P停止运动.(1)求A、B两点的坐标;(2)求PQ的长度;(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的点R的坐标;若不存在,请说明理由.28.如图,直线y=﹣2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.(1)填空:点C的坐标是(,),点D的坐标是(,);(2)设直线CD与AB交于点M,求线段BM的长;(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.29.已知△ABC,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC,AB所在直线为x轴,y 轴建立直角坐标系(如图).(1)在BD所在直线上找出一点P,使四边形ABCP为平行四边形,画出这个平行四边形,并简要叙述其过程;(2)求直线BD的函数关系式;(3)直线BD上是否存在点M,使△AMC为等腰三角形?若存在,求点M的坐标;若不存在,说明理由.30.如图,一次函数的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边△ABC,(1)求△ABC的面积;(2)如果在第二象限内有一点P(a,);试用含有a的代数式表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值;(3)在x轴上,是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.。
4.难点探究专题:一次函数与几何的综合问题(选做)

难点探究专题:一次函数与几何的综合问题(选做)◆类型一 一次函数与面积问题 一、由一次函数图象求面积1.(当涂县期末)直线y =2x -4与两坐标轴所围成的三角形面积等于( ) A .8 B .6 C .4 D .162.已知直线l 1:y 1=2x +3与直线l 2:y 2=kx -1交于A 点,A 点横坐标为-1,且直线l 1与x 轴交于B 点,与y 轴交于D 点,直线l 2与y 轴交于C 点.(1)求出A 点的坐标及直线l 2的解析式; (2)连接BC ,求出S △ABC .二、由面积求一次函数关系式3.若直线y =-2x +b (b >0)与两坐标轴围成的三角形的面积是1,则该直线的解析式为__________.4.在平面直角坐标系中,点O 是坐标原点,过点A (1,2)的直线y =kx +b 与x 轴交于点B ,且S △AOB =4.则该直线的解析式为____________________.三、一次函数上的动点与面积问题 5.(盐城中考)如图,在边长为2的正方形ABCD 中剪去一个边长为1的小正方形CEFG ,动点P 从点A 出发,沿A →D →E →F →G →B 的路线绕多边形的边匀速运动到点B 时停止(不含点A 和点B ),则△ABP 的面积S 随着时间t 变化的函数图象大致是( )6.如图所示,直线y =kx -1与x 轴、y 轴分别交于B 、C 两点,OB OC =12.(1)求B 点坐标和k 的值; (2)若点A (x ,y )是直线y =kx -1在第一象限内的部分上的一个动点,试写出在点A 运动过程中,三角形AOB 的面积S 与x 的函数表达式;(3)探索:当动点A (x ,y )可在直线y =kx -1上任意移动时,若S △AOB =14,试确定点A的位置.【易错4】◆类型二 一次函数与几何图形综合的探究性问题7.如图所示,直线y =x +1与y 轴交于点A 1,以OA 1为边作正方形OA 1B 1C 1,然后延长C 1B 1与直线y =x +1交于点A 2,得到第1个梯形A 1OC 1A 2;再以C 1A 2为边作正方形C 1A 2B 2C 2,同样延长C 2B 2与直线y =x +1交于点A 3得到第2个梯形A 2C 1C 2A 3;再以C 2A 3为边作正方形C 2A 3B 3C 3,延长C 3B 3,得到第3个梯形……则第2个梯形A 2C 1C 2A 3的面积是________;第n (n 是正整数)个梯形的面积是____________(用含n 的式子表示).第7题图 第8题图8.★如图,直角坐标系中,点P (t ,0)是x 轴上的一个动点,过点P 作y 轴的平行线,分别与直线y =12x ,直线y =-x 交于A 、B 两点,以AB 为边向右侧作正方形ABCD .(1)当t =2时,正方形ABCD 的周长是________;(2)当点(2,0)在正方形ABCD 内部时,t 的取值范围是__________________.参考答案与解析1.C2.解:(1)当x =-1时,y 1=-2+3=1,∴A 点的坐标为(-1,1).∵直线l 2:y 2=kx -1经过点A (-1,1),∴1=-k -1,∴k =-2,∴y 2=-2x -1;(2)∵直线y 1=2x +3与y 轴交于D (0,3),直线y 2=-2x -1与y 轴交于C (0,-1),∴CD =4,∴S △ADC =12×4×1=2.∵直线y 1=2x +3与x 轴交于B ⎝⎛⎭⎫-32,0,∴S △BCD =12×4×32=3,∴S △ABC =S △BCD -S △ACD =3-2=1.3.y =-2x +24.y =-23x +83或y =25x +85 解析:设B 点坐标为(m ,0),则S △AOB =12·|m |·2=|m |.又∵S △AOB=4,∴|m |=4,∴m =±4.当m =4时,由直线y =kx +b 过点A (1,2),B (4,0),得⎩⎪⎨⎪⎧2=k +b ,0=4k +b ,解得⎩⎨⎧k =-23,b =83.此时该直线的解析式为y =-23x +83;当m =-4时,由直线y =kx +b 过点A (1,2),B (-4,0),得⎩⎪⎨⎪⎧2=k +b ,0=-4k +b ,解得⎩⎨⎧k =25,b =85.此时该直线的解析式为y =25x +85.综上所述,该直线的解析式为y =-23x +83或y =25x +85.5.B 解析:当点P 在AD 上时,△ABP 的底AB 不变,高增大,所以△ABP 的面积S随着时间t 的增大而增大;当点P 在DE 上时,△ABP 的底AB 不变,高不变,所以△ABP 的面积S 不变;当点P 在EF 上时,△ABP 的底AB 不变,高减小,所以△ABP 的面积S 随着时间t 的增大而减小;当点P 在FG 上时,△ABP 的底AB 不变,高不变,所以△ABP 的面积S 不变;当点P 在GB 上时,△ABP 的底AB 不变,高减小,所以△ABP 的面积S 随着时间t 的增大而减小.故选B.6.解:(1)设B 点坐标为(m ,0).∵OB OC =12,∴C 点坐标为(0,-2m ).由直线y =kx -1与y 轴交于点C 可得C 点坐标为(0,-1),∴-2m =-1,∴m =12,∴B 点坐标为⎝⎛⎭⎫12,0.由12k -1=0得k =2; (2)∵A (x ,y )在第一象限,且y =2x -1,∴S △AOB =12OB ·y =12×12(2x -1)=12x -14⎝⎛⎭⎫x >12; (3)由题意,得12OB ·|y |=14.∵OB =12,∴y =±1.当y =1时,x =1;当y =-1时,x =0.∴A点坐标为(1,1)或(0,-1). 7.6 (2n -1+2n )·2n -28.(1)12 (2)t <-4或45<t <2解析:当t <0时,AB =-32t ,即正方形ABCD 的边长为-32t .∵点(2,0)在正方形ABCD 内部,∴-32t >2-t ,解得t <-4;当t >0时,AB =32t ,即正方形ABCD 的边长为32t ,则⎩⎪⎨⎪⎧t <2,t +32t >2,解得45<t <2.故当点(2,0)在正方形内部时,t <-4或45<t <2.。
人教版八年级数学下《一次函数与几何综合》专题练习题
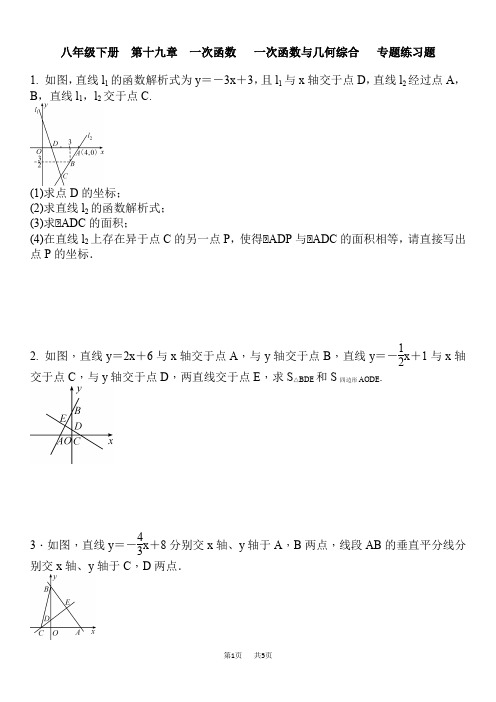
八年级下册第十九章一次函数一次函数与几何综合专题练习题1. 如图,直线l1的函数解析式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求点D的坐标;(2)求直线l2的函数解析式;(3)求△ADC的面积;(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.2. 如图,直线y=2x+6与x轴交于点A,与y轴交于点B,直线y=-12x+1与x轴交于点C,与y轴交于点D,两直线交于点E,求S△BDE和S四边形AODE.3.如图,直线y=-43x+8分别交x轴、y轴于A,B两点,线段AB的垂直平分线分别交x轴、y轴于C,D两点.(1)求点C的坐标;(2)求直线CE的解析式;(3)求△BCD的面积.4. 如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C两点,且△CBA=45°.求直线BC的解析式.5. 如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于点F,交AB于点E,BM⊥OB 交OE的延长线于点M.(1)求直线AB和直线AD的解析式;(2)求点M的坐标;(3)求点E,F的坐标.6. 如图,正方形OBAC中,O(0,0),A(-2,2),B,C分别在x轴、y轴上,D(0,1),CE⊥BD交BD延长线于点E,求点E的坐标.7. 如图,在平面直角坐标系中,A(0,1),B(3,12),P 为x 轴上一动点,则PA +PB 最小时点P 的坐标为________.8. 如图,直线y =x +4与坐标轴交于点A ,B ,点C(-3,m)在直线AB 上,在y 轴上找一点P ,使PA +PC 的值最小,求这个最小值及点P 的坐标.答案:1. 分析:(1)令y =-3x +3=0,求出x 可得点D 的坐标;(2)设直线l 2的解析式为y =kx +b ,把A ,B 的坐标代入求出k ,b 可得;(3)先求出点C 的坐标,再求S △ADC ;(4)在l 2上且到x 轴的距离等于点C 纵坐标的相反数的点即为点P.解:(1)由y =-3x +3,令y =0,得-3x +3=0,∴x =1,∴D(1,0) (2)y =32x -6 (3)由⎩⎨⎧y =-3x +3,y =32x -6,解得⎩⎪⎨⎪⎧x =2,y =-3,△C(2,-3),△AD =3,△S △ADC =12×3×|-3|=92 (4)P(6,3)2. 解:易求A (-3,0),B(0,6),C(2,0),D(0,1),△BD =5,解⎩⎨⎧y =2x +6,y =-12x +1,得⎩⎪⎨⎪⎧x =-2,y =2, △E(-2,2),△S △BDE =5,S 四边形AODE =S △AOB -S △BDE =9-5=43. 解:(1)易得A(6,0),B(0,8),设C 点坐标为(x ,0),则BC =AC =6-x ,由勾股定理得x 2+82=(6-x)2,△x =-73,△C(-73,0) (2)△点E 是AB 的中点,△点E 的坐标为(3,4),易得直线CE 的解析式为y =34x +74 (3)由CE 解析式得,点D 坐标为(0,74),S △BCD =12×(8-74)×73=175244. 分析:过点A 作AD△AB ,AD 交BC 于点D ,可得△BAD 是等腰直角三角形,再过点D 作DE△x 轴于点E ,通过证△DEA△△AOB 求出点D 的坐标,最后由点B ,D 的坐标利用待定系数法可求出直线BC 的解析式.解:过点A 作AD△AB ,AD 交BC 于点D ,可得AD =AB ,过点D 作DE△x 轴于点E ,可证△DEA△△AOB ,△DE =OA =1,EA =OB =3,△D(-4,1),可求直线BC的解析式为y =12x +35. 解:(1)AB :y =x +4,AD :y =2x +4 (2)由△OBM△△AOD 得BM =OD ,△M(-4,2) (3)由(2)得OM :y =-12x ,联立⎩⎨⎧y =-12x ,y =x +4,得E(-83,43);联立⎩⎨⎧y =2x +4,y =-12x ,得F(-85,45)6. 解:延长CE 交x 轴于点F ,则有△BOD△△COF ,△OD =OF =1,△F(1,0),△C(0,2),△CF :y =-2x +2,△B(-2,0),D(0,1),△BD :y =12x +1,由⎩⎨⎧y =12x +1,y =-2x +2,得E(25,65)7. (2,0) 分析:先作出点A 关于x 轴对称的点A′,再连接A′B 交x 轴于点P ,则点P 即为所求.由题中条件易求出直线A′B 的解析式,再求出直线A′B 与x 轴的交点坐标即可.8. 解:作点A 关于y 轴的对称点A′,连接CA′交y 轴于P ,此时PA +PC 值最小,最小值为CA′,易求C(-3,1),△A′(4,0),△CA′:y =-17x +47,△P(0,47),作CE△x 轴于E ,△CA′=CE 2+A′E 2=52。
一次函数与几何综合(垂直的函数意义)(人教版)(含答案)

一次函数与几何综合(垂直的函数意义)(人教版)一、单选题(共7道,每道14分)1.如图,直线:y=x+2与y轴交于点A,将直线绕点A旋转90°后,所得直线的表达式为( )A.y=x-2B.y=-x+2C.y=-x-2D.y=-2x-1答案:B解题思路:试题难度:三颗星知识点:一次函数与几何转化2.在平面直角坐标系中,把直线y=2x+4绕着原点O顺时针旋转90°后,所得的直线一定经过下列各点中的( )A.(2,0)B.(2,3)C.(4,2)D.(6,-1)答案:D解题思路:试题难度:三颗星知识点:一次函数与几何转化3.如图,一次函数的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,且∠BAC=90°,则AC所在直线的表达式为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:一次函数与几何综合4.如图,在平面直角坐标系中放入一张矩形纸片ABCO,已知点B的坐标为(4,-3),连接AC,作AC的垂直平分线交AB于点D,交y轴于点E.则DE所在直线的表达式为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:一次函数与几何综合5.如图,在平面直角坐标系中放入一张矩形纸片ABCO,OC=6,将纸片沿过点C的直线翻折后,点B恰好落在x轴上的点D处,折痕交AB于点E,若,则DE所在直线的解析式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数与几何综合6.如图,已知长方形纸片OABC,D是OA上的一点,且OD:AD=5:3,CD=,把△OCD 沿折痕CD向上翻折,若点O恰好与AB边上的点E重合,则CD所在直线的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转7.如图,在平面直角坐标系中放入一张矩形纸片ABCO,OC=9,将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知,则折痕B′E所在直线的解析式为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:一次函数与几何综合。
一次函数和几何综合题含答案

一次函数和几何综合题含答案1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.参考答案与试题解析一.解答题(共10小题)1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)过点B作BE⊥y轴于点E,作BF⊥x轴于点F.依题意得BF=OE=2,利用勾股定理求出OF,然后可得点B的坐标.设直线AB的解析式是y=kx+b,把已知坐标代入可求解.(2)由△ABD由△AOP旋转得到,证明△ABD≌△AOP.AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等边三角形.利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函数求出BG=BD•cos60°,DG=BD•sin60°.然后求出OH,DH,然后求出点D的坐标.(3)本题分三种情况进行讨论,设点P的坐标为(t,0):①当P在x轴正半轴上时,即t>0时,关键是求出D点的纵坐标,方法同(2),在直角三角形DBG中,可根据BD即OP的长和∠DBG的正弦函数求出DG的表达式,即可求出DH的长,根据已知的△OPD的面积可列出一个关于t的方程,即可求出t的值.②当P在x轴负半轴,但D在x轴上方时.即<t≤0时,方法同①类似,也是在直角三角形DBG用BD的长表示出DG,进而求出GF的长,然后同①.③当P在x轴负半轴,D在x轴下方时,即t≤时,方法同②.综合上面三种情况即可求出符合条件的t的值.解答:解:(1)如图1,过点B作BE⊥y轴于点E,作BF⊥x轴于点F.由已知得:BF=OE=2,OF==,∴点B的坐标是(,2)设直线AB的解析式是y=kx+b(k≠0),则有.解得.∴直线AB的解析式是y=x+4;(2)如图2,∵△ABD由△AOP旋转得到,∴△ABD≌△AOP,∴AP=AD,∠DAB=∠PAO,∴∠DAP=∠BAO=60°,∴△ADP是等边三角形,∴DP=AP=.如图2,过点D作DH⊥x轴于点H,延长EB交DH于点G,则BG⊥DH.方法(一)在Rt△BDG中,∠BGD=90°,∠DBG=60°.∴BG=BD•cos60°=×=.DG=BD•sin60°=×=.∴OH=EG=,DH=∴点D的坐标为(,)方法(二)易得∠AEB=∠BGD=90°,∠ABE=∠BDG,∴△ABE∽△BDG,∴;而AE=2,BD=OP=,BE=2,AB=4,则有,解得BG=,DG=;∴OH=,DH=;∴点D的坐标为(,).(3)假设存在点P,在它的运动过程中,使△OPD的面积等于.设点P为(t,0),下面分三种情况讨论:①当t>0时,如图,BD=OP=t,DG=t,∴DH=2+t.∵△OPD的面积等于,∴,解得,(舍去)∴点P1的坐标为(,0).②∵当D在y轴上时,根据勾股定理求出BD==OP,∴当<t≤0时,如图,BD=OP=﹣t,DG=﹣t,∴GH=BF=2﹣(﹣t)=2+t.∵△OPD的面积等于,∴,解得,,∴点P2的坐标为(,0),点P3的坐标为(,0).③当t≤时,如图3,BD=OP=﹣t,DG=﹣t,∴DH=﹣t﹣2.∵△OPD的面积等于,∴(﹣t)[﹣(2+t)]=,解得(舍去),∴点P4的坐标为(,0),综上所述,点P的坐标分别为P1(,0)、P2(,0)、P3(,0)、P4(,0).点评:本题综合考查的是一次函数的应用,包括待定系数法求解析式、旋转的性质、相似三角形的判定和性质、三角形面积公式的应用等,难度较大.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.考点:一次函数综合题.专题:压轴题.分析:(1)根据直线y=﹣x+4与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出==,据此可以求得点P的运动速度;(2)当PQ=PE时,以及当PQ=PE时,矩形PEFQ为正方形,分别求出即可;(3)根据(2)中所求得出s与t的函数关系式,进而利用二次函数性质求出即可.解答:解:(1)∵直线y=﹣x+4与坐标轴分别交于点A、B,∴x=0时,y=4,y=0时,x=8,∴==,当t秒时,QO=FQ=t,则EP=t,∵EP∥BO,∴==,∴AP=2t,∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,∴点P运动的速度是每秒2个单位长度;(2)如图1,当PQ=PE时,矩形PEFQ为正方形,则∵OQ=FQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴8﹣3t=t,解得:t=2;如图2,当PQ=PE时,矩形PEFQ为正方形,∵OQ=t,PA=2t,∴OP=8﹣2t,∴QP=t﹣(8﹣2t)=3t﹣8,∴t=3t﹣8,解得:t=4;(3)如图1,当Q在P点的左边时,∵OQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴S矩形PEFQ=QP•QF=(8﹣3t)•t=8t﹣3t2,当t=﹣=时,S矩形PEFQ的最大值为:=,如图2,当Q在P点的右边时,∵OQ=t,PA=2t,∴2t>8﹣t,∴t,∴QP=t﹣(8﹣2t)=3t﹣8,∴S矩形PEFQ=QP•QF=(3t﹣8)•t=3t2﹣8t,∵当点P、Q其中一点停止运动时,另一点也停止运动,∴<t≤4,当t=﹣=时,S矩形PEFQ的最大,∴t=4时,S矩形PEFQ的最大值为:3×42﹣8×4=16,点评:此题主要考查了二次函数与一次函数的综合应用,得出P,Q不同的位置进行分类讨论得出是解题关键.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.考点:一次函数综合题.专题:压轴题.分析:(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.解答:解:(1)解方程x2﹣14x+48=0得x1=6,x2=8.∵OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根,∴OC=6,OA=8.∴C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).由(1)知,OA=8,则A(8,0).∵点A、C都在直线MN上,∴,解得,,∴直线MN的解析式为y=﹣x+6;(3)∵A(8,0),C(0,6),∴根据题意知B(8,6).∵点P在直线MNy=﹣x+6上,∴设P(a,﹣a+6)当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);②当PC=BC时,a2+(﹣a+6﹣6)2=64,解得,a=,则P2(﹣,),P3(,);③当PB=BC时,(a﹣8)2+(a﹣6+6)2=64,解得,a=,则﹣a+6=﹣,∴P4(,﹣).综上所述,符合条件的点P有:P1(4,3),P2(﹣,)P3(,),P4(,﹣).点评:本题考查了一次函数综合题.其中涉及到的知识点有:待定系数法求一次函数解析式,一次函数图象上点的坐标特征,等腰三角形的性质.解答(3)题时,要分类讨论,防止漏解.另外,解答(3)题时,还利用了“数形结合”的数学思想.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)通过解一元二次方程x2﹣(+1)x+=0,求得方程的两个根,从而得到A、B两点的坐标,再根据两点之间的距离公式可求AB的长,根据AB:AC=1:2,可求AC的长,从而得到C点的坐标;(2)分①当点M在CB边上时;②当点M在CB边的延长线上时;两种情况讨论可求S关于t的函数关系式;(3)分AQ=AB,BQ=BA,BQ=QA三种情况讨论可求Q点的坐标.解答:解:(1)x2﹣(+1)x+=0,(x﹣)(x﹣1)=0,解得x1=,x2=1,∵OA<OB,∴OA=1,OB=,∴A(1,0),B(0,),∴AB=2,又∵AB:AC=1:2,∴AC=4,∴C(﹣3,0);(2)∵AB=2,AC=4,BC=2,∴AB2+BC2=AC2,即∠ABC=90°,由题意得:CM=t,CB=2.①当点M在CB边上时,S=2﹣t(0≤t);②当点M在CB边的延长线上时,S=t﹣2(t>2);(3)存在.①当AB是菱形的边时,如图所示,在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),②当AB为菱形的对角线时,如图所示的菱形AP4BQ4,设菱形的边长为x,则在Rt△AP4O中,AP42=AO2+P4O2,即x2=12+(﹣x)2,解得x=,所以Q4(1,).综上可得,平面内满足条件的Q点的坐标为:Q1(﹣1,0),Q2(1,﹣2),Q3(1,2),Q4(1,).点评:考查了一次函数综合题,涉及的知识点有:解一元二次方程,两点之间的距离公式,三角形面积的计算,函数思想,分类思想的运用,菱形的性质,综合性较强,有一定的难度.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.考点:一次函数综合题;解二元一次方程组;待定系数法求一次函数解析式;三角形的面积;角平分线的性质;勾股定理;菱形的性质.专题:计算题.分析:(1)根据A的坐标求出AH、OH,根据勾股定理求出即可;(2)根据菱形性质求出B、C的坐标,设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得到方程组,求出即可;(3)①过M作MN⊥BC于N,根据角平分线性质求出MN,P在AB上,根据三角形面积公式求出即可;P 在BC上,根据三角形面积公式求出即可;②求出P在AB的最大值和P在BC上的最大值比较即可得到答案.解答:(1)解:∵A(﹣3,4),∴AH=3,OH=4,由勾股定理得:AO==5,答:OA的长是5.(2)解:∵菱形OABC,∴OA=OC=BC=AB=5,5﹣3=2,∴B(2,4),C(5,0),设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得:,解得:,∴直线AC的解析式为,当x=0时,y=2.5∴M(0,2.5),答:直线AC的解析式是,点M的坐标是(0,2.5).(3)①解:过M作MN⊥BC于N,∵菱形OABC,∴∠BAC=∠OCA,∵MO⊥CO,MN⊥BC,∴OM=MN,当0≤t<2.5时,P在AB上,MH=4﹣2.5=,S=×BP×MH=×(5﹣2t)×=﹣t+,∴,当t=2.5时,P与B重合,△PMB不存在;当2.5<t≤5时,P在BC上,S=×PB×MN=×(2t﹣5)×=t﹣,∴,答:S与t的函数关系式是(0≤t<2.5)或(2.5<t≤5).②解:当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是×5×=,同理在BC上时,P与C重合时,S最大是×5×=,∴S的最大值是,答:S的最大值是.点评:本题主要考查对勾股定理,三角形的面积,菱形的性质,角平分线性质,解二元一次方程组,用待定系数法求一次函数的解析式等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.考点:一次函数综合题.专题:压轴题.分析:(1)由AO=AD,AG=AG,利用“HL”可证△AOG≌△ADG;(2)利用(1)的方法,同理可证△ADP≌△ABP,得出∠1=∠DAG,∠DAP=∠BAP,而∠1+∠DAG+∠DAP+∠BAP=90°,由此可求∠PAG的度数;根据两对全等三角形的性质,可得出线段OG、PG、BP之间的数量关系;(3)由△AOG≌△ADG可知,∠AGO=∠AGD,而∠1+∠AGO=90°,∠2+∠PGC=90°,当∠1=∠2时,可证∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,得出∠AGO=∠AGD=∠PGC=60°,即∠1=∠2=30°,解直角三角形求OG,PC,确定P、G两点坐标,得出直线PE的解析式.解答:(1)证明:∵∠AOG=∠ADG=90°,∴在Rt△AOG和Rt△ADG中,∵,∴△AOG≌△ADG(HL);(2)解:PG=OG+BP.由(1)同理可证△ADP≌△ABP,则∠DAP=∠BAP,由(1)可知,∠1=∠DAG,又∠1+∠DAG+∠DAP+∠BAP=90°,所以,2∠DAG+2∠DAP=90°,即∠DAG+∠DAP=45°,故∠PAG=∠DAG+∠DAP=45°,∵△AOG≌△ADG,△ADP≌△ABP,∴DG=OG,DP=BP,∴PG=DG+DP=OG+BP;(3)解:∵△AOG≌△ADG,∴∠AGO=∠AGD,又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,∴∠AGO=∠AGD=∠PGC,又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=60°,∴∠1=∠2=30°,在Rt△AOG中,AO=3,AG=2OG,AG2=AO2+OG2,∴OG=,则G点坐标为:(,0),CG=3﹣,在Rt△PCG中,PG=2CG=2(3﹣),PC==3﹣3,则P点坐标为:(3,3﹣3),设直线PE的解析式为y=kx+b,则,解得,所以,直线PE的解析式为y=x﹣3.点评:本题考查了一次函数的综合运用.关键是根据正方形的性质证明三角形全等,根据三角形全等的性质求角、边的关系,利用特殊角解直角三角形,求P、G两点坐标,确定直线解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.考点:一次函数综合题.专题:压轴题;探究型.分析:(1)△AOC和△BCP全等,则AO=BC=1,又∵AB=,t=AB﹣BC=﹣1;(2)过点C作x轴的平行线,交OA与直线BP于点T、H,证△OTC≌△CHP即可;(3)根据题意可直接得出b=1﹣t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1﹣),但t=0时,点C不在第一象限,所以不符合题意.解答:解:(1)△AOC和△BCP全等,则AO=BC=1,又AB=,所以t=AB﹣BC=﹣1;(2)OC=CP.证明:过点C作x轴的平行线,交OA与直线BP于点T、H.∵PC⊥OC,∴∠OCP=90°,∵OA=OB=1,∴∠OBA=45°,∵TH∥OB,∴∠BCH=45°,又∠CHB=90°,∴△CHB为等腰直角三角形,∴CH=BH,∵∠AOB=∠OBH=∠BHT=90°,∴四边形OBHT为矩形,∴OT=BH,∴OT=CH,∵∠TCO+∠PCH=90°,∠CPH+∠PCH=90°,∴∠TCO=∠CPH,∵HB⊥x轴,TH∥OB,∴∠CTO=∠THB=90°,TO=HC,∠TCO=∠CPH,∴△OTC≌△CHP,∴OC=CP;(3)①∵△OTC≌△CHP,∴CT=PH,∴PH=CT=AT=AC•cos45°=t,∴BH=OT=OA﹣AT=1﹣t,∴BP=BH﹣PH=1﹣t,∴;(0<t<)②t=0时,△PBC是等腰直角三角形,但点C与点A重合,不在第一象限,所以不符合,PB=BC,则﹣t=|1﹣t|,解得t=1或t=﹣1(舍去),∴当t=1时,△PBC为等腰三角形,即P点坐标为:P(1,1﹣).点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数的性质和点的意义表示出相应的线段的长度,再结合三角形全等和等腰三角形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.考点:一次函数综合题.专题:综合题;数形结合.分析:(1)①联立两个函数式,求解即可得出交点坐标,即为点C的坐标.②欲求△OAC的面积,结合图形,可知,只要得出点A和点C的坐标即可,点C的坐标已知,利用函数关系式即可求得点A的坐标,代入面积公式即可.(2)在OC上取点M,使OM=OP,连接MQ,易证△POQ≌△MOQ,可推出AQ+PQ=AQ+MQ;若想使得AQ+PQ存在最小值,即使得A、Q、M三点共线,又AB⊥OP,可得∠AEO=∠CEO,即证△AEO≌△CEO(ASA),又OC=OA=4,利用△OAC的面积为6,即可得出AM=3,AQ+PQ存在最小值,最小值为3.解答:解:(1)①由题意,(2分)解得所以C(4,4)(3分)②把y=0代入y=﹣2x+12得,x=6,所以A点坐标为(6,0),(4分)所以.(6分)(2)存在;由题意,在OC上截取OM=OP,连接MQ,∵OQ平分∠AOC,∴∠AOQ=∠COQ,又OQ=OQ,∴△POQ≌△MOQ(SAS),(7分)∴PQ=MQ,∴AQ+PQ=AQ+MQ,当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小.即AQ+PQ存在最小值.∵AB⊥ON,所以∠AEO=∠CEO,∴△AEO≌△CEO(ASA),∴OC=OA=4,∵△OAC的面积为6,所以AM=12÷4=3,∴AQ+PQ存在最小值,最小值为3.(9分)点评:本题主要考查一次函数的综合应用,具有一定的综合性,要求学生具备一定的数学解题能力,有一定难度.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:开放型.分析:(1)已知直线解析式,令y=0,求出x的值,可求出点A,B的坐标.联立方程组求出点P的坐标.推出AO=QO,可得出∠PAB=45°.(2)先根据CQ:AO=1:2得到m、n的关系,然后求出S△AOQ,S△PAB并都用字母m表示,根据S四边形PQOB=S△PAB ﹣S△AOQ积列式求解即可求出m的值,从而也可求出n的值,继而可推出点P的坐标以及直线PA与PB的函数表达式.(3)本题要依靠辅助线的帮助.求证相关图形为平行四边形,继而求出D1,D2,D3的坐标.解答:解:(1)在直线y=x+m中,令y=0,得x=﹣m.∴点A(﹣m,0).在直线y=﹣3x+n中,令y=0,得.∴点B(,0).由,得,∴点P(,).在直线y=x+m中,令x=0,得y=m,∴|﹣m|=|m|,即有AO=QO.又∵∠AOQ=90°,∴△AOQ是等腰直角三角形,∴∠PAB=45°.(2)∵CQ:AO=1:2,∴(n﹣m):m=1:2,整理得3m=2n,∴n=m,∴==m,而S四边形PQOB=S△PAB﹣S△AOQ=(+m)×(m)﹣×m×m=m2=,解得m=±4,∵m>0,∴m=4,∴n=m=6,∴P().∴PA的函数表达式为y=x+4,PB的函数表达式为y=﹣3x+6.(3)存在.过点P作直线PM平行于x轴,过点B作AP的平行线交PM于点D1,过点A作BP的平行线交PM于点D2,过点A、B分别作BP、AP的平行线交于点D3.①∵PD1∥AB且BD1∥AP,∴PABD1是平行四边形.此时PD1=AB,易得;②∵PD2∥AB且AD2∥BP,∴PBAD2是平行四边形.此时PD2=AB,易得;③∵BD3∥AP且AD3∥BP,此时BPAD3是平行四边形.∵BD3∥AP且B(2,O),∴y BD3=x﹣2.同理可得y AD3=﹣3x﹣12,得,∴.点评:本题的综合性强,主要考查的知识点为一次函数的应用,平行四边形的判定以及面积的灵活计算.难度较大.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:综合题.分析:(1)先求出A、B两点的坐标,再由一个角等于30°,求出AC的长,从而计算出面积;(2)过P作PD⊥x轴,垂足为D,先求出梯形ODPB的面积和△AOB的面积之和,再减去△APD的面积,即是△APB的面积;根据△APB与△ABC面积相等,求得m的值;(3)假设存在点Q,使△QAB是等腰三角形,求出Q点的坐标即可.解答:解:(1)∵一次函数的解析式为函数图象与x轴、y轴分别交于点A、B,∴A(1,0),B(0,),∴AB=2,设AC=x,则BC=2x,由勾股定理得,4x2﹣x2=4,解得x=,S△ABC==;(2)过P作PD⊥x轴,垂足为D,S△APB=S梯形ODPB+S△AOB﹣S△APD==,﹣=,解得m=;(3)∵AB==2,∴当AQ=AB时,点Q1(3,0),Q2(﹣1,0),Q3(0,﹣);当AB=BQ时,点Q4(0,+2),Q2(0,﹣2),Q2(﹣1,0);当AQ=BQ时,点Q6(0,),Q2(﹣1,0),综上可得:(0,),(0,),(﹣1,0)(3,0),(0,),(0,)点评:此题主要考查平面直角坐标系中图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.。
2024年中考数学复习重难点题型训练—一次函数与几何图形综合题一(含答案解析)

2024年中考数学复习重难点题型训练—一次函数与几何图形综合题二(含答案解析)类型一与三角形有关1.(2022·天津)如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x 轴,若AB=6,OA=OB=5,则点A的坐标是()A.(5,4)B.(3,4)C.(5,3)D.(4,3)【答案】D【分析】利用HL证明△ACO≌△BCO,利用勾股定理得到OC=4,即可求解.【详解】解:∵AB⊥x轴,∴∠ACO=∠BCO=90°,∵OA=OB,OC=OC,∴△ACO≌△BCO(HL),∴AC=BC=12AB=3,∵OA=5,∴=4,∴点A的坐标是(4,3),故选:D.【点睛】本题考查了坐标与图形,全等三角形的判定和性质,勾股定理,解题的关键是灵活运用所学知识解决问题.2.(2020·宁夏中考真题)如图,直线542y x =+与x 轴、y 轴分别交于A 、B 两点,把AOB 绕点B 逆时针旋转90°后得到11AO B ,则点1A的坐标是_____.【答案】(4,125)【解析】【分析】首先根据直线AB 来求出点A 和点B 的坐标,A 1的横坐标等于OB ,而纵坐标等于OB-OA ,即可得出答案.【详解】解:在542y x =+中,令x=0得,y=4,令y=0,得5042x =+,解得x=8-5,∴A (8-5,0),B (0,4),由旋转可得△AOB ≌△A 1O 1B ,∠ABA 1=90°,∴∠ABO=∠A 1BO 1,∠BO 1A 1=∠AOB=90°,OA=O 1A 1=85,OB=O 1B=4,∴∠OBO 1=90°,∴O 1B ∥x 轴,∴点A 1的纵坐标为OB-OA 的长,即为48-5=125;横坐标为O 1B=OB=4,故点A 1的坐标是(4,125),故答案为:(4,125).【点睛】本题主要考查了旋转的性质以及一次函数与坐标轴的交点问题,利用基本性质结合图形进行推理是解题的关键.3.(2021·广西贺州市·中考真题)如图,一次函数4y x =+与坐标轴分别交于A ,B 两点,点P ,C 分别是线段AB ,OB 上的点,且45OPC ∠=︒,PC PO =,则点P 的标为________.【答案】(--【分析】过P 作PD ⊥OC 于D ,先求出A ,B 的坐标,得∠ABO=∠OAB=45°,再证明△PCB ≌△OPA ,从而求出BD =,OD =,进而即可求解.【详解】如图所示,过P 作PD ⊥OC 于D ,∵一次函数4y x =+与坐标轴分别交于A ,B 两点,∴A(-4,0),B(0,4),即:OA=OB ,∴∠ABO=∠OAB=45°,∴△BDP 是等腰直角三角形,∵∠PBC=∠CPO=∠OAP=45°,∴∠PCB+∠BPC=135°=∠OPA+∠BPC,∴∠PCB=∠OPA,又∵PC=OP,∴△PCB≌△OPA(AAS),∴AO=BP=4,∴Rt△BDP中,BD=PD=2=2,∴OD=OB−BD=2,∴P(2,2).故答案是:P(2,2).【点睛】本题主要考查了一次函数图象上点的坐标特征以及等腰三角形的性质,结合等腰三角形的性质,判定全等三角形是解决问题的关键.4.(2022·湖北黄冈)如图1,在△ABC中,∠B=36°,动点P从点A出发,沿折线A→B→C 匀速运动至点C停止.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为y(cm),y与t的函数图象如图2所示.当AP恰好平分∠BAC时,t的值为________.【答案】252+##2+25【分析】根据函数图像可得AB=4=BC ,作∠BAC 的平分线AD ,∠B =36°可得∠B =∠DAC =36°,进而得到ADC BAC △△,由相似求出BD 的长即可.【详解】根据函数图像可得AB=4,AB+BC=8,∴BC=AB=4,∵∠B =36°,∴72BCA BAC ∠∠︒==,作∠BAC 的平分线AD ,∴∠BAD =∠DAC =36°=∠B ,∴AD=BD ,72BCA DAC ∠∠︒==,∴AD=BD=CD ,设AD BD CD x ===,∵∠DAC =∠B =36°,∴ADC BAC △△,∴AC DC BC AC =,∴x 4x 4x-=,解得:1225x =-+,225x =--,∴252AD BD CD ===,此时521AB BD t +==(s),故答案为:52.【点睛】此题考查了图形与函数图象间关系、相似三角形的判定与性质、解一元二次方程,关键是证明ADC BAC △△.5.(2020·四川内江?中考真题)如图,在平面直角坐标系中,点A (-2,0),直线33:33l y x =+与x 轴交于点B ,以AB 为边作等边1ABA ∆,过点1A 作11//A B x 轴,交直线l 于点1B ,以11A B 为边作等边112A B A ∆,过点2A 作22//A B x 轴,交直线l 于点2B ,以22A B 为边作等边223A B A ∆,以此类推……,则点2020A 的纵坐标是______________【答案】20203(21)2-【解析】【分析】如图,过A 1作A 1C ⊥AB 与C ,过A 2作A 2C 1⊥A 1B 1于C 1,过A 3作A 3C 2⊥A 2B 2于C 2,先根据直线方程与x 轴交于点B (-1,0),且与x 轴夹角为30º,则有AB=1,然后根据平行线的性质、等边三角形的性质、含30º的直角三角形的性质,分别求的A 1、A 2、A 3、的纵坐标,进而得到A n 的纵坐标,据此可得A 2020的纵坐标,即可解答.【详解】如图,过A 1作A 1C ⊥AB 与C ,过A 2作A 2C 1⊥A 1B 1于C 1,过A 3作A 3C 2⊥A 2B 2于C 2,先根据直线方程与x 轴交于点B (-1,0),与y 轴交于点D (0,33),∴OB=1,OD=33,∴∠DBO=30º由题意可得:∠A 1B 1B=∠A 2B 2B 1=30º,∠B 1A 1B=∠B 2A 2B 1=60º∴∠A 1BB 1=∠A 2B 1B 2=90º,∴AB=1,A 1B 1=2A 1B=21,A 2B 2=2A 2B 1=22,A 3B 3=2A 3B 2=23,…A n B n =2n∴A 1C=2AB=2×1,A 1纵坐标为32×1=13(21)2-;A 2C 1=32A 1B 1=1322⨯,A2的纵坐标为32×1+1322⨯=013(22)2+=332⨯=23(21)2-;A 3C 2=32A 2B 2=2322⨯,A 3的纵坐标为32×1+1322⨯+2322⨯=0123(222)2++=372⨯=33(21)2-;…由此规律可得:A n C n-1=1322n -⨯,A n 的纵坐标为01213(2222)2n -++++ =3(21)2n -,∴A 2020=20203(21)2-,故答案为:20203(21)2-【点睛】本题是一道点的坐标变化规律探究,涉及一次函数的图象、等边三角形的性质、含30º角的直角三角形的性质,数字型规律等知识,解答的关键是认真审题,观察图象,结合基本图形的有关性质,找到坐标变化规律.6.(2022·陕西)如图,ABC 的顶点坐标分别为(23)(30)(11)A B C ----,,,,,.将ABC 平移后得到A B C '''V ,且点A 的对应点是(23)A ',,点B 、C 的对应点分别是B C '',.(1)点A 、A '之间的距离是__________;(2)请在图中画出A B C '''V .【答案】(1)4(2)见解析【分析】(1)由(23)A -,,(23)A ',得,A 、A '之间的距离是2-(-2)=4;(2)根据题意找出平移规律,求出103-1B C ''(,),(,),进而画图即可.(1)解:由(23)A -,,(23)A ',得,A 、A '之间的距离是2-(-2)=4.故答案为:4.(2)解:由题意,得103-1B C ''(,),(,),如图,A B C '''V 即为所求.【点睛】本题考查了坐标系中两点之间的距离求解以及平移求点坐标画图,题目相对较简单,掌握平移规律是解决问题的关键.7.(2021·贵州毕节市·中考真题)如图,在平面直角坐标系中,点()11,1N 在直线:l y x =上,过点1N 作11N M l ⊥,交x 轴于点1M ;过点1M 作12M N x ⊥轴,交直线l 于点2N ;过点2N 作22N M l ⊥,交x 轴于点2M ;过点2M 作23M N x ⊥轴,交直线l 于点3N ;…;按此作法进行下去,则点2021M 的坐标为_____________.【答案】(20212,0).【分析】根据题目所给的解析式,求出对应的1M 坐标,然后根据规律求出n M 的坐标,最后根据题目要求求出最后答案即可.【详解】解:如图,过点N 作NM ⊥x 轴于M将1x =代入直线解析式y x =中得1y =∴1OM MN ==,MON ∠=45°∵1ONM =∠90°∴1ON NM =∵1ON NM ⊥∴11OM MM ==∴1M 的坐标为(2,0)同理可以求出2M 的坐标为(4,0)同理可以求出3M 的坐标为(8,0)同理可以求出n M 的坐标为(2n ,0)∴2021M 的坐标为(20212,0)故答案为:(20212,0).【点睛】本题主要考查了直线与坐标轴之间的关系,解题的关键在于能够发现规律.8.(2020·湖南湘西?中考真题)在平面直角坐标系中,O 为原点,点(6,0)A ,点B 在y 轴的正半轴上,30ABO ∠=︒.矩形CODE 的顶点D ,E ,C 分别在,,OA AB OB 上,2OD =.将矩形CODE 沿x 轴向右平移,当矩形CODE 与ABO 重叠部分的面积为时,则矩形CODE 向右平移的距离为___________.【答案】2【解析】【分析】先求出点B 的坐标(0,3),得到直线AB 的解析式为:33y =+,根据点D 的坐标求出OC 的长度,利用矩形CODE 与ABO 重叠部分的面积为63列出关系式求出3D G '=,再利用一次函数关系式求出OD '=4,即可得到平移的距离.【详解】∵(6,0)A ,∴OA=6,在Rt △AOB 中,30ABO ∠=︒,∴63tan 30OA OB ==∴B (0,63),∴直线AB 的解析式为:33y =+,当x=2时,y=43∴E (2,3,即DE=3∵四边形CODE 是矩形,∴OC=DE=43设矩形CODE 沿x 轴向右平移后得到矩形C O D E '''',D E ''交AB 于点G ,∴D E ''∥OB ,∴△AD G '∽△AOB ,∴∠AGD '=∠AOB=30°,∴∠EGE '=∠AGD '=30°,∴GE ''=,∵平移后的矩形CODE 与ABO 重叠部分的面积为,∴五边形C O D GE '''的面积为∴12O D O C EE GE ''''''⋅-⋅=,∴122EE ''⨯-⨯=,∴2EE '=,∴矩形CODE 向右平移的距离DD '=2EE '=,故答案为:2.【点睛】此题考查了锐角三角函数,求一次函数的解析式,矩形的性质,图形平移的性质,是一道综合多个知识点的综合题型,且较为基础的题型.9.(2021·浙江金华市·中考真题)在平面直角坐标系中,点A 的坐标为(,点B 在直线8:3l y x =上,过点B 作AB 的垂线,过原点O 作直线l 的垂线,两垂线相交于点C .(1)如图,点B ,C 分别在第三、二象限内,BC 与AO 相交于点D .①若BA BO =,求证:CD CO =.②若45CBO ∠=︒,求四边形ABOC 的面积.(2)是否存在点B ,使得以,,A B C 为顶点的三角形与BCO 相似?若存在,求OB 的长;若不存在,请说明理由.【答案】(1)①见解析;②552;(2)存在,44+-4,9,1【分析】(1)①等腰三角形等角对等边,则BAD AOB ∠=∠,根据等角的余角相等和对顶角相等,得到CDO COD ∠=∠,根据等角对等边,即可证明CD CO =;②添加辅助线,过点A 作AH OB ⊥于点H ,根据直线l 的解析式和角的关系,分别求出线段AB 、BC 、OB 、OC 的长,则11+22ABC CBO ABOC S S S AB BC OB OC =+=⨯⨯ 四边形;(2)分多钟情况进行讨论:①当点C 在第二象限内,ACB CBO ∠=∠时;②当点C 在第二象限内,ACB BCO ∠=∠时;③当点C 在第四象限内,ACB CBO ∠=∠时.【详解】解:(1)①证明:如图1,∵BA BO =,∴12∠=∠.∴BA BC ⊥,∴2590∠+∠=︒.而45∠=∠,∴2490∠+∠=︒.∵OB OC ⊥,∴1390∠+∠=︒.∴34∠=∠,∴CD CO =.②如图1,过点A 作AH OB ⊥于点H .由题意可知3tan 18∠=,在Rt AHO 中,3tan 18AH OH ∠==.设3m AH =,8m OH =.∵222AH OH OA +=,∴()()22238m m +=,解得1m =.∴38AH OH ==,.∵4590CBO ABC ∠=︒∠=︒,,∴45ABH ∠=︒,∴3,tan 45sin 45AH AH BH AB ====︒︒∴5OB OH BH =-=.∵45OB OC CBO ⊥∠=︒,,∴tan 455,cos 45OB OC OB BC =⨯︒===︒,∴111522ABC S AB BC =⨯=⨯= ,112555222CBO S OB OC =⨯=⨯⨯= :∴552ABC CBO ABOC S S S =+= 四边形.(2)过点A 作AH OB ⊥于点H ,则有38AH OH ==,.①如图2,当点C 在第二象限内,ACB CBO ∠=∠时,设OB t=∵ACB CBO ∠=∠,∴//AC OB .又∵AH OB OC OB ⊥⊥,,∴3AH OC ==.∵AH OB AB BC ⊥⊥,,∴12902390∠+∠=︒∠+∠=︒,,∴13∠=∠,∴AHB BOC ∽,∴AH HB BO OC=,∴383t t -=,整理得2890t t -+=,解得4t =±∴4OB =±②如图3,当点C 在第二象限内,ACB BCO ∠=∠时,延长AB CO ,交于点G ,则ACB GCB ≌,∴AB GB =.又∵AH OB OC OB ⊥⊥,,∴90AHB GOB ∠=∠=︒,而ABH GBO ∠=∠,∴ABH GBO ≌,∴142OB HB OH ===③当点C 在第四象限内,ACB CBO ∠=∠时,AC 与OB 相交于点E ,则有BE CE =.(a)如图4,点B 在第三象限内.在Rt ABC 中,1290,90ACB CAB ∠+∠=︒∠+∠=︒,∴2CAB∠=∠∴AE BE CE ==,又∵,AH OB OC OB ⊥⊥,∴90AHE COE ∠=∠=︒,而AEH CEO∠=∠∴AHE COE ≌,∴142HE OE OH ===∴225AE AH HE =+=,∴5BE =,∴9OB BE OE =+=(b)如图5,点B 在第一象限内.在Rt ABC 中90,90ACB CAB CBO ABE ∠+∠=︒∠+∠=︒∴CAB ABE ∠=∠,∴AE BE CE ==.又∵,AH OB OC OB ⊥⊥,∴90AHE COE ∠=∠=︒而AEH CEO ∠=∠,∴AHE COE≌∴142HE OE OH ===∴5AE ==,∴5BE =,∴1OB BE OE =-=综上所述,OB 的长为44+4,9,1.【点睛】本题涉及到等腰三角形、等角的余角相等、利用切割法求四边形的面积和相似三角形等知识,综合性较强.在题中已知两个三角形相似时,要分情况考虑.10.(2020·河南中考真题)小亮在学习中遇到这样一个问题:如图,点D 是弧BC 上一动点,线段8,BC cm =点A 是线段BC 的中点,过点C 作//CF BD ,交DA 的延长线于点F .当DCF ∆为等腰三角形时,求线段BD 的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:()1根据点D 在弧BC 上的不同位置,画出相应的图形,测量线段,,BD CD FD 的长度,得到下表的几组对应值.操作中发现:①"当点D 为弧BC 的中点时, 5.0BD cm =".则上中a 的值是②"线段CF 的长度无需测量即可得到".请简要说明理由;()2将线段BD 的长度作为自变量x CD ,和FD 的长度都是x 的函数,分别记为CD y 和FD y ,并在平面直角坐标系xOy 中画出了函数FD y 的图象,如图所示.请在同一坐标系中画出函数CD y 的图象;()3继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当DCF ∆为等腰三角形时,线段BD 长度的近似值.(结果保留一位小数).【答案】(1)①5.0;②见解析;(2)图象见解析;(3)图象见解析;3.5cm 或5.0cm 或6.3cm ;【解析】【分析】(1)①点D 为弧BC 的中点时,△ABD ≌△ACD ,即可得到CD=BD ;②由题意得△ACF ≌△ABD ,即可得到CF=BD ;(2)根据表格数据运用描点法即可画出函数图象;(3)画出CF y 的图象,当DCF ∆为等腰三角形时,分情况讨论,任意两边分别相等时,即任意两个函数图象相交时的交点横坐标即为BD 的近似值.【详解】解:(1)①点D 为弧BC 的中点时,由圆的性质可得:AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACD ,∴CD=BD=5.0,∴ 5.0a =;②∵//CF BD ,∴BDA CFA ∠=∠,∵BDA CFA BAD CAF AD AF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACF ≌△ABD ,∴CF=BD ,∴线段CF 的长度无需测量即可得到;(2)函数CD y的图象如图所示:(3)由(1)知=CF BD x =,画出CF y 的图象,如上图所示,当DCF ∆为等腰三角形时,①CF CD =,BD 为CF y 与CD y 函数图象的交点横坐标,即BD=5.0cm ;②CF DF =,BD 为CF y 与DF y 函数图象的交点横坐标,即BD=6.3cm ;③CD DF =,BD 为CD y 与DF y 函数图象的交点横坐标,即BD=3.5cm ;综上:当DCF ∆为等腰三角形时,线段BD 长度的近似值为3.5cm 或5.0cm 或6.3cm .【点睛】本题考查一次函数结合几何的应用,学会用描点法画出函数图象,熟练掌握一次函数的性质以及三角形全等的判定及性质是解题的关键.11.(2020·河北中考真题)如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN-匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持APQ B∠=∠.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将ABC∆的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当03x≤≤及39x≤≤时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角APQ∠扫描APQ∆区域(含边界),扫描器随点P从M到B再到N共用时36秒.若94AK=,请直接..写出点K被扫描到的总时长.【答案】(1)3;(2)43MP=;(3)当03x≤≤时,24482525d x=+;当39x≤≤时,33355d x=-+;(4)23t s=【解析】【分析】(1)根据当点P在BC上时,PA⊥BC时PA最小,即可求出答案;(2)过A点向BC边作垂线,交BC于点E,证明△APQ∽△ABC,可得2APQABCS APS AB∆∆⎛⎫= ⎪⎝⎭,根据SS上下=45可得24=9APQABCS APS AB∆∆⎛⎫= ⎪⎝⎭,可得23APAB=,求出AB=5,即可解出MP;(3)先讨论当0≤x≤3时,P在BM上运动,P到AC的距离:d=PQ·sinC,求解即可,再讨论当3≤x≤9时,P在BN上运动,BP=x-3,CP=8-(x-3)=11-x,根据d=CP·sinC即可得出答案;(4)先求出移动的速度=936=14,然后先求出从Q 平移到K 耗时,再求出不能被扫描的时间段即可求出时间.【详解】(1)当点P 在BC 上时,PA ⊥BC 时PA 最小,∵AB=AC ,△ABC 为等腰三角形,∴PA min =tanC·2BC =34×4=3;(2)过A 点向BC 边作垂线,交BC 于点E,S 上=S △APQ ,S 下=S 四边形BPQC ,∵APQ B ∠=∠,∴PQ ∥BC ,∴△APQ ∽△ABC ,∴AP AD PQ AB AC BC==,∴2APQABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,当S S 上下=45时,24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,∴23AP AB =,AE=2BC ·tan 3C =,根据勾股定理可得AB=5,∴2253AP MP AB +==,解得MP=43;(3)当0≤x≤3时,P 在BM 上运动,P 到AC 的距离:d=PQ·sinC ,由(2)可知sinC=35,∴d=35PQ ,∵AP=x+2,∴25AP x PQ AB BC+==,∴PQ=285x +⨯,∴d=23855x +⨯⨯=24482525x +,当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x ,d=CP·sinC=35(11-x )=-35x+335,综上()()24480325253333955x x d x x ⎧+≤≤⎪⎪=⎨⎪-+≤≤⎪⎩;(4)AM=2<AQ=94,移动的速度=936=14,①从Q 平移到K ,耗时:92414-=1秒,②P 在BC 上时,K 与Q 重合时CQ=CK=5-94=114,∵∠APQ+∠QPC=∠B+∠BAP ,APQ B∠=∠∴∠QPC=∠BAP ,又∵∠B=∠C ,∴△ABP ∽△PCQ ,设BP=y ,CP=8-y ,AB BP PC CQ =,即51184y y =-,整理得y 2-8y=554-,(y-4)2=94,解得y 1=52,y 2=112,52÷14=10秒,112÷14=22秒,∴点K 被扫描到的总时长36-(22-10)-1=23秒.【点睛】本题考查了相似三角形的判定和性质,锐角三角函数,一次函数的应用,结合知识点灵活运用是解题关键.12.(2020·湖南衡阳?中考真题)如图1,平面直角坐标系xOy 中,等腰ABC ∆的底边BC 在x 轴上,8BC =,顶点A 在y 的正半轴上,2OA =,一动点E 从(3,0)出发,以每秒1个单位的速度沿CB 向左运动,到达OB 的中点停止.另一动点F 从点C 出发,以相同的速度沿CB 向左运动,到达点O 停止.已知点E 、F 同时出发,以EF 为边作正方形EFGH ,使正方形EFGH 和ABC ∆在BC 的同侧.设运动的时间为t 秒(0t ≥).(1)当点H 落在AC 边上时,求t 的值;(2)设正方形EFGH 与ABC ∆重叠面积为S ,请问是存在t 值,使得9136S =若存在,求出t 值;若不存在,请说明理由;(3)如图2,取AC 的中点D ,连结OD ,当点E 、F 开始运动时,点M 从点O 出发,以每秒OD DC CD DO ---运动,到达点O 停止运动.请问在点E 的整个运动过程中,点M 可能在正方形EFGH 内(含边界)吗?如果可能,求出点M 在正方形EFGH 内(含边界)的时长;若不可能,请说明理由.【答案】(1)t=1;(2)存在,143t =,理由见解析;(3)可能,3455t ≤≤或4533t ≤≤或35t ≤≤理由见解析【解析】【分析】(1)用待定系数法求出直线AC 的解析式,根据题意用t 表示出点H 的坐标,代入求解即可;(2)根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4,用待定系数法求出直线AB 的解析式,求出点H 落在BC 边上时的t 值,求出此时重叠面积为169﹤9136,进一步求出重叠面积关于t 的表达式,代入解t 的方程即可解得t 值;(3)由已知求得点D (2,1),AC=,结合图形分情况讨论即可得出符合条件的时长.【详解】(1)由题意,A(0,2),B(-4,0),C(4,0),设直线AC 的函数解析式为y=kx+b ,将点A 、C 坐标代入,得:402k b b +=⎧⎨=⎩,解得:122k b ⎧=-⎪⎨⎪=⎩,∴直线AC 的函数解析式为122y x =-+,当点H 落在AC 边上时,点E(3-t ,0),点H (3-t ,1),将点H 代入122y x =-+,得:11(3)22t =--+,解得:t=1;(2)存在,143t =,使得9136S =.根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4,设直线AB 的函数解析式为y=mx+n ,将点A 、B 坐标代入,得:402m n n -+=⎧⎨=⎩,解得:122m n ⎧=⎪⎨⎪=⎩,∴直线AC 的函数解析式为122y x =+,当t ﹥4时,点E (3-t ,0)点H (3-t ,t-3),G(0,t-3),当点H 落在AB 边上时,将点H 代入122y x =+,得:13(3)22t t -=-+,解得:133t =;此时重叠的面积为221316(3)(3)39t -=-=,∵169﹤9136,∴133﹤t ﹤5,如图1,设GH 交AB 于S ,EH 交AB 于T,将y=t-3代入122y x =+得:1322t x -=+,解得:x=2t-10,∴点S(2t-10,t-3),将x=3-t 代入122y x =+得:11(3)2(7)22y t t =-+=-,∴点T 1(3,(7))2t t --,∴AG=5-t ,SG=10-2t ,BE=7-t ,ET=1(7)2t -,211(7)24BET S BE ET t ∆==- ,21(5)2ASG S AG SG t ∆==- 所以重叠面积S=AOB BET ASG S S S ∆∆∆--=4-21(7)4t --2(5)t -=2527133424t t -+-,由2527133424t t -+-=9136得:1143t =,29215t =﹥5(舍去),∴143t =;(3)可能,35≤t≤1或t=4.∵点D 为AC 的中点,且OA=2,OC=4,∴点D (2,1),AC=,易知M 点在水平方向以每秒是4个单位的速度运动;当0﹤t ﹤12时,M 在线段OD 上,H 未到达D 点,所以M 与正方形不相遇;当12﹤t ﹤1时,12+12÷(1+4)=35秒,∴t =35时M 与正方形相遇,经过1÷(1+4)=15秒后,M 点不在正方行内部,则3455t ≤≤;当t=1时,由(1)知,点F 运动到原E 点处,M 点到达C 处;当1≤t≤2时,当t=1+1÷(4-1)=43秒时,点M 追上G 点,经过1÷(4-1)=13秒,点M 都在正方形EFGH 内(含边界),4533t ≤≤当t=2时,点M 运动返回到点O 处停止运动,当t=3时,点E 运动返回到点O 处,当t=4时,点F 运动返回到点O 处,当35t ≤≤时,点M 都在正方形EFGH 内(含边界),综上,当3455t ≤≤或4533t ≤≤或35t ≤≤时,点M 可能在正方形EFGH 内(含边界).【点睛】本题考查了一次函数与几何图形的综合,涉及求一次函数的解析式、正方形的性质、直角三角形的性质、不规则图形的面积、解一元二次方程等知识,解答的关键是认真审题,提取相关信息,利用待定系数法、数形结合法等解题方法确定解题思路,进而推理、探究、发现和计算.13.(2020·黑龙江哈尔滨?中考真题)已知,在平面直角坐标系中,点O 为坐标原点,直线AB 与x 轴的正半轴交于点A ,与y 轴的负半轴交于点B ,OA OB =,过点A 作x 轴的垂线与过点O 的直线相交于点C ,直线OC 的解析式为34y x =,过点C 作CM y ⊥轴,垂足为,9M OM =.(1)如图1,求直线AB 的解析式;(2)如图2,点N 在线段MC 上,连接ON ,点P 在线段ON 上,过P 点作PD x ⊥轴,垂足为D ,交OC 于点E ,若NC OM =,求PE OD的值;(3)如图3,在(2)的条件下,点F 为线段AB 上一点,连接OF ,过点F 作OF 的垂线交线段AC 于点Q ,连接BQ ,过点F 作x 轴的平行线交BQ 于点G ,连接PF 交x 轴于点H ,连接EH ,若,DHE DPH GQ FG ∠=∠-=,求点P 的坐标.【答案】(1)12y x =-;(2)94;(3)1236(,)55P .【解析】【分析】(1)根据题意求出A ,B 的坐标即可求出直线AB 的解析式;(2)求出N (3,9),以及ON 的解析式为y=3x ,设P (a ,3a ),表达出PE 及OD 即可解答;(3)如图,设直线GF 交CA 延长线于点R ,交y 轴于点S ,过点F 作FT ⊥x 轴于点T ,先证明四边形OSRA 为矩形,再通过边角关系证明△OFS ≌△FQR ,得到SF=QR ,进而证明△BSG ≌△QRG ,得到SG=RG=6,设FR=m ,根据GQ FG -=,以及在Rt △GQR 中利用勾股定理求出m 的值,得到FS=8,AR=4,证明四边形OSFT 为矩形,得到OT=FS=8,根据∠DHE=∠DPH ,利用正切函数的定义得到DE DH DH PD=,从而得到DH=32a ,根据∠PHD=∠FHT ,得到HT=2,再根据OT=OD+DH+HT ,列出关于a 的方程即可求出a 的值,从而得到点P 的坐标.【详解】解:(1)∵CM ⊥y 轴,OM=9,∴当y=9时,394x =,解得:x=12,∴C (12,9),∵CA ⊥x 轴,则A (12,0),∴OB=OA=12,则B (0,-12),设直线AB 的解析式为y=kx+b ,∴12012k b b +=⎧⎨=-⎩,解得:112k b =⎧⎨=-⎩,∴12y x =-;(2)由题意可得,∠CMO=∠OAC=∠MOA=90°,∴四边形MOAC 为矩形,∴MC=OA=12,∵NC=OM ,∴NC=9,则MN=MC-NC=3,∴N (3,9)设直线ON 的解析式为1y k x =,将N (3,9)代入得:193k =,解得:13k =,∴y=3x ,设P (a ,3a )∵PD ⊥x 轴交OC 于点E ,交x 轴于点D ,∴3(,)4E a a ,(a,0)D ,∴PE=39344a a a -=,OD=a ,∴9944a PE OD a ==;(3)如图,设直线GF 交CA 延长线于点R ,交y 轴于点S ,过点F 作FT ⊥x 轴于点T ,∵GF ∥x 轴,∴∠OSR=∠MOA=90°,∠CAO=∠R=90°,∠BOA=∠BSG=90°,∠OAB=∠AFR ,∴∠OSR=∠R=∠AOS=∠BSG=90°,则四边形OSRA为矩形,∴OS=AR,SR=OA=12,∵OA=OB,∴∠OBA=∠OAB=45°,∴∠FAR=90°-∠AFR=45°,∴∠FAR=∠AFR,∴FR=AR=OS,∵QF⊥OF,∴∠OFQ=90°,∴∠OFS+∠QFR=90°,∵∠SOF+∠OFS=90°,∴∠SOF=∠QFR,∴△OFS≌△FQR,∴SF=QR,∵∠SFB=∠AFR=45°,∴∠SBF=∠SFB,∴BS=SF=QR,∵∠SGB=∠RGQ,∴△BSG≌△QRG,∴SG=RG=6,设FR=m,则AR=m,∴QR=SF=12-m,∴=,-=,∵GQ FG∴66m m +-=+,∵QG 2=GR 2+QR 2,即222(6)6(12)m m +=+-,解得:m=4,∴FS=8,AR=4,∵∠OAB=∠FAR ,FT ⊥OA ,FR ⊥AR ,∴FT=FR=AR=4,∠OTF=90°,∴四边形OSFT 为矩形,∴OT=FS=8,∵∠DHE=∠DPH ,∴tan ∠DHE=tan ∠DPH ,∴DE DH DH PD=,由(2)可知,DE=34a ,PD=3a ,∴343a DH DH a=,解得:DH=32a ,∴tan ∠PHD=3232PD a DH a ==,∵∠PHD=∠FHT ,∴tan ∠FHT=2TF HT =,∴HT=2,∵OT=OD+DH+HT ,∴3282a a ++=,∴a=125,∴1236(,)55P 【点睛】本题考查了一次函数与几何综合问题,涉及了一次函数解析式的求法,矩形的判定与性质,全等三角形的判定与性质以及锐角三角函数的定义等知识点,第(3)问难度较大,解题的关键是正确做出辅助线,熟悉几何的基本知识,综合运用全等三角形以及锐角三角函数的概念进行解答.类型二与平行四边形有关14.(2022·山东泰安)如图,四边形ABCD 为平行四边形,则点B 的坐标为________.【答案】()2,1--【分析】根据平行四边形的性质以及点的平移即可得出结论.【详解】解: 四边形ABCD 为平行四边形,∴DA CB ∥,即将D 点平移到A 的过程与将C 点平移到B 的过程保持一致,将D 点平移到A 的过程是::134x --=-(向左平移4各单位长度);:220y -=(上下无平移);∴将C 点平移到B 的过程按照上述一致过程进行得到()24,1B --,即()2,1B --,故答案为:()2,1--.【点睛】本题考查平行四边形的性质及点的平移,掌握点的平移的代数表示是解决问题的关键.15.(2022·甘肃武威)如图1,在菱形ABCD 中,60A ∠=︒,动点P 从点A 出发,沿折线AD DC CB →→方向匀速运动,运动到点B 停止.设点P 的运动路程为x ,APB △的面积为y ,y 与x 的函数图象如图2所示,则AB 的长为()AB .C .D .【答案】B【分析】根据图1和图2判定三角形ABD 为等边三角形,它的面积为【详解】解:在菱形ABCD 中,∠A=60°,∴△ABD 为等边三角形,设AB=a ,由图2可知,△ABD 的面积为∴△ABD 的面积24a ==解得:a=故选B【点睛】本题考查了动点问题的函数图象,根据菱形的性质和函数图象,能根据图形得出正确信息是解此题的关键.16.(2020·黑龙江牡丹江?中考真题)如图,已知直线AB 与x 轴交于点A ,与y 轴交于点B ,线段OA 的长是方程27180x x --=的一个根,12OB OA =.请解答下列问题:(1)求点A ,B 的坐标;(2)直线EF 交x 轴负半轴于点E ,交y 轴正半轴于点F ,交直线AB 于点C .若C 是EF 的中点,6OE =,反比例函数k y x=图象的一支经过点C ,求k 的值;(3)在(2)的条件下,过点C 作CD OE ⊥,垂足为D ,点M 在直线AB 上,点N 在直线CD 上.坐标平面内是否存在点P ,使以D ,M ,N ,P 为顶点的四边形是正方形?若存在,请写出点P 的个数,并直接写出其中两个点P 的坐标;若不存在,请说明理由.【答案】(1)A (9,0),B (0,92);(2)-18;(3)存在5个,(9,12)或(9,-12)或(1,0)或(-7,4)或(-15,0).【解析】【分析】(1)解一元二次方程,得到点A 的坐标,再根据12OB OA =可得点B 坐标;(2)利用待定系数法求出直线AB 的表达式,根据点C 是EF 的中点,得到点C 横坐标,代入可得点C 坐标,根据点C 在反比例函数图像上求出k 值;(3)画出图形,可得点P 共有5个位置,分别求解即可.【详解】解:(1)∵线段OA 的长是方程27180x x --=的一个根,解得:x=9或-2(舍),而点A 在x 轴正半轴,∴A (9,0),∵12OB OA =,∴B (0,92);(2)∵6OE =,∴E (-6,0),设直线AB 的表达式为y=kx+b ,将A 和B 代入,得:0992k b b =+⎧⎪⎨=⎪⎩,解得:1292k b ⎧=-⎪⎪⎨⎪=⎪⎩,∴AB 的表达式为:1922y x =-+,∵点C 是EF 的中点,∴点C 的横坐标为-3,代入AB 中,y=6,则C (-3,6),∵反比例函数k y x=经过点C ,则k=-3×6=-18;(3)存在点P ,使以D ,M ,N ,P 为顶点的四边形是正方形,如图,共有5种情况,在四边形DM 1P 1N 1中,M 1和点A 重合,∴M 1(9,0),此时P 1(9,12);在四边形DP 3BN 3中,点B 和M 重合,可知M 在直线y=x+3上,联立:31922y x y x =+⎧⎪⎨=-+⎪⎩,解得:14x y =⎧⎨=⎩,∴M (1,4),∴P 3(1,0),同理可得:P 2(9,-12),P 4(-7,4),P 5(-15,0).故存在点P 使以D ,M ,N ,P 为顶点的四边形是正方形,点P 的坐标为P 1(9,12),P 2(9,-12),P 3(1,0),P 4(-7,4),P 5(-15,0).【点睛】本题考查了解一元二次方程,一次函数表达式,正方形的性质,反比例函数表达式,难度较大,解题的关键是根据图像画出符合条件的正方形.类型三最值问题17.(2020·江苏宿迁?中考真题)如图,在平面直角坐标系中,Q是直线y=﹣12x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q',连接OQ',则OQ'的最小值为()A.455B C.523D.655【答案】B【解析】【分析】利用等腰直角三角形构造全等三角形,求出旋转后Q′的坐标,然后根据勾股定理并利用二次函数的性质即可解决问题.【详解】解:作QM⊥x轴于点M,Q′N⊥x轴于N,设Q(m,122m-+),则PM=1m﹣,QM=122m-+,∵∠PMQ=∠PNQ′=∠QPQ′=90°,∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,∴∠QPM=∠PQ′N ,在△PQM 和△Q′PN 中,'90''PMQ PNQ QPM PQ N PQ Q P ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△PQM ≌△Q′PN(AAS),∴PN=QM=122m -+,Q′N=PM=1m ﹣,∴ON=1+PN=132m -,∴Q′(132m -,1m ﹣),∴OQ′2=(132m -)2+(1m ﹣)2=54m 2﹣5m+10=54(m ﹣2)2+5,当m=2时,OQ′2有最小值为5,∴OQ′故选:B .【点睛】本题考查了一次函数图象上点的坐标特征,一次函数的性质,三角形全等的判定和性质,坐标与图形的变换-旋转,二次函数的性质,勾股定理,表示出点的坐标是解题的关键18.(2020·湖南永州?中考真题)已知点()00,P x y 和直线y kx b =+,求点P 到直线y kx b =+的距离d可用公式d =C 的圆心C 的坐标为()1,1,半径为1,直线l 的表达式为26y x =-+,P 是直线l 上的动点,Q 是C 上的动点,则PQ 的最小值是()A .355B .3515-C .6515-D .2【答案】B 【解析】【分析】过点C 作直线l 的垂线,交C 于点Q ,交直线l 于点P ,此时PQ 的值最小,利用公式计算即可.【详解】过点C 作直线l 的垂线,交C 于点Q ,交直线l 于点P ,此时PQ 的值最小,如图,∵点C 到直线l 的距离()00222116355112kx y b d k -+-⨯-+==++-,C 半径为1,∴PQ 的最小值是3515-,故选:B.【点睛】此题考查公式的运用,垂线段最短的性质,正确理解公式中的各字母的含义,确定点P与点Q最小时的位置是解题的关键.A B-,在x19.(2020·辽宁鞍山?中考真题)如图,在平面直角坐标系中,已知(3,6),(2,2)CD=,线段CD在x轴上平移,当轴上取两点C,D(点C在点D左侧),且始终保持1+的值最小时,点C的坐标为________.AD BC【答案】(-1,0)【解析】【分析】作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,得到此时AD+BC的值最小,求出直线AB″,得到点D坐标,从而可得点C坐标.【详解】解:如图,作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,可知四边形B′B″DC为平行四边形,则B′C=B″D,由对称性质可得:BC=B′C,∴AD+BC=AD+B′C=AD+B″D=AB″,则此时AB″最小,即AD+BC最小,∵A(3,6),B(-2,2),∴B′(-2,-2),∴B″(-1,-2),设直线AB″的表达式为:y=kx+b,则632k bk b=+⎧⎨-=-+⎩,解得:2kb=⎧⎨=⎩,∴直线AB″的表达式为:y=2x,令y=0,解得:x=0,即点D坐标为(0,0),∴点C坐标为(-1,0),故答案为:(-1,0).【点睛】本题考查了轴对称的性质,最短路径问题,一次函数表达式,解题的关键是找到AD+BC最小时的情形20.(2020•连云港)如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y=34x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为.【分析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.首先证明点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.求出MN,当点C与C′重合时,△C′DE的面积最小.【解析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x﹣3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,﹣3),∴OD =4,OE =3,∴DE =32+42=5,∵∠MDN =∠ODE ,∠MND =∠DOE ,∴△DNM ∽△DOE ,∴MN OE=DM DE,∴MN 3=35,∴MN =95,当点C 与C′重合时,△C′DE 的面积最小,最小值=12×5×(95−1)=2,故答案为2.21.(2020·江苏连云港?中考真题)如图,在平面直角坐标系xOy 中,半径为2的O 与x 轴的正半轴交于点A ,点B 是O 上一动点,点C 为弦AB 的中点,直线334y x =-与x 轴、y 轴分别交于点D 、E ,则CDE △面积的最小值为________.【答案】2【解析】【分析】如图,连接OB ,取OA 的中点M ,连接CM ,过点M 作MN ⊥DE 于N .首先证明点C 的运动轨迹是以M 为圆心,1为半径的⊙M ,设⊙M 交MN 于C′.求出MN ,当点C 与C′重合时,△C′DE的面积最小.【详解】解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x-3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,-3),∴OD=4,OE=3,∴5 DE===,∵∠MDN=∠ODE,∠MND=∠DOE,∴△DNM∽△DOE,∴MN DM OE DE=,∴3 35 MN=,∴95 MN=,当点C 与C′重合时,△C′DE 的面积最小,△C′DE 的面积最小值1951225⎛⎫=⨯⨯-= ⎪⎝⎭,故答案为2.【点睛】本题考查三角形的中位线定理,三角形的面积,一次函数的性质等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题,属于中考常考题型.22.(2020·北京中考真题)在平面直角坐标系xOy 中,⊙O 的半径为1,A ,B 为⊙O 外两点,AB=1.给出如下定义:平移线段AB ,得到⊙O 的弦A B ''(,A B ''分别为点A ,B 的对应点),线段AA '长度的最小值称为线段AB 到⊙O 的“平移距离”.(1)如图,平移线段AB 到⊙O 的长度为1的弦12PP 和34P P ,则这两条弦的位置关系是;在点1234,,,P P P P 中,连接点A 与点的线段的长度等于线段AB 到⊙O 的“平移距离”;(2)若点A ,B 都在直线y =+上,记线段AB 到⊙O 的“平移距离”为1d ,求1d 的最小值;(3)若点A 的坐标为32,2⎛⎫ ⎪⎝⎭,记线段AB 到⊙O 的“平移距离”为2d ,直接写出2d 的取值范围.【答案】(1)平行,P 3;(2)32;(3)233922d ≤≤。
一次函数与几何综合

一次函数与几何综合例1:如图,在平面直角坐标系xOy 中,已知矩形纸片ABCO 的顶点AC 分别在x 轴、y 轴的正半轴上,且BC =15.将纸片沿过点C 的直线折叠后,点B 恰好落在x 轴上的点B ′处,折痕交AB 于点D .若34OC OB'=则直线CD 的表达式为____________. 【思路分析】1. 由折叠性质得,△BCD ≌△B′CD ,则B′C =BC =OA =15,=2. 设AD =t ,则B′D =BD =9-t ,在Rt △B′AD 中利用勾股定理可求出t =4,故D (15,4);3. 由C (0,9),D (15,4),可通过k ,b 的几何意义得到直线CD 的表达式:193y x =-+.例2:如图,点A 的坐标为(-2,0),点B 在直线122y x =-+上运动,则当线段AB 最短时,点B 的坐标为_____________.【思路分析】1. 如图,当AB ⊥l 时,线段AB 最短;2. 因为AB ⊥l ,所以1()12AB k ⋅-=-,故k AB =2,设l AB :y =2x +b ,把A (-2,0)代入,得b =4; 3. 联立可求得点B 的坐标为(-一、知识点睛1. 一次函数表达式:y =kx +b (k ,b 为常数,k ≠0)①k 是斜率,表示倾斜程度,可以用几何中的坡度(或坡比)来解释.坡面的竖直高度与水平宽度的比叫坡度或坡比,如图所示,AM即为____________,BM 即为____________,则=AM k BM.②b 是截距,表示直线与y 轴交点的纵坐标.MAB2. 设直线l 1:y 1=k 1x +b 1,直线l 2:y 2=k 2x +b 2,其中k 1,k 2≠0.①若k 1=k 2,且b 1≠b 2,则直线l 1_____l 2; ②若k 1·k 2=_________,则直线l 1_____l 2.3. 一次函数与几何综合解题思路①要求坐标,______________________________________; ②要求函数表达式,________________________________; ③要研究几何图形,________________________________.二、精讲精练1. 如图,点B ,C 分别在直线y =2x 和y =kx 上,A ,D 是x轴上的两点,若四边形ABCD 是正方形,则k 的值为________.第1题图 第2题图 第3题图2. 如图,已知直线l:y x =x 轴交于点A ,与y 轴交于点B ,将△AOB 沿直线l 折叠,点O 落在点C 处,则直线AC 的表达式为__________________.3. 如图,在平面直角坐标系xOy 中放入一张长方形纸片ABCO ,点D 在AB 边上,将纸片沿CD4. 如图,直线l 1交x 轴、y 轴于A ,B 两点,OA =m ,OB =n ,将△AOB 绕点O 逆时针旋转90°得到△COD .CD 所在直线l 2与直线l 1交于点E ,则l 1____l 2;若直线l 1,l 2的斜率分别为k 1,k 2,则k 1·k 2=_______.5. 如图,直线483y x =-+分别交x 轴、y 轴于A ,B 两点,线段AB的垂直平分线交x 轴于点C ,交AB 于点D ,则点C 的坐标为____________.坐标几何图形一次函数6. 如图,在平面直角坐标系中,函数y =x 的图象l 是第一、三象限的角平分线.探索:若点A 的坐标为(3,1),则它关于直线l 的对称点A'的坐标为____________;猜想:若坐标平面内任一点P 的坐标为(m ,n ),则它关于直线l 的对称点P ′的坐标为____________;应用:若已知两点B (-2,-5),C (-1,-3),试在直线l 上确定一点Q ,使点Q 到B ,C 两点的距离之和最小,则此时点Q 的坐标为____________.7. 如图,已知直线l 1:2833y x =+与直线l 2:y =-2x +16相交于点C ,直线l 1,l 2分别交x 轴于A ,B 两点,矩形DEFG 的顶点DE 分别在l 1,l 2上,顶点F ,G 都在x 轴上,且点G 与点B 重合,那么S 矩形DEFG :S △ABC =_________.8. 如图,已知点A 的坐标为(2,0),点B 在直线y =-x 上运动,当线段AB 最短时,点B 的坐标为( ) A .(-1,1)B . ,C .(1,-1)D .( 9. 如图,在平面直角坐标系中,点A ,B 的坐标分别为A (4,0)B (0,-4),P 为y 轴上B 点下方的一点,且PB =m (m >0),以点P 为直角顶点,AP 为腰在第四象限内作等腰Rt △APM . (1)求直线AB 的解析式;(2)用含m 的代数式表示点M 的坐标;(3)若直线MB 与x 轴交于点Q ,求点Q 的坐标.1. 点B ,C 分别在直线y =2x 和直线y =kx 上,A ,D 是x 轴上的两点.若四边形ABCD 是长方形,且AB :AD =1:2,则k 的值为____________.2. 如图,一次函数y =-2x +4的图象与坐标轴分别交于A ,B 两点,把线段AB绕着点A 沿逆时针方向旋转90°,点B 落在点B ′处,则直线AB ′的表达式为______________________.3. 如图,在平面直角坐标系xOy 中,四边形OABC 是正方形,点A 的坐标是(4,0),P 为AB 边上一点,沿CP 折叠正方形,折叠后的点B 落在平面_____________,直线CP 的表达式为___________________.第3题图 第4题图4. 如图,点A 的坐标是(-2,0),点B 的坐标是(6,0),点C 在第一象限内,且△OBC 为等边三角形,直线BC 交y 轴于点D ,过点A 作直线AE ⊥BD ,垂足为点E ,交OC 于点F ,则点C 的坐标为_______,直线AE 的表达式为______________.5. 如图,在平面直角坐标系中,函数y =-x 的图象l 是第二、四象限的角平分线.实验与探究:由图观察易知A (0,2)关于直线l 的对称点A ′的坐标为(-2,0),请在图中分别标出B (-5,-3),C (-2,5)关于直线l 的对称点B ′,C ′的位置,并写出它们的坐标:B ′_________,C ′_________. 归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P (m ,n )关于第二、四象限的角平分线l 的对称点P ′的坐标为______________. 运用与拓广:已知两点D (0,-3),E (1,-4),试在直线l 上确定一点Q ,使点Q 到D ,E 两点的距离之和最小,并求出点Q 的坐标.。
一次函数与几何图形综合题(含答案)

一次函数与几何图形综合题(含答案)近日,举行了一次关于一次函数与几何图形综合的专题讲座。
在思想方法方面,介绍了函数方法和数形结合法。
函数方法是通过观察运动和变化来分析数量关系,并将其抽象升华为函数模型,从而解决问题的方法。
数形结合法则是将数与形结合起来,分析研究并解决问题的一种思想方法,对于与函数有关的问题,使用数形结合法能够事半功倍。
在知识规律方面,讲座介绍了常数k和b对直线y=kx+b(k≠0)位置的影响。
当b大于0时,直线与y轴的正半轴相交;当b等于0时,直线经过原点;当b小于0时,直线与y轴的负半轴相交。
当k和b异号时,即b大于0时,直线与x轴正半轴相交;当k和b同号时,即k和b的乘积小于0时,直线与x轴负半轴相交。
当k大于0且b大于0时,图象经过第一、二、三象限;当k大于0且b等于0时,图象经过第一、三象限;当b大于0且b小于0时,图象经过第一、三、四象限;当k小于0且b大于0时,图象经过第一、二、四象限;当k小于0且b等于0时,图象经过第二、四象限;当b小于0且b小于0时,图象经过第二、三、四象限。
讲座还介绍了直线y=kx+b(k≠0)与直线y=kx(k≠0)的位置关系。
当b大于0时,将直线y=kx向上平移b个单位,即可得到直线y=kx+b;当b小于0时,将直线y=kx向下平移|b|个单位,即可得到直线y=kx+b。
另外,当k1不等于k2时,y1与y2相交;当k1等于k2且b1不等于b2时,y1与y2平行但不重合;当k1等于k2且b1等于b2时,y1与y2重合。
最后,讲座还通过一个例题对知识规律进行了精讲。
题目是直线y=-2x+2与x轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB。
要求求出AC的解析式。
的性质,需要灵活运用几何知识和代数知识。
在解答过程中,要注意清晰的逻辑思路和准确的计算,避免出现错误。
2) 在OA的延长线上任取一点P,作PQ⊥BP,交直线AC于Q。
我们来探究一下BP与PQ的数量关系,并证明结论。
一次函数与几何综合(一)(K,b的几何意义)(北师版)(含答案)

学生做题前请先回答以下问题问题1:若一次函数表达式为y=kx+b(k,b为常数,k≠0),k是______,表示___________,可以用几何中的坡度来解释.坡面的____________与____________的比叫坡度或坡比.问题2:b表示____________________________.问题3:一次函数与几何综合解题思路中,求直线表达式的思路有哪些?一次函数与几何综合(一)(K,b的几何意义)(北师版)一、单选题(共8道,每道12分)1.如图,点B,C分别在直线y=3x和直线y=kx上,A,D是x轴上两点,若四边形ABCD是长方形,且,则k的值是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:k的几何意义2.如图,已知点A的坐标为(5,0),直线y=x+b(b>0)与x轴、y轴分别交于点B,C,连接AC,,则点B的坐标为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:k的几何意义3.如图,直线AP的解析式为,且点P的坐标为(4,2),PA=PB,则点B的坐标是( )A.(5,0)B.(6,0)C.(7,0)D.(8,0)答案:C解题思路:试题难度:三颗星知识点:k的几何意义4.如图,已知一条直线经过A(0,2),B(1,0)两点,将这条直线向左平移,与x轴、y 轴分别交于点C,点D.若DB=DC,则直线CD的函数解析式为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转5.已知点,B(0,0),,AE平分∠BAC,交BC于点E,则直线AE的函数表达式是( )A. B.y=x-2C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转6.如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,点C 是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,则直线CD的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转7.如图,已知长方形纸片OABC,D是OA上的一点,且OD:AD=5:3,CD=,把△OCD 沿折痕CD向上翻折,若点O恰好与AB边上的点E重合,则CD所在直线的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转8.如图,在平面直角坐标系中放入一张长方形纸片ABCO,OC=9,将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知,则折痕B′E所在直线的解析式为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:一次函数与几何综合学生做题后建议通过以下问题总结反思问题1:做完本套试题,在求解一次函数表达式的时候你有什么感触?简单列举一下!。
中考数学重难点专题12 一次函数与几何综合问题(学生版)

中考数学复习重难点与压轴题型专项突围训练(全国通用版)专题12一次函数与几何综合问题【典型例题】1.(2022·四川成都·九年级期末)如图,在平面直角坐标系中,点A,B分别在x轴,y轴正半轴上,AO=2BO,点C(3,0)(A点在C点的左侧),连接AB,过点A作AB的垂线,过点C作x轴的垂线,两条垂线交于点D,已知△ABO△△DAC,直线BD交x轴于点E.(1)求直线AD的解析式;(2)直线AD有一点F,设点F的横坐标为t,若△ACF与△ADE相似,求t的值;(3)如图2,在直线AD上找一点G,直线BD上找一点P,直线CD上找一点Q,使得四边形AQPG是菱形,求出G点的坐标.【专题训练】一、选择题1.(2022·山东龙口·七年级期末)对于函数y=-3x+1,下列结论正确的是()A.它的图象必经过点(1,3)B.y的值随x值的增大而增大C.当x>0时,y<0D.它的图象与x轴的交点坐标为(13,0)2.(2022·江苏溧阳·八年级期末)如图,直线122y x=-+与x轴、y轴交于A、B两点,在y轴上有一点C(0,4),动点M从A点发以每秒1个单位的速度沿x轴向左移动.当动到△COM与△AOB全等时,移的时间t是()A.2B.4C.2或4D.2或63.(2022·陕西·辋川乡初级中学八年级期末)数学课上,老师提出问题:“一次函数的图象经过点A(3,2),B(-1,-6),由此可求得哪些结论?”小明思考后求得下列4个结论:①该函数表达式为y=2x-4;②该一次函数的函数值随自变量的增大而增大:③点P(2a,4a-4)在该函数图象上;④直线AB与坐标轴围成的三角形的面积为8.其中错误的结论是()A.1个B.2个C.3个D.4个4.(2022·江苏启东·八年级期末)如图,在平面直角坐标系中,O为原点,点A,C,E的坐标分别为(0,4),(8,0),(8,2),点P,Q是OC边上的两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐标为()A.(2,0)B.(3,0)C.(4,0)D.(5,0)二、填空题5.(2022·江苏滨湖·八年级期末)如图,直线y=﹣43x+8与坐标轴分别交于A、B两点,P是AB的中点,则OP的长为_____.6.(2021·山东济阳·八年级期中)如图,一次函数y =x +2的图像与坐标轴分别交于A ,B 两点,点P ,C 分别是线段AB ,OB 上的点,且△OPC =45°,PC =PO ,则点P 的坐标为______.7.(2021·湖北阳新·模拟预测)如图,直线AB 的解析式为y =﹣x +b 分别与x ,y 轴交于A ,B 两点,点A的坐标为(3,0),过点B 的直线交x 轴负半轴于点C ,且31OB OC ::,在x 轴上方存在点D ,使以点A ,B ,D 为顶点的三角形与△ABC 全等,则点D 的坐标为_____.8.(2022·山东龙口·七年级期末)正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示放置,点A 1,A 2,A 3,和点C 1,C 2,C 3,…,分别在直线y =kx +b (k >0)和x 轴上,已知点B 1,B 2,B 3,B 4的坐标分别为(1,1),(3,2),(7,4),(15,8),则Bn 的坐标为_____三、解答题9.(2022·江苏海州·八年级期末)已知直线l 1经过点A (3,2)和点B (0,5),直线l 2:y =2x ﹣4经过点A 且与y 轴相交于点C .(1)求直线l 1的函数表达式;(2)已知点M 在直线l 1上,过点M 作MN //y 轴,交直线l 2于点N .若MN =6,请求出点M 的横坐标.10.(2022·广西·桂林市雁山中学九年级期末)如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=mx在第一象限的图象交于点C,CD垂直于x轴,垂足为D.如果OA=OB=OD=1,求:(1)点A、B、C的坐标;(2)这个反比例函数的表达式;(3)这个一次函数的表达式.11.(2022·江苏溧阳·八年级期末)如图,在平面直角坐标系中长方形AOBC的顶点A、B坐标分别为(0,8)、(10,0),点D是BC上一点,将△ACD沿直线AD翻折,使得点C落在OB上的点E处,点F是直线AD 与x轴的交点,连接CF.(1)点C坐标为____________;(2)求直线AD的函数表达式_______________________;(3)点P是直线AD上的一点,当△CFP是直角三角形时,请你直接写出点P的坐标.。
一次函数与几何综合一

一次函数与几何综合(一)标模块一一次函数与线段长例1(2017江岸区八下期末)如图,直线l: y=2x+4.(1)①直接写出直线l关于y轴对称的直线l i的解析式:;②直接写出直线l向右平移2个单位得到的直线12的解析式: ;(2)在(1)的基础上,点M是x轴上一点,过点M作x轴的垂线交直线l i于点Q、交直线l2于点P,若PM = 2PQ,求M 点的坐标.例2(2017斫口区八下期末)图1中两条经过原点O的射线组成的图形E表示y关于x的函数关系式.(1)直接写出图形E表示的函数解析式;(2)如图2,过直线y=3上一点P(m, 3)作x轴的垂线交图形E于点C,交直线y=- x- 1于点D.①若m>0,试比较PC与PD的大小,并证明你的结论;②若CD <3,求m的取值范围.图图2挑战压轴题(2017黄陂区八下期末第24题)如图,直线l i经过点P(2, 2),分别交x轴、y轴于点A(4, 0)、B.(1)求直线l i的解析式;(2)点C为x轴负半轴上一点,过点C的直线l2:y=mx+ n交线段AB于点D.①如图1,当点D恰与点P重合时,点Q(t, 0)为x轴上一动点,过点Q作QM,x轴,分别交直线11、12于点M、N,若m= - , MN = 2MQ,求t 的值;2②如图2,若BC=CD,试判断m、n之间的数量关系并说明理由.模块二一次函数与特殊三角形知识导航1.等腰直角三角形一三垂直全等如图,△ ABC中,AB = AC, / BAC=90°,可构造如图所示的三垂直全等模型,“△ ACD^A BAE",从而可以转化为水平线段长度与点坐标的基本计算.若已知等腰直角三角形三个顶点坐标中的两个便可通过此方法求第三顶点坐标.2.等腰三角形的存在性一两圆一中垂已知A、B为定点,C为动点,△ ABC为等腰三角形,则分下列情况:(1)若CA = CB,则点C在AB中垂线上(不与AB共线).(2)若AC = AB,则点C在以A为圆心,AB为半径的圆上(不与点B重合).(3)若BA=BC,则点C在以B为圆心,AB为半径的圆上(不与点A重合).3.直角三角形的存在性一两垂一圆已知A、B为定点,C为动点,△ ABC为直角三角形,则分下列情况:(1)若/ CAB = 90°,则点C在过点A且垂直AB的直线上(不与点A重合).(2)若/ CBA = 90°,则点C在过点B且垂直AB的直线上(不与点B重合).(3)若/ ACB = 90°,则点C在以AB为直径的圆上(不与点A、B重合).八下会把特殊三角形的顶点放在一次函数背景下讨论、计算.例3如图,在直角坐标系中,矩形OABC的两边在坐标轴上,其中点B的坐标为(4, 3),过点A的直线AD 的解析式为y=2x+3,点P是直线AD上一动点,点Q是线段BC(包才B, C两点)上一动点.若AP = AQ 且AP^AQ,求点P的坐标及直线AQ的解析式;练习如图1,在平面直角坐标系中,A(a, 0), B(0, b),且b= "a -4+”5 +16a 2(1)求直线AB的解析式;(2)如图2,若点M为直线y=mx在第一象限上一点,且^ ABM是等腰直角三角形,求m.图1 图2例4在平面直角坐标系中,直线y=kx— k经过一定点P.(1)直接写出P点坐标;(2)在y轴上有一点A(0, 2),当k = 2时,将直线y=kx—k向上平移2个单位得到直线1,在直线l上找点C,使得△ ACO为等腰三角形,求点C的坐标.练习3 ........................................... 如图,在平面直角坐标中,一次函数y= — x+ 2的图象与x轴交于A点,与y轴交于B点,在x轴上是3否存在点P,使^ PAB为等腰三角形?若存在,求出符合条件的P点的坐标;若不存在,请说明理由.3 ............... ............................ 例5如图,在平面直角坐标系中,直线y=- ^r-x+ 6与x轴、y轴分别交于B、A点,已知点C从点A出3发沿AO以每秒1cm的速度向点O运动,同时点D从点B出发沿BA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DELOB于点E.连接DC,当t为何值时,△ DEC为直角三角形?模块三一次函数与特殊四边形例61如图,已知函数y=- -x+ b的图象与x轴、y轴分别交于点A, B,与函数y=x的图象交于点E,点E的3横坐标为3.⑴求点A的坐标.1(2)在x轴上有一点F(a, 0),过点F作x轴的垂线,分别交函数y=—-x+b和y=x的图象于点C、D.若3以点B, O, C, D为顶点的四边形为平行四边形,求a的值.练习如图,在平面直角坐标系xOy中,直线y=kx+b交x轴于点A,交y轴于点B,线段AB的中点E的坐标为(2, 1).⑴求k、b的值;(2)P为直线AB上一点,PC^x轴于点C, PD^y轴于点D,若四边形PCOD为正方形,求点P的坐标.例7(2017东湖高新区八下期末)平面直角坐标系中,直线y=ax+b与x轴分别交于点B、C,且a、b满足a= *6-b + J b — 6 +3,不论k为何值,直线l: y=kx—2k都经过x轴上一定点A.(1)a =, b =, 点A 的坐标为;(2)如图1,当k= 1时,将线段BC沿某个方向平移,使点B、C对应的点M、N恰好在直线l和直线y= 2x—4上.请你判断四边形BMNC的形状,并说明理由;(3)如图2,当k的取值发生变化时,直线l: y=kx—2k绕着点A旋转,当它与直线y=ax+b相交的夹角为450时,求出相应的k的值.图1 图2拓展1平面直角坐标系中,直线li: y= —/x+3与x轴交于点A,与y轴交于点B,直线12:y=kx+2k与x轴父于点C,与直线l i交于点P.(1)当k=1时,求点P的坐标;(2)如图1,点D为PA的中点,过点D作DE^x轴于点巳交直线12于点F,若DF=2DE,求k的值.(3)如图2,点P在第二象限内,PM^x轴于M,以PM为边向左作正方形PMNQ, NQ的延长线交直线11 于点R,若PR= PC,求点P的坐标.课后作业A基础巩固1.已知点A的坐标是(2, 2),若点P在x轴上,且^ APO是等腰三角形,则点P的坐标为 .1 2.如图,P是y轴上一动点,是否存在平行于y轴的直线x=t(t>0),使它与直线y=x和直线y=-2x+2分别交于点D、E(E在D的上方),且4 PDE为等腰直角三角形.若存在,求t的值及点P的坐标;若不存在,请说明理由.3.如图,直线y=kx+b与坐标轴分别交于点A, B,且A(—4, 0), &AOB =4.(1)求直线y= kx+ b的解析式;(2)若点P为直线y=kx+b上一点,PC^x轴于C, PD^y轴于D,若四边形PCOD为正方形,求点P坐标.4 .如图,在平面直角坐标系中,直线 y=- — x+ 6与x 轴、y 轴分别交于A 、B 点,已知点C 从点A 出 3发沿AO 以每秒1cm 的速度向点O 运动,同时点D 从点B 出发沿BA 以每秒2cm 的速度向点A 运动,运 动时间为t 秒(0<t<6),过点D 作DELOB 于点E.(1)①直接写出/ ABO 的度数为②证明在C 、D 运动过程中,四边形 ACED 是平行四边形; 5 . (2017洪山区八下期末)3y=— —x+b 分别与x 轴、y 轴父于点 A 、B,且点A 坐标为(8, 0),点 4C 为AB 的中点.⑴写出点B 的坐标(2)如图1,点P 为直线AB 上的一个动点,过点 P 作x 轴的垂线,与直线 OC 交于点Q,设点P 的横坐标 为m,线段PQ 的长度为d,求d 与m 的函数解析式(请直接写出自变量 m 的取值范围);数学故事为什么2187是个幸运的数字尽管不符合常规理解的“幸运”含义,2187这个数字仍有一系列让人吃惊的特征.在纪念马丁 加德纳 100周年诞辰之际,我们来回顾他在 1997年为《数学信使》(MathematicalIntelligencer)写的一篇文章.在这篇文章中,他问他想象中的好友欧文约书亚矩阵博士(Dr. Irving JoshuaMatrix)关于数字2187的问题.欧文 约书亚 矩阵博士是“世界最著名的数字命理学家”,也是在《科学美国人》(Scientific American )"数学游戏”(Mathematical Games)专栏中经常出现的角色;而 2187,则是加德 纳儿时在美国俄克拉荷马州(Okla)塔尔萨(Tulsa)老家的门牌号码.矩阵博士立刻列举了一系列关于 2187的事实,这让加德纳感到非常兴奋: 2187,是3的7次方,它的.三进制写法是 10000000; 9999减去2187等于7812,恰好与其顺序相反;21乘以87等于1827, 27乘以81又刚好等于2187.“每个数字都有数不 尽的独特的特征,”矩阵博士点评说,同时补充道, 2187也是一个幸运数.幸运数是素数的远亲,素数是只能被1和它本身整除的正整数.尽管这两者在很多方面都不同,但它们都可以利用被称为“筛法”的方法得到.希腊数学家埃拉托斯特尼 (Eratosthenes)设计了一种在正整数序列中寻找素数的方法一一著名的埃拉托斯特尼筛法:首先删除所有除2以外2的倍数,然后删除3的倍数,然后是5, 7, 11等等.这样不断删除到无穷大,就可以得到所有素数.波兰裔美国数学家斯塔尼斯拉夫 乌拉姆(Stanislaw Ulam)在20世纪50年代中期开发出了另一种筛法:同样是从正整数序列开始,先将数列 中的第 2n 个数 (偶数 )删除,只留下奇数;这样剩下的数列中第二项是 3,因此将新数列的第 3n 个数删除;(2)当 t = 时,四边形ACED 是菱形.如图,在平面直角坐标系中,直线(3)如图2,当点P 在线段 AB 上,在第一象限内有一点 N,使得四边形 OBNP 为菱形,求出N 点坐标.B 综合训练再剩下的新数列中的第三项为7,因此将新数列的第7n 个数删除;再剩下的新数列中的第四项为9,因此将新数列的第9n 个数删除;这样继续下去,最终有一些数永远地逃离了被删除的命运而留下来,这就是为什么乌拉姆把它们称作“幸运数”.幸运数和素数有一些由奇妙的筛法得到的数字的共同特征.比如说,在小于100 的数中,有25 个素数和23 个幸运数,其中有八对孪生素数(之差为 2 的两个素数)以及七对孪生幸运数.关于素数,尚未解决的最有名的问题之一就是哥德巴赫猜想——任一大于2 的偶数,都可表示成两个素数之和.同样另一个未解决的问题是一个相似的命题——任一大于2 的偶数,都可表示成两个幸运数之和.关于2187,还有另一个有趣的事实——如下所示,等号右边的数字之和等于左边与2187 相加的排列不同的数字之和.2187 + 1234=34212187+12345= 145322187 + 123456= 1256432187 + 1234567= 12367542187+ 12345678=123478652187+ 123456789= 123458976。
一次函数与几何图形结合的问题习题

一次函数与几何图形的综合问题类型一 一次函数与面积问题1.如图,一次函数y =- x +m 的图象和y 轴交于点B ,与正比例函数y =12x 的图象交于点P (2,n ).(1)求m 和n 的值;(2)求APOB 的面积.2.如图,把Rt △ABC 放在平面直角坐标系内,其中∠CAB =90°,BC =5,点A ,B 的坐标分别为(1,0),(4,0),将△ABC 沿x 轴向右平移,当点C 落在直线y =2x -6上时,线段BC 扫过的面积为 .3.如图,直线y =-2x +3与x 轴相交于点A ,与y 轴相交于点B .[易错7](1)求A ,B 两点的坐标;(2)过B 点作直线BP 与x 轴相交于点P ,且使OP =2OA ,求△ABP 的面积.4.如图,直线y =-x +10与x 轴、y 轴分别交于点B ,C ,点A 的坐标为(8,0),点P (x ,y )是在第一象限内直线y =-x +10上的一个动点.(1)求△OPA 的面积S 与x 的函数解析式,并写出自变量x 的取值范围;(2)当△OPA 的面积为10时,求点P 的坐标.图类型二一次函数与几何图形的规律探究问题1. (2017●安顺中考)如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,..在直线l上,点B1,B2,B3,...在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,...依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn-1Bn,顶点Bn的横坐为.2.(2016●潍坊中考)在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1,.. ,正方形AnBnCnC n-1,使得点A1,A2,A3…在直线l上,点C1 ,C2,C3,...在y轴正半轴上,则点Bn的坐标是.类型三一次函数与新定义几何图形的探究1.在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2, y1≠y2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q 的“相关矩形”.下图①为点P,Q的“相关矩形”的示意图.(1)已知点A的坐标为(1,0),①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;②点B在直线x=3上.若点A,B的“相关矩形”面积是4,求点B的坐标;(2)一次函数y=-2x+b的图象经过点A,交y轴于点C,若在线段AC上存在一点D,使得点D、B的对角矩形是正方形,求m的取值范围;(3)一次函数y=k x+4的图象交y轴于点C,点A、B的对角矩形且面积是12,且m>0,要使得一次函数y=k x+4的图象与该对角矩形有交点,求k的取值范围.图①。
一次函数与几何及动点综合题(含解析)
一、选择题(题型注释)1.如图反映的过程是:矩形ABCD 中,动点P 从点A 出发,依次沿对角线AC 、边CD 、边DA 运动至点A 停止,设点P 的运动路程为x , ABP S y △.则矩形ABCD 的周长是(P )D A BC61295Oy xA .6B .12C .14D .15 【答案】C 【解析】试题分析:结合图象可知,当P 点在AC 上,△ABP 的面积y 逐渐增大,当点P 在CD 上,△ABP 的面积不变,由此可得AC=5,CD=4,则由勾股定理可知AD=3,所以矩形ABCD 的周长为:2×(3+4)=14.考点:动点问题的函数图象;矩形的性质.点评:本题考查的是动点问题的函数图象,解答本题的关键是根据矩形中三角形ABP 的面积和函数图象,求出AC 和CD 的长.2.小芳步行上学,最初以某一速度匀速前进,中途遇红灯,稍作停留后加快速度跑步去上学,到校后,她请同学们画出她行进路程s (米)与行进时间t (分钟)的函数图象的示意图.你认为正确的是( )【答案】C 【解析】试题分析:运用排除法解答本题,中间的停留路程不变,可排除BD 两项,最后的加速图象应为比最初的路程增加直线增速更快的图象,C 对3.如图,已知A 1、A 2、A 3、…、A n 、A n+1是x 轴上的点,且OA 1=A 1A 2=A 2A 3=…=A n A n+1=1,分别过点A 1、A 2、A 3、…、A n 、A n+1作x 轴的垂线交直线y=2x 于点B 1、B 2、B 3、…、B n 、B n+1,连接A 1B 2、B 1A 2、B 2A 3、…、A n B n+1、B n A n+1,依次相交于点P 1、P 2、P 3、…、P n .△A 1B 1P 1、△A 2B 2P 2、△A n B n P n 的面积依次记为S 1、S 2、S 3、…、S n ,则S n 为( )A.121nn++B.31nn-C.221nn-D.221nn+【答案】D.【解析】试题分析:∵A1、A2、A3、…、A n、A n+1是x轴上的点,且OA1=A1A2=A2A3=…=A n A n+1=1,∴A1(1,0),A2(2,0),A3(3,0),…A n(n,0),A n+1(n+1,0),∵分别过点A1、A2、A3、…、A n、A n+1,作x轴的垂线交直线y=2x于点B1、B2、B3、…、B n、B n+1,∴B1的横坐标为:1,纵坐标为:2,则B1(1,2),同理可得:B2的横坐标为:2,纵坐标为:4,则B2(2,4),B3(2,6),…B n(n,2n),B n+1(n+1,2n+2),根据题意知:P n是A n B n+1与 B n A n+1的交点,设:直线A n B n+1的解析式为:y=k1x+b1,直线B n A n+1的解析式为:y=k2x+b2,∵A n(n,0),A n+1(n+1,0),B n(n,2n),B n+1(n+1,2n+2),∴直线A n B n+1的解析式为:y=(2n+2)x﹣2n2﹣2n,直线B n A n+1的解析式为:y=﹣2n x+2n2+2n,∴P n(22221n nn++,24421n nn++)∴△A n B n P n的A n B n边上的高为:22221n nnn+-+=21nn+,△A n B n P n的面积S n为:21222121n nnn n⨯⋅=++.故选D .考点:一次函数图象上点的坐标特征. 4.如图,已知直线l :x y 33,过点A (0,1)作y 轴的垂线 交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过 点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;…;按此作法继续下去,则点A 4的坐标为 A.(0,64) B.(0,128) C.(0,256) D.(0,512)【答案】C. 【解析】试题分析:∵直线l 的解析式为;3, ∴l 与x 轴的夹角为30°, ∵AB ∥x 轴, ∴∠ABO=30°, ∵OA=1, ∴OB=2, ∴3,∵A 1B ⊥l ,∴∠ABA 1=60°, ∴A 1O=4, ∴A 1(0,4),同理可得A 2(0,16), …∴A 4纵坐标为44=256, ∴A 4(0,256). 故选C .考点:一次函数综合题.5.如图,在矩形ABCD 中,O 是对角线AC 的中点,动点P ,Q 分别从点C ,D 出发,沿线段CB ,DC 方向匀速运动,已知P ,Q 两点同时出发,并同时到达终点B ,C .连接OP ,OQ .设运动时间为t ,四边形OPCQ 的面积为S ,那么下列图象能大致刻画S 与t 之间的关系的是【答案】A . 【解析】试题分析:作OE ⊥BC 于E 点,OF ⊥CD 于F 点,如图,设BC=a ,AB=b ,点P 的速度为x ,点F 的速度为y , 则CP=xt ,DQ=yt ,所以CQ=b-yt , ∵O 是对角线AC 的中点,∴OE 、OF 分别是△ACB 、△ACD 的中位线, ∴OE=12b ,OF=12a , ∵P ,Q 两点同时出发,并同时到达终点, ∴a bx y=,即ay=bx , ∴S=S △OCQ +S △OCP =12•12a•(b-yt )+12•12b•xt=14ab-14ayt+14bxt=14ab (0<t <a x), ∴S 与t 的函数图象为常函数,且自变量的范围为0<t <ax).故选A .考点:动点问题的函数图象.6.函数321+=x y 的图象与x 、y 轴分别交于点A 、B ,点P )(y x ,为直线AB 上的一动点(0>x )过P 作PC ⊥y 轴于点C ,若使PBC ∆的面积大于AOB ∆的面积,则P的横坐标x 的取值范围是( )A 、30<<xB 、3>xC 、63<<xD 、6>x【解析】试题分析:由题意知:PC=x ,OC=132x + ∴BC=12x ∵PBC ∆的面积大于AOB ∆的面积∴x >6. 故选D.考点: 一次函数综合题.7.如图1,在直角梯形ABCD 中,动点P 从点B 出发,沿BC ,CD 运动至点D 停止.设点P 运动的路程为 ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则△BCD 的面积是( )A .3B .4C .5D .6 【答案】A 【解析】 试题分析:动点P 从直角梯形ABCD 的直角顶点B 出发,沿BC ,CD 的顺序运动,则△ABP 面积y 在BC 段随x 的增大而增大;在CD 段,△ABP 的底边不变,高不变,因而面积y 不变化.由图2可以得到:BC=2,CD=3,△BCD 的面积是12×2×3=3. 故选A .考点:动点问题的函数图象.8.如图,正方形ABCD 的边长为4,P 为正方形边上一动点,沿A →D →C →B →A 的路径匀速移动,设P 点经过的路径长为x ,△APD 的面积是y ,则下列图象能大致反映y 与x 的函数关系的是A .B .C .D .【解析】当点P 由点A 向点D 运动时,y 的值为0; 当点p 在DC 上运动时,y 随着x 的增大而增大; 当点p 在CB 上运动时,y 不变;当点P 在BA 上运动时,y 随x 的增大而减小。
一次函数与几何综合(题型齐全)

一次函数与几何图形综合考点一、面积问题一次函数求面积的常用方法:(1)直接法(公式法)适用于规则图形,三角形中至少有一边与坐标轴重合或平行时,常用直接法求面积;(2)割补法(分割求和、补形作差)适用于不规则四边形,将四边形分割成两个三角形,分别计算两个三角形的面积再求和。
或者将四边形放在一个规则图形中(需要时做辅助线),此时四边形的面积可以看作一个规则图形面积减去补充的规则图形面积;(3)铅锤法(底相同,高运算)适用于三边均不与坐标轴平行的三角形(不规则三角形);(4)平行线面积转化适用于存在平行线的情况下,利用平行线的性质,平行线间的距离处处相等做高;题型一:直接求图形面积1、正比例函数()110y k x k =≠与一次函数()220y k x b k =+≠的图象的交点坐标为()43A ,,一次函数的图象与y 轴的交点坐标为()03B -,.(1)求正比例函数和一次函数的解析式;(2)求AOB 的面积.2、如图,一次函数5y x =-+和1y kx =-的图象与x 轴分别交于A 、C 两点,与y 轴分别交于B 、D 两点,两个函数图象的交点为点E ,且E 点的横坐标为2.(1)求k 的值;(2)不解方程组,请直接写出方程组51x y kx y +=⎧⎨-=⎩的解;(3)求两函数图象与x 轴所围成的ACE △的面积.3、如图,直线443y x =-+与y 轴交于点A ,与直线4455y x =+交于点B ,且直线4455y x =+与x 轴交于点C ,求ABC 的面积.4、如图,在平面直角坐标系中,直线132x m l y =+:与直线2l 交于点()23A -,,直线2l 与x 轴交于点()40C ,,与y 轴交于点B ,将直线l 2向下平移8个单位长度得到直线3l ,3l 与y 轴交于点D ,与1l 交于点E ,连接AD .(1)求直线2l 的解析式;(2)求△ADE V 的面积;5、如图,直线l 1:y =x +m 与y 轴交于点B ,与x 轴相交于点F .直线l 2:y =kx ﹣9与x 轴交于点A ,与y 轴交于点C ,两条直线相交于点D ,连接AB ,且OA :OC :AB =1:3:.(1)求直线l 1、l 2的解析式;(2)过点C 作l 3∥l 1交x 轴于点E ,连接BE 、DE .求△BDE 的面积.5、如图,一次函数()0y kx b k =+≠的图象与正比例函数2y x =-的图象交于点A ,与x 轴交于点C ,与y 轴交于点B ,5OB =,点A 的纵坐标为4.(1)求一次函数的解析式;(2)点D 和点B 关于x 轴对称,将直线2y x =-沿y 轴向上平移8个单位后分别交x 轴,y 轴于点,M N ,与直线()0y kx b k =+≠交于点E ,连接DE ,DC ,求ECD 的面积.题型二:已知面积求点的坐标1、如图,一次函数y kx b =+与反比例函数a y x=的图象在第一象限交于点()4,3A ,与y 轴的负半轴交于点B ,且OA OB =.(1)求一次函数y kx b =+与反比例函数a y x =的表达式;(2)已知点C 在x 轴上,且ABC 的面积是8,求此时点C 的坐标;2、如图,在平面直角坐标系中直线13:2l x m +与直线2l 交于点()2,3A -,直线2l 与x 轴交于点()4,0C ,与y 轴交于点B ,过BD 中点E 作直线3l y ⊥轴.(1)求直线2l 的解析式和m 的值;(2)点P 在直线1l 上,当6PBC S = 时,求点P 坐标;。
八年级下册数学- 一次函数与几何大综合

第23讲一次函数与几何大综合【板块一】探求点的坐标或坐标关系题型一 求点的坐标【例1】已知一次函数y =2kx -3k +12(k ≠0). (1)不论k 为何值,函数图象必过一定点,求定点的坐标;(2)如图1,设(1)中的定点为P ,C 为y 轴正半轴上一点,∠CPO =45°,求S △CPC ; (3)如图2,若k =14-,函数图象与x 轴,y 轴分别交于A ,B 两点,在直线AB 上是否存在点Q ,使25QA QB =?若存在,求点Q 的坐标;若不存在,说明理由.图1针对练习11.如图1,在平面直角坐标系xOy 中,正方形ABCD 的边AB 在x 轴上,点O 是AB 的中点,直线l :y =kx -2k +4过定点C ,交x 轴于点E . (1)求正方形ABCD 的边长;(2)如图2,在直线l 上有一点N ,CN =12AB ,连接AN ,点M 为AN 的中点,连接BM ,求线段BM 的长度的最小值,并求出此时点N 的坐标.图1图22.已知一次函数y =-3x +3的图象与x 轴、y 轴交于点A ,B ,点C (3,0). ⑴求线段AB 的长度;(2)点G 和点B 关于x 轴对称,点P 在直线CG 上,若△ABP 是等腰三角形,求点P 的坐标.图2图1【板块二】 字母系数求解析式或解析式中的的值题型二求解析式或字母系数的值【例2】在平面直角坐标系中,已知点A (a ,0),C (0,b )且a ,b 满足(a +1)2=0.⑴直接写出:a =_______,b =_______;(2)如图1,点B 为x 轴正半轴上的一点:BE ⊥AC 于点E ,交y 轴于点D 连接OE ,若OE 平分∠AEB ,求直线BE 的解析式;(3)如图2,在(2)的条件下,点M 为直线BE 上的一动点:连接OM ,将线段OM 绕点M 逆时针旋转90°,点O 的对应点为N ,当点M 运动时,判断点N 的运动路线是什么图形,并说明理由.图2图1针对练习21.在平直角坐标系中,直线y =ax +b 与x 轴,y 轴分别交于点B ,C ,且a ,b 满足a +3,不论k 为何值,直线l :y =kx -2k 都经过x 轴上一定点A .⑴a =____,b =_____;点A 的坐标为________.(2)如图1,当k =1时,将线段BC 沿某个方向平移,使点B ,C 对应的点M ,N 恰好分别在直线l 和直线y =2x -4上,请你判断四边形BMNC 的形状,并说明理由;⑶图2,当k 的取值发生变化时,直线l :y =kx -2k 绕着点A 旋转,当它与直线y =ax +b 相交的夹角为45°时,求出相应的k 的值.图22.如图,直线l 1:y =2kx +4k +4交x 轴正半轴于点A ,交y 轴正半轴于点B ,经过点B 的直线l 2:y =x +4k +4交x 轴于点C .⑴若A (4,0),求两直线的解析式;⑵直线 y =-2x 交直线l 1于点M ,,交直线l 2于点N ,若S △MNB =S △NCO 求BMAB的值; ⑶直线x =k 交l 1于点D ,交l 2于点E ,若2DE -kAC =5,求k 的值.图2图1针对练习21.在平面直角坐标系中,直线y =ax +b 与x 轴,y 轴分别交于点B ,C ,且a ,b 满足a +3,不论k 为何值,直线l :y =kx 一2k 都经过x 轴上一定点A . (1)a = ,b = ;点A 的坐标为 ;(2)如图1,当k=1时,将线段BC沿某个方向平移,使点B,C对应的点M,N恰好分别在直线l和直线y=2x -4上,请你判断四边形BMNC的形状,并说明理由;(3)如图2,当k的取值发生变化时,直线l:y=kx-2k绕着点A旋转,当它与直线y=ax+b相交的夹角为45°时,求出相应的k的值.图1 图22.如图,直线l1:y=2kx+4k+4交x轴正半轴于点A,交y轴正半轴于点B,经过点B的直线l2:y=x+4k+4交x轴于点C.(1)若A(4,0),求两直线的解析式;(2)直线y=-2x交直线l1于点M,交直线l2于点N,若S△MNB=S△NCO,求BMAB的值;(3)直线x=k交l1于点D,交l2于点E,若2DE一kAC=5,求k的值.【板块三】探求点的轨迹模型三探求点的轨迹【例3】在平面直角坐标系中,点A(0,8)、C(8,0),四边形AOCB是正方形,点D(a,0)是x轴正半轴上的一动点,∠ADE=90°,DE交正方形AOCB的外角的平分线CE于点E.(1)点D(a,0)在x轴正半轴上运动,点P在y轴上,若四边形PDEB为菱形,求直线PB的解析式;(2)连接AE,点F是AE的中点,当点D在x轴正半轴上运动时,点F到CE的距离是否为定值?若为定值,求出这个值;若不是定值,请说明理由.针对练习32.已知直线l 1:y =mx -4m 交x 轴于点A ,交y 轴于点B ,直线l 2:y =nx -12m ,交x 轴于点C ,交y 轴于点D ,交l 1于点E (1)求点A 坐标;(2)如图1,若B 为线段AE 中点,求证:EC =EA ;(3)如图2,P (0,t ),将线段P A 绕点P 逆时针方向旋转90°至PF ,连接AF ,OF ,求OF +AF 的最小值.【板块四】 探求线段关系题型四 探求线段关系【例4】 直线y =kx -2k 交x 轴于点B ,交y 轴于点A(1)当k =-2时,①点P 为直线AB 上的一动点,求OP 的最小值;②若点Q 为x 轴上的一点,∠QAB =45°,求点Q 坐标;(2)若直线CD :Y =22kk x -交AB 于点D ,点C 的横坐标为-1,求AD ACBD-针对练习41.已知点C (0,-2),直线l :y =kx -2k ,无论k 取何值,直线总经过点B . (1)求定点B 的坐标;(2)若直线BC 关于x 轴对称后再向上平移5个单位得到直线B 1C 1,如图,点G (1,a )和H (6,b )是直线B 1C 1上的两点,点P (m ,n )为第一象限内(G ,H 两点除外)的一点,且mn =6,直线PG 和PH 分别交y 轴M ,N 两点,问线段OM ,ON 有什么数量关系?请证明.2.如图1,直线AB 交x 轴正半轴于点A ,交y 轴正半轴于点B ,OA =OB . (1)当AB=AB 的解析式;(2)如图2,直线y =kx 交直线AB 于点C ,点D 是AB 上的一点,过点D 分别作x 轴,y 轴的垂线交直线y =kx 于点E ,F ,若CF =2CE ,求k 的值;图1 图2。
一次函数与几何综合(习题及答案)
一次函数与几何综合(习题)1.如图,点B,C 分别在直线y=2x 和直线y=kx 上,A,D 是x轴上的两点.若四边形ABCD 是长方形,且AB:AD=1:2,则k 的值为.2.如图,一次函数y=-2x+4 的图象与坐标轴分别交于点A,B,把线段AB 绕着点A 沿逆时针方向旋转90°,点B 落在点B′ 处,则直线AB′的表达式为.3.如图,在平面直角坐标系xOy 中,四边形OABC 是正方形,点A 的坐标是(4,0),P 为AB 边上一点,沿CP 折叠正方形,折叠后的点B 落在平面内的点B′处.已知直线CB′的解析式为y =-3x +b ,则点B′的坐标为,直线CP 的表达式为.134.如图,点A 的坐标是( -,0),点B 的坐标是(6,0),点C在第一象限内,且△OBC 为等边三角形,直线BC 交y 轴于点D,过点A 作直线AE⊥BD,垂足为点E,交OC 于点F,则点C 的坐标为,直线AE 的表达式为.第4 题图第5 题图5.如图,一次函数的图象交x 轴于点B(-6,0),交正比例函数的图象于点A,且点A 的横坐标为-4,S△AOB =15,S△BOD=45,则一次函数的表达式为,正比例函数的表达式为.6.如图,在平面直角坐标系中,已知直线y =-3x + 3 与x 轴、y 4轴分别交于A,B 两点,点C(0,n)是y 轴上一点,把坐标平面沿直线AC 折叠,使点B 刚好落在x 轴上,则点C 的坐标是.7.如图,在平面直角坐标系中,函数y=-x 的图象l 是第二、四象限的角平分线.实验与探究:由图观察易知A(0,2)关于直线l 的对称点A′的坐标为(-2,0),请在图中分别标出B(-5,-3),C(-2,5)关于直线l 的对称点B′,C′的位置,并写出它们的坐标:B′,C′.归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第二、四象限的角平分线l 的对称点P′的坐标为.运用与拓广:已知两点D(0,-3),E(1,-4),试在直线l 上确定一点Q,使点Q 到D,E 两点的距离之和最小,并求出点Q 的坐标.8.如图,在平面直角坐标系中,直线y =x - 4 与x 轴、y 轴分别交于点A,B,P 为y 轴上B 点下方的一点,且PB=m(m>0),以点P 为直角顶点,AP 为腰在第四象限内作等腰Rt△APM.(1)用含m 的代数式表示点M 的坐标;(2)若直线MB 与x 轴交于点Q,求点Q 的坐标.5 5 【参考答案】➢ 巩固练习1. 252. y = 1 x + 423. (2, 4 - 2 ), y = -3 x +4 3 4. (3, 3 3 ), y =3 x + 13 5.y = x + 15 , y = - x 2 46. (0, 4 ),(0,-12)37. 实验与探究:(3,5),(-5,2) 归纳与发现:(-n ,-m )运用与拓广:点 Q 的坐标为(2,-2)8. (1)M (4+m ,-8-m )(2)Q (-4,0)3。
初二数学一次函数与综合应用(含答案)

一次函数与综合应用例题精讲一、一次函数的应用【例1】小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是()B.15分钟C.25分钟D.27分钟【答案】B【例2】有一个装有进、出水管的容器,单位时间内进、出的水量都是一定的,已知容器的容积为600升,又知单开进水管10分钟可把空容器注满,若同时打开进、出水管,20分钟可把满容器的水放完。
现已知水池内有水200升,先打开进水管5分钟,再打开出水管,两管同时开放直至把容器的水放完。
则能正确反映这一过程中容器的水量Q(升)随时间t(分钟)变化的图象是()【答案】B【例3】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,根据图中提供的信息,有下列说法:①他们都行驶了18千米;②甲在途中停留了0.5小时;③乙比甲晚出发0.5小时;④相遇后,甲的速度小于乙的速度;⑤甲、乙两人同时到达目的地。
其中符合图象描述的说法有()A.2个B.3个C.4个 D.5个Array(小时)【答案】C【例4】 某工厂用一种自动控制加工机制作一批工件,该机器运行过程分为加油过程和加工过程:加工过程中,当油箱中油量为10升时,机器自动停止加工进入加油过程,将油箱加满后继续加工,如此往复。
已知机器运行需运行185分钟才能将这批工件加工完。
如图是油箱中油量y (升)与机器运行时间x (分)之间的函数图象。
根据图象回答下列问题:⑴求在第一个加工过程中,油箱中油量y (升)与机器运行时间x (分)之间的函数关系式(不必写出自变量的取值范围)⑵机器运行多少分钟时,第一个加工过程停止? ⑶加工完这批工件,机器耗油多少升?【答案】⑴110y x =-+⑵100分钟 ⑶175升【例5】 东风商场文具部的某种毛笔每枝售价25元,书法练习本每本售价5元,该商场为促销制定了两种优惠办法.甲:买一枝毛笔就赠送一本书法练习本. 乙:按购买金额打九折付款.某校欲为校书法兴趣小组购买这种毛笔10枝,书法练习本(10)x x ≥本.⑴写出每种优惠办法实际的金额y 甲(元),y 乙(元)与x (本)之间的函数关系式; ⑵比较购买同样多的书法练习本时,按哪种优惠办法付款更省钱;⑶如果商场允许可以任意选择一种优惠办法购买,也可以同时选两种优惠办法购买,请你就购买这种毛笔10枝和书法练习本60本设计一种最省钱的购买方案.【答案】⑴25105(10)5200(10)y x x x =⨯+-=+≥甲,(25105)90% 4.5225(0)y x x x =⨯+⨯=+≥乙;⑵当购买50本书法练习本时,两种优惠办法的实际付款一样,即可任选一种办法付款;当购买本数在10~50本之间,选择的优惠办法甲付款更省钱;当购买本数大于50本时,选择优惠办法乙付款更省钱.⑶选用优惠办法甲购买10枝毛笔和10本书法练习本,再用优惠办法乙购买50本书法练习本的方案最省钱.【例6】 一次时装表演会预算中票价定位每张100元,容纳观众人数不超过2000人,毛利润y (百元)关于观众人数x (百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司交纳定额平安保险费5000元(不列入成本费用)请解答下列问题:⑴求当观众人数不超过1000人时,毛利润y (百元)关于观众人数x (百人)的函数解析式和成本费用s (百元)关于观众人数x (百人)的函数解析式;⑵若要使这次表演会获得36000元的毛利润,那么要售出多少张门票?需支付成本费用多少元?(注:当观众人数不超过1000人时,表演会的毛利润=门票收入—成本费用;当观众人数超过1000人时,表演会的毛利润=门票收入—成本费用—平安保险费)【答案】⑴由图象可知:当010x ≤≤时,设y 关于x 的函数解析100y kx =-,∵(10,400)在100y kx =-上,∴40010100k =-,解得50k = ∴50100y x =-,100(50100)s x x =--),∴50100s x =+ ⑵当1020x <≤时,设y 关于x 的函数解析式为y mx b =+, ∵(10,350),(20,850)在y mx b =+上, 1035020580m b m b +=⎧⎨+=⎩,解得50150m b =⎧⎨=-⎩∴50150y x =-,∴()100501505050100s x x s x ∴=---∴=+ ∴()()50100010501501020x x y x x ⎧-⎪=⎨-<⎪⎩≤≤≤令360y =当010x ≤≤时,50100360x -= 解得9.2x = 50100509.2100560s x =+=⨯+=当1020x <≤时,50150360x -=解得10.2x = 501005010.2100610s x =+=⨯+=.要使这次表演会获得36000元的毛利润. 要售出920张或1020张门票,相应支付的成本费用分别为56000元或61000元.二、一次函数与几何综合【例7】 如图所示,已知正比例函数y x =和3y x =,过点()20A ,作x 轴的垂线,与这两个正比例函数的图象分别交与B C ,两点,求三角形OBC 的面积(其中O 【答案】由题意,∵20A (,),AC x ⊥轴 ∴将2x =分别代入3y x y x ==、得,()()2226B C ,,,∴624BC =-=∴1142422OBC S BC OA ∆=⋅⋅=⨯⨯=【例8】 如图,直线6y kx =+与x 轴y 轴分别相交于点E F 、. 点E 的坐标为 8, 0-(), 点A 的坐标为()60-,. 点,P x y ()是第二象限内的直线上的一个动点。
一次函数与几何图形综合题(含答案)

一次函数与几何图形综合专题讲座思想方法小结 : (1)函数方法.函数方法就是用运动、变化的观点来分析题中的数量关系,抽象、升华为函数的模型,进而解决有关问题的方法.函数的实质是研究两个变量之间的对应关系,灵活运用函数方法可以解决许多数学问题.(2)数形结合法.数形结合法是指将数与形结合,分析、研究、解决问题的一种思想方法,数形结合法在解决与函数有关的问题时,能起到事半功倍的作用.知识规律小结 :(1)常数k ,b 对直线y =kx +b (k ≠0)位置的影响. ①当b >0时,直线与y 轴的正半轴相交; 当b =0时,直线经过原点;当b ﹤0时,直线与y 轴的负半轴相交. ②当k ,b 异号时,即-kb>0时,直线与x 轴正半轴相交; 当b =0时,即-kb=0时,直线经过原点; 当k ,b 同号时,即-kb﹤0时,直线与x 轴负半轴相交.③当k >O ,b >O 时,图象经过第一、二、三象限; 当k >0,b =0时,图象经过第一、三象限; 当b >O ,b <O 时,图象经过第一、三、四象限; 当k ﹤O ,b >0时,图象经过第一、二、四象限; 当k ﹤O ,b =0时,图象经过第二、四象限; 当b <O ,b <O 时,图象经过第二、三、四象限. (2)直线y =kx +b (k ≠0)与直线y =kx (k ≠0)的位置关系. 直线y =kx +b (k ≠0)平行于直线y =kx (k ≠0)当b >0时,把直线y =kx 向上平移b 个单位,可得直线y =kx +b ; 当b ﹤O 时,把直线y =kx 向下平移|b |个单位,可得直线y =kx +b . (3)直线b 1=k 1x +b 1与直线y 2=k 2x +b 2(k 1≠0 ,k 2≠0)的位置关系.①k 1≠k 2⇔y 1与y 2相交; ②⎩⎨⎧=≠2121b b k k ⇔y 1与y 2相交于y 轴上同一点(0,b 1)或(0,b 2); ③⎩⎨⎧≠=2121,b b k k ⇔y 1与y 2平行;④⎩⎨⎧==2121,b b k k ⇔y 1与y 2重合.例题精讲:1、直线y =-2x +2与x 轴、y 轴交于A 、B 两点,C 在y 轴的负半轴上,且OC =OB(1) 求AC(2) 在OA 的延长线上任取一点P ,作PQ ⊥BP ,交直线AC于Q ,试探究BP 与PQ 的数量关系,并证明你的结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数与几何综合(一)(习题)
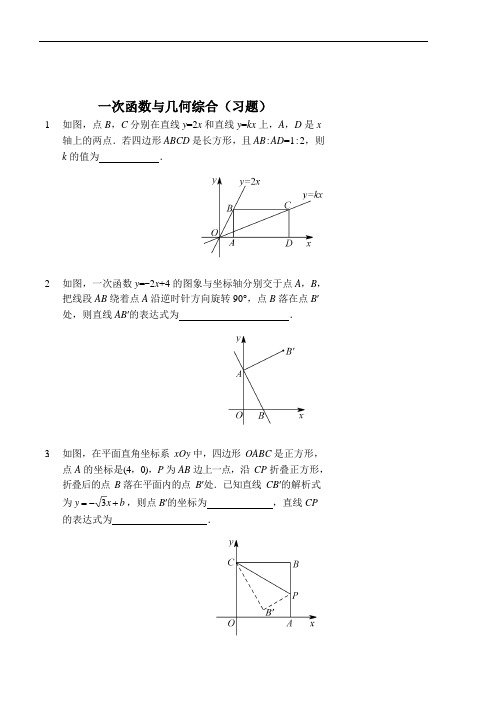
1.如图,点B,C 分别在直线y=2x 和直线y=kx 上,A,D 是x
轴上的两点.若四边形ABCD 是长方形,且AB:AD=1:2,则k 的值为.
2.如图,一次函数y=-2x+4 的图象与坐标轴分别交于点A,B,把
线段A B 绕着点A沿逆时针方向旋转90°,点B落在点B′ 处,则直线A B′的表达式为.
3.如图,在平面直角坐标系xOy 中,四边形OABC 是正方形,点A
的坐标是(4,0),P 为AB 边上一点,沿CP 折叠正方形,折叠后的点B 落在平面内的点B′处.已知直线CB′的解析式
为y=-3x +b ,则点B′的坐标为,直线C P
的表达式为.
4.如图,点A 的坐标是(-2,0),点B 的坐标是(6,0),点C 在第
一象限内,且△OBC 为等边三角形,直线B C 交y轴于点D,过点A作直线A E⊥BD,垂足为点E,交O C 于点F,则点C的坐标为,直线A E 的表达式为.
第4题图第5题图
5.如图,一次函数的图象交x轴于点B(-6,0),交正比例函数的
图象于点A,且点A的横坐标为-4,S
△AOB =15 ,S
△BOD
= 45 ,则一
次函数的表达式为,正比例函数的表达式为.
6.如图,在平面直角坐标系中,已知直线y =-3
x + 3 与x 轴、y 4
轴分别交于A,B 两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC 折叠,使点B 刚好落在x 轴上,则点C 的坐标是.
7.如图,在平面直角坐标系中,函数y=-x 的图象l 是第二、四象
限的角平分线.
实验与探究:
由图观察易知A(0,2)关于直线l 的对称点A′的坐标为(-2,0),请在图中分别标出B(-5,-3),C(-2,5)关于直线l 的对称点
B′,C′的位置,并写出它们的坐标:B′,C′.归纳与发现:
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第二、四象限的角平分线l的对称点P′的坐标为.
运用与拓广:
已知两点D(0,-3),E(1,-4),试在直线l 上确定一点Q,使点Q 到D,E 两点的距离之和最小,并求出点Q 的坐标.
8.如图,在平面直角坐标系中,直线y =x - 4 与x 轴、y 轴分别交
于点A,B,P 为y 轴上B 点下方的一点,且PB=m(m>0),以点P 为直角顶点,AP 为腰在第四象限内作等腰 Rt△APM.
(1)用含m 的代数式表示点M 的坐标;
(2)若直线MB 与x 轴交于点Q,求点Q 的坐标.
【参考答案】
巩固练习
1.
2 5
2. y = 1 x + 4
2
3. (2, 4 - 2 ), y = - 3
x + 4
3 4. (3, 3 3 ), y =
3 x + 2 3
3 35. y = 5 x +15 , y = - 5 x
2 4
6. (0, 4 ),(0,-12)
3
7. 实验与探究:(3,5),(-5,2)归纳与发现:(-n ,-m )
运用与拓广:点 Q 的坐标为(2,-2) 8.
(1)M (4+m ,-8-m )
(2)Q (-4,0)。
