运筹学第三章课后习题答案知识讲解
《运筹学教程》第三章习题答案

《运筹学教程》第三章习题答案1.影子价格是根据资源在生产中作出的贡献而做的估价。
它是一种边际价格,其值相当于在资源得到最有效利用的生产条件下,资源每变化一个单位时目标函数的增量变化。
又称效率价格。
影子价格是指社会处于某种最优状态下,能够反映社会劳动消耗、资源稀缺程度和最终产品需求状况的价格,是社会对货物真实价值的度量。
只有在完善的市场条件下才会出现,然而这种完善的市场条件是不存在的,因此现成的影子价格也是不存在的。
市场价格是物品和服务在市场上销售的实际价格,是由供求关系决定的。
2.证明:当原问题约束条件右端变为b i′时,原问题变为: maxz=∑C i X js.t. ∑a ij X i≤b i′(i=1,2,3,……,m)X j≥0 (j=1,2,3,……,n)对偶问题为: minp=∑b i′y is.t. ∑a ij y i≥C iy i≥0(i=1,2,3,……,m) (j=1,2,3,……,n) 设,当b i变为b i′原问题有最优解(X1′X2′X3′……X n-1′X n′)时,对偶问题的最优解为(y1′y2′y3′……y n-1′y n′),则有:又因为当原问题有最优解时,对偶问题也有最优解,且相等,则有:所以3(1).minp=6y1 + 2y2s.t. -y1+2y2≥-33y1+3y2≥4y1,y2≥0(2)解:令X2=X2′-X2〞,X4= X4′-X4〞,X2′,X2〞,X4′,X4〞≥0 ,原式化为:maxz=2X1 +2X2′-2X2〞-5X3 +2X4′-2X4〞s.t. 2X1 -X2′+X2〞+3X3 +3X4′-3X4〞≤-5-2X1 +X2′-X2〞-3X3 -3X4′+3X4〞≤5-6X1 -5X2′+5X2〞+X3 -5X4′+5X4〞≤-610X1 -9X2′+9X2〞+6X3 +4X4′-4X4〞≤12X1, X2′,X2〞,X3, X4′,X4〞≥0则对偶规划为:.minp= -5y1′+ 5y1〞-6y2 + 12y3s.t. 2y1′-2y1〞-6y2 + 10y3≥2-y1′+y1〞-5y2 -9y3≥2y1′-y1〞+5y2 + 9y3≥-23y1′-3y1〞+y2 + 6y3≥-53y1′-3y1〞-5y2 + 4y3≥2-3y1′+3y1〞+5y2 -4y3≥-2即:minp= -5y1′+ 5y1〞-6y2 + 12y3s.t. 2y1′-2y1〞-6y2 + 10y3≥2-y1′+y1〞-5y2 -9y3=23y1′-3y1〞+y2 + 6y3≥-53y1′-3y1〞+5y2 + 4y3=2令 y1〞- y1′= y1,得:minp= 5y1 -6y2 + 12y3s.t. -2y1-6y2 + 10y3≥2y1-5y2 -9y3=2-3y1+y2 + 6y3≥-5-3y1-5y2 + 4y3=24、试用对偶理论讨论下列原问题与他们的对偶问题是否有最优解。
运筹学胡运权第五版第三章共16页

第1年 第2年 第3年 多余 产量
期初贮存 第1年正常生产数 第1年加班生产数 第2年正常生产数 第2年加班生产数 第3年正常生产数 第3年加班生产数 需要量
40
80 120 0
2
500 540 580 0
2
570 610 650 0
3
M 600 640 0
4
M 670 710 0
2
M
M 550 0
➢ 课后题答案
3.1 表3-35 最终表如下:
销地 产地
A1 A2 A3
销量
B1
B2 B3 B4 产 量
15 5 16 10 15
12 10 15 4
25
5 5 50
5
5 15 15 10 45
注:黑色数字表最优解,红色表示对应非基变量的 检验数。即:最优值Z*=335. 亦或是:
➢ 课后题答案
1
M
M 620 0
3
3
3
4
7 17
➢ 课后题答案
最优方案为:
销 供
期初贮存 第1年正常生产数 第1年加班生产数 第2年正常生产数 第2年加班生产数 第3年正常生产数 第3年加班生产数
第1年 2 1
第2年 1 2
第3年 0
1 3
多余
3 2 2
➢ 课后题答案
3.10(a)答案
产销平衡及单价表如下:
煤矿 销量
5
0
5
50 3
注:有非基变量检验数为0,故有无穷多最优解. 此题答案不唯一,以上最优解仅作参考。
且,min Z=1390
谢谢观看
销地 产地
Ⅰ Ⅱ Ⅲ Ⅳ
销量
Ⅰ Ⅱ Ⅲ ⅣⅤ
《运筹学》课后习题答案 第3章 运输问题

一、选择题1. 2. 3. 4. 5. 6. 7.二、判断题1. 2. 3. 4. 5. 6. 7. 8. 9.三、表上作业法 3. 解:可知,有初始基本可行解1112132122230,10,20,10,35,0x x x x x x ======用闭回路法计算非基变量的检验数:1123(56)(84)10(98)(67)40σσ=+-+=-<=+-+=>因为110σ<,该解并不是最优解。
进行换基迭代,让11x 进基,考虑上述闭回路,调整量min(10,10)10θ==,调整后得到新的调运方案:A2 4 0645945销量10 45 20计算非基变量的检验数得:1223(84)(56)10(95)(47)30σσ=+-+=>=+-+=>故此方案为最优方案,最优解为:11121321222310,0,20,0,45,0x x x x x x ======最优值min 105207456460Z =⨯+⨯+⨯=用电子表格模型求解进行验算:4. 解:用西北角法求得初始基本可行解:1112131421222324313233344,0,0,0;1,2,4,2;0,0,0,4;x x x x x x x x x x x x ============ 用位势法计算检验数:1111212121131322214142233131324323243433333106()210167()861012()9455()12194()731010()47u u v u v v u v u v u u v u v v u v u v v u v u v v u v u v u σσσσσσ=⎧+==-+=⎧⎧⎪=⎪⎪⎪+==-+=⎪⎪⎪=⎪⎪++=-+=⎪⎪⇒=⇒⎨⎨⎨+==-+=-⎪⎪=-⎪⎪+==-+=-=⎪⎪+==-+=⎪⎪⎩=⎩⎪⎪⎪⎪⎪⎩因为3132,σσ小于0,该解不是最优解。
运筹学(胡运权版)第三章运输问题课后习题答案
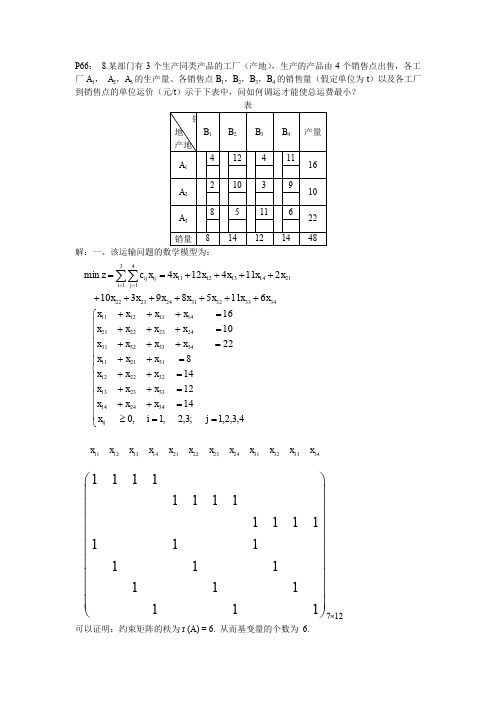
P66: 8.某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点出售,各工厂A 1, A 2,A 3的生产量、各销售点B 1,B 2,B 3,B 4的销售量(假定单位为t )以及各工厂到销售点的单位运价(元/t )示于下表中,问如何调运才能使总运费最小?表解:一、该运输问题的数学模型为:可以证明:约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解(初始调运方案)1. 最小元素法思想:优先满足运价(或运距)最小的供销业务。
其余(非基)变量全等于零。
此解满足所有约束条件,且基变量(非零变量)的个数为6(等于m+n-1=3+4-1=6).总运费为(目标函数值) ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ijij x c Z2. 伏格尔(Vogel)法伏格尔法的基本思想:运输表中各行各列的最小运价与次小运价之差值(罚数)应尽可能地小。
或者说:优先供应罚数最大行(或列)中最小运费的方格,以避免将运量分配到该行(或该列)次小运距的方格中。
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
运筹学第三章作业的参考答案

第三章作业的参考答案
99P 3、用Gomory 割平面法求解下面的ILP 问题.
⎪⎪⎩⎪⎪⎨⎧=≥≥-≤+-=.2,1,0482..5min 212121i x x x x x t s x x z i 整数, 解:将原问题标准化
⎪⎪⎩⎪⎪⎨⎧=≥=--=++-=.
4,3,2,1,0482..5min 42132121i x x x x x x x t s x x z i 整数, 将第二个等式乘以)1(-加到第一个等式,可得线性方程组的典式
⎪⎪⎩⎪⎪⎨⎧=≥=--=++-=.4,3,2,1,0443..5min 42143221i x x x x x x x t s x x z i 整数,
所以,其松驰问题(P0)的第一张单纯形表为
把零行化成检验行,得
1x 2x 3x 4x RHS z
3x 1x
以2x 为进基变量,3x 为离基变量,旋转得
所以,松驰问题(P0)的最优解为T x )0,0,3
4,316(
0=, 它不是整数向量。
所以由第一行生成的割平面条件为 31313143≥+x x .
对应的割平面为
313131143-=+--s x x .
把它加入到松驰问题(P0)的最优单纯形表中,得到改进的松弛问题(P1)的
1x 2x 3x 4x RHS z 2x 1x
利用对偶单纯形方法求解. 以1s 为离基变量,3x 为进基变量,旋转得
所以,松弛问题(P 1)的最优解为T x )0,0,1,1,5(1=。
因此,原问题的最优解为T x )1,5(*=,最优值为0. 1x 2x 3x 4x 1s RHS z
2x 1x 3x。
《管理运筹学》第四版第3章线性规划问题的计算机求解课后习题解析

《管理运筹学》第四版第3章线性规划问题的计算机求解课后习题解析第一篇:《管理运筹学》第四版第3章线性规划问题的计算机求解课后习题解析《管理运筹学》第四版课后习题解析第3章线性规划问题的计算机求解1.解:⑴甲、乙两种柜的日产量是分别是4和8,这时最大利润是2720⑵每多生产一件乙柜,可以使总利润提高13.333元⑶常数项的上下限是指常数项在指定的范围内变化时,与其对应的约束条件的对偶价格不变。
比如油漆时间变为100,因为100在40和160之间,所以其对偶价格不变仍为13.333 ⑷不变,因为还在120和480之间。
2.解:⑴不是,因为上面得到的最优解不为整数解,而本题需要的是整数解⑵最优解为(4,8).解:⑴农用车有12辆剩余⑵大于300 ⑶每增加一辆大卡车,总运费降低192元4.解:计算机得出的解不为整数解,平移取点得整数最优解为(10,8)5.解:圆桌和衣柜的生产件数分别是350和100件,这时最大利润是3100元相差值为0代表,不需要对相应的目标系数进行改进就可以生产该产品。
最优解不变,因为C1允许增加量20-6=14;C2允许减少量为10-3=7,所有允许增加百分比和允许减少百分比之和(7.5-6)/14+(10-9)/7〈100%,所以最优解不变。
6.解:(1)x1=150,x2=70;目标函数最优值103 000。
(2)1、3车间的加工工时数已使用完;2、4车间的加工工时数没用完;没用完的加工工时数为2车间330小时,4车间15小时。
(3)50,0,200,0。
含义:1车间每增加1工时,总利润增加50元;3车间每增加1工时,总利润增加200元;2车间与4车间每增加一个工时,总利润不增加。
(4)3车间,因为增加的利润最大。
(5)在400到正无穷的范围内变化,最优产品的组合不变。
(6)不变,因为在[0,500]的范围内。
(7)所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条件1的右边值在[200,440]变化,对偶价格仍为50(同理解释其他约束条件)。
管理运筹学第三章习题答案

(1)解:min 15y1 7 y2s.t. 2 y1 4 y2 105 y1 3y1 3 y2 5y1, y2 0(2)解:max 6 y1 8y2s.t. 3y1 2 y3 35y1 y2 3 y3 24 y2 7 y3 4y1 y3 02y1 y2 5 y3 2y1 0, y 2 0, y3 无限制解:例3 原问题min z x1 x 2 x3 x4 x5 x6s.t. x1 x2 70x2 x3 60x3 x4 50x4 x5 20x5 x6 30x6 x1 60x j 0, j 1, ,6对偶问题:max 70 y1 60y2 50y3 20y4 30y560y6 s.t. y1 y6 1y1 y2 1y2 y3 1y3 y4 1y4 x5 1y5 y6 1y j 0, j 1, ,6(1)由最优单纯形表可以知道原问题求max 其初始基变量为 x 4, x 5,最优基的逆阵为- - ca -3 a 23 06 3解:由P32式()()()可知bB -b,PB 4,jcjC BP j, j -,,5,其中b和 P j都是初始数据。
设bb - ,P j aj-,jI,5,C c -, C 2, C 3,贝Ub 2aj231 21 6 bb 2b 21 - 31-5-25-P23aa2aaaa 1'bB1a1222322a1 - 32 2a1- 2 1- 231 1C2 C3 2C1厶1 1C3 G 42 61C 23j C j C B P j所以原问题为:4, 4, 2 C2,0,04c2 2,解得c310G 6C3, C11,即max z 6x1 2x210x3st .X2 2x33x1 X2 X3510 X1, X2,X3min 5y1 10y2st. 3y2 6y y2 22y1 y2 10y1, y2 0对偶问题为:(2)由于对偶问题的最优解为Y* C IBIB C4,C54,2解:b 1 901 00,即 b 04 1 904b 1 90 解得0 045,所以b 1的可变范围2b 1。
运筹学习题答案(第三章)概要

90 240
210 80 410 550 330 20 70
300 100
School of Management
运筹学教程
第三章习题解答
3.8 表3-32和表3-33分别给出了各产地和各销地 的产量和销量,以及各产地至各销地的单位运价,试 用表上作业法求最优解。 表3-32 销地 产地 A1 A2 A3 销量
运筹学教程(第二版) 习题解答
运筹学教程
第三章习题解答
3.1 与一般线性规划的数学模型相比,运输问题 的数学模型具有什么特征? 答: 1、运输问题一定有有限最优解。 2、约束系数只取0或1。 3、约束系数矩阵的每列有两个1, 而且只有两个 1。前m行中有一个1,或n行中有一个1。 4、对于产销平衡的运输问题,所有的约束都取 等式。
page 13 12 November 2018
School of Management
运筹学教程
第三章习题解答
习题3.9的解答 销地 产地 B1 B2 B3 B4 B5 产量
A1
A2 A3 销量
page 14 12 November 2018
3 3
2 4 3
7
4 3 3 3 2
6
2 3 8
2 4
School of Management
运筹学教程
第三章习题解答
3.7 试判断表3-30和表3-31中给出的调运方案可 否作为表上作业法迭代时的基可行解?为什么? 答:都不是。数字格的数量不等于m+n-1。 表3-30 销地 产地 A1 A2 A3 销量
page 9 12 November 2018
page 3 12 November 2018
管理运筹学第三章习题答案

(1)解:min 15y1 7 y2s.t. 2 y1 4 y2 105 y1 3y1 3 y2 5y1, y2 0(2)解:max 6 y1 8y2s.t. 3y1 2 y3 35y1 y2 3 y3 24 y2 7 y3 4y1 y3 02y1 y2 5 y3 2y1 0, y 2 0, y3 无限制解:例3 原问题min z x1 x 2 x3 x4 x5 x6s.t. x1 x2 70x2 x3 60x3 x4 50x4 x5 20x5 x6 30x6 x1 60x j 0, j 1, ,6对偶问题:max 70 y1 60y2 50y3 20y4 30y560y6 s.t. y1 y6 1y1 y2 1y2 y3 1y3 y4 1y4 x5 1y5 y6 1y j 0, j 1, ,6(1)由最优单纯形表可以知道原问题求max 其初始基变量为 x 4, x 5,最优基的逆阵为- - ca -3 a 23 06 3解:由P32式()()()可知bB -b,PB 4,jcjC BP j, j -,,5,其中b和 P j都是初始数据。
设bb - ,P j aj-,jI,5,C c -, C 2, C 3,贝Ub 2aj231 21 6 bb 2b 21 - 31-5-25-P23aa2aaaa 1'bB1a1222322a1 - 32 2a1- 2 1- 231 1C2 C3 2C1厶1 1C3 G 42 61C 23j C j C B P j所以原问题为:4, 4, 2 C2,0,04c2 2,解得c310G 6C3, C11,即max z 6x1 2x210x3st .X2 2x33x1 X2 X3510 X1, X2,X3min 5y1 10y2st. 3y2 6y y2 22y1 y2 10y1, y2 0对偶问题为:(2)由于对偶问题的最优解为Y* C IBIB C4,C54,2解:b 1 901 00,即 b 04 1 904b 1 90 解得0 045,所以b 1的可变范围2b 1。
管理运筹学(第四版)第三章习题答案参考word

目标函数值为2×30+5×10+1×10+5×10+3×25+7×5+6×20+10×40=800目标函数值为2×30+5×10+1×10+5×10+3×25+7×5+6×20+10×40=800(2)最小元素法:先从311=c 开始分配先从325=c 开始分配,需迭代4次,具体见QM 的迭代 逼近法(结果同最小元素法——先从313=c 开始分配)vj2 2 0 u i1 2 3 产量 0 1 2 10 7 2 8 × 7 × 2 1 2 3 2 1 0 × 2 2 4 1 3 11 3 8 8 × 3 7 × 3 2 4 4 9 2 1 5 × 5 6 -2 5 0 0 0 4 0 × 2 × 4销量757目标函数值为33。
4.5第一种解法(求最大)A B C 产量 甲 18 16 21 180 乙 16 18 22 250 丙 19 14 19 320 销量 250300200用QM 解得玩 具利 润工人第二种解法(求最小)A B C产量甲526449180乙546248250丙516651320销量250300200用QM解得即甲工人做C玩具180个,乙工人做B玩具250个,丙工人做A玩具250个,做B玩具50个,做C玩具20个。
最大利润为:70×250+80×300+70×200-41390=14110元甲乙丙产量A151822400B212516450最低需求290250270最高需求320250350甲1甲2乙丙1丙2产量A1515182222400B2121251616450C M0M M070需求2903025027080用QM解得玩具费用工人地区运费厂家地区运费厂家即A厂供给甲地区化肥150万吨,供给乙地区化肥250万吨;B厂供给甲地区化肥140万吨,供给丙地区化肥310万吨,总运费为14650万元。
二三版兼用《运筹学教程》胡运权主编课后习题答案(第三章)

城市
电站
1
2
3
Ⅰ
15
18
22
Ⅱ
21
25
16
第三章习题解答
习题3.12的解答
城市 城市
电站
1-1
城市 1-2
城市2
城市 3-1
城市 3-2
产量
Ⅰ
150 15
15 250 18
22
22 400
Ⅱ
140 21
第三章习题解答
表3-35
食品厂
面粉厂
1
2
3
产量
Ⅰ
3 10
2 20
Ⅱ
4 11
8 30
Ⅲ
8 11
4 20
销量
15 25 20
第三章习题解答
习题3.10的解答
食品厂 面粉厂
Ⅰ Ⅱ Ⅲ 销量
1
3 15 4
8 15
2
10 5 11 20 11 25
3
20 2 8 4
20
4
0 10 0
0 10
产量
20 30 20
B3
B4 产量
A1 A2 A3 销量
3
7
6
45
2
4
3
22
4
3
8
56
3
3
2
2
第三章习题解答
习题3.9的解答
销地
产地
B1 B2 B3 B4 B5 产量A1源自33 7 6 24 0 5
A2
2 4 23 2 0 2
A3 销量
4 33 8 5 30 6 33223
第三章习题解答
3.10 某市有三个面粉厂,它们供给三个面食加工 厂所需的面粉。各面粉厂的产量、各面食加工厂加工 面粉的能力、各面食加工厂和各面粉厂之间的单位运 价,均表示于表3-35中。假定在第1,2和3面食加工厂 制作单位面粉食品的利润分别为12元、16元和11元, 试确定使总效益最大的面粉分配计划(假定面粉厂和面 食加工厂都属于同一个主管单位)。
运筹学习题答案(第三章)

page 8 9 July 2013
School of Management
运筹学教程
第三章习题解答
3.7 试判断表3-30和表3-31中给出的调运方案可 否作为表上作业法迭代时的基可行解?为什么? 答:都不是。数字格的数量不等于m+n-1。 表3-30 销地 产地 A1 A2 A3 销量
page 9 9 July 2013
page 4 9 July 2013
School of Management
运筹学教程
第三章习题解答
3.4 详细说明用位势法(对偶变量法)求检验数的原 理。 解:原问题的检验数也可以利用对偶变量来计 算:
ij
c ij ( u i v j )
i 1, 2 , m ; j 1, 2 , , n
运筹学教程
第三章习题解答
由于方程有m+n-1个, 而变量有m+n个。所以上 面的方程有无穷多个解。任意确定一个变量的值都可 以通过方程求出一个解。然后再利用这个解就可以求 出非基变量的检验数了。
page 6 9 July 2013
School of Management
运筹学教程
第三章习题解答
3.5 用表上作业法求解运输问题时,在什么情况 下会出现退化解?当出现退化解时应如何处理? 解:当数字格的数量小于m+n-1时,相应的解就 是退化解。如果出现了退化解,首先找到同时划去的 行和列,然后在同时划去的行和列中的某个空格中填 入数字0。只要数字格的数量保持在m+n-1个的水平即 可。
page 19 9 July 2013
School of Management
运筹学教程
第三章习题解答
运筹学第三章课后习题答案

量 1 2 34
4 51 34
6 8 302
④
A2 A3 销量
31
2
25
30 8 1 1 5
⑤
3
7 15
1 4 224 ⑥
6
5
6
3
列12 罚22 数3
vj 4
111 11 11 1
②
①⑦
③
2020/1/1
9
从上表计算知:x12=5,x13=3,x21=3,x23=2,x24=3, x33=1。总费用=5×1+3×4+3×1+2×5+3×0+ 1×5=35,在上述三种计算方法中,这种方法计算所需 运输费用是最省的。但还不知是否最优。现用闭回路法 检验如下: 闭回路法检验如下:
2020/1/1
10
第一个闭回路σ11,走4→1→5→4线路
产地 销地
A1
B1
B2
B3
45 13 4
B4
6
A2 3 1
22 5 3 0
A3 销量
3
71 5
1
6
5
6
3
产量
8 8 4
σ11=4-1+5-4=4
2020/1/1
11
第二闭回路σ14,走6→0→5→4线路
产地 销地
A1
B1
B2
B3
45 13 4
2020/1/1
17
①最小元素法求解:
销地 B1
B2
产地
A1
13
7
A2
22
4
A3
4
33
销量
3
3
B3
B4 B5 产量
6 3 28 2
1 4 30
运筹学第三版课后习题答案

运筹学第三版课后习题答案运筹学是一门研究如何在有限资源下做出最优决策的学科。
它涉及到数学、统计学、经济学等多个学科的知识,可以应用于各个领域,如物流管理、生产调度、供应链优化等。
而《运筹学》第三版是一本经典的教材,它系统地介绍了运筹学的基本概念、方法和应用。
本文将针对该教材的课后习题进行解答,帮助读者更好地理解和掌握运筹学的知识。
第一章:线性规划1. 习题1.1:求解线性规划问题的常用方法有哪些?答:求解线性规划问题的常用方法包括单纯形法、对偶理论、整数规划等。
其中,单纯形法是最常用的方法,它通过迭代寻找目标函数值最小(或最大)的解。
2. 习题1.2:什么是线性规划的对偶问题?如何求解线性规划的对偶问题?答:线性规划的对偶问题是指通过原始问题的约束条件构造一个新的问题,该问题的目标是最大化(或最小化)原始问题的目标函数值。
求解线性规划的对偶问题可以使用对偶理论,通过将原始问题转化为对偶问题的等价形式,再利用对偶问题的特性进行求解。
第二章:整数规划1. 习题2.1:什么是整数规划问题?与线性规划问题有何不同?答:整数规划问题是指决策变量的取值必须为整数的线性规划问题。
与线性规划问题相比,整数规划问题的解空间更为有限,求解难度更大。
整数规划问题在实际应用中常常涉及到资源的离散分配、路径选择等问题。
2. 习题2.2:列举几个整数规划问题的应用场景。
答:整数规划问题的应用场景包括生产调度、物流路径优化、设备配置等。
例如,在生产调度中,需要确定每个生产批次的数量和时间,以最大化产能利用率和最小化生产成本。
第三章:动态规划1. 习题3.1:什么是动态规划?它的基本思想是什么?答:动态规划是一种通过将问题划分为多个子问题,并保存子问题的解来求解原问题的方法。
其基本思想是利用子问题的解构建全局最优解,从而避免重复计算和提高求解效率。
2. 习题3.2:动态规划在哪些问题中有应用?答:动态规划在最短路径问题、背包问题、序列比对等问题中有广泛的应用。
运筹学习题答案注释(第3章)

第3章运输问题注意:本章习题解法不唯一,有的题目,最优解也可能不唯一。
3.8 表3-32和表3-33分别给出了各产地和各销地的产量和销量,以及各产地至各销地的单位运价,试用表上作业法求最优解。
表3-32解:由最小元素法求得上述运输问题的初始基可行解,其过程如下:表3.8-1由于0为最小,所以,取3与8的最小值放在x24位置上,划去B4列,得表3.8-2表3.8-2划去A2行,得表3.8-3在表3.8-3中的没画线的表格中,由于1最小,所以取8与5的最小值放在x12位置上,划去B2列,得表3.8-4在表3.8-4中没画线的表格中,由于3最小,所以取4与1的最小值放在x31位置上,划去B1列,得表3.8-5表3.8-4在表3.8-5中没画线的表格中,由于4最小,所以取3与6的最小值放在x13位置上,划去A1行,得表3.8-6在表3.8-6中没画线的表格中,由于5最小,所以取3与3的最小值放在x33位置上,划去A3行和B3列,得表3.8-7,这样就得到了一个初始基可行解,如表3.8-8所示。
在表3.8-8中,使用闭回路法计算非基变量的检验数(括弧内的数),得表3.8-9:σ11 = c11-c13 + c33-c31 = 4-4+5-3 = 2σ14 = c14-c13 + c33-c31 + c21-c24 = 6-4+5-3+1-0 = 5表3.8-7σ22 = c22 -c12 + c13 - c33 + c31 - c21 = 2-1+4-5+3-1 = 2σ23 = c23 -c33 + c31 - c21 = 5-5+3-1 = 2σ32 = c32 -c33 + c13–c12 = 7-5+4-1 = 5σ34 = c34 -c24 + c21–c13 = 1-0+1-3 = -1在表3.8-9中,由于检验数σ34 = -1≤0 ,所以表3.8-9中的解不是最优解。
选x34运筹学习题答案及注释第3页为换入变量,找到闭回路为:x34 x24 x21 x31,由于3与1的最小数为1,故调整量为1,选x31为换出变量,调整后的解如表3.8-10所示表3.8-10在表3.8-10中,使用闭回路法计算各非基变量的检验数,得表3.8-11:表3.8-11在表3.8-11中,由于所有检验数均大于等于 0 ,所以表3.8-11中的解就是最优解,其最小运价为39 。
运筹学 第3章 运输问题
第三章运输问题在生产实际中,经常需要将某种物资从一些产地运往一些销地,因而存在如何调运使总的运费最小的问题。
这类问题一般可用线性规划模型来描述,当然可以用单纯形法求解。
但由于其模型结构特殊,学者们提供了更为简便和直观的解法—-表上作业法。
此外,有些线性规划问题从实际意义上看,并非运输问题,但其模型结构类似运输问题,也可以化作运输问题进行求解。
第一节运输问题及其数学模型首先来分析下面的问题。
例3。
1农产品经销公司有三个棉花收购站,向三个纺织厂供应棉花。
三个收购站A1、A2、A3的供应量分别为50kt、45kt和65kt,三个纺织厂B1、B2、B3的需求量分别为20kt、70kt和70kt。
已知各收购站到各纺织厂的单位运价如表3-1所示(单位:千元/kt),问如何安排运输方案,使得经销公司的总运费最少?设x ij表示从A i运往B j的棉花数量,则其运输量表如下表所示。
表3—2由于总供应量等于总需求量,因此,一方面从某收购站运往各纺织厂的总棉花数量等该收购站的供应量,即x11+x12+x13 = 50x21+x22+x23 = 45x31+x32+x33 = 65另一方面从各收购站运往某纺织厂的总棉花数量等该纺织厂的需要量,即x 11+x 21+x 31 = 20 x 12+x 22+x 32 = 70 x 13+x 23+x 33 = 70因此有该问题的数学模型为min f= 4x 11+8x 12+5x 13+6x 21+3x 22+6x 23+2x 31+5x 32+7x 33x 11+x 12+x 13 = 50 x 21+x 22+x 23 = 45 x 31+x 32+x 33 = 65 x 11+x 21+x 31 = 20 x 12+x 22+x 32 = 70 x 13+x 23+x 33 = 70x ij ≥0,i=1,2,3;j=1,2,3 生产实际中的一般的运输问题可用以下数学语言描述。
运筹学第3章

§3.2 表上作业法
运输表上任何有序的至少四个以上 不同格被称为圈, 如果它们满足:
任何两个接续格在同一行或同一列; 在同一行或同一列不存在三个或三个 以上的接续格; 最后一个格应和第一个格在同一行或 同一列。
§3.3 特殊情况的处理
例3·:某农场有四种土壤,面积分别为 6 500亩、1000亩、600亩和500亩,准备将不 同的三个小麦品种播在这四种土壤上。根据 市场需求和本场的具体情况,确定这三个品 种的播种面积分别为400亩、1000亩和1200 亩,又根据过去的生产规律和未来气候的变 化以及生产物资供应的保证情况,用多元回 归方程预测得不同品种的小麦播在不同土壤 上的亩产量(公斤)如后表所示,问怎样安 排播种才能使小麦的总产量最高?
x21 x22 x23 27
s.t.
xij 0, (i 1, 2; j 1, 2,3)
例3·:一般运输问题 2 一般的运输问题可以描述为: 有 m 个供应点, n 个需求点, 第 i 个供应点的 供应量 ai ,第 j 个需求点的需求量 bj , 从 i 到 j的运费为 cij, 求费用最小的运输方 案。
6
35 10
5
0 2
工厂2 25
10
12
7
vj
8
仓库一
5
仓库三
仓库二
ui
工厂1 工厂2
7
15 10
17 +
- 174 0 6
6 12
18 35 - 10+ 27
5
5 7
0 2
25 8
管理组织运筹学(第四版)第三章知识题目解析

3.1(1)解:, 53351042..715min 212112121≥≥+≥≥++=y y y y y y y t s y y ω(2)解:无限制32132131323213121,0,0 2520474235323..86max y y y y y y y y y y y y y y y t s y y ≤≥=++≤-=+≥+--≤++=ω3.4解:例3原问题6,,1,0603020506070..min 166554433221654321 =≥≥+≥+≥+≥+≥+≥++++++=j x x x x x x x x x x x x x t s x x x x x x z j对偶问题:6,,1,0111111..603020506070max 655443322161654321 =≥≤+≤+≤+≤+≤+≤++++++=j y y y x y y y y y y y y y t s y y y y y y j ω3.5解:(1)由最优单纯形表可以知道原问题求max ,其初始基变量为54,x x ,最优基的逆阵为⎪⎪⎪⎪⎭⎫ ⎝⎛-=-31610211B 。
由P32式(2.16)(2.17)(2.18)可知b B b 1-=',5,,1,,1 ='-=='-j P C c P B P j B j j j j σ,其中b 和j P 都是初始数据。
设⎪⎪⎭⎫ ⎝⎛=21b b b ,5,,1,21 =⎪⎪⎭⎫⎝⎛=j a a P j j j ,()321,,c c c C =,则⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-⇒='-25253161021211b b b B b ,即⎪⎩⎪⎨⎧=+-=2531612521211b b b ,解得⎩⎨⎧==10521b b⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-⇒='-0211121031610212322211312111a a a a a aP B P j j ,即 ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=+-=-=+-==+-=03161121213161212113161021231313221212211111a a a a a a a a a ,解得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==-====121130231322122111a a a a a a ()()()⎪⎪⎪⎪⎭⎫⎝⎛---=---⇒'-=31612102121,0,0,2,4,4132c c c P C c j B j j σ,即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=+--=+-2314612142121113132c c c c c c ,解得⎪⎩⎪⎨⎧==-=6102132c c c 所以原问题为:,, 10352..1026max 32132132321≥≤+-≤++-=x x x x x x x x t s x x x z对偶问题为:, 102263..105min 212121221≥≥+-≥-≥+=y y y y y y y t s y y ω(2)由于对偶问题的最优解为()()()2,4,,5454*=-=-=σσσc c C Y IB IB3.6解:→j c -5 5 13 0 0B CB X b '1x2x3x4x5x5 2x 20 -1 1 3 1 0 05x10 16 0 -2 -4 1100-2-5(1)因为3x 的检验数0353≤⨯-c ,所以3c 的可变范围是153≤c 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B2
产地
A1
13
7
A2
22
4
A3 销量
4
33
3
3
B3
6 3 28 2
B4 B5 产量
A2 A3 销量
1 32 55
08
④
3
7 15 3 1 4
⑦
6
5
6
3
20
①
③
⑤
⑥
从上表计算知:x11=6,x12=2,x22=3,x23=5,x33=1, x34=3。总费用=6×4+2×1+3×2+5×5+1×5+ 3×1=65
2020/3/31
8
② 用沃格尔法求解如下:
产地
销地
A1
B1 B2 4 51
2020/3/31
2
3.3 试对给出运输问题初始基可行解的最小元素法和 Vogel法进行比较,分析给出的解之质量不同的原因。
解: 对于任意给出运输问题初始基可行解的最小元素 法和Vogel法进行比较,分析给出的两种不同的方法求出 的解确有不同的原因。初看起来,最小元素法十分合理 。但是,有时按某一最小单位运价优先安排物品调运时 ,却可能导致不得不采用运费很高的其他供销点时,从 而使整个运输费用增加。我们称各销售地或供应地的单 位运价中找出的最小单位运价和次小单位运价之差为罚 数,若罚数的值不大,当不能按最小单位运价安排运输 时造成的运费损失不大;但如果罚数很大,不按最小运 价组织运输就会造成很大损失,故应尽量按最小运价安
产地 销地
A1
B1
B2
B3
45 13 4
B4
6
A2 3 1
22 5 3 0
A3 销量
3
71 5
1
6
5
6
3
产量
8 8 4
σ32=7-1+4-5=2
2020/3/31
15
第六个闭回路σ34,走1→5→5→0线路
产地 销地
A1
B1
B2
B3
45 13 4
B4 产量
6
8
A2 3 1
22 5 3 0 8
A3
3
5
表3-29
销地 B1
B2
B3
B4
产量
产地
A1
3
7
6
4
5
A2
2
4
3
2
2
A3
4
3
8
5
6
销量
3
3
3
2
解:(1)表3-28用三种方法计算,用闭回路法检验。 ①用最小元素法计算如下表所示
2020/3/31
6
① 最小元素法求解如下:
销地 B1
B2
B3
B4
产量
产地
A1
4 5 1 34
68
⑤
A2 A3 销量
51
3.1 与一般线性规划的数学模型相比,运输问题的数 学模型具有什么特征?
答: 与一般线性规划的数学模型相比,运输问题的数 学模型具有如下特征:1.运输问题不象一般线性规划问 题那样,线性规划问题有可束条件系数矩阵的元 素等于0或1;且每一列有两个非零元素。3.运输问题的 解的个数不可能大于(m+n-1)个。
71 5
14
销量
6
5
6
3
σ34=1-5+5-0=1,至此,六个闭回路全部计算完,σ11=4, σ14=2,σ22=0,σ31=2,σ32=2,σ34=1,即全部检验数σ 均大于或等于0。即用上述三种方法计算中,用沃格尔法
计算所得结果z*=35为最优解。
2020/3/31
16
表3-29
销地 B1
B2
检验如下:
闭回路法检验如下:
2020/3/31
10
第一个闭回路σ11,走4→1→5→4线路
产地 销地
A1
B1
B2
B3
45 13 4
B4
6
A2 3 1
22 5 3 0
A3 销量
3
71 5
1
6
5
6
3
产量
8 8 4
σ11=4-1+5-4=4
2020/3/31
11
第二闭回路σ14,走6→0→5→4线路
产地 销地
A1
B1
B2
B3
45 13 4
B4
6
A2 3 1
22 5 3 0
A3
3
71 5
1
销量
6
5
6
3
产量
8 8 4
σ14=6-0+5-4=7
2020/3/31
12
第三个闭回路σ22,走2→1→4→5线路
产地 销地
A1
B1
B2
B3
45 13 4
B4
6
A2 3 1
22 5 3 0
A3 销量
3
71 5
1
6
5
6
3
3.2 运输问题的基可行解应满足什么条件?试判断形表 3-26和表3-27中给出的调运方案是否作为表上作业法迭 代时的基可行解?为什么?
2020/3/31
1
表3-26
销地 B1
B2
B3
B4
产量
产地
A1
0
A2
A3
5
销量
5
15
15
15
10
25
5
15
15
10
解:表3-26产地个数m=3,销地个数n=4,m+n-1=3+4-1=6 个,而表3-26中非零个数的分量为5个≠6个,所以表3-26不 可作为表上作业法时的基可行解。
B3
B4
产量
产地
A1
3
7
6
4
5
A2
2
4
3
2
2
A3
4
3
8
5
6
销量
3
3
2
2
解:(2)表3-29用三种方法计算,用位势法检验。因 为总产量=13,总销量=10,所以该题的总产量>总销 量,所以该题是产销不平衡的问题,故假设一销地B5 ①用最小元素法计算如下表所示
2020/3/31
17
①最小元素法求解:
销地 B1
产量
8 8 4
σ22=2-1+4-5=0
2020/3/31
13
第四个闭回路σ31,走3→1→5→5线路
产地 销地
A1
B1
B2
B3
45 13 4
B4
6
A2 3 1
22 5 3 0
A3 销量
3
71 5
1
6
5
6
3
产量
8 8 4
σ31=3-1+5-5=2
2020/3/31
14
第五个闭回路σ32,走7→1→4→5线路
B3 34
B4 产
ui
量 1 2 34
6 8 302
④
A2
31
2
25
30 8 1 1 5
⑤
A3
3
7 15
1 4 224 ⑥
销量
6
5
6
3
列12 罚22 数3
111 11 11
vj 4
1
②
①⑦
③
2020/3/31
9
从上表计算知:x12=5,x13=3,x21=3,x23=2,x24=3, x33=1。总费用=5×1+3×4+3×1+2×5+3×0+ 1×5=35,在上述三种计算方法中,这种方法计算所需 运输费用是最省的。但还不知是否最优。现用闭回路法
2
5 30 8
③
13
7 35
14
⑦
6
5
6
3
20
④
②
⑥
①
从上表计算知:x12=5,x13=3,x21=5,x24=3,x31=1, x33=3。总费用=5×1+3×4+5×1+3×0+1×3+ 3×5=40
2020/3/31
7
②西北解法计算如下:
销地 B1
B2
B3
B4
产量
产地
A1
6 4 21
4
68
②
2020/3/31
4
排运输。这就是最小元素法和沃格尔法质量不同的原因。
3.7 表3-28和表3-29分别给出了各产地和各销地的产量 和销量,以及各产地至各销地的单位运价,试用表上作业 法求最优解。
表3-28
销地 B1
B2
B3
B4
产量
产地
A1
4
1
4
6
8
A2
1
2
5
0
8
A3
3
7
5
1
4
销量
6
5
6
3
20
2020/3/31
