三次样条插值、拉格朗日插值、herminte插值
数值分析论文 ――几种插值方法的比较课程论文8(学院+专业+学号)

数值分析论文——几种插值方法的比较1.插值法概述插值法是函数逼近的重要方法之一,有着广泛的应用 。
在生产和实验中,函数或者其表达式不便于计算复杂或者无表达式而只有函数在给定点的函()x f 数值(或其导数值) ,此时我们希望建立一个简单的而便于计算的函数,使()x ϕ其近似的代替,有很多种插值法,其中以拉格朗日(Lagrange)插值和牛顿()x f (Newton)插值为代表的多项式插值最有特点,常用的插值还有Hermite 插值,分段插值和样条插值.这里主要介绍拉格朗日(Lagrange)插值和牛顿(Newton)插值和埃尔米特插值(Hermite 插值)。
2.插值方法的比较2.1拉格朗日插值2.1.1基本原理构造次多项式,这是n ()()()()()x l y x l y x l y x l y x P n n k nk k n +⋅⋅⋅++==∑=11000不超过次的多项式,其中基函数:n()x l k =)...()()...()(()...()()...()(()1110)1110n k k k k k k k n k k x x x x x x x x x x x x x x x x x x x x ----------+-+-显然满足 =()x l k ()i k x l ⎩⎨⎧≠=)(0)(1k i k i 此时,误差()()x f x P n ≈()()()=-=x P x f x R n n (x))!1()(1)1(+++n n n f ωξ其中∈且依赖于,.ξ()b a ,x ()()()()n n x x x x x x x -⋅⋅⋅--=+101ω很显然,当,插值节点只有两个,时1=n k x 1+k x ()()()x l y x l y x P k k k k i 11+++=其中基函数 = , =()x l k 11++--k k k x x x x ()x l k 1+kk kx x x x --+12.1.2优缺点可对插值函数选择多种不同的函数类型,由于代数多项式具有简单和一些良好的特性,故常选用代数多项式作为插值函数。
插值的概念和各种基本方法

插值的概念和各种基本方法插值是一种基于已知数据点的函数关系来估计未知数据点的方法。
在实际应用中,由于各种原因,我们经常只能通过有限的数据点来描述一个函数关系,而无法得到函数的精确表达式。
因此,通过插值方法,我们可以根据已知数据点推断出未知数据点的值,从而进行进一步的分析和预测。
插值的基本方法可以分为两类:多项式插值和非多项式插值。
1.多项式插值方法多项式插值是通过已知数据点构造一个多项式函数,使得该函数经过这些数据点,并且在插值区间内的其他位置也能够比较好地拟合实际数据。
常用的多项式插值方法包括拉格朗日插值和牛顿插值。
- 拉格朗日插值:拉格朗日插值是利用拉格朗日多项式来进行插值的方法。
给定 n+1 个已知数据点(x0, y0), (x1, y1), ..., (xn, yn),拉格朗日插值函数可以表示为:L(x) = Σ(yi * li(x))其中,li(x) = Π(x - xj) / Π(xi - xj),i ≠ j,函数 L(x)即为插值函数。
-牛顿插值:牛顿插值是通过对已知数据点进行差商运算来构造插值多项式的方法。
牛顿插值多项式可以表示为:N(x) = f[x0] + Σ(f[x0, x1, ..., xi] * (x - x0) * (x - x1)* ... * (x - xi-1))其中,f[x0, x1, ..., xi]表示 x0, x1, ..., xi 对应的差商。
2.非多项式插值方法非多项式插值方法是通过其他函数形式进行插值的方法,常用的非多项式插值方法包括分段线性插值和样条插值。
-分段线性插值:分段线性插值是将插值区间划分为多个小区间,然后在每个小区间内用线性函数来逼近实际数据。
具体地,给定相邻的两个已知数据点(x0,y0)和(x1,y1),分段线性插值函数可以表示为:L(x)=(y1-y0)/(x1-x0)*(x-x0)+y0-样条插值:样条插值是利用分段多项式函数来进行插值的方法。
几种常用的插值方法

几种常用的插值方法常用的插值方法包括线性插值、多项式插值、样条插值和径向基函数插值等,下面将依次介绍这些方法。
1.线性插值:线性插值是最简单的插值方法之一,它假设函数在两个已知点之间的变化是线性的。
对于给定的两个点(x0,y0)和(x1,y1),线性插值公式为:y=y0+(x-x0)*(y1-y0)/(x1-x0)其中,y是需要插值的点对应的函数值,x是插值点的横坐标。
2.多项式插值:多项式插值方法通过在给定的一组点上构建一个多项式函数来进行插值。
常用的多项式插值方法包括拉格朗日插值和牛顿插值。
- 拉格朗日插值通过构建一个n次多项式来插值n+1个给定的点。
具体来说,对于给定的n+1个点(x0, y0), (x1, y1), ..., (xn, yn),拉格朗日插值公式为:y = Σ(yk * lk(x))其中,lk(x)是拉格朗日基函数,计算公式为:lk(x) = Π((x - xj) / (xi - xj)),(j ≠ i)- 牛顿插值通过构建一个n次插值多项式来插值n+1个给定的点。
具体来说,对于给定的n+1个点(x0, y0), (x1, y1), ..., (xn, yn),牛顿插值公式为:y = Σ(Π(x - xj) / Π(xi - xj) * finDiff(yj))其中,finDiff(yj)是每个节点的差商,计算公式为:finDiff(yj) = (ΣΠ(xj - xi) * yj) / ΣΠ(xi - xj),(i ≠ j) 3.样条插值:样条插值方法通过使用分段函数来逼近给定的一组点。
常用的样条插值方法有线性样条插值和三次样条插值。
-线性样条插值在每两个相邻点之间使用线性函数进行插值,保证了插值函数的一阶导数是连续的。
-三次样条插值在每两个相邻点之间使用三次多项式进行插值,保证了插值函数的一阶和二阶导数都是连续的。
三次样条插值具有良好的平滑性和精度。
4.径向基函数插值:径向基函数插值是一种基于局部函数的插值方法,它假设函数值仅取决于与插值点的距离。
常见的插值方法及其原理

常见的插值方法及其原理1. 拉格朗日插值法(Lagrange Interpolation)拉格朗日插值法是一种基于多项式的插值方法,通过n+1个已知点的函数值来构造一个n次多项式。
具体的计算公式如下:L(x) = Σ[yk * lk(x)], k=0 to n其中yk为已知点(xi, yi)的函数值,lk(x)为拉格朗日基函数,定义为:lk(x) = Π[(x - xj)/(xi - xj)], j=0 to n, j≠k拉格朗日插值法的原理是通过构造一个通过已知点的n次多项式,来代替未知函数的近似值。
利用拉格朗日基函数的性质,可以保证插值多项式通过已知点。
2. 牛顿插值法(Newton Interpolation)牛顿插值法是一种递推的插值方法,通过已知点的函数值和差商来逐步构造插值多项式。
差商的定义如下:f[x0]=y0f[x1]=(f[x1]-f[x0])/(x1-x0)f[x2]=(f[x2]-f[x1])/(x2-x1)...f[xn] = (f[xn] - f[xn-1]) / (xn - xn-1)利用差商的定义,可以得到牛顿插值多项式的表达式:N(x) = f[x0] + f[x0, x1](x-x0) + f[x0, x1, x2](x-x0)(x-x1) + ... + f[x0, x1, ..., xn](x-x0)(x-x1)...(x-xn)牛顿插值法的原理是通过递推计算差商来得到插值多项式。
通过使用差商来处理已知点的函数值差异,可以得到更高次的插值多项式。
3. 样条插值法(Spline Interpolation)样条插值法是一种基于分段低次插值函数的插值方法,常用的是三次样条插值。
样条插值法通过寻找一组分段函数,使得满足原函数的插值条件,并要求函数在每个插值点处的函数值、一阶导数和二阶导数连续。
这样可以保证插值函数在每个插值点处的平滑性。
三次样条插值法的原理是将整个插值区间划分为多个小区间,在每个小区间内使用三次多项式进行插值。
时序预测中的时间序列插值方法分享(五)

时序预测中的时间序列插值方法分享时间序列插值方法在时序预测中扮演着重要的角色。
在实际应用中,由于各种原因,时间序列数据往往会出现缺失值的情况,这就需要我们对时间序列进行插值处理以便进行准确的预测。
本文将分享几种常用的时间序列插值方法,希望能对时序预测的实践有所帮助。
1. 线性插值线性插值是最简单、最直接的插值方法之一。
它的原理是根据已知的两个点,通过线性函数来估计缺失值点的取值。
假设已知的两个点为$(x_0, y_0)$和$(x_1, y_1)$,那么在$x_0$和$x_1$之间的任意一点$x$处的估计值$y$可以通过以下公式计算得到:$$y = y_0 + \frac{(x - x_0)(y_1 - y_0)}{x_1 - x_0}$$线性插值方法简单易行,但在实际应用中往往效果一般,因为它假设了被插值的数据点之间是线性关系,忽略了时间序列数据的趋势和周期性。
2. 拉格朗日插值拉格朗日插值是一种基于拉格朗日多项式的插值方法。
它的原理是通过已知的$n$个点$(x_0, y_0), (x_1, y_1), ..., (x_n, y_n)$构造一个$n-1$次的插值多项式$P_n(x)$,然后利用该多项式来估计缺失值点的取值。
假设要估计的点为$x$,则$P_n(x)$可以通过以下公式计算得到:$$P_n(x) = \sum_{i=0}^{n} y_i \prod_{j \neq i} \frac{x - x_j}{x_i- x_j}$$拉格朗日插值方法在理论上是一种精确的插值方法,它可以通过已知的点完全确定一个插值多项式,并且能够保证通过已知点时的取值与真实值完全一致。
但是在实际应用中,由于插值多项式的次数往往较高,容易出现龙格现象,导致插值结果的不稳定性。
3. 样条插值样条插值是一种基于样条函数的插值方法。
它的原理是将整个插值区间分成若干小段,每一小段内插值函数为一个低次多项式,然后通过对相邻小段的插值函数做一定的连接条件来得到一个整体的插值函数。
第2章-插值法(Hermite插值,样条插值)

2.5 埃尔米特插值法
Newton插值和Lagrange插值虽然构造比较简单,但都存 在插值曲线在节点处有尖点,不光滑,插值多项式在节 点处不可导等缺点
问题的提出: 不少实际问题不但要求在节点上函数值相等,而且还要 求它的导数值也相等(即要求在节点上具有一阶光滑度), 甚至要求高阶导数也相等,满足这种要求的插值多项式就是 埃尔米特(Hermite)插值多项式。下面只讨论函数值与导数 值个数相等的情况。
由 j ( x j ) 1 ,可得
Cj
1 ( x j x0 ) 2 ( x j x1 ) 2 ( x j x j 1 ) 2 ( x j x j 1 ) 2 ( x j xn ) 2
故
j ( x) ( x x j )
( x x0 ) 2 ( x x1 ) 2 ( x x j 1 ) 2 ( x x j 1 ) 2 ( x xn ) 2 ( x j x0 ) 2 ( x j x1 ) 2 ( x j x j 1 ) 2 ( x j x j 1 ) 2 ( x j xn ) 2
( x x j )l j 2 ( x)
2016/8/14 6
(ii)由条件(1)可知,x0 , x1,, x j 1, x j 1,, xn都是 j ( x)的二重根,令
j ( x) C j (ax b)( x x0 ) 2 ( x x1 ) 2 ( x x j 1 ) 2 ( x x j 1 ) 2 ( x xn ) 2
17
即
x x1 x x0 2 0 ( x) (1 2l1 ( x)) l0 ( x) 1 2 x x x0 x1 1 0
Hermite插值多项式

( xi1
4
xi )2
因此
|
Ri ( x) |
(
x i
+1
8
xi )2
max |
xi x xi1
f ( x) |
于是在[a,b]上,| R( x) ||
f
( x)
L1( x) |
h2 8
M2
优点:计算简单; 适用于光滑性要求不高的插值问题。
缺点:分段插值函数只能保证连续性, 失去了原函数的光滑性。
(1) L1(x) 在每个子区间[xi , xi+1](i=0,1,2,,n-1)上是
线性插值多项式;
(2) L1(xi ) yi , i=0,1,2,…,n (3) L1(x) 在区间[a , b]上连续; 则称 L1(x)是f(x)在[a ,b]上的分段线性插值函数。
2.分段线性插值函数的表达式
2
两点三次Hermit插值(续1)
5
直接设 H3 (x) ax3 bx2 cx d
待定系数法求出,但不易推广到高次。
3
基函数法:
令H3(x) y00 (x) y11(x) y00 (x) y11(x)
为使H3(x)是一个次数3的多项式且满足插值条件
H3 (xi ) yi , H3(xi ) yi i 0,1
并在每个 xi , xi子1区间上构造插值多项式,然后把 它们装配在一起,作为整个区间 上a,的b插值函数。
二、分段线性插值
1.问题的提法
定义 设f(x)是定义在[a,b]上的函数,在节点 a= x0< x1<x2<…<xn-1<xn=b,
的函数值为 y0 , y1 ,y2 ,…yn-1 ,yn ,若函数 L1(x)满足条件
插值算法——精选推荐
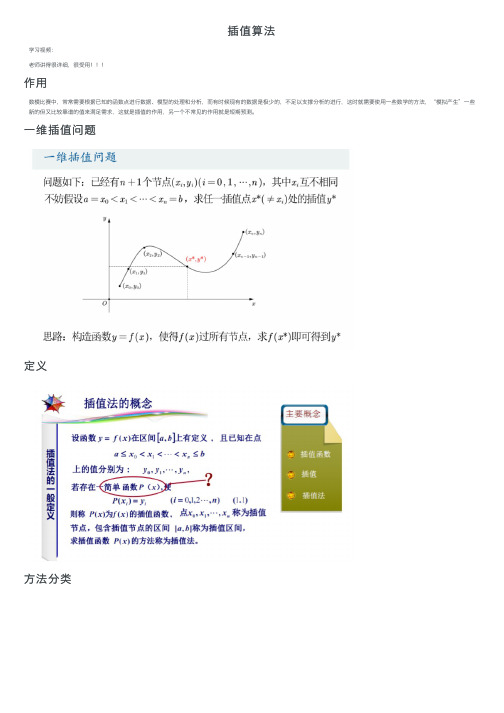
插值算法学习视频:⽼师讲得很详细,很受⽤!!!作⽤数模⽐赛中,常常需要根据已知的函数点进⾏数据、模型的处理和分析,⽽有时候现有的数据是极少的,不⾜以⽀撑分析的进⾏,这时就需要使⽤⼀些数学的⽅法,“模拟产⽣”⼀些新的但⼜⽐较靠谱的值来满⾜需求,这就是插值的作⽤,另⼀个不常见的作⽤就是短期预测。
⼀维插值问题定义⽅法分类本⽂重点介绍数学建模常⽤的两种⽅法:三次样条插值和分段三次埃尔⽶特插值插值多项式原理拉格朗⽇插值法⽅法主要有拉格朗⽇插值法,具体不介绍,它会出现龙波现象(在两端处波动极⼤,产⽣明显的震荡)。
但觉得可以出⼀个ACM题。
分段线性插值插值多项式次数⾼精度未必显著提⾼插值多项式次数越⾼摄⼊误差可能显著增⼤如何提⾼插值精度呢采⽤分段低次插值是⼀种办法概念⽜顿插值法评价与拉格朗⽇插值法相⽐,⽜顿插 值法的计算过程具有继承性。
(⽜顿插值法每次插值只和前n项 的值有关,这样每次只要在原来 的函数上添加新的项,就能够产 ⽣新的函数) 但是⽜顿插值也存在龙格现象的 问题。
致命缺点上⾯讲的两种插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值,⽽这种插值多项式却不能全⾯反映被插值函数的性态。
然⽽在许多实际问题中,不仅要求插值函数与被插值函数在所有节点处有相同的函数值,它也需要在⼀个或全部节点上插值多项式与被插函数有相同的低阶甚⾄⾼阶的导数值。
对于这些情况,拉格朗⽇插值和⽜顿插值都不能满⾜埃尔⽶特(Hermite)插值概念保持播值曲线在节点处有切线(光滑),使插值函数和被插函数的密和程度更好。
不但要求在节点上的函数值相等,⽽且还要求对应的导数值也相等,甚⾄要求 ⾼阶导数也相等,满⾜这种要求的插值多项式就是埃尔⽶特插值多项式。
缺点与改进直接使⽤Hermite插值得到的多项式次数较⾼,也存在着龙格现象, 因此在实际应⽤中,往往使⽤分段三次Hermite插值多项式(PCHIP)。
Matlab有内置的函数(实现过程已经帮我们封装好了,会调⽤就⾏了): p = pchip(x,y,new_x)x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插⼊处对应的横坐标三次样条插值Matlab有内置的函数: p = spline(x,y,new_x)x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插⼊处对应的横坐标代码% 分段三次埃尔⽶特插值x = -pi:pi; y = sin(x);new_x = -pi:0.1:pi;p = pchip(x,y,new_x);figure(1); % 在同⼀个脚本⽂件⾥⾯,要想画多个图,需要给每个图编号,否则只会显⽰最后⼀个图哦~plot(x, y, 'o', new_x, p, 'r-')% plot函数⽤法:% plot(x1,y1,x2,y2)% 线⽅式: - 实线 :点线 -. 虚点线 - - 波折线% 点⽅式: . 圆点 +加号 * 星号 x x形 o ⼩圆% 颜⾊: y黄; r红; g绿; b蓝; w⽩; k⿊; m紫; c青% 三次样条插值和分段三次埃尔⽶特插值的对⽐x = -pi:pi;y = sin(x);new_x = -pi:0.1:pi;p1 = pchip(x,y,new_x); %分段三次埃尔⽶特插值p2 = spline(x,y,new_x); %三次样条插值figure(2);plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')legend('样本点','三次埃尔⽶特插值','三次样条插值','Location','SouthEast') %标注显⽰在东南⽅向% 说明:% LEGEND(string1,string2,string3, …)% 分别将字符串1、字符串2、字符串3……标注到图中,每个字符串对应的图标为画图时的图标。
【插值】插值方法原理详解

【插值】插值⽅法原理详解插值问题详解注明出处:1.我在具体的应⽤(如数学建模竞赛)中,常常需要根据已知的函数点进⾏数据、模型的处理和分析,⽽通常情况下现有的数据是极少的,不⾜以⽀撑分析的进⾏,这时就需要使⽤⼀些数学的⽅法,“模拟产⽣”⼀些新的但⼜⽐较靠谱的值来满⾜需求。
⼀般来说,我可以去调⽤MATLAB或者Python的⼀些库函数来实现,这个功能就是“插值”。
然⽽这有个⾮常让我苦恼的问题,我可以从⼿册上知道这个函数实现“三次多项式插值”,那个函数实现“样条插值”.......但究竟在什么情况下使⽤何种插值⽅法呢?若不对插值⽅法做深⼊的学习,这个疑团恐难以解开。
于是,在这个原因驱动之下,我决定对常见、常⽤的插值⽅法⽐较深⼊的学习⼀下。
我希望读者也是基于这个原因来读这篇⽂章,希望我的总结能对你有所帮助。
2. 插值简单讲,插值就是根据已知数据点(条件),来预测未知数据点值得⽅法。
具体来说,假如你有n个已知条件,就可以求⼀个n-1次的插值函数P(x),使得P(x)接近未知原函数f(x),并由插值函数预测出你需要的未知点值。
⽽⼜n个条件求n-1次P(x)的过程,实际上就是求n元⼀次线性⽅程组。
代数插值代数插值就是多项式插值,即所求插值函数为多项式函数:显然,系数a0.....an为所求。
如果已知n+1个条件,需要n+1个⽅程组如下:这时,便可以⽤待定系数求解。
⼀、泰勒插值⾸先需要回顾泰勒多项式:因⽽,泰勒插值的条件就是已知0-n阶的导数:余项:满⾜n阶可导这个条件实在是太苛刻,导致实际上泰勒插值并不常⽤,下⾯介绍拉格朗⽇插值与⽜顿插值,这两种⽅法在本质上是相同的。
⼆、拉格朗⽇插值上⾯引论中提到,⼀般来说多项式插值就是求n-1个线性⽅程的解,拉格朗⽇插值即是基于此思想。
拉格朗⽇创造性的避开的⽅程组求解的复杂性,引⼊“基函数”这⼀概念,使得快速⼿⼯求解成为可能。
DEF:求作<=n 次多项式 p n(x),使满⾜条件p n(x i)= y i,i = 0,1,…,n.这就是所谓拉格朗⽇( Lagrange)插值先以⼀次(线性)为例,介绍基函数⽅法求解,再推⼴到任意次多项式:已知x0,x1;y0,y1,求P(x)= a0 + a1x,使得P(x)过这两点。
数值分析中常用的插值方法

数值分析中常用的插值方法在数值计算中,许多问题都可以用插值方法来近似求解,比如曲线拟合、函数逼近和图像重建等。
插值方法是指在已知数据点的情况下,通过一些数值计算技巧,在每个数据点处构造一个多项式函数,使得该函数在每个数据点处都能通过数据点。
在数据点之间计算函数值时,就可以使用这个多项式函数进行估算。
接下来,我们就来详细介绍一些常见的插值方法。
一、拉格朗日插值法拉格朗日插值法是一个经典的插值方法,它的思想是通过给定的数据点,构造一个经过这些点的多项式函数进行逼近。
具体来讲,拉格朗日插值法会首先构造一个基函数,该函数满足只在其对应的数据点处等于1,其余的数据点处等于0。
然后,根据基函数和数据点,构造一个多项式函数,使得该函数在每个数据点处都能通过数据点。
最终得到的多项式函数就是插值函数。
优点:简单易懂,使用较为广泛。
缺点:多项式次数较高时造成的误差会较大,且在数据点密集的区域可以出现龙格现象,使得插值函数在某些区间内呈现大幅度振荡。
二、牛顿插值法牛顿插值法是一种递推式的插值方法,它通过利用已知的数据点和前面已经计算出来的差商,得到一个逐步逼近的插值函数。
具体来讲,牛顿插值法会先将已知的数据点连成一条曲线,然后逐个向这条曲线添加新的数据点,每次添加一个新的数据点后,将差商计算出来并加入到之前的差商序列中,最终得到一个多项式函数,它在每个数据点处都能通过数据点。
牛顿插值法的优缺点与拉格朗日插值法相似,但是由于牛顿插值法是递推式的,可以方便的添加新的数据点,因此在数据点多变的情况下,牛顿插值法具有很大的优势。
三、分段插值法分段插值法是一种将插值区间划分为多个子区间的插值方法,在每个子区间内使用插值方法进行插值,然后将所有子区间内的插值函数拼接起来,得到最终的插值函数。
分段插值法主要分为两种:线性分段插值和三次样条插值。
1.线性分段插值线性分段插值的思路很简单,即在每个数据点处构造两条直线,在数据点之间的区间内使用一条直线作为插值函数。
常见插值算法--拉格朗日插值、三次卷积插值、三次样条插值、兰克索斯插值

常见插值算法--拉格朗⽇插值、三次卷积插值、三次样条插值、兰克索斯插值写在前⾯本⽂简单介绍了⼏种常见的插值算法并附带了相应的python代码,本⽂公式使⽤latex编写,如有错误欢迎评论指出,如果谁知道如何修改latex字号也欢迎留⾔关于⼀维、⼆维和多维插值三次卷积插值、拉格朗⽇两点插值(线性插值)、兰克索斯插值在⼆维插值时改变x和y⽅向的计算顺序不影响最终结果,这三个也是图像缩放插值时常⽤的插值算法,⽽其他插值在改变计算顺序时会产⽣明显差异,多维的情况笔者没有尝试,读者可以⾃⾏尝试或推导最近邻插值法(Nearest Neighbour Interpolation)在待求像素的四邻像素中,将距离待求像素最近的像素值赋给待求像素p_{11}p_{12}pp_{21}p_{22}python代码1def NN_interpolation(srcImg, dstH, dstW):2 scrH, scrW, _ = srcImg.shape3 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8)4for i in range(dstH - 1):5for j in range(dstW - 1):6 scrX = round(i * (scrH / dstH))7 scrY = round(j * (scrW / dstW))8 dstImg[i, j] = srcImg[scrX, scrY]9return dstImg拉格朗⽇插值(Lagrange Interpolation)拉格朗⽇插值法需要找到k个p_i(x)函数,使得每个函数分别在在x_i处取值为1,其余点取值为0,则y_ip_i(x)可以保证在x_i处取值为y_i,在其余点取值为0,因此L_k(x)能恰好经过所有点,这样的多项式被称为拉格朗⽇插值多项式,记为L_k(x)=\sum_{i=1}^ky_ip_i(x)p_i(x)=\prod_{j \neq i}^{1 \leq j \leq k}\frac{x-x_j}{x_i-x_j}以四点即三次图像插值为例,因为横坐标间隔为1,则设四个点横坐标为-1、0、1和2,可得p_1(x)、p_2(x)、p_3(x)和p_4(x)假设y_1、y_2、y_3和y_4分别为1、2、-1、4,则可得拉格朗⽇函数如下图所⽰,待插值点横坐标范围为[0,1]在K=2时在k=2时,也被称为线性插值通⽤公式p_1=\frac{x-x_2}{x_1-x_2}p_2=\frac{x-x_1}{x_2-x_1}\begin{align} L_2x &= p_1y_1+p_2y_2 \nonumber \\ &= \frac{x-x_2}{x_1-x_2}y_1 + \frac{x-x_1}{x_2-x_1}y_2 \nonumber \end{align}图像插值像素分布如图所⽰p_{11}p_{12}pp_{21}p_{22}即当x_{i+1}=x_i+1时,设p与p_{11}的横纵坐标差分别为dx和dy\begin{align} L_2x &= \frac{x-x_2}{x_1-x_2}y_1 + \frac{x-x_1}{x_2-x_1}y_2 \nonumber \\ &= (x_2-x)y_1+(x-x_1)y_2 \nonumber \\ &= (1-dx)y_1+dxy_2 \nonumber \\ &= (y_2-y_1)dx+y_1 \nonumber \end{align}L_2'x=y_2-y_1在K=3时通⽤公式p_1=\frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}p_2=\frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}p_3=\frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}\begin{align} L_3x &= p_1y_1+p_2y_2+p_3y_3 \nonumber \\ &= \frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}y_1+\frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}y_2+\frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}y_3 \nonumber \end{align}图像插值像素分布如图所⽰p_{11}p_{12}p_{13}p_{21}p_{22}p_{23}pp_{31}p_{32}p_{33}即当x_{i+1}=x_i+1时,设p与p_{11}的横纵坐标差分别为dx和dy\begin{align} L_3x &= \frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}y_1 + \frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}y_2 + \frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}y_3 \nonumber \\ &= \frac{-dx(1-dx)}{(-1)\cdot(-2)}y_1 + \frac{-(1+dx)(1-dx)}{1\cdot(-1)}y_2 + \frac{(1+dx)dx}{2\cdot 1}y_3 \nonumber \\ &= (\frac{1}{2}d^2x-\frac{1}{2}dx)y_1 - (d^2x-1)y_2 + (\frac{1}{2}d^2x+\frac{1}{2}dx)y_3 \nonumber \\ &= d^2x(\frac{1}{2}y_1-y_2+\frac{1}{2}y_3)+dx(-\frac{1}{2}y_1+\frac{1}{2}y_3)+y_2 \nonumber \end{align}L_3'x=dx(y_1-2y_2+y_3)+(\frac{1}{2}y_3-\frac{1}{2}y_1)在K=4时通⽤公式p_1=\frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}\frac{x-x_4}{x_1-x_4}p_2=\frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}\frac{x-x_4}{x_2-x_4}p_3=\frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}\frac{x-x_4}{x_3-x_4}p_4=\frac{x-x_1}{x_4-x_1}\frac{x-x_2}{x_4-x_2}\frac{x-x_3}{x_4-x_3}\begin{align} L_4x &= p_1y_1+p_2y_2+p_3y_3+p_4y_4 \nonumber \\ &= \frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}\frac{x-x_4}{x_1-x_4}y_1 + \frac{x-x_1}{x_2-x_1}\frac{x-x_3} {x_2-x_3}\frac{x-x_4}{x_2-x_4}y_2 + \frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}\frac{x-x_4}{x_3-x_4}y_3 + \frac{x-x_1}{x_4-x_1}\frac{x-x_2}{x_4-x_2}\frac{x-x_3}{x_4-x_3}y_4\nonumber \end{align}图像插值p_{11}p_{12}p_{13}p_{14}p_{21}p_{22}p_{23}p_{24}pp_{31}p_{32}p_{33}p_{34}p_{41}p_{42}p_{43}p_{44}即当x_{i+1}=x_i+1时,设p与p_{11}的横纵坐标差分别为dx和dy\begin{align} L_4x &= \frac{x-x_2}{x_1-x_2}\frac{x-x_3}{x_1-x_3}\frac{x-x_4}{x_1-x_4}y_1 + \frac{x-x_1}{x_2-x_1}\frac{x-x_3}{x_2-x_3}\frac{x-x_4}{x_2-x_4}y_2 + \frac{x-x_1}{x_3-x_1}\frac{x-x_2}{x_3-x_2}\frac{x-x_4}{x_3-x_4}y_3 + \frac{x-x_1}{x_4-x_1}\frac{x-x_2}{x_4-x_2}\frac{x-x_3}{x_4-x_3}y_4 \nonumber \\ &= \frac{dx[-(1-dx)][-(2-dx)]}{(-1)\cdot(-2)\cdot(-3)}y_1 + \frac{(1+dx)[-(1-dx)][-(2-dx)]}{1\cdot(-1)\cdot(-2)}y_2 + \frac{(1+dx)dx[-(2-dx)]}{2\cdot 1\cdot(-1)}y_3 + \frac{(1+dx)dx[-(1-dx)]}{3\cdot 2\cdot 1}y_4 \nonumber \\ &= \frac{d^3x-3d^2x+2dx}{-6}y1 + \frac{d^3x-2d^2x-dx+2}{2}y_2 + \frac{d^3x-d^2x-2dx}{-2}y_3 + \frac{d^3x-dx}{6}y_4 \nonumber \\ &= d^3x(-\frac{1}{6}y_1+\frac{1}{2}y_2-\frac{1} {2}y_3+\frac{1}{6}y_4)+d^2x(\frac{1}{2}y_1-y_2+\frac{1}{2}y_3)+dx(-\frac{1}{3}y_1-\frac{1}{2}y_2+y_3-\frac{1}{6}y_4)+y_2 \nonumber \end{align}\begin{align} L_4'x &= d^2x(-\frac{1}{2}y_1+\frac{3}{2}y_2-\frac{3}{2}y_3+\frac{1}{2}y_4)+dx(y_1-2y_2+y_3)+(-\frac{1}{3}y_1-\frac{1}{2}y_2+y_3-\frac{1}{6}y_4) \nonumber \\ &= -[\frac{1}{2}d^2x(y_1-3y_2+3y_3-y_4)-dx(y_1-2y_2+y_3)+\frac{1}{6}(2y_1+3y_2-6y_3+y_4)] \nonumber \end{align}python代码插值核计算的时候乘法和加减法计算的顺序不同可能会导致结果存在细微的差异,读者可以⾃⾏研究⼀下1class BiLagrangeInterpolation:2 @staticmethod3def LagrangeInterpolation2(x, y1, y2):4 f1 = 1 - x5 f2 = x6 result = y1 * f1 + y2 * f27return result89 @staticmethod10def LagrangeInterpolation3(x, y1, y2, y3):11 f1 = (x ** 2 - x) / 2.012 f2 = 1 - x ** 213 f3 = (x ** 2 + x) / 2.014 result = y1 * f1 + y2 * f2 + y3 * f315return result1617 @staticmethod18def LagrangeInterpolation4(x, y1, y2, y3, y4):19 f1 = - (x ** 3 - 3 * x ** 2 + 2 * x) / 6.020 f2 = (x ** 3 - 2 * x ** 2 - x + 2) / 2.021 f3 = - (x ** 3 - x ** 2 - 2 * x) / 2.022 f4 = (x ** 3 - x) / 6.023 result = y1 * f1 + y2 * f2 + y3 * f3 + y4 * f424return result2526def biLag2_2(self, srcImg, dstH, dstW):27 dstH, dstW = int(dstH), int(dstW)28 srcH, srcW, _ = srcImg.shape29 srcImg = np.pad(srcImg, ((1, 1), (1, 1), (0, 0)), 'edge')30 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8)31for dstY in range(dstH):32for dstX in range(dstW):33for channel in [0, 1, 2]:34# p11 p1235# p36# p21 p2237# 储存为 p(y, x)38 p = [dstY * srcH / dstH, dstX * srcW / dstW]39 p11 = [math.floor(p[0]), math.floor(p[1])]40 p12 = [p11[0], p11[1] + 1]4142 p21 = [p11[0] + 1, p11[1]]43 p22 = [p21[0], p12[1]]4445 diff_y, diff_x = p[0] - p11[0], p[1] - p11[1]46 r1 = grangeInterpolation2(diff_x, srcImg[p11[0], p11[1], channel], srcImg[p12[0], p12[1], channel])47 r2 = grangeInterpolation2(diff_x, srcImg[p21[0], p21[1], channel], srcImg[p22[0], p22[1], channel])4849 c = grangeInterpolation2(diff_y, r1, r2)5051 dstImg[dstY, dstX, channel] = np.clip(c, 0, 255)52return dstImg5354def biLag3_3(self, srcImg, dstH, dstW):55 dstH, dstW = int(dstH), int(dstW)56 srcH, srcW, _ = srcImg.shape57 srcImg = np.pad(srcImg, ((1, 1), (1, 1), (0, 0)), 'edge')58 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8)59for dstY in range(dstH):60for dstX in range(dstW):61for channel in [0, 1, 2]:62# p11 p12 p1363#64# p21 p22 p2365# p66# p31 p32 p3367# 储存为 p(y, x)68 p = [dstY * srcH / dstH, dstX * srcW / dstW]69 p22 = [math.floor(p[0]), math.floor(p[1])]70 p21 = [p22[0], p22[1] - 1]71 p23 = [p22[0], p22[1] + 1]7273 p11 = [p21[0] - 1, p21[1]]74 p12 = [p11[0], p22[1]]75 p13 = [p11[0], p23[1]]7677 p31 = [p21[0] + 1, p21[1]]78 p32 = [p31[0], p22[1]]79 p33 = [p31[0], p23[1]]8081 diff_y, diff_x = p[0] - p22[0], p[1] - p22[1]82 r1 = grangeInterpolation3(diff_x, srcImg[p11[0], p11[1], channel], srcImg[p12[0], p12[1], channel], srcImg[p13[0], p13[1], channel])83 r2 = grangeInterpolation3(diff_x, srcImg[p21[0], p21[1], channel], srcImg[p22[0], p22[1], channel], srcImg[p23[0], p23[1], channel])84 r3 = grangeInterpolation3(diff_x, srcImg[p31[0], p31[1], channel], srcImg[p32[0], p32[1], channel], srcImg[p33[0], p33[1], channel]) 8586 c = grangeInterpolation3(diff_y, r1, r2, r3)8788 dstImg[dstY, dstX, channel] = np.clip(c, 0, 255)89return dstImg9091def biLag4_4(self, srcImg, dstH, dstW):92 dstH, dstW = int(dstH), int(dstW)93 srcH, srcW, _ = srcImg.shape94 srcImg = np.pad(srcImg, ((1, 2), (1, 2), (0, 0)), 'edge')95 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8)96for dstY in range(dstH):97for dstX in range(dstW):98for channel in [0, 1, 2]:99# p11 p12 p13 p14100#101# p21 p22 p23 p24102# p103# p31 p32 p33 p34104#105# p41 p42 p43 p44106# 储存为 p(y, x)107 p = [dstY * srcH / dstH, dstX * srcW / dstW]108 p22 = [math.floor(p[0]), math.floor(p[1])]109 p21 = [p22[0], p22[1] - 1]110 p23 = [p22[0], p22[1] + 1]111 p24 = [p22[0], p22[1] + 2]112113 p11 = [p21[0] - 1, p21[1]]114 p12 = [p11[0], p22[1]]115 p13 = [p11[0], p23[1]]116 p14 = [p11[0], p24[1]]117118 p31 = [p21[0] + 1, p21[1]]119 p32 = [p31[0], p22[1]]120 p33 = [p31[0], p23[1]]121 p34 = [p31[0], p24[1]]122123 p41 = [p21[0] + 2, p21[1]]124 p42 = [p41[0], p22[1]]125 p43 = [p41[0], p23[1]]126 p44 = [p41[0], p24[1]]127128 diff_y, diff_x = p[0] - p22[0], p[1] - p22[1]129 r1 = grangeInterpolation4(diff_x, srcImg[p11[0], p11[1], channel], srcImg[p12[0], p12[1], channel], srcImg[p13[0], p13[1], channel], srcImg[p14[0], p14[1], channel]) 130 r2 = grangeInterpolation4(diff_x, srcImg[p21[0], p21[1], channel], srcImg[p22[0], p22[1], channel], srcImg[p23[0], p23[1], channel], srcImg[p24[0], p24[1], channel]) 131 r3 = grangeInterpolation4(diff_x, srcImg[p31[0], p31[1], channel], srcImg[p32[0], p32[1], channel], srcImg[p33[0], p33[1], channel], srcImg[p34[0], p34[1], channel]) 132 r4 = grangeInterpolation4(diff_x, srcImg[p41[0], p41[1], channel], srcImg[p42[0], p42[1], channel], srcImg[p43[0], p43[1], channel], srcImg[p44[0], p44[1], channel]) 133134 c = grangeInterpolation4(diff_y, r1, r2, r3, r4)135136 dstImg[dstY, dstX, channel] = np.clip(c, 0, 255)137return dstImg三次卷积插值法(Cubic Convolution Interpolation)使⽤上图中的卷积核进⾏加权平均计算,卷积核为u(s),四个等距(距离为1)的采样点记为x_0、x_1、x_2和x_3,采样数值记为y_0、y_1、y_2和y_3,且保证四个点均在[-2,2]区间上,计算得到g(x),假设y_1、y_2、y_3和y_4分别为1、2、-1、4,则可得三次卷积插值函数如下图所⽰,待插值点横坐标范围为[0,1]公式推导设u(s)=\begin{cases} A_1|s|^3+B_1|s|^2+C_1|s|+D_1, &0<|s|<1 \\ A_2|s|^3+B_2|s|^2+C_2|s|+D_2, &1<|s|<2 \\ 1, &s=0 \\ 0, &otherwise \end{cases}\because函数在s=0,1,2处连续\therefore\begin{cases} 1=u(0^+)=D_1 \\ 0=u(1^-)=A_1+B_1+C_1+D_1 \\ 0=u(1^+)=A_2+B_2+C_2+D_2 \\ 0=u(2^-)=8A_2+4B_2+2C_2+D_2 \end{cases} (1)\because函数在s=0,1,2处导函数连续\therefore\begin{cases} u'(0^-)=u'(0+) \\ u'(1^-)=u'(1+) \\ u'(2^-)=u'(2+)\end{cases} \Rightarrow \begin{cases} -C_1=C_1 \\ 3A_1+2B_1+C_1=3A_2+2B_2+C_2\\ 12A_2+4B_2+C+2=0 \end{cases} ~~~~ (2)联⽴⽅程组(1)(2),设A_2=a,解得\begin{cases} A_1=a+2 \\ B_1=-(a+3) \\ C_1=0 \\ D_1=1 \\ A_2=a \\ B_2=-5a \\ C_2=8a \\ D_2=-4a \end{cases}\Rightarrow u(s)=\begin{cases} (a+2)|s|^3-(a+3)|s|^2+1, &0<|s|<1 \\ A_2|s|^3+B_2|s|^2+C_2|s|+D_2, &1<|s|<2\\ 1, &s=0 \\ 0, &otherwise \end{cases}\because g(x)=\sum_kC_ku(s+j-k), ~~~~k=j-1,j, j+1,j+2且0<s<1⼜\because \begin{cases}\begin{align} u(s+1)&=as^3-2as^2+as \nonumber \\ u(s)&=(a+2)s^3-(a+3)s^2+1 \nonumber \\ u(s-1)&=-(a+2)s^3+(2a+3)s^2-as \nonumber \\ u(s-2)&=-as^3+as^2 \nonumber \end{align}\end{cases}\begin{align} \therefore g(x) &= C_{j-1}u(s+1)+C_{j}u(s)+C_{j+1}u(s-1)+C_{j+2}u(s-2) \nonumber \\ &= C_{j-1}(as^3-2as^2+as)+C_j[(a+2)s^3-(a+3)s^2+1]+C_{j+1}[-(a+2)s^3+ (2a+3)s^2-as]+C_{j+2}[-a^3+as^2] \nonumber \\ &= s^3[aC_{j-1}+(a+2)C_j-(a+2)C_{j+1}-aC_{j+2}]+s^2[-2aC_{j-1}-(a+3)C_j+(2a+3)C_{j+1}+aC_{j+2}]+s[aC_{j-1}-aC_{j+1}]+C_j \nonumber \end{align} ~~(3)f在x_j处泰勒展开得到f(x)=f(x_j)+f'(x_j)(x-x_j)+\frac{1}{2}f''(x_j)(x-x_j)^2+\cdots\therefore \begin{cases} f(x_{j+1})=f(x_j)+f'(x_j)(x_{j+1}-x_j)+\frac{1}{2}f''(x_j)(x_{j+1}-x_j)^2+\cdots \\ f(x_{j+2})=f(x_j)+f'(x_j)(x_{j+2}-x_j)+\frac{1}{2}f''(x_j)(x_{j+2}-x_j)^2+\cdots \\ f(x_{j-1})=f(x_j)+f'(x_j)(x_{j-1}-x_j)+\frac{1}{2}f''(x_j)(x_{j-1}-x_j)^2+\cdots \end{cases}令x_{j+1}-x_j=h\because x_{i+1}=x_i+1\therefore x_{j+2}-x_j=2h,x_{j-1}-x_j=-h\therefore \begin{cases} f(x_{j+2})=f(x_j)+2f'(x_j)h+2f''(x_j)h^2+\cdots \\ f(x_{j+1})=f(x_j)+f'(x_j)h+\frac{1}{2}f''(x_j)h^2+\cdots \\ f(x_{j-1})=f(x_j)-f'(x_j)h+\frac{1}{2}f''(x_j)h^2+\cdots \end{cases}\therefore \begin{cases} c_{j-1}=f(x_j)-f'(x_j)h+\frac{1}{2}f''(x_j)h^2+o(h^3) \\ c_j=f(x_j) \\ c_{j+1}=f(x_j)+f'(x_j)h+\frac{1}{2}f''(x_j)h^2+o(h^3)\\ c_{j+2}=f(x_j)+2f'(x_j)h+2f''(x_j)h^2+o(h^3) \end{cases} ~~ (4)将(4)代⼊(3),得g(x)=-(2a+1)[2hf'(x_j)+h^2f''(x_j)]s^3+[(6a+3)hf'(x_j)+\frac{4a+3}{2}h^2f''(x_j)]s^2-2ahf'(x_j)s+f(x_j)+o(h^3)\because h=1,s=x-x_J\therefore sh=x-x_j\begin{align}\therefore f(x)&= f(x_j)+f'(x_j)(x-x_j)+\frac{1}{2}f''(x_j)(x-x_j)^2+o(h^3) \nonumber \\ &= f(x_j)+f'(x_j)sh+\frac{1}{2}f''(x_j)s^2h^2+o(h^3) \nonumber \end{align}\therefore f(x)-g(x)=(2a+1)[2hf'(x_j)+h^2f''(x_j)]s^3-(2a+1)[3hf'(x_j)+h^2f''(x_j)]s^2+[(2a+1)hf'(x_j)]s+o(h^3)\because 期望f(x)-g(x)趋于0\therefore 2a+1=0 \Rightarrow a=-\frac{1}{2}\therefore u(s)=\begin{cases} \frac{3}{2}|s|^3-\frac{5}{2}|s|^2+1, &0<|s|<1 \\ -\frac{1}{2}|s|^3+\frac{5}{2}|s|^2-4|s|+2, &1<|s|<2 \\ 1, &s=0 \\ 0, &otherwise \end{cases}\therefore g(s)=s^3[-\frac{1}{2}c_{j-1}+\frac{3}{2}c_j-\frac{3}{2}c_{j+1}+\frac{1}{2}c_{j+2}]+s^2[c_{j-1}-\frac{5}{2}c_j+2c_{j+1}-\frac{1}{2}c_{j+2}]+s[-\frac{1}{2}c_{j-1}+\frac{1} {2}c_{j+1}]+c_j图像插值p_{11}p_{12}p_{13}p_{14}p_{21}p_{22}p_{23}p_{24}pp_{31}p_{32}p_{33}p_{34}p_{41}p_{42}p_{43}p_{44}python代码1class BiCubicConvInterpolation:2 @staticmethod3def CubicConvInterpolation1(p0, p1, p2, p3, s):4# ⽤g(s)公式计算,已经将四个u(s)计算完毕并整理5# as^3 + bs^2 + cs + d6 a = 0.5 * (-p0 + 3.0 * p1 - 3.0 * p2 + p3)7 b = 0.5 * (2.0 * p0 - 5.0 * p1 + 4.0 * p2 - p3)8 c = 0.5 * (-p0 + p2)9 d = p110return d + s * (c + s * (b + s * a))1112 @staticmethod13def CubicConvInterpolation2(s):14# ⽤u(s)公式计算15 s = abs(s)16if s <= 1:17return 1.5 * s ** 3 - 2.5 * s ** 2 + 118elif s <= 2:19return -0.5 * s ** 3 + 2.5 * s ** 2 - 4 * s + 220else:21return 02223def biCubic1(self, srcImg, dstH, dstW):24# p11 p12 p13 p1425#26# p21 p22 p23 p2427# p28# p31 p32 p33 p3429#30# p41 p42 p43 p4431 dstH, dstW = int(dstH), int(dstW)32 scrH, scrW, _ = srcImg.shape33 srcImg = np.pad(srcImg, ((1, 1), (1, 1), (0, 0)), 'edge')34 dstImg = np.zeros((dstH, dstW, 1), dtype=np.uint8)35for dstY in range(dstH):36for dstX in range(dstW):37for channel in [0]:38 y = dstY * scrH / dstH39 x = dstX * scrW / dstW40 y1 = math.floor(y)41 x1 = math.floor(x)4243 array = []44for i in [-1, 0, 1, 2]:45 temp = self.CubicConvInterpolation1(srcImg[y1 + i, x1 - 1, channel],46 srcImg[y1 + i, x1, channel],47 srcImg[y1 + i, x1 + 1, channel],48 srcImg[y1 + i, x1 + 2, channel],49 x - x1)50 array.append(temp)5152 temp = self.CubicConvInterpolation1(array[0], array[1], array[2], array[3], y - y1)53 dstImg[dstY, dstX, channel] = np.clip(temp, 0, 255)5455return dstImg5657def biCubic2(self, srcImg, dstH, dstW):58# p11 p12 p13 p1459#60# p21 p22 p23 p2461# p62# p31 p32 p33 p3463#64# p41 p42 p43 p4465 dstH, dstW = int(dstH), int(dstW)66 scrH, scrW, _ = srcImg.shape67 srcImg = np.pad(srcImg, ((1, 1), (1, 1), (0, 0)), 'edge')68 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8)69for dstY in range(dstH):70for dstX in range(dstW):71for channel in [0, 1, 2]:72 y = dstY * scrH / dstH73 x = dstX * scrW / dstW74 y1 = math.floor(y)75 x1 = math.floor(x)7677 array = []78for i in [-1, 0, 1, 2]:79 temp = 080for j in [-1, 0, 1, 2]:81 temp += srcImg[y1 + i, x1 + j, channel] * self.CubicConvInterpolation2(x - (x1 + j))82 array.append(temp)8384 temp = 085for i in [-1, 0, 1, 2]:86 temp += array[i + 1] * self.CubicConvInterpolation2(y - (y1 + i))87 dstImg[dstY, dstX, channel] = np.clip(temp, 0, 255)8889return dstImg三次样条插值在n-1个区间上寻找n-1个三次曲线,使其满⾜相邻曲线在端点处值相等、⼀阶导数相等,⼆阶导数相等,在加以边界条件后可得每个曲线的⽅程,然后沿x轴依次偏移对应的距离即可得到插值结果,如仅需要特定范围内的结果,则可以⼤幅减少计算量公式推导设S_i(x)=a_i+b_i(x-x_i)+c_i(x-x_i)^2+d_i(x-x_i)^3, ~~~~i=0,1,...,n-1则 \begin{cases} S_i'(x)=b_i+2c_i(x-x_i)+3d_i(x-x_i)^2\\ S_i''(x)=2c_i+6d_i(x-x_i)\\ S_i'''(x)=6d_i\\ \end{cases} ~~~~i=0,1,...,n-1设h_i(x)=x_{i+1}-x_i,可得\begin{cases} S_i(x)=a_i+b_ih_i+c_ih_i^2+d_ih_i^3\\ S_i'(x)=b_i+2c_ih_i+3d_ih_i^2\\ S_i''(x)=2c_i+6d_ih_i\\ S_i'''(x)=6d_i\\ \end{cases} ~~~~i=0,1,...,n-1\because S_i(x)过点(x_i,y_i)\therefore S_i(x)=a_i=y+i, ~~~~i=0,1,...,n-1 ~~~~~~(1)\because S_i(x)与S_{i+1}(x)在X_{i+1}处相等\therefore S_i(x_{i+1})=S_{i+1}(x_{i+1})\Rightarrow a_i+b_ih_i+c_ih_i^2+d_ih_i^3=y_{i+1}, ~~~~i=0,1,...,n-2~~~~~~(2)\because S_i'(x)与S_{i+1}'(x)在X_{i+1}处相等\therefore S_i'(x)-S_{i+1}'(x)=0\Rightarrow b_i+2c_ih_i+3d_ih_i^2-b_{i+1}=0~~~~~~(3)\because S_i''(x)与S_{i+1}''(x)在X_{i+1}处相等\therefore S_i''(x)-S_{i+1}''(x)=0\Rightarrow 2c_i+6d_ih_i-2c_{i+1}=0, ~~~~i=0,1,...,n-2~~~~~~(4)设m_i=S_i(x_i)=2c_i,即c_i=\frac{1}{2}m_i, ~~~~i=0,1,...,n-1~~~~~~(5)将(5)代⼊(4),得2c_i+6d_ih_i-2c_{i+1}=0\Rightarrow m_i+6h_id_i-m_{i+1}=0\Rightarrow d_i=\frac{m_{i+1}-m_i}{6h_i}, ~~~~i=0,1,...,n-2~~~~~~(6)将(1)(5)(6)代⼊(2),得\begin{align} &a_i+b_ih_i+c_ih_i^2+d_ih_i^3=y_{i+1} \nonumber \\ \Rightarrow&y_i+b_ih_i+\frac{1}{2}m_ih_i^2+\frac{m_{i+1}-m_i}{6h_i}h_i^3=y_{i+1} \nonumber \\\Rightarrow&b_i=\frac{y_{i+1}-y_i}{h_i}-\frac{1}{2}m_ih_i-\frac{1}{6}(m_{i+1}-m_i)h_i \nonumber \\ \Rightarrow&b_i=\frac{y_{i+1}-y_i}{h_i}-\frac{1}{3}m_ih_i-\frac{1}{6}m_{i+1}h_i, ~~~~i=0,1,...,n-2~~~~~~(7) \nonumber \end{align}将(5)(6)(7)代⼊(3),得\begin{align} &\frac{y_{i+1}-y{i}}{h_i}-\frac{1}{3}m_ih_i-\frac{1}{6}m_{i+1}h_i+2\cdot\frac{1}{2}m_ih_i+3\frac{m_{i+1}-m_i}{6h_i}h_i^2-(\frac{y_{i+2}-y_{i+1}}{h_{i+1}}-\frac{1}{3}m_{i+1}h_{i+1}-\frac{1}{6}m_{i+2}h_{i+1})=0 \nonumber \\ \Rightarrow&\frac{y_{i+1}-y{i}}{h_i}-\frac{1}{3}m_ih_i-\frac{1}{6}m_{i+1}h_i+m_ih_i+\frac{1}{2}(m_{i+1}-m_i)h_i-\frac{y_{i+2}-y_{i+1}}{h_{i+1}}+\frac{1}{3}m_{i+1}h_{i+1}+\frac{1}{6}m_{i+2}h_{i+1}=0 \nonumber \\ \Rightarrow&m_ih_i(-\frac{1}{3}+1-\frac{1}{2})+m_{i+1}h_i(-\frac{1}{6}+\frac{1} {2})+\frac{1}{3}m_{i+1}h_{i+1}+\frac{1}{6}m_{i+2}h_{i+1}=\frac{y_{i+2}-y_{i+1}}{h_{i+1}}-\frac{y_{i+1}-y_{i}}{h_{i}} \nonumber \\ \Rightarrow&\frac{1}{6}(m_ih_i+2m_{i+1}h_i+2m_{i+1}h_{i+1}+m_{i+2}h_{i+1})=\frac{y_{i+2}-y_{i+1}}{h_{i+1}}-\frac{y_{i+1}-y_{i}}{h_{i}} \nonumber \\ \Rightarrow&m_ih_i+2m_{i+1}(h_i+h_{i+1})+m_{i+2}h_{i+1}=6(\frac{y_{i+2}-y_{i+1}}{h_{i+1}}-\frac{y_{i+1}-y_{i}}{h_{i}}), ~~~~i=0,1,...,n-2~~~~~~(8) \nonumber \end{align}由(8)可知i=0,1,...,n-2,则有m_0,m_1,...,m_n,需要两个额外条件⽅程组才有解⾃然边界(Natural)m_0=0,m_n=0\begin{bmatrix} \tiny 1 & 0 & 0 & 0 & 0 & \cdots & 0\\ h_0 & 2(h_0+h_1) & h_1 & 0 & 0 & \cdots & 0\\ 0 & h_1 & 2(h_1+h_2) & h_2 & 0 & \cdots & 0\\ 0 & 0 & h_2 & 2(h_2+h_3) & h_3 & \cdots & 0\\ \vdots& & & \ddots & \ddots & \ddots & \vdots\\ 0 & \cdots & & & h_{n-2} & 2(h_{n-2}+h_{n-1}) & h_{n-1}\\ 0 & \cdots & & & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} m_0\\m_1\\m_2\\m_3\\\vdots\\m_{n-1}\\m_n \end{bmatrix}=6\begin{bmatrix} 0\\ \frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\ \frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\ \frac{y_4-y_3}{h_3}-\frac{y_3-y_2}{h_2}\\ \vdots\\ \frac{y_n-y_{n-1}}{h_{n-1}}-\frac{y_{n-1}-y_{n-2}}{h_{n-2}}\\ 0 \end{bmatrix}固定边界(Clamped)\begin{align} &\begin{cases} S_0'(x_0)=A\\ S_{n-1}'(x_n)=B \end{cases} \nonumber \\ \Rightarrow&\begin{cases} b_0=A\\ b_{n-1}+2c_{n-1}h_{n-1}+3d_{n-1}h_{n-1}^2=B\end{cases} \nonumber \\ \Rightarrow&\begin{cases} A=\frac{y_1-y_0}{h_0}-\frac{h_0}{2}m_0-\frac{h_0}{6}(m_1-m_0)\\ B=\frac{y_n-y_{n-1}}{h_{n-1}}-\frac{1}{3}m_{n-1}h_{n-1}+m_{n-1}h_{n-1}+\frac{1}{2}m_nh_{n-1}-\frac{1}{2}m_{n-1}h_{n-1} \end{cases} \nonumber \\ \Rightarrow&\begin{cases} 2h_0m_0+h_0m_1=6(\frac{y_1-y_0}{h_0}-A)\\ h_{n-1}m_{n-1}+2h_{n-1}m_{n}=6(B-\frac{y_n-y_{n-1}}{h_{n-1}}) \end{cases} \nonumber \\ \end{align}\begin{bmatrix} 2 & 1 & 0 & 0 & 0 & \cdots & 0\\ h_0 & 2(h_0+h_1) & h_1 & 0 & 0 & \cdots & 0\\ 0 & h_1 & 2(h_1+h_2) & h_2 & 0 & \cdots & 0\\ 0 & 0 & h_2 & 2(h_2+h_3) & h_3 & \cdots & 0\\ \vdots& & & \ddots & \ddots & \ddots & \vdots\\ 0 & \cdots & & & h_{n-2} & 2(h_{n-2}+h_{n-1}) & h_{n-1}\\ 0 & \cdots & & & 0 & 1 & 2 \end{bmatrix}\begin{bmatrix} m_0\\m_1\\m_2\\m_3\\\vdots\\m_{n-1}\\m_n \end{bmatrix}=6\begin{bmatrix} \frac{y_1-y_0}{h_0}-A\\ \frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\ \frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\ \frac{y_4-y_3}{h_3}-\frac{y_3-y_2}{h_2}\\ \vdots\\\frac{y_n-y_{n-1}}{h_{n-1}}-\frac{y_{n-1}-y_{n-2}}{h_{n-2}}\\ B-\frac{y_n-y_{n-1}}{h_{n-1}} \end{bmatrix}⾮节点边界(Not-A-Knot)\begin{align} &\begin{cases} S_0'''(x_1)=S_1'''(x_1)\\ S_{n-2}'''(x_{n-1})=S_{n-1}'''(x_{n-1}) \end{cases} \nonumber \\ \Rightarrow&\begin{cases} 6\cdot\frac{m_1-m_0}{6h_0}=6\cdot\frac{m_2-m_1}{6h_1}\\ 6\cdot\frac{m_{n-1}-m_{n-2}}{6h_{n-2}}=6\cdot\frac{m_n-m_{n-1}}{6h_{n-1}} \end{cases} \nonumber \\ \Rightarrow&\begin{cases} h_1(m_1-m_0)=h_0(m_2-m_1)\\ h_{n-1}(m_{n-1}-m_{n-2})=h_{n-2}(m_n-m_{n-1}) \end{cases} \nonumber \\ \Rightarrow&\begin{cases} -h_1m_0+(h_1+h_0)m_1-h_0m_2=0\\ -h_{n-1}m_{n-2}+(h_{n-1}+h_{n-2})m_{n-1}-h_{n-2}m_n=0 \end{cases} \nonumber \\ \end{align}\begin{bmatrix} -h_1 & h_0+h_1 & -h_0 & 0 & 0 & \cdots & 0\\ h_0 & 2(h_0+h_1) & h_1 & 0 & 0 & \cdots & 0\\ 0 & h_1 & 2(h_1+h_2) & h_2 & 0 & \cdots & 0\\ 0 & 0 & h_2 &2(h_2+h_3) & h_3 & \cdots & 0\\ \vdots& & & \ddots & \ddots & \ddots & \vdots\\ 0 & \cdots & & & h_{n-2} & 2(h_{n-2}+h_{n-1}) & h_{n-1}\\ 0 & \cdots & & & -h_{n-1} & h_{n-1}+h_{n-2} & -h_{n-2} \end{bmatrix}\begin{bmatrix} m_0\\m_1\\m_2\\m_3\\\vdots\\m_{n-1}\\m_n \end{bmatrix}=6\begin{bmatrix} 0\\ \frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\ \frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\ \frac{y_4-y_3}{h_3}-\frac{y_3-y_2}{h_2}\\ \vdots\\ \frac{y_n-y_{n-1}}{h_{n-1}}-\frac{y_{n-1}-y_{n-2}}{h_{n-2}}\\ 0 \end{bmatrix}在n=4时通⽤公式⾃然边界\begin{bmatrix} 1 & 0 & 0 & 0 \\ h_0 & 2(h_0+h_1) & h_1 & 0 \\ 0 & h_1 & 2(h_1+h_2) & h_2 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} m_0\\m_1\\m_2\\m_3 \end{bmatrix}=6\begin{bmatrix} 0\\ \frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\ \frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\ 0 \end{bmatrix}固定边界\begin{bmatrix} 2 & 1 & 0 & 0 \\ h_0 & 2(h_0+h_1) & h_1 & 0 \\ 0 & h_1 & 2(h_1+h_2) & h_2 \\ 0 & 0 & 1 & 2 \\ \end{bmatrix}\begin{bmatrix} m_0\\m_1\\m_2\\m_3 \end{bmatrix}=6\begin{bmatrix} \frac{y_1-y_0}{h_0}-A\\ \frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\ \frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\ B-\frac{y_3-y_2}{h_2} \end{bmatrix}⾮节点边界\begin{bmatrix} -h_1 & h_0+h_1 & -h_0 & 0 \\ h_0 & 2(h_0+h_1) & h_1 & 0 \\ 0 & h_1 & 2(h_1+h_2) & h_2 \\ 0 & -h_2 & h_1+h_2 & -h_1 \\ \end{bmatrix}\begin{bmatrix} m_0\\m_1\\m_2\\m_3 \end{bmatrix}=6\begin{bmatrix} 0\\ \frac{y_2-y_1}{h_1}-\frac{y_1-y_0}{h_0}\\ \frac{y_3-y_2}{h_2}-\frac{y_2-y_1}{h_1}\\ 0 \end{bmatrix}图像插值x_{i+1}-x_i=1 \Rightarrow h_i(x)=1在n=4时,即四个点时如下所⽰p_{11}p_{12}p_{13}p_{14}p_{21}p_{22}p_{23}p_{24}pp_{31}p_{32}p_{33}p_{34}p_{41}p_{42}p_{43}p_{44}⾃然边界(可⽤TDMA或化简计算)\begin{bmatrix} 1 & 0 & 0 & 0 \\ 1 & 4 & 1 & 0 \\ 0 & 1 & 4 & 1 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} m_0\\m_1\\m_2\\m_3 \end{bmatrix}=6\begin{bmatrix} 0\\ y_0+y_2-2y_1\\ y_1+y_3-2y_2\\ 0 \end{bmatrix}固定边界(只能⽤TDMA计算)\begin{bmatrix} 2 & 1 & 0 & 0 \\ 1 & 4 & 1 & 0 \\ 0 & 1 & 4 & 1 \\ 0 & 0 & 1 & 2 \\ \end{bmatrix}\begin{bmatrix} m_0\\m_1\\m_2\\m_3 \end{bmatrix}=6\begin{bmatrix} y_1-y_0-A\\ y_0+y_2-2y_1\\ y_1+y_3-2y_2\\ y_2-y_3+B \end{bmatrix}⾮节点边界(只能化简计算)\begin{bmatrix} -1 & 2 & -1 & 0 \\ 1 & 4 & 1 & 0 \\ 0 & 1 & 4 & 1 \\ 0 & -1 & 2 & -1 \\ \end{bmatrix}\begin{bmatrix} m_0\\m_1\\m_2\\m_3 \end{bmatrix}=6\begin{bmatrix} 0\\ y_0+y_2-2y_1\\ y_1+y_3-2y_2\\ 0 \end{bmatrix}python代码1class BiSplineInterpolation:2 @staticmethod3 def TDMA(a, b, c, d):4 n = len(d)56 c[0] = c[0] / b[0]7 d[0] = d[0] / b[0]89for i in range(1, n):10 coef = 1.0 / (b[i] - a[i] * c[i - 1])11 c[i] = coef * c[i]12 d[i] = coef * (d[i] - a[i] * d[i - 1])1314for i in range(n - 2, -1, -1):15 d[i] = d[i] - c[i] * d[i + 1]1617return d1819 @staticmethod20 def Simplified_Natural4(y1, y2, y3, y4):21 # 四点⾃然边界化简公式22 d1 = y1 + y3 - 2 * y223 d2 = y2 + y4 - 2 * y32425 k0 = 026 k1 = (4 * d1 - d2) * 0.427 k2 = (4 * d2 - d1) * 0.428 k3 = 02930return [k0, k1, k2, k3]3132 @staticmethod33 def Simplified_Not_A_Knot4(y1, y2, y3, y4):34 # 四点⾮节点边界化简公式35 d1 = y1 + y3 - 2 * y236 d2 = y2 + y4 - 2 * y33738 k0 = 2 * d1 - d239 k1 = d140 k2 = d241 k3 = 2 * d2 - d14243return [k0, k1, k2, k3]4445 # TDMA矩阵说明46 # a0 和 c3 没有实际意义,占位⽤47 # a0 [b0 c0 00 ] [x0] [d0]48 # [a1 b1 c1 0 ] [x1] = [d1]49 # [0 a2 b2 c2] [x2] [d2]50 # [00 a3 b3] c3 [x3] [d3]5152 def SplineInterpolationNatural4(self, x, y1, y2, y3, y4):53 # ⽤TDMA计算54 # matrix_a = [0, 1, 1, 0]55 # matrix_b = [1, 4, 4, 1]56 # matrix_c = [0, 1, 1, 0]57 # matrix_d = [0, 6 * (y1 + y3 - 2 * y2), 6 * (y2 + y4 - 2 * y3), 0]58 # matrix_x = self.TDMA(matrix_a, matrix_b, matrix_c, matrix_d)5960 # 化简计算61 matrix_x = self.Simplified_Natural4(y1, y2, y3, y4)6263 a = y264 b = y3 - y2 - matrix_x[1] / 3.0 - matrix_x[2] / 6.065 c = matrix_x[1] / 2.066 d = (matrix_x[2] - matrix_x[1]) / 6.06768 s = a + b * x + c * x * x + d * x * x * x69return s7071 def SplineInterpolationClamped4(self, x, y1, y2, y3, y4):72 # 仅有TDMA计算,⽆法化简73 A, B = 1, 17475 matrix_a = [0, 1, 1, 1]76 matrix_b = [2, 4, 4, 2]77 matrix_c = [1, 1, 1, 0]78 matrix_d = [6 * (y2 - y1 - A), 6 * (y1 + y3 - 2 * y2), 6 * (y2 + y4 - 2 * y3), 6 * (B - y4 + y3)]79 matrix_x = self.TDMA(matrix_a, matrix_b, matrix_c, matrix_d)8081 a = y282 b = y3 - y2 - matrix_x[1] / 3.0 - matrix_x[2] / 6.083 c = matrix_x[1] / 2.084 d = (matrix_x[2] - matrix_x[1]) / 6.08586 s = a + b * x + c * x * x + d * x * x * x87return s8889 def SplineInterpolationNotAKnot4(self, x, y1, y2, y3, y4):90 # ⽆法使⽤TDMA计算91 matrix_x = self.Simplified_Not_A_Knot4(y1, y2, y3, y4)9293 a = y294 b = y3 - y2 - matrix_x[1] / 3.0 - matrix_x[2] / 6.095 c = matrix_x[1] / 2.096 d = (matrix_x[2] - matrix_x[1]) / 6.09798 s = a + b * x + c * x * x + d * x * x * x99return s100101 def biSpline4(self, srcImg, dstH, dstW):102 dstH, dstW = int(dstH), int(dstW)103 srcH, srcW, _ = srcImg.shape104 srcImg = np.pad(srcImg, ((1, 2), (1, 2), (0, 0)), 'edge')105 dstImg = np.zeros((dstH, dstW, 3), dtype=np.uint8)106for dstY in range(dstH):107for dstX in range(dstW):108for channel in [0, 1, 2]:109 # p11 p12 p13 p14110 #111 # p21 p22 p23 p24112 # p113 # p31 p32 p33 p34114 #115 # p41 p42 p43 p44116 # 储存为 p(y, x)117 p = [dstY * srcH / dstH, dstX * srcW / dstW]118 p22 = [math.floor(p[0]), math.floor(p[1])]119 p21 = [p22[0], p22[1] - 1]120 p23 = [p22[0], p22[1] + 1]121 p24 = [p22[0], p22[1] + 2]122123 p11 = [p21[0] - 1, p21[1]]124 p12 = [p11[0], p22[1]]125 p13 = [p11[0], p23[1]]126 p14 = [p11[0], p24[1]]127128 p31 = [p21[0] + 1, p21[1]]129 p32 = [p31[0], p22[1]]130 p33 = [p31[0], p23[1]]131 p34 = [p31[0], p24[1]]132133 p41 = [p21[0] + 2, p21[1]]134 p42 = [p41[0], p22[1]]135 p43 = [p41[0], p23[1]]136 p44 = [p41[0], p24[1]]137138 diff_y, diff_x = p[0] - p22[0], p[1] - p22[1]139 r1 = self.SplineInterpolationNatural4(diff_x, srcImg[p11[0], p11[1], channel], srcImg[p12[0], p12[1], channel], srcImg[p13[0], p13[1], channel], srcImg[p14[0], p14[1], channel]) 140 r2 = self.SplineInterpolationNatural4(diff_x, srcImg[p21[0], p21[1], channel], srcImg[p22[0], p22[1], channel], srcImg[p23[0], p23[1], channel], srcImg[p24[0], p24[1], channel]) 141 r3 = self.SplineInterpolationNatural4(diff_x, srcImg[p31[0], p31[1], channel], srcImg[p32[0], p32[1], channel], srcImg[p33[0], p33[1], channel], srcImg[p34[0], p34[1], channel]) 142 r4 = self.SplineInterpolationNatural4(diff_x, srcImg[p41[0], p41[1], channel], srcImg[p42[0], p42[1], channel], srcImg[p43[0], p43[1], channel], srcImg[p44[0], p44[1], channel]) 143144 c = self.SplineInterpolationNatural4(diff_y, r1, r2, r3, r4)145146 dstImg[dstY, dstX, channel] = np.clip(c, 0, 255)。
插值法公式

插值法公式1. 什么是插值法?插值法是一种通过已知数据点之间的曲线进行估算或推测的数值方法。
它可以用来估计缺失点的数值,或者通过已知数据点之间的曲线来做出预测。
插值法在数学、统计学、计算机科学和工程等领域都有广泛的应用。
2. 常用的插值法在插值法中,有多种算法可供选择,下面介绍几种常用的插值法。
2.1 线性插值法线性插值法是一种简单但常用的插值法。
它假设两点之间的曲线是一条直线,根据已知的两个点(x₁, y₁)和(x₂, y₂)之间的线性关系,可以推断出任意两点之间的数值。
线性插值法的公式如下:y = y₁ + (y₂ - y₁) / (x₂ - x₁) * (x - x₁)其中,y是待估算的数值,x是已知的数据点。
2.2 拉格朗日插值法拉格朗日插值法是一种常用的多项式插值法。
它利用已知的数据点构造一个多项式,并通过该多项式来估算任意点的数值。
拉格朗日插值法的公式如下:L(x) = ∑[i=0~n] yᵢ * Lᵢ(x)其中,L(x)表示估算值,yᵢ表示已知数据点的y值,Lᵢ(x)表示拉格朗日基函数,定义如下:Lᵢ(x) = ∏[j=0~n, j≠i] (x - xₓ₊₀₋₀ⱼ) / (xₓ₊₀₋₀ᵢ - xₓ₊₀₋₀ⱼ)在这里,n是已知数据点的数量,xₓ₊₀₋₀ⱼ是第j个已知数据点的x值。
2.3 三次样条插值法三次样条插值法是一种更复杂的插值方法,它利用三次多项式来逼近已知数据点之间的曲线。
三次样条插值法的公式如下:S(x) = aⱼ(x - xₓ₊₂₋₂)³ + bⱼ(x - xₓ₊₂₋₂)² + cⱼ(x - xₓ₊₂₋₂) + dⱼ其中,S(x)表示估算值,aⱼ、bⱼ、cⱼ和dⱼ是通过已知数据点计算得到的系数。
3. 插值法的应用插值法在很多领域都有广泛的应用。
下面列举几个常见的应用场景:•图像处理:在图像处理中,插值法可以用来放大或缩小图像,通过已有像素点之间的颜色值来估算新的像素点的颜色值。
几种常用的插值方法

几种常用的插值方法数学系 信息与计算科学1班 李平指导老师:唐振先摘要:插值在诸如机械加工等工程技术和数据处理等科学研究中有许多直接的应用,在很多领域都要用插值的办法找出表格和中间值,插值还是数值积分微分方程数值解等数值计算的基础。
本文归纳了几种常用的插值方法,并简单分析了其各自的优缺点。
关键词:任意阶多项式插值,分段多项式插值。
引言:所谓插值,通俗地说就是在若干以知的函数值之间插入一些未知函数值,而插值函数的类型最简单的选取是代数多项式。
用多项式建立插值函数的方法主要用两种:一种是任意阶的插值多项式,它主要有三种基本的插值公式:单项式,拉格朗日和牛顿插值;另一种是分段多项式插值,它有Hermite 和spine 插值和分段线性插值。
一.任意阶多项式插值:1.用单项式基本插值公式进行多项式插值:多项式插值是求通过几个已知数据点的那个n-1阶多项式,即P n-1(X)=A 1+A 2X+…A n X n-1,它是一个单项式基本函数X 0,X 1…X n-1的集合来定义多项式,由已知n 个点(X,Y )构成的集合,可以使多项式通过没数据点,并为n 个未知系数Ai 写出n 个方程,这n 个方程组成的方程组的系数矩阵为Vandermonde 矩阵。
虽然这个过程直观易懂,但它都不是建立插值多项式最好的办法,因为Vandermonde 方程组有可能是病态的,这样会导致单项式系数不确定。
另外,单项式中的各项可能在大小上有很大的差异,这就导致了多项式计算中的舍入误差。
2.拉格朗日基本插值公式进行插值: 先构造一组插值函数L i (x )=011011()()()()()()()()i i n i i i i i i n x x x x x x x x x x x x x x x x -+-+--------,其中i=0,…n.容易看出n 次多项式L i (x )满足L i (x )=1,(i=j );L i (x )=0,(i ≠j ),其中i=0,1…n ,令L i (x )=0()ni i i y l x =∑这就是拉格朗日插值多项式。
数值分析中的插值方法

数值分析中的插值方法在数值分析中,插值是一种通过在已知数据点之间估计未知数据点的方法。
它是一种常见的数据处理技术,用于填补数据间的空白,揭示数据间的关联性,或者建立数据模型。
在本文中,我们将讨论数值分析中的几种常见的插值方法。
一、拉格朗日插值拉格朗日插值是一种基于多项式的插值方法。
假设有n个离散数据点,我们想要在这些点之间插值得到未知数据点的值。
拉格朗日插值可以通过构建一个n次多项式来实现。
例如,给定三个数据点(x0, y0),(x1, y1),(x2, y2),我们可以假定插值多项式为:P(x) = y0 * L0(x) + y1 * L1(x) + y2 * L2(x)其中,L0(x),L1(x),L2(x)是拉格朗日插值多项式的基函数,由以下公式得到:L0(x) = (x - x1) * (x - x2) / ((x0 - x1) * (x0 - x2))L1(x) = (x - x0) * (x - x2) / ((x1 - x0) * (x1 - x2))L2(x) = (x - x0) * (x - x1) / ((x2 - x0) * (x2 - x1))利用这些基函数,我们可以得到插值多项式P(x),从而计算出未知点的值。
二、牛顿插值牛顿插值是另一种常见的插值方法,也是基于多项式的。
与拉格朗日插值不同的是,牛顿插值使用了差商的概念来构建插值多项式。
差商是一种表示数据间差异的指标,它可以用于计算插值多项式的系数。
对于n个数据点,差商可以由以下递归公式计算得到:f[x0] = f(x0)f[x0, x1] = (f[x1] - f[x0]) / (x1 - x0)f[x0, x1, ..., xn] = (f[x1, x2, ..., xn] - f[x0, x1, ..., xn-1]) / (xn - x0)基于差商,我们可以得到牛顿插值多项式的表达式:P(x) = f[x0] + f[x0, x1] * (x - x0) + f[x0, x1, x2] * (x - x0) * (x - x1) + ...利用牛顿插值,我们可以通过已知数据点构建插值多项式,进而估计未知点的值。
计算方法实验二

《计算方法》实验报告实验二插值法二级学院:计算机学院专业:计算机科学与技术指导教师:爨莹班级学号:姓名:实验二插值法1、实验目的:1、掌握直接利用拉格郎日插值多项式计算函数在已知点的函数值;观察拉格郎日插值的龙格现象。
2、了解Hermite插值法、三次样条插值法原理,结合计算公式,确定函数值。
2、实验要求:1、认真分析题目的条件和要求,复习相关的理论知识,选择适当的解决方案和算法;2、编写上机实验程序,作好上机前的准备工作;3、上机调试程序,并试算各种方案,记录计算的结果(包括必要的中间结果);4、分析和解释计算结果;5、按照要求书写实验报告;3、实验内容:1、用拉格郎日插值公式确定函数值;对函数f(x)进行拉格郎日插值,并对f(x)与插值多项式的曲线作比较。
2、已知函数表:(0.56160,0.82741)、(0.56280,0.82659)、(0.56401,0.82577)、(0.56521,0.82495)用三次拉格朗日插值多项式求x=0.5635时函数近似值。
3、P129,(12)4、题目:插值法5、原理:拉格朗日插值法是以法国十八世纪数学家约瑟夫·路易斯·拉格朗日命名的一种多项式插值方法。
许多实际问题中都用函数来表示某种内在联系或规律,而不少函数都只能通过实验和观测来了解。
如对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。
这样的多项式称为拉格朗日(插值)多项式。
数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。
6、设计思想:通过拉格朗日插值法找到拉格朗日多项式,计算某个x对应的y值。
7、对应程序://Lagrange.cpp#include <stdio.h>#include <conio.h>#define N 4int checkvalid(double x[], int n);void printLag (double x[], double y[], double varx, int n);double Lagrange(double x[], double y[], double varx, int n);void main (){double x[N+1] = {0.56160, 0.56280, 0.56401, 0.56521};double y[N+1] = {0.82741, 0.82659, 0.82577, 0.82459};double varx = 0.5635;if (checkvalid(x, N) == 1){printf("\n\n插值结果: P(%f)=%f\n", varx, Lagrange(x, y, varx, N));}else{printf("结点必须互异");}getch();}int checkvalid (double x[], int n){int i,j;for (i = 0; i < n; i++){for (j = i + 1; j < n+1; j++){if (x[i] == x[j])//若出现两个相同的结点,返回-1{return -1;}}}return 1;}double Lagrange (double x[], double y[], double varx, int n){double fenmu;double fenzi;double result = 0;int i,j;printf("Ln(x) =\n");for (i = 0; i < n+1; i++){fenmu = 1;for (j = 0; j < n+1; j++){if (i != j){fenmu = fenmu * (x[i] - x[j]);}}printf("\t%f", y[i] / fenmu);fenzi = 1;for (j = 0; j < n+1; j++){if (i != j){printf("*(x-%f)", x[j]);fenzi = fenzi * (varx - x[j]);}}if (i != n){printf("+\n");}result += y[i] / fenmu * fenzi;}return result;}8、实验结果:9、实验体会:拉格朗日插值法能很好的解决生产和科研中的一些问题,计算机编程的实现有利于其更好的应用。
数值分析常用的插值方法

数值分析常用的插值方法数值分析中常用的插值方法有线性插值、拉格朗日插值、分段线性插值、Newton插值、Hermite插值、样条插值等。
下面将对这些插值方法进行详细介绍。
一、线性插值(linear interpolation)线性插值是最简单的插值方法之一、假设已知函数在两个点上的函数值,通过这两个点之间的直线来估计中间点的函数值。
线性插值公式为:f(x)=f(x0)+(x-x0)*(f(x1)-f(x0))/(x1-x0)其中,f(x)表示要求的插值点的函数值,f(x0)和f(x1)是已知的两个点上的函数值,x0和x1是已知的两个点的横坐标。
二、拉格朗日插值(Lagrange interpolation)拉格朗日插值是一种基于多项式的插值方法。
它通过多个已知点的函数值构造一个多项式,并利用这个多项式来估计其他点的函数值。
拉格朗日插值多项式的一般形式为:f(x) = Σ[f(xi) * Li(x)] (i=0,1,2,...,n)其中,f(x)表示要求的插值点的函数值,f(xi)是已知的多个点的函数值,Li(x)是拉格朗日基函数。
拉格朗日基函数的表达式为:Li(x) = Π[(x-xj)/(xi-xj)] (i≠j,i,j=0,1,2,...,n)三、分段线性插值(piecewise linear interpolation)分段线性插值是一种逐段线性近似函数的方法。
通过将整个插值区间分成多个小段,在每个小段上使用线性插值来估计函数的值。
分段线性插值的过程分为两步:首先确定要插值的点所在的小段,在小段上进行线性插值来估计函数值。
四、Newton插值(Newton interpolation)Newton插值也是一种基于多项式的插值方法。
利用差商的概念来构造插值多项式。
Newton插值多项式的一般形式为:f(x)=f(x0)+(x-x0)*f[x0,x1]+(x-x0)*(x-x1)*f[x0,x1,x2]+...其中,f(x)表示要求的插值点的函数值,f(x0)是已知的一个点的函数值,f[xi,xi+1,...,xi+k]是k阶差商。
几种常用的插值方法

几种常用的插值方法数学系 信息与计算科学1班 李平指导老师:唐振先摘要:插值在诸如机械加工等工程技术和数据处理等科学研究中有许多直接的应用,在很多领域都要用插值的办法找出表格和中间值,插值还是数值积分微分方程数值解等数值计算的基础。
本文归纳了几种常用的插值方法,并简单分析了其各自的优缺点。
关键词:任意阶多项式插值,分段多项式插值。
引言:所谓插值,通俗地说就是在若干以知的函数值之间插入一些未知函数值,而插值函数的类型最简单的选取是代数多项式。
用多项式建立插值函数的方法主要用两种:一种是任意阶的插值多项式,它主要有三种基本的插值公式:单项式,拉格朗日和牛顿插值;另一种是分段多项式插值,它有Hermite 和spine 插值和分段线性插值。
一.任意阶多项式插值:1.用单项式基本插值公式进行多项式插值:多项式插值是求通过几个已知数据点的那个n-1阶多项式,即P n-1(X)=A 1+A 2X+…A n X n-1,它是一个单项式基本函数X 0,X 1…X n-1的集合来定义多项式,由已知n 个点(X,Y )构成的集合,可以使多项式通过没数据点,并为n 个未知系数Ai 写出n 个方程,这n 个方程组成的方程组的系数矩阵为Vandermonde 矩阵。
虽然这个过程直观易懂,但它都不是建立插值多项式最好的办法,因为Vandermonde 方程组有可能是病态的,这样会导致单项式系数不确定。
另外,单项式中的各项可能在大小上有很大的差异,这就导致了多项式计算中的舍入误差。
2.拉格朗日基本插值公式进行插值: 先构造一组插值函数L i (x )=011011()()()()()()()()i i n i i i i i i n x x x x x x x x x x x x x x x x -+-+--------,其中i=0,…n.容易看出n 次多项式L i (x )满足L i (x )=1,(i=j );L i (x )=0,(i ≠j ),其中i=0,1…n ,令L i (x )=0()ni i i y l x =∑这就是拉格朗日插值多项式。
基于matlab的常见插值法及其应用

基于matlab的常见插值法及其应用郭小乐【摘要】本文就数值分析中几种常见的插值法:拉格朗日插值、牛顿插值、Hermite插值及三次样条插值,讨论其不同形式的表达式及误差,结合matlab给出具体实例,对比分析.此外还就三次样条插值的不同计算方法进行归纳、总结.【期刊名称】《赤峰学院学报(自然科学版)》【年(卷),期】2017(033)007【总页数】3页(P5-7)【关键词】拉格朗日插值;牛顿插值;Hermite插值;三次样条插值;matlab【作者】郭小乐【作者单位】宁夏大学数学统计学院,宁夏银川 750021【正文语种】中文【中图分类】O241.3在许多工程问题中,有时我们只能给出某一函数在一些离散点的值,给不出具体的函数表达式,或者函数的表达式过于复杂不利于计算,这时我们就需要构造这个函数的近似函数,数学上我们把这种方法称为插值[1].插值法作为函数逼近、数值微积分及微分方程数值解的基础,在当今社会被越来越多的学者所关注.尤其随着计算机的普及,很多学者将插值与matlab等软件结合,使得插值法得到了更广泛的应用.常用的插值法包括:拉格朗日 (Lagrange)插值、牛顿(Newton)插值、Hermite 插值、三次样条插值,本文就这四种插值法,结合matlab,从其公式的构造、余项出发,对不同的插值法通过数值实例进行对比研究.此外,还就具有良好收敛性的三次样条函数,归纳出不同的计算方法.由于代数多项式具有简单和一些良好的特性,如多项式是无穷光滑的,容易计算它的导数及积分.故本文选择代数多项式作为插值函数.下面依次就这几种插值法进行讨论.2.1 Lagrange插值所谓n次Lagrange插值即给定平面上的n+1个互不相同的插值点(xi,f(xi)),i=0,1,2,…,n,利用插值基函数构造唯一的一条次数不高于n次的插值多项式.2.1.1 n次Lagrange插值多项式形式及误差拉格朗日插值公式的优点是格式整齐和规范,在理论分析中有重要的价值.它的缺点是没有承袭性质,当需要增加插值节点时,需要重新计算所有的插值基函数,计算繁琐.2.2 Newton插值Newton插值是利用差商计算的,下面我们首先给出差商的概念.定义1[1]设x0,x1,…,xk互不相同,f(x)关于x0,x1,…,xk的k阶差商为2.2.1 n次Newton插值多项式的形式及误差牛顿插值具有拉格朗日插值没有的承袭性,当增加插值节点时,只需再计算一项即可得到相应的插值多项式.由插值多项式的唯一性可知二者是同一插值多项式的不同表达形式.2.3 Hermite插值常用Hermite插值描述如下[1]:对于f(x)具有一阶连续导数,以及插值点xi,i=0,1,…,n,xi互不相同,若有至多为2n+1次的多项式函数H2n+1(x)满足:则称H2n+1(x)为f(x)关于节点{xi}ni=0的Hermite插值多项式.2.3.1 Hermite插值多项式的形式及误差:2.4 三次样条插值在实际计算中,人们很少采用高次插值,其主要原因有两个:其一,由于受到所要通过的插值节点的约束,高次插值描绘的代数曲线是摆动的.即我们常说的Runge(龙格)现象;其二,从计算的舍入误差看,对于等距结点的差分形式,结点上函数值的微小变化可能导致高阶差分的很大变动.故在应用中主要采用的是分段低次插值.实践证明,用分段的低次插值多项式逼近被插函数比在全区间上用高次插值多项式效果好.一般来说,分段插值所描绘的曲线是不光滑的.为了能获得一条足够光滑的插值曲线,近年来人们采用了分段多项式光滑插值法,即著名的样条函数插值法.本文我们主要介绍具有良好的收敛性,具有二阶光滑性的三次样条插值.2.4.1 三次样条函数定义2[5]给定[a,b]上n+1个节点a=x0<x1<…<xn-1<xn=b以及这些点上的函数值f(xi)=yi(i=0,1,…,n).若函数s(x)满足:(1)s(xi)=yi,i=0,1,2,…,n;(2)在每个小区间[xi,xi+1]上是一个次数不超过三次的多项式;(3)s(x)、s'(x)、s"(x)在[a,b]上都连续.则称s(x)为函数f(x)关于节点x0,x1,…,xn的三次样条函数.2.4.2 三次样条插值的几种计算方法2.4.2.1 利用二阶导数为线性函数求解令s"(xj)=Mj,j=0,1,…,n.因为s(x)为分段三次多项式,故s"(x)在[xj,xj+1]上是线性函数.可表示为其中hj=xj+1-xj为了求出s(x)在[xj,xj+1]上的表达式,需要对上式积分两次,并利用s(xj)=yi及s(xj+1)=yj+1可求出积分常数.得三次样条函数表达式:再利用光滑连接条件s'(xj-0)=s'(xj+0),并对s(x)求导得为了确定唯一的Mj(j=0,1,…,N),补充三个边界条件:(1)假定s'(x0)=f'0,s'(xn)=f'n;(2)假定 s"(x0)=f"(x0),s"(xn)=f"(xn)直接得端点方程M0=f"0,Mn=f"n;(3)假定M0=MN=0,即为自然边界条件,可得M0=Mn,λnM1+μnMn-1+2Mn=dn;以上三个边界条件将其写成矩阵形式,得关于Mj(j=0,1,…,n)的三对角线性方程组,利用追赶法[2]求出唯一的Mj(j=0, 1,…,n),将其代入s(x)即可.2.4.2.2 利用特殊形式的埃尔米特插值公式求解若插值节点取为xk,xk+1,插值多项式为H3(x),则采用基函数法,令H3(x)=αk(x)yk+αk+1yk+1+βk(x)mk+βk+1(x)mk+1其中αk(x),αk+1(x),βk(x),βk+1(x)是关于插值节点 xk,xk+1的三次Hermite插值基函数.上式即为由特殊的埃尔米特插值公式推导的三次样条插值的计算方法之一.例设,x3=4.利用不同的插值法构造f(x)在[,4]上的插值多项式,使其满足P(xi)=f(xi) (i=0,1,2,3),P'(x0)=f'(x0).下图是利用matlab(2012b)编程软件绘制的上述条件下四种不同算法在[0.25,4]插值函数曲线图(a)及其相对误差曲线图(b),直观明了地展示不同插值算法的效果.从图a中可看出不同插值方法对原函数的逼近效果相差不大.但从图b中的不同插值法的相对误差大小可知,这四种插值方法中,Lagrange插值和Newton插值的效果是一样的,相对另外两种插值方法来说,这两种方法的逼近效果较差,其次是Hermite插值的逼近效果较好,而具有良好收敛性及二阶光滑性的三次样条插值来说,其误差最小,逼近效果最好.本文根据运用的插值条件的不同,对《数值分析》中常用的四种插值法进行归纳总结.通过具体的数值实例,结合matlab编程软件,通过图像直观明了地展示不同方法的逼近效果,还绘制了不同插值方法的相对误差曲线图,从误差的角度分析不同方法的效果.为不同领域的科研工作者提供理论基础.〔1〕张韵华,奚梅成,陈效群.数值计算方法与算法[M].北京:科学出版社,2006. 〔2〕李庆扬,王超能,易大义.数值分析(第五版)[M].北京:清华大学出版社,2008. 〔3〕徐利治,周蕴时,孙玉柏.逼近论[M].北京:国防工业出版社,1985.〔4〕吕晓亚,张莉.插值法在数值分析中的教学实践[J].唐山师范学院学报,2011,33(2):123-125.〔5〕张希娜,李亚红,郭中凯.关于三次样条插值的教学研究[J].长沙大学学报,2012,26(2):131-132.〔6〕张丽娟.三种插值方法的应用与比较[J].赤峰学院学报(自然科学版),2010,26(3):1-3.〔7〕林昌华,杨岩.拉格朗日插值法在工程设计及CAD中的应用[J].重庆理工大学学报(自然科学版),2013,27(12):34-37.。
插值法的推导过程

插值法生产实践中常常出现这样的问题:给出一批离散样点,要求作出一条通过这些点的光滑曲线,以便满足设计要求或进行加工。
反映在数学上,即已知函数在一些点上的值,寻求它的分析表达式。
因为由函数的表格形式不能直接得出表中未列点处的函数值,也不便于研究函数的性质。
此外,有些函数虽有表达式,但因式子复杂,不容易算其值和进行理论分析,也需要构造一个简单函数来近似它。
解决这种问题的方法有两类:一类是给出函数()x f 的一些样点值,选定一个便于计算的函数形式,如多项式、分式线性函数及三角多项式等,要求它通过已知样点,由此确定函数()x ϕ作为()x f 的近似。
这就是插值法。
另一类方法在选定近似函数的形式后,不要求近似函数过已知样点,只要求在某种意义下他在这些点上的总偏差最小。
这类方法称为曲线(数据)拟合法。
1、 拉格朗日(Lagrange )插值1. Lagrange 插值多项式先讨论只有两个节点0x ,()11=n x 的插值多项式。
由前所述,插值多项式应设为()x a a x 101+=ϕ,且满足插值条件()()0001001x f y x a a x ==+=ϕ()()1111011x f y x a a x ==+=ϕ解此方程组得1010010x x x y x y a --=,10101x x y y a --=0所以,两个节点的一次插值多项式为()x x x y y x x x y x y x 10101010011--+--=ϕ (5-6)这是用过两点()00,y x ,()11,y x 的直线()x y 1ϕ=近似曲线()x f y =,故这种插值又称为线性插值。
如果将式(5-6)改写成以下形式()01011011x x x x y x x x x y x --+--=ϕ (5-7) 式(5-7)中,()x 1ϕ被表成两个线性函数的线性组合。
记()1010x x x x x l --=,()0101x x x x x l --= 显然,它们满足()100=x l ,()010=x l ()001=x l ,()111=x l即()()10,=i x l i 在对应的插值点i x 处的取值为1,在其他点处取值为0,不难想象,以对应点处的函数值为系数对它们作线性组合所得的函数,不仅仍是线性的,且必定满足插值条件。
