2015横道中学备战中考模拟训练四[1]

合集下载

九年级上学期数学工作计划(三篇)

九年级上学期数学工作计划一、扎扎实实打好基础1、重视课本，系统复习。

初中数学基础包括基础知识和基本技能两方面。

现中考仍以基础的为主，有些基础题是课本的原型或改造，后面的大题是教材题目的引伸、变形或组合，复习时应以课本为主。

尤其课后的读一读，想一想，有些中考题就在此基础上延伸的，所以，在做题时注意方法的归纳和总结，做到举一反三。

2、充实基础，学会思考。

中考时基础分很多，所以在应用基础知识时做到熟练、正确、迅速。

上课要边听边悟，敢于质疑。

3、重视基础知识的理解和方法的学习。

基础知识既是初中所涉及的概念、公式、公理、定理等。

掌握知识间的联系，要做到理清知识结构，形成整体知识，并能综合运用。

例如：中考涉及的动点问题，既是方程、不等式与函数问题的结合，同时也涉及到几何中的相似三角形，比例推导等。

还重视数学方法的考察。

如：配方法、换元法、判别式等方法。

二、综合运用知识，提高自身的各种能力初中数学基本能力有运算能力、思维能力、空间想象能力以及体现数学与生产、生活相关学科相联系的能力等等。

1、提高综合运用数学知识解题的能力。

要求学生必须把各章节的知识联系起来，并能综合运用，做到触类旁通。

目前应根据自身的实际，有针对性地复习，查漏补缺做好知识归纳、解题方法地归纳。

我们必须了解中考的有关的政策，避免走弯路，走错路。

研读《中考说明》，看清范围，研究评分的标准，牢记每一个得分点。

避免解题中出现“跳步”现象。

三、精选习题1、初三下学期刚开始，每一周安排一次综合练习。

让学生开始接触中考题型、题量，新课结束后就每周一次综合模拟测试。

2、每天利用几分钟时间练习。

初一初二时是作为速度练习，初三时用作专题(解方程、方程组、不等式、不等式组、分解因式、代数式等)练习，在后段专门训练中考模拟试题中的选择题、填空题。

其特点是题量少，时间短，反馈快，对中考模拟试题中的选择题、填空题是反复做(打乱次序)。

3、整合习题，把握重点难点。

对中考题进行精选和整合，将重点放在第17―26题之间的基本重点部分。

河南地市、名校2024年中考语文模拟组合试卷及答案 (1)

河南地市、名校2024年中考模拟组合卷(一)
14 河南地市、名校2024年中考模拟组合卷(一)
一、(2024·洛阳三模改编)积累与运用(共23分) 开篇生肖舞蹈作品《龙舞》是此次河南春晚重点打造的节目之一，以历史悠久的“舞龙”祈福民间习俗为创作基础，融合不同地区非遗高跷、民间舞龙，还有少儿街舞等，以全新视角展示春节社火表演，让观众再次感受中华传统民俗文化的多样性。
小文：“③忽__如__一__夜__春__风__来____，④_千__树__万__树__梨__花__开__。”(岑参《白雪歌
送武判官归京》) 小豫：岑参以春意写冬景，乐观豪迈！听我的：“⑤几_处__早__莺__争__暖__树____，
⑥_谁__家__新__燕__啄__春___泥__。”(白居易《钱塘湖春行》)
意思是庆贺粮食丰收、谷物满
仓
14 河南地市、名校2024年中考模拟组合卷(一)
原创舞蹈《凤鸣朝阳》，浴火涅槃，凤舞九州，舞出中国的极致浪漫！ “凤鸣朝阳”取自《诗经·大雅》“凤凰鸣矣，于彼高冈；梧桐生矣，于彼朝阳”。舞者以充满张力的舞姿，塑造极富美感的凤凰的形象。
14 河南地市、名校2024年中考模拟组合卷(一)
4．阅读材料，完成下面的题目。(共6分) 河南春晚节目播出后，全网阅读量高达160亿，平台热搜557个，更
是登上了全国热搜榜第一的位置。网友“山河无恙”评论说：河南春晚的节目质量真的高到离谱，从
内容到形式都很高级，既有河南特色，又弘扬了中华优秀传统文化，充分彰显了泱泱中华的文化自信。
网友“国泰民安”评论说：河南春晚特效炸裂，与时俱进，包罗万象，能够传承和发扬中华优秀传统文化。
14 河南地市、名校2024年中考模拟组合卷(一)
指靠近，接触；当下，目前；即

备战中考物理真题精准训练—物理常识概念(word版含答案)

备战2022年中考物理真题精准训练—物理常识概念1. （2021阜新）下列图中，描述正确的是2. （2021玉林）由欧姆定律变形可得，以下说法正确的是A. 导体的电阻跟它两端的电压成正比B. 导体的电阻跟通过它的电流成反比C. 导体的电阻跟它两端的电压和通过它的电流无关D. 导体的电阻由它两端的电压和通过它的电流的比值决定3．（2021舟山）事物总是在变与不变中相统一。

下列有关说法错误的是（）A．气压改变时，空气的密度一定不变B．温度改变时，玻璃的导电性会发生变化C．位置改变时，物体的质量一定不变D．介质改变时，声的传播速度会发生变化4.（2021徐州）今年5月15日，我国首辆火星探测车“祝融号”成功降落在火星表面，它将开限一系列科学探究活动，下列探究不属于“祝融号”探究任务的是A．火星命名的缘由 B.火星磁场的变化C．火星土壤中存在水的证据 D.稀薄大气对火星表面的影响5. （2021济宁）如图是小明对一些知识的分类和举例，其中正确的是（）A. B.C. D.6. （2021牡丹江、鸡西）下列物理量估算不合理的是（）A. 一个中学生的重力约500NB. 人步行速度约10m/sC. 人体的正常体温约37℃D. 人体平均密度约1g/cm37．（2021岳阳）“阳光大课间”增强了学生体质，丰富了校园生活。

活动中涉及中学生的数据符合实际的是（）A．质量50kg B．体温50℃C．跑400m用时10s D．身高1.63cm8. （2021新疆）新疆1月份夜间的平均气温最接近（）A. -15°CB. 15°CC. 25°CD. 37°C9．（2021衢州）人类对天体的认识是不断深入、不断完善的。

如图所示天体系统关系图正确的是（）A B C D10.（2021淄博）下列应用中涉及的物理知识描述正确的是（）A.起钉子用的羊角锤，既省力又省距离B.病房用的消毒灯，利用红外线灭菌消毒C.驾驶员系安全带，可减轻惯性带来的伤害D.热气球升空，利用了流体压强与流速的关系11．（2021天水）对生活中物理现象的解释，下列说法正确的是（）A．自行车轮脸上有花纹，是为了增大与地面的摩擦力B．安全锤头部很尖，目的是使用时增大压力，容易击碎玻璃让人们逃生C．注射疫苗时，用针管把药液推入体内，利用了大气压强D．梳头时头发翘起来，梳子和头发带同种电荷12. （2021大庆）关于热现象，下列说法中正确的是（）A. 热传递的实质是能量从内能大的物体向内能小的物体转移的过程B. 以目前的科技水平，热机的效率无法达到100%C. 初冬季节，在家里洗澡时发现房间里充满“白气”，这些“白气”是水蒸气D. 晶体和非晶体在熔化过程中随着持续吸收热量，温度会不断升高13. （2021泰州）关于粒子和宇宙，下列说法不正确的是（）A. 摩擦起电的实质是电子的转移B. 分子间仅存在吸引力，不存在排斥力C. 宇宙中天体的位置不是恒定不变的D. 物体温度降低，分子的无规则运动速度减慢14．（2021东营）5月19日，天问一号着陆巡视器成功着陆于火屋，这标志着我国首台火星车“祝融号”开启探索之旅。

2024年中考英语考前模拟测试卷(西藏卷)(全解全析)

2024年中考英语考前模拟测试卷（西藏卷）注意事项：1. 全卷共9页，九大题，本试卷满分为100分，考试时间为120分钟。

2. 答题前，考生现将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚，将“条形码”准确粘贴在条形码区域内。

3. 回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效4. 考试结束后，将本试卷和答题卡一并交回。

一、情景交际：共两节，满分10分。

第一节情景对话（本题共5分，每小题1分，满分5分）根据上下文所表达的意思，从A、B、C和D四个选项中，选出最佳答案。

1．—How’s the weather today?—________.A．It’s Friday B．May 3rd C．It’s snowy D．It’s OK【答案】C【详解】句意：——今天天气怎么样？——下雪。

考查情景交际。

It’s Friday星期五；May 3rd五月三日；It’s snowy下雪；It’s OK没关系。

根据“How’s the weather today?”可知是询问天气，It’s snowy符合情景。

故选C。

2．—I passed the English exam.—________A．Good luck!B．Really?C．Oh, my god!D．Congratulations!【答案】D【详解】句意：——我通过了英语考试。

——恭喜！考查情景交际。

Good luck祝你好运；Really真的吗；Oh, my god天啊；Congratulations恭喜。

根据“I passed the English exam.”可知，此处应该表示祝贺。

故选D。

3．—Don’t smoke in public (公共场所).—________A．Why not?B．Pardon?C．Excuse me?D．Sorry. I won’t do that again.【答案】D【详解】句意：——不要在公共场所吸烟。

2024年中考英语仿真模拟预测卷(三)试卷

九年级英语综合模拟卷（满分：100分）听说部分（25分）Ⅰ. 听说题（25分）ⅰ）听下面短文，短文播放一遍。

你有50秒钟的时间准备，然后模仿朗读。

当听到”开始录音”的信号后，立即在50秒钟内模仿朗读短文；当听到要求”停止录音”的信号时，停止模仿朗读。

（4分）1. ________________________________________________________________________________________ ___________________________________________________________________________________________ ___________________________________________________________________________________________ⅱ）听选信息（6分）听三段对话，每段播放两遍。

请根据所听到的内容，选择正确信息。

听第一段对话，回答2—3两个问题。

( ) 2. What is the main reason John is worried about his rabbit?A. The rabbit is sick.B. The rabbit is missing.C. John is going on a business trip.( ) 3. How does Helen plan to help John with his rabbit?A. By introducing a pet store.B. By offering to take care of the rabbit.C. By sugge sting John’s son to take care of the rabbit.听第二段对话，回答4—5两个问题。

( ) 4. Where is Eric’s cousin from?A. The United States.B. The United Kingdom.C. Australia.( ) 5. What do Eric’s cousin and the girl enjoy doing?A. They both like putting on shows.B. They are both from the United Kingdom.C. They are both currently living in the United States.听第三段对话，回答6—7两个问题。

人教版高一上册数学教学工作计划例文（四篇）

人教版高一上册数学教学工作计划例文班级情况分析：一、基本情况。

总人数男生女生552827二、学习情况大部分学生对数学比较感兴趣(如郝苏湘、周叶凡等)，接受能力较强，学习态度较端正;也有部分学生自觉性不够(如郭冲、郭加林等)，不能主动去学习等，对于学习数学有一定困难。

所以在新的学期里，在端正学生学习态度的同时，应加强培养他们的各种学习数学的能力，以提高成绩。

以前对知识掌握较好部分是：1、学生的基础的知识、概念、定义掌握比较牢固。

2、学生的口算、笔算验算及脱式计算较好。

3、学生解答文字题和应用题的思路和步骤清楚。

4、学生能很好的解答几何画图形方面的题目。

5、学生书写较工整美观。

不足之处：1、学生粗心大意忘写答案。

2、运用知识不够灵活，表现在已掌握的知识，做题目时不能灵活地运用。

教材分析：这册教材包括下面地些内容：百分数的应用、圆柱和圆锥、比例、确定位置、正反比例、解决问题的策略、统计以及小学六年来所学数学内容的总复习。

本册教材的这些内容是在前几册的基础上按照完成小学数学的全部教学任务安排的，着重使学生认识一些常见的立体图形，掌握它们的体积等计算方法，进一步发展空间观念；进一步形成统计的观念，掌握用扇形统计图表示数据整理结果的方法，提高依据统计数据的分析、预测、判断能力；理解比例、正比例、反比例的概念，加深认识一些常见的数量关系，会用比例知识解答比较容易的应用题。

然后把小学数学的主要内容加以系统的整理和复习，巩固所学的数学知识，使学生能够综合运用所学的数学知识解决比较简单的实际问题；结合新的教学内容与系统的整理和复习，进一步发展思维能力，培养思维品质，进行思想品德教育。

本册教材中的圆柱和圆锥、比例都是小学数学的重要内容。

首先，认识圆柱和圆锥的特征，掌握圆柱和圆锥的一些计算，既可以为进一步学习其他形体的表面积和体积及其计算打好基础，进一步发展空间观念，也可以增强解决问题的策略和方法，逐步增强学生收集、处理信息的意识和能力。

2024年重庆市中考数学模拟试卷(预测四)

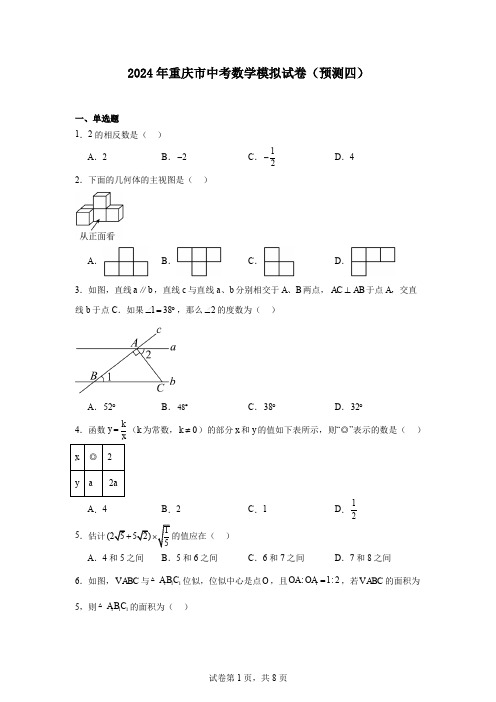
2024年重庆市中考数学模拟试卷（预测四）一、单选题1．2的相反数是（）A ．2B ．2-C ．12-D ．42．下面的几何体的主视图是（）A ．B ．C ．D ． 3．如图，直线a b ∥，直线c 与直线a 、b 分别相交于A 、B 两点，AC AB ⊥于点A ，交直线b 于点C ．如果138∠=︒，那么2∠的度数为（）A ．52︒B ．48︒C ．38︒D ．32︒ 4．函数k y =（k 为常数，0k ≠）的部分x 和y 的值如下表所示，则“◎”表示的数是（）A ．4B ．2C ．1D ．125．估计） A ．4和5之间 B ．5和6之间 C ．6和7之间 D ．7和8之间 6．如图，ABC V 与111A B C △位似，位似中心是点O ，且1:1:2OA OA =，若ABC V 的面积为5，则111A B C △的面积为（）A ．10B ．15C ．20D ．257．下列图案是用长度相同的火柴棒按一定规律拼搭而成的，图案①需要8根火柴棒，图案②需要15根火柴棒，图案③需要22根火柴棒，…．按此规律，图案⑧需要的火柴棒的根数为（）A ．50B ．54C ．57D ．648．如图，已知AB 与O e 相切于点A ，AC 是O e 的直径，连接BC 交O e 于点D ，E 为O e 上一点，连接,EC ED ，若CED α∠=，则B ∠的度数是（）A ．90α︒-B ．αC ．452α︒+ D ．2α9．如图，E 是正方形ABCD 对角线BD 上一点，连接AE ，过点E 作EF AE ⊥，交BC 于点F ．已知DE AE BF 的长为（）A ．1B ．2 CD ．10．有n 个依次排列的算式：第1项是2a ，第2项是221a a ++，用第2项减去第1项，所得之差记为1b ，将1b 加2记为2b ，将第2项与2b 相加作为第3项，将2b 加2记为3b ，将第3项与3b 相加作为第4项，……，以此类推．某数学兴趣小组对此展开研究，得到3个结论①529b a =+；②若第6项与第5项之差为4057，则2024=a ；③当n k =时，212342k b b b b b ak k +++++=+L ；其中正确的个数是（）A ．0B ．1C ．2D ．3二、填空题11．计算：()023.142π---=．12．如图，一个正方形和一个正五边形各有一边AB ，CD 在直线l 上，且只有一个公共顶点P ，则BPC ∠的度数为．13．一个不透明的口袋中有1个黄色球和3个红色球，这些球除颜色外其余均相同从中随机摸出一个球，记下颜色后放回，搅匀后再从中随机摸出一个球，则两次都摸出红球的概率是． 14．如图，某小区有一块长为15米，宽为10米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为296m ，两块绿地之间及周边留有宽度相等的人行通道．设人行通道的宽度为x 米，则所列方程是．15．长方形ABCD 中，以点A 为圆心AD 的长为半径画弧交AB 于点E ，以DC 为直径的半圆与AB 相切，切点为E ，已知4AB =，则图中阴影部分的面积为．（结果保留π）16．如图，CN 平分ABC V 的外角ACM ∠，过点A 作CN 的垂线，垂足为点D ，B BAD ∠=∠．若9AC =，6BC =，则AD 的长为．17．关于x 的一元一次不等式组32132325x x x m -+⎧≥-⎪⎨⎪->⎩至少有3个整数解，且关于y 的分式方程3222my y y y-+=--有整数解，那么符合条件的所有整数m 的和为． 18．如果一个四位自然数M 各个数位上的数字均不为0，且前两位数字之和为5，后两位数字之和为8，则称M 为“会意数”．把四位数M 的前两位数字和后两位数字整体交换得到新的四位数M '．规定()99M M F M '-=．例如：2335M =，∵235+=，358+=，∴ 2335是“会意数”．则()3523233523351299F -==．那么“会意数”4162N =，则()F N =；已知四位自然数S abcd =是“会意数”，（4b ≤，7d ≤，且a 、b 、c 、d 均为正整数），若()F S 恰好能被8整除，则满足条件的数S 的最大值是．三、解答题19．计算：（1）()()22+--x y x x y ；（2）26934222-+-⎫⎛÷+- ⎪--⎝⎭x x x x x x ． 20．如图，在Rt ABC △中，90B ??，AD 平分BAC ∠．小明在刚学完“三角形全等的判定”这节课后，想利用所学知识，推导出ABD △和ACD V 面积的比值与AB ，AC 两边比值的关系．他的思路是：过点D 作AC 的垂线，垂足为点H ，再根据三角形全等来证明ABD △和ACD V 的高相等，进一步得到ABD △和ACD V 的面积之比等于BAC ∠的两邻边边长之比．请根据小明的思路完成以下作图与填空：(1)用直尺和圆规，过点D 作AC 的垂线，垂足为点H （只保留作图痕迹）．(2)证明：∵DH AC ⊥，∴90AHD B ∠=︒=∠．∵AD 平分BAC ∠，∴ ① ．在ABD △和AHD V 中，B AHD BAD HAD ⎧∠=∠⎪∠=∠⎨⎪⎩② ∴ABD △≌AHD V ()AAS ．∴ ③ ． ∵12ABD S AB BD =⋅V ， 12ACD S AC DH =⋅△， ∴ABD ACD S AB S AC=△△．小明再进一步研究发现，只要一个三角形被其任意一内角角平分线分为两个三角形，均有此结论．请你依照题意完成下面命题：如果一个三角形满足被其任意一内角角平分线分为两个三角形，那么 ④ ．21．我校在七、八年级学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x 表示，共分成四组：A ．130135x ≤<，B ．135140x ≤<，C ．140145x ≤<，D ．145150x ≤≤），下面给出了部分信息：七年级抽取的10名学生的竞赛成绩：131，134，135，138，141，147，148，148，148，150．八年级10名学生的竞赛成绩在C 组中的数据是140，143，143，144．七、八年级抽取的学生的竞赛成绩统计表根据以上信息，解答下列问题：(1)填空：a ＝______，b ＝______，c ＝______；(2)根据以上数据分析，你认为我校七、八年级中哪个年级学生竞赛成绩较好？请说明理由（一条理由即可）；(3)我校七、八年级分别有780名、620学生参加了此次竞赛，请估计成绩达到140分及以上的学生共有多少名？22．山城步道是重庆的特色，市民可以在步道里面休闲、运动，享受美好生活．半山崖线步道沙坪坝段全长2000米，由甲、乙两个工程队合作完成，甲工程队修建的步道长度比乙工程队修建的步道长度的2倍少400米．(1)求甲、乙两工程队各修建步道多少米？(2)实际修建过程中，甲工程队每天比乙工程队多修5米，最终甲工程队完成任务时间是乙工程队完成任务时间的1.2倍，则甲工程队每天修建步道多少米？23．如图，在Rt ABC △中，90ACB ∠=︒，30A ∠=︒，4BC =．点D 是AB 中点，动点P ，Q 分别以每秒1个单位长度的速度同时运动，点P 从点C 出发，沿折线C D B →→运动，到达点B 时停止运动，点Q 从点B 出发，沿直线B A →运动，到达点A 时停止运动，设点P ，点Q 的运动时间为x 秒，点P ，Q 之间的距离为y ．(1)请直接写出y 与x 之间的函数表达式并注明自变量x 的取值范围；(2)在给定的平面直角坐标系中画出这个函数图像，并写出该函数的一条性质；(3)结合函数图像，直接写出P ，Q 两点相距大于3个单位长度时x 的值．（结果保留一位小数，误差不超过0.2）．24．如图，四边形ABCD 是某公园的休闲步道．经测量，点B 在A 的正西方向，AB =米，点D 在A 的正北方向，点C 在B 的西北方向，BC =C 在D 的南偏西60︒方向上．(1)求步道AD 的长度；（精确到个位数）；(2)小亮以90米/分的速度沿A B C D →→→的方向步行，小明骑自行车以300米/分的速度沿D C B A →→→的方向行驶．两人能否在4分钟内相遇？请说明理由．（参考数据：1.414 1.732）25．在平面直角坐标系中，抛物线22y ax bx =+-交x 轴于点()3,0A -，()1,0B ，交y 轴于点C ．(1)求抛物线的解析式；(2)如图1，在直线AC 下方的抛物线上有一点D ，作D F y ∥轴交BC 于点F ，作D E A C ⊥于E ，求DF 的最大值及此时点D 的坐标；(3)如图2，将抛物线22y ax bx =+-沿射线CBy '，在y 轴的正半轴上有一点G ，在新抛物线y '上是否存在点P ，使得2GOP BAC ∠=∠？若存在，直接写出点P 的横坐标；若不存在，说明理由．26．在ABC V 中，AB AC =，D 是边AC 上一动点，E 是ABC V 外一点，连接BD BE ，．(1)如图1，CE AB ∥，=AD CE ，若1203ABD A ∠==︒∠，求E ∠的度数； (2)如图2，CE AB ∥，2BD BE A ABD =∠=∠，，过点D 作DF AB ⊥交于点F ，若23DE DF DBC CBE =∠=∠，，求证：AB BD CE =+；(3)如图3，AE AB =，延长AE 交BC 的延长线于点F ，BE 交AC 于点G ，点D 是直线AC 上一动点，将ABD △沿BD 翻折得HBD △，连接FH ，取FH 的中点M ，连接AM ，若2EF GC AB BC ==，，当线段AM 取得最大值时，请直接写出AM AB的值．。

易错点01 亲社会行为—备战2024年中考道德与法治一轮复习易错题[001]

易错点01 亲社会行为【知识点】1．亲社会行为主要包括哪些行为?亲社会行为包括谦让、分享、帮助他人、关心社会发展等。

2．我们为什么要养成亲社会行为?(亲社会行为的意义)？（1）青少年处于走向社会的关键时期，我们应该树立积极的生活态度，关注社会，了解社会，服务社会，养成亲社会行为。

（2）有利于我们养成良好的行为习惯，塑造健康的人格，形成正确的价值观念，获得他人和社会的接纳与认可。

（3）参与社会的过程，既是体验社会生活的过程，也是在实践中发展和成就自己的过程。

（4）我们只有主动关心社会，积极融入社会，奉献社会，才能实现自己的人生价值。

3．如何养成亲社会行为？（1）要树立积极的生活态度，关注社会，了解社会。

（2）学会谦让、分享和帮助他人（3）要服务社会，奉献社会，做到:积极参加综合实活动和社会公益活动：关心社会发展，关心国家大事。

4．为什么要关爱他人?（1）关爱传递着美好情感，给人带来温暖和希望，是维系友好关系的桥梁。

（2）关爱是社会和谐稳定的润滑剂和正能量。

（3）关爱他人，收获幸福。

从一定意义上说，关爱他人也是关爱和善待自己。

5．如何关爱他人?（1）要心怀善意。

当他人遇到困难的时候，我们应该在道义上给予支持，物质上给予帮助，精神上给予关怀。

（2）要尽己所能。

关爱不分大小，贵在有爱心。

（3）要讲究策略。

帮助他人时，要考虑他人的内心感受，不伤害他人的自尊心；要增强安全防范意识和自我保护意识。

6．我们为什么要服务社会?（1）服务社会体现人生价值（2）服务社会能够促进我们全面发展。

7．人生的价值在于什么?怎样实现?（1）一个人的价值应该看他贡献什么，而不应当看他得到什么。

（2）只有积极为社会作贡献，才能得到人们的尊重和认可，实现我们自身的价值。

8．我们应该怎样服务和奉献社会?（1）服务和奉献社会，需要我们青年担当责任。

（2）服务和奉献社会，需要我们积极参与社会公活动。

（3）服务和奉献社会，需要我们热爱劳动，爱岗敬业。

数学初中必考试卷推荐教辅

摘要：本文针对初中生备战中考的需求，推荐几款优秀的数学必考试卷教辅，帮助同学们在备考过程中查漏补缺，提高解题能力。

一、教材全解《中学教材全解》（薛金星）是一本老牌教材全解教辅，适合初中生在复习过程中，全面梳理知识点，查漏补缺。

该书详细讲解了初中数学的所有知识点，并配有大量例题和练习题，帮助学生巩固所学知识。

二、教材帮《教材帮》是金星出品的一款相对年轻的教辅，内容丰富，讲解详细。

该书以教材为基础，对知识点进行系统梳理，并配以丰富的例题和练习题，帮助学生掌握解题技巧。

三、知识清单《知识清单》是曲一线——五三的出版机构出品，是一本贯穿整个初中数学知识的教辅。

该书适合在中考备考复习初期梳理知识、查漏补缺使用。

内容涵盖初中数学所有知识点，以表格形式呈现，便于学生查阅。

四、五年中考三年模拟《五年中考三年模拟》是一款针对中考的模拟试卷教辅，涵盖了近年来中考数学的所有题型和知识点。

该书以真题为基础，模拟中考题型，帮助学生熟悉考试节奏，提高应试能力。

五、五三五三教辅是初中生备考的必备神器，其中包括了《五三数学》和《五三中考模拟题》。

这两本书以真题为基础，针对中考题型进行模拟训练，帮助学生提高解题速度和准确率。

六、优胜讲义《优胜讲义》是一款针对初中数学的讲义类教辅，内容全面，讲解清晰。

该书以知识点为基础，配以大量例题和练习题，帮助学生巩固所学知识。

七、学霸笔记《学霸笔记》是一款以学霸笔记形式呈现的教辅，内容涵盖了初中数学的所有知识点。

该书以简洁明了的方式，帮助学生快速掌握知识点，提高解题能力。

总结：以上推荐的教辅都是初中生备战中考的必备良品，同学们可以根据自己的需求和实际情况，选择合适的教辅进行复习。

同时，也要注意以下几点：1. 制定合理的学习计划，确保每天有充足的时间进行复习。

2. 重视基础知识，加强对知识点和题型的理解。

3. 做好笔记，总结解题技巧和方法。

4. 定期进行模拟测试，检验自己的学习成果。

5. 保持良好的心态，相信自己，勇往直前。

备战中考数学专题训练---一元二次方程的综合题分类及答案

一、一元二次方程真题与模拟题分类汇编（难题易错题）1．已知关于x 的二次函数22(21)1y x k x k =--++的图象与x 轴有2个交点.（1）求k 的取值范围；（2）若图象与x 轴交点的横坐标为12,x x ，且它们的倒数之和是32-，求k 的值. 【答案】（1）k ＜-34 ；（2）k=﹣1 【解析】试题分析：（1）根据交点得个数，让y=0判断出两个不相等的实数根，然后根据判别式△= b 2-4ac 的范围可求解出k 的值；（2）利用y=0时的方程，根据一元二次方程的根与系数的关系，可直接列式求解可得到k 的值.试题解析：（1）∵二次函数y=x 2-（2k-1）x+k 2+1的图象与x 轴有两交点，∴当y=0时，x 2-（2k-1）x+k 2+1=0有两个不相等的实数根．∴△=b 2-4ac=[-（2k-1）]2-4×1×（k 2+1）＞0．解得k ＜-34；（2）当y=0时，x 2-（2k-1）x+k 2+1=0．则x 1+x 2=2k-1，x 1•x 2=k 2+1，∵=== 32-，解得：k=-1或k= 13-（舍去），∴k=﹣12．已知为正整数，二次方程的两根为，求下式的值：【答案】【解析】由韦达定理，有，．于是，对正整数，有原式=3．关于x的方程(k－1)x2+2kx+2=0（1）求证：无论k为何值，方程总有实数根．（2）设x1，x2是方程(k－1)x2+2kx+2=0的两个根，记S=++ x1+x2，S的值能为2吗？若能，求出此时k的值．若不能，请说明理由．【答案】（1）详见解析；（2）S的值能为2，此时k的值为2．【解析】试题分析：（1）本题二次项系数为(k－1)，可能为0，可能不为0，故要分情况讨论；要保证一元二次方程总有实数根，就必须使△＞0恒成立；（2）欲求k的值，先把此代数式变形为两根之积或两根之和的形式，代入数值计算即可．试题解析：（1）①当k-1=0即k=1时，方程为一元一次方程2x=1,x=有一个解；②当k-1≠0即k≠1时，方程为一元二次方程，△=（2k）²-4×2（k-1）=4k²-8k＋8="4(k-1)" ²＋4＞0方程有两不等根综合①②得不论k为何值，方程总有实根（2）∵x ₁＋x ₂＝,x ₁ x ₂=∴S=++ x1+x2=====2k-2=2，解得k=2，∴当k=2时，S的值为2∴S 的值能为2，此时k 的值为2．考点：一元二次方程根的判别式；根与系数的关系．4．沙坪坝区各街道居民积极响应“创文明城区”活动，据了解，某街道居民人口共有7.5万人，街道划分为A ，B 两个社区，B 社区居民人口数量不超过A 社区居民人口数量的2倍．（1）求A 社区居民人口至少有多少万人？（2）街道工作人员调查A ，B 两个社区居民对“社会主义核心价值观”知晓情况发现：A 社区有1.2万人知晓，B 社区有1.5万人知晓，为了提高知晓率，街道工作人员用了两个月的时间加强宣传，A 社区的知晓人数平均月增长率为m %，B 社区的知晓人数第一个月增长了45m %，第二月在第一个月的基础上又增长了2m %，两个月后，街道居民的知晓率达到92%，求m 的值．【答案】（1）A 社区居民人口至少有2.5万人；（2）m 的值为50．【解析】【分析】（1）设A 社区居民人口有x 万人，根据“B 社区居民人口数量不超过A 社区居民人口数量的2倍”列出不等式求解即可；（2）A 社区的知晓人数+B 社区的知晓人数=7.5×92%，据此列出关于m 的方程并解答．【详解】解：（1）设A 社区居民人口有x 万人，则B 社区有（7.5-x ）万人，依题意得：7.5-x ≤2x ，解得x ≥2.5．即A 社区居民人口至少有2.5万人；（2）依题意得：1.2（1+m %）2+1.5×（1+45m %）+1.5×（1+45m %）（1+2m %）=7.5×92%，解得m =50答：m 的值为50．【点睛】本题考查了一元二次方程和一元一次不等式的应用，解题的关键是读懂题意，找到题中相关数据的数量关系，列出不等式或方程．5．已知关于x 的一元二次方程()220x m x m -++=（m 为常数）（1）求证：不论m 为何值，方程总有两个不相等的实数根；（2）若方程有一个根是2，求m 的值及方程的另一个根．【答案】(1)见解析；(2) 即m 的值为0，方程的另一个根为0.【解析】【分析】（1）可用根的判别式，计算判别式得到△=(m+2)2−4×1⋅m=m 2+4＞0，则方程有两个不相等实数解，于是可判断不论m 为何值，方程总有两个不相等的实数根；（2）设方程的另一个根为t ，利用根与系数的关系得到2+t=21m + ,2t=m,最终解出关于t 和m 的方程组即可.【详解】(1)证明：△=(m+2)2−4×1⋅m=m 2+4，∵无论m 为何值时m 2≥0，∴m 2+4≥4＞0，即△＞0，所以无论m 为何值，方程总有两个不相等的实数根.(2)设方程的另一个根为t ， ()220x m x m -++=根据题意得2+t=21m + ,2t=m ，解得t=0，所以m=0，即m 的值为0，方程的另一个根为0.【点睛】本题考查根的判别式和根于系数关系，对于问题（1）可用根的判别式进行判断，在判断过程中注意对△的分析，在分析时可借助平方的非负性；问题（2）可先设另一个根为t ，用根于系数关系列出方程组，在求解.6．关于x 的方程()2204k kx k x +++=有两个不相等的实数根． ()1求实数k 的取值范围；()2是否存在实数k ，使方程的两个实数根之和等于两实数根之积的算术平方根？若存在，求出k 的值；若不存在，说明理由．【答案】（1）1k >-且0k ≠；（2）不存在符合条件的实数k ，使方程的两个实数根之和等于两实数根之积的算术平方根．【解析】【分析】()1由于方程有两个不相等的实数根，所以它的判别式0>，由此可以得到关于k 的不等式，解不等式即可求出k 的取值范围. ()2首先利用根与系数的关系，求出两根之和与两根之积，再由方程的两个实数根之和等于两实数根之积的算术平方根，可以得出关于k 的等式，解出k 值，然后判断k 值是否在()1中的取值范围内.【详解】解：()1依题意得2(2)404k k k =+-⋅>， 1k ∴>-，又0k ≠，k ∴的取值范围是1k >-且0k ≠；()2解：不存在符合条件的实数k ，使方程的两个实数根之和等于两实数根之积的算术平方根，理由是：设方程()2204k kx k x +++=的两根分别为1x ，2x ，由根与系数的关系有：1212214k x x k x x +⎧+=-⎪⎪⎨⎪=⎪⎩，又因为方程的两个实数根之和等于两实数根之积的算术平方根，212k k +∴-=， 43k ∴=-，由()1知，1k >-，且0k ≠，43k ∴=-不符合题意，因此不存在符合条件的实数k ，使方程的两个实数根之和等于两实数根之积的算术平方根．【点睛】本题重点考查了一元二次方程的根的判别式和根与系数的关系。

2024年广东省东莞市长安实验中学中考四模语文试题

2024年广东省东莞市长安实验中学中考四模语文试题一、名句名篇默写1．默写古诗文。

① ，。

萧关逢候骑，都护在燕然。

（王维《使至塞上》）①人生自有诗意：青年时期的杜甫，登山时则有“ ，一览众山小”的澎湃激情；而立之年的王安石，登飞来峰时则有“ ，自缘身在最高层”的潇洒自信；年近不惑的苏轼，密州出猎时则有“ ，西北望，射天狼”的雄心壮志。

①生活难免挫折：怀才不遇时，要有“长风破浪会有时，”的自信乐观；壮志未酬时，要有“了却君王天下事，”的赤胆忠心；身处逆境时，要明白“故天将降大任于是人也，必先苦其心志，，饿其体肤……曾益其所不能”的道理，勉励自己奋发有为。

①心中常忧家国：面对卷卷军帖，木兰做出了“ ，”《木兰诗》的勇敢决定。

①忽逢桃花林，夹岸数百步，中无杂树，，。

（陶渊明《桃花源记》）二、诗歌鉴赏2．诗歌比较鉴赏破阵子·为陈同甫赋壮词以寄之辛弃疾醉里挑灯看剑，梦回吹角连营。

八百里分麾下炙，五十弦翻塞外声，沙场秋点兵。

马作的卢飞快，弓如霹雳弦惊。

了却君王天下事，赢得生前身后名。

可怜白发生！十一月四日风雨大作二首陆游僵卧孤村不自哀，尚思为国戍轮台。

夜阑卧听风吹雨，铁马冰河入梦来。

请从下面两首诗中任选一首，使之与上面两首诗歌组成一组阅读材料。

你选择哪一首？为什么？残梦陆游少时铁马蹴河冰，老去摧藏百不能。

风雨满山窗未晓，只将残梦伴残灯。

从军行陆游青海长云暗雪山，孤城遥望玉门关。

黄沙百战穿金甲，不破楼兰终不还。

三、基础知识综合阅读下面的文字，完成下面小题。

青春是一段宣言，昭示着“自古英雄出少年”的激情；青春是一种姿态，“心有猛虎，细嗅蔷薇”；青春是一种勇气，跋山涉水，bùzhébùnáo，渴望找到答案。

李大钊当年在《晨钟报》创刊号上写道：“国家不可一日无青年，青年不可一日无觉醒。

”当雏鹰哺于巢穴、昂首观天之时，已yùn niàng振翅九霄的梦想；当马驹休于栏下、引颈嘶鸣之际，已蓄积chíchěng 天下的梦想。

2024年四川省成都市数学中考模拟卷C试题

2024年四川省成都市数学中考模拟卷C 试题一、单选题1．下列四个数中，最小的是（）A ．()0sin 45-︒B ．4-C ．13D ．2．下列计算正确的是（） A ．752ab a b -= B ．22211a a a a ⎛⎫ ⎪=+⎝⎭+C ．()2224236a b a b -=D ．2233a b b a ÷=3．在某校举办的“中学生钢笔字书写”比赛中，有15名同学参加比赛，初赛成绩各不相同，要取成绩前7名的同学参加决赛，小亮已经知道了自己的成绩，他想知道自己能否进入决赛，只需要再知道这15名同学成绩的（） A ．平均数 B ．中位数 C ．众数D ．以上都不对4．下列四个图中，不是正方体的表面展开图的是（）A ．B ．C ．D ．5．如图，在矩形ABCD 中，点E 在AD 上，且EC 平分BED ∠，2AB =，=45ABE ∠︒，则DE 的长为（）A ．2B 1C 1D ．6．现代办公纸张通常以01234,,,,A A A A A 等标记来表示纸张的幅面规格，一张2A 纸可截成2张3A 纸或4张4A 纸，现计划将100张2A 纸裁成3A 纸和4A 纸，两者共计300张，设可裁成3A 纸x 张，4A 纸y 张，根据题意，可列方程组（）A ．10024300x y x y +=⎧⎨+=⎩B ．30024100x y x y +=⎧⎨+=⎩C ．1001130024x y x y +=⎧⎪⎨+=⎪⎩ D ．3001110024x y x y +=⎧⎪⎨+=⎪⎩ 7．如图，A ，B ，C ，D 是O e 上的点，AB AD =，AC 与BD 交于点E ，3AE =，5EC =，BD =O e 的半径为（）A ．6 BC ．5 D．8．如图，抛物线()20y ax bx c a =++≠的对称轴为直线2x =-，且过点()1,0．现有以下结论：①0abc <；②50a c +=；③对于任意实数m ，都有224b bm a am +≤-；④若点()()1122,,,A x y B x y 是图象上任意两点，且1222x x +<+，则12y y <，其中正确的结论是（）A ．①②B ．②③④C ．①②④D ．①②③④二、填空题 9．计算． 10．已知点 ()()122,,1,A y B y --在反比例函数3y x=-的图象上，则1y 2y ．（用“<”，“>”或“=”连接）11．我国是世界四大文明古国之一，拥有五千多年的悠久文化与文明史．她位于亚洲东部，太平洋西岸，陆地面积约9600000平方千米，9600000用科学记数法可表示为．12．某商店今年7月份的销售额是5万元，9月份的销售额是7.2万元，从7月份到9月份，该店销售额平均每月的增长率是．13．如图，在ABC V 中，90,2∠=︒==ACB AC BC ，点P 是射线AB 上一动点，90CPD ∠=︒，且PC PD =，连接AD CD 、，则AD CD +的最小值是．三、解答题14．（1(1122cos602-⎛⎫+- ⎪⎝⎭︒；（2）解不等式组()2224332x x x x ⎧-≤-⎪⎨++<⎪⎩并写出它的整数解．15．为了更好的了解孩子们的体育水平，全力备战中考，某校体育组从初三年级体考成绩中随机抽查了20名男生和20名女生的体考成绩进行整理、描述和分析（成绩得分用x 表示，共分成四组：:4750A x <≤，:4447B x <≤，:4144C x <≤，:41D x ≤），下面给出了部分信息：20名男生的体考成绩（单位：分）：50，50，50，49，49，49，48，47，47，46，46，46，46，45，44，44，43，42，40，39；20名女生的体考成绩为B 等级的数据是：46，46，46，47，47，45，46．所抽取的学生体考成绩统计表所抽取的20名女生的体考成绩扇形根据以上信息，解答下列问题：(1)直接写出上述图表中b c +=______，B 组圆心角度数α=______．(2)根据以上数据，你认为该校男生的体育成绩好还是女生的体育成绩好？请说明理由（一条即可）；(3)该校初三年级共有1600名学生，参与此次体考测试，其中男女生的比例为3:2，估计初三年级参加测试的学生等级为A 的共有多少人？16．如图，小明所在的数学兴趣小组用自制的测倾器在学校教学大楼前的广场上点D 处测得楼顶A 的仰角为45︒，大楼顶端悬挂了一幅励志条幅AB ，小明他们后退3.5m 到点C 处，测得条幅底端B 的仰角为32︒，若已知条幅AB 长5m ，测倾器 1.60m EC FD ==，试求大楼的高度AH ．（参考数据sin320.53︒=，cos320.85︒=，tan 32062︒=.，结果精确到0.1m ）17．如图，AB 是O e 的弦，直径DG AB ⊥，垂足为点F ，C 为¼AG 上的一点，连接DC ，交线段AB 于点E ，作DCH AED ∠∠=，CH 交DG 延长线于点H ．(1)求证：CH 是O e 的切线；(2)若O e 的半径为5，3tan 4H =，求CD 的长．18．如图，在平面直角坐标系xOy 中，已知直线12y x b =-+与坐标轴交于C ，D 两点，反比例函数()120y x x=>的图象与直线CD 交于A ，B 两点，连结AO ，BO ，分别过点A ，B 作x 轴的垂线AE 和BF ，AE 交BO 于点G ．(1)若点B 的横坐标为12，求BDF V 的面积； (2)若阴影部分的面积为12，①记BDF V 的面积为1S ，V OGE 的面积为2S ，求证：122S S =； ②求b 的值．四、填空题19．已知实数()x y x y >，满足2222128x y x y xy +=+=，，则x y -的值为． 20．若关于x 的分式方程2344mx x=+--无解，则m 的值为． 21．如图，在ABC V 中，A m ∠=︒，ABC ∠和ACD ∠的平分线交于点1A ，得1A ∠，1A BC ∠和1ACD ∠的平分线交于点2A ，得2A ∠，…，2022A BC ∠和2022A CD ∠的平分线交于点2023A ，则2023A ∠=︒．22．矩形ABCD 中，8AB =，6BC =，对角线AC 、BD 相交于点O ，点E 为DC 上一点，将ADE V 沿AE 折叠，使点D 落在对角线AC 的点F 处，则线段OE 的长为．23．如图，在ABC V 中，5,120AB AC BAC ==∠=︒，以CA 为边在ACB ∠的另一侧作ACM ACB ∠=∠，点D 为边BC （不含端点）上的任意一点，在射线CM 上截取CE BD =，连接,,AD DE AE ．设AC 与DE 交于点F ，则线段CF 的最大值为．五、解答题24．2023年春季进入甲流高发期，保山市某学校购进A ，B 两种消毒液，用于预防甲流病毒．购买8桶A 消毒液和6桶B 消毒液，则一共需要430元；若购买7桶A 消毒液和9桶B 消毒液，则一共需要470元．(1)每桶A 消毒液、每桶B 消毒液的价格分别是多少元？(2)若该校计划购买A ，B 两种消毒液共50桶，其中A 消毒液的数量至少比B 消毒液的数量多4桶，又不大于B 消毒液的数量的2倍少4桶，怎样购买，才能使总费用最少？并求出最少费用．25．如图1，已知二次函数2y ax bx c =++（a 、b 、c 为常数，且0a ≠）的图象，与x 轴交于A 、B 两点（A 点在B 点左侧），与y 轴交于点()0,3C ，且其函数表达式可以变形为()()13y a x x =+-的形式．已知点P 为该抛物线在第一象限内的一动点，设其横坐标为m ．(1)求出点A 、点B 的坐标和该二次函数的表达式；(2)连接BC ，过点P 作PQ x ⊥轴于点Q ，交BC 于点N ，直线AP 交y 轴于点M ，连接MN ． ①求出直线AP 的函数表达式（用含有m 的代数式表示）；②设四边形MNQO 的面积为S ，求S 关于m 的函数关系式，并求S 的最大值；(3)如图2，若直线l 为该二次函数图象的对称轴，交x 轴于点H ，直线AP ，BP 分别交直线l 于点E 、F ．在点P 运动的过程中，HF HE +是否为定值？若是，请求出该定值；若不是，请说明理由．26．小明同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来则形成一组全等的三角形，小明把具有这个规律的图形称为“手拉手”图形．（1）【问题发现】：如图1，D 是等边ACB △的边BC 上的一动点，其中等边ACB △的边长为10，以AD 为边在AB 上方作等边ADE V ，小明认为AD 有最小值，那么AD 的最小值是___________．（2）①【问题探究】：如图2，若ACB △和DCE △均为等边三角形，点A 、D 、E 在同一条直线上，连接BE ，则AEB ∠的度数为___________；线段BE 与AD 之间的数量关系是___________．②【问题探究】：如图3，若ACB △和DCE △均为等腰直角三角形，90ACB DCE ∠=∠=︒，点A 、D 、E 在同一条直线上，CM 为DCE △中DE 边上的高，连接BE ，请判断AEB ∠的度数及线段CM AE BE 、、之间的数量关系并说明理由．【问题解决】（3）如图4，在四边形ABCD 中，6054AB AD BAD BC CD =∠=︒==，，，，求四边形ABCD面积的最大值．。

2023-2024学年初中历史人教版中考模拟习题及解析

2023-2024学年人教版初中历史中考模拟班级：__________ 姓名：__________ 考号：__________一、选择题（本大题共计15小题，每题3分，共计45分）1.小明把收藏了一枚钱币（如图）带到了学校，大家根据所学的知识，一致确定它发行于（）A. 隋朝B. 唐朝C. 北宋D. 清朝【答案】B【解析】材料中的货币上有“开元通宝”的字样，开元是唐玄宗统治前期的年号，因此说该钱币发行于唐朝时期。

故选B。

2.下列成就中最大程度地解放了人力，推动农业快速发展的是（）A. 青铜制造B. 铁农具的使用C. 牛耕的推广D. 兴修水利工程【答案】C【解析】春秋时期，我国开始出现牛耕，到战国时，牛耕使用范围扩大．牛耕的使用，牛耕是我国农业发展史上的一次革命，使得社会生产力显著提高，最大程度地解放了人力，推动农业快速发展．故选C．3.民族团结、民族友好是我国民族关系发展的主流，文成公主嫁给松赞干布，带去了先进的生产技术，促进了（）①吐蕃的发展与进步②唐蕃经济文化交流③汉藏两族人民的友谊④驻藏大臣的设置A. ①②③B. ①②④C. ①③④D. ①②④【答案】A【解析】唐朝时期，唐太宗把文成公主嫁给吐蕃赞普松赞干布，加强了唐蕃友好关系，促进了吐蕃经济文化发展，奠定了汉藏友好交往的基础，所以①②③是正确的选项。

④属于清朝的措施，故排除。

故选A。

4.人民日报的报道《中国建设新疆成就不容肆意抹黑歪曲一一国际人士驳斥美国所谓涉疆法案》，在网上广为传播。

新疆自古以来就是祖国不可分割的一部分，它开始隶属于中央政府管辖的历史可追溯到我国古代（）A. 秦朝B. 汉朝C. 商朝D. 周朝【答案】B【解析】结合所学知识可知，公元前60年，西汉政府在西域设置西域都护，作为管理西域的最高长官。

西域都护颁行汉朝的号令，调遣军队，征发粮草，对西域地区进行有效的管辖。

西域都护的设置，标志着西域开始正式归属中央政权，故B符合题意。

备战中招的几点做法(精)

备战中招的几点做法八里岔中学付冠华作为数学教师，我们曾羡慕过语文课上的诗情画意，羡慕过历史课的横贯古今。

作为农村中学教师，我们羡慕过县中学现代化的设备，羡慕过市中的良将精兵。

但我们相信每一朵花都有盛开的理由，我们不能选择诗歌，可以选择诗意的数学；我们不能选择精兵，可以选择培养精兵。

当各种复习方法和经验充斥在报纸里、电视中、网络上，各种资料像暴风骤雨一样不断冲击着我们。

教案、作业、试卷铺天盖地，席卷而至时，我们力图做到忙而不乱，目标明确。

备战中考我们从以下几个方面来做的。

一、做好集体教研1、研透《课标》和《中考说明》认真阅读新课标，领会新课标理念。

我们重点学习了：对教师的教学建议，具体到每一模块、每一节的目标要求是体验、感悟还是了解、理解、掌握、灵活运用？确保目标合理，方向正确，深度难度的尺度把握准确，锁定复习的核心内容。

通过阅读《2008年河南省中招考试说明与检测》，明确考试性质和命题依据，考查范围，考试要求及内容，考试的方式及试卷结构。

认真研究其中的例证性试题，帮助我们明确试题所蕴含的相关信息，加强复习的指导性、计划性和针对性。

2.研究中考试题特别是河南省近几年的中考试题，整合资源。

将05—08四年课改试卷和专家的数据分析相结合，制成表格，从而明确了在每一部分中已考查了哪些知识点，具体定位是什么，考查形式是什么？考生的答题情况是什么样的？然后从中总结出考查的热点、遗漏点。

结合上述分析来明确复习重点。

3. 研究学生学生是学习的主体，只有充分了解学生最需要的是什么，才能根据学生特点进行针对性复习，避免学生会的还在反复强调，学生不会的一带而过，出现夹生饭，炒剩饭的现象。

在教学中，我们把学生所出现的问题收集起来制定“病历档案”,重点分析清楚以下几点：概念模糊的，相关知识逻辑混乱的，图形特征直观错觉的，以偏概全的不够严谨的，对题设条件的断章取义，没有挖掘出隐含条件的，对推理运算草率马虎的。

对上述问题的处理最关键的是有针对性的把这些问题设计到练习中，让学生在解题实践中获得教训和反思。

2024年陕西师范大学附属中学中考四模数学试题(解析版)

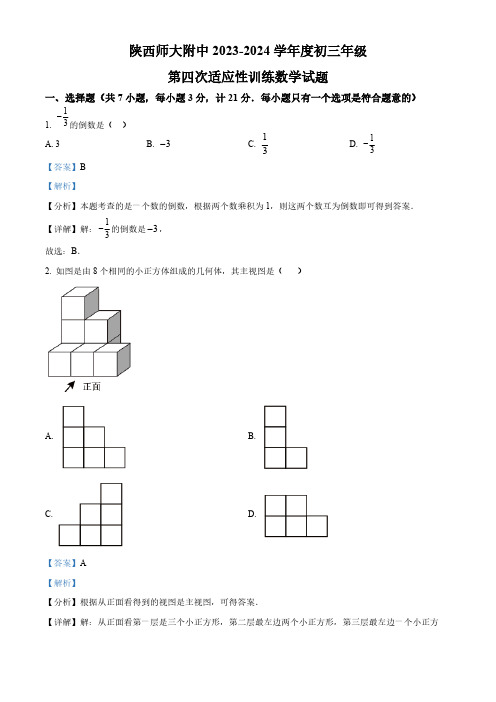
陕西师大附中2023-2024学年度初三年级第四次适应性训练数学试题一、选择题（共7小题，每小题3分，计21分．每小题只有一个选项是符合题意的）1.的倒数是（）A. 3B. C. D. 【答案】B 【解析】【分析】本题考查的是一个数的倒数，根据两个数乘积为1，则这两个数互为倒数即可得到答案．【详解】解：的倒数是，故选：B ．2. 如图是由8个相同的小正方体组成的几何体，其主视图是（）A. B.C. D.【答案】A【解析】【分析】根据从正面看得到的视图是主视图，可得答案．【详解】解：从正面看第一层是三个小正方形，第二层最左边两个小正方形，第三层最左边一个小正方13-3-1313-13-3-形，故选：A ．【点睛】本题考查了简单组合体的三视图，从正面看得到的视图是主视图．3. 如图，将含30°角的直角三角板ABC 放在平行线α和b 上，∠C ＝90°，∠A ＝30°，若∠1＝20°，则∠2的度数等于（）A. 60°B. 50°C. 40°D. 30°【答案】B【解析】【分析】根据三角形外角的性质和对顶角相等可得∠4，再根据两直线平行，同位角相等即可得出结论．【详解】解：∵∠A ＝30°，∠1＝20°，∴∠ 1= ∠ 3，∠4 = ∠3 + ∠A =20°+30°=50°，∵a ∥b ，∴∠2 =∠ 4=50° ．故选 B ．【点睛】本题考查平行线的性质、三角形外角的性质．能正确识图是解题关键．4. 在平面直角坐标系中，将直线向上平移2个单位长度，平移后的直线与两坐标轴围成的三角形面积是（）21y x =+A. B. C. D. 2【答案】B【解析】【分析】先根据图形平移的性质得出平移后的解析式，再求出此直线与x 、y 轴的交点，利用三角形的面积公式即可求解．【详解】解：将直线的图象向上平移2个单位，得到，令，得，令，得，∴平移后的直线与两坐标轴围成的三角形面积是，故选：B ．【点睛】本题考查的是一次函数的图象与几何变换，解答此题的关键是求出平移后直线的解析式及与两坐标轴的交点．5. 如图，在菱形中，对角线，相交于点O ，若，则的值为（）A. B. C. D. 【答案】C【解析】【分析】此题考查了菱形的性质、勾股定理以及锐角三角函数的定义等知识；先由菱形的性质得，，再由勾股定理求出，然后由锐角三角函数的定义即可得出答案．熟练掌握菱形的性质和锐角三角函数的定义是解题的关键．【详解】解：∵四边形是菱形，且，设，，∴，，34943221y x =+23y x =+0x =3y =0y =32x =-1393224⨯⨯=ABCD AC BD :2:3AB BD =cos BAC ∠34351322OB BD x ==AC BD ⊥OA =ABCD :2:3AB BD =2AB x =3BD x =1322OB BD x ==AC BD ⊥∴，∴，故选：C ．6. 如图，内接于，是的直径，过点C 作的切线交的延长线于点E ．若，则的度数为（）A. B. C. D. 【答案】B【解析】【分析】连接、，则，根据切线的性质可得，进而得出，根据等腰三角形的性质得出，最后根据圆的内接四边形对角互补，即可求解．【详解】解：连接、，则，∵与相切于点C ，∴，∴，∵，∴，∴，∴，故选：B ．．【点睛】本题主要考查了切线的定义，等腰三角形的性质，圆的内接四边形的性质，解题的关键是掌握圆的切线经过半径外端且垂直于半径，圆的内接四边形对角互补，等腰三角形等边对等角．OA x ===cos OA BAC AB ∠==ABC O AD O O AD 40E ∠=︒ABC ∠110︒115︒120︒125︒OC DC OC OD =90OCE ∠=︒9050COE E ∠=︒-∠=︒65ADC OCD ∠=∠=︒OC DC OC OD =CE O CE OC ⊥90OCE ∠=︒40E ∠=︒90904050COE E ∠=︒-∠=︒-︒=︒()118050652ADC OCD ∠=∠=⨯︒-︒=︒180********ABC ADC ∠=︒-∠=︒-︒=︒7. 抛物线与x 轴交于点A （－1，0），点B （3，0），交y 轴于点C ，直线经过点C ，点B （3，0），它们的图象如图所示，有以下结论：①抛物线对称轴是直线；②；③时，；④若，则．其中正确的个数为（）A. 1B. 2C. 3D. 4【答案】D【解析】【分析】根据题意易得点A 、B 关于对称轴对称，则有抛物线的对称轴为直线，把点A 代入抛物线解析式可判断②，然后由函数图形可判断③，进而把，点A （－1，0），点B （3，0）代入可求抛物线解析式，然后可得点C 的坐标，最后可判断④．【详解】解：由题意得：点A 、B 关于对称轴对称，则抛物线的对称轴为直线，故①正确；把点A （－1，0）代入解析式得：，故②正确；由图象可知当时，，故③正确；由，点A （－1，0），点B （3，0）可设二次函数解析式为，∴，∴当x =0时，则，∴点，把点B 、C 的坐标代入一次函数解析式得：，2y ax bx c =++y kx m =+1x =0a b c -+=13x -<<20ax bx c ++>1a =-1k =-1x =1a =-1312x -+==0a b c -+=13x -<<20ax bx c ++>1a =-()()13y x x =-+-223y x x =-++3y =()0,3C 303k m m +=⎧⎨=⎩解得：，故④正确；综上所述：正确的个数有4个，故选：D ．【点睛】本题主要考查二次函数的图象与性质及一次函数，熟练掌握二次函数的图象与性质及一次函数是解题的关键．二、填空题（共7小题，每小题3分，共21分）8. 比较大小：（填“＞”“＜”或“＝”）．【答案】【解析】【分析】先求出【详解】解：∵16＜20，∴．故答案为：＜．【点睛】本题考查实数大小比较，解题的关键是掌握比较有理数和根号形式无理数的大小的方法．9. 计算：______．【答案】【解析】【分析】本题考查单项式乘以单项式，直接利用相关法则计算即可．【详解】解：；故答案为：．10. 如图，分别以等边三角形的顶点A ，B ，C 为圆心，以长为半径画弧，我们把这三条弧组成的封闭图形就叫做圆弧三角形．若，则圆弧三角形的周长为______．【答案】【解析】【分析】本题考查了等边三角形的性质，弧长公式，根据弧长公式计算出每段弧的长度，即可求出圆弧三的13k m =-⎧⎨=⎩<4=4=4<()2x x -⋅=22x -()222x x x -⋅=-22x -AB 5AB =5π角形的周长．理解题意求出一段弧的长度是解题的关键．【详解】解：∵为等边三角形，∴，∵半径都为的长，∴这三段弧的长度相等，∴每段弧的长度为：，∴圆弧三角形的周长为，故答案为：．11. 如图，点A 在双曲线y=上，点B 在双曲线y=（k≠0）上，AB ∥x 轴，过点A 作AD ⊥x 轴于D ．连接OB ，与AD 相交于点C ，若AC=2CD ，则k 的值为____．【答案】12【解析】【详解】解：设点A 的坐标为（a ，），则点B 的坐标为（，），∵AB ∥x 轴，AC=2CD ，∴∠BAC=∠ODC ，∵∠ACB=∠DCO ，∴△ACB ∽△DCO ，∴，∵OD=a ，则AB=2a ，∴点B 的横坐标是3a ，∴3a=，解得：k=12.故答案为12.ABC 60∠=∠=∠=︒A B C AB 60551803ππ⨯=5353ππ⨯=5π4xk x 4a ak 44a AB AC 2DA CD 1==ak 412. 如图，在正方形中，，延长至E ，使，连接平分交于F ，连接，则长为_______．【解析】【分析】此题主要考查了正方形的判定及性质，相似三角形的判定和性质，勾股定理等，解题的关键是过点作于，作于点N ，首先证明为正方形，再设,则，然后证明，由相似三角形的性质求出a ，进而在中由勾股定理即可求出．【详解】如图，过点作于，作于点N ．∵四边形为正方形，，，∴四边形为矩形，又∵平分，，∴四边形为正方形，，设,则，，，，的ABCD 3AB =BC 2CE =AE CF ，DCE ∠AE DF DF F FM CE ⊥M FN CD ⊥CMFN CM a =FM FN CN a ===EFM EAB ∽Rt DFN DF F FM CE ⊥M FN CD ⊥ABCD 3AB =，90,3B DCB BC AB CD ∴∠=∠=︒===,,18090FM CE FN CD DCE DCB ⊥⊥∠=︒-∠=︒ CMFN CF DCE ∠FM FN ∴=CMFN FM FN CM CN ∴===CM a =FM FN CN a ===2CE = 5,BE BC CE EM CE ∴=+==-2CM a =-90,B FM CE ∠=︒⊥，，，即，解得，，，在中, ，由勾股定理得，三、解答题（共13小题，计84分．解答应写出过程）13.．【解析】【分析】本题考查了实数的混合运算，特殊角的三角函数值．代入特殊角的三角函数值，根据实数的混合运算的法则计算即可求解．．14. 解关于x 的不等式组【答案】-2<x <-1【解析】【分析】分别求出不等式组中每一个不等式的解集，再确定出公共部分，即可求解．FM AB ∴EFM EAB ∴∽FM MEAB BE ∴=235a a -=34a =FN CN ∴==3439344DN CD CN ∴=-=-=Rt DFN 9,4DN =34FN =DF ==tan 60︒1-tan 60︒1=+--1=-34423x x x x >-⎧⎪+⎨>+⎪⎩【详解】解：，解①得：x >-2，解②得：x <-1，∴-2<x <-1．【点睛】本题考查解一元一次不等式组，熟练掌握根据“大取较大，小小取较小，大小小大中间找，大大小小无处找”的原则性确定不等式组的解集是解题的关键．15. 先化简．再求值：，其中．【答案】；【解析】【分析】本题考查了分式化简求值，先根据分式的乘法进行计算，然后计算减法，最后将字母的值代入求解．解题关键是熟练运用分式运算法则进行求解．【详解】解：；当时，原式．16. 如图，已知在中，．请用尺规作图法，在边上求作一点D ，使得的周长等于．（保留作图痕迹，不写作法）34423x x x x >-⎧⎪⎨+>+⎪⎩①②221422211a a a a a a --⋅---+-13a =1a a -12-221422211a a a a a a --⋅---+-()()()22212211a a a a a a +--=⋅----2211a a a +=---1a a =-13a =13113=-12=-ABC 90ACB ∠=︒AB BCD △AB BC +【答案】见解析【解析】【分析】本题考查作图—复杂作图、线段垂直平分线的性质，作线段的垂直平分线，交于点，连接，则点即为所求．熟练掌握线段垂直平分线的性质是解答本题的关键．【详解】解：如图，作线段的垂直平分线，交于点，连接，则，∴的周长为，则点即为所求．17. 如图，在四边形中，，，，．求证：．【答案】见解析【解析】【分析】本题主要考查了全等三角形的判定和性质，根据线段之间和差关系，角度之间和差关系证得，，利用即可证明，熟练掌握全等三角形的判定和性质定理是解题的关键．【详解】证明：∵，，则，AC AB D CD D AC AB D CD CD AD =BCD △BC BD CD BC BD AD BC AB ++=++=+D ABCD BC CD =CE CF =BAF DAE ∠=∠B D ∠=∠AE AF =BE DF =BAE DAF ∠=∠AAS BC CD =CE CF =BC CE CD CF -=-∴，∵，则，∴，在和中，，∴，∴．18. 如图，正方形网格中，在平面直角坐标系中，的三个顶点为、、．（1）将向下平移5个单位长度得到，请画出；（2）画出绕点逆时针旋转后得到的，并写出点的坐标；（3）连接，，，求的面积．【答案】（1）图见解析（2）图见解析，点的坐标为（3）2【解析】【分析】本题考查平移作图、旋转作图、利用网格求三角形面积：（1）将三个顶点分别下平移5个单位长度，得到对应点，顺次连接即可；（2）将和分别绕点逆时针旋转，得到对应点，顺次连接即可；（3）利用三角形面积公式求解．BE DF =BAF DAE ∠=∠BAF EAF DAE EAF ∠∠∠∠-=-BAE DAF ∠=∠ABE ADF △BAE DAF B D BE DF ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS ABE ADF ≌△△AE AF =ABC ()1,2A ()3,1B ()2,3C ABC 111A B C △111A B C △111A B C △1C 90︒221A B C △2A 12A A 12A B 22A B 122A A B 2A ()33-，ABC 1A 1B 1C 90︒【小问1详解】解：如图，即为所求；【小问2详解】解：如图，即为所求，点的坐标为；【小问3详解】解：如图，，即的面积为2．19. 不透明的袋子里装有2个标有数字的小球，1个标有数字0的小球和若干个标有数字2的小球，这111A B C △221A B C △2A ()33-，12212222A AB S =⨯⨯= 122A A B 1-些球除颜色外都相同，从中任意摸出1个球，是标有数字的概率为．（1）袋子里标有数字2的小球有个；（2）丽丽先从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M 的横坐标、再将此球放回、摇匀，然后由静静再从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M 的纵坐标，请用树状图或表格列出点M 所有可能的坐标，并求出点M 落在坐标轴上的概率．【答案】（1）2 （2）【解析】【分析】本题考查已知概率求数量，列表或画树状图法求概率：（1）根据标有数字的小球的个数及概率求出总数，即可求解；（2）通过列表列出所有等可能的情况，从中找出满足条件的情况，再利用概率公式求解．【小问1详解】解：袋子里小球的总数为：（个），袋子里标有数字2的小球有：（个），故答案为：2；小问2详解】解：由题意列表如下：丽丽静静02222由表可知，共有25种等可能的情况，其中，，，，在坐标轴上，共有9种情况，【1-259251-2255÷=5212--=1-1-1-()1，1--()1，1--()01-，()21-，()21-，1-()1，1--()1，1--()01-，()21-，()21-，()10-，()10-，()00，()20，()20，()12-，()12-，()02，()22，()22，()12-，()12-，()02，()22，()22，()10-，()00，()20，()01-，()02，因此出点M 落在坐标轴上的概率为．20. 某“综合与实践”小组开展测量某建筑物高度的活动，他们制订了测量方案，测量报告如下．建筑物正前方有一根高度是17米的旗杆，从办公大楼顶端A 测得旗杆顶端E 的俯角为，旗杆底端D 到大楼前梯坎底边的距离是20米，梯坎坡长是9米，梯坎坡度．请根据以上测量结果，求建筑物的高度．【答案】建筑物的高度约为37.7米【解析】【分析】本题考查了解直角三角形的应用-仰角俯角问题，坡度坡角问题，如图，过点作，垂足为，延长交于点，由题意得：，，米，，，从而可得，再根据已知可设米，则米，然后在中，利用勾股定理进行计算可求出和的长，从而求出的长，最后在中，利用锐角三角函数的定义求出的长，从而利用线段的和差关系进行计算，即可解答．根据题目的已知925AB AB ED 45︒DC BC 25i =:AB AB E EG AB ⊥G AB DC H AH DH ⊥EG DH =17ED GH ==45FAE ∠=︒AF EG ∥45FAE AEG ∠=∠=︒2BH x =CH =Rt BCH △BH CH DH Rt AEG △AG条件并结合图形添加适当的辅助线是解题的关键．【详解】解：如图，过点作，垂足为，延长交于点，由题意得：，，米，，，∴，∵梯坎坡度∴∴设米，则米，在中，（米），∵米，∴，解得：，∴米，米，∵米，∴米，在中，米，∴（米），∴建筑物的高度约为37.7米．21. 某工厂生产一种正方形的合金薄板（其厚度忽略不计），每张薄板的出厂价（单位：元）由基础价和浮动价两部分组成，其中基础价与薄板的大小无关，是固定不变的，浮动价与薄板的边长成正比例，在营销过程中得到了如下表格中的数据．E EGAB ⊥G AB DC H AH DH ⊥EG DH =17ED GH ==45FAE ∠=︒AF EG ∥45FAE AEG ∠=∠=︒BC 2i=BH CH =2BH x =CH =RtBCH △3BC x ===9BC =39x =3x =6BH =CH =20DC =(20EG DH CH DC ==+=+Rt AEG △(tan 4520AG EG =⋅︒=+2017637.7AB AG GH BH =+-=++-≈AB薄板的边长x （）2030出厂价y （元/张）4565（1）求每张游板的出厂价y 与边长x 之间满足的函数关系式；（2）在营销过程中，已知出售一张边长为的薄板工厂可获得利润26元，求这张薄板的成本价．【答案】（1）（2）59元【解析】【分析】本题考查一次函数的应用，解答本题的关键是明确题意，求出相应的函数解析式．（1）根据题意和表格中的数据，可以求出每张薄板的出厂价y 与边长x 之间满足的函数关系式；（2）将代入（1）中的函数关系式，求出出厂价，然后用出厂价减利润，即可得到成本价．【小问1详解】解：每张游板的边长为，基础价为元，浮动价为元，则出厂价，由表格可得，，解得，即每张游板的出厂价y 与边长x 之间满足的函数关系式；【小问2详解】当时，，（元），答：这张薄板得成本价是59元．22. 某校为了解九年级同学的中考体育考试准备情况，随机抽查该年级部分学生进行体育模拟测试，根据测试成绩（单位：分）分为四个类别：，，，，将分类结果制成如下两幅统计图（尚不完整）．cm 40cm 25y x =+40x =x b kx y kx b =+20453065k b k b +=⎧⎨+=⎩25k b =⎧⎨=⎩25y x =+40x =240585y =⨯+=852659-=()5860A t ≤≤()5458B t ≤<()5054C t ≤<()50D t ≤根据以上信息，回答下列问题：（1）本次抽样的样本容量为；（2）补全条形统计图；（3）扇形统计图中a 的值为，圆心角的度数为；（4）若九年级有612名学生，估计测试成绩少于54分的学生有多少名？【答案】（1）60 （2）图见解析（3）20，（4）306名【解析】【分析】本题主要考查条形统计图与扇形统计图的综合应用，利用样本估计总体等，能看懂统计图是解题的关键．（1）根据D 组的人数和百分比即可求出样本容量；（2）根据C 组所占的百分比即可求出C 组的人数；（3）根据A 组的人数即可求出A 组所占的百分比，根据C 组所占的百分比即可求出对应的圆心角；（4）算出成绩少于54分的学生的比例，利用样本估计总体．【小问1详解】解：D 组的人数为6，占比，故本次抽样的样本容量为：，故答案为：60；【小问2详解】解：C 组的人数为：，补全后的条形统计图如下所示：β72︒10%610%60÷=6040%24⨯=【小问3详解】解：扇形统计图中a 的值为：，圆心角的度数为：，故答案为：20，；【小问4详解】解：（名）答：估计测试成绩少于54分的学生有306名．23. 如图，是的直径，弦于点E ，点F 为上一点，连接，交于点P ，连接，若．（1）求证：；（2）延长交延长线于点G ，若，，求的长．【答案】（1）见解析（2）10【解析】【分析】（1）连接，易得，进而得到，垂径定理得到，圆周角定理，得到，，即可得出结论；126010020÷⨯=β20%36072⨯︒=︒72︒24661230660+⨯=AB O CD AB ⊥AD CF AB ,AC AF PE BE =2BAF BAC ∠=∠CD AF 6AB=CD =GF BC BC CP =BCD FCD ∠=∠ BCBD =BAC DCB ∠=∠FAB FCB ∠=∠（2）连接，等弧对等弦，得到，圆周角定理结合勾股定理求出的长，垂径定理，求出的长，证明，列出比例式求出的长，进而求出的长，根据，求出的长，再用求出的长即可．【小问1详解】证明：连接，∵，∴，∴，∵为直径，，∴，∴，∴，∵，∴；【小问2详解】连接，BF BF CD =AF CE AEC CEB ∽BE AE cos AE AFFAB AG AB∠==AG AG AF -FG BC ,CE BP PE BE ⊥=BC CP =12FCD DCB FCB ∠=∠=∠AB AB CD ⊥ BCBD =BAC DCB ∠=∠22FCB DCB BAC ∠=∠=∠FAB FCB ∠=∠2FAB BAC ∠=∠BF由（1）可知：，∴，∴，∵为直径，，∴，，，∴，，∴，∴，∴，解得：或（不合题意，舍去）；∴，∴，∵，∴，∴，∴．BCBD DF ==»»CDBF =BF CD ==AB AB CD ⊥90AFB ACB ∠=∠=︒12CE CD ==90CEA CEB ∠=∠=︒2AF ==90CAB BCE ACE ∠=∠=︒-∠AEC CEB ∽AE CE CE BE=()26CE AE BE BE BE =⋅=-⋅2BE =4BE =2BE =4AE =cos AE AF FAB AG AB∠==426AG =12AG =10GF AG AF =-=【点睛】本题考查圆周角定理，垂径定理，弧，弦，角之间的关系，相似三角形的判定和性质，解直角三角形等知识点，综合性强，难度较大，熟练掌握相关知识点，并灵活运用，是解题的关键．24. 已知抛物线与x 轴交于点A 、B （点A 在点B 的左侧），与y 轴交于点，对称轴为直线．（1）求此二次函数表达式和点A 、点B 的坐标；（2）点P 为第四象限内抛物线上一动点，将抛物线平移得到抛物线，使得抛物线的顶点为点P ，抛物线与y 轴交于点E ，过点P 作y 轴的垂线交y 轴于点D ．是否存在这样的点P ，使得以点P 、D 、E 为顶点的三角形与相似，请你写出平移过程，并说明理由．【答案】（1），（2）存在，先向左平移个单位，再向上平移个单位【解析】【分析】（1）根据对称轴公式求出的值，将代入求出的值，进而求出抛物线的解析式，令，求出的坐标即可；（2）设，顶点式写出的解析式，进而求出点坐标，分，两种情况，进行求解即可．【小问1详解】∵抛物线的对称轴为直线，∴，把代入解析式，得：，∴抛物线的解析式为：，令，解得：，∴；【小问2详解】存在，设， ∵平移，抛物线的开口方向和大小不发生改变，∴，21:L y x bx c =++()0,3C -1x =1L 1L 2L 2L 2L AOC 2=23y x x --()()1,0,3,0A B -2349b ()0,3C-c 0y =,A B ()()2,2303P m m m m --<<2L ,D E PDE AOC △∽△EDP AOC ∽12b x =-=2b =-()0,3C -3c =-2=23y x x --2230y x x =--=123,1x x ==-()()1,0,3,0A B -()()2,2303P m m m m --<<()222:23L y x m m m =-+--∴当时，，∴，∵过点P 作y 轴的垂线交y 轴于点D ，∴，，∴，，∵，∴，当点P 、D 、E 为顶点的三角形与相似时，分两种情况，①当时，则：，即：，解得：（舍去）或（舍去）；②当时，则：，即：，解得：（舍去）或；∴，∵，∴顶点坐标为，∴平移方向为：先向左平移个单位长度，再向上平移个单位长度．【点睛】本题考查二次函数的综合应用，涉及待定系数法求函数解析式，二次函数的性质，相似三角形的判定和性质，二次函数图象的平移，综合性强，难度较大，掌握相关知识点，利用数形结合，分类讨论的思想，进行求解是解题的关键．25. （1）如图1，已知半径是4，A 是上一动点，，则的最大值是．（2）如图2，在中，，，，点D 是边上一动点，连接DB ，过点A 作于点F ，连接，求最小值．（3）如图3，某景区有一片油菜花地，形状由和以为直径的半圆两部分构成，已知米，，，为了方便游客游览，该景区计划对油菜花地进行改造，根据设计要的0x =2223y m m =--()20,223E m m --()20,23D m m --90PDE AOC ∠=︒=∠22222323DE m m m m m =---++=PD m =()(),1,00,3A C -1,3OA OC ==AOC PDE AOC △∽△PD DE OA OC =213m m =0m =3m =EDP AOC ∽PD DE OC OA =231m m =0m =13m =132,39P ⎛⎫- ⎪⎝⎭()221:2314L y x x x =--=--()1,4-12133-=324499-=O O 9OP =PA ABC 90ABC ∠=︒6AB =8BC =AC AF BD ⊥CF CF ABC BC 60BC =90ABC ∠=︒60ACB ∠=︒求，在半圆上区确定一点E ，沿修建小路，并在中点F 处修建一个凉亭，沿修建仿古长廊，由于仿古长廊造价高达1100元/米，为了控制成本，景区要求仿古长廊的长度尽可能短，在不考虑其他因素的前提下，请求出建造仿古长廊的最低费用．【答案】（1）13；（2；（3）元【解析】【分析】（1）点A 位于直线与的左侧交点时，取最大值；（2）根据可得点F 在以为直径的半圆上，设的中点为E ，连接，与点F 的运动轨迹交于点，则的长度即为的最小值；（3）连接，，取中点为M ，中点为N ，连接，，，证明，推出点F 在以为直径的左侧半圆上，连接，与点F 的运动轨迹交于点，则的长度即为的最小值．【详解】解：（1）如图，当点A 位于直线与的左侧交点时，取最大值，最大值为：，故答案为：13；（2），，点F 在以为直径的半圆上，如图，设的中点为E ，连接，与点F 的运动轨迹交于点，则的长度即为的最小值．AE AE CF CF 3-()16500-OP O PA AF BD ⊥AB AB CE F 'CF 'CF EC EB AC AB MN MF FN 90MFN CEB ︒∠=∠=MN CO F 'CF 'CF OP O PA 4913OA OP +=+= AF BD ⊥∴90AFB ∠=︒∴AB AB CE F 'CF 'CF，中点为E ，，又，，，，即．（3），，，，，．如图，连接，，取中点为M ，中点为N ，连接，，，点E 在以为直径的半圆上，，中点为M ，中点为F ，中点为N ，为的中位线，为的中位线，为的中位线，，，，，，， 6AB =∴132EB AB == 90ABC ∠=︒8BC =∴CE ===∴3CF CE EF ''=-=-CF 3- 60BC =90ABC ∠=︒60ACB ∠=︒∴30CAB ∠=︒∴2120AC BC ==∴AB ===EC EB AC AB MN MF FN BC ∴90CEB ∠=︒ AC AE AB ∴MF ACE △FN ABE MN ABC ∴MF EC ∥NF EB ∥MN BC ∥1302MN BC ==∴MFA CEA ∠=∠NFA BEA ∠=∠，，点F 在以为直径的左侧半圆上，取中点为O ，作于点K ，得矩形，连接，与点F 的运动轨迹交于点，则的长度即为的最小值．，中点O ，中点为N ，，，，，在中，，，又，，的最小值为．仿古长廊造价高达1100元/米，（元），建造仿古长廊的最低费用为元．【点睛】本题考查圆外一点到圆上点距离的最值，圆周角定理，中位线定理，勾股定理，矩形的判定和性质等，第三问有一定难度，通过作辅助线判断出点F 的运动轨迹是解题的关键．为∴MFA NFA CEA BEA ∠+∠=∠+∠∴90MFN CEB ︒∠=∠=∴MN MN OKBC ⊥ONBK CO F 'CF 'CF 1302MN BC ==MN AB =AB ∴1152ON MN ==12BN AB ==∴15KB ON ==OK BN==∴601545CK BC KB =-=-=Rt CKO222CK OK OC +=∴OC === 15OF ON '==∴15CF OC OF ''=-=∴CF 15 ()151********⨯=-∴()16500。

考点十三小说阅读(好题冲关模拟集训)-备战2024年中考语文一轮复习考点帮

考点十三小说阅读（2024·重庆涪陵·校联考一模）阅读下面的文字，完成下面小题。

邻居阿麻①我与邻居阿麻结怨已经很久了。

瞧他那副样子，够你烦心：脸麻，腿跛，背驼。

因为这副尊容，他已经四十多岁了，还是个“快乐的单身汉”。

②单身汉有空闲，管闲事管到我的头上。

我和我的伙伴们在玩的方面个个都是天才，下雪天，我们拆别人的篱笆学大人烧炭，他提起一桶水，“噗”的一声，将窑炭冲得稀烂。

“烧了镇上的房屋，你们去坐牢！”秋天，我们用“土炸药”炸别人家菜园里的南瓜，炸得“瓜肉横飞”，我们高兴得直翻跟头。

正当我们得意忘形之时，阿麻的手钳住我：“看我不告诉你们爷娘！”回家后，我们都挨了一顿打。

皮肉受苦，奇痛难忍，我们奈何不了阿麻，只能编歌谣泄恨：“麻子麻叮当，骑马上洪江，听到锣鼓响，麻子脸上痒。

”这时，麻子便要追击，我们“哗”的一声跑散，望着他一跛一跛的样子，我们开心得像喝了可口可乐。

③我们不喜欢他，小镇上的大人们也不怎么喜欢他，这中间有个缘故。

④小镇的西边有一条河，是学生上学和大人外出的必经之地。

河上有座年久失修的桥。

桥上木板朽了，常常跌倒人，木桥墩烂了，走在上面摇摇晃晃像荡秋千。

终于，一场大雨，猛涨的山溪水把它冲走，还带走了我的一个小伙伴春山。

我庆幸那天贪玩旷课，捡得了一条小命。

阿麻请人做了个小木船，干起了摆渡的行当。

第一天，过渡免费，镇里的人都说他在积德。

可是，第二天收费一角。

后来竟涨到了四角，阿麻“发”了，腰包涨鼓鼓。

有人骂他“黑良心，赚昧心钱”。

但他默默地忍受了。

⑤风里来，雨里去，阿麻摆渡六年。

操劳过度，脸色蜡黄，日渐消瘦。

人们担心，他总有一天会栽倒在小河里。

⑥后来，小河上砌起了一座石拱桥，小巧玲珑，像一把小金锁，锁住了放荡不羁的小河。

从此，小镇的人们过河如履平地，都说修桥人泽被后世。

⑦小桥落成的前两天，阿麻死了，医生说他患的是癌症。

⑧小桥落成那天，正逢小镇赶集，人山人海，好不热闹。

桥上没有彩灯，没有横幅，没有红绸。

备战中考语文文言文必考篇目之对比阅读鱼我所欲也(原卷版通用版)

鱼我所欲也（一）（2022·贵州黔东南·中考真题）阅读下面甲、乙两则文言文选段。

按要求完成下面小题。

【甲】鱼我所欲也熊掌亦我所欲也二者不可得兼舍鱼而取熊掌者也。

生，亦我所欲也；义，亦我所欲也。

二者不可得兼，舍生而取义者也。

生亦我所欲，所欲有甚于生者，故不为苟得也；死亦我所恶，所恶有甚于死者，故患有所不辟也。

如使人之所欲莫甚于生，则凡可以得生者何不用也？使人之所恶莫甚于死者，则凡可以辟患者何不为也？由是则生而有不用也，由是则可以辟患而有不为也。

是故所欲有甚于生者，所恶有甚于死者。

非独贤者有是心也，人皆有之，贤者能勿丧耳。

（节选自《鱼我所欲也》）【乙】子墨子曰：“万事莫贵于义。

今谓人曰：‘予①子②冠履③而断子之手足，子为④之乎？’必不为，何故？则冠履不若手足之贵也。

又曰：‘予子天下而杀子之身，子为之乎？’必不为，何故？则天下不若身之贵也。

争一言⑤以相杀，是贵义于其身也。

故曰：万事莫贵于义也。

”（节选自《墨子·贵义》）【注释】①予：给，送。

②子：你。

③冠履：鞋子和帽子。

④为：愿意。

⑤一言：一句话，即关系到正义与非正义的一句话。

1．下列每组句子中，加点字的意思完全相同．．．．的一项是（）A．舍生而取义．者万事皆贵于义．也B．故．不为苟得也何故．C．非独贤者有是．心也是．贵义于其身也D．人皆有之．断子之．手足2．对文中画波浪线句子断句正确．．．．的一项是（）A．鱼我/所欲也熊掌/亦我/所欲也二者/不可得兼/舍鱼而取熊掌者也。

B．鱼我/所欲也/熊掌亦我/所欲也/二者不可得/兼舍鱼而取熊掌者也。

C．鱼/我所欲也/熊掌/亦我所欲也/二者不可得兼/舍鱼而取熊掌者也。

D．鱼/我所欲也熊掌/亦我所欲也二者/不可得/兼舍鱼而取/熊掌者也。

3．对选文内容的理解、分析、概括有误．．的一项是（）A．甲文在引出“舍生而取义”的论点后，运用比喻论证，分别从“所欲”“所恶”两方面论述。

B．甲文孟子认为每个人都有“是心”，相对于“贤者”来说，普通人容易丧失。

备战2023年杭州中考数学真题分类汇编(5年中考1年模拟)4选择中档题一含详解

专题04选择中档题一1．（2022•杭州）照相机成像应用了一个重要原理，用公式111()v f f u v=+≠表示，其中f 表示照相机镜头的焦距，u 表示物体到镜头的距离，v 表示胶片（像)到镜头的距离．已知f ，v ，则(u =)A ．fv f v-B ．f v fv-C ．fv v f-D ．v f fv-2．（2022•杭州）某体育比赛的门票分A 票和B 票两种，A 票每张x 元，B 票每张y 元．已知10张A 票的总价与19张B 票的总价相差320元，则()A ．10||32019xy=B ．10||32019yx=C ．|1019|320x y -=D ．|1910|320x y -=3．（2022•杭州）如图，在平面直角坐标系中，已知点(0,2)P ，点(4,2)A ．以点P 为旋转中心，把点A 按逆时针方向旋转60︒，得点B ．在13(3M -，0)，2(3M -，1)-，3(1,4)M ，411(2,)2M 四个点中，直线PB 经过的点是()A ．1MB ．2MC ．3MD ．4M 4．（2022•杭州）已知二次函数2(y x ax b a =++，b 为常数）．命题①：该函数的图象经过点(1,0)；命题②：该函数的图象经过点(3,0)；命题③：该函数的图象与x 轴的交点位于y 轴的两侧；命题④：该函数的图象的对称轴为直线1x =．如果这四个命题中只有一个命题是假命题，则这个假命题是()A ．命题①B ．命题②C ．命题③D ．命题④5．（2021•杭州）某景点今年四月接待游客25万人次，五月接待游客60.5万人次．设该景点今年四月到五月接待游客人次的增长率为(0)x x >，则()A ．60.5(1)25x -=B ．25(1)60.5x -=C ．60.5(1)25x +=D ．25(1)60.5x +=6．（2021•杭州）某轨道列车共有3节车厢，设乘客从任意一节车厢上车的机会均等．某天甲、乙两位乘客同时乘同一列轨道列车，则甲和乙从同一节车厢上车的概率是()A ．15B ．14C ．13D ．127．（2021•杭州）在“探索函数2y ax bx c =++的系数a ，b ，c 与图象的关系”活动中，老师给出了直角坐标系中的四个点：(0,2)A ，(1,0)B ，(3,1)C ，(2,3)D ．同学们探索了经过这四个点中的三个点的二次函数图象，发现这些图象对应的函数表达式各不相同，其中a 的值最大为()A ．52B ．32C ．56D ．128．（2021•杭州）已知线段AB ，按如下步骤作图：①作射线AC ，使AC AB ⊥；②作BAC ∠的平分线AD ；③以点A 为圆心，AB 长为半径作弧，交AD 于点E ；④过点E 作EP AB ⊥于点P ，则:(AP AB =)A ．5B ．1:2C ．3D ．29．（2020•杭州）在平面直角坐标系中，已知函数(0)y ax a a =+≠的图象过点(1,2)P ，则该函数的图象可能是()A ．B ．C ．D ．10．（2020•杭州）在某次演讲比赛中，五位评委给选手圆圆打分，得到互不相等的五个分数．若去掉一个最高分，平均分为x ；去掉一个最低分，平均分为y ；同时去掉一个最高分和一个最低分，平均分为z ，则()A ．y z x>>B ．x z y>>C ．y x z>>D ．z y x>>11．（2020•杭州）设函数2()(y a x h k a =-+，h ，k 是实数，0)a ≠，当1x =时，1y =；当8x =时，8y =，()A ．若4h =，则0a <B ．若5h =，则0a >C ．若6h =，则0a <D ．若7h =，则0a >12．（2020•杭州）如图，已知BC 是O 的直径，半径OA BC ⊥，点D 在劣弧AC 上（不与点A ，点C 重合），BD 与OA 交于点E ．设AED α∠=，AOD β∠=，则()A ．3180αβ+=︒B ．2180αβ+=︒C ．390αβ-=︒D ．290αβ-=︒13．（2019•杭州）如图，在ABC ∆中，点D ，E 分别在AB 和AC 上，//DE BC ，M 为BC 边上一点（不与点B ，C 重合），连接AM 交DE 于点N ，则()A ．AD ANAN AE=B ．BD MNMN CE=C ．DN NEBM MC=D ．DN NEMC BM =14．（2019•杭州）在ABC ∆中，若一个内角等于另外两个内角的差，则()A ．必有一个内角等于30︒B ．必有一个内角等于45︒C ．必有一个内角等于60︒D ．必有一个内角等于90︒15．（2019•杭州）已知一次函数1y ax b =+和2()y bx a a b =+≠，函数1y 和2y 的图象可能是()A ．B ．C ．D ．16．（2019•杭州）如图，一块矩形木板ABCD 斜靠在墙边(OC OB ⊥，点A ，B ，C ，D ，O 在同一平面内），已知AB a =，AD b =，BCO x ∠=，则点A 到OC 的距离等于()A ．sin sin a x b x +B ．cos cos a x b x +C ．sin cos a x b x +D ．cos sin a x b x+17．（2018•杭州）某次知识竞赛共有20道题，规定：每答对一道题得5+分，每答错一道题得2-分，不答的题得0分，已知圆圆这次竞赛得了60分，设圆圆答对了x 道题，答错了y 道题，则()A ．20x y -=B ．20x y +=C ．5260x y -=D ．5260x y +=18．（2018•杭州）一个两位数，它的十位数字是3，个位数字是抛掷一枚质地均匀的骰子（六个面分别标有数字16)-朝上一面的数字，任意抛掷这枚骰子一次，得到的两位数是3的倍数的概率等于()A ．16B ．13C ．12D ．2319．（2018•杭州）如图，已知点P 是矩形ABCD 内一点（不含边界），设1PAD θ∠=，2PBA θ∠=，3PCB θ∠=，4PDC θ∠=，若80APB ∠=︒，50CPD ∠=︒，则()A ．1423()()30θθθθ+-+=︒B ．2413()()40θθθθ+-+=︒C ．1234()()70θθθθ+-+=︒D ．1234()()180θθθθ+++=︒20．（2018•杭州）四位同学在研究函数2(y x bx c b =++，c 是常数）时，甲发现当1x =时，函数有最小值；乙发现1-是方程20x bx c ++=的一个根；丙发现函数的最小值为3；丁发现当2x =时，4y =，已知这四位同学中只有一位发现的结论是错误的，则该同学是()A ．甲B ．乙C ．丙D ．丁21．（2022•上城区一模）在平面直角坐标系中，已知点(6,2)E -，(2,2)F --，以原点O 为位似中心，位似比为12，把EFO ∆缩小，则点F 的对应点F '的坐标是()A ．(1,1)--B ．(1,1)C ．(4,4)--或(4,4)D ．(1,1)--或(1,1)22．（2022•上城区一模）如图是2022年杭州亚运会徽标的示意图，若5AO =，2BO =，120AOD ∠=︒，则阴影部分面积为()A ．14πB ．7πC ．253πD ．2π23．（2022•上城区一模）斑马线前“车让人”，反映了城市的文明程度，但行人一般都会在红灯亮起前通过马路．某人行横道全长24米，小明以1.2/m s 的速度过该人行横道，行至13处时，9秒倒计时灯亮了．小明要在红灯亮起前通过马路，他的速度至少要提高到原来的()A ．1.1倍B ．1.4倍C ．1.5倍D ．1.6倍24．（2022•上城区一模）如图，在正方形ABCD 内部，以边长为斜边构造两个全等的直角三角形，已知正方形边长为5，较短的直角边长为3，则两个直角顶点之间的距离EF 为()A ．1B 2C ．1.5D 325．（2022•拱墅区一模）小皓在计算一组较大的数据的平均数和方差时，他先将原数据中的每一个数都减去某个相同的正数，然后对所得的新数据进行统计分析，新数据与原数据相比()A ．平均数不变，方差不变B ．平均数变大，方差变大C ．平均数变小，方差不变D ．平均数变小，方差变小26．（2022•拱墅区一模）已知点1(A x ，1)y ，1(1B x +，2)y 都在反比例函数(0)ky k x=<的图象上()A ．若121x -<<-，则12y y >B ．若110x -<<，则12y y <C ．若101x <<，则12y y <D ．若112x <<，则12y y >27．（2022•拱墅区一模）已知AB 是O 的弦，半径OC AB ⊥于点D ．若DO DC =，12AB =，则O 的半径为()A ．42B ．43C ．62D ．6328．（2022•拱墅区一模）如图，在ABC ∆中，AB AC >，以点A 为圆心，AC 的长为半径作弧交AB 于点D ，连接DC ；再以点D 为圆心，DC 的长为半径作弧交CB 的延长线于点E ．若BE BD =，15E ∠=︒，则()A ．2AB AC =B ．BC BD DE =+C ．2AD BE =D ．CE AB AC=+29．（2022•西湖区一模）如图，是三个反比例函数11k y x =，22ky x =，33k y x=在y 轴右侧的图象，则()A ．123k k k >>B ．213k k k >>C ．321k k k >>D ．312k k k >>30．（2022•西湖区一模）如图，在ABC ∆中，边AB ，AC 的垂直平分线交于点P ，连结BP ，CP ，若50A ∠=︒，则(BPC ∠=)A ．50︒B ．100︒C ．130︒D ．150︒31．（2022•西湖区一模）如图，已知直角坐标系中的四个点：(0,2)A ，(1,0)B ，(3,1)C ，(2,3)D ．直线AB 和直线CD 的函数表达式分别为111y k x b =+和222y k x b =+，则()A ．12k k =，12b b >B ．12k k =，12b b <C ．12k k ≠，12b b >D ．12k k ≠，12b b <32．（2022•西湖区一模）如图，已知AB 是O 的直径，弦CD 与AB 交于点E ，设ABC α∠=，ABD β∠=，AEC γ∠=，则()A ．90αβγ+-=︒B ．90βγα+-=︒C ．90αγβ+-=︒D ．180αβγ++=︒33．（2022•钱塘区一模）每年的4月23日是世界读书日．某校为了解4月份八年级学生的读书情况，随机调查了八年级50名学生读书的册数，统计数据如表格所示．关于这组数据，下列说法正确的是()册数01234人数61416122A ．众数是16B ．中位数是2C ．平均数是2D ．方差是134．（2022•钱塘区一模）如图，在ABC ∆中，D 为BC 边上一点（不与点B ，点C 重合），E ，F 分别在AB 边和AC 边上，//EF BC ，连结AD 交EF 于点G ，则()A ．AE AGAG AF=B ．EB GDGD FC=C ．EG GFBD DC=D ．EG GFDC BD=35．（2022•钱塘区一模）节假期间，几名同学合租了一辆汽车准备从市区到郊外游玩，租金为600元．出发时，又增加了2名同学，此时总人数为x 名（不超过车载额定人数）．如果汽车的租金由参加的同学平均分摊，且原先租车的几名同学平均每人少分摊了50元，由题意列方程正确的是()A ．600600502x x -=-B ．600600502x x -=+C ．600600502x x -=-D ．600600502x x -=+36．（2022•钱塘区一模）已知二次函数2221(y x mx m m m =-+--+为常数）的图象与x 轴有交点，且当3x <-时，y 随x 的增大而增大，则m 的取值范围是()A ．31m -<B ．31m -C ．31m -<<D ．3m - 或1m 37．（2022•淳安县一模）如图，AB 是O 的直径，点C 、D 在圆周上，30CAB ∠=︒，则ADC ∠的度数为()A ．30︒B ．45︒C ．60︒D ．75︒38．（2022•淳安县一模）疫情期间进入学校都要进入测温通道，体温正常才可进入学校，昌平某校有2个测温通道，分别记为A 、B 通道，学生可随机选取其中的一个通道测温进校园．某日早晨该校所有学生体温正常．小王和小李两同学该日早晨进校园时，选择同一通道测温进校园的概率是()A ．14B ．13C ．12D ．2339．（2022•淳安县一模）如图，在平面直角坐标系中，点A ，B 的坐标分别是(2,2)A ，(5,5)B ，若二次函数2y ax bx c =++的图象过A ，B 两点，且该函数图象的顶点为(,)M x y ，其中x ，y 是整数，且07x <<，07y <<，则a 的最大值是()A ．2B ．1C ．12D ．1340．（2022•淳安县一模）如图，在ABC ∆中，90ABC ∠=︒，以点A 为圆心，以AB 的长为半径作弧交AC 于点D ，连接BD ，再分别以点B ，D 为圆心，大于12BD 的长为半径作弧，两弧交于点P ，作射线AP 交BC 于点E ，连接DE ，则下列结论正确的是()A ．DE 垂直平分ACB ．ABE CBA ∆∆∽C ．2BD BC BE =⋅D ．CE AB BE CA⋅=⋅41．（2022•富阳区一模）若点1(1,)A y -，2(2,)B y ，3(3,)C y 在反比例函数6y x=-的图象上，则1y ，2y ，3y 的大小关系是()A ．123y y y >>B ．231y y y >>C ．132y y y >>D ．321y y y >>42．（2022•富阳区一模）如图，AB 是O 的直径，点D 为O 上一点，且30ABD ∠=︒，4BO =，则劣弧 BD的长为()A ．23πB ．43πC ．2πD ．83π43．（2022•富阳区一模）某辆汽车每次加油都会把油箱加满，下表记录了该车相邻两次加油时的情况．（注：“累计里程”指汽车从出厂开始累计行驶的路程）加油时间加油量（升)加油时的累计里程（千米）2022年3月10日155********年3月25日5056500在这段时间内，该车每100千米平均耗油量为()A ．7升B ．8升C ．10升D ．1007升44．（2022•富阳区一模）已知△111A B C ，△222A B C 的周长相等，现有两个判断：①若1122A B A B =，1122A C A C =，则△111A B C ≅△222A B C ；②若12A A ∠=∠，12B B ∠=∠，则△111A B C ≅△222A B C ，对于上述的两个判断，下列说法正确的是()A ．①正确，②错误B ．①错误，②正确C ．①，②都错误D ．①，②都正确45．（2022•临安区一模）学校给同学们准备了亚运吉祥物“琮琮、宸宸、莲莲”．设同学选择任意一种吉祥物的机会均等．小聪和小慧可以从三种吉祥物中任选一件，则小聪和小慧拿到同一种吉祥物的概率是(）A ．15B ．14C ．13D ．1246．（2022•临安区一模）如图，菱形OABC 的顶点A 、B 、C 在O 上，过点B 作O 的切线交OA 的延长线于点D ．若O 的半径为2，则BD 的长为()A ．3B ．3C ．23D ．447．（2022•临安区一模）如图，抛物线2(0)y ax bx c a =++≠过点(1,0)和点(0,2)-，且顶点在第三象限，设P a b c =-+，则P 的取值范围是()A ．40P -<<B ．42P -<<-C ．20P -<<D ．10P -<<48．（2022•临安区一模）如图，在等边ABC ∆的AC ，BC 边上各取一点M ，N 使AM CN =，AN ，BM 相交于点O ．若4AM =，2MO =，则BO 的长是()A ．5B ．6C ．7D ．849．（2022•钱塘区二模）下列交通标志，不是轴对称图形的是()A ．B ．C ．D ．50．（2022•钱塘区二模）如图，在矩形ABCD 中，AB m =，BAC α∠=，则OC 的长为()A ．cos mαB ．2cos m αC ．2sin m αD ．sin m α51．（2022•钱塘区二模）已知二次函数245y ax ax =-+（其中x 是自变量），当2x - 时．y 随x 的增大而增大，且65x -时，y 的最小值为7-，则a 的值为()A ．3B ．15-C ．125-D ．1-52．（2022•钱塘区二模）已知点11(P x ，1)y ，22(P x ，2)y 为抛物线24(0)y ax ax c a =-++≠上两点，且12x x <，则下列说法正确的是()A ．若124x x +<，则12y y <B ．若124x x +>，则12y y <C ．若12(4)0a x x +->，则12y y >D ．若12(4)0a x x +-<，则12y y >专题04选择中档题一1．（2022•杭州）照相机成像应用了一个重要原理，用公式111()v f f u v =+≠表示，其中f 表示照相机镜头的焦距，u 表示物体到镜头的距离，v 表示胶片（像)到镜头的距离．已知f ，v ，则(u =)A ．fvf v -B ．f vfv -C ．fvv f -D ．v ffv-【答案】C【详解】111()v f f u v=+≠，111f u v=+，111u f v=-，1v f u fv-=，fv u v f=-．故选：C ．2．（2022•杭州）某体育比赛的门票分A 票和B 票两种，A 票每张x 元，B 票每张y 元．已知10张A 票的总价与19张B 票的总价相差320元，则()A ．10||32019x y =B ．10||32019y x =C ．|1019|320x y -=D ．|1910|320x y -=【答案】C【详解】由题意可得：|1019|320x y -=．故选：C ．3．（2022•杭州）如图，在平面直角坐标系中，已知点(0,2)P ，点(4,2)A ．以点P 为旋转中心，把点A 按逆时针方向旋转60︒，得点B ．在13(3M -，0)，2(3M -，1)-，3(1,4)M ，411(2,)2M 四个点中，直线PB 经过的点是()A ．1M B ．2M C ．3M D ．4M 【答案】B 【详解】点(4,2)A ，点(0,2)P ，PA y ∴⊥轴，4PA =，由旋转得：60APB ∠=︒，4AP PB ==，如图，过点B 作BC y ⊥轴于C ，30BPC ∴∠=︒，2BC ∴=，23PC =，(2,23)B ∴+，设直线PB 的解析式为：y kx b =+，则22232k b b ⎧+=+⎪⎨=⎪⎩∴32k b ⎧=⎪⎨=⎪⎩∴直线PB 的解析式为：32y x =+，当0y =320x +=，233x =∴点13(3M ，0)不在直线PB 上，当3x =321y =-+=-，2(3M ∴-，1)-在直线PB 上，当1x =时，32y =+，3(1,4)M ∴不在直线PB 上，当2x =时，232y =，411(2,2M ∴不在直线PB 上．故选：B ．4．（2022•杭州）已知二次函数2(y x ax b a =++，b 为常数）．命题①：该函数的图象经过点(1,0)；命题②：该函数的图象经过点(3,0)；命题③：该函数的图象与x 轴的交点位于y 轴的两侧；命题④：该函数的图象的对称轴为直线1x =．如果这四个命题中只有一个命题是假命题，则这个假命题是()A ．命题①B ．命题②C ．命题③D ．命题④【答案】A【详解】假设抛物线的对称轴为直线1x =，则12a -=，解得2a =-，函数的图象经过点(3,0)，390a b ∴++=，解得3b =-，故抛物线的解析式为223y x x =--，当0y =时，得2230x x --=，解得3x =或1x =-，故抛物线与x 轴的交点为(1,0)-和(3,0)，函数的图象与x 轴的交点位于y 轴的两侧；故命题②③④都是正确，①错误，故选：A ．5．（2021•杭州）某景点今年四月接待游客25万人次，五月接待游客60.5万人次．设该景点今年四月到五月接待游客人次的增长率为(0)x x >，则()A ．60.5(1)25x -=B ．25(1)60.5x -=C ．60.5(1)25x +=D ．25(1)60.5x +=【答案】D【详解】设该景点今年四月到五月接待游客人次的增长率为(0)x x >，则25(1)60.5x +=．故选：D ．6．（2021•杭州）某轨道列车共有3节车厢，设乘客从任意一节车厢上车的机会均等．某天甲、乙两位乘客同时乘同一列轨道列车，则甲和乙从同一节车厢上车的概率是()A ．15B ．14C ．13D ．12【答案】C【详解】把3节车厢分别记为A 、B 、C ，画树状图如图：共有9种等可能的结果，甲和乙从同一节车厢上车的结果有3种，∴甲和乙从同一节车厢上车的概率为3193=，故选：C ．7．（2021•杭州）在“探索函数2y ax bx c =++的系数a ，b ，c 与图象的关系”活动中，老师给出了直角坐标系中的四个点：(0,2)A ，(1,0)B ，(3,1)C ，(2,3)D ．同学们探索了经过这四个点中的三个点的二次函数图象，发现这些图象对应的函数表达式各不相同，其中a 的值最大为()A ．52B ．32C ．56D ．12【答案】A【详解】由图象知，A 、B 、D 组成的二次函数图象开口向上，0a >；A 、B 、C 组成的二次函数开口向上，0a >；B 、C 、D 三点组成的二次函数开口向下，0a <；A 、D 、C 三点组成的二次函数开口向下，0a <；即只需比较A 、B 、D 组成的二次函数和A 、B 、C 组成的二次函数即可．设A 、B 、C 组成的二次函数为21111y a x b x c =++，把(0,2)A ，(1,0)B ，(3,1)C 代入上式得，111111120931c a b c a b c =⎧⎪++=⎨⎪++=⎩，解得156a =；设A 、B 、D 组成的二次函数为2y ax bx c =++，把(0,2)A ，(1,0)B ，(2,3)D 代入上式得，20423c a b c a b c =⎧⎪++=⎨⎪++=⎩，解得52a =，即a 最大的值为52，也可以根据a 的绝对值越大开口越小直接代入ABD 三点计算，即可求求解．故选：A ．8．（2021•杭州）已知线段AB ，按如下步骤作图：①作射线AC ，使AC AB ⊥；②作BAC ∠的平分线AD ；③以点A 为圆心，AB 长为半径作弧，交AD 于点E ；④过点E 作EP AB ⊥于点P ，则:(AP AB =)A ．5B ．1:2C ．3D ．2【答案】D【详解】AC AB ⊥ ，90CAB ∴∠=︒，AD 平分BAC ∠，190452EAB ∴∠=⨯︒=︒，EP AB ⊥ ，90APE ∴∠=︒，45EAP AEP ∴∠=∠=︒，AP PE ∴=，∴设AP PE x ==，故2AE AB ==，:22AP AB x ∴==故选：D ．9．（2020•杭州）在平面直角坐标系中，已知函数(0)y ax a a =+≠的图象过点(1,2)P ，则该函数的图象可能是()A ．B ．C ．D ．【答案】A 【详解】函数(0)y ax a a =+≠的图象过点(1,2)P ，2a a ∴=+，解得1a =，1y x ∴=+，∴直线交y 轴的正半轴于点(0,1)，且过点(1,2)，故选：A ．10．（2020•杭州）在某次演讲比赛中，五位评委给选手圆圆打分，得到互不相等的五个分数．若去掉一个最高分，平均分为x ；去掉一个最低分，平均分为y ；同时去掉一个最高分和一个最低分，平均分为z ，则()A ．y z x>>B ．x z y >>C ．y x z >>D ．z y x>>【答案】A【详解】由题意可得，若去掉一个最高分，平均分为x ，则此时的x 一定小于同时去掉一个最高分和一个最低分后的平均分为z ，去掉一个最低分，平均分为y ，则此时的y 一定大于同时去掉一个最高分和一个最低分后的平均分为z ，故y z x >>，故选：A ．11．（2020•杭州）设函数2()(y a x h k a =-+，h ，k 是实数，0)a ≠，当1x =时，1y =；当8x =时，8y =，()A ．若4h =，则0a <B ．若5h =，则0a >C ．若6h =，则0a <D ．若7h =，则0a >【答案】C【详解】当1x =时，1y =；当8x =时，8y =；代入函数式得：221(1)8(8)a h k a h k ⎧=-+⎨=-+⎩，22(8)(1)7a h a h ∴---=，整理得：(92)1a h -=，若4h =，则1a =，故A 错误；若5h =，则1a =-，故B 错误；若6h =，则13a =-，故C 正确；若7h =，则15a =-，故D 错误；故选：C ．12．（2020•杭州）如图，已知BC 是O 的直径，半径OA BC ⊥，点D 在劣弧AC 上（不与点A ，点C 重合），BD 与OA 交于点E ．设AED α∠=，AOD β∠=，则()A ．3180αβ+=︒B ．2180αβ+=︒C ．390αβ-=︒D ．290αβ-=︒【答案】D【详解】OA BC ⊥ ，90AOB AOC ∴∠=∠=︒，909090DBC BEO AED α∴∠=︒-∠=︒-∠=︒-，21802COD DBC α∴∠=∠=︒-，90AOD COD ∠+∠=︒ ，180290βα∴+︒-=︒，290αβ∴-=︒，故选：D ．13．（2019•杭州）如图，在ABC ∆中，点D ，E 分别在AB 和AC 上，//DE BC ，M 为BC 边上一点（不与点B ，C 重合），连接AM 交DE 于点N ，则()A ．AD AN AN AE =B ．BD MN MN CE =C ．DN NE BM MC =D ．DN NE MC BM=【答案】C【详解】//DN BM ，ADN ABM ∴∆∆∽，∴DNANBM AM =，//NE MC ，ANE AMC ∴∆∆∽，∴NEANMC AM =，∴DN NEBM MC =．故选：C ．14．（2019•杭州）在ABC ∆中，若一个内角等于另外两个内角的差，则()A ．必有一个内角等于30︒B ．必有一个内角等于45︒C ．必有一个内角等于60︒D ．必有一个内角等于90︒【答案】D【详解】180A B C ∠+∠+∠=︒ ，A C B ∠=∠-∠，2180C ∴∠=︒，90C ∴∠=︒，ABC ∴∆是直角三角形，故选：D ．15．（2019•杭州）已知一次函数1y ax b =+和2()y bx a a b =+≠，函数1y 和2y 的图象可能是()A ．B ．C ．D ．【答案】A【详解】A 、由图可知：直线1y ax b =+，0a >，0b >．∴直线2y bx a =+经过一、二、三象限，故A 正确；B 、由图可知：直线1y ax b =+，0a <，0b >．∴直线2y bx a =+经过一、四、三象限，故B 错误；C 、由图可知：直线1y ax b =+，0a <，0b >．∴直线2y bx a =+经过一、二、四象限，交点不对，故C 错误；D 、由图可知：直线1y ax b =+，0a <，0b <，∴直线2y bx a =+经过二、三、四象限，故D 错误．故选：A ．16．（2019•杭州）如图，一块矩形木板ABCD 斜靠在墙边(OC OB ⊥，点A ，B ，C ，D ，O 在同一平面内），已知AB a =，AD b =，BCO x ∠=，则点A 到OC 的距离等于()A．sin sina xb x+B．cos cosa xb x+C．sin cosa xb x+D．cos sina xb x+【答案】D【详解】作AE OC⊥于点E，作AF OB⊥于点F，四边形ABCD是矩形，90ABC∴∠=︒，ABC AEC∠=∠，BCO x∠=，EAB x∴∠=，FBA x∴∠=，AB a=，AD b=，cos sinFO FB BO a x b x∴=+=+，故选：D．17．（2018•杭州）某次知识竞赛共有20道题，规定：每答对一道题得5+分，每答错一道题得2-分，不答的题得0分，已知圆圆这次竞赛得了60分，设圆圆答对了x道题，答错了y道题，则()A．20x y-=B．20x y+=C．5260x y-=D．5260x y+=【答案】C【详解】设圆圆答对了x道题，答错了y道题，依题意得：52(20)060x y x y-+--⨯=．故选：C．18．（2018•杭州）一个两位数，它的十位数字是3，个位数字是抛掷一枚质地均匀的骰子（六个面分别标有数字16)-朝上一面的数字，任意抛掷这枚骰子一次，得到的两位数是3的倍数的概率等于()A．16B．13C．12D．23【答案】B【详解】根据题意，得到的两位数有31、32、33、34、35、36这6种等可能结果，其中两位数是3的倍数的有33、36这2种结果，∴得到的两位数是3的倍数的概率等于2163=，故选：B ．19．（2018•杭州）如图，已知点P 是矩形ABCD 内一点（不含边界），设1PAD θ∠=，2PBA θ∠=，3PCB θ∠=，4PDC θ∠=，若80APB ∠=︒，50CPD ∠=︒，则()A ．1423()()30θθθθ+-+=︒B ．2413()()40θθθθ+-+=︒C ．1234()()70θθθθ+-+=︒D ．1234()()180θθθθ+++=︒【答案】A【详解】矩形ABCD ，90BAD BCD ∴∠=∠=︒，190BAP θ∴∠=︒-，390DCP θ∠=︒-，ABP ∴∆中，129080180θθ︒-++︒=︒，即2110θθ-=︒，①DCP ∆中，349050180θθ︒-++︒=︒，即4340θθ-=︒，②由②-①，可得4321()()30θθθθ---=︒，即1423()()30θθθθ+-+=︒，故选：A ．20．（2018•杭州）四位同学在研究函数2(y x bx c b =++，c 是常数）时，甲发现当1x =时，函数有最小值；乙发现1-是方程20x bx c ++=的一个根；丙发现函数的最小值为3；丁发现当2x =时，4y =，已知这四位同学中只有一位发现的结论是错误的，则该同学是()A ．甲B ．乙C ．丙D ．丁【答案】B【详解】假设甲和丙的结论正确，则212434b c b ⎧-=⎪⎪⎨-⎪=⎪⎩，解得：24b c =-⎧⎨=⎩，∴抛物线的解析式为224y x x =-+．当1x =-时，2247y x x =-+=，∴乙的结论不正确；当2x =时，2244y x x =-+=，∴丁的结论正确．四位同学中只有一位发现的结论是错误的，∴假设成立．故选：B ．21．（2022•上城区一模）在平面直角坐标系中，已知点(6,2)E -，(2,2)F --，以原点O 为位似中心，位似比为12，把EFO ∆缩小，则点F 的对应点F '的坐标是()A ．(1,1)--B ．(1,1)C ．(4,4)--或(4,4)D ．(1,1)--或(1,1)【答案】D【详解】点(2,2)F --，以O 为位似中心，相似比为12，∴点F 的对应点F '的坐标为：1(22-⨯，12)2-⨯或1(2()2-⨯-，12())2-⨯-，即(1,1)--或(1,1)，故选：D ．22．（2022•上城区一模）如图是2022年杭州亚运会徽标的示意图，若5AO =，2BO =，120AOD ∠=︒，则阴影部分面积为()A ．14πB ．7πC ．253πD ．2π【答案】B 【详解】AOD BOCS S S =-阴影扇形扇形2212051202360360ππ⨯⨯=-213π=7π=，故选：B ．23．（2022•上城区一模）斑马线前“车让人”，反映了城市的文明程度，但行人一般都会在红灯亮起前通过马路．某人行横道全长24米，小明以1.2/m s 的速度过该人行横道，行至13处时，9秒倒计时灯亮了．小明要在红灯亮起前通过马路，他的速度至少要提高到原来的()A ．1.1倍B ．1.4倍C ．1.5倍D ．1.6倍【答案】C 【详解】设他的速度要提高到原来的x 倍，根据题意可得：19 1.224(1)3x ⨯⨯- ，解得：4027x ， 40 1.4827≈，∴他的速度至少要提高到原来的1.5倍．故选：C ．24．（2022•上城区一模）如图，在正方形ABCD 内部，以边长为斜边构造两个全等的直角三角形，已知正方形边长为5，较短的直角边长为3，则两个直角顶点之间的距离EF 为()A ．1B 2C ．1.5D 3【答案】B 【详解】方法一：过点F 作FM AB ⊥于点M ，过点E 作EN CD ⊥于点N ，过点F 作FO EN ⊥，交NE 的延长线于点O ，如图所示：3BF = ，5AB =，90AFB ∠=︒，根据勾股定理，得4AF =，1122ABF S AB FM AF BF ∆=⋅=⋅，AB FM AF BF ∴⋅=⋅，125FM ∴=，ABF CDE ∆≅∆ ，125NE FM ∴==，1215255OE ∴=-⨯=，在BMF ∆中，根据勾股定理，得95BM =，95ND ∴=，975255OF ∴=-⨯=，在直角OEF ∆中，根据勾股定理，得2217()()255EF =+=方法二：延长DE 交AF 于点H ，延长BF 交CE 于点G ，如图所示：在正方形ABCD 中，90ABC BCD ∠=∠=︒，AB BC =，90CBG ABF ∴∠+∠=︒，90DCE BCG ∠+∠=︒，在直角ABF ∆中，90ABF BAF ∠+∠=︒，CBG BAF ∴∠=∠，ABF CDE ∆≅∆ ，DCE BAF ∴∠=∠，BCG ABF ∴∠=∠，又AB BC = ，()ABF BCG ASA ∴∆≅∆，同理可证：()DAH ABF ASA ∆≅∆，GF FH HE EG ∴===，90GEH ∠=︒ ，∴四边形GEHF 是正方形，根据题意，得3BF =，5AB =，在AFB ∆中，根据勾股定理，得4AF =，1GF GE ∴==，根据勾股定理，得EF =，故选：B ．25．（2022•拱墅区一模）小皓在计算一组较大的数据的平均数和方差时，他先将原数据中的每一个数都减去某个相同的正数，然后对所得的新数据进行统计分析，新数据与原数据相比()A ．平均数不变，方差不变B ．平均数变大，方差变大C ．平均数变小，方差不变D ．平均数变小，方差变小【答案】C【详解】一组数据1x ，2x ，a x ⋯的每一个数都减去同一数(0)a a ≠，则新数据1x a -，2x a -，a x a ⋯-的平均数变小，但是方差不变；故选：C ．26．（2022•拱墅区一模）已知点1(A x ，1)y ，1(1B x +，2)y 都在反比例函数(0)k y k x =<的图象上()A ．若121x -<<-，则12y y >B ．若110x -<<，则12y y <C ．若101x <<，则12y y <D ．若112x <<，则12y y >【答案】C【详解】0k < ，∴反比例函数(0)k y k x=<的图象在二、四象限，在每个象限y 随x 的增大而增大，A ．若121x -<<-，则1110x -<+<，∴点1(A x ，1)y ，1(1B x +，2)y 都在第二象限，111x x <+ ，12y y ∴<，故A 不合题意；B ．若110x -<<，则1011x <+<，∴点1(A x ，1)y 在第二象限，点1(1B x +，2)y 在第四象限，12y y ∴>，故B 不合题意；C ．若101x <<，则1112x <+<，点1(A x ，1)y ，1(1B x +，2)y 都在第四象限，111x x <+ ，12y y ∴<，故C 符合题意；D ．若112x <<，则1213x <+<，点1(A x ，1)y ，1(1B x +，2)y 都在第四象限，111x x <+ ，12y y ∴<，故D 不合题意；故选C ．27．（2022•拱墅区一模）已知AB 是O 的弦，半径OC AB ⊥于点D ．若DO DC =，12AB =，则O 的半径为()A ．42B ．43C ．62D ．63【答案】B【详解】连接OA 、AC ，如图，设O 的半径为r ，OC AB ⊥ ，1112622AD DB AB ∴===⨯=，在Rt OAD ∆中，12OD CD r ==，OA r =，6AD =，2221()62r r ∴+=，解得143r =，243r =-（舍去），O ∴ 的半径为43．故选：B ．28．（2022•拱墅区一模）如图，在ABC ∆中，AB AC >，以点A 为圆心，AC 的长为半径作弧交AB 于点D ，连接DC ；再以点D 为圆心，DC 的长为半径作弧交CB 的延长线于点E ．若BE BD =，15E ∠=︒，则()A ．2AB AC =B ．BC BD DE =+C ．2AD BE =D ．CE AB AC=+【答案】D【详解】BE BD = ，15E BDE ∴∠=∠=︒，30DBC E BDE ∴∠=∠+∠=︒，DE DC = ，15E DCE ∴∠=∠=︒，45ADC DBC DCB ∴∠=∠+∠=︒，AD AC = ，45ADC ACD ∴∠=∠=︒，90A ∴∠=︒，2BC AC ∴=，2CE BE BC BE AC BD AD AC AB AC ∴=+=+=++=+，故选项D 正确，故选D ．29．（2022•西湖区一模）如图，是三个反比例函数11k y x =，22k y x =，33k y x =在y 轴右侧的图象，则()A ．123k k k >>B ．213k k k >>C ．321k k k >>D ．312k k k >>【答案】C【详解】当1x =时，11y k =，22y k =，33y k =，从图中可得123y y y <<，123k k k ∴<<，故选：C ．30．（2022•西湖区一模）如图，在ABC ∆中，边AB ，AC 的垂直平分线交于点P ，连结BP ，CP ，若50A ∠=︒，则(BPC ∠=)A ．50︒B ．100︒C ．130︒D ．150︒【答案】B 【详解】连接AP ，延长BP 交AC 于D ，BPC PDA ACP BAC ABP ACP ∴∠=∠+∠=∠+∠+∠，点P 是AB ，AC 的垂直平分线的交点，PA PB PC ∴==，ABP BAP ∴∠=∠，ACP CAP ∠=∠，2250100BPC BAC BAP CAP BAC BAC BAC ∴∠=∠+∠+∠=∠+∠=∠=⨯︒=︒，解法二：AB 、AC 中垂线角与点P ，∴点P 为ABC ∆外接圆圆心，2100BPC BAC ∴∠=∠=︒，故选B ．31．（2022•西湖区一模）如图，已知直角坐标系中的四个点：(0,2)A ，(1,0)B ，(3,1)C ，(2,3)D ．直线AB 和直线CD 的函数表达式分别为111y k x b =+和222y k x b =+，则()A ．12k k =，12b b >B ．12k k =，12b b <C ．12k k ≠，12b b >D ．12k k ≠，12b b <【答案】B 【详解】把(0,2)A ，(1,0)B 代入111y k x b =+得：11120b k b =⎧⎨+=⎩，解得1122k b =-⎧⎨=⎩，把(3,1)C ，(2,3)D 代入222y k x b =+得：22223123k b k b +=⎧⎨+=⎩，解得2227k b =-⎧⎨=⎩，12k k ∴=，12b b <，故选：B ．32．（2022•西湖区一模）如图，已知AB 是O 的直径，弦CD 与AB 交于点E ，设ABC α∠=，ABD β∠=，AEC γ∠=，则()A ．90αβγ+-=︒B ．90βγα+-=︒C ．90αγβ+-=︒D ．180αβγ++=︒【答案】B【详解】连接AC，AB 是O 的直径，90ACB BCD ACD ∴∠=∠+∠=︒，ACD ABD β∠=∠= ，90BCD β∴∠=︒-，AEC ABC BCD γ∠=∠+∠= ，ABC α∠=，90γαβ∴=+︒-，即90γβα+-=︒，故选：B ．33．（2022•钱塘区一模）每年的4月23日是世界读书日．某校为了解4月份八年级学生的读书情况，随机调查了八年级50名学生读书的册数，统计数据如表格所示．关于这组数据，下列说法正确的是()册数01234人数61416122A ．众数是16B ．中位数是2C ．平均数是2D ．方差是1【答案】B【详解】A 、众数是2册，结论错误，故A 不符合题意；B 、中位数是2册，结论正确，故B 符合题意；C 、平均数是(0611421631242)50 1.8⨯+⨯+⨯+⨯+⨯÷=（册)，结论错误，故C 不符合题意；D 、方差222221[6(0 1.8)14(1 1.8)16(2 1.8)12(3 1.8)2(4 1.8)] 1.1250=⨯⨯-+⨯-+⨯-+⨯-+⨯-=，结论错误，故D 不符合题意．故选：B ．34．（2022•钱塘区一模）如图，在ABC ∆中，D 为BC 边上一点（不与点B ，点C 重合），E ，F 分别在AB 边和AC 边上，//EF BC ，连结AD 交EF 于点G ，则()A ．AE AGAG AF=B ．EB GDGD FC=C ．EG GFBD DC=D ．EG GFDC BD=【答案】C 【详解】A 选项，AE BEAG DG=，故该选项不符合题意；B 选项，EB AEGD AG=，故该选项不符合题意；C 选项，//EF BC ，AEG B ∴∠=∠，AGE ADB ∠=∠，AEG ABD ∴∆∆∽，∴EG AGBD AD=，同理AGF ADC ∆∽，∴AG GFAD DC=，∴EG GFBD DC=，故该选项符合题意；D 选项，EG GFBD DC=，故该选项不符合题意；故选：C ．35．（2022•钱塘区一模）节假期间，几名同学合租了一辆汽车准备从市区到郊外游玩，租金为600元．出发时，又增加了2名同学，此时总人数为x 名（不超过车载额定人数）．如果汽车的租金由参加的同学平均分摊，且原先租车的几名同学平均每人少分摊了50元，由题意列方程正确的是()A ．600600502x x -=-B ．600600502x x -=+C ．600600502x x -=-D ．600600502x x -=+【答案】A【详解】出发时，又增加了2名同学，且此时总人数为x 名（不超过车载额定人数），∴原计划去郊外游玩的同学共(2)x -名．依题意得：600600502x x-=-．故选：A ．36．（2022•钱塘区一模）已知二次函数2221(y x mx m m m =-+--+为常数）的图象与x 轴有交点，且当3x <-时，y 随x 的增大而增大，则m 的取值范围是()A ．31m -<B ．31m -C ．31m -<<D ．3m - 或1m【答案】B【详解】二次函数2221(y x mx m m m =-+--+为常数）的图象与x 轴有交点，∴△0 ．22(2)4(1)(1)0m m m ∴-⨯-⨯--+ ．解得：1m．22221()1y x mx m m x m m =-+--+=---+ ，∴二次函数2221y x mx m m =-+--+的图象的对称轴为直线x m =．当3x <-时，y 随x 的增大而增大，3m ∴- ．31m ∴- ．故选：B ．37．（2022•淳安县一模）如图，AB 是O 的直径，点C 、D 在圆周上，30CAB ∠=︒，则ADC ∠的度数为()A ．30︒B ．45︒C ．60︒D ．75︒【答案】C 【详解】连接BC ，AB 是O 的直径，90ACB ∴∠=︒，30CAB ∠=︒ ，9060ABC CAB ∴∠=︒-∠=︒，60ADC ABC ∴∠=∠=︒，故选：C ．38．（2022•淳安县一模）疫情期间进入学校都要进入测温通道，体温正常才可进入学校，昌平某校有2个测温通道，分别记为A 、B 通道，学生可随机选取其中的一个通道测温进校园．某日早晨该校所有学生体温正常．小王和小李两同学该日早晨进校园时，选择同一通道测温进校园的概率是()A ．14B ．13C ．12D ．23【答案】C【详解】画树状图如图：共有4个等可能的结果，小王和小李两同学该日早晨进校园时，选择同一通道测温进校园的结果有2个，∴小王和小李两同学该日早晨进校园时，选择同一通道测温进校园的概率为2142=，故选：C ．39．（2022•淳安县一模）如图，在平面直角坐标系中，点A ，B 的坐标分别是(2,2)A ，(5,5)B ，若二次函数2y ax bx c =++的图象过A ，B 两点，且该函数图象的顶点为(,)M x y ，其中x ，y 是整数，且07x <<，07y <<，则a 的最大值是()A ．2B ．1C ．12D ．13【答案】B【详解】该函数图象的顶点为(,)M x y ，其中x ，y 是整数，且07x <<，07y <<，1y ∴=或2或5或6．根据抛物线的对称性，抛物线的顶点坐标只能是(3,1)或(2,2)或(4,6)或(5,5)．当顶点坐标为(3,1)时，设抛物线的解析式为2(3)1y a x =-+，将(2,2)代入得：2(23)12a -+=，解得：1a =；当顶点坐标为(2,2)时，设抛物线的解析式为2(2)2y a x =-+，将(5,5)代入得：2(52)25a -+=，解得：13a =；当顶点坐标为(4,6)时，设抛物线的解析式为2(4)6y a x =-+，将(2,2)代入得：2(24)62a -+=，解得：1a =-；当顶点坐标为(5,5)时，设抛物线的解析式为2(5)5y a x =-+，将(2,2)代入得：2(25)52a -+=，解得：13a =-．综上，a 的最大值是1．故选：B ．40．（2022•淳安县一模）如图，在ABC ∆中，90ABC ∠=︒，以点A 为圆心，以AB 的长为半径作弧交AC 于点D ，连接BD ，再分别以点B ，D 为圆心，大于12BD 的长为半径作弧，两弧交于点P ，作射线AP 交BC 于点E ，连接DE ，则下列结论正确的是()A ．DE 垂直平分ACB ．ABE CBA ∆∆∽C ．2BD BC BE =⋅D ．CE AB BE CA⋅=⋅【答案】D【详解】由题意可得AB AD =，AP 平分BAC ∠，AE ∴垂直平分BD ，BE DE ∴=，在ABE ∆和ADE ∆中，AB AD AE AE BE DE =⎧⎪=⎨⎪=⎩，()ABE ADE SSS ∴∆≅∆，90ABE ADE ∴∠=∠=︒，又C C ∠=∠ ，ABC EDC ∴∆∆∽，∴CE DEAC AB=，CE AB BE CA ∴⋅=⋅，故选D ．41．（2022•富阳区一模）若点1(1,)A y -，2(2,)B y ，3(3,)C y 在反比例函数6y x=-的图象上，则1y ，2y ，3y 的大小关系是()A ．123y y y >>B ．231y y y >>C ．132y y y >>D ．321y y y >>【答案】C【详解】点1(1,)A y -、2(2,)B y 、3(3,)C y 在反比例函数6y x=-的图象上，1661y ∴=-=-，2632y =-=-，3623y =-=-，又326-<-< ，。

2024年山东省潍坊市初中学业水平考试模拟试题(四)

2024年山东省潍坊市初中学业水平考试模拟试题（四）一、单选题 1．计算：()342-⨯=（） A ．6-B ．6C ．8-D ．82．如图所示的几何体的俯视图可能是（）A ．B ．C ．D ．3．已知数a 在数轴上的位置如图所示，则下列结论正确的是（）A ．22a a -<-<<B ．22a a -<-<<C ．22a a -<-<<D ．22a a -<-<<4．小颖和小亮参加数学实践活动，检验一个用断桥铝制作的窗户是否为矩形，下面的测量方法正确的是（）A ．度量窗户的两个角是否是90︒B ．测量窗户两组对边是否分别相等C ．测量窗户两条对角线是否相等D ．测量窗户两条对角线的交点到四个顶点的距离是否相等5．如图，乐器上的一根弦80cm AB =，两个端点A B ，固定在乐器面板上，支撑点C 是靠近点B 的黄金分割点，支撑点D 是靠近点A 的黄金分割点，则支撑点C D ，之间的距离为（）．（结果保留根号）A ．()160cm B ．()120cmC ．()80cmD ．()120cm6．如图是y 关于x 的一个函数图象，根据图象，下列说法不正确的是（）A ．该函数的最大值为6B ．当3x ≤时，y 随x 的增大而增大C ．当1x =时，对应的函数值3y =D ．当2x =和5x =时，对应的函数值相等二、多选题7．有一组被墨水污染的数据：4、17、7、14、★、★、★、16、10、4、4、11 ，其箱线图如下：下列说法正确的是（）A ．这组数据的下四分位数是4B ．这组数据的中位数是10C ．这组数据的上四位数是15D ．被墨水污染的数据中一个数是3，一个数是188．下列计算正确的是（）A B ．33(2)8a a -=- C ．842a a a ÷=D ．22(1)(1)4a a ab -=+- 9．如图①所示（图中各角均为直角），动点P 从点A 出发，以每秒1个单位长度的速度沿A B C D E →→→→路线匀速运动，AFP V 的面积y 随点P 运动的时间x （秒）之间的函数关系图象如图②所示，下列说法正确的是（）A ．6AF =B ．4AB =C ．3DE =D ．10EF =10．如图，矩形ABCD 中，6AB =，8AD =，点P 在对角线BD 上，过点P 作MN BD ⊥，交边AD BC ，于点M N ，，过点M 作ME AD ⊥交BD 于点E ，连接EN BM DN ，，．下列结论正确的是（）A ．EM EN =B ．四边形MBND 的面积不变C ．当1:2AM MD =：时，9625MPE S =△ D ．BM MN ND ++的最小值是20三、填空题11．分解因式：296b ab a b -+=． 12．如图，点A 在函数()20y x x =>的图象上，点B 在函数()30y x x=>的图象上，且AB ∥x 轴，BC x ⊥轴于点C ，则四边形ABCO 的面积为．13．劳动委员统计了某周全班同学的家庭劳动次数x （单位：次），按劳动次数分为4组：03x ≤<，36x <≤，69x ≤<，912x ≤<，绘制成如图所示的频数分布直方图．从中任选一名同学，则该同学这周家庭劳动次数不足6次的概率是．14．如图，在扇形AOB 中，60AOB ∠=︒，OD 平分AOB ∠交»AB 于点D ，点C 是半径OB 上一动点，若1OA =，则阴影部分周长的最小值为．四、解答题15．（1）先化简，再求值：()()()2212121x x x +---，其中2x =-；（2）若关于x 的不等式组2151922x x ax x +>+⎧⎪⎨+≥-⎪⎩所有整数解的和为14，求整数a 的值． 16．如图，矩形ABCD 的对角线AC 与BD 相交于点O ，CD OE P ，直线CE 是线段OD 的垂直平分线，CE 分别交OD ，AD 于点F ，G ，连接DE ．当4CD =时，求EG 的长．17．小王同学学习了锐角三角函数后，通过观察广场的台阶与信号塔之间的相对位置，他认为利用台阶的可测数据与在点A ，B 处测出点D 的仰角度数，可以求出信号塔DE 的高．如图，AB 的长为5m ，高BC 为3m ．他在点A 处测得点D 的仰角为45︒，在点B 处测得点D 的仰角为38.7︒，A B C D E ，，，，在同一平面内．你认为小王同学能求出信号塔DE 的高吗？若能，请求出信号塔DE 的高；若不能，请说明理由．（参考数据：sin38.70.625︒≈，cos38.70.780︒≈，tan38.70.80︒≈，结果保留整数）18．小颖妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉，为了确定售价，小颖帮妈妈调查了附近A，B，C，D，E五家花卉店近期该种盆栽花卉的售价与日销售量情况，记录如下：小颖将调查数据按照一定顺序做出了重新整理，并填写在下表中，(1)分析数据的变化规律，找出日销售量与售价间的关系．(2)根据以上信息，小颖妈妈在销售该种花卉中，①要想每天获得400元的利润，应如何定价？②售价定为多少时，每天能够获得最大利润？19．某中学九年级共有600名学生，为了了解学生信息技术操作水平，学校教学研究中心从中随机抽取了20名学生进行信息技术操作测试．【数据的收集】被抽取的20名学生的信息技术测试成绩（单位：分）如下：81 90 82 89 99 95 91 83 92 9387 92 94 88 92 87 100 86 85 96 【数据的整理与分析】(1)请按组距为5将数据分组，列出频数分布表，画出频数分布直方图；(2)①这组数据的中位数是______；这组数据的众数是． ②分析数据分布的情况（写出一条即可）_________；(3)若85分以上（不含85分）成绩为优秀等次，请预估该校九年级学生在同等难度的信息技术操作考试中达到优秀等次的人数．20．如图，点C 是以AB 为直径的O e 上一点，点D 是AB 的延长线上一点，在OA 上取一点F ，过点F 作AB 的垂线交AC 于点G ，交DC 的延长线于点E ，且EG EC =．(1)求证：DE 是O e 的切线；(2)若点F 是OA 的中点，4BD =，1sin 3D ∠=，求EC 的长． 21．如图1，小丽借助几何软件进行数学探究：第一步，画出矩形ABCD 和矩形EFGH ，点E 、F 在边AB 上（AB EF <），且点C 、D 、G 、H 在直线AB 的同侧；第二步，设置,AB EFm n AD EH==，矩形EFGH 能在边AB 上左右滑动；第三步，画出边EF 的中点O ，射线OH 与射线AD 相交于点P （点P 、D 不重合），射线OG 与射线BC 相交于点Q （点Q 、C 不重合），观测DP 、CQ 的长度．(1)如图2，小丽取4313AB EF m n ====，，，，滑动矩形EFGH ，当点E 、A 重合时，CQ =______；(2)小丽滑动矩形EFGH ，使得O 恰为边AB 的中点．她发现对于任意的m n DP CQ ≠=，总成立．请说明理由；(3)经过数次操作，小丽猜想，设定m 、n 的某种数量关系后，滑动矩形EFGH ，DP CQ =总成立．小丽的猜想是否正确？请说明理由．22．如图，已知抛物线2()40y ax bx a =++≠与x 轴交于点A （1，0）和B ，与y 轴交于点C ，对称轴为52x =．（1）求抛物线的解析式；（2）如图1，若点P 是线段BC 上的一个动点（不与点B ，C 重合），过点P 作y 轴的平行线交抛物线于点Q ，连接OQ ．当线段PQ 长度最大时，判断四边形OCPQ 的形状并说明理由．（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠=∠．在y轴上是否存在点F，使得BEFDQE ODQ2△为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．。