八数码问题代码及算法分析

合集下载

a星算法求解八数码问题python

a星算法求解八数码问题python一、介绍八数码问题是一种经典的智力游戏，也是人工智能领域中的经典问题之一。

在这个问题中，有一个3×3的棋盘，上面摆着1至8这8个数字和一个空格，初始状态和目标状态都已知。

要求通过移动数字，将初始状态变换成目标状态。

其中空格可以和相邻的数字交换位置。

为了解决这个问题，我们可以使用A*算法。

本文将详细介绍如何用Python实现A*算法来求解八数码问题。

二、A*算法简介A*算法是一种启发式搜索算法，常用于寻找最短路径或最优解等问题。

它基于Dijkstra算法，并加入了启发式函数来加速搜索过程。

在A*算法中，每个节点都有两个估价值：g值和h值。

g值表示从起点到该节点的实际代价，h值表示从该节点到目标节点的估计代价。

启发式函数f(n) = g(n) + h(n) 表示从起点到目标节点的估计总代价。

A*算法采用优先队列来保存待扩展的节点，并按照f(n)值从小到大排序。

每次取出队头元素进行扩展，并将扩展出来的新节点按照f(n)值插入队列中。

当扩展出目标节点时，算法结束。

三、八数码问题的状态表示在八数码问题中，每个状态都可以表示为一个3×3的矩阵。

我们可以用一个一维数组来表示这个矩阵，其中0表示空格。

例如，初始状态可以表示为[2, 8, 3, 1, 6, 4, 7, 0, 5]，目标状态可以表示为[1, 2, 3, 8, 0, 4, 7, 6, 5]。

四、A*算法求解八数码问题的步骤1.将初始状态加入优先队列中，并设置g值和h值为0。

2.从队头取出一个节点进行扩展。

如果该节点是目标节点，则搜索结束；否则，将扩展出来的新节点加入优先队列中。

3.对于每个新节点，计算g值和h值，并更新f(n)值。

如果该节点已经在优先队列中，则更新其估价值；否则，将其加入优先队列中。

4.重复第2步至第3步直到搜索结束。

五、Python实现以下是用Python实现A*算法求解八数码问题的代码：```import heapqimport copy# 目标状态goal_state = [1,2,3,8,0,4,7,6,5]# 启发式函数：曼哈顿距离def h(state):distance = 0for i in range(9):if state[i] == 0:continuerow = i // 3col = i % 3goal_row = (state[i]-1) // 3goal_col = (state[i]-1) % 3distance += abs(row - goal_row) + abs(col - goal_col)return distance# A*算法def A_star(start_state):# 初始化优先队列和已访问集合queue = []visited = set()# 将初始状态加入优先队列中，并设置g值和h值为0heapq.heappush(queue, (h(start_state), start_state, 0))while queue:# 取出队头元素进行扩展f, state, g = heapq.heappop(queue)# 如果该节点是目标节点，则搜索结束；否则，将扩展出来的新节点加入优先队列中。

8数码问题分析及程序代码

八数码问题1、问题描述所谓八数码问题是指：将分别标有数字1，2，3，…，8的八块正方形数码牌任意地放在一块3×3的数码盘上。

放牌时要求不能重叠。

于是，在3×3的数码盘上出现了一个空格。

现在要求按照每次只能将与空格相邻的数码牌与空格交换的原则，将任意摆放的数码盘逐步摆成某种特殊的排列。

2、问题分析首先，八数码问题包括一个初始状态(strat) 和目标状态(goal)，所谓解八数码问题就是在两个状态间寻找一系列可过渡状态（strat-> strat 1-> strat 2->...->goal ）。

这个状态是否存在表示空格）图13、数据结构定义结构体Node 如下： typedef struct{int num[9];char cur_expension; //记录是否可以扩展，Y 代表可以扩展，N 代表不可以。

char Operate; //表示不可以执行的操作，'L'代表不能左移，'R'代表不能右移， //'U'代表不能上移，'D'代表不能下移，'C'代表可以任意移动。

int father; //记录父节点的下标。

}Node;Node state[MAXSIZE]; //将搜索过的状态存储于该数组中。

4、广度优先搜索广度优先搜索是指按节点的层次进行搜索,本层的节点没有搜索完毕时,不能对下层节点进行处理,即深度越小的节点越先得到扩展,也就是说先产生的节点先得以扩展处理,直至找到目标为止。

求解八数码问题的搜索过程:如图2所示,把所有可能的算符应用到开始节点(即空格上移、空格左移、空格右移、空格下移),图2只是演示了两个扩展结点，如此继续下去,直到发现目标节点。

图2 变量定义及函数说明：1 2 3 45 6 7 8 01 2 37 4 5 8 0 61 2 34 5 67 8 0#define SUM 100//限定只搜索前50步，50步以后如果仍然没有搜索到结果，认为无解。

八数码C语言A算法详细代码

#include<iostream>#include<time.h>#include<windows.h>#include<vector>#include<cmath>using namespace std;struct node{int a[3][3]; //存放矩阵int father; //父节点的位置int gone; //是否遍历过,1为是,0为否int fn; //评价函数的值int x,y; //空格的坐标int deep; //节点深度};vector<node> store; //存放路径节点int mx[4]={-1,0,1,0};int my[4]={0,-1,0,1}; //上下左右移动数组int top; //当前节点在store中的位置bool check(int num) //判断store[num]节点与目标节点是否相同,目标节点储存在store[0]中{for(int i=0;i<3;i++){for(int j=0;j<3;j++){if(store[num].a[i][j]!=store[0].a[i][j])return false;}}return true;}bool search(int num) //判断store[num]节点是否已经扩展过 ,没有扩展返回true{int pre=store[num].father; //pre指向store[num]的父节点位置bool test=true;while(!pre){ //循环直到pre为0,既初始节点for(int i=0;i<3;i++){for (int j=0;j<3;j++){if(store[pre].a[i][j]!=store[num].a[i][j]){test=false;break;}}if(test==false) break;}if(test==true) return false;pre=store[pre].father; //pre继续指向store[pre]父节点位置}return true;}void print(int num) //打印路径,store[num]为目标节点{vector<int> temp; //存放路径int pre=store[num].father;temp.push_back(num);while(pre!=0){ //从目标节点回溯到初始节点temp.push_back(pre);pre=store[pre].father;}cout<<endl;cout<<"*********数码移动步骤*********"<<endl;int mm=1; //步数for(int m=temp.size()-1;m>=0;m--){cout<<"---第"<<mm<<"步---："<<endl;for(int i=0;i<3;i++){for(int j=0;j<3;j++){cout<<store[temp[m]].a[i][j]<<" ";}cout<<endl;}mm++;cout<<endl;}cout<<"所需步数为: "<<store[num].deep<<endl;return;}int get_fn(int num) //返回store[num]的评价函数值{int fn_temp=0; //评价函数值bool test=true;for(int i=0;i<3;i++){ //当找到一个值后,计算这个值位置与目标位置的距离差,test置为false后继续寻找下一个值for(int j=0;j<3;j++){test=true;for(int k=0;k<3;k++){for(int l=0;l<3;l++){if((store[num].x!=i||store[num].y!=j)&&store[num].a[i][j]==store[0].a[k][l]){ //寻值时排除空格位fn_temp=fn_temp+abs(i-k)+abs(j-l);test=false;}if(test==false) break;}if(test==false) break;}}}fn_temp=fn_temp+store[num].deep; //加上节点深度return fn_temp;}void kongxy(int num) //获得空格坐标{for(int i=0;i<3;i++){for(int j=0;j<3;j++){if(store[num].a[i][j]==0){store[num].x=i;store[num].y=j;}}}return;}int main(){cout<<"-----------A*算法解决8数码问题------------"<<endl;while(true){store.clear(); //清空storevector<int> open; //建立open表int i,j,m,n,f;int min; //store[min]储存fn值最小的节点int temp;bool test;top=1; //当前节点在store的位置,初始节点在store[1]int target[9];int begin[9]; //储存初始状态和目标状态,用于判断奇偶int t1=0,t2=0; //初始状态和目标状态的奇偶序数node node_temp;store.push_back(node_temp);store.push_back(node_temp); //用于创建store[0]和store[1],以便下面使用cout<<"请输入初始数码棋盘状态,0代表空格："<<endl; //输入初始状态,储存在store[1]中test=false;while(test==false){f=0;for(i=0;i<3;i++){for(j=0;j<3;j++){cin>>temp;store[1].a[i][j]=temp;begin[f++]=temp;}}test=true;for(i=0;i<8;i++){ //检查是否有重复输入,若有则重新输入for(j=i+1;j<9;j++){if(begin[i]==begin[j]){test=false;break;}}if(test==false) break;}if(test==false) cout<<"输入重复,请重新输入:"<<endl;}kongxy(1); //找出空格的坐标cout<<"请输入目标数码棋盘状态,0代表空格： "<<endl; //输入目标状态,储存在store[0]中test=false;while(test==false){f=0;for(i=0;i<3;i++){for(j=0;j<3;j++){cin>>temp;store[0].a[i][j]=temp;target[f++]=temp;}}test=true;for(i=0;i<8;i++){ //检查是否有重复输入,若有则重新输入for(j=i+1;j<9;j++){if(target[i]==target[j]){test=false;break;}}if(test==false) break;}if(test==false){cout<<"输入重复,请重新输入:"<<endl;continue; //若重复,重新输入}for(i=0;i<9;i++){ //检查目标状态与初始状态是否匹配test=false;for(j=0;j<9;j++){if(begin[i]==target[j]){test=true;break;}}if(test==false) break;}if(test==false) cout<<"输入与初始状态不匹配,请重新输入:"<<endl;}for(i=1;i<9;i++){ //判断奇偶序数是否相同,若不相同则无法找到路径for(j=1;i-j>=0;j++){if(begin[i]>begin[i-j]){if(begin[i-j]!=0) t1++;}}}for(i=1;i<9;i++){for(j=1;i-j>=0;j++){if(target[i]>target[i-j]){if(target[i-j]!=0) t2++;}}}if(!(t1%2==t2%2)){cout<<"无法找到路径."<<endl;cout<<endl;//system("pause");//return 0;continue;}LARGE_INTEGER Freg;LARGE_INTEGER Count1,Count2;QueryPerformanceFrequency(&Freg);QueryPerformanceCounter(&Count1);//获取时间Count1double d;store[1].father=0; //初始化参数store[1].gone=0;store[1].deep=0; //初始节点的父节点为0store[1].fn=get_fn(1);if(check(1)){ //判断初始状态与目标状态是否相同print(1);//system("pause");//return 0;cout<<endl;continue;}open.push_back(1); //把初始状态在store中的位置数压入open表中while(!open.empty()){ //当open表不为空时,开始寻找路径if(check(top)) break;min=top;int i_min=0;for(i=0;i<open.size();i++){ //遍历open表中元素,找出store中fn值最小的节点if(store[open[i]].fn<=store[min].fn&&store[open[i]].gone==0){min=open[i];i_min=i;}}store[min].gone=1;open.erase(open.begin()+i_min); //把最小节点标记遍历过,并从open表中删除m=store[min].x;n=store[min].y; //空格坐标for(f=0;f<4;f++){ //上下左右移动空格i=m+mx[f];j=n+my[f];if(i>=0&&i<=2&&j>=0&&j<=2){ //当变换后的空格坐标在矩阵中时,开始移动top++;store.push_back(store[min]); //把store[min]压入store中成为新增节点,位置为store[top]store[top].father=min; //新增节点的父节点为minstore[top].gone=0; //新增节点未被访问store[top].deep=store[min].deep+1; //新增节点的深度为父节点深度+1temp=store[top].a[m][n]; //交换空格与相邻数字store[top].a[m][n]=store[top].a[i][j];store[top].a[i][j]=temp;store[top].x=i; //移动后的空格坐标store[top].y=j;store[top].fn=get_fn(top); //移动后的fn值open.push_back(top); //把top压入open表中if(check(top)){ //检查是否到达目标print(top);//system("pause");//return 0;break;}if(search(top)==false){ //检查新增节点是否被访问过,若访问过,则删除此节点top--;store.pop_back();open.pop_back();}}}}QueryPerformanceCounter(&Count2);//获取时间Count2d=(double)(Count2.QuadPart-Count1.QuadPart)/(double)Freg.QuadPart*1000.0;//计算时间差，d的单位为ms.cout<<"算法时间为为"<<d<<" ms."<<endl;cout<<endl;}return 0;system("pause");}。

八数码实验报告

八数码实验报告八数码实验报告引言：八数码，也被称为滑块拼图，是一种经典的益智游戏。

在这个实验中，我们将探索八数码问题的解决方案，并分析其算法的效率和复杂性。

通过这个实验，我们可以深入了解搜索算法在解决问题中的应用，并且探讨不同算法之间的优劣势。

1. 问题描述：八数码问题是一个在3x3的方格上进行的拼图游戏。

方格中有8个方块，分别标有1到8的数字，还有一个空方块。

游戏的目标是通过移动方块，将它们按照从左上角到右下角的顺序排列。

2. 算法一：深度优先搜索（DFS）深度优先搜索是一种经典的搜索算法，它从初始状态开始，不断地向前搜索，直到找到目标状态或者无法继续搜索为止。

在八数码问题中，深度优先搜索会尝试所有可能的移动方式，直到找到解决方案。

然而，深度优先搜索在解决八数码问题时存在一些问题。

由于搜索的深度可能非常大，算法可能会陷入无限循环，或者需要很长时间才能找到解决方案。

因此，在实际应用中，深度优先搜索并不是最优的选择。

3. 算法二：广度优先搜索（BFS）广度优先搜索是另一种常用的搜索算法，它从初始状态开始，逐层地向前搜索，直到找到目标状态。

在八数码问题中，广度优先搜索会先尝试所有可能的一步移动，然后再尝试两步移动，依此类推，直到找到解决方案。

与深度优先搜索相比，广度优先搜索可以保证找到最短路径的解决方案。

然而，广度优先搜索的时间复杂度较高，尤其是在搜索空间较大时。

因此，在实际应用中，广度优先搜索可能不太适合解决八数码问题。

4. 算法三：A*算法A*算法是一种启发式搜索算法，它在搜索过程中利用了问题的启发信息，以提高搜索效率。

在八数码问题中，A*算法会根据每个状态与目标状态之间的差异，选择最有可能的移动方式。

A*算法通过综合考虑每个状态的实际代价和启发式估计值，来评估搜索路径的优劣。

通过选择最优的路径，A*算法可以在较短的时间内找到解决方案。

然而，A*算法的实现较为复杂，需要合适的启发函数和数据结构。

八数码实验报告

八数码实验报告实验名称：八数码实验目的：通过使用搜索算法和启发式算法，解决八数码问题，深入理解搜索算法原理和应用。

实验环境：使用Python语言进行编程实现，操作系统为Windows。

实验过程：1. 定义八数码问题的状态和目标状态，分别以列表的形式表示。

* 初始状态：[2, 8, 3, 1, 6, 4, 7, 0, 5]* 目标状态：[1, 2, 3, 8, 0, 4, 7, 6, 5]2. 实现深度优先搜索算法，运行程序得到结果。

通过深度优先搜索算法，得到了八数码问题的解法。

但是，由于深度优先搜索算法过于盲目，搜索时间过长，而且容易陷入无解状态，因此需要改进算法。

3. 改进算法——广度优先搜索。

在深度优先搜索的基础上，改用广度优先搜索算法，实现代码如下：```def bfs(start, target):queue = [(start, [start])]seen = {tuple(start)}while queue:node, path = queue.pop(0)for move, i in direction.items():new_node = [j for j in node]if i not in range(0, 9):continuenew_node[0], new_node[i] = new_node[i], new_node[0] if tuple(new_node) in seen:continueif new_node == target:return path + [new_node]seen.add(tuple(new_node))queue.append((new_node, path + [new_node]))```4. 改进算法——A*算法。

在广度优先搜索的基础上，使用A*算法进行优化。

进行了以下改进：* 引入估价函数，加快搜索速度；* 遍历过程中对结点进行评估，保留最优的结点。

八数码问题C代码

*********************************************************************本函数是用A*算法来实现八数码的问题***算法的步骤如下：*1、初始化两个链表open和closed，将初始状态放入open表中*2、重复下列过程，直至找到目标结点为止，如果open表为空，那* 么查找失败；*3、从open表中拿出具有最小f值的结点(将这一结点称为BESTNODE)，* 并放入closed表中；*4、如果BESTNODE为目标结点，成功求得解,退出循环；*5、如果BESTNODE不是目标结点，那么产生它的后继结点(此后继结* 点与其祖先的状态不同)，后继结点组成一个链表；*6、对每个后继结点进行以下过程：*7、建立它到BESTNODE的parent指针；*8、如果此结点在open表中，首先将open表中的结点添加进BESTNODE* 的后继结点链中，然后计算两个结点的g值，如果此结点的g值小* 于open表中的结点时，open表中的结点改变parent指针，同时将* 此结点删除；*9、如果此结点在closed表中，首先将closed表中的结点添加进BESTNODE * 的后继结点中，然后计算两个结点的g值，如果此结点的g值小于* closed表中的结点时，closed表中的结点改变parent指针；将* closed表中的结点重新放入open表中，同时将此结点删除；*10、如果此结点既不在open表中也不再closed表中，那么添加此结点至* BESTNODE的后继结点链中。

***Author: 转载作者不详。

**2011.5.16**********************************************************************/#include "stdafx.h"#include <iostream>#include <cstdlib>#include <conio.h>#define size 3using namespace std;//定义二维数组来存储数据表示某一个特定状态typedef int status[size][size];struct SpringLink;//定义状态图中的结点数据结构typedef struct Node{status data;//结点所存储的状态Node *parent;//指向结点的父亲结点SpringLink *child;//指向结点的后继结点int fvalue;//结点的总的路径int gvalue;//结点的实际路径int hvalue;//结点的到达目标的苦难程度Node *next;//指向open或者closed表中的后一个结点}NNode , *PNode;//定义存储指向结点后继结点的指针的地址typedef struct SpringLink{Node *pointData;//指向结点的指针SpringLink *next;//指向兄第结点}SPLink , *PSPLink;//定义open表和close表PNode open;PNode closed;//开始状态与目标状态status startt = {2 , 8 , 3 , 1 , 6 , 4 , 7 , 0 , 5};status target = {1 , 2 , 3 , 8 , 0 , 4 , 7 , 6 , 5};//初始化一个空链表void initLink(PNode &Head){Head = (PNode)malloc(sizeof(NNode));Head->next = NULL;}//判断链表是否为空bool isEmpty(PNode Head){if(Head->next == NULL)return true;elsereturn false;}//从链表中拿出一个数据，通过FNode返回void popNode(PNode &Head , PNode &FNode){if(isEmpty(Head)){FNode = NULL;return;}FNode = Head->next;Head->next = Head->next->next;FNode->next = NULL;}//向结点的(最终)后继结点链表中添加新的子结点void addSpringNode(PNode &Head , PNode newData) {PSPLink newNode = (PSPLink)malloc(sizeof(SPLink)); newNode->pointData = newData;newNode->next = Head->child;Head->child = newNode;}//释放状态图中存放结点后继结点地址的空间//注意传入参数PSPLink引用类型void freeSpringLink(PSPLink &Head){PSPLink tmm;while(Head != NULL){tmm = Head;Head = Head->next;free(tmm);}}//释放open表与closed表中的资源void freeLink(PNode &Head){PNode tmn;tmn = Head;Head = Head->next;free(tmn);while(Head != NULL){//首先释放存放结点后继结点地址的空间freeSpringLink(Head->child);tmn = Head;Head = Head->next;free(tmn);}}//向普通链表中添加一个结点void addNode(PNode &Head , PNode &newNode) {newNode->next = Head->next;Head->next = newNode;}//向非递减排列的链表中添加一个结点void addAscNode(PNode &Head , PNode &newNode) {PNode P;PNode Q;P = Head->next;Q = Head;while(P != NULL && P->fvalue < newNode->fvalue) {Q = P;P = P->next;}//上面判断好位置之后，下面就是简单的插入了newNode->next = Q->next;Q->next = newNode;}//计算结点额h值，当前节点与目标节点数码错位个数int computeHValue(PNode theNode){int num = 0;for(int i = 0 ; i < 3 ; i++){for(int j = 0 ; j < 3 ; j++){if(theNode->data[i][j] != target[i][j])num++;}}return num;}//计算结点的f，g，h值void computeAllValue(PNode &theNode , PNode parentNode) {if(parentNode == NULL)theNode->gvalue = 0;elsetheNode->gvalue = parentNode->gvalue + 1;theNode->hvalue = computeHValue(theNode);theNode->fvalue = theNode->gvalue + theNode->hvalue;}//初始化函数，进行算法初始条件的设置void initial(){//初始化open以及closed表initLink(open);initLink(closed);//初始化起始结点，令初始结点的父节点为空结点PNode NULLNode = NULL;PNode Start = (PNode)malloc(sizeof(NNode));for(int i = 0 ; i < 3 ; i++){for(int j = 0 ; j < 3 ; j++){Start->data[i][j] = startt[i][j];}}Start->parent = NULL;Start->child = NULL;Start->next = NULL;computeAllValue(Start , NULLNode);//起始结点进入open表addAscNode(open , Start);}//将B节点的状态赋值给A结点void statusAEB(PNode &ANode , PNode BNode) {for(int i = 0 ; i < 3 ; i++){for(int j = 0 ; j < 3 ; j++){ANode->data[i][j] = BNode->data[i][j];}}}//两个结点是否有相同的状态bool hasSameStatus(PNode ANode , PNode BNode) {for(int i = 0 ; i < 3 ; i++){for(int j = 0 ; j < 3 ; j++){if(ANode->data[i][j] != BNode->data[i][j])return false;}}return true;}//结点与其祖先结点是否有相同的状态bool hasAnceSameStatus(PNode OrigiNode , PNode AnceNode) {while(AnceNode != NULL){if(hasSameStatus(OrigiNode , AnceNode))return true;AnceNode = AnceNode->parent;}return false;}//取得方格中空的格子的位置，通过row,col返回。

八数码问题C语言代码

八数码问题源程序及注释：#include<stdio.h>#include<conio.h>int n,m;typedef struct Node{char matrix[10];/*存储矩阵*/char operate;/*存储不可以进行的操作，L代表不能左移R代表不能右移U代表不能上移D代表不能下移*/char extend;/*是否可以扩展，Y代表可以，N代表不可以*/int father;/*指向产生自身的父结点*/}Node;char start[10]={"83426517 "};/*此处没有必要初始化*/char end[10]={"1238 4765"};/*此处没有必要初始化*/Node base[4000];int result[100];/*存放结果的base数组下标号，逆序存放*/int match()/*判断是否为目标*/{int i;for(i=0;i<9;i++){if(base[n-1].matrix[i]!=end[i]){return 0;}}return 1;}void show()/*显示矩阵的内容*/{int i=1;while(m>=0){int mm=result[m];//clrscr();printf("\n\n\n 状态方格\t\t步骤 %d",i);printf("\n\n\n\n\n\t\t\t%c\t%c\t%c\n",base[mm].matrix[0],base[mm].mat rix[1],base[mm].matrix[2]);printf("\n\n\t\t\t%c\t%c\t%c\n",base[mm].matrix[3],base[mm].matrix[4],base[mm].matrix[5]);printf("\n\n\t\t\t%c\t%c\t%c\n",base[mm].matrix[6],base[mm].matrix[7] ,base[mm].matrix[8]);//sleep(1);m--;i++;}}void leave()/*推理成功后退出程序之前要执行的函数，主要作用是输出结果*/ {n--;while(base[n].father!=-1){result[m]=n;m++;n=base[n].father;}result[m]=0;result[m+1]='\0';show();//clrscr();printf("\n\n\n\n\n\n\n\n\n\t\t\t\t搜索结束\n\n\n\n\n\n\n\n\n\n"); getch();//exit(0);}int left(int x)/*把下标为X的数组中的矩阵的空格左移*/{int i,j;char ch;for(i=0;i<9;i++){if(base[x].matrix[i]==' ')break;}if(i==0||i==3||i==6||i==9){return 0;}for(j=0;j<9;j++){base[n].matrix[j]=base[x].matrix[j];}ch=base[n].matrix[i-1];base[n].matrix[i-1]=base[n].matrix[i];base[n].matrix[i]=ch;base[n].operate='R';base[n].extend='Y';base[n].father=x;base[x].extend='N';n++;if(match(i))leave();return 1;}int right(int x)/*把下标为X的数组中的矩阵的空格右移*/ {int i,j;char ch;for(i=0;i<9;i++){if(base[x].matrix[i]==' ')break;}if(i==2||i==5||i==8||i==9){return 0;}for(j=0;j<9;j++){base[n].matrix[j]=base[x].matrix[j];}ch=base[n].matrix[i+1];base[n].matrix[i+1]=base[n].matrix[i];base[n].matrix[i]=ch;base[n].operate='L';base[n].extend='Y';base[n].father=x;base[x].extend='N';n++;if(match(i))leave();return 1;}int up(int x)/*把下标为X的数组中的矩阵的空格上移*/ {int i,j;char ch;for(i=0;i<9;i++){if(base[x].matrix[i]==' ')break;}if(i==0||i==1||i==2||i==9){return 0;}for(j=0;j<9;j++){base[n].matrix[j]=base[x].matrix[j];}ch=base[n].matrix[i-3];base[n].matrix[i-3]=base[n].matrix[i];base[n].matrix[i]=ch;base[n].operate='D';base[n].extend='Y';base[n].father=x;base[x].extend='N';n++;if(match(i))leave();return 1;}int down(int x)/*把下标为X的数组中的矩阵的空格下移*/ {int i,j;char ch;for(i=0;i<9;i++){if(base[x].matrix[i]==' ')break;}if(i==6||i==7||i==8||i==9){return 0;}for(j=0;j<9;j++){base[n].matrix[j]=base[x].matrix[j];}ch=base[n].matrix[i+3];base[n].matrix[i+3]=base[n].matrix[i];base[n].matrix[i]=ch;base[n].operate='U';base[n].extend='Y';base[n].father=x;base[x].extend='N';n++;if(match(i))leave();return 1;}main(){int i;char a[20],b[20];n=1;//textcolor(LIGHTGREEN);//clrscr();/*以下是输入初始和目标矩阵，并把输入的0转换为空格*/ printf("Please input the start 9 chars:");scanf("%s",a);printf("Please input the end 9 chars:");scanf("%s",b);for(i=0;i<9;i++){if(a[i]=='0'){start[i]=' ';continue;}if(b[i]=='0'){end[i]=' ';continue;}start[i]=a[i];end[i]=b[i];}start[9]='\0';end[9]='\0';for(i=0;i<9;i++){base[0].matrix[i]=start[i];}base[0].operate='N';base[0].extend='Y';base[0].father=-1;/*以上是为第一个base数组元素赋值*/for(i=0;n<4000;i++){if(base[i].extend=='Y'){if(base[i].operate=='L'){right(i);up(i);down(i);}if(base[i].operate=='R'){left(i);up(i);down(i);}if(base[i].operate=='U'){left(i);right(i);down(i);}if(base[i].operate=='D'){left(i);right(i);up(i);}if(base[i].operate=='N'){left(i);right(i);up(i);down(i); }}}}。

A-star-算法-八数码问题-C++-报告+代码+详细注释1

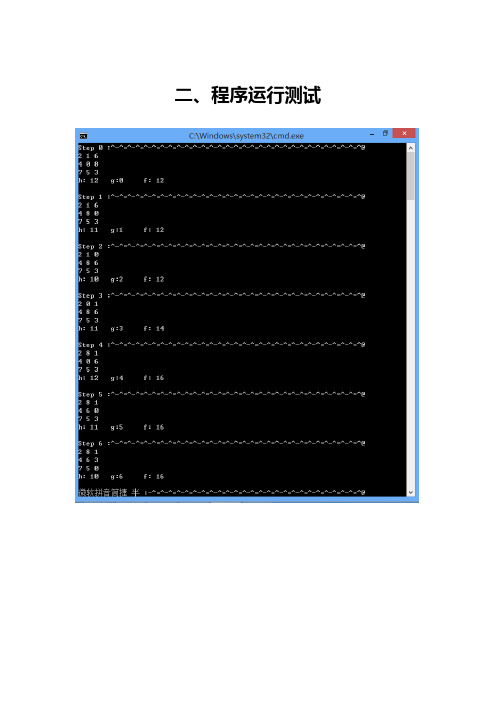
二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。

距离的定义为: “某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。

距离越小, 该节点的效果越好。

某个状态所有将牌到目标位置的距离之和用“h值”表示。

2.主要函数2.1countH（state & st）;countH函数功能是计算st状态的h值。

2.2计算过程中将会用到rightPos数组, 数组里记录的是目标状态下, 0~9每个将牌在九宫格里的位置（位置 = 行下标 * 3 + 列下标）。

2.3f（state * p）;f()=h()+level2.4look_up_dup(vector<state*> & vec, state * p);2.5在open表或close表中, 是否存在指定状态p, 当找到与p完全相等的节点时, 退出函数。

2.6search(state & start)；在open表不为空时, 按f值由小到大对open表中元素进行排序。

调用findZero()函数找到0值元素的位置。

空格可以向上下左右四个方向移动, 前提是移动后不能越过九宫格的边界线。

确定某方向可走后, 空格移动一步, 生成状态p’。

2.7此时, 检查open表中是否已有p’, 若有, 更新p’数据；检查close表中是否已有p’, 若有, 将p’从close表中删除, 添加到open表中。

2.8重复的执行这个过程, 直到某状态的h值为零。

2.9dump_solution(state * q)；在终端输出解路径。

// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数), 这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时, 若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等（对应位置元素相等）, 完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值, 对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st, 计算它的h值。

人工智能实验一_八数码问题

用A*算法解决八数码问题1 问题描述1.1 待解决问题的解释八数码游戏（八数码问题）描述为：在3×3组成的九宫格棋盘上，摆有八个将牌，每一个将牌都刻有1-8八个数码中的某一个数码。

棋盘中留有一个空格，允许其周围的某一个将牌向空格移动，这样通过移动将牌就可以不断改变将牌的布局。

这种游戏求解的问题是：给定一种初始的将牌布局或结构（称初始状态）和一个目标的布局（称目标状态），问如何移动将牌，实现从初始状态到目标状态的转变。

1.2 问题的搜索形式描述（4要素）初始状态：8个数字将牌和空格在九宫格棋盘上的所有格局组成了问题的状态空间。

其中，状态空间中的任一种状态都可以作为初始状态。

后继函数：通过移动空格（上、下、左、右）和周围的任一棋子一次，到达新的合法状态。

目标测试：比较当前状态和目标状态的格局是否一致。

路径消耗：每一步的耗散值为1，因此整个路径的耗散值是从起始状态到目标状态的棋子移动的总步数。

1.3 解决方案介绍（原理）对于八数码问题的解决，首先要考虑是否有答案。

每一个状态可认为是一个1×9的矩阵，问题即通过矩阵的变换，是否可以变换为目标状态对应的矩阵？由数学知识可知，可计算这两个有序数列的逆序值，如果两者都是偶数或奇数，则可通过变换到达，否则，这两个状态不可达。

这样，就可以在具体解决问题之前判断出问题是否可解，从而可以避免不必要的搜索。

如果初始状态可以到达目标状态，那么采取什么样的方法呢？常用的状态空间搜索有深度优先和广度优先。

广度优先是从初始状态一层一层向下找，直到找到目标为止。

深度优先是按照一定的顺序前查找完一个分支，再查找另一个分支，以至找到目标为止。

广度和深度优先搜索有一个很大的缺陷就是他们都是在一个给定的状态空间中穷举。

这在状态空间不大的情况下是很合适的算法，可是当状态空间十分大，且不预测的情况下就不可取了。

他的效率实在太低，甚至不可完成。

由于八数码问题状态空间共有9!个状态，对于八数码问题如果选定了初始状态和目标状态，有9!/2个状态要搜索，考虑到时间和空间的限制，在这里采用A*算法作为搜索策略。

八数码问题源代码

自己用宽度优先算法写的八数码问题，有代码，有注释，有截图中间动态变化过程截图省略……源代码：EightDigital.javapackage eightDigitalProblem;import java.util.*;public class EightDigital {public static void main(String[] args) {// TODO Auto-generated method stub//EightDigital ed = new EightDigital();//unch();MyFrame mf = new MyFrame();unchMyFrame();}public Node launch(int [] startData, int [] endData){//起始结点赋值283164705//结束结点赋值123804765int[] array0 = new int[9];Node s0 = new Node(array0);Node s = new Node(startData);s.setDepth(0);s.setStep(0);s.setFatherNode(s0);LinkedList<Node> open = new LinkedList<Node>(); //open集合open.add(s); //添加初始点LinkedList<Node> closed = new LinkedList<Node>(); //closed集合Node n;while(true){ //循环if(open.isEmpty()){System.out.println("fail");System.exit(0);}n = open.getFirst();if(goal(n, endData)){System.out.println("success"); //找到目标结点了break;}closed.add(n); //把结点加入到closed表中open.removeFirst(); //删除最前面的结点LinkedList<Node> m = expand(n); //扩展结点while(!m.isEmpty()){open.add(m.removeFirst());}}//找到目标结点n.display();return n;}public boolean goal(Node n, int [] endData){int[] array = new int[9];//目标结点赋初值array[0] = 1;array[1] = 2;array[2] = 3;array[3] = 8;array[4] = 0;array[5] = 4;array[6] = 7;array[7] = 6;array[8] = 5;//Node s = new Node(array); //目标结点Node s = new Node(endData); //目标结点if(s.equals(n)){return true;}else{return false;}}public LinkedList<Node> expand(Node n){ //n结点向外扩展，返回扩展的结点集合LinkedList<Node> temp = new LinkedList<Node>();int zeroPosition = n.getZeroPosition(n); //记录0(空格)的位置if(rightMove(zeroPosition)){ //空格可以向右移动Node newNode = new Node(n); //创造一个新结点newNode.getArray()[zeroPosition] = newNode.getArray()[zeroPosition+1]; //空格右移newNode.getArray()[zeroPosition+1] = 0;if( !n.getFatherNode().equals(newNode) ){ //新产生的结点不能是结点n的父节点temp.add(newNode); //将新结点添加到集合newNode.setFatherNode(n); //设置新结点的父结点newNode.setStep(n.getStep()+1); //设置新结点到此走过的步长newNode.setDepth(newNode.getFatherNode().getDepth()+1); //设置深度}}if(leftMove(zeroPosition)){ //空格可以向左移动Node newNode = new Node(n); //创造一个新结点newNode.getArray()[zeroPosition] = newNode.getArray()[zeroPosition-1]; //空格左移newNode.getArray()[zeroPosition-1] = 0;if( !n.getFatherNode().equals(newNode) ){ //新产生的结点不能是结点n的父节点temp.add(newNode); //将新结点添加到集合newNode.setFatherNode(n); //设置新结点的父结点newNode.setStep(n.getStep()+1); //设置新结点到此走过的步长newNode.setDepth(newNode.getFatherNode().getDepth()+1); //设置深度}}if(upMove(zeroPosition)){ //空格可以向上移动Node newNode = new Node(n); //创造一个新结点newNode.getArray()[zeroPosition] = newNode.getArray()[zeroPosition-3]; //空格上移newNode.getArray()[zeroPosition-3] = 0;if( !n.getFatherNode().equals(newNode) ){ //新产生的结点不能是结点n的父节点temp.add(newNode); //将新结点添加到集合newNode.setFatherNode(n); //设置新结点的父结点newNode.setStep(n.getStep()+1); //设置新结点到此走过的步长newNode.setDepth(newNode.getFatherNode().getDepth()+1); //设置深度}}if(downMove(zeroPosition)){ //空格可以向下移动Node newNode = new Node(n); //创造一个新结点newNode.getArray()[zeroPosition] = newNode.getArray()[zeroPosition+3]; //空格下移newNode.getArray()[zeroPosition+3] = 0;if( !n.getFatherNode().equals(newNode) ){ //新产生的结点不能是结点n的父节点temp.add(newNode); //将新结点添加到集合newNode.setFatherNode(n); //设置新结点的父结点newNode.setStep(n.getStep()+1); //设置新结点到此走过的步长newNode.setDepth(newNode.getFatherNode().getDepth()+1); //设置深度}}return temp;}public boolean rightMove(int p){ //判断能否空格能否向右移动if(p%3 == 2){ //第3列不能往右移动了，第3列除以3的余数为2return false;}else{ //第1，2列可以向右移动return true;}}public boolean leftMove(int p){ //判断能否空格能否向左移动if(p%3 == 0){ //第0列不能往左移动了，第1列除以3的余数为0 return false;}else{ //第2，3列可以向左移动return true;}}public boolean upMove(int p){if(p < 3){ //第一行p=0,1,2 不能往上移动了return false;}else{ //第2，3行可以向上移动return true;}}public boolean downMove(int p){if(p > 5){ //第3行p=6,7,8 不能向下移动了return false;}else{ //第1，2行可以向下移动return true;}}public LinkedList<Node> sortByDepth(LinkedList<Node> list){ LinkedList<Node> temp = new LinkedList<Node>();while(!list.isEmpty()){Node deepestNode = list.getFirst();Iterator<Node> ite = list.iterator();while(ite.hasNext()){Node node = ite.next();if(node.getDepth()>deepestNode.getDepth()){deepestNode = node;}}temp.add(deepestNode);list.remove(deepestNode);}return temp;}}MyFrame.javapackage eightDigitalProblem;import java.awt.event.ActionEvent;import java.awt.event.ActionListener;import javax.swing.*;import java.awt.*;import java.util.Stack;public class MyFrame extends JFrame implements ActionListener{ private static final long serialVersionUID = 1L;private JMenuBar jmenubar;private JMenu jmenu1;private JMenu jmenu2;private JMenuItem jmenuitem1;private JMenuItem jmenuitem2;private JPanel jpanel1;private JPanel jpanel2;private JPanel jpanel3;private JPanel jpanel4;private JLabel jlabel1; //初始值private JLabel jlabel2; //结束值private JLabel jlabel3; //提示private JLabel jlabel4; //提示private JTextField jtextfield1;private JTextField jtextfield2;private JTextField jtextfield3;private JLabel l1;private JLabel l2;private JLabel l3;private JLabel l4;private JLabel l5;private JLabel l6;private JLabel l7;private JLabel l8;private JLabel l9;private Font font;private Font font2;HelpFrame helpFrame;MyFrame(){jmenubar = new JMenuBar();jmenu1 = new JMenu("选择算法");jmenu2 = new JMenu("帮助");jmenuitem1 = new JMenuItem("宽度优先");jmenuitem2 = new JMenuItem("使用说明");jpanel1 = new JPanel();jpanel2 = new JPanel();jpanel3 = new JPanel();jpanel4 = new JPanel();jlabel1 = new JLabel("初始值：",JLabel.CENTER);jlabel2 = new JLabel("结束值：",JLabel.CENTER);jlabel3 = new JLabel("",JLabel.LEFT); //提示jlabel4 = new JLabel("",JLabel.LEFT); //提示jtextfield1 = new JTextField("283164705");jtextfield2 = new JTextField("123804765");jtextfield3 = new JTextField("步数");jtextfield3.setBackground(new Color(238,238,238));l1 = new JLabel("",JLabel.CENTER);l2 = new JLabel("",JLabel.CENTER);l3 = new JLabel("",JLabel.CENTER);l4 = new JLabel("",JLabel.CENTER);l5 = new JLabel("",JLabel.CENTER);l6 = new JLabel("",JLabel.CENTER);l7 = new JLabel("",JLabel.CENTER);l8 = new JLabel("",JLabel.CENTER);l9 = new JLabel("",JLabel.CENTER);font = new Font(Font.DIALOG,Font.BOLD,22);font2 = new Font(Font.DIALOG,Font.BOLD,14);}public void launchMyFrame(){jmenuitem1.addActionListener(this); jmenuitem2.addActionListener(this);jmenu1.add(jmenuitem1); jmenubar.add(jmenu1);jmenu2.add(jmenuitem2); jmenubar.add(jmenu2);jpanel1.setLayout(new GridLayout(1,2)); jpanel1.add(jlabel1);jpanel1.add(jtextfield1);jpanel2.setLayout(new GridLayout(1,2)); jpanel2.add(jlabel2);jpanel2.add(jtextfield2);jpanel3.setLayout(new GridLayout(3,3)); jpanel3.add(l1);jpanel3.add(l2);jpanel3.add(l3);jpanel3.add(l4);jpanel3.add(l5);jpanel3.add(l6);jpanel3.add(l7);jpanel3.add(l8);jpanel3.add(l9);jpanel4.setLayout(new GridLayout(2,2)); jpanel4.add(jpanel1);jpanel4.add(jlabel3);jpanel4.add(jpanel2);jpanel4.add(jlabel4);//设置字体l1.setFont(font);l2.setFont(font);l3.setFont(font);l4.setFont(font);l5.setFont(font);l6.setFont(font);l7.setFont(font);l8.setFont(font);l9.setFont(font);jtextfield3.setFont(font2);this.setLayout(new BorderLayout());this.add(jpanel4,BorderLayout.NORTH); //上面this.add(jpanel3,BorderLayout.CENTER); //中间this.add(jtextfield3,BorderLayout.SOUTH); //下面setJMenuBar(jmenubar);setSize(330,350); //设置大小setLocation(510,180); //设置位置setTitle("EightDigital"); //设置标题setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);setVisible(true); //设为可见}@Overridepublic void actionPerformed(ActionEvent e) {// TODO Auto-generated method stubObject source=e.getSource();if(source == jmenuitem1){boolean flag = true;EightDigital ed;int [] array1 = new int[9];int [] array2 = new int[9];int attribute = 0; //逆序数的奇偶性0-偶1-奇int reNum; //逆序数String startData = jtextfield1.getText().trim();if(startData.length() != 9){ //长度必须为9jlabel3.setText("请输入0-8的一个排列！");flag = false;jpanel3.setVisible(false);}else if(!isNumber(startData)){ //每个都必须是数字0-8 jlabel3.setText("请输入0-8的一个排列！");flag = false;jpanel3.setVisible(false);}else{jlabel3.setText("");for(int i=0; i<9; i++){ //将startData转化为整数数组Character c = startData.charAt(i);array1[i] = Integer.parseInt(c.toString());}if(repeatNum(array1)){flag = false;jlabel3.setText("有重复的数字！");jpanel3.setVisible(false);}else{reNum = reverseNum(array1);jlabel3.setText("逆序数:" + reNum);attribute = reNum%2; //0-偶1-奇}}String endData = jtextfield2.getText().trim();if(endData.length() != 9){ //长度必须为9jlabel4.setText("请输入0-8的一个排列！");flag = false;jpanel3.setVisible(false);}else if(!isNumber(endData)){ //每个都必须是数字0-8jlabel4.setText("请输入0-8的一个排列！");flag = false;jpanel3.setVisible(false);}else{jlabel4.setText("");for(int i=0; i<9; i++){ //将startData转化为整数数组Character c = endData.charAt(i);array2[i] = Integer.parseInt(c.toString());}if(repeatNum(array2)){flag = false;jlabel4.setText("有重复的数字！");jpanel3.setVisible(false);}else{reNum = reverseNum(array2);jlabel4.setText("逆序数:" + reNum);if(reNum%2 != attribute){ //两个逆序数的奇偶性不一致flag = false;jlabel4.setText("逆序数:" + reNum + " " + "奇偶不一致");jpanel3.setVisible(false);}}}if(flag){ed = new EightDigital();jpanel3.setVisible(true);showProcess(unch(array1,array2));}}else if(source == jmenuitem2){helpFrame = new HelpFrame();unchHelpFrame();}}public boolean isNumber(String data){ //判断是否是数字0-8char[] array = data.toCharArray();boolean flag = true;int temp;for(char c : array){//flag = Character.isDigit(c); //判断是否为数字if(flag = Character.isDigit(c)){Character ch = c;temp = Integer.parseInt(ch.toString());if(temp == 9){flag = false;}}if(flag == false){break;}}System.out.println("flag = " + flag); //testreturn flag;}public boolean repeatNum(int[] array){ //判断是否有重复的数字boolean flag = false;int[] temp = new int[array.length];for(int i:array){temp[i] = 1; //有数字的地方标记为1}for(int j:temp){if(j==0){flag = true; //有一个数字没有出现}}return flag;}public void showProcess(final Node n){ //展示搜索过程new Thread(new Runnable(){@Overridepublic void run() {// TODO Auto-generated method stubStack<Node> stack = new Stack<Node>();Node fatherNode = n.getFatherNode();stack.add(n);while(fatherNode != null){stack.add(fatherNode); //入栈fatherNode = fatherNode.getFatherNode();}stack.pop();while(!stack.isEmpty()){ //从栈中去结点Node cnode = stack.pop();int [] array = cnode.getArray();l1.setText(array[0]+"");l2.setText(array[1]+"");l3.setText(array[2]+"");l4.setText(array[3]+"");l5.setText(array[4]+"");l6.setText(array[5]+"");l7.setText(array[6]+"");l8.setText(array[7]+"");l9.setText(array[8]+"");jtextfield3.setText("第" + cnode.getStep() + "步"); //显示步数try{Thread.sleep(2000); //暂停一会}catch(Exception e){e.printStackTrace();}}}}).start();}public int reverseNum(int[] array){ //求逆序数int num = 0;for(int i=0; i<array.length-1; i++){for(int j=i+1; j<array.length; j++){if(array[i]>0 && array[j]>0 && array[i]>array[j]){num++;}}}return num;}}Node.javapackage eightDigitalProblem;import java.awt.event.ActionEvent;import java.awt.event.ActionListener;import javax.swing.*;import java.awt.*;import java.util.Stack;public class MyFrame extends JFrame implements ActionListener{ private static final long serialVersionUID = 1L;private JMenuBar jmenubar;private JMenu jmenu1;private JMenu jmenu2;private JMenuItem jmenuitem1;private JMenuItem jmenuitem2;private JPanel jpanel1;private JPanel jpanel2;private JPanel jpanel3;private JPanel jpanel4;private JLabel jlabel1; //初始值private JLabel jlabel2; //结束值private JLabel jlabel3; //提示private JLabel jlabel4; //提示private JTextField jtextfield1;private JTextField jtextfield2;private JTextField jtextfield3;private JLabel l1;private JLabel l2;private JLabel l3;private JLabel l4;private JLabel l5;private JLabel l6;private JLabel l7;private JLabel l8;private JLabel l9;private Font font;private Font font2;HelpFrame helpFrame;MyFrame(){jmenubar = new JMenuBar();jmenu1 = new JMenu("选择算法");jmenu2 = new JMenu("帮助");jmenuitem1 = new JMenuItem("宽度优先");jmenuitem2 = new JMenuItem("使用说明");jpanel1 = new JPanel();jpanel2 = new JPanel();jpanel3 = new JPanel();jpanel4 = new JPanel();jlabel1 = new JLabel("初始值：",JLabel.CENTER);jlabel2 = new JLabel("结束值：",JLabel.CENTER);jlabel3 = new JLabel("",JLabel.LEFT); //提示jlabel4 = new JLabel("",JLabel.LEFT); //提示jtextfield1 = new JTextField("283164705");jtextfield2 = new JTextField("123804765");jtextfield3 = new JTextField("步数");jtextfield3.setBackground(new Color(238,238,238));l1 = new JLabel("",JLabel.CENTER);l2 = new JLabel("",JLabel.CENTER);l3 = new JLabel("",JLabel.CENTER);l4 = new JLabel("",JLabel.CENTER);l5 = new JLabel("",JLabel.CENTER);l6 = new JLabel("",JLabel.CENTER);l7 = new JLabel("",JLabel.CENTER);l8 = new JLabel("",JLabel.CENTER);l9 = new JLabel("",JLabel.CENTER);font = new Font(Font.DIALOG,Font.BOLD,22);font2 = new Font(Font.DIALOG,Font.BOLD,14); }public void launchMyFrame(){jmenuitem1.addActionListener(this);jmenuitem2.addActionListener(this);jmenu1.add(jmenuitem1);jmenubar.add(jmenu1);jmenu2.add(jmenuitem2);jmenubar.add(jmenu2);jpanel1.setLayout(new GridLayout(1,2));jpanel1.add(jlabel1);jpanel1.add(jtextfield1);jpanel2.setLayout(new GridLayout(1,2));jpanel2.add(jlabel2);jpanel2.add(jtextfield2);jpanel3.setLayout(new GridLayout(3,3));jpanel3.add(l1);jpanel3.add(l2);jpanel3.add(l3);jpanel3.add(l4);jpanel3.add(l5);jpanel3.add(l6);jpanel3.add(l7);jpanel3.add(l8);jpanel3.add(l9);jpanel4.setLayout(new GridLayout(2,2));jpanel4.add(jpanel1);jpanel4.add(jlabel3);jpanel4.add(jpanel2);jpanel4.add(jlabel4);//设置字体l1.setFont(font);l2.setFont(font);l3.setFont(font);l4.setFont(font);l5.setFont(font);l6.setFont(font);l7.setFont(font);l8.setFont(font);l9.setFont(font);jtextfield3.setFont(font2);this.setLayout(new BorderLayout());this.add(jpanel4,BorderLayout.NORTH); //上面this.add(jpanel3,BorderLayout.CENTER); //中间this.add(jtextfield3,BorderLayout.SOUTH); //下面setJMenuBar(jmenubar);setSize(330,350); //设置大小setLocation(510,180); //设置位置setTitle("EightDigital"); //设置标题setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);setVisible(true); //设为可见}@Overridepublic void actionPerformed(ActionEvent e) {// TODO Auto-generated method stubObject source=e.getSource();if(source == jmenuitem1){boolean flag = true;EightDigital ed;int [] array1 = new int[9];int [] array2 = new int[9];int attribute = 0; //逆序数的奇偶性0-偶1-奇int reNum; //逆序数String startData = jtextfield1.getText().trim();if(startData.length() != 9){ //长度必须为9jlabel3.setText("请输入0-8的一个排列！");flag = false;jpanel3.setVisible(false);}else if(!isNumber(startData)){ //每个都必须是数字0-8 jlabel3.setText("请输入0-8的一个排列！");flag = false;jpanel3.setVisible(false);}else{jlabel3.setText("");for(int i=0; i<9; i++){ //将startData转化为整数数组Character c = startData.charAt(i);array1[i] = Integer.parseInt(c.toString());}if(repeatNum(array1)){flag = false;jlabel3.setText("有重复的数字！");jpanel3.setVisible(false);}else{reNum = reverseNum(array1);jlabel3.setText("逆序数:" + reNum);attribute = reNum%2; //0-偶1-奇}}String endData = jtextfield2.getText().trim();if(endData.length() != 9){ //长度必须为9jlabel4.setText("请输入0-8的一个排列！");flag = false;jpanel3.setVisible(false);}else if(!isNumber(endData)){ //每个都必须是数字0-8 jlabel4.setText("请输入0-8的一个排列！");flag = false;jpanel3.setVisible(false);}else{jlabel4.setText("");for(int i=0; i<9; i++){ //将startData转化为整数数组Character c = endData.charAt(i);array2[i] = Integer.parseInt(c.toString());}if(repeatNum(array2)){flag = false;jlabel4.setText("有重复的数字！");jpanel3.setVisible(false);}else{reNum = reverseNum(array2);jlabel4.setText("逆序数:" + reNum);if(reNum%2 != attribute){ //两个逆序数的奇偶性不一致flag = false;jlabel4.setText("逆序数:" + reNum + " " + "奇偶不一致");jpanel3.setVisible(false);}}}if(flag){ed = new EightDigital();jpanel3.setVisible(true);showProcess(unch(array1,array2));}}else if(source == jmenuitem2){helpFrame = new HelpFrame();unchHelpFrame();}}public boolean isNumber(String data){ //判断是否是数字0-8char[] array = data.toCharArray();boolean flag = true;int temp;for(char c : array){//flag = Character.isDigit(c); //判断是否为数字if(flag = Character.isDigit(c)){Character ch = c;temp = Integer.parseInt(ch.toString());if(temp == 9){flag = false;}}if(flag == false){break;}}System.out.println("flag = " + flag); //testreturn flag;}public boolean repeatNum(int[] array){ //判断是否有重复的数字boolean flag = false;int[] temp = new int[array.length];for(int i:array){temp[i] = 1; //有数字的地方标记为1}for(int j:temp){if(j==0){flag = true; //有一个数字没有出现}}return flag;}public void showProcess(final Node n){ //展示搜索过程new Thread(new Runnable(){@Overridepublic void run() {// TODO Auto-generated method stubStack<Node> stack = new Stack<Node>();Node fatherNode = n.getFatherNode();stack.add(n);while(fatherNode != null){stack.add(fatherNode); //入栈fatherNode = fatherNode.getFatherNode();}stack.pop();while(!stack.isEmpty()){ //从栈中去结点Node cnode = stack.pop();int [] array = cnode.getArray();l1.setText(array[0]+"");l2.setText(array[1]+"");l3.setText(array[2]+"");l4.setText(array[3]+"");l5.setText(array[4]+"");l6.setText(array[5]+"");l7.setText(array[6]+"");l8.setText(array[7]+"");l9.setText(array[8]+"");jtextfield3.setText("第" + cnode.getStep() + "步"); //显示步数try{Thread.sleep(2000); //暂停一会}catch(Exception e){e.printStackTrace();}}}}).start();}public int reverseNum(int[] array){ //求逆序数int num = 0;for(int i=0; i<array.length-1; i++){for(int j=i+1; j<array.length; j++){if(array[i]>0 && array[j]>0 && array[i]>array[j]){num++;}}}return num;}}HelpFrame.javapackage eightDigitalProblem;import java.awt.event.ActionEvent;import java.awt.event.ActionListener;import javax.swing.*;import java.awt.*;public class HelpFrame extends JFrame implements ActionListener{21private static final long serialVersionUID = 1L;private JTextArea jta;private String str1;private Dimension dimension1;//private String str2;HelpFrame(){jta= new JTextArea();dimension1 = new Dimension(290,290);jta.setPreferredSize(dimension1);jta.setBackground(new Color(238,238,238));str1 = "由于要实现在没有jvm的电脑上运行,搜索环境变量与\r\n";str1 = "操作步骤：\r\n" +"1.输入初始值（0-8的任意一个排列）；\r\n" +"2.输入结束值（0-8的任意一个排列）；\r\n" +"3.点击“选择算法”；\r\n" +"4.点击“宽度优先”；\r\n\r\n" +"注意事项：\r\n" +"1.初始值和结束值都必须是0-8的任意一个排列；\r\n" +"2.初始值的逆序数和结束值的逆序数奇偶性要一致；\r\n";//str2 = "使用说明xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx";}public void launchHelpFrame(){//jtf.setText(str1+"\r\n"+str2);jta.setText(str1);jta.setEditable(false);this.setLayout(new FlowLayout());this.add(jta);this.setTitle("使用说明");this.setSize(330,350);this.setLocation(880, 180);this.setVisible(true);}@Overridepublic void actionPerformed(ActionEvent e) {// TODO Auto-generated method stub22//Object source = e.getSource();}}23。

八数码C语言A算法详细代码

八数码C语言A算法详细代码以下是八数码问题的C语言A*算法的详细代码：```c#include <stdio.h>#include <stdlib.h>#define N 3typedef struct Nodeint board[N][N]; // 八数码局面struct Node *parent; // 父节点指针int f; // f(n) = g(n) + h(n)，g(n)表示起始节点到当前节点的代价，h(n)表示当前节点到目标节点的估计代价int g; // g(n)int h; // h(n)} Node;//目标局面int target[N][N] = {{1, 2, 3}, {8, 0 ,4}, {7, 6, 5}};//计算当前节点到目标节点的曼哈顿距离int manhattanDistance(int board[N][N])int distance = 0;for (int i = 0; i < N; i++)for (int j = 0; j < N; j++)if (board[i][j] != 0)int value = board[i][j] - 1;int targetI = value / N;int targetJ = value % N;distance += abs(i - targetI) + abs(j - targetJ);}}}return distance;//创建一个新节点Node* createNode(int board[N][N], int g, Node* parent) Node* node = (Node*) malloc(sizeof(Node));for (int i = 0; i < N; i++)for (int j = 0; j < N; j++)node->board[i][j] = board[i][j];}}node->parent = parent;node->g = g;node->h = manhattanDistance(board);node->f = node->g + node->h;return node;//判断两个局面是否相等int isBoardEqual(int board1[N][N], int board2[N][N]) for (int i = 0; i < N; i++)for (int j = 0; j < N; j++)if (board1[i][j] != board2[i][j])return 0;}}}return 1;//判断节点是否在开放列表中int isInOpenList(Node *node, Node **openList, int openListSize)for (int i = 0; i < openListSize; i++)if (isBoardEqual(node->board, openList[i]->board))return 1;}}return 0;//判断节点是否在关闭列表中int isInClosedList(Node *node, Node **closedList, int closedListSize)for (int i = 0; i < closedListSize; i++)if (isBoardEqual(node->board, closedList[i]->board))return 1;}}return 0;//比较两个节点的f(n)值Node *a = *(Node **)node1;Node *b = *(Node **)node2;return a->f - b->f;//输出路径void printPath(Node *node)if (node != NULL)printPath(node->parent);printf("Step %d:\n", node->g);for (int i = 0; i < N; i++)printf("%d %d %d\n", node->board[i][0], node->board[i][1], node->board[i][2]);}printf("\n");}//A*算法求解八数码问题void solvePuzzle(int initial[N][N])//创建初始节点Node* initialNode = createNode(initial, 0, NULL);//开放列表和关闭列表Node* openList[N*N*N*N];int openListSize = 0;Node* closedList[N*N*N*N];int closedListSize = 0;//将初始节点放入开放列表openList[openListSize++] = initialNode;while (openListSize > 0)//从开放列表中选择f(n)最小的节点//取出开放列表中f(n)最小的节点作为当前节点Node* currentNode = openList[0];//将当前节点从开放列表中移除for (int i = 1; i < openListSize; i++) openList[i - 1] = openList[i];}openListSize--;//将当前节点放入关闭列表closedList[closedListSize++] = currentNode; //判断当前节点是否为目标节点if (isBoardEqual(currentNode->board, target)) printf("Solution found!\n");printPath(currentNode);return;}//生成当前节点的邻居节点int i = 0, j = 0;for (i = 0; i < N; i++)for (j = 0; j < N; j++)if (currentNode->board[i][j] == 0)break;}}if (j < N)break;}}if (i > 0)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l]; }}newBoard[i][j] = newBoard[i - 1][j];newBoard[i - 1][j] = 0;if (!isInOpenList(createNode(newBoard, currentNode->g + 1, currentNode), openList, openListSize) &&!isInClosedList(createNode(newBoard, currentNode->g + 1, currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}if (i < N - 1)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l];}}newBoard[i][j] = newBoard[i + 1][j];newBoard[i + 1][j] = 0;currentNode), openList, openListSize) &&!isInClosedList(createNode(newBoard, currentNode->g + 1, currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}if (j > 0)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l];}}newBoard[i][j] = newBoard[i][j - 1];newBoard[i][j - 1] = 0;if (!isInOpenList(createNode(newBoard, currentNode->g + 1, currentNode), openList, openListSize) &&currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}if (j < N - 1)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l];}}newBoard[i][j] = newBoard[i][j + 1];newBoard[i][j + 1] = 0;if (!isInOpenList(createNode(newBoard, currentNode->g + 1, currentNode), openList, openListSize) &&!isInClosedList(createNode(newBoard, currentNode->g + 1, currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}}printf("Solution not found!\n");int maiint initial[N][N] = {{2, 8, 3}, {1, 6, 4}, {7, 0, 5}};solvePuzzle(initial);return 0;```这个代码实现了八数码问题的A*算法。

八数码问题python代码

八数码问题python代码八数码问题是一种经典的数学拼图游戏，也是人工智能搜索算法中的一个经典案例。

该问题是要将一个九宫格拼图游戏中的数字 1~8按照顺序排列，使得拼图最终呈现出从左到右、从上到下的顺序排列。

然而，因为拼图中存在一个空格，可以移动，所以这个问题有无数种解法。

在本文中，我们将使用 Python 语言来解决这个问题。

第一步，定义状态表示。

我们可以使用一个3×3 的数组来表示当前拼图的状态，以数字 0 来表示空格。

在 Python 中，可以使用列表来定义状态数组，如下所示：state = [ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 0 ] ]第二步，定义状态编号。

对于每个状态，我们需要为其分配一个唯一的编号。

在 Python 中，我们可以使用一个字典来存储每个状态和其对应的编号，代码如下：state_dict = { ( 1, 2, 3, 4, 5, 6, 7, 8, 0 ) : 0 }第三步，定义状态转移。

我们需要定义一些规则，来指导拼图的移动，以及如何表示一个状态的转移。

在本问题中，每个状态只能移动空格的位置，也就是把空格和相邻的数字进行交换。

我们可以创建一个函数来定义这个规则，如下所示：def move( state, direction ):new_state = [ row[:] for row in state ]row, col = find_blank( new_state )if direction == "up":new_state[row][col], new_state[row-1][col] =new_state[row-1][col], new_state[row][col]if direction == "down":new_state[row][col], new_state[row+1][col] =new_state[row+1][col], new_state[row][col]if direction == "left":new_state[row][col], new_state[row][col-1] =new_state[row][col-1], new_state[row][col]if direction == "right":new_state[row][col], new_state[row][col+1] =new_state[row][col+1], new_state[row][col]return tuple( [ element for row in new_state for element in row ] )这个函数首先复制了当前状态的数组，然后找到空格所在的位置，根据移动方向交换空格和相邻的数字，最后返回新的状态数组。

八数码问题代码及算法分析

八数码 Java代码//8数码类class Eight{int e[][] = {{2,8,3},{1,6,4},{7,0,5}}; //默认的起始状态int faX ,faY; //保存父状态中0的位置int f; //估价函数值Eight former ;public Eight(){faX = -1;faY=-1;f=-1;former = null;}public Eight(Eight other){for(int i = 0; i<3; i++)for(int j=0 ;j<3; j++){e[i][j] = other.e[i][j];}faX = other.faX;faY = other.faY;f = other.f;former = other.former;}public void print(){for(int i1 = 0;i1<3;i1++)for(int j1=0;j1<3;j1++){System.out.print(e[i1][j1]);if(j1==2)System.out.println();}System.out.println();}public void listAll( Eight e ){while( e.former != null ){e.former.print();e = new Eight(e.former);}return ;}}//算法实现类public class Asearch{static int dest[][] = {{1,2,3},{8,0,4},{7,6,5}}; static void Swap(Eight ee,int i,int j,int m,int n){ int temp;temp = ee.e[i][j];ee.e[i][j] = ee.e[m][n];ee.e[m][n] = temp;}static int compare(Eight a){int h =0,i,j;for(i=0;i<3;i++)for(j=0;j<3;j++){if(a.e[i][j]!=dest[i][j])h++;}return h;}//生成子状态static Queue born(Eight e){int m=1,n=1,i=0,j=0;boolean flag = true;Queue sons = new Queue();for(i=0;i<3&&flag;i++)for(j=0;j<3&&flag;j++){if(e.e[i][j]==0){flag=false;break;}}i--;if(i-1>=0){m=i-1;if(m!=e.faX){Swap(e,m,j,i,j);//e.print();Eight son1 = new Eight(e);son1.faX = i;son1.faY = j;son1.former = e;sons.addElement(son1);Swap(e,i,j,m,j);}}if(i+1<3){m=i+1;if(m!=e.faX){Swap(e,m,j,i,j);//e.print();Eight son2 = new Eight(e);son2.faX = i;son2.faY = j;son2.former = e;sons.addElement(son2);Swap(e,i,j,m,j);}}if(j-1>=0){n=j-1;if(n!=e.faY){Swap(e,i,n,i,j);//e.print();Eight son3 = new Eight(e);son3.faX = i;son3.faY = j;son3.former = e;sons.addElement(son3);Swap(e,i,j,i,n);}}if(j+1<3){n=j+1;if(n!=e.faY){Swap(e,i,n,i,j);//e.print();Eight son4 = new Eight(e);son4.faX = i;son4.faY = j;son4.former = e;sons.addElement(son4);Swap(e,i,j,i,n);}}return sons;}public static void main(String[] args){int depth=0; //深度Eight n = new Eight() ;Eight temp1 = new Eight() , temp2 = new Eight() ;//open表Queue open = new Queue();//closed表Queue closed = new Queue();//保存子状态的表Queue son = new Queue();open.addElement(n);while(!open.isEmpty()){n= open.elementAt(0);open.removeFirst( );if(compare(n)==0){n.listAll(n);System.out.println("Success!");return;}son = born(n);depth++;int count = son.size();if(count==0)continue;else for(int t=0;t<count;t++){temp1 = son.elementAt(t);if(!open.contains(temp1)&&!closed.contains(temp1)){ temp1.f = depth + compare(temp1);open.addElement(temp1);}else if(open.contains(temp1)){temp1.f = depth + compare(temp1);int pos = open.indexOf(son.elementAt(t));temp2 = open.elementAt(pos);if(temp1.f<temp2.f){open.setElementAt(temp1,pos);}}else if(closed.contains(temp1)){temp1.f = depth + compare(temp1);int pos = closed.indexOf(temp1);temp2 = closed.elementAt(pos);if( temp1.f<temp2.f ){closed.remove(son.elementAt(t));open.addElement(temp1);}}}//end forclosed.addElement(n);for(int i=open.size()-1;i>0;i--)for(int j=0;j<i;j++){temp1 = (Eight)open.elementAt(j);temp2 = (Eight)open.elementAt(j+1);if(temp1.f>temp2.f){Eight tq=new Eight();tq = open.elementAt(j);open.setElementAt(open.elementAt(j+1),j); open.setElementAt(tq,j+1);}}}//end whileSystem.out.println("Fail!");return;}//end main}class Queue extends Object{ //队列类private int size = 0;Eight qe[] = new Eight[20];public void print(){for(int i=0;i<size;i++)qe[i].print();}public void addElement(Eight e){qe[size] = e;size++;}public boolean contains(Eight e){if( size == 0 )return false;else{for(int i=0;i<size;i++){if(qe[i].equals(e))return true;}}return false;}public boolean isEmpty(){if (size == 0) {return true;}else return false;public Eight elementAt(int index){return qe[index];}public void setElementAt( Eight e,int index ){ qe[index] = e;}public int size(){return size;}public int indexOf (Eight e) {for (int i = 0; i < size; i++){if (qe[i].equals( e ))return i;}return -1;}public void removeFirst( ){for(int i=0;i<size;i++){qe[i] = qe[i+1];}size--;}public void remove( Eight e ){for( int i = 0; i < size; i++ ){if( qe[i].equals( e ))qe[i] = null;}size--;}public void removeAllElements(){for (int i = 0; i < size; i++){qe[i] = null;}size = 0;}}//八数码.java//package test;import java.io.*;import java.util.Enumeration;import java.util.Hashtable;import java.util.StringTokenizer;/** 八数码的A*算法，* 启发函数为f(x)=g(x)+h(x)，g(x)为结点x的深度，h(x)为结点x与目标结点相同元素的个数*/public class 八数码 {结点初始结点;结点目标结点;结点扩展结点[] = new 结点[4]; //保存父结点的四个子结点,顺序存储为上，下，左，右，为扩展的临时数组int f=0;//扩展结点的下标结点 open[] = new 结点[100]; //扩展结点类结点最短路径[] = new 结点[100];//相当与closed表int opennum=0;//open表中结点的个数int closednum =0;//closed表中结点的个数s八数码(int a1[],int a2[]){初始结点 = new 结点(a1);目标结点 = new 结点(a2);//初始结点.不相同结点个数 = 初始结点.不相同结点个数(目标结点);// 目标结点.不相同结点个数 = 目标结点.不相同结点个数(目标结点);// System.out.println("初始结点的不同点的个数:"+初始结点.不相同结点个数);}public class 结点{int 深度,不相同结点个数;int 数码[][] = new int[3][3];boolean 用过吗;public 结点(){用过吗 = false;}public 结点(结点 n){深度 = n.深度;for(int i=0;i<3;i++)for(int j=0;j<3;j++)数码[i][j]=n.数码[i][j];不相同结点个数 = n.不相同结点个数;用过吗 = n.用过吗;}public 结点(int a[]){int m=0;for(int i=0;i<3;i++)for(int j=0;j<3;j++){数码[i][j]=a[m];m=m+1;}用过吗 = false;深度=0;//System.out.println("测试4");//测试}public int[][] 取数值(){return 数码;}public boolean 等于(结点 st)//只是数码不相等 {int[][] s = st.取数值();int i,j;for (i = 0; i < 3; i++)for(j = 0 ; j<3 ;j++)if (s[i][j] != 数码[i][j])return false;return true;}public int[] 零点位置(){int 位置[] = new int[2];for(int i=0;i<3;i++)for(int j=0;j<3;j++)if(this.数码[i][j]==0){位置[0]=i;位置[1]=j;}return 位置;}public int 不相同结点个数(结点 a){int m = 0;for(int i=0 ; i<3 ; i++)for(int j=0; j<3 ;j++){ if( a.数码[i][j] == 数码[i][j] && a.数码[i][j]!=0 ) m=m+1;}return 8-m;}}public static void 打印结点(结点 h){for(int i=0;i<3;i++){for(int j=0;j<3;j++){System.out.print(h.数码[i][j]+" ");}System.out.println();}}public static void 输出结果(Hashtable h){Enumeration enum = h.elements();System.out.println("结果路径是:");while(enum.hasMoreElements()){System.out.println(enum.nextElement()+" ");System.out.println();}}public void 扩展_并查找结点(结点 n){结点 t = new 结点();int temp = 0; //交换数码的中间变量boolean 没找到 = true;while(没找到){if( n == 初始结点){open[opennum]=n; // （状态位置,结点对象) opennum=opennum+1;最短路径[closednum]=n;closednum=closednum+1;}int[] p= n.零点位置();//知道0的位置System.out.println("=================================待扩展的结点;================================");打印结点(n);// if(!n.等于(初始结点))// {// if(存在否(n)){System.out.println("该结点已经在open表中已经存在不用扩展");break;}// }System.out.println("0点位置:"+p[0]+" "+p[1]);if(p[0]==0 && p[1]==0)//如果0点在左上角{//展开(待扩展的结点,扩展方向,0点位置,方向行坐标,方向纵坐标,扩展临时结点数组);//向下扩展if( 展开(n,1,p,1,0,扩展结点) ) {没找到=false; break;}//向右扩展if( 展开(n,3,p,0,1,扩展结点) ) {没找到=false; break;}}else if(p[0] == 0 && p[1] == 1)//如果0点在上中间的话{System.out.println("0点在上中间");//向下扩展if( 展开(n,1,p,1,1,扩展结点) ) {没找到=false; break;}//向左扩展if( 展开(n,2,p,0,0,扩展结点) ) {没找到=false; break;}//向右扩展if( 展开(n,3,p,0,2,扩展结点) ) {没找到=false; break;}}else if(p[0] == 0 && p[1] == 2)//如果0点在右上角{System.out.println("0点在右上角");//向下扩展if( 展开(n,1,p,1,2,扩展结点) ) {没找到=false; break;}//向左扩展if( 展开(n,2,p,0,1,扩展结点) ) {没找到=false; break;}}else if(p[0] == 1 && p[1] == 0)//如果点在左边中间 {System.out.println("0点在左边中间");//向上扩展if( 展开(n,0,p,0,0,扩展结点) ) {没找到=false; break;}//向下扩展if( 展开(n,1,p,2,0,扩展结点) ) {没找到=false; break;}//向右扩展if( 展开(n,3,p,1,1,扩展结点) ) {没找到=false; break;}}else if(p[0] == 1 && p[1] == 1)//如果点在正中间{System.out.println("0点在正中间");//向上扩展if( 展开(n,0,p,0,1,扩展结点) ) {没找到=false; break;}//向下扩展if( 展开(n,1,p,2,1,扩展结点) ) {没找到=false; break;}//向左扩展if( 展开(n,2,p,1,0,扩展结点) ) {没找到=false; break;}//向右扩展if( 展开(n,3,p,1,2,扩展结点) ) {没找到=false; break;}}else if(p[0] == 1 && p[1] == 2)//如果点在右边中间 {System.out.println("0点在右边中间");//向上扩展if( 展开(n,0,p,0,2,扩展结点) ) {没找到=false; break;}//向下扩展if( 展开(n,1,p,2,2,扩展结点) ) {没找到=false; break;}//向左扩展if( 展开(n,2,p,1,1,扩展结点) ) {没找到=false; break;}}else if(p[0] == 2 && p[1] == 0)//如果点在左下角{System.out.println("0点在左下角");//向上扩展if( 展开(n,0,p,1,0,扩展结点) ) {没找到=false; break;}//向右扩展if( 展开(n,3,p,2,1,扩展结点) ) {没找到=false; break;}}else if(p[0] == 2 && p[1] == 1)//如果点在下边中间 {System.out.println("0点在下边中间");//向上扩展if( 展开(n,0,p,1,1,扩展结点) ) {没找到=false; break;}//向左扩展if( 展开(n,2,p,2,0,扩展结点) ) {没找到=false; break;}//向右扩展if( 展开(n,3,p,2,2,扩展结点) ) {没找到=false; break;}}else if(p[0] == 2 && p[1] == 2)//如果点在右下角{System.out.println("0点在右下角");//向上扩展if( 展开(n,0,p,1,2,扩展结点) ) {没找到=false; break;}//向左扩展if( 展开(n,3,p,2,1,扩展结点) ) {没找到=false; break;}}if(没找到){n = 取最优结点();System.out.println("最优结点:");打印结点(n);//测试扩展_并查找结点(n);break;}}}public boolean 存在否(结点 n){for(int i=0;i<opennum;i++){if(open[i].等于(n)) return true;}return false;}public boolean 展开(结点 n,int k,int[] z,int q,int p,结点[] 扩展结点){//展开(待扩展的结点,扩展方向,0点位置,方向行坐标,方向纵坐标,扩展临时结点数组)结点 t = new 结点(n); // 用父结点扩展int flag = 0;int temp;temp = t.数码[z[0]][z[1]];t.数码[z[0]][z[1]] = t.数码[q][p];t.数码[q][p] = temp;String msg="";if(k==0){ msg = new String("向上扩展结果");}else if(k==1){ msg = new String("向下扩展结果");}else if(k==2){ msg = new String("向左扩展结果");}else if(k==3){ msg = new String("向右扩展结果");}System.out.println(msg);打印结点(t);//测试if(!存在否(t))//如果不在open表中（测试此映射表中是否存在与指定值关联的键）{t.深度 = n.深度+1;t.不相同结点个数 = t.不相同结点个数(目标结点);if(t.等于(目标结点)){System.out.println("=======恭喜!终于找到目标结点了^-^!!!=======");打印结点(t);//测试最短路径[closednum]=t;closednum = closednum+1;return true;}else {扩展结点[f] = t;//如果在open表中不存在则装入扩展结点数组中f=f+1;}System.out.println("该结点的深度:"+t.深度+"\n该结点的不同与目标结点的个数:"+t.不相同结点个数);int r = t.深度+t.不相同结点个数;System.out.println("择优权值:"+r);System.out.println();}else{System.out.println("该结点已经分析过了");return false;}return false;}public 结点取最优结点(){结点最优;System.out.println("扩展数组的长度:"+有值的个数(扩展结点));最优 = 扩展结点[0];for(int i=0;i<有值的个数(扩展结点);i++){if((扩展结点[i].深度+扩展结点[i].不相同结点个数)<(最优.深度+最优.不相同结点个数)){最优 = 扩展结点[i];}}for(int i =0;i<有值的个数(扩展结点);i++){if(扩展结点[i]==最优) continue;open[opennum]=扩展结点[i];opennum=opennum+1;}//从open表中取出最优结点,放入closed表中最短路径[closednum]=最优;closednum = closednum+1;f=0;//重置扩展数组下标return 最优;}public static int[] 读数(){int[] a = new int[9];int i=0;BufferedReader br = new BufferedReader(new InputStreamReader(System.in));try{while(a.length<=9 && i<=8){StringTokenizer st = new StringTokenizer(br.readLine());while(st.hasMoreTokens()){if(i > 8) break;a[i]=Integer.parseInt(st.nextToken());i=i+1;}}}catch(Exception e){}return a;}public static int 有值的个数(结点 m[]){int n =0;for(int i=0;i<m.length;i++){if(m[i] != null) n=n+1;if(m[i] == null) break;}return n;}public static void main(String args[]){int a1[] =new int[9];int a2[] ={1,2,3,8,0,4,7,6,5};System.out.println("请输入初始结点:"); a1 = 八数码.读数();//System.out.println("请输入目标结点:"); //a2 = 八数码.读数();八数码 bsm = new 八数码(a1,a2);bsm.扩展_并查找结点(bsm.初始结点);System.out.println("应用程序终止");}}。

八数码难题代码与基本思路 Eight puzzles

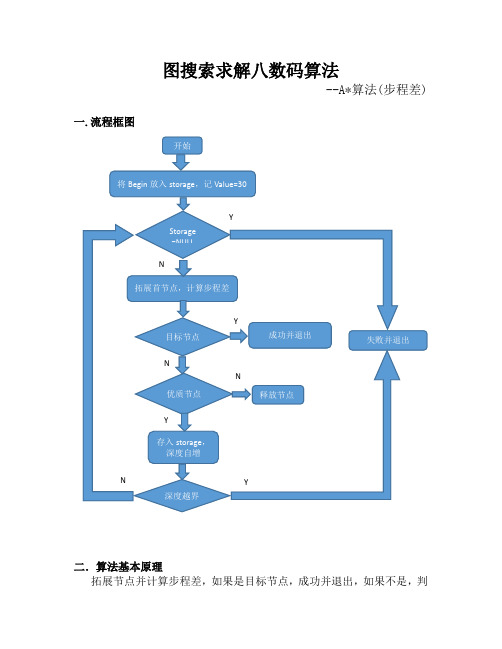
图搜索求解八数码算法--A*算法(步程差) 一.流程框图二．算法基本原理拓展节点并计算步程差，如果是目标节点，成功并退出，如果不是，判断是否为优质节点，是则拓展为子节点，否则舍弃；判断深度是否越界，是则失败，未越界则继续拓展节点，若拓展表为空，则失败退出。

八数码结构体由矩阵Array，步程差Value，屏蔽方向Undirect和父节点指针*parent四部分组成，Array存放矩阵数字状态，Value存放估值函数值，Undirect记录上一步移动方向避免逆推，*parent记录父子关系用于寻径。

三．模块分析Getgraph 键盘输入获得初始数码组并返回Graph结构体指针。

Printgraph 输入八数码结构体地址，打印矩阵数字状态与当前步程差。

Evaluate 输入目标矩阵与当前矩阵，计算步程差并返回值。

Move 输入当前矩阵与移动方向Direct，移动并返回新结构体地址。

Search 输入起始结构体与目标结构体，尝试寻径并记录路径并返回终点地址（若成功）或返回空指针（若失败）。

Main 主函数，定义目标矩阵并调用函数。

四．源代码// Eight-figure puzzle// A*#include"stdafx.h"#include<stdio.h>#include<stdlib.h>#define N 3 //数码组长度#define MAX 50 //最大搜索深度typedefstruct node//八数码结构体{int array[N][N];//数码组int Value;//评估值int Undirect;//所屏蔽方向，防止往回推到上已状态，1上2下3左4右struct node *parent;//父节点}Graph;Graph *Storage[MAX]; //拓展节点存储队列Graph *path[MAX]; //路径堆栈Graph *GetGraph(Graph *New_graph) ////////自定义初始数码组{int x;for (x = 0; x <N; x++){scanf("%d %d %d", &New_graph->array[x][0], &New_graph->array[x][1],&New_graph->array[x][2]);}New_graph->Value = 30;New_graph->Undirect = 0;New_graph->parent = NULL;return New_graph;}void PrintGraph(Graph *point_graph) /////////打印数码组{int i, j;if (point_graph == NULL)printf("NULL\n");else{printf(" ---------------\n");for (i = 0; i<N; i++){printf("| ");for (j = 0; j<N; j++){printf("%d ", point_graph->array[i][j]);}printf("|");if (i==N-1)printf(" Value %d ", point_graph->Value);//评估函数值printf("\n");}printf(" ---------------\n");}}int Evaluate(Graph *point_graph, Graph *End_graph) /////////评价函数{int value = 0;//评估值int i, j,m ,n ;for (i = 0; i<N; i++){for (j = 0; j<N; j++){for (m = 0; m <N; m++){for (n = 0; n <N; n++){if (point_graph->array[i][j] == End_graph->array[m][n])value = value + abs(i - m) + abs(j - n); //数字当前位置与目标位置步程差之和}}}}point_graph->Value = value;return value;}Graph *Move(Graph *point_graph, int Direct) /////////移动数码组{Graph *New_graph;int BlankLocate = 0;//定位空格指示int Movable = 1;//移动有效int i, j, x0, y0, x, y;for (i = 0; i<N; i++)//空格坐标i,j{for (j = 0; j<N; j++){if (point_graph->array[i][j] == 0){BlankLocate = 1;break;}}if (BlankLocate == 1)break;}x0 = i;y0 = j;switch (Direct){case 1://上x0--;if (x0<0)Movable = 0;break;case 2://下x0++;if (x0 >= N)Movable = 0;break;case 3://左y0--;if (y0<0)Movable = 0;break;case 4://右y0++;if (y0 >= N)Movable = 0;break;}if (Movable == 0)//不能移动则返回原节点return point_graph;New_graph = (Graph *)malloc(sizeof(Graph));//生成节点for (x = 0; x<N; x++){for (y = 0; y<N; y++){New_graph->array[x][y] = point_graph->array[x][y];//复制数码组}}New_graph->array[i][j] = New_graph->array[x0][y0];New_graph->array[x0][y0] = 0;return New_graph;}Graph *Search(Graph *Begin, Graph *End) /////////搜索函数{Graph *St1, *St2, *ta;int Step = 0;//深度int Direct = 0;//方向int i;int front, rear;front = rear = -1;//队列初始化ta = NULL;rear++;//入队Storage[rear] = Begin;while (rear != front)//队列不空{front++;//出队St1 = Storage[front];for (i = 1; i <= 4; i++)//分别从四个方向推导出新子节点{Direct = i;if (Direct == St1->Undirect)//跳过屏蔽方向continue;St2 = Move(St1, Direct);//移动数码组if (St2 != St1)//数码组是否可以移动{Evaluate(St2, End);//评价新的节点sif (St2->Value == 0)//为0则搜索完成{St2->parent = St1;rear++;Storage[rear] = St2;//存储节点到待处理队列ta = St2;break;}if (St2->Value <= St1->Value + 1){St2->parent = St1;//st2->Undirect=Direct>2?(Direct==3)+3:(Direct==1)+1;/屏蔽方向switch (Direct)//设置屏蔽方向，防止往回推{case 1://上St2->Undirect = 2;break;case 2://下St2->Undirect = 1;break;case 3://左St2->Undirect = 4;break;case 4://右St2->Undirect = 3;break;}rear++;Storage[rear] = St2;//存储节点到待处理队列}else{free(St2);//抛弃劣质节点St2 = NULL;}}}if (ta != NULL)//为0则搜索完成break;Step++;//统计深度if (Step>=MAX){break;}}return ta;}int main(int argc, constchar * argv[]){// 8 1 3 7 4 5 6 2 0// 4 1 3 2 7 5 8 0 6// 4 5 1 2 7 3 0 8 6 //16 steps in fact but failed//目标数码组Graph End_graph = {{{ 1, 2, 3 },{ 8, 0, 4 },{ 7, 6, 5 }}, 0, 0, NULL};//初始数码组Graph New_graph;Graph *Begin_graph;printf("Enter initial matrix line by line\n For example:\t1 3 4 ENTER\n\t\t8 2 5 ENTER\n\t\t7 6 0 ENTER\n\n");Begin_graph = GetGraph(&New_graph);Evaluate(Begin_graph, &End_graph);printf("Initial matrix:\n");PrintGraph(Begin_graph);printf("Target matrix:\n");PrintGraph(&End_graph);Graph *W, *P;int top = -1;//图搜索W = Search(Begin_graph, &End_graph);if (W){P = W; //压栈while (P != NULL){top++;path[top] = P;P = P->parent;}printf("<<<<<< The Path >>>>>>\n");//弹栈打印while (top>-1){P = path[top];top--;PrintGraph(P);}printf("<<<<< Mission Complete >>>>>\n");system("pause");}else{printf("Path not found ,Search depth is %d\n", MAX);system("pause");}return 0;}五．运行结果将初始数码组改写为 2 5 4 3 7 1 8 6 ，定义某个数前面比他小的数个数为Xi,所有数字的Xi相加为Y，因为四向移动只可能改变Y的大小，不改变其奇偶性。

基于A星算法的8数码问题程序源代码

#include "Stdio.h"#include "Conio.h"#include "stdlib.h"#include "math.h"void Copy_node(struct node *p1,struct node *p2);void Calculate_f(int deepth,struct node *p);void Add_to_open(struct node *p);void Add_to_closed(struct node *p);void Remove_p(struct node *name,struct node *p);int Test_A_B(struct node *p1,struct node *p2);struct node * Solution_Astar(struct node *p);void Expand_n(struct node *p);struct node * Search_A(struct node *name,struct node *temp);void Print_result(struct node *p);/* 定义8数码的节点状态*/typedef struct node{int s[3][3]; //当前8数码的状态int i_0; //当前空格所在行号int j_0; //当前空格所在列号int f; //当前代价值int d; //当前节点深度int h; //启发信息，采用数码“不在位”距离和struct node *father; //指向解路径上该节点的父节点struct node *next; //指向所在open或closed表中的下一个元素};struct node s_0={{3,8,2,1,0,5,7,6,4},1,1,0,0,0,NULL,NULL}; //定义初始状态struct node s_g={{1,2,3,8,0,4,7,6,5},1,1,0,0,0,NULL,NULL}; //定义目标状态struct node *open=NULL; //建立open表指针struct node *closed=NULL; //建立closed表指针int sum_node=0; //用于记录扩展节点总数int main(void){struct node s,*target;Copy_node(&s_0,&s);Calculate_f(0,&s); //拷贝8数码初始状态，初始化代价值target=Solution_Astar(&s); //求解主程序if(target) Print_result(target); //输出解路径else printf("问题求解失败！");getch();return 0;}/******************************************//* A*算法*//******************************************/struct node * Solution_Astar(struct node *p){struct node *n,*temp;Add_to_open(p); //将s_0放入open表while(open!=NULL) //只要open表中还有元素，就继续对代价最小的节点进行扩展{n=open; //n指向open表中当前要扩展的元素temp=open->next;Add_to_closed(n);open=temp;if(Test_A_B(n,&s_g)) //当前n指向节点为目标时，跳出程序结束；否则，继续下面的步骤return n;Expand_n(n); //扩展节点n}return NULL;}/*******************************************************//* 生成当前节点n通过走步可以得到的所有状态*//*******************************************************/void Expand_n(struct node *p){struct node *temp,*same;if(p->j_0>=1) //空格所在列号不小于1,可左移{temp=p->father;if(temp!=NULL&&temp->i_0==p->i_0&&temp->j_0-1==p->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(p,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0][temp->j_0-1]; //空格左移temp->s[temp->i_0][temp->j_0-1]=0;temp->j_0--;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=p; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end左移if(p->j_0<=1) //空格所在列号不大于1,可右移{temp=p->father;if(temp!=NULL&&temp->i_0==p->i_0&&temp->j_0+1==p->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(p,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0][temp->j_0+1]; //空格右移temp->s[temp->i_0][temp->j_0+1]=0;temp->j_0++;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=p; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end右移if(p->i_0>=1) //空格所在列号不小于1,上移{temp=p->father;if(temp!=NULL&&temp->i_0==p->i_0-1&&temp->j_0==p->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(p,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0-1][temp->j_0]; //空格上移temp->s[temp->i_0-1][temp->j_0]=0;temp->i_0--;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=p; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end上移if(p->i_0<=1) //空格所在列号不大于1,下移{temp=p->father;if(temp!=NULL&&temp->i_0==p->i_0+1&&temp->j_0==p->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(p,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0+1][temp->j_0]; //空格下移temp->s[temp->i_0+1][temp->j_0]=0;temp->i_0++;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=p; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end下移}/*******************************************************//* 添加p指向的节点到open表中*//*******************************************************/void Add_to_open(struct node *p){struct node *p1,*p2;p1=open; //初始时p1指向open表首部p2=NULL;if(open==NULL) //open表为空时，待插入节点即为open表第一个元素，open指向该元素{p->next=NULL;open=p;}else //open表不为空时，添加待插入节点，并保证open表代价递增的排序{while(p1!=NULL&&p->f>p1->f){p2=p1; //p2始终指向p1指向的前一个元素p1=p1->next;}if(p2==NULL) //待插入节点为当前open表最小{p->next=open;open=p;}else if(p1==NULL) //待插入节点为当前open表最大{p->next=NULL;p2->next=p;}else //待插入节点介于p2、p1之间{p2->next=p;p->next=p1;}}}/*******************************************************//* 添加p指向的节点到closed表中*//*******************************************************/void Add_to_closed(struct node *p){if(closed==NULL) //closed表为空时，p指向节点为closed表第一个元素，closed指向该元素{p->next=NULL;closed=p;}else //closed表不为空时，直接放到closed表首部{p->next=closed;closed=p;}}/**************************************************************//* 在open表或closed表中搜索与temp指向节点状态相同的节点，*//* 返回搜索到的节点地址*//**************************************************************/struct node * Search_A(struct node *name,struct node *temp){struct node *p1;p1=name; //p1指向open表或closed表while(p1!=NULL){if(Test_A_B(p1,temp)) //找到相同的节点，返回该节点地址return p1;elsep1=p1->next;}return NULL;}/**********************************************************//* 判断两个节点A、B状态是否相同，相同则返回1，否则返回0 *//**********************************************************/int Test_A_B(struct node *p1,struct node *p2){int i,j,flag;flag=1;for(i=0;i<=2;i++)for(j=0;j<=2;j++){if((p2->s[i][j])!=(p1->s[i][j])) { flag=0; return flag; }else ;}return flag;}/*******************************************************//* 从open表或closed表删除指定节点*//*******************************************************/void Remove_p(struct node *name,struct node *p){struct node *p1,*p2;p1=NULL;p2=NULL;if(name==NULL) //如果name指向的链表为空，则不需要进行删除return;else if(Test_A_B(name,p)&&name->f==p->f) //指定节点为name指向的链表的第一个元素{open=name->next;name->next=NULL;return;}else{p2=name;p1=p2->next;while(p1){if(Test_A_B(p1,p)&&p1->f==p->f) //找到指定节点{p2->next=p1->next;return;}else{p2=p1; //p2始终指向p1指向的前一个元素p1=p1->next;}}return;}}/******************************************//* 计算某个节点状态的代价值*//******************************************/void Calculate_f(int deepth,struct node *p){int i,j,temp;temp=0;for(i=0;i<=2;i++) //计算所有“不在位”数码的距离和{for(j=0;j<=2;j++){switch(p->s[i][j]){case 0: temp+=abs(i-1)+abs(j-1); break;case 1: temp+=abs(i-0)+abs(j-0); break;case 2: temp+=abs(i-0)+abs(j-1); break;case 3: temp+=abs(i-0)+abs(j-2); break;case 4: temp+=abs(i-1)+abs(j-2); break;case 5: temp+=abs(i-2)+abs(j-2); break;case 6: temp+=abs(i-2)+abs(j-1); break;case 7: temp+=abs(i-2)+abs(j-0); break;case 8: temp+=abs(i-1)+abs(j-0); break;}}}p->h=temp;p->f=deepth+p->h;}/********************************************//* 将p1指向的节点状态拷贝到p2指向的节点中*//********************************************/void Copy_node(struct node *p1,struct node *p2){int i,j;for(i=0;i<=2;i++){for(j=0;j<=2;j++){ p2->s[i][j]=p1->s[i][j]; }}p2->i_0=p1->i_0;p2->j_0=p1->j_0;p2->f=p1->f;p2->d=p1->d;p2->h=p1->h;p2->next=p1->next;p2->father=p1->father;}/********************************************//* 输出解路径*//********************************************/void Print_result(struct node *p){struct node *path[100];struct node *temp,*temp_father;int i,j,k;for(i=0;i<=99;i++) //初始化路径指针数组path[i]=0;temp=p;printf("总共扩展%d 个节点\n",sum_node);printf("总共扩展%d 层\n",temp->d);printf("*************************************************\n"); printf("解路径如下：\n");for(i=p->d;i>=0;i--) //存储解路径上各节点的地址{path[i]=temp;temp=temp->father;}for(k=0;k<=p->d;k++) //输出解路径{temp=path[k]; //建立节点指点指针printf("第%d步",temp->d);if(k-1>=0) //输出移动策略{temp_father=path[k-1];if(temp->i_0<temp_father->i_0) printf("—>上移\n");if(temp->i_0>temp_father->i_0) printf("—>下移\n");if(temp->j_0<temp_father->j_0) printf("—>左移\n");if(temp->j_0>temp_father->j_0) printf("—>右移\n");}elseprintf("\n");printf("当前：f=%d，d=%d，h=%d\n",temp->f,temp->d,temp->h);printf("当前节点状态为：\n");for(i=0;i<=2;i++){for(j=0;j<=2;j++){printf("%d ",temp->s[i][j]);}printf("\n");}printf("\n");}}。

c++算法八数码问题

c++算法八数码问题八数码问题是一种经典的智力游戏，其规则是在有限的格子中，按照一定的顺序将数字旋转移动到目标位置。

为了解决这个问题，我们可以使用算法的思想来设计一种有效的解决方案。

一、问题描述八数码问题是一个有N×N的棋盘，其中每个格子代表一个数字。

玩家需要按照一定的顺序旋转数字，将它们移动到目标位置。

目标位置是预先设定好的，玩家需要按照规则移动数字，使得棋盘上的数字按照正确的顺序排列。

二、算法思想为了解决八数码问题，我们可以使用贪心算法的思想。

首先，我们需要找到一个初始状态，这个状态应该是最简单、最容易解决的问题。

然后，我们通过循环迭代的方式，不断尝试不同的旋转方式，直到找到一个能够满足目标位置的解决方案。

三、C语言实现下面是一个简单的C语言实现，用于解决八数码问题。

这个程序使用了递归和回溯的方法，通过穷举所有可能的旋转方式来找到解决方案。

```c#include <stdio.h>#include <stdlib.h>#include <stdbool.h>#define N 3// 定义棋盘状态结构体typedef struct {int nums[N][N];int num_count[N][N]; // 记录每个数字出现的次数} Board;// 判断两个数字是否相邻bool is_adjacent(int num1, int num2) {int dx[] = {-1, 0, 1};int dy[] = {0, -1, 1};for (int i = 0; i < 3; i++) {if (abs(nums[num1][i] - nums[num2][i]) <= 1) {return true;}}return false;}// 寻找最优解函数bool find_optimal_solution(Board& board, int target_row, int target_col) {// 初始化最优解为空状态bool optimal_solution = false;int optimal_score = INT_MAX; // 最优解的得分初始化为最大整数int best_score = INT_MAX; // 最优解的当前得分初始化为最大整数加一// 对当前棋盘进行遍历for (int row = 0; row < N; row++) {for (int col = 0; col < N; col++) {// 如果当前状态为空状态，则直接跳过if (board.nums[row][col] == 0) {continue;}// 记录当前状态的信息，包括得分和旋转次数等int score = calculate_score(board, row, col); // 计算得分函数在实现中定义了旋转方式的选择和得分计算规则等具体细节，这里省略了具体实现细节。

八数码问题C语言A星算法详细实验报告含代码

一、实验容和要求八数码问题：在3×3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空的，其初始状态如图1所示，要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。

例如：(a) 初始状态(b) 目标状态图1 八数码问题示意图请任选一种盲目搜索算法（广度优先搜索或深度优先搜索）或任选一种启发式搜索方法（全局择优搜索，加权状态图搜索，A算法或A* 算法）编程求解八数码问题（初始状态任选）。

选择一个初始状态，画出搜索树，填写相应的OPEN 表和CLOSED表，给出解路径，对实验结果进行分析总结，得出结论。

二、实验目的1. 熟悉人工智能系统中的问题求解过程；2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用；3. 熟悉对八数码问题的建模、求解及编程语言的应用。

三、实验算法A*算法是一种常用的启发式搜索算法。

在A*算法中，一个结点位置的好坏用估价函数来对它进行评估。

A*算法的估价函数可表示为：f'(n) = g'(n) + h'(n)这里，f'(n)是估价函数，g'(n)是起点到终点的最短路径值（也称为最小耗费或最小代价），h'(n)是n到目标的最短路经的启发值。

由于这个f'(n)其实是无法预先知道的，所以实际上使用的是下面的估价函数：f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价，h(n)是从结点n到目标结点的最佳路径的估计代价。

在这里主要是h(n)体现了搜索的启发信息，因为g(n)是已知的。

用f(n)作为f'(n)的近似，也就是用g(n)代替g'(n)，h(n)代替h'(n)。

这样必须满足两个条件：（1）g(n)>=g'(n)（大多数情况下都是满足的，可以不用考虑），且f必须保持单调递增。

（2）h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。

启发式搜索-八数码问题

启发式搜索1. 介绍八数码问题也称为九宫问题。

在3×3的棋盘，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。

棋盘上还有一个空格〔以数字0来表示〕，与空格相邻的棋子可以移到空格中。

要求解决的问题是：给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。

所谓问题的一个状态就是棋子在棋盘上的一种摆法。

解八数码问题实际上就是找出从初始状态到达目标状态所经过的一系列中间过渡状态。

2. 使用启发式搜索算法求解8数码问题。

1) A ，A 星算法采用估价函数()()()()w n f n d n p n ⎧⎪=+⎨⎪⎩，其中：()d n 是搜索树中结点n 的深度；()w n 为结点n 的数据库中错放的棋子个数；()p n 为结点n 的数据库中每个棋子与其目标位置之间的距离总和。

2)宽度搜索采用f(i)为i 的深度，深度搜索采用f(i)为i 的深度的倒数。

3. 算法流程① 把起始节点S 放到OPEN 表中，并计算节点S 的)(S f ；② 如果OPEN 是空表，则失败退出，无解；③ 从OPEN 表中选择一个f 值最小的节点i 。

如果有几个节点值相同，当其中有一个为目标节点时，则选择此目标节点；否则就选择其中任一个节点作为节点i ； ④ 把节点i 从 OPEN 表中移出，并把它放入 CLOSED 的已扩展节点表中； ⑤ 如果i 是个目标节点，则成功退出，求得一个解；⑥ 扩展节点i ，生成其全部后继节点。

对于i 的每一个后继节点j ：计算)(j f ；如果j 既不在OPEN 表中，又不在CLOCED 表中，则用估价函数f 把它添入OPEN 表中。

从j 加一指向其父节点i 的指针，以便一旦找到目标节点时记住一个解答路径；如果j 已在OPEN 表或CLOSED 表中，则比较刚刚对j 计算过的f 和前面计算过的该节点在表中的f 值。

如果新的f 较小，则(I)以此新值取代旧值。

八数码问题解释

八数码问题解释8数码问题又称9宫问题，源于一个古老的智力游戏。

说白了就是我们小时候玩的“华容道”。

意在给定的9格棋盘的8个格子内分别放一个符号，符号之间互不相同，剩下一格做为“出口”。

我们把8个符号在棋盘上的排列顺序称作8数码的状态，游戏要求给定一个初始的状态与一个终止状态，符号要经过若干次移动后由初态变成终态，这个过程中只有“出口”附近的符号可以朝“出口”的方向移动，且每次只能移动一个符号。

如下图所示，（其中我们用0表示出口，=》表示移动一次，=》*表示移动0-n次）：初态终态1 2 3 1 2 3 0 1 24 5 6 =》 4 5 6 =》* 3 4 57 8 0 7 0 8 6 7 82 解决方案通过观察我们可以发现每一次8数码的状态都可以通过移动字符变成有限的几种其他状态，比如上图中我们可以知道初态“出口”附近有8和6可以移动，那么这个初态可以经过移动得到两个新的状态。

我们人在玩这个游戏的时候，总是要做下面几个步骤：1．看看哪个符号可以移动。

2．判断一下哪个符号的移动最有利于到达终态。

3．选定一个符号并移动它。

4．判断是否到达终态，是则结束，否则就回到第一步。

而现在我们要使用机器来模拟这一过程，其步骤与人类类似，但不同的是，人在执行第二部的时候总是能预先判断未来好几步的局势，从而选出最有利的一步，而机器则不行，它要先得到一个状态才能知道这个状态下一步将会到哪些状态而无法像我们一样一次就看到后面几步的状态。

那么基本思想就是让机器穷尽由初态出发到达所有可能状态的路径，并从中找到有终态的路径作为问题的解。

2.1 A*算法就如我们上面说到的让机器找出所有的可能来得到问题的解，看起来似乎很简单，但问题在于一旦8数问题的解达到一定规模，机器所要穷尽的路径数量将变得极为庞大，无疑会消耗大量的时间和空间。

那么如何让机器像人一样在选择移动符号的时候总是能选择最有利的那一个呢？下面就要介绍启发式搜索中的一个算法A*算法来解决这个问题。

八数码问题代码及算法分析

a星算法求解八数码问题python

8数码问题分析及程序代码

八数码C语言A算法详细代码

八数码实验报告

八数码实验报告

八数码问题C代码

八数码问题C语言代码

A-star-算法-八数码问题-C++-报告+代码+详细注释1

人工智能实验一_八数码问题

八数码问题源代码

八数码C语言A算法详细代码

八数码问题python代码

八数码问题代码及算法分析

八数码难题代码与基本思路 Eight puzzles

基于A星算法的8数码问题程序源代码

c++算法 八数码问题

八数码问题C语言A星算法详细实验报告含代码

启发式搜索-八数码问题

八数码问题解释

c++算法八数码问题