物理光学课后习题答案汇总.docx
物理光学习题答案

物理光学习题答案选择题:1.A2.D3.B4.A5.D6.A7.A8.B9.A 10.D 11.C 12.C 13.C 14.C 15.D 16.B 17.B 18.C 19.B 20.A 21.A 22.D 23. (1)(4) 24.(1)(2)(3) 25. (1)(2)(3) 26.(2)(4) 27. (1)(2)(3) 28. (2)(3) 29. (1)(2)(3) 30. (1)(4) 31. (1)(3) 32.(2)(4)作业:1. 解:根据杨氏双缝干涉明纹计算公式可得:()())(2.2104007601042.1294mm dkD x =⨯-⨯⨯⨯=-=∆--紫红λλ2. 解:某波长的光的第三级明纹和红光的第二级明纹相重合,说明它们的衍射角相等 。
根据明纹条件sin (21)2a k λϕ=±+对红光第二级明纹有5sin 2a ϕλ= 对某波长的光第三级明纹有7sin 2a ϕλ''=ϕϕ=/ /2725λλ=∴nm 4506307575/=⨯==λλ3. 解:(1)9sin (21)4sin 22a k k aλλϕϕ=±+==4429tan sin 46729x a x f f fnm afλϕϕλ=====(2)4k =∴ 从P 处来看,可分为21)9k +=(个半波带 4. (1)2400()sin 21.61sin 302k a b k k a b m λϕλμ⨯+=±=+===︒(2)紫光71410m λ-=⨯ 红光727.610m λ-=⨯1212sin sin ddλλϕϕ==第一级光谱线宽度7121212163.610(tan tan )(sin sin )0.225m 1.610f x f f d ϕϕϕϕλλ--⨯∆=-=-==⨯(-)=计算题:1. 解:(1) sin b k θλ= (1)k = 1/t g x fθ= 11()f x m m bλ== (2)sin (21)(2)2b k k λθ=+=225/(2)2.5()2f tg x fk x m m bλθ====2. .解: 由条纹间距公式D x dλ∆=中央明纹两侧的第3级明纹中心的距离为7300666 5.461107.34m m 0.134D S x dλ-=∆==⨯⨯⨯=3解:(1)()sin 21,2a k λϕ=+当1k =时,3sin 2aλϕ=()2121330.2722f f x x x cm aa λλ⎛⎫∆=-=-=⎪⎝⎭(2)由sin ,d k ϕλ= 当1k =时,sin aλϕ=()///21211.8f f x x x cm aa λλ⎛⎫∆=-=-=⎪⎝⎭4. 解:(1)中央明纹宽度7422161012mm 10f x aλ--⨯⨯⨯∆===(2)由暗纹条件2sin 2k=2sin 2a k aλλϕϕ==()则2sin tan ,sin 12mm x ftg f ϕϕϕϕϕ∴≈=≈=由很小,简述题1.用什么方法可以由普通光源获得相干光?试举出实例。
大学物理重点知识习题课解答-光学

300
600
S .. .. . . .. .. ..
I0
P2
I21
解:
P1 P3P1
P1
入射光通过偏振片I和II后,透射光强为
I1
1 2
I0
cos2
600
插入偏振片III后,其透射光强为
I2
1 2
I0
cos2
300
cos
2
300
I2 2.25I1
27
选择题1. 等倾干涉光程差公式 2d
为了12满I足0 线I偏0 振co部s2分振, 动方4向5在0 出射后“转
过”900,
只要第一个偏振片偏振化方向与入射光中线偏振
光的光振动方向夹角为450,第二个偏振片的偏振
化方向与第一偏振片偏振化方向夹角为450就行.
E
所以,只要两个偏振片就行.
P1
450
P127
I0
.
450 .
E
I0
P1
450
将有关数据代入可得
1
o
d 5 /n2 n1 8.0m
d
4
3。在折射率n3=1.52的照相机镜头表面涂有一层折射率
n2=1.38的MgF2增透膜,若此膜仅适用于波长 =550nm的
光,则此膜的最小厚度为多少?
n1 1
解:因为 光相干相
n2 1.38 d
综合效应。其中明条纹的位置由光栅方程决定,但各 明纹的强度受单缝衍射效应的调制,透射光能量的大 部分将分布在原单缝衍射中央明纹范围(中央包线) 内的各明纹上。
23
17、光栅明纹位置由d sin k 决定。单缝衍射极
小位置由 b sin k决定,当 时 ,光栅明纹
大学物理光学习题附答案
[
]
33.5649:在如图所示的夫琅禾费衍射装置中,将单缝宽
度 a 稍稍变窄,同时使会聚透镜 L 沿 y 轴正方向作微小平移(单缝与
屏幕位置不动),则屏幕 C 上的中央衍射条纹将
(A) 变宽,同时向上移动
(B) 变宽,同时向下移动
(C) 变宽,不移动
(D)
变窄,同时向上移动
(E) 变窄,不移动
[
]
34.5650:在如图所示的单缝夫琅禾费衍射装置中,设中央明
的部分
(A) 凸起,且高度为 / 4
(B) 凸起,且高度为 / 2
(C) 凹陷,且深度为 / 2
(D) 凹陷,且深度为 / 4 [
]
平玻璃
空气劈尖
工件
O
n=1.68
n=1.60 n=1.58
O
3507 图
14.3507:如图所示,平板玻璃和凸透镜构成牛顿环装置,全 部浸入 n=1.60 的液体中,凸透镜可沿 OO 移动,用波长=500 nm(1nm=109m)的单色光垂直入射。 从上向下观察,看到中心是一个暗斑,此时凸透镜顶点距平板玻璃 的距离最少是
(C) 向棱边方向平移,条纹间隔不变
(D) 向远离棱边的方向平移,条纹间隔不变
(E)
向远离棱边的方向平移,条纹间隔变小
[
]
19.5326:两块平玻璃构成空气劈形膜,左边为棱边,用单色
平行光垂直入射。若上面的平玻璃以棱边为轴,沿逆时针方向作微
小转动,则干涉条纹的
(A) 间隔变小,并向棱边方向平移
(B) 间隔变大,并向远离棱边方向平移
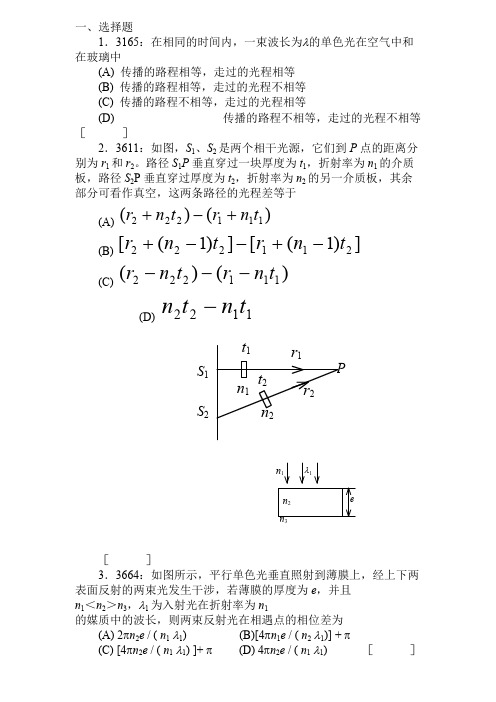
一、选择题 1.3165:在相同的时间内,一束波长为的单色光在空气中和
在玻璃中
八年级物理光学相关习题及参考答案.doc

1. 下图中,S是光源,A是不透明的物体,L是竖直墙血,试画出光源S照不到墙血的范围LAS2. 若把正在收看的电视机放在真空玻璃罩内,我们会发现()A. 图像和声音一样正常B.图像和声音同时消失C.可以听到声音,但看不到图像D.可以看到图像但听不到声音3. 太阳、月亮、荧火虫,其中不是光源的是_______ 。
“小孔成像”所成的像是_像(填“实”或“虚”),它是由于______________ 形成的。
4. “影”是我们日常生活屮常见的光现象,如做光学游戏形成的“手影”;民间皮影戏的“皮影”;湖岸景色在水中形成的“倒影”;春游时的“摄影”等。
以下列出的“影”与物理知识对应关系不正确的是A. 手影一一光的直线传播B.皮影一光的反射C.倒影一一平面镜成像D.摄影一一凸透镜成像5. 人沿看街道走向路灯,再从路灯下走远,则他的影子长短的变化是()A. 变长B.变短C.先变长再变短D.先变短再变长6. 阳光灿烂的日子,行走在绿树成荫的街道上,常常见到地面上有-•些圆形的光斑,这些光斑是()A. 树叶的实像B.树叶的虚线C.太阳的实像D.太阳的虚像7. 如图3所示的四种现彖一中,由于光的直线传摘形成的是()A・竹的倒 B.水面'折戏 D.镜中花8. 在灯光下靠近墙的地方,用手做各种姿态,在墙上会形成手影,当电灯保持静止,手向墙•靠拢时,在墙上的手影将:A. 变小;B.变大;C.不变;D.无法确定.9. 在纸上剪一个很小的方形孔,让太阳光垂冑照在方形孔上,那么地面上产生的光斑:A.是方形的;;B.是圆形的;;C.它是太阳的像;;D .是长方形的10如图所示,找一个空的易拉罐,用钉子在易拉罐底部的中央敲一个小孔,将易拉罐的顶部剪去后,蒙上一层塑料薄膜,这样就制成了一个针孔照相机,其实就是小孔成像的实验装置。
将点燃的蜡烛置于小孔前的适当位置,观察并研究小孔成像的特点:(1)__________________________ 烛焰在塑料薄膜上所成的像是_________________________ (填“实像”或“虚像”);其成像的原理是__ ;(2)如果易拉罐底部小孔是三角形,则他在半透明纸上看到的像是一9A.三角形光斑B.圆形光斑C.烛焰的正立像D.烛焰的倒立像(3)从右侧眼睛看过去,将蜡烛在孔前绕顺时针旋转,则人眼看到的塑料薄膜上的像是_(选填“顺”或“逆”)时针旋转的;(4) ______________________________________________ 为了增大烛焰所成的像,可采取的办法是::(5)晴夭太阳透过树叶缝隙形成的圆形光斑与上述原理相同,共圆形光斑大小不一的原因是_______________________________ 。
《物理光学》课后解答

第四章 光的电磁理论4-1计算由8(2)exp 610)i y t ⎡⎤=-+++⨯⎢⎥⎣⎦E i 表示的平面波电矢量的振动方向、传播方向、相位速度、振幅、频率、波长。
解:由题意:)81063(2t y x i eE x ⨯++-= )81063(32t y x i e E y ⨯++=∴3-=xy E E ∴振动方向为:j i3+-由平面波电矢量的表达式: 3=x k 1=y k∴传播方向为: j i+3平面电磁波的相位速度为光速: 8103⨯=c m/s;振幅:4)32()2(222200=+-=+=oy x E E E V/m频率:8810321062⨯=⨯==πππωf Hz 波长:πλ==fcm 4-2 一列平面光波从A 点传到B 点,今在AB 之间插入一透明薄片,薄片的厚度mm h 2.0=,折射率n =。
假定光波的波长为5500=λnm ,试计算插入薄片前后B 点光程和相位的变化。
解:设AB 两点间的距离为d ,未插入薄片时光束经过的光程为:d d n l ==01 插入薄片后光束经过的光程为:h n d nh h d n l )1()(02-+=+-= ∴光程差为:mm h n l l 1.02.05.0)1(12=⨯=-=-=∆ 则相位差为:ππλπδ6.3631.010550226=⨯⨯=∆=- (4-3 试确定下列各组光波表示式所代表的偏振态:(1))sin(0kz t E E x -=ω,)cos(0kz t E E y -=ω (2))cos(0kz t E E x -=ω,)4/cos(0πω+-=kz t E E y (3))sin(0kz t E E x -=ω,)sin(0kz t E E x --=ω 解:(1)∵)2cos()sin(00πωω--=-=kz t E kz t E E x∴2πϕϕϕ=-=x y∴ 为右旋圆偏振光。
·(2)4πϕϕϕ=-=x y∴ 为右旋椭圆偏振光,椭圆长轴沿y =x (3)0=-=x y ϕϕϕ∴ 为线偏振光,振动方向沿y =-x4-4 光束以30°角入射到空气和火石玻璃(n 2=)界面,试求电矢量垂直于入射面和平行于入射面分量的反射系数s r 和p r 。
物理光学课后习题答案-汇总

,
两式相减,可得 ,利用折射定律和小角度近似,得 ,( 为平行平板周围介质的折射率)
对于中心点,上下表面两支反射光线的光程差为 。因此,视场中心是暗点。由上式,得 ,因此,有12条暗环,11条亮环。
解:由题意,得,波列长度 ,
由公式 ,
又由公式 ,所以频率宽度
。
某种激光的频宽 Hz,问这种激光的波列长度是多少?
解:由相干长度 ,所以波列长度 。
第二章光的干涉及其应用
在与一平行光束垂直的方向上插入一透明薄片,其厚度 ,若光波波长为500nm,试计算插入玻璃片前后光束光程和相位的变化。
解:由时间相干性的附加光程差公式
,所以
。
杨氏干涉实验中,若波长 =600nm,在观察屏上形成暗条纹的角宽度为 ,(1)试求杨氏干涉中二缝间的距离(2)若其中一个狭缝通过的能量是另一个的4倍,试求干涉条纹的对比度
解:角宽度为 ,
所以条纹间距 。
由题意,得 ,所以干涉对比度
若双狭缝间距为,以单色光平行照射狭缝时,在距双缝远的屏上,第5级暗条纹中心离中央极大中间的间隔为,问所用的光源波长为多少是何种器件的光源
解:由公式 ,所以
= 。
此光源为氦氖激光器。
在杨氏干涉实验中,照明两小孔的光源是一个直径为2mm的圆形光源。光源发光的波长为500nm,它到小孔的距离为。问两小孔可以发生干涉的最大距离是多少?
解:因为是圆形光源,由公式 ,
则 。
月球到地球表面的距离约为 km,月球的直径为3477km,若把月球看作光源,光波长取500nm,试计算地球表面上的相干面积。
大学物理光学答案Word版

第十七章光的干涉一. 选择题1.在真空中波长为的单色光,在折射率为n的均匀透明介质中从月沿某一路径传播到氏若儿万两点的相位差为3 ,则路径初的长度为:(D )A. 1・ 5B. 1. onC. 3D. 1.5 /n解: △卩=二-nil = 3/r所以d= 1.52/n本题答案为D。
2.在杨氏双缝实验中, 若两缝之间的距离稍为加大,英他条件不变,则干涉条纹将(A)A. 变密B.变稀C.不变D.消失解:条纹间距= 所以/增大,Ar变小。
干涉条纹将变密。
本题答案为A。
3.在空气中做双缝干涉实验,屏幕E上的P处是明条纹。
若将缝S:盖住,并在S,、S:连线的垂直平分而上放一平面反射镜氐其它条件不变(如图),则此时(B )A.P处仍为明条纹B.P处为暗条纹C.P处位于明、暗条纹之间D.屏幕E上无干涉条纹解对于屏幕E上方的P点,从S,直接入射到屏幕E上和从出发5经平而反射镜M 反射后再入射到屏幕上的光相位差在均比原来增,因此原来是明条纹的将变为暗条纹,而原来的暗条纹将变为明条纹。
故本题答案为B。
4.在薄膜干涉实验中,观察到反射光的等倾干涉条纹的中心是亮斑,则此时透射光的等倾干涉条纹中心是(B )A.亮斑B.暗斑C.可能是亮斑,也可能是暗斑D.无法确泄解:反射光和透射光的等倾干涉条纹互补。
本题答案为&5.一束波长为的单色光由空气垂宜入射到折射率为刀的透明薄膜上,透明薄膜放在空气中,要使反射光得到干涉加强,则薄膜最小的厚度为(B )A. /4B. / (4n)C・ /2 D・/ (2n)6.在折射率为m =1.60的玻璃表而上涂以折射率沪1.38的MgF:透明薄膜,可以减少光的反射。
当波长为500. Onm的单色光垂直入射时,为了实现最小反射,此透明薄膜的最小厚度为(C )A. 5. OnmB. 30. OnmC. 90.6nmD. 250. Onm解:增透膜e min = A/4n = 90.6 nm本题答案为C。
物理光学课后部分习题答案2015

(1)由于 ,平板上下表面反射都是从低折射率介质传输到高折射率介质,半波损失的情况一样,所以上、下表面反射光的光程差为
条纹中心对应折射角 , ;
,光程差是波长的整数N个亮纹有 ,所以第10个亮条纹的角半径为 ,半径为
(3)条纹间距
14、用等厚条纹测量玻璃楔板的楔角时,在长达5cm的范围内共有15条亮条纹,玻璃楔板的折射率 ,所用光波波长 ,求楔角。
解:
条纹间隔 ;
楔角
第十三章光的衍射
5、单位振幅的单色平面波垂直照明半径为1的圆孔,试利用式(13-12)证明,圆孔后通过圆孔中心光轴上的点的光强分布为
式中,z是考察点到圆孔中心的距离。
证明:
菲涅耳衍射公式
圆孔中心轴上点x、y坐标都为零,所以其光场为
所以轴上点光强
8、波长 的单色光垂直入射到边长为3cm的方孔上,在光轴附近离孔z处观察衍射,试求夫琅和费衍射区的大致范围。
第十一章光的电磁理论基础
1、一个平面电磁波可以表示为 , , ,求:(1)该电磁波的频率、波长、振幅和原点的初相位;(2)波的传播方向和电矢量的振动方向;(3)相应的磁场 的表达式。
解:
(1)根据电磁波表达式可知振幅矢量 , ;
传播速度 ,频率 ,波长 ,初相位 。
(2)传播方向:z轴方向,电矢量振动方向:沿y轴。
(3)根据电磁波性质,电场、磁场、传输方向两两垂直,且满足 和 ,所以磁场为 , , 。
2、在玻璃中传播的一个线偏振光可以表示为 , , ,试求:(1)光的频率和波长;(2)玻璃的折射率。
解:
(1)传播速度 ,频率 ,波长
(2)折射率
8、太阳光(自然光)以 角入射到窗玻璃( )上,试求太阳光进入玻璃的透射比。
物理光学教程答案

Vϕ = −3 × 10 8 m / s
沿-z 方向传播
1.7
⎡ 2π ⎤ E ob = a1 cos ⎢ (z − V1t )⎥ ⎣λ ⎦ ⎡ 2πV1 ⎤ (z − 3) − 2π V1t + 6π ⎥ Ebc = a 2 cos ⎢ λ1 λ1 ⎦ ⎣ λ1V2
1.8
E 0 = a1
Eb − = a1 cos
3
第三章
3.1.
⎡ ⎛ π ⎞⎤ E = 6 sin (kz ) exp ⎢− j ⎜ ωt + ⎟⎥ 2 ⎠⎦ ⎣ ⎝
这是振幅为 6 的驻波,波腹位置: kz = mπ + π
2
;波节位置: kz = mπ
3.2 (1) 因 p 处是磁场的波腹位置,或电场的波节位置,说明光化学作用是由电场 E 产生. (2)
2
4.6 提示: 导出衍射强度分布 I (x ) = I (0 )sin c ⎢a⎜ ⎜ 4.7 入射光倾斜角 β 反射衍射发散角 ∆θ r (单位:rad) 折射衍射发散角 ∆θ t (单位:rad) (1) 提示: I ( x ) 的极值条件为 tan⎜ ⎜ (2) 4.9 4.10 (略) 提示:
n = 1.5385
1.24
π⎞ ⎛ E x = 20 cos⎜ 2 × 10 3 πz − 6 × 1011 πt + ⎟ 2⎠ ⎝ By =
2 π⎞ ⎛ × 10 −7 cos⎜ 2 × 10 3 π z − 6 × 1011 π t + ⎟ 3 2⎠ ⎝
1.25 1.26
E = 951 V / m N = 167 w
αe > α g
左暗右亮,
(2) α e = 3.08 × 10
(完整版)物理光学-第一章习题与答案

物理光学习题 第一章 波动光学通论一、填空题(每空2分)1、.一光波在介电常数为ε,磁导率为μ的介质中传播,则光波的速度v= 。
【εμ1=v 】2、一束自然光以 入射到介质的分界面上,反射光只有S 波方向有振动。
【布儒斯特角】3、一个平面电磁波波振动表示为 E x =E z =0, E y =cos[⎪⎭⎫⎝⎛-⨯t c x 13102π], 则电磁波的传播方向 。
电矢量的振动方向 【x 轴方向 y 轴方向】4、在光的电磁理论中,S 波和P 波的偏振态为 ,S 波的振动方向为 , 【线偏振光波 S 波的振动方向垂直于入射面】5、一束光强为I 0的自然光垂直穿过两个偏振片,两个偏振片的透振方向夹角为45°,则通过两偏振片后的光强为 。
【I 0/4】6、真空中波长为λ0、光速为c 的光波,进入折射率为n 的介质时,光波的时间频率和波长分别为 和 。
【c/λ0 λ0 /n 】7、证明光驻波的存在的维纳实验同时还证明了在感光作用中起主要作用是 。
【电场E 】8、频率相同,振动方向互相垂直两列光波叠加,相位差满足 条件时,合成波为线偏振光波。
【0 或Π】9、会聚球面波的函数表达式 。
【ikre rA r E -)(=】 10、一束光波正入射到折射率为1.5的玻璃的表面,则S 波的反射系数为 ,P 波透射系数: 。
【-0.2 0.2 】11、一束自然光垂直入射到两透光轴夹角为θ的偏振片P 1和P 2上,P 1在前,P 2在后,旋转P 2一周,出现 次消光,且消光位置的θ为 。
【2 Π/2】12、当光波从光疏介质入射到光密介质时,正入射的反射光波 半波损失。
(填有或者无) 【有】13、对于部分偏振光分析时,偏振度计算公式为 。
(利用正交模型表示) 【xy x y I I I I P +-=】二、选择题(每题2分)1.当光波从光密介质入射到光疏介质时,入射角为θ1,布儒斯特角为θB ,临界角为θC ,下列正确的是 ( )A .0<θ1<θB , S 分量的反射系数r S 有π位相突变 B .0<θ1<θB , P 分量的反射系数r P 有π位相突变C .θB <θ1<θC , S 分量的反射系数r S 有π位相突变D .θB <θ1<θC , P 分量的反射系数r P 有π位相突变 【B 】2.下面哪种情况产生驻波 ( ) A .两个频率相同,振动方向相同,传播方向相同的单色光波叠加 B .两个频率相同,振动方向互相垂直,传播方向相反的单色光波叠加 C .两个频率相同,振动方向相同,传播方向相反的单色光波叠加 D .两个频率相同,振动方向互相垂直,传播方向相同的单色光波叠加 【C 】3.平面电磁波的传播方向为k ,电矢量为E ,磁矢量为B, 三者之间的关系下列描述正确的是 ( ) A .k 垂直于E , k 平行于B B .E 垂直于B , E 平行于k C .k 垂直于E , B 垂直于k D .以上描述都不对 【C 】4、由两个正交分量]cos[0wt kz A x E x -= 和]87cos[0π+-=wt kz A y E y表示的光波,其偏振态是( )A 线偏振光B 右旋圆偏振光C 左旋圆偏振光D 右旋椭圆偏振光 【D 】5、一列光波的复振幅表示为ikre rA r E =)(形式,这是一列( )波 A 发散球面波 B 会聚球面波 C 平面波 D 柱面波 【A 】6、两列频率相同、振动方向相同、传播方向相同的光波叠加会出现现象( ) A 驻波现象 B 光学拍现象 C 干涉现象 D 偏振现象 【C 】7、光波的能流密度S 正比于( )A E 或HB E 2或H 2C E 2,和H 无关D H 2,和E 无关 【B 】8、频率相同,振动方向互相垂直两列光波叠加,相位差满足( )条件时,合成波为二、四象限线偏振光波。
物理-光学习题附答案

物理-光学习题附答案(总11页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、 选择题1、在相同时间内,一束波长为λ的单色光在空中和在玻璃中,正确的是[ ]A 、 传播的路程相等,走过的光程相等;B 、 传播的路程相等,走过的光程不相等;C 、 传播的路程不相等,走过的光程相等;D 、传播的路程不相等,走过的光程不相等。
2. 如图所示,平行单色光垂直照射到薄膜上,经上下两表面反射的两束光发生干涉,若薄膜的厚度为e ,并且n1<n2>n3,λ为入射光在真空中的波长,则两束反射光在相遇点的相位差为 [ ]A .λπe n 22 ; B. πλπ+e n 22 ;C .πλπ+e n 24; D. 2/42πλπ+e n 。
3. 在双缝干涉实验中,屏幕E 上的P 点是明条纹。
若将2S 缝盖住,并在21S S 连线的垂直平分面处放一反射镜M ,如图所示,则此时 [ ]A .P 点处仍为明条纹;B. P 点处为暗条纹;C .不能确定P 点处是明条纹还是暗条纹;D. 无干涉条纹。
4、用白光源进行双缝实验,若用一纯红色的滤光片遮盖一条缝,用一个纯蓝色的滤光片遮盖另一条缝,则 [ ]A .干涉条纹的宽度将发生变化;3n2n 1nB. 产生红光和蓝光的两套彩色干涉条纹;C.干涉条纹的位置和宽度、亮度均发生变化;D.不发生干涉条纹。
5、有下列说法:其中正确的是[]A、从一个单色光源所发射的同一波面上任意选取的两点光源均为相干光源;B、从同一单色光源所发射的任意两束光,可视为两相干光束;C、只要是频率相同的两独立光源都可视为相干光源;D、两相干光源发出的光波在空间任意位置相遇都会产生干涉现象。
6、真空中波长为λ的单色光,在折射率为n的均匀透明媒质中,从A点沿某一路径到B点,路径的长度为 L, A、B两点光振动位相差记为Δφ,则[](A) L =3λ/(2n),Δφ = 3π; ( B ) L = 3λ/(2n),Δφ = 3nπ;(C) L = 3nλ/2 , Δφ = 3π; ( D ) L = 3nλ/2 ,Δφ = 3nπ。
大学物理光学习题和解答

⼤学物理光学习题和解答光学习题和解答习题⼗六16.1 从⼀狭缝透出的单⾊光经过两个平⾏狭缝⽽照射到120cm 远的幕上,若此两狭缝相距为0.20mm ,幕上所产⽣⼲涉条纹中两相邻亮线间距离为3.60mm ,则此单⾊光的波长以mm 为单位,其数值为(A) 41050.5-?; (B) 41000.6-?; (C) 41020.6-?; (D) 41085.4-?。
答案:(B)16.2 ⽤波长为650nm 之红⾊光作杨⽒双缝⼲涉实验,已知狭缝相距410-m ,从屏幕上量得相邻亮条纹间距为1cm ,如狭缝到屏幕间距以m 为单位,则其⼤⼩为(A) 2; (B) 1.5; (C) 3.2; (D) 1.8。
答案:(B)16.3 波长λ为4106-?mm 单⾊光垂直地照到尖⾓α很⼩、折射率n 为1.5的玻璃尖劈上。
在长度l 为1cm 内可观察到10条⼲涉条纹,则玻璃尖劈的尖⾓α为(A) 24''; (B) 4.42''; (C) 3.40''; (D) 2.41''。
答案:(D)16.4 在⼀个折射率为1.50的厚玻璃板上,覆盖着⼀层折射率为1.25的丙酮薄膜。
当波长可变的平⾯光波垂直⼊射到薄膜上时,发现波长为6000nm 的光产⽣相消⼲涉。
⽽700nm 波长的光产⽣相长⼲涉,若此丙酮薄膜厚度是⽤nm 为计量单位,则为(A) 840; (B) 900; (C) 800; (D) 720。
答案:(A)16.5 当⽜顿环装置中的透镜与玻璃之间充以液体时,则第⼗个亮环的直径由1.40cm 变为1.27cm ,故这种液体的折射率为(A) 1.32; (B) 1.10; (C) 1.21; (D) 1.43。
参考答案:(C)16.6 借助于玻璃表⾯上所涂的折射率为n=1.38的2MgF 透明薄膜,可以减少折射率为60.1='n 的玻璃表⾯的反射,若波长为50000A 的单⾊光垂直⼊射时,为了实现最⼩的反射,问此透明薄膜的厚度⾄少为多少0A ?(A) 50; (B) 300; (C) 906; (D)2500; (E) 10500。
物理试题练习题教案学案课件物理光学作业习题答案.docx

物理光学作业习题答案第一章光波的基本性质(1)作业习题1、试说明下列各组光波表达式所代表的偏振态。
(1) E x= E o sin ( co t-kz), E y= E O cos ( « t-kz)⑵ E x= E O cos ( co t-kz), E y= E O cos ( « t~kz+f )(3) E x= E o sin ( co t~kz), E y=- E o sin ( co t~kz)解:(1) E x = E o sin(®r -kz) E y = E o cos(cot - kz) 71Ex = cos(M — kz~ —) 9 E ox = E oy = E°.•.5=生,.•.凡,超前所生,.•.为右旋圆偏振光2 ,2(2 ) Ex = Eq cos(仞-kz), Ey = E° cos(仞-fc + —)F8 = - , E;+E;^El,E,超前E, ^Ltga = — = 1, :.a = -4 x y u y E4_ _ 71 71 971tg2y/ = tg2a -coso = tg —-cos— , .. y/ =—为右旋椭圆偏振光,长轴在y二x方向上(3) E x = E o sin(仞-kz), E y = -E o cos(仞-kz)Ey = E Q sin(®r 一« + 兀),d = 7i , E m = E oy = E QE .丸TC % TCtga = = 1,・'・ a = —, tg2i// = tg2a-cos3 = tg — -cos n ・'・ i// = ---E°x 4 2 4 ...为线偏振光,振动方向为疔-X2、试证明:频率相同,振幅不同的右旋与左旋圆偏振光能合成一椭圆偏振光。
旋椭圆偏振光。
3、把一根截面是矩形的玻璃棒(折射率为1.5)弯成马蹄形,如图所示。
物理光学第5讲习题答案

快 x
起偏器
测定
y 快
检偏器
25.一块厚度为0.05mm的方解石波片放在两个正交的线偏振器中间,波片的光轴方 向与两线偏振器透光轴的夹角为 ,问在可见光范围内哪些波长的光不能透过这 一系统?
【解】
【解】
21.为测定波片的相位延迟角 ,采用教材图15-85所示的实验装置:使一束自然 光相继通过起偏器、待测波片、 片和检偏器。当起偏器的透光轴和 的快 轴沿x轴,待测波片的快轴与x轴成 角时,从 片透出的是线偏振光,用检偏 器确定它的振动方向便可得到待测玻片的相位延迟角。试用琼斯计算法说明这一 原理。
【Hale Waihona Puke 】19. 导出长短轴之比为2:1、且长轴沿x轴的左旋和右旋椭圆偏振光的琼斯矢量,并 计算这两个偏振光叠加的结果。
【解】
18.为了决定一束圆偏振光的旋转方向,可将 片置于检偏器之前,再将后者转 至消光位置。此时 片快轴的方位是这样的:需将它沿着逆时针方向转 才能 与检偏器的透光轴重合。问:该圆偏振光是右旋还是左旋?
【证】
15.一束线偏振的钠黄光(
)垂直通过一块厚度为
的石英晶
片。晶片折射率为
。光轴沿x方向(见教材图15-84),试对于
以下三种情况,决定出射光的偏振态。
1 入射线偏振光的振动方向与x轴成 角;
2 入射线偏振光的振动方向与x轴成 角;
3 入射线偏振光的振动方向与x轴成 角。
【解】
17.通过检偏器观察一束椭圆偏振光,其强度随着检偏器的旋转而改变。当检偏 器在某一位置时,强度为极小,此时在检偏器前插入一块 片,转动 片使 它的快轴平行于检偏器的透光轴,再把检偏器沿顺时针方向转过 就完全消光。 试问: 1 该椭圆偏振光是右旋还是左旋? 2 椭圆的长短轴之比?
物理光学练习册答案完整版

物理光学知识点汇总一、 名词:(共41个)1、 全 反 射:光从光密介质入射到光疏介质,并且当入射角大于临界角时,在两个不同介质的分界面上,入射光全部返回到原介质中的现象,就叫全反射。
2、 折射定律:①折射光位于由入射光和法线所确定的平面内。
②折射光与入射光分居在法线的两侧。
③折射角与入射角满足:n n I I '='sin sin 。
3、 瑞利判据:(注:考试时答哪个都对)定义一:一个点物衍射图样的中央极大与近旁另一点物衍射图样的第一极小重合,作为光学系统的分辨极限,认为此时系统恰好可以分辨开两个点物,称此分辨标准为瑞利判据。
定义二:两个波长的亮条纹只有当它们合强度曲线中央极小值低于两边极大值的0.81时才能被分辨开。
4、 干 涉:在两个(或多个)光波叠加的区域,某些点的振动始终加强,另一些点的振动始终减弱,形成在该区域内稳定的光强强弱分布的现象。
5、 衍 射:通俗的讲,衍射就是当入射光波面受到限制后,将会背离原来的几何传播路径,并呈现光强不均匀分布的现象。
6、 倏 逝 波:沿着第二介质表面流动的波。
7、 光拍现象:光强随时间时大时小变化的现象。
8、 相干光束会聚角:对应干涉场上某一点P 的两支相干光线的夹角)(ω。
9、 干涉孔径角:对于干涉场某一点P 的两支相干光线从光源发出时的张角)(β。
10、 缺级现象:当干涉因子的某级主极大值刚好与衍射因子的某级极小值重合,这些主极大值就被调制为零,对应级次的主极大就消失了,这种现象就是缺级。
11、 坡印亭矢量(34、辐射强度矢量):它表示单位时间内,通过垂直于传播方向的,单位面积的电磁能量的大小。
它的方向代表的是能量流动的方向,B E S⨯=μ1。
12、 相干长度:对于光谱宽度为λ∆的光源而言,能够发生干涉现象的最大光程差。
13、 发光强度:辐射强度矢量的时间平均值)(I 。
14、 全偏振现象(15、布儒斯特角):当入射光是自然光,入射角满足o 9021=+θθ时,0=P r ,0≠s r ,即反射光中只有S 波,没有P 波,这样的现象就叫全偏振现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章光的电磁理论1.1在真空中传播的平面电磁波,其电场表示为Ex=0,Ey=0,Ez=(102)Cos[π×1014(t−xc )+π2],(各量均用国际单位),求电磁波的频率、波长、周期和初相位。
解:由Ex=0,Ey=0,Ez=(102)Cos[π×1014(t−x c )+π2],则频率υ= ω2π=π×10142π=0.5×1014Hz,周期T=1/υ=2×10-14s,初相位φ0=+π/2(z=0,t=0),振幅A=100V/m,波长λ=cT=3×108×2×10-14=6×10-6m。
1.2.一个平面电磁波可以表示为Ex=0,Ey=2Cos[2π×1014(zc −t)+π2],Ez=0,求:(1)该电磁波的振幅,频率,波长和原点的初相位是多少?(2)波的传播和电矢量的振动取哪个方向?(3)与电场相联系的磁场B的表达式如何写?解:(1)振幅A=2V/m,频率υ=ω2π=2π×10142π=1014Hz,波长λ=cυ=3×1081014=3×10−6m,原点的初相位φ0=+π/2;(2)传播沿z轴,振动方向沿y轴;(3)由B=1c(e k⃗⃗⃗⃗ ×E⃗),可得By=Bz=0,Bx=2c Cos[2π×1014(zc−t)+π2]1.3.一个线偏振光在玻璃中传播时可以表示为Ey=0,Ez=0,Ex=102Cos[π×1015(z0.65c−t)],试求:(1)光的频率;(2)波长;(3)玻璃的折射率。
解:(1)υ=ω2π=π×10152π=5×1014Hz;(2)λ=2πk =2ππ×1015/0.65c=2×0.65×3×1081015m=3.9×10−7m=390nm;(3)相速度v=0.65c,所以折射率n=cv =c0.65c≈1.541.4写出:(1)在yoz平面内沿与y轴成θ角的k⃗方向传播的平面波的复振幅;(2)发散球面波和汇聚球面波的复振幅。
解:(1)由Ẽ=A exp(ik⃗∙r ),可得Ẽ= A exp[ik(ycosθ+zsinθ)];(2)同理:发散球面波Ẽ(r,t)=A r exp(ikr)= A1rexp(ikr),汇聚球面波Ẽ(r,t)=A r exp(−ikr)= A1rexp(−ikr)。
1.5一平面简谐电磁波在真空中沿正x方向传播。
其频率为4×1014Hz,电场振幅为14.14V/m,如果该电磁波的振动面与xy平面呈45º,试写出E,B 表达式。
解:E⃗=E y e y⃗⃗⃗⃗ +E z e z⃗⃗⃗ ,其中E y=10exp[i(2πλx−2πυt)]=10exp[i(2πυcx−2πυt)]=10exp[i(2π×4×10143×108x−2π×4×1014t)]=10exp[i(83×106π)(x−3×108t)],同理:E z=10exp[i(83×106π)(x−3×108t)]。
B⃗ =1c(k0⃗⃗⃗⃗ ×E⃗)=−B y e y⃗⃗⃗⃗ +B z e z⃗⃗⃗ ,其中B z=103×108exp[i(83×106π)(x−3×108t)]=B y。
1.6一个沿k方向传播的平面波表示为E=100exp{i[(2x+3y+4z)−16×105t]},试求k方向的单位矢k0。
解:|k⃗|=√22+32+42=√29,又k⃗=2e x⃗⃗⃗ +3e y⃗⃗⃗⃗ +4e z⃗⃗⃗ ,∴k0⃗⃗⃗⃗ =√29x⃗⃗⃗ +3e y⃗⃗⃗⃗ +4e z⃗⃗⃗ )。
1.9证明当入射角θ1=45º时,光波在任何两种介质分界面上的反射都有r p=r s2。
证明:r s=sin(θ1−θ2)sin(θ1+θ2)=sin45ºcosθ2−cos45ºsinθ2sin45ºcosθ2+cos45ºsinθ2=cosθ2−sinθ2cosθ2+sinθ2=1−tanθ21+tanθ2r p=tan(θ1−θ2)tan(θ1+θ2)=(tan45º−tanθ2)/(1+tan45ºtanθ2)(tan45º+tanθ2)/(1−tan45ºtanθ2)=(1−tanθ21+tanθ2)2=r s21.10证明光束在布儒斯特角下入射到平行平面玻璃片的上表面时,下表面的入射角也是布儒斯特角。
证明:由布儒斯特角定义,θ+i=90º,设空气和玻璃的折射率分别为n1和n2,先由空气入射到玻璃中则有n1sinθ=n2sin i,再由玻璃出射到空气中,有n2sinθ′=n1sin i′,又θ′=i,∴n1sin i′=n1sinθ⇒i′=θ,即得证。
1.11平行光以布儒斯特角从空气中射到玻璃(n=1.5)上,求:(1)能流反射率R p和R S;(2)能流透射率T p和T s。
解:由题意,得n=n2n1=1.5,又θ为布儒斯特角,则θ+i=90°.....①n1sinθ=n2si̇n i⇒sinθ=nsini..... ②由①、②得,θ=56.31°,i=33.69°。
(1)R p=tan2(θ−ⅈ)tan2(θ+ⅈ)=0,R s=sⅈn2(θ−ⅈ)sⅈn2(θ+ⅈ)=0.148=14.8%,(2)由R p+T p=1,可得T p=1,同理,T s=85.2%。
1.12证明光波在布儒斯特角下入射到两种介质的分界面上时,t p=1n⁄,其中n=n2∕n1。
证明:t p=2sinθ2cosθ1sin(θ1+θ2)cos(θ1−θ2),因为θ1为布儒斯特角,所以θ2+θ1=90°,t p=2sinθ2cosθ1sin90°cos(θ1−θ2)=2sinθ2cosθ1cos(90°−θ2−θ2)=2sinθ2cosθ1sin(2θ2)=2sinθ2cosθ12sinθ2cosθ2=sinθ2sinθ1,又根据折射定律n1sinθ1=n2sinθ2,得sinθ2sinθ1=n1n2=1n,则t p=1n,其中n=n2∕n1,得证。
1.17利用复数表示式求两个波E1=a cos(kx+ωt)和E2=−a cos(kx−ωt)的合成。
解:E=E1+E2=a[cos(kx+ωt)−cos(kx−ωt)] =aexp[i(kx+ωt)]−aexp[i(kx−ωt)]=aexp(ikx)(eⅈωt−e−ⅈωt)=2a sin(ωt)exp(i cos kx−sin kx)=−2aexp[i(kx+π2)]sin(ωt)。
1.18两个振动方向相同的单色波在空间某一点产生的振动分别为E1=a1cos(φ1−ωt)和E2=a2cos(φ2−ωt)。
若ω=2π×1015Hz,a1=6V/m,a2=8V/m,φ1=0,φ2=π∕2,求该点的合振动表达式。
解:E=E1+E2=a1cos(φ1−ωt)+a2cos(φ2−ωt)=6cos(−2π×1015t)+8cos(π2−2π×1015t)=6cos(2π×1015t)+8sin(2π×1015t)=10cos(arccos610−2π×1015t)=10cos(53°7′48′′−2π×1015t)。
1.20求如图所示的周期性三角波的傅立叶分析表达式。
解:由图可知,E(z)={z(0<z≤λ2⁄)−z+λ(λ∕2<z≤λ),A0=2λ∫E(z)ⅆzλ=2λ(∫zⅆzλ∕2+∫(−z+λ)ⅆzλλ∕2)=λ2,A m=2λ∫E(z)cosλ(mkz)ⅆz=2λ(∫E(z)cos mkzⅆzλ2⁄+∫E(z)cos mkzⅆzλλ2⁄)=2λ·(−22m2k2)=−8λ·λ2m2(2π)2=−2λm2(2π)2,(m为奇数),B m=2λ∫E(z)sinmkzⅆz=0λ,所以E(z)=λ4−2λπ2∑(cos mkz m2⁄)∞m=1=λ4−2λπ2(cos kz12+cos3kz32+cos5kz52+···)。
1.21试求如图所示的周期性矩形波的傅立叶级数的表达式。
解:由图可知,E(z)=1(−λ∕a<z<λ∕a),A0=2λ∫E(z)ⅆzλ=2λ(∫ⅆzλ∕a+∫ⅆzλλ−λ∕a)=4aA m=2λ∫E(z)cosλ(mkz)ⅆz=2λ(∫cos mkzⅆz+∫cos mkzⅆzλλ−λa⁄λa⁄)=2πmsin2mπa,B m=2λ∫E(z)sinmkzⅆz=0λ,所以E(z)=2a+∑2πm∞m=1sin2mπacos mkz。
1.22利用复数形式的傅里叶级数对如图所示的周期性矩形波做傅里叶分析。
解:由图可知,E (z )={1(0<z <λ2⁄)−1(λ2⁄<z <λ),A 0=2λ∫E (z )ⅆz λ0=∫ⅆz λ∕2+∫(−1)ⅆz λλ∕2=0,A m =2λ∫E (z )cos λ0(mkz )ⅆz =0,B m =2λ∫E (z )sinmkz ⅆz λ0,=2λ(∫sin mkz ⅆz λ0−∫sin mkz ⅆz λλ∕2)=1πm(2−2cos mπ),所以E (z )=1π∑1m(2−2cos mπ)∞m=1sin mkz=4π(sin kz +13sin 3kz +15sin 5kz +···)1.23氪同位素k r86放电管发出的红光波长为λ=605.7nm ,波列长度约为700mm ,试求该光波的波长宽度和频率宽度。
解:由题意,得,波列长度2L =700mm , 由公式Δλ=λ22L=605.72700×106=5.2×10−4nm ,又由公式2L =c/Δν,所以频率宽度Δν=c 2L=3×108700×10−3Hz =4.3×108Hz 。
1.24某种激光的频宽Δv =5.4×104Hz ,问这种激光的波列长度是多少? 解:由相干长度D max =λ2Δλ=c Δν,所以波列长度2L =λ2Δλ=c Δν=3×1085.4×104=5.55×103m 。
