常用图像去模糊算法分析与对比

合集下载

如何使用图像处理技术进行图像去模糊处理

如何使用图像处理技术进行图像去模糊处理图像去模糊处理是一项常见的图像处理任务，它可以提高图像的清晰度和细节，并改善图像的视觉质量。

在本文中，我们将介绍一些常用的图像处理技术，帮助您有效地去除模糊，使图像更加清晰。

了解图像模糊的原因对于进行有效的图像去模糊处理至关重要。

图像模糊通常是由于相机晃动、主体运动或镜头不聚焦等因素导致的。

根据模糊的原因，我们可以选择不同的图像处理方法。

一种常见的图像去模糊处理方法是使用图像霍夫变换（IHT）来估计模糊核。

图像霍夫变换可以帮助我们理解和分析图像中的直线、圆形、椭圆形等形状。

通过将图像转换为霍夫空间，我们可以找到对应于图像模糊的潜在模糊核。

我们可以利用找到的模糊核来进行图像去模糊处理。

另一种常用的图像去模糊处理方法是使用盲复原算法。

这种方法不需要事先知道模糊核的大小和形状，而是通过对图像进行反卷积来估计模糊核和原始图像。

盲复原算法基于图像的统计特性和先验知识来恢复模糊的图像。

这种方法在处理复杂的图像模糊时往往比较有效。

除了上述的方法，我们还可以使用一些常见的图像增强技术来改善图像的清晰度。

例如，锐化滤波器可以增强图像的边缘和细节，减少图像的模糊。

锐化滤波器可以通过增强高频分量或降低低频分量来实现。

还有一些其他的图像增强技术，如非锐化掩蔽（USM）、双边滤波（Bilateral Filter）等，它们都可以帮助我们提高图像的清晰度和细节。

在使用图像处理技术进行图像去模糊处理时，我们还应该注意一些常见的注意事项。

要根据图像的模糊程度选择合适的处理方法。

对于轻微模糊的图像，简单的滤波器可能就足够了，而对于严重模糊的图像，则可能需要更复杂的处理方法。

要注意图像去模糊处理过程中可能产生的图像伪影或噪点。

这些伪影和噪点可能会降低图像的质量，因此我们需要在处理过程中进行适当的去除或减少。

总之，图像去模糊处理是一项重要的图像处理任务，可以大大改善图像的质量和细节。

在处理图像模糊时，我们可以选择合适的图像处理技术，如图像霍夫变换、盲复原算法和图像增强技术等。

ps各种模糊的区别和用法

ps各种模糊的区别和用法
在图像处理领域，对图像应用模糊算法可以使图像变得模糊或者柔和。

下面是几种常见的模糊算法及其区别和用法：
1. 均值模糊（Mean Blur）：均值模糊是一种简单的模糊算法，通过取周围像素的平均值来模糊图像。

它可以平滑图像并去除一些细节，常用于降噪和模糊效果的应用。

2. 高斯模糊（Gaussian Blur）：高斯模糊是一种常见的模糊算法，通过在图像上应用高斯核函数来模糊图像。

使用高斯函数作为卷积核可以使得离中心越远的像素对结果的贡献越小，从而得到更柔和的效果。

高斯模糊常用于平滑图像、边缘检测前的预处理和模糊背景等应用。

3. 中值模糊（Median Blur）：中值模糊是一种基于统计的模
糊算法，通过将像素的值替换为它们相邻像素的中值来模糊图像。

它可以有效地去除孤立的噪点和小细节，对于椒盐噪声有良好的效果。

4. 运动模糊（Motion Blur）：运动模糊是一种模拟相机或物体运动造成的模糊效果的算法。

它通过在图像上应用线性模糊来模拟运动，常用于模拟摄影中的运动效果。

5. 形态学模糊（Morphological Blur）：形态学模糊是一种基于形态学操作的模糊算法，常用于去除细线、小斑点和填补一些小孔的应用。

它通过应用腐蚀和膨胀操作来模糊图像，从而改变图像的形状和结构。

这些模糊算法可以在各种图像处理软件和编程库中找到，并根据需要调整参数来达到不同的效果。

应根据具体的应用场景和需求来选择合适的模糊算法。

反模糊化常用的方法

反模糊化常用的方法
反模糊化（Deblurring）是一种用于恢复模糊图像或图像细节的方法。

下面是一些常用的反模糊化方法：
1. Wiener滤波器：Wiener滤波器是一种经典的反模糊化方法。

它基于信号和噪声的统计特性，通过频域或空域处理，对图像进行去模糊处理。

Wiener滤波器在去除模糊的同时，也会引入一定的噪声。

2. 傅里叶变换：使用傅里叶变换可以将图像从时域转换为频域，并采用频域滤波方法进行图像反模糊。

一种常用的方法是将图像通过傅里叶变换得到频域表示，然后进行滤波或修复，最后通过逆傅里叶变换得到恢复后的图像。

3. 盲去卷积：盲去卷积是一种无需事先知道模糊核的方法。

它通过迭代算法或优化过程，估计并反转模糊核，进而实现图像的反模糊。

4. 最小二乘法：最小二乘法是一种常见的数学优化方法，常用于图像反模糊。

它通过对图像进行重建，最小化重建图像与观测图像之间的均方误差，从而达到减小模糊效果的目的。

5. 统计模型：反模糊化方法中的一些技术使用统计模型来描述模糊过程和图像噪声，并通过最大似然估计或其他方法来恢复原始图像。

这些方法依靠对观测数据的统计分析，
从而实现图像的反模糊化。

需要注意的是，不同的反模糊化方法适用于不同的模糊情况和图像特点。

选择适合的反模糊化方法需要根据具体的应用场景和实际情况进行评估和选择。

此外，由于模糊是不可逆的过程，完美的反模糊化可能是不可能的，因此反模糊化结果可能仍然存在一定的模糊或伪影。

图像去模糊算法分析与研究

本科毕业设计（论文）题目: 图像去模糊算法对比分析研究学院:专业：班级:学号:学生姓名：指导教师：职称：二○一五年六月一日图像去模糊算法分析与研究摘要在数字时代,图像去模糊作为图像复原技术的一个分支，一直是一个具有挑战和吸引力的问题，具有重大的研究价值与社会意义。

图像去模糊技术近年来得到了广泛研究，在理论和算法上也愈加系统和成熟,根据图像模糊核是否已知,图像去模糊技术被分为非盲图像去模糊和盲图像去模糊两大类。

文章主要是选取几种典型的去模糊算法，在已知模糊核的基础上进行分析研究各算法的特点与去模糊效果的优劣性，即非盲去模糊算法的分析研究。

基于运动模糊和离焦模糊这两大模糊类型，对其分别在有噪声（本文指高斯白噪声）和无噪声情况下的实验结果进行分析比较。

文章首先介绍了两种主要模糊图像类型及其造成图像模糊的成因，并对各模糊类型的点扩散函数估计获取。

其次,是对图像基本退化模型的引入，从本质上了解图像模糊与去模糊的实质。

接着，我们介绍了两类典型的去模糊评价方法:峰值信噪比（Peak Signal to Noise Ratio）和平均结构相似性指数(Mean Structural Similarity Index）。

在这之后主要是算法比较，分类对几种典型的去模糊算法进行数学分析与讨论，包括用于去除运动模糊的Richardson-Lucy算法（即RL算法)和约束最小二乘法；用于去除离焦模糊的逆滤波算法和维纳滤波算法（Wiener filtering)。

最后对几种算法进行Matlab仿真实验设计，并对其结果与恢复效果分析总结。

关键词：离焦模糊；运动模糊；点扩散函数；算法比较；仿真设计AbstractIn digital times，image de—blurring as a branch of image restoration technology has been a hard and attractive problem. However, image restoration has great value of the research and social significance。

数字图像处理中的去模糊技术研究

数字图像处理中的去模糊技术研究第一章前言数字图像处理技术发展到了今天，随着硬件性能和算法的不断提升，很多以前被认为是“不可能完成”的任务都变得越来越容易了。

其中，去模糊技术就是其中之一。

去模糊技术在计算机视觉、医学影像、安防监控等领域有着广泛的应用。

本文将针对数字图像处理中的去模糊技术进行研究和探讨。

第二章基本概念2.1 模糊模糊指的是由于图像成像过程中的物理限制或非物理限制引起的图像不清晰现象。

模糊一般分为运动模糊、缩放模糊、气胶散射模糊、几何变换模糊、镜头透镜偏差模糊等多种类型。

2.2 图像去模糊图像去模糊技术旨在消除图像中的模糊现象，使得图像变得更加清晰。

图像去模糊任务可以分为盲模糊（blind deconvolution）和非盲模糊（non-blind deconvolution）两种。

2.3 盲模糊和非盲模糊盲模糊是指对于一张图像，我们并不知道图像的模糊类型和参数，需要先进行复原操作才能够获得。

非盲模糊则是指在进行模糊处理时，我们已经知道了模糊类型和参数，因此可以直接进行复原。

第三章常见的去模糊算法3.1 维纳滤波算法维纳滤波通过把图像和点传递函数（PSF）转换到频域，然后进行噪声处理，在频域中进行滤波操作。

它在处理非常强烈的噪声和平稳模糊问题时非常有效，但在强模糊情况下容易出现过度平滑的问题。

3.2 逆滤波算法逆滤波算法是指通过对模糊图像进行傅里叶变换，得到其频率分布，然后通过频率域滤波进行逆变换，得到清晰的原始图像。

但在强噪声情况下，逆滤波算法容易产生振铃现象。

3.3 去卷积算法假设模糊图像的生成过程为卷积，去卷积算法就是通过图像卷积的反向操作来进行复原。

但是由于卷积操作是不可逆的，因此去卷积算法在处理强噪声和强模糊的情况下很容易出现过度平滑的问题。

3.4 基于深度学习的方法近年来，随着深度学习技术的大力发展，去模糊算法也得到了很大的进一步。

基于深度学习的去模糊算法可以通过学习大量的清晰和模糊图像对来学习到图像的统计特性，从而达到更好的去模糊效果。

常用图像去模糊算法分析与对比

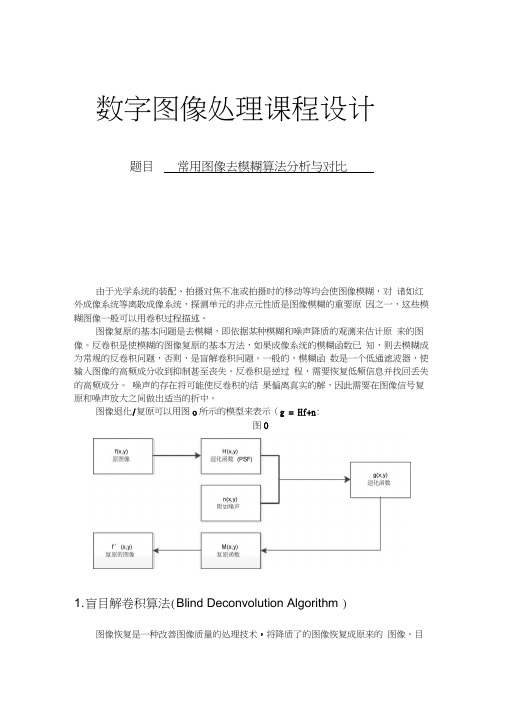
数字图像处理课程设计题目常用图像去模糊算法分析与对比由于光学系统的装配、拍摄对焦不准或拍摄时的移动等均会使图像模糊，对诸如红外成像系统等离散成像系统，探测单元的非点元性质是图像模糊的重要原因之一，这些模糊图像一般可以用卷积过程描述。

图像复原的基本问题是去模糊，即依据某种模糊和噪声降质的观测来估计原来的图像。

反卷积是使模糊的图像复原的基本方法，如果成像系统的模糊函数已知，则去模糊成为常规的反卷积问题，否则，是盲解卷积问题。

一般的，模糊函数是一个低通滤波器，使输入图像的高频成分收到抑制甚至丧失。

反卷积是逆过程，需要恢复低频信息并找回丢失的高频成分。

噪声的存在将可能使反卷积的结果偏离真实的解，因此需要在图像信号复原和噪声放大之间做出适当的折中。

图像退化/复原可以用图o所示的模型来表示（g = Hf+n:图01. 盲目解卷积算法(Blind Deconvolution Algorithm )图像恢复是一种改善图像质量的处理技术，将降质了的图像恢复成原来的图像。

目前, 图像恢复的方法很多, 然而在图像恢复过程中, 最难解决的问题之一是如何获得恢复算法中PSF勺恰当估计,那些不以PSF知识为基础的图像恢复方法统称为盲去卷积算法。

盲去卷积的方法已经受到了人们的极大重视, 对于给定的原图像, 使其退化, 得到退化图像, 再利用盲去卷积的方法使其恢复, 得到视觉质量上更好的图像。

盲解卷积的方法是以最大似然估计(MLE )为基础的，即一种用被随机噪声所干扰的量进行估计的最优化策略。

似然函数用g ( x, y ) f ( x, y )和h( x, y来加以表达, 然后问题就变成了寻求最大似然函数。

在盲解卷积中, 最优化问题用规定的约束条件并假定收敛时通过迭代来求解,得到的最大f( x, y 和 h (x, y就是还原的图像和PSF。

【函数】deconvblind【功能】使用盲解卷积算法对图像进行去模糊[J,PSF] = DECONVBLIND(I,INITPSF) deconvolves image I using maximum likelihood algorithm, returning both deblurred image J and a restoredpoint-spread function PSF. The resulting PSF is a positive array of the same size as the INITPSF, normalized so its sum adds to 1. The PSF restoration is affected strongly by the size of its initial guess, INITPSF, and less by its values (an array of ones is a safer guess).使用盲解卷积对图像I进行去模糊，得到去模糊后的图像J和重建点扩散函数矩阵PSF参量INITPS为矩阵，表示重建点扩散函数矩阵的初始值。

如何使用图像处理技术对图像进行模糊处理

如何使用图像处理技术对图像进行模糊处理图像模糊处理技术是一种常见的图像处理方法，它可以用于各种应用，如图像美化、隐私保护以及图像分析等。

图像模糊化是一种将图像中的细节信息进行模糊处理，使得图像变得模糊不清的技术。

在图像处理领域，有多种方法可以用于图像模糊处理，下面将介绍几种常用的图像模糊处理技术。

1. 高斯模糊（Gaussian Blur）高斯模糊是一种常用的图像模糊方法。

它使用了高斯滤波器对图像进行卷积处理，通过对图像中每个像素点周围的像素进行加权平均，达到模糊化的效果。

高斯模糊可以通过调整滤波器的大小和标准差来控制模糊程度。

2. 均值模糊（Mean Blur）均值模糊是另一种常见的图像模糊方法。

它使用了均值滤波器对图像进行卷积处理，通过取周围像素的平均值来模糊图像。

均值模糊可以通过调整滤波器的大小来控制模糊程度。

3. 运动模糊（Motion Blur）运动模糊是一种模拟快速运动场景中图像模糊效果的方法。

它通过对图像进行卷积操作，使用线性滤波器模拟快速运动时的模糊效果。

运动模糊可以通过调整滤波器的方向和长度来控制模糊的效果。

4. 特定形状模糊（Shape Blur）特定形状模糊是一种利用特定形状的滤波器对图像进行卷积处理的方法。

这种方法可以实现各种特定形状的模糊效果，例如圆形模糊、方形模糊等。

特定形状模糊可以通过调整滤波器的形状和大小来控制模糊程度。

5. 镜头模糊（Lens Blur）镜头模糊是一种模拟摄像机镜头焦点不准确导致图像模糊效果的方法。

它通过对图像进行卷积操作，使用不同半径和强度的滤波器模拟镜头的焦点效果。

镜头模糊可以通过调整滤波器的参数来控制模糊的效果。

在实际应用中，图像模糊处理技术可以应用于各种场景。

例如，用于保护隐私的模糊化处理可以应用于监控摄像头、照片中的人脸等，以保护个人隐私。

图像美化中的模糊处理可以用于给照片添加艺术效果，使得照片更加柔和、浪漫。

图像模糊处理还可以应用在图像分析中，通过模糊化处理提取图像的整体特征，用于图像分类、对象识别等任务。

图像去模糊算法研究与实现

图像去模糊算法研究与实现概述：图像模糊是指图像失去了清晰度和细节，使得图像看起来模糊不清。

图像去模糊算法是指通过数学和图像处理技术，尝试在一定程度上恢复被模糊的图像的清晰度和细节。

本文将研究不同的图像去模糊算法，并通过代码实现来验证其效果。

1. 图像去模糊算法的原理图像模糊是由于摄像机或者图像采集设备的光学系统或者图像采集过程中的运动模糊等造成的。

因此，图像去模糊算法的核心是根据模糊产生的原理和过程，进行数学建模和图像处理，以恢复原始图像。

1.1 维纳滤波算法维纳滤波是一种经典的图像去模糊算法，它通过对图像进行频域分析，利用频域图像的特性对模糊图像进行滤波操作。

维纳滤波算法通过加权平均滤波和反卷积操作，尽可能地减小模糊的影响，同时保留尽可能多的图像细节。

1.2 直接逆滤波算法直接逆滤波算法是一种基于频域分析的算法，它通过计算图像的傅里叶变换和逆变换，直接对图像进行滤波操作。

直接逆滤波算法能够完全去除模糊，但由于存在噪声或者其他干扰因素，可能会引入大量的伪影。

1.3 自适应模糊图像去模糊算法自适应模糊图像去模糊算法是一种基于图像分析的算法，它通过分析图像的模糊程度和模糊类型，自动选择合适的去模糊方法。

自适应模糊图像去模糊算法能够根据不同的图像特点和模糊情况，选择最适合的算法来去除图像模糊。

2. 图像去模糊算法的实现为了验证不同的图像去模糊算法的效果，在本文中将选取一些经典的算法进行实现。

2.1 维纳滤波算法的实现维纳滤波算法的实现分为以下几个步骤：- 对原始图像进行傅里叶变换，得到频域图像；- 对频域图像进行滤波操作，根据维纳滤波算法的公式进行权重计算；- 对滤波后的频域图像进行逆变换，得到去模糊的图像。

2.2 直接逆滤波算法的实现直接逆滤波算法的实现分为以下几个步骤：- 对原始图像进行傅里叶变换，得到频域图像；- 计算频域图像的逆滤波函数，根据公式进行计算；- 对滤波后的频域图像进行逆变换，得到去模糊的图像。

常用图像去噪方法比较及其性能分析

常用图像去噪方法比较及其性能分析发表时间：2019-03-15T15:13:24.833Z 来源：《信息技术时代》2018年6期作者：孟靖童王靖元[导读] 本文介绍了噪声的分类模型，之后又分别介绍了空间域去噪、傅里叶去噪算法以及小波去噪中的部分算法，并分别对相似算法进行了分析比较。

（国际关系学院，北京 100091）摘要：本文介绍了噪声的分类模型，之后又分别介绍了空间域去噪、傅里叶去噪算法以及小波去噪中的部分算法，并分别对相似算法进行了分析比较。

同时为了更好的比较出各算法之间的去噪差别针对其中部分去噪算法进行了用matlab的实现，比较了去噪的效果。

关键词：数字图像；噪声；滤波一、引言随着当今社会数字化的普及，人们传递图像信息的方式已经从之前单纯的实物传递变为当今的数字图像的传递。

然而由于各种原因会导致数字图像真实性减弱。

针对这种问题，数字图像处理技术应运而生。

数字图像处理技术的产生，不仅满足了人们的视觉，同时经过处理的图像还可以更好的应用于图像加密，图像识别等领域。

二、空间域去噪算法（一）均值滤波去噪通过计算某一滤波目标区域内的算数平均值来替代目标区域中心所对应的像素值的方法来达到去除噪声的目的。

而加权均值滤波则是在原有均值滤波的基础上，通过对某些更趋进于真实像素的点进行加权的方法来达到更好的去噪效果，使最终区域中心像素更加趋近于真实像素。

利用均值滤波可以很好的去除由高斯噪声带来的对于图像的影响，然而对于由于椒盐噪声带来的对于图像的影响，均值滤波去除的效果并不很好。

同时，由于均值滤波的算法是通过取目标范围内一小区域中点灰度值的平均值，来决定区域中心点灰度值的，所以不可避免的造成图像经过均值滤波后会导致图像部分原始真实细节被滤掉，造成视觉上细节不清楚的情况。

并且所取范围越大，图像中细节部分越不清晰，图像越平滑。

（二）中值滤波去噪通过求区域中心点及其周围点灰度值的中值，来代替该中心点的灰度值。

因此利用中值去噪的方法可以较好的弥补均值滤波对于图像边缘不清晰处理的缺点。

图像处理中的图像识别算法研究与比较分析

图像处理中的图像识别算法研究与比较分析摘要：图像识别是图像处理领域中的重要任务之一，它在各个领域都有广泛应用。

本文将深入研究和比较几种常用的图像识别算法，包括传统的人工设计算法和基于深度学习的算法。

通过比较它们的性能和适用性，为读者提供选择合适算法的参考依据。

一、引言图像识别是图像处理中一个重要的研究方向，它致力于将图像中的内容转化为可供计算机理解和处理的信息。

图像识别的应用范围非常广泛，包括人脸识别、物体检测、场景理解等。

本文将对图像处理中的图像识别算法进行研究与比较分析，以帮助读者了解各个算法的原理、性能和适用领域。

二、传统的图像识别算法1. 特征提取算法传统的图像识别算法通常基于手工设计的特征提取方法，其目标是将图像中的特定信息提取出来。

常见的特征提取算法包括灰度共生矩阵(GLCM)、Gabor滤波器、SIFT、HOG等。

这些算法通过提取图像的纹理、形状、边缘等特征信息，来描述图像的内容。

然后通过采用各种分类器或者回归模型来实现图像识别。

2. 模板匹配算法模板匹配算法是一种常用的基于相似度度量的图像识别算法。

该算法通过将输入图像与事先准备好的模板进行比较，来判断输入图像中是否存在模板目标。

模板匹配算法一般包括灰度化、归一化、匹配度量等步骤。

常见的模板匹配算法有均方差匹配法、相交匹配算法、相关匹配法等。

三、基于深度学习的图像识别算法近年来，随着深度学习的快速发展，基于深度学习的图像识别算法在图像处理领域中取得了突破性的进展。

该类算法通常利用深度神经网络进行特征提取和模式识别。

1. 卷积神经网络(CNN)卷积神经网络是一种用于图像识别的深度学习模型。

该模型通过多层卷积和池化操作来提取图像中的特征。

然后将提取到的特征输入全连接层进行分类或回归。

CNN具有参数共享和局部连接等特点，能够有效地处理图像的空间结构信息。

它在图像识别任务中表现出色，特别是对于大规模数据集和复杂问题的处理能力优秀。

2. 循环神经网络(RNN)循环神经网络是一种用于时序数据处理的深度学习模型，也可用于图像识别任务。

如何使用图像处理技术进行图像去模糊

如何使用图像处理技术进行图像去模糊图像去模糊是一种常见的图像处理技术，它可以提高图像的清晰度和细节，使得模糊的图像变得更加清晰。

在本文中，我们将探讨如何使用图像处理技术进行图像去模糊。

图像去模糊的方法取决于模糊的原因。

图像模糊通常可以分为两种类型：运动模糊和晕影模糊。

运动模糊是由于相机或拍摄对象的运动造成的，而晕影模糊则是由于光线散射或透镜问题引起的。

不同类型的模糊需要不同的处理方法。

对于运动模糊的图像，一种常见的去模糊方法是逆滤波。

逆滤波使用图像的频谱信息来恢复原始图像。

逆滤波的基本原理是将图像的频谱与模糊函数的频谱相除来消除模糊效果。

然而，逆滤波容易受到噪声的干扰，因此在实际应用中需要进行一定的处理，例如添加正则化约束或使用滤波技术来减少噪声。

另一种常见的去模糊方法是盲去卷积。

盲去卷积是一种无需事先知道模糊函数的方法，它通过估计图像和模糊核之间的关系来恢复原始图像。

盲去卷积的主要思想是在模糊图像上进行反卷积操作，并通过迭代过程来优化结果。

与逆滤波相比，盲去卷积对于噪声的鲁棒性更好。

然而，盲去卷积的计算量较大，需要较长的处理时间。

对于晕影模糊的图像，一种常用的去模糊方法是维纳滤波。

维纳滤波是一种最小化均方误差的滤波技术，它可以通过对噪声和模糊函数进行估计来恢复原始图像。

维纳滤波的主要思想是在频域上对图像进行滤波，以减小噪声和模糊效果。

维纳滤波的优点是可以提供较好的去噪和去模糊效果，但它对于边缘和细节的保持效果可能不如其他方法。

除了以上方法，还有一些其他的图像去模糊技术，例如非负矩阵分解、稀疏编码和深度学习等。

这些方法可以根据具体的应用场景选择使用，以获得更好的图像去模糊效果。

无论使用哪种方法进行图像去模糊，都需要注意合理选择参数和处理策略。

参数的选择对于去模糊结果的质量有着重要的影响，因此需要根据具体情况进行调整。

图像去模糊也需要考虑算法的效率和处理时间，以便在实际应用中能够满足实时性的要求。

三种Retinex图像去雾算法比较与分析

三种Retinex 图像去雾算法比较与分析1.引言雾气是自然环境中存在的一种常见现象，但也会对图像的质量造成一定的影响。

在照片或者其他图像应用中，需要进行去雾处理，去除图像中不必要的雾气信息，以此提高图像的清晰度和真实性。

传统的去雾方法主要有强度衰减模型和分层模型，这些方法虽然有效，但是也存在一些缺陷。

强度衰减模型往往会导致图像过度曝光或过度偏暗，同时无法有效处理图像中各种层次的雾气。

分层模型则存在对场景信息的预处理阶段，所以无法适用于实时处理环境。

近年来，Retinex 算法被引入到图像去雾领域，这种算法利用人类视觉系统的对数变换机理，对图像中的光照和颜色进行分离处理，可以有效消除图像中的雾气，提高图像的质量和视觉效果。

目前Retinex 算法在图像去雾中应用较为广泛，但其具体的表现形式和处理效果也存在差异，本篇论文将对三种Retinex 图像去雾算法进行比较和分析。

2.相关工作Retinex 算法最初被提出用于解决人类视觉系统中的色彩恒常性问题。

现有的Retinex 算法可大致分为两类：基于多尺度的Retinex 算法和基于单尺度的Retinex 算法。

基于多尺度的Retinex 算法根据图像中不同尺度的信息进行分离，从而消除图像中的雾气。

这类方法包括经典的multi-scale Retinex 和基于双边滤波器的Retinex 算法。

基于单尺度的Retinex 算法则直接对图像进行处理，常用的有原始Retinex、简单拉普拉斯Retinex（SRR）和显式Retinex 算法等。

不同于传统的强度衰减模型和分层模型，Retinex 算法在处理雾气图像的同时还能够进行去色偏和增强图像细节的效果，因此在应用中表现出更好的效果。

3.三种Retinex 图像去雾算法比较3.1.Multi-scale Retinex 算法Multi-scale Retinex 算法采用了多尺度分离的思想，先对图像进行高斯模糊，然后对每个模糊的版本进行亮度和对比度的调整，从而得到多尺度Retinex 分量。

图像处理算法在农业图像识别中的研究与对比

图像处理算法在农业图像识别中的研究与对比随着科技的迅速发展，图像处理算法在农业图像识别中的应用越来越广泛。

图像处理算法可以通过对农业图像的分析和处理，帮助农民更好地了解农作物的生长情况，优化农业生产，提高农业的效益。

本文将对几种常见的图像处理算法在农业图像识别中的研究和应用进行对比与分析。

一、图像预处理算法在使用农业图像进行识别之前，首先需要对图像进行预处理，以优化图像质量，减少噪音干扰。

常见的图像预处理算法包括灰度化、平滑滤波、边缘检测等。

1. 灰度化算法灰度化算法将彩色图像转换为灰度图像，降低了图像处理的复杂度。

常见的灰度化算法有平均值法、最大值法、最小值法等。

这些算法可以根据实际需求选择，用于农业图像中农作物的生长情况分析。

2. 平滑滤波算法平滑滤波算法可以去除图像中的噪声，提高图像质量。

常见的平滑滤波算法有均值滤波、中值滤波、高斯滤波等。

这些算法可以应用于农业图像中去除植物生长过程中可能产生的噪音。

3. 边缘检测算法边缘检测算法可以帮助农民从图像中提取出作物的边缘信息，进而进行进一步的分析。

常见的边缘检测算法有Sobel算子、Canny算子等。

这些算法可以用于检测农作物的生长状态及可能存在的异常情况。

二、图像特征提取算法图像特征提取算法可以从农业图像中提取出具有代表性的特征，用于农作物的分类和识别。

常见的图像特征提取算法包括颜色特征、纹理特征、形状特征等。

1. 颜色特征提取算法颜色特征提取算法可以提取出农作物图像中的颜色信息，用于农作物的种类分类和异常检测。

常见的颜色特征提取算法有RGB颜色模型、HSV颜色模型等。

2. 纹理特征提取算法纹理特征提取算法可以提取出农作物图像中的纹理信息，用于农作物的生长状态分析和异常检测。

常见的纹理特征提取算法有灰度共生矩阵、Gabor滤波器等。

3. 形状特征提取算法形状特征提取算法可以提取出农作物图像中的形状信息，用于农作物的分类和生长状态分析。

常见的形状特征提取算法有边界描述符、连通区域分析等。

照片模糊化处理

照片模糊化处理照片模糊化处理，顾名思义，是指通过一系列的技术手段，对照片进行模糊效果的加工。

这种处理方法在很多场景中都能够起到重要的作用，比如保护隐私、改善图像质量等。

本文将重点探讨照片模糊化处理的原理、应用以及相关的技术发展。

一、照片模糊化处理的原理照片模糊化处理的原理主要是通过对图像的像素进行模糊操作，降低图像的细节度，使得观察者无法清晰地辨识图像中的特定内容。

一般来说，照片模糊化处理可以通过以下几种方式实现：1. 高斯模糊：高斯模糊是最常用的图像模糊化处理方法之一。

该方法通过将图像中的每个像素点与周围像素的灰度值进行加权平均，从而实现模糊化效果。

这种方法能够有效地降低图像的细节度，使得图像变得更加平滑。

2. 运动模糊：运动模糊是一种通过模拟物体在相机镜头前运动而产生的模糊效果。

该方法通过在图像中添加线性模糊效果，模拟出物体在运动过程中的模糊轨迹，从而达到模糊化处理的效果。

3. 均值模糊：均值模糊是一种简单但有效的图像模糊化处理方法。

该方法通过对图像中每个像素周围的像素值进行均值计算，从而实现模糊化效果。

与高斯模糊不同的是，均值模糊使用的是一个固定的权重矩阵，而不考虑像素之间的距离关系。

二、照片模糊化处理的应用照片模糊化处理在实际应用中有着广泛的用途。

以下是几个常见的应用场景：1. 隐私保护：照片模糊化处理可以有效地保护照片中的隐私信息，比如人脸、车牌等。

通过对这些敏感信息进行模糊化处理，可以确保照片在公开或分享时不泄露个人隐私。

2. 图像融合：在图像融合领域，照片模糊化处理可以用来将两张或多张照片进行无缝衔接。

通过对边缘等进行模糊处理，可以使不同照片在融合时更加自然、平滑。

3. 图片修复：对于老照片或者损坏的照片，通过模糊化处理可以修复图像中的某些缺陷或瑕疵。

通过模糊处理，可以降低缺陷部分的明显性，使整个照片看起来更加完整和清晰。

三、照片模糊化处理的技术发展随着科技的不断进步，照片模糊化处理的技术也在不断发展。

基于深度学习的图像去模糊算法研究

基于深度学习的图像去模糊算法研究近年来，随着深度学习技术的快速发展，基于深度学习的图像处理算法在各个领域展现出了巨大的潜力和应用前景。

其中，图像去模糊算法是一项重要的研究课题，旨在恢复模糊图像的清晰度和细节，提升图像质量。

本文将对基于深度学习的图像去模糊算法进行研究和探讨。

在传统的图像去模糊算法中，常用的方法有盲去卷积、非盲去卷积和基于深度学习的方法。

与传统方法相比，基于深度学习的图像去模糊算法具有更好的性能和更广泛的适用性。

它通过利用深度神经网络对模糊图像进行建模和学习，从而实现更准确的图像去模糊效果。

首先，基于深度学习的图像去模糊算法可以通过构建卷积神经网络（CNN）来提取图像的特征信息。

CNN是一种能够自动学习特征表达的神经网络结构，通过多层卷积和池化层对输入的图像进行层层提取，最终得到图像的高维特征表示。

这种特征表示能够更好地反映图像的结构和纹理信息，为后续的图像去模糊操作提供了有力支持。

其次，基于深度学习的图像去模糊算法可以通过神经网络的训练和优化来实现图像去模糊效果的提升。

通过大量的模糊图像样本和对应的清晰图像样本进行训练，深度学习模型可以学习到模糊图像和清晰图像之间的映射关系，从而能够实现对新的模糊图像进行准确的去模糊处理。

此外，由于深度学习模型具有较强的泛化能力，即使在训练集之外的模糊图像上，也能够获得较好的去模糊效果。

在基于深度学习的图像去模糊算法中，还存在一些常用的网络结构和技术，用于进一步提升图像去模糊的性能和效果。

例如，残差连接（Residual Connection）可以有效地解决网络退化问题，提高网络的非线性建模能力；反卷积层（Deconvolutional Layer）可以实现图像的上采样和还原操作，提升图像的清晰度和细节；生成对抗网络（Generative Adversarial Network，GAN）则可以通过对抗训练的方式进一步提升图像去模糊的效果，使生成的清晰图像与真实清晰图像更加接近。

图像处理技术中的图像去模糊方法分析

图像处理技术中的图像去模糊方法分析近年来，随着数字图像技术的飞速发展，图像去模糊成为图像处理领域中广泛关注的问题之一。

随着各类高清晰度图像的需求增加，如何有效去除图像模糊成为图像处理技术研究的重要方向。

本文将对图像处理技术中的图像去模糊方法进行分析，并介绍常用的去模糊方法。

在图像处理中，图像模糊通常由多种因素引起，例如摄像机移动、镜头振动或图像采集过程中的不稳定因素等。

图像去模糊的目标是通过数学模型和算法将模糊图像转化为更加清晰、锐利的图像。

目前，已经有许多图像去模糊的方法被提出和应用，下面分别介绍以下两种常见的图像去模糊方法。

第一种方法是基于图像退化模型的去模糊方法。

这种方法假设图像模糊是由系统的退化模型引起的，通过对退化模型的建模，可以推导出图像的退化函数。

常见的图像退化模型包括运动模糊模型、模糊点扩散函数等。

基于图像退化模型的去模糊方法将模糊图像与退化模型进行反卷积处理，通过恢复退化函数来实现图像的去模糊。

然而，这种方法对退化模型的准确性和图像噪声敏感，可能导致图像产生伪影或噪点。

第二种方法是基于图像自适应方式的去模糊方法。

这种方法通常假设图像中的模糊是由局部模糊引起的，即图像不同区域的模糊程度不同。

基于图像自适应的去模糊方法通过避免对整个图像应用同样的退化模型或参数来解决图像退化问题。

常见的图像自适应去模糊方法包括基于边缘保持、基于局部图像统计特征等。

这种方法通常能够更好地保护图像细节，并减少伪影的产生。

然而，该方法需要更多的计算资源，并且在某些情况下可能无法准确判断图像退化模型。

总体而言，图像处理技术中的图像去模糊方法包括基于图像退化模型和基于图像自适应方式的方法。

每种方法都有其优势和不足，适用于不同的场景和需求。

为了获得更好的去模糊效果，有时也可以将两种方法结合起来使用。

在实际应用中，可以根据所处理图像的特点和退化程度选择合适的去模糊方法。

然而，图像去模糊问题仍然是一个具有挑战性的课题。

常用图像插值算法分析与比较

常用图像插值算法分析与比较1、引言图像几何变换包括平移、转置、镜像和缩放等。

其中前三种操作变换中，输出图像的每一个像素点在输入图像中都有一个具体的像素点与之对应。

但是，在缩放操作中，输出图像像素点坐标有可能对应于输入图像上几个像素点之间的位置，这个时候就需要通过灰度插值处理来计算出该输出点的灰度值[1]。

图像插值是图像超分辨处理的重要环节，不同的插值算法有不同的精度，插值算法的好坏也直接影响着图像的失真程度。

最常用的插值算法有三种：最近邻插值、双线性插值、立方卷积插值，其中使用立方卷积插值达到的效果是最佳的。

2、几种插值算法原理分析插值算法所应用的领域较多，对图像进行缩放处理是比较典型的应用，由于图像像素的灰度值是离散的, 因此一般的处理方法是对原来在整数点坐标上的像素值进行插值生成连续的曲面, 然后在插值曲面上重新采样以获得缩放图像像素的灰度值。

缩放处理从输出图像出发，采用逆向映射方法，即在输出图像中找到与之对应的输入图像中的某个或某几个像素，采用这种方法能够保证输出图像中的每个像素都有一个确定值，否则，如果从输入图像出发来推算输出图像，输出图像的像素点可能出现无灰度值的情况。

因为，对图像进行缩放处理时输出图像像素和输入图像之间可能不再存在着一一对应关系。

下面分别对三种算法予以介绍。

2.1 最近邻插值算法最简单的插值法是最近邻插值法，也叫零阶插值法[2]。

即选择离它所映射到的位置最近的输入像素的灰度值为插值结果。

对二维图像，是取待测样点周围4 个相邻像素点中距离最近1 个相邻点的灰度值作为待测样点的像素值。

若几何变换后输出图像上坐标为(x′,y′)的对应位置为（m，n）。

2.2 双线性插值算法双线性插值又叫一阶插值法[3]，它要经过三次插值才能获得最终结果，是对最近邻插值法的一种改进，先对两水平方向进行一阶线性插值，然后再在垂直方向上进行一阶线性插值。

2.3 立方卷积插值算法立方卷积插值又叫双三次插值[2]，是对双线性插值的改进，是一种较为复杂的插值方式，它不仅考虑到周围四个直接相邻像素点灰度值的影响，还考虑到它们灰度值变化率的影响，此法利用待采样点附近16 个像素点的灰度值作三次插值进行计算，还用到三次多项式 S( w)。

解模糊化方法

解模糊化方法解模糊化是图像处理中的一种技术，用于提高图像的清晰度和细节。

图像模糊是由于图像在捕捉或传输过程中被模糊或失真所引起的。

解模糊化是一个复杂的过程，不同的方法会应用于不同的场合，例如时间相关的问题或者在图像处理中的降噪问题。

下面我们将介绍一些常用的解模糊化方法。

1. 维纳滤波维纳滤波是一种在频域中操作的解模糊方法。

该方法通过滤波处理实现图像的恢复。

维纳滤波通过最小化噪声和失真之和的误差来实现图像恢复，同时考虑到信噪比和模糊度等参数。

该方法有时可能会导致图像中出现了一些伪影或其他问题。

2. 盲去卷积盲去卷积是一种基于信号处理的解模糊方法。

该方法的主要好处是，它不需要知道捕获或传输过程中发生的任何失真。

该方法通过计算图像的自相关矩阵来推断捕捉或传输过程中的失真，然后将图像恢复到原来的样子。

3. 基于最大后验概率(MAP)的方法基于最大后验概率的方法是一种通过概率模型来实现解模糊的技术。

该方法通过先验模型和图像模型进行建模，即在估计损失函数的同时，对图像和失真进行了建模。

基于最大后验概率的解模糊化方法可以通过损失函数进行最小化，从而实现图像的恢复。

该方法具有较高的准确度和鲁棒性。

非盲去卷积是一种可以基于已知的卷积核进行解模糊的方法。

在非盲去卷积中，通过计算捕捉或传输过程中被卷积的图像和卷积核之间的卷积，计算出白噪声和失真的实际值，然后通过滤波来恢复原始图像。

总之，解模糊化是一个具有挑战性的问题。

针对不同的场合和问题，应用各种方法进行解决。

深入了解每种技术的优缺点并适当地选择才能获得最佳的效果。

使用计算机视觉技术进行图像去模糊与增强的技巧与方法

使用计算机视觉技术进行图像去模糊与增强的技巧与方法图像去模糊与增强是计算机视觉领域的一个重要研究方向，它涉及到利用计算机视觉技术对图像中的模糊、噪声等问题进行处理，以提高图像质量和显示效果。

本文将介绍一些常用的技巧和方法，帮助读者了解图像去模糊与增强的基本原理及应用。

首先，图像去模糊是指通过使用计算机视觉技术将模糊的图像进行清晰化处理。

模糊图像通常是由于摄像机或者物体运动引起的，导致图像出现模糊不清的现象。

为了解决这个问题，一种常见的方法是使用图像复原算法，如退化模型、Wiener滤波器、最小二乘法等。

退化模型的基本思想是将模糊过程建模为线性系统，通过逆向计算得到原始图像。

Wiener滤波器则是一种优化的频谱滤波器，可以通过对频域图像进行滤波从而提高图像质量。

其次，图像增强是指通过计算机视觉技术对图像进行改善或者优化，使图像更加清晰、明亮、对比度更高等。

图像增强方法有很多种，常见的包括直方图均衡化、锐化、去噪等。

直方图均衡化是一种常用的图像增强方法，通过调整图像的像素分布，使得图像在亮度和对比度上更加均衡。

锐化是通过增强图像边缘的对比度来提高图像清晰度，常见的锐化算法有拉普拉斯算子和Sobel算子等。

去噪方法主要通过滤波器来降低图像中的噪声，如中值滤波器、均值滤波器等。

此外，图像去模糊与增强还涉及到机器学习和深度学习的应用。

在机器学习中，可以使用传统的监督学习方法，通过训练模型来预测和恢复模糊图像。

常见的算法包括支持向量机、随机森林和神经网络等。

深度学习是近年来兴起的一种强大的图像处理方法，通过构建深度神经网络，可以学习到更高级别的特征表示，从而实现更准确和有效的图像去模糊与增强。

常用的深度学习模型包括卷积神经网络（CNN）和生成对抗网络（GAN）等。

此外，图像去模糊与增强技术在实际应用中也有广泛的应用场景。

例如，在医学领域中，可以利用图像去模糊与增强技术提高医学图像的分辨率和清晰度，辅助医生进行诊断和手术操作。

去模糊化的方法

近年来，随着科技的发展，图像处理和计算机视觉技术也发生了巨变。

去模糊是其中一个非常重要的问题。

本文将介绍一些去模糊的方法。

一、基于梳理滤波的去模糊方法
基于梳理滤波的方法是一种去模糊的经典方法。

其基本思路是利用滤波器组来对模糊图像进行梳理，进而得到更清晰的图像。

这种方法能够高效、稳定地去除图像模糊，并得到较好的结果。

二、基于深度学习的去模糊方法
深度学习得益于大规模数据并行计算等技术，它在去模糊问题中也表现出了强大的能力。

研究者使用深度神经网络（DNN）进行图像去模糊。

具体地说，深度神经网络采用了专门针对图像去模糊问题设计的损失函数，能够学习到更加准确的模型。

三、基于变分贝叶斯的去模糊方法
变分贝叶斯方法是一种出色的统计学习方法。

它利用贝叶斯概率理论来描述图像及其他信号源的不确定性，通过求解变分近似来计算相应的概率分布。

这种方法准确性高、去噪效果出色。

四、基于霍尔曼滤波的去模糊方法
霍尔曼滤波在数字信号处理中得到广泛应用，其基本思路是对信号进行频域分析，并利用滤波器进行滤波处理。

这种方法可用来去除一些高斯模糊的图像。

五、基于重建方法的去模糊方法
重建方法的基础是在进行数据采集后，按照特定算法进行处理以获得图像。

进而实现图像去模糊的目的。

这种方法需要先对重建算法进行优化和选择以确保其有效性和可靠性。

综上所述，在去模糊技术中，不同的方法适用于不同类型的图像模糊。

去模糊技术的发展不仅可以用于图像处理，也可以用于视频处理等领域，对一些高精度的视觉识别和目标检测等科学研究领域的应用带来重要影响。