7年级下新人教综合测试题及答案.pptx
人教版2020—2021学年七年级数学下册全册综合复习测试题(含答案)

人教版七年级数学下册全册综合测试题一、选择题(本大题共6小题,每小题3分,共18分) 1.下列调查中,最适合用全面调查的是( ) A .检测100只灯泡的质量情况B .了解在如皋务工人员月收入的大致情况C .了解某班学生喜爱体育运动的情况D .了解全市学生观看“开学第一课”的情况 2.在平面直角坐标系中,点(-7,0)在( ) A .x 轴正半轴上B .x 轴负半轴上 C .y 轴正半轴上D .y 轴负半轴上3.不等式组⎩⎪⎨⎪⎧x -1<3,x +3≥1的解集在数轴上表示正确的是()图14.如果5x 3m -2n -2y n -m +11=0是二元一次方程,那么( ) A .m =3,n =4 B .m =1,n =2 C .m =-1,n =2 D .m =2,n =1 5.如图2,直线a∥b ,一块含60°角的三角尺ABC (∠A =60°)按图所示放置.若∠1=43°,则∠2的度数为( )图2A .101°B .103°C .105°D .107°6.如图3,一个点在第一象限及x 轴,y 轴上移动,在第一秒钟,它从原点移动到点(1,0),然后按照图中箭头所示方向移动,且每秒移动一个单位长度,即(0,0)→(1,0)→(1,1)→(0,1)→(0,2)→…,那么第2021秒时,点所在位置的坐标是( )图3A .(3,44)B .(37,44)C .(44,37)D .(44,3)二、填空题(本大题共6小题,每小题3分,共18分) 7.4的算术平方根为________.8.在平面直角坐标系中,已知点A (1,3),点B (1,5),那么AB =________.9.去年某市空气质量良好(二级以上)的天数与全年天数(365天)之比达到60%,如果今年(365天)这样的比值要超过80%,那么今年空气质量良好的天数比去年至少要增加________天.10.为了解某市13565名七年级学生每天做家庭作业所用的时间,从中随机抽取了150名学生进行调查,则本次调查的样本容量是________.11.已知⎩⎪⎨⎪⎧x =m ,y =n 是方程组⎩⎪⎨⎪⎧2x +y =6,x +2y =-3的解,则m +n 的值是________. 12.在平面直角坐标系中,三角形ABC 的面积为3,三个顶点的坐标分别为A (-1,-1),B (-3,-3),C (a ,b ),且a ,b 均为负整数,点C 在如图4所示的网格中,则点C 的坐标是____________________.图4三、解答题(本大题共5小题,每小题6分,共30分) 13.(1)计算:|-3|-(-1)+3-27-4;(2)如图5所示,EF ∥BC ,AC 平分∠BAF ,∠B =80°,求∠C 的度数.图514.解方程组:⎩⎪⎨⎪⎧3x -2(y +1)=6,3x +2y =10.15.解不等式组:⎩⎪⎨⎪⎧4x -7<5(x -1),x -13≥12x -1.16.已知2a -1的算术平方根是7,a -4b 的立方根是-4. (1)求a 和b 的值; (2)求2a +b 的平方根.17.某校进行“垃圾分一分,环境美十分”的主题宣传活动,随机调查了部分学生对垃圾分类知识的了解情况.调查选项分为“A.非常了解,B.比较了解,C.基本了解,D.不了解”四种,并将调查结果绘制成如图6所示的两幅不完整的统计图.图6请根据图中提供的信息,解答下列问题: (1)把两幅统计图补充完整; (2)本次调查了________名学生;(3)根据上述调查数据,请你提出一条合理化建议.四、解答题(本大题共3小题,每小题8分,共24分)18.如图7,已知∠A=∠ADE.(1)若∠EDC=4∠C,求∠C的度数;(2)若∠C=∠E,求证:BE∥CD.图719.如图8,已知在平面直角坐标系内,点A(-3,2),B(2,-4),把点A 向下平移4个单位长度得到点C.(1)在平面直角坐标系内画出点A,B;(2)写出点C的坐标;(3)画出三角形ABC,并求三角形ABC的面积.图820.我们定义:若整式M与N满足M+N=k(k为整数),则称M与N为关于k的平衡整式.例如,若2x+3y=4,我们称2x与3y为关于4的平衡整式.(1)若2a-5与4a+9为关于1的平衡整式,求a的值;(2)若3x-10与y为关于2的平衡整式,2x与5y+10为关于5的平衡整式,求x +y的值.五、解答题(本大题共2小题,每小题9分,共18分)21.红瓜子和萝卜干是信丰的土特产.小华去市场购买了6千克红瓜子和3千克萝卜干共用了108元;小平以同样的单价购买了5千克红瓜子和2千克萝卜干共用了88元.(1)求红瓜子和萝卜干的单价分别是多少;(2)已知小红想要购买红瓜子和萝卜干共20千克,如果她想购买红瓜子的千克数超过萝卜干的千克数的4倍,且她身上只有296元,请问她有哪几种购买方案.(红瓜子和萝卜干的千克数都取整数)22.如图9,在平面直角坐标系xOy中,长方形ABCD的四个顶点A,B,C ,D的坐标分别为(1,1),(1,2),(-2,2),(-2,1).对该长方形及其内部的每一个点都进行如下操作:把每个点的横坐标都乘同一个实数a,纵坐标都乘3,再将得到的点向右平移m(m>0)个单位长度,向下平移2个单位长度,得到长方形A′B′C′D′及其内部的点,其中点A,B,C,D的对应点分别为A′,B′,C′,D′.(1)点A′的横坐标为________(用含a,m的式子表示).(2)若点A′的坐标为(3,1),点C′的坐标为(-3,4).①求a,m的值;②若对长方形ABCD内部(不包括边界)的点E(0,y)进行上述操作后,试判断得到的对应点E′是否仍然在原来的长方形ABCD内部(不包括边界).图9六、解答题(本大题共12分)23.一个数学小组将一个直角三角形ABC(∠ACB=90°)放进平面直角坐标系中,进行探究活动.点C在第三象限,且AC过坐标原点O,AB交x轴于点G,作直线DM平行于x轴,DM交y轴于点D,交BC于点E,交AB于点F.(1)如图10①,若∠AOG=50°,求∠CEF的度数;(2)如图②,在AC上取一点N,使∠NEC+∠CEF=180°.求证:∠NEF=2∠AOG.图10参考答案1.C 2.B 3.C 4.A 5.B 6.D7. 2 8.2 9.74 10.150 11.112.(-4,-1)或(-1,-4)或(-5,-2)13.解:(1)原式=3+1-3-2=-1.(2)∵EF∥BC,∴∠B+∠BAF=180°,∠C=∠CAF.∵∠B=80°,∴∠BAF =180°-∠B =100°.∵AC 平分∠BAF ,∴∠CAF =12∠BAF =50°, ∴∠C =50°.14.解:方程组整理,得⎩⎪⎨⎪⎧3x -2y =8,①3x +2y =10.②①+②,得6x =18,解得x =3.把x =3代入①,得9-2y =8,解得y =12. ∴原方程组的解为⎩⎪⎨⎪⎧x =3,y =12.15.解:⎩⎪⎨⎪⎧4x -7<5(x -1),①x -13≥12x -1.②解不等式①,得x >-2. 解不等式②,得x≤4.∴不等式组的解集为-2<x≤4.16.解:(1)∵2a -1的算术平方根是7, ∴2a -1=(7)2=7,解得a =4. ∵a -4b 的立方根是-4,∴a -4b =(-4)3=-64,即4-4b =-64,解得b =17.(2)∵2a +b =2×4+17=25,∴2a +b 的平方根为±5.17.解:(1)调查的总人数为5÷10%=50(人).B 选项所占的百分比为25÷50×100%=50%.C 选项的人数为50×26%=13(人).D 选项的人数为50-5-25-13=7(人).D 选项所占的百分比为7÷50×100%=14%.补全的统计图如图所示.(2)50(3)答案不唯一,如根据对垃圾分类知识的了解情况,对于垃圾分类知识“非常了解”占的比例比较小,需要进一步加强宣传的力度.18.解:(1)∵∠A =∠ADE ,∴DE ∥AC , ∴∠EDC +∠C =180°.∵∠EDC =4∠C ,∴4∠C +∠C =180°, 解得∠C =36°.(2)证明:∵∠A =∠ADE , ∴DE ∥AC , ∴∠E =∠ABE. 又∵∠C =∠E , ∴∠C =∠ABE , ∴BE ∥CD.19.解:(1)如图所示,点A ,B 即为所求.(2)C(-3,-2).(3)画三角形ABC 如图.如图,过点B 作BD ⊥AC ,交AC 的延长线于点D ,则易得BD =5,∴S 三角形ABC =12AC·BD =12×4×5=10.20.解:(1)由题意,得2a -5+4a +9=1,解得a =-12.(2)由题意,得⎩⎪⎨⎪⎧3x -10+y =2,2x +5y +10=5,解得⎩⎪⎨⎪⎧x =5,y =-3,则x +y =2.21.解:(1)设红瓜子的单价为x 元/千克,萝卜干的单价为y 元/千克.依题意,得⎩⎪⎨⎪⎧6x +3y =108,5x +2y =88,解得⎩⎪⎨⎪⎧x =16,y =4. 答:红瓜子的单价为16元/千克,萝卜干的单价为4元/千克.(2)设购买红瓜子a 千克,则购买萝卜干(20-a)千克.依题意,得⎩⎪⎨⎪⎧16a +4(20-a )≤296,a >4(20-a ), 解得16<a≤18,所以a 可以取17,18.则有两种购买方案:方案一:购买红瓜子17千克,购买萝卜干3千克;方案二:购买红瓜子18千克,购买萝卜干2千克.22.解:(1)a +m(2)①由A(1,1),A ′(3,1),可得a +m =3.①由C(-2,2),C′(-3,4),可得-2a +m =-3.②联立①②,得⎩⎪⎨⎪⎧a +m =3, -2a +m =-3,解得⎩⎪⎨⎪⎧a =2,m =1, ∴a 的值为2,m 的值为1.②根据题意,得E′(1,3y -2).可知无论y 取何值,点E′一定落在直线AB 上,所以得到的对应点E′不在原来的长方形ABCD 内部.23.解:(1)如图,过点C 作CH ∥x 轴,则∠ACH =∠AOG =50°.∵∠ACB =90°,∴∠ECH =40°.∵DM ∥x 轴,∴CH ∥DM ,∴∠ECH +∠CEF =180°,∴∠CEF=180°-∠ECH=140°.(2)证明:由(1)及题意得∠AOG=∠ACH=90°-∠ECH,∠ECH+∠CEF=∠ECH+∠NEC+∠NEF=180°.∵∠NEC+∠CEF=180°,∴∠NEC=∠ECH,∴2∠ECH+∠NEF=180°,则∠NEF=180°-2∠ECH=2(90°-∠ECH)=2∠AOG.。
新人教版七年级生物下学期综合检测卷(附答案)
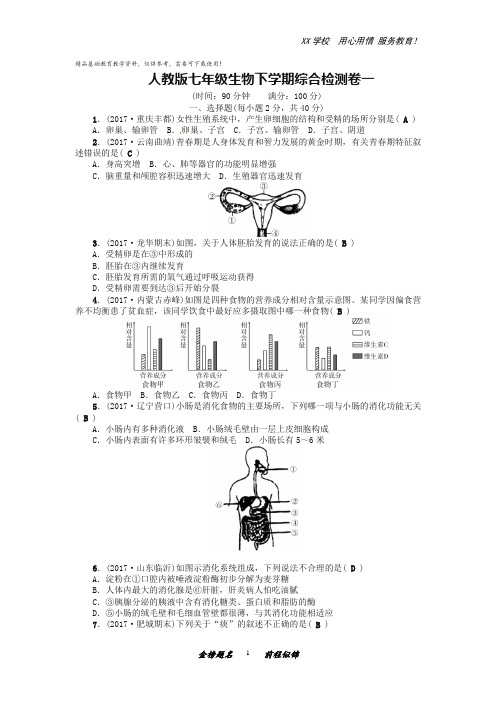
精品基础教育教学资料,仅供参考,需要可下载使用!人教版七年级生物下学期综合检测卷一(时间:90分钟满分:100分)一、选择题(每小题2分,共40分)1.(2017·重庆丰都)女性生殖系统中,产生卵细胞的结构和受精的场所分别是( A ) A.卵巢、输卵管 B.卵巢、子宫 C.子宫、输卵管 D.子宫、阴道2.(2017·云南曲靖)青春期是人身体发育和智力发展的黄金时期,有关青春期特征叙述错误的是( C )A.身高突增 B.心、肺等器官的功能明显增强C.脑重量和颅腔容积迅速增大 D.生殖器官迅速发育3.(2017·龙华期末)如图,关于人体胚胎发育的说法正确的是( B )A.受精卵是在③中形成的B.胚胎在③内继续发育C.胚胎发育所需的氧气通过呼吸运动获得D.受精卵需要到达③后开始分裂4.(2017·内蒙古赤峰)如图是四种食物的营养成分相对含量示意图。
某同学因偏食营养不均衡患了贫血症,该同学饮食中最好应多摄取图中哪一种食物( B )A.食物甲 B.食物乙 C.食物丙 D.食物丁5.(2017·辽宁营口)小肠是消化食物的主要场所,下列哪一项与小肠的消化功能无关( B )A.小肠内有多种消化液 B.小肠绒毛壁由一层上皮细胞构成C.小肠内表面有许多环形皱襞和绒毛 D.小肠长有5~6米6.(2017·山东临沂)如图示消化系统组成,下列说法不合理的是( D )A.淀粉在①口腔内被唾液淀粉酶初步分解为麦芽糖B.人体内最大的消化腺是⑥肝脏,肝炎病人怕吃油腻C.③胰腺分泌的胰液中含有消化糖类、蛋白质和脂肪的酶D.⑤小肠的绒毛壁和毛细血管壁都很薄,与其消化功能相适应7.(2017·肥城期末)下列关于“痰”的叙述不正确的是( B )A .由黏液、灰尘和细菌构成B .痰是由喉部分泌黏液C .痰经咳嗽排出体外D .避免疾病传播不要随地吐痰8.如图所示的曲线表示人体血液中某种物质含量的变化情况,有关叙述正确的是( C )A .若Ⅱ为肾小球的毛细血管网,则曲线乙可表示氧气含量的变化B .若Ⅱ为胰腺内的毛细血管网,则曲线甲可表示胰液含量的变化C .若Ⅱ为小肠壁内的毛细血管网,则曲线甲可表示营养物质含量的变化D .若Ⅱ为骨骼肌内的毛细血管网,则曲线乙表示二氧化碳含量的变化9.(2017·龙华期末)下列能正确表示肺泡与血液气体交换的是( B )A .外界空气氧气二氧化碳肺泡B .肺泡氧气二氧化碳血液C .外界空气二氧化碳氧气肺泡D .肺泡二氧化碳氧气血液10.心脏壁由心肌构成,根据右图所示心肌厚薄程度判断,左心室是( B )A .①B .②C .③D .④11.假如某人在一次事故中刺伤动脉要比刺伤静脉危险得多。
人教版数学七年级(下)期末复习综合练习题(含答案)

期末复习综合练习题一.选择题1.下列是无理数的是()A.B.C.D.2.下列命题是真命题的是()A.内错角相等B.平面内,过一点有且只有一条直线与已知直线垂直C.相等的角是对顶角D.平面内,过一点有且只有一条直线与已知直线平行3.如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC的度数为()A.40°B.60°C.80°D.100°4.下列调查方式,你认为最合适的是()A.日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式B.旅客上飞机前的安检,采用抽样调查方式C.了解深圳市居民日平均用水量,采用全面调查方式D.了解深圳市每天的平均用电量,采用抽样调查方式5.已知点P(3a,a+2)在x轴上,则P点的坐标是()A.(3,2)B.(6,0)C.(﹣6,0)D.(6,2)6.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=70°,则∠AOF等于()A.35°B.45°C.55°D.65°7.若关于x、y的二元一次方程有公共解3x﹣y=7,2x+3y=1,y=﹣kx﹣9,则k的值是()A.﹣3 B.C.2 D.﹣48.点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为()A.(5,﹣3)B.(﹣5,3)C.(3,﹣5)D.(﹣3,5)9.如图,在下列说法中错误的是()A.射线OA的方向是正西方向B.射线OB的方向是东北方向C.射线OC的方向是南偏东60°D.射线OD的方向是南偏西55°10.有一个男孩的假期有11天在下雨,这11天如果上午下雨下午就不会下雨,下午下雨上午就不下,他的假期里9个上午和12个下午是晴天,他的假期共有几天?()A.12 B.14 C.16 D.18二.填空题11.已知二元一次方程y﹣2x=1,用含x的代数式表示y,则y=.12.若x,y为实数,且|x﹣2|+=0,则(x+y)2019的值为.13.如图,将一张长方形纸条沿某条直线折叠,若∠1=116°,则∠2等于.14.如图,在平面直角坐标系中,O为坐标原点,点A(0,3)和点B(2,0)是坐标轴上两点,点C(m,n)(m≠n)为坐标轴上一点,若三角形ABC的面积为3,则C点坐标为.15.一种微波炉进价为1000元.出售时标价为1500元,双十一打折促销,但要保持利润率不低于2%,则最低可打折.16.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为.三.解答题17.解方程组:①②.18.解不等式组,并把解集在数轴上表示出来.19.先化简,再求值:2x3+4x﹣3x2﹣(x﹣3x2+2x3),其中x=﹣3.20.感知与填空:如图①,直线AB∥CD.求证:∠B+∠D=∠BED.阅读下面的解答过程,井填上适当的理由.解:过点E作直线EF∥CD∴∠2=∠D()∵AB∥CD(已知),EF∥CD,∴AB∥EF()∴∠B=∠1()∵∠1+∠2=∠BED,∴∠B+∠D=∠BED()应用与拓展:如图②,直线AB∥CD.若∠B=22°,∠G=35°,∠D=25°,则∠E+∠F =度.方法与实践:如图③,直线AB∥CD.若∠E=∠B=60°,∠F=80°,则∠D=度.21.已知关于x,y的方程组的解x,y都为正数.(1)求a的取值范围;(2)是否存在这样的整数a,使得不等式|a|+|2﹣a|<5成立?若成立,求出a的值;若不成立,并说明理由.22.春节是我国的传统节日,为了调查学生对于各地春节民俗活动的了解程度,某校随机抽取一部分学生进行问卷调查,将调查结果按“A:非常了解、B:基本了解、C:了解较少、D:不太了解”四类分别进行统计,并绘制出下面两幅不完整的统计图.请根据两幅统计图的信息,解答下列问题:(1)此次共调查了个学生;(2)扇形统计图中,A所在的扇形的圆心角度数为;(3)将上面的条形统计图补画完整.23.目前节能灯已基本普及,节能还环保,销量非常好,某商场计划购进甲、乙两种型号节能灯共1200只,这两种节能灯的进价、售价如表所示:进价(元/只)售价(元/只)甲型25 30乙型45 60(1)商场应如何进货,使进货款恰好为46000元?(2)若商场销售完节能灯后获利不超过进货价的30%,至少购进甲种型号节能灯多少只?24.在△ABC中,射线AG平分∠BAC交BC于点G,点D在BC边上运动(不与点G重合),过点D作DE∥AC交AB于点E.(1)如图1,点D在线段CG上运动时,DF平分∠EDB①若∠BAC=100°,∠C=30°,则∠AFD=;若∠B=40°,则∠AFD=;②试探究∠AFD与∠B之间的数量关系?请说明理由;(2)点D在线段BG上运动时,∠BDE的角平分线所在直线与射线AG交于点F试探究∠AFD与∠B之间的数量关系,并说明理由.参考答案一.选择题1.解:,,是有理数,是无理数,故选:B.2.解:A、内错角相等,是假命题,故此选项不合题意;B、平面内,过一点有且只有一条直线与已知直线垂直,是真命题,故此选项符合题意;C、相等的角是对顶角,是假命题,故此选项不合题意;D、平面内,过一点有且只有一条直线与已知直线平行,是假命题,故此选项不合题意;故选:B.3.解:∵∠AOE+∠BOE=180°,∠AOE=140°,∴∠2=40°,∵∠1=∠2,∴∠BOD=2∠2=80°,∴∠AOC=∠BOD=80°.故选:C.4.解:A、日光灯管厂要检测一批灯管的使用寿命,应用抽样调查,故A错误;B、旅客上飞机前的安检,采用普查方式,故B错误;C、了解深圳市居民日平均用水量,采用抽样调查方式,故C错误;D、了解深圳市每天的平均用电量,采用抽样调查方式,故D正确.故选:D.5.解:∵点P(3a,a+2)在x轴上,∴y=0,即a+2=0,解得a=﹣2,∴3a=﹣6,∴点P的坐标为(﹣6,0).故选:C.6.解:∵∠B0C=∠AOD=70°,又∵OE平分∠BOC,∴∠BOE=∠BOC=35°.∵OF⊥OE,∴∠EOF=90°.∴∠AOF=180°﹣∠EOF﹣∠BOE=55°.故选:C.7.解:解方程组得:,把代入y=﹣kx﹣9得﹣1=﹣2k﹣9,解得k=﹣4.故选:D.8.解:∵点P位于第二象限,∴点的横坐标为负数,纵坐标为正数,∵点距离x轴5个单位长度,距离y轴3个单位长度,∴点的坐标为(﹣3,5).故选:D.9.解:根据图示可知A、射线OA的方向是正西方向,正确;B、射线OB的方向是东北方向,正确;C、射线OC的方向是南偏东30°,错误;D、射线OD的方向是南偏西55°,正确.故选:C.10.解:设上午下雨是x天,下午下雨是y天,假期z天,则晴天为:(z﹣x﹣y)天由题意可得:解得:故选:C.二.填空题11.解:由y﹣2x=1,得到y=2x+1.故答案为:2x+112.解:∵x,y为实数,且|x﹣2|+=0,∴x﹣2=0,y+3=0,∴x=2,y=﹣3,∴(x+y)2019=(2﹣3)2019=﹣1,故答案为:﹣1.13.解:如图,∵AB∥CD,∴∠1=∠BAC=116°,由折叠可得,∠BAD=∠BAC=58°,∵AB∥CD,∴∠2=∠BAD=58°,故答案为:58°.14.解:∵点C(m,n)(m≠n)为坐标轴上一点,∴S△ABC=×3×|m﹣2|=3或S△ABC=×2×|n﹣3|=3,解得:m=4或0,n=6或0,∴C点坐标为(4,0)或(0,6),故答案为:(4,0)或(0,6).15.解:设打x折销售,根据题意可得:1500×≥1000(1+2%),解得:x≥6.8,故要保持利润率不低于2%,则至少可打6.8折.故答案是:6.8.16.解:过点B作BD∥l,∵直线l∥m,∴BD∥l∥m,∴∠4=∠1,∠2=∠3,∴∠1+∠2=∠3+∠4=∠ABC,∵∠ABC=45°,∴∠1+∠2=45°.故答案为:45°.三.解答题17.解:①,①+②得:4x=8,解得:x=2,将x=2代入①得:2+2y=9,解得:y=,则方程组的解为;②方程组整理得:,①﹣②得:6y=27,解得:y=,将y=代入②得:3x﹣9=9,解得:x=6,则方程组的解为.18.解:,解第一个不等式得x≥﹣1,解第二个不等式得x<3,则不等式组的解集为﹣1≤x<3,将解集表示在数轴上如下:19.解:原式=2x3+4x﹣3x2﹣x+3x2﹣2x3=3x,当x=﹣3时,原式=﹣9.20.解:感知与填空:过点E作直线EF∥CD,∴∠2=∠D(两直线平行,内错角相等),∵AB∥CD(已知),EF∥CD,∴AB∥EF(两直线都和第三条直线平行,那么这两条直线也互相平行),∴∠B=∠1(两直线平行,内错角相等),∵∠1+∠2=∠BED,∴∠B+∠D=∠BED(等量代换),故答案为:两直线平行,内错角相等;两直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;等量代换.应用与拓展:过点G作GN∥AB,则GN∥CD,如图②所示:由感知与填空得:∠E=∠B+∠EGN,∠F=∠D+∠FGN,∴∠E+∠F=∠B+∠EGN+∠D+∠FGN=∠B+∠D+∠EGF=22°+25°+35°=82°,故答案为:82.方法与实践:设AB交EF于M,如图③所示:∠AME=∠FMB=180°﹣∠F﹣∠B=180°﹣80°﹣60°=40°,由感知与填空得:∠E=∠D+∠AME,∴∠D=∠E﹣∠AME=60°﹣40°=20°,故答案为:20.21.解:(1)解方程组得,∵x>0,y>0,∴,解得a>2;(2)存在.∵a>2,而|a|+|2﹣a|<5,∴a+a﹣2<5,解得a<,∴2<a<,∵a为整数,∴a=3.22.解:(1)(19+22)÷41%=100人,故答案为:100.(2)C组人数为:100×39%=39,A组人数为:100﹣41﹣39﹣5=15,A所在的扇形的圆心角度数为:360°×=54°,故答案为:54°.(3)A组的人数:15人,其中男生15﹣5=10人,C组的人数:39人,其中女生39﹣21=18人,补全条形统计图如图所示:23.解:(1)设购进甲型节能灯x只,乙型节能灯y只,根据题意,得:,解得:,答:购进甲型节能灯400只,乙型节能灯800只,进货款恰好为46000元;(2)设商场购进甲型节能灯a只,则购进乙型节能灯(1200﹣a)只,由题意,得:(30﹣25)a+(60﹣45)(1200﹣a)≤[25a+45(1200﹣a)]×30%,解得:a≥450.答:至少购进甲种型号节能灯450只.24.解:(1)①若∠BAC=100°,∠C=30°,则∠B=180°﹣100°﹣30°=50°,∵DE∥AC,∴∠EDB=∠C=30°,∵AG平分∠BAC,DF平分∠EDB,∴∠BAG=∠BAC=50°,∠FDG=∠EDB=15°,∴∠DGF=∠B+∠BAG=50°+50°=100°,∴∠AFD=∠DGF+∠FDG=100°+15°=115°;若∠B=40°,则∠BAC+∠C=180°﹣40°=140°,∵AG平分∠BAC,DF平分∠EDB,∴∠BAG=∠BAC,∠FDG=∠EDB,∵∠DGF=∠B+∠BAG,∴∠AFD=∠DGF+∠FDG=∠B+∠BAG+∠FDG=∠B+(∠BAC+∠C)=40°+×140°=40°+70°=110°;故答案为:115°;110°;②∠AFD=90°+∠B;理由如下:由①得:∠EDB=∠C,∠BAG=∠BAC,∠FDG=∠EDB,∵∠DGF=∠B+∠BAG,∴∠AFD=∠DGF+∠FDG=∠B+∠BAG+∠FDG=∠B+(∠BAC+∠C)=∠B+(180°﹣∠B)=90°+∠B;(2)如图2所示:∠AFD=90°﹣∠B;理由如下:由(1)得:∠EDB=∠C,∠BAG=∠BAC,∠BDH=∠EDB=∠C,∵∠AHF=∠B+∠BDH,∴∠AFD=180°﹣∠BAG﹣∠AHF=180°﹣∠BAC﹣∠B﹣∠BDH=180°﹣∠BAC﹣∠B﹣∠C=180°﹣∠B﹣(∠BAC+∠C)=180°﹣∠B﹣(180°﹣∠B)=180°﹣∠B﹣90°+∠B=90°﹣∠B.。
七年级数学下册暑假综合测试卷及答案(人教版)

七年级数学下册暑假综合测试卷及答案(人教版)(全卷三个大题,共24个小题;满分100分,考试用时120分钟)姓名 班级 学号 成绩一、选择题(本大题共12小题.每小题只有一个正确选项,每小题3分,共36分)1.在2,0,-2四个数中,最小的一个数是( )A .2B .C .0D .2-2.估计1的值应在( )A .0和1之间B .1和2之间C .2和3之间D .3和4之间 3.点P (a ,2)在第一象限,则点Q (﹣2,a+1)在第( )象限. A .一 B .二 C .三 D .四4.如图,在所标识的角中,内错角是( ).A .∠1与∠4B .∠2与∠4C .∠3与∠4D .∠1与∠35.已知A ,B 两点的坐标是A(5,a),B(b ,4),若AB 平行于x 轴,且AB=3,则a+b 的值为( ) A .-1 B .9 C .12 D .6或126.如图,直线AB 、CD 、EF 相交于点O ,其中AB CD ⊥,∠1:21∠=:2,则EOD ∠=( )A .120︒B .130︒C .60︒D .150︒7.将50份数据分成3组,期中第一组和第三组的频率之和为0.7,则第二小组的频数是( ) A .0.3 B .30 C .15 D .358.某校为了了解1200名学生的视力情况,从中抽取了300名学生进行视力调查,在这个问题中,下列说法错误的是( ) A .总体是1200名学生的视力情况 B .样本是300名学生的视力情况 C .样本容量是300名 D .个体是每名学生的视力情况9.某文具店一本练习本和一支水笔的单价合计为3元,小明在该店买了20本练习本和10支水笔,共花了36元.设练习本每本为 x 元,水笔每支为 y 元,则( )A .3201036x y x y -=⎧⎨+=⎩B .3201036x y x y +=⎧⎨+=⎩C .3201036y x x y -=⎧⎨+=⎩D .3102036x y x y +=⎧⎨+=⎩10.某种品牌自行车的进价为400元,出售时标价为500元,商店准备打折出售,但要保持利润率不低于5%,则至多可打的折数是( )A .八折B .八四折C .八五折D .八八折11.已知关于x ,y 的二元一次方程组⎩⎨⎧=+=-24by ax by ax 的解 21x y =⎧⎨=⎩ ,则2a ﹣3b 的值为( )A .﹣6B .4C .6D .﹣412.不等式组⎪⎩⎪⎨⎧+++≥+2132334154x x x >的所有整数解的和为( )A .﹣1B .0C .1D .2二、填空题(本大题共4小题,每小题2分,共8分)13.比较大小:; -.14.若点()14A a a +-,在x 轴上,则点()a a -,位于第 象限. 15.小亮解方程组{2x +y =●2x −y =10的解为{x =4y =▲,由于不小心,滴上了两滴墨水,刚好遮住了两个数●和▲,请你帮他找回▲,这个数▲= .16.将直角三角板ABC 按如图所示的位置放置4590ABC ACB ∠=︒∠=︒,直线CE//AB ,BE 平分ABC ∠,在直线CE 上确定一点D ,满足40BDC ∠=︒,则EBD ∠的度数为.三、解答题(本答题共8小题,共56分) 17.求下列各式的值:(12.18.已知ABC 在88⨯方格中,位置如图所示,其中点A 的坐标为()31-,,点B 的坐标为()24-,.(1)写出点C 的坐标 ;(2)ABC 经某种变换得到A B C ''',其中点A 对应点A '的坐标为()12-,,点B 对应点B '的坐标为()05,,请在图上标出点C ';19.解不等式组()52315x x x x +⎧>⎪⎨⎪--≤⎩并在数轴上表示出它的解集.20.先阅读,然后解方程组()⎩⎨⎧=--=--5401y y x y x . 解方程组时,可由①得x ﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得01x y =⎧⎨=-⎩,这种方法被称为“整体代入法”.请用这样的方法解方程组.⎪⎩⎪⎨⎧=++-=--1225436022y y x y x21.“知识改变命运,科技繁荣祖国”,我市中小学每年都要举办一届科技运动会,下图为我市某校今年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:(1)该校参加车模、建模比赛的人数分别是人和人:(2)该校参加航模比赛的总人数是人,空模所在扇形的圆心角的度数是,并把条形统计图补充完整.(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖,今年我市中小学参加航模比赛人共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?22.已知,如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D.(1)求证:AC//DF.(2)若∠DEC=150°,求∠GBA.23.某服装专卖店计划购进A,B两种型号的精品服装.已知2件A型服装和3件B型服装共需4600元;1件A型服装和2件B型服装共需2800元.(1)求 A,B 型服装的单价;(2)专卖店要购进A,B 两种型号服装60件,其中A型件数不少于B型件数的2倍,如果B型打七五折,那么该专卖店至少需要准备多少货款?24.2021年11月,我市政府紧急组织一批物资送往新冠疫情高风险地区,现已知这批物资中,食品和矿泉水共410箱,且食品比矿泉水多110箱.(1)求食品和矿泉水各有多少箱;(2)现计划租用A,B两种货车共10辆,一次性将所有物资送到群众手中,已知A种货车最多可装食品40箱和矿泉水10箱,B种货车最多可装食品20箱和矿泉水20箱,试通过计算帮助政府设计几种运输方案;(3)在(2)的条件下,A种货车每辆需付运费600元,B种货车每辆需付运费450元,政府应该选哪种方案,才能使运费最少?最少运费是多少?参考答案:1.D 2.C 3.B 4.C 5.D 6.A 7.C 8.C 9.B 10.B 11.C 12.B 13.<;> 14.二 15.2-16.17.5︒或117.5︒ 17.(1)解:原式=2+15﹣13=4 (2)解:原式=0.5﹣74 + 14=﹣1 18.(1)()11,(2)解:∵()()3124A B --,,,的对应点分解为()()1205A B -'',,, 又321112-+=-+=, 220415-+=+=,∴A B C '''是由ABC 先向右平移2个单位,再向上平移1个单位,得到的∴C '的坐标为:()1211++,即:()32,如图所示;19.解:()()()5123152x x x x +⎧>⎪⎨⎪--≤⎩由①得,x <5由②得,x ≥-1∴不等式组的解集是-1≤x <5. 在数轴上表示如图:20.解:{2x −y −2=0①6x−3y+45+2y =12② 由①得2x ﹣y=2③ 将③代入②得3245⨯++2y=12 解得y=5把y=5代入③得x=3.5. 则方程组的解为{x =3.5y =5.21.(1)4;6(2)24;120°;(3)32÷80=0.4(1分)0.4×2485=994答:今年参加航模比赛的获奖人数约是994人 22.(1)证明:∵∠AGB =∠DGH ,∠AGB =∠EHF ∴∠DGH =∠EHF ∴//BD CE ∴∠D =∠FEC ∵∠C =∠D ∴∠FEC =∠C ∴//AC DF ;(2)解:∵由(1)知//BD CE ∴180D DEC ∠+∠︒= ∵∠DEC =150︒ ∴∠D =30︒ ∵AC//DF∴∠GBA =∠D =30︒. 23.(1)设A 型女装的单价是x 元,B 型女装的单价是y 元 依题意得: 23460022800x y x y +=⎧⎨+=⎩解得: 8001000x y =⎧⎨=⎩答:A 型女装的单价是800元,B 型女装的单价是1000元;(2)设购进A 型女装m 件,则购进B 型女装(60-m )件 根据题意,得m ≥2(60-m ) ∴m ≥40设购买A 、B 两种型号的女装的总费用为w 元 w=800m+1000×0.75×(60-m )=50m+45000 ∴w 随m 的增大而增大∴当m=40时,w 最小=50×40+45000=47000. 答:该专卖店至少需要准备47000元的贷款.24.(1)解:设食品有x 箱,矿泉水有y 箱依题意,得410110x y x y +=⎧⎨-=⎩解得260150x y =⎧⎨=⎩答:食品有260箱,矿泉水有150箱;(2)解:设租用A 种货车m 辆,则租用B 种货车(10)m -辆,依题意,得4020(10)2601020(10)150m m m m +-≥⎧⎨+-≥⎩解得:3≤m ≤5又∵m 为正整数 ∴m 可以为3,4,5 ∴共有3种运输方案方案1:租用A 种货车3辆,B 种货车7辆; 方案2:租用A 种货车4辆,B 种货车6辆; 方案3:租用A 种货车5辆,B 种货车5辆.(3)解:选择方案1所需运费为600×3+450×7=4950(元) 选择方案2所需运费为600×4+450×6=5100(元) 选择方案3所需运费为600×5+450×5=5250元). ∵4950<5100<5250∴政府应该选择方案1,才能使运费最少,最少运费是4950元。
人教版七年级下数学整册综合检测卷有答案

整册综合检测卷一、选择题(共10小题,每题3分,共30分) 1在平面直角坐标系中,点 A (- 2, 3)在()A •第一象限B •第二象限C .第三象限D .第四象限【答案】B 【解析】试题分析:利用平面直角坐标系知第一象限为( + , +),第二象限为(-,+)第三象限为(-,-)第四象限为(+ ,-).可知点A (- 2, 3)在第二象限;故选B.2 .已知点 A ( m-1 , m+4 )在y 轴上,则点 A 的坐标是()A . ( 0, 3)B . ( 0, 5)C . (5, 0)【答案】B3.和数轴上的点一 一对应的是 ( )A .整数B .有理数C .无理数【答案】D【解析】试题分析:数轴上的任意一点都可以表示 个实数, 因此,数轴上的点与实数是一一对应的;故选D .4.在 3.14,29 -、3 , 0.23, 0.2020020002-17A . 1B .2C . 3D . 4【答案】A【解析】D . ( 3, 0)D .实数反之,任何一个实数都可以用数轴上的一个点来表示,这五个数中,既是正实数也是无理数的个数是()试题分析:根据实数的分类可得,正实数有: 0.2020020002…•所以既是正实数也是无理数的是 故选A5.如图,AB // CD ,如果/ B = 20°,那么/ C 为()3.14, 29 , 0.23, 0.2020020002 …;无理数有:-3 ,17 0.2020020002 ….B. 20°C. 60D. 70°【答案】B6. 如图所示,/ 1 = 70°,有下列结论:①若/ 2= 70 °,贝U AB // CD ;②若/ 5= 70°,贝U AB // CD :③若/ 3 = 110°,贝U AB // CD;④若/ 4= 110°,贝U AB // CD .其中正确的有()A . 1个B. 2个C. 3个 D . 4个【答案】B7. 某县有近6千名考生参加中考,为了解本次中考的数学成绩,从中抽取100名考生的数学成绩进行统计分析,以下说法正确的是()组的解为[y= 10故选C.9.为了丰富同学们的课余生活,体育委员小强到体育用品商店购羽毛球拍和乒乓球拍,若购1副羽毛球拍和1副乒乓球拍共需50元,小强一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍,若设每副羽毛球拍为x元,每副乒乓球拍为y元,列二元一次方程组得()x y = 50 x y = 50 x y = 50 x y = 50A .B .C .D .$(x + y)=320 Qx+10y=320 |6x+y = 320 [10x + 6y = 320【答案】B…5x冬010 .不等式组整数解的个数是()A .这100名考生是总体的一个样本C.每位考生的数学成绩是个体【答案】Cx + 丫= 60&方程组・〜“的解是0x-2y = 30x-70 fx-90A . *B .y = —10 [y = —30【答案】C.【解析】B.近6千名考生是总体D . 100名学生是样本容量x=50= 1(}试题分析:x+y = 60®x-2y =30®①-②得: 3y=30,即y=10,将y=10代入①得:x+10=60 ,即x=50,则方程x. = 30Q - x > 0【答案】C • 二、填空题(共10小题,每题3分,共30 分) 1点P (- 5, 1),到x 轴距离为 【答案】1【解析】 试题分析:点P (- 5, 1),到x 轴距离为1.2. 如图,是象棋盘的一部分,若“帅”位于点( 2, -1) 上, “相”位于点(4,-1 )上,则“炮”所在的点 的坐标是。
部编人教版七年级语文下册全册单元测试题及答案(整理).pptx

学海无涯
A.纵然马革裹尸,魂归狼烟,也要仰天长笑,这是豪壮的选择。 B.四川九寨沟地震救灾现场出现了许多可歌可泣的事迹。 .水滴锲而不舍,日雕月琢,终于滴穿了石块,成为今天太极洞 内的一大奇观。
D.相同的鉴赏能力与博学多识使他们两个常常是一见如故。 【解析】“一见如故”指初次见面就很相投,像老朋友一样。根 据语境,两人“常常”见面,并非“初次见面”。 4.下列句子中没有语病的一项是(D)(2 分) A.糖就像烟草和酒精一样,是一种有潜在危害且容易让人上瘾。 B.没有谁不能不被消防英雄们的事迹感动。 .李爷爷种的辣椒基本上全卖完了。 D.阅读名著是启迪心智、陶冶情操的有效途径。 5.下列说法不正确的一项是(D)(2 分) A.《邓稼先》一的作者是杨振宁,邓稼先被称为“两弹”元勋。 B.《说和做》一采用夹叙夹议的写法,记述了闻一多先生作为学 者方面和作为革命家方面的说做事迹,赞扬了他为国家、为民族、为 民主献身的精神。 .《回忆鲁迅先生》是一篇回忆,作者通过叙写鲁迅先生日常生 活中的小事刻画一个真实的、富有人情味的鲁迅形象。 D.《孙权劝学》选自《资治通鉴》,是北宋司马迁主持编写的一 部国别体通史。 【解析】《资治通鉴》是司马光主持编写的一部编年体通史。
两种朗读技巧。(2 分)
示例:①要读准字音,字正腔圆;②要注重停顿,读出节奏;③ 要抑扬顿挫,读出语气语调;④要读出感情等。(指出两种朗读技巧 即可)
【读书角】 (3)阅读材料,回答问题。(2 分) 材料一 “母亲啊!天上的风雨了,鸟儿躲到它的巢里;心中的 风雨了,我只躲到你的怀里。”
诗句出自《繁星?春水(或繁星)》。(1 分) 材料二 “一跑,便喘不过气,而且嘴唇发焦,明知心里不渴, 也见水就想喝,不跑吧,那毒花花的太阳把手和脊背都要晒裂。好歹 的拉到了地方,他的裤褂全裹在了身上。拿起芭蕉扇扇扇,没用,风 是热的。”
人教版七年级下册数学综合测试卷完整版

人教版七年级下册数学综合测试卷Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】第七章综合测试卷(用时:90分钟满分:100分)一、选择题(每题2分,共20分)1.课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(D) A.(5,4) B.(4,5)C.(3,4) D.(4,3)2.在平面直角坐标系中,点(-1,m2+1)一定在(B)A.第一象限B.第二象限C.第三象限D.第四象限3.如图,下列说法正确的是(C)A.A与D的横坐标相同B.C与D的横坐标相同C.B与C的纵坐标相同D.B与D的纵坐标相同4.一个点位于x轴下方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度,那么此点的坐标是(B)A.(4,2) B.(-2,-4)C.(-4,-2) D.(2,4)5.若点P(x,y)的坐标满足xy=0,则点P的位置是(D)A.在x轴上B.在y轴上C.是坐标原点D.在x轴上或在y轴上或坐标原点6.如果点A(a,b)在第三象限,则点B(-a+1,3b-5)关于原点的对称点是(B)A.第一象限B.第二象限C.第三象限D.第四象限7.线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标为(C)A.(2,9) B.(5,3)C.(1,2) D.(-9,-4)8.已知点(2a,1-3a)在第二象限,且点到x轴的距离与到y轴的距离之和为6,则a的值为(A)A.-1 B.1C.5 D.39.小明住在学校正东200米处,从小明家出发向北走150米就到了李华家,若选取李华家为原点,分别以正东、正北方向为x,y轴正方向建立平面直角坐标系,则学校的坐标为(B)A.(-150,-200) B.(-200,-150)C.(0,-50) D.(150,200)10.已知三角形的三个顶点坐标分别是(-1,4),(1,1),(-4,-1),现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标分别是(A)A.(-2,2),(3,4),(1,7)B.(-2,2),(4,3),(1,7)C.(2,2),(3,4),(1,7)D.(2,-2),(3,3),(1,7)二、填空题(每题2分,共18分)11.如果用(8,3)表示八年级(3)班,那么九年级(6)班可表示成__(9,6)__.12.已知点P在第二象限,且横坐标与纵坐标的和为1,试写出一个符合条件的点P__(-1,2)__;点K在第三象限,且横坐标与纵坐标的积为8,写出两个符合条件的点__(-2,-4),(-1,-8)(答案不唯一)__.13.点P到x轴的距离是2,到y轴的距离是3,且在y轴的左侧,则P点的坐标是__(-3,2)或(-3,-2)__.14.在平面直角坐标系内,把点P(-5,-2)先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是__(-7,2)__.15.将点P(-3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,-1),则xy=__-10__.16.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为__(8,2)或(-2,2)__.17.已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是__4或-4__.18.如果p(a+b,ab)在第二象限,那么点Q(a,-b)在第__二__象限.19.已知线段MN=4,MN∥y轴,若点M坐标为(-1,2),则N点的坐标为__(-1,-2)或(-1,6)__.三、解答题(共62分)20.(10分)写出图中图形顶点A,B,C,D,E,F,G各点的坐标.并写出A点与E点,G点与C点的位置及它们的坐标的特点.解:A(-3,0),B(-1,-4),C(0,-2),D(3,-3),E(2,0),F(4,2),G(0,4);A,E在轴x上,纵坐标是0;C,G在轴y上,横坐标是0.21.(10分)如图,描出A(-3,-2),B(2,-2),C(-2,1),D(3,1)四个点,线段AB,CD有什么关系顺次连接A,B,C,D四点组成的图形是什么图形互相平行,平行四边形22.(10分)已知正方形的边长为8,它在平面直角坐标系中的位置如图所示.(1)直接写出点A,B,C,D四个点的坐标;(2)若将正方形向右平移4个单位长度,写出平移后A点的坐标.解:(1)因为正方形ABCD的各顶点A,B,C,D到两坐标轴的距离都相等,且A,B,C,D分别在第二、第三、第四、第一象限,正方形的边长为8,所以A,B,C,D的坐标分别是A(-4,4),B(-4,-4),C(4,-4),D(4,4).(2)(0,4).23.(10分)如图,(1)请写出在直角坐标系中的房子的A,B,C,D,E,F,G的坐标;(2)小影想把房子向下平移3个单位长度,你能帮她办到吗请作出相应图案,并写出平移后的7个点的坐标.解:(1)A(2,3),B(6,5),C(10,3),D(3,3),E(9,3),F(3,0),G(9,0).(2)A(2,0),B(6,2),C(10,0),D(3,0),E(9,0),F(3,-3),G(9,-3).图略.24.(10分)如图是某市部分简图,一个外地旅客刚走出火车站A,决定先到某超市B买些礼物,然后到老同学家C拜访,他按照同学留下的路线坐标,很快地与老同学相见了,他所走的路线如下:A(-3,0)→(-3,4)→(-4,4)→( )→(0,7)→( )→(4,4)→(3,4)→C(3,0).(1)先完成上面的填空,再画出他所走的路线,同时标出A,B,C的位置;(2)写出影院、宾馆、医院和体育场的位置坐标.(1)(0,4)或(-4,7),(4,7)或(0,4)(图略).(2)影院(-4,4),宾馆(0,0),医院(3,3),体育场(0,6).25.(12分)(1)如图1,点A坐标为(-1,1),将此小船ABCD向左平移2个单位,再向上平移3个单位得A′B′C′D′.①画出平面直角坐标系;②画出平移后的小船A′B′C′D′,写出A′,B′,C′,D′各点的坐标.(2)如图2,已知A,B两村庄的坐标分别为(2,2),(7,4),一辆汽车从原点O出发沿x轴正半轴行驶.①汽车行驶到什么位置时离A村最近写出此点的坐标.②汽车行驶到什么位置时离B村最近写出此点的坐标.③试猜想,到A,B两点距离和最近的点在x轴上有几个不要求说明理由.(3)观察图3,由①→②→③→④的变化过程,写出每一步图形的各顶点坐标是如何变化的.图3解:(1)①略.②(图略)A′(-3,4),B′(-2,2),C′(1,2),D′(2,3).(2)①图略,(2,0).②图略,(7,0).③1个,(3)①→②:A点,B 点的横坐标分别向右平移1个单位长度,2个单位长度,O点坐标不变;②→③:O,B两点坐标不变,A点纵坐标向下平移4个单位长度,横坐标不变;③→④三角形整体向下平移1个单位长度.。
(完整)人教版七年级数学下册各单元测试题及答案汇总,推荐文档

) ) )
D
E
F
1
∴∠C=∠ABD(
)
∵∠C=∠D(
)
∴∠D=∠ABD(
)
∴DF∥AC(
)
24、如图,DO 平分∠AOC,OE 平分∠BOC,若 OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________
当∠BOC=60°,∠DOE=_______________
34
2
A
B
C
第19题)
A、23° B、42° C、65° D、19°
二、填空题(本大题共 6 小题,每小题 3 分,共 18 分)
E
H
11、直线 AB、CD 相交于点 O,若∠AOC=100°,则
∠AOD=___________。 12、若 AB∥CD,AB∥EF,则 CD_______EF,其理由 是_______________________。
水面
入水点
(第14题)
度数之比是 2:7,那么这两个角分别是_______。
三 、(每题 5 分,共 15 分)
A
17、如图所示,直线 AB∥CD,∠1=75°,求∠2 的度数。
M 1B
C
D
N
2
第17题
18、如图,直线 AB 、CD 相交于 O,OD 平分∠AOF,OE⊥CD 于点 O,∠1=50°,求∠COB 、∠BOF 的度数。 F D
B
O
A
1
C (第18题) E
19、如图,在长方形 ABCD 中,AB=10cm,BC=6cm,若此长方形以 2cm/S 的速度沿着 A→B 方向移动,则经过多长 时间,平移后的长方形与原来长方形重叠部分的面积为 24?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
① ②
解:整理方程组,得
3x y 8
3x
5y
20
③ ④
③ ④,得
4y 28
解这个方程,得 y 7
把 y 7 代入①,得
3x 1 7 5
解得 x 5
x 5
所以这个方程组的解是
y
7
11 12 CB
18、60
21、解:如图所示
白棋的坐标为3,2
学无止 境
-3 -2 B
2 1 -1 0 1 -1 -2
真思考,并得出了正确结论,则下列结论中正确的是( ).
A.鸡 23只, 兔12 只 B.鸡 24 只, 兔11只 C.鸡 25 只, 兔10 只 D.鸡12 只, 兔 23只
11.如果关于 x 的不等式a 1 x a 1的解集为 x 1,那么a 的取值范围是( ).
A. a 0
B. a 0
C. a 1
∴x 2
把不等式的解集在数轴上表示为: -1 0 1 2
20、(1)
3x y 5 x 2y 15
① ②
解:由①,得
y 3x 5 ③
把③代入②,得
x 23x 5 15
解这个方程,得 x 5
把 x 5 代入①,得Fra biblioteky 10
x 5
所以这个方程组的解是
y
10
(2)
3x 5y
1 1
y5
3x
学无止 境
一、单项选择题
题号 1
2
34
5
6
7
8
9 10
选项 D B B C B D B D B A
二、填空题
13、答案不唯一,如:
x x
y y
1 3
14、 1 x 5 3 15 、 2
16 、10 17 、
三、解答题
19、解: 3x 13 x 17 2x 4
x
y
3 2
与
x
y
6 1
D. a 1
12. 如图1,在 ABC 中, AD 是 ABC 的高,B 40o,CAD 20o .则 BAC 的
度 数 为 ( ).A.20o
B. 30o
C. 50o
D. 60o
二、填空题(每小题 3 分,共 18 分)
13.写出一个解是
x
y
1 2
的二元一次方程组:
14. x 的 1 与 5 的差不小于3 ,用不等式表示为 2
22、解:依题意得:
图2
k b 2 k b 4
解这个方程组得bk
1 3
∴等式为 y x 3
当 x 2 时, y 2 3 5
答: y 的值为5 。 23、解:设 A、B 两种商品的原售价分别为 x 元和 y 元,依题意得:
x y 500 0.7x 0.9y 386
解这个方程组得
x
y
320 180
答: A、B 两种商品的原售价分别为320 元和180 元。
24、解:(1)120o (2)110o 3 AOC BOD ,理由是: ∵ AOB COD 90o ∴ AOC BOC BOD BOC 90o ∴AOC BOD
4 结论成立,理由是:
∵ AOB COD 90o ∴ AOB BOC COD BOC 即 AOC BOD
15.若 x y , 则 2x 3y . 32
.
. B
A 图1 C D
16. 根据下面所给信息,则每只玩具小猫的价格为 .
买
一 共 要 70 元
买
一 共 要 50 元
17. 方程 x 3y 9 的正整数解是:
.
18. 某种商品进价为150元,出售时标价为225 元,由于销售情况不好,商品准备降价出
89 ).
10 11 12
A. 第一象限
B. 第二象限
C. 第三象限
2.下列四个方程中,是二元一次方程组的是 ( ).
A. x 3 0
B. 2x z 5
C.3xy 5 8
3.若 5x2ab y3 与 3x6 yab 是同类项,则 a 2b ( ).
A. 3
B. 3
C. 6
4.由 x y 1。可以得到用 x 表示 y 的式子( ). 32
学无 止 境
七年级第二学期水平测试 数学科试题
(考试时间:100 分钟 满分:110 分)
题号
一
二
三
(1-12) (13-18) 19
20
21 22
得分
总分 23 24
一、单项选择题(每小题 3 分,共 36 分)
题号 1 2 3 4 5 6 7 选项
1. 在平面直角坐标系中,点 3,4 所在的象限是(
A. 675o
B. 720o
C. 900o
D.1080o
学无止 境
9.已知方程组baxx
by ay
5 2
的解是xy
4
,
3
则
(
).
A.
a b
2 3
B.
a 2 b 1
C.
a 2
b
1
D.
a b
2 1
10. 阅读材料:“今有鸡兔同笼, 上有三十五头, 下有九十四足, 问鸡兔各何”,阎伟经过认
A. y 2x 2 3
B. y 2x 1 C. y 33
2x 2 3
5.下列几对数值中哪一对是方程5x 4 y 14 的解( ).
D. 第四象限
D. 1 y 1
x
2
D. 9
D. y 2 2x 3
A.
x y
1 2
B.
x
y
2 1
C.
x y
3 2
6.不等式3x 6 的解集在数轴上表示为( ).
(1) 当 BOC 60o 时 , AOD . (2) 当 BOC 70o 时 , AOD . 3 你知道AOC 与 BOD 的大小关系吗?请说明理由. 4把三角板COD 绕点O 顺时针旋转到如图 4 的位置,(3)中的结论还成立吗?为什 么
?
A C
O
B
图3
D
A
O B
C
D
图4
七年级数学科试题参考答案
y5
3x
5
21. (本题 8 分)如图 2 的围棋盘放在平面直角坐标系内,黑棋 A 的坐标为(1,2),请在
图中画出平面直角坐标系,并写出白棋的坐标. A
B 图2
22. (本题 8 分)在等式 y kx b 中,当 x 1 时, y 2 ,当 x 1 时, y 4 ,求 当 x 2 时, y 的值.
售,但要保证利润不低于 10%,那么商店最多降
元出售此商品.
三、解答题(本大题共 66 分 19.(本题 8 分)解下列不等式,并把它的的解集在数轴上表示出来.
3x 13 x 17
学无止 境
20.解下列方程组.(每小题 5 分,共 10 分)
(1)
3x x
y 2
y
5
15
(2)
3x 5y
1 1
23. (本题 10 分)“五一”期间,某商场搞优惠促销,由顾客抽奖确定折扣,某顾客购买
学无止 境 A、B 两种商品,分别抽到七折(按售价的 70%)和九折(按售价的 90%),共付款386 元 , 这两种商品原售价之和为500 元,问这两种商品的原售价分别为多少元?
24. (本题 12 分)如图 3,将一副三角板的两个直角顶点重合在一起放置,
D.
x
y
4 1
-1 0 1 2 A
-1 0 1 2 B
-2 -1 0 1 C
-2 -1 0 1 D
7.如果等腰三角形有两边分别分别是4cm 和 8cm ,那么该等腰三角形的周长为( ).
A. 17cm B. 22cm
C. 17cm或22cm
D.以上答案都不对
8.一个多边形的每个外角都等于45o ,则这个多边形的内角和等于( ).
