思维导图之数学
小学二年级数学知识思维导图
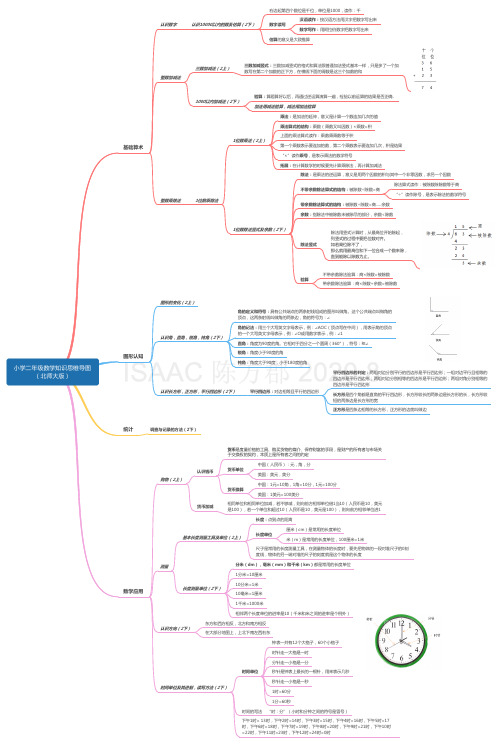
购物(2上)
认识钱币
货币单位 货币换算
中国(人民币):元,角,分 美国:美元,美分 中国:1元=10角,1角=10分,1元=100分 美国:1美元=100美分
货币加减
相同单位和相同单位加减,若不够减,则向前方相邻单位借1当10(人民币是10,美元 是100),若一个单位和超过10(人民币是10,美元是100),则向前方相邻单位进1
长度:点到点的距离
基本长度测量工具及单位(2上)
长度单位
厘米(cm)是常用的长度单位 米(m)是常用的长度单位,100厘米=1米
尺子是常用的长度测量工具,在测量物体的长度时,要先把物体的一段对准尺子的0刻 度线,物体的另一端对准的尺子的刻度就是这个物体的长度
测量
分米(dm),毫米(mm)和千米(km)都是常用的长度单位
小学二年级数学知识思维导图 (北师大版)
认识数字
认识10000以内的数及估算(2下)
右边起第四个数位是千位,单位是1000,读作:千
数字读写
汉语读作:按汉语方法用汉字把数字写出来 数字写作:用阿拉伯数字把数字写出来
估算的意义是大致推算
整数加减法
三数加减法(2上)
三数加减竖式:三数加减竖式的格式和算法跟普通加法竖式基本一样,只是多了一个加 数写在第二个加数的正下方,在横线下面的得数是这三个加数的和
直角:角度为90度的角。它相对于四分之一个圆周(360°),符号:Rt∠
锐角:角度小于90度的角
钝角:角度大于90度,小于180度的角
认识长方形,正方形,平行四边形(2下)
平行四边形:对边相等且平行的四边形
平行四边形的判定:两组对边分别平行的四边形是平行四边形;一组对边平行且相等的 四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两组对角分别相等的 四边形是平行四边形
数学乘法思维导图
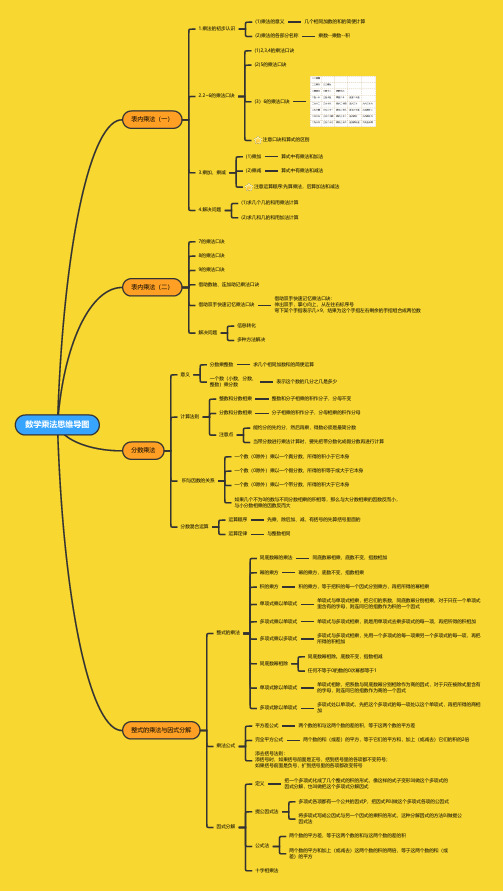
数学乘法思维导图表内乘法(一)1.乘法的初步认识(1)乘法的意义几个相同加数的和的简便计算(2)乘法的各部分名称乘数--乘数--积2.2~6的乘法口诀(1)2,3,4的乘法口诀(2)5的乘法口诀(3)6的乘法口诀注意口诀和算式的区别3.乘加、乘减(1)乘加算式中有乘法和加法(2)乘减算式中有乘法和减法注意运算顺序:先算乘法,后算加法和减法4.解决问题(1)求几个几的和用乘法计算(2)求几和几的和用加法计算表内乘法(二)7的乘法口诀8的乘法口诀9的乘法口诀借助数轴、连加助记乘法口诀借助双手快速记忆乘法口诀借助双手快速记忆乘法口诀:伸出双手,掌心向上,从左往右标序号弯下某个手指表示几×9,结果为这个手指左右剩余的手指组合成两位数解决问题信息转化多种方法解决分数乘法意义分数乘整数求几个相同加数和的简便运算一个数(小数、分数、整数)乘分数表示这个数的几分之几是多少计算法则整数和分数相乘整数和分子相乘的积作分子,分母不变分数和分数相乘分子相乘的积作分子,分母相乘的积作分母注意点能约分的先约分,然后再乘,得数必须是最简分数当带分数进行乘法计算时,要先把带分数化成假分数再进行计算积与因数的关系一个数(0除外)乘以一个真分数,所得的积小于它本身一个数(0除外)乘以一个假分数,所得的积等于或大于它本身一个数(0除外)乘以一个带分数,所得的积大于它本身如果几个不为0的数与不同分数相乘的积相等,那么与大分数相乘的因数反而小,与小分数相乘的因数反而大分数混合运算运算顺序先乘、除后加、减,有括号的先算括号里面的运算定律与整数相同整式的乘法与因式分解整式的乘法同底数幂的乘法同底数幂相乘,底数不变,指数相加幂的乘方幂的乘方,底数不变,指数相乘积的乘方积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘单项式乘以单项式单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式多项式乘以单项式单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加多项式乘以多项式多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加同底数幂相除同底数幂相除。
2020人教版八上数学思维导图(史上最新最全)

整章内容预览,梳理知识脉络,学习记忆好帮手,复习补漏好工具 目录
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十一章 三角形
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十二章 全等三角形
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十三章 轴对称
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十四章 整式的公众号“数学资料库”,更多优质内容免费领。
第十五章 分式
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
(完整版)小学数学思维导图(全)

小学数学思维导图(全)一、数的概念1. 自然数自然数是无限的,可以一直往上数。
自然数是离散的,相邻的自然数之间没有其他数。
自然数是可数的,可以一个一个地数出来。
2. 整数整数是可加的,可以相加得到新的整数。
整数是可减的,可以相减得到新的整数。
整数是可乘的,可以相乘得到新的整数。
整数是可除的,可以相除得到新的整数。
3. 分数分数有分子和分母两部分,分子表示被等分的部分,分母表示等分的总份数。
分数可以相加、相减、相乘、相除。
分数可以化简,即分子和分母同时除以它们的最大公约数。
4. 小数小数有整数部分和小数部分两部分,整数部分表示整体中的整数部分,小数部分表示整体中的小数部分。
小数可以相加、相减、相乘、相除。
小数可以化简,即去掉末尾的0。
二、数的运算1. 加法加法是可交换的,即加数的位置可以交换。
加法是可结合的,即加数可以按照任意顺序相加。
加法的结果是唯一的。
2. 减法减法的结果是唯一的。
减法的结果可以是正数、负数或0。
3. 乘法乘法是可交换的,即乘数的位置可以交换。
乘法是可结合的,即乘数可以按照任意顺序相乘。
乘法的结果是唯一的。
4. 除法除法的结果可以是正数、负数或分数。
除法的结果是唯一的。
三、几何图形1. 线段线段有长度。
线段可以测量。
线段可以比较长度。
2. 角角有大小。
角可以测量。
角可以比较大小。
3. 三角形三角形有面积。
三角形的面积可以用公式计算。
三角形的面积可以比较大小。
4. 四边形四边形有面积。
四边形的面积可以用公式计算。
四边形的面积可以比较大小。
四、数学应用1. 解决实际问题数学可以应用于解决实际问题,例如:计算购物时的找零。
计算路程和时间的关系。
计算物体的面积和体积。
2. 数学游戏数学游戏可以帮助学生提高数学思维能力和兴趣,例如:猜数字游戏。
24点游戏。
数独游戏。
3. 数学竞赛数学竞赛可以激发学生的学习兴趣和竞争意识,例如:数学奥林匹克竞赛。
华罗庚金杯赛。
小学生数学竞赛。
五、数学思维方法1. 归纳法归纳法是一种从具体事例出发,得出一般结论的思维方式。
小学五年级数学知识思维导图(无水印)

无限不循环小数
无限不循环小数指小数部分有无限多个数字,且没有依次不断地重复出现的一个数字或 几个数字的小数叫做无限不循环小数,如圆周率π=3.14159265358979323……。无 限不循环小数也就是无理数,不能化成分数形式
小数混合运算(5上)
表面积:立体图形表面所有面的面积之和
体积:物体所占空间的大小
容积:容器所能容纳的物体的体积
立方毫米:棱长为1毫米的正方体的体积
立方厘米:棱长为1厘米的正方体的体积
主要概念
体积单位
立方米:棱长为1米的正方体的体积 1000立方毫米=1立方厘米
1000立方厘米=1立方分米
1000立方分米=1立方米
体积与表面积
棱柱的体积=底面积×测棱长
体积的计算
直棱柱的体积=底面积×侧棱长 长棱长×棱长×棱长
统计
复式条形统计图(5下)
条形统计图分为单式条形统计图和复式条形统计图,前者只表示1个项目的数据,后者 可以同时表示多个项目的数据
统计图
复式折线统计图(5下)
折线统计图分单式或复式。复式的折线统计图有图例,用不同颜色或形状的线条区别开 来
两个连续整数中必有一个奇数和一个偶数
公倍数
两个或多个整数公有的倍数叫做它们的公倍数 两个或多个整数的公倍数里最小的那一个叫做它们的最小公倍数
公因数
两个或多个整数公有的因数叫做它们的公因数 两个或多个整数的公因数里最大的那一个叫做它们的最大公因数
一个大于1的整数,除了1和它自身外,不能被其他自然数整除的数叫做质数
长方体
长方体有6个面。每组相对的面完全相同。长方体有12条棱,相对的四条棱长度相等。 按长度可分为三组,每一组有4条棱。长方体有8个顶点。每个顶点连接三条棱。三条 棱分别叫做长方体的长,宽,高。长方体相邻的两条棱互相垂直
小学数学思维导图(全)
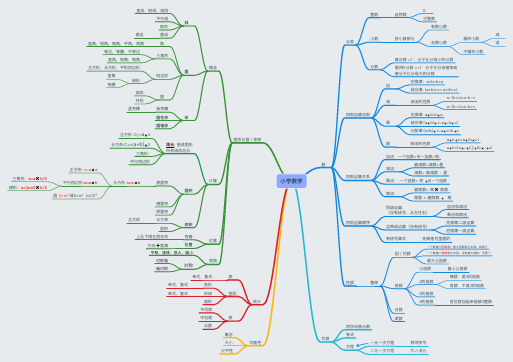
⼩小学数学数分类整数⾃自然数0正整数⼩小数按⼩小数部分有限⼩小数⽆无限⼩小数循环⼩小数纯混不不循环⼩小数分数真分数 <1 :分⼦子⽐比分⺟母⼩小的分数假(带)分数 >=1:分⼦子与分⺟母相等或者分⼦子⽐比分⺟母⼤大的分数四则运算法则加交换律律:a+b=b+a 结合律律: (a+b)+c= a+(b+c)减减法的性质a-(b+c)=a-b-c a-(b-c)=a-b +c乘交换律律: a ✖b =b ✖a结合律律:(a ✖b)✖c =a ✖(b ✖c)分配律律:(a +b)✖c =a ✖c+b ✖c除除法的性质a ➗b ➗c=a ➗(b ✖c )a ➗b=(a ✖/➗c)➗(b ✖/➗c)四则运算关系加法:⼀一个加数+另⼀一加数=和减法:被减数=减数+差减数= 被减数 - 差乘法: ⼀一个因数= 积 ➗另⼀一个因数 除法:被除数= 商✖ 除数除数 = 被除数 ➗ 商四则运算顺序同级运算, (没有括号,从左往右)加法和减法乘法和除法含两级运算(没有括号)先做第⼆二级运算后做第⼀一级运算有括号算式先做括号⾥里里⾯面的性质整除因/约数⼀一个数最⼩小因数是1, 最⼤大因数是它本身;有限个⼀一个数最⼩小倍数是它本身,没有最⼤大倍数;⽆无限个最⼤大公因数倍数公倍数最⼩小公倍数2的倍数偶数:是2的倍数奇数:不不是2的倍数5的倍数3的倍数各位数加起来能被3整除合数质数代数⽤用字⺟母表示数等式⽅方程⼀一元⼀一次⽅方程移项变号⼆二元⼀一次⽅方程代⼊入消元可能性概念⼤大⼩小公平性统计表单式,复式图形条形单式,复式折线单式,复式扇形数平均数中位数众数图形与⾯面/体积概念线直线,射线,线段平⾏行行线相交垂线垂⾜足⾯面⻆角直⻆角,锐⻆角,钝⻆角,平⻆角,周⻆角三⻆角形等边,等腰,不不等边直⻆角,锐⻆角,钝⻆角四边形正⽅方形,⻓长⽅方形,平形四边形梯形直⻆角等腰圆扇形环形体⻓长⽅方体正⽅方体圆柱体圆锥体计算周⻓长: 围成图形所有线段总⻓长正⽅方形 C 正=a ✖4⻓长⽅方形:C ⻓长=(a+b)✖2三⻆角形: 平⾏行行四边形⾯面积表⾯面积⻓长⽅方形 s=a ✖b正⽅方形: s=a ✖a平⾏行行四边形:s=a ✖h 三⻆角形:s=a ✖h/2梯形:s=(a+b)✖h/2圆 S=πr²或S=π*(d/2)²侧⾯面积底⾯面积体积⻓长⽅方体正⽅方体容积位置⽅方向上北北下南左⻄西右东位置⽅方向➕距离变换҅ ҅ ҅对称对称轴轴对称。
(word完整版)小学数学思维导图(全)
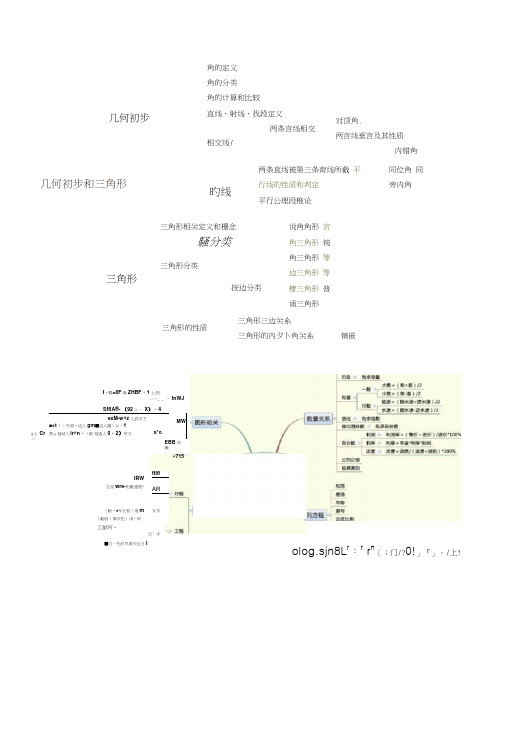
角的定义 角的分类 角的计算和比较几何初步直线、射线、找段定义两条言线相交相交线/对顶角.两言线垂言及其性质内错角几何初步和三角形旳线两条直线被第三条育线所截 平行线的性质和判定 平行公理段椎论同位角 同旁内角三角形三角形相关定义和栅念騒分类三角形分类按边分类说角角形 言角三角形 钝角三角形 等边三角形 等棲三角形 普诵三角形三角形的性质三角形三边关系 三角形的內夕卜角关系镇嵌exM-w^z 人武甲方MW ■«t ・〔外冒•边人gm ■边人徽)以・1隽u 毎沏人ir^n ・(RU 每选人0・2)甲万s*o SfflA®- (92人・ X )・4 &人 Cr 二I •稠=0F 芻ZHBF ・1 匕阿--…_ _ 一 tnWJ IRW 总及wre-炬敵連度*ftlflAR女车(軽•♦牟长和)度m(虧丽•事饮祀)/M •岸工耐阿•■力一先庐早第天生日IEBB 布魏 «715 注:水olog.sjn8L r :r r n 〔;门/?0!」『」。
/上!线射线*(51)同一平面内两条门线位诧关系田成图形的所有线]、段.曲线的总K J相似三角形的性质相似三角彤的对应角相等相似三角形的対应边成比例相似三角彤的对应高线的比等于相似比相似三角形的対应中线的比等于相似比相似三角彤的対应角平分线的比等于相似比相似相似三角形定义比例相似三角彤的周长比等于相似比相似三角彤的面枳比等于似比的平方相似三角形具有传递性形状相同、对应角相等、对应边成比例的图形两个比值相等的式子形状相同对应角相等对磁側例面枳比倉坊应边比值的平方周长比等于对应边之比相{以三角彤的定义相似三角形的定义.表示方法、相似比表示方法相似比普通三角形相似三角形的判定吉角三角形两边对应成比例夹角相等三边对应成比例两角对应相等貝备普通三角形的判定方法 F 言角边与斜边对应成比例ilMJft ia・> nj«qfl^^WKL • W %岁"诅・空輛?小・只0力匕・知_1 •方(WLt«*);何2 0) ttl* 4z 2D)全等三角形的判富角平分线的性/贵具备昔通三角形的河定方法 斜辺和 Y 直角辺(HL ) 边边边(SSS) 边角边(SAS) 角边角(ASA) 角角辺(AAS)角平分找上任盘一点到角两边的距离相等 直角三角形普逋三角形尺规作圈全等三角形找夹ft(SAS) 已知两边 拢直角(HL)拢第央(SSS) 边为角的邻辺 已m —角 全等三角形的性质找己如角的另T&SAS) 戏己知边的稠(AAS ) 找夹己知边的角(ASA ) 边为角的对边.找任越角(AAS )—如朋狭边(ASA)已溯角找锂逊AAS)对应边瞬 对应角相筹 对应中线、高和角平分线相等 面积相等百分!除以一 于乘以目例散里点苗程分配轉的应用豳分数 呼数睁以分故 分嫂混合计算 十磁昨ms 、am (a««i ■ •空回型列」衣〔分《陳<1嗷运.厂蘇l^wBsry'、.运引血"•毕!1k VSfiML定义圆的认识在T平面内,线段0甩尧固定端点O 旋转一周・另一端点确形成的图形溺性旋转不变性外接圆内切圆点在圆上点在圆外点在圆内相切相交相离相切与圆的位萱关系相交相离三角畛卜接圆和内切圍与点的位置关系圆的位置与直线的位逼关泵外切内切外离内含面积的计算圆柱体、圆锥体与圜相关的计算正多边形与圆的相关计算直线与圆的计算圆与圆的计算國周角定理与圆相关的定]圆心角垂径定理H8. KK. ttA"斗驚砂匸鸟阻”岁■两出■空L 平吞81■足 ««iM. GW. WA 甲於・ SA «无■小航亀iD.苓■・不野边■・.«• «•unn »ni» vnaifiv卄:不・环小1R三角启•形■识ttWtWF方・・距・»«Kvt用字0«^n公卩性正方律 长力“■柱上北下I •左si 右东»n平*, ftfl. ttX, ■小出11折10百分■”・MS比SEttFI. fitt«比■尺交矗" 掃・ftin BWBBttHt 比 «#K养比 fiwaiR-nas?第毎I总・aw小学数学公AMRtt.iHRB9KM««. «RUMB2 1. 5、9 4々5、S/12SBW 的畋”京曲.■分 ■賛分E!s ・vt <«3t—K —it事》费号 代人林力*) _it-走bhy^ineLcyrrLcri/zhuriio/<IEI1.每份数X份数=总数总数于每份数=份数总数2份数=每份数总数十总份数=平均数2、1倍数x倍数=几倍数几倍数"倍数=倍数几倍数十倍数=1倍数3、速度次时间=路程路程?速度=时间路程£时间=速度4、单价x数量=总价总价2单价=数量总价三数量=单价5、工作效率x工作时间=工作总量工作总量壬工作效率=工作时间工作总量三工作时间=工作效率6、加数+加数=和和 ------- 个加数=另一个加数7、被减数一减数=差被减数一差=减数差+减数=被减数8、因数乂因数=积积丰一个因数=另一个因数9、被除数m除数=商被除数三商=除数商x除数=被除数2、正方体V :体积 a:棱长表面积二棱 长X 棱长X6 S 表 =axax6体积二棱长 X 棱长X 梭长V=axaxa5三角形 S 面积2底丄髙 面积二底X 高42s=ah-r2三角形高二面积x2弓底 三角形底二面积专高4、长方体V:体积s:面积工长b:宽h:高 ⑴表面积(长X 宽#长X 高•宽X 高)x2S=2(ab+ah+bh )(2)体积二长X 宽x 高 V=abh3、长方形C 周长S 面积a 边长周长二(长璃:)X2C 二 2(3+b ) 面积二长X 离:S=ab1 X 正方形C 周长 S 面积a 边长甬长 =边长 X4C=4a 面积二边长X 边长 S 二aXa严行四辱s 面积a 底h 高 回齐只二底X 咼 S —dhS 面枳C 周长lid 二直径匸半轻 (1)周长二直轻xn=2xnx¥S C=nd=2nr (2)081=半径X 半径xn形休関形计算平行梯吃7梯形 s 面积a 上底b下 底h 高面积==(上底十下 底)*高三2s=(a+b}x h?29圆柱体V :体积h:高s;底面积「:底面半径 c:底面周长(1) 侧面积=底面周高(2) 表面诂=侧面积4底面积X2⑶体积二底面积X高(4)体积=侧面 积E2X 半径形休形甘算平行 梯形锥体h:高 s;底面积 匚底面半径 体积夢面 积乂高丰3和差问题的公式(和+差)?2=大数(和一差)-2 =小数和倍问题和一(倍数一1)=小数 小数X 倍数=大数(或者和一小数=大数)差倍问题差+ (倍数一1)=小数 小数X 倍数=大数(或小数+差=大数)追及问题盈亏问题(盈+亏)-两次分配量之差=参加分配的份数(大盈一小盈)三两次分配量之差=参加分配的份数(大亏一小亏)三两次分配量之差=参加分配的份数相遇问题相遇路程=速度和X相遇时间相遇时间=相遇路程三速度和速度和=相遇路程士相遇时间追及问题追及距离=速度差X追及时间追及时间=追及距离三速度差速度差=追及距离?追及时间流水问题顺流速度=静水速度+水流速度 逆流速度=静水速度一水流速度静水速度=(恢流速度+逆流速度>22水流速度=(顺流速度一逆流速度叶2浓度问题溶质的重量+溶剂的重量=溶液的重量'溶质的重量士溶液的重量X100% =浓度 溶液的重量X 浓度=溶质的重量溶质的重量三浓度=溶液的重量利润与折扣问题利润=售出价一成本利润率=利润十成本X100% =(售岀价十成本一1)x100% 涨跌金额二本金x 涨跌百分比 折扣=实际售价三原售价x 100%(折扣< 1) 利息=本金x 利率x 时间税后利息=本金x 利率x 时间x ( 1 — 20%)体(容)积单位换算1立方米=1000立方分米1立另分米二100 0立分■厘米1立方分米=1升1立方厘米胡毫升1立方米=1000升重量单位换算1千克=1000克1千克习公斤人垦币单位换算1元=10角1角=10分1元=100分体(容)积单位换算1立方米h 000立方分米1立方分米二1000立方!1米1立方分米了升1立方厘米=1基升1立方米=1000升重量单位换算1吨=1000千克1千克=1000克1千克胡公斤人民币单位换算1元=10角1角=10分1元=100分。
数学八下第一章思维导图

数学八下第一章思维导图
数学八下第一章思维导图如下:
拓展
一般地,形如√a的代数式叫做二次根式,其中,叫作被开方数。
当≥0时,√表示的算术平方根;当小于0时,√的值为纯虚数(在一元二次方程求根公式中,若根号下为负数,则方程有两个共轭虚根)。
判断一个二次根式是否为最简二次根式主要方法是根据最简二次根式
的定义进行,或直观地观察被开方数的每一个因数(或因式)的指数
都小于根指数2,且被开方数中不含有分母,被开方数是多项式时要先因式分解后再观察。
全套高中数学思维导图(清晰打印版)

高中数学选修 2-1 目录 第一章 常用逻辑用语 1.1 命题及其关系 1.2 充分条件与必要条件 1.3 简单的逻辑联结词 1.4 全称量词与存在量词 第二章 圆锥曲线与方程 2.1 曲线与方程 2.2 椭圆 2.3 双曲线 2.4 抛物线 第三章 空间向量与立体几何 3.1 空间向量及其运算 3.2 立体几何中的向量方法
两角和与差的正弦、余弦和正切公 式
简单的三角恒等变换
高中数学选修 1-2 目录 第一章 统计案例 1.1 回归分析的基本思想及其初 步应用 1.2 独立性检验的基本思想及其 初步应用 第二章 推理与证明 2.1 合情推理与演绎推理 2.2 直接证明与间接证明 第三章 数系的扩充与复数的引 入 3.1 数系的扩充和复数的概念 3.2 复数代数形式的四则运算 第四章 目录 第一章 解三角形 正弦定理和余弦定理 应用举例 实习作业 第二章 数列 数列的概念与简单表示法 等差数列 等差数列的前 n 项和 等比数列 等比数列的前 n 项和 第三章 不等式 不等关系与不等式 一元二次不等式及其解法 二元一次不等式(组)与简单的线 性规划问题 基本不等式
圆的方程 直线、圆的位置关系 空间直角坐标系
高中数学
思维导图
“我爱学习,学习使我妈快乐 我妈快乐,全家快乐!”
全套高中数学思维导图(清晰打印版)
高中数学必修一目录 第一章 集合与函数概念 集合 函数及其表示 函数的基本性质 第二章 基本初等函数(Ⅰ) 指数函数 对数函数 幂函数 第三章 函数的应用 函数与方程 函数模型及其应用
超实用小学数学思维导图,速掌握因数和倍数

超实用小学数学思维导图,让孩子快速掌握因数和倍数!
了解什么是因数,什么是倍数,以及数字的因数与倍数的范围最大值最小值。
对2、3、5这类比较特殊的数字,分别观察数字倍数的特征规律。
特别地,根据是否为2的倍数,可将数字划分为奇数和偶数。
质数的特征是只含1和本身两个因数,而合数除了1和本身之外还存在其他的因数。
其中1既不是质数也不是合数,最小的质数是2,最小的合数是4。
对于a×b=c(其中a,b,c都是不为0的整数),那么称a 和b都是c的因数,c是a、b的倍数,倍数和因数是相互依存的关系,不能单独的谈论谁是因数,谁是倍数。
因数针对的是非0的自然数,其数量是有限的,最小的为1,最大的为它本身。
非0整数的倍数有无限多个,最小的倍数是数字本身,数字的倍数可以无限大,不存在某个具体的最大倍数。
2、3、5的倍数有独特的特征,2的倍数个位上是0、2、4、6、8, 5的倍数个位上一般是0或5,而各个位上的数的和是3的倍数,那么这个数也是3的倍数。
根据数字是否是2的倍数,可将数字分为偶数和奇数,0是最小的偶数,1是最小的奇数。
质数的特征是只有1和它本身两个因数,而合数除了1和它本身之外还存在其他的因数。
最小的质数是2,最小的合数是4,其中1既不是质数也不是合数。
---。
