10-11 离散数学期末试卷A
离散数学期末考试试题及答案

离散数学期末考试试题及答案离散数学期末考试试题及答案离散数学是研究离散量的结构及其相互关系的数学学科,是现代数学的一个重要分支。
下面是小编整理的离散数学期末考试试题及答案,欢迎阅读参考!一、【单项选择题】(本大题共15小题,每小题3分,共45分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在答题卷相应题号处。
1、在由3个元素组成的集合上,可以有 ( ) 种不同的'关系。
[A] 3 [B] 8 [C]9 [D]272、设A1,2,3,5,8,B1,2,5,7,则AB( )。
[A] 3,8 [B]3 [C]8 [D]3,83、若X是Y的子集,则一定有( )。
[A]X不属于Y [B]X∈Y[C]X真包含于Y [D]X∩Y=X4、下列关系中是等价关系的是( )。
[A]不等关系 [B]空关系[C]全关系 [D]偏序关系5、对于一个从集合A到集合B的映射,下列表述中错误的是( )。
[A]对A的每个元素都要有象 [B] 对A的每个元素都只有一个象[C]对B的每个元素都有原象 [D] 对B的元素可以有不止一个原象6、设p:小李努力学习,q:小李取得好成绩,命题“除非小李努力学习,否则他不能取得好成绩”的符号化形式为( )。
[A]p→q [B]q→p [C]┐q→┐p [D]┐p→q7、设A={a,b,c},则A到A的双射共有( )。
[A]3个 [B]6个 [C]8个 [D]9个8、一个连通G具有以下何种条件时,能一笔画出:即从某结点出发,经过中每边仅一次回到该结点( )。
[A] G没有奇数度结点 [B] G有1个奇数度结点[C] G有2个奇数度结点 [D] G没有或有2个奇数度结点9、设〈G,*〉是群,且|G|>1,则下列命题不成立的是( )。
[A] G中有幺元 [B] G中么元是唯一的[C] G中任一元素有逆元 [D] G中除了幺元外无其他幂等元10、令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为( )[A] p→┐q [B] p∨┐q[C] p∧q [D] p∧┐q11、设G=的结点集为V={v1,v2,v3},边集为E={,}.则G的割(点)集是( )。
11离散数学a卷答案
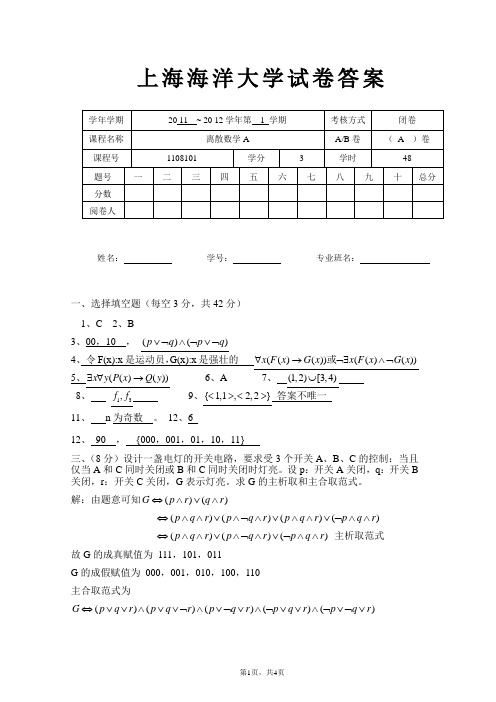
上海海洋大学试卷答案姓名: 学号: 专业班名:一、选择填空题(每空3分,共42分) 1、C 2、B3、00,10 , ()()p q p q ∨⌝∧⌝∨⌝4、 令F(x):x 是运动员,G(x):x 是强壮的 (()())(()(x F x G x x F x G x ∀→⌝∃∧⌝或5、(()())x y P x Q y ∃∀→6、A7、 (1,2)[3,⋃8、 13,f f 9、{1,1,2,2}<><> 答案不唯一 11、 n 为奇数 。
12、612、 90 , {000,001,01,10,11}三、(8分)设计一盏电灯的开关电路,要求受3个开关A 、B 、C 的控制:当且仅当A 和C 同时关闭或B 和C 同时关闭时灯亮。
设p :开关A 关闭,q :开关B 关闭,r :开关C 关闭,G 表示灯亮。
求G 的主析取和主合取范式。
解:由题意可知()()G p r q r ⇔∧∨∧()()()(p q r p q r p q r pq r⇔∧∧∨∧⌝∧∨∧∧∨⌝∧∧ ()()()p q r p q r pq r⇔∧∧∨∧⌝∧∨⌝∧∧ 主析取范式 故G 的成真赋值为 111,101,011 G 的成假赋值为 000,001,010,100,110 主合取范式为()()()()()G p q r p q r p q r p q r p q r ⇔∨∨∧∨∨⌝∧∨⌝∨∧⌝∨∨∧⌝∨⌝∨四、(8分)在自然推理系统中,构造并证明下列推理。
(命题逻辑推理证明) 若小张喜欢数学,则小李或小赵也喜欢数学。
若小李喜欢数学,则他也喜欢物理。
小张确实喜欢数学,但小李不喜欢物理。
所以,小赵喜欢数学。
证明:设p:小张喜欢数学,q:小李喜欢数学,r:小赵喜欢数学,s:小李喜欢物理 上述符号化为:前提:,,p q r q s p s →∨→∧⌝;结论:r证明:(1)p s ∧⌝ 前提 (7)q ⌝ (3)(6)拒取式 (2)p (1)化简 (8)r (5)(7)析取三段论 (3)s ⌝ (1)化简 (4)p q r →∨ 前提(5)q r ∨ (2)(4)假言推理 (6)q s → 前提五、设集合{,,,}A a b c d =,R 为A 上的二元关系,且{(,),(,),(,),(,)}R a b b c c a d d =, (1)求R 的关系矩阵;(3分) (2)求R 的性质;(3分)(3)求R 的传递闭包t (R );(4分)(4)设{(,),(,),(,)}S a c c b d c =,求1S R - ;(4分)(5)在关系R 中添加最少的有序对使其成为A 上的等价关系,不妨令该等价关系为*R ,求*R 及商集*/A R 。
离散数学期末复习题(6套)

《离散数学》期末考试题(A)一、填空题(每小题3分,共15分)1.设}}{},,{{c b a A =,}}{},,{},{{c c b a B =,则)(=⋃B A ,)(=⋂B A ,)()(=A P .2.集合},,{c b a A =,其上可定义( )个封闭的1元运算,( )个封闭的2元运算,( )个封闭的3元运算.3.命题公式1)(↑∧q p 的对偶式为( ).4.所有6的因数组成的集合为( ).5.不同构的5阶根树有( )棵.二、单选题(每小题3分,共15分)1.设A , B 是集合,若A B A =-,则(A)B = ∅ (B) A = ∅ (C)=⋂B A ∅ (D)A B A =⋂2.谓词公式)())()((x R y yQ x P x ∧∃→∀中量词x ∀的辖域为(A))())()((x R y yQ x P x ∧∃→∀ (B))()(y yQ x P ∃→(C))())()((x R y yQ x P ∧∃→ (D))()(y yQ x P ∃→和)(x R3.任意6阶群的子群的阶一定不为(A)4 (B)6 (C)2 (D)34.设n 是正整数,则有限布尔代数的元素个数为(A)2n (B)4n (C)n 2 (D)2n5.对于下列序列,可构成简单无向图的度数序列为(A)3, 3, 4, 4, 5 (B)0, 1, 3, 3, 3 (C)1, 1, 2, 2, 3 (D)1, 1, 2, 2, 2三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1. 设N N N :⨯→f ,)1,()(+=x x x f ,则f 是满射. () 2. 5男5女圆桌交替就座的方式有2880种. () 3. 设),(≤L 是格,对于L z y x ∈,,,若z x y x ⋅=⋅且z x y x +=+,则z y =. () 4. 任何树都至少2片树叶. ()5. 无向图G 有生成树的充要条件是G 为连通图. ( )四、(10分)设C B A ,,和D 是集合,证明)()()()(D B C A D C B A ⨯-⨯⊆-⨯-,并举例说明上式中不能将⊆改为 = .五、(15分)设N 是自然数集合,定义N 上的关系R 如下:y x R y x +⇔∈),(是偶数,1.证明R 是N 上的等价关系.2.求出N 关于等价关系R 的所有等价类.3.试求出一个N 到N 的函数f ,使得)}()(,N ,|),{(y f x f y x y x R =∈=.六、(10分)在实数集合R 中证明下列推理的有效性:因为R 中存在自然数,而所有自然数是整数,所以R 中存在整数.七、(10分)设R 是实数集合,令}0,R ,|),{(≠∈=a b a b a G ,定义G 上的运算如下: 对于任意G d c b a ∈),(),,(,),(),(),(b ad ac d c b a +=⋅,证明),(⋅G 是非Abel 群.八、(10分)若简单平面图G 的节点数7=n 且边数15=m ,则G 是连通图,试证明之.《离散数学》期末考试题(B)一、填空题(每小题3分,共15分)1.设,,},,{{b a b a A =∅},则-A ∅ = ( ),-A {∅} = ( ),)(A P 中的元素个数=|)(|A P ( ).2.设集合A 中有3个元素,则A 上的二元关系有( )个,其中有( )个是A 到A 的函数.3.谓词公式))()(())()((y P y Q y x Q x P x ⌝∧∃∧→∀中量词x ∀的辖域为( ), 量词y ∃的辖域为( ).4.设}24,12,8,6,4,3,2,1{24=D ,对于其上的整除关系“|”,元素( )不存在补元.5.当n ( )时,n 阶完全无向图n K 是平面图,当n 为( )时,n K 是欧拉图.二、单选题(每小题3分,共15分)1.设R 是集合A 上的偏序关系,1-R 是R 的逆关系,则1-⋃R R 是A 上的(A)偏序关系 (B)等价关系 (C)相容关系 (D)以上结论都不成立2.由2个命题变元p 和q 组成的不等值的命题公式的个数有(A)2 (B)4 (C)8 (D)163.设p 是素数且n 是正整数,则任意有限域的元素个数为(A)n p + (B)pn (C)n p (D)pn4.设R 是实数集合,≤是其上的小于等于关系,则(R, ≤)是(A)有界格 (B)分配格 (C)有补格 (D)布尔格5.3阶完全无向图3K 的不同构的生成子图有(A)2 (B)3 (C)4 (D)5 三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1.若一个元素a 既存在左逆元l a ,又存在右逆元r a ,则r l a a =. ( )2.命题联结词→不满足结合律. ( )3.在Z 8 = {0,1,2,3,4,5,6,7}中,2关于“⋅8”的逆元为4. ( )4.整环不一定是域. ( )5.任何),(m n 平面图的面数2+-=n m r . ( )四、(10分)设B A f →:且C B g →:,若g f 是单射,证明f 是单射,并举例说明g 不一定是单射.五、(15分)设},,,{d c b a A =,A 上的关系)},(),,(),,(),,(),,(),,(),,(),,(),,{(c d b d a d c c b c a c c a b a a a R =,1.画出R 的关系图R G .2.判断R 所具有的性质.3.求出R 的关系矩阵R M .六、(10分)利用真值表求命题公式))(())((p q r r q p A →→↔→→=的主析取范式和主合取范式.七、(10分) 边数30<m 的简单平面图G ,必存在节点v 使得4)deg(≤v .八、(10分) 有六个数字,其中三个1,两个2,一个3,求能组成四位数的个数.《离散数学》期末考试题(C)一、填空题(每小题3分,共15分)1. 若n B m A ==||,||,则=⨯||B A ( ),A 到B 的2元关系共有( )个,A 上的2元关系共有( )个.2. 设A = {1, 2, 3}, f = {(1,1), (2,1), (3, 1)}, g = {(1, 1), (2, 3), (3, 2)}和h = {(1, 3), (2, 1), (3,1)},则( )是单射,( )是满射,( )是双射.3. 下列5个命题公式中,是永真式的有( )(选择正确答案的番号).(1)q q p p →→∧)(;(2))(q p p ∨→;(3))(q p p ∧→;(4)q q p p →∨∧⌝)(;(5)q q p →→)(.4. 设D 24是24的所有正因数组成的集合,“|”是其上的整除关系,则3的补元( ),4的补元( ),6的补元( ).5. 设G 是(7, 15)简单平面图,则G 一定是( )图,且其每个面恰由( )条边围成,G 的面数为( ).二、单选题(每小题3分,共15分)1. 设A , B , C 是集合,则下述论断正确的是( ).(A)若A ⊆ B , B ∈ C ,则A ∈ C . (B)若A ⊆ B , B ∈ C ,则A ⊆ C .(C)若A ∈ B , B ⊆ C ,则A ∈ C . (D)若A ∈ B , B ⊆ C ,则A ⊆ C .2. 设R ⊆ A ⨯ A ,S ⊆ A ⨯ A ,则下述结论正确的是( ).(A)若R 和S 是自反的,则R ⋂ S 是自反的.(B)若R 和S 是对称的,则S R 是对称的.(C)若R 和S 是反对称的,则S R 是反对称的.(D)若R 和S 是传递的,则R ⋃ S 是传递的.3.在谓词逻辑中,下列各式中不正确的是( ).(A))()())()((x xB x xA x B x A x ∀∨∀=∨∀(B))()())()((x xB x xA x B x A x ∀∧∀=∧∀(C))()())()((x xB x xA x B x A x ∃∨∃=∨∃(D)),(),(y x xA y y x yA x ∀∃=∃∀4. 域与整环的关系为( ).(A)整环是域 (B)域是整环 (C)整环不是域 (D) 域不是整环5.设G 是(n , m )图,且G 中每个节点的度数不是k 就是k + 1,则G 中度数为k 的节点个数为( ). (A)2n . (B)n (n + 1). (C)nk . (D)m k n 2)1(-+. 三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1.设f : Z → Z ,x x x f 2||)(-=,则f 是单射. ( )2.设ϕ是群G 1到群G 2的同态映射,若G 1是Abel 群,则G 2是Abel 群. ( )3.设),(≤L 是格,对于L z y x ∈,,,若z x y x ⋅=⋅且z x y x +=+,则z y =. ( )4.元素个数相同的有限布尔代数都是同构的. ( )5.设G 是n (n ≥ 11)阶简单图,则G 或G 是非平面图. ( )四、(15分)设A 和B 是集合,使下列各式(1)A B A =⋂; (2)A B B A -=-;(3)A A B B A =-⋃-)()(成立的充要条件是什么,并给出理由.五、(10分) 设S 是实数集合R 上的关系,其定义如下∈=y x y x S ,|),{(R 且是3y x -是整数}, 证明: S 是R 上的等价关系. 六、(10分) 求谓词公式)))()(()(()(x xD y yC y B x xA ∀→∃⌝→→∃的前束范式.七、(10分) 若n 个人,每个人恰有3个朋友,则n 必为偶数,试证明之.八、(10分) 利用生成函数求解递归关系⎩⎨⎧=-+=-2)1(211a n a a n n .《离散数学》期末考试题(D)一、填空题(每小题3分,共15分)1. 设|A | = 5, |B | = 2, 则可定义A 到B 的函数( )个,其中有( )单射,( )个满射.2. 令G (x ): x 是金子,F (x ): x 是闪光的,则命题“金子都是闪光的,但闪光的未必是金子”符号化为( ).3. 设X 是非空集合,则X 的幂集P (X )关于集合的⋃运算的单位元是( ),零元是( ),P (X )关于集合的⋂运算的单位元是( ).4. 不同构的5阶无向树有( )棵.5. 对于n 阶完全无向图K n , 当n 为( )时是Euler 图,当n ≥ ( )时是Hamilton 图,当n ( )时是平面图.二、单选题(每小题3分,共15分)1. 幂集P (P (P (∅))) 为( )(A){{∅}, {∅, {∅}}}. (B){∅, {∅, {∅}}, {∅}}.(C){ ∅, {∅, {∅}}, {{∅}}, {∅}} (D){ ∅, {∅, {∅}}}.2. 设R 是集合A 上的偏序关系,则1-⋃R R 是( ).(A)偏序关系 (B)等价关系 (C)相容关系 (D)以上答案都不对3. 下列( )组命题公式是不等值的.(A))(B A →⌝与B A ⌝∧. (B) )(B A ↔⌝与)()(B A B A ∧⌝∨⌝∧.(C))(C B A ∨→与C B A →⌝∧)(. (D))(C B A ∨→与)(C B A ∨∧⌝.4.下列代数结构(G , *)中,( )是群.(A)G = {0, 1, 3, 5}, “*”是模7加法. (B) G = Q , “*”是数的乘法.(C)G = Z , “*”是数的减法. (D) G = {1, 3, 4, 5, 9}, “*”是模11乘法.5.4阶完全无向图4K 中含3条边的不同构的生成子图有(A)3 (B)4 (C)5 (D)2三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1.函数的复合运算“ ”满足结合律. ( )2. {→⌝,}是最小功能完备联结词集合. ( )3. 实数集R 关于数的乘法运算“⋅”阿贝尔群. ( )4. 任意有限域的元素个数为2n . ( )5. 设G 是n (n 为奇数)简单图,则G 与G 中度数为奇数的节点个数相同. ( )四、(10分)设A 和B 是集合,使B B A =-成立的充要条件是什么,并给出理由.五、(10分) 设R 和S 是集合A 上的对称关系,证明S R 对称的充要条件是R S S R =.六、(15分)分别利用(1)等值演算法和(2)真值表求命题公式))(())((r q p p q r A ∨→→→∨⌝=的主析取范式和主合取范式.七、(10分) 设G 是(n , m )无向图,若n m ≥,证明G 中必存在圈.八、(10分) 在初始条件f (1) = c 下,求解递归关系bn n f n f +⎪⎭⎫ ⎝⎛=22)(,其中b ,c 为常数且kn 2=,k 为正整数.《离散数学》期末考试题(E)一、填空题(每小题3分,共15分)1.设A = {2, {3}, 4, a }, B = {1, 3, 4, {a }}, 则{3}( )A ,{a }( )B ,{{a }}( )B .2. 设A = {1, 2, 3, 4, 5}上的关系R = {(1, 2), (3, 4), (2, 2)}, S = {(4, 2), (2, 5), (3, 1), (1, 3)}, 则=S R { }, =R S { }, =R R { }.3. gcd(36, 48) = ( ),lcm(36, 48) = ( ).4.任意有限布尔代数)1,0,,,,(⋅+B 均与集合代数( )同构,其元素个数为( ).5. 不同构的5阶无向树有( )棵,不同构的5阶根树有( )棵.二、单选题(每小题3分,共15分)1. 在有理数集合Q 上定义运算“*”如下:对于任意x , y ∈ Q ,y x * = x + y – xy ,则Q 关于*的单位元是( ).(A)x . (B)y . (C)1. (D)0.2. 设A = {1, 2, 3}, 下图分别给出了A 上的两个关系R 和S ,则S R 是( )关系.(A)自反. (B)对称. (C)传递. (D)等价.3.令T (x ): x 是火车,B (x ): x 是汽车,F (x , y ): x 比y 快,则“某些汽车比所有的火车慢”符号化为( ).(A)()()),()()(y x H x T x y B y →∀∧∃.(B)()()),()()(y x H x T x y B y ∧∀→∃.(C)()()),()()(y x H x T y B y x ∧→∃∀.(D)()()),()()(y x H x T x y B y →∀→∃.4. 整数集合Z 关于数的加法“+”和数的乘法“⋅”构成的代数结构(Z, +, ⋅)是( ). 1 1 22 3 3G S G R(A)域(B)域和整环(C)整环(D) 有零因子环G≅,则称G为自补图. 5阶不同构的自补图5.设G是简单图,G是G的补图,若G个数为( ).(A)0. (B)1. (C)2. (D)3.三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1. { ∅, {∅}} ∉P(P({∅})). ( )2. 非空1元及2元联结词集合的个数为29-1. ( )3. 群可分为Abel群和非Abel群. ( )4. 元素个数相同的有限域都是同构的. ( )5. 设G是简单图,则G或G是连通图. ( )四、(15分)设C,:, 若gf 是单射,证明f是单射,并举例说明g→:f→gBBA不一定是单射.五、(10分)设A = {a, b, c, d}上的关系R = {(a, b), (b, d), (c, c), (a, c)}, 画出R的关系图,并求出R的自反闭包r(R)、对称闭包s(R)和传递闭包t(R).六、(10分)用CP规则证明下列推理.⌝∨→∨(.⇒),(⌝),→pqssrqrqp→七、(10分)求谓词公式))xyByAxA∀→∨∀∧⌝∃的前束范式.zC((x()))(z(()八、(10分)任意6个人中,一定有3个人彼此认识或有3个人彼此不认识.《离散数学》期末考试题(F)一、填空题(每小题3分,共15分)1. 设A = {1, 2, 3, {1, 2}, {3}}, B = {2, {2,3}, {1}} , 则A–B = { }, B–A = { }, A⊕B = { }.2. 实数集合R关于加法运算“+”的单位元为( ), 关于乘法运算“⋅”的单位元为( ), 关于乘法运算“⋅”的零元为( ).3. 令Z(x): x是整数,O(x): x是奇数,则“不是所有整数都是奇数”符号化为( ).4. 有限域的元素个数为( ), 其中( )且( ).5. 设G 是(7, 15)简单平面图,则G 一定 ( )连通图,其每个面恰由( )条边围成,G 的面数为( ).二、单选题(每小题3分,共15分)1. 函数的复合运算“ ”满足( )(A)交换律. (B)结合律. (C)幂等律. (D)消去律.2. 设集合A 中有4个元素,则A 上的等价关系共有( )个.(A)13 (B)14 (C)15 (D)163.下列代数结构(G , *)中,( )是群.(A)G = {0, 1, 3, 5}, “*”是模7加法. (B) G = Q , “*”是数的乘法.(C)G = Z , “*”是数的减法. (D) G = {1, 3, 4, 5, 9}, “*”是模11乘法.4. 下列偏序集,( )是格.5. 不同构的(5, 3)简单无向图有( )个.(A)4 (B)5 (C)3 (D)2三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1. 设A ,B ,C 是集合,若C A B A ⊕=⊕, 则B = C . ( )2. 逻辑联结词“→”满足结合律. ( )3. 设 (L , ≤)是偏序集,若L 的任意非空子集均存在上确界和下确界,则(L , ≤)是格.( )4. 在同构意义下,有限布尔代数只有,,,),((⋂⋃X P ∅, X ). ( )5. 设G 是简单图,则G 与G 中度数为奇数的节点个数相同. ( )四、(15分) 设C B g B A f →→:,:, 若g f 是满射,证明g 是满射,并举例说明f 不一定是满射.五、(10分) 在整数集合Z 上定义关系R 如下:对于任意∈y x , Z ,y y x x R y x +=+⇔∈22),(.判断R 是否具有自反性、反自反性、对称性、反对称性及传递性.六、(10分)利用真值表求命题公式)())(q p q p A ⌝→↔→⌝=的主析取范式和主合取范式.七、(10分)证明:在至少两个人的人群中,必有两个人有相同个数的朋友.八、(10分)将6阶完全无向图K 6的边随意地涂上红色或蓝色,证明:无论如何涂法,总存在红色的K 3或蓝色的K 3.(ps :答案见离散数学期末复习题(6套)答案文档)。
离散数学期末试题A答案及评分标准

--北京工商大学离散数学试卷(A)答案及评分标准题号 一 二三 四 五 六 七总分得分一、(30分)设A ={1,2,3,4},给定A 上二元关系R 如下:R ={<1,1>, <1,2>, <2,3>, <3,3>, <4,4>}请回答以下各问题:1.写出R 的关系矩阵. (3分)2.画出R 的关系图. (3分)3.求包含R 的最小的等价关系,并写出由其确定的划分. (6分)4.分别用关系矩阵表示出R 的自反闭包r (R )、对称闭包s (R ). (6分)5.求传递闭包t (R ).(写出计算步骤)(6分)6.求R 2的关系矩阵. (3分)7.集合A 上最多可以确定多少个不同的二元关系?说明理由。
(3分)[解] (1)⎪⎪⎪⎪⎪⎭⎫⎝⎛=1000010001000011R M 。
……(3分)(2) ……(3分)(3)法一:直接由等价关系与划分之间的一一对应可知,包含R 的最小等价关系为: {<1, 2>, <1, 3>, <2, 1>,<2, 3>, <3, 1> <3, 2>}∪I A , ……(3分) 对应的划分为{{1, 2, 3},{4}}. ……(6分) 法二:包含R 的最小的等价关系就是tsr (R ), 计算过程如下:⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=100001000110001110000100001000011000010001000011)(E M M R R r,100001100111001110000110001100011000010001100011][)()()(⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=+=T R r R r R sr M M M ,3,10001110111011110000110011100111000011001110011)]([)()()]([2≥=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛⨯⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯=k M M M M k R sr R sr R sr R sr 从而,10000111011101111000011101110111100001110111011110000111011101111000011001110011432)]([)]([)]([)()(⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=+++=R sr R sr R sr R sr R tsr M M M M M即}2,3,1,3,3,2,1,2,3,1,2,1{)(><><><><><><⋃=A I R tsr =包含R 的最小的等价关系, ……(3分) 故其对应的划分为{{1, 2, 3},{4}}. ……(6分) 法三:由于4=A ,包含R 的最小的等价关系就是4131211)()()()()()(----⋃⋃⋃⋃⋃⋃⋃⋃==R R R R R R R R I R rts R tsr A ,计算过程如下:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=-⋃100001100101001110000110000100011000010001000011][1TR R R R M M M ⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=-⋃10000111011101111000011001010011)][(22)(21T R R R R M M M412131)()(33)(10000111011101111000011001010011)][(---⋃⋃⋃==⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=R R R R T R R R R M M M M M 考试纪律承诺本人自愿遵守学校考试纪律,保证以诚信认真的态度作答试卷。
2011离散数学A卷2011离散数学A卷(郑州轻工业学院)

2010-2011年第二学期 《离散数学》期末考试试卷A 专业班级:软件测试10-2一、填空题(共10题,每题3分,共30分)1. 已知256)(,64)(,3===B A P B P A ,则=B , =B A ,=-)(B A P .2. 命题公式r q p B r q p A →⌝∧=∨→=)(),(,它们关系是 A B (填写“⇔⇐⇒,,”).3.中根遍历图1中结点的次序为 .4.设函数B A f →:和函数A B g →:,且f g ⋅是A 上的恒等函数, 则f 是 射函数,g 是 射函数。
5.设有向图(图2),则其邻接矩阵为:6.一棵树有2个2度结点,1个3度结点,3个4度结点,其他为树叶结点,则它 有 个结点, 条边, 片树叶.图27.设有连通平面图有12个结点,22条边,则有 个面.8.实数集上定义二元运算*为,x*y=xy-2x-2y+6,则*的单位元为 ,零元为 ,幂等元为 .9.设有二部图如下,则其互补结点子集分别为 V 1={ }, V 2={ }.10.判别命题公式的类型:q q p ∧→⌝)(是 公式.二、选择题(共5题,每题3分,15分)1.已知四个偏序集的哈斯图如下:其中不是格的是( ).2. 集合}3,2,1{=A 上关系)}1,1(),1,2(),1,3(),3,2{(=ρ,则ρ是( )。
A .反自反 B .对称C .可传递D 自反3. 下面关于群><,*G 正确的是( )A 若><,*H 为><,*G 的子代数,则><,*H 也是群B 若对G c b a ∈∀,,,若c b ≠,则c a b a **≠C ><,*G 中除单位元外还有其他的幂等元4v 3v 2v 1v(d ) A B CDD ><,*G 中任意元素都存在有限周期4.关于下列四个无向图的命题,正确的是( )A (a )是欧拉图,(b )是哈密顿图B (a )是欧拉图,(c )是哈密顿图C (b )是欧拉图,(d )是哈密顿图D (c )是欧拉图,(d )是哈密顿图5.设集合A 上的等价关系R 1和R 2,则下列关系中是等价关系的是( ) (A )A 2-R 1; (B )R 1-R 2; (C )r(R 1-R 2);(D )R 12三、已知集合},,,{d c b a A =上的关系)},(),,(),,(),,{(d c c b a b b a R =, 求出R 的自反闭包、对称闭包。
离散数学期末试卷A卷及答案

《离散数学》试卷(A 卷)一、 选择题(共5 小题,每题 3 分,共15 分)1、设A={1,2,3},B={2,3,4,5},C={2,3},则C B A ⊕⋃)(为(C )。
A 、{1,2}B 、{2,3}C 、{1,4,5}D 、{1,2,3}2、下列语句中哪个是真命题 ( A )A 、如果1+2=3,则4+5=9;B 、1+2=3当且仅当4+5≠9。
C 、如果1+2=3,则4+5≠9;D 、1+2=3仅当4+5≠9。
3、个体域为整数集合时,下列公式( C )不是命题。
A 、)*(y y x y x =∀∀B 、)4*(=∃∀y x y xC 、)*(x y x x =∃D 、)2*(=∃∃y x y x4、全域关系A E 不具有下列哪个性质( B )。
A 、自反性B 、反自反性C 、对称性D 、传递性5、函数612)(,:+-=→x x f R R f 是( D )。
A 、单射函数B 、满射函数C 、既不单射也不满射D 、双射函数二、填充题(共 5 小题,每题 3 分,共15 分)1、设|A|=4,|P(B)|=32,|P(A ⋃B)|=128,则|A ⋂B|=ˍˍ2ˍˍˍ.2、公式)(Q P Q ⌝∨∧的主合取式为 。
3、对于公式))()((x Q x P x ∨∃,其中)(x P :x=1, )(x Q :x=2,当论域为{0,1,2}时,其真值为ˍˍˍ1ˍˍˍ。
4、设A ={1,2,3,4},则A 上共有ˍˍˍ15ˍˍˍˍ个等价关系。
5、设A ={a ,b ,c },B={1,2},则|B A |= 8 。
三、判断题(对的填T ,错的填F ,共 10 小题,每题 1 分,共计10 分)1、“这个语句是真的”是真命题。
( F )2、“刚和小强是同桌。
”是复合命题。
( F )3、))(()(r q q p p ∧⌝∧→⌝∨是矛盾式。
( T )4、)(T S R T R S R ⋂⋅⊆⋅⋃⋅。
离散数学期末考试试题

离散数学试题(A卷及答案)一、证明题(10分)1) ( -P A ( —Q A R)) V (Q A R)V (P A R)= R证明:左端 =(-P A-QAR) V ((Q V P)A R£((—P A-Q)AR)) V((Q V P)A R):=(^P V Q) A R)V(( Q V P ) A R匕(一(P V Q )V(Q V P)) A R:=(「P V Q )V( P V Q )) A fcT A R置换):=R2) x(A(x) —.B(x)) := - x A(x) _._x B(x)证明:x ( A(x) > B(x)〉= x ( f(x) V B(x))= x—A(x) V x B(x)=—- x A(x)V x B(x)=- x A(x) -l xB(x)、求命题公式(P V (Q A R)) >(P A QA R)的主析取范式和主合取范式(10分)证明:(P V (Q A R))「(P A Q A R>=— (P V (Q A R)) V (P A QA R))二(—P A ( 一QV -R) )V (P A Q A R)二(一P A — Q)V ( -P A -R)) V (P A Q A R)二(_PA _Q R) V (_P A _QA 一R) V ( _P A QA _R)) V ( _PA _QA _R)) V (P A Q R)二m0V m1V m2V m7u M3V M4V M5V M6三、推理证明题(10分)1)C V D,(C V D)》-E, -E >(A A -B), (A A证明(1) xP(x)—B)r(R V S)「:R V S(2)P(a)(1) (C V D)—;「E(3) -x(P(x) >Q(y) A R(x))证明:(2) -E >(A A -B)(4)P(a) >Q(y) A R(a)(3) (C V D)—.(A A -B)(5)Q(y) A R(a)⑷(A A -B)_. (R V S)(6)Q(y)V D)_ (R V S)(7)R(a)(5) (C⑹C V D(8)P(a)⑺R V S(9)P(a) A R(a)2)-x(P(x) —;Q(y) A R(x)) , xP(x)二Q(y) A(10) x(P(x) A R(x))x(P(x) A R(x))(11)Q(y) A x(P(x) A R(x))四、设m是一个取定的正整数,证明:在任取耐1个整数中,至少有两个整数,它们的差是m的整数倍证明设印,a2,…,a m1为任取的1个整数,用m去除它们所得余数只能是0, 1,…,m- 1,由抽屉原理可知,耳,a2,…,a m d这m+ 1个整数中至少存在两个数a s和a t,它们被m除所得余数相同,因此a s和a的差是m的整数倍。
《离散数学A》试题及答案

《离散数学A》试题及答案西南科技大学2010-2011-2学期《离散数学A》本科期末考试试卷(B卷)参考答案及评分细则一、判断题(本大题共10个小题,每小题2分,共20分)将每小题的判断结果写在答题纸上,正确的写“正确”,错误的写“错误”。
1. “3+3=6”,不是命题。
(错误)2. 命题公式(P Q Q)是偶然式。
(正确)3. 若B中不含有x,则x(A(x)B)xA(x)B。
(错误)4. 如果论述域是{a,b},则xR(x) R(a)R(b)。
(错误)5. 若集合A的基数|A|=5,则A的幂集的基数|(A)|=32。
(正确)6. 设A是一个集合,则A A=。
(错误)7. 设R是非空集合A上的二元关系,则R的传递闭包t(R)=R R0。
(错误)8. 所有欧拉图的顶点次(度)数一定是偶数。
(正确)9. 无向图G是二部图当且仅当G中所有回路的长度均为偶数。
(正确)10. K5、K3,3都是非平面图。
(正确)二、简单计算题(本大题共10个小题,每小题3分,共30分)将每小题的计算结果写在答题纸上。
1. 设P:我有时间;Q:我去镇上,用逻辑符合写出命题“只有我有时间,我才去镇上。
”。
答案:Q P2. 对命题公式:P(Q R)P Q化为仅含和的等价表达式。
答案:(P Q)3. 设S(x):x是火车,L(x):x是卡车,F(x,y):x比y快。
在谓词逻辑中符号化命题“所有火车都比所有卡车快”。
答案:?x(S(x)→?y(L(y) ∧F(x , y))4. 求谓词公式xP(x)xQ(x)的前束范式。
答案:x y(P(x)Q(x))5. 在一个班级50个学生中,有26人在第一次考试中得到A,21人在第二次考试中得到A,假如17人两次考试都没有得到A,问有多少学生在两次考试中都得到A?答案:14人。
6. 假设A是n个元素的有限集合,有多少个元素在A上的最小等价关系中?答案:n个。
7. 二元关系的关系图如下图所示,则R具有哪些特性(性质)?答案:R是反自反的、对称的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页(共5页)
浙江大学宁波理工学院2010–2011学年2学期
《 离散数学甲 》课程期末考试试卷(A)
考生姓名 学号 考生所在分院: 专业班级: .
一、 判断题
(14分,每题1分)
1 {a,b}{a,b,c,{a,b}}。 ( T )
2 “火星上可以住人”是命题。 ( T )
3 数学结构(素数 ,+,-,×,÷),加运算是封闭的。 ( F )
4 BANANA 中字母的不同排列数为6!32。 ( F )
5 ()ppq是重言式。 ( T )
6 p q的逆命题是 q p。 ( F )
7 如果关系R是非对称的,那么R是反对称的。 ( T )
8 A为某非空集合,则数学结构(P(A) ,,)中并运算的单位元是A。 ( F )
9 若是一个函数,那么是满射当且仅当处处有定义。 ( T )
10 任何偏序集都有其对偶偏序集。 ( T )
11 若是根树,那么是非对称的。 ( T )
12 无向连通图的最小生成树是唯一的。 ( F )
13 完全图不一定是正则的。 ( F )
14 如果图G有奇数度的顶点,那么在G中不可能存在欧拉回路。 ( T )
二、选择题(16分,每题2分)
1. 下面哪一个不是集合{1,2,4,7,9}A的划分?( B )。
A.{{1,2,4,7,9}} B. {{1,9},{2,4},{1,7}}
C. {{1},{2,7},{4,9}} D. {{2,4,7},{1,9}}
2. 设A 和 B 是集合U的子集. 则()ABB等于 ( D )
A. U B. A C. AB D. AB
3. *设 A = Z( 正整数 ),并且 R 为集合A上的关系: aRb当且仅当如果存在一个正整
数k,满足 a = bk. 则 R(6)是( )
第2页(共5页)
A. {1,2,3,6} B. {6}
C. {1,2,3,4,5,6} D. {6,12,18,24,...}
4. 在如下的有向图中,从V1到V4长度为3 的道路有( B )条。
A.1; B.2; C.3; D.4 。
5. 在如下各图中( B )是欧拉图。
6. ***设R为实数集合,函数:,RR2()21,xxx则 是( D ).
A. 单射而非满射 B. 满射而非单射
C. 双射 D. 既不是单射也不是满射.
7. 设和都是X上的双射函数,则为(C )。
A. B. C. D.
8. 在任何图中必定有偶数个( C )。
FA. 度数为偶数的结点 ; FB. 入度为奇数的结点 ;
C. 度数为奇数的结点 ; FD. 出度为奇数的结点 。
三、填空题(10分,每题2分)
1. 设A={{2},{1}},则|A|= 2 , P(A)= 略 。
2. 设A={1,2,4,8}, B={1,4,6,9}, aRb当且仅当a|b,
则R= 略 。
3. n个结点的无向完全图Kn的边数为 n*(n-1)/2 ,欧拉图的充要条件是
略 。
第3页(共5页)
四、解答题(共计60分)
1. 求公式(~)(~)pqpr的真值表,并判断公式的类型。(4分)
p q r ~pvq p^~r ~pvq推出p^~r
0 0 0 1 0 0
0 0 1 1 0 0
0 1 0 1 0 0
0 1 1 1 0 0
1 0 0 0 1 1
1 0 1 0 0 1
1 1 0 1 1 1
1 1 1 1 0 0
2. 证明:如果任选8个正整数,那么当用7去除时,它们当中至少有两个数有相同的余
数。(3分)
8>7
3. 序列由1232nnnaaa定义,初始条件为122,4aa,求序列的显式公式。 (4
分)
x^2+3x+2=0
x=-1,-2
an=u(-1)^n+v(-2)^n
a1=-u-2v
a2=u+4v
v=1 u=0
an= (-2)^n
第4页(共5页)
4. 设 A = {1, 2, 3, 4}。R是A上的关系,它的有向图如图1所示,
求1) 2R; 2)R (4分)
略
图 1
5. (12分) 设集合A={1, 2, 3, 4, 6, 8, 12},R是A上的整除关系,
(1) 画出偏序集(A, R)的哈塞图;
(2) 写出A的子集{2, 4, 6, 8}的上界,下界,最小上界,最大下界;
(3) 写出集合A的最大元,最小元,极大元,极小元。
略
6. (分)图给出的赋权图表示五个城市及对应两城镇间公路的长度。试给出一个最优化的设
计方案使得各城市间能够有公路连通。
3
6
3
226234455EAC
B
D
H
G
F
略
7. (12分)给出下图执行前序、中序、后序搜索的结果。
第5页(共5页)
前序:ABDEFCGHIKJ
中序:EDFBAGCKIHJ
后序:EFDBGKIJHCA
8. (10分)用Fleury算法为下图构造一条欧拉回路。
略
A
C
H
J
I
G
F
E
D
B
K
