2019版高考数学一轮复习第七章立体几何初步课时分层作业四十7.2空间几何体的表面积与体积文
2019版高考数学一轮复习第七章立体几何分层限时跟踪练(7).doc

非常考案通用版2019版高考数学一轮复习第七章立体几何分层限时跟踪练(7)一、选择题1.一个几何体的三视图如图7212所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的体积是( )图7212A .16 πB .14 πC .12 πD .8 π【解析】 由三视图可知,该几何体为一个球切去四分之一个球后剩余部分,由于球的半径为2,所以这个几何体体积为34×43π×23=8π.【答案】 D2.(2015·北京高考)某三棱锥的三视图如图7213所示,则该三棱锥的表面积是( )图7213A .2+ 5B .4+ 5C .2+2 5D .5【解析】作出三棱锥的示意图如图,在△ABC 中,作AB 边上的高CD ,连接SD .在三棱锥S ABC 中,SC ⊥底面ABC ,SC =1,底面三角形ABC 是等腰三角形,AC =BC ,AB 边上的高CD =2,AD =BD =1,斜高SD =5,AC =BC = 5.∴S表=S △ABC +S △SAC +S △SBC +S △SAB =12×2×2+12×1×5+12×1×5+12×2×5=2+2 5.【答案】 C3.(2015·全国卷Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如图7214,则截去部分体积与剩余部分体积的比值为( )图7214A.18B.17C.16D.15【解析】由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分,如图所示,截去部分是一个三棱锥.设正方体的棱长为1,则三棱锥的体积为V1=13×12×1×1×1=16,剩余部分的体积V2=13-16=56.所以V1V2=1656=15,故选D.【答案】 D4.(2015·安徽高考)一个四面体的三视图如图7215所示,则该四面体的表面积是( )图7215A.1+ 3 B.2+ 3C.1+2 2 D.2 2【解析】 根据三视图还原几何体如图所示,其中侧面ABD ⊥底面BCD ,另两侧面ABC 、ACD 为等边三角形,则S 表面积=2×12×2×1+2×34×(2)2=2+ 3. 【答案】 B5.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )A. 81π4 B .16π C .9π D.27π4【解析】 如图所示,设球半径为R ,底面中心为O ′且球心为O ,∵正四棱锥P ABCD 中AB =2,∴AO ′= 2. ∵PO ′=4, ∴在Rt △AOO ′中,AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R =94,∴该球的表面积为4πR 2=4π×⎝ ⎛⎭⎪⎫942=81π4,故选A. 【答案】 A 二、填空题6.如图7216,正方体ABCD A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1EDF 的体积为 .图7216【解析】 VD 1EDF =VF DD 1E =13 ·AB =13×12×1×1×1=16.【答案】 167.设甲、乙两个圆柱的底面积分别为S 1,S 2,体积分别为V 1,V 2,若它们的侧面积相等,且S 1S 2=94,则V 1V 2的值是 . 【解析】 设甲、乙两圆柱的底面半径分别为r 1,r 2,母线长分别为l 1,l 2,则由S 1S 2=94得r 1r 2=32.又两圆柱侧面积相等,即2πr 1l 1=2πr 2l 2,则l 1l 2=r 2r 1=23,所以V 1V 2=S 1l 1S 2l 2=94×23=32. 【答案】 328.已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图7217所示,则该几何体的体积是 .图7217【解析】 根据三视图,画出其直观图,几何体由正方体切割而成,即正方体截去一个棱台.如图所示.其中正方体棱长为2,AF =AE =1,故所求几何体体积为V =23-13×2×12×1×1+12×2×2+12×1×1×12×2×2=173. 【答案】173三、解答题9.(2015·荥阳月考)已知球的两平行截面的面积分别为5π和8π,它位于球心的同一侧,且相距为1,求这个球的体积.【解】 如图,设以r 1为半径的截面面积为5π,圆心为O 1,以r 2为半径的截面面积为8π,圆心为O 2,O 1O 2=1,球的半径为R ,设OO 2=x ,可得下列关系式:r 22=R 2-x 2,πr 22=π(R 2-x 2)=8π,r 21=R 2-(x +1)2,πr 21=π[R 2-(x +1)2]=5π,∴R 2-x 2=8,R 2-(x +1)2=5,解得R =3,∴球的体积为V =43πR 3=43π×33=36π.10.(2015·全国卷Ⅱ)如图7218,长方体ABCD A 1B 1C 1D 1中,AB =16,BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.图7218(1)在图中画出这个正方形(不必说明画法和理由); (2)求平面α把该长方体分成的两部分体积的比值. 【解】 (1)交线围成的正方形EHGF 如图所示.(2)如图,作EM ⊥AB ,垂足为M ,则AM =A 1E =4,EB 1=12,EM =AA 1=8. 因为四边形EHGF 为正方形,所以EH =EF =BC =10. 于是MH =EH 2-EM 2=6,AH =10,HB =6. 故S 四边形A 1EHA =12×(4+10)×8=56,S 四边形EB 1BH =12×(12+6)×8=72.因为长方体被平面α分成两个高为10的直棱柱, 所以其体积的比值为97⎝ ⎛⎭⎪⎫79也正确. [能 力 练]扫盲区 提素能1.(2015·山东高考)在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3 B.4π3 C.5π3D .2π【解析】 过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V 圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,选C. 【答案】 C2.如图7219,直三棱柱ABC A 1B 1C 1的六个顶点都在半径为1的半球面上,AB =AC ,侧面BCC 1B 1是半球底面圆的内接正方形,则侧面ABB 1A 1的面积为( )图7219A .2B .1 C. 2 D.22【解析】 由题意知,球心在侧面BCC 1B 1的中心O 上,BC 为截面圆的直径,∴∠BAC =90°,△ABC 的外接圆圆心N 是BC 的中点,同理△A 1B 1C 1的外心M 是B 1C 1的中点.设正方形BCC 1B 1的边长为x ,在Rt △OMC 1中,OM =x 2,MC 1=x 2,OC 1=R =1(R 为球的半径),∴⎝ ⎛⎭⎪⎫x 22+⎝ ⎛⎭⎪⎫x 22=1,即x =2,则AB =AC =1,∴S 矩形ABB 1A 1=2×1= 2.【答案】 C3.圆锥的全面积为15 π cm 2,侧面展开图的圆心角为60°,则该圆锥的体积为cm 3.【解析】 设底面圆的半径为r ,母线长为a ,则侧面积为12×(2πr )a =πra .由题意得⎩⎪⎨⎪⎧πra +πr 2=15π,πra =16πa 2,解得⎩⎪⎨⎪⎧r 2=157,a 2=36×157,故圆锥的高h =a 2-r 2=53,所以体积V =13πr 2h =13π×157×53=2537π(cm 3).【答案】2573π 4.已知正四面体的俯视图如图7220所示,其中四边形ABCD 是边长为2的正方形,则这个正四面体的表面积为 ,体积为 .图7220【解析】 由题意知正四面体的直观图E ACF 补成正方体如图所示. 由正方体棱长为2,知正四面体的棱长为22,正四面体表面积为34×(22)2×4=8 3.点E 到平面ACF 的距离为222-⎝⎛⎭⎪⎫32×22×232=433. 正四面体的体积为13×433×34×(22)2=83.【答案】 8 3835.如图7221所示,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且△ADE ,△BCF 均为正三角形,EF ∥AB ,EF =2,求该多面体的体积.图7221【解】 如图所示,分别过A ,B 作EF 的垂线,垂足分别为G ,H ,连接DG ,CH ,则原几何体分割为两个三棱锥和一个直三棱柱,∵三棱锥高为12,直三棱柱高为1,AG =12-⎝ ⎛⎭⎪⎫122=32,取AD 中点M ,则MG =22,∴S △AGD =12×1×22=24,∴V =24×1+2×13×24×12=23. 6.如图7222,已知平行四边形ABCD 中,BC =2,BD ⊥CD ,四边形ADEF 为正方形,平面ADEF ⊥平面ABCD ,G ,H 分别是DF ,BE 的中点.记CD =x ,V (x )表示四棱锥F ABCD 的体积.图7222(1)求V (x )的表达式; (2)求V (x )的最大值.【解】 (1)∵平面ADEF ⊥平面ABCD ,交线为AD 且FA ⊥AD ,∴FA ⊥平面ABCD . ∵BD ⊥CD ,BC =2,CD =x , ∴FA =2,BD =4-x 2(0<x <2), ∴S ▱ABCD =CD ·BD =x 4-x 2,∴V (x )=13S ▱ABCD ·FA =23x 4-x 2(0<x <2).(2)V (x )=23x 4-x 2=23-x 4+4x 2=23-x 2-22+4.∵0<x <2,∴0<x 2<4,∴当x 2=2,即x =2时,V (x )取得最大值,且V (x )max =43.。
全国通用近年高考数学一轮复习第七章立体几何初步课时作业四十一7.3空间点、直线、平面之间的位置关系

(全国通用版)2019版高考数学一轮复习第七章立体几何初步课时分层作业四十一7.3 空间点、直线、平面之间的位置关系文编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((全国通用版)2019版高考数学一轮复习第七章立体几何初步课时分层作业四十一7.3 空间点、直线、平面之间的位置关系文)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(全国通用版)2019版高考数学一轮复习第七章立体几何初步课时分层作业四十一7.3 空间点、直线、平面之间的位置关系文的全部内容。
课时分层作业四十一空间点、直线、平面之间的位置关系一、选择题(每小题5分,共35分)1。
给出三个命题:①若两条直线和一个平面所成的角相等,则这两条直线互相平行;②若两条直线与一个平面垂直,则这两条直线互相平行;③若两条直线与一个平面平行,则这两条直线互相平行。
其中正确的命题的个数是( )A.0B.1C.2D.3【解析】选B.若两条直线与同一个平面所成的角相等,则这两条直线与平面的法向量夹角相等,这些直线构成以法向量为轴的某个对顶圆锥。
故①错误;两条直线与平面垂直,则这两条直线与平面的法向量平行,则根据公理4,两直线平行,故②正确;两条直线与一个平面平行,这两条直线可能异面、平行或相交。
故③错误.2。
下列命题中成立的个数是()①直线l平行于平面α内的无数条直线,则l∥α;②若直线l在平面α外,则l∥α;③若直线l∥b,直线b⊂α,则l∥α;④若直线l∥b,直线b⊂α,那么直线l就平行于平面α内的无数条直线。
A。
1 B.2 C.3 D。
4【解析】选A。
直线l平行于平面α内的无数条直线,包括l⊂α和l∥α,故①不成立;直线l在平面α外,包括l与α相交和l∥α,故②不成立;直线l∥b,直线b⊂α,包括l⊂α和l∥α,故③不成立;直线l∥b,直线b⊂α,那么l平行于α内与直线b平行的所有直线,所以直线l就平行于平面α内的无数条直线,故只有④成立.3。
2019-2020年高考数学一轮复习第7章立体几何课件

[五年考情]
考点
2016 年
三视图直观 图及几何体 的表面积体 积
11,6 分(理) 14,4 分(理) 9,6 分(文)
2015 年
2,5 分(理) 2,5 分(文)
2014 年
3,5 分(理) 3,5 分(文)
2013 年
2012 年
12,4 分(理) 11,4 分(理) 5,5 分(文) 3,5 分(文)
• 常常可见到这样的同学,他们在下课前几分钟就开始看表、收拾课本文具,下课铃一响,就迫不及待地“逃离”教室。实际上,每节课刚下课时的几分 钟是我们对上课内容查漏补缺的好时机。善于学习的同学往往懂得抓好课后的“黄金两分钟”。那么,课后的“黄金时间”可以用来做什么呢?
• 一、释疑难 • 对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已
2019/7/20
最新中小学教学课件
thank
you!
2019/7/20
最新中小学教学课件
2,5 分(理)
空间点线 14,4 分(理)
面的位置 17(1),7 分(理)
关系
2,5 分(文)
18(1),7 分(文)
空间向量
及其应 17(2),8 分(理)
用、空间 14,4 分(文)
角Hale Waihona Puke 18(2),8 分(文)13,4 分(理) 17,4 分(理)
17(1),7 分(理) 20(1),7 分(理)
20(2),9 分 20(2),7 分
(理)
(理)
20(2),5 分 20(2),7 分
(文)
(文)
2019届高考数学一轮复习第七章立体几何学案理

第七章立体几何第一节空间几何体的结构特征及三视图与直观图1.简单几何体(1)多面体的结构特征名称棱柱棱锥棱台图形底面互相平行且相等多边形互相平行侧棱平行且相等相交于一点,但不一定相等延长线交于一点侧面形状平行四边形三角形梯形(2)旋转体的结构特征名称圆柱圆锥圆台球图形母线互相平行且相等,垂直于底面相交于一点延长线交于一点轴截面全等的矩形全等的等腰三角形全等的等腰梯形圆侧面展开图矩形扇形扇环2.直观图(1)画法:常用斜二测画法.(2)规则:①原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为45°(或135°),z′轴与x′轴和y′轴所在平面垂直.②原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段长度在直观图中变为原来的一半.3.三视图(1)几何体的三视图包括正视图、侧视图、俯视图,分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.说明:正视图也称主视图,侧视图也称左视图.(2)作、看三视图的3原则①位置原则:②度量原则:长对正、高平齐、宽相等(即正俯同长、正侧同高、俯侧同宽).③虚实原则:轮廓线——现则实、隐则虚.1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)有两个面平行,其余各面都是平行四边形的几何体是棱柱.( )(2)有一个面是多边形,其余各面都是三角形的几何体是棱锥.( )(3)棱台是由平行于底面的平面截棱锥所得的平面与底面之间的部分.( )(4)夹在圆柱的两个平行截面间的几何体还是圆柱.( )(5)上下底面是两个平行的圆面的旋转体是圆台.( )答案:(1)×(2)×(3)√(4)×(5)×2.用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是( )解析:选B 俯视图中显然应有一个被遮挡的圆,所以内圆是虚线,故选B.3.若一个三棱柱的三视图如图所示,其俯视图为正三角形,则这个三棱柱的高和底面边长分别为( )A.2,2 3 B.22,2C.4,2 D.2,4解析:选D 由三视图可知,正三棱柱的高为2,底面正三角形的高为23,故底面边长为4,故选D.4.(教材习题改编)如图,长方体ABCDA′B′C′D′被截去一部分,其中EH∥A′D′,则剩下的几何体是________,截去的几何体是______.答案:五棱柱三棱柱5.利用斜二测画法得到的①三角形的直观图一定是三角形;②正方形的直观图一定是菱形;③等腰梯形的直观图可以是平行四边形;④菱形的直观图一定是菱形.以上结论正确的个数是________.解析:由斜二测画法的规则可知①正确;②错误,是一般的平行四边形;③错误,等腰梯形的直观图不可能是平行四边形;而菱形的直观图也不一定是菱形,④也错误,故结论正确的个数为1.答案:1考点一空间几何体的结构特征基础送分型考点——自主练透[考什么·怎么考]空间几何体的结构特征是立体几何的基础知识,很少单独考查.多作为载体与三视图、表面积、体积等综合考查,题型为选择题或填空题,难度较低.A.圆柱B.圆锥C.球体 D.圆柱、圆锥、球体的组合体解析:选C 截面是任意的且都是圆面,则该几何体为球体.2.给出下列几个命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②底面为正多边形,且有相邻两个侧面与底面垂直的棱柱是正棱柱;③棱台的上、下底面可以不相似,但侧棱长一定相等.其中正确命题的个数是( )A.0 B.1C.2 D.3解析:选B ①错误,只有这两点的连线平行于轴时才是母线;②正确;③错误,棱台的上、下底面是相似且对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.3.给出下列命题:①棱柱的侧棱都相等,侧面都是全等的平行四边形;②若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直;③在四棱柱中,若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;④存在每个面都是直角三角形的四面体.其中正确命题的序号是________.解析:①不正确,根据棱柱的定义,棱柱的各个侧面都是平行四边形,但不一定全等;②正确,若三棱锥的三条侧棱两两垂直,则三个侧面构成的三个平面的二面角都是直二面角;③正确,因为两个过相对侧棱的截面的交线平行于侧棱,又垂直于底面;④正确,如图,正方体ABCDA1B1C1D1中的三棱锥C1ABC,四个面都是直角三角形.答案:②③④[怎样快解·准解]空间几何体概念辨析题的常用方法定义法紧扣定义,由已知构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,根据定义进行判定.反例法通过反例对结构特征进行辨析,即要说明一个结论是错误的,只要举出一个反例即可.考点二空间几何体的直观图基础送分型考点——自主练透[考什么·怎么考]单独考查空间几何体的直观图的题目很少,多与三视图、表面积、体积等综合考查,题型为选择题或填空题,难度较低.1.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是( )解析:选A 由直观图可知,在直观图中多边形为正方形,对角线长为2,所以原图形为平行四边形,位于y 轴上的对角线长为2 2.故选A.2.已知正三角形ABC 的边长为2,那么△ABC 的直观图△A ′B ′C ′的面积为________. 解析:如图,图①、图②分别表示△ABC 的实际图形和直观图. 从图②可知,A ′B ′=AB =2,O ′C ′=12OC =32,C ′D ′=O ′C ′sin 45°=32×22=64. 所以S △A ′B ′C ′=12A ′B ′·C ′D ′=12×2×64=64.答案:643.用斜二测画法画出的某平面图形的直观图如图,边AB 平行于y ′轴,BC ,AD 平行于x ′轴.已知四边形ABCD 的面积为2 2 cm 2,则原平面图形的面积为________ cm 2.解析:依题意可知∠BAD =45°,则原平面图形为直角梯形,上下底的长分别与BC ,AD 相等,高为梯形ABCD 的高的22倍,所以原平面图形的面积为8 cm 2.答案:8[怎样快解·准解]1.原图形与直观图中的“三变”与“三不变” (1)“三变”⎩⎪⎨⎪⎧坐标轴的夹角改变与y 轴平行的线段的长度改变减半图形改变(2)“三不变”⎩⎪⎨⎪⎧平行性不变与x 轴平行的线段长度不变相对位置不变2.原图形与直观图面积的关系按照斜二测画法得到的平面图形的直观图与原图形面积的关系: (1)S 直观图=24S 原图形;(2)S 原图形=22S 直观图. 考点三 空间几何体的三视图题点多变型考点——追根溯源空间几何体的三视图的辨析是高考的热点内容,一般以选择题或填空题的形式出现.常见的命题角度有:1已知几何体,识别三视图;2已知三视图,判断几何体;3已知几何体的三视图中的某两个视图,确定另一种视图.[题点全练]角度(一) 已知几何体,识别三视图1.(2018·河北衡水中学调研)如图所示,在正方体ABCD A 1B 1C 1D 1中,E 为棱BB 1的中点,用过点A ,E ,C 1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )解析:选C 如图所示,过点A ,E ,C 1的截面为AEC 1F ,则剩余几何体的侧视图为选项C 中的图形.[题型技法] 识别三视图的步骤(1)弄清几何体的结构特征及具体形状、明确几何体的摆放位置;(2)根据三视图的有关定义和规则先确定正视图,再确定俯视图,最后确定侧视图; (3)被遮住的轮廓线应为虚线,若相邻两个物体的表面相交,表面的交线是它们的分界线;对于简单的组合体,要注意它们的组合方式,特别是它们的交线位置.角度(二) 已知三视图,判断几何体2.(2017·北京高考)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )A.3 2 B.2 3C.2 2 D.2解析:选B 在正方体中还原该四棱锥如图所示,从图中易得最长的棱为AC1=AC2+CC21=22+22+22=2 3.[题型技法] 由三视图确定几何体的3步骤熟练掌握规则几何体的三视图是三视图还原几何体的基础,在明确三视图画法规则的基础上,按以下步骤可轻松解决此类问题:角度(三) 已知几何体三视图中的某两个视图,确定另外一个视图3.如图,一个三棱柱的正视图和侧视图分别是矩形和正三角形,则这个三棱柱的俯视图为( )解析:选D 由正视图和侧视图可知,这是一个水平放置的正三棱柱.故选D.[题型技法]由几何体的部分视图画出剩余视图的方法解决此类问题,可先根据已知的一部分视图,还原、推测直观图的可能形式,然后再找其剩下部分视图的可能形式.当然作为选择题,也可将选项逐项代入检验.[题“根”探求]根据几何体的三视图判断几何体的结构特征,常见的有以下几类三视图的形状对应的几何体三个三角形三棱锥两个三角形,一个四边形四棱锥两个三角形,一个圆圆锥一个三角形,两个四边形三棱柱三个四边形四棱柱两个四边形,一个圆圆柱[冲关演练]1.(2018·惠州调研)如图所示,将图①中的正方体截去两个三棱锥,得到图②中的几何体,则该几何体的侧(左)视图为( )解析:选B 从几何体的左侧看,对角线AD1在视线范围内,故画为实线,右侧面的棱C1F不在视线范围内,故画为虚线,且上端点位于几何体上底面边的中点.故选B2.(2018·石家庄质检)一个三棱锥的正(主)视图和俯视图如图所示,则该三棱锥的侧(左)视图可能为( )解析:选D 由题图可知,该几何体为如图所示的三棱锥,其中平面ACD⊥平面BCD,故选D.3.(2017·全国卷Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )A .10B .12C .14D .16解析:选B 由三视图可知该多面体是一个组合体,下面是一个底面是等腰直角三角形的直三棱柱,上面是一个底面是等腰直角三角形的三棱锥,等腰直角三角形的腰长为2,直三棱柱的高为2,三棱锥的高为2,易知该多面体有2个面是梯形,这些梯形的面积之和为2+4×22×2=12,故选B.(一)普通高中适用作业A 级——基础小题练熟练快1.如图,△A ′B ′O ′是利用斜二测画法画出的△ABO 的直观图,已知A ′B ′∥y ′轴,O ′B ′=4,且△ABO 的面积为16,过A ′作A ′C ′⊥x ′轴,则A ′C ′的长为( )A .2 2 B. 2 C .16 2D .1解析:选A 因为A ′B ′∥y ′轴,所以△ABO 中,AB ⊥OB . 又因为△ABO 的面积为16,所以12AB ·OB =16.因为OB =O ′B ′=4,所以AB =8,所以A ′B ′=4. 因为A ′C ′⊥O ′B ′于C ′,所以B ′C ′=A ′C ′, 所以A ′C ′=4·sin 45°=22,故选A.2.一几何体的直观图如图,下列给出的四个俯视图中正确的是( )解析:选B 由直观图可知,该几何体由一个长方体和一个截角三棱柱组成.从上往下看,外层轮廓线是一个矩形,矩形内部是一条水平线段连接两个三角形,故选B.3.若某几何体的三视图如图所示,则这个几何体的直观图可以是( )解析:选D 由三视图知该几何体的上半部分是一个三棱柱,下半部分是一个四棱柱.故选D.4.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图为( )解析:选D 由正视图与俯视图知,几何体是一个三棱锥与半个圆锥的组合体,故侧视图为D.5.如图,在正四棱柱ABCDA 1B1C1D1中,点P是平面A1B1C1D1内一点,则三棱锥PBCD的正视图与侧视图的面积之比为( )A.1∶1 B.2∶1C.2∶3 D.3∶2解析:选A 根据题意,三棱锥PBCD的正视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高;侧视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高.故三棱锥PBCD的正视图与侧视图的面积之比为1∶1.6.某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是( )A .2 B.92C.32D .3解析:选D 根据三视图判断几何体为四棱锥,其直观图如图所示,则体积V =13×1+22×2×x =3,解得x =3,故选D. 7.设有以下四个命题:①底面是平行四边形的四棱柱是平行六面体; ②底面是矩形的平行六面体是长方体; ③直四棱柱是直平行六面体; ④棱台的相对侧棱延长后必交于一点. 其中真命题的序号是________.解析:命题①符合平行六面体的定义,故命题①是正确的;底面是矩形的平行六面体的侧棱可能与底面不垂直,故命题②是错误的;因为直四棱柱的底面不一定是平行四边形,故命题③是错误的;命题④由棱台的定义知是正确的.答案:①④8.一个圆台上、下底面的半径分别为3 cm 和8 cm ,若两底面圆心的连线长为12 cm ,则这个圆台的母线长为________cm.解析:如图,过点A 作AC ⊥OB ,交OB 于点C . 在Rt △ABC 中,AC =12(cm),BC =8-3=5 (cm). ∴AB =122+52=13(cm). 答案:139.已知正四棱锥V ABCD 中,底面面积为16,一条侧棱的长为211,则该棱锥的高为________.解析:如图,取正方形ABCD 的中心O ,连接VO ,AO ,则VO 就是正四棱锥V ABCD 的高.因为底面面积为16,所以AO =2 2. 因为一条侧棱长为211.所以VO =VA 2-AO 2=44-8=6. 所以正四棱锥V ABCD 的高为6. 答案:610.已知某几何体的三视图如图所示,正视图和侧视图都是矩形,俯视图是正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何体的形状给出下列命题:①矩形;②有三个面为直角三角形,有一个面为等腰三角形的四面体;③两个面都是等腰直角三角形的四面体.其中正确命题的序号是________.解析:由三视图可知,该几何体是正四棱柱,作出其直观图为如图所示的四棱柱ABCDA1B1C1D1,当选择的4个点是B1,B,C,C1时,可知①正确;当选择的4个点是B,A,B1,C时,可知②正确;易知③不正确.答案:①②B级——中档题目练通抓牢1.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是( )A.8 B.7C.6 D.5解析:选C 画出直观图可知,共需要6块.2.将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧视图为( )解析:选 B 如图所示,由正视图和侧视图可知该几何体是由长方体ABCD A 1B 1C 1D 1截去三棱锥B 1A 1BC 1得到的,故其侧视图为选项B.3.已知四棱锥P ABCD 的三视图如图所示,则四棱锥P ABCD 的四个侧面中面积最大的是( )A .3B .2 5C .6D .8解析:选C 四棱锥如图所示,取AD 的中点N ,BC 的中点M ,连接PM ,PN ,则PN =5,PM =3,S △PAD =12×4×5=25,S △PAB =S △PDC =12×2×3=3, S △PBC =12×4×3=6.所以四个侧面中面积最大的是6.4.已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为________.解析:由题意可知,该几何体是三棱锥,将其放置在长方体中形状如图所示(图中棱锥P ABC ),利用长方体模型可知,此三棱锥的四个面全部是直角三角形.答案:45.如图,一立在水平地面上的圆锥形物体的母线长为4 m ,一只小虫从圆锥的底面圆上的点P 出发,绕圆锥表面爬行一周后回到点P 处.若该小虫爬行的最短路程为4 3 m ,则圆锥底面圆的半径等于________ m.解析:把圆锥侧面沿过点P 的母线展开成如图所示的扇形,由题意OP =4,PP ′=43, 则cos ∠POP ′=42+42-4322×4×4=-12,所以∠POP ′=2π3.设底面圆的半径为r ,则2πr =2π3×4,所以r =43.答案:436.已知正三棱锥V ABC 的正视图、侧视图和俯视图如图所示.(1)画出该三棱锥的直观图; (2)求出侧视图的面积. 解:(1)直观图如图所示.(2)根据三视图间的关系可得BC =23, ∴侧视图中VA =42-⎝ ⎛⎭⎪⎫23×32×232=23,∴S △VBC =12×23×23=6.7.如图,在四棱锥P ABCD 中,底面为正方形,PC 与底面ABCD 垂直,下图为该四棱锥的正视图和侧视图,它们是腰长为6 cm 的全等的等腰直角三角形.(1)根据图中所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积; (2)求PA .解:(1)该四棱锥的俯视图为(内含对角线)边长为6 cm 的正方形,如图,其面积为36 cm 2.(2)由侧视图可求得PD =PC 2+CD 2=62+62=6 2. 由正视图可知AD =6,且AD ⊥PD ,所以在Rt△APD中,PA=PD2+AD2=622+62=6 3 cm.C级——重难题目自主选做1.(2018·泉州模拟)某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是( )A.圆弧 B.抛物线的一部分C.椭圆的一部分 D.双曲线的一部分解析:选D 根据几何体的三视图可得,侧视图中的虚线部分是由平行于旋转轴的平面截圆锥所得,故侧视图中的虚线部分是双曲线的一部分,故选D.2.一只蚂蚁从正方体ABCDA1B1C1D1的顶点A出发,经正方体的表面,按最短路线爬行到顶点C1的位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )A.①② B.①③C.③④ D.②④解析:选D 由点A经正方体的表面,按最短路线爬行到达顶点C1的位置,共有6种路线(对应6种不同的展开方式).若把平面ABB1A1和平面BCC1B1展到同一个平面内,连接AC1,则AC1是最短路线,且AC1会经过BB1的中点,此时对应的正视图为②;若把平面ABCD和平面CDD1C1展到同一个平面内,连接AC1,则AC1是最短路线,且AC1会经过CD的中点,此时对应的正视图为④.而其他几种展开方式对应的正视图在题中没有出现.故选D.(二)重点高中适用作业A级——保分题目巧做快做1.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是( )解析:选B 根据直观图以及图中的辅助四边形分析可知,当正视图和侧视图完全相同时,俯视图为B,故选B.2.已知点E,F,G分别是正方体ABCDA1B1C1D1的棱AA1,CC1,DD1的中点,点M,N,Q,P分别在线段DF,AG,BE,C1B1上.以M,N,Q,P为顶点的三棱锥PMNQ的俯视图不可能是( )解析:选C 当M与F重合,N与G重合,Q与E重合,P与B1重合时,三棱锥PMNQ 的俯视图为A;当M,N,Q,P是所在线段的中点时,三棱锥PMNQ的俯视图为B;当M,N,Q,P位于所在线段的非端点位置时,存在三棱锥PMNQ,使其俯视图为D.故选C.3.已知一个三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )解析:选C 由已知条件得直观图如图所示,PC⊥底面ABC,正视图是直角三角形,中间的线是看不见的线PA形成的投影,应为虚线,故选C.4.某几何体的正视图和侧视图如图1所示,它的俯视图的直观图是如图2所示的矩形O1A1B1C1,其中O1A1=6,O1C1=2,则该几何体的侧面积为( )A .48B .64C .96D .128解析:选 C 由题意可知该几何体是一个直四棱柱,∵它的俯视图的直观图是矩形O 1A 1B 1C 1,O 1A 1=6,O 1C 1=2,∴它的俯视图是边长为6的菱形,∵棱柱的高为4, 故该几何体的侧面积为4×6×4=96.5.已知四棱锥P ABCD 的三视图如图所示,则四棱锥P ABCD 的四个侧面中面积最大的是( )A .3B .2 5C .6D .8解析:选C 四棱锥如图所示,取AD 的中点N ,BC 的中点M ,连接PM ,PN ,则PN =5,PM =3,S △PAD =12×4×5=25,S △PAB =S △PDC =12×2×3=3, S △PBC =12×4×3=6.所以四个侧面中面积最大的是6.6.一个圆台上、下底面的半径分别为3 cm 和8 cm ,若两底面圆心的连线长为12 cm ,则这个圆台的母线长为________cm.解析:如图,过点A 作AC ⊥OB ,交OB 于点C . 在Rt △ABC 中,AC =12(cm),BC =8-3=5 (cm).∴AB =122+52=13(cm). 答案:137.已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为________.解析:由题意可知,该几何体是三棱锥,将其放置在长方体中形状如图所示(图中棱锥P ABC ),利用长方体模型可知,此三棱锥的四个面全部是直角三角形.答案:48.如图,一立在水平地面上的圆锥形物体的母线长为4 m ,一只小虫从圆锥的底面圆上的点P 出发,绕圆锥表面爬行一周后回到点P 处.若该小虫爬行的最短路程为4 3 m ,则圆锥底面圆的半径等于________ m.解析:把圆锥侧面沿过点P 的母线展开成如图所示的扇形, 由题意OP =4,PP ′=43, 则cos ∠POP ′=42+42-4322×4×4=-12,所以∠POP ′=2π3.设底面圆的半径为r ,则2πr =2π3×4,所以r =43.答案:439.如图是一个几何体的正视图和俯视图. (1)试判断该几何体是什么几何体; (2)画出其侧视图,并求该平面图形的面积; (3)求出该几何体的体积.解:(1)由题意可知该几何体为正六棱锥.(2)其侧视图如图所示,其中AB =AC ,AD ⊥BC ,且BC 的长是俯视图中的正六边形对边的距离,即BC =3a ,AD 的长是正六棱锥的高,即AD =3a ,∴该平面图形的面积S =12·3a ·3a =32a 2.(3)V =13×6×34a 2×3a =32a 3.10.已知正三棱锥V ABC 的正视图、侧视图和俯视图如图所示.(1)画出该三棱锥的直观图; (2)求出侧视图的面积. 解:(1)直观图如图所示.(2)根据三视图间的关系可得BC =23, ∴侧视图中VA =42-⎝ ⎛⎭⎪⎫23×32×232=23,∴S △VBC =12×23×23=6.B 级——拔高题目稳做准做1.(2018·邵阳模拟)某四面体的三视图如图所示,该四面体的六条棱中,长度最长的棱的长是( )A .2 5B .2 6C .27D .4 2解析:选C 由三视图可知该四面体的直观图如图所示.其中AC =2,PA =2,△ABC 中,边AC 上的高为23,所以BC =42+232=27,AB=232+22=4,而PB=PA2+AB2=22+42=25,PC=PA2+AC2=22,因此在四面体的六条棱中,长度最长的是BC,其长为27,选C.2.(2018·泉州模拟)某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是( )A.圆弧 B.抛物线的一部分C.椭圆的一部分 D.双曲线的一部分解析:选D 根据几何体的三视图可得,侧视图中的虚线部分是由平行于旋转轴的平面截圆锥所得,故侧视图中的虚线部分是双曲线的一部分,故选D.3.一只蚂蚁从正方体ABCDA1B1C1D1的顶点A出发,经正方体的表面,按最短路线爬行到顶点C1的位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )A.①② B.①③C.③④ D.②④解析:选D 由点A经正方体的表面,按最短路线爬行到达顶点C1的位置,共有6种路线(对应6种不同的展开方式).若把平面ABB1A1和平面BCC1B1展到同一个平面内,连接AC1,则AC1是最短路线,且AC1会经过BB1的中点,此时对应的正视图为②;若把平面ABCD和平面CDD1C1展到同一个平面内,连接AC1,则AC1是最短路线,且AC1会经过CD的中点,此时对应的正视图为④.而其他几种展开方式对应的正视图在题中没有出现.故选D.4.某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy的最大值为________.解析:由三视图知三棱锥如图所示,底面ABC是直角三角形,AB⊥BC,PA⊥平面ABC,BC=27,PA2+y2=102,(27)2+PA2=x2,因此xy=x102-[x2-272]=x128-x2≤x2+128-x22=64,当且仅当x2=128-x2,即x=8时取等号,因此xy的最大值是64.答案:645.如图,在四棱锥PABCD中,底面为正方形,PC与底面ABCD垂直,下图为该四棱锥的正视图和侧视图,它们是腰长为6 cm 的全等的等腰直角三角形.(1)根据图中所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积;(2)求PA.解:(1)该四棱锥的俯视图为(内含对角线)边长为6 cm的正方形,如图,其面积为36 cm2.(2)由侧视图可求得PD=PC2+CD2=62+62=6 2.由正视图可知AD=6,且AD⊥PD,所以在Rt△APD中,PA=PD2+AD2=622+62=6 3 cm.6.四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(1)求四面体ABCD 的体积; (2)证明:四边形EFGH 是矩形.解:(1)由题意,BD ⊥DC ,BD ⊥AD ,AD ⊥DC ,BD =DC =2,AD =1,∵BD ∩DC =D ,∴AD ⊥平面BDC ,∴四面体ABCD 的体积V =13×12×2×2×1=23.(2)证明:∵BC ∥平面EFGH ,平面EFGH ∩平面BDC =FG ,又平面EFGH ∩平面ABC =EH , ∴BC ∥FG ,BC ∥EH , ∴FG ∥EH .同理,EF ∥AD ,HG ∥AD ,∴EF ∥HG ,∴四边形EFGH 是平行四边形. ∵AD ⊥平面BDC ,∴AD ⊥BC , ∴EF ⊥FG ,∴四边形EFGH 是矩形.第二节空间几何体的表面积与体积1.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱 圆锥 圆台侧面展开图侧面积公式 S 圆柱侧=2πrl S 圆锥侧=πrlS 圆台侧=π(r +r ′)l2.空间几何体的表面积与体积公式名称几何体 表面积体积柱体(棱柱和圆S 表面积=S 侧+2S 底 V =Sh柱) 锥体(棱锥和圆锥) S 表面积=S 侧+S 底V =13Sh台体(棱台和圆台) S 表面积=S 侧+S 上+S 下V =13(S 上+S 下+S 上S 下)h球S =4πR 2V =43πR 31.判断下列结论是否正确(请在括号中打“√”或“×”)(1)圆柱的一个底面积为S ,侧面展开图是一个正方形,那么这个圆柱的侧面积是2πS .( )(2)锥体的体积等于底面面积与高之积.( ) (3)台体的体积可转化为两个锥体的体积之差.( ) (4)球的体积之比等于半径之比的平方.( ) 答案:(1)× (2)× (3)√ (4)×2.一个球的表面积是16π,那么这个球的体积为( ) A.163π B.323πC .16πD .24π解析:选B 设球的半径为R ,则由4πR 2=16π,解得R =2,所以这个球的体积为43πR3=323π. 3.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A .20πB .24πC .28πD .32π解析:选C 由三视图知该几何体是圆锥与圆柱的组合体,设圆柱底面圆半径为r ,周长为c ,圆锥母线长为l ,圆柱高为h .由图得r =2,c =2πr =4π,h =4,由勾股定理得:。
2019-2020年高考数学大一轮复习第七章立体几何课时作业47理新人教A版

2019-2020年高考数学大一轮复习第七章立体几何课时作业47理新人教A版一、选择题1 .平面a//平面点A, C€a ,点B, D€B,则直线AC/直线BD的充要条件是()A. AB// CDB. AD// CBC. AB与CD相交D. A, B, C, D四点共面解析:充分性:A, B, C, D四点共面,由平面与平面平行的性质知AC// BD必要性显然成立.答案:D2. 一条直纟戋I上有相异三个点A、B C到平面a的距离相等,那么直线1与平面a的位置关系是()A. I / aB. I 丄aC. I 与a相交但不垂直D. I // a 或1 ?a解析:I // a时,直线I上任意点到a的距离都相等;I ? a时,直线I上所有的点到a的距离都是0;I丄a时,直线1上有两个点到a距离相等;I与a斜交时,也只能有两个点到a距离相等.故选D.答案:D3.已知不重合的两条直线I ,m和不重合的两个平面 a , 3,下列命题正确的是()A. l // m I // 3 ,则m// 3B. a n 3 =m I ? a ,贝V I // 3C. a 丄 3 , I 丄 a ,贝V I // 3D. I 丄m mL 3 , I 丄a,贝y a 丄 3解析:对于选项A, m可能在3内,故A错;对于选项B , I可能与3相交,故B错;对于选项C, I可能在3内,故C错,所以选D.答案:D4 .已知I、m是两条不同的直线, a是一个平面,则下列命题正确的是()A . 若 1 // a , m// a ,贝UI //mB . 若 1 丄m m// a,贝yI丄aC .若 1 丄m ml a ,贝y I// aD .若 1 // a , ml a ,贝UI丄m解析:A选项,I与m可能平行,异面或相交,A错;B选项,I与a可能平行,相交或l在a内,B错;C选项,I有可能在a内,C错,故选D.答案:D5. 已知a , 3是两个不同的平面,m n是两条不同的直线,给出下列命题:①若ml a , m? 3,贝U a 丄3 ;②若n? a , n? a , n i/ 3 , n // 3 ,贝U a // 3 ;③如果m? a , n? a , m n是异面直线,那么n与a相交;④若a n 3 = m n// m且n? a , n ? 3 ,贝U n // a 且n // 3 .其中正确的命题是()A. ①②B .②③C.③④D .①④解析:由面面垂直的判定定理得①正确,若m// n时,a , 3有可能相交,所以②错误.对③来说,n 可能与a平行,则③错.a n 3 = m ••• m? a , m? 3 , n? a , n // m贝u n // a , 同理n// 3 ,选D.答案:D6. 如图,正方体ABC—ABCD中,E, F分别为棱AB, CC的中点,在平面ADDA内且与平面DEF平行的直线( )A. 有无数条B. 有2条C. 有1条D. 不存在解析:因为平面DEF与平面ADD1有公共点D,所以两平面有一条过D的交线I,在平面ADD i内与I平行的任意直线都与平面DEF平行,这样的直线有无数条.答案:A二、填空题7. ____________________________________________________________________ 在正方体ABC—ABCD中,E是DD的中点,则BD与平面ACE的位置关系为 _________________ .解析:如图,连接AC BD交于O点,连接OE因为0日/ BD,而OE>平面ACE BD?平面ACE 所以BD//平面ACE答案:平行& a、 B、Y是二个平面,a、b是两条直线,有下列二个条件:①a// 丫,b? p ;②a// Y,b / B ;③ b / B,a? 丫.如果命题"a n B = a, b? Y ,且_____________ ,则a / b” 为真命题,则可以在横线处填入的条件是___________ (把所有正确的题号填上).解析:①中,a/ Y , a? B , b? B , B门丫 = b? a// b(线面平行的性质).③中,b/ B , b? Y , a? Y , B^Y = a? a// b(线面平行的性质).答案:①③9.在正四棱柱ABC—ABCD中,0为底面ABCD勺中心,P是DD的中点,设Q是CC 上的点,则点Q满足条件________________ 时,有平面DBQ//平面PAO解析:假设Q为CC的中点,因为P为DD的中点,所以QB/ PA连接DB因为P, 0分别是DD, DB的中点,所以DB// P0又DB?平面PAO Q曰平面PAO所以DB//平面PAO QB/平面PAO又DB Q QB= B,所以平面DBQ/平面PAO故Q满足条件Q为CC的中点时,有平面DBQ/平面PAO 答案:Q为CC的中点三、解答题10.如图,已知四棱锥P—ABCD的底面为直角梯形,AB// CD / DAB= 90°, PAL底面1ABCD 且PA= AD= DC= q AB= 1, M是PB的中点.(1) 求证:AM= CM(2) 若N是PC的中点,求证:DN/平面AMC1证明:(1) •••在直角梯形ABCDK AD= DC= -AB= 1,AC="j2,BC= 2,••• BC L AC 又PA!平面ABCD BC?平面ABCD••• BC L PA 又PA O AC= A,「. BCL平面PAC• BC丄PC1在Rt△ PAB中, M为PB的中点,贝U AM= §PB1在Rt△ PBC中, M为PB的中点,贝U CM= ?PB••• AM= CM⑵如图,连接DB交AC于点F,1 1 •••DC綊2AB •- DF= 2FB取PM的中点G,连接DG FM贝U DGI FM•••又DC?平面AMC FM?平面AMC•DG/ 平面AMC连接GN贝U GIN/ MC GN?平面AMC MC?平面AMC•GIN/ 平面AMC 又GN1 DG= G,•平面DNG平面AMC又DN?平面DNG•DN// 平面AMC11.如右图,在多面体ABCDEFF ,底面ABCD1边长为2的正方形,四边形BDEF是矩形, 平面BDE庄平面ABCD BF= 3 , G和H分别是CE和CF的中点.⑴求证:AC L平面BDEF(2)求证:平面BDGH平面AEF解:⑴ 因为四边形ABCD是正方形,所以ACL BD又因为平面BDE L平面ABCD平面BDEF?平面ABC B BD且AC?平面ABCD所以AC丄平面BDEF⑵ 在厶CE 冲,因为 G H 分别是CE CF 的中点,所以 GH EF,又因为 GT 平面AEF EF ?平面AEF 所以GH/平面AEF 设A8 BD= 0,连接OH在厶ACF 中,因为 OA= OC CH= HF,所以OH/ AF, 又因为OP ?平面AEF AF ?平面AEF 所以OH/平面AEF 又因为 OH P GH= H, OH GF ?平面 BDGH 所以平面BDGH 平面AEF1.下列四个正方体图形中, A , B 为正方体的两个顶点, M N, P 分别为其所在棱的中点, 能得出AB//平面MNP 勺图形的序号是()A .①③B .②③C.①④D .②④解析:对于图形①:平面MNP 与AB 所在的对角面平行, 形④:AB// PN 即可得到AB//平面MNP 图形②,③都不可以,故选 C.答案:C即可得到 AB//平面 MNP 对于图B2•如图,在长方体ABC—ABCD中,E, F, G, H分别是棱CC, CD, DD, DC的中点, N是BC的中点,点M在四边形EFGI及其内部运动,则M满足条件_________ 时,有MN/平面BBDD解析:如图,连接FH, HN FN由题意知HIN/面BBDD, FH//面BBDD且HNH FH= H,•••面NHF/ 面BBDD•••当M在线段HF上运动时,有MN/面BBDD答ME线段HF3.如图1,已知O 0的直径AB= 4,点C D为O 0上两点,且/ CAB= 45°, / DAB= 60°,F为弧BC的中点,将O 0沿直径AB折起,使两个半圆所在平面互相垂直(如图2).(1) 求证:OF// AC(2) 在弧BD上是否存在点G使得FG//平面ACD若存在,试指出点G的位置;若不存在,请说明理由.解:解法1: (1)证明:如右图,连接CO •••/ CAB= 45°,二COL AB,又••• F为弧BC的中点,•••/ FOB= 45°,「. OF// AC(2)取弧BD的中点G 连接OG FG则/ BO G / BAD= 60°,故OG/ AD由(1) OF// AC知OF//平面ACD故平面OFG平面ACD则FG//平面ACD因此,在弧BD上存在点G 使得FG/平面ACD且点G为弧BD的中点.解法2:证明:(1)如下图,以AB所在的直线为y轴,以OC所在的直线为z轴,以O为原点,作空间直角坐标系O-xyz,则A(0,- 2, 0), C(0,0,2)AC= (0,0,2) - (0,- 2,0) = (0,2,2),•••点F为弧BC的中点,•点F的坐标为(0 , 2, 2),OF= (0 , 2, 2),••• OF=爭心即OF// AC(2)设在弧BD上存在点G,使得FG//平面ACD由(1) OF// AC知OF//平面ACD二平面OFG平面ACD则有OG/ AD设O G=入AD(入>0) , ••• A D= ( 3 , 1,0) , • O G= (3 入,入,0).又T | O(G = 2, • —3- 入2+入2+ 02= 2,解得入=± 1(舍去一1) , • OG=(季,1,0),贝U G为弧BD的中占八、、♦因此,在弧BD上存在点G使得FG//平面ACD且点G为弧BD的中点.2019-2020年高考数学大一轮复习第七章立体几何课时作业49理新人教A版、选择题1 .已知点A—3,0 , —4),点A关于原点的对称点为等于(A. 12.—3 - ;! 2+ U —2+ —4-[ 2= 10.答案:D B,则|ABC. 25D . 10:点A关于原点对称的点B的坐标为(3,0,4),故|AB2.已知向量a=入,15),且a // b,则入等于()2 A.- 39 B.- 2C.解析:a // b? a= kb? ■ 2= 3k;-3= k入;155=尹2k= 3,十-9答案:3.已知向量a= (1,1,0) ,b= ( —1,0,2) ,且ka+ b与2a —b互相垂直,贝U k的值为(A. 1 1B.—53 C.57 D.7解析:ka+ b= (k —1, k, 2) , 2a—b= (3,2 , —2),由题意知,3( k —1) + 2k—4 = 0,解答案:D4.已知a= (2 , —1,3) , b= ( —1,4 , —2) , c= (7,5 ,入),若a、b、c 三个向量共面, 则实数入等于(62 6364C. ■765D.—7解析:由于a , b , c 三个向量共面,所以存在实数” 》A A A A 1 A A A 1 AAA2 A 1 A 1 A A解析:I MN= AN- AM = AN- 3AC = AB+ BN- §(AB+ AD^ AA ) = 3AB+ &AA — 3AD 二 | MN6•设A , B , c, D 是空间不共面的四个点,且满足 X B - A C = 0, Ab ・XC= 0, Ab ・AB= 0, 则厶BCD 勺形状是( )A .钝角三角形B •直角三角形 C.锐角三角形 D •无法确定 解析:—S —S—S —S—S —S—S —S —S —S —S —S —A 2 ~A 2「,BC- BD = (AC- AB •( AD - AR = AC- AD - AC- AB- AB- AM = AB >0,同理SB- A (>0,AB - Cb o ,故厶BCD 为锐角三角形•故选 C.答案:C二、填空题7.已知点P 在z 轴上,且满足| OR = 1(0为坐标原点),则点P 到点A (1,1,1)的距离为解析:由题意知,只0,0,1)或R0,0 , — 1).•••I PA =.卩-12+〔1-1 2+ 1-1 2= ,2.或I PA =.1-li2+1-2+—1-12= 6.答案:.2或6 8.已知空间四边形 OABC 点M N 分别是0A BC 的中点,且0A= a , 6B= b , A (= C ,用a ,m n 使得 c = na + nb ,即有7= 2m- n ,5=— m^ 4n , 入=3n — 2n ,解得n = 33, n =耳,65 入=7答案:D5.已知正方体 ABC —ABCD 的棱长为a,A M =空危,点N 为BB 的中点,则| MN 等于(A. B.C.D.15 3b, C表示向量A= _____________ .解析:如图,MN= 1(M BF M (C 1 IfIf=2【(OB- OM + (OC- OM =1( O B 5C - 2fM=1( OB ^ o c- O A=1( b + c - a ). 答案:2(b + c - a )9.已知 00,0,0) , A (1,2,3) , B (2,1,2) , R1,1,2),点 Q 在直线OP 上运动,当 °A- Q B 取最小值时,点 Q 的坐标是 ________ .解析:由题意,设OQ=入OP 即OQ=(入,入,2入),则QA= (1 一入,2 一入,3 — 2入),—0—0—0QB= (2 —入,1 —入,2 — 2 入),••• QA QB= (1 —入)(2 —入)+ (2 —入)(1 —入)+ (3 — 2 入)(2 4 入=3时有最小值,此时 3答案: 三、解答题10.已知 a = (1 , — 3,2) , b = ( — 2,1,1),点 A — 3,— 1, 4) , B ( — 2,— 2,2). (1)求|2 a + b | ;(2)在直线AB 上,是否存在一点 E,使得0E_ b ? (0为原点)解:(1)2 a + b = (2 , — 6,4) + ( — 2, 1,1) = (0 , — 5,5),故|2 a + b | = . 02+ —52+ 52=5 2.Q 点坐标为 性4 8)3, 3, 3 .—2 入)=6 入 2—16 入 + 10= 642-3,当3 3⑵令AE= tAB(t € R),所以0E= OA^ X E=OAb tAB= ( —3, —1,4) + t(1 , —1, —2)=(—3 + t , - 1 —t, 4- 2t),若0E1 b,则O E- b= 0,9 所以-2( —3+ t)+ ( - 1-t)+ (4 -2t)= 0,解得t = ?因此存在点E,使得OEl b,此时E点的坐标为(—6, —14, |).11. (xx •云南玉溪一中统考)如图,在三棱柱ABC-ABC中,已知ABL侧面BBCC, ABn=BC= 1, BB = 2,/ BCC^3(1) 求证:CB丄平面ABC(2) 设6E=入CC(0 w入w 1),且平面ABE与BBE所成的锐二面角的大小为30°,试求入的值.解:⑴因为AB!侧面BBGC, BC?侧面BBCC,故ABL BC,在△ BCC中,BC= 1, CCn=BB = 2,Z BCC=亍B C = B C+ CC—2BC- CC・cos/ BCC= 12+ 22—2X 1X 2X cos y- = 3,3所以BC=W,故B C+B C = cC,所以BCLBC,而B8 AB= B,所以CB丄平面ABC(2)由(1)可知,AB BC, BC两两垂直•以B为原点,BC BA BC所在直线分别为x , y , z轴建立空间直角坐标系.则B(o,o,o), A(0,1,0) , B( —1,0, ^3), C(1,0,0) , C(O,O ,萌)•所以C C= (—1,0,.3),所以6E=(—入,0 , ,3入),E(1 —入,0 , 3 入).则A E= (1 -入,-1 ,也入),AB= ( —1, —1,腑.设平面ABE的法向量为n= (x , y , z).n丄A~E ’ 1—入x—入z = 0贝汀,‘L ,3 — 3入3 丄/ 3 — 3入 3厂,y = L ,故n =(亍■厂 厂,3)是平面ABE 的一个1 .二面角a — l — 3为60°, A , B 是棱I 上的两点,AC BD 分别在半平面 a , B 内,ACL l , BDL l ,且 AB= AC= a , BD= 2a ,则 CD 的长为()A . 2a B. 5a C. aD. 3a解析:•/ AC L l , BDL l ,•••〈 AC S b = 60°,且 A C - BA = 0, X B - EBD = 0,禽 AB+ BD 2=,a 2+ a 2 + 2a 2+ 2a -2 a cos120°= 2a .答案:A2.已知空间三点 A (0,2,3),耳—2,1,6) , Q1 , — 1,5).则以AB AC 为边的平行四边形 的面积为 .解析:由题意可得: AB= (—2,— 1,3), AC= (1,一 3,2),法向量. 因为ABL 平面BBCC, BA= (0,1,0)是平面BBE 的一个法向量,B A I所以 |cos 〈n , BA> | = |I n || BA=I1X3— 3入 2—厂 +2两边平方并化简得 2入—5入+ 3= 0,所以入 3=1或入=2(舍去).•••以AB E C 为边的平行四边形的面积 1 A A A A \[3S = 2X 2l AB - AC - Sin 〈A B AG = 14X 三=7 3.答案:7 33.如图,四棱锥 S — ABCD^ , ABC [为矩形,SDL AD 且 SDL AB AD= a ( a >0), AB= 2ADSD=WAD E 为 CD 上一点,且 CE= 3DE(1) 求证:AE!平面SBD(2) M N 分别为线段 SB CD 上的点,是否存在 M N,使MN L CD 且 MN L SB 若存在,确 定M N 的位置;若不存在,说明理由.解:(1)证明:因为四棱锥 S-ABCDh ABCC 为矩形,SD L AD 且SD L AB 所以SC L 平 面 ABCDBD 就是SB 在平面ABCDb 的射影.因为AB= 2AD E 为CD 上一点,且 CE= 3DE/ DE 1 / AD 1•-tan / DAE= AD T 2,tan / DBA= AB =2,•••/ DAE=Z DBA •/ DAEb Z BDA= 90°• AE L BD •- AE! SB : SBH BD= B, • AE L 平面 SBD…cos <AB ACAB- A C - 2 + 3+ 614X 147 _ 1 14=2./• sin<A B A C = ~23(2)假设存在点 M N 满足MN L CD 且MNL SB 建立如图所示的空间直角坐标系D-xyz ,由题意可知,D (0,0,0) , A (a,0,0) , C (0,2 a, 0),B (a,2a,0) , S (0,0 , 3a ),设DM=画tBS = (a, 2a,0) +1( — a , -2a ,3a ) = (a —ta, 2a — 2ta , 3ta )( t € [0,1]),即 Ma — ta, 2a — 2ta , 3ta ) , NO , y, 0) , y € [0,2 a ],NM= (a — ta, 2a — 2ta — y,::;3ta ).[而 5C= 0,使 MNL CD 且 MNL SB 则血 B S= 0,;a — ta , 2a — 2ta — y ,^/3t ^ • I], 2a, () = 0 ,i a — ta , 2a — 2ta — y , ^3ta|— a , — 2a ,yJ 3a = 0 ,2a — 2ta — y = 0 ,a — ta — 2a 2a — 2ta — yt = 4 € [0,1] , y =|a € [0,2 a ].故存在点 M N 使MN L CD 且 MN L SB , 2a , i 3a , N 0 , 2a , 0 -2a 可得* —a+ 3ta 2= 0 ,。
高考一轮复习第7章立体几何第2讲空间几何体的表面积与体积

第二讲 空间几何体的表面积与体积知识梳理·双基自测 知识梳理知识点一 柱、锥、台和球的侧面积和体积侧面积 体积圆柱 S 侧=2πrh V =_S 底·h__=πr 2h圆锥 S 侧=_πrl __ V =13S 底·h=13πr 2h =13πr 2l 2-r 2 圆台 S 侧=π(r 1+r 2)l V =13(S 上+S 下+S 上·S 下)·h=13π(r 21+r 22+r 1r 2)h 直棱柱 S 侧=_ch__ V =_S 底h__ 正棱锥 S 侧=12ch′V =13S 底h 正棱台 S 侧=12(c +c′)h′V =13(S 上+S 下+S 上·S 下)h 球S 球面=_4πR 2V =43πR 3 (1)棱柱、棱锥、棱台的表面积就是_各面面积之和__.(2)圆柱、圆锥、圆台的侧面展开图分别是_矩形__、_扇形__、_扇环形__;它们的表面积等于_侧面积__与底面面积之和.重要结论1.长方体的外接球:球心:体对角线的交点;半径:r =_a 2+b 2+c22__(a ,b ,c 为长方体的长、宽、高).2.正方体的外接球、内切球及与各条棱相切的球: (1)外接球:球心是正方体中心;半径r =_32a__(a 为正方体的棱长); (2)内切球:球心是正方体中心;半径r =_a2__(a 为正方体的棱长);(3)与各条棱都相切的球:球心是正方体中心;半径r =_22a__(a 为正方体的棱长). 3.正四面体的外接球与内切球(正四面体可以看作是正方体的一部分):(1)外接球:球心是正四面体的中心;半径r =_64a__(a 为正四面体的棱长); (2)内切球:球心是正四面体的中心;半径r =_612a__(a 为正四面体的棱长). 双基自测题组一 走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)多面体的表面积等于各个面的面积之和.( √ ) (2)台体的体积可转化为两个锥体的体积之差.( √ ) (3)锥体的体积等于底面积与高之积.( × )(4)已知球O 的半径为R ,其内接正方体的棱长为a ,则R =32a.( √ ) (5)圆柱的一个底面积为S ,侧面展开图是一个正方形,那么这个圆柱的侧面积是2πS.( × ) 题组二 走进教材2.(必修2P 27T1)已知圆锥的表面积等于12π cm 2,其侧面展开图是一个半圆,则底面圆的半径为( B ) A .1 cm B .2 cm C .3 cmD .32cm [解析] 由条件得:⎩⎪⎨⎪⎧πrl+πr 2=12π2πrl =π,∴3r 2=12,∴r =2.题组三 走向高考3.(2020·天津卷)若棱长为23的正方体的顶点都在同一球面上,则该球的表面积为( C ) A .12π B .24π C .36πD .144π[解析] 这个球是正方体的外接球,其半径等于正方体的体对角线长的一半, 即R =232+232+2322=3,所以,这个球的表面积为S =4πR 2=4π×32=36π.故选:C .4.(2018·课标全国Ⅰ)已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( B )A .122πB .12πC .82πD .10π[解析] 设圆柱底面半径为r ,则4r 2=8,即r 2=2.∴S 圆柱表面积=2πr 2+4πr 2=12π.5.(2020·浙江卷)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm 3)是( A )A .73 B .143C .3D .6[解析] 由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,且三棱锥的一个侧面垂直于底面.棱锥的高为1,棱柱的底面为等腰直角三角形,棱柱的高为2,所以几何体的体积为:13×⎝ ⎛⎭⎪⎫12×2×1×1+⎝ ⎛⎭⎪⎫12×2×1×2=13+2=73.故选:A .考点突破·互动探究考点一 几何体的表面积——自主练透例1 (1)(2021·北京模拟)某三棱锥的三视图如图所示,则该三棱锥的表面积是( C )A .2+ 5B .4+ 5C .2+2 5D .5(2)(2021·安徽江南十校联考)已知某几何体的三视图如图所示,网格纸上小正方形的边长为1,则该几何体的表面积为( B )A .78-9π2B .78-9π4C .78-πD .45-9π2(3)(多选题)(2021·山东潍坊期末)等腰直角三角形直角边长为1,现将该三角形绕其某一边旋转一周,则所形成的几何体的表面积可以为( AB )A .2πB .(1+2)πC .22πD .(2+2)π[解析] (1)由三视图知,该几何体是底面为等腰三角形,其中一条侧棱与底面垂直的三棱锥(SA ⊥平面ABC),如图所示,由三视图中的数据可计算得S △ABC =12×2×2=2,S △SAC =12×5×1=52,S △SAB =12×5×1=52,S △SBC =12×2×5=5,所以S 表面积=2+2 5.故选C .(2)由三视图可知该几何体是一个长方体中挖去一个18球,如图所示.∴S =3×3×2+3×5×4-27π4+9π2=78-94π.故选B .(3)若绕直角边旋转一周形成的几何体是圆锥,其表面积为π+2π;若绕斜边旋转一周形成的几何体是两同底圆锥构成的组合体,其表面积为2π,故选A 、B .名师点拨空间几何体表面积的求法(1)旋转体的表面积问题注意其轴截面及侧面展开图的应用.(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.(3)已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.〔变式训练1〕(2020·河南开封二模)已知某个几何体的三视图如图所示,根据图中标出的数据,可得出这个几何体的表面积是( C )A .6B .8+4 6C .4+2 6D .4+ 6[解析] 由三视图得几何体如图所示,该几何体是一个三棱锥,底面是一个底和高均为2的等腰三角形,一个侧面是一个底和高均为2的等腰三角形,另外两个侧面是腰长为AC =AB =22+12=5, 底边AD 长为22的等腰三角形, 其高为52-22=3,故其表面积为S =2×12×22+2×12×22×3=4+2 6.故选C .考点二 几何体的体积——师生共研例2 (1)(2021·浙江金色联盟百校联考)一个空间几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )cm 3.( A )A .π6+13B .π3+16C .π6+16D .π3+13(2)(2021·云南师大附中月考)如图,某几何体的三视图均为边长为2的正方形,则该几何体的体积是( D )A .56 B .83 C .1D .163(3)(2021·湖北武汉部分学校质检)某圆锥母线长为4,其侧面展开图为半圆面,则该圆锥体积为_83π3__.(4)(2020·江苏省南通市通州区)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,P 是侧棱CC 1上一点,且C 1P =2PC .设三棱锥P - D 1DB 的体积为V 1,正四棱柱ABCD -A 1B 1C 1D 1的体积为V ,则V 1V 的值为_16__.[解析] (1)由三视图可知该几何体是由底面半径为1 cm ,高为1 cm 的半个圆锥和三棱锥S -ABC 组成的,如图,三棱锥的高为SO =1 cm ,底面△ABC 中,AB =2 cm ,AC =1 cm ,AB ⊥AC .故其体积V =13×12×π×12×1+13×12×2×1×1=⎝ ⎛⎭⎪⎫π6+13cm 3.故选A .(2)由题意三视图对应的几何体如图所示,所以几何体的体积为正方体的体积减去2个三棱锥的体积,即V =23-2×13×12×2×2×2=163,故选D .(3)该圆锥母线为4,底面半径为2,高为23, V =13×π×22×23=83π3. (4)设正四棱柱ABCD -A 1B 1C 1D 1的底面边长AB =BC =a ,高AA 1=b , 则VABCD -A 1B 1C 1D 1=S 四边形ABCD ×AA 1=a 2b ,VP -D 1DB =VB -D 1DP =13S △D 1DP·BC=13×12ab·a=16a 2b ,∴VP -D 1DB VABCD -A 1B 1C 1D 1=16,即V 1V =16.[引申]若将本例(2)中的俯视图改为,则该几何体的体积为_83__,表面积为_83__.[解析] 几何体为如图所示的正三棱锥(棱长都为22). ∴V =8-4×43=83,S =4×34×(22)2=8 3.名师点拨求体积的常用方法直接法对于规则的几何体,利用相关公式直接计算割补法首先把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算等体 积法选择合适的底面来求几何体体积,常用于求三棱锥的体积,即利用三棱锥的任一个面可作为三棱锥的底面进行等体积变换注:若以三视图的形式给出的几何体问题,应先得到直观图,再求解. 〔变式训练2〕(1)(2020·海南)已知正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点,则三棱锥A -NMD 1的体积为_13__.(2)(2021·开封模拟)如图所示,正三棱柱ABC -A 1B 1C 1的底面边长为2,侧棱长为3,D 为BC 的中点,则三棱锥A -B 1DC 1的体积为( C )A .3B .32 C .1D .32(3)(2017·浙江)某三棱锥的三视图如图所示,则该三棱锥的体积为( A )A .16 B .13 C .12D .1(4)(2021·浙北四校模拟)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是( B )A .8B .8πC .16D .16π[解析] (1)如图,∵正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点,∴S △ANM =12×1×1=12,∴VA -NMD 1=VD 1-AMN =13×12×2=13,故答案为:13.(2)如题图,在正△ABC 中,D 为BC 的中点,则有AD =32AB =3,又因为平面BB 1C 1C ⊥平面ABC ,AD ⊥BC ,AD ⊂平面ABC ,由面面垂直的性质定理可得AD ⊥平面BB 1C 1C ,即AD 为三棱锥A -B 1DC 1的底面B 1DC 1上的高,所以V 三棱锥A -B 1DC 1=13·S△B 1DC 1·AD=13×12×2×3×3=1,故选C .(3)由三视图可画出三棱锥的直观图如图所示.其底面是等腰直角三角形ACB ,直角边长为1,三棱锥的高为1,故体积V =13×12×1×1×1=16.故选A .(4)由三视图的图形可知,几何体是等边圆柱斜切一半,所求几何体的体积为:12×22π×4=8π.故选B .考点三 球与几何体的切、接问题——多维探究角度1 几何体的外接球例3 (1)(2021·河南中原名校质量测评)已知正三棱锥P -ABC 的底面边长为3,若外接球的表面积为16π,则PA =_23或2__.(2)(2020·新课标Ⅰ)已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的表面积为( A )A .64πB .48πC .36πD .32π(3)(2019·全国)已知三棱锥P -ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E 、F 分别是PA ,PB 的中点,∠CEF =90°,则球O 的体积为( D )A .86πB .46πC .26πD .6π[解析] (1)由外接球的表面积为16π,可得其半径为2,设△ABC 的中心为O 1,则外接球的球心一定在PO 1上,由正三棱锥P -ABC 的底面边长为3,得AO 1=3,在Rt △AOO 1中,由勾股定理可得(PO 1-2)2+(3)2=22,解得PO 1=3或PO 1=1,又PA 2=PO 21+AO 21,故PA =9+3=23或PA =1+3=2,故答案为:23或2.(2)由题意可知图形如图:⊙O 1的面积为4π, 可得O 1A =2, 则ABsin60°=2O 1A =4,∴AB =4sin60°=23,∴AB=BC=AC=OO1=23,外接球的半径为:R=AO21+OO21=4,球O的表面积为:4×π×42=64π,故选A.(3)∵PA=PB=PC,△ABC为边长为2的等边三角形,∴P-ABC为正三棱锥,∴PB⊥AC,又E,F分别为PA、AB中点,∴EF∥PB,∴EF⊥AC,又EF⊥CE,CE∩AC=C,∴EF⊥平面PAC,∴PB⊥平面PAC,∴∠APB=90°,∴PA=PB=PC=2,∴P-ABC为正方体一部分,2R=2+2+2=6,即R=62,∴V=43πR3=43π×668=6π.名师点拨几何体外接球问题的处理(1)解题关键是确定球心和半径,其解题思维流程是:(R—球半径,r—截面圆的半径,h—球心到截面圆心的距离).注:若截面为非特殊三角形可用正弦定理求其外接圆半径r.(2)三条侧棱两两垂直的三棱锥,可以补成长方体,它们是同一个外接球.注意:不共面的四点确定一个球面.角度2 几何体的内切球例4 (1)(2020·新课标Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_23π__. (2)(2021·安徽蚌埠质检)如图,E ,F 分别是正方形ABCD 的边AB ,AD 的中点,把△AEF ,△CBE ,△CFD 折起构成一个三棱锥P -CEF(A ,B ,D 重合于P 点),则三棱锥P -CEF 的外接球与内切球的半径之比是_26__.[解析] (1)因为圆锥内半径最大的球应该为该圆锥的内切球, 如图,圆锥母线BS =3,底面半径BC =1, 则其高SC =BS 2-BC 2=22, 不妨设该内切球与母线BS 切于点D , 令OD =OC =r ,由△SOD ∽△SBC ,则OD OS =BCBS ,即r22-r =13,解得r =22,V =43πr 3=23π,故答案为:23π.(2)不妨设正方形的边长为2a ,由题意知三棱锥P -CEF 中PC 、PF 、PE 两两垂直,∴其外接球半径R =PC 2+PF 2+PE 22=62a ,下面求内切球的半径r ,解法一(直接法):由几何体的对称性知,内切球的球心在平面PCH(H 为EF 的中点)内,M 、N 、R 、S 为球与各面的切点,又22=tan ∠CHP =tan2∠OHN , ∴tan ∠OHN =22=rNH,∴NH =2r , 又PN =2r ,∴22r =PH =22a ,∴r =a 4. 解法二(体积法):V C -PEF =13r·(S △PEF +S △PCE +S △PCF +S △CEF ),∴a 3=r·⎝ ⎛⎭⎪⎫a 22+a 2+a 2+2a 2×32a 2,∴r =a 4,故R r =6a 2·4a=2 6.名师点拨几何体内切球问题的处理(1)解题时常用以下结论确定球心和半径:①球心在过切点且与切面垂直的直线上;②球心到各面距离相等.(2)利用体积法求多面体内切球半径. 〔变式训练3〕(1)(角度1)(2020·南宁摸底)三棱锥P -ABC 中,△ABC 为等边三角形,PA = PB = PC =3,PA ⊥PB ,三棱锥P -ABC 的外接球的体积为( B )A .27π2B .273π2C .273πD .27π(2)(角度1)(2021·山西运城调研)在四面体ABCD 中,AB =AC =23,BC =6,AD ⊥平面ABC ,四面体ABCD 的体积为 3.若四面体ABCD 的顶点均在球O 的表面上,则球O 的表面积是( B )A .49π4B .49πC .49π2D .4π(3)(角度2)棱长为a 的正四面体的体积与其内切球体积之比为_63π__.[解析] (1)因为三棱锥P -ABC 中,△ABC 为等边三角形,PA =PB =PC =3,所以△PAB ≌△PBC ≌△PAC .因为PA ⊥PB ,所以PA ⊥PC ,PC ⊥PB .以PA ,PB ,PC 为过同一顶点的三条棱作正方体(如图所示),则正方体的外接球同时也是三棱锥P -ABC 的外接球.因为正方体的体对角线长为32+32+32=33,所以其外接球半径R =332.因此三棱锥P -ABC 的外接球的体积V =4π3×⎝ ⎛⎭⎪⎫3323=273π2.故选B .(2)如图,H 为BC 的中点,由题意易知AH =3,设△ABC 外接圆圆心为O 1,则|O 1C|2=32+(3-|O 1C|)2,∴|O 1C|=23,又12×6×3×|AD|3=3,∴|AD|=1,则|OA|2=|O 1C|2+⎝ ⎛⎭⎪⎫122=494,∴S 球O =4πR 2=49π,故选B .(3)如图,将正四面体纳入正方体中,显然正四面体内切球的球心O(也是外接球的球心)、△BCD 的中心O 1都在正方体的对角线上,设正四面体的棱长为a ,则|AO|=64a ,又|O 1A|=a 2-⎝⎛⎭⎪⎫33a 2=63a ,∴内切球半径|OO 1|=612a ,∴V 正四面体V 内切球=13×34a 2×63a4π3⎝ ⎛⎭⎪⎫612a 3=63π.名师讲坛·素养提升 最值问题、开放性问题例5 (1)(最值问题)(2018·课标全国Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D -ABC 体积的最大值为( B )A .12 3B .18 3C .24 3D .54 3(2)(2021·四川凉山州模拟)已知长方体ABCD -A 1B 1C 1D 1的体积V =12,AB =2,若四面体A -B 1CD 1的外接球的表面积为S ,则S 的最小值为( C )A .8πB .9πC .16πD .32π[解析] (1)设等边△ABC 的边长为a ,则有S △ABC =12a·a·sin 60°=93,解得a =6.设△ABC 外接圆的半径为r ,则2r =6sin 60°,解得r =23,则球心到平面ABC 的距离为42-232=2,所以点D 到平面ABC 的最大距离为2+4=6,所以三棱锥D -ABC 体积的最大值为13×93×6=183,故选B .(2)设BC =x ,BB 1=y ,由于V =12,所以xy =6.根据长方体的对称性可知四面体A -B 1CD 1的外接球即为长方体的外接球, 所以r =4+x 2+y22,所以S =4πr 2=π(4+x 2+y 2)≥π(4+2xy)=16π, (当且仅当x =y =6,等号成立). 故选C .名师点拨立体几何中最值问题的解法(1)观察图形特征,确定取得最值的条件,计算最值.(2)设出未知量建立函数关系,利用基本不等式或导数计算最值.例6 (开放性问题)若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值为_116⎝ ⎛⎭⎪⎫或1412等__(只需写一个可能值). [解析] 如图,若AB =AC =BD =CD =AD =2,BC =1,取AD 的中点H ,则CH =BH =3,且AH ⊥平面BCH ,又S △BCH =114,∴V A -BCD =13S △BCH ×2=116. 如图,若AB =AC =BD =CD =2,AD =BC =1,同理可求得V A -BCD =1412.〔变式训练4〕(2021·河南阶段测试)四面体ABCD 中,AC ⊥AD ,AB =2AC =4,BC =25,AD =22,当四面体的体积最大时,其外接球的表面积是_28π__.[解析] 由已知可得BC 2=AC 2+AB 2,所以AC ⊥AB ,又因为AC ⊥AD ,所以AC ⊥平面ABD ,四面体ABCD 的体积V =13AC·12AB·ADsin∠BAD ,当∠BAD =90°时V 最大,把四面体ABCD 补全为长方体,则它的外接球的直径2R 即长方体的体对角线,(2R)2=AD 2+AC 2+AB 2=28,所以外接球的表面积为4πR 2=28π.。
全国通用近年高考数学一轮复习第七章立体几何初步课时作业三十九7.1空间几何体的结构及其三视图和直观

(全国通用版)2019版高考数学一轮复习第七章立体几何初步课时分层作业三十九7.1 空间几何体的结构及其三视图和直观图文编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((全国通用版)2019版高考数学一轮复习第七章立体几何初步课时分层作业三十九7.1 空间几何体的结构及其三视图和直观图文)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(全国通用版)2019版高考数学一轮复习第七章立体几何初步课时分层作业三十九7.1 空间几何体的结构及其三视图和直观图文的全部内容。
课时分层作业三十九空间几何体的结构及其三视图和直观图一、选择题(每小题5分,共25分)1.由平面六边形沿某一方向平移形成的空间几何体是 ( )A.六棱锥B。
六棱台C.六棱柱D.非棱柱、棱锥、棱台的一个几何体【解析】选C。
平面六边形沿某一方向平移形成的空间几何体符合棱柱的定义.2.水平放置的△ABC的直观图如图,其中B′O′=C′O′=1,A′O′=,那么原△ABC是一个()A。
等边三角形B。
直角三角形C。
三边中只有两边相等的等腰三角形D.三边互不相等的三角形【解析】选A。
AO=2A′O′=2×=,在Rt△AOB中,AB==2,同理AC=2,所以BC是等边三角形.3。
一个简单几何体的正视图、侧视图分别为如图所示的矩形、正方形,则其俯视图不可能为( )A.矩形B。
直角三角形C。
椭圆 D.等腰三角形【解析】选D。
依题意,题中的几何体的俯视图的长为3、宽为2,因此结合题中选项知,其俯视图不可能是等腰三角形。
【变式备选】下列结论正确的是( )A.各个面都是三角形的几何体是三棱锥B.以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥C。
2019届高考数学一轮复习 第7单元 立体几何作业 理
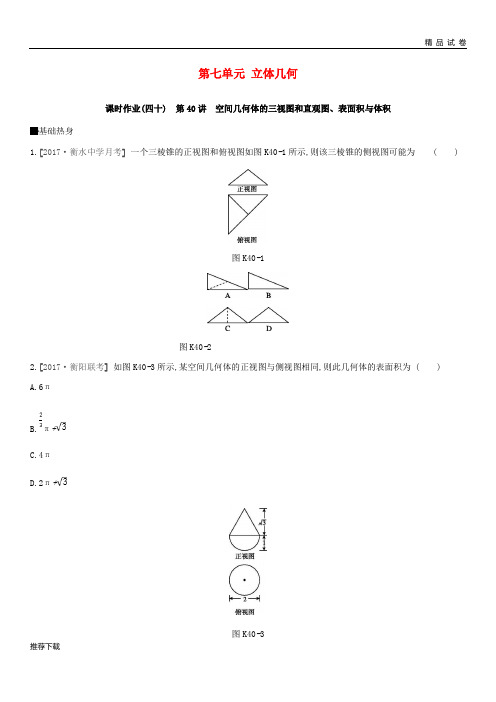
第七单元立体几何课时作业(四十)第40讲空间几何体的三视图和直观图、表面积与体积基础热身1.[2017·衡水中学月考]一个三棱锥的正视图和俯视图如图K40-1所示,则该三棱锥的侧视图可能为()图K40-1图K40-22.[2017·衡阳联考]如图K40-3所示,某空间几何体的正视图与侧视图相同,则此几何体的表面积为 ()A.6πB.π+C.4πD.2π+图K40-33.三棱锥P-ABC及其三视图中的正视图和侧视图如图K40-4所示,则PB=()图K40-4A.2B.4C.D.164.[2017·潮州四校联考]已知某多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图K40-5所示,且图中的四边形是边长为2的正方形,则该球的表面积是.图K40-55.[2017·厦门二模]某几何体的三视图如图K40-6所示,则该几何体的体积是.图K40-6能力提升6.如图K40-7,在正方体ABCD-A1B1C1D1中,P为BD1的中点,则△PAC在该正方体各个面上的射影可能是()图K40-7图K40-8A.①④B.②③C.②④D.①②7.如图K40-9,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()图K40-9A.B.C.D.8.图K40-10中,小方格是边长为1的正方形,图中粗实线画出的是某几何体的三视图,则该几何体的体积为()A.8-πB.8-πC.8-πD.8-π图K40-109.某几何体的三视图如图K40-11,其正视图中的曲线部分为半圆,则该几何体的体积是()A.4+πB.6+3πC.6+πD.12+π图K40-1110.[2017·泸州四诊]某几何体的正视图和侧视图如图K40-12(1)所示,它的俯视图的直观图是△A'B'C',如图K40-12(2)所示,其中O'A'=O'B'=2,O'C'=,则该几何体的表面积为 ()(1)(2)图K40-12A.36+12B.24+8C.24+12D.36+811.某几何体的三视图如图K40-13所示,则该几何体的表面积为.图K40-1312.[2017·蚌埠质检]已知边长为的正三角形ABC的三个顶点都在球O的表面上,且OA与平面ABC所成的角为60°,则球O的表面积为.13.[2017·淮北二模]我国古代数学经典名著《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的三棱锥称为鳖臑(biēnào).若三棱锥P-ABC为鳖臑,且PA⊥平面ABC,PA=AB=2,且该鳖臑的外接球的表面积为24π,则该鳖臑的体积为.14.(12分)如图K40-14所示,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,求该多面体的体积.图K40-1415.(13分)某几何体按比例绘制的三视图如图K40-15所示(单位:m).(1)试画出该几何体的直观图;(2)求该几何体的表面积和体积.图K40-15难点突破16.(5分)[2017·石家庄二模]如图K40-16是一个底面半径为1的圆柱被平面截开所得的几何体,截面与底面所成的角为45°,过圆柱的轴的平面截该几何体所得的四边形ABB'A'为矩形,若沿AA'将其侧面剪开,则其侧面展开图的形状大致为()图K40-16图K40-1717.(5分)祖暅是我国齐梁时代的数学家,他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图K40-18所示,将底面直径皆为2b,高皆为a的半椭球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面在距平面β任意高度d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.据此,短轴长为4 cm,长轴长为6 cm 的椭球体的体积是cm3.图K40-18加练一课(五) 空间几何体与球的切﹑接问题一、选择题(本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.某正四棱锥的顶点都在同一球面上,若该正四棱锥的高为4,底面边长为2,则该球的表面积为()A.B.16πC.9πD.2.一块石材表示的几何体的三视图如图L5-1所示,将石材切削、打磨、加工成球,则能得到的最大球的半径为()A.1B.2C.3D.4图L5-13.[2017·山西三区八校二模]在矩形ABCD中,AC=2,现将△ABC沿对角线AC折起,使点B到达点B'的位置,得到三棱锥B'-ACD,则三棱锥B'-ACD的外接球的表面积是()A.πB.2πC.4πD.与点B'的位置有关图L5-24.若一个底面是正三角形的三棱柱的正视图如图L5-3所示,其顶点都在一个球面上,则该球的表面积为()A.πB.πC.πD.π图L5-35.四面体A-BCD的四个顶点都在球O的球面上,AB⊥平面BCD,△BCD是边长为3的等边三角形.若AB=2,则球O的表面积为()A. 12πB.16πC.D.32π6.[2017·马鞍山质检]某几何体的三视图如图L5-4所示,则该几何体的外接球的表面积为()图L5-4A.25πB.26πC.32πD.36π7.空间四边形ABCD的四个顶点都在同一球面上,E,F分别是AB,CD的中点,且EF⊥AB,EF⊥CD,若AB=8,CD=EF=4,则该球的半径为()A.B.C.D.8.[2017·黄冈质检]某一简单几何体的三视图如图L5-5所示,则该几何体的外接球的表面积是 ()图L5-5A.13πB.16πC.25πD.27π9.[2017·湛江二模]底面是边长为1的正方形,侧面是等边三角形的四棱锥的外接球的体积为()A.B.C.D.二、填空题(本大题共7小题,每小题5分,共35分.把答案填在题中横线上)10.若正方体的外接球的表面积为6π,则该正方体的表面积为.11.设正三棱锥A-BCD的所有顶点都在球O的球面上, E, F分别是AB, BC的中点, EF⊥DE,且EF=1,则球O的表面积为.12.[2017·洛阳三模]已知直三棱柱ABC-A1B1C1中,AB=3,AC=4,AB⊥AC,AA1=2,则该三棱柱内切球的表面积与外接球的表面积的和为.13.[2017·唐山三模]直角三角形ABC的三个顶点都在球O的球面上, AB=AC=2,若球O的表面积为12π,则球心O 到平面ABC的距离等于.14.球O内切于棱长为的正方体ABCD-A1B1C1D1,以A为顶点,以平面B1CD1被球O所截的圆面为底面的圆锥的侧面积为.15.[2017·宁德二检]已知菱形ABCD的边长为6,∠A=60°.沿对角线BD将该菱形折成锐二面角A-BD-C,连接AC.若三棱锥A-BCD的体积为,则该三棱锥的外接球的表面积为.16.[2017·山西大学附中二模]正三棱锥的高为1,底面边长为2,正三棱锥内有一个球与其四个面都相切,则该球的表面积是,体积是.课时作业(四十一)第41讲空间点、直线、平面之间的位置关系基础热身1.[2017·闽南八校二联]已知直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”是“平面α和平面β相交”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.[2017·郑州一模]已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b,c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面3.下面四个说法中正确的个数为()(1)如果两个平面有四个公共点,那么这两个平面重合;(2)两条直线可以确定一个平面;(3)若M∈α,M∈β,α∩β=l,则M∈l;(4)在空间中,相交于同一点的三条直线在同一平面内.A.1B.2C.3D.44.[2017·佛山模拟]如图K41-1所示,在正三棱柱ABC-A1B1C1中,D是AC的中点,AA1∶AB=∶1,则异面直线AB1与BD所成的角为.图K41-15.如图K41-2是某个正方体的展开图,l1,l2是两条侧面对角线,则在正方体中,下面关于l1与l2的四个结论中正确的是.(填序号)①互相平行;②异面垂直;③异面且夹角为;④相交且夹角为.图K41-2能力提升6.l1,l2表示空间中的两条直线,若p:l1,l2是异面直线;q:l1,l2不相交,则()A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件7.已知正方体ABCD-A1B1C1D1中,O是BD1的中点,直线A1C交平面AB1D1于点M,则下列结论错误的是()A.A1,M,O三点共线B.M,O,A1,A四点共面C.A1,O,C,M四点共面D.B,B1,O,M四点共面8.[2017·济南模拟]设a,b,c是两两不同的三条直线,下面四个说法中正确的是()A.若直线a,b异面,b,c异面,则a,c异面B.若直线a,b相交,b,c相交,则a,c相交C.若a∥b,则a,b与c所成的角相等D.若a⊥b,b⊥c,则a∥c9.已知m,n为异面直线,m⊥平面α,n⊥平面β,若直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l10.异面直线l与m成60°角,异面直线l与n成45°角,则异面直线m与n所成角的取值范围是()A.[15°,90°]B.[60°,90°]C.[15°,90°)D.[15°,60°]11.正四棱锥P-ABCD中,四条侧棱长均为2,底面ABCD是正方形,E为PC的中点,若异面直线PA与BE所成的角为45°,则该四棱锥的体积是 ()A.4B.2C. D.12.已知集合A={直线},B={平面},C=A∪B.若a∈A,b∈B,c∈C,给出下列四个说法:①若a∥b,c∥b,则a∥c;②若a⊥b,c⊥b,则a∥c;③若a∥b,c⊥b,则a⊥c;④若a⊥b,c∥b,则a⊥c.其中正确说法的序号是.13.如图K41-3所示是正方体和正四面体,P,Q,R,S分别是其所在棱的中点,则四个点共面的图形是.图K41-314.(12分)如图K41-4,平面ABEF⊥平面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC AD,BE FA,G,H分别为FA,FD的中点.(1)求证:四边形BCHG是平行四边形.(2)C,D,F,E四点是否共面?为什么?图K41-415.(13分)[2017·成都七中月考]如图K41-5所示,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点.已知∠BAC=,AB=2,AC=2,PA=2.(1)求三棱锥P-ABC的体积;(2)求异面直线BC与AD所成角的余弦值.图K41-5难点突破16.(5分)[2017·包头十校联考]在正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,则异面直线CP与BA1所成的角θ的取值范围是()图K41-6A.0<θ<B.0<θ≤C.0≤θ≤D.0<θ≤17.(5分)在直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为.课时作业(四十二)第42讲直线、平面平行的判定与性质基础热身1.[2017·江西六校联考]设α,β是两个不同的平面,m是直线,且m⊂α,则“m∥β”是“α∥β”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件2.[2017·潮州三校联考]在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则()A.BD∥平面EFG,且四边形EFGH是平行四边形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是平行四边形D.EH∥平面ADC,且四边形EFGH是梯形3.[2017·保定模拟]有下列四个说法:①若直线l平行于平面α内的无数条直线,则直线l∥α;②若直线a在平面α外,则a∥α;③若直线a∥b,b∥α,则a∥α;④若直线a∥b,b∥α,则a平行于平面α内的无数条直线.其中正确说法的个数是()A.1B.2C.3D.44.如图K42-1是正方体的平面展开图,关于这个正方体有以下判断:图K42-1①ED与NF所成的角为60°;②CN∥平面AFB;③BM∥DE;④平面BDE∥平面NCF.其中正确判断的序号是()A.①③B.②③C.①②④D.②③④5.如图K42-2,四棱锥P-ABCD的底面是直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为.图K42-2能力提升6.若平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是()A.AB∥CDB.AD∥CBC.AB与CD相交D.A,B,C,D四点共面7.已知直线a与平面α,β,若α∥β,a⊂α,点B∈β,则在β内过点B的所有直线中()A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一一条与a平行的直线8.[2017·长郡中学质检]在如图K42-3所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于DE,则DE与AB 的位置关系是()A.异面B.平行C.相交D.以上均有可能图K42-39.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列说法中正确的是()A.若m∥α,n∥α,则m∥nB.若α⊥γ,β⊥γ,则α∥βC.若m∥α,m∥β,则α∥βD.若m⊥α,n⊥α,则m∥n10.[2017·浙江金丽衢十二校联考]已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于点A,C,过点P的直线n与α,β分别交于点B,D,且PA=6,AC=9,PD=8,则BD=()A.16B.24或C.14D.2011.如图K42-4是某长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为.图K42-412.已知a,b为两条不同的直线,α,β,γ为三个不同的平面,给出以下三个说法:①若a∥b,b⊂α,则a∥α;②若a∥b,a∥α,则b∥α;③若α∩β=a,b⊂γ,且b∥β,a⊂γ,则a∥b.其中正确说法的序号是.13.在正四棱柱ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,则点Q满足条件时,有平面D1BQ∥平面PAO.14.(10分)[2017·宜春二模]在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC 的中点,又PA=AB=4,∠CDA=120°,点N在PB上,且PN=.求证:MN∥平面PDC.图K42-515.(13分)[2017·石家庄二模]如图K42-6,在三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=,BC=.点F在平面ABED内的正投影为G,且G在AE上,FG=,点M在CF上,且CM=CF.(1)证明:直线GM∥平面DEF;(2)求三棱锥M-DEF的体积.图K42-6难点突破16.(12分)[2018·南昌模拟]如图K42-7所示,在四棱锥P-ABCD中, ∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA ⊥平面ABCD,PA=2,AB=1.设M,N分别为PD,AD的中点.(1)求证:平面CMN∥平面PAB;(2)求三棱锥P-ABM的体积.图K42-7课时作业(四十三)第43讲直线、平面垂直的判定与性质基础热身1.[2017·湖南六校联考]已知m和n是两条不同的直线,α和β是两个不重合的平面,下面给出的条件中一定能推出m⊥β的是()A.α⊥β且m⊂αB.α⊥β且m∥αC.m∥n且n⊥βD.m⊥n且α∥β2.[2017·唐山三模]已知平面α⊥平面β,则“直线m⊥平面α”是“直线m∥平面β”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.[2017·深圳四校联考]若平面α,β满足α⊥β,α∩β=l,P∈α,P∉l,则下列说法中不正确的是()A.过点P垂直于平面α的直线平行于平面βB.过点P垂直于直线l的直线在平面α内C.过点P垂直于平面β的直线在平面α内D.过点P且在平面α内垂直于l的直线必垂直于平面β4.[2017·龙岩二模]已知三个不同的平面α,β,γ满足α⊥γ,β⊥γ,则α与β的关系是.5.在三棱锥P-ABC中,点P在平面ABC内的射影为点O,若PA⊥PB,PB⊥PC,PC⊥PA,则点O是△ABC的心.能力提升6.[2017·南昌二模]已知直线m,n与平面α,β,γ满足α⊥β,α∩β=m,n⊥α,n⊂γ,则下列判断一定正确的是()A.m∥γ,α⊥γB.n∥β,α⊥γC.β∥γ,α⊥γD.m⊥n,α⊥γ7.将图K43-1①中的等腰直角三角形ABC沿斜边BC的中线AD折起,得到空间四面体ABCD(如图②),则在空间四面体ABCD中,AD与BC的位置关系是 ()图K43-1A.相交且垂直B.相交但不垂直C.异面且垂直D.异面但不垂直8.[2017·临汾三模]已知α为平面,a,b为两条不同的直线,则下列说法中正确的是()A.若直线a,b与平面α所成角都是30°,则直线a,b平行B.若直线a,b与平面α所成角都是30°,则直线a,b不可能垂直C.若直线a,b平行,则直线a,b中至少有一条与平面α平行D.若直线a,b垂直,则直线a,b与平面α不可能都垂直9.如图K43-2所示,在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点,则下列说法错误的是()A.当AE⊥PB时,△AEF一定为直角三角形B.当AF⊥PC时,△AEF一定为直角三角形C.当EF∥平面ABC时,△AEF一定为直角三角形D.当PC⊥平面AEF时,△AEF一定为直角三角形图K43-210.[2017·肇庆三模]在棱长为1的正方体ABCD-A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的动点,给出下列说法:①OE⊥BD1;②OE∥平面A1C1D;③三棱锥A1-BDE的体积为定值;④OE与A1C1所成的最大角为90°.其中说法正确的个数是()A.1B.2C.3D.411.[2017·邯郸二模]如图K43-3,在矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折到△A1DE(A1∉平面ABCD)的位置.若M,O分别为线段A1C,DE的中点,则在△ADE的翻折过程中,下列说法错误的是()A.与平面A1DE垂直的直线必与直线BM垂直B.过E作EG∥BM,G∈平面A1DC,则∠A1EG为定值C.一定存在某个位置,使DE⊥MOD.三棱锥A1-ADE外接球半径与棱AD的长之比为定值图K43-312.已知a,b,l表示三条不同的直线,α,β,γ表示三个不同的平面,有下列四个说法:①若α∩β=a,β∩γ=b,且a∥b,则α∥γ;②若a,b相交,且都在α,β外,a∥α,a∥β,b∥α,b∥β,则α∥β;③若α⊥β,α∩β=a,b⊂β,a⊥b,则b⊥α;④若a⊂α,b⊂α,l⊥a,l⊥b,l⊄α,则l⊥α.其中正确说法的序号是.13.[2017·厦门二模]正方体ABCD-A1B1C1D1的棱和六个面的对角线共有24条,其中与体对角线AC1垂直的有条.14.(10分)[2017·徐州、宿迁、连云港、淮安四市三模]如图K43-4,在四棱锥P-ABCD中,底面ABCD是矩形,点E 在棱PC上(异于点P,C),平面ABE与棱PD交于点F.(1)求证:AB∥EF;(2)若平面PAD⊥平面ABCD,求证:AF⊥EF.图K43-415.(13分)如图K43-5,在正三棱柱A1B1C1-ABC中,点D,E分别是A1C,AB的中点.(1)求证:ED∥平面BB1C1C;(2)若AB=BB1,求证:A1B⊥平面B1CE.图K43-5难点突破16.(12分)[2018·昆明检测]如图K43-6,在三棱柱ABC-A1B1C1中,侧棱CC1⊥底面ABC,M为BC的中点,AC=AB=3,BC=2,CC1=.(1)证明:B1C⊥平面AMC1;(2)求点A1到平面AMC1的距离.图K43-6课时作业(四十四)第44讲空间向量及其运算和空间位置关系基础热身1.[2017·上饶期中]如图K44-1所示,三棱锥O-ABC中,M,N分别是AB,OC的中点,设=a,=b,=c,用a,b,c 表示,则=()图K44-1A.(-a+b+c)B.(a+b-c)C.(a-b+c)D.(-a-b+c)2.[2017·唐山统考]已知正方体ABCD-A1B1C1D1的棱长为a,点M在AC1上,且=,N为B1B的中点,则||为()A.aB.aC.aD.a3.[2018·黑龙江齐齐哈尔实验中学期中]设ABCD-A1B1C1D1是棱长为a的正方体,则有()A.·=a2B.·=a2C.·=a2D.·=a24.已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三个向量共面,则实数λ= .5.在空间直角坐标系中,以点A(4,1,9),B(10,-1,6),C(x,4,3)为顶点的△ABC是以BC为斜边的等腰直角三角形,则实数x的值为.能力提升6.[2017·台州统考]已知向量a=(2m+1,3,m-1),b=(2,m,-m),且a∥b,则实数m的值等于()A.B.-2C.0D.或-27.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则·的值为()A.a2B.a2C.a2D.a28.如图K44-2所示,在平行六面体ABCD-A1B1C1D1中,AM=MC,A1N=2ND.设=a,=b,=c,=xa+yb+zc,则x+y+z=()A. B.C. D.图K44-29.如图K44-3所示,已知PA⊥平面ABC,∠ABC=120°,PA=AB=BC=6,则||等于()A.6B.6C.12D.144图K44-310.已知空间向量a,b满足|a|=|b|=1,且a,b的夹角为,O为空间直角坐标系的原点,点A,B满足=2a+b,=3a-b,则△OAB的面积为()A.B.C.D.11.[2017·泉州四校联考]O为空间中任意一点,A,B,C三点不共线,且=++t,若P,A,B,C四点共面,则实数t= .12.设A1,A2,A3,A4,A5是空间中给定的5个不同的点,则使=0成立的点M的个数为.13.[2017·北京西城区模拟]如图K44-4所示,正方体ABCD-A1B1C1D1的棱长为1,若动点P在线段BD1上运动,则·的取值范围是.图K44-414.(10分)如图K44-5所示,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB,BC上的动点,且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz.(1)写出点E,F的坐标;(2)求证:A1F⊥C1E;(3)若A1,E,F,C1四点共面,求证:=+.图K44-515.(13分)如图K44-6所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G分别是AB,AD,CD的中点.计算:(1)·;(2)EG的长;(3)异面直线AG与CE所成角的余弦值.图K44-6难点突破16.(12分)如图K44-7所示,正三角形ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC的中点,现将△ABC沿CD翻折成直二面角A-DC-B.(1)试判断直线AB与平面DEF的位置关系,并说明理由.(2)在线段BC上是否存在一点P,使AP⊥DE?如果存在,求出的值;如果不存在,请说明理由.图K44-7课时作业(四十五)第45讲第1课时空间角的求法基础热身1.如图K45-1所示,已知正方体ABCD-A1B1C1D1,E,F分别是A1C1和AD1的中点,则EF和CD所成的角是 ()A.30°B.45°C.60°D.90°图K45-12.[2018·河北枣强中学月考]已知向量m,n分别是直线l的方向向量和平面α的法向量,若cos<m,n>=-,则l与α所成的角为()A.30°B.60°C.120°D.150°3.[2017·郑州模拟]过正方形ABCD的顶点A作线段PA⊥平面ABCD,若AB=PA,则平面ABP与平面CDP所成的锐二面角为()A.30°B.45°C.60°D.90°4.已知直三棱柱ABC-A1B1C1,∠ACB=90°,CA=CB=CC1,D为B1C1的中点,则异面直线BD和A1C所成角的余弦值为.5.在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为.能力提升6.[2017·东营质检]已知A(1,0,0),B(0,-1,1),O为坐标原点,+λ与的夹角为120°,则λ的值为()A.±B.C.-D.±7.如图K45-2所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是()A.30°B.45°C.60°D.90°图K45-28.[2017·邯郸一模]如图K45-3,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AA1=2,AC=,过BC的中点D作平面ACB1的垂线,交平面ACC1A1于点E,则BE与平面ABB1A1所成角的正切值为()A.B.C.D.图K45-39.[2017·浙江五校联考]如图K45-4所示,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O 为AB的中点,OD⊥PC,若PD与平面PAB所成的角为30°,则二面角D-PC-B的余弦值是()图K45-4A.B.-C. D.-10.[2017·珠海模拟]在正方体ABCD-A1B1C1D1中,O是BD的中点,点P在线段B1D1上,直线OP与平面A1BD所成的角为α,则sin α的取值范围是()A.,B.,C.,D.,11.[2017·衡阳二联]如图K45-5所示,在正方体ABCD-A1B1C1D1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)= .图K45-512.如图K45-6所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.设二面角D-AE-C为60°,AP=1,AD=,则三棱锥E-ACD的体积为.图K45-613.如图K45-7,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC 的中点.设异面直线EM与AF所成的角为θ,则cos θ的最大值为.图K45-714.(10分)[2017·南通一模]如图K45-8所示,在棱长为2的正方体ABCD-A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).(1)若λ=,求AP与AQ所成角的余弦值;(2)若直线AA1与平面APQ所成的角为45°,求实数λ的值.图K45-815.(13分)[2017·泉州质检]如图K45-9所示,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.(1)求证:AC⊥BE;(2)若二面角E-BA-D的余弦值为,求三棱锥A-BCD的体积.图K45-9难点突破16.(12分)[2017·河南六市二联]如图K45-10所示,AB是半圆O的直径,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB=.(1)证明:平面ADE⊥平面ACD;(2)当三棱锥C-ADE的体积最大时,求二面角D-AE-B的余弦值的绝对值.图K45-10课时作业(四十五)第45讲第2课时空间向量的应用基础热身1.(12分)[2017·郴州三模]如图K45-11所示,C是以AB为直径的圆上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.(1)求证:直线l⊥平面PAC.(2)直线l上是否存在点Q,使直线PQ分别与平面AEF,直线EF所成的角互余?若存在,求出AQ的值;若不存在,请说明理由.图K45-112.(12分)[2017·北京丰台区一模]如图K45-12①所示,平面五边形ABCDE中,AB∥CD,∠BAD=90°,AB=2,CD=1,△ADE 是边长为2的正三角形.现将△ADE沿AD折起,得到四棱锥E-ABCD(如图②),且DE⊥AB.(1)求证:平面ADE⊥平面ABCD.(2)求平面BCE和平面ADE所成锐二面角的大小.(3)在棱AE上是否存在点F,使得DF∥平面BCE?若存在,求的值;若不存在,请说明理由.图K45-12能力提升3.(12分)[2017·濮阳一模]如图K45-13所示,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2,DA=.(1)线段BC上是否存在一点E,使平面PBC⊥平面PDE?若存在,请求出的值,并进行证明;若不存在,请说明理由.(2)若PD=,线段PC上有一点F,且PC=3PF,求直线AF与平面PBC所成角的正弦值.图K45-134.(12分)[2017·天津河西区一模]如图K45-14所示,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD 满足AB⊥AD,BC∥AD,BC=4,点M为PC的中点,点E为BC边上的动点,且=λ.(1)求证:DM∥平面PAB.(2)求证:平面ADM⊥平面PBC.(3)是否存在实数λ,使得二面角P-DE-B的余弦值为?若存在,试求出实数λ的值;若不存在,说明理由.图K45-145.(12分)[2017·玉溪民族中学模拟]直三棱柱ABC-A1B1C1中, AA1=AB=AC=1, E,F分别是CC1,BC的中点, 且AE⊥A1B1,(1)证明: AB⊥平面A1ACC1.(2)棱A1B1上是否存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为?若存在,说明点D的位置;若不存在,说明理由.图K45-15难点突破6.(12分)[2017·北京昌平区二模]如图K45-16所示,三棱柱ABC-A1B1C1中,BC垂直于正方形A1ACC1所在平面,AC=2,BC=1,D为AC中点,E为线段BC1上的一点(端点除外),平面AB1E与BD交于点F.(1)若E不是BC1的中点,求证:AB1∥EF.(2)若E是BC1的中点,求AE与平面BC1D所成角的正弦值.(3)在线段BC1上是否存在点E,使得A1E⊥CE?若存在,求出的值;若不存在,请说明理由.图K45-16课时作业(四十)1.D[解析] 由题图可知,该几何体为如图所示的三棱锥,其中平面ACD⊥平面BCD,该三棱锥的侧视图可能为等腰三角形,故选D.2.C[解析] 此几何体为一个组合体,上面部分为一个圆锥,下面部分为一个半球.故此几何体的表面积为S=×12+×2×2π×1=4π,故选C.3.B[解析] 由正视图和侧视图可知,AC=4,PC=4,AB=BC==4,则PB===4,故选B.4.12π[解析] 由三视图知,该组合体为正方体内接于球,正方体的棱长为2,设球的半径为R,则2R=2,即R=,则该球的表面积S=4πR2=4π×3=12π.5.[解析] 由三视图可知该几何体是三棱柱割去一个三棱锥后剩下的部分(如图),则该几何体的体积为×2×2×2-××1×1×2=4-=.6.A[解析] 由所给的正方体的直观图知,△PAC在该正方体上、下底面上的射影是①中图形,△PAC在该正方体前、后、左、右侧面上的射影是④中图形,故选A.7.C[解析] 由题意知,该几何体是由一个半圆柱与一个半球组成的组合体,其中半圆柱的底面半径为1,高为4,半球的半径为1,则该几何体的体积为×π×13+π×12×4=π,故选C.8.D[解析] 由三视图得,该几何体是正方体挖去一个半圆锥后剩余的部分,故该几何体的体积V=23-×π×12×2=8-,故选D.9.C[解析] 由三视图可知,该几何体是由半圆柱与三棱柱组成的,则该几何体的体积V=π×12×3+×2×2×3=6+π.10.C[解析] 由俯视图的直观图可得该几何体的底面是边长为4的等边三角形,由正视图与侧视图可得该几何体是高为6的三棱锥(如图所示的三棱锥P-ABC),其中PC⊥底面ABC,∴该几何体的表面积S=×42+2××4×6+×4×=24+12,故选C.11.11+2[解析] 由三视图知,该几何体是一个直四棱柱,上、下底面为直角梯形,直角梯形斜腰长为=,则底面周长为4+,故侧面积为2×(4+)=8+2,又两底面的面积和为2××1×(1+2)=3,所以该几何体的表面积为8+2+3=11+2.12.16π[解析] 边长为的正三角形ABC的外接圆的半径r=1,则球O的半径R==2,则球O的表面积S=4πR2=16π.13.[解析] 根据题意,三棱锥P-ABC为鳖臑,且PA⊥平面ABC,PA=AB=2,如图所示,可得∠PAB=∠PAC=∠ABC=∠PBC=90°.易知PC为外接球的直径,设外接球的半径为R.又该鳖臑的外接球的表面积为24π,则R2==6,则BC==4,则该鳖臑的体积为××2×4×2=.14.解:分别过A,B作EF的垂线,垂足分别为G,H,连接DG,CH,则原几何体被分割为两个三棱锥和一个直三棱柱.易知三棱锥的高为,直三棱柱的高为1,AG==,取AD的中点M,连接MG,则MG=,∴S△AGD=×1×=,∴V多面体ABCDEF=×1+2×××=.15.解:(1)直观图如图所示.(2)由三视图可知该几何体是长方体被截去一个三棱柱后剩余的部分,且该几何体的体积是以A1A,A1D1,A1B1为棱的长方体的体积的,∴该几何体的体积V=×1×2×1=(m3).在直角梯形AA1B1B中,作BE⊥A1B1于E,则四边形AA1EB是正方形,AA1=BE=1.在Rt△BEB1中,BE=1,EB1=1,∴BB1=,∴该几何体的表面积S=S正方形ABCD++2++=1+2×1+2××(1+2)×1+1×+1=7+(m2),∴该几何体的表面积为(7+)m2,体积为 m3.16.A[解析] 用排除法.首先截线不可能是直线,排除B中图形;又圆柱被平面截开所得的截面是椭圆,而侧面展开图为平面图,不可能是圆或椭圆,排除C,D中的图形.故选A.17.16π[解析] 因为总有S圆=S环,所以半椭球体的体积为V圆柱-V圆锥=πb2a-πb2a=πb2a.又2a=6,2b=4,即a=3,b=2,所以椭球体的体积V=πb2a=π×22×3=16π.加练一课(五)1.A[解析] 由题意易知,球心在正四棱锥的高上,设球的半径为R,则(4-R)2+()2=R2,解得R=,所以该球的表面积为4π×=π,故选A.2.B[解析] 由三视图可得该几何体为三棱柱,能得到的最大球为三棱柱的内切球,球的半径为正视图中直角三角形内切圆的半径r.由切线长的性质,得(8-r)+(6-r)=,得r=2,故选B.3.C[解析] 三棱锥B'-ACD中,△AB'C和△ACD是有公共斜边AC的直角三角形,取AC的中点O,则有OB'=OA=OC=OD,∴O为三棱锥B'-ACD的外接球的球心,外接球半径R=OA=1,则三棱锥B'-ACD的外接球的表面积是4πR2=4π,故选C.。
2019届高考数学一轮复习第7单元立体几何作业理

第七单元立体几何课时作业(四十)第40讲空间几何体的三视图和直观图、表面积与体积基础热身1.[2017·衡水中学月考]一个三棱锥的正视图和俯视图如图K40-1所示,则该三棱锥的侧视图可能为()图K40-1图K40-22.[2017·衡阳联考]如图K40-3所示,某空间几何体的正视图与侧视图相同,则此几何体的表面积为()A.6πB.π+C.4πD.2π+图K40-33.三棱锥P-ABC及其三视图中的正视图和侧视图如图K40-4所示,则PB=()图K40-4A.2B.4C.D.164.[2017·潮州四校联考]已知某多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图K40-5所示,且图中的四边形是边长为2的正方形,则该球的表面积是.图K40-55.[2017·厦门二模]某几何体的三视图如图K40-6所示,则该几何体的体积是.图K40-6能力提升6.如图K40-7,在正方体ABCD-A1B1C1D1中,P为BD1的中点,则△PAC在该正方体各个面上的射影可能是()图K40-7图K40-8A.①④B.②③C.②④D.①②7.如图K40-9,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()图K40-9A.B.C.D.8.图K40-10中,小方格是边长为1的正方形,图中粗实线画出的是某几何体的三视图,则该几何体的体积为()A.8-πB.8-πC.8-πD.8-π图K40-109.某几何体的三视图如图K40-11,其正视图中的曲线部分为半圆,则该几何体的体积是()A.4+πB.6+3πC.6+πD.12+π图K40-1110.[2017·泸州四诊]某几何体的正视图和侧视图如图K40-12(1)所示,它的俯视图的直观图是△A'B'C',如图K40-12(2)所示,其中O'A'=O'B'=2,O'C'=,则该几何体的表面积为()(1)(2)图K40-12A.36+12B.24+8C.24+12D.36+811.某几何体的三视图如图K40-13所示,则该几何体的表面积为.图K40-1312.[2017·蚌埠质检]已知边长为的正三角形ABC的三个顶点都在球O的表面上,且OA 与平面ABC所成的角为60°,则球O的表面积为.13.[2017·淮北二模]我国古代数学经典名著《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的三棱锥称为鳖臑(biēnào).若三棱锥P-ABC为鳖臑,且PA⊥平面ABC,PA=AB=2,且该鳖臑的外接球的表面积为24π,则该鳖臑的体积为.14.(12分)如图K40-14所示,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,求该多面体的体积.图K40-1415.(13分)某几何体按比例绘制的三视图如图K40-15所示(单位:m).(1)试画出该几何体的直观图;(2)求该几何体的表面积和体积.图K40-15难点突破16.(5分)[2017·石家庄二模]如图K40-16是一个底面半径为1的圆柱被平面截开所得的几何体,截面与底面所成的角为45°,过圆柱的轴的平面截该几何体所得的四边形ABB'A'为矩形,若沿AA'将其侧面剪开,则其侧面展开图的形状大致为()图K40-16图K40-1717.(5分)祖暅是我国齐梁时代的数学家,他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图K40-18所示,将底面直径皆为2b,高皆为a的半椭球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面在距平面β任意高度d处可横截得到S圆及S环两截面,可以证明S圆=S环总成立.据此,短轴长为4 cm,长轴长为6 cm的椭球体的体积是cm3.图K40-18加练一课(五) 空间几何体与球的切﹑接问题一、选择题(本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.某正四棱锥的顶点都在同一球面上,若该正四棱锥的高为4,底面边长为2,则该球的表面积为()A.B.16πC.9πD.2.一块石材表示的几何体的三视图如图L5-1所示,将石材切削、打磨、加工成球,则能得到的最大球的半径为()A.1B.2C.3D.4图L5-13.[2017·山西三区八校二模]在矩形ABCD中,AC=2,现将△ABC沿对角线AC折起,使点B到达点B'的位置,得到三棱锥B'-ACD,则三棱锥B'-ACD的外接球的表面积是()A.πB.2πC.4πD.与点B'的位置有关图L5-24.若一个底面是正三角形的三棱柱的正视图如图L5-3所示,其顶点都在一个球面上,则该球的表面积为()A.πB.πC.πD.π图L5-35.四面体A-BCD的四个顶点都在球O的球面上,AB⊥平面BCD,△BCD是边长为3的等边三角形.若AB=2,则球O的表面积为()A.12πB.16πC.D.32π6.[2017·马鞍山质检]某几何体的三视图如图L5-4所示,则该几何体的外接球的表面积为()图L5-4A.25πB.26πC.32πD.36π7.空间四边形ABCD的四个顶点都在同一球面上,E,F分别是AB,CD的中点,且EF⊥AB,EF⊥CD,若AB=8,CD=EF=4,则该球的半径为()A.B.C.D.8.[2017·黄冈质检]某一简单几何体的三视图如图L5-5所示,则该几何体的外接球的表面积是()图L5-5A.13πB.16πC.25πD.27π9.[2017·湛江二模]底面是边长为1的正方形,侧面是等边三角形的四棱锥的外接球的体积为()A.B.C.D.二、填空题(本大题共7小题,每小题5分,共35分.把答案填在题中横线上)10.若正方体的外接球的表面积为6π,则该正方体的表面积为.11.设正三棱锥A-BCD的所有顶点都在球O的球面上, E, F分别是AB, BC的中点, EF⊥DE,且EF=1,则球O的表面积为.12.[2017·洛阳三模]已知直三棱柱ABC-A1B1C1中,AB=3,AC=4,AB⊥AC,AA1=2,则该三棱柱内切球的表面积与外接球的表面积的和为.13.[2017·唐山三模]直角三角形ABC的三个顶点都在球O的球面上, AB=AC=2,若球O的表面积为12π,则球心O到平面ABC的距离等于.14.球O内切于棱长为的正方体ABCD-A1B1C1D1,以A为顶点,以平面B1CD1被球O所截的圆面为底面的圆锥的侧面积为.15.[2017·宁德二检]已知菱形ABCD的边长为6,∠A=60°.沿对角线BD将该菱形折成锐二面角A-BD-C,连接AC.若三棱锥A-BCD的体积为,则该三棱锥的外接球的表面积为.16.[2017·山西大学附中二模]正三棱锥的高为1,底面边长为2,正三棱锥内有一个球与其四个面都相切,则该球的表面积是,体积是.课时作业(四十一)第41讲空间点、直线、平面之间的位置关系基础热身1.[2017·闽南八校二联]已知直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”是“平面α和平面β相交”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.[2017·郑州一模]已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b,c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面3.下面四个说法中正确的个数为()(1)如果两个平面有四个公共点,那么这两个平面重合;(2)两条直线可以确定一个平面;(3)若M∈α,M∈β,α∩β=l,则M∈l;(4)在空间中,相交于同一点的三条直线在同一平面内.A.1B.2C.3D.44.[2017·佛山模拟]如图K41-1所示,在正三棱柱ABC-A1B1C1中,D是AC的中点,AA1∶AB=∶1,则异面直线AB1与BD所成的角为.图K41-15.如图K41-2是某个正方体的展开图,l1,l2是两条侧面对角线,则在正方体中,下面关于l1与l2的四个结论中正确的是.(填序号)①互相平行;②异面垂直;③异面且夹角为;④相交且夹角为.图K41-2能力提升6.l1,l2表示空间中的两条直线,若p:l1,l2是异面直线;q:l1,l2不相交,则()A.p是q的充分条件,但不是q的必要条件B.p是q的必要条件,但不是q的充分条件C.p是q的充分必要条件D.p既不是q的充分条件,也不是q的必要条件7.已知正方体ABCD-A1B1C1D1中,O是BD1的中点,直线A1C交平面AB1D1于点M,则下列结论错误的是 ()A.A1,M,O三点共线B.M,O,A1,A四点共面C.A1,O,C,M四点共面D.B,B1,O,M四点共面8.[2017·济南模拟]设a,b,c是两两不同的三条直线,下面四个说法中正确的是()A.若直线a,b异面,b,c异面,则a,c异面B.若直线a,b相交,b,c相交,则a,c相交C.若a∥b,则a,b与c所成的角相等D.若a⊥b,b⊥c,则a∥c9.已知m,n为异面直线,m⊥平面α,n⊥平面β,若直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l10.异面直线l与m成60°角,异面直线l与n成45°角,则异面直线m与n所成角的取值范围是()A.[15°,90°]B.[60°,90°]C.[15°,90°)D.[15°,60°]11.正四棱锥P-ABCD中,四条侧棱长均为2,底面ABCD是正方形,E为PC的中点,若异面直线PA与BE所成的角为45°,则该四棱锥的体积是()A.4B.2C.D.12.已知集合A={直线},B={平面},C=A∪B.若a∈A,b∈B,c∈C,给出下列四个说法:①若a∥b,c∥b,则a∥c;②若a⊥b,c⊥b,则a∥c;③若a∥b,c⊥b,则a⊥c;④若a⊥b,c∥b,则a⊥c.其中正确说法的序号是.13.如图K41-3所示是正方体和正四面体,P,Q,R,S分别是其所在棱的中点,则四个点共面的图形是.图K41-314.(12分)如图K41-4,平面ABEF⊥平面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC AD,BE FA,G,H分别为FA,FD的中点.(1)求证:四边形BCHG是平行四边形.(2)C,D,F,E四点是否共面?为什么?图K41-415.(13分)[2017·成都七中月考]如图K41-5所示,在三棱锥P-ABC中,PA⊥底面ABC,D 是PC的中点.已知∠BAC=,AB=2,AC=2,PA=2.(1)求三棱锥P-ABC的体积;(2)求异面直线BC与AD所成角的余弦值.图K41-5难点突破16.(5分)[2017·包头十校联考]在正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,则异面直线CP与BA1所成的角θ的取值范围是()图K41-6A.0<θ<B.0<θ≤C.0≤θ≤D.0<θ≤17.(5分)在直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为.课时作业(四十二)第42讲直线、平面平行的判定与性质基础热身1.[2017·江西六校联考]设α,β是两个不同的平面,m是直线,且m⊂α,则“m∥β”是“α∥β”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件2.[2017·潮州三校联考]在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则()A.BD∥平面EFG,且四边形EFGH是平行四边形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是平行四边形D.EH∥平面ADC,且四边形EFGH是梯形3.[2017·保定模拟]有下列四个说法:①若直线l平行于平面α内的无数条直线,则直线l∥α;②若直线a在平面α外,则a∥α;③若直线a∥b,b∥α,则a∥α;④若直线a∥b,b∥α,则a平行于平面α内的无数条直线.其中正确说法的个数是()A.1B.2C.3D.44.如图K42-1是正方体的平面展开图,关于这个正方体有以下判断:图K42-1①ED与NF所成的角为60°;②CN∥平面AFB;③BM∥DE;④平面BDE∥平面NCF.其中正确判断的序号是()A.①③B.②③C.①②④D.②③④5.如图K42-2,四棱锥P-ABCD的底面是直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E 为PC的中点,则BE与平面PAD的位置关系为.图K42-2能力提升6.若平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是()A.AB∥CDB.AD∥CBC.AB与CD相交D.A,B,C,D四点共面7.已知直线a与平面α,β,若α∥β,a⊂α,点B∈β,则在β内过点B的所有直线中()A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一一条与a平行的直线8.[2017·长郡中学质检]在如图K42-3所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于DE,则DE与AB的位置关系是()A.异面B.平行C.相交D.以上均有可能图K42-39.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列说法中正确的是()A.若m∥α,n∥α,则m∥nB.若α⊥γ,β⊥γ,则α∥βC.若m∥α,m∥β,则α∥βD.若m⊥α,n⊥α,则m∥n10.[2017·浙江金丽衢十二校联考]已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于点A,C,过点P的直线n与α,β分别交于点B,D,且PA=6,AC=9,PD=8,则BD=()A.16B.24或C.14D.2011.如图K42-4是某长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为.图K42-412.已知a,b为两条不同的直线,α,β,γ为三个不同的平面,给出以下三个说法:①若a∥b,b⊂α,则a∥α;②若a∥b,a∥α,则b∥α;③若α∩β=a,b⊂γ,且b∥β,a⊂γ,则a∥b.其中正确说法的序号是.13.在正四棱柱ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,则点Q满足条件时,有平面D1BQ∥平面PAO.14.(10分)[2017·宜春二模]在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC 与BD的交点M恰好是AC的中点,又PA=AB=4,∠CDA=120°,点N在PB上,且PN=.求证:MN∥平面PDC.图K42-515.(13分)[2017·石家庄二模]如图K42-6,在三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=,BC=.点F在平面ABED内的正投影为G,且G在AE上,FG=,点M在CF上,且CM=CF.(1)证明:直线GM∥平面DEF;(2)求三棱锥M-DEF的体积.图K42-6难点突破16.(12分)[2018·南昌模拟]如图K42-7所示,在四棱锥P-ABCD中, ∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.设M,N分别为PD,AD的中点.(1)求证:平面CMN∥平面PAB;(2)求三棱锥P-ABM的体积.图K42-7课时作业(四十三)第43讲直线、平面垂直的判定与性质基础热身1.[2017·湖南六校联考]已知m和n是两条不同的直线,α和β是两个不重合的平面,下面给出的条件中一定能推出m⊥β的是()A.α⊥β且m⊂αB.α⊥β且m∥αC.m∥n且n⊥βD.m⊥n且α∥β2.[2017·唐山三模]已知平面α⊥平面β,则“直线m⊥平面α”是“直线m∥平面β”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.[2017·深圳四校联考]若平面α,β满足α⊥β,α∩β=l,P∈α,P∉l,则下列说法中不正确的是()A.过点P垂直于平面α的直线平行于平面βB.过点P垂直于直线l的直线在平面α内C.过点P垂直于平面β的直线在平面α内D.过点P且在平面α内垂直于l的直线必垂直于平面β4.[2017·龙岩二模]已知三个不同的平面α,β,γ满足α⊥γ,β⊥γ,则α与β的关系是.5.在三棱锥P-ABC中,点P在平面ABC内的射影为点O,若PA⊥PB,PB⊥PC,PC⊥PA,则点O 是△ABC的心.能力提升6.[2017·南昌二模]已知直线m,n与平面α,β,γ满足α⊥β,α∩β=m,n⊥α,n⊂γ,则下列判断一定正确的是()A.m∥γ,α⊥γB.n∥β,α⊥γC.β∥γ,α⊥γD.m⊥n,α⊥γ7.将图K43-1①中的等腰直角三角形ABC沿斜边BC的中线AD折起,得到空间四面体ABCD(如图②),则在空间四面体ABCD中,AD与BC的位置关系是()图K43-1A.相交且垂直B.相交但不垂直C.异面且垂直D.异面但不垂直8.[2017·临汾三模]已知α为平面,a,b为两条不同的直线,则下列说法中正确的是()A.若直线a,b与平面α所成角都是30°,则直线a,b平行B.若直线a,b与平面α所成角都是30°,则直线a,b不可能垂直C.若直线a,b平行,则直线a,b中至少有一条与平面α平行D.若直线a,b垂直,则直线a,b与平面α不可能都垂直9.如图K43-2所示,在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点,则下列说法错误的是()A.当AE⊥PB时,△AEF一定为直角三角形B.当AF⊥PC时,△AEF一定为直角三角形C.当EF∥平面ABC时,△AEF一定为直角三角形D.当PC⊥平面AEF时,△AEF一定为直角三角形图K43-210.[2017·肇庆三模]在棱长为1的正方体ABCD-A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的动点,给出下列说法:①OE⊥BD1;②OE∥平面A1C1D;③三棱锥A1-BDE的体积为定值;④OE与A1C1所成的最大角为90°.其中说法正确的个数是()A.1B.2C.3D.411.[2017·邯郸二模]如图K43-3,在矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折到△A1DE(A1∉平面ABCD)的位置.若M,O分别为线段A1C,DE的中点,则在△ADE的翻折过程中,下列说法错误的是()A.与平面A1DE垂直的直线必与直线BM垂直B.过E作EG∥BM,G∈平面A1DC,则∠A1EG为定值C.一定存在某个位置,使DE⊥MOD.三棱锥A1-ADE外接球半径与棱AD的长之比为定值图K43-312.已知a,b,l表示三条不同的直线,α,β,γ表示三个不同的平面,有下列四个说法:①若α∩β=a,β∩γ=b,且a∥b,则α∥γ;②若a,b相交,且都在α,β外,a∥α,a∥β,b∥α,b∥β,则α∥β;③若α⊥β,α∩β=a,b⊂β,a⊥b,则b⊥α;④若a⊂α,b⊂α,l⊥a,l⊥b,l⊄α,则l⊥α.其中正确说法的序号是.13.[2017·厦门二模]正方体ABCD-A1B1C1D1的棱和六个面的对角线共有24条,其中与体对角线AC1垂直的有条.14.(10分)[2017·徐州、宿迁、连云港、淮安四市三模]如图K43-4,在四棱锥P-ABCD 中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.(1)求证:AB∥EF;(2)若平面PAD⊥平面ABCD,求证:AF⊥EF.图K43-415.(13分)如图K43-5,在正三棱柱A1B1C1-ABC中,点D,E分别是A1C,AB的中点.(1)求证:ED∥平面BB1C1C;(2)若AB=BB1,求证:A1B⊥平面B1CE.图K43-5难点突破16.(12分)[2018·昆明检测]如图K43-6,在三棱柱ABC-A1B1C1中,侧棱CC1⊥底面ABC,M为BC的中点, AC=AB=3,BC=2,CC1=.(1)证明:B1C⊥平面AMC1;(2)求点A1到平面AMC1的距离.图K43-6课时作业(四十四)第44讲空间向量及其运算和空间位置关系基础热身1.[2017·上饶期中]如图K44-1所示,三棱锥O-ABC中,M,N分别是AB,OC的中点,设=a,=b,=c,用a,b,c表示,则= ()图K44-1A.(-a+b+c)B.(a+b-c)C.(a-b+c)D.(-a-b+c)2.[2017·唐山统考]已知正方体ABCD-A 1B1C1D1的棱长为a,点M在AC1上,且=,N 为B1B的中点,则||为()A.aB.aC.aD.a3.[2018·黑龙江齐齐哈尔实验中学期中]设ABCD-A1B1C1D1是棱长为a的正方体,则有()A.·=a2B.·=a2C.·=a2D.·=a24.已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三个向量共面,则实数λ=.5.在空间直角坐标系中,以点A(4,1,9),B(10,-1,6),C(x,4,3)为顶点的△ABC是以BC为斜边的等腰直角三角形,则实数x的值为.能力提升6.[2017·台州统考]已知向量a=(2m+1,3,m-1),b=(2,m,-m),且a∥b,则实数m的值等于()A.B.-2C.0D.或-27.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则·的值为()A.a2B.a2C.a2D.a28.如图K44-2所示,在平行六面体ABCD-A1B1C1D1中,AM=MC,A1N=2ND.设=a,=b,=c,=xa+yb+zc,则x+y+z= ()A.B.C.D.图K44-29.如图K44-3所示,已知PA⊥平面ABC,∠ABC=120°,PA=AB=BC=6,则||等于()A.6B.6C.12D.144图K44-310.已知空间向量a,b满足|a|=|b|=1,且a,b的夹角为,O为空间直角坐标系的原点,点A,B 满足=2a+b,=3a-b,则△OAB的面积为()A.B.C.D.11.[2017·泉州四校联考]O为空间中任意一点,A,B,C三点不共线,且=++t,若P,A,B,C四点共面,则实数t= .12.设A1,A2,A3,A4,A5是空间中给定的5个不同的点,则使=0成立的点M的个数为.13.[2017·北京西城区模拟]如图K44-4所示,正方体ABCD-A1B1C1D1的棱长为1,若动点P 在线段BD1上运动,则·的取值范围是.图K44-414.(10分)如图K44-5所示,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB,BC上的动点,且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz.(1)写出点E,F的坐标;(2)求证:A1F⊥C1E;(3)若A1,E,F,C1四点共面,求证:=+.图K44-515.(13分)如图K44-6所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G 分别是AB,AD,CD的中点.计算:(1)·;(2)EG的长;(3)异面直线AG与CE所成角的余弦值.图K44-6难点突破16.(12分)如图K44-7所示,正三角形ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC的中点,现将△ABC沿CD翻折成直二面角A-DC-B.(1)试判断直线AB与平面DEF的位置关系,并说明理由.(2)在线段BC上是否存在一点P,使AP⊥DE?如果存在,求出的值;如果不存在,请说明理由.图K44-7课时作业(四十五)第45讲第1课时空间角的求法基础热身1.如图K45-1所示,已知正方体ABCD-A1B1C1D1,E,F分别是A1C1和AD1的中点,则EF和CD所成的角是()A.30°B.45°C.60°D.90°图K45-12.[2018·河北枣强中学月考]已知向量m,n分别是直线l的方向向量和平面α的法向量,若cos<m,n>=-,则l与α所成的角为()A.30°B.60°C.120°D.150°3.[2017·郑州模拟]过正方形ABCD的顶点A作线段PA⊥平面ABCD,若AB=PA,则平面ABP 与平面CDP所成的锐二面角为()A.30°B.45°C.60°D.90°4.已知直三棱柱ABC-A1B1C1,∠ACB=90°,CA=CB=CC1,D为B1C1的中点,则异面直线BD和A1C 所成角的余弦值为.5.在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为.能力提升6.[2017·东营质检]已知A(1,0,0),B(0,-1,1),O为坐标原点,+λ与的夹角为120°,则λ的值为()A.±B.C.-D.±7.如图K45-2所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E,F 分别是棱AB,BB1的中点,则直线EF和BC1所成的角是()A.30°B.45°C.60°D.90°图K45-28.[2017·邯郸一模]如图K45-3,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AA1=2,AC=,过BC的中点D作平面ACB1的垂线,交平面ACC1A1于点E,则BE与平面ABB1A1所成角的正切值为()A.B.C.D.图K45-39.[2017·浙江五校联考]如图K45-4所示,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC,若PD与平面PAB所成的角为30°,则二面角D-PC-B的余弦值是()图K45-4A.B.-C.D.-10.[2017·珠海模拟]在正方体ABCD-A1B1C1D1中,O是BD的中点,点P在线段B1D1上,直线OP与平面A1BD所成的角为α,则sin α的取值范围是()A.,B.,C.,D.,11.[2017·衡阳二联]如图K45-5所示,在正方体ABCD-A1B1C1D1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)= .图K45-512.如图K45-6所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.设二面角D-AE-C为60°,AP=1,AD=,则三棱锥E-ACD的体积为.图K45-613.如图K45-7,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ 上,E,F分别为AB,BC的中点.设异面直线EM与AF所成的角为θ,则cos θ的最大值为.图K45-714.(10分)[2017·南通一模]如图K45-8所示,在棱长为2的正方体ABCD-A1B1C1D1中,P 为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).(1)若λ=,求AP与AQ所成角的余弦值;(2)若直线AA1与平面APQ所成的角为45°,求实数λ的值.图K45-815.(13分)[2017·泉州质检]如图K45-9所示,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.(1)求证:AC⊥BE;(2)若二面角E-BA-D的余弦值为,求三棱锥A-BCD的体积.图K45-9难点突破16.(12分)[2017·河南六市二联]如图K45-10所示,AB是半圆O的直径,C是半圆O上除A,B 外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB=.(1)证明:平面ADE⊥平面ACD;(2)当三棱锥C-ADE的体积最大时,求二面角D-AE-B的余弦值的绝对值.图K45-10课时作业(四十五)第45讲第2课时空间向量的应用基础热身1.(12分)[2017·郴州三模]如图K45-11所示,C是以AB为直径的圆上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.(1)求证:直线l⊥平面PAC.(2)直线l上是否存在点Q,使直线PQ分别与平面AEF,直线EF所成的角互余?若存在,求出AQ的值;若不存在,请说明理由.图K45-112.(12分)[2017·北京丰台区一模]如图K45-12①所示,平面五边形ABCDE中,AB∥CD,∠BAD=90°,AB=2,CD=1,△ADE是边长为2的正三角形.现将△ADE沿AD折起,得到四棱锥E-ABCD(如图②),且DE⊥AB.(1)求证:平面ADE⊥平面ABCD.(2)求平面BCE和平面ADE所成锐二面角的大小.(3)在棱AE上是否存在点F,使得DF∥平面BCE?若存在,求的值;若不存在,请说明理由.图K45-12能力提升3.(12分)[2017·濮阳一模]如图K45-13所示,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2,DA=.(1)线段BC上是否存在一点E,使平面PBC⊥平面PDE?若存在,请求出的值,并进行证明;若不存在,请说明理由.(2)若PD=,线段PC上有一点F,且PC=3PF,求直线AF与平面PBC所成角的正弦值.图K45-134.(12分)[2017·天津河西区一模]如图K45-14所示,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD,BC=4,点M为PC的中点,点E为BC边上的动点,且=λ.(1)求证:DM∥平面PAB.(2)求证:平面ADM⊥平面PBC.(3)是否存在实数λ,使得二面角P-DE-B的余弦值为?若存在,试求出实数λ的值;若不存在,说明理由.图K45-145.(12分)[2017·玉溪民族中学模拟]直三棱柱ABC-A1B1C1中, AA1=AB=AC=1, E,F分别是CC1,BC的中点, 且AE⊥A1B1,(1)证明: AB⊥平面A1ACC1.(2)棱A1B1上是否存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为?若存在,说明点D的位置;若不存在,说明理由.图K45-15难点突破6.(12分)[2017·北京昌平区二模]如图K45-16所示,三棱柱ABC-A1B1C1中,BC垂直于正方形A1ACC1所在平面,AC=2,BC=1,D为AC中点,E为线段BC1上的一点(端点除外),平面AB1E 与BD交于点F.(1)若E不是BC1的中点,求证:AB1∥EF.(2)若E是BC1的中点,求AE与平面BC1D所成角的正弦值.(3)在线段BC1上是否存在点E,使得A1E⊥CE?若存在,求出的值;若不存在,请说明理由.图K45-16课时作业(四十)1.D[解析] 由题图可知,该几何体为如图所示的三棱锥,其中平面ACD⊥平面BCD,该三棱锥的侧视图可能为等腰三角形,故选D.2.C[解析] 此几何体为一个组合体,上面部分为一个圆锥,下面部分为一个半球.故此几何体的表面积为S=×12+×2×2π×1=4π,故选C.3.B[解析] 由正视图和侧视图可知,AC=4,PC=4,AB=BC==4,则PB===4,故选B.4.12π[解析] 由三视图知,该组合体为正方体内接于球,正方体的棱长为2,设球的半径为R,则2R=2,即R=,则该球的表面积S=4πR2=4π×3=12π.5.[解析] 由三视图可知该几何体是三棱柱割去一个三棱锥后剩下的部分(如图),则该几何体的体积为×2×2×2-××1×1×2=4-=.6.A[解析] 由所给的正方体的直观图知,△PAC在该正方体上、下底面上的射影是①中图形,△PAC在该正方体前、后、左、右侧面上的射影是④中图形,故选A.7.C[解析] 由题意知,该几何体是由一个半圆柱与一个半球组成的组合体,其中半圆柱的底面半径为1,高为4,半球的半径为1,则该几何体的体积为×π×13+π×12×4=π,故选C.8.D[解析] 由三视图得,该几何体是正方体挖去一个半圆锥后剩余的部分,故该几何体的体积V=23-×π×12×2=8-,故选D.9.C[解析] 由三视图可知,该几何体是由半圆柱与三棱柱组成的,则该几何体的体积V=π×12×3+×2×2×3=6+π.10.C[解析] 由俯视图的直观图可得该几何体的底面是边长为4的等边三角形,由正视图与侧视图可得该几何体是高为6的三棱锥(如图所示的三棱锥P-ABC),其中PC⊥底面ABC,∴该几何体的表面积S=×42+2××4×6+×4×=24+12,故选C.11.11+2[解析] 由三视图知,该几何体是一个直四棱柱,上、下底面为直角梯形,直角梯形斜腰长为=,则底面周长为4+,故侧面积为2×(4+)=8+2,又两底面的面积和为2××1×(1+2)=3,所以该几何体的表面积为8+2+3=11+2.12.16π[解析] 边长为的正三角形ABC的外接圆的半径r=1,则球O的半径R==2,则球O的表面积S=4πR2=16π.13.[解析] 根据题意,三棱锥P-ABC为鳖臑,且PA⊥平面ABC,PA=AB=2,如图所示,可得∠PAB=∠PAC=∠ABC=∠PBC=90°.易知PC为外接球的直径,设外接球的半径为R.又该鳖臑的外接球的表面积为24π,则R2==6,则BC==4,则该鳖臑的体积为××2×4×2=.14.解:分别过A,B作EF的垂线,垂足分别为G,H,连接DG,CH,则原几何体被分割为两个三棱锥和一个直三棱柱.易知三棱锥的高为,直三棱柱的高为1,AG==,取AD的中点M,连接MG,则MG=,∴S△AGD=×1×=,∴V多面体ABCDEF=×1+2×××=.15.解:(1)直观图如图所示.(2)由三视图可知该几何体是长方体被截去一个三棱柱后剩余的部分,且该几何体的体积是以A1A,A1D1,A1B1为棱的长方体的体积的,∴该几何体的体积V=×1×2×1=(m3).在直角梯形AA1B1B中,作BE⊥A1B1于E,则四边形AA1EB是正方形,AA1=BE=1.在Rt△BEB1中,BE=1,EB1=1,∴BB1=,∴该几何体的表面积S=S正方形ABCD++2++=1+2×1+2××(1+2)×1+1×+1=7+ (m2),∴该几何体的表面积为(7+)m2,体积为 m3.16.A[解析] 用排除法.首先截线不可能是直线,排除B中图形;又圆柱被平面截开所得的截面是椭圆,而侧面展开图为平面图,不可能是圆或椭圆,排除C,D中的图形.故选A.17.16π[解析] 因为总有S圆=S环,所以半椭球体的体积为V圆柱-V圆锥=πb2a-πb2a=πb2a.又2a=6,2b=4,即a=3,b=2,所以椭球体的体积V=πb2a=π×22×3=16π.加练一课(五)1.A[解析] 由题意易知,球心在正四棱锥的高上,设球的半径为R,则(4-R)2+()2=R2,解得R=,所以该球的表面积为4π×=π,故选A.2.B[解析] 由三视图可得该几何体为三棱柱,能得到的最大球为三棱柱的内切球,球的半径为正视图中直角三角形内切圆的半径r.由切线长的性质,得(8-r)+(6-r)=,得r=2,故选B.3.C[解析] 三棱锥B'-ACD中,△AB'C和△ACD是有公共斜边AC的直角三角形,取AC的中点O,则有OB'=OA=OC=OD,∴O为三棱锥B'-ACD的外接球的球心,外接球半径R=OA=1,则三棱锥B'-ACD的外接球的表面积是4πR2=4π,故选C.4.C[解析] 由正视图知,三棱柱的底面边长为2,高为1.易知外接球的球心O在上、下底面两个三角形中心连线的中点上,连接球心和任意一个顶点的线段长即为球O的半径,则R2=+=(其中R为球O的半径),则球O的表面积S=4πR2=4π×=π,故选C.5.B[解析] 将四面体A-BCD补形成正三棱柱,则其外接球的球心为上、下底面的中心连线的中点.易得△BCD的外接圆半径为,所以外接球球O的半径R==2,所以球O的表面积S=4πR2=16π,故选B.6.C[解析] 由三视图可知,该几何体是以俯视图为底面,一条侧棱与底面垂直的三棱锥,如图中三棱锥A-BCD所示,设该几何体外接球的球心为O.由勾股定理可得CD==2,tan∠CBD=,即∠CBD=30°.由正弦定理可得△BCD的外接圆直径2r==4.设球O的半径为R,易知O为AD的中点,则由勾股定理得4R2=AB2+4r2=32,所以该几何体的外接球的表面积S=4πR2=32π,故选C.。
高考数学一轮总复习第七章 立体几何与空间向量第1节 立体图形及其直观图、简单几何体的表面积与体积

C.圆锥、圆台的底面都是圆,母线都与底面垂直
D.位于上方的面是棱台的上底面,位于下方的面是棱台的下底面
解析:(1)一个矩形以其对边中点的连线为旋转轴,旋转180°所形
成的几何体是圆柱,所以A正确;
根据圆台的定义,可得圆锥截去一个小圆锥后剩余的部分是圆台,
所以B正确;
圆锥、圆台的母线都不与底面垂直,所以C错误;
②分割法:把不规则的几何体分割成规则的几何体.当规则的几何
体用公式不易求出时,可将其分割转化成比较好求体积的几何体.
大多数情况下,可以把不规则几何体分割为三棱锥或四棱锥,从四
棱锥底面对角线或几何体表面四边形对角线处寻找分割的
“刀口”.
[针对训练]
(1)(角度一)在△ABC中,已知AB⊥BC,AB=BC=2.现将△ABC绕边AC旋
FC⊥平面ABCD,ED=2FC=2,则四面体A-BEF的体积为(
A.
B.
√
C.1 D.
)
解析:(2)因为 ED⊥平面 ABCD,且 AD⊂平面 ABCD,所以 ED⊥AD.
因为在正方形 ABCD 中,AD⊥DC,而 DC∩ED=D,DC⊂平面 CDEF,ED⊂平面 CDEF,
所以 AD⊥平面 CDEF.连接 EC,DF(图略),
1.空间几何体的结构特征
(1)多面体的结构特征
名称
棱柱
棱锥
棱台
互相 平行 且 全等 .
多边形
互相 平行 且相似
图形
底面
侧棱
平行且相等 .
侧面形状
平行四边形 .
相交于 一点 但不
一定相等
三角形.
延长线交于 一点 .
近年高考数学一轮复习第7章立体几何7.2空间几何体的表面积与体积课后作业理(2021年整理)

2019版高考数学一轮复习第7章立体几何7.2 空间几何体的表面积与体积课后作业理编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2019版高考数学一轮复习第7章立体几何7.2 空间几何体的表面积与体积课后作业理)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2019版高考数学一轮复习第7章立体几何7.2 空间几何体的表面积与体积课后作业理的全部内容。
7。
2 空间几何体的表面积与体积[基础送分提速狂刷练]一、选择题1.(2017·东北五校联考)如左图所示,在三棱锥D-ABC中,已知AC=BC =CD=2,CD⊥平面ABC,∠ACB=90°.若其正视图、俯视图如右图所示,则其侧视图的面积为( )A.错误!B.2C.错误!D。
错误!答案D解析由几何体的结构特征和正视图、俯视图,得该几何体的侧视图是一个直角三角形,其中一直角边为CD,其长度为2,另一直角边为底面三角形ABC的边AB上的中线,其长度为错误!,则其侧视图的面积为S=错误!×2×错误!=错误!,故选D.2.某几何体的三视图如图所示,则该几何体的体积为( )A.16+8π B.8+8πC.16+16π D.8+16π答案A解析由三视图可知该几何体由长方体和圆柱的一半组成(如图所示),其中长方体的长、宽、高分别为4,2,2,圆柱的底面半径为2,高为4.所以该几何体的体积V=4×2×2+错误!π×22×4=16+8π.故选A.3.(2018·合肥质检)一个几何体的三视图如图所示(其中正视图的弧线为四分之一圆周),则该几何体的表面积为( )A.72+6π B.72+4πC.48+6π D.48+4π答案A解析由三视图知,该几何体由一个正方体的错误!部分与一个圆柱的错误!部分组合而成(如图所示),其表面积为16×2+(16-4+π)×2+4×(2+2+π)=72+6π。
全国通用版2019版高考数学一轮复习第七章立体几何课时分层作业四十七7.7.1利用空间向量证明空间中

课时分层作业四十七利用空间向量证明空间中的位置关系一、选择题(每小题5分,共25分)1.向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),下列结论正确的是()A.a∥b,a∥cB.a∥b,a⊥cC.a∥c,a⊥bD.以上都不对【解析】选C.因为a·b=0,c=2a,所以a∥c,a⊥b.【变式备选】设a=(x,4,3),b=(3,2,z),且a∥b,则xz等于()A.-4B.9C.-9D.【解析】选B.因为a∥b,所以= = ,所以x=6,z= ,所以xz=9.2.(2018·泰安模拟)已知长方体ABCD-A1B1C1D1,下列向量的数量积一定不为0的是()A. ·B. ·C. ·D. ·【解析】选D.当侧面BCC1B1是正方形时可得·=0,所以排除A.当底面ABCD是正方形时,AC垂直于对角面BD1,所以排除B.显然排除C.由图可得BD1与BC所成的角小于90°.3.(2018·淮安模拟)如图,正方体ABCD-A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN= ,则MN与平面BB1C1C的位置关系是()A.相交B.平行C.垂直D.不能确定【解题指南】利用向量垂直条件求解.【解析】选B.因为正方体棱长为a,A1M=AN= ,所以= , = ,- 1 -所以= + + = + += ( + )+ + ( + )= + .又因为是平面B1BCC1的法向量,且·= ·=0,所以⊥,所以MN∥平面B1BCC1.【变式备选】在正方体ABCD-A1B1C1D1中,若E为A1C1中点,则直线CE垂直于() A.AC B.BD C.A1D D.A1A【解析】选B.以A为原点,AB,AD,AA1所在直线分别为x,y,z轴建立空间直角坐标系,设正方体棱长为1,则A(0,0,0),C(1,1,0),B(1,0,0),D(0,1,0),A1(0,0,1),E ,所以= , =(1,1,0),=(-1,1,0), =(0,1,-1), =(0,0,-1).显然·= - +0=0,所以⊥,即CE⊥BD.4.(2018·石家庄模拟)如图所示,正方体ABCD-A1B1C1D1中,E,F分别在A1D,AC上,且A1E=A1D,AF= AC,则()A.EF至多与A1D,AC之一垂直- 2 -B.EF⊥A1D,EF⊥ACC.EF与BD1相交D.EF与BD1异面【解题指南】建立空间直角坐标系,用向量法求解.【解析】选B.以D点为坐标原点,以DA,DC,DD1所在直线分别为x,y,z轴建立空间直角坐标系, 设正方体棱长为1,则A1(1,0,1),D(0,0,0),A(1,0,0),C(0,1,0),E ,F ,B(1,1,0),D1(0,0,1),=(-1,0,-1), =(-1,1,0),= , =(-1,-1,1),=- , ·= ·=0,从而EF∥BD1,EF⊥A1D,EF⊥AC.5.已知三点A(2,1,2),B(1,2,3),C(1,1,1),O是坐标原点,点Q在直线OC上运动,则当·取得最小值时,点Q的坐标是()A. B.C. D.【解析】选B.设=λ=(λ,λ,λ),则·=(2-λ,1-λ,2-λ)·(1-λ,2-λ,3-λ)=3λ2-11λ+10,λ= 时取得最小值,Q坐标为.二、填空题(每小题5分,共15分)6.点B( ,0,0)是点A(m,2,5)在x轴上的射影,则点A到原点的距离为________.【解析】点B( ,0,0)是点A(m,2,5)在x轴上的射影,所以m= ,所以点A到原点的距离为d= = =4 .- 3 -答案:47.(2018·南阳模拟)已知平面α内的三点A(0,0,1),B(0,1,0),C(1,0,0),平面β的一个法向量n=(-1,-1,-1),则不重合的两个平面α与β的位置关系是________.【解析】设平面α的法向量为m=(x,y,z),由m·=0,得x·0+y-z=0⇒y=z,由m·=0,得x-z=0⇒x=z ,取x=1,所以m=(1,1,1),m=-n,所以m∥n,所以α∥β.答案:α∥β8.已知点P是平行四边形ABCD所在的平面外一点,如果=(2,-1,-4), = (4,2,0),=(-1,2,-1).对于结论:①AP⊥AB;②AP⊥AD;③是平面ABCD的法向量;④∥.其中正确的是________.【解析】因为·=0, ·=0,所以AB⊥AP,AD⊥AP,则①②正确.又与不平行,所以是平面ABCD的法向量,则③正确.因为= - =(2,3,4), =(-1,2,-1),所以与不平行,故④错.答案:①②③三、解答题(每小题10分,共20分)9.在棱长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.应用空间向量方法求解下列问题.(1)求EF的长.(2)证明:EF∥平面AA1D1D.【解析】(1)如图,建立空间直角坐标系,- 4 -则A1(2,0,2),A(2,0,0),B(2,2,0),C(0,2,0),D1(0,0,2),E(2,1,0),F(1,1,1).=(-1,0,1),| |= ,即EF= .(2)连接AD1,因为=(-2,0,2),所以AD1∥EF.而EF⊄平面ADD1A1,所以EF∥平面AA1D1D.10.如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD的中点.(1)求证:B1E⊥AD1.(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE.若存在,求AP的长;若不存在,说明理由. 【解析】(1)以A为原点, , , 的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系(如图).设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),E ,B1(a,0,1),故=(0,1,1), = ,=(a,0,1), = .因为·=- ×0+1×1+(-1)×1=0,所以B1E⊥AD1.(2)假设在棱AA1上存在一点P(0,0,z0),- 5 -。
(全国通用版)高考数学一轮复习第七章立体几何初步课时分层作业四十7.2空间几何体的表面积与体积文
课时分层作业四十空间几何体的表面积与体积一、选择题 ( 每题 5 分, 共 35 分)1. 某几何体的三视图如下图( 图中网格的边长为 1 个单位 ), 此中俯视图为扇形, 则该几何体的体积为()A. B. C. D.【分析】选 B. 由三视图知几何体是圆锥的一部分, 由俯视图可得: 底面扇形的圆心角为120°, 又由侧视图知几何体的高为 3, 底面圆的半径为 2, 所以几何体的体积 V=2× × π ×2×3=.2. 已知一个空间几何体的三视图如下图, 此中俯视图是边长为 6的正三角形 , 若这个空间几何体存在独一的一个内切球 ( 与该几何体各个面都相切), 则这个几何体的表面积是()A.18B.36C.45D.54【分析】选 D. 由三视图知 , 几何体为正三棱柱 .因为俯视图是边长为 6 的正三角形 ,所以几何体的内切球的半径R=6××=, 所以三棱柱的侧棱长为2.所以几何体的表面积S=2×× 6×6×+3× 6× 2=54.3.已知某几何体的外接球的半径为, 其三视图如下图 , 图中均为正方形 , 则该几何体的体积为 ()A.16B.C.D.8【分析】选 C. 由该三视图可知: 该几何体是一个正方体, 切去四个角所得的正四周体, 其外接球等同于该正方体的外接球, 设正方体的棱长为a, 则有=,a=2, 故该正四周体的体积为33V=2 -×4× ×2= .【变式备选】已知三棱锥的三视图如下图, 此中侧视图是边长为的正三角形 , 则该几何体的外接球的体积为 ()A. B. C.4 D.16π【分析】选 B. 由已知中的三视图, 可得该几何体的直观图如下图:取 AB 的中点 F,AF 的中点 E,由三视图可得:AB 垂直平面 CDE,且平面 CDE是边长为的正三角形,AB=1+3=4,所以 AF=BF=2,EF=1,所以 CF=DF==2,故 F 即为棱锥外接球的球心, 半径 R=2,故外接球的体积V=π R3=.4. 已知在长方体ABCD-A1B1C1D1中 , 底面是边长为 2 的正方形 , 高为 4, 则点 A1到截面 AB1D1的距离是()A. B. C. D.【分析】选 C. 设点 A1到截面 AB1D1的距离是h, 由=, 可得· h=· AA1,解得h=.【一题多解】选 C.取B1D1的中点E1,连结A1E1,AE1,依据几何体的构造特点, 可知 , 作 A1H⊥ AE1, 垂足为 H,A1H⊥平面 AB1D1,A 1H即为所求 .A 1E1=,A 1A=4,A 1A⊥ A1E1,A 1H= ( 等面积法 ).【变式备选】如图,在四棱锥P-ABCD中, 底面 ABCD是矩形 ,PD⊥底面 ABCD,M,N分别为 AB,PC 的中点 ,PD=AD=2,AB=4. 则点 A 到平面 PMN的距离为 ____________ .【分析】取 PD的中点 E, 连结 AE,NE,则因为四棱锥P-ABCD中 , 底面 ABCD是矩形 ,M,N 分别为 AB,PC的中点 ,所以 NE∥ AM,NE=AM,所以四边形AENM是平行四边形 , 所以 AE∥ MN,所以点 A 到平面 PMN的距离等于点 E 到平面 PMN的距离 , 设为 h, 在△ PMN中 ,PN=,PM=2,MN=, 所以 S△PMN=×2×=,由 V E-PMN=V M-PEN, 可得×h=××1× 2× 2,所以 h=.答案 :【方法技巧】求点到平面的距离(1) 能作出高线的则直接作出高线, 转变为求线段的长度;(2)不可以直接求时, ①可转变为与平面平行的直线上一点到平面的距离. ②或利用等体积法求解., ∠AOB=90°,C为该球面上的动点, 若三棱锥O-ABC体积的最大值为36,则5. 已知A,B 是球O的球面上两点()球 O的表面积为A.36 πB.64 πC.144 πD.256 π【分析】选 C. 如下图 , 当点 C位于垂直于面AOB的直径端点时 , 三棱锥 O-ABC的体积最大 , 设球 O的半径为 R, 此时 V O-ABC=V C-AOB=×R2×R= R3=36, 故 R=6,则球 O的表面积为S=4π R2=144π .6. 某几何体的三视图如下图, 其内切球的体积为()A. π【分析】选B. πC. A. 依据图示可得几何体为正八面体π, 内切球心为D.O, 过πO作OH垂直AD于点H, 连结S1H, 作OR垂直 S1H,OR即为内切球O的半径 . 所以 R=,V 0=π .7.如图 , 在透明塑料制成的长方体 ABCD-A1B1C1D1容器内灌进一些水 ( 未满 ), 现将容器底面一边 BC固定在底面上 , 再将容器倾斜 , 跟着倾斜度的不一样 , 有以下四种说法 :①水的部分一直呈棱柱状;②水面四边形EFGH的面积为定值;③棱 A1D1一直与水面EFGH平行 ;④若 E∈ AA1,F ∈ BB1, 则 AE+BF是定值 .则此中正确命题的个数是()A.1个B.2个C.3个D.4个【分析】选 C. 联合题设中供给的图形信息可知: 当容器底面一边BC固准时,BC∥ FG∥A1 D1 , 故由线面平行的判断定理可知结论“棱A1D1一直与水面EFGH平行”建立 ; 同时因为四边形ABFE≌四边形DCGH,且相互平行 ,则由棱柱的定义可知结论“水的部分一直呈棱柱状”正确; 如图 , 因为水平搁置时, 水的高度是定值, 所以当一部分上涨的同时, 另一面降落同样的高度, 因为 BF=h-FD,AE=h+D1E 且 FD=D1E, 所以BF+AE=h-FD+h+D1E=2h( 定值 ),即结论“若E∈AA1,F∈BB1,则AE+BF是定值” 是正确的; 因为水面四边形EFGH的边长在变化是正确的 ., 所以其面积是变化的, 故结论“水面四边形EFGH的面积为定值” 的说法不正确. 即命题①③④【题目溯源】此题根源于人教 A 版必修 2P29A 组第 4 题 .【变式备选】水平桌面上搁置着一个容积为V 的密闭长方体玻璃容器ABCD-A1B1C1D1, 此中装有以下操作与结论:①把容器一端慢慢提起, 使容器的一条棱BC保持在桌面上 , 这个过程中 , 水的状态一直是柱体②在①中的运动过程中, 水面一直是矩形;③把容器提离桌面, 任意转动 , 水面一直过长方体内一个定点;④在③中的转动中水与容器的接触面积一直不变.以上说法正确的选项是__________ .( 把全部正确命题的序号都填上)【分析】①水的部分一直呈棱柱状; 从棱柱的特点及平面ABFE平行平面DCGH即可判断①正确②在①中的运动过程中, 水面四边形EFGH的对边一直保持平行, 且 EF⊥ FG,故水面一直是矩形V的水,给出;; 如图,, ②是正确的 ;③因为一直装有V 的水 , 而均分长方体体积的平面必然经过长方体的中心, 即水面一直过长方体内一个定点 ; 所以结论③正确;④在③中的转动中水与容器接触时, 因为水的体积是定值, 所以水与容器的接触面的面积是正方体表面积的一半 , 故一直保持不变, 所以④正确 .答案 : ①②③④二、填空题 ( 每题 5 分, 共 15 分)8.如图直三棱柱 ABC-A1B1C1的六个极点都在半径为 1 的半球面上 ,AB=AC,侧面 BCC1B1是半球底面圆的内接正方形 , 则侧面 ABB1A1的面积为 ______________ .【分析】由题意知 , 球心在侧面BCC1B1的中心 O上 ,BC 为截面圆的直径, 所以∠B AC=90°, △ ABC的外接圆圆心 N 是 BC的中点 , 同理△ A1B1C1的外心 M是 B1C1的中点 . 设正方形 BCC1B1的边长为 x. 在 Rt△ OMC1中 ,OM= ,MC1= ,OC1=R=1(R 为球的半径 ),所以即 x=+, 则=1,AB=AC=1,所以=× 1=.答案 :9.(2016·浙江高考) 某几何体的三视图如下图( 单位:cm),则该几何体的表面积是______cm2,体积是________cm3.【分析】几何体为两个同样长方体组合而成, 长方体的长、宽、高分别为4,2,2,所以体积为2×(2 ×2×4)=32(cm 3), 因为两个长方体重叠部分为一个边长为 2 的正方形 , 所以表面积为2(2 ×2×2+2×4×4) - 2×2×2=72(cm 2).答案:72 3210.一个圆锥的表面积为π , 它的侧面睁开图是圆心角为120°的扇形 , 则该圆锥的高为 __________ .【分析】设圆锥底面半径是r, 母线长为l ,所以πr2+πr l =π,即r2+r l =1,依据圆心角公式π =, 即l =3r,所以解得r=, l = , 那么高 h==.答案 :【变式备选】已知圆锥侧面睁开图的圆心角为90°, 则该圆锥的底面半径与母线长的比为__________.【分析】设圆锥的母线长是R,则扇形的弧长是=,设底面半径是r,则=2πr,所以 r=,所以圆锥的底面半径与母线长的比为1∶4.答案 :1.(5分)如图,网格纸上小正方形的边长为1, 粗实线画出的是某多面体的三视图, 则该多面体的表面积为()A.18+36B.54+18C.90D.81【解题指南】依据三视图作出原几何体是重点.【分析】选 B. 依据三视图可知原几何体是一个斜四棱柱, 上下底面为边长为 3 的正方形 , 左右为宽为3, 长为 3的矩形,前后为底边长为3, 且底边上的高为 6 的平行四边形, 所以S=9+9+18+18+9+9=54+18.2.(5 分 ) 如图 , 网格纸上小正方形的边长为1, 粗实线画出的是某几何体的三视图, 该几何体由一平面将一圆柱截去一部分所得, 则该几何体的体积为()A.90 πB.63 πC.42πD.36π【分析】选 B. 由三视图知 , 该几何体为一个底面半径为3, 高为 4 的圆柱和一个底面半径为3, 高为 6 的圆柱的一半 , 故其体积为22V= × π ×3×6+π ×3×4=63π .3.(10 分 ) 已知一个平放的各棱长为 4 的三棱锥内有一个小球, 现从该三棱锥顶端向锥内灌水, 小球慢慢上调 .时 , 小球恰与该三棱锥各侧面及水面相切( 小球完整浮在水面上方),当注入的水的体积是该三棱锥体积的求小球的表面积.【分析】由题意 , 没有水的部分的体积是三棱锥体积的,因为三棱锥的各棱长均为4, 所以三棱锥体积为×× 42×=,所以没有水的部分的体积是,a, 则×a2×a=,设其棱长为所以 a=2.设小球的半径为r, 则 4××× 22r=,所以 r=,所以小球的表面积S=4π ·=π .。
高考数学(文)一轮复习精练:第七章 立体几何 课时作业 40 Word含解析

课时作业40空间点、直线、平面之间的位置关系[基础达标]一、选择题1.[2019·江西七校联考]已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面解析:依题意,直线b和c的位置关系可能是相交、平行或异面.答案:D2.若直线a⊥b,且直线a∥平面α,则直线b与平面α的位置关系是()A.b⊂αB.b∥αC.b⊂α或b∥αD.b与α相交或b⊂α或b∥α解析:b与α相交或b⊂α或b∥α都可以.答案:D3.如图所示,ABCD-A1B1C1D1是正方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是()A.A,M,O三点共线B.A,M,O,A1不共面C.A,M,C,O不共面D.B,B1,O,M共面解析:连接A1C1,AC(图略),则A1C1∥AC,∴A1,C1,A,C四点共面,∴A1C⊂平面ACC1A1.∵M∈A1C,∴M∈平面ACC1A1.又M∈平面AB1D1,NO ,AO ,MN ,因为12B 1C 1,因为M ,MN =12B 1C 1,所以11A 1作A 1M ⊥AC 于点M ,连接60°,得AM =1,BM =3,ABC ,A 1M ⊂平面A 1ACC 1,所以的中点,连接MB ,为原点,MA →,MB →,MA →二、填空题6.设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列四个命题,其中正确命题的序号是________.①P∈a,P∈α⇒a⊂α;②a∩b=P,b⊂β⇒a⊂β;③a∥b,a⊂α,P∈b,P∈α⇒b⊂α;④α∩β=b,P∈α,P∈β⇒P∈b.解析:当a∩α=P时,P∈a,P∈α,但a⊄α,∴①错;a∩β=P时,②错;如图∵a∥b,P∈b,∴P∉a,∴由直线a与点P确定唯一平面α,又a∥b,由a与b确定唯一平面γ,但γ经过直线a与点P,∴γ与α重合,∴b⊂α,故③正确;两个平面的公共点必在其交线上,故④正确.答案:③④7.如图所示,G,H,M,N分别是三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有________(填上所有正确答案的序号).解析:图(1)中,直线GH∥MN;图(2)中,G,H,N三点共面,但M∉平面GHN,因此直线GH 与MN异面;图(3)中,连接MG,HN,GM∥HN,因此GH与MN共面;图(4)中,G,M,N共面,但H∉平面GMN,因此GH与MN异面.所以图(2),(4)中GH与MN异面.所成角的大小为________.的中点P ,连接PM =12CD .AB 与CD 所成的角,则 中,已知AB ∥E ,G ,H ,F ,求证:又因为AB∩α=E,AB⊂β,所以E∈α,E∈β,即E为平面α与β的一个公共点.同理可证F,G,H均为平面α与β的公共点,因为若两个平面有公共点,那么它们有且只有一条通过公共点的公共直线,所以E,F,G,H四点必定共线.10.如图,已知不共面的三条直线a,b,c相交于点P,A∈a,B∈a,C∈b,D∈c,求证:AD与BC是异面直线.证明:假设AD和BC共面,所确定的平面为α,那么点P,A,B,C,D都在平面α内,∴直线a,b,c都在平面α内,与已知条件a,b,c不共面矛盾,假设不成立.∴AD和BC是异面直线.[能力挑战]11.[2019·武汉调研]在棱长为3的正方体ABCD-A1B1C1D1中,E,F分别在棱AB,CD上,且AE=CF=1.(1)求异面直线A1E与C1F所成角的余弦值;(2)求四面体EFC1A1的体积.解析:(1)如图,在正方体ABCD-A1B1C1D1中,=1,则AE綊CM 綊AC綊A1C1,连接。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时分层作业四十空间几何体的表面积与体积一、选择题(每小题5分,共35分)1.某几何体的三视图如图所示(图中网格的边长为1个单位),其中俯视图为扇形,则该几何体的体积为( )A. B. C. D.【解析】选B.由三视图知几何体是圆锥的一部分,由俯视图可得:底面扇形的圆心角为120°,又由侧视图知几何体的高为3,底面圆的半径为2,所以几何体的体积V=××π×22×3=.2.已知一个空间几何体的三视图如图所示,其中俯视图是边长为6的正三角形,若这个空间几何体存在唯一的一个内切球(与该几何体各个面都相切),则这个几何体的表面积是 ( )A.18B.36C.45D.54【解析】选D.由三视图知,几何体为正三棱柱.因为俯视图是边长为6的正三角形,所以几何体的内切球的半径R=6××=,所以三棱柱的侧棱长为2.所以几何体的表面积S=2××6×6×+3×6×2=54.3.已知某几何体的外接球的半径为,其三视图如图所示,图中均为正方形,则该几何体的体积为( )A.16B.C.D.8【解析】选C.由该三视图可知:该几何体是一个正方体,切去四个角所得的正四面体,其外接球等同于该正方体的外接球,设正方体的棱长为a,则有=,a=2,故该正四面体的体积为V=23-×4××23=. 【变式备选】已知三棱锥的三视图如图所示,其中侧视图是边长为的正三角形,则该几何体的外接球的体积为( )A. B. C.4 D.16π【解析】选B.由已知中的三视图,可得该几何体的直观图如图所示:取AB的中点F,AF的中点E,由三视图可得:AB垂直平面CDE,且平面CDE是边长为的正三角形,AB=1+3=4,所以AF=BF=2,EF=1,所以CF=DF==2,故F即为棱锥外接球的球心,半径R=2,故外接球的体积V=πR3=.4.已知在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )A. B. C. D.【解析】选C.设点A1到截面AB1D1的距离是h,由=,可得·h=·AA1,解得h=.【一题多解】选C.取B1D1的中点E1,连接A1E1,AE1,根据几何体的结构特征,可知,作A1H⊥AE1,垂足为H,A1H⊥平面AB1D1,A1H即为所求.A1E1=,A1A=4,A1A⊥A1E1,A1H=(等面积法).【变式备选】如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为____________.【解析】取PD的中点E,连接AE,NE,则因为四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为AB,PC的中点,所以NE∥AM,NE=AM,所以四边形AENM是平行四边形,所以AE∥MN,所以点A到平面PMN的距离等于点E到平面PMN的距离,设为h,在△PMN中,PN=,PM=2,MN=,所以S△PMN=×2×=,由V E-PMN=V M-PEN,可得×h=××1×2×2,所以h=.答案:【方法技巧】求点到平面的距离(1)能作出高线的则直接作出高线,转化为求线段的长度;(2)不能直接求时,①可转化为与平面平行的直线上一点到平面的距离.②或利用等体积法求解.5.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )A.36πB.64πC.144πD.256π【解析】选C.如图所示,当点C位于垂直于面AOB的直径端点时,三棱锥O-ABC的体积最大,设球O的半径为R,此时V O-ABC=V C-AOB=×R2×R=R3=36,故R=6,则球O的表面积为S=4πR2=144π.6.某几何体的三视图如图所示,其内切球的体积为 ( )A.πB.πC.πD.π【解析】选A.根据图示可得几何体为正八面体,内切球心为O,过O作OH垂直AD于点H,连接S1H,作OR垂直S1H,OR即为内切球O的半径.所以R=,V0=π.7.如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水(未满),现将容器底面一边BC固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:①水的部分始终呈棱柱状;②水面四边形EFGH的面积为定值;③棱A1D1始终与水面EFGH平行;④若E∈AA1,F∈BB1,则AE+BF是定值.则其中正确命题的个数是( )A.1个B.2个C.3个D.4个【解析】选C.结合题设中提供的图形信息可知:当容器底面一边BC固定时,BC∥FG∥A1D1,故由线面平行的判定定理可知结论“棱A1D1始终与水面EFGH平行”成立;同时由于四边形ABFE≌四边形DCGH,且互相平行,则由棱柱的定义可知结论“水的部分始终呈棱柱状”正确;如图,由于水平放置时,水的高度是定值,所以当一部分上升的同时,另一面下降相同的高度,因为BF=h-FD,AE=h+D1E且FD=D1E,所以BF+AE=h-FD+h+D1E=2h(定值),即结论“若E∈AA1,F∈BB1,则AE+BF是定值”是正确的;因为水面四边形EFGH 的边长在变化,因此其面积是变化的,故结论“水面四边形EFGH的面积为定值”的说法不正确.即命题①③④是正确的.【题目溯源】本题来源于人教A版必修2P29A组第4题.【变式备选】水平桌面上放置着一个容积为V的密闭长方体玻璃容器ABCD-A1B1C1D1,其中装有V的水,给出下列操作与结论:①把容器一端慢慢提起,使容器的一条棱BC保持在桌面上,这个过程中,水的状态始终是柱体;②在①中的运动过程中,水面始终是矩形;③把容器提离桌面,随意转动,水面始终过长方体内一个定点;④在③中的转动中水与容器的接触面积始终不变.以上说法正确的是__________.(把所有正确命题的序号都填上)【解析】①水的部分始终呈棱柱状;从棱柱的特征及平面ABFE平行平面DCGH即可判断①正确;如图,②在①中的运动过程中,水面四边形EFGH的对边始终保持平行,且EF⊥FG,故水面始终是矩形,②是正确的;③由于始终装有V的水,而平分长方体体积的平面必定经过长方体的中心,即水面始终过长方体内一个定点;所以结论③正确;④在③中的转动中水与容器接触时,由于水的体积是定值,所以水与容器的接触面的面积是正方体表面积的一半,故始终保持不变,所以④正确.答案:①②③④二、填空题(每小题5分,共15分)8.如图直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为______________.【解析】由题意知,球心在侧面BCC1B1的中心O上,BC为截面圆的直径,所以∠BAC=90°,△ABC的外接圆圆心N是BC的中点,同理△A1B1C1的外心M是B1C1的中点.设正方形BCC1B1的边长为x.在Rt△OMC1中,OM=,MC1=,OC1=R=1(R为球的半径),所以+=1,即x=,则AB=AC=1,所以=×1=.答案:9.(2016·浙江高考)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm2,体积是________cm3.【解析】几何体为两个相同长方体组合而成,长方体的长、宽、高分别为4,2,2,所以体积为2×(2×2×4)=32(cm3),由于两个长方体重叠部分为一个边长为2的正方形,所以表面积为2(2×2×2+2×4×4)-2×2×2=72(cm2).答案:72 3210.一个圆锥的表面积为π,它的侧面展开图是圆心角为120°的扇形,则该圆锥的高为__________. 【解析】设圆锥底面半径是r,母线长为l,所以πr2+πr l=π,即r2+r l=1,根据圆心角公式π=,即l=3r,所以解得r=,l=,那么高h==.答案:【变式备选】已知圆锥侧面展开图的圆心角为90°,则该圆锥的底面半径与母线长的比为__________.【解析】设圆锥的母线长是R,则扇形的弧长是=,设底面半径是r,则=2πr,所以r=,所以圆锥的底面半径与母线长的比为1∶4.答案:1.(5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A.18+36B.54+18C.90D.81【解题指南】根据三视图作出原几何体是关键.【解析】选B.根据三视图可知原几何体是一个斜四棱柱,上下底面为边长为3的正方形,左右为宽为3,长为3的矩形,前后为底边长为3,且底边上的高为6的平行四边形,所以S=9+9+18+18+9+9=54+18.2.(5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为 ( )A.90πB.63πC.42πD.36π【解析】选B.由三视图知,该几何体为一个底面半径为3,高为4的圆柱和一个底面半径为3,高为6的圆柱的一半,故其体积为V=×π×32×6+π×32×4=63π.3.(10分)已知一个平放的各棱长为4的三棱锥内有一个小球,现从该三棱锥顶端向锥内注水,小球慢慢上浮.当注入的水的体积是该三棱锥体积的时,小球恰与该三棱锥各侧面及水面相切(小球完全浮在水面上方),求小球的表面积.【解析】由题意,没有水的部分的体积是三棱锥体积的,因为三棱锥的各棱长均为4,所以三棱锥体积为××42×=,所以没有水的部分的体积是,设其棱长为a,则×a2×a=,所以a=2.设小球的半径为r,则4×××22r=,所以r=,所以小球的表面积S=4π·=π.。
