高中数学第一章解三角形测试卷新人教版必修5

合集下载

(word完整版)高中数学必修5解三角形测试题及,文档

高中数学必修 5 解三角形测试题及答案一、选择题：〔每题 5 分，共 60 分〕1．在 VABC 中， AB 3, A 45 , C 75 ，那么 BC=A ．33B ．2 C ．2D ．332．以下关于正弦定理的表达或变形中错误的是．．A ．在 VABC 中 ,a:b:c=sinA:sinB:sinCB ． VABC 中 ,a=bsin2A=sin2B a =b+cC ． VABC 中,sinAsinB+sinCD ． VABC 中 , 正弦值较大的角所对的边也较大sin Acos B B 的值为 3． VABC 中 , 假设 a,那么bA ．30B ． 45C ． 60D ． 90ab c，那么 VABC 是4．在VABC 中，假设 =cosCcosA cosBA ．直角三角形B ．等边三角形C ．钝角三角形5．以下命题正确的选项是A ．当 a=4,b=5,A= 30 时，三角形有一解。

B ．当 a=5,b=4,A= 60 时，三角形有两解。

（ A 〕（ B 〕（ B 〕〔 B 〕D ．等腰直角三角形（ D 〕C ．当 a= 3 ,b= 2 ,B= 120 时，三角形有一解。

D ．当 a=3 6 ,A= 60 时，三角形有一解。

2 ,b=26． ABC 中 ,a=1,b=3 , ∠A=30 °,那么∠ B 等于〔 B 〕A ． 60°B ． 60°或 120°C ． 30°或 150°D ． 120°7 ．符合下列条件的三角形有且只有一个的是〔D〕A ． a=1,b=2 ,c=3B ． a=1,b= 2 ,∠ A=30 °C ． a=1,b=2, ∠ A=100 °D ． b=c=1, ∠ B=45 °8 ．假设 (a+b+c)(b+c－a)=3abc, 且sinA=2sinBcosC, 那么 ABC是〔B〕A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰直角三角形9．在ABC 中，角 A 、 B 、C 的对边分别为 a 、b 、c ， A=,a= 3 ,b=1，3c=那么(B)(A)1(B)2(C)3 －1(D)3uur10 ．〔 2021 重庆理〕设ABC 的三个内角 A, B, C ，向量 m( 3 sin A,sin B) ，ruur r1 cos( AB) ，那么 C =〔n (cos B,3 cos A) ，假设 m gn C 〕A ．B ．2 5C ．D ．66 3 311．等腰 △ ABC 的腰为底的 2 倍，那么顶角 A 的正切值是〔 D 〕Ａ． 3Ｂ． 3Ｃ． 15Ｄ．1528712．如图： D,C,B 三点在地面同素来线上 ,DC=a, 从 C,D 两点测得A 点仰角分别是β ,α (α <β ),那么 A 点离地面的高度 AB 等于〔 A 〕Aa sin sina sin sin A ．) B ．)sin(cos(a sin cosacos sin C ．)D ．)sin(cos(αβBDC题号 123 4567891011 12答案二、填空题：〔每题 5 分，共 20 分〕13．a2 ，那么a b c _______2_______sin Asin Bsin A sin C14．在ABC 1 (a 2+b 2－ c 2),那么角∠ C=______.中，假设 S ABC =4415．〔广东 2021 理〕点 A, B, C 是圆 O 上的点，且AB 4, ACB450 ，那么圆 O 的面积等于8．rrr rr r 16． a2, b4, a 与b 的夹角为3，以 a,b 为邻边作平行四边形，那么此平行四边形的两条对角线中较短的一条的长度为____ 2 3 ________三、解答题：〔 17 题 10 分，其余小题均为 12 分〕17．在ABC 中， c 2 ,b2 3 , B 450 ，解三角形 ABC 。

人教版高中数学必修5第一章解三角形测试题及答案

必修五第一章解三角形测试(总分150)一、选择题(每题5分，共50分)1、在△ABC 中，a ＝3，b ＝7，c ＝2，那么B 等于（）A ． 30°B ．45°C ．60°D ．120°2、在△ABC 中，a ＝10，B=60°,C=45°,则c 等于（）A ．310+B ．()1310-C ．13+D ．3103、在△ABC 中，a ＝32，b ＝22，B ＝45°，则A 等于（）A ．30°B ．60°C ．30°或120°D ． 30°或150°4、在△ABC 中，3=AB ,1=AC ,∠A ＝30°，则△ABC 面积为（）A ．23 B ．43 C ．23或3 D ．43 或23 5、在△ABC 中，已知bc c b a ++=222，则角A 为（）A ．3πB ．6πC ．32πD ． 3π或32π6、在△ABC 中,面积22()Sa b c =--,则sin A 等于（）A ．1517B ．817C ．1315D ．13177、已知△ABC 中三个内角为A 、B 、C 所对的三边分别为a 、b 、c ，设向量(,)p a c b =+ ，(,)q b a c a =-- .若//p q，则角C 的大小为（）A ．6π B ．3π C ．2π D ．23π8、已知锐角三角形的边长分别为1，3，a ，则a 的范围是（）A ．()10,8B ．()10,8C ．()10,8D ．()8,109、在△ABC 中，已知C B A sin cos sin 2=,那么△ABC 一定是 ( )A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．正三角形 10、在△ABC 中,3,4ABBC AC ===,则AC 上的高为（）A ．BC ．32D ．二、填空题（每小题5分，共20分）11、在△ABC 中，若∠A:∠B:∠C=1:2:3,则=c b a :: 12、已知三角形两边长为11，则第三边长为13、若三角形两边长为1和3，第三边上的中线长为1，则三角形的外接圆半径为 14、在△ABC 中BC=1，3Bπ=，当△ABC tan C =三、解答题（本大题共小题6小题，共80分）15、（本小题14分）在△ABC 中，已知210=AB ，A ＝45°，在BC 边的长分别为20，3320，5的情况下，求相应角C 。

必修5解三角形第一单元测试题 (含答案)

数学必修5解三角形单元测试题（时间120分钟，满分150分）一、选择题：（每小题5分，共计60分）1.在△ABC 中，若BA sin sin >，则A 与B 的大小关系为（） A. B A > B. B A < C. A ≥B D. A 、B 的大小关系不能确定 2. 在△ABC 中，b=3，c=3，B=300，则a 等于（）A ．3B ．123C ．3或23D ．2 3. 不解三角形，下列判断中正确的是（）A ．a=2，b=4，A=300有两解B ．a=30，b=25，A=1500有一解C ．a=6，b=9，A=450有两解D ．a=9，c=10，B=600无解4. 已知△ABC 的周长为9，且4:2:3sin :sin :sin =C B A ，则cosC 的值为（）A ．41-B ．41 C ．32-D ．32 5. 在△ABC 中，A ＝60°，b ＝1，其面积为3，则CB A cb a sin sin sin ++++等于( )A ．33B ．3392C ．338D ．2396．（2013年高考湖南卷）在锐角中ABC ∆,角,A B 所对的边长分别为,a b 若2sin 3,a B b A =则角等于（） A.12π B.6π C.4π D.3π 7.已知锐角三角形的边长分别为1，3，a ，则a 的范围是（）A ．()10,8B ．()8,10 C ． ()10,8D ．()10,88.在△ABC 中，若cCb B a A sin cos cos ==，则△ABC 是（） A ．有一内角为30°的直角三角形B ．等腰直角三角形C ．有一内角为30°的等腰三角形D ．等边三角形9. △ABC 中，若c=ab b a ++22，则角C 的度数是( ) A.60°或120° B.60° C. 45° D.120° 10. 在△ABC 中，若b=22,a=2，且三角形有解，则A 的取值范围是( ) A.0°＜A ＜30° B.0°＜A ≤45° C.0°＜A ＜90° D.30°＜A ＜60°11. 已知△ABC 的三边长6,5,3===c b a ，则△ABC 的面积为（）A ． 14B ．15C ． 142D ．15212.（2013年高考陕西卷）设△ABC 的内角A , B , C 所对的边分别为a , b , c ,若cos cos sin b C c B a A +=, 则△ABC 的形状为（）(A) 锐角三角形 (B)直角三角形 (C)钝角三角形 (D) 不确定二、填空题（每小题5分，满分20分）13.（2013新课标Ⅱ）设θ为第二象限角,若1tan()42πθ+=,则sin cos θθ+=______. 14. 在等腰三角形 ABC 中，已知sinA ∶sinB=1∶2，底边BC=10，则△ABC 的周长是 .15. 在△ABC 中，已知sinA ∶sinB ∶sinC=3∶5∶7,则此三角形的最大内角的度数等于________.16. 已知△ABC 的三边分别是a 、b 、c ，且面积4222c b a S -+=，则角C=_______．三、解答题（70分）17. (本题满分10分)已知a ＝33，c ＝2，B ＝150°，求边b 的长及三角形面积．18. （本题满分12分）在△ABC 中，已知a-b=4,a+c=2b ，且最大角为120°，求△ABC 的三边长.19. （本题满分12分）在△ABC 中，证明：2222112cos 2cos ba b B a A -=-。

高一数学必修五第一章试题——解三角形(带答案)

高一数学必修五第一章试题——解三角形一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．设a ，b ，c 分别是△ABC 中∠A ，∠B ，∠C 所对边的边长，则直线x sin A ＋ay ＋c ＝0与bx －y sin B ＋sin C ＝0的位置关系是( )A ．平行B ．重合C ．垂直D ．相交但不垂直2．在△ABC 中，已知a －2b ＋c ＝0，3a ＋b －2c ＝0，则sin A ∶sin B ∶sin C 等于( )A ．2∶3∶4B ．3∶4∶5C ．4∶5∶8D ．3∶5∶73．△ABC 的三边分别为a ，b ，c ，且a ＝1，B ＝45°，S △ABC ＝2，则△ABC 的外接圆的直径为( )A ．4 3B ．5C ．5 2D ．624．已知关于x 的方程x 2－x cos A ·cos B ＋2sin 2C2＝0的两根之和等于两根之积的一半，则△ABC 一定是( )A ．直角三角形B ．钝角三角形C ．等腰三角形D ．等边三角形5．△ABC 中，已知下列条件：①b ＝3，c ＝4，B ＝30°；②a ＝5，b ＝8，A ＝30°；③c ＝6，b ＝33，B ＝60°；④c ＝9，b ＝12，C ＝60°．其中满足上述条件的三角形有两解的是( )A ．①②B ．①④C ．①②③D ．③④6．在△ABC 中，a ，b ，c 分别为内角A ，B ，C 所对的边，若a ＝1，sin B ＝32，C ＝π6，则b 的值为( )A ．1B ．32C ．3或32 D ．±17．等腰△ABC 底角B 的正弦与余弦的和为62，则它的顶角是( ) A ．30°或150° B ．15°或75°C ．30°D ．15°8．若G 是△ABC 的重心，a ，b ，c 分别是角A ，B ，C 的对边，且aGA →＋bGB →＋33cGC →＝0，则角A ＝( )A ．90°B ．60°C ．45°D ．30°9．在△ABC 中，B ＝60°，C ＝45°，BC ＝8，D 为BC 上一点，且BD →＝3－12BC→，则AD 的长为( ) A ．4(3－1) B ．4(3＋1) C ．4(3－3)D ．4(3＋3)10．在△ABC 中，B A →·B C →＝3，S △ABC ∈⎣⎢⎡⎦⎥⎤32，332，则B 的取值范围是( ) A ．⎣⎢⎡⎦⎥⎤π4，π3 B ．⎣⎢⎡⎦⎥⎤π6，π4 C ．⎣⎢⎡⎦⎥⎤π6，π3 D ．⎣⎢⎡⎦⎥⎤π3，π211．在△ABC 中，三内角A ，B ，C 所对边分别为a ，b ，c ，若(b －c )sin B ＝2c sin C 且a ＝10，cos A ＝58，则△ABC 面积等于( )A ．392 B ．39 C ．313 D ．312．锐角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若2sin A (a cos C ＋c cos A )＝3b ，则cb 的取值范围是( )A ．⎝ ⎛⎭⎪⎫12，2 B ．⎝ ⎛⎭⎪⎫32，233 C ．(1，2) D ．⎝ ⎛⎭⎪⎫32，1二、填空题(本大题共4小题，每小题5分，共20分)13．已知在△ABC 中，a ＋b ＝3，A ＝π3，B ＝π4，则a 的值为________．14．在△ABC 中，AB ＝2，点D 在边BC 上，BD ＝2DC ，cos ∠DAC ＝31010，cos C ＝255，则AC ＋BC ＝________．15．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ．已知a ＝23，C ＝45°，1＋tan A tan B ＝2cb ，则边c 的值为________．16．在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，且a ，b ，c 满足2b ＝a ＋c ，B ＝π4，则cos A －cos C ＝________．三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(本小题满分10分)如图，△ACD 是等边三角形，△ABC 是等腰直角三角形，∠ACB ＝90°，BD 交AC 于E ，AB ＝2． (1)求cos ∠CBE 的值； (2)求AE ．18．(本小题满分12分)在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，且cos A a ＋cos B b ＝sin C c ．(1)证明：sin A sin B ＝sin C ； (2)若b 2＋c 2－a 2＝65bc ，求tan B ．19．(本小题满分12分)为保障高考的公平性，高考时每个考点都要安装手机屏蔽仪，要求在考点周围1 km内不能收到手机信号．检查员抽查青岛市一考点，在考点正西约 3 km有一条北偏东60°方向的公路，在此处检查员用手机接通电话，以12 km/h的速度沿公路行驶，最长需要多少时间，检查员开始收不到信号，并至少持续多长时间该考点才算合格？20．(本小题满分12分)已知△ABC的内角A，B，C的对边分别为a，b，c，a2＋b2＝λab．(1)若λ＝6，B＝5π6，求sin A；(2)若λ＝4，AB边上的高为3c6，求C．21．(本小题满分12分)已知锐角三角形ABC中，角A，B，C所对的边分别为a，b，c，且tan A＝3cbc2＋b2－a2．(1)求角A的大小；(2)当a＝3时，求c2＋b2的最大值，并判断此时△ABC的形状．22．(本小题满分12分)在海岸A处，发现北偏东45°方向，距A处(3－1) n mile的B处有一艘走私船，在A处北偏西75°的方向，距离A处2 n mile的C处的缉私船奉命以10 3 n mile/h的速度追截走私船．此时，走私船正以10 n mile/h 的速度从B处向北偏东30°方向逃窜，问缉私船沿什么方向能最快追上走私船？一、选择题1．答案 C解析 ∵k 1＝－sin A a ，k 2＝bsin B ，∴k 1k 2＝－1，∴两直线垂直．故选C ． 2．答案 D解析因为a －2b ＋c ＝0，3a ＋b －2c ＝0，所以c ＝73a ，b ＝53a ．a ∶b ∶c ＝3∶5∶7．所以sin A ∶sin B ∶sin C ＝3∶5∶7．故选D ． 3．答案 C解析 ∵S △ABC ＝12ac sin B ＝2，∴c ＝42．由余弦定理b 2＝a 2＋c 2－2ac cos B ＝25， ∴b ＝5．由正弦定理2R ＝bsin B ＝52(R 为△ABC 外接圆的半径)．故选C ． 4．答案 C解析由题意知：cos A ·cos B ＝sin 2C2，∴cos A ·cos B ＝1－cos C 2＝12－12cos [180°－(A ＋B )]＝12＋12cos(A ＋B )， ∴12(cos A ·cos B ＋sin A ·sin B )＝12， ∴cos(A －B )＝1．∴A －B ＝0，∴A ＝B ，∴△ABC 为等腰三角形．故选C ． 5．答案 A解析 ①c sin B <b <c ，故有两解； ②b sin A <a <b ，故有两解； ③b ＝c sin B ，有一解； ④c <b sin C ，无解．所以有两解的是①②．故选A ． 6．答案 C解析在△ABC 中，sin B ＝32，0＜B ＜π， ∴B ＝π3或2π3，当B ＝π3时，△ABC 为直角三角形， ∴b ＝a ·sin B ＝32；当B ＝2π3时，A ＝C ＝π6，a ＝c ＝1．由余弦定理得b 2＝a 2＋c 2－2ac cos 2π3＝3， ∴b ＝3．故选C ． 7．答案 A解析由题意：sin B ＋cos B ＝62．两边平方得sin2B ＝12，设顶角为A ，则A ＝180°－2B ．∴sin A ＝sin(180°－2B )＝sin2B ＝12，∴A ＝30°或150°．故选A ． 8．答案 D解析由重心性质可知GA →＋GB →＋GC →＝0，故GA →＝－GB →－GC →，代入aGA →＋bGB→＋33cGC →＝0中，即 (b －a )GB →＋33c －aGC →＝0，因为GB →，GC →不共线，则⎩⎨⎧b －a ＝0，33c －a ＝0，即⎩⎨⎧b ＝a ，c ＝3a ，故由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝32．因为0<A <180°，所以A ＝30°．故选D ．9．答案 C解析由题意知∠BAC ＝75°，根据正弦定理，得AB ＝BC sin45°sin75°＝8(3－1)，因为BD →＝3－12BC →，所以BD ＝3－12BC ．又BC ＝8，所以BD ＝4(3－1)．在△ABD 中，AD ＝AB 2＋BD 2－2AB ·BD ·cos60°＝4(3－3)．故选C ． 10．答案 C解析由题意知ac ·cos B ＝3，所以ac ＝3cos B ， S △ABC ＝12ac ·sin B ＝12×3cos B ×sin B ＝32tan B ．因为S △ABC ∈⎣⎢⎡⎦⎥⎤32，332，所以tan B ∈⎣⎢⎡⎦⎥⎤33，3，所以B ∈⎣⎢⎡⎦⎥⎤π6，π3．故选C ．11．答案 A解析由正弦定理，得(b －c )·b ＝2c 2，得b 2－bc －2c 2＝0，得b ＝2c 或b ＝－c (舍)．由a 2＝b 2＋c 2－2bc cos A ，得c ＝2，则b ＝4．由cos A ＝58知，sin A ＝398．S △ABC ＝12bc sin A ＝12×4×2×398＝392．故选A ． 12．答案 A解析 2sin A (a cos C ＋c cos A )＝3b ⇔2sin A ·(sin A cos C ＋sin C cos A )＝3sin B ⇔2sin A sin(A ＋C )＝3sin B ⇔2sin A sin B ＝3sin B ⇔sin A ＝32，因为△ABC 为锐角三角形，所以A ＝π3，a 2＝b 2＋c 2－bc ， ① a 2＋c 2＞b 2， ② a 2＋b 2＞c 2， ③由①②③可得2b 2＞bc ，2c 2＞bc ，所以12＜cb ＜2．故选A ．二、填空题(本大题共4小题，每小题5分，共20分) 13．答案 33－32解析由正弦定理，得b ＝a sin B sin A ＝63a ．由a ＋b ＝a ＋63a ＝3，解得a ＝33－32．14．答案 3＋5解析 ∵cos ∠DAC ＝31010，cos C ＝255， ∴sin ∠DAC ＝1010，sin C ＝55， ∴sin ∠ADC ＝sin(∠DAC ＋∠C ) ＝1010×255＋31010×55＝22．由正弦定理，得AC sin ∠ADC ＝DCsin ∠DAC，得AC ＝5DC ．又∵BD ＝2DC ，∴BC ＝3DC ．在△ABC 中，由余弦定理，得 AB 2＝AC 2＋BC 2－2AC ·BC cos C＝5DC 2＋9DC 2－25DC ·3DC ·255＝2DC 2．由AB ＝2，得DC ＝1，从而BC ＝3，AC ＝5．即AC ＋BC ＝3＋5． 15．答案 22解析在△ABC 中，∵1＋tan A tan B ＝1＋sin A cos Bcos A sin B ＝ cos A sin B ＋sin A cos B cos A sin B ＝sin (A ＋B )cos A sin B ＝sin C cos A sin B ＝2cb ．由正弦定理得c b cos A ＝2c b ，∴cos A ＝12，∴A ＝60°．又∵a ＝23，C ＝45°．由a sin A ＝c sin C 得2332＝c 22，∴c ＝22．16．答案 ±42 解析 ∵2b ＝a ＋c ，由正弦定理得2sin B ＝sin A ＋sin C ，又∵B ＝π4，∴sin A ＋sin C ＝2，A ＋C ＝3π4．设cos A －cos C ＝x ，可得(sin A ＋sin C )2＋(cos A －cos C )2＝2＋x 2，即sin 2A ＋2sin A sin C ＋sin 2C ＋cos 2A －2cos A cos C ＋cos 2C ＝2－2cos(A ＋C )＝2－2cos 3π4＝2＋x 2．则(cos A －cos C )2＝x 2＝－2cos 3π4＝2， ∴cos A －cos C ＝±42．三、解答题 17．解 (1)∵∠BCD ＝90°＋60°＝150°，CB ＝AC ＝CD ， ∴∠CBE ＝15°．∴cos ∠CBE ＝cos15°＝cos(45°－30°)＝6＋24． (2)在△ABE 中，AB ＝2，由正弦定理，得AE sin (45°－15°)＝2sin (90°＋15°)，故AE ＝2sin30°sin75°＝2×126＋24＝6－2．18．解 (1)证明：由正弦定理a sin A ＝b sin B ＝c sin C ，可知原式可以化为cos A sin A ＋cos Bsin B ＝sin Csin C ＝1，因为A 和B 为三角形内角，所以sin A sin B ≠0，则两边同时乘以sin A sin B ，可得sin B cos A ＋sin A cos B ＝sin A sin B ，由和角公式可知，sin B cos A ＋sin A cos B ＝sin(A ＋B )＝sin(π－C )＝sin C ，原式得证．(2)因为b 2＋c 2－a 2＝65bc ，根据余弦定理可知，cos A ＝b 2＋c 2－a 22bc ＝35．因为A 为三角形内角，A ∈(0，π)，sin A >0，则sin A ＝1－⎝ ⎛⎭⎪⎫352＝45，即cos A sin A ＝34，由(1)可知cos A sin A ＋cos B sin B ＝sin C sin C ＝1，所以cos B sin B ＝1tan B ＝14，所以tan B ＝4．19．解如右图所示，考点为A ，检查开始处为B ，设公路上C ，D 两点到考点的距离为1 km ．在△ABC 中，AB ＝3≈1．732，AC ＝1，∠ABC ＝30°，由正弦定理，得sin ∠ACB ＝AB sin30°AC ＝32，∴∠ACB ＝120°(∠ACB ＝60°不符合题意)， ∴∠BAC ＝30°，∴BC ＝AC ＝1．在△ACD 中，AC ＝AD ，∠ACD ＝60°， ∴△ACD 为等边三角形，∴CD ＝1．∵BC 12×60＝5，∴在BC 上需要5 min ，CD 上需要5 min ．∴最长需要5 min 检查员开始收不到信号，并至少持续5 min 该考点才算合格．20．解 (1)由已知B ＝5π6，a 2＋b 2＝6ab ，综合正弦定理得4sin 2A －26sin A ＋1＝0．于是sin A ＝6±24，∵0＜A ＜π6，∴sin A ＜12，∴sin A ＝6－24．(2)由题意可知S △ABC ＝12ab sin C ＝312c 2，得12ab sin C ＝312(a 2＋b 2－2ab cos C )＝312(4ab －2ab cos C )，从而有3sin C ＋cos C ＝2即sin ⎝ ⎛⎭⎪⎫C ＋π6＝1．又π6＜C ＋π6＜7π6，∴C ＝π3．21．解 (1)由已知及余弦定理，得sin A cos A ＝3cb 2cb cos A ，sin A ＝32，因为A 为锐角，所以A ＝60°． (2)解法一：由正弦定理，得a sin A ＝b sin B ＝c sin C ＝332＝2，所以b ＝2sin B ，c ＝2sin C ＝2sin(120°－B )．c 2＋b 2＝4[sin 2B ＋sin 2(120°－B )] ＝41－cos2B 2＋1－cos (240°－2B )2＝4－cos2B ＋3sin2B＝4＋2sin(2B －30°)．由⎩⎨⎧0°<B <90°，0°<120°－B <90°，得30°<B <90°，所以30°<2B －30°<150°．当sin(2B －30°)＝1，即B ＝60°时，(c 2＋b 2)max ＝6，此时C ＝60°，△ABC 为等边三角形．解法二：由余弦定理得(3)2＝b 2＋c 2－2bc cos60°＝b 2＋c 2－bc ＝3．∵bc ≤b 2＋c 22(当且仅当b ＝c 时取等号)，∴b 2＋c 2－b 2＋c 22≤3，即b 2＋c 2≤6(当且仅当b ＝c 时等号)．故c 2＋b 2的最大值为6，此时△ABC 为等边三角形．22．解设缉私船用t 小时在D 处追上走私船．在△ABC 中，由余弦定理，得BC 2＝AB 2＋AC 2－2AB ·AC ·cos ∠CAB ＝(3－1)2＋22－2×(3－1)×2×cos120°＝6，∴BC ＝6．在△BCD 中，由正弦定理，得sin ∠ABC ＝AC BC sin ∠BAC ＝22，∴∠ABC ＝45°，∴BC 与正北方向垂直．∴∠CBD ＝120°．在△BCD 中，由正弦定理，得CD sin ∠CBD ＝BD sin ∠BCD， ∴103t sin120°＝10t sin ∠BCD ， ∴sin ∠BCD ＝12，∴∠BCD ＝30°．故缉私船沿北偏东60°的方向能最快追上走私船．。

高中数学必修五解三角形测试题及答案

高中数学必修五解三角形测试题及答案1.在三角形ABC中，如果C=90度，a=6，B=30度，那么c-b的值是多少？选项：A。

1 B。

-1 C。

2/3 D。

-2/32.如果A是三角形ABC的内角，那么下列函数中一定取正值的是什么？选项：A。

XXX3.在三角形ABC中，角A和角B都是锐角，并且cosA>sinB，那么三角形ABC的形状是什么？选项：A。

直角三角形 B。

锐角三角形 C。

钝角三角形 D。

等腰三角形4.在等腰三角形中，一条腰上的高为3，这条高与底边的夹角为60度，那么底边的长度是多少？选项：A。

2 B。

3 C。

3/2 D。

2/35.在三角形ABC中，如果b=2sinB，那么角A等于多少？选项：A。

30度或60度 B。

45度或60度 C。

120度或60度 D。

30度或150度6.边长为5、7、8的三角形的最大角与最小角的和是多少？选项：A。

90度 B。

120度 C。

135度 D。

150度填空题：1.在直角三角形ABC中，如果C=90度，那么sinAsinB 的最大值是1/4.2.在三角形ABC中，如果a=b+bc+c，那么角A的大小是60度。

3.在三角形ABC中，如果b=2，B=30度，C=135度，那么a的大小是2.4.在三角形ABC中，如果5.在三角形ABC中，如果AB=2(6-2)，C=30度，那么AC+BC的最大值是5.解答题：1.在三角形ABC中，如果acosA+bcosB=ccosC，那么三角形ABC是等腰三角形。

2.在三角形ABC中，证明：b-a/c = c-b/a。

3.在锐角三角形ABC中，证明：XXX>XXX。

4.在三角形ABC中，如果a+c=2b，A-C=π/3，那么sinB 的值是1/2.1.在△ABC中，若 $\log(\sin A) - \log(\cos B) - \log(\sin C) = \log 2$，则△ABC的形状是（）A。

直角三角形 B。

高中数学必修5第一章解三角形测试题

高中数学必修5第一章解三角形测试题一选择题：（共12小题，每题5分，共60分，四个选项中只有一个符合要求)1．在ABC ∆中,若b 2+ c 2= a 2+ bc , 则A =( )A ．30︒B ．45︒C ．60︒D ．120︒2．在ABC ∆中，若20sin A sin BcosC -=，则ABC ∆必定是（）A 、钝角三角形B 、等腰三角形C 、直角三角形D 、锐角三角形3．在△ABC 中，已知，，则的值为（） A 、 B 、 C 、或 D 、4．不解三角形，确定下列判断中正确的是（）A.30,14,7===A b a ，有两解 B.150,25,30===A b a ,有一解 C.45,9,6===A b a ，有两解 D.60,10,9===A c b ，无解5．飞机沿水平方向飞行，在A 处测得正前下方地面目标C 的俯角为30°，向前飞行10000米，到达B 处，此时测得目标C 的俯角为75°，这时飞机与地面目标的距离为A ．5000米B ．米 C ．4000米 D．米 6．已知ABC △中，a =b =60B =，那么角A 等于A ．135B ．90C ．45D ．45或135 7．在△ABC 中，60A ∠=︒，2AB =，且△ABC的面积ABC S ∆=，则边BC 的长为（） A．3 CD ．7 8．已知△ABC 中，2cos c b A =，则△ABC 一定是A 、等边三角形B 、等腰三角形C 、直角三角形D 、等腰直角三角形9．在△ABC 中，角C B A ,,的对边分别为,,a b c ，若22241c b a +=，则cBa cos 的值为（） A.41 B. 45 C. 85 D.83 10．设△ABC 的内角A,B,C 所对边的长分别为a,b,c,若b+c=2a,3sinA=5sinB,则角C 等于( )(A)π3 (B) 2π3 (C)3π4 (D)5π611．三角形三内角A 、B 、C 所对边分别为a 、b 、c ，且4tan 3C =，8c =，则△ABC 外接圆半径为（）A ．10B ．8C ．6D ．5 12．在△ABC 中，cos22B ＝2a c c + (a 、b 、c 分别为角A 、B 、C 的对边)，则△ABC 的形状为( )A ．等边三角形B ．直角三角形C ．等腰三角形或直角三角形D ．等腰直角三角形二、填空题：13．在ABC 中，已知sinA:sinB:sinC=3：5：7，则此三角形最大内角度数为为14．在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，设S 为△ABC 的面积，222)S a b c +-，则C 的大小为___________15．在△中，角所对的边分别为，已知，，．则= .16．在中，若2B A =，:a b =A =_____三，解答题：17．在中，角、、的对边分别为、、，且．（Ⅰ）求角的大小；（Ⅱ）求的取值范围.5cos 13A =3sin 5B =cosC 16655665166556651665-∆ABC ,,A B C ,,a b c 2a =3c =60B =︒b ABC ∆ABC ∆A B C a b c cos (2)cos b C a c B=-B sin sin A C +18．（本小题满分12分）已知在△ABC 中，AC=2，BC=1，（1）求AB 的值；（2）求的值。

高中数学必修五第一章《解三角形》单元测试卷及答案

高中数学必修五第一章《解三角形》单元测试卷及答案（2套）单元测试题一一、选择题（本大题共12个小题，每小题5分，共60分，每小题有4个选项，其中有且仅有一个是正确的，把正确的选项填在答题卡中） 1．在ABC △中，::1:2:3A B C =，则::a b c 等于（）A ．1:2:3B ．3:2:1C ．2D ．22．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且A >B ，则一定有（） A ．cos A >cos BB ．sin A >sin BC ．tan A >tan BD ．sin A <sin B3．△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ，2sin sin cos a A B b A +，则ba =（）A ．B ．C D4．在△ABC 中，∠A ＝60°，a =，b ＝4．满足条件的△ABC （） A ．无解B ．有一解C ．有两解D ．不能确定5．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且222a b c =-，则角B 的大小是（） A ．45°B ．60°C ．90°D ．135°6．在△ABC 中，内角A 、B 、C 的对边分别是a 、b 、c ，若22a b -，sin C B =，则A ＝（） A ．30°B ．60°C ．120°D ．150°7．在△ABC 中，∠A ＝60°，b ＝1，△ABC sin aA为（）A B C D ．8．在△ABC 中，sin 2A ≤sin 2B ＋sin 2C －sin B sin C ，则A 的取值范围是（）A ．0,6π⎛⎤ ⎥⎝⎦B ．,6π⎡⎫π⎪⎢⎣⎭C ．0,3π⎛⎤ ⎥⎝⎦D ．,3π⎡⎫π⎪⎢⎣⎭9．在△ABC 中，已知B ＝45°，c =，b =A 的值是（） A ．15°B ．75°C ．105°D ．75°或15°10．在锐角三角形ABC 中，b ＝1，c ＝2，则a 的取值范围是（）A ．1<a <3B ．1a <<C a <D ．不确定11．在△ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，且2cos 22A b cc+=，则 △ABC 的形状为（） A ．直角三角形B ．等腰直角三角形C ．等腰或直角三角形D ．等边三角形12．如图所示，在△ABC 中，已知∠A ∶∠B ＝1∶2，角C 的平分线CD 把三角形面积分为3∶2两部分，则cos A 等于（）A ．13B ．12C ．34D ．0二、填空题（本大题共4个小题，每空5分，共20分，把正确答案填在题中横线上） 13．等腰三角形的底边长为6，腰长为12，其外接圆的半径为________． 14．在△ABC 中，若a 2＋b 2<c 2，且3sin C ，则∠C ＝________． 15．在△ABC 中，a ＝3，26b =B ＝2∠A ，则cos A ＝________．16．某人在C 点测得塔AB 在南偏西80°，仰角为45°，沿南偏东40°方向前进10 m 到O ，测得塔A 仰角为30°，则塔高为________．三、解答题(本大题共6个小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(10分)在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ．已知()cos cos 3sin cos 0C A A B +=．（1）求角B 的大小；（2）若a ＋c ＝1，求b 的取值范围．18．(12分)在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ．（1）若sin 2cos 6A A π⎛⎫+= ⎪⎝⎭，求A 的值；（2）若1cos 3A =，b ＝3c ，求sin C 的值．19．(12分)在△ABC 中，角A 、B 、C 对应的边分别是a 、b 、c ，已知cos2A －3cos(B ＋C )＝1．（1）求角A 的大小；（2）若△ABC 的面积S =b ＝5，求sin B sin C 的值．20．(12分)在△ABC 中，内角A 、B 、C 的对边分别是a 、b 、c ，且222a b c +=．（1）求C ；（2）设cos cos A B =，()()2cos cos cos A B ααα++，求tan α的值．21．(12分)在△ABC 中，2C A π-=，1sin 3B =．（1）求sin A 的值；（2）设6AC =，求△ABC 的面积．22．(12分)如图，已知扇形AOB ，O 为顶点，圆心角AOB 等于60°，半径为2，在弧AB 上有一动点P ，过P 引平行于OB 的直线和OA 相交于点C ，设∠AOP ＝θ，求△POC 面积的最大值及此时θ的值．答案一、选择题（本大题共12个小题，每小题5分，共60分，每小题有4个选项，其中有且仅有一个是正确的，把正确的选项填在答题卡中） 1．【答案】C 【解析】6A π=，3B π=，2C π=，132::sin :sin :sin 3222a b c A B C ===，故选C ． 2．【答案】B【解析】∵A B >，∴a b >，由正弦定理，得sin sin A B >，故选B ．3．【答案】D【解析】本小题考查内容为正弦定理的应用．∵2sin sin cos a A B b A +=，∴22sin sin sin cos A B B A A +=，sin B A =，∴b =，∴ba．故选D ． 4．【答案】A【解析】4sin 60⨯︒=<a <b sin A ，∴△ABC 不存在．故选A ． 5．【答案】A【解析】∵222a b c =-，∴222a c b +-=，由余弦定理，得222cos 2a c b B ac +-===0°<B <180°，所以B ＝45°．故选A ． 6．【答案】A【解析】由sin C B =及正弦定理，得c =，∴2226a b b -=，即a 2＝7b 2．由余弦定理，2222222cos2b c a A bc +-===，又∵0°<A <180°，∴A ＝30°．故选A ． 7．【答案】B【解析】由1sin 2bc A =c ＝4．由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝13，故a =sin a A ==B ． 8．【答案】C【解析】本题主要考查正余弦定理，∵sin 2A ≤sin 2B ＋sin 2C －sin B sin C ， ∴由正弦定理得：a 2≤b 2＋c 2－bc ，即b 2＋c 2－a 2≥bc ，由余弦定理得：2221cos 222b c a bc A bc bc +-==≥=，∴03A π<≤，故选C ．9．【答案】D 【解析】∵sin sin b cB C =，∴sin sin c B C b ==． ∵0°＜C ＜180°．∴C ＝60°或120°，∴A ＝75°或15°．故选D ． 10．【答案】C【解析】∵b <c ，△ABC 为锐角三角形，∴边c 与边a 所对的角的余弦值大于0，即b 2＋a 2－c 2>0且b 2＋c 2－a 2>0，∴22140140a a ⎧+->⎪⎨+->⎪⎩．∴3<a 2<5，∴35a <<．故选C ． 11．【答案】A【解析】由21cos cos 222A A b c c ++==，整理得cos bA c=．又222cos 2b c a A bc +-=，联立以上两式整理得c 2＝a 2＋b 2，∴C ＝90°．故△ABC 为直角三角形．故选A ． 12．【答案】C【解析】在△ABC 中，设∠ACD ＝∠BCD ＝β，∠CAB ＝α，由∠A ∶∠B ＝1∶2，得∠ABC ＝2α．∵∠A <∠B ，∴AC >BC ，∴S △ACD >S △BCD ，∴S △ACD ∶S △BCD ＝3∶2，∴1sin 3212sin 2AC DC BC DC ββ⋅⋅⋅=⋅⋅⋅，∴32AC BC =．由正弦定理得sin sin AC BC B A =，sin 2sin 2sin cos sin AC BC AC BCααααα=⇒=， ∴133cos 2224AC BC α==⨯=，即3cos 4A =．故选C ．二、填空题（本大题共4个小题，每空5分，共20分，把正确答案填在题中横线上） 13．815【解析】设△ABC 中，AB ＝AC ＝12，BC ＝6，由余弦定理222222121267cos 2212128AB AC BC A AB AC +-+-===⋅⨯⨯．∵()0,A ∈π，∴15sin A =，∴外接圆半径8152sin BC r A == 14．【答案】23π【解析】∵a 2＋b 2<c 2，∴a 2＋b 2－c 2<0，即cos C <0．又3sin C ，∴23C π∠=． 15．6【解析】∵a ＝3，26b =，∠B ＝2∠A ，由正弦定理326sin sin 2A A=， ∴2sin cos 26sin 3A A A =，∴6cos 3A =． 16．【答案】10 m【解析】画出示意图，如图所示，CO ＝10，∠OCD ＝40°，∠BCD ＝80°，∠ACB ＝45°， ∠AOB ＝30°，AB ⊥平面BCO ，令AB ＝x ，则BC ＝x ，3BO x ，在△BCO 中，由余弦定理得)()223100210cos 8040xx x =+-⨯⨯︒+︒，整理得25500x x -=-，解得10x =，5x =-(舍去)，故塔高为10 m ．三、解答题(本大题共6个小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．【答案】（1）3B π=；（2）112b ≤<．【解析】（1）由已知得()cos cos cos 3cos 0A B A B A B -++-=，即有sin sin 3sin cos 0A B A B =．因为sin A ≠0，所以sin 30B B =．又cos B ≠0，所以tan 3B =．又0<B <π，所以3B π=．（2）由余弦定理，有b 2＝a 2＋c 2－2ac cos B ．因为a ＋c ＝1，1cos 2B =，有2211324b a ⎛⎫=-+ ⎪⎝⎭．又0<a <1，于是有2114b ≤<，即有112b ≤<． 18．【答案】（1）3A π=；（2）1sin 3C =．【解析】（1）由题设知sin cos cos sin 2cos 66A A A ππ+=．从而sin 3A A ，所以cos A ≠0，tan A =．因为0<A <π，所以3A π=．（2）由1cos 3A =，b ＝3c 及a 2＝b 2＋c 2－2bc cos A ，得a 2＝b 2－c 2，故△ABC 是直角三角形，且2B π=．所以1sin cos 3C A ==． 19．【答案】（1）3A π=；（2）5sin sin 7B C =．【解析】（1）由cos2A －3cos(B ＋C )＝1，得2cos 2A ＋3cos A －2＝0，即(2cos A －1)(cos A ＋2)＝0，解得1cos 2A =或cos A ＝－2(舍去)．因为0<A <π，所以3A π=．（2）由11sin sin 223S bc A bc π====bc ＝20，又b ＝5，知c ＝4．由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝25＋16－20＝21，故a =．又由正弦定理得222035sin sin sin sin sin 2147b c bc B C A A A a a a =⋅==⨯=．20．【答案】（1）34C π=；（2）tan α＝1或tan α＝4．【解析】（1）因为222a b c +=，由余弦定理有222cos 2a b c C ab +-===34C π=．（2）由题意得()()2sin sin cos cos sin sin cos cos cos A A B B ααααα--，因此()()tan sin cos tan sin cos A A B B αα--=，()2tan sin sin tan sin cos cos sin cos cos A B A B A B A B αα-++=，()2tan sin sin tan sin cos cos A B A B A B αα-++=因为34C π=，4A B π+=，所以()sin A B +=因为cos(A ＋B )＝cos A cos B －sin A sin B ，即sin sin 52A B -=，解得sin sin 5210A B =-=．由①得tan 2α－5tan α＋4＝0，解得tan α＝1或tan α＝4． 21．【答案】（1）sin A ；（2）ABC S =△．【解析】（1）由2C A π-=和A ＋B ＋C ＝π，得22A B π=-，04A π<<． ∴cos2A ＝sinB ，即2112sin 3A -=，∴sin A =．（2）由（1）得cos A sin sin BC AC A B =，∴sin 31sin 3AC ABC B===∵2C A π-=，∴2C A π=+，∴sin sin cos 2C A A π⎛⎫=+== ⎪⎝⎭，∴11sin 22ABC S AC BC C =⋅⋅==△． 22．【答案】当θ＝30°时，S (θ)．【解析】∵CP ∥OB ，∴∠CPO ＝∠POB ＝60°－θ，∠OCP ＝120°．在△OCP 中，由正弦定理，得sin sin OP CP OCP θ=∠，即2sin120sin CPθ=︒，∴CP θ．又()2sin 60sin120CO θ=︒-︒，∴()60OC θ=︒-．故△POC 的面积是()1sin1202S CP CO θ=⋅⋅︒()()160sin si 2n 60θθθθ=︒-︒-()1sin sin 21cos 2602θθθθ⎫⎤=-︒=-⎪-⎥⎪⎝⎦⎭，()0,60θ∈︒︒， ∴当θ＝30°时，S (θ)单元测试题二一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的）1．在ABC △中，若90C =︒，6a =，30B =︒，则c b -等于（）A ．1B ．1-C ．D ．-2．在ABC △中，3AB =，2AC =，BC =BA ·AC 等于（）A ．32-B ．23-C ．23D ．323．在△ABC 中，已知a =，b =A ＝30°，则c 等于（）A ．BC ．D ．以上都不对4．根据下列情况，判断三角形解的情况，其中正确的是（） A ．a ＝8，b ＝16，A ＝30°，有两解 B ．b ＝18，c ＝20，B ＝60°，有一解 C ．a ＝5，c ＝2，A ＝90°，无解 D ．a ＝30，b ＝25，A ＝150°，有一解5．△ABC 的两边长分别为2,3，其夹角的余弦值为13，则其外接圆的半径为（）A B C D ．6．在△ABC 中，2cos 22A b cc+⋅=(a 、b 、c 分别为角A 、B 、C 的对边)，则△ABC 的形状为（） A ．直角三角形 B ．等腰三角形或直角三角形 C ．等腰直角三角形D ．正三角形7．已知△ABC 中，A 、B 、C 的对边分别为a 、b 、c ．若a c =A ＝75°，则b 等于（）A ．2B -C ．4-D ．4+8．在△ABC 中，已知b 2－bc －2c 2＝0，a =7cos 8A =，则△ABC 的面积S 为（）A B C D ．9．在△ABC 中，AB ＝7，AC ＝6，M 是BC 的中点，AM ＝4，则BC 等于（）A B C D10．若sin cos cos A B Ca b c==，则△ABC 是（） A ．等边三角形 B ．有一内角是30°的直角三角形 C ．等腰直角三角形D ．有一内角是30°的等腰三角形11．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若()222tan 3a c b B ac +-=，则角B 的值为（） A ．6π B ．3π C ．6π或56π D ．3π或23π12．△ABC 中，3A π=，BC ＝3，则△ABC 的周长为（） A ．43sin 33B π⎛⎫++ ⎪⎝⎭B ．43sin 36B π⎛⎫++ ⎪⎝⎭C ．6sin 33B π⎛⎫++ ⎪⎝⎭D ．6sin 36B π⎛⎫++ ⎪⎝⎭二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上） 13．在△ABC 中，2sin sin sin a b cA B C--=________． 14．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若2223a c b ac +-=，则角B 的值为________．15．已知a ，b ，c 分别是△ABC 的三个内角A ，B ，C 所对的边．若a ＝1，3b =， A ＋C ＝2B ，则sin C ＝________．16．钝角三角形的三边为a ，a ＋1，a ＋2，其最大角不超过120°，则a 的取值范围是________．三、解答题（本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．(10分)如图所示，我艇在A 处发现一走私船在方位角45°且距离为12海里的B 处正以每小时10海里的速度向方位角105°的方向逃窜，我艇立即以14海里/小时的速度追击，求我艇追上走私船所需要的时间．18．(12分)在△ABC 中，角A 、B 、C 所对的边长分别是a 、b 、c ，且4cos 5A =．（1）求2sin cos22B CA ++的值；（2）若b ＝2，△ABC 的面积S ＝3，求a ．19．(12分)如图所示，△ACD 是等边三角形，△ABC 是等腰直角三角形，∠ACB ＝90°，BD 交AC 于E ，AB ＝2．（1）求cos ∠CBE 的值；（2）求AE ．20．(12分)已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a ＝2，3cos 5B =．（1）若b ＝4，求sin A 的值；（2）若△ABC 的面积S △ABC ＝4，求b ，c 的值．21．(12分)在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且2a sin A ＝(2b ＋c )sin B ＋(2c ＋b )sin C ．（1）求A 的大小；（2）若sin B ＋sin C ＝1，试判断△ABC 的形状．22．(12分)已知△ABC 的角A 、B 、C 所对的边分别是a 、b 、c ，设向量(),a b m =， ()sin ,sin B A =n ，()2,2b a --p =．（1）若m ∥n ，求证：△ABC 为等腰三角形；（2）若m ⊥p ，边长c ＝2，角3C π=，求△ABC 的面积．答案一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的） 1．【答案】C【解析】tan 30ba=︒，tan30b a =︒=2c b ==，c b -= 故选C ． 2．【答案】A【解析】由余弦定理得22294101cos 2124AB AC BC A AB AC +-+-===⋅．∴13cos 3242AB AC AB AC A ⋅=⋅⋅=⨯⨯=．∴32BA AC AB AC ⋅=-⋅=-．故选A ．3．【答案】C【解析】∵a 2＝b 2＋c 2－2bc cos A ，∴2515c c =+-．化简得：2100c -+=，即(0c c -=，∴c =c = 故选C ． 4．【答案】D 【解析】A 中，因sin sin a b A B =，所以16sin30sin 18B ⨯︒==，∴90B =︒，即只有一解；B 中，20sin 60sin 18C ︒==c b >，∴C B >，故有两解； C 中，∵A ＝90°，a ＝5，c ＝2，∴b = 故A 、B 、C 都不正确．故选D ． 5．【答案】C【解析】设另一条边为x ，则2221232233x =+-⨯⨯⨯，∴29x =，∴3x =．设1cos 3θ=，则sin θ=．∴32sinR θ==，R =C ． 6．【答案】A【解析】由2cos cos 22A b c b A c c+⋅=⇒⋅=，又222cos 2b c a A bc +-⋅=， ∴b 2＋c 2－a 2＝2b 2⇒a 2＋b 2＝c 2，故选A ． 7．【答案】A【解析】()sin sin 75sin 3045A =︒=︒+︒，由a ＝c 知，C ＝75°，B ＝30°．1sin 2B =．由正弦定理：4sin sin b aB A===．∴b ＝4sin B ＝2．故选A ．8．【答案】A【解析】由b 2－bc －2c 2＝0可得(b ＋c )(b －2c )＝0． ∴b ＝2c ，在△ABC 中，a 2＝b 2＋c 2－2bc cos A ，即22276448c c c =+-⋅．∴c ＝2，从而b ＝4．∴11sin 4222ABCS bc A ==⨯⨯△A ． 9．【答案】B【解析】设BC ＝a ，则2aBM MC ==．在△ABM 中，AB 2＝BM 2＋AM 2－2BM ·AM ·cos ∠AMB ，即22217424cos 42aa AMB =+-⨯⨯⋅∠ ①在△ACM 中，AC 2＝AM 2＋CM 2－2AM ·CM ·cos ∠AMC即22216424cos 42aa AMB =++⨯⨯⋅∠ ②①＋②得：22222176442a +=++，∴a =B ．10．【答案】C 【解析】∵sin cos A Ba b=，∴a cos B ＝b sin A ， ∴2R sin A cos B ＝2R sin B sin A,2R sin A ≠0．∴cos B ＝sin B ，∴B ＝45°．同理C ＝45°，故A ＝90°．故C 选项正确． 11．【答案】D【解析】∵()222tan a c b B +-，∴222tan 2a c b B ac +-⋅=，即cos tan sin B B B ⋅=0<B <π，∴角B 的值为3π或23π．故选D ． 12．【答案】D 【解析】3A π=，BC ＝3，设周长为x ，由正弦定理知2sin sin sin BC AC ABR A B C ===，由合分比定理知sin sin sin sin BC AB BC ACA ABC ++=++，=，∴()sin sin B A B x ⎤+++=⎥⎦，即3sin sin 3sin sin cos cos sin 333x B B B B B π⎤ππ⎛⎫⎫=+++=+++ ⎪⎪⎥⎝⎭⎭⎦133sin sin 3sin 22B B B B B ⎫⎫=+++=++⎪⎪⎪⎪⎭⎭136cos 36sin 26B B B ⎫π⎛⎫=++=++⎪ ⎪⎪⎝⎭⎝⎭．故选D ．二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上） 13．【答案】0 14．【答案】6π【解析】∵222a cb +-=，∴222cos 2a c b B ac +-==6B π=． 15．【答案】1【解析】在△ABC 中，A ＋B ＋C ＝π，A ＋C ＝2B ．∴3B π=．由正弦定理知，sin 1sin 2a B A b ==．又a <b ．∴6A π=，2C π=．∴sin 1C =． 16．【答案】332a ≤< 【解析】由()()()()()()22222212120121212a a a a a a a a a a a ⎧⎪++>+⎪⎪++-+<⎨⎪++-+⎪≥-⎪+⎩，解得332a ≤<．三、解答题（本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．【答案】2小时．【解析】设我艇追上走私船所需时间为t 小时，则BC ＝10t ，AC ＝14t ，在△ABC 中，由∠ABC ＝180°＋45°－105°＝120°，根据余弦定理知：(14t )2＝(10t )2＋122－2·12·10t cos 120°，∴2t =．答：我艇追上走私船所需的时间为2小时． 18．【答案】（1）5950；（2）a = 【解析】（1）()221cos 1cos 59sin cos2cos22cos 122250B C B C A A A A -++++=+=+-=．（2）∵4cos 5A =，∴3sin 5A =．由1sin 2ABC S bc A =△，得133225c =⨯⨯，解得c ＝5．由余弦定理a 2＝b 2＋c 2－2bc cos A ，可得24425225135a =+-⨯⨯⨯=，∴a = 19．【答案】（1；（2）AE=．【解析】（1）∵∠BCD ＝90°＋60°＝150°，CB ＝AC ＝CD ， ∴∠CBE ＝15°．∴()cos cos 4530CBE ∠=︒-︒= （2）在△ABE 中，AB ＝2，由正弦定理得sin sin AE ABABE AEB=∠∠，即()()2sin 4515sin 9015AE =︒-︒︒+︒，故122sin 30cos15AE ⨯︒===︒20．【答案】（1）2sin 5A =；（2）b =5c =．【解析】（1）∵3cos 05B =>，且0<B <π，∴4sin 5B ==．由正弦定理得sin sin a bA B=，42sin 25sin 45a B Ab ⨯===．（2）∵1sin 42ABC S ac B ==△，∴142425c ⨯⨯⨯=，∴5c =．由余弦定理得2222232cos 25225175b a c ac B =+-=+-⨯⨯⨯=，∴b =21．【答案】（1）120A =︒；（2）△ABC 为等腰钝角三角形．【解析】（1）由已知，根据正弦定理得2a 2＝(2b ＋c )b ＋(2c ＋b )c ，即a 2＝b 2＋c 2＋bc ．由余弦定理得a 2＝b 2＋c 2－2bc cos A ，故1cos 2A =-，120A =︒．（2）方法一由（1）得sin 2A ＝sin 2B ＋sin 2C ＋sin B sin C ，又A ＝120°，∴223sin sin sin sin 4B C B C ++=， ∵sin B ＋sin C ＝1，∴sin C ＝1－sin B ． ∴()()223sin 1sin sin 1sin 4B B B B +-+-=，即21sin sin 04B B -+=．解得1sin 2B =．故1sin 2C =．∴B ＝C ＝30°．所以，△ABC 是等腰的钝角三角形．方法二由（1）A ＝120°，∴B ＋C ＝60°，则C ＝60°－B ， ∴sin B ＋sin C ＝sin B ＋sin(60°－B) 11sin sin sin 22B B B B B =-=＝sin(B ＋60°)＝1， ∴B ＝30°，C ＝30°．∴△ABC 是等腰的钝角三角形．22．【答案】（1）见解析；（2）ABC S =△ 【解析】（1）证明 ∵m ∥n ，∴a sin A ＝b sin B ，即22a ba b R R⋅=⋅，其中R 是△ABC 外接圆半径，∴a ＝b ．∴△ABC 为等腰三角形．（2）解由题意知m ·p ＝0，即a (b －2)＋b (a －2)＝0．∴a ＋b ＝ab ．由余弦定理可知，4＝a 2＋b 2－ab ＝(a ＋b )2－3ab ，即(ab )2－3ab －4＝0．∴ab ＝4(舍去ab ＝－1)，∴11sin 4sin 223ABC S ab C π==⨯⨯=△．。

(新人教A版)高中数学第一章解三角形1.2应用举例第1课时距离问题练习必修5

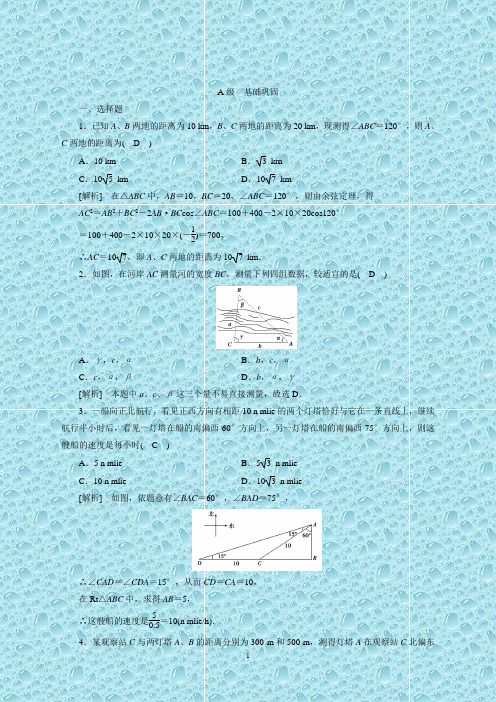
A 级基础巩固一、选择题1．已知A 、B 两地的距离为10 km ，B 、C 两地的距离为20 km ，现测得∠ABC ＝120°，则A 、C 两地的距离为( D )A ．10 kmB ． 3 kmC ．10 5 kmD ．107 km[解析] 在△ABC 中，AB ＝10，BC ＝20，∠ABC ＝120°，则由余弦定理，得 AC 2＝AB 2＋BC 2－2AB ·BC cos ∠ABC ＝100＋400－2×10×20cos120° ＝100＋400－2×10×20×(－12)＝700，∴AC ＝107，即A 、C 两地的距离为107 km ．2．如图，在河岸AC 测量河的宽度BC ，测量下列四组数据，较适宜的是( D )A ．γ，c ，αB ．b ，c ，αC ．c ，α，βD ．b ，α，γ[解析] 本题中a 、c 、β这三个量不易直接测量，故选D ．3．一船向正北航行，看见正西方向有相距10 n mlie 的两个灯塔恰好与它在一条直线上，继续航行半小时后，看见一灯塔在船的南偏西60°方向上，另一灯塔在船的南偏西75°方向上，则这艘船的速度是每小时( C )A ．5 n mlieB ．5 3 n mlieC ．10 n mlieD ．10 3 n mlie[解析] 如图，依题意有∠BAC ＝60°，∠BAD ＝75°，∴∠CAD ＝∠CDA ＝15°，从而CD ＝CA ＝10，在Rt △ABC 中，求得AB ＝5， ∴这艘船的速度是50.5＝10(n mlie/h)．4．某观察站C 与两灯塔A 、B 的距离分别为300 m 和500 m ，测得灯塔A 在观察站C 北偏东30°，灯塔B 在观察站C 正西方向，则两灯塔A 、B 间的距离为( C )A ．500 mB ．600 mC ．700 mD ．800 m[解析] 根据题意画出图形如图．在△ABC 中，BC ＝500，AC ＝300，∠ACB ＝120°，由余弦定理得，AB 2＝AC 2＋BC 2－2AC ·BC cos120° ＝3002＋5002－2×300×500×(－12)＝490 000，∴AB ＝700(m)．5．要直接测量河岸之间的距离(河的两岸可视为平行)，由于受地理条件和测量工具的限制，可采用如下办法：如图所示，在河的一岸边选取A 、B 两点，观察对岸的点C ，测得∠CAB ＝45°，∠CBA ＝75°，且AB ＝120 m 由此可得河宽为(精确到1m)( C )A ．170 mB ．98 mC ．95 mD ．86 m[解析] 在△ABC 中，AB ＝120，∠CAB ＝45°，∠CBA ＝75°，则∠ACB ＝60°，由正弦定理，得BC ＝120sin45°sin60°＝406．设△ABC 中，AB 边上的高为h ，则h 即为河宽， ∴h ＝BC ·sin ∠CBA ＝406×sin75°≈95(m)．6．甲船在湖中B 岛的正南A 处，AB ＝3 km ，甲船以8 km/h 的速度向正北方向航行，同时乙船从B 岛出发，以12 km/h 的速度向北偏东60°方向驶去，则行驶15 min 时，两船的距离是( B )A ．7 kmB ．13 kmC ．19 kmD ．10－3 3 km[解析] 由题意知AM ＝8×1560＝2，BN ＝12×1560＝3，MB ＝AB －AM ＝3－2＝1，所以由余弦定理，得MN 2＝MB 2＋BN 2－2MB ·BN cos120°＝1＋9－2×1×3×(－12)＝13，所以MN ＝13 km ．二、填空题7．在相距2km 的A ，B 两点处测量目标点C ，若∠CAB ＝75°，∠CBA ＝60°，则A ，C 两点之间的距离是__6__km ．[解析] 如图所示，由题意易知C ＝45°，由正弦定理得AC sin60°＝2sin45°，从而AC ＝222·32＝6(km)．8．一只蜘蛛沿东北方向爬行x cm 捕捉到一只小虫，然后向右转105°，爬行10 cm 捕捉到另一只小虫，这时它向右转135°爬行回它的出发点，则x ＝__1063__cm ．[解析] 如图，由题意知，∠BAC ＝75°，∠ACB ＝45°.∠B ＝60°，由正弦定理，得x sin ∠ACB ＝10sin B ，∴x ＝10sin ∠ACB sin B ＝10×sin45°sin60°＝1063．三、解答题9．如图，我炮兵阵地位于地面A 处，两观察所分别位于地面点C 和D 处，已知CD ＝6 000 m ．∠ACD ＝45°，∠ADC ＝75°，目标出现于地面B 处时测得∠BCD ＝30°，∠BDC ＝15°.求炮兵阵地到目标的距离．(结果保留根号)[解析] 在△ACD 中，∠CAD ＝60°， AD ＝CD ·sin45°sin60°＝63CD ．在△BCD 中，∠CBD ＝135°，BD ＝CD ·sin30°sin135°＝22CD ，∠ADB ＝90°．在Rt △ABD 中，AB ＝AD 2＋BD 2＝426CD ＝1 00042(m)．10．一艘船以32.2 n mile/h 的速度向正北航行．在A 处看灯塔S 在船的北偏东20°的方向，30 min 后航行到B 处，在B 处看灯塔在船的北偏东65°的方向，已知距离此灯塔6.5 n mile 以外的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？[解析] 在△ASB 中，∠SBA ＝115°，∠S ＝45°.由正弦定理，得SB ＝AB sin20°sin45°＝16.1sin20°sin45°≈7.787(n mile)．设点S 到直线AB 的距离为h ，则h ＝SB sin65°≈7.06(n mile)．∵h >6.5 n mile ，∴此船可以继续沿正北方向航行．B 级素养提升一、选择题1．已知船A 在灯塔C 北偏东85°且到C 的距离为2 km ，船B 在灯塔C 西偏北25°且到C 的距离为 3 km ，则A 、B 两船的距离为( D )A ．2 3 kmB ．3 2 kmC ．15 kmD ．13 km[解析] 如图可知∠ACB ＝85°＋(90°－25°)＝150°，AC ＝2，BC ＝3，∴AB 2＝AC 2＋BC 2－2AC ·BC ·cos150°＝13， ∴AB ＝13．2．一船自西向东匀速航行，上午10时到达一座灯塔P 的南偏西75°距塔68 n mile 的M 处，下午2时到达这座灯塔的东南方向的N 处，则这只船的航行速度为( A )A ．1762 n mile/hB ．34 6 n mile/hC ．1722n mile/hD ．34 2 n mile/h[解析] 如图所示，在△PMN 中，PM sin45°＝MNsin120°，∴MN ＝68×3222＝346，∴v ＝MN 4＝1762(n mile/h)．3．如图，货轮在海上以40 km/h 的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为140°的方向航行．为了确定船的位置，船在B 点观测灯塔A 的方位角为110°，航行12 h 到达C 点，观测灯塔A 的方位角是65°，则货轮到达C 点时，与灯塔A 的距离是( B )A ．10 kmB ．10 2 kmC ．15 kmD ．15 2 km[解析] 在△ABC 中，BC ＝40×12＝20( km)，∠ABC ＝140°－110°＝30°，∠ACB ＝(180°－140°)＋65°＝105°，则A ＝180°－(30°＋105°)＝45°．由正弦定理，得AC ＝BC ·sin ∠ABC sin A ＝20·sin30°sin45°＝102( km)．二、填空题4．海上一观测站测得方位角240°的方向上有一艘停止航行待修的商船，在商船的正东方有一艘海盗船正向它靠近，速度为每小时90 n mile.此时海盗船距观测站107 n mile ，20 min 后测得海盗船距观测站20 n mlie ，再过__403__min ，海盗船到达商船．[解析] 如下图，设开始时观测站、商船、海盗船分别位于A 、B 、C 处，20 min 后，海盗船到达D 处，在△ADC 中，AC ＝107，AD ＝20，CD ＝30，由余弦定理，得cos ∠ADC ＝AD 2＋CD 2－AC 22AD ·CD ＝400＋900－7002×20×30＝12．∴∠ADC ＝60°，在△ABD 中，由已知得∠ABD ＝30°， ∠BAD ＝60°－30°＝30°， ∴BD ＝AD ＝20，2090×60＝403(min)．5．如图，一艘船上午8∶00在A 处测得灯塔S 在它的北偏东30°处，之后它继续沿正北方向匀速航行，上午8∶30到达B 处，此时又测得灯塔S 在它的北偏东75°处，且与它相距4 2 n mile ，则此船的航行速度是__16__n mile/h ．[解析] 在△ABS 中，∠A ＝30°，∠ABS ＝105°， ∴∠ASB ＝45°，∵BS ＝42，BS sin A ＝ABsin ∠ASB ，∴AB ＝BS ·sin ∠ASBsin A ＝42×2212＝8，∵上午8∶00在A 地，8∶30在B 地， ∴航行0.5小时的路程为8 n mile ， ∴此船的航速为16 n mile/h ．三、解答题6．如图，为了解某海域海底构造，在海平面内一条直线上的A 、B 、C 三点进行测量，已知AB ＝50 m ，BC ＝120 m ，于A 处测得水深AD ＝80 m ，于B 处测得水深BE ＝200 m ，于C 处测得水深CF ＝110 m ，求∠DEF 的余弦值．[解析] 由题意可得DE 2＝502＋1202＝1302， DF 2＝1702＋302＝29 800， EF 2＝1202＋902＝1502，由余弦定理，得cos ∠DEF ＝1665．C 级能力拔高1．为了测量两山顶M 、N 间的距离，飞机沿水平方向在A 、B 两点进行测量，A 、B 、M 、N 在同一个铅垂平面内(如图)．能够测量的数据有俯角和A 、B 间的距离．请设计一个方案，包括：①指出需要测量的数据(用字母表示，并在图中标出)；②用文字和公式写出计算M 、N 间的距离的步骤．[解析] 方案一：①需要测量的数据有：点A 到点M 、N 的俯角α1、β1；点B 到点M 、N 的俯角α2、β2；A 、B 间的距离d (如图)．②第一步：计算AM ，由正弦定理，得AM ＝d sin α2sin α1＋α2；第二步：计算AN ，由正弦定理，得AN ＝d sin β2sin β2－β1；第三步：计算MN ，由余弦定理，得 MN ＝AM 2＋AN 2－2AM ·AN cos α1－β1．方案二：①需要测量的数据有：点A 到点M 、N 的俯角α1、β1；点B 到点M 、N 的俯角α2、β2；A 、B 间的距离d (如图)．②第一步：计算BM ，由正弦定理，得BM ＝d sin α1sin α1＋α2；第二步：计算BN ，由正弦定理，得BN ＝d sin β1sin β2－β1；第三步：计算MN ，由余弦定理，得 MN ＝BM 2＋BN 2＋2BM ·BN cos β2＋α2．2．已知海岛B 在海岛A 的北偏东45°方向上，A 、B 相距10 n mile ，小船甲从海岛B 以2 n mile/h的速度沿直线向海岛A 移动，同时小船乙从海岛A 出发沿北偏西15°方向也以2 n mile/h 的速度移动．(1)经过1 h 后，甲、乙两小船相距多少海里？(2)在航行过程中，小船甲是否可能处于小船乙的正东方向？若可能，请求出所需时间，若不可能，请说明理由．[解析] 经过1 h 后，甲船到达M 点，乙船到达N 点， AM ＝10－2＝8，AN ＝2，∠MAN ＝60°，所以MN 2＝AM 2＋AN 2－2AM ·AN cos60°＝64＋4－2×8×2×12＝52．所以MN ＝213．所以经过1 h 后，甲、乙两小船相距213海里．(2)设经过t (0<t <5)h 小船甲处于小船乙的正东方向，则甲船与A 距离为AE ＝(10－2t )n mile ，乙船与A 距离为AF ＝2t n mile ，∠EAF ＝60°，∠EF A ＝75°，则由正弦定理，得AF sin45°＝AE sin75°，即2tsin45°＝10－2t sin75°，则t ＝10sin45°2sin75°＋2sin45°＝103＋3＝53－33<5．答：经过53－33小时小船甲处于小船乙的正东方向．。

新版高中数学人教A版必修5习题：第一章解三角形检测B

第一章检测(B )(时间:90分钟满分:120分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1已知腰长为定值的等腰三角形的最大面积为2,则等腰三角形的腰长为( ).A .12B.1 C.2D.3解析:设该等腰三角形的腰长为a ,顶角为θ,则该等腰三角形的面积为12a2sin θ,易知当θ=90°时,该等腰三角形的面积取得最大值12a2=2,则a=2,故腰长为2.答案:C2在△ABC 中,b =√3,c =3,B =30°,则a 的值为( ). A .√3B.2√3 C .√3或2√3D.2 解析:∵sin C =sinBb ·c =√32,∴C=60°或C=120°.∴A=90°或A=30°.当A=30°时,a=b =√3;当A=90°时,a =√b 2+c 2=2√3. 答案:C3在△ABC 中,∠ABC =π4,AB =√2,BC =3,则sin ∠BAC=( ).A .√1010B.√105C .3√1010 D.√55解析:在△ABC 中,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC cos ∠ABC=2+9-2×√2×3×√22=5,即得AC =√5.由正弦定理AC sin∠ABC =BC sin∠BAC ,√5√22=3sin∠BAC ,所以sin ∠BAC =3√1010. 答案:C4在△ABC 中,A ,B ,C 的对边分别为a ,b ,c ,且a>b>c ,a 2<b 2+c 2,则A 的取值范围是( ).A .(π2,π)B.(π4,π2)C .(π3,π2)D.(0,π2)解析:cos A =b 2+c 2-a 22bc>0,∴A <π2.又a>b>c ,∴A>B>C.∴A >π3,故选C .答案:C5在△ABC 中,sin A =34,a =10,则边长c 的取值范围是( ).A .(152,+∞)B.(10,+∞)C.(0,10)D .(0,403]解析:由正弦定理得,asinA =csinC ,c =asinA ·sin C =1034sin C =403sin C ≤403.又c>0,故0<c ≤403.答案:D6路边一树干被台风吹断后,树尖与地面成45°角,树干也倾斜为与地面成75°角,树干底部与树尖着地处相距20 m,则折断点与树干底部的距离是( ).A .20√63mB.10√6 m C .10√63 mD.20√2 m解析:如图,设树干底部为O ,树尖着地处为B ,折断点为A ,则∠ABO=45°,∠AOB=75°,∴∠OAB=60°.由正弦定理知,AOsin45°=20sin60°,∴AO =20sin45°sin60°=20√63(m).答案:A7在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c.已知b=c ,a 2=2b 2(1-sin A ),则A=( ).A .3π4B.π3 C .π4D.π6解析:由余弦定理可得a 2=b 2+c 2-2bc cos A ,又因为b=c ,所以a 2=b 2+b 2-2b×b cos A=2b 2(1-cos A ). 由已知a 2=2b 2(1-sin A ), 所以sin A=cos A , 因为A ∈(0,π),所以A =π4. 答案:C8在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若tan A=7tan B ,a 2-b2c=3,则c 等于( ).A.4B.3C.7D.6解析:由tan A=7tan B ,得sinAcosA =7sinBcosB ,即sin A cos B=7sin B cos A ,所以sin A cos B+sin B cos A=8sin B cos A , 即sin(A+B )=sin C=8sin B cos A.由正、余弦定理可得c=8b ·b 2+c 2-a 22bc ,即c 2=4b 2+4c 2-4a 2.又a 2-b 2c=3,所以c 2=4c ,即c=4.答案:A9在△ABC中,角A,B,C所对的边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2-c2,则tan C等于().A.34B.43C.−34D.−43解析:由2S=(a+b)2-c2,得2S=a2+b2+2ab-c2,即2×12absin C=a2+b2+2ab-c2,所以ab sin C-2ab=a2+b2-c2.由余弦定理可知cos C=a 2+b2-c22ab=absinC-2ab2ab=sinC2−1,所以cos C+1=sinC2,即2cos2C2=sin C2cos C2,所以ta n C2=2.所以tan C=2tan C21-tan2C2=2×21-22=−43.答案:D10甲船在B岛的正南方10 km处,且甲船以4 km/h的速度向正北方向航行,同时乙船自B岛出发以6 km/h的速度向北偏东60°的方向行驶,当甲、乙两船相距最近时它们航行的时间是().A.1507 minB.157hC.21.5 minD.2.15 h解析:如图,设经过x h 后甲船处于点P 处,乙船处于点Q 处,两船的距离为s ,则在△BPQ 中,BP=10-4x ,BQ=6x ,∠PBQ=120°,由余弦定理可知s 2=PQ 2=BP 2+BQ 2-2BP ·BQ ·cos ∠PBQ , 即s 2=(10-4x )2+(6x )2-2(10-4x )·6x ·cos120°=28x 2-20x+100.当x=−-202×28=514时s 最小, 此时x =514(h)=1507(min). 答案:A二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)11设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.若b+c=2a ,3sin A=5sin B ,则角C= . 解析:∵3sin A=5sin B ,∴3a=5b.① 又∵b+c=2a ,②∴由①②可得,a =53b,c =73b,∴cos C =b2+a 2-c 22ab=b 2+(53b )2-(73b )22×53b×b =−12,∴C =2π3. 答案:2π312已知△ABC 的面积为S ,且|BC⃗⃗⃗⃗⃗ |2=CA ⃗⃗⃗⃗⃗ ·CB ⃗⃗⃗⃗⃗ +2S,则B = .解析:设AB=c ,BC=a ,AC=b ,则∵|BC⃗⃗⃗⃗⃗ |2=CA ⃗⃗⃗⃗⃗ ·CB ⃗⃗⃗⃗⃗ +2S, ∴a 2=ab cos C+ab sin C ,即a=b sin C+b cos C.由正弦定理得sin A=sin B sin C+sin B cos C. 又sin A=sin(B+C )=sin B cos C+cos B sin C ,∴sin B=cos B ,即tan B=1,B =π4. 答案:π413在△ABC 中,BC=1,B =π3,当△ABC 的面积等于√3时,sin C = . 解析:设AB=c ,AC=b ,BC=a ,则△ABC 的面积S =12acsin B =√3,解得c=4, 所以b =√a 2+c 2-2accosB =√13.所以cos C =a 2+b 2-c 22ab=−√1313.所以sin C =2√3913. 答案:2√391314在△ABC 中,已知b=1,sin C =35,bcos C +ccos B =2,则AC⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ = . 解析:由余弦定理的推论知cos C =a 2+b 2-c 22ab,cos B =a 2+c 2-b22ac .∵b cos C+c cos B=2,∴a2+b2-c22a+a2+c2-b22a=2.∴a=2,即|BC⃗⃗⃗⃗⃗ |=2.又b=1,∴|AC⃗⃗⃗⃗⃗ |=1.∵sin C=35,0°<C<180°,∴cos C=45或cos C=−45.∴AC⃗⃗⃗⃗⃗ ·BC⃗⃗⃗⃗⃗ =85或AC⃗⃗⃗⃗⃗ ·BC⃗⃗⃗⃗⃗ =−85.答案:85或−8515在△ABC中,角A,B,C的对边分别为a,b,c,若1+tanAtanB =2cb,则A=.解析:由正弦定理,得2cb =2sinCsinB.又因为1+tanAtanB =tanB+tanAtanB=sinBcosA+cosBsinAsinBcosA=sin(A+B)sinBcosA=sinCsinBcosA,所以sinCsinBcosA =2sinCsinB.则cos A=12.又因为0°<A<180°,所以A=60°.答案:60°三、解答题(本大题共5小题,共45分.解答时应写出文字说明、证明过程或演算步骤)16(8分)在△ABC 中,已知AB=2,AC=3,A=60°. (1)求BC 的长; (2)求sin 2C 的值.解(1)由余弦定理知,BC 2=AB 2+AC 2-2AB ·AC ·cos A=4+9-2×2×3×12=7,所以BC =√7.(2)由正弦定理知,AB sinC =BCsinA ,所以sin C =ABBC ·sin A =√7=√217.因为AB<BC ,所以C 为锐角,则cos C =√1-sin 2C =√1-37=2√77. 因此sin2C=2sin C ·cos C=2×√217×2√77=4√37. 17(8分)在△ABC 中,∠A =3π4,AB =6,AC =3√2,点D 在BC 边上,AD =BD,求AD 的长. 解设△ABC 的内角A ,B ,C 所对边的长分别是a ,b ,c.由余弦定理得a 2=b 2+c 2-2bc cos ∠BAC=(3√2)2+62−2×3√2×6×cos 3π4=18+36−(−36)=90,所以a=3√10.又由正弦定理得sin B =bsin∠BACa=3√10=√1010,由题设知0<B <π4,所以cos B =√1-sin 2B =√1-110=3√1010.在△ABD 中,由正弦定理得AD =AB ·sinB sin (π-2B )=6sinB 2sinBcosB=3cosB=√10.18(9分)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a>c.已知BA⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =2,cos B =13,b =3,求: (1)a 和c 的值; (2)cos(B-C )的值.解(1)由BA ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =2得c ·a cos B=2.又cos B =13,所以ac=6.由余弦定理,得a 2+c 2=b 2+2ac cos B. 又b=3,所以a 2+c 2=9+2×2=13.解{ac =6,a 2+c 2=13,得a=2,c=3或a=3,c=2.因为a>c ,所以a=3,c=2. (2)在△ABC 中,sin B =√1-cos 2B=√1-(13)2=2√23,由正弦定理,得sin C =cb sin B =23×2√23=4√29. 因为a=b>c ,所以C 为锐角,因此cos C =√1-sin 2C =√1-(4√29)2=79.于是cos(B-C )=cos B cos C+sin B sin C=13×79+2√23×4√29=2327.19(10分)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c.已知a-c =√66b,sin B =√6sin C. (1)求cos A 的值;(2)求co s (2A -π6)的值.解(1)在△ABC 中,由b sinB =c sinC ,及sin B =√6sin C ,可得b =√6c.又由a-c =√66b,有a=2c.所以cos A =b 2+c 2-a 22bc =2222√6c 2=√64. (2)在△ABC 中,由cos A =√64,可得sin A =√104.于是cos2A=2cos 2A-1=−14,sin 2A=2sin A ·cos A =√154.所以co s (2A -π6)=cos 2A ·co s π6+sin 2A ·si n π6=√15-√38.20(10分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c.已知a=3,cos A =√63,B =A +π2. (1)求b 的值;(2)求△ABC 的面积.解(1)在△ABC 中,由题意知sin A =√1-cos 2A =√33,又因为B=A +π2,所以sin B=si n (A +π2)=cos A =√63.由正弦定理可得b=asinBsinA=3×√63√33=3√2.(2)由B=A+π2,得cos B=co s(A+π2)=−sin A=−√33.由A+B+C=π,得C=π-(A+B),所以sin C=sin[π-(A+B)]=sin(A+B) =sin A cos B+cos A sin B=√33×(-√33)+√63×√63=13.因此△ABC的面积S=12absin C=12×3×3√2×13=3√22.。

（完整）新课标人教A版高中数学必修五第一章《解三角形》单元测试题

（完整）新课标⼈教A版⾼中数学必修五第⼀章《解三⾓形》单元测试题解三⾓形第Ⅰ卷（选择题共60分）⼀、选择题（共12⼩题，每⼩题5分，只有⼀个选项正确）：1.在△ABC 中，若∠A ＝60°，∠B ＝45°，BC ＝23，则AC ＝( ) A ．43 B ．22 C ．3 D ．32.在△ABC 中，AB ＝5，BC ＝6，AC ＝8，则△ABC 的形状是( )A ．锐⾓三⾓形B ．直⾓三⾓形C ．钝⾓三⾓形D ．⾮钝⾓三⾓形 3.在△ABC 中，已知a ＝11，b ＝20，A ＝130°，则此三⾓形( )A ．⽆解B ．只有⼀解C ．有两解D ．解的个数不确定4. 海上有A 、B 两个⼩岛相距10海⾥，从A 岛望C 岛和B 岛成60ο的视⾓，从B 岛望C 岛和A岛成75ο视⾓，则B 、C 两岛的距离是（）海⾥A. 65B. 35C. 25D. 5 5.边长为3、7、8的三⾓形中，最⼤⾓与最⼩⾓之和为 ( ) A ．90° B ．120° C ．135° D ．150°6.如图，设A ，B 两点在河的两岸，⼀测量者在A 的同侧，在所在的河岸边选定的⼀点C ，测出AC 的距离为502m ，45ACB ∠=?，105CAB ∠=?后，就可以计算出A ，B 两点的距离为 ( )A. 100mB. 3mC. 1002mD. 200mB ．2 C. 2 D. 38.如图，四边形ABCD中，B＝C＝120°，AB＝4，BC＝CD＝2，则该四边形的⾯积等于( )A. 3 B．5 3C．6 3 D．7 39.在△ABC中，A＝120°，AB＝5，BC＝7，则sin Bsin C的值为( )A.85B.58C.53D.3510.某海上缉私⼩分队驾驶缉私艇以40 km/h的速度由A处出发，沿北偏东60°⽅向航⾏，进⾏海⾯巡逻，当⾏驶半⼩时到达B处时，发现北偏西45°⽅向有⼀艘船C，若C船位于A处北偏东30°⽅向上，则缉私艇B与船C的距离是( )A．5(6＋2) km B．5(6－2) kmC．10(6＋2) km D．10(6－2) km11.△ABC 的周长为20，⾯积为A ＝60°，则BC 的长等于( ) A ．5 B.6 C ．7D ．812.在ABC △中，⾓A B C 、、所对的边分别为,,a b c ，若120,C c ∠=?=，则（） A ．a b > B ．a b <C ．a b =D ．a 与b 的⼤⼩关系不能确定第Ⅱ卷（⾮选择题共90分）⼆、填空题（共4⼩题，每⼩题5分）：13.三⾓形的两边分别是5和3，它们夹⾓的余弦值是⽅程06752=--x x 的根，则此三⾓形的⾯积是。

高一必修5解三角形练习题及答案

高一必修5解三角形练习题及答案第一章解三角形一、选择题BC中，(1)b1．在A2ainB;(2)(abc)(bca)(22)bc,(3)a32,c3,C300;(4)inBbcoAa;则可求得角A450的是（）A．（1）、（2）、（4）B．（1）、（3）、（4）C．（2）、（3）D．（2）、（4）2．在ABC中，根据下列条件解三角形，其中有两个解的是（）A．b10，A45，C70B．a60，c48，B60C．a14，b16，A45D．a7，b5，A803．在ABC中，若bc21，C45，B30，则（）A．b1,c2；B．b2,c1；C．b222,c12；D．b1222,c24．在△ABC中，已知coA513，inB35，则coC的值为（）A.1665或5665B.16561665C.65D.655．如果满足ABC60，AC12，BCk的△ABC恰有一个，那么k的取值范围是（A．k83B．0k12C．k12D．0k12或k83二、填空题6．在ABC中，a5，A60，C15，则此三角形的最大边的长为．7．在ABC中，已知b3，c33，B30，则a__．8．若钝角三角形三边长为a1、a2、a3，则a的取值范围是．9．在△ABC中，AB=3，BC=13，AC=4，则边AC上的高为10.在△ABC中，（1）若inCin(BA)in2A，则△ABC的形状是.（2）若inA=inBinCcoBcoC，则△ABC的形状是.）三、解答题11.已知在ABC中,coA63,a,b,c分别是角A,B,C所对的边.(Ⅰ)求tan2A；(Ⅱ)若in(2B)223,c22,求ABC的面积.解:12.在△ABC中，a,b,c分别为角A、B、C的对边，a2c2b28bc5，a=3,△ABC的面积为6，D为△ABC内任一点，点D到三边距离之和为d。

⑴求角A的正弦值；⑵求边b、c；⑶求d的取值范围解：213．在ABC中，A,B,C的对边分别为a,b,c,且acoC,bcoB,ccoA成等差数列.（I）求B的值；（II）求2in2Aco(AC)的范围。

人教版高中数学必修5解三角形测试题ABC卷

（数学5必修）第一章：解三角形[基础训练A 组]一、选择题1．在△ABC 中，若0030,6,90===B a C ，则b c -等于（）A ．1B ．1-C ．32D ．32-2．若A 为△ABC 的内角，则下列函数中一定取正值的是（）A ．A sinB ．A cosC ．A tanD ．Atan 1 3．在△ABC 中，角,A B 均为锐角，且,sin cos B A >则△ABC 的形状是（）A ．直角三角形B ．锐角三角形C ．钝角三角形D ．等腰三角形4．等腰三角形一腰上的高是3，这条高与底边的夹角为060，则底边长为（）A ．2B ．23 C ．3 D ．32 5．在△ABC 中，若B a b sin 2=，则A 等于（）A ．006030或B ．006045或C ．0060120或D ．0015030或6．边长为5,7,8的三角形的最大角与最小角的和是（）A ．090B ．0120C ．0135D ．0150 二、填空题1．在Rt △ABC 中，090C =，则B A sin sin 的最大值是_______________。

2．在△ABC 中，若=++=A c bc b a 则,222_________。

3．在△ABC 中，若====a C B b 则,135,30,200_________。

4．在△ABC 中，若sin A ∶sin B ∶sin C =7∶8∶13，则C =_____________。

5．在△ABC 中，,26-=AB 030C =，则AC BC +的最大值是________。

三、解答题1．在△ABC 中，若,cos cos cos C c B b A a =+则△ABC 的形状是什么？2．在△ABC 中，求证：)cos cos (a A b B c a b b a -=-3．在锐角△ABC 中，求证：C B A C B A cos cos cos sin sin sin ++>++。

新人教版必修5解三角形测试题ABC卷

(数学5必修)第一章:解三角形[基础训练A 组]一、选择题1．在△ABC 中，若0030,6,90===B a C ，则b c -等于( )A ．1B ．1-C ．32D ．32-2．若A 为△ABC 的内角，则下列函数中一定取正值的是( )A ．A sinB ．A cosC ．A tanD ．Atan 1 3．在△ABC 中，角,A B 均为锐角，且,sin cos B A >则△ABC 的形状是( )A ．直角三角形B ．锐角三角形C ．钝角三角形D ．等腰三角形4．等腰三角形一腰上的高是3，这条高与底边的夹角为060，则底边长为( )A ．2B ．23 C ．3 D ．32 5．在△ABC 中，若B a b sin 2=，则A 等于( )A ．006030或B ．006045或C ．0060120或D ．0015030或6．边长为5,7,8的三角形的最大角与最小角的和是( )A ．090B ．0120C ．0135D ．0150 二、填空题1．在Rt △ABC 中，090C =，则B A sin sin 的最大值是_______________。

2．在△ABC 中，若=++=A c bc b a 则,222_________。

3．在△ABC 中，若====a C B b 则,135,30,200_________。

4．在△ABC 中，若sin A ∶sin B ∶sin C =7∶8∶13，则C =_____________。

5．在△ABC 中，,26-=AB 030C =，则AC BC +的最大值是________。

三、解答题1．在△ABC 中，若,cos cos cos C c B b A a =+则△ABC 的形状是什么？2．在△ABC 中，求证:)cos cos (aA bB c a b b a -=-3．在锐角△ABC 中，求证:C B A C B A cos cos cos sin sin sin ++>++。

高中数学第一章解三角形测试卷新人教版必修5

一、选择题：1. 在ABC ∆中，若::1:2:3A B C ∠∠∠=，则::a b c 等于（）A.1:2:3B.3:2:1C.2:3:1D.1:3:22．在△ABC 中，222a b c bc =++ ，则A 等于（）A ．60°B ．45°C ．120°D ．30°3．有一长为1公里的斜坡，它的倾斜角为20°，现要将倾斜角改为10°，则坡底要伸长（）A. 1公里B. sin10°公里C. cos10°公里D. cos20°公里4．等腰三角形一腰上的高是3，这条高与底边的夹角为060，则底边长=（）A ．2B ．23C ．3D ．325．已知锐角三角形的边长分别为2、3、x ，则x 的取值范围是（）A ．135<<xB ．13＜x ＜5C ．2＜x ＜5D ．5＜x ＜56．在ABC ∆中，60A ∠=，6a =，3b =，则ABC ∆解的情况（）A. 无解B. 有一解C. 有两解D. 不能确定7．边长为5、7、8的三角形的最大角与最小角之和为（）A. 90B. 120C. 135D. 1508．在200米高的山顶上，测得山下一塔顶与塔底的俯角分别为30°、60°，则塔高为（） A. 3400米 B. 33400米 C. 2003米 D. 200米9．在△ABC 中，若)())((c b b c a c a +=-+，则∠A=（）A ．090B ．060C ．0120D ．015010．某人朝正东方向走x km 后，向右转150°，然后朝新方向走3km ，结果他离出发点恰好3km ，那么x 的值为（）A. 3B. 23C. 23或3D. 3二、填空题： 12．在ABC ∆中，三边a 、b 、c 所对的角分别为A 、B 、C ，已知23a =，2b =，ABC ∆的面积S=3，则C = 13．在△ABC 中，已知AB =4，AC =7，BC 边的中线72AD =，那么BC = 14．在△ABC 中，|AB |＝3，|AC |＝2，AB 与AC 的夹角为60°，则|AB -AC |＝________15．一船以每小时15km 的速度向东航行,船在A 处看到一个灯塔B 在北偏东60，行驶４h 后，船到达C 处，看到这个灯塔在北偏东15，这时船与灯塔的距离为 km ．16．三角形的一边长为14，这条边所对的角为60，另两边之比为8：5，则这个三角形的面积为。

高中数学必修5第一章解三角形单元测试题有答案

高二周末测试〔一〕第一卷〔选择题共60分〕一选择题：〔本大题共12小题，每题5分，共60分。

在每题的四个选项中，只有一项为哪一项符合题目要求的〕1.△ABC中，A30o，C105o，b8，那么等于〔〕A4B42C43D 4 52.△ABC中，B45o，C60o，c1，那么最短边的边长等于〔〕6613 3B2C2D23 .长为5、7、8的三角形的最大角与最小角之和为()A90°B 120°C135°D150°a b c4.△ABC中，cosAcosBcosC，那么△ABC一定是〔〕A直角三角形B钝角三角形C等腰三角形D等边三角形5.△ABC中，B60o，b2ac，那么△ABC一定是〔〕A 锐角三角形B钝角三角形C等腰三角形D等边三角形6.△ABC中，∠A=60°,a=6,b=4,那么满足条件的△ABC()A 有一个解B有两个解C无解D不能确定7 .△ABC中，b8，c83，S VABC163，那么A等于〔〕A30o B60o C30o或150o D60o或120obc8.△ABC中，假设A60o，a3，那么sinAsinB sinC等于〔〕1A2B23D29 .△ABC中，A:B1:2，C的平分线CD把三角形面积分成3:2两局部，那么cosA〔〕A1B13D032410.如果把直角三角形的三边都增加同样的长度，那么这个新的三角形的形状为〔〕A 锐角三角形B直角三角形C钝角三角形D由增加的长度决定11在200米高的山顶上，测得山下一塔顶与塔底的俯角分别为30°、60°，那么塔高为〔〕12 A.米 B. 米米米13海上有A、B两个小岛相距10海里，从A岛望C岛和B岛成60°的视角，从B岛望C岛和A岛成75°的视角，那么B、C间的距离是()海里海里C.56 海里 3 海里第二卷〔非选择题共90分〕二、填空题：〔本大题共4小题，每题5分，共20分〕13.在△ABC中，如果sinA:sinB:sinC2:3:4，那么cosC等于。

高中数学 第一章 解三角形测试卷 新人教版必修5

(word完整版)高中数学必修5解三角形测试题及,文档

人教版高中数学必修5第一章解三角形测试题及答案

必修5解三角形第一单元测试题 (含答案)

高一数学必修五第一章试题——解三角形(带答案)

高中数学必修五解三角形测试题及答案

高中数学必修5第一章解三角形测试题

高中数学必修五第一章《解三角形》单元测试卷及答案

(新人教A版)高中数学第一章解三角形1.2应用举例第1课时距离问题练习必修5

新版高中数学人教A版必修5习题：第一章解三角形 检测B

（完整）新课标人教A版高中数学必修五第一章《解三角形》单元测试题

高一必修5解三角形练习题及答案

人教版高中数学必修5解三角形测试题ABC卷

新人教版必修5解三角形测试题ABC卷

高中数学 第一章 解三角形测试卷 新人教版必修5

高中数学必修5第一章解三角形单元测试题有答案

高中数学第一章解三角形测试卷新人教版必修5

新版高中数学人教A版必修5习题：第一章解三角形检测B

高中数学第一章解三角形测试卷新人教版必修5