采用循环双向链表, 能实现多个长整型进行加法运算
python实现双向循环链表

python实现双向循环链表最近⾝边的朋友在研究⽤python来实现数据结构。
遇到⼀个问题就是双向循环链表的实现,改指向的时候总是发蒙。
我⾃⼰尝实现了⼀个python的双向循环链表。
附上代码,希望对⼤家有帮助。
如果不懂什么是双向循环链表的伙伴,需要补习⼀下数据结构的基础之后哦~~~在python当中⽤⼀个类Node 来实现链表的节点,节点数据有三个变量: prev:前驱指针:⽤于指向当前节点前⼀个节点 next: 后继指针⽤于指向当前节点后⼀个节点 item:值,⽤于存储该节点要存的数值 当前节点的前⼀个节点我们叫他前驱,后⼀个节点我们叫他后继。
在链表类当中,我们有⼀个变量head是链表的头指针我们拿着链表的头head,就可以对他进⾏⼀些列操作:(由于是双向循环链表,修改指针特别容易出错,我尽量说的细致,⽅便⼤家参考)判断空: is_empty() 如果头指针head没有指向则链表是空的否则不是空的在头部添加元素: add(item) 1 新建⼀个节点⾥⾯的值是item。
2 放⼊头部: 2.1 如果链表是空的,node的next和prev都指向⾃⼰,然后head再指向node在尾部添加元素: append(item) 1 创建⼀个新节点node ⾥⾯的值是item 2 放⼊尾部: 2.1 如果链表空,则执⾏头部添加add就可以 2.2 链表⾮空: 2.2.1 node的next指向head 2.2.2 node的prev指向head的prev 2.2.3 head的prev元素的next指向node 2.2.4 head的prev指向改为node 2.2.5 head指向node 更换了头部指定位置添加元素: insert( pos , item ) 1 新建⼀个节点node ⾥⾯的值是item 2 找到合适的位置插进去: 2.1 如果pos <= 0 还⼩,那就执⾏头插⽅法 add() 2.2 如果pos >= 链表长度, 那就执⾏尾部插⼊ append() 2.3 如果pos位置在链表的中间: 2.3.1 定义⼀个临时变量temp 按照传⼊的pos找到要插⼊的位置的前⼀个元素 2.3.2 node的prev设为temp,node的next设为temp的next 2.3.3 temp的next指向的节点的prev改为node 2.3.4 temp的next改为node得到链表长度: length() 1 我们设置⼀个临时变量temp初始设为head ,设置⼀个计数器count 初始为 0 2 令count⾃增1 然后temp改指向⾃⼰的下⼀个元素⼀直到temp遇到None 为⽌,temp到了链表的最后⼀个元素 通过这样的⽅式,统计出⼀共有多少个节点返回遍历链表数据: travelji() 1 设置⼀个临时变量temp初始化设为head 2 temp 每次输出⾃⼰指向元素的值,然后在指向⾃⼰的下⼀个元素,⼀直temp为None 说明到了列表的尾部删除链表元素: remove( item ) 1 开启temp临时变量初始化为head , 2 temp不断指向⾃⼰的下⼀个元素,每次指向⼀个元素都检查当前值是不是item,如果找到item则删除它返回True,如果没找到就到尾部了就返回False 2.1 删除过程: 2.1.1 temp的前⼀个元素的next改为temp的后⼀个元素 2.1.2 temp的后⼀个元素的prev改为前⼀个元素查询是否有元素:search() 设置⼀个临时变量temp从head开始,不断指向⾃⼰下⼀个,每次都检查⼀下⾃⼰的值如果和item相同返回True结束 如果temp变成None 则到尾部了都没找到返回False上代码!1#链表的节点2class Node(object):3def__init__(self , item ):4 self.item = item #节点数值5 self.prev = None #⽤于指向前⼀个元素6 self.next = None #⽤于指向后⼀个元素7#双向循环链表8class DoubleCircleLinkList(object):9def__init__(self):10 self.__head = None #初始化的时候头节点设为空、11#判断链表是否为空,head为None 的话则链表是空的12def is_empty(self):13return self.__head is None14#头部添加元素的⽅法15def add(self,item):16 node = Node(item) #新建⼀个节点node ⾥⾯的值是item17# 如果链表是空的,则node的next和prev都指向⾃⼰(因为是双向循环),head指向node18if self.is_empty():19 self.__head = node20 node.next = node21 node.prev = node22# 否则链表不空23else:24 node.next = self.__head#node的next设为现在的head25 node.prev = self.__head.prev #node的prev 设为现在head的prev26 self.__head.prev.next = node #现在head的前⼀个元素的next设为node27 self.__head.prev = node #现在head的前驱改为node28 self.__head = node #更改头部指针29#尾部添加元素⽅法30def append(self , item):31#如果当前链表是空的那就调⽤头部插⼊⽅法32if self.is_empty():33 self.add(item)34#否则链表不为空35else :36 node = Node(item) #新建⼀个节点node37#因为是双向循环链表,所以head的prev其实就是链表的尾部38 node.next = self.__head#node的下⼀个设为头39 node.prev = self.__head.prev #node的前驱设为现在头部的前驱40 self.__head.prev.next = node #头部前驱的后继设为node41 self.__head.prev = node #头部⾃⼰的前驱改为node42#获得链表长度节点个数43def length(self):44#如果链表是空的就返回045if self.is_empty():46return 047#如果不是空的48else:49 cur = self.__head#临时变量cur表⽰当前位置初始化设为头head50 count = 1 #设⼀个计数器count,cur每指向⼀个节点,count就⾃增1 ⽬前cur指向头,所以count初始化为1 51#如果cur.next不是head,说明cur⽬前不是最后⼀个元素,那么count就1,再让cur后移⼀位52while cur.next is not self.__head:53 count += 154 cur = cur.next55#跳出循环说明所有元素都被累加了⼀次返回count就是⼀共有多少个元素56return count57#遍历链表的功能58def travel(self):59#如果当前⾃⼰是空的,那就不遍历60if self.is_empty():61return62#链表不空63else :64 cur = self.__head#临时变量cur表⽰当前位置,初始化为链表的头部65#只要cur的后继不是头说明cur不是最后⼀个节点,我们就输出当前值,并让cur后移⼀个节点66while cur.next is not self.__head:67print( cur.item,end="" )68 cur = cur.next69#当cur的后继是head的时候跳出循环了,最后⼀个节点还没有打印值在这⾥打印出来70print( cur.item )7172#置顶位置插⼊节点73def insert(self, pos , item ):74#如果位置<=0 则调⽤头部插⼊⽅法75if pos <= 0:76 self.add(item)77#如果位置是最后⼀个或者更⼤就调⽤尾部插⼊⽅法78elif pos > self.length() - 1 :79 self.append(item)80#否则插⼊位置就是链表中间81else :82 index = 0 #设置计数器,⽤于标记我们后移了多少步83 cur = self.__head#cur标记当前所在位置84#让index每次⾃增1 ,cur后移,当index=pos-1的时候说明cur在要插⼊位置的前⼀个元素,这时候停下 85while index < pos - 1 :86 index += 187 cur = cur.next88#跳出循环,cur在要插⼊位置的前⼀个元素,将node插⼊到cur的后⾯89 node = Node(item) #新建⼀个节点90 node.next = cur.next #node的后继设为cur的后继91 node.prev = cur #node的前驱设为cur92 cur.next.prev = node #cur后继的前驱改为node93 cur.next = node #cur后继改为node94#删除节点操作95def remove(self,item):96#如果链表为空直接不操作97if self.is_empty():98return99#链表不为空100else:101 cur = self.__head#临时变量标记位置,从头开始102#如果头结点就是要删除的元素103if cur.item == item:104#如果只有⼀个节点链表就空了 head设为None105if self.length() == 1:106 self.__head = None107#如果多个元素108else:109 self.__head = cur.next #头指针指向cur的下⼀个110 cur.next.prev= cur.prev #cur后继的前驱改为cur的前驱111 cur.prev.next = cur.next #cur前驱的后继改为cur的后继112#否则头节点不是要删除的节点我们要向下遍历113else:114 cur = cur.next #把cur后移⼀个节点115#循环让cur后移⼀直到链表尾元素位置,期间如果找得到就删除节点,找不到就跳出循环,116while cur is not self.__head:117#找到了元素cur就是要删除的118if cur.item == item:119 cur.prev.next = cur.next #cur的前驱的后继改为cur的后继120 cur.next.prev = cur.prev #cur的后继的前驱改为cur的前驱121 cur = cur.next122#搜索节点是否存在123def search(self , item):124#如果链表是空的⼀定不存在125if self.is_empty():126return False127#否则链表不空128else:129 cur = self.__head#设置临时cur从头开始130# cur不断后移,⼀直到尾节点为⽌131while cur.next is not self.__head:132#如果期间找到了就返回⼀个True 结束运⾏133if cur.item == item:134return True135 cur = cur.next136# 从循环跳出来cur就指向了尾元素看⼀下为元素是不是要找的是就返回True137if cur.item ==item:138return True139#所有元素都不是就返回False 没找到140return False141142143if__name__ == "__main__":144 dlcl = DoubleCircleLinkList()145print(dlcl.search(7))146 dlcl.travel()147 dlcl.remove(1)148print(dlcl.length())149print(dlcl.is_empty())150 dlcl.append(55)151print(dlcl.search(55))152 dlcl.travel()153 dlcl.remove(55)154 dlcl.travel()155print(dlcl.length())156 dlcl.add(3)157print(dlcl.is_empty())158 dlcl.travel()159 dlcl.add(4)160 dlcl.add(5)161 dlcl.append(6)162 dlcl.insert(-10,1)163 dlcl.travel()164print(dlcl.length())165 dlcl.remove(6)166 dlcl.travel()167168print(dlcl.search(7) )169 dlcl.append(55)170 dlcl.travel()各种数据结构主要是思想,不同的⼈实现⽅式都不⼀定⼀样,同⼀个⼈多次实现也不⼀定⼀样。
c语言中双向循环列表原理

c语言中双向循环列表原理A doubly linked list, also known as a double-ended queue, is a data structure that consists of a set of sequentially linked records called nodes. Each node contains two fields, called links, that are references to the previous and next nodes in the sequence of nodes. This data structure allows for efficient insertion and removal of elements at both the beginning and end of the list, making it a versatile and practical choice for many programming tasks.双向循环列表,也称为双端队列,是一种数据结构,它由一组连续链接的记录组成,称为节点。
每个节点包含两个字段,称为链接,它们是对节点序列中前一个和后一个节点的引用。
这种数据结构允许在列表的开始和结尾有效地插入和删除元素,使其成为许多编程任务的一种多才多艺且实用的选择。
From a technical perspective, a doubly linked list is implemented using a combination of nodes and references. Each node contains data and two reference fields, usually called prev and next, that point to the previous and next nodes in the sequence. This allows for traversing the list in both forward and backward directions, providing flexibility in data access and manipulation. Additionally, the conceptof a circular doubly linked list means that the "next" reference of the last node points back to the first node, creating a continuous loop structure.从技术角度来看,双向循环列表是使用节点和引用的组合来实现的。
双链表的各种基本算法

双链表的各种基本算法双链表是一种常见的数据结构,它由节点组成,每个节点除了包含一个数据元素外,还有两个指针,分别指向前一个节点和后一个节点。
双链表具有插入、删除、遍历等基本操作,下面将介绍双链表的各种基本算法。
一、双链表的插入操作双链表的插入操作可以在指定位置插入一个新节点。
插入操作分为三种情况:在表头插入、在表尾插入和在指定位置插入。
1. 在表头插入:将新节点的next指针指向原表头节点,将原表头节点的prev指针指向新节点,更新表头指针为新节点。
2. 在表尾插入:将新节点的prev指针指向原表尾节点,将原表尾节点的next指针指向新节点,更新表尾指针为新节点。
3. 在指定位置插入:找到要插入位置的节点,将新节点的next指针指向该节点的next节点,将新节点的prev指针指向该节点,将该节点的next节点的prev指针指向新节点,将该节点的next指针指向新节点。
二、双链表的删除操作双链表的删除操作可以删除指定位置的节点。
删除操作分为三种情况:删除表头节点、删除表尾节点和删除指定位置节点。
1. 删除表头节点:将表头指针指向表头节点的next节点,将新的表头节点的prev指针置为空。
2. 删除表尾节点:将表尾指针指向表尾节点的prev节点,将新的表尾节点的next指针置为空。
3. 删除指定位置节点:找到要删除位置的节点,将该节点的prev 节点的next指针指向该节点的next节点,将该节点的next节点的prev指针指向该节点的prev节点。
三、双链表的查找操作双链表的查找操作可以根据给定的条件查找满足条件的节点。
查找操作分为两种:按值查找和按位置查找。
1. 按值查找:从表头开始遍历双链表,逐个比较节点的数据元素与给定值是否相等,直到找到满足条件的节点或遍历结束。
2. 按位置查找:从表头开始遍历双链表,遍历到指定位置的节点。
四、双链表的遍历操作双链表的遍历操作可以按顺序访问双链表中的每个节点。
带头结点的双向循环链表操作集

带头结点的双向循环链表操作集带头结点的双向循环链表操作集1. 链表的定义链表是一种数据结构,它由一系列节点组成,每个节点存储数据和指向下一个节点的指针。
链表可以分为单向链表和双向链表。
在双向链表中,每个节点有两个指针,一个指向前一个节点,另一个指向后一个节点。
2. 链表的基本操作2.1 链表的创建创建一个带头结点的双向循环链表,可以按照以下步骤进行:1. 创建头结点2. 将头结点的前指针和后指针均指向自身,完成循环链接的闭合3. 将头结点作为链表的起始节点2.2 链表的遍历链表的遍历是指按照某种顺序遍历链表中的所有节点。
可以使用循环或递归的方法进行遍历,其具体步骤如下:1. 先将指针指向链表的起始节点2. 依次访问每个节点,并将指针指向下一个节点,直到指针指向空节点为止2.3 链表的插入链表的插入是指将一个新的节点插入到链表中的某个位置。
如果要在第i个位置插入一个新节点,需要进行以下操作:1. 新建一个节点,并将要插入的数据存储在其中2. 找到第i-1个节点,并将它的后指针指向新节点3. 将新节点的前指针指向第i-1个节点,后指针指向第i个节点4. 如果插入位置是链表的末尾,则需要将新节点的后指针指向头结点,完成循环链接的闭合2.4 链表的删除链表的删除是指将链表中某个节点删除。
如果要删除第i个节点,需要进行以下操作:1. 找到第i个节点2. 将第i-1个节点的后指针指向第i+1个节点3. 将第i+1个节点的前指针指向第i-1个节点4. 释放第i个节点所占用的内存空间3. 链表的应用链表常常被用于各种算法和数据结构中,如栈、队列、哈希表、图等。
链表具有无需预先分配内存空间,插入和删除操作效率高等优点,在某些场合可以取代数组进行操作。
4. 链表的优化在实际使用中,链表的优化也是非常重要的,可以采用以下方法进行优化:1. 在插入和删除操作频繁的场合,可以选用跳表、B树等数据结构进行优化2. 在查询操作频繁的场合,可以选用哈希表等数据结构进行优化3. 可以使用链表的迭代器进行遍历操作,比单纯使用指针更加方便和安全5. 总结带头结点的双向循环链表是一种常用的数据结构,具有插入和删除操作效率高、可以减少分配内存空间等优点。
便于插入和删除的数据结构,双链表,循环链表

便于插入和删除的数据结构:双链表、循环链表1.双链表双链表是一种常见的数据结构,它的每个节点包含两个指针,一个指向前一个节点,一个指向后一个节点。
相比于单链表,双链表能够更方便地进行插入和删除操作。
1.1双链表的节点结构双链表的节点结构可以定义如下:```m ar kd ow ns t ru ct No de{T d at a;//存储的数据N o de*p re v;//指向前一个节点的指针N o de*n ex t;//指向后一个节点的指针};```1.2双链表的插入操作在双链表中插入一个节点,需要将该节点的前后指针分别指向前一个节点和后一个节点,并将前一个节点的后指针和后一个节点的前指针分别指向待插入节点。
具体步骤如下:1.创建一个新节点,并给新节点赋值。
2.将新节点的前指针指向前一个节点,后指针指向后一个节点。
3.将前一个节点的后指针指向新节点,后一个节点的前指针指向新节点。
1.3双链表的删除操作在双链表中删除一个节点,需要将该节点的前后节点的指针重新连接起来,并释放待删除节点的内存空间。
具体步骤如下:1.找到待删除节点。
2.将待删除节点的前一个节点的后指针指向待删除节点的后一个节点。
3.将待删除节点的后一个节点的前指针指向待删除节点的前一个节点。
4.释放待删除节点的内存空间。
2.循环链表循环链表是一种特殊的链表,它的最后一个节点的后指针指向头节点,形成一个循环。
循环链表同样可以便于插入和删除操作。
2.1循环链表的节点结构循环链表的节点结构与单链表的节点结构相似,只是在最后一个节点的后指针处做了特殊处理:```m ar kd ow ns t ru ct No de{T d at a;//存储的数据N o de*n ex t;//指向下一个节点的指针};```2.2循环链表的插入操作循环链表的插入操作与单链表类似,只需要将插入节点的后指针指向下一个节点,并将上一个节点的后指针指向插入节点。
循环链表长度

循环链表长度介绍循环链表是一种特殊的链表结构,它与普通链表的区别在于尾节点指针不为null,而是指向链表的头节点,形成一个循环链表。
循环链表可以解决一些特定的问题,比如在某些场景下需要循环遍历链表或者需要快速访问链表的最后一个节点。
在这篇文章中,我们将重点讨论循环链表的长度计算方法,以及一些相关的问题和应用场景。
计算循环链表长度的方法计算循环链表的长度可以通过遍历链表的方式来实现,也可以通过记录链表的节点数来实现。
下面将介绍两种方法。
方法一:遍历链表遍历链表是一种直观的方法,通过从链表的头节点开始,依次遍历下一个节点,直到回到头节点。
在遍历的过程中,我们可以用一个计数器来记录遍历的节点数,最终的计数器值就是循环链表的长度。
具体的实现步骤如下: 1. 初始化计数器count为0; 2. 从链表的头节点开始,依次遍历下一个节点,每遍历一个节点,计数器count加1; 3. 当遍历到头节点时,停止遍历; 4. 返回计数器count的值,即为循环链表的长度。
遍历链表的代码示例:count = 0current = headwhile True:count += 1current = current.nextif current == head:breakreturn count方法二:记录节点数在循环链表中,每个节点都可以通过其下一个节点来访问到,因此可以通过每个节点的next指针来记录链表的节点数。
具体做法是,从链表的头节点开始,依次遍历下一个节点,每访问到一个节点,节点数加1,直到再次回到头节点为止。
具体的实现步骤如下: 1. 初始化节点数为1; 2. 从链表的头节点开始,依次遍历下一个节点,每访问到一个节点,节点数加1; 3. 当节点的next指针指向头节点时,停止遍历; 4. 返回节点数,即为循环链表的长度。
记录节点数的代码示例:count = 1current = head.nextwhile current != head:count += 1current = current.nextreturn count循环链表长度的应用场景循环链表长度的计算方法可以在一些特定的问题中得到应用。
双向链表也叫双链表

一、循环链表循环链表是与单链表一样,是一种链式的存储结构,所不同的是,循环链表的最后一个结点的指针是指向该循环链表的第一个结点或者表头结点,从而构成一个环形的链。
循环链表的运算与单链表的运算基本一致。
所不同的有以下几点:1、在建立一个循环链表时,必须使其最后一个结点的指针指向表头结点,而不是象单链表那样置为NULL。
此种情况还使用于在最后一个结点后插入一个新的结点。
2、在判断是否到表尾时,是判断该结点链域的值是否是表头结点,当链域值等于表头指针时,说明已到表尾。
而非象单链表那样判断链域值是否为NULL。
二、双向链表双向链表其实是单链表的改进。
当我们对单链表进行操作时,有时你要对某个结点的直接前驱进行操作时,又必须从表头开始查找。
这是由单链表结点的结构所限制的。
因为单链表每个结点只有一个存储直接后继结点地址的链域,那么能不能定义一个既有存储直接后继结点地址的链域,又有存储直接前驱结点地址的链域的这样一个双链域结点结构呢?这就是双向链表。
在双向链表中,结点除含有数据域外,还有两个链域,一个存储直接后继结点地址,一般称之为右链域;一个存储直接前驱结点地址,一般称之为左链域。
在c语言中双向链表结点类型可以定义为:typedef struct node{int data; /*数据域*/struct node *llink,*rlink; /*链域,*llink是左链域指针,*rlink是右链域指针*/}JD;当然,也可以把一个双向链表构建成一个双向循环链表。
双向链表与单向链表一样,也有三种基本运算:查找、插入和删除。
双向链表的基本运算:1、查找假若我们要在一个带表头的双向循环链表中查找数据域为一特定值的某个结点时,我们同样从表头结点往后依次比较各结点数据域的值,若正是该特定值,则返回指向结点的指针,否则继续往后查,直到表尾。
下例就是应用双向循环链表查找算法的一个程序。
#include <stdio.h>#include <malloc.h>#define N 10typedef struct node{char name[20];struct node *llink,*rlink;}stud;stud * creat(int n){stud *p,*h,*s;int i;if((h=(stud *)malloc(sizeof(stud)))==NULL) {printf("不能分配内存空间!");exit(0);}h->name[0]=’\0’;h->llink=NULL;h->rlink=NULL;p=h;for(i=0;i<n;i++){if((s= (stud *) malloc(sizeof(stud)))==NULL) {printf("不能分配内存空间!");exit(0);}p->rlink=s;printf("请输入第%d个人的姓名",i+1);scanf("%s",s->name);s->llink=p;s->rlink=NULL;p=s;}h->llink=s;p->rlink=h;return(h);}stud * search(stud *h,char *x){stud *p;char *y;p=h->rlink;while(p!=h){y=p->name;if(strcmp(y,x)==0)return(p);else p=p->rlink;}printf("没有查找到该数据!"); }void print(stud *h){int n;stud *p;p=h->rlink;printf("数据信息为:\n"); while(p!=h){printf("%s ",&*(p->name));p=p->rlink;}printf("\n");}main(){int number;char studname[20];stud *head,*searchpoint;number=N;clrscr();head=creat(number);print(head);printf("请输入你要查找的人的姓名:"); scanf("%s",studname);searchpoint=search(head,studname);printf("你所要查找的人的姓名是:%s",*&searchpoint->name);}/* 线性表的双向链表存储结构*/typedef struct DuLNode{ElemType data;struct DuLNode *prior,*next;}DuLNode,*DuLinkList;/*带头结点的双向循环链表的基本操作(14个) */void InitList(DuLinkList *L){ /* 产生空的双向循环链表L */*L=(DuLinkList)malloc(sizeof(DuLNode));if(*L)(*L)->next=(*L)->prior=*L;elseexit(OVERFLOW);}void DestroyList(DuLinkList *L){ /* 操作结果:销毁双向循环链表L */ DuLinkList q,p=(*L)->next; /* p指向第一个结点*/ while(p!=*L) /* p没到表头*/{q=p->next;free(p);p=q;}free(*L);*L=NULL;}void ClearList(DuLinkList L) /* 不改变L */{ /* 初始条件:L已存在。
c++实现任意长整数的四则运算

else if (s>='1'&&s<='9'){}
else if(a[0]=='0'&&a[1]=='\0') return true;
else return false;
while (a[i]!='\0')
{
Jud=IsNum(a[i]);
if (Jud==0) return false;
void Display();//任意长度整数的标准化输出
};
说明:数据的存储,无外乎顺序或者链表。顺序存储时,定义数组无法实现任意长度,而且需要预设一个maxsize,不是特别的方便。所以采用链式存储方式。而且任意长数据通过字符串输入。在链表的每一个结点中,数据域是在该数位上的数字大小。
2.主要功能模块的功能
return i;
}
class DblList { //定义一个双向链表类,存储任意长度的数字
private: //并可以进行标准化输出和加法,乘法。
DblNode *head, *tail;
DblNode *current;
int sign;
public:
DblList(); //构造函数
~DblList(); //析构函数
break;
}
else if (choose=="#")
{
return;
}
else
{
cout<<"输入有误,请重新输入!!"<<endl;
双向循环链表解释

双向循环链表解释
双向循环链表是一种特殊的链表结构,它与单向链表的区别在于,双向循环链表中的每个节点都有两个链接,一个指向前一个节点,另一个指向下一个节点。
这种结构使得双向循环链表在某些操作上更为高效,例如在查找中间节点或从链表两端插入或删除节点时。
在双向循环链表中,第一个节点的前一个节点是最后一个节点,最后一个节点的下一个节点是第一个节点,形成一个闭环。
这种结构使得在双向循环链表中的任何位置插入或删除节点变得简单,而无需像单向链表那样从头节点开始遍历。
双向循环链表通常使用四个字段来存储数据:两个链接字段用于存储指向前一个和下一个节点的链接,一个数据字段用于存储实际的数据,还有一个哨兵字段用于指示链表的开始和结束。
双向循环链表的主要操作包括插入节点、删除节点、查找节点等。
在插入节点时,需要更新前一个和后一个节点的链接,以使新节点成为正确的链表部分。
在删除节点时,需要更新前一个和后一个节点的链接,以移除被删除的节点。
在查找节点时,可以从任何位置开始遍历链表,直到找到所需的节点或到达链表的另一端。
双向循环链表的优点是操作效率高,可以在O(1)时间内完成插入、删除和查找等操作。
但是,与单向链表相比,双向循环链表需要更多的存储空间来存储额外的链接信息。
总之,双向循环链表是一种高效的链表结构,适用于需要在链表中频繁进行中间插入和删除操作的情况。
双向循环链表的结构与定义

双向循环链表的结构与定义双向循环链表是一种常见的数据结构,它可以在链表中添加、删除、查找节点,并且可以在任意位置进行操作。
与单向链表不同的是,双向循环链表每个节点都有两个指针,一个指向前一个节点,一个指向后一个节点。
这种数据结构的优点是可以快速地在任意位置插入或删除节点。
双向循环链表的结构与定义如下:1. 结构双向循环链表由多个节点组成,每个节点包含三部分:数据域、前驱指针和后继指针。
其中,数据域存储节点的数据信息;前驱指针指向该节点的前一个节点;后继指针指向该节点的后一个节点。
2. 定义通常情况下,我们会定义一个双向循环链表类来实现这种数据结构。
类中包含以下几个基本元素:(1)头结点:头结点是一个特殊的哨兵节点,它不存储实际数据信息。
头结点的作用是方便对链表进行操作,并且可以避免处理空链表时出现异常情况。
(2)尾结点:尾结点也是一个特殊的哨兵节点,它与头结点类似,不存储实际数据信息。
尾结点的作用是方便对链表进行操作,并且可以避免处理空链表时出现异常情况。
(3)节点数目:节点数目表示当前链表中实际存储的节点数目。
当链表为空时,节点数目为0。
(4)构造函数:构造函数用于创建一个新的双向循环链表对象,并初始化头结点和尾结点。
(5)析构函数:析构函数用于销毁双向循环链表对象,并释放占用的内存资源。
(6)插入操作:插入操作可以在任意位置插入一个新的节点。
具体实现方式包括在头部插入、在尾部插入、在指定位置插入等。
(7)删除操作:删除操作可以删除任意位置的一个节点。
具体实现方式包括删除头部节点、删除尾部节点、删除指定位置的节点等。
(8)查找操作:查找操作可以根据指定条件查找符合要求的节点。
具体实现方式包括按照数据域查找、按照位置查找等。
总之,双向循环链表是一种非常重要的数据结构,它广泛应用于各种算法和程序设计中。
掌握双向循环链表的结构与定义,对于提高程序设计能力和算法水平都有很大帮助。
long类型加法

long类型加法
长整型加法是一种计算机程序设计中常见的数值计算方法,主要用于处理大整数之间的加法运算。
在实际应用中,普通的整数类型可能无法满足对大整数进行精确计算的需求,因此引入了长整型数据类型以解决这一问题。
长整型加法就是基于这种数据类型进行的计算,它可以实现对任意大小的整数进行加法运算。
长整型加法的运算规则主要包括以下几个方面:
1. 运算数的表示:长整数一般采用字符串形式表示,例如:"12345678901234567890"。
2. 运算规则:长整型加法遵循普通整数加法的运算规则,即对应位相加,如果有进位则加到下一位。
3. 进位处理:在长整型加法中,进位处理尤为重要。
因为长整数的位数很多,所以进位可能会出现在任意位置。
在计算过程中,需要对每一位的进位进行正确处理,以确保计算结果的准确性。
c++中双链表的用法

c++中双链表的用法在C++中,双链表是一种常用的数据结构,它由一系列节点组成,每个节点包含两个部分:数据和指向下一个节点的指针。
双链表可以用来存储具有顺序关系的数据,并且可以在常数时间内完成插入、删除和查找等操作。
以下是使用C++实现双链表的基本步骤:1. 定义节点结构体```c++struct Node {int data;Node* next;};```2. 创建双链表类```c++class LinkedList {private:Node* head;public:LinkedList() {head = nullptr;}// 添加节点到链表末尾void addNode(int data) {Node* newNode = new Node();newNode->data = data;newNode->next = nullptr;if (head == nullptr) {head = newNode;} else {Node* temp = head;while (temp->next != nullptr) {temp = temp->next;}temp->next = newNode;}}// 删除指定数据的节点void removeNode(int data) {if (head == nullptr) {return;}if (head->data == data) {head = head->next;delete temp;return;}Node* prev = head;Node* curr = head->next;while (curr != nullptr && curr->data != data) { prev = curr;curr = curr->next;}if (curr == nullptr) {return;}prev->next = curr->next;delete curr;}// 打印链表中的数据void printList() {Node* temp = head;while (temp != nullptr) {cout << temp->data << " ";}cout << endl;}};```。
数据结构循环双链表

数据结构循环双链表数据结构是计算机科学中非常重要的一个概念,它用来组织和存储数据,以便于高效地操作和管理。
循环双链表是一种常见的数据结构之一,它在实际应用中有着广泛的用途。
循环双链表是双向链表的一种扩展形式,它的特点是链表的头节点和尾节点相互连接,形成一个环形结构。
相比于单向链表和双向链表,循环双链表具有更强的表达能力和更高的灵活性。
循环双链表的结构包含三个重要的部分:节点、指针和操作。
节点是链表中的基本单元,它包含两个指针,分别指向前一个节点和后一个节点。
指针是用来连接各个节点的,它们指示了节点之间的关系。
操作是对链表进行增删改查等操作的方法,通过操作可以实现对链表中数据的管理和处理。
循环双链表的优点之一是可以实现快速的插入和删除操作。
由于节点之间的指针连接,插入和删除一个节点只需要修改少量的指针,而不需要像数组那样移动大量的元素。
这使得循环双链表在需要频繁插入和删除操作的场景下具有较高的效率。
另一个优点是可以实现双向遍历。
由于每个节点都有指向前一个节点和后一个节点的指针,所以可以从头节点或尾节点开始,沿着指针的方向依次遍历整个链表。
这种双向遍历的特性使得循环双链表在需要正向和反向遍历操作的场景下十分便利。
除了基本的插入、删除和遍历操作,循环双链表还可以实现其他一些功能。
比如,可以通过指针的调整实现链表的反转,可以通过指针的交换实现节点的位置互换,可以通过指针的移动实现链表的拆分和合并等。
这些功能的实现都依赖于循环双链表的结构特点和操作方法。
在实际应用中,循环双链表有着广泛的用途。
比如,在操作系统中,循环双链表可以用来管理进程或线程的控制块;在图形学中,循环双链表可以用来管理图形的顶点和边;在网络通信中,循环双链表可以用来管理数据包的缓冲区等。
这些应用场景都需要高效地组织和操作数据,循环双链表正好满足了这些需求。
循环双链表是一种重要的数据结构,它具有高效的插入和删除操作、双向遍历的特性以及丰富的功能实现。
c语言长整数加法运算 -回复

c语言长整数加法运算-回复C语言是一种广泛应用于计算机编程中的高级编程语言,其功能强大且灵活。
在C语言中,提供了各种数据类型来满足不同的需求。
其中,长整数是一种用于表示较大整数的数据类型。
在日常编程中,经常会遇到需要对长整数进行加法运算的情况。
因此,掌握C语言中长整数的加法运算方法是非常重要的。
首先,我们需要了解C语言中长整数的表示方法。
在C语言中,长整数使用关键字"long"来定义。
它的存储范围通常比整数类型更大,因此可以容纳较大的整数值。
具体的存储范围取决于所使用的编译器和计算机体系结构。
在C语言中,长整数的加法运算可以使用"+"运算符来实现。
以下是一个示例代码,演示了如何进行长整数的加法运算:cinclude <stdio.h>int main() {long num1, num2, sum;printf("请输入第一个长整数:");scanf("ld", &num1);printf("请输入第二个长整数:");scanf("ld", &num2);sum = num1 + num2;printf("两个长整数的和为:ld", sum);return 0;}在这段代码中,我们首先定义了三个变量:num1、num2和sum,它们分别用于存储第一个长整数、第二个长整数和它们的和。
然后,通过使用"printf"和"scanf"函数,我们可以从用户那里获取两个长整数的值,并将它们分别存储在num1和num2中。
接下来,我们使用"+"运算符来计算num1和num2的和,并将结果存储在sum变量中。
最后,我们使用"printf"函数将sum的值打印到屏幕上。
C++双向循环链表实现
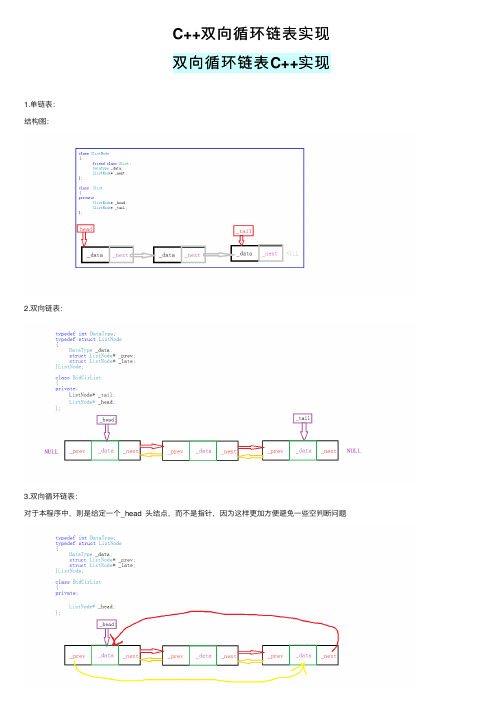
BidCirList& operator = (BidCirList& list)
{ if (this != &list) { BidCirList S(list);
Swap(S); } return *this; }
//反向打印 void PrintPrev() {
ListNode* cur = _head._prev; while (cur) {
if (cur == &_head) break;
cout << cur->_data << " -> "; cur = cur->_prev; } cout << " Over! " << endl; } //正向打印 void PrintLate() { ListNode* cur = _head._late;
if (del == NULL) {
//删除头之前 _head._prev = _head._prev->_prev; delete _head._prev->_late;
_head._prev->_late = &_head; } else {
del->_prev = del->_prev->_prev; delete del->_prev->_late;
while (cur) {
if (cur == &_head) break;
cout << cur->_data << " -> "; cur = cur->_late; } cout << " Over! " << endl; }
循环双链表特点

循环双链表特点循环双链表是一种特殊的数据结构,它具有循环和双向链表的特点。
循环双链表中的每个节点都包含两个指针,一个指向前一个节点,一个指向后一个节点。
最后一个节点的后指针指向头节点,头节点的前指针指向最后一个节点,从而形成了一个闭环。
循环双链表的特点如下:1. 双向性:每个节点都有两个指针,分别指向前一个节点和后一个节点。
这样可以方便地在任意位置插入或删除节点,而不需要像单链表那样需要遍历找到前驱节点。
2. 循环性:循环双链表是一个闭环,即最后一个节点的后指针指向头节点,头节点的前指针指向最后一个节点。
这样可以方便地进行循环遍历,不需要判断是否到达了链表的末尾。
3. 动态性:循环双链表可以动态地增加或删除节点,而不需要预先指定链表的长度。
4. 灵活性:循环双链表可以在任意位置插入或删除节点,不受限于只能在链表的头部或尾部进行操作。
这样可以方便地实现栈、队列等数据结构。
5. 代码实现简单:相比于其他数据结构,循环双链表的代码实现相对简单,只需要处理好节点之间的指针关系即可。
循环双链表的应用领域非常广泛,特别是在需要频繁插入和删除节点的场景中,循环双链表能够提供高效的插入和删除操作。
下面以几个具体的应用场景来展开对循环双链表的解释和扩展。
1. 缓存替换算法:循环双链表可以用于实现LRU(Least Recently Used)缓存替换算法。
LRU算法中,当缓存满时,需要替换掉最近最少使用的数据。
循环双链表可以维护数据的访问顺序,每次访问一个数据时,将其移到链表的头部;当缓存满时,删除链表尾部的数据即可。
这样就可以保证链表头部的数据是最近访问的数据,尾部的数据是最久未访问的数据。
2. 轮播图:循环双链表可以用于实现轮播图功能。
轮播图需要循环展示多张图片,循环双链表正好可以满足这个需求。
每个节点表示一张图片,节点之间通过指针连接起来形成一个循环链表。
通过不断地遍历链表,可以实现图片的自动切换。
3. 约瑟夫环问题:循环双链表可以用于解决约瑟夫环问题。
双链表和循环链表

结点类型与非 循环单链表的
相同
结点类型与非 循环双链表的
相同
17/29
1、循环单链表
逻辑结构
L
存储结构
线性表 (a1,a2,…,ai,…an)
映射
a1
a2
…
an
带头结点循环单链表示意图
18/29
与非循环单链表相比,循环单链表:
链表中没有空指针域 p所指结点为尾结点的条件:p->next==L
L
p
s->data=a[i];
//创建数据结点*s
s->next=L->next;
//将*s插入到头结点之后
if (L->next!=NULL) //若L存在数据结点,修改前驱指针
L->next->prior=s;
L->next=s;
s->prior=L;
}
}
L
∧
插入 ∧
s
ai
9/29
尾插法建立双链表:由含有n个元素的数组a创建带头结 点的双链表L。
{ DLinkNode *p=L->next,*q;//p指向开好结点
L->next=NULL;
//构造只有头结点的双链表L
while (p!=NULL)
//扫描L的数据结点
{ q=p->next;
//用q保存其后继结点
p->next=L->next; if (L->next!=NULL)
L->next->prior=p; L->next=p; p->prior=L;
14/29
【例2-9】 有一个带头结点的双链表L,设计一个算法
long类型加法

long类型加法
【原创实用版】
目录
1.长整型加法的概念
2.长整型加法的运算规则
3.长整型加法的应用实例
4.长整型加法的优点与局限性
正文
1.长整型加法的概念
长整型加法是一种计算机程序设计中的数值计算方法,主要用于处理非常大的整数。
在许多编程语言中,长整型是一种数据类型,可以表示比整数范围更大的整数值。
长整型加法就是对两个长整数进行相加的运算。
2.长整型加法的运算规则
长整型加法的运算规则与普通整数加法相似,不同之处在于它需要处理更大的数值范围。
长整型加法遵循交换律和结合律,即对于任意的长整数 a、b、c,有:
a +
b = b + a
(a + b) + c = a + (b + c)
3.长整型加法的应用实例
长整型加法在许多实际应用场景中有广泛的应用,例如:
- 密码学:在现代密码学中,长整型加法常用于实现公钥加密算法,如 RSA 加密算法。
- 大数据处理:在处理海量数据时,长整型加法可以提高计算效率,避免数据溢出问题。
- 数学建模:在解决一些复杂的数学问题时,长整型加法有助于简化计算过程。
4.长整型加法的优点与局限性
长整型加法的优点在于可以处理更大的整数值,避免了普通整数加法中的溢出问题。
然而,长整型加法也有其局限性,例如计算速度较慢,存储空间需求较大等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
采用循环双向链表,能实现多个长整型进行加法运算/**文件名: 1_2.c*实验环境: Turbo C 2.0*完成时间: 2003年2月17日*--------------------------------------------------------------------*改进说明:采用循环双向链表,能实现多个长整型进行加法运算. */#include <math.h>#include <conio.h>#include <stdio.h>#include <stdlib.h>#include <string.h>#define TRUE 1#define FALSE 0#define OPERAND_NUM 2#define POSITIVE 1#define NEGATIVE 0typedef int ElemType;typedef int status;typedef struct NodeType{ElemType data;struct NodeType *prior;struct NodeType *next;} NodeType, *LinkType;status CreateOpHeadBuff(LinkType **, int);status CreateOperandList(LinkType *, int);void CreateResultList(LinkType *, LinkType *, int);status DeleteZero(LinkType *);status PushDataToList(LinkType *, int, int);status AppendNodeToList(LinkType *, LinkType);LinkType ComputePNList(LinkType, LinkType, int);LinkType ComputePPNNList(LinkType, LinkType, int);status MakeNode(LinkType *, ElemType);status PrintList(LinkType);status ClearMemory(LinkType *, int);status DeleteList(LinkType);status ErrorProcess(char[], int);int main(void){int iCounter,iOpNum = 2;/*操作数的个数,默认为2 */char strNum[10], cOrder[5];LinkType ResultList = NULL, /*结果链表的头指针*/*ListHeadBuff = NULL; /*指向操作数头指针缓冲*/do{printf("请输入需要的操作数的个数,注意至少为2: "); gets(strNum);iOpNum = atoi(strNum);} while (iOpNum < 2);/*构造操作数链表的头指针缓冲区*/ CreateOpHeadBuff(&ListHeadBuff, iOpNum);/*提示用户输入数据,并构造操作数链表*/while (!CreateOperandList(ListHeadBuff, iOpNum)){printf("\n出现非法输入,需要退出吗?\n");printf("键入Y则退出,键入N重新输入(Y/N):");gets(cOrder);if (cOrder[0] == 'Y' || cOrder[0] == 'y'){ClearMemory(ListHeadBuff, iOpNum);return 0;}}printf("打印输入情况:\n");for (iCounter = 0; iCounter < iOpNum; iCounter++){printf("- - -第%d个操作数- - -\n", iCounter + 1); DeleteZero(ListHeadBuff + iCounter);PrintList(*(ListHeadBuff + iCounter));}/*相加所有操作数链表的结果,并存放在ResultList中*/ CreateResultList(&ResultList, ListHeadBuff, iOpNum); printf("打印结果:\n");PrintList(ResultList);ClearMemory(ListHeadBuff, iOpNum);DeleteList(ResultList);printf("运算完毕!");getch();return 0;}status CreateOpHeadBuff(LinkType **pBuff, int size){int iCounter;*pBuff = (LinkType *)malloc(sizeof(LinkType) * size);if (!*pBuff){printf("Error, the memory is overflow!\n");return FALSE;}for (iCounter = 0; iCounter < size; iCounter++)*(*pBuff + iCounter) = NULL;return TRUE;}status CreateOperandList(LinkType *headBuff, int iOpNum){int iCounter = 0, iTemp = 0,iNodeNum = 0, /*记录每一个操作数链表中加入的操作数个数*/ iSign = POSITIVE; /*标识操作数的正(1)负(0),初始为正的*/ char strScrNum[150], /*用户输入的所有操作数字符*/*cpCurr, /*当前操作数字符尾*/*cpCurrNum, /*当前操作数字符头*/strTsl[7]; /*准备转换的操作数字符*/LinkType NewNode;printf("请输入所有操作数\n");printf("例如输入3个操作数: \n\1111, 2222; -3333, 4444; -3333, 9999, 0202;\n: ");gets(strScrNum);/*检测输入正确性*/if (!ErrorProcess(strScrNum, iOpNum)) return FALSE;for (cpCurr = cpCurrNum = strScrNum; *cpCurr != '\0'; cpCurr++) {if (*cpCurr == ',' || *cpCurr == ';'){if (*(cpCurr + 1) == '\0') cpCurr++;strncpy(strTsl, cpCurrNum, cpCurr - cpCurrNum); strTsl[cpCurr - cpCurrNum] = '\0';iTemp = atol(strTsl);/*异常处理,如strTsl=="-3333","10000" */if (0 > iTemp || iTemp > 9999){printf("\n出现非法输入2!\n");return FALSE;}/*为操作数链表加入结点*/MakeNode(&NewNode, iTemp); AppendNodeToList(headBuff + iCounter, NewNode); iNodeNum++; /*当前链表已经加入的一个结点*/if (*cpCurr == ';'){/*将控制结点插在链表头*/PushDataToList(headBuff + iCounter, iNodeNum, iSign); iNodeNum = 0; /*逻辑结点个数初始化为0 */iSign = POSITIVE; /*符号标识默认为正的*/if ((iCounter + 1) < iOpNum)iCounter++; /*标识下一个链表头指针*/}cpCurrNum = cpCurr + 1;}else if (*cpCurr == '-'){iSign = NEGATIVE; /*符号标识改为负的*/cpCurr++;cpCurrNum = cpCurr;}else if (*cpCurr == '+');/*读完后停止构造操作数链表*/if (*cpCurr == '\0'){PushDataToList(headBuff + iCounter, iNodeNum, iSign); break;}} /* end for */return TRUE;}/**正正,结果为正的.*负负,结果为负的.*长正短负,结果为正的.*长负短正,要变为长正短负,结果为负的.*异号时同样长*注意要删除每次算出的中间链表,最后传回Result*/void CreateResultList(LinkType *ResultHead,LinkType *headBuff, int iOpNum){int iCounter, iSign;LinkType ResultList = NULL, TempList, CurrNode_1, CurrNode_2;for (ResultList = *headBuff, iCounter = 1;iCounter < iOpNum; iCounter++){TempList = ResultList;if (ResultList->data > 0 &&(*(headBuff + iCounter))->data > 0)/*正正,结果为正的*/ ResultList = ComputePPNNList(TempList, *(headBuff + iCounter), POSITIVE);else if (ResultList->data < 0 &&(*(headBuff + iCounter))->data < 0)/*负负,结果为负的*/ ResultList = ComputePPNNList(TempList, *(headBuff + iCounter), NEGA TIVE);else{if (ResultList->data + (*(headBuff + iCounter))->data == 0){ /*异号时同样长*/CurrNode_1 = ResultList;CurrNode_2 = *(headBuff + iCounter);do{ /*直到找到第一个不等值的结点*/if (CurrNode_1->data > CurrNode_2->data){iSign = (ResultList->data > 0) ?POSITIVE : NEGATIVE;ResultList = ComputePNList(TempList, *(headBuff + iCounter), iSign);break;}else if (CurrNode_1->data < CurrNode_2->data)iSign = ((*(headBuff + iCounter))->data > 0) ?POSITIVE : NEGATIVE;ResultList = ComputePNList(*(headBuff + iCounter), TempList, iSign);break;}CurrNode_1 = CurrNode_1->next;CurrNode_2 = CurrNode_2->next;} while (CurrNode_1 != ResultList);}else if (fabs(ResultList->data) >fabs((*(headBuff + iCounter))->data)){iSign = (ResultList->data > 0) ? POSITIVE : NEGA TIVE;ResultList = ComputePNList(TempList, *(headBuff + iCounter), iSign);}else if (fabs(ResultList->data) <fabs((*(headBuff + iCounter))->data)){iSign = ((*(headBuff + iCounter))->data > 0) ?POSITIVE : NEGATIVE;ResultList = ComputePNList(*(headBuff + iCounter), TempList, iSign);}}if (*headBuff > TempList || TempList > *(headBuff + iCounter)) DeleteList(TempList); /*清除上次的中间链表*//*删除多出的0,如删除0000,0010,3333中的0000为0010,3333*/ DeleteZero(&ResultList);}*ResultHead = ResultList;}/**每次只处理两个操作数链表,符号相异时List_1为正的, List_2为负的*如果两个操作数链表不一样长则List_1为长的结果链表的结构和操作*数链表一样,最后返回结果链表*/LinkType ComputePNList(LinkType List_1, LinkType List_2, int iSign) {int iResult = 0, iBorrow = 0, iResultNodeNum = 0;LinkType CurrNodeArray[2],NewNode = NULL, ResultList = NULL;/*初始为每一个操作数链表的尾结点地址*/ CurrNodeArray[0] = (List_1)->prior;CurrNodeArray[1] = (List_2)->prior;while ((CurrNodeArray[0] != List_1)|| (CurrNodeArray[1] != List_2)){if (iBorrow < 0) /*处理前一位的借位*/if (CurrNodeArray[0]->data > 0){iBorrow = 0;iResult = -1;}else if (CurrNodeArray[0]->data == 0){iBorrow = -1; /*继续向高位借1位*/iResult = 9999;}if ((CurrNodeArray[0] != List_1)&& (CurrNodeArray[1] != List_2)){if ((CurrNodeArray[0]->data < CurrNodeArray[1]->data) && iBorrow == 0){iBorrow = -1; /*不够减则向高位借1位*/iResult += 10000;}iResult += CurrNodeArray[0]->data -CurrNodeArray[1]->data;CurrNodeArray[0] = CurrNodeArray[0]->prior; CurrNodeArray[1] = CurrNodeArray[1]->prior;}else if (List_1 != CurrNodeArray[0]) /*处理剩下的链表*/ {iResult += CurrNodeArray[0]->data;CurrNodeArray[0] = CurrNodeArray[0]->prior;}/*将算好的结点加入结果链表*/PushDataToList(&ResultList, iResult, POSITIVE);iResultNodeNum++;if ((CurrNodeArray[0] == List_1)&& (CurrNodeArray[1] == List_2)){/*在链表头插入控制结点*/MakeNode(&NewNode, iResultNodeNum);PushDataToList(&ResultList, iResultNodeNum, iSign);}iResult = 0; /*准备计算下一个结点*/}return ResultList;}/*每次只处理两个操作数链表,正正,结果为正的,负负,结果为负的*/ LinkType ComputePPNNList(LinkType List_1, LinkType List_2, int iSign) {int iResult = 0, iCarry = 0, iResultNodeNum = 0;LinkType CurrNodeArray[2],NewNode = NULL, ResultList = NULL;/*初始为每一个操作数链表的尾结点地址*/CurrNodeArray[0] = (List_1)->prior;CurrNodeArray[1] = (List_2)->prior;while (TRUE){if (iCarry > 0) /*处理前一位的进位*/{iResult += iCarry;iCarry = 0;}if (CurrNodeArray[0] != List_1 &&CurrNodeArray[1] != List_2){iResult += CurrNodeArray[0]->data + CurrNodeArray[1]->data; CurrNodeArray[0] = CurrNodeArray[0]->prior;CurrNodeArray[1] = CurrNodeArray[1]->prior;}else if (CurrNodeArray[0] != List_1){iResult += CurrNodeArray[0]->data;CurrNodeArray[0] = CurrNodeArray[0]->prior;}else if (CurrNodeArray[1] != List_2){iResult += CurrNodeArray[1]->data;CurrNodeArray[1] = CurrNodeArray[1]->prior;}if (iResult >= 10000){iCarry = iResult / 10000;iResult = iResult % 10000;}PushDataToList(&ResultList, iResult, POSITIVE); iResultNodeNum++;if (iCarry == 0 && CurrNodeArray[0] == List_1&& CurrNodeArray[1] == List_2){MakeNode(&NewNode, iResultNodeNum); PushDataToList( &ResultList, iResultNodeNum, iSign); break;}iResult = 0; /*准备计算下一个结点*/}return ResultList;}/**删除多出的0,如删除0000,0010,3333中的0000为0010,3333 * ,但链表为只有一个逻辑结点为0时则不删除.*/status DeleteZero(LinkType *List){LinkType CurrNode, DelNode;/**一旦遇到第一个不为0的结点则退出,但*链表为只有一个逻辑结点为0时则不删除*/CurrNode = DelNode = (*List)->next;while (fabs((*List)->data) > 1 && CurrNode->data == 0){(*List)->next = CurrNode->next;CurrNode->next->prior = *List;DelNode = CurrNode;CurrNode = CurrNode->next;free(DelNode);/*控制结点减少一个逻辑结点的个数*/(*List)->data += ((*List)->data > 0) ? -1 : 1;}return TRUE;}status PushDataToList(LinkType *head, int iNodeNum, int sign) {LinkType NewNode;/* sign为1时为正的, sign为0时为负的*/iNodeNum *= (sign == POSITIVE) ? 1 : -1;MakeNode(&NewNode, iNodeNum);if (*head != NULL){/*将NewNode所指的结点插入链表,使成为头结点*/ NewNode->next = *head;NewNode->prior = (*head)->prior;(*head)->prior = NewNode;NewNode->prior->next = NewNode;}*head = NewNode;return TRUE;}status AppendNodeToList(LinkType *head, LinkType NewNode) {static LinkType CurrNode = NULL;if (*head == NULL)*head = CurrNode = NewNode;else{/*在链表尾部添加结点*/NewNode->next = CurrNode->next;CurrNode->next = NewNode;NewNode->prior = CurrNode;NewNode->next->prior = NewNode;/*当前指针向前一步*/CurrNode = CurrNode->next;}return TRUE;}status MakeNode(LinkType *p, ElemType e){*p = (LinkType)malloc(sizeof(NodeType) * 1);if (!(*p)){printf("Error, the memory is overflow!\n");return FALSE;}(*p)->data = e;(*p)->prior = (*p)->next = (*p);return TRUE;}status PrintList(LinkType head){/* LinkType CurrNode = head; use for debug */ LinkType CurrNode = head->next;if (head == NULL) return FALSE;if (head->data < 0) printf("-");while (TRUE){printf(" %04d", CurrNode->data);CurrNode = CurrNode->next;if (CurrNode == head) break;printf("%c", ',');}printf("\n");return TRUE;}status ClearMemory(LinkType *headBuff, int iOpNum)int iCounter;for (iCounter = 0; iCounter < iOpNum; iCounter++) DeleteList(*(headBuff + iCounter));free(headBuff);return TRUE;}status DeleteList(LinkType head){LinkType CurrNode;if (head == NULL) return FALSE;while (1){CurrNode = head;CurrNode->next->prior = CurrNode->prior; CurrNode->prior->next = CurrNode->next;if (head == head->next){free(CurrNode);break;}head = head->next;free(CurrNode);}return TRUE;}/*输入异常处理*/status ErrorProcess(char strScrNum[], int iOpNum) {int iTemp = 0;char *cpCurr;if (!strlen(strScrNum)){printf("你没有输入数据!");return FALSE;}for (cpCurr = strScrNum; *cpCurr != '\0'; cpCurr++)if (!(*cpCurr == ' ' || *cpCurr == ',' || *cpCurr == ';' || *cpCurr == '-' || *cpCurr == '+'|| ('0' <= *cpCurr && *cpCurr <= '9'))|| (*(cpCurr + 1) == '\0' && *cpCurr != ';')|| (*(cpCurr + 1) == '+' && *cpCurr == '-')|| (*(cpCurr + 1) == '-' && *cpCurr == '+')|| (*(cpCurr + 1) == '-' && *cpCurr == '-')|| (*(cpCurr + 1) == '+' && *cpCurr == '+')){printf("\n出现非法输入1!\n");return FALSE;}if (*cpCurr == ';') iTemp++;}if (iTemp != iOpNum) return FALSE;return TRUE;}。
